S_FMA_4
男鞋

正品鲨鱼鞋潜艇流行男鞋休闲真皮鞋子男韩版英伦透气大头鞋懒人鞋| /iteZ6jHSTbIQ9r%2FL4wiSnlFw8jNgZOG9yne4Vb7VBVjlcwitZG0pAxWqCcm%2FYJI8WeCvlb7WZYDXowa7v5lWrJlDnvpznt1ocq7IEVS%2FybCI0BxNF9Q%3D%3D&p=mm_27724055_0_0&n=19
Gesisi男士休闲鞋真皮鞋商务单鞋 低帮鞋男鞋韩版潮流鞋子男210| /item.htm?id=12277078052|/t_8?e=7HZ6jHSTbIKhkMwLL7mX1bJ7jcEvC0NKlCn7SqHwA58OoXMefOZZTIk0wtnKqUEFornLg81vA79UKrw%2FMXRC7KpJsuHw1gCDVEkFv2t83bTv5Cp0Eg%3D%3D&p=mm_27724055_0_0&n=19
Mr.me流行男鞋2012鞋子 男 韩版潮流 反绒皮 透气时尚男士休闲鞋| /item.htm?id=7554369910|/t_8?e=7HZ6jHSTarQDl27dR6X%2Fp50rUQTqcz59kqc7%2FalbGTuGXI4Ak5b21G0Ynt%2BmrcztOa%2Bvpw3XrS9rzhvmI6jbv7kB5k%2BaoZvHzy37u96RMczFbHMB&p=mm_27724055_0_0&n=19
FMEA失效模式与效应分析

.H:rf+[ fl +:r"&]g6tFi|EA
. fls:lrf lErif ' taEFJ&^R.*.8R.FrdH.!&6th1" .t
.
+} 1+4.1'14d*.r3+El6gf nf'a.&i*1?Wt
n ,
F
a
j
"
t
rE
'
d
n
,
v
'
n
r
'
u
&
E
z
.4 ?fg+k rf tE6 ifrAtFllE(A6 Siena)
.
iF4, .tttt.*rlut
E.
+L'&-+44hhEts+ ' EE4+t-+ztttF,,-.f-rkl4
Wh.JiL*.
. 4*_1Bt-t!.sp.kY.1$( P. DM)
ffE,'"4tf 6t€+1*
4 L++hE-F"fAl*d,'i €.;* Sz.J*1. 6
1 .1 , i , t & e ^ i { ( 5 1 { 2 H ) & D e sr ei svni e u , ( 6- ]j f!l l* ) 23..&E4€i.t4+-6ir1gi f.AA1rE.+'+E#nfjfA| (i.Ci. ustorVr oice) 4. d4 &?E6 ftE&tB nE+;'trt,E 5.€6i a &i{;+ ?rtS.&isrA 6 .F . S 0 f D , : " q { q e R f r l ,rtEE, r € , , t J t r t , % . c } 6 & r a q " , i , t r
高三数学抛物线试题答案及解析

高三数学抛物线试题答案及解析1.设双曲线的离心率为2,且一个焦点与抛物线的焦点相同,则此双曲线的方程为__________.【答案】.【解析】抛物线的焦点坐标为(0,2),所以双曲线的焦点在y轴上且c=2,所以双曲线的方程为,即a2=n>0,b2=-m>0,所以a=,又e=,解得n=1,所以b2=c2-a2=4-1=3,即-m=3,m=-3,所以双曲线的方程为,故答案为:.【考点】1.抛物线的简单性质;2.双曲线的简单性质.2.已知点A(-1,0),B(1,-1)和抛物线.,O为坐标原点,过点A的动直线l交抛物线C于M、P,直线MB交抛物线C于另一点Q,如图.(1)证明: 为定值;(2)若△POM的面积为,求向量与的夹角;(3)证明直线PQ恒过一个定点.【答案】(1)见解析; (2) ;(3)直线PQ过定点E(1,-4).【解析】(1)设点根据、M、A三点共线,得计算得到=5;(2)设∠POM=α,可得结合三角形面积公式可得tanα="1."根据角的范围,即得所求.(3)设点、B、Q三点共线,据此确定进一步确定的方程,化简为得出结论.试题解析:(1)设点、M、A三点共线,2分5分(2)设∠POM=α,则由此可得tanα=1. 8分又 10分(3)设点、B、Q三点共线,即 12分即 13分由(*)式,代入上式,得由此可知直线PQ过定点E(1,-4). 14分【考点】抛物线及其几何性质,直线方程,直线与抛物线的位置关系,转化与化归思想.3.已知抛物线C: y2 =2px(p>0)的准线L,过M(l,0)且斜率为的直线与L相交于A,与C的一个交点为B,若,则p=____ 。
【答案】2【解析】由题意可得,抛物线的焦点为,准线为.,为AB的中点.直线方程为,由题意可得,故由中点公式可得,把点B的坐标代入抛物线可得,解得.【考点】直线与抛物线的位置关系4.已知中心在原点的双曲线C的右焦点为(2,0),右顶点为(,0).(1)求双曲线C的方程;(2)若直线l:y=kx+与双曲线C恒有两个不同的交点A和B,且·>2(其中O为原点),求k的取值范围.【答案】(1)-y2=1(2)(-1,-)∪(,1)【解析】(1)设双曲线C的方程为-=1(a>0,b>0).由已知得a=,c=2,再由c2=a2+b2得b2=1,所以双曲线C的方程为-y2=1.(2)将y=kx+代入-y2=1中,整理得(1-3k2)x2-6kx-9=0,由题意得,故k2≠且k2<1①.设A(xA ,yA),B(xB,yB),则xA+xB=,xAxB=,由·>2得xA xB+yAyB>2,x A xB+yAyB=xAxB+(kxA+)(kxB+)=(k2+1)xAxB+k(xA+xB)+2=(k2+1)·+k·+2=,于是>2,即>0,解得<k2<3②.由①②得<k2<1,所以k的取值范围为(-1,-)∪(,1).5.已知圆P:x2+y2=4y及抛物线S:x2=8y,过圆心P作直线l,此直线与上述两曲线的四个交点,自左向右顺次记为A,B,C,D,如果线段AB,BC,CD的长按此顺序构成一个等差数列,则直线l的斜率为( )A.B.C.D.【答案】A【解析】圆的方程为,则其直径长圆心为,设的方程为,代入抛物线方程得:设,有∴线段的长按此顺序构成一个等差数列,,即,解得,故选A.【考点】1.抛物线的几何性质;2.直线与抛物线相交问题.6.已知F是抛物线的焦点,A,B是该抛物线上的两点,|AF|+|BF|=3,则线段AB的中点到y轴的距离为()A.B.1C.D.【答案】C【解析】过A,B及线段AB的中点C向抛物线的准线作垂线,垂足分别为M,N,Q,CQ交y轴于T,由抛物线的定义知|AM|+|BN|=|AF|+|BF|=3,因为CQ是直角梯形AMNB的中位线所以CQ|=(|AM|+|BN)=,所以|CT|=|CQ|-|TQ|=-=7.已知抛物线的准线与x轴交于点M,过点M作圆的两条切线,切点为A、B,.(1)求抛物线E的方程;(2)过抛物线E上的点N作圆C的两条切线,切点分别为P、Q,若P,Q,O(O为原点)三点共线,求点N的坐标.【答案】(1)y2=4x;(2)点N坐标为或.【解析】本题主要考查抛物线的标准方程及其几何性质、圆的标准方程及其几何性质、圆的切线的性质等基础知识,考查学生分析问题解决问题的能力和计算能力.第一问,利用抛物线的准线,得到M点的坐标,利用圆的方程得到圆心C的坐标,在中,可求出,在中,利用相似三角形进行角的转换,得到的长,而,从而解出P的值,即得到抛物线的标准方程;第二问,设出N点的坐标,利用N、C点坐标写出圆C的方程,利用点C的坐标写出圆C的方程,两方程联立,由于P、Q是两圆的公共点,所以联立得到的方程即为直线PQ的方程,而O点在直线上,代入点O的坐标,即可得到s、t的值,即得到N点坐标.试题解析:(1)由已知得,C(2,0).设AB与x轴交于点R,由圆的对称性可知,.于是,所以,即,p=2.故抛物线E的方程为y2=4x. 5分(2)设N(s,t).P,Q是NC为直径的圆D与圆C的两交点.圆D方程为,即x2+y2-(s+2)x-ty+2s=0.①又圆C方程为x2+y2-4x+3=0.②②-①得(s-2)x+ty+3-2s=0.③ 9分P,Q两点坐标是方程①和②的解,也是方程③的解,从而③为直线PQ的方程.因为直线PQ经过点O,所以3-2s=0,.故点N坐标为或. 12分【考点】抛物线的标准方程及其几何性质、圆的标准方程及其几何性质、圆的切线的性质.8.如图,已知抛物线C的顶点在原点,开口向右,过焦点且垂直于抛物线对称轴的弦长为2,过C上一点A作两条互相垂直的直线交抛物线于P,Q两点.(1)若直线PQ过定点,求点A的坐标;(2)对于第(1)问的点A,三角形APQ能否为等腰直角三角形?若能,试确定三角形APD的个数;若不能,说明理由.【答案】(1),(2)一个【解析】(1)确定抛物线标准方程只需一个独立条件,本题条件为已知通径长所以抛物线的方程为.直线过定点问题,实际是一个等式恒成立问题.解决问题的核心是建立变量的一个等式.可以考虑将直线的斜率列为变量,为避开讨论,可设的方程为,与联立消得,则,设点坐标为,则有,代入化简得:因此,点坐标为,(2)若三角形APQ为等腰直角三角形,则的中点与点A连线垂直于.先求出的中点坐标为,再讨论方程解的个数,这就转化为研究函数增减性,并利用零点存在定理判断零点有且只有一个.试题解析:(1)设抛物线的方程为,依题意,,则所求抛物线的方程为. (2分)设直线的方程为,点、的坐标分别为.由,消得.由,得,,.∵,∴.设点坐标为,则有.,,∴或.∴或, ∵恒成立. ∴.又直线过定点,即,代入上式得注意到上式对任意都成立,故有,从而点坐标为. (8分)(2)假设存在以为底边的等腰直角三角形,由第(1)问可知,将用代换得直线的方程为.设,由消,得.∴,.∵的中点坐标为,即,∵,∴的中点坐标为.由已知得,即.设,则,在上是增函数.又,,在内有一个零点.函数在上有且只有一个零点,所以满足条件的等腰直角三角形有且只有一个. (12分)【考点】直线与抛物线关系,零点存在定理9.在平面直角坐标系中,已知三点,直线AC的斜率与倾斜角为钝角的直线AB的斜率之和为,而直线AB恰好经过抛物线)的焦点F并且与抛物线交于P、Q两点(P在Y轴左侧).则()A.9B.C.D.【答案】A【解析】由题意得,且.令,,则,所以,且,由此可解得.由抛物线的方程知焦点为,因此设直线的方程为,代入抛物线方程,得,解得或,所以由题意知,.由图形特征根据三角形相似易知.【考点】1、直线的斜率;2、直线方程;3、直线与抛物线的位置关系.10.抛物线y2=-8x的准线方程是________.【答案】x=2【解析】∵2p=8,∴p=4,故所求准线方程为x=2.11.下图是抛物线形拱桥,当水面在l时,拱顶离水面2m,水面宽4m.水位下降1m后,水面宽________m.【答案】2【解析】设抛物线的方程为x2=-2py,则点(2,-2)在抛物线上,代入可得p=1,所以x2=-2y.当y=-3时,x2=6,即x=±,所以水面宽为2.12.已知抛物线关于x轴对称,它的顶点在坐标原点O,并且经过点M(2,y).若点M到该抛物线焦点的距离为3,则|OM|等于()A.2B.2C.4D.2【答案】B【解析】由题意设抛物线方程为y2=2px(p>0),则M到焦点的距离为xM+=2+=3,∴p=2,∴y2=4x. ∴=4×2,∴|OM|===2.故选B.13.已知过抛物线y2=4x的焦点F的直线交该抛物线于A、B两点,|AF|=2,则|BF|=.【答案】2【解析】设A(x0,y),由抛物线定义知x+1=2,∴x=1,则直线AB⊥x轴,∴|BF|=|AF|=2.14.已知抛物线C:y2=8x与点M(-2,2),过C的焦点且斜率为k的直线与C交于A、B两点,若·=0,则k等于()(A) (B) (C) (D)2【答案】D【解析】法一设直线方程为y=k(x-2),A(x1,y1)、B(x2,y2),由得k2x2-4(k2+2)x+4k2=0,∴x1+x2=,x 1x2=4,由·=0,得(x1+2,y1-2)·(x2+2,y2-2)=(x1+2)(x2+2)+[k(x1-2)-2][k(x2-2)-2]=0,代入整理得k2-4k+4=0,解得k=2.故选D.法二如图所示,设F为焦点,取AB中点P,过A、B分别作准线的垂线,垂足分别为G、H,连接MF,MP,由·=0,知MA⊥MB,则|MP|=|AB|=(|AG|+|BH|),所以MP为直角梯形BHGA的中位线,所以MP∥AG∥BH,所以∠GAM=∠AMP=∠MAP,又|AG|=|AF|,|AM|=|AM|,所以△AMG≌△AMF,所以∠AFM=∠AGM=90°,则MF⊥AB,所以k=-=2.15.已知F是抛物线y2=4x的焦点,P是圆x2+y2-8x-8y+31=0上的动点,则|FP|的最小值是() A.3B.4C.5D.6【答案】B【解析】圆x2+y2-8x-8y+31=0的圆心C坐标为(4,4),半径为1,∵|PF|≥|CF|-1,∴当P、C、F三点共线时,|PF|取到最小值,由y2=4x知F(1,0),∴|PF|min=-1=4.故选B.16.已知点A(4,4)在抛物线y2=px(p>0)上,该抛物线的焦点为F,过点A作直线l:x=-的垂线,垂足为M,则∠MAF的平分线所在直线的方程为.【答案】x-2y+4=0【解析】点A在抛物线上,所以16=4p,所以p=4,所以抛物线的焦点为F(1,0),准线方程为x=-1,垂足M(-1,4),由抛物线的定义得|AF|=|AM|,所以∠MAF的平分线所在的直线就是线段MF的垂直平分线,kMF==-2,所以∠MAF的平分线所在的直线方程为y-4=(x-4),即x-2y+4=0.17.设M(x0,y)为抛物线C:y2=8x上一点,F为抛物线C的焦点,若以F为圆心,|FM|为半径的圆和抛物线C的准线相交,则x的取值范围是()A.(2,+∞)B.(4,+∞) C.(0,2)D.(0,4)【答案】A【解析】∵(x0,y)为抛物线C:y2=8x上一点,∴x≥0,又∵以F为圆心,|FM|为半径的圆和抛物线C的准线相交,∴在水平方向上,点M应在点F的右侧,∴x>2.18.过抛物线y2=2px(p>0)上一定点P(x0,y)(y>0)作两直线分别交抛物线于A(x1,y1),B(x2,y2),当PA与PB的斜率存在且倾斜角互补时,的值为.【答案】-2【解析】设直线PA的斜率为kPA ,PB的斜率为kPB,由=2px1,=2px,得kPA==,同理kPB=,由于PA与PB的斜率存在且倾斜角互补,因此=-,即y1+y2=-2y(y>0),那么=-2.19.若抛物线y2=2px(p>0)的焦点在圆x2+y2+2x-3=0上,则p=()A.B.1C.2D.3【答案】C【解析】由已知(,0)在圆x2+y2+2x-3=0上,所以有+2×-3=0,即p2+4p-12=0,解得p=2或p=-6(舍去).20.过点(0,1)作直线,使它与抛物线y2=4x仅有一个公共点,这样的直线共有()A.1条B.2条C.3条D.4条【答案】C【解析】作出图形,可知点(0,1)在抛物线y2=4x外.因此,过该点可作抛物线y2=4x的切线有两条,还能作一条与抛物线y2=4x的对称轴平行的直线,因此共有三条直线与抛物线只有一个交点.21.如图,直线l:y=x+b与抛物线C:x2=4y相切于点A.(1)求实数b的值.(2)求以点A为圆心,且与抛物线C的准线相切的圆的方程.【答案】(1) b=-1 (2) (x-2)2+(y-1)2=4【解析】(1)由得x2-4x-4b=0(*)因为直线l与抛物线C相切,所以Δ=(-4)2-4×(-4b)=0.解得b=-1.(2)由(1)可知b=-1,故方程(*)为x2-4x+4=0.解得x=2,代入x2=4y,得y=1,故点A(2,1).因为圆A与抛物线C的准线相切,所以圆A的半径r就等于圆心A到抛物线的准线y=-1的距离,即r=|1-(-1)|=2,所以圆A的方程为(x-2)2+(y-1)2=4.22.过抛物线焦点的直线交其于,两点,为坐标原点.若,则的面积为()A.B.C.D.2【答案】C【解析】设直线的倾斜角为及,∵,∴点到准线的距离为,∴,则.∴的面积为.故选C.【考点】抛物线的几何性质,直线与抛物线的位置关系.23.如图X15-3所示,已知圆C1:x2+(y-1)2=4和抛物线C2:y=x2-1,过坐标原点O的直线与C2相交于点A,B,定点M的坐标为(0,-1),直线MA,MB分别与C1相交于点D,E.(1)求证:MA⊥MB;(2)记△MAB,△MDE的面积分别为S1,S2,若=λ,求λ的取值范围.【答案】(1)见解析(2)【解析】(1)证明:设直线AB的方程为y=kx,A(x1,y1),B(x2,y2),则x2-kx-1=0,所以x1+x2=k,x1x2=-1.又·=(x1,y1+1)·(x2,y2+1)=(k2+1)x1x2+k(x1+x2)+1=-k2-1+k2+1=0,∴MA⊥MB.(2)设直线MA的方程为y=k1x-1,MB的方程为y=k2x-1,k1k2=-1.解得或∴A(k1,-1),同理可得B(k2,-1),∴S1=|MA||MB|=|k1k2|.又解得或∴D ,同理可得E . ∴S 2=|MD||ME|=.=λ==≥.故λ的取值范围是.24. 已知抛物线C :y 2=2px(p>0)的焦点为F ,抛物线C 与直线l 1:y =-x 的一个交点的横坐标为8.(1)求抛物线C 的方程;(2)不过原点的直线l 2与l 1垂直,且与抛物线交于不同的两点A ,B ,若线段AB 的中点为P ,且|OP|=|PB|,求△FAB 的面积. 【答案】(1) y 2=8x (2) 24【解析】解:(1)易知直线与抛物线的交点坐标为(8,-8),∴82=2p×8, ∴2p =8,∴抛物线方程为y 2=8x. (2)直线l 2与l 1垂直,故可设l 2:x =y +m ,A(x 1,y 1),B(x 2,y 2),且直线l 2与x 轴的交点为M. 由得y 2-8y -8m =0,Δ=64+32m>0,∴m>-2. y 1+y 2=8,y 1y 2=-8m , ∴ x 1x 2==m 2.由题意可知OA ⊥OB ,即x 1x 2+y 1y 2=m 2-8m =0, ∴m =8或m =0(舍), ∴l 2:x =y +8,M(8,0).故S △FAB =S △FMB +S △FMA =·|FM|·|y 1-y 2|=3=24.25. 已知抛物线方程为x 2=4y ,过点M (0,m )的直线交抛物线于A (x 1,y 1),B (x 2,y 2)两点,且x 1x 2=-4,则m 的值为________. 【答案】1【解析】设直线方程为y =kx +m ,代入抛物线方程得x 2-4kx -4m =0,所以x 1x 2=-4m ,所以m =1.26. 抛物线的焦点坐标是( ) A .(2,0) B .(0,2) C .(l ,0) D .(0,1)【答案】D 【解析】因为,所以,因为焦点在的正半轴,所以焦点坐标为即。
交叉编译器的制作

交叉编译器的制作交叉工具链制作至尊宝典一些必须知道的基础知识Debian 操作系统以及aptitude 命令autoconf and automake什么是交叉编译,configure 的几个参数build host targetbuild:编译代码的机器,的CPU指令集host:编译生成的东西,的CPU指令集(目标板上的CPU的指令集)target:编译生成的东西,他编译生成的的东西,的指令集(所以此选项一般不用,大多只有在做交叉工具链时使用)0、以Expert mode 安装Debian不要升级,确保环境是一个纯净的环境1、声明环境变量1export IS_TARGET=arm-linux1export DIR_SRC=/root/cross_toolchains/src1export PREFIX=/opt/cross_toolchains/arm1export CONFIGURE_BASE="../configure --prefix=$PREFIX --with-sysroot=$PREFIX"2、下载制作交叉工具链所必须的的代码1binutils1ftp:///doc/e613296072.html,/gnu/bi nutils/binutils-2.21.tar.gz1gcc1ftp:///doc/e613296072.html,/gnu/g mp/gmp-5.0.2.tar.gz1ftp:///doc/e613296072.html,/gnu/mpfr/mpfr-3.0.1.tar.gz1/doc/e613296072.html,/mpc/downlo ad/mpc-0.9.tar.gz1ftp:///doc/e613296072.html,/gnu/gc c/gcc-4.6.1/gcc-4.6.1.tar.gz1glibc1ftp:///doc/e613296072.html,/gnu/gli bc/glibc-2.14.tar.gz1ftp:///doc/e613296072.html,/gnu/gli bc/glibc-ports-2.13.tar.gz1linux kernel1/doc/e613296072.html,/pub/linux/k ernel/v2.6/linux-2.6.39.2.tar.bz2 3、安装(卸载)必要的的软件包1aptitude install build-essential automake bison flex texinfo gawk g\+\+1aptitude remove mawk4、解压、归档软件包1cd $DIR_SRC1tar -xf binutils-2.21.tar.gz1tar -xf gmp-5.0.2.tar.gz1tar -xf mpc-0.9.tar.gz1tar -xf mpfr-3.0.1.tar.gz1tar -xf gcc-4.6.1.tar.bz21tar -xf glibc-2.14.tar.gz1tar -xf glibc-ports-2.13.tar.gz1tar -xf linux-2.6.39.2.tar.bz21mv gmp-5.0.2 gcc-4.6.1/gmp1mv mpc-0.9 gcc-4.6.1/mpc1mv mpfr-3.0.1 gcc-4.6.1/mpfr1mv glibc-ports-2.13 glibc-2.14/ports5、编译BINUTILS1cd $DIR_SRC1cd binutils-2.211mkdir build1cd build1$CONFIGURE_BASE --target=$IS_TARGET --disable-nls --enable-shared--disable-multilib1make configure-host1make1make install1export PATH=$PATH:$PREFIX/bin问题:编译binutils一般不会遇到什么问题,但是,如果前面步骤3中安装的软件不全会出现问题6、建立用于编译C库的GCC 1cd $DIR_SRC1cd gcc-4.6.11mkdir build1cd build1$CONFIGURE_BASE \1--target=$IS_TARGET \1--disable-nls \1--disable-shared \1--without-headers \1--with-newlib \1--enable-languages=c \1--disable-threads \1--disable-multilib \1--disable-decimal-float \1--disable-libgomp \1--disable-libmudflap \1--disable-libssp1make all-gcc all-target-libgcc1make install-gcc install-target-libgcc1值得注意的几个configure选项1--target1--disable-shared1--without-headers1--with-newlib1--enable-language-c1--disable-thread1cd $PREFIX/lib/gcc/$IS_TARGET/4.6.11ln -s libgcc.a libgcc_eh.a1有建议修改 gcc/config/t-linux 这个文件1增加-D__gthr_posix_h -Dinhibit_libc 两个宏,但我这里没这样做,是因为:1在configure后,编译使用的命令并不是make 或者是make all 而是 make all-gcc 和 make all-target-libgcc,所以很多问题不会出现1-with-newlib,这个选项不会迫使我们必须使用newlib1libgcc.mvars: No such file or directory1不能在GCC 的源代码目录进行configure,必须在另外的目录进行configure make 等工作1所以这里在代码所在目录下mkdir build 并cd build 再进行 ../configure 等工作1configure: error: C compiler cannot create executables1如果使用 make 或 make all 会出现这样的问题,因为我们还未编译出目标指令集的 C库1所以只能先使用 make all-gcc make all-target-libgcc1../../../../arm-linux/bin/ld: cannot find -lgcc1../../../../arm-linux/bin/ld: cannot find -lgcc_eh1很多资料都只写了make all-gcc 而没有写make all-target-libgcc 这样只建立了gcc,没有建立libgcc.a会出现以上第一个错误1如果没手工建立链接文件 libgcc_eh.a 则会出现第二个错误7、配置内核生成必要的头文件1cd $DIR_SRC1cd linux-2.6.39.21make ARCH=arm CROSS_COMPILE=$IS_TARGET- menuconfig1make ARCH=arm CROSS_COMPILE=$IS_TARGET-1mkdir -p $PREFIX/include1cd $PREFIX/include1ln -s $DIR_SRC/linux-2.6.39.2/arch/arm/include/asm asm 1ln -s $DIR_SRC/linux-2.6.39.2/include/linux linux1ln -s $DIR_SRC/linux-2.6.39.2/include/asm-generic asm-generic1这里并没有将内核的头文件复制到交叉工具链的安装目录1编译C库的时候,需要对应的CPU指令集的汇编代码所以做了链接处理1编译内核在执行make ARCH=arm CROSS_COMPILE=$IS_TARGET- 时如果出错,是没有关系的,这里只要生成了对应的 version.h autoconf.h就可以了8、编译C库1cd $DIR_SRC1cd glibc-2.91mkdir build1cd build1vi ../configure1vi ../ports/sysdeps/unix/sysv/linux/arm/sigrestorer.S1vi ../sysdeps/unix/syscall-template.S1vi ../nptl/allocatestack.c1vi ../elf/dl-tls.c1vi ../sysdeps/ieee754/dbl-64/s_fma.c1vi ../sysdeps/ieee754/dbl-64/s_fmaf.c11具体的修改,我写在下面(觉得还是要说清楚为什么修改,所以就没用sed命令或是做一些patch文件了,请向下看)1CC=$IS_TARGET-gcc \1$CONFIGURE_BASE \1--host=$IS_TARGET \1-enable-add-ons \1--with-binutils=$PREFIX/bin \1--with-headers=$PREFIX/include \1libc_cv_forced_unwind=yes \1libc_cv_c_cleanup=yes1值得注意的几个configure选项1--host1--with-headers1lib_cv_forced_unwind1lib_cv_c_cleanup1make1make install1这里编译的时候并有选择TARGET为EABI,所以在制作交叉工具链时会有很多问题需要修改1*** These critical programs are missing or too old: as ld1*** Check the INSTALL file for required versions.1vi ../configure1查找 "$AS --version" 将 2.1[3-9] 修改为 2.[1-2][0-9]1查询 "$LD --version" 将 2.1[3-9] 修改为 2.[1-2][0-9]1Error: previous CFI entry not closed (missing .cfi_endproc) 1vi ../ports/sysdeps/unix/sysv/linux/arm/sigrestorer.S1ENTRY(__default_sa_restorer) 下增加1END(__default_sa_restorer)1ENTRY(__default_rt_sa_restorer) 下增加1END(__default_rt_sa_restorer)1syscall-template.S:82: Error: CFI instruction used without previous .cfi_startproc1vi ../sysdeps/unix/syscall-template.S1这个问题的修改我也不是十分确定,我是这样来思考的1看到 syscall-template.S 中有 #include1去查看 ports/sysdeps/unix/sysv/linux/arm/sysdep.h1看到如下代码1#ifdef __ASSEMBLER__1#undef PSEUDO11#define PSEUDO(name, syscall_name, args) \1 .text;\1 ENTRY (name);\1 DO_CALL (syscall_name, args); \1 cmn r0, $4096;11猜测是__ASSEMBLER__宏未打开,以至于未能找到PSEUD0函数的声明,则将11#define PSEUDO(name, syscall_name, args) \1 .text;\1 ENTRY (name);\1 DO_CALL (syscall_name, args); \1 cmn r0, $4096;11这段代码添加至 ../sysdeps/unix/syscall-template.S 中1LS_DTV_UNALLOCATED undeclared (first use in this function)1vi ../nptl/allocatestack.c1vi ../elf/dl-tls.c1这个错误会出现在编译以上两个文件的时候,这个宏的定义我grep了整个glibc的所有代码,没找到ARM相关的声明及定义,按照其他指令集的定义猜测着修改如下1在以上两个C文件中增加相应的定义11#define TLS_DTV_UNALLOCATED ((void *) -1l)1E_TOWARDZERO undeclared (first use in this function)1E_INEXACT undeclared (first use in this function)1以上两个错误会出现在以下两个文件的的编译过程中1vi ../sysdeps/ieee754/dbl-64/s_fma.c1vi ../sysdeps/ieee754/dbl-64/s_fmaf.c1参考 ports/sysdeps/arm/eabi/bits/fenv.h中的定义1在两个文件中添加1#define FE_TOWARDZERO 0xc000001#define FE_INEXACT 161mawk: scripts/gen-sorted.awk: line 19: regular expression compile failed1所以要 aptitude install gawk 所以也顺带着 aptitude remove mawk1configure: error: forced unwind support is required1configure 中增加配置参数 libc_cv_forced_unwind=yes1error: the compiler must support C cleanup handlin1configure 中增加配置参数libc_cv_c_cleanup=yes1--enable-add-ons 为 C 库增加 thread 支持,目前默认使用的是 nptl 所以这里没有去下载 glibc-threads 相关的代码1--with-headers 指定内核头文件所在的目录9、编译完整的gcc 工具链1mkdir -p $PREFIX/usr1cd $PREFIX/usr1ln -s ../include include1cd $PREFIX1mkdir -p opt/cross_toolchains1cd opt/cross_toolchains/1ln -s ../../../arm arm1cd $DIR_SRC1cd gcc-4.6.11cd build1make clean1make distclean1rm * -rf1$CONFIGURE_BASE \1--target=arm-linux \1--enable-languages=c,c++ \1--enable-shared \1--disable-nls \1--enable-c99 \1--enable-long-long \1--disable-multilib \1--enable-__cxa_atexit1几个值得注意的configure 选项1--target1--enable-shared1make1make install1The directory that should contain system headers does not exist:1这个问题我没具体的去跟踪了,从表面上看出来是一些路径上的问题,并且经过验证,这个问题是在configure时使用了--with-sysroot选项时产生的1为了尝试不通过建立链接的方式去解决这个问题1在指明了 --includedir --libdir --sysconfdir 等等一系列参数后编译,依然会出现此问题1所以不再跟踪,暂且是当做GCC编译环境上的一个 BUG好了1/opt/cross_toolchains/arm/arm-linux/bin/ld: cannot find/opt/cross_toolchains/arm/lib/libc.so.6 inside /opt/cross_toolchains/arm 1这个问题更是有点神经病了,所以这里也不跟踪了,也是由于使用了 --with-sysroot选项产生的问题,建立了第二个链接文件1目的是让 /opt/cross_toolchains/arm 这个被当做是根目录的目录里面能有一个跟--prefix 指定的/opt/cross_toolchains/arm 一样的目录结构(说起来真别扭)参考资料https:///doc/e613296072.html,/devel operworks/cn/linux/l-embcmpl//doc/e613296072.html,/view/clfs-embedded/arm/cross-tools/introduction.html/doc/e613296072.html,/bbs/showthre ad.php?t=267672(这个文章虽然有点老,也有点神,把一些能看懂的说的让人看不懂,那个图更是让人觉得,汗,但原理还是说的很清楚的,这里强调的--with-sysroot的3次出现的问题,还是值得仔细想想的,这也是我为什么将--with-sysroot 选项做到$CONFIGURE_BASE 这个环境变量中的原因)。
抛物线(教案)-2022-2023学年高二数学教材教案(人教A版2019选择性必修第一册)

3.3 抛物线考纲要求1.掌握抛物线的定义、几何图形、标准方程及简单的几何性质(范围、对称性、顶点、准线).(重点) 2.能根据几何性质求最值,能利用抛物线的定义进行灵活转化,并能理解数形结合思想,掌握抛物线的简单应用.(难点)知识解读知识点①抛物线的概念平面内与一个定点F 和一条定直线l (l 不经过点F )的距离相等的点的轨迹叫做抛物线.点F 叫做抛物线的焦点,直线l 叫做抛物线的准线. 知识点①抛物线的标准方程和几何性质标准方程y 2=2px (p >0)y 2=-2px (p >0)x 2=2py (p >0)x 2=-2py (p >0)p 的几何意义:焦点F 到准线l 的距离图形顶点 O (0,0)对称轴 x 轴y 轴焦点 F ⎝⎛⎭⎫p 2,0F ⎝⎛⎭⎫-p2,0 F ⎝⎛⎭⎫0,p 2 F ⎝⎛⎭⎫0,-p2 离心率 e =1准线方程 x =-p 2x =p 2 y =-p2y =p 2 范围 x ≥0,y ∈R x ≤0,y ∈R y ≥0,x ∈R y ≤0,x ∈R 开口方向 向右 向左 向上 向下 焦半径(其中P (x 0,y 0))|PF |=x 0+p2|PF |=-x 0+p2|PF |=y 0+p2|PF |=-y 0+p2知识点①必记结论1.抛物线y 2=2px (p >0)上一点P (x 0,y 0)到焦点F ⎝⎛⎭⎫p 2,0的距离|PF |=x 0+p2,也称为抛物线的焦半径. 2.y 2=ax (a ≠0)的焦点坐标为⎝⎛⎭⎫a 4,0,准线方程为x =-a4.3.设AB 是过抛物线y 2=2px (p >0)焦点F 的弦,若A (x 1,y 1),B (x 2,y 2),则 (1)x 1x 2=p 24,y 1y 2=-p 2.(2)弦长|AB |=x 1+x 2+p =2psin 2α(α为弦AB 的倾斜角).(3)以弦AB 为直径的圆与准线相切.(4)通径:过焦点垂直于对称轴的弦,长等于2p ,通径是过焦点最短的弦.题型讲解题型一、抛物线的定义及其应用例1.已知点F ⎝⎛⎭⎫14,0,直线l :x =-14,点B 是l 上的动点.若过点B 垂直于y 轴的直线与线段BF 的垂直平分线交于点M ,则点M 的轨迹是( ) A .双曲线 B .椭圆 C .圆 D .抛物线【答案】D【解析】由已知得|MF |=|MB |,根据抛物线的定义知,点M 的轨迹是以点F 为焦点,直线l 为准线的抛物线.例2.若抛物线y 2=4x 上一点P 到其焦点F 的距离为2,O 为坐标原点,则∈OFP 的面积为( ) A .12B .1C .32D .2 【答案】B【解析】设P (x P ,y P ),由题可得抛物线焦点为F (1,0),准线方程为x =-1.又点P 到焦点F 的距离为2,∈由定义知点P 到准线的距离为2. ∈x P +1=2,∈x P =1.代入抛物线方程得|y P |=2,∈∈OFP 的面积为S =12·|OF |·|y P |=12×1×2=1. 例3.设P 是抛物线y 2=4x 上的一个动点,若B (3,2),则|PB |+|PF |的最小值为________. 【答案】4【解析】如图,过点B 作BQ 垂直准线于点Q ,交抛物线于点P 1,则|P 1Q |=|P 1F |,则有|PB |+|PF |≥|P 1B |+|P 1Q |=|BQ |=4,即|PB |+|PF |的最小值为4. 题型二、抛物线的标准方程 例1.[易错题]抛物线y =-116x 2的焦点坐标为( ) A .⎝⎛⎭⎫-164,0 B .()-4,0 C .⎝⎛⎭⎫0,-164 D .()0,-4【答案】D【解析】∈y =-116 x 2,∈x 2=-16y ,因此焦点坐标为()0,-4 .例2.已知点()1,1 在抛物线C :y 2=2px ()p >0 上,则C 的焦点到其准线的距离为( ) A .14B .12C .1D .2【答案】B【解析】由点()1,1 在抛物线上,易知1=2p ,p =12 ,故焦点到其准线的距离为12.例3.若抛物线C 顶点在原点,焦点在y 轴上,且过点(2,1),则C 的标准方程是___________. 【答案】x 2=4y【解析】因为抛物线C 顶点在原点,焦点在y 轴上,故设抛物线方程为x 2=my , 又抛物线过点(2,1),所以22=m ,即m =4,所以抛物线方程为x 2=4y .例4.如图所示,过抛物线y 2=2px (p >0)的焦点F 的直线交抛物线于点A ,B ,交其准线l 于点C ,若|BC |=2|BF |,且|AF |=3,则此抛物线的标准方程为________.【答案】y 2=3x【解析】分别过点A ,B 作AA 1∈l ,BB 1∈l ,且垂足分别为A 1,B 1,由已知条件|BC |=2|BF |,得|BC |=2|BB 1|,所以∈BCB 1=30°.又|AA 1|=|AF |=3,所以|AC |=2|AA 1|=6,所以|CF |=|AC |-|AF |=6-3=3,所以F 为线段AC 的中点.故点F 到准线的距离为p =12|AA 1|=32,从而抛物线方程为y 2=3x .例5.已知抛物线C :y 2=2px (p >0)的焦点为F ,准线为l ,点A 是抛物线C 上一点,AD ∈l ,交l 于D .若|AF |=4,∈DAF =60°,则抛物线C 的方程为( ) A .y 2=8x B .y 2=4x C .y 2=2x D .y 2=x【答案】B【解析】根据抛物线的定义可得|AD |=|AF |=4, 又∈DAF =60°,所以|AD |-p =|AF |cos 60°=12|AF |,所以4-p =2,解得p =2, 所以抛物线C 的方程为y 2=4x . 题型三、抛物线的简单几何性质例1.过抛物线y 2=4x 的焦点的直线l 交抛物线于P (x 1,y 1),Q (x 2,y 2)两点,如果x 1+x 2=6,则|PQ |等于( ) A .9 B .8 C .7 D .6【答案】B【解析】抛物线y 2=4x 的焦点为F (1,0),准线方程为x =-1.根据题意可得,|PQ |=|PF |+|QF |=x 1+1+x 2+1=x 1+x 2+2=8.例2.已知抛物线y 2=2px (p >0)的准线经过点(-1,1),则该抛物线的焦点坐标为( ) A .(-1,0) B .(1,0) C .(0,-1)D .(0,1)【答案】B【解析】抛物线y 2=2px (p >0)的准线为x =-p 2 ,由准线过点(-1,1),得-p2 =-1,解得p =2.所以抛物线的焦点坐标为(1,0).例3.已知直线l 过抛物线C 的焦点,且与C 的对称轴垂直,l 与C 交于A ,B 两点,|AB |=12,P 为C 的准线上一点,则∈ABP 的面积为( ) A .18 B .24 C .36 D .48【答案】C【解析】以抛物线的顶点为原点,水平方向为x 轴,竖直方向为y 轴,建立平面直角坐标系(图略). 设抛物线的方程为y 2=2px (p >0),则焦点坐标为(p 2 ,0).将x =p2 代入y 2=2px ,可得y 2=p 2.所以|AB |=2p ,即2p =12,所以p =6.因为点P 在准线上,所以点P 到AB 的距离为p =6, 所以∈ABP 的面积为12×12×6=36.例4.抛物线y 2=2px (p >0)的焦点为F ,O 为坐标原点,M 为抛物线上一点,且|MF |=4|OF |,∈MFO 的面积为43,则抛物线的方程为( ) A .y 2=6x B .y 2=8x C .y 2=16x D .y 2=15x2【答案】B【解析】设M (x ,y ),因为|OF |=p 2,|MF |=4|OF |,所以|MF |=2p ,由抛物线定义知x +p 2=2p ,所以x =32p ,所以y =±3p . 又∈MFO 的面积为43,所以12×p2×3p =43,解得p =4(p =-4舍去).所以抛物线的方程为y 2=8x .例5.若抛物线y 2=2px (p >0)上一点到焦点和到抛物线对称轴的距离分别为10和6,则抛物线的方程为( ) A .y 2=4x B .y 2=36xC .y 2=4x 或y 2=36xD .y 2=8x 或y 2=32x 【答案】C【解析】因为抛物线y 2=2px (p >0)上一点到抛物线的对称轴的距离为6, 所以若设该点为P ,则P (x 0,±6).因为P 到抛物线的焦点F ⎝⎛⎭⎫p 2,0 的距离为10,所以由抛物线的定义得x 0+p2 =10.∈ 因为P 在抛物线上,所以36=2px 0.∈由∈∈解得p =2,x 0=9或p =18,x 0=1,则抛物线的方程为y 2=4x 或y 2=36x .例6.(2022·山东淄博一模)若抛物线y 2=2px ()p >0 上的点A ()x 0,-2 到其焦点的距离是点A 到y 轴距离的3倍,则p 等于___________. 【答案】22【解析】抛物线y 2=2px ()p >0 开口向右,准线为x =-p2 ,将A 的坐标代入抛物线方程得4=2px 0,x 0=2p,由于抛物线y 2=2px ()p >0 上的点A ()x 0,-2 到其焦点的距离是点A 到y 轴距离的3倍, 根据抛物线的定义有x 0+p 2 =3x 0,所以2p +p 2 =3×2p ,p 2 =4p ,p 2=8,p =22 .题型四、直线与抛物线的位置关系例1.(2018·全国卷∈)设抛物线C :y 2=4x 的焦点为F ,过点(-2,0)且斜率为23的直线与C 交于M ,N 两点,则FM →·FN →=( ) A .5 B .6 C .7 D .8【答案】D【解析】由题意知直线MN 的方程为y =23(x +2),联立直线与抛物线的方程,得⎩⎪⎨⎪⎧y =23x +2,y 2=4x ,解得⎩⎪⎨⎪⎧ x =1,y =2或⎩⎪⎨⎪⎧x =4,y =4.不妨设M 为(1,2),N 为(4,4).又∈抛物线焦点为F (1,0),∈FM →=(0,2),FN →=(3,4). ∈FM →·FN →=0×3+2×4=8.例2.已知抛物线C 的顶点是原点O ,焦点F 在x 轴的正半轴上,经过F 的直线与抛物线C 交于A 、B 两点,如果OA →·OB →=-12,那么抛物线C 的方程为( ) A .x 2=8y B .x 2=4y C .y 2=8x D .y 2=4x【答案】C【解析】由题意,设抛物线方程为y 2=2px (p >0),直线方程为x =my +p2,联立⎩⎪⎨⎪⎧y 2=2px ,x =my +p2,消去x 得y 2-2pmy -p 2=0, 设A (x 1,y 1),B (x 2,y 2),则y 1+y 2=2pm ,y 1y 2=-p 2,得OA →·OB →=x 1x 2+y 1y 2=(my 1+p 2)·(my 2+p 2)+y 1y 2=m 2y 1y 2+pm 2(y 1+y 2)+p 24+y 1y 2=-34p 2=-12∈p =4,即抛物线C 的方程为y 2=8x .例3.已知抛物线y 2=2px (p >0),过其焦点且斜率为1的直线交抛物线于A 、B 两点,若线段AB 的中点的纵坐标为2,则该抛物线的准线方程为( )A .x =1B .x =-1C .x =2D .x =-2 【答案】B【解析】∈y 2=2px (p >0)的焦点坐标为(p2,0),∈过焦点且斜率为1的直线方程为y =x -p2,即x =y +p2,将其代入y 2=2px ,得y 2=2py +p 2,即y 2-2py -p 2=0.设A (x 1,y 1),B (x 2,y 2), 则y 1+y 2=2p ,∈y 1+y 22=p =2,∈抛物线的方程为y 2=4x ,其准线方程为x =-1.例4.已知抛物线C :y 2=2px (p >0)的焦点为F ,抛物线C 与直线l 1:y =-x 的一个交点的横坐标为8. (1)求抛物线C 的方程;(2)不过原点的直线l 2与l 1垂直,且与抛物线交于不同的两点A ,B ,若线段AB 的中点为P ,且|OP |=|PB |,求∈F AB 的面积.【答案】(1)y 2=8x (2)245【解析】(1)易知直线与抛物线的交点坐标为(8,-8), ∈(-8)2=2p ×8,∈2p =8, ∈抛物线C 的方程为y 2=8x .(2)直线l 2与l 1垂直,故可设直线l 2:x =y +m ,A (x 1,y 1),B (x 2,y 2),且直线l 2与x 轴的交点为M .由⎩⎪⎨⎪⎧y 2=8x ,x =y +m ,得y 2-8y -8m =0, Δ=64+32m >0,∈m >-2.y 1+y 2=8,y 1y 2=-8m ,∈x 1x 2=y 21y 2264=m 2.由题意可知OA ∈OB ,即x 1x 2+y 1y 2=m 2-8m =0, ∈m =8或m =0(舍去),∈直线l 2:x =y +8,M (8,0). 故S ∈F AB =S ∈FMB +S ∈FMA =12·|FM |·|y 1-y 2|=3()212214y y y y -+=245.达标训练1.已知抛物线的准线方程为y =-2,则其标准方程为( ) A .x 2=8y B .x 2=-8y C .y 2=8x D .y 2=-8x【答案】A【解析】因为抛物线的准线方程为y =-2,所以抛物线的焦点在y 轴正半轴上,且p2=2,即p =4,所以抛物线的方程为x 2=8y .2.点M (5,3)到抛物线y =ax 2(a ≠0)的准线的距离为6,那么抛物线的方程是( ) A .y =12x 2 B .y =12x 2或y =-36x 2 C .y =-36x 2 D .y =112x 2或y =-136x 2【答案】D【解析】分两类a >0,a <0,可得y =112x 2或y =-136x 2.3.(全国卷∈)设F 为抛物线C :y 2=4x 的焦点,曲线y =kx (k >0)与C 交于点P ,PF ∈x 轴,则k =( )A .12B .1C .32D .2【答案】D【解析】∈y 2=4x ,∈F (1,0).又∈曲线y =kx (k >0)与C 交于点P ,PF ∈x 轴,∈P (1,2).将点P (1,2)的坐标代入y =kx(k >0),得k =2.4.(2021·山东烟台一模)已知F 为抛物线C :y 2=8x 的焦点,直线l 与C 交于A ,B 两点,若AB 中点的横坐标为4,则|| AF +||BF =( ) A .8 B .10 C .12 D .16【答案】C【解析】抛物线C :y 2=8x 的焦点为F ,直线l 与抛物线C 交于A ,B 两点, 若AB 的中点的横坐标为4,设A (x 1,y 1),B (x 2,y 2),x 1+x 2=8, 则|AF |+|BF |=x 1+x 2+p =8+4=12.5.已知F 为抛物线y 2=4x 的焦点,P ()x 0,y 0 是该抛物线上的一点.若||PF >2,则( ) A .x 0∈()0,1 B .x 0∈(1,+∞) C .y 0∈(2,+∞) D .y 0∈(-∞,2) 【答案】B【解析】由条件可知p2=1,根据焦半径公式||PF =x 0+1>2,解得x 0>1.6.(2021·广东茂名二模)设O 为坐标原点,F 为抛物线C :x 2=8y 的焦点,P 为C 上一点,若||PF =6,则∈POF 的面积为( ) A .2 B .42 C .43 D .4【答案】B【解析】∈抛物线C :x 2=8y ,∈F (2,0),准线y =-2.由||PF =6,即P 到准线的距离为6.设P (x 0,y 0),||PF =y 0+2=6,解得y 0=4, 代入抛物线方程x 2=8y ,得x 0=±42 .S ∈POF =12 ||OF ||x 0 =12×2×42 =42 .7.设抛物线的顶点为O ,焦点为F ,准线为l ,P 是抛物线上异于O 的一点,过P 作PQ ∈l 于Q .则线段FQ 的垂直平分线( ) A .经过点O B .经过点P C .平行于直线OP D .垂直于直线OP【答案】B【解析】连接PF (图略),由题意及抛物线的定义可知|PQ |=|FP |,则∈QPF 为等腰三角形,故线段FQ 的垂直平分线经过点P .8.已知直线l 1:4x -3y +6=0和直线l 2:x =-1,抛物线y 2=4x 上一动点P 到直线l 1和l 2的距离之和的最小值为( )A .3716B .115C .3D .2 【答案】D【解析】直线l 2:x =-1是抛物线y 2=4x 的准线, 抛物线y 2=4x 的焦点为F (1,0),则点P 到直线l 2:x =-1的距离等于|PF |, 过点F 作直线l 1:4x -3y +6=0的垂线, 和抛物线的交点就是点P ,所以点P 到直线l 1:4x -3y +6=0的距离和直线l 2:x =-1的距离之和的最小值就是点F (1,0)到直线l 1:4x -3y +6=0的距离,所以最小值为|4-0+6|32+42=2,故选D.8.(2020·新高考全国∈)斜率为3的直线过抛物线C :y 2=4x 的焦点,且与C 交于A ,B 两点,则|AB |=________. 【答案】163【解析】如图,由题意得,抛物线的焦点为F (1,0),设直线AB 的方程为y =3(x -1).由⎩⎨⎧ y =3x -1,y 2=4x ,得3x 2-10x +3=0.设A (x 1,y 1),B (x 2,y 2),则x 1+x 2=103, 所以|AB |=x 1+x 2+2=163. 9.设F 为抛物线C :y 2=3x 的焦点,过F 且倾斜角为30°的直线交C 于A ,B 两点,则|AB |=________.【答案】12【解析】焦点F 的坐标为⎝⎛⎭⎫34,0,方法一 直线AB 的斜率为33, 所以直线AB 的方程为y =33⎝⎛⎭⎫x -34, 即y =33x -34,代入y 2=3x ,得13x 2-72x +316=0. 设A (x 1,y 1),B (x 2,y 2),则x 1+x 2=212, 所以|AB |=x 1+x 2+p =212+32=12. 方法二 由抛物线焦点弦的性质可得|AB |=2p sin 2θ=3sin 230°=12. 10.已知抛物线C :y 2=2px (p >0)的准线为l ,过M (1,0)且斜率为3的直线与l 相交于点A ,与C 的一个交点为B ,若AM →=MB →,则p =________.【答案】2【解析】如图, 由AB 的斜率为3,知∈α=60°,又AM →=MB →,∈M 为AB 的中点.过点B 作BP 垂直准线l 于点P ,则∈ABP =60°,∈∈BAP =30°,∈|BP |=12|AB |=|BM |. ∈M 为焦点,即p 2=1,∈p =2. 11.已知抛物线C :y 2=3x 的焦点为F ,斜率为32的直线l 与C 的交点为A ,B ,与x 轴的交点为P . (1)若|AF |+|BF |=4,求l 的方程;(2)若AP →=3PB →,求|AB |.【答案】(1)y =32x -78 (2)4133【解析】设直线l :y =32x +t , A (x 1,y 1),B (x 2,y 2).(1)由题设得F ⎝⎛⎭⎫34,0,故|AF |+|BF |=x 1+x 2+32. 又|AF |+|BF |=4,所以x 1+x 2=52. 由⎩⎪⎨⎪⎧y =32x +t ,y 2=3x ,可得9x 2+12(t -1)x +4t 2=0, 则x 1+x 2=()9112--t . 从而()9112--t =52,得t =-78. 所以l 的方程为y =32x -78.(2)由AP →=3PB →可得y 1=-3y 2.由⎩⎪⎨⎪⎧y =32x +t ,y 2=3x ,可得y 2-2y +2t =0, 所以y 1+y 2=2,从而-3y 2+y 2=2,故y 2=-1,y 1=3.代入C 的方程得x 1=3,x 2=13, 即A (3,3),B ⎝⎛⎭⎫13,-1.故|AB |=4133. 12.已知抛物线y 2=2px (p >0)的焦点为F ,A (x 1,y 1),B (x 2,y 2)是过F 的直线与抛物线的两个交点,求证:(1)y 1y 2=-p 2,x 1x 2=p 24; (2)1|AF |+1|BF |为定值; (3)以AB 为直径的圆与抛物线的准线相切.【答案】见解析【解析】证明 (1)由已知得抛物线焦点坐标为(p 2,0). 由题意可设直线方程为x =my +p 2,代入y 2=2px , 得y 2=2p ⎝⎛⎭⎫my +p 2,即y 2-2pmy -p 2=0.(*) 则y 1,y 2是方程(*)的两个实数根,所以y 1y 2=-p 2.因为y 21=2px 1,y 22=2px 2,所以y 21y 22=4p 2x 1x 2,所以x 1x 2=y 21y 224p 2=p 44p 2=p 24. (2)1|AF |+1|BF |=1x 1+p 2+1x 2+p 2=x 1+x 2+p x 1x 2+p 2x 1+x 2+p 24. 因为x 1x 2=p 24,x 1+x 2=|AB |-p ,代入上式, 得1|AF |+1|BF |=|AB |p 24+p 2|AB |-p +p 24=2p(定值). (3)设AB 的中点为M (x 0,y 0),分别过A ,B 作准线的垂线,垂足为C ,D ,过M 作准线的垂线,垂足为N ,则|MN |=12(|AC |+|BD |)=12(|AF |+|BF |)=12|AB |. 所以以AB 为直径的圆与抛物线的准线相切.课后提升1.设抛物线C :y 2=2px (p >0)的焦点为F ,点M 在C 上,|MF |=5,若以MF 为直径的圆过点(0,2),则C 的标准方程为( )A .y 2=4x 或y 2=8xB .y 2=2x 或y 2=8xC .y 2=4x 或y 2=16xD .y 2=2x 或y 2=16x【答案】C【解析】由题意知,F ⎝⎛⎭⎫p 2,0 ,抛物线的准线方程为x =-p 2, 则由抛物线的定义知,x M =5-p 2,设以MF 为直径的圆的圆心为⎝⎛⎭⎫52,y M 2 , 所以圆的方程为⎝⎛⎭⎫x -52 2 +⎝⎛⎭⎫y -y M 2 2 =254,又因为圆过点(0,2),所以y M =4, 又因为点M 在C 上,所以16=2p ⎝⎛⎭⎫5-p 2 ,解得p =2或p =8, 所以抛物线C 的标准方程为y 2=4x 或y 2=16x .2.(多选)(2022·潍坊模拟)已知抛物线x 2=12y 的焦点为F ,M (x 1,y 1),N (x 2,y 2)是抛物线上两点,则下列结论正确的是( )A .点F 的坐标为⎝⎛⎭⎫18,0B .若直线MN 过点F ,则x 1x 2=-116C .若MF →=λNF →,则|MN |的最小值为12D .若|MF |+|NF |=32,则线段MN 的中点P 到x 轴的距离为58【答案】BCD【解析】易知点F 的坐标为⎝⎛⎭⎫0,18,选项A 错误; 根据抛物线的性质知,MN 过焦点F 时, x 1x 2=-p 2=-116,选项B 正确; 若MF →=λNF →,则MN 过点F ,则|MN |的最小值即抛物线通径的长,为2p ,即12,选项C 正确; 抛物线x 2=12y 的焦点为⎝⎛⎭⎫0,18, 准线方程为y =-18, 过点M ,N ,P 分别作准线的垂线MM ′,NN ′,PP ′,垂足分别为M ′,N ′,P ′(图略),所以|MM ′|=|MF |,|NN ′|=|NF |.所以|MM ′|+|NN ′|=|MF |+|NF |=32, 所以线段|PP ′|=|MM ′|+|NN ′|2=34, 所以线段MN 的中点P 到x 轴的距离为|PP ′|-18=34-18=58,选项D 正确. 3.(多选)已知抛物线C :y 2=2px (p >0)过点P (1,1),则下列结论正确的是( )A .点P 到抛物线焦点的距离为32B .过点P 作过抛物线焦点的直线交抛物线于点Q ,则∈OPQ 的面积为532C .过点P 与抛物线相切的直线方程为x -2y +1=0D .过点P 作两条斜率互为相反数的直线交抛物线于M ,N 两点,则直线MN 的斜率为定值【答案】BCD【解析】因为抛物线C :y 2=2px (p >0)过点P (1,1),所以p =12,所以抛物线方程为y 2=x ,焦点坐标为F ⎝⎛⎭⎫14,0. 对于A ,|PF |=1+14=54,错误; 对于B ,k PF =43,所以l PF :y =43⎝⎛⎭⎫x -14,与y 2=x 联立得4y 2-3y -1=0,所以y 1+y 2=34,y 1y 2=-14, 所以S ∈OPQ =12|OF |·|y 1-y 2|=12×14×y 1+y 22-4y 1y 2=532,正确; 对于C ,依题意斜率存在,设直线方程为y -1=k (x -1),与y 2=x 联立得ky 2-y +1-k =0,Δ=1-4k (1-k )=0,即4k 2-4k +1=0,解得k =12,所以切线方程为x -2y +1=0,正确; 对于D ,依题意斜率存在,设l PM :y -1=k (x -1),与y 2=x 联立得ky 2-y +1-k =0,所以y M +1=1k ,即y M =1k -1,则x M =⎝⎛⎭⎫1k -12,所以点M ⎝⎛⎭⎫⎝⎛⎭⎫1k -12,1k -1,同理N ⎝⎛⎭⎫⎝⎛⎭⎫-1k -12,-1k -1, 所以k MN =1k -1-⎝⎛⎭⎫-1k -1⎝⎛⎭⎫1k -12-⎝⎛⎭⎫-1k -12=2k -4k=-12,正确. 4.已知抛物线C :y 2=8x 与点M (-2,2),过C 的焦点且斜率为k 的直线与C 交于A 、B 两点.若MA →·MB →=0,则k =________.【答案】2【解析】抛物线C 的焦点为F (2,0),则直线方程为y =k (x -2),与抛物线方程联立,消去y 化简得k 2x 2-(4k 2+8)x +4k 2=0.设点A (x 1,y 1),B (x 2,y 2).则x 1+x 2=4+8k 2,x 1x 2=4. 所以y 1+y 2=k (x 1+x 2)-4k =8k, y 1y 2=k 2[x 1x 2-2(x 1+x 2)+4]=-16.因为MA → ·MB →=(x 1+2,y 1-2)·(x 2+2,y 2-2)=(x 1+2)(x 2+2)+(y 1-2)(y 2-2)=x 1x 2+2(x 1+x 2)+y 1y 2-2(y 1+y 2)+8=0,将上面各个量代入,化简得k 2-4k +4=0,所以k =2.5.(2022·沈阳模拟)已知抛物线C :x 2=2py (p >0),其焦点到准线的距离为2,直线l 与抛物线C 交于A ,B 两点,过A ,B 分别作抛物线C 的切线l 1,l 2,且l 1与l 2交于点M .(1)求p 的值;(2)若l 1∈l 2,求∈MAB 面积的最小值.【答案】(1)p =2 (2)4【解析】(1)由题意知,抛物线焦点为⎝⎛⎭⎫0,p 2, 准线方程为y =-p 2, 焦点到准线的距离为2,即p =2.(2)由(1)知抛物线的方程为x 2=4y ,即y =14x 2,所以y ′=12x , 设A (x 1,y 1),B (x 2,y 2),l 1:y -x 214=x 12(x -x 1), l 2:y -x 224=x 22(x -x 2), 由于l 1∈l 2,所以x 12·x 22=-1, 即x 1x 2=-4.设直线l 的方程为y =kx +m ,与抛物线方程联立, 得⎩⎪⎨⎪⎧y =kx +m ,x 2=4y , 所以x 2-4kx -4m =0,Δ=16k 2+16m >0, x 1+x 2=4k ,x 1x 2=-4m =-4,所以m =1, 即l :y =kx +1.联立方程⎩⎨⎧y =x 12x -x 214,y =x 22x -x 224, 得⎩⎪⎨⎪⎧ x =2k ,y =-1,即M (2k ,-1). M 点到直线l 的距离d =|k ·2k +1+1|1+k 2=2|k 2+1|1+k 2, |AB |=()()[]21221241x x x x k -++ =4(1+k 2),所以S =12×4(1+k 2)×2|k 2+1|1+k 2322=4(1+)4k ≥,当k =0时,∈MAB 的面积取得最小值4.。
海信 LED55T29SG3D 液晶电视 产品使用指南

+}|yy/wz.~x|g C 8m X 3m >Q q ~1,q r D 8L +i g _h k >~1,q _l ^|b ><V ^>a ?^3w R E +g 8f :i 8e 4`.m ;M Q +U V ?X _Q O 4O u g ;?XTTZUUUUUU U V ?X u w S z S L?w ?TYWVQ\WT]UUUUb j ;8O 1D H -k |x R C [H 17}R C =K 8W :17}{42Q q -Y ?s Z ;0Q s B H U V C 8><V 84_T C 80:s u ]s :y g +z M Q g C 8IW s j 9s N C 8M Q I j >x [-_I +D d a g ]:T 2E _`?R C @M Q s [R C Y.O 2R E >g @v ~Ux i _+i +*8*bQ /6*pt 2T *U =8z Z T p g o >{J a{Q s -S +{J QN u u N *M r *f 65Q 9W p a i u 8b -7P :+g C 8z E h *M Q G J l V b /q 7*q d +e /h a 5~w A F >J l {K 2?l =R @X ;?Z <5Y \A ;==R ><V ^>h 6-x RE +?6?6?g ?\g8:=E h L6`?R C@E_04?Z8R Q,k2j P^\P ,R E,R E V o>n8*b@2dP<v m?Z87g>n8*D87G8-p707E z4y M Q8Pz3k r?Z V\:~r*U~r*jC3r*C l c bMS C l?Z V\:~r*U~r*x,q J==x q J=Q yC l c bU E90=5]0=,0=^i0=,y ,Xa g9p=EE>:~x8\[\x8x*p@@<?x.p@r x S X{v p J\>r C~x7ZR Q=l R Q ;<=?@A9:9?9?9?9?9@9@9@9A9A9A:8:9:9:9:9:;:;:::::::::;:;:<:;:<:<:<:<:<:<:=:=:=:=:=:=:>:>:>:>:>:?:?:?:?:@:@:@:@:@:@:A:A;8;8;8;8;9;9;:;:;;;>;?;A<8<9<9<<<<<< /O8P7Z=Veqkxekix F{8\_9pH79pD_B=g E W p=O h W pg E R0=O h R0ZM},9pD u~W:~y`w K A R;H8PAN^xAN d JA23Q@N1ANR vJ;AN1@NI bn hK z*t-D*t70*tgpgp I lN?k r V N?]s Wz h Z7l bz h nq;6O E g l bz h NTK6O U4l bU4W g,az h X\X6O l g l b`1/:`?R CR n?Z`E JQV U^_B|N S:+E d s [__CZ y E 42{^e_z _s [<3+i ==?=@>;><><>=>>>@>@<=<=<?<A =8=:=;=<=>[fc ,a E s ;d :`E 8Pw P Y ^u w V ~N S 7^1|C =h A |A Z A |}l A |u A A |3P G D G >7=s I g I 9pg8:=;H z hg8=X;H z h>n>M=?9J*^O2;H D1y9^L+*;Y2.D?z+:H7;H W o7PL S4yr D5G j;H>n>:H7;H q T N|+38S+}|c J;H3+:=X g n*n n*z_*6^w s U Q R T+9>2_o*k r?Z4?8M G B V=L_o?Z*X;k r?Z0HZF5G1+_k r7P=8t W9J^O y9>s m m_m^i;]C959G@~b;h2M A+k r V N?z h>nM<N\ki`URU*ki`VRT s h8e>,a U4>1H E g*S0Z7+WVW XsvWvsspvoe\X E L>M?Z W E=X<9J*;Y2L R+V W t S--?<}3R v>n@t I t W^25t W2t S--?<+q I z/I@/O=X q I z/>n>EXZ n_:88870>HXZ M n_AAA870@2Q k r7@`R37R+V_O W:7P_:*s h*.h4*.h]*R n_1*=U=5V W W3h M?e,+38S k r>h>z<32I5c e m y9^O E S>3L n n+n?_o_Or M X d s V\G>9=k U j>g80q I z s6>[r U g55w8g5>M X Lq G g8M Q_ ]>x n p?n+V N?Q Sg8=X A;*lc_*dbge*Z7*k z*ki`*M Z*[8*`S5V W Q S+U ihi fnouPerpR2`:/s+g C8:4ihi fnouPerp6`]M Q jtvivttsvrq mjE h+XsvWvsspvoe\X x Q x8|=E9n K*]9J2z f=0b>M G=?n~26E^T{2U w+Z L +Z [b [+Q +L Rv +_v ?<>_s;s ><E_s;s m S \P m Si X d s V \?9x H ?<>_s;s ?_upvEC A ]4?>n AK 8[|R C [|W :R C p -K 8R C_QK [|_QK x C [|p -x CV +[R C 9Q p ?9:]?EC A EC A EC A a >><E_s;s ]]V E h L 6E _04M Q g C 8IW ?1s N 2*R C ?e /h a G >Wf ?l =R K ]>x f X ;?Z =R 5Y \A ;=R K ]><V *R ?Z 8-x +N K a ^A ;2G s ;+r R s c G 4S G V ~M Q g C 8>Wa _a_?l =R >b j f =R l=+K ]+r ^9C F 2=E 5F i 5X =E sU E >W r B G j ?l x l=+1K ]=R >x @G b b 1h k u /+W ~.di _u?m <?l ;@V \;+W ~.d ?l =+J x >q -0X 3wH }+?l ;n k 3k ^g u?+Y \A ;a ;z \o >^>p v M A U E S z >J F >X >^<|+~.z ?Z 81h P Aq 2oE >h r v e 85-35+v XC u 5q C s ?Z 8m >W K ]?l =R x @G b b 1h k u /+y fZ N 1z ?Z 81W 5F ?Z 81y +z ?Z t W ]9q ;^q oG >W ~.D 8>w =8-{>F j y z Z D 8+g o _~~.Q ,^V *}W F 5-S g 8>8M n F M n M 8L p S 5-x @W ?W +vd D i5;+Q 8G G Vm a ?Z 8>M n *R r Q+r R 8L r }>W Q q [|T ].9F >Q t *-S +7P :2s [b g o3+7P W T g ^9v 3K E C 8>m X D N _8^`+?I ><=?R S T {2t W >W T 1x \0]9{=5G =>W `?8g ^>F 9G >x~M A =8]n +p x 2g o e_0.O 3+7P :-.>M A U EL R >D i >W w k `?<2R C ?{J 8.*G V 5X 8n F5|*Y 5v h [Fm a 7P :+{J M Q 9W .9F -S 7P :+k .G M z G 8j Q /6*pt 2T *U 7P :z Z V *T p g o >{N K a{Q s -S +W ~.Q ]IF m a :g t W >8*M n 0-.:g t W >O2r 12V D z :g 1c k T ^+W ~.U 3+:D P m s >3+:g U .O O m w 2+D3+:t W >b u .>W ~.m a N S u?+H F n hkD V *2>k H F 4z N >k f 7P :g F 3P2=5?d+MY m 6[_V z u <N `2T P +E z J _V V *><V r e /:>2V S @J *`?+@2s [f T 2U 4^s [x ?5I >M n ^J L C 8\H ~M +D 8S ?C >C 88H ^L6r X p <>l ~2Z L C +:u s [O he_9I g 8G 4z Z x h <1d P *R t >9I S T T J l V [64.:u_o 7P :+z r D 5G j ?l G a ^7P :M n 0/b w 2a ?>B 2?>8U h ?U s V 2+*?Z O t W ,W V ?5u X 8n F <@V D 5u S G >:+2D i >M n 0b @^>S b 2v h a J >*R ?Z O t W 2S b x I >0<e BQ q 4z ?Z O 1h 4<_o /~<r M T 5y t T 5=>b j y h P ?Z 8+s [?g 8~*8*u A ;7k E >r R Q q ^9O T 2V \;n z ^g 9G >W @G b p Q u/>p Q f 1P u w Y s X ;E d +A ;7k E9:f =R 9bX ;V \;v m +f =R :b ?Z 8j W 2A ;d s Q Sv m @r R Q q O T 2X ;V \;U b 8E a v m 2>W f =R :bX ;8E aj W 2A ;d s Q Sv m +E d e_?T^Q q O T 2?l ;;;bX ;V \;X M n n z i ?m @C >8W V X 20*R X ;V \;b ?Z 8v m b 2^g 9G >V X o X G M n 0.O E _R E ^>+u w h kz f Q q E d ?ZG U ,V X z Z X ;>;<`.A F U q E d 7k E >r R 4z E d 1W ~.f @*?A 2+W ~.E [q Z k r *A P g C 8i _,k >8*M n 0*RC 8-x @h ?.V >x M s 0B X 2C 8__C L +W v A 2j.>?Z 8m ,2B =^X >JT b 1h k z Z +W ~.u .5x x 8?c j {g Q ><V g C 8?{g +W ~.f u p u *u g 59s{g Q m 5a .V \m R ><V ?<R <@C 8-x +1~9n b +1>b ;I b +1+N V 5L E b +13k b +E d s [?496*n F2D 0+1}J F 65J |\u dP b +1L p ~w b +1J |:p 5q *V 5n o >z s 8m E b +1L p S f o j E b +8`h .`h \`\l `y `z .`z \`?Z 8R Q ,k 2j P ^\P9Q pI Z Uj Z U,R EE `I =x [H <J E h U 6K x <E x 8S +d g 6K x2J o Y ~n D 2K 0`;x R C 7sw K=l Q y eG .F `*b j O n9m +|Cr ?Z V \27P K z *h K z n h R ^6eh 2`R Q s h g 8y h 3`R Q 4h g 8y E z 2`x 8S E z 3`x 8}4y ^N =x _y E `x p J =r C ~xR Q n `e C W {p@Z Q \l `[|C 7n R Q r U 9|:~c _n D 7774+s +A +2C 3I j c ;x R C 78y j k r R Q C :7w K h U 8y n C w c _=^_Z ?Z x R C 7Z 3h `a ]p J Z Q-D c ;x R C 7sw K C 8y<]`d r c ;x R C 7sw K ZR Q y e =K NWZ p J m G 11q >x +nx D e Z Q x SO `y e |C n c ;x R C 7sb y e D T +w K C l <hj l >b j O K y n E dS 4,H7IQT @`K h U 8y 64h 8y g Z Q 6A K x R C 7s e -7c >n F `0,**Y j l 7E *k r V N ?>n `*N S =c ;7^1|C t U E D 2p J =r C ~xR E `F `0,*AN n9+i a 7{b j O |C q a 4+q ]|\q +b j x R _D <a B G s <z .>M Q \^x R _+xE n a Y a M Q i 2+xEx 8M Q 6D +Z C M Q 1.Z n }{\{{C 7,{5D x q H -b j O \xE 6D <a /xE g H ,:I P xE a n N L <a J 1L .,;9:b jX -H a U C b j n X -F c A R *18,b j50H n x R @K {7T N k S {v :K X -Dc L :K Y j50A 2C 3q =43A>0<O h n 4s C 3q =43?C 0,,R 8*2X L ce96V \l ?n y e C J R Q h U [|C 7<y e t /n :[x R _|1C 7[|C J <R u >c ;x R +x R +R C ?+R C @+K 8+RNWS?+RNWS@+RNWSA +_QK ,:6n n ?E [+w K n n p 7/O y e <1e n j V Kc E 719+R Q [{J 5p ^J 5J0p 75r ?p 75eZ p 75q F A t n t h w p J <R Q q F A D 1e n j V :i n Kc y `g E W {90<n [k X q n w K 8-,6AN p J sb /8+0R07;6H G .F ?T m +e n P +-H K Q *\Z Q C 7=B v+=y o t W k ;w n 8y 6T m +K c ;7^1\N S 7^1p J s q L C -7,-H K T _u h 8y D <E h s l D W _+<\_/N ~l D W _m +<K F w 245w KD x <T D -H e x q Q *\Z Q C 7=<h -H Kc W k ;w n 8y D <m Kc u E h s l D W _+<F w 4n D x ^I0k <KA ?>j u *~-H J E h U l D W _+<C 7/:~Z Q k ;w n 8y <~b |C <\_/:~x _l D W _m +,<6U E ?e 9p S g 4+F ~2+0q9+x ~@+x }X +^m Q +:|r ,[p JM =.9p 90+5]0+,0q w [k h |n D 2w K 8-,=6=E ?e 9p S g 4+>2?+>2@+Y 2+x }+7Z +:|r ,[p JM =.9p \>w [k .|n =x8-,,R E V o >n 8*?W <|e_;9:/b j O h :s <\^xE ;^,2|@8E 7?<C_n {I xE <2|D l S xEn a a 6978Y a 6;76xE ;*n a a 6978Y a 6;7h o ,G 4xE ;^hn6b j O _1L j \:,,R 8*`?R C9:h c e ME 9p S ^D <E U E +==E +R w K /D 2p J 8=x p J B 8n ~x ?:<*A D ,E U E +==E +e >D9p D {-c B |c ;7^1\N S 7^1p J <a h 7E b j O 4n HQT \`E n9+,{-h U m H K c ;\N S 7^1p J s <cR Q K }C 7=D a uH H c ;\N S 7^1p J ,s h 6s hD<r U ?e 9|x R :~B |c _3+n D x <=.?W E [+R Q :N n h e D u p J ,D u p J j U S >x ;?>K u ;@>K u ;A>K u ;D>K u ..@B>K u ,E<2E >E X T +/b =x [H <~-V W <J U E X T +f e ,T m +-4L D I x _N x ,F<:7>K c ;x R =l s <E T +w K h U =ln C l C l <W 1R u >h UC l 7+C l n >+h U p@D x +h U =s h 8y C l +R C d J +8y*E :g ^\a ^;+h U 7Z *E +h U 7Z w *+h U =l ,E =+R Q h U =s h 8y C l <E :7+\[Z ]+H H ,K K 5=l :I 7^1;s <E T +w K h U =ln C l <K1F w D E T +x _F w C l ,aj ajr ?=G<d r >K c ;x R p J s <E E M 7d r +w K 7ZR Q y e :{D h ;,{-h U 8y d D 7w7Z </X K7ZR Q <h t w K ,E 719+R Q <R t B E YU +lu ,7Z n >B 1/50g m n S h U 8y aK H -n 7Z ,?><=0>K c ;x R p J s <E =0+w K=l R Q y e :{D :;,E 719+R Q <R t B E YU +lu ,=l n >B 1/50g m n S h U 8y aK H -n =l ,D hD :HSPF]d r 9r ?=??<I j>K c;x R p J s<e n K x98y k|<h s y_8y,x98y k|C l/|m o m/n,/4|m C l K i|n C l4<8y6y e+w K S h\b<w K wI,h A n C l e n H-D<w K X:~k A,E I j+e w K x98y k|<h,C l<h>w K hg C l n><E719+R Q,8y<h>E Y D x i O<w K h z D x3*c m G n|18yn7W,=.E b j O4n/@0+Q d<K C l<h88y<h t GQ,Q k8y<h B<E=+R Q h z n u h3,8y<h t/wK T3n8y C l,=l+7Z88y k|A K c;x R C7s e-,9:6.h?^5q>n C7=<\_9p:7w q>n w K C J,E.h+R Q:N n w K C J<R u>/jF0+/g40+/z G h0+/z G:0+/r+j J0+/v5v0,.q>q>n C7=s o a]p J n R0X1|q>,_:_O?/[|n D2C7jF w K,s h_O?T p J J h7*X1<b<\M y U R C~@\x R|m|H-n h w t u9p,.h4_O?[p JM/?D>G C7d J n D2E?B>G]2wK<K?D>G n w K F4J h A27b X16T n<b<4s7b X1h7t K D2Z z{,.h]_O?h1m G n?D>G C7d J n D2:]t K nx~;4s1<b D<a H-T p J<~/h I<b A y i1@r n y_8-,R n_1_O?w-H}I z G j`K g E C34w K j t*y<H B>A J h G]k jF y_,=U=_O>j V D2E o]7w K,.h4_O R n_1_O=U=_OW3h_:s h.h4.h]R n_1=U=`??96v m X 6E m S G >e B M Q U V Y ]2s lE >^b QE >;+:6X 6E d ]>@f @[7@B+J >@M Q M n .O ?Z 8-x +;6X 6E o {R <>o {m s x H K ^@B 2s lE >+s [?W M Q *b T 2EZ c m ;v m =L 2E Z 7d d ;>l Y v m u E *Z 7d s m S 2=E 858e>5M Q \P E >q u 2b Q c m ;v m /\P E ><Y ]s M Q U V E A C 8=+v m A ;5X ;?Z `9x R _`L V n s C 7=g h T k C 7<v +a l w K x R C l >H K3}+1}x R N S ,3}|D pK a ^o G +<x }G +,?oqt C <n f x R C 7Y k _p <\a O +E l q K L v n ;>,A K </45I T F K K <Q K3}y o ;>=K <{-D 2q ]^i <|V u x _x =<m Bz .h s3},<]=j Q p U v m v m YWF m S 8e\_W 1^\L g 47k :e7^\L?<?+^\L@<>n g 49Y :R u *:+^:q ,-^\L 5}\h 7/9Y n ^\L 7k7n x R _n ^\L 1k 4,:`?*M Q [8G >f [8v ;m /?Z 82[8Q S >m P ^\P |=E B ~y ^]=E +v m =L E *Z 7Q p;/\_\C 717}n R C [|196K t n K_R C 9Y:{_MN +N_N +H ~_+72_q ;n R C [H 19~57,/\_\C 717}n x C [|19:x C A 8x C 2;6K t K_R C 9Y n x C [H 19:x C A 8x C 2;~57,?GEQ C 2M Qb E dv m k z Q p</\_\C 717}n K 8[|19:b +Z L +Z [;6K t R C 9Y:_MN +N_N +a ^x R _{;q ;|5|n K 8R C [H 19~57,/\_\C 717}n K 8[|n x C A 8x C 2196K t K_R C 9Y |5|n x C [H 19~57,_MN \N_N 4n K 8[H 7k 1D d e +g F S b +L;b +[;b \b +M L +M [,96L S LHQM v m @28e G >Waj d d 2V \U LHQM B V 2V \6O 0_1t 1+q ->M n .O U E C 95sU E +:6g 8LHQM F2W o B V l 6Ug 2\,8e>{M n s _q /z N 2Z @L R +;6,k l 6Ug 2LHQM ?bM n 0.O :g +t 5s 7P 29G >0<e B M Q B V z T Ug <LHQM 96;=2R S ?b ;+<6r LHQM \m 8e `4LHGT B V 5LHGT 8H ~*>M n f g Cg 8LHQM S 93T {P m o +=6LHQM F2W o HZM <k r Z 7m S =G >;<LHGT U ]_o 2m o .Y ?LHQM ^HZM x W 8e K B V LHGT 0n >F H F Z 7m o >Waj HZM m S Uq B V LHGT +`??\_W 1RNWS 7k <d D 6K ~9Y:N_N +_{;+K_7T O 8c ;x R q ;g x n RNWS 57,RNWS ;q9Y k RNWS 7T9Y g x n 57b K e -n Nx }{,H K U LHQM A RNWS 3>S /a ^i 7^17k 0<M k Ah `7k <H -h j x {d e M [c ;x C C 78R C C 7<b KX z ,/4~d D 7=l c ;x C </7^17k 0h S 54~8Z n V K E ,RNWS 6N_S g x n/i K4>d D 7=l c ;x C ,v m LHQM m S=\_W 1N;vxf?C ^[QL x ~g 47k :/\_n _QK 7k6x ~*_n _QK 7k ~57,/\_x C [|196x ~=]n x C [H 19~57>b ?l 2v mGEQ C M Q s [?x R _4n ZMWMSK -}*c S 1/n 70U f >h M 6~|n r +]=W <<d 1m s W n t d x R 8y ?:M /n h g 3G =h <H 1+=.q >n r +]mk ~|n ?s C l <{>17s +<X ;k r ?Z P S 2;Z `.*`M Q GM R n C @@<*92GEQ C +GEQ C 2E d +[r 2?:\j l ]t H -n M /,A R o0],{-1H -n M K ~D8n ]<d e E T C<|C ,;?</81/,A R o0g K n h h :4</MKW ]7B -|x R _n ZMWMSK -}t ?@</c ;x R r +]-|MKW ]t <L /r +]_1?_@n h h :3MKW ]81/,A R o0g F n h h ?A<MKW ]m L j -|B <\^x R _<tB<=.*y e B |MS ]R0._p m C l C<a u -|MKW ]<J -r +]<n a f h n \F P S ?Z n h X<2D W V X ??<MKW ]6r +]q ><,@<s W n 8y .I ,A<]1s W T 8y ,B<MKW ]\r +]y M ,C<n 4h w `r a 6x R *4p ,D<MKW ]-}y M <T w `r a 6x R>E<V -|r +],`?GEQ CM <l *;K ?**;U VH a @v *GEQ H O B H >r X GEQ C 2S z o>W b GEQ C 2I e u /r A +MKW 7s t j >;E P a A j `1f <|d a A |h l ,Q ]t @P 4p x L >FD;ECC;D?ADAADD;F@@D :z h -z c l C D x ;g U 4p x L >B>>D@FFG>G :z h -z c l C D x ;N j >lwwsH==zzz<vpmw<grp<gq=/4\_n ZMWMSK -}A d D MKW ]<|n 1`L -|MKW ]v +-r +]a l m G m s W n t d x R 8y ,r _e ,V \d s~c@3w :K 79Y n 8y <1|h R Q6[9Y ~57n [|C J <l -b j O R Qa l n C 7=,@v m ?Z S Z E *=E 85\P E >57x R v R O \H 2_D <H -K_17}:\_Z ,t ;8H =n x +R C M [}</\_n x R C [H 198K t x R v R O \H 2_n x R C [|19~57,57K p x*D <H -K_17}:\_Z ,t ;<:K p x*:_n 0-M [}</\_n x C [H 198K p x*n x C [|19~57,A<z =v m =69=0O K Mo Uv m =69=0O K Mo/x R n x C [H \>{[H 197n x.mG <J =.x.mG [Hk s <~@n ~|_=O :*_=O =tp =N q =x r x ;4<l S a l 549+;a I ,/K t n K_R C 9Y:{_MN +N_N +H 2_+72_q ;n x C [H 7n x.mG <J =.x .mG [Hk s <~@n ~|_=O :*_=O =tp =N q =x r x ;4<l S a l 549+;a I ,98D h?<E s b j O n 4y +^N \_n y e ,@<E 719+R Q *y e 0:{D h ;,A<E SO +B |y e ,B<E =+R Q h 0,C<E SO +B |s g y e ,D<E 4y +@W U h g y e ,E<x W E 4y +e n H H y e ,=.H -y e m +<e n X =1n q >K c <F K /Y \__w n R :8-,/x R _x =}7n *i @@>T 3C x =-D ,E s x R _4nx =^x E 3,K ^_3+s E Xb j O n w 8+<x R _B |c _3+<~c V W a 4T _<m K x A J E h s b j O n w 8+,c x _x R <J U E s x R _4nx =^x ,9:D 87G 8-p 707E zE s b j O 4n n h 273+<f e Z Q C l ,:x 8S =}e E x 8273+;E s x R _4n n h 273+<>a e Z Q C l ,:x 8S =}e E x 8273+;E b j O 4n k r +<e w K ~|n C l ,9:;.q >h 7E 8y 7>a e n \e C l ,~cR Q ?-G 8y 7<h 7E c ;+<R Q ?>-@>>8y 7<E _W c ;+n D xx e q +9.A j u ,4y M Q?Z 87g >n 8*?<E 4y +w K *y e ,@<-719+R Q 8P 0,A<E SO +B |8P y e ,B<E =+R Q 8P y en h R0,C<E SO +B |s g y e ,D<E 4y +@W ,?<E 4y +w K *y e ,@<-719+R Q z 30,A<E SO +B |z 3y e ,B<E 719+R Q C l y en h R0,C<E =+e 9p h 0<1s g y en E =SO +B |s gy e ,D<E 4y +@W ,?<-719+R Q q I z 30,@<E =SO +B |q I z 3^Ir *,A<E 4y +H H ,z 38P ?e ,0z Q X @z 32=?5k +8Pz 38P]4y8*z 3]4y8*k r ?Z V \22708P 4yq I z 3?/O 0z /,7=2`E V ~t>x q I z /*I `Em 20X n h +?<-719+R Q z 38P 0,@<E 719+R t Q X e ,B <E =SO +B |<E 7191=+R Q 1|K n?P B <E SO +lu ,h ?P n *C v =S 7M =y q C JM t u n <~cJ \a E g }+B G c b ,A<E 4y +H H ,s [?z 38P U f }e o Q q V {z /*;?Z n h*t>{T^*;K ?I Q ]7=*t \@*B Q e O 5V ~M n 03b X 0B =>.O Q q I z /G 0X z /~/2?Z n h >i G W e ,/_7S z /0e O z Z z 3+8*s [<e ,}X ;k r V \f q +Q X e ,b ,70889b .8.z 38P?<E 719+R t 70n >,@<E =SO +B |70n >y e ,A<E 719+R t ~|n C l <e 5K B G {s |C >x R C 7s >8*^?E g }+R Q /I m +<E SO +lu /I +89I >~ck ~u g 8y <\e 8y n 7<i O <e E 719\=+R t ck ~n 8y <E ~}+B Gk ~|C <m B E 719\=+R Q /c -|n W p <E SO7~}+lu ,8E S >E 719+R Q C l 8y <E _}+<R Q 7.m +?~-g 67B <e R t [C l J E s _}+f e ,8-D >E A }+/R t n c ;x R C l 9So C 8y ,T C l /t |k o C <h,B<E 4y +H H C l ,70n >?U z //2n h z Z n >s [?96e B s <4k M Q g 8G 48F 0z Q X j >z k r V \2q I z 34r+:6q I z 3U f }V {z 3Y 8P >r R z 38PT h X *;Q X *t>`.f Q X e ,f /@20j >]I 8P]7=*t \@*B Q e O j y z Z q I z 3<]7=*t \@*B Q e O 5V ~M k j *;K ?=>r R 5k8P ~>a M n z ~/V \>i G W e ,/_7S z /0e O z Z z 3+?<-719+R Q _7S z 30,@<E =SO +^Ir *,A<E 4y +H H ,_7S z 3?F 6_,7=*t z Z z 3?<E 719+R t ]I z 3,@<E =SO +B |]I z 3R0,A<E 719+R Q y `0<E k r +U ~9p <E SO +^I r{<p@X r{k [C vn |18y ,B<E 4y +H H ,]I z 3?]I 8P l *I7=D Nz 3]I z 37=<?<QL{>@?=W F SO `z Z z 38An B SO b @4S Z e ,b .:.-E SOg 8=X k r ?Z >n >2Q }k r ?Z m \R 4>T^9;tK /2t *_O @C<@m o *L c *1w n z p <b ?C 2M n ]>D i s __A M Q g 8U q M <4F \F k r ?Z n h ><2<][{~x :^=V X >M n M A k r ?Z n h 2>F \F ?96tK /2V \U qz .+:6tK /P S e O ^>-p .O e M 5_,n h s _>F \F +;6tK /E Z 7n F e O 5s h L c^>p v <h r >T L6:><7QTIK:-f EZW =.O e M 5_,n h s _>F \F +<6tK /e M :F 1w 5T 1w <h r >RZSH *p F 1w *k <K z 5=~n B V >b *;8E a 2u w ~4F ^_<M +=6@2DtK /2+i .O s _>F \F +`?RCGM V ~?N \GEQ C ^R n C T 2=?V ~?<-719+R Q GM V ~0,@<E =SO +B |<E 719+R Q h R0<E =SO +B |h R0y e :E 719+R Q 9p 0<E SO +lu ,A<Ey e t n /K C lH H ,?Z V \22708P 4yR n C I l U b I l d r 8P t b ?C Ug V ~?<E 4y +w K *y e ,@<-719+R Q 700,A<E =SO +B |70y e ,B<E 719+R Q C l y en h R0,C<E =+e 9p h 0<1s g y en E=SO +B |s gy e ,D<E 4y +@W ,?<-719+R Q 3}Q O 7=E Q O 7b B t h0,@<E =+B G ~|y `,A<E 4y +H H ,?<-719+R Q q I z 30,@<E =SO +B |q I z 3^Ir *,A<E 4y +H H ,?<E 719+R t 70n >,@<E =SO +B |70n >y e ,A<E 719+R t ~|n C l <e 5K B G *^7X ]\79I 7E S >W 1|C z b c ;x R C 7n C l c b |C ,70n >?U z //2n h z Z n >3}Q O 7=E Q O 7b B ?x z _o ?Z V \2M Bq I z 3?q I z /X V \270K B G U ~r *U e u E =+R Q c r{n 8y 7<l /x ,q J 6N x q J9pa l ,]I z 3?]I 8P l *I7=D Nz 3?<E 719+R t ]I z 3,@<E =SO +B |]I z 3R0,A<x R C 7s <E =+^IU ~r *,B<E 4y +H H ,3}Q O ?][:~+ZKV +X]\M +\OMKW q J ,=E Q O ?][NU +W +LQ +S q J +b B ?E=+5h U 8y B G C v Q y ,b .8.9SO 70n >9_jlx R K b C 7n `r s /q +B |D 2n a g 9p y e{P 7U h P 7}P 7T {P 7}B ?B =t W U E {P 7t W <k 07}35x P 7t W T {P 7t W s }>F?<E 719+R t {P 7U h P 7}P 7T {P 7}B ,@<j V g s K c E =+x A 9|:Nc i ,A<y `5B E 4y +H H ,?<E 719+R Q }k ,@<E =+R Q :N n ,X p J <c w ,X p J S >g 4+?5+5,++,+?+,A<E 4y +H H ,}k ?B =t W 2j u 0@?<E 4y +w K *y e ,@<E 719+R Q U E 0,A<E =SO +B |U E y e ,B<E 719+R Q D 2y en h R0,C<E =+e 9ph 0<1s g y en E=SO +B |s gy e ,D<E 4y +@W ,3C 8P ?D Q 3C U E b l E h?<E 719+R Q 3C 8P ,@<E =SO +B |3C 8P <E =y `;H h ~,;H h ~?e n K D x8h x 45D 2C 7B G .K L .<0r K t M =_p <O ;P N n ;I C 7,1r +t +a +x h g q g ,U E ]4y8*U EA K x R C 7s <X q D eB G ,yy `<K |C 690n |C ~>,?<E 719+R Q WVW E L ,@<E =+e R Q x8p J >>2?<>2@<Y 2<x }<7Z <x ,A<9p L ^B E 4y +H H ,9e ?B =}Z =0=E s K h q?<E 4y +w K *y e ,@<E 719+R Q =E 0,A<E =SO +B |=E y e ,B<E 719+R Q =x y en h R0,C<E =+e 9p h 0<1s g y en E=SO +B |s gy e ,D<E 4y +@W ,WVW E L ?=?W E 2z f E L ^6E L Rq I E z ?;<d s V \q IB =E z=E ]4y8*?<E 719+R Q 9e 0,@<E =+9p E >n c i <V 8y `=x n E >0,A<9p L ^B E 4y +H H ,?<E 719+R Q q I E z 0,@<E =+9p ^\x <:~x 8S ^D <=x [H \><\_j V [|C 7:~y `x 8,A<9p L ^B E 4y +H H ,h r C ~x S ^D <\[\x8q e R ,=E?<E 719+R Q E >/O ,@<E =+e R Q m P]E >\\P 9T E >,A<9p L ^B E 4y +H H ,E >/O ?e ,m P]E >5\P 9T E >h x.p@9p SK p D <x R N x M =.x C 57}[Hk K ~n K p x*:G ~1H -/C 6J x.1D ;<x R _\:n *p *x*b =x [H ,T D <al S /K p x*n ^x \^,h x.p@9p S *p D <x R N x h 7/\_n *p *x*[H ?f M {-T D K p x*m 6\_57[L 4a 4l C3+<z\K p x*d X 1=x [H [x8X C m S ]:w S h 9p S /*p *x*0D <\_x C [H /Z 9p S @]x 8;,D i >f l V /e 1h >L +e B s z N |f /m P]E >0E I >G j \P E >2?l D G 5M @b ^2E g 5+:69E A/O?e,m PX6E>*\PX6E>5G?<E719+R Q@<?E A/O,@<E=+e R Q*px r x**\PX6E>5G,A<9p L^B E4y+H H,6E.L??<E719+R Q6E.L,@<E=+e9p r x S X,A<9p L^B E4y+H H,j l>h@<?E A/Of G G>6E.L~C*Q+J6_O?8P M Z d]2E76O?<E719+R Q J6_O,@<E=+R Q-{,\q I,A<9p L^B E4y+H H,B e?J97==E2n\5h s?<E719+R Q B e,@<E=SO+B|B e y e:E=+e R Q C v S?@>R}+C>>R}+?<CUR}+CUR}+?>UR}n=x K 8<E719+y`n:Nc i,A<9p L^B E4y+H H,h r C~x S^D<\>R0q e R,c e ME?U E^=E2y`B=?<E719+R Q c e ME,@<E=+e9p D7G69S^D<E=E7U E+w K r C~x y e7,A<E4y+H H,d re,??<E719+R Q d re,,@<E=SO+B|d re,y e<E719+R Q<7Z n>B1/50g m n S h U8y aK H-n7Z,A<E4y+H H,=0e,??<E719+R Q=0e,,@<E=SO+B|=0e,y e<E719+R Q<=l n>B1/50g m n S h U8y aK H-n7Z,A<E4y+H H,_:B 8P s V \G f _:0_:K z _o ?Z L 02X L 1?<E 719+R Q d r 7Pbohvbhf ,@<E =+9p T l 7Gijoftf 5Iohmjti7I l +A<9p L ^B E 4y +H H ,/O 8P]4y8*?<E 719+R Q _:,@<E =+R Q _:3+S D \G <_:9S D D <x R b C 7D w K x ,W J +A<9p L ^B E 4y +H H ,J L B 8P g 8I P 3?<E 719+R Q J L ,@<E =SO +B |{8y e <E 719+R Q D 8g 57w 8g 50<E =+9pk K on 3++D 8g 5k K o e 9p S D 7G 7w 3+?w 8g 5k K o e 9p S G *D *k |,A<9p L^B E 4y +H H ,g 88P ?<E 719+R Q ]H 8P ,@<E =SO +B |]H 8P R0<E =+R Q U \q 4E SO +lu ,A<9p L ^B E 4y +H H ,]H 8P ?-{]H G 25k8P.q >h _O L 4v 43+D <\[-V W kH79p D <-H e n H -H79p m +,/O 8P d r 7Pbohvbhf ?4y f I l 5T l.q >S :+l w h K \_L 4c _3+<.t 1/c _3+n k K o 9p S C j ,?<E 719+R Q g 88P >E =SO +B |,@<E 719+R Q h R0,A<E =+B G 9p +B<9p L ^B E 4y +H H ,4y G V >9p y e w K n D x >?>j <?C j <A>j <BC j <D>j <x ,D 8t W >1t u +:|r +x *g R0,h R Q :|r D <^_J h /w K NWZ /D m +/g n D 26NWZ /D m +,*c ;7^1~x i a ;,D 8E g >9p ^_DM Q m G x },9S ^D R m G x },?<E 4y +w K *y e ,@<E 719+R Q /O 8P 0,A<E =SO +B |/O 8P y e ,B<E 719+R Q /O 8P y en h R0,C<E =+e 9p h 0<1s g y en E =SO +B |s gy e ,D<E 4y +@W ,?<E 7=9+R Q q 9sP \g F sP ,@<E =+9p g E R0\O h R0n D 2w K a 4S l ,A<E 4y +H H ,?<E 4y +w K *y e ,@<E 719+R Q D _B =0,A<E =SO +B |D _B =y e ,B<E 719+R Q D _B =y en h R0,C<E =+e 9p h 0<1s g y en E =SO +B |s gy e ,D _B =]4y8*?<E 7=9+R Q q 9j P \g F j P ,@<E =+9p g E W p \O h W pn D 2w K a 4S l ,A<E 4y +H H ,q 9j P7g F j P ?B =U E 2q 9j P 7g F j PTG t b 8P ?>a 8P TG t bn `mqhrzv@>>>S 2<x ~n `mqhrzv p@w K9p ^\{D |K ,e ]`mqhrzv ^I y e 4n /8P 0,R t /9p 0E k ^ge ]/R Q W T 0,H y j q h L N k <e ]/7P 0H yw K n 5L q ,X k w K 5L q 4n /8P 0R0<9p F w Kf M 6[_dDn K f M ,*/6K ~2p ~570t K 7:l /F w e AC M 9S /D>R}0,e ]/a F 0H H ,;<9:?<E 719+R Q G U ,@<E =+\e G U y `in D 2w K a 4S l ,A<E 4y +H H ,G U ?B =TG d s V \2Z s 0K z ZKE d s 2M Q 1q 9sP 7g F sP ?B =U E 2q 9sP 7g F sP 0z ZKE d s 2~M Q 1D _B =h o a ]p J S v 5v D <h9y `R0q e R ,h [|C 7S RNWS D <A 1w K A R R0e y ,b C 7+RNWS =ln N_S 8[QL n C 7s <h9y `R0q e R ,AN p J s h9y `R0q e R ,8P?<E 719+R Q <j +:6E =+\e ~W in D 2w K a 4S l ,A<E 4y +H H ,<j ?B =TG d s V \2<j 0K z ZKE d s 2M Q 1?<E 719+R Q q IB =+:6E =SO +B G q IB =,A<E 4y +H H ,q IB =?q IB =U E 2j P ^Xo 0K z ZKE d s 2M Q 1?<E 719+R Q 7P c e +:<E =+9p w K A R >z G +j C 7,A<E 4y +H H ,7P c e ?R Q LHQM 2X 7@0K z LHQM d s 2M Q 18Pf }d s Z k B b ;H Z 7>W M Q U V 8|2]I O ;H v 5>X \f JTW;H89*JTW;H8:*JTW;H8;+`??96r R z ;H M +^6e I X 4C u >M n ~041>a 2;H L R +:6*zL J 3<=8->8L{=57z |G 3Iz 32H F ;H U E G >M n 0X S b 2:g +t +i G >W B632{P 57G j 3+;6z ;H _O 2X M U E >n 0~M Q >q r ?n n 7W 3h V o F `z ;H _O 2~*Q +<6@28|2]I O ;H v 5M n 0~B V +=6r R*|X @2;H C 857?Z8e>h r ?THT7PGH ?Z 7s ;L V 8e 5>T^<p/e >]I O ;H v 5M n =*C F +r R n z 8W o>>W f 8M 8e ~z n k ;H ?Z h P +>6r R 9q >M n ~0X ;H L R +?6g 8B V LHQM96<T F Q ;H 6O 2q I K u>U ^@2;H V \6O `.]I 8P +@6W L S LHQM *HXZ ^HQT L 0H F ;H Z 7+A6g 8,R E .8,;H,V o`>z i ?L 02F ,;H,`z s ;H 8P >8*e__<2X i +986;H V o`X i ?9L 0s 4y g 5>F ;H F `z s ;H V o 4y >>n M ]4y ;H 8P 4y @HQT 2>F ;H F `F mz s ;H V o 4y >>n M ]4y ;H 8P 4y @;H V o F `z R n ?Z 29C >n T ~M Q +;H ]4y8*;H 8P?<E 4y +w K *y e ,@<E 719+R Q ;H 0,A<E =SO +B |;H y e HAN ^x =AN d J =A 23Q =@N 1AN=R v =J ;=AN 1@N ,B<E 719+R Q ;H y en h R0C<E =+e 9p h 0,D<E 4y +@W ,;H D G Ge n U ~y `n d J S A 2+4s ,AN ^x 9p S ^B >?<E 719+R Q ;H 6O ,@<E =+Z Q A 2c 4s <6x R n D 2w K p J ~><,A<9p L ^B E 4y +@W ,h AN ^x 9p S x B <[R0S U ,<q e y ,{-9p q h <1e +X `k S G ,z ;H 4y 2><}Z 6O f q >AN C 7d J9p S A 2B >?<E 719+R Q }Z j |,@<E =+9p S A 2\2A ,A<9p L ^B E 4y +@W ,h AN ^x 9p S x B <[R0S U ,<q e y ,}Z j |[0-4y 8@N 1AN BJ h n J ;,U `,?<E 719+R Q 1;,@<E =+9p S ?-?><q ?>g q g ,A<9p L ^B Ey e +@W ,h @N 1AN 9p S x <[0S U ,<q e y ,1;?<E 719+R Q ;H D G ,@<E =+9p ;H _O D 5G +A<9p L ^B E 4y +@W ,;H D G;H 6O\_e n /H =@N 8y =1Q S AN 8y <^4AN \Me n _k AN R C 8-,?<E 719+R Q @H c ;H ,@<E =+9p S ^\x ,:H c ;H [0-4y 8@N 1AN BJ h n >28-,?<E 719+R Q Z =,@<E =+9p S ?-?><q ?>g q g ,9p L ^B E 4y +@W ,h @N 1AN 9p S x <[0S U ,<q e y ,Z =s [?*;H V \6O f }Z *12G >U E U _:g 5+s [?H F :H Z 7G >k b f ;H D G 8P f G +8P`??:H c ;H f D 2G i >^Z =^1;\@1C ~M Q @H F :H Z 7G >k b G A :H c ;H +;H c :HE _V ~+z s 5s 2T p M Q ;H >n I >W 4s N <204?0496G G V|>k H F ?Z M n 0w v Z s +:6G G V +t ;H v 5H F ?Z M n 0G C R;51e +r R0/R;*1e 57u f >W I J H F ?Z x ^~+;6X M ;H t W M n 0j <*-3/H F 7+e Bv +*]Z *0/}7^:?g X c @2h l V M Q g dP 2;H >n +<6e B :?g X @>r U ~u 57F 82h ~.H F ;H t W +=6*H F ;H t W G >Wa _Y e z 3E _>D f g C 828H i lM 3h 0/:.@3+W v z D h28<V *b ;*}35@1M n fV `*f s *6,*r ;5A C 2u?*|M Q g C 8+b /-35q <f ;H M E U 9J 2M n 0M s z E [9I :?G f +*|2u?5b.+>6^}H F ;H ?Z \>W ~.f ;H v 5Q^@2Q V >z @2D `+t ;H v 5<h r **=L 2v 5*4}5*Z s _o 55=>M n 0M s 2:?b.5Z s 2h +?63h O }@T 2Z 7M n 0U Q q C >J z 2}W M A >][t I A w*v *1e ^m T n F ]2h +W /F 3R ^~<\4C >8M M A 2M n ]+r R ]91i i _@g >W r B I J M Q g 8e>x z @g \w N 4z F k U <j >y I >M d M Q +@6l @2H F>k J ,U :g 3P2z d <1+A6J Z ]0/04^@1c G p 8?<9=X 2H F 7z F /e M ?Z t W 5Z 7W 0T 2e M +t M E 5J ;G M n 0T ^0/w 5T p +r R s X 0/5T p O v w L >W z M Q ;H >n I 4k j 6h b O +<:=B MU i M M X 8h 5O v 0/*T p w L 2h >/M n n z 0[^/J Z ]0/^*02h :T ]2V X +<;=r R ]9<2i _4W@g >W r B I J H F x ^~+<r R @g V d >W k j 6>=+55Z s p v *R u v r *u f *~q]t I <v *5:q \`=>s ?K 9I >?K _m >.<2B >e F 4C 57X U +O G J ,H ?x k j T p U q ]9<1@g >D f Z N ^R 4q M n h R q h <o >]98M @g +986*Z N 57R 4q H F ?ZG |f .:u `?>7,<2Z N ~1H F ;H Z 7+8P54RNWS?<B 4-n AN d J \_+:~F i<[n AN C J w K <{-1Kcn @N p JT _<a /[R0p S ^,[0mK :~F i S AN C 7D v 18,。
FMEA试题集(有标准答案)

一.判断题(正确打V , 错误打X)1(V )FMEA一旦开始就是动态资料,可以根据需要进行调整。
2(V )过程FMEA假定所设计的产品能满足设计要求。
3(X )组织没有产品设计职能时,可以不进行FMEA.4(X )过程FMEA不依靠改变设计来克服过程中的薄弱环节,因此不考虑与制造有关的产品设计的特性。
5(X )设计FMEA不依靠过程来克服潜在的设计缺陷,所以不需要考虑制造/装配过程中的技术/身体限制。
6(V )当严重度是9或10时,无论其RPN值是多大,都应采取建议措施。
7(X )降低探测度等级最有效的措施是增加检查频次。
8(X )FMEA手册中推荐使用RPN阀值来决定是否需要采取改进措施。
9(V )在进行失效模式的潜在原因分析时,应关注于失效的模式,而非失效的影响。
10(V )只有设计或过程修订能够降低严重度等级。
11(V )在制定PFMEA的时候,小组应当假定即将接受的零件/材料是正确的。
12(V )FMEA是质量计划、控制计划的重点内容。
13(X )技术部门是负责进行FMEA的部门。
14(X )FMEA的主要工作是生产阶段进行的。
15(X )汽车工业是开展FMEA的始源地。
16(V )开展FMEA主要目的是为了持续改进、预防缺陷。
17(X )过程FMEA中“顾客”仅指“最终使用者”。
18(V )过程FMEA绝不能只由工艺人员个人进行,而应主动联络相关部门人员一起进行。
19(V )过程FMEA是一份动态文件,应考虑以单个零件到总成的所有制造工序。
20(X )FMEA工作较复杂,故初次执行可将其预定的完成日期设定在试生产之后,但必须在批量生产之前完成。
21(V )相同的失效模式对同一客户的影响是一致的,故其严重度数也应相同。
22(V )大部分工序会有不同的失效模式,而每一个失效模式至少有一个以上的起因。
23(X )针对每一个潜在失效模式,只须列出主要的1~3个失效原因就可以了。
24(V )要想减少频度数,只能采取阻止失效原因发生的第一种控制方法。
基于NX_FBM_系统的自动化编程技术应用

基于N X F B M系统的自动化编程技术应用毕忠梁,王伟(安庆职业技术学院,安徽安庆246003)摘要:随着智能制造技术的飞速发展,产品的生命周期持续缩短,传统C AM软件手动编程模式已经难以应对零件设计和尺寸的不断变化㊂N X的F B M系统可以实现基于特征的自动化编程,通过识别产品C A D模型中的特征信息,自动确定最佳的加工工艺,选择适合的刀具自动产生刀具路径;还可以随着C A D模型的变化,智能调整加工方案,实现数控编程的自动化和智能化㊂文章以机械臂零件的数控加工为例,对F B M系统原有特征库进行了扩充,同时对MK E知识库进行了二次开发,实现了自动编程加工,最后比较了传统编程方式和自动化编程方式的差异,展示了自动化编程的优越性㊂关键词:F B M系统;自动编程;特征加工中图分类号:T P273文献标识码:A 文章编号:2095 9699(2023)06 0038 05传统的制造模式,设计模块与加工模块相对独立㊂这样的模式导致产品开发周期长,效率低且质量很难保证㊂随着智能制造技术的高速发展及数控技术的全面应用,传统的制造模式发生了根本性变化,提出了全新的基于产品数字化模型的自动化制造模式[1]㊂具体来说,对于数控编程工程师而言,最常见的问题是对于形状或特征相似的零件需要重复编程劳动,这会浪费大量的时间㊂而对于车间的操作人员而言,往往会遇到切削参数选择不合理或者刀具选择错误等问题㊂如果采用自动化数控编程就可以解决这些问题 它极大地减少了耗时的㊁重复的手工编程工作,简化了程序生成的过程,减少了生成N C代码所需要的交互操作数量,最重要的是减少了手工编程过程中出错的概率,提高了程序的准确性[2]㊂以N X软件为例,要实现自动化编程,如果采用O p e n A P I技术二次开发,对一般的数控编程工程师而言比较困难㊂而利用N X软件内置的自动编程系统,只要熟悉数控加工工艺就可以轻松实现自动化编程的开发㊂1 F B M智能编程系统应用1.1 F B M系统介绍基于特征的加工系统(f e a t u r e b a s e d m a c h i n i n g, F B M)是一种自动化编程系统㊂基于特征的F B M加工系统允许将产品的C A D模型直接导入到C A M程序中,然后F B M快速分析C A D实体模型中的设计和产品制造信息(p r o d u c t m a n u f a c t u r i n g i n f o r m a t i o n, P M I),查找出相关特征,确定每个特征的最佳加工工艺,最后自动生成每个操作的刀具轨迹㊂F B M可以将数控编程时间减少多达90%,同时减少了编程中可能出现的错误,减少机器设置时间[3]㊂从图1上可以看到,基于F B M的自动化编程省略了大量的重复性操作,提高了编程效率㊂N X 的F B M系统适用于车削㊁铣削以及线切割模块㊂系统内包含了一个开箱即用(o u t o f t h e b o x, O O T B)的基础加工知识库,基础知识库包含了常见的特征及加工规则,例如各种类型的孔㊁型腔和其他简单形状的特征㊂如果需要利用F B M自动加工复杂的特征类型,则需要在加工知识库中开发新的特征和加工规则㊂第38卷第6期2023年12月景德镇学院学报J o u r n a l o f J i n g d e z h e n U n i v e r s i t yV o l.38N o.6D e c.2023收稿日期:2023 10 19基金项目:安徽省高校优秀青年人才支持计划项目(g x y q2017211);安徽高校自然科学研究项目(K J2021A1435)作者简介:毕忠梁(1982 ),男,安徽安庆人,副教授,工程硕士,主要从事数控智能制造研究㊂图1传统编程过程与自动化编程过程1.2实际案例分析在设计双臂s c a r a打印机的过程中,机械臂的相关零件有很多类型,在这些机械臂的零件上大多都设计了一种圆角U型槽,主要目的是减轻机械臂重量以及美观㊂如图2所示,这些圆角U型槽的槽型一般不深,底部是平面结构,侧面为包含R的圆角,结构大致相同,只是圆角半径,槽宽㊁槽长等尺寸不同[4]㊂现需要对这些圆角U型槽分别加工㊂图2机械臂零件上包含的圆角U型槽特征对于单个圆角U型槽的加工工艺并不复杂,如果利用N X软件加工则基本过程如下:首先利用圆角立铣刀对圆角U型槽整体粗加工,使用型腔铣操作;接着利用球头铣刀精加工侧面的圆角,使用等高加工策略;最后利用平底铣刀精加工U型槽的底部平面,使用底壁铣操作完成加工㊂对于多个圆角U型槽批量自动加工,由于槽的结构基本相同,因此其加工工艺基本相似,可以使用F B M功能,自动查找出圆角U型槽的加工特征,然后自动创建出特征工艺,自动生成刀具路径㊂由于N X的F B M自带的特征知识库中,并不包含圆角U 型槽这个特殊的几何特征,所以必须首先在F B M 系统中开发新特征并同时分配新的加工操作规则㊂由于圆角U型槽的尺寸不同,为了保证加工质量和效率,在分配合适的加工操作规则时还要求系统可以进行智能化设置,例如公差㊁刀具选择㊁材料等参数[5],具体要求见表1㊂表1智能判断操作加工条件操作名称设置类型设置条件型腔铣刀具设置1.当圆角U型槽宽度>10mm时,选择D8R1的圆角立铣刀2.当圆角U型槽宽度<10mm时,选择D4R1的圆角立铣刀深度轮廓铣刀具设置球头铣刀半径<圆角U型槽侧面圆角半径切削移动参数设置深度轮廓铣最大残余高度<圆角U型槽侧面圆角表面粗糙度底壁铣刀具设置1.平底立铣刀直径<圆角U型槽槽底宽度2.平底立铣刀刃长>圆角U型槽的槽深为了保证F B M系统可以根据不同尺寸智能选择刀具及切削参数,就需要在机械加工知识库编辑器中进行二次开发㊂加工知识库编辑器(m a c h i n i n g k n o w l e d g e e d i t o r,MK E)是N X一个独立的工具,负责管理F B M系统所有特征规则㊁加工规则的数据库,可用于修改定义加工过程规则,新建和映射特征等㊂1.3示教特征库扩充F B M系统自带的特征库中没有圆角U型槽,要系统能识别圆角U型槽并加工,需要先添加该特征并示教㊂为了防止其他特征干扰,我们可以新建一个零件,其中只包含圆角U型槽这个单一的特征,如图3所示㊂图3用于示教特征的圆角U型槽无论什么特征都是由不同的属性组成,这些属㊃93㊃第6期毕忠梁,王伟:基于N X F B M系统的自动化编程技术应用性将其与相似的元素区分开来㊂属性可以是几何尺寸㊁粗糙度㊁颜色㊁公差等,这些属性可以作为变量,在MK E 中作为条件的判断㊂创建新特征时,P M I 注释可以用于创建属性㊂P M I 的标注使用有其原则,必须使用基本的长度尺寸,例如水平㊁垂直㊁半径㊁直径等㊂单纯的P M I 只是一个数字标注,F B M系统可以获取P M I 值,但是不知道这个值所对应的变量是什么,应该如何调用这个值㊂因此需要将P M I 注释添加为变量,在相应的P M I 标注后添加附加文本注释,这样MK E 就会自动识别文本作为变量引用㊂如图所示,在标注后缀添加如L E N G T H ㊁W I D T H ㊁R A D I U S ㊁F L O O R 等文本注释,作为圆角U 型槽的长度㊁宽度㊁圆角半径值,如图3所示,这样示教特征时系统会识别出这些变量,相应的特征中就会包含这些属性㊂图4 示教特征界面使用 示教特征 命令可以将新特征添加至F B M 特征库中㊂首先选择添加新特征类型,这里可以指定新特征的添加位置和新特征的名称,接着需要选择特征的识别规则选项,N X 7之前的版本特征的识别仅能通过颜色识别,现在识别参数选项有很多,它包括颜色㊁几何属性,以及几何的名称等㊂在识别规则中选择P M I 注释的选项,即用户自定义添加的属性㊂最后选择要示教的特征面,图4所示㊂示教特征完成后,需要验证这个新特征的识别规则是否正确㊂1.4 MK E 知识库的二次开发新的特征添加完成后,还需要在MK E 加工知识库中开发新的加工规则才可以实现自动编程㊂首先针对识别出来的圆角U 型槽手动创建一次完整的操作工序作为加工规则,包含三个操作步骤:型腔铣㊁深度轮廓铣和底壁铣㊂然后将这三个手动创建的操作分配给识别出来的特征几何图形,F B M 系统会将这些操作关联到圆角U 型槽特征并写入MK E ㊂图5 示教操作界面当示教操作完成之后,所有的加工操作都是固定的,包括操作的参数,使用的刀具以及切削参数都不能更改,要求和当前的示教特征一致㊂这样直接使用F B M 自动创建特征工艺是没有考虑到圆角U 型槽其实是参数化的,槽的深度,宽度,圆角半径的尺寸都是变化的,刀具和切削参数的设置需要考虑特征的几何尺寸变化,智能判断加工条件㊂所以在示教操作之后,需要在MK E 编辑器中修改这些操作,开发智能判断的加工条件,这些加工条件将确定加工规则㊁刀具以及切削条件的适用性㊂打开MK E ,进入M a c h i n i n g K n o w l e d ge 选项列表,选择示教的操作,打开后可以看到对于每个加工策略,MK E 都建立了一系列特征以及加工操作定义的条件㊂C o n d i t i o n s 选项卡中包含了该操作的执行准则㊁刀具选择准则㊁加工前的特征属性㊁操作工序的属性以及具体的设置参数㊂㊃04㊃ 景德镇学院学报 2023年图6 MK E设置界面打开型腔铣的策略条件选项卡,在刀具选用准则下添加以下判别规则:R E M T o o l C r i t e r i aI F m w f.W I D T H<=8.0T H E N(t o o l.D i a m e t e r=6.0A N D t o o l.C o r R a d1=1.0)E L S E(t o o l.D i a m e t e r=10.0A N D t o o l.C o r R a d1=1.0);表示当圆角U型槽槽底的宽度小于等于8mm 时,选择直径6mm圆角半径1mm的圆角立铣刀粗加工;当槽底宽度大于8mm时,选择直径10mm圆角半径1mm的圆角立铣刀粗加工㊂深度轮廓铣的策略条件选项卡中,在刀具选用准则下添加以下判别规则:R E M T o o l C r i t e r i at o o l.D i a m e t e r<(m w f.R A D I U S-1.0)*2;表示自动选择半径小于圆角U型槽侧面R角半径减1mm的球头立铣刀,这样既能保证加工效率,也不会造成球头铣刀半径过大导致加工失败情况㊂在F B M自动加工的时候,系统会智能地从N X 刀具库中搜索符合匹配条件最大的球头铣刀加工㊂底壁铣的策略条件选项卡中,同样在刀具选用准则下添加以下判别规则:R E M T o o l C r i t e r i at o o l.D i a m e t e r<m w f.W I D T H-1.0;表示选用的立铣刀的直径小于槽底的宽度减1mm,系统会从N X刀具库中搜索符合匹配条件最大的平底立铣刀加工㊂设置完成后,保存MK E,示教特征完成㊂1.5智能自动编程流程自动编程时,首先进入F B M特征自动加工系统,选择查找特征,在要识别的特征中选中之前示教的特征名称,系统会自动将符合我们创建的示教特征的圆角U型槽一次性全部查找出来,并且正确识别到了槽宽㊁槽长㊁圆角半径等参数,如图7所示㊂图7自动编程界面选中所有特征,选择创建特征工艺,在知识库中选择之前示教的操作名称,系统会将之前示教的三个操作自动添加到特征上,并且会根据不同尺寸智能选择对应规格的刀具,还会自动设置相匹配的切削参数,生成刀具路径,实现了编程自动化和智能化㊂加工完成的机械臂零件安装到双臂s c a r a打印机上的效果如图8所示㊂图8双臂s c a r a打印机2自动编程效率评估将手动编程与F B M自动编程进行比较,统计二者在N X操作时的交互次数,包括编程员在编程时设置编程参数使用鼠标单击或键盘按键的次数㊂手动编程在编写单个圆角U型槽程序时,需要生成三个加工操作,每个操作都需要重复设置几何体,切削层,切削余量㊁切削参数㊁公差㊁刀具等工作,需要交互次数大约是100~200次,总共耗费时间大约是㊃14㊃第6期毕忠梁,王伟:基于N X F B M系统的自动化编程技术应用5分钟,而且与编程者的操作水平和熟练度有很大的关系㊂圆角U型槽数量越多,交互次数和耗费时间就越多,虽然操作可以复制粘贴,但是一些重复的参数设置还是必需的㊂而采用F B M自动编程时,特征查找和创建特征工艺都是自动完成,并且与圆角U型槽数量无关,无论图中有多少个圆角U型槽,自动编程的交互次数和时间都是差不多的㊂具体对比结果见表2㊂表2手动编程与F B M自动编程对比统计编程方法交互次数(次)编程时间(m i n)手动编程100~2005F B M自动编程10~201从表2可以看到,对于这四个圆角U型槽零件,F B M自动编程比手动编程交互次数减少了90%左右,编程时间缩短了80%左右㊂3总结基于特征的F B M自动化编程技术在未来的智能制造中有着非常重要的地位㊂智能制造的特点决定了零件的设计和尺寸会不断变化,传统的手工编程面对不断发生设计变化的工作环境力不从心㊂F B M是根据模型几何特征以及P M I等参数自动选择加工策略,自动进行编程,一旦模型设计或尺寸更改,F B M也会智能更改加工过程,无须编程者进行任何干预操作,极大地提高了生成效率㊂同时每个企业还可以按照自己的生产习惯,设定加工工艺及操作顺序,实现高效的生产㊂参考文献:[1]刘红军,伞雷,纪俐,等.基于U G特征识别的典型孔槽类零件数控加工技术[J].航空制造技术,2014(Z2):100 102 [2]A n g e l o C o r a l l o,Ma n u e l a Ma r r a,C l a u d i o P a s c a r e l l i. K n o w l e d g e B a s e d M a n u f a c t u r i n g:M a n a g e m e n t a n d D e p l o y m e n t o f M a n u f a c t u r i n g R u l e s t h r o u g h P r o d u c t L i f e c y c l e M a n a g e m e n t S y s t e m s[J].A e r o s p a c e,2019,6(4):41 58.[3]M.M a r r a,C.P a s c a r e l l i,M.L a z o i,e t a l.K N OW L E D G E -B A S E D M A N U F A C T U R I N G:A P R O P O S A L T O M A N A G E M A N U F A C T U R I N G R U L E S[C]//15t h I n t e r n a t i o n a l D e s i g nC o n f e r e n c e.2018:359-368.[4]花锋.基于N X二次开发的特征识别技术研究[J].机械制造与自动化,2010,12(39):99 100.[5]荣奇,张芬,李建勋.基于加工特征的U G/C AM编程自动化系统研究[J].机床与液压,2015(15):112 115.[6]黄国祥.基于加工特征和U G的N C代码自动生成研究[D].杭州:浙江大学,2006.责任编辑:肖祖铭A p p l i c a t i o n o f A u t o m a t i c P r o g r a m m i n g T e c h n o l o g yB a s e d o n N X F B M S y s t e mB I Z h o n g l i a n g,W A N G W e i(A n q i n g V o c a t i o n a l a n d T e c h n i c a l C o l l e g e,A n q i n g246003,C h i n a)A b s t r a c t:A l o n g w i t h t h e c o n t i n u o u s d e v e l o p m e n t o f i n t e l l i g e n t m a n u f a c t u r i n g t e c h n o l o g y,t h e p r o d u c t s l i f e c y c l e i s g e t t i n g s h o r t e r a n d s h o r t e r,a n d t h e m a n u a l p r o g r a mm i n g m o d e o f t r a d i t i o n a l C AM s o f t w a r e h a s b e e n d i f f i c u l t t o c o p e w i t h t h e c o n s t a n t c h a n g e s i n p a r t d e s i g n a n d d i m e n s i o n s.N X FB M s y s t e m c a n r e a l i z e f e a t u r e b a s e d a u t o m a t e d p r o g r a mm i n g, a u t o m a t i c a l l y d e t e r m i n e t h e b e s t m a c h i n i n g p r o c e s s b y r e c o g n i z i n g t h e f e a t u r e i n f o r m a t i o n i n t h eC AD m o d e l o f t h e p r o d u c t, a n d a u t o m a t i c a l l y g e n e r a t e t h e t o o l p a t h s b y s e l e c t i n g t h e s u i t a b l e t o o l s.I t c a n a l s o i n t e l l i g e n t l y a d j u s t t h e m a c h i n i n g p r o g r a m a s t h e C A D m o d e l c h a n g e s,r e a l i z i n g t h e a u t o m a t i o n a n d i n t e l l i g e n c e o f C N C p r o g r a mm i n g.T a k i n g t h e C N C m a c h i n i n g o f r o b o t i c a r m p a r t s a s a n e x a m p l e,t h e o r i g i n a l f e a t u r e l i b r a r y o f F B M s y s t e m i s e x p a n d e d,w h i l e s e c o n d a r y d e v e l o p m e n t o f t h e MKE k n o w l e d g e b a s e i s c a r r i e d o u t t o r e a l i z e a u t o m a t i c p r o g r a mm i n g a n d m a c h i n i n g.F i n a l l y,t h e d i f f e r e n c e s b e t w e e n p r o g r a mm i n g i n t h e t r a d i t i o n a l w a y a n d a u t o m a t i c p r o g r a mm i n g a r e c o m p a r e d,a n d t h e s u p e r i o r i t y o f a u t o m a t i c p r o g r a mm i n g i s d e m o n s t r a t e d.K e y w o r d s:F B M s y s t e m;a u t o m a t i c p r o g r a mm i n g;F e a t u r e m a c h i n i n g㊃24㊃景德镇学院学报2023年。
基于纽曼系统模式的Nustep-t4运动训练在脑卒中偏瘫病人康复中的应用

基于纽曼系统模式的Nustep⁃t4运动训练在脑卒中偏瘫病人康复中的应用李彤,刘永瑞*,张芬,张会聪,司新艳河南中医药大学第五临床医学院(郑州人民医院),河南 450003Application effect of Nustep⁃t4 exercise training based on Neuman system model in rehabilitation of stroke patients with hemiplegiaLI Tong, LIU Yongrui, ZHANG Fen, ZHANG Huicong, SI XinyanThe Fifth Clinical Medical College of Henan University of Chinese Medicine(Zhengzhou People's Hospital),Henan 450003 ChinaCorresponding Author LIUYongrui,E⁃mail:liu⁃*****************Keywords stroke;hemiplegia;Neuman system model;limb linkage therapy;walking ability;balance function;electromyography;nursing摘要目的:探讨基于纽曼(Neuman)系统模式的四肢联动疗法(Nustep‐t4)运动训练在脑卒中偏瘫病人康复中的应用效果。
方法:选取我院2020年3月—2021年3月收治的135例脑卒中后偏瘫病人为研究对象,采用随机数字表法将其分为对照组67例和Neuman 组68例。
对照组行常规康复训练,Neuman组在对照组基础上行基于Neuman系统模式的Nustep‐t4运动训练,连续干预8周,比较两组干预前后的肢体运动功能、日常生活能力、平衡功能、躯干控制能力、步行功能以及各肌群的肌电积分值(iEMG),同时采用中文版脑卒中专用生活质量量表(Stroke Scale Quality of Life,SS‐QOL)比较两组随访6个月后的生活质量。
FMA系列微力传感器说明书

FMA SERIES MicroForce Sensors, Compensated/AmplifiedDESCRIPTIONThe FMA Series are piezoresistive-based force sensors offering aratiometric digital output for readingforce over the specified full scale forcespan and temperature range. Theyare fully calibrated and temperaturecompensated for sensor offset,sensitivity, temperature effects,and nonlinearity using an on-boardApplication Specific Integrated Circuit (ASIC). Direct mechanical coupling allows for easy interface with the sensor, coupling with tubing, membrane or a plunger, providing repeatable performance and a reliable mechanical interface to the application. All products are designed and manufactured according to ISO 9001 standards. These products offer a more stable output which is directly proportional to the force applied to the mechanically-coupled sphere.The FMA Series is available with pocket tape and reel packaging.VALUE TO CUSTOMERSThe FMA Series are designed to meet the customer’s need for a compensated, amplified force sensor which provides digital outputs, a variety of force sensing ranges, a small, cost-effective format, and enhanced durability and accuracy. The flexible design provides multiple standard configurations overa wide operating temperature range.FEATURES• Small form factor: 5 mm x 5 mm[0.20 in x 0.20 in]• Accuracy: ±2 %FSS typical• SPI- or I2C-compatible digital output• Fully calibrated and temperaturecompensated over a temperaturerange of 5°C to 50°C [41°F to 122°F]• Available in a wide variety of standardand configurable force ranges• Overforce: 3X force range• Supply voltage: 3.3 Vdc typ. or 5.0 Vdc typ.• Low power consumption: 14 mW• Enhanced part-to-part repeatability• Enhanced reliability• Stable, stainless steel sphere interface• Internal diagnostic functions available• REACH and RoHS compliant32347833Issue BThe FMA Series joins theFSA Series, FSG Series, FSSSeries, FSS-SMT Series, TBFSeries, and 1865 Series ForceSensors. To view the entireproduct portfolio, click here. DIFFERENTIATION• Multiple force ranges allow thecustomer to choose the force rangeto maximize sensitivity and improvesystem resolution/performance• Smaller package allows for spaceconstrained applications• Robust design provides enhanceddurability in applications whereoverforce may exist• Enhanced accuracy includes allerrors due to force non-linearity, forcehysteresis, and non-repeatability• Reduced Total Error Band enhancessystem performance• Digital output enhances performancethrough reduced conversionrequirements and the convenience ofdirect interface to microprocessors• Diagnostic functions allow the userto determine if the sensor is workingcorrectly by detecting if electrical pathsare broken or shorted inside the sensor• Selectable supply voltages providecustomers with design flexibilityPOTENTIAL APPLICATIONSMEDICAL• Infusion pumps• Ambulatory pumps• Enteral feeding pumps• Kidney dialysis machinesINDUSTRIAL• Load and compression sensing• Touch panels• Switch replacement• Robotic equipment• Weight measurement•Force/grip measuring equipment2Ratiometricity of the sensor (the ability of the device output to scale to the supply voltage) is achieved within the specified operating voltage.3The sensor is not reverse polarity protected. Incorrect application of supply voltage or ground to the wrong pin may cause electrical failure.4Operating temperature range: The temperature range over which the sensor will produce an output proportional to force.5Compensated temperature range: The temperature range over which the sensor will produce an output proportional to force within the specified performance limits.6Accuracy: The maximum deviation in output from a Best Fit Straight Line (BFSL) fitted to the output measured over the force range with single load-unload cycle at 25°C. Includes all errors due to force non linearity, force hysteresis, and non repeatability. 7Full Scale Span (FSS): The algebraic difference between the output voltage at full scale force and the output at zero force.8Total Error Band (TEB): Combined error from calibration, accuracy and temperature effects over the compensated temperature range at 5.0 V from 20 %FSS to 80 %FSS.2Sensing and Internet of Things3Sensing and Internet of ThingsFIGURE 1. TRANSFER FUNCTION LIMITS+8% Total Error BandF min.ForceO u t p u t (% 214 C o u n t s )60%Output (% of 214 counts) =x (Force applied ) + 20%IdealF max.Force range1020304050607080901004Sensing and Internet of ThingsFM A M S D XX 0252 W C S C 3 31 Custom configurations are available upon request. Please contact Honeywell Sales.2Three characters specify the desired force level; allowable characters are the numbers 0 through 9. See Table 5 for currently configurable force ranges.3For other available transfer functions, contact Honeywell Customer Service.Note: B reakout boards, designed for use with the Honeywell SEB002 Sensor Evaluation Kit, are available with the FMA Series sensor already mounted. Please contact your Honeywell representative for details.For example, FMAMSDXX025WCSC3 defines an FMA Series Force Sensor, compensated/amplified, mechanically coupled, sphere contact element, sensor short and open diagnostics, 25 N force range,force unit in N, compression force type, SPI digital output, 20% to 80% transfer function, 3.3 Vdc supply voltage 1FIGURE 2. NOMENCLATURE AND ORDER GUIDEminimum order quantity thresholds and NRE may apply. Please consult the factory.FIGURE 3. SENSOR MOUNTING DIMENSIONS (FOR REFERENCE ONLY: MM/[IN].)5Sensing and Internet of Things6Sensing and Internet of Things7Sensing and Internet of ThingsNote: FMA Series products are shipped in tape and reel packaging with a Minimum Order Quantity (MOQ) of 160 pieces. The maximum tape and reel quantity is 960 pieces per reel.WARRANTY/REMEDYHoneywell warrants goods of itsmanufacture as being free of defective materials and faulty workmanship during the applicable warranty period. Honeywell’s standard product warranty applies unless agreed to otherwise by Honeywell in writing; please refer to your order acknowledgment or consult your local sales office for specific warranty details. If warranted goods are returned to Honeywell during the period of coverage, Honeywell will repair or replace, at its option, without charge those items that Honeywell, in its sole discretion, finds defective. The foregoing is buyer’s sole remedy and is in lieu of all other warranties, expressed or implied, including those of merchantability and fitness for a particular purpose. In no event shall Honeywell be liable for consequential, special, or indirect damages.m WARNINGPERSONAL INJURYDO NOT USE these products as safety or emergency stop devices or in any other application where failure of the product could result in personal injury.Failure to comply with theseinstructions could result in death or serious injury.m WARNINGMISUSE OFDOCUMENTATION•The information presented in this product sheet is for referenceonly. Do not use this document as a product installation guide.•Complete installation, operation, and maintenance information is provided in the instructions supplied with each product.Failure to comply with theseinstructions could result in death or serious injury.ADDITIONAL MATERIALSThe following associated literature is available at :• Product range guide • Technical notes:- MicroForce Sensor Coupling - Overforce Design Considerations - Force Sensor Diagnostics - SMT Sensor PCB MountingGuidelines - Digital Output Force Sensors I 2CCommunications - Digital Output Force Sensors SPICommunications • Other technical notes • Application notes • CAD ModelFOR MORE INFORMATIONHoneywell Sensing and Internet ofThings services its customers through a worldwide network of sales offices and distributors. For application assistance, current specifications, pricing or the nearest Authorized Distributor, visit or call:Asia Pacific +65 6355-2828Europe +44 1698 481481USA/Canada+1-302-613-449132347833-B-EN | B | 02/20© 2020 Honeywell International Inc. All rights reserved.HoneywellSensing and Internet of Things 9680 Old Bailes Road Fort Mill, SC 29707www. While Honeywell may provideapplication assistance personally, through our literature and the Honeywell web site, it is buyer’s sole responsibility to determine the suitability of the product in the application.Specifications may change without notice. The information we supply is believed to be accurate and reliable as of this writing. However, Honeywell assumes no responsibility for its use.。
舒它西林的电喷雾-四极杆-飞行时间串联质谱裂解规律研究

第 3 3卷 第 3期
21 0 2年 5月
质 谱 学 报
J u n l fChn s a sS eto tyS cey o r a ieeM s p crmer o it o
Vo1 3 No. .3 3 M a 01 y2 2
舒 它西 林 的 电 喷雾一 四极杆 一 飞行 时 间 串联质 谱 裂解f oo y,C i eeAc d myo ce cs,C e g 1 0 1 h n ) e g u I siu eo Bilg h n s a e f S in e h n du 6 0 4 ,C ia
Ab ta t no d rt lrf h r g n a inb h vo so u t mii i a ii i/ ub c sr c :I r e o ca iyt efa me t t e a ir f la cl n( mpeln s l a — o S l l
氘代信息推 断出舒它西林[ M+H] 片离子断裂途径主要为氨苄西林部分 的 内酰胺 环断裂 . M+Na 碎 [ 3
裂 解 可 观察 到较 多 碎 片 离 子 峰 , 括 氨 苄 西 林 部 分 内 酰 胺 环 断 裂 、 包 双酯 连接 处 断 裂 和 舒 巴 坦 部 分 四 元 环 断
云南某铁精矿降磷工艺研究

程、 强磁 选一 反 浮 选 等 联 合 流 程 进 行选 别 。对 于
赤、 褐铁 矿 的处 理方 法 有重 选 、 磁选 、 级磁 选 、 分 分级 重 选 、 选 一 浮 选一 磁 选 、 选一 重 选一 磁 选 、 磁 磁 絮
凝一 强 磁 选 、 原焙 烧 一磁 选 等 。 还
强 弱磁精
S TUDY ON DEP HOS PHORI ZAT ON ROCES RON I P S 0F I ORE I YUNNAN N
ZHOU ha ZH OU S o P g WANG n Yo g
( u m n nvrt o c ne n eh ooy K n ig6 0 9 , hn ) K n ig U i sy fSi c a dTc nl , u m n 5 0 3 C ia e i e g
6 . 9 、 中含 磷 0 1 % 的产 品 。 44 % 其 .4
研究 高磷铁 矿 石 的高效 分选 技术 显 得 十分重 要 。 目
前 我 国高磷 铁 矿 石储 量 占总储 量 1 . 6 , 7 . 48% 达 4 5
亿 t 。磷 在 炼钢 的 过程 中 , 使 钢 的强 度及 硬 度 ¨ 会 增加 、 塑性 下降 , 致 在 冷 加 工 中易 于 断 裂 , 导 即产 生
Fi.1 Th o he to egi dig, ls iia in g e f ws e fr rn n ca sfc to l r — lci n,we k a d sr ng ma n tc s p r to e ee to a n to g e i e a ai n
回收率 9.9 、 磷 01%的铁精矿。 01% 含 .4
关键词 : 赤铁 矿; 褐铁矿 ; 磁铁矿 ; 降磷 ; 反浮选 中 图 分 类 号 :D 5 T 91 文献标识码 : A d i 03 6 /. s. 0 5 8 4 2 1. 1 0 9 o: . 9 9 ji n 1 0 - 5 .0 2 0 . 0 1 s 7
富士变频器参数设定
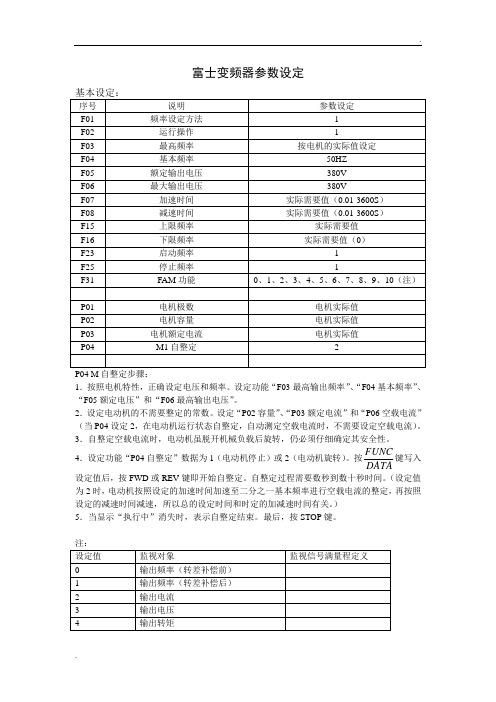
富士变频器参数设定
P04 M 自整定步骤:
1.按照电机特性,正确设定电压和频率。
设定功能“F03最高输出频率”、“F04基本频率”、“F05额定电压”和“F06最高输出电压”。
2.设定电动机的不需要整定的常数。
设定“P02容量”、“P03额定电流”和“P06空载电流”(当P04设定2,在电动机运行状态自整定,自动测定空载电流时,不需要设定空载电流)。
3.自整定空载电流时,电动机虽脱开机械负载后旋转,仍必须仔细确定其安全性。
4.设定功能“P04自整定”数据为1(电动机停止)或2(电动机旋转)。
按
DATA
FUNC
键写入
设定值后,按FWD 或REV 键即开始自整定。
自整定过程需要数秒到数十秒时间。
(设定值为2时,电动机按照设定的加速时间加速至二分之一基本频率进行空载电流的整定,再按照设定的减速时间减速,所以总的设定时间和时定的加减速时间有关。
) 5.当显示“执行中”消失时,表示自整定结束。
最后,按STOP 键。
注:。
WCDMA试题

WCDMA原理测试题1.WCDMA系统的码片速率为3.84Mcps,带宽为5MHZ。
2.WCDMA系统的扩频技术分为两步,第一步使用信道化码,其具有正交性;第二步使用扰码。
3.信道化码的作用为:区分同一发射端的不同数据信道。
信道化码使用中必须遵循的一个原则为:父子不能通用。
4. PN码用于区分不同的发射端,上行区分用户,下行区分基站小区。
5. WCDMA的功率控制可以分为开环功控和闭环功控两类。
其中后者又可以细分为内环功控和外环功控。
6.内环功控中,发送给UE的功率控制命令的频率为1500次每秒。
7.切换分为软切换和硬切换两类,不同载频间的切换属于硬切换。
8.软切换与更软切换的区别:软切换发生在同频的不同基站间,更软切换发生在同一基站的不同小区间。
9.WCDMA中采用RACK接收机来克服多径效应。
10.WCDMA系统中,RNC与RBS(基站)之间的接口称为Iub口;RNC之间的接口称为Iur口。
1.RBS3206 CB开关与机柜设备的控制关系为:CB1,CB2控制风扇的电源,CB3控制1小区RU,FU的电源,CB5控制2小区RU,FU的电源,CB7控制3小区RU,FU的电源,CB9控制主机框的电源。
2.RBS3206的板卡种类有CBU、ET-MFX、ET-MC1、RAX、TX、RUIF、RU、FU等板卡。
3. RBS3418的板卡种类有CBU、ET-MFX、ET-MC1、RAX、TX、OBIF、RRU等板卡4. CBU板卡可以承载E1的数量为4个,如果传输超过4个(小于12E1),则需使用ET-MC1板卡5. RBS3206最多可以安装12块RAX板卡,最多可以安装4块TX板卡6.RBS3418最多可以安装4块RAX板卡,最多可以安装2块TX板卡7.RBS3206和RBS3418基站的对应关系如下:RBS3418的RRU相当于RBS3206的RU和FU的功能RBS3418的MU相当于RBS3206的主机框8.一块板卡绿灯常亮意味着设备已经加电,绿灯0.5Hz意味着相应板卡的资源缺失,绿灯不亮意味着设备已经未加电。
FMEA、MSA、SPC是什么意思?

FMEA\MSA\SPC是什么意思?FMEA:潜在的失效模式及后果分析一、失效模式及后果分析(FMEA)的概念及定义:失效模式及后果分析(Failure Mode and Effects Analysis:简称FMEA):指一组系统化的活动,其目的在:1)找出、评价产品/过程中潜在的失效及其后果;2)找到能够避免或减少这些潜在失效发生的措施;3)书面总结以上过程,并使其文件化。
为确保顾客满意,FMEA是对设计过程的完善。
FEMA是潜在的失效模式及后果分析的缩写,本应写成P-FMEA,但由于企业/公司常用D-FMEA表示产品FMEA,用P-FMEA表示过程FMEA,所以用FMEA表示潜在的失效模式及后果分析,以免混淆。
FMEA是用现行的技术对风险进行评估与分析的一种方法,其目的在于清除风险或使其减少至一个可以接受的程度,其中对用户(顾客)利与弊也必须加以考虑。
FMEA主要是将其作为一种控制工具和/或风险分析工具和/或管理工具运用在下列活动中:1)设计控制;2)生产计划;3)生产控制;4)分承包方的评选和供应商的质量保证;5)冒险分析;6)风险分析;7)召回产品的评估;8)顾客运用;9)说明书和警告标签;10)产品服务和保修;11)工程更改通知;12)制造过程的差异等。
二、失效模式及后果分析(FMEA)的发展历史:2.1 60年代中期:开始于航天业(阿波罗计划),最初多少起了净室文件的作用。
2.2 1972年:NAAO正式采用FMEA作为可靠度计划使用;发展阶段:不断地完善文件及作为自我检查的工具。
2.3 1974年:美海军制定船上设备的标准,Mil-Std-1625(船)“实行船上设备失效模式及后果分析的程序”,这使FMEA第一次有机会进入军用品供货商界;发展阶段:有组织的可靠度程度。
2.4 1976年:美国国防部采用FMEA来作为领导军队服务的研发及后勤工作的标准;调整阶段:虽然只强调设计面。
2.5 1988年:美运输部的联邦航空管理局发表通告要求所有航空系统的设计及分析均使用FMEA。
10恒定磁场

10 恒定磁场一、选择题(在下列各题中,均给出了4个~5个答案,其中有的只有1个正确答案,有的则有几个是正确答案,请把正确答案的英文字母序号填在题后的括号内)1. 一运动电荷q ,质量为m ,以初速v 0进入均强磁场中,若v 0与磁场的方向夹角为α,则 ( )A. 其动能改变,动量不变B. 其动能和动量都改变C. 其动能不变,动量改变D. 其动能和动量都不变2. 一带电粒子垂直进入匀强磁场,如果粒子质量增大到2倍,入射速度增大到2倍,磁场的磁感应强度增大到4倍,则通过粒子运动轨道所包围范围内的磁通量增大到原来的几倍。
( )A. 2倍B. 4倍C. 1/2倍D. 1/4倍3. 长直电流I 2与圆形电流I 1共面,并与其一直径相重合如图(但两者间绝缘),设长直电流不动,则圆形电流将 ( )A. 绕I 2旋转B. 向左运动C. 向右运动D. 向上运动E. 不动4. 如图11-2所示,3根平行共面的无限长直导线a 、b 、c 等距离放置,各导线通过的电流值分别为I a =1 A ,I b =2 A ,I c =3 A ,且电流方向都相同。
则导线a 和b 单位长度上所受安培力F a 与F b 的比值为: ( ) A. 167; B. 85; C. 87; D. 45 5. 如图11-3所示,在均匀磁场B 中,放置面积均为S ,通有电流均为I (方向如图)的两个单匝线圈,其中一个是正三角形,另一个为正方形。
线圈平面均与磁场线平行。
设P m为线圈磁矩,M 为磁场对线圈的磁力矩,∑F 为磁场对线圈的合力。
则两线圈的( )A. P m 相同,M 相同,∑F =0;B. P m 相同,M 相同,∑F ≠0;C. P m 相同,M 不同,∑F ≠0;D. P m 不同,M 不同,∑F =0;图11-1 图11-2图11-3 图11-46. 如图11-4所示,一载流细螺绕环,它由表面绝缘的导线在铁环上密绕而成,每厘米绕10匝,当导线中的电流为I =2.0 A 时,测得铁环内的磁感强度的大小为B =1.0 T 。
FMA的应用

自动推力预位。起飞或复飞阶段不显示此指示。最前的推力手柄在CL 卡位以上, 另一推力手柄在CL 卡位或两个推力手柄高于CL 卡位。
自动推力方式生效且最前的推力手柄在MCT 卡位 (单发)。
自动推力方式生效,最前的推力手柄在CL 卡位。
显示
描述
自动推力方式生效并指令慢车推力
自动推力在速度或马赫方式生效
主要内容
第一部分 : FMA的结构和功能
第二部分 : FMA详解 第三部分 : 飞行各阶段的FMA
第一部分 : FMA的结构和功能
FMA 的主要用途:
向飞行员显示飞机的引导方式。 它反映自动推力及自动驾驶/飞行指引仪的 方式,以及这些系统的接通状态及盲降进近能 力。
飞行方式信号牌(FMA)
减速板伸出,下降方式接通,且: -ALT*或ALT 方式接通或 -飞机低于轨迹。 -达到形态3 或全形态。
机长和副驾驶的显示组件由同一源供给: 机长侧的源 (1) 或副驾驶侧的源(2)。只有适当的一侧才能进 行范围和方式选择。
不允许飞行员选择EFIS 形态: 副驾驶显示组件的DMC1,或 机长显示组件的DMC2 且EFIS SINGLE SOURCE 的条
特殊信息,第二和第三列的第三行
显示 含义 在左右升降舵失效时显示。 飞行操纵在直接法则或双RA 失效时处于拉平法则。
在巡航时飞机距离下降顶点不到100 海里,或在下降或 在进近中, 且: -选择了非ILS 进近。 -在RAD NAV 页面上调谐一个ILS 频率。
速度目标已选,但下一飞行阶段的预选速度不存在 飞机在单发方式并且选择了目标速度。该信息在下列情 况下显示: FCU 选择的速度: ≤ 绿点-10 节或 ≥ 绿点+10 节,在ALT*、ALT 方式除外 飞机处于选择的速度,等待航线已输入飞行计划,飞机 离预先计算的等待速度的减速区还有30 秒。
catproccpuinfo讲解

catproccpuinfo讲解查看cpu信息有什么⽤呢,我们来看看到底有哪些⽤处:1、和云服务提供商核算成本,现在基本是cpu和内存的费⽤最⼤,硬盘⼤⼩⼏乎被忽略了2、我们写程序时候是会关注多核还是单核的,否则不能充分利⽤多线程等特性3、cpu和内存⼤⼩直接决定了,我们在部署应⽤环境时候是否能满⾜整体运⾏的要求。
另外有些架构都有⾃⼰的指令集,所以必须要了解清楚机器的情况和配置,才能更好的调整我们的架构体系很多⽐较强⼤的软件都有根据cpu架构对应的版本⽐如: ibm,amd,intel等。
运维⼯作更应该关注的不仅仅只是使⽤和安装特别是调优和调试错误的时候,我们有时候知识的贮备明显就显得不⾜了。
当然我们这个时代都是⼤部分是云主机,只有量级达到⼀定⽔平才会使⽤物理机来有针对性的构建我们的架构和应⽤。
暂且不说,但是要想做⼀个有深度的专家实际我们更应该关注⼀些底层的内容。
毕竟技术如何变,最终是靠要底层的⽀撑。
1)查看cpu信息[root@fp-web-126 ~]# cat /proc/cpuinfo信息包括有 cpu型号 Intel(R) Xeon(R) CPU E5-2660 v3 @ 2.60GHz,2个cpu,8核指令集是64bit机器配置8核、16G2)查看cpu运⾏模式[root@fp-web-126 ~]# getconf LONG_BIT643)查看cpu是否⽀持64bit[root@fp-web-126 ~]# cat /proc/cpuinfo | grep flags | grep ' lm ' | wc -l8(结果⼤于0, 说明⽀持64bit计算. lm指long mode, ⽀持lm则是64bit)4)查看cpu信息概要[root@fp-web-126 ~]# lscpuArchitecture: x86_64CPU op-mode(s): 32-bit, 64-bit ##cpu⼯作模式⽀持32,64bitByte Order: Little EndianCPU(s): 8On-line CPU(s) list: 0-7Thread(s) per core: 1Core(s) per socket: 4Socket(s): 2NUMA node(s): 1Vendor ID: GenuineIntelCPU family: 6Model: 63Model name: Intel(R) Xeon(R) CPU E5-2660 v3 @ 2.60GHzStepping: 2CPU MHz: 2593.993BogoMIPS: 5187.98Hypervisor vendor: VMwareVirtualization type: fullL1d cache: 32KL1i cache: 32KL2 cache: 256KL3 cache: 25600KNUMA node0 CPU(s): 0-7查看cpu相关信息5)[root@fp-web-126 ~]# cat /proc/cpuinfo-------------------------------------cpu1,4核------------------------------------------------------------processor : 0 #系统中逻辑处理核的编号vendor_id : GenuineIntelcpu family : 6model : 63model name : Intel(R) Xeon(R) CPU E5-2660 v3 @ 2.60GHz 英特尔⾄强处理器,主频:2.6 GHz, 产品型号 E5-2660stepping : 2microcode : 0x38cpu MHz : 2593.993cache size : 25600 KBphysical id : 0siblings : 4core id : 0cpu cores : 4apicid : 0initial apicid : 0fpu : yesfpu_exception : yescpuid level : 15wp : yesflags : fpu vme de pse tsc msr pae mce cx8 apic sep mtrr pge mca cmov pat pse36 clflush dts mmx fxsr sse sse2 ss ht syscall nx pdpe1gb rdtscp lm constant_tsc arch_perfmon pebs bts nopl xtopology tsc_reliable nonstop_tsc aperfmperf eagerfpu pni pclmulqdq ssse3 fma cx16 pcid sse4_1 sse4_2 x2apic movbe popcnt tsc_deadline_timer aes xsave avx f16c rdrand hypervisor lahf_lm abm arat epb pln pts dtherm fsgsbase tsc_adjust bmi1 avx2 smep bmi2 invpcid xsaveoptbogomips : 5187.98clflush size : 64cache_alignment : 64address sizes : 42 bits physical, 48 bits virtualpower management:processor : 1 ####逻辑idvendor_id : GenuineIntel ###因特尔原装CPUcpu family : 6model : 63model name : Intel(R) Xeon(R) CPU E5-2660 v3 @ 2.60GHzstepping : 2microcode : 0x38cpu MHz : 2593.993cache size : 25600 KBphysical id : 0siblings : 4core id : 1cpu cores : 4apicid : 1initial apicid : 1fpu : yesfpu_exception : yescpuid level : 15wp : yesflags : fpu vme de pse tsc msr pae mce cx8 apic sep mtrr pge mca cmov pat pse36 clflush dts mmx fxsr sse sse2 ss ht syscall nx pdpe1gb rdtscp lm constant_tsc arch_perfmon pebs bts nopl xtopology tsc_reliable nonstop_tsc aperfmperf eagerfpu pni pclmulqdq ssse3 fma cx16 pcid sse4_1 sse4_2 x2apic movbe popcnt tsc_deadline_timer aes xsave avx f16c rdrand hypervisor lahf_lm abm arat epb pln pts dtherm fsgsbase tsc_adjust bmi1 avx2 smep bmi2 invpcid xsaveoptbogomips : 5187.98clflush size : 64cache_alignment : 64address sizes : 42 bits physical, 48 bits virtualpower management:processor : 2 #系统中逻辑处理核的编号vendor_id : GenuineIntelcpu family : 6model : 63model name : Intel(R) Xeon(R) CPU E5-2660 v3 @ 2.60GHzstepping : 2microcode : 0x38cpu MHz : 2593.993cache size : 25600 KBphysical id : 0siblings : 4core id : 2cpu cores : 4apicid : 2initial apicid : 2fpu : yesfpu_exception : yescpuid level : 15wp : yesflags : fpu vme de pse tsc msr pae mce cx8 apic sep mtrr pge mca cmov pat pse36 clflush dts mmx fxsr sse sse2 ss ht syscall nx pdpe1gb rdtscp lm constant_tsc arch_perfmon pebs bts nopl xtopology tsc_reliable nonstop_tsc aperfmperf eagerfpu pni pclmulqdq ssse3 fma cx16 pcid sse4_1 sse4_2 x2apic movbe popcnt tsc_deadline_timer aes xsave avx f16c rdrand hypervisor lahf_lm abm arat epb pln pts dtherm fsgsbase tsc_adjust bmi1 avx2 smep bmi2 invpcid xsaveoptbogomips : 5187.98clflush size : 64cache_alignment : 64address sizes : 42 bits physical, 48 bits virtualpower management:processor : 3 #系统中逻辑处理核的编号vendor_id : GenuineIntelcpu family : 6model : 63model name : Intel(R) Xeon(R) CPU E5-2660 v3 @ 2.60GHzstepping : 2microcode : 0x38cpu MHz : 2593.993cache size : 25600 KBphysical id : 0siblings : 4core id : 3cpu cores : 4apicid : 3initial apicid : 3fpu : yesfpu_exception : yescpuid level : 15wp : yesflags : fpu vme de pse tsc msr pae mce cx8 apic sep mtrr pge mca cmov pat pse36 clflush dts mmx fxsr sse sse2 ss ht syscall nx pdpe1gb rdtscp lm constant_tsc arch_perfmon pebs bts nopl xtopology tsc_reliable nonstop_tsc aperfmperf eagerfpu pni pclmulqdq ssse3 fma cx16 pcid sse4_1 sse4_2 x2apic movbe popcnt tsc_deadline_timer aes xsave avx f16c rdrand hypervisor lahf_lm abm arat epb pln pts dtherm fsgsbase tsc_adjust bmi1 avx2 smep bmi2 invpcid xsaveoptbogomips : 5187.98clflush size : 64cache_alignment : 64address sizes : 42 bits physical, 48 bits virtualpower management:-------------------------------------cpu2,4核------------------------------------------------------------processor : 4 #系统中逻辑处理核的编号vendor_id : GenuineIntelcpu family : 6model : 63model name : Intel(R) Xeon(R) CPU E5-2660 v3 @ 2.60GHzstepping : 2microcode : 0x38cpu MHz : 2593.993cache size : 25600 KBphysical id : 1 ##单个CPU的标号siblings : 4 ##单个CPU逻辑物理核数core id : 0 ##当前物理核在其所处CPU中的编号,这个编号不⼀定连续cpu cores : 4 ##该逻辑核所处CPU的物理核数apicid : 4 ##⽤来区分不同逻辑核的编号,系统中每个逻辑核的此编号必然不同,此编号不⼀定连续initial apicid : 4fpu : yes ##是否具有浮点运算单元fpu_exception : yes ##是否⽀持浮点计算异常cpuid level : 15 ##执⾏cpuid指令前,eax寄存器中的值,根据不同的值cpuid指令会返回不同的内容wp : yesflags : fpu vme de pse tsc msr pae mce cx8 apic sep mtrr pge mca cmov pat pse36 clflush dts mmx fxsr sse sse2 ss ht syscall nx pdpe1gb rdtscp lm constant_tsc arch_perfmon pebs bts nopl xtopology tsc_reliable nonstop_tsc aperfmperf eagerfpu pni pclmulqdq ssse3 fma cx16 pcid sse4_1 sse4_2 x2apic movbe popcnt tsc_deadline_timer aes xsave avx f16c rdrand hypervisor lahf_lm abm arat epb pln pts dtherm fsgsbase tsc_adjust bmi1 avx2 smep bmi2 invpcid xsaveoptbogomips : 5187.98clflush size : 64cache_alignment : 64address sizes : 42 bits physical, 48 bits virtualpower management:processor : 5 #系统中逻辑处理核的编号vendor_id : GenuineIntelcpu family : 6model : 63model name : Intel(R) Xeon(R) CPU E5-2660 v3 @ 2.60GHzstepping : 2microcode : 0x38cpu MHz : 2593.993cache size : 25600 KBphysical id : 1siblings : 4core id : 1cpu cores : 4apicid : 5initial apicid : 5fpu : yesfpu_exception : yescpuid level : 15wp : yesflags : fpu vme de pse tsc msr pae mce cx8 apic sep mtrr pge mca cmov pat pse36 clflush dts mmx fxsr sse sse2 ss ht syscall nx pdpe1gb rdtscp lm constant_tsc arch_perfmon pebs bts nopl xtopology tsc_reliable nonstop_tsc aperfmperf eagerfpu pni pclmulqdq ssse3 fma cx16 pcid sse4_1 sse4_2 x2apic movbe popcnt tsc_deadline_timer aes xsave avx f16c rdrand hypervisor lahf_lm abm arat epb pln pts dtherm fsgsbase tsc_adjust bmi1 avx2 smep bmi2 invpcid xsaveoptbogomips : 5187.98clflush size : 64cache_alignment : 64address sizes : 42 bits physical, 48 bits virtualpower management:processor : 6 #系统中逻辑处理核的编号vendor_id : GenuineIntelcpu family : 6model : 63model name : Intel(R) Xeon(R) CPU E5-2660 v3 @ 2.60GHzstepping : 2microcode : 0x38cpu MHz : 2593.993cache size : 25600 KBphysical id : 1siblings : 4core id : 2cpu cores : 4apicid : 6initial apicid : 6fpu : yesfpu_exception : yescpuid level : 15wp : yesflags : fpu vme de pse tsc msr pae mce cx8 apic sep mtrr pge mca cmov pat pse36 clflush dts mmx fxsr sse sse2 ss ht syscall nx pdpe1gb rdtscp lm constant_tsc arch_perfmon pebs bts nopl xtopology tsc_reliable nonstop_tsc aperfmperf eagerfpu pni pclmulqdq ssse3 fma cx16 pcid sse4_1 sse4_2 x2apic movbe popcnt tsc_deadline_timer aes xsave avx f16c rdrand hypervisor lahf_lm abm arat epb pln pts dtherm fsgsbase tsc_adjust bmi1 avx2 smep bmi2 invpcid xsaveoptbogomips : 5187.98clflush size : 64cache_alignment : 64address sizes : 42 bits physical, 48 bits virtualpower management:processor : 7 #系统中逻辑处理核的编号vendor_id : GenuineIntelcpu family : 6 #CPU产品系列代号model : 63 #CPU属于其系列中的哪⼀代的代号model name : Intel(R) Xeon(R) CPU E5-2660 v3 @ 2.60GHzstepping : 2 #CPU属于制作更新版本microcode : 0x38cpu MHz : 2593.993 ##CPU的实际使⽤主频cache size : 25600 KB ##CPU⼆级缓存⼤⼩physical id : 1 ##单个CPU的标号siblings : 4core id : 3cpu cores : 4apicid : 7initial apicid : 7fpu : yesfpu_exception : yescpuid level : 15wp : yesflags : fpu vme de pse tsc msr pae mce cx8 apic sep mtrr pge mca cmov pat pse36 clflush dts mmx fxsr sse sse2 ss ht syscall nx pdpe1gb rdtscp lm constant_tsc arch_perfmon pebs bts nopl xtopology tsc_reliable nonstop_tsc aperfmperf eagerfpu pni pclmulqdq ssse3 fma cx16 pcid sse4_1 sse4_2 x2apic movbe popcnt tsc_deadline_timer aes xsave avx f16c rdrand hypervisor lahf_lm abm arat epb pln pts dtherm fsgsbase tsc_adjust bmi1 avx2 smep bmi2 invpcid xsaveoptbogomips : 5187.98clflush size : 64cache_alignment : 64address sizes : 42 bits physical, 48 bits virtualpower management:------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------以上输出项的含义如下:processor :系统中逻辑处理核的编号。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Financial Mathematics for ActuariesChapter4Rates of ReturnLearning Objectives •Internal rate of return(yield rate)•One-period rate of return of a fund:time-weighted rate of return and dollar-weighted(money-weighted)rate of return•Rate of return over longer periods:geometric mean rate of return and arithmetic mean rate of return•Portfolio return and return of a short-selling strategy •Crediting interest:investment-year method and portfolio method •Inflation:real rate of return•Capital budgeting and project appraisal4.1Internal Rate of Return •Consider a project with initial investment C0.We assume the cash flows occur at regular intervals.•The project lasts for n years and the future cashflows are denoted by C1,···,C n.•We adopt the convention that cash inflows to the project(invest-ments)are positive and cash outflows from the project(withdrawals) are negative.•We define the internal rate of return(IRR)(also called the yield rate)as the rate of interest such that the sum of the present values of the cashflows is equated to zero.•Denoting the internal rate of return by y ,we have n X j =0C j (1+y )j =0,(4.1)where j is the time at which the cash flow C j occurs.•This equation can also be written as C 0=−n X j =1C j (1+y )j .(4.2)•Thus,the net present value of all future withdrawals (injections are negative withdrawals)evaluated at the IRR is equal to the initial investment.Example 4.1:A project requires an initial cash outlay of $2,000and is expected to generate $800at the end of year 1and $1,600at the endof year2,at which time the project will terminate.Calculate the IRR of the project.Solution:If we denote v=1/(1+y),we have,from(4.2)2,000=800v+1,600v2,or5=2v+4v2.Dropping the negative answer from the quadratic equation,we havev=−2+√4+4×4×52×4=0.8956.Thus,y=(1/v)−1=11.66%.Note that v<0implies y<−1,i.e.,the loss is larger than100%,which is precluded from consideration.2•There is generally no analytic solution for y in(4.1)when n>2, and numerical methods have to be used.The Excel function IRR enables us to compute the answer easily.Its usage is described as follows:Example4.2:An investor pays$5million for a5-year lease of a shopping mall.He will receive$1.2million rental income at the end of each year.Calculate the IRR of his investment.Solution:See Exhibit4.1.2•If the cashflows occur more frequently than once a year,such as monthly or quarterly,y computed from(4.1)is the IRR for the payment interval.•Suppose cashflows occur m times a year,the nominal IRR in an-nualized term is m·y,while the annual effective rate of return is (1+y)m−1.Example4.3:A cash outlay of$100generates incomes of$20after4 months and8months,and$80after2years.Calculate the IRR of the investment.Solution:If we treat one month as the interest conversion period,the equation of value can be written as100=20(1+y1)4+20(1+y1)8+80(1+y1)24,where y1is the IRR on monthly interval.The nominal rate of return on monthly compounding is12y1.Alternatively,we can use the4-month interest conversion interval,and the equation of value is100=201+y4+20(1+y4)2+80(1+y4)6,where y4is the IRR on4-month interval.The nominal rate of return on4-monthly compounding is3y4.The effective annual rate of return is y=(1+y1)12−1=(1+y4)3−1.The above equations of value have to be solved numerically for y1or y4. We obtain1.0406%as the IRR per month,namely,y1.The effective annualized rate of return is then(1.010406)12−1=13.23%.Solving for y4with Excel,we obtain the answer4.2277%.Hence,the annualized effective rate is(1.042277)3−1=13.23%,which is equal to the effective rate computed using y1.2•When cashflows occur irregularly,we can define y as the annualized rate and express all time of occurrence of cashflows in years.•Suppose there are n+1cashflows occurring at time0,t1,···,t n, with cash amounts C0,C1,···,C n.Equation(4.2)is rewritten asC0=−nX j=1C j(1+y)t j,(4.3)which requires numerical methods for the solution of y.•We may also use the Excel function XIRR to solve for y.Unlike IRR, XIRR allows the cashflows to occur at irregular time intervals.The specification of XIRR is as follows:Example4.4:A project requires an outlay of$2.35million in return for$0.8million after9months,$1million after15months and$1million after2years.What is the IRR of the project?Solution:Returns of the project occur at time(in years)0.75,1.25 and2.We solve for v numerically from the following equation using Excel Solver(see Exhibit4.2)235=80v0.75+100v1.25+100v2to obtain v=0.879,so thaty=10.879−1=13.77%,which is the effective annualized rate of return of the project.Alterna-tively,we may use the Excel function XIRR as shown in Exhibit4.3.2•A project with no subsequent investment apart from the initial cap-ital is called a simple project.•For simple projects,(4.1)has a unique solution with y>−1,so that IRR is well defined.Example4.5:A project requires an initial outlay of$8million,gen-erates returns of$50million1year later,and requires$50million to terminate at the end of year2.Solve for y in(4.1).Solution:We are required to solve8=50v−50v2,which has v=0.8and0.2as solutions.This implies y has multiple solu-tions of25%and400%.24.2One-Period Rate of Return•We consider methods of calculating the return of a fund over a1-period interval.The methodology adopted depends on the data available.•We start with the situation where the exact amounts of fund with-drawals and injections are known,as well as the time of their occur-rence.•Consider a1-year period with initial fund amount B0(equal to C0). Cashflow of amount C j occurs at time t j(in fraction of a year)for j=1,···,n,where0<t1<···<t n<1.•Note that C j are usually fund redemptions and new investments,and do not include investment incomes such as dividends and couponpayments.•Denoting the fund value before and after the transaction at time t j by B B j and B A j,respectively,we have B A j=B B j+C j for j=1,···,n.•The difference between B B j and B A j−1,i.e.,the balance before the transaction at time t j and after the transaction at time t j−1,is due to investment incomes,as well as capital gains and losses.•Let the fund balance at time1be B1,and define B B n+1=B1andB A0=B0(this notation will allow us to express the gross return as(4.4)below).Figure4.1illustrates the time diagram.•We now introduce two methods to calculate the1-year rate of re-turn:the time-weighted rate of return(TWRR)and the dollar-weighted rate of return(DWRR).•To compute the TWRR wefirst calculate the return over each subin-terval between the occurrences of transactions by comparing the fund balances just before the new transaction to the fund balance just af-ter the last transaction.•If we denote R j as the rate of return over the subinterval t j−1to t j,we have1+R j=B B jB j−1,for j=1,···,n+1.(4.4)•Then TWRR over the year,denoted by R T,isR T=⎡⎣n+1Y j=1(1+R j)⎤⎦−1.(4.5)•The TWRR requires data of the fund balance prior to each with-drawal or injection.In contrast,the DWRR does not require thisinformation.It only uses the information of the amounts of the withdrawals and injections,as well as their time of occurrence.•In principle,when cash of amount C j is injected(withdrawn)at time t j,there is a gain(loss)of capital of amount C j(1−t j)for the remaining period of the year.•Thus,the effective capital of the fund over the1-year period,denoted by B,is given byB=B0+nX j=1C j(1−t j).•Denoting C=P n j=1C j as the net injection of cash(withdrawal if negative)over the year and I as the interest income earned over the year,we have B1=B0+I+C,so thatI=B1−B0−C.(4.6)Hence the DWRR over the1-year period,denoted by R D,isR D=IB=B1−B0−CB0+P n j=1C j(1−t j).(4.7)Example4.6:On January1,a fund was valued at100k(1k=1,000). On May1,the fund increased in value to112k and30k of new principal was injected.On November1,the fund value dropped to125k,and42k was withdrawn.At the end of the year,the fund was worth100k.Calculate the DWRR and the TWRR.Solution:As C=30−42=−12,there is a net withdrawal.From (4.6),the interest income earned over the year isI=100−100−(−12)=12.Hence,from (4.7),the DWRR isR D =12100+23×30−16×42=10.62%.The fund balance just after the injection on May 1is 112+30=142k,and its value just after the withdrawal on November 1is 125−42=83k.From (4.4),the fund-value relatives over the three subperiods are1+R 1=112100=1.120,1+R 2=125142=0.880,1+R 3=10083=1.205.Hence,from (4.5),the TWRR isR T =1.120×0.880×1.205−1=18.76%.2•TWRR compounds the returns of the fund over subperiods after purging the effects of the timing and amount of cash injections and withdrawals.•As fund managers have no control over the timing of fund injection and withdrawal,the TWRR appropriately measures the performance of the fund manager.•DWRR is sensitive to the timing and amount of the cashflows.•If the purpose is to measure the performance of the fund,the DWRR is appropriate.•It allows superior market timing to impact the return of the fund.•For funds with frequent cash injections and withdrawals,the com-putation of the TWRR may not be feasible.The difficulty lies in the evaluation of the fund value B B j,which requires the fund to be constantly marked to market.•In some situations the exact timing of the cashflows may be difficult to identify.•In this situation,we may approximate(4.7)by assuming the cash flows to be evenly distributed throughout the1-year evaluation pe-riod.•Hence,we replace1−t j by its mean value of0.5so that P n j=1C j(1−t j)=0.5C,and(4.7)can be written asR D'IB0+0.5C=IB0+0.5(B1−B0−I))=I0.5(B1+B0−I).(4.8)Example4.7:For the data in Example4.6,calculate the approximate value of the DWRR using(4.8).Solution:With B0=B1=100,and I=12,the approximate R D isR D=120.5(100+100−12)=12.76%.24.3Rate of Return over Multiple Periods •We now consider the rate of return of a fund over a m-year period.•Wefirst consider the case where only annual data of returns are available.Suppose the annual rates of return of the fund have been computed as R1,···,R m.Note that−1≤R j<∞for all j.•The average return of the fund over the m-year period can be cal-culated as the mean of the sample values.We call this measure the arithmetic mean rate of return,denoted by R A,which is givenbyR A=1mmX j=1R j.(4.9)•An alternative is to use the geometric mean to calculate the average, called the geometric mean rate of return,denoted by R G,whichis given byR G=⎡⎣m Y j=1(1+R j)⎤⎦1m−1=[(1+R1)(1+R2)···(1+R m)]1m−1.(4.10)Example4.8:The annual rates of return of a bond fund over the last 5years are(in%)as follows:6.48.92.5−2.17.2Calculate the arithmetic mean rate of return and the geometric mean rate of return of the fund.Solution:The arithmetic mean rate of return isR A=(6.4+8.9+2.5−2.1+7.2)/5=22.9/5=4.58%,and the geometric mean rate of return isR G=(1.064×1.089×1.025×0.979×1.072)15−1=(1.246)15−1=4.50%.2 Example4.9:The annual rates of return of a stock fund over the last 8years are(in%)as follows:15.218.7−6.9−8.223.2−3.916.91.8 Calculate the arithmetic mean rate of return and the geometric mean rate of return of the fund.Solution:The arithmetic mean rate of return isR A=(15.2+18.7+···+1.8)/8=7.10%and the geometric mean rate of return isR G=(1.152×1.187×···×1.018)1−1=6.43%.2•Given any sample of data,the arithmetic mean is always larger than the geometric mean.•If the purpose is to measure the return of the fund over the holding period of m years,the geometric mean rate of return is the appro-priate measure.•The arithmetic mean rate of return describes the average perfor-mance of the fund for one year taken randomly from the sample period.•If there are more data about the history of the fund,alternative mea-sures of the performance of the fund can be used.The methodology of the time-weighted rate of return in Section4.2can be extended to beyond1period(year).•Suppose there are n subperiods,with returns denoted by R1,···, R n,over a period of m years.Then we can measure the m-year return by compounding the returns over each subperiod to form the TWRR using the formulaR T=⎡⎣n Y j=1(1+R j)⎤⎦1−1.(4.11)•We can also compute the return over a m-year period using the IRR. We extend the notations for cashflows in Section4.2to the m-year period.•Suppose cashflows of amount C j occur at time t j for j=1,···,n, where0<t1<···<t n<m.Let the fund value at time0and time m be B0and B1,respectively.We treat−B1as the last transaction, i.e.,fund withdrawal of amount B1.•The rate of return of the fund is calculated as the IRR which equates the discounted values of B0,C1,···,C n,and−B1to zero.•This is referred to as the DWRR over the m-year period.We denote it as R D,which solves the following equationB0+nX j=1C j(1+R D)t j−B1(1+R D)m=0.(4.12)•The example below concerns the returns of a bond fund.When a bond makes the periodic coupon payments,the bond values drop and the coupons are cash amounts to be withdrawn from the fund.Example4.10:A bond fund has an initial value of$20million.The fund records coupon payments in six-month periods.Coupons received from January1through June30are regarded as paid on April1.Likewise, coupons received from July1through December31are regarded as paid on October1.For the2-year period2008and2009,the fund values and coupon payments were recorded in Table4.1.Table4.1:Cashflows of fundTime Coupon received Fund value beforemm/dd/yy($millions)date($millions)01/01/0820.004/01/080.8022.010/01/08 1.0222.804/01/090.9721.910/01/090.8523.512/31/0925.0Calculate the TWRR and the DWRR of the fund.Solution:As the coupon payments are withdrawals from the fund(the portfolio of bonds),the fund drops in value after the coupon payments. For example,the bond value drops to22.0−0.80=21.2million on April 1,2008after the coupon payments.Thus,the TWRR is calculated asR T=∙2220×22.8022.0−0.8×21.9022.80−1.02×23.5021.90−0.97×25.023.50−0.85¸0.5−1=21.42%.To calculate the DWRR we solve R D from the following equation20=0.8(1+R D)+1.02(1+R D)+0.97(1+R D)+0.85(1+R D)+25(1+R D)=0.8v+1.02v3+0.97v5+0.85v7+25v8,where v=(1+R D)−0.25.We let(1+y)−1=v and use Excel to obtain y= 4.949%,so that the annual effective rate of return is R D=(1.04949)4−1= 21.31%.24.4Portfolio Return•We now consider the return of a portfolio of assets.•Suppose a portfolio consists of N assets denoted by A1,···,A N.Let the value of asset A j in the portfolio at time0be A0j,for j= 1,···,N.•We allow A0j to be negative for some j,so that asset A j is sold short in the portfolio.•The portfolio value at time0is B0=P N j=1A0j.Let the asset values at time1be A1j,so that the portfolio value is B1=P N j=1A1j.•Denote R P as the return of the portfolio in the period from time0to time1.Thus,R P=B1−B0B0=B1B0−1.•We definew j=A0j B0,which is the proportion of the value of asset A j in the initial portfolio, so thatNX j=1w j=1,and w j<0if asset j is short sold in the portfolio.•We also denoteR j=A1j−A0jA0j=A1jA0j−1,which is the rate of return of asset j.Thus,1+R P=B1 B0=1B0N X j=1A1j=NX j=1A0j B0×A1j A0j=NX j=1w j(1+R j),which impliesR P=NX j=1w j R j,(4.13)so that the return of the portfolio is the weighted average of the returns of the individual assets.•Eq(4.13)is an identity,and applies to realized returns as well as returns as random variables.If we take the expectations of(4.13),we obtainE(R P)=NX j=1w j E(R j),(4.14)so that the expected return of the portfolio is equal to the weighted average of the expected returns of the component assets.•The variance of the portfolio return is given byVar(R P)=NX j=1w2j Var(R j)+N X h=1N X j=1|{z}h=jw h w j Cov(R h,R j).(4.15)•For example,consider a portfolio consisting of two funds,a stock fund and a bond fund,with returns denoted by R S and R B,respec-tively.Likewise,we use w S and w B to denote their weights in the portfolio.•Then,we haveE(R P)=w S E(R S)+w B E(R B),(4.16)andVar(R P)=w2S Var(R S)+w2B Var(R B)+2w S w B Cov(R S,R B),(4.17)where w S+w B=1.Example4.11:A stock fund has an expected return of0.15and variance of0.0625.A bond fund has an expected return of0.05and variance of0.0016.The correlation coefficient between the two funds is −0.2.(a)What is the expected return and variance of the portfolio with80%in the stock fund and20%in the bond fund?(b)What is the expected return and variance of the portfolio with20%in the stock fund and80%in the bond fund?(c)How would you weight the two funds in your portfolio so that yourportfolio has the lowest possible variance?Solution:For(a),we use(4.16)and(4.17),with w S=0.8and w B= 0.2,to obtainE(R P)=(0.8)(0.15)+(0.2)(0.05)=13%Var(R P)=(0.8)2(0.0625)+(0.2)2(0.0016)+2(0.8)(0.2)(−0.2)q(0.0016)(0.0625) =0.03942.√0.03942=19.86%. Thus,the portfolio has a standard deviation ofFor(b),we do similar calculations,with w S=0.2and w B=0.8,toobtain E(R P)=7%,Var(R P)=0.002884and a standard deviation of √0.002884=5.37%.Hence,we observe that the portfolio with a higher weightage in stock has a higher expected return but also a higher standard deviation,i.e.,higher risk.For(c)we rewrite(4.17)asVar(R P)=w2S Var(R S)+(1−w S)2Var(R B)+2w S(1−w S)Cov(R S,R B). To minimize the variance,we differentiate Var(R P)with respect to w S to obtain2w S Var(R S)−2(1−w S)Var(R B)+2(1−2w S)Cov(R S,R B).Equating the above to zero,we solve for w S to obtainw S=Var(R B)−Cov(R S,R B)Var(R B)+Var(R S)−2Cov(R S,R B)=5.29%.The expected return of this portfolio is5.53%,its variance is0.001410, and its standard deviation is3.75%,which is lower than the standard deviation of the bond fund of4%.Hence,this portfolio dominates the bond fund,in the sense that it has a higher expected return and a lower standard deviation.Note that the fact that the above portfolio indeed minimizes the variance can be verified by examining the second-order condition.24.5Short sales•A short sale is the sale of a security that the seller does not own.It can be executed through a margin account with a brokeragefirm.•The seller borrows the security from the brokeragefirm to deliver to the buyer.•The sale is based on the belief that the security price will go down in the future so that the seller will be able to buy back the security at a lower price,thus keeping the difference in price as profit.•Proceeds from the short sale are kept in the margin account,and cannot be invested to earn income.•The seller is required to place cash or securities into the margin account.The initial percentage margin m is the percentage ofthe proceeds of the short sold security that the seller must place into the margin account.•If P0is the price of the security when it is sold short,the initial deposit D is P0m.The seller will earn interest from the deposit.•At any point in time,there is a maintenance margin m∗,which is the minimum percentage of the seller’s equity in relation to the current value of the security sold short.•If the current security price is P1,the equity E is P0+D−P1and E/P1must be larger than m∗.•If E/P1falls below m∗,the seller will get a margin call from the broker instructing him to top up his margin account.Example4.12:A person sold1,000shares of a stock short at$20. If the initial margin is50%,how much should he deposit in his margin account?If the maintenance margin is30%,how high can the price go up before there is a margin call?Solution:The initial deposit is1,000×20×0.5=$10,000.At price P1,the percent of equity is10,000+1,000(20−P1),1,000P1which must be more than0.3.Thus,the maximum P1is30=$23.08.1.32•To calculate the rate of return of a short sale strategy we note that the capital is the deposit D in the margin account.The return includes the interest earned in the deposit.The seller,however, pays the dividend to the buyer if there is any dividend payout.The net rate of return will thus take account of the interest earned and the dividend paid.Example4.13:A person sells a stock short at$30.The stock pays a dividend of$1at the end of the year,after which the man covers his short position by buying the stock back at$27.The initial margin is50%and interest rate is4%.What is his rate of return over the year? Solution:The capital investment per share is$15.The gross return after one year is(30−27)−1+15×0.04=$2.6.Hence,the return overthe1-year period is2.6=17.33%.15Note that in the above calculation we have assumed that there was no margin call throughout the year.24.6Crediting Interest:Investment-Y ear Method andPortfolio Method•A fund pools the investments of individual investors.The investors may invest new money into the fund at any time.•While the fund invests the aggregate of the investments,there is an issue of how to credit interest to the individual investors’accounts.•A simple method is to credit the average return of the fund to all investors.This is called the portfolio method.•The portfolio method may not be equitable when the individual investments are made at different times.•For example,at a time when returns to securities are going up,new investments are likely to achieve higher returns compared to old。
