常用软考算法大全内附实例
软考挣值计算题大全 项目管理软考

软考挣值计算题大全项目管理软考软考挣值计算题是项目管理软考中的一个重要部分,也是考生们备考时经常遇到的难题之一。
挣值管理是项目管理中的一种重要的成本和进度控制技术,通过对项目的成本和进度进行实时跟踪和评估,为项目管理决策提供重要依据。
掌握挣值管理方法,对于提高项目管理水平,提升个人能力都具有重要意义。
挣值管理中最常见的题目类型就是挣值计算题,通过计算实际成本、计划成本以及挣值三个指标之间的关系,来评估项目的成本和进度的执行情况。
下面将通过全面的评估,深入分析挣值计算题,为大家进行解析和总结。
一、挣值计算题的基本概念1.实际成本(Actual Cost,AC):项目执行阶段实际完成某项工作所花费的费用。
2.计划成本(Planned Value,PV):预定在某一时间段内,完工的预控成本。
3.挣值(Earned Value,EV):在某一时间点上实际完成的工作量所对应的成本。
这三个指标是挣值管理中的基本概念,也是求解挣值计算题时需要用到的核心数据。
二、挣值计算题的解题步骤1.要根据题目所给的数据,找出实际成本、计划成本和挣值的具体数值。
2.利用挣值计算公式进行计算,计算出实际成本、计划成本和挣值的具体数值。
其中,挣值计算公式为:实际成本(AC)= 实际费用计划成本(PV)= 计划费用挣值(EV)= 计划工作量× 完成工作百分比3.通过比较实际成本、计划成本和挣值的数值,分析项目的执行情况,评估项目的成本和进度表现。
三、挣值计算题的常见形式1.给定实际成本和计划成本,求解挣值。
2.给定实际成本和挣值,求解计划成本。
3.给定计划成本和挣值,求解实际成本。
4.根据实际成本、计划成本和挣值,分析项目的执行情况。
四、挣值计算题的实际应用挣值计算题不仅仅是理论知识,更是实际项目管理中的重要工具。
通过挣值计算,可以及时了解项目的成本和进度执行情况,及时调整项目管理策略,确保项目按时按质完成。
挣值计算也是评估项目经理个人能力的重要指标,能够帮助项目经理及时发现问题并采取措施,提升项目管理水平。
常用算法举例范文

常用算法举例范文在计算机科学中,算法是解决问题的一系列有序步骤,它能够帮助我们解决各种各样的问题。
以下是一些常用的算法及其举例:1.排序算法:-冒泡排序:通过比较相邻元素并交换位置来将最大的元素逐渐移动到数组的末尾。
-快速排序:选择一个基准元素,将数组分为两部分,左边的元素小于基准,右边的元素大于基准,然后递归地对两部分进行快速排序。
-归并排序:将数组划分为两个子数组,对每个子数组分别进行归并排序,然后将两个有序子数组合并成一个有序数组。
2.查找算法:-二分查找:对于有序数组,通过与中间元素进行比较,将查找范围缩小一半,直到找到目标元素或确定不存在。
-哈希查找:通过将关键字映射到数组的索引位置来进行查找,可以在常数时间内找到目标元素。
3.图算法:-广度优先(BFS):从起始节点开始,逐层遍历图中的节点,直到找到目标节点。
-深度优先(DFS):从起始节点开始,沿着一条路径一直向下,直到找到目标节点或无法继续为止。
4.动态规划算法:-背包问题:给定一组物品和一个容量限制,选择一些物品放入背包中,使得总价值最大。
-最长公共子序列(LCS):给定两个字符串,找到它们的最长公共子序列的长度。
5.数学算法:-欧几里得算法:计算两个整数的最大公约数。
-快速幂算法:计算一个数的幂运算,通过将指数进行二进制拆分来减少计算次数。
6.字符串处理算法:-KMP算法:通过利用已匹配字符的信息来避免不必要的回溯,实现高效的字符串匹配。
- Boyer-Moore算法:利用模式串中的信息来进行快速的字符串匹配。
7.图像处理算法:-图像平滑算法:通过对图像进行滤波处理,去除图像中的噪声,使其更加平滑。
-图像边缘检测算法:通过检测图像中的边缘信息,突出物体的轮廓。
8.机器学习算法:-K均值聚类算法:将数据集划分为K个簇,使得同一个簇内的数据点之间的距离最小化。
-支持向量机(SVM):将数据集映射到高维空间,并通过找到最优的超平面来实现分类。
软考中项计算题公式

软考中项计算题公式软考中的计算题公式软考是指软件职业资格考试,是由中国电子学会主办的一项全国性的技术职业资格认证考试。
其中,项计算题是软考中的一种题型,要求考生掌握各个领域的计算公式。
本文将介绍软考中项计算题常见的公式。
1. 网络技术计算公式1.1 带宽计算公式带宽(kbps) = 8 * 带宽(bps)其中,带宽为bit/s,可通过将其转换为kbps来方便计算。
1.2 时延计算公式时延(s) = 数据长度 / 带宽其中,数据长度以bit为单位,时延以秒为单位。
2. 数据库计算公式2.1 总记录数计算公式总记录数 = (平均记录长度 * 块长度) / (块内记录长度)其中,平均记录长度为每条记录的平均长度,块长度为块的大小,块内记录长度为每个记录在块中占据的空间。
节点数 = 总记录数 / 每个节点的最大键数其中,总记录数为数据库中的总记录数,每个节点的最大键数为树节点中能够包含的最大键的数量。
3. 软件工程计算公式3.1 代码行数计算公式代码行数 = 注释行数 + 空白行数 + 有效代码行数其中,注释行数为代码中的注释行数,空白行数为代码中的空行数,有效代码行数为代码中的实际执行代码行数。
3.2 平均构造率计算公式平均构造率 = 实际构造率 / 理想构造率其中,实际构造率为实际构造的代码行数占全部代码行数的比例,理想构造率为按照预估时间应该构造的代码行数占全部代码行数的比例。
4. 操作系统计算公式4.1 磁盘存储容量计算公式存储容量 = 磁道数 * 每条磁道的扇区数 * 每个扇区的字节数其中,磁道数为磁盘上的磁道数量,每条磁道的扇区数为每个磁道上的扇区数量,每个扇区的字节数为每个扇区上可存储的字节数。
页面引用串长度 = 总访问命令数 * 每个命令访问的页面数其中,总访问命令数为对页面的总访问命令数量,每个命令访问的页面数为每个访问命令需要访问的页面数量。
以上是软考中项计算题常见的公式,掌握这些公式能够帮助考生在考试中更好地解决计算题。
软考中项、高项常见计算题详解

选择题:一、决策树分析(EMV)2011年下半年例题1:某公司希望举办一个展销会以扩大市场,选择北京、天津、上海、深圳作为候选会址。
获利情况除了会址关系外,还与天气有关。
天气可分为晴、多云、多雨三种。
通过天气预报,估计三种天气情况可能发生的概率为0.25、0.50、0.25,其收益(单位:人民币万元)情况见下表。
使用决策树进行决策的结果为(61)。
(61)A.北京B.天津C.上海D.深圳答案:B解析:北京的期望货币值为 4.5×0.25+4.4×0.5+1×0.25=3.575 天津 5×0.25+4×0.5+1.6×0.25=3.65上海 6×0.25+3×0.5+1.3×0.25=3.325深圳 5.5×0.25+3.9×0.5+0.9×0.25=3.55例题2 (2008上)某电子商务公司要从A地向B地的用户发送一批价值90000元的货物。
从A地到B地有水、陆两条路线。
走陆路时比较安全,其运输成本为10000元;走水路时一般情况下的运输成本只要7000元,不过一旦遇到暴风雨天气,则会造成相当于这批货物总价值的10%的损失。
根据历年情况,这期间出现暴风雨天气的概率为1/4,那么该电子商务公司_(70)。
A.应选择走水路B.应选择走陆路C.难以选择路线D.可以随机选择路线答案: A。
陆路10000水路7000×3/4+(7000+90000×10%)×1/4=9250例题3二、盈亏平衡点盈亏平衡点(Break Even Point,简称BEP)又称零利润点、保本点、盈亏临界点、损益分歧点、收益转折点。
通常是指全部销售收入等于全部成本时(销售收入线与总成本线的交点)的产量。
以盈亏平衡点的界限,当销售收入高于盈亏平衡点时企业盈利,反之,企业就亏损。
盈亏平衡点可以用销售量来表示,即亏平衡点的销售量;也可以用销售额来表示,即盈亏平衡点的销售额。
软考中级软件设计师算法题

软考中级软件设计师算法题软考中级软件设计师考试中,算法题是一个重要的考点,也是考生容易失分的地方。
本文将介绍一些常见的软考中级软件设计师算法题,并给出解题思路和算法实现,以帮助考生更好地备考。
一、选择排序算法题目描述:给定一个包含n个元素的数组,对其进行选择排序,找出最小元素的下标,并输出其下标。
解题思路:选择排序的基本思想是在每一趟遍历过程中,找出最小元素,将其放到已排序序列的末尾。
具体步骤如下:1.从数组的第一个元素开始,依次遍历数组;2.记录当前遍历到的最小元素的下标min_index;3.将当前遍历到的元素与min_index对应的元素进行交换;4.将min_index向前移动一位,继续遍历下一个元素;5.重复步骤2-4,直到遍历完整个数组。
算法实现:```c++intmin_index(intarr[],intn){intmin_index=0;for(inti=1;i<n;i++){if(arr[i]<arr[min_index]){min_index=i;}}returnmin_index;```二、最长递增子序列问题题目描述:给定一个长度为n的数组,求其最长递增子序列的长度。
解题思路:可以使用动态规划来解决该问题。
定义一个长度为n+1的数组dp,其中dp[i]表示以arr[i]结尾的最长递增子序列的长度。
初始时,所有元素都为1,除了最后一个元素外。
然后从左到右遍历数组,对于每个元素arr[j],如果它比前一个元素arr[i]大,则将dp[j]更新为max(dp[j],dp[i]+1)。
最终,dp[n]就是最长递增子序列的长度。
算法实现:```c++intlongest_increasing_subsequence(intarr[],intn){intdp[n+1];for(inti=1;i<=n;i++){dp[i]=1;for(intj=0;j<i;j++){if(arr[i]>arr[j]){dp[i]=max(dp[i],dp[j]+1);}}}returndp[n];```三、最长公共子序列问题题目描述:给定两个长度为n和m的序列,求它们的最长公共子序列的长度。
软考计算题进度类考点公式汇总

软考计算题进度类考点公式汇总一、PERT三点估算1、β分布期望持续时间/成本=(最悲观+最可能*4+最乐观)/62、三角分布期望持续时间/成本=(最悲观+最可能+ 最乐观)/33、标准差= (最悲观时间-最乐观时间)/64、正负西格玛1(68%)、2(95%)、3(99%)二、单代号网络图(会画图)1、画图正推法:最早,取最大逆推法:最迟,取最小2、找关键路径从起点到终点所有路径活动之和最大的路径;可能有多条关键路径;3、计算总工期关键路径上所有活动持续时间之和;4、总时差画图:最迟最早不画图:关键路径长度-经过这个活动最大非关键路径长度5、自由时差画图:min{紧后工作最早开始时间} -本工作最早完成时间不画图:紧后工作是关键工作:自由时差= 总时差紧后工作不是关键工作或者既有关键工作也有非关键工作:自由时差= 06、工期压缩压缩关键路径上的工作;压缩可以压缩的活动;压缩花费代价最小的活动;注意关键路径变化的问题;注意是否有间接费用的节约;三、双代号网络图(会画图)1、关键路径从起点到终点所有路径活动之和最大的路径2、总工期关键路径上所有活动持续时间之和3、总时差关键路径长度-经过这个活动最大非关键路径长度4、自由时差用标号法结合网络图去求解;四、双代号时标网络图(会画图)1、画图会看图、画图;是资源平衡/平滑类计算题解题神器,需要会算最少几个人的问题;2、找关键路径持续时间最长的路径【虽有波形线但是时间最长也是关键路径】3、计算总工期关键路径上所有活动持续时间之和4、总时差以该工作为起点,到终点,可能有很多条路径,把每条路径的波浪线的长度的和求出来,和的最小值就是自由时差;该工作完成节点到项目全部完成时的节点之间波形线投影值之和的最小值+ 该工作的自由时差;5、自由时差该工作箭线上波形线投影的长度6、工期压缩同单代号网络图五、横道图1、关键路径从后往前推,能够收尾相连的2、总工期关键路径上所有活动持续时间之和3、总时差和自由时差图上看不出来,可结合单双代号网络图进行计算六、其他类1、EMV决策树计算EMV = 盈利百分比*影响值-风险百分比*影响值EMV = 各活动Σ净利润(收入-成本)×%2、沟通渠道计算n(n-1)/2,n代表干系人数量3、自制/外购分析对比成本大小、技术、涉密、长期使用等方面对比;自制的成本算出来,外购的成本算出来,比较大小就好;4、加权系统n项分值之和除以n,乘以权重比例;5、系统可用性可用时间/总时间平均无故障时间/(平均无故障时间+平均维修时间)*100%6、运筹学计算具体看我发的视频资料;7、其他净现值投资回收期(静态) = (T-1)+ 第(T-1)年累计现金流量绝对值/第T年现金流量投资回收期(动态) = (T-1)+ 第(T-1)年累计折现值/第T年折现值ROI投资收益率分析= (总的折现收益-总的折现成本)/折现成本ROI投资收益率分析(第4版的公式) = 项目达产后正常年份的利润/投资总额。
软考中级系统集计算题公式

软考中级系统集计算题公式
在软考中级系统集计算题中,常见的公式包括:
1. 机器周期(TP)= 主频(MHz)/ 时钟周期(ns)
其中,主频表示CPU的工作频率,时钟周期表示CPU完成一个基本操作所需的时间。
2. CPU执行时间(Texec)= TP × CPI × IC
其中,TP表示机器周期,CPI表示每指令周期数,IC表示指令数。
3. 系统吞吐率(Throughput)= 1 / Tavg
其中,Tavg表示平均响应时间。
4. 计算机存储器存取时间(Tmem)= Tcache × Ha + Tmain ×(1-Ha)
其中,Tcache表示高速缓存存取时间,Tmain表示主存存取时间,Ha表示高速缓存的命中率。
5. 磁盘平均访问时间(Tdisk)= (1-P) × Tseek + P ×Trotation + Ttransfer
其中,P表示盘块命中率,Tseek表示寻道时间,Trotation表示旋转延迟时间,Ttransfer表示传输时间。
6. 系统响应时间(Tresp)= Tcpu + Tmem + Tdisk + Tio
其中,Tcpu表示CPU执行时间,Tmem表示存储器存取时间,Tdisk 表示磁盘访问时间,Tio表示输入输出设备的响应时间。
以上是一些常见的公式,根据具体的题目要求,还可能会需要其
他的计算公式。
常见算法及其运算实例分析

常见算法及其运算实例分析算法是计算机科学中最重要的一部分。
算法既是计算机科学的基础,又是计算机编程的核心。
了解算法,可以让我们更深入地理解计算机的运行原理,以及如何利用计算机处理各种问题。
本文将为大家介绍几个常见的算法及其运算实例分析。
一、递归算法递归算法是一种函数调用自身的算法。
递归算法具有简单、直观、可理解等优点。
但同时也存在着栈溢出、时间复杂度高等问题。
递归算法通常包含有一些关键参数,如递归的次数和递归深度等,这些参数的变化对于程序的运行和结果都有着重要的影响。
实例:斐波那契数列我们可以通过递归算法来实现斐波那契数列。
斐波那契数列的定义如下:F(0)=0,F(1)=1,F(n)=F(n-1)+F(n-2)(n>=2)。
通过递归算法,可以很容易地实现斐波那契数列。
我们只需要以递归方式调用F函数即可,代码如下:```def F(n):if n==0:return 0elif n==1:return 1else:return F(n-1)+F(n-2)```二、分治算法分治算法是将问题分解成若干个子问题,然后递归地分别解决每个子问题,最终合并成一个整体的算法。
分治算法通常解决的问题都具备“可分解性”和“合并性”的特征。
实例:二分查找二分查找可以用分治算法来实现。
二分查找的思想是将数组分成两个区间,分别判断目标值是否在每个区间中。
如果目标值存在于某个区间中,则继续在该区间中进行查找;否则在另一个区间中进行查找。
通过分治算法,我们可以将二分查找优化成O(log n)的时间复杂度。
代码如下:```def binary_search(arr, left, right, target):if left > right:return -1mid = (left + right) // 2if arr[mid] == target:return midelif arr[mid] < target:return binary_search(arr, mid+1, right, target)else:return binary_search(arr, left, mid-1, target)```三、贪心算法贪心算法可以理解为通过每步选择中的局部最优解,从而达到全局最优的解决方案。
软考网络工程师常用计算公式汇总

软考网络工程师常用计算公式汇总1.网络带宽计算:
带宽=网络吞吐量/传输时间
2.网络传输时间计算:
传输时间=数据量/带宽
3.网络时延计算:
总时延=传播时延+传输时延+排队时延
其中,传播时延=传输距离/传播速度
传输时延=数据长度/传输速率
排队时延=排队长度/排队速率
4.网络利用率计算:
利用率=传输时延/(传输时延+传播时延)
5.IP地址计算:
IP地址=网络号+主机号
6.网络号计算:
网络号=IP地址&子网掩码
7.子网掩码计算:
子网掩码=网络号位数为1,主机号位数为0的二进制数
8.网络中设备数量计算:
主机数=2^(主机位数)-2
9.平均排队长度计算:
平均排队长度=平均到达率*平均服务时间
10.斐波那契数列计算:
F(n)=F(n-1)+F(n-2)
以上是软考网络工程师常用的计算公式的汇总。
这些公式涉及到网络带宽、传输时间、网络时延、网络利用率、IP地址、子网掩码、设备数量、排队长度、斐波那契数列等方面的计算。
掌握这些公式可以帮助你在软考网络工程师考试和实际工作中更好地应对各种计算问题。
软考计算题公式

软考计算题公式
软考计算题要用到的公式很多,以下列举一些常用的:
1. 等比数列通项公式:An=A1*q^(n-1),其中A1为首项,q为公比,An为第n 项。
2. 等差数列通项公式:An=A1+(n-1)*d,其中A1为首项,d为公差,An为第n 项。
3. 算术平均数公式:平均数=(数列中所有数的和)/总数
4. 平行四边形面积公式:S=a*h,其中a为底边长,h为高。
5. 三角形面积公式:S=(底边长×高)/2。
6. 直角三角形勾股定理:c^2=a^2+b^2,其中c为斜边长,a和b为直角边长。
7. 一元二次方程求根公式:x=[-b±√(b^2-4ac)]/(2a),其中a、b、c为方程
ax^2+bx+c=0的系数。
8. 正弦定理:a/sinA=b/sinB=c/sinC,其中a、b、c为三角形的边长,A、B、C 为对应的角度。
9. 余弦定理:c^2=a^2+b^2-2abcosC,其中a、b、c为三角形的边长,C为夹角的余弦值。
10. 数据的标准差公式:s=√(∑(x-x)²/n),其中x为平均数,n为样本数。
软考中项的计算题公式 软考项目管理

软考中项的计算题公式软考项目管理
软考项目管理中的计算题主要涉及以下几个公式:
1. 离散概率分布的期望值(Expected Value):
期望值(E)= P1 * X1 + P2 * X2 + ... + Pn * Xn
其中,P1、P2...Pn为概率,X1、X2...Xn为对应的随机变量。
2. 项目管理中的成本管理公式:
成本偏差(Cost Variance,CV)= EV(挣值)- AC(实际成本)
成本绩效指数(Cost Performance Index,CPI)= EV(挣值)/ AC(实际成本)
3. 项目管理中的进度管理公式:
进度偏差(Schedule Variance,SV)= EV(挣值)- PV(计划价值)
进度绩效指数(Schedule Performance Index,SPI)= EV(挣值)/ PV(计划价值)
4. 项目管理中的风险管理公式:
风险影响(Risk Impact)= 风险概率 * 风险事件影响
风险影响概率值(Risk Impact Probability Value)= 风险影响 * 风险概率
5. 项目管理中的质量管理公式:
质量计划可行性(Quality Plan Feasibility)= 可行的质量计划数 / 所有质量计划数
质量成本(Cost of Quality,COQ)= 预防成本 + 检查成本 + 再制造成本
以上是软考项目管理中常见的一些计算题公式,根据具体的题目要求,可能会涉及到其他公式或计算方法。
建议多练习相关的计算题,熟悉公式的应用,提高解题能力。
软考计算复习资料
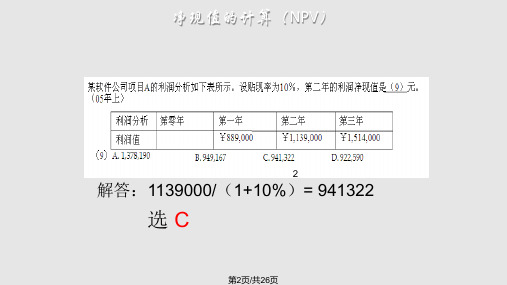
列式:
(3-1)+
|(-925.93+428.67+396.92) | = 2.27
367.51
0 -925.93
1
2
3
2.27
第4页/共26页
选C
PERT(计划评审技术)计算
μ
第5页/共26页
PERT(计划评审技术)计算
第6页/共26页
PERT(计划评审技术)计算
例1:公司的某项目即将开始,项目经理估计该项目10天即可完 成,如果出现问题耽搁了也不会超过20天完成,最快6天即可完 成。根据项目历时估计中的三点估算法,你认为该项目的历时为 (37)该项目历时的估算标准差为(38) 。 (37)A.10天 B.11天 C.12天 D.13天 (38)A.2.1天 B.2.2天 C.2.3天 D.2.4天
第23页/共26页
决策树分析
80x65%+(-30)x35%
第24页/共26页
70x65%+10x35%
谢谢!再见! 祝大家取得好成绩!
第25页/共26页
感谢您的观看!
第26页/共26页
—CV、SV、EAC、ETC —CPI、SPI
公式:CV=EV‐AC, SV=EV‐PV CPI=EV/AC(支出), SPI=EV/PV(进度)
型偏差
预测技术: ETC=(BAC‐EV) 当前偏差被看做是非典型的 ETC=(BAC‐EV)/CPI 当前偏差被看做是代表未来的典型偏差 EAC=AC+ETC ‐‐‐‐衍化为下面两个公式 EAC=AC+BAC‐EV 当前偏差被看做是非典型的 EAC=AC+(BAC‐EV)/CPI 当前偏差被看做是代表未来的典
软件设计师常考计算公式总结
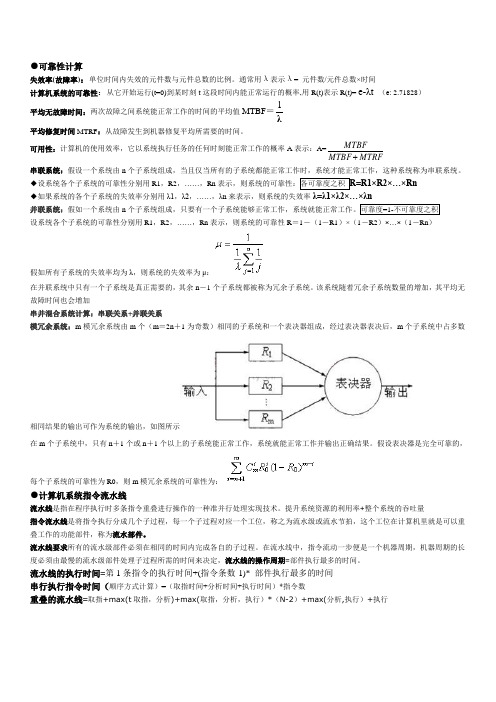
●可靠性计算失效率(故障率):单位时间内失效的元件数与元件总数的比例。
通常用λ表示λ= 元件数/元件总数×时间计算机系统的可靠性:从它开始运行(t=0)到某时刻t 这段时间内能正常运行的概率,用R(t)表示R(t)= e-λt (e: 2.71828) 平均无故障时间:两次故障之间系统能正常工作的时间的平均值MTBF =λ1 平均修复时间MTRF :从故障发生到机器修复平均所需要的时间。
可用性:计算机的使用效率,它以系统执行任务的任何时刻能正常工作的概率A 表示:A=MTRF MTBF MTBF串联系统:假设一个系统由n 个子系统组成,当且仅当所有的子系统都能正常工作时,系统才能正常工作,这种系统称为串联系统。
◆设系统各个子系统的可靠性分别用R1,R2,……,Rn◆如果系统的各个子系统的失效率分别用λ1,λ2,……,λn 来表示,则系统的失效率λ=λ1×λ2×…×λn并联系统:假如一个系统由n 设系统各个子系统的可靠性分别用R1,R2,……,Rn 表示,则系统的可靠性R =1-(1-R1)×(1-R2)×…×(1-Rn ) 假如所有子系统的失效率均为λ,则系统的失效率为μ:在并联系统中只有一个子系统是真正需要的,其余n -1个子系统都被称为冗余子系统。
该系统随着冗余子系统数量的增加,其平均无故障时间也会增加串并混合系统计算:串联关系+并联关系模冗余系统:m 模冗余系统由m 个(m =2n +1为奇数)相同的子系统和一个表决器组成,经过表决器表决后,m 个子系统中占多数相同结果的输出可作为系统的输出,如图所示 在m 个子系统中,只有n +1个或n +1个以上的子系统能正常工作,系统就能正常工作并输出正确结果。
假设表决器是完全可靠的,每个子系统的可靠性为R0,则m 模冗余系统的可靠性为:●计算机系统指令流水线流水线是指在程序执行时多条指令重叠进行操作的一种准并行处理实现技术。
软考高项计算题公式

软考高项计算题公式
软考高项计算题的公式主要包括以下几个方面:
1. 折扣公式:常用于计算优惠后的价格、打折后的金额等。
公式为:折扣 = 折扣额 / 原价。
2. 面积和体积计算公式:用于计算常见图形的面积和体积。
例如:矩形的面积公式为:面积 = 长 * 宽;圆的面积公式为:
面积= π * 半径的平方。
3. 利息、利润和损益计算公式:用于计算贷款、投资等的利息,以及计算利润和损益。
例如:利息公式为:利息 = 本金 * 年
利率 * 时间;利润公式为:利润 = 销售额 - 成本;损益公式为:损益 = 收入 - 支出。
4. 阶乘和组合公式:用于计算阶乘和组合问题。
例如:阶乘公式为:n! = n * (n-1) * (n-2) * ... * 1;组合公式为:C(n, m) = n! / (m! * (n-m)!)。
5. 等比数列和等差数列的求和公式:用于计算等比数列和等差数列的和。
例如:等差数列和公式为:Sn = (a1 + an) * n / 2;
等比数列和公式为:Sn = a1 * (1 - q^n) / (1 - q)。
以上只是软考高项计算题常用的公式之一,具体的公式还会根据题目要求的不同而有所变化。
考生在备考过程中应该熟练掌握常用的计算公式,并灵活运用到解题过程中。
软考网工常用计算公式

软考网工常用计算公式下面是软考网工常用计算公式的一些例子:1.TCP/IP数据报长度计算公式:
IP数据报长度=首部长度+数据部分长度
2.数据传输速率计算公式:
数据传输速率=数据传输量/传输时间
3.网络传输延迟计算公式:
网络传输延迟=传输距离/传输速度
4.最大网络传输速度计算公式(理论最大速度):最大网络传输速度=信道带宽/信噪比
5.TCP/IP传输时间计算公式:
传输时间=数据量/带宽
6.电路延迟计算公式:
电路延迟=电路长度/电信速度
7.确定控制帧的额外开销计算公式:
额外开销=控制帧长度-原始数据帧长度
8.平均传输时间计算公式:
平均传输时间=平均传输延迟+平均等待时间9.密钥的比特长度计算公式:
密钥比特长度=密钥的信息比特长度+冗余比特长度
10.程序运行时间计算公式:
程序运行时间=CPU执行时间+IO交互时间
11.网络吞吐量计算公式:
网络吞吐量=数据传输量/(传输时间+等待时间)
12.碰撞域的计算公式:
碰撞域=(交换机的个数+集线器的个数)*交换机的端口数量
13.CRC校验位计算公式:
CRC校验位=余数/生成多项式
14.电源功率计算公式:
电源功率=电源电压*电源电流
15.总功率损耗计算公式:
总功率损耗=线路阻抗*电流的平方*线路长度
这些公式可以帮助工程师在网络工程、传输技术、计算机网络和通信等领域进行计算和分析,从而更好地设计和优化网络。
软考高项计算公式汇总

软考高项计算公式汇总软考高级考试是我国计算机软件职业资格证书的一种,是考察候选人在计算机软件领域专业知识和实践能力的能力证明。
在软考高级考试中,高级计算机应用能力是其中的一个重要考核项。
高级计算机应用能力要求候选人具备计算机软件开发、测试、运维等领域的专业知识,并能够灵活运用各种计算机软件工具和技术解决实际问题。
在软考高级计算机应用能力考试中,计算公式的运用是其中一个重要的考点。
候选人需要熟悉并掌握常见的计算公式,能够准确地运用这些公式解决实际问题。
下面将对常见的高级计算机应用能力考试中的计算公式进行汇总和总结。
一、数据库相关公式1. 数据库表的存储空间计算公式数据库表的存储空间计算公式为:存储空间 = 行大小× 行数其中,行大小可以通过各列的数据类型和长度来确定,行数可以通过查询得到。
2. 数据库索引的存储空间计算公式数据库索引的存储空间计算公式为:存储空间= 索引键长度× 索引记录数其中,索引键长度可以通过索引字段的数据类型和长度来确定,索引记录数可以通过查询得到。
二、网络相关公式1. 带宽利用率计算公式带宽利用率计算公式为:带宽利用率 = 实际传输速率 / 理论传输速率× 100%其中,实际传输速率可以通过测量得到,理论传输速率可以通过带宽和信号传输速率来计算。
2. 网络延迟计算公式网络延迟计算公式为:延迟 = 传输时延 + 处理时延 + 排队时延 + 传播时延其中,传输时延是指数据从发送端到接收端所需的时间,处理时延是指数据在路由器或交换机上进行处理所需的时间,排队时延是指数据在网络中等待传输所需的时间,传播时延是指数据在传输介质中传播所需的时间。
三、软件工程相关公式1. 代码行数估算公式代码行数估算公式为:代码行数 = 逻辑行数× 系数其中,逻辑行数是指程序中的逻辑代码行数,系数是根据具体项目的特点和开发人员的经验确定的。
2. 软件缺陷密度计算公式软件缺陷密度计算公式为:缺陷密度 = 缺陷数 / 代码行数× 100%其中,缺陷数可以通过测试和代码审查等方法得到,代码行数可以通过统计代码行数得到。
软考 已知分布密度函数,求随机数算法

软考已知分布密度函数,求随机数算法在软件工程中,有时需要生成一些随机数,这些随机数可以用于模拟测试或者其他应用。
如果已知随机数的分布密度函数,可以使用一些算法生成符合该分布的随机数。
以下是几种常见的随机数生成算法。
1. 均匀分布如果随机数的分布符合均匀分布,可以使用线性同余法生成随机数。
该算法需要一个起始值和一个系数,通过不断迭代生成随机数。
代码如下:```int random(int seed, int a, int b) {seed = (a * seed + b) % m;return seed;}```其中,seed是起始值,a和b是系数,m是一个很大的质数。
生成的随机数在[a,b]区间内均匀分布。
2. 正态分布如果随机数的分布符合正态分布,可以使用Box-Muller变换生成随机数。
该算法需要生成两个均匀分布的随机数,然后通过一些计算得到正态分布的随机数。
代码如下:```double random_normal() {double u1 = (double) rand() / RAND_MAX;double u2 = (double) rand() / RAND_MAX;double z = sqrt(-2 * log(u1)) * cos(2 * PI * u2);return z;}```其中,rand()函数生成均匀分布的随机数,PI是圆周率。
生成的随机数符合标准正态分布。
3. 指数分布如果随机数的分布符合指数分布,可以使用逆变换法生成随机数。
该算法需要一个均匀分布的随机数,然后通过一些计算得到指数分布的随机数。
代码如下:```double random_exponential(double lambda) {double u = (double) rand() / RAND_MAX;double x = -1.0 / lambda * log(1 - u);return x;}```其中,lambda是指数分布的参数。
全国软考-一个决策树算法案例分析

建中型楼。
14
§4.5 效用与风险分析(Utility and Risk Analysis)
以前所述的决策分析方法是按照最好的货币期望值选择方案,但在决策 分析中除了要考虑方案的货币益损因素以外,还要考虑风险程度,包括决策 人对待风险的态度这一主观偏好因素。因而,往往单从货币益损期望值选择 的方案,不一定是最佳方案。本节将介绍决策分析中的期望效用。 所谓效用是一种特定结果的总价值的相对尺度,它反映决策者面对诸如 利润、损失和风险等因素集合的态度。
2
为了进行决策分析,必须做好以下两项工作:
(1)市场调研,综合楼被市场接受的程度如何?亦即市场的需求如何? 对此问题,公司管理者通过调研认为,只有两种市场接受状态,称为决策 者无法控制的自然
状态:
S1——高的市场接受程度,对楼房有显著需求; S2——低的市场接受程度,对楼房需求有限。 (2)要根据工程设计与造价核算以及销售价格计算出不同方案,不同自然状 态时,楼房的盈 亏(益损)表。对该问题,经计算得到如下益损矩阵Vij:
各方案dj的益损期望值为:
EV (d i ) P( S j ) * Vij
j 1 n
益损期望值为最大者对应的方案,可选为最佳方案。 对本问题而言,若已知:P(S1)=0.8,P(S2)=0.2,则 有: EV(d1)=0.8×800+0.2×700=780万 EV(d2)=0.8×1400+0.2×500=1220万 EV(d3)=0.8×2000+0.2×(-900)=1420万
P( S i | I K ) P( S i ) P( I K | S i )
P( S ) P( I
i 1 i
n
K
| Si )
软件设计师常考算法知识点

软件设计师常考算法知识点在软件设计师岗位的面试过程中,算法知识是常常考察的一个重要方面。
算法作为计算机科学的基础,是软件设计师必不可少的技能之一。
下面将介绍一些软件设计师常考的算法知识点。
一、排序算法1. 冒泡排序冒泡排序是一种简单的交换排序算法,通过重复遍历待排序序列,比较相邻元素并交换位置来实现排序。
具体步骤如下:(1)比较相邻的两个元素,如果前者大于后者,则交换位置;(2)重复步骤(1),直到遍历完整个序列,此时最大的数会被移到最后一位;(3)重复步骤(1)和(2),直到所有元素都排序完成。
2. 快速排序快速排序是一种常见的基于“分治”思想的排序算法,通过递归地将待排序序列划分为较小和较大的两个子序列,再分别对子序列进行排序。
具体步骤如下:(1)选择一个基准元素,通常选择第一个元素;(2)将比基准元素小的元素移到基准元素的左边,比基准元素大的元素移到右边;(3)对左右子序列分别重复步骤(1)和(2),直到所有元素排序完成。
二、查找算法1. 二分查找二分查找是一种高效的查找算法,要求待查找的序列必须是有序的。
具体步骤如下:(1)选择序列的中间元素;(2)如果中间元素等于目标值,则查找成功;(3)如果中间元素大于目标值,则在左侧子序列中继续进行二分查找;(4)如果中间元素小于目标值,则在右侧子序列中继续进行二分查找;(5)重复步骤(1)至(4),直到找到目标值或遍历完整个序列。
2. 哈希查找哈希查找是通过哈希函数将要查找的元素映射到一个位置,进而直接访问该位置的元素来实现查找。
具体步骤如下:(1)构建一个哈希表,将元素与对应的位置进行关联;(2)根据哈希函数将要查找的元素映射到哈希表中的某个位置;(3)如果该位置存在元素,则查找成功;(4)如果该位置不存在元素,则查找失败。
三、图算法1. 广度优先搜索广度优先搜索是一种用于图的遍历的算法,通过逐层扩展访问顶点,直到遍历完所有与起始顶点连通的顶点。
软考高级《信息系统项目管理师》计算公式汇总(考前必背)

软考高级《信息系统项目管理师》计算公式汇总一、进度计算关键路径:项目中时间最长的活动顺序。
总浮动时间:本活动的最迟完成时间-本活动最早完成时间(注:关键路径总浮动时间为零)。
自由浮动时间:紧后活动最早开始时间的最小值-本活动的最早完成时间(当紧后活动只有一个的时候自由浮动时间为0,当有2 个紧后活动时取最小值)。
三点估算法:(乐观时间+4 最可能时间+悲观时间)/6。
二、成本计算(1)偏差指标进度偏差SV=EV-PVSV>0:进度提前SV=0:进度符合预期SV<0:进度落后成本偏差CV=EV-ACCV>0:成本节约CV=0:成本符合预期CV<0:成本超支(2)绩效指标进度绩效指数SPI=EV/PVSPI>0:进度提前SPI=0:进度符合预期SPI<0:进度落后成本绩效指数CPI=EV/ACCPI>0:成本节约CPI=0:成本符合预期CPI<0:成本超支(3)完工尚需估算典型ETC=(BAC-EV)/CPI非典型ETC=BAC-EV(4)完工估算典型:EAC=AC+(BAC-EV)/CPI非典型:EAC=AC+(BAC-EV)进度成本同时作用EAC=(BAC-EV)/(CPI*SPI)V AC(完工偏差)=BAC-EAC(5)完工尚需绩效指数TCPI=(BAC-EV)/(BAC-AC)TCPI=(BAC-EV)/(EAC-AC)(BAC 不可行,分母变EAC)三、单选计算净现值分析:净现值分析是指把所有预期的未来现金流入与流出都折算成现值,以计算一个项目预期的净货币收益与损失。
净现值越大越好!(1)确定项目现金流现金流(利润)=现金流入-现金流出=收益-成本(2)计算净现值:t:现金流持续时间A:每年的现金流量r:折现率投资收益率分析:投资收益率是将净收入除以投资额的所得值。
计算多年份项目的投资收益率时,对收益和投资进行折现。
投资收益率ROI=(总的折现收益-总的折现成本)/折现成本=折现利润/折现成本ROI越大越好。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
河南大学软件学院 计算机应用 单付尚 2009-3-9常用算法大全【程序1-1】欧几里德递归算法 (1)【程序1-2】欧几里德迭代算法 (1)【程序1-3】 Gcd的连续整数检测算法 (1)【程序1-4】求F n (1)【程序1-5】逆序输出正整数的各位数 (2)【程序1-6】汉诺塔问题 (2)【程序1-7】排列产生算法 (2)【程序2-1】求数组元素累加之和的迭代程序 (3)【程序2-2】求数组元素累加之和的递归程序 (3)【程序2-3】矩阵乘法 (3)【程序3-1】伸展树类 (4)【程序3-2】旋转函数 (4)【程序3-3】伸展树插入 (5)【程序3-4】跳表结点类 (6)【程序3-5】跳表类 (7)【程序3-6】构造函数 (7)【程序3-7】级数分配 (8)【程序3-8】插入运算 (8)【程序4-1】 ENode类 (9)【程序4-2】图的广度优先遍历 (10)【程序4-3】图的深度优先搜索 (10)【程序4-4】计算d和Low (11)【程序4-5】求双连通分量 (11)【程序4-6】与或树及其结点类型 (12)【程序4-7】判断与或树是否可解算法 (13)【程序4-8】广度优先生成解树的算法框架 (13)【程序5-1】分治法 (14)【程序5-2】一分为二的分治法 (14)【程序5-3】可排序表类 (15)【程序5-4】求最大最小元 (15)【程序5-5】分治法求最大、最小元 (16)【程序5-6】二分搜索算法框架 (16)【程序5-7】对半搜索递归算法 (17)【程序5-8】对半搜索的迭代算法 (17)【程序5-9】 Merge函数 (17)【程序5-10】两路合并排序 (18)【程序5-11】分划函数 (18)【程序5-12】快速排序 (18)【程序5-13】 Select函数 (19)【程序5-14】线性时间选择算法 (19)【程序6-1】贪心法 (20)【程序6-2】背包问题的贪心算法 (21)【程序6-3】带时限作业排序的贪心算法 (21)【程序6-4】带时限的作业排序程序 (22)【程序6-5】使用并查集的带时限作业排序程序 (22)【程序6-6】两路合并最佳模式的贪心算法 (23)【程序6-7】最小代价生成树的贪心算法 (24)【程序6-8】普里姆算法 (24)【程序6-9】克鲁斯卡尔算法 (26)【程序6-10】迪杰斯特拉算法 (26)【程序6-11】多带最优存储 (28)【程序7-1】多段图的向前递推算法 (28)【程序7-2】弗洛伊德算法 (29)【程序7-3】矩阵连乘算法 (29)【程序7-4】矩阵连乘的备忘录方法 (30)【程序7-5】求LCS的长度 (32)【程序7-6】构造最长公共子序列 (32)【程序7-7】构造最优二叉搜索树 (33)【程序7-8】 0/1背包的递归算法 (33)【程序7-9】 0/1背包算法的粗略描述 (34)【程序7-10】 0/1背包最优解值算法 (35)【程序7-11】 0/1背包最优解算法 (36)【程序7-12】Johnson算法 (37)【程序8-1】递归回溯法 (37)【程序8-2】迭代回溯法 (38)【程序8-3】蒙特卡罗算法 (38)【程序8-4】n-皇后问题的回溯算法 (38)【程序8-5】子集和数的回溯算法 (39)【程序8-6】图的m-着色算法 (40)【程序8-7】哈密顿环算法 (40)【程序8-8】 0/1背包算法 (42)【程序8-9】批处理作业调度算法 (43)【程序9-1】分枝限界算法 (44)【程序9-2】基于上下界函数的FIFO分枝限界法 (45)【程序9-3】基于上下界的LC分枝限界法 (46)【程序9-4】带时限的作业排序 (47)【程序9-5】类声明 (49)【程序9-6】上下界函数 (50)【程序9-7】 0/1背包问题的LC分枝限界法 (50)【程序9-8】批作业类和活结点结构 (51)【程序9-9】下界函数 (53)【程序9-10】批处理作业调度LCBB算法 (53)【程序10-1】不确定搜索算法 (54)【程序10-2】不确定排序算法 (54)【程序10-3】最大集团判定问题不确定算法 (55)【程序10-4】可满足性问题的不确定算法 (55)【程序11-1】标识重复元素的拉斯维加斯算法 (55)【程序11-2】伪素数测试 (56)【程序11-3】合数性检测 (56)【程序11-4】素数测试的蒙特卡罗算法 (57)【程序11-5】快速排序舍伍德算法 (57)【程序12-1】平面图着色近似算法 (57)【程序12-2】最小顶点覆盖近似算法 (57)【程序12-3】集合覆盖近似算法 (58)【程序12-4】子集和数算法 (58)【程序12-5】修正表L为新表 (58)【程序12-6】子集和数近似方案 (58)【程序1-1】欧几里德递归算法v o i d S w a p(i n t&a,i n t&b){i n t c=a;a=b;b=c;}i n t R G c d(i n t m,i n t n){i f(m==0)r e t u r n n;r e t u r n R G c d(n%m,m);}i n t G c d(i n t m,i n t n){i f(m>n)S w a p(m,n);r e t u r n R G c d(m,n);}【程序1-2】欧几里德迭代算法i n t G c d(i n t m,i n t n){i f(m==0)r e t u r n n;i f(n==0)r e t u r n m;i f(m>n)S w a p(m,n);w h i l e(m>0){i n t c=n%m;n=m;m=c;}r e t u r n n;}【程序1-3】Gc d的连续整数检测算法i n t G c d(i n t m,i n t n){i f(m==0)r e t u r n n;i f(n==0)r e t u r n m;i n t t=m>n?n:m;w h i l e(m%t||n%t)t--;r e t u r n t;}【程序1-4】求F nl o n g F i b(l o n g n){i f(n<=1)r e t u r n n;e l s e r e t u r n F i b(n-2)+F i b(n-1);}【程序1-5】逆序输出正整数的各位数#i n c l u d e<i o s t r e a m.h>v o i d P r i n t D i g i t(u n s i g n e d i n t n){//设k位正整数为d1d2 d k,按各位数的逆序d k d k 1 d1形式输出c o u t<<n%10;//输出最后一位数d ki f(n>=10)P r i n t D i g i t(n/10);//以逆序输出前k-1位数}v o i d m a i n(){u n s i g n e d i n t n;c i n>>n;P r i n t D i g i t(n);}【程序1-6】汉诺塔问题#i n c l u d e<i o s t r e a m.h>e n u m t o w e r{A='X',B='Y',C='Z'};v o i d M o v e(i n t n,t o w e r x,t o w e r y){//将第n个圆盘从塔座x移到塔座y的顶部c o u t<<"T h ed i s k"<<n<<"i s m o ve df r o m"<<c h a r(x)<<"t o t o p o f t o w e r"<<c h a r(y)<<e n d l;}v o i d H a n o i(i n t n,t o w e r x,t o w e r y,t o w e r z){//将塔座x上部的n个圆盘移到塔座y上,顺序不变。
i f(n){H a n o i(n-1,x,z,y);//将前n-1个圆盘从塔座x移到塔座z,塔座y为中介M o v e(n,x,y);//将第n个圆盘从塔座x移到塔座yH a n o i(n-1,z,y,x);//将塔座z上的n-1个圆盘移到塔座y上,塔座x为中介}}v o i d m a i n(){H a n o i(4,A,B,C);//假定n=4}【程序1-7】排列产生算法t e m p l a t e<c l a s s T>v o i d P e r m(T a[],i n t k,i n t n){i f(k==n-1){//输出一种排列f o r(i n t i=0;i<n;i++)c o u t<<a[i]<<"";c o u t<<e nd l;}e l s e//产生{a[k],…,a[n-1]}各种排列f o r(i n t i=k;i<n;i++){T t=a[k];a[k]=a[i];a[i]=t;P e r m(a,k+1,n);//产生{a[k+1],…,a[n-1]}各种排列t=a[k];a[k]=a[i];a[i]=t;}}【程序2-1】求数组元素累加之和的迭代程序f l o a t S u m(f l o a t l i s t[],c o n s t i n t n){f l o a t t e m p s u m=0.0;c o u n t++;//针对赋值语句f o r(i n t i=0;i<n;i++){c o u n t++;//针对f o r循环语句t e m p s u m+=l i s t[i];c o u n t++;//针对赋值语句}c o u n t++;//针对f o r的最后一次执行c o u n t++;//针对r e t u r n语句r e t u r n t e m p s u m;}【程序2-2】求数组元素累加之和的递归程序f l o a t R S u m(f l o a t l i s t[],c o n s t i n t n){c o u n t++;//针对i f条件i f(n){c o u n t++;//针对R S u m调用和r e t u r n语句r e t u r n R S u m(l i s t,n-1)+l i s t[n-1];}c o u n t++;//针对r e t u r n语句r e t u r n0;}【程序2-3】矩阵乘法f o r(i=0;i<n;i++)//n+1f o r(j=0;j<n;j++){//n(n+1)c[i][j]=0;//n2f o r(k=0;k<n;k++)//n2(n+1)c[i][j]+=a[i][k]*b[k][j];//n3 }【程序3-1】伸展树类#i n c l u d e<i o s t r e a m.h>e n u m R e s u l t C o d e{U n d e rf l o w,O v e r f l o w,S u c c e s s,D u p l i c a t e,F a i l,N o t P r e s e n t};t e m p l a t e<c l a s s T>s t r u c t B T N o d e{//二叉树结点类B T N o d e(c o n s t T&x){e l e m e n t=x;l C h i l d=r C h i l d=N U L L;}T e l e m e n t;B T N o d e*lC h i l d,*r C h i l d;};t e m p l a t e<c l a s s T,c l a s s K>c l a s s S P T r e e{//伸展树类p u b l i c:S P T r e e(){r o o t=N U L L;}R e s u l t C o d e I n s e r t(T x);p r o t e c t e d:B T N o d e<T>*r o o t;p r i v a t e:R e s u l t C o d e I n s e r t(B T N o d e<T>*&p,T x);v o i d L R o t(B T N o d e<T>*&p);v o i d R R o t(B T N o d e<T>*&p);};【程序3-2】旋转函数t e m p l a t e<c l a s s T>v o i d S P T r e e<T>::L R o t(B T N o d e<T>*&p){//前置条件:p有右孩子,实现向左旋转B T N o d e<T>*r=p->rC h i l d;p->r C h i l d=r->l C h i l d;r->l C h i l d=p;p=r;//p的右孩子成为子树根}t e m p l a t e<c l a s s T>v o i d S P T r e e<T>::R R o t(B T N o d e<T>*&p){//前置条件:p有左孩子,实现向右旋转B T N o d e<T>*r=p->lC h i l d;p->l C h i l d=r->r C h i l d;r->r C h i l d=p;p=r;//p的左孩子成为子树根}【程序3-3】伸展树插入t e m p l a t e<c l a s s T,c l a s s K>R e s u l t C o d e S P T r e e<T,K>::I n s e r t(T x){r e t u r n I n s e r t(r o o t,x);}t e m p l a t e<c l a s s T,c l a s s K>R e s u l t C o d e S P T r e e<T,K>::I n s e r t(B T N o d e<T>*&p,T x){//假定T类上已重载了关系运算符或类型转换运算符①R e s u l t C o d e r e s u l t=S u c c e s s;B T N o d e<T>*r;i f(p==N U L L){//插入新结点p=n e w B T N o d e<T>(x);r e t u r n r e s u l t;}i f(x==p->e l e m e n t){r e s u l t=D u p l i c a t e;r e t u r n r e s u l t;}i f(x<p->e l e m e n t){r=p->l C h i l d;i f(r==N U L L){//z i g旋转r=n e w B T N o d e<T>(x);r->r C h i l d=p;p=r;r e t u r n r e s u l t;}e l s e i f(x==r->e l e m e n t){//z i g旋转R R o t(p);r e s u l t=D u p l i c a t e;r e t u r n r e s u l t;①一个类上通过重载关系运算符或类型转换运算符,将结构间的比较视为关键字间的比较。
