1_AMC10入学测评卷 V1 from
2015美国数学竞赛10年级试题

American Mathematics Competitions
WRITE TO US!
Correspondence about the problems and solutions for this AMC 10 and orders for publications should be addressed to:
Students who score 120 or above or finish in the top 2.5% on this AMC 10 will be invited to take the 33rd annual American Invitational Mathematics Examination (AIME) on Thursday, March 19, 2015 or Wednesday, March 25, 2015. More details about the AIME and other information are on the back page of this test booklet.
MAA American Mathematics Competitions
are supported by Academy of Applied Science Akamai Foundation American Mathematical Society American Statistical Association Art of Problem Solving, Inc. Casualty Actuarial Society Conference Board of the Mathematical Sciences The D.E. Shaw Group Google IDEA MATH, LLC Jane Street Capital Math for America Inc. Mu Alpha Theta National Council of Teachers of Mathematics Simons Foundation Society for Industrial & Applied Mathematics
amc10真题与答案解析

amc10真题与答案解析AMC10真题与答案解析美国数学竞赛(AMC)是一项极具挑战性的数学竞赛,旨在推动学生的数学学习和解决问题的能力。
其中AMC10是为中学生设计的竞赛,是很多学生展现才华并锻炼数学素养的重要机会。
本文将对一道AMC10真题进行解析,帮助读者理解和掌握解题技巧。
以下是一道来自AMC10的真题:"In the xy-plane, the graph of$\log_{16}x+\log_{16}y=\tfrac{3}{2}$ is drawn. The line$y=x$ intersects the graph at points $A$ and $B$. What is the length of segment $AB$?"这道题目涉及了对数的性质和直线与曲线的交点问题。
首先,我们先来理解题目所给出的等式。
$\log_{16}x$表示以16为底的对数,可以简化为$\log_2x^4$。
同样地,$\log_{16}y$可以简化为$\log_2y^4$。
所以等式可以写为$\log_2x^4 + \log_2y^4 =\frac{3}{2}$。
我们可以将等式进一步简化为$\log_2 (x^4y^4) =\frac{3}{2}$。
根据对数的性质,我们可以将等式转化为指数形式,得到$x^4y^4 = 2^{\frac{3}{2}}$。
然后我们来解决直线$y=x$与曲线$y=x^4$的交点问题。
我们可以将$x$代入曲线方程中,得到$y=x^4$。
因此,我们可以将交点问题转化为求解以下方程组:$x^4 =x$和$x^4y^4 = 2^{\frac{3}{2}}$。
首先,我们来解原方程$x^4 = x$。
很明显,$x=0$和$x=1$是方程的两个根。
我们可以进一步分析,当$x>1$时,$x^4$的增长速度比$x$快,所以方程没有其他解。
然后,我们来解方程$x^4y^4 = 2^{\frac{3}{2}}$。
AMC 美国数学竞赛 2001 AMC 10 试题及答案解析

USA AMC 10 20011The median of the listis . What is the mean?Solution2A number is more than the product of its reciprocal and its additive inverse. In which interval does the number lie?Solution3The sum of two numbers is . Suppose 3 is added to each number and then each of the resulting numbers is doubled. What is the sum of the final two numbers?Solution4What is the maximum number of possible points of intersection of a circle and a triangle?Solution5How many of the twelve pentominoes pictured below have at least one line of symettry?Solution6Let and denote the product and the sum, respectively, of thedigits of the integer . For example, and . Supposeis a two-digit number such that . What is the units digit of ?Solution7When the decimal point of a certain positive decimal number is moved four places to the right, the new number is four times the reciprocal of the original number. What is the original number?Solution8Wanda, Darren, Beatrice, and Chi are tutors in the school math lab. Their schedule is as follows: Darren works every third school day, Wanda works every fourth school day, Beatrice works every sixth school day, and Chi works every seventh school day. Today they are all working in the math lab. In how many school days from today willthey next be together tutoring in the lab?Solution9The state income tax where Kristin lives is levied at the rate of of the first of annual income plus of any amount above . Kristin noticed that the state income tax she paid amounted to of her annual income. What was her annual income?Solution10If , , and are positive with , , and , then isSolution11Consider the dark square in an array of unit squares, part of which is shown. The first ring of squ ares around this center square contains unit squares. The second ring contains unit squares. If we continue this process, the number of unit squares in the ring isSolution12Suppose that is the product of three consecutive integers and that is divisible by . Which of the following is not necessarily a divisor of Solution13A telephone number has the form , where each letter represents a different digit. The digits in each part of the numbers are in decreasing order; that is, , , and . Furthermore, , , and are consecutive even digits; , , , and are consecutive odd digits; and . Find .Solution14A charity sells 140 benefit tickets for a total of . Some tickets sell for full price (a whole dollar amount), and the rest sells for half price. How much money is raised by the full-price tickets?Solution15A street has parallel curbs feet apart. A crosswalk bounded by two parallel stripes crosses the street at an angle. The length of the curb between the stripes is feet and each stripe is feet long. Find the distance, in feet, between the stripes.Solution16The mean of three numbers is 10 more than the least of the numbers and 15 less than the greatest. The median of the three numbers is 5. What is their sum?Solution17Which of the cones listed below can be formed from a sector of a circle of radius by aligning the two straight sides?A cone with slant height of and radiusA cone with height of and radiusA cone with slant height of and radiusA cone with height of and radiusA cone with slant height of and radiusSolution18The plane is tiled by congruent squares and congruent pentagons as indicated. The percent of the plane that is enclosed by the pentagons is closest toSolution19Pat wants to buy four donuts from an ample supply of three types of donuts: glazed, chocolate, and powdered. How many different selections are possible?Solution20A regular octagon is formed by cutting an isosceles right triangle from each of the corners of a square with sides of length . What is the length of each side of the octagon?Solution21A right circular cylinder with its diameter equal to its height is inscribed in a right circular cone. The cone has diameter and altitude , and the axes of the cylinder and cone coincide. Find the radius of the cylinder.Solution22In the magic square shown, the sums of the numbers in each row, column, and diagonal are the same. Five of these numbers are represented by , , , , and . Find .Solution23A box contains exactly five chips, three red and two white. Chips are randomly removed one at a time without replacement until all the red chips are drawn or all the white chips are drawn. What is the probability that the last chip drawn is white?Solution24In trapezoid , and are perpendicular to , with, , and . What is ?Solution25How many positive integers not exceeding are multiples of or but not ?。
2023年AMC10美国数学竞赛A卷附中文翻译和答案

2023AMC10美国数学竞赛A卷1. A cell phone plan costs $20 each month, plus 5¢ per text message sent, plus 10¢ for each minute used over 30 hours. In January Michelle sent 100 text messages and talked for 30.5 hours. How much did she have to pay?(A) $24.00 (B) $24.50 (C) $25.50 (D) $28.00 (E) $30.002. A small bottle of shampoo can hold 35 milliliters of shampoo, Whereas a large bottle can hold 500 milliliters of shampoo. Jasmine wants to buy the minimum number of small bottles necessary to completely fill a large bottle. How many bottles must she buy?(A) 11 (B) 12 (C) 13 (D) 14 (E) 153. Suppose [a b] denotes the average of a and b, and {a b c} denotes the average of a, b, and c. What is {{1 1 0} [0 1] 0}?(A) (B)(C)(D) (E)4. Let X and Y be the following sums of arithmetic sequences:X= 10 + 12 + 14 + …+ 100.Y= 12 + 14 + 16 + …+ 102.What is the value of(A) 92 (B) 98 (C) 100 (D) 102 (E) 1125. At an elementary school, the students in third grade, fourth grade, and fifth grade run an average of 12, 15, and 10 minutes per day, respectively. There are twice as many third graders as fourth graders, and twice as many fourth graders as fifth graders. What is the average number of minutes run per day by these students?(A) 12 (B) (C) (D) 13 (E) 146. Set A has 20 elements, and set B has 15 elements. What is the smallest possible number of elements in A∪B, the union of A and B?(A) 5 (B) 15 (C) 20 (D) 35 (E) 3007. Which of the following equations does NOT have a solution?(A) (B) (C)(D) (E)8. Last summer 30% of the birds living on Town Lake were geese, 25% were swans, 10% were herons, and 35% were ducks. What percent of the birds that were not swans were geese?(A) 20 (B) 30 (C) 40 (D) 50 (E) 609. A rectangular region is bounded by the graphs of the equations y=a, y=-b, x=-c, and x=d, where a, b, c, and d are all positive numbers. Which of the following represents the area of this region?(A) ac + ad + bc + bd (B) ac – ad + bc – bd (C) ac + ad – bc – bd(D) –ac –ad + bc + bd (E) ac – ad – bc + bd10. A majority of the 20 students in Ms. Deameanor’s class bought pencils at the school bookstore. Each of these students bought the same number of pencils, and this number was greater than 1. The cost of a pencil in cents was greater than the number of pencils each student bought, and the total cost of all the pencils was $17.71. What was the cost of a pencil in cents?(A) 7 (B) 11 (C) 17 (D) 23 (E) 7711. Square EFGH has one vertex on each side of square ABCD. Point E is on AB with AE=7·EB. What is the ratio of the area of EFGH to the area of ABCD?(A) (B)(C)(D) (E)12. The players on a basketball team made some three-point shots, some two-point shots, some one-point free throws. They scored as many points with two-point shots as with three-point shots. Their number of successful free throws was one more than their number of successful two-point shots. The team’s total score was 61 points. How many free throws did they make?(A) 13 (B) 14 (C) 15 (D) 16 (E) 1713. How many even integers are there between 200 and 700 whose digits are alldifferent and come from the set {1, 2, 5, 7, 8, 9}?(A) 12 (B)20 (C)72 (D) 120 (E) 20014. A pair of standard 6-sided fair dice is rolled once. The sum of the numbers rolled determines the diameter of a circle. What is the probability that the numerical value of the area of the circle is less than the numerical value of the circle’s circumference?(A) (B)(C)(D) (E)15. Roy bought a new battery-gasoline hybrid car. On a trip the car ran exclusively on its battery for the first 40 miles, then ran exclusively on gasoline for the rest of the trip, using gasoline at a rate of 0.02 gallons per mile. On the whole trip he averaged55 miles per gallon. How long was the trip in miles?(A) 140 (B) 240 (C) 440 (D) 640 (E) 84016. Which of the following in equal to(A) (B) (C) (D) (E)17. In the eight-term sequence A, B, C, D, E, F, G, H, the value of C is 5 and the sum of any three consecutive terms is 30. What is A + H?(A) 17 (B) 18 (C) 25 (D) 26 (E) 4318. Circles A, B, and C each have radius 1. Circles A and B share one point of tangency. Circle C has a point of tangency with the midpoint of AB. What is the area inside Circle C but outside Circle A and Circle B?(B) (C) (D) (E)(A)19. In 1991 the population of a town was a perfect square. Ten years later, after an increase of 150 people, the population was 9 more than a perfect square. Now, in 2023, with an increase of another 150 people, the population is once again a perfect square. Which of the following is closest to the percent growth of the town’s popu lation during this twenty-year period?(A) 42 (B) 47 (C) 52 (D) 57 (E) 6220. Two points on the circumference of a circle of radius r are selected independently and at random. From each point a chord of length r is drawn in a clockwise direction. What is the probability that the two chords intersect?(A) (B) (C) (D) (E)21. Two counterfeit coins of equal weight are mixed with 8 identical genuine coins. The weight of each of the counterfeit coins is different from the weight of each of the genuine coins. A pair of coins is selected at random without replacement from the 10 coins. A second pair is selected at random without replacement from the remaining 8coins. The combined weight of the first pair is equal to the combined weight of the second pair. What is the probability that all 4 selected coins are genuine?(A) (B) (C) (D) (E)22. Each vertex of convex pentagon ABCDE is to be assigned a color. There are 6 colors to choose from, and the ends of each diagonal must have different colors. How many different colorings are possible?(A) 2500 (B) 2880 (C) 3120 (D) 3250 (E) 375023. Seven students count from 1 to 1000 as follows:·Alice says all the numbers, except she skips the middle number in each consecutive group of thre e numbers. That is Alice says 1, 3, 4, 6, 7, 9, …, 997, 999, 1000.·Barbara says all of the numbers that Alice doesn’t say, except she also skips the middle number in each consecutive grope of three numbers.·Candice says all of the numbers that neither Alice nor Barbara says, except she also skips the middle number in each consecutive group of three numbers. ·Debbie, Eliza, and Fatima say all of the numbers that none of the students with the first names beginning before theirs in the alphabet say, except each also skips the middle number in each of her consecutive groups of three numbers.·Finally, George says the only number that no one else says.What number does George say?(A) 37 (B) 242 (C) 365 (D) 728 (E) 99824. Two distinct regular tetrahedra have all their vertices among the vertices of the same unit cube. What is the volume of the region formed by the intersection of the tetrahedra?(A) (B) (C) (D) (E)an integer. A point X in the interior of R is25. Let R be a square region andcalled n-ray partitional if there are n rays emanating from X that divide R into N triangles of equal area. How many points are 100-ray partitional but not 60-ray partitional?(A) 1500 (B) 1560 (C) 2320 (D) 2480 (E) 25002023AMC10美国数学竞赛A卷1. 某通讯公司手机每月基本费为20美元, 每传送一则简讯收 5美分(一美元=100 美分)。
美国AMC10中文版试题及答案

2000到20XX年AMC10美国数学竞赛0 0P 0 A 0 B 0 C 0D 0 全美中学数学分级能力测验(AMC 10)2000年 第01届 美国AMC10 (2000年2月 日 时间75分钟)1. 国际数学奥林匹亚将于 在美国举办,假设I 、M 、O 分别表示不同的正整数,且满足I ⨯M ⨯O =2001,则试问I +M +O 之最大值为 。
(A) 23 (B) 55 (C) 99 (D) 111 (E) 6712. 2000(20002000)为 。
(A) 20002001 (B) 40002000 (C) 20004000 (D) 40000002000 (E) 200040000003. Jenny 每天早上都会吃掉她所剩下的聪明豆的20%,今知在第二天结束时,有32颗剩下,试问一开始聪明豆有 颗。
(A) 40 (B) 50 (C) 55 (D) 60 (E) 754. Candra 每月要付给网络公司固定的月租费及上网的拨接费,已知她12月的账单为12.48元,而她1月的账单为17.54元,若她1月的上网时间是12月的两倍,试问月租费是 元。
(A) 2.53 (B) 5.06 (C) 6.24 (D) 7.42 (E) 8.775. 如图M ,N 分别为PA 与PB 之中点,试问当P 在一条平行AB 的直 在线移动时,下列各数值有 项会变动。
(a) MN 长 (b) △P AB 之周长 (c) △P AB 之面积 (d) ABNM 之面积(A) 0项 (B) 1项 (C) 2项 (D) 3项 (E) 4项 6. 费氏数列是以两个1开始,接下来各项均为前两项之和,试问在费氏数列各项的个位数字中, 最后出现的阿拉伯数字为 。
(A) 0 (B) 4 (C) 6 (D) 7 (E) 97. 如图,矩形ABCD 中,AD =1,P 在AB 上,且DP 与DB 三等分∠ADC ,试问△BDP 之周长为 。
amc 10 2023 题目

【主题】解析AMC 10 2023年数学竞赛题目【内容】一、导言2023年AMC 10数学竞赛作为一项备受关注的数学竞赛,吸引了众多中学生的参与。
在本文中,我们将对2023年AMC 10数学竞赛的题目进行一一解析,帮助读者更好地理解和掌握其中的数学知识和解题技巧。
二、数学竞赛概况AMC(American Mathematics Competitions)是由美国数学协会(MAA)主办的一项全国性数学竞赛。
AMC 10是专门面向中学生的数学竞赛,旨在激发学生对数学的兴趣,培养其数学能力和解决问题的能力。
每年举办的AMC 10数学竞赛题目涵盖了数学中的各个领域,要求考生具有扎实的数学基础和灵活的思维能力。
三、2023年AMC 10数学竞赛题目解析1. 第一道题目题目:求下列无理数的整数部分:$\sqrt{129}+\sqrt{189}-\sqrt{144}-\sqrt{121}$解析:我们可以将每个无理数的平方根表示成对应的整数和余数的形式,然后进行合并化简,经过一系列运算,最终得到答案。
2. 第二道题目题目:设函数$f(x)=\frac{ax+b}{cx+d}$,其中$a,b,c,d$是常数,$ad-bc\neq0$,且$c\neq0$。
若对任意实数$x$恒有$f(f(x))=x$,则$f(x)$的表达式是什么?解析:通过设定函数$f(x)$,并根据题目给出的条件,我们可以利用函数的复合运算和方程的求解,来确定$f(x)$的表达式。
3. 第三道题目题目:在平面直角坐标系中,曲线$C$的方程为$x^2+y^2-4x-6y+9=0$,则曲线$C$的图像是什么?解析:通过将方程进行配方完全平方,消去一次项,得到标准方程,然后结合圆的性质,来描述曲线$C$的图像特征。
4. 第四道题目题目:若正实数$a,b,c$满足$a+b+c=1$,则$\frac{1+a}{1-a}+\frac{1+b}{1-b}+\frac{1+c}{1-c}$的值是多少?解析:题目中给出的条件可以让我们有一个开始,然后我们可以通过利用分式的化简和求和规律来得出最终的结果。
美国高中数学竞赛 AMC10 2001年试题解答

where
1
1
(x + 5 + y) = x + 10 and (x + 5 + y) + 15 = y.
3
3
If we add these equations, we get
2 (x + 5 + y) + 15 = x + y + 10,
3
and solving for x + y gives x + y = 25. Hence, the sum of the numbers is x + 5 + y = 30.
p
p+2
p + 0.25
· 28000 +
· (x − 28000) =
· x.
100
100
100
Multiplying by 100 and expanding yields
28000p + px + 2x − 28000p − 56000 = px + 0.25x.
So,
1.75x
=
7 4
Hale Waihona Puke x=56000
3
2nd AMC 10
2001
13. (E) The last four digits (GHIJ) are either 9753 or 7531, and the remaining odd digit (either 1 or 9) is A, B, or C. Since A + B + C = 9, the odd digit among A, B, and C must be 1. Thus the sum of the two even digits in ABC is 8. The three digits in DEF are 864, 642, or 420, leaving the pairs 2 and 0, 8 and 0, or 8 and 6, respectively, as the two even digits in ABC. Of those, only the pair 8 and 0 has sum 8, so ABC is 810, and the required first digit is 8. The only such telephone number is 810-642-9753.
AMC10美国数学竞赛真题 xx年

AMC10美国数学竞赛真题 xx年Problem 1The median of the lististhe mean?Solution. What isProblem 2A number is more than the product of its reciprocal and its additive inverse. In which interval does the number lie?SolutionProblem 3The sum of two numbers is . Suppose is added to each number and then each of the resulting numbers is doubled. What is the sum of the final two numbers?SolutionProblem 4What is the maximum number for the possible points of intersection of a circle and a triangle?SolutionProblem 5How many of the twelve pentominoes pictured below have at least one line of symmetry?SolutionProblem 6Letanddenote the product and the sum, respectively, of the digits ofand. Supposeis athe integer . For example,two-digit number such that . What is the units digit ofSolutionProblem 7When the decimal point of a certain positive decimal number is moved four places to the right, thenew number is four times the reciprocal of the original number. What is the original number?SolutionProblem 8Wanda, Darren, Beatrice, and Chi are tutors in the school math lab. Theirschedule is as follows: Darren works every third school day, Wanda works every fourth school day, Beatrice works every sixth school day, and Chi works every seventh school day. Today they are all working in the math lab. In how many school days from today will they next be together tutoring in the lab?SolutionProblem 9The state income tax where Kristin lives is levied at the rate ofof annual income plusof any amount aboveof the first. Kristin of hernoticed that the state income tax she paid amounted to annual income. What was her annual income?Problem 10If ,, and are positive withis,, andSolution, thenProblem 11Consider the dark square in an array of unit squares, part of which is shown. The ?rst ring of squares around this center square contains unit squares. The second ring contains unit squares. If we continue this process, the number of unit squares in the ring isSolutionProblem 12Suppose that is the product of three consecutive integers and that by . Which of the following is not necessarily a divisor of ?is divisibleProblem 13A telephone number has the form , where each letter represents a different digit. The digits in each partof the numbers are in decreasing order; that is, , , and . Furthermore, , , and are consecutive even digits; , , , and are consecutive odd digits; and . Find . SolutionProblem 14A charity sells benefit tickets for a total of . Some tickets sell for full price (a whole dollar amount), and the rest sells for half price. How much money is raised by the full-price tickets?SolutionProblem 15A street has parallel curbs feet apart. A crosswalk bounded by two parallel stripes crosses the street atan angle. The length of the curb between the stripesis feet and each stripe is feet long. Find the distance,in feet, between the stripes?SolutionProblem 16The mean of three numbers is more than the least of the numbers and less than the greatest. The median of the three numbers is . What is their sum?SolutionProblem 17Which of the cones listed below can be formed froma radius by aligning the two straight sides?sector of a circle ofSolutionProblem 18The plane is tiled by congruent squares and congruent pentagons as indicated. The percent of the plane that is enclosed by the pentagons is closest toSolutionProblem 19Pat wants to buy four donuts from an ample supply of three types of donuts: glazed, chocolate, and powdered. How many different selections are possible? SolutionProblem 20A regular octagon is formed by cutting an isosceles right triangle from each of the corners of a square with sides of length . What is the length of each side of the octagon?SolutionProblem 21A right circular cylinder with its diameter equal to its height is inscribed in a right circular cone. The cone has diameter and altitude , and the axes of the cylinder and cone coincide. Find the radius of the cylinder.SolutionProblem 22In the magic square shown, the sums of the numbersin each row, column, and diagonal are the same. Five of these numbers are represented by , , , , and . Find .SolutionProblem 23A box contains exactly five chips, three red and two white. Chips are randomly removed one at a timewithout replacement until all the red chips are drawn or all the white chips are drawn. What is the probability that the last chip drawn is white?SolutionProblem 24In trapezoid, ,andare perpendicular to , and . What is, withSolutionProblem 25How many positive integers not exceeding ?are multiples of or but notSolutionProblem 1The median of the lististhe mean?Solution. What isProblem 2A number is more than the product of its reciprocal and its additive inverse. In which interval does the number lie?SolutionProblem 3The sum of two numbers is . Suppose is added to each number and then each of the resulting numbers is doubled. What is the sum of the final two numbers?SolutionProblem 4What is the maximum number for the possible points of intersection of a circle and a triangle?SolutionProblem 5How many of the twelve pentominoes pictured below have at least one line of symmetry?SolutionProblem 6Letanddenote the product and the sum, respectively, of the digits ofand. Supposeis athe integer . For example,two-digit number such that . What is the units digit ofSolutionProblem 7When the decimal point of a certain positive decimal number is moved four places to the right, the new number is four times the reciprocal of the original number. What is the original number?SolutionProblem 8Wanda, Darren, Beatrice, and Chi are tutors in the school math lab. Theirschedule is as follows: Darren works every thirdschool day, Wanda works every fourth school day, Beatrice works every sixth school day, and Chi works every seventh school day. Today they are all working in the math lab. In how many school days from today will they next be together tutoring in the lab?SolutionProblem 9The state income tax where Kristin lives is levied at the rate ofof annual income plusof any amount aboveof the first. Kristin of hernoticed that the state income tax she paid amounted to annual income. What was her annual income?SolutionProblem 10If ,, and are positive withis,, and, thenProblem 11Consider the dark square in an array of unit squares, part of which is shown. The ?rst ring of squares around this center square contains unit squares. The second ring contains unit squares. If we continue this process, the number of unit squares in the ring isSolutionProblem 12Suppose that is the product of three consecutive integers and that by . Which of the following is not necessarily a divisor of ?is divisibleSolutionProblem 13A telephone number has the form , where each letter represents a different digit. The digits in each partof the numbers are in decreasing order; that is, , , and . Furthermore, , , and are consecutive even digits; , , , and are consecutive odd digits; and . Find .Problem 14A charity sells benefit tickets for a total of . Some tickets sell for full price (a whole dollar amount), and the rest sells for half price. How much money is raised by the full-price tickets?SolutionProblem 15A street has parallel curbs feet apart. A crosswalk bounded by two parallel stripes crosses the street at an angle. The length of the curb between the stripes is feet and each stripe is feet long. Find the distance, in feet, between the stripes?SolutionProblem 16The mean of three numbers is more than the least of the numbers and less than the greatest. The median of the three numbers is . What is their sum?SolutionProblem 17Which of the cones listed below can be formed from a radius by aligning the two straight sides?sector of a circle ofSolutionProblem 18The plane is tiled by congruent squares and congruent pentagons as indicated. The percent of the plane that is enclosed by the pentagons is closest toSolutionProblem 19Pat wants to buy four donuts from an ample supply of three types of donuts: glazed, chocolate, and powdered. How many different selections are possible? SolutionProblem 20A regular octagon is formed by cutting an isosceles right triangle from each of the corners of a square with sides of length . What is the length of each side of the octagon?。
amc10数学竞赛试卷

amc10数学竞赛试卷
以下是一份AMC10数学竞赛的试卷样题,供您参考。
答题时间:120分钟
满分:150分
一、选择题(每题5分,共75分)
1.题目:一个等腰三角形的顶角是120°,则它的底角是:
2. A. 30° B. 45° C. 60° D. 90°
3.题目:如果两个数的和为6,且这两个数的积最大,则这两个数应为:
4. A. 1和5 B. 2和4 C. 3和3 D. 4和2
5.题目:一个正方形的面积为9,则它的边长为:
6. A. 3 B. -3 C. ±3 D. 以上都不对
(此处省略部分题目)
二、填空题(每题5分,共25分)
1.题目:若x = ___时,分式 x^2 - 1/x - 2 的值为零。
2.题目:已知 |x| = 5,y = 3,则 x - y =或。
3.题目:若 a/b = c/d = e/f = ... = m/n = k,则 (a + c + ... + m)/(b + d
+ ... + n) = ___。
以上是一份AMC10数学竞赛的试卷样题,包括选择题和填空题两个部分。
此试卷仅供参考,实际考试题目可能会有所不同。
amc10典型题目

amc10典型题目AMC 10(美国数学竞赛10)是一项面向中学生的数学竞赛,旨在提高学生的数学解题能力和思维能力。
以下是一些典型的AMC 10题目,供你参考:1. 题目,一个正方形的边长为10。
从正方形的一个顶点出发,每次只能向右或向上移动一个单位。
求到达对角线上另一个顶点的最短路径长度。
解答,通过观察可以发现,每次移动都会使横坐标或纵坐标增加1,因此最短路径长度为10。
2. 题目,若a、b、c是满足a+b+c=10的正整数,且abc的最大值为多少?解答,根据AM-GM不等式,当a=b=c时,abc的值最大。
因此,a=b=c=10/3,所以abc的最大值为(10/3)^3。
3. 题目,已知等差数列的前四项之和为10,且公差为2,求该等差数列的第一项。
解答,设等差数列的第一项为a,则根据等差数列的性质,前四项之和为4a+6。
将其与题目中给出的和10相等,得到4a+6=10。
解方程可得a=1,所以该等差数列的第一项为1。
4. 题目,在平面直角坐标系中,点A(3, 4)和点B(-1, 2)的中点坐标为多少?解答,中点的横坐标等于两点横坐标之和的一半,中点的纵坐标等于两点纵坐标之和的一半。
因此,中点的坐标为((3 + (-1))/2, (4 + 2)/2),即(1, 3)。
5. 题目,一个数与它的平方之和等于90,求这个数。
解答,设这个数为x,根据题目条件可得x + x^2 = 90。
解这个二次方程可得x = 9或x = -10。
因为题目中没有指定数的范围,所以这两个解都是可能的。
以上是一些AMC 10的典型题目,希望对你有所帮助。
请注意,这只是一小部分题目,实际的AMC 10考试还包含更多类型的数学问题。
高中一年级美国数学竞赛试题(简称AMC10)2012年B卷39617197
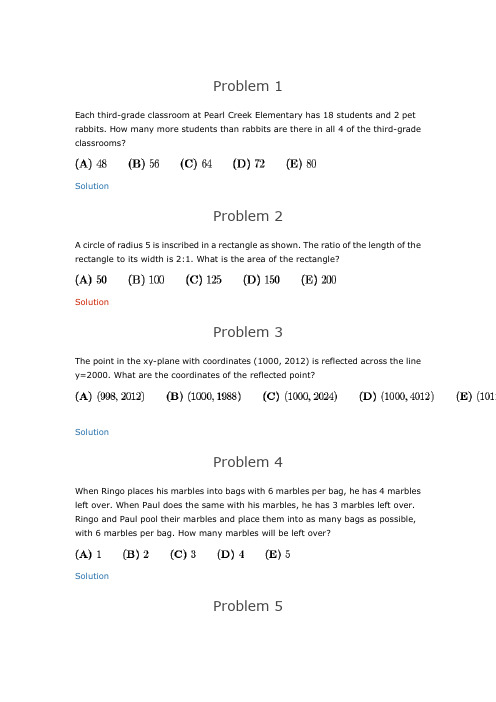
Problem 1Each third-grade classroom at Pearl Creek Elementary has 18 students and 2 pet rabbits. How many more students than rabbits are there in all 4 of the third-grade classrooms?SolutionProblem 2A circle of radius 5 is inscribed in a rectangle as shown. The ratio of the length of the rectangle to its width is 2:1. What is the area of the rectangle?SolutionProblem 3The point in the xy-plane with coordinates (1000, 2012) is reflected across the line y=2000. What are the coordinates of the reflected point?SolutionProblem 4When Ringo places his marbles into bags with 6 marbles per bag, he has 4 marbles left over. When Paul does the same with his marbles, he has 3 marbles left over. Ringo and Paul pool their marbles and place them into as many bags as possible, with 6 marbles per bag. How many marbles will be left over?SolutionProblem 5Anna enjoys dinner at a restaurant in Washington, D.C., where the sales tax on meals is 10%. She leaves a 15% tip on the price of her meal before the sales tax is added, and the tax is calculated on the pre-tip amount. She spends a total of 27.50 dollars for dinner. What is the cost of her dinner without tax or tip in dollars?SolutionProblem 6In order to estimate the value of x-y where x and y are real numbers with x > y > 0, Xiaoli rounded x up by a small amount, rounded y down by the same amount, and then subtracted her rounded values. Which of the following statements is necessarily correct?A) Her estimate is larger than x-y B) Her estimate is smaller than x-y C) Her estimate equals x-y D) Her estimate equals y - x E) Her estimate is 0SolutionProblem 7For a science project, Sammy observed a chipmunk and a squirrel stashing acorns in holes. The chipmunk hid 3 acorns in each of the holes it dug. The squirrel hid 4 acorns in each of the holes it dug. They each hid the same number of acorns, although the squirrel needed 4 fewer holes. How many acorns did the chipmunk hide?SolutionProblem 8What is the sum of all integer solutions to ?SolutionProblem 9Two integers have a sum of 26. When two more integers are added to the first two integers the sum is 41. Finally when two more integers are added to the sum of the previous four integers the sum is 57. What is the minimum number of even integers among the 6 integers?SolutionProblem 10How many ordered pairs of positive integers (M,N) satisfy the equation =SolutionProblem 11A dessert chef prepares the dessert for every day of a week starting with Sunday. The dessert each day is either cake, pie, ice cream, or pudding. The same dessert may not be served two days in a row. There must be cake on Friday because of a birthday. How many different dessert menus for the week are possible?SolutionProblem 12Point B is due east of point A. Point C is due north of point B. The distance betweenpoints A and C is , and = 45 degrees. Point D is 20 meters due Northof point C. The distance AD is between which two integers?SolutionProblem 13It takes Clea 60 seconds to walk down an escalator when it is not operating, and only 24 seconds to walk down the escalator when it is operating. How many seconds does it take Clea to ride down the operating escalator when she just stands on it?SolutionProblem 14Two equilateral triangles are contained in square whose side length is . The bases of these triangles are the opposite side of the square, and their intersection is a rhombus. What is the area of the rhombus?SolutionProblem 15In a round-robin tournament with 6 teams, each team plays one game against each other team, and each game results in one team winning and one team losing. At the end of the tournament, the teams are ranked by the number of games won. What is the maximum number of teams that could be tied for the most wins at the end on the tournament?SolutionProblem 16Three circles with radius 2 are mutually tangent. What is the total area of the circles and the region bounded by them, as shown in the figure?SolutionProblem 17Jesse cuts a circular paper disk of radius 12 along two radii to form two sectors, the smaller having a central angle of 120 degrees. He makes two circular cones, using each sector to form the lateral surface of a cone. What is the ratio of the volume of the smaller cone to that of the larger?SolutionProblem 18Suppose that one of every 500 people in a certain population has a particular disease, which displays no symptoms. A blood test is available for screening for this disease. For a person who has this disease, the test always turns out positive. For aperson who does not have the disease, however, there is a false positive rate--inother words, for such people, of the time the test will turn out negative, butof the time the test will turn out positive and will incorrectly indicate that the person has the disease. Let be the probability that a person who is chosen at random from this population and gets a positive test result actually has the disease. Which of the following is closest to ?SolutionProblem 19In rectangle , , , and is the midpoint of . Segmentis extended 2 units beyond to point , and is the intersection of and. What is the area of ?SolutionProblem 20Bernardo and Silvia play the following game. An integer between 0 and 999, inclusive, is selected and given to Bernardo. Whenever Bernardo receives a number, he doubles it and passes the result to Silvia. Whenever Silvia receives a number, she adds 50 to it and passes the result to Bernardo. The winner is the last person who produces a number less than 1000. Let be the smallest initial number that resultsin a win for Bernardo. What is the sum of the digits of ?SolutionProblem 21Four distinct points are arranged on a plane so that the segments connecting them have lengths , , , , , and . What is the ratio of to ?SolutionProblem 22Let be a list of the first 10 positive integers such that for eacheither or or both appear somewhere before in the list. How many such lists are there?SolutionProblem 23A solid tetrahedron is sliced off a wooden unit cube by a plane passing through two nonadjacent vertices on one face and one vertex on the opposite face not adjacent to either of the first two vertices. The tetrahedron is discarded and the remaining portion of the cube is placed on a table with the cut surface face down. What is the height of this object?SolutionProblem 23A solid tetrahedron is sliced off a wooden unit cube by a plane passing through two nonadjacent vertices on one face and one vertex on the opposite face not adjacent to either of the first two vertices. The tetrahedron is discarded and the remaining portion of the cube is placed on a table with the cut surface face down. What is the height of this object?SolutionProblem 24Amy, Beth, and Jo listen to four different songs and discuss which ones they like. No song is liked by all three. Furthermore, for each of the three pairs of the girls, there is at least one song liked by those girls but disliked by the third. In how many different ways is this possible?SolutionProblem 25A bug travels from to along the segments in the hexagonal lattice picturedbelow. The segments marked with an arrow can be traveled only in the direction of the arrow, and the bug never travels the same segment more than once. How many different paths are there?Retrieved from"/Wiki/index.php/2012_AMC_10B_Problems"。
amc10 25题对16题

amc10 25题对16题AMC10是美国数学竞赛中学生组的一项考试。
该考试由数学协会(AMC)主办,旨在评估参赛学生在数学方面的能力和解决问题的技巧。
在AMC10考试中,有25道选择题,本文将对第25题与第16题进行比较和分析。
首先,让我们来看一下第25题。
这道题可能是AMC10中最具挑战性的一道题目。
它通常要求学生在给定的条件下,利用数学知识和解决问题的能力,找到最佳的解决方案。
相比之下,第16题的难度较低。
这道题可能要求学生在给定的条件下,进行一些简单的计算或者找到一些基本的数学关系。
虽然这道题不太复杂,但它可以帮助学生巩固和应用基本的数学知识。
比较这两道题的不同之处,可以发现第25题通常需要更深入的数学思考和推理。
它可能涉及到更复杂的数学概念和技巧,需要学生能够将这些概念和技巧应用到实际问题中。
而第16题更注重学生对基本概念的理解和应用,它可能是通过一些简单的计算或者数学推理来解决问题。
在准备AMC10考试时,对这两道题的对比和分析对于学生的备考是非常有帮助的。
学生可以通过研究解决这些问题的方法和技巧,提高他们的数学解题能力。
对于第25题,学生可以通过加强数学理论知识的学习来提高解题能力。
他们可以学习更高级的数学概念和技巧,如数列和级数、概率和统计等。
此外,学生还可以通过刷题来增加解题经验,掌握解决不同类型问题的方法和技巧。
对于第16题,学生可以通过对基础数学知识的巩固来提高解题能力。
他们可以复习和巩固数学的基本概念,如代数、几何、函数等。
同时,他们还可以通过解决类似的简单问题,来提高他们的计算和推理能力。
总的来说,对于AMC10考试中的第25题和第16题,学生应该根据题目的要求和难度,采取不同的解题策略和方法。
通过研究和解决这些问题,学生可以提高他们的数学思考能力和解题技巧。
此外,学生还应该注重对基本数学知识的巩固和应用,这将有助于他们在考试中取得更好的成绩。
在备考过程中,学生还可以参加数学竞赛培训班或者参考一些备考资料,以获取更多的解题技巧和方法。
AMC10的真题答案及中文翻译

AMC10的真题答案及中文翻译
1、一张展览票原价为20美元。
Susan使用优惠券购买4张票,享受75折优惠。
Pam使用优惠券购买5张票,享受7折优惠。
Pam比Susan多花了多少美元?
2、一个养鱼缸的底部为矩形,长100cm,宽40cm,高50cm。
水位高度为40cm。
将一个底部为矩形,长40cm,宽20cm,高10cm的砖块放入缸中。
水位上升了多少厘米?
3、两个连续的奇数中,较大的数是较小的数的3倍。
它们的和是多少?
4、一个学校商店售卖7支铅笔和8个笔记本需要4.15美元,售卖5支铅笔和3个笔记本需要1.77美元。
那么16支铅笔和10个笔记本需要多少钱?
5、Euclid高中在2002年有60名学生参加AMC10,在2003年有66名,2004年有70名,2005年有76名,2006年有78名,2007年有85名。
在相邻的哪两年中人数增长的百分率最大?
6、去年,John Q. Public先生继承了一笔遗产。
他需要支付20%的联邦税和剩下的部分中10%的州税。
他需要支付美元的总税费。
这笔遗产有多少美元?
答案:(C) 美元
有多少个正整数对(m, n),满足m > n且它们的平方差是96?。
AMC10的真题答案及中文翻译

AMC10的真题及中文翻译1、One ticket to a show costs $20 at full price. Susan buys 4 tickets using a coupon that gives her a 25% discount. Pam buys 5 tickets using a coupon that gives her a 30% discount. How many more dollars does Pam pay than Susan?(A) 2 (B) 5 (C) 10 (D) 15 (E) 20中文:一张展览票全价为20美元。
Susan用优惠券买4张票打七五折。
Pam用优惠券买5张票打七折。
Pam比Susan多花了多少美元?2、An aquarium has a rectangular base that measures 100cm by 40cm and has a height of 50cm. It is filled with water to a height of 40cm. A brick with a rectangular base that measures 40cm by 20cm and a height of 10cm is placed in the aquarium. By how many centimeters does that water rise?(A) 0.5 (B) 1 (C) 1.5 (D) 2 (E)2.5中文:一个养鱼缸有100cm×40cm的底,高为50cm。
它装满水到40cm的高度。
把一个底为40cm×20cm,高为10cm的砖块放在这个养鱼缸里。
鱼缸里的水上升了多少厘米?3、The larger of two consecutive odd integers is three times the smaller. What is their sum?(A) 4 (B) 8 (C) 12 (D) 16 (E) 20中文:2个连续的奇整数中较大的数是较小的数的3倍。
amc10 2023 题目

amc10 2023 题目
AMC10 2023年的题目设计覆盖了代数、几何、数论和排列组合与概率等主要数学领域。
具体来说:
1. 代数题:共有5道,这些题目考察了参赛者的代数知识,包括多项式、方程、不等式等内容。
2.几何题:共有11道,是本次竞赛中数量最多的题型,涵盖了平面几何、立体几何以及坐标几何等领域。
3. 数论题:共有6道,涉及整数的性质、因数与倍数、质数等概念。
4. 排列组合与概率题:有3道,虽然数量上偏少,但也是衡量学生综合运用数学知识解决问题能力的重要部分。
此外,AMC10和AMC12的考题在一定程度上存在重合,特别是在基础题目部分,这可能使得两个考试的难度体现出一定的差异化。
对于准备参加或对数学竞赛感兴趣的学生来说,分析这些考题不仅有助于了解AMC10的题型和难度分布,还可以作为未来准备类似竞赛的参考。
amc10a 2023 透题

AMC10A 2023 透题一、考试概况1.1 AMC10A 2023是美国数学竞赛(American Mathematics Competitions,以下简称AMC)中的一场考试。
该考试是由美国数学学会(Mathematical Association of America,以下简称MAA)主办的,旨在激发学生对数学的兴趣,提高数学解决问题的能力,培养数学人才。
1.2 AMC10A 2023考试分为A、B两部分,每部分75分钟,共150分钟,共计25道选择题。
考试内容涵盖了基础数学知识、运算技巧、逻辑推理等多个方面,题目类型多样,难度适中。
1.3 考生可以通过学校或注册机构参加AMC10A 2023考试,成绩可以用于评选AMC奖项、参加本人ME、申请美国大学等。
二、考题特点2.1 知识点覆盖广泛。
AMC10A 2023考题覆盖了基础的代数、几何、概率、数论等数学知识点,要求考生具备全面的数学基础。
2.2 题型多样。
考题既有需要灵活运用数学知识解决问题的计算题,也有需要逻辑推理和数学思维能力的证明题,题型多样,考查面广。
2.3 难度适中。
AMC10A 2023考题难度适中,不会设置过于复杂的题目,但也能考查考生的数学解题能力。
三、备考建议3.1 夯实基础。
备考AMC10A 2023考试,首先要夯实数学基础知识,掌握代数、几何、概率、数论等知识点,熟练掌握相关的运算和解题技巧。
3.2 多做题。
通过多做真题和模拟题,可以熟悉考试题型和考点,培养解题技巧和逻辑思维能力,提高解题效率。
3.3 注重综合能力。
除了掌握基础知识和解题技巧,备考AMC10A 2023还要注重综合能力的培养,提高数学思维的灵活性和逻辑推理能力。
3.4 注意时间管理。
考试时间较短,需要考生在有限的时间内完成众多的题目,因此要注重时间管理,合理安排时间,确保每道题都能得到充分的解答。
3.5 多参加训练营和辅导班。
参加数学竞赛的训练营和辅导班,可以帮助考生系统地学习数学知识和解题技巧,提高备考效率。
十级入学测试卷

十级入学测试卷
(满分100分,附加题20分。
考试用时30分钟。
)姓名:年级:
1、(1+0.1)+(2+0.1×2)+(3+0.1×3)+…+(99+0.1×99)(20分)
2、在一个四位数的某一位数字前面添一个小数点,再和原来的数相减,差是
2009.7,则原来的数是多少?(20分)
3、、甲、乙两个运输员先后开车从北师大出版社出发前往北师大奥小,已知两车行驶的速度相同。
现在甲行驶在乙的前方,乙行驶了1500米,当乙追上甲时,甲已经行驶了2660米,甲现在离起点多少米?(20分)
4、、由七巧板拼成的正方形如图,如果正方形的边长是20厘米,问其中的一块平行四边形(图中阴影部分)的面积是多少?(20分)
5、、如图,已知△ABC、△ACD、△ADE、△AEF都是等腰直角三角形,EF=8厘米,梯形ABCD的面积是多少平方厘米?(20分)
附加题(20分):最后谁能胜(请写出推理过程)
有一个乡村,每年庆祝丰收的时候都会进行拔河比赛。
今年的比赛出现了这样的现象:
四个胖小伙与五个胖姑娘拉平。
两个胖姑娘加上一个胖小伙可以与一对瘦孪生兄弟对抗。
现在,这对瘦孪生兄弟和三个胖姑娘对一个胖姑娘和4个胖小伙,请问哪队能赢?。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
AMC10 入学模考卷(考试时间75分钟) 090117 v1 Problem 1What is the value of ?SolutionProblem 2For what value of does ?SolutionProblem 3For every dollar Ben spent on bagels, David spent cents less. Ben paid more than David.How much did they spend in the bagel store together?SolutionProblem 4The remainder can be defined for all real numbers and with bywhere denotes the greatest integer less than or equal to . What is the value of ?SolutionProblem 5A rectangular box has integer side lengths in the ratio . Which of the following could be thevolume of the box?SolutionProblem 6Ximena lists the whole numbers through once. Emilio copies Ximena's numbers, replacing eachoccurrence of the digit by the digit . Ximena adds her numbers and Emilio adds his numbers. How much larger is Ximena's sum than Emilio's?SolutionProblem 7The mean, median, and mode of the data values are all equal to .What is the value of ?SolutionProblem 8Trickster Rabbit agrees with Foolish Fox to double Fox's money every time Fox crosses the bridge by Rabbit's house, as long as Fox pays coins in toll to Rabbit after each crossing. The payment ismade after the doubling, Fox is excited about his good fortune until he discovers that all his money is gone after crossing the bridge three times. How many coins did Fox have at the beginning?SolutionProblem 9A triangular array of coins has coin in the first row, coins in the second row, coins in thethird row, and so on up to coins in the th row. What is the sum of the digits of ?SolutionProblem 10A rug is made with three different colors as shown. The areas of the three differently colored regions form an arithmetic progression. The inner rectangle is one foot wide, and each of the two shaded regions is foot wide on all four sides. What is the length in feet of the inner rectangle?SolutionProblem 11What is the area of the shaded region of the given rectangle?SolutionProblem 12Three distinct integers are selected at random between and , inclusive. Which of the following isa correct statement about the probability that the product of the three integers is odd?SolutionProblem 13Five friends sat in a movie theater in a row containing seats, numbered to from left to right. (Thedirections "left" and "right" are from the point of view of the people as they sit in the seats.) During the movie Ada went to the lobby to get some popcorn. When she returned, she found that Bea had moved two seats to the right, Ceci had moved one seat to the left, and Dee and Edie had switched seats, leaving an end seat for Ada. In which seat had Ada been sitting before she got up?SolutionHow many ways are there to write as the sum of twos and threes, ignoring order? (Forexample, and are two such ways.)SolutionProblem 15Seven cookies of radius inch are cut from a circle of cookie dough, as shown. Neighboring cookiesare tangent, and all except the center cookie are tangent to the edge of the dough. The leftover scrap is reshaped to form another cookie of the same thickness. What is the radius in inches of the scrap cookie?SolutionProblem 16A triangle with vertices , , and is reflected about the -axis, then the image is rotated counterclockwise about the origin by to produce . Whichof the following transformations will return to ?counterclockwise rotation about the origin by .clockwise rotation about the origin by .reflection about the -axisreflection about the linereflection about the -axis.SolutionLetbe a positive multiple of . One red ball andgreen balls are arranged in a line in randomorder. Let be the probability that at least of the green balls are on the same side of the red ball.Observe that and that approaches asgrows large. What is the sum of the digitsof the least value ofsuch that?SolutionProblem 18Each vertex of a cube is to be labeled with an integer through , with each integer being used once,in such a way that the sum of the four numbers on the vertices of a face is the same for each face. Arrangements that can be obtained from each other through rotations of the cube are considered to be the same. How many different arrangements are possible?SolutionProblem 19In rectangle and . Point between and , andpoint between and are such that .Segments and intersect at and , respectively. The ratio can bewritten as where the greatest common factor of and is 1. What is?SolutionProblem 20For some particular value of , when is expanded and like terms arecombined, the resulting expression contains exactly terms that include all fourvariables and , each to some positive power. What is ?SolutionProblem 21Circles with centers and , having radii and , respectively, lie on the same side ofline and are tangent to at and , respectively, with between and . The circle withcenter is externally tangent to each of the other two circles. What is the area of triangle ?SolutionProblem 22For some positive integer , the number has positive integer divisors, including and thenumber . How many positive integer divisors does the number have?SolutionProblem 23A binary operation has the properties that and that for allnonzero real numbers and . (Here represents multiplication). The solution to theequation can be written as , where and are relatively prime positive integers. What isSolutionProblem 24A quadrilateral is inscribed in a circle of radius . Three of the sides of this quadrilateral have length . What is the length of the fourth side?SolutionProblem 25How many ordered triples of positive integerssatisfy and ?Solution答题卡:。
