定积分的证明题44题word文档良心出品
01-客户服务题库(word文档良心出品)

单项选择题(50题)1、下面的(C)属于《供电服务规范》内容。
(A)用电检查服务规范(B)装表接电服务规范(C)“95598”服务规范(D)抄核收服务规范2、下面的(D)属于《供电服务规范》内容。
(A)用电检查服务规范(B)装表接电服务规范(C)抄核收服务规范(D)投诉举报处理服务规范3、《供电服务规范》要求接待客户时,应面带微笑,目光专注,做到(B)。
(A)满足客户要求(B)来有迎声、去有送声(C)提高服务水平(D)迎三步4、办理居民客户收费业务的时间一般每件不超过(C)分钟。
(A)3 (B)4 (C)5 (D)65、办理客户用电业务的时间一般每件不超过(D)。
(A)5 (B)10 (C)15 (D)206、如前一位客户业务办理时间过长,应对下一位客户(B)(A)不理睬(B)致歉(C)说明原因(D)优先办理7、当有特殊情况必须暂时停办业务时,应列示(A)标牌。
(A)暂停营业(B)停止营业(C)请稍侯(D)暂停办理8、下班时如仍有等候办理业务的客户,应(C)。
(A)暂停营业(B)停止营业(C)继续办理(D)暂停办理9、对客户投诉,应做到(A)跟踪投诉受理全过程。
(A)100% (B)98% (C)96% (D)95%10、《供电服务规范》中现场服务是对客户侧用电情况开展(B)。
(A)检查(B)巡查(C)抢修(D)维护11、对产权不属于供电企业的电力设施进行维护和抢修实行(D)的原则。
(A)无偿服务(B)产权归属(C)公平公正(D)有偿服务12、应客户要求进行有偿服务的,电力修复或更换电气材料的费用,执行(C)物价管理部门核定的收费标准。
(A)自治区、直辖市(B)地市(县级)(C)省(自治区、直辖市)(D)省(直辖市、地市)13、进行有偿服务工作时,客户付费后,应开具(C)。
(A)服务性收据(B)政府公益事业性收据(C)正式发票(D)白条14、国家电网公司员工服务“十个不准”规定,不准对外泄漏客户的( D )。
习题课_定积分的应用(解答)

中的 x0 唯一。
证明: (1)构造函数 g( x ) x f (t )dt ,对 g ( x ) 用罗尔定理即 可得证 。
x 1
(2) 考虑 g '( x) 的单调性来证明。
11
dx dx dx 2 2 2 2 0 1 2cos x 1 2cos x 2 1 2cos x
令 tan x t dx d tan x dt 2 2 而 ; 0 1 2cos 2 x 0 3 tan 2 x 0 3 t2 2 3
S S1 S2 (2 x x )dx ( x 2 2 x )dx 2
y x2 2 x
V y [(1 1 y )2 12 ]dy
1
0
[33 (1 1 y )2 ]dy 9
0
3 2 2 1 1
3
S2
1
o
3 2
d tan x 令 tan x t 0 dx dt 2 1 2cos2 x 2 3 tan2 x 3 t 2 2 3 ;
故原式
3
15
定积分的物理应用:
常 数 ,长度为 L 的细杆, 1.如图,x 轴上有一线密度为
有一质量为 m 的质点到杆右端的距离为 a ,已知引力 系数为 k,则质点和细杆之间引力的大小为( A ) (A) L
3
5. 设曲线 y f ( x ) 在 x 轴的上方,并过点 (1,1) ,该曲线与直线
x 1 , y 0 及动直线 x b(b 1) 所围图形绕 y 轴旋转所得的旋
(完整word版)算法设计试题(word文档良心出品)

一、选择题(15*2分)1.算法分析是( C)A.将算法用某种程序设计语言恰当地表示出来B.在抽象数据集合上执行程序,以确定是否会产生错误的结果C.对算法需要多少计算时间和存储空间作定量分析D.证明算法对所有可能的合法输入都能算出正确的答案2.算法与程序的区别在于算法具有(C )A.能行性B.确定性C.有穷性D.输入和输出3.记号Ω的定义正确的是(B)A.O(g(n)) = { f(n) | 存在正常数c和n0使得当n≥n0 有f(n) ≤ cg(n) }B.O(g(n)) = { f(n) | 存在正常数c和n0使得当n≥n0有 cg(n) ≤ f(n) }>0使得对所有n≥n0 C.(g(n)) = { f(n) | 对于任何正常数c>0,存在正数和n有f(n)<cg(n) }D.(g(n)) = { f(n) | 对于任何正常数c>0,存在正数和n>0使得对所有n≥n0有cg(n) < f(n) }4.衡量一个算法好坏的标准是(C )A.运行速度快B. 占用空间少C.时间复杂度低D. 代码短5.二分搜索算法是利用(A)实现的算法。
A.分治法B.动态规划法C.贪心法D.回溯法6.下面问题(B )不能使用贪心法解决。
A. 单源最短路径问题B. N皇后问题C. 最小代价生成树问题D. 背包问题7.用贪心法设计算法的关键是( B )。
A.将问题分解为多个子问题来分别处理B.选好最优量度标准C.获取各阶段间的递推关系式D.满足最优性原理8.找最小生成树的算法Kruskal的时间复杂度为( D )(其中n为无向图的结点数,m为边数)A.O(n2) B.O(mlogn) C.O(nlogm) D.O(mlogm)9.回溯法搜索状态空间树是按照(C )的顺序。
A.中序遍历B.广度优先遍历C.深度优先遍历D.层次优先遍历10. 一个问题可用动态规划算法或贪心算法求解的关键特征是问题的( B )A.重叠子问题B.最优子结构性质C.最优量度标准性质D.定义最优解11.程序块(A)是回溯法中遍历排列树的算法框架程序。
定积分证明题

x 0
F ( x ) f (t )dt xf ( x ) xf ( x ) f (t )dt
0 x x 0
x
x
F ( x )与( x )都是 f (t )dt的原函数
F ( x )=( x ) C F (0)=(0) 0 C 0 F ( x )=( x )
0
T
F ( a)
a T a
f ( x)dx
0
F (a ) f (a T ) f (a ) 0
F (a) C F (0) f ( x)dx
0 T
于是
a T a
f ( x)dx f ( x)dx
0
T
例5. 设 f C a, b , f x 0, x a, b ,
2 x
[ 12dt ][
a
a x
f ( x) dx] a
x
2
( x a) [ f (t )]2 dt
x
( x a) [ f ( x)]2dx,
a
a b
f ( x )dx [ f ( x )] dx ( x a )dx
2 2 a a a
M.
例 10 若 f (x) 在[a,b]上连续可导,且 f(a)=0, 2 b b 1 2 2 则 f ( x )dx (b a ) f ( x ) dx . a a 2 x , 证 显然 f ( x ) a 1 f (t )dt由柯西-施瓦兹不等式, 则
f ( x) [ 1 f (t )dt )]2
由广义积分中值定理
n 1
x 1 1 1 n 1 xdx 1 x dx 1 n 1 0 0
江苏专转本高等数学 定积分 例题加习题

- 106 -第四章 定积分本章主要知识点● 定积分计算● 特殊类函数的定积分计算 ● 变限积分● 定积分有关的证明题 ● 广义积分敛散性 ● 定积分应用(1)面积 (2)旋转体体积一、定积分计算定积分计算主要依据牛顿—莱伯尼兹公式:设⎰+=C x F dx x f )()(,则()()()()bb a af x dx F b F a F x =-=⎰。
其主要计算方法与不定积分的计算方法是类似的,也有三个主要方法,但需要指出的是对于第Ⅱ类直接交换法,注意积分限的变化:()111()()()()()(())x t bb aa t x f x dx f t t dt ϕϕϕϕϕϕ---=='=⎰⎰。
例4.1.111)edx x ⎰解:原式=e11)ln d x ⎰=32125((ln )ln )|33ex x +=例4.2.30dx ⎰ 解:原式t x t x =+-==11222 1121t tdt t -+⎰=32 121t t dt t -+⎰=322125()|33t t -= 例4.3.⎰22sin πxdx x- 107 -解:原式=⎰-22cos 21πx xd =⎰+-2022cos 21|2cos 21ππxdx x x =20|2sin 414ππx +=4π 二、特殊类函数的定积分计算1.含绝对值函数利用函数的可拆分性质,插入使绝对值为0的点,去掉绝对值,直接积分即可。
例4.4.⎰--21|1|dx x解:原式=121 1(1)(1)x dx x dx --+-⎰⎰=212|)2(2x x -+=)121(02--+=25例4.5.⎰--++22|)1||1(|dx x x解:原式=112211(|1||1|)(|1||1|)(|1||1|)x x dx x x dx x x dx ---++-+++-+++-⎰⎰⎰=112211(11)(11)(11)x x dx x x dx x x dx ------++++-+++-⎰⎰⎰=112211222xdx dx xdx ----++⎰⎰⎰=212122|4|x x ++---=)14(4)41(-++--=102.分段函数积分例4.6.⎩⎨⎧≤+>=0,10,)(2x x x x x f ,求⎰-11)(dx x f解:原式=⎰⎰-+0110)()(dx x f dx x f =⎰⎰-++01102)1(dx x dx x =103012|31|)2(x x x ++- =31)121(+--=65- 108 -例4.7.⎩⎨⎧≤>+=1,1,12)(x x x x x f ,求⎰-+12)1(dx x f解:原式11221(1)()u x f x dx f u du =+--=+==⎰⎰1211()()f u du f u du -+⎰⎰1222111(21)0()udu u du u u -=++=++⎰⎰624=-=3.奇函数积分如果 ()f x 为定义在[],a a -的奇函数,则()0aaf x dx -≡⎰,这是一个很重要考点。
定积分的证明题

又x3 > 0,∴ 4 − x2 − x3 > 4 − x2
∴1 <
1
<1
2 4 − x2 + x3 4 − x2
∫1 1dx = 1
02 2
∫1 dx = π
0 4 − x2 6
∫ ∴ 1 < 1
dx
< π。
2 0 4 − x2 + x3 6
∫ ∫ ∫ 6. 设函数f (x)和g(x)在[a,b]上连续,证明: [ b f (x)g(x)dx]2 ≤ b f 2(x)dx ⋅ b g2(x)dx 。
dx a = − f (a) + f (x) = f (x) − f (a)。
∫ 2. 设函数f (x)在[a,b]内可导,且f (a) = 0, b f (x)dx = 0, 证明:在[a, b]内至少存在一点ξ , a
使f ′(ξ ) = 0。
证明:
由积分中值定理,在(a, b)存在一点ξ
,使
1
∫ 1. 证明 d x (x − t) f ′(t)dt = f (x) − f (a) 。
dx a 证明:
∫ x (x − t) f ′(t)dt a x
= ∫a (x − t)df (t)
xx
= (x − t) f (t) a + ∫a f (t)dt
x
= (a − x) f (a) + ∫a f (t)dt ∫ ∴ d x (x − t) f ′(t)dt
即f (a) − (x − a) ≤ f (x) ≤ f (a) + (x − a) 由定积分的不等性质, 有
b
b
b
∫a [ f (a) − (x − a)]dx ≤ ∫a f (x)dx ≤ ∫a [ f (a) + (x − a)]dx
(完整版)定积分应用题附答案

《定积分的应用》复习题一.填空:1.曲线ln ,ln ,ln (0)y x y a y b a b y ===<<及轴所围成的平面图形的面积为A =ln ln by ae dy ⎰=b-a______2.2y x y ==曲线和 ____13____二.计算题:1.求由抛物线 y 2 = 2x 与直线 2x + y – 2 = 0 所围成的图形的面积。
解:(1)确定积分变量为y ,解方程组2222y x y x ⎧=⎨=-+⎩ 得12121/22,12x x y y ==⎧⎧⎨⎨==-⎩⎩ 即抛物线与直线的交点为(21,1)和( 2 , - 2 ).故所求图形在直线y = 1和y = - 2 之间,即积分区间为[-2,1 ]。
(2)在区间[-2,1]上,任取一小区间为[ y , y + dy ],对应的窄条面积近似于高为[(1-21y )-21y 2 ],底为dy 的矩形面积,从而得到面积元素 dA = [(1-21y)- 21y 2 ]dy (3)所求图形面积 A =⎰-12[(1- 21y )-21y 2 ]dy = [y - 41y 2 – 61y 3]12-= 942.求抛物线 y = - x 2 + 4x - 3 及其在点(0,- 3)和(3,0)处的切线所围成的图形的面积。
解:由y = - x 2 + 4x – 3 得 '24,'(0)4,'(3)2y x y y =-+==-。
抛物线在点(0,- 3)处的切线方程为 y = 4x – 3 ;在点(3,0)处的切线方程为 y = - 2x + 6 ; 两切线的交点坐标为 ( 32,3 )。
故 面积A =332223029[(43)(43)][(26)(43)]4x x x dx x x x dx --+-+-+-+-=⎰⎰3.求由摆线 x = a (t – sint) , y = a( 1- cost) 的一拱(02t π≤≤)与横轴所围成的图形的面积。
(完整word版)选择填空题库(word文档良心出品)

选择填空1、单选题(1)html中的注释标签是()A、 <-- -->B、<--! -->C、<!-- -->D、<-- --!>(2)<strong>…</strong>标签的作用是()A、斜体B、下划线C、上划线D、加粗(3)网页中的空格在html代码里表示为()A、&B、 C、"D、<(4)定义锚记主要用到<a>标签中的()属性。
A、nameB、targetC、onclickD、onmouseover(5)要在新窗口中打开所点击的链接,实现方法是将<a>标签的target属性设为()A、_blankB、_selfC、_parentD、_top(6)下列代表无序清单的标签是()A、 <ul>…<li>…</ul>B、<ol>…<li>…</ol>C、<hl>…<li>…</hl>D、< li >…< ol >…</ li >(7)要实现表单元素中的复选框,input标签的type属性应设为()A、radioB、checkboxC、selectD、text(8)要实现表单元素中的单选框,input标签的type属性应设为()A、radioB、checkboxC、selectD、text(9)要使表单元素(如文本框)在预览时处于不可编辑状态,显灰色,要在input中加()属性A、selectedB、disabledC、typeD、checked2、多选题(选错、多选、少选都不给分)(5*2)(1)定义表格常用的3个标签是()A、tableB、trC、tdD、tp(2)哪两个属性可用于表格的合并单元格()A、colspanB、trspanC、tdspanD、rowspan(3)实现下拉列表框,要用到一下哪几个标签()A、inputB、selectC、optionD、radio(4)定义框架要用到以下的哪个标签()A、frameworkB、framesetC、frameD、framespace(5)要在网页中加入音乐或背景音乐,以下哪个标签可以实现()A、embedB、objectC、bgsoundD、sound3、填空题(1*8)(1)、可用p标签定义段落。
(完整word版)定积分的证明题44题(word文档良心出品)

题目1证明题容易d x证明(x -t) f (t)dt = f (x) - f (a) dx」a题目2证明题容易JI利用积分中值定理证明:lim 4 sin n xdx ^0 b=0题目3证明题一般b设函数f(x)在[a,b]内可导,且f(a) =0, a 证明:在[a,b]内至少存在一点•使f ()f (x)dx = 0 =0。
题目4证明题一般设f (x) = f (x +a),na证明:当n为正整数时° f (x)dxan 0f (x)dx。
题目5证明题一般1 1 证明:oX m (1-x)n dxx n (1-x)m dx o 题目6证明题 一般设f (x)在[a,b ]上有定义,且对[a,b ]上任意两点x, y,有 f (x) — f (y) _ x — y.则f (x)在[a,b ]上可积,且1题目7证明题一般 设f (x)在[a,b ]上的连续,在(a,b)内可导,且f(a) = f (b) =0.b 2 证明:4 | f (x)dx 兰 M (b —a),其中 M = sup f "(x)。
a *x :bb[f (x)dx —(b —a) f (a)兰一(b —a)题目8证明题一般设f(x)在[a,b]上正值,连续,则在(a,b)内至少存在一点t ,b 1 b使f(x)dx = f(x)dx f(x)dx 。
■ a ' 2 ■ a题目9证明题一般jc 丑证明:0:::2sin n1xdx ::刁sin n xdx。
题目10证明题一般11 dx 二求证2°4-x2 x3 6题目11证明题一般设f(x)在区间(a,b)上连续,且在(a,b)内任一闭区间上积分为零,证明f(x)在(a,b)内恒等于零。
题目12证明题一般若函数f (x)在[0,1]上连续,a 3 2 1 a2证明:o x f(x )dx xf (x)dx (a 0)。
题目13证明题一般设函数f(x)和g(x)在[a,b]上连续,b 2 b 2 b 2证明:[f(x)g(x)dx]2乞f2(x)dx g2(x)dxa a a题目14证明题一般设f (x)在[0,1]上连续,证明:02f (sin2 Jcos「d = 04f(sin2 J(cos「sin「)d「题目15证明题一般设f (x)在[a,b]上可导,且 f (x)玄M, f(a) =0,b Me证明:a f(x)dx^3(b—a)2。
定积分复习

e
(10)ò -
1022)(1xmdx ;(11)ò
p
lnx dx ;(12)ò 20x cos xdx .
1
e
1
11.已知.. f(0) = 1, f (2) = 3, f ¢(2) = 5 ,试计算ò0
xf ¢
¢¢(2x)dx .
35 6
b
1
15
1
(5) -ln |1+ 3 cos x | +C; (6) -(3 -2x) + C; (7) -3 -2x + C; (8) -ln |1 -10 x | +C;
3 cosxx +
(9) -ln |1 -3e | +C; (10) ln | x -5x + 7| +C; (11) -e + C; (12) 2eC;
211
(arcsin x2)
dx ;(2)ò-
332423sinxx dx .
21-xx + 2x +1
7.计算下列定积分:
(1)ò
p
xdx;(2)ò xdx;(3)òp
2 12 sin
1
dx ;(4)ò
p
-322cos1pxdx;
203cossinx1022(x +1)1 xx
12.设.. f(x) 在区间[a, b] 上具有二阶连续导数,且.. f(a) = f (b) = 0 ,证明:..
1
f ¢¢(x)(x -a)(x -b)dx
ò 2 ò=
babaxdxf()
习题课十一 定积分的计算(解答)

1 2
1 2
1 sin3 3
x
1
2 1
2
1
2
1 1 (椭圆的一半面积) 2
2 sin3 3
1
24
4.
设
f
(
x)
1, x1
1 ex 1,
x0
,求
2
f ( x 1)dx .
0
x0
解:2 f ( x 1)dx令x 1 t 0
1
f (t)dt
1
01
1
et
dt 1
11 dt
0 t1
令x tan t
6
sec2 tdt
0 (2 tan2 t 1)sec t
6
costdt
0 2sin2t cos2t
6
dsint
0 1sin2t
arctan(sint
)
6
arctan1
0
2
7
3.
1 2
[cos
x(ln 1
x
sin2
x)
1 4x2 ]dx
1 2
1 x
1
1
2 cos x sin2 xdx 2 1 4x2 dx (对称区间奇函数性质)
t
ln(1 et )
0 1
+ln(1+t )
1 0
1
ln(1
e1 )+ln2
8
三、解答题
1.设 f ( x)
x2 et2 dt ,求
1
xf ( x)dx.
1
0
2. 已知 f (0) 1, f (2) 3, f (2) 5,求 1 xf (2 x)dx 。 0
7定积分的证明题

20]上连续且单调递增,
证明:
b
ab
xf (x)dx
b
f (x)dx
a
2a
3.设f (x)在[0, 1]上连续且递减,
证明:当0 a 1时,
a
f (x)dx a
1
f (x)dx
0
0
2020/9/10
2
例4:. 设f (x)a,+上连续,且单调增加
1
a
a
f [u(t)]dt
0
f
1 a
a 0
u(t
)dt
2020/9/10
9
15.设
S(
x
)
x
0
cos t
dt ,
(1)当 n 为正整数,且 n x ( n 1)时,
证明:2n S( x ) 2( n 1);
(2)求lim S( x ) . x x
2
2020/9/10
10
1例6.: 当f (x)是以2为周期的连续函数时,
证明 2,4,使2 f ( ) (1 ) f ( )
2020/9/10
7
12.
2020/9/10
8
13.设f (x)在[0,1]上二次可微,且f (x) 0
证明:01 f (xn )dx
f( 1 ) n 1
14. 设函数处处二阶可导且 f ( x) 0,
u(t )为任意连续函数,
证明:对任意常数a 0有
(2)
已知f
(
x)=
4
sinx cos2
x
2 xf ( x)dx,求f ( x)
0
2020/9/10
16
证明:函数G( x) 20x f (t)dt-x02 f (t)dt
证明题

十六章1、(10分)证明函数f(x,y)=x y y x x y x y x y sin sin ,,,110000000+≠≠=≠≠=⎧⎨⎪⎩⎪当当或在原点的极限是0. 2、(8分)证明lim()x y x xy y →→++=222173、证明: f x y x y y x x y x y x y (,)sin sin ,,,,,=+≠≠=≠≠=⎧⎨⎪⎩⎪110000000当当或在(0,0)的极限为零。
(10分) 4.设f(x,y) 在集合G ⊂R 2 上对x 连续,对y 满足利普希茨条件即f x y f x y L y y (,)(,)'-''≤'-''试证 f 在G 上处处连续十七章1、设ϕ,ψ 是任意的二阶可导函数,证明z=x y x y xϕψ()()+ 满足022222222=++y z y y x z xy x z x ∂∂∂∂∂∂∂ 2、(8分)设z=12224a tex b a tπ()- 证明∂∂∂∂z t a z t =2223、(10分)设z=sinx+F(u),u=siny-sinx 证明sec xz x ∂∂+secy ∂∂zy=1 4.证明函数2222222(,),0;(,)0,0x y f x y x y f x y x y x y=+≠=+=+在点(0,0)连续且偏导数存在,但在此点不可微.5. 证明函数222222(,)(0;(,)0,0f x y x y x y f x y x y =++≠=+=在点(0,0)连续且偏导数存在,但在此点偏导数不连续,而f 在(0,0)可微.6.证明:若二元函数f 在点00(,)P x y 的某邻域()U P 内的偏导函数x f 与y f 有界,则f 在()U P 内连续.7.证明:可微函数(,,)F x y z 为k 次齐次函数的充要条件是:(,,)(,,)(,,)(,,)x y z xF x y z yF x y z zF x y z kF x y z ++=8.设(,)f x y 可微,(,)(cos sin ,sin cos )g u v f u v u v θθθθ=-+,求证2222()()()()x y u v f f g g +=+9.设(,)f x y 可微,1l 与2l 是2R 上的一组线性无关向量.试证明:若(,)0(1,2)i l f x y i ≡=,则(,)f x y ≡常数.10.若(,)f x y 在区域D 上存在偏导数,且0x y f f =≡,则(,)f x y ≡常数.11.设,x y f f 和yx f 在点00(,)x y 的某领域内存在, yx f 在点00(,)x y 连续,证明00(,)xy f x y 也存在,且0000(,)(,)xy yx f x y f x y =.12. 设,x y f f 在点00(,)x y 的某领域内存在且在点00(,)x y 可微,则有0000(,)(,)x y y x f x y f x y =. 13.设f 在点000(,)P x y 可微,且在0P 给定了n 个向量(1,2,,)i l i n = ,相邻两个向量之间的夹角为2n π.证明:01()0i nl i f P ==∑.14.设(,)f x y 为n 次齐次函数,证明()(1)(1)m xy f n n n m f x y∂∂+=--+∂∂ . 十八章1、(10分)试证:所有切于曲面z xf y x=()的平面都相交于一点。
定积分及应用

∫
2 0
x 2 − 4 x + 4dx
2
解
∫
2
0
x − 4x + 4dx = ∫
2
x
0
1 (x − 2) dx = ∫ x − 2 dx = ∫ (2 − x)dx = (2x − x2 ) = 2 0 0 2 0
2 2 2
2
例 10
∫ t (t + sin t )dt 求 lim ∫ t dt
)
此题属于
0 型未定式的极限,由洛必达法则有 0
原式= lim
sin x 2 1 = x →0 3x 2 3
例6
∫
a
−a
x sin 8 xdx = (
)
解 例7
因 x sin 8 x 为奇函数且积分区间[-a,a]关于原点对称,故
∫
a
−a
x sin 8 xdx =0
d x 1 + t 4 dt = ( dx ∫ 0
0
a2
1 2 t
π
0
dt = ∫ tf (t )dt = ∫ xf ( x)dx
π
例2
设
∫
x 0
f ( t )dt = x sin x ,则 f(x)=(
(B)sinx-xcosx,
x 0
) (D) -(sinx+xcosx)
(A)sinx+xcosx, 解 例3 由
(C)xcosx-sinx,
∫
x 0
f (t )dt = x sin x ,则 ( ∫ f (t )dt )′ = ( x sin x)′ ,即 f(x)=sinx+xcosx,应选 B。
(完整word版)高等数学试题及答案(word文档良心出品)

《高等数学》一.选择题1. 当0→x 时,)1ln(x y +=与下列那个函数不是等价的 ( )A)、x y = B)、x y sin = C)、x y cos 1-= D)、1-=x e y2. 函数f(x)在点x 0极限存在是函数在该点连续的( )A )、必要条件B )、充分条件C )、充要条件D )、无关条件3. 下列各组函数中,)(x f 和)(x g 不是同一函数的原函数的有( ).A)、()()()2221,21)(x x x x e e x g e e x f ---=-=B)、(())()ln ,ln f x x g x x ==-C)、()()x x g x x f --=-=1arcsin 23,12arcsin )( D)、()2tan,sec csc )(xx g x x x f =+= 4. 下列各式正确的是( )A )、2l n 2x xx dx C =+⎰ B )、s i n c o s t d t t C =-+⎰C )、2a r c t a n 1dxdx x x =+⎰ D )、211()dx C x x-=-+⎰ 5. 下列等式不正确的是( ).A )、()()x f dx x f dx d b a =⎥⎦⎤⎢⎣⎡⎰ B )、()()()[]()x b x b f dt x f dx d x b a '=⎥⎦⎤⎢⎣⎡⎰ C )、()()x f dx x f dx d x a =⎥⎦⎤⎢⎣⎡⎰ D )、()()x F dt t F dx d x a '=⎥⎦⎤⎢⎣⎡'⎰ 6. 0ln(1)limxx t dt x→+=⎰( )A )、0B )、1C )、2D )、47. 设bx x f sin )(=,则=''⎰dx x f x )(( )A )、C bx bx b x +-sin cos B )、C bx bx b x+-cos cos C )、C bx bx bx +-sin cos D )、C bx b bx bx +-cos sin8. 10()()bx xa e f e dx f t dt =⎰⎰,则( )A )、1,0==b aB )、e b a ==,0C )、10,1==b aD )、e b a ==,19. 23(sin )x x dx ππ-=⎰( )A )、0B )、π2C )、1D )、22π10. =++⎰-dx x x x )1(ln 2112( )A )、0B )、π2C )、1D )、22π11. 若1)1(+=x xxf ,则dx x f ⎰10)(为( )A )、0B )、1C )、2ln 1-D )、2ln12. 设)(x f 在区间[]b a ,上连续,⎰≤≤=xa b x a dt t f x F )()()(,则)(x F 是)(x f 的( ).A )、不定积分B )、一个原函数C )、全体原函数D )、在[]b a ,上的定积分13. 设1sin 2y x x =-,则dxdy=( ) A )、11c o s2y - B )、11c o s2x - C )、22c o sy- D )、22c o sx-14. )1ln(1lim 20x e x xx +-+→=( )A 21-B 2C 1D -115. 函数x x y +=在区间]4,0[上的最小值为( )A 4;B 0 ;C 1;D 3二.填空题1. =+++∞→2)12(lim xx x x ______.2. 2-=⎰3. 若⎰+=C e dx e x f xx 11)(,则⎰=dx x f )(4. =+⎰dt t dx d x 26215. 曲线3y x =在 处有拐点 三.判断题 1. xxy +-=11ln是奇函数. ( ) 2. 设()f x 在开区间(),a b 上连续,则()f x 在(),a b 上存在最大值、最小值.( ) 3. 若函数()f x 在0x 处极限存在,则()f x 在0x 处连续. ( ) 4. 0sin 2xdx π=⎰. ( )5. 罗尔中值定理中的条件是充分的,但非必要条件.( )四.解答题1. 求.cos 12tan lim20xxx -→ 2. 求nxmxx sin sin limπ→,其中n m ,为自然数.3. 证明方程01423=+-x x 在(0,1)内至少有一个实根.4. 求cos(23)x dx -⎰.5. 求⎰+dx xx 321.6. 设21sin ,0()1,0x x f x x x x ⎧<⎪=⎨⎪+≥⎩,求()f x '7.求定积分4⎰8. 设)(x f 在[]1,0上具有二阶连续导数,若2)(=πf ,⎰=''+π5sin )]()([xdx x f x f ,求)0(f ..9. 求由直线0,1,0===y x x 和曲线x e y =所围成的平面图形绕x 轴一周旋转而成的旋转体体积《高等数学》答案一.选择题1. C2. A3. D4. B5. A6. A7. C8. D9. A 10. A 11. D 12. B 13. D14. A15. B 二.填空题 1. 21e 2. 2π 3. C x+1 4. 412x x + 5. (0,0) 三.判断题 1. T 2. F 3. F 4. T 5. T 四.解答题 1. 82. 令,π-=x t nmn nt m mt nx mx n m t x -→→-=++=)1()sin()sin(lim sin sin lim 0πππ3. 根据零点存在定理.4.1cos(23)cos(23)(23)31sin(23)3x dx x d x x C-=---=--+⎰⎰5. 令t x =6,则dt t dx t x 566,==原式⎰⎰⎰++-=+=+=dt )t111t (6dt t 1t 6dt t t t 62435 C t 1ln t 2t 62+⎪⎭⎫⎝⎛++-= C x x x +++⋅-⋅=6631ln 6636. 222sin 2cos ,0()1,00x x x x f x x x ⎧-+<⎪⎪⎪'=>⎨⎪=⎪⎪⎩不存在,7. 42ln3-8. 解:⎰⎰⎰''--=-=ππππ0sin )()0()()cos ()(sin )(xdx x f f f x d x f xdx x f所以3)0(=f9. V=())1(2121)2(212102102102210-====⎰⎰⎰e e x d e dx e dx exx xxπππππ 《高等数学》试题2一.选择题1. 当0→x 时,下列函数不是无穷小量的是 ( )A )、x y =B )、0=yC )、)1ln(+=x yD )、x e y =2. 设12)(-=x x f ,则当0→x 时,)(x f 是x 的( )。
(完整word版)综合题(word文档良心出品)
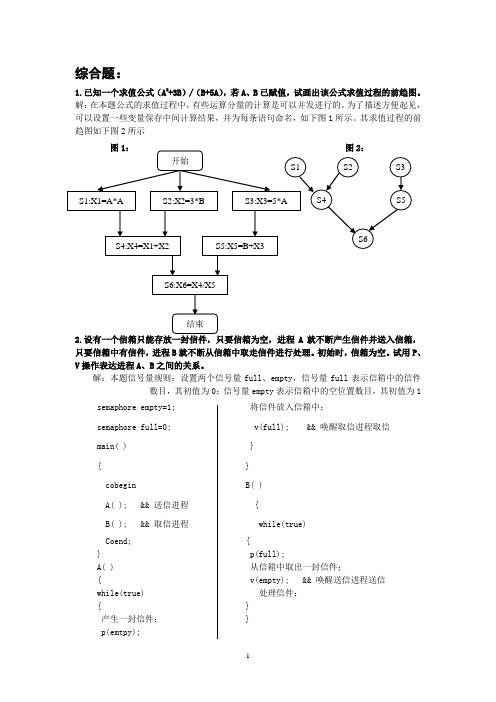
综合题:1.已知一个求值公式(A2+3B)/(B+5A),若A、B已赋值,试画出该公式求值过程的前趋图。
解:在本题公式的求值过程中,有些运算分量的计算是可以并发进行的。
为了描述方便起见,可以设置一些变量保存中间计算结果,并为每条语句命名,如下图1所示。
其求值过程的前趋图如下图2所示只要信箱中有信件,进程B就不断从信箱中取走信件进行处理。
初始时,信箱为空。
试用P、V操作表达进程A、B之间的关系。
解:本题信号量规则:设置两个信号量full、empty,信号量full表示信箱中的信件数目,其初值为0;信号量empty表示信箱中的空位置数目,其初值为1 semaphore empty=1; 将信件放入信箱中;semaphore full=0; v(full); && 唤醒取信进程取信main( ) }{ }cobegin B( )A( ); && 送信进程 {B( ); && 取信进程 while(true)Coend; {} p(full);A( ) 从信箱中取出一封信件;{ v(empty); && 唤醒送信进程送信while(true) 处理信件;{ }产生一封信件; }p(emtpy);3.有两个程序,A程序按顺序使用CPU 10秒,使用设备甲5秒,使用CPU 5秒,使用设备乙10秒,最后使用CPU 10秒。
B程序按顺序使用设备甲10秒,使用CPU 10秒,使用设备乙5秒,使用CPU 5秒,使用设备乙10秒。
在顺序执行环境下,先执行A程序,再执行B 程序,问CPU的利用率是多少?解:有题目所给条件可知,两个程序顺序执行,先执行程序A,后执行程序B。
A程序的执行时间为:10+5+5+10+10=40秒其中使用CPU的时间为:10+5+10=25秒B程序的执行时间为:10+10+5+5+10=40秒其中使用CPU的时间为:10+5=15秒两个程序的总执行时间为:40+40=80秒其中使用CPU时间为:15+25=40秒故CPU利用率为:40/80*100%=50%4.某虚拟存储器的用户编程空间共32个页面,每页为1KB,内存为16KB。
定积分证明题方法总结

定积分证明题方法总结定积分证明题方法总结「篇一」一、原函数定义1 如果对任一xI,都有F(x)f(x) 或 dF(x)f(x)dx则称F(x)为f(x)在区间I 上的原函数。
例如:(sinx)cosx,即sinx是cosx的原函数。
[ln(xx2)原函数存在定理:如果函数f(x)在区间I 上连续,则f(x)在区间I 上一定有原函数,即存在区间I 上的可导函数F(x),使得对任一xI,有F(x)f(x)。
注1:如果f(x)有一个原函数,则f(x)就有无穷多个原函数。
设F(x)是f(x)的原函数,则[F(x)C]f(x),即F(x)C也为f(x)的原函数,其中C为任意常数。
注2:如果F(x)与G(x)都为f(x)在区间I 上的原函数,则F(x)与G(x)之差为常数,即F(x)G(x)C(C为常数)注3:如果F(x)为f(x)在区间I 上的一个原函数,则F(x)C(C为任意常数)可表达f(x)的任意一个原函数。
1x2,即ln(xx2)是1x2的原函数。
二、不定积分定义2 在区间I上,f(x)的带有任意常数项的原函数,成为f(x)在区间I上的不定积分,记为f(x)dx。
如果F(x)为f(x)的一个原函数,则f(x)dxF(x)C,(C为任意常数)三、不定积分的几何意义图 5—1 设F(x)是f(x)的一个原函数,则yF(x)在平面上表示一条曲线,称它为f(x)f(x)的不定积分表示一族积分曲线,它们是由f(x)的某一条积分曲线沿着y轴方向作任意平行移动而产生的所有积分曲线组成的.显然,族中的每一条积分曲线在具有同一横坐标x的点处有互相平行的切线,其斜率都等于f(x).在求原函数的具体问题中,往往先求出原函数的一般表达式yF(x)C,再从中确定一个满足条件 y(x0)y0 (称为初始条件)的原函数yy(x).从几何上讲,就是从积分曲线族中找出一条通过点(x0,y0)的积分曲线.四、不定积分的性质(线性性质)[f(x)g(x)]dxf(x)dxg(x)dxk为非零常数) kf(x)dxkf(x)dx(五、基本积分表∫ a dx = ax + C,a和C都是常数∫ x^a dx = [x^(a + 1)]/(a + 1) + C,其中a为常数且 a ≠ -1 ∫ 1/x dx = ln|x| + C∫ a^x dx = (1/lna)a^x + C,其中a > 0 且 a ≠ 1∫ e^x dx = e^x + C∫ cosx dx = sinx + C∫ sinx dx = - cosx + C∫ cotx dx = ln|sinx| + C = - ln|cscx| + C∫ tanx dx = - ln|cosx| + C = ln|secx| + C∫ secx dx =ln|cot(x/2)| + C= (1/2)ln|(1 + sinx)/(1 - sinx)| + C= - ln|secx - tanx| + C = ln|secx + tanx| + C ∫ cscx dx = ln|tan(x/2)| + C= (1/2)ln|(1 - cosx)/(1 + cosx)| + C= - ln|cscx + cotx| + C = ln|cscx - cotx| + C ∫ sec^2(x) dx = tanx + C∫ csc^2(x) dx = - cotx + C∫ secxtanx dx = secx + C∫ cscxcotx dx = - cscx + C∫ dx/(a^2 + x^2) = (1/a)arctan(x/a) + C∫ dx/√(a^2 - x^2) = arcsin(x/a) + C∫ dx/√(x^2 + a^2) = ln|x + √(x^2 + a^2)| + C∫ dx/√(x^2 - a^2) = ln|x + √(x^2 - a^2)| + C∫ √(x^2 - a^2) dx = (x/2)√(x^2 - a^2) - (a^2/2)ln|x + √(x^2 - a^2)| + C ∫ √(x^2 + a^2) dx = (x/2)√(x^2 + a^2) + (a^2/2)ln|x +√(x^2 + a^2)| + C ∫ √(a^2 - x^2) dx = (x/2)√(a^2 - x^2) +(a^2/2)arcsin(x/a) + C六、第一换元法(凑微分)设F(u)为f(u)的原函数,即F(u)f(u) 或 f(u)duF(u)C 如果 u(x),且(x)可微,则 dF[(x)]F(u)(x)f(u)(x)f[(x)](x) dx即F[(x)]为f[(x)](x)的原函数,或f[(x)](x)dxF[(x)]C[F(u)C]u(x)[f(u)du]因此有定理1 设F(u)为f(u)的原函数,u(x)可微,则f[(x)](x)dx[f(u)du]公式(2-1)称为第一类换元积分公式。
【数学】证明题

有些题目中关于单调性与有界性的证明有先后次序之分,需要及时调整证明次序(证明单调性时需用有界性,从而必先证明数列有界;或证明 有界性时需用单调性,从而必先证明数列的单调性)
1
1
Hale Waihona Puke f(x) = f(0) + f′(0)x + 2!f″(0)x2 + 3!f‴(ξ)x3
,ξ在0与x之间 在上式中分别取x=1和x=-1 1=f(1)=f(0)+... 0=f(-1)=f(0)+... 两式相减得,f'''(ξ1)+f'''(ξ2)=6,即(f'''(ξ1)+f'''(ξ2))/2=3 由于f'''(x)连续,则f'''(x)在闭区间[ξ1,ξ2]上有最大值M和最小值m m≤(f'''(ξ1)+f'''(ξ2))/2≤M 由连续函数介值定理知,存在ξ∈[ξ1,ξ2]⊆(-1,1),使f'''(ξ)=(f'''(ξ1)+f'''(ξ2))/2=3
目的:寻找一个辅助函数G(x),使G'(x)=F[ξ,f(ξ),f'(ξ)]或者G'(x)={F[ξ,f(ξ),f'(ξ)]}g(x);这样就可使得G'(x)的零点与F[]的零点一 致。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
题目1证明题 容易
d x 证明丄 f (X _t) f Tt)dt = f(X)_ f (a)。
dx 'a
题目2证明题 容易
题目3证明题 一般
b
设函数 f(x)在[a,b ]内可导,且 f(a)=0,[ f(x)dx
= 0 证明:在[a,b ]内至少存在一点E 使f(E )=0。
题目4证明题 一般
设f(X)= f(X +a).
na
证明:当n 为正整数时 L f(x)dx= nj0f(x)dx 。
利用积分中值定理证明 :lim f 4 sin n
xdx = 0。
」0
1 1
证明:x m (1-x)n dx = Lx n (1 —x)m dx 。
题目6证明题 一般
设f (x)在[a,b ]上有定义,且对[a,b ]上任意两点x, y,
x — y |.则f (x)在[a,b ]上可积,且
1 2
题目7证明题 一般
设f(X)在[a,b ]上的连续,在(a,b)内可导,且f(a) = f (b) =0. 证明:4a|f(x)|dx<M(b —a)2,其中M = sup f'(x)。
f(x)dx —(b —a)f(a) <?(b —a)。
f(X)。
(a,b)内至少存在一点匕,设f (x)在[a,b]上正值,连续,则在
£ b 1 b
使J a f (x)dx = J E f (x)dx = —J a f (x)dx。
■* 2
题目9证明题一般
丑丑
证明:0<FsinXxdxc『sin n xdx。
题目10证明题一般
1/ dx 兀
求证:一<〔<-。
20 2,3 6
2V4 —X +x 6
题目11证明题一般
设f(x)在区间(a,b)上连续,且在(a,b)内任一闭区间上积分为零,证明f(x)在(a,b)内恒等于零。
题目12证明题一般
若函数f(x)在[0,1]上连续,
a 3 2 1 a2
(a A O)。
证明:J0x f(x )dx=5 J o xf (x)dx
题目13证明题一般
设函数f(x)和g(x)在[a,b]上连续,
b 2 b 2 b 2
证明:[f f(x)g(x)dx]< f f (x)dx 订g (x)dx。
a a a
题目14证明题一般
设f (x)在[0,1]上连续,
丑丑
证明:『f (sin2®)cos® d W = J; f (sin2W)(cos® +sin
申)d W 。
题目15证明题一般
设f(X)在[a,b]上可导,且f(X)<M, f(a) =0, 证明:a
f(x)dx<M(b-a)2。
题目16证明题一般
设f(x)在[Q2a],(a >0)上连续,
2a a
证明:f(x)dx= .0[f(x) + f(2a—x)]dx。
题目17证明题一般
设k为正整数,证明:
(1H 兀cos2 kxdx =兀
(2H^si n 2kxdx =兀
,-n;
题目18证明题一般
设f(x)在[0,1]上有一阶连续导数•且f(1) - f(0) =1.
2
1
试证:[[f '(X)] dx 3。
题目19证明题一般
若m为正整数,
迟1
fcos E xdx。
证明:『cos m x sin m xdx =班
若函数f(x)在区间[a,b]上连续,
b b
贝y L f(x)dx=(b-a) Jaf[a+(b-a)x]dx。
题目21证明题一般
设函数f(x)在[0,1]上连续,
1 2兀
证明:『f(
cosx|)dx =;)0 f (cosx )dx。
题目22证明题一般
x
若函数f(x)在R连续,且f(x)=l' f(t)dt,则f(x)三0。
・a
设f(x)是以;I 为周期的连续函数,
2 吓 -TT-
证明:『(sinx + x)f (x)dx =+ (x)dx o
题目24证明题 一般
设f (x)在[0,1]上连续且单调递减, 试证明:对于任何q€[0,1],都有不等式 q 1 、
Jo f (x)dx >q L f (x)dx 成立。
题目25证明题 一般
设f(X)在[a,b ]上单调增加且f "(X)>0.
、 b 证明:(b-a) f (a) C J a f(x)dx v(b-a)
f(a)+ f(b) --------- o
设函数f(x)在[a, b]上连续且单调递增。
1 X
F(x)[ f (t)dt ,(a c x<b)
X - a 'a
F(a) = f(a), 证明:F(x)在[a,b]上单调增.。
题目27证明题一般
设f (X)在[a,b]上二阶可导且f 7x) c O, b a + b
证明:a f (x)dx <(b -a) f (^^)。
题目28证明题一般
设f (x)在[a,b]上连续,在[a,b]可导,且f'(x)vO,证明函数
F(X)=广丄%
'a X -a
在(a,b)内满足 F '(X)<0。
试证:如果f(x)在[a,b]上连续,且对于一切X忘[a,b],
f(x)>0
” b
同时至少存在一点©引a, b],使f(©);>0,则f f(x)dx;>0。
*■ a
题目30证明题一般
b c _a
试证 f f (c —x)dx = f f (x)dx。
■a・c_b
题目31证明题一般
设函数f(x)在[0,1]上可微,且满足等式:
1
f(1)—2fxf(x)dx =0
试证在(0,1)内至少存在一点©,使f佗)=-響
J
设f(x)在[a,b]上连续,并且对于每一个在[a,b] b
上的连续函数g(x).都有[g(x) f (x)dx = 0 证明:f(x)=O
(a<x<b)。
题目33证明题难
b — a b ' 2
则J a|f(x)「(x)|dx J a[ f (x)]
设函数f(x)在[a,b]上有连续导数f'(x,且f(a) = O,
一 . b
J a
题目34证明题难
设f(x)在[a,b]上二阶连续可微,其中acOcb,则在该区间上必存在一个E,使
b 1
2 2
f(x)dx=bf(b)—af(a)—2![bf(b)—af(a)]
a
+»)*)。
题目35证明题难
若f(x)关于X =T对称,且acTcb,
b b 2T』
贝y J a f (x)dx =2 J T f (x)dx + J a f (x)dx。
2
x .
1 ~A 4 dx= L
1+x 242
题目37证明题难
证明奇函数的一切原函
偶函数的原函数中有一
数皆为偶函数,
为奇函数。
X X 4 设f(X)在[a,b]上连续,且f(x)〉O,又F(x) = Ja f
(t)dt + Jb〒話dt
证明:F(X)= 0在[a, b]内有且仅有一个实根。
题目39证明题难
a a 2 1 a
a
2 1
证明:当a A1 时,有f f(X2+-2) — dx= f f(x+—)—dx。
1X X 1X X
题目41证明题 难
证明:若 f f 2(x )dx =0则f (X )=0
a
题目40证明
题 难 f (X )在[0,+=c ]连
续,且
lim f(X)= A, 则:lim X T^X -r f (t)dt = A 。
「0 \ /
X 忘[a,b ]。
设函数f(x)在[a,b]上连续,
1 x
证明:I迪¥ J a[f(t +h)-f(t)]dt = f(x)-f(a) (a e x
<b)。
题目43证明题难
设f(x)处处二阶可导,且f“(x)30又u(t)为任一连续函
数,
1 a 1 a
(a》0)。
证明:一0 f[u(t)]dt > f[- f u(t)dt]
a 0 a 0
证明:若函数f (x)在[0^)一致连续,
-4^
且无穷积分J o「f(x)dX攵敛,则lim f(x)=0。
