小学数学平行四边形和梯形精选练习

合集下载

小学五年级数学多边形面积精选题目重难点题目练习题

五年级数学多边形面积经典题目一一、填空1.一个三角形的面积是25平方厘米，和它等底等高的平行四边形的面积是( )平方厘米。

2.平行四边形的底长16米，高是12米，它的面积是（）平方米。

3.在一个长9厘米，周长26厘米的长方形内画一个最大的三角形，这个三角形的面积是( )平方厘米。

4.三角形的底扩大3倍，高扩大2倍，面积扩大（）倍。

5.一个三角形与梯形的高相等，它们的面积也相等。

那梯形的上底与下底的和等于三角形( )的长度。

6.右图中阴影部分的面积是15平方厘米，长方形的面积是( )平方厘米。

7..一个平行四边形的底是6厘米，高是14厘米，它的面积是（）平方厘米，与它等底等高的三角形面积是（）平方厘米。

8.如图，每个方格的边长为1厘米，这只小鱼的面积是（）平方厘米。

9.有一个长方形长15厘米，宽8厘米，另一直角梯形上底长7厘米，下底长6厘米，高8厘米，将它们拼成一个梯形，梯形的面积是( )平方厘米。

10.一个平行四边形，底为10分米，高是4分米，如果底不变，高增加2分米，则面积增加（）平方分米；若高不变，底增加2分米，则面积增加（）平方分米。

11.将木条订成的长方形后拉成一个平行四边形（如图），原来长方形的面积是（）平方厘米，现在平行四边形的面积是（）平方厘米，现在平行四边形的周长是（）厘米。

12、4.6m2=（）dm2 3200cm2=（）dm213、用字母表示三角形的面积公式S=（）。

14、一个平行四边形的底和高都是1.6m，它的面积是（）m2，和它等底等高的三角形的面积是（）m2。

15、一个直角三角形的两条直角边分别是6cm和8cm，斜边长10cm，这个直角三角形的面积是（）cm2。

16、两个完全一样的梯形可以拼成一个（）。

二、判定题（每题2分，共10分）1．两个面积相等的三角形，一定能拼成一个平行四边形.（）2．平行四边形的面积等于一个三角形面积的2倍.（）3．两个完全一样的梯形，能拼成一个平行四边形.（）4．把一个长方形的框架挤压成一个平行四边形，面积减少了.（）5．两个三角形面积相等，底和高也一定相等。

人教版五年级上册数学《梯形面积》精选练习(含答案)

人教版五年级上册数学《梯形面积》精选练习练习一一、单选题1.下图中，平行线间梯形A，B的面积相等，梯形B的下底是（）cm。

A. 5B. 3C. 3.3D. 无法确定2.一个梯形的面积是18m2，它的上底是3m，高是4m，求它的下底。

下面( )是正确的。

A. 18÷4-3=1.5B. 18×2÷4-3=6 C. 18×2÷4+3=12 D. 无法计算3.利用篱笆和一面墙围成了如右图所示的小菜园，篱笆长64m，小菜园的面积是（）m2。

A. 217B. 294.5C. 315D. 4754.等腰梯形的周长是48厘米，面积是96平方厘米，高是8厘米，则腰长是（）。

A. 24厘米B. 12厘米C. 18厘米 D. 36厘米二、判断题5.．平行四边形的面积是梯形面积的2倍（）6.面积相同的两个梯形，形状完全相同。

（）7.一个梯形的上底是6米，下底是8米，面积是42平方米，它的高是6米。

（）8.面积相等的梯形和平行四边形的高不一定相等。

（）三、填空题9.看图计算(单位：米)梯形的面积S=________平方米10.一个梯形的上底扩大2倍，下底也扩大2倍，它的面积就扩大________倍。

11.一个直角梯形，如果把上底延长5厘米，面积就增加25平方厘米，而且变成一个正方形，原来梯形的面积是________平方厘米．12.计算下列图形的面积是________四、解答题13.下图是一个平行四边形和一个阴影三角形组合成的梯形，梯形面积是25平方厘米，求阴影三角形面积。

单位：cm14.求出下列图形阴影部分的面积．五、应用题15. 梯形的上底是3.8厘米，高是4厘米，已知它的面积是20平方厘米，下底是多少厘米？练习二一、单选题（共5题；共10分）1.一个梯形的上底与高的积是24，下底与高的积是40。

这个梯形的面积是（）。

A. 32B. 44C. 52D. 642.王大伯用46米篱笆在河边围了一块梯形的地种菜（如图，河岸不要篱笆）。

小学五年级上册数学练习题人教版

小学五年级上册数学练习题人教版（经典版）编制人：__________________审核人：__________________审批人：__________________编制单位：__________________编制时间：____年____月____日序言下载提示：该文档是本店铺精心编制而成的，希望大家下载后，能够帮助大家解决实际问题。

文档下载后可定制修改，请根据实际需要进行调整和使用，谢谢!并且，本店铺为大家提供各种类型的经典范文，如演讲致辞、规章制度、策划方案、合同协议、条据文书、心得体会、职业规划、教学资料、作文大全、其他范文等等，想了解不同范文格式和写法，敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!Moreover, our store provides various types of classic sample essays for everyone, such as speeches, rules and regulations, planning plans, contract agreements, documentary evidence, insights, career planning, teaching materials, complete essays, and other sample essays. If you want to learn about different sample formats and writing methods, please pay attention!小学五年级上册数学练习题人教版小学五年级上册数学练习题人教版（18篇）五年级数学老师在数学教学中要结合教学内容向学生传授数学学习和记忆的方法。

平行四边形性质和判定综合习题精选(答案详细)

第十九章平行四边形性质和判定综合习题精选一．解答题（共30小题）1．（2011•资阳）如图，已知四边形ABCD为平行四边形，AE⊥BD于E，CF⊥BD于F．（1）求证：BE=DF；（2）若M、N分别为边AD、BC上的点，且DM=BN，试判断四边形MENF的形状（不必说明理由）．2．（2011•昭通）如图所示，▱AECF的对角线相交于点O，DB经过点O，分别与AE，CF交于B，D．求证：四边形ABCD是平行四边形．3．（2011•徐州）如图，在四边形ABCD中，AB=CD，BF=DE，AE⊥BD，CF⊥BD，垂足分别为E，F．（1）求证：△ABE≌△CDF；（2）若AC与BD交于点O，求证：AO=CO．4．（2011•铜仁地区）已知：如图，在△ABC中，∠BAC=90°，DE、DF是△ABC的中位线，连接EF、AD．求证：EF=AD．5．（2011•泸州）如图，已知D是△ABC的边AB上一点，CE∥AB，DE交AC于点O，且OA=OC，猜想线段CD与线段AE的大小关系和位置关系，并加以证明．6．（2010•恩施州）如图，已知，▱ABCD中，AE=CF，M、N分别是DE、BF的中点．7．（2009•永州）如图，平行四边形ABCD，E、F两点在对角线BD上，且BE=DF，连接AE，EC，CF，FA．求证：四边形AECF是平行四边形．8．（2009•来宾）在▱ABCD中，分别以AD、BC为边向内作等边△ADE和等边△BCF，连接BE、DF．求证：四边形BEDF是平行四边形．9．（2006•黄冈）如图所示，DB∥AC，且DB=AC，E是AC的中点，求证：BC=DE．10．（2006•巴中）已知：如图，在梯形ABCD中，AD∥BC，AD=24cm，BC=30cm，点P自点A向D以1cm/s的速度运动，到D点即停止．点Q自点C向B以2cm/s的速度运动，到B点即停止，直线PQ截梯形为两个四边形．问当P，Q同时出发，几秒后其中一个四边形为平行四边形？11．（2002•三明）如图：已知D、E、F分别是△ABC各边的中点，求证：AE与DF互相平分．12．已知：如图，在▱ABCD中，对角线AC交BD于点O，四边形AODE是平行四边形．求证：四边形ABOE、四边形DCOE都是平行四边形．13．如图，已知四边形ABCD中，点E，F，G，H分别是AB、CD、AC、BD的中点，并且点E、F、G、H有在同一条直线上．求证：EF和GH互相平分．14．如图：▱ABCD中，MN∥AC，试说明MQ=NP．15．已知：如图所示，平行四边形ABCD的对角线AC，BD相交于点O，EF经过点O并且分别和AB，CD相交于点E，F，点G，H分别为OA，OC的中点．求证：四边形EHFG是平行四边形．16．如图，已知在▱ABCD中，E、F是对角线BD上的两点，BE=DF，点G、H分别在BA和DC的延长线上，且AG=CH，连接GE、EH、HF、FG．（1）求证：四边形GEHF是平行四边形；（2）若点G、H分别在线段BA和DC上，其余条件不变，则（1）中的结论是否成立？（不用说明理由）17．如图，在△ABC中，D是AC的中点，E是线段BC延长线一点，过点A作BE的平行线与线段ED的延长线交于点F，连接AE、CF．（1）求证：AF=CE；（2）如果AC=EF，且∠ACB=135°，试判断四边形AFCE是什么样的四边形，并证明你的结论．18．如图平行四边形ABCD中，∠ABC=60°，点E、F分别在CD、BC的延长线上，AE∥BD，EF⊥BF，垂足为点F，DF=2（1）求证：D是EC中点；（2）求FC的长．19．（2010•厦门）如图，已知△ABC是等边三角形，点D、F分别在线段BC、AB上，∠EFB=60°，DC=EF．（1）求证：四边形EFCD是平行四边形；（2）若BF=EF，求证：AE=AD．20．（2010•滨州）如图，四边形ABCD，E、F、G、H分别是AB、BC、CD、DA的中点．（1）请判断四边形EFGH的形状？并说明为什么；（2）若使四边形EFGH为正方形，那么四边形ABCD的对角线应具有怎样的性质？21．（2008•佛山）如图，△ACD、△ABE、△BCF均为直线BC同侧的等边三角形．（1）当AB≠AC时，证明：四边形ADFE为平行四边形；（2）当AB=AC时，顺次连接A、D、F、E四点所构成的图形有哪几类？直接写出构成图形的类型和相应的条件．22．如图，以△ABC的三边为边，在BC的同侧分别作三个等边三角形即△ABD、△BCE、△ACF，那么，四边形AFED是否为平行四边形？如果是，请证明之，如果不是，请说明理由．23．（2007•黑龙江）在△ABC中，AB=AC，点P为△ABC所在平面内一点，过点P分别作PE∥AC交AB于点E，PF∥AB交BC于点D，交AC于点F．若点P在BC边上（如图1），此时PD=0，可得结论：PD+PE+PF=AB．请直接应用上述信息解决下列问题：当点P分别在△ABC内（如图2），△ABC外（如图3）时，上述结论是否成立？若成立，请给予证明；若不成立，PD，PE，PF与AB之间又有怎样的数量关系，请写出你的猜想，不需要证明．24．（2006•大连）如图1，P为Rt△ABC所在平面内任意一点（不在直线AC上），∠ACB=90°，M为AB边中点．操作：以PA、PC为邻边作平行四边形PADC，连续PM并延长到点E，使ME=PM，连接DE．探究：（1）请猜想与线段DE有关的三个结论；（2）请你利用图2，图3选择不同位置的点P按上述方法操作；（3）经历（2）之后，如果你认为你写的结论是正确的，请加以证明；如果你认为你写的结论是错误的，请用图2或图3加以说明；（注意：错误的结论，只要你用反例给予说明也得分）（4）若将“Rt△ABC”改为“任意△ABC”，其他条件不变，利用图4操作，并写出与线段DE有关的结论（直接写答案）．25．（2005•贵阳）在一次数学实践探究活动中，小强用两条直线把平行四边形ABCD分割成四个部分，使含有一组对顶角的两个图形全等；（1）根据小强的分割方法，你认为把平行四边形分割成满足以上全等关系的直线有_________组；（2）请在图中的三个平行四边形中画出满足小强分割方法的直线；（3）由上述实验操作过程，你发现所画的两条直线有什么规律？26．如图，在直角梯形ABCD中，AB∥CD，∠BCD=Rt∠，AB=AD=10cm，BC=8cm．点P从点A出发，以每秒3cm的速度沿折线ABCD方向运动，点Q从点D出发，以每秒2cm的速度沿线段DC方向向点C运动．已知动点P、Q同时发，当点Q运动到点C时，P、Q运动停止，设运动时间为t．（1）求CD的长；（2）当四边形PBQD为平行四边形时，求四边形PBQD的周长；（3）在点P、点Q的运动过程中，是否存在某一时刻，使得△BPQ的面积为20cm2？若存在，请求出所有满足条件的t的值；若不存在，请说明理由．27．已知平行四边形的三个顶点的坐标分别为O（0，0）、A（2，0）、B（1，1），则第四个顶点C的坐标是多少？28．已知平行四边形ABCD的周长为36cm，过D作AB，BC边上的高DE、DF，且cm，，求平行四边形ABCD的面积．29．如图，在平面直角坐标系中，已知O为原点，四边形ABCD为平行四边形，A、B、C的坐标分别是A（﹣3，），B（﹣2，3），C（2，3），点D在第一象限．（1）求D点的坐标；（2）将平行四边形ABCD先向右平移个单位长度，再向下平移个单位长度所得的四边形A1B1C1D1四个顶点的坐标是多少？（3）求平行四边形ABCD与四边形A1B1C1D1重叠部分的面积？30．如图所示．▱ABCD中，AF平分∠BAD交BC于F，DE⊥AF交CB于E．求证：BE=CF．三角形的中位线练习题姓名1．连结三角形___________的线段叫做三角形的中位线．2．三角形的中位线______于第三边，并且等于_______．3．一个三角形的中位线有_________条．4.如图△ABC中，D、E分别是AB、AC的中点，则线段CD是△ABC的＿＿＿，线段DE是△ABC＿＿＿＿＿＿＿5、如图，D、E、F分别是△ABC各边的中点（1）如果EF＝4cm，那么BC＝＿＿cm如果AB＝10cm，那么DF＝＿＿＿cm（2）中线AD与中位线EF的关系是＿＿＿6．如图1所示，EF是△ABC的中位线，若BC=8cm，则EF=_______cm．(1) (2) (3) (4)7．三角形的三边长分别是3cm，5cm，6cm，则连结三边中点所围成的三角形的周长是_________cm．8．在Rt△ABC中，∠C=90°，AC=•5，•BC=•12，•则连结两条直角边中点的线段长为_______．9．若三角形的三条中位线长分别为2cm，3cm，4cm，则原三角形的周长为（）A．4.5cm B．18cm C．9cm D．36cm10．如图2所示，A，B两点分别位于一个池塘的两端，小聪想用绳子测量A，B间的距离，但绳子不够长，一位同学帮他想了一个主意：先在地上取一个可以直接到达A，B的点C，找到AC，BC的中点D，E，并且测出DE 的长为10m，则A，B间的距离为（）A．15m B．25m C．30m D．20mA 、20081B 、20091C 、220081D 、22009112．如图3所示，已知四边形ABCD ，R ，P 分别是DC ，BC 上的点，E ，F 分别是AP ，RP 的中点，当点P 在BC 上从点B 向点C 移动而点R 不动时，那么下列结论成立的是（）A ．线段EF 的长逐渐增大B ．线段EF 的长逐渐减少C ．线段EF 的长不变D ．线段EF 的长不能确定13．如图4,在△ABC 中，E ，D ，F 分别是AB ，BC ，CA 的中点，AB=6，AC=4，则四边形AEDF •的周长是（）A ．10B ．20C ．30D ．4014．如图所示，□ ABCD 的对角线AC ，BD 相交于点O ，AE=EB ，求证：OE ∥BC ．15．如图所示，在△ABC 中，点D 在BC 上且CD=CA ，CF 平分∠ACB ，AE=EB ，求证：EF=12BD ．16．如图所示，已知在□ABCD 中，E ，F 分别是AD ，BC 的中点，求证：MN ∥BC ．17．已知：如图，四边形ABCD 中，E 、F 、G 、H 分别是AB 、BC 、CD 、DA 的中点．求证：四边形EFGH 是平行四边形．18．已知：△ABC 的中线BD 、CE 交于点O ，F 、G 分别是OB 、OC 的中点．求证：四边形DEFG 是平行四边形．C19．已知：如图，E 为□ABCD 中DC 边的延长线上的一点，且CE ＝DC ，连结AE分别交BC 、BD 于点F 、G ，连结AC 交BD 于O ，连结OF ．求证：AB ＝2OF ．1、已知在四边形ABCD 中，AB=CD ，E 、F 、G 分别是BD 、AC 、BC 的中点，H 是EF 的中点.求证：EF ⊥GH.3、如图所示，△ABC 中，AB ＞AC ，AD 平分∠BAC ，CD ⊥AD ，点E 是BC 的中点。

平行四边形与梯形练习

平行四边形与梯形练习
1、画出下面图形底边对应的高。

2、为了实现“村村通有线电视”的承诺，某县政府决定分别为幸福村和移民村接通有线电视信号。

从哪里接入主干线最省材料呢？请画出来。

5．(变式题)如下图，小鹿在A点，小熊在B点，它们都渴极了，想要到河边喝水，请你分别为它们设计出到河边最短的路线，并在图上画出来。

4、过点O分别画直线l的垂线。

5．小明家门前有一个平行四边形的鱼塘，鱼塘两条邻边的长分别是80米和60米，爷爷每天绕鱼塘走3圈，他每天走多少米？
班级：姓名：
6．在一个等腰梯形的花坛周围围栏杆，栏杆长42米，这个梯形的上底是12米，下底是16米，这个等腰梯形的腰长多少米？
7．一个平行四边形的纸板沿4厘米的高剪开，分成两个梯形，这两个梯形的周长之和比原来平行四边形的周长长多少厘米？。

小学奥数任意四边形、梯形与相似模型(二) 精选例题练习习题(含知识点拨)

板块二梯形模型的应用梯形中比例关系(“梯形蝴蝶定理”)：A BCDO ba S 3S 2S 1S 4①2213::S S a b =②221324::::::S S S S a b ab ab =； ③S 的对应份数为()2a b +．梯形蝴蝶定理给我们提供了解决梯形面积与上、下底之间关系互相转换的渠道，通过构造模型，直接应用结论，往往在题目中有事半功倍的效果．(具体的推理过程我们可以用将在第九讲所要讲的相似模型进行说明)【例 1】如图，22S =，34S =，求梯形的面积．【巩固】如下图，梯形ABCD 的AB 平行于CD ，对角线AC ，BD 交于O ，已知AOB △与BOC △的面积分别为25 平方厘米与35平方厘米，那么梯形ABCD 的面积是________平方厘米．3525OABCD【巩固】如图所示，在梯形ABCD 中，AB ∥CD ，对角线AC ，BD 相交于点O 。

已知AB =5，CD =3，且梯形ABCD 的面积为4，求三角形OAB 的面积。

例题精讲任意四边形、梯形与相似模型A BCDO【例 2】梯形ABCD 的对角线AC 与BD 交于点O ，已知梯形上底为2，且三角形ABO 的面积等于三角形BOC 面积的23，求三角形AOD 与三角形BOC 的面积之比．OA B CD【例 3】如下图，四边形ABCD 中，对角线AC 和BD 交于O 点，已知1AO =，并且35ABD CBD =三角形的面积三角形的面积，那么OC 的长是多少？ABCDO【例 4】梯形的下底是上底的1.5倍，三角形OBC 的面积是29cm ，问三角形AOD 的面积是多少？A BCDO【巩固】如图，梯形ABCD 中，AOB ∆、COD ∆的面积分别为1.2和2.7，求梯形ABCD 的面积．OD CBA【例5】在梯形ABCD中，上底长5厘米，下底长10厘米，20=∆BOCS平方厘米，则梯形ABCD的面积是平方厘米。

梯形练习题精选

梯形练习题精选（基础题）一．判断题一．判断题（1）只有一组对边平行的四边形是梯形）只有一组对边平行的四边形是梯形（）（2）梯形的内角最多有两个是锐角）梯形的内角最多有两个是锐角（）（3）等腰梯形的两条对角线相等）等腰梯形的两条对角线相等（）（4）等腰梯形的对角互补）等腰梯形的对角互补（）（5）我们通常把梯形中较短的底叫上底，较长的底叫下底（）（6）梯形的高一定小于腰的长度）梯形的高一定小于腰的长度（）（7）如果一个梯形是轴对称图形，则它一定是等腰梯形（）（8）对角互补的梯形为等腰梯形）对角互补的梯形为等腰梯形（）（9）如果梯形的一组对角互补，则另一组对角也互补）如果梯形的一组对角互补，则另一组对角也互补（）（10）延长等腰梯形的两腰交于一点后形成的图形中的三角形一定是等腰三角形（）二．选择题二．选择题（1）下列说法正确的是（）下列说法正确的是（）A ．平行四边形是一种特殊的梯形．平行四边形是一种特殊的梯形B ．等腰梯形的两底角相等C ．等腰梯形不可能是直角梯形．等腰梯形不可能是直角梯形D ．有两邻角相等的梯形是等腰梯形（2）在等腰梯形中，下列结论：①两腰相等；②两底平行；③对角线相等；④两底角相等．其中正确的有（中正确的有（）个）个 A ．1 B ．2 C ．3 D ．4 （3）等腰梯形的上底、下底、高之比为1∶3∶1，则下底角的度数是（，则下底角的度数是（）A ．30°B ．45°C ．60°D ．75°（4）等腰梯形ABCD 中，BC AD //，AC 与BD 交于O 点，图中全等三角形有（点，图中全等三角形有（） A ．两对．两对 B ．四对．四对 C 一对一对 D ．三对．三对（5）等腰梯形中，下列判断正确的是（）等腰梯形中，下列判断正确的是（）A 两底相等两底相等B 两个角相等两个角相等C 同底上两底角互补同底上两底角互补D 对角线交点在对称轴上（6）下列命题中：）下列命题中：①有两个角相等的梯形是等腰梯形①有两个角相等的梯形是等腰梯形 ②有两条边相等的梯形是等腰梯形②有两条边相等的梯形是等腰梯形③两条对角线相等的梯形是等腰梯形③两条对角线相等的梯形是等腰梯形 ④等腰梯形上、下底中点连线，把梯形分成面积相等的两部分。

人教版五年级数学上册《平行四边形的面积》》精选练习(含答案)

人教版五年级数学上册《平行四边形的面积》精选练习（附答案）练习一一、判断题1..一个平行四边形的底是8cm，高是4cm．一个底和面积与它相等的三角形，高一定是2cm2.一个平行四边形的面积是56平方厘米，高是7厘米，底是8厘米。

3.三角形的面积一定等于平行四边形面积的一半。

（）4.火眼金睛。

（1）把一个梯形分成2个三角形，这2个三角形的面积一定不相等。

（2）一个平行四边形的底增加2 cm，对应的高减少2 cm，这个平行四边形的面积不变。

（3）三角形的面积等于平行四边形面积的一半。

（4）一个平行四边形停车场，底为64 m，高为26 m，平均每辆车占地15 m2，则这个停车场最多可停放111辆车。

二、填空题5.看图计算（单位：米）面积S=________平方米6.一个平行四边形的底是15厘米，该底边上的高是8厘米，它的面积是________平方厘米，与它等底等高的三角形面积是________平方厘米。

7.一个正方形的周长是24厘米，把它割补成一个平行四边形，这个平行四边形的面积是________平方厘米。

8.如图1至图4各图形中，面积是平行四边形A一半的有________（填序号）三、单选题9.选择题。

（1）平行四边形的底扩大到原来的3倍，高不变，面积( )。

A.扩大到原来的3倍B.缩小到原来的（2）如果这个平行四边形的底扩大到原来的3倍，高扩大到原来的2倍，则面积( )。

A.扩大到原来的6倍B.缩小到原来的10.兴华小区有一块平行四边形的空地，底是80米，高是60米，其中2880平方米的地方种草，其余的地方种花，花占地（）平方米。

A. 4800B. 3600C. 1920D. 288011.下图的面积是（）A. 8B. 9C. 12D. 1012.三角形与平行四边形的底和面积都相等，已知平行四边形的高是8厘米，三角形的高是（）A. 4厘米B. 8厘米 C. 16厘米四、解答题13.下图中，四边形ABCD是一个直角梯形。

小学五年级上册数学《总复习》练习题精选

小学五年级上册数学《总复习》练习题精选篇一：一、我会填空。

1.17个0.25的和是（），0.5的4倍是（）。

2.在3.1415926…，12.383，9.1666…中，（）是有限小数，（）是无限小数，（）是循环小数。

3.商店进了a个书包，平均每天售出m个，卖了4天，还剩（）个。

如果a＝120，m＝25，那么还剩（）个。

4.一个梯形的上底是5.8厘米，下底是6.2厘米，高是2.5厘米，它的面积是（）平方厘米。

5.一个平行四边形，底是8厘米，高是2厘米，如果底不变，髙增加2厘米，则面积增加（）平方厘米；如果底和高都扩大到原来的10倍，它的面积就扩大到原来的（）倍。

6.如果x＋5＝21，那么2.3x－16＝（）。

7.从王林家到公路有一条长90m的小路。

王林要在小路的一侧每隔15m栽一棵白杨树，两端都栽，一共要栽（）棵白杨树。

二、我会判断。

1.一个不等于0的数除以2.5，商一定比这个数大。

（）2.两个等底等高的三角形，面积相等，并且一定能重合。

（）3.因为x2＝x▪x，所以x2＝2x。

（）4.24×（x＋5）＝24x＋24×5（）5.1.8÷4的商是0.4，余数是0.2。

（）6.鱼儿不可能在天上飞。

（）三、我会选择。

1.因为65×39＝2535，所以下列各式错误的是（）。

A.6.5×39＝253.5B.0.65×3.9＝0.2535C.65×0.39＝25.35D.6.5×3.9＝25.352.一个数与a的和的4倍比9.8少2，求这个数。

设这个数为x，则所列方程为（）。

A.x＋4a－9.8＝2B.x＋4a＝9.8－2C.4（x＋a）＝9.8－2D.4（x＋a）－2＝9.83.图中，空白部分的面积是阴影部分面积的（）。

A.一半B.1倍C.2倍4.4.3减去 2.01与 2.2的和，然后除以0.2，商是多少？列式为（）。

A.4.3－（2.01＋2.2）÷0.2B.[（4.3－2.01）＋2.2]÷0.2C.[4.3－（2.01＋2.2）]÷0.25.一个梯形的上底是9分米，下底是15分米，高是6分米，在这个梯形里面画一个的三角形，这个三角形的面积是（）平方分米。

八年级数学平行四边形梯形和平行性质的证明题

⼋年级数学平⾏四边形梯形和平⾏性质的证明题A C BD学⽣姓名彭年级初三授课时间教师姓名刘课时 2课题四边形教学⽬标掌握特殊四边形的性质和判定⽅法重点特殊四边形的性质和判定⽅法难点综合应⽤平⾏、三⾓形全等、四边形性质进⾏综合的证明【知识点】：(必须熟记在⼼)1、平⾏四边形定义：有两组对边分别平⾏的四边形叫做平⾏四边形。

平⾏四边形的性质：平⾏四边形的对边相等；平⾏四边形的对⾓相等。

平⾏四边形的对⾓线互相平分。

平⾏四边形的判定1.两组对边分别相等的四边形是平⾏四边形2.对⾓线互相平分的四边形是平⾏四边形；3.两组对⾓分别相等的四边形是平⾏四边形；4.⼀组对边平⾏且相等的四边形是平⾏四边形。

2、矩形的定义：有⼀个⾓是直⾓的平⾏四边形。

矩形的性质：矩形的四个⾓都是直⾓；矩形的对⾓线平分且相等。

AC=BD 矩形判定定理： 1.有⼀个⾓是直⾓的平⾏四边形叫做矩形。

2.对⾓线相等的平⾏四边形是矩形。

3.有三个⾓是直⾓的四边形是矩形。

直⾓三⾓形斜边上的中线等于斜边的⼀半。

3、菱形的定义：邻边相等的平⾏四边形。

菱形的性质：菱形的四条边都相等；菱形的两条对⾓线互相垂直，并且每⼀条对⾓线平分⼀组对⾓。

菱形的判定定理： 1.⼀组邻边相等的平⾏四边形是菱形。

2.对⾓线互相垂直的平⾏四边形是菱形。

3.四条边相等的四边形是菱形。

S 菱形=1/2×ab （a 、b 为两条对⾓线）4、正⽅形定义：⼀个⾓是直⾓的菱形或邻边相等的矩形。

正⽅形的性质：四条边都相等，四个⾓都是直⾓。

正⽅形既是矩形，⼜是菱形。

正⽅形判定定理： 1.邻边相等的矩形是正⽅形。

2.有⼀个⾓是直⾓的菱形是正⽅形。

5、梯形的定义：⼀组对边平⾏，另⼀组对边不平⾏的四边形叫做梯形。

直⾓梯形的定义：有⼀个⾓是直⾓的梯形等腰梯形的定义：两腰相等的梯形。

等腰梯形的性质：等腰梯形同⼀底边上的两个⾓相等；等腰梯形的两条对⾓线相等。

等腰梯形判定定理：同⼀底上两个⾓相等的梯形是等腰梯形。

苏教版四年级下册三角形,平行四边形和梯形精选试卷练习(含答案)2

评卷人
得分
三、判断题
31．一个梯形最多有2个直角。（______）
32．小强画了一个三个角分别是80°、70°、50°的锐角三角形。（______）
33．在很多电信塔支架里能找到三角形，是因为三角形具有稳定性。（______）
34．用三根长度分别是4厘米、4厘米和8厘米的小棒一定能拼成一个等腰三角形。（________）
27．平移不改变图形的________和________，只改变图形的________
28．如图，∠3＝（______）度。
29．一个等腰三角形的顶角是80°．这个三角形的一个底角是（_____）°．
30．一个等腰三角形的一个底角是35°，它的顶角是（______）°，按角分这个三角形是一个（______）三角形。
35．梯形的上底与下底一定不相等。（______）
36．已知三角形最大内角的度数，就可以确定这个三角形按角分类是哪种三角形。（______）
37．三条同样长的线段一定能围成一个三角形。（______）
38．一个三角形中，最大的角是锐角，那么，这个三角形就一定是锐角三角形．（____）
39．在梯形的上、下底之间最多可以画2条高。（______）
22．过一个多边形的任意一个顶点可以作6条对角线，则此多边形的内角和是（________）º。
23．一个三角形中，最多有（______）个直角，最多有（______）个钝角，最少有（______）个锐角。
24．把一个等边三角形沿其中一条高剪开，分成两个直角三角形，其中一个直角三角形的两个锐角分别是（____）和（____）。
47．三角形ABC是等边三角形，如果∠CAE＝20º，求∠E的度数。
48．王兵绕一个等边三角形的场地散步，走了8圈，一共走了4800米，这个等边三角形场地的边长是多少米？

小学奥数基本图形的面积计算精选练习例题含答案解析(附知识点拨及考点)

小学数学平面图形计算公式：1 、正方形：周长＝边长×4；面积=边长×边长2 、正方体：表面积=棱长×棱长×6；体积=棱长×棱长×棱长3 、长方形：周长=(长+宽)×2；面积=长×宽4 、长方体：表面积(长×宽+长×高+宽×高)×2；体积=长×宽×高 5、三角形：面积=底×高÷2 6 平行四边形：面积=底×高 7 梯形：面积=(上底+下底)×高÷ 2模块一、基本公式的应用【例 1】如图，两个正方形边长分别是5厘米和4厘米，图中阴影部分为重叠部分。

则两个正方形的空白部分的面积相差多少平方厘米？【考点】基本图形的面积计算【难度】2星【题型】解答【关键词】华杯赛，五年级，决赛，第9题，10分【解析】 5×5－4×4=9（平方厘米），两个正方形的空白部分的面积相差9平方厘米。

【答案】9平方厘米【巩固】如图12，边长为4cm 的正方形将边长为3cm 的正方形遮住了一部分，则空白部分的面积的差等于 2cm 。

【考点】基本图形的面积计算【难度】2星【题型】填空【关键词】希望杯，4年级，初赛，19题【解析】空白部分的面积差等于两个正方形的面积差，即⨯-⨯=44337（平方厘米）。

【答案】7平方厘米【例 2】在一个正方形水池的四周，环绕着一条宽2米的路(如图)，这条路的面积是120平方米，那么水池的面积是______ 平方米。

水池例题精讲知识点拨4-2-1.基本图形的面积计算【考点】基本图形的面积计算【难度】2星【题型】填空【关键词】希望杯，4年级，初赛，19题【解析】四个边角的面积和为2×2×4=16，则水池的边长为：104÷2÷4=13，所以水池的面积是：13×13=169平方米。

【精选】苏教版四年级下册数学期末复习《图形与几何》专项练习(含答案)

【精选】苏教版四年级下册数学期末复习《图形与几何》专项练习（含答案）一、填空。

(每空1分，共24分)1．把一根18cm长的铁丝折成一个等边三角形铁框，铁框的一条边( )cm，若折成一个腰长为5cm的等腰三角形铁框，铁框的底边长( )cm。

2．有四根小棒，长度分别是20厘米、10厘米、8厘米、10厘米。

从中选择三根围成一个三角形，围成的是( )三角形，它的周长是( )厘米。

3．右图是用一个等腰直角三角形和一个直角三角形拼成的一个四边形，则∠1＝( )°，这个四边形的内角和是( )°。

4．选用三根整厘米长的小棒摆三角形，如果先选的两根长度分别是11厘米和( )厘米，那么第三根最长可以选27厘米的小棒，最短可以选( )厘米的小棒。

5．一个直角梯形的上底是2厘米，一腰长10厘米，把它的上底增加6厘米，就变成了一个正方形。

这个直角梯形的周长是( )厘米。

6．五边形的内角和是( )°，( )边形的内角和是900°。

7．(1)小汽车图向( )平移了( )格；(2)房子图先向右平移了( )格，再向( )平移了( )格；(3)小船图向( )平移了( )格；(4)图形A和图形B的组合图形是( )图形；(5)图形D是图形C绕点O按( )时针方向旋转90°得到的。

8．妈妈去超市买水果，超市的台秤最多能称4千克的物品，妈妈先挑了几个水蜜桃，称量后发现指针指向2，她又添了一些水蜜桃，指针顺时针旋转了90°。

已知水蜜桃每千克3元，妈妈一共要付( )元。

9．如右图，如果“一”字所在的位置用数对表示为(3，2)，则“塔”字所在的位置用数对表示为( )，数对(4，3)表示的汉字是( )。

10．右面方格图中的阴影部分表示160，整个长方形表示( )。

二、选择。

(每小题2分，共10分)1．下面说法正确的有( )。

①平行四边形是轴对称图形，有2条对称轴。

②将一个等腰梯形顺时针旋转180°可以与原图形重合。

人教版四年级数学上册《平行四边形与梯形》画图专项练习

平行四边形与梯形专项练习——操作题
1.分别过下面的点作已知直线的垂线
2.A村要修修一条公路，怎样修最近？请画出来。

3.王刚家要安装自来水管，怎样安装最节省材料？
4.画一个和下面大小、形状都相同的图形，再把所画的图形分成一个平行四边形和一个三角形。

5.过M点画已知直线的垂线和平行线。

6.画出指定底边的高。

7.在点子图上画出一个平行四边形，再画出它的高，标出这条高对应的底。

在画一个等腰梯形，并标出它的上底、下底和腰。

8.画出线段AB ，射线BC ，直线AC ，并在直线AC 上截取长为2cm 的线段
9.甲乙两村各要修一条公路连接主路，怎样修最
近？
10.过A 点分别画出OB 、OC 的垂线11.画一个高为3厘米的等腰梯形和一个边长为4厘米的正方形。

（每个格子的面积是1
平方厘米）
12.利用下面的平行线画一个长方形和正方形。

13.
将下列图形改成平行四边形。

A B
C。

平行四边形证明练习题#精选.

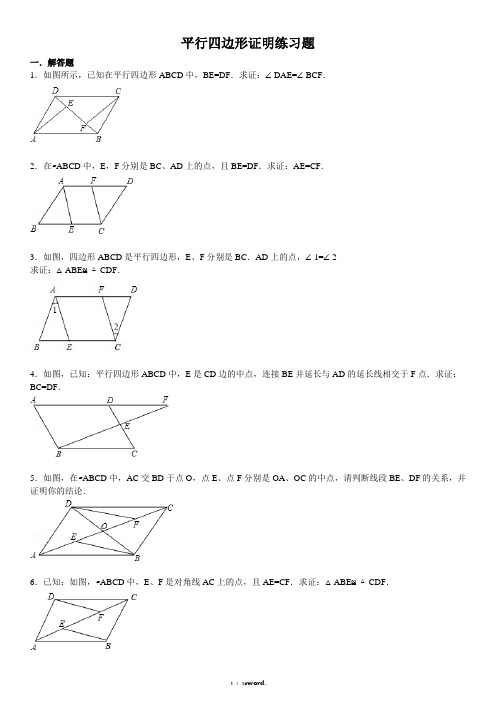
平行四边形证明练习题一．解答题1．如图所示，已知在平行四边形ABCD中，BE=DF．求证：∠DAE=∠BCF．2．在▱ABCD中，E，F分别是BC、AD上的点，且BE=DF．求证：AE=CF．3．如图，四边形ABCD是平行四边形，E、F分别是BC．AD上的点，∠1=∠2求证：△ABE≌△CDF．4．如图，已知：平行四边形ABCD中，E是CD边的中点，连接BE并延长与AD的延长线相交于F点．求证：BC=DF．5．如图，在▱ABCD中，AC交BD于点O，点E、点F分别是OA、OC的中点，请判断线段BE、DF的关系，并证明你的结论．6．已知：如图，▱ABCD中，E、F是对角线AC上的点，且AE=CF．求证：△ABE≌△CDF．7．如图，已知在▱ABCD中，过AC中点的直线交CD，AB于点E，F．求证：DE=BF．8．如图，在等腰梯形ABCD中，AD∥BC，AB=CD=AE．四边形AECD是平行四边形吗？为什么？9．如图，E、F是平行四边形ABCD的对角线AC上的两点，AE=CF．求证：DE=BF．10．如图，四边形ABCD中，AD=BC，AE⊥BD，CF⊥BD，垂足为E、F，AE=CF，求证：四边形ABCD是平行四边形．11．如图，在△ABC中，AD是中线，点E是AD的中点，过A点作BC的平行线交CE的延长线于点F，连接BF．求证：四边形AFBD是平行四边形．12．如图，在等腰梯形ABCD中，AD∥BC，AB=DC，DE∥AB，AD+DC=BC．求证：（1）DE=DC；（2）△DEC是等边三角形．13．已知：如图，E、F是平行四边形ABCD的对角线AC上的两点，AE=CF．求证：（1）△ADF≌△CBE；（2）连接DE、BF，试判断四边形DEBF的形状，并说明理由．14．如图，平行四边形ABCD中，点E、F、G、H分别在AB、BC、CD、AD边上且AE=CG，AH=CF．求证：四边形EFGH是平行四边形．15．如图，在平行四边形ABCD中，E、F是对角线AC上的点，且AE=CF．（1）猜想探究：BE与DF之间的关系：_________（2）请证明你的猜想．16．如图，E、F是平行四边形ABCD对角线AC上的两点，且BE∥DF．求证：∠1=∠2．17．如图，已知E，F分别是▱ABCD的边AB，CD的中点．求证：ED=BF．18．如图，BD是▱ABCD的对角线，∠ABD的平分线BE交AD于点E，∠CDB的平分线DF交BC于点F．求证：四边形DEBF为平行四边形．19．如图，在▱ABCD中，对角线AC与BD交于点O，已知点E、F分别为AO、OC的中点，证明：四边形BFDE 是平行四边形．20．如图所示，A，E，F，C在一条直线上，AE=CF，过E，F分别作DE⊥AC，BF⊥AC，若AB=CD，可以得到BD平分EF，为什么？说明理由．21．如图，△ABC的中线BD、CE交于点O，F、G分别是OB、OC的中点．求证：EF=DG且EF∥DG．22．已知如图所示，▱ABCD的对角线AC、BD交于O，GH过点O，分别交AD、BC于G、H，E、F在AC上且AE=CF，求证：四边形EHFG是平行四边形．平行四边形证明练习题参考答案与试题解析一．解答题（共22小题）1．如图所示，已知在平行四边形ABCD中，BE=DF．求证：∠DAE=∠BCF．考点：平行四边形的性质；平行线的性质；全等三角形的判定与性质．分析：根据平行四边形性质求出AD∥BC，且AD=BC，推出∠ADE=∠CBF，求出DE=BF，证△ADE≌△CBF，推出∠DAE=∠BCF即可．解答：证明：∵四边形ABCD为平行四边形，∴AD∥BC，且AD=BC，∴∠ADE=∠CBF又∵BE=DF，∴BF=DE，∵在△ADE和△CBF中，∴△ADE≌△CBF，∴∠DAE=∠BCF．点评：本题考查了平行四边形性质，平行线性质，全等三角形的性质和判定的应用，关键是求出证出△ADE和△CBF全等的三个条件，主要考查学生的推理能力．2．在▱ABCD中，E，F分别是BC、AD上的点，且BE=DF．求证：AE=CF．考点：平行四边形的性质；全等三角形的判定与性质．分析：根据平行四边形的性质得出AB=CD，∠B=∠D，根据SAS证出△ABE≌△CDF即可推出答案．解答：证明：∵四边形ABCD是平行四边形，∴AB=CD，∠B=∠D，∵BE=DF，∴△ABE≌△CDF，∴AE=CF．点评：本题主要考查对平行四边形的性质，全等三角形的性质和判定等知识点的理解和掌握，能根据性质证出△ABE≌△CDF是证此题的关键．3．如图，四边形ABCD是平行四边形，E、F分别是BC．AD上的点，∠1=∠2求证：△ABE≌△CDF．考点：平行四边形的性质；全等三角形的判定．分析：利用平行四边形的性质和题目提供的相等的角可以为证明三角形全等提供足够的条件．解答：证明：∵四边形ABCD是平行四边形，∴∠B=∠D，AB=CD，∴在：△ABE与△CDF中，∴△ABE≌△CDF（ASA）点评：本题考查了平行四边形的性质及全等三角形的判定，根据平行四边形找到证明全等三角形足够的条件是解决本题的关键．4．如图，已知：平行四边形ABCD中，E是CD边的中点，连接BE并延长与AD的延长线相交于F点．求证：BC=DF．考点：平行四边形的性质；全等三角形的判定与性质．分析：由四边形ABCD是平行四边形，可得AD∥BC，根据平行线的性质即可求得∠EBC=∠F，∠C=∠EDF，又由E是CD边的中点，根据AAS即可求得△EBC≌△EFD，则问题得证．解答：证明：∵四边形ABCD是平行四边形，∴AD∥BC，∴∠EBC=∠F，∠C=∠EDF，又∵EC=ED，∴△EBC≌△EFD（AAS），∴BC=DF．点评：此题考查了平行四边形的性质以及全等三角形的判定与性质．此题难度不大，解题的关键是要注意数形结合思想的应用．5．（2013•莒南县二模）如图，在▱ABCD中，AC交BD于点O，点E、点F分别是OA、OC的中点，请判断线段BE、DF的关系，并证明你的结论．考点：平行四边形的性质；全等三角形的判定与性质．分析：根据平行四边形的性质对角线互相平分得出OA=OC，OB=OD，利用中点的意义得出OE=OF，从而利用平行四边形的判定定理“对角线互相平分的四边形是平行四边形”判定BFDE是平行四边形，从而得出BE=DF，BE∥DF．解答：解：由题意得：BE=DF，BE∥DF．理由如下：连接DE、BF．∵ABCD是平行四边形，∴OA=OC，OB=OD，∵E，F分别是OA，OC的中点，∴OE=OF，∴BFDE是平行四边形，∴BE=DF，BE∥DF．点评：本题考查了平行四边形的基本性质和判定定理的运用．性质：①平行四边形两组对边分别平行；②平行四边形的两组对边分别相等；③平行四边形的两组对角分别相等；④平行四边形的对角线互相平分．判定：①两组对边分别平行的四边形是平行四边形；②两组对边分别相等的四边形是平行四边形；③两组对角分别相等的四边形是平行四边形；④对角线互相平分的四边形是平行四边形；⑤一组对边平行且相等的四边形是平行四边形．6．已知：如图，▱ABCD中，E、F是对角线AC上的点，且AE=CF．求证：△ABE≌△CDF．考点：平行四边形的性质；平行线的性质；全等三角形的判定．分析：根据平行四边形的性质得出AB∥DC，AB=CD，根据平行线的性质推出∠BAC=∠DCF，根据SAS证出即可．解答：证明：∵四边形ABCD是平行四边形，∴AB∥DC，AB=CD，∴∠BAC=∠DCF，∵AE=CF，∴△ABE≌△CDF．点评：本题主要考查对平行四边形的性质，全等三角形的判定，平行线的性质等知识点的理解和掌握，能推出证△ABE≌△CDF的三个条件是解此题的关键．7．如图，已知在▱ABCD中，过AC中点的直线交CD，AB于点E，F．求证：DE=BF．考点：平行四边形的性质；平行线的性质；全等三角形的判定与性质．分析：根据平行四边形的性质得到DC=AB，DC∥AB，根据平行线的性质得到∠ECA=∠BAC，∠CEO=∠AFO，能推出△AOF≌△COE，得到CE=AF，即可证出答案．解答：证明：∵四边形ABCD 是平行四边形，∴DC=AB，DC∥AB，∴∠ECA=∠BAC，∠CEO=∠AFO，∵OA=OC，∴△AOF≌△COE，∴CE=AF，∵DC=AB，∴DE=BF．点评：本题主要考查对平行四边形的性质，平行线的性质，全等三角形的性质和判定等知识点的理解和掌握，解此题的关键是根据平行四边形的性质证出△AOF和△COE全等．8．如图，在等腰梯形ABCD中，AD∥BC，AB=CD=AE．四边形AECD是平行四边形吗？为什么？考点：等腰梯形的性质；平行线的判定与性质；等腰三角形的性质；平行四边形的判定．分析：根据等腰三角形性质求出∠B=∠C，根据等腰三角形性质推出∠AEC=∠B=∠C，推出AE∥CD，根据平行四边形的判定推出即可．解答：解：是平行四边形，理由：∵四边形ABCD是等腰梯形，AD∥BC，∴AB=DC，∠B=∠C，∵AB=AE，∴∠AEB=∠B，∴∠AEB=∠C，∴AE∥DC，又∵AD∥BC，∴四边形AECD是平行四边形．点评：本题考查了等腰三角形的性质，等腰梯形的性质，平行线的性质和判定，平行四边形的判定等知识点的应用，关键是根据题意推出AE∥CD，培养了学生分析问题和解决问题的能力，题目较好，综合性比较强．9．如图，E、F是平行四边形ABCD的对角线AC上的两点，AE=CF．求证：DE=BF．考点：平行四边形的性质；全等三角形的判定与性质；平行四边形的判定．分析：连接BE，DF，BD，BD交AC于O，根据平行四边形性质求出OA=OC，OD=OB，推出OE=OF，根据平行四边形的判定推出四边形BEDF是平行四边形即可．解答：证明：连接BE，DF，BD，BD交AC于O，∵四边形ABCD是平行四边形，∴OA=OC，OD=OB，∵AE=CF，∴OE=OF，∴四边形BEDF是平行四边形，∴DE=BF．点评：本题考查了平行四边形的性质和判定等应用，关键是能熟练地运用平行四边形的性质和判定进行推理，此题的证明方法二是证△AED≌△CFB，推出DE=BF．10．如图，四边形ABCD中，AD=BC，AE⊥BD，CF⊥BD，垂足为E、F，AE=CF，求证：四边形ABCD是平行四边形．考点：平行四边形的判定；平行线的性质；全等三角形的判定与性质．分析：求出∠AED=∠CFB=90°，根据HL证Rt△AED≌Rt△CFB，推出∠ADE=∠CBD，得到AD∥BC，根据平行四边形的判定判断即可．解答：证明：∵AE⊥BD，CF⊥BD，∴∠AED=∠CFB=90°，在Rt△AED和Rt△CFB中，∴Rt△AED≌Rt△CFB（HL），∴∠ADE=∠CBD，∴AD∥BC，∵AD=BC，∴四边形ABCD是平行四边形．点评：本题考查了平行四边形的判定，平行线的性质，全等三角形的性质和判定等知识点的应用，关键是推出AD∥BC，主要考查学生运用性质进行推理的能力．11．如图，在△ABC中，AD是中线，点E是AD的中点，过A点作BC的平行线交CE的延长线于点F，连接BF．求证：四边形AFBD是平行四边形．考点：平行四边形的判定；全等三角形的判定与性质．专题：证明题．分析：求出AE=DE，∠AFE=∠DCE，证△AEF≌△CED，推出AF=DC，得出AF∥BD，AF=BD，根据平行四边形的判定推出即可．解答：证明：∵E为AD中点，∴AE=DE，∵AF∥BC，∴∠AFE=∠DCE，在△AEF和△CED中∵，∴△AEF≌△CED（AAS），∴AF=DC，∵AD是△ABC的中线，∴BD=DC，∴AF=BD，即AF∥BD，AF=BD，故四边形AFBD是平行四边形．点评：本题考查了平行四边形的性质和判定，全等三角形的性质和判定，关键是推出AF=DC=BD．12．如图，在等腰梯形ABCD中，AD∥BC，AB=DC，DE∥AB，AD+DC=BC．求证：（1）DE=DC；（2）△DEC是等边三角形．考点：等腰梯形的性质；等边三角形的判定；平行四边形的判定与性质．分析：（1）证出平行四边形ABED，推出DE=AB，即可推出答案；（2）根据BE=AD，AD+DC=BC，BE+EC=BC，推出DC=EC即可证出答案．解答：证明：（1）∵AD∥BC，DE∥AB，∴四边形ABED是平行四边形，∴DE=AB，∵AB=DC，∴DE=DC．（2）证明：∵BE=AD，AD+DC=BC，BE+EC=BC，∴DC=EC，由（1）知：DE=DC，∴DE=DC=EC，∴△DEC是等边三角形．点评：本题主要考查对等腰梯形的性质，平行四边形的性质和判定，等边三角形的判定等知识点的理解和掌握，证出平行四边形ABED和DC=EC是解此题的关键．13．已知：如图，E、F是平行四边形ABCD的对角线AC上的两点，AE=CF．求证：（1）△ADF≌△CBE；（2）连接DE、BF，试判断四边形DEBF的形状，并说明理由．考点：平行四边形的判定与性质；全等三角形的判定与性质．分析：（1）根据平行四边形的性质对边平行且相等得到AD与BC平行且相等，由AD与BC平行得到内错角∠DAF 与∠BCA相等，再由已知的AE=CF，根据“SAS”得到△ADF与△CBE全等；（2）由（1）证出的全等，根据全等三角形的性质得到DF与EB相等且∠DFA与∠BEC相等，由内错角相等两直线平行得到DF与BE平行，根据一组对边平行且相等的四边形为平行四边形即可得到四边形DEBF 的形状．解答：证明：（1）∵ABCD是平行四边形，∴AD=BC，AD∥BC（1分）∴∠DAF=∠BCA（2分），∵AE=CF，∴AE+EF=CF+EF，即AF=CE（3分）∴△ADF≌△CBE（4分）（2）四边形DEBF是平行四边形（5分）∵△ADF≌△CBE，∴∠DFA=∠BEC，DF=BE，∴DF∥BE，∴四边形DEBF是平行四边形（6分）点评：本题综合考查了全等三角形的判断与性质，以及平行四边形的判断与性质．其中第2问是一道先试验猜想，再探索证明的新型题，其目的是考查学生提出问题，解决问题的能力，这类几何试题将成为今后中考的热点试题．14．如图，平行四边形ABCD中，点E、F、G、H分别在AB、BC、CD、AD边上且AE=CG，AH=CF．求证：四边形EFGH是平行四边形．考点：平行四边形的判定与性质；全等三角形的判定与性质．分析：易证得△AEH≌△CGF，从而证得对应边BE=DG、DH=BF．故有△BEF≌△DGH，根据两组对边分别相等的四边形是平行四边形而得证．解答：证明：在平行四边形ABCD中，∠A=∠C（平行四边形的对边相等）；又∵AE=CG，AH=CF（已知），∴△AEH≌△CGF（SAS），∴EH=GF（全等三角形的对应边相等）；在平行四边形ABCD中，AB=CD，AD=BC（平行四边形的对边相等），∴AB﹣AE=CD﹣CG，AD﹣AH=BC﹣CF，即BE=DG，DH=BF．又∵在平行四边形ABCD中，∠B=∠D，∴△BEF≌△DGH；∴GH=EF（全等三角形的对应边相等）；∴四边形EFGH是平行四边形（两组对边分别相等的四边形是平行四边形）．点评：本题考查了平行四边形的判定和性质、全等三角形的判定和性质．平行四边形的判定方法共有五种，应用时要认真领会它们之间的联系与区别，同时要根据条件合理、灵活地选择方法．15．如图，在平行四边形ABCD中，E、F是对角线AC上的点，且AE=CF．（1）猜想探究：BE与DF之间的关系：平行且相等（2）请证明你的猜想．考点：平行四边形的判定与性质．分析：（1）BE平行且等于DF；（2）连接BD交AC于O，根据平行四边形的性质得出OA=OC，OD=OB，推出OE=OF，得出平行四边形BEDF即可．解答：（1）解：BE和DF的关系是：BE=DF，BE∥DF，故答案为：平行且相等．（2）证明：连接BD交AC于O，∵ABCD是平行四边形，∴OA=OC，OB=OD，∵AE=CF，∴OE=OF，∴BFDE是平行四边形，∴BE=DF，BE∥DF．点评：本题考查了平行四边形的性质和判定的应用，主要检查学生能否熟练地运用平行四边形的性质和判定进行推理，题型较好，通过此题培养了学生分析问题和解决问题的能力，同时培养了学生的观察能力和猜想能力．16．如图，E、F是平行四边形ABCD对角线AC上的两点，且BE∥DF．求证：∠1=∠2．考点：平行四边形的判定与性质；全等三角形的判定与性质．分析：由三角形全等（△ABE≌△CDF）得到BE=DF，所以四边形BFDE是平行四边形，根据对角相等即可得证．解答：证明：∵四边形ABCD是平行四边形（已知），∴AB=CD，AB∥CD（平行四边形的对边平行且相等），∴∠BAE=∠DCF（两直线平行，内错角相等）；∵BE∥DF（已知），∴∠BEF=∠DFE（两直线平行，内错角相等），∴∠AEB=∠CFD（等量代换），∴△ABE≌△CDF（AAS）；∴BE=DF（全等三角形的对应边相等），∵BE∥DF，∴四边形BEDF是平行四边形（对边平行且相等的四边形是平行四边形），∴∠1=∠2（平行四边形的对角相等）．点评：本题主要考查平行四边形的性质和三角形全等的判定，需要熟练掌握并灵活运用．平行四边形的判定定理：对边平行且相等的四边形是平行四边形．17．如图，已知E，F分别是▱ABCD的边AB，CD的中点．求证：ED=BF．考点：平行四边形的判定与性质．分析：根据平行四边形的性质得到AB∥CD，AB=CD，根据线段的中点的定义得到EB=AB，DF=CD，即BE=DF，BE∥DF，得到平行四边形EBFD，根据平行四边形的性质即可得到答案．解答：证明：∵四边形ABCD是平行四边形，∴AB∥CD，AB=CD，∵E，F分别是▱ABCD的边AB，CD的中点，∴EB=AB，DF=CD，∴BE=DF，∵BE∥DF，∴四边形EBFD是平行四边形，∴ED=BF．点评：本题主要考查对平行四边形的性质和判定的理解和掌握，能灵活运用平行四边形的性质和判定进行证明是解此题的关键．18．如图，BD是▱ABCD的对角线，∠ABD的平分线BE交AD于点E，∠CDB的平分线DF交BC于点F．求证：四边形DEBF为平行四边形．考点：平行四边形的判定与性质；角平分线的定义．分析：根据平行四边形性质和角平分线定义求出∠FDB=∠EBD，推出DF∥BE，根据平行四边形的判定判断即可．解答：解：∵四边形ABCD是平行四边形，∴AD∥BC，AB∥CD，∴∠CDB=∠ABD，∵DF平分∠CDB，BE平分∠ABD，∴∠FDB=∠CDB，∠EBD=∠ABD，∴∠FDB=∠EBD，∴DF∥BE，∵AD∥BC，即ED∥BF，∴四边形DEBF是平行四边形．点评：本题考查了角平分线定义，平行四边形的性质和判定等的应用，关键是推出DF∥BE，主要检查学生能否运用定理进行推理，题型较好，难度适中．19．如图，在▱ABCD中，对角线AC与BD交于点O，已知点E、F分别为AO、OC的中点，证明：四边形BFDE 是平行四边形．考点：平行四边形的判定与性质；全等三角形的判定与性质．分析：利用“平行四边形的对角线互相平分”的性质推知OA=OC，OB=OD；然后由已知条件“点E、F分别为AO、OC的中点”可以证得OE=OF；最后根据平行四边形的判定定理“对角线相互平分的四边形为平行四边形”即可证得结论．解答：证明：∵四边形ABCD是平行四边形，∴OA=OC，OB=OD（平行四边形的对角线互相平分）．又∵点E、F分别为AO、OC的中点，∴OE=OF．∴四边形BFDE是平行四边形（对角线相互平分的四边形为平行四边形）．点评：本题考查了平行四边形的判定与性质．平行四边形的判定方法共有五种，应用时要认真领会它们之间的联系与区别，同时要根据条件合理、灵活地选择方法．20．如图所示，A，E，F，C在一条直线上，AE=CF，过E，F分别作DE⊥AC，BF⊥AC，若AB=CD，可以得到BD平分EF，为什么？说明理由．考点：全等三角形的判定与性质；垂线；直角三角形全等的判定；平行四边形的判定与性质．分析：求出∠AFB=∠CED=90°，DE∥BF，推出AF=CE，连接BE、DF，根据HL证Rt△ABF≌Rt△CDE，推出DE=BF，得出平行四边形DEBF，根据平行四边形的性质推出即可．解答：解：BD平分EF，理由是：证法一、连接BE、DF．∵DE⊥AC，BF⊥AC，∴∠AFB=∠CED=90°，DE∥BF，∵AE=CF，∴AE+EF=CF+EF，即AF=CE，在Rt△ABF和Rt△CDE中，∴Rt△ABF≌Rt△CDE，∴DE=BF，∵DE∥BF，∴四边形DEBF是平行四边形，∴BD平分EF；证法二、∵DE⊥AC，BF⊥AC，∴∠AFB=∠CED=90°，DE∥BF，∵AE=CF，∴AE+EF=CF+EF，即AF=CE，在Rt△ABF和Rt△CDE中，∴Rt△ABF≌Rt△CDE，∴DE=BF，∵在△BFG和△DEG中，∴△BFG≌△DEG（AAS），∴EG=FG，即BD平分EF．点评：本题考查了平行四边形的性质和判定，垂线，全等三角形的性质和判定等知识点的运用，关键是得出平行四边形DEBF，题目比较好，难度适中．21．如图，△ABC的中线BD、CE交于点O，F、G分别是OB、OC的中点．求证：EF=DG且EF∥DG．考点：三角形中位线定理；三角形的角平分线、中线和高；平行四边形的判定与性质．分析：根据三角形的中位线推出DE∥BC，DE=BC，GF∥BC，GF=BC，推出GF=DE，GF∥DE，得出平行四边形DEFG，根据平行四边形的性推出即可．解答：证明：∵BD、CE是△ABC的中线，∴DE∥BC，DE=BC，同理：GF∥BC，GF=BC，∴GF=DE，GF∥DE，∴四边形DEFG是平行四边形，∴EF=DG，EF∥DG．点评：本题考查了平行四边形的性质和判定，三角形的中位线，三角形的中线等知识点，主要检查学生能否熟练的运用性质进行推理，题目比较典型，难度适中，通过做此题培养了学生分析问题和解决问题的能力．22．已知如图所示，▱ABCD的对角线AC、BD交于O，GH过点O，分别交AD、BC于G、H，E、F在AC上且AE=CF，求证：四边形EHFG是平行四边形．考点：平行四边形的判定与性质．分析：根据平行四边形性质得出OA=OC，AD∥BC，推出OE=OF，∠GAO=∠HCO，∠AGO=∠CHO，根据AAS 证△AGO≌△CHO，推出OG=OH，根据平行四边形的判定推出即可．解答：证明：∵四边形ABCD是平行四边形，∴OA=OC，AD∥BC，∵AE=CF，∴OE=OF，∵AD∥BC，∴∠GAO=∠HCO，∠AGO=∠CHO，在△AGO和△CHO中，∴△AGO≌△CHO（AAS），∴OG=OH，∵OE=OF，∴四边形EHFG是平行四边形．点评：本题考查了全等三角形的性质和判定，平行线的性质，平行四边形的性质和判定等知识点，注意：平行四边形的对角线互相平分，对角线互相平分的四边形是平行四边形．最新文件仅供参考已改成word文本。

几何图形的包含关系

圆形的包含关系&1 几何图形的定义&主题1四边形的定义(用最少性质描述)1.长方形(矩)形：有四个直角的四边形。

2.正方形：四边等长且四个直角的四边形。

3.菱形：四边等长的四边形。

4.平行四边形：两组对边平行的四边形。

5.鸢(筝)形：两组邻边等长且内角均小于180°的四边形。

6.镖形：两组邻边等长且有一个内角大于180°的四边形。

7.梯形：只有一组对边平行的四边形。

试说明一个四边形，其两组对边等长，则此四边形为一平行四边形。

试说明一个四边形，其两组对角相等，则此四边形为一平行四边形。

试说明一个四边形，其两邻角互补，则此四边形为一平行四边形。

试说明一个四边形，其两对角线互相平分，则此四边形为一平行四边形。

试说明一个四边形，其任一对角线可将它分割成两个全等三角形，则此四边形为一平行四边形。

具有下列性质的四边形，我们称之为「平行四边形」：甲：两组对边平行乙：两组对边等长丙：两组对角相等丁：两邻角互补戊：两对角线互相平分己：任一对角线可将它分割成两个全等三角形(A) (B) (C) (D)(E) (F) (G)(1)试问上列七个图形中，哪些图形是平行四边形？(2)试问上列六个性质中，找出以最少的性质来定义平行四边形。

下列各性质中，哪些可以最少的性质来定义「正方形」？甲：四个角都是直角乙：两组对边平行丙：两组对边等长丁：两组对角相等戊：四边等长己：两对角线互相垂直平分庚：一对角线将它分割成两个等腰三角形试问一矩形至少有一组邻边等长，则此四边形为何形状？若有一平行四边形至少有一个内角是直角，则此四边形为何形状？试问一菱形有一个内角为直角，则此四边形为何形状？下列各性质中，哪些可以最少的性质来定义「梯形」？甲：一组对角互补乙：有两组邻角互补丙：只有一组对边平行丁：有二组对边平行戊：只有一组对边等长，另一组对边不等长己：一组对角相等庚：两对角线等长具有下列性质的四边形，我们称之为「筝形」（或鸢形）：甲：两组邻边等长乙：对角线互相垂直丙：内角均小于180°丁：一组对角相等戊：具有对称性己：一条对角线可将它分割成两个等腰三角形庚：至少一条对角线被另一条对角线所平分(A) (B) (C) (D)(E) (F) (G)(1)试问上列七个图形中，哪些图形是筝形？(2)试问上列七个性质中，找出以最少的性质来定义「筝形」。

人教版数学五上书后第六单元精选练习

第六单元多边形的面积1.计算下面图形的面积。

2.有一块麦田的形状是平行四边形。

它的底是250m，高是84m，共收小麦14.7吨。

这块麦田有多少公顷？平均每公顷收小麦多少吨？3.下图中正方形的周长是32m。

请你求出平行四边形的面积。

4.下图中大平行四边形的面积是48cm2。

A、B是上、下两边的中点。

你能求出图中小平行四边行（涂色部分）的面积吗？5.一块玻璃的形状是一个三角形，它的底是12.5dm，高是7.8dm。

每平方米玻璃的价钱是68元，买这块玻璃要用多少钱？6.已知一个三角形的面积和底（如下图），求高。

7. 图中的平行四边形被分成两个三角形，它们的面积都是270㎡，求平行四边形的周长。

8. 右面平行四边形底边的中点是A，它的面积是48 m 2。

求涂色的三角形的面积。

9. 科技小组制作飞机模型，机翼的平面图是由两个完全相同的梯形组成的（如下图）。

机翼的面积是多少？10. 靠墙边围成一个花坛，围花坛的篱笆长46m，求这个花坛的面积。

11. 已知一个梯形的面积是15cm 2。

它的上底是4.5cm，高是3cm，下底是多少厘米？（列方程解决。

）12. 我们经常见到圆木、钢管等堆成像下图的形状。

通常用下面的方法求总根数：（顶层根数+底层根数）×层数÷2 算出图中圆木的总根数。

13.在下面的梯形中减去一个最大的平行四边形，剩下的面积是多少？有几种求法？14.一面中国少年先锋队中队旗的面积是多少？你能想出几种算法？ 15.在一块梯形的地中间有一个长方形的游泳池，其余的地方是草地。

草地的面积是多少平方米？16.图中每个小方格的面积是1 cm2，计算阴影部分的面积。

17.图中每个小方格的面积为1 m2，请你估计这个池塘的面积？18.图中是教室的一面墙。

如果砌这面墙平均每平方米用砖185块，一共需要用多少块砖？ 19.有一台收割机，作业宽度是1.8m。

每小时行5km，大约多少小时可以收割完左边这块地？。