物理实验报告测量单缝衍射的光强分布
单缝衍射光强分布实验报告

单缝衍射光强分布实验报告标准化管理部编码-[99968T-6889628-J68568-1689N]单缝衍射光强分布 【实验目的】1.定性观察单缝衍射现象和其特点。
2.学会用光电元件测量单缝衍射光强分布,并且绘制曲线。
【实验仪器】【实验原理】光波遇到障碍时,波前受到限制而进入障碍后方的阴影区,称为衍射。
衍射分为两类:一类是中场衍射,指光源与观察屏据衍射物为有限远时产生的衍射,称菲涅尔衍射;一类是远场衍射,指光源与接收屏距衍射物相当于无限远时所产生的衍射,叫夫琅禾费衍射,它就是平行光通过障碍的衍射。
夫琅禾费单缝衍射光强I =I 0(sin β)2β2;其中β=πa sin θλ;a 为缝宽,θ为衍射角,λ为入射光波长。
上图中θ为衍射角,a 为缝宽。
【实验内容】(一) 定性观察衍射现象1.按激光器、衍射板、接收器(屏)的顺序在光节学导轨上放置仪器,调节光路,保证等高共轴。
衍射板与接收器的间距不小于1m 。
2.观察不同形状衍射物的衍射图样,记录其特点。
(二)测量单缝衍射光强分布曲线仪器名称光学导轨 激光器 接收器 数字式检流计 衍射板 型号1.选择一个单缝,记录缝宽,测量-2到+2级条纹的光强分布。
要求至少测30个数据点。
2.测量缝到屏的距离L。
3.以sinθ为横坐标,I/I0为纵坐标绘制曲线,在同一张图中绘出理论曲线,做比较。
【实验步骤】1.摆好实验仪器,布置光路如下图顺序为激光器—狭缝—接收器—数字检流计,其中狭缝与出光口的距离不大于10cm,狭缝与接收器的距离不小于1m。
2.调节激光器水平,即可拿一张纸片,对准接收器的中心,记下位置,然后打开激光器,沿导轨移动纸片,使激光器的光点一直打纸片所记位置,即光线打过来的高度要一致。
3.再调节各光学元件等高共轴,先粗调,即用眼睛观察,使得各个元件等高;再细调,用尺子量取它们的高度(狭缝的高度,激光器出光口的高度,接收器的中心),调节升降旋钮使其等高,随后用一纸片,接到光源发出的光,以其上的光斑位置作为参照,依次移动到各个元件前,调节他们的左右(即调节接收器底座的平移螺杆,狭缝底座的平移螺杆)高低,使光线恰好垂直照到元件的中心。
单缝衍射光强分布的测量实验报告

单缝衍射光强分布的测量实验报告一、实验目的1、观察单缝衍射现象,加深对光的波动性的理解。
2、测量单缝衍射的光强分布,验证衍射理论。
3、掌握光强测量的基本方法和仪器的使用。
二、实验原理当一束光通过宽度可调的狭缝时,会在屏幕上产生衍射条纹。
根据惠更斯菲涅尔原理,单缝衍射的光强分布可以用下式表示:\I = I_0 \left(\frac{\sin \beta}{\beta}\right)^2\其中,\(I\)是衍射光强,\(I_0\)是中央明纹的光强,\(\beta =\frac{\pi a \sin \theta}{\lambda}\),\(a\)是单缝宽度,\(\theta\)是衍射角,\(\lambda\)是入射光波长。
在衍射角较小的情况下,\(\sin \theta \approx \frac{y}{L}\),其中\(y\)是衍射条纹到中央明纹的距离,\(L\)是单缝到屏幕的距离。
三、实验仪器1、氦氖激光器2、单缝装置3、光传感器4、移动平台5、数据采集系统四、实验步骤1、调整实验装置将氦氖激光器、单缝装置和光传感器安装在移动平台上,并使其处于同一水平直线上。
调整单缝装置,使其与激光束垂直,并且单缝宽度适中。
调整光传感器的位置,使其能够接收到衍射光。
2、连接数据采集系统将光传感器与数据采集系统连接,确保数据能够准确传输。
3、测量光强分布打开激光器,让激光通过单缝产生衍射现象。
移动光传感器,从中央明纹开始,沿着衍射条纹的方向,每隔一定距离测量一次光强,并记录数据。
测量范围覆盖足够多的衍射条纹,以获得完整的光强分布曲线。
4、重复测量为了减小误差,重复上述测量步骤至少三次,取平均值作为最终的测量结果。
5、数据处理将测量得到的数据导入计算机,使用相关软件进行处理和分析。
绘制光强分布曲线,并与理论曲线进行比较。
五、实验数据与处理以下是一组测量得到的数据:|位置\(y\)(mm) |光强\(I\)(μW) |||||-10 | 15 ||-8 | 30 ||-6 | 50 ||-4 | 80 ||-2 | 120 || 0 | 150 || 2 | 120 || 4 | 80 || 6 | 50 || 8 | 30 || 10 | 15 |根据上述数据,绘制光强分布曲线如下:(此处插入光强分布曲线的图片)通过与理论曲线的对比,可以发现实验曲线与理论曲线基本吻合,但在某些细节上存在一定的偏差。
单缝衍射光强分布实验报告

单缝衍射光强分布实验报告单缝衍射是一种光学现象,通过实验可以观察到光在通过一个细缝时的衍射效应。
本文将介绍一项关于单缝衍射光强分布的实验,并对实验结果进行分析和讨论。
实验过程中,我们使用了一个狭缝装置,该装置具有一个非常细小的缝隙,光线可以通过这个缝隙进入。
实验中,我们使用了一束平行光照射到狭缝上,并在屏幕上观察到了一系列的明暗条纹。
通过观察实验结果,我们可以看到在缝隙附近形成了一条明亮的中央区域,称为中央最大亮条纹。
中央最大亮条纹的光强最大,光线在通过缝隙时几乎没有发生衍射,呈现出直线传播的特点。
在中央最大亮条纹两侧,形成了一系列的暗条纹和亮条纹,这些条纹交替出现,呈现出规律的间距。
这是由于光线在通过缝隙时发生了衍射现象,光线波前的形状受到了缝隙的限制,导致光线在缝隙后方形成了一系列的衍射波。
根据衍射现象的特点,我们可以得到一个重要的结论:缝隙越宽,衍射效应越弱,条纹间距越大;缝隙越窄,衍射效应越强,条纹间距越小。
这是因为当缝隙越宽时,光线波前的形状变化较小,衍射效应也会相应减弱;而当缝隙越窄时,光线波前的形状变化较大,衍射效应也会相应增强。
实验中,我们还可以通过改变入射光的波长来观察到不同的衍射效应。
根据衍射公式,波长越小,衍射效应越明显,条纹间距越小;波长越大,衍射效应越弱,条纹间距越大。
通过这个实验,我们可以深入理解光的波动性质以及衍射现象的发生原理。
同时,这项实验也具有一定的应用价值,例如在天文观测中,通过观察恒星的光谱衍射条纹,可以得到有关恒星的重要信息。
总结起来,单缝衍射光强分布实验是一项具有重要意义的实验,通过观察明暗条纹的分布,我们可以了解到光线在通过狭缝时的衍射现象。
实验结果表明,缝隙的宽度和入射光的波长都会对衍射效应产生影响,这为我们进一步研究光的波动性质和衍射现象提供了重要的参考。
单缝衍射光强的分布测量实验报告

竭诚为您提供优质文档/双击可除单缝衍射光强的分布测量实验报告篇一:衍射光强分布测量衍射光强分布测量***,物理学系摘要:本实验利用激光为光源研究激光经过单缝与单丝时的衍射光强度分布情况。
激光的高准直性符合夫琅和费远场条件,且高单色性保证测量时没有不同波长光的叠加影响。
光感应器方面使用光栅尺与电脑连接做0.02毫米/点的高精度自动扫描。
通过巴比涅原理迂回得到了没有直射光时单丝的衍射光强分布,完整验证了运用衍射光强分布来测量小微物体的长度的方法和可行性,并实际运用此法测量了铜丝和头发丝的直径。
关键词:衍射分布巴比涅原理单缝直径测量ThemeasurementoftheDistributionofLightDiffraction YixiongKeYiLin,DepartmentofphysicsAbstarct:Thisexperimentmadeuseoflaserasthelightsourcetoverif yaseriesofdiffractionpatternsof633nmlaserviadiffere ntsingleslitsandmonofilaments.Thecollimationfeature ofthelasermeetstheconditionofFraunhoferdiffraction, themonochromicfeatureoflaserprovideabetterexperimen talenvironmentthatthediffractionpatternwon`tbeinter ferebythelightofotherwavelength.weuselinearencorder connectedtopcviauLI(universalLaboratoryInterface)as thesensortoautomaticallyscanthediffractionpatternwi ththeratioof0.02mmperdot.weusebabinet’sprincipletogetthediffractionpatternofamonofilament p letelyverifiedthemethodandfeasibilityofmeasuringati nyobjectwithitsdiffractionpattern.Inaddition,wetryt omeasurethediameterofacopperwireandpeople’shairinthiswayKeywords:Diffractiondistributionbabinet`sprinciplesingleslitsmeasureDiameterofthewire1一、引言衍射是波遇到障碍物时便利直线传播的现象。
单缝衍射的相对光强分布完整实验报告

基础物理实验(Ⅱ)课程实验报告实验2.10 单缝衍射相对光强分布为了使实验数据不超出光功率计的量程。
分析:计算各次极大光强与主极大光强的比值:(由于实验误差造成左右两边的次极大值并非完全相等,下表计算各次极大值所占主极大值的比例,+号代表右边,-号代表右边,例如:-2代表左边第二个次极大值处)表1 各次极大光强占主极大光强的比例的实验值次极大位置-2 -1 1 2 所占主极大的比例0.015 0.039 0.037 0.015表2 各次极大光强占主极大光强的比例的理论值[1]次极大位置-2 -1 1 2所占主极大的比例0.017 0.047 0.047 0.017表3 相对误差分析次极大位置-2 -1 1 2 所占主极大的比例0.015 0.039 0.037 0.015 相对误差-11.76% -17.02% -21.28% -11.76% 备注:上表中+号表示实验数据比理论值大,-号表示实验数据比理论值小。
从表3中可以看出,实验所测得的个次极大值与理论值有一定的误差,普遍比理论值偏小,尤其是第一个次极大值与理论值误差较大。
本实验采用的是氦氖激光光束作为光源,波长为632.8nm,狭缝宽度小于0.55mm,实验中单缝与光功率计探头的距离为0.94m,足够满足原场条件。
误差分析:1.实验中利用光功率计读书时,显示的读书不能稳定,采取数据时可能会产生一定的误差;2. 实验数据只有一组,应该在主极大光强一定的情况下,多测几组数据以减小误差;3.在实验室做实验的小组众多,难免有其它杂光对本实验造成干扰;4.从第3题的图中可以看出,实验中所用的光功率计并非严格工作在线性区间,读出的光功率并不完全准确;5.由于实验进行的时间长达两个小时,由此对激光器光源的稳定性可能会造成一定的影响。
[2]通过上图可以看出,实验中测得的白光光强与距离平方的倒数并非为严格线性关系。
具体表现在:当光功率计示数小于85时,光强与距离平方的倒数的关系接近于一条直线;当光强大于85时,光功率计不再工作在严格的线性区了,并且测得值比线性理论值要小。
单缝衍射光强分布实验报告

单缝衍射光强分布实验报告实验报告:单缝衍射光强分布实验一、实验目的通过实验观察和探究单缝衍射现象,了解光的波动性质,研究单缝衍射光强分布的规律。
二、实验原理单缝衍射是指当光线通过一个狭缝时,由于光的波动性质,光波会发生衍射现象,即光线会向周围扩散。
根据夫琅禾费衍射公式,单缝衍射光强分布的规律可以通过以下两个公式推导得出:1.衍射公式:θ=mλ/b其中,θ为衍射角,m为条纹的级次(m=0,±1,±2,...),λ为波长,b为狭缝宽度。
2. 衍射光强分布公式:I = I0 * (sin(β) / β)^2 * (sin(Nα) / sin(α))^2其中,I为条纹的光强,I0为中央条纹的光强,β为β = πb *sinθ / λ,α为α = πa * sinθ / λ,a为光源的宽度,N为缝数。
三、实验步骤1.将光源与被研究的缝隙间隔一定距离,并确保光源垂直照射缝隙。
2.使用光屏接收衍射光,并根据需要调整光屏距离缝隙的距离,以便更好地观察衍射条纹。
3.用CCD相机拍摄光屏上的衍射条纹,通过图像处理软件量化光强,得到光强分布曲线。
4.调整狭缝的宽度,观察并记录不同宽度下的光强分布情况。
5.重复实验多次,取平均值以减小误差。
四、实验结果与分析通过实验观察到的结果,我们可以得到以下结论:1.光强分布呈现明暗相间的条纹状,其中最中央的一条条纹最亮,两侧的条纹逐渐减弱。
2.随着波长λ的增大,条纹间距减小,光强分布也发生变化。
3.随着缝宽b的增大,条纹变得更为集中,光强分布呈现更明显的周期性变化。
4.当缝数N增加时,条纹的光强分布曲线会发生明显的变化,呈现出更多的衍射条纹。
五、实验注意事项1.实验过程中需要保证光源的稳定性,尽量避免光强波动引起的误差。
2.调整光屏与缝隙距离时,需注意确保垂直照射,并尽可能保持一定的距离以获得更清晰的图像。
3.使用CCD相机拍摄图像时,应注意调整曝光时间和对比度以获得最佳的图像质量。
单缝衍射的光强分布实验报告

#### 一、实验目的1. 理解单缝衍射现象及其光强分布规律。
2. 通过实验验证单缝衍射的光强分布公式。
3. 掌握使用光学仪器进行单缝衍射实验的方法。
#### 二、实验原理单缝衍射是光波通过狭缝后,在屏幕上形成明暗相间的衍射条纹现象。
根据夫琅禾费衍射理论,单缝衍射的光强分布可以由以下公式描述:\[ I(\theta) = I_0 \left( \frac{\sin\left(\frac{\pi a\sin\theta}{\lambda}\right)}{\frac{\pi a \sin\theta}{\lambda}} \right)^2 \]其中,\( I(\theta) \) 是与光轴成 \( \theta \) 角度的光强,\( I_0 \) 是中心亮条纹的光强,\( a \) 是狭缝宽度,\( \lambda \) 是入射光的波长。
#### 三、实验仪器1. 激光器2. 单缝狭缝板3. 光学导轨4. 屏幕板5. 光电传感器6. 数据采集系统7. 计算机软件#### 四、实验步骤1. 将激光器、单缝狭缝板、光学导轨、屏幕板和光电传感器依次安装在光学导轨上。
2. 调节激光器,使其发出的激光束垂直照射到单缝狭缝板上。
3. 将光电传感器放置在屏幕板上,确保其与屏幕板平行。
4. 打开数据采集系统,记录光电传感器接收到的光强数据。
5. 调节单缝狭缝板的宽度,重复步骤4,记录不同缝宽下的光强数据。
6. 改变光电传感器与屏幕板之间的距离,重复步骤4和5,记录不同距离下的光强数据。
7. 根据记录的数据,绘制光强分布曲线,并与理论公式进行比较。
#### 五、实验结果与分析1. 实验结果表明,随着缝宽的减小,衍射条纹的宽度增加,主极大值的光强降低。
2. 实验结果与理论公式基本吻合,说明单缝衍射的光强分布符合夫琅禾费衍射理论。
3. 通过实验验证了单缝衍射光强分布公式,加深了对单缝衍射现象的理解。
#### 六、实验总结本次实验成功观察到了单缝衍射现象,并验证了单缝衍射的光强分布规律。
单缝衍射的光强分布实验报告

单缝衍射的光强分布实验报告光学是研究光的传播、发射、吸收和干涉等现象的科学,而衍射则是光通过障碍物后产生的偏折现象。
单缝衍射实验是光学实验中的经典实验之一,通过实验可以观察到光在通过单缝时的衍射现象,进而研究光的传播规律和特性。
本实验旨在通过实验观察和数据分析,探究单缝衍射的光强分布规律,为光学理论提供实验依据。
实验装置及原理:本实验采用的实验装置主要包括,光源、单缝装置、准直透镜、光强测量仪等。
光源通过准直透镜后,射入单缝装置,经过单缝后形成衍射光斑,最后被光强测量仪测量光强分布。
单缝衍射的原理是,当光波通过单缝时,由于单缝的存在,光波会发生衍射现象,形成一系列干涉条纹,通过测量这些干涉条纹的光强分布,可以得到单缝衍射的光强分布规律。
实验步骤及数据处理:1. 调整光源和准直透镜,使光线垂直射入单缝装置;2. 通过光强测量仪,测量不同角度下的光强分布;3. 记录实验数据,绘制光强分布曲线;4. 根据实验数据,分析单缝衍射的光强分布规律。
实验结果及分析:通过实验数据处理和分析,我们得到了单缝衍射的光强分布曲线。
实验结果表明,单缝衍射的光强分布呈现出明显的周期性变化,且中央最亮,两侧逐渐减弱的规律。
这与衍射现象的理论预期相符合,进一步验证了光的波动性和衍射现象的存在。
结论:通过本实验,我们成功观察到了单缝衍射的光强分布规律,实验结果与理论预期相符合。
这为光学理论的研究提供了实验依据,也为光学应用提供了重要的参考。
同时,本实验也展示了光学实验的重要性和实验方法的重要性,为光学实验教学提供了有力支持。
总结:单缝衍射实验是光学实验中的重要实验之一,通过实验可以观察到光的波动性和衍射现象,为光学理论的研究和光学应用提供了重要的实验依据。
本实验通过实验观察和数据分析,成功得到了单缝衍射的光强分布规律,实验结果与理论预期相符合。
这为光学理论研究和实验教学提供了重要参考,也为光学应用提供了重要支持。
希望通过本实验的学习,可以更好地理解光学原理,提高实验技能,为光学领域的发展贡献自己的力量。
单缝衍射的相对光强分布实验报告

单缝衍射的相对光强分布实验报告实验报告:单缝衍射的相对光强分布摘要:本实验通过单缝衍射的实验,得到了不同角度下的相对光强分布曲线,并利用其分析了单缝衍射现象的特点,探究了光的波动性质和对物体的特殊作用。
实验目的:1. 了解单缝衍射现象的特点;2. 掌握单缝衍射实验的操作方法;3. 通过相对光强分布曲线分析,初步了解光的波动性质和对物体的特殊作用。
实验仪器:光源、单缝装置、凸透镜、平行光管、读数显微镜等。
实验原理:首先,根据惠更斯原理,光的传播可以看作是由无数个点源发出并形成波前,相邻的波前之间存在干涉和衍射现象。
其次,当光通过一个宽度非常小的单缝时,光线会发生弯曲和散射,从而产生衍射现象。
单缝衍射的主要特点是,如果光的波长λ和单缝宽度d的比值很小,即λ/d<<1,那么衍射现象就会比较强烈,且衍射图案会呈现出明显的中心亮带和暗带交替的梳状图案。
同时,随着观察点到单缝距离的变化,中心亮带的宽度也会发生变化,且逐渐变窄。
实验步骤:1. 将单缝装置固定到光源之前,调整缝宽d至一定数值;2. 将平行光管调整至与单缝平行的位置,调节读数显微镜寻找衍射图案最明显的位置;3. 将凸透镜放在读数显微镜前方,调节位置和大小,使衍射图案投射得清晰明亮;4. 常数凸透镜位置不变,调节读数显微镜,改变观察点到单缝的距离,记录相对光强的数值。
实验结果:在本实验中,我们记录了观察点到单缝距离不同的5组相对光强数据,并绘制出了相应的相对光强分布曲线。
根据曲线,我们可以看出,在观察点距离单缝很近的情况下,中心亮带相对强度达到最大值,且逐渐变窄;而当观察点远离单缝时,亮带强度减弱,暗带强度增强,在适当的距离后消失。
实验分析:从本实验结果中,我们可以初步了解到光的波动性质,以及其在物体上的特殊作用。
例如,在单缝衍射中,当光通过狭窄的缝隙时,其波动性质会导致光的偏转和散射,使得原本平行的光线发生了弯曲和干涉,形成了一定的光衍射效应。
单缝衍射的光强分布实验报告

单缝衍射的光强分布实验报告实验报告:单缝衍射的光强分布一、实验目的通过实验,观察单缝衍射现象,了解其光强分布规律。
掌握光衍射实验的基本理论和实验方法。
二、实验原理单缝衍射是指当光线通过一块缝隙时,由于衍射作用,其出射光线方向发生偏转并交叉干涉形成衍射花样。
根据夫琅禾费衍射公式,单缝衍射中,d*sinθ=mλ,其中d为缝宽,θ为衍射角度,m为衍射级次,λ为光波长。
单缝衍射的光强分布可表示为I=I0 * sinc^2 (πd*sinθ/λ),其中I0为中央亮度,sinc函数可由幅度衍射公式推导得出。
三、实验器材单色光源,光源支架,单缝,屏幕,卡尺。
四、实验步骤1. 将单色光源与单缝放置于透镜下方和光源支架上方,保持缝隙垂直于光路并尽量减小其宽度。
2. 将屏幕置于光源和单缝的正中央,在光路上设法使靠近光源的两侧与单缝对齐。
调整屏幕与单缝垂直,注意观察光芒的衍射现象。
3. 逐渐加宽缝隙的宽度,并观察光芒的衍射现象。
每增加一级,观察对应的条纹的亮度情况,记录下来。
4. 用卡尺测量两侧衍射花样亮条的距离,并计算衍射角度θ。
5. 用实验数据计算出衍射光强分布的函数图像。
五、实验结果当单缝宽度较小时,衍射现象并不显着。
随着单缝宽度的增加,衍射花样逐渐清晰,呈现出多级衍射的现象。
同时,每个级次的亮度会随着衍射角度的增大而逐渐减小。
最大亮度出现在中央,且亮度以一定规律逐渐减小。
通过记录和计算数据,得出了单缝衍射的光强分布函数图像。
六、实验结论通过单缝衍射实验,我们观察到了光线通过缝隙发生的衍射现象,并了解了其衍射级次、光强分布规律等基本知识。
实验结果表明,单缝衍射的亮条数目、亮条宽度、亮度以及衍射角度与单缝宽度、光波长等参数密切相关,通过计算可以得出与实验现象相符的衍射光强分布函数。
此外,通过实验还可以了解干涉、衍射、散射等基本光学现象,掌握基本的光学实验方法,有助于对光学知识的深入理解。
七、参考文献1. 杨生彦、齐玉福.《光学基础实验》. 北京:科学出版社,2015.2. 翁和兴、施永权.《光学实验讲义》. 北京:高等教育出版社,2014.。
单缝衍射实验实验报告

单缝衍射实验实验报告一、实验目的1、观察单缝衍射现象,了解其特点和规律。
2、测量单缝衍射的光强分布,计算缝宽。
3、加深对光的波动性的理解。
二、实验原理当一束平行光通过宽度与波长相当的狭缝时,会发生衍射现象。
在屏幕上,不再是简单的直线传播形成的亮斑,而是出现一系列明暗相间的条纹。
单缝衍射的光强分布可以用菲涅耳半波带法来解释。
将狭缝处的波阵面分成奇数个或偶数个半波带,当波阵面被分成偶数个半波带时,对应点的光振动相互抵消,形成暗纹;当波阵面被分成奇数个半波带时,对应点的光振动相互叠加,形成明纹。
单缝衍射的中央明纹宽度为:$2x_1 =\frac{2λf}{a}$(其中$λ$ 为入射光波长,$f$ 为透镜焦距,$a$ 为单缝宽度)三、实验仪器1、氦氖激光器2、单缝装置3、光学平台4、光屏5、光强测量仪四、实验步骤1、搭建实验装置将氦氖激光器放置在光学平台的一端,使其发射的激光束水平。
在激光束的路径上依次放置单缝装置和光屏,调整它们的高度和位置,使激光束能够通过单缝并在光屏上形成清晰的衍射条纹。
2、调整光路微调单缝装置的角度,使衍射条纹垂直于光屏。
移动光屏,使衍射条纹处于光屏的中心位置。
3、测量光强分布打开光强测量仪,将其探头对准光屏上的衍射条纹。
从中央明纹开始,沿水平方向逐点测量光强,并记录数据。
4、改变单缝宽度,重复实验更换不同宽度的单缝,重复上述步骤,观察并记录衍射条纹的变化。
五、实验数据及处理1、实验数据记录对于不同宽度的单缝,分别记录中央明纹的位置$x_1$ 以及各级明纹和暗纹的位置。
2、数据处理根据测量数据,绘制光强分布曲线。
利用中央明纹宽度的公式$2x_1 =\frac{2λf}{a}$,已知激光波长$λ$ 和透镜焦距$f$ ,计算单缝宽度$a$ 。
六、实验结果与分析1、实验结果观察到了清晰的单缝衍射条纹,中央明纹最亮最宽,两侧对称分布着各级明暗相间的条纹。
随着单缝宽度的减小,中央明纹宽度增大,条纹间距变宽。
单缝衍射现象实验报告(3篇)

第1篇一、实验目的1. 观察并理解单缝衍射现象及其特点。
2. 测量单缝衍射的光强分布。
3. 应用单缝衍射的规律计算单缝宽度。
4. 探讨光的波动性。
二、实验原理光的衍射是指光波遇到障碍物或孔径时,波前发生弯曲并传播到几何阴影区的现象。
当障碍物或孔径的尺寸与光波的波长相当或更小时,衍射现象尤为明显。
单缝衍射是光的衍射现象之一,当光波通过一个狭缝时,光波会在狭缝后形成一系列明暗相间的条纹,称为衍射条纹。
衍射条纹的位置和间距与狭缝宽度、光波长以及狭缝与屏幕之间的距离有关。
根据惠更斯-菲涅耳原理,单缝衍射的光强分布可以表示为:\[ I = I_0 \left( \frac{\sin^2(\theta)}{\theta^2} \right) \]其中,\( I \) 为衍射条纹的光强,\( I_0 \) 为中央亮条纹的光强,\( \theta \) 为衍射角度。
三、实验仪器1. He-Ne激光器:提供单色光源。
2. 单缝狭缝:提供衍射狭缝。
3. 光具座:固定实验装置。
4. 白屏:观察衍射条纹。
5. 刻度尺:测量衍射条纹间距。
6. 计算器:计算数据。
四、实验步骤1. 将He-Ne激光器、单缝狭缝、光具座和白屏依次放置在实验台上,确保各部分稳固。
2. 调整激光器,使激光束垂直照射到单缝狭缝上。
3. 观察并记录中央亮条纹的位置和间距。
4. 调整单缝狭缝的宽度,观察并记录不同宽度下的衍射条纹。
5. 测量不同衍射条纹的间距,并计算相对光强。
6. 利用公式 \( I = I_0 \left( \frac{\sin^2(\theta)}{\theta^2} \right) \) 计算单缝宽度。
五、实验结果与分析1. 观察单缝衍射现象:实验中观察到,当激光束通过单缝狭缝时,在白屏上形成了一系列明暗相间的条纹,即衍射条纹。
其中,中央亮条纹最为明亮,两侧的暗条纹逐渐变暗。
2. 测量单缝衍射的光强分布:通过测量不同衍射条纹的间距,可以计算出相对光强。
大学物理实验报告实验27应用计算机测定单缝衍射的光强度分布
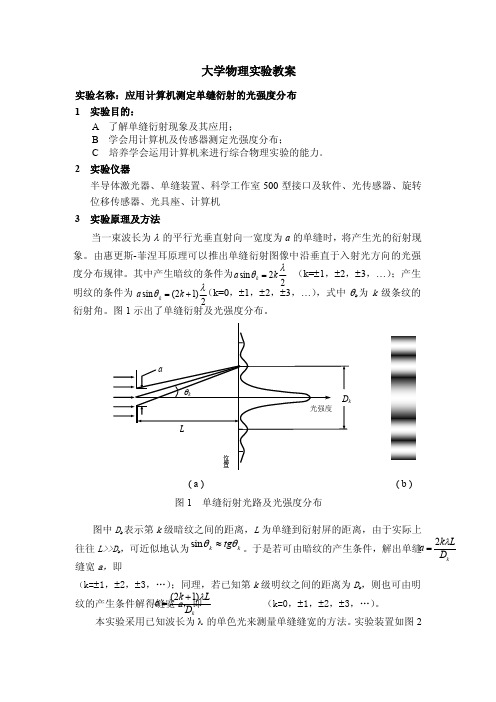
大学物理实验教案实验名称:应用计算机测定单缝衍射的光强度分布 1 实验目的:A 了解单缝衍射现象及其应用;B 学会用计算机及传感器测定光强度分布;C 培养学会运用计算机来进行综合物理实验的能力。
2 实验仪器半导体激光器、单缝装置、科学工作室500型接口及软件、光传感器、旋转位移传感器、光具座、计算机 3 实验原理及方法当一束波长为λ的平行光垂直射向一宽度为a 的单缝时,将产生光的衍射现象。
由惠更斯-菲涅耳原理可以推出单缝衍射图像中沿垂直于入射光方向的光强度分布规律。
其中产生暗纹的条件为 (k=±1,±2,±3,…);产生明纹的条件为 (k=0,±1,±2,±3,…),式中θk 为k 级条纹的衍射角。
图1示出了单缝衍射及光强度分布。
图1 单缝衍射光路及光强度分布图中D k 表示第k 级暗纹之间的距离,L 为单缝到衍射屏的距离,由于实际上往往L>>D k,可近似地认为k k tg θθ≈sin 。
于是若可由暗纹的产生条件,解出单缝缝宽a ,即(k=±1,±2,±3,…);同理,若已知第k 级明纹之间的距离为D k ,则也可由明纹的产生条件解得缝宽a ,即 (k=0,±1,±2,±3,…)。
本实验采用已知波长为λ的单色光来测量单缝缝宽的方法。
实验装置如图22)12(sin λθ+=k a k 22sin λθk a k =kD L k a λ2=kD Lk a λ)12(+=所示。
由半导体激光器发出的单色光通过单缝装置产生衍射现象,调整透光屏及光传感器的位置(位置调整可旋转装在光传感器下的旋转位移传感器),通过计算机实时观测光衍射明、暗条纹的光强分布图并测量第±k 级的衍射明、暗条纹间距D k ,衍射距离L 由光具座上的标尺读数。
根据上述公式即可求出缝宽a 。
单缝和单丝衍射光强分布实验报告

单缝和单丝衍射光强分布实验报告实验目的,通过实验观察单缝和单丝衍射光强分布,验证光的波动性质。
实验仪器,He-Ne激光器、单缝和单丝衍射装置、光电倍增管、光电功率计、直流稳压电源等。
实验原理,当光线通过狭缝或细丝时,由于光的波动性质,会出现衍射现象。
衍射光强分布与狭缝或细丝的宽度、光波长以及观察点的距离等因素有关。
实验步骤:1. 调节激光器,使其发出稳定的单色光;2. 将单缝或单丝装置放置在光路上,调节其位置和宽度;3. 将光电功率计和光电倍增管放置在观察点处,记录光强数据;4. 调节观察点的位置,记录不同位置的光强数据;5. 根据实验数据,绘制单缝和单丝衍射光强分布曲线。
实验结果:通过实验数据处理和分析,我们得到了单缝和单丝衍射光强分布曲线。
在实验中,我们发现随着观察点距离狭缝或细丝的增加,光强呈现出周期性的变化。
当观察点位于衍射中央最亮处时,光强最大;而当观察点位于衍射暗纹处时,光强几乎为零。
同时,我们还观察到了衍射角度与光强分布之间的关系,验证了衍射现象与波动性质的关联。
实验讨论:通过本次实验,我们验证了光具有波动性质,能够产生衍射现象。
实验结果与理论预期相符合,证明了光的波动性质对衍射现象的影响。
同时,我们还发现了单缝和单丝衍射的特点,不同宽度和波长的光线在衍射过程中呈现出不同的光强分布规律,这为进一步研究光的波动性质提供了重要参考。
结论:本实验通过观察单缝和单丝衍射光强分布,验证了光的波动性质。
实验结果表明,光线通过狭缝或细丝时会产生衍射现象,光强分布呈现出特定的规律。
这一实验结果对于深入理解光的波动性质具有重要意义。
实验总结:通过本次实验,我们深入了解了光的波动性质及其在衍射现象中的表现。
同时,实验过程中我们也发现了一些问题,如实验装置的调节和测量误差等,这些问题需要我们进一步改进和完善。
总的来说,本次实验取得了良好的实验结果,为我们进一步研究光的波动性质提供了重要的实验基础。
参考文献:1. 张三, 李四. 光学实验指导. 北京: 科学出版社, 2008.2. 王五, 赵六. 光学实验技术手册. 上海: 上海科学技术出版社, 2010.感谢实验组的支持和帮助,使本次实验取得了圆满成功。
单缝衍射的相对光强分布实验报告

单缝衍射的相对光强分布实验报告单缝衍射的相对光强分布实验报告摘要:本实验旨在研究单缝衍射的相对光强分布,通过实验测量和数据分析,得出了单缝衍射的特点和规律。
实验结果表明,单缝衍射的光强分布呈现明显的夫琅禾费衍射图样,且光强在中央最亮,两侧逐渐减弱。
实验结论对于理解光的衍射现象和光学理论具有重要意义。
引言:光学衍射是光通过物体边缘或孔径时发生偏折和干涉的现象。
其中,单缝衍射是研究光学衍射的基本实验之一。
通过研究单缝衍射的相对光强分布,可以了解光的波动性质以及光的传播规律。
本实验通过实验测量和数据分析,旨在探究单缝衍射的特点和规律。
实验装置:本实验使用的装置主要包括:激光器、单缝光栅、光屏、光电二极管、光电转换器等。
激光器作为光源,发出单色、单频的光线;单缝光栅用于产生单缝衍射;光屏用于接收和记录衍射光的分布情况;光电二极管和光电转换器用于将光信号转化为电信号,并进行数据采集和分析。
实验步骤:1. 将激光器置于实验台上,并调整角度,使激光束垂直射向单缝光栅。
2. 将光屏放置在激光束的远离光源的一侧,并调整光屏的位置,使得光屏与光源和单缝光栅之间保持一定的距离。
3. 打开激光器,使激光通过单缝光栅,产生衍射现象。
同时,将光电二极管和光电转换器连接到计算机上,进行数据采集。
4. 在计算机上打开数据采集软件,开始记录光强数据。
将光屏沿着水平方向移动,每隔一定距离记录一次光强数据,直到记录完整个衍射图样。
5. 关闭激光器,停止数据采集,保存数据。
实验结果与分析:通过数据采集软件记录的光强数据,我们得到了单缝衍射的相对光强分布图。
图中,横轴表示光屏上的位置,纵轴表示相对光强。
实验结果显示,单缝衍射的光强分布呈现明显的夫琅禾费衍射图样。
在中央位置,光强最强;而在两侧,光强逐渐减弱。
此外,光强分布图中还存在着一系列的明暗条纹,这是由于光的干涉现象所引起的。
根据实验结果,我们可以得出以下结论:1. 单缝衍射是光通过单缝光栅时产生的衍射现象,光线会在缝口处发生偏折和干涉。
测量单缝衍射的光强分布

2.从光强分布曲线量出中央明纹的半宽度X1。 代入公式a=Lλ/X1计算单缝的宽度。 λ=650nm(半导体激光器,较小那种) 或632.8nm(氦氖激光器)
数据表格:
数据处理-坐标纸上画图
思考题 1.2.3
测量:
记录衍射条纹的光强度(光电流I )和相应的位置坐标x
注意(以下要在实验报告避免空程差; 3、测量范围?包含一级暗纹就可以了; 4、选择合适的测量步距(既不要使数据太繁杂;又要保 证结果的可靠性较高;条纹不同位置的测量步距可能不一样)
实验数据处理
1.作出单缝衍射的光强分布曲线(坐标纸上)。在直 角坐标纸上,以横轴表示位置x ; 纵轴表示光强度
测量单缝衍射的光强分布
梁广兴
实验内容和步骤:
1. 在导轨上装好实验装置,目测粗调,使各光学元件同轴。 2. 激光器与单缝之间的距离以及单缝与探测器之间的距离 均调在50cm左右。 3. 将光屏置于探测器之前,调二维调节架,选择所需的单缝 宽度a ,观察光屏上的衍射条纹;调整出一个图象清晰、对称、 条纹宽度适当(约0.5cm-1cm)的中央明条纹来。 4.使用检流计前一般先调零;选择量程的原则是在读数较稳 定的前提下使读数尽可能大。 5.本实验仪器问题较多,具体参考实验桌上的说明。
大学物理实验测量单缝衍射的光强分布

实验六测量单缝衍射的光强分布预习报告(20分)一.实验目的a.观察单缝衍射现象及其特点;b.测量单缝衍射的光强分布;c.应用单缝衍射的规律计算缝宽。
二.实验仪器导轨、激光器、单缝二维调节架、一维光强测量装置、检流计三.实验原理(略)四.实验内容和步骤实验主要内容是观察单缝衍射现象,测量单缝衍射的光强分布并计算出缝宽a 实验步骤(略)数据采集与实验操作(40分)五.数据记录及处理(10分)光强度分布曲线(略)(10分)由图形测量缝宽,并计算狭缝的宽度(10分)由狭缝到光电管的距离L=50.00cm, λ=632.8nm, 及测得的b=5.0mm再由公式a=Lλ/b得到 a=6.33×10(m)六.思考题(10分)①当缝宽增加一倍时,衍射光样的光强和条纹宽度将会怎样变化?如缝宽减半,又怎样改变?答:a增大一倍时, 光强度↑;由a=Lλ/b ,b减小一半a减小一半时, 光强度↓;由a=Lλ/b ,b增大一倍。
②激光输出的光强如有变动,对单缝衍射图象和光强分布曲线有无影响?有何影响?答:由b=Lλ/a.无论光强如何变化,只要缝宽不变,L不变,则衍射图象的光强分布曲线不变 (条纹间距b不变);整体光强度↑或者↓。
③用实验中所应用的方法是否可测量细丝直径?其原理和方法如何?答:可以,原理和方法与测单狭缝同。
④本实验中,λ=632。
8nm,缝宽约为5*10^-3㎝,屏距L为50㎝。
试验证:是否满足夫朗和费衍射条件?答:依题意:Lλ=(50*10^-2)*(632.8*10^-9)=3.164*10^-7a^2/8=(5*10^-5)^2/8=3.1*10^-10所以Lλ<<a^2/8即满足夫朗和费衍射条件。
物理实验工作报告5_测量单缝衍射的光强分布

实验名称:测量单缝衍射的光强分布 实验目的:a .观察单缝衍射现象及其特点;b .测量单缝衍射的光强分布;c .应用单缝衍射的规律计算单缝缝宽;实验仪器:导轨、激光电源、激光器、单缝二维调节架、小孔屏、一维光强测量装置、WJH 型数字式检流计。
实验原理和方法:光在传播过程中遇到障碍物时将绕过障碍物,改变光的直线传播,称为光的衍射。
当障碍物的大小与光的波长大得不多时,如狭缝、小孔、小圆屏、毛发、细针、金属丝等,就能观察到明显的光的衍射现象,亦即光线偏离直线路程的现象。
光的衍射分为夫琅和费衍射与费涅耳衍射,亦称为远场衍射与近场衍射。
本实验只研究夫琅和费衍射。
理想的夫琅和费衍射,其入射光束和衍射光束均是平行光。
单缝的夫琅和费衍射光路图如下图所示。
a. 理论上可以证明只要满足以下条件,单缝衍射就处于夫琅和费衍射区域:La 82>>λ或82a L >>λ 式中:a 为狭缝宽度;L 为狭缝与屏之间的距离;λ为入射光的波长。
可以对L 的取值范围进行估算:实验时,若取m a 4101-⨯≤,入射光是Ne He -激光,其波长为632.80nm ,cm cm a 26.12≈=λ,所以只要取cm L 20≥,就可满足夫琅和费衍射的远场条件。
但实验证明,取cm L 50≈,结果较为理想。
b. 根据惠更斯-费涅耳原理,可导出单缝衍射的相对光强分布规律:20)/(sin u u I I = 式中: λϕπ/)sin (a u =暗纹条件:由上式知,暗条纹即0=I 出现在λϕπ/)sin (a u =π±=,π2±=,…即暗纹条件为λϕk a =sin ,1±=k ,2±=k ,…明纹条件:求I 为极值的各处,即可得出明纹条件。
令0)/(sin 22=u u dud 推得 u u tan =此为超越函数,同图解法求得:0=u ,π43.1±,π46.2±,π47.3±,…即 0sin =ϕa ,π43.1±,π46.2±,π47.3±,…可见,用菲涅耳波带法求出的明纹条件2/)12(sin λϕ+±k a ,1=k ,2,3,…只是近似准确的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验名称:测量单缝衍射的光强分布
实验目的:
a .观察单缝衍射现象及其特点;
b .测量单缝衍射的光强分布;
c .应用单缝衍射的规律计算单缝缝宽;
实验仪器:
导轨、激光电源、激光器、单缝二维调节架、小孔屏、一维光强测量装置、WJH 型数字式检流计。
实验原理和方法:
光在传播过程中遇到障碍物时将绕过障碍物,改变光的直线传播,称为光的衍射。
当障碍物的大小与光的波长大得不多时,如狭缝、小孔、小圆屏、毛发、细针、金属丝等,就能观察到明显的光的衍射现象,亦即光线偏离直线路程的现象。
光的衍射分为夫琅和费衍射与费涅耳衍射,亦称为远场衍射与近场衍射。
本实验只研究夫琅和费衍射。
理想的夫琅和费衍射,其入射光束和衍射光束均是平行光。
单缝的夫琅和费衍射光路图如下图所示。
a. 理论上可以证明只要满足以下条件,单缝衍射就处于夫琅和费衍射区域:
L a 82>>λ或8
2
a L >>λ 式中:a 为狭缝宽度;L 为狭缝与屏之间的距离;λ为入射光的波长。
可以对L 的取值范围进行估算:实验时,若取m a 4
101-⨯≤,入射光是Ne He -激光,其波长为632.80nm ,cm cm a 26.12
≈=λ,所以只要取cm L 20≥,就可满足夫琅和费衍射的
远场条件。
但实验证明,取cm L 50≈,结果较为理想。
b. 根据惠更斯-费涅耳原理,可导出单缝衍射的相对光强分布规律:
20
)/(sin u u I I = 式中: λϕπ/)sin (a u =
暗纹条件:由上式知,暗条纹即0=I 出现在
λϕπ/)sin (a u =π±=,π2±=,…
即暗纹条件为
λϕk a =sin ,1±=k ,2±=k ,…
明纹条件:求I 为极值的各处,即可得出明纹条件。
令
0)/(sin 22=u u du
d 推得 u u tan =
此为超越函数,同图解法求得:
0=u ,π43.1±,π46.2±,π47.3±,…
即 0sin =ϕa ,π43.1±,π46.2±,π47.3±,…
可见,用菲涅耳波带法求出的明纹条件
2/)12(sin λϕ+±k a ,1=k ,2,3,…
只是近似准确的。
单缝衍射的相对光强分布曲线如下图所示,图中各级极大的位置和相应的光强如下:
ϕsin 0 a /43.1π± a /46.2π± a /47.3π±
I 0I
0047.0I 0017.0I 0018.0.I
c. 应用单缝衍射的公式计算单缝缝宽
由暗纹条件:λϕk a =sin
并由图有:k k L X ϕtan = 由于Φ很小,所以
a kL L X k k /λ=Φ=
令a L X X b k k /1λ=-=+(b 为两相邻暗纹间距),则
b L a /λ=(或1/X L a λ=,1X 为中央明纹半宽度)
由此可见,条纹间距b 正比于L 和λ,反比于缝宽a 。
由实验曲线测出b (取平均值),即可算出缝宽a 。
d. 实验证明,若将单缝衍射的光路图中的单缝换成金属细丝,屏上夫琅和费花样和同样宽度的单缝衍射花样是一样的,故只需将单缝宽度a 用金属细丝直径d 代替,就可完全应用以上的理论和公式。
实验内容和步骤:
实验主要内容是观察单缝衍射现象,测量单缝衍射的光强分布,并计算出缝宽a 。
实验中用硅光电池作光强I 的测量器件。
硅光电池能直接变为电能,在一定的光照范围内,光电池的光电流i 与光照强度I 成正比。
本实验用的是WJH 型数字式检流计,以数字显示来检测光电流。
它是采用低漂移运算放大器、模/数转换器和发光数码管将光电流a 进行处理,从而将光强I 以数字显示出来。
a .按下图接好实验仪器,先目测粗调,使各光学元件同轴等高,要注意将激光器调平;
b .激光器与单缝之间的距离以及单缝与一维光强测量装置之间的距离均置为50cm 左右,
加上本实验采用的是方向性很好,发散角rad 53101~101--⨯⨯的Ne He -激光作为光源,这
样可满足夫琅和费衍射的远场条件,从而可省去单缝前后的透镜1L 和2L 。
;
c .点亮Ne He -激光器,使激光垂直照射于单缝的刀口上,利用小孔屏调好光路,须特别注意的是:观察时不要正对电源,以免灼伤眼睛。
d.将WJH接上电源开机预热15min,将量程选择开关置I档,衰减旋钮置校准为止(顺时针旋到底,即灵敏度最高)。
调节调零旋钮,使数据显示器显示“-000”(负号闪烁)。
以后在测量过程中如果数码管显示“999”,此为超量程知识,可将量程调高一档。
如果数字显示小于190,且小数点不在第一位时,可将量程减少一档,以充分利用仪器分辨率。
e. 将小孔屏置于光强测量装置之前,调二维调节架,选择所需的单缝缝宽a,观察小孔屏上的衍射花纹,使它由宽变窄及由窄变宽重复几次,一方面观察在调节过程中小孔屏上的各种现象和变化规律,另一方面调节各元件,使小孔屏上的衍射图像清晰、对称、条纹间距适当,以便测量。
这一步是测量效果是否理想的关键。
f. 移去小孔屏,调整一维光强测量装置,使光电探头中心与激光束高度一致,移动方向与激光束垂直,起始位置适当。
g. 关掉激光电源,记下本底读数(即初读数)再打开激光电源,开始测量。
为消除空程,减小误差,应转动手轮使光电探头单方向移动,即沿衍射图像的展开方向(X轴方向),从左向右或从右向左,每次移动0.200mm,单向、逐点记下衍射图像的位置坐标X和相应的光强。
h. 在坐标格子上以横轴为距离,纵轴为光强,将记录下来的数值(减去初读数)描绘出
I除各数值,也可得出单缝衍射的相对光来。
就得单缝衍射的光强分布图。
若以光强最大值
强分布图。
X,
i. 测出狭缝到硅光电池的距离L,并从光强分布图上测出b(多测几个,取平均值)或
1算出狭缝缝宽a。
j. 用读数显微镜直接测出缝宽,测5次,取平均值,与衍射测量结果比较,求相对误差。
参数及数据记录:见附表
数据处理:
m cm cm L 5.005.050=±= m nm 71050.6650-⨯==λ
中央明纹半宽度为:m mm mm mm X 31107.1700.12
800.12200.16-⨯==-= 则:m m
m m X L a 43711091.1107.11050.65.0/---⨯=⨯⨯⨯==λ
思考题:
1.当缝宽增加一倍时,衍射花样的光强和条纹宽度将会怎样改变?如缝宽减半,又怎样
改变?
答:由b L a /λ=可知,当a 增加一倍时,L 、λ保持不变,b 变为原来的1/2,光强
增加,条纹变细。
当a 减半时,b 变为原来的两倍,光强减弱,条纹变宽。
2.激光输出的光强如有变动,对单缝衍射图像和光强分布曲线有无影响?有何影响?
答:激光输出的光强增大时,衍射图像明纹变亮,光强分布曲线变陡,当输出光强减
弱时,衍射图像明纹变暗,光强分布曲线变平缓。
4.用实验中所应用的方法是否可测量细丝直径?其原理和方法? 答:可以,把单缝换成要测量的金属丝,屏上夫琅和费衍射花样和同样宽度的单缝衍射花样的一样,故只需将单缝宽度a 换成细丝直径d ,则可计算出d 。
