71Credit Default Swap V3

合集下载

《草民经济学》-南勇

《草民经济学》-南勇名词解释GDPGDP，就是英文GrossDomesticProduct的简称，翻译成中文意思就是“国内生产总值”。

它是指在一定时期内(比如一个季度或一年)，一个国家或地区的经济中所生产出的全部最终产品和劳务的价值，常被公认为衡量国家经济状况，即经济表现如何、国民财富的多寡、国家实力强弱的最佳指标。

GNP“国民生产总值”(英文简称为GNP)这个概念，要把你的人在外国创造，然后汇回国内来的收入都算进去，而将外国人在你的国家所创造的，却要汇回人家地盘的收入刨掉。

汇率汇率说白了就是一个国家货币的“价格”，当然参照物是别的国家的货币。

决定价格的因素是“供需关系”，汇率也不例外。

避险式储蓄老百姓为了应付充满了不确定性的生活压力而不得已为之的事。

供需关系价格是由供需关系决定的。

当某种东西买的多、卖的少，即“供不应求”的时候，价格就会上涨;反之，价格就会下降。

通货膨胀当通胀来临的时候，通常都意味着一个国家的经济形势相当不错，经济发展、收入增加、工作好找、生活稳定，大家都放开了花钱，抢着买东西，从而使该国的经济生活总体上呈现出一种由需求旺盛带来的“供不应求”局面。

因此，适度的通胀，预示着一个国家的生活水平总体上不错，是一个值得高兴的信号。

通缩通缩意味着所有的东西都降价，降价也没多少人买，所以经济长期处在一种物价过于低迷，货币购买力过强的局面。

消费者物价指数-CPI用来反映与居民生活有关的商品及劳务价格变动情况的指标。

CPI超过3%就可以算通胀，超过5%就基本上属于“较严重通胀”的范畴了。

生产者物价指数-PPI用来衡量工业企业产品出厂价格变动趋势和变动程度的指标。

它就站在CPI的前边，直接影响着CPI的变动。

就是说，一个物件儿从“工厂”到“商场”是需要一个过程的，“工厂”这边涨价(或降价)，迟早会影响到“商场”那边的价格变化。

采购经理人指数-PMI用来监测制造业生产活动的活跃度的指标，就是说，可以用来反映一国经济还处在“工厂生产”阶段时的景气度。

credit default swap 通俗解释

credit default swap 通俗解释信用违约互换（Credit Default Swap，CDS）是指一种金融衍生品，通过将信用风险从一方转嫁给另一方，用于对冲信用违约风险。

信用违约互换是由债券市场衍生而来的金融产品，最早在20世纪90年代出现，并在其后几十年中迅速发展。

这篇文章将试图通过通俗的方式解释信用违约互换的概念、作用、运作机制以及其在金融市场中的影响。

信用违约互换是一种合约，通常由两个相互信任的当事人签订，即买方和卖方。

买方支付一定的保费给卖方，以换取其对一份特定债券债务违约风险的保护。

如果债务发行人（即债券发行方）违约，买方将获得赔偿，相当于债务违约的损失。

与此同时，卖方则承担相应的风险，并在发生违约时向买方支付赔偿。

信用违约互换的作用是用于对冲信用违约风险。

投资者可以利用这种工具来降低持有债务所面临的风险。

例如，一家银行持有大量的债券，但担心债券发行方可能违约，导致损失。

为了对冲这种风险，该银行可以购买信用违约互换，以便在债务违约时获得赔偿。

通过购买信用违约互换，银行可以降低其持有债务的风险，从而保护其财务状况。

信用违约互换的运作机制可以简单解释如下。

假设投资者A购买了一份债券，且担心发行方会违约。

投资者A可以与投资者B签订信用违约互换合约。

根据合约的内容，投资者A将支付给投资者B一定的保费。

如果发行方违约，投资者A将向投资者B索赔，获得赔偿。

通常情况下，合约中还规定了其他一些条款，比如违约定义、赔偿金额计算方法等。

这样，投资者A通过购买信用违约互换，实际上在投资者B那里获得了对债务违约的保护。

信用违约互换在金融市场中扮演着重要的角色。

它不仅对投资者降低风险提供了有力的工具，同时也对金融系统的稳定性起到了促进作用。

然而，信用违约互换也存在一些问题和风险。

首先，由于信用违约互换市场规模巨大且高度复杂，管理和监控这一市场变得更加困难。

其次，信用违约互换的流动性也可能受到影响。

Credit Default Swap函数包用户指南说明书

Package‘credule’October12,2022Version0.1.4Date2020-05-09Title Credit Default Swap FunctionsMaintainer Bertrand Le Nezet<**************************>Depends R(>=2.14.1)DescriptionIt provides functions to bootstrap Credit Curves from market quotes(Credit Default Swap-CDS-spreads)and price Credit Default Swaps-CDS.License MIT+ﬁle LICENSEURL https:///blenezet/creduleBugReports https:///blenezet/credule/issuesSuggests knitrVignetteBuilder knitrNeedsCompilation yesAuthor Bertrand Le Nezet[cre,aut,cph],Richard Brent[ctb,cph],John Burkardt[ctb,cph]Repository CRANDate/Publication2020-05-1021:20:12UTCR topics documented:credule-package (2)bootstrapCDS (3)priceCDS (6)Index912credule-package credule-package Credit Default Swap pricing and Credit Curve bootstrappingDescriptionCredit Curve boostrapping from market quotes(Credit Default Swap-CDS-spreads)and Credit Default Swap-CDS-pricingDetailsPackage:creduleType:PackageVersion:0.1.3Date:2015-08-03License:MIT+ﬁle LICENSEA Credit Default Swap(CDS)is aﬁnancial swap agreement that the seller of the CDS will com-pensate the buyer(usually the creditor of the reference loan)in the event of a loan default(by the debtor)or other credit event.This is to say that the seller of the CDS insures the buyer against some reference loan defaulting.The buyer of the CDS makes a series of payments(the CDS"fee"or "spread")to the seller and,in exchange,receives a payoff if the loan defaults.It was invented by Blythe Masters from JP Morgan in1994.April82009saw a"Big Bang"in the market for credit default swap(CDS)contracts and the way in which they are traded.Both contract and convention changes were implemented simultaneously.These changes were designed to make CDS more standardised to help support efforts for central clearing of CDS trades,make strides towards T+0trade processing and facilitate operational efﬁ-ciency.The CDS"Big Bang"has introduced standardized coupon dates and maturity dates.The functions provided in this package do not use these"new"conventions(i.e.they use the conventions pre-April2008);therefore it’s not recommended to use them in a production context.In most cases the differences are marginal,therefore these functions are good enough for preliminary research.See vignette("credule")for more details.Note.I’m planning to update this package with proper CDS ISDA conventions handling at a later stage.Author(s)Bertrand Le Nezet Maintainer:Bertrand Le Nezet<bertrand dot lenezet at gmail dot com>ReferencesISDA Standard CDS Example /cdsmodel/assets/cds-model/docs/ Standard%20CDS%20Examples.pdfCDS Bing Bang /assets/en/docs/markit-magazine/issue-4/60-cds-big-bang.pdfExampleslibrary(credule)yieldcurveTenor=c(1,2,3,4,5,7)yieldcurveRate=c(0.0050,0.0070,0.0080,0.0100,0.0120,0.0150)creditcurveTenor=c(1,3,5,7)creditcurveSP=c(0.99,0.98,0.95,0.92)cdsTenors=c(1,3,5,7)cdsSpreads=c(0.0050,0.0070,0.00100,0.0120)premiumFrequency=4defaultFrequency=12accruedPremium=TRUERR=0.40#CDS pricingres_price=priceCDS(yieldcurveTenor,yieldcurveRate,creditcurveTenor,creditcurveSP,cdsTenors,RR,premiumFrequency,defaultFrequency,accruedPremium)res_price#Credit curve bootstrapping from CDS spreadsres_bootstrap=bootstrapCDS(yieldcurveTenor,yieldcurveRate,res_price$tenor,res_price$spread,RR,premiumFrequency,defaultFrequency,accruedPremium)res_bootstrapbootstrapCDS Bootstrap a Credit CurveDescriptionA function that bootstrap a credit curve from a set of Credit Default Swap spreads givent for variousmaturity.UsagebootstrapCDS(yieldcurveTenor,yieldcurveRate,cdsTenors,cdsSpreads,recoveryRate,numberPremiumPerYear=c(4,2,1,12),numberDefaultIntervalPerYear=12,accruedPremium=c(TRUE,FALSE))ArgumentsyieldcurveTenorA double vector.Each value represents a tenor of the yield curve expressed inyear(e.g.1.0for1Y,0.5for6M)yieldcurveRate A double vector.Each value represents the discount rate(continuously com-pounded)for a partical tenor(e.g.0.005means0.5%,0.02means2 cdsTenors A double vector.Each value represents the maturity expressed in year of a Credit Default Swap which we want to price(e.g5.0means5Y)cdsSpreads A double vector.Each value represents the CDS spread(expressed in decimal,e.g.0.0050represent0.5%or50bp)for a given maturityrecoveryRate A double.It represents the Recovery Rate in case of default(e.g0.40means 40%recovery which is a standard value for Senior Unsecured debt) numberPremiumPerYearAn Integer.It represents the number of premiums paid per year.CDS premiumspaid quaterly(i.e.numberPremiumPerYear=4)and sometimes semi-annually(i.e.numberPremiumPerYear=2)numberDefaultIntervalPerYearAn Integer.It represents the number of timesteps used to perform the numeri-cal integral required while computing the default leg value.It is shown that amonthly discretisation usually gives a good approximation(Ref.Valuation ofCredit Default Swaps,Dominic O Kane and Stuart Turnbull) accruedPremium A boolean.If set to TRUE,the accrued premium will be taken into account in the calculation of the premium leg value.DetailsIn brief,a CDS is used to transfer the credit risk of a reference entity(corporate or sovereign)from one party to another.In a standard CDS contract one party purchases credit protection from another party,to cover the loss of the face value of an asset following a credit event.A credit event isa legally deﬁned event that typically includes bankruptcy,failure-to-pay and restructuring.Thisprotection lasts until some speciﬁed maturity date.To pay for this protection,the protection buyer makes a regular stream of payments,known as the premium leg,to the protection seller.This size of these premium payments is calculated from a quoted default swap spread which is paid on the face value of the protection.These payments are made until a credit event occurs or until maturity, whichever occursﬁrst.Modeling Credit Using a Reduced-Form Approach The world of credit modelling is divided into two main approaches,one called the structural and the other called the reduced-form.In the struc-tural approach,the idea is to characterize the default as being the consequence of some company event such as its asset value being insufﬁcient to cover a repayment of debt.Structural models are generally used to say at what spread corporate bonds should trade based on the internal structure of theﬁrm.They therefore require information about the balance sheet of the ﬁrm and can be used to establish a link between pricing in the equity and debt markets.However, they are limited in at least three important ways:they are hard to calibrate because internal company data is only published at most four times a year;they generally lack theﬂexibility toﬁt exactly a given term structure of spreads;and they cannot be easily extended to price credit derivatives.In the reduced-form approach,the credit event process is modeled directly by modeling the prob-ability of the credit event ing a security pricing model based on this approach,this prob-ability of default can be extracted from market prices.Reduced form models also generally have theﬂexibility to reﬁt the prices of a variety of credit instruments of different maturities.They can also be extended to price more exotic credit derivatives.It is for these reasons that they are used for credit derivative pricing.See vignette("credule")for more details.ValueReturns a Dataframe with3columns:tenor,survprob and hazrate.The tenor column contains the tenor value given in parameter cdsTenors,the survprob column gives the survival probability(in decimal)for each tenor(e.g.0.98menas98%)and the hazrate column gives the non-cumulative hazard rate(intensity of the poisson process)for each tenor(e.g.0.01means1%hazard rate). Author(s)Bertrand Le NezetExampleslibrary(credule)yieldcurveTenor=c(1,2,3,4,5,7)yieldcurveRate=c(0.0050,0.0070,0.0080,0.0100,0.0120,0.0150)cdsTenors=c(1,3,5,7)cdsSpreads=c(0.0050,0.0070,0.0090,0.0110)premiumFrequency=4defaultFrequency=12accruedPremium=TRUERR=0.40bootstrapCDS(yieldcurveTenor,yieldcurveRate,cdsTenors,cdsSpreads,RR,premiumFrequency,defaultFrequency,accruedPremium)priceCDS Credit Default Swap PricingDescriptionA function that calculates the spreads of several Credit Default Swaps(different maturities)from ayield curve and a credit curve.UsagepriceCDS(yieldcurveTenor,yieldcurveRate,creditcurveTenor,creditcurveSP,cdsTenors,recoveryRate,numberPremiumPerYear=c(4,2,1,12),numberDefaultIntervalPerYear=12,accruedPremium=c(TRUE,FALSE))ArgumentsyieldcurveTenorA double vector.Each value represents a tenor of the yield curve expressed inyear(e.g.1.0for1Y,0.5for6M)yieldcurveRate A double vector.Each value represents the discount rate(continuously com-pounded)for a partical tenor(e.g.0.005means0.5%,0.02means2%) creditcurveTenorA double vector.Each value represents a tenor of the credit curve expressed inyear(e.g.1.0for1Y,0.5for6M)creditcurveSP A double vector.Each value represents the survival probability for a partical tenor(e.g.0.98means98%)cdsTenors A double vector.Each value represents the maturity expressed in year of a Credit Default Swap which we want to price(e.g5.0means5Y)recoveryRate A double.It represents the Recovery Rate in case of default(e.g0.40means 40%recovery which is a standard value for Senior Unsecured debt) numberPremiumPerYearAn Integer.It represents the number of premiums paid per year.CDS premiumspaid quaterly(i.e.numberPremiumPerYear=4)and sometimes semi-annually(i.e.numberPremiumPerYear=2)numberDefaultIntervalPerYearAn Integer.It represents the number of timesteps used to perform the numeri-cal integral required while computing the default leg value.It is shown that amonthly discretisation usually gives a good approximation(Ref.Valuation ofCredit Default Swaps,Dominic O Kane and Stuart Turnbull) accruedPremium A boolean.If set to TRUE,the accrued premium will be taken into account in the calculation of the premium leg value.DetailsIn brief,a CDS is used to transfer the credit risk of a reference entity(corporate or sovereign)from one party to another.In a standard CDS contract one party purchases credit protection from another party,to cover the loss of the face value of an asset following a credit event.A credit event isa legally deﬁned event that typically includes bankruptcy,failure-to-pay and restructuring.Thisprotection lasts until some speciﬁed maturity date.To pay for this protection,the protection buyer makes a regular stream of payments,known as the premium leg,to the protection seller.This size of these premium payments is calculated from a quoted default swap spread which is paid on the face value of the protection.These payments are made until a credit event occurs or until maturity, whichever occursﬁrst.Modeling Credit Using a Reduced-Form Approach The world of credit modelling is divided into two main approaches,one called the structural and the other called the reduced-form.In the struc-tural approach,the idea is to characterize the default as being the consequence of some company event such as its asset value being insufﬁcient to cover a repayment of debt.Structural models are generally used to say at what spread corporate bonds should trade based on the internal structure of theﬁrm.They therefore require information about the balance sheet of the ﬁrm and can be used to establish a link between pricing in the equity and debt markets.However, they are limited in at least three important ways:they are hard to calibrate because internal company data is only published at most four times a year;they generally lack theﬂexibility toﬁt exactly a given term structure of spreads;and they cannot be easily extended to price credit derivatives.In the reduced-form approach,the credit event process is modeled directly by modeling the prob-ability of the credit event ing a security pricing model based on this approach,this prob-ability of default can be extracted from market prices.Reduced form models also generally have theﬂexibility to reﬁt the prices of a variety of credit instruments of different maturities.They can also be extended to price more exotic credit derivatives.It is for these reasons that they are used for credit derivative pricing.See vignette("credule")for more details.ValueReturns a Dataframe with2columns:tenor and spread.The tenor column contains the tenor value given in parameter cdsTenors,the spread column give the Credit Default Swap spreads(in decimal) for each tenor(e.g.0.0050is equivalent to0.5%or50bp).Author(s)Bertrand Le NezetExampleslibrary(credule)yieldcurveTenor=c(1,2,3,4,5,7)yieldcurveRate=c(0.0050,0.0070,0.0080,0.0100,0.0120,0.0150)creditcurveTenor=c(1,3,5,7)creditcurveSP=c(0.99,0.98,0.95,0.92)cdsTenors=c(1,3,5,7)cdsSpreads=c(0.0050,0.0070,0.00100,0.0120)premiumFrequency=4 defaultFrequency=12 accruedPremium=TRUERR=0.40priceCDS(yieldcurveTenor,yieldcurveRate,creditcurveTenor,creditcurveSP,cdsTenors,RR,premiumFrequency,defaultFrequency,accruedPremium)Index∗CDS spreadbootstrapCDS,3credule-package,2priceCDS,6∗Credit Default Swaps bootstrapCDS,3credule-package,2priceCDS,6∗Credit Default SwapbootstrapCDS,3credule-package,2priceCDS,6∗bootstrappingbootstrapCDS,3credule-package,2priceCDS,6∗credit curvebootstrapCDS,3credule-package,2priceCDS,6∗default probabilitiesbootstrapCDS,3credule-package,2priceCDS,6∗default probabilitybootstrapCDS,3credule-package,2priceCDS,6∗hazard ratebootstrapCDS,3credule-package,2priceCDS,6∗poisson processbootstrapCDS,3credule-package,2priceCDS,6∗pricingbootstrapCDS,3credule-package,2priceCDS,6∗survival probabilitiesbootstrapCDS,3credule-package,2priceCDS,6∗survival probabilitybootstrapCDS,3credule-package,2priceCDS,6bootstrapCDS,3credule-package,2priceCDS,69。

信用联结票据运作流程

信用联结票据运作流程Credit linking bills, also known as credit linked notes, are financial instruments that combine a debt obligation with a derivative component, typically a credit default swap. With the emergence of credit linked notes in the late 1990s, this financial product has become increasingly popular in the global financial markets.信用联结票据，也称为信用联结债券，是将债务义务与衍生品部分（通常是信用违约掉期）相结合的金融工具。

随着信用联结票据于20世纪90年代后期的出现，这种金融产品在全球金融市场上变得越来越受欢迎。

From an operational perspective, the process of credit linking bills involves several key steps. First, the issuer of the credit linked notes enters into a credit default swap agreement with a counterparty, typically a financial institution or another institutional investor. This agreement serves as the derivative component of the credit linked notes, allowing the issuer to transfer the credit risk associated with a specific reference entity to the counterparty.从运作的角度来看，信用联结票据的流程涉及几个关键步骤。

金融行业必备的100个专业名词

进入金融行业必须知道的100个专有名词1. 股票(Stock): 公司的所有权证券，持有股票意味着持有公司的一部分所有权。

2. 债券(Bond): 债务工具，投资者购买债券即借钱给发行者，预期在未来获得利息和本金回报。

3. 资产配置(Asset Allocation): 投资组合中不同资产类别的分配，以实现风险和回报的平衡。

4. 流动性(Liquidity): 资产能够迅速买卖并转化为现金的能力，流动性越高，市场风险越低。

5. 市盈率(P/E Ratio): 股票价格与每股收益之比，用于衡量一家公司的估值。

6. 资本市场(Capital Market): 提供长期融资的市场，包括股票和债券市场。

7. 衍生品(Derivative): 派生自其他资产的金融合约，如期货合约和期权。

8. 投资组合(Portfolio): 拥有多种资产的集合，旨在实现投资目标。

9. 财务杠杆(Financial Leverage): 利用借款来增加投资回报的策略。

10. 通货膨胀(Inflation): 货币购买力下降的过程，影响资产和投资的价值。

11. 市值(Market Capitalization): 公司的总市场价值，等于其股票价格乘以已发行股票的总数。

12. 利率(Interest Rate): 借款或存款的价格，通常以百分比形式表示。

13. 复利(Compound Interest): 利息在每个计息周期内基于原始本金和之前利息的计算。

14. 企业治理(Corporate Governance): 确保公司管理层履行职责，保护股东权益的体系和原则。

15. 信用评级(Credit Rating): 评估借款人信用风险的分级系统，影响债券和贷款的利率。

16. 流通股(Outstanding Shares): 公司已发行并在市场上交易的股票总数。

17. 市场风险(Market Risk): 由市场波动引起的投资损失的风险。

信用衍生性金融商品简介

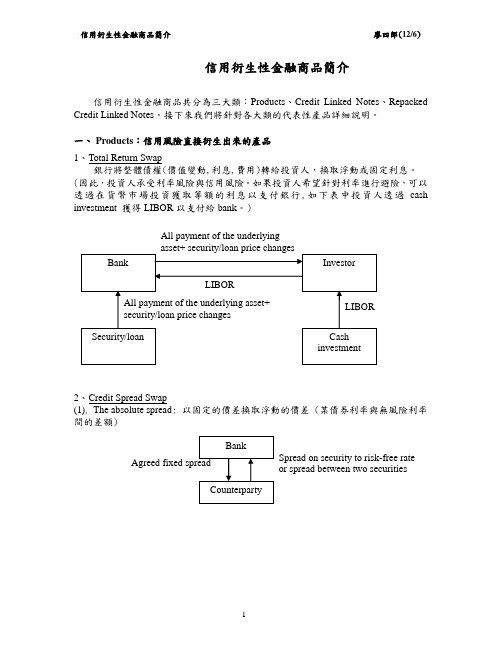
信用衍生性金融商品簡介信用衍生性金融商品共分為三大類：Products 、Credit Linked Notes 、Repacked Credit Linked Notes 。

接下來我們將針對各大類的代表性產品詳細說明。

一、 Products ：信用風險直接衍生出來的產品 1、Total Return Swap銀行將整體債權(價值變動,利息,費用)轉給投資人，換取浮動或固定利息。

(因此，投資人承受利率風險與信用風險。

如果投資人希望針對利率進行避險，可以透過在貨幣市場投資獲取等額的利息以支付銀行,如下表中投資人透過cash investment 獲得LIBOR 以支付給bank 。

)2、Credit Spread Swap(1). The absolute spread : 以固定的價差換取浮動的價差 (某債券利率與無風險利率間的差額)All payment of the underlying Spread on security to risk-free rate or spread between two securities(2). The relative spread: 以浮動換取浮動 (例: 以甲債券與無風險利率間的利差換取乙債券與無風險利率間的利差)3、Credit Default Swap避險銀行透過支付對手銀行固定的費用, 將該公司承受的信用風險轉由對手銀行承擔。

當發生倒閉時對手銀行須支付避險銀行該債券的倒閉損失。

(EX: the default payment is: (national amount)(fair market value of reference bond before default - fair market value of reference bond after default))4、Basket- Linked Credit Default Swap是Credit Default Swap 的一種，但是標的信用資產為一籃子債券或債權,因此使整體信用品質較單一標的Credit Default Swap 之信用品質低。

英语语法词汇详解default

英语语法词汇详解defaultdefault英[dɪˈfɔːlt]美[dɪˈfɔːlt]n.不履行；违约；拖欠；未到庭；默认值v.不履行；拖欠；未到庭；自动转到；因未到场而取消…参赛资格第三人称单数：defaults现在分词：defaulting过去式：defaulted过去分词：defaulted英文释义：1. [uncountable, countable] failure to do something that must be done by law, especially paying a debt【不可数，可数】未能做法律规定必须做的事情，尤指偿还债务2. [uncountable, countable, usually singular] (computing) what happens or appears if you do not make any other choice or change【不可数，可数，通常单数】(计算)如果你不做任何其他选择或改变，会发生或出现什么举个例子：1.When you start a fresh letter the system will default to its own style.你要重新写封信的时候，系统会自动转到默认格式。

2.It will have to restructure its debts to avoid default.必须重新整合债务才能避免拖欠。

3.I became a presenter by default rather than by design.我成为主持人是因为当时我未考虑其他选择就接受了，并非我刻意要求得此职。

常用短语：1.by default(比赛)因其他参赛者不到场, 由于对手缺席(而胜出)2.in default拖欠违约；不出庭罪3.in default of因缺少；在缺乏…时；由于没有协议；租金将由房产稽查员决定4.go by default因一方未提出反对而判另一方获胜5.judgement in default缺席审判6.default value默认值7.default gateway默认网关；缺省网关8.default setting默认设置；默认设定；缺省设置9.default risk违约风险；违约的风险10.credit default swaps信用违约互换；信用违约掉期；信贷违约互换11.default interest拖欠利息；违约利息；过期罚金12.default option默认选项；默认选择；违约期权13.default rate违约率；拖欠率；交易违约率14.credit default swap信用违约互换；信贷违约互换15.default position默认立场；默认位置；默认的观点。

CDS简介

信用违约互换简介一、什么是CDS信用风险缓释(Credit Risk Mitigation, CRM)是指金融机构运用信用衍生工具等方式转移或降低信用风险。

信用风险缓释功能体现为违约概率、违约损失率或违约风险暴露的下降。

常用的信用风险缓释工具包括信用违约互换(Credit Default Swap, CDS)、总收益互换(Total Return Swap, TRS)、信用价差期权(Credit Spread Option, CSO)以及其他信用衍生产品。

按照市场规模来看，CDS 市值规模占全部信用衍生工具市场的97%以上，是最为重要的CRM工具。

CDS又被称为信贷违约掉期和贷款违约保险（第三种名称更为贴近产品的本意），是信用衍生工具的一种，是用来防止特定公司或产品破产的一种保险安排。

一般情况下，CDS的购买者拥有一种权力，在发行某种债券或金融产品的特定公司破产的时候，持有该公司债券或金融产品并购买了CDS合约的人，就可以以原债券或金融产品的面值出售或按一定的市场价位赎回现金。

特定公司所发行的特定债券或金融产品，被称为“推荐义务”（Reference Obligation,RO），在CDS合约下可出售的债券或金融产品的总面值，被称为是CDS合约的“名义本金”（Notional Principal,NP）。

二、CDS发展历程1992年，国际互换与衍生品协会（ISDA）提出了信用衍生品的原理和机制，探索分散、转移或对冲信用风险。

这种衍生品常用模式是信用保障买方向卖方支付一笔固定费用，一旦发生买卖双方所指定的信用问题，信用保障卖方就按合同约定赔偿对方损失。

信用违约互换最初形成于1993年，当时，美国信孚银行为了防止其向日本银行提供的贷款遭受损失，与金融衍生品的交易对手达成了一项合同：由交易商对日本银行的违约行为予以保护，如果日本银行发生信用问题、出现还款困难等问题，交易商将对信孚银行予以补偿，但信孚银行需要向交易商支付一笔固定费用。

cre-dio的原理

cre-dio的原理英文回答：The principle of cre-dio, also known as credit default swap (CDS) index options, is to provide investors with a way to hedge against credit risk. It is a financial derivative that allows investors to protect themselves against the possibility of default on a specific credit instrument, such as a bond or a loan.The cre-dio works by allowing investors to buy or sell CDS index options, which are contracts that provide protection against default on a basket of credit instruments. These credit instruments are typically grouped together based on their credit rating or industry sector. By purchasing CDS index options, investors can effectively transfer the risk of default from the underlying credit instruments to the seller of the options.When an investor buys a CDS index option, they areessentially paying a premium to the seller in exchange for the right to receive a payout if any of the credit instruments in the index default. The payout is typically based on the difference between the face value of thecredit instrument and its market value at the time of default.On the other hand, when an investor sells a CDS index option, they are taking on the risk of default. In exchange for assuming this risk, the seller receives a premium from the buyer. If none of the credit instruments in the index default, the seller keeps the premium as profit. However,if any of the credit instruments default, the seller is obligated to pay the buyer the agreed-upon payout.CDS index options provide investors with a way to hedge against credit risk because they allow them to transfer the risk of default to someone else. By purchasing these options, investors can protect themselves against the potential losses that could occur if the credit instruments in their portfolio default. This can be especially useful for investors who have exposure to a large number of creditinstruments or who are concerned about the creditworthiness of a specific industry or sector.中文回答：cre-dio的原理，也被称为信用违约互换指数期权（CDS index options），是为投资者提供对冲信用风险的一种方式。

swap3概念 -回复

swap3概念-回复什么是swap3？Swap3（第三代跨链流动性协议）是一种全新的跨链流动性解决方案，专为去中心化金融（DeFi）应用而设计。

它旨在解决当前跨链资产流动性问题，提供更高效、更便捷的跨链交易服务，并将不同区块链网络之间的资产连接起来。

Swap3的核心特点是支持多链互操作性和高效的资产转移。

它通过创建一个统一的桥接层来连接不同的区块链网络，使得用户可以在不同的链上实现资产的自由流动。

这个桥接层是由Swap3的智能合约构建的，可以便捷地处理不同链上的资产映射和转移。

Swap3的实现主要依赖于两个关键技术：跨链资产映射和桥接层的构建。

首先，跨链资产映射是Swap3实现跨链流动性的基础。

不同的区块链网络之间存在资产的不兼容性，这使得跨链交易变得复杂。

Swap3通过引入资产映射机制，将不同链上的资产进行一对一的映射，使得它们可以在桥接层之间进行转换。

例如，用户可以将以太坊上的ERC-20代币映射到波卡网络上的等值代币，并在两个链上自由地进行交易。

其次，桥接层的构建是Swap3实现高效资产转移的关键。

这个桥接层由Swap3的智能合约构建，它既可以运行在以太坊上，也可以运行在其他支持智能合约的区块链上。

桥接层负责处理资产的锁定、解锁和转移等操作。

当用户在一个链上发起跨链交易时，资产将被锁定在桥接层上，然后相应的等值代币将在目标链上解锁。

这个过程是通过Swap3的智能合约实现的，它确保了交易的安全性和可靠性。

Swap3的应用场景非常广泛。

首先，它可以解决不同区块链网络之间的资产流动性问题。

目前，不同的区块链网络之间很难实现资产的跨链转移，这导致了流动性的局限。

Swap3的出现可以打破这种限制，为用户提供更多的交易选择和更高效的交易体验。

其次，Swap3可以促进DeFi应用的发展。

当前的DeFi市场主要集中在以太坊上，这限制了不同区块链网络之间的资产流动。

Swap3的出现将使得不同链上的DeFi应用能够互通有无，共享流动性，推动整个DeFi生态系统的发展。

虚拟子账户V3版使用手册

八、虚拟子账户虚拟子账户是企业网上银行为企业客户提供的账户记账信息分类管理功能.企业客户可以通过本行的企业网上银行系统为账户设定从010000－999989最多共近一百万个虚拟子账户,原已新增4位序号有效状态的虚拟子账户仍保留使用,但不可进行新增，新增只能为6位序号虚拟子账户。

账户设定成功后企业可以操纵不同的子账户实现资金的转入与转出,网上银行提供自动区分每笔转入与转出资金及流水归属相应的虚拟子账户的功能，网银与柜面均支持子账户的查询与资金转出功能。

企业可以使用管理员和主管角色自行为企业自身的账户签约虚拟子账户业务,设定若干个虚拟子账户,并对操作员的虚拟子账户权限进行管理。

虚拟子账户增加成功后,经办、复核和授权人员就能够登录企业网上银行系统对虚拟子账户的实际应用进行操作了。

1账户管理管理员通过该模块对虚拟子账户进行签约、增加、修改、删除、查询的操作,管理员通过该模块的所有设置都必须要主管授权后才能生效。

频道功能子功能使用角色账户管理虚拟子账户签约管理管理员虚拟子账户设置管理员待签约指令撤销管理员待授权指令撤销管理员授权子账户设置主管授权子账户签约主管1。

1签约管理➢管理员登陆企业网银系统，进入“账户管理“频道，打开“虚拟子账户”菜单，如下图所示:➢点击“签约管理”功能项：➢账户选择“子账户签约情况"为“未签约”的主账户，然后点击“签约”按钮,系统提示“签约虚拟子账户成功，经授权后生效"。

等待主管授权。

1.2授权子账户签约➢管理员签约虚拟子账户后,必须由主管授权生效。

主管进入“账户管理”频道:➢点击“授权子账户签约"功能项:➢选择需要授权的主账户,点击“授权”按钮，再次点击“确认”后，授权成功，该主账户签约虚拟子账户业务成功。

➢只有签约成功的主账户才可办理虚拟子账户的新增业务.➢签约成功后系统自动新增户名分别为“待清分子账户"和“默认子账户”，序号分别为“999998”和“999999”的子账户。

Bec高级第三版

Bec1.翻译10乘2’=202.选词填空5乘2‘=103.对错5乘2’=104.简答题4乘5’=205.Report writing 301.Entitlement generation: 养尊处优的一代EntitleVt. 称做…；定名为…；给…称号；使…有权利（授权，entitle ..to…）[ 过去式entitled 过去分词entitled 现在分词entitling ]2.Instant gratification 即时性满足3.Coddling parents 溺爱孩子的父母4.Executiveadj. 行政的；经营的；执行的，经营管理的n. 经理；执行委员会；执行者；经理主管人员chief executive officer 首席执行官；总裁5.Executevt. 实行；执行；处死[ 过去式executed 过去分词executed 现在分词executing ]6.Corporateadj. 法人的；共同的，全体的；社团的n. corporation公司；法人（团体）；社团；大腹便便；市政当局vt. corporatize使…企业化7．Cooperatevi. 合作，配合；协力[ 过去式cooperated 过去分词cooperated 现在分词cooperating ] 8．Veterann. 老兵；老手；富有经验的人；老运动员；adj. 经验丰富的；老兵的9．Bury oneself in cubicle: 在办公室默默无闻10.Appetite n. 食欲；嗜好11.Spoilvt. 溺爱；糟蹋；掠夺vi. 掠夺；变坏；腐败n. 次品；奖品12.Break our backs for you 为其拼搏奋斗13.Subsidiary adj. 附属的；辅助的n. 子公司；辅助14.entrepreneur [,ɔntrəprə'nə:]n. 企业家；承包人；主办者[ 复数entrepreneurs ]15.Expertise n. 专门知识；专门技术；专家的意见expert专家；行家；能手16.Read between lines字里行间17.Anonymous adj. 匿名的，无名的；无个性特征的18.Pilot n. 飞行员；领航员adj. 试点的 v. 驾驶；领航；试用19.Prospective adj. 未来的；预期的n. 预期；展望20.Perspective n. 观点；远景；透视图adj. 透视的ply with 照做，遵守abide by/obey/observe22.Quarter(fiscal year) 财政年度23.Bargaining power 议价能力谈判能力24.Licensing fee 许可费25.Synergy n. 协同；协同作用；合力26.Cost saving节约成本27.Consolidation n. 巩固；合并；团结28.Customer base 客户基础29.Mandate n. 授权；命令，指令；委托管理；受命进行的工作vt. 授权；托管Mandatory adj. 强制的；托管的；命令的n. 受托者（等于mandatary）30.Preconceivedadj. 预想的；（思想或观点）事先形成的v. 预想（preconceive的过去式和过去分词）Preconception n. 偏见；先入之见；预想（forecast, bias，prejudice）31.Integratevt. 使…完整；使…成整体；求…的积分；表示…的总和vi. 求积分；取消隔离；成为一体adj. 整合的；完全的n. 一体化；集成体integration n. 集成；综合integrity n. 完整；正直；诚实；廉正32.Omit vt. 省略；遗漏；删除；疏忽[ 过去式omitted 现在分词omitting ]第二章Growing the company33.B＆D division( business and development ) 业务拓展部34.R&D (Research & Development) 研发部35.Purchasing Department 采购部36.Sales Promotion Department 促销部37.Headquarters 总部boratory(lab) n,实验室39.Warehouse n. 仓库；货栈；大商店vt. 储入仓库；以他人名义购进（股票）40.Main plant 工厂41．Division/department 部门42.Bills 法案43.Parliament=congress 议会、国会44.Critical infrastructure 关键的基础设施45.Infrared n. 红外线adj. 红外线的46.Deteriorate vi. 恶化，变坏vt. 恶化y off=fire=make redundant=dismiss 解雇、辞退Make redundant更多是裁员48.acquired=take over 接管、接收49.grow=expand 扩大50.created=set up=establish 建立51be listed on the Stock Exchange =go public 上市52.go bankrupt= go out of business 破产y(过去式laid 过去分词laid 现在分词laying)…off= make redundant54.close=shut down 关闭55.divest=sell off 【商业】(削价)出售56.blockbustern. 轰动；巨型炸弹；一鸣惊人者57.acquisition 收购58.squarely adv. 直角地；诚实地；正好；干脆地；正当地59.rival 竞争对手plement n. 补语；余角；补足物vt. 补足，补助61.implement vt. 实施，执行；实现，使生效n. 工具，器具；手段动词的各种时态Present perfect tense:现在完成时When you ask about something that started in the past but continues to the present time, you use the Present Perfect tense, e.g.当你谈论从过去开始一直持续到现在的某件事时，用现在完成法时态。

信用联结票据运作流程

信用联结票据运作流程英文文档内容：The operation process of credit-linked notes involves several key steps.Firstly, the issuer identifies the need for credit protection and determines the appropriate credit risk to be hedged.Then, a credit default swap (CDS) is entered into with a counterparty, which transfers the credit risk from the issuer to the counterparty.The proceeds from the sale of the credit-linked notes are used to pay the premium on the CDS.If a credit event occurs, such as a default by the reference entity, the issuer can trigger the CDS and receive compensation from the counterparty.The amount of compensation is typically equal to the face value of the credit-linked notes.The issuer then uses these funds to make payments to the noteholders, who have been exposed to the credit risk.Throughout the process, the issuer is responsible for managing the credit risk and ensuring that the CDS is properly executed.The noteholders receive a return on their investment, which is adjusted to reflect the credit risk associated with the reference entity.中文文档内容：信用联结票据的运作流程包括几个关键步骤。

credit default swap 通俗解释

credit default swap 通俗解释信用违约掉期（Credit Default Swap，简称CDS）的通俗解释
信用违约掉期（CDS）是一种金融衍生品，用于衡量借款人无法如约偿还债务
的风险。

通俗地说，CDS类似于保险合同，它提供了一种保障，以防止借款人无
法履行其负债承诺。

CDS的工作原理是这样的：债权人（通常是金融机构或投资者）购买CDS合同，作为对其投资进行保险的一种方式。

当债务人无法按约定偿还债务时，CDS
合同就会生效。

在这种情况下，CDS的卖方会向债权人支付一笔赔偿金，以弥补
其遭受的损失。

CDS的价值取决于债务人违约的可能性。

如果债务人信用风险较高，CDS的
价格就会上涨，因为购买CDS合同的成本增加了。

相反，如果债务人信用风险较低，CDS的价格就会下降。

CDS具有重要的市场和经济作用。

它提供了一种衡量和管理信用风险的方式，使投资者能够通过购买CDS合同来对冲其投资组合中的风险。

此外，CDS还促进
了市场流动性，提高了债券市场的效率。

然而，CDS也存在一些争议和风险。

一些人担心，CDS市场过于庞大，可能
导致金融体系的不稳定，因为CDS合同的规模超过了实际风险需要的范围。

此外，CDS的买卖也存在一定的不透明性，可能导致市场操纵和信息不对称的问题。

总的来说，信用违约掉期是一种用于衡量和管理信用风险的金融工具。

它在市
场中发挥着重要的作用，但也需要被监管和管理，以确保其对金融系统的稳定起到积极的作用。

Counterparty Credit Risk and Credit Value Adjustment

ReferencesAcharya,V.,Engle,R.F.,Figlewski,S.,Lynch,A.W.and Subrahmanyam,M.G.(2009)Centralized Clearing for Credit Derivatives,in Restoring Financial Stability:How to Repair a Failed System ,Acharya,V .and Richardson,M.(eds),John Wiley &Sons Inc.Albanese,C.,D’Ippoliti,F.and Pietroniero,G.(2011)Margin Lending and Securitization:Regulators,Modelling and Technology,working paper.Altman,E.(1968)Financial Ratios,Discriminant Analysis and the Prediction of Corporate Bankruptcy.Journal of Finance ,23,589–609.Altman,E.(1989)Measuring Corporate Bond Mortality and Performance,Journal of Finance ,44(4,September),909–922.Altman,E.and Kishore,V.(1996)Almost Everything You Wanted to Know About Recoveries on Defaulted Bonds,Financial Analysts Journal ,Nov/Dec.Amdahl,G.(1967)Validity of the Single Processor Approach to Achieving Large-Scale Computing Capabilities,AFIPS Conference Proceedings,30,483–485.Andersen,L.and Piterbarg,V .(2010a)Interest Rate Modelling Volume 1:Foundations and Vanilla Models ,Atlantic Financial Press.Andersen,L.and Piterbarg,V.(2010b)Interest Rate Modelling Volume 2:Term Structure Models ,Atlantic Financial Press.Andersen,L.and Piterbarg,V .(2010c)Interest Rate Modelling Volume 3:Products and Risk Manage-ment ,Atlantic Financial Press.Andersen,L.,Sidenius,J.and Basu,S.(2003)All your hedges in one basket,Risk Magazine ,November.Arvanitis,A.and Gregory,J.(2001)Credit:The Complete Guide to Pricing,Hedging and Risk Man-agement ,Risk Books.Arvanitis,A.,Gregory,J.and Laurent,J.-P.(1999)Building Models for Credit Spreads,Journal of Derivatives ,6(3,Spring),27–43.Baird,D.G.(2001)Elements of Bankruptcy ,3rd edition,Foundation Press,New York,NY .Basel Committee on Banking Supervision (BCBS)(2004)An Explanatory Note on the Basel II IRB Risk Weight Functions,October,.Basel Committee on Banking Supervision (BCBS)(2005)The Application of Basel II to Trading Activities and the Treatment of Double Default,.Basel Committee on Banking Supervision (BCBS)(2006)International Convergence of Capital Measurement and Capital Standards,A Revised Framework –Comprehensive Version,June,.Basel Committee on Banking Supervision (BCBS)(2009)Strengthening the resilience of the banking sector,Consultative document,December,.Basel Committee on Banking Supervision (BCBS)(2010a)Basel III:A global regulatory framework for more resilient banks and banking systems,December (Revised June (2011),.Basel Committee on Banking Supervision (BCBS)(2010b)Basel III counterparty credit risk –Frequently asked questions,November,.Basel Committee on Banking Supervision (BCBS)(2011)Capitalisation of bank exposures to central counterparties,December,." / . ओ * # $ 7 9 3 ओ 3 ओ436ReferencesBasurto,M.S.and Singh,M.(2008)Counterparty Risk in the Over-the-Counter Derivatives Market, November.IMF Working Papers,1–19,Available at SSRN:/abstract¼1316726. Bates,D.and Craine,R.(1999)Valuing the Futures Market Clearinghouse’s Default Exposure during the1987Crash,Journal of Money,Credit&Banking,31(2,May),248–272.Bliss,R.R.and Kaufman,G.G.(2005)Derivatives and Systemic Risk:Netting,Collateral,and Closeout (May10th),FRB of Chicago Working Paper No.(2005)-03.Available at SSRN:/ abstract¼730648.Black,F.and Cox,J.(1976)Valuing Corporate Securities:Some Effects of Bond Indenture Provisions, Journal of Finance,31,351–67.Black,F.and Scholes,M.(1973)The Pricing of Options and Corporate Liabilities,Journal of Political Economy,81(3),637–654.Bluhm,C.,Overbeck,L.and Wagner,C.(2003)An Introduction to Credit Risk Modeling,Chapman and Hall.Brace,A.,Gatarek,D.and Musiela,M.(1997)The Market Model of Interest Rate Dynamics, Mathematical Finance,7(2),127–154.Brady,N.(1988)Report of the Presidential Task Force on Market Mechanisms,US Government Printing Ofﬁce,Washington DC.Brigo,D.and Masetti,M.(2005a)Risk Neutral Pricing of Counterparty Risk,in Counterparty Credit Risk Modelling,Pykhtin,M.(ed.),Risk Books.Brigo,D.and Masetti,M.(2005b)A Formula for Interest Rate Swaps Valuation under Counterparty Risk in presence of Netting Agreements,www.damianobrigo.it.Brigo,D.and Morini,M.(2010)Dangers of Bilateral Counterparty Risk:the fundamental impact of closeout conventions,working paper.Brigo,D.and Morini,M.(2011)Closeout convention tensions,Risk,December,86–90.Brigo,D.,Chourdakis K.and Bakkar,I.(2008)Counterparty Risk Valuation for Energy Commodities Swaps:Impact of Volatilities and Correlation.Available at SSRN:/ abstract¼1150818.Burgard,C.and Kjaer,M.(2011a)Partial differential equation representations of derivatives with coun-terparty risk and funding costs,The Journal of Credit Risk,7(3),1–19.Burgard,C.and Kjaer,M.(2011b)In the balance,Risk,November,72–75.Burgard,C.and Kjaer,M.(2012)A Generalised CVA with Funding and Collateral,working paper. /abstract¼2027195.Canabarro,E.and Dufﬁe,D.(2003)Measuring and Marking Counterparty Risk,in Asset/Liability Management for Financial Institutions,Tilman,L.(ed.),Institutional Investor Books. Canabarro,E.,Picoult,E.and Wilde,T.(2003)Analyzing counterparty risk,Risk,16(9),117–122. Cesari,G.,Aquilina,J.,Charpillon,N.,Filipovic,Z.,Lee,G.and Manda,I.(2009)Modelling,Pricing, and Hedging Counterparty Credit Exposure,Springer Finance.Collin-Dufresne,P.,Goldstein,R.S.and Martin,J.S.(2001)The Determinants of Credit Spread Changes,Journal of Finance,56,2177–2207.Cooper,I.A.and Mello,A.S.(1991)The default risk of swaps,Journal of Finance,46,597–620. Das,S.(2008)The Credit Default Swap(CDS)Market–Will It Unravel?,February2nd,http:// /Article3.1018þM583ca062a10.0.html.Das,S.and Sundaram,R.(1999)Of smiles and smirks,a term structure perspective,Journal of Finan-cial and Quantitative Analysis,34,211–239.De Prisco,B.and Rosen,D.(2005)Modelling Stochastic Counterparty Credit Exposures for Deriva-tives Portfolios,in Counterparty Credit Risk Modelling,Pykhtin,M.(ed.),Risk Books. Downing,C.,Underwood,S.and Xing,Y.(2005)Is liquidity risk priced in the corporate bond market?, Working paper,Rice University.Duffee,G.(1998)The Relation Between Treasury Yields and Corporate Bond Yield Spreads,The Journal of Finance,LIII(6,December).Duffee,G.R.(1996a)Idiosyncratic Variation of Treasury Bill Yields,Journal of Finance,51,527–551.References437 Duffee,G.R.(1996b)On measuring credit risks of derivative instruments,Journal of Banking and Finance,20(5),805–833.Dufﬁe,D.(1999)Credit Swap Valuation,Financial Analysts Journal,January-February,73–87.Dufﬁe,D.(2011)On the clearing of foreign exchange derivatives,working paper.Dufﬁe,D.and Huang,M.(1996)Swap rates and credit quality,Journal of Finance,51,921–950.Dufﬁe,D.and Singleton,K.J.(2003)Credit Risk:Pricing,Measurement,and Management,Princeton University Press.Dufﬁe,D.and Zhu,H.(2009)Does a Central Clearing Counterparty Reduce Counterparty Risk?, working paper.Edwards F.R.and Morrison,E.R.(2005)Derivatives and the Bankruptcy Code:Why the Special Treatment?,Yale Journal on Regulation,22,91–122.Ehlers,P.and Sch€o nbucher,P.(2006)The Inﬂuence of FX Risk on Credit Spreads,working paper. Engelmann,B.and Rauhmeier,R.(eds)(2006)The Basel II Risk Parameters:Estimation,Validation, and Stress Testing,Springer.Figlewski,S.(1984)Margins and Market Integrity:Margin Setting for Stock Index Futures and Options,Journal of Futures Markets,13(4),389–408.Financial Times(2008)Banks face$10bn monolines charges,June10th.Finger,C.(1999)Conditional Approaches for CreditMetrics Portfolio Distributions,CreditMetrics Monitor,April.Finger,C.(2000)Towards a better understanding of wrong-way credit exposure,RiskMetrics working paper number99-05,February.Finger,C.,Finkelstein,V.,Pan,G.,Lardy,J.-P.and Tiemey,J.(2002)CreditGrades technical document. RiskMetrics Group.Fitzpatrick,K.(2002)Spotlight on counterparty risk,International Financial Review,99,November 30th.Fleck,M.and Schmidt,A.(2005)Analysis of Basel II Treatment of Counterparty Risk,in Counter-party Credit Risk Modelling,Pykhtin,M.(ed.),Risk Books.Fons,J.S.(1987)The Default Premium and Corporate Bond Experience,Journal of Finance,42 (1March),81–97.Garcia-Cespedes,J.C.,de Juan Herrero,J.A.,Rosen,D.and Saunders,D.(2010)Effective Modelling of Wrong-Way Risk,CCR Capital and Alpha in Basel II,Journal of Risk Model Validation,4(1),71–98. Garcia-Cespedes,J.C.,Keinin,A.,de Juan Herrero,J.A.and Rosen,D.(2006)A Simple Multi-Factor ‘Factor Adjustment’for Credit Capital Diversiﬁcation,Special issue on Risk Concentrations in Credit Portfolios(Gordy,M.ed.)Journal of Credit Risk,Fall.Gemen,H.(2005)Commodities and commodity derivatives,John Wiley&Sons Ltd.Geman,H.and Nguyen,V.N.(2005)Soy bean inventory and forward curve dynamics,Management science,51(7,July),1076–1091.Gemmill,G.(1994)Margins and the Safety of Clearing Houses,Journal of Banking and Finance,18 (5),979–996.Ghosh,A.,Rennison,G.,Soulier,A.,Sharma,P.and Malinowska,M.(2008)Counterparty risk in credit markets,Barclays Capital Research Report.Gibson,M.S.(2005)Measuring counterparty credit risk exposure to a margined counterparty,in Coun-terparty Credit Risk Modelling,Pykhtin,M.(ed),Risk Books.Giesecke,K.,Longstaff,F.A.,Schaefer,S.and Strebulaev,I.(2010)Corporate Bond Default Risk: A150ÀYear Perspective,NBER Working Paper No.15848,March.Glasserman,P.and Li,J.(2005)Importance Sampling for Portfolio Credit Risk,Management Science, 51(11,November),1643–1656.Glasserman,P.and Yu,B.(2002)Pricing American options by simulation:regression now or regression later?,in Monte Carlo and Quasi-Monte Carlo Methods,Niederreiter,H.(ed),Springer.Gordy,M.(2002)Saddlepoint approximation of credit riskþ,Journal of Banking and Finance,26, 1335–1353.438ReferencesGordy,M.(2004)Granularity Adjustment in Portfolio Credit Risk Management,in Risk Measures for the21st Century,Szeg€o,G.P.(ed.),John Wiley&Sons.Gordy,M.and Howells,B.(2006)Procyclicality in Basel II:can we treat the disease without killing the patient?,Journal of Financial Intermediation,15,395–417.Gordy,M.and Juneja,S.(2008)Nested Simulation in Portfolio Risk Measurement,working paper. Gregory,J.(2008a)A trick of the credit tail,Risk,March,88–92.Gregory,J.(2008b)A free lunch and the credit crunch,Risk,August,74–77.Gregory,J.(2009a)Being two faced over counterparty credit risk,Risk,22(2),86–90.Gregory,J.(2009b)Counterparty credit risk:the new challenge for globalﬁnancial markets,John Wiley and Sons.Gregory,J.(2010)Counterparty casino:The need to address a systemic risk,European Policy Forum working paper.www.epﬂ.Gregory J.(2011)Counterparty risk in credit derivative contracts,in,The Oxford Handbook of Credit Derivatives,Lipton,A.and Rennie,A.(eds),Oxford University Press.Gregory,J.and German,I.(2012)Closing out DV A,working paper.Gregory,J.and Laurent,J.-P.(2003)I will survive,Risk,June,103–107.Gregory,J.and Laurent,J.-P.(2004)In the core of correlation,Risk,October87–91.Gupton,G.M.,Finger C.C.and Bhatia,M.(1997)CreditMetrics Technical Document,Morgan Guaranty Trust Company,New York.Hamilton,D.T.,Gupton,G.M.and Berthault,A.(2001)Default and Recovery Rates of Corporate Bond Issuers:(2000),Moody’s Investors Service,February.Hardouvelis,G.and Kim,D.(1995)Margin Requirements:Price Fluctuations,and Market Participa-tion in Metal Futures,Journal of Money,Credit and Banking,27(3),659–671.Hartzmark,M.(1986)The Effects of Changing Margin Levels on Futures Market Activity,the Compo-sition of Traders in the Market,and Price Performance,Journal of Business,59(2),S147–S180. Hille,C.T.,Ring J.and Shimanmoto,H.(2005)Modelling Counterparty Credit Exposure for Credit Default Swaps,in Counterparty Credit Risk Modelling,Pykhtin,M.(ed.),Risk Books.Hills,B.,Rule,D.,Parkinson,S.and Young,C.(1999)Central Counterparty Clearing Houses and Financial Stability,Bank of England Financial Stability Review,June,22–133.Hughston,L.P.and Turnbull,S.M.(2001)Credit risk:constructing the basic building block,Economic Notes,30(2),257–279.Hull,J.(2010)OTC Derivatives and Central Clearing:Can All Transactions Be Cleared?,working paper,April.Hull,J.and White,A.(1990)Pricing interest-rate derivative securities,The Review of Financial Stud-ies,3(4),573–592.Hull,J.and White,A.(1999)Pricing interest rate derivative securities,Review of Financial Studies, 3(4),573–92.Hull,J.and White,A.(2004)Valuation of a CDO and an nth to Default CDS without Monte Carlo Simulation,Working paper,September.Hull,J.and White,A.(2011)CVA and Wrong Way Risk,Working Paper,University of Toronto. Hull,J.,Predescu,M.and White,A.(2004)The Relationship Between Credit Default Swap Spreads, Bond Yields,and Credit Rating Announcements,Journal of Banking&Finance,28(11November), 2789–2811.Hull,J.,Predescu,M.and White,A.(2005a)Bond Prices,Default Probabilities and Risk Premiums, Journal of Credit Risk,1(2Spring),53–60.Hull,J.,Predescu,M.and White,A.(2005b)The valuation of correlation-dependent credit derivatives using a structural model,Journal of Credit Risk,6(3),99–132.Hull,J.,Predescu,M.and White,A,(2005c)The Valuation of Correlation-Dependent Credit Derivatives Using a Structural Model.Available at SSRN:/abstract¼686481. International Swaps and Derivatives Association(ISDA)(2009)ISDA close-out protocol,available at .References439 Jamshidian,F.and Zhu,Y.(1997)Scenario Simulation:Theory and methodology,Finance and Sto-chastics,1,43–67.Jarrow,R.A.and Turnbull,S.M.(1992)Drawing the analogy,Risk,5(10),63–70.Jarrow,R.A.and Turnbull,S.M.(1995)Pricing options onﬁnancial securities subject to default risk, Journal of Finance,50,53–86.Jarrow,R.and Turnbull,S.M.(1997)When swaps are dropped,Risk,10(5),70–75.Jarrow,R.A.and Yu,F.(2001)Counterparty risk and the pricing of defaultable securities,Journal of Finance,56,1765–1799.Johnson,H.and Stulz,R.(1987)The pricing of options with default risk,Journal of Finance,42, 267–280.Jorion,P.(2007)Value-at-Risk:The new benchmark for managingﬁnancial risk,3rd edition, McGraw-Hill.Kealhofer,S.(1995)Managing Default Risk in Derivative Portfolios,in Derivative Credit Risk: Advances in Measurement and Management,Jameson,R.(ed.),Renaissance Risk Publications. Kealhofer,S.(2003)Quantifying credit risk I:Default prediction,Financial Analysts Journal,January/ February,30–44.Kealhofer,S.and Kurbat,M.(2002)The Default Prediction Power of the Merton Approach,Relative to Debt Ratings and Accounting Variables,KMV LLC,Mimeo.KMV Corporation(1993)Portfolio management of default risk,San Francisco:KMV Corporation. Kenyon,C.(2010)Completing CVA and Liquidity:Firm-level positions and collateralized trades, working paper,.Kolb,R.W.and Overdahl,J.A.(2006)Understanding Futures Markets,Wiley-Blackwell. Kroszner,R.(1999)Can the Financial Markets Privately Regulate Risk?The Development of Deriva-tives Clearing Houses and Recent Over-the-Counter Innovations,Journal of Money,Credit,and Banking,August,569–618.Laurent,J.-P.and Gregory,J.(2005)Basket Default Swaps,CDOs and Factor Copulas,Journal of Risk, 7(4),103–122.Leland,H.(1994)Corporate Debt Value,Bond Covenants,and Optimal Capital Structure,Journal of Finance,49,1213–1252.Levy,A.and Levin,R.(1999)Wrong-way exposure,Risk,July.Li,D.X.(1998)Constructing a credit curve,Credit Risk:A RISK special report,November,40–44. Li,D.X.(2000)On Default Correlation:A Copula Function Approach,Journal of Fixed Income, 9(4March),43–54.Lomibao,D.and Zhu,S.(2005)A Conditional Valuation Approach for Path-Dependent Instruments,in Counterparty Credit Risk Modelling,Pykhtin,M.(ed),Risk Books.Longstaff,F.A.and Schwartz,S.E.(1995)A Simple Approach to Valuing Risky Fixed and Floating Rate Debt,The Journal of Finance,L(3July).Longstaff,F.A.and Schwarz,S.E.(2001)Valuing American options by simulation:A simple least squares approach,The review ofﬁnancial studies,14(1),113–147.Martin,R.,Thompson,K.and Browne,C.(2001)Taking to the saddle,Risk,June,91–94.Mashal,R.and Naldi,M.(2005)Pricing multiname default swaps with counterparty risk,Journal of Fixed Income,14(4),3–16.Matthews,R.A.J.(1995)Tumbling Toast,Murphy’s Law and the Fundamental Constants,European Journal of Physics,16,172–176.McKenzie,D.(2006)An Engine,Not a Camera:How Financial Models Shape Markets,MIT Press. Meese,R.and Rogoff,K.(1983)Empirical Exchange Rate Models of the Seventies,Journal of Inter-national Economics,14,3–24.Mercurio,F.(2010)A LIBOR Market Model with Stochastic Basis,available at SSRN:/ abstract¼1583081.Merton,R.C.(1974)On the Pricing of Corporate Debt:The Risk Structure of Interest Rates,Journal of Finance,29,449–70.440ReferencesMilne,A.(2012)Central Counterparty Clearing and the management of Systemic Default Risk, working paper,Loughborough University School of Business and Economics.Moody’s Investors Service(2007)Corporate Default and Recovery Rates:1920-(2006),Moody’s Special Report,New York,February.Morini,M.and Prampolini,A.(2010)Risky Funding:A uniﬁed framework for counterparty and liquidity charges,working paper./abstract¼1669930.O’Kane, D.(2007)Approximating Independent Loss Distributions with an Adjusted Binomial Distribution,EDHEC working paper.O’Kane,D.(2008)Modelling Single-name and Multi-name Credit Derivatives,John Wiley&Sons Ltd.Ong,M.K.(ed.)(2006)The Basel Handbook:A Guide for Financial Practitioners,2nd edition, Risk Books.Picoult,E.(2002)Quantifying the Risks of Trading,in Risk Management:Value at Risk and Beyond, Dempster,M.A.H.(ed.),Cambridge University Press.Picoult,E.(2005)Calculating and Hedging Exposure,Credit Value Adjustment and Economic Capital for Counterparty Credit Risk,in Counterparty Credit Risk Modelling,Pykhtin,M.(ed.),Risk Books. Pindyck,R.(2001)The dynamics of commodity spot and futures markets:A primer,Energy Journal, 22(3),1–29.Pirrong,C.(2000)A Theory of Financial Exchange Organization,Journal of Law and Economics,437. Pirrong,C.(2009)The Economics of Clearing in Derivatives Markets:Netting,Asymmetric Informa-tion,and the Sharing of Default Risks Through a Central Counterparty.Available at SSRN:http:// /abstract¼1340660.Pirrong,C.(2011)The Economics of Central Clearing:Theory and Practice,ISDA Discussion Papers Series Number One(May).Piterbarg,V.(2010)Funding beyond discounting:Collateral agreements and derivatives pricing,Risk, 2,97–102.Polizu,C.,Neilson F.L.and Khakee,N.(2006)Criteria for Rating Global Credit Derivative Product Companies,Standard&Poor’s working paper.Press,W.H.,Teukolsky,S.A.,Vetterling W.T.and Flannery,B.P.(2007)Numerical Recipes:The Art of Scientiﬁc Computing,3rd Edition,Cambridge University Press.Pugachevsky,D.(2005)Pricing counterparty risk in unfunded synthetic CDO tranches,in Counter-party Credit Risk Modelling,Pykhtin,M.(ed.),Risk Books.Pykhtin,M.(2003)Unexpected recovery risk,Risk,16(8),74–78.Pykhtin,M.(2012)Model foundations of the Basel III standardised CV A charge,Risk,July,60–66. Pykhtin,M.and Sokol,A.(2012)If a Dealer Defaulted,Would Anybody Notice?,working paper. Pykhtin,M.and Zhu,S.(2007)A Guide to Modelling Counterparty Credit Risk,GARP Risk Review, July/August,16–22.Rebonato,R.(1998)Interest Rate Options Models,2nd edition,John Wiley and Sons,Ltd. Reimers,M.and Zerbs,M.(1999)A multi-factor statistical model for interest rates,Algo Research Quarterly,2(3),53–64.Remeza,A.(2007)Credit Derivative Product Companies Poised to Open for Business,Moody’s Inves-tor Services special report.Rosen,D.and Pykhtin,M.(2010)Pricing Counterparty Risk at the Trade Level and CVA Allocations, Journal of Credit Risk,6(Winter),3–38.Rosen,D.and Saunders,D.(2010)Measuring Capital Contributions of Systemic Factors in Credit Portfolios,Journal of Banking and Finance,34,336–349.Rowe,D.(1995)Aggregating Credit Exposures:The Primary Risk Source Approach,in Derivative Credit Risk,Jameson,R.(ed.),Risk Publications,13–21.Rowe,D.and Mulholland,M.(1999)Aggregating Market-driven Credit Exposures:A Multiple Risk Source Approach,in Derivative Credit Risk,2nd edition,Incisive Media,141–147.References441 Sarno,L.(2005)Viewpoint:Towards a Solution to the Puzzles in Exchange Rate Economics:Where do we Stand?,Canadian Journal of Economics,38,673–708.Sarno,L.and Taylor,M.P.(2002)The Economics of Exchange Rates,Cambridge University Press. Segoviano,M.A.and Singh,M.(2008)Counterparty Risk in the Over-the-Counter Derivative market, IMF working paper,November.Shadab,H.B.(2009)Guilty by Association?Regulating Credit Default Swaps,Entrepreneurial Busi-ness Law Journal,August19,forthcoming.Available at SSRN:/abstract¼1368026. Shelton,D.(2004)Back to Normal,Proxy Integration:A fast accurate method for CDO and CDO-squared pricing,Citigroup Structured Credit Research,August.Singh,M.(2010)Collateral,Netting and Systemic Risk in the OTC Derivatives Market,IMF working paper,November.Singh,M.and Aitken,J.(2009)Deleveraging after Lehman–Evidence from Reduced Rehypotheca-tion,March,IMF Working Papers,1–11,available at SSRN:/abstract¼1366171. Sokol,A.(2010)A Practical Guide to Monte Carlo CVA,in Lessons From the Crisis,Berd,A.(ed.), Risk Books.Sorensen,E.H.and Bollier,T.F.(1994)Pricing Swap Default Risk,Financial Analysts Journal,50 (3May/June),23–33.Soros,G.(2009)My three steps toﬁnancial reform,Financial Times,June17th.Standard&Poor’s(2007)Ratings Performance:2006Stability and Transition,New York,S&P,16th February.Standard&Poor’s(2008)Default,Transition,and Recovery:2008Annual Global Corporate Default Study and Rating Transitions,April2nd.Tang,Y.and Williams,A.(2010)Funding beneﬁt and funding cost,in Counterparty Credit Risk, Canabarro,E.(ed.),Risk Books.Tavakoli,J.M.(2008)Structured Finance and Collateralized Debt Obligations:New Developments in Cash and Synthetic Securitization,John Wiley&Sons,Inc.Tennant,J.,Emery,K.and Cantor,R.(2008)Corporate one-to-ﬁve-year rating transition rates, Moody’s Investor Services Special Comment.Thompson,J.R.(2009)Counterparty Risk in Financial Contracts:Should the Insured Worry About the Insurer?,available at SSRN:/abstract¼1278084.Turnbull,S.(2005)The Pricing Implications of Counterparty Risk for Non-Linear Credit Products,in Counterparty Credit Risk Modelling,Pykhtin,M.(ed.),Risk Books.Tzani,R.and Chen,J.J.(2006)Credit Derivative Product Companies,Moody’s Investor Services, March.Vasicek,O.(1997)The Loan Loss Distribution,KMV Corporation.Vrins,F.and Gregory,J.(2011)Getting CV A up and running,Risk,October.Wilde,T.(2001)The regulatory capital treatment of credit risk arising from OTC derivatives exposures in the trading and the banking book,in ISDA’s response to the Basel Committee On Banking Supervision’s Consultation on The New Capital Accord,May(2001),Annex1.Wilde,T.(2005)Analytic Methods for Portfolio Counterparty Risk,in Counterparty Credit Risk Modelling,Pykhtin,M.(ed.),Risk Books.。