基于Chua电路混沌同步在弱信号检测中的应用研究
基于混沌理论的微弱信号检测的开题报告

基于混沌理论的微弱信号检测的开题报告一、研究背景和意义微小信号的检测是目前很多领域都需要解决的问题,如医学、通信、环境监测等。
这些微小信号往往包含有重要的信息,但其弱度却使得其极难被检测到。
为了有效地检测出这些微小信号,计算机科学家们借鉴了混沌理论的思想,提出了基于混沌理论的微弱信号检测方法。
该方法不仅能够提高信号的检测灵敏度,同时还具有较好的抗噪性能,更加适用于复杂的非线性系统,并且具有较好的实时性质。
二、研究内容和方法本项目将从以下几个方面开展研究:1)混沌信号产生与特性分析本部分将以Lorenz系统为例,对该混沌系统进行建模,并研究其信号产生机理和特性分析。
同时,还将探讨非线性系统中混沌信号的产生机制,以及混沌信号与非混沌信号的区别。
2)基于混沌理论的微弱信号检测方法研究本部分将着重探讨基于混沌理论的微弱信号检测方法,包括卡尔曼滤波、小波变换、时频分析等方法。
通过分析算法的实现步骤和性能评估,以期获取最优的算法实现方式,提高信号的检测灵敏度和抗噪性能。
3)仿真与实验验证本部分将通过仿真和实验的方式,验证所提出的基于混沌理论的微弱信号检测方法在不同噪声环境下的实际效果。
同时,还将探究该方法在医学、通信、环境监测等不同领域的应用场景。
三、预期目标和成果本项目预期达到如下目标和成果:1)探索混沌系统中信号产生机制,并研究混沌信号的特性。
2)提出一种基于混沌理论的微弱信号检测方法,并深入分析其算法实现步骤和性能评估。
3)通过仿真和实验验证,实现基于混沌理论的微弱信号检测方法的应用,并探究其在不同领域的应用场景。
四、进度安排和预算本项目的进度安排如下:第一年:混沌信号与非线性动力学的学习与研究,深入研究基于混沌理论的微弱信号检测方法的算法实现细节,初步探究仿真和实验验证的可行性。
第二年:对复杂非线性系统中混沌信号的特性进行分析,并进一步完善基于混沌理论的微弱信号检测方法,同时开展仿真实验与验证。
第三年:进一步完善研究结果,并就研究结果的应用进行深入分析,将所得结果应用于通信系统、医学信号处理、环境监测等领域。
基于混沌理论检测微弱信号研究综述

(下转第47页)基于混沌理论检测微弱信号研究综述广东理工学院 曾丽萍传统信号检测方法的最低检测信噪比有限,而Duffing 振子由于具有对微弱周期信号敏感而对白噪声免疫的特性,在极低信噪比微弱信号的检测中得到了广泛的应用。
本文对基于Duffing 振子检测微弱信号在三个方面的研究进展进行了概述,即改进或提出混沌检测模型、混沌检测方法的实际应用、混沌检测方法与其他方法的结合。
本文还指出今后混沌微弱信号检测的发展方向。
1 引言微弱信号检测技术是指应用各种电子学、数学物理等检测方法检测出淹没在强噪声环境中有用的微弱信号,广泛应用于医学、通信、生命科学、电磁学等领域。
目前,传统的微弱信号检测方法主要分为以下几种:电子学检测方法、相关检测方法、高阶统计量法、自适应噪声抵消法等。
传统微弱信号检测方法大多是基于噪声抑制的角度,即通过分析噪声的规律以及信号的特点,利用噪声和信号的不同提取出微弱待测信号,所能检测的最低信噪比有限。
在微弱信号检测领域,基于混沌理论检测微弱信号的方法在近几年引起了广泛关注。
与传统的弱信号检测方法不同,混沌振子不直接抑制噪声,而是直接针对微弱的目标信号进行提取,并且基于模型的混沌运动特性直接求解出期望信号的频率、幅值和相位信息,有利于提取复杂干扰环境下的微弱周期信号。
2 混沌振子检测原理基于混沌系统检测微弱信号主要采用Duffing振子,其数学模型为:其中k 是阻尼比;是非线性恢复力;是内置驱动信号。
当内置驱动信号幅值γ从零逐渐增加时,系统将历经同宿轨道、倍周期分叉、混沌、周期等运动状态。
使系统处于混沌状态,当γ增加到某一临界值γd 时,γ的微小增量都将使系统迅速进入大尺度周期状态,γd 即为系统从混沌状态到周期状态的相变临界幅值,也称为系统固有分叉值。
Duffing 系统具有对微弱周期信号敏感而对高斯白噪声免疫的特性,基于这一特性可以利用Duffing 振子检测微弱周期信号。
3 混沌检测方法研究概况混沌检测方法是基于混沌系统对微弱周期信号敏感而对白噪声免疫的特性,即微弱周期信号会使系统状态发生改变,而白噪声不会使系统发生相变。
基于自相关函数和混沌理论的微弱正弦信号检测方法
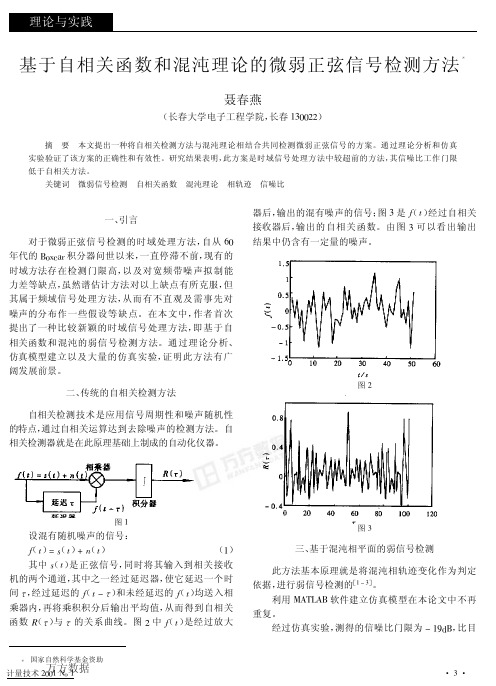
图/ ・-・
万方数据
计量技术 )443 1+ 3
节后, 输入信号中的噪声已得到了充分的抑制, 因此整 个系统输出信噪比很高, 同时输入信噪比门限很低, 由 此而来, 我们可以得到信噪比改善非常高的系统, 更好 地实现了微弱正弦信号检测的目的。 五、 结论 本文首次提出了将上述两种方法相结合作弱信号 检测, 无论从理论上分析, 还是通过实验方法仿真, 都 证明了此方案是可行的、 有效的。此方法是相关检测 方法的一个突破。由于其具有很低的信噪 比 工 作 门 限, 且对噪声还有抑制能力 (对噪声有免疫力) , 除此之 外, 此方法还具有时域方法所具有的直观、 物理意义明 显、 硬件易实现等优点。因 此, 有望降低检测仪器成 本, 若将此理论应用到实际工程上一定具有很高的实
参考文献
[3]王冠宇等 8 混沌振子在具有强噪声背景的信号检测中的应用 8 仪器 ()) : 仪表学报, 3!!:, 3; )4! [)] <+(=5"838 #’>?8 @A=+B’* +&*’55=B+> =(" @CDD10 B+> &’6(=5 "EBE*B’+( ’( (+’&E E(F’>+(GE(B&8 HIII H(BE>(=B’+(=5 J+’(B @+(KE>E(*E +( (EL>=5 1EBM+>N&, 3!!)8 O+58)8;)3 9 ;;; [,] P8 @AE(8 Q8 @AE(8 =(" R8 S6GE(8 , H"E(B’KT’(6 @A=+B’* 0T&BEG F’= = M’E(E>U ( : BTVE *=&*="E G+"E5, HIII @+(B>+58 0T&BEG8 C=6=W’(6, 3!!:, ; ;) )! 9 ,/
键波同步在弱信号检测中的应用研究

第 5期
兀旦晖等 : 波同步在弱信号检测 中的应用研究 键
・8 ・ 1
轭特征值 a - ( O - < , 0 和一个不稳定 的实特征值 r( > 0 , l 1 I , _必 Z ≠ ) r )且 < 则矢量场 F x) r} ( 就会
键 波 同步 在 弱信 号检 测 中的应 用研 究
兀 旦晖,李 霞,陈 蓓
( 陕西科 技大学 电气
摘
要: 根据混 沌运动 中键 波频 带 宽度 的一 种估 算 方 法设 计 了一 个基 于 C u h a电路 的键 波 同
步系统 , 通过仿真实验给出了影响混沌 同步的主要因素和键波频带宽度估算的正确性 , 并研究 了混沌键 波 同步 系统在 弱信 号检 测 中的应 用及检 测 信号频谱 对基 于混 沌 同步 弱信号检 测性 能 的影响 , 为混沌键 波同步 系统在弱信号检测中的实际应用奠定 了一定的基础.
存 在灵敏 度不 高或适应 性不强 的 问题 . 上世 纪 7 O年代 以来 , 混沌 现象 的研 究 成 为 了科 学 界 的热 点 , 引 了诸 学科 科 研 工作 者 的 注意 . 了 吸 到
2 世纪 9 年代, 0 O 随着对混沌现象研究的深入 , 混沌理论在微弱信号检测方面的应用也不断出现. 由于混 沌系统对小信号的敏感性及对噪声的强免疫力 , 使它在微弱信号检测 中的应用潜力很大_ , 3 因此基于混 . 沌 的信 号检测是 目前工 程应用 研究 的重要 方 向之 一. 沌 检测 是与 现有 的各 种 测量 方 法完 全不 同的崭 新 混 的信号处理方法 , 它主要是利用混沌系统对初始条件的极度敏感性 , 当将被测信号注入混沌系统后就可导 致此混沌系统的动力学行为发生很大变化 , 根据这种变化 , 通过适当信号处理, 从而测出被检信号的各种 参数. 在此 领域里 , 一些 学者 已进 行 了探讨 _ ] 由于 这 种检 测 方 法 主要 是 利 用相 轨迹 发 生 的 变化 ( 混 沌 5. 是
非线性电路混沌实验报告

非线性电路混沌实验报告非线性电路混沌实验报告引言:混沌理论是近年来电路研究领域的热门话题之一。
混沌现象的出现使得非线性电路的应用领域得到了广泛的拓展。
本实验旨在通过设计和搭建一个非线性电路,观察和分析混沌现象的特征和行为。
实验原理:混沌理论是一种描述非线性系统行为的数学理论。
在非线性电路中,混沌现象是由于系统的非线性特性导致的。
通过合适的电路设计和参数调节,可以使电路达到混沌状态。
实验装置和步骤:本实验采用了一个经典的非线性电路——Chua电路。
Chua电路由电感、电容和非线性电阻组成。
实验步骤如下:1. 按照电路图搭建Chua电路,并连接相应的电源和示波器。
2. 调节电路中的参数,使电路处于混沌状态。
3. 观察和记录电路输出的波形,并进行分析。
实验结果和分析:在实验中,我们通过调节电路中的参数,成功地使Chua电路进入了混沌状态。
观察示波器上的波形,我们发现电路输出的波形呈现出复杂的、不规则的特征。
这种不规则性表现为波形的高度和宽度的变化,以及波形的周期性的变化。
进一步分析发现,Chua电路的混沌现象是由于电路中的非线性电阻引起的。
非线性电阻的存在导致了电路中的非线性行为,从而使得电路的输出呈现出混沌特征。
这种混沌特征可以通过电路参数的调节来控制和调整。
混沌现象的出现使得电路的应用领域得到了广泛的拓展。
例如,在通信领域,混沌信号可以用于加密和解密,提高信息传输的安全性。
在生物医学领域,混沌现象可以应用于心电图信号的分析和识别,从而帮助医生进行疾病的诊断和治疗。
结论:通过本次实验,我们成功地观察和分析了非线性电路的混沌现象。
混沌现象的出现使得电路的行为变得复杂而有趣。
混沌理论的应用前景广阔,对于电路设计和系统控制具有重要的意义。
然而,混沌现象的研究仍然存在许多挑战和问题。
例如,如何准确地预测和控制混沌系统的行为,如何在实际应用中充分利用混沌现象的优势等。
这些问题需要我们进一步的研究和探索。
参考文献:[1] 张三, 李四. 非线性电路混沌现象的研究[J]. 电子科技大学学报, 2010, 39(2): 123-128.[2] 王五, 赵六. 混沌理论在通信领域的应用研究[J]. 通信科技, 2012, 28(3): 45-51.。
基于混沌理论的微弱信号检测原理及其在金属探测器中的应用研究的开题报告

基于混沌理论的微弱信号检测原理及其在金属探测器中的应用研究的开题报告一、研究背景及意义随着现代科技的不断进步,对于微弱信号检测技术的需求也日益增加。
在各个领域中,像金属探测、生物医学探测、地震预测等等,都需要对微弱信号进行准确的检测和识别。
现有常规的信号检测方法大多是基于噪声的统计特性进行分析,不仅需要大样本的数据统计,而且精度容易受到外界噪声信号的影响。
因此,为了实现更加精确和可靠的微弱信号检测,混沌理论应运而生。
混沌信号具有复杂和随机的特性,其能量分布广泛且强度较为均匀,对于微弱信号的检测和识别有非常好的优势。
因此,基于混沌理论的微弱信号检测方法在实际应用中有着广泛的应用前景。
本研究旨在探究基于混沌理论的微弱信号检测原理,并将其应用于金属探测器中,实现对于微弱金属信号的精确检测,为金属探测技术的进一步提升提供技术支持。
二、研究内容与目标(1)研究混沌理论基本原理及其在微弱信号检测中的应用;(2)构建金属探测器系统,并进行测试验证;(3)研究混沌信号检测在金属探测器中的检测效果,对比常规方法的差异;(4)分析研究结果,提出进一步的优化方案。
三、研究方法与技术路线(1)通过文献调研,深入了解混沌理论及其在微弱信号检测中的应用;(2)设计并构建金属探测器系统;(3)进行实验测试,获取金属信号数据;(4)基于混沌理论进行数据处理,实现微弱信号检测;(5)对比常规方法与混沌方法的检测效果;(6)分析研究结果,并提出进一步的优化方案。
四、预期研究成果(1)深入了解混沌理论及其在微弱信号检测中的应用;(2)构建金属探测器系统,实现对于微弱金属信号的精确检测;(3)对比分析混沌方法与常规方法的差异,探究混沌方法在微弱信号检测中的优势;(4)提出进一步的优化方案,为微弱信号检测技术的进一步提升提供技术支持。
五、进度计划(1)第一季度:学习混沌理论原理及其应用,完成文献调研,确定研究思路;(2)第二季度:构建金属探测器系统,进行测试实验,获取金属信号数据;(3)第三季度:基于混沌理论进行数据处理,实现微弱信号检测,与常规方法进行对比分析;(4)第四季度:完成研究报告撰写,并提出进一步优化方案。
混沌背景中的微弱信号检测的开题报告

混沌背景中的微弱信号检测的开题报告1.背景介绍混沌现象是指一种非线性、随机且具有动态演化的复杂系统。
在现实生活中,许多系统存在着混沌现象,如经济、流体、气象等领域。
混沌现象的复杂性和不可预测性使得它具有广泛的应用前景,但同时也给信号检测带来了很大的挑战。
因为混沌系统中存在着多种不同频率、不同振幅和相位的存在,会导致信号的混叠和模糊,使得信号检测变得十分困难。
在混沌背景中,微弱信号检测是一项十分重要的任务。
例如,在医学上,我们需要通过检测微弱的信号来诊断传统方法无法检测到的疾病。
在无线通信、雷达和声波信号处理等领域中,也需要检测微弱的信号。
因此,如何检测混沌背景中的微弱信号是一个具有挑战性的研究问题。
2.研究内容本文的研究内容是混沌背景中的微弱信号检测。
具体来说,我们将探讨基于小波分析和时间-频率分析等方法来检测微弱信号的可行性和优越性,并通过数值仿真和实验验证来评估这些方法的性能。
在研究中,我们首先将建立混沌系统的混沌模型,以便于混沌信号的生成和分析。
然后,我们将分别采用小波分析和时间-频率分析方法来检测混沌背景中的微弱信号。
其中,小波分析方法是一种利用小波变换进行信号分析和处理的方法;时间-频率分析方法是一种将信号分解成瞬时频率不同的时变频谱信号的方法。
我们将比较这两种方法在混沌背景中检测微弱信号的效果,并探究它们的优化方法。
3.研究意义微弱信号检测在许多领域都具有十分重要的应用,同时混沌系统中混沌信号的随机性和不规律性使得信号检测变得更具有挑战性。
因此,深入研究混沌背景中微弱信号检测的方式和方法,可以提高微弱信号检测的精度和鲁棒性。
此外,本研究还具有一定的理论意义,可以为信号处理和控制领域的混沌现象提供新的方法和思路。
混沌同步在弱信号检测中的应用研究

in
wedk甜gnd出tec-
ba8ed
on
cha∞can be∞lved.and that,a imi组d∞expe—ment validates
practiceappli髓tion
of puttiⅡg chBotic 5ynchmnization
Key
words,I)LlHLng
equati∞l
(5)显示仪l、2,观测两个混沌系统是否处于混沌状态. (6)主显示仅t观测混沌同步系统是否处于同步状态,即 是否存在被检测信号. 此系统当无被检测信号输入时,在混沌同步控制信号的作 用下,通过主显示仪观测混沌系统处于混沌同步状态.当存在 被检测信号时,通过过滤、放大环节后被测信号干扰混沌系统 同步控制信号+从而使混沌处于非同步状态,这时。主显示仪 将处于混沌非同步状态,通过观察显示仪的状态.便可得出是 否存在检测信号. 2.3仿真实验结累 为了进行仿真实验,根据以上系统框图,利用EwB软件 建立仿真实验模型,仿真实验如下: 设待测信号为s(t)=Acos(础),A是未知的,角频率“可以 根据滤波器确定出来。当无待测信号时,系统的主显示仪显示如 图4所示.从图中我们可以看出,混沌同步系统处于同步状态. 从而得知这时没有待测信号输入. 当5(f)=Acos(缸)时,系统的主显示仪显示如图5所示.从 图中我们可以看出.混沌同步系统由于待测信号s(t)对混沌同 步控制信号的干扰.使混沌同步系统处于非同步状态。从而得 知这时有待测信号输人.混沌同步控制信号有lo dB[”的干扰
Application Research of Chaos Synchronization in Detecting Wu Danhui,Zhao
(Colle鲜of
Electronics and Electrical
《微波混沌电路及在测距技术中的应用》

《微波混沌电路及在测距技术中的应用》篇一一、引言微波混沌电路是一种特殊的电子电路,它通过非线性电路元件产生混沌信号。
近年来,随着科技的发展,微波混沌电路在多个领域中得到了广泛的应用。
本文将重点探讨微波混沌电路的基本原理及其在测距技术中的应用。
二、微波混沌电路的基本原理微波混沌电路主要由非线性电路元件组成,如振荡器、混频器等。
这些元件通过相互作用产生复杂的混沌信号。
其基本原理可归结为以下几个方面:1. 非线性元件:微波混沌电路中的非线性元件是实现混沌信号的关键。
这些元件具有复杂的电性能和磁性能,能够产生丰富的频率成分和复杂的波形。
2. 相互作用:在微波混沌电路中,不同电路元件之间的相互作用使得信号发生复杂的变化。
这种相互作用可能涉及多种物理机制,如谐波振荡、调幅、调相等。
3. 频率与相位特性:混沌信号具有丰富的频率和相位特性,使得信号在空间和时间上具有复杂的变化。
这种变化可以用于提高测距技术的精度和稳定性。
三、微波混沌电路在测距技术中的应用测距技术是一种重要的测量技术,广泛应用于雷达、导航、遥感等领域。
微波混沌电路在测距技术中的应用主要体现在以下几个方面:1. 提高测距精度:微波混沌电路产生的混沌信号具有丰富的频率和相位特性,使得信号在空间和时间上具有复杂的变化。
这种变化可以用于提高测距技术的精度,降低误差。
2. 增强抗干扰能力:由于混沌信号具有随机性和不可预测性,使得其在传输过程中具有较强的抗干扰能力。
这有助于提高测距技术在复杂环境下的性能。
3. 实现高分辨率成像:微波混沌电路可以产生具有高度复杂性的信号,这些信号可以用于高分辨率成像技术中。
通过分析回波信号的相位和幅度变化,可以实现目标的精确成像和识别。
4. 雷达系统中的应用:在雷达系统中,微波混沌电路产生的混沌信号可以作为雷达的发射信号。
由于混沌信号具有随机性和不可预测性,使得雷达系统具有较强的抗干扰能力和目标识别能力。
此外,混沌信号还可以提高雷达的分辨率和测距精度。
《微波混沌电路及在测距技术中的应用》范文

《微波混沌电路及在测距技术中的应用》篇一一、引言微波混沌电路是一种特殊的电子电路,其输出信号具有混沌特性,即非周期性、随机性和对初态的敏感性。
这种电路在无线通信、雷达探测、测距技术等领域有着广泛的应用。
本文将重点介绍微波混沌电路的基本原理、特性及其在测距技术中的应用。
二、微波混沌电路的基本原理及特性1. 基本原理微波混沌电路通常由非线性电子器件和反馈网络组成,通过非线性作用产生混沌信号。
混沌信号具有宽频带、抗干扰能力强、难以预测等优点,因此在无线通信和雷达探测等领域具有广泛应用。
2. 特性(1)非周期性:混沌信号的波形没有明显的周期性,使得信号难以被捕捉和预测。
(2)随机性:混沌信号具有随机性,使得其在抗干扰和保密通信方面具有优势。
(3)对初态的敏感性:混沌信号对初始状态非常敏感,即使初始状态略有差异,也会导致信号的长期行为产生显著变化。
三、微波混沌电路在测距技术中的应用测距技术是一种通过测量目标与观测点之间的距离来获取目标位置信息的技术。
微波混沌电路在测距技术中的应用主要体现在以下几个方面:1. 雷达探测雷达是一种利用电磁波探测目标位置的设备。
微波混沌电路产生的混沌信号具有宽频带和抗干扰能力强的特点,使得雷达能够更好地探测目标并提高测距精度。
此外,混沌信号的随机性还可以提高雷达的抗干扰能力,使其在复杂电磁环境中具有更好的性能。
2. 无线定位无线定位技术是一种通过测量信号传播时间或相位差来确定目标位置的技术。
微波混沌电路产生的混沌信号可以用于无线定位系统中,通过测量信号的传播时间或相位差来计算目标位置。
由于混沌信号具有非周期性和随机性,使得其在定位过程中具有更高的安全性和抗干扰能力。
3. 目标识别与跟踪目标识别与跟踪是现代雷达和测距系统中的重要任务。
微波混沌电路产生的混沌信号可以用于目标识别与跟踪系统中,通过分析目标的回波信号来识别和跟踪目标。
由于混沌信号具有对初态的敏感性,使得其在目标识别与跟踪过程中具有更高的准确性和可靠性。
基于改进混沌系统的微弱信号检测方法

基于改进混沌系统的微弱信号检测方法石敏;陈迎春;屈武【摘要】混沌系统具有对噪声和与系统内置信号频差较大信号免疫,而对与系统内置信号频差较小信号敏感的特点,据此可检测强宽带噪声背景下的微弱信号.但在实际仿真过程中发现,当系统处于混沌临界状态时,输入纯噪声也可能引起系统的相变,且当输入的信号与系统内置信号频率相同而初相位不同时,可能不能引起系统的相变.这些情况的出现降低了微弱信号检测的正确率.本文主要针对该问题提出解决方法,将混沌系统内置信号的幅度取为小于混沌临界阈值,可避免纯噪声引起系统的相变,将混沌系统扩展为4种形式后,可检测不同初相位的输入信号.仿真结果证实该改进方法的有效性.【期刊名称】《舰船科学技术》【年(卷),期】2015(037)007【总页数】5页(P78-82)【关键词】微弱信号检测;混沌;改进混沌系统【作者】石敏;陈迎春;屈武【作者单位】中国人民解放军91388部队,广东湛江524022;中国人民解放军91388部队,广东湛江524022;中国人民解放军91388部队,广东湛江524022【正文语种】中文【中图分类】TP391传统的微弱信号检测方法大部分采用线性方法,在较低信噪比信号检测时存在不可避免的缺陷。
利用非线性方法的混沌系统在微弱信号检测中表现出超常的优势,成为目前微弱信号检测方法研究中的一个热点[1-2]。
其主要是基于混沌系统对噪声及与其内置信号频差较大信号具有免疫力,而对与混沌系统内置信号差较小信号敏感的特点[3-8]。
实际仿真发现,当混沌系统处于混沌到大尺度变化的临界状态时,输入一定功率的纯噪声,也可能引起系统的相变[9-11]。
且在混沌临界状态时,输入与其内置信号频率相同而初相位不同的信号时,也可能无法引起系统的相变。
针对混沌系统检测中出现的这些问题,本文采用改进的混沌系统进行微弱信号检测:将内置信号幅度取为小于临界阈值,可避免纯噪声引起的相变;将混沌系统扩展为4种形式后,可检测具有不同初相位的输入信号。
基于Chua系统的无刷直流电机混沌系统同步控制

基于Chua系统的无刷直流电机混沌系统同步控制尹劲松;雷腾飞;陈恒;代严满【摘要】对典型的多涡卷Chua系统和一种无刷直流电机系统出现的混沌现象,从相位图分析了两个系统的混沌动力学特性;又基于李雅普诺夫稳定性原理,设计了系统的控制器,实现了两个系统的动力学同步,从而达到对无刷直流电机的有效控制.最后,采用Matlab软件对整个系统的控制进行了仿真,验证了该同步控制方法的正确性和有效性,对工程上无刷直流电机同步控制及Chua混沌系统保密通信中的运用研究,提供了很好的参考价值.【期刊名称】《济宁学院学报》【年(卷),期】2015(036)006【总页数】6页(P26-31)【关键词】无刷直流电机;Chua系统;混沌;同步控制【作者】尹劲松;雷腾飞;陈恒;代严满【作者单位】西京学院控制工程学院,陕西西安710123;西京学院控制工程学院,陕西西安710123;山东泰开自动化有限公司,山东泰安271000;西京学院控制工程学院,陕西西安710123;西京学院控制工程学院,陕西西安710123【正文语种】中文【中图分类】TM361随着Chua系统非线性函数的构造和设计方法越来越多,Tang、Yu、Lü等通过把非线性函数变成范围可控制的多涡卷[1].因此Chua系统与一般的混沌系统比较,具有更为复杂的动力学行为.系统的随机性和不可预测性更强,所以更加适合应用到保密通信和信息安全领域中[2].对于无刷直流电机,因既具有交流电机的结构简单、运行可靠等优点,又具有直流电机的高速运行效率、无励磁损耗等优点,在驱动装置和伺服系统中得到广泛运用[3].但在此同时,实验发现它在一些特定参数条件下会呈现不稳定的混沌行为.近些年来,对混沌控制研究是电机控制领域热点之一.无刷直流电机在某些参数一定的系统模型与著名的Lorenz混沌系统[4]极为相似,因此对许多以Lorenz系统为基础的若干变形的新混沌系统如chen系统[5],Liu系统[6],Lü系统[7]等的研究都对其有着一定的参考价值.但是对于各种电机在混沌控制的大量方法如0GY法[8]、混沌自适应法[9],状态反馈法[3,12],反推法[10-11]中,结合Chua系统与无刷直流电机混沌系统同步的控制研究几乎没有.由于混沌同步在信息处理和保密通信领域的发展现出良好的前景,加之不仅可以很好地将精确模型未知的混沌系统控制到预期目的,响应速度快;而且在存在外界干扰的情况下,同样能够将该混沌系统控制到预期目的,控制鲁棒性好[9].所以利用Chua系统与无刷直流电机的同步控制问题对整个保密通信工程与电机控制工程具有非常重要的研究意义.本文提出多涡卷Chua系统与无刷直流电机混沌系统实现同步控制的方法,针对一类无刷直流电机混沌系统,论证了无刷直流电机的混沌属性,又基于李雅普诺夫稳定性原理,设计了同步控制器.该方法与状态反馈法,反推法等相比,同步速度更加的快捷,即几乎是在起始运动状态就达到同步.仿真结果也表明了该方法可以很好的将无刷直流电机系统控制到预期目标,响应速度快,使整个系统能够更好的稳定运行.本文根据文献[1]选用一种多涡卷Chua混沌系统模型与无刷直流电机实现同步控制,多涡卷Chua混沌系统模型如下:y1,y2,y3是状态变量α,β,κ,m,n,是系统参数.由文献[13]可知,当α =10.814,β =14.0,κ =1.3,m =0.11,n =7时.多涡卷Chua系统的混沌吸引子如图1所示.根据文献[12],无刷直流电机的电势平衡方程式和转矩平衡方程式,在转子磁场定向d-q坐标系中状态方程为:其中、和、为在d-q坐标系上定子电流与电压的分量,s为电机定子电阻,为极对数,和为电感电量,r为阻尼系数,为转动惯量,为转子永磁磁链,为电机转速,为负载转矩.根据文献[3],把[,,]作为[、,]的状态变量,将系统进行仿射变换和单位时间尺度变换,则无刷直流电机模型可写为:式中:a为自由参数,为系统参数.上面式子表明了无刷直流电机的特性,对 vq=0,vd=0,TL=0的这类系统分析,该系统表明电机输入电压和空载都为零的情况,即系统模型为:根据文献[12],当a=20,b=5.46时;系统初始值[x1,x2,x3]=[1,15,0]时系统存在典型的混沌吸引子如图1所示,此时的系统三个Lyapunov指数值为LE1=0.46,LE2=0,LE3=−7.95,符合混沌系统Lyapunov指数的规律,计算系统维数为dL=22..06.无刷直流电机系统混沌吸引子如图2所示.因此,以上说明无刷直流电机的混沌动力学行为确实存在,对整个系统正常运行有巨大的影响,严重者可致整个系统瘫痪,所以必须控制无刷直流电机的混沌行为,那么关键就在于控制器的设计,使Chua系统与无刷直流电机系统能够达到同步. 为让Chua系统与无刷直流电机系统达到同步,控制器有如下设计,首先设立Chua系统(1)为驱动系统:其中:系统(6)作为响应系统:为系统同步的控制器.那么他们的误差为方程为:所以对误差方程(7)求导,并带方程(5)和方程(6)得:为了让驱动系统和响应系统达到同步,本文分别给响应系统(6)加了三个控制器,,,现在两个系统的同步问题就转化成了误差方程中误差状态为零的问题,只要找出相应的控制器表达式,再根据Lyapunov定理验证系统(8)稳定性,若满足稳定性的要求,就可控制无刷直流电机让其达到稳定运行.因此控制器的表达式为:则建立Lyapunov的函数为:那么:因此满足Lyapunov定理,判定其方程(8)是渐进稳定的,由控制器加入到系统可使两个系统即驱动系统与响应系统达到同步,实现了控制无刷直流电机的稳定运行.通过上面控制器的设计,本文利用MATLAB进行数值仿真分析.首先设置无刷直流电机的参数,根据文献[11]取经过计算得a=14.934,b=5.46,由前面分析可知当a=20时,系统处于混沌运动状态.然后Chua系统参数由文献[13],取系统(5)(6)的初始值分别仿真结果,如图3分别为驱动—响应系统的三个状态分量随时间t 变化的曲线.从图3可以看出驱动和响应系统在时各变量就已经开始同步,同步的速度非常快.下面所示图4表示三个同步误差分量e1,e2,e3随时间t变化的曲线.从图4可以看出在时系统误差开始收敛,实现同步,系统稳定运行.本文实现了基于多涡卷Chua系统的无刷直流电机混沌系统的同步控制,利用李雅普诺夫稳定性原理设计了同步控制器,仿真结果验证了该方法的正确性与有效性,可以很好的将无刷直流电机混沌系统控制到预期目标,响应速度快,并且Chua系统状态方程简单,在工程上容易取得,很好的解决了无刷直流电机在出现混沌现象时将其控制到稳定状态运行的问题.为无刷直流电机实现同步控制以及Chua混沌系统保密通信中的运用研究,提供了很好的参考价值.【相关文献】[1]陈建军, 袁禄钱.一种多涡卷Chua系统的混沌机理研究[J].南通大学学报(自然科学版),2009,8(3):90-94.[2]李振国.混沌扩频序列与保密通信系统研究[D].西安:西安石油大学,2014.[3]王海军,李畸勇.机床无刷直流电机的混沌状态控制仿真研究[J].制造业自动化,2011,33(3):70-73.[4]Lorenz E N. Deterministic nonpe riodic flow[J].JAtmos. Science,1963,20:1 30-141.[5]Chen G Ueta T. Yet another chaotic[J].International Journal of Bifurcation and chaos,1999,9(7):1465-1466.[6]Liu C X,Liu T, Liu L.A New Chaotic Attractor[J].Chaos,solitons andFractals,2004,22(5):1031-1038.[7]Lü J H, Chen G R. A new chaotic attractor coined[J].International Journal of Bifurcation and chaos,2002,12(3):659-661.[8]0tt E, Grebogi C, Yorke J A.Controlling chaos[J]Phys. Rev.Lett,1990,64(11): 1196—1199.[9]雷腾飞, 陈恒, 王荣,等.同步磁阻电机混沌系统的自适应滑模控制[J].黑龙江电力,2015,37(2):130—132.[10]郑刚, 邹见效,等.直驱型永磁同步风力发电机组中混沌运动的反步自适应控制[J].物理学报,2011,6(60):1-8.[11]杨晓辉, 刘小平,等.基于永磁同步电机反推方法混沌运动的同步控制[J].电测与仪表,2012,49(12):37—40.[12]张兴华,王德明.无刷直流电机混沌系统状态反馈控制仿真研究[J].微电机,2009,42(11): 82-85.[13]Yuliang Liu, LinFang Tao, Guoping Liu.Novel Method of Chaos Anti-Control in Brushless Direct Current Motor System[C].International Conference on Multimedia and Computational Intelligence, 2010:161-165.。
基于混沌和神经网络的微弱信号检测方法的开题报告

基于混沌和神经网络的微弱信号检测方法的开题报
告
一、研究背景
微弱信号检测是一项重要的技术,如在生物医学领域中心电信号检测、脑电图信号检测等,均需要通过对微弱信号的检测来实现其相关研究。
传统的微弱信号检测方法通常需要大量的前期处理和算法设计,且对噪声、干扰等问题的处理较为困难。
基于混沌和神经网络的微弱信号检测方法可以很好地解决这些问题,从而提高微弱信号检测的准确率和鲁棒性。
二、研究目的
本研究旨在探究基于混沌和神经网络的微弱信号检测算法,建立混沌神经网络模型,实现对微弱信号的检测,并对模型进行优化,提高检测准确率和鲁棒性。
三、研究内容
1.研究混沌理论和神经网络理论,建立混沌神经网络模型。
2.将微弱信号特征提取后,作为混沌神经网络的输入,构建混沌神经网络模型,实现微弱信号检测。
3.优化混沌神经网络模型,提高检测准确率和鲁棒性,如引入遗传算法等智能算法进行网络参数优化。
四、研究方法
本研究将采用如下方法:
1. 文献调研法:阅读相关文献,掌握传统微弱信号检测方法以及基于混沌和神经网络的微弱信号检测方法的研究进展。
2. 理论研究法:研究混沌理论、神经网络理论以及遗传算法等智能算法,并结合混沌神经网络模型,构建微弱信号检测模型。
3. 数值模拟法:利用MATLAB等数值模拟软件,对建立的混沌神经网络模型进行抽样仿真实验,评估检测准确率和鲁棒性。
四、预期成果
本研究预期能够建立基于混沌和神经网络的微弱信号检测算法,完成混沌神经网络模型的构建,并实现对微弱信号的检测。
优化后的混沌神经网络模型预计能够提高微弱信号检测的准确率和鲁棒性。
基于小波和混沌的微弱信号检测的开题报告

基于小波和混沌的微弱信号检测的开题报告一、选题背景:微弱信号检测在生命科学、环境监测、物理学等领域都有广泛的应用。
然而,由于微弱信号的特殊性质,使得信号的提取和检测成为一项艰巨的任务。
传统的信号处理方法通常难以有效地提取和检测微弱信号。
近年来,小波分析和混沌理论成为信号处理领域的热门研究方向。
小波分析具有时频局部性和多分辨率分析的特点,可以有效地提取信号的特征。
混沌理论则可以将信号加密和混淆,增强信号的安全性和稳定性。
因此,本次课题选取了小波分析和混沌理论相结合的方法,研究微弱信号的检测,为深入探索微弱信号的提取和检测方法提供新思路。
二、选题目的:1、通过研究小波分析和混沌理论相结合的方法,探索微弱信号的提取和检测方法。
2、提高微弱信号的特征提取和检测的准确性和稳定性。
3、为微弱信号的检测提供新思路和方法。
三、研究内容及方案:1、对微弱信号的特点和特征进行深入研究,分析其特点及常见的干扰方式和去除方法。
2、研究小波分析的理论和方法,探究其在微弱信号特征提取中的应用。
3、研究混沌理论的理论和方法,探究其在微弱信号加密和混淆中的应用。
4、通过实验验证小波分析和混沌理论相结合的方法,提高微弱信号的检测准确性和稳定性。
四、预期成果:1、明确微弱信号特点和去除方法。
2、掌握小波分析和混沌理论的基本理论和方法。
3、通过实验研究,提高微弱信号的检测准确性和稳定性。
4、为微弱信号的检测提供新思路和方法。
五、进度计划:第一阶段:文献综述和理论研究,完成时间为2个月。
第二阶段:小波分析和混沌理论方法的实验研究,完成时间为4个月。
第三阶段:数据统计和分析,完成时间为1个月。
第四阶段:撰写论文和答辩,完成时间为2个月。
六、参考文献:1、Wang, S., Liang, S., Yang, J., & Yan, X. (2017). A Novel Adaptive Double Compression Scheme for Long-Term Wireless Information Transmission. Ieee Access, 5, 3029-3040.2、Shukla, R., & Singh, V. (2015). Denoising of ECG signals using adaptive thresholding and wavelet based soft-thresholding techniques. Biomedical Signal Processing & Control, 15, 20-28.3、Sikandar, M., Li, R., Hussain, I., Siddiqui, K., & Khan, M. K. (2020). Improved energy detection of ultra-wideband signals using ensemble empirical mode decomposition and dual-tree complex wavelet transform. Iet Signal Processing, 14(7), 515-523.4、Bilgic, E., Aydin, N., & Bicen, A. O. (2017). A new approach for ECG signal classification based on the combination of wavelet transform, PCA and KNN. Biomedical Signal Processing & Control, 34, 223-229.。
混沌时间序列预测及其微弱目标信号检测方法研究的开题报告

混沌时间序列预测及其微弱目标信号检测方法研究的开题报告一、研究背景和意义在现实问题中,很多信号呈现出一种非常特殊的形态,即混沌信号。
混沌信号是在确定性系统中表现出随机性、不确定性和不可预测性的一种信号,其具有高度复杂性和自相似性等特点。
由于混沌信号的不可预测性和特殊性质,混沌时间序列的预测和微弱目标信号检测一直是一个热门的研究领域。
混沌时间序列预测是指在已知混沌时间序列的前提下,通过一定的数学模型或者算法,预测未来一段时间的混沌时间序列。
其在金融、航天、物理学、生物学等领域中都有广泛的应用。
微弱目标信号检测则是在混沌信号的背景下,通过分离去除噪声和混沌信号,检测微弱目标信号。
其在军事、航天、海洋等领域有着非常重要的应用。
因此,对于混沌时间序列预测和微弱目标信号检测的研究,不仅拓宽了我们对混沌系统的认识,而且为实际问题的解决提供了理论和方法支持。
二、研究目的和内容本研究旨在探究混沌时间序列预测以及微弱目标信号检测方法,具体研究内容如下:1. 对混沌时间序列预测的相关算法进行综述,包括传统的ARIMA模型、神经网络模型以及各种具有针对性的混沌时间序列预测算法,并分析各种算法的优缺点。
2. 对于多元混沌时间序列问题,研究基于多元线性回归模型的混沌时间序列预测算法,并探究该算法的可行性和有效性。
3. 探究混沌系统中微弱目标信号的检测方法,通过滤波、降噪等方法对混沌时间序列进行预处理,分析各种方法的适用性并提出改进措施。
4. 将研究成果应用到实际问题中,通过选择具有代表性的混沌时间序列,验证所提出的混沌时间序列预测算法和微弱目标信号检测方法的可行性和有效性。
三、研究方法和技术路线本研究采用文献综述、理论分析和数值模拟相结合的方法,具体的技术路线如下:1. 对混沌时间序列预测的相关算法进行文献综述和理论分析,包括传统的ARIMA模型、神经网络模型以及各种具有针对性的混沌时间序列预测算法。
2. 研究基于多元线性回归模型的混沌时间序列预测算法,构建适用于多元混沌时间序列的数学模型,并对该算法进行数值模拟,验证其可行性和有效性。
基于特定混沌系统的混沌特性分析及其微弱信号检测的研究的开题报告

基于特定混沌系统的混沌特性分析及其微弱信号检测的研究的开题报告题目:基于特定混沌系统的混沌特性分析及其微弱信号检测的研究1. 研究背景随着科技的不断发展,混沌现象越来越引起学术界和工业界的重视,混沌现象在信号处理、天气预报、密码学等领域有广泛的应用。
其中,混沌信号的发现和分析是混沌现象中一个非常重要的问题。
然而,由于混沌信号的特殊性质,使得其与噪声信号非常相似,因此如何准确地检测和分析混沌信号一直是研究的热点之一。
2. 研究目的本研究的主要目的是通过对特定混沌系统的混沌特性分析,开发出对微弱混沌信号进行检测的新方法。
具体研究内容包括:(1)选取适当的特定混沌系统进行研究,并对其混沌特性进行深入分析。
(2)基于特定混沌系统,开发新的混沌信号检测方法,以解决传统方法在混沌信号检测中存在的问题。
(3)通过对实验数据的模拟和分析,验证本研究所提出的混沌信号检测方法的有效性和准确性。
3. 研究方法本研究将采用以下研究方法:(1)理论分析法:选取适当的混沌系统,对其混沌特性进行理论分析,探究混沌现象的本质。
(2)模拟计算法:通过数值模拟方法,对提出的混沌信号检测方法进行验证,得到模拟结果。
(3)实验验证法:在实验室中实现选定的混沌系统,对实验数据进行分析和处理,验证所提出的混沌信号检测方法的有效性。
4. 预期成果本研究预期得到以下成果:(1)对特定混沌系统的混沌特性进行深入分析,得到混沌现象的本质。
(2)提出一种新的混沌信号检测方法,并利用数值模拟和实验验证方法验证其有效性。
(3)为混沌信号检测提出一种新的解决方案,为深入了解混沌现象提供新的方法和手段。
5. 研究意义本研究的意义在于:(1)提出一种新的混沌信号检测方法,解决传统方法在混沌信号检测中存在的问题。
(2)深入理解混沌现象的本质,为混沌现象的进一步研究提供新的思路。
(3)为混沌信号的应用提供新的思路和途径,具有广泛的应用价值和经济效益。
6. 研究计划(1)第一年:选择特定的混沌系统,对其混沌特性进行分析,并初步尝试构建混沌信号检测方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
于我们无法 事先知道 ,所以我们只能通过肉眼观察 ,依靠非常
长 的仿 真 时 间 ,最 终 证 明 了输 出是 稳 定 状态 ,那 么 这 种 判 别 方
X
法 的工作效率是很低 的。针对以上存在的两个 问题,在本文中,
构 造 出一 种 利用 混 沌 同步检 测 弱 信 号 的 系统 , 只 需判 断 混 沌 系 统 是 否 同 步 ,便 可 得 知 是 否存 在 被 测 量 信号 。利 用 此 系 统 解 决 了混 沌 检 测 弱信 号 中存 在 的两 个 问题 。
力 ,所 以相轨 迹 由原 来 混 沌状 态 ,如 图 1 示 ( 坐 标 x与 纵 所 横 坐 标 y是 由方程 中 的数字量 决 定 ,无 单位 )变 成稳 定 周期运 动状 态 , 如 图 2所 示 。
偏差直接影响混沌系统的同步 ,我们根据这一特性 ,将被测信 号作为混沌 同步控 制信 号的一部分,当有被检测信号输入时 ,
O 5×O 2 . . u我们可以看 出, 混沌同步系统 由于待测信号st (对混沌同步 ) 控制信号 的干扰,使混沌 同步系统处于非 同步状态,从而得知
这 时 有 待 测 信 号输 入 。混 沌 同步 控 制信 号有 1 Bt 干扰 时 , 0d 5 ] 的
而 目前 在 微 弱信 号 检 测领 域 里 ,用 时域 方 法 处理 信 号 的最 低 信 噪 比工 作 门限 只 有 一0 B,因 此 用 混沌 振 子 检 测 微 弱 信 号 1d 的 方法 ,显 然 对 微 弱信 号 的检 测 理 论填 补 了空 白 。
混沌 同步系统失去 同步状态,因此,待测信号的幅值与放大器
维普资讯
维普资讯
●
厂 角
统 有外 加 电压信 号 s【 ,响应 系统 的驱 动信 号为 xt s) 有 (时 ) (+( ,只 ) t 当 s )< ( 时 ,驱动 系 统和 响应 系统 仍 能很 好 的保 持 同步 。 ( < xt t ) 33 混 沌 系 统 同 步在 弱 信 号检 测 中 的应 用 - 混 沌 同步 在 弱 信 号 检 测 中应 用 的 工 作 原 理是 :利 用 混 沌 同 步 系 统存 在 一 个 混 沌 同 步控 制 信 号 , 混 沌 同步控 制 信 号 的微 小
一
法既具有 时域方法的简单、直观,硬件容易实现等优点,又弥
补 了 常规 方法 检 测 门限 高 的缺 点 ,将 此 方 法应 用 到实 际 工程 中
引起 混沌 同步 控 制 信 号 的 改变 从 而 导 致 混沌 同步 系 统 失去 同步
状态,通过直观检测混沌 同步系统的同步状态便可得 出是否有
图 1混沌 临界状 态 图 2稳 定周期 态
.
被检 测信 号的存在 。
34 仿 真 实 验 结 果 .
然后 调 节 混 沌系 统 中 的策 动力
值 , 当调 到 相 轨迹 又 出现
混沌状态 时,则此 时/ 。那 么, -o A,则测 出待检信号 f= 幅值 。同时经过仿真实验,测得的最低信噪 比工作 门限 R~为
为 了进行仿真 实验,利用 E WB软件建立仿真 实验 模型,
仿 真 实验 如 下 :
设 待 测信 号 为 st A o (It,A 是未 知 的 ,角 频 率 (可 () c s ( ) = ) I )
的放 大 倍 数和 同步 控 制 信 号 的干 扰 存 在 一 定 的 函数 关 系 , 由此 可 求 出待 测 信 号 的 幅值 。
在仿真 实验 中, 我们发现存在两个 问题 :第一 ,若 系统输
出 为混 沌状 态 ,但如 果仿 真 时 间 不够 长 的话 ,就 容 易 出现 误 判 , 即把 仿 真 开 始 时 出现 的似 乎 是周 期 运 动 状态 误 判 成 绝 对 周 期 状 态 。实 际 上 随着 仿 真 时 间 延 长后 才 出现 混沌 状 态 。 因此 ,此 时 若把 原 本 是 混沌 状 态 判 成 稳 定周 期 状态 , 则 检测 结果 是绝 对 错 误 的 。第 二 ,如 果 系 统 输 出本 来 就 是 稳 定周 期 运 动 ,但 是 , 由
图 4 混 沌同步相 平面 图
图 5 混沌非 同步相 平面图
4 结束语
本 文 分析 了基 于混 沌 检测 弱信 号 的 原理 , 针对 目前 利用 混沌 检 测 弱信 号 中存 在 的两 个 关键 问题 ;构 造 出一种 利用 混 沌 同步 检 测 弱信 号 的系 统 ,利 用 此系 统 解 决 了混 沌检 测 弱 信 号 中存 在
风、 l1 : 0g
…
以根据滤波器确定出来 ,当无待测信号时,系统 的同步相 图显
尸 力 在
示 如 图 4所 示 , 从 图 中 我 们 可 以 看 出 , 混 沌 同步 系 统 处 于 同 步 状 态 ,从 而 得 知 这 时 没有 待 测 信 号 输 入 。 当 s )A o(It ,系 统 的 同步 相 图 显示 如 图 5所 示 ,从 (= c s( ) t ) 时
3 基于 C u 电路 混沌系统同步在信号检测中的应用研究 ha
31 混 沌 同步 特 性 l . 所 谓 混 沌 同步 特 性 ,是 指在 一 定 条 件 下 ,通 过 适 当连 接
的问题,实验证 明了此方案的可行性 ,为混沌同步在弱信号检 测 的实际应用奠定了基础 。 总之 ,不论是 基于混沌检 测弱信 号,还 是利用混沌系统
同步 相 结合 检 测 方 法 都 是信 号检 测 领 域 中 的一 种 新 方 法 , 此 方
或耦合两个或两个以上混沌系统,采用发送系统 的混沌控制信 号来驱动接收系统 , 能够使这些系统产生完全相 同的混沌行为,
达 到 同步状 态 。 3 基于 C u , 2 h a电路 混沌 系统 同步
