12.3等腰1练习9.2

合集下载

12.3 等腰三角形课课练(含答案)课时训练

12.3 等腰三角形第1课时◆名师导航本课重点内容是等腰三角形的两个重要性质：性质1，等腰三角形的两个底角相等；性质2，等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合．实际上，由于等腰三角形是轴对称图形，可以发现等腰三角形中许多相等的线段或角，如两底角平分线、两腰的中线、两腰的高，以及教科书安排的“讨论”栏目中提到的一些线段和角等，这些结论用全等三角形和等腰三角形的性质可以比较容易的证明．◆典例精析【例1】（2007年重庆市）已知一个等腰三角形两内角的度数之比为1∶4，则这个等腰三角形顶角的度数为（）（A）200（B）1200（C）200或1200（D）360【思路点拨】结合等腰三角形底角相等的性质，要分类讨论该三角形三个内角的比可能为1：1：4或1：4：4，于是这个三角形顶角可为200或1200．【简解】C．【规律总结】本题是一道经典考题，主要考查三角形内角和定理及分类讨论的思想意识．【例2】如图所示，Rt△ABC中，∠BC A是直角，D是AB上的一点，BD=BC，过D⊥．点作AB的垂线交AC于点．，CD、B．交于点F，求证：C D BECEFA D B【思路点拨】由已知得△BDC是等腰三角形，要证C D BE⊥，只要证BF是顶角∠C BD 的平分线或是底边CD上的中线，所以只要证，或证DF=FC即可．已EDCABHFG知DE BD CE BC EB EB ⊥⊥=，，，可从证Rt ED B Rt ECB ∆∆≅入手．【证明】 D E AB ⊥∴∠=∠===∴≅∴∠=∠=∴∴⊥E D B B C A BD BC BE BE Rt EBD Rt EC B EBD EBC BD BCBD C BE C D 90°，是等腰三角形∆∆∆【规律总结】本题主要考查三角形全等、等腰三角形三线合一等知识的综合运用．在运用三线合一性质时，通常是证明在等腰三角形中，顶角的平分线、底边上的中线，底边上的高三条中具有一条性质时，则它必同时具有另两条性质，而不是证这三条线段重合，在证题时不能混淆． ◆跟踪训练1．等腰三角形的对称轴是（）A ．顶角的平分线B ．底边上的高C ．底边上的中线D ．底边上的高所在的直线 2．等腰三角形有两条边长为4cm 和9cm ，则该三角形的周长是（） A ．17cm B ．22cm C ．17cm 或22cm D ．18cm 3．等腰三角形的顶角是80°，则一腰上的高与底边的夹角是（） A ．40° B ．50° C ．60° D ．30° 4．等腰三角形的一个外角是80°，则其底角是（）A ．100°B ．100°或40°C ．40°D ．80° 5．如图，C 、E 和B 、D 、F 分别在∠GAH 的两边上，且AB=BC=CD=DE=EF ，若∠A=18°，则∠GEF 的度数是（） A ．80° B ．90° C ．100° D ．108°6．等腰△ABC 的底角是60°，则顶角是________度．ED CABF7．等腰三角形“三线合一”是指___________．8．等腰三角形的顶角是n °，则两个底角的角平分线所夹的钝角是_________． 9．如图，△ABC 中AB=AC ，EB=BD=DC=CF ，∠A=40°，则∠EDF•的度数是_____． 10．△ABC 中，AB=AC ．点D 在BC 边上. （1）∵AD 平分∠BAC ，∴_______=________；________⊥_________；（2）∵AD 是中线，∴∠________=∠________；________⊥________；（3）∵AD ⊥BC ，∴∠________=∠_______；_______=_______．参考答案1．D 2．B 3．A 4．C 5．B 6．607．等腰三角形底边上的高、底边上的中线、顶角的平分线互相重合 8．（90+ 12n ）° 9．70° 10．略12.3 等腰三角形第2课时◆名师导航本课的重点是探究了等腰三角形的判定方法：等角对等边．这也是证明两条线段相等的重要方法，它是把三角形中角的相等关系转化为边的相等关系的重要依据，同学们注意掌握这个技能，这也是全章重点所在．另外还要注意体会的是“等边对等角”与“等角对等边”是不一样的两个结论，它们的题设与结论正好相反，实际上是互逆命题，也前面平行线的判定与性质及全等三角形的判定与性质类似，具体应用时要注意不能混淆，这也是一个难点．◆典例精析【例题】如图，△ABC中，AB=AC，过BC上一点D作BC的垂线，交BA的延长线于P，交AC于Q，试判断△APQ的形状，并证明你的结论.【思路点拨】判断三角形的形状，其探索思路是根据图形结合我们学习过的特殊的三角形（如等腰三角形，等边三角形，直角三角形等）进行探究.【解析】△APQ是等腰三角形.证明：因为AB=AC，所以∠B=∠C，又PD⊥BC，所以∠BDP=∠PDC，所以∠P=∠DQC，又因为∠DQC=∠AQP，所以∠AQP=∠P，所以△APQ为等腰三角形.【规律总结】解决和等腰三角形有关的探索型试题，需要根据等腰三角形的特征，结合已知条件进行.◆跟踪训练1．如图1，已知OC平分∠AOB，CD∥OB，若OD=3cm，则CD等于（）A．3cm B．4cm C．1.5cm D．2cmD CABEDABFEDCA BHF（1） (2) (3)2．△ABC中AB=AC，∠A=36°，BD平分∠ABC交AC于D，则图中的等腰三角形有（） A．1个 B．2个 C．3个 D．4个3．如图2，△ABC中，∠ABC与∠ACB的平分线交于点F，过点F作DE∥BC交AB于点D，交AC于点E，那么下列结论：①△BDF和△CEF都是等腰三角形；②DE=BD+CE；•③△ADE 的周长等于AB与AC的和；④BF=CF．其中正确的有（）A．①②③ B．①②③④ C．①② D．①4．如图3，Rt△ABC中，CD是斜边AB上的高，角平分线AE交CD于H，EF⊥AB于F，则下列结论中不正确的是（）A．∠ACD=∠B B．CH=CE=EF C．CH=HD D．AC=AF二、填空题5．△ABC中，∠A=65°，∠B=50°，则AB：BC=_________．6．已知AD是△ABC的外角∠EAC的平分线，要使AD•∥BC，•则△ABC•的边一定满足________．7．△ABC中，∠C=∠B，D、E分别是AB、AC上的点，•AE=•2cm，•且DE•∥BC，•则AD=________．8．一灯塔P在小岛A的北偏西25°，从小岛A沿正北方向前进30海里后到达小岛，•此时测得灯塔P在北偏西50°方向，则P与小岛B相距________．三、解答题9．如图，已知AB=AC，E、D分别在AB、AC上，BD与CE交于点F，•且∠ABD=•∠ACE，求证：BF=CF．E DAF10．如图，△ABC 中BA=BC ，点D 是AB 延长线上一点，DF ⊥AC 于F 交BC 于E ，•求证：△DBE 是等腰三角形．ED CABF参考答案1．A 2．C 3．A 4．C 5．1 6．AB=AC 7．2cm 8．30海里9．连接BC ，∵AB=AC ，∴∠ABC=∠ACB ，又∵∠ABD=∠ACE ，∴∠FBC=∠FCB ，∴FB=FC 10．证明∠D=∠BED12.3 等腰三角形第3课时◆名师导航本课重点是等边三角形的性质、判定方法及直角三角形的一个性质．等边三角形是一种特殊的等腰三角形，它的性质实际上也是等边对等角问题，由于它三条边都相等，于是它的三个角都相等为60度；第一个判定正三角形的方法也是等角对等边的问题，只是三个角都相等，所对的三个边都相等，从而它是等边三角形，第2个判定方法告诉我们，在等腰三角形中，只要有一个角为60度，不论这个角是顶角还是底角，这个三角形就是等边三角形，这也给证明三角形中边相等带来方便．◆典例精析【例题】已知△ABC为等边三角形，在图①中，点M是线段BC上任意一点，点N 线段CA上任意一点，且BM=CN，直线BN与AM相交于Q点．（1）请猜一猜：图①中∠BQM等于多少度？（2）若M、N两点分别在线段BC、CA的延长线上，其它条件不变，如图②所示，（1）中的结论是否仍然成立？如果成立，请加以证明；如不成立，请说明理由．【思路点拨】（1）题通过猜想、测量或证明等方法不难发现∠BQM=60°，而且这一结论在图形发生变化后仍然成立．【简解】（1）∠BQM=60°；（2）题的证明思路如下：先证△ACM≌△BAN，得到∠M=∠N，所以∠BQM=∠N+∠QAN=∠M+∠CAM=∠ACB=60°．【规律总结】随着几何学习的深入，经常会出现规律探究题，要求同学们在运动变化中探求图形某些不变的性质或变化的规律，培养同学们运动变化的观念，以及发现和解决问题的能力．◆跟踪训练1．正△ABC的两条角平分线BD和CE交于点I，则∠BIC等于（）A．60° B．90° C．120° D．150°2．下列三角形：①有两个角等于60°；②有一个角等于60°的等腰三角形；•③三个外角（每个顶点处各取一个外角）都相等的三角形；•④一腰上的中线也是这条腰上的高的等腰三角形．其中是等边三角形的有（）A．①②③ B．①②④ C．①③ D．①②③④3．如图，D、E、F分别是等边△ABC各边上的点，且AD=BE=CF，则△DEF•的形状是（） A．等边三角形 B．腰和底边不相等的等腰三角形C．直角三角形 D．不等边三角形DA B F21EDCAB第3题第5题4．Rt△ABC中，CD是斜边AB上的高，∠B=30°，AD=2cm，则AB的长度是（）A．2cm B．4cm C．8cm D．16cm5．如图，E是等边△ABC中AC边上的点，∠1=∠2，BE=CD，则对△ADE的形状最准备的判断是（）A．等腰三角形 B．等边三角形 C．不等边三角形 D．不能确定形状6．△ABC中，AB=AC，∠A=∠C，则∠B=_______．7．已知AD是等边△ABC的高，BE是AC边的中线，AD与BE交于点F，则∠AFE=______．8．等边三角形是轴对称图形，它有______条对称轴，分别是_____________．9．△ABC中，∠B=∠C=15°，AB=2cm，CD⊥AB交BA的延长线于点D，•则CD•的长度是_______．10．已知D、E分别是等边△ABC中AB、AC上的点，且AE=BD，求BE与CD•的夹角是多少度？参考答案1．C 2．D 3．A 4．C 5．B 6．60° 7．60°8．三；三边的垂直平分线 9．1cm 10．60°或120°AB P Q C12.3 等腰三角形第4课时◆名师导航本课安排一节习题课，综合应用等腰三角形的性质、判定与等边三角形的性质与判定，还有直角三角形的一个重要性质，灵活地选择性质进行求解． ◆典例精析【例题】如图所示，P 、Q 是△ABC 边BC 上的两点，且BP=PQ=QC=AP=AQ ，求∠B A C 的度数．【思路点拨】由已知△APQ 为等边三角形，故可求得它的外角的度数，又由等腰三角形的性质求得底角的度数．【解析】 PA PQ AQ ==（已知）∴∠=∠=∠=APQ PQA QAP 60°（等边三角形三个角都为60°） PA PB =∴∠=∠B PAB （等边对等角）又°∠+∠=B PAB 60（三角形的一个外角等于和它不相邻的两个内角和）．∴∠=∠=∠=∴∠=∠+∠+∠=++=PBA PAB Q AC BAC BAP PAQ Q AC 3030306030120°，同理°°°°°【规律总结】（1）几何计算的目的通常是找量与量的关系，等腰三角形的两底角相等，等边三角形三内角均为60°，等腰三角形三线合一的性质等都是建立量与量的关系的依据．（2）几何计算通常用列方程（组）来解决． ◆跟踪训练1．如图，等腰三角形ABC 中，A B A C =，∠A =44°，C D ⊥A B 于D ，则∠D C B 等于（）A ．44°B ．68°C ．46°D ．22°BEAB DC第1题第3题第4题2．已知∠AOB=30°，点P 在∠AOB 内部，P 1与P 关于OB 对称，P 2与P 关于OA 对称，则P 1，O ，P 2三点所构成的三角形是（） A ．直角三角形B ．钝角三角形C ．等腰三角形D ．等边三角形3．如图所示，在等腰三角形ABC 中，12cm A B A C ==，30ABC = ∠，那么底边上的高AD = cm ．4．（教材变型题）如图,是屋架设计图的一部分,点D 是斜梁AB 的中点,立柱BC 、DE 垂直于横梁AC,BC=4m,∠A=30°,则DE 等于 ( ) (A)1m (B) 2m (C)3m (D) 4m5．如图，ABC △中，A B A C =，30A ∠= ，D E 垂直平分A C ，则BCD ∠的度数为（）Ａ．80Ｂ．75 Ｃ．65 Ｄ．45第5题第7题6．一个等腰三角形的两边分别为8cm 和6cm ，则它的周长为 cm ．7．聪明的亮亮用含有30的两个完全相同的三角板拼成如图所示的图案，并发现图中有等ＡＢＤＣD腰三角形，请你帮他找出两个等腰三角形．8．已知等腰三角形ABC 中，AB AC D ，为B C 边上一点，连接A D ，若A C D △和ABD △都是等腰三角形，则C ∠的度数是．9．小明将两个全等且有一个角为60 的直角三角形拼成如图所示的图形，其中两条较长直角边在同一直线上，则图中有个等腰三角形．10．如图所示，A ，B 是4×5网格中的格点，网格中的每个小正方形的边长都是1．请在图中清晰标出使以A ，B ，Ｃ为顶点的三角形是等腰三角形的所有格点Ｃ的位置．参考答案1．D 2．D 3．6 4．B 5．Ｄ 6．22或20 7．ABE BEC CED ，，△△△ 8．36 或459．3 10．AFCDH BMEG BAB。

人教版八年级上册数学等腰三角形的性质与判定练习题及答案

13.3.1 第1课时等腰三角形的性质一．选择题（共8小题）1．如图，△ABC中，∠C=90°，AC=3，∠B=30°，点P是BC边上的动点，则AP长不可能是（）A． 3.5 B． 4.2 C． 5.8 D．7第1题第2题第3题2．如图，在△ABC中，∠B=30°，BC的垂直平分线交AB于E，垂足为D．若ED=5，则CE的长为（）A．10 B．8 C． 5 D． 2.53．如图，Rt△ABC中，∠C=90°，以点B为圆心，适当长为半径画弧，与∠ABC的两边相交于点E，F，分别以点E和点F为圆心，大于的长为半径画弧，两弧相交于点M，作射线BM，交AC于点D．若△BDC的面积为10，∠ABC=2∠A，则△ABC的面积为（）A．25 B．30 C．35 D．404．在Rt△ABC中，∠C=90°，∠B=30°，斜边AB的长为2cm，则AC长为（）A．4cm B．2cm C．1cm D．m5．如图，△ABC中，∠ACB=90°，CD是高，∠A=30°，则BD与AB的关系是（）A．BD=AB B．BD=AB C．BD=AB D．BD=AB第5题第6题第7题第8题6．如图是屋架设计图的一部分，立柱BC垂直于横梁AC，AB=10m，∠A=30°，则立柱BC的长度是（）A．5m B．8m C．10m D．20m7．如图，一棵树在一次强台风中于离地面3米处折断倒下，倒下部分与地面成30°角，这棵树在折断前的高度为（）A．6米 B．9米C．12米 D．15米8．如图，已知∠ABC=60°，DA是BC的垂直平分线，BE平分∠ABD交AD于点E，连接CE．则下列结论：①BE=AE；②BD=AE；③AE=2DE；④S△ABE=S△CBE，其中正确的结论是（）A．①②③B．①②④ C．①③④ D．②③④二．填空题（共10小题）9．如图，在Rt△ABC中，∠ACB=90°，AB的垂直平分线DE交AC于E，交BC的延长线于F，若∠F=30°，DE=1，则BE的长是_________．10．如图，∠AO E=∠BOE=15°，EF∥OB，EC⊥OB，若EC=1，则EF=_________．11．如图，在△ABC中，∠C=90°，∠B=60°，AB=10，则BC的长为_________．12．如图，在等腰三角形ABC中，AB=AC=12cm，∠ABC=30°，底边上的高AD=_______cm．第9题第10题第11题第12题13．如图，在△ABC中，AB=BC，∠B=120°，AB的垂直平分线交AC于点D．若AC=6cm，则AD=_________cm．第13题第14题第15题第16题14．如图，在△ABC中．∠B=90°，∠BAC=30°．AB=9cm，D是BC延长线上一点．且AC=DC．则AD=_________cm．15．如图是某超市一层到二层滚梯示意图．其中AB、CD分别表示超市一层、二层滚梯口处地面的水平线，∠ABC=150°，BC的长约为12米，则乘滚梯从点B到点C上升的高度h约为_________米．16．在△ABC中，已知A B=4，BC=10，∠B=30°，那么S△ABC=_________．17．如图，△ABC是等边三角形，AD⊥BC，DE⊥AC，若AB=12cm，则CE=______cm．18．有一轮船由东向西航行，在A处测得西偏北15°有一灯塔P．继续航行20海里后到B 处，又测得灯塔P在西偏北30°．如果轮船航向不变，则灯塔与船之间的最近距离是_________海里．三．解答题（共5小题）19．如图，在△ABC中，∠C=90°，AD平分∠CAB，交CB于点D，过点D作DE⊥AB于点E．（1）求证：△ACD≌△AED；（2）若∠B=30°，CD=1，求BD的长．20．如图，在△ABC中，BA=BC，∠B=120°，AB的垂直平分线MN交AC于D，求证：AD=DC．21．如图，△ABC中，∠C=90°，∠ABC=60°，BD平分∠ABC，若AD=6，求AC的长．22．如图，△ABC中，∠ACB=90°，CD是△ABC的高，∠A=30°，AB=4，求BD长．23．如图，已知∠MAN=120°，AC平分∠MAN．B、D分别在射线AN、AM上．（1）在图（1）中，当∠ABC=∠ADC=90°时，求证：AD+AB=AC．（2）若把（1）中的条件“∠ABC=∠ADC=90°”改为∠ABC+∠ADC=180°，其他条件不变，如图（2）所示．则（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由．一、DABCCABC二、9、2；10、2；11、5；12、6；13、2；14、18；15、6；16、10；17、3；18、10三、19、（1）证明：∵AD平分∠CAB，DE⊥AB，∠C=90°，∴CD=ED，∠DEA=∠C=90°，∵在Rt△ACD和Rt△AED中∴Rt△ACD≌Rt△A ED（HL）；（2）解：∵DC=DE=1，DE⊥AB，∴∠DEB=90°，∵∠B=30°，∴BD=2DE=2．20、解：如图，连接DB．∵MN是AB的垂直平分线，∴AD=DB，∴∠A=∠ABD，∵BA=BC，∠B=120°，∴∠A=∠C=（180°﹣120°）=30°，∴∠ABD=30°，又∵∠ABC=120°，∴∠DBC=120°﹣30°=90°，∴BD=DC，∴AD=DC．21、解：∵△ABC中，∠C=90°，∠ABC=60°，BD平分∠ABC，∴∠2=∠3=30°；在Rt△BCD中，CD= BD，∠4=90°﹣30°=60°（直角三角形的两个锐角互余）；∴∠1+∠2=60°（外角定理），∴∠1=∠2=30°，∴AD=BD（等角对等边）；∴AC=AD+CD=AD；又∵AD=6，∴AC=9．22、解：∵△ABC中，∠ACB=90°，∠A=30°，AB=4，∴BC=AB=×4=2，∵CD是△A BC的高，∴∠CDA=∠ACB=90°，∠B=∠B，故∠BCD=∠A=30°，∴在Rt△BCD中，BD=BC=×2=1，∴BD=1．23、（1）证明：∵∠MAN=120°，AC平分∠MAN，∴∠DAC=∠BAC=60°∵∠ABC=∠ADC=90°，∴∠DCA=∠BCA=30°，在Rt△ACD中，∠DCA=30°，Rt△ACB中，∠BCA=30°∴AC=2AD，AC=2AB，∴AD+AB=AC；（2）解：结论AD+AB=AC成立．理由如下：在AN上截取AE=AC，连接CE，∵∠BAC=60°，∴△CAE为等边三角形，∴AC=CE，∠AEC=60°，∵∠DAC=60°，∴∠DAC=∠AEC，∵∠ABC+∠ADC=180°，∠ABC+∠EBC=180°，∴∠ADC=∠EBC，∴△ADC≌△EBC，∴DC=BC，DA=BE，∴AD+AB=AB+BE=AE，∴AD+AB=AC．13.3.1 第2课时等腰三角形的判定一、填空题1．如图（1），△ABC 中，AB=AC ，DE 是AB 的中垂线，△BCE 的周长为14，BC=6，则AB 的长为。

中考数学复习----《等腰三角形》知识点总结与专项练习题(含答案解析)

中考数学复习----《等腰三角形》知识点总结与专项练习题（含答案解析）知识点总结1.等腰三角形的定义：有两条边相等的三角形叫做等腰三角形。

其中相等的两边叫做腰，另一边叫做底。

两腰构成的夹角叫做顶角，腰与底构成的夹角叫做底角。

2.等腰三角形的性质：①等腰三角形的两腰相等。

②等腰三角形的两底角相等。

（简称“等边对等角”）③等腰三角形底边的中线、高线以及顶角平分线相互重合。

（简称底边上三线合一）3.等腰三角形的判定：①有两条边相等的三角形是等腰三角形。

②有两个底角相等的三角形是等腰三角形。

（等角对等边）③若一个三角形某一边上存在“三线合一”，则三角形是等腰三角形。

练习题1、（2022•黑龙江）如图，△ABC中，AB＝AC，AD平分∠BAC与BC相交于点D，点E是AB的中点，点F是DC的中点，连接EF交AD于点P．若△ABC的面积是24，PD＝1.5，则PE的长是（）A．2.5 B．2 C．3.5 D．3【分析】如图，过点E作EG⊥AD于G，证明△EGP≌△FDP，得PG＝PD＝1.5，由三角形中位线定理可得AD的长，由三角形ABC的面积是24，得BC的长，最后由勾股定理可得结论．【解答】解：如图，过点E作EG⊥AD于G，∵AB＝AC，AD平分∠BAC，∴AD⊥BC，BD＝CD，∴∠PDF＝∠EGP＝90°，EG∥BC，∵点E是AB的中点，∴G是AD的中点，∴EG＝BD，∵F是CD的中点，∴DF＝CD，∴EG＝DF，∵∠EPG＝∠DPF，∴△EGP≌△FDP（AAS），∴PG＝PD＝1.5，∴AD＝2DG＝6，∵△ABC的面积是24，∴•BC•AD＝24，∴BC＝48÷6＝8，∴DF＝BC＝2，∴EG＝DF＝2，由勾股定理得：PE＝＝2.5．故选：A．2、（2022•淄博）某城市几条道路的位置关系如图所示，道路AB∥CD，道路AB与AE的夹角∠BAE＝50°．城市规划部门想新修一条道路CE，要求CF＝EF，则∠E的度数为（）A．23°B．25°C．27°D．30°【分析】先根据平行线的性质，由AB∥CD得到∠DFE＝∠BAE＝50°，根据等腰三角形的性质得出∠C＝∠E，再根据三角形外角性质计算∠E的度数．【解答】解：∵AB∥CD，∴∠DFE＝∠BAE＝50°，∵CF＝EF，∴∠C＝∠E，∵∠DFE＝∠C+∠E，∴∠C＝∠DFE＝×50°＝25°，故选：B．3、（2022•鞍山）如图，在△ABC中，AB＝AC，∠BAC＝24°，延长BC到点D，使CD＝AC，连接AD，则∠D的度数为（）A．39°B．40°C．49°D．51°【分析】利用等边对等角求得∠B＝∠ACB＝78°，然后利用三角形外角的性质求得答案即可．【解答】解：∵AB＝AC，∠BAC＝24°，∴∠B＝∠ACB＝78°．∵CD＝AC，∠ACB＝78°，∠ACB＝∠D+∠CAD，∴∠D＝∠CAD＝∠ACB＝39°．故选：A．4、（2022•荆州）如图，直线l1∥l2，AB＝AC，∠BAC＝40°，则∠1+∠2的度数是（）A．60°B．70°C．80°D．90°【分析】过点C作CD∥l1，利用平行线的性质可得∠1+∠2＝∠ACB，再由等腰三角形的性质可得∠ACB＝∠ABC，从而可求解．【解答】解：过点C作CD∥l1，如图，∵l1∥l2，∴l1∥l2∥CD，∴∠1＝∠BCD，∠2＝∠ACD，∴∠1+∠2＝∠BCD+∠ACD＝∠ACB，∵AB＝AC，∴∠ACB＝∠ABC，∵∠BAC＝40°，∴∠ACB＝（180°﹣∠BAC）＝70°，∴∠1+∠2＝70°．故选：B．5、（2022•台湾）如图，△ABC中，D点在AB上，E点在BC上，DE为AB的中垂线．若∠B＝∠C，且∠EAC＞90°，则根据图中标示的角，判断下列叙述何者正确？（）A．∠1＝∠2，∠1＜∠3 B．∠1＝∠2，∠1＞∠3C．∠1≠∠2，∠1＜∠3 D．∠1≠∠2，∠1＞∠3【分析】根据线段垂直平分线的性质，等腰三角形的性质解答即可．【解答】解：∵DE为AB的中垂线，∴∠BDE＝∠ADE，BE＝AE，∴∠B＝∠BAE，∴∠1＝∠2，∵∠EAC＞90°，∴∠3+∠C＜90°，∵∠B+∠1＝90°，∠B＝∠C，∴∠1＞∠3，∴∠1＝∠2，∠1＞∠3，故选：B．6、（2022•宜宾）如图，在△ABC中，AB＝AC＝5，D是BC上的点，DE∥AB交AC于点E，DF∥AC交AB于点F，那么四边形AEDF的周长是（）A．5 B．10 C．15 D．20【分析】由于DE∥AB，DF∥AC，则可以推出四边形AFDE是平行四边形，然后利用平行四边形的性质可以证明▱AFDE的周长等于AB+AC．【解答】解：∵DE∥AB，DF∥AC，∴四边形AFDE是平行四边形，∠B＝∠EDC，∠FDB＝∠C∵AB＝AC，∴∠B＝∠C，∴∠B＝∠FDB，∠C＝∠EDC，∴BF＝FD，DE＝EC，∴▱AFDE的周长＝AB+AC＝5+5＝10．故选：B．7、（2022•宿迁）若等腰三角形的两边长分别是3cm和5cm，则这个等腰三角形的周长是（）A．8cm B．13cm C．8cm或13cm D．11cm或13cm 【分析】题目给出等腰三角形有两条边长为3cm和5cm，而没有明确腰、底分别是多少，所以要进行讨论，还要应用三角形的三边关系验证能否组成三角形．【解答】解：当3cm是腰长时，3，3，5能组成三角形，当5cm是腰长时，5，5，3能够组成三角形．则三角形的周长为11cm或13cm．故选：D．8、（2022•天津）如图，△OAB的顶点O（0，0），顶点A，B分别在第一、四象限，且AB ⊥x轴，若AB＝6，OA＝OB＝5，则点A的坐标是（）A．（5，4）B．（3，4）C．（5，3）D．（4，3）【分析】根据等腰三角形的性质求出AC，根据勾股定理求出OC，根据坐标与图形性质写出点A的坐标．【解答】解：设AB与x轴交于点C，∵OA＝OB，OC⊥AB，AB＝6，∴AC＝AB＝3，由勾股定理得：OC＝＝＝4，∴点A的坐标为（4，3），故选：D．9、（2022•泰安）如图，l1∥l2，点A在直线l1上，点B在直线l2上，AB＝BC，∠C＝25°，∠1＝60°．则∠2的度数是（）A．70°B．65°C．60°D．55°【分析】利用等腰三角形的性质得到∠C＝∠BAC＝25°，利用平行线的性质得到∠BEA＝95°，再根据三角形外角的性质即可求解．【解答】解：如图，∵AB＝BC，∠C＝25°，∴∠C＝∠BAC＝25°，∵l1∥l2，∠1＝60°，∴∠BEA＝180°﹣60°﹣25°＝95°，∵∠BEA＝∠C+∠2，∴∠2＝95°﹣25°＝70°．故选：A．10、（2022•自贡）等腰三角形顶角度数比一个底角度数的2倍多20°，则这个底角的度数是（）A．30°B．40°C．50°D．60°【分析】设底角的度数是x°，则顶角的度数为（2x+20）°，根据三角形内角和是180°列出方程，解方程即可得出答案．【解答】解：设底角的度数是x°，则顶角的度数为（2x+20）°，根据题意得：x+x+2x+20＝180，解得：x＝40，故选：B．11、（2022•广安）若（a﹣3）2+5−b＝0，则以a、b为边长的等腰三角形的周长为．【分析】先求a，b．再求第三边c即可．【解答】解：∵（a﹣3）2+＝0，（a﹣3）2≥0，≥0，∴a﹣3＝0，b﹣5＝0，∴a＝3，b＝5，设三角形的第三边为c，当a＝c＝3时，三角形的周长＝a+b+c＝3+5+3＝11，当b＝c＝5时，三角形的周长＝3+5+5＝13，故答案为：11或13．12、．（2022•岳阳）如图，在△ABC中，AB＝AC，AD⊥BC于点D，若BC＝6，则CD＝．【分析】根据等腰三角形的性质可知D是BC的中点，即可求出CD的长．【解答】解：∵AB＝AC，AD⊥BC，∴CD＝BD，∵BC＝6，∴CD＝3，故答案为：3．13、（2022•苏州）定义：一个三角形的一边长是另一边长的2倍，这样的三角形叫做“倍长三角形”．若等腰△ABC是“倍长三角形”，底边BC的长为3，则腰AB的长为．【分析】由等腰△ABC是“倍长三角形”，可知AB＝2BC或BC＝2AB，若AB＝2BC＝6，可得AB的长为6；若BC＝3＝2AB，因1.5+1.5＝3，故此时不能构成三角形，这种情况不存在；即可得答案．【解答】解：∵等腰△ABC是“倍长三角形”，∴AB＝2BC或BC＝2AB，若AB＝2BC＝6，则△ABC三边分别是6，6，3，符合题意，∴腰AB的长为6；若BC＝3＝2AB，则AB＝1.5，△ABC三边分别是1.5，1.5，3，∵1.5+1.5＝3，∴此时不能构成三角形，这种情况不存在；综上所述，腰AB的长是6，故答案为：6．14、（2022•云南）已知△ABC是等腰三角形．若∠A＝40°，则△ABC的顶角度数是．【分析】分∠A是顶角和底角两种情况讨论，即可解答．【解答】解：当∠A是顶角时，△ABC的顶角度数是40°；当∠A是底角时，则△ABC的顶角度数为180°﹣2×40°＝100°；综上，△ABC的顶角度数是40°或100°．故答案为：40°或100°．15、（2022•滨州）如图，屋顶钢架外框是等腰三角形，其中AB＝AC，立柱AD⊥BC，且顶角∠BAC＝120°，则∠C的大小为．【分析】根据等腰三角形的性质和三角形内角和得到∠B＝∠C＝30°．【解答】解：∵AB＝AC且∠BAC＝120°，∴∠B＝∠C＝（180°﹣∠BAC）＝×60°＝30°．故答案为：30°．11。

人教版数学八年级上册13.3 等腰三角形同步练习(解析版)

人教版数学八年级上册13.3：等腰三角形同步练习一．选择题（共15小题）1．在Rt△ABC中，∠C＝90°，∠B＝30°，斜边AB的长为2cm，则AC长为（）A．4 cm B．2 cm C．1 cm D．cm2．一个等腰三角形但不是等边三角形，它的角平分线、高线、中线总数共（）条．A．9B．7C．6D．33．如图，△ABC是等边三角形，AE⊥BC于E，AD⊥CD于D，AB∥CD，则图中60°的角有（）A．3个B．4个C．5个D．6个4．下列判断不正确的是（）A．等腰三角形的两底角相等B．等腰三角形的两腰相等C．等边三角形的三个内角都是60°D．两个内角分别为120°、40°的三角形是等腰三角形5．在△ABC中，∠ACB＝90°，∠B＝30°，CD⊥AB于D，若AC＝6，则BD等于（）A．6B．3C．9D．126．等腰三角形的对称轴，最多可以有（）A．1条B．3条C．6条D．无数条7．等腰三角形两边的长分别为2cm和5cm，则这个三角形的周长是（）A．9cm B．12cmC．9cm或12cm D．在9cm或12cm之间8．如图，在△ABC中，AB＝AC，D为BC的中点，E为AC边上一点，且AE＝AD，∠BAC ＝40°，则∠EDC的度数是（）A．10°B．20°C．30°D．40°9．一个三角形有两条边相等，这个三角形一边等于5cm，一边等于10cm，则另一边等于（）A．5cm B．10cm C．15cm D．12cm10．如图，△ABC是等腰三角形，AD是底边BC上的高线，DE⊥AB于E，DF⊥AC于F，图中除AB＝AC外，相等的线段共有（）A．1对B．2对C．3对D．4对11．等腰三角形一腰上的高与底边所夹的角为a，则这个等腰三角形的顶角为（）A．a B．90°﹣a C．12a D．2a12．等腰三角形的底角为a，则a的取值范围是（）A．a≤45°B．0°＜a＜90°C．45°＜a＜90°D．0°≤a＜90°13．如图，在等边三角形ABC中，三条中线AE，BD，CF相交于点O，则等边三角形ABC 中，从△BOF到△COD需要经过的变换是（）A．轴对称变换B．旋转变换C．平移变换D．相似变换14．如果以4cm长的线段为底组成一个等腰三角形，腰长x的取值范围是（）A．x＞4cm B．x＞2cm C．x≥4cm D．x≥2cm15．等腰三角形周长是32cm，一边长为10cm，则其他两边的长分别为（）A．10cm，12cm B．11cm，11cmC．11cm，11cm或10cm，12cm D．不能确定二．填空题（共6小题）16．若等腰三角形的一腰上的高与另一腰的夹角等于50°，则其顶角的度数为．若等腰三角形的一腰上的高与底边的夹角等于50°，则其顶角的度数为．17．一个等腰三角形的腰长为3cm，则底边长的取值范围是．18．如图，AB＝AC，∠A＝100°，AB∥CD，则∠BCD＝度．19．等腰三角形的顶角与底角的度数之比为4：1，则它的各内角度数为．20．△ABC中，∠A：∠B：∠C＝1：2：3，AB＝10，则BC＝．21．（1）等腰三角形的一个角为100°，那么另外两个角分别为．（2）等腰三角形的一个角为50°，则底角是．三．解答题（共9小题）22．已知等腰三角形的周长为28cm，其中的一边长是另一边长的倍，求这个等腰三角形各边的长．23．如图，已知AB＝AC，D为BC边中点，你能说出AD与BC的位置关系吗？请说明理由．24．如图，△ABC是等腰三角形，且AB＝AC，试作出BC边上的中线和高以及∠A的平分线，从中你发现了什么？与其他同学进行交流．25．如图，在△ABC中，AB＝AC，∠C＝2∠A，BD平分∠ABC．请找出图中其他的等腰三角形，并选择其中的一个说明理由．26．已知D是等腰△ABC底边BC上的一个点，DE⊥AB于E，DF⊥AC于F，当D点在什么位置时，DE＝DF，并加以证明．27．如图，AD是等腰△ABC顶角的外角的平分线，那么AD与BC平行吗？为什么？28．如图，在△ABC中，AD平分∠BAC，G是CA延长线上一点，GE∥AD交AB于F．交BC于E，试判断△AGF的形状并加以证明．29．如图，在等腰△ABC中，AB＝AC，AD是BC边上的高，点E、F分别是边AB、AC上的点，且EF∥BC．（1）试说明△AEF是等腰三角形；（2）试比较DE与DF的大小关系，并说明理由．30．已知：如图，△ABC中，AB＝AC，D是BC延长线上一点，E是AC延长线上一点，且DE∥AB，求证：ED＝EC．人教版数学八年级上册13.3：等腰三角形同步练习参考答案一．选择题（共15小题）1．在Rt△ABC中，∠C＝90°，∠B＝30°，斜边AB的长为2cm，则AC长为（）A．4 cm B．2 cm C．1 cm D．cm【解答】解：∵∠C＝90°，∠B＝30°，∴AB＝2AC，∵AB＝2cm，∴AC＝AB＝1cm，故选：C．2．一个等腰三角形但不是等边三角形，它的角平分线、高线、中线总数共（）条．A．9B．7C．6D．3【解答】解：由于任意一个三角形都有三条角平分线、三条高线、三条中线，而等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合，所以一个等腰三角形但不是等边三角形，它的角平分线、高线、中线总数共7条．故选：B．3．如图，△ABC是等边三角形，AE⊥BC于E，AD⊥CD于D，AB∥CD，则图中60°的角有（）A．3个B．4个C．5个D．6个【解答】解：∵△ABC是等边三角形，∴∠ABC＝∠ACB＝∠CAB＝60°∵AB∥CD，∴∠ACD＝∠CAB＝60°，∵AD⊥CD，∴∠DAB＝90°，∵AE⊥BC，∴∠BAE＝∠CAE＝30°，∴∠DAE＝60°∴图中60°的角有5个，故选：C．4．下列判断不正确的是（）A．等腰三角形的两底角相等B．等腰三角形的两腰相等C．等边三角形的三个内角都是60°D．两个内角分别为120°、40°的三角形是等腰三角形【解答】解：A、等腰三角形的两底角相等，正确，故本选项错误；B、等腰三角形的两腰相等，正确，故本选项错误；C、等边三角形的三个内角都是60°，正确，故本选项错误；D、两个内角分别为120°、40°的三角形的第三个内角为20°，不是等腰三角形，故本选项正确．故选：D．5．在△ABC中，∠ACB＝90°，∠B＝30°，CD⊥AB于D，若AC＝6，则BD等于（）A．6B．3C．9D．12【解答】解：∵∠ACB＝90°，CD⊥AB，∴∠ACD＝∠B＝30°，∵AC＝6，∴AD＝AC＝×6＝3，AB＝2AC＝2×6＝12，∴BD＝AB﹣AD＝12﹣3＝9．故选：C．6．等腰三角形的对称轴，最多可以有（）A．1条B．3条C．6条D．无数条【解答】解：等腰三角形为等边三角形时对称轴最多，可以有3条．故选：B．7．等腰三角形两边的长分别为2cm和5cm，则这个三角形的周长是（）A．9cm B．12cmC．9cm或12cm D．在9cm或12cm之间【解答】解：当腰长是2cm时，因为2+2＜5，不符合三角形的三边关系，应排除；当腰长是5cm时，因为5+5＞2，符合三角形三边关系，此时周长是12cm．故选：B．8．如图，在△ABC中，AB＝AC，D为BC的中点，E为AC边上一点，且AE＝AD，∠BAC ＝40°，则∠EDC的度数是（）A．10°B．20°C．30°D．40°【解答】解：∵在△ABC中，D为BC中点，AB＝AC，∴AD⊥BC，AD是∠BAC的角平分线，又∵AD＝AE，∠BAC＝40°，∴∠ADE＝80°∴∠EDC＝∠ADC﹣∠ADE＝90°﹣80°＝10°．故选：A．9．一个三角形有两条边相等，这个三角形一边等于5cm，一边等于10cm，则另一边等于（）A．5cm B．10cm C．15cm D．12cm【解答】解：当第三边是5cm时，则5+5＝10，不能构成三角形，当另一边长是10cm时，能构成三角形．故选：B．10．如图，△ABC是等腰三角形，AD是底边BC上的高线，DE⊥AB于E，DF⊥AC于F，图中除AB＝AC外，相等的线段共有（）A．1对B．2对C．3对D．4对【解答】解：∵△ABC是等腰三角形，AD是底边BC上的高线，∴BD＝CD，∠BAD＝∠CAD，∵DE⊥AB，DF⊥AC，∴DE＝DF，∠BED＝∠DFC＝90°，在Rt△BED和Rt△CFD中，，∴Rt△BED≌Rt△CFD（HL），∴BE＝CF，∵AB＝AC，∴AE＝AF．故图中除AB＝AC外，相等的线段共有4对．故选：D．11．等腰三角形一腰上的高与底边所夹的角为a，则这个等腰三角形的顶角为（）A．a B．90°﹣a C．12a D．2a【解答】解：如图，AB＝AC，BD是腰AC的高，则∠DBC＝α∴∠C＝90°﹣α∴∠A＝180°﹣2（90°﹣α）＝2α故选：D．12．等腰三角形的底角为a，则a的取值范围是（）A．a≤45°B．0°＜a＜90°C．45°＜a＜90°D．0°≤a＜90°【解答】解：∵等腰三角形的底角为a，且三角形的内角和等于180°，∴0°＜2a＜180°，∴0°＜a＜90°．故选：B．13．如图，在等边三角形ABC中，三条中线AE，BD，CF相交于点O，则等边三角形ABC 中，从△BOF到△COD需要经过的变换是（）A．轴对称变换B．旋转变换C．平移变换D．相似变换【解答】解：∵△BOF与△COD是关于OE的轴对称图形，∴从△BOF到△COD需要经过轴对称变换．故选A14．如果以4cm长的线段为底组成一个等腰三角形，腰长x的取值范围是（）A．x＞4cm B．x＞2cm C．x≥4cm D．x≥2cm【解答】解：此等腰三角形的底为4cm，则有2x＞4，解得x＞2，故选：B．15．等腰三角形周长是32cm，一边长为10cm，则其他两边的长分别为（）A．10cm，12cm B．11cm，11cmC．11cm，11cm或10cm，12cm D．不能确定【解答】解：当该边是腰时，底边是32﹣20＝12cm，则另外两边是10cm，12cm；当该边是底时，则腰的长为：（32﹣10）÷2＝11cm，则另外两边是11cm，11cm；经检验，两种情况都符合三角形的三边关系．故选：C．二．填空题（共6小题）16．若等腰三角形的一腰上的高与另一腰的夹角等于50°，则其顶角的度数为40°或140°．若等腰三角形的一腰上的高与底边的夹角等于50°，则其顶角的度数为100°．【解答】解：（1）①当为锐角三角形时可以画图，高与右边腰成50°夹角，由三角形内角和为180°可得，顶角为40°；②当为钝角三角形时可画图，此时垂足落到三角形外面，因为三角形内角和为180°，由图可以看出等腰三角形的顶角的补角为40°，三角形的顶角为140°．（2）如图，①顶角是钝角时，∠B＝90°﹣50°＝40°，则顶角＝180°﹣2×40°＝100°，是钝角，符合；②顶角是锐角时，∠B＝90°﹣50°＝40°，∠A＝180°﹣2×40°＝100°，是钝角，不符合．故答案为：40°或140°；100°．17．一个等腰三角形的腰长为3cm，则底边长的取值范围是0＜底边＜6cm．【解答】解：∵3﹣3＝0，3+3＝6cm，∴底边的取值范围是0＜底边＜6cm．故答案为：0＜底边＜6cm．18．如图，AB＝AC，∠A＝100°，AB∥CD，则∠BCD＝40度．【解答】解：∵AB＝AC∴∠B＝∠ACB＝（180﹣∠A）＝40°∵AB∥CD∴∠BCD＝∠B＝40°．故填40．19．等腰三角形的顶角与底角的度数之比为4：1，则它的各内角度数为120°，30°，30°．【解答】解：设等腰三角形的各角为4x，x，x∵4x+x+x＝180°∴x＝30°∴三个内角分别是120°，30°，30°．故填120°，30°，30°．20．△ABC中，∠A：∠B：∠C＝1：2：3，AB＝10，则BC＝5．【解答】解：由∠A：∠B：∠C＝1：2：3，可设∠A＝x°，则∠B＝2x°，∠C＝3x°．∵∠A+∠B+∠C＝180°，∴x+2x+3x＝180，∴x＝30，∴∠A＝30°，∠B＝60°，∠C＝90°，∴BC＝AB＝×10＝5．故答案为5．21．（1）等腰三角形的一个角为100°，那么另外两个角分别为40°，40°．（2）等腰三角形的一个角为50°，则底角是50°，65°．【解答】解：（1）∵等腰三角形的一个角为100°∴两底角的和＝180°﹣100°＝80°又∵等腰三角形的两底角相等∴两底角都为40°．（2）当50°的角是底角，则底角就为50°；当50°的角是顶角，则两底角的和等于130°，所以底角等于65°．故填40°，40°；50°，65°．三．解答题（共9小题）22．已知等腰三角形的周长为28cm，其中的一边长是另一边长的倍，求这个等腰三角形各边的长．【解答】解：设等腰三角形的一边长为xcm，则另一边长为xcm，则等腰三角形的三边有两种情况：xcm，xcm，xcm或xcm，xcm，xcm，则有：①x+x+x＝28，得x＝8cm，所以三边为：8cm、8cm、12cm；②x+x+x＝28，得x＝7cm，所以三边为7cm、10.5cm、10.5cm．因此等腰三角形的三边的长为：8cm，8cm，12cm或7cm，10.5cm，10.5cm．23．如图，已知AB＝AC，D为BC边中点，你能说出AD与BC的位置关系吗？请说明理由．【解答】解：AD⊥BC．理由如下：∵AB＝AC，D为BC边中点，∴AD⊥BC．24．如图，△ABC是等腰三角形，且AB＝AC，试作出BC边上的中线和高以及∠A的平分线，从中你发现了什么？与其他同学进行交流．【解答】解：如图，过点A作AD⊥BC于点D，在Rt△ABD和Rt△ACD中，∵AB＝AC，AD＝AD，∴Rt△ABD≌Rt△ACD（HL）∴BD＝CD，即AD也是中线，∴∠BAD＝∠CAD，即AD又是高线，所以等腰三角形底边上的中线、高以及顶角的角平分线重合．25．如图，在△ABC中，AB＝AC，∠C＝2∠A，BD平分∠ABC．请找出图中其他的等腰三角形，并选择其中的一个说明理由．【解答】解：△ABD、△BCD．理由：∵在△ABC中，AB＝AC，∠C＝2∠A，∴∠ABC＝∠C＝2∠A，∵∠A+∠ABC+∠C＝180°，∴∠A+2∠A+2∠A＝180°，解得：∠A＝36°，∴∠ABC＝∠C＝72°，∵BD平分∠ABC，∴∠ABD＝∠DBC＝36°，∴∠A＝∠ABD＝36°，∠BDC＝∠C＝72°，∴△ABD与△BCD是等腰三角形．26．已知D是等腰△ABC底边BC上的一个点，DE⊥AB于E，DF⊥AC于F，当D点在什么位置时，DE＝DF，并加以证明．【解答】解：当D是BC中点时DE＝DF，理由：∵AB＝AC，∴∠B＝∠C；∵∠BED＝∠CFD＝90°，BD＝CD；∴△BDE≌△CDF；∴DE＝DF．27．如图，AD是等腰△ABC顶角的外角的平分线，那么AD与BC平行吗？为什么？【解答】解：AD∥BC．∵△ABC是等腰三角形，∴∠B＝∠C，又∵∠EAC是△ABC的一个外角，∴∠EAC＝∠B+∠C＝2∠B，∵AD是等腰△ABC顶角的外角的平分线，∴2∠DAC＝∠EAC，∴∠C＝∠DAC，∴AD∥BC（内错角相等，两直线平行）．28．如图，在△ABC中，AD平分∠BAC，G是CA延长线上一点，GE∥AD交AB于F．交BC于E，试判断△AGF的形状并加以证明．【解答】解：△AGF是等腰三角形；理由：∵GE∥AD，∴∠G＝∠CAD，∠BAD＝∠GF A，∵AD平分∠BAC，∴∠CAD＝∠BAD，∴∠G＝∠GF A，∴AG＝AF，∴△AGF是等腰三角形．29．如图，在等腰△ABC中，AB＝AC，AD是BC边上的高，点E、F分别是边AB、AC上的点，且EF∥BC．（1）试说明△AEF是等腰三角形；（2）试比较DE与DF的大小关系，并说明理由．【解答】解：（1）∵EF∥BC，∴∠AEF＝∠B，∠AFE＝∠C．又∵AB＝AC，∴∠B＝∠C，∴∠AEF＝∠AFE，∴AE＝AF，即△AEF是等腰三角形；（2）DE＝DF．理由如下：∵AD是等腰三角形ABC的底边上的高，∴AD也是∠BAC的平分线．又∵△AEF是等腰三角形，∴AG是底边EF上的高和中线，∴AD⊥EF，GE＝GF，∴AD是线段EF的垂直平分线，∴DE＝DF．30．已知：如图，△ABC中，AB＝AC，D是BC延长线上一点，E是AC延长线上一点，且DE∥AB，求证：ED＝EC．【解答】证明：∵AB＝AC，∴∠B＝∠ACB，∵AB∥ED，∴∠B＝∠D，∴∠ACB＝∠D，又∵∠ACB＝∠ECD，∴∠ECD＝∠D，∴ED＝EC．。

北师大八级下《等腰三角形》课时练习含答案解析

北师大数学八年级下册第一章三角形的证明第1节等腰三角形练习一、选择题1．等腰三角形的一个角是80°，则它顶角的度数是（）A ．80°B ．80°或20°C ．80°或50°D ．20° 答案：B解析：解答：当80°的角是底角时，等腰三角形两底角相等，根据三角形内角和定理得到顶角为20°；另一种情况是80°是顶角.分析：等腰三角形等边对等角，结合三角形内角和为180°，从而得出两种结果.2．已知等腰三角形的两边长分别是3和5，则该三角形的周长是（）A ．8B ．9C ．10或12D ．11或13答案：D解析：解答：当3是腰时，两腰和为6加上底边5，周长为11；当5是腰时，两腰和为10加上底边3，周长为13.分析：等腰三角形两腰相等，结合三角形中两小边和大于第三边.3．在等腰△ABC 中，AB =AC ，中线BD 将这个三角形的周长分为15和12两个部分，则这个等腰三角形的底边长为（）A ．7B ．11C ．7或11D ．7或10答案：C解析：解答：设AB =AC =x BC =y则有12,2152x x x y +=+=⎧⎨⎩或者12,2152x x x y +=+=⎧⎨⎩ 所以x =8， y =11或者x =10，y =7.即三角形AB =AC =8，BC =11.或AB =AC =10，BC =7.故选C.分析：等腰三角形两腰相等，会解二元一次方程.4．等腰三角形一腰上的高与另一腰的夹角为30°，则顶角的度数为（）A ．60°B ．120°C ．60°或150°D ．60°或120°答案：D解析：解答：分两种情况：一种是这个高在三角形内,即此三角形是锐角三角形顶角=180°-90°-30°=60°，另一种是这个高落在一腰延长线上,即此三角形为钝角三角形顶角的补角=180°-90°-30°=60°，顶角=180°-60°=120°.分析：此题要注意分两种情况，要考虑锐角三角形和钝角三角形.5.在等腰△ABC中，AB=AC，BD⊥AC，∠ABC=72°，则∠ABD=（）A．36°B．54°C．18 °D．64°答案：B解析：解答：∵AB=AC，∠ABC=72°，∴∠ABC=∠ACB=72°，∴∠A=36°.∵BD⊥AC，∴∠ABD=90°-36°=54°.分析：根据等腰三角形的性质由已知可求得∠A的度数，再根据垂直的定义和三角形内角和定理不难求得∠ABD的度数.6. 在△ABC中，D是BC上的点，AB=AD=DC，∠B=70°，则∠C的度数为（）A．35°B．40°C．45°D．50°答案：A解析：解答：∵AB=AD, ∴∠ADB=∠B=70°.∵AD=DC，∴12C DAC ADB∠=∠=∠=35°.分析：等腰三角形两底角相等，再根据三角形的外角等于和它不相邻的两个内角和.7. 在△ABC中，∠B=∠C，AB=5，则AC的长为（）A．2 B．3 C．4 D．5答案：D解析：解答：∵∠B=∠C，∴AB=AC=5．分析：等腰三角形的性质可得AB=AC，继而得出AC的长．8. 在矩形ABCD中，AB＜BC，AC，BD相交于点O，则等腰三角形的个数是（）A．8 B．6 C．4 D．2答案：C解析：解答：∵四边形ABCD是矩形，∴AO=BO=CO=DO，∴△ABO，△BCO，△DCO，△ADO都是等腰三角形.分析：根据矩形的对角线相等且互相平分可得AO=BO=CO=DO，进而得到等腰三角形.9. 在等腰△ABC中，AB=AC，其周长为20 cm，则AB边的取值范围是（）A．1 cm＜AB＜4 cm B．5 cm＜AB＜10 cm C．4 cm＜AB＜8 cm D．4 cm＜AB＜10cm 答案：B解析：解答：∵在等腰△ABC中，AB=AC，其周长为20cm，∴设AB=AC=x cm，则BC=（20-2x）cm，∴2x＞20−2x，即20−2x＞0.解得5 cm＜x＜10 cm．分析：设AB=AC=x，则BC=20-2x，根据三角形的三边关系即可得出结论.10. 在△ABC中，∠ACB=90°，BE平分∠ABC，ED⊥AB于D．如果∠A=30°，AE=6cm，那么CE等于（）A. 4 cm B．2 cm C. 3 cm D.1 cm答案：C解析：解答：∵ED⊥AB，∠A=30°，∴AE=2ED，∵AE=6cm，∴ED=3cm.∵∠ACB=90°，BE平分∠ABC，∴ED=CE，∴CE=3cm.分析：根据在直角三角形中，30度所对的直角边等于斜边的一半得出AE=2ED，求出ED，再根据角平分线到两边的距离相等得出ED=CE，即可得出CE的值11.在平面直角坐标系xOy中，A（0，2），B（0，6），动点C在直线y=x上．若以A、B、C三点为顶点的三角形是等腰三角形，则点C的个数是( )A．2 B．3 C．4 D．5答案B解析：解答：AB的垂直平分线与直线y=x相交于点C1，∵A（0，2），B（0，6），∴AB=6-2=4，点A为圆心，以AB的长为半径画弧，与直线y=x的交点为C2，C3∴点B到直线y=x的距离为=∵4，∴以点B为圆心，以AB的长为半径画弧，与直线y=x没有交点，所以，点C的个数是1+2=3．分析：根据线段垂直平分线上的点到线段两端点的距离相等可得AB的垂直平分线与直线y=x 的交点为点C再求出AB的长，以点A为圆心，以AB的长为半径画弧，与直线y=x的交点为点C，求出点B到直线y=x的距离可知以点B为圆心，以AB的长为半径画弧，与直线没有交点12. 在△ABC中，AB=20 cm，AC=12 cm，点P从点B出发以每秒3 cm的速度向点A运动，点Q从点A同时出发以每秒2 cm的速度向点C运动，其中一个动点到达端点时，另一个动点也随之停止运动，当△APQ是以PQ为底的等腰三角形时，运动的时间是（）A．秒B．3秒C．秒D．4秒答案：D解析：解答：设运动的时间为x cm/s，在△ABC中，AB=20cm，AC=12cm点P从点B出发以每秒3cm的速度向点A运动，点Q从点A同时出发以每秒2cm的速度向点C运动当△APQ是等腰三角形时，AP=AQ，AP=20-3x，AQ=2x即20-3x=2x，解得x=4．分析：设运动的时间为x，则AP=20-3x，当APQ是等腰三角形时，AP=AQ，则20-3x=2x，解得x即可.13. 等腰但不等边的三角形的角平分线、高线、中线的总条数是（）A．3 B．5 C．7 D．9答案：C解析：解答：等腰但不等边的三角形底边上的角平分线、中线、高线三线重合成一条；腰上的三条线不重合，因而共有7条线.分析：画出图形，根据等腰三角形的性质进行分析即可得到答案14. 已知△ABC中，三边a，b，c满足|b-c|+（a-b）2=0，则∠A等于（）A. 60°B．45°C．90°D．不能确定答案：A解析：解答：△ABC中，三边a，b，c满足|b-c|+（a-b）2=0∴b-c=0，a-b=0，∴a=b=c，∴三角形是等边三角形，∴∠A=60°.分析：根据非负数的性质列式求解得到a=b=c，然后选择答案即可.15.等腰三角形周长为36cm，两边长之比为4：1，则底边长为（）A．16cm B．4cm C．20cm D．16cm或4cm答案：B解析：解答：因为两边长之比为4：1，所以设较短一边为x，则另一边为4x；(1)假设x为底边，4x为腰；则8x+x=36，x=4，即底边为4；(2)假设x为腰，4x为底边，则2x+4x=36，x=6，4x=24；∵6+6＜24，∴该假设不成立．所以等腰三角形的底边为4cm．分析：题中只给出了两边之比，没有明确说明哪个是底哪个是腰，所以应该分两种情况进行分析，再结合三角形三边的关系将不合题意的解舍去.二、填空题16. 等腰三角形的一个外角为110°，则底角的度数可能是_______.答案：70°或55°解析：解答：当110°是等腰三角形底角的外角时，底角为70°；当110°是等腰三角形顶角的外角时，因为等腰三角形两底角相等，所以一个底角的度数等于外角110°的一半，即55°分析：外角与它相邻的内角互补，外角等于和它不相邻的两个内角和.17. 等腰三角形的对称轴是____________.答案：底边上的高(顶角平分线或底边的中线)所在的直线解析：解答：根据等腰三角形的性质，等腰三角形的对称轴是底边上的高（顶角平分线或底边的中线）所在的直线．分析：本题根据等腰三角形是轴对称图形，其对称轴是底边上的高所在的直线，因为等腰三角形底边上的高，顶角平分线，底边上的中线三线合一，所以等腰三角形的对称轴是底边上的高（顶角平分线或底边的中线）所在的直线．18.△ABC中，AB=AC，∠A=36°，BD平分∠ABC，则∠1 =_______度，此三角形有_______个等腰三角形．答案：72°/3解析：解答：∵AB=AC，∠A=36°，∴△ABC是等腰三角形，∠C=∠ABC=（180°−36°）12⨯=72°.∵BD为∠ABC的平分线，∴∠ABD=∠A=∠DBC=36°，∴AD=BD，△ADB是等腰三角形，∴∠1=180°-36°-72°=72°=∠C，∴BC=BD，△CDB是等腰三角形.图中共有3个等腰三角形．分析：由已知条件，根据三角形内角和等于180、角的平分线的性质求得各个角的度数，然后利用等腰三角形的判定进行找寻，注意做到由易到难，不重不漏.19. 在△ABC中，与∠A相邻的外角是100°，要使△ABC是等腰三角形，则∠B的度是_________.答案：80°或50°或20°解析：解答：∵∠A的相邻外角是100°，∴∠A=80°．分两种情况：（1）当∠A为底角时，另一底角∠B=∠A=80°；（2）当∠A为顶角时，则底角∠B=∠C=(180°−80°)12⨯=50°（3）当∠B是顶角时，∠B=180°-2∠A=20°．综上所述，∠B的度数是80°或50°或20°.分析：已知给出了∠A的相邻外角是100°，没有明确是顶角还是底角，所以要进行分类讨论，分类后还有用内角和定理去验证每种情况是不是都成立.20. 在△ABC中，若∠A=80°，∠B=50°，AC=5，则AB=_______.答案：5解析：解答：∵∠A=80°，∠B=50°，∴∠C=180°-80°-50°=50°.∴AB=AC=5.分析：由已知条件先求出∠C的度数是50°，根据等角对等边的性质求解即可.三、解答题.21.在△ABC中，AB=AC，AD是BC边上的高，∠C=63°，BC=4，求∠BAD的度数及DC的长.答案：27°/2 解答：∵AB =AC ，∠C =63°，∴∠B =∠C =63°，∴∠BAC =180°-63°-63°=54°. 又∵AD 是BC 边上的高，∴AD 是∠BAC 的平分线，AD 是BC 边上的中线，∴∠BAD =12∠BAC =27°，DC =12BC =2. 解析：分析：根据等腰三角形的两个底角相等求出顶角∠BAC 的度数，再由等腰三角形的三线合一性质即可求出∠BAD =12∠BAC =27°，DC =12BC =2. 22.在△ABC 中，AB =AC ，BD ⊥AC 于D ，CE ⊥AB 于E ，BD 、CE 相交于F .求证：AF 平分∠BAC答案：证明：∵AB =AC ，∴∠ABC =∠ACB .又∵BD ⊥AC ，CE ⊥AB ，∴∠BEC =∠CDB =90°. 在△BCE 和△CBD 中，∠ABC =∠ACB ，∠BEC =∠CDB ，BC =BC.∴△BCE ≌△CBD （AAS ）.∴BE =CD.∵AB =AC ，BE =CD ，∴AB -BE =AC -CD ，∴AE =AD.∴在△AEF 和△ADF 中，AE =AD , AF =AF.△AEF ≌△ADF （HL ）.∴∠EAF =∠DAF ，AF 平分∠BAC.解析：分析：要通过两次三角形全等，再结合等腰三角形的性质得出结论.23.如图，已知点B 、C 、D 在同一条直线上，△ABC 和△CDE 都是等边三角形.BE 交AC 于F ，AD 交CE 于H ，求证：（1）△BCE ≌△ACD ；答案：证明：∵△ABC 和△CDE 都是等边三角形，∴∠BCA =∠DCE =60°，BC =AC =AB ，EC =CD =ED ，∴∠BCE =∠ACD .在△BCE 和△ACD 中，,,,BC AC BCE ACD CE CD =⎧∠=∠=⎪⎨⎪⎩∴△BCE ≌△ACD （S A S ）；（2）CF =CH ；答案：∵△BCE ≌△ACD ，∴∠CBF =∠CAH ．∵∠ACB =∠DCE =60°，在△BCF 和△ACH 中，∴∠ACH =60°，∴∠BCF =∠ACH ，,,,CBF CAH BC AC BCF ACH ∠=∠=∠=∠⎧⎪⎨⎪⎩∴△BCF ≌△ACH （A S A ），∴CF =CH ；（3）△FCH 是等边三角形；答案：∵CF =CH ，∠ACH =60°，∴△CFH 是等边三角形．（4）FH ∥BD.答案：证明：∵△CHF 为等边三角形∴∠FHC =60°，∵∠HCD =60°，∴FH ∥BD解析：分析：由等边三角形的三边相等，三角都是60°，再根据平角的关系，就能证明△BCE ≌△ACD ；由△BCE ≌△ACD 得出对应角相等，结合等边三角形的边角特点证明△BCF ≌△ACH ，能得出CF =CH ；两边等，加上一个角60°推出△CFH 是等边三角形；根据内错角相等，两直线平行推出FH ∥BD .24. 如图，已知AB =AC =AD ，且AD ∥BC ，求证：∠C =2∠D答案：证明：∵AB=AC=AD，∴∠C=∠ABC，∠D=∠ABD.∴∠ABC=∠CBD+∠D.∵AD∥BC，∴∠CBD=∠D，∴∠ABC=∠D+∠D=2∠D，又∵∠C=∠ABC，∴∠C=2∠D.解析：分析：首先根据AB=AC=AD，∵AD∥BC，∴∠D=∠DBC可得∠C=∠ABC，∠D=∠ABD，∠ABC=∠CBD+∠D；然后根据AD∥BC，可得∠CBD=∠D，据此判断出∠ABC=2∠D，再根据∠C=∠ABC，即可判断出∠C=2∠D25.如图，在△ABC中，∠B与∠C的平分线交于点O，过O点作DE∥BC，分别交AB、AC于D、E，若AB=5，AC=4，求△ADE的周长.答案：解答：∵在△ABC中，∠B与∠C的平分线交于点O，∴∠DBO=∠CBO，∠ECO=∠BCO，∵DE∥BC，∴∠DOB=∠CBO，∠EOC=∠BCO，∴∠DBO=∠DOB，∠ECO=∠EOC，∴OD=BD，OE=CE，∵AB=5，AC=4，∴△ADE的周长为：AD+DE+AE=AD+DO+EO+AE=AD+DB+EC+AE=AB+AC=5+4=9.解析：分析：由在△ABC中，∠B与∠C的平分线交于点O，过点O作DE∥BC，易证得△DOB与△EOC是等腰三角形，即DO=DB，EO=EC，继而可得△ADE的周长等于AB+AC，即可求得答案．北师大版数学八年级课时练习一、选择题1．如图，△ABC中，AB=5，AC=6，BC=4，边AB的垂直平分线交AC于点D，则△BDC 的周长是（）A. 8B. 9C. 10D.11答案：C解析：解：∵ED是AB的垂直平分线，∴AD=BD，∵△BDC的周长=DB+BC+CD，∴△BDC的周长=AD+BC+CD=AC+BC=6+4=10．故选C.分析：由ED是AB的垂直平分线，可得AD=BD，又由△BDC的周长=DB+BC+CD，即可得△BDC的周长=AD+BC+CD=AC+BC.2.如图，△ABC中，BD平分∠ABC，BC的中垂线交BC于点E，交BD于点F，连接CF．若∠A=60°，∠ABD=24°，则∠ACF的度数为（）A. 48°B. 36°C. 30°D. 24°答案：A解析：解：∵BD平分∠ABC，∴∠DBC=∠ABD=24°，∵∠A=60°，∴∠ACB=180°－60°－24°×2=72°，∵BC的中垂线交BC于点E，∴BF=CF，∴∠FCB=24°，∴∠ACF=72°－24°=48°，故选：A.分析：根据角平分线的性质可得∠DBC=∠ABD=24°，然后再计算出∠ACB的度数，再根据线段垂直平分线的性质可得BF=CF，进而可得∠FCB=24°，然后可算出∠ACF的度数. 3．如图，在等腰△ABC中，一腰AB的垂直平分线交另一腰AC于点G，若已知AB=10，△GBC的周长为17，则底BC的长为（）A. 10B. 9C. 7D. 5答案：C解析：解：如图，∵在等腰△ABC中，一腰AB的垂直平分线交另一腰AC于点G，∴AG=BG，∵AB=10，△GBC的周长为17，∴CG+BG+BC=CG+AG+BC=AC+BC=17，AC=AB=10，∴BC=7．故选C.分析：首先根据题意在等腰△ABC中，一腰AB的垂直平分线交另一腰AC于点G，根据线段垂直平分线的性质，可得AG=BG，继而可得△GBC的周长=AC+BC=17，则可求得答案. 4．如图，AB=AC，∠A=40°，AB的垂直平分线DE交AC于点E，垂足为D，则∠EBC的度数是（）A. 30°B. 40°C. 70°D. 80°答案：A解析：解：∵AB的垂直平分线DE交AC于点E，∴AE=BE，∴∠ABE=∠A=40°，∵AB=AC，∴∠ABC=∠C=70°，∴∠EBC=∠ABC－∠ABE=30°．故选A.分析：由AB的垂直平分线DE交AC于点E，可得AE=BE，继而求得∠ABE=∠A=40°，然后由AB=AC，求得∠ABC的度数，继而求得答案.5．如图，在△ABC中，AB的垂直平分线分别交AB，AC于D，E两点，且AC=10，BC=4，则△BCE的周长为（）A. 6B. 14C. 18D. 24答案：B解析：解：∵AC=10，BC=4，∴AC+BC=10+4=14，∵DE是线段AB的垂直平分线，∴AE=BE，∴△BCE的周长=（BE+CE）+BC=AC+BC=14．故选B.分析：先根据AC=10，BC=4，可得出AC+BC的长，再根据DE是线段AB的垂直平分线可得到AE=BE，进而可得出答案.6．如图，在Rt△ABC中，∠C=90°，AC=12，AB=13，AB边的垂直平分线分别交AB、AC 于N、M两点，则△BCM的周长为（）A. 18B. 16C. 17D. 无法确定答案：C解析：解：在Rt△ABC中，∠C=90°，AC=12，AB=13，由勾股定理得，BC=5，∵MN是AB的垂直平分线，∴MB=MA，∴△BCM的周长=BC+CM+MB=BC+CM+MA=BC+CA=17，故选：C分析：根据勾股定理求出BC的长，根据线段垂直平分线的性质得到MB=MA，根据三角形的周长的计算方法代入计算即可.7．如果三角形三条边的中垂线的交点在三角形的外部，那么，这个三角形是（）A. 直角三角形B. 锐角三角形C. 钝角三角形D. 等边三角形答案：C解析：解：如图，O是边AB和边AC的垂直平分线的交点，则AO=OB，AO=OC，所以∠OAB=∠OBA，∠OAC=∠OCA，∵∠BAC=∠OAB+∠OAC=∠OBA+∠OCA，∴∠BAC＞∠ABC+∠ACB，∵∠BAC+∠ABC+∠ACB=180°，∴∠BAC＞90°，即△ABC是钝角三角形，故选C分析：先根据题意画出图形，再根据线段垂直平分线性质、等腰三角形的性质、三角形的内角和定理求出∠BAC＞90°即可.8. 已知MN是线段AB的垂直平分线，C，D是MN上任意两点，则∠CAD和∠CBD之间的大小关系是（）A．∠CAD＜∠CBD B．∠CAD=∠CBD C．∠CAD＞∠CBD D.无法确定答案：B解析：解：∵MN是线段AB的垂直平分线，C，D是MN上任意两点，∴AC=BC，AD=BD，∴∠DAB=∠CBA，∠DAB=∠DBA，如图1，∠CAD=∠CAB+∠DAB，∠CBD=∠CBA+∠DBA，∴∠CAD=∠CBD；如图2，∠CAD=∠CAB－∠DAB，∠CBD=∠CBA－∠DBA，∴∠CAD=∠CBD．故选B.分析：首先根据题意画出图形，然后由MN是线段AB的垂直平分线，C，D是MN上任意两点，根据线段垂直平分线的性质可得：AC=BC，AD=BD，则可证得∠DAB=∠CBA，∠DAB=∠DBA，继而求得答案.9. 已知△ABC中，AB=AC，AB的垂直平分线交AC于D，△ABC和△DBC的周长分别是60 cm和38 cm，则△ABC的腰和底边长分别为（）A．24 cm和12 cm B．16 cm和22 cm C．20 cm和16 cm D．22 cm和16 cm答案：D解析：解：如图，连接BD，∵D在线段AB的垂直平分线上，∴BD=AD，∴BD+DC+BC=AC+BC=38 cm，且AB+AC+BC=60 cm，∴AB=60 cm－38 cm =22 cm，∴AC=22 cm，∴BC=38 cm－AC=38 cm－22 cm =16 cm，即等腰三角形的腰为22 cm，底为16 cm，故选D.分析：连接BD，根据线段垂直平分线的性质可得到BD=AD，可知两三角形周长差为AB，结合条件可求得腰长，再由周长可求得BC，可得出答案.10．如图，地面上有三个洞口A、B、C，老鼠可以从任意一个洞口跑出，猫为能同时最省力地顾及到三个洞口（到A、B、C三个点的距离相等），尽快抓到老鼠，应该蹲守在（）A．△ABC三边垂直平分线的交点B．△ABC三条角平分线的交点C．△ABC三条高所在直线的交点D．△ABC三条中线的交点答案：A解析：解：∵三角形三边垂直平分线的交点到三个顶点的距离相等，∴猫应该蹲守在△ABC三边垂直平分线的交点处．故选A分析：根据题意，知猫应该到三个洞口的距离相等，则此点就是三角形三边垂直平分线的交点.11. 三角形内有一点到三角形三顶点的距离相等，则这点一定是三角形的（）A．三条中线的交点B．三边垂直平分线的交点C．三条高的交点D．三条角平分线的交点答案：B解析：解：三角形内有一点到三角形三顶点的距离相等，则这点一定是三角形的三边垂直平分线的交点，故选：B.分析：根据线段垂直平分线的性质：线段垂直平分线上任意一点，到线段两端点的距离相等可得答案.12. △ABC中，AB=AC，AB的垂直平分线与直线AC相交所成锐角为40°，则此等腰三角形的顶角为（）A．50°B．60°C．150°D．50°或130°答案：D解析：解：（1）当AB的中垂线MN与AC相交时易得∠A=90°－40°=50°，（2）当AB的中垂线MN与CA的延长线相交时，易得∠DAB=90°－40°=50°，∴∠A=130°，故选D.分析：此题根据△ABC中∠A为锐角与钝角分为两种情况解答.13. 如图，在Rt△ABC中，∠C=90°，直线DE是斜边AB的垂直平分线交AC于D．若AC=8，BC=6，则△DBC的周长为（）A．12 B．14 C．16 D．无法计算答案：B解析：解：∵DE是AB的垂直平分线，∴DA=DB，∴△DBC的周长为CB+CD+DB=CB+CD+DA=BC+CA=6+8=14，故选：B分析：根据线段的垂直平分线上的点到线段的两个端点的距离相等得到DA=DB，根据三角形周长公式求出周长.14. 如图，在△ABC中，AB=A，AC=B，BC边上的垂直平分线DE交BC、BA分别于点D、E，则△AEC的周长等于（）A．A+B B．A－B C．2A+B D．A+2B答案：A解析：解：∵ED垂直且平分BC，∴BE=CE．∵AB=A，AC=B，∴AB=AE+BE=AE+CE=A．∴△AEC的周长为：AE+EC+AC=A+B．故选A分析：要求三角形的周长，知道AC=B，只要求得AE+EC即可，由DE是BC的垂直平分线，结合线段的垂直平分线的性质，知EC=BE，这样三角形周长的一部分AE+EC=AE+BE=AB，代入数值，答案可得.15. 如图，有A、B、C三个居民小区的位置成三角形，现决定在三个小区之间修建一个购物超市，使超市到三个小区的距离相等，则超市应建在（）A．在AC，BC两边高线的交点处B．在AC，BC两边中线的交点处C．在AC，BC两边垂直平分线的交点处D．在∠A，∠B两内角平分线的交点处答案：C解析：解：根据线段的垂直平分线的性质：线段的垂直平分线上的点到线段的两个端点的距离相等．则超市应建在AC，BC两边垂直平分线的交点处．故选C.分析：要求到三小区的距离相等，首先思考到A小区、B小区距离相等，根据线段垂直平分线定理的逆定理知满足条件的点在线段AB的垂直平分线上，同理到B小区、C小区的距离相等的点在线段BC的垂直平分线上，于是到三个小区的距离相等的点应是其交点，答案可得.二、填空题16．△ABC中，AB=AC，∠BAC=120°，AC的垂直平分线EF交AC于E，交BC于F．若FC=3 cm，则BF=_________．答案：6 cm解析：解：连接AF．∵AB=AC，∠BAC=120°，∴∠B=∠C=30°；∵AC的垂直平分线EF交AC于点E，交BC于点F，∴CF=AF，∠FAC=30°，∴∠BAF=90°，∴BF=2AF（30°直角边等于斜边的一半），∴BF=2CF=6 cm．故答案是：6 cm分析：利用辅助线，连接AF，求出CF=AF，∠BAF=90°，再根据AB=AC，∠BAC= 120°可求出∠B的度数，由直角三角形的性质即可求出BF=2AF=2CF=6 cm.17. 如图，ED为△ABC的AC边的垂直平分线，且AB=5，△BCE的周长为8，则BC=________．答案：3解析：解：∵ED为AC上的垂直平分线，∴AE=EC，∵AB=AE+EB=5，△BCE的周长=AE+BE+BC=AB+BC=8，∴BC=8－5=3．故答案为：3分析：根据ED为AC上的垂直平分线，得出AE=CE，再根据AB=5，△BCE的周长为AB+BC=8，即可求得BC.18．如图，已知在△ABC中，AB=AC=10，DE垂直平分AB，垂足为E，DE交AC于D，若△BDC的周长为16，则BC=__________ ．答案：6解析：解：∵DE垂直平分AB，∴AD=BD，∴AD+CD=BD+CD，即AC=BD+CD，∵AC=10，△BDC的周长为16，∴BC=16－AC=16－10=6．故答案为：6分析：先根据DE垂直平分AB可知，AD=BD，即AC=BD+CD，再由AC=10，△BDC的周长为16即可求出答案.19. 如图，在等腰三角形ABC中，AB=AC，DE垂直平分AB，已知∠ADE=40°，则∠DBC=答案：15解析：解：∵DE垂直平分AB，∴AD=BD，∠AED=90°，∴∠A=∠ABD，∵∠ADE=40°，∴∠A=90°－40°=50°，∴∠ABD=∠A=50°，∵AB=AC，∴∠ABC=∠C=65°，∴∠DBC=∠ABC－∠ABD=65°－50°=15°，故答案为：15分析：根据线段垂直平分线求出AD=BD，推出∠A=∠ABD=50°，根据三角形内角和定理和等腰三角形性质求出∠ABC，即可得出答案.20.点P在线段AB的垂直平分线上，PA=7，则PB= _________．答案：7解析：解：∵点P在线段AB的垂直平分线上，PA=7，∴PB=PA=7，故答案为：7分析：根据线段垂直平分线的性质得出PA=PB，代入即可求出答案．三、解答题21. 某公园有海盗船、摩天轮、碰碰车三个娱乐项目，现要在公园内建一个售票中心，使三个娱乐项目所处位置到售票中心的距离相等，请在图中确定售票中心的位置．答案：解：如图，①连接AB，AC，②分别作线段AB，AC的垂直平分线，两垂直平分线相较于点P，则P即为售票中心解析：由三个娱乐项目所处位置到售票中心的距离相等，可得售票中心是海盗船、摩天轮、碰碰车三个娱乐场组成三角形的三边的垂直平分线的交点.22．如图，在△ABC中，∠C=90°，DE垂直平分AB，分别交AB，BC于D，E．若∠CAE=∠B+30°，求∠AEB的度数答案：140°解析：解：∵DE垂直平分AB，∴AE=BE，∴∠B=∠EAB.∵∠C=90°，∠CAE=∠B+30°，∴∠B+30°+∠B+∠B=90°，∴∠B=20°，∴∠AEB=180°－20°－20°=140°.分析：根据线段垂直平分线求出AE=BE，推出∠B=∠EAB，根据已知和三角形内角和定理得出∠B+30°+∠B+∠B=90°，求出∠B，即可得出答案.23．如图，在△ABC中，AB=AC，AB的垂直平分线MN交AC于点D，交AB于点E．（1）求证：△ABD是等腰三角形；（2）若∠A=40°，求∠DBC的度数；（3）若AE=6，△CBD的周长为20，求△ABC的周长答案：（1）证明：∵AB的垂直平分线MN交AC于点D，∴DB=DA，∴△ABD是等腰三角形.（2）30°（3）32解析：解：（1）证明：∵AB的垂直平分线MN交AC于点D，∴DB=DA，∴△ABD是等腰三角形；（2）∵△ABD是等腰三角形，∠A=40°，∴∠ABD=∠A=40°，∠ABC=∠C=（180°－40°）÷2=70°.∴∠BDC=∠ABC－∠ABD=70°－40°=30°.（3）∵AB的垂直平分线MN交AC于点D，AE=6，∴AB=2AD=12.∵△CBD的周长为20，∴AC+BC=20，∴△ABC的周长=AB+AC+BC=12+20=32．分析：（1）根据线段的垂直平分线到线段两端点的距离相等即可得证；（2）首先利用三角形内角和求得∠ABC的度数，然后减去∠ABD的度数即可得到答案；（3）将△ABC的周长转化为AB+AC+BC的长即可求得.24．如图所示，在△ABC中，DE是边AB的垂直平分线，交AB于E，交AC于D，连接BD．（1）若∠ABC=∠C，∠A=50°，求∠DBC的度数．（2）若AB=AC，且△BCD的周长为18 cm，△ABC的周长为30 cm，求BE的长.答案：（1）15°；（2）6 cm解析：解：（1）∵∠A=50°，∴∠ABC=∠C=65°.又∵DE垂直平分AB，∴∠A=∠ABD=50°，∴∠DBC=∠ABC－∠ABD=15°．（2）∵DE是AB的垂直平分线，∴AD=BD，AE=BE，∴△BCD的周长=BC+CD+BD=BC+CD+AD=BC+AC=18 cm．∵△ABC的周长=30 cm，∴AB=30－18=12 cm，∴BE=AE=6 cm．分析：（1）已知∠A=50°，易求∠ABC的度数．又因为DE垂直平分AB根据线段垂直平分线的性质易求出∠DBC的度数．（2）同样利用线段垂直平分线的性质：垂直平分线上任意一点，和线段两端点的距离相等可解．25．已知：如图，在△ABC中，MN是边AB的中垂线，∠MAC=50°，∠C=3∠B，求∠B 的度数=26°答案：B解析：解：∵MN是边AB的中垂线，∴AM=BM，∴∠BAM=∠B.设∠B=x，则∠BAM=x，∵∠C=3∠B，∴∠C=3x，在△ABC中，由三角形内角和定理，得x+x+3x+50°=180°，∴x=26°，即∠B=26°分析：根据线段垂直平分线性质得出AM=BM，推出∠BAM=∠B，设∠B=x，则∠BAM=x，∠C=3x，在△ABC中，由三角形内角和定理得出方程x+x+3x+50°=180°，求出即可。

人教版八年级下册数学专题复习及练习(含解析)：等腰三角形

专题13.3 等腰三角形知识点1：等腰三角形1.等腰三角形的定义：有两条边相等的三角形叫做等腰三角形．相等的两边叫做腰，另一边叫做底边，两腰所夹的角叫做顶角，底边与腰的夹角叫底角．2.等腰三角形的性质：（1）等腰三角形的两个底角相等（简写成“等边对等角”）．（2）等腰三角形的顶角平分线，底边上的中线、底边上的高互相重合（通常称作“三线合一”）．3.等腰三角形的判定定理：如果一个三角形有两个角相等，那么这两个角所对的边也相等（简写成“等角对等边”）．知识点2：等边三角形1.定义：三条边相等的三角形叫做等边三角形．2.等边三角形的性质和判定：（1）等边三角形的三个内角都相等，并且每一个角都等于60°。

（2）三个角都相等的三角形是等边三角形。

（3）有一个角是60°的等腰三角形是等边三角形。

知识点3：直角三角形的一个定理在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半．【例题1】如图，在△ABC中，AB=AC，点D在AC上，且BD=BC=AD，求：△ABC各角的度数．【例题2】证明：在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半．已知：如图，在Rt △ABC 中，∠C=90°，∠BAC=30°．求证：BC=AB ．【例题7】已知等边三角形的边长为3，点P 为等边三角形内任意一点，则点P 到三边的距离之和为（）A ．B ．C ．D ．不能确定【例题3】如图，已知AC ⊥BC ，BD ⊥AD ，AC 与BD 交于点O ，AC=BD.求证：(1)BC=AD ；(2)△OAB 是等腰三角形.一、选择题1.已知等边三角形的边长为3，点P 为等边三角形内任意一点，则点P 到三边的距离之和为（）12C AA．B．C．D．不能确定2.如图所示，点D是△ABC的边AC上一点（不含端点），AD=BD，则下列结论正确的是（）A．AC＞BC B．AC=BC C．∠A＞∠ABC D．∠A=∠ABC3．如图，∠AOB=120°，OP平分∠AOB，且OP=2．若点M，N分别在OA，OB上，且△PMN 为等边三角形，则满足上述条件的△PMN有（）A．1个B．2个C．3个D．3个以上4.如图所示，底边BC为2，顶角A为120°的等腰△ABC中，DE垂直平分AB于D，则△ACE的周长为（）A．2+2B．2+C．4 D．3二、解答题5.已知：在△ABC中，AB=AC，D为AC的中点，DE⊥AB，DF⊥BC，垂足分别为点E，F，且DE=DF．求证：△ABC是等边三角形．6.如图，在△ABC中，过C作∠BAC的平分线AD的垂线，垂足为D，DE∥AB交AC于E．求证：AE=CE．7.求证：如果三角形一个外角的平分线平行于三角形的一边，那么这个三角形是等腰三角形．已知：∠CAE 是△ABC 的外角，∠1=∠2，AD ∥BC （如图）．求证：AB=AC ．8.已知：如图，AD ∥BC ，BD 平分∠ABC ．求证：AB=AD ．9.证明：等腰三角形两底角的平分线相等．已知：如图，在△ABC 中，AB=AC ，BD 、CE 是△ABC 的平分线．求证：BD=CE ．10.证明：等腰三角形两腰上的高相等．已知：如图，在△ABC 中，AB=AC ，BE 、CF 分别是△ABC 的高．E DCAB11.证明：等腰三角形两腰上的中线相等．已知：如图，在△ABC 中，AB=AC ，BD 、CE 分别是两腰上的中线．求证：BD=CE ．12.已知：如图，在△ABC 中，AB=AC=2a ，∠ABC=∠ACB=15°，CD 是腰AB 上的高．求：CD 的长．13．已知：如图，△ABC 中，∠ACB=90°，CD 是高，∠A=30°．求证：BD=AB ．14.已知直角三角形的一个锐角等于另一个锐角的2倍，这个角的平分线把对边分成两条线段．求证：其中一条是另一条的2倍．已知：在Rt △ABC 中，∠A=90°，∠ABC=2∠C ，BD 是∠ABC 的平分线．1415.已知：如图，在Rt △ABC 中，∠C=90°，BC=AB ．求证：∠BAC=30°．16.已知，如图，点C 为线段AB 上一点，△ACM 、△CBN 是等边三角形．求证：AN=BM ．17．一个直角三角形房梁如图所示，其中BC ⊥AC ，∠BAC=30°，AB=10cm ， CB 1⊥AB ，B 1C ⊥AC 1，垂足分别是B 1、C 1，那么BC 的长是多少？18.如图，△ABC 中，AB=AC ，∠A=36°，AC 的垂直平分线交AB 于E ，D 为垂足，连接EC ．（1）求∠ECD 的度数；（2）若CE=5，求BC 长．12专题13.3 等腰三角形知识点1：等腰三角形1.等腰三角形的定义：有两条边相等的三角形叫做等腰三角形．相等的两边叫做腰，另一边叫做底边，两腰所夹的角叫做顶角，底边与腰的夹角叫底角．2.等腰三角形的性质：（1）等腰三角形的两个底角相等（简写成“等边对等角”）．（2）等腰三角形的顶角平分线，底边上的中线、底边上的高互相重合（通常称作“三线合一”）．3.等腰三角形的判定定理：如果一个三角形有两个角相等，那么这两个角所对的边也相等（简写成“等角对等边”）．知识点2：等边三角形1.定义：三条边相等的三角形叫做等边三角形．2.等边三角形的性质和判定：（1）等边三角形的三个内角都相等，并且每一个角都等于60°。

12.3 等腰三角形水平测试(含答案)

12.3 等腰三角形一、选择题题号一1 二2 三3 四4 五5 六6 七7 八8 得分度的反复训练才能取得跟多的收获，我们设计的试卷主要就是从这点出发，所以从你下载这张试卷开始，就与知识接近了一步。

1．等腰三角形的周长为26㎝，一边长为6㎝，那么腰长为（）Ａ．6㎝Ｂ．10㎝Ｃ．6㎝或10㎝Ｄ．14㎝2．已知△ABC，AB =AC，∠B=65°，∠C度数是( )A．50°B．65°C．70°D．75°3．等腰三角形是轴对称图形，它的对称轴是（）A．过顶点的直线B．底边的垂线C．顶角的平分线所在的直线D．腰上的高所在的直线二、填空题4．等腰三角形的两个_______相等（简写成“____________”）．5．已知△ABC，AB =AC，∠A=80°，∠B度数是_________．6．等腰三角形的两个内角的比是1：2，则这个等腰三角形的顶角的度数是_______________．7．等腰三角形的腰长是6，则底边长5，周长为__________．三、解答题8．如图AB=AD，AD∥BC，求证：BD平分∠ABC．（写出每步证明的重要依据）9．如图，在△ABC中，AB=AC，D、E分别在AC、AB边上，且BC=BD，AD=DE=EB。

求∠A的度数参考答案一、选择题1．B2．B3．C二、填空题4．底角，等边对等角5．50°6．36°或90°7．16或17三、解答题8．如图AB=AD，AD∥BC，求证：BD平分∠ABC．证明：∵AB=AD（已知）∴∠ABD=∠ADB（等边对等角）∵AD∥BC（已知）∴∠ADB=∠CBD（两直线平行，内错角相等）∴∠ABD=∠CBD（等量代换）∴BD平分∠ABC．（角平分线定义）9．4512.3.2等边三角形一、选择题1．△ABC是等边三角形，D、E、F为各边中点，则图中共．有正三角形( ) A．2个B．3个C．4个D．5个2．△ABC中，∠A：∠B：∠C=1：2：3，则BC：AB等于( )A．2：1 B．1：2 C．1：3 D．2 ：3二、填空题3．等边三角形的周长为6㎝，则它的边长为________．4．等边三角形的两条高线相交所成钝角的度数是__________．5．在△ABC中，∠A=∠B=∠C，则△ABC是_____三角形．6．△ABC中，∠AC B=90°∠B=60°，BC=3㎝，则AB=_______．三、解答题7．△ABC是等边三角形，点D在边BC上，DE∥AC，△BDE是等边三角形吗？试说明理由．8．已知：如图，P，Q是△ABC边上BC上的两点，且BP=PQ=QC=AP=AQ。

中考数学复习《等腰、等边及直角三角形》经典题型(含答案)

中考数学复习《等腰、等边及直角三角形》经典题型（含答案）知识点一：等腰和等边三角形1.等腰三角形定义：有两条边相等的三角形叫等腰三角形（1）性质①等边对等角：两腰相等，底角相等，即AB＝AC ∠B＝∠C；②三线合一：顶角的平分线、底边上的中线和底边上的高互相重合;③对称性：等腰三角形是轴对称图形，直线AD是对称轴.（2）判定①定义：有两边相等的三角形是等腰三角形；注意：1.实际解题中的一个常用技巧是，构造等腰三角形，进而利用等腰三角形的性质为解题服务，常用的构造方法有：1）、“角平分线+平行线”构造等腰三角形。

2）、“角平分线+垂线”构造等腰三角形。

3）、用“垂直平分线”构造等腰三角形；4）、用“三角形中角的2倍关系”构造等腰三角形。

2.当等腰三角形的腰和底不明确时，需分类讨论.变式练习1：如若等腰三角形ABC的一个内角为30°，则另外两个角的度数为30°、120°或75°、75°.3.三角形中“垂线、角平分线、中线、等腰”四个条件中，只要满足其中两个，其余均成立.变式练习2：如右图，已知AD⊥BC,D为BC的中点，则三角形的形状是等腰三角形.②等角对等边：即若∠B＝∠C，则△ABC是等腰三角形.变式练习3：一个等腰三角形的两边长分别为3和7，则它的周长为( ) A. 17 B. 15 C. 13 D. 13或17【解析】A ①当等腰三角形的腰为3，底为7时，3＋3＜7不能构成三角形；②当等腰三角形的腰为7，底为3时，周长为3＋7＋7＝17，故这个等腰三角形的周长是17.变式练习4：如图，O为数轴原点，A，B两点分别对应－3，3，作腰长为4的等腰△ABC，连接OC，以O为圆心，CO长为半径画弧交数轴于点M，则点M对应的实数为 __7__．变式练习5：一个等腰三角形的两边长分别为4，8，则它的周长为( C )A．12 B．16 C．20 D．16或202.等边三角形（1）性质①边角关系：三边相等，三角都相等且都等于60°.即AB＝BC＝AC，∠BAC＝∠B＝∠C＝60°；②对称性：等边三角形是轴对称图形，三条高线(或角平分线或中线)所在的直线是对称轴.（2）判定①定义：三边都相等的三角形是等边三角形；②三个角都相等（均为60°）的三角形是等边三角形；③任一内角为60°的等腰三角形是等边三角形.即若AB＝AC，且∠B＝60°，则△ABC是等边三角形.变式练习1：△ABC中，∠B=60°，AB=A C，BC=3，则△ABC的周长为9.变式练习2：在等边△ABC中，点D，E分别在边BC，AC上，若CD＝2，过点D 作DE∥AB，过点E作EF⊥DE，交BC的延长线于点F，求EF的长．解：∵△ABC是等边三角形，∴∠B＝∠ACB＝60°，∵DE∥AB，∴∠EDC＝∠B＝60°，∴△EDC是等边三角形，∴DE＝DC＝2，在Rt△DEF，∵∠DEF＝90°，DE＝2，∴DF＝2DE＝4，∴EF＝DF2－DE2＝42－22＝2 3.变式练习3：如图，△ABC是等边三角形，BD平分∠ABC，点E在BC的延长线上，且CE＝1，∠E＝30°，则BC＝__2__.知识点二：角平分线和垂直平分线1.角平分线（1）性质：角平分线上的点到角的两边的距离相等．即若∠1 ＝∠2，PA⊥OA，PB⊥OB，则PA＝PB.（2）判定：角的内部到角的两边的距离相等的点在角的角平分线上．4.垂直平分线图形（1）性质：线段的垂直平分线上的点到这条线段的两端点距离相等．即若OP垂直且平分AB，则PA＝PB.（2）判定：到一条线段两端点距离相等的点在这条线段的垂直平分线上．21P C OBAPCO B A注意：（1）等边三角形是特殊的等腰三角形，所以等边三角形也满足“三线合一”的性质.（2）等边三角形有一个特殊的角60°，所以当等边三角形出现高时，会结合直角三角形30°角的性质，即BD=1/2AB.变式练习：如图，△ABC中，∠C=90°，∠A=30°，AB的垂直平分线交AC于D，交AB于E，CD=2，则AC=6.知识点三：直角三角形的判定与性质1.直角三角形的性质(1)两锐角互余.即∠A＋∠B＝90°；(2) 30°角所对的直角边等于斜边的一半.即若∠B＝30°则AC＝12AB；(3)斜边上的中线长等于斜边长的一半．即若CD是中线，则CD＝12AB.(4)勾股定理：两直角边a、b的平方和等于斜边c的平方．即a2＋b2＝c2 .2.直角三角形的判定(1) 有一个角是直角的三角形是直角三角形.即若∠C＝90°，则△ABC是Rt△；(2) 如果三角形一条边的中线等于这条边的一半，那么这个三角形是直角三角形．即若AD＝BD＝CD，则△ ABC是Rt△(3) 勾股定理的逆定理：若a2＋b2＝c2，则△ABC是Rt△.3.直角三角形相似判定定理1).斜边与一条直角边对应成比例的两直角三角形相似。

八年级数学12.3等腰三角形水平测试题及答案

12.3等腰三角形水平测试题一.选择题(每小题3分；共24分)1. 小明将两个全等且有一个角为60的直角三角形拼成如图1所示的图形；其中两条较长直角边在同一直线上；则图中等腰三角形的个数是（）Ａ．4 Ｂ．3 Ｃ．2 Ｄ．12、已知等腰三角形的一个角等于42°；则它的底角为（）． A 、42 ° B 、69° C 、69°或84° D 、42°或69°3、如图；ABC △中；AB AC =；30A ∠=；DE 垂直平分AC ；则BCD ∠的度数为（）Ａ．80 Ｂ．75 Ｃ．65 Ｄ．454、等腰三角形的顶角是80°；则一腰上的高与底边的夹角是（） A ．40° B ．50° C ．60° D ．30°5、如图；已知等边三角形ABC 中；BD CE =；AD 与BE 交于点P ；则APE ∠的度数是（） A ．45B ．55C ．60D ．756、如图是一个等边三角形木框；甲虫P 在边框AC 上爬行（A ；C 端点除外）；设甲虫P 到另外两边的距离之和为d ；等边三角形ABC 的高为h ；则d 与h 的大小关系是（）Ａ．d h > Ｂ．d h < Ｃ．d h = Ｄ．无法确定7. 如图；15A =∠；AB BC CD DE EF ====；则DEF ∠等于（）A F C H BME G AD EE DC AB F A ．90 B ．75C ．70D ．608、如图；△MNP 中； ∠P=60°；MN=NP ；MQ ⊥PN ；垂足为Q ；延长MN 至G ；取NG=NQ ；若△MNP 的周长为12；MQ=a ；则△MGQ 周长是（）PQMNGA ．8+2aB ．8+aC ．6+aD ．6+2a二.选择题(每小题3分；共24分)1. 在△ABC 中；AB=AC ；若∠B=56º；则∠C=__________．2.等腰三角形底边中点与一腰的距离为6；则腰上的高为______．3.如图；在△ABC 中；AB=AC ；CD 平分∠ACB 交AB 于点D ；AE ∥DC 交BC 的延长线于点E ；已知∠E=36°；则∠B= ．4.如图；在ABC △中；点D 是BC 上一点；80BAD ∠=°；AB AD DC ==；则C ∠= ．5. 等腰三角形至少有a 条对称轴；至多有b 条对称轴；则b a -＝．6. 有一个等腰三角形；三边分别是3x －2；4x －3；6－2x ；则等腰三角形的周长＿＿＿．7. 如图；△ABC 中AB=AC ；EB=BD=DC=CF ；∠A=40°；则∠EDF•的度数是_____．8.在△ABC 中；B C ⊥AC ；D E ⊥AC ；D 是AB 的中点；若∠A=300；AB=8；则BC= ；DE= 。

八年级上册数学人教版课时练《13.3.1 等腰三角形》02(含答案解析)

答卷时应注意事项１、拿到试卷，要认真仔细的先填好自己的考生信息。

２、拿到试卷不要提笔就写，先大致的浏览一遍，有多少大题，每个大题里有几个小题，有什么题型，哪些容易，哪些难，做到心里有底；３、审题，每个题目都要多读几遍，不仅要读大题，还要读小题，不放过每一个字，遇到暂时弄不懂题意的题目，手指点读，多读几遍题目，就能理解题意了；容易混乱的地方也应该多读几遍，比如从小到大，从左到右这样的题；４、每个题目做完了以后，把自己的手从试卷上完全移开，好好的看看有没有被自己的手臂挡住而遗漏的题；试卷第１页和第２页上下衔接的地方一定要注意，仔细看看有没有遗漏的小题；５、中途遇到真的解决不了的难题，注意安排好时间，先把后面会做的做完，再来重新读题，结合平时课堂上所学的知识，解答难题；一定要镇定，不能因此慌了手脚，影响下面的答题；６、卷面要清洁，字迹要清工整，非常重要；７、做完的试卷要检查，这样可以发现刚才可能留下的错误或是可以检查是否有漏题，检查的时候，用手指点读题目，不要管自己的答案，重新分析题意，所有计算题重新计算，判断题重新判断，填空题重新填空，之后把检查的结果与先前做的结果进行对比分析。

亲爱的小朋友，你们好!经过两个月的学习，你们一定有不小的收获吧，用你的自信和智慧，认真答题，相信你一定会闯关成功。

相信你是最棒的！《13．3．1等腰三角形》课时练一、选择题1．下列命题中，属于假命题的是()A．等腰三角形底边上的高是它的对称轴B．有两个角相等的三角形是等腰三角形C．等腰三角形底边上的中线平分顶角D．等边三角形的每一个内角都等于60∘2．如图，在△ABC中，∠B=∠C， AB=5，则AC的长为（）A．2B．3C．4D．53．如图：等腰直角△ABC中，若∠ACB=90∘，CD=DE=CE，则∠DAB 的度数为（）A．60∘B．30∘C．45∘D．15∘4．等腰三角形的一腰上的高与另一腰的夹角是48∘，它的一个底角的度数是()A．48∘B．21∘或69∘C．21∘D．48∘或69∘5．已知等腰三角形的两边长分别为5㎝、2㎝，则该等腰三角形的周长是（）A．7㎝B．9㎝C．12㎝或者9㎝D．12㎝6．等腰直角三角形的底边长为5，则它的面积是()A．25B．12．5C．10D．6．257．如图，△ABC中，∠ABC=90∘，∠C=30∘，AD是角平分线，DE⊥AC 于E，AD、BE相交于点F，则图中的等腰三角形有（）A．2个B．3个C．4个D．5个8．一个角是60∘的等腰三角形是（）A．等腰直角三角形B．等边三角形C．直角三角形D．上述都正确9．以下关于等边三角形的判定：①三条边相等的三角形是等边三角形；②有一个角是60∘的等腰三角形是等边三角形；③有两个角为60∘的三角形是等边三角形④三个角相等的三角形是等边三角形其中正确的是（）A．只有①②③B．只有①②④C．只有①③④D．①②③④10．如图，在△ABC中，∠B=60∘，AB=9，BP=3，AP=AC，则BC 的长为（）A．8B．7C．6D．511．等腰三角形一腰上的高等于该三角形另一边长的一半．则其顶角等于（）A．30∘B．30∘或150∘C．120∘或150∘D．120∘、30∘或150∘12．等腰三角形的一个角比另一个角的2倍少20度，等腰三角形顶角的度数是()A．140∘B．20∘或80∘C．44∘或80∘D．140∘或44∘或80∘二、填空题13．等腰三角形一腰的高等于腰长的一半，则其顶角的度数为________．14．如图，△ABC是边长为8的等边三角形，点D在BC的延长线上，做DF⊥AB，垂足为F，若CD=6，则AF的长等于________．15．如图所示的图形由4个等腰直角形组成，其中直角三角形（1）的腰长为1cm，则直角三角形（4）的斜边长为________．16．如图等边三角形ABC中，AB=3，D、E是BC上的两点，AD、AE把△ABC分割成周长相等的三个三角形，则CD=________．17．如图，在△ABC中，∠ABC＝∠C，∠A＝100∘，BD平分∠ABC交AC于点D，点E是BC上一个动点．若△DEC是直角三角形，则∠BDE的度数是________．三、解答题18．从①∠B=∠C；②∠BAD=∠CDA；③AB=DC；④BE=CE四个等式中选出两个作为条件，证明△AED是等腰三角形（写出一种即可）．已知：________(只填序号)，求证：△AED是等腰三角形．19．如图，BD//AC，BD=BC，点E在BC上，且BE=AC．求证：D=∠ABC．20．如图所示，在矩形ABCD中，DE⊥CE，∠ADE=30∘，DE=4，求这个矩形的周长．21．如图，在△ABC中，∠ACB−∠B=90∘，∠BAC的平分线交BC于点E，∠BAC的外角∠CAD的平分线交BC的延长线于点F，试判断△AEF的形状．22．（1）如图①，△ABC是等边三角形，△ABC所在平面上有一点P，使△PAB，△PBC，△PAC都是等腰三角形，问：具有这样性质的点P有几个？在图中画出来．（2）如图②，正方形ABCD所在的平面上有一点P，使△PAB，△PBC，△PCD，△PDA都是等腰三角形，问：具有这样性质的点P有几个？在图中画出来．参考答案题号12345678910答案A D D B D D C B D C 题号1112答案D D13．30∘或150∘14．115．416．−3+3331617．30∘或70∘18．证明：选择的条件是：①∠B=∠C②∠BAD=∠CDA（或①③，①④，②③）；证明：在△BAD和△CDA中，∵∠B=∠C，∠BAD=∠CDA，AD=DA，∴△BAD≅△CDA(AAS)，∴∠ADB=∠DAC，即在△AED中∠ADE=∠DAE，∴AE=DE，△AED为等腰三角形．19．证明：∵BD//AC，∴∠EBD=∠C，BD=BC，BE=AC，∴△EDB≅ABC SAS，∴∠D=∠ABC20．解：∵四边形ABCD是矩形，∴∠A=∠B=90∘，AD=BC．在Rt△ADE中，∵∠A=90∘，∠ADE=30∘，DE=4，∴AE=12DE=2，AD=3AE=23．∵DE⊥CE，∠A=90∘，∴∠BEC=∠ADE=90∘−∠AED=30∘．在Rt△BEC中，∵∠B=90∘，∠BEC=30∘，BC=AD=23，∴BE=3BC=6，∴AB=AE+BE=2+6=8，∴矩形ABCD的周长=2(AB+AD)=2(8+23)=16+43．21．解：△AEF是等腰直角三角形；理由如下：如图所示：∵AE平分∠BAC，AF平分∠CAD，∴∠EAC=12∠BAC，∠FAC=12∠CAD，∵∠BAC+∠CAD=180∘，∴∠EAC+∠FAC=12(∠BAC+∠CAD)=90∘，即∠EAF=90∘，∵∠ACB−∠B=90∘，∴∠ACB=90∘+∠B，∴∠1=90∘−∠B=∠B+∠BAC，∴∠B=12(90∘−∠BAC)，∴∠4=∠B+∠AEF，∵AE平分∠DAC，∴∠3=∠4=∠B+∠AEF，∵∠BAC+∠3+∠4=180∘，∴2(∠B+∠AEF)+∠BAC=2[12(90∘−∠BAC)+∠AEF]+∠BAC=180∘，∴∠AEF=45∘，∴∠AFE=45∘，∴△AEF是等腰直角三角形．22．【解答】（1）10个，如解图①，当点P在△ABC内部时，P是边AB．BC．CA的垂直平分线的交点：当点P在△ABC外部时，P是以三角形各顶点为圆心，边长为半径的圆与三条垂直平分线的交点每条垂直平分线上得3个交点，故具有这样性质的点P共有10个．（2）9个，如解图③．两条对角线的交点是1个，以正方形各顶点为圆心，边长为半径画圆，在正方形里面和外面的交点一共有8个，故具有这样性质的点P共有9个．。

八年级上册数学人教版课时练《13.3.1 等腰三角形》01(含答案解析)

答卷时应注意事项１、拿到试卷，要认真仔细的先填好自己的考生信息。

亲爱的小朋友，你们好!经过两个月的学习，你们一定有不小的收获吧，用你的自信和智慧，认真答题，相信你一定会闯关成功。

相信你是最棒的！《13．3．1等腰三角形》课时练一、单选题1．有下列说法：①等腰三角形的腰相等；②等腰三角形的两底角相等，③等腰三角形的中线、高线和角平分线互相重合；④等腰三角形两底角的平分线相等；⑤等腰三角形的腰一定大于腰上的高线其中正确的有（）个A ．1B ．2C ．3D ．42．如果一个三角形的外角平分线平行于三角形的一边，那么这个三角形是（）A ．等腰直角三角形B ．等腰三角形C ．直角三角形D ．锐角三角形3．如图，已知,ABC AB AC =，以点B 为圆心，BC 长为半径画弧，交腰AC 于点E ，则下列结论一定正确的是（）A ．BC EC =B ．AE BE =C ．EBC BAC Ð=ÐD ．EBC ABE Ð=Ð4．如图，ABC 中，BA BC =，DE 是边AB 的垂直平分线，分别交BC 、AB 于点D 、E ，连接AD ，若AD 恰好为BAC Ð的平分线，则B Ð的度数是（）A ．60°B ．45°C ．36°D ．30°5．如图，在△ABC 中，∠ABC ＝90°，AB ＝CB ，F 为AB 延长线一点，点E 在BC 上，且AE ＝CF ，∠CAE ＝30°，则∠ACF 的度数是（）A ．75°B ．60°C ．55°D ．45°6．如图，ABC 中，AB ＝AC ，AD ⊥BC 于点D ，DE ⊥AB 于点E ，BF ⊥AC 于点F ，DE ＝2，则BF 的长为（）A ．4B ．3C ．5D ．67．在ABC 中，AB BC =，两个完全一样的三角尺按如图所示摆放．它们一组较短的直角边分别在AB ，BC 上，另一组较长的对应边的顶点重合于点P ，BP 交边AC 于点D ，则下列结论错误的是（）A ．BP 平分ABC ÐB ．AD DC =C ．BD 垂直平分AC D ．2AB AD=8．如图，在5×5的正方形网格中，每个小正方形的边长均为1，线段AB 的端点在格点上，若画以AB 为边的等腰三角形ABC ，使得点C 在格点上，则点C 的个数是（）A ．3B ．4C ．5D ．89．如图，在ABC 中，36B C Ð=Ð=°，D ，E 是边BC 上的两点，且有72ADE AED Ð=Ð=°，则图中等腰三角形的个数是（）A ．2B ．6C ．5D ．710．如图，在ABC 中，BO 平分ABC Ð，CO 平分ACB Ð，EF 经过点O 且//EF BC ，若7AB =，8AC =，9BC =，则AEF 的周长是（）A ．15B ．16C ．17D ．2411．如图，在Rt ABC △中，90BAC °Ð=，AD BC ^于点D ，AE 平分BAD Ð交BC 于点E ，则下列结论一定成立的是（）A ．AC AE =B ．EC AE =C ．BE AE =D ．AC EC=12．如图，在△ABC 中，点D 、E 分别在边AB 、AC 上，BE 与CD 相交于点O ，如果已知∠ABC =∠ACB ，补充下列一个条件后，仍无法判定△ABE ≌△ACD 的是（）A ．AD ＝AEB ．BE ＝CDC ．OB ＝OCD ．∠BDC ＝∠CEB 13．如图，在△ABC 中，∠BAC ＝90°，AD 是高，BE 是中线，CF 是角平分线，CF 交AD 于点G ，交BE 于点H ，下面说法：①△ABE 的面积＝△BCE 的面积；②∠AFG ＝∠AGF ；③∠F AG ＝2∠ACF ；④BH ＝CH ．其中正确的是（）A ．①②③④B ．①②③C ．②④D ．①③14．如图，在△ABC 中，∠CAB 的平分线AD 与BC 的垂直平分线DE 交于点D ，DM ⊥AB 于点M ，DN ⊥AC 交AC 的延长线于点N ，连接BD 、CD ．以下结论：①BM ＝CN ；②∠DBC＝∠DAN ；③∠BAC +∠BDC ＝180°；④点D 到△ABC 各顶点的距离相等．正确的是（）A ．①②④B ．②③④C ．①②③D ．①③④15．如图，在4×4的正方形网格中，记∠ABF ＝a ，∠FCH ＝b ，∠DGE ＝g ，则（）A ．b ＜a ＜gB ．b ≤g ＜aC ．a ＜g ＜bD ．a ＜b ＜g二、填空题16．一个等腰三角形的底角是顶角的2倍，则顶角的大小是____．17．如图，ABC 中，8cm AB BC ==，将ABC 沿BC 平移3cm 得到DEF ，AC 与DE 相交于点G ，则GE 的长为________cm ．18．如图，∠ABC 的平分线BF 与△ABC 中∠ACB 的相邻外角∠ACG 的平分线CF 相交于点F ，过F 作DF ∥BC ，交AB 于D ，交AC 于E ，若BD ＝7cm ，DE ＝3cm ，求CE 的长为______cm ．19．如图，ABC DEC ≌△△，60DCE Ð=°，100ACE Ð=°，点D 恰好落在线段AB 上，则A Ð的度数为________度．20．如图，在△ABC 中，∠ACB ＝90°，∠A ＜∠B ，点D 为AB 边上一点且不与A 、B 重合，将△ACD 沿CD 翻折得到△ECD ，直线CE 与直线AB 相交于点F ．若∠A ＝40°，当△DEF 为等腰三角形时，∠ACD ＝__________________．三、解答题21．一个三角形的两边b ＝2，c ＝7．（1）当各边均为整数时，有几个三角形？（2）若此三角形是等腰三角形，则其周长是多少？22．如图，DE ∥BC ，CG ＝GB ，∠1＝∠2，求证：△DGE 是等腰三角形．23．如图，在ABC 中，2AB AC ==，50B Ð=°，点D 是边BC 上一点，2CD =，作50ADE Ð=°，D 交边AC 于点E ．求证：BD CE =．24．如图，在等腰△ABC 中，BA ＝BC ，点F 在AB 边上，延长CF 交AD 于点E ，BD ＝BE ，∠ABC ＝∠DBE ．（1）求证：AD ＝CE ；（2）若∠ABC ＝30°，∠AFC ＝45°，求∠EAC 的度数．25．已知：如图，在△ABC中，∠BAC＝90°，AB＝AC，BD平分∠ABC，交AC于D，AE⊥BD 于F，交BC于E．求证：（1）AB＝BE；∠ABC；（2）∠CAE＝12（3）AD＝CE；（4）CD＋CE＝AB．参考答案1．C2．B3．C4．C5．B6．A7．D8．D9．B 10．A11．D12．B13．B14．C15．A16．36°17．518．419．7020．30°或15°或60°21．（1）a=6或7或8，有三个三角形；（2）周长为16．解：（1）设第三边长为a，则5＜a＜9由于三角形的各边均为整数，则a=6或7或8，因此有三个三角形；（2）当a=7时，有a=7=c，由2+7>7,所以周长为7+7+2=16;当a=2时，有a=2=c，由2+2<7,故不能构成三角形，综上其周长只能为16 22．见详解解：连接AG，∵DE∥BC，∴∠ABC＝∠1，∠ACB＝∠2．又∵∠1＝∠2，∴∠ABC＝∠ACB．∴AB=AC，又∵G为BC中点，∴AG⊥BC．∴AG ⊥DE∵∠1＝∠2，∴AD =AE ，∴AG 垂直平分DE ，∴DG ＝GE ．∴△DGE 是等腰三角形．23．证明见解析证明：∵AB AC =，50B Ð=°，∴50C B Ð=Ð=°，∵2CD =，∴CD AB AC ==，∴65DAC ADC Ð=Ð=°，∵ADC B BAD ADE CDE Ð=Ð+Ð=Ð+Ð，50ADE Ð=°，∴BAD CDE Ð=Ð，在BAD 和CDE △中，BAD CDE AB CDB C Ð=Ðìï=íïÐ=Ðî，∴BAD ≌CDE △，∴BD CE =．24．（1）证明见解析；（2）90°解：（1）∵∠ABC ＝∠DBE ，∴ABC ABE DBE ABE Ð+Ð=Ð+Ð，即ABD CBE Ð=Ð，在ABD △和CBE △中，BA BC ABD CBE BD BE =ìïÐ=Ðíï=î，∴ABD △≌CBE △，∴AD ＝CE ；（2）∵∠ABC ＝30°，∠AFC ＝45°，∴15BCF Ð=°，∵ABD △≌CBE △，∴15EAB Ð=°∵BA ＝BC ，∴75BAC BCA Ð=Ð=°，∴90EAC EAB BAC Ð=Ð+Ð=°．25．（1）见详解；（2）见详解；（3）见详解；（4）见详解证明：（1）∵BD 平分∠ABC ，AE ⊥BD ，∴∠ABF ＝∠EBF ，∠AFB ＝∠EFB ＝90°，在△ABF 和△EBF 中，ABF EBF BF BFAFB EFB Ð=Ðìï=íïÐ=Ðî，∴△ABF ≌△EBF （ASA ），∴AB ＝BE ；（2）∵∠BAC ＝90°，∴∠CAE ＋∠BAF ＝90°，而∠BAF ＋∠ABF ＝90°，∴∠CAE ＝∠ABF ＝12∠ABC ；（3）连接DE，在△ABD 和△EBD 中∵AB BE ABF EBF BD BD ìïÐÐíïî＝＝＝，∴△ABD ≌△EBD （SAS ），∴AD＝DE，∠DEC＝∠BAC＝90°，∵∠BAC＝90°，AB＝AC，∴∠C＝45°，∴CE＝DE，∴AD＝CE；（4）由（3）可得AD＝CE，∴CD＋CE=CD＋AD＝AC＝AB．。

12.3.1 等腰三角形(二)及答案

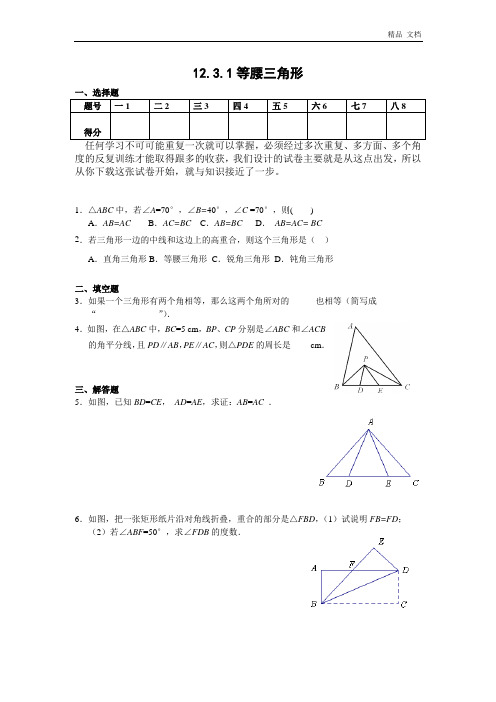
12.3.1等腰三角形题号一1 二2 三3 四4 五5 六6 七7 八8 得分度的反复训练才能取得跟多的收获，我们设计的试卷主要就是从这点出发，所以从你下载这张试卷开始，就与知识接近了一步。

1．△ABC中，若∠A=70°，∠B=40°，∠C =70°，则( )A．AB=AC B．AC=BC C．AB=BC D．AB=AC=BC2．若三角形一边的中线和这边上的高重合，则这个三角形是（）A．直角三角形B．等腰三角形C．锐角三角形D．钝角三角形二、填空题3．如果一个三角形有两个角相等，那么这两个角所对的______也相等（简写成“______________”）．4．如图，在△ABC中，BC=5cm，BP、CP分别是∠ABC和∠ACB的角平分线，且PD∥AB，PE∥AC，则△PDE的周长是____ cm．三、解答题5．如图，已知BD=CE，AD=AE，求证：AB=AC．6．如图，把一张矩形纸片沿对角线折叠，重合的部分是△FBD，（1）试说明FB=FD；（2）若∠ABF=50°，求∠FDB的度数．7．已知四边形ABCD、EFGC为全等的矩形，B、C、E在一条直线上，试判断三角形△ACF 的形状，并说明理由．参考答案一、选择题1．C2．B二、填空题3．边，等边对等角4．5三、解答题5．过A做AF⊥BC，垂足为F，∵AD=AE∴DF=EF，又∵BD=CE∴BF=CF ∴AB=AC．6．（1）证明略（2）20°7．△ACF是等腰直角三角形，提示：证明△ABC≌△CE F，再零用三角形全等的性质This document is collected from the Internet, which is convenient for readers to use. Ifthere is any infringement, please contact the author and delete it immediately.可以编辑的试卷（可以删除）。

(完整版)等腰三角形三线合一专题练习[1]

等腰三角形三线合一专题训练1例1 如图，四边形ABCD中，AB // DC, BE、CE分别平分/ ABC、/ BCD，且点E在AD上。

求BC=AB+DC 。

变 1 如图，AB // CD，/ A = 90° AB = 2, BC = 3, CD = 1, E 是AD 边中点。

求证：CE丄BE。

变2：如图，四边形ABCD中，AD / BC, E是CD上一点，且AE、BE分别平分/ BAD、/ ABC.(1)求证：AE丄BE; (2)求证：E是CD的中点；(3)求证：AD+BC=AB.A n变3:\ ABC是等腰直角三角形，/ BAC=90 ,AB=AC.⑴若D为BC的中点，过D作DM丄DN分别交AB、AC 于M、N，求证：（1）DM = DN。

A⑵若DM丄DN分别和BA、AC延长线交于M、N。

问DM和DN有何数量关系。

|\/|⑴已知：如图，AB=AC , E为AB上一点，F是AC延长线上一点，且BE=CF , EF交BC于点D .求证：DE=DF .⑵已知：如图，AB=AC , E为AB上一点，F是AC延长线上一点，且，EF交BC于点D，且D为EF的中点. 求证：BE=CF .利用面积法证明线段之间的和差关系1、如图，在△ ABC中, AB=AC P为底边BC上的一点，PC L AB于D, PEL AC于E, ?CF丄AB于F,那么PD+PE与CF相等吗？变1若P点在直线BC上运动，其他条件不变，则PD、PE与CF的关系又怎样，请你作图，证明。

1、已知等腰三角形的两边长分别为4、9,则它的周长为（）A 17B 22C 17 或22D 13根据等腰三角形的性质寻求规律1 1例1.在△ ABC中，AB=AC /仁一 / ABC / 2= —/ ACB BD与CE相交于点0,如图，/ B0C勺大小2 2与/A的大小有什么关系？1 1若/ 1= / ABC / 2= / ACB则/ BOC WZ A大小关系如何？3 31 1若/ 1= / ABC / 2= / ACB则/ B0C与Z A大小关系如何?n n会用等腰三角形的判定和性质计算与证明例2.如图，等腰三角形ABC中，AB=AC —腰上的中线BD?各这个等腰三角形周长分成15和6两部分,利用等腰三角形的性质证线段相等例3.如图，P是等边三角形ABC内的一点，连结PA PB PC, ?以BP为边作/ PBQ=60，且BQ=BP 连结CQ （1）观察并猜想AP与CQ之间的大小关系，并证明你的结论.2）若PA PB: PC=3: 4: 5,连结PQ试判断△ PQC的形状，并说明理由.例1、等腰三角形底边长为5cm,腰上的中线把三角形周长分为差是3cm的两部分，则腰长为（）A、2cm B 、8cm C 、2cm 或8cm D 、不能确定例2、已知AD^^ ABC的高，AB=AC △ ABC周长为20cm,A ADC的周长为14cm,求AD的长。

12.3.1 等腰三角形(1)(含答案)-

12.3.1 等腰三角形(1)第1课时角度的反复训练才能取得跟多的收获，我们设计的试卷主要就是从这点出发，所以从你下载这张试卷开始，就与知识接近了一步。

◆课前预习1．等腰三角形是有________相等的三角形．2．等腰三角形的性质（1）性质1：等腰三角形的_______相等，简称“等边对等角”．（2）性质2：等腰三角形的________，_______，________相互重合，•简称“等腰三角形三线合一”．◆互动课堂（一）基础热点【例1】已知一个等腰三角形的两角分别为（2x-2）°，（3x-5）°，•求这个等腰三角形各角的度数．解：（1）当（2x-2）°作为顶角时，三角形三个角的度数分别为46°，67°，67°．（2）当（3x-5）°为顶角时，三角形三个角的度数分别为：52°，52°，76°．（3）当以上两个角均为底角时，即（2x-2）=（3x-5），解得x=3，因此，•三角形的三个内角分别为4°，4°，172°．点拨：利用等腰三角形的性质解题时易犯考虑不周全的错误，解题时应认真审题，分析已知条件，分清是顶角还是底角．（二）易错疑难【例2】如图，已知AB=AC，BD⊥AC于D，求证：∠BAC=2∠DBC．分析：利用等腰三角形“三线合一”的性质．解：作∠BAC的平分线AE，交BC于E，则∠1=∠2=12∠BAC．又∵AB=AC（已知）∴AE⊥BC∴∠2+∠ACB=90°∵BD⊥AC（已知）∴∠DBC+∠ACB=90°∴∠2=∠DBC∴∠BAC=2∠DBC（三）中考链接【例3】如图，在△ABC中，AB=AC，DE是AB的垂直平分线，垂足为D，交AC于E，连接BE．（1）如果∠ABE=40°，求∠C的度数；（2）若△ABC的周长为82cm，一边为30cm，求△BCE的周长．解：（1）由已知得∠ABE=∠A=40°，∴∠C=12（180°-40°）=70°．（2）在△BCE中，BE+EC=AC，由三角形两边之和大于第三边得AC>BC，∴AC为30cm，•BC为22cm，∴△BCE的周长为52cm．名师点津在等腰三角形中，常常需要作底边上的高，运用等腰三角形“三线合一”的性质，对于解决所有的问题能起到事半功倍的效果．◆跟进课堂1．已知等腰三角形的一个角为50°，则其余两个角的度数为______．2．已知等腰三角形的一个外角为120°，则它的另外两个角的度数为_______．3．已知等腰三角形的一个内角是另一个内角的7倍，则它的三个内角的度数分别为_________．4．已知等腰三角形的两边长为7和3，则它的周长为________．5．如图1，在△ABC中，∠A=36°，∠C=72°，BD是∠ABC的平分线，则图中共有______个等腰三角形．6．在△ABC中，AB=AC，如果∠A=100°，那么∠B为（）．A．100° B．80° C．40° D．120°7．如图2所示，∠A=15°，AB=BC=CD=DE=EF=，那么∠FEM等于（）．A．90° B．75° C．70° D．60°(1) (2) (3)8．一等腰三角形的周长为20，两条边的比为1：2，那么其底边长为（）．A．10 B．4 C．4或10 D．5或89．一等腰三角形的底边长为5，周长被一腰上的中线分成的两部分的差为3，则腰长为（）． A．2 B．8 C．2或8 D．710．（2007，荆门）如图3，D是等腰Rt△ABC内一点，BC是斜边，如果将△ABD绕点A逆时针方向旋转到△ACD′的位置，则∠ADD′的度数是（）．A．25° B．30° C．35° D．45°◆漫步课外11．如图，在△ABC中，AB=AD=DC，∠BAD=26°，求∠B和∠C的度数．12．在△ABC中，AB=AC，D是BC上的一点，若BD=AB，CD=AD，求△ABC三个内角的度数．13．（2008，内江）如图，在△ABC中，点E在AB上，点D在BC上，BD=BE，∠BAD=•∠BCE，AD与CE相交于点F，试判断△AFC的形状，并说明理由．◆挑战极限14．如图①，在等腰△ABC中，底边BC上有任意一点，过点P作PE⊥AC，PD⊥AB，垂足为E、E，再过C作CF⊥AB于点F；（1）求证：PD+PE=CF；（2）若点P在BC•的延长线上，如图②，则PE、PD、CF之间存在什么样的等量关系，请写出你的猜想，并证明．答案:1．50°，80°或65° 2．60°，60°3．12°，84°，84°或140°，20°，20•° •4．17 5．3 6．C 7．B 8．B 9．B 10．D11．∠B=77°，∠C=38.5° •12．•∠BAC=108°，∠ABC=∠ACB=36°13．△AFC是等腰三角形，证明略．14．（1）提示：连接AP；（2）PD-PE=CF，连接AP，证明略．可以编辑的试卷（可以删除）。

八年级数学等腰三角形同步练习1新课标人教版

等腰三角形同步练习1新课指南1.知识与技能：（1）经历获得知识的过程，并通过观察、分析、想象、探索，掌握等腰三角形的性质及判定；（2）了解等边三角形的性质和判定等知识的形成过程，培养丰富的想像力，增强审美意识.2.过程与方法：经历探索等腰（边）三角形的性质及判定，探索应用等腰三角形知识解决实际问题，尤其是用轴对称的性质来解释等腰（或等边）三角形的相关性质，进一步体会从一般到特殊，再从特殊到一般的研究事物的辩证方法.3.情感态度与价值观：培养学生合作交流、体验成功、体验审美、增强自信心，同时，充分体会分类讨论数学思想在解决问题中的广泛应用.4.重点与难点；重点是等腰三角形的性质和判定.难点是由轴对称知识来理解和掌握等腰三角形的性质和判定.教材解读精华要义数学与生活如图14－61所示，位于在海上A，B两处的两艘救生船接到O处遇险船只的报警，当时测得∠A=∠B，如果这两艘救生船以同样的速度同时出发，能不能大约同时赶到出事地点（不考虑风浪因素）？思考讨论如果两艘船以同样的速度同时出发，并且同时赶到出事地点，说明两艘船的航程相同，即OA=OB，而已知∠A=∠B，能直接由此判断出OA=OB吗？知识详解知识点1 等腰三角形的概念有两条边相等的三角形，叫做等腰三角形，相等的两条边叫做腰，另一条边叫做底边，两腰所夹的角叫做顶角，底边与腰的夹角叫做底角.如图14－62所示，在△ABC中，若AB=AC，则△ABC是等腰三角形，其中AB，AC叫做腰，BC叫做底边，∠A叫做顶角，∠B和∠C叫做底角.知识点2 等腰三角形的性质性质1：等腰三角形的两个底角相等（简写成“等边对等角”）.性质2：等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.【说明】等腰三角形的两个性质都可以由证明两个三角形全等而证实.例如：如图14－63所示，在△∠B=∠C.证明：过点A作BC边上的中线AD.∴BD=DC.在△ABD和△ACD中，∴△ABD≌△ACD（SSS）.∴∠B=∠C（全等三角形的对应角相等）.探究交流上例中并没有直接全等的三角形，而是通过作辅助线“BC边上的中线AD”来构造出两个全等的三角形，再用全等三角形的性质证明出“∠B=∠C”.想一想，本题还有没有作其他辅助线的方法？在本题中能否进一步证明AD是∠BAC的平分线和BD边上的高？试试看.点拨由等腰三角形的性质2可知，等腰三角形是轴对称图形，它的对称轴是底边上的中线（顶角平分线、底边上的高）所在直线.知识点3 等腰三角形的判定定理如果一个三角形有两个角相等，那么这两个角所对的边也相等（简写成“等角对等边”）.例如：图14－64所示，在△ABC中，∠B=∠C.求证AB=AC.证明：作AD⊥BC，垂足为D.∴∠ADB=∠ADC=90°.在Rt△ADB和Rt△ADC中，∴Rt△ADB≌Rt△ADC（AAS）.∴AB=AC（全等三角形的对应边相等）.知识点4 等边三角形的概念三条边都相等的三角形，叫做等边三角形.知识点5 等边三角形的性质和判定Ⅰ.等边三角形的性质和判定.（1）等边三角形的三个内角都相等，并且每一个内角都等于60°（2）三个角都相等的三角形是等边三角形（3）有一个角是60°的等腰三角形是等边三角形Ⅱ.在直角三角形中，如果一个锐角等于30°那么它所对的直角边等于斜边的一半.典例剖析师生互动基础知识应用题本节知识的基础应用主要包括：（1）等腰三角形的性质和判定；（2）等边三角形的性质；（3）三角形的内角和；（4）三角形三边关系.例1 已知三角形的一个内角是110°，求另外两个角的度数.(分析)因为等腰三角形的内角和是180°，若110°是底角，则110°×2=220°＞180°，所以110°2110180︒-︒=35°.解：由题意可知，110°是顶角，设底角为α，则2α+110°=180°，∴α=35°.∴这个三角形另外两个角是35°，35°.例2 等腰三角形的一个内角是80°，求它的另外两个角.°，则设底角为α，由三角形内角和得2α+80°=180°，∴α=50°.若底角是80°则设项角为β，由三角形内角和得2×80°+β=180°，∴β=20°.解：①若顶角是80°，设底角为α，则有2α+80°=180°，∴α=50°.②若底角是80°，设顶角为β，则有80°×2+β=180°，∴β=20。

八年级数学上册等腰三角形课后练习二(含详解)(新版)苏科版

等腰三角形重难点易错点解析题一：题面：下列说法：①顶角相等的两个等腰三角形的底角一定相等；②底边相等的两个等腰三角形全等；③腰长相等且有一个角是20°的两个等腰三角形全等．其中正确的有 .金题精讲题一：题面：如图，在△ABC中，AB=AC，点D是BC的中点，点E在AD上.求证：(1)△ABD≌△ACD；(2)BE=CE题二：题面：如图，a∥b，点A在直线a上，点C在直线b上，∠BAC=900，AB=AC.若∠1=20°，则∠2的度数为( )A. 25°B. 65°C. 70°D. 75°题三：题面：如图，△ABC中，AB=AC=10，BC=8，AD平分∠BAC交BC于点D，点E为AC的中点，连接DE，则△CDE的周长为( )A. 20B. 12C. 14D. 13题四：题面：如图，在△ABC中，∠BAC的平分线与BC的垂直平分线PQ相交于点P，过点P分别作PN⊥AB于N，PM⊥AC于点M，求证：BN=CM．思维拓展题面：如图，∠AOB是一建筑钢架，∠AOB=10°，为使钢架更加稳固，需在内部添加一些钢管EF、FG、GH、HI、IJ，添加钢管的长度都与OE相等，则∠BIJ= .课后练习详解重难点易错点解析题一：答案：①．详解：①两个等腰三角形的顶角相等，根据三角形内角和定理可知底角一定相等，故是正确的；②底边相等的两个等腰三角形，不满足两个三角形全等的条件，故是错误的；③腰长相等且有一个角是20°的两个等腰三角形，不满足两个三角形全等的条件，故是错误的．故答案为：①．金题精讲题一：答案：见详解详解：(1)∵D是BC的中点，∴BD=CD.在△ABD和△ACD中，∵BD=CD，AB=AC，AD=AD(公共边)，∴△ABC≌△ACD(SSS).(2)由(1)知△ABD≌△ACD，∴∠BAD=∠CAD，即∠BAE=∠CAE.在△ABE和△ACE中，∵AB=AC，∠BAE=∠CAD，AE=AE，∴△ABE≌△ACE(SAS).∴BE=CE(全等三角形的对应边相等).题二：答案：B.详解：∵∠BAC=90°，AB=AC，∴∠ACB=45°.∵∠1=20°，∴∠ACB＋∠1=65°.又∵a∥b，∴∠2=∠ACB＋∠1=65°.故选B.题三：答案：C.详解：∵AB=AC，AD平分∠BAC，BC=8，∴根据等腰三角形三线合一的性质得AD⊥BC，C D=BD=12BC=4.∵点E为AC的中点，∴根据直角三角形斜边上的中线等于斜边的一半得DE=CE=12AC=5.∴△CDE的周长=CD+DE+CE=4+5+5=14.故选C. 题四：答案：见详解详解：连接PB，PC，∵AP是∠BAC的平分线，PN⊥AB，PM⊥AC，∴PM=PN，∠PMC=∠PNB=90°，∵P在BC的垂直平分线上，∴PC=PB，在Rt△PMC和Rt△PNB中PC＝PB，PM＝PN，∴Rt△PMC≌Rt△PNB(HL)，∴BN=CM．思维拓展答案：60°.详解：∵OE=EF=FG=GH=HI=IJ，∴∠1=∠AOB=10°，∠2=∠3，∠4=∠5，∠6=∠7，∠8=∠9，∴∠2=∠O+∠1=20°=∠3，∴∠4=∠O+∠3=30°=∠5，∠6=∠O+∠5=40°=∠7，∠8=∠O+∠7=50°=∠9，∠BIJ=∠O+∠9=60°。