北大测试全套课件和教案 32. 第11章第1讲

合集下载

北大测试全套课件和教案 8. 第4章第2讲

《软件测试基础》授课教案授课内容：第四章白盒测试技术授课课次：第8次课授课时数：2学时授课日期: 上课教室:目的与要求：掌握白盒测试的概念；掌握逻辑覆盖的基本思想，能够独立分析程序的逻辑，设计路经覆盖测试用例。

教学重点：逻辑覆盖教学难点：条件组合覆盖教学方式：1.运用《白盒测试技术》课件进行课堂讲授，让学生理解白盒测试的概念；2.通过讲述白盒测试，拓宽学生们的测试思维，掌握白盒测试中最普遍的逻辑覆盖法。

3.进行课堂练习，加深对覆盖测试的理解和使用。

教学内容：1．语句覆盖2．判定覆盖3．条件覆盖4．判定-条件覆盖5．条件组合覆盖6．路经覆盖。

内容提要及时间分配：1、课前引导（5分钟）◆为什么要进行静态测试。

◆白盒测试有什么意义。

2、本课内容（78分钟）◆语句覆盖（10分钟）◆判定覆盖（13分钟）◆条件覆盖（15分钟）◆判定-条件覆盖（10分钟）◆条件组合覆盖（20分钟）◆路经覆盖（10分钟）3、课后小结（5分钟）4、布置作业（2分钟）教学参考书：1.软件测试方法和技术朱少民清华大学出版社2.软件测试Paul C.Jorgensen 机械工业出版社讨论与思考：为伪代码三角形程序开发条件组合覆盖的测试用例。

作业:写出“直接插入排序”的算法，画出流程图，并用逻辑覆盖法，写出测试用例。

复问题目：教学内容与方法步骤4．2 白盒测试方法引言：白盒测试作为测试人员常用的一种测试方法，越来越受到测试工程师的重视。

白盒测试并不是简单的按照代码设计用例，而是需要根据不同的测试需求，结合不同的测试对象，使用适合的方法进行测试。

因为对于不同复杂度的代码逻辑，可以衍生出许多种执行路径，只有适当的测试方法，才能帮助我们从代码的迷雾森林中找到正确的方向。

白盒测试与程序内部结构相关，需要利用程序结构的实现细节等知识，才能有效进行测试用例的设计工作。

白盒测试方法有程序控制流分析、数据流分析、逻辑驱动测试、域测试、符号测试、路径测试、程序插桩及程序变异等。

最新北师大版高中数学选修2-1课时同步讲义(全册共312页)

最新北师大版高中数学选修2-1课时同步讲义（全册共312页）目录第一章常用逻辑用语§1命题(一)§2充分条件与必要条件§3全称量词与存在量词3．1全称量词与全称命题3．2存在量词与特称命题§4逻辑联结词“且”“或”“非”4．1逻辑联结词“且”4．2逻辑联结词“或”第二章空间向量与立体几何§1从平面向量到空间向量§2空间向量的运算(一)§2空间向量的运算(二)§3向量的坐标表示和空间向量基本定理(一)3．1空间向量的标准正交分解与坐标表示3．2空间向量基本定理3.3空间向量运算的坐标表示§4用向量讨论垂直与平行第1课时用空间向量解决立体几何中的平行问题第2课时用空间向量解决立体几何中的垂直问题§5夹角的计算§6距离的计算第三章圆锥曲线与方程§1椭圆1．1椭圆及其标准方程1.2椭圆的简单性质(一)§2抛物线2．1抛物线及其标准方程§3双曲线3．1双曲线及其标准方程3．2双曲线的简单性质§4曲线与方程4．1曲线与方程§1 命题(一)学习目标 1.理解命题的概念.2.能判断命题的真假.3.了解命题的构成形式，能将命题改写为“若p ，则q ”的形式.4.了解四种命题的概念，会写出所给命题的逆命题、否命题和逆否命题．知识点一命题的概念及分类思考下列语句有什么共同特征？(1)空集是任何集合的子集．(2)单位向量的模为1.(3)垂直于同一条直线的两条直线平行．答案共同特征是：都是陈述句，都可以判断真假．梳理 (1)命题的概念：在数学中，我们把用语言、符号或式子表达的，可以判断真假的陈述句叫作命题．(2)命题定义中的两个要点：“可以判断真假”和“陈述句”．我们学习过的定理、推论都是命题．(3)分类命题⎩⎪⎨⎪⎧ 真命题：判断为真的语句，假命题：判断为假的语句. 知识点二命题的结构(1)命题的一般形式为“若p ，则q ”．其中p 叫作命题的条件，q 叫作命题的结论．(2)确定命题的条件和结论时，常把命题改写成“若p ，则q ”的形式．知识点三四种命题四种命题的定义如下表所示1．命题均能判断其真假．(√)2．我们所学习过的定理均为命题．(√)3．命题：若函数f (x )为区间D 上的奇函数，则f (0)＝0，为真命题．(×)4．命题：若sin A ＞sin B ，则A ＞B ，其逆命题为真命题．(×)类型一命题的概念及真假判断命题角度1 命题的概念例1 判断下列语句是不是命题，并说明理由．(1)π3是有理数； (2)3x 2≤5；(3)梯形是不是平面图形呢？(4)若x ∈R ，则x 2＋4x ＋5≥0；(5)一个数的算术平方根一定是负数；(6)若a 与b 是无理数，则ab 是无理数．考点命题的定义及分类题点命题的定义解 (1)“π3是有理数”是陈述句，并且它是假的，所以它是命题． (2)因为无法判断“3x 2≤5”的真假，所以它不是命题．(3)“梯形是不是平面图形呢？”是疑问句，所以它不是命题．(4)“若x ∈R ，则x 2＋4x ＋5≥0”是陈述句，并且它是真的，所以它是命题．(5)“一个数的算术平方根一定是负数”是陈述句，并且它是假的，所以它是命题．(6)“若a 与b 是无理数，则ab 是无理数”是陈述句，并且它是假的，所以它是命题．反思与感悟判断一个语句是不是命题的三个关键点(1)一般来说，陈述句才是命题，祈使句、疑问句、感叹句等都不是命题．(2)语句表述的结构可以判断真假，含义模糊不清，无法判断真假的语句不是命题．(3)对于含有变量的语句，要注意根据变量的取值范围，看能否判断真假，若能，就是命题；否则就不是命题．跟踪训练1 下列语句是命题的是( )①三角形内角和等于180°；②2＞3；③一个数不是正数就是负数；④x ＞2；⑤这座山真险啊！A ．①②③B ．①③④C ．①②⑤D ．②③⑤考点命题的定义及分类题点命题的定义答案 A解析依据命题定义，得①②③为命题．命题角度2 命题真假的判断例2 给定下列命题：①若a >b ，则2a >2b ；②命题“若a ，b 是无理数，则a ＋b 是无理数”是真命题；③直线x ＝π2是函数y ＝sin x 的一条对称轴； ④在△ABC 中，若AB →·BC →>0，则△ABC 是钝角三角形．其中为真命题的是________．考点命题的真假判断题点命题真假的判断答案 ①③④解析结合函数f (x )＝2x 的单调性，知①为真命题；而函数y ＝sin x 的对称轴方程为x ＝π2＋k π，k ∈Z ，故③为真命题；又因为AB →·BC →＝|AB →||BC →|cos(π－B )＝－|AB →||BC →|cos B >0，故得cos B <0，从而得B 为钝角，所以④为真命题；②中，若a ＝－2，b ＝2，则a ＋b ＝0，是有理数，故②是假命题．引申探究1．本例中命题④变为：若AB →·BC →<0，则△ABC 是锐角三角形，该命题还是真命题吗？解不是真命题，AB →·BC →<0只能说明∠B 是锐角，其他两角的情况不确定．只有三个角都是锐角，才可以判定三角形为锐角三角形．2．本例中命题④改为：若AB →·BC →＝0，则△ABC 是________三角形．答案直角解析由AB →·BC →＝0，得∠B ＝90°，故该三角形为直角三角形．反思与感悟一个命题要么为真命题，要么为假命题，且必居其一．欲判断一个命题为真命题，需进行论证，而要判断一个命题为假命题，只需举出一个反例即可．跟踪训练2 (1)下列命题中假命题的个数为( )①多边形的外角和与边数有关；②如果数量积a ·b ＝0，那么向量a ＝0或b ＝0；③二次方程a 2x 2＋2x －1＝0有两个不相等的实根；④函数f (x )在区间[a ，b ]内有零点，则f (a )·f (b )<0.A ．1B ．2C ．3D ．4考点命题的真假判断题点命题真假的判断答案 C解析因为Δ＝4＋4a 2>0，故③正确，而①②④都错误，均可举出反例．(2)下列命题中为真命题的是( )A ．若ln x ＜1，则x ＜eB ．若向量a ，b ，c 满足a ∥b ，b ∥c ，则a ∥cC ．已知数列{a n }满足a n ＋1－2a n ＝0，则该数列为等比数列D ．在△ABC 中，设角A ，B ，C 所对的边分别为a ，b ，c ，若满足a cos B ＝b cos A ，则该三角形为等腰三角形考点命题的真假判断题点命题真假的判断答案 D解析对于A ，需满足x ＞0；对于B ，若b ＝0，其结论不成立；对于C ，若a n ＝0，则结论不成立．类型二命题的结构形式例3 将下列命题写成“若p ，则q ”的形式．(1)末位数是0或5的整数，能被5整除；(2)方程x 2－x ＋1＝0有两个实数根．考点命题的结构形式题点改写成标准的若p 则q 形式解 (1)若一个整数的末位数字是0或5，则这个数能被5整除．(2)若一个方程是x 2－x ＋1＝0，则它有两个实数根．反思与感悟将命题改写为“若p ，则q ”形式的方法及原则跟踪训练3将下列命题改写成“若p，则q”的形式，并判断其真假．(1)正n边形(n≥3)的n个内角全相等；(2)负数的立方是负数；(3)已知x，y为正整数，当y＝x－5时，y＝－3，x＝2.考点命题的结构形式题点改写成标准的若p则q形式解(1)若一个多边形是正n边形，则这个正n边形的n个内角全相等，是真命题．(2)若一个数是负数，则这个数的立方是负数，是真命题．(3)已知x，y为正整数，若y＝x－5，则y＝－3，x＝2，是假命题．类型三四种命题的概念及真假判断命题角度1四种命题的概念例4(1)命题“两对角线相等的四边形是矩形”是命题“矩形是两条对角线相等的四边形”的() A．逆命题B．否命题C．逆否命题D．等价命题答案 A(2)写出命题“若抛物线y＝ax2＋bx＋c的图像开口向下，则集合{x|ax2＋bx＋c＜0}≠∅”的逆命题、否命题、逆否命题．考点四种命题的概念题点四种命题定义的应用解逆命题：若集合{x|ax2＋bx＋c＜0}≠∅，则抛物线y＝ax2＋bx＋c的图像开口向下．否命题：若抛物线y＝ax2＋bx＋c的图像开口向上，则集合{x|ax2＋bx＋c＜0}＝∅.逆否命题：若集合{x|ax2＋bx＋c＜0}＝∅，则抛物线y＝ax2＋bx＋c的图像开口向上．反思与感悟四种命题的转换方法(1)逆命题：交换原命题的条件和结论，所得命题是原命题的逆命题．(2)否命题：同时否定原命题的条件和结论，所得命题是原命题的否命题．(3)逆否命题：交换原命题的条件和结论，并且同时否定，所得命题是原命题的逆否命题．跟踪训练4写出下列命题的逆命题、否命题、逆否命题．(1)实数的平方是非负数；(2)等底等高的两个三角形是全等三角形．考点四种命题的概念题点四种命题定义的应用解 (1)逆命题：若一个数的平方是非负数，则这个数是实数．否命题：若一个数不是实数，则它的平方不是非负数．逆否命题：若一个数的平方不是非负数，则这个数不是实数．(2)逆命题：若两个三角形全等，则这两个三角形等底等高．否命题：若两个三角形不等底或不等高，则这两个三角形不全等．逆否命题：若两个三角形不全等，则这两个三角形不等底或不等高．命题角度2 四种命题的真假判断例5 写出下列命题的逆命题、否命题、逆否命题，并判断其真假．(1)若a >b ，则ac 2>bc 2；(2)若四边形的对角互补，则该四边形是圆的内接四边形．考点四种命题的概念题点判断四种命题的真假解 (1)逆命题：若ac 2>bc 2，则a >b .真命题．否命题：若a ≤b ，则ac 2≤bc 2.真命题．逆否命题：若ac 2≤bc 2，则a ≤b .假命题．(2)逆命题：若四边形是圆的内接四边形，则该四边形的对角互补．真命题．否命题：若四边形的对角不互补，则该四边形不是圆的内接四边形．真命题．逆否命题：若四边形不是圆的内接四边形，则该四边形的对角不互补．真命题．反思与感悟若原命题为真命题，则它的逆命题、否命题可能为真命题，也可能为假命题．原命题与逆否命题互为逆否命题，否命题与逆命题互为逆否命题．互为逆否命题的两个命题的真假性相同．在原命题及其逆命题、否命题、逆否命题中，真命题的个数要么是0，要么是2，要么是4.跟踪训练5 已知命题“若2m －1＜x ＜3m ＋2，则1＜x ＜3”的逆命题为真命题，则m 的取值范围是________．考点四种命题的概念题点判断四种命题的真假答案 ⎣⎡⎦⎤13，1解析其逆命题为若1＜x ＜3，则2m －1＜x ＜3m ＋2.该命题为真命题，需满足⎩⎪⎨⎪⎧2m －1≤1，3m ＋2≥3，解得13≤m ≤1，故m 的取值范围为⎣⎡⎦⎤13，1.1．下列语句为命题的是()A．2x＋5≥0 B．求证对顶角相等C．0不是偶数D．今天心情真好啊考点命题的定义及分类题点命题的定义答案 C解析结合命题的定义知C为命题．2．下列说法中错误的是()A．命题“a，b，c中至少有一个等于0”的否命题是“a，b，c中没有一个等于0”B．命题“若x＞1，则x2－1＞0”的否命题是“若x≤1，则x2－1＜0”C．命题“面积相等的三角形全等”的否命题是“面积不相等的三角形不全等”D．命题“若x＝－4，则x是方程x2＋3x－4＝0的根”的否命题是“若x1≠－4，则x不是方程x2＋3x－4＝0的根”考点四种命题的概念题点按要求写命题答案 B解析由否命题的定义知B是错误的．3．命题“若a≥b，则a＋b＞2017且a＞－b”的逆否命题是()A．若a＋b≤2017且a≤－b，则a＜bB．若a＋b≤2017且a≤－b，则a＞bC．若a＋b≤2017或a≤－b，则a＜bD．若a＋b≤2017或a≤－b，则a≤b考点四种命题的概念题点按要求写命题答案 C解析将原命题的条件与结论互换的同时，对条件和结论进行否定即得逆否命题．“若a≥b，则a＋b＞2 017且a＞－b”的逆否命题为“若a＋b≤2 017或a≤－b，则a＜b”．故选C.4．命题“函数y＝log2(x2－mx＋4)的值域为R”为真命题，则实数m的取值范围为________________．考点命题的定义及分类题点由命题的真假求参数的取值范围答案(－∞，－4]∪[4，＋∞)解析由题意可知，满足条件时，需方程x2－mx＋4＝0的判别式Δ≥0，即(－m)2－4×4≥0，解得m≤－4或m≥4.5．命题：3mx2＋mx＋1>0恒成立是真命题，求实数m的取值范围．考点命题的定义及分类题点由命题的真假求参数的取值范围解“3mx2＋mx＋1>0恒成立”是真命题，需对m进行分类讨论．当m＝0时，1>0恒成立，所以m＝0满足题意；当m>0，且Δ＝m2－12m<0，即0<m<12时，3mx2＋mx＋1>0恒成立，所以0<m<12满足题意．综上所述，实数m的取值范围是[0,12)．1．根据命题的定义，可以判断真假的陈述句是命题．命题的条件与结论之间属于因果关系，真命题需要给出证明，假命题只需举出一个反例即可．2．任何命题都是由条件和结论构成的，可以写成“若p，则q”的形式．含有大前提的命题写成“若p，则q”的形式时，大前提应保持不变，且不写在条件p中．一、选择题1．命题“垂直于同一条直线的两个平面平行”的条件是()A．两个平面B．一条直线C．垂直D．两个平面垂直于同一条直线考点命题的结构形式题点区分命题的条件和结论答案 D解析所给的命题可以改为“如果两个平面垂直于同一条直线，那么它们互相平行”，故选D.2．下列命题为假命题的是()A．若a·b＝0(a≠0，b≠0)，则a⊥bB．若|a|＝|b|，则a＝bC．0是偶数D．5＞3考点命题的真假判断题点命题真假的判断答案 B解析结合向量的有关知识知A为真命题，B为假命题．C，D显然是真命题．3．命题“若x2＞1，则x＜－1或x＞1”的逆否命题是()A．若x2＞1，则－1≤x≤1B．若－1≤x≤1，则x2≤1C．若－1＜x＜1，则x2＜1D．若x＜－1或x＞1，则x2＞1考点四种命题的概念题点按要求写命题答案 B解析结合逆否命题的定义知B正确．4．下列命题是真命题的是()A．若ab＝0，则a2＋b2＝0B．若a>b，则ac>bcC．若M∩N＝M，则N⊆MD．若M⊆N，则M∩N＝M考点命题的真假判断题点命题真假的判断答案 D解析A中，a＝0，b≠0时，a2＋b2＝0不成立；B中，c≤0时不成立；C中，M∩N＝M说明M⊆N.故A，B，C均错误．5．已知a，b为两条不同的直线，α，β为两个不同的平面，且a⊥α，b⊥β，则下列命题中的假命题是() A．若a∥b，则α∥βB．若α⊥β，则a⊥bC．若a，b相交，则α，β相交D．若α，β相交，则a，b相交考点命题的真假判断题点命题真假的判断答案 D解析D中如果α，β相交，a和b可以相交，也可以异面．6．对任意平面向量a，b，下列关系式中不恒成立的是()A．|a·b|≤|a||b| B．|a－b|≤||a|－|b||C．(a＋b)2＝|a＋b|2D．(a＋b)·(a－b)＝a2－b2考点命题的真假判断题点命题真假的判断答案 B解析设向量a，b的夹角为θ，因为a·b＝|a||b|cosθ，所以|a·b|＝|a||b||cosθ|≤|a||b|，A成立；由向量的运算律易知C，D成立．故选B.7．设m，n是两条不同的直线，α，β，γ是三个不同的平面，给出下列四个命题：①若m⊥α，n∥α，则m⊥n；②若α∥β，β⊥γ，则α∥γ；③若m⊥α，n⊥α，则m∥n；④若α⊥γ，β⊥γ，则α∥β.其中为真命题的是()A．①②B．②③C．③④D．①③考点命题的真假判断题点命题真假的判断答案 D解析结合线面、面面位置关系易知①③为真命题．8．对于原命题“正弦函数不是分段函数”，下列说法正确的是()A．否命题是“正弦函数是分段函数”B．逆否命题是“分段函数不是正弦函数”C．逆否命题是“分段函数是正弦函数”D．以上都不正确考点四种命题题点四种命题的判断答案 B解析否命题为“不是正弦函数的函数是分段函数”，所以A错误；B正确；C不正确，故选B.二、填空题 9．有下列命题： ①22340能被5整除；②不存在x ∈R ，使得x 2＋x ＋1＜0； ③对任意的实数x ，均有x ＋1＞x ； ④方程x 2－2x ＋3＝0有两个不等的实根．其中假命题有________．(填序号) 考点命题的真假判断题点命题真假的判断答案 ④解析易知①②③为真命题，④中Δ＝4－12＜0，方程x 2－2x ＋3＝0无实根，因而④为假命题．10．命题“当a ＞0，a ≠1时，若函数f (x )＝log a x 在其定义域内是减函数，则log a 2＜0”的逆否命题是______________________________________________________________________ ________________________________________________________________________. 考点四种命题的概念题点按要求写命题答案当a ＞0，a ≠1时，若log a 2≥0，则函数f (x )＝log a x 在其定义域内不是减函数．11．已知p ：关于x 的不等式x 2＋2ax ＋4＞0对一切x ∈R 恒成立，q ：函数f (x )＝－(5－2a )x 是减函数，若p ，q 中有且只有一个是真命题，则实数a 的取值范围是________．考点命题的真假判断题点由命题的真假求参数的取值范围答案 (－∞，－2]解析 p 为真命题时，Δ＝4a 2－16＜0，解得－2＜a ＜2.q 为真命题时，5－2a ＞1，解得a ＜2.当p 真q 假时，⎩⎪⎨⎪⎧－2＜a ＜2，a ≥2，a ∈∅.当p 假q 真时，⎩⎪⎨⎪⎧a ≤－2或a ≥2，a ＜2，即a ≤－2.故实数a 的取值范围为(－∞，－2]．三、解答题12．把下列命题改写成“若p ，则q ”的形式，并判断命题的真假． (1)当ac >bc 时，a >b ；(2)当m >14时，mx 2－x ＋1＝0无实根；(3)当ab ＝0时，a ＝0或b ＝0. 考点命题的结构形式题点改写成标准的若p 则q 形式，并判断命题的真假解 (1)若ac >bc ，则a >b .∵ac >bc ，c <0时，a <b ，∴该命题是假命题． (2)若m >14，则mx 2－x ＋1＝0无实根．∵Δ＝1－4m <0，∴该命题是真命题．(3)若ab ＝0，则a ＝0或b ＝0，该命题是真命题．13．判断命题“已知a ，x 为实数，若关于x 的不等式x 2＋(2a ＋1)x ＋a 2＋2≤0的解集非空，则a ≥1”的逆否命题的真假．考点四种命题的概念题点判断四种命题的真假解其逆否命题：已知a ，x 为实数，若a ＜1，则关于x 的不等式x 2＋(2a ＋1)x ＋a 2＋2≤0的解集是空集． ∵a ＜1，∴Δ＝(2a ＋1)2－4×(a 2＋2)＝4a ＋1－8＝4a －7＜0，即不等式x 2＋(2a ＋1)x ＋a 2＋2≤0的解集是空集， ∴原命题的逆否命题是真命题．四、探究与拓展14．命题“ax 2－2ax ＋3>0恒成立”是假命题，则实数a 的取值范围是( ) A ．a <0或a ≥3 B ．a ≤0或a ≥3 C ．a <0或a >3 D ．0<a <3考点命题的真假判断题点由命题的真假求参数的取值范围答案 A解析若命题“ax 2－2ax ＋3>0恒成立”是真命题，当a ＝0时，3>0符合题意，当a ≠0时，则a >0且Δ<0，解得0<a <3，综上可知，当0≤a <3时，命题“ax 2－2ax ＋3>0恒成立”是真命题，故当a <0或a ≥3时，命题“ax 2－2ax ＋3>0恒成立”是假命题．15．写出命题“当2m ＋1＞0时，如果m ＋32m －1＞0，那么m 2－5m ＋6＜0”的逆命题、否命题和逆否命题，并分别指出四种命题的真假．考点四种命题的概念题点判断四种命题的真假解由2m ＋1＞0，得m ＞－12.由m ＋32m －1＞0，得m ＜－3或m ＞12，又m ＞－12，所以m ＞12.由m 2－5m ＋6＜0，得2＜m ＜3，又m ＞－12，所以2＜m ＜3.由此可知，原命题可变为“如果m ＞12，那么2＜m ＜3”，显然原命题是假命题．逆命题为“当2m ＋1＞0时，如果m 2－5m ＋6＜0，那么m ＋32m －1＞0”，即“如果2＜m ＜3，那么m ＞12”，它是真命题．否命题为“当2m ＋1＞0时，如果m ＋32m －1≤0，那么m 2－5m ＋6≥0”，因为⎩⎪⎨⎪⎧2m ＋1＞0，m ＋32m －1≤0，所以⎩⎨⎧m ＞－12，－3≤m ＜12，所以－12＜m ＜12，由⎩⎪⎨⎪⎧2m ＋1＞0，m 2－5m ＋6≥0，得⎩⎪⎨⎪⎧m ＞－12，m ≤2或m ≥3，即－12＜m ≤2或m ≥3，所以否命题可表述为“如果－12＜m ＜12，那么－12＜m ≤2或m ≥3”，它是真命题．逆否命题为“当2m ＋1＞0时，如果m 2－5m ＋6≥0，那么m ＋32m －1≤0”，则逆否命题可表述为“如果－12＜m ≤2或m ≥3，那么－12＜m ＜12”，它是假命题．§2 充分条件与必要条件学习目标 1.理解充分条件、必要条件、充要条件的定义.2.会求某些简单问题成立的充分条件、必要条件、充要条件.3.能够利用命题之间的关系判定充要关系或进行充要条件的证明．知识点一充分条件与必要条件(1)“若p ，则q ”为真命题，是指由p 通过推理可以得出q .这时，我们就说，由p 可推出q ，记作p ⇒q ，并且说p 是q 的充分条件，q 是p 的必要条件．(2)若p ⇒q ，但q ⇏p ，称p 是q 的充分不必要条件，若q ⇒p ，但p ⇏q ，称p 是q 的必要不充分条件．知识点二充要条件思考在△ABC 中，角A ，B ，C 为它的三个内角，则“A ，B ，C 成等差数列”是“B ＝60°”的什么条件？答案因为A ，B ，C 成等差数列，故2B ＝A ＋C ，又因为A ＋B ＋C ＝180°，故B ＝60°，反之，亦成立，故“A ，B ，C 成等差数列”是“B ＝60°”的充要条件．梳理 (1)一般地，如果既有p ⇒q ，又有q ⇒p ，就记作p ⇔q ，此时，我们说，p 是q 的充分必要条件，简称充要条件．(2)充要条件的实质是原命题“若p ，则q ”和其逆命题“若q ，则p ”均为真命题，如果p 是q 的充要条件，那么q 也是p 的充要条件，即如果p ⇔q ，那么p 与q 互为充要条件． (3)从集合的角度判断充分条件、必要条件和充要条件.的充分不必要的必要不充分的必要条件其中p ：A ＝{x |p (x )成立}，q ：B ＝{x |q (x )成立}．1．q是p的必要条件时，p是q的充分条件．(√)2．若p是q的充要条件，则p和q是两个相互等价的命题．(√)3．q不是p的必要条件时，“p⇏q”成立．(√)类型一充分条件、必要条件、充要条件的判定例1下列各题中，试分别指出p是q的什么条件．(1)p：两个三角形相似，q：两个三角形全等；(2)p：一个四边形是矩形，q：四边形的对角线相等；(3)p：A⊆B，q：A∩B＝A；(4)p：a＞b，q：ac＞bc.考点充分条件、必要条件的判断题点充分、必要条件的判断解(1)∵两个三角形相似⇏两个三角形全等，但两个三角形全等⇒两个三角形相似，∴p是q的必要不充分条件．(2)∵矩形的对角线相等，∴p⇒q，而对角线相等的四边形不一定是矩形，∴q⇏p，∴p是q的充分不必要条件．(3)∵p⇒q，且q⇒p，∴p既是q的充分条件，又是q的必要条件．(4)∵p⇏q，且q⇏p，∴p是q的既不充分又不必要条件．反思与感悟充分条件、必要条件的两种判断方法(1)定义法①确定谁是条件，谁是结论；②尝试从条件推结论，若条件能推出结论，则条件为充分条件，否则就不是充分条件；③尝试从结论推条件，若结论能推出条件，则条件为必要条件，否则就不是必要条件．(2)命题判断法①如果命题：“若p，则q”为真命题，那么p是q的充分条件，同时q是p的必要条件；②如果命题：“若p，则q”为假命题，那么p不是q的充分条件，同时q也不是p的必要条件．跟踪训练1指出下列各题中，p是q的什么条件？(1)p：ax2＋ax＋1>0的解集是R，q：0<a<4；(2)p：|x－2|<3，q：6x－5<－1；(3)p ：A ∪B ＝A ，q ：A ∩B ＝B ；(4)p ：⎩⎪⎨⎪⎧ α>2，β>2，q ：⎩⎪⎨⎪⎧α＋β>4，αβ>4.考点充分条件、必要条件的判断题点充分、必要条件的判断解 (1)当a ＝0时，1>0满足题意；当a ≠0时，由⎩⎪⎨⎪⎧Δ＝a 2－4a <0，a >0，可得0<a <4.故p 是q 的必要不充分条件． (2)易知p ：－1<x <5，q ：－1<x <5，所以p 是q 的充要条件．(3)因为A ∪B ＝A ⇔A ∩B ＝B ，所以p 是q 的充要条件．(4)由⎩⎪⎨⎪⎧ α>2，β>2，根据同向不等式相加、相乘的性质，有⎩⎪⎨⎪⎧α＋β>4，αβ>4，即p ⇒q ，但⎩⎪⎨⎪⎧ α＋β>4，αβ>4⇏⎩⎪⎨⎪⎧α>2，β>2，比如，当α＝1，β＝5时，⎩⎪⎨⎪⎧α＋β＝6>4，αβ＝5>4，而α<2，所以q ⇏p ，所以p 是q 的充分不必要条件．类型二充要条件的探求与证明命题角度1 充要条件的探求例2 求ax 2＋2x ＋1＝0至少有一个负实根的充要条件是什么？考点充要条件的概念及判断题点寻求充要条件解 (1)当a ＝0时，原方程变为2x ＋1＝0，即x ＝－12，符合要求．(2)当a ≠0时，ax 2＋2x ＋1＝0为一元二次方程，它有实根的充要条件是Δ≥0，即4－4a ≥0，∴a ≤1.①方程ax 2＋2x ＋1＝0只有一个负根的充要条件是⎩⎪⎨⎪⎧Δ≥0，x 1x 2<0，即⎩⎪⎨⎪⎧a ≤1，1a<0，∴a <0.②方程ax 2＋2x ＋1＝0有两个负根的充要条件是⎩⎪⎨⎪⎧Δ≥0，x 1＋x 2<0，x 1x 2>0，即⎩⎪⎨⎪⎧a ≤1，－2a<0，1a >0，∴0<a ≤1.综上所述，ax2＋2x＋1＝0至少有一个负实根的充要条件是a≤1.反思与感悟探求一个命题的充要条件，可以利用定义法进行探求，即分别证明“条件⇒结论”和“结论⇒条件”，也可以寻求结论的等价命题，还可以先寻求结论成立的必要条件，再证明它也是其充分条件．跟踪训练2已知数列{a n}的前n项和S n＝(n＋1)2＋t(t为常数)，试问t＝－1是否为数列{a n}是等差数列的充要条件？请说明理由．考点充要条件的概念及判断题点寻求充要条件解是充要条件．(充分性)当t＝－1时，S n＝(n＋1)2－1＝n2＋2n.a1＝S1＝3，当n≥2时，a n＝S n－S n－1＝2n＋1.又a1＝3符合上式，∴a n＝2n＋1(n∈N＋)，又∵a n＋1－a n＝2(常数)，∴数列{a n}是以3为首项，2为公差的等差数列．故t＝－1是{a n}为等差数列的充分条件．(必要性)∵{a n}为等差数列，则2a2＝a1＋a3，∵a1＝S1＝4＋t，a2＝S2－S1＝5，a3＝S3－S2＝7，∴10＝11＋t，解得t＝－1，故t＝－1是{a n}为等差数列的必要条件．综上，t＝－1是数列{a n}为等差数列的充要条件．命题角度2充要条件的证明例3求证：一元二次方程ax2＋bx＋c＝0有一正根和一负根的充要条件是ac＜0.考点充要条件的概念及判断题点充要条件的证明证明充分性(由ac＜0推证方程有一正根和一负根)，∵ac＜0，∴一元二次方程ax2＋bx＋c＝0的判别式Δ＝b2－4ac＞0，∴原方程一定有两不等实根，不妨设为x1，x2，则x1x2＝ca＜0，∴原方程的两根异号，即一元二次方程ax 2＋bx ＋c ＝0有一正根和一负根．必要性(由方程有一正根和一负根推证ac ＜0)， ∵一元二次方程ax 2＋bx ＋c ＝0有一正根和一负根，不妨设为x 1，x 2，∴由根与系数的关系得x 1x 2＝ca ＜0，即ac ＜0，此时Δ＝b 2－4ac ＞0，满足原方程有两个不等实根．综上可知，一元二次方程ax 2＋bx ＋c ＝0有一正根和一负根的充要条件是ac ＜0.反思与感悟对于充要条件性命题证明，需要从充分性和必要性两个方面进行证明，需要分清条件和结论．跟踪训练3 求证：方程x 2＋(2k －1)x ＋k 2＝0的两个根均大于1的充要条件是k ＜－2. 考点充要条件的概念及判断题点充要条件的证明证明必要性：若方程x 2＋(2k －1)x ＋k 2＝0有两个大于1的根，不妨设两个根为x 1，x 2，则⎩⎪⎨⎪⎧Δ＝(2k －1)2－4k 2≥0，(x 1－1)＋(x 2－1)＞0，(x 1－1)(x 2－1)＞0，即⎩⎪⎨⎪⎧k ≤14，(x 1＋x 2)－2＞0，x 1x 2－(x 1＋x 2)＋1＞0.即⎩⎪⎨⎪⎧k ≤14，－(2k －1)－2＞0，k 2＋(2k －1)＋1＞0，解得k ＜－2. 充分性：当k ＜－2时，Δ＝(2k －1)2－4k 2＝1－4k ＞0. 设方程x 2＋(2k －1)x ＋k 2＝0的两个根为x 1，x 2.则(x 1－1)(x 2－1)＝x 1x 2－(x 1＋x 2)＋1＝k 2＋2k －1＋1＝k (k ＋2)＞0. 又(x 1－1)＋(x 2－1)＝(x 1＋x 2)－2＝－(2k －1)－2＝－2k －1＞0， ∴x 1－1＞0，x 2－1＞0，∴x 1＞1，x 2＞1.综上可知，方程x 2＋(2k －1)x ＋k 2＝0有两个大于1的根的充要条件为k ＜－2. 类型三利用充分条件、必要条件求参数的值(或范围)例4 设命题p ：x (x －3)＜0，命题q ：2x －3＜m ，已知p 是q 的充分不必要条件，则实数m 的取值范围为________．考点充分、必要条件的综合应用题点由充分、必要条件求参数的范围答案 [3，＋∞)解析 p ：x (x －3)＜0，即0＜x ＜3； q ：2x －3＜m ，即x ＜m ＋32.由题意知p ⇒q ，q ⇏p ，则在数轴上表示不等式如图所示，则m ＋32≥3，解得m ≥3，即实数m 的取值范围为[3，＋∞)．反思与感悟 (1)在有些含参数的充要条件问题中，要注意将条件p 和q 转化为集合，从而转化为两集合之间的子集关系，再转化为不等式(或方程)，从而求得参数的取值范围． (2)根据充分条件或必要条件求参数范围的步骤 ①记集合M ＝{x |p (x )}，N ＝{x |q (x )}；②若p 是q 的充分不必要条件，则M ?N ，若p 是q 的必要不充分条件，则N ?M ，若p 是q 的充要条件，则M ＝N ；③根据集合的关系列不等式(组)； ④求出参数的范围．跟踪训练4 设A ＝⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫y ⎪⎪y ＝2x 2x ＋1，x ∈R，B ＝⎩⎨⎧⎭⎬⎫y ⎪⎪y ＝13x ＋m ，x ∈[－1，1]，记命题p ：“y ∈A ”，命题q ：“y ∈B ”，若p 是q 的必要不充分条件，则m 的取值范围为______________．考点充分、必要条件的综合应用题点由充分、必要条件求参数的范围答案 ⎝⎛⎭⎫13，23解析由题意知A ＝{y |0＜y ＜1}．， B ＝⎩⎨⎧⎭⎬⎫y | m －13≤y ≤m ＋13，依题意，得B ?A ，故⎩⎨⎧m －13>0，m ＋13<1，∴13<m <23.1．“x ＞0”是“x 2＋x ＞0”的( )A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分又不必要条件考点充分条件、必要条件的判断题点充分、必要条件的判断答案 A解析由x 2＋x ＞0⇔x ＜－1或x ＞0，由此判断A 符合要求．2．对于非零向量a ，b ，“a ＋b ＝0”是“a ∥b ”的( )A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分又不必要条件答案 A解析当a ＋b ＝0时，得a ＝－b ，所以a ∥b ，但若a ∥b ，不一定有a ＋b ＝0.3．“关于x 的不等式x 2－2ax ＋a ＞0，x ∈R 恒成立”的一个必要不充分条件是( )A ．0＜a ＜1B ．0≤a ≤1C ．0＜a ＜12D ．a ≥1或a ≤0 考点充分条件、必要条件的概念及判断题点充分、必要条件的判断答案 B解析当关于x 的不等式x 2－2ax ＋a ＞0，x ∈R 恒成立时，应有Δ＝4a 2－4a ＜0，解得0＜a ＜1.所以一个必要不充分条件是0≤a ≤1.4．设p ：1≤x ＜4，q ：x ＜m ，若p 是q 的充分条件，则实数m 的取值范围是________．(用区间表示) 考点充分条件的概念及判断题点由充分条件求取值范围答案 [4，＋∞)解析因为p 为q 的充分条件，所以[1,4)⊆(－∞，m )，得m ≥4.5．设p ：|x |＞1，q ：x ＜－2或x ＞1，则q 是p 的__________条件．(填“充分不必要”“必要不充分”“既不充分又不必要”“充要”)考点充分条件、必要条件的判断题点充分、必要条件的判断答案充分不必要。

北大测试全套课件和教案 7. 第4章第1讲

---------------------------------------------------------------最新资料推荐------------------------------------------------------ 北大测试全套课件和教案7. 第4章第1讲《软件测试基础》授课教案授课内容：第四章白盒测试技术授课课次：第 7 次课授课时数：2 学时授课日期: 上课教室: 目的与要求：了解静态测试的必要性；理解静态测试的方法，包括代码检查、静态结构分析、代码质量度量。

教学重点：代码检查和编程风格教学难点：代码质量度量教学方式：1. 运用《白盒测试技术》课件进行课堂讲授，了解静态测试的必要性；2. 通过讲述静态测试，拓宽学生们对测试的理解，测试不光是设计用例，执行用例观察结果，测试的工作也包括不实际运行软件，对软件评估。

3. 展开课堂讨论，怎们样做静态测试。

教学内容：1．代码检查 2．静态结构分析 3．代码质量度量 4．课堂讨论。

内容提要及时间分配：1、课前引导（5 分钟）什么叫做静态测试和动态测试？1 / 12什么叫做白盒测试和黑盒测试。

2、代码检查（50 分钟）代码走查（10 分钟）编程风格与规范（25 分钟）代码审查（15 分钟） 3、静态结构分析（5 分钟） 4、代码质量度量（5 分钟） 5、课堂讨论（20分钟）在做静态测试的时候，我们可能会遇到什么困难？怎样解决呢？ 6、课后小结和布置作业（5 分钟）教学参考书：1. 软件测试方法和技术朱少民清华大学出版社 2. 软件测试 Paul C.Jorgensen 机械工业出版社讨论与思考：为什么要做静态测试，在做静态测试的时候，我们可能会遇到什么困难？怎样解决呢？作业: 试写 c++语言编程中变量和常量的命名规范。

复问题目：序号题目学生成绩 1 2 3 教学内容与方法步骤 4.1 静态测试引言：静态测试包括包括代码检查、静态结构分析、代码质量度量等。

北师版高中同步学考数学选修1-1精品课件第一章 §2 充分条件与必要条件

p 不能推出 q,
且 q 不能推出 p
结论
p 是 q 的充分不必要条件
p 是 q 的必要不充分条件
p 是 q 的充要条件
p 是 q 的既不充分也不必要条件
-6-
§2充分条件与必要条件
首页
自主预习
【做一做2】下列各项中,p是q的充要条件的是(
探究学习
当堂检测
)
A.p: பைடு நூலகம் ,q:a=b

同理x2+2cx-b2=0可化为x2+2cx-a2+c2=0,
即(x+a+c)(x+c-a)=0,
所以两根分别为x1=-a-c,x2=a-c.
故两个方程有公共根-a-c.
-16-
§2充分条件与必要条件
探究一
探究二
首页
自主预习
探究学习
当堂检测
思维辨析
(2)(必要性)
设两个方程有公共根α,则α2+2aα+b2=0,α2+2cα-b2=0,显然α≠0.
∴A+C=2B.
又A+B+C=180°,
∴3B=180°.
∴B=60°.
故A,B,C成等差数列的充要条件是B=60°.
-19-
§2充分条件与必要条件
探究一
探究二
首页
自主预习
探究学习
当堂检测
思维辨析
考虑不周致误
【典例】 “直线l在y轴上的截距是在x轴上的截距的2倍”是“直线
l的斜率等于-2”的(
)
A.充分不必要条件
首页
自主预习
探究学习
当堂检测
思维辨析
解析:若直线l的斜率等于-2,则直线l在y轴上的截距一定是它在x

《走向高考》：高三数学一轮复习课件11-1(北师大)

第U章统计、统计案例ZSWL知识网络抽签法简单随机抽样线性回归方程变量间的相关关系整理、分析赠估计，推断 (随机抽样)收集数回归分析统计案例独立性检验MTFX命题分析•统计和统计案例主要以应用题为命题背景,考查分层抽样、系统抽样的有关计算，或三种抽样方法的区别.以及茎叶图频率分布表、频率分布直方图的识图及运用，少部分涉及到回归分析和独立性检验.一般以选择题、填空题考查，少有大题，有些只是解答题中的一问.主要是通过案例体会运用统计方法解决实际问题的思想和方法.FXJY复习建议•复习中要注意以下几点：• (1)合理选用三种抽样方法•在三种抽样中，简单随机抽样是最简单、最基本的抽样•方法，其他两种抽样方法是建立在它的基础上的，三种抽样方法的共同点：它们都是等概率抽样，体现了抽样的公平性；三种抽样方法各有其特点和适用范围，在抽样实践中要根据具体情况选用相应的抽样方法.• (2)正确运用频率分布条形图和直方图•由于总体分布通常不易知道，我们往往用样本的频率分布去估计总体分布，一般地 ,样本容量越大，估计越精确.•①当总体中个体取不同数值很少时，其频率分布表由所取的样本的不同数值及相应频率表示，其几何表示就是相应的条形图•②当总体中个体取不同数值很少时，用频率分布直方图来表示相应样本的频率分布• (3)分析两个变量相关关系的常用方法•①利用散点图进行判断：把样本数据表示的点在平面直角坐标系中作岀，从而得到散点图，如果这些点大致分布在通过散点图中心的一条直线附近，那么就说这两个变量之间具有线性相关关系.•②利用相关系数成行判断:|^1而且M 越接近于1,相关程度越大；州越接近于0 ，相关程度越小•(4)独立性检验的一般步骤①根据样本数据制成2X2列联表°②根据公式/2> n(ad~bc)、+皆—(a + b)(a + c)(b+d)(c+d)，'的值.③比较于与临界值的大小关系作统计推断.抽样方法GKMB咼考目标•考纲解读•1・理解随机抽样的必要性和重要性.•2.会用简单随机抽样方法从总体中抽取样本；了解分层抽样和系统抽样方法.•考向预测•1.本节主要考查学生在应用问题中构造抽样模型、识别模型、选择适当的抽样方法抽取样本.KQZZYX课前自主预习•知识梳理• 1.简单随机抽样•⑴定义：设一个总体含有2个个褚T从中放豎_________ 抽取门个个体作为样本,如果每次抽取时总体内酌各个个体被抽到的概翠都______ ,就把这种抽样方法叫做简单随机抽样. 抽签法•（刼最常用的简单随机抽样的方法:•2.系统抽样(等距抽样或机械抽样)的步骤•假设要从容量为/V的总体畔1抽取容量为门白勺木羊2$ •分段间隔k分段N•⑴先将总体的/V个个体进行______ 〃・•(2)确定_____ ?机対编号进行______ ,当是整数时，取•(3)在第1段用________ 确定第一个样本编号/(辰k).廿/+农•(4)按照一定的规则抽取样本，通常是将/ 加上间隔昭到第2个个体编号_______ ,再•3.分层抽样•(1)定义：将总体按其属性特征分成若干类型(有时称作层)严燃培腔寒吩类型中_ ______________ 定的样本.这种抽样方法通常叫做分层抽样，有时也称为类型抽样. •(2)分层抽样的应笛倔分•当总体是由____________________ 组成时，往往选用分层抽样.•基础自测• 1・（2010 •四川文）一个单位职工800人，其中具有咼级职称的160人，具有中级职称的320人，具有初级职称的200人，其余人员120人，为了解职工收入情况，决定采用分层抽样的方法，从中抽取容量为40的样本，则从上述各层中依次抽取的人数分别是（）• A. 12,24,15,9B.9,12,12,7• C・ 8,15,12,5 D.懈析］本题考查分层抽样的概念和应用，利用分层10,40X 翳=6.抽样抽取人数时，首先应计算抽样比.从各层中依次抽160 320 , 200 40X 800 = 8940X 800= 16940X 800=取的人数分别是• 2・（教材改编题）在抽样过程中，每次抽取的个体不再放回总体的为不放回抽样，则分层抽样、简单随机抽样、系统抽样中 ,为不放回抽样的有（）•A. 1 个•C. 3 个B. 2个D. 0个•［答案］C•解析］三种抽样都是不放回抽样・•3・（2011 •威海摸拟）老师在班级50名学生中，依次抽取学号为5,10,15,20,25,30,35,40,45,50 的学生进行作业检查，这种抽样方法是（）•A.随机抽样 B.分层抽样•C.系统抽样 D.以上都不是•［答案］C•［解析］因为所抽取学生的学号成等差数列,即为等距离抽样,属于系统抽样・•4 •某校高三年级有男生500人，女生400 人，为了解该年级学生的健康情况，从男生中任意抽取25人，从女生中任意抽取20人进行调查.这种抽样方法是（）•A.简单随机抽样法 B.抽签法•C.随机数表法 D.分层抽样法•［答案］D•［解析］本小题主要考查抽样方法.若总体由差异明显的几部分组成时z经常采用分层抽样的方法进行抽样,故选D.• 5・当前，国家正在分批修建经济适用房以解决低收入家庭住房紧张问题，统计数据表示，甲、乙、丙三个社区现分别有低收入家庭180户、150户、90户，若第一批经济适用房中有70套用于解决这三个社区中70户低收入家庭的住房问题，现采用分层抽样的方法决定各社区的户数，抽;麺娈法7辭应A甲社区中抽取的低收入家庭的户数为盲」6+?+i X70=3°-• 6・某单位200名职工的年龄分布情况如图所示，现要从中抽取40名职工作样本 ,用系统抽样法，将全体职工随机按1〜200编号，并按编号顺序平均分为40组（1 〜5号，6〜10号…，196〜200号）.若第5组抽岀的号码为22,则第8组抽血的号码应是_______________ ・若用分层抽样方法，贝何0岁以下年苗函兀______________［解析］考查随机抽样概念及方法.由分组可知，抽号的间隔为5,又因为第5组抽出的号码为22,所以第6组抽出的号码为27,第7组抽出的号码为32,第8组抽出的号码为37.40岁以下年龄段的职工数为200X0.5 = 100,则应抽取40的人数为555X100 = 20人.•7 .从某厂生产的905辆家用轿车中随机抽取90辆测试某项性能,请合理选择抽样方法进行抽样,并写出抽样过程.•解析］可用系统抽样法进行抽样,抽样步骤如下：•⑴将905辆轿车用随机方式编号；•（2）从总体中剔除5辆（剔除法可用随机数表法）,将剩下的900辆轿车重新编号（分另0为001,002，…,900）并分成90段；（3）在第一段001,002 z…,010这十个编号中用简单随机抽样抽出一个作为起课堂典例讲练•［例1］某班共有60名学生，领到10张电命题方向简单随机抽样影票.现在用抽签法和随机数表法把10 张电影票分下去，试写岀过程.•［分析］结合抽签法和随机数表法的步骤来解决.•［解析］(1)抽签法.•第一步/先将60名学生编号・编号为01,02,03 , (60)•第二步，准备抽签工具.把号码写在形状、大小相同的号签上,将这些号签放在同一个不透明箱子里.•第三步,实施抽签.抽签前先将放在箱子里的号签搅拌均匀,抽签时每次从中抽出—号签,连续抽10次,根据抽到的10个号码对应10名学生「0张电影票就分给10名被抽到的学生・• (2)随机数表法.•第一步/先将60名学生编号z分另0为00,01,02,03 z…z 59.•第二步,由于总体的编号为两位数,在随机数表中选取两列组成两位数.从随机数表中的任意一个位置,按一定顺序开始读数・如果读至啲数小于59 ,则将它取出；若读到的数大于59 ,则舍去；重复的数字只取一个,直到取满10个不超过59 的数为止・将10张电影票分给抽到10名相应编号的学生.•比如,从随机数表第6行的第3列和第4列开始读数,从上至下分别是35,11,48,77,79,64,58,89,31,55,00,93,80 , 46,66,12,11,10 ,…•其中11重复出现, 77,79,64,89,93,80,66超过59不能取z这样选取的10个样本号码分别为35,11,48,58,31,55,00,46,12,10.Slhb ,可把10张电影票分给编号为上述号码的10 名学生.•［点评］利用抽签法进行简单随机抽样的步骤可分为五个步骤,事实上有些步骤明显地可以合并两个为一个,无论怎样合并,只要把过程按正确的顺序叙述、符合抽签的规则就行•随机数表法同理・跟踪练习❶•••有一批机器，编号为1,2,3,…，112,为调查机器的质量问题，打算抽取10台入样，问此样本若采用简单随机抽样方法将如何获得？•［分析］简单随机抽样方法有抽签法和随机数表法，因为样本的容量为10,因此 ,两种方法均可以.•［解析］方法一首先，把机器都编上号码001,002,003 z - z 112 z如用抽签法，则把门2个形状、大小相同的号签放在同一个箱子里，进行均匀搅拌，抽签时，每次从中抽出1个号签,连续抽取10次z 就得到一个容量为10的样本.•方法二第一步，将原来的编号调整为000,001,002,003 , - z 111.•第二步，在随机数表中的任选F作为开始，任选一方向作为读数方向，比如：选第9行第7个数“3〃 ,向右读•三次,凡不在000 ~ 111中的数跳过去不读,前面已经读过的也跳过去不读,依次可得到074,100,094,052,080,003,105,107,083, 092.•第四步,对应原来编号74,100,94,52,80,3,105,107,83,92白勺机器便是要抽取的对象.•［点评］(1)—个抽样试验能否用抽签法/关键看两点：一是制签是否方便；二是号签是否易搅匀,_般地,当总体容量和• (2)随机数表中共随机出现0丄2 , (9)个数字,也就是说,在表中的每个位置上出现各个数字的机会都是相等的・在使用随机数表时,如遇到三位数或四位数时, 可从选择的随机数表中的某行某列的数字计起，每三个或每四个作为一个单位,自左向右选取,有超过总体号码或出现重复号码的数字舍去.命题方向蜜系统抽样10100,然后再利用系统抽样的方法进行.名工人，使得总体容量能被样本容量整除，取k= 1 000 •［例2］某工厂有1 003名工人，从中抽取10人参加体检，试用系统抽样进行具体采施f ・］由于总体容量较大，因此，采用系统抽样法进行抽样，又因总体容量不能被样本容量整除，需先剔除3•解析］(1 )将每个人随机编一个号由0001至1003.• (2)利用随机数法找到3个号,将这3名工人剔除■•⑶将剩余的1 000名工人重新随机编号0001至1000.•(4)分段,取间隔k二=100 ,将总体均分为10段，每段含100名工人.•(5)从第一段即为0001至0100号中随机抽取—个号L.•［点评］⑴系统抽样时，为保证“等距” 分段,应先将多余个体剔除,然后再按系统抽样步9聚睡行.•⑵因为每个个体被剔除的可能性也是相等的z所以能保证每个个体被抽到的可能性是相等的.跟踪练习❷•某单位共有在岗职工人数为624人，为了调查工人上班时，从离开家到单位平均所用的时间，决定抽取10%的工人调查这一情况，如何采用系统抽样的方法完成这一抽禅？•［分析］总体中的每个个体，都必须等可能地入样，为了实现“等距”入样，且又等概率，因此，应先剔除，再“分段”，后定起始位.•解析］第一步,将在岗的工人624人,用随机方式编号（如按出生年阿顺序）,_ _ 6 2 _000,001,002 z…,623第二步,由题意知,应抽取62人的样本,因为不是整数,所以应从总体中剔除4人（剔除方法用随机数表法,随机定一起始数，向右取三位数.如起始数为课本附表1中第8行, 第19列数,则为1 •向右取三位数为199 , 即编号199被剔除,若三位数恰大于623 或是已被剔除之数,则重新定起始数,反•［点评］当总体容量不能被样本容量整除时,可以先从总体中随机地剔除几个个体，使得总体中剩余的个体数能被样本容量整除命题方向鼻分层抽样•［例3］某单位最近组织了一次健身活动,活动分为登山组和游泳组，且每个职工至多参加其中一组.在参加活动的职工中 ,青年人占42.5%,中年人占47十％,老年人占10%.登山组的职工占参加活动总人数的，且该组中，青年人占50%,中年人占40%,老年人占10%.为了了解各组不同年龄层次的职工对本次活动的满意程度，现用分层抽样方法从参加活动的全体职工中抽取一个容量为200的样本•试• (1)游泳组中，青年人、中年人、老年人分别所占的比例；• (2)游泳组中，青年人、中年人、老年人分别应抽取的人数.［解析］(1)设登山组人数为兀，游泳组中，青年人、10%> ~I -3xc=47.5%, ------- =10%,解得 b = 50%，c=10%.故a=100% —50%—10%=40%,即游泳组中，青年人、中年人、老年人各占比例分别为40%、50%、10%.中年人、老年人各占比例分别为a 、b 、c, 则有上40% + 3妙3(2)游泳组中，抽取的青年人数为200X|X40% = 60(A),3抽取的中年人数为200X-X50% = 75(A);抽取的老年人数为3 ,200X-X10%=15(人).跟踪练习❸•••(1)某市力、B、C三个区共有高中学生20000人，其中力区高中学生7000人，现采用分层抽样的方法从这三个区所有高中学生中抽取一个容量为600人的样本进行学习兴趣调查，则力区应抽取()•A. 200人 B. 205人• C. 210人 D. 215人•［轡篥|耕分层抽样的特点,4区应抽取的人数为7000 , x20000 X 600 = 210人・• (2)防疫站对学生进行身体健康调查，采用分层抽样法抽取，红星中学共有学生1600名，抽取一个容量为200的样本，已知女生比男生少抽了10人，则该校的女生总共人数为. •［答刺设欽较女生共有兀人，则男生为1600—兀人，女生抽了y人，则男生抽了y+10人.y+(j+10) = 200 y 200x 1600$=95x=760 •X.雌蜩磴》抽样方法的综合应用•［例4］为『考查某校的教学水平，将抽查这个学校高三年级的部分学生本年度的考试成绩.为了全面反映实际情况，采取以下三种方式进行抽查（已知该校高三年级共有20个班，并且每个班内的学生已经按随机方式编好了学号，假定该校每班学生的人数相同）：①从高三年级20个班中任意抽取一个班，再从该班中任意抽取20名学生，考察他们的学习成绩；②每个班抽取1人，共计20人，考察这20名学生的成绩；③把学生按成绩分成优秀、良•普通三个级别，从其中共抽取100名学生进行考察(已知该校高三学生共1000人，若按成绩分，其中优秀生共150人，良好生共600人，普通生共250人)•根据上面的叙述，试回答下列问题：•(1)上面三种抽取方式的总体、个体、样本分别是什么？每一种抽取方式抽取的样本中，样本容量分别是多少？•(2)上面三种抽取方式各自采用的是何种抽取样本的方法？•(3)试分别写出上面三种抽取方式各自抽取。

2018版高考数学文北师大版大一轮复习讲义教师版文档第十一章概率 11.1 含答案精品

1．随机事件和确定事件(1)在条件S下，一定会发生的事件，叫作相对于条件S的必然事件．(2)在条件S下，一定不会发生的事件，叫作相对于条件S的不可能事件．(3)必然事件与不可能事件统称为相对于条件S的确定事件．(4)在条件S下可能发生也可能不发生的事件，叫作相对于条件S的随机事件．(5)确定事件和随机事件统称为事件，一般用大写字母A，B，C…表示．2．频率与概率在相同的条件下，大量重复进行同一试验时，随机事件A发生的频率会在某个常数附近摆动，即随机事件A发生的频率具有稳定性．这时，我们把这个常数叫作随机事件A的概率，记作P(A)．3．事件的关系与运算互斥事件：在一个随机试验中，我们把一次试验下不能同时发生的两个事件A与B称作互斥事件．事件A＋B：事件A＋B发生是指事件A和事件B至少有一个发生．对立事件：不会同时发生，并且一定有一个发生的事件是相互对立事件．4．概率的几个基本性质(1)概率的取值范围：0≤P(A)≤1.(2)必然事件的概率P(E)＝1.(3)不可能事件的概率P(F)＝0.(4)互斥事件概率的加法公式①如果事件A与事件B互斥，则P(A＋B)＝P(A)＋P(B)．②若事件A 与事件A 互为对立事件，则P (A )＝1－P (A )．【知识拓展】互斥事件与对立事件的区别与联系互斥事件与对立事件都是两个事件的关系，互斥事件是不可能同时发生的两个事件，而对立事件除要求这两个事件不同时发生外，还要求二者之一必须有一个发生，因此，对立事件是互斥事件的特殊情况，而互斥事件未必是对立事件．【思考辨析】判断下列结论是否正确(请在括号中打“√”或“×”) (1)事件发生频率与概率是相同的．( × ) (2)随机事件和随机试验是一回事．( × )(3)在大量重复试验中，概率是频率的稳定值．( √ ) (4)两个事件的和事件是指两个事件都得发生．( × )(5)对立事件一定是互斥事件，互斥事件不一定是对立事件．( √ ) (6)两互斥事件的概率和为1.( × )1．从{1,2,3,4,5}中随机选取一个数a ，从{1,2,3}中随机选取一个数b ，则b >a 的概率是( ) A.45 B.35 C.25 D.15 答案 D解析基本事件的个数为5×3＝15，其中满足b >a 的有3种，所以b >a 的概率为315＝15.2．(教材改编)将一枚硬币向上抛掷10次，其中“正面向上恰有5次”是( ) A ．必然事件 B ．随机事件 C ．不可能事件 D ．无法确定答案 B解析抛掷10次硬币正面向上的次数可能为0～10，都有可能发生，正面向上5次是随机事件．3．从某班学生中任意找出一人，如果该同学的身高小于160 cm 的概率为0.2，该同学的身高在[160,175](单位：cm)内的概率为0.5，那么该同学的身高超过175 cm 的概率为( ) A ．0.2 B ．0.3 C ．0.7 D ．0.8答案 B解析因为必然事件发生的概率是1，所以该同学的身高超过175 cm 的概率为1－0.2－0.5＝0.3，故选B.4．给出下列三个命题，其中正确的命题有________个．①有一大批产品，已知次品率为10%，从中任取100件，必有10件是次品；②做7次抛硬币的试验，结果3次出现正面，因此正面出现的概率是37；③随机事件发生的频率就是这个随机事件发生的概率．答案 0解析 ①错，不一定是10件次品；②错，37是频率而非概率；③错，频率不等于概率，这是两个不同的概念．5．(教材改编)袋中装有9个白球，2个红球，从中任取3个球，则①恰有1个红球和全是白球；②至少有1个红球和全是白球；③至少有1个红球和至少有2个白球；④至少有1个白球和至少有1个红球．在上述事件中，是对立事件的为________．答案 ②解析 ①是互斥不对立的事件，②是对立事件，③④不是互斥事件．题型一事件关系的判断例1 (1)从1,2,3，…，7这7个数中任取两个数，其中： ①恰有一个是偶数和恰有一个是奇数； ②至少有一个是奇数和两个都是奇数； ③至少有一个是奇数和两个都是偶数； ④至少有一个是奇数和至少有一个是偶数．上述事件中，是对立事件的是( ) A ．① B ．②④ C ．③ D ．①③(2)设条件甲：“事件A 与事件B 是对立事件”，结论乙：“概率满足P (A )＋P (B )＝1”，则甲是乙的( )A ．充分不必要条件B ．必要不充分条件C．充要条件D．既不充分也不必要条件(3)在5张电话卡中，有3张移动卡和2张联通卡，从中任取2张，若事件“2张全是移动卡”的概率是310，那么概率是710的事件是()A．至多有一张移动卡B．恰有一张移动卡C．都不是移动卡D．至少有一张移动卡答案(1)C(2)A(3)A解析(1)③中“至少有一个是奇数”即“两个奇数或一奇一偶”，而从1～7中任取两个数根据取到数的奇偶性可认为共有三个事件：“两个都是奇数”、“一奇一偶”、“两个都是偶数”，故“至少有一个是奇数”与“两个都是偶数”是对立事件，易知其余都不是对立事件．(2)若事件A与事件B是对立事件，则A＋B为必然事件，再由概率的加法公式得P(A)＋P(B)＝1.设掷一枚硬币3次，事件A：“至少出现一次正面”，事件B：“3次出现正面”，则P(A)＝78，P(B)＝18，满足P(A)＋P(B)＝1，但A，B不是对立事件．(3)至多有一张移动卡包含“一张移动卡，一张联通卡”，“两张全是联通卡”两个事件，它是“2张全是移动卡”的对立事件．思维升华(1)准确把握互斥事件与对立事件的概念①互斥事件是不可能同时发生的事件，但可以同时不发生．②对立事件是特殊的互斥事件，特殊在对立的两个事件不可能都不发生，即有且仅有一个发生．(2)判断互斥、对立事件的方法判断互斥事件、对立事件一般用定义判断，不可能同时发生的两个事件为互斥事件；两个事件，若有且仅有一个发生，则这两事件为对立事件，对立事件一定是互斥事件．下列命题：①将一枚硬币抛两次，设事件M：“两次出现正面”，事件N：“只有一次出现反面”，则事件M与N互为对立事件；②若事件A与B互为对立事件，则事件A与B为互斥事件；③若事件A与B为互斥事件，则事件A与B为对立事件；④若事件A与B互为对立事件，则事件A＋B为必然事件．其中，真命题是()A．①②④B．②④C ．③④D ．①②答案 B解析对①，将一枚硬币抛两次，共出现{正，正}，{正，反}，{反，正}，{反，反}四种结果，则事件M 与N 是互斥事件，但不是对立事件，故①错；对②，对立事件首先是互斥事件，故②正确；对③，互斥事件不一定是对立事件，如①中两个事件，故③错；对④，事件A 、B 为对立事件，则在一次试验中A 、B 一定有一个要发生，故④正确．题型二随机事件的频率与概率例2 (2016·全国甲卷)某险种的基本保费为a (单位：元)，继续购买该险种的投保人称为续保人，续保人本年度的保费与其上年度出险次数的关联如下：随机调查了该险种的200名续保人在一年内的出险情况，得到如下统计表：(1)记A 为事件：“一续保人本年度的保费不高于基本保费”，求P (A )的估计值；(2)记B 为事件：“一续保人本年度的保费高于基本保费但不高于基本保费的160%”，求P (B )的估计值；(3)求续保人本年度的平均保费的估计值．解 (1)事件A 发生当且仅当一年内出险次数小于2.由所给数据知，一年内出险次数小于2的频率为60＋50200＝0.55，故P (A )的估计值为0.55.(2)事件B 发生当且仅当一年内出险次数大于1且小于4.由所给数据知，一年内出险次数大于1且小于4的频率为30＋30200＝0.3，故P (B )的估计值为0.3.(3)由所给数据得调查的200名续保人的平均保费为0.85a ×0.30＋a ×0.25＋1.25a ×0.15＋1.5a ×0.15＋1.75a ×0.10＋2a ×0.05＝1.192 5a .因此，续保人本年度平均保费的估计值为1.192 5a . 思维升华 (1)概率与频率的关系频率反映了一个随机事件出现的频繁程度，频率是随机的，而概率是一个确定的值，通常用概率来反映随机事件发生的可能性的大小，有时也用频率作为随机事件概率的估计值． (2)随机事件概率的求法利用概率的统计定义求事件的概率，即通过大量的重复试验，事件发生的频率会逐渐趋近于某一个常数，这个常数就是概率．(2015·北京)某超市随机选取1 000位顾客，记录了他们购买甲、乙、丙、丁四种商品的情况，整理成如下统计表，其中“√”表示购买，“×”表示未购买.(1)估计顾客同时购买乙和丙的概率；(2)估计顾客在甲、乙、丙、丁中同时购买3种商品的概率；(3)如果顾客购买了甲，则该顾客同时购买乙、丙、丁中哪种商品的可能性最大？解 (1)从统计表可以看出，在这1 000位顾客中有200位顾客同时购买了乙和丙，所以顾客同时购买乙和丙的概率可以估计为2001 000＝0.2.(2)从统计表可以看出，在这1 000位顾客中，有100位顾客同时购买了甲、丙、丁，另有200位顾客同时购买了甲、乙、丙，其他顾客最多购买了2种商品．所以顾客在甲、乙、丙、丁中同时购买3种商品的概率可以估计为100＋2001 000＝0.3.(3)与(1)同理，可得顾客同时购买甲和乙的概率可以估计为2001 000＝0.2，顾客同时购买甲和丙的概率可以估计为100＋200＋3001 000＝0.6，顾客同时购买甲和丁的概率可以估计为1001 000＝0.1.所以，如果顾客购买了甲，则该顾客同时购买丙的可能性最大．题型三互斥事件、对立事件的概率命题点1 互斥事件的概率例3 袋中有12个小球，分别为红球、黑球、黄球、绿球，从中任取一球，得到红球的概率是13，得到黑球或黄球的概率是512，得到黄球或绿球的概率也是512，试求得到黑球、黄球和绿球的概率各是多少？解方法一从袋中选取一个球，记事件“摸到红球”“摸到黑球”“摸到黄球”“摸到绿球”分别为A ，B ，C ，D ，则有 P (A )＝13，P (B ＋C )＝P (B )＋P (C )＝512，P (C ＋D )＝P (C )＋P (D )＝512，P (B ＋C ＋D )＝P (B )＋P (C )＋P (D )＝1－P (A )＝1－13＝23，解得P (B )＝14，P (C )＝16，P (D )＝14，因此得到黑球、黄球、绿球的概率分别是14，16，14. 方法二设红球有n 个，则n 12＝13，所以n ＝4，即红球有4个．又得到黑球或黄球的概率是512，所以黑球和黄球共5个．又总球数是12，所以绿球有12－4－5＝3(个)．又得到黄球或绿球的概率也是512，所以黄球和绿球共5个，而绿球有3个，所以黄球有5－3＝2(个)．所以黑球有12－4－3－2＝3(个)．因此得到黑球、黄球、绿球的概率分别是 312＝14，212＝16，312＝14. 命题点2 对立事件的概率例4 某商场有奖销售中，购满100元商品得1张奖券，多购多得.1 000张奖券为一个开奖单位，设特等奖1个，一等奖10个，二等奖50个．设1张奖券中特等奖，一等奖，二等奖的事件分别为A ，B ，C ，求： (1)P (A )，P (B )，P (C )； (2)1张奖券的中奖概率；(3)1张奖券不中特等奖且不中一等奖的概率．解 (1)P (A )＝11 000，P (B )＝101 000＝1100，P (C )＝501 000＝120. 故事件A ，B ，C 的概率分别为11 000，1100，120. (2)1张奖券中奖包含中特等奖，一等奖，二等奖．设“1张奖券中奖”这个事件为M ，则M ＝A ＋B ＋C .∵A ，B ，C 两两互斥，∴P (M )＝P (A ＋B ＋C )＝P (A )＋P (B )＋P (C ) ＝1＋10＋501 000＝611 000.故1张奖券的中奖概率为611 000. (3)设“1张奖券不中特等奖且不中一等奖”为事件N ，则事件N 与“1张奖券中特等奖或中一等奖”为对立事件，∴P (N )＝1－P (A ＋B )＝1－⎝⎛⎭⎫11 000＋1100＝9891 000. 故1张奖券不中特等奖且不中一等奖的概率为9891 000.思维升华求复杂事件的概率的两种方法求概率的关键是分清所求事件是由哪些事件组成的，求解时通常有两种方法： (1)将所求事件转化成几个彼此互斥的事件的和事件，利用概率加法公式求解概率；(2)若将一个较复杂的事件转化为几个互斥事件的和事件时，需要分类太多，而其对立面的分类较少，可考虑利用对立事件的概率公式，即“正难则反”．它常用来求“至少”或“至多”型事件的概率．经统计，在某储蓄所一个营业窗口等候的人数相应的概率如下：求：(1)至多2人排队等候的概率； (2)至少3人排队等候的概率．解记“无人排队等候”为事件A ，“1人排队等候”为事件B ，“2人排队等候”为事件C ，“3人排队等候”为事件D ，“4人排队等候”为事件E ，“5人及5人以上排队等候”为事件F ，则事件A 、B 、C 、D 、E 、F 彼此互斥．(1)记“至多2人排队等候”为事件G ，则G ＝A ＋B ＋C ，所以P(G)＝P(A＋B＋C)＝P(A)＋P(B)＋P(C)＝0.1＋0.16＋0.3＝0.56.(2)方法一记“至少3人排队等候”为事件H，则H＝D＋E＋F，所以P(H)＝P(D＋E＋F)＝P(D)＋P(E)＋P(F)＝0.3＋0.1＋0.04＝0.44.方法二记“至少3人排队等候”为事件H，则其对立事件为事件G，所以P(H)＝1－P(G)＝0.44.22．用正难则反思想求互斥事件的概率典例(12分)某超市为了了解顾客的购物量及结算时间等信息，安排一名员工随机收集了在该超市购物的100位顾客的相关数据，如下表所示.已知这100位顾客中一次购物量超过8件的顾客占55%.(1)确定x，y的值，并估计顾客一次购物的结算时间的平均数；(2)求一位顾客一次购物的结算时间不超过．．．2分钟的概率．(将频率视为概率)思想方法指导若某一事件包含的基本事件多，而它的对立事件包含的基本事件少，则可用“正难则反”思想求解．规范解答解(1)由已知得25＋y＋10＝55，x＋30＝45，所以x＝15，y＝20.[2分]该超市所有顾客一次购物的结算时间组成一个总体，所收集的100位顾客一次购物的结算时间可视为总体的一个容量为100的简单随机样本，顾客一次购物的结算时间的平均数可用样本平均数估计，其估计值为1×15＋1.5×30＋2×25＋2.5×20＋3×10100＝1.9(分钟)．[6分](2)记A 为事件“一位顾客一次购物的结算时间不超过2分钟”，A 1，A 2分别表示事件“该顾客一次购物的结算时间为2.5分钟”，“该顾客一次购物的结算时间为3分钟”，将频率视为概率得P (A 1)＝20100＝15，P (A 2)＝10100＝110.[9分]P (A )＝1－P (A 1)－P (A 2)＝1－15－110＝710.[11分]故一位顾客一次购物的结算时间不超过2分钟的概率为710.[12分]1．(2016·天津)甲、乙两人下棋，两人下成和棋的概率是12，甲获胜的概率是13，则甲不输的概率为( ) A.56 B.25 C.16 D.13答案 A解析事件“甲不输”包含“和棋”和“甲获胜”这两个互斥事件，所以甲不输的概率为12＋13＝56. 2．(教材改编)袋中装有3个白球，4个黑球，从中任取3个球，则①恰有1个白球和全是白球；②至少有1个白球和全是黑球；③至少有1个白球和至少有2个白球；④至少有1个白球和至少有1个黑球．在上述事件中，是对立事件的为( ) A ．① B ．② C ．③ D ．④ 答案 B解析至少有1个白球和全是黑球不同时发生，且一定有一个发生．∴②中两事件是对立事件．3．(2016·安阳模拟)从一箱产品中随机地抽取一件，设事件A ＝{抽到一等品}，事件B ＝{抽到二等品}，事件C ＝{抽到三等品}，且已知P (A )＝0.65，P (B )＝0.2，P (C )＝0.1，则事件“抽到的产品不是一等品”的概率为( )A．0.7 B．0.65 C．0.35 D．0.5答案 C解析“抽到的产品不是一等品”与事件A是对立事件，∴所求概率P＝1－P(A)＝0.35.4．(2016·襄阳模拟)有一个游戏，其规则是甲、乙、丙、丁四个人从同一地点随机地向东、南、西、北四个方向前进，每人一个方向．事件“甲向南”与事件“乙向南”是()A．互斥但非对立事件B．对立事件C．相互独立事件D．以上都不对答案 A解析由于每人一个方向，故“甲向南”意味着“乙向南”是不可能的，故是互斥事件，但不是对立事件，故选A.5．(2016·蚌埠模拟)从一篮子鸡蛋中任取1个，如果其重量小于30克的概率为0.3，重量在[30,40]克的概率为0.5，那么重量不小于30克的概率为()A．0.8 B．0.5 C．0.7 D．0.3答案 C解析由互斥事件概率公式知重量大于40克的概率为1－0.3－0.5＝0.2，又∵0.5＋0.2＝0.7，∴重量不小于30克的概率为0.7.6．对一批产品的长度(单位：mm)进行抽样检测，下图为检测结果的频率分布直方图．根据标准，产品长度在区间[20,25)上的为一等品，在区间[15,20)和[25,30)上的为二等品，在区间[10,15)和[30,35)上的为三等品．用频率估计概率，现从该批产品中随机抽取一件，则其为二等品的概率为()A．0.09 B．0.20 C．0.25 D．0.45答案 D解析设区间[25,30)对应矩形的高为x，则所有矩形面积之和为1，即(0.02＋0.04＋0.06＋0.03＋x )×5＝1，解得x ＝0.05.产品为二等品的概率为0.04×5＋0.05×5＝0.45. 7．在200件产品中，有192件一级品，8件二级品，则下列事件： ①在这200件产品中任意选出9件，全部是一级品； ②在这200件产品中任意选出9件，全部是二级品； ③在这200件产品中任意选出9件，不全是二级品．其中________是必然事件；________是不可能事件；________是随机事件．答案 ③ ② ①8．已知某运动员每次投篮命中的概率都为40%，现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率：先由计算器产生0到9之间取整数值的随机数，指定1,2,3,4表示命中，5,6,7,8,9,0表示不命中；再以每三个随机数为一组，代表三次投篮的结果．经随机模拟产生了如下20组随机数：907 966 191 925 271 932 812 458 569 683 431 257 393 027 556 488 730 113 537 989据此估计，该运动员三次投篮恰有两次命中的概率为________．答案 0.25解析 20组随机数中表示三次投篮恰好有两次命中的是191,271,932,812,393，其频率为520＝0.25，以此估计该运动员三次投篮恰有两次命中的概率为0.25.9．若随机事件A ，B 互斥，A ，B 发生的概率均不等于0，且P (A )＝2－a ，P (B )＝4a －5，则实数a 的取值范围是________________．答案 (54，43]解析由题意可知⎩⎪⎨⎪⎧0<P (A )<1，0<P (B )<1，P (A )＋P (B )≤1⇒⎩⎪⎨⎪⎧0<2－a <1，0<4a －5<13a －3≤1，⇒⎩⎪⎨⎪⎧1<a <2，54<a <32，a ≤43⇒54<a ≤43. 10．若A ，B 互为对立事件，其概率分别为P (A )＝4x ，P (B )＝1y ，且x >0，y >0，则x ＋y 的最小值为________．答案 9解析由题意可知4x ＋1y ＝1，则x ＋y ＝(x ＋y )(4x ＋1y )＝5＋(4y x ＋x y )≥9，当且仅当4y x ＝xy，即x ＝2y时等号成立．11．某保险公司利用简单随机抽样方法，对投保车辆进行抽样，样本车辆中每辆车的赔付结果统计如下：(1)若每辆车的投保金额均为2 800元，估计赔付金额大于投保金额的概率；(2)在样本车辆中，车主是新司机的占10%，在赔付金额为4 000元的样本车辆中，车主是新司机的占20%，估计在已投保车辆中，新司机获赔金额为4 000元的概率．解(1)设A表示事件“赔付金额为3 000元”，B表示事件“赔付金额为4 000元”，以频率估计概率得P(A)＝1501 000＝0.15，P(B)＝1201 000＝0.12.由于投保金额为2 800元，赔付金额大于投保金额对应的情形是赔付金额为3 000元和4 000元，所以其概率为P(A)＋P(B)＝0.15＋0.12＝0.27.(2)设C表示事件“投保车辆中新司机获赔4 000元”，由已知，样本车辆中车主为新司机的有0.1×1 000＝100(辆)，而赔付金额为4 000元的车辆中，车主为新司机的有0.2×120＝24(辆)，所以样本车辆中新司机车主获赔金额为4 000元的频率为24100＝0.24，由频率估计概率得P(C)＝0.24.12．国家射击队的队员为在射击世锦赛上取得优异成绩，正在加紧备战，经过近期训练，某队员射击一次命中7～10环的概率如下表所示：求该射击队员射击一次：(1)射中9环或10环的概率；(2)命中不足8环的概率．解记事件“射击一次，命中k环”为A k(k∈N，k≤10)，则事件A k之间彼此互斥．(1)记“射击一次，射中9环或10环”为事件A，那么当A9，A10之一发生时，事件A发生，由互斥事件的加法公式得P(A)＝P(A9)＋P(A10)＝0.28＋0.32＝0.6.(2)设“射击一次，至少命中8环”的事件为B ，则B 表示事件“射击一次，命中不足8环”．又B ＝A 8＋A 9＋A 10，由互斥事件概率的加法公式得 P (B )＝P (A 8)＋P (A 9)＋P (A 10) ＝0.18＋0.28＋0.32＝0.78.故P (B )＝1－P (B )＝1－0.78＝0.22.因此，射击一次，命中不足8环的概率为0.22.13.一盒中装有12个球，其中5个红球，4个黑球，2个白球，1个绿球．从中随机取出1球，求：(1)取出1球是红球或黑球的概率； (2)取出1球是红球或黑球或白球的概率．解方法一 (利用互斥事件求概率) 记事件A 1＝{任取1球为红球}，A 2＝{任取1球为黑球}，A 3＝{任取1球为白球}，A 4＝{任取1球为绿球}，则P (A 1)＝512，P (A 2)＝412＝13，P (A 3)＝212＝16，P (A 4)＝112.根据题意知，事件A 1，A 2，A 3，A 4彼此互斥，由互斥事件的概率公式，得 (1)取出1球为红球或黑球的概率为 P (A 1＋A 2)＝P (A 1)＋P (A 2) ＝512＋412＝34. (2)取出1球为红球或黑球或白球的概率为 P (A 1＋A 2＋A 3)＝P (A 1)＋P (A 2)＋P (A 3) ＝512＋412＋212＝1112. 方法二 (利用对立事件求概率)(1)由方法一知，取出1球为红球或黑球的对立事件为取出1球为白球或绿球，即A 1＋A 2的对立事件为A 3＋A 4，所以取出1球为红球或黑球的概率为P (A 1＋A 2)＝1－P (A 3＋A 4)＝1－P (A 3)－P (A 4)＝1－212－112＝34.(2)因为A 1＋A 2＋A 3的对立事件为A 4，1 12＝1112.所以P(A1＋A2＋A3)＝1－P(A4)＝1－。

北大测试全套课件和教案,第3章第1讲

《软件测试基础》授课教案授课内容：第三章单元测试授课课次：第6次课授课时数：2学时授课日期: 上课教室:目的与要求：要求学生掌握单元测试的概念，了解单元测试的方法和相关的基本知识。

教学重点：1.单元测试的概念2.单元测试的过程3.单元测试常用的方法教学难点：单元测试环境单元测试的概念教学方式：1.运用《单元测试》课件进行课堂讲授，加强学生对测试的理解。

教学内容：1.为什么要进行单元测试2.单元测试的基本概念3.单元测试过程4.白盒测试和黑盒测试比较内容提要及时间分配：1、课前引入（5分钟）◆通常我们写完代码，习惯性做的第一件事情是什么？2、单元测试的重要性（30分钟）◆对单元测试的一些错误认识◆单元测试的重要性◆实行单元测试的好处3、单元测试的基本概念（30分钟）◆单元测试的内容◆单元测试的环境构成◆单元测试的常用方法4、单元测试的过程（15分钟）5、白盒测试和黑盒测试比较（5分钟）6、课后小节和布置作业（5分钟））教学参考书：1.软件测试方法和技术朱少民清华大学出版社2.软件测试 Paul C.Jorgensen 机械工业出版社3.Visual Basic.编程导论 David I.Schneider 电子工业出版社讨论与思考：1.单元测试中单元的概念讨论。

作业:1．什么是单元测试？2．单元测试主要采用什么测试方法？复问题目：教学内容与方法步骤引言：我们每天都在做单元测试。

你写了一个函数，除了极简单的外，总是要执行一下，看看功能是否正常，有时还要想办法输出些数据，如弹出信息窗口什么的，这，就是单元测试，可以把这种单元测试称为临时单元测试。

只进行了临时单元测试的软件，针对代码的测试很不完整，代码覆盖率要超过70%都很困难，未覆盖的代码可能遗留大量的细小的错误，这些错误还会互相影响，当BUG暴露出来的时候难于调试，大幅度提高后期测试和维护成本，也降低了开发商的竞争力。

可以说，进行充分的单元测试，是提高软件质量，降低开发成本的必由之路。

清华北大十一分班考试班教师版

1.如图，BD ，FB ，FC 将长方形ABC D 分成5块，白色三角形面积是1平方厘米，兰色三角形面积是2平方厘米，红色三角形的面积是多少平方厘米?蓝红白FEDCBA【分析】白色三角形和蓝色三角形面积比为1:2，所以:1:2FE EC =，那么::1:2,F D B C F EE C ==说明F为AD 的中点，即A F FD =，红色三角形面积就等于白色三角形和蓝色三角形的面积之和，即123+=。

2.一张长方形纸片，把它的右上角往下折叠(如图甲)阴影部分面积占原纸片面积的27；再把左下角往上折叠(如图乙)，乙图中阴影部分面积占原纸片面积的________(答案用分数表示)。

甲乙【分析】甲图阴影面积占原纸面积27，设原纸的长为7，说明阴影的宽为2，原纸的空白部分为边长5的正方形，即原纸的宽为5，左下角折叠的三角形打开为边长2的正方形，523,326-=⨯=为乙图阴影面积，原纸面积为7535⨯=，所以乙图中阴影面积占原纸面积的635。

第二讲几何3.有甲、乙、丙三个梯形，他们的高之比是1:2:3，上底之比依次是6:9:4，下底之比依次是12:15:10．已知甲梯形的面积是30平方厘米，那么乙与丙两个梯形的面积之和是多少平方厘米?【分析】设甲梯形的高为x ，上底的长为6y ，下底的长为12z ，那么根据甲梯形的面积公式得到等式：()612230y z x +÷=，整理为210xy xz +=，而乙梯形的面积为()91522915y z x xy xz +⨯÷=+，丙梯形的面积为()41032615y z x xy xz +⨯÷=+，乙丙两个梯形的面积之和为 1530xy xz +=()1521510150xy xz +=⨯=平方厘米。

4.如图，ABC G 是4×7的长方形，D EFG 是2×10长方形，那么，三角形形BC M 的面积与D EM 的面积之差是_______。

北大测试全套课件和教案第1-6章习题与解答

第1章习题解答1．为何说软件缺陷的最大来源是产品说明书？解答：产品说明书没有写，我们要记得说不出来就做不出来；产品说明书不完整、不停更改，难以和开发人员沟通。

2．简述软件质量保证和软件测试的关系。

解答：软件质量保证（SQA）是建立一套有计划，有系统的方法，来向管理层保证拟定出的标准、步骤、实践和方法能够正确地被所有项目所采用。

软件测试流程包括项目计划检查、测试计划创建、测试设计、执行测试、更新测试文档和测试评估；SQA的活动可总结为协调度量、风险管理、文档检查、促进／协助流程改进、监察测试工作。

软件质量保证和软件质量控制之间的界限越来越模糊了。

软件测试是SQA中的重要手段，SQA的主要功能在软件测试中得到体现，集中在静态测试中，两者的关系越来越紧密。

3．在了解软件测试职业及其素质要求后，对你从事软件职业的生涯设计有何影响？略。

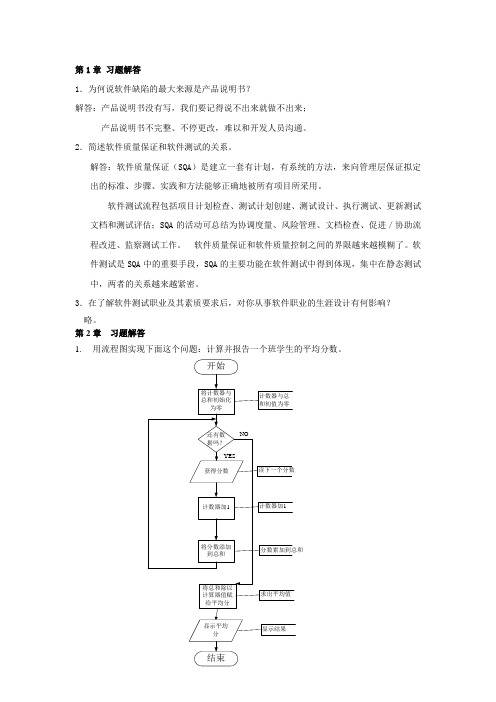
第2章习题解答1.用流程图实现下面这个问题：计算并报告一个班学生的平均分数。

2.用伪代码实现下面这个问题：输入一年中的某月，然后给出该月的天数，如果是2月，用户将回答这年是否是闰年。

#include<iostream.h>void main(){int month,year;bool Isleap;cout<<"please input year:(1812-2012)";cin>>year;if((year%4==0)&&(year%100!=0)||(year%100!=0)&&(year%400==0)){ Isleap=true;cout<<"是闰年";}else{Isleap=false;cout<<"不是闰年";}cout<<"please input the month:(1-12)";cin>>month;switch( month){case 1:case 3:case 5:case 7:case 8:case 10:case 12:cout<<"31天.";break;case 4:case 6:case 9:case 11:cout<<"30天.";break;case 2:if(Isleap)cout<<"29天.";else cout<<"28天";break;default:cout<<"erroe!";}}3.PriorDate是NextDate的逆函数，参照NextDate，写出PriorDate的伪代码。

北师版高中同步学考数学选修1-1精品课件模块复习课第1课时常用逻辑用语

a·b=|a||b|或a·b=-|a||b|,所以“a·b=|a||b|”是“a∥b”的充分不必要条
件,故选A.
(2)由a⊥b知a·b=0,即2(x-1)+2=0,所以x=0.
而当x=0时,a=(-1,2),b=(2,1),必有a⊥b,所以a⊥b的充要条件是
x=0.
(3)要使不等式x2-2ax+a>0的解集为R,应有Δ=(-2a)2-4a<0,即4a24a<0,所以0<a<1,此为“关于x的不等式x2-2ax+a>0的解集为R”的
不必要条件;
④已知p,q为两个命题,若p∨q为假命题,则( p)∧( q)为真命题.
其中所有真命题的序号是
.
-12-
第1课时
专题归纳
J基础梳理 Z专题整合
常用逻辑用语
ICHU SHU LI
高考体验
专题一
专题二
专题三
HUANTIZHENGHE
专题四
答案:①②④
解析:①∵x-3=0⇒x-3≤0,∴原命题为真命题.
打“×”.
(1)“x2+2x-3<0”是命题.(
)
(2)“sin 45°=1”是真命题.(
)
(3)命题“若p,则q”的否命题是“若p,则 q”.(
)
(4)若原命题为真,则这个命题的否命题、逆命题、逆否命题中至
少有一个为真.(
)
(5)当q是p的必要条件时,p是q的充分条件.(
)
(6)当p是q的充要条件时,也可说成q成立当且仅当p成立.(
充要条件,因此一个必要不充分条件是0≤a≤1.
-15-
第1课时
专题归纳
J基础梳理 Z专题整合

北师版高中同步学考数学选修1-1精品课件第一章 §1 命题

(2)如果x=1,那么x>3;
(3)方程x2-5x+6=0的根是x=2;
(4)x2-5x+6=0;
(5)一个实数不是正数就是负数;
(6)矩形是平行四边形;
(7)把这道题解出来;
(8)正方形是平行四边形吗?
-13-
§1命题
探究一
首页
探究二
探究三
自主预习
探究学习
当堂检测
思维辨析
分析判断一个语句是否为命题,应把握住这个语句能否判断真假.
质”(即分别否定)后,可以构成其他三种不同形式的命题.
设原命题:若p,则q.
则逆命题:将条件和结论“换位”,即“若q,则p”.
否命题:将条件和结论都“换质”,即分别否定.
逆否命题:将条件和结论“换位”又“换质”,即互换位置,且分别否
定.
-6-
§1命题
首页
自主预习
探究学习
当堂检测
特别提醒1.一定要分清命题的条件和结论,注意大前提是不能作
(2)“对顶角相等”的逆命题;
(3)“直角三角形的两个锐角互为余角”的逆否命题;
(4)若a≥0或b≥0,则a+b≥0.
分析可以先根据要求写出每个命题,再判断真假.也可以不写出
命题,而利用四种命题之间的等价关系进行判断.
-20-
§1命题
探究一
首页
探究二
探究三
自主预习
探究学习
当堂检测
思维辨析
解(1)(方法一)“若x+y=0,则x,y互为相反数”的否命题是“若x+y≠0,
§1 命题
-1-
§1命题
首页
课标阐释
自主预习
探究学习
当堂检测

【高中课件】高中数学北师大版选修11命题导学课件ppt.ppt

中小学精编教育课件
第一章常用逻辑用语
知识点命题及其关系充分条件与必要条件简单的逻辑联结词全称量词与存在量词
新课程标准的要求
层次要求
领域目标要求
1.了解命题的概念及命题的四种
形式(即原命题、逆命题、否命题、
逆否命题)
2.会分析四种命题间的相互关系
和等价关系
3.能根据已知命题写出它的逆命
叫作互否命题.如果把其中一个命题叫作原命题,那么另一个命题就叫作原命题的否命题 .
对于两个命题,其中一个命题的条件和结论恰好是另一个命题
的
结论的否定和
条件的否定 ,我们把这样的两个命
题叫作互为逆否命题 .如果把其中的一个命题叫作原命题,那么另一个命题就叫作原命题的逆否命题 .
问题3 四种命题之间的相互关系
问题4 四种命题的真假性的判断情况:
原命题逆命题否命题逆题否命
真
真
真
真
真
假
假
真
假
真
真
假
假
假
假
假
说明:(1)原命题与逆否命题,否命题与逆命题具有相同的真假 ; (2)互逆命题和互否命题,它们的真假性没有关系; (3)在判断一些命题的真假时,如果不容易直接判断,可以通过判断
其逆否命题的真假来判断原命题的真假.
有一家主人是一个不善言辞的木讷之人,一天主人邀请张三、李四、王五三人吃饭聊天,时间到了,只有张三、李四
准时赴约,王五打电话说:“临时有急事不能来了.”主人听到随口说了一句:“你看看,该来的没来.”张三听到,脸色一
沉,起来一声不吭地走了,主人愣了片刻,又道了句:“哎,不
该走的走了.”李四一听大怒,拂袖而去,主人尴尬不知所措.

高中数学(北师大版,选修11)：第一章常用逻辑用语+课件+同步测试+本章整合+综合素质检测(12份

第一章§3一、选择题1．下列命题中，全称命题的个数为()①平行四边形的对角线互相平分；②梯形有两边平行；③存在一个菱形，它的四条边不相等．A．0 B．1C．2 D．3[答案] C[解析]①②是全称命题，③是特称命题．2．下列特称命题中真命题的个数是()①存在x∈R，x≤0；②至少有一个整数，它既不是合数，也不是素数；③存在x∈{x|x是整数}，x2是整数．A．0 B．1C．2 D．3[答案] D[解析]①②③都是真命题．3．下列命题为特称命题的是()A．偶函数的图像关于y轴对称B．正四棱柱都是平行六面体C．不相交的两条直线是异面直线D．存在实数大于等于3[答案] D[解析]分清各命题中含有的量词是全称量词还是存在量词，其中选项A，B，C都是全称命题．4．下列命题中是全称命题的是()A．所有的正方形都是菱形B．有两个实数x，使得x2＋3x＋2＝0C．存在两条相交直线平行于同一个平面D．存在一无理数x，使得x2也是无理数[答案] A[解析]B，C，D是特称命题．5．下列命题中，真命题是()A．存在m∈R，使函数f(x)＝x2＋mx(x∈R)是偶函数B ．存在m ∈R ，使函数f (x )＝x 2＋mx (x ∈R )是奇函数C ．对任意m ∈R ，函数f (x )＝x 2＋mx (x ∈R )都是偶函数D ．对任意m ∈R ，函数f (x )＝x 2＋mx (x ∈R )都是奇函数[答案] A[解析] 显然当m ＝0时，f (x )＝x 2为偶函数，故选A.6．设函数f (x )的定义域为R ，有下列三个命题：①若存在常数M ，使得对任意x ∈R ，有f (x )≤M ，则M 是函数f (x )的最大值；②若存在x 0∈R ，使得对任意x ∈R ，且x ≠x 0，有f (x )≤f (x 0)，则f (x 0)是函数f (x )的最大值； ③若存在x 0∈R ，使得对任意x ∈R ，有f (x )≤f (x 0)，则f (x 0)是函数f (x )的最大值．这些命题中，真命题的个数是( )A ．0个B ．1个C ．2个D ．3个 [答案] C[解析] 对于①，M 不一定在函数f (x )的值域内，故①不正确；对于②③，所取值x 0在其定义域内，f (x 0)在函数f (x )的值域内，f (x 0)为函数f (x )的最大值，故②③正确，故应选C.二、填空题7．(2014·高州四中质量检测)已知函数f (x )＝x 2＋mx ＋1，若命题“存在x 0>0，f (x 0)<0”为真，则m 的取值范围是________．[答案] (－∞，－2)[解析] 由条件知⎩⎪⎨⎪⎧－m 2>0，m 2－4>0，∴m <－2.8．下列命题中真命题为________，假命题为________．①末位是0的整数，可以被2整除；②角平分线上的点到这个角的两边的距离相等；③有的实数是无限不循环小数；④有些三角形不是等腰三角形；⑤所有的菱形都是正方形[答案] ①②③④ ⑤9．下列语句：①能被7整除的数都是奇数；②|x －1|<2；③存在实数a 使方程x 2－ax ＋1＝0成立；④等腰梯形对角线相等且不互相平分．其中是全称命题且为真命题的序号是________．[答案] ④[解析] ①是全称命题，但为假命题，②不是命题，③是特称命题，只有④是全称命题且为真命题．三、解答题10．判断下列命题是全称命题还是特称命题，并判断其真假．(1)存在两个相交平面垂直于同一条直线；(2)有些整数只有两个正因数；(3)对任意实数α，有sin2α＋cos2α＝1；(4)存在一条直线，其斜率不存在；(5)对所有的实数a、b，方程ax＋b＝0都有唯一解．[答案](1)(2)(4)为特称命题(3)(5)为全称命题(2)(3)(4)真(1)(5)假[解析](1)是特称命题．因为垂直于同一条直线的两个平面是互相平行的，因此不存在两个相交的平面垂直于同一条直线．所以特称命题“存在两个相交平面垂直于同一条直线”是假命题．(2)是特称命题．因为存在整数2只有两个正因数1和2，所以特称命题“有些整数只有两个正因数”是真命题．(3)是全称命题，由三角函数知识知“对任意α∈R，sin2α＋cos2α＝1都成立”，故此命题是真命题．(4)是特称命题，因为垂直于x轴的直线斜率不存在，所以“存在直线l，l的斜率不存在”，是真命题．(5)是全称命题，因为0x＋3＝0无解，所以“对任意a、b∈R，方程ax＋b＝0都有唯一解”，是假命题.一、选择题11．命题“任意x>1，log2x<0”的否定是()A．任意x>1，log2x≥0 B．任意x≤1，log2x>0C．存在x>1，log2x≥0 D．存在x≤1，log2x>0[答案] C[解析]全称命题的否定是特称命题，故选C.12．给出下列四个命题，其中为真命题的是()A．任意x∈R，x2＋3<0 B．任意x∈N，x2≥1C．存在x∈Z，使x5<1 D．存在x∈Q，x2＝3[答案] C[解析]由于任意x∈R，都有x2≥0，因而有x2＋3≥3，所以命题“任意x∈R，x2＋3<0”为假命题；由于0∈N，当x＝0时，x2≥1不成立，所以命题“任意x∈N，x2≥1”是假命题；由于－1∈Z，当x＝－1时，x5<1，所以命题“存在x∈Z，使x5<1”为真命题；由于使x2＝3成立的数只有±3，而它们都不是有理数，因此没有任何一个有理数的平方能等于3，所以命题“存在x∈Q，x2＝3”是假命题．故选C.13．下列命题中的假命题是()A．存在实数α和β，使cos(α＋β)＝cosαcosβ＋sinαsinβB．不存在无穷多个α和β，使cos(α＋β)＝cosαcosβ＋sinαsinβC．对任意α和β，使cos(α＋β)＝cosαcosβ－sinαsinβD．不存在这样的α和β，使cos(α＋β)≠cosαcosβ－sinαsinβ[答案] B[解析]cos(α＋β)＝cosα·cosβ－sinα·sinβ，显然C、D为真；sinα·sinβ＝0时，A为真；B为假．故选B.14．(2014·福州市八县联考)命题“有些实数的绝对值是正数”的否定是()A．对任意x∈R，|x|>0B．存在x0∈R，|x0|>0C．对任意x∈R，|x|≤0 D．存在x0∈R，|x0|≤0[答案] C[解析]由词语“有些”知原命题为特称命题，故其否定为全称命题，因为命题的否定只否定结论，所以选C.15．(2014·甘肃临夏中学期中)命题“存在x∈Z，使x2＋2x＋m≤0成立”的否定是()A．存在x∈Z，使x2＋2x＋m>0B．不存在x∈Z，使x2＋2x＋m>0C．对于任意x∈Z，都有x2＋2x＋m≤0D．对于任意x∈Z，都有x2＋2x＋m>0[答案] D[解析]特称命题的否定是全称命题．16．(2014·海南省文昌市检测)下列命题中是假命题．．．的是()A．存在m∈R，使f(x)＝(m－1)·xm2－4m＋3是幂函数，且在(0，＋∞)上单调递减B．对任意a>0，函数f(x)＝ln2x＋ln x－a有零点C．存在α、β∈R，使cos(α＋β)＝cosα＋sinβD．对任意φ∈R，函数f(x)＝sin(2x＋φ)都不是偶函数[答案] D[解析] ∵f (x )为幂函数，∴m －1＝1，∴m ＝2，f (x )＝x －1，∴f (x )在(0，＋∞)上递减，故A 真；∵y ＝ln 2x ＋ln x 的值域为[－14，＋∞)，∴对任意a >0，方程ln 2x ＋ln x －a ＝0有解，即f (x )有零点，故B 真；当α＝π6，β＝2π时，cos(α＋β)＝cos α＋sin β成立，故C 真；当φ＝π2时，f (x )＝sin(2x ＋φ)＝cos2x 为偶函数，故D 为假命题．二、填空题17．已知命题“存在x ∈R ，使2x 2＋(a －1)x ＋12≤0”是假命题，则实数a 的取值范围是________． [答案] －1<a <3[解析] 由条件得命题“任意x ∈R ，使2x 2＋(a －1)x ＋12>0”是真命题．所以Δ＝(a －1)2－4<0，解得－1<a <3.三、解答题18．指出下列命题是全称命题还是特称命题，并判断其真假：(1)在平面直角坐标系中，任意有序实数对(x ，y )，都对应一点P ；(2)存在一个函数，既是偶函数又是奇函数；(3)每一条线段的长度都能用正有理数表示；(4)存在一个实数，使等式x 2＋x ＋8＝0成立．[答案] (1)全称命题，真命题；(2)特称命题，真命题；(3)全称命题，假命题；(4)特称命题，假命题．。

北京大学国际象棋课程 ppt课件

课后练习
双方仅用兵和王作战，
练习兵的使用
课后消遣
轮到白方走棋，
要设法和棋
（注意，黑方不笨）
例如10分钟包干、1小时包干、1’+0”
温和一点的时制: （需要电子钟）加秒制：双方各给定一定初始时间，每走完一步棋补偿若干秒
例如5’+3” , 2’+12” , 0’+1”
用时
大赛时制：分段计时，在一定时限内完成若干步棋，然后携带剩余时间进入下一时限
例如：第一时限：2小时完成40步棋第二时限：1小时完成20步棋第三时限：1小时包干
棋钟位置
白方先行，略占优势。
为了照顾黑方，棋钟一般应摆在黑方的右手方向
棋钟位置
如果想刺激一点，
不妨把棋钟放在距离棋盘10 米远的地方
开钟
双方握手后，
由黑方先按钟，
使白方开始倒计时
然后白方开始走出第一步棋……
按钟
每方走完棋后要按钟，使己方停止倒计时，对方开始倒计时
某次大赛上的裁判席特写，注意那堆备用的棋子
补充知识：关于和棋
例如：双方都只剩下单王
或一方还剩单象（或
对方
B. 逼和
C. 三次重复局面
D. 无休无止的长将
有导致棋局
E. 连续50回合双方未吃永无休止的嫌疑
子且没有走兵
F. 双方同意和棋
关于时间
棋子的时间
如图黑方超时但如果黑方多一兵反而要判为黑为他有被杀的可能性21课后练习任意方先行课上出现过的这个局面需要亲自练习仔细体会占领关键22课后练习双方仅用兵和王作战练习兵的使23课后消遣轮到白方走棋要设法和24课后消遣轮到白方走棋白方要将

【素材】高中数学北师大版选修11第一章教材点拨充分条件与必要条件word素材

【关键字】素材充分条件与必要条件教材点拨一、充分条件命题的条件和结论是构成命题的两个部分，并且条件和结论可以互相转化。

当一个命题为假命题时，可以说条件不能推出结论；而当命题为真命题时，可以说由此条件能推出结论。

所以一个命题从条件和结论的角度看，条件与结论有着一定的关系，即：由条件能否推出结论？如果由命题的条件能推出结论，那么命题就是真命题，此时条件就叫结论的充分条件。

物理模型的直观解释：如图电路图，当开关A紧闭时，灯泡B亮，而当灯泡B亮时，开关A却不一定是紧闭的；即要使灯泡B亮，只要开关A紧闭着一个条件就够了，我们就称“开关A紧闭”是“灯泡B亮”的充分条件。

一般地，“若，则”是一个真命题，是指由通过推理可以得出，即由可推出，记作，那么，就称条件是结论的充分条件（sufficient condition）。

“若，则”是一个真命题，是指由通过推理可以得出，即由可推出，记作，那么，就称是的充分条件（sufficient condition）。

例如：①，那么，“”是“”成立的充分条件；②，那么，“”是“”成立的充分条件；③三边对应相等的两个三角形全等：“三边对应相等”是“两个三角形全等”的充分条件；④“”是函数为幂函数的充分条件；警示：充分条件就是某一个结论成立应该具备的条件，当命题具备此条件时，就可以得出此结论，或者要是此结论成立，只要具备此条件就够了，而当命题不具备此条件时，结论也有可能成立。

例如，当时，成立，但是，当时，也可以成立，即时，也成立，所以，是成立的充分条件，也是成立的充分条件。

【例】仿照示例改写下列命题，并判断条件是否为充分条件：示例：若，则，可以改写成：；是充分条件；（1）个位数字是0的自然数能被5整除；（2）对角线相等的四边形是矩形；（3）与同一平面所成的角相等的两条直线平行；（4）若定义域为的函数为奇函数，则解：（1）个位数字是0的自然数这个自然数能被5整除；是充分条件；（2）四边形的对角线相等这个四边形是矩形；不是充分条件；（3）两条直线与同一平面所成的角相等这两条直线平行；不是充分条件；（4）定义域为的函数为奇函数；是充分条件。

最新-2021学年北师大版高中数学选修11课件：第一章常用逻辑用语 1 精品

[边听边记]
序号结论
理由
(1) 是真命题满足指数函数定义
(2) 不是命题因为不能判断“x－2>0”的真假
因为集合{a，b，c}有∅，{a}，{b}，{c}， (3) 是假命题 {a，b}，{a，c}，{b，c}，{a，b，c}共8个
子集
(4) 不是命题因为是感叹句
(5)
是假命题
因为当x，y为无理数，且互为相反数时，x ＋y＝0，x＋y是有理数，而x，y不是有理数.
【错解】 “若p，则q”的形式：若a＞0，则函数y＝ax ＋b的值随x的增大而增大；否命题；若a≤0，则函数y＝ax＋b 的值随x的不增大而不增大．
【错因】原命题有两个条件：“a＞0”和“x增大”，其中“a＞0”是前提条件，在写原命题、逆命题、否命题、逆否命题时，都要把 “ a ＞ 0” 置于 “ 若 ” 字的前面，把 “ x 增大”作为原命题的条件．错解中对否命题的写法，把“a＞0” 和“x增大”都否定了，从而改变了一次函数的性质，特别是当a＝0时，便失去了研究“增”与“不增”的意义了，应在不改变函数性质的前提下完成解答．
第一章
常用逻辑用语
§1 命题
学课前预习学案
分析下列语句： (1)两个全等的三角形的面积相等； (2)5能被3整除； (3)今天天气真好啊！ (4)请把门关上！ (5)2是质数吗？ (6)若x＝3，则x2＝9. 其中哪些语句能判断为真？哪些语句能判断为假？哪些语句不能判断真假？提示： (1)与(6)为真，(2)为假，(3)(4)(5)无法判断真假．
表述形式若p，则q _若__q_，__则__p__ 若__¬_p_，__则__¬__q 若__¬_q_，__则__¬__p

北大测试全套课件和教案 32. 第11章 第1讲

北大测试全套课件和教案 8. 第4章 第2讲

最新北师大版高中数学选修2-1课时同步讲义(全册 共312页)

北大测试全套课件和教案 7. 第4章 第1讲

北师版高中同步学考数学选修1-1精品课件 第一章 §2 充分条件与必要条件

《走向高考》：高三数学一轮复习课件11-1(北师大)

2018版高考数学文北师大版大一轮复习讲义教师版文档 第十一章 概率 11.1 含答案 精品

北大测试全套课件和教案,第3章 第1讲

清华北大十一分班考试班 教师版

北大测试全套课件和教案 第1-6章习题与解答

北师版高中同步学考数学选修1-1精品课件 模块复习课 第1课时 常用逻辑用语

北师版高中同步学考数学选修1-1精品课件 第一章 §1 命 题