ADF检验

adf检验临界值

adf检验临界值adf检验临界值在经济学领域中，我们常常需要对时间序列数据进行分析，以了解其特征及其变化趋势。

而对于非平稳时间序列数据的检验，则需要用到ADF（Augmented Dickey-Fuller）检验方法。

而在ADF检验中，临界值的选择非常重要，因此本文将从概述ADF检验的基本原理、几种常见的ADF检验方法以及临界值选择等方面，来深入解读ADF检验临界值的重要性。

ADF检验简介ADF检验，全称Augmented Dickey-Fuller Test，是检验时间序列数据是否平稳的经典方法之一。

在这个方法中，我们会设置一个基准假设，即时间序列数据是不平稳的。

如果我们找不到反驳这个基准假设的证据，那么我们就确定了时间序列数据是不平稳的。

反之，如果我们找到了证据反驳这个基准假设，那么我们就可以符合地断定时间序列数据是平稳的。

ADF检验方法ADF检验其实有几种常见的方法，这里列举以下：1. ADF-OLS（ordinary least squares）检验：这种方法是最常见的ADF 检验方法。

其适用于没有确定趋势的时间序列数据。

2. ADF-GLS（generalized least squares）检验：这种方法是应用于数据确定趋势的情况下。

它基于一种称为Generalized Least Squares的方法来消除数据中的趋势。

3. ADF-WM（weighted mean）检验：这种方法则可以在数据不平稳的情况下使用，它首先对数据进行标准化，然后使用加权均值来计算数据的趋势，最后通过与残差进行比较确定序列的平稳性。

三种ADF检验方法的原理都非常精妙，各有优缺点，但对于临界值的选择来说，它们都具有相同的依据和标准。

ADF检验临界值在ADF检验中，我们会使用t统计量来衡量我们的样本与平稳随机游走（RW）之间的距离。

在这个过程中，我们需要参照一组临界值来判断我们的样本t统计量所处位置是否超出了这个随机游走的范畴。

adf检验名词解释

ADF检验名词解释1. 什么是ADF检验？ADF（Augmented Dickey-Fuller）检验是一种用于时间序列数据的单位根检验方法。

单位根是指时间序列数据中存在非随机趋势，即数据具有持续性的特征。

ADF检验可以帮助我们判断一个时间序列数据是否具有单位根，从而确定其是否为稳定的平稳过程。

2. 单位根和平稳过程单位根是时间序列数据中的非随机趋势，它表示数据存在长期依赖关系，即过去的值对未来值有预测能力。

相反，平稳过程是指时间序列数据的统计特性在时间上保持不变，不受外部因素影响。

在经济学和金融学中，平稳过程是进行预测和建模的基础。

如果一个时间序列数据包含单位根，则其统计性质会发生变化，使得预测和建模变得困难。

3. ADF检验的原理ADF检验基于Dickey-Fuller回归模型，在该模型中，被解释变量是时间序列数据的差分值（将原始数据进行一阶差分），解释变量包括差分值、滞后差分值以及其他可能影响时间序列数据的因素。

ADF检验的原假设（H0）是存在单位根，即时间序列数据是非平稳的。

备择假设（H1）是不存在单位根，即时间序列数据是平稳的。

通过对回归模型进行估计和假设检验，我们可以判断原假设是否成立，并得出结论。

4. ADF检验的步骤步骤1：提取差分值首先，我们需要对原始时间序列数据进行差分操作，获得一阶差分值。

这样做可以消除数据中的线性趋势。

步骤2：构建ADF回归模型在ADF检验中，我们使用自回归模型（AR）来对差分后的数据进行建模。

这个模型包括一个滞后项和其他可能影响时间序列数据的因素。

步骤3：估计ADF模型参数通过最小二乘法估计ADF模型中的参数，并计算出参数的标准误差。

这些参数和标准误差将用于后续的统计推断。

步骤4：进行假设检验在ADF检验中，我们需要对回归系数进行假设检验。

常见的方法是计算t统计量，并与相应的临界值进行比较。

如果t统计量大于临界值，则可以拒绝原假设，认为时间序列数据是平稳的。

adf检验通俗解释

adf检验通俗解释
ADF检验，即单位根检验（Augmented Dickey-Fuller Test），是一种经济学时间序列分析中常用的统计方法。

它用来判断一个时间序列数据是否存在单位根，即是否存在趋势。

通俗地说，单位根检验用来判断时间序列数据的变化趋势是否随机性的，或者说是否存在长期趋势。

如果数据存在长期趋势，就不能用简单的方法进行分析和预测，因为数据变化是有规律的。

而单位根检验可以帮助我们识别数据是否存在长期趋势，从而选择合适的模型来进行进一步分析。

ADF检验的思路是将时间序列数据拆分成趋势项、季节项、残差项等不同部分，然后分别对这些部分进行统计检验。

如果残差项（即剔除了趋势项和季节项后的数据）不存在单位根，那么我们可以认为原始数据也不存在单位根，即没有长期趋势。

通过ADF检验，我们可以得到一个统计量，根据这个统计量的显著性水平，来判断时间序列是否存在单位根。

如果统计量的值小于某个阈值，即p值小于显著性水平，那么我们可以拒绝存在单位根的假设，认为数据不存在长期趋势。

总之，ADF检验是一种用来判断时间序列数据是否存在长期趋势的方法，通过检验序列的残差项是否存在单位根，来判断原始数据是否存在单位根。

引自Ruey S. Tsay著，王辉、潘家柱译《金融时间序列分析》（第2版）DF检验为了检验资产的对数价格p t是否服从一个随机游动或一个带漂移的随机游动，对模型p t=ϕ1p t−1+e t (1)p t=ϕ0+ϕ1p t−1+e t (2)其中e t为误差项。

考虑原假设H0:ϕ1=1;H1:ϕ1<1，即是一个单位根检验问题。

一个方便的检验统计量就是在原假设下ϕ1的最小二乘估计的t−比。

对(1)式，由最小二乘法得ϕ1=p t−1p tTt=1t−1Tt=1,σe2=p t−ϕ1p t−12Tt=1其中p0=0，T为样本容量。

t−比为DF≡t−比=ϕ1−1ϕ1的标准差=p eTσe p t−12Tt=1这个t−比检验通常称为DF检验。

若e t为一个白噪声序列，其稍高于二阶的矩是有限的，则当T⟶∞时DF统计量趋于一个标准布朗运动的函数。

如果ϕ0=0但我们采用了(2)式，则所得的检验ϕ1=1的t−比将趋于另一种非标准的渐进分布。

上述两种情形都是用模拟方法来得到检验统计量的临界值。

然而如果ϕ0≠0且使用的是(2)式，则用来检验ϕ1=1的t−比是渐进正态的，但此时将需要很大的样本容量来保证渐进正态分布的使用。

ADF检验用x t表示一个AR(p)时间序列，为了验证序列是否存在单位根，通常人们采用ADF检验来验证，即可以用如下回归来进行假设检验（H0:β=1;H1:β<1）：x t=c t+βx t−1+ϕiΔx t−i+e tp−1i=1其中c t是关于时间t的确定性函数，Δx j=x j−x j−1是x t的差分序列。

在实际中，c t可以是常数或者c t=ω0+ω1t。

β−1的t−比为ADF−检验=β−1β的标准差其中β为β的最小二乘估计，上述t−比就是著名的ADF检验。

注意到由于一阶差分，上面x t的式子等价于一个带确定性函数c t的AR(p)模型，可以改写为Δx t=c t+βc x t−1+ϕiΔx t−i+e tp−1i=1其中βc=β−1，相应的检验为H0:βc=0;H1:βc<0。

平稳序列检验方法

平稳序列检验方法平稳序列检验是判断一个时间序列是否具有平稳性的方法。

平稳序列是指序列的统计特性在时间上不发生变化，即均值、方差和自协方差与时间无关。

判断一个序列是否平稳很重要，因为只有平稳序列才能进行许多经济和统计分析。

平稳序列检验方法主要有单位根检验、ADF检验和KPSS检验等。

单位根检验是最常用的平稳序列检验方法之一，其基本思想是判断一个序列是否具有单位根。

单位根的存在意味着序列是非平稳的。

ADF检验是单位根检验的一种常用方法，它是在一个线性回归模型的基础上构建的。

具体而言，假设要检验的序列为Yt，则在ADF检验中，我们构建以下的回归模型：Yt = α+ β*t + γ*Yt-1 + δ1(ΔYt-1) + δ2(ΔYt-2) + …+ δp(ΔYt-p) + et其中，ΔYt表示序列的一阶差分，α、β、γ和δ分别是模型中的系数，et是随机误差项。

在ADF检验中，我们假设序列Yt具有单位根，即H0:γ=0，然后通过假设检验来判断是否拒绝原假设。

如果在检验的过程中发现γ显著不等于0，则拒绝原假设，即序列Yt是平稳的。

ADF检验的统计量是基于t统计量计算的，一般会提供临界值用于判断统计量的显著性。

如果统计量的值小于临界值，则拒绝原假设，序列是平稳的。

除了ADF检验外，还有KPSS检验也是一种用于判断平稳序列的方法。

与ADF 检验不同的是，KPSS检验是在原假设下进行的，即假设序列是平稳的。

KPSS检验的原假设是H0:序列是平稳的，备择假设是H1:序列是非平稳的。

具体而言，KPSS检验是基于单位根检验的思想，即检验序列的观测值是否围绕一个常数进行波动。

如果序列的波动围绕一个常数，则序列是平稳的；如果波动围绕着一个随时间增长的函数，则序列是非平稳的。

KPSS检验的统计量也是基于t统计量计算的，一般会提供临界值用于判断统计量的显著性。

如果统计量的值大于临界值，则拒绝原假设，序列是非平稳的。

除了单位根检验，还有一些其他的平稳序列检验方法，如Ljung-Box检验和ARCH检验等。

ADF检验

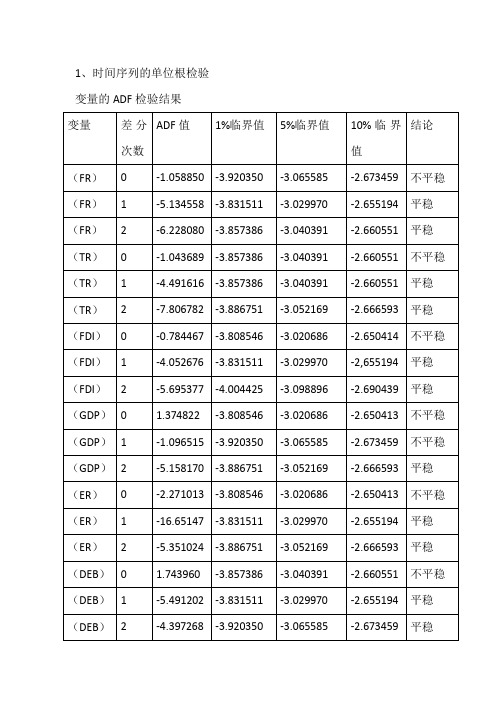
1、时间序列的单位根检验变量的ADF检验结果
说明：差分次数0代表未对数据进行差分；1代表数据的一阶差分；2代表数据的二阶差分
本文运用ADF（Augmented Dickey-Fuller test statistic）对时间序列进行单位根检验，检验Lg（FR）、Lg（TR）、Lg（FDI）、Lg（GDP）、Lg（ER）、Lg（DEB）、Lg（M2）的平稳性，并确定其单整阶数，单位根方程不包括常数项和时间序列项。

具体检验结果如上图所示。

从检验的结果来看，FR、TR、FDI、GDP、ER、DEB、M2均为原阶非平稳，FR、TR、FDI、ER、DEB、M2均为一阶平稳。

但是全体7组数据均为二阶单整。

2、时间序列的协整检验
通过ADF检验得知，FR、TR、FDI、GDP、ER、DEB、M2经过对数变换后都是二阶平稳序列，这是判定Lg（FR）、Lg（TR）、Lg（FDI）、Lg （GDP）、Lg（ER）、Lg（DEB）、Lg（M2）之间是否存在协整关系的前提条件。

adf检验拒绝原假设的条件

adf检验拒绝原假设的条件
ADF检验是判断时间序列数据是否具有平稳性的一种常用方法。

当ADF 检验的统计值小于所设定的临界值时，我们拒绝原假设，即认为该时间序列不存在单位根，即该时间序列是平稳的。

那么ADF检验拒绝原假设的条件有哪些呢？
一、样本容量
首先，在进行ADF检验时，需要确保时间序列的样本容量足够大。

如果样本容量过小，可能会导致统计结果不可靠。

一般来说，样本容量应当大于50，最好是100以上。

二、数据的平稳性
在进行ADF检验之前，需要先对数据进行平稳性检验。

如果数据本身已经是平稳的，那么进行ADF检验的结果显然没有什么意义。

因此，需要对数据进行一定程度的平稳性处理，例如差分或对数变换等。

三、临界值的选择
ADF检验中，临界值的选择非常重要。

不同的置信水平和不同阶数的ADF检验所对应的临界值也不同。

因此，在进行ADF检验时，需要特别注意临界值的选择，以保证检验结果的准确性。

四、模型的选择
在进行ADF检验时，需要选择合适的模型。

如果模型选择不当，可能会影响到检验结果的准确性。

一般来说，需要根据数据的特点选择相应的模型，例如ARIMA模型、VAR模型等。

综上所述，ADF检验拒绝原假设的条件主要包括：样本容量足够大、数据具有一定的平稳性、选择合适的临界值和模型。

只有在以上条件都满足的情况下，我们才能够对时间序列的平稳性进行有效的判断。

ADF检验通俗解释

ADF检验通俗解释
ADF检验，全名为Augmented DickeyFuller检验，是一种用于检验时间序列数据中单位根存在性的统计检验方法。

单位根表示时间序列数据具有非平稳性，即均值或方差可能随时间变化。

以下是对ADF检验的通俗解释：
单位根的概念：在时间序列中，如果一个变量具有单位根，意味着它的变化随时间的推移而保持在某一水平上。

这使得时间序列变量呈现出一种趋势，而不是随机波动。

平稳性的重要性：在统计学和经济学中，我们通常假设数据是平稳的，即它们的均值和方差在时间上是恒定的。

如果时间序列具有单位根，就可能导致违反这个平稳性假设。

ADF检验的目的：ADF检验的目的是确定一个时间序列是否具有单位根，从而判断该序列是否是平稳的。

如果序列是平稳的，就更容易应用许多统计方法，因为这些方法通常基于数据的稳定性。

检验的步骤：
提出假设：ADF检验的零假设是序列具有单位根，即非平稳。

备择假设是序列是平稳的。

进行统计检验：通过比较计算出的检验统计量与临界值，来判断是否拒绝零假设。

如果拒绝了零假设，就认为序列是平稳的。

ADF统计量的解释：ADF检验的统计量反映了单位根的存在性。

如果ADF统计量的值小于某个阈值（即临界值），那么我们可能拒绝
零假设，认为序列是平稳的。

总体而言，ADF检验是一种用于检验时间序列平稳性的工具，它帮助我们判断一个变量是否随时间保持在某一水平上，从而影响到我们在统计建模和分析中如何处理这个变量。

stata中进行adf检验的命令

在Stata中进行ADF检验（Augmented Dickey-Fuller Test）是研究单位根（unit root）存在与否的一种常用方法。

单位根指的是时间序列数据中的根（根是指方程的解），如果单位根存在，意味着时间序列数据具有非平稳性。

而ADF检验则是用来检验单位根是否存在的统计方法。

在Stata中，进行ADF检验可以使用dfuller命令。

下面将详细介绍如何使用这个命令进行ADF检验。

1. 环境设置在使用dfuller命令之前，需要先加载Stata的时间序列数据扩展包（timeseries package）。

通过输入以下命令加载扩展包：ssc install tsset2. 数据准备在进行ADF检验之前，需要准备好相关的时间序列数据。

可以使用tsset命令将数据设置为Stata的时间序列数据格式。

tsset date这里的date是数据中表示日期的变量名，需要将其替换为实际使用的日期变量名。

3. 进行ADF检验使用dfuller命令可以进行ADF检验。

下面是该命令的基本语法：dfuller dependent_variable [if] [in], [options]其中，dependent_variable是要进行ADF检验的变量名。

可以使用if子句和in子句进行数据筛选。

在进行ADF检验时，需要考虑以下两个核心问题： - 是否包含截距项（constant）：使用-c选项来指定。

如果添加了-c选项，表示模型中包含截距项。

如果没有添加该选项，则表示模型中不包含截距项。

- 是否包含时间趋势项（trend）：使用-t选项来指定。

同样地，如果添加了-t选项，表示模型中包含时间趋势项。

如果没有添加该选项，则表示模型中不包含时间趋势项。

如果要进行包含截距项和时间趋势项的ADF检验，可以使用以下命令：dfuller dependent_variable, lags(#) trend其中，#需要用实际的滞后阶数替换，表示在ADF检验中使用的滞后阶数。

ADF检验

仍以日本人口序列y t为例（数据见3.3）。

在工作文件窗口中双击y t序列，从而打开y t数据窗口。

点击View键，选择Unit Root Test功能，如下图，则会弹出一个单位根检验对话框。

其中共有4种选项。

（1）检验方法（缺省选择是ADF检验），（2）所检验的序列（缺省选择是对原序列（Level）做单位根检验）。

（3）选择不同检验式（缺省选择是检验式中只包括截距项。

其他两种选择是检验式中包括趋势项和截距项，检验式中不包括趋势项和截距项。

（4）ADF检验式中选择差分项的最大滞后期数。

这里做的选择是（1）ADF 检验，（2）对原序列y t做单位根检验，（3）检验式中不包括趋势项和截距项。

点击OK 键。

得ADF检验结果如下。

相应的检验式是∆= 0.0041 y t-1 + 0.2197∆ y t-1 + 0.1366∆ y t-1 + 0.2159∆ y t-1(2.9) (2.4) (1.4) (2.3) DW = 2.05输出的最上部分给出了检验结果。

因为ADF = 2.9283，分别大于不同检验水平的三个临界值，所以日本人口序列y t是一个非平稳序列。

在此情形下，应该继续对y t的差分序列进行单位根检验。

在序列y t窗口（即显示单位根检验结果的窗口）中，点击View键，选择Unit Root Test 功能，再次得到单位根检验对话框。

这时第二项选择应选1st difference，即检验∆y t。

第三项选择含截距项，第四项选择滞后2期。

点击OK键。

得ADF检验结果如下。

见输出结果的最上部分。

因为ADF = 3.5602，分别小于不同检验水平的三个临界值，所以日本人口差分序列∆ y t是一个平稳序列。

因此y t~ (1)。

3.对两个时间序列分别做ADF检验。

1.eviews中选取时间序列P4，右键=》open。

在新的窗口中点击view=》unit root test。

2.ADF检验需要对3个模型依次检验，所以在unit root test窗口中先①选：level、trend and intercept。

adf单位根检验的原理

adf单位根检验的原理ADF单位根检验是一种常用于时间序列数据的统计分析方法，用于判断一个时间序列是否具有随机漂移或趋势，即是否有趋势性或非平稳性。

如果时间序列具有趋势或非平稳性，那么进行进一步的分析和预测就会出现较大误差和不确定性。

因此，ADF单位根检验是时间序列分析中非常重要的一部分。

ADF单位根检验的原理可以从以下步骤来阐述：第一步，假设时间序列模型为：$y_t = \alpha + \beta t + \gamma y_{t-1} + \epsilon_t$其中，$y_t$为时间序列的观测值，$\epsilon_t$为残差项，$\alpha$为常数项，$\beta$为$t$的系数，$\gamma$为$y_{t-1}$的系数。

第二步，进行零假设和备择假设的设定：零假设（$H_0$）：时间序列具有单位根，即$\gamma = 1$；备择假设（$H_1$）：时间序列不具有单位根，即$\gamma < 1$。

第三步，进行统计检验，即对时间序列进行回归和残差分析：①对上述模型进行回归分析，得到回归系数$\hat{\alpha}$、$\hat{\beta}$和$\hat{\gamma}$，并计算残差$e_t=y_t-\hat{\alpha}-\hat{\beta}t-\hat{\gamma}y_{t-1}$；②计算残差的自相关系数$r_k$，并进行估计值的偏误调整，得到$t$统计量：$t=\frac{\hat{\gamma}-1}{SE(\hat{\gamma})}$其中，$SE(\hat{\gamma})$为$\hat{\gamma}$的标准误，可以通过样本自相关系数的估计值进行计算；③按照给定的显著性水平和自由度，查找$t$分布表，计算$t$统计量的临界值；④比较$t$统计量和临界值，得出结论。

如果$t$统计量的绝对值大于临界值，则拒绝零假设，即时间序列不具有单位根；反之，则无法拒绝零假设，即时间序列可能具有单位根。

ADF检验——精选推荐

ADF检验摘⾃：⼀、简介在ARMA/ARIMA这样的⾃回归模型中，模型对时间序列数据的平稳是有要求的，因此，需要对数据或者数据的n阶差分进⾏平稳检验，⽽⼀种常见的⽅法就是ADF检验，即单位根检验⼆、平稳随机过程在数学中，平稳随机过程（Stationary random process）或者严平稳随机过程，⼜称狭义平稳过程，是在固定时间和位置的概率分布与所有时间和位置的概率分布相同的随机过程：即随机过程的统计特性不随时间的推移⽽变化。

这样，数学期望和⽅差这些参数也不随时间和位置变化平稳在理论上⼜严平稳和宽平稳两种，在实际应⽤上宽平稳使⽤较多。

宽平稳的数学定义为：给定⼆阶矩过程（⼆阶矩存在）X（t），t属于T，如果X(t)，的均值函数u(t)是常数，相关函数R(t1,t2)=f(t2-t1)即相关函数只与时间间隔相关，则称为宽平稳过程。

严平稳定义：给定随机过程X(t)，t属于T，其有限纬分布组为F(x1, x2,.... xn, t1, t2,...., tn), t1,t2,....tn属于T，对任意n任意的t1, t2, ...., tn属于T，任意满⾜t1+h, t2+h, .... tn+h，称此过程严平稳。

简单点说严平稳是⼀种条件⽐较苛刻的平稳性定义，它认为只有当序列所有的统计性质都不会随着时间的推移⽽发⽣变化时，该序列才能被认为平稳。

⼀般关系严平稳条件⽐宽平稳条件苛刻，通常情况下，低阶矩存在的严平稳成⽴，⽽宽平稳序列不能反推严平稳成⽴。

三、单位根检验单位根检验是指检验序列中是否存在单位根，因为存在单位根就是⾮平稳时间序列了。

单位根就是指单位根过程，可以证明，序列中存在单位根过程就不平稳。

迪基-福勒检验(Dickey-Fuller test)和扩展迪基-福勒检验可以测试⼀个⾃回归模型是否存在单位根。

adf检验的辅助回归方程

ADF检验的辅助回归方程引言ADF（Augmented Dickey-Fuller）检验是一种常用的时间序列分析方法，用于检验一个时间序列是否具有单位根。

在进行ADF检验时，通常需要构建一个辅助回归方程。

本文将详细介绍ADF检验的原理和步骤，并探讨辅助回归方程在ADF检验中的作用。

ADF检验原理ADF检验是基于Dickey-Fuller单位根检验的扩展，用于判断一个时间序列是否具有单位根，即是否是非平稳的。

单位根存在的话，时间序列将具有持续的趋势，而不存在单位根的时间序列则具有平稳性。

ADF检验的原理是通过构建一个回归模型来判断时间序列是否具有单位根。

具体来说，ADF检验的原假设是时间序列具有单位根，备择假设是时间序列不存在单位根。

如果ADF检验的统计量小于一定的临界值，就可以拒绝原假设，即认为时间序列不存在单位根。

ADF检验步骤ADF检验的步骤如下：步骤一：构建辅助回归方程ADF检验需要构建一个辅助回归方程，该方程包括待检验的时间序列和其滞后差分项。

辅助回归方程的一般形式如下：Δy t=α+βt+γy t−1+δ1Δy t−1+⋯+δp−1Δy t−p+1+εt其中，Δy t是时间序列的一阶差分，α是截距，β是时间趋势系数，γ是系数表示时间序列的长期依赖性，δ1,…,δp−1是系数表示时间序列的短期依赖性，εt是误差项。

步骤二：计算ADF统计量利用辅助回归方程的残差项，可以计算ADF统计量。

ADF统计量的计算公式如下：ADF=γ̂SE(γ̂)其中，γ̂是回归方程中γ的估计值，SE(γ̂)是该估计值的标准误。

步骤三：判断统计显著性根据ADF统计量的大小，可以判断时间序列的单位根假设。

如果ADF统计量小于临界值，就可以拒绝原假设，认为时间序列不存在单位根，即是平稳的。

反之，如果ADF统计量大于临界值，则无法拒绝原假设，时间序列可能具有单位根，即是非平稳的。

辅助回归方程的作用辅助回归方程在ADF检验中的作用是帮助判断时间序列是否具有单位根。

ADF检验——精选推荐

ADF检验单位根检验是指检验序列中是否存在，因为存在单位根就是⾮平稳时间序列了。

单位根就是指单位根过程，可以证明，序列中存在单位根过程就不平稳，会使回归分析中存在。

from statsmodels.tsa.stattools import adfullerimport pandas as pdimport numpy as np#湖北省1978年⾄2010年GDPdata = pd.Series([151.0, 188.46, 199.38, 219.75, 241.55, 262.58, 328.22, 396.26, 442.04, 517.77, 626.52, 717.08, 824.38, 913.38, 1088.39, 1325.83, 1700.92, 2109.38, 2499.77, 2856.47, 3114.02, 3229.29, 3545.39, 3880.53, 4212.82, 4757.45, 56 print(adfuller(data))结果： (-0.04391111656553232, 0.9547464774274733, 10, 22, {'1%': -3.769732625845229, '5%': -3.005425537190083, '10%': -2.6425009917355373}, 291.54354258641223)第⼀个是adt检验的结果，简称为T值，表⽰t统计量。

第⼆个简称为p值，表⽰t统计量对应的概率值。

第三个表⽰延迟。

第四个表⽰测试的次数。

第五个是配合第⼀个⼀起看的，是在99%，95%，90%置信区间下的临界的ADF检验的值。

第⼀点，1%、%5、%10不同程度拒绝原假设的统计值和ADF Test result的⽐较，ADF Test result同时⼩于1%、5%、10%即说明⾮常好地拒绝该假设。

ADF单位的根检验具体操作

：ADF检验
单位根检验，把数据输入Eviews之后，点击左上角的View--Unit Root Test,
（但好像更好用一些），之后可以选择一阶、二阶差分之后的序列是否存在单
位根，同时可以选检验的方程中是否存在存在趋势项、常数项等。

一般进行ADF检验要分3步：
1 对原始时间序列进行检验，此时第二项选level，第三项选None.如果没通过检验，说明原始时间序列不平稳；
2 对原始时间序列进行一阶差分后再检验，即第二项选1st difference，第三
项选intercept,若仍然未通过检验，则需要进行二次差分变换；
3 二次差分序列的检验，即第二项选择2nd difference ，第四项选择Trend and intercept.一般到此时间序列就平稳了！
看结果：
1%，5%，10%指的是显著水平，如果ADF检验值（t值）大于某显著水平值（一般是5%），则不通
过检验，即存在单位根（不平稳），此时，可通过一阶差分再来查看单位根是否平稳，p值指的
是接受原假设的概率。

在报告上的写法：
H：r=0 0H: r=1
1如果ADF检验值>临界值，则接受H，序列有单位根，非平缓。

反之 0
（注：H的写法，选中要设置为下标的字母，点击菜单栏格式——字体，选择效
果中的下标，确定。

或直接选中的那个红色项进行格式设置）
/line&symbol 操作：图。

ADF检验

ADF检验
1数据输入file——--new---——workfile——-—出现以下窗口
输入起始年份和结束年份
点击ok出现以下窗口
在总窗口点击object--——new objeck出现如下窗口
选择poold点击ok
在此窗口中另起一行输入n，代表年份点击sheet
输入y？x？后点击ok（两者之间空一格)
点击edit+/-输入数据。

对两组数据取对数，得新的数据：p=log（y),q=log（x）。

可在eviews中点击Genr输入p=log(y)可自动产生对数数列。

对两个时间序列分别做ADF检验.
1。

eviews中选取时间序列P4，右键=》open.在新的窗口中点击view=》unit root test。

2.ADF检验需要对3个模型依次检验,所以在unit root test窗口中先①选:level、trend and intercept。

然后确认=》得到
第一行是所得t值，下面3行是临界值。

t=—2.0665〉临界值，因此非平稳.因此要继续检验②：level、intercept,假设还是非平稳。

继续检验③：level none.假设还是非平稳,则做一阶差分，即将level换成1st difference,将之前①②③从新来过，一旦t<临界值就可以停止了。

若level时，t值均大于临界值，则为非平稳序列.若1st difference的一阶差分时,变为平稳的，就是1阶单整，记为I（1）,依次类推.。

r语言adf检验代码

r语言adf检验代码ADF检验是一种常用的时间序列分析方法，用于检验一个时间序列是否具有单位根。

单位根表示时间序列具有随机漂移，即序列中的值是随机游走的，没有明显的趋势。

如果时间序列存在单位根，则说明序列是非平稳的，难以进行进一步的分析和预测。

而ADF检验可以帮助我们判断一个时间序列是否平稳，从而为后续的分析提供基础。

在R语言中，我们可以使用“ur.df()”函数来进行ADF检验。

该函数位于“urca”包中，因此我们需要先安装并加载该包，然后才能使用该函数。

下面是一段示例代码，演示了如何使用R语言进行ADF检验：```R# 加载urca包library(urca)# 生成一个随机游走序列set.seed(123)random_walk <- cumsum(rnorm(100))# 进行ADF检验adf_test <- ur.df(random_walk, type = "trend", selectlags = "AIC")# 显示ADF检验结果summary(adf_test)```在上面的代码中，我们首先使用“cumsum()”函数生成了一个随机游走序列，该序列具有单位根。

然后，我们使用“ur.df()”函数对该序列进行ADF检验。

参数“type”指定了模型类型，这里我们选择了“trend”，表示模型中包含趋势项。

参数“selectlags”指定了滞后阶数的选择标准，这里我们选择了“AIC”准则。

最后，我们使用“summary()”函数显示了ADF检验的结果。

在结果中，我们关注的是测试统计量（Test Statistic）和p值（p-value）。

测试统计量用于判断时间序列是否具有单位根，如果测试统计量的绝对值大于对应的临界值，就可以拒绝单位根存在的假设，即序列是平稳的。

而p值则用于判断检验统计量是否显著，通常取0.05作为显著性水平。

如果p值小于0.05，则可以拒绝单位根存在的假设，即序列是平稳的。

ADF检验和FO估计值模型

ADF检验和FO估计值模型
一、DF检验：随机游走序列Xt=Xt-1+μt是非平稳的，其中μt 是白噪声。

而该序列可看成是随机模型Xt=ρXt-1+μt中参数ρ=1时的情形。

零假设H0：δ=0；备择假设H1：δ<0可通过OLS法估计
Xt=α+δXt-1+μt并计算t统计量的值，与DF分布表中给定显著性水平下的临界值比较：如果：t<临界值，则拒绝零假设H0：δ=0，认为时间序列不存在单位根，是平稳的。

二、ADF检验：在DF检验中，实际上是假定了时间序列是由具有白噪声随机误差项的一阶自回归过程AR（1）生成的。

但在实际检验中，时间序列可能由更高阶的自回归过程生成的，或者随机误差项并非是白噪声，为了保证DF检验中随机误差项的白噪声特性，Dicky和Fuller对DF检验进行了扩充，形成了ADF （AugmentDickey-Fuller）检验。

四格表资料的卡方检验用于进行两个率或两个构成比的比较。

1、专用公式：
若四格表资料四个格子的频数分别为a，b，c，d，则四格表资料卡方检验的卡方值=n(ad-bc)^2/(a+b)(c+d)(a+c)(b+d)，（或者使用拟合度公式）
自由度v=（行数-1）（列数-1）=1
2、应用条件：
要求样本含量应大于40且每个格子中的理论频数不应小于5。

当样本含量大于40但有1=<理论频数<5时，卡方值需要校正，当样本含量小于40或理论频数小于1时只能用确切概率法计算概率。

以上内容参考：百度百科-卡方检验。

adf二阶差分检验python

adf二阶差分检验pythonADF二阶差分检验是一种常用的时间序列分析方法，用于判断时间序列数据是否平稳。

本文将介绍ADF二阶差分检验的原理及其在Python中的应用。

时间序列分析是研究随时间变化的数据的统计方法。

在金融、经济学等领域，时间序列分析被广泛应用于预测、建模和决策等方面。

其中，平稳性是时间序列分析的基本假设之一。

平稳时间序列具有恒定的均值和方差，且自相关性不随时间变化而改变。

ADF（Augmented Dickey-Fuller）检验是一种常用的平稳性检验方法。

它基于Dickey-Fuller单位根检验（DF检验）的扩展，使用单位根的存在与否来判断时间序列数据是否平稳。

ADF检验的原假设是时间序列具有单位根，即非平稳；备择假设是时间序列不具有单位根，即平稳。

在进行ADF二阶差分检验之前，我们首先要了解二阶差分的概念。

一阶差分是指将序列中每个元素与其前一个元素的差值作为新的序列元素，而二阶差分则是对一阶差分结果再进行一次差分。

二阶差分可以进一步减小序列的趋势和季节性变动，将非平稳的时间序列转化为平稳序列。

在Python中，我们可以使用statsmodels库进行ADF二阶差分检验。

首先，我们需要导入需要的库：import pandas as pdfrom statsmodels.tsa.stattools import adfuller接下来，我们可以使用pandas库读取时间序列数据，并将其转化为pandas的Series对象：data = pd.read_csv('data.csv') # 读取时间序列数据series = pd.Series(data['value']) # 转化为Series对象然后，我们可以使用adf函数进行ADF二阶差分检验：result = adfuller(series.diff().diff().dropna()) # 进行ADF二阶差分检验我们可以输出ADF检验的结果：print('ADF Statistic: %f' % result[0]) # ADF检验统计量print('p-value: %f' % result[1]) # p-value值print('Critical Values:')for key, value in result[4].items(): # 输出临界值print('\t%s: %.3f' % (key, value))通过观察ADF检验的p-value值，我们可以判断时间序列数据的平稳性。

单位根公式

单位根公式
ADF检验的单位根公式如下： Δyt = α + βt + γyt-1 + δ1Δyt-1 + δ2Δyt-2 + ... + δpΔyt-p + εt 其中，Δyt是时间序列yt的一阶差分，α是常数项，βt是时间趋势项，γ是系数，δ1到δp 是滞后差分项的系数，εt是误差项。
除了ADF检验，还有其他的单位根检验方法，如Phillips-Perron检验、KPSS检验等，它们都是用来判断时间序列的平稳性和非平稳性的重析中常用的概念，用于判断一个时间序列是否具有单位根（即非平稳性）。单位根表示序列中存在一种趋势，使得序列在长期内不会回归到其均值。
单位根公式有几种常见的形式，其中最常用的是ADF（Augmented Dickey-Fuller）检验。ADF检验的原假设是序列具有单位根，即非平稳性，而备择假设是序列是平稳的。ADF 检验的统计量会与一个临界值进行比较，如果统计量小于临界值，则可以拒绝原假设，认为序列是平稳的。