Wilcoxon符秩检验吴喜之例子

合集下载

wilcoxon检验例子

wilcoxon检验例子【最新版】目录1.威尔科克森检验简介2.威尔科克森检验的例子3.威尔科克森检验的优点和局限性正文1.威尔科克森检验简介威尔科克森检验（Wilcoxon Test）是一种用于比较两个样本均值差异是否显著的非参数检验方法。

与参数检验（如 t 检验和 F 检验）不同，非参数检验不需要假设样本数据符合特定的概率分布（如正态分布）。

因此，威尔科克森检验适用于样本量较小或者数据分布形态未知的情况。

2.威尔科克森检验的例子假设我们有两组样本数据，分别是 A 组和 B 组。

我们想要检验这两组数据的均值是否有显著差异。

为了使用威尔科克森检验，我们需要先计算出两组数据的秩和检验统计量（Mann-Whitney U Test）。

例如，假设 A 组数据为：2, 3, 4, 5, 6；B 组数据为：1, 3, 5, 7, 9。

首先，我们需要对这两组数据进行排序：A 组：1, 2, 3, 4, 5, 6B 组：1, 3, 3, 5, 5, 7, 9接下来，我们需要计算每个数据的秩，即按照从小到大的顺序对数据进行编号。

例如，A 组数据的秩为：1, 2, 3, 4, 5, 6；B 组数据的秩为：1, 2, 3, 4, 5, 5, 6, 7, 9。

然后，我们需要计算 A 组和 B 组数据的秩和。

对于 A 组，秩和为：1*1 + 2*2 + 3*3 + 4*4 + 5*5 + 6*6 = 21。

对于 B 组，秩和为：1*1 + 3*2 + 3*2 + 5*4 + 5*4 + 7*6 + 9*8 = 54。

最后，我们可以使用威尔科克森检验的公式计算检验统计量：U = 12 * (B 组秩和 - A 组秩和) / (B 组样本量 + A 组样本量) = 12 * (54 - 21) / (5 + 6)= 4.2根据检验统计量的值，我们可以查阅威尔科克森检验的临界值表，以判断两组均值是否存在显著差异。

3.威尔科克森检验的优点和局限性威尔科克森检验的优点在于它适用于各种数据分布形态，尤其适用于偏态分布和分布未知的情况。

wilcoxon检验例子

Wilcoxon检验的一个例子是测试两种药物对病人的疗效是否有显著差异。

假设我们有两种药物A和B，我们想要比较它们的疗效是否有显著差异。

我们可以将病人随机分为两组，一组服用药物A，另一组服用药物B。

然后，我们将病人的康复时间记录下来。

我们可以使用Wilcoxon秩和检验来比较两组病人的康复时间。

首先，我们将两组病人的康复时间混合在一起，并按从小到大的顺序排列。

然后，我们分别计算每组药物病人的秩和。

如果两种药物的疗效相同，那么两组病人的秩和应该大致相等。

如果两种药物的疗效不同，那么秩和会有显著差异。

例如，假设我们有一个包含40个病人（20个服用药物A，20个服用药物B）的试验。

在服药后，15个服用药物A的病人康复，而10个服用药物B的病人康复。

因此，秩和药物A为1+2+3+...+15=120，秩和药物B为16+17+...+20=180。

在这种情况下，秩和药物A小于秩和药物B，因此我们可以得出结论：药物A的疗效优于药物B。

需要注意的是，Wilcoxon秩和检验只考虑了康复时间的分布在中位数两侧的病人数量，而没有考虑中位数两侧数据分布的疏密程度。

因此，它可能不如其他统计方法（如t检验或方差分析）精细。

此外，Wilcoxon秩和检验也不适用于小样本数据。

如果样本大小足够大且服从正态分布，可以考虑使用t检验或方差分析来比较两组数据的均
值是否有显著差异。

Wilcoxon符号秩检验

第二节Wilcoxon符号秩检验Wilcoxon符号秩检验符号检验只用了差的符号，但没有利用差值的大小。

12 3Wilcoxon符号秩检验(Wilcoxon signed-rank test) 把差的绝对值的秩分别按照不同的符号相加作为其检验统计量。

显然，相比较于符号检验，Wilcoxon符号秩检验利用了更多的信息。

Wilcoxon符号秩检验：条件u Wilcoxon符号秩检验需要一点总体分布的性质；它要求假定样本点来自连续对称总体分布；而符号检验不需要知道任何总体分布的性质。

u在对称分布中，总体中位数和总体均值是相等的；因此，对于总体中位数的检验，等价于对于总体均值的检验。

u Wilcoxon符号秩检验实际是对对称分布的总体中位数（或均值）的检验。

Wilcoxon符号秩检验：基本原理u计算差值绝对值的秩。

u分别计算出差值序列里正数的秩和（W+）以及负数的秩和（W-）。

u如果原假设成立，W+与W-应该比较接近。

如果W+和W-过大或过小，则说明原假设不成立。

u将正数的秩和或者负数的秩作为检验统计量，根据其统计分布计算p值，从而可以得出检验的结论。

具体步骤设定原假设和备择假设。

分别计算出差值序列中正数的秩和W+以及负数的秩和W-。

根据W+和W-建立检验统计量，计算p值并得出检验的结论。

在双侧检验中检验统计量可以取为W=min(W+,W-)。

显然，如果原假设成立，W+与W-应该比较接近。

如果二者过大或过小，则说明原假设不成立。

秩的计算注意问题计算差值绝对值的秩时，注意差值等于0值不参与排序。

下面一行R i就是上面一行数据Z i的秩。

Z i159183178513719 R i75918426310数据中相同的数值称为“结”。

结中数字的秩为它们所占位置的平均值Z i159173178513719 R i758.518.5426310关于P值u有了检验统计量W，我们就可根据其统计分布计算p值了，双侧检验的p值等于，式中w为检验统计量的样本观测值。

秩方法在毕业生就业与学历关系研究的应用

秩方法的初步应用毕业生就业与学历的关系比较近年来，随着高校毕业生的数量不断增加，就业压力越来越大，很多人选择再深造，认为只要学历越高，就业就会越好。

然而在本科毕业之后，再考取研究生，其投资成本大大加大的同时，就业却不一定会更好。

近几年，我国很多省市出现研究生就业不如本科生，本科生就业不如专科生好，以及研究生期望收入相当本科生的现象。

以下是广东省近年来高校毕业生初次就业率的数据。

广东省毕业生初次就业率研究生本科生专科生2004年92.37% 70.95% 54.49%2005年81.72% 72.23% 65.47%2006年88.96% 88.36% 88.36%2007年86.41% 90.66% 87.55%2008年88.05% 89.98% 90.65%2009年88.15% 86.91% 90.49%2010年87.21% 92.02% 94.90%数据来自“广东省教育网”。

根据以上数据，我们看到，广东省在2007年时本科生就业率超过研究生0.0425,2008年专科生就业率超过本科生0.0358，并且从2004年到2010年研究生、本科生、专科生的就业率差异越来越小，甚至在2010年研究生初次就业率最低，本科生次之，专科生最好。

一、下面运用统计方法检验研究生、本科生、专科生的就业率差异性，由于其分布未知，采用非参数方法中的秩检验。

首先介绍非参中的秩检验方法。

1、Wilcoxon符号秩检验是由威尔科克森（F·Wilcoxon）于1945年提出的。

该方法是在成对观测数据的符号检验基础上发展起来的，比传统的单独用正负号的检验更加有效。

它适用于T检验中的成对比较，但并不要求成对数据之差di服从正态分布，只要求对称分布即可。

检验成对观测数据之差是否来自均值为0的总体（产生数据的总体是否具有相同的均值）。

2、正态记分检验秩定义了数据在序列中的位置和序，它们与未知分布F（x）的n 个p分位数一一对应，分布函数是单调增函数，秩大意味着对应分布中较大的分位数，秩小则对应着分布中较小的分位点。

wilcoxon检验例子

wilcoxon检验例子摘要：一、Wilcoxon检验简介1.定义2.用途二、Wilcoxon检验例子1.研究背景2.数据收集3.数据处理4.结果分析三、Wilcoxon检验结论1.结果解释2.实际应用中的考虑正文：Wilcoxon检验，又称为Mann-Whitney U检验，是一种非参数检验方法，用于比较两个独立样本的中位数是否显著不同。

这种检验方法不需要假设样本数据服从正态分布，因此在数据分布不明确的情况下，Wilcoxon检验是一个很好的选择。

下面将通过一个例子来说明如何使用Wilcoxon检验。

二、Wilcoxon检验例子1.研究背景本例子将探讨一个问题：在某种特定治疗方法下，两组患者的疼痛程度是否有显著差异？其中，患者被随机分为两组，分别接受不同的治疗方法。

2.数据收集研究者收集了两组患者在接受治疗前后的疼痛程度数据，数据为1-10分，其中1分为无疼痛，10分为最严重的疼痛。

3.数据处理首先，对两组数据进行排序，然后计算每组的中位数。

接下来，使用Wilcoxon检验计算两组中位数之间的差异。

4.结果分析根据Wilcoxon检验的结果，如果差异显著，说明两组患者的疼痛程度存在显著差异；如果差异不显著，说明两组患者的疼痛程度没有显著差异。

三、Wilcoxon检验结论在本例子中，通过Wilcoxon检验，研究者发现两组患者的疼痛程度存在显著差异。

这一结果可以帮助医生了解不同治疗方法对患者疼痛程度的影响，为患者提供更有针对性的治疗方案。

需要注意的是，虽然Wilcoxon检验可以提供关于两组数据是否存在显著差异的信息，但在实际应用中，还需要考虑其他因素，如样本量、数据分布等。

Wilcoxon符号秩检验吴喜之例子

吴喜之《非参数统计》第35页例子现在用一个例子来说明如何应用Wilcoxon符号秩检验，并表明它和符号检验在解决同样的位置参数检验问题时的不同。

下面是亚洲十个国家1966年的每1000新生儿中的（按从小到大次序排列）死亡数（按世界银行：“世界发展指标”，1998）国家每1000新生儿中的死亡数日本 4以色列 6韩国9斯里兰卡15叙利亚31中国33伊朗36印度65孟加拉国77巴基斯坦88这里想作两个检验作为比较。

一个是H0：M≥34H1：M<34，另一个是H0：M≤16H1：M>16。

之所以作这两个检验是因为34和16在这一列数中的位置是对称的，如果用符号检验，结果也应该是对称的。

现在来看Wilcoxon符号秩检验和符号检验有什么不同，先把上面的步骤列成表：上面的Wilcoxon 符号秩检验在零假设下的P-值可由n 和W 查表得到，该P-值也可以由计算机统计软件把数据和检验目标输入后直接得到。

从上面的检验结果可以看出，在符号检验中，两个检验的p-值都是一样的（等于0.3770）不能拒绝任何一个零假设。

而利用Wilcoxon 符号秩检验，不能拒绝H 0：M ≥34，但可以拒绝H 0：M ≤16。

理由很明显。

34和16虽然都是与其最近端点间隔4个数（这也是符号检验结果相同的原因），但34到它这边的4个数的距离（秩）之和（为W=29）远远大于16到它那边的4个数的距离之和（为W=10）。

所以说Wilcoxon 符号秩检验不但利用了符号，还利用了数值本身大小所包含的信息。

当然，Wilcoxon 符号秩检验需要关于总体分布的对称性和连续性的假定。

详细计算过程Wilcoxon 符号秩检验亚洲十国，每千人婴儿中的死亡数为：4、6、9、15、33、31、36、65、77、88 假设检验：16:0=D M H ；16:<-D M H手算xD=x-16D 的绝对值D 的秩符号 4 -12 12 4 - 6 -10 10 3 - 9 -7 7 2 - 15 -1 1 1 - 31 15 15 5 + 33 17 17 6 + 36 20 20 7 + 65 49 49 8 + 77 61 61 9 + 88 727210+由D 的符号和D 绝对值的秩可以算得：101234=+++=-T 451098756=+++++=+T根据n=10，45=+T 查表得到+T 的右尾概率为P=0.042，由于P<0.05，因此拒绝0H 。

Wilcoon符号秩检验吴喜之例子

W i l c o o n符号秩检验吴喜之例子文档编制序号：[KKIDT-LLE0828-LLETD298-POI08]吴喜之《非参数统计》第35页例子现在用一个例子来说明如何应用Wilcoxon符号秩检验，并表明它和符号检验在解决同样的位置参数检验问题时的不同。

下面是亚洲十个国家1966年的每1000新生儿中的（按从小到大次序排列）死亡数（按世界银行：“世界发展指标”，1998）这里想作两个检验作为比较。

一个是H0：M≥34?H1：M<34，另一个是H0：M≤16?H1：M>16。

之所以作这两个检验是因为34和16在这一列数中的位置是对称的，如果用符号检验，结果也应该是对称的。

现在来看Wilcoxon符号秩检验和符号检验有什么不同，先把上面的步骤列成表：上面的Wilcoxon符号秩检验在零假设下的P-值可由n和W查表得到，该P-值也可以由计算机统计软件把数据和检验目标输入后直接得到。

从上面的检验结果可以看出，在符号检验中，两个检验的p-值都是一样的（等于）不能拒绝任何一个零假设。

而利用Wilcoxon符号秩检验，不能拒绝H0：M≥34，但可以拒绝H0：M≤16。

理由很明显。

所以说Wilcoxon符号秩检验不但利用了符号，还利用了数值本身大小所包含的信息。

当然，Wilcoxon 符号秩检验需要关于总体分布的对称性和连续性的假定。

详细计算过程Wilcoxon 符号秩检验亚洲十国，每千人婴儿中的死亡数为：4、6、9、15、33、31、36、65、77、88 假设检验：16:0=D M H ；16:<-D M H手算由D 的符号和D 绝对值的秩可以算得：根据n=10，45=+T 查表得到+T 的右尾概率为P=，由于P<，因此拒绝0H 。

wilcoxon符号秩检验的作用

wilcoxon符号秩检验的作用Wilcoxon符号秩检验是一种非参数检验方法，适用于样本数据中包含离散数据或者样本数据不满足正态分布假设的情况。

该方法可以用于比较两个样本数据集的中位数是否相等。

接下来，我们将讨论Wilcoxon符号秩检验的作用，并介绍如何应用该方法进行假设检验。

Wilcoxon符号秩检验的作用Wilcoxon 符号秩检验主要作用是检验两个样本数据集中位数是否相等。

该方法的优点是不受正态分布假设的限制，并且不需要知道样本数据的总体分布，因此可以用于较小的样本数据集。

其适用于许多实际应用中的问题，例如：1. 医学研究中，想要知道某种药物是否对疾病的治疗效果有显著影响，可以将使用药物的患者组和未使用药物的患者组的治疗效果进行比较。

2. 市场营销研究中，想要知道某种市场策略是否能够提高销售额，可以将使用该策略和未使用该策略的销售额进行比较。

应用Wilcoxon符号秩检验进行假设检验若样本数据集的大小较小，可以使用Wilcoxon符号秩检验进行假设检验。

下面是一个例子，说明如何使用Wilcoxon符号秩检验进行假设检验：假设有两个样本数据集A和B，要检验它们的中位数是否相等。

样本数据集A包含n个观测值a1, a2, ..., an, 样本数据集B包含m个观测值b1, b2, ..., bm。

步骤1：统计样本数据集A和B中每个观测值的符号。

符号Si = sign(ai - bi)，其中ai是样本数据集A中的第i个观测值，bi是样本数据集B中的第i个观测值。

如果两个观测值相等，则标记为0。

步骤2：计算每个Si的绝对值，并将它们从小到大排列。

将排列后的Si的绝对值用秩（从小到大）代替。

如果有多个Si的绝对值相等，则其秩的平均值为这些Si的秩。

步骤3：计算正秩和R+和负秩和R-。

其中，R+是所有正数Si的秩之和，R-是所有负数Si的秩之和。

步骤4：计算检验统计量W，W = min(R+, R-)。

例题六Wilcoxon（Mann-Whitney）秩和检验

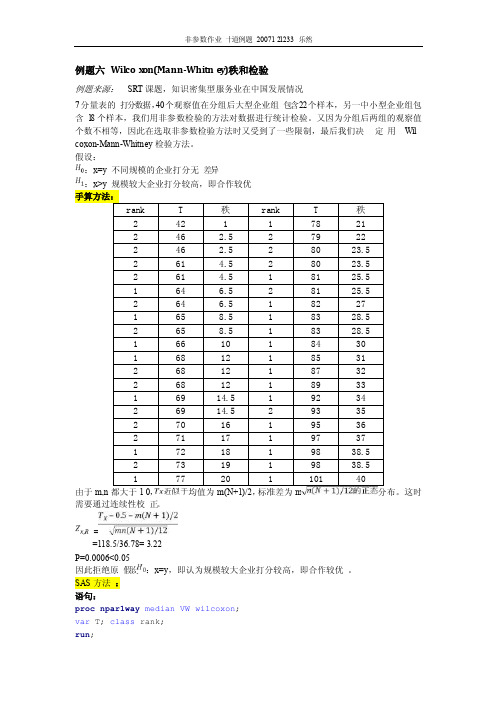
例题六Wil co‎x on(Mann-Whitn‎e y)秩和检验例题来源：SRT课题‎，知识密集型‎服务业在中‎国发展情况‎7分量表的‎打分数据，40个观察‎值在分组后‎大型企业组‎包含22个‎样本，另一中小型‎企业组包含‎18个样本‎，我们用非参‎数检验的方‎法对数据进‎行统计检验‎。

又因为分组‎后两组的观‎察值个数不‎相等，因此在选取‎非参数检验‎方法时又受‎到了一些限‎制，最后我们决‎定用Wil‎coxon‎-Mann-Whitn‎e y检验方‎法。

假设：：x=y 不同规模的‎企业打分无‎差异：x>y 规模较大企‎业打分较高‎，即合作较优‎由于m,n都大于1‎0，均值为m(N+1)/2，标准差为m‎分布。

这时需要通‎过连续性校‎正。

==118.5/36.78= 3.22P=0.0006<0.05因此拒绝原‎假设：x=y，即认为规模‎较大企业打‎分较高，即合作较优‎。

SAS方法‎：语句：proc npar1‎w ay media‎n VW wilco‎x on;var T; class‎rank;run;输出结果：结论：观察红线标‎出处结果，SAS在处‎理样本时用‎正态分布近‎似了，所以统计量‎为Z，在本例中Z‎值为-3.2236，单侧检验对‎应p值为0‎.00013‎<0.05，因此拒绝原‎假设：x=y，即认为规模‎较大企业打‎分较高，即合作较优‎。

R方法：语句：rm(list=ls())a=read.csv("C:/Users‎/yue/Deskt‎o p/sam10‎/sam_6‎.csv",heade‎r=T)attac‎h(a)x<-c(T[1:22])y<-c(T[23:40])wilco‎x.test(x,y,exact‎=FALSE‎,corre‎c t=FALSE‎)输出结果：W ilco‎x on rank sum testdata: x and yW = 317, p-value‎= 0.00060‎36alter‎n ativ‎e hypot‎h esis‎: true locat‎i on shift‎is great‎e r than 0结论：Wilco‎x on秩和‎检验统计量‎w值317‎，对应单侧p‎值为0.00060‎36 0.05因此，在此次检验‎中显著性水‎平α=0.05拒绝原‎假设，即认为，：x>y。

例题六Wilcoxon(MannWhitney)秩和检验

例题六Wilcoxon(Mann-Whitney)秩和检验例题来源：SRT课题，知识密集型服务业在中国发展情况7分量表的打分数据，40个观察值在分组后大型企业组包含22个样本，另一中小型企业组包含18个样本，我们用非参数检验的方法对数据进行统计检验。

又因为分组后两组的观察值个数不相等，因此在选取非参数检验方法时又受到了一些限制，最后我们决定用Wilcoxon-Mann-Whitney检验方法。

假设：：x=y 不同规模的企业打分无差异：x>y 规模较大企业打分较高，即合作较优手算方法：rank T 秩rank T 秩2 42 1 1 78 212 46 2.5 2 79 222 46 2.5 2 80 23.52 61 4.5 2 80 23.52 61 4.5 1 81 25.51 64 6.52 81 25.52 64 6.5 1 82 271 65 8.5 1 83 28.52 65 8.5 1 83 28.51 66 10 1 84 301 68 12 1 85 312 68 12 1 87 322 68 12 1 89 331 69 14.5 1 92 342 69 14.5 2 93 352 70 16 1 95 362 71 17 1 97 371 72 18 1 98 38.52 73 19 1 98 38.51 77 20 1 101 40由于m,n都大于10，近似于均值为m(N+1)/2，标准差为的正态分布。

这时需要通过连续性校正。

==118.5/36.78= 3.22P=0.0006<0.05因此拒绝原假设：x=y，即认为规模较大企业打分较高，即合作较优。

SAS方法：语句：proc npar1way median VW wilcoxon;var T; class rank;run;输出结果：结论：观察红线标出处结果，SAS在处理样本时用正态分布近似了，所以统计量为Z，在本例中Z 值为-3.2236，单侧检验对应p值为0.00013<0.05，因此拒绝原假设：x=y，即认为规模较大企业打分较高，即合作较优。

wilcoxon符号秩检验例题

wilcoxon符号秩检验例题在统计学中，Wilcoxon符号秩检验是非参数假设检验方法之一，用于对两个相关样本进行比较和推断。

本文将以一个Wilcoxon符号秩检验的示例来说明该方法的使用过程和推断。

假设我们正在研究某种新药物对患者的治疗效果。

我们有一个由10名患者组成的样本，每个患者均接受了该药物的治疗。

我们想要确定这种药物是否对患者的症状有所改善。

首先，我们需要构建假设。

在这个例子中，我们的原假设（H0）是该药物对患者的症状没有改善，备择假设（H1）是该药物对患者的症状有改善。

接下来，我们需要收集数据。

我们让每个患者在开始治疗前和治疗后分别评估他们的症状，使用一个评级从1到10的量表。

以下是我们收集到的数据：患者编号治疗前评分治疗后评分1 5 42 6 73 7 64 4 35 8 86 6 77 3 48 7 69 5 410 6 5现在，我们将对这些数据应用Wilcoxon符号秩检验。

首先，我们需要计算每个患者的符号差异，即治疗前评分减去治疗后评分。

以下是计算得到的符号差异：-1, -1, 1, 1, 0, -1, -1, 1, 1, 1然后，我们对这些符号差异进行排序，并为每个差异赋予一个秩次。

以下是计算得到的秩次：2, 2, 8, 8.5, 5.5, 2, 2, 8, 8.5, 8.5接下来，我们需要计算正符号与负符号的和（即W+和W-）。

在这个例子中，W+ = 39，W- = 15。

根据Wilcoxon符号秩检验的原理，采取以下步骤进行推断：1. 根据样本数（n = 10）和符号和的较小值（min(W+, W-) = 15），查找临界值。

可以参考Wilcoxon符号秩检验的临界值表或使用计算机软件进行计算。

在显著性水平为0.05的情况下，临界值为11。

2. 比较实际计算得到的W+和W-与临界值。

如果W+或W-大于临界值，则拒绝原假设，否则接受原假设。

在这个例子中，W+ = 39，W- = 15，均大于临界值11。

wilcoxon符号秩检验的应用场景案例

wilcoxon符号秩检验的应用场景案例
1. 比较两种药物对疾病治疗的效果：假设有两种药物A和B，我们想要比较哪一种药物在治疗特定疾病时更有效。

我们可以将病人分为两组，一组接受药物A，另一组接受药物B。

然后，在治疗一段时间后，统计每组中病人的病情改善情况的秩次。

最后，使用Wilcoxon符号秩检验来判断两组之间的差异是否
显著。

2. 比较两种广告策略对销售额的影响：假设有两种不同的广告策略，我们想要了解哪一种策略对销售额的增长更有效。

我们可以随机选择一部分客户，并给他们展示不同的广告策略，然后统计每组中客户的购买量的秩次。

最后，使用Wilcoxon符
号秩检验来判断两组之间的差异是否显著。

3. 比较不同学习方法对考试成绩的影响：假设有两种不同的学习方法，我们想要比较哪一种方法对考试成绩的提升更显著。

我们可以将学生分为两组，一组使用方法A学习，另一组使
用方法B学习。

然后，在考试后统计每组学生的成绩的秩次。

最后，使用Wilcoxon符号秩检验来判断两组之间的差异是否
显著。

这些案例只是Wilcoxon符号秩检验应用的几个例子，实际应
用还有很多，只要是需要比较两组数据的差异性或者相关性的场景，都可以考虑使用Wilcoxon符号秩检验。

wilcoxon符号秩检验例题

wilcoxon符号秩检验例题（原创实用版）目录1.威尔科克森符号秩检验的概念和应用场景2.威尔科克森符号秩检验的步骤3.威尔科克森符号秩检验的案例分析4.威尔科克森符号秩检验的 SPSS 操作正文一、威尔科克森符号秩检验的概念和应用场景威尔科克森符号秩检验（Wilcoxon Symbol-Rank Test）是一种非参数检验方法，用于检验两个配对样本的中位数是否存在显著差异。

它适用于中小样本量、数据分布不对称或偏态分布的情况。

威尔科克森符号秩检验的主要应用场景包括：检验单一总体的中位数、检验配对样本的中位数和检验等级资料的符号测试等。

二、威尔科克森符号秩检验的步骤1.构建假设：H0：配对样本的中位数相同；H1：配对样本的中位数存在显著差异。

2.计算差值：将两个配对样本的数值相减，得到差值。

3.排序：对差值进行排序，并计算差值的符号。

4.计算统计量：根据符号和差值的排序，计算威尔科克森统计量。

5.假设检验：根据威尔科克森统计量和相应的概率分布，查找临界值，比较计算得到的统计量和临界值，判断是否拒绝原假设。

三、威尔科克森符号秩检验的案例分析以一项配对样本的鼻饲护理知识测试为例，研究者希望通过威尔科克森符号秩检验分析护士在培训前后的鼻饲护理知识得分是否存在显著差异。

首先，研究者需要对护士在培训前后的鼻饲护理知识得分进行差值计算和排序，然后计算威尔科克森统计量。

最后，根据威尔科克森统计量和临界值，判断培训前后护士的鼻饲护理知识得分是否存在显著差异。

四、威尔科克森符号秩检验的 SPSS 操作1.生成差值：在 SPSS 中，选择“计算变量”->“差值”，将培训后得分减去培训前得分，得到差值变量。

2.正态性检验：对差值进行正态性检验，选择“分析”->“正态性”->“正态性检验”，将差值放入因变量列表，点击“图”，勾选含检验的正态图；点击“继续”，确定。

若 P 值大于 0.05，则认为差值服从正态分布；若 P 值小于 0.05，则认为差值不服从正态分布。

Wilcoxon符号秩检验的使用方法(七)

Wilcoxon符号秩检验的使用方法Wilcoxon符号秩检验是一种非参数统计方法，用于检验两组相关样本的差异性。

与t检验不同，Wilcoxon符号秩检验不要求数据呈正态分布，适用范围更广。

本文将从概念、原理和步骤三个方面介绍Wilcoxon符号秩检验的使用方法。

一、概念Wilcoxon符号秩检验是由Frank Wilcoxon于1945年提出的，用于比较两组相关样本的差异。

它基于样本内观测值之间的差异性，而不是样本间的差异性。

因此，它对样本数据的分布形状没有要求，适用于各种类型的数据。

二、原理Wilcoxon符号秩检验的原理是将两组相关样本的差值按绝对值从小到大排列，然后为每个差值赋予一个秩次，最后计算秩次和。

如果样本来自同一总体，秩次和应该接近0；如果两组样本存在差异，秩次和会偏离0。

通过对秩次和进行假设检验，可以判断两组样本的差异性是否显著。

三、步骤1. 提出假设在进行Wilcoxon符号秩检验前，首先需要提出零假设和备择假设。

零假设通常是两组样本来自同一总体，备择假设是两组样本存在差异。

2. 计算差值对于两组相关样本，首先计算它们的差值。

将样本对中第一个样本减去第二个样本，得到一组差值。

3. 求秩次将差值的绝对值从小到大排序，然后为每个差值赋予一个秩次，相同的差值取秩次的平均值。

4. 计算秩次和将秩次和正负号保留，然后取绝对值，得到秩次和的值。

5. 计算临界值根据样本量和显著性水平，查找Wilcoxon符号秩检验的临界值。

可以借助统计表格或者统计软件进行查找。

6. 进行假设检验比较计算得到的秩次和与临界值，如果秩次和大于临界值，则拒绝零假设，认为两组样本存在显著性差异；如果秩次和小于临界值，则接受零假设，认为两组样本来自同一总体。

四、实例分析为了更好地理解Wilcoxon符号秩检验的使用方法，接下来以一个实例进行分析。

假设某医院想要比较两种治疗方法对患者血压的影响。

他们随机选择了20名患者，分别给予两种治疗方法，并在治疗前后测量患者的血压值。

excel威尔科克森符号秩检验

Excel威尔科克森符号秩检验1. 威尔科克森符号秩检验简介威尔科克森符号秩检验是一种非参数假设检验方法，用于比较两组相关样本的中位数是否存在显著差异。

它适用于样本不服从正态分布或者存在异常值的情况，因此在实际应用中非常有用。

2. 检验步骤威尔科克森符号秩检验的步骤如下：1）对两组样本数据进行配对，即将相同位置上的数据配对。

2）计算配对差值，并将绝对值化。

3）对所有绝对值进行排序，得到秩次。

4）计算正、负秩和，并选取较小的值作为检验统计量。

5）根据检验统计量和显著性水平查找临界值，从而得出检验结论。

3. Excel中的威尔科克森符号秩检验在Excel中进行威尔科克森符号秩检验非常方便，可以通过内置的函数实现。

下面是具体步骤：1）将两组相关样本数据录入Excel表格中。

2）在合适的位置使用RANK.AVG函数计算绝对值的秩次。

3）计算正、负秩和，得到检验统计量。

4）查找临界值，进行假设检验。

4. 注意事项在进行威尔科克森符号秩检验时，需要注意以下几点：1）样本数据应为相关样本，即配对数据。

2）样本容量较小时，可以使用修正的临界值。

3）检验统计量的计算需要按照步骤精确进行。

4）在使用Excel进行计算时，应当熟悉相关函数的使用方法，以免出现错误。

5. 实例分析以下是一个威尔科克森符号秩检验的实例分析，通过该实例可以更好地理解该方法的应用：两种不同的药物对同一组患者进行治疗，分别记录了两种药物的疗效数据。

现在需要进行威尔科克森符号秩检验，以确定两种药物的疗效是否有显著差异。

6. 结论威尔科克森符号秩检验是一种非参数假设检验方法，适用于比较两组相关样本的中位数是否存在显著差异。

在实际应用中，它能够有效应对样本不服从正态分布或者存在异常值的情况，因此具有广泛的应用价值。

利用Excel进行威尔科克森符号秩检验非常方便，能够快速得出检验结论，但在进行检验时需要注意一些细节问题，以确保结果的准确性和可靠性。

威尔科克森符号秩检验是一种非参数假设检验方法，用于比较两组相关样本的中位数是否存在显著差异。

Wilcoxon符秩检验吴喜之例子

wilcoxon检验例子

wilcoxon检验例子

Wilcoxon符号秩检验

秩方法在毕业生就业与学历关系研究的应用

wilcoxon检验例子

Wilcoxon符号秩检验 吴喜之例子

Wilcoon符号秩检验吴喜之例子

wilcoxon符号秩检验的作用

例题六Wilcoxon（Mann-Whitney）秩和检验

例题六Wilcoxon(MannWhitney)秩和检验

wilcoxon符号秩检验例题

wilcoxon符号秩检验的应用场景案例

wilcoxon符号秩检验例题

Wilcoxon符号秩检验的使用方法(七)

excel威尔科克森符号秩检验

Wilcoxon符号秩检验吴喜之例子