查找与及其应用实验报告
计算机信息检索实验报告(6个)

实验一网上中文搜索引擎及其使用一、实验心得在电脑已经成为生活必备品的现在,日常搜索是一件很平常的事情。
俗话说,天天百度知识丰富。
当然,我国国内主要的搜索引擎除了百度,还有谷歌、雅虎、搜狗、网易、新浪。
一般来说,百度和谷歌是最多人用的。
不同的搜索引擎,不同的搜索方法,得到搜索结果的速度和准确度也不一样。
所以我觉得学习计算机信息检索的主要目的就是更好地提高自己搜索的速度和准确度。
在这次实验当中,我们主要学习和掌握以下搜索技巧的运用。
「“”」的基本用法、「+」或「空格」的基本用法、「+」的基本用法、「-」的基本用法、「OR」的基本用法、「site」的基本用法、「inurl」的基本用法、「intitle」的基本用法、「filetype」的基本用法。
比起以前直接把整个问题打上去然后从网页中寻找满意的答案,灵活使用这些搜索技巧可以更快地找到准确率高的答案。
这些技巧在现实生活中具有高度的可操作性和便捷性。
二、实验结果(一)请使用Google或百度搜索引擎完成以下知识测验:(请将检索结果复制到题干之后,并把所有有关的网页都下载到你的作业文件夹中,以作为本作业评分的依据。
)1.谁根据小仲马的《茶花女》改编了同名歌剧( B )/b/7602599.htmlA.奥斯汀 B.威尔第 C.福楼拜2."生存还是死亡,这是一个问题。
"出自莎士比亚的哪部作品?( A )/question/25934693.htmlA.《哈姆雷特》 B.《李尔王》 C.《麦克白》3."侦探福尔摩斯"第一次出现是在下列哪部作品中: ( A )/question/1306083005651.htmlA.《血字的研究》B.《东方快车谋杀案》C.《尼罗河上的惨案》D.《难逃一生》4.李清照词中名句"寻寻觅觅,冷冷清清,凄凄惨惨戚戚"的词牌名是: ( D ) /wenda/thread?tid=7c29ad4f072df739&hl=cnA.醉花阴B.一剪梅C.如梦令D.声声慢(二)请在网上寻找如下列图片。
信息检索课程实验报告

一、实验背景随着信息技术的飞速发展,信息检索已成为信息时代的重要技能。
为了提高我们的信息素养,培养我们在海量信息中快速、准确地找到所需信息的能力,我们开展了信息检索课程实验。
本实验旨在让我们熟悉信息检索的基本流程,掌握各种检索工具的使用方法,并学会运用检索策略进行信息获取。
二、实验目的1. 熟悉信息检索的基本概念和流程。
2. 掌握搜索引擎和数据库的使用方法。
3. 学会运用检索策略提高检索效率。
4. 培养信息素养,提高信息获取能力。
三、实验内容1. 信息检索基本概念(1)信息检索:指根据信息用户的需求,利用一定的检索工具或联机网络,从大量的文献中迅速准确地查找、筛选、整理和利用所需信息的过程。
(2)检索工具:包括搜索引擎、数据库、图书馆等。
(3)检索策略:指在检索过程中,针对特定需求,选择合适的检索词、检索式和检索途径,以达到快速、准确地获取所需信息的目的。
2. 搜索引擎的使用(1)以百度为例,介绍搜索引擎的基本操作。
(2)演示如何利用关键词进行精确检索、组合检索和高级检索。
(3)讲解如何使用搜索技巧,如排除法、使用引号等。
3. 数据库的使用(1)以CNKI为例,介绍学术数据库的基本操作。
(2)演示如何利用数据库的高级检索功能,如主题检索、作者检索、机构检索等。
(3)讲解如何筛选和整理检索结果,提高信息获取效率。
4. 检索策略的应用(1)针对特定课题,分析检索需求,确定检索策略。
(2)运用关键词、布尔逻辑运算符、位置运算符等构建检索式。
(3)根据检索结果,调整检索策略,提高检索效果。
四、实验步骤1. 熟悉实验内容,了解信息检索的基本概念和流程。
2. 登录百度搜索引擎,进行关键词检索、组合检索和高级检索实验。
3. 登录CNKI学术数据库,进行主题检索、作者检索、机构检索等实验。
4. 根据实验需求,构建检索式,进行检索实验。
5. 分析检索结果,调整检索策略,提高检索效果。
6. 撰写实验报告,总结实验心得。
实验四 搜索 实验报告

实验四搜索实验报告一、实验目的本次实验的主要目的是深入了解和掌握不同的搜索算法和技术,通过实际操作和分析,提高对搜索问题的解决能力,以及对搜索效率和效果的评估能力。
二、实验环境本次实验使用的编程语言为 Python,使用的开发工具为 PyCharm。
实验中所需的数据集和相关库函数均从网络上获取和下载。
三、实验原理1、线性搜索线性搜索是一种最简单的搜索算法,它从数据的开头开始,依次比较每个元素,直到找到目标元素或者遍历完整个数据集合。
2、二分搜索二分搜索则是基于有序数组的一种搜索算法。
它每次将数组从中间分割,比较目标值与中间元素的大小,然后在可能包含目标值的那一半数组中继续进行搜索。
3、广度优先搜索广度优先搜索是一种图搜索算法。
它从起始节点开始,逐层地访问相邻节点,先访问距离起始节点近的节点,再访问距离远的节点。
4、深度优先搜索深度优先搜索也是一种图搜索算法,但它沿着一条路径尽可能深地访问节点,直到无法继续,然后回溯并尝试其他路径。
四、实验内容及步骤1、线性搜索实验编写线性搜索函数,接受一个列表和目标值作为参数。
生成一个包含随机数的列表。
调用线性搜索函数,查找特定的目标值,并记录搜索所用的时间。
2、二分搜索实验先对列表进行排序。
编写二分搜索函数。
同样生成随机数列表,查找目标值并记录时间。
3、广度优先搜索实验构建一个简单的图结构。
编写广度优先搜索函数。
设定起始节点和目标节点,进行搜索并记录时间。
与广度优先搜索类似,构建图结构。
编写深度优先搜索函数。
进行搜索并记录时间。
五、实验结果与分析1、线性搜索结果在不同规模的列表中,线性搜索的时间消耗随着列表长度的增加而线性增加。
对于较小规模的列表,线性搜索的效率尚可,但对于大规模列表,其搜索时间明显较长。
2、二分搜索结果二分搜索在有序列表中的搜索效率极高,其时间消耗增长速度远低于线性搜索。
即使对于大规模的有序列表,二分搜索也能在较短的时间内找到目标值。
3、广度优先搜索结果广度优先搜索能够有效地遍历图结构,并找到最短路径(如果存在)。
查找排序实验报告

查找排序实验报告一、实验目的本次实验的主要目的是深入理解和比较不同的查找和排序算法在性能和效率方面的差异。
通过实际编程实现和测试,掌握常见查找排序算法的原理和应用场景,为今后在实际编程中能够选择合适的算法解决问题提供实践经验。
二、实验环境本次实验使用的编程语言为 Python,开发环境为 PyCharm。
计算机配置为:处理器_____,内存_____,操作系统_____。
三、实验内容1、查找算法顺序查找二分查找2、排序算法冒泡排序插入排序选择排序快速排序四、算法原理1、顺序查找顺序查找是一种最简单的查找算法。
它从数组的一端开始,依次比较每个元素,直到找到目标元素或者遍历完整个数组。
其时间复杂度为 O(n),在最坏情况下需要遍历整个数组。
2、二分查找二分查找适用于已排序的数组。
它通过不断将数组中间的元素与目标元素进行比较,将查找范围缩小为原来的一半,直到找到目标元素或者确定目标元素不存在。
其时间复杂度为 O(log n),效率较高。
3、冒泡排序冒泡排序通过反复比较相邻的两个元素并交换它们的位置,将最大的元素逐步“浮”到数组的末尾。
每次遍历都能确定一个最大的元素,经过 n-1 次遍历完成排序。
其时间复杂度为 O(n^2)。
4、插入排序插入排序将数组分为已排序和未排序两部分,每次从未排序部分取出一个元素,插入到已排序部分的合适位置。
其时间复杂度在最坏情况下为 O(n^2),但在接近有序的情况下性能较好。
5、选择排序选择排序每次从待排序数组中选择最小的元素,与当前位置的元素交换。
经过 n-1 次选择完成排序。
其时间复杂度为 O(n^2)。
6、快速排序快速排序采用分治的思想,选择一个基准元素,将数组分为小于基准和大于基准两部分,然后对这两部分分别递归排序。
其平均时间复杂度为 O(n log n),在大多数情况下性能优异。
五、实验步骤1、算法实现使用Python 语言实现上述六种查找排序算法,并分别封装成函数,以便后续调用和测试。
文献检索的实验报告

一、实验目的1. 掌握文献检索的基本方法与技巧。
2. 培养查找相关文献的能力,提高学术研究水平。
3. 了解学术资源数据库的特点与使用方法。
二、实验时间2023年10月25日三、实验地点图书馆电子阅览室四、实验内容1. 确定检索主题:以“人工智能在医疗领域的应用”为检索主题。
2. 选择检索工具:使用中国知网(CNKI)进行文献检索。
3. 确定检索策略:采用关键词检索、主题词检索和分类检索相结合的方式。
五、实验步骤1. 打开中国知网(CNKI)官方网站,点击“高级检索”。
2. 在检索框中输入关键词“人工智能”、“医疗领域”。
3. 选择检索范围:全文、标题、关键词等。
4. 设置检索时间范围:2010年至今。
5. 选择文献类型:期刊、学位论文、会议论文等。
6. 点击“检索”按钮,查看检索结果。
六、实验结果与分析1. 检索结果:共检索到相关文献123篇,其中期刊论文89篇,学位论文20篇,会议论文14篇。
2. 文献分析:(1)人工智能在医疗领域的应用研究主要集中在以下几个方面:a. 辅助诊断:利用人工智能技术对医学影像进行分析,提高诊断准确率。
b. 辅助治疗:根据患者的病情,制定个性化的治疗方案。
c. 医疗资源优化:通过人工智能技术,实现医疗资源的合理配置。
(2)研究方法:a. 数据挖掘:通过对大量医疗数据的挖掘,发现疾病规律。
b. 深度学习:利用深度学习技术,实现对医学图像的自动识别。
c. 自然语言处理:通过自然语言处理技术,实现医疗文本的自动分析。
(3)研究现状:a. 人工智能在医疗领域的应用已取得一定成果,但仍存在一些问题,如数据质量、算法精度等。
b. 未来发展趋势:随着技术的不断发展,人工智能在医疗领域的应用将更加广泛。
七、实验结论1. 通过本次实验,掌握了文献检索的基本方法与技巧。
2. 提高了查找相关文献的能力,为学术研究提供了有力支持。
3. 了解了学术资源数据库的特点与使用方法,为今后的学术研究奠定了基础。
文件检索实验报告

文件检索实验报告一、引言文件检索是一种通过关键词或查询语句来查找和检索目标文件的方法。
它在信息检索领域有着广泛的应用,包括大规模文本搜索、网络搜索引擎等。
本实验旨在通过设计和实现一个简单的文件检索系统,来探讨文件检索的原理和实现方法。
二、文件检索系统设计2.1 系统架构文件检索系统主要包括以下三个组件:1.文本预处理器:负责对待检索的文件进行预处理,包括文本分词、去除停用词等。
2.索引构建器:将预处理后的文本构建成倒排索引,以便后续的查询操作。
3.查询处理器:接收用户的查询请求,根据倒排索引进行检索,并返回与查询相关的文件列表。
2.2 文件预处理文件预处理是文件检索的第一步,目的是将待检索的文件转化为可以建立索引的形式。
常见的预处理步骤包括:1.分词:将文本切分成一个个单词或词组,常用的方法有基于规则的切分和基于统计的切分。
2.去除停用词:将一些常见且无实际检索意义的词汇去除,例如“的”、“是”等。
3.大小写转换:将文本中的英文字母统一转换为小写,以方便后续的索引构建和查询处理。
2.3 索引构建索引构建是文件检索的核心步骤,其目的是根据预处理后的文本构建倒排索引。
倒排索引是一种将单词映射到包含该单词的文件列表的数据结构。
索引构建的过程主要包括以下几个步骤:1.单词统计:对预处理后的文本进行单词的统计,得到每个单词在不同文档中的出现次数。
2.倒排列表生成:根据单词的统计信息,生成每个单词对应的倒排列表,记录该单词在哪些文档中出现。
3.索引存储:将生成的倒排列表存储到磁盘上,以便后续的查询操作。
2.4 查询处理查询处理是文件检索的关键步骤,通过用户的查询请求,在倒排索引中查找与查询相关的文档列表,并按照相关性进行排序。
查询处理的过程主要包括以下几个步骤:1.查询解析:将用户的查询请求解析为一组关键词,例如对查询语句进行分词。
2.查询扩展:根据倒排索引,将查询中的关键词进行扩展,找到与之相关的同义词或相关词。
计算机信息检索实验报告(6个)

实验一网上中文搜索引擎及其使用一、实验心得在电脑已经成为生活必备品的现在,日常搜索是一件很平常的事情。
俗话说,天天百度知识丰富。
当然,我国国内主要的搜索引擎除了百度,还有谷歌、雅虎、搜狗、网易、新浪。
一般来说,百度和谷歌是最多人用的。
不同的搜索引擎,不同的搜索方法,得到搜索结果的速度和准确度也不一样。
所以我觉得学习计算机信息检索的主要目的就是更好地提高自己搜索的速度和准确度。
在这次实验当中,我们主要学习和掌握以下搜索技巧的运用。
「“”」的基本用法、「+」或「空格」的基本用法、「+」的基本用法、「-」的基本用法、「OR」的基本用法、「site」的基本用法、「inurl」的基本用法、「intitle」的基本用法、「filetype」的基本用法。
比起以前直接把整个问题打上去然后从网页中寻找满意的答案,灵活使用这些搜索技巧可以更快地找到准确率高的答案。
这些技巧在现实生活中具有高度的可操作性和便捷性。
二、实验结果(一)请使用Google或百度搜索引擎完成以下知识测验:(请将检索结果复制到题干之后,并把所有有关的网页都下载到你的作业文件夹中,以作为本作业评分的依据。
)1.谁根据小仲马的《茶花女》改编了同名歌剧( B )/b/7602599.html A.奥斯汀B.威尔第C.福楼拜2."生存还是死亡,这是一个问题。
"出自莎士比亚的哪部作品?( A )/question/25934693.html A.《哈姆雷特》 B.《李尔王》 C.《麦克白》 3."侦探福尔摩斯"第一次出现是在下列哪部作品中: ( A ) /question/1306083005651.html A.《血字的研究》 B.《东方快车谋杀案》 C.《尼罗河上的惨案》D.《难逃一生》4.李清照词中名句"寻寻觅觅,冷冷清清,凄凄惨惨戚戚"的词牌名是: ( D ) /wenda/thread?tid=7c29ad4f072df739&hl=cn A.醉花阴 B.一剪梅 C.如梦令 D.声声慢(二)请在网上寻找如下列图片。
文献检索与利用作业(一)
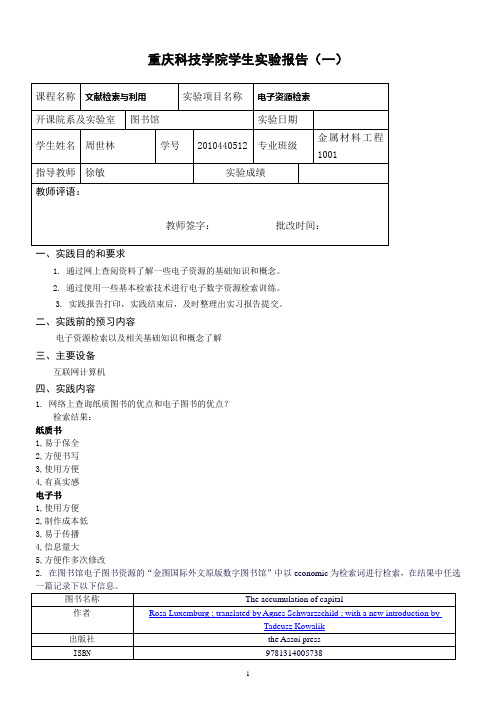
重庆科技学院学生实验报告(一)一、实践目的和要求1. 通过网上查阅资料了解一些电子资源的基础知识和概念。
2. 通过使用一些基本检索技术进行电子数字资源检索训练。
3. 实践报告打印,实践结束后,及时整理出实习报告提交。
二、实践前的预习内容电子资源检索以及相关基础知识和概念了解三、主要设备互联网计算机四、实践内容1. 网络上查询纸质图书的优点和电子图书的优点?检索结果:纸质书1,易于保全2,方便书写3,使用方便4,有真实感电子书1,使用方便2,制作成本低3,易于传播4,信息量大5,方便作多次修改2.在图书馆电子图书资源的“金图国际外文原版数字图书馆”中以economic为检索词进行检索,在结果中任选一篇记录下以下信息。
3. 在图书馆电子图书资源的“时代圣典数字图书馆”中检索作者为“王燕”,书名含“四级”的电子图书信息。
4.在图书馆电子图书资源的“超星数字图书馆”中检索作者姓“赵”,书名含“冶金”的2009年出版的电子图检索结果:( 4 )条书信息,记录下检索结果数量并任选一个记录以下信息。
★此项要填>>6.在图书馆电子图书资源的“书生之家数字图书馆”中利用分类检索来查找“冶金与金属-> 炼钢-> 炼钢炉”下的电子图书数量并任选一个记录以下信息。
★此项要填>> 检索结果:( 1 )条56348. 在图书馆电子图书资源的“九羽数字图书馆”中,高级搜索以ISBN号为7-80153-961-3来检索并记录。
9.在图书馆电子图书资源的“博图外文电子图书”中,高级检索书名含“economy”,出版社为“State University of New Y ork Press”的任意一条结果并记录结果中的书名、作者和ISBN信息。
图书名称:A Comparative Political Economy of Tunisia and Morocco : On the Outside of Europe Looking in作者:White, Gregory.ISBN:0791450279/079145027910. 图书馆的CNKI中国学术期刊全文数据库中的中国期刊全文数据库中寻找题名为“国内铜硫浮选分离研究现状”的文章并下载打开记录其结论段落三点内容任意其一。
实验报告

实验报告书课程名称:《数据库原理及应用》实验题目:实验四SQL Server 数据查询班级:学号:姓名:指导教师:一、实验目的(1)掌握使用Transact-SQL的SELECT语句进行基本查询的方法。
(2)掌握使用SELECT语句进行条件查询的方法。
(3)掌握SELECT语句的GROUP BY、ORDER BY以及UNION子句的作用和使用方法。
(4)掌握嵌套查询的方法。
(5)掌握连接查询的操作方法。
二、实验内容及步骤1.启动 SQL Server 管理平台,在对象资源管理器中展开studentsdb数据库文件夹。
2.在studentsdb数据库中使用SELECT语句进行基本查询。
(1)在student_info表中,查询每个学生的学号、姓名、出生日期信息。
(2)查询学号为0002 的学生的姓名和家庭住址。
(3)找出所有男同学的学号和姓名。
3.使用SELECT语句进行条件查询(1)在grade表中查找分数在80~90范围内的学生的学号和分数。
(2)在grade表中查询课程编号为0003的学生的平均分。
(3)在grade表中查询学习各门课程的人数。
(4)将学生按出生日期由大到小排序。
(5)查询所有姓“张”的学生的学号和姓名。
4.对student_info表,按性别顺序列出学生的学号、姓名、性别、出生日期及家庭住址,性别相同的按学号由小到大排序。
5.使用GROUP BY查询子句列出各个学生的平均成绩。
6.使用UNION运算符将student_info表中姓“张”的学生的学号、姓名与curriculum表的课程编号、课程名称返回在一个表中,且列名为u_编号、u_名称,如图8所示。
图联合查询结果集7.嵌套查询(1)在student_info表中查找与“刘卫平”性别相同的所有学生的姓名、出生日期。
(2)使用IN子查询查找所修课程编号为0002、0005的学生学号、姓名、性别。
(3)列出学号为0001的学生的分数比0002号的学生的最低分数高的课程编号和分数。
实习检索报告

实习检索报告
标题:实习检索报告
一、引言
在本次实习期间,我参与了一项检索任务。
本报告将详细介绍我进行实习检索的目的、方法、结果和总结。
二、目的
本次实习的检索任务是为了解决一个特定领域的问题。
我们的目标是收集和整理相关
文献,以便为该问题提供有用的信息和解决方案。
三、方法
在实施检索任务之前,我首先进行了问题的分析和理解。
然后,我制定了检索策略和
关键词,并在相关数据库和搜索引擎中进行了检索。
我使用了多种检索工具和技术,
包括关键词检索、高级检索和筛选。
四、结果
通过我的检索努力,我收集到了大量与问题相关的文献。
这些文献涵盖了不同的领域
和专业知识,并提供了多种解决方案和观点。
我整理和归纳了这些文献,为问题的深
入研究提供了基础。
五、总结
通过参与实习检索任务,我深入了解了检索的方法和技巧,提高了我的信息搜集和整
理能力。
通过阅读大量文献,我也对特定领域的知识有了更加全面和深入的了解。
这
次实习对我的学术和职业发展都具有积极的影响。
六、建议
在今后的实习中,我建议加强对检索工具和技术的了解和应用。
我还建议进一步扩大检索范围,并利用更多的有效资源和渠道来收集文献。
此外,与其他实习生或专业人士交流和合作,将有助于开拓视野和提高研究能力。
七、致谢
最后,我要感谢实习导师和团队对我的指导和支持。
他们的专业知识和经验对我的实习检索任务起到了重要的帮助和影响。
感谢他们的辛勤工作和付出。
《网络信息资源检索与利用》课内实验二.doc

实验结果:
一.请分别针对网络资源目录使用的分类方法进行举例。
主题分类法:如yahoo
学科分类法:如sohu的社会科学分类
图书分类法:如中国图书馆图书分类法
c.其他
6.如果你是小王的话,在无法找到自己所需资源时你会向他人求助吗?()
a.会(请做第7题)
b.不会(请做第8题)
7.如果会的话,你会通过哪些途径向别人求助?
8.为什么不向别人求助?()
a.不知道如何向别人求助
b.不相信别人能够帮你解决问题
9.你有向别人求助的经历吗?是通过何种途径求助的?求助的效果如何?
6.相关检索词智能推荐技术。在用户第一次检索后,会提示相关的检索词,帮助用户查找更相关的结果,统计表明可以促进检索量提升10-20%。
7.运用多线程技术、高效的搜索算法、稳定的UNIX平台、短检索的响应时间(一个检索的平均响应时间小于0.5秒)
3.智能相关度算法。采用了基于内容和基于超链分析相结合的方法进行相关度评价,能够客观分析网页所包含的信息,从而最大限度保证了检索结果相关性。
4.检索结果能标示丰富的网页属性(如标题、网址、时间、大小、编码、摘要等),并突出用户的查询串)。可在上次检索结果中继续检索,逐步缩小查找范围,直至达到最小、最准确的结果集。利于用户更加方便地在海量信息中找到自己真正感兴趣的内容。
《网络信息资源检索与利用》课程实验第2次实验报告
实验内容及基本要求:
实验项目名称:网络搜索引擎的应用
实验类型:验证
每组人数:1
实验内录使用的分类方法进行举例。
顺序查找法实验报告

一、实验目的1. 理解顺序查找法的原理和过程。
2. 掌握顺序查找法的实现方法。
3. 通过实验验证顺序查找法的效率和适用场景。
二、实验环境1. 操作系统:Windows 102. 编程语言:Python3.83. 实验数据:一组随机生成的整数序列三、实验原理顺序查找法是一种简单的查找算法,其基本思想是从线性表的第一个元素开始,逐个比较,直到找到待查找的元素或者比较到序列的末尾。
如果找到待查找的元素,则返回该元素的位置;如果比较到序列的末尾仍未找到,则返回-1表示查找失败。
顺序查找法的时间复杂度为O(n),空间复杂度为O(1),适用于数据量较小或者无序的线性表。
四、实验步骤1. 导入Python的random模块,用于生成随机整数序列。
2. 定义一个顺序查找函数,接收线性表和待查找元素作为参数。
3. 在主函数中,生成一个随机整数序列,并设置待查找元素。
4. 调用顺序查找函数,并输出查找结果。
五、实验代码```pythonimport randomdef sequential_search(arr, target):for i in range(len(arr)):if arr[i] == target:return ireturn -1def main():# 生成随机整数序列arr = [random.randint(1, 100) for _ in range(20)] print("随机整数序列:", arr)# 设置待查找元素target = random.randint(1, 100)print("待查找元素:", target)# 调用顺序查找函数result = sequential_search(arr, target)# 输出查找结果if result != -1:print("查找成功,元素位置:", result)else:print("查找失败")if __name__ == "__main__":main()```六、实验结果与分析1. 运行实验程序,生成随机整数序列和待查找元素。
信息检索(实验报告)

信息检索(实验报告)徐州工程学院管理学院实验报告实验课程名称:信息存储与检索实验地点:经济管理实验教学中心 2012 年月至 2012 年 12 月专业信息管理与信息系统班级 10信管学生姓名 xx学号 20101511215指导老师 xxx2、使用数字照相机(或具有近似功能的设备,如摄像功能手机)获取本人实验用的计算机显示器上显示的任一屏幕图像,保存成JPG格式图片,粘贴到实验报告上。
并用文字简要叙述你所使用设备的工作原理。
(实验目的不同,请不要用计算机本身的屏幕抓图功能)数字照相机的工作原理:数码相机是集光学、机械、电子、电功一体化的产品。
它集成了影像信息的转换、存储和传输等部件,具有数字化存取模式,与电脑交互处理和实时拍摄等特点。
光线通过镜头或者镜头组进入相机,通过成像元件转化为数字信号,数字信号通过影像运算芯片储存在存储设备中。
数码相机的成像元件是CCD或者COMS,该成像元件的特点是光线通过时,能根据光线的不同转化为电子信号。
佳能数码照像机3、够读取条形码的设备有哪些?任意选取一种,并将其图片粘贴到实验报告中,并在图片下方给出设备名称信息。
读取条形码的设备:光笔、条码卡槽、扫描枪、激光全向扫描台、扫描仪、扫描器条形码扫描设备:手持式激光条码扫描器LS2208(摩托罗拉)4、叙述一下本人触摸屏手机(没有的可以借用同学的)的触摸屏类型(电容式、电阻式…)及其工作原理。
并用图片说明。
手机信息:步步高vivio S3, Android OS 2.3系统,电容屏。
5、叙述一下本人手写板手机(没有的可以借用同学的)的手写板类型及其工作原理。
并用图片说明。
手机信息:三星Galaxy Tab P1000,7.0英寸超大电容触摸屏工作原理:数位电磁板和压感式电磁板的工作原理都是采用了电磁感应技术。
它由手写笔发射出电磁波,由写字板上排列整齐的传感器感应到后,计算出笔的位置后报告给计算机,然后由计算机做出移动光标或其它的相应动作。
信息检索实验报告_2

信息检索实验报告信息检索试验报告以下是为大家收拾的信息检索试验报告的相关范文,本文关键词为信息,检索,试验,报告,,您可以从右上方搜寻框检索更多琴试验指导教师:崔新华完成日期:20XX年06月10日名目1.文献检索的意义....................................................32.检索主题......................................................... .33.课程试验地点......................................................44.检索主题分析 (4)4.1各主题分析...................................................44.2各主题检索策略...............................................55.检索步骤的制订. (7)5.1手工检索.....................................................75.2计算机检索...................................................86.检索内容 (10)6.1图书馆专业图书检索..........................................106.2中文科技期刊信息检索........................................106.3网络科技信息检索(含报纸和网络)............................257.检索主题结果的分析与总结.........................................298.信息资源检索课程心得 (31)1.文献检索的意义文献检索是教导讨论过程中必不行少的一环。
查找和排序 实验报告

查找和排序实验报告查找和排序实验报告一、引言查找和排序是计算机科学中非常重要的基础算法之一。
查找(Search)是指在一组数据中寻找目标元素的过程,而排序(Sort)则是将一组数据按照特定的规则进行排列的过程。
本实验旨在通过实际操作和实验验证,深入理解查找和排序算法的原理和应用。
二、查找算法实验1. 顺序查找顺序查找是最简单的查找算法之一,它的基本思想是逐个比较待查找元素与数据集合中的元素,直到找到目标元素或遍历完整个数据集合。
在本实验中,我们设计了一个包含1000个随机整数的数据集合,并使用顺序查找算法查找指定的目标元素。
实验结果显示,顺序查找的时间复杂度为O(n)。
2. 二分查找二分查找是一种高效的查找算法,它要求待查找的数据集合必须是有序的。
二分查找的基本思想是通过不断缩小查找范围,将待查找元素与中间元素进行比较,从而确定目标元素的位置。
在本实验中,我们首先对数据集合进行排序,然后使用二分查找算法查找指定的目标元素。
实验结果显示,二分查找的时间复杂度为O(log n)。
三、排序算法实验1. 冒泡排序冒泡排序是一种简单但低效的排序算法,它的基本思想是通过相邻元素的比较和交换,将较大(或较小)的元素逐渐“冒泡”到数列的一端。
在本实验中,我们设计了一个包含1000个随机整数的数据集合,并使用冒泡排序算法对其进行排序。
实验结果显示,冒泡排序的时间复杂度为O(n^2)。
2. 插入排序插入排序是一种简单且高效的排序算法,它的基本思想是将数据集合分为已排序和未排序两部分,每次从未排序部分选择一个元素插入到已排序部分的适当位置。
在本实验中,我们使用插入排序算法对包含1000个随机整数的数据集合进行排序。
实验结果显示,插入排序的时间复杂度为O(n^2)。
3. 快速排序快速排序是一种高效的排序算法,它的基本思想是通过递归地将数据集合划分为较小和较大的两个子集合,然后对子集合进行排序,最后将排序好的子集合合并起来。
网络信息资源检索与利用第二次作业.doc

《网络信息资源检索与利用》课程实验第 2 次实验报告
实验内容及基本要求:
实验项目名称:网络搜索引擎的应用
实验类型:验证
每组人数: 1
实验内容及要求:
1. 请分别针对网络资源目录使用的分类方法进行举例。
2. 在yahoo的分类目录中找到一条路径指向网站论文:/Summer98/koumoutsakos.pdf。
3. 在新浪网的分类目录中找到一条路径指向学校的网站:
4. 在sohu的分类目录中找到一条路径指向网页:/newbook/
5. 请指出yahoo,sina,sohu的分类目录之间的异同和优劣(500字以内)
6. 请了解google和baidu在进行关键词检索中语法的异同,并说明这两者在针对某一主题进行检索时检索结果的差异以及对检索意图理解准确度的差异。
实验结果:
1. 请分别针对网络资源目录使用的分类方法进行举例。
(1)主题分类法
(2)学科分类法
(3)图书分类法
(4)分面组配法
2. 在yahoo的分类目录中找到一条路径指向网站论文:/Summer98/koumoutsakos.pdf。
3. 在新浪网的分类目录中找到一条路径指向学校的网站:
4. 在sohu的分类目录中找到一条路径指向网页:/newbook/
5. 请指出yahoo,sina,sohu的分类目录之间的异同和优劣(500字以内)。
大学计算机实验6 实验报告

大学计算机实验6 实验报告一、实验目的本次大学计算机实验 6 的目的在于深入了解和掌握计算机系统中的某些关键技术和应用,通过实际操作和实践,提高我们对计算机知识的理解和应用能力,培养我们解决实际问题的思维和方法。
二、实验环境本次实验在学校的计算机实验室进行,使用的计算机配置为_____,操作系统为_____,安装了所需的实验软件,包括_____等。
三、实验内容(一)操作系统的基本操作1、文件和文件夹的管理熟练掌握了文件和文件夹的创建、复制、移动、删除、重命名等操作。
通过实际操作,了解了文件和文件夹的属性设置,如只读、隐藏等,以及如何查找和筛选特定的文件和文件夹。
2、任务管理器的使用学会了使用任务管理器查看系统中正在运行的进程、CPU 和内存的使用情况。
能够通过任务管理器结束无响应的进程,优化系统资源的分配。
(二)办公软件的应用1、 Word 文档的编辑使用 Word 进行了文档的排版,包括字体、字号、颜色、段落格式的设置。
学会了插入图片、表格、页眉页脚等元素,以及如何进行文档的页面设置和打印预览。
2、 Excel 数据处理在 Excel 中,掌握了数据的输入、编辑和格式化。
学会了使用函数和公式进行数据的计算和统计,如求和、平均值、最大值、最小值等。
还掌握了数据的排序、筛选和图表的创建,能够将数据以直观的方式呈现出来。
(三)网络应用1、浏览器的使用熟悉了常用浏览器的操作,如网页的浏览、书签的添加和管理、历史记录的查看等。
学会了设置浏览器的主页、隐私和安全选项。
2、电子邮件的收发通过实验,掌握了电子邮箱的注册和设置,能够熟练地发送和接收电子邮件,包括添加附件、设置邮件格式和优先级等。
(四)多媒体软件的使用1、图片处理软件使用图片处理软件对图片进行了裁剪、调整大小、色彩调整、添加文字和特效等操作,提高了图片的质量和美观度。
2、音频和视频播放软件学会了使用音频和视频播放软件播放各种格式的文件,掌握了播放控制、音量调节、画面调整等基本操作。
串的应用实验报告小结

串的应用实验报告小结实验目的:本实验旨在探索串的应用,并通过实际操作,加深对串的理解和应用能力。
实验原理:串是计算机中常用的数据类型,表示一个字符序列。
在实际应用中,串具有很强的灵活性和实用性,可以用于字符串的处理、文本处理、数据传输等场景。
串的基本操作包括串的定义、串的赋值、串的连接、串的比较、串的查找、串的替换等。
实验仪器和材料:编程环境:本实验使用Python编程语言进行实验操作。
实验过程中需要使用字符串处理相关的函数和方法。
实验步骤:1. 串的定义与赋值:首先介绍串的定义方法,并进行一些基本的赋值操作,包括直接赋值和通过输入获取串的赋值。
2. 串的连接:实现两个串的连接操作,了解串的拼接方式及其应用场景。
3. 串的比较:通过比较两个串的内容,了解串的比较操作及其返回值的含义。
4. 串的查找与替换:实现对串的查找和替换操作,掌握相关函数的用法并思考其实际应用。
实验结果:通过本次实验,我对串的相关操作有了更深入的了解。
掌握了串的基本定义、赋值、连接、比较、查找和替换等操作,并能够将其应用到实际问题中。
在实验过程中,我学会了如何利用串来处理文本数据,进行查找和替换操作,以及如何利用串的连接来构造更复杂的字符串。
这些知识和实践经验对我的编程能力和问题解决能力都有所提高。
实验总结:通过本次实验,我对串的基本概念和相关应用有了更深入的了解。
串作为计算机中重要的数据类型,在实际应用中有着广泛的应用场景,掌握了串的相关操作,将对我的日常编程工作和问题解决能力产生积极的影响。
串的处理能力将对字符串处理、文本处理、数据传输等方面有很大帮助。
结语:本次实验使我更加深入地理解了串的概念及其在实际应用中的作用。
通过在实验中动手操作,我对串的相关操作有了更深入的了解,相信这将对我的编程能力和问题解决能力有所提升。
我也意识到了串在计算机领域的重要性和广泛的应用前景,将积极应用串的相关知识到我的日常工作和学习中。
文件检索实验报告

文件检索实验报告一、研究背景在现代社会,随着信息技术的快速发展,越来越多的文件被电子化存储。
但是,如何进行高效的文件检索依然是一个挑战。
为了解决这一问题,本实验旨在探索不同文件检索方法的性能和效果,并提出一种更好的文件检索机制。
二、实验目的本实验的目的是:1.比较不同文件检索方法在检索准确性和效率方面的差异。
2.评估现有文件检索机制的局限性和改进空间。
3.提出一种改进的文件检索机制,以提高检索的效率和准确性。
三、实验方法1.数据收集从多个来源收集一定量的文本文件作为实验材料,并对其进行分类和标记,以便于后续的检索实验。
2.实验设计选择不同的文件检索方法,并进行对比实验。
本实验选择了以下三种方法进行比较:- 关键词搜索:根据用户输入的关键词,在文件中进行全文搜索,并返回与关键词相关的文档。
- 文档分类:通过对文件进行分类和标记,在用户输入查询条件时,通过匹配文档的分类标签来返回相应的文档。
- 相似度匹配:利用自然语言处理技术,计算用户查询与文档之间的相似度,并按照相似度进行排序,返回相似度最高的文档。
3.实验操作使用实验室提供的文件检索系统,依次输入不同的查询条件,并记录下每种方法的检索结果和所花费的时间。
四、实验结果与分析1.检索准确性比较根据实验中的查询条件,比较三种不同的文件检索方法的准确性。
结果显示,相似度匹配方法的准确性较高,因为它考虑了文档的整体内容和结构,而不仅仅是关键词的匹配。
关键词搜索和文档分类方法在准确性方面存在一定的局限性,容易受到关键词选择和分类标签的限制。
2.检索效率比较比较三种不同的文件检索方法的效率。
结果显示,关键词搜索方法最为快速,因为它只需在文档中进行简单的匹配操作。
相似度匹配方法由于需要进行复杂的相似度计算,所以相对耗时。
文档分类方法的效率受到分类标签的数量和质量的影响,当分类系统复杂时,其效率可能会较低。
3.改进方案在分析实验结果的基础上,提出一种改进的文件检索机制:结合关键词搜索和相似度匹配的方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
{printf("%d ",R[i].key);i++; //从表头往后找}if (i>=n)return -1;else{printf("%d",R[i].key);return i;}}int main(){SeqList R;int n=10,i;KeyType k=5;int a[]={3,6,2,10,1,8,5,7,4,9};for (i=0;i<n;i++) //建立顺序表R[i].key=a[i];printf("关键字序列:");for (i=0;i<n;i++)printf("%d ",R[i].key);printf("\n");printf("查找%d所比较的关键字:\n\t",k);if ((i=SeqSearch(R,n,k))!=-1)printf("\n元素%d的位置是%d\n",k,i);elseprintf("\n元素%d不在表中\n",k);printf("\n");}代码片段2:#include <stdio.h>#define MAXL 100//定义表中最多记录个数typedef int KeyType;typedef char InfoType[10];typedef struct{KeyType key;//KeyType为关键字的数据类型InfoType data;//其他数据} NodeType;typedef NodeType SeqList[MAXL];//顺序表类型int BinSearch(SeqList R,int n,KeyType k)//二分查找算法{int low=0,high=n-1,mid,count=0;while (low<=high){mid=(low+high)/2;printf("第%d次比较:在[%d,%d]中比较元素R[%d]:%d\n",++count,low,high,mid,R[mid].key);if (R[mid].key==k)//查找成功返回return mid;if (R[mid].key>k)//继续在R[low..mid-1]中查找high=mid-1;elselow=mid+1;//继续在R[mid+1..high]中查找}return -1;}int main(){SeqList R;KeyType k=9;int a[]={1,2,3,4,5,6,7,8,9,10},i,n=10;for (i=0;i<n;i++)//建立顺序表R[i].key=a[i];printf("关键字序列:");for (i=0;i<n;i++)printf("%d ",R[i].key);printf("\n");printf("查找%d的比较过程如下:\n",k);if ((i=BinSearch(R,n,k))!=-1)printf("元素%d的位置是%d\n",k,i);elseprintf("元素%d不在表中\n",k);return 0;}代码片段3:#include <stdio.h>#include <malloc.h>#define MaxSize 100typedef int KeyType;//定义关键字类型typedef char InfoType;typedef struct node //记录类型{KeyType key; //关键字项InfoType data; //其他数据域struct node *lchild, *rchild;//左右孩子指针} BSTNode;int path[MaxSize];//全局变量,用于存放路径void DispBST(BSTNode *b);//函数说明int InsertBST(BSTNode *&p, KeyType k);BSTNode *CreatBST(KeyType A[], int n);void DispBST(BSTNode *bt);int JudgeBST(BSTNode *bt);int SearchBST(BSTNode *bt, KeyType k);void Delete1(BSTNode *p, BSTNode *&r);void Delete(BSTNode *&p);int DeleteBST(BSTNode *&bt, KeyType k);int InsertBST(BSTNode *&p, KeyType k)//在以*p为根节点的BST中插入一个关键字为k的节点{if (p == NULL)//原树为空, 新插入的记录为根节点{p = (BSTNode *)malloc(sizeof(BSTNode));p->key = k; p->lchild = p->rchild = NULL;return 1;}else if (k == p->key)return 0;else if (k<p->key)return InsertBST(p->lchild, k);//插入到*p的左子树中elsereturn InsertBST(p->rchild, k); //插入到*p的右子树中}BSTNode *CreatBST(KeyType A[], int n)//由数组A中的关键字建立一棵二叉排序树{BSTNode *bt = NULL; //初始时bt为空树int i = 0;while (i<n)if (InsertBST(bt, A[i]) == 1)//将A[i]插入二叉排序树T中{printf(" 第%d步,插入%d:", i + 1, A[i]);DispBST(bt); printf("\n");i++;}return bt; //返回建立的二叉排序树的根指针}void DispBST(BSTNode *bt)//以括号表示法输出二叉排序树bt{if (bt != NULL){printf("%d", bt->key);if (bt->lchild != NULL || bt->rchild != NULL){printf("(");DispBST(bt->lchild);if (bt->rchild != NULL) printf(",");DispBST(bt->rchild);printf(")");}}}KeyType predt = -32767; //predt为全局变量,保存当前节点中序前趋的值,初值为-∞int JudgeBST(BSTNode *bt)//判断bt是否为BST{int b1, b2;if (bt == NULL) //空二叉树是排序二叉树return 1;else{b1 = JudgeBST(bt->lchild); //返回对左子树的判断,不是返回0,否则返回1if (b1 == 0 || predt >= bt->key) //当左子树不是二叉排序树,或中序前趋(全局变量)大于当前根结点时return 0; //返回“不是二叉排序树”predt = bt->key; //记录当前根为右子树的中序前趋b2 = JudgeBST(bt->rchild); //对右子树进行判断return b2;}}int SearchBST(BSTNode *bt, KeyType k)//以递归方式输出从根节点到查找到的节点的路径{if (bt == NULL)return 0;else if (k == bt->key){printf("%3d", bt->key);return 1;}else if (k<bt->key)SearchBST(bt->lchild, k); //在左子树中递归查找elseSearchBST(bt->rchild, k); //在右子树中递归查找printf("%3d", bt->key);}void Delete1(BSTNode *p, BSTNode *&r)//当被删*p节点有左右子树时的删除过程{BSTNode *q;if (r->rchild != NULL)Delete1(p, r->rchild);//递归找最右下节点else//找到了最右下节点*r{p->key = r->key;//将*r的关键字值赋给*pq = r;r = r->lchild;//将*r的双亲节点的右孩子节点改为*r的左孩子节点free(q);//释放原*r的空间}}void Delete(BSTNode *&p)//从二叉排序树中删除*p节点{BSTNode *q;if (p->rchild == NULL)//*p节点没有右子树的情况{q = p; p = p->lchild; free(q);}else if (p->lchild == NULL)//*p节点没有左子树的情况{q = p; p = p->rchild; free(q);}else Delete1(p, p->lchild);//*p节点既有左子树又有右子树的情况}int DeleteBST(BSTNode *&bt, KeyType k)//在bt中删除关键字为k的节点{if (bt == NULL) return 0;//空树删除失败else{if (k<bt->key)return DeleteBST(bt->lchild, k);//递归在左子树中删除关键字为k的节点else if (k>bt->key)return DeleteBST(bt->rchild, k);//递归在右子树中删除关键字为k的节点else//k=bt->key的情况{Delete(bt);//调用Delete(bt)函数删除*bt节点return 1;}}}int main(){BSTNode *bt;KeyType k = 6;int a[] = { 4, 9, 0, 1, 8, 6, 3, 5, 2, 7 }, n = 10;printf("创建一棵BST树:");printf("\n");bt = CreatBST(a, n);printf("BST:"); DispBST(bt); printf("\n");printf("bt%s\n", (JudgeBST(bt) ? "是一棵BST" : "不是一棵BST"));printf(" 查找%d关键字(递归,逆序):", k); SearchBST(bt, k);//SearchBST(bt, k, path, -1);printf("\n删除操作:\n");printf(" 原BST:"); DispBST(bt); printf("\n");printf(" 删除节点4:");DeleteBST(bt, 4);DispBST(bt); printf("\n");printf(" 删除节点5:");实验结果:1.2.3:总结体会:通过本次实验学会了顺序查找和二分查找的区别,认清了两种方法的不同之处,相比之下,二分查找比顺序查找更能节约空间和时间,利用二分查找要优越与顺序查找,也更符合人们的思想,对排序的算法有了更深的认识,体会到了算法的优越。
