浙江版2018年高考数学一轮复习专题5.3平面向量的数量积及其应用测

合集下载

(浙江专用)2018年高考数学总复习第五章平面向量、复数第3讲平面向量的数量积及其应用学案

第3讲平面向量的数量积及其应用最新考纲 1.理解平面向量数量积的含义及其物理意义；2.了解平面向量的数量积与向量投影的关系；3.掌握数量积的坐标表达式，会进行平面向量数量积的运算；4.能运用数量积表示两个向量的夹角，会用数量积判断两个平面向量的垂直关系；5.会用向量的方法解决某些简单的平面几何问题；6.会用向量方法解决简单的力学问题与其他一些实际问题.知识梳理1.平面向量数量积的有关概念(1)向量的夹角：已知两个非零向量a 和b ，记OA →＝a ，OB →＝b ，则∠AOB ＝θ(0°≤θ≤180°)叫做向量a 与b 的夹角.(2)数量积的定义：已知两个非零向量a 与b ，它们的夹角为θ，则数量|a ||b |cos__θ 叫做a 与b 的数量积(或内积)，记作a ·b ，即a ·b ＝|a ||b |cos__θ，规定零向量与任一向量的数量积为0，即0·a ＝0.(3)数量积的几何意义：数量积a ·b 等于a 的长度|a |与b 在a 的方向上的投影|b |cos__θ的乘积.2.平面向量数量积的性质及其坐标表示设向量a ＝(x 1，y 1)，b ＝(x 2，y 2)，θ为向量a ，b 的夹角. (1)数量积：a ·b ＝|a ||b |cos θ＝x 1x 2＋y 1y 2. (2)模：|a |＝a ·a ＝x 21＋y 21. (3)夹角：cos θ＝a ·b |a ||b |＝x 1x 2＋y 1y 2x 21＋y 21·x 22＋y 22. (4)两非零向量a ⊥b 的充要条件：a ·b ＝0⇔x 1x 2＋y 1y 2＝0.(5)|a ·b |≤|a ||b |(当且仅当a ∥b 时等号成立)⇔|x 1x 2＋y 1y 2|≤ x 21＋y 21·x 22＋y 22. 3.平面向量数量积的运算律 (1)a ·b ＝b ·a (交换律).(2)λa ·b ＝λ(a ·b )＝a ·(λb )(结合律). (3)(a ＋b )·c ＝a ·c ＋b ·c (分配律).诊断自测1.判断正误(在括号内打“√”或“×”)(1)两个向量的夹角的范围是⎣⎢⎡⎦⎥⎤0，π2.( )(2)向量在另一个向量方向上的投影为数量，而不是向量.( )(3)两个向量的数量积是一个实数，向量的加、减、数乘运算的运算结果是向量.( ) (4)若a ·b ＞0，则a 和b 的夹角为锐角；若a ·b ＜0，则a 和b 的夹角为钝角.( ) (5)a ·b ＝a ·c (a ≠0)，则b ＝c .( ) 解析 (1)两个向量夹角的范围是[0，π].(4)若a ·b >0，a 和b 的夹角可能为0；若a ·b <0，a 和b 的夹角可能为π.(5)由a ·b ＝a ·c (a ≠0)得|a ||b |cos 〈a ，b 〉＝|a ||c |cos 〈a ，c 〉，所以向量b 和c 不一定相等.答案 (1)× (2)√ (3)√ (4)× (5)×2.(2015·全国Ⅱ卷)向量a ＝(1，－1)，b ＝(－1，2)，则(2a ＋b )·a 等于( ) A.－1B.0C.1D.2解析因为a ＝(1，－1)，b ＝(－1，2)，所以2a ＋b ＝2(1，－1)＋(－1，2)＝(1，0)，得(2a ＋b )·a ＝(1，0)·(1，－1)＝1，选C. 答案 C3.(2017·湖州模拟)已知向量a ，b ，其中|a |＝3，|b |＝2，且(a －b )⊥a ，则向量a 和b 的夹角是________.解析因为(a －b )⊥a ，所以(a －b )·a ＝|a |2－|a ||b |·cos〈a ，b 〉＝3－23×cos〈a ，b 〉＝0，解得cos 〈a ，b 〉＝32，由于〈a ，b 〉∈[0，π].则向量a ，b 的夹角为π6. 答案π64.(2016·石家庄模拟)已知平面向量a ，b 的夹角为2π3，|a |＝2，|b |＝1，则|a ＋b |＝________.解析 ∵|a ＋b |2＝|a |2＋2a ·b ＋|b |2＝4＋2|a ||b |cos 2π3＋1＝4－2＋1＝3，∴|a ＋b |＝ 3.答案35.(必修4P104例1改编)已知|a |＝5，|b |＝4，a 与b 的夹角θ＝120°，则向量b 在向量a 方向上的投影为________.解析由数量积的定义知，b 在a 方向上的投影为 |b |cos θ＝4×cos 120°＝－2. 答案－26.(2017·瑞安一中检测)已知a ，b ，c 是同一平面内的三个向量，其中a ＝(1，2)，|b |＝1，且a ＋b 与a －2b 垂直，则向量a ·b ＝________；a 与b 的夹角θ的余弦值为________. 解析 ∵(a ＋b )⊥(a －2b )，∴(a ＋b )·(a －2b )＝0，即|a |2－a ·b －2|b |2＝0，∴5－a ·b －2＝0，∴a ·b ＝3，∴cos θ＝a ·b |a |·|b |＝355.答案 3355考点一平面向量的数量积及在平面几何中的应用【例1】 (1)(2015·四川卷)设四边形ABCD 为平行四边形，|AB →|＝6，|AD →|＝4，若点M ，N 满足BM →＝3MC →，DN →＝2NC →，则AM →·NM →等于( ) A.20B. 15C.9D.6(2)(2016·天津卷)已知△ABC 是边长为1的等边三角形，点D ，E 分别是边AB ，BC 的中点，连接DE 并延长到点F ，使得DE ＝2EF ，则AF →·BC →的值为( ) A.－58B.18C.14D.118解析 (1)取AB →，AD →为一组基底.∵BM →＝3MC →，∴AM →＝AB →＋BM →＝AB →＋34BC →＝AB →＋34AD →，NM →＝CM →－CN→＝－14AD →＋13AB →，∴AM →·NM →＝14(4AB →＋3AD →)·112(4AB →－3AD →)＝148(16AB →2－9AD →2)＝148(16×62－9×42)＝9，选C.(2)法一如图所示，根据已知得，DF →＝34AC →，所以AF →＝AD →＋DF →＝12AB →＋34AC →，BC →＝AC →－AB →，则AF →·BC →＝⎝ ⎛⎭⎪⎫12AB →＋34AC →·(AC →－AB →)＝12AB →·AC →－12AB →2＋34AC →2－34AC →·AB →＝34AC →2－12AB →2－14AC →·AB →＝34－12－14×1×1×cos 60°＝18.故选B. 法二建立如图所示的平面直角坐标系.则B ⎝ ⎛⎭⎪⎫－12，0，C ⎝ ⎛⎭⎪⎫12，0， A ⎝ ⎛⎭⎪⎫0，32，所以BC →＝(1，0).易知DE ＝12AC ，∠FEC ＝∠ACE ＝60°，则EF ＝14AC ＝14，所以点F 的坐标为⎝ ⎛⎭⎪⎫18，－38，则AF →＝⎝ ⎛⎭⎪⎫18，－538，所以AF →·BC →＝⎝ ⎛⎭⎪⎫18，－538·(1，0)＝18.故选B.答案 (1)C (2)B规律方法 (1)求两个向量的数量积有三种方法：利用定义；利用向量的坐标运算；利用数量积的几何意义.(2)解决涉及几何图形的向量数量积运算问题时，可先利用向量的加减运算或数量积的运算律化简再运算.但一定要注意向量的夹角与已知平面角的关系是相等还是互补.【训练1】 (1)(2017·义乌市调研)在Rt△ABC 中，∠A ＝90°，AB ＝AC ＝2，点D 为AC 的中点，点E 满足BE →＝13BC →，则AE →·BD →＝________.(2)(2017·宁波质检)已有正方形ABCD 的边长为1，点E 是AB 边上的动点，则DE →·CB →的值为________；DE →·DC →的最大值为________.解析 (1)法一因为AE →＝AB →＋BE →＝AB →＋13BC →＝AB →＋13(AC →－AB →)＝23AB →＋13AC →，BD →＝BA →＋AD →＝－AB→＋12AC →.因为AB ⊥AC ，所以AB →·AC →＝0，所以AE →·BD →＝⎝ ⎛⎭⎪⎫23AB →＋13AC →·⎝ ⎛⎭⎪⎫－AB →＋12AC →＝－23|AB →|2＋16|AC →|2＝－23×22＋16×22＝－2. 法二建立如图所示的平面直角坐标系，则A (0，0)，B (2，0)，D (0，1)，E ⎝ ⎛⎭⎪⎫43，23，所以AE →＝⎝ ⎛⎭⎪⎫43，23，BD →＝(－2，1)，所以AE →·BD →＝⎝ ⎛⎭⎪⎫43，23·(－2，1)＝43×(－2)＋23×1＝－2.(2)法一如图，DE →·CB →＝(DA →＋AE →)·CB →＝DA →·CB →＋AE →·CB →＝DA →2＝1，DE →·DC →＝(DA →＋AE →)·DC → ＝DA →·DC →＋AE →·DC →＝AE →·DC →＝|AE →|·|DC →|≤|DC →|2＝1.法二以射线AB ，AD 为x 轴，y 轴的正方向建立平面直角坐标系，则A (0，0)，B (1，0)，C (1，1)，D (0，1)，设E (t ，0)，t ∈[0，1]，则DE →＝(t ，－1)，CB →＝(0，－1)，所以DE →·CB →＝(t ，－1)·(0，－1)＝1.因为DC →＝(1，0)，所以DE →·DC →＝(t ，－1)·(1，0)＝t ≤1，故DE →·DC →的最大值为1.法三由图知，无论E 点在哪个位置，DE →在CB →方向上的投影都是CB ＝1，∴DE →·CB →＝|CB →|·1＝1.当E 运动到B 点时，DE →在DC →方向上的投影最大即为DC ＝1， ∴(DE →·DC →)max ＝|DC →|·1＝1. 答案 (1)－2 (2)1 1 考点二平面向量的夹角与垂直【例2】 (1)(2016·全国Ⅱ卷)已知向量a ＝(1，m )，b ＝(3，－2)，且(a ＋b )⊥b ，则m ＝( ) A.－8B.－6C.6D.8(2)若向量a ＝(k ，3)，b ＝(1，4)，c ＝(2，1)，已知2a －3b 与c 的夹角为钝角，则k 的取值范围是________.解析 (1)由题知a ＋b ＝(4，m －2)，因为(a ＋b )⊥b ，所以(a ＋b )·b ＝0，即4×3＋(－2)×(m －2)＝0，解之得m ＝8，故选D. (2)∵2a －3b 与c 的夹角为钝角， ∴(2a －3b )·c <0，即(2k －3，－6)·(2，1)<0，解得k ＜3. 又若(2a －3b )∥c ，则2k －3＝－12，即k ＝－92.当k ＝－92时，2a －3b ＝(－12，－6)＝－6c ，即2a －3b 与c 反向.综上，k 的取值范围为⎝ ⎛⎭⎪⎫－∞，－92∪⎝ ⎛⎭⎪⎫－92，3. 答案 (1)D (2)⎝⎛⎭⎪⎫－∞，－92∪⎝ ⎛⎭⎪⎫－92，3 规律方法 (1)根据平面向量数量积的性质：若a ，b 为非零向量，cos θ＝a ·b|a ||b |(夹角公式)，a ⊥b ⇔a ·b ＝0等，可知平面向量的数量积可以用来解决有关角度、垂直问题.(2)数量积大于0说明不共线的两向量的夹角为锐角，数量积等于0说明不共线的两向量的夹角为直角，数量积小于0且两向量不共线时两向量的夹角为钝角.【训练2】 (1)(2016·全国Ⅲ卷)已知向量BA →＝⎝ ⎛⎭⎪⎫12，32，BC →＝⎝ ⎛⎭⎪⎫32，12，则∠ABC ＝( )A.30°B.45°C.60°D.120°(2)(2016·全国Ⅰ卷)设向量a ＝(m ，1)，b ＝(1，2)，且|a ＋b |2＝|a |2＋|b |2，则m ＝________. 解析 (1)|BA →|＝1，|BC →|＝1，c os∠ABC ＝BA →·BC →|BA →|·|BC →|＝32.由〈BA →，BC →〉∈[0°，180°]，得∠ABC ＝30°.(2)由|a ＋b |2＝|a |2＋|b |2，得a ⊥b ，所以m ×1＋1×2＝0，得m ＝－2. 答案 (1)A (2)－2考点三平面向量的模及其应用【例3】 (1)(2017·云南统一检测)已知平面向量a 与b 的夹角等于π3，若|a |＝2，|b |＝3，则|2a －3b |＝( ) A.57 B.61 C.57D.61(2)(2016·浙江卷)已知向量a ，b ，|a |＝1，|b |＝2.若对任意单位向量e ，均有|a ·e |＋|b ·e |≤6，则a ·b 的最大值是________. 解析 (1)由题意可得a ·b ＝|a |·|b |cos π3＝3，所以|2a －3b |＝（2a －3b ）2＝4|a |2＋9|b |2－12a ·b ＝16＋81－36＝61，故选B. (2)由已知可得：6≥|a ·e |＋|b ·e |≥|a ·e ＋b ·e |＝|(a ＋b )·e | 由于上式对任意单位向量e 都成立. ∴6≥|a ＋b |成立.∴6≥(a ＋b )2＝a 2＋b 2＋2a ·b ＝12＋22＋2a ·b .即6≥5＋2a ·b ，∴a ·b ≤12.答案 (1)B (2)12规律方法 (1)求向量的模的方法：①公式法，利用|a |＝a ·a 及(a ±b )2＝|a |2±2a ·b ＋|b |2，把向量的模的运算转化为数量积运算；②几何法，利用向量的几何意义，即利用向量加减法的平行四边形法则或三角形法则作出向量，再利用余弦定理等方法求解.(2)求向量模的最值(范围)的方法：①代数法，把所求的模表示成某个变量的函数，再用求最值的方法求解；②几何法(数形结合法)，弄清所求的模表示的几何意义，结合动点表示的图形求解.【训练3】 (1)在平面直角坐标系中，O 为原点，A (－1，0)，B (0，3)，C (3，0)，动点D 满足|CD →|＝1，则|OA →＋OB →＋OD →|的最大值是________.(2)已知直角梯形ABCD 中，AD ∥BC ，∠ADC ＝90°，AD ＝2，BC ＝1，P 是腰DC 上的动点，则|PA →＋3PB →|的最小值为________.解析 (1)设D (x ，y )，由|CD →|＝1，得(x －3)2＋y 2＝1，向量OA →＋OB →＋OD →＝(x －1，y ＋3)，故|OA →＋OB →＋OD →|＝（x －1）2＋（y ＋3）2的最大值为圆(x －3)2＋y 2＝1上的动点到点(1，－3)距离的最大值，其最大值为圆(x －3)2＋y 2＝1的圆心(3，0)到点(1，－3)的距离加上圆的半径，即（3－1）2＋（0＋3）2＋1＝1＋7.(2)以D 为原点，分别以DA ，DC 所在直线为x 轴，y 轴建立如图所示的平面直角坐标系，设DC ＝a ，DP ＝x (0≤x ≤a )，∴D (0，0)，A (2，0)，C (0，a )，B (1，a )，P (0，x ).PA →＝(2，－x )，PB →＝(1，a －x )，32∴PA →＋3PB →＝(5，3a－4x )，|PA →＋3PB →|2＝25＋(3a －4x )2≥25，当x ＝3a 4时取等号.∴|PA →＋3PB →|的最小值为5.答案 (1)1＋7 (2)5[思想方法]1.计算数量积的三种方法：定义、坐标运算、数量积的几何意义，要灵活选用，与图形有关的不要忽略数量积几何意义的应用.2.求向量模的常用方法：利用公式|a |2＝a 2，将模的运算转化为向量的数量积的运算. 3.利用向量垂直或平行的条件构造方程或函数是求参数或最值问题常用的方法与技巧.[易错防范]1.数量积运算律要准确理解、应用，例如，a·b＝a·c(a≠0)不能得出b＝c，两边不能约去一个向量.2.两个向量的夹角为锐角，则有a·b＞0，反之不成立；两个向量夹角为钝角，则有a·b＜0，反之也不成立.。

2018高考数学(浙江省专用)复习专题测试：第五章平面向量与解三角形 §5-2 平面向量的数量积及其应用

OC OD

2.(2017课标全国Ⅱ,12,5分)已知△ABC是边长为2的等边三角形,P为平面ABC内一点,则 · ( + )的最小值是 ( A.-2 答案 B.-
3 2
PC

PA

PB

C.-
4 3
) D.-1
B 本题考查向量的坐标运算,考查利用数形结合的方法求解最值问题.
以AB所在直线为x轴,AB的中点为原点建立平面直角坐标系,如图,
A.I1<I2<I3 B.I1<I3<I2 C.I3<I1<I2 D.I2<I1<I3
பைடு நூலகம்
答案
C 本题考查向量的数量积,共线向量定理,解三角形,考查运算能力和逻辑推理能力.
如图,建立直角坐标系,则B(0,0),A(0,2),C(2,0).
设D(m,n), 由AD=2和CD=3,
m2 (n 2) 2 4, 2 2 得 (m 2) n 9, 5 从而有n-m= 4 >0,∴n>m.

6.(2016天津,7,5分)已知△ABC是边长为1的等边三角形,点D,E分别是边AB,BC的中点,连接DE并延长到点F,使得DE=2EF,则 · 的值为 ( A.-
5 8
AF BC

B.
1 8
C.
1 4
D.
11 8
)
答案
B 建立平面直角坐标系,如图.
则B
1 1 ,0 ,0 2 2 1 ,C ,A 2
五年高考
考点一
O.记I1= · , I 2= · , I 3= · ,则 (
OA OB OB OC

高考数学一轮复习(浙江版)专题5.3平面向量的数量积及应用(测)含解析

第03节平面向量的数量积及应用班级__________ 姓名_____________ 学号___________ 得分__________一、选择题：本大题共10小题，每小题4分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1.【2018届广西柳州高级中学5月模拟】已知向量，则是的（）A．充分不必要条件 B．必要不充分条件 C．充分必要条件 D．既不充分也不必要条件【答案】A【解析】【分析】先化简，再利用充要条件的定义判断是的什么条件.2.【2018届黑龙江省仿真模拟（四）】若向量，满足：，，，则（）A． B． C． D．【答案】B【解析】【分析】利用向量垂直的性质直接求解．【详解】∵向量，满足：，，，∴，解得=．故选：B ．3.【陕西省咸阳市2018年高考5月信息专递】已知两个向量和的夹角为，，则向量在方向上的正射影的数量为（）A ．B ．C ．D ．【答案】D4. ,2,1==b 且⊥+)(，则与的夹角为（） A.30 B.60 C.120 D.150 【答案】C【解析】由⊥+)(知，()a b a +∙ =2a a b +∙ =0，所以2a b a ∙=- =-1，所以cos ,a b =||||a ba b ∙ =12-，所以与的夹角为120，故选C.5.【2018届山东省沂水县第一中学三轮考】设向量，且，则（）A ． 2B ．C ．D ． 4【答案】A【分析】6.【2018届北京市石景山区一模】已知平面向量满足，与的夹角为，若，则实数的值为（）A． B． C． D．【答案】D【解析】因为与的夹角为，所以，因为，所以，解得，故选D．7.【2018届河北省武邑中学五模】非零向量满足：，，则与夹角的大小为( )A． B． C． D．【答案】A【解析】【分析】根据题意，设=，=，则﹣=﹣=，结合题意分析可得△OAB为等腰直角三角形，结合向量夹角的定义分析可得答案．根据题意，设=，=，则﹣=﹣=，若||=||，，即||=||，且⊥，则△OAB为等腰直角三角形，则与的夹角为180°﹣45°=135°，故选：A．8．【浙江省金华市浦江县2018年高考适应性考试】已知平面向量，满足且，则的最大值为（）A． 1 B． 2 C． 3 D． 4【答案】B9．【2018届浙江省杭州市第二次检测】记的最大值和最小值分別为和.若平面向量满足则（）A． B．C． D．【答案】A10.【2018届浙江省台州市高三上学期期末】已知m ， n是两个非零向量，且1m = ， 23m n +=，则m n n ++的最大值为A ．． C ． 4 D ． 5 【答案】B 【解析】()221,23,24419m m n m n n m n =+=∴+=+⋅+= ,22n m n ∴+⋅=,()2222m n m m n n ∴+=+⋅+25n =- ,m n n n ∴++= ，令(()0,n x x f x x =<≤=,则()'1f x =+，令()'0f x =，得x =∴当0x << ()'0f x >x <<时， ()'0f x <， ∴当x =时， ()f x 取得最大值2f ⎛= ⎝⎭B. 二、填空题：本大题共7小题，共36分．11.【2018届安徽省六安市第一中学高三下学期适应性考试】已知平面向量，的夹角为，且，，则__________．【答案】12.【2018届浙江省温州市一模】设向量，，且，，则的最大值是__________；最小值是__________．【答案】9 1 【解析】设的夹角为，由，可得，化简得，可得，即的最大值是，最小值是，故答案为.13.【2018届浙江省名校协作体高三上学期考试】已知在ABC ∆中, 3AB =, BC =2AC =，且O是ABC ∆的外心，则AO AC ⋅= ___， AO BC ⋅=_____________【答案】2 52-【解析】设外接圆半径为,32R AB BC AC AO CO R == ＝，＝，224122R R cos OAC R R+-∠==⋅则122 AO AC AO AC cos CAO RR ⋅=⋅∠=⨯⨯=.14.【2018届浙江省教育绿色评价联盟5月适应性考试】已知，，则的最大值为______，最小值为______．【答案】615.【2018届黑龙江省仿真模拟（五）】已知向量，，则当时，的取值范围是__________．【答案】.【解析】【分析】，因此，其模为，根据的范围可求模的取值范围．【详解】，因此，故．因为，故，所以填．16.【2018届浙江省金丽衢十二校第二次联考】已知向量满足的夹角为，则=_____；与的夹角为_____．【答案】17.【2018届湖北省宜昌市一中考前训练2】在中，，点是所在平面内一点，则当取得最小值时，__________．【答案】24.【解析】分析：由，可得，可得，以为坐标原点建立坐标系，设，由展开后配方整理，可得当时取得最小值，求得，再由数量积的坐标运算求解.详解：三、解答题：本大题共5小题，共74分．解答应写出文字说明、证明过程或演算步骤．18.已知两个单位向量的夹角为60°.（1）若，且，求的值；（2）求向量在方向上的投影.【答案】（1）或；（2）【解析】分析：（1），求解即可；（2）向量在方向上的投影为，计算即可.详解：（1）,所以或；（2）向量在方向上的投影为..19.已知向量，，满足.（1）求的值；（2）求向量与向量夹角的余弦值.【答案】（1）4；（2）【解析】【分析】（1）运用向量的加减运算和向量垂直的条件：数量积为0，解方程可得；（2）求得向量与的模，由向量的夹角公式，计算即可得到所求值．【详解】20．已知两个非零向量.（Ⅰ）若向量是夹角为120°的单位向量，试确定实数，使和垂直；（Ⅱ）若，，，求证：三点共线.【答案】（Ⅰ）；（Ⅱ）详见解析.【解析】【分析】：（Ⅰ）令，可确定实数.（Ⅱ）由，，可得根据向量共线的条件建立等式关系即可得到结论．【详解】：（Ⅰ）∵和垂直21．已知是同一平面内的两个向量，其中.（1）若，求向量的坐标；（2）若，求与的夹角的值.【答案】(1)或.(2).【解析】【分析】⑴可设，根据条件建立关于的方程组，求出的值，从而得到向量的坐标⑵根据条件可以得到），根据可以求得的值，然后求出的值，最后得到结果【详解】（1）设，根据条件，则：解得或；∴或.（2）∴.解得∴∴∵∴.22．已知向量，，（1）若，求向量、的夹角；（2）若，求函数的最值以及相应的的取值. 【答案】（1）；（2）见解析所以所以，的最小值为，，的最小值为1.。

浙江专版高考数学一轮复习第五章平面向量第三节平面向量的数量积与平面向量应用举例课件

4．在用|a |＝ a2求向量的模时，一定要把求出的 a 2再进行开方．
[小题纠偏] 1．若a ，b 是两个互相垂直的非零向量，给出以下式子：①a ·b
＝0；②a ＋b ＝a －b ；③|a ＋b |＝|a －b |；④a 2＋b 2＝(a ＋b )2.
其中正确的个数是
()
A．1
B．2
C．3
D．4
解析：因为a ，b 是两个互相垂直的非零向量，所以a ·b ＝
0；所以(a ＋b )2＝a 2＋b 2＋2a ·b ＝a 2＋b 2；(a －b )2＝a 2＋b 2
－2a ·b ＝a 2＋b 2；所以(a ＋b )2＝(a －b )2，即|a ＋b |＝|a －b |. 故①③④是正确的，②是错误的．答案：C
答案：2
5．已知正方形ABCD的边长为2，E为CD的中点，则―A→E ·―B→D
＝________. 解析：选向量的基底为―A→B ，―A→D ，则―B→D ＝―A→D － ―A→B ，
―A→E ＝―A→D ＋12―A→B ，所以―A→E ·―B→D ＝―A→D ＋12
―→ AB
―→ ·( AD
2．(2016·北京高考)已知向量a ＝(1， 3)，b ＝( 3，1)，则a 与b 夹角的大小为________．
解析：由题意得|a |＝ 1＋3＝2，|b |＝ 3＋1＝2，
a ·b ＝1× 3＋ 3×1＝2 3.
设 a 与 b 的夹角为 θ，则 cos θ＝22×32＝ 23.
∵θ∈[0，π]，∴θ＝π6.
＝32a 2，故选 D. 答案：D
3．已知向量a 与b 的夹角为60°，且a ＝(－2，－6)，|b |＝ 10，则a ·b ＝________；(2a －b )·(a ＋b )＝__________. 解析：因为 a ＝(－2，－6)，所以|a |＝－22＋－62＝2 10，又|b |＝ 10，向量 a 与 b 的夹角为 60°，所以 a ·b ＝|a |·|b |·cos 60°＝2 10× 10×12＝10. (2a －b )·(a ＋b )＝2a 2＋a ·b －b 2＝80＋10－10＝80. 答案：10 80

高考数学导与练一轮复习(浙江版)知识梳理第八章第三节平面向量的数量积及应用

第三节平面向量的数量积及应用一、数量积的定义及意义(1)定义已知两个非零向量a和b,作OA=a,OB=b,如图所示,则∠AOB=θ叫做向量a与b的夹角,也可记作<a,b>=θ.(2)范围向量夹角θ的范围是[0,π],a与b同向时,夹角θ=0;a与b反向时,夹角θ=π.(3)垂直关系如果非零向量a与b的夹角是90°,我们说a与b垂直,记作a⊥b. 已知两个非零向量a与b,它们的夹角为θ,则数量|a||b|cos θ叫做a与b的数量积(或内积),记作a·b.规定:零向量与任一向量的数量积为0.两个非零向量a与b垂直的充要条件是a·b=0.数量积a·b等于a的长度|a|与b在a的方向上的投影|b|cos θ的乘积.(1)在平面图形中运算向量的数量积要注意向量夹角的取值,注意区分平面图形中的角和向量夹角的区别.(2)理解数量积的概念可以和物理中功的公式相联系,加深对概念的理解.(3)向量a与b的夹角为锐角⇔a·b>0且a与b不共线,a,b夹角为钝角⇔a·b<0且a与b不共线..(1)a在b方向上的投影:|a|·cos θ或a bb(2)|a·b|≤|a||b|,“=”当且仅当a与b共线时取到.二、数量积的性质与运算律(1)e·a=a·e=|a|cos θ(e为单位向量,θ为a与e的夹角);(2)非零向量a,b,a⊥b⇔a·b=0;(3)当a与b同向时,a·b=|a||b|;当a 与b 反向时,a ·b=|a||b|,a ·a=|a|2,(4)cos θ=a b a b⋅(θ为a 与b 的夹角).(1)a ·b=b ·a(交换律);(2)(λa)·b=λ(a ·b)=a ·(λb)(λ为实数); (3)(a+b)·c=a ·c+b ·c.已知非零向量a=(x 1,y 1),b=(x 2,y 2),θ为向量a,b 的夹角. (1)a ·b=x 1x 2+y 1y 2.(3)cos θ.(1)0·a=0,0·a=0.(2)a ·b=b ·c ⇔b=0或b ⊥(ac). A(x 1,y 1),B(x 2,y 2),则AB 的中点坐标为(122xx +,122yy +),AB 的两个三等分点坐标为(1223x x +,1223y y+)和(1223x x +,1223yy +).1.对于向量a,b,c 和实数λ,下列命题中正确的是( B ) (A)若a ·b=0,则a=0或b=0 (B)若λa=0,则λ=0或a=0 (C)若a 2=b 2,则a=b 或a=b (D)若a ·b=a ·c,则b=c解析:当a ⊥b 时,a ·b=0,故A 错;当a ⊥b,|a|=|b|=1时,a 2=b 2,故C 错;当a ⊥b,a ⊥c 时,a ·b=a ·c=0,故D 错.故选B.2.(2018·全国Ⅱ卷)已知向量a,b 满足|a|=1,a ·b=1,则a ·(2ab)等于( B )(A)4 (B)3 (C)2 (D)0解析:a·(2ab)=2a2a·b=2|a|2a·b.因为|a|=1,a·b=1,所以原式=2×12+1=3.故选B.AB与AC的夹角为120°,且|AB|=3,| AC AP=λAB+AC,且AP⊥BC,则实数λ的值为.解析:因为AP⊥BC,所以AP·BC=0,所以(λAB+AC)·(AC AB)=0,即2ACλ2AB+(λ1)AB·AC=0,又因为AB·AC=3×2×(12)=3,所以49λ3(λ1)=0.所以λ=712.答案:7124.(2019·江苏卷)如图,在△AB·AC=6AO·EC,则ABAC的值是.解析:如图,过点D作DF∥CE交AB于点F,由D是BC的中点,可知F为BE的中点.又BE=2EA,则知EF=EA,从而可得AO=OD,则有AO=12AD=14(AB+AC),EC=AC AE=AC13AB,所以6AO·EC=32(AB+AC)·(AC13AB)=3 2AC212AB+AB·AC=AB·AC,整理可得2AB=32AC,所以AB AC=3.答案:3考点一平面向量数量积的运算[例1] (2018·天津卷)在如图的平面图形中,已知OM=1,ON=2,∠MON= 120°,BM=2MA,CN=2NA,则BC·OM的值为( )(A)15 (B)9 (C)6 (D)0解析:如图,连接MN.因为BM=2MA,CN=2NA,所以AMAB =13=ANAC,所以MN∥BC,且MNBC =13,所以BC=3MN=3(ON OM),所以BC·OM=3(ON·OM2OM)=3(2×1×cos 120°12)=6.故选C.(1)求两个向量的数量积,有三种方法:利用定义;利用向量的坐标运算;利用数量积的几何意义.(2)解决涉及几何图形的数量积运算问题时,可先利用向量的加减运算或数量积的运算律化简再运算,但要注意向量的夹角与已知平面角的关系是相等还是互补.(2018·嘉兴模拟)如图,B,D是以AC为直径的圆上的两点,其中1t+2t+,则AC·BD等于( A )(A)1 (B)2(C)t (D)2t解析:AC·BD=AC·(AD AB)=AC·AD AC·AB=|AC||AD|cos ∠DAC|AC||AB|cos ∠BAC=2AD2AB=(t+2)(t+1)=1.考点二平面向量的夹角[例2] 已知单位向量e1,e2的夹角为α,且cos α=13,向量a=3e12e2与b=3e1e2的夹角为β,则cos β= .解析:由已知得e1·e2=1×1×13=13,a·b=(3e12e2)·(3e1e2)=9+29e1·e2=113=8.又因为a2=(3e12e2)2=9+412e1·e2=134=9, 得|a|=3,b2=(3e1e2)2=9+16e1·e2=102=8,得所以cos β=a ba b⋅=答案:223根据平面向量数量积的性质,若a,b 为非零向量,则cos<a,b>=a b a b⋅,a ⊥b ⇔a ·b=0等,可知利用平面向量的数量积可解决有关角度、垂直问题.1.(2019·金丽衢十二校第一次联考)已知向量a=(4, 3),b=3),则a 与b 的夹角为( C )(A)30° (B)45° (C)60° (D)90° 解析:cos<a,b>=a b a b⋅19219⋅=12, 所以<a,b>=60°.故选C.2.(2018·浙江台州期末统考)设非零向量a,b,则“a,b 的夹角为锐角”是“|a+b|>|ab|”的( A ) (A)充分不必要条件 (B)必要不充分条件 (C)充要条件(D)既不充分也不必要条件解析:由于|a+b|>|ab|等价于a ·b>0,若a,b 的夹角为锐角,则a ·b>0,所以|a+b|>|ab|成立,反之不一定成立,如a,b 夹角为0,不一定为锐角,所以“a,b 的夹角为锐角”是“|a+b|>|ab|”的充分不必要条件.故选A.考点三平面向量的模[例3] (1)设a,b 为单位向量,若向量c 满足|c(a+b)|=|ab|,则|c|的最大值是( )(A)22 (B)2 (C)2 (D)1(2)(2018·π3,向量b 满足b 24e ·b+3=0,则|ab|的最小值是( ) (A)31 (B)3+1 (C)2 (D)23OA =a,OB =b,OC =c,则a+b=OD ,ab=BA , 由已知得|OC OD |=|BA |,又由|BA|=|OC OD|≥|OC||OD|得|c|=|OC|≤|OD |+|BA |=|a+b|+|ab|,由已知得|a+b|2+|ab|2=2(|a|2+|b|2)=4, 而2a b a b++-≤222a b a b++-=2,故|c|≤22.故选A. 解析:(2)由b 24e ·b+3=0得b 24e ·b+3e 2=(be)·(b3e)=0.设b=OB ,e=OE ,3e=OF , 所以be=EB ,b3e=FB ,所以EB ·FB =0,取EF 的中点为C,则B 在以C 为圆心,EF 为直径的圆上.如图,设a=OA ,作射线OA,使得∠AOE=π3,所以|ab|=|(a2e)+(2eb)|≥|a2e||2eb|=|CA ||BC |≥31.故选A.(1)求向量模的常用方法:利用公式|a|2=a 2,将模的运算转化为数量积的运算.(2)求模也可将向量置于特殊图形中,利用图形解决向量的模. (2019·温州2月模拟)在平面上,e 1,e 2是方向相反的单位向量,|a|= 2,(be 1)·(be 2)=0,则|ab|的最大值为( D )(A)1(D)3解析:由题意得(be1)·(be2)=0⇒b2b·(e1+e2)+e1·e2=0,e1,e2是方向相反的单位向量,所以e1+e2=0,e1·e2=1,b21=0⇒|b|=1,所以|ab|≤|a|+|b|=3,|ab|的最大值为3.故选D.考点四平面向量的应用[例4] (1)已知点O,N,P在△ABC所在平面内,且|OA|=|OB|=|OC|, NA+NB+NC=0,PA·PB=PB·PC=PC·PA,则点O,N,P依次是△ABC的( )(A)重心、外心、垂心(B)重心、外心、内心(C)外心、重心、垂心(D)外心、重心、内心(2)(2019·浙江卷)已知正方形A B C D的边长为1,当每个λi (i=1,2,3,4,5,6)取遍±1时,|λ1AB+λ2BC+λ3CD+λ4DA+λ5AC+ λ6BD|的最小值是,最大值是.解析:(1)由|OA|=|OB|=|OC|知点O到A,B,C距离相等,为外心;由NA+NB+NC=0,即NA=(NB+NC)知N为△ABC三条中线交点即重心;由PA·PB=PB·PC,即PB·(PA PC)=0得PB·PC=0,即PB⊥PC,同理PC⊥AB,PA⊥BC,即P为垂心,故选C.解析:(2)如图,以A 为原点,AB 所在直线为x 轴,AD 所在直线为y 轴建立平面直角坐标系,则AB =(1,0),AD =(0,1). 设a=λ1AB +λ2BC +λ3CD +λ4DA + λ5AC +λ6BD=λ1AB +λ2AD λ3AB λ4AD +λ5(AB +AD )+λ6(AD AB )=(λ1λ3+λ5λ6)AB +(λ2λ4+λ5+λ6)AD =(λ1λ3+λ5λ6,λ2λ4+λ5+λ6). 故|a|=2213562456()()λλλλλλλλ-+-+-++.因为λi (i=1,2,3,4,5,6)取遍±1,所以当λ1λ3+λ5λ6=0,λ2λ4+λ5+λ6=0时,|λ1AB +λ2BC +λ3CD +λ4DA +λ5AC +λ6BD |取得最小值0.考虑到λ5λ6,λ5+λ6有相关性,要确保所求模最大,只需使|λ1λ3+λ5λ6|,|λ2λ4+λ5+λ6|尽可能取到最大值,即当λ1λ3+λ5λ6=2,λ2λ4+λ5+λ6=4时可取到最大值,所以|λ1AB +λ2BC +λ3CD +λ4DA +λ5AC +λ6BD |的最大值为416+=25.答案:(1)C (2)0 25以向量为载体求相关变量的取值范围是向量与函数、不等式、三角函数等相结合的一类综合问题,通过几何图形的分析,转化为不等式解集或函数值域等问题.已知圆O:x 2+y 2=4上有三个不同的点P,A,B,且满足AP =x OB 12OA (其中x>0),则实数x 的取值范围是 . 解析:因为AP =x OB12OA ,所以OP OA=x OB12OA,即x OB=OP12OA,两边平方得4x2=4+1OP·OA,设<OP,OA>=α,则4x2=54cos α, 因为1<cos α<1,所以1<54cos α<9,即1<4x2<9,因为x>0,所以12<x<32.即实数x的取值范围是(12,32).答案:(12,32)类型一平面向量数量积的运算1.(2019·衢州二中第一次模拟)在梯形ABCD中,AD∥BC,BC=2AB=2AD=2DC=4,AC与BD相交于O,过点A作AE⊥BD于E,则AE·AC等于( C )解析:如图,由题意知BD⊥DC,∠ADC=120°,所以∠ADB=30°,∠ACD=30°,由题意得AE∥CD,所以∠EAO=30°,AC=2,AE=1,AE·AC=|AE|·|AC|·cos30°=1×故选C.类型二平面向量的夹角2.(2019·浙江省模拟)设θ是两个非零向量a,b的夹角,已知对任意实数t,|b+ta|的最小值为1,则( B )(A)若θ确定,则|a|唯一确定(B)若θ确定,则|b|唯一确定(C)若|a|确定,则θ唯一确定(D)若|b|确定,则θ唯一确定解析:|b+ta|2=b 2+2ta ·b+t 2a 2,令g(t)=b 2+2ta ·b+t 2a 2,二次函数图象开口向上,所以最小值为222244()4a b a b a -⋅=|b|2|b|2cos 2θ=|b|2sin 2θ=1,故当θ确定,则|b|唯一确定.故选B.3.(2019·余高、缙中、长中5月模拟)已知平面向量a,b 不共线,且|a|=1,a ·b=1,记b 与2a+b 的夹角是θ,则θ最大时,|ab|等于( C )(A)1解析:设|b|=x,则b ·(2a+b)=2a ·b+b 2=x 2+2,(2a+b)2=4a 2+4a ·b+b 2=x 2+8,cos θ=(2)2b a b b a b⋅+⋅+2所以cos 2θ=2222(2)(8)x x x ++ =22211241(2)2x x -++++ =2111412()263x --++,即当x 2=4,x=2时,cos 2θ取到最小值,则θ取到最大值,此时|ab|2= a 2-2a ·b+b 2=12+4=3,所以故选C.类型三平面向量的模△ABC 中,|BC |=10,AB ·AC =16,D 为边BC 的中点,则|AD |等于( D )(A)6 (B)5 (C)4 (D)3解析:因为AB ·AC =16,BC = AC AB , 所以|BC |=|AC AB |, 所以|AC AB |2=|BC |2=100, 所以2AC +2AB 2AC ·AB =100,所以2AC +2AB =68, 又因为AD =12AB +12AC , 所以|AD |2=14(2AB +2AC +2AB ·AC ) =14×(6832) =9.所以|AD |=3.类型四平面向量的应用5.(2019·浙江三校第一次联考)如图,圆O 是半径为1的圆,OA=12,设B,C 是圆上的任意2个点,则AC ·BC 的取值范围是( A ) (A)[18,3] (B)[1,3] (C)[1,1] (D)[18,1] 解析:由题意,设<OA ,BC >=θ, AC ·BC =(OC OA )·BC =OC ·BC OA ·BC=|OC |·|BC |cos ∠BCO|OA |·|BC |cos θ =212BC |OA |·|BC |cos θ=212BC 12|BC |cos θ,又因为cos θ≤1,所以212BC 12|BC |cos θ ≥212BC 12|BC |=12(|BC |12)218, 又因为|BC |∈[0,2],所以当|BC |=12时,AC ·BC 取到最小值为18, 当|BC |=2,cos θ=1,AC ·BC 取到最大值为3. 故选A.△ABC 满足|AB|=3,|AC|=4,O 是△ABC 的外心,且AO =λAB +12AC λ-(λ∈R),则△ABC 的面积是 . 解析:由AO =λAB +12AC λ-, 得221,21,2AO AB AB AC AB AO AC AB AC AC λλλλ-⎧⋅=+⋅⎪⎪⎨-⎪⋅=⋅+⎪⎩即()()9181,881,AC AB AB AC λλλλ⎧=+-⋅⎪⎨=-+⋅⎪⎩解方程组得8,1,10AB AC λ⎧⋅=⎪⎨=⎪⎩或0,9,AB AC λ=⎧⎪⎨⋅=⎪⎩ 当AB ·AC =9时,cos A=34, 所以S △ABC =12×3×4当AB ·AC =8时,cos A=23所以S △ABC =12×3×4所以△ABC 的面积是.答案或。

1高考数学一轮复习浙江专用课件：5 平面向量的数量积及其应用讲解部分

(3)(a+b)·c=a·c+b·c.
4.平面向量的数量积的坐标表示 (1)若a=(x1,y1),b=(x2,y2),则a·b=x1x2+y1y2. (2)若a=(x,y),则a·a=a2=|a|2=x2+y2,|a|= x2 y2 . (3)若A(x1,y1),B(x2,y2),则| AB|= (x2 -x1)2 (y2 -y1)2 ,这就是平面内两点间的距离公式. (4)若a=(x1,y1),b=(x2,y2),则a⊥b⇔x1x2+y1y2=0. 5.向量中的重要不等式若a=(x1,y1),b=(x2,y2),则-|a||b|≤a·b≤|a||b|⇔- x12 y12 · x22 y22 ≤x1x2+y1y2≤
高考数学浙江专用
5.2 平面向量的数量积及其应用
考点清单
考点一平面向量的数量积
考向基础 1.向量的数量积的定义 (1)向量a与b的夹角已知两个非零向量a和b,过O点作OOAA=a, OB=b,则∠AOB=θ(0°≤θ≤180°)叫做向量a与b的夹角. 当θ=90°时,a与b垂直,记作a⊥b;当θ=0°时,a与b同向;当θ=180°时,a与b反向. (2)a与b的数量积已知两个非零向量a和b,它们的夹角为θ,则把|a|·|b|·cos θ叫做a和b的数量积 (或内积),记作a·b=|a|·|b|·cos θ.
(3)规定:0·a=0. (4)a·b的几何意义 a.一个向量在另一个向量方向上的投影设θ是非零向量a与b的夹角,则|a|cos θ叫做a在b的方向上的投影,|b|cos θ叫做b在a的方向上的投影.b在a的方向上的投影是一个实数,而不是向量.当0 °≤θ<90°时,它是正值;当90°<θ≤180°时,它是负值;当θ=90°时,它是0. b.a·b等于a的长度|a|与b在a的方向上的投影|b|cos θ的乘积. 2.向量的数量积的性质设a、b都是非零向量,e是与b方向相同的单位向量,θ是a与e的夹角,则 (1)e·a=a·e=|a|·cos θ. (2)a⊥b⇔a·b=0.

2018浙江新课改新人教版A高考一轮复习第三节平面向量的数量积及其应用

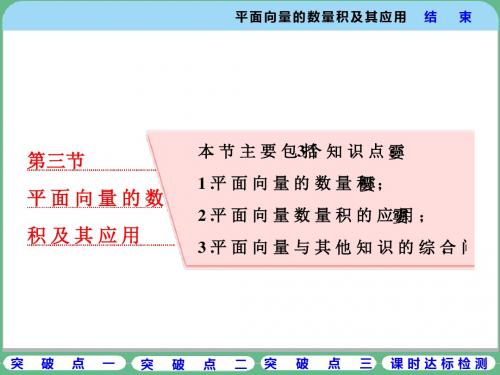
2 7 25 1 2 29 2 ×4－1 8 ×2×1×2＋3＝1 8 . BA · BC ＋3| BC | ＝1 2
突破点一突破点二突破点三
[答案]
29 18
课时达标检测
平面向量的数量积及其应用
结
束
[易错提醒]
(1 ) 解决涉及几何图形的向量数量积运算问题时
结
束
3．平面向量数量积的运算律
· a ( 1a )· b＝_b _ __( _ 交换律 )．
a· (λb ( 2 λa ) · b＝_λ_ _ _ __ _ _ _) _( _ 结合律 )． (a · b )＝
· c_ ＋ c ( 3 )a( ＋b)· c＝_a_ _ _b _· __ ( 分配律 ).
一定要注意向量的夹角与已知平面角的关系是相等是互补． ( 2两 ) 向量 a ， b的数量积 a· b与代数中 a ， b的乘积写法不同，不能漏掉其“ 中 · ”．的
点
一
突
破
点
二
突
破
点
三
课时达标检测
平面向量的数量积及其应用
结
束
2．根据定义计算数量积的两种思路 ( 1若 ) 两个向量共起点，则两向量的夹角直接可得
定义即可求得数量积；若两向量的起点不同，需要通使它们的起点重合，然后再计算． ( 2根 ) 据图形之间的关系，用长度和相互之间的夹
[ 解析 ]
a ＋ 2b ＝ ( － 1 , 2＋ )2( m,1 ) ＝ ( － 1 ＋ 2m,4 ) ， 2a － b ＝
2( －1 , 2－ ) (m,1 ) ＝(－2－m,3 ) ，由题意得 3 ( －1＋2m)－4(－2－

(浙江专用)2018年高考数学一轮复习第五章平面向量与解三角形 5.2 平面向量的数量积及其应用

t
| m || n |
4m n =- 4 = 1 ,所以t=-4.故选B.
3 | n |2 3t 3
评析本题主要考查了非零向量垂直的充要条件和夹角公式,属中档题.
8.(2015安徽,8,5分)△ABC是边长为2的等边三角形,已知向量a,b满足 AB=2a, AC =2a+b,则下列结论正确的是 ( ) A.|b|=1 B.a⊥b C.a·b=1 D.(4a+b)⊥ BC

=-λ2 OA(λ2>1),
从而I3= OC

·O D

=λ1λ2 OA

· OB
=λ1λ2I1,
又λ1λ2>1,I1<0,I3<0,∴I3<I1,∴I3<I1<I2.故选C.
2.(2017课标全国Ⅱ,12,5分)已知△ABC是边长为2的等边三角形,P为平面ABC内一点,则 PA·( PB
解法二:设P(x,y),则 AO· AP=(2,0)·(x+2,y)=2x+4,由题意知-1≤x≤1,∴x=1时, AO· AP取最大值6,∴ AO· AP的最大值为6.
13.(2017课标全国Ⅰ理,13,5分)已知向量a,b的夹角为60°,|a|=2,|b|=1,则|a+2b|=
答案 D 当|a|=|b|≠0时,|a+b|=|a-b|⇔(a+b)2=(a-b)2⇔a·b=0⇔a⊥b,推不出|a|=|b|.同样,由|a|=|b|也不能推出a⊥b.故选D.
解后反思由向量加法、减法的几何意义知,当a、b不共线,且|a|=|b|时,a+b与a-b垂直;当a⊥b时, |a+b|=|a-b|.
4.(2016课标全国Ⅱ,3,5分)已知向量a=(1,m),b=(3,-2),且(a+b)⊥b,则m= ( ) A.-8 B.-6 C.6 D.8

(浙江版)2018年高考数学复习：专题5.3 平面向量的数量积及其应用(测)

第03节平面向量的数量积及其应用班级__________ 姓名_____________ 学号___________ 得分__________一、选择题（本大题共12小题，每小题5分，在每小题给出的四个选择中，只有一个是符合题目要求的。

）1.【北京卷】设a ，b 是非零向量，“a b a b ⋅= ”是“//a b ”的（）A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件【答案】A【解析】||||cos ,a b a b a b ∙=∙<> ，由已知得cos ,1a b <>= ，即,0a b <>= ，//a b .而当//a b 时，,a b <> 还可能是π，此时||||a b a b ∙=- ，故“a b a b ⋅= ”是“//a b ”的充分而不必要条件，故选A.2.【福建卷】设(1,2)a = ，(1,1)b = ，c a kb =+ ．若b c ⊥ ，则实数k 的值等于（）A ．32-B ．53-C ．53D ．32【答案】A3.【2017浙江温州模拟】已知为单位向量，，则在的投影为 A. B. C. D. 【答案】C【解析】由题设可得，即，则，即，又，故，应选答案C.4. ,2,1==b 且a b a ⊥+)(，则与的夹角为（）A. 30B. 60C. 120D. 150【答案】C5.【重庆卷】已知向量(,3),(1,4),(2,1)a k b c === ，且(23)a b c -⊥ ，则实数k =（）9.2A - .0B .C 3 D.152【答案】C【解析】因为()(),3,1,4,a k b == 所以()2323,6a b k -=-- ，又因为()23a b c -⊥ ，所以，()230a b c -⋅= ，所以，()()22360k -+-=，解得：3k =，故选C.6.【辽宁卷】设,,a b c 是非零向量，已知命题P ：若0a b ⋅= ，0b c ⋅= ，则0a c ⋅= ；命题q ：若//,//a b b c ，则//a c ，则下列命题中真命题是（）A ．p q ∨B ．p q ∧C ．()()p q ⌝∧⌝D ．()p q ∨⌝【答案】A【解析】若0a b ⋅= ，0b c ⋅= ，则,a b b c ⊥⊥ ，故//a c ，故命题p 是假命题；若//,//a b b c ，则//a c ，故命题q 是真命题，由复合命题真假判断知，p q ∨是真命题，选A ．7.【2017四川宜宾二诊】若非零向量,a b ，满足a b =， ()20a b a -⋅=，则a 与b 的夹角为 A. 6π B. 3π C. 23π D. 56π【答案】B【解析】由()2220a b a a a b -⋅=-⋅= ，即22a ab ⋅= ，所以由向量的夹角公式可得1cos ,22a a b a b a a a b ⋅〈〉===⋅⋅ ，又(),0,a b π〈〉∈ ，所以,3a b π〈〉= ，故选B. 8．【2017陕西师范附属二模】已知向量()1,1a = ， ()24,2a b += ，则向量,a b的夹角的余弦值为（）B.-【答案】C9．【2017四川成都二诊】已知平面向量a ， b 夹角为3π，且1a = ， 12b = ，则2a b + 与b 的夹角是（） A. 6π B. 56π C. 4π D. 34π 【答案】A【解析】由题意可知： 111cos 234a b π⋅=⨯⨯= ，则： ()2113222444a b b a b b +⋅=⋅+=+⨯= ，且：2a b +== ，设所求向量的夹角为θ ，有： ()2cos 22a b b a b b θ+⋅==+⨯ ，则2a b + 与b 的夹角是6π . 本题选择A 选项.10. 设a ，b ， c 为同一平面内具有相同起点的任意三个非零向量，且满足a 与b 不共线，a ⊥c ，|a |＝|c |，则||b c ⋅ 的值一定等于( )。

【步步高】2018版高考数学(浙江·文理通用)大一轮教师文档讲义：第五章5.3平面向量的数量积

1．向量的夹角已知两个非零向量a 和b ，作OA →＝a ，OB →＝b ，则∠AOB 就是向量a 与b 的夹角，向量夹角的范围是[0，π]． 2．平面向量的数量积3.平面向量数量积的性质设a ，b 都是非零向量，e 是单位向量，θ为a 与b (或e )的夹角．则 (1)e ·a ＝a ·e ＝|a |cos θ. (2)a ⊥b ⇔a ·b ＝0.(3)当a 与b 同向时，a ·b ＝|a ||b |；当a 与b 反向时，a ·b ＝－|a ||b |.特别地，a ·a ＝|a |2或|a |(4)cos θ＝a ·b |a ||b |.(5)|a ·b |≤|a ||b |.4．平面向量数量积满足的运算律 (1)a·b ＝b·a ；(2)(λa )·b ＝λ(a·b )＝a ·(λb )(λ为实数)； (3)(a ＋b )·c ＝a·c ＋b·c .5．平面向量数量积有关性质的坐标表示设向量a ＝(x 1，y 1)，b ＝(x 2，y 2)，则a·b ＝x 1x 2＋y 1y 2，由此得到 (1)若a ＝(x ，y )，则|a |2＝x 2＋y 2或|a |＝x 2＋y 2.(2)设A (x 1，y 1)，B (x 2，y 2)，则A ，B 两点间的距离AB ＝|AB →|(3)设两个非零向量a ，b ，a ＝(x 1，y 1)，b ＝(x 2，y 2)，则a ⊥b ⇔x 1x 2＋y 1y 2＝0. (4)若a ，b 都是非零向量，θ是a 与b 的夹角，则cos θ＝a ·b|a ||b |＝x 1x 2＋y 1y 2x 21＋y 21 x 22＋y 22. 【知识拓展】1．两个向量a ，b 的夹角为锐角⇔a·b >0且a ，b 不共线；两个向量a ，b 的夹角为钝角⇔a·b <0且a ，b 不共线． 2．平面向量数量积运算的常用公式 (1)(a ＋b )·(a －b )＝a 2－b 2.(2)(a ＋b )2＝a 2＋2a·b ＋b 2. (3)(a －b )2＝a 2－2a·b ＋b 2. 【思考辨析】判断下列结论是否正确(请在括号中打“√”或“×”)(1)向量在另一个向量方向上的投影为数量，而不是向量．( √ )(2)两个向量的数量积是一个实数，向量的加、减、数乘运算的运算结果是向量．( √ ) (3)由a ·b ＝0可得a ＝0或b ＝0.( × ) (4)(a ·b )c ＝a (b ·c )．( × )(5)两个向量的夹角的范围是[0，π2]．( × )1．(教材改编)已知向量a ＝(2,1)，b ＝(－1，k )，a·(2a －b )＝0，则k 等于( ) A ．－12 B ．6 C ．－6 D ．12答案 D解析 ∵2a －b ＝(4,2)－(－1，k )＝(5,2－k )，由a ·(2a －b )＝0，得(2,1)·(5,2－k )＝0， ∴10＋2－k ＝0，解得k ＝12.2．(2016·临安质检)已知向量a 与b 的夹角为30°，且|a |＝1，|2a －b |＝1，则|b |等于( ) A. 6 B. 5 C. 3 D. 2答案 C解析由题意可得a·b ＝|b |cos 30°＝32|b |,4a 2－4a·b ＋b 2＝1，即4－23|b |＋b 2＝1，由此求得|b |＝3，故选C.3．(2016·温州调研)若平面四边形ABCD 满足AB →＋CD →＝0，(AB →－AD →)·AC →＝0，则该四边形一定是( ) A ．直角梯形 B ．矩形 C ．菱形 D ．正方形答案 C解析由AB →＋CD →＝0得平面四边形ABCD 是平行四边形，由(AB →－AD →)·AC →＝0得DB →·AC →＝0，故平行四边形的对角线垂直，所以该四边形一定是菱形，故选C.4．(2016·北京)已知向量a ＝(1，3)，b ＝(3，1)，则a 与b 夹角的大小为________．答案 π6解析设a 与b 的夹角为θ，则cos θ＝a·b|a ||b |＝1×3＋1×312＋(3)2·12＋(3)2＝234＝32，又因为θ∈[0，π]，所以θ＝π6.题型一平面向量数量积的运算例1 (1)(2016·天津)已知△ABC 是边长为1的等边三角形，点D ，E 分别是边AB ，BC 的中点，连接DE 并延长到点F ，使得DE ＝2EF ，则AF →·BC →的值为( ) A ．－58B.18C.14D.118(2)已知正方形ABCD 的边长为1，点E 是AB 边上的动点，则DE →·CB →的值为________；DE →·DC →的最大值为________．答案 (1)B (2)1 1解析 (1) 如图，由条件可知BC →＝AC →－AB →，AF →＝AD →＋DF →＝12AB →＋32DE →＝12AB →＋34AC →，所以BC →·AF →＝(AC →－AB →)·(12AB →＋34AC →)＝34AC →2－14AB →·AC →－12AB →2. 因为△ABC 是边长为1的等边三角形，所以|AC →|＝|AB →|＝1，∠BAC ＝60°，所以BC →·AF →＝34－18－12＝18.(2)方法一以射线AB ，AD 为x 轴，y 轴的正方向建立平面直角坐标系，则A (0，0)，B (1,0)，C (1,1)，D (0,1)，设E (t,0)，t ∈[0,1]，则DE →＝(t ，－1)，CB →＝(0，－1)，所以DE →·CB →＝(t ，－1)·(0，－1)＝1. 因为DC →＝(1,0)，所以DE →·DC →＝(t ，－1)·(1,0)＝t ≤1，故DE →·DC →的最大值为1. 方法二由图知，无论E 点在哪个位置，DE →在CB →方向上的投影都是CB ＝1，∴DE →·CB →＝|CB →|·1＝1，当E 运动到B 点时，DE →在DC →方向上的投影最大，即为DC ＝1， ∴(DE →·DC →)max ＝|DC →|·1＝1.思维升华平面向量数量积的三种运算方法(1)当已知向量的模和夹角时，可利用定义法求解，即a·b ＝|a ||b |cos 〈a ，b 〉．(2)当已知向量的坐标时，可利用坐标法求解，即若a ＝(x 1，y 1)，b ＝(x 2，y 2)，则a·b ＝x 1x 2＋y 1y 2.(3)利用数量积的几何意义求解．(1)(2016·全国丙卷)已知向量BA →＝⎝⎛⎭⎫12，32，BC →＝⎝⎛⎭⎫32，12，则∠ABC 等于( )A ．30°B ．45°C ．60°D ．120°(2)(2015·天津)在等腰梯形ABCD 中，已知AB ∥DC ，AB ＝2，BC ＝1，∠ABC ＝60°.点E 和F 分别在线段BC 和DC 上，且BE →＝23BC →，DF →＝16DC →，则AE →·AF →的值为________．答案 (1)A (2)2918解析 (1)∵|BA →|＝1，|BC →|＝1， cos ∠ABC ＝BA →·BC →|BA →||BC →|＝32，又∵0°≤∠ABC ≤180°，∴∠ABC ＝30°.(2)在等腰梯形ABCD 中，AB ∥DC ，AB ＝2，BC ＝1， ∠ABC ＝60°，∴CD ＝1，AE →＝AB →＋BE →＝AB →＋23BC →，AF →＝AD →＋DF →＝AD →＋16DC →，∴AE →·AF →＝⎝⎛⎭⎫AB →＋23BC →·⎝⎛⎭⎫AD →＋16DC →＝AB →·AD →＋AB →·16DC →＋23BC →·AD →＋23BC →·16DC →＝2×1×cos 60°＋2×16＋23×12×cos 60°＋23×16×12×cos 120°＝2918.题型二平面向量数量积的应用命题点1 求向量的模例2 (1)(2016·宁波模拟)已知平面向量a ，b 的夹角为π6，且|a|＝3，|b |＝2，在△ABC 中，AB→＝2a ＋2b ，AC →＝2a －6b ，D 为BC 的中点，则|AD →|＝________.(2)在平面直角坐标系中，O 为原点，A (－1,0)，B (0，3)，C (3,0)，动点D 满足|CD →|＝1，则|OA →＋OB →＋OD →|的最大值是________．答案 (1)2 (2)7＋1 解析 (1)因为AD →＝12(AB →＋AC →)＝12(2a ＋2b ＋2a －6b ) ＝2a －2b ，所以|AD →|2＝4(a －b )2＝4(a 2－2b·a ＋b 2) ＝4×(3－2×2×3×cos π6＋4)＝4，所以|AD →|＝2.(2)设D (x ，y )，由CD →＝(x －3，y )及|CD →|＝1，知(x －3)2＋y 2＝1，即动点D 的轨迹为以点C 为圆心的单位圆．又OA →＋OB →＋OD →＝(－1,0)＋(0，3)＋(x ，y )＝(x －1，y ＋3)，∴|OA →＋OB →＋OD →|＝(x －1)2＋(y ＋3)2.问题转化为圆(x －3)2＋y 2＝1上的点与点P (1，－3)间距离的最大值． ∵圆心C (3,0)与点P (1，－3)之间的距离为(3－1)2＋(0＋3)2＝7，故(x －1)2＋(y ＋3)2的最大值为7＋1. 即|OA →＋OB →＋OD →|的最大值是7＋1.命题点2 求向量的夹角例3 (1)已知单位向量e 1与e 2的夹角为α，且cos α＝13，向量a ＝3e 1－2e 2与b ＝3e 1－e 2的夹角为β，则cos β＝________.(2)若向量a ＝(k,3)，b ＝(1,4)，c ＝(2,1)，已知2a －3b 与c 的夹角为钝角，则k 的取值范围是________________．答案 (1)223 (2)⎝⎛⎭⎫－∞，－92∪⎝⎛⎭⎫－92，3 解析 (1)因为a 2＝(3e 1－2e 2)2 ＝9－2×3×2×12×cos α＋4＝9，所以|a |＝3，因为b 2＝(3e 1－e 2)2＝9－2×3×1×12×cos α＋1＝8，所以|b |＝22，又a ·b ＝(3e 1－2e 2)·(3e 1－e 2)＝9e 21－9e 1·e 2＋2e 22＝9－9×1×1×13＋2＝8，所以cos β＝a ·b |a ||b |＝83×22＝223.(2)∵2a －3b 与c 的夹角为钝角， ∴(2a －3b )·c ＜0，即(2k －3，－6)·(2,1)＜0， ∴4k －6－6＜0， ∴k ＜3.又若(2a －3b )∥c ，则2k －3＝－12，即k ＝－92.当k ＝－92时，2a －3b ＝(－12，－6)＝－6c ，即2a －3b 与c 反向．综上，k 的取值范围为⎝⎛⎭⎫－∞，－92∪⎝⎛⎭⎫－92，3. 思维升华平面向量数量积求解问题的策略(1)求两向量的夹角：cos θ＝a·b|a||b |，要注意θ∈[0，π]． (2)两向量垂直的应用：两非零向量垂直的充要条件是a ⊥b ⇔a·b ＝0⇔|a －b |＝|a ＋b |.(3)求向量的模：利用数量积求解长度问题的处理方法有①a 2＝a·a ＝|a |2或|a |＝a·a .②|a ±b |＝(a ±b )2＝a 2±2a·b ＋b 2.③若a ＝(x ，y )，则|a |＝x 2＋y 2.(1)(2015·湖北)已知向量OA →⊥AB →，|OA →|＝3，则OA →·OB →＝________.(2)(2016·绍兴二模)已知单位向量a 和b 满足|a ＋b |＝2|a －b |，则a 与b 夹角的余弦值为( ) A ．－13B ．－23C.13D.23(3)在△ABC 中，若A ＝120°，AB →·AC →＝－1，则|BC →|的最小值是( ) A. 2 B ．2 C. 6D ．6答案 (1)9 (2)C (3)C解析 (1)因为OA →⊥AB →，所以OA →·AB →＝0.所以OA →·OB →＝OA →·(OA →＋AB →)＝OA →2＋OA →·AB →＝|OA →|2＋0＝32＝9.(2)由|a |＝|b |＝1，|a ＋b |＝2|a －b |，得2＋2a·b ＝2(1－2a·b ＋1)，即a·b ＝13，cos 〈a ，b 〉＝a·b |a||b |＝13.(3)∵AB →·AC →＝－1， ∴|AB →|·|AC →|·cos 120°＝－1，即|AB →|·|AC →|＝2，∴|BC →|2＝|AC →－AB →|2＝AC →2－2AB →·AC →＋AB →2 ≥2|AB →|·|AC →|－2AB →·AC →＝6， ∴|BC →|min ＝ 6.题型三平面向量与三角函数例4 (2015·广东)在平面直角坐标系xOy 中，已知向量m ＝⎝⎛⎭⎫22，－22，n ＝(sin x ，cos x )，x ∈⎝⎛⎭⎫0，π2. (1)若m ⊥n ，求tan x 的值； (2)若m 与n 的夹角为π3，求x 的值．解 (1)因为m ＝⎝⎛⎭⎫22，－22，n ＝(sin x ，cos x )，m ⊥n . 所以m ·n ＝0，即22sin x －22cos x ＝0，所以sin x ＝cos x ，所以tan x ＝1. (2)因为|m |＝|n |＝1，所以m ·n ＝cos π3＝12，即22sin x －22cos x ＝12，所以sin ⎝⎛⎭⎫x －π4＝12，因为0<x <π2，所以－π4<x －π4<π4，所以x －π4＝π6，即x ＝5π12.思维升华平面向量与三角函数的综合问题的解题思路(1)题目条件给出向量的坐标中含有三角函数的形式，运用向量共线或垂直或等式成立等，得到三角函数的关系式，然后求解．(2)给出用三角函数表示的向量坐标，要求的是向量的模或者其他向量的表达形式，解题思路是经过向量的运算，利用三角函数在定义域内的有界性，求得值域等．(1)已知O 为坐标原点，向量OA →＝(3sin α，cos α)，OB →＝(2sin α，5sin α－4cos α)，α∈⎝⎛⎭⎫3π2，2π，且OA →⊥OB →，则tan α的值为( ) A ．－43B ．－45C.45D.34(2)已知向量a ＝(－12，32)，OA →＝a －b ，OB →＝a ＋b ，若△OAB 是以O 为直角顶点的等腰直角三角形，则△OAB 的面积为________．答案 (1)A (2)1解析 (1)由题意知6sin 2α＋cos α·(5sin α－4cos α)＝0，即6sin 2α＋5sin αcos α－4cos 2α＝0，上述等式两边同时除以cos 2α，得6tan 2α＋5tan α－4＝0，由于α∈⎝⎛⎭⎫3π2，2π，则tan α＜0，解得tan α＝－43，故选A.(2)由题意得，|a |＝1，又△OAB 是以O 为直角顶点的等腰直角三角形，所以OA →⊥OB →，|OA →|＝|OB →|.由OA →⊥OB →得(a －b )·(a ＋b )＝|a |2－|b |2＝0，所以|a |＝|b |，由|OA →|＝|OB →|得|a －b |＝|a ＋b |，所以a·b ＝0. 所以|a ＋b |2＝|a |2＋|b |2＝2，所以|OB →|＝|OA →|＝2，故S △OAB ＝12×2×2＝1.5．利用数量积求向量夹角典例已知直线y ＝2x 上一点P 的横坐标为a ，直线外有两个点A (－1,1)，B (3,3)．求使向量P A →与PB →夹角为钝角的充要条件．错解展示现场纠错解错解中，cos θ<0包含了θ＝π，即P A →，PB →反向的情况，此时a ＝1，故P A →，PB →夹角为钝角的充要条件是0<a <2且a ≠1.纠错心得利用数量积的符号判断两向量夹角的范围时，不要忽视两向量共线的情况．1．(2016·北师大附中模拟)已知向量a ＝(x －1,2)，b ＝(2,1)，则a ⊥b 的充要条件是( ) A ．x ＝－12B ．x ＝－1C ．x ＝5D ．x ＝0答案 D2．若向量a ，b 满足|a |＝|b |＝2，a 与b 的夹角为60°，则|a ＋b |等于( )A ．22＋ 3B ．2 3C ．4D ．12答案 B解析 |a ＋b |2＝|a |2＋|b |2＋2|a ||b |cos 60°＝4＋4＋2×2×2×12＝12，|a ＋b |＝2 3.3．(2016·山西四校联考)已知平面向量a ，b 满足a ·(a ＋b )＝3，且|a |＝2，|b |＝1，则向量a 与b 夹角的正弦值为( ) A ．－12 B ．－32 C.12 D.32答案 D解析 ∵a ·(a ＋b )＝a 2＋a ·b ＝22＋2×1×cos 〈a ，b 〉＝4＋2cos 〈a ，b 〉＝3， ∴cos 〈a ，b 〉＝－12，又〈a ，b 〉∈[0，π]，∴sin 〈a ，b 〉＝1－cos 2〈a ，b 〉＝32. 4. 在△ABC 中，如图，若|AB →＋AC →|＝|AB →－AC →|，AB ＝2，AC ＝1，E ，F 为BC 边的三等分点，则AE →·AF →等于( )A.89B.109C.259D.269 答案 B解析若|AB →＋AC →|＝|AB →－AC →|，则AB →2＋AC →2＋2AB →·AC →＝AB →2＋AC →2－2AB →·AC →，即有AB →·AC →＝0.又E ，F 为BC 边的三等分点，则AE →·AF →＝(AC →＋CE →)·(AB →＋BF →) ＝⎝⎛⎭⎫AC →＋13CB →·⎝⎛⎭⎫AB →＋13BC → ＝⎝⎛⎭⎫23AC →＋13AB →·⎝⎛⎭⎫13AC →＋23AB → ＝29AC →2＋29AB →2＋59AB →·AC → ＝29×(1＋4)＋0＝109.故选B. 5．(2016·驻马店质检)若O 为△ABC 所在平面内任一点，且满足(OB →－OC →)·(OB →＋OC →－2OA →)＝0，则△ABC 的形状为( ) A ．正三角形B ．直角三角形C ．等腰三角形D ．等腰直角三角形答案 C解析因为(OB →－OC →)·(OB →＋OC →－2OA →)＝0，即CB →·(AB →＋AC →)＝0，因为AB →－AC →＝CB →，所以(AB →－AC →)·(AB →＋AC →)＝0，即|AB →|＝|AC →|，所以△ABC 是等腰三角形，故选C.*6.若△ABC 外接圆的圆心为O ，半径为4，OA →＋2AB →＋2AC →＝0，则CA →在CB →方向上的投影为( ) A ．4 B.15 C.7 D ．1答案 C解析如图所示，取BC 的中点D ，连接AD ，OD ，则由平面向量的加法的几何意义得 AB →＋AC →＝2AD →. 又由条件得，AB →＋AC →＝－12OA →＝12AO →，所以2AD →＝12AO →，即4AD →＝AO →，所以A ，O ，D 共线．所以OA ⊥BC ，所以CD 为CA →在CB →方向上的投影．因为|AO →|＝|CO →|＝4，所以|OD →|＝3，所以|CD →|＝|OC →|2－|OD →|2＝7.7．(2016·绍兴柯桥区二模)已知平行四边形ABCD 中，AC ＝3，BD ＝2，则AB →·AD →＝________. 答案 54解析 ▱ABCD 中，AC →＝AB →＋AD →，DB →＝AB →－AD →， ∴|AB →＋AD →|＝3，|AB →－AD →|＝2， ∴(AB →＋AD →)2－(AB →－AD →)2＝5， ∴AB →·AD →＝54.8．在△ABC 中，AB →·BC →＝3，△ABC 的面积S ∈[32，32]，则AB →与BC →夹角的取值范围是________．答案 [π6，π4]解析由三角形面积公式及已知条件知 32≤S △ABC ＝12AB ·BC sin B ≤32，所以3≤AB ·BC sin B ≤3，①由AB →·BC →＝3，知AB ·BC cos(π－B )＝3，所以AB ·BC ＝－3cos B ，代入①得，3≤－3sin Bcos B≤3，所以－1≤tan B ≤－33，所以3π4≤B ≤5π6，而AB →与BC →的夹角为π－B ，其取值范围为[π6，π4]．9．(2017·临安中学调研)已知在直角三角形ABC 中，∠ACB ＝90°，AC ＝BC ＝2，点P 是斜边AB 上的中点，则CP →·CB →＋CP →·CA →＝________. 答案 4解析由题意可建立如图所示的坐标系，可得A (2,0)，B (0,2)，P (1,1)，C (0，0)，则CP →·CB →＋CP →·CA →＝CP →·(CB →＋CA →)＝2CP →2＝4.10．(2015·杭州模拟)已知AB →⊥AC →，|AB →|＝1t ，|AC →|＝t ，若点P 是△ABC 所在平面内的一点，且AP →＝AB →|AB →|＋4AC →|AC →|，则PB →·PC →的最大值等于________．答案 13解析建立如图所示坐标系，则B ⎝⎛⎭⎫1t ，0，C (0，t )，AB →＝⎝⎛⎭⎫1t ，0， AC →＝(0，t )，AP →＝AB →|AB →|＋4AC →|AC →|＝t ⎝⎛⎭⎫1t ，0＋4t (0，t )＝(1,4)，∴P (1,4)，PB →·PC →＝⎝⎛⎭⎫1t －1，－4·(－1，t －4) ＝17－⎝⎛⎭⎫1t ＋4t ≤17－21t·4t ＝13. 11．在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，向量m ＝(cos(A －B )，sin(A －B ))，n ＝(cos B ，－sin B )，且m ·n ＝－35.(1)求sin A 的值；(2)若a ＝42，b ＝5，求角B 的大小及向量BA →在BC →方向上的投影．解 (1)由m ·n ＝－35，得cos(A －B )cos B －sin(A －B )sin B ＝－35，所以cos A ＝－35.因为0＜A ＜π，所以sin A ＝1－cos 2A ＝1－⎝⎛⎭⎫－352＝45. (2)由正弦定理，得a sin A ＝bsin B ，则sin B ＝b sin A a ＝5×4542＝22，因为a ＞b ，所以A ＞B ，则B ＝π4.由余弦定理得(42)2＝52＋c 2－2×5c ×⎝⎛⎭⎫－35，解得c ＝1，故向量BA →在BC →方向上的投影为|BA →|cos B ＝c cos B ＝1×22＝22. 12．(2017·杭州高三第一次质检)在△ABC 中，角A ，B ，C 所对的边分别记为a ，b ，c .若A ＝π6，(1＋3)c ＝2b . (1)求C ；(2)若CB →·CA →＝1＋3，求a ，b ，c .解 (1)在△ABC 中，由正弦定理b sin B ＝c sin C ，得(1＋3)sin C ＝2sin B ，又因为2sin B ＝2sin(5π6－C )＝cos C ＋3sin C ，所以sin C ＝cos C ，又C ∈(0，56π)，所以C ＝π4. (2)因为CB →·CA →＝22ab ，所以ab ＝2(1＋3)．由正弦定理得2a ＝c ，由余弦定理c 2＝a 2＋b 2－2ab cos C ，得c 2＝a 2＋b 2－2ab ＝12c 2＋(1＋3)24c 2－2(1＋3) ＝3＋32c 2－2(1＋3)，解得c ＝2，所以a ＝2，b ＝1＋ 3.*13.(2016·萧山中学模拟)在平面直角坐标系中，O 为坐标原点，已知向量a ＝(－1,2)，又点A (8,0)，B (n ，t )，C (k sin θ，t )(0≤θ≤π2)．(1)若AB →⊥a ，且|AB →|＝5|OA →|，求向量OB →；(2)若向量AC →与向量a 共线，当k >4，且t sin θ取最大值4时，求OA →·OC →.解 (1)由题设知AB →＝(n －8，t )，∵AB →⊥a ，∴8－n ＋2t ＝0.又∵5|OA →|＝|AB →|，∴5×64＝(n －8)2＋t 2＝5t 2，得t ＝±8.当t ＝8时，n ＝24；当t ＝－8时，n ＝－8，∴OB →＝(24,8)或OB →＝(－8，－8)．(2)由题设知AC →＝(k sin θ－8，t )，∵AC →与a 共线，∴t ＝－2k sin θ＋16，t sin θ＝(－2k sin θ＋16)sin θ＝－2k (sin θ－4k )2＋32k. ∵k >4，∴0<4k<1， ∴当sin θ＝4k 时，t sin θ取得最大值32k. 由32k＝4，得k ＝8，此时θ＝π6，OC →＝(4,8)， ∴OA →·OC →＝(8,0)·(4,8)＝32.。

浙江版2018年高考数学一轮复习专题5.3平面向量的数量积及其应用练20171128389

第 03节平面向量的数量积及其应用A 基础巩固训练1.若向量 a2,0,b1,1，则下列结论正确的是（）A ． a b 1 B.| a || b | C ． (a b ) b D ． a //b【答案】C 【解析】计算得 a b 2 ，| a | 2| b |， a b (1,1), (a b )b 11 0 ，故选C .2.若 a 1， b 2，且a ba，则 a 与b 的夹角是（）A.6B.3 C.5 6D.2 3【答案】D3.ABC 中，D 是 BC 中点， AD m ， BC n ，则 AB AC 等于（） A ． m 21 n2 B ． m 2 1 n 2 C ． 1 m 2 n 2D ． 122mn4444【答案】A n 【解析】由已知BD DC， DCDB ， 2222n 221 2AB AC (AD DB )(AD DC ) (AD DB )(AD DB ) AD DBm ( ) m n24.4.【湖北卷】已知向量OA AB ，| OA | 3，则OA OB.【答案】9【解析】因为OA AB，|OA|3，- 1 -所以OA OB OA(OA AB ) | OA |2 OA OB | OA |2 32 9 .5.【 2017课标 1，理 13】已知向量 a ， b 的夹角为 60°， |a |=2， |b |=1，则 | a +2 b |=.【答案】 2 3B 能力提升训练1.【重庆卷】已知非零向量 a ,b 满足|b |=4|a |，且a(2a +b ) 则 a 与b 的夹角为（） A.3B.2C.2 3D. 56【答案】C2【解析】由已知可得 a (2a b ) 0 2a a b 0，设 a 与b 的夹角为，则有222 a 4 a122a ab cos，又因为[0, ]，所以cos 0，故选 C.2232.【2017浙江台州 10月】已知O 为原点，点 A ， B 的坐标分别为 (a ,0)， (0,a )，其中常数a ，点 P 在线段 AB 上，且 AP t AB (0 t 1) ，则OA OP 的最大值是（）aB.a2A.C.2aD.3a【答案】A.【解析】∵AP t AB，∴OP OA t(OB OA)OP(1t)OA tOB，- 2 -OAOPt OA tOBOAt a ，∴当t0时，OA OP 的最大值是 a 2 ，故选[(1 )](1 )2∴ A.3.已知O 是边长为1的正三角形 ABC 的中心,则 (OA OB ) (OA OC ) __________【答案】 1 6【解析】， a 2 ， b 3，且 a 2b 与 a b 垂直，则实数的值为.4.已知 ab9【答案】．2【解析】由已知得， (a2b )(ab ) 0，则有a (2 1)a b2b 022，，又因为 a b则 a b 0 ，所以4 18 0 ，9． 25.【2016高考浙江理数】已知向量 a 、b , ｜a ｜ =1，｜b ｜ =2，若对任意单位向量 e ，均有｜a ·e ｜+｜b ·e ｜ 6 ,则 a ·b 的最大值是．【答案】12【解析】| (a b) | | a | | b | 6 | a b |6 | a |2 | b |2 2a b 6 a b 1 e e e2，即最大值为12.C 思维拓展训练11.【福建卷】已知AB AC,AB ,ACtt ，若P点是ABC所在平面内一点，且- 3 -APAB 4AC，则 PB PC 的最大值等于（）ABACA ．13B ．15C ．19D ．21【答案】A1即t时取等号．22.在边长为 2 的正方形 ABCD 中, 动点 M 和 N 分别在边 BC 和CD 上, 且1 BMBC , DNDC41,则的最小值为．AM BN【答案】 1【解析】B N BD DNAD ABDC4 1因为 AM AB BMABBC , 4.注意到AB DC , AB BC242432,所以,令AM BN BC AB4()414125441t t41t1tt t4,则,当且仅当取等AM BN t54512,号.- 4 -3.已知在直角三角形ABC中，ACB90，AC BC2，点P是斜边AB上的一个三等分点，则CP CB CP CA．【答案】4.4.【上海卷】已知平面向量a、b、c满足a b，且{|a|,|b|,|c|}{1,2,3}，则|a b c|的最大值是.【答案】35【解析】因为a b，设a(1,0)，b(0,2)，c(3cos,3sin)，[0,2)，所以a b c(13cos,23sin)，所以|a b c|2(13cos)2(23sin)21465sin()，其中65sin ，655所以当sin()1时，|a b c|取得最大值，即146535.5.【2017河北定州】已知向量a1,2，b3,4．- 5 -（1）求a b与a b的夹角；（2）若a a b，求实数的值．3【答案】（1）；（2）．14【解析】- 6 -。

高中数学(人教A版浙江)一轮参考课件5.3 平面向量的数量积ppt版本

=
1 2
��
=
12(b-a),
��
=
3 2
��
=
34(b-a),��
=
��
+
�� =-12a+34(b-a)=-54a+34b.
故��
·�� =-54a·b+34b2=-58
-8-
考点一
考点二
考点三
平面向量数量积的运算(考点难度★★)
例 1(1)(2016·天津高考)已知△ABC 是边长为 1 的等边三角形,
点 D,E 分别是边 AB,BC 的中点,连接 DE 并延长到点 F,使得 DE=2EF,
则�� ·��的值为( B )
A.-58
是
(-∞,-6)∪
-6,
3 2
.
解析:由 a·b<0,即 2λ-3<0,解得 λ<32.
由 a∥b,得 6=-λ,即 λ=-6.因此 λ<32,且 λ≠-6.
知识梳理
-7-
知识梳理双击自测
自测点评 1.对于两个非零向量a与b,由于当θ=0°时,a·b>0,所以a·b>0是两个向量a,b夹角为锐角的必要而不充分条件;a·b=0也不能推出a=0 或b=0,因为a·b=0时,有可能a⊥b. 2.在实数运算中,若a,b∈R,则|ab|=|a|·|b|;若a·b=a·c(a≠0),则b=c. 但对于向量a,b却有|a·b|≤|a|·|b|;若a·b=a·c(a≠0),则b=c不一定成立. 原因是a·b=|a||b|cos θ,都是cos θ “惹的祸”. 3.向量数量积的运算不满足乘法结合律,即(a·b)·c不一定等于 a·(b·c),这是由于(a·b)·c表示一个与c共线的向量,而a·(b·c)表示一个与a共线的向量,而c与a不一定共线.

(浙江专用)高考数学一轮总复习专题5 平面向量与解三角形 5.2 平面向量的数量积及其应用检测-人

5.2 平面向量的数量积及其应用挖命题【考情探究】考点内容解读5年考情预测热度考题示例考向关联考点平面向量的数量积1.理解平面向量数量积的含义及其物理意义.2.掌握向量夹角概念及其X围,掌握向量长度的表示.3.了解平面向量的数量积与向量投影的关系.4.掌握平面向量的数量积的坐标表达式,会进行平面向量的数量积的运算.5.理解平面向量的数量积的性质,并能灵活运用.2018某某,9平面向量的模的求法平面向量的模的最值★★★2017某某,10平面向量的数量积的计算平面向量的数量积的大小比较2016某某,15平面向量的数量积的计算平面向量的数量积的最大值2015某某文,13平面向量的模的求法数量积的计算2014某某,8平面向量的模的求法向量模的大小比较向量的综合应用1.会运用数量积解决两向量的夹角问题和长度问题.2.会用数量积判断两个向量的平行与垂直关系.3.会用向量方法解决某些简单的平面几何问题、力学问题以及一些实际问题.2018某某,9平面向量的模、夹角平面向量的模的最值★★★2017某某,15平面向量的模的求法2016某某,15,文15分析解读 1.向量的数量积是高考命题的热点,主要有以下几个方面:(1)平面向量的运算、化简、证明及其几何意义;(2)平面向量垂直的充要条件及其应用;(3)平面向量的综合应用,向量的坐标是代数与几何联系的桥梁,它融数、形于一体,具有代数形式和几何形式的双重身份,是中学数学知识的重要交汇点,常与平面几何、解析几何、三角函数等内容交叉渗透.2.预计2020年高考试题中,向量的数量积仍是高考的热点,应高度重视.破考点【考点集训】考点一平面向量的数量积1.(2018某某某某二模(3月),9)已知向量a,b满足|a|=1,且对任意实数x,y,|a-xb|的最小值为,|b-ya|的最小值为,则|a+b|=( )A. B.C.或D.或答案 C2.(2017某某名校(某某二中)交流卷三)已知向量a=(cos2A,-sin2A),b=,其中A 为△ABC的最小内角,且a·b=-,则角A等于 ( )A. B.C. D.或答案 C考点二向量的综合应用1.(2018某某名校协作体期初,12)在△ABC中,AB=3,BC=,AC=2,且O是△ABC的外心,则·=,·=.答案2;-2.(2018某某某某高三3月适应性模拟,16)已知正三角形ABC的边长为4,O是平面ABC上的动点,且∠AOB=,则·的最大值为.答案炼技法【方法集训】方法1 利用数量积求长度和夹角的方法1.(2017某某镇海中学模拟卷三,13)已知向量a,b满足|a-b|=1且|a|=2|b|,则a·b的最小值为,此时a与b的夹角是.答案-;π2.(2018某某“七彩阳光”联盟期初联考,16)若向量a,b满足a2+a·b+b2=1,则|a+b|的最大值为.答案方法2 利用向量解决几何问题的方法1.(2018某某新高考调研卷二(镇海中学),9)已知点P在边长为2的正方形ABCD的边上,点M 在以P为圆心,1为半径的圆上运动,则·的最大值是( )A.2B.1+C.1+2D.2+2答案 C2.(2018某某某某二中期中,16)在半径为1的扇形AOB中,∠AOB=60°,C为弧AB上的动点,AB 与OC交于点P,则·的最小值是.答案-过专题【五年高考】A组自主命题·某某卷题组考点一平面向量的数量积1.(2017某某,10,4分)如图,已知平面四边形ABCD,AB⊥BC,AB=BC=AD=2,CD=3,AC与BD交于点O.记I1=·,I2=·,I3=·,则( )A.I1<I2<I3B.I1<I3<I2C.I3<I1<I2D.I2<I1<I3答案 C2.(2014某某,8,5分)记max{x,y}=min{x,y}=设a,b为平面向量,则( )A.min{|a+b|,|a-b|}≤min{|a|,|b|}B.min{|a+b|,|a-b|}≥min{|a|,|b|}C.max{|a+b|2,|a-b|2}≤|a|2+|b|2D.max{|a+b|2,|a-b|2}≥|a|2+|b|2答案 D3.(2016某某文,15,4分)已知平面向量a,b,|a|=1,|b|=2,a·b=1.若e为平面单位向量,则|a·e|+|b·e|的最大值是.4.(2015某某文,13,4分)已知e1,e2是平面单位向量,且e1·e2=,若平面向量b满足b·e1=b·e2=1,则|b|=.答案考点二向量的综合应用1.(2018某某,9,4分)已知a,b,e是平面向量,e是单位向量.若非零向量a与e的夹角为,向量b满足b2-4e·b+3=0,则|a-b|的最小值是( )A.-1B.+1C.2D.2-答案 A2.(2017某某,15,6分)已知向量a,b满足|a|=1,|b|=2,则|a+b|+|a-b|的最小值是,最大值是.答案4;23.(2016某某,15,4分)已知向量a,b,|a|=1,|b|=2.若对任意单位向量e,均有|a·e|+|b·e|≤,则a·b的最大值是.答案B组统一命题、省(区、市)卷题组考点一平面向量的数量积1.(2018课标全国Ⅱ理,4,5分)已知向量a,b满足|a|=1,a·b=-1,则a·(2a-b)=( )A.4B.3C.2D.0答案 B2.(2017课标全国Ⅱ,12,5分)已知△ABC是边长为2的等边三角形,P为平面ABC内一点,则·(+)的最小值是( )A.-2B.-C.-D.-1答案 B3.(2016课标全国Ⅱ,3,5分)已知向量a=(1,m),b=(3,-2),且(a+b)⊥b,则m=( )A.-8B.-6C.6D.84.(2018文,9,5分)设向量a=(1,0),b=(-1,m).若a⊥(ma-b),则m=.答案-15.(2017课标全国Ⅰ理,13,5分)已知向量a,b的夹角为60°,|a|=2,|b|=1,则|a+2b|=. 答案26.(2015某某,16,12分)在平面直角坐标系xOy中,已知向量m=,n=(sin x,cos x),x∈.(1)若m⊥n,求tan x的值;(2)若m与n的夹角为,求x的值.解析(1)因为m⊥n,所以m·n=sin x-cos x=0.即sin x=cos x,又x∈,所以tan x==1.(2)易求得|m|=1,|n|==1.因为m与n的夹角为,所以cos==,则sin x-cos x=sin=.又因为x∈,所以x-∈.所以x-=,解得x=.考点二向量的综合应用1.(2018理,6,5分)设a,b均为单位向量,则“|a-3b|=|3a+b|”是“a⊥b”的( )A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件答案 C2.(2018某某文,8,5分)在如图的平面图形中,已知OM=1,ON=2,∠MON=120°,=2,=2,则·的值为( )A.-15B.-9C.-6D.0答案 C3.(2018某某理,8,5分)如图,在平面四边形ABCD中,AB⊥BC,AD⊥CD,∠BAD=120°,AB=A D=1.若点E为边CD上的动点,则·的最小值为( )A. B. C. D.3答案 A4.(2016某某,10,5分)在平面内,定点A,B,C,D满足||=||=||,·=·=·=-2,动点P,M满足||=1,=,则||2的最大值是( )A. B.C. D.答案 B5.(2017某某,12,5分)如图,在同一个平面内,向量,,的模分别为1,1,,与的夹角为α,且tan α=7,与的夹角为45°.若=m+n(m,n∈R),则m+n=.答案 36.(2014某某,14,5分)已知单位向量e1与e2的夹角为α,且cos α=,向量a=3e1-2e2与b=3e1-e2的夹角为β,则cos β=.答案C组教师专用题组考点一平面向量的数量积1.(2016,4,5分)设a,b是向量,则“|a|=|b|”是“|a+b|=|a-b|”的( )A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件答案 D2.(2016某某,7,5分)已知△ABC是边长为1的等边三角形,点D,E分别是边AB,BC的中点,连接DE并延长到点F,使得DE=2EF,则·的值为( )A.-B.C.D.答案 B3.(2016某某,8,5分)已知非零向量m,n满足4|m|=3|n|,cos<m,n>=.若n⊥(tm+n),则实数t 的值为( )A.4B.-4C.D.-答案 B4.(2015某某,9,5分)已知⊥,||=,||=t.若点P是△ABC所在平面内的一点,且=+,则·的最大值等于( )A.13B.15C.19D.21答案 A5.(2015某某,4,5分)已知菱形ABCD的边长为a,∠ABC=60°,则·=( )A.-a2B.-a2C.a2D.a2答案 D6.(2015某某,8,5分)△ABC是边长为2的等边三角形,已知向量a,b满足=2a,=2a+b,则下列结论正确的是( )A.|b|=1B.a⊥bC.a·b=1D.(4a+b)⊥答案 D7.(2015某某,6,5分)若非零向量a,b满足|a|=|b|,且(a-b)⊥(3a+2b),则a与b的夹角为( )A. B. C. D.π答案 A8.(2014大纲全国,4,5分)若向量a、b满足:|a|=1,(a+b)⊥a,(2a+b)⊥b,则|b|=( )A.2B.C.1D.答案 B9.(2014某某,7,5分)平面向量a=(1,2),b=(4,2),c=ma+b(m∈R),且c与a的夹角等于c与b 的夹角,则m=( )A.-2B.-1C.1D.2答案 D10.(2014某某,8,5分)已知菱形ABCD的边长为2,∠BAD=120°,点E,F分别在边BC,DC 上,BE=λBC,DF=μDC.若·=1,·=-,则λ+μ=()A. B. C. D.答案 C11.(2014课标Ⅱ,3,5分)设向量a,b满足|a+b|=,|a-b|=,则a·b=()A.1B.2C.3D.5答案 A12.(2017课标全国Ⅲ文,13,5分)已知向量a=(-2,3),b=(3,m),且a⊥b,则m=.答案 213.(2017文,12,5分)已知点P在圆x2+y2=1上,点A的坐标为(-2,0),O为原点,则·的最大值为.答案 614.(2017某某理,12,5分)已知e1,e2是互相垂直的单位向量.若e1-e2与e1+λe2的夹角为60°,则实数λ的值是.答案15.(2016课标全国Ⅰ,13,5分)设向量a=(m,1),b=(1,2),且|a+b|2=|a|2+|b|2,则m=.答案-216.(2016某某,13,5分)如图,在△ABC中,D是BC的中点,E,F是AD上的两个三等分点,·=4,·=-1,则·的值是.答案17.(2015某某,11,5分)已知向量⊥,||=3,则·=.答案918.(2015某某,14,5分)在等腰梯形ABCD中,已知AB∥DC,AB=2,BC=1,∠ABC=60°.动点E和F分别在线段BC和DC上,且=λ,=,则·的最小值为.答案19.(2014某某,12,5分)如图,在平行四边形ABCD中,已知AB=8,AD=5,=3,·=2,则·的值是.答案2220.(2014某某,15,5分)已知两个不相等的非零向量a,b,两组向量x1,x2,x3,x4,x5和y1,y2,y3,y4,y5均由2个a和3个b排列而成.记S=x1·y1+x2·y2+x3·y3+x4·y4+x5·y5,S min表示S所有可能取值中的最小值.则下列命题正确的是(写出所有正确命题的编号).①S有5个不同的值;②若a⊥b,则S min与|a|无关;③若a∥b,则S min与|b|无关;④若|b|>4|a|,则S min>0;⑤若|b|=2|a|,S min=8|a|2,则a与b的夹角为.答案②④考点二向量的综合应用1.(2016课标全国Ⅲ,3,5分)已知向量=,=,则∠ABC=()A.30°B.45°C.60°D.120°答案 A2.(2015某某,8,5分)已知点A,B,C在圆x2+y2=1上运动,且AB⊥BC.若点P的坐标为(2,0),则|++|的最大值为( )A.6B.7C.8D.9答案 B3.(2017课标全国Ⅰ文,13,5分)已知向量a=(-1,2),b=(m,1).若向量a+b与a垂直,则m=. 答案74.(2015某某,14,5分)设向量a k=cos,sin+cos(k=0,1,2,…,12),则(a k·a k+1)的值为.答案9【三年模拟】一、选择题(每小题4分,共24分)1.(2019届某某某某普通高中适应性测试,9)已知向量a,b满足|a|=2,a2+2a·b+2b2=8,则a·b的取值X围是( )A.[2-2,2+2]B.[-2-2,2-2]C.[-1,+1]D.[--1,-1]答案 B2.(2019届某某、某某、某某三地教学质量检测,8)如图,△OA1B1,△A1A2B2,△A2A3B3是边长相等的等边三角形,且O,A1,A2,A3四点共线.若点P1,P2,P3分别是边A1B1,A2B2,A3B3上的动点(不含端点),记I1=·,I2=·,I3=·,则( )A.I1>I2>I3B.I2>I3>I1C.I2>I1>I3D.I3>I1>I2答案 B3.(2018某某嵊州第一学期期末质检,10)如图,已知矩形ABCD中,AB=3,BC=2,该矩形所在的平面内一点P满足||=1,记I1=·,I2=·,I3=·,则( )A.存在点P,使得I1=I2B.存在点P,使得I1=I3C.对任意的点P,有I2>I1D.对任意的点P,有I3>I1答案 C4.(2018某某某某第一学期期末质检,9)已知m,n是两个非零向量,且|m|=1,|m+2n|=3,则|m+n|+|n|的最大值为( )A.B. C.4 D.5答案 B5.(2018某某某某第一次调考(4月),9)已知单位向量e1,e2,且e1·e2=-,若向量a满足(a-e1)·(a-e2)=,则|a|的取值X围为( )A. B.C. D.答案 B6.(2018某某某某第二次教学质量检测(4月),9)记 M 的最大值和最小值分别为 M max 和 M min.若平面向量a,b,c 满足|a|=|b|=a·b=c·(a+2b-2c)=2,则( )A.|a-c|max=B.|a+c|max=C.|a-c|min=D.|a+c|min=答案 A二、填空题(单空题4分,多空题6分,共16分)7.(2019届某某名校新高考研究联盟第一次联考,16)已知向量a,b满足|a|=2|b|,|a-b|=2,则a·b的取值X围为.答案8.(2019届某某中学第一次模拟,14)已知向量a,b满足|a|=2,|b|=1,a,b的夹角为,则a与a-2b的夹角为.答案9.(2019届镇海中学期中,15)已知两个不共线的非零向量a,b满足|a|=2,|a-b|=1,则向量a,b的夹角的最大值是.答案30°10.(2018某某某某十校第一学期期末调研,17)已知平面向量a,b,c满足|a|≤1,|b|≤1,|2c-(a+b)|≤|a-b|,则|c|的最大值为.答案。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

）1.【北京卷】设a ，b 是非零向量，“a b a b ⋅=”是“//a b ”的（） A ．充分而不必要条件 B ．必要而不充分条件 C ．充分必要条件 D ．既不充分也不必要条件【答案】A【解析】||||cos ,a b a b a b •=•<>，由已知得cos ,1a b <>=，即,0a b <>=，//a b .而当//a b 时，,a b <>还可能是π，此时||||a b a b •=-，故“a b a b ⋅=”是“//a b ”的充分而不必要条件，故选A.2.【福建卷】设(1,2)a =，(1,1)b =，c a kb =+．若b c ⊥，则实数k 的值等于（） A ．32-B ．53-C ．53D ．32【答案】A3.【2017浙江温州模拟】已知为单位向量，，则在的投影为A. B. C. D.【答案】C 【解析】由题设可得，即，则，即，又，故，应选答案C.4. ,2,1==b a 且⊥+)(，则与的夹角为（） A.30 B.60 C.120 D.150 【答案】C5.【重庆卷】已知向量(,3),(1,4),(2,1)a k b c ===，且(23)a b c -⊥，则实数k =（） 9.2A -.0B .C 3 D.152【答案】C【解析】因为()(),3,1,4,a k b ==所以()2323,6a b k -=--，又因为()23a b c -⊥，所以，()230a b c -⋅=，所以，()()22360k -+-=，解得：3k =，故选C.6.【辽宁卷】设,,a b c 是非零向量，已知命题P ：若0a b ⋅=，0b c ⋅=，则0a c ⋅=；命题q ：若//,//a b b c ，则//a c ，则下列命题中真命题是（）A ．p q ∨B ．p q ∧C ．()()p q ⌝∧⌝D ．()p q ∨⌝ 【答案】A【解析】若0a b ⋅=，0b c ⋅=，则,a b b c ⊥⊥，故//a c ，故命题p 是假命题；若//,//a b b c ，则//a c ，故命题q 是真命题，由复合命题真假判断知，p q ∨是真命题，选A ．7.【2017四川宜宾二诊】若非零向量,a b ，满足a b =， ()20a b a -⋅=，则a 与b 的夹角为 A.6π B. 3π C. 23π D. 56π 【答案】B【解析】由()2220a b a a a b -⋅=-⋅=，即22aa b ⋅=，所以由向量的夹角公式可得1cos ,22a a b a b a aa b⋅〈〉===⋅⋅，又(),0,a b π〈〉∈，所以,3a b π〈〉=，故选B. 8．【2017陕西师范附属二模】已知向量()1,1a =， ()24,2a b +=，则向量,a b 的夹角的余弦值为（）A.310 10B.31010- C.22D.22-【答案】C9．【2017四川成都二诊】已知平面向量a ，b夹角为3π，且1a=，12b=，则2a b+与b的夹角是（）A.6πB.56πC.4πD.34π【答案】A【解析】由题意可知：111cos234a bπ⋅=⨯⨯=，则：()2113222444a b b a b b+⋅=⋅+=+⨯=，且：()22222443a b a b a a b b+=+=+⋅+=，设所求向量的夹角为θ，有：()23cos2a b ba b bθ+⋅==+⨯，则2a b+与b的夹角是6π.本题选择A选项.10. 设a ，b，c为同一平面内具有相同起点的任意三个非零向量，且满足a与b 不共线，a⊥c，|a|＝|c|，则||b c⋅的值一定等于( )A．以a，b为两边的三角形的面积B．以b，c为两边的三角形的面积C．以a，b为邻边的平行四边形的面积D．以b，c为邻边的平行四边形的面积【答案】C．平行四边形的面积．11.【重庆卷】若非零向量a ，b 满足|a |=223|b |，且（a -b ）⊥（3a +2b ），则a 与b 的夹角为（） A 、4π B 、2π C 、34π D 、π 【答案】A【解析】由题意22()(32)320a b a b a a b b -⋅+=-⋅-=，即223cos 20a a b b θ--=，所以222223(2033θ⨯--=，2cos 2θ=，4πθ=，选A .12.【2017课标II ，理12】已知ABC ∆是边长为2的等边三角形，P 为平面ABC 内一点，则()PA PB PC ⋅+的最小是（）A.2-B.32-C. 43- D.1- 【答案】B 【解析】二、填空题（本大题共4小题，每小题5分，共20分。

把答案填在题中的横线上。

） 13.已知不共线的平面向量满足若向量,且,，则__________．【答案】14.【2017福建4月质检】设向量()()1,3,,3a b m ==，且,a b 的夹角为3π，则实数m =__________．【答案】-1【解析】由题得： cos a b a b θ⋅=得2132312m m m +=+⇒=-15.已知,AD BE 分别是ABC ∆的中线，若1AD BE ==，且23AB AC ⋅=，则AD 与BE 的夹角为 . 【答案】0120 【解析】由题设222AD AB AC BE AC AB⎧=+⎪⎨=-⎪⎩,解之得2()32(2)3AB AD BE AC AD BE ⎧=-⎪⎪⎨⎪=+⎪⎩,因23AB AC ⋅=,即42()(2)93AD BE AD BE -+=,也即22322AD BE AD BE --⋅=,故12AD BE ⋅=-,即21cos -=α,所以0120,>=<BE AD ,应填0120.16.【2017浙江台州中学10月】在ABC ∆中，16AB AC ⋅=，sin sin cos A B C =，D 线段AB 上的动点（含端点），则DA DC ⋅的取值范围是．【答案】[4,0]-. 【解析】三、解答题（本大题共4小题，共70分.解答应写出文字说明、证明过程或演算步骤.） 17.在ABC ∆中，点M 是边BC 的中点.若1120,2A AB AC ∠=⋅=-，求AM 的最小值. 【答案】21 【解析】试题分析：设,AB c AC b ==，由1120,2A AB AC ∠=⋅=-，即有1cos1202bc =-，得1bc =，点M 是BC 的中点，则()12AM AB AC =+，()()22222112144AM AB AC AB AC c b =++⋅=+-()()11121211444bc ≥-=⨯-=．当且仅当1b c ==取得最小值，且为14．则AM 的最小值为12．18.已知向量(cos ,sin )a αα=，(1+cos ,sin )b ββ=-. （1）若3πα=，(0,)βπ∈，且a b ⊥，求β；（2）若=βα，求a b ⋅的取值范围.【答案】（1）3πβ=；（2）a b ⋅的取值范围为9[,2]8-.整理得1cos()32πβ+=- 3分 ∴2233k ππβπ+=+过42,33k k z ππβπ+=+∈ 4分 ∵(0,)βπ∈∴3πβ=6分（2）222cos cos sin cos 2cos 1a b ααααα⋅=+-=+- 8分令[]cos ,1,1t t α=∈- 2219212()48a b t t t ⋅=+-=+-9分 ∴当1t =时，max 2a b ⋅=，当14t =-时，98min a b ⋅=- 11分∴a b ⋅的取值范围为9[,2]8-. 12分19.已知向量)7,1(1-=a ，)1,1(=d ，对任意*N n ∈都有d a a n n +=+1. （1）求||n a 的最小值；（2）求正整数,m n ,使m n a a ⊥ 【答案】（1）|n a |的最小值为2（2）212m n =⎧⎨=⎩或320m n =⎧⎨=⎩ 122m n =⎧⎨=⎩ 203m n =⎧⎨=⎩．【解析】(1)设(),n n n a x y =,由1n a +=n a +d 得 1111n n n n x x y y ++=+⎧⎨=+⎩∴{x n }、{y n }都是公差为1的等差数列 .3分 ∵1a =（1，7）∴,8n n x n y n ==-, (),8n a n n =-222||(8)2(4)3242n a n n n =+-=-+≥|n a |的最小值为2分∴212m n =⎧⎨=⎩或320m n =⎧⎨=⎩ 122m n =⎧⎨=⎩ 203m n =⎧⎨=⎩． ..12分20.已知→→b a ,是两个单位向量．（1）若323=-→→b a ，试求→→+b a 3的值；（2）若→→b a ,的夹角为o60，试求向量→→→+=b a m 2与→→→-=a b n 2的夹角的余弦.【答案】（1）23 ；.（2）3212cos 14||||73m n m n θ⋅===⋅ 【解析】试题分析：（1）由题为,a b →→单位向量，且323a b →→-=，可利用向量乘法运算的性质；22a a →→=，化为向量的乘法运算，求出13a b ⋅=，进而可求得3a b →→+229||124||9a a b b ∴-⋅+=，即13a b ⋅=． 221|3|9||6||9161233a b a a b b ∴+=+⋅+=⨯+⨯+= （2）22221||(2)4||4||414172m a b a a b b =+=+⋅+=⨯+⨯+=222|(2)4||4||41-4n b a b a b a =-=-⋅+=⨯223(2)(2)2||32||2m n a b b a b a b a ⋅=+⋅-=+⋅-=， 32||||7m nm n ⋅=⋅。