专练04 实验题(原卷版)
专题04 一元二次方程的应用(八大类型)(题型专练)(原卷版)

专题04 一元二次方程的应用(八大类型)【题型1 一元二次方程应用-变化率】【题型2 一元二次方程应用-传染问题】【题型3 一元二次方程应用-分支问题】【题型4 一元二次方程应用-比赛问题及迁移运用】【题型5 一元二次方程应用-销售问题】【题型6 一元二次方程应用-每每问题】【题型7 一元二次方程应用-几何面积问题】【题型8 一元二次方程应用-几何动态问题】【题型1 一元二次方程应用-变化率】1.(2023春•鄞州区期中)某商品经过连续两次降价,价格由100元降为64元.已知两次降价的百分率都是x,则x满足的方程是()A.64(1﹣2x)=100B.100(1﹣x)2=64C.64(1﹣x)2=100D.100(1﹣2x)=64 2.(2023•东莞市校级一模)某旅游景点8月份共接待游客25万人次,10月份共接待游客64万人次,设游客每月的平均增长率为x,则下列方程正确的是()A.25(1+x)2=64B.25(1+x2)=64C.64(1﹣x)2=25D.64(1﹣x2)=253.(2021·松北期末)某机械厂七月份生产零件50万个,第三季度生产零件196万个.设该厂八、九月份平均每月的增长率为x,那么x满足的方程是()A.50(1+x2)=196 B.50+50(1+x2)=196C.50+50(1+x)+50(1+x2)=196 D.50+50(1+x)+50(1+2x)=196 4.(2023•沭阳县模拟)某商品原价每件75元,两次降价后每件48元,则平均每次的降价百分率是.5.(2022秋•确山县期中)2022年是中国共产党建党101周年,全国各地积极开展“弘扬红色文化,重走长征路”主题教育学习活动,某市“红二方面军长征出发地纪念馆”成为重要的活动基地.据了解,今年8月份该基地接待参观人数10万人,10月份接待参观人数增加到12.1万人.(1)求这两个月参观人数的月平均增长率;(2)按照这个增长率,预计11月份的参观人数能否突破13.5万人?6.(2022春•沂源县校级月考)受益于国家支持新能源汽车发展等多重利好因素,我市某汽车零部件生产企业的利润逐年提高.据统计,2016年利润为2亿元,2018年利润为2.88亿元.(1)求该企业从2016年到2018年利润的年平均增长率.(2)若2019年保持前两年利润的年平均增长率不变,该企业2019年的利润能否超过3.4亿元?【题型2 一元二次方程应用-分支问题】7.(2022秋•青川县期末)某数学活动小组在开展野外项目实践时,发现一种植物的主干长出若干数目的枝干,每个枝干又长出同样数目的小分枝,主干、枝干和小分枝的总数是31,则这种植物每个枝干长出的小分支个数是()A.4B.5C.6D.7 8.(2022秋•澄海区期末)某校“生物研学”活动小组在一次野外研学实践时,发现某种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支.若主干、支干和小分支的总数是91,求这种植物每个支干长出的小分支个数是多少?【题型3 一元二次方程应用-传染问题】9.(2022春•南谯区校级期中)新冠肺炎病毒是一种传染性极强的急性呼吸道传染病,感染者的临床以发热、乏力、干咳为主要表现.在“新冠肺炎”疫情初期,有1人感染了“新冠肺炎病毒”,如若得不到有效控制,经过两轮传染后共有196人感染了“新冠肺炎病毒”,则每轮传染中平均一个人传染了()A.12人B.13人C.14人D.15人10.(2023•兴庆区校级一模)有一个人患流感,经过两轮传染后共有81个人患流感,每轮传染中平均一个人传染几个人?设每轮传染中平均一个人传染x 个人,可到方程为()A.1+2x=81B.1+x2=81C.1+x+x2=81D.(1+x)2=81 11.(2022秋•沈丘县月考)若有2个人患了流感,经过两轮传染后共有50人患了流感(这2个人在第二轮传染中仍有传染性),则每轮传染中平均一个人传染人.12.(2023•城关区一模)有一人患了流感,经过两轮传染后共有169人患了流感,每轮传染中平均一个人传染了人.13.(2022秋•天河区校级期末)截止到2022年1月,新冠肺炎疫情在中国已经得到有效控制,但在全球却持续蔓延,这是对人类的考验,将对全球造成巨大影响.新冠肺炎具有人传人的特性,若一人携带病毒,未进行有效隔离,经过两轮传染后共有196人患新冠肺炎,求每轮传染中平均每个人传染了几个人?14.(2022秋•甘井子区校级期末)有一个人患了流感,经过两轮传染后共有144个人患了流感.(1)每轮传染中平均一个人传染了几个人?(2)如果按照这样的传染速度,经过三轮传染后共有多少个人患流感?【题型4 一元二次方程应用-比赛问题及迁移运用】15.(2023•东莞市二模)2022年北京冬奥会女子冰壶比赛有若干支队伍参加了单循环比赛,单循环比赛共进行了45场,共有多少支队伍参加比赛?()A.7B.8C.9D.1016.(2021秋•虎林市校级期末)2021年虎林市教育局组织开展了全市中学生篮球联赛,比赛采用单循环赛制(每两队之间进行一场比赛),共进行了66场比赛,则参加比赛的队伍数量是()A.10B.11C.12D.1317.(2022•黑龙江模拟)某校八年级组织篮球赛,若每两班之间赛一场,共进行了28场,则该校八年级有()个班级.A.8B.9C.10D.11 18.(2023•惠东县一模)2022年北京冬奥会女子冰壶比赛有若干支队伍参加了单循环比赛,单循环比赛共进行了45场,则本次比赛共有参赛队伍()A.8支B.9支C.10支D.11支19.(2022秋•于洪区期末)一次会议上,每两个参加会议的人都相互握了一次手.有人统计一共握了66次手,这次会议到会的人数有多少人()A.8B.10C.12D.14 20.(2022秋•南平期中)生物兴趣小组的学生,将自己收集的标本向本组其他成员各赠送一件,全组共互赠了182件,那么全组有()名同学.A.12B.13C.14D.1521.(2022秋•和平区期末)一次会议上,每两个参加会议的人都相互握了一次手,经统计所有人一共握了10次手,则这次会议到会的人数是人.22.(2022秋•荔湾区校级期末)卡塔尔足球世界杯小组赛,每两队之间进行一场比赛,小组赛共进行了6场比赛,则该小组有支球队.23.(2023春•安徽月考)网课期间小夏写了封保护眼睛的倡议书,用微博转发的方式传播,设计了如下转发规则:将倡议书发表在自己的微博上,然后邀请x个好友转发,每个好友转发之后,又邀请x个互不相同的好友转发,已知经过两轮转发后,共157人参与了此次活动,则x为人.24.(2022秋•蔚县校级期末)一个小组有若干人,新年互送贺卡一张,共送贺卡72张,共有人.25.(2022秋•白云区期末)一次足球联赛,赛制为双循环形式(每两队之间都赛两场),共要比赛90场,共有多少个队参加比赛?【题型5 一元二次方程应用-销售问题】26.(2023春•盐都区月考)某商店分别花20000元和30000元先后两次以相同的进价购进某种商品,且第二次的数量比第一次多500千克.(1)该商品的进价是多少?(2)已知该商品每天的销售量y(千克)与销售单价x(元/千克)之间的函数关系式为:y=﹣10x+500,若想销售该商品每天获利2000元,该商店需将商品的售价定为多少?27.(2023•中山市一模)某超市以每千克40元的价格购进菠萝蜜,计划以每千克60元的价格销售,为了让顾客得到实惠.现决定降价销售,已知这种菠萝蜜销售量y(千克)与每千克降价x(元)(0<x<20)之间满足一次函数关系,其图象如图所示.(1)求y与x之间的函数关系式.(2)若超市要想获利2400元,且让顾客获得更大实惠,这种菠萝蜜每千克应降价多少元?28.(2022秋•九龙坡区期末)某图书店在2022年国庆节期间举行促销活动,某课外阅读书进货价为每本8元,标价为每本15元.(1)该图书店举行了国庆大回馈活动,连续两次降价,每次降价的百分率相同,最后以每本9.6元的价格售出,求图书店每次降价的百分率;(2)在九月底该书店老板去进货该书500本,按照(1)两次降价后的价格在国庆节全部售出;国庆节后老板去进货发现进货价上涨了a%,进货量比九月底增加3a%,以标价的八折全部售出后,比国庆节的总利润多1200元,求a%的值.29.(2022秋•平遥县期末)某商店通过网络在一源头厂家进一种季节性小家电,由于疫情影响以及市场竞争,该厂家不得不逐年下调出厂价;(1)2019年这个小家电出厂价是每台62.5元,到2021年同期该品牌小家电出厂价下调为40元,若每年下调幅度相同,请你计算该小家电出厂价平均每年下调的百分率;(2)若明年商场计划按每台40元购一批该品牌小家电,经市场预测,销售定价为50元时,每月可售出500台,销售定价每增加1元,销售量将减少10台.因受库存的影响,每月进货台数不得超过300台;商家若希望月获利8750元,则应进货多少台?销售定价多少元?30.(2023•桂林一模)小王计划经营某种时尚产品的专卖店,已知该产品的进货价为70元/件,售价不能低于80元/件,专卖店每月有800元的固定成本开支,根据市场调研,产品的销售量y(件)随着产品的售价x(元/件)的变化而变化,销售量y与售价x之间的部分对应关系如表:80828486…售价x(元/件)500490480470…销售量y(件)(1)求销售量y(件)与售价x(元/件)的函数关系式;(2)小王预计每月盈利8200元,为尽可能让利于顾客,则该产品的售价每件应定为多少元?31.(2022秋•通川区期末)为了满足社区居民强身健体的需要,政府准备采购若干套健身器材免费提供给社区,经过考察了解,飞跃公司有A,B两种型号的健身器材可供选择,已知飞跃公司2020年每套A型健身器材的售价为2.5万元,2020年每套B型健身器材的售价为2万元,2022年每套A型健身器材售价为1.6万元,每套A型,B型健身器材的年平均下降率相同.(1)求2020年到2022年每套A型健身器材年平均下降率;(2)2022年政府经过招标,决定年内采购并安装飞跃公司A,B两种型号的健身器材共80套,政府采购专项经费总计不超过115.2万元,并且采购A型器材费用不能少于B型器材的费用,请求出所需经费最少的采购方案.32.(2023•抚州一模)某超市经销一种商品,每千克成本为30元,经试销发现,该种商品的每天销售量y(千克)与销售单价x(元/千克)满足一次函数关系,其每天销售单价,销售量的四组对应值如表所示:40455560销售单价x(元/千克)80705040销售量y(千克)(1)求y(千克)与x(元/千克)之间的函数表达式;(2)若商店按销售单价不低于成本价,且不高于60元的价格销售,要使销售该商品每天获得的利润为800元,求每天的销售量应为多少千克?33.(2022春•莱芜区期末)某农户生产经营一种农产品,已知这种农产品的成本价为每千克20元,经市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)之间满足一次函数关系,其图象如图所示.(1)求y与x之间的函数关系式;(2)该农户想要每天获得150元的利润,又要让利消费者,销售价应定为每千克多少元?【题型6 一元二次方程应用-每每问题】34.(2023春•沙坪坝区校级月考)将进货价格为38元的商品按单价45元售出时,能卖出300个.已知该商品单价每上涨1元,其销售量就减少5个.设这种商品的售价上涨x元时,获得的利润为2300元,则下列关系式正确的是()A.(x﹣38)(300﹣5x)=2300B.(x+7)(300+5x)=2300C.(x﹣7)(300﹣5x)=2300D.(x+7)(300﹣5x)=230035.(2021秋•纳溪区期末)某商场经营某种品牌的玩具,购进时的价格是30元/件,根据市场调查:在一段时间内,当销售价格是40元/件时,销售量是600件,当销售单价每涨1元,就会少售出10件玩具.(1)不妨设该种品牌玩具的销售价格为x元/件(x>40),请你分别用含x 的代数式来表示销售量y件和销售该品牌玩具获得的利润w元.(2)在第(1)间的条件下,若商场获得了10000元的销售利润,求该玩具的销售价格应定为多少元/件.36.(2022秋•东明县期末)2022年北京冬季奥运会于2月4日至2月20日在北京市和河北省张家口市联合举行,冬奥会吉祥物为“冰墩墩”.(1)据市场调研发现,某工厂今年二月份共生产500个“冰墩墩”,为增大生产量,该工厂平均每月生产量增加20%,则该工厂在四月份能生产多少个“冰墩墩”?(2)已知某商店“冰墩墩”平均每天可销售20个,每个盈利40元,在每个降价幅度不超过10元的情况下,每下降2元,则每天可多售10件.如果每天要盈利1440元,则每个“冰墩墩”应降价多少元?37.(2022秋•龙岗区期末)“双十一”期间,某网店直接从工厂购进A,B两款保温杯,进货价和销售价如表:(注:利润=销售价﹣进货价)A款保温杯B款保温杯进货价(元/个)3528销售价(元/个)5040(1)若该网店用1540元购进A,B两款保温杯共50个,求两款保温杯分别购进的个数.(2)“双十一”后,该网店打算把B款保温杯降价销售,如果按照原价销售,平均每天可售出4个,经调查发现,每降价1元,平均每天可多售出2个,则将B款保温杯的销售价定为每个多少元时,才能使B款保温杯平均每天的销售利润为96元?38.(2023春•长沙期中)春节是中国的传统节日,每年元旦节后是购物的高峰期,2023年元月某水果商从农户手中购进A、B两种红富士苹果,其中A种红富士苹果进货价为28元/件,销售价为42元/件,其中B种红富士苹果进货价为22元/件,销售价为34元/件.(注:利润=销售价﹣进货价)(1)水果店第一次用720元购进A、B两种红富士苹果共30件,求两种红富士苹果分别购进的件数;(2)第一次购进的红富士苹果售完后,该水果店计划再次购进A、B两种红富士苹果共80件(进货价和销售价都不变),且进货总费用不高于2000元.应如何设计进货方案,才能获得最大销售利润,最大销售利润是多少?(3)春节临近结束时,水果店发现B种红富士苹果还有大量剩余,决定对B 种红富士苹果调价销售.如果按照原价销售,平均每天可售4件.经调查发现,每降价1元,平均每天可多售2件,为了尽快减少库存,将销售价定为每件多少元时,才能使B种红富士苹果平均每天销售利润为90元?39.(2023春•北仑区期中)某超市于今年年初以每件25元的进价购进一批商品.当商品售价为40元时,一月份销售256件.二、三月该商品十分畅销.销售量持续走高.在售价不变的基础上,三月底的销售量达到400件.设二、三这两个月的月平均增长率不变.(1)求二、三这两个月的月平均增长率;(2)从四月份起,商场决定采用降价促销的方式回馈顾客,经调查发现,该商品每降价1元,销售量增加5件,当商品降价多少元时,商场获利4250元?【题型7 一元二次方程应用-几何面积问题】40.(2023春•温州期中)如图,在长为32米,宽为20米的长方形地面上修筑同样宽的小路(图中阴影部分),余下部分种植草坪,要使小路的面积为100平方米,设小路的宽为x米,则下面所列方程正确的是()A.32×20﹣32x﹣20x=100B.32x+20x﹣x2=100C.(32﹣x)(20﹣x)+x2=100D.(32﹣x)(20﹣x)=100 41.(2022春•凭祥市期中)如图,在长为30m,宽为15m的长方形地面上修筑同样宽的道路(图中阴影部分),其余部分铺设草坪,要使草坪的面积为406m2,则小路的宽度应为多少()A.1B.1.5C.2D.442.(2023•两江新区一模)如图,某小区居民休闲娱乐中心是一块长方形(长60米,宽40米)场地,被3条宽度相等的绿化带分为总面积为1750平方米的活动场所,如果设绿化带的宽度为x米,由题意可列方程为()A.(60﹣x)(40﹣x)=1750B.(60﹣2x)(40﹣x)=1750C.(60﹣2x)(40﹣x)=2400D.(60﹣x)(40﹣2x)=1750 43.(2023春•涡阳县期中)如图,长方形铁皮的长为10cm,宽为8cm,现在它的四个角上剪去边长为xcm的正方形,做成底面积为24cm2的无盖的长方体盒子,则x的值为()A.2B.7C.2或7D.3或6 44.(2023春•永嘉县校级期中)如图,在高3m,宽4m的长方形墙面上有一块长方形装饰板(图中阴影部分),装饰板的上面和左右两边都留有宽度为x (m)的空白墙面.若长方形装饰板的面积为4m2,则以下方程正确的是()A.(3﹣x)(4﹣x)=4B.(3﹣x)(4﹣2x)=4C.(3﹣2x)(4﹣x)=4D.(3﹣2x)(4﹣2x)=4 45.(2023•碑林区校级模拟)如图,把一块长AB为40cm的长方形硬纸板的四角剪去四个边长为5cm的小正方形,然后把纸板沿虚线折起,做成一个无盖长方体纸盒.若纸盒的体积是1500cm3,则长方形硬纸板的宽为多少?46.(2022秋•城固县期末)如图,现有一块长11cm,宽7cm的长方形硬纸板,在它的四个角分别剪去一个大小完全相同的小正方形,用剩余的部分(图中阴影部分)做成一个底面积为21cm2的无盖长方体盒子,请求出剪去的小正方形的边长.47.(2023•政和县模拟)为培养学生正确的劳动价值观和良好的劳动品质.某校为此规划出矩形苗圃ABCD.苗圃的一面靠墙(墙最大可用长度为15米)另三边用木栏围成,中间也用垂直于墙的木栏隔开分成面积相等的两个区域,并在如图所示的两处各留1米宽的门(门不用木栏),修建所用木栏总长28米,设矩形ABCD的一边CD长为x米.(1)矩形ABCD的另一边BC长为米(用含x的代数式表示);(2)矩形ABCD的面积能否为80m2,若能,请求出AB的长;若不能,请说明理由.48.(2022秋•从化区期末)某农场要建一个矩形动物场,场地的一边靠墙(墙AB长度不限),另外三边用木栏围成,木栏总长20米,设动物场CD边的长为xm,矩形面积为ym2.(1)矩形面积y=(用含x的代数式表示);(2)当矩形动物场面积为48m2时,求CD边的长.(3)能否围成面积为60m2矩形动物场?说明理由.【题型8 一元二次方程应用-几何动态问题】49.(2022秋•舞钢市期中)如图,矩形ABCD中,AB=21cm,BC=8cm,动点E从A出发,以3cm/s的速度沿AB向B运动,动点F从C出发,以2cm/s 的速度沿着CD向D运动,当点E到达点B时,两个点同时停止.则EF的长为10cm时点E的运动时间是()A.3s B.s C.3s或s D.2.5s50.(2022•晋中期中)如图,在△ABC中,∠ABC=90°,AB=8cm,BC=6cm,动点P,Q分别从点A,B同时开始移动(移动方向如图所示),点P的速度为1cm/s,点Q的速度为2cm/s,点Q移动到C点后停止,点P也随之停止运动,当四边形APQC的面积为9cm2时,则点P运动的时间是()A.3s B.3s或5s C.4s D.5s51.(2022•方城县期末)如图,已知等边三角形ABC的边长为6cm,点P从点A出发,沿A→C→B的方向以2cm/s的速度向终点B运动,同时点Q从点B出发,沿B→A的方向以1cm/s的速度向终点A运动.当点P运动到点B时,两点均停止运动.运动时间记为ts,请解决下列问题:若点P在边AC上,当t为何值时,△APQ为直角三角形?52.(2022秋•江门期末)如图,在△ABC中,∠B=90°,AB=5cm,BC=8cm.点P从点A开始沿AB边向点B以1cm/s的速度移动、同时点Q从点B开始沿BC边向点C以2cm/s的速度移动,当其中一点到达终点时,另外一点也随之停止运动.(1)△PQB的面积能否等于9cm2?请说明理由.(2)几秒后,四边形APQC的面积等于16cm2?请写出过程.53.(2021秋•城关区月考)如图,在△ABC中,∠B=90°,AB=5cm,BC=7cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动.若P,Q两点同时出发,当点Q运动到点C 时,P,Q两点同时停止运动.求:(1)几秒后,PQ的长度等于2cm?(2)△PBQ的面积能否等于7cm2?说明理由.54.(2023春•蚌埠月考)△ABC中,∠B=90°,AB=5cm,BC=6cm,点P 从点A开始沿边AB向终点B以1cm/s的速度移动,与此同时,点Q从点B 开始沿边BC向终点C以2cm/s的速度移动,如果点P、Q分别从点A、B同时出发,当点Q运动到点C时,两点停止运动.设运动时间为t秒.(1)填空:BQ=,PB=(用含t的代数式表示);(2)是否存在t的值,使得△PBQ的面积等于4cm2?若存在,请求出此时t 的值;若不存在,请说明理由.。
专题04光现象-2024年中考物理【热点·重点·难点】专练(江苏专用)(原卷版)

专题04 光现象2023年考点与往年变化不大,考法上更加注重对学生能力的考查,在生活生产实例中运用物理知识解决问题。
如:探究光的反射实验、探究平面镜成像特点实验、作反射光路图、平面镜成像图仍是高频考点,占分比较重;小孔成像、反射、折射、散射、漫反射、不透明物理的颜色也是常考点。
预测今年中考考点不会变化太大,考点还是会延续之前的考点。
考查方式会进一步突出对能力的考查,即用所学知识解决问题,情景设置上更加新颖、贴近生活、加入最近科技信息,考有所依,学有所用。
(建议用时:20分钟)一、单选题1.(2023·江苏镇江·二模)皮影戏是中国民间古老的传统艺术。
表演时,艺人们操纵鲁皮制作的人物剪影,在灯光照射下,屏幕上就会出现活动的影子。
下列现象与皮影戏的光学原理相同是()A.月食的形成B.湖面的倒影C.海市蜃楼D.用放大镜看报纸2.(2023·江苏南通·二模)小明妈妈在回家的路上通过手机APP开启了家中电热水器,其指令信息的传递依靠()A.紫外线B.红外线C.电磁波D.超声波3.(2023·江苏徐州·一模)云龙公园是我市一道亮丽的风景线。
如图所示,1.5m深的荷花池内,一只立于荷尖上的蜻蜓距水面0.6m,蜻蜓在水中的像()A.是一个倒立的像B.是比蜻蜓略小的虚像C.在水面下0.9m深处D.与蜻蜓相距1.2m4.(2023·江苏扬州·模拟预测)如图,夜色中的五亭桥流光溢彩,让游客小明流连忘返。
下列说法正确的是()A.小明看到桥在水中的倒影,是因为光从水中折射入空气,再进入小张的眼睛B.小明取下近视眼镜,看到桥变模糊了,是因为廊桥的像成在了视网膜的后面C.小明拿出携带的放大镜观看远处的桥,发现看到一个倒立桥,这个像是虚像D.小明用手指组成方框“取景”,方框离眼睛越远,“取景”范围越小,是因为光沿直线传播5.(2023·江苏扬州·一模)生活处处皆物理,下列生活实例说法错误的是()A.发光二极管是由半导体材料制作而成B.家里炒菜的锅导热性比较好C.家用测温枪利用红外线测量体温D.人耳可以直接听到响度足够大的次声波6.(2023·江苏扬州·二模)“禾下乘凉梦”是袁隆平先生的中国梦,意思是水稻下面可乘凉,这是因为水稻下面形成了阴影区域,下列现象与阴影的形成原理相同的是()A.湖光倒“影”B.杯弓蛇“影”C.毕业合“影”D.形“影”不离7.(2023·江苏盐城·二模)如图所示,小海同学在“探究光的反射规律”实验时,利用红、绿、蓝三种色光的激光笔进行实验,他将位于同一平面内的白色纸板A、B立在平面镜上。
2023学年浙江七年级数学上学期专题训练专题04一元一次方程单元综合提优(含详解)

A.0.4B.2.5C.-0.4D.-2.5
【答案】B
【详解】
∵P=2y-2,Q=2y+3,且3P-Q=1,
∴3(2y-2)-(2y+3)=1,
化简、整理得:4y-9=1,解得:y=2.5.
故选B.
3.(2021·山东七年级期末)某商店有两个进价不同的计算器都卖了80元,其中一个赢利60%,另一个亏本20%,在这次买卖中,这家商店()
(1)小海从小嘉家开车到高速路口 需要多少时间?
(2)求小海在高速上的行驶速度.
(3)在返回过程中为节省高速路费,小海从 下高速,先送小嘉回家后再返回自己家,发现整个返回过程与整个前往景区过程的时间相同,求小嘉家与小海家之间的距离.
15.(2021·浙江宁波市·七年级期末)为节约用水,宁波市居民生活用水实行按级收费,居民用水价格(含污水处理费)按用水量分为三级,下表是宁波市目前实行的水费收费标准:
(3)十二月份,小江、小北两家用水情况如下:①小江家用水量比小北家少;②两家用水量达到的级别不同;③两家用水量总共 立方米;④水费共 元.请根据以上信息,算一算:小江、小北两家用水量分别是多少立方米?
16.(2021·浙江七年级期末)某市居民生活用电峰谷电价如下表:
高峰时间段用电价格表
低谷时间段用电价格表
D.当b=-1时,方程 无解,,故此选项不正确;
故选:C
【点睛】
本题考查了方程的解的定义,方程的解就是能使方程左右两边相等的未知数的值.
5.(2021·浙江九年级一模)已知 ,则()
A. 2B.
C. D.
【答案】C
【分析】
选择专练04(概念全面辨析40题)-2022年中考化学常考点专题必杀集训(人教版)(原卷版)

2022年中考化学常考点专题必杀集训选择专练04(概念全面辨析)1.推理是学习化学的一种重要方法,下列推理合理的是()A.离子是带电荷的粒子,则带电荷的原子一定是离子B.单质是由同种元素组成的,则含一种元素的物质一定是单质C.中和反应有盐和水生成,则有盐和水生成的反应一定是中和反应D.碱的溶液能使无色酚酞试液变红,所以能使无色酚酞试液变红的一定是碱的溶液2.下列类比和推理正确的是()A.单质中只含有一种元素,所以含有一种元素的物质一定是单质B.由金属离子和酸根离子构成的化合物是盐,所以盐中一定含有金属元素C.点燃氢气之前需要验纯,所以点燃甲烷之前也需要验纯D.有机物是含碳元素的化合物,所以含碳元素的化合物一定是有机物3.逻辑推理是学好化学的重要思维方法,下面是从小明同学学习笔记中摘录出来的一些推理,你认为正确的一句是A.同种元素的原子具有相同质子数,所以具有相同质子数的两种粒子一定是同种元素B.由同种分子构成的物质是纯净物,所以纯净物一定由同种分子构成C.中和反应生成了盐和水,所以能生成盐和水的反应一定是中和反应D.金属活动性强的金属能将较弱的金属从其化合物溶液中置换出来,金属铁能与硫酸铜溶液反应,所以铁的活动性强于铜的活动性4.分析推理是化学学习过程中的常用方法,下列推理中,正确的是()A.物质和氧气发生的反应是氧化反应,所以发生氧化反应一定有氧气参加B.溶液具有均一、稳定的特征,所以均一、稳定的物质一定是溶液C.化合物是含有不同元素的纯净物,所以含不同种元素的纯净物一定是化合物D.分子、原子都是构成物质微粒,所以物质一定都是由分子、原子构成的5.分析推理是化学中常用的思维方法,下列分析推理中正确的是()A.碳酸氢钠溶于水后显碱性,所以它是一种碱B.白醋的pH值小于7,所以它呈酸性C.某物质在20℃时溶解度是30g,所以在20℃时,溶质为30g的该物质的溶液一定是饱和溶液D.氧化物是指氧元素与另一种化学元素组成的化合物,所以含有氧元素的化合物都是氧化物6.比较、推理是化学学习常用的方法,以下是根据一些反应事实推导出的影响化学反应的因素,其中推理不合理的是序号化学反应事实影响反应的因素A 二氧化碳与水反应生成碳酸,但通过光合作用可生成葡萄糖反应条件B 木炭在常温下不与氧气发生反应,而在点燃时与氧气反应反应温度C 铜片在空气中很难燃烧,钠米铜粉在空气中较易燃烧反应物的种类D 双氧水常温下分解缓慢,而加入二氧化锰后就迅速分解催化剂7.运用推理、归纳、类比、对比的方法得出下列结论,其中合理的是A.水沸腾时可冲起壶盖,说明温度升高分子会变大B.水和过氧化氢的组成元素相同,则两者的化学性质相同C.同温下分解氯酸钾,加催化剂的反应速率快,说明催化剂可以改变反应速率D.Na+、Cl﹣的最外层电子数均为8,由此得出离子的最外层电子数均为88.分析推理是化学常用的一种学习方法。
专题04 竖直上抛运动规律及相遇问题(原卷版)-2024年高考物理一轮综合复习
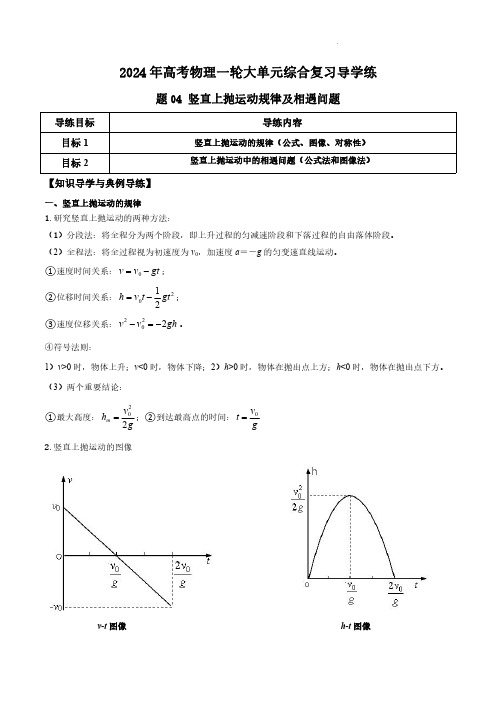
2024年高考物理一轮大单元综合复习导学练题04竖直上抛运动规律及相遇问题导练目标导练内容目标1竖直上抛运动的规律(公式、图像、对称性)目标2竖直上抛运动中的相遇问题(公式法和图像法)【知识导学与典例导练】一、竖直上抛运动的规律1.研究竖直上抛运动的两种方法:(1)分段法:将全程分为两个阶段,即上升过程的匀减速阶段和下落过程的自由落体阶段。
(2)全程法:将全过程视为初速度为v 0,加速度a =-g 的匀变速直线运动。
①速度时间关系:0v v gt =-;②位移时间关系:2012h v t gt =-;③速度位移关系:2202v v gh -=-。
④符号法则:1)v >0时,物体上升;v <0时,物体下降;2)h >0时,物体在抛出点上方;h <0时,物体在抛出点下方。
(3)两个重要结论:①最大高度:202m v h g =;②到达最高点的时间:0vt g=2.竖直上抛运动的图像v-t 图像h-t 图像3.竖直上抛运动的对称性时间对称物体上升到最高点所用时间与物体从最高点落回到原抛出点所用时间相等物体在上升过程中经过某两点之间所用的时间与下降过程中经过该两点之间所用的时间相等速度对称物体上抛时的初速度与物体又落回原抛出点时的速度大小相等、方向相反物体在上升阶段和下降阶段经过同一个位置时的速度大小相等、方向相反能量对称竖直上抛运动物体在上升和下降过程中经过同一位置时的动能、重力势能及机械能分别相等【例1】甲同学在一楼房的地面上以15m/s 的初速度上竖直上抛小球,乙同学站在阳台上正好接住小球,已知接住小球的瞬时速度大小正好为5m/s ,则在这一过程中,下列判断正确的是()A .乙同学接住小球位置的高度为10mB .小球在空中的运动时间一定是2sC .小球的平均速度一定是10m/sD .小球运动的路程可能是12.5m【针对训练1】近年来有一种测g 值的方法叫“对称自由下落法”,将真空长直管沿竖直方向放置,自其中O 点向上抛小球又落至原处的时间为2T ,在小球运动过程中经过比O 点高H 的P 点,小球离开P 点至又回到P 点所用的时间为1T ,测得1T 、2T 和H ,可求得g 等于()A .()2218HT T -B .()2214-HT T C .22218HT T -D .()2214H T T -二、竖直上抛运动中的相遇问题1.竖直上抛运动与自由落体运动相遇问题公式法:(1)同时运动,相遇时间:22011()22gt v t gt H +-=,解得:0H t v =(2)上升、下降过程中相遇中的临界条件:①若在a 球上升时两球相遇,临界条件:0v t g<,即:00H v v g <,解得:②若在a 球下降时两球相遇,临界条件:002v vt g g<<,即0002v H v g v g <<,解得:图像法:左图(在a 球上升时两球相遇);右图(在a球下降时两球相遇)【例2】自高为H 的塔顶自由落下A 物体的同时B 物体自塔底以初速度v 0竖直上抛,且A 、B 两物体在同一直线上运动,重力加速度为g ,下列说法正确的是()A.若0v >B 正在下降途中B.若0v =C0v <,两物体相遇时B 物体正在空中下落D.若0v =【针对训练2】如图所示,长度为0.55m 的圆筒竖直放在水平地面上,在圆筒正上方距其上端1.25m 处有一小球(可视为质点)。
专题04有理数的混合运算(计算题专项训练)(沪科版)(原卷版+解析)

专题04 有理数的混合运算1.(2023秋·河南商丘·七年级统考期末)计算:(1)(−3)2−(12−23+14)×12 (2)−12022−[(−4)2−(1−32)×2]÷(−8)2.(2022秋·七年级单元测试)计算:(1)−12+20−(−2)+(−3)(2)−14+(−112−38+712)×(−24)(3)(−2)3×[−0.75+(−38)]−|−3|2÷(−32)(4)|−(−23)2+(−59)|−(−1)1000−2.45×8+2.55×(−8)3.(2022秋·辽宁抚顺·七年级统考期中)计算:(1)(−49)−(+91)−(−5)+(−9);(2)(14+38−712)÷124;(3)(−1)2021×|−112|−(0.5)÷(−13).(4)−23×(−8)−(−12)3×(−16)+49×(−3)24.(2022秋·四川巴中·七年级校考阶段练习)计算(1)[2−(1−0.5×23)]×[5−(−1)](2)−32+(−212)2+|−2|(3)(−48)÷(−2)3−(−25)×(−4)+(−2)2(4)57×34−(−57)×12+57×(−14)5.(2022秋·河南驻马店·七年级统考期中)计算:(1)(1112−76+34−1324)×(−48);(2)−9+5×|−3|−(−2)2÷4;(3)−18+(−4)2÷14−(1−32)×(13−0.5).6.(2022秋·海南海口·七年级校考期中)计算:(1)−8−(−8)−10+5;(2)2×(−3)2+6÷(−2)×(−13); (3)(34−56+712)×(−24);(4)−52×1(−5)2+|−4|+(−2)÷(−12)3; (5)−23÷|−43|−(−3)2×(−1)2023.7.(2022秋·吉林长春·七年级校考期末)计算:(1)−(3−5)+32×(1−3)(2)(−1)2023+|−22+4|−(12−14+18)×(−24)8.(2022秋·河南安阳·七年级统考期中)计算:(1)−22×|−5|−6÷(12−13)×56; (2)(−56+13−34)×(−24);(3)(−1)2023×[−24×(−34)2−1];(4)24−12022×(−2)3−5.5÷415×(−815).9.(2022秋·全国·七年级专题练习)计算:(1)−32÷[−23×(−32)2−(−2)3]; (2)100÷52−14−(12−23+14)×12.10.(2022秋·辽宁沈阳·七年级统考期中)计算(1)(−3)2−(112)3×39−6÷23(2)−12×(−5)÷[(−3)2+2×(−5)](3)(−2)3−2×(−3)−(−5)+|2−5|−(−1)2020(4)−32+214×(−23)+4−22×(−13)11.(2022秋·湖北恩施·七年级校考阶段练习)计算.(1)−1100−(1−0.5)×13×|3−(−3)2|; (2)25÷(−225)−821×(−134)−0.5÷2×12.12.(2022秋·河南鹤壁·七年级统考期末)计算:(1)(−1)2021×|112|−(0.5)÷(−13); (2)−32÷34×(−12)−[1+(−2)3]−|−6|.13.(2023秋·河南南阳·七年级校考期末)计算下列各题:(1)(79−56+718)×2×32−74÷(−1.75)(2)−14−(1−0×4)÷13×[(−2)2−6]−614.(2022秋·江苏苏州·七年级校考期中)计算(1)−43÷(−2)2×15 (2)−1.53×0.75+0.53×34−2.6×0.75(3)−(1−0.5)÷13×[2+(−4)2] (4)(−5)3×(−35)+32÷(−22)×(−114) (5)136÷(−34−59+712)(6)−12−[317+(−12)÷6]2×(−34)315.(2022秋·安徽蚌埠·七年级校考期中)计算:(1)−22−(1−23)÷213×[6+(−3)3] (2)(14−15−56)÷(−160)−22+3×(−1)202216.(2022秋·重庆长寿·七年级统考期末)计算:(1)−22−|−7|+3−2×(−12);(2)−14+[4−(38+16−34)×24]÷5.17.(2022秋·吉林长春·七年级校考阶段练习)计算:(1)(−2)2−(13+14+16)×12(2)−14−16×[2−(−3)2]÷(−7)18.(2023秋·重庆垫江·七年级统考期末)计算下列各题(1)2×(−3)3−4×(−3)+15;(2)(−34+59−712)÷136−(−3−1)2×(−12+178).19.(2023秋·山东淄博·六年级统考期末)计算(1)−22−8÷(−12)×2(2)[(−35)−53]÷[(−3)2+|2−3|]20.(2023秋·山东枣庄·七年级统考期末)计算:(1)−23−[−3+(−3)2÷(−16)](2)−|−52|−(−3)3−(23−14−38)×2421.(2023春·黑龙江哈尔滨·六年级哈尔滨市第四十七中学校考阶段练习)计算下列各题(1)−0.5+(−15)−(−17)−|−12|(2)(13−37+56)÷(−142)(3)25×34+(−25)×12−25×(−14) (4)−12−(1−12)÷3×[2−(−3)2]22.(2022秋·河南焦作·七年级焦作市实验中学校考期中)计算:(1)−0.5−(−314)+2.75−(+712)(2)12÷(13+14−16)(3)−32×[−32×(−23)2−|−2|3](4)−14−(1−0.5)×13×[2−(−3)2]23.(2022秋·河南南阳·七年级期中)计算.(1)[(−1)2022−(1−0.5×13)]×[2−(−3)3]; (2)−32−13[(−5)2×(−35)−240÷(−4)×14].24.(2022秋·七年级课时练习)计算:(1)(−323)−(−2.4)+(−13)−(+425)(2)[−23+(−35)]+[1+(−23)×(−35)](3)(−1)4−{35−[(13)2+0.4×(−112)÷(−2)2]} (4)[(223+334)(223−334)+(223−334)2]÷(334−223)专题04 有理数的混合运算1.(2023秋·河南商丘·七年级统考期末)计算:(1)(−3)2−(12−23+14)×12 (2)−12022−[(−4)2−(1−32)×2]÷(−8)【思路点拨】(1)先计算平方运算,用乘法分配律计算出积,再求差;(2)先算乘方,再算括号里的,然后求商,最后算加法;【解题过程】(1)解:原式=9−(12×12−23×12+14×12)=9−(6−8+3)=8; (2)原式=−1−[16−(−8)×2]÷(−8)=−1−32÷(−8)=−1+4=3.2.(2022秋·七年级单元测试)计算:(1)−12+20−(−2)+(−3)(2)−14+(−112−38+712)×(−24)(3)(−2)3×[−0.75+(−38)]−|−3|2÷(−32)(4)|−(−23)2+(−59)|−(−1)1000−2.45×8+2.55×(−8) 【思路点拨】(1)去括号,进行有理数加减运算,即可求解;(2)用乘方及乘法分配律展开后,即可求解;(3)分别进行乘方,去绝对值运算后,再按有理数混合步骤进行运算即可;(4)分别进行乘方,去绝对值运算及乘法分配律的逆用运算后,再按有理数混合步骤进行运算即可.【解题过程】(1)解:原式=−12+20+2−3=7.(2)解:原式=−1+(−32)×(−24)+(−38)×(−24)+712×(−24)=−1+36+9−14=30.(3)解:原式=(−8)×(−34−38)−9÷(−9)=(−8)×(−98)+1 =10.(4)解:原式=|−49−59|−1−(2.45+2.55)×8=1−1−5×8=−40.3.(2022秋·辽宁抚顺·七年级统考期中)计算:(1)(−49)−(+91)−(−5)+(−9);(2)(14+38−712)÷124; (3)(−1)2021×|−112|−(0.5)÷(−13). (4)−23×(−8)−(−12)3×(−16)+49×(−3)2 【思路点拨】(1)统一成省略加号和括号的和的形式,再结合有理数加法法则解答;(2)先转化为乘法,再利用乘法分配律解答;(3)先乘方,再乘除,最后计算加减;(4)先乘方,再乘除,最后计算加减、注意负号的作用;【解题过程】(1)(−49)−(+91)−(−5)+(−9)=-49+5-91-9=-44-100=-144(2)(14+38−712)÷124 =14×24+38×24−712×24=6+9-14=1(3)(−1)2021×|−112|−(0.5)÷(−13)=−1×32−12×(−3)=0(4)−23×(−8)−(−12)3×(−16)+49×(−3)2 =64+18×(-16)+4=64-2+4=66.4.(2022秋·四川巴中·七年级校考阶段练习)计算(1)[2−(1−0.5×23)]×[5−(−1)] (2)−32+(−212)2+|−2| (3)(−48)÷(−2)3−(−25)×(−4)+(−2)2(4)57×34−(−57)×12+57×(−14) 【思路点拨】(1)根据有理数四则混合运算法则计算即可.(2)先算乘方,后算加减.(3)先算乘方,后算乘除,最后算加减.(4)根据有理数四则混合运算法则计算即可.【解题过程】(1)[2−(1−0.5×23)]×[5−(−1)] =(2−1+13)×6 =43×6 =8(2)−32+(−212)2+|−2|=−9+254+2 =−34(3)(−48)÷(−2)3−(−25)×(−4)+(−2)2=−48÷(−8)−100+4=6−100+4=−90(4)57×34−(−57)×12+57×(−14)=57×34+57×12−57×14=57×34+57×12−57×14=57×34−57×14+57×12=57×12+57×12=57.5.(2022秋·河南驻马店·七年级统考期中)计算:(1)(1112−76+34−1324)×(−48);(2)−9+5×|−3|−(−2)2÷4;(3)−18+(−4)2÷14−(1−32)×(13−0.5).【思路点拨】(1)根据乘法分配律计算即可;(2)先算乘方,再算乘除法,最后算加减即可;(3)先算乘方和括号内的式子,然后再计算括号外的乘除法,最后算加减法即可.【解题过程】(1)(1112−76+34−1324)×(−48)=1112×(−48)−76×(−48)+34×(−48)−1324×(−48)=−44+56+(−36)+26=2(2)−9+5×|−3|−(−2)2÷4=−9+5×3−4÷4=−9+15−1=5(3)−18+(−4)2÷14−(1−32)×(13−0.5)=−1+64−(−8)×(−1 6 )=−1+64−4 3=612 36.(2022秋·海南海口·七年级校考期中)计算:(1)−8−(−8)−10+5;(2)2×(−3)2+6÷(−2)×(−13);(3)(34−56+712)×(−24);(4)−52×1(−5)2+|−4|+(−2)÷(−12)3;(5)−23÷|−43|−(−3)2×(−1)2023.【解题过程】(1)解:原式=−8+8−10+5=0−10+5 =−5;(2)解:原式=2×9+(−3)×(−13)=18+1 =19;(3)解:原式=34×(−24)−56×(−24)+712×(−24)=−18+20−14=−12;(4)解:原式=−25×125+4+(−2)÷(−18)=−1+4+(−2)×(−8)=−1+4+16=19;(5)解:原式=−8÷43−9×(−1)=−8×34+9=−6+9=3.7.(2022秋·吉林长春·七年级校考期末)计算: (1)−(3−5)+32×(1−3)(2)(−1)2023+|−22+4|−(12−14+18)×(−24) 【思路点拨】(1)先计算平方,再计算括号里面的,再做乘除,最后做加减即可;(2)先计算乘方和平方,再计算绝对值和括号里面的,再做乘法,最后做加减即可. 【解题过程】(1)解:−(3−5)+32×(1−3) =−(3−5)+9×(1−3) =−(−2)+9×(−2) =2−18 =−16;(2)解:(−1)2023+|−22+4|−(12−14+18)×(−24)=−1+|−4+4|−(12−14+18)×(−24) =−1+0−(48−28+18)×(−24)=−1−38×(−24) =−1+9 =8.8.(2022秋·河南安阳·七年级统考期中)计算: (1)−22×|−5|−6÷(12−13)×56; (2)(−56+13−34)×(−24); (3)(−1)2023×[−24×(−34)2−1]; (4)24−12022×(−2)3−5.5÷415×(−815). 【思路点拨】(1)根据有理数的乘方以及四则运算求解即可; (2)根据有理数乘法分配律求解即可; (3)根据有理数的乘方以及四则运算求解即可; (4)根据有理数的乘方以及四则运算求解即可. 【解题过程】(1)解:−22×|−5|−6÷(12−13)×56=−4×5−6×6×56=−20−30=−50;(2)解:(−56+13−34)×(−24)=−56×(−24)+13×(−24)−34×(−24)=20−8+18=30; (3)解:(−1)2023×[−24×(−34)2−1]=−1×(−16×916−1) =−1×(−10)=10;(4)解:24−12022×(−2)3−5.5÷415×(−815)=24−1×(−8)−5.5×154×(−815) =24−(−8)−(−11)=24+8+11=43.9.(2022秋·全国·七年级专题练习)计算: (1)−32÷[−23×(−32)2−(−2)3]; (2)100÷52−14−(12−23+14)×12. 【思路点拨】(1)原式先算中括号中的乘方,乘法,以及减法,再算括号外的除法即可得到结果; (2)原式先算乘方,再算乘除,最后算加减即可得到结果. 【解题过程】(1)原式=−32÷(−8×94+8)=−32÷(−18+8)=−32×(−110)=320;(2)原式=100÷25−1−(12×12−23×12+14×12)=4−1−(6−8+3)=4−1−1=2.10.(2022秋·辽宁沈阳·七年级统考期中)计算 (1)(−3)2−(112)3×39−6÷23 (2)−12×(−5)÷[(−3)2+2×(−5)](3)(−2)3−2×(−3)−(−5)+|2−5|−(−1)2020 (4)−32+214×(−23)+4−22×(−13)【解题过程】(1)解:(−3)2−(112)3×39−6÷23=9−278×39−6×32=9−98−9=−98,(2)−12×(−5)÷[(−3)2+2×(−5)] =−1×(−5)÷(9−10) =5÷(−1) =−5;(3)(−2)3−2×(−3)−(−5)+|2−5|−(−1)2020 =−8+6+5+3−1=5;(4)−32+214×(−23)+4−22×(−13)=−9+94×(−23)+4−4×(−13)=−9−32+4+43=−5−16=−516.11.(2022秋·湖北恩施·七年级校考阶段练习)计算.(1)−1100−(1−0.5)×13×|3−(−3)2|;(2)25÷(−225)−821×(−134)−0.5÷2×12.【思路点拨】(1)先计算乘方和绝对值,再计算乘法,最后计算加减法,有括号先计算括号即可;(2)先计算乘除,再计算加减,有括号先计算括号即可.【解题过程】(1)解:原式=−1−12×13×|3−9|=−1−16×|−6|=−1−16×6=−1−1=−2;(2)解:原式=25×(−512)−821×(−74)−12×12×12=−16+23−18=−424+1624−324=38.12.(2022秋·河南鹤壁·七年级统考期末)计算: (1)(−1)2021×|112|−(0.5)÷(−13);(2)−32÷34×(−12)−[1+(−2)3]−|−6|.【思路点拨】(1)先计算乘方、绝对值、将除法转化为乘法,再计算乘法,最后计算加法即可;(2)先计算乘方、将除法转化为乘法、计算括号内的运算,再计算乘法,最后计算加减即可. 【解题过程】(1)原式=−1×32−12×(−3)=−32+32 =0;(2)原式=−9×43×(−12)−(1−8)−6 =6−(−7)−6 =6+7−6 =7.13.(2023秋·河南南阳·七年级校考期末)计算下列各题: (1)(79−56+718)×2×32−74÷(−1.75) (2)−14−(1−0×4)÷13×[(−2)2−6]−6【思路点拨】(1)先计算乘方,并将除法部分的小数与分数进行形式的统一,再利用乘法分配律以及除法法则计算即可; (2)先计算乘方和括号,再利用有理数的运算法则计算即可. 【解题过程】(1)原式=(79×18−56×18+718×18)−1.75÷(−1.75)=14−15+7+1=7;(2)原式=−1−1×3×(4−6)−6=−1−3×(−2)−6=−1+6−6=−1.14.(2022秋·江苏苏州·七年级校考期中)计算 (1)−43÷(−2)2×15(2)−1.53×0.75+0.53×34−2.6×0.75(3)−(1−0.5)÷13×[2+(−4)2] (4)(−5)3×(−35)+32÷(−22)×(−114) (5)136÷(−34−59+712)(6)−12−[317+(−12)÷6]2×(−34)3【解题过程】(1)解:−43÷(−2)2×15=−64÷4×15=−16×15=−165;(2)解:−1.53×0.75+0.53×34−2.6×0.75=−1.53×34+0.53×34−2.6×34=34×(−1.53+0.53−2.6) =34×(−3.6) =−2.7;(3)解:−(1−0.5)÷13×[2+(−4)2]=−12×3×(2+16)=−12×3×18=−27;(4)解:(−5)3×(−35)+32÷(−22)×(−114)=125×35+32÷4×54=75+8×54=75+10=85;(5)解:136÷(−34−59+712)=136÷(−2736−2036+2136) =136÷(−2636) =−136×3626=−126;(6)解:−12−[317+(−12)÷6]2×(−34)3=−1−(227−2)2×(−2764)=−1−(87)2×(−2764)=−1+6449×2764=−1+2749=−2249.15.(2022秋·安徽蚌埠·七年级校考期中)计算: (1)−22−(1−23)÷213×[6+(−3)3](2)(14−15−56)÷(−160)−22+3×(−1)2022 【思路点拨】(1)(2)按照先计算乘方,再计算乘除法,最后计算加减,有括号先计算括号的运算顺序求解即可. 【解题过程】(1)解:原式=−4−13×37×(6−27)=−4−17×(−21)=−4−(−3)=−4+3 =−1;(2)解:原式=(14−15−56)×(−60)−4+3×1=14×(−60)−15×(−60)−56×(−60)−4+3=−15+12+50−4+3=46.16.(2022秋·重庆长寿·七年级统考期末)计算:(1)−22−|−7|+3−2×(−12);(2)−14+[4−(38+16−34)×24]÷5.【思路点拨】按照先计算乘方,再计算乘除法,最后计算加减法,有括号先计算括号的运算顺序求解即可.【解题过程】(1)解:原式=−4−7+3−(−1)=−4−7+3+1=−7.(2)解:原式=−1+(4−38×24−16×24+34×24)÷5=−1+(4−9−4+18)÷5 =−1+9÷5=−1+9 5=45.17.(2022秋·吉林长春·七年级校考阶段练习)计算:(1)(−2)2−(13+14+16)×12(2)−14−16×[2−(−3)2]÷(−7)【思路点拨】(1)按照先计算乘方,再计算乘法,最后计算加减法的运算顺序求解即可;(2)按照先计算乘方,再计算乘除法,最后计算加减法,有括号先计算括号的运算顺序求解即可.【解题过程】(1)解:原式=4−13×12−14×12−16×12=4−4−3−2=−5;(2)解:原式=−1−16×(2−9)÷(−7)=−1−16×(−7)×(−17)=−1−16×1=−1−1 6=−116.18.(2023秋·重庆垫江·七年级统考期末)计算下列各题(1)2×(−3)3−4×(−3)+15;(2)(−34+59−712)÷136−(−3−1)2×(−12+178).【解题过程】(1)解:2×(−3)3−4×(−3)+15=2×(−27)−4×(−3)+15=−54+12+15=−27(2)解:(−34+59−712)÷136−(−3−1)2×(−12+178)=(−34+59−712)×36−(−4)2×(−1+178)=−27+20−21−16×78=−27+20−21−14=−4219.(2023秋·山东淄博·六年级统考期末)计算(1)−22−8÷(−12)×2(2)[(−35)−53]÷[(−3)2+|2−3|] 【思路点拨】按照先计算乘方,再计算乘除法,最后计算加减法,有括号先计算括号的运算顺序求解即可.【解题过程】(1)解:原式=−4−8×(−2)×2=−4−(−16)×2=−4−(−32)=−4+32=28;(2)解:原式=(−35−53)÷(9+|−1|)=(−35−53)÷(9+1) =(−915−2515)÷10 =−3415×110=−1775 20.(2023秋·山东枣庄·七年级统考期末)计算:(1)−23−[−3+(−3)2÷(−16)](2)−|−52|−(−3)3−(23−14−38)×24【思路点拨】 (1)按照有理混合运算的运算顺序进行运算,即可求得结果;(2)按照有理混合运算的运算顺序及运算律进行运算,即可求得结果.【解题过程】(1)解:−23−[−3+(−3)2÷(−16)]=−8−[−3+9×(−6)]=−8+57=49(2)解:−|−52|−(−3)3−(23−14−38)×24=−25−(−27)−(23×24−14×24−38×24) =−25+27−(16−6−9)=2−1=121.(2023春·黑龙江哈尔滨·六年级哈尔滨市第四十七中学校考阶段练习)计算下列各题(1)−0.5+(−15)−(−17)−|−12|(2)(13−37+56)÷(−142)(3)25×34+(−25)×12−25×(−14) (4)−12−(1−12)÷3×[2−(−3)2] 【思路点拨】(1)先对数进行化简,后根据法则计算.(2)化除法我乘法,后根据分配律计算即可.(3)逆向运用分配律计算即可.(4)按照混合运算的顺序依次计算即可.【解题过程】(1)−0.5+(−15)−(−17)−|−12|=−0.5−15+17−12=−0.5−10+(−5+17−12)=−10.5+0=−10.5.(2)(13−37+56)÷(−142) =(13−37+56)×(−42) =−14+18−35=−31.(3)25×34+(−25)×12−25×(−14)=25×[34−12+14]=25×[1−12]=252. (4)−12−(1−12)÷3×[2−(−3)2] =−1−12×13×[2−9] =−1+76=16.22.(2022秋·河南焦作·七年级焦作市实验中学校考期中)计算:(1)−0.5−(−314)+2.75−(+712)(2)12÷(13+14−16)(3)−32×[−32×(−23)2−|−2|3](4)−14−(1−0.5)×13×[2−(−3)2]【思路点拨】(1)根据有理数加减计算法则求解即可;(2)根据有理数四则混合计算法则求解即可;(3)(4)按照先计算乘方,再计算乘除法,最后计算加减法,有括号先计算括号的运算顺序求解即可.【解题过程】(1)解:原式=(−0.5−712)+(314+2.75) =−8+6=−2;(2)解:原式=12÷(412+312−212)=12÷512=1445;(3)解:原式=−32×(−9×49−8)=−32×(−4−8) =−32×(−12) =18;(4)解:原式=−1−12×13×(2−9) =−1−16×(−7) =−1+76=16.23.(2022秋·河南南阳·七年级期中)计算.(1)[(−1)2022−(1−0.5×13)]×[2−(−3)3];(2)−32−13[(−5)2×(−35)−240÷(−4)×14].【思路点拨】(1)先算括号内的运算和乘方运算,再算乘除;(2)先算括号内的和乘方运算,再算乘除,最后算加减.【解题过程】(1)解:原式=[1−(1−16)]×(2+27) =(1−56)×29 =16×29 =296(2)原式=−9−13×[25×(−35)−(−60)×14]=−9−13×(−15+15) =−9−13×0 =−9−0=−924.(2022秋·七年级课时练习)计算:(1)(−323)−(−2.4)+(−13)−(+425)(2)[−23+(−35)]+[1+(−23)×(−35)](3)(−1)4−{35−[(13)2+0.4×(−112)÷(−2)2]}(4)[(223+334)(223−334)+(223−334)2]÷(334−223)【思路点拨】(1)先算同分母分数,再计算加减法;(2)先算乘法,再去括号,再算同分母分数,再计算加减法;(3)先算乘方,再算乘除,最后算加减;如果有括号,要先做括号内的运算;(4)根据乘法分配律简便计算.【解题过程】(1)解:(−323)−(−2.4)+(−13)−(+425) 原式=(−323)+2.4−13−4.4 =(−323−13)+(2.4−4.4)=−4−2=−6(2)解:[−23+(−35)]+[1+(−23)×(−35)] 原式=−23−35+(1+25) =−23−35+1+25 =(−23+1)+(−35+25)=13−15 =215(3)解:(−1)4−{35−[(13)2+0.4×(−112)÷(−2)2]}原式=1−{35−[19+25×(−32)÷4]}=1−[35−(19−320)]=1−(35−19+320)=1−[(35+320)−19]=1−(34−19)=1−34+19=14+19=1336(4)解:[(223+334)(223−334)+(223−334)2]÷(334−223)原式=(223+334+223−334)(223−334)÷(334−223)=513×(223−334)÷(334−223)=513×(−1)=−513.。
专题04 离子反应(高考押题)(原卷版)

高考押题专练1.下列离子或分子能够在指定的分散系中大量共存的是( )A .与铝反应生成大量氢气的溶液中:Mg 2+、K +、HCO -3、NO -3 B .0.1 mol/L 的NaNO 3溶液中:K +、I -、Cl -、SO 2-4 C .铁与稀硫酸反应后的溶液中:[Fe(CN)6]3-、NH +4、Cl -、NO -3 D .空气中:SO 2、NO 、N 2、NH 32.常温下,下列各组离子一定能在指定溶液中大量共存的是( )A .pH =1的溶液:Ag +、Al 3+、Cl -、SO 2-4 B .能使酚酞试液变红的溶液:Na +、K +、HCO -3、S 2-C.c (OH -)c (H +)=10-12的溶液:NH +4、Cu 2+、NO -3、Cl - D .水电离产生的c (OH -)=10-12mol/L 的溶液:K +、Fe 2+、SO 2-4、NO -3 3.常温下,下列各组离子在指定溶液中一定能大量共存的是( )A .0.1 mol·L -1NaOH 溶液:K +、Na +、SO 2-4、CO 2-3 B .0.1 mol·L -1Na 2CO 3溶液:K +、Ba 2+、NO -3、Cl -C .0.1 mol·L -1FeCl 3溶液:K +、NH +4、I -、SCN -D .c (H +)/c (OH -)=1×1014的溶液:Ca 2+、Na +、ClO -、NO -3 4.常温下,下列各组离子在指定溶液中可能大量共存的是( )A .滴入甲基橙显红色的溶液中:Na +、NO -3、I -、SO 2-4 B .水电离出的c (H +)=10-12 mol/L 的溶液中:K +、AlO -2、CH 3COO -、SiO 2-3 C .c (H +)/c (OH -)=1012的水溶液中:K +、ClO -、SO 2-4、S 2O 2-3D .加入SCN -呈红色的溶液中:OH -、K +、NO -3、Cl -5.能大量共存于同一溶液中,且当加入另一种强电解质使水电离出的c (H +)=1×10-13mol/L 时又一定能发生反应的离子组是( )①Na +、Ba 2+、Cl -、HCO -3 ②K +、NH +4、CH 3COO -、SO 2-4 ③Ca 2+、Cu 2+、NO -3、SO 2-3 ④Fe 3+、Na +、SCN -、Cl - ⑤Al 3+、Na +、HCO -3、NO -3 ⑥Fe 2+、Na +、NO -3、I - ⑦Ag +、NH +4、OH -、NO -3 ⑧Na +、K +、CH 3COO -、NO -3A .①②⑥B .②③⑥C .①④⑧D .③⑤⑦6.下列离子方程式或电离方程式正确的是( )A.NaHSO3溶液呈酸性:NaHSO3=Na++H++SO2-3B.向Na2SiO3溶液中通入少量CO2:SiO2-3+CO2+H2O=H2SiO3↓+CO2-3C.将一小块钠投入稀醋酸中:2Na+2H+=2Na+H2D.在Na2S2O3溶液中滴加稀硝酸:2H++S2O2-3=S+SO2+H2O7.能正确表示下列反应的离子方程式是()A.Fe2O3溶于过量氢碘酸溶液中:Fe2O3+6H++2I-=2Fe2++I2+3H2OB.0.1 mol/L NH4Al(SO4)2溶液与0.2 mol/L Ba(OH)2溶液等体积混合:Al3++2SO2-4+2Ba2++4OH-=2BaSO4+AlO-2+2H2OC.用浓盐酸酸化的KMnO4溶液与H2O2反应,证明H2O2具有还原性:2MnO-4+6H++5H2O2=2Mn2++5O2↑+8H2OD.向次氯酸钠溶液中通入足量SO2气体:ClO-+SO2+H2O===HClO+HSO-38.下列各组物质或物质间反应可能包括多步反应,其总的离子方程式正确的是()A.向NaClO溶液中通入过量SO2:ClO-+SO2+H2O===HClO+HSO-3B.Na 2S投入水中:S2-+2H2O H2S+2OH-C.向含1 mol AlCl3溶液中投入4 mol Na:Al3++4Na+2H2O===AlO-2+4Na++2H2↑D.向明矾溶液中滴加Ba(OH)2溶液,恰好使SO2-4沉淀完全:2Al3++3SO2-4+3Ba2++6OH-===Al(OH)3↓+3BaSO4↓9.下列选项中,离子方程式书写正确的是()A.向Fe(NO3)2和KI混合溶液中加入少量稀盐酸:3Fe2++4H++NO-3===3Fe3++2H2O+NO↑B.泡沫灭火器的灭火原理:2Al3++3CO2-3+3H2O2Al(OH)3↓+3CO2↑C.向硝酸银溶液中加入足量的氨水:Ag++2NH3·H2OAg(NH3)+2+2H2OD.用足量的氨水处理硫酸工业的尾气:SO2+NH3·H2O===NH+4+HSO-310.下列离子方程式正确的是()A.金属钠与水反应:Na+H2O=Na++H2B.氯化铵溶液显酸性的原因:NH+4+H2O=NH3·H2O+H+C.AlCl3溶液中加入足量氨水:Al3++4NH3·H2O=AlO-2+4NH+4+2H2OD.氯化铁溶液中滴加少量的硫化氢溶液:2Fe3++H2S=2Fe2++S↓+2H+11.某固体混合物,可能含有FeCl2、NaNO2、Ba(OH)2、AlCl3、Na2SO3中的若干种,取适量该混合物加入适量水充分搅拌,得到白色沉淀A与无色溶液B。
专练04 完形填空二 备战2024年中考英语之题型专项练(通用版)(原卷版)

专练04 完形填空二备战2024年中考英语之题型专项练(通用版)一、完形填空阅读下面短文,理解其大意,然后从各题所给的A、B、C、D四个选项中选出最佳选项。
There is nothing more wonderful than the smell of the Adirondack air! Every summer, my father would plan a 1 to one of those wonderful lakes which are among the forests of the Adirondack Mountains.One trip that I will never 2 was a visit to a lake at the foot of the mountains. After arriving at the lake, we emptied the car full of 3 things, carrying them through a wooded path to the picnic place. Then my dad, my sister and I 4 ran into the water. Dad let us dive (跳水) from his knee, throwing 5 up in the air and turning us over like thick pancakes on a grill (烤架). This amazing game went on and on as we 6 “more, more”.When we were finally 7 of our games, my dad stopped to watch my sister. She loved artistic swimming and started 8 skills that her team used in competition. My father paid all his attention to her. I was 9 that no one watched or played with me. I decided to swim by myself in deeper water. The waves were getting 10 , but I didn’t care. I just wanted to do what my 11 could do so that I could catch dad’s attention.As I tried to dive, a huge wave hit me. I tried to stand up but 12 . I thought I was dying.Suddenly, I felt a strong catch on my arm. It was my dad! He hugged me tightly and carried me back to a place where I could 13 . He gave me a warm hug and a big smile 14 he knew I was all right. He was watching me all the time! He had never taken his eye 15 me. He had protected me!Being told by someone that you are loved is great, but experiencing that love is even better.1.A.trip B.party C.lesson D.meeting2.A.mind B.finish C.forget D.enjoy3.A.sports B.farm C.school D.picnic4.A.quietly B.suddenly C.seriously D.quickly5.A.them B.us C.it D.her6.A.shouted out B.worried about C.gave up D.fell down7.A.sure B.tired C.proud D.afraid8.A.playing B.choosing C.comparing D.practicing9.A.sad B.relaxed C.excited D.scared10.A.smaller B.quieter C.stronger D.smoother11.A.father B.sister C.mother D.brother12.A.stayed B.failed C.stopped D.moved13.A.stand B.swim C.walk D.push14.A.if B.before C.because D.although15.A.on B.from C.off D.into阅读下面的短文,掌握其大意,然后从短文后各题所给的A、B、C、D四个选项中,选择最佳选项。
专题04分式单元综合提优专练(原卷版)(人教版)

专题04分式单元综合提优专练(原卷版)学校:___________姓名:___________班级:___________考号:___________一、单选题1.(2021·陕西九年级专题练习)方程14233x x x -+=-- 的解是( ) A .0 B .2 C .3 D .无解 2.(2021·河北八年级月考)如果分式||11x x -+的值为0,那么x 的值为( ) A .-1 B .1 C .-1或1 D .1或0 3.(2021·河南)十堰即将跨入高铁时代,钢轨铺设任务也将完成.现还有6000米的钢轨需要铺设,为确保年底通车,如果实际施工时每天比原计划多铺设20米,就能提前15天完成任务.设原计划每天铺设钢轨x 米,则根据题意所列的方程是( ) A .600060001520x x -=+ B .600060001520x x -=+ C .600060002015-=-x x D .600060002015-=-x x4.(2021·全国九年级专题练习)已知关于x 的分式方程213x m x -=-的解是非正数,则m 的取值范围是( )A .3m ≤B .3m <C .3m >-D .3m ≥-5.(2021·浙江七年级专题练习)化简2111x x x ---的结果是( ) A .x+1B .11x +C .x -1D .1x x -二、填空题 6.(2018·南昌市第十九中学八年级期末)(2011贵州安顺,14,4分)某市今年起调整居民用水价格,每立方米水费上涨20%,小方家去年12月份的水费是26元,而今年5月份的水费是50元.已知小方家今年5月份的用水量比去年12月份多8立方米,设去年居民用水价格为x 元/立方米,则所列方程为________________.7.(2021·安徽九年级三模)若关于x 的分式方程2222x m m x x+=--有增根,则m 的值为_______.8.(2021·全国九年级专题练习)甲、乙两辆汽车同时从A 地出发,开往相距200km 的B 地,甲、乙两车的速度之比是4:5,结果乙车比甲车早30分钟到达B 地,则甲车的速度为_____/km h .三、解答题9.(2021·江苏九年级零模)班级组织同学乘大巴车前往“研学旅行”基地开展爱国教育活动,基地离学校有90公里,队伍8:00从学校出发.苏老师因有事情,8:30从学校自驾小车以大巴1.5倍的速度追赶,追上大巴后继续前行,结果比队伍提前15分钟到达基地.问:(1)大巴与小车的平均速度各是多少?(2)苏老师追上大巴的地点到基地的路程有多远?10.(2021·广东九年级专题练习)已知T 229633a a a a a -=+++()(). (1)化简T ;(2)若正方形ABCD 的边长为a ,且它的面积为9,求T 的值.11.(2021·广水市教学研究室八年级期末)为了创建全国卫生城市,某社区要清理一个卫生死角内的垃圾,租用甲、乙两车运送,两车各运12趟可完成,需支付运费4800元.已知甲、乙两车单独运完此堆垃圾,乙车所运趟数是甲车的2倍,且乙车每趟运费比甲车少200元.(1)求甲、乙两车单独运完此堆垃圾各需运多少趟?(2)若单独租用一台车,租用哪台车合算?12.(2021·陕西八年级期末)某商家预测一种应季衬衫能畅销市场,就用13200元购进了一批这种衬衫,面市后果然供不应求.商家又用28800元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但单价贵了10元.(1)该商家购进的第一批衬衫是多少件?(2)若两批衬衫按相同的标价销售,最后剩下50件按八折优惠卖出,如果两批衬衫全部售完后利润率不低于25%(不考虑其它因素),那么每件衬衫的标价至少是多少元? 13.(2021·全国)小华想复习分式方程,由于印刷问题,有一个数“?”看不清楚:1322x x+=--. (1)她把这个数“?”猜成5,请你帮小华解这个分式方程;(2)小华的妈妈说:“我看到标准答案是:方程的增根是2x =,原分式方程无解”,请你求出原分式方程中“?”代表的数是多少?14.(2020·广西八年级期末)老师在黑板上书写了一个代数式的正确计算结果,随后用字母A 代替了原代数式的一部分,如下:22112111x x x A x x x x ⎛⎫-+-÷= ⎪-++-⎝⎭(1)求代数式A ,并将其化简;(2)原代数式的值能等于1-吗?请说明理由.15.(2021·广东九年级专题练习)先化简231(1)244x x x x --÷+++,再将1x =-代入求值. 16.(2021·全国九年级专题练习)某中学开学初在商场购进A 、B 两种品牌的足球,购买A 品牌足球花费了2500元,购买B 品牌足球花费了2000元,且购买A 品牌的足球数量是购买B 品牌足球数量的2倍,已知购买一个B 品牌足球比购买一个A 品牌足球多花30元(1)求购买一个A 品牌、一个B 品牌的足球各需多少元?(2)该中学响应习总书记足球进校园号召,决定两次购进A 、B 两种品牌足球共50个,恰逢商场对两种品牌足球的售价进行调整,A 品牌足球售价比第一次购买时提高了8%,B 品牌足球按第一次购买时售价的9折出售,如果这所中学此次购买A 、B 两种品牌足球的总费用不超过3240元,那么该中学此次最多可购买多少个B 品牌足球? 17.(2021·全国九年级专题练习)已知关于x 的分式方程()()211122mx x x x x +=--++, (1)若方程的增根为x=1,求m 的值(2)若方程有增根,求m 的值(3)若方程无解,求m 的值. 18.(2021·全国八年级课时练习)若a ,b 为实数,且()2221604a b b -+-=+,求3a ﹣b 的值.19.(2021·全国八年级课时练习)若a >0,M =12a a ++,N =23a a ++. (1)当a =3时,计算M 与N 的值;(2)猜想M 与N 的大小关系,并证明你的猜想.20.(2021·全国九年级专题练习)若关于x 的方程221933m x x x +=-+-有增根,则增根是多少?并求方程产生增根时m 的值.。
北师大版四年级数学上册期末典例专练04:角度计算问题“综合版”(原卷版+解析)

2023-2024学年四年级数学上册典型例题系列期末典例专练04:角度计算问题“综合版”一、填空题。
1.已知∠1+∠2=180°,如果∠1=80°,那么∠2=( )。
2.55°的角是( )角,55°的2倍的角是( )角,180°的一半的角是( )角。
3.小星画了一个65度的锐角,如果要把它改成一个平角要增加( )度,如果要改成一个钝角至少要增加( )度。
(结果取整数)4.钟面上2时整时,时针和分针所夹的最小角是( )°;9时,时针和分针所夹的角是一个( )角。
5.( )时整时,时针和分针成平角;( )时整时,时针和分针成直角,9点半时,分针和时针成( )角。
6.从“3”走到“9”,分针旋转了( )°,形成的角是( )角。
从“6”走了一圈又回到“6”,分针旋转了( )°形成的角是( )角。
7.已知∠1+∠2=140°,那么∠2=( )°,∠3=( )。
8.计算下面图形中角的度数。
(已知∠2=25°)那么∠1=( ),∠3=( ),∠4=( )。
9.图中,已知∠1=75°,∠2=( ),∠3=( )。
10.如图是一正方形纸折起来以后的图形,∠2=( )°。
二、解答题。
11.两个正方形相交如图,已知∠1=32°,求∠2、∠3各是多少度。
12.如图,已知∠1=35°,那么∠2、∠3和∠5各是多少度?13.测量下面各角的度数,你发现了什么?∠1=( ),∠2=( ),∠3=( ),∠4=( )。
14.测量下面各角的度数,你发现了什么?∠1=( ),∠2=( ),∠3=( )。
发现:15.已知∠2=60°,请求出∠3、∠4的度数。
16.如下图所示,将一张正方形纸沿AB折叠,如果∠2=40°,那么∠1是多少度?17.如图是把一张长方形纸折起来以后形成的图形,∠1=35°,求∠2的度数。
04含有滑轮组复杂装置的浮力综合计算-【压轴必刷】2022中考物理力学压轴计算题难题专练 (原卷版)

04含有滑轮组复杂装置的浮力综合计算1.如图所示,某考古队用滑轮组将重4.8×103N,体积为100dm3的文物打捞出水,定滑轮重100N.滑轮组上共有三根绳子a,b和c,其中a是悬挂定滑轮,b绕在定滑轮和动滑轮上,c悬挂文物,整个打捞过程始终缓慢匀速提升文物,文物完全浸没在水中时,滑轮组的机械效率为95%(ρ水=1×103kg/m3,g=10N/kg,绳重、滑轮与轴的摩擦以及水的阻力均忽略不计).请解答下列问题:(1)文物浸没在水中时受到的浮力是多大?(2)动滑轮的重力是多大?(3)在整个打捞过程中,a、b、c三根绳中哪根绳承受的拉力最大?该绳至少要承受多大的拉力?2.如图,水平桌面上放有一薄壁柱形容器,容器底面积为0.03m2,容器中装有水,质量为0.25kg、体积为1×10-3m3的正方体木块漂浮在水面上.现将细绳的一端绕过定滑轮后固定在木块下表面,并用竖直向上的拉力F缓慢匀速拉动细绳另一端,使木块从漂浮状态逐渐浸没入水中,木块不接触滑轮.不计摩擦与水的阻力,忽略绳重与体积的影响,g取10N/kg.求:(1)木块漂浮时受到的浮力;(2)若水深为0.3m,则容器底受到的水的压强;(3)拉力F的最大值;(4)木块从漂浮到被细绳拉到完全浸没,容器底部受到水的压强的变化量.3.如图所示,工人用滑轮组缓慢地打捞沉没在水下的重物,打捞过程中当重物全部在水中时,拉力F为160N,滑轮组的机械效率为80%.当重物离开水面后拉力F′为480N,整个装置的摩擦和绳重不计.(ρ水=1.0×103kg/m 3,g 取10N/kg )求:(1)当重物上升到距水面以下2.5米时受到水的压强为多少?(2)动滑轮的重力;(3)物体的重力;(4)重物的密度.4.如图所示,用动滑轮打捞水中的物体A .物体A 的体积是0.1m 3,重2500N ,在卷扬机对绳子拉力F 的作用下,物体A 在水面以下以1m/s 的速度匀速上升.(水对物体A 的阻力不计,g =10N/kg )求:(1)物体A 浸没在水中时所受的浮力.(2)如果物体A 在水面下被匀速竖直向上拉起过程中滑轮组的机械效率是75%,拉力F 的功率多大?5.某提升装置中,杠杆AB 能绕固定点O 在竖起平面内转动,水平地面上的配重乙通过经细绳竖直拉着杠杆B 端.已知:2:5AO OB =,配重乙与地面的接触面积为S 且2200cm S =.当在动滑轮下面挂上重1000N 的物体甲静止时(甲未浸入水中),竖直向下拉绳子自由端的力为1T ,杠杆在水平位置平衡,此时配重乙对地面的压强为1P 且41 3.510Pa P =⨯;如果在动滑轮下挂一个质量为动滑轮质量5倍的物体丙,并把物体丙浸没在水中静止时,如图甲所示,竖直向上拉绳子自由端的力为2T ,杠杆在水平位置平衡.此时配重乙对地面的压强为2P 且42 5.610Pa P =⨯.已知物体丙的质量与体积的关系的图像如图乙所示,如果不计杠杆重、绳重和滑轮轴间摩擦,图中两个滑轮所受重力相同取10N/kg g =.配重乙的体积为23510m -⨯,求配重乙的密度.6.如图所示,图甲是使用滑轮组从水中打捞一正方体物体的简化示意图,在打捞过程中物体始终以0.1m/s的速度匀速竖直上升,物体未露出水面前滑轮组的机械效率为75%,图乙是打捞过程中拉力F随时间t变化的图象.(不计绳重,忽略摩擦和水的阻力,g取10Nkg)求:(1)物体的边长;(2)物体浸没在水中时受到的浮力;(3)物体的重力.7.体重为550N的小宇使用如图甲所示的滑轮组匀速提升底面积为0.01m2的重物A。
【易失分点】专练04:《红岩》(原卷版)

七年级下册【易失分点解读】【易失分点“避雷”】【注意事项】人物形象江姐:江姐是《红岩》中比较丰满的艺术典型。
作为一个坚定的共产主义战士,她视死如归,宁折不屈。
面对敌人惨无人道的酷刑,她忍受百般折磨,对党的秘密守口如瓶。
行将就义,她神态平静,举止从容,梳理头发,整理衣衫,吻别“监狱之花”,始终带着胜利的笑容。
她稳重精细深沉坚强,处处表现出纯洁的党性和对革命事业的无比忠贞,深受同志们的爱戴,是无产阶级真善美的化身。
许云峰:是一个工人出身,长期从事地下党领导工作,有着丰富斗争经验的党的领导人形象。
他足智多谋,立场坚定,具有非凡的胆识和善于应付瞬息万变的局势的才能。
在狱中,他巧妙地引导徐鹏飞作出错误的判断,承担《挺进报》的领导责任,保护了地下党组织。
面对敌人惊心设计的酒宴,随机应变,戳穿了敌人的阴谋,把筵席变成了揭露敌人的讲台,机智地引出特务头子毛人凤出场。
表现出共产党人的无敌力量。
许云峰具有压倒任何敌人而不被敌人压倒的大无畏气概和勇于献身的崇高精神。
在狱中,他与徐鹏飞进行了针锋相对的斗争,他赤手空拳以顽强的毅力挖通了监狱通向狱外的洞口,并把它留给了战友,自己带着必胜的信念从容就义。
成岗:16岁加入中国共产党。
参加地下刊物《挺进报》的编辑、印刷和发行工作,在工作间被捕,关押于渣滓洞、白公馆看守所,在敌人的威逼利诱下坚持自己的气节,在狱中坚持出版《挺进报》。
后被枪杀。
刘思扬:他虽然出身于大地主家庭,但却投身革命,为信仰劳碌奔波。
是知识分子中的楷模。
他有着丰富的内心世界和坚定的革命信仰,至死没有玷污党的荣誉。
小萝卜头:在敌人的监狱里长大的,不知道外面的世界是什么样。
6岁时在黄将军的帮助下学习。
学习非常刻苦,记忆力很强,非常尊敬老师,经常帮助大人做秘密工作。
遇害时不满9岁,但在监狱中关了八年。
甫志高:原为重庆地下党员,后因被捕不堪严刑拷打而叛变,交出了许云峰、江雪琴等人对地下党网络造成了极大的破坏,是贪图享乐,没有革命精神的典型。
专题04 一元二次方程的定义及方程的解压轴题六种模型全攻略(原卷版)

专题04一元二次方程的定义及方程的解压轴题六种模型全攻略【考点导航】目录【典型例题】 (1)【考点一一元二次方程的判别】 (1)【考点二一元二次方程的一般形式、各项系数】 (1)【考点三利用一元二次方程的定义求参数的值】 (2)【考点四已知一元二次方程的解求参数的值】 (2)【考点五已知一元二次方程的解求式子的值】 (2)【考点六一元二次方程的解的估算】 (3)【过关检测】 (4)【典型例题】【考点一一元二次方程的判别】【变式训练】【考点二一元二次方程的一般形式、各项系数】例题:(2023春·湖南长沙·八年级湖南师大附中博才实验中学校考期末)一元二次方程2450x x --=的二次项系数、一次项系数和常数项分别是()A .1,4,5B .0,4-,5-C .1,4-,5D .1,4-,5-【变式训练】1.(2023春·黑龙江大庆·八年级统考期末)关于x 的一元二次方程251x x =-的二次项系数、一次项系数、常数项分别是()A .1,5-,1-B .1-,5-,1-C .1,5-,1D .1,5,12.(2023春·黑龙江大庆·八年级统考阶段练习)将一元二次方程2351x x =-化成一般式后,二次项系数和一次项系数分别为()A .3,5B .3,1C .23x ,5x-D .3,5-【考点三利用一元二次方程的定义求参数的值】【考点四已知一元二次方程的解求参数的值】例题:(2023春·黑龙江哈尔滨·八年级哈尔滨市第六十九中学校校考阶段练习)关于x 的一元二次方程2210x x a ++-=的一个根是0,则a 的值为______.【变式训练】1.(2023秋·湖南株洲·九年级统考期末)已知方程230x kx +-=的一个根是=1x -,则k 值是________.2.(2023春·湖北武汉·八年级统考期末)3x =是一元二次方程220x x m -+=的一个根,则m 的值是__________.【考点五已知一元二次方程的解求式子的值】例题:(2023春·浙江宁波·八年级统考期末)若关于x 的一元二次方程210+-=ax bx 有一个根为2-,则2a b -=______.【变式训练】1.(2023·山东枣庄·统考中考真题)若3x =是关x 的方程26ax bx -=的解,则202362a b -+的值为___________.2.(2023·甘肃平凉·统考二模)若m 是方程22310x x -+=的一个根,则2692023m m -+的值为______.【考点六一元二次方程的解的估算】【变式训练】【过关检测】一、选择题1.(2023春·黑龙江大庆·九年级校考期末)下列方程中是关于x 的一元二次方程的是()A .221x x +B .20ax bx c ++=C .()()121x x -+=D .223250x xy y --=2.(2023·江苏·九年级假期作业)将方程2235x x =-化成一般形式(二次项系数为正)后,它的一次项系数与常数项分别是()A .3,5-B .3-,5-C .3-,5D .3,53.(2023春·安徽合肥·八年级合肥寿春中学校考期末)如果关于x 的一元二次方程210ax bx ++=的一个解是=1x -,则代数式a b -的值为()A .1-B .1C .2-D .24.(2023春·北京门头沟·八年级统考期末)关于x 的方程()21130mm x x +-+-=是一元二次方程,则()A .1m =-B .1m =C .1m =±D .2m =5.(2023春·山东青岛·八年级统考期末)根据下表的对应值,试判断一元二次方程20ax bx c ++=的一个解的取值范围是()x3-1-142ax bx c++0.060.020.03-0.07-A .31x -<<-B .0.030.02x -<<C .11x -<<D .0.070.03x -<<-二、填空题6.(2023春·浙江·八年级专题练习)一元二次方程2213x x +=化为一般形式是.7.(2023·全国·九年级假期作业)写出一个以1-和5为两根且二次项系数为1的一元二次方程:.8.(2023秋·福建泉州·九年级统考期末)如果关于x 的方程230x x k -+=有一个根为1,那么k =.9.(2023春·浙江宁波·八年级统考期末)若a 是方程2530x x -+=的一个根,则代数式21210a a -+的值是.10.(2023春·八年级课时练习)若关于x 的方程||1(1)450k k x x +--+=是一元二次方程,则k =.三、解答题11.(2023·上海·八年级假期作业)下列方程中,哪些是一元二次方程?哪些不是一元二次方程.。
专练04 微观粒子题 (原卷版)-备战2021年中考化学压轴题专练(广东广州专用)

专练04 微观粒子题1.(2021•华师附中一模)化学与生活、生产密切相关。
(1)氯化钠是重要的工业原料。
工业氯化钠中常混有有毒的亚硝酸钠,其中氮元素的化合价为+3,亚硝酸钠的化学式为________。
(2)工业上通过氯气与消石灰反应制备漂白粉。
漂白粉主要成分是氯化钙和次氯酸钙(Ca(ClO)2)。
使用漂白粉时,将它与水混合配成溶液,吸收空气中的二氧化碳,便会产生具有漂白作用的次氯酸(HClO)。
①Ca(ClO)2中氯元素的化合价为________;②写出上述操作中使漂白粉溶液转化为次氯酸的反应的化学方程式________;③次氯酸是一种弱酸,溶于水时部分次氯酸分子会发生解离。
HCl溶于水时能全部解离出离子(如下图所示)。
在下图中画出次氯酸溶液中的微观粒子组成示意图(不用画水分子)。
________2.(2021•广大附中一模)符号和模型是表征和探析微观世界的重要工具。
(1)硫元素可以形成多种硫单质,图所示为“皇冠硫”分子,其构成单质的化学式为______。
(2)图中能反映水在空气中放置发生变化的微观示意图是______(填字母序号)3.(2021•荔湾区一模)氨气(NH3)是极易溶于水的无色气体,其水溶液叫氨水.(1)在充满氨气的试管中,放入用紫色石蕊浸染过的干燥纸条,无明显现象;再向试纸上滴水,现象是____________。
(2)向盛有氯化铁粉末的试管中通入氨气,无明显现象;停止通气,再加入适量水,产生红褐色沉淀,则发生复分解反应的化学方程式是______________________。
(3)画出氨气(NH3)和氨水的微观粒子组成示意图,并进行必要的标注(水分子不用画出______4.(2021•增城区一模)氮化镓(GaN)是支撑5G、人工智能、工业互联网等“新基建”的核心材料,以氮化镓和碳化硅(SiC)为首的第三代半导体及以氧化镓和金刚石为代表的第四代半导体材料,近年来愈发受到关注。
(1)GaN是由Ga3+和_______构成,写出Ga的氧化物化学式_______。
人教版三年级数学上册专题提升第一单元专练篇04:时间计算问题和时间推算问题综合版(原卷版+解析)

人教版2024-2025学年三年级数学上册专题提升第一单元专练篇·04:时间计算问题和时间推算问题综合版1.请看以下钟面所显示的小华上学相关信息,解决数学问题。
(1)小华上学路上用了多长时间?(2)小华明天值日,必须7:00到校,他最晚什么时候在家出发?2.如图是两个小区的停电通知。
(1)哪个小区的停电时间长些?(2)王奶奶9:30买菜回到家,发现家里停电,5分钟后来电了。
王奶奶住在哪个小区?3.下图是彤彤一家假期去青岛旅游的部分时间安排。
(1)他们参观栈桥用了多长时间?(2)他们中午吃饭用了30分钟,在什么时候吃完午餐?4.根据下面的“停电预告”回答问题。
(1)哪个小区的停电时间长?停了多长时间?(2)小欣中午12:00回到家,发现家里停电。
她家住在什么小区,还要等多长时间才能有电?5.张明早上8:40离开家去图书馆,9:10坐上地铁,9:35下地铁后又步行5分钟到达图书馆。
(1)他坐地铁用了多长时间?他从家到图书馆一共用了多长时间?(2)如果按照去的线路,下午4:10从图书馆出发,几时几分能回到家?6.下面有一条停电通知。
停电通知:上午9:00——11:30西城区下午1:30——3:30东城区(1)哪个城区停电时间长?停电多长时间?(2)明明11点回到家时,发现家里停电,你知道明明的家住在哪儿吗?还要多长时间来电?7.(1)上午禁止机动车通行的时间有多长?(2)王叔叔下午5:10开车经过这条路,他违反交通规则了吗?8.以下是三年级4个班到学校展厅参观科技展览的时间安排表。
(1)上午9:15三年()班在参观科技展览,他们班共参观了()分钟。
(2)小华是三年(3)班的学生,她从教室到展厅要走5分钟,再排队“准备”10分钟,她最晚什么时候从教室出发?请通过计算说明理由。
(3)请你根据规律,在上面的安排表中填出三年(4)班参观的时间。
9.认真观察下面的表格后回答问题。
(1)上午第一节课用了多长时间?(2)如果新华小学的一名学生从家到学校需要15分钟,他最晚什么时候从家里出发?(3)你能发现上课时间规律吗?请你填出第四节课的上课时间。
专题04 图形的位似(五大类型)(题型专练)(原卷版)

专题04 图形的位似(五大类型)【题型1位似图形性质】【题型2 位似图形的点坐标】【题型3 判定位似中心】【题型4 位似图形-作图】【题型5 平移、轴对称、旋转和位似综合】【题型1位似图形性质】1.(2023春•乳山市期末)如图,以点O为位似中心,将△OAB放大后得到△OCD,OA=3,AC=5,则=()A.B.C.D.2.(2023•开州区校级模拟)如图,△ABC与△DEF位似,点O是位似中心,且OD=2AD,则S△ABC :S△DEF=()A.3:2B.9:4C.9:1D.4:1 3.(2023•衡南县三模)如图,四边形ABCD与四边形EFGH位似,其位似中心为点O,且,则()A.B.C.D.4.(2023•宿豫区三模)如图,△ABC与△DEF是位似图形,位似中心为O,OA:AD=3:4,S△ABC=9,则△DEF的面积为()A.12B.16C.21D.49 5.(2023•大理州模拟)如图,△ABC与△DEF位似,点O为位似中心,位似比为2:3,若△ABC的面积为4,则△DEF的面积是()A.6B.9C.12D.16 6.(2023春•石景山区期中)如图,四边形ABCD与四边形EFGH是位似图形,点O是位似中心.若,四边形ABCD的面积是100,则四边形EFGH 的面积是()A.4B.16C.36D.7.(2023•汇川区模拟)如图,△ABC和△DEF是位似三角形,点O是位似中心,且AC=9,DF=3,OA=6,则OD=()A.2B.4C.6D.8 8.(2023春•太仓市期末)如图,在平面直角坐标系中,将△OAB以原点O为位似中心放大后得到△OCD,若A(1,0),C(3,0),则△OAB与△OCD 的面积比是()A.1:2B.1:3C.1:4D.1:9 9.(2023•岳麓区校级模拟)如图所示,△ABC与△DEF是位似图形,点O为位似中心.若AD=3OA,△ABC的周长为5,则△DEF的周长为()A.10B.15C.25D.125【题型2 位似图形的点坐标】9.(2022秋•江北区校级期末)如图,在平面直角坐标系中△ABC与△A'B'C'位似,且原点O为位似中心,其位似比1:2,若点B(﹣2,﹣1),则其对应点B'的坐标为()A.(2,4)B.(4,2)C.(2,1)D.(1,2)10.(2023•舟山三模)在平面直角坐标系中,已知点A(﹣4,2),B(﹣6,﹣4),以原点O为位似中心,相似比为,把△ABO缩小,则点A的对应点A′的坐标是()A.(﹣2,1)B.(2,﹣1)C.(﹣8,4)或(8,﹣4)D.(﹣2,1)或(2,﹣1)11.(2023•市南区校级二模)如图,在平面直角坐标系中,等边三角形OAB的顶点O(0,0),B(2,0),已知△OA'B′与△OAB位似,位似中心是原点O,且△OA'B′的面积是△OAB面积的4倍,则点A对应点A′的坐标为()A.B.或C.D.或12.(2023春•岱岳区期末)如图,△OAB和△OCD是以点O为位似中心的位似图形,已知A(﹣4,2),△OAB与△OCD的相似比为2:1,则点C的坐标为()A.(2,﹣1)B.(﹣2,1)C.(1,﹣2)D.(﹣1,2)13.(2023春•肥城市期末)如图,矩形OABC与矩形ODEF是位似图形,点P 是位似中心.若点B的坐标为(2,3),点E的横坐标为﹣1,则点P的坐标为()A.(﹣2,0)B.(0,﹣2)C.D.14.(2023春•长寿区校级期中)如图,线段AB两个端点坐标分别为A(6,9),B(9,3),以原点O为位似中心,在第三象限内将线段AB缩小为原来的后,得到线段CD,则点C的坐标为()A.(﹣2,﹣3)B.(﹣3,﹣2)C.(﹣3,﹣1 )D.(﹣2,﹣1)15.(2023•杜集区校级模拟)如图,在平面直角坐标系中,△A'B'C'与△ABC 位似,位似中心为原点O,已知点A(﹣1,﹣1),C(﹣4,﹣1),A'C'=6,则点C'的坐标为()A.(2,2)B.(4,2)C.(6,2)D.(8,2)【题型3 判定位似中心】16.(2022秋•泉州期末)如图,在8×8网格中,△ABC和△A'B'C'位似,则位似中心为()A.点O B.点P C.点Q D.点R 17.(2023•长安区模拟)图中的两个三角板是位似图形,则位似中心可能是()A.点A B.点B C.点C D.点D 18.(2022秋•青县期末)如图中的两个三角形是位似图形,点M的坐标为(3,2),则它们位似中心的坐标是()A.(0,2)B.(0,3)C.(2,﹣1)D.(2,3 )19.(2023春•烟台期末)如图,点A的坐标为(﹣3,1),点B的坐标为(﹣1,1),点C的坐标为(0,﹣1).(1)求出△ABC的面积;(2)请以点O为位似中心作一个与△ABC位似的△A1B1C1,使得△A1B1C1的面积为18.20.(2022秋•未央区期末)如图,在平面直角坐标系中,△ABO的顶点都在正方形网格顶点上.以原点O为位似中心,相似比为1:2,在y轴的右侧,画出将△ABO放大后得到的△A1B1O.【题型4 位似图形-作图】21.(2023春•福山区期末)已知,△ABC在平面直角坐标系的位置如图所示,点A,B,C的坐标分别为(1,0),(4,﹣1),(3,2).△A1B1C1与△ABC是以点P为位似中心的位似图形.(1)请画出点P的位置,并写出点P的坐标;(2)以点O为位似中心,在y轴左侧画出△ABC的位似图形△A2B2C2,使相似比为1:1,若点M(a,b)为△ABC内一点,则点M在△A2B2C2内的对应点的坐标为.【题型5 平移、轴对称、旋转和位似综合】22.(2023•碑林区校级模拟)如图,在平面直角坐标系中,△AOB的顶点均在网格格点上,且点A、B的坐标分别为A(3,1),B(2,﹣1).(1)在y轴的左侧以原点O为位似中心作△OAB的位似图形△OA1B1(点A、B的对应点分别为A1,B1)使△OA1B1与△OAB的相似比为2:1;(2)在(1)的条件下,计算△OA1B1的面积为.23.(2023•南山区校级一模)在平面直角坐标系内,△ABC的位置如图所示.(1)将△ABC绕点O顺时针旋转90°得到△A1B1C1,作出△A1B1C1.(2)以原点O为位似中心,在第四象限内作出△ABC的位似图形△A2B2C2,且△A2B2C2与△ABC的相似比为2:1.24.(2023春•荣成市期末)如图,在边长为1的小正方形组成的网格中,△ABC 的顶点在格点(网格线的交点)上,以点O为原点建立平面直角坐标系,点B的坐标为(1,0).(1)将△ABC向左平移5个单位长度,得到△A1B1C1,画出△A1B1C1;(2)以点O为位似中心,将△A1B1C1放大到两倍(即新图与原图的相似比为2),得到△A2B2C2,在所给的方格纸中画出△A2B2C2;(3)若点M是AB的中点,经过(1)、(2)两次变换,M的对应点M2的坐标是.25.(2023•碑林区校级模拟)如图,在由边长为1的小正方形组成的网格中,△ABC的三个顶点坐标分别为A(﹣2,﹣2),B(﹣5,﹣4),C(﹣1,﹣5).(1)请在网格中画出△ABC关于x轴对称的△A1B1C1.(2)以点O为位似中心,将△ABC放大为原来的2倍,得到△A2B2C2,请在网格中画出△A2B2C2.(3)①点B1的坐标为;②求△A2B2C2的面积.26.(2022秋•青羊区期中)已知O是坐标原点,A、B的坐标分别为(3,1)、(2,﹣1).(1)画出△OAB绕点O顺时针旋转90°后得到的△OA1B1;(2)在y轴的左侧以O为位似中心作△OAB的位似图形△OA2B2,使新图与原图相似比为2:1;(3)求出△OA2B2的面积.。
专项04 化学观念、科学思维、科学态度-【专项专练】中考化学专项考点培优训练(原卷版)

专项04 化学观念、科学思维、科学态度一、单选题1.构建化学基本观念是学好化学的基础。
下列对化学基本观念的认识,不正确的是A.结构观:金刚石和石墨的物理性质不同,因为它们碳原子的排列方式不同B.分类观:根据组成元素的异同,可将纯净物分为单质和化合物C.变化观:在一定条件下,CO2和O2可以相互转化D.微粒观:所有原子的原子核都是由质子和中子构成2.化学观念可以让我们更全面的认识物质。
以下说法正确的是A.微粒观:氧气和氯化钠都是由分子构成B.能量观:化学反应中不通过燃烧也能获得热量C.结构观:石墨转化成金刚石改变了碳原子的排列方式,是物理变化D.元素观:大麻酚是一种毒品,化学式为C21H26O2,它由3个元素组成3.构建化学基本观念是学好化学的基础,下列对化学基本观念的认识错误的是A.元素观:一氧化碳、二氧化碳都是由碳元素和氧元素组成的B.微粒观:保持水化学性质的最小粒子是水分子C.转化观:氧化汞在一定条件下可生成金属汞D.守恒观:4g氢气和16g氧气反应,应该生成20g水4.下列涉及的化学观点,说法错误的是A.微粒观:保持硫酸铜化学性质的最小微粒是铜离子和硫酸根离子B.结构观:金刚石、石墨、C60的碳原子排列方式不同,决定其性质也不同C.守恒观:镁条在空气中燃烧,所得固体质量增重,遵守质量守恒定律D.转化观:氧气和二氧化碳在一定条件下可以相互转化5.化学观念是核心素养的重要组成部分。
下列有关叙述中,不正确的是A.物质是由元素组成的B.物质的结构决定物质的性质C.物质发生化学变化时会伴随能量变化D.只含有一种元素的物质是纯净物6.构建化学基本观念是学好化学的基础,下列对化学基本观念的认识不正确的是A.元素观:水、过氧化氢都是由氢元素和氧元素组成的B.微粒观:金刚石和石墨都是由碳原子直接构成的单质C.守恒观:1L氢气和1L氧气反应生成2L水D.转化观:在一定条件下,二氧化碳和碳酸可以相互转化7.构建化学基本观念是学好化学的基础。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专练04 实验题一、机械运动、声、光、物态变化、质量和密度1.(2020•衡阳模拟)在同一粗糙水平面固定两个不同斜面,小华同学研究相同的两个小球A、B分别沿不同的斜面运动,用频闪照相机每隔0.1s拍摄了小球滚动时的不同位置,图上数字为闪光时刻编号,位置间距如图所示。
(1)甲图中A球在斜面上运动的速度(选填“增大”“减小”或“不变”)。
(2)乙图中小球B从2位置运动到4位置的这段时间内平均速度v=m/s,小球B沿斜面运动过程中的动能(选填“增加”“减少”或“不变”)。
(3)若两个小球从斜面上运动到斜面底部时与相同的木块碰撞,碰撞之后图(选填“甲”或“乙”)中木块运动距离较大。
2.(2020•济南模拟)图中一枚纽扣的直径是cm;正确测量物体质量时,盘中砝码和游码位置如图所示,则物体的质量为g。
3.(2019秋•莘县期末)“测平均速度”实验:(1)实验中为了方便计时,应使斜面的坡度较(填“大”或“小”)。
(2)在实验前必须熟练使用电子表,如果小车到达金属挡板后还没有停止计时,则会使所测量的平均速度偏(3)为了测量小车运动过程中下半程的平均速度,某同学让小车从斜面中点由静止释放。
测出小车到达斜面底端的时间,从而计算出小车运动过程中下半程的平均速度。
他的做法正确吗?(4)若小车通过上半段和下半段路程的平均速度分别为v1,v2,则两者大小关系为v1v2 4.(2019秋•九龙坡区期末)小明在“测小车的平均速度”的实验中,设计了如图所示的实验装置:小车从带有刻度的斜面顶端由静止滑下,图中的方框内是小车到达A、B、C三处时电子表的时间显示(数字分别表示“时:分:秒”)。
(1)该实验是根据公式进行测量的。
(2)实验中应使斜面坡度较(选填“大”或“小”),目的是(选填“延长”或“缩短”)运动时间,减小测量时间的误差。
(3)请根据图中信息回答:s AC=cm,v BC=m/s。
(4)为了测量小车运动过程中下半程的平均速度,同组的小琦同学让小车从B点由静止释放,测出小车到达C点的时间,从而计算出小车在下半程运动的平均速度,请你判断:小琦的做法是(选填“正确”或“错误”)的。
5.(2019秋•金湖县期末)如图甲所示,是研究气泡的运动规律所用注水玻璃管。
(1)要达到实验目的,还需要的实验工具是(手表/秒表)。
(2)0cm刻度线离玻璃管末端较远的好处是。
(3)判断气泡到达每个刻度线的标准是。
(4)要比较准确地测出气泡从0cm分别到10cm、20cm、30cm、40cm、50cm的运动的时间,让气泡在同样的情况下向上运动次。
(5)根据测量的数据作出s﹣t图线如图乙,气泡从0cm到50cm的运动近似为运动,速度为(保留1位小数)cm/s。
6.(2019秋•莲湖区期末)按要求完成填空。
(1)如图1所示,读数时视线正确的是(选填“A”或“B”)。
物体的长度为cm.图2中秒表的读数是s。
(2)如图3所示的是“研究气泡的运动规律”实验装置。
要正确判断气泡是否做匀速直线运动,需要对气泡运动时的路程和时间进行测量,为便于测量,要使气泡在管内运动得较(选填“快”或“慢”),气泡的运动如果是匀速运动,收集到的数据特点是:运动的路程和时间成(选填“正”或“反”)比,若测得气泡从0到80cm,所用的时间为10s,则在这个过程中气泡的速度为m/s。
7.(2019秋•龙岩期末)如图所示是一小球从A点静止开始沿直线运动到F点的频闪照片,频闪照相机每隔0.2s闪拍一次。
分析照片可知:(1)该小球在做(选填“匀速”或“变速”)直线运动;(2)EF两点之间的距离为cm;(3)该小球从B点运动到D点的平均速度为m/s;(4)该小球在两点间的平均速度最大;(5)图中四个速度随时间的关系图象,能反映出该小球运动的v﹣t图象是。
8.(2019秋•东方期末)小浩在“测小车的平均速度”的实验中,设计了如图所示的实验装置:小车从带刻度的斜面顶端由静止下滑,图中的圆圈是小车到达A、B、C三处时电子表的显示(格式为:时:分:秒)。
(1)该实验的公式是,需要测量的物理量是和,分别用和测量;(2)实验中为了便于测量时间,应使斜面的坡度较(选填“大”或“小”);(3)请根据图中所给信息回答:小车在AB段的路程。
时间和速度分别为:s AB=m,t AB =s,v AB=m/s;(4)由实验可以得出的结论是:小车在斜面下滑时做运动(选填“匀速”或“变速”)。
9.(2019秋•市北区期末)测量小车的平均速度提出问题:小车在哪段路程的平均速度大?猜想:小宇猜测全程的平均速度比上半程的大实验过程和数据:保持斜面坡度不变,分别测出小车通过全程AC和上半程AB段的路程及所用的时间填入表,请算出对应的平均速度。
路段路程s/cm 时间t/s 速度v/m•s﹣1AC 120 5AB 3实验结果证明小宇的猜想是的。
10.(2019秋•福清市期末)如图(a)所示,小欣用刻度尺测出玩具小甲虫的长度为cm.接着她又想测量玩具小甲虫上了发条之后在水平面上运动的速度。
于是,她在水平放置的长木板上做了两个标记A、B,如图(b)所示。
用刻度尺测出A、B间的距离s=32.00cm,并标出AB的中点M.接着,她让上了发条的玩具小甲虫从A点开始运动,同时用秒表开始计时,测出小甲虫运动到M点所用的时间t1=3.2s,以及小甲虫运动到B点所用的时间t2=7.2s,则小甲虫在MB段的平均速度为cm/s,小甲虫在AB间做(选填“匀速”或“变速”)直线运动。
11.(2019秋•丹东期末)在探究声音的产生与传播时,小明和小华一起做了下面的实验:(1)如图甲,用悬挂着的乒乓球接触正在发声的音叉,可观察到乒乓球弹跳起来,这个现象说明,此研究过程中用到的主要物理研究方法是。
(2)如图乙,敲响右边的音叉,左边完全相同的音叉也会发声,并且把泡沫塑料球弹起。
该实验能说明可以传声,还能说明声波具有。
(3)如图丙,把正在响铃的闹钟放在玻璃罩内,逐渐抽出其中的空气,听到的声音会逐渐变小,甚至最后听不到声音,这个实验说明了不能传声,用到的主要物理研究方法是。
12.(2019秋•盱眙县期末)如图所示,用钢尺做探究实验,把钢尺紧按在桌面上,一端伸出桌边,拨动钢尺,听它发出的声音,同时注意观察钢尺振动的快慢,改变钢尺伸出桌边的长度,再次拨动,使钢尺每次的振动幅度大致相同。
(1)本实验中应该听的声音是。
A.钢尺伸出桌面部分振动发出的B.钢尺拍打桌面发出的(2)实验时,钢尺伸出桌面的长度越长,振动越(选填“快”或“慢”),发出声音的音调越。
说明:音调的高低与声源振动的有关。
(3)小华同学发现钢尺伸出桌面的长度太长时,可以明显看到钢尺在振动,但却听不到声音,这是因为。
13.(2019秋•清江浦区期末)在探究声音的产生与传播的实验中:(1)石头落入水中,产生的水波向四周传播:发声的音叉接触水面,激起水波向四周传播。
通过水波来研究声波,这种研究问题的方法是;(选填序号)A.推理法B.类比法C.控制变量法D.转换法(2)如图甲所示,用竖直悬挂的乒乓球接触发声的音叉时,乒乓球会被弹起,这个现象说明;乒乓球在实验中起到的作用是;(3)敲击图乙右边的音叉,左边完全相同的音叉会把乒乓球弹起,这个现象说明。
14.(2019秋•覃塘区期末)如图甲所示,用竖直悬挂的泡沫塑料球接触发声的音叉时,泡沫塑料球被弹起,这个现象说明声音是物体产生的,敲击音叉的力增大,泡沫塑料球被弹起的幅度(填“增大”或“减小”),同时声音更洪亮,说明声音的与振幅有关;如图乙所示;敲击右边的音叉,左边完全相同的音叉把泡沫塑料球弹起,这个现象说明空气传声。
(选填“能”或“不能”)。
15.(2019秋•建平县期末)如图所示是探究“声音的传播”实验装置:(1)交流讨论:①在玻璃钟罩内的木塞上,放一个正在发声的音乐闹铃,此时我们能听到音乐。
②用抽气设备抽钟罩内空气,在抽气的过程中,你听到音乐声将会(选填“变大”“不变”或“变小”)。
③如果把钟罩内空气完全抽出我们将(选填“能”或“不能”)听到声音。
(2)实验结论:声音的传播需要,声音在中不能传播。
(3)通常人们会从噪声的产生、传播及接收三个环节控制噪声。
下列控制噪声的措施中,与上述实验结论相符合的是(填序号)A.摩托车安装消声器 B.在高噪声环境下工作的人戴耳罩C.临街的房屋安装双层真空玻璃 D.学校附近禁止汽车鸣笛16.(2019秋•长春期末)如图所示,在探究“声音的产生”的实验中,将正在发声的音叉紧靠悬线下的轻质小球,发现小球被多次弹开,音叉停止发声时,小球就不能被弹开了,由此证明了振动(选填“是”或“不是”)产生声音的条件;该实验中,使用小球的目的是为了。
A.将音叉的振动时间延迟B.使音叉的振动尽快停下来C.使声波被多次反射形成回声D.将音叉的微小振动反映出来,便于观察17.(2019秋•松江区期末)某同学在学过声音的特征以后,到学校物理实验室借了两个不同的音叉,用同一示波设备,做了三次实验,并记录了每次实验的波型图,如图(a)、(b)、(c)所示。
根据我们所学过的知识可知,在上述三个波形图中,响度最小的是图,音调最高的是图。
18.(2019秋•卫辉市期末)如图是被文化部授予“中国民间绝艺王”称号的安徽南卫东制作的胡萝卜排箫,它根据胡萝卜的粗细,孔的大小、高低,然后利用口腔吹气产生的震动来演奏曲目,为了探究发生体音调的高低与哪些因素有关,物理课代表在家找一个胡萝卜,用电钻在胡萝卜的一端转一个浅孔,用嘴对着胡萝卜下口部吹气,使其发出声音,用电钻继续钻深一些(未钻透),用嘴对着胡萝卜下口部吹气,比较发现发出声音比第一次低沉一些。
(1)胡萝卜发声是利用(选填“空气柱”或“胡萝卜”)的振动发声的;(2)他逐渐用力吹同一个胡萝卜孔,响度(选填“增大”或“不变”或“降低”);(3)南卫东制作的胡萝卜排萧从左向右钻的孔逐渐变浅,用相同的力逐个吹一下,发现最右边声音的音调最;演出时,后排观众能听到声音,声音是通过传播到人耳的。
19.(2019秋•河池期末)在探究声音的产生与传播时,小明和小华一起做了如图所示的实验:(1)如图①所示,用悬挂着的乒乓球接触正在发声的音叉。
此探究中悬挂着的乒乓球的作用是。
本实验说明。
(2)如图②所示,为了验证(1)中的探究结论,小华同学用手使劲敲桌子,桌子发出了很大的声响,但他几乎没有看到桌子的振动,为了明显地看到实验现象,你的改进方法是:。
(3)如图③所示,敲响右边的音叉,左边完全相同的音叉也会发声,并且把泡沫塑料球弹起,该实验能说明可以传声,(4)如图④所示,把正在响铃的闹钟放在玻璃党内,逐渐抽出其中的空气,听到的声音会逐渐(选填“变大“、“变小”或“不变”)。
这个实验说明了。
20.(2019秋•奉节县期末)在学习吉他演奏的过程中,小华发现琴弦发出声音的音调高低是受各种因素影响的,他决定对此进行研究,经过和同学们讨论,提出了以下猜想:猜想一:琴弦发出声音的音调高低,可能与琴弦的横截面积有关;猜想二:琴弦发出声音的音调高低,可能与琴弦的长短有关;猜想三:琴弦发出声音的音调高低,可能与琴弦的材料有关。
