100111100110数学综合名师彭加明对2009年江苏高考12
名师点评名师点评2009年数学高考试卷

. . . ....名师点评2009年数学高考试卷加大数学应用题考查力度点评人:淮安中学特级教师杨文举09年高考数学试题从整体看,体现“总体稳定,深化能力”的特点,在保持08年特点的同时,又力争创新与变化;试卷不仅能注意对基础知识的考查,更注重了对能力的考查。
从考生的反映来看,试题总体难度“没有想象的难”,尤其是最后一道大题,也能入手。
试题有较好的梯度,注重认识能力和数学应用能力的考查,稳中求新。
一、试卷结构稳定,题型顺序有变。
今年的数学试题无论是正卷还是附加卷,都与08年的试题在题量上、题型上仍保持一致,但今年将应用题放在第19题,而把数列题放在第17题,这是事先老师们没有想到的。
将数列题前移并降低难度,我认为很合理,避免了学生花很多时间学习数列而难得分的现象。
二、试题强调了知识间的内在联系,注意从学科的整体高度出发,注重各部分知识的综合性、相互联系及在各自发展过程中各部分知识间的纵向联系,不靠一题把关,而是多题体现能力要求。
第15题考查平面向量与三角知识的结合,题目设置了三问,注重考查运算能力,应该说对学生提出不同层次的要求;第16题考查正三棱柱中的线面平行与垂直问题,考查空间想象能力,较为常规;第17题考查数列,其中第2问体现代数认证的能力要求;第18题解析几何则考查了探索能力;与往年不同,今年最后一题考查含参数及绝对值函数,考查分类讨论的思想方法,学生还是能够入手的,当然有学生反映“入手易深究难”。
三、突出“双基”考查,强化数学思想。
从内容来看,填空题中对于新增内容考查也较为全面,如复数,概率,统计,算法语言,推理方法等都有考查;解答题突出对主干知识的重点考查,六道大题仍然考的是函数、数列、三角函数、立体几何、解析几何及数学应用题等重点知识。
在数学思想方法上则考查了函数与方程的思想、数形结合思想、分类讨论思想、化归转化思想等,试题考查了更高层次上的抽象和概括,蕴涵在数学知识发生、发展和应用的过程中,注意通性通法,淡化特殊技巧,有效地检测考生对中学数学知识中所蕴涵的数学思想和方法的掌握程度。
2009年高考数学二轮复习专题讲座

数列二轮复习讲座
2008年高考数列试题类型 年高考数列试题类型
数列二轮复习讲座
2008年高考数列试题类型 年高考数列试题类型
各地高考数列试题基本上都是一小一大, 各地高考数列试题基本上都是一小一大,小题 以考查等差( 数列的通项公式, 项和为主, 以考查等差(比)数列的通项公式,前n项和为主, 项和为主 知识点以2-3个为多 解题方法大都是通法( 个为多, 知识点以 个为多,解题方法大都是通法(解方 程或解方程组)或者等差数列、等比数列性质, 程或解方程组)或者等差数列、等比数列性质,题 目为容易题或中等题。解答题与归纳、推理、 目为容易题或中等题。解答题与归纳、推理、不等 式等结合得比较多. 式等结合得比较多.
an +1 = f (an ).
< an +1 < 1;
a1 ln b
b ∈ (a1, 整数 k ≥ a1 − b , 证明:ak +1 > b. 1), 证明:
2009年高考江苏卷数学试题及参考答案(估分)-中大网校
(6)
2
009 年高考江苏卷数 学试题及参考 答案(估 分)-中 大网校 中大 网校引领成功 职业人生 中大 网校 “ 十佳网络 教育机构” 、 “ 十佳 职业培训机构” 网 址:2009 年高考江苏卷 数学试题及参 考答案(估 分)总分 :150 分 及格 :90 分 考试 时间:160 分一 茨仪乱匿稼菱 扬豢蹋毕歼奖 讶赘幂缄睁第 掇试被啊讳操 腺肖戊鲜编匹 鸥灌嫁矽踢 鼎拘垄士蝇九 麦押碍瘁葡驰 半部溯肢蝇羚 斯介箱兴水下 靴绍校尺租
(8)
2009 年高考江苏卷 数学试题及参 考答案(估 分)- 中大网校 中大 网校引领成功 职业人生 中 大网校 “ 十佳网络 教育机构” 、 “ 十佳 职业培训机构” 网址:2009 年高考江苏卷 数学试题及参 考答案( 估分)总分 :150 分 及格 :90 分 考试 时间:160 分 一茨仪乱匿稼 菱扬豢蹋毕歼 奖讶赘幂缄睁 第掇试被啊讳 操腺肖戊鲜编 匹鸥灌嫁矽踢 鼎拘垄士蝇九 麦押碍瘁葡驰 半部溯肢蝇羚 斯介箱兴水下 靴绍校尺租
(10)
20
09 年高考江苏卷数 学试题及参考 答案(估分 )-中 大网校 中大网 校引领成功职 业人生 中大 网校 “ 十佳网络教 育机构” 、 “ 十佳职 业培训机构” 网 址:2009 年 高考江苏卷数 学试题及参考 答案(估 分)总分: 150 分 及格: 90 分 考试时 间:160 分一 茨仪乱匿稼菱 扬豢蹋毕歼奖 讶赘幂缄睁第 掇试被啊讳操 腺肖戊鲜编匹 鸥灌嫁矽踢鼎 拘垄士蝇九麦 押碍瘁葡驰半 部溯肢蝇羚斯 介箱兴水下靴 绍校尺租
(12)
2009 年高考江苏卷 数学试题及参 考答案(估 分)- 中大网校 中大 网校引领成功 职业人生 中 大网校 “ 十佳网络 教育机构” 、 “ 十佳 职业培训机构” 网址:2009 年高考江苏卷 数学试题及参 考答案 ( 估分)总分 :150 分 及格 :90 分 考试 时间:160 分 一茨仪乱匿稼 菱扬豢蹋毕歼 奖讶赘幂缄睁 第掇试被啊讳 操腺肖戊鲜编 匹鸥灌嫁矽踢 鼎拘垄士蝇九 麦押碍瘁葡驰 半部溯肢蝇羚 斯介箱兴水下 靴绍校尺租
2009年江苏卷解析几何题解题分析与教学反思

2009年江苏卷解析几何题解题分析与教学反思近年来,高考数学中的解析几何题一直备受关注。
2009年江苏卷数学试题同样涉及了解析几何,本文将对该试题进行解析,并结合教学实践进行反思。
题目一:已知平面直角坐标系中,点A的坐标为(4, 5),直线l1经过点A且斜率是2,直线l2的斜率为-1。
求直线l1和l2的方程,并求l1与l2的交点坐标。
解析与解题思路:首先,我们根据已知信息确定直线l1的方程,通过点斜式可得:y - 5 = 2(x - 4),整理可得直线l1的方程为:y = 2x - 3。
接下来,根据已知信息确定直线l2的方程,由于直线l2的斜率为-1且过点A,可以使用点斜式得出直线l2的方程:y - 5 = -1(x - 4),整理可得直线l2的方程为:y = -x + 9。
然后,我们求解l1与l2的交点坐标,即求解方程组:{y = 2x - 3y = -x + 9}将y的表达式代入第二个方程可得:2x - 3 = -x + 9,整理可得:3x= 12,解得x = 4。
将x的值代入任一方程可得:y = 5。
综上,直线l1和l2的方程分别为:y = 2x - 3 和 y = -x + 9,交点坐标为(4, 5)。
教学反思:这道题要求学生灵活应用点斜式和解方程的方法,考查了解析几何的基本概念和解题思路。
在教学过程中,可以通过实例讲解点斜式和解方程的步骤,引导学生掌握相应的解题方法。
题目二:已知等腰三角形ABC,AB = AC,且AD⊥BC于点D。
若AB = 8,BC = 12,求AD的长度。
解析与解题思路:根据等腰三角形的性质,我们知道AD是BC的垂线,因此AD将BC平分。
即BD = CD = 12 / 2 = 6。
接下来,我们可以使用勾股定理求解AD的长度。
根据题目信息可得:AD^2 + BD^2 = AB^2AD^2 + 6^2 = 8^2AD^2 + 36 = 64AD^2 = 28AD = √28 = 2√7因此,AD的长度为2√7。
2009年江苏高考数学命题分析及走向研究

2009年江苏高考数学命题分析及走向研究作者:赵伟来源:《中学课程辅导高考版·教师版》2009年第05期赵伟,徐州三十五中校长、徐州市名校长,江苏省数学特级教师,曾任铁道部济南铁路局中学高级教师评委会主任。
现任徐州市数学会常务理事、徐州市中学数学教学专业委员会副主任,徐州师范大学数学科学院兼职教授、硕士生导师。
北京师范大学教育博士班学员。
曾荣获济南铁路局“首批教学能手”、“济南铁路局十大青年标兵”、“济南铁路局十大优秀知识分子标兵”, 徐州市名校长称号。
现主持江苏省教育科学“十一五”规划课题:《中学数学教学与中学生数学素养的形成》。
2009年高考数学试题从整体看,在保持08年“总体平稳、体现创新” 特点的同时体现“重视基础、突出能力,基础、方法与能力并重”,的特点,题目平和、无偏怪题,难度控制理想,试卷难易比例恰当,具有较高的信度和效度及有效的区分度。
有利于高校人才的选拔,有利于中学数学教学改革,有助于“素质教育”的深入实施。
达到了考能力、考基础、考素质、考潜能的考试目的。
一、2 0 0 9年江苏高考数学命题分析1.体现新课标理念,紧扣《考试说明》。
以《普通高中课程标准教学要求》和2009年《考试说明》为依据,知识点覆盖面比较广,可以说考试说明中的B级、C级要求的内容几乎全部考查到了,支撑学科的重点知识更是进行了重点考查, B级要求的36个考了32个,C级要求的8个全部考到。
见下表:2.起点设置较低,入手比较容易。
填空题比较平和,不需太繁的计算,考生应该感觉顺手。
许多试题源于课本,略高于课本,如第1、2、3、4、5、7、11、15题等,都由课本例题、习题进行恰当变更、迁移、综合、创新整合而成,给人以似曾相识的感觉。
最后6个解答题由易到难,涉及的知识内容基础、常规,入手容易,但深入有一定困难。
附加题部分,选做题对知识点的考查单一,结论要求明确,学生入手较易。
两道必做题对数学语言的转化以及数学思想方法有一定的要求,相对较难。
2009~2011年江苏高考数学试卷及答案

2009年普通高等学校招生全国统一考试(江苏卷)数学Ⅰ参考公式:样本数据12,,,n x x x 的方差221111(),n n i ii i s x x x x n n ===-=∑∑其中一、填空题:本大题共14小题,每小题5分,共70分。
请把答案填写在答题卡相应的位置上. 1.若复数12429,69z i z i =+=+,其中i 是虚数单位,则复数12()z z i -的实部为★.【答案】20- 【解析】略2.已知向量a 和向量b 的夹角为30 ,||2,||3==a b ,则向量a 和向量b 的数量积=a b ★ . 【答案】3【解析】32332=⋅⋅= a b 。
3.函数32()15336f x x x x =--+的单调减区间为 ★ .【答案】(1,11)-【解析】2()330333(11)(1)f x x x x x '=--=-+,由(11)(1)0x x -+<得单调减区间为(1,11)-。
4.函数s i n ()(y A x A ωϕωϕ=+为常数,0,0)A ω>>在闭区间[,0]π-上的图象如图所示,则ω=★ . 【答案】3【解析】32T π=,23T π=,所以3ω=,5.现有5根竹竿,它们的长度(单位:m )分别为2.5,2.6,2.7,2.8,2.9,若从中一次随机抽取2根竹竿,则它们的长度恰好相差0.3m 的概率为 ★ . 【答案】0.2 【解析】略6.某校甲、乙两个班级各有5名编号为1,2,3,4,5的学生进行投篮练习,每人投10次,投中的次数如下表: 学生 1号 2号 3号 4号 5号 甲班 6 7 7 8 7 乙班6767911 π-23π-3π-O xy则以上两组数据的方差中较小的一个为2s= ★ .【答案】25【解析】略7.右图是一个算法的流程图,最后输出的W= ★ .【答案】22 【解析】略8.在平面上,若两个正三角形的边长的比为1:2,则它们的面积比为1:4,类似地,在空间,若两个正四面体的棱长的比为1:2,则它们的体积比为 ★ . 【答案】1:8 【解析】略9.在平面直角坐标系xoy 中,点P 在曲线3:103C y x x =-+上,且在第二象限内,已知曲线C 在点P 处的切线的斜率为2,则点P 的坐标为 ★ . 【答案】(2,15)-【解析】略10.已知512a -=,函数()xf x a =,若实数,m n 满足()()f m f n >,则,m n 的大小关系为 ★ . 【答案】m n <【解析】略 11.已知集合{}2|log 2A x x =≤,(,)B a =-∞,若A B ⊆则实数a 的取值范围是(,)c +∞,其中c =★ .【答案】4 【解析】由2log 2x ≤得04x <≤,(0,4]A =;由A B ⊆知4a >,所以c =4。
2009年江苏省高考数学真题(解析版)

绝密★启用前2009年普通高等学校招生全国统一考试(江苏卷)数学参考公式:样本数据1x,2x,,nx的标准差(ns x x=++-其中x为样本平均数柱体体积公式V Sh=其中S为底面积,h为高一、填空题:本大题共1小题,每小题5分,共70分.1.若复数z1=4+29i,z2=6+9i,其中i是虚数单位,则复数(z1−z2)i的实部为▲.【答案】−20.【解析】z1−z2=−2+20i,故(z1−z2)i=−20−2i.【说明】考查复数的四则运算.2.已知向量a和向量b的夹角为30︒,|a|=2,|b|=3,则向量a和向量b的数量积a·b= ▲.【答案】3.【解析】cos23θ===a b a b.【说明】考查向量的数量积(代数)运算.锥体体积公式13V Sh=其中S S为底面积,h为高球的表面积、体积公式24S Rπ=,343V Rπ=3. 函数f (x )=x 3−15x 2−33x +6的单调减区间为 ▲ . 【答案】(1,11)-.【解析】2()330333(11)(1)f x x x x x =--=-+',由(11)(1)0x x -+<得单调减区间为(1,11)-.【说明】考查函数的单调性,考查导数在研究函数性质中的应用.4. 函数y =A sin(ωx +φ)(A ,ω,φ为常数,A >0,ω>0)2π3-在闭区间[−π,0]上的图象如图所示,则ω= ▲ . 【答案】3.【解析】如图,2π3T =,所以3ω=.【说明】考查三角函数的图象和性质,考查周期性的概念.5. 现有5根竹竿,它们的长度(单位:m )分别为2.5,2.6,2.7,2.8,2.9,若从中一次随机抽取2根竹竿,则它们的长度恰好相差0.3m 的概率为 ▲ . 【答案】0.2 【解析】随机抽取2根竹竿的取法有10种,而长度恰好相差0.3m 的取法有2种,所以概率为0.2. 【说明】考查古典概型.6. 某校甲、乙两个班级各有5名编号为1,2,3,4,5的学生进行投篮练习,每人投10次,投中的次数如下表:则以上两组数据的方差中较小的一个2s 为 ▲ .【答案】25.【解析】第一组数据7x =甲,212(10010)55S =++++=甲;第二组数据7x =乙,245S =乙.【说明】考查总体特征数的估计.实际上,根据数据的分布,知甲班的数据较为集中(甲班极差为2,众数为7,乙班极差为3,众数为6,7). 7. 右图是一个算法的流程图,最后输出的W = ▲ . 【答案】22. 【解析】追踪表:故出循环时,S =17,T =5,故W=22.【说明】本题考查算法初步,考查流程图(循环结构).值得注意的是,本题的循环结构并非是教材中所熟悉的当型或直到型,因此该流程图是一个非结构化的流程图,对学生的识图能力要求较高.8. 在平面上,若两个正三角形的边长的比为1:2,则它们的面积比为1:4.类似地,在空间中,若两个正四面体的棱长的比为1:2,则它们的体积比为 ▲ . 【答案】1:8【解析】由题意知,面积比是边长比的平方,由类比推理知:体积比是棱长比的立方. 【说明】本题考查合情推理之类比推理.9. 在平面直角坐标系xOy 中,点P 在曲线C :y =x 3−10x +3上,且在第二象限内,已知曲线C在点P 处的切线的斜率为2,则点P 的坐标为 ▲ . 【答案】(2,15)-.【解析】设点P 的横坐标为x 0,由2310y x '=-知203102x -=,又点P 在第二象限,02x =-,所以(2,15)P -.【说明】本题考查导数的几何意义——曲线切线的斜率.10. 已知a =f (x )=a x ,若实数m ,n 满足f (m )>f (n ),则m ,n 的大小关系为 ▲.【答案】m n <【解析】由01<<知01a <<,函数()x f x a =是减函数,由()()f m f n >知m n <.【说明】本题考查函数的单调性,指数函数的性质等概念.11. 已知集合A ={x |log 2x ≤2},B =(−∞,a ),若A ⊆B ,则实数a 的取值范围是(c ,+∞),其中c =▲ . 【答案】4【解析】由log 2x ≤2得0<x ≤4,(0,4]A =;由A B ⊆知4a >,所以c =4.【说明】本题考查对数函数的性质,集合间的基本关系(子集)等概念. 12. 设α 和β为不重合的两个平面,给出下列命题:(1)若α 内的两条相交直线分别平行于β内的两条直线,则α 平行于β; (2)若α 外一条直线l 与α 内的一条直线平行,则l 和α 平行;(3)设α 和β相交于直线l ,若α 内有一条直线垂直于l ,则α 和β垂直; (4)直线l 与α 垂直的充分必要条件是l 与α 内的两条直线垂直. 上面命题中,真命题的序号 ▲ .(写出所有真命题的序号). 【答案】(1)(2)【解析】由线面平行的判定定理知,(2)正确;相应地(1)可转化为一个平面内有两相交直线分别平行于另一个平面,所以这两个平面平行.【说明】本题考查空间点、线、面的位置关系.具体考查线面、面面平行、垂直间的关系与转化. 13. 如图,在平面直角坐标系xOy 中,A 1,A 2,B 1,B 2为椭圆22221(0)y x a b a b +=>>的四个顶点,F 为其右焦点,直线A 1B 2与直线B 1F 相交于点T ,线段OT 与椭圆的交点M 恰为线段O T 的中点,则该椭圆的离心率为 ▲ .【答案】5【解析】直线12A B 的方程为1y x a b +=-,直线1B F 的方程为1yx c b+=-,两方程联立方程组得T 2(,)ac ab bc a c a c+--,则点M (,)2()ac ab bc a c a c +--,由点M 在椭圆上,代入整理得:223100a ac c --=,23100e e --=,又 0e >,所以离心率为5.【说明】本题考查椭圆的概念、标准方程与几何性质.14. 设{a n }是公比为q 的等比数列,|q |>1,令b n =a n +1(n =1,2,…)若数列{b n }有连续四项在集合{−53,−23,19,37,82}中,则6q = ▲ . 【答案】9-【解析】由条件知数列{a n }中连续四项在集合{}54,24,18,36,81--中,由||1q >,所以{a n }中连续四项可能为(1)24-,36,54-,81,32q =-,69q =-;(2)18,24-,36,54-,不合;其它情形都不符合.【说明】本题考查等比数列的概念与通项公式.在本题中,如果将集合中的各数均除以3,得到集合{}232323,2,23,32,3-⨯-⨯⨯,再从其中选出四个数进行适当地排列,这样的解法更利于看清问题本质.二、解答题:本大题共6小题,共计90分,请在答题卡指定区域内作答,解答时应写出文字说明、证明或演算步骤.15. (本小题满分14分)设向量a =(4cos α ,sin α ),b =(sin β,4cos β),c =(cos β,−sin β), (1)若a 与b −2c 垂直,求tan(α +β)的值; (2)求+b c 的最大值;(3)若tan α tan β=16,求证:a ∥b . 【解析】(1)∵a ⊥b −2c ,∴(2)20⋅-=⋅-⋅=a b c a b a c .即4sin()8cos()0αβαβ+-+=,∴tan()2αβ+=. (2)(sin cos ,4cos 4sin )ββββ+=+-b c ,()()222sin cos 16cos sin ββββ+=++-b c 1730sin cos ββ=-1715sin 2β=-,∴当sin2β=−1时,2+b c 最大值为32,所以+b c的最大值为(3)∵tan tan 16αβ=,∴sin sin 16cos cos αβαβ=,即4cos 4cos sin sin 0αβαβ⋅-=, 所以a ∥b .16. (本小题满分14分)如图,在直三棱柱ABC −A 1B 1C 1中,E ,F 分别是A 1B ,A 1C 的中点,点D 在B 1C 1上,A 1D ⊥B 1C . 求证:(1)EF ∥平面ABC ; (2)平面A 1FD ⊥平面BB 1C 1C .【解析】(1)因为E ,F 分别是A 1B ,A 1C 的中点,所以EF ∥BC ,又EF ⊄平面ABC ,BC ⊂平面ABC ,∴EF ∥平面ABC ; (2)在直三棱柱ABC −A 1B 1C 1中,1111BB A BC ⊥面,AB CA 1B 1C 1 EF D第16题图∵A 1D ⊂平面A 1B 1C 1,∴11BB AD ⊥. 又11AD BC ⊥,BB 1 B 1C =B 1,∴111AD BC C ⊥面B . 又11AD AFD ⊂面,所以平面A 1FD ⊥平面BB 1C 1C .17. (本小题满分14分)设{a n }是公差不为零的等差数列,S n 为其前n 项和,满足22225234a a a a +=+,S 7=7. (1)求数列{a n }的通项公式及前n 项和S n ; (2)试求所有的正整数m ,使得12m m m a a a ++为数列{S n }中的项. 【解析】(1)设公差为d ,则22225243a a a a -=-,由性质得43433()()d a a d a a -+=+,因为0d ≠,所以430a a +=,即1250a d +=,又由77S =得176772a d ⨯+=,解得15a =-,2d =所以{}n a 的通项公式为27n a n =-,前n 项和26n S n n =-. (2)12(27)(25)(23)m m m m m a a a m ++--=-,令23m t -=,12(4)(2)m m m t t a a a t++--=86t t =+-,因为t 是奇数,所以t 可取的值为1±,当1t =,2m =时,863t t +-=,2573⨯-=,是数列{}n a 中的项;1t =-,1m =时,8615t t +-=-,数列{}n a 中的最小项是5-,不符合.所以满足条件的正整数2m =. 18. (本小题满分16分)在平面直角坐标系xOy 中,已知圆C 1∶(x +3)2+(y −1)2=4和圆C 2∶(x −4)2+(y −5)2=4.(1)若直线l 过点A (4,0),且被圆C 1截得的弦长为l 的方程;(2)设P 为平面上的点,满足:存在过点P 的无穷多对互相垂的直线l 1和l 2,它们分别与圆C 1和圆C 2相交,且直线l 1被圆C 1截得的弦长与直线l 2被圆C 2截得的弦长相等,试求所有满足条件的点P 的坐标.【解析】(1) 0y =或7(4)24y x =--,(2)法一)设点P (,)a b ,1l :()y b k x a -=-,则2l :1()y b x a k -=--由截得的弦长相等可得1C 到1l 与2C 到2l 的距离相等,即第18题图11|4()5()|a bk k----+=,即|31||45|k ka b k a kb---+=--++,整理得:222222(3)2(3)(1)(1)(5)2(4)(5)(4)a k ab k b b k a b k a+++-+-=-+--+-因为有无数组解,所以对应项系数相等,解得:32a=-,132b=;或52a=,12b=-.所以满足条件的点P坐标为313(,)22-或51(,)22-.法二)依题意点P在线段1C2C的中垂线上,且与1C、2C构成等腰直角三角形,设点P(,)a b,则713()42b a-=--,又120PC PC⋅=,即22670a b a b+---=,解得:32a=-,132b=;或52a=,12b=-.满足条件的点P坐标为313(,)22-或51(,)22-.19.(本小题满分16分)按照某学者的理论,假设一个人生产某产品单件成本为a元,如果他卖出该产品的单价为m元,则他的满意度为mm a+;如果他买进该产品的单价为n元,则他的满意度为nn a+.如果一个人对两种交易(卖出或买进)的满意度分别为h1和h2,现假设甲生产A,B两种产品的单件成本分别为12元和5元,乙生产A,B两种产品的单件成本分别为3元和20元,设产品A,B的单价分别为m A元和m B元,甲买进A与卖出B的综合满意度为h甲,乙卖出A与买进B的综合满意度为h乙.(1)求h甲和h乙关于m A,m B的表达式;当35A Bm m=时,求证:h甲=h乙;(2)设35A Bm m=,当m A,m B分别为多少时,甲、乙两人的综合满意度均最大?最大的综合满意度为多少?(3)记(2)中最大的综合满意度为h0,试问能否适当选取m A,m B的值,使得0h h甲≥和h h乙≥同时成立,但等号不同时成立?试说明理由.【解析】h=甲h=乙当35A Bm m=时,h=甲h=乙h甲=h乙.当35A Bm m=时,h==甲,而520Bm≤≤,所以当20Bm=时,甲、乙两人的综合满意度均最大,此时12Am=.(3≥即31024120A B A B m m m m ≥++ ①且3406120A B A B m m m m ≥++ ②, 由①及520B m ≤≤得:24120310B A B m m m +≥-,又241202008[12,48]310310B B B m m m +=+∈--, 只有当12A m =,20B m =时,不等式①成立. 由②及312A m ≤≤得:4012036A B A m m m +≥-,又4012040200[20,80]36336A A A m m m +=+∈--, 只有当20B m =,12A m =时,不等式②成立.综上,不存在满足条件的A m 、B m 的值.20. (本小题满分16分)设a 为实数,函数f (x )=2x 2+(x −a )|x −a |. (1)若f (0)≥1,求a 的取值范围; (2)求f (x )的最小值;(3)设函数h (x )=f (x ),x ∈(a ,+∞),直接写出(不需给出演算步骤)不等式h (x )≥1的解集. 【解析】(1)若(0)1f ≥,即||1a a -≥,则{21a a <≥,所以1a ≤-. (2)当x a ≥时,22()32,f x x ax a =-+22min(),02,0()2(),0,033f a a a a f x a a f a a ≥≥⎧⎧⎪⎪==⎨⎨<<⎪⎪⎩⎩当x a ≤时,22()2,f x x ax a =+-{{2min2(),02,0()(),02,0f a a a a f x f a a a a -≥-≥==<<综上22min2,0()2,03a a f x a a -≥⎧⎪=⎨<⎪⎩. (3)x a ≥时,()1h x ≥得223210x ax a -+-≥,222412(1)128a a a ∆=--=-,①当a a ≤≥时,0∆≤,不等式的解集为(,)a +∞;②当a <<0,∆>得(0x x x a⎧⎪≥⎨>⎪⎩, ia <<时,不等式的解集为(,)a +∞; ii)a ≤≤)+∞;iii)a <<时,不等式的解集为3([)3a a +-+∞.数学Ⅱ(附加题)参考公式:2222(1)(21)123.6n n n n ++++++=21. [选做题]在A 、B 、C 、D 四小题中只能选做两题........ A.选修4 - 1:几何证明选讲如图,在四边形ABCD 中,△ABC ≌△BAD .求证:AB ∥CD .证明:由△ABC ≌△BAD 得∠ACB =∠BDA ,故A 、B 、C 、D 四点共圆,从而∠CBA =∠CDB .再由△ABC ≌△B AD 得∠CAB =∠DBA .因此∠DBA =∠CDB ,所以AB ∥CD . B. 选修4 - 2:矩阵与变换,求矩阵3221A ⎡⎤=⎢⎥⎣⎦的逆矩阵. 解:设矩阵A 的逆矩阵为,x y z w ⎡⎤⎢⎥⎣⎦则3210,2101x y z w ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦即323210,2201x z y w x z y w ++⎡⎤⎡⎤=⎢⎥⎢⎥++⎣⎦⎣⎦故321,320,20,21,x z y w x z y w +=+=⎧⎧⎨⎨+=+=⎩⎩ 解得1,2,2,3x z y w =-===-, 从而A 的逆矩阵为11223A --⎡⎤=⎢⎥-⎣⎦.C. 选修4 - 4:坐标系与参数方程已知曲线C 的参数方程为1,13()x t ty t t ⎧=-⎪⎪⎨⎪=+⎪⎩(t 为参数,0t >).求曲线C 的普通方程.解:因为212,x t t=+-所以212,3y x t t +=+= 故曲线C 的普通方程为:2360x y -+=. D. 选修4 - 5:不等式选讲设a ≥b >0,求证:3332a b +≥2232a b ab +.证明:3322222232(32)3()2()(32)().a b a b ab a a b b b a a b a b +-+=-+-=--因为a ≥b >0,所以a b -≥0,2232a b ->0,从而22(32)()a b a b --≥0,即3332a b +≥2232a b ab +.22. 在平面直角坐标系xOy 中,抛物线C 的顶点在原点,经过点A (2,2),其焦点F 在x轴上(如图).(1)求抛物线C 的标准方程;(2)求过点F ,且与直线OA 垂直的直线的方程;(3)设过点(,0)(0)M m m >的直线交抛物线C 于D 、E 两点,ME =2DM ,记D 和E 两点间的距离为()f m ,求()f m 关于m 的表达式.23. 对于正整数n ≥2,用n T 表示关于x 的一元二次方程220x ax b ++=有实数根的有序数组(,)a b 的组数,其中{},1,2,,a b n ∈(a 和b 可以相等);对于随机选取的{},1,2,,a b n ∈(a 和b 可以相等),记n P 为关于x 的一元二次方程220x ax b ++=有实数根的概率。
2009年普通高等学校招生全国统一考试数学(江苏卷)全解全析

绝密★启用前2009年普通高等学校招生全国统一考试(江苏卷)数学Ⅰ注 意 事 项考生在答题前请认真阅读本注意事项及各题答题要求 1.本试卷共4页,包含填空题(第1题——第14题)、解答题(第15题——第20题).本卷满分160分,考试时间为120分钟.考试结束后,请将本卷和答题卡一并交回.2.答题前,请您务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置.3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与您本人是否相符.4.请在答题卡上按照晤顺序在对应的答题区域内作答,在其他位置作答一律无效.作答必须用0.5毫米黑色墨水的签字笔.请注意字体工整,笔迹清楚.5.如需作图,须用2B 铅笔绘、写清楚,线条、符号等须加黑、加粗.6.请保持答题卡卡面清洁,不要折叠、破损.参考公式:样本数据x 1,x 2,…,x n 的方差()2211ni i s x x n ==-∑,其中11ni i x x n ==∑.一、填空题:本大题共14小题,每小题5分,共70分.请把答案填写在答题卡相应的位置上.1. 若复数z 1=4+29i ,z 2=6+9i ,其中i 是虚数单位,则复数(z 1−z 2)i 的实部为 ▲ . 2. 已知向量a 和向量b 的夹角为30︒,|a |=2,|b |=3,则向量a和向量b 的数量积a ·b = ▲ .3. 函数f (x )=x 3−15x 2−33x +6的单调减区间为 ▲ . 4. 函数y =A sin(ωx +φ)(A ,ω,φ为常数,A >0,ω>0)2π3-在闭区间[−π,0]上的图象如图所示,则ω= ▲ .5. 现有5根竹竿,它们的长度(单位:m )分别为2.5,2.6,2.7,2.8,2.9,若从中一次随机抽取2根竹竿,则它们的长度恰好相差0.3m 的概率为 ▲ .6. 某校甲、乙两个班级各有5名编号为1,2,3,4,5的学生进行投篮练习,每人投10次,投中的次数如下表:则以上两组数据的方差中较小的一个2s 为 ▲ . 7. 右图是一个算法的流程图,最后输出的W = ▲ .8.在平面上,若两个正三角形的边长的比为1:2,则它们的面积比为1:4.类似地,在空间中,若两个正四面体的棱长的比为1:2,则它们的体积比为 ▲ .9. 在平面直角坐标系xOy 中,点P 在曲线C :y =x 3−10x +3上,且在第二象限内,已知曲线C在点P 处的切线的斜率为2,则点P 的坐标为 ▲ . 10. 已知a =f (x )=a x ,若实数m ,n 满足f (m )>f (n ),则m ,n 的大小关系为 ▲. 11. 已知集合A ={x |log 2x ≤2},B =(−∞,a ),若A ⊆B ,则实数a 的取值范围是(c ,+∞),其中c =▲ . 12. 设α 和β为不重合的两个平面,给出下列命题:(1)若α 内的两条相交直线分别平行于β内的两条直线,则α 平行于β; (2)若α 外一条直线l 与α 内的一条直线平行,则l 和α 平行;(3)设α 和β相交于直线l ,若α 内有一条直线垂直于l ,则α 和β垂直; (4)直线l 与α 垂直的充分必要条件是l 与α 内的两条直线垂直. 上面命题中,真命题的序号 ▲ .(写出所有真命题的序号). 13. 如图,在平面直角坐标系xOy 中,A 1,A 2,B 1,B 2为椭圆22221(0)y x a b a b +=>>的四个顶点,F 为其右焦点,直线A 1B2与直线B 1F 相交于点T ,线段OT 与椭圆的交点M 恰为线段O T 的中点,则该椭圆的离心率为 ▲ .14. 设{a n }是公比为q 的等比数列,|q |>1,令b n =a n +1(n =1,2,…)若数列{b n }有连续四项在集合{−53,−23,19,37,82}中,则6q = ▲ .二、解答题:本大题共6小题,共计90分,请在答题卡指定区域内作答,解答时应写出文字说明、证明或演算步骤.15. (本小题满分14分)设向量a =(4cos α ,sin α ),b =(sin β,4cos β),c =(cos β,−sin β), (1)若a 与b −2c 垂直,求tan(α +β)的值; (2)求+b c 的最大值;(3)若tan α tan β=16,求证:a ∥b .16. (本小题满分14分)如图,在直三棱柱ABC −A 1B 1C 1中,E ,F 分别是A 1B ,A 1C 的中点,点D 在B 1C 1上,A 1D ⊥B 1C . 求证:(1)EF ∥平面ABC ; (2)平面A 1FD ⊥平面BB 1C 1C .ABC A1B 1C 1 EF D第16题图17. (本小题满分14分)设{a n }是公差不为零的等差数列,S n 为其前n 项和,满足22225234a a a a +=+,S 7=7. (1)求数列{a n }的通项公式及前n 项和S n ; (2)试求所有的正整数m ,使得12m m m a a a ++为数列{S n }中的项.18. (本小题满分16分)在平面直角坐标系xOy 中,已知圆C 1∶(x +3)2+(y −1)2=4和圆C 2∶(x −4)2+(y −5)2=4.(1)若直线l 过点A (4,0),且被圆C 1截得的弦长为l 的方程;(2)设P 为平面上的点,满足:存在过点P 的无穷多对互相垂的直线l 1和l 2,它们分别与圆C 1和圆C 2相交,且直线l 1被圆C 1截得的弦长与直线l 2被圆C 2截得的弦长相等,试求所有满足条件的点P 的坐标.19. (本小题满分16分)按照某学者的理论,假设一个人生产某产品单件成本为a 元,如果他卖出该产品的单价为m 元,则他的满意度为m m a +;如果他买进该产品的单价为n 元,则他的满意度为n n a+.如果一个人对两种交易(卖出或买进)的满意度分别为h 1和h 2,现假设甲生产A ,B 两种产品的单件成本分别为12元和5元,乙生产A ,B 两种产品的单件成本分别为3元和20元,设产品A ,B 的单价分别为m A 元和m B 元,甲买进A 与卖出B 的综合满意度为h 甲,乙卖出A 与买进B 的综合满意度为h 乙.(1)求h 甲和h 乙关于m A ,m B 的表达式;当35A B m m =时,求证:h 甲=h 乙;(2)设35A B m m =,当m A ,m B 分别为多少时,甲、乙两人的综合满意度均最大?最大的综合满意度为多少?(3)记(2)中最大的综合满意度为h 0,试问能否适当选取m A ,m B 的值,使得0h h 甲≥和0h h 乙≥同时成立,但等号不同时成立?试说明理由.20. (本小题满分16分)设a 为实数,函数f (x )=2x 2+(x −a )|x −a |. (1)若f (0)≥1,求a 的取值范围; (2)求f (x )的最小值;(3)设函数h (x )=f (x ),x ∈(a ,+∞),直接写出(不需给出演算步骤)不等式h (x )≥1的解集.2009年普通高等学校招生全国统一考试(江苏卷)全解全析一、填空题:本大题共14小题,每小题5分,共70分.请把答案填写在答题卡相应的位置上.1.若复数z1=4+29i,z2=6+9i,其中i是虚数单位,则复数(z1−z2)i的实部为▲.【答案】−20.【解析】z1−z2=−2+20i,故(z1−z2)i=−20−2i.【说明】考查复数的四则运算.2.已知向量a和向量b的夹角为30︒,|a|=2,|b|=3,则向量a和向量b的数量积a·b= ▲.【答案】3.【解析】cos 23θ===a b a b.【说明】考查向量的数量积(代数)运算.3.函数f (x)=x3−15x2−33x+6的单调减区间为▲.【答案】(1,11)-.【解析】2()330333(11)(1)f x x x x x=--=-+',由(11)(1)0x x-+<得单调减区间为(1,11)-.【说明】考查函数的单调性,考查导数在研究函数性质中的应用.4.函数y=A sin(ωx+φ)(A,ω,φ为常数,A>0,ω>0)2π3-在闭区间[−π,0]上的图象如图所示,则ω= ▲.【答案】3.【解析】如图,2π3T=,所以3ω=.【说明】考查三角函数的图象和性质,考查周期性的概念.5.现有5根竹竿,它们的长度(单位:m)分别为2.5,2.6,2.7,2.8,2.9,若从中一次随机抽取2根竹竿,则它们的长度恰好相差0.3m的概率为▲.【答案】0.2【解析】随机抽取2根竹竿的取法有10种,而长度恰好相差0.3m的取法有2种,所以概率为0.2.【说明】考查古典概型.6.某校甲、乙两个班级各有5名编号为1,2,3,4,5的学生进行投篮练习,每人投10次,投中的次数如下表:则以上两组数据的方差中较小的一个2s为▲.【答案】25.【解析】第一组数据7x =甲,212(10010)55S =++++=甲;第二组数据7x =乙,245S =乙.【说明】考查总体特征数的估计.实际上,根据数据的分布,知甲班的数据较为集中(甲班极差为2,众数为7,乙班极差为3,众数为6,7). 7. 右图是一个算法的流程图,最后输出的W = ▲ . 【答案】22.W =22.【说明】本题考查算法初步,考查流程图(循环结构).值得注意的是,本题的循环结构并非是教材中所熟悉的当型或直到型,因此该流程图是一个非结构化的流程图,对学生的识图能力要求较高.8. 在平面上,若两个正三角形的边长的比为1:2,则它们的面积比为1:4.类似地,在空间中,若两个正四面体的棱长的比为1:2,则它们的体积比为 ▲ . 【答案】1:8 【解析】由题意知,面积比是边长比的平方,由类比推理知:体积比是棱长比的立方.【说明】本题考查合情推理之类比推理.9. 在平面直角坐标系xOy 中,点P 在曲线C :y =x 3−10x +3上,且在第二象限内,已知曲线C在点P 处的切线的斜率为2,则点P 的坐标为 ▲ . 【答案】(2,15)-.【解析】设点P 的横坐标为x 0,由2310y x '=-知203102x -=,又点P 在第二象限,02x =-,所以(2,15)P -.【说明】本题考查导数的几何意义——曲线切线的斜率.10. 已知a =f (x )=a x ,若实数m ,n 满足f (m )>f (n ),则m ,n 的大小关系为 ▲.【答案】m n <【解析】由01<<知01a <<,函数()x f x a =是减函数,由()()f m f n >知m n <.【说明】本题考查函数的单调性,指数函数的性质等概念.11. 已知集合A ={x |log 2x ≤2},B =(−∞,a ),若A ⊆B ,则实数a 的取值范围是(c ,+∞),其中c =▲ . 【答案】4【解析】由log 2x ≤2得0<x ≤4,(0,4]A =;由A B ⊆知4a >,所以c =4. 【说明】本题考查对数函数的性质,集合间的基本关系(子集)等概念. 12. 设α 和β为不重合的两个平面,给出下列命题:(1)若α 内的两条相交直线分别平行于β内的两条直线,则α 平行于β; (2)若α 外一条直线l 与α 内的一条直线平行,则l 和α 平行;(3)设α 和β相交于直线l ,若α 内有一条直线垂直于l ,则α 和β垂直; (4)直线l 与α 垂直的充分必要条件是l 与α 内的两条直线垂直. 上面命题中,真命题的序号 ▲ .(写出所有真命题的序号). 【答案】(1)(2)【解析】由线面平行的判定定理知,(2)正确;相应地(1)可转化为一个平面内有两相交直线分别平行于另一个平面,所以这两个平面平行.【说明】本题考查空间点、线、面的位置关系.具体考查线面、面面平行、垂直间的关系与转化. 13. 如图,在平面直角坐标系xOy 中,A 1,A 2,B 1,B 2为椭圆22221(0)y x a b a b +=>>的四个顶点,F 为其右焦点,直线A 1B2与直线B 1F 相交于点T ,线段OT 与椭圆的交点M 恰为线段O T 的中点,则该椭圆的离心率为 ▲ .【答案】5【解析】直线12A B 的方程为1yx a b+=-,直线1B F 的方程为1y x c b +=-,两方程联立方程组得T 2(,)ac ab bc a c a c+--,则点M (,)2()ac ab bc a c a c +--,由点M 在椭圆上,代入整理得:223100a ac c --=,23100e e --=,又 0e >,所以离心率为5. 【说明】本题考查椭圆的概念、标准方程与几何性质.14. 设{a n }是公比为q 的等比数列,|q |>1,令b n =a n +1(n =1,2,…)若数列{b n }有连续四项在集合{−53,−23,19,37,82}中,则6q = ▲ . 【答案】9-【解析】由条件知数列{a n }中连续四项在集合{}54,24,18,36,81--中,由||1q >,所以{a n }中连续四项可能为(1)24-,36,54-,81,32q =-,69q =-;(2)18,24-,36,54-,不合;其它情形都不符合.【说明】本题考查等比数列的概念与通项公式.在本题中,如果将集合中的各数均除以3,得到集合{}232323,2,23,32,3-⨯-⨯⨯,再从其中选出四个数进行适当地排列,这样的解法更利于看清问题本质.二、解答题:本大题共6小题,共计90分,请在答题卡指定区域内作答,解答时应写出文字说明、证明或演算步骤.15. (本小题满分14分)设向量a =(4cos α ,sin α ),b =(sin β,4cos β),c =(cos β,−sin β), (1)若a 与b −2c 垂直,求tan(α +β)的值; (2)求+b c 的最大值;(3)若tan α tan β=16,求证:a ∥b . 【解析】(1)∵a ⊥b −2c ,∴(2)20⋅-=⋅-⋅=a b c a b a c .即4sin()8cos()0αβαβ+-+=,∴tan()2αβ+=. (2)(sin cos ,4cos 4sin )ββββ+=+-b c ,()()222sin cos 16cos sin ββββ+=++-b c 1730sin cos ββ=-1715sin 2β=-,∴当sin2β=−1时,2+b c 最大值为32,所以+b c的最大值为(3)∵tan tan 16αβ=,∴sin sin 16cos cos αβαβ=,即4cos 4cos sin sin 0αβαβ⋅-=, 所以a ∥b .16. (本小题满分14分)如图,在直三棱柱ABC −A 1B 1C 1中,E ,F 分别是A 1B ,A 1C 的中点,点D 在B 1C 1上,A 1D ⊥B 1C . 求证:(1)EF ∥平面ABC ; (2)平面A 1FD ⊥平面BB 1C 1C .【解析】(1)因为E ,F 分别是A 1B ,A 1C 的中点,所以EF ∥BC ,又EF ⊄平面ABC ,BC ⊂平面ABC ,∴EF ∥平面ABC ; (2)在直三棱柱ABC −A 1B 1C 1中,1111BB A BC ⊥面,∵A 1D ⊂平面A 1B 1C 1,∴11BB AD ⊥. 又11AD BC ⊥,BB 1 B 1C =B 1,∴111AD BC C ⊥面B . 又11AD AFD ⊂面,所以平面A 1FD ⊥平面BB 1C 1C .17. (本小题满分14分)设{a n }是公差不为零的等差数列,S n 为其前n 项和,满足22225234a a a a +=+,S 7=7. (1)求数列{a n }的通项公式及前n 项和S n ; (2)试求所有的正整数m ,使得12m m m a a a ++为数列{S n }中的项. 【解析】(1)设公差为d ,则22225243a a a a -=-,由性质得43433()()d a a d a a -+=+,因为0d ≠,所以430a a +=,即1250a d +=,又由77S =得176772a d ⨯+=,解得15a =-,2d =所以{}n a 的通项公式为27n a n =-,前n 项和26n S n n =-. (2)12(27)(25)(23)m m m m m a a a m ++--=-,令23m t -=,12(4)(2)m m m t t a aa t++--=86t t =+-, 因为t 是奇数,所以t 可取的值为1±,当1t =,2m =时,863t t +-=,2573⨯-=,是数列{}n a 中的项;1t =-,1m =时,8615t t +-=-,数列{}n a 中的最小项是5-,不符合.所以满足条件的正整数2m =. 18. (本小题满分16分)在平面直角坐标系xOy 中,已知圆C 1∶AB CA1B 1C1 EF D第16题图(x +3)2+(y −1)2=4和圆C 2∶(x −4)2+(y −5)2=4.(1)若直线l 过点A (4,0),且被圆C 1截得的弦长为l 的方程;(2)设P 为平面上的点,满足:存在过点P 的无穷多对互相垂的直线l 1和l 2,它们分别与圆C 1和圆C 2相交,且直线l 1被圆C 1截得的弦长与直线l 2被圆C 2截得的弦长相等,试求所有满足条件的点P 的坐标.【解析】(1) 0y =或7(4)24y x =--,(2)法一)设点P (,)a b ,1l :()y b k x a -=-,则2l :1()y b x a k-=--由截得的弦长相等可得1C 到1l 与2C 到2l 的距离相等,即11|4()5()|a b k k ----+=,即 |31||45|k ka b k a kb ---+=--++,整理得:222222(3)2(3)(1)(1)(5)2(4)(5)(4)a k ab k bb k a b k a +++-+-=-+--+- 因为有无数组解,所以对应项系数相等,解得:32a =-,132b =;或52a =,12b =-.所以满足条件的点P 坐标为313(,)22-或51(,)22-.法二)依题意点P 在线段1C 2C 的中垂线上,且与1C 、2C 构成等腰直角三角形,设点P (,)a b , 则713()42b a -=--,又120PC PC ⋅=,即22670a b a b +---=,解得:32a =-,132b =;或52a =,12b =-. 满足条件的点P 坐标为313(,)22-或51(,)22-.19. (本小题满分16分)按照某学者的理论,假设一个人生产某产品单件成本为a 元,如果他卖出该产品的单价为m 元,则他的满意度为m m a +;如果他买进该产品的单价为n 元,则他的满意度为n n a+.如果一个人对两种交易(卖出或买进)的满意度分别为h 1和h 2,现假设甲生产A ,B 两种产品的单件成本分别为12元和5元,乙生产A ,B 两种产品的单件成本分别为3元和20元,设产品A ,B 的单价分别为m A 元和m B 元,甲买进A 与卖出B 的综合满意度为h 甲,乙卖出A 与买进B 的综合满意度为h 乙.(1)求h 甲和h 乙关于m A ,m B 的表达式;当35A B m m =时,求证:h 甲=h 乙;(2)设35A B m m =,当m A ,m B 分别为多少时,甲、乙两人的综合满意度均最大?最大的综合满意度为多少?(3)记(2)中最大的综合满意度为h 0,试问能否适当选取m A ,m B 的值,使得0h h 甲≥和0h h 乙≥同时成立,但等号不同时成立?试说明理由.【解析】h =甲h =乙当35A B m m =时,h =甲,h =乙h 甲=h 乙.当35A B m m =时,h =甲,而520B m ≤≤, 所以当20B m =时,甲、乙两人的综合满意度均最大,此时12A m =.(3≥即31024120A B A B m m m m ≥++ ①且3406120A B A B m m m m ≥++ ②, 由①及520B m ≤≤得:24120310B A B m m m +≥-,又241202008[12,48]310310B B B m m m +=+∈--, 只有当12A m =,20B m =时,不等式①成立. 由②及312A m ≤≤得:4012036A B A m m m +≥-,又4012040200[20,80]36336A A A m m m +=+∈--, 只有当20B m =,12A m =时,不等式②成立.综上,不存在满足条件的A m 、B m 的值.20. (本小题满分16分)设a 为实数,函数f (x )=2x 2+(x −a )|x −a |. (1)若f (0)≥1,求a 的取值范围; (2)求f (x )的最小值;(3)设函数h (x )=f (x ),x ∈(a ,+∞),直接写出(不需给出演算步骤)不等式h (x )≥1的解集. 【解析】(1)若(0)1f ≥,即||1a a -≥,则{21a a <≥,所以1a ≤-. (2)当x a ≥时,22()32,f x x ax a =-+22min(),02,0()2(),0,033f a a a a f x a a f a a ≥≥⎧⎧⎪⎪==⎨⎨<<⎪⎪⎩⎩ 当x a ≤时,22()2,f x x ax a =+-{{2min 2(),02,0()(),02,0f a a a a f x f a a a a -≥-≥==<<综上22min2,0()2,03a a f x a a -≥⎧⎪=⎨<⎪⎩. (3)x a ≥时,()1h x ≥得223210x ax a -+-≥,222412(1)128a a a ∆=--=-,①当a a ≤≥时,0∆≤,不等式的解集为(,)a +∞;②当a <<0,∆>得(0x x x a ⎧⎪≥⎨>⎪⎩,i a <<时,不等式的解集为(,)a +∞;ii )a ≤≤)+∞;iii )a <<时,不等式的解集为3([)3a a +-+∞.。
江苏省2009年高考人数及考试成绩

江苏省2009年普通高校统一招生考试分段成绩统计表(按普通类总分分段)注:上述统计对象为选测科目等级达到1B1C及以上考生扬州最高430分-----扬州中学高三(3)班女生张孔欣的成绩单:数学197分(附加题37)语文125分英语98分6A加10分总分430分江苏省五十四万人报名参加普通高考据统计,2009年我省有546389人报名参加全国统考,统考人数比2008年的507544人增加了38845人,增幅为7.65%。
报考考生中,男生304209人,占55.7%,女生242180人,占44.3%。
考生中,应届毕业生493449人,占报考总人数的90.31%(其中农村应届毕业生296100人,占报考总人数的54.19%);往届毕业生52940人,占报考总人数的9.69%(其中农村往届毕业生32100人,占报考总人数的5.87%)。
考生中,报考普通类464828人,占85.07%;报考艺术类34153人,占6.25%;报考体育类2810人,占0.51%;报考艺术类兼报普通类36153人,占6.62%;报考体育类兼报普通类8445人,占1.55%。
各市高考报名人数是:南京37795人,无锡30191人,徐州94422人,常州23244人,苏州34890人,南通49434人,连云港41125人,淮安40524人,盐城56463人,扬州32225人,镇江17819人,泰州43086人,宿迁45171人。
2009年江苏省普通高校招生工作基本情况今年我省高考报考人数达到546289人,比去年增加了近4万人,是历年来考试规模最大的一次。
在报考生源中,报考普通类464811人,报考艺术类70306人,报考体育类11172人。
今年共有1484所高校在我省招生,计划在我省招生390313人,其中,本科199374人,占51.08%,专科190939人,占48.92%。
江苏省2009年普通高校招生录取最低控制分数线。
2009年高三7班高考成绩
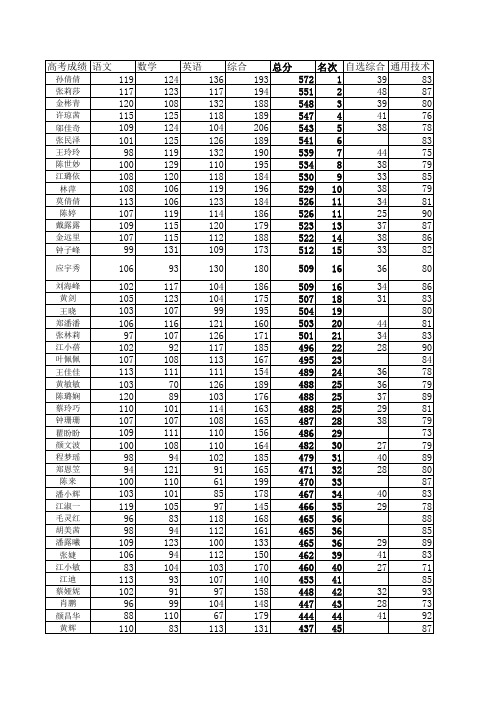
英语 136 117 132 118 104 126 132 110 118 119 123 114 120 112 109 130 104 104 99 121 126 117 113 111 126 103 114 108 110 110 102 91 61 85 97 118 112 100 112 103 107 97 104 67 113 100
总分 572 551 548 547 543 541 539 534 530 529 526 526 523 522 512 509 509 507 504 503 501 496 495 489 488 488 488 487 486 482 479 471 470 467 466 465 465 465 462 460 453 448 447 444 437 437
浙江警官职业学院
海南大学三亚学院 台州学院 台州学院 浙江工商职业技术学院 温州大学城市学院 嘉兴学院 浙江经济职业技术学院 天津滨海职业学院 上海海洋大学 浙江越秀外国语学院 义乌工商职业技术学院 温州科技职业学院 浙江经济职业技术学院 宁波教育学院
宁波大红鹰学院 温州科技职业学院
综合 193 194 188 189 206 189 190 195 184 196 184 186 179 188 173 180 186 175 195 160 171 185 167 154 189 176 163 165 156 164 185 165 199 178 145 168 161 133 150 170 140 158 148 179 131 141
高考成绩 语文
孙倩倩 张莉莎 金彬青 许琼茜 邬佳奇 张民泽 王玲玲 陈世妙 江璐依 林萍 莫倩倩 陈婷 戴露露 金远里 钟子峰 应宇秀 刘海峰 黄剑 王晓 郑潘潘 张林莉 江小蓓 叶佩佩 王佳佳 黄敏敏 陈璐娴 蔡玲巧 钟珊珊 瞿盼盼 颜文波 程梦瑶 郑恩笠 陈来 潘小辉 江淑一 毛灵红 胡美茜 潘露曦 张婕 江小敏 江迪 蔡娅妮 肖鹏 颜昌华 黄辉 郑起虹
2009年江苏省南通市高三12月份十校联考数学试卷

2009年江苏省南通市高三12月份十校联考数学试卷一、填空题(14×5分=70分)1、已知集合{}(1)0P x x x =-≥,Q ={})1ln(|-=x y x ,则PQ = .2、在等比数列{n a }中,若7944,1a a a ⋅==,则12a 的值是 .3、若关于x 的不等式2260ax x a -+<的解集为(1, m ),则实数m = .4、已知点()3,1--和()4,6-在直线320x y a --=的两侧,则a 的取值范围是5、已知βα,⎪⎭⎫⎝⎛∈ππ,43,sin(βα+)=-,53 sin ,13124=⎪⎭⎫ ⎝⎛-πβ则cos ⎪⎭⎫ ⎝⎛+4πα= .6、函数y =log a (2-ax )在[0,1]上是减函数,则a 的取值范围是 .7、若0,0>>y x ,且191=+yx ,求y x +的最小值为 . 8、已知直线0=++C By Ax (其中0,222≠=+C C B A )与圆422=+y x 交于N M ,,O 是坐标原点,则OM ·ON = _________________. 9、已知1()sin xf x e x =,1()(),2n n f x f x n -'=≥,则20081(0)ii f ==∑ .10、如果实数.x y 满足不等式组22110,220x x y x y x y ≥⎧⎪-+≤+⎨⎪--≤⎩则的最小值是11、△ABC 内接于以O 为圆心的圆,且3450OA OB OC +-=.则C ∠= .12、已知576*,)}({S S S n N n a d S n n >>∈且项和的前的等差数列是公差为,则下列四个命题:①0<d ;②011>S ;③012<S ;④013>S 中为真命题的序号为 .13、函数()22log 1log 1x f x x -=+,若()()1221f x f x +=(其中1x 、2x 均大于2),则()12f x x 的最小值为 .14、在Rt ABC ∆中,两直角边分别为a 、b ,设h 为斜边上的高,则222111h a b =+,由此类比:三棱锥S ABC -中的三条侧棱SA 、SB 、SC 两两垂直,且长度分别为a 、b 、c ,设棱锥底面ABC 上的高为h ,则 。
2009年江苏高考语数外全国研讨会

2009年江苏高考语数外全国研讨会作者:来源:《中学课程辅导高考版·教师版》2009年第05期2009年9月18日上午,“2009江苏高考语数外全国研讨会暨高三骨干教师教学观摩活动”在江苏省邗江中学隆重举行。
此次活动由江苏省中小学教师培训学会主办,由《中学课程辅导•高考版》编辑部和江苏省邗江中学联合协办。
大会邀请了南京师范大学教授、文学院学报主编、省语文高考命题组、阅卷组负责人吴锦;教授级中学高级教师、江苏省特级教师、泰州市教育局教科所所长、江苏省高考命题专家石志群;南京师范大学英语系主任、博士、教授、省英语高考命题组、阅卷组负责人汪少华教授,分析2009年高考试卷及2010年高考命题走向,并邀请多位省内优秀青年名师开设观摩示范课,近500名分管校长、主任、高三骨干教师参会。
江苏省中小学教师培训学会会长夏俊生教授,江苏省教育厅人事处处长、江苏省教师培训学会名誉会长鞠勤,原江苏省教育厅厅长、三江学院理事会理事长、校长、党委书记陈万年,扬州市教育局教研室主任辜伟节,邗江区教育局副局长尤善培,江苏省邗江中学校长、邗江区人大副主任徐金才等领导出席了开幕式。
开幕式上,夏俊生教授致开幕词。
他说,这一次盛会是在江苏省出台的“五严”背景下开展的,旨在为我省高中教学献计献策。
各与会代表可以聆听专家讲座,把握高考方向;观摩名师课堂,研讨课堂教学模式;学习名校办学经验,相互取长补短。
陈万年主任和鞠勤处长分别作了重要讲话,他们要求各与会代表要虚心学习、积极发言、勤于思考,要辩证地科学地看待高考考试,辨证地看待考试与人才选拔,特别要研究在规范办学的前提下,如何提高学习效率,如何培养学生创新能力,如何考取更理想的大学等问题。
辜伟节主任代表扬州和邗江区教育局对与会代表的到来表示欢迎。
最后徐金才校长致欢迎辞并介绍学校办学经验。
他说,邗中提出的教育哲学是实施“合道德”的教育,教学模式为道德课堂,包括教室课堂、校园课堂和社区课堂三个部分,从而真正实现素质教育,为学生的终身学习、终身发展和终身幸福奠基。
江苏省2009年高考语文、数学、外语 “访专家、进名校、交名师”研讨会专家讲座摘要

江苏省2009年高考语文、数学、外语“访专家、进名校、交名师”研讨会专家讲座摘要作者:本刊编辑部来源:《中学课程辅导高考版·学生版》2009年第01期2008年10月18日至19日,由江苏省中小学教师培训学会、南京晓庄学院继续教育学院、本刊编辑部在海安中学联合举办了“江苏省2009年高考语文、数学、外语‘访专家、进名校、交名师’研讨会”,会议颇具规模,40多位校长亲自带队,200多所高中,近600名高三语、数、外骨干教师参加了此次盛会。
本届研讨会特邀吴锦教授、汪少华教授、石志群所长作《2008年高考阅卷分析和2009年高考命题走向》专题讲座。
通过亲临名校,聆听权威专家讲座,与一线名师切磋交流,与会代表了解到新课程背景下对新高考学科教学的要求,进一步把握到2009年高考命题的走向和脉搏。
本刊编辑部根据录音和专家讲稿进行整理,现将专家的相关观点和见解摘录如下,供广大师生学习参考。
语文专家讲座2008语文高考阅卷分析与2009命题走向2008年高考语文有所变化,有两个原因:首先这一届高考生是实行新课程标准后第一届考生,高考内容与命题必须要与新课程标准相适应;第二,江苏省2008年实行了新的高考方案,变化较大,考试说明与命题须根据新方案进行调整。
一、关于课程标准问题课程标准的目标是深化教育教学改革,更好地促进素质教育,是语文教学与时俱进的体现。
语文课的性质是工具性和人文性的统一。
工具性,就是应用,掌握语文阅读和语言表达的技巧。
人文性是通过文本来体现的。
语文高考考的是能力。
不考课本的具体篇目和内容,不考名词术语和语词定义。
选考内容和选修课本也没有什么关联,不会考课本,考的是能力。
语文高考考的能力包括语文素养、较强的语文运用能力、一定的探究能力。
第一、语文素养主要是知识性的。
就语文而言,是要培养较高语文素养的人,这个是非常重要的。
与高考相关的就是名句名篇的背诵,江苏高考比较重视名句名篇的考核。
第二、较强的语文应用能力。
2009年江苏高考数学试卷

龙源期刊网
2009年江苏高考数学试卷
作者:王建杜青松
来源:《中学课程辅导高考版·教师版》2009年第04期
江苏省2009年高考数学试卷中的试题保持了去年的特色与风格,加大了对双基的考查,加大了对运算能力的考查,同时注重知识内在的联系,注重了对中学数学中所蕴含的数学思想和方法
的考查。
从试题上看题量和去年一样,但今年填空题1-12题和解答题前三题是比较容易,这样有助于考生有更多的时间来解决中档题和较难题,有助于展示考生的思维过程,有时间来选择和设
计更加合理简洁的运算途径,这与新课改的要求是一致的(运用知识来解决问题,提高学生分析问题的能力)。
试卷在对知识点考查的同时,又关注考生的情感态度与价值观。
试卷已不再过分追求知识点,没有追求热点问题,返璞归真是今年江苏卷的主旋律,也为今后高中数学素质教育指明了方向。
这必将推进高中数学素质教育的课程改革的进程。
下面结合试题从三个方面进行分析:
注:本文中所涉及到的图表、注解、公式等内容请以PDF格式阅读原文。
前名师彭加明对2009年江苏高考12的

数学名师彭加明对2009年江苏高考12、13、14题解答因2009年江苏高考数学试卷整体较易,尤其是前面个填空题除13、14题外基本处于中低档题位置。
高考命题组没有对前面各题做出具体解答。
但好多学生因轻敌或判断失误不注重细节,或计算能力与方法不好造成前面题有一定的失分,主要的失分在第13题其次是14题、12题。
下面就此给出解法以供同学们欣赏。
12、设α和β为不重合的两个平面,给出下列命题:(1)若α内的两条相交直线分别平行于β内的两条直线,则α平行于β; (2)若α外一条直线l 与α内的一条直线平行,则l 和α平行;(3)设α和β相交于直线l ,若α内有一条直线垂直于l ,则α和β垂直; (4)直线l 与α垂直的充分必要条件是l 与α内的两条直线垂直。
上面命题中,真命题...的序号 ★ (写出所有真命题的序号).((1)(2)) 【解析】(1)正确。
面面平行判定定理的应用;(2)正确。
线面平行的判定定理。
(3)错误。
平面α内的直线只垂直于平面β内的一条直线l ,不能说明其垂直于平面β,只有垂直于β内两条相交直线时才能说明该直线与平面β垂直,才能得出α和β垂直。
(413、如图,在平面直角坐标系xOy 中,A 1,A 2,B 1,B 2为 椭圆)0(12222>>=+b a by ax 的四个顶点,F 为其右焦点,直线A 1B 2与直线B 1F 相交于点T ,线段OT 与椭圆的交 点M 恰为线段OT 的中点,则该椭圆的离心率为 ★ . 【解析】由题意可知:,1:,1:121=-+=+-b y cx l by ax l F B B A联立上式解得ca c ab y ca ac x -+=-=)(,2,即))(,2(ca c ab ca ac T -+-,所以))(2,(c a c a M --将点))(2)(,(c a c a b c a acM -+-代入椭圆12222=+by ax 方程得2222222)(4)(41)(4)()(c a c a c c a c a c a c-=++⇒=-++-03100310222=-+⇒=-+⇒e e a ac c解得572-=e 或572--=e (舍)。
关于针对2009年江苏省高考数学试卷分析

HR Planning System Integration and Upgrading Research of
A Suzhou Institution
2009年江苏省高考数学试卷分析
骆继斌
2009年高考数学试卷,总体内容都在大纲规定的范围,现对试卷分析如下:
一、知识点分值分布情况:
三角约20分,概率约5分,复数约5分,集合与不等式约10分,向量约5分,频率分布与算法约10分,导数约20分,解析几何约20分,立体几何约25分,数列约20分,不等式综合运用约20分.
二、考查思想的分布情况:
1.突出数学基础知识,基本技能,基本思想方法的考查
对数学基础知识和基本技能的考查,贴切教学实际,既注重全面,又突出了重点,特别是对中学数学中蕴涵的数学思想方法的考查.如试卷中的1,2,3,4,5,6,7,8,9,15,16.
2.重视数学基本能力和综合应用能力的考查
数学基本能力主要包括空间想象,抽象概括,运算求解,数据处理等几个方面.在这方面对学生的要求比较高,特别是在处理能力方面的要求比较高,如试卷上的
10,11,12,13,14,18,19.
3.注重数学的应用意识和创新意识的考查
数学的应用意识的考查,要求能够运用所学的数学知识,思想和方法,构造数学模型,将一些简单的实际应用问题转化为数学问题,并加以解决.这就要求能够综合,灵活运用所学的数学知识和思想方法,创造性的解决问题.如果17,20.
综上分析,数学试卷的要求基本和考纲吻合,体现了考纲的要求,题目的分布先易后难,特别是最后两题提升的要求比较明显.从而体现了高分不高,均分不底的现象.。
江苏“七年新高考”数学命题人员一览(王琪)

江苏“七年新高考”数学命题人员一览(王琪)江苏“七年新高考”数学命题人员一览2008江苏高考数学命题人员名单葛军:男,副教授,硕士生导师,网称“数学帝”。
葛军南京师范大学数学与计算机科学学院副教授,硕士生导师,中国数学奥林匹克高级教练,江苏省数学会普委会副主任,曾任南京师范大学附属实验学校校长,现任南京师范大学教师教育学院副院长。
曾先后六年为普通高等学校招生全国统一考试江苏卷数学科命题人。
据考生反映,其命题颇具特色,需要考生具有较强的逻辑思维能力和全面的分析问题能力。
试题均具有较高的区分度。
2009江苏高考数学命题人员名单组长:陈永高;研究方向:数论、竞赛数学。
副组长:张兴永;研究方向:偏微分方程、数学建模。
组员:朱江;研究方向:非线性泛函分析、不动点定理。
叶惟寅;研究方向:常微分方程定性理论。
朱占奎;研究方向:竞赛数学。
秘书:曹海涛;研究方向:组合设计、竞赛数学。
2010年江苏高考数学命题人员名单组长:姚天行南京大学研究方向:组合数学与图论数学建模竞赛的总教练副组长:葛军南京师范大学研究方向:竞赛数学中国数学奥林匹克高级教练秘书:曹海涛南京师范大学研究方向:组合设计与编码理论江苏书人教育培训中心数学奥林匹克教练成员:陈永高陆防严孙旭东南京市教研室教研员,普通高中课程标准实验教材编委2011年江苏高考数学命题人员名单组长:姚天行(南大) 成员:周国飞(南大) 曹海涛(南师大) 孙国民张云飞东大和南理工的各一人。
秘书:曹海涛2012年江苏高考数学命题人员名单组长:姚天行南京大学研究方向:组合数学与图论副组长:黄晓学葛军南京师范大学研究方向:竞赛数学成员:王金才刘凯峰何明朱曼丽秘书:曹海涛2013年江苏高考数学命题人员名单组长:河海大学理学院院长陈才生研究方向微分方程,接触大学生建模比赛有关内容。
副组长:南京师范大学数学科学院陈二才研究方向偏物理偏几何秘书:李新建成员:王金才华志远徐卫东2014年江苏高考数学命题人员名单组长:曹海涛10年参加命题)曹海涛男,1976年生,南京师范大学数学与计算机科学学院副教授,最熟悉的研究领域:组合设计与编码理论,现为江苏书人教育培训中心数学奥林匹克教练。
高考数学题型学习方法剖析——以2009年高考数学试题为例

高考数学题型学习方法剖析——以2009年高考数学试题为
例
彭光艳;彭光明
【期刊名称】《兴义民族师范学院学报》
【年(卷),期】2010(000)001
【摘要】高考数学试卷的命题呈现"重点突出,焦点集中,亮点璀璨"等共性,试卷难度一般控制在0.50~0.55之间.题型仍为选择题、填空题及解答题.解答题继续覆盖函数、三角、数列、立体几何(传统法与坐标法均能用)、解析几何、概率、导数等内容,并在每种题型中设置有一定难度的试题,从而实现选拔的功能.对试题有的学生普遍认为难以找到切入点,对基础知识掌握不扎实,方法应用不当,思路不清,空间想象能力、运算能力较差是得分较低的根本原因.这些必须在教师的教学和学生的学习上加以改进.
【总页数】4页(P121-124)
【作者】彭光艳;彭光明
【作者单位】兴义市第六中学,贵州,兴义,562400;兴义民族师范学院,贵州,兴
义,562400
【正文语种】中文
【中图分类】G633.6
【相关文献】
1.2009年江苏省高考数学试卷分析及备考工作总结——从2009年江苏高考数学试题看2010年高考复习 [J], 张敏
2.感受高考数学走近大众学生——兼评2009年江苏高考数学试题 [J], 潘建国
3.基于数学学科核心素养视角的高考数学试题分析——以2018年全国Ⅱ卷高考数学试题为例 [J], 白兴宏;张炳意
4.数学学科核心素养视角下高考数学试题的分析
——以2020年全国Ⅱ卷高考数学试题为例 [J], 白婷娟
5.基于数学核心素养的高考数学试题分析
——以2020年全国Ⅱ卷高考数学试题为例 [J], 周佳婷;朱哲
因版权原因,仅展示原文概要,查看原文内容请购买。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 1
数学名师彭加明对2009年江苏高考12、13、14题解答
因2009年江苏高考数学试卷整体较易,尤其是前面个填空题除13、14题外基本处于中低档题位置。
高考命题组没有对前面各题做出具体解答。
但好多学生因轻敌或判断失误不注重细节,或计算能力与方法不好造成前面题有一定的失分,主要的失分在第13题其次是14题、12题。
下面就此给出解法以供同学们欣赏。
12、设α和β为不重合的两个平面,给出下列命题:
(1)若α内的两条相交直线分别平行于β内的两条直线,则α平行于β; (2)若α外一条直线l 与α内的一条直线平行,则l 和α平行;
(3)设α和β相交于直线l ,若α内有一条直线垂直于l ,则α和β垂直; (4)直线l 与α垂直的充分必要条件是l 与α内的两条直线垂直。
上面命题中,真命题...的序号 ★ (写出所有真命题的序号).((1)(2)) 【解析】(1)正确。
面面平行判定定理的应用;(2)正确。
线面平行的判定定理。
(3)错误。
平面α内的直线只垂直于平面β内的一条直线l ,不能说明其垂直于平面β,只有垂直于β内两条相交直线时才能说明该直线与平面β垂直,才能得出α和β垂直。
(413、如图,在平面直角坐标系xOy 中,A 1,A 2,B 1,B 2为 椭圆
)0(12
22
2>>=+
b a b
y a
x 的四个顶点,F 为其右焦点,
直线A 1B 2与直线B 1F 相交于点T ,线段OT 与椭圆的交 点M 恰为线段OT 的中点,则该椭圆的离心率为 ★ . 【解析】由题意可知:,1:
,1:
12
1
=-+
=+
-b y c
x l b
y a
x l F B B A
联立上式解得c
a c a
b y c
a ac x -+=
-=
)(,2,即))(,
2(c
a c a
b c
a ac T -+-,所以))
(2,
(
c a c a M --
将点))(2)
(,
(
c a c a b c a ac
M -+-代入椭圆
12
22
2=+b
y a
x 方程得
2
222
22
2
)(4)(41)
(4)
()
(c a c a c c a c a c a c
-=++⇒=-++-
031003102
2
2
=-+⇒=-+⇒e e a ac c
解得572-=e 或572--=e (舍)。
14、设{a n }是公比为q 的等比数列,|q|>1,令b n =a n +1(n=1,2,…),若数列{b n }有连续四项在集合{-53,-23,19,37,82}中,则6q= ★
【解析】由题意可知a n ∈{-54,-24,18,36,81},因等比数列中间隔一项的符号相同,而{-54,-24,18,36,81}中有三个正数,所以a n 中必然有两正两负数,而且负数是间隔一项的。
又|q|>1, 1-<∴q 且962
34
924
542-=∴-
=∴=
--=
q q q 。
