第1章 算法初步 复习
《算法初步》复习

一般而言 对一类问题的机械的统 , 一的求解方法称为 算法
a lg orithm
描述算法主要有三种方式:
自然语言 流程图 程序设计语言
1、找到某种算法是指使用一系列运算规则,能在有限
步骤内求解某类问题,并且其中的每条规则必须是明 确定义的、可行的。
2、算法从初始步骤开始,每一个步骤只能有一个确定
如图, 虚线框内是一个顺序结构.其中A 和B两个框是依次执行的.顺序结构是 一种最简单、最基本的结构.
A B
先根据条件作出判断, 再决定执行哪 一种操作的结构称为 选择结构 ( selection structure) 或称为" 分支结构" .
如图所示, 虚线框内是一个选择结 , 构 它包含一个判断框当条件 p 成立(或 , 称为" 真" ) 时执行 A , 否则执行 B .
四、循环语句
当循环的次数已经确定 可用 For " 语句表示." For" , " 语句的一般形式为 : For I From " 初值"To " 终值" Step "步长" End For .
当循环次数不能确定时可 , 用"While " 语句来实现循环 . "While "的一般形式为 While A End While , 其中A表示判断执 行循环 的条件.
条 件 结 构
循 句
循 环 语 句
()
算法的基本思想就是探 求解决问题的一般方法 , 并将解决问题的步骤用 具体化、程序化的语言 加以表述.
描述算法的方式经历了 从简单的自然语言向高 级的计算机程序语言的 发展过程自然语言通俗 . 易懂, 直接明了 流 程图直观 形象, 能 体现算法过 ; 程的结构特征; 伪代 码 将 流 程图的各结构用接 近计算机程序语言的算 法语句进行表述 为编制 , 算机程序提供了便利 .
人教版高中(必修3)第1章算法初步 第1章 算法初步 章末复习课

章末复习课【画一画知识网络、结构更完善】【填要点、记疑点】1.算法的概念算法可以理解为由基本运算及规定的运算顺序所构成的完整的解题步骤,或看成按要求设计好的有限的、确切的计算序列,并且这样的步骤或序列能够解决一类问题.2.程序框图(1)程序框图又称流程图,是一种用规定的图形、流程线及文字说明来准确、直观地表示算法的图形.(2)程序框图由程序框和流程线组成.一个或几个程序框的组合表示算法中的一个步骤:流程线是带方向箭头的指向线,按照算法进行的顺序将程序框连接起来.(3)在利用循环结构画程序框图前,常确定三件事:一是确定循环变量的初始条件;二是确定算法中的循环体;三是循环终止的条件.3.程序设计自然语言表述的算法和程序框图是程序设计的基础,程序框图侧重于直观性,而程序则倾向于计算机执行的实用性.【探题型、提能力】题型一算法设计算法设计应注意:(1)与解决问题的一般方法有联系,从中提炼出算法;(2)将解决问题的过程分为若干个可执行步骤;(3)引入有关的参数或变量对算法步骤加以表达;(4)用最简练的语言将各个步骤表达出来;(5)算法的执行要在有限步内完成.例1 已知平面直角坐标系中两点A (-1,0),B (3,2),写出求线段AB 的垂直平分线方程的一个算法.解 第一步,计算x 0=-1+32=1,y 0=0+22=1,得AB 的中点N (1,1). 第二步,计算k 1=2-03-(-1)=12,得AB 斜率. 第三步,计算k =-1k 1=-2,得AB 垂直平分线的斜率. 第四步,由点斜式得直线AB 的垂直平分线的方程,并输出.跟踪训练1 某工厂2019年生产小轿车200万辆,技术革新后预计每年的生产能力比上一年增加5%,问最早哪一年该厂生产的小轿车数量超过300万辆?写出解决该问题的一个算法.解 算法如下:第一步,令n =0,a =200,r =0.05.第二步,T =ar(计算年增量).第三步,a =a +T(计算年产量).第四步,如果a ≤300,那么n =n +1,返回第二步:否则执行第五步.第五步,N =2 012+n.第六步,输出N.题型二 程序框图及设计算法的设计是画程序框图的基础,我们通过对问题的分析,写出相应的算法步骤.画程序框图之前应先对算法问题设计的合法性和合理性进行探讨,然后分析算法的逻辑结构和各步骤的功能(输入、输出、判断、赋值和计算),画出相应的程序框图.例2 给出以下10个数:5,9,80,43,95,73,28,17,60,36.要求把大于40的数找出来并输出.试画出该问题的算法程序框图.解 程序框图如下:跟踪训练2阅读如图所示的程序框图,运行相应的程序,如果输入某个正整数n后,输出的s∈(10,20),那么n的值为()A.3 B.4C.5 D.6答案B解析逐项验证.若n=3,输出s=7∉(10,20).若n=4时,s=15∈(10,20),选B.题型三算法语句的设计基本算法语句有输入语句、输出语句、赋值语句、条件语句、循环语句五种,它们对应于算法的三种逻辑结构:顺序结构、条件结构、循环结构.用基本语句编写程序时要注意各种语句的格式要求,特别是条件语句和循环语句,应注意这两类语句中条件的表达以及循环语句中有关变量的取值范围.例3给出30个数:1,2,4,7…,其规律是:第1个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第4个数比第3个数大3,依此类推,要计算第30个数的大小,现在已给出了该问题算法的程序框图(如下图)(1)请在图中判断框①处和执行框②处填上合适的语句,使之能完成该题算法功能.(2)根据程序框图写出程序.解(1)①i>30?②P=P+i(2)程序如下:P=1S=0i=1DOS=S+PP=P+ii=i+1LOOP UNTIL i>30PRINT SEND跟踪训练3试设计一个程序来求解这个正三棱柱的表面积和体积,并画出程序框图.解程序如下:INPUT “a=”;aINPUT “h=”;hS=SQR(3)*a^2/4V=S*hC=3PRINT “体积:”;VPRINT “表面积:”;PEND程序框图如图所示,【呈重点、现规律】从近三年高考各省市试题中可以看出,本部分命题呈现以下特点:(1)考题以选择题、填空题为主,属中低档题.(2)考查内容是程序框图,或者要求补充完整框图,或者要求出按程序框图执行后的结果.程序框图中主要以条件结构和循环结构为主,其中循环结构是重点.(3)对基本算法语句仅在2019年江苏、福建高考卷中以填空题的形式出现过;算法案例没有考查.。
知识点总结第一章算法初步

知识点总结第一章算法初步
1.1算法的基本定义
算法(algorithm)定义为一组使机器可以达到特定目标的指令,它是计算机程序的一种基础。
它可以是通过演绎的过程创建出来的,也可以是通过纯粹的归纳的方法创建出来的。
一个典型的算法由不同步骤组成,每个步骤都有一定的功能和有效的设计思想。
1.2算法的实现
算法的实现通常需要使用一定的编程语言进行编程,比如C语言、Java等。
编程语言提供了许多有效的指令,可以用来实现不同的算法。
一般来说,实现算法的步骤有:设计,即把算法的概念写出来;编写,即把设计好的算法代码写出来;测试,即测试程序的正确性;调试,即改正程序中的缺陷。
1.3算法的分析
对于一个算法来说,它执行的时间和空间都是有限的,可以通过空间复杂度和时间复杂度来衡量一个算法的优劣。
一般来说,时间复杂度和空间复杂度可以分别衡量算法中计算和存储资源的消耗情况。
另外,为了使算法的运行效率更好,还可以使用存储技术、排序技术、技术等技术来改进算法的性能。
1.4实例
为了更好的理解算法,下面给出一个实例:输出1到100内的所有自然数。
解法一:使用循环语句,将1到100分别赋值给变量i。
第一章算法的初步

1.1.1算法的概念
例1 设计一个算法,判断1997是否为质数. 第一步,令i=2. 第二步,用i除1997.得到余数r. 第三步,若r=0,则1997不是质数,算法结束,否则给r增加 1仍用i表示. 第四步,判断i>1996是否成立,若是,则1997是质数,算法 结束,否则返回第二步.
1.1.1算法的概念
(1) (2)
的求解步骤
第一步, 1 b2 2 b1,得 a1b2 a2b1 x b2c1 b1c2 . 第二步,解(3)得 x b2c1 b1c2 .
a1b2 a2b1
(3)
第三步, 2 a1 1 a2 , 得 a b a b y a c a c . 1 2 2 1 1 2 2 1
例1 设计一个算法,判断1997是否为质数. 第一步,用2除1997,得到余数1,因为余数不为0,所以2不 能整除1997. 第二步,用3除1997,得到余数1,因为余数不为0,所以3不 能整除1997.
第三步,用4除1997,得余数3,因为余数不为0,所以4不能 整除1997.
…… 第四步,用 5除1997,得到余数2,因为余数不为0,所以5不 能整除1997. 第一九九五步,用1996除1997,得到余数1,因为余数不为0, 所以1996不能整除1997.因此1997是质数.
你能写出“判断整数n(n>2)是否为质数”的算法吗? 第一步,给定一个大于2的整数n 第二步,令i=2 第三步,用i除n,得到余数r 第四步,判断“r=0”是否成立.若是,则n不是质数, 结束算法;否则,将i的值增加1,仍用i表示. 第五步,判断“i>(n-1)”是否成立.若是,则n是质数, 结束算法;否则返回第三步.
7 ,得到余数3.因为余数不为0,所以4不能整除 7 第三步,用4除 35 35. 第四步,用5除 35 ,得到余数2 .因为余数 不 为0,所以5 不 能整除35 0 7. 因此,35不是质数 第五步,用 6除7,得到余数1.因为余数不为0,所以6不能整除7. 因此,7是质数.
第一章算法初步复习总结

第一章算法初步全章小结1、算法概念:在数学上,算法通常是指可以解决的一类问题是程序或步骤,这些程序或步骤必须是,而且能够在。
.2、程序框图基本概念:(1)程序构图的概念:程序框图又称流程图,是一种用规定的图形、指向线及文字说明来准确、直观地表示算法的图形。
(2)构成程序框的图形符号及其作用(3)、算法的三种基本逻辑结构◇:描述的是最简单的算法结构,语句与语句之间,框与框之间按从上到下的顺序进行。
例:◇:是依据指定条件选择执行不同指令的控制结构。
例:◇:根据指定条件决定是否重复执行一条或多条指令的控制结构。
例:3、基本算法语句◇:用来表明赋给某一个变量一个具体的确定的语句叫做赋值语句。
一般格式:变量名=表达式。
注意:赋值号左边只能是变量名字,而不是表达式;如:2=X是错误的。
赋值号左右不能对换;如“A=B”“B=A”的含义运行结果是不同。
不能利用赋值语句进行代数式的演算;(如化简、因式分解、解方程等)赋值号与数学中的等号意义不同。
◇:一般格式:input“提示内容”;变量◇:一般格式:print“提示内容”;表达式◆ :处理条件分支逻辑结构的算法语句。
◆:处理算法中的循环结构。
(1)WHILE 语句的一般格式是(2)UNTIL语句的一般格式是4、算法案例(1)辗转相除法,更相减损之术(求两个正整数最大公约数的算法) 例题1:用两种方法求161与253的最大公约数. 【解析】方法一:辗转相除法253=161×1+92, 161=92×1+69, 92=69×1+23, 69=23×3+0.∴161与253的最大公约数为23.方法二:更相减损术253-161=92, 161-92=69, 92-69=23, 69-23=46, 46-23=23.∴161与253的最大公约数为23.(2)秦九韶算法:求多项式的值时,首先计算最内层括号内依次多项式的值,然后由内向外逐层计算一次多项式的值例题2:已知一个5次多项式为14325)(2345-+-++=x x x x x x f ,用秦九韶算法求这个多项式当x=2时的值.5:进位制例题3:把二进制数234(2),转化为五进制数(先转化为十进制数)。
算法基础知识点复习

第一单元算法基础1.算法的概念及特点。
(1)复述算法的概念;答:答案1:书P6——算法是在有限步骤内求解某一问题所使用的具有精确定义的一系列操作规则。
答案2:——为解决某一问题而设计的确定的有限的步骤称为算法。
(2)解释算法的主要特点;答:书P61、有穷性:指每一个算法都应该在一定的时间和步骤内完成。
2、确定性:指算法的每个步骤必须有确切的含义,而不应当是含糊的、模棱两可的。
3、可行性:指算法中的每一个步骤都必须是实际能做的,而且能在有限的时间内完成。
4、有0个或多个输入:指算法的执行需要从外界获取信息,为算法的某些阶段建立初试状态。
如果建立初试状态所需要的信息已经包含在算法中,那就不再需要输人。
5、有1个或多个输出:指算法用来解决问题的结果应以一定的方式输出,即使问题“无”解答,也需要输出相关信息。
(3)描述用算法解决问题的一般过程。
答:书P3答案1:1、分析问题→2、设计算法→3、编写程序→4、运行程序答案2:1、需求分析→2、设计算法→3、编写程序→4、上机调试与维护2.算法的描述方法;流程图的绘制方法;用流程图来描述算法。
(1)列举算法的描述方法(用自然语言描述、用流程图描述、用程序语言描述实现);答:书P8,1、自然语言描述;2、流程图描述;3、伪代码或直接用计算机程序描述(2)列举常用的流程图符号(起止框、输入输出框、处理框、判断框、流程线等);答:书P 8—P 9开始结束框(即:起止框)判断框输入、输出框流程线处理框连接框(3)根据需要使用合适的流程图符号描述算法;和)(4)描述绘制流程图的基本要求。
3.常量和变量的区别。
(1)复述常量和变量的概念;答:书P57常量——常量是在程序运行过程中值不变的数据或存储单元。
变量——变量用来表示数据的存数区,在程序运行过程中,这些存储区中的值是可以改变的。
(2)比较常量与变量的不同;答:在程序运行过程中,常量的值不变,变量的值可以改变(3)列举数据的基本类型(整型、实数型、字符型、逻辑型等)。
算法初步复习

算法初步复习一、算法1、算法的含义在数学中,算法通常是指。
现在,算法通常可以。
2、算法的特征①;②;③;④;⑤。
二,程序框图1、程序框图又称,是一种用。
2、基本的程序框与它们所表示的功能三,算法的基本逻辑结构1、顺序结构程序框图:程序语句:(1)输入语句(2)输出语句(3)赋值语句2、条件结构程序框图: 程序语句:IF -THEN 格式IF -THEN -ELSE 格式3、循环语句程序框图: 程序语句:① 直到型循环结构 UNTIL 语句② 当型循环结构 WHILE 语句注:常用的运算符号在程序语句中的表示方法:a +b;a -b ;a ⅹb ;a b;a 2 ∣a a 除以b 的余数 ;a 除以b < ;> ;≤ ;≠3 < a < 10 ;a ≤-4或a ≥2四,经典算法案例案例1 绘制计算函数3238257y x x x =-++函数值的程序框图,并编写程序。
案例2 绘制计算函数函数值的程序框图,并编写程序。
案例3 绘制使任意输入的3个正整数按从小到大的顺序输出的程序框图,并编写程序。
案例4绘制计算数列{}3n 的前n 项和S 的程序框图,并编写程序。
2(2)(0)x x +<4(0)x =2(2)(0)x x ->y =案例5 绘制用“二分法”求方程01043=-+x x 的近似解的程序框图,并编写程序。
案例6 绘制判定一个大于2的正整数是否为质数的程序框图,并编写程序。
案例7 利用辗转相除法或更相减损术求下列两数的最大公约数(1)228,1995; (2)5280,12155;案例8 利用秦九韶算法求多项式 765432()765432f x x x x x x x x =++++++当3x =时的值;并指出共进行了多少次乘法与加法运算案例9 完成下列进位制之间的转化(1)10212(3)= (10); (2)2376(8)= (10);(3)119(10)= (6); (4)412(5)= (7);。
算法初步复习(教案)
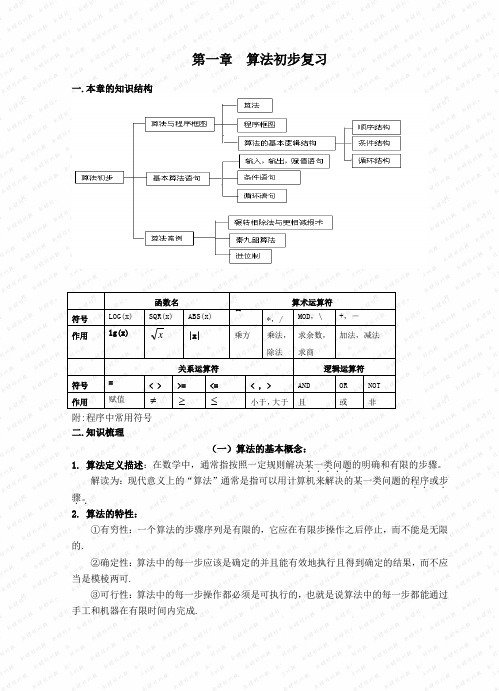
算法初步复习一.本章的知识结构附:程序中常用符号二.知识梳理(一)算法的基本概念:1. 算法定义描述:在数学中,通常指按照一定规则解决某一类问题.....的明确和有限的步骤。
解读为:现代意义上的“算法”通常是指可以用计算机来解决的某一类问题的程序..或步.骤。
..2. 算法的特性:①有穷性:一个算法的步骤序列是有限的,它应在有限步操作之后停止,而不能是无限的.②确定性:算法中的每一步应该是确定的并且能有效地执行且得到确定的结果,而不应当是模棱两可.③可行性:算法中的每一步操作都必须是可执行的,也就是说算法中的每一步都能通过手工和机器在有限时间内完成.函数名 算术运算符符号 LOG(x) SQR(x)ABS(x) ^*,/MOD ,\+,- 作用lg(x)x|x|乘方乘法,除法求余数,求商加法,减法关系运算符 逻辑运算符符号 = < >>=<=< , >ANDOR NOT 作用赋值≠ ≥ ≤小于,大于 且或非3.算法的表示:例1:已知平面直角坐标系中的两点A(-1,0)B(3,2),写出求线段AB的垂直平分线方程的一个算法。
(二)画程序框图三种基本逻辑结构1. 顺序结构2. 条件结构3. 循环结构1)当型循环2)直到型循环(三)编写程序五种基本算法语句1)输入语句INPUT“提示内容”;变量INPUT“提示内容1,提示内容2,…”;变量1,变量2,…2)输出语句PRINT“提示内容”;表达式3)赋值语句变量=表达式4)条件语句IF-THEN-ELSE格式IF-THEN格式IF条件THEN语句1ELSE语句2END IFIF条件THEN语句END IF5)循环语句(1)WHILE语句(2)UNTIL语句WHILE条件循环体WENDDO循环体LOOP UNTIL条件(二)三种基本逻辑结构和五种基本算法语句解读例2 某公司出售软磁盘,购买500片及以上者每片4.5元计价,否则每片按5元计价。
必修知识点总结:第一章算法初步

1、程序框图基本概念:
(一)程序构图的概念:程序框图又称流程图,是一种用规定的图形、指向线及文字说明来准确、直观地表
示算法的图形。
一个程序框图包括以下几部分:表示相应操作的程序框;带箭头的流程线;程序框外必要文字说明。
(二)构成程序框的图形符号及其作用
程起始和结束,是任何流程图不可少 的。
必修知识点总结:第一章-算法 初步
———————————————————————————————— 作者: ———————————————————————————————— 日期:
1.1.1 算法的概念
高中数学必修 3 知识点总结
第一章 算法初步
1、算法概念:
在数学上,现代意义上的“算法”通常是指可以用计算机来解决的某一类问题是程序或步骤,这些程序或步
式 式;(5)提示内容与变量之间用分号“;”隔开,若输入多个变量,变量与变量之间用逗号“,”隔开。
2、输出语句
(1)输出语句的一般格式
PRINT“提示内容”;表达式
图形 计算
Disp “提示内容”,变量
(2)输出语句的作用是实现算法的输出结果功能;(3)“提示内容”提示用户输入什么样的信息,表达式是
3、循环结构:在一些算法中,经常会出现从某处开始,按照一定条件,反复执行某一处理步骤的情况,这就
是循环结构,反复执行的处理步骤为循环体,显然,循环结构中一定包含条件结构。循环结构又称重复结构,
循环结构可细分为两类:
(1)、一类是当型循环结构,如下左图所示,它的功能是当给定的条件 P 成立时,执行 A 框,A 框执行完毕后,
骤必须是明确和有效的,而且能够在有限步之内完成.
2. 算法的特点:
(1)有限性:一个算法的步骤序列是有限的,必须在有限操作之后停止,不能是无限的.
第一章算法初步

第一章算法初步一、算法与程序框图1、算法的概念:在数学中,算法通常指按照一定规则解决某一类...问题明确的...和有限的...步骤。
注意:(1)算法不等同于....某个具体问题的解题过程,它必须能解决一类问题。
(2)解决某类问题的算法不是唯一的。
2、算法的特征:(1)确定性:指一个算法中每一步操作都是明确的,不能模糊或有歧义,算法执行后一定产生明确的结果;(2)有穷性:指一个算法必须能够在有限个步骤之内把问题解决,不能无限的执行下去;(3)可行性:指一个算法对于某一类问题的解决都必须是有效的,切实可行的,并且能够重复使用.3、程序框图定义:程序框图又称流程图,是一种用规定的程序框、流程线及文字说明来准确、直观地表示算法的图形。
程序框名称功能起止框表示一个算法的起始和结束,是任何流程图不可少的。
输入、输出框表示一个算法输入和输出的信息,可用在算法中任何需要输入、输出的位置。
处理框赋值、计算,算法中处理数据需要的算式、公式等分别写在不同的用以处理数据的处理框内。
判断框判断某一条件是否成立,成立时在出口处标明“是”或“Y”;不成立时标明“否”或“N”。
流程线连接程序框连接点连接程序框图的两部分(此表重点掌握)二、算法的三种基本逻辑结构与算法语句(重点)1、顺序结构与输入语句、输出语句、赋值语句顺序结构:由若干个依次执行的步骤组成的算法结构。
输入语句对应输入框;输出语句对应输出框;赋值语句对应处理框。
程序框图:算法语句:注意:(1)输入语句输入的值只能是具体的常数。
(2)赋值语句中的“=”称为赋值号。
(3)赋值语句右边必须是一个数据、常量和算式,左边必须是变量,不能为表达式。
一个赋值语句只能给一个变量赋值;不能连续赋值。
2、条件结构与条件语句条件结构:在算法中通过对条件的判断,根据条件是否成立有不同流向的算法结构。
条件语句中的条件对应程序框图中的条件框。
程序框图: 算法语句:注意:(1)IF 与END IF 要配对使用.(2)END IF 是结束条件语句,END 则是结束整个程序.3、循环结构与循环语句循环结构:需要重复执行某一操作的算法结构。
第一节 算法初步

A.3
B.4
C.5
D.6
解析:执行程序框图,i=1,S=12=1,N =(1+1)(1+2)=6,S≠N;i=2,S=1+22=5, N=(2+1)(2+2)=12,S≠N;i=3,S=5+32= 14,N=(3+1)(3+2)=20,S≠N;i=4,S=14 +42=30,N=(4+1)(4+2)=30,S=N.输出的i
第一节 算法初步
【知识重温】
一、必记6个知识点 1.算法通常是指按照一定规则解决某一类问题的①__明_确___和② ___有__限___的步骤. 2 . 程 序 框 图 又 称 ③__流__程_图___ , 是 一 种 用 ④__程__序__框__ 、 ⑤ ___流_程__线__及⑥_文__字__说_明__来表示算法的图形.通常程序框图由程序框和 流程线组成,一个或几个程序框的组合表示算法中的一个步骤:⑦ ___流_程__线__带方向箭头,按照算法步骤的执行顺序将⑧__程__序_框___连接起 来.
二、教材改编 2.如图所示程序框图的运行结果为____2._5_____.
解析:因为a=2,b=4,所以输出S=24 + 42=2.5.
3.执行下面的程序框图,输出K的值为( )
A.99
B.98
C.100
D.101
解析:执行程序框图,得K=1,S=0;S=0+lg
1+1=
1
lg
2,K=2;S=lg
四、走进高考 6.[2020·全国卷Ⅱ]执行下面的程序框图,若输入的k=0,a=0, 则输出的k为( )
A.2 B.3 C.4 D.5
解析:输入k=0,a=0,第一次循环,a=1, k=1,a<10,第二次循环,a=3,k=2,a<10,第 三次循环,a=7,k=3,a<10,第四次循环,a= 15,k=4,a>10,结束循环,输出k=4.
人教版数学高一-第一章算法初步课件章末复习课

INPUT t IF t<=8 THEN
c=0.2 ELSE
c=0.2+0.1*(t-3) END IF PRINT c END
t=8满足条件“t<=8”,执行c=0.2.
12345
5.用辗转相除法求210和162的最大公约数,并用更相减损术检验. 解答 辗 转 相 除 法 : (210,162)→(48,162)→(18,48)→(12,18)→(6,12) , 12 = 2×6 , 故 210 和 162 的 最 大 公 约 数 为 6. 用 更 相 减 损 术 检 验 : (210,162)→(105,81)→(24,81)→(24,57)→(24,33)→(24,9)→(15,9)→(6,9)→ (6,3)→(3,3), 故210和162的最大公约数为2×3=6.
√C.12+14+16+…+210
D.12+212+213+…+2110
12345
3.两个二进制数101(2)与110(2)的和用十进制数表示为_1_1__. 答案 解析 101(2)=1×22+0×21+1×20=5,110(2)=1×22+1×21+0×20=6.
12345
4.若输入t=8,则下列程序执行后输出的结果是_0_.2__. 答案 解析
反思与感悟
算法的设计与一般意义上的解决问题并不相同,它是对一类问题一般解 法的抽象与概括.我们将一般问题划分为数值型问题和非数值型问题两 类;对于数值型问题,我们可以采用数值分析的方法进行处理,数值分 析中许多现成的固定算法,我们可以直接使用,当然我们也可以根据问 题的实际情况设计算法;对于非数值型问题,可以根据过程模型分析算 法并进行处理,也可以选择一些成熟的办法进行处理,如排序、递推等.
跟踪训练2 执行如图所示的程序框图,若输入x=2,则输出y的值为 __2_3__. 答案 解析
必修三(第一章)算法初步

含条件结构。
循环结构可细分为两类:①当型循环结构
②直到型循环结构
注意:
(1)循环结构要在某个条件下终止循环,这就需要条件结构来判断。因此,循环结构中一定包含条件结构,但不允
许“死循环”。
(2)在循环结构中都有一个计数变量和累加变量。计数变量用于记录循环次数,累加变量用于输出结果。计数变量
和累加变量一般是同步执行的,累加一次,计数一次。
(二)程序框图
4、输入、输出语句和赋值语句:
图形计
(1)输入语句:
算器格式
INPUT“提示内容”;变
INPUT “提示内容”,变
•
作用是实现算法的输入信息功能;
•
“提示内容”提示用户输入什么样的信息,变量是指程序在运行时其值是可以变化的量;
•
输入语句要求输入的值只能是具体的常数,不能是函数、变量或表达式;
(5)在图形符号内描述的语言要非常简练清楚
类型一:求输出结果的程序框图
【例题1】(2015·高考湖南卷)执行如图所示的程序框图,如果输入n=3,则输出的S=(
输入 = 3
= 1, = 0
1
1
=0+
=
1∙3 3
=2
否
∴=
)
6
A.
7
3
B.
7
8
C.
9
4
D.
9
=
1
1
+
3 3∙5
=3
否
=
当x≤2时,y= 2 =x,解得x1=0,x2=1
当2<x≤5时,y=2x-3=x,解得x3=3
18-19 阶段复习课 第1章 算法初步

返 首 页
[规律方法] 算法设计和程序框图是设计程序的基础.编写程序的基本方法是
“自上而下逐步求精”,步骤如下:
1把一个复杂的大问题分解成若干相对独立的小问题.若小问题仍较复杂,则可
以把小问题分解成若干个子问题.这样不断地分解,使小问题或子问题简单到能
直接用程序的三种基本结构甚至是五种基本语句表达清楚为止.
专 题 强
S4 由点斜式得直线 AB 的垂直平分线的方程,并输出.
化 训
练
返 首 页
[规律方法]
1.算法设计与一般意义上的解决问题不同,它是对一类问题的一般解法的抽象
与概括,它往往是把问题的解法划分为若干个可执行的步骤,有时是重复多次,
专
但最终都必须在有限个步骤之内完成.
题 强
化
训
练
返 首 页
2.对于给定的问题,设计其算法时应注意以下五点:
专
程序框图如图.
题 强
化
训
练
返 首 页
[规律方法] 在解答某些数学问题时,有时会有多种情况,需对各种情况加以
分类,并逐类求解,然后综合得结论,这就是分类讨论思想.在具体问题的算
法设计中,往往需要根据条件进行逻辑判断,并进行不同的处理(如条件分支结
专
构和循环结构),这实际上运用了分类讨论的数学思想方法.
专 题 强 化 训 练
图 1-2
A.1
B.2
C.3
D.4
返
首
页
B [开始 a=1,b=1,k=0;
第一次循环 a=-12,k=1;
第二次循环 a=-2,k=2;
专
题
第三次循环 a=1,条件判断为“是”,跳出循环,此时 k=2.]
第一章 算法初步:算法小结复习(1)

(A)k<8?
(B)k≤8?
(C)k≥8?
(D)k>8?
11.如图所示,程序框图(算法流程图)
的输出结果是___1_5__.
12.阅读如图所示的程序框图,运
行相应的程序,输出的结果是( B )
(A)3
(B)11
(C)38
(D)123
A. c > x
B. x > c
B. C. c > b D. b > c
开始
输入a,b,c
x=a
b>x 否
否
是
x=b
是 x=c
输出x
结束
图5
5.如图,若N=5,则输出结果S=___1_2_0_.
6.阅读如图所示的程序框图,
运行相应的程序,输出的结果是( B)
(A)3
(B)11
(C)38
(D)123ຫໍສະໝຸດ 1.阅读如图所示的程序框图, 若运行该程序后,输出的y值为 则输入的实数x的值为______.
3.执行右面的框图,若输出 结果为3,则可输入的实数 值的个数为( C )
A.1 C.3
B.2 D.4
4.右面的程序框图,如果输入三 个实数a、b、c,要求输出这三 个数中最大的数,那么在空白的 判断框中,应该填入下面四个选 项中的(A ).
连接程序框
连接点
连接程序框图的两部分
3.算法的三种基本逻辑结构: (1) 顺序结构-----是由若干个依次执行的处理步骤组成 的.这是任何一个算法都离不开的基本结构.
用程序框图可以表示为:
步骤n
步骤n+1
特征:由若干个依次执行的处理步骤组成的,任何 一个算法都离不开的基本结构.
(2)条件结构---在一个算法中,经常会遇到一些条件 的判断,算法的流向根据条件是否成立有不同的流向. 条件结构就是处理这种过程的结构. 两种常见形式:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第1章 算法初步 复习
【明目标、知重点】
1.加深对算法概念的理解,提高把具体问题的求解转化为算法步骤的能力; 2.理解并掌握画程序框图的规则;
3.在具体问题的解决过程中,理解程序框图的三种基本逻辑结构; 4.能正确选择并运用三种逻辑结构框图表示具体问题的算法. 【探题型、提能力】
题型一 算法的设计,画程序框图,写程序语言
例1 已知函数y =⎩
⎪⎨⎪⎧
-x 2-1 (x ≤-1)
x 3 (x >-1),试设计一个算法,输入x 的值,求对应的函数
值,画出框图并写出程序语句.
跟踪训练 已知函数y =⎩⎪⎨⎪
⎧
2x
-1 (x ≤-1)log 2(x +1) (-1<x <2)
x 2 (x ≥2),试设计一个算法,输入x 的值,求对应
的函数值,画出框图并写出程序语句.
例2画出求12-22+32-42+…+992-1002的值的程序框图并写出程序语句.
跟踪训练设计求1×2×3×4×…×2 013×2 014的值的算法,并画出程序框图并写出程序语句.
例 3.以下是某次考试中某班15名同学的数学成绩:72,91,58,63,84,88,90,55,61,73,64,77,82,94,60,画出求80分以上的同学的平均分的程序框图.
跟踪训练 乘坐火车时,可以托运货物.从甲地到乙地,规定每张火车客票托运费计算方法:
行李质量不超过50 kg 时按0.25元/kg ;超过50 kg 而不超过100 kg 时,其超过部分按0.35元/kg ;超过100 kg 时,其超过部分按0.45元/kg .设计输入行李质量,计算出托运的费用的算法,并画出程序框图.
【呈重点、现规律】
1.在一个问题中经常要进行多次判断,这就需要条件结构嵌套来进行解决.
2.直到型循环结构是先执行一次循环体,然后再判断是否继续执行循环体,当型循环结构是先判断是否执行循环体;直到型循环结构是在条件不满足时执行循环体,当型循环结构是在条件满足时执行循环体.要掌握这两种循环结构,必须抓住它们的区别.
3.算法问题经常涉及到与现实生活有关的题目,解答时,首先根据题意写出内含的表达式,选择适合的结构,设计程序框图,因此,解题的关键是写出函数解析式. 题型二 算法案例
例1.(1)294与84的最大公约数为 ,最小公倍数为
(2)把88化为五进制数是 ,化为六进制数是
(3)求多项式()765432
765432f x x x x x x x x =++++++当3x =的值时
V3=_____________.
跟踪训练
1.三个数72,120,168的最大公约数是____________,最小公倍数为_____________.
2.若六进数()613502m 化为十进数为12710,则
_____m =,把12710化为八进数为____________.
3.完成下列进位制之间的转化.
()21011001=_____________()10=_____________()5 ()8105=_________()10=_____________()5
()5312=_________()7 ()320212=_________()10
(3)用秦九韶方法求多项式1510105)(2345+++++=x x x x x x f 当x=-2时的值。
课时达标训练
1.用二分法求方程的近似根,精确度为δ,用直到型循环结构的终止条件是 ( ) A .|x 1-x 2|>δ B .|x 1-x 2|<δ C .x 1<δ<x 2 D .x 1=x 2=δ
2.阅读如图所示的程序框图,运行相应的程序,则输出的i 值等于 ( )
A .2
B .3
C .4
D .5
3.阅读下边的程序框图,若输出s的值为-7,则判断框内可填写()
A.i<3? B.i<4? C.i<5? D.i<6?
4.根据条件把图中的程序框图补充完整,求区间[1,1 000]内所有奇数的和,(1)处填________;(2)处填________.
5.下图是一个程序框图,则输出的k的值是________.
6.画出求满足12+22+32+…+i2>106的最小正整数n的程序框图.。
