人教中考数学压轴题解题模型几何图形之半角模型含解析汇报
中考数学必会几何模型:半角模型

中考数学必会几何模型:半角模型半角模型是指存在两个角度是一半关系,并且这两个角共顶点的模型。
通过先旋转全等再轴对称全等,一般结论是证明线段和差关系。
常见的半角模型是90°含45°,120°含60°。
例如,已知正方形ABCD中,∠MAN=45°,它的两边分别交线段CB、DC于点M、N。
要求证:BM+DN=MN,以及作AH⊥XXX于点H,求证:AH=AB。
证明过程如下:1.延长ND到E,使DE=BM。
由四边形ABCD是正方形,得AD=AB。
在△ADE和△ABM中,有AD=AB,∠ADE=∠BAM,DE=BM,因此△ADE≌△ABM。
得AE=AM,∠XXX∠BAM。
由∠MAN=45°,得∠BAM+∠NAD=45°,因此∠MAN=∠EAN=45°。
在△AMN和△AEN中,有MA=EA,∠MAN=∠EAN,AN=AN,因此△AMN≌△AEN。
得MN=EN。
因此BM+DN=DE+DN=EN=MN。
2.由(1)得△AMN≌△XXX。
因此S△AMN=S△AEN,即AH×MN=AD×EN。
又因为MN=EN,得AH=AD。
因此AH=AB。
在等边△ABC的两边AB、AC上分别有两点M、N,D为△ABC外一点,且∠MDN=60°,∠BDC=120°,BD=DC。
要探究当M、N分别在线段AB、AC上移动时,BM、NC、MN之间的数量关系。
1) 当DM=DN时,BM、NC、MN之间的数量关系是BM+NC=MN。
2) 猜想:当DM≠DN时,仍有BM+NC=MN。
证明如下:延长AC至E,使CE=BM,连接DE。
因为BD=CD,且∠BDC=120°,所以△BDC是等边三角形。
因此BD=DC=CE=BM,得△BDE是等边三角形,∠BED=60°。
因此△DEN和△DME是等腰三角形,得DN=EN,DM=EM。
2024年中考数学几何模型归纳(全国通用):全等与相似模型-半角模型(教师版)

专题16全等与相似模型-半角模型全等三角形与相似三角形在中考数学几何模块中占据着重要地位。
相似三角形与其它知识点结合以综合题的形式呈现,其变化很多,难度大,是中考的常考题型。
如果大家平时注重解题方法,熟练掌握基本解题模型,再遇到该类问题就信心更足了。
本专题就半角模型进行梳理及对应试题分析,方便掌握。
模型1.半角模型半角模型概念:过多边形一个顶点作两条射线,使这两条射线夹角等于该顶角一半。
思想方法:通过旋转(或截长补短)构造全等三角形,实现线段的转化。
解题思路一般是将半角两边的三角形通过旋转到一边合并成新的三角形,从而进行等量代换,然后证明与半角形成的三角形全等,再通过全等的性质得到线段之间的数量关系。
半角模型(题中出现角度之间的半角关系)利用旋转——证全等——得到相关结论。
【模型展示】1)正方形半角模型条件:四边形ABCD是正方形,∠ECF=45°;结论:①△BCE≌△DCG;②△CEF≌△CGF;③EF=BE+DF;④ AEF的周长=2AB;⑤CE、CF分别平分∠BEF和∠EFD。
2)等腰直角三角形半角模型条件: ABC是等腰直角三角形,∠DAE=45°;结论:①△BAD≌△CAG;②△DAE≌△GAE;③∠ECG==90°;④DE2=BD2+EC2;3)等边三角形半角模型(120°-60°型)条件: ABC 是等边三角形, BDC 是等腰三角形,且BD =CD ,∠BDC =120°,∠EDF =60°;结论:①△BDE ≌△CDG ;②△EDF ≌△GDF ;③EF =BE +FC ;④ AEF 的周长=2AB ;⑤DE 、DF 分别平分∠BEF 和∠EFC 。
4)等边三角形半角模型(60°-30°型)条件: ABC 是等边三角形,∠EAD =30°;结论:①△BDA ≌△CFA ;②△DAE ≌△FAE ;③∠ECF =120°;④DE 2=(12BD +EC)2+2;5)半角模型(2 - 型)条件:∠BAC =2 ,AB =AC ,∠DAE = ;结论:①△BAD ≌△CAF ;②△EAD ≌△EAF ;③∠ECF=180°-2 。
九年级中考几何模型之半角模型详解

中考几何模型之半角模型【模型由来】半角模型是指:共顶点的两个一大一小的角,其中小角是大角的一半。
如下图中:若小角∠EAD等于大角∠BAC的一半,我们习惯上称之为“半角模型”。
【模型思想】通过旋转变化后构造全等三角形,实线边的转化。
【基本模型】类型一、90°中夹45°(正方形中的半角模型)条件:在正方形ABCD中,E、F分别是BC、CD边上的点,∠EAF=45°,BD为对角线,交AE于M点,交AF于N点。
结论①:图1、2中,EF=BE+FD;证明:如图3中,将AF绕点A顺时针旋转90°,F点落在F’处,连接BF’,∴∠EAF’=90°-∠EAF=90°-45°=45°=∠EAF,且AE=AE,AF=AF’,∴△FAE≌△F’AE(SAS),∴EF=EF’,又∠D=∠ABF’=90°,∠ABE=90°,∴∠ABE+∠ABF’=90°+90°=180°,∴F’、B、E三点共线,∴EF’=BE+BF’=BE+DF。
结论②:图2中MN²=BM²+DN²;证明:如图4中,将AN绕点A顺时针旋转90°,N点落在N’处,连接AN’、BN’、MN’,∴∠N’AM=90°-∠EAF=90°-45°=45°=∠MAN,且AM=AM,AN=AN’,∴△MAN’≌△MAN(SAS),∴MN=MN’,又∠ADN=45°=∠ABN ’,∠ABD=45°,∴∠MBN ’=∠ABD+∠ABN ’=45°+45°=90°,∴在Rt △MBN ’中,MN ’²=BM ²+BN ’²,即MN ²=BM ²+BN ’²。
结论③:图1、2中EA 平分∠BEF ,FA 平分∠DFE 。
数学中考复习——半角模型

A
D
45°
F
B
E
C
二、运用模型
⑤ 若点E、F分别在CB、DC的延长线上,∠EAF=45°,那么线段EF、 DF、BE之间有怎样的数量关系?
三、深化模型
正方形ABCD,边长为a,E、F分别为BC、CD上的点,∠EAF=45°, 连接BD交AE于点M,交AF于点N,那么线段DN,MN,BM之间有 什么数量关系?
分别是BC,CD上的点,且∠EAF=60°,探究图中线段BE,EF,FD之间的数量关
系.小王同学探究此问题的方法是,延长FD到点G,使DG=BE,连结AG,先证明
△ABE≌△ADG,再证明△AEF≌△AGF.可得出结论,他的结论是
。
探索延伸:如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是BC,
课堂小结:
这节课你都有哪些收获?
中考链接
数学模型二、坐标系中的等腰直角三角形
——畅想思维飞扬之梦
平面直角坐标系中,△ABC为等腰直角三角形,∠B=90°,点B
坐标为(3,1),求点A的坐标。
y
A
思路剖析: 构造“k型” 全等或“弦图” 全等 解题策略:
过直角顶点和另外一个顶点做
B
坐标轴的垂线
O
中考复习专题
“半角”模型
——奏响思维“直通车”之歌
学习目标:
1.在解题过程中提炼解题策略、经验、方法、技巧。 2.在学习过程中树立模型意识,充分关注模型、提炼 模型、运用模型、深化模型、升华模型。 3.通过导师引领,小组合作,提高学习效率。
一、提炼模型
正方形ABCD,边长为a,E、F分别为BC、CD上的点,∠EAF=45°, 求证:①EF=BE+DF ②∠AEF=∠AEB,∠AFD=∠AFE;③△ECF的周长为正 方形边长的2倍;④点A到EF的距离等于正方形边长。
初中数学突破中考压轴题几何模型之正方形的半角模型教案有答案

初中数学突破中考压轴题几何模型之正方形的半角模型教案有答案 WTD standardization office【WTD 5AB- WTDK 08- WTD 2C】1.掌握正方形的定义,弄清正方形与平行四边形、菱形、矩形的关系。
2.掌握正方形的性质定理1和性质定理2。
3.正确运用正方形的性质解题。
4.通过四边形的从属关系渗透集合思想。
5.通过理解四种四边形内在联系,培养学生辩证观点。
正方形的性质因为正方形是特殊的平行四边形,还是特殊的矩形,特殊的菱形,所以它具有这些图形性质的综合,因此正方形有以下性质(由学生和老师一起总结)。
正方形性质定理1:正方形的四个角都是直角,四条边相等。
正方形性质定理2:正方形的两条对角线相等并且互相垂直平分,每一条对角线平分一组对角。
说明:定理2包括了平行四边形,矩形,菱形对角线的性质,一个题设同时有四个结论,这是该定理的特点,在应用时需要哪个结论就用哪个结论,并非把结论写全。
小结:(1)正方形与矩形,菱形,平行四边形的关系如上图(2)正方形的性质:①正方形对边平行。
②正方形四边相等。
③正方形四个角都是直角。
④正方形对角线相等,互相垂直平分,每条对角线平分一组对角。
例1.如图,折叠正方形纸片ABCD,先折出折痕BD,再折叠使AD边与对角线BD 重合,得折痕DG,使2AD=,求AG.【解析】:作GM⊥BD,垂足为M.由题意可知∠ADG=GDM,则△ADG≌△MDG.∴DM=DA=2. AC=GM又易知:GM=BM.而BM=BD-DM=22-2=2(2-1),∴AG=BM=2(2-1).例2 .如图,P为正方形ABCD内一点,10==,并且P点到CD边的距离也PA PB等于10,求正方形ABCD的面积?【解析】:过P作EF AB⊥于F交DC于E.设PF x =,则10EF x =+,1(10)2BF x =+.由222PB PF BF =+.可得:222110(10)4x x =++.故6x =.216256ABCD S ==.例3. 如图,E 、F 分别为正方形ABCD 的边BC 、CD 上的一点,AM EF ⊥,•垂足为M ,AM AB =,则有EF BE DF =+,为什么? 【解析】:要说明EF=BE+DF ,只需说明BE=EM ,DF=FM 即可,而连结AE 、AF .只要能说明△ABE ≌△AME ,△ADF ≌△AMF 即可.理由:连结AE 、AF .由AB=AM ,AB ⊥BC ,AM ⊥EF ,AE 公用, ∴△ABE ≌△AME . ∴BE=ME .同理可得,△ADF ≌△AMF . ∴DF=MF .∴EF=ME+MF=BE+DF .例4.如下图E 、F 分别在正方形ABCD 的边BC 、CD 上,且45EAF ︒∠=,试说明EF BE DF =+。
中考数学几何专题——半角模型(几何压轴)
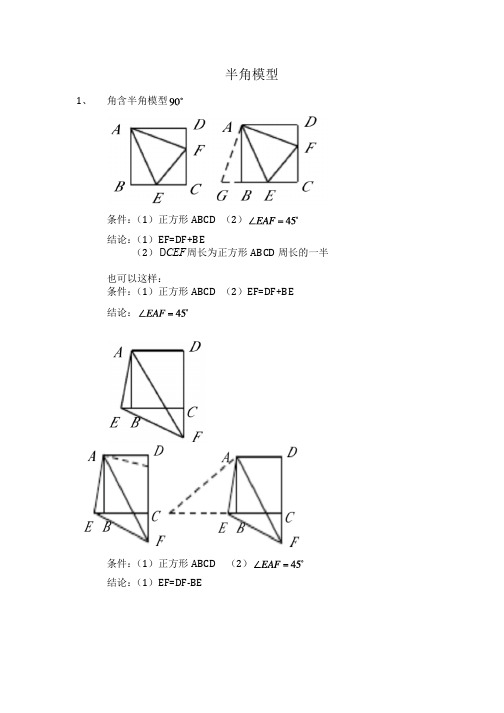
半角模型1、角含半角模型条件:(1)正方形ABCD (2)结论:(1)EF=DF+BE(2)D CEF周长为正方形ABCD周长的一半也可以这样:条件:(1)正方形ABCD (2)EF=DF+BE结论:条件:(1)正方形ABCD (2)结论:(1)EF=DF-BE条件:(1)结论:D AHE为等腰直角三角形证明:连接AC\ÐDAH=ÐCAE\D ADH相似于D ACE\DAAH=ACAE\D AHE相似于D ADC条件:(1)等腰直角D ABC(2)结论:BD2+CE2=DE2若ÐDAE旋转到D ABC外部时结论:BD2+CE2=DE2经典例题1.如图,正方形ABCD中,E、F分别在BC、DC上,且∠EAF=45°.求证:BE+DF=EF.2.如图,在正方形ABCD中,E和F分别是BC和CD上的点,AG⊥EF,∠EAF=45°,求证:AG=AD.3、已知:正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB、DC(或它们的延长线)于点M、N,AH⊥MN于点H.(1)如图①,当∠MAN绕点A旋转到BM=DN时,请你直接写出AH与AB的数量关系:;(2)如图②,当∠MAN绕点A旋转到BM≠DN时,(1)中发现的AH与AB的数量关系还成立吗?如果不成立请写出理由,如果成立请证明;(3)如图③,已知∠MAN=45°,AH⊥MN于点H,且MH=2,NH=3,求AH的长.(可利用(2)得到的结论)4、如图①△ABC是正三角形,△BDC是等腰三角形,BD=CD,∠BDC=120°,以D为顶点作一个60°角,角的两边分别交AB、AC边于M、N,连接MN.(1)探究BM、MN、NC之间的关系,并说明理由.(2)若△ABC的边长为2,求△AMN的周长.(3)若点M、N分别是AB、CA延长线上的点,其它条件不变,在图②中画出图形,并说出BM、MN、NC之间的关系.5.(2014秋•安阳校级期中)在△ABC中,∠BAC=90°,AB=AC,点D和点E均在边BC 上,且∠DAE=45°,试猜想BD.DE.EC应满足的数量关系,并写出推理过程.6.在△ABC中,∠BAC=90°,AB=AC,D、E在直线BC上,∠DAE=45°,(1)写出图中的相似三角形;(2)求证:BE•CD=2S△ABC,并探究BD、DE、CE之间的数量关系,给以证明.7.已知在△ABC中,AB=AC,点D、E在边BC上,将△ABD绕着点A旋转,得到△ACD′,接连D′E交AC于点O.(1)如图1,当△BAC=120°,△DAE=60°时,求证:DE=D′E;(2)如图2,当△DAE=45°,△BAC=90°,BD=DE时,在不舔加任何辅助线的情况下,请直接写出图2中的所有的全等三角形.8.(2014秋•通山县期中)如图1,在Rt△ABC中,∠BAC=90°,AB=AC,点D、E是BC 边上的任意两点,且∠DAE=45°.(1)将△ABD绕点A逆时针旋转90°,得到△ACF,请在图(1)中画出△ACF.(2)在(1)中,连接EF,探究线段BD,EC和DE之间有怎样的数量关系?写出猜想,并说明理由.(3)如图2,M、N分别是正方形ABCD的边BC、CD上一点,且BM+DN=MN,试求△MAN 的大小.9.△ABC的边BC在直线l上,点D,E是直线l上的两点,且BA=BD,CA=CE(1)如图1,若AB=AC,△BAC=90°,求△CAE的度数;(2)如图2,若△BAC=90°,求△CAE的度数;(3)如图3,设△BAC=α,△DAE=β,请直接写出α与β的关系式.10.(2011秋•朝阳区期末)已知,在△ABC中,∠BAC=90°,AB=AC,BC=,点D、E在BC边上(均不与点B、C重合,点D始终在点E左侧),且∠DAE=45°.(1)请在图△中找出两对相似但不全等的三角形,写在横线上,;(2)设BE=m,CD=n,求m与n的函数关系式,并写出自变量n的取值范围;(3)如图△,当BE=CD时,求DE的长;(4)求证:无论BE与CD是否相等,都有DE2=BD2+CE2.11.(2014•平谷区一模)(1)如图1,点E、F分别是正方形ABCD的边BC、CD上的点,∠EAF=45°,连接EF,则EF、BE、FD之间的数量关系是:EF=BE+FD.连结BD,交AE、AF于点M、N,且MN、BM、DN满足MN2=BM2+DN2,请证明这个等量关系;(2)在△ABC中,AB=AC,点D、E分别为BC边上的两点.△如图2,当△BAC=60°,△DAE=30°时,BD、DE、EC应满足的等量关系是;△如图3,当△BAC=α,(0°<α<90°),△DAE=时,BD、DE、EC应满足的等量关系是.[参考:sin2α+cos2α=1]12.(2015•海宁市模拟)(1)探究:如图1和2,四边形ABCD中,已知AB=AD,∠BAD=90°,点E、F分别在BC、CD上,∠EAF=45°.△如图1,若△B、△ADC都是直角,把△ABE绕点A逆时针旋转90°至△ADG,使AB与AD重合,则能证得EF=BE+DF,请写出推理过程;△如图2,若△B、△D都不是直角,则当△B与△D满足数量关系时,仍有EF=BE+DF;(2)拓展:如图3,在△ABC中,△BAC=90°,AB=AC=2,点D、E均在边BC上,且△DAE=45°.若BD=1,求DE的长.13.(2015•滑县一模)(1)问题发现如图1,点E、F分别在正方形ABCD的边BC、CD上,△EAF=45°,连接EF、则EF=BE+DF,试说明理由;(2)类比引申如图2,在四边形ABCD中,AB=AD,△BAD=90°,点E、F分别在边BC、CD上,△EAF=45°,若△B,△D都不是直角,则当△B与△D满足等量关系时,仍有EF=BE+DF;(3)联想拓展如图3,在△ABC中,△BAC=90°,AB=AC,点D、E均在边BC上,且△DAE=45°,猜想BD、DE、EC满足的等量关系,并写出推理过程.14.(2014•山西校级模拟)已知△ABC中,AB=AC,D、E是BC边上的点,将△ABD绕点A旋转,得到△ACD′,连结D′E.(1)如图1,当△BAC=120°,△DAE=60°时,求证:DE=D′E;(2)如图2,当DE=D′E时,△DAE与△BAC有怎样的数量关系?请写出,并说明理由.(3)如图3,在(2)的结论下,当△BAC=90°,BD与DE满足怎样的数量关系时,△D′EC 是等腰直角三角形?(直接写出结论,不必说明理由)。
中考数学压轴题专题角含半角模型

专题15 角含半角模型破题策略1. 等腰直角三角形角含半角如图,在△ABC 中,AB =AC ,∠BAC =90°,点D ,E 在BC 上且∠DAE =45° (1) △BAE ∽△ADE ∽△CDA(2)BD 2+CE 2=DE 2.45°EA BCD证明(1)易得∠ADC =∠B +∠BAD =∠EAB , 所以△BAE ∽△ADE ∽△CD A .(2)方法一(旋转法):如图1,将△ABD 绕点A 逆时针旋转90°得到△ACF ,连结EF .45°FEA BCD则∠EAF =∠EAD =45°,AF =AD , 所以△ADE ∽△FAE ( SAS ). 所以DE = EF .而CF =BD ,∠FCE =∠FCA +∠ACE =90°,所以BD 2+ CE 2=CF 2+CE 2=EF 2=DE 2.方法二(翻折法):如图2,作点B 关于AD 的对称点F ,连结AF ,DF ,EF .45°EA BCD因为∠BAD +∠EAC =∠DAF +∠EAF , 又因为∠BAD =∠DAF ,则∠FAE =∠CAE ,AF =AB =AC , 所以△FAE ∽△CAE (SAS ). 所以EF = E C .而DF =BD , ∠DFE =∠AFD + ∠AFE =90°,所以BD 2+ EC 2= FD 2+ EF 2= DE 2. 【拓展】①如图,在△ ABC 中,AB =AC ,∠BAC =90°,点D 在BC 上,点E 在BC 的延长线上,且∠DAE =45°,则BD 2+CE 2=DE 2.ED可以通过旋转、翻折的方法来证明,如图:EADFEAD②将等腰直角三角形变成任意的等腰三角形:如图,在△ABC 中,AB =AC ,点D ,E 在BC 上,且∠DAE =12∠BAC ,则以BD ,DE ,EC 为三边长的三角形有一个内角度数为180°-∠BA C .B可以通过旋转、翻折的方法将BD ,DE ,EC 转移到一个三角形中,如图:BCEBD2. 正方形角含半角如图1,在正方形ABCD 中,点E ,F 分别在边BC ,CD 上,∠EAF =45°,连结EF ,则:45°图1F ABCD E图2GF E A B DC45°图3H F EABDC(1)EF =BE +DF;(2)如图2,过点A 作AG ⊥EF 于点G ,则AG =AD ;(3)如图3,连结BD 交AE 于点H ,连结FH . 则FH ⊥AE .(1)如图4,将△ABE 绕点A 逆时针旋转90°得到△ADI 证明.图4IF EAB DC则∠IAF =∠EAF =45°,AI =AE , 所以△AEF ∽△AIF (SAS ),所以EF =IF =DI +DF =BE +DF .(2)因为△AEF ∽△AIF ,AG ⊥EF ,AD ⊥IF , 所以AG =A D .(3)由∠HAF =∠HDF =45°可得A ,D ,F ,H 四点共圆, 从而∠AHF =180°-∠ADF =90°, 即FH ⊥AE .【拓展】①如图,在正方形ABCD 中,点E ,F 分别在边CB ,DC 的延长线上,∠EAF =45°,连结EF ,则EF =DF -BE .F BC E可以通过旋转的方法来证明.如图:EBC DAF G②如图,在一组邻边相等、对角互补的四边形ABCD 中,AB =AD ,∠BAD +∠C =180 °,点E ,F 分别在BC 、CD 上,∠EAF =12∠BAD ,连结EF ,则EF=BE+DF. ABFDCE可以通过旋转的方法来证明.如图:ABFDCE G例题讲解例1 如图1,点E 、F 分别在正方形ABCD 的边BC 、CD 上,∠EAF =45°.(1) 试判断BE 、EF 、FD 之间的数量关系.(2) 如图2,在四边形ABCD 中,∠BAD ≠90°,AB =AD .∠B +∠D =180°,点E 、F 分别在BC 、CD 上,则当∠EAF 与∠BAD 满足 关系时,仍有EF =BE +FD .(3)如图3.在某公园的同一水平面上,四条通道围成四边形ABCD .已知AB =AD =80m ,∠B =60°,∠ADC =120°,∠BAD =150°,道路BC ,CD 上分别有景点 E ,F ,且AE ⊥AD .DF =40(3-1)m .现要在E 、F 之间修一条笔直的道路,求这条道路EF 的长.(2=1.413=1.73)图1FA D CBE图2ABD CEF图3FCA EBD解: (1)由“正方形内含半角模型”可得EF =BE +FD . (2)∠BAD =2∠EAF ,理由如下:如图4,延长CD 至点G ,使得DG =BE .连结AG. 易证△ABE ≌△ADG (SAS ). 所以AE =AG ,即EF =BE +DF =DG +DF =GF . 从而证得△AEF ≌△AGF ( SSS ).所以∠EAF =∠GAF =12∠EAG =12∠BAD . 图4AD CF图5HFCGA BED(3)如图5,将△ABE 绕点A 逆时针旋转1 50°至△ADG .连结AF .由题意可得∠BAE =60°所以△ABE 和△ADG 均为等腰直角三角形. 过点A 作 AH ⊥DG 于点H .则DH =12AD =40m ,AH =32 AD =3 m.而DF =4031)m. 所以∠EAF =∠GAF =45°.可得△EAF ≌△GAF (SAS ).所以EF =GF =80m+403l )m ≈109. 2m.例2如图,正方形ABCD 的边长为a ,BM 、DN 分别平分正方形的两个外角,且满足∠MA N =45°.连结MC 、NC 、MN .(1)与△ABM 相似的三角形是 ,BM DN = (用含有a 的代数式表示); (2)求∠MCN 的度数;(3)请你猜想线段BM 、DN 和MN 之间的等量关系,并证明你的结论. NADC BM解:(1)△NDA ,2a . (2)由(1)可得BM ABAD ND=, 所以BM DCBC DN=. 易证∠CBM =∠NDC =45°, 所以△BCM ∽△DNC . 则∠BCM =∠DNC ,所以∠MCN =360°一∠BCD 一∠BCM 一∠DCN =270°- (∠DNC +∠DCN ) =270°-(180°-∠DNC ) =135°.(3) 222BM DN MN +=,证明如下:如图,将△ADN 绕点A 顺时针旋转90°,得到△ABE ,连结EM. 易得AE =AN . ∠MAE =∠MAN =45°,∠EBM =90°, 所以△A ME ≌△AMN .(SAS ). 则ME =MN .在Rt △BME 中,222BM BE EM += 所以222BM DN EM +=.ENBC DAM倒3 如图,在四边形ABCD 中,AD ∥BC ,∠BCD =90°,AB =BC +AD ,∠DAC =45°,E 为CD 上一点,且∠BAE =45°.若CD =4,求△ABE 的面积.图1BADCE解:如图1.过点A 作CB 的垂线,交CB 的延长线于点F .由∠DAC =45°,∠ADC =90°,可得AD =CD.所以四边形ADCF 为正方形. 从而AF = FC =4.令BC =m ,则AB =4+m ,BF =4-m .在Rt △AFB 中,有16+(4-m )2一(4+m )2所以AB =5,BF =3.如图2.将△ADE 绕点A 逆时针旋转90°至△AFG. 易证△AGH ≌△AEB .令DE =n ,则CE =4 -n ,BE =BG =3+n在Rt △BCE 中,有1+(4-n )2=(3+n )2,解得n =47. 所以BG =257. 从而15027ABE ABG S S AF BG ∆∆===. 图2FBADCEG进阶训练1.如图,等边△ABC 的边长为1,D 是△ABC 外一点且∠BDC =120°,BD =CD ,∠MDN =60°,求△AMN 的周长.NDABCM△AMN 的周长是2【提示】如图,延长AC 至点E ,使得CE =BM ,连结DE .先证△BMD ≌△CED ,再证△MDN ≌△EDN 即可.ENDAC BM2.如图,在正方形ABCD 中,连结BD ,E 、F 是边BC ,CD 上的点,△CEF 的周长是正方形ABCD 周长的一半,AE 、AF 分别与BD 交于M 、N ,试判断线段BM 、DN 和MN 之间的数量关系,并证明.NMCDFE BA解:BM 2+DN 2=MN 2.【提示】由△CEF 周长是正方形ABCD 周长的一半,想到“正方形角含半角”,从而旋转构造辅助线解决问题(如图1),证△AEF ≌△AGF ,得∠MAN =12∠BAD =4,然后,再由“等腰直角三角形含半角”(如图2)即可证得.H G G图2图1ABE FDCM NNMCDFE BA3.如图,在△ABC 中,∠ACB =90°,点D 在边AB 上,DE ⊥BC 于点E ,且DE =BC ,点F 在边AC 上,连结BF 交DE 于点G ,若∠DBF =45°,DG =275,BE =3,求CF 的长. G F EDCBA解:CF =125. 【提示】如图,将DE 向左平移至BH ,连结HD 并延长交AC 于点I ,则四边形HBCI 为正方形.将△BHD 绕点B 顺时针旋转90°至△BCJ ,则点J 在AC 的延长线上.连结DF ,由“正方形角含半角模型”可得DF =DH +CF ,∠DFB =∠JFB =∠DGF ,所以DF =DG ,从而求得CF 的长.JIHABC DEF G。
中考数学常见几何模型专题02 全等模型-半角模型(解析版)

专题02 全等模型--半角模型全等三角形在中考数学几何模块中占据着重要地位,也是学生必须掌握的一块内容,本专题就半角模型进行梳理及对应试题分析,方便掌握。
模型1.半角模型【模型解读】过等腰三角形顶点 两条射线,使两条射线的夹角为等腰三角形顶角的一半这样的模型称为半角模型。
【常见模型及证法】常见的图形为正方形,正三角形,等腰直角三角形等,解题思路一般是将半角两边的三角形通过旋转到一边合并成新的三角形,从而进行等量代换,然后证明与半角形成的三角形全等,再通过全等的性质得到线段之间的数量关系。
半角模型(题中出现角度之间的半角关系)利用旋转——证全等——得到相关结论. 1.(2022·湖北十堰·中考真题)【阅读材料】如图①,四边形ABCD 中,AB AD =,180B D ∠+∠=︒,点E ,F 分别在BC ,CD 上,若2BAD EAF ∠∠=,则EF BE DF =+.【解决问题】如图②,在某公园的同一水平面上,四条道路围成四边形ABCD .已知100m CD CB ==,60D ∠=︒,120ABC ∠=︒,150BCD ∠=︒,道路AD ,AB 上分别有景点M ,N ,且100m DM =,)501m BN =,若在M ,N 之间修一条直路,则路线M N →的长比路线M A N →→的长少_________m 1.7≈).【答案】370【分析】延长,AB DC 交于点E ,根据已知条件求得90E ∠=︒,进而根据含30度角的直角三角形的性质,求得,EC EB ,,AE AD ,从而求得AN AM +的长,根据材料可得MN DM BN =+,即可求解.【详解】解:如图,延长,AB DC 交于点E ,连接,CM CN ,60D ∠=︒,120ABC ∠=︒,150BCD ∠=︒,30A ∴∠=︒,90E ∠=︒,100DC DM ==DCM ∴是等边三角形,60DCM ∴∠=︒,90BCM ∴∠=︒,在Rt BCE 中,100BC =,18030ECB BCD ∠=︒-∠=︒,1502EB BC ==,EC ==100DE DC EC ∴=+=+Rt ADE △中,2200AD DE ==+150AE ==,∴200100100AM AD DM =-=+=+()AN AB BN AE EB BN =-=--())15050501=--150=,100150250AM AN ∴+=+=+Rt CMB △中,BM =)50501EN EB BN EC =+=+==ECN ∴是等腰直角三角形()1752NCM BCM NCB BCM NCE BCE DCB ∴∠=∠-∠=∠-∠-∠=︒=∠由阅读材料可得))100501501MN DM BN =+=+=,∴路线M N →的长比路线M A N →→的长少)250501200370+=+≈m .答案:370. 【点睛】本题考查了含30度角的直角三角形的性质,勾股定理,理解题意是解题的关键.2.(2022·河北邢台·九年级期末)学完旋转这一章,老师给同学们出了这样一道题:“如图1,在正方形ABCD 中,∠EAF =45°,求证:EF =BE +DF .”小明同学的思路:∠四边形ABCD 是正方形,∠AB =AD ,∠B =∠ADC =90°.把∠ABE 绕点A 逆时针旋转到ADE '△的位置,然后证明AFE AFE '≌△△,从而可得=EF E F '. E F E D DF BE DF ''=+=+,从而使问题得证.(1)【探究】请你参考小明的解题思路解决下面问题:如图2,在四边形ABCD 中,AB =AD ,∠B =∠D =90°,12EAF BAD ∠=∠,直接写出EF ,BE ,DF 之间的数量关系.(2)【应用】如图3,在四边形ABCD 中,AB =AD ,∠B +∠D =180°,12EAF BAD ∠=∠,求证:EF =BE +DF .(3)【知识迁移】如图4,四边形ABPC 是O的内接四边形,BC 是直径,AB =AC ,请直接写出PB +PC 与AP 的关系. ADE ,证明∠AEF EAF ='E AF ∠先利用圆内接四边形的性质证明为等腰直角三角形,等量代换即得结论.AD 重合,点ADE=180°知,BAD,∠∠BAF=∠EAF=∠,∠EF=E F'∠ABE绕点【点睛】本题考查了旋转与全等三角形的综合应用、直径所对的圆周角是直角、圆内接四边形的性质、等腰直角三角形的判定及性质等知识点.解题关键是利用旋转构造全等三角形.3.(2022·福建·龙岩九年级期中)(1)【发现证明】如图1,在正方形ABCD 中,点E ,F 分别是BC ,CD 边上的动点,且45EAF ∠=︒,求证:EF DF BE =+.小明发现,当把ABE △绕点A 顺时针旋转90°至ADG ,使AB 与AD 重合时能够证明,请你给出证明过程.(2)【类比引申】①如图2,在正方形ABCD 中,如果点E ,F 分别是CB ,DC 延长线上的动点,且45EAF ∠=︒,则(1)中的结论还成立吗?若不成立,请写出EF ,BE ,DF 之间的数量关系______(不要求证明) ②如图3,如果点E ,F 分别是BC ,CD 延长线上的动点,且45EAF ∠=︒,则EF ,BE ,DF 之间的数量关系是_____(不要求证明).(3)【联想拓展】如图1,若正方形ABCD 的边长为6,AE =求AF 的长.180ADF ADG ∴∠+∠=︒,F ∴,D ,G 三点共线,45EAF ∠=︒,45BAE FAD ∴∠+∠=︒,45DAG FAD ∴∠+∠=︒,EAF FAG ∴∠=∠,AF AF =,()EAF GAF SAS ∴∆≅∆,EF FG DF DG ∴==+,EF DF BE ∴=+;(2)①不成立,结论:EF DF BE =-;证明:如图2,将ABE ∆绕点A 顺时针旋转90︒至ADM ∆,EAB MAD ∴∠=∠,AE AM =,90EAM =︒∠,BE DM =,45FAM EAF ∴∠=︒=∠,AF AF =,()EAF MAF SAS ∴∆≅∆,EF FM DF DM DF BE ∴==-=-;②如图3,将ADF ∆绕点A 逆时针旋转90︒至ABN ∆,AN AF ∴=,90NAF ∠=︒,45EAF ∠=︒,45NAE ∴∠=︒,NAE FAE ∴∠=∠,AE AE =,()AFE ANE SAS ∴∆≅∆,EF EN ∴=,BE BN NE DF EF ∴=+=+.正方形Rt EFC中,2CF CE+解得:2x=.2DF∴=,226AF AD DF=+=【点睛】本题属于四边形综合题,主要考查了正方形的性质、旋转的性质、全等三角形的判定与性质以及勾股定理的综合应用,解题的关键是作辅助线构造全等三角形,根据全等三角形的对应边相等进行推导.4.(2022·山东省青岛第二十六中学九年级期中)【模型引入】当几何图形中,两个共顶点的角所在角度是公共大角一半的关系,我们称之为“半角模型”【模型探究】(1)如图1,在正方形ABCD中,E、F分别是AB、BC边上的点,且∠EDF=45°,探究图中线段EF,AE,FC之间的数量关系.【模型应用】(2)如图2,如果四边形ABCD中,AB=AD,∠BAD=∠BCD=90°,∠EAF=45°,且BC=7,DC=13,CF=5,求BE的长.【拓展提高】(3)如图3,在四边形ABCD中,AB=AD,∠ABC与∠ADC互补,点E、F分别在射线CB、DC上,且∠EAF12=∠BAD.当BC=4,DC=7,CF=1时,CEF的周长等于.(4)如图4,正方形ABCD中,AMN的顶点M、N分别在BC、CD边上,AH∠MN,且AH=AB,连接BD分别交AM、AN于点E、F,若MH=2,NH=3,DF=EF的长.(5)如图5,已知菱形ABCD中,∠B=60°,点E、F分别是边BC,CD上的动点(不与端点重合),且∠EAF=60°.连接BD分别与边AE、AF交于M、N,当∠DAF=15°时,求证:MN2+DN2=BM2.又AH=AN,AB=AD,∠∠ABH∠∠ADN(SAS),∠DN=BH,∠ABH=∠ADN,∠∠B=60°,且∠EAF=60°.∠∠BAD=120°,∠∠DAF+∠BAE=∠EAF=60°,∠∠BAG+∠BAE=∠EAF,即∠MAH=∠MAN,而AH=AN,AM=AM,∠∠AMH∠∠AMN(SAS),∠MN=MH,∠AMN=∠AMH,∠菱形ABCD,∠B=60°,∠∠ABD=∠ADB=30°,∠∠HBD=∠ABH+∠ABD=60°,∠∠DAF=15°,∠EAF=60°,∠∠ADM中,∠DAM=∠AMD=75°,∠∠AMN=∠AMH=75°,∠∠HMB=180°-∠AMN-∠AMH=30°,∠∠BHM=90°,∠BH2+MH2=BM2,∠DN2+MN2=BM2.【点睛】本题是四边形综合题,主要考查了旋转的性质、正方形的性质、等腰直角三角形的性质、全等三角形的判定和性质、勾股定理等知识,解题关键是学会用旋转法添加辅助线,构造全等三角形解决问题,学会利用探究的结论解决新的问题,属于中考压轴题.课后专项训练:1.(2022·重庆市育才中学二模)回答问题(1)【初步探索】如图1:在四边形ABCD中,AB=AD,∠B=∠ADC=90°,E、F分别是BC、CD上的点,且EF=BE+FD,探究图中∠BAE、∠F AD、∠EAF之间的数量关系.小王同学探究此问题的方法是:延长FD到点G,使DG=BE.连接AG,先证明△ABE∠∠ADG,再证明△AEF∠∠AGF,可得出结论,他的结论应是_______________;(2)【灵活运用】如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E、F分别是BC、CD上的点,且EF=BE+FD,上述结论是否仍然成立,并说明理由;(3)【拓展延伸】知在四边形ABCD中,∠ABC+∠ADC=180°,AB=AD,若点E在CB的延长线上,点F在CD的延长线上,如图3所示,仍然满足EF=BE+FD,请直接写出∠EAF与∠DAB的数量关系.2.(2022·江西九江·一模)如图(1),在四边形ABCD 中,180B D ∠+∠=︒,AB AD =,以点A 为顶点作EAF ∠,且12EAF BAD ∠=∠,连接EF .(1)观察猜想 如图(2),当90BAD B D ∠=∠=∠=︒时,①四边形ABCD 是______(填特殊四边形的名称);②BE ,DF ,EF 之间的数量关系为______.(2)类比探究 如图(1),线段BE ,DF ,EF 之间的数量关系是否仍然成立?若成立,请加以证明;若不成立,请说明理由.(3)解决问题 如图(3),在ABC 中,90BAC ∠=︒,4AB AC ==,点D ,E 均在边BC 上,且45DAE ∠=︒,若BD =,求DE 的长.证得ABE ADG ≌,得出证得AEF AGF ≌,之间的数量关系;(2)同(1)②即可得出,证得ABD ACM ≌,同(证得AEF AGF ≌,在Rt ECM 中,由勾股定理可解得90BAD B D =∠=∠=︒,ABCD 是矩形,又∠AB AD ,∠矩形CD 至点G ,使得DG=BE 90ADG ADF =∠=︒,∠∠,∠ABE ADG ≌,DG ,BAE DAG ∠=∠BAD ∠,∠BAE DAF ∠+∠∠AEF AGF ≌,∠EF DG EF =∠BE FD +在ABC 中,B ACB ∠=∠∠ABD ACM ≌,同(1)②的证明方法得DE ME =, 2BD =,22+BC AB AC ==DE ME =x -,Rt ECM 中,2EM ,2(2)(32+【点睛】本题考查了特殊的平行四边形的判定、全等三角形的性质和判定及勾股定理的应用,熟练应用相关定理和性质是解决本题的关键.3.(2022·山东聊城·九年级期末)(1)如图1,点E ,F 分别在正方形ABCD 的边BC ,CD 上,45EAF ∠=︒,连接EF ,求证:EF BE DF =+,试说明理由.(2)类比引申:如图2,四边形ABCD 中,AB AD =,90BAD ∠=︒,点E ,F 分别在边BC ,CD 上,∠EAF =45°,若B 、D ∠都不是直角,则当B 与D ∠满足等量关系______时,仍有EF BE DF =+,试说明理由.(3)联想拓展:如图3,在∠ABC 中,90BAC ∠=︒,AB AC =,点D ,E 均在边BC 上,且∠DAE =45,若1BD =,2EC =,求DE 的长.AB AD =∠ADC =∠B =90°∠则DAG ∠∠F AG =∠F AD理由:AB AD==∠BAE DAG∠=︒,BAD90∠+∠=ADC B在∠AFE和∠AFG∴=EF FG()3将∠ACE∠=BAC又∠∠F AB=∠则在∠ADF∠∠ADF∠∠∠∠C+∠ABD4.(2022·黑龙江九年级阶段练习)已知:正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB、DC(或它们的延长线)于点M、N.当∠MAN绕点A旋转到BM=DN时,(如图1),易证BM+DN=MN.(1)当∠MAN 绕点A 旋转到BM ≠DN 时(如图2),线段BM 、DN 和MN 之间有怎样的数量关系?写出猜想,并加以证明;(2)当∠MAN 绕点A 旋转到如图3的位置时,线段BM 、DN 和MN 之间又有怎样的数量关系?请直接写出你的猜想. 【答案】(1)BM DN MN +=,理由见解析;(2)DN BMMN -=,理由见解析【分析】(1)把ADN ∆绕点A 顺时针旋转90︒,得到ABE ∆,然后证明得到AEM ANM ∆∆≌,从而证得ME MN =,可得结论;(2)首先证明ADQ ABM ∆∆≌,得DQ BM =,再证明AMN AQN ∆∆≌,得MN QN =,可得结论; (1)解:BM DN MN +=.理由如下:如图2,把ADN ∆绕点A 顺时针旋转90︒,得到ABE ∆,90ABE ADN ∴∠=∠=︒,AE AN =,BE DN =,180ABE ABC ∴∠+∠=︒,∴点E ,点B ,点C 三点共线,90904545EAM NAM ∴∠=︒-∠=︒-︒=︒,又45NAM ∠=︒,在AEM ∆与ANM ∆中,AE AN EAM NAM AM AM =⎧⎪∠=∠⎨⎪=⎩,AEM ANM ∴∆∆≌(SAS ),ME MN ∴=, ME BE BM DN BM =+=+,DN BM MN ∴+=;(2)解:DN BM MN -=.理由如下:在线段DN 上截取DQ BM =,在ADQ ∆与ABM ∆中,AD AB ADQ ABM DQ BM =⎧⎪∠=∠⎨⎪=⎩,ADQ ABM ∴∆∆≌(SAS ),DAQ BAM ∴∠=∠,QAN MAN ∴∠=∠.在AMN ∆和AQN ∆中,AQ AM QAN MAN AN AN =⎧⎪∠=∠⎨⎪=⎩,AMN AQN ∴∆∆≌(SAS ),MN QN ∴=,DN BM MN ∴-=.【点睛】本题是四边形综合题,考查正方形的性质,旋转变换,全等三角形的判定和性质,勾股定理等知识,解题的关键是学会利用旋转法添加辅助线,构造全等三角形解决问题.5.(2022·重庆南川·九年级期中)如图,正方形ABCD 中,45MAN ∠=︒,MAN ∠绕点A 顺时针旋转,它的两边分别交BC 、DC (或它们的延长线)于点M 、N .(1)当MAN ∠绕点A 旋转到BM DN =时(如图1),证明:2MN BM =;(2)绕点A 旋转到BM DN ≠时(如图2),求证:MN BM DN =+;(3)当MAN ∠绕点A 旋转到如图3位置时,线段BM 、DN 和MN 之间有怎样的数量关系?请写出你的猜想并证明.【答案】(1)见解析(2)见解析(3)DN BM MN -=,见解析【分析】(1)把ADN △绕点A 顺时针旋转90︒,得到ABE △,证得B 、E 、M 三点共线,即可得到AEM △∠ANM ,从而证得ME MN =;(2)证明方法与(1)类似;(3)在线段DN 上截取DQ BM =,判断出ADQ △∠ABM ,同(2)的方法,即可得出结论.(1)证明:如图1,∠把ADN △绕点A 顺时针旋转90︒,得到ABE △,ABE ∴∠ADN △,AE ANM ∴=,ABE D ∠=∠,四边形ABCD 是正方形,90ABC D ∴∠=∠=︒,90ABE ABC ∴∠=∠=︒,∴点E 、B 、M 三点共线.90904545EAM NAM ∴∠=︒-∠=︒-︒=︒,又45NAM ∠=︒,在AEM △与ANM 中,AE AN EAM NAM AM AM =⎧⎪∠=∠⎨⎪=⎩,AEM ∴△∠()ANM SAS ,ME MN ∴=,ME BE BM DN BM =+=+,DN BM MN ∴+=,BM DN =,2MN BM ∴=.(2)证明:如图2,把ADN △绕点A 顺时针旋转90︒,得到ABE △,ABE ∴∠ADN △,AE ANM ∴=,ABE D ∠=∠,四边形ABCD 是正方形,90ABC D ∴∠=∠=︒,90ABE ABC ∴∠=∠=︒,∴点E 、B 、M 三点共线.90904545EAM NAM ∴∠=︒-∠=︒-︒=︒,又45NAM ∠=︒,在AEM △与ANM 中,AE AN EAM NAM AM AM =⎧⎪∠=∠⎨⎪=⎩,AEM ∴△∠()ANM SAS ,ME MN ∴=,ME BE BM DN BM =+=+,DN BM MN ∴+=. (3)解:DN BM MN -= 理由如下:如图3,在线段DN 上截取DQ BM =,连接AQ ,在ADQ △与ABM中,AD AB ADQ ABM DQ BM =⎧⎪∠=∠⎨⎪=⎩,ADQ ∴∠()ABM SAS ,DAQ BAM ∴∠=∠,QAN MAN ∴∠=∠.在AMN 和AQN △中,AQ AM QAN MAN AN AN =⎧⎪∠=∠⎨⎪=⎩,AMN ∴∠()AQN SAS ,MN QN ∴=,DN BM MN ∴-=.【点睛】本题是四边形综合题,考查正方形的性质,旋转变换,全等三角形的判定和性质,勾股定理等知识,学会利用旋转法添加辅助线,构造全等三角形是解题的关键.6.(2022·江西景德镇·九年级期中)(1)【特例探究】如图1,在四边形ABCD 中,AB AD =,90ABC ADC ∠=∠=︒,100BAD ∠=︒,50EAF ∠=︒,猜想并写出线段BE ,DF ,EF 之间的数量关系,证明你的猜想;(2)【迁移推广】如图2,在四边形ABCD 中,AB AD =,180ABC ADC ∠+∠=︒,2BAD EAF ∠∠=.请写出线段BE ,DF ,EF 之间的数量关系,并证明;(3)【拓展应用】如图3,在海上军事演习时,舰艇在指挥中心(O 处)北偏东20°的A 处.舰艇乙在指挥中心南偏西50°的B 处,并且两舰艇在指挥中心的距离相等,接到行动指令后,舰艇甲向正西方向以80海里/时的速度前进,同时舰艇乙沿北偏西60°的方向以90海里/时的速度前进,半小时后,指挥中心观测到甲、乙两舰艇分别到达C ,D 处,且指挥中心观测两舰艇视线之间的夹角为75°.请直接写出此时两舰艇之间的距离.【答案】(1)EF =BE +DF ,理由见解析;(2)EF =BE +DF ,理由见解析;(3)85海里【分析】(1)延长CD 至点G ,使DG =BE ,连接AG ,可证得∠ABE ∠∠ADG ,可得到AE =AG ,∠BAE =∠DAG ,再由100BAD ∠=︒,50EAF ∠=︒,可证得∠AEF ∠∠AGF ,从而得到EF =FG ,即可求解;(2)延长CD 至点H ,使DH =BE ,连接AH ,可证得∠ABE ∠∠ADH ,可得到AE =AH ,∠BAE =∠DAH ,再由2BAD EAF ∠∠=,可证得∠AEF ∠∠AHF ,从而得到EF =FH ,即可求解;(3)连接CD ,延长AC 、BD 交于点M ,根据题意可得∠AOB =2∠COD ,∠OAM +∠OBM =70°+110°=180°,再由(2)【迁移推广】得:CD =AC +BD ,即可求解.【详解】解:(1)EF =BE +DF ,理由如下:如图,延长CD 至点G ,使DG =BE ,连接AG ,∠90ABC ADC∠=∠=︒,∠∠ADG=∠ABC=90°,∠AB=AD,∠∠ABE∠∠ADG,∠AE=AG,∠BAE=∠DAG,∠100BAD∠=︒,50EAF∠=︒,∠∠BAE+∠DAF=50°,∠∠F AG=∠EAF=50°,∠AF=AF,∠∠AEF∠∠AGF,∠EF=FG,∠FG=DG+DF,∠EF=DG+DF=BE+DF;(2)EF=BE+DF,理由如下:如图,延长CD至点H,使DH=BE,连接AH,∠180ABC ADC∠+∠=︒,∠ADC+∠ADH=180°,∠∠ADH=∠ABC,∠AB=AD,∠∠ABE∠∠ADH,∠AE=AH,∠BAE=∠DAH,∠2BAD EAF∠∠=∠∠EAF=∠BAE+∠DAF=∠DAF+∠DAH,∠∠EAF=∠HAF,∠AF=AF,∠∠AEF∠∠AHF,∠EF=FH,∠FH=DH+DF,∠EF=DH+DF=BE+DF;(3)如图,连接CD,延长AC、BD交于点M,根据题意得:∠AOB=20°+90°+40°=150°,∠OBD=60°+50°=110°,∠COD=75°,∠OAM=90°-20°=70°,OA=OB,∠∠AOB=2∠COD,∠OAM+∠OBM=70°+110°=180°,∠OA=OB,∠由(2)【迁移推广】得:CD=AC+BD,∠AC=80×0.5=40,BD=90×0.5=45,∠CD=40+45=85海里.即此时两舰艇之间的距离85海里.【点睛】此题是三角形综合题,主要考查了全等三角形的判定和性质、勾股定理的运用、等腰直角三角形的性质,题目的综合性较强,难度较大,解题的关键是正确的作出辅助线构造全等三角形,解答时,注意类比思想的应用.7.(2022·上海·九年级专题练习)小明遇到这样一个问题:如图1,在Rt∠ABC中,∠BAC=90°,AB=AC,点D,E在边BC上,∠DAE=45°.若BD=3,CE=1,求DE的长.小明发现,将∠ABD 绕点A 按逆时针方向旋转90º,得到∠ACF ,联结EF (如图2),由图形旋转的性质和等腰直角三角形的性质以及∠DAE =45°,可证△F AE ∠△DAE ,得FE =DE .解△FCE ,可求得FE (即DE )的长.(1)请回答:在图2中,∠FCE 的度数是 ,DE 的长为 .参考小明思考问题的方法,解决问题:(2)如图3,在四边形ABCD 中,AB =AD ,∠B +∠D =180°.E ,F 分别是边BC ,CD 上的点,且∠EAF =12∠BAD .猜想线段BE ,EF ,FD 之间的数量关系并说明理由. )根据旋转的性质,可得ADB AFC ≌,勾股定理解按逆时针方向旋转,使AB 与AD 重合,FG =DG +FD =BE +按逆时针方向旋转90º,得到∠ACF ∠ADB AFC ≌ACF ∴∠,90AB AC BAC ∠==45ACF ABD ∴∠=∠=在Rt FCE 中,BD 2EF CF ∴=+(2)猜想:EF =BE 如图,将∠ABE8.(2022·黑龙江·哈尔滨市九年级阶段练习)已知四边形ABCD 是正方形,一个等腰直角三角板的一个锐角顶点与A 点重合,将此三角板绕A 点旋转时,两边分别交直线BC ,CD 于M ,N .(1)如图1,当M ,N 分别在边BC ,CD 上时,求证:BM +DN =MN(2)如图2,当M ,N 分别在边BC ,CD 的延长线上时,请直接写出线段BM ,DN ,MN 之间的数量关系(3)如图3,直线AN 与BC 交于P 点,MN =10,CN =6,MC =8,求CP 的长.【答案】(1)见解析;(2)BM DN MN -=;(3)3【分析】(1)延长CB 到G 使BG DN=,连接AG ,先证明AGB AND ≅△△,由此得到AG AN =,GAB DAN ∠=∠,再根据45MAN ∠=︒,90BAD ∠=︒,可以得到45GAM NAM ∠=∠=︒,从而证明AMN AMG △≌△,然后根据全等三角形的性质即可证明BM DN MN +=;(2)在BM 上取一点G ,使得BG DN =,连接AG ,先证明AGB AND ≅△△,由此得到AG AN =,GAB DAN ∠=∠,由此可得90GAN BAD ∠=∠=︒,再根据45MAN ∠=︒可以得到45GAM NAM ∠=∠=︒,从而证明AMN AMG △≌△,然后根据全等三角形的性质即可证明BM DN MN -=;(3)在DN 上取一点G ,使得DG BM =,连接AG ,先证明ABM ADG ≌,再证明AMN AGN △≌△,设DG BM x ==,根据DC BC =可求得2x =,由此可得6AB BC CD CN ====,最后再证明ABP NCP △≌△,由此即可求得答案.【详解】(1)证明:如图,延长CB 到G 使BG DN =,连接AG ,∠四边形ABCD 是正方形,∠AB AD =,90ABG ADN BAD ∠=∠=∠=︒,在ABG 与ADN △中,AB AD ABG ADN BG DN =⎧⎪∠=∠⎨⎪=⎩, ()AGB AND SAS ∴△≌△,AG AN ∴=,GAB DAN ∠=∠,45MAN ∠=︒,90BAD ∠=︒,∠45DAN BAM BAD MAN ∠+∠=∠-∠=︒,45GAM GAB BAM DAN BAM ∴∠=∠+∠=∠+∠=︒,GAM NAM ∴∠=∠,在AMN 与AMG 中,AM AM GAM NAM AN AG =⎧⎪∠=∠⎨⎪=⎩, ()AMN AMG SAS ∴△≌△,MN GM ∴=,又∠BM GB GM +=,BG DN =,BM DN MN ∴+=;(2)BM DN MN -=,理由如下:如图,在BM 上取一点G ,使得BG DN =,连接AG ,∠四边形ABCD 是正方形,∠AB AD =,90ABG ADN BAD ∠=∠=∠=︒,在ABG 与ADN △中,AB AD ABG ADN GB DN =⎧⎪∠=∠⎨⎪=⎩,()AGB AND SAS ∴△≌△,AG AN ∴=,GAB DAN ∠=∠,∠GAB GAD DAN GAD ∠+∠=∠+∠,∠90GAN BAD ∠=∠=︒,又45MAN ∠=︒,45GAM GAN MAN MAN∴∠=∠-∠=︒=∠,在AMN 与AMG 中,AM AM GAM NAM AN AG =⎧⎪∠=∠⎨⎪=⎩,()AMN AMG SAS ∴△≌△,MN GM ∴=,又∠BM BG GM -=,BG DN =,∠BM DN MN -=,故答案为:BM DN MN -=;(3)如图,在DN 上取一点G ,使得DG BM =,连接AG ,∠四边形ABCD 是正方形,∠AB AD BC CD ===,90ABM ADG BAD ∠=∠=∠=︒,//AB CD ,在ABM 与ADG 中,AB AD ABM ADG BM DG =⎧⎪∠=∠⎨⎪=⎩, ()ABM ADG SAS ∴△≌△,AM AG ∴=,MAB GAD ∠=∠,∠MAB BAG GAD BAG ∠+∠=∠+∠,∠90MAG BAD ∠=∠=︒,又45MAN ∠=︒,45GAN MAG MAN MAN ∴∠=∠-∠=︒=∠,在AMN 与AGN 中,AM AG MAN GAN AN AN =⎧⎪∠=∠⎨⎪=⎩, ()AMN AGN SAS ∴△≌△,10MN GN ∴==,设DG BM x ==,∠6CN =,8MC =,∠1064DC DG GN CN x x =+-=+-=+,8BC MC BM x =-=-, ∠DC BC =,∠48x x +=-,解得:2x =,∠6AB BC CD CN ====,∠//AB CD ,∠BAP CNP ∠=∠,在ABP △与NCP 中,APB NPC BAP CNP AB CN ∠=∠⎧⎪∠=∠⎨⎪=⎩, ()ABP NCP AAS ∴△≌△,9.(2022·浙江·九年级阶段练习)如图1,等腰直角三角板的一个锐角顶点与正方形ABCD的顶点A重合,将此三角板绕点A旋转,使三角板中该锐角的两条边分别交正方形的两边BC,DC于点E,F,连接EF.(1)猜想BE、EF、DF三条线段之间的数量关系,并证明你的猜想;(2)在图1中,过点A作AM∠EF于点M,请直接写出AM和AB的数量关系;∠BAD,(3)如图2,将Rt∠ABC沿斜边AC翻折得到Rt∠ADC,E,F分别是BC,CD边上的点,∠EAF=12连接EF,过点A作AM∠EF于点M,试猜想AM与AB之间的数量关系.并证明你的猜想.10.(2022·北京四中九年级期中)如图,在∠ABC中,∠ACB=90°,CA=CB,点P在线段AB上,作射线CP (0°<∠ACP<45°),射线CP绕点C逆时针旋转45°,得到射线CQ,过点A作AD∠CP于点D,交CQ于点E,连接BE.(1)依题意补全图形;(2)用等式表示线段AD,DE,BE之间的数量关系,并证明.【答案】(1)作图见解析.(2)结论:AD+BE=DE.证明见解析.【分析】(1)根据要求作出图形即可.(2)结论:AD+BE=DE.延长DA至F,使DF=DE,连接CF.利用全等三角形的性质解决问题即可.(1)解:如图所示:(2)结论:AD+BE=DE.理由:延长DA至F,使DF=DE,连接CF.∠AD∠CP,DF=DE,∠CE=CF,∠∠DCF=∠DCE=45°,∠∠ACB=90°,∠∠ACD+∠ECB=45°,∠∠DCA+∠ACF=∠DCF=45°,∠∠FCA=∠ECB,在∠ACF和∠BCE中,CA CB ACF BCE CF CE =⎧⎪∠=∠⎨⎪=⎩,∠∠ACF ∠∠BCE (SAS ),∠AF =BE ,∠AD +BE =DE .【点睛】本题考查作图-旋转变换,全等三角形的判定和性质,等腰直角三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.。
中考数学解题的基本模型半角模型
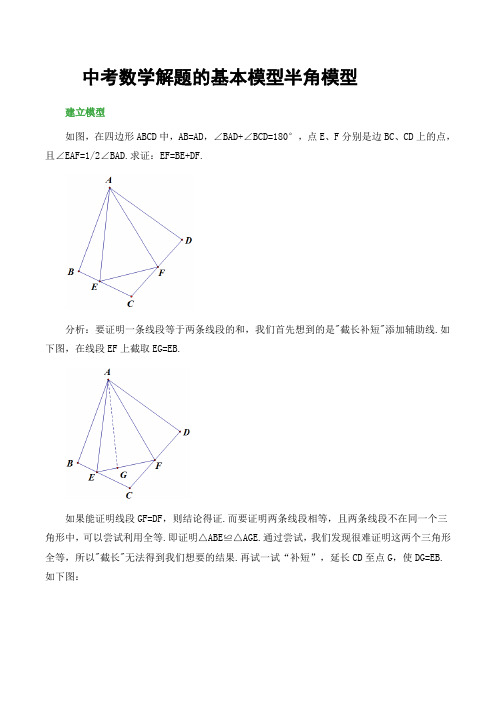
中考数学解题的基本模型半角模型建立模型如图,在四边形ABCD中,AB=AD,∠BAD+∠BCD=180°,点E、F分别是边BC、CD上的点,且∠EAF=1/2∠BAD.求证:EF=BE+DF.分析:要证明一条线段等于两条线段的和,我们首先想到的是"截长补短"添加辅助线.如下图,在线段EF上截取EG=EB.如果能证明线段GF=DF,则结论得证.而要证明两条线段相等,且两条线段不在同一个三角形中,可以尝试利用全等.即证明△ABE≌△AGE.通过尝试,我们发现很难证明这两个三角形全等,所以"截长"无法得到我们想要的结果.再试一试“补短”,延长CD至点G,使DG=EB.如下图:此时若能证明FG=FE,则FE=FG=FD+DG=FD+BE.结论得证.而要证明FE=FG,只需证明△AEF≌AGF即可.证明:延长FD至点G,使DG=BE.易证△ABE≌△ADG(SAS),∴AE=AG,∠BAE=∠DAG.∴∠EAF=1/2∠BAD=∠BAE+∠FAD=∠DAG+∠FAD=∠GAF又∵AF=AF,∴△EAF≌△GAF.∴EF=GF=DF+DG=DF+BE反思:1、本题中的辅助线:延长DG=BE,也可以通过旋转来实现(实际上就是将三角形ABE绕点A逆时针旋转∠BAD的度数).需要指出的是,如果用旋转,需说明C、D、G三点共线(证明∠ADG+∠ADC=180°即可).2、题中有三个非常重要的元素:(1)∠EAF=1/2∠BAD(半角模型名称的由来);(2)AB=AD. 共端点的两条线段相等,这点尤为关键,它为下一步的旋转提供了条件.当题中出现一个角等于另一角的一半,且共端点的线段相等时,常采用旋转,将分散的条件集中起来,为下一步的证明做好铺垫. (3)对角互补.由于对角互补的存在,通过旋转,两边的两个三角形可拼成一个大三角形,进而可证明三角形全等.一、半角结构之90°与45°先来看一道题目:如图,在正方形ABCD中,点E,F分别在BC,CD上,∠EAF=45°.求证:EF=BE+DF.证明:证明:∵四边形ABCD是正方形∴AB=AD且∠ABE+∠ADF=180°将△ABE绕点A逆时针旋转90°得到△ADG,此时点C、D、G三点共线.∴∠BAE=∠DAG,AE=AG. ∵∠EAF=45°∴∠BAE+∠DAF=∠DAG+∠DAF=∠GAF=45°∴∠EAF=∠GAF. 又∵AF=AF.∴△EAF≌△GAF.∴EF=GF=DF+DG=DF+BE.模型应用1:如图,在正方形ABCD中,点E,F分别在边BC,CD上,∠EAF=45°.BE=2cm,DF=3cm.求正方形的边长.分析:根据上题的结论可知EF=BE+DF=5.设正方形的边长为x,那么CE=x-2,CF=x-3.在Rt△CEF中,根据勾股定理得,CE^2+CF^2=EF^2,即(x-2)^2+(x-3)^2=5^2,解得,x=6.所以正方形的边长为6以上的半角结构主要发生在四边形中,再次回顾半角结构中的重要元素:(1)半角(2)邻边相等(3)对角互补. 半角模型中经常通过旋转将分散的条件集中起来,进而通过三角形的全等进行证明.在三角形中同样存在半角模型,下面以一道题为例来说明三角形中的半角模型.如图,在△ABC中,∠BAC=90°,AB=AC.点D,E是BC边上两点且∠DAE=45°求证:BD^2+CE^2=DE^2分析:看到这个结论,相信大部分同学首先想到的是勾股定理,但DE,BD,CE不在同一个三角形中.所以要想办法将他们集中在一个三角形里面,根据题中条件AB=AC,共端点的两条线段相等,可以尝试旋转.证明:因为AB=AC,且∠BAC=90°.将△ABD绕点A逆时针旋转90°得到△ACG,连接EG. 如下图:由旋转的性质可知,△ABD≌△ACG.∴AD=AG,∠BAD=∠CAG,∠ABD=∠ACG=45°.∵∠DAE=45°,∴∠BAD+∠EAC=∠CAG+∠EAC=45°∴∠DAE=∠GAE∴△DAE≌△GAE(SAS)∴DE=GE在Rt△GCE中CE^2+CG^2=GE^2∵BD=CG,DE=CG∴BD^2+CE^2=DE^2反思:对于本题,我们通过旋转将分散的条件集中起来,进而得到结论。
备战中考数学二轮专题归纳提升真题几何模型—半角模型(解析版)
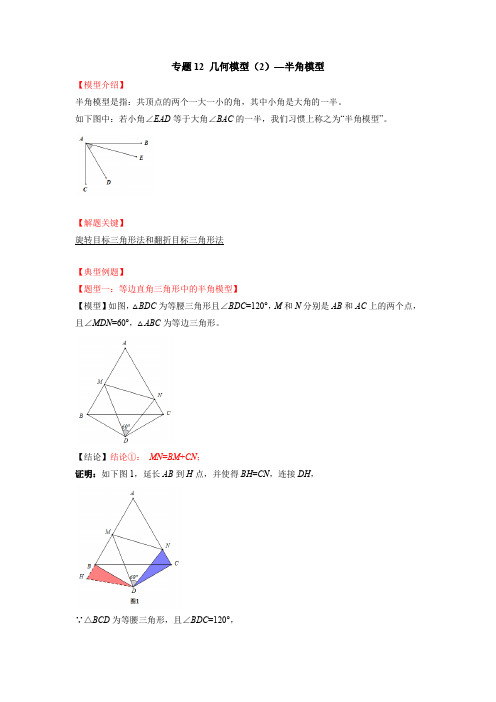
专题12 几何模型(2)—半角模型【模型介绍】半角模型是指:共顶点的两个一大一小的角,其中小角是大角的一半。
如下图中:若小角∠EAD等于大角∠BAC的一半,我们习惯上称之为“半角模型”。
【解题关键】旋转目标三角形法和翻折目标三角形法【典型例题】【题型一:等边直角三角形中的半角模型】【模型】如图,△BDC为等腰三角形且∠BDC=120°,M和N分别是AB和AC上的两个点,且∠MDN=60°,△ABC为等边三角形。
【结论】结论①:MN=BM+CN;证明:如下图1,延长AB到H点,并使得BH=CN,连接DH,∵△BCD为等腰三角形,且∠BDC=120°,∴∠DBC=∠DCB=30°,∵△ABC为等边三角形,∴∠ABC=∠ACB=60°,∴∠ABD=∠ABC+∠DBC=60°+30°=90°=∠ACD,即∠HBD=∠NCD=90°,在△HBD和△NC D中:{BH=CN∠HBD=∠NCD=90∘DB=DC∴△HBD≌△NCD(SAS),∴DH=DN,∠HDB=∠CDN,又∠BDC=120°,∠MDN=60°,∴∠BDM+∠CDN=60°,即∠BDM+∠HDB=60°,∴∠HDM=∠NDM=60°,在△HDM和△NDM中:{HD=DN∠HDM=∠NDM=60∘MD=MD∴△HDM≌△NDM(SAS),∴MN=MH=MB+BH=MB+CN。
证明完毕!结论②:如上图1中:△AMN的周长=2倍等边△ABC的边长;或者说成:3倍△AMN的周长=2倍等边三角形的周长。
证明:由结论①知:MN=MB+CN,CΔAMN=AM+AN+MN=AM+AN+(MB+CN)=(AM+MB)+(AN+NC)=AB+AC=2AB【例】如图,△ABC是边长为2的等边三角形,△BDC是顶角为120°的等腰三角形,以点D 为顶点作∠MDN=60°,点M、N分别在AB、AC上.(1)如图①,当MN//BC时,则△AMN的周长为______;(2)如图②,求证:BM+NC=MN.【答案】(1)4;(2)证明见解析【解析】解:(1)∵△ABC 是等边三角形,MN //BC ,∴∠AMN =∠ABC =60°,∠ANM =∠ACB =60°∴△AMN 是等边三角形,∴AM =AN ,则BM =NC ,∵△BDC 是顶角∠BDC =120°的等腰三角形,∴∠DBC =∠DCB =30°,∴∠DBM =∠DCN =90°在△BDM 和△CDN 中,{BM =CN,∠MBD =∠DCN,BD =CD,∴△BDM ≌△CDN (SAS )∴DM =DN ,∠BDM =∠CDN ,∵∠MDN =60°,∴△DMN 是等边三角形,∠BDM ∠CDN =30°,∴NC =BM =12DM =12MN∴MN =MB +NC ,∴△AMN 的周长=AB +AC =4.(2)如图,延长AC 至点E ,使得CE =BM ,连接DE ,∵△ABC 是等边三角形,△BDC 是顶角∠BDC =120°的等腰三角形,∴∠ABC =∠ACB =60°,∠DBC =∠DCB =30°,∴∠ABD =∠ACD =90°,∴∠DCE =90°,在△BDM 和△CDE 中,{BD =CD,∠MBD =∠ECD,BM =CE,∴△BDM ≌△CDE (SAS ),∴MD =ED ,∠MDB =∠EDC∴∠MDE=120°-∠MDB+∠EDC=120°,∵∠MDN=60°,∴∠EDN=60°,在△MDN和△EDN中,{MD=ED,∠MDN=∠NDE=60°,DN=DN,∴△NDM≌△NDE(SAS),∴MN=NE,又∵NE=NC+CE=NC+BM,∴BM+NC=MN.【练1】如图,△ABC是边长为3的等边三角形,△BDC是等腰三角形,且∠BDC=120°,以D为顶点作一个60°角,使其两边分别交AB于点M,交AC于点N,连接MN,求△AMN的周长.【答案】△AMN的周长为6.【解析】解:∵△BDC是等腰三角形,且∠BDC=120°∴∠BCD=∠DBC=30°∵△ABC是边长为3的等边三角形∴∠ABC=∠BAC=∠BCA=60°∴∠DBA=∠DCA=90°延长AB至F,使BF=CN,连接DF,在Rt△BDF和Rt△CN D中,BF=CN,DB=DC∴△BDF≌△CDN,∴∠BDF=∠CDN,DF=DN∵∠MDN=60°∴∠BDM+∠CDN=60°∴∠BDM+∠BDF=60°,∠FDM=60°=∠MDN,DM为公共边∴△DMN≌△DMF,∴MN=MF∴△AMN的周长是:AM+AN+MN=AM+MB+BF+AN=AB+AC=6.【练2】在等边△ABC的两边AB、AC所在直线上分别有两点M、N,D为△ABC外一点,且∠MDN=60°,∠BDC=120°,BD=D C.探究:当M、N分别在直线AB、AC上移动时,BM、NC、MN之间的数量关系及△AMN的周长Q与等边△ABC的周长L的关系.(1)如图1,当点M、N边AB、AC上,且DM=DN时,BM、NC、MN之间的数量关系=;是;此时QL(2)如图2,点M、N在边AB、AC上,且当DM≠DN时,猜想(I)问的两个结论还成立吗?若成立请直接写出你的结论;若不成立请说明理由.(3)如图3,当M、N分别在边AB、CA的延长线上时,探索BM、NC、MN之间的数量关系如何?并给出证明.【答案】(1)BM+NC=MN,2;3(2)结论仍然成立,详见解析;(3)NC﹣BM=MN,详见解析【解析】(1)如图1,BM、NC、MN之间的数量关系BM+NC=MN.此时QL =23.理由:∵DM=DN,∠MDN=60°,∴△MDN是等边三角形,∵△ABC是等边三角形,∴∠A=60°,∵BD=CD,∠BDC=120°,∴∠DBC=∠DCB=30°,∴∠MBD=∠NCD=90°,∵DM=DN,BD=CD,∴Rt△BDM≌Rt△CDN,∴∠BDM=∠CDN=30°,BM=CN,∴DM=2BM,DN=2CN,∴MN=2BM=2CN=BM+CN;∴AM=AN,∴△AMN是等边三角形,∵AB=AM+BM,∴AM:AB=2:3,∴QL =23;(2)猜想:结论仍然成立.证明:在NC的延长线上截取CM1=BM,连接DM1.∵∠MBD=∠M1CD=90°,BD=CD,∴△DBM≌△DCM1,∴DM=DM1,∠MBD=∠M1CD,M1C=BM,∵∠MDN=60°,∠BDC=120°,∴∠M1DN=∠MDN=60°,∴△MDN≌△M1DN,∴MN=M1N=M1C+NC=BM+NC,∴△AMN的周长为:AM+MN+AN=AM+BM+CN+AN=AB+AC,∴QL =23;(3)证明:在CN上截取CM1=BM,连接DM1.∵∠MBD=∠M1CD=90°,BD=CD,∴△DBM≌△DCM1,∴DM=DM1,∠MBD=∠M1CD,M1C=BM,∵∠MDN=60°,∠BDC=120°,∴∠M1DN=∠MDN=60°,∴△MDN≌△M1DN,∴MN=M1N.∴NC﹣BM=MN.【题型二:等腰直角三角形中的半角模型】【模型】:如图,在△AB C中,AB=AC,∠BAC=90°,点D,E在BC上,且∠DAE=45°作法1:将△ABD旋转90°作法2:分别翻折△ABD,△ACE【结论】BD 2+CE 2=DE 2(证明与正方形中的半角模型类似)【例】如图,等腰直角三角形AB C 中,∠BAC = 90°,AB =AC ,点M ,N 在边BC 上,且∠MAN =45°.若BM = 1,CN =3,求MN 的长.【答案】√10【解析】解:如图,过点C 作CE ⊥BC ,垂足为点C ,截取CE ,使CE =BM .连接AE 、EN .∵AB =AC ,∠BAC =90°,∴∠B =∠ACB =45°.∵CE ⊥BC ,∴∠ACE =∠B =45°.在△ABM 和△ACE 中{AB =AC∠B =∠ACE BM =CE,∴△ABM ≌△ACE (SAS ).∴AM =AE ,∠BAM =∠CAE .∵∠BAC =90°,∠MAN =45°,∴∠BAM +∠CAN =45°.于是,由∠BAM =∠CAE ,得∠MAN =∠EAN =45°.在△MAN 和△EAN 中{AM =AE∠MAN =∠EAN AN =AN,∴△MAN ≌△EAN (SAS ).∴MN =EN .在Rt △EN C 中,由勾股定理,得EN 2=EC 2+NC 2.∴MN 2=BM 2+NC 2.∵BM =1,CN =3,∴MN 2=12+32,∴MN =√10.【练1】如图,在四边形ABC D 中,AB =AD ,BC =CD ,∠ABC =∠ADC =90°,∠MAN =∠BA D .(1)如图1,将∠MAN 绕着A 点旋转,它的两边分别交边BC 、CD 于M 、N ,试判断这一过程中线段BM 、DN 和MN 之间有怎样的数量关系?直接写出结论,不用证明;(2)如图2,将∠MAN 绕着A 点旋转,它的两边分别交边BC 、CD 的延长线于M 、N ,试判断这一过程中线段BM 、DN 和MN 之间有怎样的数量关系?并证明你的结论;(3)如图3,将∠MAN 绕着A 点旋转,它的两边分别交边BC 、CD 的反向延长线于M 、N ,试判断这一过程中线段BM 、DN 和MN 之间有怎样的数量关系?直接写出结论,不用证明.【答案】证明见解析【解答】解:(1)证明:如图,延长MB 到G ,使BG =DN ,连接AG .∵∠ABG=∠ABC=∠ADC=90°,AB=AD,∴△ABG≌△ADN.∴AG=AN,BG=DN,∠1=∠4.∠BA D.∴∠1+∠2=∠4+∠2=∠MAN=12∴∠GAM=∠MAN.又AM=AM,∴△AMG≌△AMN.∴MG=MN.∵MG=BM+BG.∴MN=BM+DN.(2)MN=BM﹣DN.证明:如图,在BM上截取BG,使BG=DN,连接AG.∵∠ABC=∠ADC=90°,AD=AB,∴△ADN≌△ABG,∴AN=AG,∠NAD=∠GAB,∠DAB,∴∠MAN=∠NAD+∠BAM=12∠BAD,∴∠MAG=12∴∠MAN=∠MAG,∴△MAN≌△MAG,∴MN=MG,∴MN=BM﹣DN.(3)MN=DN﹣BM.【练2】已知:如图(1)在Rt△AB C中,∠BAC=90°,AB=AC,点D、E分别为线段BC 上两动点,若∠DAE=45°.探究线段BD、DE、EC三条线段之间的数量关系:(1)猜想BD、DE、EC三条线段之间存在的数量关系式,直接写出你的猜想;(2)当动点E在线段BC上,动点D运动在线段CB延长线上时,如图(2),其它条件不变,(1)中探究的结论是否发生改变?请说明你的猜想并给予证明;(3)已知:如图(3),等边三角形AB C中,点D、E在边AB上,且∠DCE=30°,请你找出一个条件,使线段DE、AD、EB能构成一个等腰三角形,并求出此时等腰三角形顶角的度数.【答案】(1)DE2=BD2+EC2;(2)关系式DE2=BD2+EC2仍然成立,详见解析;(3)当AD=BE时,线段DE、AD、EB能构成一个等腰三角形,且顶角∠DFE为120°.【解析】解:(1)DE2=BD2+EC2;证明:如图,将△ADB沿直线AD对折,得△AFD,连FE,∴△AFD≌△ABD,∴AF=AB,FD=DB,∠F AD=∠BAD,∠AFD=∠ABD,∵∠BAC=90°,∠DAE=45°∴∠BAD+∠CAE=45°,∠F AD+∠F AE=45°,∴∠CAE=∠F AE又AE=AE,AF=AB=AC∴△AFE≌△ACE,∴∠DFE=∠AFD+∠AFE=45°+45°=90°,∴DE2=FD2+EF2∴DE2=BD2+EC2;(2)关系式DE2=BD2+EC2仍然成立.证明:将△ADB沿直线AD对折,得△AFD,连FE∴△AFD≌△ABD,∴AF=AB,FD=DB,∠F AD=∠BAD,∠AFD=∠ABD,又∵AB=AC,∴AF=AC,∵∠F AE=∠F AD+∠DAE=∠F AD+45°,∠EAC=∠BAC﹣∠BAE=90°﹣(∠DAE﹣∠DAB)=45°+∠DAB,∴∠F AE=∠EAC,又∵AE=AE,∴△AFE≌△ACE,∴FE=EC,∠AFE=∠ACE=45°,∠AFD=∠ABD=180°﹣∠ABC=135°∴∠DFE=∠AFD﹣∠AFE=135°﹣45°=90°,∴在Rt△DFE中,DF2+FE2=DE2,即DE2=BD2+EC2;(3)当AD=BE时,线段DE、AD、EB能构成一个等腰三角形.如图,与(2)类似,以CE为一边,作∠ECF=∠ECB,在CF上截取CF=CB,可得△CFE≌△CBE,△DCF≌△DC A.∴AD=DF,EF=BE.∴∠DFE=∠1+∠2=∠A+∠B=120°.若使△DFE为等腰三角形,只需DF=EF,即AD=BE,∴当AD=BE时,线段DE、AD、EB能构成一个等腰三角形,且顶角∠DFE为120°.【题型三:正方形中的半角模型】【模型】在正方形ABC D中,E、F分别是BC、CD边上的点,∠EAF=45°,BD为对角线,交AE于M点,交AF于N点。
中考必会几何模型:半角模型
3.已知,在等边△ABC 中,点 O 是边 AC、BC 的垂直平分线的交点,M、N 分别在直线 AC、BC 上,且∠MON=60°. (1)如图①,当 CM=CN 时,M、N 分别在边 AC、BC 上时,请写出 AM、CN、MN 三 者之间的数量关系; (2)如图②,当 CM≠CN 时,M、N 分别在边 AC、BC 上时,(1)中的结论是否仍然 成立?若成立,请你加以证明;若不成立,请说明理由; (3)如图③,当点 M 在边 AC 上,点 N 在 BC 的延长线上时,请直接写出线段 AM、
图①
图②
【答案】 解答:(1)猜想:DE2=BD2+EC2. 证明:将△AEC 绕点 A 顺时针旋转 90°得到△ABE′,如图①
∴△ACE≌△ABE′. ∴BE′=EC,AE′=AE,∠C=∠ABE′,∠EAC=∠E′AB. 在 Rt△ABC 中, ∵AB=AC, ∴∠ABC=∠ACB=45°. ∴∠ABC+∠ABE′=90°,即∠E′BD=90°. ∴E′B2+BD2=E′D2. 又∵∠DAE=45°, ∴∠BAD+∠EAC=45°. ∴∠E′AB+∠BAD=45°,即∠E′AD=45°.
5
∴△ABM≌△ADE. ∴MN=EN. ∵DN-DE=EN. ∴DN-BM=MN.
WANG
2.已知,如图①在 Rt△ABC 中,∠BAC=90°,AB=AC,点 D、E 分别为线段 BC 上两动 点,若∠DAE=45°,探究线段 BD、DE、EC 三条线段之间的数量关系. 小明的思路是:把△AEC 绕点 A 顺时针旋转 90°,得到△ABE′,连接 E′D 使问题得到解 决.请你参考小明的思路探究并解决以下问题: (1)猜想 BD、DE、EC 三条线段之间的数量关系式,并对你的猜想给予证明; (2)当动点 E 在线段 BC 上,动点 D 运动到线段 CB 延长线上时,如图②,其他条件不 变,(1)中探究的结论是否发生改变?请说明你的猜想并给予证明.
半角模型(初三数学最全最详细半角模型)

几何模型07——半角模型一、正方形中夹半角模型(45°)例1.如图,已知正方形ABCD中,E、F分别是BC、CD上的点,且∠EAF=45°.求证:(1)EF=BE+DF;变式1.如图,已知正方形ABCD的边长为6,E,F分别是AB、BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.(1)求证:EF=MF(2)若AE=2,求FC的长.变式2.在四边形ABCD中,AD∥BC(BC>AD),∠A=∠B=90°,AB=BC=20,E是AB上一点,且∠DCE=45°,BE=4,求DE的长.变式3.已知,正方形ABCD,M在CB延长线上,N在DC延长线上,∠MAN=45°.求证:MN=DN﹣BM.变式4.在平面直角坐标系中,已知A(x,y),点A作AB⊥y轴,垂足为B.若在x轴正半轴上取一点M,连接BM并延长至N,以BN为直角边作等腰Rt △BNE,∠BNE=90°,过点A作AF∥y轴交BE于点F,连接MF,设OM =a,MF=b,AF=c,试证明:=.例2.如图所示,过正方形ABCD的顶点A在正方形ABCD的内部作∠EAF=45°,E、F分别在BC、CD上,连接EF,作AH⊥EF于点H求证:AH=AB.变式1.已知△AMN中,∠MAN=45°,AH⊥MN于点H,且MH=3,NH=7,求AH的长.变式2.已知:如图,在正方形ABCD中,M在CB延长线上,N在DC延长线上,∠MAN=45°,AH⊥MN,垂足为H,求证:AH=AB.二、等腰直角三角形中的夹半角模型(45°)例3.已知Rt△ABC中,∠ACB=90°,AC=BC,点D、E在斜边AB上,且∠DCE=45°,证明:DE2=BE2+AD2;.变式1.如图,等腰直角三角形ABC中,∠BAC=90°,AB=AC,点M,N在边BC上,且∠MAN=45°.若BM=1,CN=3,则MN的长为.变式2.如图,在△ABC中,AB=AC,点E,F是边BC所在直线上与点B,C不重合的两点.∠BAC=90°,∠EAF=135°,证明:EF2=EC2+BF2三、其他半角模型例4.在等边△ABC的两边AB,AC上分别有两点M,N,点D为△ABC外一点,且∠MDN=60°,∠BDC=120°,BD=DC,DM≠DN,证明:MN=BM+NC.变式1.如图,在△ABC中,AB=AC,点E,F是边BC所在直线上与点B,C不重合的两点.∠BAC=60°,∠EAF=30°,已知BE=3,CF=5,求线段EF的长度;例5.如图,在四边形ABCD中,AB=AD,∠B=∠D=90°,E、F分别是边BC、CD上的点,且∠EAF=∠BAD.求证:EF=BE+FD;变式1.如图,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是边BC、CD上的点,且∠EAF=∠BAD.求证:EF=BE+FD;变式2.如图,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E、F分别是边BC、CD延长线上的点,且∠EAF=∠BAD.证明:EF=BE﹣FD,变式3.已知,如图,在四边形ABCD中,∠B+∠D=180°,AB=AD,E,F分别是线段BC,CD上的点,且BE+FD=EF.求证:∠EAF=∠BAD.变式4.已知△ABC中,AB=AC,∠BAC=120°.点M在BC上,点N在BC 的上方,且∠MBN=∠MAN=60°,求证:MC=BN+MN;。
2024专题3.3旋转---半角模型-中考数学二轮复习必会几何模型剖析(全国通用)

A
D
2
2
⑤CE= 2 DM,DF= BG,EF= GM, ⑥ = =
CE FC 2
M
⑦△AEF的边EF上的高等于正方形的边长;
⑧△EFC的周长等于正方形的边长的2倍.
F
角度之间的关系: ①∠AEB=∠AEF,∠AFE=∠AFD
G
O
②根据下面共圆,每个共圆都至少可以得到四队相等的角.
四点共圆:①ABEM ②ADFG ③GEFM ④CEMF ⑤CEGMF
=
=
= .
A
(1)∵∠MEN=∠MFN=45º,∴M、N、F、E四点共圆
D
45º
∴∠ANM=∠AEF,∠AMN=∠AFE,
∴△AMN∽△AFE.
N
F
M
B
E
C
变式训练
考点3-1
半角模型---90°+45°
【变式6】如图,E,F是正方形ABCD的两边上的点,∠EAF=45º,BD交AE,AF于
A
上且∠EDF=60º.求证:EF=BE+CF.
【分析】将△BDN绕点D顺时针旋转120º得△DCG,
E
F
易证:△DBE≌△DCG(SAS)→DE=DG,∠FDG=∠FDE=60º
易证:△DFE≌△DFG(SAS)→EF=GF,
∴EF=GF=GC+CF=BE+CF.
B
60º
D
C
针对训练
考点3-2
半角模型---120°+60°
图形示例
A
模型分析
当一个角包含着这个角的半角
等边三角形
,常将半角两边的三角形通过
中考数学压轴题重难点突破十 几何图形综合题 类型一:与全等三角形有关的问题

∠CRD=12∠ARB=45°.∴∠MON=135°.
此时,P,O,B 在一条直线上,△PAB 为直角三角 PQ= 2PQ,则PQ= 2.
1.如图,在△ABC 和△ADE 中,AB=AC,AD=AE,∠BAC=∠DAE,F 为 BD,CE 的交点. (1)求证:BD=CE; (2)连接 AF,求证:AF 平分∠BFE.
Ⅲ)∵∠EMD=45°,∠DGM=90°, ∴∠DMG=∠GDM,∴DG=GM, 又∵DM=6 2, ∴DG=GM=6, ∵DE=12, ∴EG= ED2-DG2=6 3, ∴EM=GM+EG=6+6 3.
模型二:半角模型
如图,在正方形 ABCD 中,点 E,F 分别在边 BC,CD 上,分别连接 EF, AE,AF,∠EAF=45°.求证: (1)EF=BE+DF; (2)AF 平分∠EFD.
证明:(1)将△ADF 绕点 A 顺时针旋转 90°, 得到△ABG, ∵四边形 ABCD 为正方形, ∴∠BAD=∠D=∠ABC=90°,
出现等顶角,共顶点,等线段就能构造全等型手拉手.
1.(2016·安徽第 23 题 14 分)如图①,A,B 分别在射线 OM,ON 上,且 ∠MON 为钝角.现以线段 OA,OB 为斜边向∠MON 的外侧作等腰直角三角 形,分别是△OAP,△OBQ,点 C,D,E 分别是 OA,OB,AB 的中点. (1)求证:△PCE≌△EDQ; (2)延长 PC,QD 交于点 R. Ⅰ)如图②,若∠MON=150°,求证:△ABR 为等边三角形; Ⅱ)如图③,若△ARB∽△PEQ,求∠MON 的大小和APBQ的值.
(2)Ⅰ)证明:如图②,连接 OR. ∵PR 与 QR 分别为线段 OA 与 OB 的中垂线, ∴AR=OR=BR,∠ARC=∠ORC,∠ORD=∠BRD. 在四边形 OCRD 中, ∠OCR=∠ODR=90°,∠MON=150°, ∴∠CRD=30°. ∴∠ARB=∠ARO+∠BRO =2∠CRO+2∠ORD =2∠CRD=60°. ∴△ABR 为等边三角形.
中考数学压轴题分析:半角模型

中考数学压轴题分析:半角模型等腰直角三角形的直角内含有一个45°的角,形成了倍半的关系。
这样的图形也会出现在正方形之中。
其实等腰直角三角形可以看成正方形的一半,而正方形有时候也可以看出两个等腰直角三角形拼成的图形。
等腰直角三角形中常常需要利用三线合一进行解题。
主要是得到3个等腰直角三角形,进而得到边与角的等量关系。
【中考真题】(2020·襄阳)在△ABC中,∠BAC═90°,AB=AC,点D在边BC 上,DE⊥DA且DE=DA,AE交边BC于点F,连接CE.(1)特例发现:如图1,当AD=AF时,①求证:BD=CF;②推断:∠ACE=°;(2)探究证明:如图2,当AD≠AF时,请探究∠ACE的度数是否为定值,并说明理由;(3)拓展运用:如图3,在(2)的条件下,当EF/AF=1/3时,过点D作AE的垂线,交AE于点P,交AC于点K,若CK=16/3,求DF的长.【分析】题(1)的第①小问用全等即可证明。
第②小问通过目测观察或者尺子一量就出来了。
当然,要证明也不难。
因为这里面有一个8字形。
所以比较容易得到一个等量关系。
可以得到∠DAE=∠DCE,那么结论就出来了。
其实本质是四点共圆。
题(2)就是在题(1)②的基础上面用二次相似就可以了。
当然,要用四点共圆说明也可以。
题(3)因为DP与AE垂直,所以可以考虑过点C作CG⊥AE,那么就可以得到一个8字形与一个A字形。
有两个相似再加上等腰直角三角形的三线合一。
进而可以得出边长的比例关系。
设GF=x,再表示出其它线段,表示出CK的长,进而得到x的值。
就可以在△DPF中利用勾股定理得到DF的长度了。
当然,本题也可以像上图,连接EK。
得到AK与EK是相等的,因为DK是AE的垂直平分线。
在△DKC中设未知数利用勾股定理,可以求出AK、EK和EC的长度。
再求出AE、DP和PF的长度就可以了。
【答案】(1)①证明:如图1中,∵AB=AC,∴∠B=∠ACF,∵AD=AF,∴∠ADF=∠AFD,∴∠ADB=∠AFC,∴△ABD≌△ACF(AAS),∴BD=CF.②结论:∠ACE=90°.理由:如图1中,∵DA=DE,∠ADE=90°,AB=AC,∠BAC=90°,∴∠ACD=∠AED=45°,∴A,D,E,C四点共圆,∴∠ADE+∠ACE=180°,∴∠ACE=90°.故答案为90.(2)结论:∠ACE=90°.理由:如图2中,∵DA=DE,∠ADE=90°,AB=AC,∠BAC=90°,∴∠ACD=∠AED=45°,∴A,D,E,C四点共圆,∴∠ADE+∠ACE=180°,∴∠ACE=90°.(3)如图3中,连接EK.∵∠BAC+∠ACE=180°,∴AB∥CE,∴EC/AB=EF/AF=1/3,设EC=a,则AB=AC=3a,AK=3a-16/3,∵DA=DE,DK⊥AE,∴AP=PE,∴AK=KE=3a-16/3,∵EK²=CK²+EC²,∴(3a-16/3)²=(16/3)²+a²,解得a=4或0(舍弃),∴EC=4,AB=AC=12,∴AE=√(AC²+EC² )=√(4²+12² )=4√10,∴DP=PA=PE=1/2AE=2√10,EF=1/4AE=√10,∴PF=FE=√10,∵∠DPF=90°,∴DF=√(DP²+PF² )=√((2√10 )²+(√10 )² )=5√2.。
2022年中考数学复习专题三半角模型及其例题解析

专题03 半角模型半角模型:是指有公共顶点,锐角等于较大的角的一半,且较大的角的两边相等(不等),通过旋转,可将角进行等量转化,构造全等(相似)的三角形的几何模型。
主要解法:一、经典之旋转法。
二、创新之翻折法。
三、常规之补短法。
熟练掌握:正方形的10个结论。
学会变通:矩形通过截或补变成正方形。
含60°角的菱形除旋转外,还可以借助对角线,构成等边三角形,利用三边相等,构造全等。
模型总讲:如图,已知在正方形ABCD 中,∠EAF =45°,连接BD 与AM ,AN 分别交于E 、F 两点。
1. BE+DF=EF ;2. △CEF 的周长等于正方形的边长的2倍。
3. S △ABE +S △ADF =S △AEF4. 点A 到MN 的距离等于正方形的边长;即AH=AD5. MN 2=MB 2+DN 2;6. 点A,M,F,D 四点共圆。
点A,B,E,N 四点共圆. 点M,E,F,N四点共圆。
点N,F,C,E,M 五点共圆。
7. 证明△AFM 和△AEN 为等腰直角三角形。
8.MN EF=√229. S △AMF =2S △AEF 10. 5组相似△HMN ∼△DFN(图9) △HMN ∼△BME(图10) △AMN ∼△BNA(图11) △AMN ∼△DMA(图12) △ AMN∽△ AFE证明如下: 结论1(图1)将△ABE 逆时针旋转90°,与△ADE'重合. 则AE=AE', ∠BAE=∠DAE’,易得 ∠EAF=∠E'AF=45° 又∵ AF=AF∴△EAF ≌ △E'AF (SAS )(图2) ∴EF=E'F=DE'+DF ∴BE+DF=EF(结论1成立) 结论2 由结论1可得:AO HN M EBCD FAE'OEBCD F图1C △CEF =CE+CF+EF= CE+CF+BE+DF=BC+CD=2BC即△CEF 的周长等于正方形的边长的2倍。
人教中考数学压轴题解题模型几何图形之半角模型含解析汇报

论,这是该定理的特点,在应用时需要哪个结论就用哪个结论,并非把结论写全。
小结:(1)正方形与矩形,菱形,平行四边形的关系如上图(2)正方形的性质:①正方形对边平行。
②正方形四边相等。
③正方形四个角都是直角。
④正方形对角线相等,互相垂直平分,每条对角线平分一组对角。
典型例题精讲例1.如图,折叠正方形纸片ABCD,先折出折痕BD,再折叠使AD边与对角线BD重合,得折痕DG,使2AD ,求AG.【解析】:作GM⊥BD,垂足为M.由题意可知∠ADG=GDM,则△ADG≌△MDG.∴DM=DA=2. AC=GM又易知:GM=BM.而BM=BD-DM=22-2=2(2-1),∴AG=BM=2(2-1).例2 .如图,P 为正方形ABCD 内一点,10PA PB ==,并且P 点到CD 边的距离也等于10,求正方形ABCD 的面积?【解析】:过P 作EF AB ⊥于F 交DC 于E .设PF x =,则10EF x =+,1(10)2BF x =+. 由222PB PF BF =+.可得:222110(10)4x x =++. 故6x =.216256ABCD S ==.例3. 如图,E 、F 分别为正方形ABCD 的边BC 、CD 上的一点,AM EF ⊥,•垂足为M ,AM AB =,则有EF BE DF =+,为什么?【解析】:要说明EF=BE+DF ,只需说明BE=EM ,DF=FM 即可,而连结AE 、AF .只要能说明△ABE ≌△AME ,△ADF ≌△AMF 即可. 理由:连结AE 、AF .由AB=AM ,AB ⊥BC ,AM ⊥EF ,AE 公用,∴△ABE ≌△AME .∴BE=ME.同理可得,△ADF≌△AMF.∴DF=MF.∴EF=ME+MF=BE+DF.例4.如下图E、F分别在正方形ABCD的边BC、CD上,且45∠=,试说明EAF︒EF BE DF=+。
【解析】:将△ADF旋转到△ABC,则△ADF≌△ABG∴AF=AG,∠ADF=∠BAG,DF=BG∵∠EAF=45°且四边形是正方形,∴∠ADF﹢∠BAE=45°∴∠GAB﹢∠BAE=45°即∠GAE=45°∴△AEF≌△AEG(SAS)∴EF=EG=EB﹢BG=EB﹢DF例 5. 如图,在正方形ABCD的BC、CD边上取E、F两点,使45∠=,AG EFEAF=⊥于G. 求证:AG AB【解析】:欲证 AG=AB ,就图形直观来看,应证Rt △ABE 与Rt △AGE 全等,但条件不够.∠EAF=45°怎么用呢?显然∠1+∠2=45°,若把它们拼在一起,问题就解决了.【证明】:把 △A FD 绕A 点旋转90°至△AHB.∵∠EAF=45°,∴∠1+∠2=45°.∵∠2=∠3,∴∠1+∠3=45°.又由旋转所得 AH=AF ,AE=AE.∴ △AEF ≌△AEH.例6.(1) 如图1,在正方形ABCD 中,点E ,F 分别在边BC ,CD 上,AE ,BF 交于点O ,90AOF ︒∠=.求证:BE CF =.(2) 如图2,在正方形ABCD 中,点E ,H ,F ,G 分别在边AB ,BC ,CD ,DA 上,EF ,GH 交于点O ,90FOH ︒∠=,4EF =.求GH 的长.1.已知点E ,H ,F ,G 分别在矩形ABCD 的边AB ,BC ,CD ,DA 上,EF ,GH 交于点O ,90FOH ︒∠=,4EF =. 直接写出下列两题的答案:①如图3,矩形ABCD 由2个全等的正方形组成,求GH 的长;②如图4,矩形ABCD 由n 个全等的正方形组成,求GH 的长(用n 的代数式表示).【解析】(1) 证明:如图1,∵ 四边形ABCD 为正方形,∴ AB =BC ,∠ABC =∠BCD =90°,∴ ∠EAB +∠AEB =90°.∵ ∠EOB =∠AOF =90°,∴ ∠FBC +∠AEB =90°,∴ ∠EAB =∠FBC ,∴ △ABE ≌△BCF , ∴ BE =CF .(2) 解:如图2,过点A 作AM //GH 交BC 于M ,过点B 作BN //EF 交CD 于N ,AM 与BN 交于点O /,则四边形AMHG和四边形BNFE均为平行四边形,∴EF=BN,GH=AM,∵∠FOH=90°, AM//GH,EF//BN, ∴∠NO/A=90°,故由(1)得, △ABM≌△BCN,∴AM=BN,∴GH=EF=4.(3) ① 8.② 4n.巩固训练【双基训练】1. 如图6,点A在线段BG上,四边形ABCD与DEFG都是正方形,•其边长分别为3cm和cm.5cm,则CDE∆的面积为________2(6) (7)2.你可以依次剪6张正方形纸片,拼成如图7所示图形.•如果你所拼得的图形中正方形①的面积为1,且正方形⑥与正方形③的面积相等,•那么正方形⑤的面积为________.3.如图9,已知正方形ABCD的面积为35平方厘米,E、F分别为边AB、BC上的点.AF、CE相交于G,并且ABF∆的面积为5平方厘米,•那么四∆的面积为14平方厘米,BCE边形BEGF的面积是________.4.如图,A、B、C三点在同一条直线上,2=。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
人教中考数学压轴题解题模型几何图形之半角模型含解析汇报The pony was revised in January 2021说明:定理2包括了平行四边形,矩形,菱形对角线的性质,一个题设同时有四个结论,这是该定理的特点,在应用时需要哪个结论就用哪个结论,并非把结论写全。
小结:(1)正方形与矩形,菱形,平行四边形的关系如上图(2)正方形的性质:①正方形对边平行。
②正方形四边相等。
③正方形四个角都是直角。
④正方形对角线相等,互相垂直平分,每条对角线平分一组对角。
典型例题精讲例1.如图,折叠正方形纸片ABCD,先折出折痕BD,再折叠使AD边与对角线BD重合,得折痕DG,使2AD ,求AG.【解析】:作GM⊥BD,垂足为M.由题意可知∠ADG=GDM,则△ADG≌△MDG.∴DM=DA=2. AC=GM又易知:GM=BM.而BM=BD-DM=22-2=2(2-1),∴AG=BM=2(2-1).例2 .如图,P 为正方形ABCD 内一点,10PA PB ==,并且P 点到CD 边的距离也等于10,求正方形ABCD 的面积?【解析】:过P 作EF AB ⊥于F 交DC 于E .设PF x =,则10EF x =+,1(10)2BF x =+. 由222PB PF BF =+.可得:222110(10)4x x =++. 故6x =.216256ABCD S ==.例3. 如图,E 、F 分别为正方形ABCD 的边BC 、CD 上的一点,AM EF ⊥,•垂足为M ,AM AB =,则有EF BE DF =+,为什么?【解析】:要说明EF=BE+DF ,只需说明BE=EM ,DF=FM 即可,而连结AE 、AF .只要能说明△ABE ≌△AME ,△ADF ≌△AMF 即可.理由:连结AE、AF.由AB=AM,AB⊥BC,AM⊥EF,AE公用,∴△ABE≌△AME.∴BE=ME.同理可得,△ADF≌△AMF.∴DF=MF.∴EF=ME+MF=BE+DF.例4.如下图E、F分别在正方形ABCD的边BC、CD上,且45∠=,试说明EAF︒=+。
EF BE DF【解析】:将△ADF旋转到△ABC,则△ADF≌△ABG∴AF=AG,∠ADF=∠BAG,DF=BG∵∠EAF=45°且四边形是正方形,∴∠ADF﹢∠BAE=45°∴∠GAB﹢∠BAE=45°即∠GAE=45°∴△AEF≌△AEG(SAS)∴EF=EG=EB ﹢BG=EB ﹢DF例5. 如图,在正方形ABCD 的BC 、CD 边上取E 、F 两点,使45EAF ∠=,AG EF ⊥于G . 求证:AG AB =【解析】:欲证 AG=AB ,就图形直观来看,应证Rt △ABE 与Rt △AGE 全等,但条件不够.∠EAF=45°怎么用呢显然∠1+∠2=45°,若把它们拼在一起,问题就解决了.【证明】:把 △A FD 绕A 点旋转90°至△AHB.∵∠EAF=45°,∴∠1+∠2=45°.∵∠2=∠3,∴∠1+∠3=45°.又由旋转所得 AH=AF ,AE=AE.∴ △AEF ≌△AEH.例6.(1) 如图1,在正方形ABCD 中,点E ,F 分别在边BC ,CD 上,AE ,BF 交于点O ,90AOF ︒∠=.求证:BE CF =.(2) 如图2,在正方形ABCD 中,点E ,H ,F ,G 分别在边AB ,BC ,CD ,DA 上,EF ,GH 交于点O ,90FOH ︒∠=,4EF =.求GH 的长.1.已知点E ,H ,F ,G 分别在矩形ABCD 的边AB ,BC ,CD ,DA 上,EF ,GH 交于点O ,90FOH ︒∠=,4EF =. 直接写出下列两题的答案:①如图3,矩形ABCD 由2个全等的正方形组成,求GH 的长;②如图4,矩形ABCD 由n 个全等的正方形组成,求GH 的长(用n 的代数式表示).【解析】(1) 证明:如图1,∵ 四边形ABCD 为正方形,∴ AB =BC ,∠ABC =∠BCD =90°,∴ ∠EAB +∠AEB =90°.∵ ∠EOB =∠AOF =90°,∴ ∠FBC +∠AEB =90°,∴ ∠EAB =∠FBC ,∴△ABE≌△BCF,∴BE=CF.(2) 解:如图2,过点A作AM如图6,点A在线段BG上,四边形ABCD与DEFG都是正方形,•其边长分别为3cm和cm.5cm,则CDE∆的面积为________2(6) (7)2.你可以依次剪6张正方形纸片,拼成如图7所示图形.•如果你所拼得的图形中正方形①的面积为1,且正方形⑥与正方形③的面积相等,•那么正方形⑤的面积为________.3.如图9,已知正方形ABCD的面积为35平方厘米,E、F分别为边AB、BC上的点.AF、CE相交于G,并且ABF∆的面积为5平方厘∆的面积为14平方厘米,BCE米,•那么四边形BEGF的面积是________.4.如图,A、B、C三点在同一条直线上,2=。
分别以AB BCAB、BC为边作正方形ABEF和正方形BCMN,连接FN,EC。
求证:FN EC=。
5.如图,ABCD是正方形.G是BC上的一点,DE AG⊥于E,⊥于F.BF AG(1)求证:ABF DAE△≌△;8.提示:延长AE交GF于点M,DC,使CH=DG,连接HF,证四边形对角互补,法2:延长FE,AE证全等三角形9.(1)略(2)45(3)作CM⊥DG,证DM=AG=专题(1)定义:有一组邻边相等且有一个角是直角的平行四边形叫做正方形。
(2)特征:边:两组对边分别平行;四条边都相等;内角:四个角都是90°;对角线:对角线互相垂直;对角线相等且互相平分;每条对角线平分一组对角。
(3)主要识别方法:1:对角线相等的菱形是正方形2:对角线互相垂直的矩形是正方形3:四边相等,有一个角是直角的四边形是正方形4:一组邻边相等的平行四边形是正方形5:一组邻边相等且有一个角是直角的平行四边形是正方形依次连接四边形各边中点所得的四边形称为中点四边形。
不。
2AIC,可得由△BFH ≌△CBI ,可得FH=BI 。
从而可得PQ= 2AIBI = 2AB , 从而得证。
例4. 如图,四边形ABCD 为正方形,DE AC ∥,AE AC =,AE 与CD 相交于F .求证:CE CF =.【证明】:顺时针旋转△ADE ,到△ABG ,连接CG.由于∠ABG=∠ADE=900+450=1350从而可得B ,G ,D 在一条直线上,可得△AGB ≌△CGB 。
推出AE=AG=AC=GC ,可得△AGC 为等边三角形。
∠AGB=300,既得∠EAC=300,从而可得∠A EC=750。
又∠EFC=∠DFA=450+300=750.可证:CE=CF 。
例6. 设P 是正方形ABCD 一边BC 上的任一点,PF AP ⊥,CF 平分DCE ∠.求证:PA PF =.【证明】:作FG ⊥CD ,FE ⊥BE ,可以得出GFEC 为正方形。
令AB=Y ,BP=X ,CE=Z ,可得PC=Y-X 。
tan ∠BAP=tan ∠EPF=X Y =Z Y X Z ,可得YZ=XY-X 2+XZ ,即Z(Y-X)=X(Y-X) ,既得X=Z ,得出△ABP ≌△PEF ,得到PA =PF ,得证 。
例7. 已知:P 是边长为1的正方形ABCD 内的一点,求PA PB PC ++的最小值.【证明】:顺时针旋转△BPC 600 ,可得△PBE 为等边三角形。
既得PA+PB+PC=AP+PE+EF 要使最小只要AP ,PE ,EF 在一条直线上, 即如下图:可得最小PA+PB+PC=AF 。
既得AF=213(1)42 = 23= 4232A CB P D= 2(31)2 = 2(31)2= 622 。
例8. P 为正方形ABCD 内的一点,并且PA a =,2PB a =,3PC a =,求正方形的边长.【证明】顺时针旋转△ABP 900 ,可得如下图:既得正方形边长L =2222(2)()22a = 522a 。
【双基训练】 1.如图,四边形ABCD 是正方形,对角线AC 、BD 相交于O ,四边形BEFD 是菱形,若正方形的边长为6,则菱形的面积为________.2.如图,ABCD 是正方形,E 为BF 上一点,四边形AFEC •恰是一个菱形,•则EAB ∠=________.【纵向应用】3.如图,四边形ABCD 是边长为a 的正方形,点G ,E 分别是边AB ,BC 的中点,ACBP D90∠=,且EF交正方形外角的平分线CF于点F.AEF︒(1)证明:BAE FEC∠=∠;(2)证明:AGE ECF∆≅∆;(3)求AEF∆的面积.【横向拓展】4.如图,四边形ABCD是正方形,ABE∆是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60︒得到BN,连接EN、AM、CM.⑴求证:AMB ENB∆≅∆;⑵①当M点在何处时,AM CM+的值最小;②当M点在何处时,AM BM CM++的值最小,并说明理由;3+时,求正方形的边长.⑶当AM BM CM++的最小值为1【练习题答案】1.362.【解析】连结BD交AC于点O,作EM⊥AC于点M.设正方形边长为a,则AC=BD=AE=2a。
