中考压轴题3
专题3 填空压轴题之几何求值-备战2022年中考数学满分真题模拟题分类之压轴题汇编(深圳专用解析版)
专题03 填空压轴题之几何求值1.(2021•深圳)如图,在ABC ∆中,D ,E 分别为BC ,AC 上的点,将CDE ∆沿DE 折叠,得到FDE ∆,连接BF ,CF ,90BFC ∠=︒,若//EF AB ,43AB =,10EF =,则AE 的长为 .【答案】1043-【详解】如图,延长ED 交FC 于G ,延长BA ,DE 交于点M ,将CDE ∆沿DE 折叠,得到FDE ∆,EF EC ∴=,DF DC =,FED CED ∠=∠,EG CF ∴⊥,又90BFC ∠=︒,//BF EG ∴,//AB EF ,∴四边形BFEM 是平行四边形,10BM EF ∴==,1043AM BM AB ∴=-=-,//AB EF ,M FED∴∠=∠,M CED AEM∴∠=∠=∠,1043 AE AM∴==-2.(2020•深圳)如图,在四边形ABCD中,AC与BD相交于点O ,90ABC DAC∠=∠=︒,1tan2ACB∠=,43BOOD=,则ABDCBDSS∆∆=.【答案】332【详解】如图,过点D作//DM BC,交CA的延长线于点M,延长BA交DM于点N,//DM BC,ABC ANM∴∆∆∽,OBC ODM∆∆∽,∴1tan2AB ANACBBC NM==∠=,43BC OBDM OD==,又90ABC DAC∠=∠=︒,90BAC NAD∴∠+∠=︒,90BAC BCA∠+∠=︒,NAD BCA∴∠=∠,ABC DAN∴∆∆∽,∴12AB DNBC NA==,设4BC a=,由43BC OBDM OD==得,3DM a=,2AB a∴=,35DN a=,65AN a=,616255NB AB AN a a a∴=+=+=,∴22313521323225ABDBCDaAB DNSS BC NB a∆∆⋅===⋅.3.(2019•深圳)如图,在正方形ABCD 中,1BE =,将BC 沿CE 翻折,使B 点对应点刚好落在对角线AC 上,将AD 沿AF 翻折,使D 点对应点刚好落在对角线AC 上,求EF = .【答案】6 【详解】如图,作FM AB ⊥于点M .四边形ABCD 是正方形,45BAC CAD ∴∠=∠=︒.将BC 沿CE 翻折,B 点对应点刚好落在对角线AC 上的点X ,1EX EB AX ∴===,90EXC B ∠=∠=︒,222AE AX EX ∴=+=.将AD 沿AF 翻折,使D 点对应点刚好落在对角线AC 上的点Y ,1AM DF YF ∴===,∴正方形的边长21AB FM ==+,21EM =-,2222(21)(21)6EF EM FM ∴=+=-++=.4.(2018•深圳)在Rt ABC ∆中,90C ∠=︒,AD 平分CAB ∠,BE 平分ABC ∠,AD 、BE 相交于点F ,且4AF =,2EF =,则AC = .【答案】8105 【详解】如图,过点E 作EG AD ⊥于G ,连接CF , AD ,BE 是分别是BAC ∠和ABC ∠的平分线, CAD BAD ∴∠=∠,CBE ABE ∠=∠,90ACB ∠=︒,2()90BAD ABE ∴∠+∠=︒,45BAD ABE ∴∠+∠=︒,45EFG BAD ABE ∴∠=∠+∠=︒,在Rt EFG ∆中,2EF =,1FG EG ∴==,4AF =,3AG AF FG ∴=-=,根据勾股定理得,2210AE AG EG =+=,AD 平分CAB ∠,BE 平分ABC ∠,CF ∴是ACB ∠的平分线,45ACF AFE ∴∠=︒=∠,CAF FAE ∠=∠,AEF AFC ∴∆∆∽,∴AE AF AF AC=, 216810510AF AC AE ∴===5.(2017•深圳)如图,在Rt ABC ∆中,90ABC ∠=︒,3AB =,4BC =,Rt MPN ∆,90MPN ∠=︒,点P 在AC 上,PM 交AB 于点E ,PN 交BC 于点F ,当2PE PF =时,AP = .【答案】3【详解】如图作PQ AB ⊥于Q ,PR BC ⊥于R .90PQB QBR BRP ∠=∠=∠=︒,∴四边形PQBR 是矩形,90QPR MPN ∴∠=︒=∠,QPE RPF ∴∠=∠,QPE RPF ∴∆∆∽, ∴2PQ PE PR PF ==, 22PQ PR BQ ∴==,//PQ BC ,::::3:4:5AQ QP AP AB BC AC ∴==,设4PQ x =,则3AQ x =,5AP x =,2BQ x =, 233x x ∴+=,35x ∴=, 53AP x ∴==.6.(2021•深圳模拟)如图,在四边形ABCD 中,AE 平分BAD ∠交CD 于点E ,且AB AE =,12CBA D BAD ∠=∠+∠,过点E 作EG AB ⊥,垂足为G .延长BC 和AE 交于点F ,若:2:1BF ED =,2EG =,三角形ABF 的面积为7,则AD = .【答案】72 【详解】解法一: 如图,过A 作AM BF ⊥于M ,作AN CD ⊥于N ,过E 作EH AD ⊥于H ,90AMB ANE ∴∠=∠=︒,AE 平分BAD ∠交CD 于点E ,12BAE DAE BAD ∴∠=∠=∠, 12CEA DAE ADE BAD ADE ∠=∠+∠=∠+∠, 12CBA D BAD ∠=∠+∠, CEA CBA ∴∠=∠,AED ABM ∴∠=∠,AB AE =,()ABM AEN AAS ∴∆≅∆,AM AN ∴=,12ABF S BF AM ∆=⋅,12AED S DE AN ∆=⋅,且2BF ED =, 2ABF AED S S ∆∆∴=, 7ABF S ∆=,72AED S ∆∴=, AE 平分BAD ∠,EG AB ⊥,EH AD ⊥,2EH EG ∴==,1722AED S AD EH ∆∴=⋅=, 72AD ∴=; 解法二:过D 作DM AE ⊥于M ,过F 作FN AB ⊥,交AB 的延长线于N , AE 平分BAD ∠交CD 于点E ,12BAE DAE BAD ∴∠=∠=∠, 12CEA DAE ADE BAD ADE ∠=∠+∠=∠+∠, 12CBA D BAD ∠=∠+∠, CEA CBA ∴∠=∠,AED FBN ∴∠=∠,90DME FNB ∠=∠=︒,DME FNB ∴∆∆∽,∴12ED DM BF FN ==, 2FN DM ∴=,112722ABF S AB FN AE DM ∆=⋅=⋅=, 7AE DM ∴⋅=,BAE DAE ∠=∠,90AGE AMD ∠=∠=︒,AGE AMD ∴∆∆∽,∴EG AE DM AD =, ∴2AE DM AD=,722DM AE AD ⋅∴==.7.(2021•龙岩模拟)将含30︒角且大小不等的两个三角板按如图摆放,使直角顶点重合,连接AE 、BD ,则AE BD = .【答案】3【详解】EDC ∆与ACB ∆为两个直角三角形,且30DEC BAC ∠=∠=︒,90ACB ECD ∠=∠=︒, ACB DCA ECD DCA ∴∠+∠=∠+∠,DCB ECA ∴∠=∠,在Rt ACB ∆中,tan tan30BC CAB AC∠==︒, 在Rt ECD ∆中,tan tan30DC CED EC ∠==︒, ∴BC DC AC EC=, ∴在ECA ∆与DCB ∆中,DC BC EC AC=, DCB ECA ∠=∠,ECA DCB ∴∆∆∽,∴AE AC BD BC=,在Rt ACB ∆中,tan tan 603AC ABC BC =∠=︒= 8.(2021•南山区一模)如图,在Rt ABC ∆中,90C ∠=︒,BE ,AF 分别是ABC ∠,CAB ∠平分线,BE ,AF 交于点O ,OM AB ⊥,10AB =,8AC =,则OM = .【答案】2【详解】过O 作OG AC ⊥于G ,OH BC ⊥于H ,连接OC ,AF 平分CAB ∠,BE 平分ABC ∠,OG OH OM ∴==,90C ∠=︒,10AB =,8AC =,221086BC ∴=-=11112222ABC S AC BC AB OM AC OG BC OH ∆∴=⋅=⨯⋅+⋅+⋅, ∴11118610862222OM OG OH ⨯⨯=⨯⨯+⨯⨯+⨯⨯, 2OM ∴=9.(2021•深圳模拟)如图,在ABC ∆中,45B ∠=︒,62AB =,D 、E 分别是AB 、AC 的中点,连接DE ,在直线DE 和直线BC 上分别取点F 、G ,连接BF 、DG .若3BF DG =,且直线BF 与直线DG 互相垂直,则BG 的长为 .【答案】4或2【详解】如图,过点B 作BT BF ⊥交ED 的延长线于T ,过点B 作BH DT ⊥于H .DG BF ⊥,BT BF ⊥,//DG BT ∴,AD DB =,AE EC =,//DE BC ∴,∴四边形DGBT 是平行四边形,BG DT ∴=,DG BT =,45BDH ABC ∠=∠=︒, 32AD DB ==, 3BH DH ∴==, 90TBF BHF ∠=∠=︒,90TBH FBH ∴∠+∠=︒,90FBH F ∠+∠=︒,TBH F ∴∠=∠,1tan tan 3BT DG F TBH BF BF ∴∠=∠===, ∴13TH BH =, 1TH ∴=,134DT TH DH ∴=+=+=,4BG ∴=.当点F 在ED 的延长线上时,同法可得312DT BG ==-=.10.(2021•福田区二模)如图,点M 是Rt ABC ∆斜边AB 的中点,过点M 作DM CM ⊥,交AC 于点D ,若2AD =,5BC =,则CD = .【答案】29【详解】延长CM,使CM MN=,连接AN,点M是Rt ABC∆斜边AB的中点,AM BM∴=,在AMN∆和BMC∆中,AM BMAMN BMCMN CM=⎧⎪∠=∠⎨⎪=⎩,()AMN BMC SAS∴∆≅∆,5BC AN∴==,NAM B∠=∠,//AN BC∴,90BCA∠=︒,90NAD∴∠=︒,22225229DN AN AD∴=+=+=,DM CM⊥,CM MN=,29CD DN∴==.11.(2021•深圳模拟)如图,在Rt ABC∆中,90BAC∠=︒,D为BC的中点,过点D作DE DF⊥,交BA的延长线于点E,交AC的延长线于点F.若72CF=,4AC=,2AB=.则AE=.【答案】10【详解】延长FD 至G ,使GD FD =,连接BG ,如图所示: D 为BC 的中点,BD CD ∴=,在BDG ∆和CDF ∆中,BD CD BDG CDF GD FD =⎧⎪∠=∠⎨⎪=⎩,()BDG CDF SAS ∴∆≅∆,72BG CF ∴==,G F ∠=∠, //BG CF ∴, BGH AFH ∴∆∆∽, ∴77271542GH BH BG FH AH AF ====+, ∴411DH FD =,15152211AH AB ==, 90BAC ∠=︒,152AF AC CF =+=, 221515755()()21122HF ∴=+=, 41051511DH FH ∴==, DE DF ⊥,90EDH BAC ∴∠=︒=∠,90E EHD F EHD ∴∠+∠=∠+∠=︒,E F ∴∠=∠,DHE AHF ∴∆∆∽,∴HE DH HF AH=,即10511157551122HE=,解得:12511HE=,12515101111AE HE AH∴=-=-=;12.(2021•宝安区二模)如图,在等腰Rt ABC∆中,90B∠=︒,BA BC=,D为BC上一点,且3BD=,E为AD上一点,连接CE,45CED∠=︒,2CE AE=,则CE的长为.【答案】1855【详解】过A作AN CE⊥的延长线于N,过C作CM AD⊥交AD延长线于M,2CE AE=,∴设AE a=,则2CE a=,3445∠=∠=︒,AN NE ∴=,45ECM ∠=︒,90B ∠=︒,BA BC =,45ACD ∴∠=︒,12∴∠=∠,AEN ∴∆,CEM ∆都是等腰直角三角形, 2CE a =,AE a =, CM EM a ∴==,22AN NE a ==, 12∠=∠,CDM CAN ∴∆∆∽,∴CM CD CN AC=, 22NE a =,2CE a =, 322NC a ∴=, 222213255222AC AN NC a a a a ∴=+=+==, ∴3252aCD a a =,103CD a ∴=, 1033BC a ∴=+, 在Rt ABC ∆中,45BAC ∠=︒,sin BC BAC AC∴∠=, sin45BC AC ∴=︒⋅,即1023532a a +=⨯, 9105a ∴=, 9101852255CE a ∴==⨯=. 13.(2021•宝安区期末)如图,在ABC ∆中,AB AC =,点D 、E 是BC 边上两点,连接AD ,以AD 为腰作等腰直角ADF ∆,90ADF ∠=︒,作FE BC ⊥于点E ,FE CE =,若2BD =,5CE =,则CDF S ∆=. 【答案】30 【详解】过点A 作AH BC ⊥于H ,90AHD ∴∠=︒,FE BC ⊥,90DEF ∴∠=︒,ADF ∆是等腰直角ADF ∆,AD DF ∴=,90ADF ADH EDF ∠=∠+∠=︒,90ADH DAH ∴∠+∠=︒,EDF DAH ∴∠=∠,在ADH ∆和DFE ∆中,DAH EDF AHD DEF AD FD ∠=∠⎧⎪∠=∠⎨⎪=⎩,()ADH DFE AAS ∴∆≅∆,5CE =,5DH EF ∴==,7BH CH ∴==(三线合一), ∴12CDF S DC EF ∆=⨯⨯11252=⨯⨯30=.14.(2021•罗湖区期末)如图,在ABC∆中,90ACB∠=︒,点D 是BC上的一点,AC DC=,AB AE⊥,且AE AB=,连接DE交AC的延长线于点F,32ACCF=,则BDCD=.【答案】43【详解】在DC上截取CG CF=,连接AG,32ACCF=,设3AC x=,2CF x=,AC DC=,3CD x∴=,CG CF=,2CG x∴=,90ACB∠=︒,在Rt ACG∆和Rt DCF∆中,AC CDACD DCFCG CF=⎧⎪∠=∠⎨⎪=⎩,()ACG DCF SAS∴∆≅∆,CAG CDF∴∠=∠,90AGB CAG∠=∠+︒,90EFA CDF∠=︒+∠,AGB EFA∴∠=∠,AB AE⊥,90EAB∴∠=︒,90ACD∠=︒,AC CD=,45CAD∴∠=︒,45EAF BAD ∴∠+∠=︒,45ADC ABC BAD ∠=︒=∠+∠,EAF ABC ∴∠=∠,在EAF ∆和ABG ∆中,EAF ABC EFA AGB AE AB ∠=∠⎧⎪∠=∠⎨⎪=⎩,()EAF ABG AAS ∴∆≅∆,5BG AF x ∴==,32GD x x x =-=,4BD x ∴=, ∴43BDCD =15.(2020•崇州市模拟)如果点P 是ABC ∆内一点,且它到三角形的三个顶点距离之和最小,则P 点叫ABC ∆的费马点.已经证明:在三个内角均小于120︒的ABC ∆中,当120APB APC BPC ∠=∠=∠=︒时,P 就是ABC ∆的费马点.若点P 是腰长为2的等腰直角三角形DEF 的费马点,则PD PE PF ++= .【答案】31+【详解】如图:过点D 作DM EF ⊥于点M ,在BDE ∆内部过E 、F 分别作30MEP MFP ∠=∠=︒,则120EPF FPD EPD ∠=∠=∠=︒,点P 就是费马点, 在等腰Rt DEF ∆中,2DE DF ==,DM EF ⊥,22EF DE ∴==1EM DM ∴==, 故cos30EM PE ︒=, 解得:233PE =,则33PM =, 故313DP =-,同法可得233PF = 则233213133PD PE PF ++=⨯+-=+.16.(2021•深圳模拟)如图,在ABC ∆中,5AB AC ==,45BC =,D 为边AB 上一动点(B 点除外),以CD 为一边作正方形CDEF ,连接BE ,则BDE ∆面积的最大值为 .【答案】8【详解】过点C 作CG BA ⊥于点G ,作EH AB ⊥于点H ,作AM BC ⊥于点M . 5AB AC ==,45BC =,25BM CM ∴==,易证AMB CGB ∆∆∽,∴BM AB GB CB=, 即25545GB = 8GB ∴=,设BD x =,则8DG x =-,易证()EDH DCG AAS ∆≅∆,8EH DG x ∴==-,2111(8)(4)8222BDE S BD EH x x x ∆∴==-=--+, 当4x =时,BDE ∆面积的最大值为8.17.(2021•光明区二模)如图,扇形OPQ 可以绕着正六边形ABCDEF 的中心O 旋转,若120POQ ∠=︒,OP 等于正六边形ABCDEF 边心距的2倍,2AB =,则阴影部分的面积为 .【答案】423π-【详解】连接OE ,OD ,OC .设EF 交OP 于T ,CD 交OQ 于J .120POQ EOC ∠=∠=︒,EOT COJ ∴∠=∠,OE OJ =,60OET OCJ ∠=∠=︒,()EOT COJ ASA ∴∆≅∆,2322234OTEDJ OEDC S S ∴==⨯⨯=五边形四边形, 2120(23)23423360OPQ OTEDJ S S S ππ⋅⋅∴=-=-=-阴扇形五边形 18.(2021•深圳二模)如图Rt ABC ∆中,90BAC ∠=︒,3AB =,4AC =,点P 为BC 上任意一点,连接PA ,以PA ,PC 为邻边作平行四边形PAQC ,连接PQ ,则PQ 的最小值为.【答案】12 5【详解】90BAC∠=︒,3AB=,4AC=,225BC AC AB∴=+=,四边形APCQ是平行四边形,PO QO∴=,CO AO=,PQ最短也就是PO最短,∴过O作BC的垂线OP',ACB P CO∠=∠',90CP O CAB∠'=∠=︒,CAB∴∆∽△CP O',∴CO OP BC AB'=,∴253OP' =,65 OP∴'=,∴则PQ的最小值为1225 OP'=,方法二:不用相似的方法,只利用等面积得,OC AB BC OP'=,求得OP',而其他部分的步骤共用.19.(2020•九龙坡区校级月考)如图,Rt ABC∆中,AB BC⊥,6AB=,4BC=,点D是ABC∆内一个动点,且满足DAB DBC∠=∠,当线段CD取最小值时,记BCDα∠=,线段AB 上一动点E绕着点D顺时针旋转得到点F,且满足EDFα∠=,则AF的最小值 .【答案】125 【详解】AB BC ⊥,6AB =、4BC =, 90DBC ABD ∴∠+∠=︒,DAB DBC ∠=∠,设DAB DBC β∠=∠=,90DAB ABD ∴∠+∠=︒,90ADB ∴∠=︒,∴点D 在以AB 为直径的圆上,设圆心为O ,半径为132AB =,则当O 、D 、C 三点共线时CD 最小,3OD OB OA ∴===,225OC OB BC ∴=+=,将DA 绕点D 逆时针旋转α,得到DG ,连接GE ,DG DA ∴=,GDA EDF α∠=∠=,GDE ADF ∴∠=∠,DE DF =,()GDE ADF SAS ∴∆≅∆,GE AF ∴=,∴当GE AB ⊥时,GE 最小,即AF 最小,过点D 作DM AB ⊥于M ,过点G 作GH DM ⊥,交DM 的延长线于点H ,//DM BC ∴,四边形GHME 为矩形.OMD OBC ∴∆∆∽,GE HM =,∴DM OM OD BC OB OC ==, ∴3435DM OM ==, 125DM ∴=,95OM =, 924355AM OM OA ∴=+=+=, DAB DBC β∠=∠=,OA OD =,ODA OAD β∴∠=∠=,2BOC ODA OAD β∴∠=∠+∠=.在Rt OBC ∆中,90OCB BOC ∠=︒-∠,902αβ∴=︒-,90MAD MDA ∠+∠=︒,90GDH βα∴++∠=︒,GDH DAM β∴∠==∠,90DHG AMD ∠=∠=︒,AD DG =,()GDH DAM AAS ∴∆≅∆.245DH AM ∴==, 125HM DH DM ∴=-=,即AF 的最小值为125. 20.(2021•南山区二模)矩形ABCD 中,4AB =,6BC =,点E 为BC 的中点,沿AE 将AEB ∆翻折得到AFE ∆,sin FCE ∠= .【答案】45【详解】如图,过E 作EH CF ⊥于H ,由折叠的性质得:BE EF =,BEA FEA ∠=∠,点E 是BC 的中点,3CE BE ∴==,3EF CE ∴==,FEH CEH ∴∠=∠,90AEB CEH ∴∠+∠=︒,在矩形ABCD 中,90B ∠=︒,90BAE BEA ∴∠+∠=︒,BAE CEH ∴∠=∠,B EHC ∠=∠,ABE EHC ∴∆∆∽, ∴AB AE EH CE =, 22435AE =+=,125EH ∴=, 4sin 5EH ECF CE ∴∠==. 21.(2021•龙岗区二模)如图,已知在菱形ABCD ,9BC =,60ABC ∠=︒,点E 在BC 上,且6BE =,将ABE ∆沿AE 折叠得到△AB E ',其中B E '交CD 于点F ,则CF = .【答案】95【详解】过点A 作AG BC ⊥交BC 于G ,取HG 使HG GE =,过H 作HM AE ⊥于H ,过F 作FN BC ⊥交BC 延长线于N ,四边形ABCD 是菱形,在Rt ABG ∆中,60B ∠=︒, 3sin sin 602AG B AB ∴=︒==, 39322AG AB ∴==, 1cos cos602BG B AB =︒==, 1922BG AB ∴==, 6BE =,922()2(6)32HE GE BE BG ∴==-=⨯-=, 在Rt AGE ∆中,222439633744AE AG GE =+=+==, 1122AHE S HE AG AE HM ∆=⨯⨯=⨯⨯, ∴131337222HM ⨯⨯=⨯⨯, 解得,92114HM =, HG GE =,AG HE ⊥,AHE ∴∆是等腰三角形,AH AE ∴=,AHE HEA ∠=∠,在Rt AHM ∆中,222229211064739763()1419614AM AH HM AE HM =-=-=-==, //AB CD ,60FCN B ∴∠=∠=︒,∴tan 603FN CN=︒=, 折叠,AEB HEA ∴∠'=∠,在Rt AHE ∆中,1801802HAE HEA AHE HEA ∠=︒-∠-∠=︒-∠,又1801802FEN HEA AEB HEA ∠=︒-∠-∠'=︒-∠,设CN x =,3FN x =, tan tan FN HM FEC HAM EN AM ∠=∠==,∴921314339714x x =+, ∴333313x x =+, 910x ∴=, 9931010CN FN ∴==, 22189105CF CN FN ∴=+==. 22.(2021•深圳模拟)如图,矩形ABCD 中,13AE AD =,将ABE ∆沿BE 折叠后得到GBE ∆,延长BG 交CD 于F 点,若3CF FD ==,则BC 的长为 .【答案】66【详解】延长BF 交AD 的延长线于点H ,四边形ABCD 是矩形,AD BC ∴=,//AD BC ,90A BCF ∠=∠=︒, H CBF ∴∠=∠,在BCF ∆和HDF ∆中,CBF H BCF DFH CF DF ∠=∠⎧⎪∠=∠⎨⎪=⎩,()BCF HDF AAS ∴∆≅∆,将ABE ∆沿BE 折叠后得到GBE ∆,90A BGE ∴∠=∠=︒,AE EG =,90EGH ∴∠=︒, 13AE AD =, ∴设AE EG x ==,则3AD BC DH x ===, 2ED x ∴=,5EH ED DH x ∴=+=, 在Rt EGH ∆中,1sin 55EG x H EH x ∠===, 1sin 5CF CBF BF ∴∠==, ∴315BF =, 15BF ∴=,222215366BC BF CF ∴=-=-=23.(2021•葫芦岛二模)如图,在矩形ABCD 中,15AB =,8AD =,E 为AB 边上一点,将BEC ∆沿CE 翻折,点B 落在点F 处,当AEF ∆为直角三角形时,AE = .【答案】7或515【详解】①如图,若90AEF ∠=︒,90B BCD AEF ∠=∠=︒=∠,∴四边形BCFE 是矩形,将BEC ∆沿着CE 翻折,∴四边形BCFE 是正方形,8BE BC AD ∴===,1587AE AB BE ∴=-=-=;②如图,若90AFE ∠=︒,将BEC ∆沿着CE 翻折,8CB CF ∴==,90B EFC ∠=∠=︒,BE EF =, 180AFE EFC ∠+∠=︒,∴点A ,点F ,点C 三点共线, 222215817AC AB BC ∴=+=+=,9AF AC CF ∴=-=,222AE AF EF =+,2281(15)AE AE ∴=+-,515AE ∴=, ③若90EAF ∠=︒,158CD CF BC =>==,∴点F 不可能落在直线AD 上,∴不存在90EAF ∠=︒,综上所述:7AE =或515. 24.(2020•青羊区校级期末)如图1,在矩形ABCD 中,8AB =,10BC =,P 是边AD 上一点,将ABP ∆沿着直线BP 翻折得到△A BP '.当8AP =时,A D '= .如图2,连接A C ',当2AP =时,此时△A BC '的面积为 .【答案】217;60017 【详解】如图1,当8AP =时,由折叠知AB AP =,APB BPA '∠=∠,ABP A BP '∠=∠,90A BA P '∠=∠=︒, ∴四边形ABA P '是正方形,8A P '∴=,2PD =,222282217A D A P PD ''∴=+=+=.如图2,当2AP =时,过点A '作//MN AB ,交AD 于点M ,交BC 于点N ,∴四边形ABNM 为矩形,8AB MN ∴==,AM BN =,90AMN BNM ∠=∠=︒, 设A M x '=,则8A N x '=-,设BN y =,则2PM y =-, 在Rt PMA '∆中,222PM A M PA ''+=,222(2)2y x ∴-+=①,在Rt BNA '∆中,222BN A N A B ''+=,222(8)8y x ∴+-=②,由①②可得,4y x =,把4y x =代入①得,222(42)2x x -+=, 解得,1617x =, 1612081717A N '∴=-=, 1112060010221717A BC S BC A N ''∴=⨯⨯=⨯⨯=. 25.(2021•坪山区二模)如图,在ABC ∆和ADE ∆中,90BAC DAE ∠=∠=︒,60C E ∠=∠=︒,点D 在BC 边上,AC 与DE 相交于点F ,3DF CF =,则AD BD= .【答案】3【详解】连接EC ,如图,90BAC DAE ∠=∠=︒,60ACB AED ∠=∠=︒, AED ACB ∴∆∆∽,∴AE AD AC AB=, 即AE AC AD AB=, 90BAC DAE ∠=∠=︒,BAC CAD DAE CAD ∴∠-∠=∠-∠,EAC DAB ∴∠=∠,EAC DAB ∴∆∆∽,∴AD BD AE EC=,ACE ABD ADE ∠=∠=∠, 在Rt EAD ∆中,60AED ∠=︒,∴3AD AE=,∴3BD EC =, ∴33EC BD=,EFCAFD ∠=∠,ECF ADF ∠=∠, EFC AFD ∴∆∆∽,∴3AD DF EC CF==, ∴3333AD AD EC BD EC BD =⋅=⨯= 26.(2021•深圳模拟)如图所示的网格是正方形网格,则BAC DAE ∠-∠= ︒(点A ,B ,C ,D ,E 是网格线交点).【答案】45【详解】如图,连接CG 、AG ,由勾股定理得:2222125AC AG ==+=,2221310CG =+=, 222AC AG CG ∴+=,90CAG ∴∠=︒,CAG ∴∆是等腰直角三角形,45ACG ∴∠=︒,//CF AB ,ACF BAC ∴∠=∠,在CFG ∆和ADE ∆中,90CF AD CFG ADE FG DE =⎧⎪∠=∠=︒⎨⎪=⎩,()CFG ADE SAS∴∆≅∆,FCG DAE∴∠=∠,45BAC DAE ACF FCG ACG∴∠-∠=∠-∠=∠=︒27.(2021•深圳模拟)如图,矩形ABCD中,E是AB上一点,连接DE,将ADE∆沿DE翻折,恰好使点A落在BC边的中点F处,在DF上取点O,以O为圆心,OF长为半径作半圆与CD相切于点G.若4AD=,则图中阴影部分的面积为.【答案】23 9【详解】连接OG,QG,将ADE∆沿DE翻折,恰好使点A落在BC边的中点F处,4AD DF∴==,2BF CF==,矩形ABCD中,90DCF∠=︒,30FDC∴∠=︒,60DFC∴∠=︒,O与CD相切于点G,OG CD∴⊥,BC CD⊥,//OG BC∴,DOG DFC∴∆∆∽,∴DO OG DF FC=,设OG OF x==,则442x x-=,解得:43x =,即O 的半径是43. 连接OQ ,作OH FQ ⊥, 60DFC ∠=︒,OF OQ =, OFQ ∴∆为等边三角形;同理OGQ ∆为等边三角形; 60GOQ FOQ ∴∠=∠=︒,32323OH OQ ==, 3232333QH ∴=⨯=, 23CQ ∴= 四边形OHCG 为矩形,233OH CG ∴==, 232311222339CGQ S S CQ CG ∆∴==⨯⨯=⨯⨯=阴影. 28.(2020•扬州)如图,在ABCD 中,60B ∠=︒,10AB =,8BC =,点E 为边AB 上的一个动点,连接ED 并延长至点F ,使得14DF DE =,以EC 、EF 为邻边构造EFGC ,连接EG ,则EG 的最小值为 .【答案】93【详解】作CH AB ⊥于点H ,在ABCD 中,60B ∠=︒,8BC =,43CH ∴=,四边形ECGF 是平行四边形,//EF CG ∴,EOD GOC ∴∆∆∽,∴EO DO ED GO OC GC==,14DF DE =, ∴45DE EF =, ∴45ED GC =, ∴45EO GO =, ∴当EO 取得最小值时,EG 即可取得最小值,当EO CD ⊥时,EO 取得最小值,CH EO ∴=,43EO ∴=,53GO ∴=,EG ∴的最小值是9329.(2021•锡山区一模)如图,在平行四边形ABCD 中,60B ∠=︒,4BC =,点E 为边AB上的一个动点,连接ED 并延长至点F ,使得13DF DE =,以EC 、EF 为邻边构造平行四边形EFGC ,连接EG ,则EG 的最小值为 .【答案】1433【详解】作CH AB ⊥于点H ,在ABCD 中,60B ∠=︒,4BC =,23CH ∴=,四边形ECGF 是平行四边形,//EF CG ∴,EOD GOC ∴∆∆∽, ∴EO DO ED GO CO GC ==, 13DF DE =, ∴34DE EF =, ∴34ED GC =, ∴34EO GO =, ∴当EO 取得最小值时,EG 即可取得最小值,当EO CD ⊥时,EO 取得最小值,CH EO ∴=,23EO ∴=,833GO ∴=, EG ∴的最小值是814233333+=30.(2021•龙岗区校级一模)如图,在矩形ABCD 中,5AC =,AE 平分DAC ∠交CD 于E ,CF 平分ACD ∠交AE 于点F ,且:1:2EF AF =,则CF = .【答案】10【详解】作FG AC ⊥于点G ,作FM CD ⊥于点M ,作FN AD ⊥于点N , CF 平分ACD ∠交AE 于点F ,且:1:2EF AF =,:1:2CE CA ∴=,5AC =, 52CE ∴=, AE 平分DAC ∠,CF 平分ACD ∠, FG FM FN ∴==, FM CD ⊥,AD CD ⊥,:1:2EF AF =, EMF EDA ∴∆∆∽,∴13MF EF DA EA ==, 设FM x =,则3AD x =,同理可得,ANF AED ∆∆∽,则32DE x =, 5322CD x ∴=+, 90D ∠=︒,3AD x =,5AC =, 22253()(3)522x x ∴++=, 解得11x =,253x =-(舍去), 1FM ∴=,5311322CM =+⨯-=, 又90CMF ∠=︒,221310CF ∴=+=,故答案为:10.。
福建中考压轴题解题技巧(3)—证三点共线与三线共点的基本思路

福建中考压轴题解题技巧(3)—证三点共线与三线共点的基本思路一、证明三点共线(一)证明方法(1)平角模型:图1,要证明A 、B 、C 三点共线,可以选择一条过B 点的直线PBQ ,并连接AB 、CB ,证明∠ABP+∠CBP=180°;(2)重合模型:先做过其中两点的直线,再证第三点过此直线; (图1)(3)函数模型:①构建平面直角坐标系,求出三个点坐标,其中两个点构建一次函数模型,判断第三个点是否在函数图像上,满足则共线。
②利用21k k =,其中(βαtan tan 21==k k ,),得两直线平行,由此得出三点共线。
(二)典例剖析23.(2020年)如图,C 为线段AB 外一点.(1)求作四边形ABCD ,使得CD//AB ,且CD=2AB ;(要求:尺规作图,不写作法,保留作图痕迹)(2)在(1)的四边形ABCD 中,AC ,BD 相交于点P ,AB ,CD 的中点分别为M ,N ,求证:M ,P ,N 三点在同一条直线上.24. (2023年)已知抛物线23y ax bx =++交x 轴于A (1,0)、B (3,0)两点,C 、D 为抛物线上不与A 、B 重合的相异两点,记AB 中点为E ,.(2)若()34,3,,4C D m ⎛⎫-⎪⎝⎭,且2m <,求证:C 、D 、E 三点共线。
25.(2019年)已知点A 是抛物线122+-=x x y 的顶点。
(2)直线l :y =kx +1-k 与抛物线交于点B 、C ,直线BD 垂直于直线y =-1,垂足为D .证明:对于每个给定的实数k ,都有A 、D 、C 三点共线。
4、已知:A (-m,m) ,B (n,0),其中m>0,n>0,点C在第一象限内,∠ABC=90°,AB=BC,延长CB至P,使BP=BQ,求证:A,O,P三点共线.二、证明三线共点(一)证明方法①先假设其中两条直线交于一点,再证明第三条直线经过这一点;②证明三条线中两条线的交点和另外两条线的交点是同一个。
中考数学“三类压轴题”专题——选择题压轴题

第1讲 中考数学“三类压轴题"专题——选择题压轴题题型一 方程、等式、不等式类代数变形或计算1.(2012襄阳)如果关于x 的一元二次方程2kx2k 1x 10-++=有两个不相等的实数根,那么k 的取值范围是( ) A .k <12 B .k <12且k≠0 C.﹣12≤k<12 D .﹣12≤k<12且k≠0 2. (2008武汉)下列命题:其中正确的是( ) ①若0a b c ++=,则240b ac -≥;②若b a c >+,则一元二次方程20ax bx c ++=有两个不相等的实数根;③若23b a c =+,则一元二次方程20ax bx c ++=有两个不相等的实数根;④若240b ac ->,则二次函数的图像与坐标轴的公共点的个数是2或3.A.只有①②③ B.只有①③④ C.只有①④ D. 只有②③④.题型二 函数类代数计算3.(2012宜昌)已知抛物线y=ax 2﹣2x+1与x 轴没有交点,那么该抛物线的顶点所在的象限是( )A .第四象限B .第三象限C .第二象限D .第一象限4. (2012天门、仙桃、潜江、江汉油田)已知二次函数y=ax 2+bx+c 的图象如图所示,它与x 轴的两个交点分别为(﹣1,0),(3,0).对于下列命题:①b﹣2a=0;②abc<0;③a﹣2b+4c <0;④8a+c>0.其中正确的有( )A .3个B .2个C .1个D .0个 题型三 坐标几何类图像信息题5.(2012柳州)小兰画了一个函数的图象如图,那么关于x 的分式方程的解是( )A .x=1B .x=2C .x=3D .x=46.(2012宁波)勾股定理是几何中的一个重要定理。
在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载。
如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理。
图2是由图1放入矩形内得到的,∠BAC=90O ,AB=3,AC=4,点D ,E ,F ,G ,H ,I 都在矩形KLMJ 的边上,则矩形KLMJ 的面积为( )A 、 90B 、 100C 、 110D 、 121(第7题) C D E F A B O x y 4 4 A . O x y 4 4 B . O x y 4 4 C . O x y 4 4 D . O A F CE B7。
云南省曲靖市初中物理中考压轴题-专题三:物态变化

云南省曲靖市初中物理中考压轴题-专题三:物态变化姓名:________ 班级:________ 成绩:________一、单选题 (共12题;共24分)1. (2分)下列关于蒸发和沸腾的说法中,正确的是()A . 蒸发和沸腾都只能在液体表面发生B . 沸腾需要吸热,而蒸发不需要吸热C . 蒸发和沸腾是汽化的两种方式D . 蒸发和沸腾都只能在一定温度下发生2. (2分)下列自然现象中,属于液化现象的是()A . 暖春,麦田里白雪消融B . 初夏,草地上露珠晶莹C . 深秋,操场上轻霜涂抹D . 严冬,池塘里厚厚寒冰3. (2分)很冷的冬天,戴眼镜的人从室外走进温暖的室内,眼镜变模糊了,这是因为()A . 室内的水蒸气遇到冷的镜片凝华成的小水珠附着在眼镜上B . 眼镜上有灰尘C . 室内的水蒸气遇到冷的镜片液化成小水珠附着在眼镜片上D . 镜片导致水发生汽化蒙在玻璃上4. (2分) (2017九上·成都期中) 质量相同的甲、乙两种物质从固态开始加热,它们在相同时间内吸收的热量相等,加热时间都为6分钟,它们的温度随时间变化的图象如图所示.下列说法正确的是()A . 甲在3~6min内是液态B . 甲是非晶体,乙是晶体C . 在4~6min内,甲的内能保持不变D . 在固态时,甲的比热容小于乙的比热容5. (2分)炎热的夏天,小红从冰箱冷冻室中取出一些冰块放入可乐杯中,经过一段较长时间后,杯中的冰块全部变成了液态,下面的图像能正确反映冰块物态变化过程的是()A .B .C .D .6. (2分)(2018·青海) 如图所示,从中得出的结论错误的一项是A . 在AB段,物质处于固态B . 这是某种晶体的熔化图象C . 该物质熔化过程历时6分钟D . 该物质的熔点是7. (2分)(2017·海拉尔模拟) 某同学对冰加热,他将冰熔化成水直到沸腾的过程,绘制成如图所示的温度随时间变化的图象,下列分析正确的是()A . 冰的升温比水快,说明冰的比热容比水小B . 冰熔化时温度不变,内能不变C . 水沸腾时温度不变,说明沸腾不需要吸热D . 图中DE段表示冰的熔化过程8. (2分)(2021·广西壮族自治模拟) 如图所示,下列现象中,与烧水时壶口出现的“白气”,属于同种物态变化的是()A . ①②B . ①④C . ②③D . ③④9. (2分) (2017八上·鹤岗期中) 下列四个图象中,能够表示晶体凝固的是()A .B .C .D .10. (2分) (2018八上·滨州期中) 生活中常用碗炖食物,如图所示。
2021年中考九年级数学一轮专题复习:圆 压轴题综合练习(三)()

2021年中考九年级数学一轮专题复习:圆压轴题综合练习(三)1、如图,AB是半圆O的直径,点P是BA延长线上一点,PC是⊙O的切线,切点为C. 过点B作BD⊥PC交PC的延长线于点D,连接BC. 求证:(1)∠PBC =∠CBD; (2)BC2=AB·BD2、如图,已知⊙O的直径AB=10,弦AC=6,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E.(1)求证:DE是⊙O的切线.(2)求DE的长.3、如图,⊙O中,点C为的中点,∠ACB=120°,OC的延长线与AD交于点D,且∠D=∠B.(1)求证:AD与⊙O相切;(2)若点C到弦AB的距离为2,求弦AB的长.4、如图,AB是⊙O的直径,点C是⊙O上一点,连接AC,∠MAC=∠CAB,作CD ⊥AM,垂足为D.(1)求证:CD是⊙O的切线;(2)若∠ACD=30°,AD=4,求图中阴影部分的面积.5、如图,在△ABC中,∠C=90°,D是BC边上一点,以DB为直径的⊙O经过AB 的中点E,交AD的延长线于点F,连结EF.(1)求证:∠1=∠F.(2)若CD的长.6、如图,以AB边为直径的⊙O经过点P,C是⊙O上一点,连结PC交AB于点E,且∠ACP=60°,PA=PD.(1)试判断PD与⊙O的位置关系,并说明理由;(2)若点C是弧AB的中点,已知AB=4,求CE•CP的值.7、如图,在⊙O中,点C是直径AB延长线上一点,过点C作⊙O的切线,切点为D,连结BD.(1)求证:∠A=∠BDC;(2)若CM平分∠ACD,且分别交AD、BD于点M、N,当DM=1时,求MN的长.8、已知:如图,在△ABC 中,AC =BC ,以 BC 为直径的⊙O 交AB 于点D ,过点D作DE ⊥AC 于点E ,交BC 的延长线于点F 。
(1)求证:AD =BD ;(2)求证:DF 是⊙O 的切线;(3)若⊙O 的半径为3,sin ∠F =53,求DE 的长。
2022年中考数学挑战压轴题《解答题三》

中考数学冲刺挑战压轴题专题汇编(解答题三)1.(2019•江西)在图1,2,3中,已知▱ABCD,∠ABC=120°,点E为线段BC上的动点,连接AE,以AE 为边向上作菱形AEFG,且∠EAG=120°.(1)如图1,当点E与点B重合时,∠CEF=°;(2)如图2,连接AF.①填空:∠F AD∠EAB(填“>”,“<“,“=”);②求证:点F在∠ABC的平分线上;(3)如图3,连接EG,DG,并延长DG交BA的延长线于点H,当四边形AEGH是平行四边形时,求的值.2.(2018•江西)在菱形ABCD中,∠ABC=60°,点P是射线BD上一动点,以AP为边向右侧作等边△APE,点E的位置随着点P的位置变化而变化.(1)如图1,当点E在菱形ABCD内部或边上时,连接CE,BP与CE的数量关系是,CE与AD 的位置关系是;(2)当点E在菱形ABCD外部时,(1)中的结论是否还成立?若成立,请予以证明;若不成立,请说明理由(选择图2,图3中的一种情况予以证明或说理);(3)如图4,当点P在线段BD的延长线上时,连接BE,若AB=2,BE=2,求四边形ADPE的面积.3.(2017•江西)我们定义:如图1,在△ABC看,把AB点绕点A顺时针旋转α(0°<α<180°)得到AB',把AC绕点A逆时针旋转β得到AC',连接B'C'.当α+β=180°时,我们称△A'B'C'是△ABC的“旋补三角形”,△AB'C'边B'C'上的中线AD叫做△ABC的“旋补中线”,点A叫做“旋补中心”.特例感知:(1)在图2,图3中,△AB'C'是△ABC的“旋补三角形”,AD是△ABC的“旋补中线”.①如图2,当△ABC为等边三角形时,AD与BC的数量关系为AD=BC;②如图3,当∠BAC=90°,BC=8时,则AD长为.猜想论证:(2)在图1中,当△ABC为任意三角形时,猜想AD与BC的数量关系,并给予证明.拓展应用(3)如图4,在四边形ABCD,∠C=90°,∠D=150°,BC=12,CD=2,DA=6.在四边形内部是否存在点P,使△PDC是△P AB的“旋补三角形”?若存在,给予证明,并求△P AB的“旋补中线”长;若不存在,说明理由.1.如图1,边长为4的正方形ABCD中,点E在AB边上(不与点A,B重合),点F在BC边上(不与点B、C重合).第一次操作:将线段EF绕点F顺时针旋转,当点E落在正方形上时,记为点G;第二次操作:将线段FG绕点G顺时针旋转,当点F落在正方形上时,记为点H;依此操作下去…(1)图2中的△EFD是经过两次操作后得到的,其形状为,求此时线段EF的长;(2)若经过三次操作可得到四边形EFGH.①请判断四边形EFGH的形状为,此时AE与BF的数量关系是;②以①中的结论为前提,设AE的长为x,四边形EFGH的面积为y,求y与x的函数关系式及面积y的取值范围.2.(发现证明)如图1,点E,F分别在正方形ABCD的边BC,CD上,∠EAF=45°,试判断BE,EF,FD之间的数量关系.小聪把△ABE绕点A逆时针旋转90°至△ADG,通过证明△AEF≌△AGF;从而发现并证明了EF=BE+FD.(类比引申)(1)如图2,点E、F分别在正方形ABCD的边CB、CD的延长线上,∠EAF=45°,连接EF,请根据小聪的发现给你的启示写出EF、BE、DF之间的数量关系,并证明;(联想拓展)(2)如图3,如图,∠BAC=90°,AB=AC,点E、F在边BC上,且∠EAF=45°,若BE=3,EF=5,求CF 的长.3.(1)问题发现如图1,在△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=40°,连接AC,BD交于点M.填空:①ACBD的值为;②∠AMB的度数为.(2)类比探究如图2,在△OAB和△OCD中,∠AOB=∠COD=90°,∠OAB=∠OCD=30°,连接AC交BD的延长线于点M.请判断ACBD的值及∠AMB的度数,并说明理由;(3)拓展延伸在(2)的条件下,将△OCD绕点O在平面内旋转,AC,BD所在直线交于点M,若OD=1,OB直接写出当点C与点M重合时AC的长.1.(1)(问题发现)如图1,在Rt△ABC中,AB=AC=2,∠BAC=90°,点D为BC的中点,以CD为一边作正方形CDEF,点E 恰好与点A重合,则线段BE与AF的数量关系为(2)(拓展研究)在(1)的条件下,如果正方形CDEF绕点C旋转,连接BE,CE,AF,线段BE与AF的数量关系有无变化?请仅就图2的情形给出证明;(3)(问题发现)当正方形CDEF旋转到B,E,F三点共线时候,直接写出线段AF的长.2.综合与实践﹣四边形旋转中的数学“智慧”数学小组在课外数学活动中研究了一个问题,请帮他们解答.任务一:如图1,在矩形ABCD中,AB=6,AD=8,E,F分别为AB,AD边的中点,四边形AEGF为矩形,连接CG.(1)请直接写出CG的长是______.(2)如图2,当矩形AEGF绕点A旋转(比如顺时针旋转)至点G落在边AB上时,请计算DF与CG的长,通过计算,试猜想DF与CG之间的数量关系.(3)当矩形AEGF绕点A旋转至如图3的位置时,(2)中DF与CG之间的数量关系是否还成立?请说明理由.任务二:“智慧”数学小组对图形的旋转进行了拓展研究,如图4,在▱ABCD中,∠B=60°,AB=6,AD=8,E,F分别为AB,AD边的中点,四边形AEGF为平行四边形,连接CG.“智慧”数学小组发现DF与CG 仍然存在着特定的数量关系.(4)如图5,当▱AEGF绕点A旋转(比如顺时针旋转),其他条件不变时,“智慧”数学小组发现DF与CG 仍然存在着这一特定的数量关系.请你直接写出这个特定的数量关系.3.△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B,C重合),以AD为边在AD 右侧作正方形ADEF,连接CF,(1)观察猜想如图1,当点D在线段BC上时,①BC与CF的位置关系为:.②BC,CD,CF之间的数量关系为:;(将结论直接写在横线上)(2)数学思考如图2,当点D在线段CB的延长线上时,结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.(3)拓展延伸如图3,当点D在线段BC的延长线上时,延长BA交CF于点G,连接GE,若已知AB CD=14 BC,请求出GE的长.4.如图(1),已知点G在正方形ABCD的对角线AC上,GE⊥BC,垂足为点E,GF⊥CD,垂足为点F.(1)证明与推断:①求证:四边形CEGF是正方形;②推断:AGBE的值为:(2)探究与证明:将正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°),如图(2)所示,试探究线段AG与BE之间的数量关系,并说明理由:(3)拓展与运用:正方形CEGF在旋转过程中,当B,E,F三点在一条直线上时,如图(3)所示,延长CG交AD于点H.若AG=6,GH BC=.。
2020年数学中考复习,几何代数综合压轴题解析(三)

2020年数学中考复习,几代综合压轴题解析(三)1.(2019.眉山)如图,在平面直角坐标系中,抛物线y=-94x 2+bx+c 经过点A(-5,0)和点B (1,0).(1)求抛物线的解析式及顶点D 的坐标;(2)点P 是抛物线上A 、D 之间的一点,过点P 作PE ⊥x 轴于点F ,当矩形PEFG 的周长最大时,求点P 的横坐标;(3)如图连接AD 、BD ,点M 在线段AB 上(不与A 、B 重合),作∠DMN=∠DBA ,MN 交线段AD 于点N ,是否存在这样点M ,使得△DMN 为等腰三角形?若存在,求AN 的长;若不存在,请说明理由。
解析:(1)将A(-5,0)和点B (1,0)代入y=-94x 2+bx+c ,可得b=-916,c=920∴抛物线的解析式:y=-94x 2-916x+920,D (-2,4).(2)设P (m,-94m 2-916m+920),根据对称性可得GP=-4-2m 。
矩形PEFG 的周长=2(PE+PG )=2(-94m 2-916m+920-4-2m )=-98(m+417)2+18225 当m=-417时,矩形PEFG 的周长有最大值,即P 的点的横坐标为m=-417。
(3)由A(-5,0)和点B (1,0),D (-2,4)可求得AB=6,AD=DB=5。
①当MD=MN 时,由∠DBA=∠MAB,∠BDM=∠AMN.可证得△MBD ≌△NAM, ∴AN=MB.又∠DMN=∠DBA=∠DAB ,∠MDN=∠ADM,∴∠DNM=∠AMD ∴△ADM 是等腰三角形,即AM=AD=5,∴AN=MB=6-5=1②当ND=MN 时,∠NDM=∠DMN=∠DBA,又∠DAM 是公共角, ∴△ADM ∽△ABD ,∴AD 2=AM ·AB,可求得AM=625,BM=611 又△ANM ∽△BMD,∴DBAM=MB AN , 可得AN=3655。
③当ND=MD 时,可得∠DNM=∠DMN,又知∠DMN=∠DBA=∠DAB ,而发生了∠PNM=∠PAM,显然 这种情况不成立。
2021年中考数学复习《中考压轴题:轴对称之线段最短问题》经典题型靶向提升练习(三)

2021年中考数学复习《中考压轴题:轴对称之线段最短问题》经典题型靶向提升练习(三)1.如图,点P是∠AOB内部一点,现有一只蚂蚁要从P点出发,先到OA,再到OB,最后返回到点P.请作出蚂蚁爬行的最短路径(要求:保留作图痕迹,不写作法.)2.在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD 的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.(1)如图①,若∠ADE=60°,AB=AC=2,点D在线段BC上,①∠BCE和∠BAC之间是有怎样的数量关系?不必说明理由;②当四边形ADCE的周长取最小值时,直接写出BD的长;(2)若∠BAC≠60°,当点D在射线BC上移动,如图②,则∠BCE和∠BAC之间有怎样的数量关系?并说明理由.3.如图,在矩形ABCD中,E是对角线BD上一点(不与点B、D重合),过点E作EF∥AB,且EF=AB,连接AE、BF、CF.(1)若DE=DC,求证:四边形CDEF是菱形;(2)若AB=,BC=3,当四边形ABFE周长最小时,四边形CDEF的周长为.4.如图,在Rt△ABC中,∠A=90°,∠ACB=30°,AC=10,CD是角平分线.(1)如图1,若E是AC边上的一个定点,在CD上找一点P,使P A+PE的值最小;(2)如图2,若E是AC边上的一个动点,在CD上找一点P,使P A+PE的值最小,并直接写出其最小值.5.如图,要在燃气管道l上修建一个泵站,分别向A,B两城镇供气,泵站修在管道的什么位置可使所用的输气管线最短?6.如图,在7×7网格中,每个小正方形边长都为1.建立适当的平面直角坐标系,使点A (3,4)、C(4,2).(1)判断△ABC的形状,并求图中格点△ABC的面积;(2)在x轴上有一点P,使得P A+PC最小,则P A+PC的最小值为.7.如图,平面直角坐标系内,A(﹣5,4),B(3,0),C(2,3)按下列要求解答.(1)如图1,在x轴上标出点D的位置,使AD=BD,直接写出点D的坐标.(2)如图2,在x轴上标出点E的位置,使AE+CE最短,直接写出点E的坐标.8.如图,一牧童的家在点A处,他和哥哥一起在点C处放马,点A,C到河岸的距离分别是AB=500m,CD=700m,且B,D两地间的距离为600m.夕阳西下,弟兄俩准备从C 点将马牵到河边去饮水,再赶回家,为了使所走的路程最短.(1)他们应该将马赶到河边的什么地点?请在图中画出来.(2)请求出他们至少要走的路程.9.如图,等边△ABC的边长为4,AD是BC边上的中线,F是AD边上的动点,E是AC 边上一点,若AE=2,当EF+CF取得最小值时,则∠ECF的度数为多少?10.如图,在▱ABCD中,AD的垂直平分线经过点B,与CD的延长线交于点E,AD与BE 相交于点O,连接AE,BD.(1)求证:四边形ABDE为菱形;(2)若AD=8,问在BC上是否存在点P,使得PE+PD最小?若存在,求线段BP的长;若不存在,请说明理由.参考答案1.解:如图,作点P关于OA、OB的对称点P′、P″,连接P′P″与OA、OB交于点M、N,则蚂蚁爬行的最短路径为:PM+MN+PN=P′M+MN+P″N=P′P″.2.解:(1)①∠BCE+∠BAC=180°;②如图1∵△ABD≌△ACE,∴BD=EC,∵四边形ADCE的周长=AD+DC+CE+AE=AD+DC+BD+AE=BC+2AD,∴当AD最短时,四边形ADCE的周长最小,即AD⊥BC时,周长最小;∵AB=AC,∴BD=BC=1;(2)∠BCE+∠BAC=180°;理由如下:如图2,AD与CE交于F点,∵∠BAC=∠DAE,∴∠BAD=∠CAE,∵AB=AC,AD=AE,∴△ABD≌△ACE,∴∠ADB=∠AEC,∵∠AFE=∠CFD,∴∠EAF=∠ECD,∵∠BAC=∠F AE,∠BCE+∠ECD=180°,∴∠BCE+∠BAC=180°;3.解:(1)∵矩形ABCD中,∴AB∥CD,AB=CD,∵EF∥AB,EF=AB,∴EF∥CD,EF=CD,∴四边形CDEF是平行四边形,∵DE=DC,∴四边形CDEF是菱形;(2 )∵AB=CD,AB∥CD∥EF,EF=AB,∴AB∥EF,AB=EF,∴四边形ABFE是平行四边形,∵四边形ABFE周长=2(BF+EF)=2(AB+BF),∴当BF⊥BD时,四边形ABFE周长最小;∵AB=,BC=3,∴∠CBD=∠ADB=30°,∵∠AEB=∠FBE=90°,∴∠DAE=60°,∴∠BAE=30°,∴AE=,∴BF=,∵AE=,AD=3,∠ADE=30°,∴DE=,∴四边形CDEF的周长=2(CD+DE)=2(+)=5.故答案为:5.4.解:(1)如图,作点E关于CD的对称点F连接AF交CD于点P,则此时,P A+PE的值最小;点P即为所求;(2)如图,过D作DF⊥BC于F,过F作EF⊥AC交CD于P,则此时,P A+PE的值最小;P A+PE的最小值=EF,∵CD是角平分线,∠BAC=90°,∴DA=DF,即点A与点F关于CD对称,∴CF=AC=10,∵∠ACB=30°,∴EF=CF=5.5.解:作A关于直线l的对称点A′,连接A′B交直线l于P,连接AP,则泵站修在管道的P点处,可使所用的输气管线AP+BP最短.理由如下:在直线l上任取一点E,连接AE、BE、A′E,∵A、A′关于直线l对称,∴AP=A′P,同理AE=A′E,∵AP+BP=A′P+BP=A′B,AE+BE=A′E+BE>A′B,∴AP+BP<A′E+BE,∵E是任意取的一点,∴AP+BP最短.6.解:(1)△ABC是直角三角形,理由:∵AC2+BC2=25,AB2=25,∴AC2+BC2=AB2,∴△ABC是直角三角形;△ABC的面积=××=5;(2)如图所示,作点C关于x轴的对称点C',连接AC'交x轴于P,连接CP,则CP=C'P,∴P A+PC的最小值为AC'的长,∵AC'==,∴P A+PC的最小值为,故答案为:.7.解:(1)如图1所示,点D即为所求,D(﹣2,0);(2)如图2所示,点E即为所求,E(﹣1,0).故答案为:(﹣2,0);(﹣1,0).8.解:(1)作A点关于河岸的对称点A′,连接CA′交河岸与P,则PC+P A=PC+P A′=CA′最短,故牧童应将马牵到河边的P地点.(2)作DB′=BA′,且DB′⊥BD,∵DB′=BA′,DB′⊥BD,CB′∥A′A,∴四边形A′B′CA是矩形,∴B'A'=BD,在Rt△CB′A′中,连接A′B′,则CB′=CD+DB′=1200(m),∴CA′==600(m).9.解:过E作EM∥BC,交AD于N,∵AC=4,AE=2,∴EC=2=AE,∴AM=BM=2,∴AM=AE,∵AD是BC边上的中线,△ABC是等边三角形,∴AD⊥BC,∵EM∥BC,∴AD⊥EM,∵AM=AE,∴E和M关于AD对称,连接CM交AD于F,连接EF,则此时EF+CF的值最小,∵△ABC是等边三角形,∴∠ACB=60°,AC=BC,∵AM=BM,∴∠ECF=∠ACB=30°.10.(1)证明:∵BE垂直平分AD,.∴AO=DO,AD⊥BE.∵四边形ABCD是平行四边形,∴AB∥CD.∴∠ABE=∠BED.∵∠AOB=∠DOE,又AO=DO,∴△AOB≌△DOE(AAS),∴BO=EO.又AO=DO,∴四边形ABDE是平行四边形.∵AD⊥BE,∴四边形ABDE是菱形;(2)解:如图所示:作点D关于BC的对称点D',DD′交BC于点G,延长EB,过D'作DM⊥BE于点M,连接ED'交BC于点P,此时PD+PE最小;∵∠B0D=∠OBC=∠BGD=90°,∴四边形ODGB是矩形.∴BO=DG.同理BM=GD.∴MD'=DO=AD=4.又BO=EO,∴BO=EO=BM.∵∠EBP=∠M=90°,∠BEP=∠MED',∴△BEP∽△MED′,∴==,∴=,即BP=.。
初三中考数学压轴题精选100题(含答案)

初三中考数学压轴题精选100题(含答案)一、中考压轴题1.在△ABC中,AB=BC,将△ABC绕点A沿顺时针方向旋转得△A1B1C1,使点C1落在直线BC上(点C1与点C不重合),(1)如图,当∠C>60°时,写出边AB1与边CB的位置关系,并加以证明;(2)当∠C=60°时,写出边AB1与边CB的位置关系(不要求证明);(3)当∠C<60°时,请你在如图中用尺规作图法作出△AB1C1(保留作图痕迹,不写作法),再猜想你在(1)、(2)中得出的结论是否还成立并说明理由.【分析】(1)AB1∥BC.因为等腰三角形,两底角相等,再根据平行线的判定,内错角相等两直线平行,可证明两直线平行.(2)当∠C=60°时,写出边AB1与边CB的位置关系也是平行,证明方法同(1)题.(3)成立,根据旋转变换的性质画出图形.利用三角形全等即可证明.【解答】解:(1)AB1∥BC.证明:由已知得△ABC≌△AB1C1,∴∠BAC=∠B1AC1,∠B1AB=∠C1AC,∵AC1=AC,∴∠AC1C=∠ACC1,∵∠C1AC+∠AC1C+∠ACC1=180°,∴∠C1AC=180°﹣2∠ACC1,同理,在△ABC中,∵BA=BC,∴∠ABC=180°﹣2∠ACC1,∴∠ABC=∠C1AC=∠B1AB,∴AB1∥BC.(5分)(2)如图1,∠C=60°时,AB1∥BC.(7分)(3)如图,当∠C<60°时,(1)、(2)中的结论还成立.证明:显然△ABC≌△AB1C1,∴∠BAC=∠B1AC1,∴∠B1AB=∠C1AC,∵AC1=AC,∴∠AC1C=∠ACC1,∵∠C1AC+∠AC1C+∠ACC1=180°,∴∠C1AC=180°﹣2∠ACC1,同理,在△ABC中,∵BA=BC,∴∠ABC=180°﹣2∠ACC1,∴∠ABC=∠C1AC=∠B1AB,∴AB1∥BC.(13分)【点评】考查图形的旋转,等腰三角形的性质,平行线的判定.本题实质是考查对图形旋转特征的理解,旋转前后的图形是全等的.2.我们学习了利用函数图象求方程的近似解,例如:把方程2x﹣1=3﹣x的解看成函数y =2x﹣1的图象与函数y=3﹣x的图象交点的横坐标.如图,已画出反比例函数y=在第一象限内的图象,请你按照上述方法,利用此图象求方程x2﹣x﹣1=0的正数解.(要求画出相应函数的图象;求出的解精确到0.1)【分析】根据题意可知,方程x2﹣x﹣1=0的解可看做是函数y=和y=x﹣1的交点坐标,所以根据图象可知方程x2﹣x﹣1=0的正数解约为1.1.【解答】解:∵x≠0,∴将x2﹣x﹣1=0两边同时除以x,得x﹣1﹣=0,即=x﹣1,把x2﹣x﹣1=0的正根视为由函数y=与函数y=x﹣1的图象在第一象限交点的横坐标.如图:∴正数解约为1.1.【点评】主要考查了反比例函数和一元二次方程之间的关系.一元二次方程的解都可化为一个反比例函数和一次函数的交点问题求解.3.汽车产业的发展,有效促进我国现代化建设.某汽车销售公司2005年盈利1500万元,到2007年盈利2160万元,且从2005年到2007年,每年盈利的年增长率相同.(1)该公司2006年盈利多少万元?(2)若该公司盈利的年增长率继续保持不变,预计2008年盈利多少万元?【分析】(1)需先算出从2005年到2007年,每年盈利的年增长率,然后根据2005年的盈利,算出2006年的利润;(2)相等关系是:2008年盈利=2007年盈利×每年盈利的年增长率.【解答】解:(1)设每年盈利的年增长率为x,根据题意得1500(1+x)2=2160解得x1=0.2,x2=﹣2.2(不合题意,舍去)∴1500(1+x)=1500(1+0.2)=1800答:2006年该公司盈利1800万元.(2)2160(1+0.2)=2592答:预计2008年该公司盈利2592万元.【点评】本题的关键是需求出从2005年到2007年,每年盈利的年增长率.等量关系为:2005年盈利×(1+年增长率)2=2160.4.如图,△ABC内接于⊙O,AB=6,AC=4,D是AB边上一点,P是优弧BAC的中点,连接P A、PB、PC、PD.(1)当BD的长度为多少时,△P AD是以AD为底边的等腰三角形?并证明;(2)在(1)的条件下,若cos∠PCB=,求P A的长.【分析】(1)根据等弧对等弦以及全等三角形的判定和性质进行求解;(2)过点P作PE⊥AD于E.根据锐角三角函数的知识和垂径定理进行求解.【解答】解:(1)当BD=AC=4时,△P AD是以AD为底边的等腰三角形.∵P是优弧BAC的中点,∴=.∴PB=PC.又∵∠PBD=∠PCA(圆周角定理),∴当BD=AC=4,△PBD≌△PCA.∴P A=PD,即△P AD是以AD为底边的等腰三角形.(2)过点P作PE⊥AD于E,由(1)可知,当BD=4时,PD=P A,AD=AB﹣BD=6﹣4=2,则AE=AD=1.∵∠PCB=∠P AD(在同圆或等圆中,同弧所对的圆周角相等),∴cos∠P AD=cos∠PCB=,∴P A=.【点评】综合运用了等弧对等弦的性质、全等三角形的判定和性质、锐角三角函数的知识以及垂径定理.5.广安市某楼盘准备以每平方米6000元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望,房地产开发商为了加快资金周转,对价格经过两次下调后,决定以每平方米4860元的均价开盘销售.(1)求平均每次下调的百分率.(2)某人准备以开盘价均价购买一套100平方米的住房,开发商给予以下两种优惠方案以供选择:①打9.8折销售;②不打折,一次性送装修费每平方米80元,试问哪种方案更优惠?【分析】(1)根据题意设平均每次下调的百分率为x,列出一元二次方程,解方程即可得出答案;(2)分别计算两种方案的优惠价格,比较后发现方案①更优惠.【解答】解:(1)设平均每次下调的百分率为x,则6000(1﹣x)2=4860,解得:x1=0.1=10%,x2=1.9(舍去),故平均每次下调的百分率为10%;(2)方案①购房优惠:4860×100×(1﹣0.98)=9720(元);方案②可优惠:80×100=8000(元).故选择方案①更优惠.【点评】本题主要考查一元二次方程的实际应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解,属于中档题.6.如图,已知直径为OA的⊙P与x轴交于O、A两点,点B、C把三等分,连接PC并延长PC交y轴于点D(0,3).(1)求证:△POD≌△ABO;(2)若直线l:y=kx+b经过圆心P和D,求直线l的解析式.【分析】(1)首先连接PB,由直径为OA的⊙P与x轴交于O、A两点,点B、C把三等分,可求得∠APB=∠DPO=60°,∠ABO=∠POD=90°,即可得△P AB是等边三角形,可得AB=OP,然后由ASA,即可判定:△POD≌△ABO;(2)易求得∠PDO=30°,由OP=OD•tan30°,即可求得点P的坐标,然后利用待定系数法,即可求得直线l的解析式.【解答】(1)证明:连接PB,∵直径为OA的⊙P与x轴交于O、A两点,点B、C把三等分,∴∠APB=∠DPO=×180°=60°,∠ABO=∠POD=90°,∵P A=PB,∴△P AB是等边三角形,∴AB=P A,∠BAO=60°,∴AB=OP,∠BAO=∠OPD,在△POD和△ABO中,∴△POD≌△ABO(ASA);(2)解:由(1)得△POD≌△ABO,∴∠PDO=∠AOB,∵∠AOB=∠APB=×60°=30°,∴∠PDO=30°,∴OP=OD•tan30°=3×=,∴点P的坐标为:(﹣,0)∴,解得:,∴直线l的解析式为:y=x+3.【点评】此题考查了圆周角定理、全等三角形的判定与性质、直角三角形的性质、等边三角形的判定与性质以及待定系数法求一次函数的解析式.此题综合性较强,难度适中,注意准确作出辅助线,注意数形结合思想的应用.7.如图1,在直角坐标系中,点A的坐标为(1,0),以OA为边在第四象限内作等边△AOB,点C为x轴的正半轴上一动点(OC>1),连接BC,以BC为边在第四象限内作等边△CBD,直线DA交y轴于点E.(1)试问△OBC与△ABD全等吗?并证明你的结论;(2)随着点C位置的变化,点E的位置是否会发生变化?若没有变化,求出点E的坐标;若有变化,请说明理由;(3)如图2,以OC为直径作圆,与直线DE分别交于点F、G,设AC=m,AF=n,用含n的代数式表示m.【分析】(1)由等边三角形的性质知,OBA=∠CBD=60°,易得∠OBC=∠ABD,又有OB=AB,BC=BD故有△OBC≌△ABD;(2)由1知,△OBC≌△ABD⇒∠BAD=∠BOC=60°,可得∠OAE=60°,在Rt△EOA 中,有EO=OA•tan60°=,即可求得点E的坐标;(3)由相交弦定理知1•m=n•AG,即AG=,由切割线定理知,OE2=EG•EF,在Rt△EOA中,由勾股定理知,AE==2,故建立方程:()2=(2﹣)(2+n),就可求得m与n关系.【解答】解:(1)两个三角形全等.∵△AOB、△CBD都是等边三角形,∴OBA=∠CBD=60°,∴∠OBA+∠ABC=∠CBD+∠ABC,即∠OBC=∠ABD;∵OB=AB,BC=BD,△OBC≌△ABD;(2)点E位置不变.∵△OBC≌△ABD,∴∠BAD=∠BOC=60°,∠OAE=180°﹣60°﹣60°=60°;在Rt△EOA中,EO=OA•tan60°=,或∠AEO=30°,得AE=2,∴OE=∴点E的坐标为(0,);(3)∵AC=m,AF=n,由相交弦定理知1•m=n•AG,即AG=;又∵OC是直径,∴OE是圆的切线,OE2=EG•EF,在Rt△EOA中,AE==2,()2=(2﹣)(2+n)即2n2+n﹣2m﹣mn=0解得m=.【点评】命题立意:考查圆的相交弦定理、切线定理、三角形全等等知识,并且将这些知识与坐标系联系在一起,考查综合分析、解决问题的能力.8.我国年人均用纸量约为28公斤,每个初中毕业生离校时大约有10公斤废纸;用1吨废纸造出的再生好纸,所能节约的造纸木材相当于18棵大树,而平均每亩森林只有50至80棵这样的大树.(1)若我市2005年4万名初中毕业生能把自己离校时的全部废纸送到回收站使之制造为再生好纸,那么最少可使多少亩森林免遭砍伐?(2)我市从2000年初开始实施天然林保护工程,大力倡导废纸回收再生,如今成效显著,森林面积大约由2003年初的50万亩增加到2005年初的60.5万亩.假设我市年用纸量的20%可以作为废纸回收、森林面积年均增长率保持不变,请你按全市总人口约为1000万计算:在从2005年初到2006年初这一年度内,我市因回收废纸所能保护的最大森林面积相当于新增加的森林面积的百分之几?(精确到1%)【分析】(1)因为每个初中毕业生离校时大约有10公斤废纸,用1吨废纸造出的再生好纸,所能节约的造纸木材相当于18棵大树,而平均每亩森林只有50至80棵这样的大树,所以有40000×10÷1000×18÷80,计算出即可求出答案;(2)森林面积大约由2003年初的50万亩增加到2005年初的60.5万亩,可先求出森林面积年均增长率,进而求出2005到2006年新增加的森林面积,而因回收废纸所能保护的最大森林面积=1000×10000×28×20%÷1000×18÷50,然后进行简单的计算即可求出答案.【解答】解:(1)4×104×10÷1000×18÷80=90(亩).答:若我市2005年4万名初中毕业生能把自己离校时的全部废纸送到回收站使之制造为再生好纸,那么最少可使90亩森林免遭砍伐.(2)设我市森林面积年平均增长率为x,依题意列方程得50(1+x)2=60.5,解得x1=10%,x2=﹣2.1(不合题意,舍去),1000×104×28×20%÷1000×18÷50=20160,20160÷(605000×10%)≈33%.答:在从2005年初到2006年初这一年度内,我市因回收废纸所能保护的最大森林面积相当于新增加的森林面积的33%.【点评】本题以保护环境为主题,考查了增长率问题,阅读理解题意,并从题目中提炼出平均增长率的数学模型并解答的能力;解答时需仔细分析题意,利用方程即可解决问题.9.一个不透明的口袋里有红、黄、绿三种颜色的球(除颜色外其余都相同),其中红球有2个,黄球有1个,任意摸出一个黄球的概率为.(1)试求口袋里绿球的个数;(2)若第一次从口袋中任意摸出一球(不放回),第二次任意摸出一球,请你用树状图或列表法,求出两次都摸到红球的概率.【分析】(1)根据概率的求解方法,利用方程求得绿球个数;(2)此题需要两步完成,所以采用树状图法或者列表法都比较简单,解题时要注意是放回实验还是不放回实验,此题为不放回实验.【解答】解:(1)设口袋里绿球有x个,则,解得x=1.故口袋里绿球有1个.(2)红一红二黄绿红一红二,红一黄,红一绿,红一红二红一,红二黄,红一绿,红二黄红一,黄红二,黄绿,黄绿红一,绿红二,绿黄,绿故,P(两次都摸到红球)=.【点评】(1)解题时要注意应用方程思想;(2)列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.10.如图,在矩形ABCD中,AB=8,AD=6,点P、Q分别是AB边和CD边上的动点,点P从点A向点B运动,点Q从点C向点D运动,且保持AP=CQ.设AP=x.(1)当PQ∥AD时,求x的值;(2)当线段PQ的垂直平分线与BC边相交时,求x的取值范围;(3)当线段PQ的垂直平分线与BC相交时,设交点为E,连接EP、EQ,设△EPQ的面积为S,求S关于x的函数关系式,并写出S的取值范围.【分析】(1)根据已知条件,证明四边形APQD是矩形,再根据矩形的性质和AP=CQ 求x即可;(2)连接EP、EQ,则EP=EQ,设BE=y,列出等式(8﹣x)2+y2=(6﹣y)2+x2然后根据函数的性质来求x的取值范围;(3)由图形的等量关系列出方程,再根据函数的性质来求最值.【解答】解:(1)当PQ∥AD时,则∠A=∠APQ=90°,∠D=∠DQP=90°,又∵AB∥CD,∴四边形APQD是矩形,∴AP=QD,∵AP=CQ,AP=CD=,∴x=4.(2)如图,连接EP、EQ,则EP=EQ,设BE=y.∴(8﹣x)2+y2=(6﹣y)2+x2,∴y=.∵0≤y≤6,∴0≤≤6,∴≤x≤.(3)S△BPE=•BE•BP=••(8﹣x)=,S△ECQ==•(6﹣)•x=,∵AP=CQ,∴S BPQC=,∴S=S BPQC﹣S△BPE﹣S△ECQ=24﹣﹣,整理得:S==(x﹣4)2+12(),∴当x=4时,S有最小值12,当x=或x=时,S有最大值.∴12≤S≤.【点评】解答本题时,涉及到了矩形的判定、矩形的性质、勾股定理以及二次函数的最值等知识点,这是一道综合性比较强的题目,所以在解答题目时,一定要把各个知识点融会贯通,这样解题时才会少走弯路.11.某公司经营杨梅业务,以3万元/吨的价格向农户收购杨梅后,分拣成A、B两类,A 类杨梅包装后直接销售;B类杨梅深加工后再销售.A类杨梅的包装成本为1万元/吨,根据市场调查,它的平均销售价格y(单位:万元/吨)与销售数量x(x≥2)之间的函数关系如图;B类杨梅深加工总费用s(单位:万元)与加工数量t(单位:吨)之间的函数关系是s=12+3t,平均销售价格为9万元/吨.(1)直接写出A类杨梅平均销售价格y与销售量x之间的函数关系式;(2)第一次,该公司收购了20吨杨梅,其中A类杨梅有x吨,经营这批杨梅所获得的毛利润为w万元(毛利润=销售总收入﹣经营总成本).①求w关于x的函数关系式;②若该公司获得了30万元毛利润,问:用于直销的A类杨梅有多少吨?(3)第二次,该公司准备投入132万元资金,请设计一种经营方案,使公司获得最大毛利润,并求出最大毛利润.【分析】(1)这是一个分段函数,分别求出其函数关系式;(2)①当2≤x<8时及当x≥8时,分别求出w关于x的表达式.注意w=销售总收入﹣经营总成本=w A+w B﹣3×20;②若该公司获得了30万元毛利润,将30万元代入①中求得的表达式,求出A类杨梅的数(3)本问是方案设计问题,总投入为132万元,这笔132万元包括购买杨梅的费用+A类杨梅加工成本+B类杨梅加工成本.共购买了m吨杨梅,其中A类杨梅为x吨,B类杨梅为(m﹣x)吨,分别求出当2≤x<8时及当x≥8时w关于x的表达式,并分别求出其最大值.【解答】解:(1)①当2≤x<8时,如图,设直线AB解析式为:y=kx+b,将A(2,12)、B(8,6)代入得:,解得,∴y=﹣x+14;②当x≥8时,y=6.所以A类杨梅平均销售价格y与销售量x之间的函数关系式为:y=;(2)设销售A类杨梅x吨,则销售B类杨梅(20﹣x)吨.①当2≤x<8时,w A=x(﹣x+14)﹣x=﹣x2+13x;w B=9(20﹣x)﹣[12+3(20﹣x)]=108﹣6x∴w=w A+w B﹣3×20=(﹣x2+13x)+(108﹣6x)﹣60=﹣x2+7x+48;当x≥8时,w A=6x﹣x=5x;w B=9(20﹣x)﹣[12+3(20﹣x)]=108﹣6x∴w=w A+w B﹣3×20=(5x)+(108﹣6x)﹣60=﹣x+48.∴w关于x的函数关系式为:w=.②当2≤x<8时,﹣x2+7x+48=30,解得x1=9,x2=﹣2,均不合题意;当x≥8时,﹣x+48=30,解得x=18.∴当毛利润达到30万元时,直接销售的A类杨梅有18吨.(3)设该公司用132万元共购买了m吨杨梅,其中A类杨梅为x吨,B类杨梅为(m﹣x)吨,则购买费用为3m万元,A类杨梅加工成本为x万元,B类杨梅加工成本为[12+3(m﹣x)]∴3m+x+[12+3(m﹣x)]=132,化简得:x=3m﹣60.①当2≤x<8时,w A=x(﹣x+14)﹣x=﹣x2+13x;w B=9(m﹣x)﹣[12+3(m﹣x)]=6m﹣6x﹣12∴w=w A+w B﹣3×m=(﹣x2+13x)+(6m﹣6x﹣12)﹣3m=﹣x2+7x+3m﹣12.将3m=x+60代入得:w=﹣x2+8x+48=﹣(x﹣4)2+64∴当x=4时,有最大毛利润64万元,此时m=,m﹣x=;②当x≥8时,w A=6x﹣x=5x;w B=9(m﹣x)﹣[12+3(m﹣x)]=6m﹣6x﹣12∴w=w A+w B﹣3×m=(5x)+(6m﹣6x﹣12)﹣3m=﹣x+3m﹣12.将3m=x+60代入得:w=48∴当x>8时,有最大毛利润48万元.综上所述,购买杨梅共吨,其中A类杨梅4吨,B类吨,公司能够获得最大毛利润,最大毛利润为64万元.【点评】本题是二次函数、一次函数的综合应用题,难度较大.解题关键是理清售价、成本、利润三者之间的关系.涉及到分段函数时,注意要分类讨论.12.⊙O1与⊙O2相交于A、B两点,如图(1),连接O2O1并延长交⊙O1于P点,连接P A、PB并分别延长交⊙O2于C、D两点,连接CO2并延长交⊙O2于E点.已知⊙O2的半径为R,设∠CAD=α.(1)求CD的长(用含R、α的式子表示);(2)试判断CD与PO1的位置关系,并说明理由;(3)设点P’为⊙O1上(⊙O2外)的动点,连接P’A、P’B并分别延长交⊙O2于C’、D’,请你探究∠C’AD’是否等于α?C’D’与P’O1的位置关系如何?并说明(注:图(2)与图(3)中⊙O1和⊙O2的大小及位置关系与图(1)完全相同,若你感到继续在图(1)中探究问题(3),图形太复杂,不便于观察,可以选择图(2)或图(3)中的一图说明理由).【分析】(1)作⊙O2的直径CE,连接DE.根据圆周角定理的推论,得∠E=∠CAD=α,再利用解直角三角形的知识求解;(2)连接AB,延长PO1与⊙O1相交于点E,连接AE.根据圆内接四边形的性质,得∠ABP′=∠C′,根据圆周角定理的推论,得∠ABP′=∠E,∠EAP′=90°,从而证明∠AP′E+∠C′=90°,则CD与PO1的位置关系是互相垂直;(3)根据同弧所对的圆周角相等,则说明∠C’AD’等于α;根据(2)中的证明过程,则可以证明C’D’与P’O1的位置关系是互相垂直.【解答】解:(1)连接DE.根据圆周角定理的推论,得∠E=∠CAD=α.∵CE是直径,∴∠CDE=90°.∴CD=CE•sin E=2R sinα;(2)CD与PO1的位置关系是互相垂直.理由如下:连接AB,延长PO1与⊙O1相交于点E,连接AE.∵四边形BAC′D′是圆内接四边形,∴∠ABP′=∠C′.∵P′E是直径,∴∠EAP′=90°,∴∠AP′E+∠E=90°.又∠ABP′=∠E,∴∠AP′E+∠C′=90°,即CD与PO1的位置关系是互相垂直;(3)根据同弧所对的圆周角相等,则说明∠C’AD’等于α;根据(2)中的证明过程,则可以证明C’D’与P’O1的位置关系是互相垂直.【点评】此题综合运用了圆周角定理及其推论、直角三角形的性质、圆内接四边形的性质.注意:连接两圆的公共弦、构造直径所对的圆周角都是圆中常见的辅助线.13.已知⊙O1与⊙O2相交于A、B两点,点O1在⊙O2上,C为⊙O2上一点(不与A,B,O1重合),直线CB与⊙O1交于另一点D.(1)如图(1),若AD是⊙O1的直径,AC是⊙O2的直径,求证:AC=CD;(2)如图(2),若C是⊙O1外一点,求证:O1C丄AD;(3)如图(3),若C是⊙O1内的一点,判断(2)中的结论是否成立?【分析】(1)连接C01,利用直径所对圆周角等于90度,以及垂直平分线的性质得出即可;(2)根据已知得出四边形AEDB内接于⊙O1,得出∠ABC=∠E,再利用=,得出∠E=∠AO1C,进而得出CO1∥ED即可求出;(3)根据已知得出∠B=∠EO1C,又∠E=∠B,即可得出∠EO1C=∠E,得出CO1∥ED,即可求出.【解答】(1)证明:连接C01∵AC为⊙O2直径∴∠AO1C=90°即CO1⊥AD,∵AO1=DO1∴DC=AC(垂直平分线的性质);(2)证明:连接AO1,连接AB,延长AO1交⊙O1于点E,连接ED,∵四边形AEDB内接于⊙O1,∴∠E+∠ABD=180°,∵∠ABC+∠ABD=180°,∴∠ABC=∠E,又∵=,∴∠ABC=∠AO1C,∴∠E=∠AO1C,∴CO1∥ED,又AE为⊙O1的直径,∴ED⊥AD,∴O1C⊥AD,(3)(2)中的结论仍然成立.证明:连接AO1,连接AB,延长AO1交⊙O1于点E,连接ED,∵∠B+∠AO1C=180°,∠EO1C+∠AO1C═180°,∴∠B=∠EO1C,又∵∠E=∠B,∴∠EO1C=∠E,∴CO1∥ED,又ED⊥AD,∴CO1⊥AD.【点评】此题主要考查了圆周角定理以及相交两圆的性质和圆内接四边形的性质,根据圆内接四边形的性质得出对应角之间的关系是解决问题的关键.14.如图,已知△BEC是等边三角形,∠AEB=∠DEC=90°,AE=DE,AC,BD的交点为O.(1)求证:△AEC≌△DEB;(2)若∠ABC=∠DCB=90°,AB=2 cm,求图中阴影部分的面积.【分析】(1)在△AEC和△DEB中,已知AE=DE,BE=CE,且夹角相等,根据边角边可证全等.(2)由图可知,在连接EO并延长EO交BC于点F,连接AD之后,整个图形是一个以EF所在直线对称的图形.即△AEO和△DEO面积相等,只要求出其中一个即可,而三角形AEO面积=•OE•FB,所以解题中心即为求出OE和FB,有(1)中结论和已知条件即可求解.【解答】(1)证明:∵∠AEB=∠DEC=90°,∴∠AEB+∠BEC=∠DEC+∠BEC,即∠AEC=∠DEB,∵△BEC是等边三角形,∴CE=BE,又AE=DE,∴△AEC≌△DEB.(2)解:连接EO并延长EO交BC于点F,连接AD.由(1)知AC=BD.∵∠ABC=∠DCB=90°,∴∠ABC+∠DCB=180°,∴AB∥DC,AB==CD,∴四边形ABCD为平行四边形且是矩形,∴OA=OB=OC=OD,又∵BE=CE,∴OE所在直线垂直平分线段BC,∴BF=FC,∠EFB=90°.∴OF=AB=×2=1,∵△BEC是等边三角形,∴∠EBC=60°.在Rt△AEB中,∠AEB=90°,∠ABE=∠ABC﹣∠EBC=90°﹣60°=30°,∴BE=AB•cos30°=,在Rt△BFE中,∠BFE=90°,∠EBF=60°,∴BF=BE•cos60°=,EF=BE•sin60°=,∴OE=EF﹣OF==,∵AE=ED,OE=OE,AO=DO,∴△AOE≌△DOE.∴S△AOE=S△DOE∴S阴影=2S△AOE=2וEO•BF=2×××=(cm2).【点评】考查综合应用等边三角形、等腰三角形、解直角三角形、直角三角形性质,进行逻辑推理能力和运算能力.15.经统计分析,某市跨河大桥上的车流速度v(千米/小时)是车流密度x(辆/千米)的函数,当桥上的车流密度达到220辆/千米时,造成堵塞,此时车流速度为0千米/小时;当车流密度不超过20辆/千米时,车流速度为80千米/小时,研究表明:当20≤x≤220时,车流速度v是车流密度x的一次函数.(1)求大桥上车流密度为100辆/千米时的车流速度;(2)在交通高峰时段,为使大桥上的车流速度大于40千米/小时且小于60千米/小时,应控制大桥上的车流密度在什么范围内?(3)车流量(辆/小时)是单位时间内通过桥上某观测点的车辆数,即:车流量=车流速度×车流密度.求大桥上车流量y的最大值.【分析】(1)当20≤x≤220时,设车流速度v与车流密度x的函数关系式为v=kx+b,根据题意的数量关系建立方程组求出其解即可;(2)由(1)的解析式建立不等式组求出其解即可;(3)设车流量y与x之间的关系式为y=vx,当x<20和20≤x≤220时分别表示出函数关系由函数的性质就可以求出结论.【解答】解:(1)设车流速度v与车流密度x的函数关系式为v=kx+b,由题意,得,解得:,∴当20≤x≤220时,v=﹣x+88,当x=100时,v=﹣×100+88=48(千米/小时);(2)由题意,得,解得:70<x<120.∴应控制大桥上的车流密度在70<x<120范围内;(3)设车流量y与x之间的关系式为y=vx,当0≤x≤20时y=80x,∴k=80>0,∴y随x的增大而增大,∴x=20时,y最大=1600;当20≤x≤220时y=(﹣x+88)x=﹣(x﹣110)2+4840,∴当x=110时,y最大=4840.∵4840>1600,∴当车流密度是110辆/千米,车流量y取得最大值是每小时4840辆.【点评】本题考查了车流量=车流速度×车流密度的运用,一次函数的解析式的运用,一元一次不等式组的运用,二次函数的性质的运用,解答时求出函数的解析式是关键.16.如图,菱形、矩形与正方形的形状有差异,我们将菱形、矩形与正方形的接近程度称为“接近度”.在研究“接近度”时,应保证相似图形的“接近度”相等.(1)设菱形相邻两个内角的度数分别为m°和n°,将菱形的“接近度”定义为|m﹣n|,于是|m﹣n|越小,菱形越接近于正方形.①若菱形的一个内角为70°,则该菱形的“接近度”等于40;②当菱形的“接近度”等于0时,菱形是正方形.(2)设矩形相邻两条边长分别是a和b(a≤b),将矩形的“接近度”定义为|a﹣b|,于是|a﹣b|越小,矩形越接近于正方形.你认为这种说法是否合理?若不合理,给出矩形的“接近度”一个合理定义.【分析】(1)根据相似图形的定义知,相似图形的形状相同,但大小不一定相同,相似图形的“接近度”相等.所以若菱形的一个内角为70°,则该菱形的“接近度”等于|m﹣n|;当菱形的“接近度”等于0时,菱形是正方形;(2)不合理,举例进行说明.【解答】解:(1)①∵内角为70°,∴与它相邻内角的度数为110°.∴菱形的“接近度”=|m﹣n|=|110﹣70|=40.②当菱形的“接近度”等于0时,菱形是正方形.(2)不合理.例如,对两个相似而不全等的矩形来说,它们接近正方形的程度是相同的,但|a﹣b|却不相等.合理定义方法不唯一.如定义为,越接近1,矩形越接近于正方形;越大,矩形与正方形的形状差异越大;当时,矩形就变成了正方形,即只有矩形的越接近1,矩形才越接近正方形.【点评】正确理解“接近度”的意思,矩形的“接近度”|a﹣b|越小,矩形越接近于正方形.这是解决问题的关键.17.如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点B的坐标为(1,0)①画出△ABC关于x轴对称的△A1B1C1;②画出将△ABC绕原点O按逆时针旋转90°所得的△A2B2C2;③△A1B1C1与△A2B2C2成轴对称图形吗?若成轴对称图形,画出所有的对称轴;④△A1B1C1与△A2B2C2成中心对称图形吗?若成中心对称图形,写出所有的对称中心的坐标.【分析】(1)将三角形的各顶点,向x轴作垂线并延长相同长度得到三点的对应点,顺次连接;(2)将三角形的各顶点,绕原点O按逆时针旋转90°得到三点的对应点.顺次连接各对应点得△A2B2C2;(3)从图中可发现成轴对称图形,根据轴对称图形的性质画出对称轴即连接两对应点的线段,做它的垂直平分线;(4)成中心对称图形,画出两条对应点的连线,交点就是对称中心.【解答】解:如下图所示:(3)成轴对称图形,根据轴对称图形的性质画出对称轴即连接两对应点的线段,作它的垂直平分线,或连接A1C1,A2C2的中点的连线为对称轴.(4)成中心对称,对称中心为线段BB2的中点P,坐标是(,).【点评】本题综合考查了图形的变换,在图形的变换中,关键是找到图形的对应点.18.如图,矩形ABCD的边AD、AB分别与⊙O相切于点E、F,(1)求的长;(2)若,直线MN分别交射线DA、DC于点M、N,∠DMN=60°,将直线MN沿射线DA方向平移,设点D到直线的距离为d,当时1≤d≤4,请判断直线MN与⊙O的位置关系,并说明理由.【分析】(1)连接OE、OF,利用相切证明四边形AFOE是正方形,再根据弧长公式求弧长;(2)先求出直线M1N1与圆相切时d的值,结合1≤d≤4,划分d的范围,分类讨论.【解答】解:(1)连接OE、OF,∵矩形ABCD的边AD、AB分别与⊙O相切于点E、F,∴∠A=90°,∠OEA=∠OF A=90°∴四边形AFOE是正方形∴∠EOF=90°,OE=AE=∴的长==π.(2)如图,将直线MN沿射线DA方向平移,当其与⊙O相切时,记为M1N1,切点为R,交AD于M1,交BC于N1,连接OM1、OR,∵M1N1∥MN∴∠DM1N1=∠DMN=60°∴∠EM1N1=120°∵MA、M1N1切⊙O于点E、R∴∠EM1O=∠EM1N1=60°在Rt△EM1O中,EM1===1∴DM1=AD﹣AE﹣EM1=+5﹣﹣1=4.过点D作DK⊥M1N1于K在Rt△DM1K中DK=DM1×sin∠DM1K=4×sin∠60°=2即d=2,∴当d=2时,直线MN与⊙O相切,当1≤d<2时,直线MN与⊙O相离,当直线MN平移到过圆心O时,记为M2N2,点D到M2N2的距离d=DK+OR=2+=3>4,∴当2<d≤4时,MN直线与⊙O相交.【点评】本题考查的是直线与圆的位置关系,解决此类问题可通过比较圆心到直线距离d 与圆半径大小关系完成判定.19.如图,在Rt△ABC中,∠C=90°,Rt△BAP中,∠BAP=90°,已知∠CBO=∠ABP,BP交AC于点O,E为AC上一点,且AE=OC.(1)求证:AP=AO;(2)求证:PE⊥AO;(3)当AE=AC,AB=10时,求线段BO的长度.【分析】(1)根据等角的余角相等证明即可;(2)过点O作OD⊥AB于D,根据角平分线上的点到角的两边的距离相等可得CO=DO,利用“SAS”证明△APE和△OAD全等,根据全等三角形对应角相等可得∠AEP=∠ADO=90°,从而得证;(3)设C0=3k,AC=8k,表示出AE=CO=3k,AO=AP=5k,然后利用勾股定理列式求出PE=4k,BC=BD=10﹣4k,再根据相似三角形对应边成比例列式求出k=1然后在Rt △BDO中,利用勾股定理列式求解即可.【解答】(1)证明:∵∠C=90°,∠BAP=90°∴∠CBO+∠BOC=90°,∠ABP+∠APB=90°,又∵∠CBO=∠ABP,∴∠BOC=∠APB,∵∠BOC=∠AOP,∴∠AOP=∠APB,∴AP=AO;(2)证明:如图,过点O作OD⊥AB于D,∵∠CBO=∠ABP,∴CO=DO,∵AE=OC,∴AE=OD,∵∠AOD+∠OAD=90°,∠P AE+∠OAD=90°,∴∠AOD=∠P AE,在△AOD和△P AE中,,∴△AOD≌△P AE(SAS),∴∠AEP=∠ADO=90°∴PE⊥AO;(3)解:设AE=OC=3k,∵AE=AC,∴AC=8k,∴OE=AC﹣AE﹣OC=2k,∴OA=OE+AE=5k.由(1)可知,AP=AO=5k.如图,过点O作OD⊥AB于点D,∵∠CBO=∠ABP,∴OD=OC=3k.在Rt△AOD中,AD===4k.∴BD=AB﹣AD=10﹣4k.∵OD∥AP,∴,即解得k=1,∵AB=10,PE=AD,∴PE=AD=4K,BD=AB﹣AD=10﹣4k=6,OD=3在Rt△BDO中,由勾股定理得:BO===3.【点评】本题考查了全等三角形的判定与性质,角平分线上的点到角的两边的距离相等的性质,勾股定理,相似三角形的判定与性质,(2)作辅助线构造出过渡线段DO并得到全等三角形是解题的关键,(3)利用相似三角形对应边成比例求出k=1是解题的关键.20.下框中是小明对一道题目的解答以及老师的批改.题目:某村计划建造如图所示的矩形蔬菜温室,要求长与宽的比为2:1,在温室内,沿前侧内墙保留3m的空地,其他三侧内墙各保留1m的通道,当温室的长与宽各为多少时,矩形蔬菜种植区域的面积是288m2?解:设矩形蔬菜种植区域的宽为xm,则长为2xm,根据题意,得x•2x=288.解这个方程,得x1=﹣12(不合题意,舍去),x2=12所以温室的长为2×12+3+1=28(m),宽为12+1+1=14(m)答:当温室的长为28m,宽为14m时,矩形蔬菜种植区域的面积是288m2.我的结果也正确!小明发现他解答的结果是正确的,但是老师却在他的解答中画了一条横线,并打了一个?.结果为何正确呢?(1)请指出小明解答中存在的问题,并补充缺少的过程:变化一下会怎样…(2)如图,矩形A′B′C′D′在矩形ABCD的内部,AB∥A′B′,AD∥A′D′,且AD:AB=2:1,设AB与A′B′、BC与B′C′、CD与C′D′、DA与D′A′之间的距离分别为a、b、c、d,要使矩形A′B′C′D′∽矩形ABCD,a、b、c、d应满足什么条件?请说明理由.。
7.20几何压轴题(第3部分)-2018年中考数学试题分类汇编(word解析版)

第七部分专题拓展7.20 几何压轴题【一】知识点清单【二】分类试题汇编及参考答案与解析一、选择题1.(2018年贵州省遵义市-第12题-3分)如图,四边形ABCD中,AD∥BC,∠ABC=90°,AB=5,BC=10,连接AC、BD,以BD为直径的圆交AC于点E.若DE=3,则AD的长为()A.5 B.4 C.D.【知识考点】勾股定理;相似三角形的判定与性质.【思路分析】先求出AC,进而判断出△ADF∽△CAB,即可设DF=x,AD=x,利用勾股定理求出BD,再判断出△DEF∽△DBA,得出比例式建立方程即可得出结论.【解答过程】解:如图,在Rt△ABC中,AB=5,BC=10,∴AC=5过点D作DF⊥AC于F,∴∠AFD=∠CBA,∵AD∥BC,∴∠DAF=∠ACB,∴△ADF∽△CAB,∴,∴,设DF=x,则AD=x,在Rt△ABD中,BD==,∵∠DEF=∠DBA,∠DFE=∠DAB=90°,∴△DEF∽△DBA,∴,∴,∴x=2,∴AD=x=2,故选:D.【总结归纳】此题主要考查了勾股定理,相似三角形的判定和性质,平行线的性质,正确作出辅助线是解本题的关键.2.(2018年内蒙古鄂尔多斯市-第6题-3分)如图,在菱形ABCD中,按以下步骤作图:①分别以点C和点D为圆心,大于12CD为半径作弧,两弧交于点M,N;②作直线MN,且MN恰好经过点A,与CD交于点E,连接BE,则下列说法错误的是()A.∠ABC=60°B.S△ABE=2S△ADEC.若AB=4,则BE D.sin∠CBE【知识考点】三角形的面积;线段垂直平分线的性质;菱形的性质;作图—基本作图;解直角三角形.【思路分析】由作法得AE垂直平分CD,则∠AED=90°,CE=DE,于是可判断∠DAE=30°,∠D=60°,从而得到∠ABC=60°;利用AB=2DE得到S△ABE=2S△ADE;作EH⊥BC于H,如图,若AB=4,则可计算出CH=CE=1,EH=CH=,利用勾股定理可计算出BE=2;利用正弦的定义得sin∠CBE==.【解答过程】解:由作法得AE垂直平分CD,∴∠AED=90°,CE=DE,∵四边形ABCD为菱形,∴AD=2DE,∴∠DAE=30°,∠D=60°,∴∠ABC=60°,所以A选项的说法正确;∵AB=2DE,∴S△ABE=2S△ADE,所以B选项的说法正确;作EH⊥BC于H,如图,若AB=4,在Rt△ECH中,∵∠ECH=60°,∴CH=CE=1,EH=CH=,在Rt△BEH中,BE==2,所以C选项的说法错误;sin∠CBE===,所以D选项的说法正确.故选:C.【总结归纳】本题考查了基本作图:熟练掌握基本作图(作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线).也考查了菱形的性质和解直角三角形.3.(2018年江苏省无锡市-第8题-3分)如图,矩形ABCD中,G是BC的中点,过A、D、G三点的圆O与边AB、CD分别交于点E、点F,给出下列说法:(1)AC与BD的交点是圆O的圆心;(2)AF与DE的交点是圆O的圆心;(3)BC与圆O相切,其中正确说法的个数是()A.0 B.1 C.2 D.3【知识考点】矩形的性质;切线的判定.【思路分析】连接DG、AG,作GH⊥AD于H,连接OD,如图,先确定AG=DG,则GH垂直平分AD,则可判断点O在HG上,再根据HG⊥BC可判定BC与圆O相切;接着利用OG=OG可判断圆心O不是AC与BD的交点;然后根据四边形AEFD为⊙O的内接矩形可判断AF与DE的交点是圆O的圆心.【解答过程】解:连接DG、AG,作GH⊥AD于H,连接OD,如图,∵G是BC的中点,∴AG=DG,∴GH垂直平分AD,∴点O在HG上,∵AD∥BC,∴HG⊥BC,∴BC与圆O相切;∵OG=OG,∴点O不是HG的中点,∴圆心O不是AC与BD的交点;而四边形AEFD为⊙O的内接矩形,∴AF与DE的交点是圆O的圆心;∴(1)错误,(2)(3)正确.故选:C.【总结归纳】本题考查了三角形内切圆与内心:三角形的内心到三角形三边的距离相等;三角形的内心与三角形顶点的连线平分这个内角.也考查了矩形的性质.4.(2018年山东省潍坊市-第6题-3分)如图,木工师傅在板材边角处作直角时,往往使用“三弧法”,其作法是:(1)作线段AB,分别以A,B为圆心,以AB长为半径作弧,两弧的交点为C;(2)以C为圆心,仍以AB长为半径作弧交AC的延长线于点D;(3)连接BD,BC.下列说法不正确的是()A.∠CBD=30°B.S△BDC=AB2C.点C是△ABD的外心D.sin2A+cos2D=l【知识考点】作图—基本作图;线段垂直平分线的性质;三角形的外接圆与外心;解直角三角形的应用.【思路分析】根据等边三角形的判定方法,直角三角形的判定方法以及等边三角形的性质,直角三角形的性质一一判断即可;【解答过程】解:由作图可知:AC=AB=BC,∴△ABC是等边三角形,由作图可知:CB=CA=CD,∴点C是△ABD的外心,∠ABD=90°,BD=AB,∴S △ABD =AB 2,∵AC=CD , ∴S △BDC =AB 2,故A 、B 、C 正确, 故选:D .【总结归纳】本题考查作图﹣基本作图,线段的垂直平分线的性质,三角形的外心等知识,直角三角形等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型. 5.(2018年四川省南充市-第10题-3分)如图,正方形ABCD 的边长为2,P 为CD 的中点,连结AP ,过点B 作BE ⊥AP 于点E ,延长CE 交AD 于点F ,过点C 作CH ⊥BE 于点G ,交AB 于点H ,连接HF .下列结论正确的是( )A .B .EF=2 C .cos ∠CEP=5D .HF 2=EF•CF 【知识考点】相似三角形的判定与性质;全等三角形的判定与性质;正方形的性质;解直角三角形. 【思路分析】首先证明BH=AH ,推出EG=BG ,推出CE=CB ,再证明△CEH ≌△CBH ,Rt △HFE ≌Rt △HFA ,利用全等三角形的性质即可一一判断. 【解答过程】解:连接EH .∵四边形ABCD 是正方形, ∴CD=AB═BC=AD=2,CD ∥AB , ∵BE ⊥AP ,CH ⊥BE , ∴CH ∥PA ,∴四边形CPAH 是平行四边形, ∴CP=AH , ∵CP=PD=1, ∴AH=PC=1, ∴AH=BH ,在Rt△ABE中,∵AH=HB,∴EH=HB,∵HC⊥BE,∴BG=EG,∴CB=CE=2,故选项A错误,∵CH=CH,CB=CE,HB=HE,∴△ABC≌△CEH,∴∠CBH=∠CEH=90°,∵HF=HF,HE=HA,∴Rt△HFE≌Rt△HFA,∴AF=EF,设EF=AF=x,在Rt△CDF中,有22+(2﹣x)2=(2+x)2,∴x=,∴EF=,故B错误,∵PA∥CH,∴∠CEP=∠ECH=∠BCH,∴cos∠CEP=cos∠BCH==,故C错误.∵HF=,EF=,FC=∴HF2=EF•FC,故D正确,故选:D.【总结归纳】本题考查正方形的性质、全等三角形的判定和性质、勾股定理、锐角三角函数等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考选择题中的压轴题.二、填空题1.(2018年内蒙古鄂尔多斯市-第16题-3分)如图1,AF,BE是△ABC的中线,AF⊥BE,垂足为点P,设BC=a,AC=b,AB=c,则a2+b2=5c2,利用这一性质计算.如图2,在▱ABCD中,E,F,G分别是AD,BC,CD的中点,EB⊥EG于点E,AD=8,AB=则AF=.【知识考点】勾股定理;三角形中位线定理;平行四边形的性质.【思路分析】连接AC交EF于H,设BE与AF的交点为P,由点E、G分别是AD,CD的中点,得到EG是△ACD的中位线于是证出BE⊥AC,由四边形ABCD是平行四边形,得到AD∥BC,根据E,F分别是AD,BC的中点,得到AE=BF=CF=AD,证出四边形ABFE是平行四边形,证得EH=FH,推出EH,AH分别是△AFE的中线,由题目中的结论得即可得到结果.【解答过程】解:如图2,连接AC,EF交于H,AC与BE交于点Q,设BE与AF的交点为P,∵点E、G分别是AD,CD的中点,∴EG∥AC,∵BE⊥EG,∴BE⊥AC,∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC=8,∴∠EAH=∠FCH,∵E,F分别是AD,BC的中点,∴AE=AD,BF=BC,∴AE=BF=CF=AD=4,∵AE∥BF,∴四边形ABFE是平行四边形,∴EF=AB=2,AP=PF,在△AEH和△CFH中,,∴△AEH≌△CFH(AAS),∴EH=FH,∴EP,AH分别是△AFE的中线,由a2+b2=5c2得:AF2+EF2=5AE2,∴AF2=5×42﹣(2)2=60,∴AF=2.故答案为:2.【总结归纳】本题考查了平行四边形的性质,勾股定理,三角形的中位线的性质,正确的作出辅助线是解题的关键.2.(2018年贵州省遵义市-第18题-4分)如图,在菱形ABCD中,∠ABC=120°,将菱形折叠,使点A恰好落在对角线BD上的点G处(不与B、D重合),折痕为EF,若DG=2,BG=6,则BE的长为.【知识考点】菱形的性质;翻折变换(折叠问题).【思路分析】作EH⊥BD于H,根据折叠的性质得到EG=EA,根据菱形的性质、等边三角形的判定定理得到△ABD为等边三角形,得到AB=BD,根据勾股定理列出方程,解方程即可.【解答过程】解:作EH⊥BD于H,由折叠的性质可知,EG=EA,由题意得,BD=DG+BG=8,∵四边形ABCD是菱形,∴AD=AB,∠ABD=∠CBD=∠ABC=60°,∴△ABD为等边三角形,∴AB=BD=8,设BE=x,则EG=AE=8﹣x,在Rt△EHB中,BH=x,EH=x,在Rt△EHG中,EG2=EH2+GH2,即(8﹣x)2=(x)2+(6﹣x)2,解得,x=2.8,即BE=2.8,故答案为:2.8.【总结归纳】本题考查的是翻转变换的性质、菱形的性质、勾股定理、解直角三角形,掌握翻转变换是一种对称变换,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等是解题的关键.3.(2018年湖北省咸宁市-第16题-3分)如图,已知∠MON=120°,点A,B分别在OM,ON上,且OA=OB=a,将射线OM绕点O逆时针旋转得到OM′,旋转角为α(0°<α<120°且α≠60°),作点A关于直线OM′的对称点C,画直线BC交OM′于点D,连接AC,AD,有下列结论:①AD=CD;②∠ACD的大小随着α的变化而变化;③当α=30°时,四边形OADC为菱形;④△ACD2;其中正确的是.(把你认为正确结论的序号都填上).【知识考点】等边三角形的性质;菱形的判定与性质;轴对称的性质;旋转的性质.【思路分析】①根据对称的性质:对称点的连线被对称轴垂直平分可得:OM'是AC的垂直平分线,再由垂直平分线的性质可作判断;②作⊙O,根据四点共圆的性质得:∠ACD=∠E=60°,说明∠ACD是定值,不会随着α的变化而变化;③当α=30°时,即∠AOD=∠COD=30°,证明△AOC是等边三角形和△ACD是等边三角形,得OC=OA=AD=CD,可作判断;④先证明△ACD是等边三角形,当AC最大时,△ACD的面积最大,当AC为直径时最大,根据面积公式计算后可作判断.【解答过程】解:①∵A、C关于直线OM'对称,∴OM'是AC的垂直平分线,∴CD=AD,故①正确;②连接OC,由①知:OM'是AC的垂直平分线,∴OC=OA,∴OA=OB=OC,以O为圆心,以OA为半径作⊙O,交AO的延长线于E,连接BE,则A、B、C都在⊙O上,∵∠MON=120°,∴∠BOE=60°,∵OB=OE,∴△OBE是等边三角形,∴∠E=60°,∵A、C、B、E四点共圆,∴∠ACD=∠E=60°,故②不正确;③当α=30°时,即∠AOD=∠COD=30°,∴∠AOC=60°,∴△AOC是等边三角形,∴∠OAC=60°,OC=OA=AC,由①得:CD=AD,∴∠CAD=∠ACD=∠CDA=60°,∴△ACD是等边三角形,∴AC=AD=CD,∴OC=OA=AD=CD,∴四边形OADC为菱形;故③正确;④∵CD=AD,∠ACD=60°,∴△ACD是等边三角形,当AC最大时,△ACD的面积最大,∵AC是⊙O的弦,即当AC为直径时最大,此时AC=2OA=2a,α=90°,∴△ACD面积的最大值是:AC2==,故④正确,所以本题结论正确的有:①③④故答案为:①③④.【总结归纳】本题是圆和图形变换的综合题,考查了轴对称的性质、四点共圆的性质、等边三角形的判定、菱形的判定、三角形面积及圆的有关性质,有难度,熟练掌握轴对称的性质是关键,是一道比较好的填空题的压轴题.4.(2018年江苏省无锡市-第18题-2分)如图,已知∠XOY=60°,点A在边OX上,OA=2.过点A作AC⊥OY于点C,以AC为一边在∠XOY内作等边三角形ABC,点P是△ABC围成的区域(包括各边)内的一点,过点P作PD∥OY交OX于点D,作PE∥OX交OY于点E.设OD=a,OE=b,则a+2b的取值范围是.【知识考点】等边三角形的性质;含30度角的直角三角形;平行四边形的判定与性质.【思路分析】作辅助线,构建30度的直角三角形,先证明四边形EODP是平行四边形,得EP=OD=a,在Rt△HEP中,∠EPH=30°,可得EH的长,计算a+2b=2OH,确认OH最大和最小值的位置,可得结论.【解答过程】解:过P作PH⊥OY交于点H,∵PD∥OY,PE∥OX,∴四边形EODP是平行四边形,∠HEP=∠XOY=60°,∴EP=OD=a,Rt△HEP中,∠EPH=30°,∴EH=EP=a,∴a+2b=2(a+b)=2(EH+EO)=2OH,当P在AC边上时,H与C重合,此时OH的最小值=OC=OA=1,即a+2b的最小值是2;当P在点B时,OH的最大值是:1+=,即(a+2b)的最大值是5,∴2≤a+2b≤5.【总结归纳】本题考查了等边三角形的性质、直角三角形30度角的性质、平行四边形的判定和性质,有难度,掌握确认a+2b的最值就是确认OH最值的范围.5.(2018年江苏省苏州市-第18题-3分)如图,已知AB=8,P为线段AB上的一个动点,分别以AP,PB为边在AB的同侧作菱形APCD和菱形PBFE,点P,C,E在一条直线上,∠DAP=60°.M,N分别是对角线AC,BE的中点.当点P在线段AB上移动时,点M,N之间的距离最短为(结果留根号).【知识考点】垂线段最短;三角形中位线定理;菱形的性质;梯形.【思路分析】连接PM、PN.首先证明∠MPN=90°设PA=2a,则PB=8﹣2a,PM=a,PN=(4﹣a),构建二次函数,利用二次函数的性质即可解决问题;【解答过程】解:连接PM、PN.∵四边形APCD,四边形PBFE是菱形,∠DAP=60°,∴∠APC=120°,∠EPB=60°,∵M,N分别是对角线AC,BE的中点,∴∠CPM=∠APC=60°,∠EPN=∠EPB=30°,∴∠MPN=60°+30°=90°,设PA=2a,则PB=8﹣2a,PM=a,PN=(4﹣a),∴MN===,∴a=3时,MN有最小值,最小值为2,故答案为2.【总结归纳】本题考查菱形的性质、勾股定理二次函数的性质等知识,解题的关键是学会添加常用辅助线,构建二次函数解决最值问题.6.(2018年辽宁省大连市-第16题-3分)如图,矩形ABCD中,AB=2,BC=3,点E为AD上一点,且∠ABE=30°,将△ABE沿BE翻折,得到△A′BE,连接CA′并延长,与AD相交于点F,则DF 的长为.【知识考点】矩形的性质;翻折变换(折叠问题).【思路分析】如图作A′H⊥BC于H.由△CDF∽△A′HC,可得=,延长构建方程即可解决问题;【解答过程】解:如图作A′H⊥BC于H.∵∠ABC=90°,∠ABE=∠EBA′=30°,∴∠A′BH=30°,∴A′H=BA′=1,BH=A′H=,∴CH=3﹣,∵△CDF∽△A′HC,∴=,∴=,∴DF=6﹣2,故答案为6﹣2.【总结归纳】本题考查翻折变换、矩形的性质、勾股定理、直角三角形30度角性质、相似三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.6.(2018年山东省潍坊市-第17题-3分)如图,点A1的坐标为(2,0),过点A1作x轴的垂线交直线l:y 于点B1,以原点O为圆心,OB1的长为半径画弧交x轴正半轴于点A2;再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,以OB2的长为半径画弧交x轴正半轴于点A3;….按A B的长是.此作法进行下去,则20192018【知识考点】弧长的计算;规律型:点的坐标;一次函数图象上点的坐标特征.【思路分析】先根据一次函数方程式求出B1点的坐标,再根据B1点的坐标求出A2点的坐标,得出B2的坐标,以此类推总结规律便可求出点A2019的坐标,再根据弧长公式计算即可求解,.【解答过程】解:直线y=x,点A1坐标为(2,0),过点A1作x轴的垂线交直线于点B1可知B1点的坐标为(2,2),以原O为圆心,OB1长为半径画弧x轴于点A2,OA2=OB1,OA2==4,点A2的坐标为(4,0),这种方法可求得B2的坐标为(4,4),故点A3的坐标为(8,0),B3(8,8)以此类推便可求出点A2019的坐标为(22019,0),则的长是=.故答案为:.【总结归纳】本题主要考查了一次函数图象上点的坐标特征,做题时要注意数形结合思想的运用,是各地的中考热点,学生在平常要多加训练,属于中档题.8.(2018年浙江省嘉兴市舟山市-第16题-4分)如图,在矩形ABCD中,AB=4,AD=2,点E在CD上,DE=1,点F是边AB上一动点,以EF为斜边作Rt△EFP.若点P在矩形ABCD的边上,且这样的直角三角形恰好有两个,则AF的值是.【知识考点】矩形的性质;勾股定理.【思路分析】先根据圆周角定理确定点P在以EF为直径的圆O上,且是与矩形ABCD的交点,先确定特殊点时AF的长,当F与A和B重合时,都有两个直角三角形.符合条件,即AF=0或4,再找⊙O与AD和BC相切时AF的长,此时⊙O与矩形边各有一个交点或三个交点,在之间运动过程中符合条件,确定AF的取值.【解答过程】解:∵△EFP是直角三角形,且点P在矩形ABCD的边上,∴P是以EF为直径的圆O与矩形ABCD的交点,①当AF=0时,如图1,此时点P有两个,一个与D重合,一个交在边AB上;②当⊙O与AD相切时,设与AD边的切点为P,如图2,此时△EFP是直角三角形,点P只有一个,当⊙O与BC相切时,如图4,连接OP,此时构成三个直角三角形,则OP⊥BC,设AF=x,则BF=P1C=4﹣x,EP1=x﹣1,∵OP∥EC,OE=OF,∴OG=EP1=,∴⊙O的半径为:OF=OP=,在Rt△OGF中,由勾股定理得:OF2=OG2+GF2,∴,解得:x=,∴当1<AF<时,这样的直角三角形恰好有两个,③当AF=4,即F与B重合时,这样的直角三角形恰好有两个,如图5,综上所述,则AF的值是:0或1<AF或4.故答案为:0或1<AF或4.【总结归纳】本题考查了矩形的性质的运用,勾股定理的运用,三角形中位线定理的运用,圆的性质的运用,分类讨论思想的运用,解答时运用勾股定理求解是关键,并注意运用数形结合的思想解决问题.三、解答题1.(2018年内蒙古鄂尔多斯市-第24题-12分)(1)【操作发现】如图1,将△ABC绕点A顺时针旋转60°,得到△ADE,连接BD,则∠ABD=度.(2)【类比探究】如图2,在等边三角形ABC内任取一点P,连接PA,PB,PC,求证:以PA,PB,PC的长为三边必能组成三角形.(3)【解决问题】如图3ABC内有一点P,∠APC=90°,∠BPC=120°,求△APC 的面积.(4)【拓展应用】如图4是A,B,C三个村子位置的平面图,经测量AC=4,BC=5,∠ACB=30°,P为△ABC 内的一个动点,连接PA,PB,PC.求PA+PB+PC的最小值.【知识考点】几何变换综合题.【思路分析】(1)【操作发现】:如图1中,只要证明△DAB是等边三角形即可;(2)【类比探究】:如图2中,以PA为边长作等边△PAD,使P、D分别在AC的两侧,连接CD.利用全等三角形的性质以及三角形的三边关系即可解决问题;(3)【解决问题】:如图3中,将△APB绕点A按逆时针方向旋转60°,得到△AP′C′,只要证明∠PP′C=90°,利用勾股定理即可解决问题;(4)【拓展应用】:如图4中,先由旋转的性质得出△APC≌△EDC,则∠ACP=∠ECD,AC=EC=4,∠PCD=60°,再证明∠BCE=90°,然后在Rt△BCE中,由勾股定理求出BE的长度,即为PA+PB+PC的最小值;【解答过程】(1)【操作发现】解:如图1中,连接BD.∵△ABC绕点A顺时针旋转60°,得到△ADE,∴AD=AB,∠DAB=60°,∴△DAB是等边三角形,∴∠ABD=60°故答案为60.(2)【类比探究】证明:如图2中,以PA为边长作等边△PAD,使P、D分别在AC的两侧,连接CD.∵∠BAC=∠PAD=60°,∴∠BAP=∠CAD,∵AB=AC,AP=AD,∴△PAB≌△ACD(SAS),∴BP=CD,在△PCD中,∵PD+CD>PC,又∵PA=PD,∴AP+BP>PC.∴PA,PB,PC的长为三边必能组成三角形.(3)【解决问题】解:如图3中,∵将△APB绕点A按逆时针方向旋转60°,得到△AP′C′,∴△APP′是等边三角形,∠AP′C=∠APB=360°﹣90°﹣120°=150°,∴PP′=AP,∠AP′P=∠APP′=60°,∴∠PP′C=90°,∠P′PC=30°,∴PP′=PC,即AP=PC,∵∠APC=90°,∴AP2+PC2=AC2,即(PC)2+PC2=()2,∴PC=2,∴AP=,∴S△APC=AP•PC=××2=.(4)【拓展应用】解:如图4中,将△APC绕点C顺时针旋转60°,得到△EDC,连接PD、BE.∵将△APC绕点C顺时针旋转60°,得到△EDC,∴△APC≌△EDC(旋转的性质),∴∠ACP=∠ECD,AC=EC=4,∠PCD=60°,∴∠ACP+∠PCB=∠ECD+∠PCB,∴∠ECD+∠PCB=∠ACB=30°,∴∠BCE=∠ECD+∠PCB+∠PCD=30°+60°=90°,在Rt△BCE中,∵∠BCE=90°,BC=5,CE=4,∴BE===,即PA+PB+PC的最小值为;【总结归纳】本题属于几何变换综合题,考查了旋转变换,等边三角形的性质,勾股定理等知识,解题的关键是添加常用辅助线,构造全等三角形解决问题,用转化的思想思考问题,属于中考压轴题.2.(2018年湖北省襄阳市-第24题-10分)如图(1),已知点G在正方形ABCD的对角线AC上,GE⊥BC,垂足为点E,GF⊥CD,垂足为点F.(1)证明与推断:①求证:四边形CEGF是正方形;②推断:AGBE的值为:(2)探究与证明:将正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°),如图(2)所示,试探究线段AG与BE 之间的数量关系,并说明理由:(3)拓展与运用:正方形CEGF在旋转过程中,当B,E,F三点在一条直线上时,如图(3)所示,延长CG交AD于点H.若AG=6,GH=BC=.【知识考点】相似形综合题.【思路分析】(1)①由GE⊥BC、GF⊥CD结合∠BCD=90°可得四边形CEGF是矩形,再由∠ECG=45°即可得证;②由正方形性质知∠CEG=∠B=90°、∠ECG=45°,据此可得=、GE∥AB,利用平行线分线段成比例定理可得;(2)连接CG,只需证△ACG∽△BCE即可得;(3)证△AHG∽△CHA得==,设BC=CD=AD=a,知AC=a,由=得AH= a、DH=a、CH=a,由=可得a的值.【解答过程】解:(1)①∵四边形ABCD是正方形,∴∠BCD=90°,∠BCA=45°,∵GE⊥BC、GF⊥CD,∴∠CEG=∠CFG=∠ECF=90°,∴四边形CEGF是矩形,∠CGE=∠ECG=45°,∴EG=EC,∴四边形CEGF是正方形;②由①知四边形CEGF是正方形,∴∠CEG=∠B=90°,∠ECG=45°,∴=,GE∥AB,∴==,故答案为:;(2)连接CG,由旋转性质知∠BCE=∠ACG=α,在Rt△CEG和Rt△CBA中,=cos45°=、=cos45°=,∴==,∴△ACG∽△BCE,∴==,∴线段AG与BE之间的数量关系为AG=BE;(3)∵∠CEF=45°,点B、E、F三点共线,∴∠BEC=135°,∵△ACG∽△BCE,∴∠AGC=∠BEC=135°,∴∠AGH=∠CAH=45°,∵∠CHA=∠AHG,∴△AHG∽△CHA,∴==,设BC=CD=AD=a,则AC=a,则由=得=,∴AH=a,则DH=AD﹣AH=a,CH==a,∴=得=,解得:a=3,即BC=3,故答案为:3.【总结归纳】本题主要考查相似形的综合题,解题的关键是掌握正方形的判定与性质、相似三角形的判定与性质等知识点.3.(2018年湖南省湘潭市-第25题-10分)如图,AB是以O为圆心的半圆的直径,半径CO⊥AO,点M是AB上的动点,且不与点A、C、B重合,直线AM交直线OC于点D,连结OM与CM.(1)若半圆的半径为10.①当∠AOM=60°时,求DM的长;②当AM=12时,求DM的长.(2)探究:在点M运动的过程中,∠DMC的大小是否为定值?若是,求出该定值;若不是,请说明理由.【知识考点】圆的综合题.【思路分析】(1)①当∠AOM=60°时,所以△AMO是等边三角形,从而可知∠MOD=30°,∠D=30°,所以DM=OM=10;②过点M作MF⊥OA于点F,设AF=x,OF=10﹣x,利用勾股定理即可求出x的值.易证明△AMF∽△ADO,从而可知AD的长度,进而可求出MD的长度.(2)根据点M的位置分类讨论,然后利用圆周角定理以及圆内接四边形的性质即可求出答案.【解答过程】解:(1)①当∠AOM=60°时,∵OM=OA,∴△AMO是等边三角形,∴∠A=∠MOA=60°,∴∠MOD=30°,∠D=30°,∴DM=OM=10②过点M作MF⊥OA于点F,设AF=x,∴OF=10﹣x,∵AM=12,OA=OM=10,由勾股定理可知:122﹣x2=102﹣(10﹣x)2∴x=,∴AF=,∵MF∥OD,∴△AMF∽△ADO,∴,∴,∴AD=∴MD=AD﹣AM=(2)当点M位于之间时,连接BC,∵C是的中点,∴∠B=45°,∵四边形AMCB是圆内接四边形,此时∠CMD=∠B=45°,当点M位于之间时,连接BC,由圆周角定理可知:∠CMD=∠B=45°综上所述,∠CMD=45°【总结归纳】本题考查圆的综合问题,涉及圆周角定理,勾股定理,相似三角形的判定与性质,含30度角的直角三角形性质,解方程等知识,综合程度较高,需要学生灵活运用所学知识.4.(2018年湖南邵阳市-第25题-8分)如图1所示,在四边形ABCD中,点O,E,F,G分别是AB,BC,CD,AD的中点,连接OE,EF,FG,GO,GE.(1)证明:四边形OEFG是平行四边形;(2)将△OGE绕点O顺时针旋转得到△OMN,如图2所示,连接GM,EN.①若OG=1,求ENGM的值;②试在四边形ABCD中添加一个条件,使GM,EN的长在旋转过程中始终相等.(不要求证明)【知识考点】相似形综合题.【思路分析】(1)连接AC,由四个中点可知OE∥AC、OE=AC,GF∥AC、GF=AC,据此得出OE=GF、OE=GF,即可得证;(2)①由旋转性质知OG=OM、OE=ON,∠GOM=∠EON,据此可证△OGM∽△OEN得==;②连接AC、BD,根据①知△OGM∽△OEN,若要GM=EN只需使△OGM≌△OEN,添加使AC=BD 的条件均可以满足此条件.【解答过程】解:(1)如图1,连接AC,∵点O、E、F、G分别是AB、BC、CD、AD的中点,∴OE∥AC、OE=AC,GF∥AC、GF=AC,∴OE=GF,OE=GF,∴四边形OEFG是平行四边形;(2)①∵△OGE绕点O顺时针旋转得到△OMN,∴OG=OM、OE=ON,∠GOM=∠EON,∴=,∴△OGM∽△OEN,∴==.②添加AC=BD,如图2,连接AC、BD,∵点O、E、F、G分别是AB、BC、CD、AD的中点,∴OG=EF=BD、OE=GF=BD,∵AC=BD,∴OG=OE,∵△OGE绕点O顺时针旋转得到△OMN,∴OG=OM、OE=ON,∠GOM=∠EON,∴OG=OE、OM=ON,在△OGM和△OEN中,∵,∴△OGM≌△OEN(SAS),∴GM=EN.【总结归纳】本题主要考查相似形的综合题,解题的关键是熟练掌握中位线定义及其定理、平行四边形的判定、旋转的性质、相似三角形与全等三角形的判定与性质等知识点.5.(2018年江苏省淮安市-第26题-12分)如果三角形的两个内角α与β满足2α+β=90°,那么我们称这样的三角形为“准互余三角形”.(1)若△ABC是“准互余三角形”,∠C>90°,∠A=60°,则∠B=°;(2)如图①,在Rt△ABC中,∠ACB=90°,AC=4,BC=5.若AD是∠BAC的平分线,不难证明△ABD是“准互余三角形”.试问在边BC上是否存在点E(异于点D),使得△ABE也是“准互余三角形”?若存在,请求出BE的长;若不存在,请说明理由.(3)如图②,在四边形ABCD中,AB=7,CD=12,BD⊥CD,∠ABD=2∠BCD,且△ABC是“准互余三角形”,求对角线AC的长.【知识考点】四边形综合题.【思路分析】(1)根据“准互余三角形”的定义构建方程即可解决问题;(2)只要证明△CAE∽△CBA,可得CA2=CE•CB,由此即可解决问题;(3)如图②中,将△BCD沿BC翻折得到△BCF.只要证明△FCB∽△FAC,可得CF2=FB•FA,设FB=x,则有:x(x+7)=122,推出x=9或﹣16(舍弃),再利用勾股定理求出AC即可;【解答过程】解:(1)∵△ABC是“准互余三角形”,∠C>90°,∠A=60°,∴2∠B+∠A=60°,解得,∠B=15°,故答案为:15°;(2)如图①中,在Rt△ABC中,∵∠B+∠BAC=90°,∠BAC=2∠BAD,∴∠B+2∠BAD=90°,∴△ABD是“准互余三角形”,∵△ABE也是“准互余三角形”,∴只有2∠A+∠BAE=90°,∵∠A+∠BAE+∠EAC=90°,∴∠CAE=∠B,∵∠C=∠C=90°,∴△CAE∽△CBA,可得CA2=CE•CB,∴CE=,∴BE=5﹣=.(3)如图②中,将△BCD沿BC翻折得到△BCF.∴CF=CD=12,∠BCF=∠BCD ,∠CBF=∠CBD , ∵∠ABD=2∠BCD ,∠BCD+∠CBD=90°, ∴∠ABD+∠DBC+∠CBF=180°, ∴A 、B 、F 共线, ∴∠A+∠ACF=90° ∴2∠ACB+∠CAB≠90°, ∴只有2∠BAC+∠ACB=90°, ∴∠FCB=∠FAC ,∵∠F=∠F , ∴△FCB ∽△FAC , ∴CF 2=FB•FA ,设FB=x , 则有:x (x+7)=122, ∴x=9或﹣16(舍弃), ∴AF=7+9=16, 在Rt △ACF 中,AC===20.【总结归纳】本题考查四边形综合题、相似三角形的判定和性质、“准互余三角形”的定义等知识,解题的关键是理解题意,学会利用翻折变换添加辅助线,构造相似三角形解决问题,学会利用已知模型构建辅助线解决问题,属于中考压轴题.6.(2018年江苏省无锡市-第27题-10分)如图,矩形ABCD 中,AB=m ,BC=n ,将此矩形绕点B 顺时针方向旋转θ(0°<θ<90°)得到矩形A 1BC 1D 1,点A 1在边CD 上. (1)若m=2,n=1,求在旋转过程中,点D 到点D 1所经过路径的长度;(2)将矩形A 1BC 1D 1继续绕点B 顺时针方向旋转得到矩形A 2BC 2D 2,点D 2在BC 的延长线上,设边A 2B 与CD 交于点E ,若11A E EC =,求nm的值.【知识考点】轨迹;旋转的性质.【思路分析】(1)作A1H⊥AB于H,连接BD,BD1,则四边形ADA1H是矩形.解直角三角形,求出∠ABA1,得到旋转角即可解决问题;(2)由△BCE∽△BA2D2,推出==,可得CE=由=﹣1推出=,推出AC=•,推出BH=AC==•,可得m2﹣n2=6•,可得1﹣=6•,由此解方程即可解决问题;【解答过程】解:(1)作A1H⊥AB于H,连接BD,BD1,则四边形ADA1H是矩形.∴AD=HA1=n=1,在Rt△A1HB中,∵BA1=BA=m=2,∴BA1=2HA1,∴∠ABA1=30°,∴旋转角为30°,∵BD==,∴D到点D1所经过路径的长度==π.(2)∵△BCE∽△BA2D2,∴==,∴CE=∵=﹣1∴=,∴AC=•,∴BH=AC==•,∴m2﹣n2=6•,∴m4﹣m2n2=6n4,1﹣=6•,∴=(负根已经舍弃).【总结归纳】本题考查轨迹,旋转变换、解直角三角形、弧长公式等知识,解题的关键是理解题意,灵活运用所学知识解决问题,属于中考常考题型.7.(2018年江苏省苏州市-第27题-10分)问题1:如图①,在△ABC中,AB=4,D是AB上一点(不与A,B重合),DE∥BC,交AC于点E,连接CD.设△ABC的面积为S,△DEC的面积为S′.(1)当AD=3时,SS'=;(2)设AD=m,请你用含字母m的代数式表示SS'.问题2:如图②,在四边形ABCD中,AB=4,AD∥BC,AD=12BC,E是AB上一点(不与A,B重合),EF∥BC,交CD于点F,连接CE.设AE=n,四边形ABCD的面积为S,△EFC的面积为S′.请你利用问题1的解法或结论,用含字母n的代数式表示SS'.【知识考点】三角形中位线定理;相似三角形的判定与性质.【思路分析】问题1:(1)先根据平行线分线段成比例定理可得:,由同高三角形面积的比等于对应底边的比,则==,根据相似三角形面积比等于相似比的平方得:==,可得结论;(2)解法一:同理根据(1)可得结论;解法二:作高线DF、BH,根据三角形面积公式可得:=,分别表示和的值,代入可得结论;问题2:解法一:如图2,作辅助线,构建△OBC,证明△OAD∽△OBC,得OB=8,由问题1的解法可知:===,根据相似三角形的性质得:=,可得结论;解法二:如图3,连接AC交EF于M,根据AD=BC,可得=,得:S△ADC=S,S△ABC=,由问题1的结论可知:=,证明△CFM∽△CDA,根据相似三角形面积比等于相似比的平方,根据面积和可得结论.【解答过程】解:问题1:(1)∵AB=4,AD=3,∴BD=4﹣3=1,∵DE∥BC,∴,∴==,∵DE∥BC,∴△ADE∽△ABC,∴==,∴=,即,故答案为:;(2)解法一:∵AB=4,AD=m,∴BD=4﹣m,∵DE∥BC,∴==,∴==,∵DE∥BC,∴△ADE∽△ABC,∴==,∴===,即=;解法二:如图1,过点B作BH⊥AC于H,过D作DF⊥AC于F,则DF∥BH,∴△ADF∽△ABH,∴=,∴===,即=;问题2:如图②,解法一:如图2,分别延长BD、CE交于点O,∵AD∥BC,∴△OAD∽△OBC,∴,∴OA=AB=4,∴OB=8,∵AE=n,∴OE=4+n,∵EF∥BC,由问题1的解法可知:===,∵==,∴=,∴===,即=;解法二:如图3,连接AC交EF于M,∵AD∥BC,且AD=BC,∴=,∴S△ADC=,∴S△ADC=S,S△ABC=,由问题1的结论可知:=,∵MF∥AD,∴△CFM∽△CDA,∴===,∴S△CFM=×S,∴S△EFC=S△EMC+S△CFM=+×S=,∴=.。
2023年中考数学压轴题培优教案专题03 对角互补模型(含答案解析)

【压轴必刷】2023年中考数学压轴大题之经典模型培优案专题3对角互补模型模型1:全等形——90°对角互补模型模型2:全等形——120°对角互补模型模型3:全等形——任意角对角互补模型模型4:相似形——90°对角互补模型【例1】.(2021·全国·1,在四边形ABCD 中,AB=AD,∠B+∠ADC=180°,点E,F 分别在四边形ABCD 的边BC,CD 上,∠EAF=12∠BAD,连接EF,试猜想EF,BE,DF 之间的数量关系.(1)思路梳理将△ABE 绕点A 逆时针旋转至△ADG,使AB 与AD 重合,由∠B+∠ADC=180°,得∠FDG=180°,即点F,D,G 三点共线,易证△AFG ≌△AFE,故EF,BE,DF 之间的数量关系为__;(2)类比引申如图2,在图1的条件下,若点E,F 由原来的位置分别变到四边形ABCD 的边CB,DC 延长线上,∠EAF=12∠BAD,连接EF,试猜想EF,BE,DF之间的数量关系,并给出证明.(3)联想拓展如图3,在△ABC中,∠BAC=90°,AB=AC,点D,E均在边BC上,且∠DAE=45°,若BD=1,EC=2,直接写出DE的长为________________.【例2】.(2019·山东枣庄·中考真题)在ΔABC中,∠BAC=90°,AB=AC,AD⊥BC于点D,(1)如图1,点M,N分别在AD,AB上,且∠BMN=90°,当∠AMN=30°,AB=2时,求线段AM的长;(2)如图2,点E,F分别在AB,AC上,且∠EDF=90°,求证:BE=AF;(3)如图3,点M在AD的延长线上,点N在AC上,且∠BMN=90°,求证:AB+AN=√2AM;【例3】.(2022·江苏·八年级课时练习)(1)如图①,在四边形ABCD中,AB=AD,∠B=∠D=90°,E,F分别是∠BAD.请直接写出线段EF,BE,FD之间的数量关系:__________;边BC,CD上的点,且∠EAF=12∠BAD,(2)如图②,在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是边BC,CD上的点,且∠EAF=12(1)中的结论是否仍然成立?请写出证明过程;(3)在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是边BC,CD所在直线上的点,且∠EAF=1∠BAD.请画出图形(除图②外),并直接写出线段EF,BE,FD之间的数量关系.2【例4】.(2022·全国·八年级课时练习)四边形ABCD是由等边ΔABC和顶角为120°的等腰ΔABD排成,将一个60°角顶点放在D处,将60°角绕D点旋转,该60°交两边分别交直线BC、AC于M、N,交直线AB于E、F两点.(1)当E、F都在线段AB上时(如图1),请证明:BM+AN=MN;(2)当点E在边BA的延长线上时(如图2),请你写出线段MB,AN和MN之间的数量关系,并证明你的结论;(3)在(1)的条件下,若AC=7,AE=2.1,请直接写出MB的长为.一、解答题1.(2022·陕西·西安市第三中学七年级期末)回答问题(1)【初步探索】如图1:在四边形ABCD中,AB=AD,∠B=∠ADC=90°,E、F分别是BC、CD上的点,且EF=BE+FD,探究图中∠BAE、∠F AD、∠EAF之间的数量关系.FD到点G,使DG=BE.连接AG,先证明△ABE≌△ADG,再证明△AEF ≌△AGF,可得出结论,他的结论应是_______________;(2)【灵活运用】如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E、F分别是BC、CD上的点,且EF=BE+FD,上述结论是否仍然成立,并说明理由;(3)【拓展延伸】知在四边形ABCD中,∠ABC+∠ADC=180°,AB=AD,若点E在CB的延长线上,点F在CD 的延长线上,如图3所示,仍然满足EF=BE+FD,请直接写出∠EAF与∠DAB的数量关系.2.(2021·陕西·交大附中分校八年级开学考试)问题探究((1)如图①,已知∠A=45°,∠ABC=30°,∠ADC=40°,则∠BCD的大小为___________;(2)如图②,在四边形ABCD中,AB=BC,∠ABC=∠ADC=90°,对角线BD=6.求四边形ABCD的面积;小明这样来计算.延长DC,使得CE=AD,连接BE,通过证明△ABD≌△CBE,从而可以计算四边形ABCD的面积.请你将小明的方法完善.并计算四边形ABCD的面积;问题解决(3)如图③,四边形ABCD是正在建设的城市花园,其中AB=BC,∠ABC=60°,∠ADC=30°,DC=40米,AD=30米.请计算出对角线BD的长度.3.(2021·福建三明·八年级期中)感知:如图①,AD平分∠BAC,∠B+∠C=180°,∠B=90°.判断DB与DC的大小关系并证明.探究:如图②,AD平分∠BAC,∠ABD+∠ACD=180°,∠ABD<90°,DB与DC的大小关系变吗?请说明理由.应用:如图③,四边形ABDC中,∠B=45°,∠C=135°,DB=DC=m,则AB与AC差是多少(用含m的代数式表示)4.(2021·辽宁大连·九年级期中)如图1,正方形ABCD中,BD是对角线,点E在AB上,点F在BC上,连接EF(EF 与BD不垂直),点G是线段EF的中点,过点G作GH⊥EF交线段BD于点H.(1)猜想GH与EF的数量关系,并证明;(2)探索AE,CF,DH之间的数量关系,并证明;(3)如图2,若点E在AB的延长线上,点F在BC的延长线上,其他条件不变,请直接写出AE,CF,DH之间的数量关系.5.(2020·河南洛阳·八年级期中)在∠MAN内有一点D,过点D分别作DB⊥AM,DC⊥AN,垂足分别为B,C.且BD=CD,点E,F分别在边AM和AN上.(1)如图1,若∠BED=∠CFD,请说明DE=DF;(2)如图2,若∠BDC=120°,∠EDF=60°,猜想EF,BE,CF具有的数量关系,并说明你的结论成立的理由.6.(2020·江西萍乡·八年级期末)【课题研究】旋转图形中对应线段所在直线的夹角(小于等于90°的角)与旋转角的关系.【问题初探】线段AB绕点O顺时针旋转得到线段CD,其中点A与点C对应,点B与点D对应,旋转角的度数为α,且0°<α<180°.(1)如图①,当α=60°时,线段AB、CD所在直线夹角(锐角)为;(2)如图②,当90°<α<180°时,直线AB与直线CD所夹锐角与旋转角α存在怎样的数量关系?请说明理由;【形成结论】旋转图形中,当旋转角小于平角时,对应线段所在直线的夹角与旋转角.【运用拓广】运用所形成的结论解决问题:(3)如图③,四边形ABCD中,∠ABC=60°,∠ADC=30°,AB=BC,CD=3,BD=√19,求AD的长.7.(2021··九年级专题练习)如图,在△ABC中,∠ACB=120°,BC>AC,点E在BC上,点D在AB上,CE=CA,连接DE,∠ACB+∠ADE=180°,CH⊥AB,垂足为H.证明:DE+AD=2√3CH.8.(2020·湖南湘西·中考真题)问题背景:如图1,在四边形ABCD中,∠BAD=90°,∠BCD=90°,BA= BC,∠ABC=120°,∠MBN=60°,∠MBN绕B点旋转,它的两边分别交AD、DC于E、F.探究图中线段AE,CF,EF之间的数量关系.小李同学探究此问题的方法是:延长FC到G,使CG=AE,连接BG,先证明△BCG≌△BAE,再证明△BFC≌△BFE,可得出结论,他的结论就是_______________;探究延伸1:如图2,在四边形ABCD中,∠BAD=90°,∠BCD=90°,BA=BC,∠ABC=2∠MBN,∠MBN绕B点旋转,它的两边分别交AD、DC于E、F.上述结论是否仍然成立?请直接写出结论(直接写出“成立”或者“不成立”),不要说明理由.探究延伸2:如图3,在四边形ABCD中,BA=BC,∠BAD+∠BCD=180°,∠ABC=2∠MBN,∠MBN绕B点旋转,它的两边分别交AD、DC于E、F.上述结论是否仍然成立?并说明理由.实际应用:如图4,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等接到行动指令后,舰艇甲向正东方向以75海里/小时的速度前进,同时舰艇乙沿北偏东50°的方向以100海里/小时的速度前进,1.2小时后,指挥中心观测到甲、乙两舰艇分别到达E、F处,且指挥中心观测两舰艇视线之间的夹角为70°,试求此时两舰艇之间的距离.9.(2019·重庆·西南大学附中八年级阶段练习)如图1,四边形ABCD中,BD⊥AD,E为BD上一点,AE=BC,CE⊥BD,CE=ED(1)已知AB=10,AD=6,求CD;(2)如图2,F为AD上一点,AF=DE,连接BF,交BF交AE于G,过G作GH⊥AB于H,∠BGH=75°.求证:BF=2√2GH+√2EG.10.(2021·全国·九年级专题练习)探究问题:(1)方法感悟:如图①,在正方形ABCD中,点E,F DC,BC边上的点,且满足∠BAF=45°,连接EF,求证DE+BF=EF.感悟解题方法,并完成下列填空:将△ADE绕点A顺时针旋转90°得到△ABG,此时AB与AD重合,由旋转可得:AB=AD,BG=DE,∠1=∠2,∠ABG=∠D=90°,∴∠ABG+∠ABF=90°+90°=180°,因此,点G,B,F在同一条直线上.∵∠EAF=45°∴∠2+∠3=∠BAD-∠EAF=90°-45°=45°.∵∠1=∠2,∠1+∠3=45°.即∠GAF=∠________.又AG=AE,AF=AE∴△GAF≌△________.∴_________=EF,故DE+BF=EF.(2)方法迁移:∠DAB.试猜想如图②,将Rt△ABC沿斜边翻折得到△ADC,点E,F分别为DC,BC边上的点,且∠EAF=12DE,BF,EF之间有何数量关系,并证明你的猜想.11.(2021·全国·八年级专题练习)我们规定:一组邻边相等且对角互补的四边形叫作“完美四边形”.(1)在①平行四边形,②菱形,③矩形,④正方形中,一定为“完美”四边形的是(请填序号);(2)在“完美”四边形ABCD中,AB=AD,∠B+∠D=180°,连接AC.①如图1,求证:AC平分∠BCD;小明通过观察、实验,提出以下两种想法,证明AC平分∠BCD:想法一:通过∠B+∠D=180°,可延长CB到E,使BE=CD,通过证明△AEB≌△ACD,从而可证AC平分∠BCD;想法二:通过AB=AD,可将△ACD A顺时针旋转,使AD与AB重合,得到△AEB,可证C,B,E三点在条直线上,从而可证AC平分∠BCD.请你参考上面的想法,帮助小明证明AC平分∠BCD;②如图2,当∠BAD=90°,用等式表示线段AC,BC,CD之间的数量关系,并证明.12.(2019·全国·九年级专题练习)如图,△ABC是边长为4的等边三角形,点D是线段BC的中点,∠EDF=120°,把∠EDF绕点D旋转,使∠EDF的两边分别与线段AB、AC交于点E、F.(1)当DF⊥AC时,求证:BE=CF;(2)在旋转过程中,BE+CF是否为定值?若是,求出这个定值;若不是,请说明理由13.(2022·全国·八年级专题练习)如图所示,ΔABC为等边三角形,边长为4,点O为BC边中点,∠EOF=120°,其两边分别交AB和CA的延长线于E,F,求AE−AF的值.14.(2019·全国·九年级专题练习)如图所示,ΔABC中,AB=BC=1,∠ABC=90°,把一块含30°角的直角三角板DEF的直角顶点D放在AC的中点上(直角三角板的短直角边为DF,长直角边为DE),将三角板DEF绕D点按逆时针方向旋转.(1)在如图所见中,DE交AB于M,DF交BC于N,证明DM=DN;(2)继续旋转至如图所见,延长AB交DE于M,延长BC交DF于N,证明DM=DN.15.(2019·江西·南昌市第十九中学九年级阶段练习)一位同学拿了两块45°三角尺ΔMNK,ΔACB做了一个探究活动:将ΔMNK的直角顶点M放在ΔACB的斜边AB的中点处,设AC=BC=4.(1)如图1所示,两三角尺的重叠部分为ΔACM ,则重叠部分的面积为______,周长为______.(2)将如图1所示中的ΔMNK 绕顶点M 逆时针旋转45°,得到如图2所示,此时重叠部分的面积为______,周长为______.(3)如果将ΔMNK 绕M 旋转到不同于如图1所示和如图2所示的图形,如图3所示,请你猜想此时重叠部分的面积为______.(4)在如图3所示情况下,若AD =1,求出重叠部分图形的周长.16.(2019·江苏常州·一模)我们定义:有一组对角为直角的四边形叫做“对直角四边形”.(1)如图①,四边形ABCD 为对直角四边形,∠B=90°,若AB 2-AD 2=4,求CD 2-BC 2的值;(2)如图②,四边形ABCD 中,∠ABC=90°,AB=BC,若BD 平分∠ADC,求证:四边形ABCD 为对直角四边形;(3)在(2)的条件下,如图③,连结AC,若S △ACDS △ABC =35,求tan ∠ACD 的值.17.(2021·全国·九年级专题练习)阅读下面材料:小炎遇到这样一个问题:如图1,点E 、F 分别在正方形ABCD 的边BC,CD 上,∠EAF=45°,连结EF,则EF=BE+DF,试说明理由.小炎是这样思考的:要想解决这个问题,首先应想办法将这些分散的线段相对集中.她先后尝试了翻折、旋转、平移的方法,最后发现线段AB,AD是共点并且相等的,于是找到解决问题的方法.她的方法是将△ABE 绕着点A逆时针旋转90°得到△ADG,再利用全等的知识解决了这个问题(如图2).参考小炎同学思考问题的方法,解决下列问题:(1)如图3,四边形ABCD中,AB=AD,∠BAD=90°点E,F分别在边BC,CD上,∠EAF=45°.若∠B,∠D都不是直角,则当∠B与∠D满足_ 关系时,仍有EF=BE+DF;(2)如图4,在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠DAE=45°,若BD=1, EC=2,求DE 的长.18.(2021·全国·八年级专题练习)已知:∠ABC=∠ADC=90°,AD=DC,求证:BC+AB=√2BD.【例1】.(2021·全国·九年级专题练习)如图1,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,点E,F分别在四边形ABCD的边BC,CD上,∠EAF=12∠BAD,连接EF,试猜想EF,BE,DF之间的数量关系.(1)思路梳理将△ABE绕点A逆时针旋转至△ADG,使AB与AD重合,由∠B+∠ADC=180°,得∠FDG=180°,即点F,D,G三点共线,易证△AFG≌△AFE,故EF,BE,DF之间的数量关系为__;(2)类比引申如图2,在图1的条件下,若点E,F由原来的位置分别变到四边形ABCD的边CB,DC延长线上,∠EAF=12∠BAD,连接EF,试猜想EF,BE,DF之间的数量关系,并给出证明.(3)联想拓展如图3,在△ABC中,∠点D,E均在边BC上,且∠DAE=45°,若BD=1,EC=2,直接写出DE的长为________________.【答案】(1)EF=BE+DF;(2)EF=DF−BE;证明见解析;(3)√5.【分析】(1)将△ABE绕点A逆时针旋转至△ADG,使AB与AD重合,首先证明F,D,G三点共线,求出∠EAF=∠GAF,然后证明△AFG≌△AFE,根据全等三角形的性质解答;(2)将△ABE绕点A逆时针旋转,使AB与AD重合,得到△ADE',首先证明E',D,F三点共线,求出∠EAF=∠E'AF,然后证明△AFE≌△AFE',根据全等三角形的性质解答;(3)将△ABD绕点A逆时针旋转至△ACD',使AB与AC重合,连接ED',同(1)可证△AED≌AED',求出∠ECD'=90°,再根据勾股定理计算即可.【详解】解:(1)将△ABE绕点A逆时针旋转至△ADG,使AB与AD重合,∵∠B+∠ADC=180°,∴∠FDG=180°,即点F,D,G三点共线,∵∠BAE=∠DAG,∠EAF=12∠BAD,∴∠EAF=∠GAF,在△AFG和△AFE中,{AE=AG∠EAF=∠GAFAF=AF,∴△AFG≌△AFE,∴EF=FG=DG+DF=BE+DF;(2)EF=DF−BE;证明:将△ABE绕点A逆时针旋转,使AB与AD重合,得到△ADE',则△ABE≌ADE',∴∠DAE'=∠BAE,AE'=AE,DE'=BE,∠ADE'=∠ABE,∵∠ABC+∠ADC=180°,∠ABC+∠ABE=180°,∴∠ADE'=∠ADC,即E',D,F三点共线,∵∠EAF=12∠BAD,∴∠E'AF=∠BAD−(∠BAF+∠DAE')=∠BAD−(∠BAF+∠BAE)=∠BAD−∠EAF=12∠BAD,∴∠EAF=∠E'AF,在△AEF和△AE'F中,{AE=AE′∠EAF=∠E′AFAF=AF,∴△AFE≌△AFE'(SAS),∴FE=FE',又∵FE'=DF−DE',∴EF=DF−BE;(3)将△ABD绕点A逆时针旋转至△ACD',使AB与AC重合,连接ED',同(1)可证△AED≌AED',∴DE=D'E.∵∠ACB=∠B=∠ACD'=45°,∴∠ECD'=90°,在Rt△ECD'中,ED'=√EC2+D′C2=√EC2+BD2=√5,即DE=√5,故答案为:√5.【点睛】本题考查的是旋转变换的性质、全等三角形的判定和性质以及勾股定理等知识,灵活运用利用旋转变换作图、掌握全等三角形的判定定理和性质定理是解题的关键.【例2】.(2019·山东枣庄·中考真题)在ΔABC中,∠BAC=90°,AB=AC,AD⊥BC于点D,(1)如图1,点M,N分别在AD,AB上,且∠BMN=90°,当∠AMN=30°,AB=2时,求线段AM的长;(2)如图2,点E,F分别在AB,AC上,且∠EDF=90°,求证:BE=AF;(3)如图3,点M在AD的延长线上N在AC上,且∠BMN=90°,求证:AB+AN=√2AM;;(2)见解析;(3)见解析.【答案】(1) AM=√2−2√33【分析】(1)根据等腰三角形的性质、直角三角形的性质得到AD=BD=DC=√2,求出∠MBD=30°,根据勾股定理计算即可;(2)证明△BDE≌△ADF,根据全等三角形的性质证明;(3)过点M作ME∥BC交AB的延长线于E,证明△BME≌△AMN,根据全等三角形的性质得到BE=AN,根据等腰直角三角形的性质、勾股定理证明结论.【详解】(1)解:∵∠BAC=90°,AB=AC,AD⊥BC,【点睛】本题考查的是等腰直角三角形的性质、全等三角形的判定和性质、直角三角形的性质,掌握全等三角形的判定定理和性质定理是解题的关键.【例3】.(2022·江苏·八年级课时练习)(1)如图①,在四边形ABCD中,AB=AD,∠B=∠D=90°,E,F分别是∠BAD.请直接写出线段EF,BE,FD之间的数量关系:__________;边BC,CD上的点,且∠EAF=12∠BAD,(2)如图②,在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是边BC,CD上的点,且∠EAF=12(1(3)在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是边BC,CD所在直线上的点,且∠EAF=1∠BAD.请画出图形(除图②外),并直接写出线段EF,BE,FD之间的数量关系.2【答案】(1)EF=BE+FD;(2)成立,理由见解析;(3)图形见解析,EF=BE−FD【分析】(1)延长EB到G,使BG=DF,连接AG.证明△AGE和△AEF全等,则EF=GE,则EF=BE+DF,证明△ABE和△AEF中全等,那么AG=AF,∠1=∠2,∠1+∠3=∠2+∠3=∠EAF=1∠BAD.从而得出EF=GE;2(2)思路和作辅助线的方法同(1);(3)根据(1)的证法,我们可得出DF=BG,GE=EF,那么EF=GE=BE-BG=BE-DF.【详解】(1)延长EB至G,使BG=DF,连接AG,∵∠ABG=∠ABC=∠D=90°,AB=AD,∴△ABG≌△ADF,∴AG=AF,∠1=∠2,∴∠1+∠3=∠2+∠3=∠EAF=12∠BAD,∴∠GAE=∠EAF,在△GAE和△FAE中,∵{AG=AF∠GAE=∠EAFAE=AE,∴△GAE≌△FAE(SAS),∴EG=EF,∵EG=BE+BG,∴EF=BE+FD.故答案为:EF=BE+FD(2)(1)中的结论仍成立,证明:延长CB至M,使BM=DF,∵∠ABC+∠D=180°,∠1+∠ABC=180°,∴∠1=∠D,在△ABM和△ADF中,{AB=AD ∠1=∠D BM=DF,∴△ABM≌△ADF(SAS),∴AF=AM,∠2=∠3,∵∠EAF=12∠BAD,∴∠2+∠4=12∠BAD=∠EAF,∴∠3+∠4=∠EAF即∠MAE=∠EAF,在△AME和△AFE中,{AM=AF∠MAE=∠EAFAB=AE,∴△AME≌△AFE(SAS),∴EF=ME,即EF=BE+BM.(3)EF=BE−FD,证明:在BE上截取BG使BG=DF,连接AG,∵∠B+∠ADC=180°,∠ADF+∠ADC=180°,∴∠B=∠ADF,∵在△ABG和△ADF中,{AB=AD∠ABG=∠ADFBG=DF,∴△ABG≌△ADF(SAS),∴∠BAG=∠DAF,AG=AF,∴∠BAG+∠EAD=∠DAF+∠EAD=∠EAF=12∠BAD,∴∠GAE=∠EAF,在△AEG和△AEF中,{AG=AF∠GAE=∠EAFAE=AE,∴△AEG≌△AEF(SAS),∴EG=EF,∵EG=BE−BG,∴EF=BE−FD.【点睛】此题主要考查了三角形全等的判定与性质,通过全等三角形来实现线段的转换是解题关键,没有明确的全等三角形时,要通过辅助线来构建与已知和所求条件相关联的全等三角形.【例4】.(2022·全国·八年级课时练习)四边形ABCD是由等边ΔABC和顶角为120°的等腰ΔABD排成,将一个60°角顶点放在D处,将60°角绕D,该60°交两边分别交直线BC、AC于M、N,交直线AB于E、F两点.(1)当E、F都在线段AB上时(如图1),请证明:BM+AN=MN;(2)当点E在边BA的延长线上时(如图2),请你写出线段MB,AN和MN之间的数量关系,并证明你的结论;(3)在(1)的条件下,若AC=7,AE=2.1,请直接写出MB的长为.【答案】(1)证明见解析;(2)MB=MN+AN.证明见解析;(3)2.8.【分析】(1)把△DBM绕点D逆时针旋转120°得到△DAQ,根据旋转的性质可得DM=DQ,AQ=BM,∠ADQ=∠BDM,然后求出∠QDN=∠MDN,利用“边角边”证明△MND和△QND全等,根据全等三角形对应边相等可得MN=QN,再根据AQ+AN=QN整理即可得证;(2)把△DAN绕点D顺时针旋转120°得到△DBP,根据旋转的性质可得DN=DP,AN=BP,根据∠DAN=∠DBP=90°可知点P在BM上,然后求出∠MDP=60°,然后利用“边角边”证明△MND和△MPD全等,根据全等三角形对应边相等可得MN=MP,从而得证;(3)过点M作MH∥AC交AB于G,交DN于H,可以证明△BMG是等边三角形,根据等边三角形的性质可得BM=MG=BG,根据全等三角形对应角相等可得∠QND=∠MND,再根据两直线平行,内错角相等可得∠QND=∠MHN,然后求出∠MND=∠MHN,根据等角对等边可得MN=MH,然后求出AN=GH,再利用“角角边”证明△ANE和△GHE全等,根据全等三角形对应边相等可得AE=GE,再根据BG=AB-AE-GE代入数据进行计算即可求出BG,从而得到BM的长.【详解】解:(1)证明:把△DBM绕点D逆时针旋转120°得到△DAQ,则DM=DQ,AQ=BM,∠ADQ=∠BDM,∠QAD=∠CBD=90°,∴点Q在直线CA上,∵∠QDN=∠ADQ+∠ADN=∠BDM+∠ADN=∠ABD-∠MDN=120°-60°=60°,∴∠QDN=∠MDN=60°,∵在△MND和△QND中,{DM=DQ∠QDN=∠MDNDN=DN,∴△MND≌△QND(SAS),∴MN=QN,∵QN=AQ+AN=BM+AN,∴BM+AN=MN;(2):MB=MN+AN.理由如下:如图,把△DAN绕点D顺时针旋转120°得到△DBP,则DN=DP,AN=BP,∵∠DAN=∠DBP=90°,∴点P在BM上,∵∠MDP=∠ADB-∠ADM-∠BDP=120°-∠ADM-∠ADN=120°-∠MDN=120°-60°=60°,∴∠MDP=∠MDN=60°,∵在△MND和△MPD中,{DN=DP∠MDP=∠MDNDM=DM,∴△MND≌△MPD(SAS),∴MN=MP,∵BM=MP+BP,∴MN+AN=BM;(3)如图,过点M作MH∥AC交AB于G,交DN于H,∵△ABC 是等边三角形,∴△BMG 是等边三角形,∴BM =MG =BG ,根据(1)△MND ≌△QND 可得∠QND =∠MND ,根据MH ∥AC 可得∠QND =∠MHN ,∴∠MND =∠MHN ,∴MN =MH ,∴GH =MH -MG =MN -BM =AN ,即AN =GH ,∵在△ANE 和△GHE 中,{∠QND =∠MHN∠AEN =∠GEH AN =GH,∴△ANE ≌△GHE (AAS ),∴AE =EG =2.1,∵AC =7,∴AB =AC =7,∴BG =AB -AE -EG =7-2.1-2.1=2.8,∴BM =BG =2.8.故答案为:2.8【点睛】本题考查了全等三角形的判定与性质及等腰三角形的性质,根据等边三角形的性质,旋转变换的性质作辅助线构造全等三角形是解题的关键,(3)作平行线并求出AN =GH 是解题的关键,也是本题的难点.一、解答题1.(2022·陕西·西安市第三中学七年级期末)回答问题(1)【初步探索】如图1:在四边形ABCD中,AB=AD,∠B=∠ADC=90°,E、F分别是BC、CD上的点,且EF=BE+FD,探究图中∠BAE、∠F AD、∠EAF之间的数量关系.小王同学探究此问题的方法是:延长FD到点G,使DG=BE.连接AG,先证明△ABE≌△ADG,再证明△AEF ≌△AGF,可得出结论,他的结论应是_______________;(2)【灵活运用】如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E、F分别是BC、CD上的点,且EF=BE+FD,上述结论是否仍然成立,并说明理由;(3)【拓展延伸】知在四边形ABCD中,∠ABC+∠ADC=180°,AB=AD,若点E在CB的延长线上,点F在CD 的延长线上,如图3所示,仍然满足EF=BE+FD,请直接写出∠EAF与∠DAB的数量关系.【答案】(1)∠BAE+∠F AD=∠EAF;(2)仍成立,理由见解析;(3)∠EAF=180°-12∠DAB【分析】(1)延长FD到点G,使DG=BE,连接AG,可判定△ABE≌△ADG,进而得出∠BAE=∠DAG,AE=AG,再判定△AEF≌△AGF,可得出∠EAF=∠GAF=∠DAG+∠DAF=∠BAE+∠DAF,据此得出结论;(2)延长FD到点G,使DG=BE,连接AG,先判定△ABE≌△ADG,进而得出∠BAE=∠DAG,AE=AG,再判定△AEF≌△AGF,可得出∠EAF=∠GAF=∠DAG+∠DAF=∠BAE+∠DAF;(3)在DC延长线上取一点G,使得DG=BE,连接AG,先判定△ADG≌△ABE,再判定△AEF≌△AGF,得出∠F AE=∠F AG,最后根据∠F AE+∠F AG+∠GAE=360°,推导得到2∠F AE+∠DAB=360°,即可得出结论.【详解】解:(1)∠BAE+∠F AD=∠EAF.理由:如图1,延长FD到点G,使DG=BE,连接AG,∵∠B=∠ADF=90°,∠ADG=∠ADF=90°,∴∠B=∠ADG=90°,又∵AB=AD,∴△ABE≌△ADG(SAS),∴∠BAE=∠DAG,AE=AG,∵EF=BE+FD=DG+FD=GF,AF=AF,∴△AEF≌△AGF(SSS),∴∠EAF=∠GAF=∠DAG+∠DAF=∠BAE+∠DAF;故答案为:∠BAE+∠F AD=∠EAF;(2)仍成立,理由:如图2,延长FD到点G,使DG=BE,连接AG,∵∠B+∠ADF=180°,∠ADG+∠ADF=180°,∴∠B=∠ADG,又∵AB=AD,∴△ABE≌△ADG(SAS),∴∠BAE=∠DAG,AE=AG,∵EF=BE+FD=DG+FD=GF,AF=AF,∴△AEF≌△AGF(SSS),∴∠EAF=∠GAF=∠DAG+∠DAF=∠BAE+∠DAF;∠DAB.(3)∠EAF=180°-12证明:如图3,在DC延长线上取一点G,使得DG=BE,连接AG,∵∠ABC+∠ADC=180°,∠ABC+∠ABE=180°,∴∠ADC=∠ABE,又∵AB=AD,∴△ADG≌△ABE(SAS),∴AG=AE,∠DAG=∠BAE,∵EF=BE+FD=DG+FD=GF,AF=AF,∴△AEF≌△AGF(SSS),∴∠F AE=∠F AG,∵∠F AE+∠F AG+∠GAE=360°,∴2∠F AE+(∠GAB+∠BAE)=360°,∴2∠F AE+(∠GAB+∠DAG)=360°,即2∠F AE+∠DAB=360°,∴∠EAF=180°-1∠DAB.2【点睛】本题属于三角形综合题,主要考查了全等三角形的判定以及全等三角形的性质的综合应用,解决问题的关键是作辅助线构造全等三角形,根据全等三角形的对应角相等进行推导变形.解题时注意:同角的补角相等.2.(2021·陕西·交大附中分校八年级开学考试)问题探究((1)如图①,已知∠A=45°,∠ABC=30°,∠ADC=40°,则∠BCD的大小为___________;(2)如图②,在四边形ABCD中,AB=BC,∠ABC=∠ADC=90°,对角线BD=6.求四边形ABCD的面积;小明这样来计算.延长DC,使得CE=AD,连接BE,通过证明△ABD≌△CBE,从而可以计算四边形ABCD的面积.请你将小明的方法完善.并计算四边形ABCD的面积;问题解决(3)如图③,四边形ABCD是正在建设的城市花园,其中AB=BC,∠ABC=60°,∠ADC=30°,DC=40米,AD=30米.请计算出对角线BD的长度.在四边形ABCD中,∠ABC=∠ADC=90°,∴∠A+∠BCD=180°,∵∠BCE+∠BCD=180°,∴∠A=∠BCE,在△ABD和△CBE中,{AB=BC ∠A=∠BCE AD=CE,∴△ABD≌△CBE,∴BE=BD,∠ABD=∠CBE,S△ABD=S△CBE,∵∠ABC=90°,即∠ABD+∠DBC=90°,∴∠CBE+∠DBC=90°,即∠DBE=90°,∵BD=BE=6,∠DBE=90°,∴S△BDE=12×BE×BD=18,∴S△BDE=S△CBE+S△DBC=S△ABD+S△DBC=S四边形ABCD=18;(4)如图,将△BCD绕点B逆时针旋转60°,得到△BAF,连接FD,∴△BCD≌△BAF,∠FBD=60°,∴BF=BD,AF=CD=40,∠BDC=∠BF A,∴△BFD是等边三角形,∴BF=BD=DF,∵∠ADC=30°,∴∠ADB+∠BDC=30°,∴∠BF A+∠ADB=30°,∵∠FBD+∠BF A+∠BDA+∠AFD+∠ADF=180°,∴60°+30°+∠AFD+∠ADF=180°,∴∠AFD+∠ADF=90°,∴∠F AD=90°,∴DF=√AF2+AD2=√402+302=50,∴BD=50(米).答:对角线BD的长度为50米.【点睛】本题考查了旋转的性质,全等三角形的判定和性质,等边三角形的判定和性质,勾股定理等知识,添加辅助线构造全等三角形是本题的关键.3.(2021·福建三明·八年级期中)感知:如图①,AD平分∠BAC,∠B+∠C=180°,∠B=90°.判断DB与DC的大小关系并证明.探究:如图②,AD平分∠BAC,∠ABD+∠ACD=180°,∠ABD<90°,DB与DC的大小关系变吗?请说明理由.应用:如图③,四边形ABDC中,∠B=45°,∠C=135°,DB=DC=m,则AB与AC差是多少(用含m的代数式表示)【答案】感知:DB=DC,证明见详解;探究:DB与DC的大小关系不变,理由见详解;应用:AB与AC差是与BD不垂直),点G是线段EF的中点,过点G作GH⊥EF交线段BD于点H.(1)猜想GH与EF的数量关系,并证明;(2)探索AE,CF,DH之间的数量关系,并证明;(3)如图2,若点E在AB的延长线上,点F在BC的延长线上,其他条件不变,请直接写出AE,CF,DH之间的数量关系.∴HI=HJ,∵HG垂直平分EF,∴HE=HF,∵∠HIE=∠HJF=90°,∴△HIE≌△HJF(HL),∴∠IHE=∠JHF,又∵∠IHJ=∠IHE+∠EHJ=90°,∴∠EHF=∠JHF+EHJ=90°,∴△HEF为等腰直角三角形,∵G为斜边的中点,∴GH=1EF.2(2)AE+CF=√2DH,理由如下:由(1)中△HIE≌△HJF(HL),∴EI=FJ,由下图:∠A=∠AIH=∠AKH=90°,∴四边形AIHK为矩形,∴AI=KH,在△DHK中,由正方形的性质知,∠HDK=45°,∵∠HKD=90°,∴∠DHK=90°−45°=45°∴△DKH为等腰直角三角形,又∴∠D=∠HKD=∠HLD=90°,∴四边形HKDL为正方形,∴HL=KH,同理四边形HLCJ为矩形,∴HL=JC∴AI=KH=HL=JC,AE=AI+EI,CF=JC−FJ,∴AE+CF=AI+JC=2AI=2KH,在△DHK中,由正方形的性质知,∠HDK=45°,∵∠HKD=90°,∴∠DHK=90°−45°=45°∴△DKH为等腰直角三角形,∴DH=√2KH,∴AE+CF=√2DH.(3)AE−CF=√2DH,理由如下:过点H作AB,BC垂线,分别交AB,BC,CD,AD于I,J,L,K,连接HE,HF,∵HI=HJ,HE=HF,∠HIE=∠HJF=90°,∴△HIE≌△HJF,∴EI=FJ,由(2)得AI=KH=HL=JC,CF=FJ−JC,AE=AI+EI,∴AE−CF=AI+JC=2AI=2KH,由(2)可得:DH=√2KH,△DKH为等腰直角三角形,∴AE−CF=√2DH.【点睛】本题考查了正方形的性质、三角形全等的判定及性质、等腰直角三角形、解题的关键是添加适当的辅助线,掌握相关的知识点,通过等量代换的思想进行求解.5.(2020·河南洛阳·八年级期中)在∠MAN内有一点D,过点D分别作DB⊥AM,DC⊥AN,垂足分别为B,C.且BD=CD,点E,F分别在边AM和AN上.(1)如图1,若∠BED=∠CFD,请说明DE=DF;(2)如图2,若∠BDC=120°,∠EDF=60°,猜想EF,BE,CF具有的数量关系,并说明你的结论成立的理由.理由:过点D作∠CDG=∠BDE,交AN于点G,在ΔBDE和ΔCDG中,{∠EBD=∠GCDBD=CD∠BDE=∠CDG,∴ΔBDE≅ΔCDG(ASA),∴DE=DG,BE=CG.∵∠BDC=120°,∠EDF=60°,∴∠BDE+∠CDF=60°.∴∠FDG=∠CDG+∠CDF=60°,∴∠EDF=∠GDF.在ΔEDF和ΔGDF中,{DE=DG∠EDF=∠GDFDF=DF,∴ΔEDF≅ΔGDF(SAS).∴EF=GF,∴EF=FC+CG=FC+BE.【点睛】本题考查全等三角形的判定、解答本题的关键是明确题意,利用数形结合的思想解答.6.(2020·江西萍乡·八年级期末)【课题研究】旋转图形中对应线段所在直线的夹角(小于等于90°的角)与旋转角的关系.【问题初探】线段AB绕点O顺时针旋转得到线段CD,其中点A与点C对应,点B与点D对应,旋转角的度数为α,且0°<α<180°.(1)如图①,当α=60°时,线段AB、CD所在直线夹角(锐角)为;(2)如图②,当90°<α<180°时,直线AB与直线CD所夹锐角与旋转角α存在怎样的数量关系?请说明理由;【形成结论】旋转图形中,当旋转角小于平角时,对应线段所在直线的夹角与旋转角.【运用拓广】运用所形成的结论解决问题:(3)如图③,四边形ABCD中,∠ABC=60°,∠ADC=30°,AB=BC,CD=3,BD=√19,求AD的长.【答案】(1)60°;(2)互补,理由见解析;【形成结论】相等或互补;(3)√10【分析】(1)由旋转的性质可得AB=CD,OA=OC,BO=DO,可证ΔAOB≅ΔCOD(SSS),可得∠B=∠D,由三角形内角和定理可求解;(2)由旋转的性质可得AB=CD,OA=OC,BO=DO,可证ΔAOB≅ΔCOD(SSS),可得∠B=∠D,由平角的定义和四边形内角和定理可求解;【形成结论】由(1)(2)可知对应线段所在直线的所夹锐角角与旋转角:相等或互补;【运用拓广】(3)将ΔBCD绕点B顺时针旋转60°,得到ΔBAF,连接FD,由旋转的性质可得BF=BD,AF=CD=3,由三角形内角和定理可求∠FAD=90°,由勾股定理可求解.【详解】解:(1)如图1,延长DC交AB于F,交BO于E,∵α=60°,∴∠BOD=60°,∵线段AB绕点O顺时针旋转得线段CD,∴AB=CD,OA=OC,BO=DO,∴ΔAOB≅ΔCOD(SSS),∴∠B=∠D,∵∠B=∠D,∠OED=∠BEF,∴∠BFE=∠EOD=60°,故答案为:60°;(2)直线AB与直线CD所夹锐角角与旋转角α互补,理由如下:如图2,延长AB,DC交于点E,∵线段AB绕点O顺时针旋转得线段CD,∴AB=CD,OA=OC,BO=DO,∴ΔAOB≅ΔCOD(SSS),∴∠ABO=∠D,∵∠ABO+∠EBO=180°,∴∠D+∠EBO=180°,∵∠EBO+∠E+∠D+∠BOD=360°,∴∠E+∠BOD=180°,∴直线AB与直线CD所夹锐角角与旋转角α互补.形成结论由(1)(2)(3)可知:旋转图形中,当旋转角小于平角时,对应线段所在直线的所夹锐角角与旋转角:相等或互补.故答案为:相等或互补.运用拓广(3)如图3,将ΔBCD绕点B顺时针旋转60°,得到ΔBAF,连接FD,延长FA,DC交于点E,∴旋转角∠ABC=60°,∵ΔBCD≅ΔBAF,∴∠AED=∠ABC=60°,AF=CD=3,BD=BF,∵∠ADC=30°,∴∠FAD=∠AED+∠ADC=90°,又∵∠FBD=∠ABC=60°,BF=BD,∴ΔBFD是等边三角形,∴BF=BD=DF,∴在RtΔDAF中,AD=√DF2−AF2=√19−9=√10.【点睛】本题是几何变换综合题,考查了旋转的性质,全等三角形的判定和性质,等边三角形的判定和性质等知识,添加辅助线构造全等三角形是本题的关键.7.(2021··九年级专题练习)如图,在△ABC中,∠ACB=120°,BC>AC,点E在BC上,点D在AB上,CE=CA,连接DE,∠ACB+∠ADE=180°,CH⊥AB,垂足为H.证明:DE+AD=2√3CH.【答案】见解析【分析】如图,延长BA到点F,使AF=DE,连接CF、CD,根据四边形的内角和和邻补角互补可得∠CAF=∠CED,进而可根据SAS证明△AFC≌△EDC,可得CF=CD,∠ACF=∠ECD,进一步即可求得∠FCD=120°,然后利用等腰三角形的性质和解直角三角形的知识即可证得结论.【详解】证明:如图,延长BA到点F,使AF=DE,连接CF、CD,∵∠ACB+∠ADE=180°,∴∠CAD+∠CED=360°−180°=180°,∵∠CAD+∠CAF=180°,∴∠CAF=∠CED,∵AC=EC,AF=ED,∴△AFC≌△EDC,。
2021年九年级中考数学第三轮压轴题专题冲刺复习:四边形综合(含答案)

2021年中考数学第三轮压轴题专题冲刺复习:四边形综合1、如图,四边形ABCD中,AD∥BC,AD=CD,E是对角线BD上一点,且EA=EC.(1)求证:四边形ABCD是菱形;(2)如果BE=BC,且∠CBE:∠BCE=2:3,求证:四边形ABCD是正方形.2、如图,四边形ABCD中,AB=AC=AD,AC平分∠BAD,点P是AC延长线上一点,且PD⊥AD.(1)证明:∠BDC=∠PDC;(2)若AC与BD相交于点E,AB=1,CE:CP=2:3,求AE的长.3、如图,在△ABC中,过点C作CD∥AB,E是AC的中点,连接DE并延长,交AB于点F,交CB的延长线于点G,连接AD,CF.(1)求证:四边形AFCD是平行四边形.(2)若GB=3,BC=6,BF=,求AB的长.4、给出定义,若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称该四边形为勾股四边形.(1)在你学过的特殊四边形中,写出两种勾股四边形的名称;(2)如图,将△ABC绕顶点B按顺时针方向旋转60°得到△DBE,连接AD,DC,CE,已知∠DCB=30°.①求证:△BCE是等边三角形;②求证:DC2+BC2=AC2,即四边形ABCD是勾股四边形.5、如图1,将一张矩形纸片ABCD沿着对角线BD向上折叠,顶点C落到点E处,BE交AD于点F.(1)求证:△BDF是等腰三角形;(2)如图2,过点D作DG∥BE,交BC于点G,连接FG交BD于点O.①判断四边形BFDG的形状,并说明理由;②若AB=6,AD=8,求FG的长.6、如图,正方形ABCD的边CD在正方形ECGF的边CE上,连接DG,过点A作AH∥DG,交BG于点H.连接HF,AF,其中AF交EC于点M.(1)求证:△AHF为等腰直角三角形.(2)若AB=3,EC=5,求EM的长.7、如图1,四边形ABCD的对角线AC,BD相交于点O,OB=OD,OC=OA+AB,AD=m,BC=n,∠ABD+∠ADB=∠ACB.(1)填空:∠BAD与∠ACB的数量关系为;(2)求的值;(3)将△ACD沿CD翻折,得到△A′CD(如图2),连接BA′,与CD相交于点P.若CD=,求PC的长.8、如图,四边形ABCD是平行四边形,AD=AC,AD⊥AC,E是AB的中点,F是AC 延长线上一点.(1)若ED⊥EF,求证:ED=EF;(2)在(1)的条件下,若DC的延长线与FB交于点P,试判定四边形ACPE是否为平行四边形?并证明你的结论(请先补全图形,再解答);(3)若ED=EF,ED与EF垂直吗?若垂直给出证明.9、在四边形ABCD中,︒∠.B,对角线AC平分BADD∠180=∠+(1)如图1,若︒∠90=B,试探究边AD、AB与对角线AC=∠120DAB,且︒的数量关系并说明理由.(2)如图2,若将(1)中的条件“︒B”去掉,(1)中的结论是否成立?∠90=请说明理由.(3)如图3,若︒DAB,探究边AD、AB与对角线AC的数量关系并说明∠90=理由.10、如图,在正方形ABCD中,点G在对角线BD上(不与点B,D重合),GE⊥DC于点E,GF⊥BC于点F,连结AG.(1)写出线段AG,GE,GF长度之间的数量关系,并说明理由;(2)若正方形ABCD的边长为1,∠AGF=105°,求线段BG的长.11、如图1,菱形ABCD 的顶点A ,D 在直线上,∠BAD =60°,以点A 为旋转中心将菱形ABCD 顺时针旋转α(0°<α<30°),得到菱形AB ′C ′D ′,B ′C ′交对角线AC 于点M ,C ′D ′交直线l 于点N ,连接MN .(1)当MN ∥B ′D ′时,求α的大小.(2)如图2,对角线B ′D ′交AC 于点H ,交直线l 与点G ,延长C ′B ′交AB 于点E ,连接EH .当△HEB ′的周长为2时,求菱形ABCD 的周长.12、已知正方形的对角线,相交于点.(1)如图1,,分别是,上的点,与的延长线相交于点.若,求证:;(2)如图2,是上的点,过点作,交线段于点,连结交于点,交于点.若,①求证:;②当时,求的长.CD AB C A D B O E G OB C O C E DG F DF C ⊥E G OE =O H C B H C EH ⊥B OB E D H C E F C O G G OE =O DG C ∠O =∠O E 1AB =C H13、已知正方形ABCD,点M为边AB的中点.(1)如图1,点G为线段CM上的一点,且90∠=︒,延长AG,BG分别AGB与边BC,CD交于点E,F.①求证:BE CF=;②求证:2=⋅.BE BC CE(2)如图2,在边BC上取一点E,满足2=⋅,连接AE交CM于点G,BE BC CE连接BG延长交CD于点F,求tan CBF∠的值.14、如图,在Rt△ABC中,∠ACB=90°,∠A=45°,AB=4cm.点P从点A出发,以2cm/s的速度沿边AB向终点B运动.过点P作PQ⊥AB交折线ACB于点Q,D 为PQ中点,以DQ为边向右侧作正方形DEFQ.设正方形DEFQ与△ABC重叠部分图形的面积是y(cm2),点P的运动时间为x(s).(1)当点Q 在边AC 上时,正方形DEFQ 的边长为 cm (用含x 的代数式表示);(2)当点P 不与点B 重合时,求点F 落在边BC 上时x 的值;(3)当0<x <2时,求y 关于x 的函数解析式;(4)直接写出边BC 的中点落在正方形DEFQ 内部时x 的取值范围.15、如图AM 是ABC ∆的中线,D 是线段AM 上一点(不与点A 重合),AB DE //交AC 于点F ,AM CE //,连结AE .(1)如图1,当点D 与M 重合时,求证:四边形ABDE 是平行四边形;(2)如图2,当点D 不与M 重合时,(1)中的结论还成立吗?请说明理由.(3)如图3,延长BD 交AC 于点H ,若AC BH ⊥,且AM BH =.当3=FH ,4=DM 时,求DH 的长.16、在四边形ABCD 中,对角线AC 、BD 交于点O .若四边形ABCD 是正方形如图1:则有AC=BD ,AC ⊥BD .旋转图1中的Rt △COD 到图2所示的位置,AC ′与BD ′有什么关系?(直接写出)若四边形ABCD 是菱形,∠ABC=60°,旋转Rt △COD 至图3所示的位置,AC ′与BD ′又有什么关系?写出结论并证明.17、在平面直角坐标系中,点A的坐标为(0,3),点B和点D的坐标分别为(m,0),(n,4),且m>0,四边形ABCD是矩形.(1)如图1,当四边形ABCD为正方形时,求m,n的值;(2)在图2中,画出矩形ABCD,简要说明点C,D的位置是如何确定的,并直接用含m的代数式表示点C的坐标;(3)探究:当m为何值时,矩形ABCD的对角线AC的长度最短.参考答案2021年中考数学第三轮压轴题专题冲刺复习:四边形综合1、如图,四边形ABCD中,AD∥BC,AD=CD,E是对角线BD上一点,且EA=EC.(1)求证:四边形ABCD是菱形;(2)如果BE=BC,且∠CBE:∠BCE=2:3,求证:四边形ABCD是正方形.【解答】证明:(1)在△ADE与△CDE中,,∴△ADE≌△CDE,∴∠ADE=∠CDE,∵AD∥BC,∴∠ADE=∠CBD,∴∠CDE=∠CBD,∴BC=CD,∵AD=CD,∴BC=AD,∴四边形ABCD为平行四边形,∵AD=CD,∴四边形ABCD是菱形;(2)∵BE=BC∴∠BCE=∠BEC,∵∠CBE:∠BCE=2:3,∴∠CBE=180×=45°,∵四边形ABCD是菱形,∴∠ABE=45°,∴∠ABC=90°,∴四边形ABCD是正方形.2、如图,四边形ABCD中,AB=AC=AD,AC平分∠BAD,点P是AC延长线上一点,且PD⊥AD.(1)证明:∠BDC=∠PDC;(2)若AC与BD相交于点E,AB=1,CE:CP=2:3,求AE的长.【解答】(1)证明:∵AB=AD,AC平分∠BAD,∴AC⊥BD,∴∠ACD+∠BDC=90°,∵AC=AD,∴∠ACD=∠ADC,∴∠ADC+∠BDC=90°,∴∠BDC=∠PDC;(2)解:过点C作CM⊥PD于点M,∵∠BDC=∠PDC,∴CE=CM,∵∠CMP=∠ADP=90°,∠P=∠P,∴△CPM∽△APD,∴=,设CM=CE=x,∵CE:CP=2:3,∴PC=x,∵AB=AD=AC=1,∴=,解得:x=,故AE=1﹣=.3、如图,在△ABC中,过点C作CD∥AB,E是AC的中点,连接DE并延长,交AB于点F,交CB的延长线于点G,连接AD,CF.(1)求证:四边形AFCD是平行四边形.(2)若GB=3,BC=6,BF=,求AB的长.【解答】解:(1)∵E是AC的中点,∴AE=CE,∵AB∥CD,∴∠AFE=∠CDE,在△AEF和△CED中,∵,∴△AEF≌△CED(AAS),∴AF=CD,又AB∥CD,即AF∥CD,∴四边形AFCD是平行四边形;(2)∵AB∥CD,∴△GBF∽△GCD,∴=,即=,解得:CD=,∵四边形AFCD是平行四边形,∴AF=CD=,∴AB=AF+BF=+=6.4、给出定义,若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称该四边形为勾股四边形.(1)在你学过的特殊四边形中,写出两种勾股四边形的名称;(2)如图,将△ABC绕顶点B按顺时针方向旋转60°得到△DBE,连接AD,DC,CE,已知∠DCB=30°.①求证:△BCE是等边三角形;②求证:DC2+BC2=AC2,即四边形ABCD是勾股四边形.解:(1)正方形、矩形、直角梯形均可;证明:(2)①∵△ABC≌△DBE,∴BC=BE,∵∠CBE=60°,∴△BCE是等边三角形;②∵△ABC≌△DBE,∴BE=BC,AC=ED;∴△BCE为等边三角形,∴BC=CE,∠BCE=60°,∵∠DCB=30°,∴∠DCE=90°,在Rt△DCE中,DC2+CE2=DE2,∴DC2+BC2=AC2.5、如图1,将一张矩形纸片ABCD沿着对角线BD向上折叠,顶点C落到点E处,BE交AD于点F.(1)求证:△BDF是等腰三角形;(2)如图2,过点D作DG∥BE,交BC于点G,连接FG交BD于点O.①判断四边形BFDG的形状,并说明理由;②若AB=6,AD=8,求FG的长.【解答】(1)证明:如图1,根据折叠,∠DBC=∠DBE,又AD∥BC,∴∠DBC=∠ADB,∴∠DBE=∠ADB,∴DF=BF,∴△BDF是等腰三角形;(2)①∵四边形ABCD是矩形,∴AD∥BC,∴FD∥BG,又∵DG∥BE,∴四边形BFDG是平行四边形,∵DF=BF,∴四边形BFDG是菱形;②∵AB=6,AD=8,∴BD=10.∴OB=BD=5.假设DF=BF=x,∴AF=AD﹣DF=8﹣x.∴在直角△ABF中,AB2+AF2=BF2,即62+(8﹣x)2=x2,解得x=,即BF=,∴FO===,∴FG=2FO=.6、如图,正方形ABCD的边CD在正方形ECGF的边CE上,连接DG,过点A作AH∥DG,交BG于点H.连接HF,AF,其中AF交EC于点M.(1)求证:△AHF为等腰直角三角形.(2)若AB=3,EC=5,求EM的长.【解答】证明:(1)∵四边形ABCD,四边形ECGF都是正方形∴DA∥BC,AD=CD,FG=CG,∠B=∠CGF=90°∵AD∥BC,AH∥DG∴四边形AHGD是平行四边形∴AH=DG,AD=HG=CD∵CD=HG,∠ECG=∠CGF=90°,FG=CG∴△DCG≌△HGF(SAS)∴DG=HF,∠HFG=∠HGD∴AH=HF,∵∠HGD+∠DGF=90°∴∠HFG+∠DGF=90°∴DG⊥HF,且AH∥DG∴AH⊥HF,且AH=HF∴△AHF为等腰直角三角形.(2)∵AB=3,EC=5,∴AD=CD=3,DE=2,EF=5∵AD∥EF∴=,且DE=2∴EM=7、如图1,四边形ABCD的对角线AC,BD相交于点O,OB=OD,OC=OA+AB,AD=m,BC=n,∠ABD+∠ADB=∠ACB.(1)填空:∠BAD与∠ACB的数量关系为∠BAD+∠ACB=180°;(2)求的值;(3)将△ACD沿CD翻折,得到△A′CD(如图2),连接BA′,与CD相交于点P.若CD=,求PC的长.【解答】解:(1)如图1中,在△ABD中,∵∠BAD+∠ABD+∠ADB=180°,又∵∠ABD+∠ADB=∠ACB,∴∠BAD+∠ACB=180°,故答案为∠BAD+∠ACB=180°.(2)如图1中,作DE∥AB交AC于E.∴∠DEA=∠BAE,∠OBA=∠ODE,∵OB=OD,∴△OAB≌△OED,∴AB=DE,OA=OE,设AB=DE=CE=CE=x,OA=OE=y,∵∠EDA+∠DAB=180°,∠BAD+∠ACB=180°,∴∠EDA=∠ACB,∵∠DEA=∠CAB,∴△EAD∽△ABC,∴===,∴=,∴4y2+2xy﹣x2=0,∴()2+﹣1=0,∴=(负根已经舍弃),∴=.(3)如图2中,作DE∥AB交AC于E.由(1)可知,DE=CE,∠DCA=∠DCA′,∴∠EDC=∠ECD=∠DCA′,∴DE∥CA′∥AB,∴∠ABC+∠A′CB=180°,∵△EAD∽△ACB,∴∠DAE=∠ABC=∠DA′C,∴∠DA′C+∠A′CB=180°,∴A′D∥BC,∴△PA′D∽△PBC,∴==,∴=,即=∵CD=,∴PC=1.8、如图,四边形ABCD是平行四边形,AD=AC,AD⊥AC,E是AB的中点,F是AC 延长线上一点.(1)若ED⊥EF,求证:ED=EF;(2)在(1)的条件下,若DC的延长线与FB交于点P,试判定四边形ACPE是否为平行四边形?并证明你的结论(请先补全图形,再解答);(3)若ED=EF,ED与EF垂直吗?若垂直给出证明.【解答】(1)证明:在▱ABCD中,∵AD=AC,AD⊥AC,∴AC=BC,AC⊥BC,连接CE,∵E是AB的中点,∴AE=EC,CE⊥AB,∴∠ACE=∠BCE=45°,∴∠ECF=∠EAD=135°,∵ED⊥EF,∴∠CEF=∠AED=90°﹣∠CED,在△CEF和△AED中,,∴△CEF≌△AED,∴ED=EF;(2)解:由(1)知△CEF≌△AED,CF=AD,∵AD=AC,∴AC=CF,∵DP∥AB,∴FP=PB,∴CP=AB=AE,∴四边形ACPE为平行四边形;(3)解:垂直,理由:过E 作EM ⊥DA 交DA 的延长线于M ,过E 作EN ⊥FC 交FC 的延长线于N , 在△AME 与△CNE 中,,∴△AME ≌△CNE ,∴∠ADE=∠CFE ,在△ADE 与△CFE 中,, ∴△ADE ≌△CFE ,∴∠DEA=∠FEC ,∵∠DEA+∠DEC=90°,∴∠CEF+∠DEC=90°,∴∠DEF=90°,∴ED ⊥EF .9、在四边形ABCD 中,︒=∠+∠180D B ,对角线AC 平分BAD ∠.(1)如图1,若︒=∠120DAB ,且︒=∠90B ,试探究边AD 、AB 与对角线AC的数量关系并说明理由.(2)如图2,若将(1)中的条件“︒=∠90B ”去掉,(1)中的结论是否成立?请说明理由.(3)如图3,若︒=∠90DAB ,探究边AD 、AB 与对角线AC 的数量关系并说明理由.解:(1)AB AD AC +=.证明如下: 在四边形ABCD 中,︒=∠+∠180B D ,︒=∠90B ,∴ ︒=∠90D .︒=∠120DAB ,AC 平分DAB ∠, ∴ 60=∠=∠BAC DAC ,︒=∠90B ,∴AC AB 21=,同理AC AD 21=. ∴AB AD AC +=.(2)(1)中的结论成立,理由如下:以C 为顶点,AC 为一边作 60=∠ACE , ACE ∠的另一边交AB 延长线于点E , 60=∠BAC ,∴AEC ∆为等边三角形, ∴CE AE AC ==,︒=∠+∠180B D ,︒=∠120DAB ,∴ 60=∠DCB , ∴BEC DAC ∆≅∆,∴BE AD =,∴AB AD AC +=.(3)AC AB AD 2=+.理由如下:过点C 作AC CE ⊥交AB 的延长线于点E , ︒=∠+∠180B D ,︒=∠90DAB ,∴ 90=DCB , 90=∠ACE ,∴BCE DCA ∠=∠, 又AC 平分DAB ∠,∴ 45=∠CAB ,∴ 45=∠E . ∴CE AC =.又︒=∠+∠180B D ,CBE D ∠=∠,∴CBE CDA ∆≅∆,∴BE AD =,∴AE AB AD =+.在ACE Rt ∆中, 45=∠CAB ,∴AC cos ACAE 245==, ∴AC AB AD 2=+.10、如图,在正方形ABCD 中,点G 在对角线BD 上(不与点B ,D 重合),GE ⊥DC 于点E ,GF ⊥BC 于点F ,连结AG .(1)写出线段AG ,GE ,GF 长度之间的数量关系,并说明理由; (2)若正方形ABCD 的边长为1,∠AGF=105°,求线段BG 的长.【答案】(1)结论:AG 2=GE 2+GF 2. 理由:连接CG .∵四边形ABCD 是正方形, ∴A 、C 关于对角线BD 对称,∵点G 在BD 上, ∴GA=GC ,∵GE ⊥DC 于点E ,GF ⊥BC 于点F , ∴∠GEC=∠ECF=∠CFG=90°, ∴四边形EGFC 是矩形, ∴CF=GE ,在Rt △GFC 中,∵CG 2=GF 2+CF 2, ∴AG 2=GF 2+GE 2.解得,[来源:学科网ZXXK] ∴, ∴BG=BN ÷cos30°=.11、如图1,菱形ABCD 的顶点A,D 在直线上,∠BAD =60°,以点A 为旋转中心将菱形ABCD 顺时针旋转α(0°<α<30°),得到菱形AB ′C ′D ′,B ′C ′6交对角线AC于点M,C′D′交直线l于点N,连接MN.(1)当MN∥B′D′时,求α的大小.(2)如图2,对角线B′D′交AC于点H,交直线l与点G,延长C′B′交AB于点E,连接EH.当△HEB′的周长为2时,求菱形ABCD的周长.【解答】解:(1)∵四边形AB′C′D′是菱形,∴AB′=B′C′=C′D′=AD′,∵∠B′AD′=∠B′C′D′=60°,∴△AB′D′,△B′C′D′是等边三角形,∵MN∥B′C′,∴∠C′MN=∠C′B′D′=60°,∠CNM=∠C′D′B′=60°,∴△C′MN是等边三角形,∴C′M=C′N,∴MB′=ND′,∵∠AB′M=∠AD′N=120°,AB′=AD′,∴△AB′M≌△AD′N(SAS),∴∠B′AM=∠D′AN,∵∠CAD=∠BAD=30°,∠DAD′=15°,∴α=15°.(2)∵∠C′B′D′=60°,∴∠EB′G=120°,∵∠EAG=60°,∴∠EAG+∠EB′G=180°,∴四边形EAGB′四点共圆,∴∠AEB ′=∠AGD ′,∵∠EAB ′=∠GAD ′,AB ′=AD ′, ∴△AEB ′≌△AGD ′(AAS ), ∴EB ′=GD ′,AE =AG , ∵AH =AH ,∠HAE =∠HAG , ∴△AHE ≌△AHG (SAS ), ∴EH =GH ,∵△EHB ′的周长为2,∴EH +EB ′+HB ′=B ′H +HG +GD ′=B ′D ′=2, ∴AB ′=AB =2, ∴菱形ABCD 的周长为8.12、已知正方形的对角线,相交于点.(1)如图1,,分别是,上的点,与的延长线相交于点.若,求证:;(2)如图2,是上的点,过点作,交线段于点,连结交于点,交于点.若,①求证:; ②当时,求的长.CD AB C A D B O E G OB C O C E DG F DF C ⊥E G OE =O H C B H C EH ⊥B OB E D H C E F C O G G OE =O DG C ∠O =∠O E 1AB =CH∴∠DOG=∠COE=90°∴∠OEC+∠OCE=90°∵DF⊥CE∴∠OEC+∠ODG=90°∴∠ODG=∠OCE∴△DOG≌△COE(ASA)∴OE=OG②解:设CH=x,∵四边形ABCD是正方形,AB=1 ∴BH=1-x∠DBC=∠BDC=∠ACB=45°∵EH⊥BC∴∠BEH=∠EBH=45°∴EH=BH=1-x∵∠ODG=∠OCE∴∠BDC-∠ODG=∠ACB-∠OCE ∴∠HDC=∠ECH∵EH⊥BC∴∠EHC=∠HCD=90° ∴△CHE ∽△DCH ∴∴HC 2=EH ·CD 得x 2+x-1=0 解得,(舍去) ∴13、已知正方形ABCD,点M 为边AB 的中点.(1)如图1,点G 为线段CM 上的一点,且90AGB ∠=︒,延长AG ,BG 分别与边BC ,CD 交于点E ,F .①求证:BE CF =; ②求证:2BE BC CE =⋅.(2)如图2,在边BC 上取一点E ,满足2BE BC CE =⋅,连接AE 交CM 于点G ,连接BG 延长交CD 于点F ,求tan CBF ∠的值.解答:(1)①证明:∵四边形ABCD 为正方形,∴AB BC ,90ABC BCF ∠∠°, 又90AGB ∠°,∴90BAE ABG ∠∠°,又90ABG CBF ∠∠°,∴BAE CBF ∠∠,∴ABE BCF △≌△(ASA),∴BE CF .EH HCHC CD=1x =1x =②证明:∵90AGB ∠°,点M 为AB 中点,∴MG MA MB ,∴GAM AGM ∠∠,又∵CGE AGM ∠∠,从而CGE CGB ∠∠,又ECG GCB ∠∠,∴CGE CBG △∽△, ∴CE CGCGCB,即2CG BC CE ,由CFG GBMCGF ∠∠∠,得CFCG .由①知,BE CF ,∴BE CG ,∴2BE BC CE . (2)解:(方法一)延长AE ,DC 交于点N (如图1),由于四边形ABCD 是正方形,所以AB CD ∥, ∴N EAB ∠∠,又CEN BEA ∠∠,∴CEN BEA △∽△, 故CE CNBEBA,即BE CN AB CE ,∵AB BC ,2BE BC CE ,∴CN BE ,由AB DN ∥知,CN CG CFAM GM MB, 又AM M B ,∴FC CN BE ,不妨假设正方形边长为1, 设BE x ,则由2BE BC CE ,得211x x , 解得1512x ,2512x (舍去),∴512BEBC, 于是51tan 2FC BE CBFBC BC ∠,(方法二)不妨假设正方形边长为1,设BE x ,则由2BE BC CE ,得211x x , 解得1512x ,2512x (舍去),即512BE , 作GN BC ∥交AB 于N (如图2),则MNG MBC △∽△,∴12MN MB NGBC , 设MN y ,则2GN y ,5GM y ,∵GN AN BEAB ,即121y,解得125y,∴12GM,从而GM MAMB ,此时点G 在以AB 为直径的圆上,∴AGB △是直角三角形,且90AGB ∠°, 由(1)知BE CF ,于是51tan 2FC BE CBFBCBC∠.14、如图,在Rt△ABC中,∠ACB=90°,∠A=45°,AB=4cm.点P从点A出发,以2cm/s的速度沿边AB向终点B运动.过点P作PQ⊥AB交折线ACB于点Q,D 为PQ中点,以DQ为边向右侧作正方形DEFQ.设正方形DEFQ与△ABC重叠部分图形的面积是y(cm2),点P的运动时间为x(s).(1)当点Q在边AC上时,正方形DEFQ的边长为cm(用含x的代数式表示);(2)当点P不与点B重合时,求点F落在边BC上时x的值;(3)当0<x<2时,求y关于x的函数解析式;(4)直接写出边BC的中点落在正方形DEFQ内部时x的取值范围.试题解析:(1)∵∠ACB=90°,∠A=45°,PQ⊥AB,∴∠AQP=45°,∴PQ=AP=2x,∵D为PQ中点,∴DQ=x,∵D为PQ中点,∴DQ=x,∴GP=2x,∴2x+x+2x=4,∴x=45;(3)如图②,当0<x≤45时,y=S正方形DEFQ=DQ2=x2,∴y=x2;如图③,当45<x≤1时,过C作CH⊥AB于H,交FQ于K,则CH=12AB=2,∵PQ=AP=2x,CK=2﹣2x,∴MQ=2CK=4﹣4x,FM=x﹣(4﹣4x)=5x﹣4,∴y=S正方形DEFQ ﹣S△MNF=DQ2﹣12FM2,∴y=x2﹣12(5x﹣4)2=﹣232x2+20x﹣8,∴y=﹣232x2+20x﹣8;∴DQ=2﹣x ,∴y=S △DEQ =12DQ 2,∴y=12(2﹣x )2,∴y=12x 2﹣2x+2;(4)当Q 与C 重合时,E 为BC 的中点, 即2x=2, ∴x=1,当Q 为BC 的中点时, PB=1, ∴AP=3, ∴2x=3,∴x=32,∴边BC 的中点落在正方形DEFQ 内部时x 的取值范围为:1<x <32.15、如图AM 是ABC ∆的中线,D 是线段AM 上一点(不与点A 重合),AB DE //交AC 于点F ,AM CE //,连结AE .(1)如图1,当点D 与M 重合时,求证:四边形ABDE 是平行四边形; (2)如图2,当点D 不与M 重合时,(1)中的结论还成立吗?请说明理由. (3)如图3,延长BD 交AC 于点H ,若AC BH ⊥,且AM BH =.当3=FH ,DM时,求DH的长.4【答案】:(1)证明:∵DE//AB,∴∠EDC=∠ABM,∵CE//AM,∴∠ECD=∠ADB,又∵AM是△ABC的中线,且D与M重合,∴BD=DC,∴△ABD≅△EDC,∴AB=ED,又∵AB//ED,∴四边形ABDE为平行四边形。
2021年九年级中考数学第三轮压轴题冲刺专题复习:圆的综合 专项练习题

2021年中考数学第三轮压轴题冲刺专题复习:圆的综合专项练习题1、如图,O是ABC∆的外接圆,其切线AE与直径BD的延长线相交于点E,=.且AE AB(1)求ACB∠的度数;DE=,求O的半径.(2)若22、如图,AB是半圆O的直径,C,D是半圆O上不同于A,B的两点,AD BC=,AC与BD相交于点F.BE是半圆O所在圆的切线,与AC的延长线相交于点E.(1)求证:CBA DAB∆≅∆;(2)若BE BF=,求证:AC平分DAB∠.3、如图,AG是∠HAF的平分线,点E在AF上,以AE为直径的⊙O交AG于点D,过点D作AH的垂线,垂足为点C,交AF于点B.(1)求证:直线BC是⊙O的切线;(2)若AC=2CD,设⊙O的半径为r,求BD的长度.4、如图,在Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,点O在AB 上,⊙O经过A、D两点,交AC于点E,交AB于点F.(1)求证:BC是⊙O的切线;(2)若⊙O的半径是2cm,E是的中点,求阴影部分的面积(结果保留π和根号)5、如图,CE是⊙O的直径,BC切⊙O于点C,连接OB,作ED∥OB交⊙O于点D,BD的延长线与CE的延长线交于点A.(1)求证:AB是⊙O的切线;(2)若⊙O的半径为1,tan∠DEO=,tan∠A=,求AE的长.6、如图,点O是△ABC的边AB上一点,⊙O与边AC相切于点E,与边BC,AB 分别相交于点D,F,且DE=EF.(1)求证:∠C=90°;(2)当BC=3,sinA=时,求AF的长.7、如图,已知A 、B 是⊙O 上两点,△OAB 外角的平分线交⊙O 于另一点C ,CD ⊥AB 交AB 的延长线于D .(1)求证:CD 是⊙O 的切线;(2)E 为的中点,F 为⊙O 上一点,EF 交AB 于G ,若tan ∠AFE=,BE=BG ,EG=3,求⊙O 的半径.8、如图,已知AB 是O 的直径,C 是O 上的一点,D 是AB 上的一点,DE AB ⊥于D ,DE 交BC 于F ,且EF EC =.(1)求证:EC 是O 的切线;(2)若4BD =,8BC =,圆的半径5OB =,求切线EC 的长.9、如图,AB 是⊙O 的直径,点E 为线段OB 上一点(不与O ,B 重合),作EC ⊥OB ,交⊙O 于点C ,作直径CD ,过点C 的切线交DB 的延长线于点P ,作AF ⊥PC 于点F ,连接CB .(1)求证:AC 平分∠FAB ;(2)求证:BC 2=CE•CP ;(3)当AB=4且=时,求劣弧的长度.10、已知⊙O 的直径AB=2,弦AC 与弦BD 交于点E .且OD ⊥AC ,垂足为点F .(1)如图1,如果AC=BD ,求弦AC 的长;(2)如图2,如果E 为弦BD 的中点,求∠ABD 的余切值;(3)联结BC 、CD 、DA ,如果BC 是⊙O 的内接正n 边形的一边,CD 是⊙O 的内接正(n +4)边形的一边,求△ACD 的面积.11、如图,AB 为O 的直径,四边形ABCD 内接于O ,对角线AC ,BD 交于点E ,O 的切线AF 交BD 的延长线于点F ,切点为A ,且CAD ABD ∠=∠.(1)求证:AD CD =;(2)若4AB =,5BF =,求sin BDC ∠的值.12、如图,AB 为⊙O 的直径,C 、D 为⊙O 上的两个点,AĈ=CD ̂=DB ̂,连接AD ,过点D 作DE ⊥AC 交AC 的延长线于点E .(1)求证:DE 是⊙O 的切线.(2)若直径AB =6,求AD 的长.13、如图,在△ABC 中,O 为AC 上一点,以O 为圆心,OC 长为半径作圆,与BC 相切于点C ,过点A 作AD ⊥BO 交BO 的延长线于点D ,且∠AOD =∠BAD .(1)求证:AB 为⊙O 的切线;(2)若BC =6,tan ∠ABC =43 ,求AD 的长.14、如图,⊙O 是△ABC 的外接圆,点O 在BC 边上,∠BAC 的平分线交⊙O 于点D ,连接BD 、CD ,过点D 作BC 的平行线与AC 的延长线相交于点P .(1)求证:PD 是⊙O 的切线;(2)求证:△ABD ∽△DCP ;(3)当AB=5cm ,AC=12cm 时,求线段PC 的长.C B15、如图,AB 为⊙O 的直径,且AB=4,点C 在半圆上,OC ⊥AB ,垂足为点O ,P 为半圆上任意一点,过P 点作PE ⊥OC 于点E ,设△OPE 的内心为M ,连接OM 、PM .(1)求∠OMP 的度数;(2)当点P 在半圆上从点B 运动到点A 时,求内心M 所经过的路径长.16、如图,AB 是半圆O 的直径,C 是AB 延长线上的点,AC 的垂直平分线交半圆于点D ,交AC 于点E ,连接DA ,DC .已知半圆O 的半径为3,BC=2.(1)求AD 的长.(2)点P 是线段AC 上一动点,连接DP ,作∠DPF=∠DAC ,PF 交线段CD 于点F .当△DPF 为等腰三角形时,求AP 的长.17、如图所示:O 与ABC 的边BC 相切于点C ,与AC 、AB 分别交于点D 、E ,//DE OB .DC 是O 的直径.连接OE ,过C 作//CG OE 交O 于G ,连接DG 、EC ,DG 与EC 交于点F .(1)求证:直线AB与O相切;(2)求证:AE ED AC EF⋅=⋅;(3)若13,tan2EF ACE=∠=时,过A作//AN CE交O于M、N两点(M在线段AN上),求AN的长.18、如图1,⊙I与直线a相离,过圆心I作直线a的垂线,垂足为H,且交⊙I 于P、Q两点(Q在P、H之间).我们把点P称为⊙I关于直线a的“远点”,把PQ PH⋅的值称为⊙I关于直线a的“特征数”.(1)如图2,在平面直角坐标系xOy中,点E的坐标为()0,4,半径为1的⊙O 与两坐标轴交于点A、B、C、D.⊙过点E画垂直于y轴的直线m,则⊙O关于直线m的“远点”是点_________(填“A”、“B”、“C”或“D”),⊙O关于直线m的“特征数”为_________;⊙若直线n的函数表达式为4y=+,求O关于直线n的“特征数”;(2)在平面直角坐标系xOy 中,直线l 经过点()1,4M ,点F 是坐标平面内一点,以F ⊙F .若⊙F 与直线l 相离,点()1,0N -是⊙F 关于直线l 的“远点”,且⊙F 关于直线l 的“特征数”是l 的函数表达式.参考答案2021年中考数学第三轮压轴题冲刺专题复习:圆的综合 专项练习题1、如图,O 是ABC ∆的外接圆,其切线AE 与直径BD 的延长线相交于点E ,且AE AB =.(1)求ACB ∠的度数;(2)若2DE =,求O 的半径.解:(1)如图,连接OA .∵AE 是O 的切线,∴90OAE ∠=︒.又∵OB OA =,∴12∠=∠.∵AB AE =,∴1E ∠=∠,∴212AOE E ∠=∠=∠.又∵在Rt AOE ∆中,90AOE E ∠+∠=︒,∴390E ∠=︒.∴30E ∠=︒.∴120AOB ∠=︒.∴1602ACB AOB ∠=∠=︒. (2)设O 的半径为r ,在Rt OAE ∆中,∵30E ∠=︒,∴2OE OA =.∴2OD DE OA +=.∴22r r +=,∴2r =.∴O 的半径是2.2、如图,AB 是半圆O 的直径,C ,D 是半圆O 上不同于A ,B 的两点,AD BC =,AC 与BD 相交于点F .BE 是半圆O 所在圆的切线,与AC 的延长线相交于点E .(1)求证:CBA DAB ∆≅∆;(2)若BE BF =,求证:AC 平分DAB ∠.【解答】(1)证明:AB 是半圆O 的直径,90ACB ADB ∴∠=∠=︒,在Rt CBA ∆与Rt DAB ∆中,BC AD BA AB =⎧⎨=⎩, Rt CBA Rt DAB(HL)∴∆≅∆; (2)解:BE BF =,由(1)知BC EF ⊥,E BFE ∴∠=∠, BE 是半圆O 所在圆的切线,90ABE ∴∠=︒,90∴∠+∠=︒,E BAE由(1)知90∠=︒,D∴∠+∠=︒,DAF AFD90∠=∠,AFD BFE∴∠=∠,AFD E∠=︒-∠,BAF E∴∠=︒-∠,9090DAF AFD∴∠=∠,DAF BAF∴平分DABAC∠.3、如图,AG是∠HAF的平分线,点E在AF上,以AE为直径的⊙O交AG于点D,过点D作AH的垂线,垂足为点C,交AF于点B.(1)求证:直线BC是⊙O的切线;(2)若AC=2CD,设⊙O的半径为r,求BD的长度.【解答】(1)证明:连接OD,∵AG是∠HAF的平分线,∴∠CAD=∠BAD,∵OA=OD,∴∠OAD=∠ODA,∴∠CAD=∠ODA,∴OD∥AC,∵∠ACD=90°,∴∠ODB=∠ACD=90°,即OD⊥CB,∵D在⊙O上,∴直线BC是⊙O的切线;(4分)(2)解:在Rt△ACD中,设CD=a,则AC=2a,AD=a,连接DE,∵AE是⊙O的直径,∴∠ADE=90°,由∠CAD=∠BAD,∠ACD=∠ADE=90°,∴△ACD∽△ADE,∴,即,∴a=,由(1)知:OD∥AC,∴,即,∵a=,解得BD=r.(10分)4、如图,在Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,点O在AB 上,⊙O经过A、D两点,交AC于点E,交AB于点F.(1)求证:BC是⊙O的切线;(2)若⊙O的半径是2cm,E是的中点,求阴影部分的面积(结果保留π和根号)【解答】解:(1)连接OD.、∵OA=OD,∴∠OAD=∠ODA,∵∠OAD=∠DAC,∴∠ODA=∠DAC,∴OD∥AC,∴∠ODB=∠C=90°,∴OD⊥BC,∴BC是⊙O的切线.(2)连接OE,OE交AD于K.∵=,∴OE⊥AD,∵∠OAK=∠EAK,AK=AK,∠AKO=∠AKE=90°,∴△AKO≌△AKE,∴AO=AE=OE,∴△AOE是等边三角形,∴∠AOE=60°,∴S阴=S扇形OAE﹣S△AOE=﹣×22=﹣.5、如图,CE是⊙O的直径,BC切⊙O于点C,连接OB,作ED∥OB交⊙O于点D,BD的延长线与CE的延长线交于点A.(1)求证:AB是⊙O的切线;(2)若⊙O的半径为1,tan∠DEO=,tan∠A=,求AE的长.【解答】解:(1)连接OD,如图.∵ED∥OB,∴∠1=∠4,∠2=∠3,∵OD=OE,∴∠3=∠4,∴∠1=∠2.在△DOB与△COB中,,∴△DOB≌△COB,∴∠ODB=∠OCB,∵BC切⊙O于点C,∴∠OCB=90°,∴∠ODB=90°,∴AB是⊙O的切线;(2)∵∠DEO=∠2,∴tan∠DEO=tan∠2==,∵⊙O的半径为1,OC=1,∴BC=,tan∠A==,∴AC=4BC=4,∴AE=AC﹣CE=4﹣2.6、如图,点O是△ABC的边AB上一点,⊙O与边AC相切于点E,与边BC,AB 分别相交于点D,F,且DE=EF.(1)求证:∠C=90°;(2)当BC=3,sinA=时,求AF的长.【解答】解:(1)连接OE,BE,∵DE=EF,∴∴∠OBE=∠DBE∵OE=OB,∴∠OEB=∠OBE∴∠OEB=∠DBE,∴OE∥BC∵⊙O与边AC相切于点E,∴OE⊥AC∴BC⊥AC∴∠C=90°(2)在△ABC,∠C=90°,BC=3,sinA=∴AB=5,设⊙O的半径为r,则AO=5﹣r,在Rt△AOE中,sinA===∴r=∴AF=5﹣2×=7、如图,已知A、B是⊙O上两点,△OAB外角的平分线交⊙O于另一点C,CD ⊥AB交AB的延长线于D.(1)求证:CD是⊙O的切线;(2)E为的中点,F为⊙O上一点,EF交AB于G,若tan∠AFE=,BE=BG,EG=3,求⊙O的半径.【解答】(1)证明:连接OC,如图,∵BC平分∠OBD,∴∠OBD=∠CBD,∵OB=OC,∴∠OBC=∠OCB,∴∠OCB=∠CBD,∴OC∥AD,而CD⊥AB,∴OC⊥CD,∴CD 是⊙O 的切线;(2)解:连接OE 交AB 于H ,如图,∵E 为的中点,∴OE ⊥AB ,∵∠ABE=∠AFE ,∴tan ∠ABE=tan ∠AFE=,∴在Rt △BEH 中,tan ∠HBE==设EH=3x ,BH=4x ,∴BE=5x ,∵BG=BE=5x ,∴GH=x ,在Rt △EHG 中,x 2+(3x )2=(3)2,解得x=3, ∴EH=9,BH=12,设⊙O 的半径为r ,则OH=r ﹣9,在Rt △OHB 中,(r ﹣9)2+122=r 2,解得r=, 即⊙O 的半径为.8、如图,已知AB 是O 的直径,C 是O 上的一点,D 是AB 上的一点,DE AB ⊥于D ,DE 交BC 于F ,且EF EC =.(1)求证:EC 是O 的切线;(2)若4BD =,8BC =,圆的半径5OB =,求切线EC 的长.【解答】解:(1)连接OC,OC OB=,OBC OCB∴∠=∠,DE AB⊥,90OBC DFB∴∠+∠=︒,EF EC=,ECF EFC DFB∴∠=∠=∠,90OCB ECF∴∠+∠=︒,OC CE∴⊥,EC∴是O的切线;(2)AB是O的直径,90ACB∴∠=︒,5OB=,10AB∴=,6 AC∴==,cosBD BC ABCBF AB∠==,∴8410BF=,5BF∴=,3CF BC BF∴=-=,90ABC A∠+∠=︒,90ABC BFD∠+∠=︒,BFD A∴∠=∠,A BFD ECF EFC∴∠=∠=∠=∠,OA OC=,OCA A BFD ECF EFC∴∠=∠=∠=∠=∠,OAC ECF∴∆∆∽,∴EC CFOA AC=,53562 OA CFECAC⨯∴===.9、如图,AB是⊙O的直径,点E为线段OB上一点(不与O,B重合),作EC ⊥OB,交⊙O于点C,作直径CD,过点C的切线交DB的延长线于点P,作AF ⊥PC于点F,连接CB.(1)求证:AC平分∠FAB;(2)求证:BC2=CE•CP;(3)当AB=4且=时,求劣弧的长度.【解答】(1)证明:∵AB是直径,∴∠ACB=90°,∴∠BCP+∠ACF=90°,∠ACE+∠BCE=90°,∵∠BCP=∠BCE,∴∠ACF=∠ACE,(2)证明:∵OC=OB,∴∠OCB=∠OBC,∵PF是⊙O的切线,CE⊥AB,∴∠OCP=∠CEB=90°,∴∠PCB+∠OCB=90°,∠BCE+∠OBC=90°,∴∠BCE=∠BCP,∵CD是直径,∴∠CBD=∠CBP=90°,∴△CBE∽△CPB,∴=,∴BC2=CE•CP;(3)解:作BM⊥PF于M.则CE=CM=CF,设CE=CM=CF=3a,PC=4a,PM=a,∵∠MCB+∠P=90°,∠P+∠PBM=90°,∴∠MCB=∠PBM,∵CD是直径,BM⊥PC,∴∠CMB=∠BMP=90°,∴△BMC∽△PMB,∴=,∴BM2=CM•PM=3a2,∴BM=a,∴tan∠BCM==,∴∠BCM=30°,∴∠OCB=∠OBC=∠BOC=60°,∠BOD=120°∴的长==π.10、已知⊙O的直径AB=2,弦AC与弦BD交于点E.且OD⊥AC,垂足为点F.(1)如图1,如果AC=BD,求弦AC的长;(2)如图2,如果E为弦BD的中点,求∠ABD的余切值;(3)联结BC、CD、DA,如果BC是⊙O的内接正n边形的一边,CD是⊙O的内接正(n+4)边形的一边,求△ACD的面积.【解答】解:(1)∵OD⊥AC,∴=,∠AFO=90°,又∵AC=BD,∴=,即+=+,∴=,∴==,∴∠AOD=∠DOC=∠BOC=60°,∵AB=2,∴AO=BO=1,∴AF=AOsin∠AOF=1×=,则AC=2AF=;(2)如图1,连接BC,∵AB为直径,OD⊥AC,∴∠AFO=∠C=90°,∴OD∥BC,∴∠D=∠EBC,∵DE=BE、∠DEF=∠BEC,∴△DEF≌△BEC(ASA),∴BC=DF、EC=EF,又∵AO=OB,∴OF是△ABC的中位线,设OF=t,则BC=DF=2t,∵DF=DO﹣OF=1﹣t,∴1﹣t=2t,解得:t=,则DF=BC=、AC===,∴EF=FC=AC=,∵OB=OD,∴∠ABD=∠D,则cot∠ABD=cot∠D===;(3)如图2,∵BC是⊙O的内接正n边形的一边,CD是⊙O的内接正(n+4)边形的一边,∴∠BOC=、∠AOD=∠COD=,则+2×=180,解得:n=4,∴∠BOC=90°、∠AOD=∠COD=45°,∴BC=AC=,∵∠AFO=90°,∴OF=AOcos ∠AOF=, 则DF=OD ﹣OF=1﹣, ∴S △ACD =AC•DF=××(1﹣)=.11、如图,AB 为O 的直径,四边形ABCD 内接于O ,对角线AC ,BD 交于点E ,O 的切线AF 交BD 的延长线于点F ,切点为A ,且CAD ABD ∠=∠.(1)求证:AD CD =;(2)若4AB =,5BF =,求sin BDC ∠的值.【解答】解:(1)证明:CAD ABD ∠=∠,又ABD ACD ∠=∠,ACD CAD ∴∠=∠,AD CD ∴=;(2)AF 是O 的切线,90FAB ∴∠=︒, AB 是O 的直径,90ACB ADB ADF ∴∠=∠=∠=︒,90ABD BAD BAD FAD ∴∠+∠=∠+∠=︒,ABD FAD ∴∠=∠,ABD CAD ∠=∠,FAD EAD ∴∠=∠,AD AD =,()ADF ADE ASA ∴∆≅∆,AF AE ∴=,DF DE =,4AB =,5BF =,3AF ∴=,3AE AF ∴==,1122ABF S AB AF BF AD ∆==, ∴431255AB AF AD BF ⨯===,95DE ∴==, 725BE BF DE ∴=-=, AED BEC ∠=∠,90ADE BCE ∠=∠=︒,BEC AED ∴∆∆∽,∴BE BC AE AD =, ∴2825BE AD BC AE ==, ∴7sin 25BC BAC AB ∠==, BDC BAC ∠=∠,∴7sin 25BDC ∠=.12、如图,AB 为⊙O 的直径,C 、D 为⊙O 上的两个点,AĈ=CD ̂=DB ̂,连接AD ,过点D 作DE ⊥AC 交AC 的延长线于点E .(1)求证:DE 是⊙O 的切线.(2)若直径AB =6,求AD 的长.【解答】(1)证明:连接OD,̂=CD̂=DB̂,∵AC×180°=60°,∴∠BOD=13̂=DB̂,∵CD∠BOD=30°,∴∠EAD=∠DAB=12∵OA=OD,∴∠ADO=∠DAB=30°,∵DE⊥AC,∴∠E=90°,∴∠EAD+∠EDA=90°,∴∠EDA=60°,∴∠EDO=∠EDA+∠ADO=90°,∴OD⊥DE,∴DE是⊙O的切线;(2)解:连接BD,∵AB为⊙O的直径,∴∠ADB=90°,∵∠DAB=30°,AB=6,AB=3,∴BD=12∴AD=√62−32=3√3.13、如图,在△ABC中,O为AC上一点,以O为圆心,OC长为半径作圆,与BC相切于点C,过点A作AD⊥BO交BO的延长线于点D,且∠AOD=∠BAD.(1)求证:AB为⊙O的切线;(2)若BC=6,tan∠ABC=43,求AD的长.【解析】(1)作OE⊙AB于点E∵⊙O切BC于点C∴OC⊙BC ⊙ACB=90°∵ AD⊙BD ∴⊙D=90°∴⊙ABD+⊙BAD =90°⊙CBD+⊙BOC=90°∵⊙BOC=⊙AOD ⊙AOD=⊙BAD∴⊙BOC=⊙BAD∴⊙ABD=⊙CBD在⊙OBC和⊙OBE中{∠OEA=∠OCB ∠ABD=∠CBD OB=OB∴△OBC⊙⊙OBE∴OE=OC ∴OE是⊙O的半径. ∵OE⊙AB ∴AB为⊙O的切线.(2)∵tan⊙ABC=ACBC =43,BC=6B⊙AC=8 ⊙AB=√62+82=10∵BE=BC=6 ⊙AE=4∵⊙AOE=⊙ABC ⊙tan⊙AOE=AEEO =43⊙EO=3∴AO=5 OC=3 ⊙BO=√62+32=3√5在△AOD和△BOC中{∠AOD=∠BOC∠ADOE=∠BCO∴△AOD⊙△BOC ∴AOBO =ADBC即3√5=AD6∴AD=2√514、如图,⊙O是△ABC的外接圆,点O在BC边上,∠BAC的平分线交⊙O于点D,连接BD、CD,过点D作BC的平行线与AC的延长线相交于点P.(1)求证:PD是⊙O的切线;(2)求证:△ABD∽△DCP;(3)当AB=5cm,AC=12cm时,求线段PC的长.【解答】解:(1)如图,连接OD,∵BC是⊙O的直径,∴∠BAC=90°,∵AD平分∠BAC,∴∠BAC=2∠BAD,∵∠BOD=2∠BAD,∴∠BOD=∠BAC=90°,∵DP∥BC,∴∠ODP=∠BOD=90°,∴PD⊥OD,∵OD是⊙O半径,∴PD是⊙O的切线;(2)∵PD∥BC,∴∠ACB=∠P,∵∠ACB=∠ADB,∴∠ADB=∠P,∵∠ABD+∠ACD=180°,∠ACD+∠DCP=180°,∴∠DCP=∠ABD,∴△ABD∽△DCP,(3)∵BC是⊙O的直径,∴∠BDC=∠BAC=90°,在Rt△ABC中,BC==13cm,∵AD平分∠BAC,∴∠BAD=∠CAD,∴∠BOD=∠COD,∴BD=CD,在Rt△BCD中,BD2+CD2=BC2,∴BC=CD=BC=,∵△ABD∽△DCP,∴,∴,∴CP=16.9cm.15、如图,AB为⊙O的直径,且AB=4,点C在半圆上,OC⊥AB,垂足为点O,P为半圆上任意一点,过P点作PE⊥OC于点E,设△OPE的内心为M,连接OM、PM.(1)求∠OMP的度数;(2)当点P在半圆上从点B运动到点A时,求内心M所经过的路径长.【解答】解:(1)∵△OPE的内心为M,∴∠MOP=∠MOC,∠MPO=∠MPE,∴∠PMO=180°﹣∠MPO﹣∠MOP=180°﹣(∠EOP+∠OPE),∵PE⊥OC,即∠PEO=90°,∴∠PMO=180°﹣(∠EOP+∠OPE)=180°﹣(180°﹣90°)=135°,(2)如图,∵OP=OC,OM=OM,而∠MOP=∠MOC,∴△OPM≌△OCM,∴∠CMO=∠PMO=135°,所以点M在以OC为弦,并且所对的圆周角为135°的两段劣弧上(和);点M在扇形BOC内时,过C、M、O三点作⊙O′,连O′C,O′O,在优弧CO取点D,连DA,DO,∵∠CMO=135°,∴∠CDO=180°﹣135°=45°,∴∠CO′O=90°,而OA=4cm,∴O′O=OC=×4=2,∴弧OMC的长==π(cm),同理:点M在扇形AOC内时,同①的方法得,弧ONC的长为πcm,所以内心M所经过的路径长为2×π=2πcm.16、如图,AB是半圆O的直径,C是AB延长线上的点,AC的垂直平分线交半圆于点D,交AC于点E,连接DA,DC.已知半圆O的半径为3,BC=2.(1)求AD的长.(2)点P是线段AC上一动点,连接DP,作∠DPF=∠DAC,PF交线段CD于点F.当△DPF为等腰三角形时,求AP的长.【解答】解:(1)如图1,连接OD,∵OA=OD=3,BC=2,∴AC=8,∵DE是AC的垂直平分线,∴AE=AC=4,∴OE=AE﹣OA=1,在Rt△ODE中,DE==2;在Rt△ADE中,AD==2;(2)当DP=DF 时,如图2,点P 与A 重合,F 与C 重合,则AP=0;当DP=PF 时,如图4,∴∠CDP=∠PFD ,∵DE 是AC 的垂直平分线,∠DPF=∠DAC ,∴∠DPF=∠C ,∵∠PDF=∠CDP ,∴△PDF ∽△CDP ,∴∠DFP=∠DPC ,∴∠CDP=∠CPD ,∴CP=CD ,∴AP=AC ﹣CP=AC ﹣CD=AC ﹣AD=8﹣2;当PF=DF 时,如图3,∴∠FDP=∠FPD ,∵∠DPF=∠DAC=∠C ,∴△DAC ∽△PDC ,∴, ∴, ∴AP=5,即:当△DPF 是等腰三角形时,AP 的长为0或5或8﹣2.17、如图所示:O 与ABC 的边BC 相切于点C ,与AC 、AB 分别交于点D 、E ,//DE OB .DC 是O 的直径.连接OE ,过C 作//CG OE 交O 于G ,连接DG 、EC,DG与EC交于点F.(1)求证:直线AB与O相切;(2)求证:AE ED AC EF⋅=⋅;(3)若13,tan2EF ACE=∠=时,过A作//AN CE交O于M、N两点(M在线段AN上),求AN的长.【详解】(1)⊙DE//OB,⊙⊙BOC=⊙EDC,⊙CG//OE,⊙⊙DEO=⊙BOE,又⊙⊙DEO=⊙EDC,⊙⊙DEO=⊙BOE,由题意得:EO=CO,BO=BO,⊙⊙BOE⊙⊙BOC(SAS),⊙⊙BEO=⊙BCO=90°,⊙AB是⊙O的切线.(2)如图所示DG与OE交点作为H点,⊙EO//GC,⊙⊙EHD=⊙DGC=90°,又由(1)所知⊙AEO=90°,⊙AE//DF,⊙⊙AEC⊙⊙DFC, ⊙AE DF AC DC=, 由圆周角定理可知⊙EDG=⊙ECG,⊙EOD=2⊙ECD,⊙DO//GC,⊙⊙EOD=⊙GCD=⊙GCE+⊙ECD,⊙⊙ECD=⊙GCE=⊙EDF,又⊙⊙FED=⊙DEC,⊙⊙FED⊙⊙DEC, ⊙DF EF DC ED=, ⊙AE EF AC ED=,即AE ED AC EF ⋅=⋅. (3)⊙13,tan 2EF ACE =∠=,与⊙ACE 相等角的tan 值都相同. ⊙ED=6,则EC=12,根据勾股定理可得CD ===⊙EO=DO=CO=由(2)可得12AE EF AC ED ==, 在Rt⊙AEO 中,可得222AO AE EO =+,即()222AC OC AE EO -=+,⊙((2222AE AE -=+,解得AE=则AC=连接ON,延长BO 交MN 于点I,根据垂径定理可知OI⊙MN,⊙AN//CE,⊙⊙CAN=⊙ACE .在Rt⊙AIO 中,可得222AO AI IO =+,即(()2222OI OI =+, 解得OI=5,则AI=10,在Rt⊙OIN 中, 222ON IN IO =+,即(2225IN =+,解得IN=⊙AN=AI+IN=10+18、如图1,⊙I 与直线a 相离,过圆心I 作直线a 的垂线,垂足为H ,且交⊙I于P 、Q 两点(Q 在P 、H 之间).我们把点P 称为⊙I 关于直线a 的“远点”,把PQ PH ⋅的值称为⊙I 关于直线a 的“特征数”.(1)如图2,在平面直角坐标系xOy 中,点E 的坐标为()0,4,半径为1的⊙O 与两坐标轴交于点A 、B 、C 、D .⊙过点E 画垂直于y 轴的直线m ,则⊙O 关于直线m 的“远点”是点_________(填“A ”、“B ”、“C ”或“D ”),⊙O 关于直线m 的“特征数”为_________;⊙若直线n 的函数表达式为4y =+,求O 关于直线n 的“特征数”;(2)在平面直角坐标系xOy 中,直线l 经过点()1,4M ,点F 是坐标平面内一点,以F ⊙F .若⊙F 与直线l 相离,点()1,0N -是⊙F 关于直线l 的“远点”,且⊙F 关于直线l 的“特征数”是l 的函数表达式.【详解】解:(1)⊙⊙O 关于直线m 的“远点”是点D ,⊙O 关于直线m 的“特征数”为DB·DE=2×5=10;⊙如下图:过圆心O 作OH⊙直线n ,垂足为点H ,交⊙O 于点P 、Q ,⊙直线n 的函数表达式为4y =+,当x=0时,y=4;当y=0时,x=3-,⊙直线n 经过点E (0,4),点F (3-,0),在Rt⊙EOF 中,⊙tan⊙FEO=FO EO =34=3, ⊙⊙FEO=30°,⊙⊙EFO=60°,Rt⊙HOF 中,⊙sin⊙HFO=HO FO, ⊙HO= sin⊙HFO·FO=2,⊙PH=HO+OP=3,⊙PQ·PH=2×3=6,⊙⊙O 关于直线n 的“特征数”为6;(2)如下图,⊙点F 是圆心,点()1,0N -是“远点”,⊙连接NF 并延长,则直线NF⊙直线l ,设NF 与直线l 的交点为点A (m ,n ),设直线l 的解析式为y=kx+b 1(k≠0),将点()1,4M 与A (m ,n )代入y=kx+b 1中,114=k b n mk b +⎧⎨=+⎩①② ⊙-⊙得:n -4=mk -k ,⊙又⊙直线NF⊙直线l ,⊙设直线NF 的解析式为y=1k-x+b 2(k≠0), 将点()1,0N -与A (m ,n )代入y=1k -x+b 2中, 2210=b k m n b k ⎧+⎪⎪⎨⎪=-+⎪⎩④⑤ ⊙-⊙得:-n=1k +m k,⊙ 联立方程⊙与方程⊙,得:41n mk k m n k k -=-⎧⎪⎨-=+⎪⎩解得:222411421k k m k k n k ⎧--=⎪⎪+⎨-⎪=⎪+⎩, ⊙点A 的坐标为(22411k k k --+,2421k k -+); 又⊙⊙F 关于直线l 的“特征数”是⊙F⊙NB·NA=即解得:,⊙[m -(-1)]2+(n -0)2)2, 即(m+1)2+n 2=10, 把222411421k k m k kn k ⎧--=⎪⎪+⎨-⎪=⎪+⎩代入,解得k=-3或k=13; 当k=-3时,m=2,n=1, ⊙点A 的坐标为(2,1),把点A (2,1)与点()1,4M 代入y=kx+b 1中,解得直线l 的解析式为y=-3x+7;当k=13时,m=-2,n=3, ⊙点A 的坐标为(-2,3),把点A (-2,3)与点()1,4M 代入y=kx+b 1中,解得直线l 的解析式为y=13x+113. ⊙直线l 的解析式为y=-3x+7或y=13x+113.。
2018年中考数学选择填空压轴题专题3函数的几何综合问题

专题03函数的几何综合问题例1.如图,在平面直角坐标系中,直线 l : y= W3x — #与x 轴交于点B i ,以OB 为边长作等边三角 形A l OB |,过点A i 作A i B 2平行于x 轴,交直线l 于点B2 ,以A i B 2为边长作等边三角形 A 2A 1B 2,过点A 2 作A 2B 3平行于x 轴,交直线l 于点B 3 ,以A 2B 3为边长作等边三角形 A3A2B3 ,…,则点A 2017的横坐标同类题型1.1如图,直线l : y= x+1交y 轴-于点A i ,在x 轴正方向上取点B i ,使OB = OA ;过点B i 作A 2B i ,x 轴,交l 于点A 2 ,在x 轴正方向上取点B 2 ,使B i B 2=B 1A 2 ;过点 也彳^。
改,x 轴,交l 于点A 3 ,在 x 轴正方向上取点B 3 ,使B 2B3=E 2A 3 ;…记△ 0AB i 面积为S 1, △ B]A 2B 2面积为S 2 ,△ B 2A 3B 3面积为S3 ,…则S 2017等于 ( )同类题型1.2如图,已知直线| : y= W3 x,过点A (0, 1)作y 轴的垂线交直线l 于点B,过点B 作直 3 线l 的垂线交y 轴于点A 1 ;过点A 1作y 轴的垂线交直线l 于点B 1 ,过点B 1作直线l 的垂线交y 轴于点 A2 ;…;按此作法继续下去,则点 A 4的坐标为( )A. (0, 128)B. (0, 256)C. (0, 512)D. (0, 1024)八 c4030 A. 24031B. 2C. 240324033D. 2同类题型1.3如图,在平面直角坐标系中,直线 l : y= g 3 x+1交x 轴于点B,交y 轴于点A,过点A 作AB1 LAB 交x 轴于点M ,过点'彳^B1A 1,x 轴交直线l 于点A 2…依次作下去,则点 牛 的横坐标为例2.高速公路上依次有 3个标志点A 、R C,甲、乙两车分别从 A C 两点同时出发,匀速行驶,甲车从-B-C,乙车从 OB-A,甲、乙两车离 B 的距离y 1、V2 (千米)与行驶时间 x (小时)之间的函数关 系图象如图所示.观察图象,给出下列结论:① A C 之间的路程为690千米;②乙车比甲车每小时快30千米;③4.5小时两车相遇;④点 E 的坐标为(7, 180),「其中正确的有 号都填在横线上).2「千羽450同类题型2.1甲、乙两辆汽车沿同一路线从 A 地前往B 地,甲车以a 千米/时的速度匀速行驶,途中出现 故障后停车维修,修好后以 2a 千米/时的速度继续行驶;乙车在甲车出发 2小时后匀速前往 B 地,比甲车 早30分钟到达.到达 B 地后,乙车按原速度返回 A 地,甲车以2a 千米/时的速度返回 A 地.设甲、乙两 车与A 地相距s (千米),甲车离开 A 地的时间为t (小时),s 与t 之间的函数图象如图所示.下列说法:①a=40;②甲车维修所用时间为 1小时;③两车在途中第二次相遇时 相距40千米,其中不正确的个数为一…一、- 7 . 一、,(1) a=40, n^ 1; (2)乙的速度是 80km/h ; (3)甲比乙迟-h 到达B 地;240t 的值为5.25 ;④当t = 3时,两车 ( ) C. 2个D. 3个甲车比乙车早行驶 2h,并且甲车的函数图象.则下列结论:(把所有正确结论的序并以各自的速度匀速行驶, y (km)与时间x (h)50km.正确的个数是C. 3D. 4同类题型2.3甲、乙两人从科技馆出发, 沿相同的路线分别以不同的速度匀速跑向极地馆, 程后,乙开始出发,当乙超出甲 150米时,乙停在此地等候甲,两人相遇后乙又继续以原来的速度跑向极1例3.如图,已知动点P 在函数y= — (x>0)的图象上运动,PML x 轴于点 MPN! y 轴于点N,线段2xPM PN 分别与直线 AB : y=—x+ 1交于点E, F,则AF. BE 的值为6,,点D 在AB 的右侧,△ OA 丽△BCDTB 是等腰直角三角形,/ OAB= / BCD= 90 ,若函数y= - (x>0)的 x甲先跑一段路 地馆.如图是甲、乙两人在跑步的全过程中经过的路程下列四种说法:①甲的速度为 1.5米/秒;②a=750; 相遇时乙跑了 375米.其中正确的个数是 y (米)与甲出发的时间 x (秒)的函数图象.则 ③乙在途中等候甲 100秒;④乙出发后第一次与甲 疝眯900C.D.「4 个A. 4B. 2C. 1同类题型3.1如图,,一 一 一一 3 ,,一 ,,,, ,」在反比例函数y=法的图象上有一动点A,连接 AO 并延长交图象的另一支于点 B,在第二象限内有一点 C,满足AC= BC 当点A 运动时,点C 始终在函数 k ....... ................... y=x 的图象上运动,若tan/CABC. — 9D. — 12A 在x 轴的正半轴上,点B 在第一象限,点C 在线段AB 上,A. 1个B. 2个150A=2,则k 的值为同类题型3.2如图,在平面直角坐标系中,点一 6图象经过点 D,则^ OABW △ BCD 勺面积之差为( A. 12 B . 6 C. 3 D . 2一 .一 ................. .. ................ ......................... . . 1 一 9同类题型3.3如图,在平面直角坐标系 xOy 中,已知直线y = kx (k>0)分别交反比例函数y= -和丫= - x x在第一象限的图象于点 A, B,过点B 作BDLx 轴于点D,交y=1的图象于点C,连结AC.若△ABB 等x例4.如图,一次函,数y = x+b 的图象与反比例函数y= k 的图象交于点 A (3, 6)与点B,且与 x.... ___ k ............. ................................... ...............................................点C,右点P 是反比例函数y= -图象上的一个动点,作直线 AP 与x 轴、y 轴分别交于点 M N,x2同类题型4.2方程x 2 +3x —1 = 0的根可视为函数y=x+3的图象与函数....... 一 .、一一 2 .......... ............ ........ ....那么用此方法可推断出方程 x 2 +2x- 1=0的实数根x o 所在的范围是( )2 2例5.在平面直角坐标系 xOy 中,抛物线y= —x +2mx- m - 1父y 轴于点为A,顶点为D,对称轴与 x 轴交于点H.当抛物线顶点 D 在第二象限时,如果/ ADH / AHO 则m=.y 轴交于连结BNA. b> 2 2 , 9B. bv 2C. b<3D. 2 V2<b<1 . ................... ...... y=;的图象交点的横坐标,A. - 1<x 0 <0B. 0<xo <1C. 1<xo <2D. 2<xo <3A取值范围为AP1 ,点在函数y= x 的图象下万,同类题型5.1已知抛物线y= 4x 2 +1具有如下性质:该抛物线上任意一点到定点 F (0, 2)的距离与到12x 轴的距离始终相等,如图,点M 的坐标为(木,3), P 是抛物线丫= 4x 2 +1上一个动点,则4 PMF周长的最小值是()A. 3B. 4C. 5D. 6同类题型5.2抛物线y=ax2+bx+3 (aw0)经过点A(—1, 0), B( 2 , 0),且与y 轴相交于点C.设点D 是所求抛物线第一象限上一点,且在对称轴的右侧,点AOCf 似时,求点 D 的坐标.同类题型5.3小明家的洗手盆上装有一种抬启式水龙头(如图 1),完全开启后,水流路线呈抛物线,把手端点A,出水口 B 和落水点C 恰好在同一直线上,点 A 至出水管BD 的距离为12cm,洗手盆及水龙头的相 关数据如图2所示,现用高10.2cm 的圆柱型水杯去接水,若水流所在抛物线经过点 D 和杯子上底面中心 E, 则点E 到洗手盆内侧的距离 EH 为 cm.E 在线段 AC 上,且 DEL AG 当△ DCE^A图1图2参考答案例1 .如图,在平面直角坐标系中,直线l :y= W3x—率与x轴交于点B i ,以OB为边长作等边三角形々0耳,过点A1作A1B2平行于x轴,交直线l于点B2 ,以A1B2为边长作等边三角形A2A l B2,过点为作A2B3平行于x轴,交直线l于点B3 ,以A2B3为边长作等边三角形A3A2B3 ,…,则点A2017的横坐标是.Bi ,可得Bi (1, 0), D (0,—・•.OB =1, / OB D= 30 ,1一1如图所不,过A1作A1Al OB于A,则OA= 2。
2021年九级中考数学压轴题 –几何综合问题(圆的专题)(三)

2021年九级中考数学压轴题满分训练–几何综合问题(圆的专题)(三)1.如图所示,AC与⊙O相切于点C,线段AO交⊙O于点B.过点B作BD∥AC交⊙O 于点D,连接CD、OC,且OC交DB于点E.若∠CDB=30°,DB=4cm.(1)求⊙O的半径长;(2)求由弦CD、BD与弧BC所围成的阴影部分的面积.(结果保留π)2.如图,△ABC内接于⊙O,且AB为⊙O的直径,OE⊥AB交AC于点E,在OE的延长线上取点D,使得DE=DC.(1)求证:CD是⊙O的切线;(2)若AC=2,BC=,求CD的长.3.如图,四边形ABCD内接于⊙O,BC为⊙O的直径,⊙O的切线AP与CB的延长线交于点P.(1)求证:∠PAB=∠ACB;(2)若AB=12,cos∠ADB=,求PB的长.4.如图,△ABC内接于⊙O,AH⊥BC于点H,若AC=24,AH=18,⊙O的半径OC =13,过点O作OD⊥AC于点D.(1)求证:∠B=∠COD;(2)求AB的长.5.如图,AB是⊙O的直径,AE是弦,C是弧AE的中点,过点C作⊙O的切线交BA 的延长线于点G,过点C作CD⊥AB于点D,交AE于点F.(1)求证:GC∥AE;(2)若sin∠EAB=,OD=3,求AE的长.6.如图,AD与⊙O相切于点D,点A在直径CB的延长线上.(1)求证:∠DCB=∠ADB;(2)若∠DCB=30°,AC=3,求AD的长.7.如图1,在⊙O中,弦AB⊥弦CD,垂足为点E,连接AD、BC、AO,AD=AB.(1)求证:∠CAO=2∠CDB;(2)如图2,过点O作OH⊥AD,垂足为点H,求证:2OH+CE=DE;(3)如图3,在(2)的条件下,延长DB、AC交于点F,过点D作DM⊥AC,垂足为M交AB于N,若BC=12,AF=3BF,求MN的长.8.如图,在△ABC中,∠ABC=90°,AB=8,BC=6.以BC为直径的⊙O交AC于D,E是AB的中点,连接ED并延长交BC的延长线于点F.(1)求证:DE是⊙O的切线;(2)求DB的长.9.如图,在Rt△ABC中,∠ACB=90°,AB=10,AC=6,点D为BC边上的一个动点,以CD为直径的⊙O交AD于点E,过点C作CF∥AB,交⊙O于点F,连接CE、CF、EF.(1)当∠CFE=45°时,求CD的长;(2)求证:∠BAC=∠CEF;(3)是否存在点D,使得△CFE是以EF为腰的等腰三角形,若存在,求出此时CD 的长;若不存在,试说明理由.10.直线l与⊙O相离,OB⊥l于点B,且OB=5,OB与⊙O交于点P,A为圆上一点,AP的延长线交直线l于点C,且AB=BC.(1)求证:AB是⊙O的切线;(2)若⊙O的半径为3,求线段AP的长.11.如图,已知直线l与⊙O无公共点,OA⊥l于点A,交⊙O于点P,点B是⊙O上一点,连接BP并延长交直线l于点C,使得AB=AC.(1)求证:AB是⊙O的切线;(2)若BP=2,sin∠ACB=,求AB的长.12.如图,在△ABC中,AB=AC.以AB为直径的⊙O分别与BC、AC相交于点D、E,连接AD.过点D作DF⊥AC,垂足为点F,(1)求证:DF是⊙O的切线;(2)若⊙O的半径为4,∠CDF=22.5°,求图中阴影部分的面积.13.如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交BC于点D,交CA的延长线于点E,过点D作DH⊥AC,垂足为点H,连接DE,交AB于点F.(1)求证:DH是⊙O的切线;(2)若⊙O的半径为4,①当AE=FE时,求的长(结果保留π);②当时,求线段AF的长.14.如图,AB是⊙O的直径,点C和点D分别在AB和⊙O上,且AC=AD,DC的延长线交⊙O于点E,过E作AC的平行线交⊙O于点F,连接AF,DF.(1)求证:四边形ACEF是平行四边形;(2)当sin∠EDF=,BC=4时,求⊙O的半径.15.如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D 作DE⊥AC,分别交AC、AB的延长线于点E,F.(1)求证:EF是⊙O的切线;(2)若AC=6,CE=2,求CB的长.参考答案1.解:(1)∵AC与⊙O相切于点C,∴∠ACO=90°.∵BD∥AC,∴∠BEO=∠ACO=90°,∴DE=EB=BD==2(cm)∵∠D=30°,∴∠O=2∠D=60°,在Rt△BEO中,sin60°=,=.∴OB=5,即⊙O的半径长为5cm.(2)由(1)可知,∠O=60°,∠BEO=90°,∴∠EBO=∠D=30°.在△CDE与△OBE中,.∴△CDE≌△OBE(AAS).∴S阴影=S扇OBC=π•42=(cm2),答:阴影部分的面积为cm2.2.(1)证明:连接OC,如图1,∵DC=DE,∴∠DCE=∠DEC,∵∠DEC=∠AEO,∴∠DCE=∠AEO,∵OA⊥OE,∴∠A+∠AEO=90°,∴∠DCE+∠A=90°,∵OA=OC,∴∠A=∠ACO,∴∠DCE+∠ACO=90°,∴OC⊥DC,∴CD是⊙O的切线;(2)如图2,过点D作DF⊥CE于点F,∵AC=2,BC=,∴AB===5,∵AB为⊙O的直径,∴∠ACB=90°,∴∠ACB=∠AOE,又∵∠A=∠A,∴△AOE∽△ACB,∴,∴,∴AE=,∴CE=AC﹣AE=2﹣=,∵CD=DE,∴CF=CE=,∠DEC=∠DCE,∵∠DEC=∠AEO,∠AEO=∠B,∴∠DCE=∠B,又∵∠DFC=∠ACB,∴△DFC∽△ACB,∴,∴,∴DC=.3.解:(1)证明:如图,连接OA,∵AP为⊙O的切线,∴OA⊥AP,∴∠OAP=90°,∴∠OAB+∠PAB=90°,∵OA=OB,∴∠OAB=∠OBA,∴∠OBA+∠PAB=90°,∵BC为⊙O的直径,∴∠ACB+∠OBA=90°,∴∠PAB=∠ACB;(2)由(1)知∵∠PAB=∠ACB,且∠ADB=∠ACB,∴∠PAB=∠ACB=∠ADB,∴,∵AB=12,∴AC=16,∴,∴OB=10,过B作BF⊥AP于F,∵∠ADB=∠FAB,,∴,∴,∴在Rt△ABF中,,∵OA⊥AP,BF⊥AP,∴BF∥OA,∴△PBF∽△POA,∴,∴,∴.答:PB的长为.4.解:(1)作直径AE,连接CE,∴∠ACE=90°,∴∠CAE+∠E=90°,∵OA=OC,∴∠CAE=∠OCD,∴∠OCD+∠E=90°,∵OD⊥AC,∴∠OCD+∠COD=90°,∴∠COD=∠E,∵∠B=∠E,∴∠B=∠COD;(2)∵AH⊥BC,∴∠AHB=90°,∴∠ACE=∠AHB,∵∠B=∠E,∴△ABH∽△AEC,∴=,∴AB=,∵AC=24,AH=18,AE=2OC=26,∴AB==.5.(1)证明:连接OC,交AE于点H.∵C是弧AE的中点,∴OC⊥AE.∵GC是⊙O的切线,∴OC⊥GC,∴∠OHA=∠OCG=90°,∴GC∥AE;(2)解:∵OC⊥GC,GC∥AE,∴OC⊥AE,∵CD⊥AB,∴∠CHF=∠FDA=90°,∵∠CFH=∠AFD,∴∠OCD=∠EAB.∴.在Rt△CDO中,OD=3,∴OC=5,∴AB=10,连接BE,∵AB是⊙O的直径,∴∠AEB=90°.在Rt△AEB中,∵,∴BE=6,∴AE=8.6.(1)证明:如图,连接OD,∵AD与⊙O相切于点D,∴OD⊥AD,∴∠ODB+∠ADB=90°,∵CB是直径,∴∠CDB=90°,∴∠ODB+∠ODC=90°,∴∠ODC=∠ADB,∵OD=OC,∴∠ODC=∠OCD,∴∠C=∠ADB;(2)解:∵∠DCB=∠ADB,∠DAC=∠CAD,∴△ADB∽△ACD,∴=,∵CB是直径,∴∠CDB=90°,∠DCB=30°,∴tan∠DCB==,∴=,∵AC=3,∴AD=3.7.解:(1)如图,连接AO、DO,∵AB=AD,∴,∴∠AOB=∠AOD,∴AO=OB,AO=OD,∴△AOB≌△AOD,∴∠BAO=∠DAO,延长AO交BD于点H,∵AB=AD,∴AH⊥BD,∴∠AHB=∠AHD=90°,∵,∴∠ACD=∠ABD,∴∠CAB=∠BAO=∠OAD,∴∠CAO=2∠CDB.(2)过点O作OT⊥CD,则CT=DT,∵CD⊥AB,CD⊥OT,OQ⊥AB,∴∠OQB=∠OTE=∠AED=90°,∴四边形OTEQ为矩形,∴OQ=ET,∵TD=CT=ET+CE,∵AB=AD,∴OQ=OH,∴2OH+CE=DE.(3)如图,∵∠ACB+∠ADB=180°,∠FCB+∠ACB=180°,∴∠ADB=∠FCB,∵∠F=∠F,∴△FCB∽△FDA,∵CB=12,∴AB=AD=36,∵∠BCD=∠BAD,∠AEB=∠AED,∴△CEB∽△AED,∴,设BE=x,则AE=36﹣x,ED=3x,∵AB⊥CD,∴∠AED=90°,则在Rt△AED中,AE2+ED2=AD2,(36﹣x)2+(3x)2=362,解得:,∴BD=∵CD⊥AB,∴∠BED=90°,∠NMA=90°,∠ANM=∠END,∴∠NED=∠MAN,∴∠BDE=∠EDN,∵ED=ED,∴△BED≌△NED,∴,∵∠CDB=∠CAB,∠NMA=∠BED,∴△AMN∽△DEB,∴,∴,8.(1)证明:连接BD,DO,∵BC是⊙O的直径,∴∠ADB=90°.∴∠CDB=90°,又∵E为AB的中点,∴DE=EB=EA,∴∠EDB=∠EBD.∵OD=OB,∴∠ODB=∠OBD.∵∠ABC=90°,∴∠EDB+∠OBD=90°.即OD⊥DE.∴DE是⊙O的切线.(2)解:在Rt△ABC中,AB=8,BC=6,∴AC===10,∵,∴.9.解:(1)∵∠CFE=90°,∠CFE=∠CDE,∴∠CDE=45°,∵∠ACB=90°,∴∠DAC=45°,∴∠DAC=∠ADC,∴AC=CD=6;(2)证明:∵∠ACB=90°,∴∠BAC+∠B=90°,∵CF∥AB,∴∠B=∠FCB,又∵∠FCB=∠DEF,∴∠BAC+∠DEF=90°,∵CD为⊙O的直径,∴∠CED=90°,∴∠DEF+∠CEF=90°,∴∠BAC=∠CEF;(3)①如图1,当EF=CE时,则∠EFC=∠ECF,∵四边形CEDF为圆内接四边形,∴∠ADG=∠ECF,又∵∠CDE=∠CFE,∴∠ADG=∠CDE,∵CD为⊙O的直径,∴∠DFC=90°,∵FC∥AB,∴∠FGA=90°,∴∠FGA=∠ACD,∵AD=AD,∴△AGD≌△ACD(AAS),∴DG=CD,在Rt△BDG中,设CD=x,∵BG2+DG2=BD2,∴42+x2=(8﹣x)2,∴x=3,即CD=3;②如图2,当EF=CF时,则∠CEF=∠ECF,∵四边形CEDF为圆内接四边形,∴∠ADG=∠ECF,又∵∠CEF=∠CDF=∠BDG,∴∠ADG=∠BDG,∵FC∥AB,∠DFC=90°,∴∠FGA=90°,∴∠FGA=∠ACD,∵GD=GD,∴△BGD≌△AGD(ASA),∴BD=AD,在Rt△ACD中,设CD=x,∵CD2+AC2=AD2,∴x2+62=(8﹣x)2,∴x=,即CD=;综合以上可得CD的长为3或.10.证明:(1)连接OA,∵OA=OP,∴∠OPA=∠OAP=∠BPC,∵AB=BC,∴∠BAC=∠ACB,∵OB⊥l,∴∠ACB+∠BPC=90°,∴∠BAC+∠OAP=90°,即OA⊥AB,∴AB与⊙O相切;(2)解:如图,连接AO并延长交⊙O于D,连接PD,则∠APD=90°,∵OB=5,OP=3,∴PB=2,∴BC=AB==4,在Rt△PBC中,PC==2,∵∠DAP=∠CPB,∠APD=∠PBC=90°,∴△DAP∽△CPB,∴,即,解得,AP=.11.(1)证明:连接OB,如图1,∵AB=AC,∴∠ABC=∠ACB,∵OA⊥l,∴∠ACB+∠APC=90°,∵OB=OP,∴∠OBP=∠OPB,∵∠OPB=∠APC,∴∠OBP+∠ACB=90°,∴∠OBP+∠ABC=90°,即∠OBA=90°,∴OB⊥AB,∴AB是⊙O的切线;(2)解:作直径BD,连接PD,则∠BPD=90°,如图2,∵AB是⊙O的切线,∴∠ABC=∠D,∵∠ABC=∠ACB,∴∠D=∠ABC=∠ACB,∵sin∠ACB=,∴sin∠D==,∵BP=2,∴BD=10,∴OB=OP=5,∵sin∠ACB=,∴=,∴=,设PA=x,则AB=AC=2x,在Rt△AOB中,AB=2x,OB=5,OA=5+x,∴(2x)2+52=(5+x)2,解得x=,∴AB=2x=.12.(1)证明:连接AD.∵AB是⊙O的直径,∴∠ADB=90°,∴AD⊥BC.又AB=AC=13,BC=10,D是BC的中点,∴BD=5.连接OD;由中位线定理,知DO∥AC,又DF⊥AC,∴DF⊥OD.∴DF是⊙O的切线;(2)连接OE,∵DF⊥AC,∠CDF=22.5°,∴∠ABC=∠ACB=67.5°,∴∠BAC=45°,∵OA=OE,∴∠AOE=90°,∵⊙O的半径为4,∴S扇形AOE=4π,S△AOE=8∴S阴影=S扇形AOE﹣S△AOE=4π﹣8.13.证明:(1)连接OD,如图1,∵OB=OD,∴△ODB是等腰三角形,∠OBD=∠ODB①,在△ABC中,∵AB=AC,∴∠ABC=∠ACB②,由①②得:∠ODB=∠OBD=∠ACB,∴OD∥AC,∵DH⊥AC,∴DH⊥OD,∴DH是圆O的切线;(2)①∵AE=EF,∴∠EAF=∠EAF,设∠B=∠C=α,∴∠EAF=∠EFA=2α,∵∠E=∠B=α,∴α+2α+2α=180°,∴α=36°,∴∠B=36°,∴∠AOD=72°,∴的长==;②连接AD,∵AB为⊙O的直径,∴∠ADB=∠ADC=90°,∵⊙O的半径为4,∴AB=AC=8,∵,∴=,∴AD=2,∵AD⊥BC,DH⊥AC,∴△ADH∽△ACD,∴=,∴=,∴AH=3,∴CH=5,∵∠B=∠C,∠E=∠B,∴∠E=∠C,∴DE=DC,∵DH⊥AC,∴EH=CH=5,∴AE=2,∵OD∥AC,∴∠EAF=∠FOD,∠E=∠FDO,∴△AEF∽△ODF,∴=,∴=,∴AF=.14.(1)证明:∵AC=AD,∴∠ADC=∠ACD,∵AC∥EF,∴∠ACD=∠E,∴∠ADC=∠E,∴=,∴=,∴AD=EF,∵AD=AC,∴AC=EF,∵AC∥EF,∴四边形ACEF是平行四边形;(2)解:连接BD,∵四边形ACEF是平行四边形,∴AF∥CE,∴∠EDF=∠AFD,∵所对圆周角∠B和∠AFD,∴∠AFD=∠B,∴∠B=∠EDF,∵AB是⊙O的直径,∴∠ADB=90°,∵sin∠EDF=,∴sin B=sin∠EDF==,∴设AD=2x,AB=3x,∵AC=AD,BC=4,∴3x﹣2x=4,解得:x=4,即AB=3x=3×4=12,∵AB为⊙O的直径,∴⊙O的半径是6.15.(1)证明:连接OD交BC于H,如图所示:∵OA=OD,∴∠OAD=∠ODA,∵AD平分∠BAC,∴∠OAD=∠DAC,∴∠ODA=∠DAC,∴OD∥AE,∵DE⊥AC,∴OD⊥EF,∵OD是⊙O的半径,∴EF是⊙O的切线;(2)解:∵AB为⊙O的直径,∴∠ACB=90°,∴∠HCE=90°,又∵DE⊥AC,∴∠E=90°,由(1)得:OD⊥EF,∴∠HDE=90°,∴四边形CEDH是矩形,∴HD=CE=2,∴∠CHD=90°,∴∠OHB=90°,∴OD⊥BC,∴OH平分BC,∴OH是△ABC的中位线,∴OH=AC=3,∴OB=OD=OH+HD=5,∴AB=2OB=10,∴CB===8.。
2021年九年级中考数学第三轮压轴题冲刺:统计与概率的综合 专题复习练习(含答案)

2021年中考数学第三轮压轴题冲刺:统计与概率的综合专题复习练习1、某校“校园主持人大赛”结束后,将所有参赛选手的比赛成绩(得分均为整数)进行整理,并分别绘制成扇形统计图和频数直方图.部分信息如下:(1)本次比赛参赛选手共有人,扇形统计图中“79.5~89.5”这一范围的人数占总参赛人数的百分比为;(2)补全图2频数直方图;(3)赛前规定,成绩由高到低前40%的参赛选手获奖.某参赛选手的比赛成绩为88分,试判断他能否获奖,并说明理由;(4)成绩前四名是2名男生和2名女生,若从他们中任选2人作为该校文艺晚会的主持人,试求恰好选中1男1女为主持人的概率.2、为了解某校九年级学生的体质健康状况,随机抽取了该校九年级学生的10%进行测试,将这些学生的测试成绩()x分为四个等级:优秀85100x<;不及x<;及格6075x;良好7585格060x<,并绘制成如图两幅统计图.根据以上信息,解答下列问题:(1)在抽取的学生中不及格人数所占的百分比是;(2)计算所抽取学生测试成绩的平均分;(3)若不及格学生的人数为2人,请估算出该校九年级学生中优秀等级的人数.3、端午节是中国的传统节日.今年端午节前夕,遂宁市某食品厂抽样调查了河东某居民区市民对A、B、C、D四种不同口味粽子样品的喜爱情况,并将调查情况绘制成如图两幅不完整统计图:(1)本次参加抽样调查的居民有人.(2)喜欢C种口味粽子的人数所占圆心角为度.根据题中信息补全条形统计图.(3)若该居民小区有6000人,请你估计爱吃D种粽子的有人.(4)若有外型完全相同的A、B、C、D棕子各一个,煮熟后,小李吃了两个,请用列表或画树状图的方法求他第二个吃的粽子恰好是A种粽子的概率.4、某校对九年级学生进行一次综合文科中考模拟测试,成绩x分(x为整数)评定为优秀、良好、合格、不合格四个等级(优秀、良好、合格、不合格分别用A、B、C、D表示),A等级:90100x<,D等级:060x<.该校随机抽取了x<,C等级:6080x,B等级:8090一部分学生的成绩进行调查,并绘制成如图不完整的统计图表.请你根据统计图表提供的信息解答下列问题:(1)上表中的a,b=,m=.(2)本次调查共抽取了多少名学生?请补全条形图.(3)若从D等级的4名学生中抽取两名学生进行问卷调查,请用画树状图或列表的方法求抽取的两名学生恰好是一男一女的概率.5、某校为了响应市政府号召,在“创文创卫”活动周中,设置了“A:文明礼仪;B:环境保护;C;卫生保洁;D:垃圾分类”四个主题,每个学生选一个主题参与;为了解活动开展情况,学校随机抽取了部分学生进行调查,并根据调查结果绘制了如下条形统计图和扇形统计图.⑴.本次调查的学生人数是人,m= ;⑵.请补全条形统计图;⑶.学校要求每位同学从星期一至星期五选择两天参加活动,如果小张同学随机选择连续两天,其中有一天是星期一的概率是;小李同学星期五要参加市演讲比赛,他在其余四天中随机选择两天,其中一天是星期三的概率是.6、为了了解本校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,课题小组随机选取该校部分学生进行了问卷调査(问卷调査表如图1所示),并根据调查结果绘制了图2、图3两幅统计图(均不完整),请根据统计图解答下列问题.(1)本次接受问卷调查的学生有________名.(2)补全条形统计图.(3)扇形统计图中B类节目对应扇形的圆心角的度数为________.(4)该校共有2000名学生,根据调查结果估计该校最喜爱新闻节目的学生人数.7、某中学为了了解本校学生对排球、篮球、毽球、羽毛球和跳绳五项“大课间”活动的喜欢情况,随机抽查了部分学生进行问卷调查(每名学生只选择一项),将调查结果整理并绘制成如图所示不完整的统计图表.请结合统计图表解答下列问题:抽样调查学生喜欢大课间活动人数的统计表(1)本次抽样调查的学生有人,请补全条形统计图;(2)求扇形统计图中,喜欢毽球活动的学生人数所对应圆心角的度数;(3)全校有学生1800人,估计全校喜欢跳绳活动的学生人数是多少?8、我市某中学举行“法制进校园”知识竞赛,赛后将学生的成绩分为A、B、C、D四个等级,并将结果绘制成如图所示的条形统计图和扇形统计图.请你根据统计图解答下列问题.(1)成绩为“B等级”的学生人数有名;(2)在扇形统计图中,表示“D等级”的扇形的圆心角度数为,图中m的值为;(3)学校决定从本次比赛获得“A等级”的学生中选出2名去参加市中学生知识竞赛.已知“A等级”中有1名女生,请用列表或画树状图的方法求出女生被选中的概率.9、遵义市各校都在深入开展劳动教育,某校为了解七年级学生一学期参加课外劳动时间(单位:)h的情况,从该校七年级随机抽查了部分学生进行问卷调查,并将调查结果绘制成如下不完整的频数分布表和频数分布直方图.课外劳动时间频数分布表:020t<t<2040t<4060t<6080t<80100解答下列问题:(1)频数分布表中a=,m=;将频数分布直方图补充完整;(2)若七年级共有学生400人,试估计该校七年级学生一学期课外劳动时间不少于60h的人数;(3)已知课外劳动时间在6080<的男生人数为2人,其余为女生,现从该组中任选2人h t h代表学校参加“全市中学生劳动体验”演讲比赛,请用树状图或列表法求所选学生为1男1女的概率.10、每年6月26日是“国际禁毒日”.某中学为了让学生掌握禁毒知识,提高防毒意识,组织全校学生参加了“禁毒知识网络答题”活动.该校德育处对八年级全体学生答题成绩进行统计,将成绩分为四个等级:优秀、良好、一般、不合格;并绘制成如下不完整的统计图.请你根据图1、图2中所给的信息解答下列问题:(1)该校八年级共有_________名学生,“优秀”所占圆心角的度数为_________.(2)请将图1中的条形统计图补充完整.(3)已知该市共有15000名学生参加了这次“禁毒知识网络答题”活动,请以该校八年级学生答题成绩统计情况估计该市大约有多少名学生在这次答题中成绩不合格?(4)德育处从该校八年级答题成绩前四名甲、乙、丙、丁学生中随机抽取2名同学参加全市现场禁毒知识竞赛,请用树状图或列表法求出必有甲同学参加的概率.11、广元市某中学举行了“禁毒知识竞赛”,王老师将九年级(1)班学生成绩划分为A、B、C、D、E五个等级,并绘制了图1、图2两个不完整的统计图,请根据图中的信息解答下列问题:(1)求九年级(1)班共有多少名同学?(2)补全条形统计图,并计算扇形统计图中的“C”所对应的圆心角度数;(3)成绩为A类的5名同学中,有2名男生和3名女生;王老师想从这5名同学中任选2名同学进行交流,请用列表法或画树状图的方法求选取的2名同学都是女生的概率.12、为了丰富学生们的课余生活,学校准备开展第二课堂,有四类课程可供选择,分别是“A.书画类、B.文艺类、C.社会实践类、D.体育类”.现随机抽取了七年级部分学生对报名意向进行调查,并根据调查结果绘制了两幅不完整的统计图,请你根据图表信息回答下列问题:(1)本次被抽查的学生共有_____________名,扇形统计图中“A .书画类”所占扇形的圆心角的度数为___________度; (2)请你将条形统计图补全;(3)若该校七年级共有600名学生,请根据上述调查结果估计该校学生选择“C .社会实践类”的学生共有多少名?(4)本次调查中抽中了七(1)班王芳和小颖两名学生,请用列表法或画树状图法求她们选择同一个项目的概率.13、根据公安部交管局下发的通知,自2020年6月1日起,将在全国开展“一带一盔”安全守护行动,其中就要求骑行摩托车、电动车需要佩戴头盔.某日我市交警部门在某个十字路口共拦截了50名不带头盔的骑行者,根据年龄段和性别得到如下表的统计信息,根据表中信息回答下列问题:(1)统计表中m 的值为_______;(2)若要按照表格中各年龄段的人数来绘制扇形统计图,则年龄在“3040x ≤<”部分所对应扇形的圆心角的度数为_______;(3)在这50人中女性有______人;x<”的4人中随机抽取2人参加交通安全知识学习,请用列表或画树(4)若从年龄在“20状图的方法,求恰好抽到2名男性的概率.14、为了提高学生的综合素养,某校开设了五门手工活动课,按照类别分为:A“剪纸”、B “沙画”、C“葫芦雕刻”、D“泥塑”、E“插花”.为了了解学生对每种活动课的喜爱情况,随机抽取了部分同学进行调查,将调查结果绘制成如图两幅不完整的统计图.根据以上信息,回答下列问题:(1)本次调查的样本容量为;统计图中的a=,b=;(2)通过计算补全条形统计图;(3)该校共有2500名学生,请你估计全校喜爱“葫芦雕刻”的学生人数.15、为了丰富同学们的课余生活,冬威中学开展以“我最喜欢的课外活动小组”为主题的调查活动,围绕“在绘画、剪纸、舞蹈、书法四类活动小组中,你最喜欢哪一类?(必选且只选一类)”的问题,在全校范围内随机抽取部分学生进行问卷调查,将调查结果整理后绘制成如图所示的不完整的条形统计图,其中最喜欢绘画小组的学生人数占所调查人数的30%.请你根据图中提供的信息回答下列问题:(1)在这次调查中,一共抽取了多少名学生?(2)请通过计算补全条形统计图;(3)若冬威中学共有800名学生,请你估计该中学最喜欢剪纸小组的学生有多少名.16、“新冠病毒”疫情防控期间,我市积极开展“停课不停学”网络教学活动,了了解和指导学生有效进行网络学习,某校对学生每天在家网络学习时间进行了随机问卷调查(问卷调查表如图所示),并用调查结果绘制了图①,图②两幅统计图(均不完整),请根据统计图解答以下问题:(1)本次接受问卷调查的学生共有___________人;(2)请补全图①中的条形统计图;(3)图②中,D选项所对应的扇形圆心角为_________度;(4)若该校共有1500名学生,请你估计该校学生“停课不停学”期间平均每天利用网络学习时间在C选项的有多少人?17、为了解天水市民对全市创建全国文明城市工作的满意程度,某中学数学兴趣小组在某个小区内进行了调查统计.将调查结果分为不满意,一般,满意,非常满意四类,回收、整理好全部问卷后,得到下列不完整的统计图.请结合图中的信息,解决下列问题:(1)此次调查中接受调查的人数为__________人;(2)请你补全条形统计图;(3)扇形统计图中“满意”部分的圆心角为__________度;(4)该兴趣小组准备从调查结果为“不满意”的4位市民中随机选择2位进行回访,已知这4位市民中有2位男性,2位女性.请用画树状图的方法求出选择回访的市民为“一男一女”的概率.参考答案2021年中考数学第三轮压轴题冲刺:统计与概率的综合 专题复习练习1、某校“校园主持人大赛”结束后,将所有参赛选手的比赛成绩(得分均为整数)进行整理,并分别绘制成扇形统计图和频数直方图.部分信息如下:(1)本次比赛参赛选手共有 50 人,扇形统计图中“79.5~89.5”这一范围的人数占总参赛人数的百分比为 ; (2)补全图2频数直方图;(3)赛前规定,成绩由高到低前40%的参赛选手获奖.某参赛选手的比赛成绩为88分,试判断他能否获奖,并说明理由;(4)成绩前四名是2名男生和2名女生,若从他们中任选2人作为该校文艺晚会的主持人,试求恰好选中1男1女为主持人的概率.【解答】解:(1)本次比赛参赛选手共有:(84)24%50+÷=(人), “59.5~69.5”这一范围的人数占总参赛人数的百分比为23100%10%50+⨯=, 79.5~89.5∴”这一范围的人数占总参赛人数的百分比为100%24%10%30%36%---=;故答案为:50,36%;(2) “69.5~79.5”这一范围的人数为5030%15⨯=(人),∴ “69.5~74.5”这一范围的人数为1587-=(人),“79.5~89.5”这一范围的人数为5036%18⨯=(人),∴ “79.5~84.5”这一范围的人数为18810-=(人);补全图2频数直方图:(3)能获奖.理由如下:本次比赛参赛选手50人,∴成绩由高到低前40%的参赛选手人数为5040%20⨯=(人),又8884.5>,∴能获奖;(4)画树状图为:共有12种等可能的结果数,其中恰好选中1男1女的结果数为8,所以恰好选中1男1女的概率82==.1232、为了解某校九年级学生的体质健康状况,随机抽取了该校九年级学生的10%进行测试,将这些学生的测试成绩()x分为四个等级:优秀85100x<;不及x;良好7585x<;及格6075格060x<,并绘制成如图两幅统计图.根据以上信息,解答下列问题:(1)在抽取的学生中不及格人数所占的百分比是 5% ; (2)计算所抽取学生测试成绩的平均分;(3)若不及格学生的人数为2人,请估算出该校九年级学生中优秀等级的人数. 【解答】解:(1)在抽取的学生中不及格人数所占的百分比120%25%50%5%=---=, 故答案为5%.(2)所抽取学生测试成绩的平均分9050%7825%6620%425%79.81⨯+⨯+⨯+⨯==(分).(3)由题意总人数25%40=÷=(人),4050%20⨯=,2010%200÷=(人)答:该校九年级学生中优秀等级的人数约为200人.3、端午节是中国的传统节日.今年端午节前夕,遂宁市某食品厂抽样调查了河东某居民区市民对A 、B 、C 、D 四种不同口味粽子样品的喜爱情况,并将调查情况绘制成如图两幅不完整统计图:(1)本次参加抽样调查的居民有 600 人.(2)喜欢C 种口味粽子的人数所占圆心角为 度.根据题中信息补全条形统计图. (3)若该居民小区有6000人,请你估计爱吃D 种粽子的有 人.(4)若有外型完全相同的A 、B 、C 、D 棕子各一个,煮熟后,小李吃了两个,请用列表或画树状图的方法求他第二个吃的粽子恰好是A 种粽子的概率. 【解答】解:(1)24040%600÷=(人), 所以本次参加抽样调查的居民有60人;(2)喜欢B 种口味粽子的人数为60010%60⨯=(人),喜欢C种口味粽子的人数为60018060240120---=(人),所以喜欢C种口味粽子的人数所占圆心角的度数为12036072︒⨯=︒;600补全条形统计图为:(3)600040%2400⨯=,所以估计爱吃D种粽子的有2400人;故答案为600;72;2400;(4)画树状图为:共有12种等可能的结果数,其中他第二个吃的粽子恰好是A种粽子的结果数为3,所以他第二个吃的粽子恰好是A种粽子的概率31==.1244、某校对九年级学生进行一次综合文科中考模拟测试,成绩x分(x为整数)评定为优秀、良好、合格、不合格四个等级(优秀、良好、合格、不合格分别用A、B、C、D表示),A等级:90100x<.该校随机抽取了x<,D等级:060x,B等级:8090x<,C等级:6080一部分学生的成绩进行调查,并绘制成如图不完整的统计图表.请你根据统计图表提供的信息解答下列问题:(1)上表中的a8 ,b=,m=.(2)本次调查共抽取了多少名学生?请补全条形图.(3)若从D等级的4名学生中抽取两名学生进行问卷调查,请用画树状图或列表的方法求抽取的两名学生恰好是一男一女的概率.【解答】解:(1)1640%20%8a=÷⨯=,1640%(120%40%10%)12b=÷⨯---=,120%40%10%30%m=---=;故答案为:8,12,30%;(2)本次调查共抽取了410%40÷=名学生;补全条形图如图所示;(3)将男生分别标记为A,B,女生标记为a,b,共有12种等可能的结果,恰为一男一女的有8种,∴抽得恰好为“一男一女”的概率为82 123=.5、某校为了响应市政府号召,在“创文创卫”活动周中,设置了“A:文明礼仪;B:环境保护;C;卫生保洁;D:垃圾分类”四个主题,每个学生选一个主题参与;为了解活动开展情况,学校随机抽取了部分学生进行调查,并根据调查结果绘制了如下条形统计图和扇形统计图.⑴.本次调查的学生人数是人,m= ;⑵.请补全条形统计图;⑶.学校要求每位同学从星期一至星期五选择两天参加活动,如果小张同学随机选择连续两天,其中有一天是星期一的概率是;小李同学星期五要参加市演讲比赛,他在其余四天中随机选择两天,其中一天是星期三的概率是.【详解】(1)1220%60÷=,∴本次调查的学生人数为60人,1830%60=,故m=30.故答案为:60,m=30.(2)C的人数为:60-18-12-9=21(人),补全图形如下所示:(3)星期一到星期五连续的两天为(星期一、星期二),(星期二、星期三),(星期三、星期四),(星期四、星期五)共4种情况,符合题意的只有(星期一、星期二)这一种情况,故概率为14;在星期一到星期四任选两天的所有情况如下:(星期一、星期二),(星期一、星期三),(星期一、星期四),(星期二、星期三)、(星期二、星期四),(星期三、星期四)共6种情况,其中有一天是星期三的情况有:(星期一、星期三),(星期二、星期三),(星期三、星期四)共3种情况,所以概率是31 62 =.故答案为:14,12.6、为了了解本校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,课题小组随机选取该校部分学生进行了问卷调査(问卷调査表如图1所示),并根据调查结果绘制了图2、图3两幅统计图(均不完整),请根据统计图解答下列问题.(1)本次接受问卷调查的学生有________名.(2)补全条形统计图.(3)扇形统计图中B类节目对应扇形的圆心角的度数为________.(4)该校共有2000名学生,根据调查结果估计该校最喜爱新闻节目的学生人数.【详解】(1)本次接受问卷调查的学生有:3636%100÷=(名),故答案为100;(2)喜爱C的有:10082036630----=(人),补全的条形统计图如右图所示;(3)扇形统计图中B类节目对应扇形的圆心角的度数为:2036072100︒︒⨯=,故答案为72︒;(4)82000160100⨯=(人),答:该校最喜爱新闻节目的学生有160人.7、某中学为了了解本校学生对排球、篮球、毽球、羽毛球和跳绳五项“大课间”活动的喜欢情况,随机抽查了部分学生进行问卷调查(每名学生只选择一项),将调查结果整理并绘制成如图所示不完整的统计图表.请结合统计图表解答下列问题:抽样调查学生喜欢大课间活动人数的统计表(1)本次抽样调查的学生有50 人,请补全条形统计图;(2)求扇形统计图中,喜欢毽球活动的学生人数所对应圆心角的度数;(3)全校有学生1800人,估计全校喜欢跳绳活动的学生人数是多少?【解答】解:(1)612%50m=----=(人),÷=(人),5018410612故答案为:50;补全条形统计图如图所示:(2)103607250︒⨯=︒,答:喜欢“毽球”所在的圆心角的度数为72︒;(3)18180064850⨯=(人),答:全校1800名学生中喜欢跳绳活动的有648人.8、我市某中学举行“法制进校园”知识竞赛,赛后将学生的成绩分为A、B、C、D四个等级,并将结果绘制成如图所示的条形统计图和扇形统计图.请你根据统计图解答下列问题.(1)成绩为“B等级”的学生人数有名;(2)在扇形统计图中,表示“D等级”的扇形的圆心角度数为,图中m的值为;(3)学校决定从本次比赛获得“A等级”的学生中选出2名去参加市中学生知识竞赛.已知“A等级”中有1名女生,请用列表或画树状图的方法求出女生被选中的概率.【详解】(1)学生总人数为3÷15%=20(人)∴成绩为“B等级”的学生人数有20-3-8-4=5(人)故答案为:5;(2)“D等级”扇形的圆心角度数为436072 20⨯︒=︒m=810040 20⨯=,故答案为:72°;40;(3)根据题意画树状图如下:∴P(女生被选中)=42 63 =.9、遵义市各校都在深入开展劳动教育,某校为了解七年级学生一学期参加课外劳动时间(单位:)h的情况,从该校七年级随机抽查了部分学生进行问卷调查,并将调查结果绘制成如下不完整的频数分布表和频数分布直方图.课外劳动时间频数分布表:020t<2040t<4060t<6080t<80100t<解答下列问题:(1)频数分布表中a= 5 ,m=;将频数分布直方图补充完整;(2)若七年级共有学生400人,试估计该校七年级学生一学期课外劳动时间不少于60h的人数;(3)已知课外劳动时间在6080h t h<的男生人数为2人,其余为女生,现从该组中任选2人代表学校参加“全市中学生劳动体验”演讲比赛,请用树状图或列表法求所选学生为1男1女的概率.【分析】(1)根据频数分布表所给数据即可求出a,m;进而可以补充完整频数分布直方图;(2)根据样本估计总体的方法即可估计该校七年级学生一学期课外劳动时间不少于60h的人数;(3)根据题意画出用树状图即可求所选学生为1男1女的概率.【解答】解:(1)(20.1)0.255a=÷⨯=,m=÷=,4200.2补全的直方图如图所示:故答案为:5,0.2;(2)400(0.250.15)160⨯+=(人);(3)根据题意画出树状图,由树状图可知:共有20种等可能的情况, 1男1女有12种,故所选学生为1男1女的概率为:123205P ==. 10、每年6月26日是“国际禁毒日”.某中学为了让学生掌握禁毒知识,提高防毒意识,组织全校学生参加了“禁毒知识网络答题”活动.该校德育处对八年级全体学生答题成绩进行统计,将成绩分为四个等级:优秀、良好、一般、不合格;并绘制成如下不完整的统计图.请你根据图1、图2中所给的信息解答下列问题:(1)该校八年级共有_________名学生,“优秀”所占圆心角的度数为_________. (2)请将图1中的条形统计图补充完整.(3)已知该市共有15000名学生参加了这次“禁毒知识网络答题”活动,请以该校八年级学生答题成绩统计情况估计该市大约有多少名学生在这次答题中成绩不合格?(4)德育处从该校八年级答题成绩前四名甲、乙、丙、丁学生中随机抽取2名同学参加全市现场禁毒知识竞赛,请用树状图或列表法求出必有甲同学参加的概率. 【详解】(1)由条形统计图知:等级“良好”的人数为:200名 由扇形统计图知:等级“良好”的所占的比例为:40% 则该校八年级总人数为:20040%500÷=(名) 由条形统计图知:等级“优秀”的人数为:150名 其站该校八年级总人数的比例为:15050030%÷= 所以其所对的圆心角为:36030%108︒︒⨯= 故答案为:500,108°(2)等级“一般”的人数为:50015020050100---=(名) 补充图形如图所示:(3)该校八年级中不合格人数所占的比例为:5010% 500=故该市15000名学生中不合格的人数为:1500010%1500⨯=(名)(4)从甲,乙,丙,丁四名学生中任取选出两人,所得基本事件有:共计12种,其中必有甲同学参加的有6种,必有甲同学参加的概率为:61 122=.11、广元市某中学举行了“禁毒知识竞赛”,王老师将九年级(1)班学生成绩划分为A、B、C、D、E五个等级,并绘制了图1、图2两个不完整的统计图,请根据图中的信息解答下列问题:(1)求九年级(1)班共有多少名同学?(2)补全条形统计图,并计算扇形统计图中的“C”所对应的圆心角度数;(3)成绩为A类的5名同学中,有2名男生和3名女生;王老师想从这5名同学中任选2名同学进行交流,请用列表法或画树状图的方法求选取的2名同学都是女生的概率.【详解】解:(1)由题意可知总人数=10÷20%=50名;(2)补全条形统计图如图所示:扇形统计图中C等级所对应扇形的圆心角=15÷50×100%×360°=108°;(3)列表如下:得到所有等可能的情况有20种,其中恰好抽中2名同学都是女生的情况有6种,所以恰好选到2名同学都是女生的概率=620=310.12、为了丰富学生们的课余生活,学校准备开展第二课堂,有四类课程可供选择,分别是“A.书画类、B.文艺类、C.社会实践类、D.体育类”.现随机抽取了七年级部分学生对报名意向进行调查,并根据调查结果绘制了两幅不完整的统计图,请你根据图表信息回答下列问题:(1)本次被抽查的学生共有_____________名,扇形统计图中“A.书画类”所占扇形的圆心角的度数为___________度;(2)请你将条形统计图补全;(3)若该校七年级共有600名学生,请根据上述调查结果估计该校学生选择“C.社会实践类”的学生共有多少名?(4)本次调查中抽中了七(1)班王芳和小颖两名学生,请用列表法或画树状图法求她们选择同一个项目的概率.【详解】解:(1)本次被抽查的学生共有:20÷40%=50名,扇形统计图中“A.书画类”所占扇形的圆心角的度数为103607250⨯︒=︒;故答案为:50,72;(2)B类人数是:50-10-8-20=12名,补全条形统计图如图所示:(3)86009650⨯=名,答:估计该校学生选择“C.社会实践类”的学生共有96名;(4)所有可能的情况如下表所示:由表格可得:共有16种等可能的结果,其中王芳和小颖两名学生选择同一个项目的结果有4种,∴王芳和小颖两名学生选择同一个项目的概率41 164==.13、根据公安部交管局下发的通知,自2020年6月1日起,将在全国开展“一带一盔”安全。
《2020年中考数学保A必刷压轴题(湖南长沙专版)》(三):几何新定义专题(原卷版)

《2020年中考数学保A必刷压轴题(湖南长沙专版)》(三)几何新定义专题1.(2019•咸宁)定义:有一组邻边相等且对角互补的四边形叫做等补四边形.理解:(1)如图1,点A,B,C在⊙O上,⊙ABC的平分线交⊙O于点D,连接AD,CD.求证:四边形ABCD是等补四边形;探究:(2)如图2,在等补四边形ABCD中,AB=AD,连接AC,AC是否平分⊙BCD?请说明理由.运用:(3)如图3,在等补四边形ABCD中,AB=AD,其外角⊙EAD的平分线交CD的延长线于点F,CD =10,AF=5,求DF的长.2.(2019•达州)箭头四角形,模型规律,如图1,延长CO交AB于点D,则⊙BOC=⊙1+⊙B=⊙A+⊙C+⊙B.因为凹四边形ABOC形似箭头,其四角具有“⊙BOC=⊙A+⊙B+⊙C”这个规律,所以我们把这个模型叫做“箭头四角形”.模型应用(1)直接应用:⊙如图2,⊙A+⊙B+⊙C+⊙D+⊙E+⊙F=.⊙如图3,⊙ABE、⊙ACE的2等分线(即角平分线)BF、CF交于点F,已知⊙BEC=120°,⊙BAC=50°,则⊙BFC=.⊙如图4,BO i、CO i分别为⊙ABO、⊙ACO的2019等分线(i=1,2,3,…,2017,2018).它们的交点从上到下依次为O1、O2、O3、…、O2018.已知⊙BOC=m°,⊙BAC=n°,则⊙BO1000C=度.(2)拓展应用:如图5,在四边形ABCD中,BC=CD,⊙BCD=2⊙BAD.O是四边形ABCD内一点,且OA=OB=OD.求证:四边形OBCD是菱形.3.(2019•天水)如图1,对角线互相垂直的四边形叫做垂美四边形.(1)概念理解:如图2,在四边形ABCD中,AB=AD,CB=CD,问四边形ABCD是垂美四边形吗?请说明理由;(2)性质探究:如图1,四边形ABCD的对角线AC、BD交于点O,AC⊙BD.试证明:AB2+CD2=AD2+BC2;(3)解决问题:如图3,分别以Rt⊙ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连结CE、BG、GE.已知AC=4,AB=5,求GE的长.4.(2019•嘉兴)小波在复习时,遇到一个课本上的问题,温故后进行了操作、推理与拓展.(1)温故:如图1,在⊙ABC中,AD⊙BC于点D,正方形PQMN的边QM在BC上,顶点P,N分别在AB,AC上,若BC=6,AD=4,求正方形PQMN的边长.(2)操作:能画出这类正方形吗?小波按数学家波利亚在《怎样解题》中的方法进行操作:如图2,任意画⊙ABC,在AB上任取一点P',画正方形P'Q'M'N',使Q',M'在BC边上,N'在⊙ABC内,连结BN'并延长交AC于点N,画NM⊙BC于点M,NP⊙NM交AB于点P,PQ⊙BC于点Q,得到四边形PPQMN.小波把线段BN称为“波利亚线”.(3)推理:证明图2中的四边形PQMN是正方形.(4)拓展:在(2)的条件下,在射线BN上截取NE=NM,连结EQ,EM(如图3).当tan⊙NBM=时,猜想⊙QEM的度数,并尝试证明.请帮助小波解决“温故”、“推理”、“拓展”中的问题.5.定义:在三角形中,若有两条中线互相垂直,则称该三角形为中垂三角形.(1)如图(1),ABC ∆是中垂三角形,BD ,AE 分别是AC ,BC 边上的中线,且BD AE ⊥于点O ,若45BAE ∠=︒,求证:ABC ∆是等腰三角形.(2)如图(2),在中垂三角形ABC 中,AE ,BD 分别是边BC ,AC 上的中线,且AE BD ⊥于点O ,猜想2AB ,2BC ,2AC 之间的数量关系,并加以证明.(3)如图(3),四边形ABCD 是菱形,对角线AC ,BD 交于点O ,点M ,N 分别是OA ,OD 的中点,连接BM ,CN 并延长,交于点E .⊙求证:BCE ∆是中垂三角形;⊙若AB =22BE CE +的值.6.(2020•长沙模拟)定义:有一个内角为90︒,且对角线相等的四边形称为准矩形.(1)⊙如图1,准矩形ABCD 中,90ABC ∠=︒,若2AB =,3BC =,则BD⊙如图2,直角坐标系中,(0,3)A ,(5,0)B ,若整点P 使得四边形AOBP 是准矩形,则点P 的坐标是 ;(整点指横坐标、纵坐标都为整数的点)(2)如图3,正方形ABCD 中,点E 、F 分别是边AD 、AB 上的点,且CF BE ⊥,求证:四边形BCEF 是准矩形;(3)已知,准矩形ABCD 中,90ABC ∠=︒,60BAC ∠=︒,2AB =,当ADC ∆为等腰三角形时,请直接写出这个准矩形的面积是 .7.(2019秋•雨花区校级月考)新定义:我们把两个面积相等但不全等的三角形叫做偏等积三角形.(1)如图1,已知等腰直角ABC ∆,90ACB ∠=︒,4AC BC ==,P 为AC 上一点,当AP = 2 时,ABP ∆与CBP ∆为偏等积三角形.(2)如图2,ABD ∆与ACD ∆为偏等积三角形,2AB =,6AC =,且线段AD 的长度为正整数,过点C 作//CE AB 交AD 的延长线于点E ,求AE 的长度(3)如图3,已知ACD ∆为直角三角形,90ADC ∠=︒,以AC ,AD 为边问外作正方形ACFB 和正方形ADGE ,连结BE ,求证:ACD ∆与ABE ∆为偏等积三角形.8.(2019•岳麓区校级三模)定义:在凸四边形中,我们把两组对边乘积的和等于对角线的乘积的四边形称为“完美四边形”(1)在“正方形”、“矩形”、“菱形”中,一定是“完美四边形”的是 .(2)如图1,在ABC ∆中,2AB =,52BC =,3AC =,D 为平面内一点,以A 、B 、C 、D 四点为顶点构成的四边形为“完美四边形”,若DA ,DC 的长是关于x 的一元二次方程221(3)(5213)04x m x m m -++-+=(其中m 为常数)的两个根,求线段BD 的长度. (3)如图2,在“完美四边形” EFGH 中,90F ∠=︒,6EF =,8FG =,求“完美四边形” EFGH 面积的最大值.9.(2017•宁波)有两个内角分别是它们对角的一半的四边形叫做半对角四边形.(1)如图1,在半对角四边形ABCD 中,12B D ∠=∠,12C A ∠=∠,求B ∠与C ∠的度数之和; (2)如图2,锐角ABC ∆内接于O ,若边AB 上存在一点D ,使得BD BO =,OBA ∠的平分线交OA 于点E ,连结DE 并延长交AC 于点F ,2AFE EAF ∠=∠.求证:四边形DBCF 是半对角四边形;(3)如图3,在(2)的条件下,过点D 作DG OB ⊥于点H ,交BC 于点G ,当DH BG =时,求BGH ∆与ABC ∆的面积之比.10.(2014•鞍山二模)我们给出如下定义:有一组相邻内角相等的四边形叫做等邻角四边形.请解答下列问题:(1)写出一个你所学过的特殊四边形中是等邻角四边形的图形的名称;(2)如图1,在ABC ∆中,AB AC =,点D 在BC 上,且CD CA =,点E 、F 分别为BC 、AD 的中点,连接EF 并延长交AB 于点G .求证:四边形AGEC 是等邻角四边形;(3)如图2,若点D 在ABC ∆的内部,(2)中的其他条件不变,EF 与CD 交于点H ,图中是否存在等邻角四边形,若存在,指出是哪个四边形,不必证明;若不存在,请说明理由.。
2021年中考数学第三轮压轴题强化训练:三角形 专题复习(含答案)
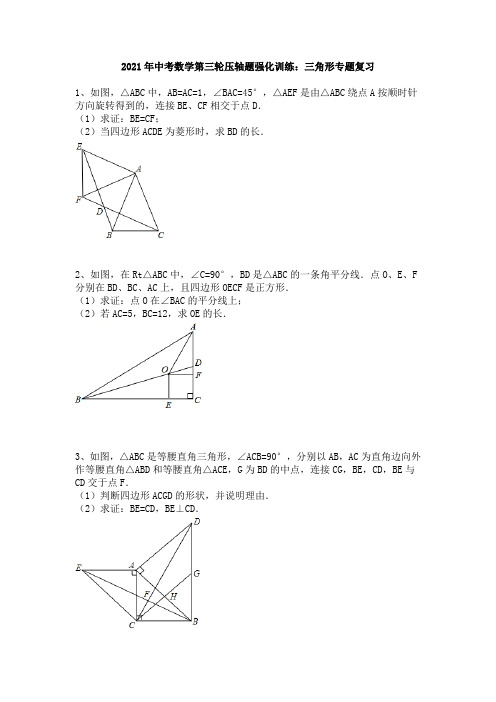
2021年中考数学第三轮压轴题强化训练:三角形专题复习1、如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的,连接BE、CF相交于点D.(1)求证:BE=CF;(2)当四边形ACDE为菱形时,求BD的长.2、如图,在Rt△ABC中,∠C=90°,BD是△ABC的一条角平分线.点O、E、F 分别在BD、BC、AC上,且四边形OECF是正方形.(1)求证:点O在∠BAC的平分线上;(2)若AC=5,BC=12,求OE的长.3、如图,△ABC是等腰直角三角形,∠ACB=90°,分别以AB,AC为直角边向外作等腰直角△ABD和等腰直角△ACE,G为BD的中点,连接CG,BE,CD,BE与CD交于点F.(1)判断四边形ACGD的形状,并说明理由.(2)求证:BE=CD,BE⊥CD.4、如图1,在四边形ABCD中,点E、F分别是AB、CD的中点,过点E作AB的垂线,过点F作CD的垂线,两垂线交于点G,连接AG、BG、CG、DG,且∠AGD=∠BGC.(1)求证:AD=BC;(2)求证:△AGD∽△EGF;(3)如图2,若AD、BC所在直线互相垂直,求的值.5、如图,是一副学生用的三角板,在△ABC 中,∠C=90°,∠A=60°,∠B=30°;在△A1B1C1中,∠C1=90°,∠A1=45°,∠B1=45°,且A1B1=CB.若将边A1C1与边CA重合,其中点A1与点C重合.将三角板A1B1C1绕点C(A1)按逆时针方向旋转,旋转过的角为α,旋转过程中边A1C1与边AB的交点为M,设AC=a.(1)计算A1C1的长;(2)当α=30°时,证明:B1C1∥AB;(3)若a=,当α=45°时,计算两个三角板重叠部分图形的面积;(4)当α=60°时,用含a的代数式表示两个三角板重叠部分图形的面积.(参考数据:sin15°=,cos15°=,tan15°=2﹣,sin75°=,cos75°=,tan75°=2+)6、如图,两个全等的△ABC和△DFE重叠在一起,固定△ABC,将△DEF进行如下变换:(1)如图1,△DEF沿直线CB向右平移(即点F在线段CB上移动),连接AF、AD、BD.请直接写出S△ABC 与S四边形AFBD的关系;(2)如图2,当点F平移到线段BC的中点时,若四边形AFBD为正方形,那么△ABC应满足什么条件?请给出证明;(3)在(2)的条件下,将△DEF沿DF折叠,点E落在FA的延长线上的点G处,连接CG,请你在图3的位置画出图形,并求出sin∠CGF的值.7、如图1,在△ABC中,∠ACB=90°,AC=BC,∠EAC=90°,点M为射线AE上任意一点(不与A重合),连接CM,将线段CM绕点C按顺时针方向旋转90°得到线段CN,直线NB分别交直线CM、射线AE于点F、D.(1)直接写出∠NDE的度数;(2)如图2、图3,当∠EAC为锐角或钝角时,其他条件不变,(1)中的结论是否发生变化?如果不变,选取其中一种情况加以证明;如果变化,请说明理由;(3)如图4,若∠EAC=15°,∠ACM=60°,直线CM与AB交于G,BD=,其他条件不变,求线段AM的长.8、我们把两条中线互相垂直的三角形称为“称为中垂三角形”,例如图1,图2,图3中,AF,BE是△ABC的中线,AF⊥BE,垂足为P,像△ABC这样的三角形均称为“中垂三角形”,设BC=a,AC=b,AB=c.特例探索(1)如图1,当∠ABE=45°,c=2时,a= ,b= .如图2,当∠ABE=30°,c=4时,a= ,b= .归纳证明(2)请你观察(1)中的计算结果,猜想a2,b2,c2三者之间的关系,用等式表示出来,并利用图3证明你发现的关系式.拓展应用(3)如图4,在▱ABCD中,点E、F、G分别是AD,BC,CD的中点,BE⊥EG,AD=2,AB=3,求AF的长.9、如图1,在Rt△ABC中,∠B=90°,BC=2AB=8,点D、E分别是边BC、AC的中点,连接DE,将△EDC绕点C按顺时针方向旋转,记旋转角为α.(1)问题发现①当α=0°时,= ;②当α=180°时,= .(2)拓展探究试判断:当0°≤α<360°时,的大小有无变化?请仅就图2的情形给出证明.(3)问题解决当△EDC旋转至A,D,E三点共线时,直接写出线段BD的长.10、已知点P是线段AB上与点A不重合的一点,且AP<PB.AP绕点A逆时针旋转角α(0°<α≤90°)得到AP1,BP绕点B顺时针也旋转角α得到BP2,连接PP1、PP2.(1)如图1,当α=90°时,求∠P1PP2的度数;(2)如图2,当点P2在AP1的延长线上时,求证:△P2P1P∽△P2PA;(3)如图3,过BP的中点E作l1⊥BP,过BP2的中点F作l2⊥BP2,l1与l2交于点Q,连接PQ,求证:P1P⊥PQ.11、两个三角板ABC,DEF,按如图所示的位置摆放,点B与点D重合,边AB与边DE在同一条直线上(假设图形中所有的点,线都在同一平面内).其中,∠C=∠DEF=90°,∠ABC=∠F=30°,AC=DE=6cm.现固定三角板DEF,将三角板ABC 沿射线DE方向平移,当点C落在边EF上时停止运动.设三角板平移的距离为x (cm),两个三角板重叠部分的面积为y(cm2).(1)当点C落在边EF上时,x= cm;(2)求y关于x的函数解析式,并写出自变量x的取值范围;(3)设边BC的中点为点M,边DF的中点为点N.直接写出在三角板平移过程中,点M与点N之间距离的最小值.12、已知∠MAN=135°,正方形ABCD绕点A旋转.(1)当正方形ABCD旋转到∠MAN的外部(顶点A除外)时,AM,AN分别与正方形ABCD的边CB,CD的延长线交于点M,N,连接MN.①如图1,若BM=DN,则线段MN与BM+DN之间的数量关系是;②如图2,若BM≠DN,请判断①中的数量关系是否仍成立?若成立,请给予证明;若不成立,请说明理由;(2)如图3,当正方形ABCD旋转到∠MAN的内部(顶点A除外)时,AM,AN分别与直线BD交于点M,N,探究:以线段BM,MN,DN的长度为三边长的三角形是何种三角形,并说明理由.13、已知:△ABC是等腰三角形,动点P在斜边AB所在的直线上,以PC为直角边作等腰三角形PCQ,其中∠PCQ=90°,探究并解决下列问题:(1)如图①,若点P在线段AB上,且AC=1+,PA=,则:①线段PB= ,PC= ;②猜想:PA2,PB2,PQ2三者之间的数量关系为;(2)如图②,若点P在AB的延长线上,在(1)中所猜想的结论仍然成立,请你利用图②给出证明过程;(3)若动点P满足=,求的值.(提示:请利用备用图进行探求)参考答案2021年中考数学第三轮压轴题强化训练:三角形专题复习1、如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的,连接BE、CF相交于点D.(1)求证:BE=CF;(2)当四边形ACDE为菱形时,求BD的长.(1)证明:∵△AEF是由△ABC绕点A按顺时针方向旋转得到的,∴AE=AB,AF=AC,∠EAF=∠BAC,∴∠EAF+∠BAF=∠BAC+∠BAF,即∠EAB=∠FAC,∵AB=AC,∴AE=AF,∴△AEB可由△AFC绕点A按顺时针方向旋转得到,∴BE=CF;(2)解:∵四边形ACDE为菱形,AB=AC=1,∴DE=AE=AC=AB=1,AC∥DE,∴∠AEB=∠ABE,∠ABE=∠BAC=45°,∴∠AEB=∠ABE=45°,∴△ABE为等腰直角三角形,∴BE=AC=,∴BD=BE﹣DE=﹣1.2、如图,在Rt△ABC中,∠C=90°,BD是△ABC的一条角平分线.点O、E、F 分别在BD、BC、AC上,且四边形OECF是正方形.(1)求证:点O在∠BAC的平分线上;(2)若AC=5,BC=12,求OE的长.解答:(1)证明:过点O作OM⊥AB,∵BD是∠ABC的一条角平分线,∴OE=OM,∵四边形OECF是正方形,∴OE=OF,∴OF=OM,∴AO是∠BAC的角平分线,即点O在∠BAC的平分线上;(2)解:∵在Rt△ABC中,AC=5,BC=12,∴AB===13,设OE=CF=x,BE=BM=y,AM=AF=z,∴,解得:,∴OE=2.3、如图,△ABC是等腰直角三角形,∠ACB=90°,分别以AB,AC为直角边向外作等腰直角△ABD和等腰直角△ACE,G为BD的中点,连接CG,BE,CD,BE与CD交于点F.(1)判断四边形ACGD的形状,并说明理由.(2)求证:BE=CD,BE⊥CD.解答:(1)解:∵△ABC是等腰直角三角形,∠ACB=90°,∴AB=BC,∵△ABD和△ACE均为等腰直角三角形,∴BD==BC=2BC,∵G为BD的中点,∴BG=BD=BC,∴△CBG为等腰直角三角形,∴∠CGB=45°,∵∠ADB=45°,AD∥CG,∵∠ABD=45°,∠ABC=45°∴∠CBD=90°,∵∠ACB=90°,∴∠CBD+∠ACB=180°,∴AC∥BD,∴四边形ACGD为平行四边形;(2)证明:∵∠EAB=∠EAC+∠CAB=90°+45°=135°,∠CAD=∠DAB+∠BAC=90°+45°=135°,∴∠EAB=∠CAD,在△DAC与△BAE中,,∴△DAC≌△BAE,∴BE=CD;∵∠EAC=∠BCA=90°,EA=AC=BC,∴四边形ABCE为平行四边形,∴CE=AB=AD,在△BCE与△CAD中,,∴△BCE≌△CAD,∴∠CBE=∠ACD,∵∠ACD+∠BCD=90°,∴∠CBE+∠BCD=90°,∴∠CFB=90°,即BE⊥CD.4、如图1,在四边形ABCD中,点E、F分别是AB、CD的中点,过点E作AB的垂线,过点F作CD的垂线,两垂线交于点G,连接AG、BG、CG、DG,且∠AGD=∠BGC.(1)求证:AD=BC;(2)求证:△AGD∽△EGF;(3)如图2,若AD、BC所在直线互相垂直,求的值.解答(1)证明:∵GE是AB的垂直平分线,∴GA=GB,同理:GD=GC,在△AGD和△BGC中,,∴△AGD≌△BGC(SAS),∴AD=BC;(2)证明:∵∠AGD=∠BGC,∴∠AGB=∠DGC,在△AGB和△DGC中,,∴△AGB∽△DGC,∴,又∵∠AGE=∠DGF,∴∠AGD=∠EGF,∴△AGD∽△EGF;(3)解:延长AD交GB于点M,交BC的延长线于点H,如图所示:则AH⊥BH,∵△AGD≌△BGC,∴∠GAD=∠GBC,在△GAM和△HBM中,∠GAD=∠GBC,∠GMA=∠HMB,∴∠AGB=∠AHB=90°,∴∠AGE=∠AGB=45°,∴,又∵△AGD∽△EGF,∴==.5、如图,是一副学生用的三角板,在△ABC 中,∠C=90°,∠A=60°,∠B=30°;在△A1B1C1中,∠C1=90°,∠A1=45°,∠B1=45°,且A1B1=CB.若将边A1C1与边CA重合,其中点A1与点C重合.将三角板A1B1C1绕点C(A1)按逆时针方向旋转,旋转过的角为α,旋转过程中边A1C1与边AB的交点为M,设AC=a.(1)计算A1C1的长;(2)当α=30°时,证明:B1C1∥AB;(3)若a=,当α=45°时,计算两个三角板重叠部分图形的面积;(4)当α=60°时,用含a的代数式表示两个三角板重叠部分图形的面积.(参考数据:sin15°=,cos15°=,tan15°=2﹣,sin75°=,cos75°=,tan75°=2+)解:(1)在Rt△ABC中,∠B=30°,AC=a,由特殊锐角三角函数可知:,∴BC=.∴B1C=在Rt△A1B1C1,∠B1=∠45°,∴.∴A1C1==.(2)∵∠ACM=30°,∠A=60°,∴∠BMC=90°.∴∠C1=∠BMC.∴B1C1∥AB.(3)如下图:由(1)可知:A1C1===3+∴△A1B1C1的面积==∵∠A1B1C1=45°,∠ABC=30°∴∠MBC1=15°在Rt△BC1M中,C1M=BCtan15°=(3+)(2﹣)=3﹣,∴Rt△BC1M的面积===3.∴两个三角板重叠部分图形的面积=△A1B1C1的面积﹣△BC1M的面积=3+3.(4)由(1)可知:BC=,A1C1=,∴C1F=A1C1•tan30°=a,∴==×a×a=a2,∵∠MCA=60°,∠A=60°,∴∠AMC=60°∴MC=AC=MA=a.∴C1M=C1A1﹣MC=.∵∠MCA=60°,∴∠C1A1B=30°,∴∠C1MD=∠B+∠C1A1B=60°在Rt△DC1M中,由特殊锐角三角函数可知:C1D=C1M•tan60°=a,∴=C1M•C1D=a2,两个三角板重叠部分图形的面积=﹣=C1M=a2﹣a2=a2.6、如图,两个全等的△ABC和△DFE重叠在一起,固定△ABC,将△DEF进行如下变换:(1)如图1,△DEF沿直线CB向右平移(即点F在线段CB上移动),连接AF、AD、BD.请直接写出S△ABC 与S四边形AFBD的关系;(2)如图2,当点F平移到线段BC的中点时,若四边形AFBD为正方形,那么△ABC应满足什么条件?请给出证明;(3)在(2)的条件下,将△DEF沿DF折叠,点E落在FA的延长线上的点G处,连接CG,请你在图3的位置画出图形,并求出sin∠CGF的值.解:(1)S△ABC =S四边形AFBD,理由:由题意可得:AD∥EC,则S△ADF =S△ABD,故S△ACF =S△ADF=S△ABD,则S△ABC =S四边形AFBD;(2)△ABC为等腰直角三角形,即:AB=AC,∠BAC=90°,理由如下:∵F为BC的中点,∴CF=BF,∵CF=AD,∴AD=BF,又∵AD∥BF,∴四边形AFBD为平行四边形,∵AB=AC,F为BC的中点,∴AF⊥BC,∴平行四边形AFBD为矩形,∵∠BAC=90°,F为BC的中点,∴AF=BC=BF,∴四边形AFBD为正方形;(3)如图3所示:由(2)知,△ABC为等腰直角三角形,AF⊥BC,设CF=k,则GF=EF=CB=2k,由勾股定理得:CG=k,sin∠CGF===.7、如图1,在△ABC中,∠ACB=90°,AC=BC,∠EAC=90°,点M为射线AE上任意一点(不与A重合),连接CM,将线段CM绕点C按顺时针方向旋转90°得到线段CN,直线NB分别交直线CM、射线AE于点F、D.(1)直接写出∠NDE的度数;(2)如图2、图3,当∠EAC为锐角或钝角时,其他条件不变,(1)中的结论是否发生变化?如果不变,选取其中一种情况加以证明;如果变化,请说明理由;(3)如图4,若∠EAC=15°,∠ACM=60°,直线CM与AB交于G,BD=,其他条件不变,求线段AM的长.解:(1)∵∠ACB=90°,∠MCN=90°,∴∠ACM=∠BCN,在△MAC和△NBC中,,∴△MAC≌△NBC,∴∠NBC=∠MAC=90°,又∵∠ACB=90°,∠EAC=90°,∴∠NDE=90°;(2)不变,在△MAC≌△NBC中,,∴△MAC≌△NBC,∴∠N=∠AMC,又∵∠MFD=∠NFC,∠MDF=∠FCN=90°,即∠NDE=90°;(3)作GK⊥BC于K,∵∠EAC=15°,∴∠BAD=30°,∵∠ACM=60°,∴∠GCB=30°,∴∠AGC=∠ABC+∠GCB=75°,∠AMG=75°,∴AM=AG,∵△MAC≌△NBC,∴∠MAC=∠NBC,∴∠BDA=∠BCA=90°,∵BD=,∴AB=+,AC=BC=+1,设BK=a,则GK=a,CK=a,∴a+a=+1,∴a=1,∴KB=KG=1,BG=,AG=,∴AM=.8、我们把两条中线互相垂直的三角形称为“称为中垂三角形”,例如图1,图2,图3中,AF,BE是△ABC的中线,AF⊥BE,垂足为P,像△ABC这样的三角形均称为“中垂三角形”,设BC=a,AC=b,AB=c.特例探索(1)如图1,当∠ABE=45°,c=2时,a= 2,b= 2.如图2,当∠ABE=30°,c=4时,a= 2,b= 2.归纳证明(2)请你观察(1)中的计算结果,猜想a2,b2,c2三者之间的关系,用等式表示出来,并利用图3证明你发现的关系式.拓展应用(3)如图4,在▱ABCD中,点E、F、G分别是AD,BC,CD的中点,BE⊥EG,AD=2,AB=3,求AF的长.解:(1)∵AH⊥BE,∠ABE=45°,∴AP=BP=AB=2,∵AF,BE是△ABC的中线,∴EF∥AB,EF=AB=,∴∠PFE=∠PEF=45°,∴PE=PF=1,在Rt△FPB和Rt△PEA中,AE=BF==,∴AC=BC=2,∴a=b=2,如图2,连接EF,同理可得:EF=×4=2,∵EF∥AB,∴△PEF~△ABP,∴,在Rt△ABP中,AB=4,∠ABP=30°,∴AP=2,PB=2,∴PF=1,PE=,在Rt△APE和Rt△BPF中,AE=,BF=,∴a=2,b=2,故答案为:2,2,2,2;(2)猜想:a2+b2=5c2,如图3,连接EF,设∠ABP=α,∴AP=csinα,PB=ccosα,由(1)同理可得,PF=PA=,PE==,AE2=AP2+PE2=c2sin2α+,BF2=PB2+PF2=+c2cos2α,∴=c2sin2α+,=+c2cos2α,∴+=+c2cos2α+c2sin2α+,∴a2+b2=5c2;(3)如图4,连接AC,EF交于H,AC与BE交于点Q,设BE与AF的交点为P,∵点E、G分别是AD,CD的中点,∴EF∥AC,∵BE⊥EG,∴BE⊥AC,∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC=2,∴∠EAH=∠FCH,∵E,F分别是AD,BC的中点,∴AE=AD,BF=BC,∴AE=BF=CF=AD=,∵AE∥BF,∴四边形ABFE是平行四边形,∴EF=AB=3,AP=PF,在△AEH和△CFH中,,∴△AEH≌△CFH,∴EH=FH,∴EH,AH分别是△AFE的中线,由(2)的结论得:AF2+EF2=5AE2,∴AF2=5﹣EF2=16,∴AF=4.9、如图1,在Rt△ABC中,∠B=90°,BC=2AB=8,点D、E分别是边BC、AC的中点,连接DE,将△EDC绕点C按顺时针方向旋转,记旋转角为α.(1)问题发现①当α=0°时,= ;②当α=180°时,= .(2)拓展探究试判断:当0°≤α<360°时,的大小有无变化?请仅就图2的情形给出证明.(3)问题解决当△EDC旋转至A,D,E三点共线时,直接写出线段BD的长.解:(1)①当α=0°时,∵Rt△ABC中,∠B=90°,∴AC=,∵点D、E分别是边BC、AC的中点,∴,∴.②如图1,,当α=180°时,可得AB∥DE,∵,∴=.故答案为:.(2)如图2,,当0°≤α<360°时,的大小没有变化,∵∠ECD=∠ACB,∴∠ECA=∠DCB,又∵,∴△ECA∽△DCB,∴.(3)①如图3,,∵AC=4,CD=4,CD⊥AD,∴AD==,∵AD=BC,AB=DC,∠B=90°,∴四边形ABCD是矩形,∴.②如图4,连接BD,过点D作AC的垂线交AC于点Q,过点B作AC的垂线交AC 于点P,,∵AC=4,CD=4,CD⊥AD,∴AD==,在△ABC和△CDA中,∴BP=DQ,BP∥DQ,PQ⊥DQ,∴四边形BDQP为矩形,∴BD=PQ=AC﹣AP﹣CQ==.综上所述,BD的长为4或10、已知点P是线段AB上与点A不重合的一点,且AP<PB.AP绕点A逆时针旋转角α(0°<α≤90°)得到AP1,BP绕点B顺时针也旋转角α得到BP2,连接PP1、PP2.(1)如图1,当α=90°时,求∠P1PP2的度数;(2)如图2,当点P2在AP1的延长线上时,求证:△P2P1P∽△P2PA;(3)如图3,过BP的中点E作l1⊥BP,过BP2的中点F作l2⊥BP2,l1与l2交于点Q,连接PQ,求证:P1P⊥PQ.解答:(1)解:由旋转的性质得:AP=AP1,BP=BP2.∵α=90°,∴△PAP1和△PBP2均为等腰直角三角形,∴∠APP1=∠BPP2=45°,∴∠P1PP2=180°﹣∠APP1﹣∠BPP2=90°;(2)证明:由旋转的性质可知△PAP1和△PBP2均为顶角为α的等腰三角形,∴∠APP1=∠BPP2=90°﹣,∴∠P1PP2=180°﹣(∠APP1+∠BPP2)=180°﹣2(90°)=α,在△PP2P1和△P2PA中,∠P1PP2=∠PAP2=α,又∵∠PP2P1=∠AP2P,∴△P2P1P∽△P2PA.(3)证明:如图,连接QB.∵l1,l2分别为PB,P2B的中垂线,∴EB=BP,FB=BP2.又BP=BP2,∴EB=FB.在Rt△QBE和Rt△QBF中,,∴Rt△QBE≌Rt△QBF,∴∠QBE=∠QBF=∠PBP2=,由中垂线性质得:QP=QB,∴∠QPB=∠QBE=,由(2)知∠APP1=90°﹣,∴∠P1PQ=180°﹣∠APP1﹣∠QPB=180°﹣(90°﹣)=90°,即 P1P⊥PQ.11、两个三角板ABC,DEF,按如图所示的位置摆放,点B与点D重合,边AB与边DE在同一条直线上(假设图形中所有的点,线都在同一平面内).其中,∠C=∠DEF=90°,∠ABC=∠F=30°,AC=DE=6cm.现固定三角板DEF,将三角板ABC 沿射线DE方向平移,当点C落在边EF上时停止运动.设三角板平移的距离为x (cm),两个三角板重叠部分的面积为y(cm2).(1)当点C落在边EF上时,x= 15 cm;(2)求y关于x的函数解析式,并写出自变量x的取值范围;(3)设边BC的中点为点M,边DF的中点为点N.直接写出在三角板平移过程中,点M与点N之间距离的最小值.解:(1)如图1所示:作CG⊥AB于G点.,在Rt△ABC中,由AC=6,∠ABC=30,得BC==6.在Rt△BCG中,BG=BC•cos30°=9.四边形CGEH是矩形,CH=GE=BG+BE=9+6=15cm,故答案为:15;(2)①当0≤x<6时,如图2所示.,∠GDB=60°,∠GBD=30°,DB=x,得DG=x,BG=x,重叠部分的面积为y=DG•BG=×x×x=x2②当6≤x<12时,如图3所示.,BD=x,DG=x,BG=x,BE=x﹣6,EH=(x﹣6).重叠部分的面积为y=S△BDG ﹣S△BEH=DG•BG﹣BE•EH,即y=×x×x﹣(x﹣6)(x﹣6)化简,得y=﹣x2+2x﹣6;③当12<x≤15时,如图4所示.,AC=6,BC=6,BD=x,BE=(x﹣6),EG=(x﹣6),重叠部分的面积为y=S△ABC ﹣S△BEG=AC•BC﹣BE•EG,即y=×6×6﹣(x﹣6)(x﹣6),化简,得y=18﹣(x2﹣12x+36)=﹣x2+2x+12;综上所述:y=;(3)如图5所示作NG⊥DE于G点.(4),点M在NG上时MN最短,NG是△DEF的中位线,NG=EF=.MB=CB=3,∠B=30°,MG=MB=,MN最小=3﹣=.12、已知∠MAN=135°,正方形ABCD绕点A旋转.(1)当正方形ABCD旋转到∠MAN的外部(顶点A除外)时,AM,AN分别与正方形ABCD的边CB,CD的延长线交于点M,N,连接MN.①如图1,若BM=DN,则线段MN与BM+DN之间的数量关系是MN=BM+DN ;②如图2,若BM≠DN,请判断①中的数量关系是否仍成立?若成立,请给予证明;若不成立,请说明理由;(2)如图3,当正方形ABCD旋转到∠MAN的内部(顶点A除外)时,AM,AN分别与直线BD交于点M,N,探究:以线段BM,MN,DN的长度为三边长的三角形是何种三角形,并说明理由.解:(1)①如图1,若BM=DN,则线段MN与BM+DN之间的数量关系是MN=BM+DN.理由如下:在△ADN与△ABM中,,∴△ADN≌△ABM(SAS),∴AN=AM,∠NAD=∠MAB,∵∠MAN=135°,∠BAD=90°,∴∠NAD=∠MAB=(360°﹣135°﹣90°)=67.5°,作AE⊥MN于E,则MN=2NE,∠NAE=∠MAN=67.5°.在△ADN与△AEN中,,∴△ADN≌△AEN(AAS),∴DN=EN,∵BM=DN,MN=2EN,∴MN=BM+DN.故答案为MN=BM+DN;②如图2,若BM≠DN,①中的数量关系仍成立.理由如下:延长NC到点P,使DP=BM,连结AP.∵四边形ABCD是正方形,∴AB=AD,∠ABM=∠ADC=90°.在△ABM与△ADP中,,∴△ABM≌△ADP(SAS),∴AM=AP,∠1=∠2=∠3,∵∠1+∠4=90°,∴∠3+∠4=90°,∵∠MAN=135°,∴∠PAN=360°﹣∠MAN﹣(∠3+∠4)=360°﹣135°﹣90°=135°.在△ANM与△ANP中,,∴△ANM≌△ANP(SAS),∴MN=PN,∵PN=DP+DN=BM+DN,∴MN=BM+DN;(2)如图3,以线段BM,MN,DN的长度为三边长的三角形是直角三角形.理由如下:∵四边形ABCD是正方形,∴∠BDA=∠DBA=45°,∴∠MDA=∠NBA=135°.∵∠1+∠2=45°,∠2+∠3=45°,∴∠1=∠3.在△ANB与△MAD中,,∴△ANB∽△MAD,∴=,∴AB2=BN•MD,∵AB=DB,∴BN•MD=(DB)2=BD2,∴BD2=2BN•MD,∴MD2+2MD•BD+BD2+BD2+2BD•BN+BN2=MD2+BD2+BN2+2MD•BD+2BD•BN+2BN•MD,∴(MD+BD)2+(BD+BN)2=(DM+BD+BN)2,即MB2+DN2=MN2,∴以线段BM,MN,DN的长度为三边长的三角形是直角三角形.13、已知:△ABC是等腰三角形,动点P在斜边AB所在的直线上,以PC为直角边作等腰三角形PCQ,其中∠PCQ=90°,探究并解决下列问题:(1)如图①,若点P在线段AB上,且AC=1+,PA=,则:①线段PB= ,PC= 2 ;②猜想:PA2,PB2,PQ2三者之间的数量关系为PA2+PB2=PQ2;(2)如图②,若点P在AB的延长线上,在(1)中所猜想的结论仍然成立,请你利用图②给出证明过程;(3)若动点P满足=,求的值.(提示:请利用备用图进行探求)解:(1)如图①:①∵△ABC是等腰直直角三角形,AC=1+∴AB===+,∵PA=,∴PB=,作CD⊥AB于D,则AD=CD=,∴PD=AD﹣PA=,在RT△PCD中,PC==2,故答案为,2;②如图1.∵△ACB为等腰直角三角形,CD⊥AB,∴CD=AD=DB.∵AP2=(AD﹣PD)2=(DC﹣PD)2=DC2﹣2DC•PD+PD2,PB2=(DB+PD)2=(DC+DP)2=CD2+2DC •PD+PD2∴AP2+BP2=2CD2+2PD2,∵在Rt△PCD中,由勾股定理可知:PC2=DC2+PD2,∴AP2+BP2=2PC2.∵△CPQ为等腰直角三角形,∴2PC2=PQ2.∴AP2+BP2=PQ2(2)如图②:过点C作CD⊥AB,垂足为D.∵△ACB为等腰直角三角形,CD⊥AB,∴CD=AD=DB.∵AP2=(AD+PD)2=(DC+PD)2=CD2+2DC•PD+PD2,PB2=(DP﹣BD)2=(PD﹣DC)2=DC2﹣2DC•PD+PD2,∴AP2+BP2=2CD2+2PD2,∵在Rt△PCD中,由勾股定理可知:PC2=DC2+PD2,∴AP2+BP2=2PC2.∵△CPQ为等腰直角三角形,∴2PC2=PQ2.∴AP2+BP2=PQ2.(3)如图③:过点C作CD⊥AB,垂足为D.①当点P位于点P处时.1∵,∴.∴.D中,由勾股定理得:==DC,在Rt△CP1在Rt△ACD中,由勾股定理得:AC===DC,∴=.处时.②当点P位于点P2∵=,∴.D中,由勾股定理得:==,在Rt△CP2在Rt△ACD中,由勾股定理得:AC===DC,∴=.综上所述,的比值为或已知∠MAN=135°,正方形ABCD绕点A旋转.。
2021年九年级数学中考第三轮压轴题冲刺:三角形 典型题训练

2021年九年级数学中考第三轮压轴题冲刺:三角形 典型题训练1、如图,在锐角三角形 ABC 中,点D ,E 分别在边 AC ,AB 上,AG ⊥BC 于点G ,AF ⊥DE 于点F ,∠EAF=∠GAC .(1)求证:△ADE ∽△ABC ;(2)若 A D=3,AB=5,求的值.2、如图,△ABC 中,AB =AC ,∠B 的平分线交AC 于D ,AE ∥BC 交BD 的延长线于点E ,AF ⊥AB 交BE 于点F .(1)若∠BAC =40°,求∠AFE 的度数; (2)若AD =DC =2,求AF 的长.3、如图,ABC ∆和CDE ∆都是等边三角形,点B 、C 、E 三点在同一直线上,连接BD ,AD ,BD 交AC 于点F .(1)若2AD DF DB =⋅,求证:AD BF =; (2)若90BAD ∠=︒,6BE =. ①求tan DBE ∠的值;②求DF 的长.4、已知:如图,在Rt △ABC 中,∠ACB=90°,点M 是斜边AB 的中点,MD ∥BC ,且MD=CM ,DE ⊥AB 于点E ,连结AD 、CD . (1)求证:△MED ∽△BCA ; (2)求证:△AMD ≌△CMD ;(3)设△MDE 的面积为S 1,四边形BCMD 的面积为S 2,当S 2=S 1时,求cos ∠ABC 的值.5、如图,ADE ∆由ABC ∆绕点A 按逆时针方向旋转90︒得到,且点B 的对应点D 恰好落在BC 的延长线上,AD ,EC 相交于点P .(1)求BDE ∠的度数;(2)F 是EC 延长线上的点,且∠=∠CDF DAC . ①判断DF 和PF 的数量关系,并证明;②求证:=EP PCPF CF.6、如图1,已知在Rt △ABC 中,∠ACB =90°,AC =BC =4,点D 为边BC 上一动点(与点B 、C 不重合),点E 为边AB 上一点,∠EDB =∠ADC ,过点E 作EF ⊥AD ,垂足为G ,交射线AC 于点F .(1)如果点D 为BC 的中点,求∠DAB 的正切值;(2)当点F 在边AC 上时,设CD =x ,CF =y ,求y 关于x 的函数解析式及定义域;(3)联结DF ,如果△CDF 与△AGE 相似,求线段CD 的长.7、感知:如图 1,AD 平分∠BAC .∠B+∠C=180°,∠B=90°,易知:DB=DC . 探究:如图 2,AD 平分∠BAC ,∠ABD+∠ACD=180°,∠ABD <90°,求证:DB=DC应用:如图 3,四边形ABCD 中,∠B=45°,∠C=135°,DB=DC=a ,则 AB ﹣AC= (用含 a 的代数式表示)8、如图1,已知△ABC≌△EBD,∠ACB=∠EDB=90°,点D在AB上,连接CD 并延长交AE于点F.(1)猜想:线段AF与EF的数量关系为;(2)探究:若将图1的△EBD绕点B顺时针方向旋转,当∠CBE小于180°时,得到图2,连接CD并延长交AE于点F,则(1)中的结论是否还成立?若成立,请证明;若不成立,请说明理由;(3)拓展:图1中,过点E作EG⊥CB,垂足为点G.当∠ABC的大小发生变化,其它条件不变时,若∠EBG=∠BAE,BC=6,直接写出AB的长.9、已知Rt△ABC中,∠ACB=90°,点D、E分别在BC、AC边上,连结BE、AD交于点P,设AC=kBD,CD=kAE,k为常数,试探究∠APE的度数:(1)如图1,若k=1,则∠APE的度数为;(2)如图2,若k=,试问(1)中的结论是否成立?若成立,请说明理由;若不成立,求出∠APE的度数.(3)如图3,若k=,且D、E分别在CB、CA的延长线上,(2)中的结论是否成立,请说明理由.10、在△ABC 中,E、F 分别为线段AB、AC 上的点(不与 A、B、C 重合).如图 1,若 EF∥BC,求证:如图 2,若 EF 不与 BC 平行,(1)中的结论是否仍然成立?请说明理由;如图 3,若 EF 上一点 G 恰为△ABC 的重心,,求的值.11、在等腰ABC 中,AB BC =,点D ,E 在射线BA 上,BD DE =,过点E 作//EF BC ,交射线CA 于点F .请解答下列问题:(1)当点E 在线段AB 上,CD 是ACB △的角平分线时,如图①,求证:AE BC CF +=;(提示:延长CD ,FE 交于点M .)(2)当点E 在线段BA 的延长线上,CD 是ACB △的角平分线时,如图②;当点E 在线段BA 的延长线上,CD 是ACB △的外角平分线时,如图③,请直接写出线段AE ,BC ,CF 之间的数量关系,不需要证明;(3)在(1)、(2)的条件下,若26DE AE ==,则CF =___________.12、在等腰△ABC 中,∠B=90°,AM 是△ABC 的角平分线,过点M 作MN ⊥AC 于点N ,∠EMF=135°.将∠EMF 绕点M 旋转,使∠EMF 的两边交直线AB 于点E ,交直线AC 于点F ,请解答下列问题:(1)当∠EMF 绕点M 旋转到如图①的位置时,求证:BE+CF=BM ;(2)当∠EMF 绕点M 旋转到如图②,图③的位置时,请分别写出线段BE ,CF ,BM 之间的数量关系,不需要证明;(3)在(1)和(2)的条件下,tan∠BEM=,AN=+1,则BM= ,CF= .13、在△ABC中,AB=BC,点O是AC的中点,点P是AC上的一个动点(点P不与点A,O,C重合).过点A,点C作直线BP的垂线,垂足分别为点E和点F,连接OE,OF.(1)如图1,请直接写出线段OE与OF的数量关系;(2)如图2,当∠ABC=90°时,请判断线段OE与OF之间的数量关系和位置关系,并说明理由(3)若|CF﹣AE|=2,EF=2,当△POF为等腰三角形时,请直接写出线段OP的长.14、如图,△OAB 是边长为2+的等边三角形,其中O 是坐标原点,顶点B 在y轴正方向上,将△OAB 折叠,使点A 落在边OB 上,记为A ′,折痕为EF . (1)当A ′E ∥x 轴时,求点A ′和E 的坐标;(2)当A ′E ∥x 轴,且抛物线y=﹣x 2+bx+c 经过点A ′和E 时,求抛物线与x 轴的交点的坐标;(3)当点A ′在OB 上运动,但不与点O 、B 重合时,能否使△A ′EF 成为直角三角形?若能,请求出此时点A ′的坐标;若不能,请你说明理由.15、【初步尝试】(1)如图①,在三角形纸片ABC 中,90ACB ∠=︒,将ABC 折叠,使点B 与点C 重合,折痕为MN ,则AM 与BM数量关系为 ;【思考说理】(2)如图②,在三角形纸片ABC 中,6AC BC ==,10AB =,将ABC 折叠,使点B 与点C 重合,折痕为MN ,求AMBM的值.【拓展延伸】(3)如图③,在三角形纸片ABC 中,9AB =,6BC =,2ACB A ∠=∠,将ABC 沿过顶点C 的直线折叠,使点B 落在边AC 上的点B '处,折痕为CM . ①求线段AC 的长;②若点O 是边AC 的中点,点P 为线段OB '上的一个动点,将APM △沿PM 折叠得到A PM ',点A 的对应点为点A ',A M '与CP 交于点F ,求PFMF的取值范围.。
