广州中考圆压轴题专题#(精选.)

合集下载

中考数学压轴题专题圆的综合的经典综合题附详细答案

中考数学压轴题专题圆的综合的经典综合题附详细答案中考数学压轴题专题：圆的综合一、圆的综合1.如图，⊙O的半径为6cm，经过⊙O上一点C作⊙O的切线交半径OA的延长于点B，作∠ACO的平分线交⊙O于点D，交OA于点F，延长DA交BC于点E。

1) 求证：AC∥OD；2) 如果DE⊥BC，求AC的长度。

答案】(1) 证明见解析；(2) 2π。

解析】试题分析：(1) 由OC=OD，CD平分∠ACO，易证得∠ACD=∠ODC，即可证得AC∥OD；(2) BC切⊙O于点C，DE⊥BC，易证得平行四边形ADOC是菱形，继而可证得△AOC是等边三角形，则可得：∠AOC=60°，继而求得弧AC的长度。

试题解析：1) 证明：因为OC=OD，所以∠OCD=∠XXX。

因为CD平分∠ACO，所以∠XXX∠ACD。

因此，∠ACD=∠ODC，即可证得AC∥OD。

2) 因为BC切⊙XXXC，所以XXX。

因为DE⊥BC，所以OC∥DE。

因为AC∥OD，所以四边形ADOC是平行四边形。

因为OC=OD，所以平行四边形ADOC是菱形，所以OC=AC=OA。

因为△AOC是等边三角形，所以∠AOC=60°，因此弧AC的长度为2π。

点睛：本题考查了切线的性质、等腰三角形的判定与性质、菱形的判定与性质以及弧长公式。

此题难度适中，注意掌握数形结合思想的应用。

2.(类比概念) 三角形的内切圆是以三个内角的平分线的交点为圆心，以这点到三边的距离为半径的圆，则三角形可以称为圆的外切三角形，可以得出三角形的三边与该圆相切。

以此类推，如图1，各边都和圆相切的四边形称为圆外切四边形。

性质探究) 如图1，试探究圆外切四边形的ABCD两组对边AB，CD与BC，AD之间的数量关系。

猜想结论：(要求用文字语言叙述)写出证明过程（利用图1，写出已知、求证、证明）性质应用)①初中学过的下列四边形中哪些是圆外切四边形(填序号)：A：平行四边形；B：菱形；C：矩形；D：正方形。

中考各省压轴之圆综合问题(9考点39题)—2024年中考数学压轴题(全国通用)(解析版)

中考各省压轴之圆综合问题（9考点39题）一．圆周角定理（共3小题）1．如图，在⊙O中，将沿弦AB翻折，使恰好经过圆心O，C是劣弧AB上一点．已知AE＝2，tan∠CBA＝，则AB的长为（）A．B．6C．D．【答案】C【解答】解：连接EO并延长交⊙O于点H，连接AH，过点O作OF⊥AB于F，延长OF交⊙O于点G，连接OB，∵EH是⊙O的直径，∴∠EAH＝90°，∴tan∠AHE＝，∵∠AHE＝∠CBA，tan∠CBA＝，∴tan∠AHE＝tan∠CBA＝，∴＝，∵AE＝2，∴AH＝4，∴EH＝＝2，∴⊙O的半径为，∴OG＝OB＝，∵OG⊥AB于F，∴AB＝2BF，根据折叠的性质得，OF＝GF，∴OF＝OG＝，∴BF＝＝，∴AB＝，故选：C．2．如图，AB是半圆的直径，点C是弧AB的中点，点E是弧AC的中点，连接EB，CA交于点F，则＝（）A．B．C．1﹣D．【答案】D【解答】解：方法1：连接AE、CE．作AD∥CE，交BE于D．∵点E是弧AC的中点，∴可设AE＝CE＝1，根据平行线的性质得∠ADE＝∠CED＝45°．∴△ADE是等腰直角三角形，则AD＝，BD＝AD＝．所以BE＝+1．再根据两角对应相等得△AEF∽△BEA，则EF＝＝﹣1，BF＝2．所以＝．方法2：过点C作CO⊥AB于点O，∵AB是半圆的直径，点C是弧AB的中点，∴点O是圆心．连接OE，BC，OE与AC交于点M，∵E为弧AC的中点，易证OE⊥AC，∵∠ACB＝90°，∠AOE＝45°，∴OE∥BC，设OM＝1，则AM＝1，∴AC＝BC＝2，OA＝，∴OE＝，∴EM＝﹣1，∵OE∥BC，∴＝＝．故选：D．3．如图，MN是⊙O的直径，MN＝2，点A在⊙O上，∠AMN＝30°，B为弧AN的中点，P是直径MN上一动点，则P A+PB的最小值为．【答案】见试题解答内容【解答】解：作点B关于MN的对称点C，连接AC交MN于点P，连接OB，则P点就是所求作的点．此时P A+PB最小，且等于AC的长．连接OA，OC，∵∠AMN＝30°，∴∠AON＝60°，∵＝∴∠AOB＝∠BON＝30°，∵MN⊥BC，∴＝，∴∠CON＝∠NOB＝30°，则∠AOC＝90°，又OA＝OC＝1，则AC＝．二．切线的性质（共1小题）4．为了测量一个圆形铁环的半径，小华采用了如下方法：将铁环平放在水平桌面上，用一个锐角为30°的直角三角板和一个刻度尺，按如图所示的方法得到有关数据，进而求得铁环的半径，若测得AB＝10cm，则铁环的半径是．【答案】见试题解答内容【解答】解：如图所示：连接OB，OC，OA，∵AB为圆O的切线，∴OB⊥AB，即∠OBA＝90°，又AC为圆O的切线，∴OC⊥AC，即∠OCA＝90°，在Rt△ADE中，∠E＝30°，∠ADE＝90°，∴∠EAD＝60°，∠BAC＝120°，∵AC及AB为圆O的切线，∴OA为∠BOC的平分线，则∠BAO＝∠OAC，可得∠BOA＝∠COA，又∠OBA＝∠OCA＝90°，∴∠OAB＝∠OAC＝∠BAC＝60°，在Rt△OBA中，∠OBA＝90°，∠OAB＝60°，AB＝10cm，∴tan60°＝，即＝，则圆的半径OB＝10cm．故答案为：10cm三．切线的判定与性质（共2小题）5．如图，点C在以AB为直径的半圆上，AB＝4，∠CBA＝30°，点D在线段AB上运动，点E与点D关于AC对称，DF⊥DE于点D，并交EC的延长线于点F．下列结论：①∠F＝30°；②CE＝CF；③线段EF的最小值为2；④当AD＝1时，EF与半圆相切；⑤当点D从点A运动到点B时，线段EF扫过的面积是8．其中正确的结论的序号为．【答案】②③④．【解答】解：①连接CD，如图1所示．∵点E与点D关于AC对称，∴CE＝CD．∴∠E＝∠CDE．∵DF⊥DE，∴∠EDF＝90°．∴∠E+∠F＝90°，∠CDE+∠CDF＝90°．∴∠F＝∠CDF．只有当CD⊥AB时，∠F＝∠CDF＝∠CBA＝30°，故①错误；②又∵∠F＝∠CDF，∴CD＝CF，∴CE＝CD＝CF．故②正确；③当CD⊥AB时，如图2所示．∵AB是半圆的直径，∴∠ACB＝90°，∵AB＝4，∠CBA＝30°，∴∠CAB＝60°，AC＝2，BC＝2，∵CD⊥AB，∠CBA＝30°，∴CD＝BC＝，根据“点到直线之间，垂线段最短”可得：点D在线段AB上运动时，CD的最小值为．∵CE＝CD＝CF，∴EF＝2CD．∴线段EF的最小值为2．故③正确；④当AD＝1时，连接OC，如图3所示，∵OA＝OC，∠CAB＝60°，∴△OAC是等边三角形．∴CA＝CO，∠ACO＝60°．∵AO＝2，AD＝1，∴DO＝1．∴AD＝DO，∴∠ACD＝∠OCD＝30°，∵点E与点D关于AC对称，∴∠ECA＝∠DCA，∴∠ECA＝30°，∴∠ECO＝90°，∴OC⊥EF，∵EF经过半径OC的外端，且OC⊥EF，∴EF与半圆相切．故④正确；⑤∵点D与点E关于AC对称，点D与点F关于BC对称，∴当点D从点A运动到点B时，点E的运动路径AM与AB关于AC对称，点F的运动路径NB与AB关于BC对称．∴EF扫过的图形就是图5中阴影部分．∴S阴影＝2S△ABC＝2×•AC•BC＝4．故⑤错误．故答案为②③④．6．如图，⊙O是Rt△ABC的外接圆，AB为直径，∠ABC＝30°，CD⊥OC于C，ED⊥AB 于F，（1）判断△DCE的形状；（2）设⊙O的半径为1，且OF＝，求证：△DCE≌△OCB．【答案】见试题解答内容【解答】解：（1）△DCE为等腰三角形，理由为：∵∠ABC＝30°，圆周角∠ABC与圆心角∠AOC都对，∴∠AOC＝2∠ABC＝60°，又∵OA＝OC，∴△OAC为等边三角形，∴∠OAC＝∠OCA＝60°，∵OC⊥CD，∴∠OCD＝90°，∴∠DCE＝180°﹣90°﹣60°＝30°，又∵EF⊥AF，∴∠AFE＝90°，∴∠E＝180°﹣90°﹣60°＝30°，∴∠DCE＝∠E，∴DC＝DE，则△DCE为等腰三角形；（2）∵OA＝OB＝1，OF＝，∴AF＝AO+OF＝1+＝，OA＝AC＝OC＝1，在Rt△AEF中，∠E＝30°，∴AE＝2AF＝+1，∴CE＝AE﹣AC＝+1﹣1＝，又∵AB为圆O的直径，∴∠ACB＝90°，在Rt△ABC中，∠B＝30°，∴cos30°＝，即BC＝AB cos30°＝，∴CB＝CE＝，在△OBC和△DCE中，∵，∴△OBC≌△DCE（ASA）．四．三角形的内切圆与内心（共1小题）7．如图，Rt△ABC中，∠C＝90°，AC＝8，BC＝6，I为Rt△ABC的内心，若M、N分别是斜边AB和直角边AC上的动点，连接IM、MN，则IM+MN的最小值为．【答案】5.2．【解答】解：分别作ID⊥BC，IE⊥AC，IF⊥AB，垂足分别为点D、E、F，延长IF到I'，使I'F＝IF，作I'N⊥AC于点N，交AB于点M，延长DI，交I'N于点G，连接BI，∵IF⊥AB，I'F＝IF，∴IM＝I'M，∴IM+MN＝I'M+MN，当I'、M、N三点共线，且I'N⊥AC时，I'N最短，即IM+MN的值最小．∵I为Rt△ABC的内心，ID⊥BC，IE⊥AC，IF⊥AB，∴ID＝IE＝IF，设ID＝IE＝IF＝r，又∵ID⊥BC，IE⊥AC，∠C＝90°，∴四边形CEID是正方形，∴CD＝IE＝CE＝ID＝r，∵Rt△ABC中，∠C＝90°，AC＝8，BC＝6，∴AB＝10，∴BD＝6﹣r，AE＝8﹣r，在Rt△BID和Rt△BIF中，，∴Rt△BID≌Rt△BIF（HL），∴BD＝BF，同理AE＝AF，∵AB＝AF+BF，∴6﹣r+（8﹣r）＝10，解得r＝2，∵I'F＝IF，∴II'＝4，∵IF⊥AB，I'N⊥AC，∠FMI'＝∠NMA，∴∠I'＝∠A，又∵∠C＝90°，I'N⊥AC，∴BC∥I'N，∵ID⊥BC，∴IG⊥I'N，∴四边形CDGN为矩形，△II'G∽△BAC，∴GN＝CD＝2，，即，∴I'G＝3.2，∴I'N＝I'G+GN＝3.2+2＝5.2，∴IM+MN的最小值为5.2．故答案为：5.2．五．圆与圆的位置关系（共1小题）8．如图，⊙O1和⊙O2的半径为1和3，连接O1O2，交⊙O2于点P，O1O2＝8，若将⊙O1绕点P按顺时针方向旋转360°，则⊙O1与⊙O2共相切次．【答案】见试题解答内容【解答】解：两圆相切时，O1O2之间的距离等于4（外切）或者2（内切）时即可，当⊙O1绕P点顺时针旋转时360°时，O1O2的变化范围从8到2再到8，其中有两次外切和一次内切．可以用尺规作图的方法来做，以P为圆心做一个半径为5的圆，再以O2为圆心，做一个半径为4的圆，两者相交即为外切，然后以O2为圆心做一个半径为2的圆，两者相交即为内切．故答案为：3．六．弧长的计算（共1小题）9．一位小朋友在粗糙不打滑的“Z”字形平面轨道上滚动一个半径为10cm的圆盘，如图所示，AB与CD是水平的，BC与水平面的夹角为60°，其中AB＝60cm，CD＝40cm，BC ＝40cm，那么该小朋友将圆盘从A点滚动到D点其圆心所经过的路线长为 cm．【答案】见试题解答内容【解答】解：A点滚动到D点其圆心所经过的路线＝（60+40+40）﹣+＝（cm）．故答案为：（）．七．扇形面积的计算（共1小题）10．如图，在△ABC中，AB＝8cm，BC＝4cm，∠ABC＝30°，把△ABC以点B为中心按逆时针方向旋转，使点C旋转到AB边的延长线上的C′′处，那么AC边扫过的图形（图中阴影部分）的面积是 cm2（结果保留π）．【答案】见试题解答内容【解答】解：×（64﹣16）＝20πcm2．八．圆锥的计算（共3小题）11．现有30%圆周的一个扇形彩纸片，该扇形的半径为40cm，小红同学为了在“六一”儿童节联欢晚会上表演节目，她打算剪去部分扇形纸片后，利用剩下的纸片制作成一个底面半径为10cm的圆锥形纸帽（接缝处不重叠），那么剪去的扇形纸片的圆心角为．【答案】见试题解答内容【解答】解：20π＝解得：n＝90°，∵扇形彩纸片是30%圆周，因而圆心角是108°∴剪去的扇形纸片的圆心角为108°﹣90°＝18°．剪去的扇形纸片的圆心角为18°．故答案为18°．12．如图，有一直径为4的圆形铁皮，要从中剪出一个最大圆心角为60°的扇形ABC．用此剪下的扇形铁皮围成一个圆锥，该圆锥的侧面积为．【答案】见试题解答内容【解答】解：连接OA，过点O作OD⊥AB，∵∠CAB＝60°，∴∠OAD＝30°，∵AO＝2，∴DO＝1，∴AD＝，∴AB＝2，∴S阴影＝＝2π．故答案为：2π．13．如图，圆锥的母线长是3，底面半径是1，A是底面圆周上一点，从A点出发绕侧面一周，再回到A点的最短的路线长是．【答案】3．【解答】解：∵图扇形的弧长是2π，根据弧长公式得到2π＝，∴n＝120°即扇形的圆心角是120°，∴弧所对的弦长AA′＝2×3sin60°＝3，故答案为3．九．圆的综合题（共26小题）14．如图，半径为4的⊙O中，CD为直径，弦AB⊥CD且过半径OD的中点，点E为⊙O 上一动点，CF⊥AE于点F．当点E从点B出发顺时针运动到点D时，点F所经过的路径长为（）A．B．C．D．【答案】C【解答】解：连接AC，AO，∵AB⊥CD，∴G为AB的中点，即AG＝BG＝AB，∵⊙O的半径为4，弦AB⊥CD且过半径OD的中点，∴OG＝2，∴在Rt△AOG中，根据勾股定理得：AG＝＝2，又∵CG＝CO+GO＝4+2＝6，∴在Rt△AGC中，根据勾股定理得：AC＝＝4，∵CF⊥AE，∴△ACF始终是直角三角形，点F的运动轨迹为以AC为直径的半圆，当E位于点B时，CG⊥AE，此时F与G重合；当E位于D时，CA⊥AE，此时F与A 重合，∴当点E从点B出发顺时针运动到点D时，点F所经过的路径长，在Rt△ACG中，tan∠ACG＝＝，∴∠ACG＝30°，∴所对圆心角的度数为60°，∵直径AC＝4，∴的长为＝π，则当点E从点B出发顺时针运动到点D时，点F所经过的路径长为π．故选：C．15．定义：如果一个三角形中有两个内角α，β满足α+2β＝90°，那我们称这个三角形为“近直角三角形”．（1）若△ABC是“近直角三角形”，∠B＞90°，∠C＝50°，则∠A＝度；（2）如图1，在Rt△ABC中，∠BAC＝90°，AB＝3，AC＝4．若BD是∠ABC的平分线，①求证：△BDC是“近直角三角形”；②在边AC上是否存在点E（异于点D），使得△BCE也是“近直角三角形”？若存在，请求出CE的长；若不存在，请说明理由．（3）如图2，在Rt△ABC中，∠BAC＝90°，点D为AC边上一点，以BD为直径的圆交BC于点E，连接AE交BD于点F，若△BCD为“近直角三角形”，且AB＝5，AF＝3，求tan∠C的值．【答案】见试题解答内容【解答】解：（1）∠B不可能是α或β，当∠A＝α时，∠C＝β＝50°，α+2β＝90°，不成立；故∠A＝β，∠C＝α，α+2β＝90°，则β＝20°，故答案为20；（2）①如图1，设∠ABD＝∠DBC＝β，∠C＝α，则α+2β＝90°，故△BDC是“近直角三角形”；②存在，理由：在边AC上是否存在点E（异于点D），使得△BCE是“近直角三角形”，AB＝3，AC＝4，则BC＝5，则∠ABE＝∠C，则△ABC∽△AEB，即，即，解得：AE＝，则CE＝4﹣＝；（3）①如图2所示，当∠ABD＝∠DBC＝β时，则AE⊥BF，则AF＝FE＝3，则AE＝6，AB＝BE＝5，过点A作AH⊥BC于点H，设BH＝x，则HE＝5﹣x，则AH2＝AE2﹣HE2＝AB2﹣HB2，即52﹣x2＝62﹣（5﹣x）2，解得：x＝；cos∠ABE＝＝＝cos2β，则tan2β＝，则tanα＝；②如图3所示，当∠ABD＝∠C＝β时，过点A作AH⊥BE交BE于点H，交BD于点G，则点G是圆的圆心（BE的中垂线与直径的交点），∵∠AEB＝∠DAE+∠C＝α+β＝∠ABC，故AE＝AB＝5，则EF＝AE﹣AF＝5﹣3＝2，∵DE⊥BC，AH⊥BC，∴ED∥AH，则AF：EF＝AG：DE＝3：2，则DE＝2k，则AG＝3k＝R（圆的半径）＝BG，点H是BE的中点，则GH＝DE＝k，在△BGH中，BH＝＝2k，在△ABH中，AB＝5，BH＝2k，AH＝AG+HG＝4k，∵∠C+∠ABC＝90°，∠ABC+∠BAH＝90°，∴∠C＝∠BAH，∴tan C＝tan∠BAH＝＝＝，综上，tan C的值为或．16．四边形ABCD内接于⊙O，AC是⊙O的直径，连结BD交AC于点G，AF⊥BD，垂足为E．（1）如图1，若AF交BC于点F．①求证：∠BAF＝∠CAD；②若⊙O的直径为10，，BF：CG＝3：5，求AF的长．（2）如图2，若AF交CD于点F，连结OD，若OD∥AB，，DF＝2CF，求⊙O 的直径．【答案】（1）①见解析；②AF＝．（2）⊙O的直径为．【解答】（1）①证明：∵AC是⊙O的直径，AF⊥BD，∴∠ABC＝90°＝∠AEB，∴∠ABE+∠CBD＝90°，∠ABE+∠BAF＝90°，∴∠CBD＝∠BAF，又∵，∴∠CBD＝∠CAD，∴∠BAF＝∠CAD．②解：如图，过点G作GK⊥BC于点K，在Rt△ABC中，AC＝10，cos∠BCA＝，∴BC＝8，由勾股定理得AB＝＝＝6，∴sin∠BCA＝＝，tan∠BCA＝＝，在Rt△GKC中，sin∠KCG＝sin∠BCA＝＝，tan∠KCG＝tan∠BCA＝＝，又∵BF：CG＝3：5，∴BF＝GK，在△ABF和△BKG中，，∴△ABF≌△BKG（AAS），∴AB＝BK＝6，∴CK＝BC﹣BK＝8﹣6＝2，∴KG＝CK•tan∠KCG＝2×＝，即BF＝KG＝，∴AF＝＝＝．（3）解：如图，设AF交OD于点Q，过点O作OH⊥AF于点H，链接BO并延长交AF 于点P，延长AF交⊙O于点G，连接CG，∵AF⊥BD，OH⊥AF，∴∠OHO＝∠BEG＝90°，∴OH∥BD，∴∠QOH＝∠ODB，∠POH＝∠OBD，又∵OB＝OD，∴∠ODB＝∠OBD，∴∠QOH＝∠POH，∴QH＝PH，∵AC为⊙O的直径，∴∠AGC＝90°＝∠OHQ＝∠AEB，∴CG∥OH∥BD，∴△AOH∽△ACG⇒⇒CG＝2OH，△DEF∽△CGF⇒＝⇒DE＝2CG⇒DE＝4OH，△DEQ∽△OHQ⇒＝＝4⇒QE＝4PH，DQ＝4OQ⇒EP＝6PH，DQ＝，△OPH∽△BPE⇒＝⇒BE＝6OH，∴，∵OD∥AB，∴△ABE∽△QDE，∴⇒QE＝⇒AQ＝＝，∵，OD＝OC，∴∠OCD＝∠ABD＝∠ODC，∴∠BAE＝90°﹣∠ABD＝90°﹣∠ODC＝∠ODA，∵OD∥AB，OA＝OD，∴∠AQD＝∠BAQ＝∠ODA＝∠OAD，∴AD＝AQ＝，△DAQ∽△DOA，∴，即AD2＝OD•DQ，设⊙O的半径为r，则OD＝r，DQ＝，∴＝，∴r＝，∴⊙O的直径为．17．如图，在平面直角坐标系xOy中，点S（﹣1，0），T（1，0）．对于一个角α（0°＜α≤180°），将一个图形先绕点S顺时针旋转α，再绕点T逆时针旋转α，称为一次“α对称旋转”．（1）点R在线段ST上，则在点A（1，﹣1），B（3，﹣2），C（2，﹣2），D（0，﹣2）中，有可能是由点R经过一次“90°对称旋转”后得到的点是；（2）x轴上的一点P经过一次“α对称旋转”得到点Q．①当α＝60°时，PQ＝；②当α＝30°时，若QT⊥x轴，求点P的坐标；（3）以点O为圆心作半径为1的圆．若在⊙O上存在点M，使得点M经过一次“α对称旋转”后得到的点在x轴上，直接写出α的取值范围．【答案】（1）B，C；（2）①2；②P（﹣1+，0）．（3）0°＜α≤30°或150°≤α≤180°．【解答】解：（1）如图，当点R与点O重合时，点R绕点S顺时针旋转90°得到点R′，点R′绕点T逆时针旋转90°得到点C；当点R与点T重合时，点R绕点S顺时针旋转90°得到点R″，点R″绕点T逆时针旋转90°得到点B；故答案为：B，C；（2）①当α＝60°时，如图，∵x轴上的一点P经过一次“α对称旋转”得到点Q，∴△SPP′和△TQP′均为等边三角形，∴SP′＝PP′，TP′＝QP′，∠SP′P＝∠TP′Q＝60°，∴∠SP′T+∠TP′P＝∠TP′P+∠PP′Q，∴∠SP′T＝∠PP′Q，∴△P′ST≌△P′PQ（SAS），∴PQ＝ST＝2，故答案为：2；②当α＝30°时，设点P绕点S顺时针旋转30°得到点P′，则SP′＝SP，如图，将x轴作一次“α对称旋转”后得到直线y＝﹣1，∵QT⊥x轴，点P经过一次“α对称旋转”得到点Q，∴点Q的坐标为Q（1，﹣1），∵点P′绕点T逆时针旋转30°得到点Q，∴P′T＝QT＝1，∠P′TQ＝30°，∴∠STP′＝90°﹣∠P′TQ＝60°，∵∠TSP′＝30°，∴∠SP′T＝180°﹣∠STP′﹣∠TSP′＝90°，∵ST＝2，∴SP′＝＝，∴SP＝SP′＝，∴点P的坐标为P（﹣1+，0）．（3）点M在⊙O上，则M绕S顺时针旋转α度以后的M′的轨迹为O绕S顺时针旋转α度以后的⊙O′上，M′关于T逆时针旋转α度以后得到点N，则N在O′关于T逆时针旋转α度以后的⊙O″上，若满足题意，只需⊙O′与x轴有交点O″在粉弧上，且O′T＝O″T，如图，⊙O″与x轴相切，则O″H＝1，在x轴上取点R，连接O″R，使O″R＝2，″∴HR＝，∴∠O″RH＝30°，TR＝O′S＝1，O″R＝ST＝2，O″T＝O′T，∴△O″TR≌△TO′S（SSS），∴∠TSO′＝∠O″RT＝30°，故0°＜α≤30°；如图，⊙O″与x轴相切，则O″H＝1，在x轴上取点R，连接O″R，使O″R＝2，∴∠HRO″＝30°，ST＝O″R，∴∠TRO″＝150°，∵∠SO′T+∠STO′＝∠STO′+∠RTO″，∴∠SO′T＝∠RTO″，∵O′T＝TO″，∴△O′ST≌△TRO″（SAS），∴∠O′ST＝∠TRO″＝150°，∴α＝150°，∴150°≤α≤180°；综上所述，0°＜α≤30°或150°≤α≤180°．18．问题提出（1）如图①，已知直线a∥b，点A，B在直线a上，点C，D在直线b上，则S△ACD S（填“＞”“＜”或“＝”）；△BCD问题探究（2）如图②，⊙O的直径为20，点A，B，C都在⊙O上，AB＝12，求△ABC面积的最大值；问题解决（3）如图③，在△ABC中，∠ACB＝90°，AB＝20，BC＝10，根据设计要求，点D为∠ABC内部一点，且∠ADB＝60°，过点C作CE∥AD交BD于点E，连接AE，CD，试求满足设计要求的四边形ADCE的最大面积．【答案】（1）＝；（2）△ABC面积的最大值为108；（3）四边形ADCE的最大面积是75．【解答】解：（1）如图①所示，分别过A、B两点向直线b作垂线，垂足为M、N.∵a∥b，∴∠MAB＝∠AMN＝90°，∴四边形AMNB是矩形，∴AM＝BN，∴CD•AM＝CD•BN又S△ACD＝CD•AM，S△BCD＝CD•BN，∴S△ACD＝S△BCD；故答案为：＝；（2）取优弧的中点记为C1，过C1作AB的垂线，垂足为D，由垂径定理知C1D过O 且AD＝BD，如图②所示.过点C作AB的平行线a，∵当直线a向上平移时，a距AB的距离增大，即△ABC的AB边上的高增大，∴当a运动到最高点C时，△ABC的AB边上的高最大，又∵AB为常数，∴当C运动到C1时，△ABC的面积最大，下面计算△ABC1的面积：连接OB，在Rt△OBD中，∵AB＝12，⊙O的直径为20，∴BD＝6，BO＝10，OC1＝10，由勾股定理得：OD＝＝＝8，∴C1D＝OD+OC1＝8+10＝18，∴△ABC1的面积为：AB•C1D＝×12×18＝108，∴△ABC面积的最大值为108；（3）过点C作CF∥BD交AD的延长线于F，如图③﹣1所示，∵CF∥BD，∴∠F＝∠ADB＝60°，∵AD∥CE，∴四边形DECF是平行四边形，∴DF＝CE，FC＝DE，∵DC＝CD∴△DFC≌△CED（SSS），∴S△DFC＝S△CED，又由（1）的结论知S△DAC＝S△DAE，∴S四边形ADCE＝S△DAE+S△CED＝S△DAC+S△DFC＝S△AFC，所以只需求得S△AFC最大值即得S四边形ADCE的最大值.以AC为边向△ABC外作等边△AGC，再作等边△AGC的外接圆，过G作GJ⊥AC于J，如图③﹣2所示，∵∠F＝60°，∴点F在△AGC的外接圆上，由第（2）问的解决知，当F运动到点G时，S△AFC最大＝S△ACG；在Rt△ABC中：由勾股定理得AC＝＝＝10，∴AJ＝AC＝5，∴GJ＝×10＝15，∴S△ACG＝AC×GJ＝×10×15＝75；∴四边形ADCE的最大面积是75．19．课本再现（1）在圆周角和圆心角的学习中，因为圆内接四边形的每一个角都是圆周角，所以我们可以利用圆周角定理，来研究圆内接四边形的角之间的关系．如图1，四边形ABCD为⊙O的内接四边形，AC为直径，则∠B＝∠D＝度，∠BAD+∠BCD＝度．（2）如果⊙O的内接四边形ABCD的对角线AC不是⊙O的直径，如图2、图3，请选择一个图形证明：圆内接四边形的对角互补．知识运用（3）如图4，等腰三角形ABC的腰AB是⊙O的直径，底边和另一条腰分别与⊙O交于点D，E．点F是线段CE的中点，连接DF，求证：DF是⊙O的切线．【答案】（1）90，180；（2）证明见解答；（3）证明见解答．【解答】（1）解：∵四边形ABCD为⊙O的内接四边形，AC为直径，∴∠B＝∠D＝90°，∴∠BAD+∠BCD＝360°﹣（∠B+∠D）＝360°﹣180°＝180°，故答案为：90，180；（2）证明：如图2，连接OB，OD，∵＝，∴∠BOD＝2∠C，∠1＝2∠A，∵∠BOD+∠1＝360°，∴2∠C+2∠A＝360°，∴∠C+∠A＝180°，在四边形ABCD中，∠ABC+∠ADC＝360°﹣（∠A+∠C）＝180°，即圆内接四边形的对角互补；如图3，连接OA，OC，∵＝，∴∠AOC＝2∠B，∠1＝2∠D，∵∠AOC+∠1＝360°，∴2∠B+2∠D＝360°，∴∠B+∠D＝180°，在四边形ABCD中，∠BAD+∠DCB＝360°﹣（∠B+∠D）＝180°，即圆内接四边形的对角互补；（3）证明：连接OD，DE，如图4，∵OB＝OD，∴∠B＝∠ODB，∵AB＝AC，∴∠B＝∠C，∴∠ODB＝∠C，∴OD∥AC，∵四边形ABDE是圆内接四边形，∴∠B+∠AED＝180°，∵∠DEC+∠AED＝180°，∴∠B＝∠DEC，∴∠C＝∠DEC，∴DC＝DE，∵点F是线段CE的中点，∴DF⊥AC，∴OD∥AC，∴DF⊥OD，∵OD是⊙O的半径，∴DF是⊙O的切线．20．如图，以Rt△ABC的直角边AB为直径作⊙O，交斜边AC于点D，点E是BC的中点，连接OE、DE．（1）求证：DE是⊙O的切线；（2）若sin C＝，DE＝5，求AD的长；（3）求证：2DE2＝CD•OE．【答案】（1）证明见解答；（2）AD的长为；（3）证明见解答．【解答】（1）证明：连接OD，BD，在Rt△ABC中，∠ABC＝90°，∵AB是⊙O的直径，∴∠ADB＝90°，∴∠BDC＝180°﹣∠ADB＝90°，∵点E是BC的中点，∴DE＝BE＝EC，∵OB、OD是⊙O的半径，∴OB＝OD，又∵OE＝OE，∴△ODE≌△OBE（SSS），∴∠ODE＝∠OBE＝90°，∴半径OD⊥DE，∴DE是⊙O的切线；（2）解：连接BD，如图，由（1）知：DE＝BE＝EC，∠ADB＝∠BDC＝∠ABC＝90°，∵DE＝5，∴BC＝10，∵sin C＝，∴＝，∴BD＝8，∵∠C+∠CBD＝∠ABD+∠CBD＝90°，∴∠ABD＝∠C，∴sin∠ABD＝sin∠C＝，∴＝，设AD＝4x，则AB＝5x，∵AD2+BD2＝AB2，∴（4x）2+82＝（5x）2，解得：x＝（负值舍去），∴AD＝4x＝4×＝；（3）证明：连接BD，由（1）（2）得：∠BDC＝∠OBE＝90°，BE＝DE，∵点O是AB的中点，点E是BC的中点，∴OE∥AC，BC＝2BE，∴∠C＝∠OEB，∴△BCD∽△OEB，∴＝，即＝，∴2DE2＝CD•OE．21．已知在Rt△ABC中，∠ACB＝90°，BC＝6，AC＝8，以边AC为直径作⊙O，与AB 边交于点D，点M为边BC的中点，连接DM．（1）求证：DM是⊙O的切线；（2）点P为直线BC上任意一动点，连接AP交⊙O于点Q，连接CQ．①当tan∠BAP＝时，求BP的长；②求的最大值．【答案】（1）证明见解答；（2）①BP的长为或；②的最大值为．【解答】（1）证明：如图，连接OD，CD，∵AC是⊙O的直径，∴∠ADC＝90°，∴∠BDC＝180°﹣∠ADC＝90°，∵点M为边BC的中点，∴MC＝MD，∴∠MDC＝∠MCD，∵OC＝OD，∴∠ODC＝∠OCD，∵∠ACB＝90°，即∠MCD+∠OCD＝90°，∴∠MDC+ODC＝∠MCD+∠OCD＝90°，即∠ODM＝90°，∴DM⊥OD，∵OD是⊙O的半径，∴DM是⊙O的切线；（2）①当点P在线段BC上时，如图，过点P作PT⊥AB于点T，在Rt△ABC中，AB＝＝＝10，设PT＝x，∵tan∠BAP＝，∴＝，∴AT＝3PT＝3x，∴BT＝AB﹣AT＝10﹣3x，∵tan∠ABC＝＝，∴＝，解得：x＝，∴PT＝，∵sin∠ABC＝＝，即＝，∴BP＝；当点P在CB的延长线上时，如图，过点B作BK⊥AP于点K，∵tan∠BAP＝，∴＝，设BK＝a，则AK＝3a，在Rt△ABK中，AK2+BK2＝AB2，即（3a）2+a2＝102，解得：a1＝，a2＝﹣（舍去），∴AK＝3，BK＝，∵S△ABP＝AP•BK＝BP•AC，∴＝＝，设BP＝m，则AP＝m，在Rt△ACP中，AC2+CP2＝AP2，即82+（m+6）2＝（m）2，解得：m1＝，m2＝﹣（舍去），∴BP＝；综上所述，BP的长为或；②设CP＝n，则AP＝＝，如图，∵AC是⊙O的直径，∴CQ⊥AP，∵CQ•AP＝AC•CP，∴CQ＝＝，∴＝，∵n＞0，∴（n﹣8）2≥0，∴64+n2≥16n，∴＝≤＝，∴的最大值为．22．如图（1），已知在Rt△ABC中，∠ACB＝90°，以AC为直径的圆O交斜边AC于点E，点D为BC中点，连接DE．（1）求证：DE是圆O的切线；（2）如图（2），EH⊥AC，垂足为H，若AC＝6，BC＝8，求EH的长；（3）如图（3），在⊙O上取一点P，使PE＝CE，连接PE，AP，试探究AP、AH、HC 之间的数量关系，并说明理由．【答案】见试题解答内容【解答】（1）连结OE，∵AC是直径，∴∠AEC＝90°∴∠CEB＝90°，∵D是BC的中点，∴CD＝DE，∴∠DCE＝∠DEC，∵∠ACB＝90°，∴∠DCE+∠OCE＝90°，∵OE＝OC，∴∠OCE＝∠OEC，∴∠OEC+∠DEC＝90°，∴OE⊥DE，∵OE是圆O的半径，∴DE是圆O的切线；（2）连结CE，∵AC＝6，BC＝8，∴，∵∠B＝∠B，∠CEB＝∠ACB＝90°，∴△CEB∽△ACB，∴，∴，∵HE⊥AC，∴∠EHC＝90°，∴，∴，∴；（3）在AC上取点M，使CM＝AP，∵PE＝CE，∠P＝∠MCE∴△APE≌△MCE（SAS）∴AE＝ME∵EH⊥AC∴AH＝MH∴CM＝CH﹣MH＝CH﹣AH，∴AP＝CH﹣AH．23．在平面直角坐标系xOy中，⊙O的半径为1，A为任意一点，B为⊙O上任意一点．给出如下定义：记A，B两点间的距离的最小值为p（规定：点A在⊙O上时，p＝0），最大值为q，那么把的值称为点A与⊙O的“关联距离”，记作d（A，⊙O）．（1）如图，点D，E，F的横、纵坐标都是整数．①d（D，⊙O）＝；②若点M在线段EF上，求d（M，⊙O）的取值范围；（2）若点N在直线y＝上，直接写出d（N，⊙O）的取值范围；（3）正方形的边长为m，若点P在该正方形的边上运动时，满足d（P，⊙O）的最小值为1，最大值为，直接写出m的最小值和最大值．【答案】（1）①2；②2≤d（M，⊙O）≤3；（2）d（N，⊙O）≥；（3）m的最小值为﹣，最大值为．【解答】解：（1）①∵D（0，2）到⊙O的距离的最小值p＝1，最大值q＝3，∴d（D，⊙O）＝＝2，故答案为：2；②当M在点E处，d（E，⊙O）＝2，当M在点F处，d（F，⊙O）＝＝3，∴2≤d（M，⊙O）≤3；（2）设ON＝d，∴p＝d﹣r＝d﹣1，q＝d+r＝d+1，∴d（N，⊙O）＝＝＝d，∵点N在直线y＝上，设直线交x轴于点B，交y轴于点A，如图1，则x＝0时，y＝2，y＝0时，x＝﹣2，∴A（0，2），B（﹣2，0），∴OA＝2，OB＝2，∴AB＝＝4，当ON⊥AB时，d（N，⊙O）最小，∴S△AOB＝OA•OB＝AB•ON，即×2×2＝×4ON，∴ON＝，∵ON无最大值，∴d（N，⊙O）≥；（3）如图2，∵d（P，⊙O）的最小值为1，最大值为，∴两个同心圆中，小圆的半径为1，大圆的半径为，∵KL＝﹣1，∴m的最小值是＝﹣，在Rt△OMH中，OM＝，OH＝m﹣1，MH＝m，∴（m﹣1）2+（m）2＝（）2，解得：m＝﹣2（舍去）或m＝；∴m的最小值为﹣，最大值为．24．在⊙O中＝，顺次连接A、B、C．（1）如图1，若点M是的中点，且MN∥AC交BC延长线于点N，求证：MN为⊙O 的切线；（2）如图2，在（1）的条件下，连接MC，过点A作AP⊥BM于点P，若BP＝a，MP ＝b，CM＝c，则a、b、c有何数量关系？（3）如图3，当∠BAC＝60°时，E是BC延长线上一点，D是线段AB上一点，且BD ＝CE，若BE＝5，△AEF的周长为9，请求出S△AEF的值？【答案】（1）证明见解答；（2）a＝b+c；（3）．【解答】解：（1）如图1，连接OM，∵M是的中点，∴OM⊥AC，∵MN∥AC，∴OM⊥MN，∵OM为⊙O的半径，∴MN为⊙O的切线；（2）如图2，连接OM交AC于K，连结AM，∵M是的中点，∴＝，∴AM＝CM＝c，∵AP⊥BM，∴∠APM＝∠APB＝90°，∴AP2＝AM2﹣PM2＝c2﹣b2，∴AB2＝AP2+BP2＝c2﹣b2+a2，∴AC＝AB＝，∵M是的中点，∴OM⊥AC，∴AK＝CK＝AC＝，∵∠APB＝∠CKM＝90°，∠ABP＝∠MCK，∴△ABP∽△MCK，∴＝，∴BP•CM＝CK•AB，∴ac＝•，∴2ac＝c2﹣b2+a2，∴（a﹣c）2﹣b2＝0，∴（a+b﹣c）（a﹣b﹣c）＝0，∵a+b﹣c＞0，∴a﹣b﹣c＝0，∴a＝b+c；（3）过点B作BH∥AC，过点D作DH∥BC，BH与DH交于点H，连接CH，则∠BDH＝∠ABC＝60°，∠DBH＝∠ACB＝60°，∴△BDH是等边三角形，∴BH＝BD，∠DBH＝60°，∴BH＝CE，∠CBH＝∠ABC+∠DBH＝60°+60°＝120°，∵∠ACE＝180°﹣∠ACB＝120°＝∠CBH，AC＝BC，∴△ACE≌△CBH（SAS），∴∠CAE＝∠BCH，AE＝CH，∵DH∥BC，DH＝CE，∴四边形CEDH是平行四边形，∴CE∥ED，CH＝ED，∴∠BCH＝∠BED，CH＝AE，∴∠BED＝∠CAE，AE＝ED，过点E作ET⊥AB于点T，交AC于点L，连接DL，则AT＝TD＝AD，AL＝DL，∵∠BAC＝60°，∴△ADL是等边三角形，∴∠ALD＝60°＝∠ACB，∴DL∥BC，即HD与DL在同一直线上，∴四边形BCLH是平行四边形，∴CL＝BH＝BD＝CE，LH＝BC，设CE＝x，则CL＝x，BC＝AC＝5﹣x，AD＝DL＝AL＝AC﹣CL＝5﹣2x，AT＝，∵DF∥CH，∴＝，即＝，∴LF＝，∴AF＝AL+LF＝5﹣2x+＝，在Rt△BET中，ET＝BE•sin60°＝，∵AE2＝AT2+ET2，∴AE2＝（）2+（）2＝x2﹣5x+25，延长BH，ED交于点R，则∠RHD＝∠FCE，∠R＝∠CFE，DH＝CE，∴△HDR≌△CEF（AAS），∴DR＝EF，∴ER＝ED+DR＝AE+EF＝9﹣AF＝9﹣＝，∵CH∥ED，∴＝，∴CH＝•ER＝×＝，∴AE＝，∴x2﹣5x+25＝（）2，解得：x1＝5（舍去），x2＝，∴AD＝5﹣2×＝，AF＝＝10﹣＝2，作DM⊥AL于点M，则DM＝AD•sin60°＝×＝，∴S△AEF＝S△ADE﹣S△ADF＝AD•ET﹣AF•DM＝××﹣×2×＝．25．在平面直角坐标系xOy中，⊙O的半径为1，AB＝1，且A，B两点中至少有一点在⊙O 外．给出如下定义：平移线段AB，得到线段A′B′（A′，B′分别为点A，B的对应点），若线段A′B′上所有的点都在⊙O的内部或⊙O上，则线段AA′长度的最小值称为线段AB到⊙O的“平移距离”．（1）如图1，点A1，B1的坐标分别为（﹣3，0），（﹣2，0），线段A1B1到⊙O的“平移距离”为，点A2，B2的坐标分别为（﹣，），（，），线段A2B2到⊙O的“平移距离”为；（2）若点A，B都在直线y＝x+2上，记线段AB到⊙O的“平移距离”为d，求d的最小值；（3）如图2，若点A坐标为（1，），线段AB到⊙O的“平移距离”为1，画图并说明所有满足条件的点B形成的图形（不需证明）．【答案】（1）2，；（2）．（3）所有满足条件的点B形成的图形是以A为圆心圆心角为120°的．【解答】解：（1）根据“平移距离”的定义可得：线段A1B1到⊙O的“平移距离”为2，如图1，设A2B2与y轴交于E，线段A2B2向下平移得到⊙O的弦A′2B′2，线段A′2B′2与y轴交于点F，则A′2F＝，OA′2＝1，OE＝，∴OF＝，∴A2A′2＝EF＝OE﹣OF＝﹣＝，∴线段A2B2到⊙O的“平移距离”为，故答案为：2，；（2）如图2中，作等边△OEF，点E在x轴上，OE＝EF＝OF＝1，设直线y＝x+2交x轴于M，交y轴于N．则M（﹣2，0），N（0，2），过点E作EH⊥MN于H，∵OM＝2，ON＝2，∴tan∠NMO＝，∴∠NMO＝60°，∴EH＝EM•sin60°＝，观察图象可知，线段AB到⊙O的“平移距离”为d1的最小值为．（3）如图3，连接OA，交⊙O于点A′，则OA＝＝2，∴OA到⊙O任意一点距离的最小值为OA′＝OA﹣1＝1，∴点A′（，），设平移后圆上另一点为B′，由题意得：A′B′＝1，有三种情况：①点B′与点O重合，则点B的坐标为（，）；②点B′与点（1，0）重合，则点B的坐标为（，）；③点B′与点（﹣，）重合，则点B的坐标为（0，）；如图可知所有满足条件的点B形成的图形是以A为圆心圆心角为120°的．26．【了解概念】定义：在平面直角坐标系xOy中，组成图形的各点中，与点P连线段最短的点叫做点P 于这个图形的短距点，这条最短线段的长度叫做点P这个图形的短距．【理解运用】（1）已知点P（﹣3，0），以原点为圆心，1半径作⊙O，则点P于⊙O的短距点的坐标是；（2）如图，点P（3，），等边三角形OAB的顶点A的坐标为（6，0），顶点B在第一象限，判断点P于△OAB的短距点的个数，并说明理由；【拓展提升】（3）已知P（p，﹣p+6），A（6，0），B（0，6），点C在第一象限内，且∠CBO＝75°，∠ACB＝90°，若点P到四边形OACB的短距大于2，请直接写出p的取值范围．【答案】（1）（﹣1，0）；（2）3个，理由见解答过程；（3）p＜﹣或2＜p＜4或p＞6+．【解答】解：（1）如图：根据短距点定义，点P于⊙O的短距点为A，坐标是（﹣1，0），故答案为：（﹣1，0）；（2）点P关于△OAB的短距点有3个，理由如下：过P作PC⊥OA于C，PE⊥AB于E，PD⊥OB于D，如图：∵P（3，），∴OC＝3，PC＝，∴tan∠POC＝，∴∠POC＝30°，∵△OAB是等边三角形，∴∠BOC＝60°，OA＝6，∴∠BOP＝∠POC＝30°，又PC⊥OA，PD⊥OB，∴PD＝PC＝，∵AC＝OA﹣OC＝3，PC＝，∴tan∠P AC＝，∴∠P AC＝30°，同理∠P AE＝∠P AC＝30°，PE＝PC，∴PC＝PD＝PE，即点P关于△OAB的短距点有C、D、E，∴点P关于△OAB的短距点有3个；（3）∵P（p，﹣p+6），∴P在直线y＝﹣x+6上，直线经过A（6，0）、B（0，6），且∠ABO＝∠BAO＝45°，①当p＜0时，过P作PD⊥x轴于D，过B作PE⊥PD于E，如图：△PBE是等腰直角三角形，若PB＝2，则BE＝PE＝，而DE＝OB＝6，∴PD＝6+，∴P（﹣，6+），由图可知：此时p＜﹣，点P到四边形OACB的短距大于2，②当0≤p≤6时，过P作PD⊥BC于D，设PD＝2，作PE⊥OB，PF⊥OA，过P'作P'G ⊥OA，设P'G＝2，如图：∵∠PBD＝∠OBC﹣∠ABC＝30°，PD＝2，∴BP＝4，∵△PBE是等腰直角三角形，∴BE＝PE＝2，PF＝OE＝OB﹣BE＝6﹣2，。

专题06-圆专题(解析版)-2021年中考数学保A必刷压轴题(广东专用)

专题06 圆专题1．（2019•黄石）如图，AB是⊙O的直径，点D在AB的延长线上，C、E是⊙O上的两点，CE＝CB，∠BCD＝∠CAE，延长AE交BC的延长线于点F．（1）求证：CD是⊙O的切线；（2）求证：CE＝CF；（3）若BD＝1，CD＝，求弦AC的长．【分析】（1）连接OC，可证得∠CAD＝∠BCD，由∠CAD+∠ABC＝90°，可得出∠OCD＝90°，即结论得证；（2）证明△ABC≌△AFC可得CB＝CF，又CB＝CE，则CE＝CF；（3）证明△DCB∽△DAC，可求出DA的长，求出AB长，设BC＝a，AC＝a，则由勾股定理可得AC的长．【解析】（1）连接OC，∵AB是⊙O的直径，∴∠ACB＝90°，∴∠CAD+∠ABC＝90°，∵CE＝CB，∴∠CAE＝∠CAB，∵∠BCD＝∠CAE，∴∠CAB＝∠BCD，∵OB＝OC，∴∠OBC＝∠OCB，∴∠OCB+∠BCD＝90°，∴∠OCD＝90°，∴CD是⊙O的切线；（2）∵∠BAC＝∠CAE，∠ACB＝∠ACF＝90°，AC＝AC，∴△ABC≌△AFC（ASA），∴CB＝CF，又∵CB＝CE，∴CE＝CF；（3）∵∠BCD＝∠CAD，∠ADC＝∠CDB，∴△DCB∽△DAC，∴，∴，∴DA＝2，∴AB＝AD﹣BD＝2﹣1＝1，设BC＝a，AC＝a，由勾股定理可得：，解得：a＝，∴．2．（2019•包头）如图，在⊙O中，B是⊙O上的一点，∠ABC＝120°，弦AC＝2，弦BM平分∠ABC 交AC于点D，连接MA，MC．（1）求⊙O半径的长；（2）求证：AB+BC＝BM．【分析】（1）连接OA、OC，过O作OH⊥AC于点H，由圆内接四边形的性质求得∠AMC，再求得∠AOC，最后解直角三角形得OA便可；（2）在BM上截取BE＝BC，连接CE，证明BC＝BE，再证明△ACB≌△MCE，得AB＝ME，进而得结论．【解析】（1）连接OA、OC，过O作OH⊥AC于点H，如图1，∵∠ABC＝120°，∴∠AMC＝180°﹣∠ABC＝60°，∴∠AOC＝2∠AMC＝120°，∴∠AOH＝∠AOC＝60°，∵AH＝AC＝，∴OA＝，故⊙O的半径为2．（2）证明：在BM上截取BE＝BC，连接CE，如图2，∵∠MBC＝60°，BE＝BC，∴△EBC是等边三角形，∴CE＝CB＝BE，∠BCE＝60°，∴∠BCD+∠DCE＝60°，∵∠ACM＝60°，∴∠ECM+∠DCE＝60°，∴∠ECM＝∠BCD，∵∠ABC＝120°，BM平分∠ABC，∴∠ABM＝∠CBM＝60°，∴∠CAM＝∠CBM＝60°，∠ACM＝∠ABM＝60°，∴△ACM是等边三角形，∴AC＝CM，∴△ACB≌△MCE，∴AB＝ME，∵ME+EB＝BM，∴AB+BC＝BM．3．（2019•聊城）如图，△ABC内接于⊙O，AB为直径，作OD⊥AB交AC于点D，延长BC，OD交于点F，过点C作⊙O的切线CE，交OF于点E．（1）求证：EC＝ED；（2）如果OA＝4，EF＝3，求弦AC的长．【分析】（1）连接OC，由切线的性质可证得∠ACE+∠A＝90°，又∠CDE+∠A＝90°，可得∠CDE＝∠ACE，则结论得证；（2）先根据勾股定理求出OE，OD，AD的长，证明Rt△AOD∽Rt△ACB，得出比例线段即可求出AC 的长．【解析】（1）证明：连接OC，∵CE与⊙O相切，为C是⊙O的半径，∴OC⊥CE，∴∠OCA+∠ACE＝90°，∵OA＝OC，∴∠A＝∠OCA，∴∠ACE+∠A＝90°，∵OD⊥AB，∴∠ODA+∠A＝90°，∵∠ODA＝∠CDE，∴∠CDE+∠A＝90°，∴∠CDE＝∠ACE，∴EC＝ED；（2）∵AB为⊙O的直径，∴∠ACB＝90°，在Rt△DCF中，∠DCE+∠ECF＝90°，∠DCE＝∠CDE，∴∠CDE+∠ECF＝90°，∵∠CDE+∠F＝90°，∴∠ECF＝∠F，∴EC＝EF，∵EF＝3，∴EC＝DE＝3，∴OE＝＝5，∴OD＝OE﹣DE＝2，在Rt△OAD中，AD＝＝2，在Rt△AOD和Rt△ACB中，∵∠A＝∠A，∠ACB＝∠AOD，∴Rt△AOD∽Rt△ACB，∴，即，∴AC＝．4．（2019•成都）如图，AB为⊙O的直径，C，D为圆上的两点，OC∥BD，弦AD，BC相交于点E．（1）求证：＝；（2）若CE＝1，EB＝3，求⊙O的半径；（3）在（2）的条件下，过点C作⊙O的切线，交BA的延长线于点P，过点P作PQ∥CB交⊙O于F，Q两点（点F在线段PQ上），求PQ的长．【分析】（1）由等腰三角形的性质和平行线的性质可得∠OBC＝∠CBD，即可证＝；（2）通过证明△ACE∽△BCA，可得，可得AC＝2，由勾股定理可求AB的长，即可求⊙O的半径；（3）过点O作OH⊥FQ于点H，连接OQ，通过证明△APC∽△CPB，可得，可求P A＝，即可求PO的长，通过证明△PHO∽△BCA，可求PH，OH的长，由勾股定理可求HQ的长，即可求PQ的长．【解析】证明：（1）∵OC＝OB∴∠OBC＝∠OCB∵OC∥BD∴∠OCB＝∠CBD∴∠OBC＝∠CBD∴（2）连接AC，∵CE＝1，EB＝3，∴BC＝4∵∴∠CAD＝∠ABC，且∠ACB＝∠ACB∴△ACE∽△BCA∴∴AC2＝CB•CE＝4×1∴AC＝2，∵AB是直径∴∠ACB＝90°∴AB＝＝2∴⊙O的半径为（3）如图，过点O作OH⊥FQ于点H，连接OQ，∵PC是⊙O切线，∴∠PCO＝90°，且∠ACB＝90°∴∠PCA＝∠BCO＝∠CBO，且∠CPB＝∠CP A∴△APC∽△CPB∴∴PC＝2P A，PC2＝P A•PB∴4P A2＝P A×（P A+2）∴P A＝∴PO＝∵PQ∥BC∴∠CBA＝∠BPQ，且∠PHO＝∠ACB＝90°∴△PHO∽△BCA∴即∴PH＝，OH＝∴HQ＝＝∴PQ＝PH+HQ＝5．（2019•鄂州）如图，P A是⊙O的切线，切点为A，AC是⊙O的直径，连接OP交⊙O于E．过A点作AB⊥PO于点D，交⊙O于B，连接BC，PB．（1）求证：PB是⊙O的切线；（2）求证：E为△P AB的内心；（3）若cos∠P AB＝，BC＝1，求PO的长．【分析】（1）连结OB，根据圆周角定理得到∠ABC＝90°，证明△AOP≌△BOP，得到∠OBP＝∠OAP，根据切线的判定定理证明；（2）连结AE，根据切线的性质定理得到∠P AE+∠OAE＝90°，证明EA平分∠P AD，根据三角形的内心的概念证明即可；（3）根据余弦的定义求出OA，证明△P AO∽△ABC，根据相似三角形的性质列出比例式，计算即可．【解析】（1）证明：连结OB，∵AC为⊙O的直径，∴∠ABC＝90°，∵AB⊥PO，∴PO∥BC∴∠AOP＝∠C，∠POB＝∠OBC，OB＝OC，∴∠OBC＝∠C，∴∠AOP＝∠POB，在△AOP和△BOP中，，∴△AOP≌△BOP（SAS），∴∠OBP＝∠OAP，∵P A为⊙O的切线，∴∠OAP＝90°，∴∠OBP＝90°，∴PB是⊙O的切线；（2）证明：连结AE，∵P A为⊙O的切线，∴∠P AE+∠OAE＝90°，∵AD⊥ED，∴∠EAD+∠AED＝90°，∵OE＝OA，∴∠OAE＝∠AED，∴∠P AE＝∠DAE，即EA平分∠P AD，∵P A、PB为⊙O的切线，∴PD平分∠APB∴E为△P AB的内心；（3）∵∠P AB+∠BAC＝90°，∠C+∠BAC＝90°，∴∠P AB＝∠C，∴cos∠C＝cos∠P AB＝，在Rt△ABC中，cos∠C＝＝＝，∴AC＝，AO＝，∵△P AO∽△ABC，∴，∴PO＝＝＝5．6．（2018•孝感）如图，△ABC中，AB＝AC，以AB为直径的⊙O交BC于点D，交AC于点E，过点D作DF⊥AC于点F，交AB的延长线于点G．（1）求证：DF是⊙O的切线；（2）已知BD＝2，CF＝2，求AE和BG的长．【分析】（1）连接OD，AD，由圆周角定理可得AD⊥BC，结合等腰三角形的性质知BD＝CD，再根据OA＝OB知OD∥AC，从而由DG⊥AC可得OD⊥FG，即可得证；（2）连接BE．BE∥GF，推出△AEB∽△AFG，可得＝，由此构建方程即可解决问题；【解析】（1）连接OD，AD，∵AB为⊙O的直径，∴∠ADB＝90°，即AD⊥BC，∵AB＝AC，∴BD＝CD，又∵OA＝OB，∴OD∥AC，∵DG⊥AC，∴OD⊥FG，∴直线FG与⊙O相切；（2）连接BE．∵BD＝2，∴，∵CF＝2，∴DF＝＝4，∵AB是直径，∴∠AEB＝∠CEB＝90°，∴BE⊥AC，∵DF⊥AC，∴DF∥BE，∴EF＝FC，∴BE＝2DF＝8，∵cos∠C＝cos∠ABC，∴＝，∴＝，∴AB＝10，∴AE＝＝6，∵BE⊥AC，DF⊥AC，∴BE∥GF，∴△AEB∽△AFG，∴＝，∴＝，∴BG＝．7．（2019•恩施州）如图，在⊙O中，AB是直径，BC是弦，BC＝BD，连接CD交⊙O于点E，∠BCD＝∠DBE．（1）求证：BD是⊙O的切线．（2）过点E作EF⊥AB于F，交BC于G，已知DE＝2，EG＝3，求BG的长．【分析】（1）连接AE，由条件可得出∠AEB＝90°，证明∠C＝∠DBE，得出∠ABE+∠DBE＝90°，即∠ABD＝90°，结论得证；（2）延长EF交⊙O于H，证明△EBC∽△GBE，得出，求出BE长，求出CG＝GE＝3，则BC ＝BG+3，可得出，解出BG＝5．【解析】（1）证明：如图1，连接AE，则∠A＝∠C，∵AB是直径，∴∠AEB＝90°，∴∠A+∠ABE＝90°，∵∠C＝∠DBE，∴∠ABE+∠DBE＝90°，即∠ABD＝90°，∴BD是⊙O的切线（2）如图2，延长EF交⊙O于H，∵EF⊥AB，AB是直径，∴，∴∠ECB＝∠BEH，∵∠EBC＝∠GBE，∴△EBC∽△GBE，∴，∵BC＝BD，∴∠D＝∠C，∵∠C＝∠DBE，∴∠D＝∠DBE，∴BE＝DE＝2，又∠AFE＝∠ABD＝90°，∴BD∥EF，∴∠D＝∠CEF，∴∠C＝∠CEF，∴CG＝GE＝3，∴BC＝BG+CG＝BG+3，∴，∴BG＝﹣8（舍）或BG＝5，即BG的长为5．8．（2019•莱芜区）如图，已知AB是⊙O的直径，CB⊥AB，D为圆上一点，且AD∥OC，连接CD，AC，BD，AC与BD交于点M．（1）求证：CD为⊙O的切线；（2）若CD＝AD，求的值．【分析】（1）连接OD，设OC交BD于K．想办法证明△ODC≌△OBC（SSS）即可解决问题．（2）由CD＝AD，可以假设AD＝a，CD＝a，设KC＝b．由△CDK∽△COD，推出＝，推出＝整理得：2（）2+（）﹣4＝0，解得＝或（舍弃），由此即可解决问题．【解析】（1）证明：连接OD，设OC交BD于K．∵AB是直径，∴∠ADB＝90°，∴AD⊥BD，∵OC∥AD，∴OC⊥BD，∴DK＝KB，∴CD＝CB，∵OD＝OB，OC＝OC，CD＝CB，∴△ODC≌△OBC（SSS），∴∠ODC＝∠OBC，∵CB⊥AB，∴∠OBC＝90°，∴∠ODC＝90°，∴OD⊥CD，∴CD是⊙O的切线．（2）∵CD＝AD，∴可以假设AD＝a，CD＝a，设KC＝b．∵DK＝KB，AO＝OB，∴OK＝AD＝a，∵∠DCK＝∠DCO，∠CKD＝∠CDO＝90°，∴△CDK∽△COD，∴＝，∴＝整理得：2（）2+（）﹣4＝0，解得＝或（舍弃），∵CK∥AD，∴＝＝＝．9．（2019•广安）如图，在Rt△ABC中，∠ACB＝90°，AC＝6，BC＝8，AD平分∠BAC，AD交BC于点D，ED⊥AD交AB于点E，△ADE的外接圆⊙O交AC于点F，连接EF．（1）求证：BC是⊙O的切线；（2）求⊙O的半径r及∠3的正切值．【分析】（1）由垂直的定义得到∠EDA＝90°，连接OD，则OA＝OD，得到∠1＝∠ODA，根据角平分线的定义得到∠2＝∠1＝∠ODA，根据平行线的性质得到∠BDO＝∠ACB＝90°，于是得到BC是⊙O 的切线；（2）由勾股定理得到AB＝＝＝10，推出△BDO∽△BCA，根据相似三角形的性质得到r＝，解直角三角形即可得到结论．【解析】（1）证明：∵ED⊥AD，∴∠EDA＝90°，∵AE是⊙O的直径，∴AE的中点是圆心O，连接OD，则OA＝OD，∴∠1＝∠ODA，∵AD平分∠BAC，∴∠2＝∠1＝∠ODA，∴OD∥AC，∴∠BDO＝∠ACB＝90°，∴BC是⊙O的切线；（2）在Rt△ABC中，由勾股定理得，AB＝＝＝10，∵OD∥AC，∴△BDO∽△BCA，∴，即，∴r＝，在Rt△BDO中，BD＝＝＝5，∴CD＝BC﹣BD＝8﹣5＝3，在Rt△ACD中，tan∠2＝＝＝，∵∠3＝∠2，∴tan∠3＝tan∠2＝．10．（2019•泸州）如图，AB为⊙O的直径，点P在AB的延长线上，点C在⊙O上，且PC2＝PB•P A．（1）求证：PC是⊙O的切线；（2）已知PC＝20，PB＝10，点D是的中点，DE⊥AC，垂足为E，DE交AB于点F，求EF的长．【分析】（1）连接OC，△PBC∽△PCA，得出∠PCB＝∠P AC，由圆周角定理得出∠ACB＝90°，证出∠PCB+∠OCB＝90°，即OC⊥PC，即可得出结论；（2）连接OD，由相似三角形的性质得出＝＝2，设BC＝x，则AC＝2x，在Rt△ABC中，由勾股定理得出方程，得出BC＝6，证出DE∥BC，得出△DOF∽△ACB，得出＝＝，得出OF＝OD＝，即AF＝，再由平行线得出＝＝，即可得出结果．【解析】（1）证明：连接OC，如图1所示：∵PC2＝PB•P A，即＝，∵∠P＝∠P，∴△PBC∽△PCA，∴∠PCB＝∠P AC，∵AB为⊙O的直径，∴∠ACB＝90°，∴∠A+∠ABC＝90°，∵OC＝OB，∴∠OBC＝∠OCB，∴∠PCB+∠OCB＝90°，即OC⊥PC，∴PC是⊙O的切线；（2）连接OD，如图2所示：∵PC＝20，PB＝10，PC2＝PB•P A，∴P A＝＝＝40，∴AB＝P A﹣PB＝30，∵△PBC∽△PCA，∴＝＝2，设BC＝x，则AC＝2x，在Rt△ABC中，x2+（2x）2＝302，解得：x＝6，即BC＝6，∵点D是的中点，AB为⊙O的直径，∴∠AOD＝90°，∵DE⊥AC，∴∠AEF＝90°，∵∠ACB＝90°，∴DE∥BC，∴∠DFO＝∠ABC，∴△DOF∽△ACB，∴＝＝，∴OF＝OD＝，即AF＝，∵EF∥BC，∴＝＝，∴EF＝BC＝．11．（2019•雅安）如图，已知AB是⊙O的直径，AC，BC是⊙O的弦，OE∥AC交BC于E，过点B作⊙O 的切线交OE的延长线于点D，连接DC并延长交BA的延长线于点F．（1）求证：DC是⊙O的切线；（2）若∠ABC＝30°，AB＝8，求线段CF的长．【分析】（1）连接OC，根据平行线的性质得到∠1＝∠ACB，由圆周角定理得到∠1＝∠ACB＝90°，根据线段垂直平分线的性质得到DB＝DC，求得∠DBE＝∠DCE，根据切线的性质得到∠DBO＝90°，求得OC⊥DC，于是得到结论；（2）解直角三角形即可得到结论．【解析】（1）证明：连接OC，∵OE∥AC，∴∠1＝∠ACB，∵AB是⊙O的直径，∴∠1＝∠ACB＝90°，∴OD⊥BC，由垂径定理得OD垂直平分BC，∴DB＝DC，∴∠DBE＝∠DCE，又∵OC＝OB，∴∠OBE＝∠OCE，即∠DBO＝∠OCD，∵DB为⊙O的切线，OB是半径，∴∠DBO＝90°，∴∠OCD＝∠DBO＝90°，即OC⊥DC，∵OC是⊙O的半径，∴DC是⊙O的切线；（2）在Rt△ABC中，∠ABC＝30°，∴∠3＝60°，又OA＝OC，∴△AOC是等边三角形，∴∠COF＝60°，在Rt△COF中，tan∠COF＝，∴CF＝4．12．（2019•十堰）如图，△ABC中，AB＝AC，以AC为直径的⊙O交BC于点D，点E为AC延长线上一点，且∠CDE＝∠BAC．（1）求证：DE是⊙O的切线；（2）若AB＝3BD，CE＝2，求⊙O的半径．【分析】（1）根据圆周角定理得出∠ADC＝90°，按照等腰三角形的性质和已知的2倍角关系，证明∠ODE为直角即可；（2）通过证得△CDE∽△DAE，根据相似三角形的性质即可求得．【解析】（1）如图，连接OD，AD，∵AC是直径，∴∠ADC＝90°，∴AD⊥BC，∵AB＝AC，∴∠CAD＝∠BAD＝∠BAC，∵∠CDE＝∠BAC．∴∠CDE＝∠CAD，∵OA＝OD，∴∠CAD＝∠ADO，∵∠ADO+∠ODC＝90°，∴∠ODC+∠CDE＝90°∴∠ODE＝90°又∵OD是⊙O的半径∴DE是⊙O的切线；（2）∵AB＝AC，AD⊥BC，∴BD＝CD，∵AB＝3BD，∴AC＝3DC，设DC＝x，则AC＝3x，∴AD＝＝2x，∵∠CDE＝∠CAD，∠DEC＝∠AED，∴△CDE∽△DAE，∴＝，即＝＝∴DE＝4，x＝，∴AC＝3x＝14，∴⊙O的半径为7．13．（2017•十堰）已知AB为⊙O的直径，BC⊥AB于B，且BC＝AB，D为半圆⊙O上的一点，连接BD并延长交半圆⊙O的切线AE于E．（1）如图1，若CD＝CB，求证：CD是⊙O的切线；（2）如图2，若F点在OB上，且CD⊥DF，求的值．【分析】（1）连接DO，CO，易证△CDO≌△CBO，即可解题；（2）连接AD，易证△ADF∽△BDC和△ADE∽△BDA，根据相似三角形对应边成比例的性质即可解题．【解析】（1）连接DO，CO，∵BC⊥AB于B，∴∠ABC＝90°，在△CDO与△CBO中，，∴△CDO≌△CBO，∴∠CDO＝∠CBO＝90°，∴OD⊥CD，∴CD是⊙O的切线；（2）连接AD，∵AB是直径，∴∠ADB＝90°，∴∠ADF+∠BDF＝90°，∠DAB+∠DBA＝90°，∵∠BDF+∠BDC＝90°，∠CBD+∠DBA＝90°，∴∠ADF＝∠BDC，∠DAB＝∠CBD，∵在△ADF和△BDC中，，∴△ADF∽△BDC，∴＝，∵∠DAE+∠DAB＝90°，∠E+∠DAE＝90°，∴∠E＝∠DAB，∵在△ADE和△BDA中，，∴△ADE∽△BDA，∴＝，∴＝，即＝，∵AB＝BC，∴＝1．14．（2019•孝感）如图，点I是△ABC的内心，BI的延长线与△ABC的外接圆⊙O交于点D，与AC交于点E，延长CD、BA相交于点F，∠ADF的平分线交AF于点G．（1）求证：DG∥CA；（2）求证：AD＝ID；（3）若DE＝4，BE＝5，求BI的长．【分析】（1）根据三角形内心的性质得∠2＝∠7，再利用圆内接四边形的性质得∠ADF＝∠ABC，则∠1＝∠2，从而得到∠1＝∠3，则可判断DG∥AC；（2）根据三角形内心的性质得∠5＝∠6，然后证明∠4＝∠DAI得到DA＝DI；（3）证明△DAE∽△DBA，利用相似比得到AD＝6，则DI＝6，然后计算BD﹣DI即可．【解析】（1）证明：∵点I是△ABC的内心，∴∠2＝∠7，∵DG平分∠ADF，∴∠1＝∠ADF，∵∠ADF＝∠ABC，∴∠1＝∠2，∵∠3＝∠2，∴∠1＝∠3，∴DG∥AC；（2）证明：∵点I是△ABC的内心，∴∠5＝∠6，∵∠4＝∠7+∠5＝∠3+∠6，即∠4＝∠DAI，∴DA＝DI；（3）∵∠3＝∠7，∠AED＝∠BAD，∴△DAE∽△DBA，∴AD：DB＝DE：DA，即AD：9＝4：AD，∴AD＝6，∴DI＝6，∴BI＝BD﹣DI＝9﹣6＝3．15．（2019•滨州）如图，在△ABC中，AB＝AC，以AB为直径的⊙O分别与BC，AC交于点D，E，过点D 作DF⊥AC，垂足为点F．（1）求证：直线DF是⊙O的切线；（2）求证：BC2＝4CF•AC；（3）若⊙O的半径为4，∠CDF＝15°，求阴影部分的面积．【分析】（1）如图所示，连接OD，证明∠CDF+∠ODB＝90°，即可求解；（2）证明△CFD∽△CDA，则CD2＝CF•AC，即BC2＝4CF•AC；（3）S阴影部分＝S扇形OAE﹣S△OAE即可求解．【解析】（1）如图所示，连接OD，∵AB＝AC，∴∠ABC＝∠C，而OB＝OD，∴∠ODB＝∠ABC＝∠C，∵DF⊥AC，∴∠CDF+∠C＝90°，∴∠CDF+∠ODB＝90°，∴∠ODF＝90°，∴直线DF是⊙O的切线；（2）连接AD，则AD⊥BC，则AB＝AC，则DB＝DC＝，∵∠CDF+∠C＝90°，∠C+∠DAC＝90°，∴∠CDF＝∠DCA，而∠DFC＝∠ADC＝90°，∴△CFD∽△CDA，∴CD2＝CF•AC，即BC2＝4CF•AC；（3）连接OE，∵∠CDF＝15°，∠C＝75°，∴∠OAE＝30°＝∠OEA，∴∠AOE＝120°，S△OAE＝AE×OE sin∠OEA＝×2×OE×cos∠OEA×OE sin∠OEA＝4，S阴影部分＝S扇形OAE﹣S△OAE＝×π×42﹣4＝﹣4．16．（2018•成都）如图，在Rt△ABC中，∠C＝90°，AD平分∠BAC交BC于点D，O为AB上一点，经过点A，D的⊙O分别交AB，AC于点E，F，连接OF交AD于点G．（1）求证：BC是⊙O的切线；（2）设AB＝x，AF＝y，试用含x，y的代数式表示线段AD的长；（3）若BE＝8，sin B＝，求DG的长，【分析】（1）连接OD，由AD为角平分线得到一对角相等，再由等边对等角得到一对角相等，等量代换得到内错角相等，进而得到OD与AC平行，得到OD与BC垂直，即可得证；（2）连接DF，由（1）得到BC为圆O的切线，由弦切角等于夹弧所对的圆周角，进而得到三角形ABD 与三角形ADF相似，由相似得比例，即可表示出AD；（3）连接EF，设圆的半径为r，由sin B的值，利用锐角三角函数定义求出r的值，由直径所对的圆周角为直角，得到EF与BC平行，得到sin∠AEF＝sin B，进而求出DG的长即可．【解析】（1）证明：如图，连接OD，∵AD为∠BAC的角平分线，∴∠BAD＝∠CAD，∵OA＝OD，∴∠ODA＝∠OAD，∴∠ODA＝∠CAD，∴OD∥AC，∵∠C＝90°，∴∠ODC＝90°，∴OD⊥BC，∴BC为圆O的切线；（2）连接DF，由（1）知BC为圆O的切线，∴∠FDC＝∠DAF，∴∠CDA＝∠CFD，∴∠AFD＝∠ADB，∵∠BAD＝∠DAF，∴△ABD∽△ADF，∴＝，即AD2＝AB•AF＝xy，则AD＝；（3）连接EF，在Rt△BOD中，sin B＝＝，设圆的半径为r，可得＝，解得：r＝5，∴AE＝10，AB＝18，∵AE是直径，∴∠AFE＝∠C＝90°，∴EF∥BC，∴∠AEF＝∠B，∴sin∠AEF＝＝，∴AF＝AE•sin∠AEF＝10×＝，∵AF∥OD，∴＝＝＝，即DG＝AD，∴AD＝＝＝，则DG＝×＝．17．（2017•成都）如图，在△ABC中，AB＝AC，以AB为直径作圆O，分别交BC于点D，交CA的延长线于点E，过点D作DH⊥AC于点H，连接DE交线段OA于点F．（1）求证：DH是圆O的切线；（2）若A为EH的中点，求的值；（3）若EA＝EF＝1，求圆O的半径．【分析】（1）根据同圆的半径相等和等边对等角证明：∠ODB＝∠OBD＝∠ACB，则DH⊥OD，DH是圆O的切线；（2）如图2，先证明∠E＝∠B＝∠C，则H是EC的中点，设AE＝x，EC＝4x，则AC＝3x，由OD是△ABC的中位线，得：OD＝AC＝，证明△AEF∽△ODF，列比例式可得结论；（3）如图2，设⊙O的半径为r，即OD＝OB＝r，证明DF＝OD＝r，则DE＝DF+EF＝r+1，BD＝CD ＝DE＝r+1，证明△BFD∽△EF A，列比例式为：，则＝，求出r的值即可．【解析】证明：（1）连接OD，如图1，∵OB＝OD，∴△ODB是等腰三角形，∠OBD＝∠ODB①，在△ABC中，∵AB＝AC，∴∠ABC＝∠ACB②，由①②得：∠ODB＝∠OBD＝∠ACB，∴OD∥AC，∵DH⊥AC，∴DH⊥OD，∴DH是圆O的切线；（2）如图2，在⊙O中，∵∠E＝∠B，∴由（1）可知：∠E＝∠B＝∠C，∴△EDC是等腰三角形，∵DH⊥AC，且点A是EH中点，设AE＝x，EC＝4x，则AC＝3x，连接AD，则在⊙O中，∠ADB＝90°，AD⊥BD，∵AB＝AC，∴D是BC的中点，∴OD是△ABC的中位线，∴OD∥AC，OD＝AC＝×3x＝，∵OD∥AC，∴∠E＝∠ODF，在△AEF和△ODF中，∵∠E＝∠ODF，∠OFD＝∠AFE，∴△AEF∽△ODF，∴，∴＝＝，∴＝；（3）如图2，设⊙O的半径为r，即OD＝OB＝r，∵EF＝EA，∴∠EF A＝∠EAF，∵OD∥EC，∴∠FOD＝∠EAF，则∠FOD＝∠EAF＝∠EF A＝∠OFD，∴DF＝OD＝r，∴DE＝DF+EF＝r+1，∴BD＝CD＝DE＝r+1，在⊙O中，∵∠BDE＝∠EAB，∴∠BFD＝∠EF A＝∠EAB＝∠BDE，∴BF＝BD，△BDF是等腰三角形，∴BF＝BD＝r+1，∴AF＝AB﹣BF＝2OB﹣BF＝2r﹣（1+r）＝r﹣1，在△BFD和△EF A中，∵，∴△BFD∽△EF A，∴，∴＝，解得：r1＝，r2＝（舍），综上所述，⊙O的半径为．18．（2016•成都）如图，在Rt△ABC中，∠ABC＝90°，以CB为半径作⊙C，交AC于点D，交AC的延长线于点E，连接BD，BE．（1）求证：△ABD∽△AEB；（2）当＝时，求tan E；（3）在（2）的条件下，作∠BAC的平分线，与BE交于点F，若AF＝2，求⊙C的半径．【分析】（1）要证明△ABD∽△AEB，已经有一组对应角是公共角，只需要再找出另一组对应角相等即可．（2）由于AB：BC＝4：3，可设AB＝4，BC＝3，求出AC的值，再利用（1）中结论可得AB2＝AD•AE，进而求出AE的值，所以tan E＝＝．（3）设AB＝4x，BC＝3x，由于已知AF的值，构造直角三角形后利用勾股定理列方程求出x的值，即可知道半径3x的值．【解析】（1）∵∠ABC＝90°，∴∠ABD＝90°﹣∠DBC，由题意知：DE是直径，∴∠DBE＝90°，∴∠E＝90°﹣∠BDE，∵BC＝CD，∴∠DBC＝∠BDE，∴∠ABD＝∠E，∵∠A＝∠A，∴△ABD∽△AEB；（2）∵AB：BC＝4：3，∴设AB＝4，BC＝3，∴AC＝＝5，∵BC＝CD＝3，∴AD＝AC﹣CD＝5﹣3＝2，由（1）可知：△ABD∽△AEB，∴＝＝，∴AB2＝AD•AE，∴42＝2AE，∴AE＝8，在Rt△DBE中tan E＝＝＝＝；（3）过点F作FM⊥AE于点M，∵AB：BC＝4：3，∴设AB＝4x，BC＝3x，∴由（2）可知；AE＝8x，AD＝2x，∴DE＝AE﹣AD＝6x，∵AF平分∠BAC，∴＝，∴＝＝，∵tan E＝，∴cos E＝，sin E＝，∴＝，∴BE＝，∴EF＝BE＝，∴sin E＝＝，∴MF＝，∵tan E＝，∴ME＝2MF＝，∴AM＝AE﹣ME＝，∵AF2＝AM2+MF2，∴4＝+，∴x＝，∴⊙C的半径为：3x＝．另由上述知tan∠F AM＝＝，∵BC＝DC＝CE，＝，∴AD：DM：ME＝2：3：3，∵tan∠E＝＝，设FM＝a，则AM＝3a，ME＝2a，∴AE＝5a，∴DC＝AE＝a，由勾股定理可知：AF＝a，∵AF＝2，∴a＝，∴DC＝。

2024中考备考数学重难点05 圆的综合压轴题(6大题型+满分技巧+限时分层检测

重难点05 圆的综合压轴题中考数学中《圆的综合压轴题》部分主要考向分为六类：一、圆中弧长和面积的综合题二、圆与全等三角形的综合题三、圆的综合证明问题四、圆与等腰三角形的综合题五、圆的阅读理解与新定义问题六、圆与特殊四边形的综合题圆的综合问题是中考数学中的压轴题中的一类，也是难度较大的一类，所以，对应的训练很有必要。

考向一：圆中弧长与面积的综合题1．（2023•河北）装有水的水槽放置在水平台面上，其横截面是以AB为直径的半圆O，AB＝50cm，如图1和图2所示，MN为水面截线，GH为台面截线，MN∥GH．计算：在图1中，已知MN＝48cm，作OC⊥MN于点C.（1）求OC的长．操作：将图1中的水槽沿GH向右作无滑动的滚动，使水流出一部分，当∠ANM＝30°时停止滚动．如图2．其中，半圆的中点为Q，GH与半圆的切点为E，连接OE交MN于点D．探究：在图2中．（2）操作后水面高度下降了多少？（3）连接OQ并延长交GH于点F，求线段EF与的长度，并比较大小．2．（2023•乐山）在学习完《图形的旋转》后，刘老师带领学生开展了一次数学探究活动．【问题情境】刘老师先引导学生回顾了华东师大版教材七年级下册第121页“探索”部分内容：如图1，将一个三角形纸板△ABC绕点A逆时针旋转θ到达的位置△AB′C′的位置，那么可以得到：AB＝AB′，AC＝AC′，BC＝B′C′；∠BAC＝∠B′AC′，∠ABC＝∠AB′C′，∠ACB＝∠AC′B′．（_____）刘老师进一步谈到：图形的旋转蕴含于自然界的运动变化规律中，即“变”中蕴含着“不变”，这是我们解决图形旋转的关键．故数学就是一门哲学．【问题解决】（1）上述问题情境中“（_____）”处应填理由：；（2）如图2，小王将一个半径为4cm，圆心角为60°的扇形纸板ABC绕点O逆时针旋转90°到达扇形纸板A′B′C′的位置．①请在图中作出点O；②如果BB′＝6cm，则在旋转过程中，点B经过的路径长为；【问题拓展】小李突发奇想，将与（2）中完全相同的两个扇形纸板重叠，一个固定在墙上，使得一边位于水平位置．另一个在弧的中点处固定，然后放开纸板，使其摆动到竖直位置时静止．此时，两个纸板重叠部分的面积是多少呢？如图3所示，请你帮助小李解决这个问题．考向二：圆与全等三角形综合题1．（2023•济宁）如图，已知AB是⊙O的直径，CD＝CB，BE切⊙O于点B，过点C作CF⊥OE交BE于点F，EF＝2BF．（1）如图1，连接BD，求证：△ADB≌△OBE；（2）如图2，N是AD上一点，在AB上取一点M，使∠MCN＝60°，连接MN．请问：三条线段MN，BM，DN有怎样的数量关系？并证明你的结论．2．（2023•哈尔滨）已知△ABC内接于⊙O，AB为⊙O的直径，N为的中点，连接ON交AC于点H．（1）如图①，求证：BC＝2OH；（2）如图②，点D在⊙O上，连接DB，DO，DC，DC交OH于点E，若DB＝DC，求证OD∥AC；（3）如图③，在（2）的条件下，点F在BD上，过点F作FG⊥DO，交DO于点G，DG＝CH，过点F 作FR⊥DE，垂足为R，连接EF，EA，EF：DF＝3：2，点T在BC的延长线上，连接AT，过点T作TM ⊥DC，交DC的延长线于点M，若FR＝CM，AT＝4，求AB的长．3．（2023•长春）【感知】如图①，点A、B、P均在⊙O上，∠AOB＝90°，则锐角∠APB的大小为45度．【探究】小明遇到这样一个问题：如图②，⊙O是等边三角形ABC的外接圆，点P在弧AC上（点P不与点A、C重合），连接PA、PB、PC．求证：PB＝PA+PC．小明发现，延长PA至点E，使AE＝PC，连接BE，通过证明△PBC≌△EBA．可推得△PBE是等边三角形，进而得证．下面是小明的部分证明过程：证明：延长PA至点E，使AE＝PC，连接BE．∵四边形ABCP是⊙O的内接四边形，∴∠BAP+∠BCP＝180°，∵∠BAP+∠BAE＝180°，∴∠BCP＝∠BAE，∵△ABC是等边三角形，∴BA＝BC，∴△PBC≌△EBA（SAS）．请你补全余下的证明过程．【应用】如图③，⊙O是△ABC的外接圆，∠ABC＝90°，AB＝BC，点P在⊙O上，且点P与点B在AC的两侧，连接PA、PB、PC，若，则的值为．考向三：圆的综合证明问题1．（2023•黄石）如图，AB为⊙O的直径，DA和⊙O相交于点F，AC平分∠DAB，点C在⊙O上，且CD ⊥DA，AC交BF于点P．（1）求证：CD是⊙O的切线；（2）求证：AC•PC＝BC2；（3）已知BC2＝3FP•DC，求的值．2．如图，在⊙O中，直径AB垂直弦CD于点E，连接AC，AD，BC，作CF⊥AD于点F，交线段OB于点G（不与点O，B重合），连接OF．（1）若BE＝1，求GE的长．（2）求证：BC2＝BG•BO．（3）若FO＝FG，猜想∠CAD的度数，并证明你的结论．3．（2023•永州）如图，以AB为直径的⊙O是△ABC的外接圆，延长BC到点D．使得∠BAC＝∠BDA，点E在DA的延长线上，点M在线段AC上，CE交BM于N，CE交AB于G．（1）求证：ED是⊙O的切线；（2）若，BD＝5，AC＞CD，求BC的长；（3）若DE•AM＝AC•AD，求证：BM⊥CE．4．（2023•广东）综合探究如图1，在矩形ABCD中（AB＞AD），对角线AC，BD相交于点O，点A关于BD的对称点为A′．连接AA′交BD于点E，连接CA′．（1）求证：AA'⊥CA'；（2）以点O为圆心，OE为半径作圆．①如图2，⊙O与CD相切，求证：；②如图3，⊙O与CA′相切，AD＝1，求⊙O的面积．考向四：圆与等腰三角形的综合1．（2023•宁波）如图，在Rt△ABC中，∠C＝90°，E为AB边上一点，以AE为直径的半圆O与BC相切于点D，连结AD，BE＝3，BD＝3．P是AB边上的动点，当△ADP为等腰三角形时，AP的长为．2．（2023•上海）如图（1）所示，已知在△ABC中，AB＝AC，O在边AB上，点F是边OB中点，以O 为圆心，BO为半径的圆分别交CB，AC于点D，E，连接EF交OD于点G．（1）如果OG＝DG，求证：四边形CEGD为平行四边形；（2）如图（2）所示，连接OE，如果∠BAC＝90°，∠OFE＝∠DOE，AO＝4，求边OB的长；（3）连接BG，如果△OBG是以OB为腰的等腰三角形，且AO＝OF，求的值．3．（2023•泰州）已知：A、B为圆上两定点，点C在该圆上，∠C为所对的圆周角．知识回顾（1）如图①，⊙O中，B、C位于直线AO异侧，∠AOB+∠C＝135°．①求∠C的度数；②若⊙O的半径为5，AC＝8，求BC的长；逆向思考（2）如图②，若P为圆内一点，且∠APB＜120°，PA＝PB，∠APB＝2∠C．求证：P为该圆的圆心；拓展应用（3）如图③，在（2）的条件下，若∠APB＝90°，点C在⊙P位于直线AP上方部分的圆弧上运动．点D在⊙P上，满足CD＝CB﹣CA的所有点D中，必有一个点的位置始终不变．请证明．考向五：圆的阅读理解与新定义问题1．（2023•青海）综合与实践车轮设计成圆形的数学道理小青发现路上行驶的各种车辆，车轮都是圆形的．为什么车轮要做成圆形的呢？这里面有什么数学道理吗？带着这样的疑问，小青做了如下的探究活动：将车轮设计成不同的正多边形，在水平地面上模拟行驶．（1）探究一：将车轮设计成等边三角形，转动过程如图1，设其中心到顶点的距离是2，以车轮转动一次（以一个顶点为支点旋转）为例，中心的轨迹是，BA＝CA＝DA＝2，圆心角∠BAD＝120°．此时中心轨迹最高点是C（即的中点），转动一次前后中心的连线是BD（水平线），请在图2中计算C 到BD的距离d1．（2）探究二：将车轮设计成正方形，转动过程如图3，设其中心到顶点的距离是2，以车轮转动一次（以一个顶点为支点旋转）为例，中心的轨迹是，BA＝CA＝DA＝2，圆心角∠BAD＝90°．此时中心轨迹最高点是C（即的中点），转动一次前后中心的连线是BD（水平线），请在图4中计算C到BD的距离d2（结果保留根号）．（3）探究三：将车轮设计成正六边形，转动过程如图5，设其中心到顶点的距离是2，以车轮转动一次（以一个顶点为支点旋转）为例，中心的轨迹是，圆心角∠BAD＝．此时中心轨迹最高点是C（即的中点），转动一次前后中心的连线是BD（水平线），在图6中计算C 到BD的距离d3＝（结果保留根号）．（4）归纳推理：比较d1，d2，d3大小：，按此规律推理，车轮设计成的正多边形边数越多，其中心轨迹最高点与转动一次前后中心连线（水平线）的距离（填“越大”或“越小”）．（5）得出结论：将车轮设计成圆形，转动过程如图7，其中心（即圆心）的轨迹与水平地面平行，此时中心轨迹最高点与转动前后中心连线（水平线）的距离d＝.这样车辆行驶平稳、没有颠簸感．所以，将车轮设计成圆形．2．（2023•陕西）（1）如图①，∠AOB＝120°，点P在∠AOB的平分线上，OP＝4．点E，F分别在边OA，OB上，且∠EPF＝60°，连接EF．求线段EF的最小值；（2）如图②，是一个圆弧型拱桥的截面示意图．点P是拱桥的中点，桥下水面的宽度AB＝24m，点P到水面AB的距离PH＝8m．点P1，P2均在上，＝，且P1P2＝10m，在点P1，P2处各装有一个照明灯，图中△P1CD和△P2EF分别是这两个灯的光照范围．两灯可以分别绕点P1，P2左右转动，且光束始终照在水面AB上．即∠CP1D，∠EP2F可分别绕点P1，P2按顺（逆）时针方向旋转（照明灯的大小忽略不计），线段CD，EF在AB上，此时，线段ED是这两灯照在水面AB上的重叠部分的水面宽度．已知∠CP1D＝∠EP2F＝90°，在这两个灯的照射下，当整个水面AB都被灯光照到时，求这两个灯照在水面AB上的重叠部分的水面宽度．（可利用备用图解答）3．（2023•北京）在平面直角坐标系xOy中，⊙O的半径为1．对于⊙O的弦AB和⊙O外一点C给出如下定义：若直线CA，CB中一条经过点O，另一条是⊙O的切线，则称点C是弦AB的“关联点”．（1）如图，点A（﹣1，0），B1（，），B2（，）．①在点C1（﹣1，1），C2（，0），C3（0，）中，弦AB1的“关联点”是；②若点C是弦AB2的“关联点”，直接写出OC的长；（2）已知点M（0，3），N（，0），对于线段MN上一点S，存在⊙O的弦PQ，使得点S是弦PQ的“关联点”．记PQ的长为t，当点S在线段MN上运动时，直接写出t的取值范围．4．在探究“四点共圆的条件”的数学活动课上，小霞小组通过探究得出：在平面内，一组对角互补的四边形的四个顶点共圆．请应用此结论，解决以下问题：如图1，△ABC中，AB＝AC，∠BAC＝α（60°＜α＜180°）．点D是BC边上的一动点（点D不与B，C重合），将线段AD绕点A顺时针旋转α到线段AE，连接BE．（1）求证：A，E，B，D四点共圆；（2）如图2，当AD＝CD时，⊙O是四边形AEBD的外接圆，求证：AC是⊙O的切线；（3）已知α＝120°，BC＝6，点M是边BC的中点，此时⊙P是四边形AEBD的外接圆，直接写出圆心P与点M距离的最小值．考向六：圆与特殊四边形综合1．（2023•威海）已知：射线OP平分∠MON，A为OP上一点，⊙A交射线OM于点B，C，交射线ON 于点D，E，连接AB，AC，AD．（1）如图1，若AD∥OM，试判断四边形OBAD的形状，并说明理由；（2）如图2，过点C作CF⊥OM，交OP于点F；过点D作DG⊥ON，交OP于点G．求证：AG＝AF．2．（2023•益阳）如图，线段AB与⊙O相切于点B，AO交⊙O于点M，其延长线交⊙O于点C，连接BC，∠ABC＝120°，D为⊙O上一点且的中点为M，连接AD，CD．（1）求∠ACB的度数；（2）四边形ABCD是否是菱形？如果是，请证明；如果不是，请说明理由；（3）若AC＝6，求的长．（建议用时：80分钟）1．（2023•宜昌）如图1，已知AB是⊙O的直径，PB是⊙O的切线，PA交⊙O于点C，AB＝4，PB＝3．（1）填空：∠PBA的度数是，PA的长为；（2）求△ABC的面积；（3）如图2，CD⊥AB，垂足为D．E是上一点，AE＝5EC．延长AE，与DC，BP的延长线分别交于点F，G，求的值．2．（2023•台州）我们可以通过中心投影的方法建立圆上的点与直线上点的对应关系，用直线上点的位置刻画圆上点的位置．如图，AB是⊙O的直径，直线l是⊙O的切线，B为切点．P，Q是圆上两点（不与点A重合，且在直径AB的同侧），分别作射线AP，AQ交直线l于点C，点D．（1）如图1，当AB＝6，弧BP长为π时，求BC的长；（2）如图2，当，时，求的值；（3）如图3，当，BC＝CD时，连接BP，PQ，直接写出的值．3．（2023•遂宁）如图，四边形ABCD内接于⊙O，AB为⊙O的直径，AD＝CD，过点D的直线l交BA的延长线于点M．交BC的延长线于点N且∠ADM＝∠DAC．（1）求证：MN是⊙O的切线；（2）求证：AD2＝AB•CN；（3）当AB＝6，sin∠DCA＝时，求AM的长．4．（2023•丽水）如图，在⊙O中，AB是一条不过圆心O的弦，点C，D是的三等分点，直径CE交AB于点F，连结AD交CF于点G，连结AC，过点C的切线交BA的延长线于点H．（1）求证：AD∥HC；（2）若＝2，求tan∠FAG的值；（3）连结BC交AD于点N，若⊙O的半径为5．下面三个问题，依次按照易、中、难排列．请根据自己的认知水平，选择其中一道问题进行解答．①若OF＝，求BC的长；②若AH＝，求△ANB的周长；③若HF•AB＝88，求△BHC的面积．5．（2023•长沙）如图，点A，B，C在⊙O上运动，满足AB2＝BC2+AC2，延长AC至点D，使得∠DBC ＝∠CAB，点E是弦AC上一动点（不与点A，C重合），过点E作弦AB的垂线，交AB于点F，交BC 的延长线于点N，交⊙O于点M（点M在劣弧上）．（1）BD是⊙O的切线吗？请作出你的判断并给出证明；（2）记△BDC，△ABC，△ADB的面积分别为S1，S2，S，若S1•S＝（S2）2，求（tan D）2的值；（3）若⊙O的半径为1，设FM＝x，FE•FN•＝y，试求y关于x的函数解析式，并写出自变量x的取值范围．6．（2023•宁波）如图1，锐角△ABC内接于⊙O，D为BC的中点，连结AD并延长交⊙O于点E，连结BE，CE，过C作AC的垂线交AE于点F，点G在AD上，连结BG，CG，若BC平分∠EBG且∠BCG ＝∠AFC．（1）求∠BGC的度数．（2）①求证：AF＝BC．②若AG＝DF，求tan∠GBC的值．（3）如图2，当点O恰好在BG上且OG＝1时，求AC的长．（建议用时：80分钟）1．（2023•东营区校级一模）如图，PA、PB是⊙O的切线，切点分别为A、B，BC是⊙O的直径，PO交⊙O于E点，连接AB交PO于F，连接CE交AB于D点．下列结论：①PA＝PB；②OP⊥AB；③CE 平分∠ACB；④；⑤E是△PAB的内心；⑥△CDA≌△EDF．其中一定成立的有（）个．A．5B．4C．3D．22．（2023•鹿城区校级三模）如图1，在△ABC中，∠ACB＝90°，BC＝2AC＝2，过BC上一点D作DE ⊥BC，交AB于点E，以点D为圆心，DE的长为半径作半圆，交AC，AB于点F，G，交直线BC于点H，I（点I在H左侧）．当点D与点C重合时（如图2），GH＝；当EF＝GH时，CD＝．3．（2023•湖北模拟）如图，AB是⊙O的直径，点C是⊙O上一点，AD与过点C的切线垂直，垂足为D，直线DC与AB的延长线交于点P，弦CE平分∠ACB，交AB于点F，连接BE，BE＝7，下列四个结论：①AC平分∠DAB；②PF2＝PB•PA；③若BC＝OP，则阴影部分的面积为；④若PC＝24，则tan∠PCB＝；其中，所有正确结论的序号是．4．（2024•鄞州区校级一模）如图1，AB，CD是⊙O的两条互相垂直的弦，垂足为E，连结BC，BD，OC．（1）求证：∠BCO＝∠ABD．（2）如图2，过点A作AF⊥BD，交CD于G，求证：CE＝EG．（3）如图3，在（2）的条件上，连结BG，若BG恰好经过圆心O，若⊙O的半径为5，，求AB的长．5．（2024•常州模拟）对于⊙C和⊙C上的一点A，若平面内的点P满足：射线AP与⊙C交于点Q（点Q 可以与点P重合，且，则点P称为点A关于⊙C的“阳光点”．已知点O为坐标原点，⊙O 的半径为1，点A（﹣1，0）．（1）若点P是点A关于⊙O的“阳光点”，且点P在x轴上，请写出一个符合条件的点P的坐标；（2）若点B是点A关于⊙O的“阳光点”，且，求点B的横坐标t的取值范围；（3）直线与x轴交于点M，且与y轴交于点N，若线段MN上存在点A关于⊙O的“阳光点”，请直接写出b的取值范围是或．6．（2024•广东一模）如图1，在⊙O中，AB为⊙O的直径，点C为⊙O上一点，点D在劣弧BC上，CE ⊥CD交AD于E，连接BD．（1）求证：△ACE～△BCD；（2）若cos∠ABC＝m，求；（用含m的代数式表示）（3）如图2，DE的中点为G，连接GO，若BD＝a，cos∠ABC＝，求OG的长．7．（2024•镇海区校级模拟）在矩形ABCD中，M、N分别在边BC、CD上，且AM⊥MN，以MN为直径作⊙O，连结AN交⊙O于点H，连结CH交MN于点P，AB＝8，AD＝12．（1）求证：∠MAD＝∠MHC；（2）若AM平分∠BAN，求MP的长；（3）若△CMH为等腰三角形，直接写出BM的长．8．（2024•浙江一模）如图，在⊙O中，AB是一条不过圆心O的弦，C，D是的三等分点，直径CE交AB于点F，连结BD交CF于点G，连结AC，DC，过点C的切线交AB的延长线于点H．（1）求证：FG＝CG．（2）求证：四边形BDCH是平行四边形．（3）若⊙O的半径为5，OF＝3，求△ACH的周长．9．（2024•五华区校级模拟）如图，AB，CD是⊙O的两条直径，且AB⊥CD，点E是上一动点（不与点B，D重合），连接DE并延长交AB的延长线于点F，点P在AF上，且∠PEF＝∠DCE，连接AE，CE分别交OD，OB于点M，N，连接AC，设⊙O的半径为r．（1）求证：PE是⊙O的切线；（2）当∠DCE＝15°时，求证：AM＝2ME；（3）在点E的移动过程中，判断AN•CM是否为定值，若是，求出该定值；若不是，请说明理由．10．（2024•福建模拟）已知：如图，⊙O内两条弦AB、CD，且AB⊥CD于E，OA为⊙O半径，连接AC、BD．（1）求证：∠OAC＝∠BCD；（2）作EN⊥BD于N，延长NE交AC于点H．求证：AH＝CH；（3）在（2）的条件下，作∠EHF＝60°交AB于点F，点P在FE上，连接PC交HN于点L，当EL＝HF＝，CL＝8，BE＝2PF时，求⊙O的半径．11．（2024•鹿城区校级一模）如图1，锐角△ABC内接于⊙O，点E是AB的中点，连结EO并延长交BC 于D，点F在AC上，连结AD，DF，∠BAD＝∠CDF．（1）求证：DF∥AB．（2）当AB＝9，AF＝FD＝4时，①求tan∠CDF的值；②求BC的长．（3）如图2，延长AD交⊙O于点G，若，求的值．12．（2024•正阳县一模）【材料】自从《义务教育数学课程标准（2022年版）》实施以来，九年级的晏老师通过查阅新课标获悉：切线长定理由“选学”改为“必学”，并新增“会过圆外的一个点作圆的切线”，在学习完《切线的性质与判定》后，她布置一题：“已知：如图所示，⊙O及⊙O外一点P．求作：直线PQ，使PQ与⊙O相切于点Q．李蕾同学经过探索，给出了如下的一种作图方法：（1）连接OP，分别以O、P为圆心，以大于的长为半径作弧，两弧分别交于A、B两点（A、B 分别位于直线OP的上下两侧）；（2）作直线AB，AB交OP于点C；（3）以点C为圆心，CO为半径作⊙C，⊙C交⊙O于点Q（点Q位于直线OP的上侧）；（4）连接PQ，PQ交AB于点D，则直线PQ即为所求．【问题】（1）请按照步骤完成作图，并准确标注字母（尺规作图，保留作图痕迹）；（2）结合图形，说明PQ是⊙O切线的理由；（3）若⊙O半径为2，OP＝6．依据作图痕迹求QD的长．13．（2024•泌阳县一模）小贺同学在数学探究课上，用几何画板进行了如下操作：首先画一个正方形ABCD，一条线段OP（OP＜AB），再以点A为圆心，OP的长为半径，画⊙A分别交AB于点E．交AD于点G．过点E，G分别作AB，AD的垂线交于点F，易得四边形AEFG也是正方形，连接CF．（1）【探究发现】如图1，BE与DG的大小和位置关系：．（2）【尝试证明】如图2，将正方形AEFG绕圆心A转动，在旋转过程中，上述（1）的关系还存在吗？请说明理由．（3）【思维拓展】如图3，若AB＝2OP＝4，则：①在旋转过程中，点B，A，G三点共线时，CF的值为；②在旋转过程中，CF的最大值是．14．（2024•秦都区校级一模）问题提出：（1）如图①，⊙O的半径为4，弦AB＝4，则点O到AB的距离是．问题探究：（2）如图②，⊙O的半径为5，点A、B、C都在⊙O上，AB＝6，求△ABC面积的最大值．问题解决：（3）如图③，是一圆形景观区示意图，⊙O的直径为60m，等边△ABP的边AB是⊙O的弦，顶点P在⊙O内，延长AP交⊙O于点C，延长BP交⊙O于点D，连接CD．现准备在△PAB和△PCD 区域内种植花卉，圆内其余区域为草坪．按照预算，草坪的面积尽可能大，求草坪的最大面积．（提示：花卉种植面积尽可能小，即花卉种植面积S△PAB +S△PCD的最小值）15．（2024•碑林区校级一模）问题探究（1）寒假期间，乐乐同学参观爸爸的工厂，看到半径分别为2和3的两个圆形零件⊙A、⊙B按如图1所示的方式放置，点A到直线m的距离AC＝4，点B到直线m的距离BD＝6，CD＝5，M是⊙A上一点，N是⊙B上一点，在直线m上找一点P，使得PM+PN最小．请你在直线m上画出点P的位置，并直接写出PM+PN的最小值．问题解决（2）如图2，乐乐爸爸的工厂欲规划一块花园，如图所示的矩形ABCD，其中米，BC＝30米，点E、F为花园的两个入口，米，DF＝10米．若在△BCD区域内设计一个亭子G（亭子大小忽略不计），满足∠BDG＝∠GBC，从入口到亭子铺设两条景观路．已知铺设小路EG所用的景观石材每米的造价是400元，铺设小路FG所用的景观石材每米的造价是200元，你能否帮乐乐同学分析一下，是否存在点G，使铺设小路EG和FG的总造价最低？若存在，求出最低总造价，并求出此时亭子G到边AB的距离；若不存在，请说明理由．16．（2024•雁塔区校级一模）问题发现（1）在△ABC中，AB＝2，∠C＝60°，则△ABC面积的最大值为；（2）如图1，在四边形ABCD中，AB＝AD＝6，∠BCD＝∠BAD＝90°，AC＝8，求BC+CD的值．问题解决（3）有一个直径为60cm的圆形配件⊙O，如图2所示．现需在该配件上切割出一个四边形孔洞OABC，要求∠O＝∠B＝60°，OA＝OC，并使切割出的四边形孔洞OABC的面积尽可能小．试问，是否存在符合要求的面积最小的四边形OABC？若存在，请求出四边形OABC面积的最小值及此时OA的长；若不存在，请说明理由．17．（2024•东莞市校级一模）如图①，点C，D在线段AB上，点C在点D的左侧，若线段AC，CD，DB 满足AC2+BD2＝CD2，称C，D是线段AB的勾股点．（1）如图②，C，D是线段AB的勾股点，分别以线段AC，CD，DB为边向AB的同侧作正△ACE，正△CDF，正△DBG，已知正△ACE、正△CDF的面积分别是3，5，则正△DBG的面积是；（2）如图①，AB＝12，C，D是线段AB的勾股点，当AC＝AB时，求CD的长；（3）如图③，C，D是线段AB的勾股点，以CD为直径画⊙O，P在⊙O上，AC＝CP，连接PA，PB，若∠A＝2∠B，求∠B的度数．18．（2023•西湖区模拟）如图，已知CE是圆O的直径，点B在圆O上，且BD＝BC，过点B作弦CD的平行线与CE的延长线交于点A．（1）若圆O的半径为2，且点D为弧EC的中点时，求线段CD的长度；（2）在（1）的条件下，当DF＝a时，求线段BD的长度；（答案用含a的代数式表示）（3）若AB＝3AE，且CD＝12，求△BCD的面积．19．古希腊数学家毕达哥拉斯认为：“一切平面图形中最美的是圆”．小明决定研究一下圆，如图，AB是⊙O的直径，点C是⊙O上的一点，延长AB至点D，连接AC、BC、CD，且∠CAB＝∠BCD，过点C 作CE⊥AD于点E．（1）求证：CD是⊙O的切线；（2）若OB＝BD，求证：点E是OB的中点；（3）在（2）的条件下，若点F是⊙O上一点（不与A、B、C重合），求的值．。

广东省2024年九年级中考数学一轮复习：圆模拟练习(含解析)

2024年广东省九年级数学一轮复习：圆模拟练习一、单选题1．（2023·广东广州·中考真题）如图，的内切圆与，，分别相切于点D，E，F，若的半径为r，，则的值和的大小分别为（）A．2r，B．0，C．2r，D．0，2．（2023·广东·中考真题）如图，是的直径，，则（）A．B．C．D．3．（2023·广东清远·二模）如图，在边长为4正方形中，点E在以B为圆心的弧上，射线交于F，连接，若，则（）．A．2B．C．D．4．（2023·广东河·一模）如图，为⊙O的直径，是⊙O的弦，点是上的一点，且．若，，则的长为（）A．B．C．D．5．（2023·广东湛江·一模）如图，、是的直径，弦，弧为，则的度数为（）A．B．C．D．6．（2023·广东佛山·一模）如图，点A、B、C在上，，则（）A．18°B．36°C．72°D．144°7．（2023·广东深圳·模拟预测）下列说法中正确的一项是（）A．经过三点有且只有一个圆B．在圆中，长度相等的弦所对的圆心角相等C．有一组对边平行，一组对角相等的四边形是平行四边形D．有两条边相等的直角三角形全等8．（2023·广东清远·模拟预测）如图，是半的直径，点在半上，．是上的一个动点，连接，过点作于，连接．在点移动的过程中，的最小值为（）A．B．C．D．29．（2023·广东云浮·一模）如图，切于C，点D从C出发，以每秒的速度沿方向运动，运动1秒时，运动2秒时长是（）A．B．C．D．10．（2023·广东深圳·二模）如图，在中，，，，D是上一动点，于E，交于点F，则的最大值是（）A．B．C．D．11．（2023·广东阳江·二模）如果一个正多边形的中心角是，那么这个正多边形的边数是（）A．4B．6C．8D．1012．（2023·广东广州·二模）如图，正六边形内接于，点是上的一点，则的度数为（）A．B．C．D．13．（2023·广东深圳·模拟预测）如图，在中，，以点B为圆心，长为半径画弧，交边于点D，则的长为（）A．B．C．D．14．（2023·广东珠海·一模）如图，切于两点，若，的半径为，则阴影部分的面积为（）A．B．C．D．二、填空题15．（2023·广东深圳·中考真题）如图，在中，为直径，C为圆上一点，的角平分线与交于点D，若，则°．16．（2023·广东东莞·一模）如图，四边形为的内接四边形，，则的度数为．17．（2023·广东广州·一模）如图，是的弦，交于点P，过点B的直线交的延长线于点C，若，，，则的长为．18．（2023·广东梅州·一模）如图，是上的三个点，，则度数是．19．（2023·广东东莞·一模）如图，在平面直角坐标系中，已知，以点C为圆心的圆与y轴相切，点A、B在x轴上，且．点P为上的动点，，则长度的最小值为．20．（2023·广东广州·一模）如图，在中，为直径，点M为延长线上的一点，与相切于点C，圆周上有另一点D与点C分居直径两侧，且使得，连接．现有下列结论：①与相切；②四边形是菱形；③；④．其中正确的结论是（填序号）．21．（2023·广东揭阳·一模）一个正多边形的中心角为36°，则这个正多边形的内角和为度．22．（2023·广东东莞·三模）如图，和是两个完全重合的直角三角板，，斜边长为三角板绕直角顶点顺时针旋转，当点落在边上时，则点所转过的路径长为．23．（2023·广东潮州·一模）如图，正方形的边长为2，分别以为圆心，以正方形的边长为半径的圆相交于点，那么图中阴影部分的面积为．三、解答题24．（2023·广东广州·中考真题）如图，在平面直角坐标系v中，点，，所在圆的圆心为O．将向右平移5个单位，得到（点A平移后的对应点为C）．(1)点D的坐标是___________，所在圆的圆心坐标是___________；(2)在图中画出，并连接，；(3)求由，，，首尾依次相接所围成的封闭图形的周长．（结果保留）25．（2023·广东·中考真题）综合探究如图1，在矩形中，对角线相交于点，点关于的对称点为，连接交于点，连接．(1)求证：；(2)以点为圆心，为半径作圆．①如图2，与相切，求证：；②如图3，与相切，，求的面积．26．（2023·广东东莞·一模）如图，在中，，延长到点D，以为直径作，交的延长线于点E，延长到点F，使．(1)求证：是的切线；(2)若的半径为5，，，求的长．27．（2023·广东汕头·一模）如图，内接于．是直径，过点作直线，且是的切线．(1)求证：．(2)设是弧的中点，连接交于点，过点作于点，交于点．①求证：．②若，，试求的长．28．（2023·广东肇庆·二模）如图，在中，，平分交于点，为上一点，经过点，的分别交，于点，连接交于点．(1)求证：是的切线；(2)若，半径为4，在圆O上取点P，使，求点P到直线的距离．29．（2023·广东茂名·一模）张师傅要将一张残缺的圆形轮片恢复原貌（如图），已知轮片的一条弦的垂直平分线交弧于点，交弦于点，测得，．(1)请你帮张师傅找出此残片所在圆的圆心（尺规作图，不写作法，保留作图痕迹）；(2)求（1）中所作圆的半径．30．（2023·广东河·三模）【发现问题】爱好数学的小明在做作业时碰到这样的一道题目：如图，点为坐标原点，的半径为，点．动点在上，连接，作等边（，，为顺时针顺序），求的最大值；【解决问题】小明经过多次的尝试与探索，终于得到解题思路：在图中，连接，以为边在的左侧作等边，连接．（）请你找出图中与相等的线段，并说明理由；（）线段的最大值为．【灵活运用】（）如图，在平面直角坐标系中，点的坐标为，点的坐标为，点为线段外一动点，且，，，求线段长的最大值及此时点的坐标．【迁移拓展】（）如图③，，点是以为直径的半圆上不同于的一个动点，以为边作等边，请直接写出的最值．参考答案：1．D【分析】如图，连接．利用切线长定理，圆周角定理，切线的性质解决问题即可．【详解】解：如图，连接．∵的内切圆与，，分别相切于点D，E，F，∴，∴，，∴，∴．故选：D．【点睛】本题考查三角形的内切圆与内心，圆周角定理，切线的性质等知识，解题的关键是掌握切线的性质，属于中考常考题型．2．B【分析】根据圆周角定理可进行求解．【详解】解：∵是的直径，∴，∵，∴，∵，∴；故选B．【点睛】本题主要考查圆周角的相关性质，熟练掌握直径所对圆周角为直角是解题的关键．3．B【分析】如图，连接，过点B作于点H，根据圆的性质和等腰三角形的性质可定，再结合正方形的性质可得；再证可得，即；然后再根据勾股定理列方程即可解答．【详解】解：如图，连接，过点B作于点H，∵点E在以B为圆心的弧上，∴，∵，∴，∵四边形是正方形，∴，∴，∵，∴，∴，∴，在中，，∴，∴或（舍去）．故选：B．【点睛】本题主要考查了圆的基本性质、全等三角形的判定与性质、等腰三角形的性质、勾股定理等知识点，灵活运用相关知识成为解答本题的关键．4．B【分析】连接，交于，根据垂径定理推论，再由垂径定理，再由勾股定理计算，的长，从而求得的长，此题考查了圆周角定理，垂径定理和勾股定理的性质，正确作出辅助线是解题的关键．【详解】解：连接，交于，∵，∴点是的中点，∴，，∴，∵，∴，∴，∴，∵为的直径，∴，∴，故选：．5．C【分析】连接，利用等边对等角，弦，圆心角，弧的关系，平行线的性质计算即可.【详解】连接，解：∵弧为，∴，∵，∴，∵，∴，故选：C．【点睛】本题考查了等边对等角，弦，圆心角，弧的关系，平行线的性质，熟练掌握平行线的性质，圆的性质是解题的关键.6．C【分析】本题考查圆周角定理，根据对边对等角，三角形的内角和定理，求出的度数，根据同弧所对的圆周角等于圆心角的一半，即可得出结果．【详解】解：∵点A、B、C在上，∴，∴，∴，∴；故选C．7．C【分析】根据确定圆的条件对A进行判断；根据弦与圆心角关系对B进行判断；根据平行四边形的判定方法对C进行判断；根据全等三角形的判定对D进行判断．【详解】解：A、经过不在同一直线上的三点有且只有一个圆，故此选项错误；B、在同圆或等圆中，长度相等的弦所对的圆心角相等，故此选项错误；C、有一组对边平行，一组对角相等的四边形是平行四边形，故此选项正确；D、有两条边相等的直角三角形不一定全等，故此选项错误．故选：C．【点睛】此题主要考查了确定圆的条件、弦与圆心角的关系、平行四边形的判定及全等三角形的判定方法等知识，正确有关图形的判定与性质是解题关键．8．D【分析】以为直径画圆，圆心为，连接、，在点移动的过程中，点在以为直径的圆上运动，当、、共线时，的值最小，最小值为，利用勾股定理求出即可解决问题．【详解】解：如图，以为直径画圆，圆心为，连接、，，∵，∴，∴在点移动的过程中，点在以为直径的圆上运动，∵是直径，∴，在中，∵，∴，在中，，∵，∴当、、共线时，的值最小，最小值为，故选：D．【点睛】本题主要考查了勾股定理、点与圆的位置关系等知识，解题的关键是确定点的运动轨迹是在以为直径的圆上运动，属于中考填空题中的压轴题．9．C【分析】本题考查切线的性质、勾股定理，掌握切线性质是关键．先证得，再利用勾股定理求解即可．【详解】解：∵切于C，∴，∵点D从C出发，以每秒的速度沿方向运动，∴运动1秒时，又∵运动1秒时，∴在中，由勾股定理得：，∵运动2秒时长为，∴此时．故选：C．10．B【分析】取的中点O，连接，，延长交于T．证明，推出点E在以O为圆心，为半径的圆上运动，推出当与相切时，的值最大，根据切线的性质、平行线的性质及含30度角的直角三角形的性质即可得出答案．【详解】解：如图，取的中点O，连接，，延长交于T．∵，，，∴，∴，，∵，∴，∴E在上，∵，∴，∴点E在以O为圆心，为半径的圆上运动，∵，∴当与相切时，的值最大，∵直线，直线都是的切线，∴，∴，∵，，∴，∵，，∴，∴，∵，，∴，∵，∴，∴，∴，∴，∴的最大值为．故选：B．【点睛】本题考查直角三角形角的性质、直线与圆的位置关系、线段的垂直平分线的性质等知识，解题的关键是发现点E在以O为圆心，为半径的圆上运动，并推出与相切时，的值最大．11．C【分析】根据正多边形的边数周角中心角，计算即可得解．【详解】解：这个多边形的边数是，故选：C．【点睛】本题考查的是正多边形的中心角的有关计算；熟记正多边形的中心角与边数的关系是解题的关键．12．B【分析】利用圆内接正多边形中心角及同弧所多对的圆周角是圆心角一半定理即可．【详解】如图，连接，，∵六边形是圆内接正六边形，∴，∴，故选：．【点睛】本题考查圆内接正多边形和圆周角定理，解此题的关键是熟练掌握圆内接正多边形中心角计算和圆周角定理角度计算．13．B【分析】根据直角三角形的性质得到，根据已知条件得到是等边三角形，由等边三角形的性质即可得到结论．【详解】解：连接，，，，，，以点为圆心，长为半径画弧，交边于点，是等边三角形，，，故选：B．【点睛】本题考查了含角的直角三角形的性质，等边三角形的判定和性质及弧长公式，熟练掌握直角三角形的性质是解题的关键．14．B【分析】如图所示，连接，可证，，，根据含角的直角三角形的性质可计算出的值，由此可算出四边形的面积，再根据四边形的性质，算出的角度，可算出扇形的面积，由此即可求解．【详解】解：如图所示，连接，∵切于，，∴，，∴是的角平分线，则，∵，是公共边，∴，∴，在中，，∴，∴，∴，在四边形中，，∴，∴，∴，故选：．【点睛】本题主要考查扇形，不规则图像面积的计算方法，掌握圆的基础知识，扇形的面积计算方法，不规则图形面积的计算方法是解题的关键．15．35【分析】由题意易得，，则有，然后问题可求解．【详解】解：∵是的直径，∴，∵，，∴，∴，∵平分，∴；故答案为35．【点睛】本题主要考查圆周角的性质，熟练掌握直径所对圆周角为直角是解题的关键．16．/70度【分析】本题考查圆内接四边形的性质，掌握圆内接四边形对角互补是解题关键．直接利用圆内接四边形对角互补与邻补角的性质推导可得出答案．【详解】解：∵四边形为的内接四边形，，即，，故答案为：．17．4【分析】由垂直定义得，根据等腰三角形的性质由得，根据对顶角相等得，所以，而，所以，设，则，在中，根据勾股定理得到，然后解方程即可．【详解】解：连接，如图所示：∵，∴，∴，∵，∴，而，∴，∵，∴，∴，∴为直角三角形，设，则，在中，，，∵，∴，解得：，即的长为4．故答案为：4．【点睛】本题考查了圆的基本知识，等腰三角形的性质以及勾股定理，垂线定义理解，正确应用勾股定理求出的长是解题关键．18．【分析】由圆周角定理即可得到答案．【详解】解：，，故答案为：．【点睛】本题主要考查了圆周角定理，熟练掌握圆周角定理：同弧所对的圆周角等于圆心角的一半，是解题的关键．19．4【分析】本题考查了切线的性质，坐标和图形的性质，圆周角定理，找到的最小值是解题的关键．连接，交上一点P，以O为圆心，以为半径作，交x轴于A、B，此时的长度最小，根据勾股定理和题意求得，则的最小长度为4．【详解】解：连接，交⊙C上一点P，以O为圆心，以为半径作，交x轴于A、B，此时的长度最小，∵，∴，∵以点C为圆心的圆与y轴相切．∴的半径为3，∴，∴，∵是直径，∴，∴长度的最小值为4，故答案为：4．20．①②③④【分析】本题考查了全等三角形的判定及性质、切线的判定及性质、菱形的判定及性质、含角的直角三角形的特征，利用得，可得，再根据切线的判定及性质可判断①，利用三角形的判定及性质得，再根据菱形的判定即可判断②，利用含角的直角三角形的特征可判断③，利用菱形的性质可判断④，熟练掌握相关的判定及性质是解题的关键．【详解】解：连接，，，，，，，与相切于点C，，，是的直径，与相切；故①正确；，，，，，，，∴四边形是菱形，故②正确；，，，，，，，，故③正确；∵四边形是菱形，，，故④正确；故答案为：①②③④．21．1440【分析】依据正多边形的中心角和为求得边数，再依据多边形内角和公式代入求解即可．【详解】解：因为正多边形的中心角为36°，且中心角和为，所以这个多边形边数：，则这个多边形的内角和为：．故答案为：．【点睛】本题考查了正多边形内角和公式、中心角性质，通过中心角求得边数是解题的关键．22．【分析】本题主要考查了旋转的性质，求弧长，等边三角形的性质与判定，含30度角的直角三角形的性质，根据三角形内角和和含度的直角三角形三边的关系得到，，再根据旋转的性质得，于是可判断为等边三角形，所以，然后根据弧长公式计算弧的长度即可．【详解】解：，，，，，三角板绕直角顶点顺时针旋转，点落在边上，∴，∴为等边三角形，∴弧的长度，即点所转过的路径长．故答案为：．23．【分析】本题考查了等边三角形的判定与性质、扇形面积、弓形面积的计算，连接，过点作，易得为等边三角形，从而利用割补法求得阴影部分的面积即可，准确识图，添加适当的辅助线构造规则图形是解此题的关键．【详解】解：如图，连接，过点作，由题意可得，为等边三角形，，，，，，∴弓形的面积为，∴空白部分的面积为，∴阴影部分的面积为，故答案为：．24．(1)，(2)见解析(3)【分析】（1）根据平移的性质，即可解答；（2）以点为圆心，2为半径画弧，即可得出；（3）根据弧长公式求出，根据平移的性质得出，根据勾股定理求出，最后相加即可．【详解】（1）解：∵，所在圆的圆心为，∴，所在圆的圆心坐标是，故答案为：，；（2）解：如图所示：即为所求；（3）解：连接，∵，，∴的半径为2，∴，∵将向右平移5个单位，得到，∴，∴，∴由，，，首尾依次相接所围成的封闭图形的周长．【点睛】本题主要考查了平移的性质，求弧长，勾股定理，解题的关键是掌握平移前后对应点连线相等，弧长公式，以及勾股定理的内容．25．(1)见解析(2)①见解析；②【分析】（1）由点关于的对称点为可知点E是的中点，，从而得到是的中位线，继而得到，从而证明；（2）①过点O作于点F，延长交于点G，先证明得到，由与相切，得到，继而得到，从而证明是的角平分线，即，，求得，利用直角三角形两锐角互余得到，从而得到，即，最后利用含度角的直角三角形的性质得出；②先证明四边形是正方形，得到，再利用是的中位线得到，从而得到，，再利用平行线的性质得到，从而证明是等腰直角三角形，，设，求得，在中，即，解得，从而得到的面积为．【详解】（1）∵点关于的对称点为，∴点E是的中点，，又∵四边形是矩形，∴O是的中点，∴是的中位线，∴∴，∴（2）①过点O作于点F，延长交于点G，则，∵四边形是矩形，∴，，∴，．∵，，，∴，∴．∵与相切，为半径，，∴，∴又∵即，，∴是的角平分线，即，设，则，又∵∴∴又∵，即是直角三角形，∴，即解得：，∴，即，在中，，，∴，∴；②过点O作于点H，∵与相切，∴，∵∴四边形是矩形，又∵，∴四边形是正方形，∴，又∵是的中位线，∴∴∴又∵，∴又∵，∴又∵，∴是等腰直角三角形，，设，则∴在中，，即∴∴的面积为：【点睛】本题考查矩形的性质，圆的切线的性质，含度角的直角三角形的性质，等腰直角三角形的性质与判定，中位线的性质定理，角平分线的判定定理等知识，掌握相关知识并正确作出辅助线是解题的关键．26．(1)见详解(2)【分析】（1）连接，根据，，可得，，再根据，，可得，即有半径，问题得证；（2）连接，过O点作于点，利用垂径定理可得，，即，再证明，即有，设，即，在和中，有，，即，解方程即可求解．【详解】（1）证明：连接，如图，∵，，∴，，∵，∴，∵，，，∴，∴半径，∴是的切线；（2）解：连接，过O点作于点，如图，∵，，，的半径为5，∴，，即：，∵，，，∴，∴，设，即，∵，，∴在中，有；在中，有∴，解得：，∴．【点睛】本题考查了切线的判定与性质，等边对等角，全等三角形的判定与性质以及勾股定理等知识，掌握切线的判定与性质是解答本题的关键．27．(1)见解析(2)①见解析；②1【分析】（1）由直径所对的圆周角等于得出，由切线的性质定理得出，即可得出结论；（2）①由等弧所对的圆周角相等得出，由直角所对的圆周角为90°得出，由垂直的定义得出，等量代换得出，即可得出结论；②连接、，作，交的延长线于点，由角平分线的性质得出，由全等三角形的判定得出和，得出，，代入计算即可求出的值．【详解】（1）证明：是直径，，；是的切线；∴，，∴；（2）解：①是弧的中点，，是直径，，∵，，，，．②连接、，作，交的延长线于点．，，，，在与中，，，，是弧的中点，，在与中，，．．，即，．【点睛】本题考查了圆周角定理，切线的性质，全等三角形的性质和判定，角平分线的性质，熟练掌握各性质定理是解答此题的关键．28．(1)见解析(2)或【分析】（1）连接，可得，从而可证，即可求证；（2）①过点作交的延长线于点，并连接、，，过作交于，可求，从而可求，，进而可求，即可求解；②连接，，，过点作交于点，连接，同理可求，，可证，可得与重合，可求，即可求解．【详解】（1）解：如图，连接，，，是的平分线，，，，，点在上，是的切线；（2）解：①如图，过点作交的延长线于点，并连接、，，过作交于，，，，，，是的平分线，，，，，，，在中，，，，在中，，，，，，，点到直线的距离是；②如图，连接，，，过点作交于点，连接，同理可求，，，，，与重合，，在中，，，，，，点到直线的距离是；综上所述：或．【点睛】本题考查了切线的判定，勾股定理，等腰三角形的性质，直角三角形的特征，根据题意作出辅助线，掌握相关的性质是解题的关键．29．(1)见解析(2)【分析】（1）由垂径定理知，垂直于弦的直径是弦的中垂线，故作，的中垂线交于点，则点是弧所在圆的圆心；（2）在中，由勾股定理得出方程，解方程可求得半径的长．【详解】（1）解：作弦的垂直平分线与弦的垂直平分线交于点，以为圆心长为半径作圆就是此残片所在的圆，如图1所示．（2）连接，如图2所示：设，∵，，∴，则根据勾股定理列方程：，解得：．答：圆的半径为．【点睛】本题考查了作图，垂径定理，中垂线的性质，勾股定理；熟练掌握垂径定理，由勾股定理得出方程是解决问题（2）的关键．30．（）结论：，理由见解析；（）；（），；（）的最大值为，的最小值为．【分析】()结论：．只要证明即可；()利用三角形的三边关系即可解决问题；()连接，将绕着点顺时针旋转得到，连接，得到是等腰直角三角形，根据全等三角形的性质得到，，根据当在线段的延长线时，线段取得最大值，即可得到最大值为；过作轴于，根据等腰直角三角形的性质，即可得到结论；()如图中，以为边作等边三角形，由，推出，推出欲求的最大值，只要求出的最大值即可，由定值，，推出点在以为直径的上运动，由图象可知，当点在上方，时，的值最大．【详解】解：（）如图中，结论：，理由：∵、都是等边三角形，∴，，，∴，∴，∴；（）在中，，∴当共线，∴的最大值为，∴的最大值为．故答案为：；（）如图，连接，∵将绕着点顺时针旋转得到，连接，则是等腰直角三角形，∴，，∵的坐标为，点的坐标为，∴，，∴，∴线段长的最大值线段长的最大值，∴当在线段的延长线时，线段取得最大值（如图中），最大值，∵，∴最大值为；如图，过作轴于，∵是等腰直角三角形，∴，∴，∴；（）如图中，以为边作等边三角形，∵，∴，∵，，∴，∴，∴欲求的最大值，只要求出的最大值即可，∵定值，，∴点在以为直径的半圆上运动，由图象可知，当点在上方，时，的值最大，最大值，∴AC的最大值为；当点在线段的右侧时，以为边作等边，∵，∴，且，，∴，∴，∴欲求的最小值，只要求出的最小值即可，∵定值，，∴点在以为直径的上运动，由图象可知，当点在的上方，时，的值最小，的最小值，∴的最小值为；综上所述，的最大值为，AC的最小值为．【点睛】本题考查了圆的有关知识、等边三角形的性质、等腰直角三角形的性质、全等三角形的判定和性质，正确的作出辅助线构造全等三角形是解题的关键．。

专题03 圆的综合计算压轴题-备战2022年中考数学满分真题模拟题分类汇编(广州专用)(原卷版)

专题03 圆的综合计算压轴题1．（2021•广州）如图，在平面直角坐标系xOy中，直线1:42l y x=+分别与x轴，y轴相交于A、B两点，点(,)P x y为直线l在第二象限的点．（1）求A、B两点的坐标；（2）设PAO∆的面积为S，求S关于x的函数解析式，并写出x的取值范围；（3）作PAO∆的外接圆C，延长PC交C于点Q，当POQ∆的面积最小时，求C的半径．2．（2020•广州）如图，O为等边ABC∆的外接圆，半径为2，点D在劣弧AB上运动（不与点A，B重合），连接DA，DB，DC．（1）求证：DC是ADB∠的平分线；（2）四边形ADBC的面积S是线段DC的长x的函数吗？如果是，求出函数解析式；如果不是，请说明理由；（3）若点M，N分别在线段CA，CB上运动（不含端点），经过探究发现，点D运动到每一个确定的位置，DMN∆的周长有最小值t，随着点D的运动，t的值会发生变化，求所有t值中的最大值．3．（2021•海珠区一模）如图，等边三角形ABE∆和矩形ABCD有共同的外接圆O，且30AB =．（1）求证：120CED ∠=︒；（2）在劣弧AB 上有动点F ，连接DF 、CF 、BF ，DF 分别交AE 、AB 于点M 、P ，CF 交BE 于点N ．①设MNF ∆与CDF ∆的周长分别为1C 和2C ，试判断21C C -的值是否发生变化，若不变则求出该值；若变化请说明理由； ②若53PN =，求BF 的长．4．（2021•江北区模拟）定义：两个角对应互余，且这两个角的夹边对应相等的两个三角形叫做余等三角形．如图1，在ABC ∆和DEF ∆中，若90A E B D ∠+∠=∠+∠=︒，且AB DE =，则ABC ∆和DEF ∆是余等三角形．（1）图2，等腰直角ABC ∆，其中90ACB ∠=︒，AC BC =，点D 是AB 上任意一点（不与点A 、B 重合），则图中△ 和△ 是余等三角形，并求证：2222AD BD CD +=．（2）图3，四边形ABCD 是O 的内接四边形，O 的半径为5，且22100AD BC +=， ①求证：ABC ∆和ADC ∆是余等三角形．②图4，连接BD 交AC 于点I ，连接OI ，E 为AI 上一点，连接EO 并延长交BI 于点F ，若67.5ADB ∠=︒，IE IF =，设OI x =，EIF S y ∆=，求y 关于x 的函数关系式．5．（2021•花都区一模）已知，AB 是O 的直径，42AB =，AC BC =．（1）求弦BC 的长；（2）若点D 是AB 下方O 上的动点（不与点A ，B 重合），以CD 为边，作正方形CDEF ，如图1所示，若M是DF的中点，N是BC的中点，求证：线段MN的长为定值；（3）如图2，点P是动点，且2AP=，连接CP，PB，一动点Q从点C出发，以每秒2个单位的速度沿线段CP匀速运动到点P，再以每秒1个单位的速度沿线段PB匀速运动到点B，到达点B后停止运动，求点Q的运动时间t的最小值．6．（2020•长沙）如图，半径为4的O中，弦AB的长度为43，点C是劣弧AB上的一个动点，点D是弦AC的中点，点E是弦BC的中点，连接DE、OD、OE．（1）求AOB∠的度数；（2）当点C沿着劣弧AB从点A开始，逆时针运动到点B时，求ODE∆的外心P所经过的路径的长度；（3）分别记ODE ∆，CDE ∆的面积为1S ，2S ，当221221S S -=时，求弦AC 的长度．7．（2021•越秀区校级模拟）AB 为O 的直径，点C 、D 为O 上的两个点，AD 交BC 于点F ，点E 在AB 上，DE 交BC 于点G ，且DGF CAB ∠=∠．（1）如图1．求证：DE AB ⊥．（2）如图2．若AD 平分CAB ∠．求证：2BC DE =．（3）如图3．在（2）的条件下，连接OF ，若45AFO ∠=︒，8AC =，求OF 的长．8．（2021•广西一模）在图1至图3中，O的直径30BC=，AC切O于点C，40AC=，连接AB交O于点D，连接CD，P是线段CD上一点，连接PB．（1）如图1，当点P，O的距离最小时，求PD的长；（2）如图2，若射线AP过圆心O，交O于点E，F，求tan F的值；（3）如图3，作DH PB⊥于点H，连接CH，直接写出CH的最小值．9．（2021•白云区二模）如图，在Rt ABC ∆中，90C ∠=︒，6AC =，8BC =，过点C 的圆与斜边AB 相切于点D ，与AC ，BC 边分别交于点E ，F （异于C 的交点）．（1）求sin A 的值；（2）EF 的长是否有最小值？如果有，请求出该值；如果没有，请说明理由；（3）若CEF ∆与ABC ∆相似，连接DE ，求ADE ∆的面积．10．（2021•滨湖区模拟）如图，在平面直角坐标系中，矩形OABC 的顶点A 、C 的坐标分别为(0,5)A 与(10,0)C -，经过点A 的直线1:2l y x b =-+与x 轴交于点D ．将矩形OABC 绕点O 顺时针旋转，旋转角为(0180)a α︒<<︒，旋转后，矩形的顶点A 、B 、C 的对应点分别记作A '、B '、C '．（1）求直线l 所对应的函数表达式；（2）点A '是否会落在直线l 上？若会，请求出此时点C '的坐标；若不会，请说明理由；（3）在旋转的过程中，当△OA D '的外心落在△OA D '内部时，请直接写出旋转角α的范围．11．（2021•姑苏区一模）如图①，周长为12的矩形ABCD 内接于O ，设AB 的长为x ．（1）当2x =时，O 的半径为；（2）如图②，D 是弧AC 的中点，设阴影部分的面积为S ，求S 的值；（3）如图③，连接AC 并延长，试问在AC 的延长线上是否存在一点E ，连接DE ，使得DE 与O 相切，且12CE AC =，若存在，求出此时x 的值；若不存在，请说明理由．12．（2021•碑林区校级模拟）问题提出（1）如图①，在中，，．过点作直线，再分别过点、作于，于．则线段、、之间的数量关系为；（2）如图②，在中，，，，点在上，点、分别是边、上，且，．设，求四边形的面积与之间的函数关系式；（3）如图③是一个圆形广场，其中四边形规划为园林绿化区（四个顶点均在圆上），Rt ABC ∆90ACB ∠=︒AC BC =C l A B AM l ⊥M BN l ⊥N MN AM BN Rt ABC ∆90C ∠=︒30AC =40BC =P AB E F AC BC ABC FPB ∠=∠PE PF ⊥BP x =CEPF y x ACBD且要求，米，米，连接、交于点．为了更好的美化环境，需要在、边上分别确定点、，且满足，．为了整体布局，计划在四边形内种植花卉，在四边形剩余区域种植草坪．已知花卉每平方米的价格是60元，草坪每平方米的价格是90元，从实用角度希望四边形的面积最大．根据设计要求，求出当四边形的面积最大时种植花卉和草坪的总费用．13．（2021•广州模拟）定义：数学活动课上，李老师给出如下定义：如果一个三角形有一边上的中线等于这条边的一半，那么称这个三角形为“智慧三角形”．理解：（1）如图1，已知、是上两点，请在圆上找出满足条件的点，使为“智慧三角形”（画出点的位置，保留作图痕迹）；（2）如图2，在正方形中，是的中点，是上一点，且，试判90ACB ∠=︒30AC =40BC =AB CD P AC BC E F ABC FPB ∠=∠PE PF ⊥CEPF ACBD CEPFCEPF A B O C ABC ∆C ABCD E BC F CD 14CF CD =断是否为“智慧三角形”，并说明理由；运用：（3）如图3，在平面直角坐标系中，的半径为1，点是直线上的一点，若在上存在一点，使得为“智慧三角形”，当其面积取得最小值时，直接写出此时点的坐标．14．（2021•宁波模拟）如图，已知是的直径，弦于点．点是劣弧上任一点（不与点，重合），交于点，与的延长相交于点．（1）设，，求证：；（2）若，设，． ①求的度数；②求关于的函数表达式及自变量的取值范围． AEF ∆xOy O Q 3y =O P OPQ ∆P AB O CD AB ⊥E P AD A D CP AB M AP CD F CPF α∠=BDC β∠=90αβ=+︒OE BE =tan AFC x ∠=AM y BM=APC ∠y x x15．（2021•拱墅区二模）已知：为的直径，点，在上，，连接，．（1）如图1，求证：；（2）如图2，过点作于点，求证：；（3）如图3，在（2）的条件下，点在上，且，连接并延长交于点，过点作于点，连接，若，，求的长．AB O C D O BC CD =AD OC //AD OC C CE AB ⊥E 2AD OE =F OC OF BE =DF O G G GH AD ⊥H CH 135CFG ∠=︒3CE =CH16．（2021•南沙区一模）如图，的直径为，弦为．（1）作的角平分线交于点，连接、（尺规作图．并保留作图痕迹）；（2）求线段的长度；（3）若点在劣弧上由点运动到点时，求弦的中点运动的路径长．O AB 10cm AC 6cm ACB O D AD BD CD G BD B D CG K17．（2021•青羊区校级模拟）如图，中，，，，以为直径的交斜边于点．（1）如图1，若是的中点，求证：是的切线；（2）如图2，设是延长线上一动点，交于点，交于点，连接．若，求和的长；Rt ABC ∆90ABC ∠=︒8AB =6BC =AB O AC D M BC DM O E BC AE O F BF AC G DF ()i GB GC =CE DF求的最大值为．（直接写出结果）18．（2021•阿城区一模）内接于，于点，交于点，连接，．（1）如图1，求证：；（2）如图2，作射线，交线段于点，求证：；（3）如图3，在（2）的条件下，连接并延长，交于点，连接，交弦于点，连接、，若，，求线段的长．()ii BFAEABC ∆O BD AC ⊥D O E AE 2AEB ABE ∠=∠AC BC =CO BD F DE DF =BO O G AG BE H EG CH EG DH =15BCF S ∆=CH19．（2021•越秀区模拟）如图，在中，，为的外接圆，且的半径为3，过作，交于，连接交于点．（1）尺规作图：延长至点，使，连接（保留作图痕迹，不写作法）；（2）在（1）的条件下，①求证：是的切线；②当点在上运动时，求的最大值．ABC ∆AB AC =O ABC ∆O C //CD AB CD O D AD BC E DC F CF AC =AF AF O C O AB FD ⋅20．（2020•海珠区一模）圆内接四边形，点是的中点，．（1）求的度数，并求证：；（2）连接，相交于点，如图1，若，，求的值；（3）在（2）的条件下，点是四边形内一动点，点在线段上，且，，以点为旋转中心，将逆时针旋转，并缩短得到线段，使得，如图2，连接，试探索的长是否有最小值，若有请求出该值；若没有，请说明理由．ABCD A BD 120ADC ∠=︒ABC ∠AB DC BC +=AC BD H 3AD =5BC =HD AC ⋅E ABCD P BC 1PE =3PC =D DE 120︒DF 23DF DE =PF PF21．（2021•江西模拟）如图所示，是的直径，点是半圆上的一动点不与，重合），弦平分，过点作交射线于点．（1）求证：与相切：（2）若，，求长；（3）若，长记为，长记为，求与之间的函数关系式，并求出的最大值．AB O F (F A B AD BAF ∠D DE AF ⊥AF AF DE O 8AE =10AB =DE 10AB =AF x EF y y x AF EF ⋅22．（2021•松北区模拟）如图，四边形内接于，为直径，和交于点，．（1）求的度数；（2）过作的平行线，交于，试判断线段，，之间满足的等量关系，并说明理由；（3）在（2）条件下过，分别作，的垂线，垂足分别为，，连接，ABCD O AC AC BD E AB BC =ADB ∠B AD AC F EA CF EF E F AB BC G H GH交于，若，，求的半径．23．（2020•天河区校级模拟）如图1，已知、、、是上四点，的直径，．为的中点，延长到点．使，连接．（1）求线段的长；（2）求证：直线是的切线．（3）如图2，连交于点，延长交于另一点，连、，求的值．BO M 3AG =:8:9AGMO CHMO S S =四边形四边形O A B D E O O 23BE =60BAD ∠=︒A BE BA P BA AP =PE BD PE O PO O F O C EF EC tan ECF ∠24．（2020•花都区一模）如图1，已知、、是上的三点，，．（1）求证：的半径；（2）如图2，若点是所对弧上的一动点，连接，，． ①探究，，三者之间的数量关系，并说明理由；②若，点与关于对称，连接，点是的中点，当点从点运动到点时，求点的运动路径长．A B C O AB AC =120BAC ∠=︒O R AB =D BAC ∠DA DB DC DA DB DC 3AB =C 'C AD C D 'E C D 'D B C E25．（2020•越秀区校级二模）如图，是的直径，点是上一点，过点作的切线与的延长线相交于点，弦平分，交于点，连接．（1）利用尺规作图，过点作于点（保留作图痕迹，不写作法）；（2）求证：是等腰三角形；（3）若，，求线段的长． AB O C O C O AB P CE ACB ∠AB F BE A AD CP ⊥D PCF ∆4tan 3ABC ∠=72BE =PC26．（2020•黄埔区一模）如图，是的直径，与相切于点，．（1）尺规作图，在上找一点，使．（2）在（1）所作的图形中，求证：与相切．（3）在（1）所作的图形中，点是线段上一点（与端点，不重合），连接，，当的值最小时，求的值． AB O CB O B 25AB =2BC =O D CD CB =CD O E OB O B ED EC CE DE +CEDE27．（2021•深圳一模）如图所示，是的直径，点为线段上一点（不与，重合），作，交于点，垂足为点，作直径，过点的切线交的延长线于点，作于点，连接．（1）求证：平分．（2）求证：．（3）当时，求劣弧长度（结果保留． AB O E OB O B CE OB ⊥O C E CD C DB P AF PC ⊥F CB AC FAB ∠2BC CE CP =⋅3434CF AB CP ==且BC )π28．（2021•罗湖区模拟）已知的直径，点是上一个动点，是弦的中点，连接．（1）如图1，过点作的切线交直径的延长线于点，且； ①；②求证：；（2）如图2，是弧的中点，且、分别位于直径的两侧，连接、．在点运动过程中，当是等腰三角形时，求的长．O 6AB =C O D AC BD C O AB E 3tan 4E =BE =45CDB ∠=︒F AB C F AB DF BF C BDF ∆AC29．（2020•白云区一模）某数学学习小组在复习线段垂直平分线性质时，提出了以下几个问题，请你帮他们解决：【数学理解】（1）点是线段垂直平分线上的一点，则的值为．【拓展延伸】（2）在平面直角坐标系中，点，点在轴上，且，则点的坐标为．P AB :PA PB xOy (6,0)C Q x :2:1QO QC Q（3）经小组探究发现，如图1，延长线段到点，使，以点为圆心，长为半径作圆，则对于上任一点，都有，请你证明这个结论．【问题解决】（4）如图2，某人乘船以25千米时的速度沿一笔直的河从码头到码头，再立即坐车沿一笔直公路以75千米时的速度回到住处，已知乘船和坐车所用的时间相等，请在河边上确定码头的位置．（请画出示意图并简要说明理由）30．（2020•白云区模拟）如图，是的直径，，，点是上不与点，重合的点．（1）请判断的形状，并证明你的结论；（2）利用尺规作的平分线，交于点，交于点，连接；（保留作图痕迹，不写作法） ①求弧的长度；②求与的面积比．DE F 13EF DE =F 2EFF T 2TD TE =/lG M /H lM AB O 4AB =30ABC ∠=︒C O A B AOC ∆ACB ∠CD AB E O D BD AD ACE ∆BDE ∆。

中考数学临考题号押广东卷16题(与圆有关的计算)(解析版)

押广东卷第16题与圆有关的计算中考对与圆有关的计算的考查要求较高，在填空题中一般在第16题中进行考查，2021年是第13题。

一般难度不大，要求考生熟练掌握与与圆有关的基础知识．纵观近几年的中考考试题，主要考查以下两个方面：一是考查阴影部分面积，弧长．二是考查角度问题．在备考中应掌握圆的相关概念与计算，包括圆周角，圆心角的角度计算，圆的关系性质，圆的面积，扇形面积及周长，圆锥侧面积等。

1．（2021广东）如图，等腰直角三角形ABC 中，90,4A BC ∠=︒=．分别以点B 、点C 为圆心，线段BC 长的一半为半径作圆弧，交AB 、BC 、AC 于点D 、E 、F ，则图中阴影部分的面积为____．【分析】根据等腰直角三角形的性质可求出AC 的长，根据S 阴影=S △ABC -2S 扇形CEF 即可得答案．【详解】∵等腰直角三角形ABC 中，90,4A BC ∠=︒=，∴AC =AB =2222BC =，∠B =∠C =45°， ∴S 阴影=S △ABC -2S 扇形CEF =2145222360AC AB π⨯⋅-⨯=4π-，故答案为：4π-2．（2020广东）如题16图，从一块半径为1m 的圆形铁皮上剪出一个圆周角为120°的扇形ABC ，如果将剪下来的扇形围成一个圆锥，则该圆锥的底面圆的半径为______m ．【分析】根据弧长公式、圆锥底面周长公式即可求解【解析】连接BO 、AO 可得△ABO 为等边，可知AB=1，l=32π，2πr=32π得r=31故答案为：313．（2019广州）如图放置的一个圆锥，它的主视图是直角边长为2的等腰直角三角形，则该圆锥侧面展开扇形的弧长为．（结果保留π）【分析】根据圆锥侧面展开扇形的弧长＝底面圆的周长即可解决问题．【解答】解：∵某圆锥的主视图是一个腰长为2的等腰直角三角形， ∴斜边长为22，则底面圆的周长为22π，∴该圆锥侧面展开扇形的弧长为22π，故答案为：22π．4．（2018广东）如图，矩形ABCD 中，BC=4，CD=2，以AD 为直径的半圆O 与BC 相切于点E ，连接BD ，则阴影部分的面积为．（结果保留π）【分析】连接OE ，如图，利用切线的性质得OD=2，OE ⊥BC ，易得四边形OECD 为正方形，先利用扇形面积公式，利用S 正方形OECD ﹣S 扇形EOD 计算由弧DE 、线段EC 、CD 所围成的面积，然后利用三角形的面积减去刚才计算的面积即可得到阴影部分的面积．【解答】解：连接OE ，如图，∵以AD 为直径的半圆O 与BC 相切于点E ， ∴OD=2，OE ⊥BC ，易得四边形OECD 为正方形，∴由弧DE 、线段EC 、CD 所围成的面积=S 正方形OECD ﹣S 扇形EOD =22﹣=4﹣π，∴阴影部分的面积=×2×4﹣（4﹣π）=π．故答案为π．1．（2022年广东省佛山市禅城区中考一模）如图，小明利用半径为40cm 的扇形纸片制作成一个圆锥形纸帽（接缝忽略不计），若圆锥底面半径为10cm ，那么这个圆锥的侧面积是 _____cm 2．（结果用含π的式子表示）【分析】圆锥的底面圆的周长等于侧面展开扇形的弧长，再利用扇形的面积公式计算即可．【详解】解：∵圆锥底面半径为10cm ，∴圆锥底面圆的周长为221020r πππ=⨯=cm ，∴扇形纸片的弧长20l π=， ∴圆锥的侧面积11204040022lR ππ==⨯⨯=cm 2．故答案为：400π2．（广东省韶关市南雄市第一次质检数学试题）如图，△ABC 内接于⊙O ，∠A ＝72°，则∠OBC ＝_____．【分析】连接OC ，根据圆周角定理得求出∠BOC ，根据等腰三角形的性质、三角形内角和定理计算得到答案．【详解】解：如图，连接OC ，由圆周角定理得，∠BOC=2∠A=144°， ∵OB=OC ，∴∠OBC=（180°-144°）÷2=18°，故答案为18°．1．（2021佛山市禅城区一模）如图，正方形ABCD 内接于⊙O ，⊙O 的半径为2，以点A 为圆心，以AC 为半径画弧交AB 的延长线于点E ，交AD 的延长线于点F ，则图中阴影部分的面积是．【分析】利用对称性可知：阴影部分的面积＝扇形AEF 的面积﹣△ABD 的面积．【解答】解：利用对称性可知：阴影部分的面积＝扇形AEF 的面积﹣△ABD 的面积＝×4×2＝4π﹣4，故答案为：4π﹣43．（2021惠州市一模）若圆锥的侧面积是15π，母线长是5，则该圆锥底面圆的半径是．【分析】设该圆锥底面圆的半径是为r ，利用圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长和扇形面积公式得到125152r ππ⨯⨯⨯=，然后解关于r 的方程即可．【解答】解：设该圆锥底面圆的半径是为r ，根据题意得125152r ππ⨯⨯⨯=，解得3r =．即该圆锥底面圆的半径是3．故答案为3．4．（2021佛山市大沥镇一模）如图，在 Rt △ABC 中，∠ACB=90°，∠ABC=30°，AC=6，以C 为圆心，以AC 的长为半径作弧，交AB 于点D ，交BC 于点E ，则图中阴影部分的面积是_____________；（结果保留π）【分析】连接CD ．首先证明AD=BD=6，根据S 阴=12S △ABC -S 扇形CDE ，计算即可．【详解】解：如图，连接CD ． ∵∠ACB=90°，∠B=30°，AC=6， ∴∠BAC=60°，3 ∵CA=CD ，∴△ACD 是等边三角形 ∴∠ACD=60°，∠ECD=30°， ∵AB=2AC=12，AC=AD ， ∴AD=BD=6，∴S 阴=12S △ABC -S 扇形CDE =12×12×6×3－2306360π33π．故答案为：33π．5．（2021深圳市光明区二模）如图，扇形OPQ可以绕着正六边形ABCDEF的中心O旋转，若∠POQ＝120°，OP等于正六边形ABCDEF边心距的2倍，AB＝2，则阴影部分的面积为．【分析】连接OE，OD，OC．设EF交OP于T，CD交OQ于J．证明△EOT≌△COJ （ASA），推出S五边形OTEDJ＝S四边形OEDC＝2××22＝2，根据S阴＝S扇形OPQ﹣S五边形OTEDJ，求解即可．解：连接OE，OD，OC．设EF交OP于T，CD交OQ于J．∵∠POQ＝∠EOC＝120°，∴∠EOT＝∠COD，∵OE＝OJ，∠OET＝∠OCJ＝60°，∴△EOT≌△COJ（ASA），∴S＝S四边形OEDC＝2××22＝2，五边形OTEDJ∴S＝S扇形OPQ﹣S五边形OTEDJ＝＝4π﹣2，阴故答案为：4π﹣2．6．（2021汕头市金平区一模）如图，扇形ABC的圆心角为120°，半径为8，将扇形ABC绕点C顺时针旋转得到扇形EDC，点B，A的对应点分别为点D，E．若点D刚好落在上，则阴影部分的面积为．【分析】证明△BCD是等边三角形，根据S阴＝S扇形DCE﹣（S扇形BDC﹣S△BCD）计算即可．【解答】解：如图，连接BD．由题意：CD＝CB＝BD，∴△BCD是等边三角形，∴∠DBC＝60°，∴S阴＝S扇形DCE﹣（S扇形BDC﹣S△BCD）＝﹣（﹣×82）＝+16，故答案为+16．1．（2022·广东江门·一模）如图，P A，PB分别与⊙O相切于点A，B，⊙O的切线EF分别交P A，PB于点E，F，切点C在弧AB上，若P A长为8，则△PEF的周长是_____．【答案】16 【解析】【分析】由切线长定理知，AE ＝CE ，FB ＝CF ，P A ＝PB ＝12，然后根据△PEF 的周长公式即可求出其结果．【详解】解：∵P A 、PB 、EF 分别与⊙O 相切于点A 、B 、C ， ∴AE ＝CE ，FB ＝CF ，P A ＝PB ＝8， ∴△PEF 的周长＝PE +EF +PF ＝P A +PB ＝16．故答案为：16．2．（2022·广东·模拟预测）已知圆锥的高是4,cm 圆锥的底面半径是3,cm 则该圆锥的侧面积是______2cm ．【答案】15π 【解析】【分析】由已知中圆锥的底面半径和高，求出圆锥的母线长，代入圆锥侧面积公式，可得答案．【详解】解:由勾股定理得:圆锥的母线长=22345cm圆锥的底面周长为2236,r cm πππ=⨯= ∴圆锥的侧面展开扇形的弧长为6,cm π ∴圆锥的侧面积为：2165 15.2cm ππ⨯⨯=故答案为: 15π.3．（2022·广东·江门市新会东方红中学模拟预测）如图，BC 是⊙O 的直径，点A 在圆上，连接AO ，AC ，∠AOB=64°，则∠ACB=____．【答案】32°．【解析】【详解】 ∵AO=OC ，∴∠ACB=∠OAC ， ∵∠AOB=64°， ∴∠ACB+∠OAC=64°， ∴∠ACB=64°÷2=32°．故答案为32°. 4．（2021·广东·佛山市第四中学三模）如图，等边三角形ABC 中，AB =4，圆O 与三角形内切，则阴影部分的面积为________．4349π【解析】【分析】首先连接圆心和切点，结合等边三角形的性质可以得到CD =12AC =2，OD =DC ·tan ∠OCD 2343OECD S 四边形22312043609ODES ππ⎝⎭==扇形，最后利用阴影部分面积=-OECD S 四边形ODE S 扇形得出结果. 【详解】解：设圆O 分别与AC 和CB 的切点为点D 和E ，连接OD 、OE 、OC ，OC 交圆O 于点F ， ∴∠ODC =∠OEC =90°，∴∠OCD =∠OCE =12∠DCE =30°，又∵CD =12AC =2， ∴OD =DC ·tan ∠OCD 23∴112323=222ODCSOD DC ⋅=⨯= ，同理23OECS =， ∴43OECD S 四边形223120343609ODES ππ⎛⎫ ⎪⎝⎭==扇形 , 所以阴影部分的面积=434-39π，故答案为434-39π.5．（2021·广东云浮·一模）如图，两个圆都是以点O 为圆心，大圆的弦AB 是小圆的切线，点P 为切点，10AB =，则图中圆环的面积为_________．【答案】25π 【解析】【分析】连接OP ，OA ，根据切线的性质得到OP ⊥AB ，根据垂径定理求出AP =5，最后根据圆的面积公式计算即可达到答案. 【详解】解：连接OP ，OA ，∵大圆的弦AB 是小圆的切线，∴OP ⊥AB ， ∴12AP AB =，又AB =10，∴AP =5，在Rt AOP △中，222OA OP AP -=，∴2225OA OP -=，∴圆环的面积为2222()25OA OP OA OP ππππ⨯-⨯=⨯-=．故答案为25π．6．（2021·广东·东莞市南开实验学校一模）如图，已知⊙O 是正六边形ABCDEF 的外接圆，且半径为2，则阴影部分的面积为____．【答案】2π33【解析】【分析】由⊙O 是正六边形ABCDEF 的外接圆可求得∠AOB ，进而求得圆的半径为OA ，由扇形的面积公式求得S 扇形OAB ，由三角形的面积公式求出S △OAB ，根据S 阴影=S 扇形OA B -S △OAB 即可求得结果．【详解】解：∵⊙O 是正六边形ABCDEF 的外接圆，∴∠AOB =360°÷6=60°，∵OA=OB ，∴△OAB 是等边三角形，∴OA=AB =2，∴S 扇形OAB =26022π3603π⨯⨯=，过O 作OH ⊥AB 于H ，如下图所示：∴∠AOH =12∠AOB =30°，∴AH =12AB =1，∴OH =223OA AH -=，∴S △OAB =12AB×OH =123=32⨯⨯， ∴S 阴影=S 扇形OA B -S △OAB =2π33-，故答案为：2π33-． 7．（2021·广东广州·一模）如图，⊙O 的直径CD 为6cm ，OA ，OB 都是⊙O 的半径，∠AOD ＝2∠AOB ＝60°，点P 在直径CD 上移动，则AP +BP 的最小值为______．【答案】32【解析】【分析】如图，过点B 作BE ⊥CD ，交⊙O 于E ，连接AE ，交CD 于P ，连接BP ，OE ，根据垂径定理可得CD 垂直平分线BE ，根据垂直平分线的性质可得BP =PE ，可得P A +PB =P A +PE ，即可得出AE为AP+BP的最小值，根据∠AOD＝2∠AOB＝60°可得∠BOD=30°，根据等腰三角形“三线合一”的性质可得∠DOE=∠BOD=30°，可得∠AOE=90°，根据CD为直径可得OA 的长，根据等腰直角三角形的性质求出AE的长即可得答案．【详解】如图，过点B作BE⊥CD，交⊙O于E，连接AE，交CD于P，连接BP，OE，∵CD是⊙O的直径，BE⊥CD，∴CD垂直平分线BE，∴BP=PE，∴P A+PB=P A+PE，∴AE为AP+BP的最小值，∵∠AOD＝2∠AOB＝60°，∴∠BOD=30°，∵OB=OE，OD⊥BE，∴∠DOE=∠BOD=30°，∴∠AOE=90°，∴△AOE是等腰直角三角形，∵CD=6，CD=3，∴OA=12∴AE=2OA=32，∴AP+BP的最小值为32．故答案为：32【点睛】本题考查垂径定理、等腰三角形的性质及线段垂直平分线的性质，垂直弦的直径平分弦，且平分这条弦所对的两条弧；线段垂直平分线上的点到线段两端点的距离相等；熟练掌握相关性质及定理是解题关键．8．（2021·广东河源·二模）如图，半径为4的⊙O中，CD为直径，弦AB⊥CD且过半径OD 的中点，点E为⊙O上一动点，CF⊥AE于点F，当点E从点B出发顺时针运动到点D时，点F所经过的路径长为____．【答案】233π 【解析】【分析】由90AFC ∠=︒得点F 在以AC 为直径的圆上运动，当点E 与B 重合时，此时点F 与G 重合，当点E 与D 重合时，此时点F 与A 重合，则点E 从点B 出发顺时针运动到点D 时，点F 所经过的路径长为AG 的长，然后根据条件求出AG 所在圆的半径和圆心角，从而解决问题．【详解】解：CF AE ⊥，90AFC ∴∠=︒，∴点F 在以AC 为直径的圆上运动，以AC 为直径画半圆AC ，连接OA ，确定出AC 的中点P ，连接PG ，当点E 与B 重合时，此时点F 与G 重合，当点E 与D 重合时，此时点F 与A 重合，∴点E 从点B 出发顺时针运动到点D 时，点F 所经过的路径长的AG 的长，∵点G 为OD 的中点，11222OG OD OA ∴===． OG AB ⊥，60AOG ∴∠=︒，23AG =OA OC =，30ACG ∴∠=︒，23AC AG ∴==AG ∴所在圆的半径为23，所对的圆心角260APG ACG ∠=∠=︒，AG ∴的长为602323=1803ππ⨯．故答案为：233π． 9．（2021·广东·二模）如图，在扇形AOB 中，∠AOB ＝90°，点C 是AB 的中点，过点C 的切线交OB 的延长线于点E ，当BE ＝42233-时，则阴影部分的面积为 __________________．【答案】49π- 【解析】【分析】分析：由∠AOB ＝90°，点C 是AB 的中点可得∠COE ＝45°，由CE 与圆O 相切得△OCE 为等腰直角三角形，根据BE 的长度求得OC 的长，用S △OCE ﹣S 扇形OCB ，即得阴影部分面积．【详解】解：∵∠AOB ＝90°，点C 是AB 的中点，∴∠COE ＝45°，∵CE 与圆O 相切，∴△OCE 为等腰直角三角形，设OC ＝CE ＝x ，则OB ＝x ，OE 2，∵OE ﹣OB ＝BE ，BE ＝422332﹣x ＝42233解得：x 22， ∴阴影部分的面积＝S △OCE ﹣S 扇形OCB ＝222(45122223233360π⨯⨯⨯-＝49π-，故答案为：49π-． 10．（2022·广东广州·一模）如图AB 与圆O 相切于A ，D 是圆O 内一点，DB 与圆相交于C ．已知BC ＝DC ＝3，OD ＝2，AB ＝6，则圆的半径为_____．【答案】22【解析】【分析】连接BC 并延长，交圆于F ，过O 作OE ⊥BF ，连接,,AC OA AF ，证明ABC FBA ∽，则可得AB 2＝BC •BF ，进而求得DE ＝32，OD ＝2，勾股定理求解即可．【详解】解：连接BC 并延长，交圆于F ，过O 作OE ⊥BF ，连接,,AC OA AF∵BA 是圆O 的切线，切点为A ，90OAB ︒∴∠=90OAC CAB ∴∠+∠=︒AC AC =12AOC AFC ∴∠=∠ 在AOC △中，OA OC =2180AOC OAC ∴∠+∠=︒则22180AFC OAC ∠+∠=︒90AFC OAC ∴∠+∠=︒AFC CAB ∴∠=∠又B B ∠=∠ABC FBA ∴∽AB BC FB AB ∴=∴AB 2＝BC •BF ，∵BC ＝DC ＝3，AB ＝6，∴BF ＝12，CF ＝9，∴DE ＝32，OD ＝2， ∴OE ＝22OD DE -＝944-＝72，CE ＝92， ∴OC ＝22OE CE +＝78144+＝22．故答案为：22． 11．（2021·广东阳江·二模）如图，在Rt △ABC 中，∠ACB ＝90°，∠ABC ＝30°，AC ＝2，以C 为圆心，以AC 的长为半径作弧，交AB 于点D ，交BC 于点E ，则图中阴影部分的面积是_________________．（结果保留根号和π）【答案】33π-【解析】【分析】连接CD ，如图，先根据含30度的直角三角形三边的关系得到23BC =，4AB =，则判断ACD △为等边三角形得到60ACD ︒∠=，所以30DCE ︒∠=，然后根据三角形面积公式和扇形的面积公式，利用阴影部分的面积ABE AED DEE S S S ∆∆∆=--进行计算．【详解】解：连接CD ，如图，90ACB ︒∠=，30ABC ︒∠=，323BC AC ∴==24AB AC ==，60BAC ︒∠=，CA CD =，60CAD ︒∠=，ACD ∴∆为等边三角形，60ACD ︒∴∠=，30DCE ︒∴∠=，阴影部分的面积ABE AED DEE S S S ∆∆∆=-- 221330222322360π⨯⨯=⨯⨯- 133π=． 313π．。

2021年广东省中考数学总复习《圆》压轴题200道

2021年广东省中考数学总复习《圆》压轴题200道
第一组
1．⊙O是△ABC的外接圆，AB是直径，过的中点P作⊙O的直径PG交弦BC于点D，连接AG、CP、PB．
（1）如图1，若D是线段OP的中点，求∠BAC的度数；
（2）如图2，在DG上取一点K，使DK＝DP，连接CK，求证：四边形AGKC是平行四边形；
（3）如图3，取CP的中点E，连接ED并延长ED交AB于点H，连接PH，求证：PH ⊥AB．
【分析】（1）由垂径定理得出PG⊥BC，CD＝BD，再由三角函数求出∠BOD＝60°，证出AC∥PG，得出同位角相等即可；
（2）先由SAS证明△PDB≌△CDK，得出CK＝BP，∠OPB＝∠CKD，证出AG＝CK，再证明AG∥CK，即可得出结论；
（3）先证出DH∥AG，得出∠OAG＝∠OHD，再证OD＝OH，由SAS证明△OBD≌△HOP，得出∠OHP＝∠ODB＝90°，即可得出结论．
【解答】（1）解：∵点P为的中点，AB为⊙O直径，
∴BP＝PC，PG⊥BC，CD＝BD，
∴∠ODB＝90°，
∵D为OP的中点，
∴OD＝OP＝OB，
∴cos∠BOD＝＝，
∴∠BOD＝60°，
∵AB为⊙O直径，
1/ 519。

近三年广州中考数学几何压轴题真题汇编

2011 25.如图7，⊙O 中AB 是直径，C 是⊙O 上一点，∠ABC=450，等腰直角三角形DCE 中∠DCE 是直角，点D 在线段AC 上。

（1）证明：B 、C 、E 三点共线；（2）若M 是线段BE 的中点，N 是线段AD 的中点，证明：MN=2OM ；（3）将△DCE 绕点C 逆时针旋转α（00<α<900）后，记为△D 1CE 1（图8），若M 1是线段BE 1的中点，N 1是线段AD 1的中点，M 1N 1=2OM 1是否成立？若是，请证明：若不是，说明理由。

2012 25. 如图10，在平行四边形ABCD 中，A B=5,BC =10,F 为AD 的中点。

C E ⊥AB 于点E ,设∠ABC=α(600≤<α<900). （1）、当α=600时，求CE 的长。

（2）、当600≤<α<900时， ①是否存在正整数k ，使得∠EFD=k ∠A EF ?若存在，求出k 的值；若不存在，请说明理由。

②连接CF ，当CE 2-CF 2取最大值时，求tan ∠DCF 的值。

2013 24. 已知AB 是⊙O 的直径，AB=4，点C 在线段AB 的延长线上运动，点D 在⊙O 上运动（不与点B 重合），连接CD ，且CD=OA.(1)当OC=12），求证：CD 是⊙O 的切线；（2）当OC＞CD 所在直线于⊙O 相交，设另一交点为E ，连接AE .①当D 为CE 中点时，求△ACE 的周长;②连接OD ,是否存在四边形AODE 为梯形？若存在，请说明图12梯形个数并求此时AE·ED的值；若不存在，请说明理由。

When you are old and grey and full of sleep,And nodding by the fire, take down this book,And slowly read, and dream of the soft lookYour eyes had once, and of their shadows deep;How many loved your moments of glad grace,And loved your beauty with love false or true,But one man loved the pilgrim soul in you,And loved the sorrows of your changing face;And bending down beside the glowing bars,Murmur, a little sadly, how love fledAnd paced upon the mountains overheadAnd hid his face amid a crowd of stars.The furthest distance in the worldIs not between life and deathBut when I stand in front of youYet you don't know thatI love you.The furthest distance in the worldIs not when I stand in front of youYet you can't see my loveBut when undoubtedly knowing the love from both Yet cannot be together.The furthest distance in the worldIs not being apart while being in loveBut when I plainly cannot resist the yearningYet pretending you have never been in my heart. The furthest distance in the worldIs not struggling against the tidesBut using one's indifferent heartTo dig an uncrossable riverFor the one who loves you.。

年中考数学压轴题之圆题例题(完整版)资料

年中考数学压轴题之圆题例题（完整版）资料(可以直接使用，可编辑优秀版资料，欢迎下载）广东中考数学专题训练（二）：几何综合题（圆题）例题训练1．如图，⊙O 为∆ABC 外接圆，BC 为⊙O 直径，BC =4．点D 在⊙O 上，连接OA 、CD 和BD ，AC 与BD 交于点E ，并作AF ⊥BC 交BD于点G ，点G 为BE 中点，连接OG ．（1）求证：OA ∥CD ；（2）若∠DBC =2∠DBA ，求BD 的长；（3）求证：FG =2DE ．2．如图，⊙O 为∆ABC 外接圆，AB 为⊙O 直径，AB =4．⊙O 切线CD 交BA 延长线于点D ，∠ACB 平分线交⊙O 于点E ，并以DC 为边向下作∠DCF =∠CAB 交⊙O 于点F ，连接AF ．（1）求证：∠DCF =∠D +∠B ；（2）若AF =32，AD =52，求线段AC 的长；（3）若CE=AB ⊥CF ．3．如图，⊙O为 ABC外接圆，BC为⊙O直径．作AD=AC，连接AD、CD和BD，AB与CD交于点E，过点B作⊙O切线，并作点E作EF⊥DC交切线于点G．（1）求证：∠DAC=∠G+90°；（2）求证：CF=GF；（3）若EFBD =23，求证：AE=DE．4．如图，⊙O为 ABC外接圆，AB为⊙O直径．连接CO，并作AD∥CO交⊙O于点D，过点D 作⊙O切线DE交CO延长线于点E ，连接BE ，作AF ⊥CO 交BC 于点G ，交BE 于点H ，连接OG ．（1）若CF =2，OF =3，求AC 的长；（2）求证：BE 是⊙O 的切线；（3）若2AFAH DE =23，求证：OG ⊥AB ．一线三等角CB EDAP点评：此题是典型的图形变式题，记住口诀：“图形改变，方法不变”。

动点在线段上时，通过哪两个三角形相似求解，当动点在线段的延长线上时，还是找原来的两个三角形，多数情况下这两个三角形还是相似的，还是可以沿用原来的方法求解。

2024年中考数学高频压轴题训练——圆-动点问题及参考答案

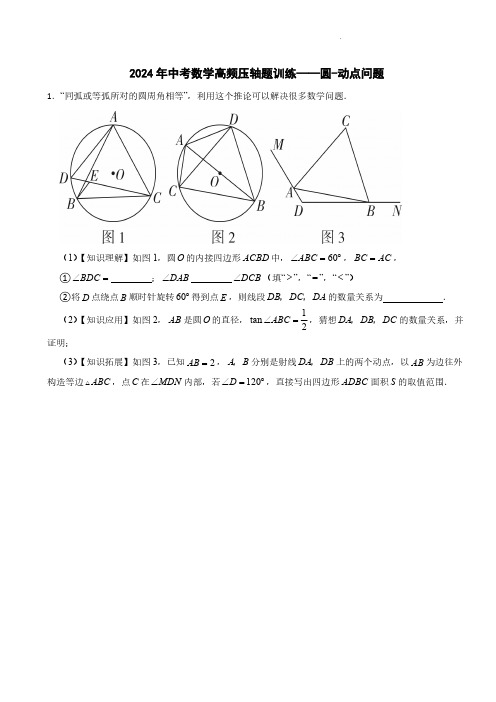
2024年中考数学高频压轴题训练——圆-动点问题1．“同弧或等弧所对的圆周角相等”，利用这个推论可以解决很多数学问题．（1）【知识理解】如图1，圆O 的内接四边形ACBD 中，60ABC ∠=︒，BC AC =，①BDC ∠=；DAB ∠DCB ∠（填“>”，“=”，“<”）②将D 点绕点B 顺时针旋转60︒得到点E ，则线段DB DC DA ，，的数量关系为．（2）【知识应用】如图2，AB 是圆O 的直径，1tan 2ABC ∠=，猜想DA DB DC ，，的数量关系，并证明；（3）【知识拓展】如图3，已知2AB =，A B ，分别是射线DA DB ，上的两个动点，以AB 为边往外构造等边ABC ，点C 在MDN ∠内部，若120D ∠=︒，直接写出四边形ADBC 面积S 的取值范围．2．如图1，对于PMN 的顶点P 及其对边MN 上的一点Q ，给出如下定义：以P 为圆心，PQ 为半径的圆与直线MN 的公共点都在线段MN 上，则称点Q 为PMN 关于点P 的内联点．在平面直角坐标系xOy 中：（1）如图2，已知点(70)A ，，点B 在直线1y x =+上．①若点(34)B ，，点(30)C ，，则在点O ，C ，A 中，点是AOB 关于点B 的内联点；②若AOB 关于点B 的内联点存在，求点B 纵坐标n 的取值范围；（2）已知点(20)D ，，点(42)E ，，将点D 绕原点O 旋转得到点F ．若EOF 关于点E 的内联点存在，直接写出点F 横坐标m 的取值范围．3．在平面直角坐标系xOy 中，O 的半径为1，对于点A 和线段BC ，给出如下定义：若将线段BC 绕点A 旋转可以得到O 的弦B C ''（B C ''，分别是B C ，的对应点），则称线段BC 是O 的以点A 为中心的“关联线段”．（1）如图，点112233A B C B C B C ，，，，，，的横､纵坐标都是整数．在线段112233B C B C B C ，，中，O 的以点A 为中心的“关联线段”是；（2）ABC 是边长为1的等边三角形，点()0A t ，，其中0t ≠．若BC 是O 的以点A 为中心的“关联线段”，求t 的值；（3）在ABC 中，12AB AC ==，．若BC 是O 的以点A 为中心的“关联线段”，直接写出OA 的最小值和最大值，以及相应的BC 长．4．已知：点C 为⊙O 的直径AB 上一动点，过点C 作CD ⊥AB ，交⊙O 于点D 和点E ，连接AD 、BD ，∠DBA 的角平分线交⊙O 于点F ．（1）若DF ＝BD ，求证：GD ＝GB ；（2）若AB ＝2cm ，在（1）的条件下，求DG 的值；（3）若∠ADB 的角平分线DM 交⊙O 于点M ，交AB 于点N ．当点C 与点O 重合时，AD BD DM+＝；据此猜想，当点C 在AB （不含端点）运动过程中，AD BD DM +的值是否发生改变？若不变，请求其值；若改变，请说明理由．5．在平面直角坐标系xOy 中，O 的半径为1，对于ABC 和直线l 给出如下定义：若ABC 的一条边关于直线l 的对称线段PQ 是O 的弦，则称ABC 是O 的关于直线l 的“关联三角形”，直线l 是“关联轴”．（1）如图1，若ABC 是O 的关于直线l 的“关联三角形”，请画出ABC 与O 的“关联轴”（至少画两条）；（2）若ABC 中，点A 坐标为(23)，，点B 坐标为(41)，，点C 在直线3y x =-+的图像上，存在“关联轴l ”使ABC 是O 的关联三角形，求点C 横坐标的取值范围；（3）已知A ，将点A 向上平移2个单位得到点M ，以M 为圆心MA 为半径画圆，B ，C 为M 上的两点，且2AB =（点B 在点A 右侧），若ABC 与O 的关联轴至少有两条，直接写出OC 的最小值和最大值，以及OC 最大时AC 的长．6．如图，在⊙O 中，AB 为弦，CD 为直径，且AB ⊥CD ，垂足为E ，P 为 AC 上的动点（不与端点重合），连接PD ．（1）求证：∠APD ＝∠BPD ；（2）利用尺规在PD 上找到点I ，使得I 到AB 、AP 的距离相等，连接AD （保留作图痕迹，不写作法）．求证：∠AIP+∠DAI ＝180°；（3）在（2）的条件下，连接IC 、IE ，若∠APB ＝60°，试问：在P 点的移动过程中，IC IE 是否为定值？若是，请求出这个值；若不是，请说明理由．7．在平面直角坐标系xOy 中，已知线段AB 和点P ，给出如下定义：若PA PB =且点P 不在线段AB 上，则称点P 是线段AB 的等腰顶点．特别地，当90APB ∠≥︒时，则称点P 是线段AB 的非锐角等腰顶点．（1）已知点(20)A ，，(42)B ，．①在点(40)C ，，(31)D ，，(15)E -，，(05)F ，中，是线段AB 的等腰顶点的是▲；②若点P 在直线3(0)y kx k =+≠上，且点P 是线段AB 的非锐角等腰顶点，求k 的取值范围；（2）直线33y x =-+与x 轴交于点M ，与y 轴交于点N ．⊙P 的圆心为(0)P t ，，半径为，若⊙P 上存在线段MN 的等腰顶点，请直接写出t 的取值范围．8．在平面直角坐标系xOy中，⊙O的半径为1，T（0，t）为y轴上一点，P为平面上一点．给出如下定义：若在⊙O上存在一点Q，使得△TQP是等腰直角三角形，且∠TQP＝90°，则称点P为⊙O的“等直点”，△TQP为⊙O的“等直三角形”．如图，点A，B，C，D的横、纵坐标都是整数．（1）当t＝2时，在点A，B，C，D中，⊙O的“等直点”是；（2）当t＝3时，若△TQP是⊙O“等直三角形”，且点P，Q都在第一象限，求CPOQ的值．9．综合与实践动手操作利用正方形纸片的折叠开展数学活动．探究体会在正方形折叠过程中，图形与线段的变化及其蕴含的数学思想方法．如图1，点E 为正方形ABCD 的AB 边上的一个动点，3AB =，将正方形ABCD 对折，使点A 与点B 重合，点C 与点D 重合，折痕为MN ．思考探索（1）将正方形ABCD 展平后沿过点C 的直线CE 折叠，使点B 的对应点B '落在MN 上，折痕为EC ，连接DB '，如图2．①点B '在以点E 为圆心，的长为半径的圆上；②B M '=；③DB C ' 为三角形，请证明你的结论．（2）拓展延伸当3AB AE =时，正方形ABCD 沿过点E 的直线l （不过点B ）折叠后，点B 的对应点B '落在正方形ABCD 内部或边上．①ABB ' 面积的最大值为；②连接AB '，点P 为AE 的中点，点Q 在AB '上，连接PQ AQP AB E ∠=∠'，，则2B C PQ '+的最小值为．10．在平面直角坐标系xOy 中，过⊙T （半径为r ）外一点P 引它的一条切线，切点为Q ，若0＜PQ≤2r ，则称点P 为⊙T 的伴随点．（1）当⊙O 的半径为1时，①在点A(4，0)，B(0，)，C(1，)中，⊙O 的伴随点是▲；②点D 在直线y ＝x+3上，且点D 是⊙O 的伴随点，求点D 的横坐标d 的取值范围；（2）⊙M 的圆心为M(m ，0)，半径为2，直线y ＝2x ﹣2与x 轴，y 轴分别交于点E ，F ．若线段EF 上的所有点都是⊙M 的伴随点，直接写出m 的取值范围．11．定义：在平面直角坐标系xOy 中，点P 为图形M 上一点，点Q 为图形N 上一点．若存在OP OQ =，则称图形M 与图形N 关于原点O “平衡”．（1）如图，已知⊙A 是以()1,0为圆心，2为半径的圆，点()1,0C -，()2,1D -，()3,2E ．①在点C ，D ，E 中，与⊙A 关于原点O “平衡”的点是；②点H 为直线y x =-上一点，若点H 与⊙A 关于原点O “平衡”，点H 的横坐标的取值范围为：；（2）如图，已知图形G 是以原点O 为中心，边长为2的正方形．⊙K 的圆心在x 轴上，半径为2．若⊙K 与图形G 关于原点O “平衡”，请直接写出圆心K 的横坐标的取值范围．12．阅读下列材料，并按要求解答相关问题：【思考发现】根据直径所对的圆周角是直角，我们可以推出“如果一条定边所对的角始终为直角，那么所有满足条件的直角顶点组成的图形是以定边为直径的圆或圆弧（直径的两个端点除外）”这一正确的结论．如图1，若AB 是一条定线段，且90APB ∠=︒，则所有满足条件的直角顶点P 组成的图形是定边AB 为直径的O （直径两端点A 、B 除外）（1）已知：如图2，四边形ABCD 是边长为8的正方形，点E 从点B 出发向点C 运动，同时点F 从点C 出发以相同的速度向点D 运动，连接AE ，BF 相交于点P ．①当点E 从点B 运动到点C 的过程中，APB ∠的大小是否发生变化？若发生变化，请说明理由；若不发生变化，请直接写出APB ∠的度数．②当点E 从点B 运动到点C 的过程中，点P 运动的路径是（）A ．线段；B ．弧；C ．半圆；D ．圆③点P 运动的路经长是▲．（2）已知：如图3，在图2的条件下，连接CP ，请直接写出E 、F 运动过程中，CP 的最小值．13．对于平面内的图形1G 和图形2G ，记平面内一点P 到图形1G 上各点的最短距离为1d ，点P 到图形2G 上各点的最短距离为2d ，若12d d =，就称点P 是图形1G 和图形2G 的一个“等距点”．在平面直角坐标系xOy 中，已知点()60A ，，(0B ．（1）在()30R ，，()20S ，，(1T 三点中，点A 和点B 的等距点是；（2）已知直线2y =-．①若点A 和直线2y =-的等距点在x 轴上，则该等距点的坐标为▲；②若直线y a =上存在点A 直线2y =-的等距点，求实数a 的取值范围；（3）记直线AB 为直线1l ，直线2l ：33y x =-，以原点O 为圆心作半径为r 的O ．若O 上有m 个直线1l 和直线2l 的等距点，以及n 个直线1l 和y 轴的等距点（0m ≠，0n ≠），求m n ≠时，求r 的取值范围．14．如图，平面上存在点P 、点M 与线段AB ．若线段AB 上存在一点Q ，使得点M 在以PQ 为直径的圆上，则称点M 为点P 与线段AB 的共圆点．已知点P （0，1），点A （﹣2，﹣1），点B （2，﹣1）．（1）在点O （0，0），C （﹣2，1），D （3，0）中，可以成为点P 与线段AB 的共圆点的是；（2）点K 为x 轴上一点，若点K 为点P 与线段AB 的共圆点，请求出点K 横坐标x K 的取值范围；（3）已知点M （m ，﹣1），若直线y ＝12x +3上存在点P 与线段AM 的共圆点，请直接写出m 的取值范围．15．如图，在ABC 中，AB BC =，30CAB ∠=︒，8AC =，半径为2的O 从点A 开始（如图1）沿直线AB 向右滚动，滚动时始终与直线AB 相切（切点为D ），当O 与ABC 只有一个公共点时滚动停止，作OG AC ⊥于点G ．（1）图1中，O 在AC 边上截得的弦长AE =；（2）当圆心落在AC 上时，如图2，判断BC 与O 的位置关系，并说明理由．（3）在O 滚动过程中，线段OG 的长度随之变化，设AD x =，OG y =，求出y 与x 的函数关系式，并直接写出x 的取值范围．16．在平面直角坐标系xOy 中，给出如下定义：若点P 在图形M 上，点Q 在图形N 上，称线段PQ 长度的最小值为图形M ，N 的“近距离”，记为d(M ，N)，特别地，若图形M ，N 有公共点，规定d(M ，N)＝0．已知：如图，点A(2-，0)，B(0，．（1）如果⊙O 的半径为2，那么d(A ，⊙O)＝，d(B ，⊙O)＝．（2）如果⊙O 的半径为r ，且d （⊙O ，线段AB ）=0，求r 的取值范围；（3）如果C(m ，0)是x 轴上的动点，⊙C 的半径为1，使d （⊙C ，线段AB ）<1，直接写出m 的取值范围．17．在平面直角坐标系xOy 中，对于点()P m n ，，我们称直线y mx n =+为点P 的关联直线.例如，点()24P ，的关联直线为24y x =+．（1）已知点()12A ，．①点A 的关联直线为；②若O 与点A 的关联直线相切，则O 的半径为；（2）已知点()02C ，，点()0.D d ，点M 为直线CD 上的动点．①当2d =时，求点O 到点M 的关联直线的距离的最大值；②以()11T -，为圆心，3为半径作.T 在点M 运动过程中，当点M 的关联直线与T 交于E ，F 两点时，EF 的最小值为4，请直接写出d 的值．18．在平面直角坐标系xOy 中，给定圆C 和点P ，若过点P 最多可以作出k 条不同的直线，且这些直线被圆C 所截得的线段长度为正整数，则称点P 关于圆C 的特征值为.k 已知圆O 的半径为2，（1）若点M 的坐标为()11，，则经过点M 的直线被圆O 截得的弦长的最小值为，点M 关于圆O 的特征值为；（2）直线y x b =+分别与x ，y 轴交于点A ，B ，若线段AB 上总存在关于圆O 的特征值为4的点，求b 的取值范围；（3）点T 是x 轴正半轴上一点，圆T 的半径为1，点R ，S 分别在圆O 与圆T 上，点R 关于圆T 的特征值记为r ，点S 关于圆O 的特征值记为.s 当点T 在x 轴正轴上运动时，若存在点R ，S ，使得3r s +=，直接写出点T 的横坐标t 的取值范围．答案解析部分1．【答案】（1）60︒；=；DC DB DA=+（2）解：在AB 上取一点E ，使ADE BDC ∠=∠，如图所示：∵AB 是圆O 的直径，1tan 2ABC ∠=，∴1tan 2AC ABC BC BC =∠⋅=，∴在Rt ACB 中，52AB BC ==，∵ BD BD =，∴DAB DCB ∠=∠，∵ADE BDC ∠=∠，∴ADE CDB ∽，∴ADAECD CB =，∴AD CB CD AE ⋅=⋅，∵ AD AD =，∴DBA DCA ∠=∠，∵ADE CDE CDB CDE ∠-∠=∠-∠，即ADC BDE ∠=∠，∴BDE CDA ∽，∴BDBECD AC =，∴BD AC CD BE ⋅=⋅，∴()AD CB AC BD CD AE CD BE CD AE BE CD AB⋅+⋅=⋅+⋅=⋅+=⋅，∴AB CD AC DB AD BC ⋅=⋅+⋅，∴122BC CD BC DB AD BC ⋅=⋅+⋅，∴5122CD DB AD ⋅=⋅+，∴5122CD DB AD =+，即2DB AD =+，故答案为：2DB AD =+．（3）解：∵A B ，分别是射线DA DB ，上的两个动点，120D ∠=︒，ABC 是等边三角形，∴四边形ADBC 的两个对角180ADB ACB ∠+∠=︒，∴构造四边形ADBC 的外接圆，∴根据四边形外接圆的性质可得：当点A 和点D 重合时，四边形ADBC 面积S 最小；当CD AB ⊥时，四边形ADBC 面积S 最大，①当点A 和点D 重合时，四边形ADBC 面积S 最小，∵CBD 时等边三角形，且2AB =，∴60CBD ∠=︒，2AB BD BC ===∴1sin 602CBD S BC BD =⋅⋅⋅= ，②当CD AB ⊥时，四边形ADBC 面积S 最大，∵CBD 时等边三角形，且2AB =，∴30ACD ∠=︒，2AC =，∴tan 233AD ACD AC =∠⋅==，∴11232322233ADC S AD DC =⋅⋅=⨯= ，∴23ADC ADBC S S == 四边形；433S <≤．2．【答案】（1）解：①O ，C ②当点B 的坐标为（0，1）时，如图，此时以BO 为半径的B 与线段OA 相切于点O ，∴点O 是OAB 关于点B 的内联点；当点B 移动到在y 轴左侧时，作图发现B 与x 轴有相交，且有一个交点不在线段OA 上，∴不再有OAB 关于点B 的内联点；当点B 的坐标为（7，8）时，以BA 为半径的B 与x 轴相切于点A ，∴点A 是OAB 关于点B 的内联点；当点B 直线x=7的右侧时，以BA 为半径的B 与x 轴相交，且有一个交点不在线段OA 上∴不再有OAB 关于点B 的内联点；综上所述，若AOB 关于点B 的内联点存在，求点B 纵坐标n 的取值范围为18n ≤≤；（2）80m 555m -≤≤≤≤或3．【答案】（1）22B C （2）解：由题意可得：当BC 是O 的以点A 为中心的“关联线段”时，则有AB C '' 是等边三角形，且边长也为1，当点A 在y 轴的正半轴上时，如图所示：设B C ''与y 轴的交点为D ，连接OB '，易得B C y ''⊥轴，∴12B D DC ''==，∴32OD ==，32==，∴OA =，∴t =；当点A 在y 轴的正半轴上时，如图所示：同理可得此时的OA =，∴t =；（3）当1min OA =时，此时BC =；当2max OA =时，此时2BC =．4．【答案】（1）证明：∵CD ⊥直径AB ，∴ BDBE =，∵DF ＝BD ，∴ DFBD =，∴ BEDF =，∴∠1＝∠2，∴DG ＝BG（2）解：∠DBA 的角平分线交⊙O 于点F ，∴∠2＝∠3，由（1）知，∠1＝∠2，∴∠1＝∠2＝∠3，∵∠BCD ＝90°，∴∠1+∠2+∠3＝90°，∴∠1＝∠2＝∠3＝30°，∵AB 是⊙O 的直径，∴∠ADB ＝90°，∴∠4＝90°﹣∠2﹣∠3＝30°，∵AB ＝2，∴BD ＝1，在Rt △BCD 中，∠1＝30°，∴BC ＝12BD ＝12，在Rt △BCG 中，∠3＝30°，∴CG ＝＝6，∴BG ＝2CG ＝33，由（1）知，DG ＝BG ＝33（3）5．【答案】（1）解：如图1，作BM ⊥x 轴，垂足为M ，根据题意AB=AE=EF=BF=，且∠EFO=∠BFM=45°，∴∠EFB=90°，∴四边形ABFE 是正方形，∴边AE ，BF 的中点所在直线就是ABC 与O 的一条“关联轴”；∵O 的半径为1，∴，且∠EFG=90°，∴四边形EFGH 是正方形，∵∠EFG+∠EFB=180°，∴B 、F 、G 三点共线，∴直线EF 是ABC 与O 的一条“关联轴”．（2）解：如图2，根据A （2，3），B （4，1），C （4，1），计算2=，故AB 不能落在圆的内部；过点A 作AN ⊥y 轴，垂足为N ，则AN=2，等于圆的直径，存在“关联轴l ”使ABC 是O 的关联三角形，此时0C x =；作点B 关于x 轴的对称点P ，此时BP=2，等于圆的直径，存在“关联轴l ”使ABC 是O 的关联三角形，此时4C x =，综上所述，点C 横坐标的范围是04C x ≤≤．（3）解：OC 的最小值为2-；OC 最大，根据勾股定理，AC=4.6．【答案】（1）证明：∵直径CD ⊥弦AB ，∴ AD BD=，∴∠APD=∠BPD ；（2）解：如图，作∠BAP 的平分线，交PD 于I ，证：∵AI 平分∠BAP ，∴∠PAI=∠BAI ，∴∠AID=∠APD+∠PAI=∠APD+BAI ，∵ AD BD=，∴∠DAB=∠APD ，∴∠DAI=∠DAB+∠BAI=∠APD+∠BAI ，∴∠AID=∠DAI ，∵∠AIP+∠DAI=180°，∴∠AIP+∠DAI=180°；（3）解：如图2，连接BI ，AC ，OA ，OB ，∵AI 平分∠BAP ，PD 平分∠APB ，∴BI 平分∠ABP ，∠BAI=12∠BAP ，∴∠ABI=12∠ABP ，∵∠APB=60°，∴∠PAB+∠PBA=120°，∴∠BAI+∠ABI=12（∠BAP+∠ABP ）=60°，∴∠AIB=120°，∴点I 的运动轨迹是 AB ，∴DI=DA ，∵∠AOB=2∠APB=120°，∵AD ⊥AB ，∴ AD BD=，∴∠AOB=∠BOD=60°，∵OA=OD ，∴△AOD 是等边三角形，∴AD=AO ，∵CD 是⊙O 的直径，∴∠DAC=90°，∵CD ⊥AB ，∴∠AED=90°，∴∠AED=∠CAD ，∵∠ADC=∠ADE ，∴△ADE ∽△CDA ，∴AD DE CD AD=，∴AD 2=DE•CD ，∵DI′=DI=AD ，∴DI 2=DE•CD ，∵∠I′DE 是公共角，∴△DIE ∽△DCI ，∴2IC CD IE DI==．7．【答案】（1）解：①C(4，0)，E(-1，5)；②（Ⅰ）当点(40)，在直线3y kx =+上时，430k +=，34k =-；（Ⅱ）当点(31)，在直线3y kx =+上时，331k +=，23k =-；（Ⅲ）当点(22)，在直线3y kx =+上时，232k +=，12k =-；结合图象可得3142k -≤≤-且23k ≠-；（2）解：直线333y x =-+与x 轴的交点M 坐标为()30，，与y 轴交点N 的坐标为(03，，∴tan 3NMO ∠=，∴30NMO ∠=︒，如图，作出线段MN 的垂直平分线，如图为两个临界情况：，利用待定系数法求得MN 垂直平分线解析式为y =，∴(0R -，，12230ORQ P RQ ∠=∠=︒，∴1112PR PQ ==，2222P R P Q ==，∴(10P ，(20P -，，∴t -≤<．8．【答案】（1）A 、B 、D（2）解：如图，依题意作⊙O 的“等直三角形”△TQP∴TQ=PQ ，∠TQP=90°过Q 点作MH //x 轴，交y 轴于M 点，过点P 作PH ⊥MH 于H 点∴∠TMQ=∠QHP=90°∴∠TQM+∠MTQ=∠TQM+∠HQP=90°∴∠MTQ=∠HQP∴△TMQ ≌△QHP （AAS ）∴TM=QH ，MQ=HP设Q （x ，y ）∴HM=MQ+QH=MQ+TM=x+3-y ，PH=MQ=x∴P （x-y+3，x+y ）∵C （3，0）∴∵∴CP OQ ．9．【答案】（1）BE ；3332-；等边；证明：B′D=BC CD ==，∴△DB'C 为等边三角形（2）310．【答案】（1）B ，C ；解：②如图2中，设点D 的坐标为(3)d d +，当过点D 的切线长为22r =时，OD ==由两点之间的距离公式得：OD =解得1221d d =-=-，结合图象可知，点D 的横坐标d 的取值范围是21d -≤≤-；（2）解：对于22y x =-当0y =时，220x -=，解得1x =，则点E 的坐标为(10)E ，当0x =时，2y =-，则点F 的坐标为(02)F -，⊙M 的半径为2，⊙M 的圆心为(0)M m ，24r ∴=，OM m=由题意，由以下两种情况：如图3-1中，点M 在点E 的右侧设FT 是⊙M 的切线则有两个临界位置：4FT =和点E 对应的切线长为0当4FT =时，则4OM m FT ===当点E 对应的切线长为0，即2EM =12EM m ∴=-=解得3m =结合图象得，当34m <≤时，线段EF 上的所有点都是⊙M 的伴随点②如图3-2和3-3中，点M 在点E 的左侧则有如下两个临界位置：如图3-2，设ET 是⊙M 的切线，连接MT ，则90MTE ∠=︒当4ET =时，2222245EM MT ET =+=+此时15m -=解得15m =-如图3-3，当⊙M 在直线EF 的左侧与EF 相切时，设切点为T ，连接MT∵(10)(02)E F -，，，∴12OE OF ==，∴22125EF =+=∵EF 是切线∴EF MT⊥∴90MTE FOE ∠=∠=︒∵MET FEO∠=∠∴MTE FOE~ ∴EM MTEF OF =，即22=解得EM =，即1m -=解得1m =-结合图象得，当11m -≤<-时，线段EF 上的所有点都是⊙M 的伴随点综上，m 的取值范围是11m -≤<-或34m <≤．11．【答案】（1）点C 、D ；22H x -≤≤-或22H x ≤≤（2）解：图形G 是以原点O 为中心，边长为2的正方形，∴原点O 到正方形的最短距离是1d =，最长距离是d =，⊙K 与图形G 关于原点O “平衡”，∴原点O 到⊙K 上一点的距离1d ≤≤，⊙K 的圆心在x 轴上，半径为2，∴当⊙K 在x 轴正半轴时，圆心K 的横坐标的取值范围为：22x -≤≤+，当⊙K 在x 轴负半轴时，圆心K 的横坐标的取值范围为：22x --≤≤，综上所述，圆心K 的横坐标的取值范围22x -≤≤+或22x --≤≤．12．【答案】（1）解：①90°；②B ；③2π（2）解：413．【答案】（1）S(2，0)（2）解：①（4，0）或（8，0）；②如图，设直线y a =上的点Q 为点A 和直线2y =-的等距点，连接QA ，过点Q 作直线2y =-的垂线，垂足为点C ．点Q 为点A 和直线2y =-的等距点，QA QC ∴=．22QA QC ∴=．点Q 在直线y a =上，∴可设点Q 的坐标为()Q x a ，．()()22262x a a ∴-+=--⎡⎤⎣⎦．整理得2123240x x a -+-=．由题意得关于x 的方程2123240x x a -+-=有实数根．()()()212413241610a a ∴∆=--⨯⨯-=+≥．解得1a ≥-．（3）解：如图．直线l 1和直线l 2的等距点在直线l 3：33y x =-+上，直线l 1和y 轴的等距点在直线4l y =+：或33y x =+上，点O 与l 4的距离为32，点O 与l 3的距离为，点O 与l 5的距离为3，当r ＜时，n=0不符合题意，当r=时，m=2，n=0，符合题意，当＜r ＜3时，m=n=2，不符合题意，当r≥3时，m=2，n=3或4，符合题意，综上所述，r=或r≥3.14．【答案】（1）C（2）解：∵P （0，1），点A （﹣2，﹣1），点B （2，﹣1）．∴AP ＝BP ＝＝2，如图2，分别以PA 、PB 为直径作圆，交x 轴于点K 1、K 2、K 3、K 4，∵OP＝OG＝1，OE∥AB，∴PE＝AE＝，∴OE＝12AG＝1，∴K1（﹣1﹣，0），k2（1﹣，0），k3（﹣1，0），k4（1+，0），∵点K为点P与线段AB的共圆点，∴﹣1﹣≤x k≤1﹣或﹣1≤x k≤1+（3）解：分两种情况：①如图3，当M在点A的左侧时，Q为线段AM上一动点，以PQ为直径的圆E与直线y＝12x+3相切于点F，连接EF，则EF⊥FH，当x＝0时，y＝3，当y＝0时，y＝12x+3＝0，x＝﹣6，∴ON＝3，OH＝6，∵tan∠EHF＝ON EFOH FH＝36＝12，设EF＝a，则FH＝2a，EH＝a，∴OE＝6﹣a，Rt △OEP 中，OP ＝1，EP ＝a ，由勾股定理得：EP 2＝OP 2+OE 2，∴2221(6)a =+-，解得：a ＝2+（舍去）或2，∴QG ＝2OE ＝2（6﹣a ）＝﹣3+2，∴m≤3﹣2；②如图4，当M 在点A 的右侧时，Q 为线段AM 上一动点，以PQ 为直径的圆E 与直线y ＝12x+3相切于点F ，连接EF ，则EF ⊥FH ，同理得QG ＝3+2，∴m≥3+2，综上，m 的取值范围是m≤3﹣2或m≥3+215．【答案】（1）2（2）解：BC 与O 相切；理由：如图2，过点O 作OH BC ⊥于H ，连接OD ，∵O 与AB 相切于D ，∴OD AB ⊥，在Rt AOD 中，30BAC ∠=︒，∴24OA OD ==，∵8AC =，∴4OC =，在ABC 中，AB BC =，∴30C BAC ∠=∠=︒，在Rt OHC 中，30C ∠=︒，∴122OH OC OD ===，∴BC 与O 相切，（3）解：①当点O 在AC 的左侧时，连接OD 交AC 于F ，如备用图1，∵O 与AB 相切于D ，∴OD AB ⊥，∵OG AC ⊥，∴30FOG BAC ∠=∠=︒，在Rt FDA 中，tan FD BAC AD ∠=，∴tan 3FD AD BAC x =⋅∠=，∴23OF x =-，在Rt FOG 中，331cos 2322y OG OF FOG ⎛⎫==⋅∠=-⨯-+ ⎪ ⎪⎝⎭，即12y x =-+，此时x 的取值范围为0x ≤≤；②当点O 在AC 的右侧时，连接DO 并延长交AC 于F ，如备用图2，同①的方法得，33FD x =，∴23OF x =-，∵FD AB ⊥，∴90BAC AFD ∠+∠=︒，∴30FOG BAC ∠=∠=︒，在Rt FOG 中，331cos 2322y OG OF FOG x x ⎛⎫==⋅∠=-⨯- ⎪⎪⎝⎭，即12y x =-，此时x 的取值范围为1433x ≤≤．16．【答案】（1）0；2-（2）解：过点O 作OD ⊥AB 于点D ，∵点A(2-，0)，B(0，．∴2OA OB ==，，∴4AB ==，∵1122OA OB AB OD ⋅=⋅，∴112422OD ⨯⨯=⨯⨯∴DO =，∵d （⊙O ，线段AB ）=0，∴当⊙O 的半径等于OD 时最小，当⊙O 的半径等于OB 时最大，∴r r ≤≤（3）43423m -<<-17．【答案】（1）2y x =+（2）解：①当2d =时，()20D ，，设直线CD 的解析式为：y kx b =+，()02C ，，202k b b +=⎧∴⎨=⎩，解得：12k b =-⎧⎨=⎩，∴直线CD 的解析式为：y x =-+，设点M 的坐标为()2m m -+，，∴点M 的关联直线为：()212y mx m m x =-+=-+，∴点M 的关联直线经过定点()12N ，，如图2，过点O 作直线2y mx m =--+的垂线，垂足为H ，连接ON ，ON OH ∴≥，∴当点H与点N重合时，OH最大，即点O到点M的关联直线的距离最大，∴点O到点M=；2 d=②或2 3-18．【答案】（1）；3（2）解：设点G是O的特征值为4的点，∴经过一点G且弦长为4(最长弦)的直线有1条，弦长为3的直线有2条，弦长为2的直线有且只有1条，经过点G的直线被O截得的弦长的最小值为2，=，∴关于O的特征值为4的所有点都在以O为半径的圆周上，直线y x b=+分别与x，y轴交于点A、B，()0A b∴-，，()B b，，OA OB b∴==，45OBH∴∠=︒，当0b>时，线段AB与以O为半径的圆相切时，点G特征值为4，设切点为为H，连接OH，则OH=，OB∴==，b∴=，设以O 为半径的圆与y 轴正半轴的交点记为1B ，则1OB =，当线段AB 与以O 1B 时，可得b =，b ≤≤同理可求当0b <时，b ≤≤，综上，b b b ≤≤-≤（3）当372122t -≤≤+时，存在点R ，S ，使得3r s +=。

中考数学圆-经典压轴题(带答案)

1.如图，四边形ABCD内接于⊙O，AB是⊙O的直径，AC和BD相交于点E，且DC2=CE•CA．（1）求证：BC=CD；（2）分别延长AB，DC交于点P，过点A作AF⊥CD交CD的延长线于点F，若PB=OB，CD =，求DF的长．2.如图，AB是⊙O的直径，弦CD⊥AB于H，过CD延长线上一点E作⊙O的切线交AB的延长线于F．切点为G，连接AG交CD于K．（1）求证：KE=GE；（2）若=KD·GE，试判断AC与EF的位置关系，并说明理由；（3）在（2）的条件下，若sinE=，AK=，求FG的长．4.5.已知：如图，在半径为4的⊙O中，AB，CD是两条直径，M为OB的中点，CM的延长线交⊙O于点E，且EM＞MC，连结DE，DE=。

（1）求证：AM·MB=EM·MC；（2）求EM的长；（3）求sin∠EOB的值。

6.如图，AE切⊙O于点E，AT交⊙O于点M，N，线段OE交AT于点C，OB⊥AT于点B，已知∠EAT=30°，AE=3，MN=2．（1）求∠COB的度数；（2）求⊙O的半径R；（3）点F在⊙O上（是劣弧），且EF=5，把△OBC经过平移、旋转和相似变换后，使它的两个顶点分别与点E，F重合．在EF的同一侧，这样的三角形共有多少个？你能在其中找出另一个顶点在⊙O上的三角形吗？请在图中画出这个三角形，并求出这个三角形与△OBC的周长之比．7.如图，AB是半径O的直径，AB=2．射线AM、BN为半圆O的切线．在AM上取一点D，连接BD交半圆于点C，连接AC．过O点作BC的垂线OE，垂足为点E，与BN相交于点F．过D点作半圆O的切线DP，切点为P，与BN相交于点Q．（1）求证：△ABC∽△OFB；（2）当△ABD与△BFO的面枳相等时，求BQ的长；（3）求证：当D在AM上移动时（A点除外），点Q始终是线段BF的中点8.如图，在⊙O的内接△ABC中，∠ACB=90°，AC=2BC，过C作AB的垂线l交⊙O于另一点D，垂足为E.设P是上异于A,C的一个动点，射线AP交l 于点F，连接PC与PD，PD交AB于点G.（1）求证：△PAC∽△PDF；（2）若AB=5，，求PD的长；（3）在点P运动过程中，设，求与之间的函数关系式.（不要求写出的取值范围）∴=∴=∴=4==2，∴=中有，2解：（1）如答图1，连接OG ．∵EG 为切线，∴∠KGE+∠OGA=90°，∵CD ⊥AB ，∴∠AKH+∠OAG=90°，又OA=OG ，∴∠OGA=∠OAG ，∴∠KGE=∠AKH=∠GKE ，∴KE=GE ．（2）AC ∥EF ，理由为：连接GD ，如答图2所示．∵KG 2=KD GE ，即=，∴=，又∠KGE=∠GKE ，∴△GKD ∽△EGK ，∴∠E=∠AGD ，又∠C=∠AGD ，∴∠E=∠C ，∴AC∥EF；（3）连接OG，OC，如答图3所示．sinE=sin∠ACH=，设AH=3t，则AC=5t，CH=4t，∵KE=GE，AC∥EF，∴CK=AC=5t，∴HK=CK﹣CH=t．在Rt△AHK中，根据勾股定理得AH2+HK2=AK2，即（3t）2+t2=（）2，解得t=．设⊙O半径为r，在Rt△OCH中，OC=r，OH=r﹣3t，CH=4t，由勾股定理得：OH2+CH2=OC2，即（r﹣3t）2+（4t）2=r2，解得r=t=．∵EF为切线，∴△OGF为直角三角形，在Rt△OGF中，OG=r=，tan∠OFG=tan∠CAH==，∴FG===．.45.6.7.8.。

押广东广州卷第22-23题(几何图形中的尺规作图求证、圆的综合)(原卷版)-备战2024年中考数学

押广东广州卷第22-23题押题方向一：几何图形中的尺规作图求证3年广东广州卷真题考点命题趋势2023年广东广州卷第23题菱形、尺规作图、求证求解从近年广东广州中考来看，几何图形中的尺规作图求证求解是近三年的必考题，考查了实际操作能力和几何运算或几何推理的能力；预计2024年广东广州卷还将继续重视对何图形中的尺规作图求证求解的考查。

2022年广东广州卷第22题圆、尺规作图、求解2021年广东广州卷第22题等腰三角形、尺规作图、求证1．（2023·广东广州·中考真题）如图，AC 是菱形ABCD 的对角线．（1）尺规作图：将ABC ∆绕点A 逆时针旋转得到ADE ∆，点B 旋转后的对应点为D （保留作图痕迹，不写作法）；（2）在（1）所作的图中，连接BD ，CE ．①求证：~ABD ACE ∆∆；②若1tan 3BAC ∠=，求cos DCE ∠的值．2．（2022·广东广州·中考真题）如图，AB 是⊙O 的直径，点C 在⊙O 上，且AC =8，BC =6．(1)尺规作图：过点O 作AC 的垂线，交劣弧 AC 于点D ，连接CD （保留作图痕迹，不写作法）；(2)在（1）所作的图形中，求点O 到AC 的距离及sin ∠ACD 的值．3．（2021·广东广州·中考真题）如图，在四边形ABCD 中，90ABC ∠=︒，点E 是AC 的中点，且AC AD =（1）尺规作图：作CAD ∠的平分线AF ，交CD 于点F ，连结EF 、BF （保留作图痕迹，不写作法）；（2）在（1）所作的图中，若45BAD ∠=︒，且2CAD BAC ∠=∠，证明：BEF △为等边三角形．1.考查尺规作图、旋转的性质、菱形的性质、全等三角形的判定与性质、相似三角形的判定与性质、勾股定理、锐角三角函数与解直角三角形等知识，此题综合性强，难度较大，属于考试压轴题．2.考查了圆的基本性质、垂径定理及其推论、勾股定理、线段垂直平分线的尺规作图、锐角三角函数等，属于综合题，欲求某角的某三角函数值，首先想到的应该是能否在直角三角形中进行，如果没有现成的直角三角形，则需要设法构造(作辅助图形)．3.考查了基本作图和等腰三角形性质以及与三角形中点有关的两个定理，解题关键是掌握等腰三角形三线合一定理、直角三角形斜边中线等于斜边一半以及三角形中位线定理．1．如图，在ABCD Y 中，30DCB ∠=︒．(1)操作：用尺规作图法过点D 作AB 边上的高DE ；(保留作图痕迹，不要求写作法)(2)计算∶在（1）的条件下，若4=AD ，6AB =，求梯形EBCD 的面积．2．如图，ABCD 为O 内接四边形，AC 为O 的直径， AB BD =，点E 为 AD 上一点，且 EAEC =．(1)求作点E ，连接ED ，延长ED ，BC 交于点F （尺规作图，保留作图痕迹，不写作法）；(2)在（1）所作的图中，连接CE ．①求证：CEF △为等腰三角形；②若5FC =，15BC =，求弦DE 的长．3．如图所示，在ABC 中，23AB AC ==30B ∠=︒，点O 为边BC 上一点，以O 为圆心的圆经过点A ，B ．(1)求作圆O （尺规作图，保留作图痕迹，不写作法）；(2)求证：AC 是O 的切线；(3)若点P 为圆O 上一点，且弧PA =弧PB ，连接PC ，求线段PC 的长．4．如图，AB 为经过圆心O 的一条线段，且与O 交于E 点．(1)过B 在AB 的上方作O 的切线，切点为D ，过A 作AC BD ⊥，垂足为C ，AC 与O 交于F 点．请尺规作图，不用写作图的详细步骤．(2)求证：AD 平分BAC ∠；(3)若3BD =，1tan 2CAD ∠=，求O 的半径．5．数学中的轴对称就像镜子一样，可以展现出图形对称的美，初中常见的轴对称图形有：等腰三角形、菱形、圆等．如图，在等腰ABC 中，AB BC =．(1)尺规作图：作ABC 关于直线AC 对称的ADC △（保留作图痕迹，不写作法）；(2)连接BD ，交AC 于点O ，若2BD =，四边形ABCD 周长为45ABCD 的面积．6．如图，在ABC 中，C ∠是钝角．(1)尺规作图：在AB 上取一点O ，以O 为圆心，作出O ，使其过A 、C 两点，交AB 于点D ，连接CD ；（不写作法，保留作图痕迹）(2)在（1）所作的图中，若BCD A ∠=∠，1tan 3A =，9BC =．①求证：BC 是O 的切线；②求弦AC 的长．7．如图，在菱形ABCD 中，对角线AC BD ，相交于点O ．(1)尺规作图：在菱形ABCD 的边AD 上方找一点E ，使得AED BOC ≌；（不写作法，保留作图痕迹）；(2)判断四边形AODE 的形状，并给出证明．8．如图，AB 是O 的直径，C 是O 上的一点．(1)作AOC ∠的角平分线OM ，交弧AC 于点P ；（要求：尺规作图并保留作图痕迹，不写作法）(2)在（1）的条件下，连接AP ，AC ，若10,6AP AC ==，求P 到AC 的距离及cos BAC ∠的值．9．已知正方形ABCD 中，3BC =，E 是边AB 上的动点，连接AC 和CE ．(1)尺规作图：在图中分别作线段AC 和CE 的中点F 和G ，连接FG ；（不写作法，不说明理由，写明结论并保留作图痕迹）(2)当2CE AE =时，求（1）中所作的线段FG 的长度．10．如图，四边形ABCD 是矩形，以点B 为圆心，BA 长为半径的半圆，交BC 于点M ．(1)作线段BC 的垂直平分线交BC 于点O ；（要求：尺规作图，不写作法，保留作图痕迹）(2)以点O 为圆心，以OB 为半径作O ，交弧AM 于点E （要求：尺规作图，不写作法，保留作图痕迹），证明：BE CE ⊥；(3)在（2）的条件下，延长线段CE 交AD 于点F ，从条件①或者条件②这两个条件中选择一个作为已知条件，求cos EBC ∠的值．条件①：:1:3AF DF =；条件②：3CDF ABF S S =△△；注明：如果选择条件①与条件②分别作答，按第一个解答计分．押题方向二：圆中的综合问题3年广东广州卷真题考点命题趋势2023年广东广州卷第19题圆与平面直角坐标系从近年广东广州中考来看，圆通常会在平面直角坐标考查，与一次函数结合一起考查；预计2024年广东广州卷还将继续重视对圆的考查。

2020广东省中考数学圆压轴(原卷版)-2020年中考数学保A必刷压轴题(广东专版)

2020广东省中考数学圆压轴1．（2020•丰台区模拟）如图，AB是⊙O的直径，AC⊥AB，BC交⊙O于点D，点E在劣弧BD上，DE的延长线交AB的延长线于点F，连接AE交BD于点G．（1）求证：∠AED＝∠CAD；（2）若点E是劣弧BD的中点，求证：ED2＝EG•EA；（3）在（2）的条件下，若BO＝BF，DE＝2，求EF的长．2．（2020•光明区一模）在图1至图3中，⊙O的直径BC＝30，AC切⊙O于点C，AC＝40，连接AB交⊙O 于点D，连接CD，P是线段CD上一点，连接PB．（1）如图1，当点P，O的距离最小时，求PD的长；（2）如图2，若射线AP过圆心O，交⊙O于点E，F，求tan F的值；（3）如图3，作DH⊥PB于点H，连接CH，直接写出CH的最小值．3．（2020•香坊区模拟）△ABC内接⊙O，AD⊥BC与D，连接OA．（1）如图1，求证：∠BAO＝∠CAD；（2）如图2，作BE⊥AC交CA延长线于E交⊙O于F，延长AD交⊙O于G，连接AF，求证：AD+AF ＝DG；（3）在第（2）问的条件下，如图3，OA交BC于点T，CA＝CT，AD＝2AF，AB＝4，求DT长．4．（2020•中山市校级模拟）如图F为⊙O上的一点，过点F作⊙O的切线与直径AC的延长线交于点D，过圆上的另一点B作AO的垂线，交DF的延长线于点M，交⊙O于点E，垂足为H，连接AF，交BM 于点G．（1）求证：△MFG为等腰三角形．（2）若AB∥MD，求证：FG2＝EG•MF．（3）在（2）的条件下，若DF＝6，tan∠M＝，求AG的长．5．（2020•盐田区二模）如图，△ABC内接于⊙O，AC＝BC，弦CD与AB交于E，AB＝CD，过A作AF⊥BC于F．（1）判断AC与BD的位置关系，并说明理由；（2）求证：AC＝2CF+BD；（3）若S△CF A＝S△CBD，求tan∠BDC的值．6．（2020•锦江区模拟）如图1，AB是⊙O的直径，C是⊙O上一点，CD⊥AB于D，E是BA廷长线上一点，连接CE，∠ACE＝∠ACD，K是线段AO上一点，连接CK并延长交⊙O于点F．（1）求证：CE是⊙O的切线；（2）若AD＝DK，求证：AK•AO＝KB•AE；（3）如图2，若AE＝AK，＝，点G是BC的中点，AG与CF交于点P，连接BP．请猜想P A，PB，PF的数量关系，并证明．7．（2020•梅列区一模）如图，AB是⊙O的直径，CD⊥AB，交⊙O于C、D两点，交AB点E、F是弧BD 上一点，过点F作一条直线，交CD的延长线于点G，交AB的延长线于点M．连结AF，交CD于点H，GF＝GH．（1）求证：MG是⊙O的切线；（2）若弧AF＝弧CF，求证：HC＝AC；（3）在（2）的条件下，若tan G＝，AE＝6，求GM的值．8．（2020•成都模拟）如图，在⊙O的内接△ABC中，∠CAB＝90°，AB＝2AC，过点A作BC的垂线m交⊙O于另一点D，垂足为H，点E为上异于A，B的一个动点，射线BE交直线m于点F，连接AE，连接DE交BC于点G．（1）求证：△FED∽△AEB；（2）若＝，AC＝2，连接CE，求AE的长；（3）在点E运动过程中，若BG＝CG，求tan∠CBF的值．。

2025年广东中考数学题型专练++++专练9 解答题之圆的综合题

在Rt△ADE中，由勾股定理，得x2＋[( －1)x]2＝12，∴x2＝
∴S☉O
+
2
＝π·OE ＝
.

+
.

返回
目录
分类·精讲
4．(2024·绥化)如图1，O是正方形ABCD对角线上一点，以O为圆心，OC
长为半径的☉O与AD相切于点E，与AC相交于点F.
(1)求证：AB与☉O相切.
明理由.
解：AF＝AD，AF⊥AD，理由如下：
∵四边形ABCD是菱形，∴AB＝AD，∠BAD＝∠C＝120°.
∵△ABE和△AFE关于AE对称，∴AB＝AF.∴AF＝AD.
∵∠BAF＝30°，∴∠DAF＝∠BAD－∠BAF＝90°.∴AF⊥AD.
∴AF＝AD，AF⊥AD.
返回
目录
分类·精讲
(2)若AB＝6＋6 ，☉O为△AEF的外接圆，设☉O的半径为r.

由折叠的性质，得AC＝AD＝a，∴PC＝PA＋AC＝4a.

在Rt△PCB中，tan∠CPB＝＝，∴BD＝CB＝ PC＝ a.
∵AD⊥BD，GA⊥AB，∴∠AGB＝90°－∠GAD＝∠DAB.

∴tan∠AGB＝tan∠DAB＝＝＝

.
返回
目录
分类·精讲
证明两直线平行的方法：(1)根据平行线的判定方法证明(同位角相等或内
角三角形，考虑相似三角形或锐角三角函数；(3)若有特殊角(30°，45°，
60°或15°，22.5°，75°等)，或出现三角函数(sin α，cos α，tan α)，考虑锐
角三角函数.
返回

2024年广州市中考数学压轴题

选择题在直角坐标系中，点A(3,4)关于x轴对称的点的坐标是：A. (-3,4)B. (3,-4)（正确答案）C. (4,3)D. (-4,-3)已知二次函数y = ax2 + bx + c的图像经过点(1,0)，(0,3)，且对称轴为直线x = 2，则a的值为：A. 1B. -1（正确答案）C. 2D. -2若圆O的半径为5，圆心O到直线l的距离为3，则直线l与圆O的位置关系是：A. 相离B. 相切C. 相交（正确答案）D. 无法确定已知等腰三角形的两边长分别为3和7，则这个等腰三角形的周长为：A. 13B. 17（正确答案）C. 13或17D. 无法确定在平行四边形ABCD中，AB = 5，AD = 8，∠BAD的平分线AE交BC于点E，则BE的长为：A. 3B. 5C. 2或3（正确答案）D. 2或5已知关于x的一元二次方程x2 - (2k + 1)x + 4(k - 1/2) = 0有两个相等的实数根，则k的值为：A. 1B. 2C. 3（正确答案）D. 4已知点P(x,y)在第四象限，且满足x2 + y2 = 25和x - y = 7，则点P的坐标为：A. (3,-4)B. (4,-3)（正确答案）C. (-3,4)D. (-4,3)已知函数y = (m - 2)x(m2 - 2)是关于x的二次函数，则m的值为：A. ±2B. 2C. -2（正确答案）D. 4在矩形ABCD中，AB = 6，BC = 8，点E是BC的中点，点F在边CD上，且CF = 2，连接AE、EF、AF，则∠AEF的面积是：A. 12B. 16C. 20（正确答案）D. 24。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1.如图甲，分别以两个彼此相邻的正方形OABC与CDEF的边OC、OA 所在直线为x轴、y轴建立平面直角坐标系（O、C、F三点在x轴正半轴上）．若⊙P过A、B、E三点（圆心在x轴
上），抛物线y=1
4
x2+bx+c经过A、C两点，与x轴的另一交点为G，M是FG的中点，正方形
CDEF的面积为1．
（1）求B点坐标；
（2）求证：ME是⊙P的切线；
2.如图，△ABC内接于⊙O，AD⊥BC，OE⊥BC，OE=1
2 BC．
（1）求∠BAC的度数；
（2）将△ACD沿AC折叠为△ACF，将△ABD沿AB折叠为△ABG，延长FC和GB相交于点H；求证：四边形AFHG是正方形；
（3）若BD=6，CD=4，求AD的长．
3.如图1所示，以点M（-1，O）为圆心的圆与y轴、x轴分别交于点A，B，C，D，直线y=
3
-x-
53
与⊙M相切于点H，交x轴于点E，交y轴于点F．
（1）请直接写出OE、⊙M的半径r、CH的长；
（2）如图2所示，弦HQ交x轴于点P，且DP：PH=3：2，求cos∠QHC的值；
（3）如图3所示，点K为线段EC上一动点（不与E，C重合），连接BK交⊙M于点T，弦A T交x轴于点N．是否存在一个常数a，始终满足MN•MK=a，如果存在，请求出a的值；如果不存在，请说明
理由．
4.如图，E点为x轴正半轴上一点，⊙E交x轴于A、B两点，交y轴于C、D两点，P点
为劣弧»BC上一个动点，且A（-1，0），E（1，0）．
（1）求点C的坐标；
（2）连接PA，PC．若CQ平分∠PCD交PA于Q点，当P点在运动时，线段AQ的长度是否发生变化；
若不变求出其值，若发生变化，求出变化的范围；
（3）连接PD，当P点在运动时（不与B、C两点重合），求证：PC PD
PA
的值不变
5.直线y=-x+m与直线y=
3
-x+2相交于y轴上的点C，与x轴分别交于点A、B．
（1）求A、B、C三点的坐标；
（2）经过上述A、B、C三点作⊙E，求∠ABC的度数，点E的坐标和⊙E的半径；
（3）若点P是第一象限内的一动点，且点P与圆心E在直线AC的同一侧，直线PA、PC分别交⊙E于点M、N，设∠APC=θ，试求点M、N的距离．（可用含θ的三角函数式表示）
6.如图1，⊙O中AB是直径，C是⊙O上一点，∠ABC=45°，等腰直角三角形DCE中∠DCE是直角，点D在线段AC上．
（1）若M是线段BE的中点，N是线段AD的中点，证明：MN= 2OM；
（2）将△DCE绕点C逆时针旋转α（0°＜α＜90°）后，记为△D1CE1（图2），若M1是线段BE1的
中点，N1是线段AD1的中点，M1N1= 2OM1是否成立？若是，请证明；若不是，说明理由．
7.在平面直角坐标系xoy中，点M在x轴的正半轴上，⊙M交x轴于A、B两点，交y轴
于C、D两点，且C为»AE
的中点，AE交y轴于G点，若点A的坐标为（-2，0），AE=8．
（1）求点C的坐标；
（2）连接MG、BC，求证：MG∥BC；
（3）过点D作⊙M的切线，交x轴于点P．动点F在⊙M的圆周上运动时，OF
PF
的比值是否发生变化？
若不变，求出比值；若变化，说明变化规律．
最新文件仅供参考已改
成word文本。

方便更改。