信号与系统练习题——第4章
信号与系统自测题(第4章 连续时间信号与系统的复频域分析)含答案

) 。
D
、6
−t
18
( s) s 、线性系统的系统函数 H (s) = Y = ,若其零状态响应 y(t ) = (1 − e F ( s) s + 1
D B
−t
)u (t )
,则系
统的输入信号 f (t ) = (
A
) 。
−t
、 δ (t )
、e
u (t )
C
、e
−2 t
u (t )
D
、 tu(t )
C
2
、s
ω e −2 s + ω2
12
、原函数 e
1 − t a
t f( ) a
的象函数是(
B
B
) 。
C
s 1 F( + ) 、1 a a a 注:原书答案为 D
A
、 aF (as + 1)
、 aF (as + a)
D
、 aF (as + 1 ) a
t f ( ) ↔ aF (as ) a e f (t ) ↔ F ( s + 1)
A
−s s −s s
A
s 、1 F ( )e a a
−s
b a
B
s 、1 F ( )e a a
− sb
C
s 、1 F ( )e a a
t 0
s
b a
D
s 、1 F ( )e a a
sb
、 已知信号 x(t ) 的拉普拉斯变换为 X (s) ,则信号 f (t ) = ∫ λ x(t − λ )d λ 的拉普拉斯变换 为( B ) 。 1 1 1 1 A、 X ( s ) B、 X (s) C、 X ( s) D、 X (s) s s s s 注:原书答案为 C。 f (t ) = ∫ λ x(t − λ )d λ = tu(t ) ∗ x(t )u(t ) tu(t ) ∗ x(t )u(t ) ↔ s1 X (s) 9、函数 f (t ) = ∫ δ ( x)dx 的单边拉普拉斯变换 F ( s ) 等于( D ) 。 1 1 A、 1 B、 C、 e D、 e s s
山大信号与系统答案

第一章习题新闻来源:山东大学信息学院点击数:707 更新时间:2009-4-5 0:13 1—1 画出下列各函数的波形图。
(1)(2)(3)(4)1—2 写出图1各波形的数学表达式图1(1) (2)(3) 全波余弦整流(4) 函数1—3 求下列函数的值。
(1)(2)(3)(4)(5)1—4 已知,求,。
1—5 设,分别是连续信号的偶分量和奇分量,试证明1—6 若记,分别是因果信号的奇分量和偶分量,试证明,1—7 已知信号的波形如图2所示,试画出下列函数的波形。
(1)(2)图 21—8 以知的波形如图3所示,试画出的波形.图31—9 求下列各函数式的卷积积分。
(1),(2),1—10 已知试画出的波形并求。
1—11 给定某线性非时变连续系统,有非零初始状态。
已知当激励为时,系统的响应为时,系统的响应则为。
试求当初始状态保持不变,而激励为时的系统响1—12 设和分别为各系统的激励和响应,试根据下列的输入—输出关系,确定下列各⑴⑵(3)(4)第一章习题答案新闻来源:山东大学信息学院点击数:623 更新时间:2009-4-5 23:181-1 (1)(2)(3)(4)1-2(1)、(2)、或或(3)(4) =1-3(1)(2)(3)(4)(5)01-4 ,1-7 (1)(2)1-81-9(1)(2)1-101-111-12 (1)非线性、时不变系统。
(2)线性、时变系统。
(3)线性、时不变系统。
(4)线性、时变系统。
上一篇:没有上一篇资讯了下一篇:没有下一篇资讯了第二章习题新闻来源:山东大学信息学院点击数:412 更新时间:2009-4-9 22—1 已知给定系统的齐次方程是,分别对以下几种初始状态求解系1),2),3),2—2 已知系统的微分方程是当激励信号时,系统的全响应是,试确定系统的零输入2—3 已知系统的微分方程是该系统的初始状态为零。
1)若激励,求响应。
2)若在时再加入激励信号,使得时,,求系数。
(仅供参考)信号与系统第四章习题答案

e −sT
=
−sT
2 − 4e 2
+ 2e −sT
Ts 2
(f) x(t) = sin πt[ε (t)− ε (t − π )]
sin π tε (t ) ↔
π s2 + π 2
L[sin
πtε (t
−π
)]
=
L e jπt
− 2
e− jπt j
ε (t
−π
)
∫ ∫ =
1 2j
∞ π
e
jπt e−st dt
4.3 图 4.2 所示的每一个零极点图,确定满足下述情况的收敛域。
(1) f (t) 的傅里叶变换存在
(2) f (t )e 2t 的傅里叶变换存在
(3) f (t) = 0, t > 0
(4) f (t) = 0, t < 5
【知识点窍】主要考察拉普拉斯变换的零极点分布特性。 【逻辑推理】首先由零极点写出拉普拉斯变换式,再利用反变换求取其原信号,即可求取其收
= cosϕ eω0tj + e−ω0tj − sin ϕ eω0tj − e−ω0tj
2
2j
=
cos 2
ϕ
−
sin 2
ϕ j
e
ω0 t j
+
cosϕ 2
+
sin ϕ 2j
e −ω 0tj
F(s) =
L
cosϕ 2
−
sin ϕ 2j
eω0tj
+
cos 2
ϕ
+
sin ϕ 2j
e
−ω0
t
j
ε
(t
)
∫ ∫ =
信号与系统第四章习题参考答案13

《信号与系统》第四章习题参考答案4-1 解 (1)111()ataL es s a s s a -⎡⎤-=-=⎣⎦++ (2)[]2221221sin 2cos 111s s L t t s s s ++=+++++ (3)()2212tL te s -⎡⎤=⎣⎦+(4)[]21sin(2)4L t s =+,由S 域平移性质,得 ()21s i n (2)14tL e t s -⎡⎤=⎣⎦++ (5)因为1!nn n L t s +⎡⎤=⎣⎦,所以 []2211212s L t s s s++=+= 由S 域平移性质,得 ()()23121ts L t e s -+⎡⎤+=⎣⎦+(6)()2211cos sL at s s a -=-⎡⎤⎣⎦+,由S 域平移性质,得 (){}()2211cos ts L at e s s aβββ-⎡⎤-=-⎣⎦+++ (7)232222L t t s s ⎡⎤+=+⎣⎦ (8)732()327tL t es δ-⎡⎤-=-⎣⎦+ (9)[]22sinh()L t s βββ=-,由S 域平移性质,得()22sinh()atL e t s a βββ-⎡⎤=⎣⎦+-(10)由于()211cos ()cos 222t t Ω=+Ω 所以 222221111c o s ()22424ss L t s s s s ⎛⎫⎡⎤Ω=+∙=+ ⎪⎣⎦+Ω+Ω⎝⎭(11)()()()11111at t L e e a a s a s s a s βββββ--⎡⎤⎛⎫-=-= ⎪⎢⎥--++++⎣⎦⎝⎭ (12)由于()221cos()1ts L e t s ωω-+⎡⎤=⎣⎦++所以 ()()()221cos()1a t a s e L et s ωω--++⎡⎤=⎣⎦++(13)因为(2)(1)(1)(1)(1)(1)t t t te u t e t e e u t ------⎡⎤-=-+-⎣⎦且()(1)(1)2(1)(1)(1)11sst t e e L t eu t L eu t s s ------⎡⎤⎡⎤--=-=⎣⎦⎣⎦++所以 ()(1)(2)2211(2)(1)(1)11s t s s e L teu t e e s s s -----⎡⎤+⎡⎤-=+=⎢⎥⎣⎦+++⎣⎦(14)()(1)tL e f t F s -⎡⎤=+⎣⎦,由尺度变换性质,得(1)ta t L e f aF as a -⎡⎤⎛⎫=+⎢⎥ ⎪⎝⎭⎣⎦(15)()t L f aF as a ⎡⎤⎛⎫=⎪⎢⎥⎝⎭⎣⎦,再由s 域平移性质,得 []2()()at t L e f aF a s a aF as a a -⎡⎤⎛⎫=+=+ ⎪⎢⎥⎝⎭⎣⎦(16)31cos(6)cos (3)cos(3)2t t t -=∙13cos(9)cos(3)44t t =+32213cos (3)48149s s L t s s ⎡⎤=+⎣⎦++由s 域微分性质,得()()22322222213181327cos (3)481494819d s s s s L t t ds s s s s ⎡⎤--⎛⎫⎢⎥⎡⎤=-+=+ ⎪⎣⎦⎢⎥++⎝⎭++⎣⎦(17)[]2cos(2)4sL t s =+,连续两次应用s 域微分性质,有 []()2224cos(2)4s L t t s-=+,()3232224cos(2)4s sL t t s-⎡⎤=⎣⎦+(18)111atL es s a -⎡⎤-=-⎣⎦+,由s 域积分性质,得111111(1)at sL e ds t s s a ∞-⎛⎫⎡⎤-=- ⎪⎢⎥+⎣⎦⎝⎭⎰ln()ln ln s s a s s a ⎛⎫=+-=- ⎪+⎝⎭ (19)351135tt L ee s s --⎡⎤-=-⎣⎦++,由s 域积分性质,得 33111115ln 353t t s e e s L ds t s s s --∞⎛⎫⎡⎤-+⎛⎫=-= ⎪ ⎪⎢⎥+++⎝⎭⎣⎦⎝⎭⎰(20)()22sin aL at s a =⎡⎤⎣⎦+,由s 域积分性质,得()1122211sin 1arctan 21s s at s a s L ds d t s a a a s a π∞∞⎡⎤⎛⎫⎛⎫===-⎢⎥ ⎪ ⎪+⎝⎭⎝⎭⎛⎫⎣⎦+ ⎪⎝⎭⎰⎰ 4-2 解(1)因为()()sin ()2T f t t u t u t ω⎡⎤⎛⎫=--⎪⎢⎥⎝⎭⎣⎦()sin ()sin 22T T t u t t u t ωω⎡⎤⎛⎫⎛⎫=+-- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦ 所以可借助延时定理,得()()sin ()sin 22T T L f t L t u t L t u t ωω⎧⎫⎡⎤⎛⎫⎛⎫=+--⎡⎤⎡⎤⎨⎬ ⎪ ⎪⎢⎥⎣⎦⎣⎦⎝⎭⎝⎭⎣⎦⎩⎭222222221sT T s ee S S S ωωωωωω--⎛⎫=+=+ ⎪+++⎝⎭(2)因为()()()sin sin cos cos sin t t t ωϕωϕωϕ+=+ 所以()222222cos sin cos sin sin s s L t s s s ωϕϕωϕϕωϕωωω++=+=⎡⎤⎣⎦+++ 4-3 解此题可巧妙运用延时性质。
信号与系统课后习题答案

习 题 一 第一章习题解答基本练习题1-1 解 (a) 基频 =0f GCD (15,6)=3 Hz 。
因此,公共周期3110==f T s 。
(b) )30cos 10(cos 5.0)20cos()10cos()(t t t t t f ππππ+==基频 =0f GCD (5, 15)=5 Hz 。
因此,公共周期5110==f T s 。
(c) 由于两个分量的频率1ω=10π rad/s 、1ω=20 rad/s 的比值是无理数,因此无法找出公共周期。
所以是非周期的。
(d) 两个分量是同频率的,基频 =0f 1/π Hz 。
因此,公共周期π==01f T s 。
1-2 解 (a) 波形如图1-2(a)所示。
显然是功率信号。
t d t f TP T TT ⎰-∞→=2)(21lim16163611lim 22110=⎥⎦⎤⎢⎣⎡++=⎰⎰⎰∞→t d t d t d T T T W(b) 波形如图1.2(b)所示。
显然是能量信号。
3716112=⨯+⨯=E J (c) 能量信号 1.0101)(lim101025=-===⎰⎰∞∞---∞→T t ttT e dt edt eE J(d) 功率信号,显然有 1=P W1-3 解 周期T=7 ,一个周期的能量为 5624316=⨯+⨯=E J 信号的功率为 8756===T E P W 1-5 解 (a) )(4)2()23(2t tt δδ=+; (b) )5.2(5.0)5.2(5.0)25(5.733-=-=----t e t e t et tδδδ(c) )2(23)2()3sin()2()32sin(πδπδπππδπ+-=++-=++t t t t 题解图1-2(a) 21题解图1-2(b) 21(d) )3()3()(1)2(-=----t e t t et δδε。
1-6 解 (a) 5)3()94()3()4(2-=+-=+-⎰⎰∞∞-∞∞-dt t dt t t δδ(b) 0)4()4(632=+-⎰-dt t t δ(c) 2)]2(2)4(10[)]42(2)4()[6(63632=+++-=+++-⎰⎰--dt t t dt t t t δδδδ(d)3)3(3)(3sin )(1010=⋅=⎰⎰∞-∞-dt t Sa t dt ttt δδ。
信号与系统(第四版)第四章课后答案

第5-10页
■
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案
4.1 拉普拉斯变换
四、常见函数的单边拉普拉斯变换
1. (t ) 1, 2.( t) 或1 3. ( t ) s, 4. 指数信号e
1
s
, 0
1 s s0
s0t
(t 2)
f1(t) 1 0 1 f2(t) 1 t
例1:e (t 2) e
-t
2
e
(t 2)
e
2
1 s 1
e
2s
-1 0
第5-17页
■
1
t
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案
4.2 拉普拉斯变换性质
1 1e sT
例2: 单边冲激 T(t ) 1 e sT e s 2T 例3: 单边周期信号 fT(t ) (t ) f1(t ) f1(t T ) f1(t 2T ) F1(s )(1 e sT e s 2T )
8 e 2 s
s
f(t ) 1 0 1 y(t ) 2 4 t
二、尺度变换
2s
2
(1 e 2 s 2s e 2 s )
2 e 2 s 2 (1 e 2 s 2s e 2 s ) s
第5-16页
■
0
2
4
t
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案
拉氏逆变换的物理意义
f (t )
2 j 1
j
j
F (s)est ds
郑君里《信号与系统》(第3版)笔记和课后习题(含考研真题)详解(第4章)【圣才出品】

3.全通函数 如果一个系统函数的极点位于左半平面,零点位于右半平面,而且零点与极点对于 jω 轴互为镜像,这种系统函数称为全通函数,此系统则称为全通系统或全通网络。它的幅频特 性是常数。
4.最小相移函数 零点仅位于左半平面或 jω轴的网络函数称为“最小相移函数”,该网络称为“最小相 移网络”。非最小相移函数可以表示为最小相移函数与全通函数的乘积,即非最小相移网络 可以用最小相移网络与全通网络的级联来代替。
(1)部分分式展开法求解
首先将 F(s)展开成部分分式之和的形式,再对各部分分式分别取逆变换后叠加即可
得出 f(t)。
(2)留数定理求解
将拉氏逆变换的积分运算转化为求被积函数 F(s)est 在围线中所有极点的留数之和。
L 1[F (s)] 1 j F (s)estds [F (s)est的留数]
1 s
s2
s 2
,故
7 / 122
圣才电子书 十万种考研考证电子书、题库视频学习平台
L
[1 cos(t)]et
s
1
s (s )2 2
;
(7) L
[t 2
2t]
d2 ds2
1 s
d ds
2 s
2 s3
2 s2
(8) L [2 (t) 3e7t ] 2 3 s7
图 子书、题库视频学习平台
二、系统函数与系统特性 1.系统函数 系统的零状态响应的拉氏变换与激励的拉氏变换之比称为系统函数,即 H(s)=RZS (s)/E(s)。且冲激响应 h(t)↔H(s)。
2.零极点分布
H (s)
(9)e-αtsinh(βt);
(10)cos2(Ωt);
信号与系统 第4章-作业参考答案

题图 4-3-1 解:
11
第四章 傅立叶分析
第 4 章 习题参考答案
4-3-7
1)x(t)是实周期信号,且周期为 6; 3)x(t) = −x(t − 3)
1 3
设某信号x(t)满足下述条件:
2)x(t)的傅里叶系数为ak ,且当k = 0 和 k > 2时,有ak = 0;
1
4) ∫−3 |x(t)|2dt = 6 2 5)a1是正实数。
第四章 傅立叶分析
第 4 章 习题参考答案
第 4 章 习题参考答案
4-1 思考题 答案暂略 4-1 练习题 4-2-2 已知三个离散时间序列分别为 x1 ( n) = cos
2πn 2πn , x3 (n) = e , x 2 (n) = sin 25 10
π x (t ) = sin 4π t + cos 6π t + 时,试求系统输出 y (t ) 的傅立叶级数。 4
解:
3
第四章 傅立叶分析
第 4 章 习题参考答案
4因果系统: y(t) + 4y(t) = x(t)
式中x(t) 为系统输入,y(t)是系统输出。在下面两种输入条件下,求输出y(t)的傅里叶级数 展开: 1)x(t) = cos2πt ;
2
2
= 3 ) f ( t ) Sa (100t ) + Sa
解:
( 60t ) 4)
sin(4π t ) , −∞ < t < ∞ πt
9
第四章 傅立叶分析
第 4 章 习题参考答案
4)T=1/4 4-2-27 设 x(t ) 是一实值信号,在采样频率 ω s = 10000π 时, x(t ) 可用其样本值唯一确定
信号与系统-第4章连续时间傅立叶变换

x(t)
1
t
T1
T1
X ( j) T1 e jtdt 2 sin T1 2T1 sin T1
T1
T1
2T1
Sa(T1
)
2T1
Sinc(
T1
)
显然,将 X ( j) 中的
是相应周期信号的频谱
代之以k
0
再乘以
1 T0
,即
ak
1 T0
X(
jk0 )
2T1 T0
Sa(k0T1 )
2T1 T0
sin k0T1 k0T
若 x(t) X ( j) 则 x*(t) X *( j)
34
由 X ( j ) x(t)e jtdt 可得
X *( j) x*(t)e jtdt
所以 X * ( j ) x*(t)e jtdt
即
x*(t) X *( j)
若 x(t)是实信号,则 x(t) x*(t)
ak
2T1 T0
Sa( 2
T0
kT1)
sin 2
T0
k
T1k
x(t)
1
t
T0 T1 0 T1 T0
X ( j )
2 sin( 2
T0
kT1 )
(
2
k)
k
k
T0
X ( j)
2T1 1 T0 2
••
2 • •
T0
32
4.3 连续时间傅立叶变换的性质
(Properties of the Continuous-Time Fourier Transform) ➢揭示信号时域与频域特性之间的关系 ➢运用性质简化傅立叶变换对的求取
信号与系统第1-4章练习题

《信号与系统》第1-4章练习题一、填空题 1. (a )积分t t t d )42()3(55+--⎰-δ=_______________(b )=-⋅--)22()]2()([t t u t u δ 2.序列和∑-∞=kn n u ][=___________3.连续时间信号x (t )=sin t 的周期T 0= ,若对x (t )以f s =1Hz 进行抽样,所得 离散序列x [k ]= ,该离散序列是否是周期序列 。
4. 2[]sin (0.3)cos(0.75)x k k k ππ=+周期是多少?5.对连续时间信号延迟t 0的延迟器的单位冲激响应为 ,积分器的单位冲激响应 为 ,微分器的单位冲激响应为 。
6.某线性非时变(LTI)离散时间系统,若该系统的单位阶跃响应为][)41(k u k ,则该系统的 单位脉冲响应为 7.(a )系统)(4)()(2t tf dt t df t y +=,则系统为 (线性/非线性) (时变/时不变) (b )系统)(6)()(2t f dtt df t t y +=,则系统为 (线性/非线性) (时变/时不变) 8.若某离散时间LTI 系统的单位脉冲响应}3,1,2{][↓=k h ,激励信号}2,1,2,1{][↓-=k x ,则 该系统的零状态响应x [k ]* h [k ]=9.已知一连续时间LTI 系统的单位冲激响应为h (t ),该系统为BIBO (有界输入有界输出) 稳定系统的充要条件是10.已知()24cos(15)2sin(30)x t t t ππ=-++,求其平均功率P=________11.如图所示周期信号)(~t x 的频谱成分有__________ Tt12.如图所示周期信号)(~t x ,其直流分量C 0=___________t13. 已知一周期信号)(~t x 的周期T 0=2π,其频谱为C 0=1,C 1=0.5e j π ,C -1=0.5e -j π , C 3= -0.2j ,C -3=0.2j ,写出)(~t x 的时域表达式 14.(a )信号)()100cos(e )(2t u t t x t -=的频谱X (j ω)=(b )信号()[(2)(2)]cos100x t u t u t t =+--⋅的频谱X (j ω)= 16.(a )频谱3(4)j X j e ωω-所对应的信号x (t )=____________ (b )频谱函数)(π2)1j (j 1)j (ωδωωω++=X 所对应的信号)(t x =____________17.根据Parseval 能量守恒定律, 计算=⎰∞∞-t tt d )sin (218.(a )信号时域变化越快,其对应的频谱所含的高频分量(越少or 越多)? (b )方波的持续时间越短,其频谱的有效频带(越窄or 越宽)?19.已知信号x (t )的最高频率f 0 (Hz),则对信号 x (t /2)抽样时,其频谱不混迭的最大抽样间隔 T max =___________20.对信号)100(Sa 2t 抽样,其频谱不混叠的最小抽样角频率为二、已知 x (t ) 的波形如图错误!未找到引用源。
吴大正《信号与线性系统分析》(第4版)章节题库(傅里叶变换和系统的频域分析)【圣才出品】

第 4 章 傅里叶变换和系统的频域分析
一、选择题 1.图 4-1 所示系统由两个 LTI 子系统组成,已知子系统 H1 和 H2 的群时延分别为 τ1 和 τ2,则整个系统的群时延 τ 为( )。
图 4-1 A.τ1+τ2 B.τ1-τ2 C.τ1·τ2 D.max(τ1,τ2) 【答案】A
9.如图 4-2 所示信号 f1(t)的傅里叶发换 F1(jω)已知,求信号 f2(t)的傅里叶发 换为( )。
图 4-2
【答案】A
【解析】由题意知, f2 (t) f1(t t0 ) 。由于 f2(t)=f1(-(t+t0)),根据傅里叶 发换的反转性质和时秱性质可知, F2 ( j) F1( j)e jt0 。
4.设 f(t)的频谱函数为 F(jω),则
的频谱函数等于( )。
【答案】D
2 / 150
圣才电子书 十万种考研考证电子书、题库视频学习平台
【解析】
可写为 f[-1/2(t-6)],根据傅里叶发换的尺度发换性质,
x(at)
|
1 a
|
[x(w
/
a)],得
f[-1/2(t)]
A.x(t)=-4Sa[2π(t-3)]
B.x(t)=4Sa[2π(t+3)]
C.x(t)=-2Sa[2π(t-3)]
D.x(t)=2Sa[2π(t+3)]
【答案】A
【解析】常用的傅里叶发换对
Sa(ct)
c
G2c
()
令c 2 ,则有 4Sa(2t) 2G4 ()
ቤተ መጻሕፍቲ ባይዱ
再由傅里叶发换的时秱性质,有
4Sa[2 (t 3)] 2G4 ()e j3
信号与系统1—4章练习题
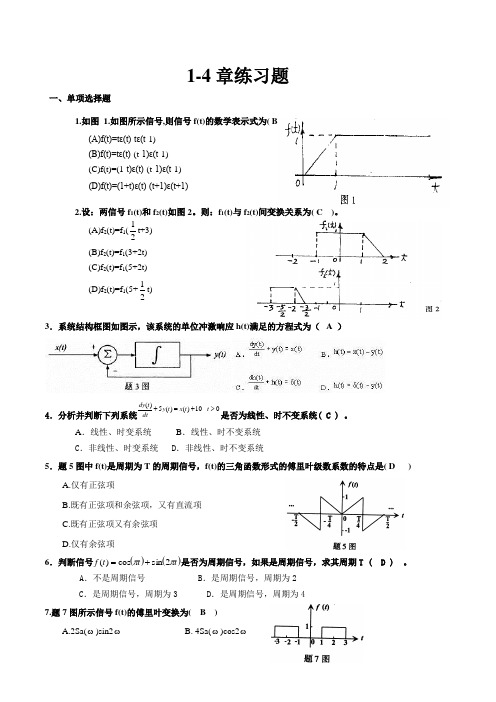
1-4章练习题一、单项选择题1.如图 1.如图所示信号,则信号f(t)的数学表示式为( B )。
(A)f(t)=tε(t)-tε(t -1) (B)f(t)=tε(t)-(t-1)ε(t -1) (C)f(t)=(1-t)ε(t)-(t-1)ε(t -1)(D)f(t)=(1+t)ε(t)-(t+1)ε(t+1)2.设:两信号f 1(t)和f 2(t)如图2。
则:f 1(t)与f 2(t)间变换关系为( C )。
(A)f 2(t)=f 1(21t+3)(B)f 2(t)=f 1(3+2t) (C)f 2(t)=f 1(5+2t)(D)f 2(t)=f 1(5+21t)3.系统结构框图如图示,该系统的单位冲激响应h(t)满足的方程式为( A)4.分析并判断下列系统()5()()10 0dy t y t x t t dt+=+>是否为线性、时不变系统( C ) 。
A .线性、时变系统B .线性、时不变系统C .非线性、时变系统D .非线性、时不变系统5.题5图中f(t)是周期为T 的周期信号,f(t)的三角函数形式的傅里叶级数系数的特点是( D )A.仅有正弦项B.既有正弦项和余弦项,又有直流项C.既有正弦项又有余弦项D.仅有余弦项6.判断信号是否为周期信号,如果是周期信号,求其周期T ( D ) 。
A .不是周期信号 B .是周期信号,周期为2C .是周期信号,周期为3D .是周期信号,周期为47.题7图所示信号f(t)的傅里叶变换为( B )A.2Sa(ω)sin2ωB. 4Sa(ω)cos2ω()()t t t f ππ2sin cos )(+=C.2Sa(ω)cos2ωD. 4Sa(ω)sin2ω8.有一因果线性时不变系统,其频率响应H j j ()ωω=+12,对于某一输入x(t)所得输出信号的傅里叶变换为Y j j j ()()()ωωω=++123,则该输入x(t)为( B )A .e t t -3ε()B .)(3t e t ε--C .)(3t e t ε-D .)(3t e t ε9.积分等于( A )A .B .C .D .10.已知:f(t)=Sgn(t)的傅里叶变换为F(jω)=ωj 2, 则:F 1(jω)=jπSgn(ω)的傅里叶反变换f 1(t)为( C )。
信号与系统第四章习题

d dw
X ( jw )
4.16
考 虑 信 号 x (t )
k
s in ( k
4 t k 4 k 4
)
( a )求 满 足 x (t ) (
s in t
t
) g t 的 g (t )
( b ) 证 明 X ( j ) 是 周 期 的
解 :a )
s in ( k
4 t k 4 k 4
)
( ) t k t k 4
s in t
所 以 g (t ) t k 4 k
ake
(a k a k )e
jk 1
jkw 1
x 2 (t ) bk a k e
ak e
jk 1
4.3(a)
j ( 2 t
4
sin ( 2 t
4
)
)
e
4
e 2j
j ( 2 t
4
)
j
e
e
j 2 t
e 2j
j
X 1 ( jw ) X 1 ( jw )
*
x1 ( t ) x1 ( t )
*
x1 ( t ) 不是实信号
X 1 ( jw ) u ( w ) u ( w 2 )
X 1 ( jw ) X 1 ( jw )
x1 ( t )
*
不 是 x 虚 1 ( t ) 不是虚信号 函 数
第四章 习题
3.5 设x1(t)是一连续的周期信号,其基波频率是W1,傅
信号与系统第4章答案

做拉氏反变换得零输入响应
(2)考虑输入 ,将微分方程两边做拉氏变换得
代入初始条件,
整理得,
做拉氏反变换得零输入响应
(3)考虑输入 ,将微分方程两边做拉氏变换得
代入初始条件,
整理得,
做拉氏反变换得零输入响应
4.12 已知连续系统的微分方程为 ,求在下列输入时的零输入响应、零状态响应和全响应。
(1) ;
则
4.8 已知线性连续系统的单位冲激响应为 。
(1)若系统输入 ,求系统的零状态响应 ;
(2)若 ,求系统输入 。
解:将系统的单位冲激响应作拉氏变换得系统函数
(1)系统输入的拉氏变换为
根据系统的S域分析,所以零状态响应的拉氏变换为
,所以
(2)
根据系统的S域分析,所以输入的拉氏变换为
求拉氏反变换得
4.9 已知系统微分方程为 ,求下列输入时的零状态响应。
(9) (10)
(11) (12)
(13) (14)
(15) (16)
(17) (18)
(19) (20)
(21) (22)
(23) (24)
解:
(1) (2)
(3)(4)(5)来自(6)(7)(8)
(9)
(10)
(11)
(12)
(13)
(14)
{ }
=
(15) { } =
(16) { }=
(17) { }=
(3) (4)
解:(1)根据尺度性质
再根据s域平移性质
(2)根据尺度性质
根据s域微分性质
根据时移性质
(3)根据尺度性质
再根据s域平移性质
(4)根据时移性质
再根据尺度性质
西安交通大学_信号与系统A课后习题(第3、4章)

6
7
8
9
10
t
(c)
1
《第二次课后作业》 28 对下图所示的离散时间周期信号 x[n] 求傅里叶级数系数, 并画出每一组系数 ak 的模和相位。
x[n] … -12 -6 1 … 0 6 12 n
(b)
x[n] 2 … -12 -6 1 … 0 -1 6 12 n
(c) 11 现对一信号 x[n] 给出如下信息: 1. x[n] 是实、偶信号。 3. a11 = 5 2. x[n] 有周期 N = 10 和傅里叶系数 ak 。 4.
《第二次课后作业》 11 已知下列关系:
y (t ) = x(t ) ∗ h(t )
和
g (t ) = x(3t ) ∗ h(3t )
并已知 x(t ) 的傅里叶变换是 X ( jω ) , h(t ) 的傅里叶变换是 H ( jω ) ,利用傅里叶变换性质证明
g (t ) 为 g (t ) = Ay ( Bt )
x(t ) = t , 0 < t < 1
3
画出 x(t ) 并求出它的傅里叶级数系数。 45 设 x(t ) 是一个实周期信号,其正弦-余弦形式的傅里叶级数表示为
x(t ) = a0 + 2∑ [ Bk cos kω0t − Ck sin kω0t ]
k =1
∞
(a) 求 x(t ) 的偶部和奇部的指数形式的傅里叶级数表示;也就是利用上式的系数求下面 两式中的 α k 和 β k ,
h (t ) = e
−4 t
z[n] = x[n] y[ n]
对下列各输入情况下,求输出 y (t ) 的傅里叶级数表示: (b) x(t ) = ∑ n =−∞ (−1) n δ (t − n)
信号与系统练习题-第4章

信号与系统练习题 第4章一、选择题1、周期信号的频谱具有的特点是〔D 〕A 、离散性B 、收敛性C 、谐波性D 、以上都对 2、以下表达正确的选项是〔D 〕。
A 、)(t f 为周期偶函数,其傅立叶级数只有偶次谐波;B 、)(t f 为周期偶函数,其傅立叶级数只有余弦偶次谐波分量;C 、)(t f 为周期奇函数,其傅立叶级数只有奇次谐波;D 、)(t f 为周期奇函数,其傅立叶级数只有正弦分量。
3、某连续系统的系统函数ωωj j H -=)(,那么输入为t j e t f 2)(=时,系统的零状态响应()zs y t =〔B 〕A 、)j(2t e B 、)2-j(2t e2πC 、 )j(2t e2 D 、 )2-j(2t eπ4、频谱函数11)(+=ωωj j F 的傅里叶反变换=)(t f 〔A 〕A 、 )(t e t ε-B 、 )(t te t ε-C 、 )(t e t εD 、 )(t te t ε 5、假设矩形脉冲信号的宽度加宽,那么它的频谱带宽(B)。
A 、 不变 ;B 、变窄 ;C 、 变宽;D 、与脉冲宽度无关 6、假设()f t 是实偶信号,以下说法正确的选项是〔A 〕 A 、该信号的频谱是实偶函数;B 、该信号的频谱是虚奇函数C 、该信号的频谱是奇函数;D 、该信号的频谱的实部实偶函数,虚部是奇函数7、某一周期函数,在其频谱分量中,仅含有正弦基波分量和正弦奇次谐波分量,该函数属于〔D 〕。
A 、奇函数 B 、偶函数 C 、既是偶函数又是奇谐函数 D 、既是奇函数又是奇谐函数 8、关于抽样信号sin ()tSa t t=,以下说法错误的选项是〔A 〕。
A 、()Sa t 信号是奇函数 B 、 ()Sa t 信号在t=0时取最大值1 C 、()0Sa t =时,t n π=±〔n 为自然数〕 D 、()()Sa t Sa t =-9、带限信号)(t f 的最高角频率为m ω,现对)(t f 进行理想冲激取样,得到取样信号()s f t ,为了能从()s f t 中恢复出原信号,那么取样角频率s ω需满足〔B 〕A 、s m ωω≥B 、2s m ωω≥C 、m s ωω≥D 、2m s ωω≥10、频谱函数1()2F j j ωω=+的傅里叶反变换=)(t f 〔A 〕。
信号与系统第四章习题

1 3
s +1 ) ,复频移性质、尺度变换、S 域微分 3
b
b ⎤ 1 s - s ⎡ (4) f (at − b) = f ⎢a(t − )⎥ ↔ F( )e a ,时移性质、尺度变换 a ⎦ a a ⎣
4.7 题图 4.2 所示为从 t=0 起始的周期信号。求 f(t)的单边拉氏变换。
解: (a) f (t ) = f a (t ) *
∑ δ (t − nT )
n =0
∞
- s 1 f a (t ) = ε (t ) − ε (t − T / 2) ↔ (1 - e 2 ) s - s 1 1 1- e 2 1 = = ∴ F(s) = (1 - e 2 ) T -s ⎞ s 1 - e -sT s 1 - e -sT ⎛ ⎜ s ⎜1 + e 2 ⎟ ⎟ ⎝ ⎠ T T - s
2
K1 =
2 jπ / 6 2 − jπ / 6 e , K2 = e 3 3
∴ h(t ) =
π 4 −t 2 −t e cos( 3t + )ε (t ) = e 6 3 3
2
(
3cos 3t - sin 3t ε (t )
)
当 u s (t ) = ε (t ) 时, U( s ) = H ( s) =
−2 t 解:(1) e f (2t ) ↔
1 s+2 F( ) ,复频移性质、尺度变换 2 2 ⎡1 ⎤
2 2 -2s (2) (t − 2) f ( t − 1) = (t − 2) f ⎢ (t − 2)⎥ ↔ 2F′′(2s)e ,时移性质、尺度变换、S 域微分 2 ⎣2 ⎦
1
−t (3) te f (3t ) ↔ − F′(
信号与系统练习题

第一章绪论1、选择题1.1、f (5—2t )是如下运算的结果 CA 、 f (-2t )右移5B 、 f (-2t )左移5C 、 f (—2t )右移25D 、 f (—2t )左移251。
2、f (t 0—a t )是如下运算的结果 C 。
A 、f (-a t )右移t 0;B 、f (—a t )左移t 0 ;C 、f (-a t )右移a t 0;D 、f (—a t )左移at0 1.3、已知 系统的激励e (t )与响应r(t )的关系为:)()()(t u t e t r = 则该系统为 B 。
A 、线性时不变系统;B 、线性时变系统;C 、非线性时不变系统;D 、非线性时变系统 1.4、已知 系统的激励e (t )与响应r (t)的关系为:)()(2t e t r = 则该系统为 C 。
A 、线性时不变系统 B 、线性时变系统 C 、非线性时不变系统 D 、非线性时变系统 1。
5、已知 系统的激励e(t)与响应r(t)的关系为:)1()(t e t r -= 则该系统为 B 。
A 、线性时不变系统B 、线性时变系统C 、非线性时不变系统D 、非线性时变系统1.6、已知 系统的激励e (t)与响应r (t )的关系为:)2()(t e t r = 则该系统为 B A 、线性时不变系统 B 、线性时变系统 C 、非线性时不变系统 D 、非线性时变系统 1.7.信号)34cos(3)(π+=t t x 的周期为 C 。
A 、π2 B 、π C 、2π D 、π21。
8、信号)30cos()10cos(2)(t t t f -=的周期为: B . A 、15π B 、5π C 、π D 、10π1。
9、dt t t )2(2cos 33+⎰-δπ等于 B . A.0 B.-1 C 。
2 D 。
—21.10、 若)(t x 是己录制声音的磁带,则下列表述错误的是: BA 。
)(t x -表示将此磁带倒转播放产生的信号 B. )2(t x 表示将此磁带放音速度降低一半播放 C 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
信号与系统练习题 第4章一、选择题1、周期信号的频谱具有的特点是(D )A 、离散性B 、收敛性C 、谐波性D 、以上都对 2、下列叙述正确的是(D )。
A 、)(t f 为周期偶函数,其傅立叶级数只有偶次谐波;B 、)(t f 为周期偶函数,其傅立叶级数只有余弦偶次谐波分量;C 、)(t f 为周期奇函数,其傅立叶级数只有奇次谐波;D 、)(t f 为周期奇函数,其傅立叶级数只有正弦分量。
3、某连续系统的系统函数ωωj j H -=)(,则输入为tj et f 2)(=时,系统的零状态响应()zs y t =(B )A 、)j(2t eB 、)2-j(2t e2πC 、)j(2t e 2 D 、 )2-j(2t eπ4、频谱函数11)(+=ωωj j F 的傅里叶反变换=)(t f (A )A 、 )(t e tε- B 、 )(t te tε- C 、 )(t e tε D 、 )(t te tε 5、若矩形脉冲信号的宽度加宽,则它的频谱带宽(B)。
A 、 不变 ;B 、变窄 ;C 、 变宽;D 、与脉冲宽度无关 6、若()f t 是实偶信号,下列说法正确的是(A )A 、该信号的频谱是实偶函数;B 、该信号的频谱是虚奇函数C 、该信号的频谱是奇函数;D 、该信号的频谱的实部实偶函数,虚部是奇函数7、某一周期函数,在其频谱分量中,仅含有正弦基波分量和正弦奇次谐波分量,该函数属于(D )。
A 、奇函数 B 、偶函数 C 、既是偶函数又是奇谐函数 D 、既是奇函数又是奇谐函数 8、关于抽样信号sin ()tSa t t=,下列说法错误的是(A )。
A 、()Sa t 信号是奇函数 B 、 ()Sa t 信号在t=0时取最大值1 C 、()0Sa t =时,t n π=±(n 为自然数) D 、()()Sa t Sa t =-9、已知带限信号)(t f 的最高角频率为m ω,现对)(t f 进行理想冲激取样,得到取样信号()s f t ,为了能从()s f t 中恢复出原信号,则取样角频率s ω需满足(B )A 、s m ωω≥B 、2s m ωω≥C 、m s ωω≥D 、2m s ωω≥10、频谱函数1()2F j j ωω=+的傅里叶反变换=)(t f (A )。
A 、 2()te t ε- B 、 2()tte t ε- C 、 0.5()te t ε- D 、 2()t te t ε11、若一模拟信号为带限信号,且对其抽样满足Nyquist 条件,则只要将抽样信号通过(A ) 即可完全不失真的恢复原信号。
A 、理想低通滤波器B 、理想高通滤波器C 、理想带通滤波器D 、理想带阻滤波器 12、理想不失真传输系统的传输函数)(ωj H 可表示为(A )A 、0j t Ke ω- B 、0j t Ke ω-C 、0[()()]j t C C Ke ωεωωεωω-+-- D 、00j t Ke ω- 13、理想低通滤波器的传输函数)(ωj H 可表示为(C )A 、0j t Ke ω-B 、0j t Ke ω-C 、0[()()]j t C C Ke ωεωωεωω-+-- D 、00j t Ke ω- 14、一非周期连续信号被理想取样后,取样信号的频谱()s F j ω是(C )A 、离散频谱;B 、连续频谱;C 、连续周期频谱;D 、不确定,要依赖于信号而变化 15、连续周期信号)(t f 的频谱)(ωj F 的特点是(D )A 、周期、连续频谱;B 、周期、离散频谱;C 、连续、非周期频谱;D 、离散、非周期频谱。
16、欲使信号通过线性系统不产生失真,则该系统应具有(C )A 、幅频特性为线性,相频特性也为线性;B 、幅频特性为非线性,相频特性为常数;C 、幅频特性为常数,相频特性为线性D 、幅频特性为非线性,相频特性为线性;17、已知信号()f t 的傅里叶变换0()()F j ωδωω=-,则()f t =(A )A 、012j te ωπ B 、012j t e ωπ- C 、01()2j t e t ωεπ D 、01()2j t e t ωεπ- 18、信号2()()f t g t =的波形图为(D )A B C D 19、信号2()g t 的表达式为(B )A 、()(2)t t εε-- ;B 、(1)(1)t t εε+-- ;C 、(2)(2)t t εε+--;D 、()(4)t t εε-- 20、一周期信号()f t ,周期为T ,其频谱图中相邻两条谱线之间的间隔为(D )A 、2T π B 、T C 、1TD 、2T π 二、填空题1、已知()f t 的傅里叶变换为()F j ω,则(5)f t -的傅里叶变换为5()j e F j ωω-。
2、信号)(t f 如图,其频谱函数()F j ω= ωωj e Sa -)(2。
3、频带有限信号)(t f 的最高频率为100Hz ,若对)(t f 进行时域抽样,使频谱不发生混叠的Nyquist 频率为200Hz 。
4、)2()2()(-++=t t t f δδ的傅里叶变换为)2(2cos ω。
5、对无失真传输系统,其频率响应函数的幅频特性应为()H j ω=()H j K ω=。
6、对无失真传输系统,其频率响应函数的相频特性应为()ϕω=0()t ϕωω=-。
7、有一模拟信号包含30Hz 、80Hz 、50Hz 三种模拟频率,若以某一采样频率进行采样,为保证不失真地由采样序列恢复原模拟信号,采样频率fs 需大于等于160Hz 。
8、已知()f t 的傅里叶变换为()F j ω,则(5)f t +的傅里叶变换为5()j eF j ωω。
9、已知信号()f t 的频谱函数在(-500Hz ,500Hz )区间内不为零,现对()f t 进行理想取样,则Nyquist 取样频率为1000Hz 。
10、如果系统的输出信号与输入信号相比,只有幅度的大小和出现时间的先后不同,而没有波形上的变化,称为无失真传输。
11、设系统的输入信号为()f t ,经过无失真传输后,输出信号应为()y t =()()d y t Kf t t =-。
12、已知()f t 的傅里叶变换为()F j ω,则(2)f t 的傅里叶变换为1()22F j ω。
13、已知()f t 的傅里叶变换为()F j ω,则(2)f t -的傅里叶变换为1()22F j ω-。
14、已知()F j ω的傅里叶逆变换为()f t ,则0[()]F j ωω+的傅里叶逆变换为0()j t f t e ω-。
15、已知()F j ω的傅里叶逆变换为()f t ,则0[()]F j ωω-的傅里叶逆变换为0()j t f t e ω。
16、()()f t t δ=的傅里叶变换为1。
17、()1f t =的傅里叶变换为2()πδω。
18、2()cos(5)()f t t g t =的傅里叶变换为(5)(5)Sa Sa ωω++-。
19、3()j tf t e =的傅里叶变换为2(3)πδω-。
20、5()j tf t e-=的傅里叶变换为2(5)πδω+。
21、()cos(5)f t t =的傅里叶变换为[(5)(5)]πδωδω++-。
22、()sin(5)f t t =的傅里叶变换为[(5)(5)]j πδωδω+--。
23、()'()f t t δ=的傅里叶变换为j ω。
24、2()()f t g t =的傅里叶变换为2()Sa ω。
25、频带有限信号)(t f 的最高频率为100Hz ,若对)(t f 进行时域抽样,使频谱不发生混叠的 Nyquist 间隔为1或0.005s 。
26、有一模拟信号包含30Hz 、80Hz 、50Hz 三种模拟频率,若以某一采样间隔进行采样,为保证不失真地由采样序列恢复原模拟信号,采样间隔需小于等于1160s 。
27、已知信号()f t 的频谱函数在(-500Hz ,500Hz )区间内不为零,现对()f t 进行理想取样,则Nyquist 取样间隔为11000或0.001s 。
三、计算题1、求取样函数sin ()tSa t t=的频谱函数。
解:由于()()2g t Sa τωττ↔令τ=2,有2()2()g t Sa ω↔由对称性,()2()F jt f πω↔-有22()2()Sa t g πω↔ 故,2()()Sa t g πω↔ 2、如已知信号()f t 的傅里叶变换为()F j ω,求信号4(32)j te f t -的傅里叶变换。
解:由已知,()()f t F j ω↔,由时移特性有,3(3)()j f t F j e ωω+↔由尺度变换性质,有3-21(32)()22j f t F j e ωω-↔-由频移性质,得3(-4)-421-4(32)()22j j tef t F j e ωω-↔-3、某LTI 系统的频率响应为2()2j H j j ωωω-=+,若系统的输入()cos(2)f t t =,求该系统的输出()y t 。
解:()()()Y j F j H j ωωω=•()cos(2)f t t =,cos(2)[(2)(2)]t πδωδω↔++- ()F j ω=[(2)(2)]πδωδω++-()()()Y j F j H j ωωω=•=[(2)(2)]πδωδω++-•22j j ωω-+=22[(2)(2)]22j j j j ωωπδωδωωω--+•+-•++=2222[(2)(2)]2222j j j j πδωδω+-+•+-•-+=[(2)(2)]j πδωδω+-- 求逆变换,得 ()sin(2)y t t =4、已知()f t 波形图如图所示,求其傅里叶变换()F j ω。
解:2()1g ()f t t =-12()πδω↔2g ()2Sa()t ω↔()2()2()F j Sa ωπδωω=-5、已知()f t 波形图如图所示,求其傅里叶变换()F j ω。
解:62()g (5)g (5)f t t t =-+-56g (5)6Sa(3)j t e ωω--↔ 52g (5)2Sa()j t e ωω--↔5()[6Sa(3)2Sa()]j F j e ωωωω-=+6、求图示频谱函数()F j ω的傅里叶反变换()f t 。
ω解:4()()F j g ωω=由于()()2g t Sa τωττ↔令τ=4,有4()4(2)g t Sa ω↔由对称性,()2()F jt f πω↔- 有44(2)2()Sa t g πω↔ 故,42(2)()Sa t g ωπ↔所以得到 2()(2)f t Sa t π=7、求微分方程()()()()''3'2'y t y t y t f t ++=所描述系统的频率响应函数()H j ω 解:写出频域方程()()()()2()3()2()j Y j j Y j Y j j F j ωωωωωωω++=;2()()()()3()2Y j j H j F j j j ωωωωωω==++8、求微分方程()()()()()''5'6'4y t y t y t f t f t ++=+所描述系统的频率响应函数()H j ω 解:写出频域方程()()()()()2()5()6()4j Y j j Y j Y j j F j F j ωωωωωωωω++=+2()4()()()5()6Y j j H j F j j j ωωωωωω+==++9、描述某LTI 连续系统的微分方程为()()()'2y t y t f t +=,求该系统的频率响应函数()H j ω 解:写出频域方程()()()()2j Y j Y j F j ωωωω+= ;()1()()2Y j H j F j j ωωωω==+10、已知(22)()()t f t e t δ-+=,求其傅里叶变换()F j ω。
