椭圆的知识点分类基础练习
椭圆知识点总结及练习

椭圆知识点总结及典型方法知识点一:椭圆的定义平面内一个动点P 到两个定点1F 、2F 的距离之和等于常数)2(2121F F a PF PF >=+ ,这个动点P 的轨迹叫椭圆.这两个定点叫椭圆的焦点,两焦点的距离叫作椭圆的焦距.知识点二:椭圆的标准方程1.当焦点在x 轴上时,椭圆的标准方程:12222=+by a x )0(>>b a ,其中222b a c -=2.当焦点在y 轴上时,椭圆的标准方程:12222=+bx a y )0(>>b a ,其中222b a c -=;知识点三:椭圆的简单几何性质椭圆:12222=+by a x )0(>>b a 的简单几何性质(1)对称性:对于椭圆标准方程12222=+b y a x )0(>>b a :说明:把x 换成x -、或把y 换成y -、或把x 、y 同时换成x -、y -、原方程都不变,(2)范围:椭圆上所有的点都位于直线a x ±=和b y ±=所围成的矩形内,所以椭圆上点的坐标满足a x≤,b y ≤。
(3)顶点:①椭圆的对称轴与椭圆的交点称为椭圆的顶点。
②椭圆12222=+by a x )0(>>b a 与坐标轴的四个交点即为椭圆的四个顶点,坐标分别为 )0,(1a A -,)0,(2a A ,),0(1b B -,),0(2b B③线段21A A ,21B B 分别叫做椭圆的长轴和短轴,a A A 221=,b B B 221=。
a 和b 分别叫做椭圆的长半轴长和短半轴长。
(4)离心率:①椭圆的焦距与长轴长度的比叫做椭圆的离心率,用e 表示,记ac a c e ==22。
知识点四:椭圆12222=+b y a x 与 12222=+bx a y )0(>>b a 的区别和联系知识点五: 椭圆的第二定义:平面内与一个定点(焦点)和一定直线(准线)的距离的比为常数e ,(0<e <1)的点的轨迹为椭圆。
椭圆考点练习题

椭圆考点练习题一、选择题1. 椭圆的焦点为F1,F2,如果椭圆的长轴长为2a,短轴长为2b,则F1F2的距离是:A. 2aB. aC. 2bD. b2. 椭圆的离心率为e,长轴长为2a,与椭圆相应的直角双曲线的离心率是:A. eB. 1/eC. e^2D. 1/e^23. 椭圆的焦点为F1,F2,点P为椭圆上一点,F1P与F2P的夹角为90度,则椭圆的离心率为:A. 0B. 1C. 2D. 无法确定4. 椭圆水平长轴的标准方程为x^2/a^2 + y^2/b^2 = 1,若椭圆的离心率为2/3,短轴长为6,则长轴长a为:A. 9B. 18C. 12D. 6二、填空题1. 椭圆的标准方程为x^2/16 + y^2/9 = 1,焦点在x轴上,离心率为2/3,则焦点的坐标为(_____, 0)和(_____,0)。
答:(8,0)和(-8,0)2. 椭圆的离心率为1/2,焦点在x轴上,则椭圆的标准方程可以表示为x^2/____ + y^2/5 = 1。
答:36三、解答题1. 某椭圆的焦点分别为F1(-2,0)和F2(2,0),离心率为1/2。
求该椭圆的标准方程。
解:由椭圆的标准方程可知,离心率e满足e = c/a,其中c为焦点到原点的距离,a为椭圆的半长轴。
由题意可知,c = 2,e = 1/2。
代入公式得:1/2 = 2/a,解得a = 4。
由焦点到原点的关系可知,c = a关于y轴的旋转角度(逆时针),所以c = 4。
椭圆的标准方程为x^2/16 + y^2/4 = 1。
2. 某椭圆的长轴长为10,短轴长为6,求该椭圆的离心率。
解:椭圆的离心率e满足e = c/a,其中c为焦点到原点的距离,a 为椭圆的半长轴。
由题意可知,长轴长2a = 10,短轴长2b = 6。
解得a = 5,b = 3。
由焦点到原点的关系可知,c = a关于x轴的旋转角度(逆时针),所以c = 5。
椭圆的离心率e = c/a = 5/5 = 1。
椭圆基础练习题

椭圆基础练习题一、选择题1. 椭圆的长轴和短轴长度分别为2a和2b,其中a和b的关系是()。
A. a > bB. a < bC. a = bD. 无法确定2. 椭圆的焦点到椭圆上任意一点的距离之和等于()。
A. 2aB. 2bC. a + bD. a - b3. 如果椭圆的方程是 \( \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \),其中a和b是常数,那么a和b的单位是什么?A. 米B. 秒C. 无单位D. 角度4. 椭圆的离心率e的取值范围是()。
A. 0 ≤ e < 1B. 0 ≤ e ≤ 1C. 0 < e < 1D. 1 < e ≤ 25. 椭圆的面积公式是()。
A. πabB. π(a + b)C. π(a - b)D. π(a^2 + b^2)二、填空题6. 椭圆的中心点坐标是(____,____)。
7. 椭圆的离心率e定义为____,其中c是焦点到中心的距离。
8. 如果一个椭圆的长轴是10,短轴是6,那么它的面积是____。
9. 椭圆的焦点坐标可以表示为(____,0)和(____,0)。
10. 椭圆的方程 \( \frac{x^2}{16} + \frac{y^2}{9} = 1 \) 中,a 和b的值分别是____和____。
三、简答题11. 描述椭圆的基本性质,并给出一个实际生活中椭圆的应用例子。
12. 解释为什么椭圆的离心率总是小于1。
13. 如果一个椭圆的长轴是20,短轴是10,求出它的焦点坐标。
四、计算题14. 给定一个椭圆的方程 \( \frac{x^2}{25} + \frac{y^2}{16} = 1 \),求出它的离心率e。
15. 已知一个椭圆的长轴是26,短轴是15,求出它的面积和离心率。
五、证明题16. 证明椭圆上任意一点到两个焦点的距离之和是一个常数。
17. 证明椭圆的中心点到长轴和短轴的距离相等。
椭圆综合练习知识点总结

椭圆综合练习知识点总结1. 椭圆的基本性质椭圆是一种闭曲线,其定义是平面上距离两个固定点的距离之和等于常数的轨迹。
这个点到两个固定点的距离分别为d1和d2,那么椭圆的定义可以表示为d1+d2=2a,其中a为椭圆的半长轴。
根据这个定义,我们可以得到椭圆的一些基本性质:a) 椭圆的离心率e满足0<e<1;b) 椭圆的中心C是两个焦点的连线的中点;c) 椭圆的两条对称轴互相垂直,且相交于中心;d) 椭圆的短轴长为2b,满足b^2=a^2*(1-e^2);e) 椭圆的焦点到椭圆上任意一点的连线在该点处的角度等于这条连线的斜率。
2. 椭圆的方程式椭圆的方程式可以分为标准方程和一般方程两种形式。
标准方程是指椭圆的中心在坐标原点,且长轴平行于坐标轴的方程。
一般方程是指椭圆的中心不在坐标原点,且长轴不平行于坐标轴的方程。
标准方程为x^2/a^2+y^2/b^2=1,其中a为长轴的半径,b为短轴的半径;一般方程为A(x-h)^2+B(y-k)^2=1,其中(h,k)为椭圆的中心坐标。
3. 椭圆的参数方程椭圆的参数方程可以表示为:x = a * cos(t)y = b * sin(t)其中t为参数,a和b分别为长轴和短轴的半径。
参数方程可以描述椭圆上的任意一点的坐标,并且可以方便地进行参数方程曲线的相关计算。
4. 椭圆的焦点和离心率椭圆的焦点是指两个固定点F1和F2,这两个点到椭圆上任意一点的距离之和等于椭圆的长轴长度。
离心率e定义为焦点到中心的距离与长轴的长度之比,满足e=c/a,其中c为焦点到中心的距离。
5. 椭圆的焦距和直径椭圆的焦距是指两个焦点之间的距离,等于2ae。
椭圆的直径是指椭圆上任意两个对称点之间的距离,满足等于2a或2b。
6. 椭圆的焦准线椭圆的焦准线是指通过两个焦点的直线,它们与椭圆的交点为椭圆上所有点的切线。
焦准线的斜率与椭圆上各点处的切线的斜率成反比关系,即斜率的乘积为-1。
在实际的应用中,椭圆可以描述行星、卫星、电子轨道、轮廓设计等许多现实世界中的问题。
椭圆知识点总结及经典习题练习

第二部分 圆锥曲线(一)---椭圆知识点一:1、平面内与两个定点1F ,2F 的距离之和等于常数(大于12F F )的点的轨迹称为椭圆.即:|)|2(,2||||2121F F a a MF MF >=+。
注意:若)(2121F F PF PF =+,则动点P 的轨迹为线段21F F ;这两个定点称为椭圆的焦点,两焦点的距离称为椭圆的焦距.注意:椭圆122=+b y a x ,122=+bx a y )0(>>b a 的相同点:形状、大小都相同;参数间的关系都有)0(>>b a 和)10(<<=e ac e ,222c b a +=;不同点:两种椭圆的位置不同;它们的焦点坐标也不相同。
知识点二:椭圆的标准方程1.当焦点在x 轴上时,椭圆的标准方程:12222=+b y a x )0(>>b a ,其中222b a c -=2.当焦点在y 轴上时,椭圆的标准方程:12222=+bx a y )0(>>b a ,其中222b a c -=;注意:1.只有当椭圆的中心为坐标原点,对称轴为坐标轴建立直角坐标系时, 才能得到椭圆的标准方程;2.在椭圆的两种标准方程中,都有)0(>>b a 和222b a c -=; 3.椭圆的焦点总在长轴上.当焦点在x 轴上时,椭圆的焦点坐标为)0,(c ,)0,(c -; 当焦点在y 轴上时,椭圆的焦点坐标为),0(c ,),0(c -知识点三:椭圆的简单几何性质椭圆:12222=+by a x )0(>>b a 的简单几何性质(1)对称性:对于椭圆标准方程12222=+by a x )0(>>b a :说明:把x 换成x -、或把y 换成y -、或把x 、y 同时换成x -、y -、原方程都不变,所以椭圆12222=+by a x 是以x 轴、y 轴为对称轴的轴对称图形,并且是以原点为对称中心的中心对称图形,这个对称中心称为椭圆的中心。
椭圆高中练习题及讲解

椭圆高中练习题及讲解椭圆是圆锥曲线的一种,其定义为平面上所有到两个固定点(焦点)距离之和为常数的点的集合。
这个常数称为椭圆的长轴长度,而长轴长度的一半称为椭圆的长半轴。
椭圆的另一个重要参数是短半轴,它的长度是长半轴的一半乘以椭圆的离心率的倒数。
### 练习题1. 椭圆的基本性质给定一个椭圆,其长半轴为6,短半轴为4,求椭圆的离心率。
2. 椭圆的方程已知椭圆的中心在原点,焦点在x轴上,求椭圆的方程,其中长半轴a=5,短半轴b=3。
3. 椭圆的切线若点P(2,3)在椭圆x²/16 + y²/9 = 1上,求过点P的椭圆切线的方程。
4. 椭圆与直线的位置关系直线y=2x+4与椭圆x²/25 + y²/16 = 1相交于两点,求这两点的坐标。
5. 椭圆的面积求椭圆x²/100 + y²/64 = 1的面积。
### 讲解1. 椭圆的基本性质离心率e定义为焦点到椭圆上任意一点的距离与长半轴的比值。
由于椭圆上任意一点到两个焦点的距离之和等于长轴长度,设长轴长度为2a,那么离心率e = √(1 - (b²/a²))。
对于本题,a=6,b=4,所以e = √(1 - (4²/6²)) = √(1 - 4/9) = √(5/9)。
2. 椭圆的方程当椭圆的中心在原点,焦点在x轴上时,椭圆的方程为x²/a² + y²/b² = 1。
代入a=5,b=3,得到椭圆的方程为x²/25 + y²/9 = 1。
3. 椭圆的切线对于椭圆上的点P(2,3),切线斜率可以通过椭圆的梯度求得。
首先求椭圆在点P处的梯度,然后切线的斜率是梯度的负倒数。
具体计算过程涉及到求导和使用点斜式方程。
4. 椭圆与直线的位置关系将直线方程代入椭圆方程,得到一个关于x的二次方程,解此方程可得x的值,再代回直线方程求得y的值,从而得到交点的坐标。
椭圆练习题带答案,知识点总结(基础版)

椭圆练习题带答案,知识点总结(基础版)椭圆是平面内与两个定点F1、F2的距离的和等于常数2a (其中2a>F1F2)的点的轨迹。
这两个定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距。
当椭圆焦点在x轴上时,标准方程为x^2/a^2+y^2/b^2=1(a>b>0)。
当椭圆焦点在y轴上时,标准方程为x^2/b^2+y^2/a^2=1(a>b>0)。
椭圆的范围为-a≤x≤a,-b≤y≤b。
椭圆有x轴和y轴两条对称轴,对称中心为坐标原点O(0,0)。
椭圆的长轴长为2a,短轴长为2b。
椭圆的顶点坐标为(±a,0),(0,±b)。
椭圆的焦点坐标为(±c,0),其中c^2=a^2-b^2.椭圆的离心率为e=c/a(其中0<e<1)。
a、b、c、e的几何意义:a叫做长半轴长;b叫做短半轴长;c叫做半焦距;a、b、c之间满足a^2=b^2+c^2.e叫做椭圆的离心率,e可以刻画椭圆的扁平程度,e越大,椭圆越扁,e 越小,椭圆越圆。
对于椭圆上任一点P和椭圆的一个焦点F,PF_max=a+c,PF_min=a-c。
当点P在短轴端点位置时,∠F1PF2取最大值(余弦定理)。
椭圆方程常用三角换元为x=acosθ,y=bsinθ。
弦长公式为:设直线y=kx+b交椭圆于P1(x1,y1),P2(x2,y2),则|P1P2|=√(1+k^2(x1-x2)^2)或|P1P2|=√(1+(y1-y2)^2/k^2)(k≠0)。
判断点P(x,y)是否在椭圆内,当且仅当x^2/a^2+y^2/b^21.若椭圆x^2/a^2+y^2/b^2=1(a>b>0)的离心率为c/a,短轴长为4√2,则它的长轴长为2a=6.1.在椭圆$x^2/a^2+y^2=1$的内部,点$A(a,1)$,则$a$的取值范围是$-2<a<2$。
2.已知椭圆方程$x^2/16+y^2/8=1$,焦点为$F_1,F_2$,点$P$在椭圆上且$\angle F_1PF_2=\pi/3$。
椭圆知识点总结及经典习题

圆锥曲线与方程--椭圆知识点一.椭圆及其标准方程1.椭圆的定义:平面内与两定点F1,F2距离的和等于常数()212F F a >的点的轨迹叫做椭圆,即点集M={P| |PF 1|+|PF 2|=2a,2a >|F 1F 2|=2c};这里两个定点F 1,F 2叫椭圆的焦点,两焦点间的距离叫椭圆的焦距2c 。
(212F F a =时为线段21F F ,212F F a <无轨迹)。
2.标准方程: 222ca b =-①焦点在x 轴上:12222=+by a x (a>b>0); 焦点F(±c,0)②焦点在y 轴上:12222=+bx a y (a >b >0);焦点F(0, ±c)注意:①在两种标准方程中,总有a>b>0,并且椭圆的焦点总在长轴上;②两种标准方程可用一般形式表示:221x y m n+= 或者 mx 2+ny 2=1 二.椭圆的简单几何性质: 1.范围(1)椭圆12222=+by a x (a>b>0) 横坐标-a ≤x ≤a ,纵坐标-b ≤x≤b(2)椭圆12222=+bx a y (a>b >0) 横坐标-b ≤x ≤b,纵坐标-a ≤x ≤a2.对称性椭圆关于x 轴y 轴都是对称的,这里,坐标轴是椭圆的对称轴,原点是椭圆的对称中心,椭圆的对称中心叫做椭圆的中心 3.顶点(1)椭圆的顶点:A 1(-a,0),A 2(a,0),B 1(0,-b),B 2(0,b )(2)线段A 1A 2,B 1B 2 分别叫做椭圆的长轴长等于2a,短轴长等于2b ,a和b 分别叫做椭圆的长半轴长和短半轴长。
4.离心率(1)我们把椭圆的焦距与长轴长的比22ca,即a c 称为椭圆的离心率,ﻫ记作e (10<<e ),22221()be a a==-ce 0=是圆;e 越接近于0 (e越小),椭圆就越接近于圆;e 越接近于1 (e 越大),椭圆越扁;注意:离心率的大小只与椭圆本身的形状有关,与其所处的位置无关。
椭圆的几何性质知识点归纳及典型例题及练习(付答案)

(一)椭圆的定义:1、椭圆的定义:平面与两个定点F i 、F 2的距离之和等于定长(大于 IRF 2I )的点的轨迹叫做椭圆。
这两个定点 F i 、F 2叫做椭圆的 焦点,两焦点的距离 厅汀2|叫做椭圆的 焦距。
对椭圆定义的几点说明:(1) “在平面”是前提,否则得不到平面图形(去掉这个条件,我们将得到一个椭球面); (2) “两个定点”的设定不同于圆的定义中的“一个定点” ,学习时注意区分;(3) 作为到这两个定点的距离的和的 “常数”,必须满足大于| F i F 2|这个条件。
若不然, 当这个“常数”等于| F i F 2|时,我们得到的是线段 F 1F 2;当这个“常数”小于| F i F 2|时,无 轨迹。
这两种特殊情况,同学们必须注意。
(4) 下面我们对椭圆进行进一步观察,发现它本身具备对称性,有两条对称轴和一个 对称中心,我们把它的两条对称轴与椭圆的交点记为 A i , A 2, B i , B 2,于是我们易得| A i A 2|的值就是那个“常数”,且|B 2F 2|+|B 2F i |、|B i F 2|+|B i F i |也等于那个“常数”。
同学们想一想 其中的道理。
(5)中心在原点、焦点分别在 x 轴上,y 轴上的椭圆标准方程分别为:2 2 2 2i (a b 0),77i (a b 0),a ba b2 2 2相同点是:形状相同、大小相同;都有 a > b > 0, a c b 。
不同点是:两种椭圆相对于坐标系的位置不同, 它们的焦点坐标也不同(第一个椭圆的 焦点坐标为(一c , 0)和(c , 0),第二个椭圆的焦点坐标为(0,— c )和(0, c )。
椭圆的 焦点在x 轴上 标准方程中x 2项的分母较大;椭圆的焦点在 y 轴上标准方程中y 2项的分母较大。
(二)椭圆的几何性质:椭圆的几何性质可分为两类:一类是与坐标系有关的性质,如顶点、焦点、中心坐标; 一类是与坐标系无关的本身固有性质,如长、短轴长、焦距、离心率.对于第一类性质,只2 2要X 2 每 i (a b 0)的有关性质中横坐标x 和纵坐标y 互换,就可以得出 a b2 2^2 —2 i (a b 0)的有关性质。
高中数学-椭圆常考题型汇总及练习

高中数学-椭圆常考题型汇总及练习高中数学-椭圆常考题型汇总及练第一部分:复运用的知识一)椭圆几何性质椭圆的第一定义是:平面内与两定点F1、F2距离和等于常数(大于F1F2)的点的轨迹叫做椭圆。
两个定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距(2c)。
椭圆的几何性质以x^2/a^2 + y^2/b^2 = 1为例:范围由标准方程可知,椭圆上点的坐标(x,y)都适合不等式2≤x^2/a^2 + y^2/b^2 ≤1,即abx≤a,y≤b。
这说明椭圆位于直线x=±a和y=±b所围成的矩形里(封闭曲线)。
该性质主要用于求最值、轨迹检验等问题。
椭圆还有以下对称性:关于原点、x轴、y轴对称,坐标轴是椭圆的对称轴,原点是椭圆的对称中心。
椭圆的顶点(椭圆和它的对称轴的交点)有四个:A1(-a,0)、A2(a,0)、B1(0,-b)、B2(0,b)。
长轴为A1A2,长度为2a;短轴为B1B2,长度为2b。
椭圆的离心率e有以下几个性质:(1)椭圆焦距与长轴的比e=c/a,其中c为焦距;(2)a^2=b^2+c^2,即a是长半轴长,b是短半轴长;(3)椭圆的圆扁程度由离心率的大小确定,与焦点所在的坐标轴无关。
当e接近于1时,椭圆越扁;当e接近于0时,椭圆越接近圆。
椭圆还有通径(过椭圆的焦点且垂直于长轴的弦)和焦点三角形等性质。
二)运用的知识点及公式在解题过程中,我们需要掌握以下知识点和公式:1、两条直线.2、XXX定理:若一元二次方程ax^2+bx+c=0(a≠0)有两个不同的根x1,x2,则2bc/(a(x1+x2))=-1,x1+x2=-b/a。
1.中点坐标公式:对于点A(x1,y1)和点B(x2,y2),它们的中点坐标为(x,y),其中x=(x1+x2)/2,y=(y1+y2)/2.2.弦长公式:如果点A(x1,y1)和点B(x2,y2)在直线y=kx+b(k≠0)上,则y1=kx1+b,y2=kx2+b。
椭圆基础题10道-含答案

故选;A
4.设椭圆
C:x2
y2 b2
10 b
1 的左焦点为
F,下顶点为
B,点
P
在
C
上,则
PFห้องสมุดไป่ตู้
PB
的最大值为( )
A.1
B.b
C.3
D.3b
【答案】C
【分析】利用椭圆的定义,结合两点间线段最短进行求解即可.
【详解】设该椭圆的右焦点为 Q ,
因为点 P 在 C 上,所以 PF PQ 2a 2 PF 2 PQ ,
5
B. 3 3
C.
1 2
D. 6 3
试卷第 1页,共 3页
4.设椭圆
C:x2
y2 b2
10 b
1 的左焦点为
F,下顶点为
B,点
P
在
C
上,则
PF
PB
的最大值为( )
A.1
B.b
C.3
D.3b
5.已知椭圆的中心在原点,焦点在 x 轴上,焦距为 2,长轴长是短轴长的 2 倍,则该
椭圆的标准方程为( )
准方程为( ) A. x2 y2 1
9
B. x2 y2 1 3
C. x2 y2 1 9
D. 4x2 4 y2 1 9
3.已知
A
是椭圆
x a
2 2
y2 b2
1a
b
0 的上顶点,若过 A 的直线 l 与圆 x2
y2
c2 相切,
且 l 的倾斜角为120 ,则椭圆的离心率是( )
A. 5
A. 6,
B. 2,6
C. , 2
D. 2,6
9.已知圆 (x 2)2 y2 36 的圆心为 M,设 A 是圆上任意一点, N (2, 0) ,线段 AN 的垂
“椭圆”知识点及配套练习

《椭圆》知识点及配套练习【知识点1】椭圆上任一点到两焦点距离之和为常量(椭圆的长轴长)1、已知椭圆2212516x y +=上一点P 到椭圆一个焦点的距离为3,则P 到另一焦点距离为 2、椭圆两焦点间的距离为16,且椭圆上某一点到两焦点的距离分别等于9和15,则椭圆的标准方程 是 .3、设定点1(0,3)F -、2(0,3)F ,动点P 满足条件129PF PF a a+=+(0a >),则点P 的轨迹是 A .椭圆 B .线段 C .不存在D .椭圆或线段4、椭圆13622=+y x 中,1F 、2F 为左、右焦点,弦AB 过左焦点F 1,则2ABF ∆的周长为 5、若椭圆的两焦点为(-2,0)和(2,0),且椭圆过点53(,)22-,则椭圆方程是 【知识点2】(1)当椭圆的焦点在x 轴上,则其标准方程为22221x y a b +=(0a b >>),焦点坐标为(,0)c ±(2)当椭圆的焦点在y 轴上,则其标准方程为22221y x a b+=(0a b >>),焦点坐标为(0,)c ±以上,,a b c 满足222a b c =+6、已知椭圆06322=-+m y mx 的一个焦点为(0,2),则m 的值为7、如果方程222x ky +=表示焦点在y 轴上的椭圆,那么实数k 的取值范围是8、椭圆2214x y m+=的焦距为2,则实数m 的值为【知识点3】(1)椭圆2222221x y a t b t +=++(0a b >>)与椭圆22221x y a b+=(0a b >>)共焦点; (2)椭圆方程的一般式:221Ax By +=(0,0,A B A B >>≠)9、过点(3,2)-,且与椭圆224936x y +=有相同的焦点的椭圆的标准方程是10、求经过点1(4,P 和2P 的椭圆的标准方程.点P 为椭圆22221x y a b+=(0a b >>)上一点,1F 、2F 为其两个焦点,(1)若12F PF θ∠=,则12PF F ∆的面积为2tan2θb ; (2)若点P 在长轴上的射影为椭圆的焦点,且点P 到长轴的距离为2b a.11、椭圆2214924x y +=上一点P 与椭圆的两个焦点1F 、2F 的连线互相垂直,则△12PF F 的面积为 12、1F 、2F 是椭圆22197x y +=的两个焦点,A 为椭圆上一点,且∠124πAF F =,则Δ12AF F 的面积为13、已知点P 是椭圆22154x y +=上的一点,且以点P 及焦点1F ,2F 为顶点的三角形的面积等于1,则点P 的坐标为 .14、点P 为椭圆221123x y +=上一点,椭圆焦点为1F 和2F ,,若线段1PF 的中点在y 轴上,那么1PF 是2PF 的 倍.15、已知椭圆221259x y +=的左、右焦点分别为F 1、F 2,点P 在椭圆上,若P 、F 1、F 2是一个直角三角形的三个顶点,则点P 到x 轴的距离为16、椭圆22194x y +=的焦点1F 、2F ,点P 为其上的动点,当∠12F PF 为钝角时,点P 横坐标的取值范围是17、已知动圆C 过点(3,0)A -,且在定圆B :22(3)64x y -+=的内部与定圆相切,求动圆圆心C 的轨迹方程.(1)直线与椭圆的位置关系:相交、相切、相离 (2)直线与椭圆位置关系的判断方法:把直线方程与椭圆方程联立方程组,消去一个未知数,转化成关于x (或y )的二元一次方程,再利用“∆”来判断.0∆>⇔直线与椭圆相交; 0∆=⇔直线与椭圆相切; 0∆<⇔直线与椭圆相离.18、直线230x y -+=与椭圆13422=+y x 的位置关系是19、直线1y kx =+与焦点在x 轴上的椭圆1522=+m y x 恒有公共点,则实数m 的取范围是 20、判断直线03=+-y kx 与椭圆141622=+y x 的位置关系.【知识点6】直线与椭圆相交时,研究弦长. (1)当直线的斜率存在时,弦AB 的长212212111y y k x x k AB -+=-+=(其中k 表示直线的斜率)或者,A B =或AB =(其中k 为直线的斜率,m 为二次项系数)(2)直线的斜率不存在时,弦AB 的长12AB y y =-如果直线过焦点,还可以利用焦半径公式求弦长.1P c P F ax a =+,2P cP F a x a=- 21、直线1y =被椭圆12422=+y x 截得的线段长为 22、过椭圆4222=+y x 的左焦点且倾角为3π的弦AB ,则AB =23、已知椭圆1422=+y x 及直线m x y +=.(1)当m 为何值时,直线与椭圆有公共点?(2)若直线被椭圆截得的弦长为5102,求直线的方程.【知识点7】研究与弦中点有关的问题,常用方法:(1)韦达定理;(2)“点差法”24、椭圆12422=+y x 中过(1,1)P 的弦恰好被点P 平分,则此弦的直线方程 25、中心在原点,焦点坐标为(0, 25±)的椭圆被直线320x y --=截得的弦中点的横坐标为21,求椭圆方程.26、已知椭圆221164x y +=,求过点(1,1)M 的弦的中点的轨迹方程.。
椭圆练习题带答案,知识点总结(基础版)

椭圆重难点复习椭圆:平面内与两个定点1F 、2F 的距离的和等于常数2a (其中122a F F >)的点的轨b a bab 、c 之间满足222a b c =+. e 叫做椭圆的离心率,ce a=且01e <<,e 可以刻画椭圆的扁平程度,e 越大,椭圆越扁,e 越小,椭圆越圆.2.点P 是椭圆上任一点,F 是椭圆的一个焦点,则max PF a c =+,min PF a c =-.3.点P 是椭圆上任一点,当点P 在短轴端点位置时,12F PF ∠取最大值.(余弦定理)4.椭圆方程22221(0)x y a b a b+=>> 常用三角换元为cos ,sin x a y b θθ==.5、(1)点00(,)P x y 在椭圆内2200221x y a b⇔+<(含焦点)(2)点00(,)P x y 在椭圆上2200221x y a b⇔+=(3)点00(,)P x y 在椭圆外2200221x y a b ⇔+>6.弦长公式:设直线y kx b =+交椭圆于111222(,),(,)P x y P x y则1212||PP x =-,或1212||PP y =-(0)k ≠1.则它的长轴长为( )A. 3 【答案】D【解析】所以得3,1a c == 故长轴长为2a=6 2.点(),1A a 在椭圆A. 11a -<< D. , 、2F 为椭圆上的两个焦点,点P 在C 上且.2222216,8,8a b c a b ==∴=-=,设128t t +=, ① ,由余弦定理得2212122cos6032t t t t +-⋅=, ② 由 ①平方-②可得,83603=)22y +( )A. B. 2y C.平分线交BF 于P ,则动点P 的轨迹方程为( )A. x 212+y 211=1 B. x 236−y 235=1 C. x 23−y 22=1 D. x 23+y 22=1 【答案】D由题意得|PA|=|PB| ,∴|PA|+|PF|=|PB|+|PF|=r =2√3>|AF|=2 ,∴P 点轨迹是以A 、F 为焦点的椭圆,a =√3,c =1 ,∴b =√2 ,∴动点P 的轨迹方为程x 23+y 22=1,故选:D .6.设椭圆的中心在原点,对称轴为坐标轴,且长轴长是短轴长的2倍.又点P (4,1)在椭圆上,求该椭圆的方程.【答案】22205x y +=1或2246565x y +=1 解:①当椭圆的焦点在x 轴上时,设方程为+=1(a >b >0).∵椭圆过点P (4,1),∴+=1,∵长轴长是短轴长的2倍,∴2a=2×2b,即a=2b ,可得a=2,b=,此时椭圆的方程为+=1;②当椭圆的焦点在y 轴上时,设方程为+=1(m >n >0).∵椭圆过点P (4,1),∴+=1,∵长轴长是短轴长的3倍,可得a=2b ,解得m=,n=,此时椭圆的方程为=1.7.已知(4,2)是直线l 被椭圆所截得的线段的中点,则l 的方程是( )A.x +2y+8=0B.x +2y -8=0C.x-2y -8=0D.x-2y+8=0【答案】B【解析】设直线l 与椭圆相交于A(x 1,y 1),B(x 2,y 2). 则,且,两式相减得又x 1+x 2=8,y 1+y 2=4, 所以,故直线l 的方程为y -2=(x -4),即x +2y -8=0.故选B .8.中心在原点的椭圆长轴右顶点为(2 , 0),直线y =x −1与椭圆相交于M ,N 两点,MN 中点的横坐标为23,则此椭圆标准方程是() A. x 22+y 24=1 B.x 24+y 23=1 C.x 23+y 22=1 D.x 24+y 22=1【答案】D【解析】设椭圆方程为x 2a 2+y 2b 2=1(a >b >0),由椭圆长轴右顶点为(2 , 0)可得a =2,∴椭圆方程可以化为x 24+y 2b 2=1,把直线y =x −1代入得(4+b 2)x 2−8x +4−4b 2=0,设M (x 1,y 1),N (x 2,y 2),则x 1+x 2=84+b 2,∵MN 的中点的横坐标为23,∴12×84+b 2=23,解得b 2=2,∴椭圆的标准方程是x 2+y 2=1,故选D.9.若点O 和点F 分别为椭圆点P 为椭圆上的任意一点,则OP FP ⋅的最小值为A .1.已知点12,F F 是椭圆2222x y +=的左、右焦点,点P 是该椭圆上的一个动点,那12PF PF +的最小值是( ) C. 0 D. 1 2的中线,即有()1212PO PF PF =+,则122PF PF PO +=,可设1,即有2222211122x x PO x y x =+=+-=+≥,当x =12PF PF +的最小值为2,故选A.)在椭圆2211612x y +=上,则2x y +的最大值为( ) 6 C .7 D .8 【答案】D试题分析:(4cos ,23sin P α2x y +的最大值为12.则椭圆的离心率是( )A.C. D. D则有a=3b ,则,则椭圆的离心率13A ,B ,且过C ,DA.B. 【答案】D【解析】设正方形椭圆过C , D 两点14.已知F 是椭圆 A 为右顶点, P 是椭圆上的一点, PF x ⊥轴,若 )A. A22433b a ac =- 22430c ac a +-= ,由于01e <<,所以15.点P 在椭圆x 2a 2+y 2b 2=1(a >b >0)上,F 1,F 2是椭圆的两个焦点,∠F 1PF 2=600,且ΔF 1PF 2的三条边|PF 2|,|PF 1|,|F 1F 2|成等差数列,则此椭圆的离心率是( ) A. 45 B. 34 C. 23 D. 12 【答案】D【解析】设|PF 1|=r 1, |PF 2|=r 2,由椭圆的定义得:r 1+r 2=2a ,∵△F 1PF 2的三条边|PF 2|, |PF 1|, |F 1F 2|成等差数列,∴2r 1=2c +r 2,联立r 1+r 2=2a ,2r 1=2c +r 2,解得 r 1=2a+2c 3,r 2=4a−2c 3,由余弦定理得:(2c)2=r 12+r 22−2r 1r 2 · cos60°,将 r 1=2a+2c3,r 2=4a−2c3代入(2c)2=r 12+r 22−2r 1r 2 · cos60°可得,4c 2=(2a+2c 3)2+(4a−2c 3)2−2 · 2a+2c3 · 4a−2c 3 · 12,整理得:2c 2+ac −a 2=0,由e =ca ,得2e 2+e −1=0,解得:e =1或e =−1(舍去),故选D .16.过椭圆C :的左顶点A 且斜率为k 的直线交椭圆C 于另一点B ,且点B 在x 轴上的射影恰好为右焦点2F ,则椭圆C 的离心率的取值范围是()121212)(,1)3,30,则椭圆的离心率为(【答案】D【解析】∵线段PF 1的中点在y 轴上设P 的横坐标为x ,F 1(﹣c ,0), ∴﹣c+x=0,∴x=c ;∴P 与F∴PF 2⊥x ∵∠PF 1PF 1+PF 2=2a ,∴PF 2=tan ∠PF 13,∴e=a =319是椭圆的两个焦点,满足12·0MF MF =的点M 总在椭圆的内部,则椭A. ()0,1 B. D. 2,12⎡⎫⎪⎢⎪⎣⎭【答案】C【解析】设椭圆的半长轴、半短轴、半焦距分别为,,a b c 。
椭圆知识点及习题分类

椭圆知识点及习题分类一、椭圆的定义平面内与两个定点$F_1$,$F_2$的距离之和等于常数(大于$|F_1F_2|$)的点的轨迹叫做椭圆。
这两个定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距。
若$M$为椭圆上任意一点,$F_1$,$F_2$为椭圆的焦点,则有$|MF_1| +|MF_2| = 2a$($2a >|F_1F_2| = 2c$)。
二、椭圆的标准方程1、焦点在$x$轴上的椭圆标准方程:$\frac{x^2}{a^2} +\frac{y^2}{b^2} = 1$($a > b > 0$),其中$a$为椭圆的长半轴长,$b$为椭圆的短半轴长,$c =\sqrt{a^2 b^2}$为半焦距。
2、焦点在$y$轴上的椭圆标准方程:$\frac{y^2}{a^2} +\frac{x^2}{b^2} = 1$($a > b > 0$)。
三、椭圆的性质1、范围对于焦点在$x$轴上的椭圆:$a \leq x \leq a$,$b \leq y \leq b$;对于焦点在$y$轴上的椭圆:$b \leq x \leq b$,$a \leq y \leq a$。
2、对称性椭圆关于$x$轴、$y$轴和原点对称。
3、顶点焦点在$x$轴上的椭圆顶点坐标为$(\pm a, 0)$,$(0, \pm b)$;焦点在$y$轴上的椭圆顶点坐标为$(0, \pm a)$,$(\pm b, 0)$。
4、离心率椭圆的离心率$e =\frac{c}{a}$($0 < e < 1$),它反映了椭圆的扁平程度,$e$越接近$1$,椭圆越扁;$e$越接近$0$,椭圆越接近于圆。
四、椭圆习题分类1、求椭圆的标准方程此类题目通常会给出椭圆的一些几何特征,如焦点坐标、长轴或短轴的长度、离心率等,要求根据这些条件确定椭圆的标准方程。
例 1:已知椭圆的焦点在$x$轴上,焦距为$4$,离心率为$\frac{2}{3}$,求椭圆的标准方程。
解:因为焦距$2c = 4$,所以$c = 2$。
312 椭圆的简单几何性质(基础知识+基本题型)(含解析)2022高二数学(选择性必修第一册)

3.1.2椭圆的简单几何性质(基础知识+基本题型)知识点一椭圆的范围以椭圆22221(0)x y a b a b +=>>为例.由标准方程可知,椭圆上点的坐标(,)x y 都适合不等式22221,1x y a b≤≤,即2222,x a y b ≤≤,所以||,||x a y b ≤≤.这说明椭圆位于直线x a =±和y b =±所围成的矩形框内(如图2.2-8).拓展(1)确定了曲线的范围后,用描点法作图时,就可以不取范围之外的点了,在解析几何中,讨论曲线的范围就是确定方程中变量的取值范围.(2)如果将椭圆的标准方程22221(0)x y a b a b+=>>变形为y =,那么这个椭圆的方程可以分成y =,y =两个函数式,研究椭圆的范围,就是讨论这两个函数的定义域和值域,这也是讨论椭圆范围的一种方法.知识点二椭圆的对称性以椭圆22221(0)x y a b a b+=>>为例.1.椭圆的对称轴:坐标轴.2.椭圆的对称中心:原点(0,0)O ,椭圆的对称中心叫做椭圆的中心.通过观察椭圆的形状,可以发现椭圆既是轴对称图形,又是中心对称图形.提示:(1)在方程22221(0)x y a b a b+=>>中,将x 换成x -,方程显然不变,这就是说椭圆上的点(,)x y 关于y 轴的对称点(,)x y -也在椭圆上,故椭圆关于y 轴对称;将方程中的y 换成y -,方程也不变,故椭圆关于x 轴对称;同理,将,x y 分别换成,x y --时,方程也不变,故椭圆关于原点对称.(2)椭圆的中心是焦点连线的中点,对称轴是焦点的连线及它的垂直平分线.(3)椭圆关于x 轴、y 轴成轴对称,关于原点成中心对称,原点为椭圆的中心.知识点三椭圆的顶点与长轴、短轴以椭圆22221(0)x y a b a b+=>>为例.1.椭圆的顶点令0x =,得y b =±,令0y =,得x a =±.这说明12(,0),(,0)A a A a -是椭圆与x 轴的两个交点,1(0,)B b -,2(0,)B b 是椭圆与y 的两个交点,因为x 轴、y 轴是椭圆的对称轴,所以椭圆和它的对称轴有四个交点.这四个交点叫做椭圆的顶点.2.椭圆的长轴、短轴线段12A A 叫做椭圆的长轴,它的长为2a ,a 叫做椭圆的长半轴长.线段12B B 叫做椭圆的短轴,它的长为2b ,b 叫做椭圆的短半轴长.提示明确,a b 的几何意义,a 是长半轴长,b 是短半轴长,由222c a b =-,得“已知椭圆的四个顶点求焦点”的几何作法,只要以短轴的端点1B (或2B )为圆心,以a 为半径作弧,交长轴于两点,这两点就是焦点.知识点四椭圆的离心率1.定义:椭圆的焦距与长轴长的比称为椭圆的离心率,记作22c c e a a==.2.范围:因为0a c >>,所以01ca<<,即(0,1)e ∈.拓展对椭圆离心率的理解(1)01e <<,越趋近于1,椭圆越扁;越趋近于0,椭圆越接近于圆.(2)当趋近于0时,c 趋近于0,椭圆变圆,直至成为圆,此时也可认为圆在椭圆在0e =时的特例.(3)当趋近于1时,c 趋近于a ,椭圆变扁,直至成为线段12F F ,此时也可认为12F F 为椭圆在1e =时的特例.(4)2221b e a=-.知识点五直线与椭圆的位置关系1.直线与椭圆的三种位置关系:(1)相交;(2)相切;(3)相离.2.直线与椭圆的位置关系的判断;直线与椭圆的位置关系,可通过讨论椭圆方程与直线方程组成的方程组的实数解的个数来确定,通常用消元后的关于x (或y )的一元二次方程的判别式∆来判定;0∆>⇔直线与椭圆相交;0∆=⇔直线与椭圆相切;0∆<⇔直线与椭圆相离.3.弦长公式一条直线被椭圆所截得的线段叫做椭圆的弦,若直线y kx b =+与椭圆相交于不同的两点11(,)A x y ,22(,)B x y ,则直线被椭圆所截得的弦长公式为12|||AB x x =-或12|||AB y y =-.考点一由方程求椭圆的几何性质例1.求椭圆22925225x y +=的长轴长、短轴长、离心率、焦点和顶点坐标,并用描点法画出这个椭圆.解:将椭圆的方程化为标准形式为221259x y +=,得5,3a b ==,则4c ==因此,长轴长210a =,短轴长26b =,离心率40.85c e a ===.焦点坐标为1(4,0)F -和2(4,0)F ,顶点坐标为1212(5,0),(5,0),(0,3),(0,3)A A B B --.将方程变形为55)y x =-≤≤,根据5)y x =≤≤可求出椭圆的两个顶点及其在第一象限内一些点的坐标(,)x y ,列表如下:x 012345y32.942.752.41.8先描点画出第一象限内的图形,再利用椭圆的对称性画出整个椭圆.将椭圆的方程化成标准方程易得5,3a b ==,则椭圆位于四条直线5x =±,3y =±所围成的矩形框内,又因为椭圆以两坐标轴为对称轴,所以只要画出椭圆在第一象限内的图形,就可以利用对称性画出整个椭圆.考点二由椭圆的几何性质求方程例2.已知椭圆C 以坐标轴为对轴称、长轴长是短轴长的5倍,且经过点(5,0)A ,求此椭圆的标准方程.解:方法1:若椭圆的焦点在x 轴上,设其标准方程为22221(0)x y a b a b +=>>由题意,得22252,2501,a b a b =⨯⎧⎪⎨+=⎪⎩解得5,1.a b =⎧⎨=⎩故所求椭圆的标准方程为22125x y +=,若椭圆的焦点在y 轴上,设其标准方程为22221(0)y x a b a b +=>>,由题意,得22252,0251,a b a b =⨯⎧⎪⎨+=⎪⎩解得25,5.a b =⎧⎨=⎩故所求椭圆的标准方程为22162525y x +=.综上所述,所求椭圆的标准方程为22125x y +=或22162525y x +=.方法2:设椭圆方程为221(0,0,)x y m n m n m n +=>>≠.由题意,得2501,5m n ⎧+=⎪⎨⎪=⨯⎩或2501,5m n⎧+=⎪⎨⎪=⨯⎩解得25,1m n =⎧⎨=⎩或25,625.m n =⎧⎨=⎩故所求椭圆的标准方程为22125x y +=或22162525y x +=.(1)利用椭圆的几何性质求椭圆的标准方程,通常利用待定系数法.(2)根据已知条件求椭圆的标准方程的思路是“选标准,定参数”,其一般步骤:①确定焦点所在的坐标轴;②求出22,a b 的值;③写出标准方程.考点三求椭圆的离心率例3.若一个椭圆的长轴长、短轴长和焦距成等差数列,求该椭圆的离心率.分析:解答本题的关键是先由椭圆长轴长、短轴长和焦距成等差数列,列出,,a b c 的关系式,再转化成,a c 间的关系式,从而求出.解:因为椭圆的长轴长、短轴长和焦距成等差数列,所以2b a c =+,①所以224()b a c =+,即22242b a ac c =++.②又因为222a b c =+,所以22224()2a c a ac c -=++,③即225230c ac a +-=.两边同除以2a ,得25230e e +-=.④解得35e =或1e =-(舍去).故该椭圆的离心率为35.求椭圆的离心率,关键是寻找a 与c 的关系,一般地,(1)若已知,a c ,则直接代入ce a=求解;(2)若已知,a b,则由e =(3)若已知,,a b c 的关系,则可先转化为,a c 的齐次式,再转化为含的方程,求解即可.例4.若椭圆22221(0)x y a b a b+=>>上存在一点M ,使1290F MF ∠=︒(12,F F 为椭圆的两焦点),求椭圆的离心率的取值范围.解:设点M 的坐标是00(,)x y ,则220022222001,.x y a b x y c ⎧+=⎪⎨⎪+=⎩消去0y ,得222202()a cb xc -=.因为2200x a ≤≤②所以222222222()0,().a c b c a c b a c ⎧-≥⎪⎪⎨-⎪≤⎪⎩①②由①,得22c b ≥,即222c a c ≥+,所以222a c ≤,所以22212c e a =≥.又因为01e <<,所以2[2e ∈,由②,得222c b c -≤,此式恒成立.综上所述,所求椭圆的离心率的取值范围是2[2.(1)解析几何中求参数的取值范围是一类常见而又较困难的题型,其基本的解题思路有:①建立目标函数,运用求函数值域的方法求解;②建立目标变量的不等式,解不等式求解.(2)本题在用基本量表示出椭圆上的点的坐标后,借助椭圆的范围(||,||)x a y b ≤≤建立了一个关于基本量的不等式组.考点四点与椭圆的位置关系例5.直线1()y kx k R =+∈与焦点在x 轴上的椭圆2215x y m+=总有公共点,求m 的取值范围.解:方法1,直线1y kx =+恒过定点(0,1),直线与椭圆总有公共点等价于点(0,1)在椭圆内或椭圆上,所以20115m+≤,即1m ≥.又由于5m <,故[1,5)m ∈,方法2:由221,15y kx x y m=+⎧⎪⎨+=⎪⎩,得22(5)105(1)0m k x kx m +++-=,则2210020(1)(5)0k m m k ∆=--+≥对k R ∈恒成立,即2250mk m m +-≥对k R ∈恒成立.因为0m >,所以251k m ≥-对k R ∈恒成立,故10m -≤,即1m ≥.又因为5m <,所以[1,5)m ∈.点与椭圆的位置关系(1)点00(,)P x y 在椭圆22221(0)x y a b a b +=>>上2200221x y a b ⇔+=;(2)点00(,)P x y 在椭圆22221(0)x y a b a b +=>>外⇔2200221x y a b +>;(3)点00(,)P x y 在椭圆22221(0)x y a b a b +=>>内2200221x y a b⇔+<.考点五直线与椭圆的位置关系例6.已知椭圆2241x y +=及直线y x m =+.(1)当直线与椭圆有公共点时,求实数m 的取值范围;(2)求直线被椭圆截得的最长弦的长度.解:由方程组2241,x y y x m⎧+=⎨=+⎩消去y 并整理,得225210x mx m ++-=.(1)因为直线与椭圆有公共点,所以222420(1)20160m m m ∆=--=-≥.解得m ≤故实数m 的取值范围是55[]22.(2)由根与系数的关系,得1225m x x +=-,21215m x x -⋅=,则弦长12||d x x =-===故当0m =时,d.(1)利用方程讨论直线与椭圆的位置关系设直线方程为y kx m =+,椭圆方程为22221(0)x y a b a b +=>>,联立方程,得2222,1.y kx m x y ab =+⎧⎪⎨+=⎪⎩消去方程组中的一个变量,得到关于另一变量的一元二次方程,写出判别式∆,则0∆>⇔直线与椭圆相交⇔有两个公共点;0∆=⇔直线与椭圆相切⇔有且只有一个公共点;0∆<⇔直线与椭圆相离⇔无公共点.(2)弦长问题设直线:y kx m =+交椭圆22221(0)x y a b a b+=>>于111(,)P x y ,222(,)P x y 两点,则1212||||PP x x =-=或1212||||PP y y =-=考点六椭圆中弦的中点问题例7焦点分别为和的椭圆截直线32y x =-所得椭圆的弦的中点的横坐标为12,求此椭圆方程.分析:设椭圆的方程→联立椭圆的方程与直线的方程→利用根与系数的关系设而不求→由中点列出方程→已知焦点→求出方程.解析:设22221(0)y x a b a b+=>>依题意,有22250a b -==.①由22221,32y x a b y x ⎧+=⎪⎨⎪=-⎩消去y 并整理,得2222222(9)1240a b x b x b a b +-+-=.因为12122x x +=,所以2226192b a b =+.所以223a b =.②由①②,得275a =,225b =.经检验,此时0∆>.所以椭圆方程为2217525y x +=.弦的中点问题的解决方法关于中点的问题,我们一般可以采用两种方法解决:(1)联立方程、消元,利用根与系数进行设而不求,从而简化运算过程;(2)利用“点差法”,求出与中点、斜率有关的式子,进而求解.不管应用何种方法,我们都必须要注意判别式∆的限制.考点七椭圆中的最值问题例8设椭圆的中心是坐标原点,长轴在x轴上,离心率e =3(0,2P 到这个椭圆P的点的坐标.分析:本题是解析几何与代数中的最大值的综合题.解题关键是怎样运用“最远距离是”这个条件,可尝试用两点间的距离公式,转化为函数的最大值问题来解.解析:设所求椭圆方程为22221x y a b +=(a >b >0).由c e a ==,得a =2b .①设椭圆上任一点M 的坐标为(x ,y ),点M 到点P 的距离为d ,则22222a y x a b =-,且2222222233()()22a d x y a y yb =+-=-+-2222913343()4342y y b y b =--++=-+++,其中b y b -≤≤.若12b <,则当y =-b 时,2d 取得最大值223()2b =+.解得3122b =>,与12b <矛盾.若12b ≥,则当12y =-时,2d 取得最大值2243b =+.②由①②,得b =1,a =2.故所求椭圆方程为2214x y +=.由12y =-,得椭圆上到点P 的点为1()2-,12-.本题是一道考查椭圆知识和函数最值的综合性问题,需要全面的掌握基础知识和基本方法,在建立二次函数求最值时,要特别注意通过椭圆的范围来确定自变量的取值范围.考点八与椭圆相关的实际问题例9在大西北的荒漠上,A ,B 两地相距2km ,正在准备在荒漠上围成一片以AB 为一条对角线的平行四边形区域,建立农艺园.按照规划,围墙总长度为8km .(1)农艺园的最大面积能达到多少?(2)该荒漠上有一条直线型水沟刚好过点A ,且与AB 成45︒角,现要对整条水沟进行加固改造,但考虑到今后农艺园内的水沟要重新设计改造,因此该水沟可能被农艺园围住的部分暂不加固,那么暂不加固的部分有多长?分析:(1)如图2.2-12所示,求农艺园的最大面积,实际就是求平行四边形ADBC 的面积的最大值.结合图形和椭圆的几何性质,易知当点C 位于短轴端点时,ACB ∆的面积最大,即平行四边形ADBC 的面积最大;(2)实质就是求弦长.解析:(1)如图2.2-12所示,由题意,知平行四边形相邻两边长之和为4km ,另两个端点C ,D 在以A ,B 为焦点的椭圆上.以AB 所在的直线为x 轴,以AB 的垂直平分线为y 轴建立平面直角坐标系,则椭圆方程为22143x y +=(0y ≠).因为max ()ABC S ∆=(点C 在短轴端点),所以农艺园的最大面积为2km .(2)由题可知,直线型水沟的方程是y =x +1,暂时不加固的部分的长度即直线被椭圆所截得的弦长.把直线方程代入椭圆方程,得27880x x +-=.1224|7x x -=.所以暂时不加固的部分长为247km .椭圆是天文学和日常生产、生活中常见的一个模型,因此,我们必须熟练掌握利用代数方法解决与椭圆有关的问题的技巧.。
椭圆 知识点+例题+练习
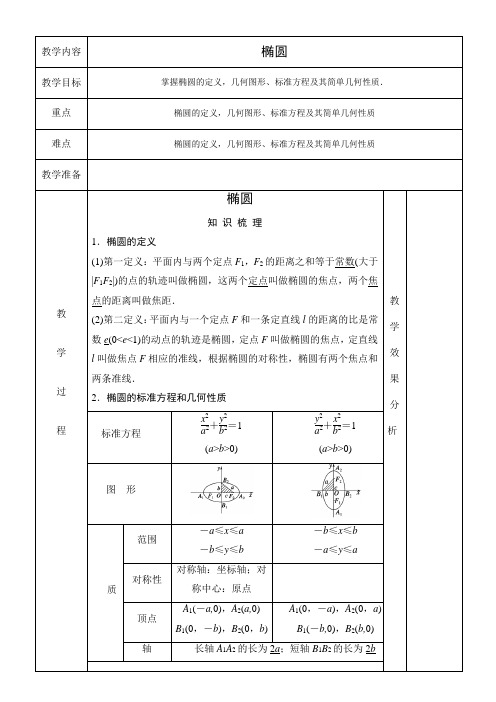
教学内容椭圆教学目标掌握椭圆的定义,几何图形、标准方程及其简单几何性质.重点椭圆的定义,几何图形、标准方程及其简单几何性质难点椭圆的定义,几何图形、标准方程及其简单几何性质教学准备教学过程椭圆知识梳理1.椭圆的定义(1)第一定义:平面内与两个定点F1,F2的距离之和等于常数(大于|F1F2|)的点的轨迹叫做椭圆,这两个定点叫做椭圆的焦点,两个焦点的距离叫做焦距.(2)第二定义:平面内与一个定点F和一条定直线l的距离的比是常数e(0<e<1)的动点的轨迹是椭圆,定点F叫做椭圆的焦点,定直线l叫做焦点F相应的准线,根据椭圆的对称性,椭圆有两个焦点和两条准线.2.椭圆的标准方程和几何性质标准方程x2a2+y2b2=1(a>b>0)y2a2+x2b2=1(a>b>0)图形性质范围-a≤x≤a-b≤y≤b-b≤x≤b-a≤y≤a对称性对称轴:坐标轴;对称中心:原点顶点A1(-a,0),A2(a,0)B1(0,-b),B2(0,b)A1(0,-a),A2(0,a)B1(-b,0),B2(b,0)轴长轴A1A2的长为2a;短轴B1B2的长为2b教学效果分析教学过程考点二椭圆的几何性质【例2】已知F1、F2是椭圆的两个焦点,P为椭圆上一点,∠F1PF2=60°.(1)求椭圆离心率的范围;(2)求证:△F1PF2的面积只与椭圆的短轴长有关.规律方法(1)椭圆上一点与两焦点构成的三角形,称为椭圆的焦点三角形,与焦点三角形有关的计算或证明常利用正弦定理、余弦定理、|PF1|+|PF2|=2a,得到a,c的关系.(2)椭圆的离心率是椭圆最重要的几何性质,求椭圆的离心率(或离心率的取值范围),常见有两种方法:①求出a,c,代入公式e=ca;②只需要根据一个条件得到关于a,b,c的齐次式,结合b2=a2-c2转化为a,c的齐次式,然后等式(不等式)两边分别除以a或a2转化为关于e的方程(不等式),解方程(不等式)即可得e(e的取值范围).【训练2】(1)(2013·四川卷改编)从椭圆x2a2+y2b2=1(a>b>0)上一点P向x轴作垂线,垂足恰为左焦点F1,A是椭圆与x轴正半轴的交点,B是椭圆与y轴正半轴的交点,且AB∥OP(O是坐标原点),则该椭圆的离心率是________.(2)(2012·安徽卷)如图,F1,F2分别是椭圆C:x2a2+y2b2=1(a>b>0)的左、右焦点,A教学效果分析教学过程设条件建立有关参变量的等量关系.(2)涉及到直线方程的设法时,务必考虑全面,不要忽略直线斜率为0或不存在等特殊情形.【训练3】(2014·山东省实验中学诊断)设F1,F2分别是椭圆:x2a2+y2b2=1(a>b>0)的左、右焦点,过F1倾斜角为45°的直线l与该椭圆相交于P,Q两点,且|PQ|=43a.(1)求该椭圆的离心率;(2)设点M(0,-1)满足|MP|=|MQ|,求该椭圆的方程.1.椭圆的定义揭示了椭圆的本质属性,正确理解掌握定义是关键,教学效果分析|BF |=8,cos ∠ABF =45,则C 的离心率为________.6.(2014·无锡模拟)设椭圆x 2m 2+y 2n 2=1(m >0,n >0)的右焦点与抛物线y 2=8x 的焦点相同,离心率为12,则此椭圆的方程为________. 7.已知F 1,F 2是椭圆C :x 2a 2+y 2b 2=1(a >b >0)的两个焦点,P 为椭圆C 上的一点,且PF 1→⊥PF 2→.若△PF 1F 2的面积为9,则b =________. 8.(2013·福建卷)椭圆Γ:x 2a 2+y 2b 2=1(a >b >0)的左,右焦点分别为F 1,F 2,焦距为2c .若直线y =3(x +c )与椭圆Γ的一个交点M 满足∠MF 1F 2=2∠MF 2F 1,则该椭圆的离心率等于________.二、解答题9.已知椭圆的两焦点为F 1(-1,0),F 2(1,0),P 为椭圆上一点,且2|F 1F 2|=|PF 1|+|PF 2|. (1)求此椭圆的方程;(2)若点P 在第二象限,∠F 2F 1P =120°,求△PF 1F 2的面积.10.(2014·绍兴模拟)如图,椭圆x 2a 2+y 2b 2=1(a >b >0)的左、右焦点分别为F 1(-c,0),F 2(c,0).已知点M ⎝ ⎛⎭⎪⎫3,22在椭圆上,且点M 到两焦点距离之和为4. (1)求椭圆的方程;。
椭圆知识点总结加例题

椭圆知识点总结加例题一、椭圆的定义和性质1.1 椭圆的定义在平面上,椭圆的定义为:对于给定的两个不重合的实点F1和F2,以及一个实数2a (a>0),定义为到点F1和点F2的距离的和等于2a的点的轨迹,这个轨迹就是椭圆。
1.2 椭圆的几何性质(1)焦点性质:椭圆上到焦点的距离之和是一个常数2a。
(2)长短轴性质:椭圆有两个互相垂直的对称轴,其中较长的轴称为长轴,较短的轴称为短轴。
(3)离心率性质:椭圆的离心率e定义为焦距与长轴的比值,介于0和1之间。
(4)焦点到顶点的连线和短轴的交点为端点的线段称为短轴的焦径。
(5)焦点到顶点的连线和长轴的交点为端点的线段称为长轴的焦径。
1.3 椭圆的方程和标准方程椭圆的一般方程为:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$, 其中a、b分别为椭圆长轴和短轴的半轴长。
通过坐标平移和旋转,可以得到椭圆的标准方程:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$, 椭圆长轴在x轴上,且椭圆的中心为原点。
1.4 椭圆的参数方程和极坐标方程椭圆的参数方程:$\begin{cases}x=a\cos \theta\\ y=b\sin \theta\end{cases}$, $\theta \in [0, 2\pi)$。
椭圆的极坐标方程:$r(\theta)=\frac{ab}{\sqrt{b^2\cos^2\theta+a^2\sin^2\theta}}$。
二、椭圆的相关性质2.1 椭圆的离心率和焦距的关系设椭圆的长轴和短轴分别为2a和2b,焦点到几点段为2c,则椭圆的离心率e满足关系:$e=\frac{c}{a}$。
2.2 椭圆的面积和周长椭圆的面积:$S=\pi ab$。
椭圆的周长:$L=4aE(e)$,其中E(e)为第二类完全椭圆积分。
2.3 椭圆的切线和法线对于椭圆上任一点P(x,y),其切线的斜率为$k=-\frac{b^2x}{a^2y}$,切线的方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$,且斜率为$k$的切线方程为$y-kx+ka^2=0$。
椭圆知识点及例题

四.直线和椭圆的位置关系
1.位置关系的判断:判别式法
2.相交弦:
(1)弦长公式:
(2)中点弦问题:点差法
3、点M(x0,y0)与椭圆 的位置关系:
点M在椭圆内:
点M在椭圆外:
五、例题
1、椭圆定义的应用
(1)椭圆 + =1的焦点为F1、F2,点P在椭圆上,若|PF1|=4,则|PF2|=?;求cos∠F1PF2
(1)2-(2)得:|PF1| | PF2| =2b2/(1+cosθ)
∴S=b2tanθ/2
二、椭圆的标准方程
三、椭圆的几何性质
以焦点在X轴的标准方程为例
1、范围:
|x| a,|y| b 即椭圆位于直线x= a、y= b围成的矩形里。
2、对称性
对称中心:O (0,0),对称轴方程:x=0,y=0.
∠F1PF2=60º,则∆PF1F2的面积是?
2、椭圆几何性质的应用
(1)过椭圆 (a>b>0)的左焦点F1作x轴的垂线交椭圆与点P,F2为右焦点,若∠F1PF2=600,则椭圆的离心率为?
(2)已知椭圆C: (a>b>0)的离心率e= ,短轴的一个端点到右焦点的距离为 ,求椭圆C的方程。
(3)已知椭圆 +y2=1的焦点为F1、F2,点M在该椭圆上,由 =0,则点M到y轴的距离为?
(2)已知F是椭圆5x2+9y2=45的左焦点,p是椭圆上的点,A(1,1)是一定点,则|PA|+|PF|的最大值和最小值分别为?
(3)一动圆与已知圆O1:(x+3)2+y2=1外切,与圆O2:(x-3)2+y2=1内切,则动圆圆心的轨迹方程为?
(4)已知椭圆x2+9y2=9的两个焦点分别为F1,F2,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
椭圆基础与分类导学训练案1
一:椭圆的定义填空:
平面内一个动点P 到两个定点1F 、2F 的距离之和等于常数)2(2121F F a PF PF >=+ ,这个动点 P 的轨迹叫_________.这两个定点叫椭圆的焦点,两焦点的距离叫作椭圆的_____________. 注意:若)(2121F F PF PF =+,则动点P 的轨迹为__________________; 若)(2121F F PF PF <+,则动点P 的轨迹_________________. 二:椭圆的标准方程填空:
1.当焦点在x 轴上时:12222=+b y a x )0(>>b a ,其中2
22b a c -=
2.当焦点在y 轴上时:12222=+b
x a y )0(>>b a ,其中2
22b a c -=;
阅读下面的材料并注意记忆:)0(>>b a ,)10(<<=
e a
c
e ,222c b a +=,a r r 221=+等隐含条件。
1.方程均不为零)
C B A C By Ax ,,(22=+是表示椭圆的条件方程C By Ax =+22可化为12
2=+C
By C Ax ,即122=+B
C By A C x ,所以(只有A 、B 、C 同号,且A ≠B 时),方程表示椭圆。
当B C A C >时,椭圆的焦点在x 轴上;当
B
C
A C <时,椭圆的焦点在y 轴上。
2、e 越小,椭圆越圆;e 越大,椭圆越扁。
3. 椭圆22
221x y a b
+=上任意一点P (x ,y )(y ≠0)与两焦点F 1(-c,0),F 2 (c,0),设12F PF θ∠=
(1) 构成的△PF 1F 2称为焦点三角形,其周长为2(a +c ),其面积122
tan 2
PF F S b θ
=△
(2) a-c ≤|PF 1|≤a+c (3)b 2
≤ |PF 1||PF 2|≤a 2
(4)()()121212min max 0,F PF F PF F B F ∠=∠=∠ (5)过焦点F 1的弦AB ,则△ABF 2的周长为4a .
(6)与122
22=+b y a x (a >b >0)共焦点的椭圆为12222=+++k
b y k a x
三.完成下组的问题1:
1.已知圆(x +2)2+y 2=36的圆心为M ,设A 为圆上任一点,N (2,0),线段AN 的垂直平分线交MA 于点P ,则动点P 的轨迹是
( )
A .圆
B .椭圆
C .双曲线
D .抛物线
如果22
2
=+ky x 表示焦点在y 轴上的椭圆,那么实数k 的取值范围是
2.设椭圆的两个焦点分别为F 1、、F 2,过F 2作椭圆长轴的垂线交椭圆于点P ,若△F 1PF 2为等腰直角三角形,则椭圆的离心率是
3.椭圆3
122
2y x +
=1的焦点为F 1和F 2,点P 在椭圆上.如果线段PF 1的中点在y 轴上,那么|PF 1|是|PF 2|的 倍
4.若椭圆2215x y m +=的离心率e =,则m 的值______________________
5..椭圆13
42
2=+y x 的右焦点到直线x y 3=的距离________________________
6.与椭圆22
143
x y +=具有相同的离心率且过点(2,__________________ 7.(选用)椭圆
14
162
2=+y x 上的点到直线022=-+y x 的最大距离是_______________________ 8. 已知P 点在以坐标轴为对称轴的椭圆上,点P 到两焦点的距离分别为354和3
5
2,过P 点作焦点所在轴的垂线,它恰好过椭圆的一个焦点,求椭圆方程.
四.以小组提问的形式展示以上的答案并记录小组成绩。
四.完成下面的问题2
求椭圆的标准方程(先定型,后定量,各班根据自身情况酌情取舍)
1.若椭圆的两焦点为(-2,0)和(2,0),且椭圆过点)2
3,25(-,则椭圆方程是
2.与椭圆4 x 2 + 9 y 2 = 36 有相同的焦点,且过点(-3,2)的椭圆方程为_______________.
3.求中心在原点,对称轴为坐标轴,且经过)2,3(-A 和)1,32(-B 两点的椭圆方程.
4.已知椭圆的中心在原点,且经过点()03,P ,b a 3=,求椭圆的标准方程.
5.求经过点(3,0)和(0,-4)的椭圆的标准方程
6、焦点在x 轴上,一个焦点与短轴的两端连线相互垂直,且半焦距是6,求椭圆的标准方程。
五.以小组黑板的形式展示以上的答案并讲评然后记录小组成绩。
椭圆基础与分类导学训练案2
学习目标:1.通过自行填空与归类,达到总结整体把握知识系统的目的;2.通过练习培养学生克服困难的勇气与信心,进而培养学生思维与运算能力。
一 求参数的取值范围:
1.已知方程1352
2-=-+-k
y k x 表示椭圆,求k 的取值范围.
2.已知1cos sin 22=-ααy x )0(πα≤≤表示焦点在y 轴上的椭圆,求α的取值范围.
3.设)2,0(π
α∈,方程
1cos sin 2
2=+α
αy x 表示焦点在x 轴上的椭圆,则α∈
4.(选用)已知()y x P ,是椭圆125
1442
2=+y x 上的点,则y x +的取值范围是________________ .
二.以小组黑板的形式展示以上的答案并讲评然后记录小组成绩。
三 焦点三角形类型的练习:
1、已知椭圆
124
492
2=+y x 上一点P 与两焦点连线的夹角是直角,求21PF PF ⋅的值。
2.椭圆x 2100+y 2
64=1的焦点为F 1、F 2,椭圆上的点P 满足∠F 1PF 2=60°, ,求21PF PF ⋅的值。
3.已知椭圆方程()0122
22>>=+b a b
y a x ,长轴端点为1A ,2A ,焦点为1F ,2F ,P 是椭圆上一点,
θ=∠21PA A ,α=∠21PF F .求:21PF F ∆的面积(用a 、b 、α表示).
探究提升4.椭圆122
22=+b
y a x (a>b>0)的二个焦点F 1(-c ,0),F 2(c ,0),M 是椭圆上一点,且021=⋅F F 。
求离心率e 的取值范围.
四.以小组黑板的形式展示以上的答案并讲评然后记录小组成绩。
五 课后习题:
已知△ABC 的顶点B 、C 在椭圆2
213
x y +=上,顶点A 是椭圆的一个焦点,且椭圆的另外一个焦点在BC 边上,则△ABC 的周长是:
2.椭圆142
2
=+y x 的离心率___________________
3.已知椭圆中心在原点,一个焦点为F (-23,0),且长轴长是短轴长的2倍,则该椭圆的标准方程是
4. 已知椭圆1982
2=++y k x 的离心率21=e ,则k 的值为
5.求经过点35
(,)22
-,且229445x y +=与椭圆有共同焦点的椭圆方程。
6.已知椭圆以坐标轴为对称轴,且长轴长是短轴长的3倍,点P (3,0)在该椭圆上,求椭圆的方程。
7.点A 、B 分别是椭圆
120
362
2=+y x 长轴的左、右端点,点F 是椭圆的右焦点,点P 在椭圆上,且位于x 轴上方,PF PA ⊥.(1)求点P 的坐标;(2)设M 是椭圆长轴AB 上的一点,M 到直线AP 的距离等于||MB ,求椭圆上的点到点M 的距离d 的最小值。
