轴向均布载荷下压杆稳定问题的DQ解
工程力学第16章压杆稳定问题
(为什么A 、B 不能同时等于0 ?)
sinkl 0
kl n
n22EI
F l2 (n1,2,...)
由于临界载荷是F 的最小值,所以取n = 1
两端铰支细长压杆的临界载荷
Fcr
2EImin
l2
当截面对不同方向弯曲中性轴的惯性矩不一样时
应取Imin的方向计算。
二、两端非铰支细长压杆的临界载荷
解:在正视图平面(xy 平 面)内失稳,A 、B 处可自 由转动,即两端为铰链约束
1
iz
Iz A
bh3/12 h
bh 2 3
z izl
12.32 3 60103 132.8
在俯视图平面(xz 平面)内失稳,A 、B 处不可自由转动,即两 端为固定约束
0.5
iy
Iy A
hb3/12 b
bh 2 3
y
l 0.52.32
iy
40103
399.6
z y
压杆在正视图平面内失稳定
z 132.8P 属于大柔度杆,用欧拉公式计算临界载荷
F c rc r A 2 z 2 E b h 2 1 2 3 0 2 5 .8 2 1 0 9 4 0 6 0 1 0 6 2 7 5 k N
解:根据欧拉公式
2 E I 3 E d 4 3 2 0 0 1 0 9 2 0 4 1 0 1 2
F c r (l) 2 6 4 (l) 2 6 4 ( 1 0 .8 ) 2
2 4 .2 k N
此时横截面上的正应力
F A cr 4 2 2 4 0 .2 2 1 1 0 0 3 677M P aP
专升本工程力学压杆稳定

计算杆在不同方向失稳时的临界力。I 为其相应的对
中性轴的惯性矩。
12
例题 2: 图示各杆材料和截面均相同,试问哪一根杆能承 受的压力最大, 哪一根的最小?
F F
F 因为 l1 l2 l3
又
2 EI
Fcr l 2
可知
0 < p
因此
可用直线公式.
Fcr cr A (a b )A
(304 1.12 77) 106 d 2
4
462KN
37
例4
解: CD梁 M C 0
F 2000 FN sin 30 1500
得 FN 26.6kN
AB杆 l
i
1
1.5
l cos 30 1.732m
2
Pc
r
2 一端固定另端绞支
A
l
0.7l
C
B
C为拐点
Fcr
2EI
(0.7l)
2
7
3 两端固定
Pcr
C,D为拐点
AD
Fcr
2EI
(0.5l)
2
l
C
B
8
4 一端固定,另端自由
Fcr
2EI
(2l)2
l 2l
9
10
欧拉公式 的统一形式
F
cr
2 EI (l)2
为压杆的长度系数; l 为相当长度。
讨论:
(1)相当长度 l 的物理意义
1 压杆失稳时,挠曲线上两拐点间的长度就是压杆的相当
长度 l 。
2 l 是各种支承条件下,细长压杆失稳时,挠曲线中相当于
《材料力学》课后习题答案详细

《材料力学》课后习题答案详细在学习《材料力学》这门课程时,课后习题是巩固知识、检验理解程度的重要环节。
一份详细准确的课后习题答案不仅能够帮助我们确认自己的解题思路是否正确,还能进一步加深对知识点的理解和掌握。
材料力学是一门研究材料在各种外力作用下产生的应变、应力、强度、刚度和稳定性的学科。
它对于工程领域的学生来说至关重要,无论是机械工程、土木工程还是航空航天工程等,都离不开材料力学的知识支撑。
对于课后习题的解答,我们首先要明确每个问题所涉及的核心概念和原理。
比如,在研究杆件的拉伸和压缩问题时,需要清楚胡克定律的应用条件和计算公式。
胡克定律指出,在弹性限度内,杆件的伸长或缩短量与所受的拉力或压力成正比。
以一道常见的拉伸习题为例:一根直径为 20mm 的圆杆,受到100kN 的拉力,材料的弹性模量为 200GPa,求杆的伸长量。
解题思路如下:首先,根据圆杆的直径计算出横截面积 A =π×(d/2)^2 ,其中 d 为直径。
然后,根据胡克定律ΔL = FL/EA ,其中F 为拉力,L 为杆长,E 为弹性模量,A 为横截面积,代入已知数据进行计算。
在计算过程中,要注意单位的统一。
拉力的单位通常为牛顿(N),长度的单位要与弹性模量的单位相匹配,面积的单位要为平方米(m²)。
再来看一个关于梁的弯曲问题。
梁在受到横向载荷作用时,会产生弯曲变形。
在解答这类习题时,需要运用到弯矩方程、挠曲线方程等知识。
例如:一简支梁,跨度为 L,承受均布载荷 q,求梁的最大弯矩和最大挠度。
解题时,首先要根据梁的支座情况列出弯矩方程。
然后,通过积分求出挠曲线方程,再根据边界条件确定积分常数。
最后,求出最大弯矩和最大挠度的位置及数值。
在求解过程中,要理解弯矩和挠度的物理意义,以及它们与载荷、梁的几何形状和材料性质之间的关系。
对于扭转问题,要掌握扭矩的计算、切应力的分布规律以及扭转角的计算方法。
比如,一根轴受到扭矩 T 的作用,已知轴的直径和材料的剪切模量,求轴表面的最大切应力和扭转角。
8第十章压杆稳定问题PPT课件

2
§11-3 两端非铰支细长压杆的临界载荷
解析法确定临界载荷:铰支-固支压杆 类比法确定临界载荷 相当长度与长度因素 例题
3
一、解析法确定临界载荷
1. 固支-自由压杆
根据微弯临界平衡状态
建立微分方程
A
l
M (x)F(w)
d 2w M (x)
dx2 EI
Fcr
B 0.7l
13
3. 两端固支压杆:
拐点
拐点
F cr
l4
l2
l4
Fcr
(l
2 EI / 2)2
F cr
F cr
l2
14
三、欧拉公式的统一表达式:
Fcr
EI l2
1
EI Fcr (2l )2
2
Fcr
l
EI
/ 22
1 2
EI Fcr (0.7l )2
0.7
欧拉公式可以写成统一形式: Fcr
从数学观点看,压杆微分方程与梁弯曲方程有着根本区别:前者是本征值问 题,其本征函数(即屈曲模态)均含有一个不确定的系数(如最大挠度等)。 其物理根源是在临界载荷作用下,压杆处于中性平衡状态(或称为随遇平衡 状态),所以即使对应一定的屈曲模态,位移的大小是不确定的。与梁不同,
梁弯曲时载荷与挠度无关,挠度是完全确定的。(如果考虑大挠度问题,位
(k2 F ) EI
考虑位移边界条件:
x0,w0
B
FR l EIk 2
0
x0,w'0
Ak
FR EIk 2
0
FR
F x
l
xl,w0 A s in k l B c o s k l 0
工程力学(静力学与材料力学)第15章压杆稳定问题

其他形式的稳定问题
F ≥ Fcr
单辉祖:材料力学教程
8
§2 两端铰支细长压杆的临界载荷
临界载荷的欧拉公式 临界载荷的欧拉公式 小挠度理论与理想压杆 模型的实际意义 例题
单辉祖:材料力学教程
9
临界载荷的欧拉公式
求解思路
Fcr-使压杆在微弯条件下保持平衡的最小轴向压力
方法:使压杆微弯, 方法:使压杆微弯, 再求能 微弯 保持其平衡的最小轴向压力 保持其平衡的最小轴向压力 平衡 临界载荷公式
第 9 章 压杆稳定问题
本章主要研究: :
压杆稳定概念 压杆临界载荷的确定 压杆稳定条件与合理设计
单辉祖:材料力学教程 1
§1 §2 §3 §4 §5
稳定性概念 两端铰支细长压杆的临界载荷 两端非铰支细长压杆的临界载荷 中、小柔度杆的临界应力 压杆稳定条件与合理设计
单辉祖:材料力学教程
2
§1 稳定性概念
引言 稳定与不稳定平衡 压杆稳定概念 其他形式的稳定问题
单辉祖:材料力学教程
3
引 言
轴向受压细长杆, 轴向受压细长杆,当所受压力 F 达到或超过一定数 值时,杆将突然变弯,即产生失稳 失稳现象 值时,杆将突然变弯,即产生失稳现象
杆件失稳往往产生显著弯曲变形, 杆件失稳往往产生显著弯曲变形,甚至导致系统局 部或整体破坏。 部或整体破坏。
单辉祖:材料力学教程
15
类比法确定临界载荷
π2EI Fcr = (2l )2
π2EI Fcr = 4l 2
单辉祖:材料力学教程
π2EI Fcr = 2 l 2
4π2EI Fcr = l2
16
相当长度与长度因数
材力公式总结完美版

失效原因:脆性材料在其强度极限bσ破坏,塑性材料在其屈服极限sσ时失效。
二者统称为极限应力理想情形。
塑性材料、脆性材料的许用应力分别为:[]3n sσσ=,[]bb n σσ=,强度条件:[]σσ≤⎪⎭⎫⎝⎛=maxmax A N ,等截面杆[]σ≤AN m a x轴向拉伸或压缩时的变形:杆件在轴向方向的伸长为:ll l-=∆1,沿轴线方向的应变和横截面上的应力分别为:ll ∆=ε,AN =σ。
横向应变为:bb b bb -=∆=1'ε,横向应变与轴向应变的关系为:μεε-='。
胡克定律:当应力低于材料的比例极限时,应力与应变成正比,即εσE =,这就是胡克定律。
E 为弹性模量。
将应力与应变的表达式带入得:EANl l =∆圆轴扭转时的应力圆轴扭转时的应力:tpW T R I T ==maxτ;圆轴扭转的强度条件: ][maxττ≤=tW T ,可以进行强度校核、截面设计和确定许可载荷。
圆轴扭转时的变形:;等直杆:pGITl =ϕ圆轴扭转时的刚度条件:∏⨯=='180pGIT dxd ϕϕ,][max maxϕϕ'≤='pGIT弯曲内力与分布载荷q 之间的微分关系)()(x q dxx dQ =;()()x Q dxx dM =;()()()x q dxx dQ dxx M d ==22Q 、M 图与外力间的关系a )梁在某一段内无载荷作用,剪力图为一水平直线,弯矩图为一斜直线。
b )梁在某一段内作用均匀载荷,剪力图为一斜直线,弯矩图为一抛物线。
c )在梁的某一截面。
()()0==x Q dxx dM ,剪力等于零,弯矩有一最大值或最小值。
d )由集中力作用截面的左侧和右侧,剪力Q 有一突然变化,弯矩图的斜率也发生突然变化形成一个转折点。
梁的正应力和剪应力强度条件[]σσ≤=WMmaxmax,[]ττ≤max提高弯曲强度的措施:梁的合理受力(降低最大弯矩maxM,合理放置支座,合理布置载荷,合理设计截面形状塑性材料:[][]c t σσ=,上、下对称,抗弯更好,抗扭差。
关于稳定性问题的讨论

关于稳定性问题的研究土木工程0503刘瑞琦一、什么是稳定性问题呢?稳定性是受压杆件的一个异常异常的力知识题,对压杆稳定性的理解应该分为以下几个方面:首先,当理想压杆两端受到的压力较小时,压杆能够保持稳定的和唯一的直线平衡状态,即便是有侧向干扰力把压杆推弯,但当干扰力撤除之后被推弯了的压杆依然恢复成直线平衡状态。
我们从轴向拉压变形知道,杆件在轴向压力作用下保持直线平衡(轴向有压缩变形)是压杆的常态,因此,我们把压杆的这种平衡状态称为是稳定的。
第二,当理想压杆两端受到的压力增大到某一个异常值时,压杆无疑依然保持直线平衡,只是若有侧向干扰力把压杆推弯,而再把干扰力撤除之后被推弯了的压杆就会在微弯的曲线状态下保持平衡了,无法恢复直线平衡状态。
从轴向拉压变形知道,这种现象显然不是压杆的常态,因此,我们把压杆的这种现象称为是失稳。
不能认为压杆失稳了就无法保持直线平衡状态了,只是说直线平衡状态不再是压杆的稳定的和唯一的平衡状态了,压杆既可以在直线状态下保持平衡也可以在微弯的曲线状态下保持平衡。
从实际的工程应用角度来讲,压杆不再能保持唯一的只发生轴向压缩变形的直线平衡,还可能变成曲线了,那绝对是不允许的。
固然压杆稳定问题的异常性并不在于曲线平衡本身,因为失稳时两端的压力对中间的横截面产生了偏心,横截面上除了有轴力之外还有弯矩存在,此时杆件顺势而弯是可以想象的,其实此时已经有轴压问题改变为弯曲问题了。
压杆稳定第1 页/共7 页问题的异常性主要在于存在一个异常的压力值,当压杆两端的压力达到该压力值时才会发生失稳现象,那么研究这个压力值就异常有价值了,因为对于细长的压杆来讲,这个压力值有可能低于杆件由强度决定的承载力。
二、稳定性计算与强度和刚度的检算有何异同?相同之处就在于稳定性与强度和刚度一样,都是构件必须满意的设计条件。
就问题的分析和求解策略而言,稳定性问题与强度和刚度有所不同,强度和刚度问题分析和求解的重点是对构件实际工作状态下的受力(包括内力和应力)和变形举行分析和计算,这部分内容常常是问题的重点和难点,而强度和刚度的控制参数,如许用应力和刚度条件往往都是已知的。
工程力学(静力学与材料力学)压杆稳定问题资料重点

π 2 EI l2
16
例 3-2 试确定图示细 长压杆的临界载荷
解: 微弯平衡, 最 小轴向压力
EI
d2w dx 2
M(x)
M ( x) Fw FR (l x)
EI
d2w dx 2
Fw
FR
(l
x)
d2w dx 2
F EI
w
FR EI
(l
x)
w
Asinkx
B coskx
FR EIk 2
(l
x)
方法:使压杆微弯, 再求能 保持其平衡的最小轴向压力
临界载荷公式
微弯, 且 max p 时
d2w dx 2
M(x EI
)
M ( x)Fw
d2w dx 2
F EI
w
0
注意:M(x) , w - 设正法
w Asin
单辉祖:材料力学教程
F EI
x
Bcos
F EI
x
(a)
A,B,F 待定
9
w Asin
( k 2 F / EI )
单辉祖:材料力学教程
x 0, w 0 x 0, w' 0 x l, w 0
B
FR l EIk 2
0
Ak
FR EIk 2
0
Asin kl B cos kl 0
关于 A, B, FR 的 线性齐次方程组
17
B
FR l EIk 2
0
Ak
FR EIk 2
0
Asinkl B coskl 0
Fcr
π EI
l 2
2
Fcr
4π EI l2
14
相当长度与长度因数
压杆稳定

Fcr n nst FN 2
柔度:
l 2 1 0 .6 80 d2 / 4 i2
0 < p
可用直线公式.
因此
Fcr cr A2 (a b ) A2
6
2 (304 1.12 80) 10 d 2 4
151.47 KN
二、细长压杆的临界力
1、两端铰支的细长压杆的临界力 2、其他杆端约束细长压杆的临界力
材料力学
压杆稳定问题/细长压杆的临界力
1、两端铰支的细长压杆的临界力 考察微弯状态下局部压杆的平衡
FBx Fp
材料力学
y
压杆稳定问题/细长压杆的临界力
若 p , 则压杆的弯曲变形为 d2y EI 2 M ( x) Fp y dx Fp y d2y 2 dx EI Fp 2 设k , 则 EI
二、压杆的稳定条件:
P A
材料力学
例
杆的 AB 杆为圆松木,长 L= 6m,[ ] =11MPa 直径 d = 0.3m,试此杆的容许压力 解:折减系数法
B
①最大柔度
T1 T2
x y面内, =1.0
A
y W
xy
1 6 4 80 i 0.3
L
z y面内, =2.0
l2 y(x)=a sin nx l —欧拉公式
F cr =
材料力学
2EI
l2
压杆稳定问题/细长压杆的临界力
• 分析
1)、I 如何确定 ?
压杆总是在抗弯能力最小的纵向平面内弯曲
I I min
F h b
y
x
F
z 例如矩形截面压杆首先在哪个平面内失稳弯曲? (绕哪个轴转动)
工程力学第16章(压杆稳定问题)
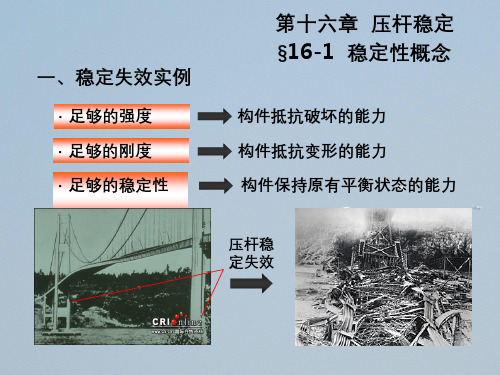
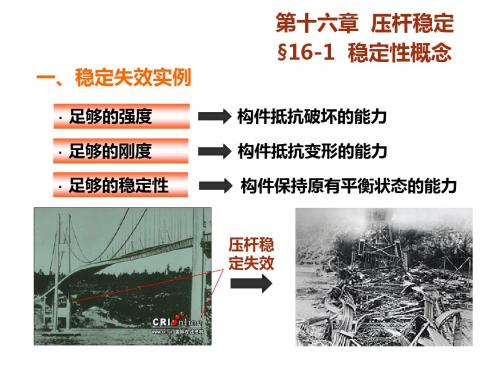
·足够的强度 ·足够的刚度 ·足够的稳定性
第十六章 压杆稳定 §16-1 稳定性概念
构件抵抗破坏的能力 构件抵抗变形的能力 构件保持原有平衡状态的能力
压杆稳 定失效
二、平衡的稳定性
稳定的平衡
非稳定的平衡
三、压杆的稳定性问题
当压力小于某值,压 杆保持直线平衡,在任 意小的扰动下,压杆偏 离直线平衡位置。但当 扰动除去后,压杆回到 原来直线平衡位置。
属于大柔度杆,欧拉公式计算临界载荷
2 E 2 2 0 5 1 0 9 1 6 0 1 0 3
F c r 1 c r 1 A 2A 1
1 2 5 2
4
2 6 0 0 k N
两端固支约束的压杆
21 d 81601 8 103112.5P
属于大柔度杆,欧拉公式计算临界载荷
2 E 2 2 0 5 1 0 9 1 6 0 2 1 0 6 F c r 2 c r 2 A 2 2A 1 1 2 .5 2 4 3 2 1 0 k N
解:⑴ 计算柔度,判断临界应力大者
圆截面 i d 4
两端铰支约束的压杆
1 1
1
1l1
i
20 d
两端固支约束的压杆
1
2
2
0.5
cr
2
2E 2
2l2 18
id
cr1 cr2
所以两端固支的压杆具有较大的临界压力。
⑵ 计算给定参数下压杆的临界载荷
两端铰支约束的压杆
12 d 01602 0 10 3125P101
中柔度杆发生弹塑性失稳,欧拉公式不适用。临界 应力一般采用经验公式计算。
·直线经验公式
cr ab
(a 、b是与材料性质有关的 常数,可查阅有关工程手册)
工程力学中的稳定性分析有哪些方法?

工程力学中的稳定性分析有哪些方法?在工程力学领域,稳定性分析是至关重要的一个环节,它关乎着结构和系统在各种载荷和条件下能否安全、可靠地运行。
稳定性分析旨在确定结构或系统在受到干扰后是否能够恢复到初始平衡状态,或者是否会发生不可控的变形或破坏。
接下来,让我们一起探讨一下工程力学中常见的稳定性分析方法。
首先,静力平衡法是一种基础且常用的方法。
它基于结构在平衡状态下的静力条件进行分析。
通过研究结构所受的外力和内力,建立平衡方程,判断在给定的载荷条件下结构是否能够保持稳定。
例如,对于简单的梁柱结构,可以通过计算其受压杆件的临界载荷来评估其稳定性。
如果所施加的载荷小于临界载荷,结构被认为是稳定的;反之,如果超过临界载荷,结构可能会发生失稳现象。
能量法也是稳定性分析中的重要手段之一。
这种方法基于能量原理,通过比较结构在不同状态下的总势能来判断稳定性。
当结构处于稳定平衡状态时,其总势能具有极小值;而在不稳定平衡状态下,总势能具有极大值。
能量法在处理复杂结构和非线性问题时具有一定的优势,能够提供较为准确的稳定性判据。
瑞利里兹法是一种近似分析方法。
它通过假设结构的位移函数,并将其代入能量表达式中,然后通过求解特征值问题来确定结构的稳定性。
这种方法在处理具有复杂边界条件和几何形状的结构时非常有用,可以得到较为接近实际情况的结果。
有限元法在现代工程力学稳定性分析中扮演着关键角色。
它将连续的结构离散化为有限个单元,通过建立单元刚度矩阵和总体刚度矩阵,求解线性或非线性方程组,从而得到结构的位移和应力分布。
通过对不同载荷条件下的计算结果进行分析,可以评估结构的稳定性。
有限元法能够处理非常复杂的结构和载荷情况,并且可以直观地展示结构的变形和应力分布,为工程设计提供详细的参考。
动力分析法主要用于研究结构在动态载荷作用下的稳定性。
通过建立结构的运动方程,并求解其特征值和特征向量,可以得到结构的固有频率和振型。
如果动态载荷的频率接近结构的固有频率,可能会引起共振现象,导致结构失稳。
《工程力学》课件——22 压杆稳定问题

Z
Y
《工程力学》
《 压杆稳定问题 》
PART
1
压杆稳定的概念
压杆稳定的概念
问题思考 已知: • 木杆横截面积 = 150mm2 • 抗压强度极限 σb = 40MPa • 短木杆长度 = 30mm • 长木杆长度 = 1000mm
长木杆折断破坏: 细长压杆承载能力不仅取决于轴向压缩抗压 强度 且与杆件在轴向压力作用下突然变弯,丧失 原有直线形状有关
压杆稳定的概念
加拿大魁北克省圣劳伦斯河钢铁结构大桥 事故照片 经验教训:桥梁等结构设计必须考虑强度、刚度与稳定性并重的体系
压杆稳定的概念
压杆的稳定性
稳定平衡状态: 当 P < Pcr 时杆件保持直线平衡状态 微小横向力干扰 → 杆件弯曲 干扰力去掉 → 杆件恢复原有直线状态
压杆稳定的概念
cr a b
式中:λ 为压杆的柔度,α为与材料有关的系数
➢ 抛物线型经验公式
• 我国钢结构规范中规定采用抛物线经验公式: cr s 2
式中:a、b 值是与材料性能有关的常数 适用于合金钢、铝合金、铸铁与松木等
X
Z
Y
感谢聆听!
《 压杆稳定问题 》
平衡状态稳定性与压力大小有关: P < Pcr 时为稳定平衡 P > Pcr 时是不稳定的 P = Pcr 时为临界状态
PART
2
临界力的欧拉公式
临界力的欧拉公式
临界状态: 压杆从稳定平衡过渡到不稳定平衡的特定状态
临界力 Pcr: 压杆处于临界状态时所受的轴向压力
临界力欧拉公式: 临界力的稳定性
临界平衡状态: 当 P 增加到 Pcr 时对 微小横向力干扰 → 杆件弯曲 干扰力去掉 → 杆件不能恢复原来直线形状 (压杆将保持一种微弯的平衡状态)
考虑轴向均布载荷时压杆的稳定性计算

考虑轴向均布载荷时压杆的稳定性计算黄开志;陈小亮【摘要】为了求得压杆同时承受轴向均布载荷和集中载荷时,临界载荷的计算公式,首先对仅承受轴向均布载荷的压杆,用初参数法,导出了临界载荷特征方程,由软件分析特征方程发现,"固支-定向"、"固支-自由"、"铰支-定向"支承的压杆,轴向均布载荷对其稳定性有明显影响,并求得了临界载荷的近似解;其次采用载荷换算与叠加的方法,求得了压杆同时承受轴向均布载荷和集中载荷时,临界载荷计算的经验公式;最后就"固支-自由"支承的压杆,与其他一些研究结果进行了比较,本文结果与"平均结果"较吻合.【期刊名称】《力学与实践》【年(卷),期】2015(037)006【总页数】6页(P744-749)【关键词】材料力学;压杆;稳定性;临界载荷;经验公式;欧拉公式【作者】黄开志;陈小亮【作者单位】重庆科技学院数理学院,重庆 401331;重庆科技学院数理学院,重庆401331【正文语种】中文【中图分类】O341对同时承受轴向均布载荷和集中载荷的压杆稳定性问题,文献[1]指出,难以求得临界载荷的精确解,该文作者采用摄动法得到了临界载荷的特征方程,给出了临界载荷的一些数值解;文献[2]首先假设了压杆挠曲线近似为正弦函数,然后用能量原理得到了临界载荷的解答;文献[3]用幂级数法求得了临界载荷的解答.在这些近似方法中,较详细研究了“固支--自由”支承的情况,对其他支承情况,没有提供详实的临界载荷公式.本文拟先导出压杆仅承受轴向均布载荷q时,其临界载荷的近似解,并根据不同的支承情况作载荷换算,再与压杆轴向集中载荷叠加,以求得压杆同时承受轴向均布载荷和集中载荷时,其临界载荷计算的经验公式.设长为l、抗弯刚度为E I的压杆,仅承受轴向均布载荷q时处于微弯曲平衡状态,其受力和变形情况可简化为图1所示模型.1.1 变形方程在微弯曲平衡状态的压杆中取d x微段,因小变形,可视d x段为直线,按材料力学习惯设内力为正,其受力情况如图2所示,则静力平衡方程为因小变形,故sin w′(x)≈w′(x),并略去二阶微量,上述二式简化为对式(2)求一阶导数并考虑到式(1)得挠曲线近似微分方程对式(4)求一阶导数并考虑到式(2)得对式(5)求一阶导数并考虑到式(1)得令,上式变为求解式(6)得挠曲线方程对式(7)求一阶导数得转角w′(x)满足方程1.2 变形边界条件在式(7)~式(8)中令x=0,得到A端的变形满足在式(7)~式(8)中令x=l,得到B端的变形满足1.3 内力边界条件对式(8)求一阶导数并考虑到式(4),得对式(13)求一阶导数并考虑到式(2),得在式(13)~式(14)中令x=0,得到A端的内力满足在式(13)~式(14)中令x=l,得到B端的内力满足1.4 特征方程根据表1所述不同支承情况的压杆,由变形和内力为零的边界条件,选用式(9)~式(12),式(15)~式(18)中的4个,构成关于初参数C1,C2,C3,C4的齐次线性方程组.因初参数C1,C2,C3,C4不全为0,则方程组的系数行列式必为0,由此得到临界载荷q cr的特征方程.1.4.1 固支--固支由式(9)~式(12)及表1所述该支承情况下为零的边界条件,得特征方程为1.4.2 固支--铰支由式(9)~式(11)和式(17)及表1所述该支承情况下为零的边界条件,得特征方程为1.4.3 固支--定向定向支承是指仅对压杆的转角作刚性约束,即该处压杆的转角为0,而不限制其挠度,即该处压杆的剪力为0.由式(9),式(10),式(12),式(18)及表1所述该支承情况下为0的边界条件,得特征方程为1.4.4 固支--自由由式(9),式(10),式(17),式(18)及表1所述该支承情况下为零的边界条件,得特征方程为1.4.5 铰支--铰支由式(9),式(11),式(15),式(17)及表1所述该支承情况下为零的边界条件,得特征方程为1.4.6 铰支--定向由式(9),式(12),式(15),式(18)及表1所述该支承情况下为零的边界条件,得特征方程为1.5 临界载荷近似解对1.4.1~1.4.6所述的特征?方程求解,若其有最小正数解(kl)cr,则由k3得临界载荷qcr=用软件如《Maple》等绘制1.4.1~1.4.6所述的6种压杆的临界载荷特征方程曲线,见图3,每条曲线在k l轴上的所有截距均为相应的特征方程的解,取第一截距即最小正数值(kl)cr计算临界载荷.软件分析表明,易失稳的压杆为图中虚线表示的情况.(1)1.4.3所述固支--定向支承压杆第一截距(kl)cr≈3.02,则该式表明,将大小为q cr l且沿压杆轴向均布施加的载荷,换算成大小为0.35833q cr l的集中载荷施将式(19)换算为欧拉公式形式,即加在压杆端部时,二者对压杆的稳定性影响是等效的.(2)1.4.4所述固支--自由支承和1.4.6所述“铰支--定向”支承压杆二者特征方程曲线重合,第一截距(k l)cr≈1.85,则将式(21)换算为欧拉公式形式,即该式表明,将大小为q cr l且沿压杆轴向均布施加的载荷,换算成大小为0.38969q cr l的集中载荷施加在压杆端部时,二者对压杆的稳定性影响是等效的. 设压杆处于临界状态时,轴向均布载荷为q,轴向集中载荷为F;设F cr为未考虑轴向均布载荷q时,按欧拉公式计算的临界载荷.不妨令F= K cr F cr,且称K cr 为F cr的修正因子.(1)对1.4.3所述固支--定向支承压杆采用载荷换算与叠加的方法,结合式(20)得q和F同时作用时,临界载荷经验公式为即,得其中(2)对1.4.4所述固支--自由支承和1.4.6所述铰支--定向支承压杆采用载荷换算与叠加的方法,结合式(22)得q和F同时作用时,临界载荷经验公式为即得其中由于文献[1-3]及Bessel函数法(源于文献[1])仅研究了本文所述固支--自由支承的压杆,且研究范围是ql/F cr介于0与0.5之间,故这里仅就该可比情况进行比较.先分别按文献[1-3]、Bessel函数法及本文方法得到的公式或数据计算出F cr 的修正因子K cr(本文应按式(26)计算K cr),再计算出K cr的平均值cr,最后计算出各K cr与cr的偏差δcr(%),结果见表2.表2中带下划线及粗体数字表明:(1)当ql/F cr=0时,5种方法研究结果一致;(2)当ql/F cr在0.05左右时,文献[2-3]的研究结果与平均结果较吻合,文献[1]次之;(3)当ql/F cr介于0.10~0.20时,本文研究结果与平均结果较吻合,Bessel函数法次之;(4)当ql/F cr介于0.25~0.5时,本文研究结果与平均结果较吻合,文献[3]次之.由文献[1]知,工程中一般0.1≤ql/F cr≤0.25.由表2知,当0.1≤ql/F cr≤0.5时,本文研究结果与平均结果较吻合.对固支--定向、固支--自由和铰支--定向支承的压杆,q对其稳定性有明显影响.压杆处于临界状态时,q和F依次满足经验式(23)和式(25).当F计算结果为负时,表示需要施加拉力,才可能避免压杆失稳.其他支承的压杆,q对其稳定性无明显影响.显然,对于完全理想支承的压杆,参照经验公式计算临界载荷是比较安全的,其中u为压杆的长度因数,其值取决于压杆的支承情况.【相关文献】1吴晓,杨立军,郑长成.轴向压力和均布载荷作用下压杆的屈曲研究.四川建筑科学研究,2008,34(5):34-35,652张平占.BHA受压失稳的模型及临界钻压公式.煤田地质与勘探,1995,23(5):59-623马肖,韩春民.具有较大初始位移的拼组柱在分布与集中荷载共同作用下的承载能力分析.四川建筑科学研究,2009,35(3):27-29。
工程力学精品课程压杆稳定.ppt

压杆稳定
Stability of columns
一。稳定性概念
细长杆件承受轴向压缩载荷作用时,会表现出与强度失效性质全然不同的失效现象, 即将会由于平衡的不稳定性而发生失效,这种失效称为稳定性失效,简称失稳,又称为 屈曲失效。
内燃机配气机构中的挺杆
磨床液压装置的活塞杆
细长压杆随受力的改变,平衡的稳定性会发生改变,由稳定平衡转为不稳定平衡的 临界值称为压杆的临界压力或临界力;它是压杆保持稳定的直线平衡的最大值,或是 压杆保持微曲平衡的最小值。
b
经验公式: cr a b
其中,a,b是由杆件材料决定的常数
2)小柔度杆的临界应力
小柔度杆或短杆: λ < λ2 此时压杆属强度问题,临界应力就是屈服极限或强度极限,即
cr s
或
b
3) 临界应力总图
σ σcr=σs
σs σp
σcr=a-bλ σcr=π2E/λ2
O
λ2
λ1
可以明显地看出,短杆的临界应力与柔度λ无关,而中、长杆的临界应力则随柔度 λ的增加而减小。
例10-4图示钢结构,承受载荷F作用,试校核斜撑杆的稳定性。已知载荷F=12kN,其
外径D=45mm,内径d=36 mm,稳定安全系数nst=2.5。斜撑杆材料是Q235钢,弹性模 量E=210 GPa, σp=200 MPa, σs=235 MPa,
1m A
1m B
F 解:(a) 受力分析。以梁AC为研究对象,由静力
1.减小压杆的支承长度;因为临界应力与杆长平方成反比,因此可以显著地提高压杆承 载能力。 2. 改变压杆两端的约束;使长度系数减小,相应地减小柔度,从而增大临界应力。 3. 选择合理的截面形状;可以在不增加截面面积的情况下,增加横截面的惯性矩I, 从而减小压杆柔度,起到提高压杆稳定性的作用。图10.10是起重臂合理截面。
压杆稳定公式

压杆稳定公式压杆稳定公式是结构设计中非常重要的一部分,它能够帮助我们预测和控制结构在压力作用下的稳定性。
下面就让我们通过全面的介绍和详细的指导,来探究压杆稳定公式的来龙去脉和应用方法。
一、什么是压杆稳定公式?压杆稳定公式就是描述杆件在压力作用下稳定性的数学公式。
其中,稳定性指杆件在受到压力时,能否保持不失稳、不弯曲、不塑性变形,从而保证整个结构的安全可靠。
二、为什么需要压杆稳定公式?在结构设计中,压杆是经常使用的一种构件。
然而,如果压杆不稳定,就会导致结构的整体稳定性受到威胁。
因此,进行压杆稳定性分析,有助于预测和控制结构在压力作用下的承载能力和稳定性,是非常必要的。
三、如何计算压杆稳定系数?计算压杆稳定系数的具体方法取决于压杆的截面形状。
下面我们以圆形截面为例进行介绍。
1.圆杆稳定系数的计算公式如果压杆的截面为圆形,我们可以采用欧拉公式的方法来计算其稳定系数。
具体公式如下:k = (π²E) / (l/r)²其中,k表示压杆稳定系数,E表示弹性模量,l表示压杆的长度,r表示压杆截面的半径。
2.圆形压杆稳定系数的应用在实际工程中,我们可以利用上述公式来计算圆形压杆的稳定系数,从而判断其稳定性。
一般来说,当k的值大于1时,说明压杆稳定;当k的值小于1时,说明压杆失稳。
四、如何提高压杆的稳定性?为了提高压杆的稳定性,我们可以采取以下措施:1. 选择合适的材料和截面形状。
2. 缩小压杆的长度。
3. 增加压杆的直径或截面积。
4. 增加支撑结构的刚度和强度,以减少结构的变形。
5. 控制压力大小和作用方向,避免压力超过压杆承受范围。
总之,对于结构设计中的压杆稳定问题,我们需要掌握其计算公式和计算方法,并且采取相应措施来提高压杆的稳定性,以确保整个结构的安全可靠。
