2013浙江省高等数学微积分竞赛(数学类)含答案
年浙江省大学生高等数学(微积分)竞赛试题.

2005年浙江省大学生高等数学(微积分)竞赛试题(数学类)一. 计算题(每小题12分,满分60分)1.计算()()23400sin ln(1)38sin 1lim x x x x x t t dt x x e →+−+−−∫ 2.计sin 3cos 4sin x dx x x+∫ 3.计算2200501tan dx xπ+∫ 4.设()f x 在点二阶可导,且0x =()011cos lim x f x x→=−,求,和的值。
()0f ()0f ′()0f ′′5.设()(),z f x y x y g x ky =−+++,f ,g 具有二阶连续偏导数,且,如果0g ′′≠22222222z z z 4f x x y y∂∂∂′′++≡∂∂∂∂,求常数k 的值。
二. (本题满分20分)在某平地上向下挖一个半径为R 的半球形池塘,若某点泥土的密度为22r R e ρ=,其中r 为此点离球心的距离,试求挖此池塘需作的功。
三 (本题满分20分)判别级数()111.n n∞=−∑的收敛性 四 (本题满分20分)证明对任意连续函数()f x ,有 ()(){}112211max sin ,cos 1x x f x dx x f x dx −−−−−∫∫≥ 五 (本题满分15分)对下列函数()f x ,分别说明是否存在一个区间[],a b ,,使(0a >)()[]{}[]{},,f x x a b x x a b ∈=∈,并说明理由。
()()21133f x x =+2 ()()12f x x = ()()131f x x =−六(本题15分) 设()f x 在[]1,1−上二阶导数连续,证明()()()112133xf x dx f f ξξξ−′′′=+∫。
2012浙江省高等数学微积分竞赛(经管类)含答案.

2012浙江省高等数学(微积分)竞赛试题经管类一、计算题(每小题14分,满分70分)1求极限lim log ()abx x x x →+∞+。
2.设()sin ax f x e bx =(,a b R ∈为常数),求()(0)n f 。
装 订 线3.计算 0sin d n x x x π⎰(n 为正整数)。
4.求积分2241d 1x x x x+++⎰5.设函数21()2af x x x=+,0x >,常数0a >,试求最小的常数a ,使得()6f x ≥。
二、(满分20分)证明:111ln 1lnni n n n i =+<<+∑,n +∈三、(满分20分)求2211(21)2nn nn C n ∞=-∑的值。
四、(满分20分)在草地中间有一个半径为R 的圆形池塘,池塘边拴着一只山羊,拴山羊的绳子长为,(02)kR k <<,求山羊能吃到草的草地面积。
五、(满分20分)(1)求极限lim 2coscos cos 482n n n πππ→∞(2)证明2π=经管类一、计算题 1、若a b ≥l i m l o g (a b x x x x →+∞+l i m l o g(1)l i m l o g (1a b ab a x xx x x x a x a --→+∞→+∞=+=++= 同理,当a b <时,l i m l o ga b x x x x →+∞+b=,所以l i m l o g a b x x x x →+∞+m a x (a b = 2、解:()sin cos ax ax f x ae bx be bx e bx bx ⎫'=+=+⎪⎭)()cos sin sin cos sin ax e bx bx bx θθθ=+=+arcsin θ⎛⎫==⎝同理)()sin()cos()f x ea bxb bx θθ''=+++22()sin(2)ax a b e bx θ=++可得()()()()()()/2/222()22sin()0sin()n n nax n f x a b e bx n f a b n θθ=++⇒=+3、解:sin d n x x x π⎰()011sin sin nnj j j j x x dx x j xdx ππππππ-====+-∑∑⎰⎰()()201sin d 21212nj n x x x j n n n n n n πππππ==+-=++-=+∑⎰4、解:2442222121(1)(1)x x x x x x x x x ++=++-=+++-()()22242221111111d d d 121121/23/41/23/4x x x x x x x x x x x x ⎛⎫+⎛⎫∴=+=+ ⎪ ⎪ ⎪++++-+⎝⎭++-+⎝⎭⎰⎰⎰1r c t a r C =5、解:2()0a f x x x '=-=0x = 032()10a f x x ''=+> ()f x ∴f==6= 即8a =时 ()6f x ≥,且在02x =时,(2)6f = 所以min 8a =二、证明:显然11111d d j j jj x x x j x+-<<⎰⎰ 2j ≥1 1122111111d 1d 1ln nn n j n j j j j x x n j j x x -===∴=+<+=+=+∑∑∑⎰⎰另一方面111111111111d ln nn n j j j j j x n j jn x n n --+====+>+=+∑∑∑⎰三、解:[]2222221221(2)!(22)!(22)!1(21)2(21)2(!)2!(1)!22(1)!nn n n n n n n n C n n n n n nn ----===---- 而2212(21)122n n n n -=- 122222222111(21)222nn nn n n nn n C C C n ---∴=-- 而22102nn n C → ∴原级数1=四、解:以过拴羊点与池塘圆心为x 轴,拴山羊点为原点,则池塘边界圆为222()x R y R -+=而羊能跑的最大圆周为2222x y k R +=,易知在22R x k =时,两圆有两个交点2222012d 2R k S k R x π∴=+⎰222222arcsin (arcsin 22x x R R k R k R x R R k kR R π-⎛⎫=+-- ⎪⎝⎭2222arcsin 22k k R k R π=+222221arcsin 14222k k R R R π⎛⎫⎛⎫---- ⎪ ⎪⎝⎭⎝⎭2222222arcsin arcsin 12222k k k R R k R R ππ⎛⎫=+-- ⎪⎝⎭五(1)解:cos cos cos cos cos cos sin /sin 48248222n n n n n πππππππ=1121111cos cos cos sin cos sin 4822442sin 2sin 2sin 222n n n n n n nn ππππππππ----===∴原极限22lim2sin2n n nππ→∞==(2)cos4π=c o s 8π===c o s 2n π==2cos cos cos 482n ππππ==书中横卧着整个过去的灵魂——卡莱尔人的影响短暂而微弱,书的影响则广泛而深远——普希金人离开了书,如同离开空气一样不能生活——科洛廖夫书不仅是生活,而且是现在、过去和未来文化生活的源泉——库法耶夫书籍把我们引入最美好的社会,使我们认识各个时代的伟大智者———史美尔斯书籍便是这种改造灵魂的工具。
2013年浙江卷数学试题及答案(理)

2013·浙江卷(理科数学)1. 已知i 是虚数单位,则(-1+i)(2-i)=( ) A .-3+i B .-1+3i C .-3+3i D .-1+i1.B [解析] (-1+i)(2-i)=-2+i +2i +1=-1+3i ,故选择B. 2. 设集合S ={x |x >-2},T ={x |x 2+3x -4≤0},则(∁S )∪T =( ) A .(-2,1] B .(-∞,-4] C .(-∞,1] D .[1,+∞)2.C [解析] ∁S ={x |x ≤-2},T ={x |(x +4)(x -1)≤0}={x |-4≤x ≤1},所以(∁S )∪T =(-∞,1].故选择C.3., 已知x ,y 为正实数,则( )A .2lg x +lg y =2lg x +2lg yB .2lg(x +y )=2lg x ·2lg yC .2lg x ·lg y=2lg x +2lg y D .2lg(xy )=2lg x ·2lg y3.D [解析] ∵lg(xy )=lg x +lg y ,∴2lg(xy )=2lg x +lg y =2lg x 2lg y ,故选择D. 4. 已知函数f (x )=A cos(ωx +φ)(A >0,ω>0,φ∈),则“f (x )是奇函数”是“φ=π2”的( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件4.B [解析] f (x )=A cos(ωx +φ)是奇函数的充要条件是f (0)=0,即cos φ=0,φ=k π+π2,k ∈,所以“f (x )是奇函数”是“φ=π2”的必要不充分条件,故选择B.5. 某程序框图如图1-1所示,若该程序运行后输出的值是95,则( )图1-1A .a =4B .a =5C .a =6D .a =75.A [解析] S =1+11×2+12×3+…+1k (k +1)=1+1-12+12-13+…+1k -1k +1=1+1-1k +1=2-1k +1=95,故k =4,k =k +1=5,满足k >a 时,即5>a 时,输出S ,所以a=4,选择A.6. 已知α∈,sin α+2cos α=102,则tan 2α=( ) A.43 B.34 C .-34 D .-43 6.C [解析] 由(sin α+2cos α)2=1022'得sin 2α+4sin αcos α+4cos 2α=104=52,4sin αcos α+1+3cos 2α=52,2sin 2α+1+3×1+cos 2α2=52,故2sin 2α=-3cos 2α2,所以tan 2α=-34,选择C. 7. 设△ABC ,P 0是边AB 上一定点,满足P 0B =14AB ,且对于边AB 上任一点P ,恒有PB →·PC →≥P 0B →·P 0C →,则( )A .∠ABC =90°B .∠BAC =90°C .AB =ACD .AC =BC7.D [解析] 建立以AB 的中点O 为原点的坐标系,如图所示,PB →·PC →=(c -x ,0)·(a -x ,b )=x 2-(a +c )x +ac ,当x =a +c 2时,PB →·PC →最小,而已知P 0B →·P 0C →最小,所以c 2=a +c 2,此时a =0,所以AC =BC ,选择D.8. 已知e 为自然对数的底数,设函数f (x )=(e x -1)(x -1)k (k =1,2),则( ) A .当k =1时,f (x )在x =1处取到极小值 B .当k =1时,f (x )在x =1处取到极大值 C .当k =2时,f (x )在x =1处取到极小值 D .当k =2时,f (x )在x =1处取到极大值8.C [解析] 当k =1时,f (x )=(e x -1)(x -1),f ′(x )=e x (x -1)+(e x -1)=x e x -1,则在x =1处取不到极值.当k =2时,f (x )=(e x -1)(x -1)2,f ′(x )=e x (x -1)2+(e x -1)×2(x -1)=(x -1)(x e x +e x -2),f ′(1)=0,f ′(2)>0,f ′12<0,所以在x =1处取得极小值.图1-29., 如图1-2,F 1,F 2是椭圆C 1:x 24+y 2=1与双曲线C 2的公共焦点,A ,B 分别是C 1,C 2在第二、四象限的公共点.若四边形AF 1BF 2为矩形,则C 2的离心率是( )A. 2B. 3C.32D.629.D [解析] 设双曲线实半轴长为a ,焦半距为c ,|AF 1|=m ,|AF 2|=n ,由题意知c =3,⎩⎪⎨⎪⎧m +n =4,m 2+n 2=(2c )2=12,2mn =(m +n )2-(m 2+n 2)=4,(m -n )2=m 2+n 2-2mn =8,2a =m -n =2 2,a =2,则双曲线的离心率e =c a =32=62,选择D.10. 在空间中,过点A 作平面π的垂线,垂足为B ,记B =f π(A ).设α,β是两个不同的平面,对空间任意一点P ,Q 1=f β[f α(P )],Q 2=f α[f β(P )],恒有PQ 1=PQ 2,则( )A .平面α与平面β垂直B .平面α与平面β所成的(锐)二面角为45°C .平面α与平面β平行D .平面α与平面β所成的(锐)二面角为60°10.A [解析] 当α⊥β,且α∩β=b ,设f α(P )=A ,则P A ⊥α,Q 1=f β[f α(P )]=f β(A ),故AQ 1⊥β;同理设f β(P )=B ,则PB ⊥β,Q 2=f α[f β(P )]=f α(B ),故BQ 2⊥α,故AQ 1∥PB ,P A ∥BQ 2,所以Q 1和Q 2重合,恒有PQ 1=PQ 2,选择A.11. 设二项式x -13x5的展开式中常数项为A ,则A =________.11.-10 [解析] T r +1=C r 5x 5-r 2(-1)r x -r 3=(-1)r C r 5x 15-5r 6,则15-5r 6=0,r =3,故常数项A =T 4=(-1)3C 35=-10.12. 若某几何体的三视图(单位:cm)如图1-3所示,则此几何体的体积等于________cm 3.图1-312.24 [解析] 此几何体知直观图是一个直三棱柱挖去一个三棱锥而得,如图所示,则体积为12×3×4×5-13×12×3×4×3=24.13. 设z =kx +y ,其中实数x ,y 满足⎩⎪⎨⎪⎧x +y -2≥0,x -2y +4≥0,2x -y -4≤0.若z 的最大值为12,则实数k =________.13.2 [解析] 不等式组表示的可行区域为如图所示的三角形ABC 及其内部,A (2,0),B (4,4),C (0,2),要使z 的最大值为12,只能经过B 点,此时12=4k +4,k =2.14. 将A ,B ,C ,D ,E ,F 六个字母排成一排,且A ,B 均在C 的同侧,则不同的排法共有________种(用数字作答).14.480 [解析] 先在6个位置找3个位置,有C 36种情况,A ,B 均在C 的同侧,有CAB ,CBA ,ABC ,BAC ,而剩下D ,E ,F 有A 33种情况,故共有4C 36A 33=480种.15. 设F 为抛物线C :y 2=4x 的焦点,过点P (-1,0)的直线l 交抛物线C 于A ,B 两点,点Q 为线段AB 的中点.若|FQ |=2,则直线l 的斜率等于________.15.±1 [解析] 设直线l :my =x +1,代入y 2=4x 得y 2-4my +4=0,则y A +y B =4m ,因为Q 为线段AB 的中点,则y Q =y A +y B2=2m ,x Q =my Q -1=2m 2-1,故Q (2m 2-1,2m ),又|FQ |2=4,(2m 2-2)2+(2m )2=4⇒m 4-m 2=0,所以m =±1.16. 在△ABC 中,∠C =90°,M 是BC 的中点.若sin ∠BAM =13,则sin ∠BAC =________.16.63 [解析] 设△ABC 的三边长为a ,b ,c ,tan ∠BAM =12 2.而tan ∠BAM =tan(∠BAC -∠CAM )=tan ∠BAC -tan ∠CAM1+tan ∠BAC ·tan ∠CAM=a b -a 2b 1+a b ·a 2b =a 2b 1+a 22b 2=12 2,则2a b =1+a 22b 2⇒a 2b 2-22a b +2=0⇒a b -22=0,故a b =2⇒sin ∠BAC =a c =aa 2+b 2=2b 3b =63. 17. 设1,2为单位向量,非零向量=x 1+y 2,x ,y ∈若1,2的夹角为π6,则|x ||b |的最大值等于________.17.2 [解析] |x ||b |=|x |2|b |2=x 2x 2e 21+2xy e 1·e 2+y 2e 22=x 2x 2+2xy ×32+y 2=11+3y x +y x2=1y x +322+14≤114=2. 18. 在公差为d 的等差数列{a n }中,已知a 1=10,且a 1,2a 2+2,5a 3成等比数列.(1)求d ,a n ;(2)若d <0,求|a 1|+|a 2|+|a 3|+…+|a n |. 18.解:(1))由题意得a 1·5a 3=(2a 2+2)2, 即d 2-3d -4=0. 所以d =-1或d =4.所以a n =-n +11,n ∈*或a n =4n +6,n ∈*.(2)设数列{a n }的前n 项和为S n .因为d <0,由(1)得d =-1,a n =-n +11,则 当n ≤11时,|a 1|+|a 2|+|a 3|+…+|a n | =-12n 2+212n .当n ≥12时, |a 1|+|a 2|+|a 3|+…+|a n |=-S n +2S 11=12n 2-212n +110.综上所述,|a 1|+|a 2|+|a 3|+…+|a n|=⎩⎨⎧-12n 2+212n ,n ≤11,12n 2-212n +110,n ≥12.19. 设袋子中装有a 个红球,b 个黄球,c 个蓝球,且规定:取出一个红球得1分,取出一个黄球得2分,取出一个蓝球得3分.(1)当a =3,b =2,c =1时,从该袋子中任取(有放回,且每球取到的机会均等)2个球,记随机变量ξ为取出此2球所得分数之和,求ξ的分布列;(2)从该袋子中任取(每球取到的机会均等)1个球,记随机变量η为取出此球所得分数.若Eη=53,Dη=59,求a ∶b ∶c .19.解:(1)由题意得,ξ=2,3,4,5,6.P (ξ=2)=3×36×6=14,P (ξ=3)=2×3×26×6=13,P (ξ=4)=2×3×1+2×26×6=518.P (ξ=5)=2×2×16×6=19,P (ξ=6)=1×16×6=136,所以ξ的分布列为ξ 2 3 4 5 6 P141351819136(2)由题意知η的分布列为η 1 2 3 Paa +b +cba +b +cca +b +c所以Eη=a a +b +c +2b a +b +c +3c a +b +c =53,Dη=1-532·a a +b +c +2-532·b a +b +c +3-532·c a +b +c =59,化简得⎩⎪⎨⎪⎧2a -b -4c =0,a +4b -11c =0,解得a =3c ,b =2c ,故a ∶b ∶c =3∶2∶1.图1-4 20., 如图1-4所示,在四面体A -BCD 中,AD ⊥平面BCD ,BC ⊥CD ,AD =2,BD =2 2,M 是AD 的中点,P 是BM 的中点,点Q 在线段AC 上,且AQ =3QC . (1)证明:PQ ∥平面BCD .(2)若二面角C -BM -D 的大小为60°,求∠BDC 的大小.20.解:方法一:(1)证明:取BD 的中点O ,在线段CD 上取点F ,使得DF =3FC .联结OP ,OF ,FQ .因为AQ =3QC ,所以QF ∥AD ,且QF =14AD .因为O ,P 分别为BD ,BM 的中点,所以OP 是△BDM 的中位线,所以 OP ∥DM ,且OP =12DM .又点M 为AD 的中点,所以OP ∥AD ,且OP =14AD .从而OP ∥FQ ,且OP =FQ ,所以四边形OPQF 为平行四边形,故PQ ∥OF .又PQ ⊄平面BCD ,OF ⊂平面BCD ,所以PQ ∥平面BCD . (2)作CG ⊥BD 于点G ,作GH ⊥BM 于点H ,联结CH . 因为AD ⊥平面BCD ,CG ⊂平面BCD ,所以AD ⊥CG .又CG ⊥BD ,AD ∩BD =D ,故CG ⊥平面ABD ,又BM ⊂平面ABD ,所以CG ⊥BM . 又GH ⊥BM ,CG ∩GH =G ,故BM ⊥平面CGH ,所以CH ⊥BM . 所以∠CHG 为二面角C -BM -D 的平面角,即∠CHG =60°. 设∠BDC =θ,在Rt △BCD 中, CD =BD cos θ=2 2cos θ, CG =CD sin θ=2 2cos θsin θ, BG =BC sin θ=2 2sin 2θ,在Rt △BDM 中,HG =BG ·DM BM =2 2sin 2 θ3.在Rt △CHG 中,tan ∠CHG =CG HG =3cos θsin θ= 3. 所以tan θ=3,从而θ=60°, 即∠BDC =60°.方法二:(1)证明:如图所示,取BD 的中点O ,以O 为原点,OD ,OP 所在射线为y ,z 轴的正半轴,建立空间直角坐标系O -xyz .由题意知A (0,2,2),B (0,-2,0),D (0,2,0).设点C 的坐标为(x 0,y 0,0),因为AQ →=3QC →,所以Q34x 0,24+34y 0,12. 因为M 为AD 的中点,故M (0,2,1).又P 为BM 的中点,故P 0,0,12.所以PQ →=34x 0,24+34y 0,0. 又平面BCD 的一个法向量为=(0,0,1),故PQ →·=0. 又PQ ⊄平面BCD ,所以PQ ∥平面BCD .(2)设=(x ,y ,z )为平面BMC 的一个法向量. 由CM →=(-x 0,2-y 0,1),BM →=(0,2 2,1),知⎩⎨⎧-x 0x +(2-y 0)y +z =0,2 2y +z =0.取y =-1,得=y 0+2x 0,-1,2 2.又平面BDM 的一个法向量为=(1,0,0),于是|cos 〈,〉|=|m·n ||m||n|=y 0+2x 09+y 0+2x 02=12,即y 0+2x 02=3.① 又BC ⊥CD ,所以CB →·CD →=0,故(-x 0,-2-y 0,0)·(-x 0,2-y 0,0)=0,即x 20+y 20=2.② 联立①②,解得⎩⎨⎧x 0=0,y 0=-2(舍去)或⎩⎨⎧x 0=±62,y 0=22.所以tan ∠BDC =x 02-y 0= 3.又∠BDC 是锐角,所以∠BDC =60°.图1-521., 如图1-5所示,点P (0,-1)是椭圆C 1:x 2a 2+y 2b 2=1(a >b >0)的一个顶点,C 1的长轴是圆C 2:x 2+y 2=4的直径.l 1,l 2是过点P 且互相垂直的两条直线,其中l 1交圆C 2于A ,B 两点,l 2交椭圆C 1于另一点D .(1)求椭圆C 1的方程;(2)求△ABD 面积取得最大值时直线l 1的方程.21.解:(1)由题意得⎩⎪⎨⎪⎧b =1,a =2,所以椭圆C 的方程为x 24+y 2=1.(2)设A (x 1,y 1),B (x 2,y 2),D (x 0,y 0).由题意知直线l 1的斜率存在,不妨设其为k ,则直线l 1的方程为y =kx -1.又圆C 2:x 2+y 2=4,故点O 到直线l 1的距离d =1k 2+1,所以|AB |=24-d 2=24k 2+3k 2+1. 又l 2⊥l 1,故直线l 2的方程为x +ky +k =0.由⎩⎪⎨⎪⎧x +ky +k =0,x 2+4y 2=4. 消去y ,整理得(4+k 2)x 2+8kx =0. 故x 0=-8k 4+k 2,所以|PD |=8k 2+14+k 2.设△ABD 的面积为S ,则S =12·|AB |·|PD |=8 4k 2+34+k 2,所以S =324k 2+3+134k 2+3≤3224k 2+3·134k 2+3=16 1313,当且仅当k =±102时取等号.所以所求直线l 1的方程为y =±102x -1. 22. 已知a ∈,函数f (x )=x 3-3x 2+3ax -3a +3. (1)求曲线y =f (x )在点(1,f (1))处的切线方程; (2)当x ∈[0,2]时,求|f (x )|的最大值.22.解:(1)由题意 f ′(x )=3x 2-6x +3a ,故 f ′(1)=3a -3. 又f (1)=1,所以所求的切线方程为y =(3a -3)x -3a +4. (2)由于f ′(x )=3(x -1)2+3(a -1),0≤x ≤2,故①当a ≤0时,有f ′(x )≤0,此时f (x )在[0,2]上单调递减,故 |f (x )|max =max {|f (0)|,|f (2)|}=3-3a .②当a ≥1时,有f ′(x )≥0,此时f (x )在[0,2]上单调递增,故 |f (x )|max =max {|f (0)|,|f (2)|}=3a -1.③当0<a <1时,设x 1=1-1-a ,x 2=1+1-a ,则 0<x 1<x 2<2,f ′(x )=3(x -x 1)(x -x 2). 列表如下: x 0 (0,x 1) x 1 (x 1,x 2) x 2 (x 2,2) 2 f ′(x ) + 0 - 0 + f (x ) 3-3a单调 递增极大值 f (x 1)单调 递减极小值 f (x 2)单调 递增3a -1由于f (x 1)=1+2(1-a )1-a ,f (x 2)=1-2(1-a )1-a , 故f (x 1)+f (x 2)=2>0,f (x 1)-f (x 2)=4(1-a )1-a >0. 从而f (x 1)>|f (x 2)|.所以|f (x )|max =max{f (0),|f (2)|,f (x 1)}. (Ⅰ)当0<a <23时,f (0)>|f (2)|.又f (x 1)-f (0)=2(1-a )1-a -(2-3a )=a 2(3-4a )2(1-a )1-a +2-3a >0,故|f (x )|max =f (x 1)=1+2(1-a )1-a .(Ⅱ)当23≤a <1时,|f (2)|=f (2),且f (2)≥f (0).又f (x 1)-|f (2)|=2(1-a )1-a -(3a -2)=a 2(3-4a )2(1-a )1-a +3a -2.所以(i)当23≤a <34时,f (x 1)>|f (2)|.故f (x )max =f (x 1)=1+2(1-a )1-a . (ii)当34≤a <1时,f (x 1)≤|f (2)|.故f (x )max =|f (2)|=3a -1. 综上所述,|f (x )|max=⎩⎪⎨⎪⎧3-3a ,a ≤0;1+2(1-a )1-a ,0<a <34;3a -1,a ≥34.自选模块1. (1)解不等式|x -1|+|x -4|≥5.(2)求函数y =|x -1|+|x -4|+x 2-4x 的最小值.1.解:(1)当x <1时,1-x +4-x ≥5,得x ≤0,此时x ≤0; 当1≤x ≤4时,x -1+4-x ≥5,得3≥5,此时x ∈∅; 当x >4时,x -1+x -4≥5,得x ≥5,此时x ≥5.综上所述,原不等式的解集是(-∞,0]∪[5,+∞). (2)因为|x -1|+|x -4|≥|(x -1)-(x -4)|=3, 当且仅当1≤x ≤4时取等号;x 2-4x =(x -2)2-4≥-4,当且仅当x =2时取等号.故|x -1|+|x -4|+x 2-4x ≥3-4=-1,当x =2时取等号.所以y =|x -1|+|x -4|+x 2-4x 的最小值为-1.2., 已知a ∈“矩阵与变换和坐标系与参数方程”模块(1)以极坐标系Ox 的极点O 为原点,极轴Ox 为x 轴正半轴建立平面直角坐标系xOy ,并在两种坐标系中取相同的长度单位.把极坐标方程cos θ+ρ2sin θ=1化成直角坐标方程.(2)在直角坐标系xOy 中,曲线C :⎩⎨⎧x =2cos θ,y =sin θ(θ为参数),过点P (2,1)的直线与曲线C 交于A ,B 两点.若|P A |·|PB |=83,求|AB |的值. 2.解:(1)极坐标方程两边同乘以ρ得ρcos θ+ρ3sin θ=ρ.又在直角坐标系下,ρcos θ=x ,ρsin θ=y ,ρ2=x 2+y 2,故化成直角坐标方程为x +y (x 2+y 2)=x 2+y 2.又(0,0)满足原极坐标方程.故所求的直角坐标方程为x +y (x 2+y 2)=x 2+y 2.(2)由题意,曲线C 的直角坐标方程为x 2+2y 2=2.设过点P (2,1),倾斜角为α的直线的参数方程为⎩⎪⎨⎪⎧x =2+t cos α,y =1+t sin α(t 为参数). 及点A ,B 对应的参数分别为t 1,t 2.将直线的参数方程代入x 2+2y 2=2得(2+t cos α)2+2(1+t sin α)2-2=0.即(1+sin 2α)t 2+4(sin α+cos α)t +4=0.则Δ=16(2sin αcos α-sin 2 α)>0,且t 1+t 2=-4(sin α+cos α)1+sin 2 α,t 1t 2=41+sin 2 α, 由|P A |·|PB |=83得|t 1t 2|=41+sin 2 α=83. 故sin 2 α=12.又由Δ>0得0<tan α<2. 故t 1+t 2=8 23,t 1t 2=83. 所以|AB |=|t 1-t 2|=(t 1+t 2)-4t 1t 2=4 23.。
2012浙江省高等数学微积分竞赛(经管类)含答案
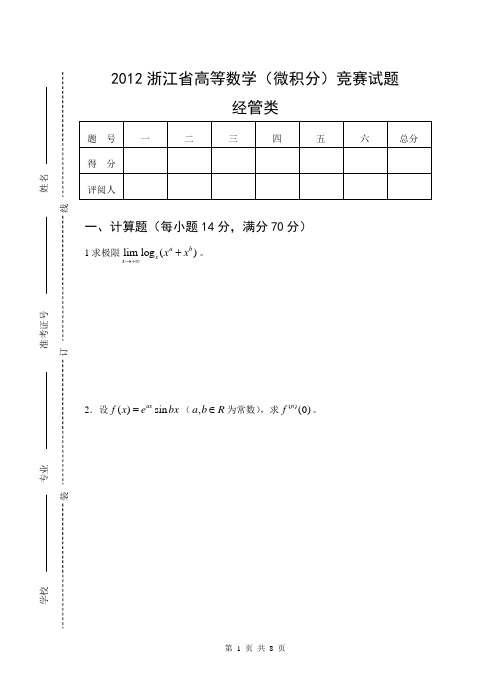
2012浙江省高等数学(微积分)竞赛试题经管类一、计算题(每小题14分,满分70分)1求极限lim log ()abx x x x →+∞+。
2.设()sin ax f x e bx =(,a b R ∈为常数),求()(0)n f 。
装 订线3.计算 0sin d n x x x π⎰(n 为正整数)。
4.求积分2241d 1x x x x+++⎰5.设函数21()2af x x x=+,0x >,常数0a >,试求最小的常数a ,使得()6f x ≥。
二、(满分20分)证明:111ln 1lnni n n n i =+<<+∑,n +∈三、(满分20分)求2211(21)2nn nn C n ∞=-∑的值。
四、(满分20分)在草地中间有一个半径为R 的圆形池塘,池塘边拴着一只山羊,拴山羊的绳子长为,(02)kR k <<,求山羊能吃到草的草地面积。
五、(满分20分)(1)求极限lim 2coscos cos 482nn n πππ→∞(2)证明2π=经管类一、计算题 1、若a b ≥l i m l o g (a b x x x x →+∞+l i m l o g(1)l i m l o g (1a b ab ax xx x x x a x a --→+∞→+∞=+=++= 同理,当a b<时,l i m l o ga b x x x x →+∞+b=, 所以l i m l o g a b x x x x →+∞+m a x (a b = 2、解:()sin cos ax ax f x ae bx be bx e bx bx ⎫'=+=⎪⎭)()cos sin sin cos sin ax e bx bx bx θθθ=+=+θ⎛⎫==⎝同理)()sin()cos()f x ea bxb bx θθ''=+++ 22()sin(2)ax a b e bx θ=++可得()()()()()()/2/222()22sin()0sin()n n n ax n fx a b e bx n f a b n θθ=++⇒=+3、解:sin d n x x x π⎰()011sin sin nnj j j j x x dx x j xdx ππππππ-====+-∑∑⎰⎰()()201sin d 21212nj n x x x j n n n n n n πππππ==+-=++-=+∑⎰4、解:2442222121(1)(1)x x x x x x x x x ++=++-=+++-()()22242221111111d d d 121121/23/41/23/4x x x x x x x x x x x x ⎛⎫+⎛⎫∴=+=+ ⎪ ⎪ ⎪++++-+⎝⎭++-+⎝⎭⎰⎰⎰1r c t a r C =+5、解:2()0a f x x x '=-=0x = 032()10a f x x ''=+> ()f x ∴f==6= 即8a =时 ()6f x ≥,且在02x =时,(2)6f = 所以min 8a =二、证明:显然11111d d j j jj x x x j x+-<<⎰⎰ 2j ≥1 1122111111d 1d 1ln nn n j n j j j j x x n j j x x -===∴=+<+=+=+∑∑∑⎰⎰另一方面111111111111d ln nn n j j j j j x n j jn x n n --+====+>+=+∑∑∑⎰三、解:[]2222221221(2)!(22)!(22)!1(21)2(21)2(!)2!(1)!22(1)!nn n n n n n n n C n n n n n nn ----===---- 而2212(21)122n n n n -=- 122222222111(21)222nn nn n n n n n C C C n ---∴=-- 而22102nn n C → ∴原级数1=四、解:以过拴羊点与池塘圆心为x 轴,拴山羊点为原点,则池塘边界圆为222()x R y R -+=而羊能跑的最大圆周为2222x y k R +=,易知在22R x k =时,两圆有两个交点2222012d 2R k S k R x π∴=+⎰222222arcsin (arcsin 22x x R R k R k R x R R k kR R π-⎛⎫=+-- ⎪⎝⎭2222arcsin 22k k R k R π=222221arcsin 14222k k R R R π⎛⎫⎛⎫---- ⎪ ⎪⎝⎭⎝⎭2222222arcsin arcsin 12222k k k R R k R R ππ⎛⎫=++-- ⎪⎝⎭五(1)解:coscos cos cos cos cos sin /sin 48248222n n n n n πππππππ= 1121111cos cos cos sin cos sin 4822442sin 2sin 2sin 222n n n n n n nn ππππππππ----===∴原极限22lim2sin2n n nππ→∞==(2)cos42π=c o s 8π===c o s 2n π==2cos cos cos 482n ππππ==。
历年浙江省高等数学(微积分)竞赛--工科类试题
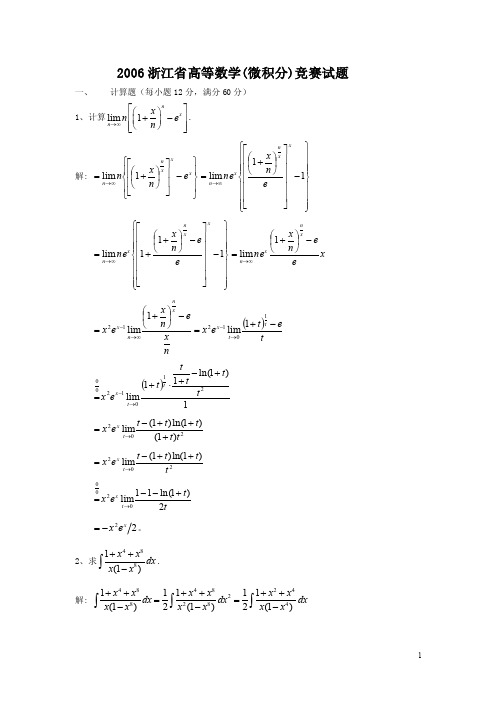
2006浙江省高等数学(微积分)竞赛试题一、计算题(每小题12分,满分60分)1、计算lim 1n x n x n e n →∞⎡⎤⎛⎫+-⎢⎥ ⎪⎝⎭⎢⎥⎣⎦.解: ⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧-⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+=∞→x x x n n e n x n 1lim ⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧-⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+=∞→11lim x x n x n e n x ne ⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧-⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡-⎪⎭⎫ ⎝⎛++=∞→111lim x x n x n e e n x ne x ee n x ne xnx n -⎪⎭⎫⎝⎛+=∞→1limn x en x e x xnn x -⎪⎭⎫ ⎝⎛+=∞→-1lim 12()te t e x t t x -+=→-10121lim()1)1ln(11lim2101200t t t tt e x t t x +-+⋅+=→- 202)1()1ln()1(lim t t t t t e x t x +++-=→ 22)1ln()1(limtt t t e x t x ++-=→ tt e x t x 2)1ln(11lim0200+--=→22x e x -=。
2、求4881(1)x x dx x x ++-⎰. 解: 4848242828411111(1)2(1)2(1)x x x x x x dx dx dx x x x x x x ++++++==---⎰⎰⎰242224211114(1)4(1)x x x x dx dx x x x x ++++==--⎰⎰ 3111122411411A B C dx dx x x x x x x ⎛⎫--⎪⎛⎫=++=++ ⎪ ⎪-+-+⎝⎭ ⎪⎝⎭⎰⎰ 131ln(1)ln ln(1)422x x x C ⎡⎤=--+-++⎢⎥⎣⎦311ln(1)ln ln(1)848x x x C =--+-++.3、求22110x y y e dy e dx x ⎡⎤-⎢⎥⎢⎥⎣⎦⎰⎰.解: 2222111111000x x y y y y ye e dy e dx dy dx dy e dx x x ⎡⎤-=-⎢⎥⎢⎥⎣⎦⎰⎰⎰⎰⎰⎰2211100x xy y e dx dy dy e dx x =-⎰⎰⎰⎰2221111(1)2x y x e e dx y e dy xe dx -=--==⎰⎰⎰. 4、求过(1,2,3)且与曲面3()z x y z =+-的所有切平面皆垂直的平面方程.解:令3(,,)()F x y z x y z z =+--则(,,)1x F x y z '=,2(,,)3()y F x y z y z '=-,2(,,)3()1z F x y z y z '=--- 令所求平面方程为: (1)(2)(3)0A x B y C z -+-+-=,在曲面3()z x y z =+-上取一点(1,1,1),则切平面的法向量为{1,0,1}-, 则0A C -=在曲面3()z x y z =+-上取一点(0,2,1),则切平面的法向量为{1,3,4}-, 则340A B C +-=. 解得: A B C ==即所求平面方程为: 6x y z ++=.二、(15分)设3()6xx f x e =-,问()0f x =有几个实根?并说明理由.解: 当0x ≤, 306xx e >≥当0x >, 00e >且xe 的增长速度要比36x 来得快!所以()0f x =无实根.三、(满分20分)求31n n x ∞=⎛⎫⎪⎝⎭∑中20x 的系数.解: 当1x <时, 33331111n n x x x x x ∞=⎛⎫⎛⎫⎛⎫==⋅ ⎪ ⎪ ⎪--⎝⎭⎝⎭⎝⎭∑3301122n n x x x x ∞=''''⎛⎫⎛⎫=⋅=⋅ ⎪ ⎪-⎝⎭⎝⎭∑ 322(1)2n n x n n x ∞-==-∑ 故31n n x ∞=⎛⎫ ⎪⎝⎭∑中20x 的系数为171.四、(20分) 计算C xyds ⎰,其中C 是球面2222x y z R ++=与平面0x y z ++=的交线. 解: 2222()()2()CCCx y z ds x y z ds xy yz zx ds ++=+++++⎰⎰⎰而2()0Cx y z ds ++=⎰,22223()2CCx y z ds R ds R π++==⎰⎰, CCCxyds yzds zxds ==⎰⎰⎰,故33CR xyds π=-⎰.五、(20分)设12,,,n a a a 为非负实数,试证:1sin sin nkk akx x =≤∑的充分必要条件为11nkk ka=≤∑.证明:必要性 由于1sin sin nk k akx x =≤∑,则1sin sin nkk kx xax x=≤∑, 0x ≠0011sin sin lim lim 1nnk k x x k k kx xa ka x x →→==⇒=≤=∑∑. 充分性;要证明1sin sin nkk akx x =≤∑,只需证明:1sin 1sin nkk akxx=≤∑,这里sin 0x ≠,若sin 0x =,不等式显然成立;即只需证明:1sin 1sin nkk kxa x=≤∑, 而11sin sin sin sin nnk kk k kx kx a a x x ==≤∑∑,11nk k ka =≤∑ 故只要说明:sin sin kxk x≤,即sin sin kx k x ≤, 当1k =时,显然成立;假设当k n =时,也成立,即sin sin nx n x ≤;当1k n =+时, sin(1)sin()sin cos sin cos n x nx x nx x x nx +=+=+sin sin (1)sin nx x n x ≤+≤+六、(15分)求最小的实数c ,使得满足1()1f x dx =⎰的连续函数()f x 都有1f dx c ≤⎰.解:1111)2()2()2f dx f dx t f t dx f t dx ≤=≤=⎰⎰⎰⎰,取2y x =,显然1()1f x dx =⎰,而110024233f dx ==⋅=⎰⎰,取(1)ny n x =+,显然1()1f x dx =⎰,而111(1)22,2nn f dx n dx n n +=+=⋅→→∞+⎰⎰, 故最小的实数2c =.2007浙江省高等数学(微积分)竞赛试题(解答)一.计算题(每小题12分,满分60分) 1、求9dx .解:9551155==1111555u t =+==-312222155u u C =-+ C x x ++-+215235)1(52)1(152。
2010浙江省高等数学(微积分)竞赛试题

2010浙江省大学生高等数学(微积分)竞赛试题(数学类)一、计算题(每小题14分,满分70分)1.求极限1lim 2n →+∞+⎦2.计算()22222exp 21R x xy y dxdy ρρ⎡⎤-+⎢⎥--⎢⎥⎣⎦⎰⎰. 其中01ρ≤< 3.请用,a b 描述圆 222x y y +≤ 落在椭圆 22221x y a b+= 内的充分必要条件,并求此时椭圆的最小面积。
4.已知分段光滑的简单闭曲线Γ(约当曲线)落在平面π:10ax by cz +++=上,设Γ在π上围成的面积为A ,求()()()bz cy dx cx az dy ay bx dzax by czΓ-+-+-++⎰Ñ其中n Γr与的方向成右手系。
5.设f 连续,满足()()() 22 02exp xf x x x t f t dt =--⎰且()11/f e =,求()()1n f 的值。
二、(满分20)定义数列{}n a 如下:{},,max ,211011dx x a a a n n ⎰-==Λ,4,3,2=n ,求n n a ∞→lim 。
三、(满分20分)设函数)(2R C f ∈,且0)(lim =∞→x f x ,1)(≤''x f ,证明:0)(lim ='∞→x f x 。
四、(满分20分)设非负函数f 在[0,1]上满足)()()(,,y f x f y x f y x +≥+∀且1)1(=f ,证明:(1)]1,0[,2)(∈≤x x x f (2)21)(1≤⎰dx x f五、(满分20分)设全体正整数集合为+N ,若集合+⊂N G 对加法封闭(即G y x G y x ∈+⇒∈∀,),且G 内所有元素的最大公约数为1,证明:存在正整数N ,当正整数n >N 时,G n ∈(工科类)一、计算题(每小题14分,满分70分)1.求极限1lim 2n →+∞+⎦2.计算()() +22 122dxx x x ∞-∞+-+⎰3.设ABC ∆为锐角三角形,求sin sin sin cos cos cos A B C A B C ++---的最大值和最小值。
2013年浙江专升本高等数学真题与答案解析(详细)

浙江省 2013 年选拔优秀高职高专毕业生进入本科学习统一考试高等数学请考生按规定用笔将所有试题的答案涂、写在答题纸上。
选择题部分注意事项:1.答题前,考生务必将自己的姓名、 准考证号用黑色字迹的签字笔或钢笔填写在答题纸规定的位置上。
2.每小题选出答案后,用2B 铅笔把答题纸上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。
不能答在试题卷上。
一、选择题: 本大题共5小题,每小题4分,共 20分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设()sin(cos 2),x f x x =-∞<<+∞,则此函数是 AA.有界函数B.奇函数C.偶函数D.周期函数 解:正弦函数都是有界的。
2.若函数y=f(x)是区间[1,5]上的连续函数,则该函数一定 A A.在区间[1,5]上可积 B 在区间(1,5)上有最小值 C.在区间(1,5)上可导 D.在区间(1,5)上有最大值 解:连续必定可积。
3.π0cos x xdx ⎰= DA. 0B.1C.-1D.-2解:000cos sin sin sin cos 2x xdx xd x x x xdx x πππππ==-==-⎰⎰⎰4.由曲线y =y x =所围成的平面图形的面积是 D A.3/2 B.1/2 C.1/3 D.1/6 解:交点为()()0,0,1,1,)13122002121132326S x dx x x ⎛⎫==-=-= ⎪⎝⎭⎰5.二阶微分方程263sin cos x y y y e x x '''+-=,则其特解的形式为B A 2(cos sin )x e a x b x + B.)2sin 2cos (2x b x a e x +C.2(cos sin )x xe a x b x +D.2(cos 2sin 2)xxe a x b x + 解:22363sin cos sin 22xx y y y e x x e x '''+-==,齐次方程的特征方程为:212603,2r r r r +-=⇒=-=,而2λ=,所以22ϖ±不是特征根,故选择B非选择题部分注意事项:1.用黑色字迹的签字笔或钢笔将答案写在答题纸上,不能答在试题卷上。
微积分竞赛试题答案

湖州师范学院高等数学(微积分)竞赛试题答案(数学专业)一、 计算题(每小题15分,满分60分)1. 计算:222sin )(cos 112lim2xe x xxxx -+-+→。
解:),(082114422x xxx+-+=+)(0811124422x x x x+=+-+。
又 )(023)](01[)](0211[cos 2222224x x x x x x e x x+-=++-+-=-,故 222sin )(cos 112lim2xe x xxxx -+-+→121sin )(023)(081lim sin 1)(023)(081lim 222244022222440-=⋅+-+=⋅⋅+-+=→→x x xx x x x x x x x x x x x 2.设2006)1(lim=--∞→ββαn nn n ,试求βα,的值。
解:ββα)1(--n n n=)1(0))1(01(1)11(11nn nnn nnn⋅+=+--=--+---βββαβαββα,显然由条件知0≠β,而⎪⎪⎩⎪⎪⎨⎧<+-=+->+-∞=⋅++-∞→,01,0,01,1,01,)1(0lim1βαβαββαββαn n n n 因此有,01=+-βα且20061=β,故20061,20062005=-=βα3. 求积分⎰+π2cos1sin dx xx x解:⎰+π2cos1sin dx xx x =⎰+22cos1sin πdx xx x +⎰+ππ22cos1sin dx xx x令t x -=π,有⎰⎰⎰+-=-+---=+222222c o s 1s i n )()(c o s 1)s i n ()(c o s 1s i n ππππππππdt tt t dt t t t dx xx x=⎰⎰+-+2222cos1sin cos1sin πππdx xx x dx xx所以⎰+π2cos1sin dx xx x =4|)(cos cos1sin 2222πππππ=-=+⎰x arctg dx xx4.计算二重积分⎰⎰Dy x dxdy e},max(22,其中}10,10|),{(≤≤≤≤=y x y x D 。
2013年浙江省高中数学竞赛试题解答 (2)

2013年浙江省高中数学竞赛试题解答一、选择题(本大题共有10小题,每题只有一个正确答案,将正确答案的序号填入题干后的括号里,多选、不选、错选均不得分,每题5分,共50分)1. 集合{,11P x x R x =∈-<},{,1},Q x x R x a =∈-≤且P Q ⋂=∅,则实数a 取值范围为( )A. 3a ≥B. 1a ≤-.C. 1a ≤-或 3a ≥D. 13a -≤≤答案 C {02},{11},P x x Q x a x a =<<=-<<+要使P Q ⋂=∅,则12a -≥或10a +≤。
解得1a ≤-或 3a ≥。
2. 若,,R αβ∈ 则90αβ+= 是sin sin 1αβ+>的( )A. 充分而不必要条件B. 必要而不充分条件C. 充要条件D. 既不充分也不必要条件答案 D 若0,90sin sin 1αβαβ==⇒+= 。
当60sin sin 1αβαβ==⇒+=> ,但90αβ+≠ 。
3. 已知等比数列{a n }:,31=a 且第一项至第八项的几何平均数为9,则第三项是( )A. D.答案 B 计算得2733,q a ==4. 已知复数(,,z x yi x y R i =+∈为虚数单位),且28z i =,则z =( )A.22z i =+B. 22z i =--C. 22,z i =-+或22z i =-D. 22,z i =+或22z i =--答案 D5. 已知直线AB 与抛物线24y x =交于,A B 两点,M 为AB 的中点,C 为抛物线上一个动点,若0C 满足00min{}C A C B CA CB ∙=∙,则下列一定成立的是( )。
A. 0C M AB ⊥B. 0,C M l ⊥其中l 是抛物线过0C 的切线C. 00C A C B ⊥D. 012C M AB =答案 B2()()()CA CB CM AM CM BM CM CM AM BM AM BM ∙=-∙-=-++∙22min min{}CM AM CA CB CM CM l =-⇒∙=⇔⊥。
2013年浙江省高等数学竞赛(数学类)参考答案

一、计算题(每小题 14 分,满分 70 分)
k - sin 2 k é 1.求极限 lim å ln ( n + k - sin 2 k ) - ln n ù 2 ë û。 n ®+¥ n k =1
n
k - 1 1 解:记 f ( x ) = x ln(1 + x ) , xk = , Dx k = n n
1 ( n ) 1 f n ( ) n n !
ln x + x n -1
( n -1)
( f n ( x ))( ) = ( nx n -1 ln x + x n -1 )
= n( f n -1 ( x ))(
n -1 )
+ ( n - 1) !
第 2 页 共 4 页
第 3 页 共 4 页
h ( t1 ) < h ( t2 )
所以 f ( x ) 严格单调增。
五、 (满分 20 分)
设 x1 = 1 , sin xn = xn cos xn +1
+¥ຫໍສະໝຸດ xn +1 Î ( 0, p / 2 ) ,证明:
n 收敛
1) lim xn = 0 。2)级数
0
1
1 1 1 x 2 1 ln 2 - ò dx = 2 2 0 x + 1 4
2.求异面面直线 L1 : 的方程。
x - 5 y - 1 z + 1 x + 2 y - 2 z - 4 = = 与 L2 : = = 的公垂线 L 4 -3 1 -2 9 2
解: l1 ´ l2 = -5{3, 2, -6} ,公垂线 L 法矢量为 l = {3, 2, -6}
2013年专升本高数真题答案解析(浙江)

浙江省2013年选拔优秀高职高专毕业生进入本科学习统一考试高等数学参考答案选择题部分一、选择题:本大题共5小题,每小题4分,共20分。
题号12345答案AADDB1.A 解析:因为1)2sin(cos1≤≤-x,所以函数)2sin(cos )(x x f =是有界函数,而且是非奇非偶函数,非周期函数,所以选项A 正确。
2.A 解析:由可积的充要条件可知,函数)(x f 在闭区间]5,1[上的连续,可推得)(x f 在闭区间]5,1[上可积,所以选项A 正确。
3.D 解析:()()2cos sin sin )(sin cos 0000-==-==⎰⎰⎰πππππx xdx x x x xd xdx x ,可见选项D 正确。
4.D 解析:根据题意可知:6121322132211231=-=-⎪⎪⎭⎫ ⎝⎛=-⎰x dx x ,所以选项D 正确。
5.B 解析:21x e x f x 2sin 23)(2=,(利用公式x x x 2sin 21cos sin =),故设特解为:)2sin 2cos(2x b x a e y x +=*,可见选项B 正确。
非选择题部分二、填空题:本大题共10小题,每小题4分,共40分。
6.0解析:0)cos(2lim )()sin()cos(2lim 1)sin(ln lim )sin(ln lim 2022202020=-=-⋅==→→→→x x x x x x xx x x x x x x7.[]()2,(21)ππ+∈k k k z 解析:由0sin 1≤≤x ,解得()2(21)ππ≤≤+∈k x k k z 8.2-解析:000(1)(1)(1)(1)(1)(1)limlim lim ∆→∆→∆→-∆-+∆-∆--+∆=+∆∆∆x x x f x f x f x f f f x x x x0(1)(1)(1)(1)limlim 2(1)2∆→∆→-∆--+∆'=--=-=--∆-∆x x f x f f f x f x x9.yxe e y ycos 1sin sin -解析:隐函数方程求导可知,方程sin 1=+yy xe两边同时对x 求导,得:sin sin cos ''=+⋅yyy e xey y ,即:yxe e y y ycos 1sin sin -='10.C x +ln ln (C 为任意常数)解析:(ln )ln ln ln ln ==+⎰⎰dx d x x C x x x (C 为任意常数)11.1sin ⎰x xdx解析:利用定积分的定义求极限可知,原式10111122331lim (sin sin sin sin1)lim sin sin →∞→∞==+++⋅⋅⋅+=⋅=∑⎰n n n i n i i x xdxn n n n n n n n n nn 12.(1,1)-解析:2123211lim )()(lim )(x x n n x x u x u x n n n nn n =⋅+==++∞→+∞→ρ,令1)(2<=x x ρ,解得:()1,1-∈x ,因此收敛区间为:()1,1-13.])([1)()(C dx e x Q eydx x P dxx P +⎰⎰⋅-⎰=-(C 为任意常数)解析:由伯努利方程,令y z 1=,z y 1=,dxdzz dx dy ⋅-=21,所以原方程可化为:221)(1)(1z x Q z x P dx dz z ⋅=⋅+⋅-,即:)()(x Q z x P dxdz -=⋅-,由一阶线性微分方程的通解公式可得:])([)()(C dx e x Q e z dx x P dx x P +⎰⎰⋅-⎰=-,即:])([1)()(C dx e x Q eydxx P dxx P +⎰⎰⋅-⎰=-(C 为任意常数)14.0323=-+-z y x 解析:由点法式可知,平面方程为:0)1(2)0(3)1(=-+---z y x ,即:0323=-+-z y x 15.264-解析:球心坐标为:)2,0,0(,半径2=R ,球心到平面2260+-+=x y z 的距离为:64)1(12262222=-+++-=h ,故所求距离为:264-=-=R h d三、计算题:本题共有8小题,其中16-19小题每小题7分,20-23小题每小题8分,共60分。
2012年浙江省高等数学(微积分)竞赛试题及答案 工科类

2012年浙江省高等数学(微积分)竞赛试题 工科类 一:计算题(每小题14分,共70分)1:计算:()+lim log +a ba n x x →∞2设函数f :R R →可导,且,x y R ∀∈,满足:()()+++f x y f x y xy ≥,求()f x 的表达式。
3计算: 0sin ,n x xdx n Z π*∈⎰4计算:{}-min ,2Dx y x y dxdy ⎰⎰,其中D 是2=y x 和2=x y 所围成的封闭区域。
5求曲线{33=cos =sin x a y a θθ()0,>0a θπ≤≤的形心。
二:(本题满分20分)证明:=111+ln <<1+ln ,ni n n n Z n i *∈∑三:(本题满分20分)设2:u RR →,且u 具有二阶连续偏导,求证当u 可以表示成:()()(),=u x y f x f y 的充分必要条件是:2=u u uu x y y y∂∂∂∂∂∂∂ 。
四:(本题满分20分)在空旷的草地上有一个地面半径为3的圆柱体,在墙角栓有一头山羊,其绳长为π,求山羊能吃到草地的面积。
五:(本题满分20分)求证:()-1=1=111-1C =,k nn k nk k n Z k k*∈∑∑参考答案一、计算题1、若a b ≥ l i m l o g(a bx x x x →+∞+l i m l o g(1)l i m l o g (1a b ab ax xx x x x a x a --→+∞→+∞=+=++= 同理,当a b <时,lim log ()a b x x x x →+∞+b =, 所以lim log ()a bx x x x →+∞+max(,)a b =2、解:由假设,0y ∀>,有()()1f x y f x x y+-≥+ f 可导()1f x x +'⇒≥+同理()1()1f x x f x x -''≤+⇒=+ 2()/2f x x x c =++ 3、解:sin d n x x x π⎰()011sin sin nnj j j j x x dx x j xdx ππππππ-====+-∑∑⎰⎰()()201sin d 21212nj n x x x j n n n n n n πππππ==+-=++-=+∑⎰4、解:(){}(){}12,1,,/2,01/2D x y x y x D x y x y x x =≤≤≤≤=≤≤≤≤(){}(){}2234,,1/21,,/2,01/2D x y xy x x D x y xy x x =≤≤≤≤=≤≤≤≤原积分12()d d ()d d D D y x x x y x y x x y =-+-⎰⎰⎰⎰34()d d ()d d D D x y x x y x y y x y +-+-⎰⎰⎰⎰211102d )d d ()d xxxx y x x y x x y x y =-+-⎰⎰⎰21112221002d ()d d ()2d xx xx x y x x y x x y y y +-+-⎰⎰⎰⎰11341456142210021211111()678851232x x x x x x x =-++-++146720112()24621x x x +-+111124724532245=++⨯⨯⨯⨯112533216642117920++=⨯⨯ 5、解:/0c LLx xds ds ==⎰⎰,d /d c LLy y s s =⎰⎰而d 3sin cos d s a θθθθ== 2d 3sin cos d sin cos 3Ls a ba d a ππθθθθθθ/===⎰⎰⎰/2324206d sin 3sin cos d 6sin cos d 5Ly s a x a a a ππθθθθθθθ===⎰⎰⎰0c x ∴= 25c y a =二、证明:显然11111d d j j jj x x x jx +-<<⎰⎰ 2j ≥1 1122111111d 1d 1ln nn n j n j j j j x x n j j x x -===∴=+<+=+=+∑∑∑⎰⎰另一方面111111111111d ln nn n j j j j j x n j jn x n n --+====+>+=+∑∑∑⎰三、证明:()()u f x g y =时,显然有xy x y uu u u = 反之,若xy x y uu u u =成立,即有2()/()0xxy x y y u uu u u u u-== 1/()x u u f x ⇒= 也即1121ln ()d ()()()u f x x g y f x g y =+=+⎰ ()()u f x g y ∴=四、解:(方法一)以圆柱形旁子的圆心为原点,拴羊点在x 轴上3x =点,则羊跑最远的曲线在3x <的区域内是渐开线 即 3(cos (/3)sin )x t t t π=-- 3(sin (/3)cos )y t t t π=+- 记在3x <山羊能吃到草的草地面积为1S3/30213/2/32d 29sin d 2(3sin (3)cos )(3)cos d S y x t t t t t t t t ππππ=-=+--⎰⎰⎰/32029sin d t t π-⎰/32223(3)sin cos (3)cos d t t t t t t πππ⎡⎤=-+-⎣⎦⎰/32029sin d t t π-⎰/322013(3)sin (3)(sin 2)2t t t t t πππ⎡⎤=-+-+⎢⎥⎣⎦/32016(3)(sin 2)9sin d 2t t t t t ππ⎡⎤+-+-⎢⎥⎣⎦⎰()/3/3/322000191133cos 2sin 29cos 2d 2222t t t t t t t t ππππ⎛⎫⎛⎫⎛⎫=----+- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎰33/319sin 2349t t ππ⎛⎫=+-=⎪⎝⎭所以山羊能吃到草的草地面积333119218S πππ=+= (方法二) 山羊能吃到草的草地面积S 可表示为一半圆与绳子绕向房子所能到达的面积1S 和 绳子绕向房子时转过θ∆ 其扫过的面积可近似为扇形22r θ∆()2/33103/9S d ππθθπ=-=⎰所以311/18S π=五、证明:111110011111(1)(1)d (1)d nn n k k k k k k k knn n k k k C C t t C t t k t ---===--=-=-∑∑∑⎰⎰ 1100(1)11(1)d d n n t t t t t t ----==⎰⎰101d 1nx x x -=-⎰ 而11100111d d 1nnn k k k t t t t k t -==1-==-∑∑⎰⎰ ∴等式成立。
2013年浙江专升本高等数学真题与答案解析(详细)

浙江省 2013 年选拔优秀高职高专毕业生进入本科学习统一考试高等数学请考生按规定用笔将所有试题的答案涂、写在答题纸上。
选择题部分注意事项:1.答题前,考生务必将自己的姓名、 准考证号用黑色字迹的签字笔或钢笔填写在答题纸规定的位置上。
2.每小题选出答案后,用2B 铅笔把答题纸上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。
不能答在试题卷上。
一、选择题: 本大题共5小题,每小题4分,共 20分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设()sin(cos 2),x f x x =-∞<<+∞,则此函数是 AA.有界函数B.奇函数C.偶函数D.周期函数 解:正弦函数都是有界的。
2.若函数y=f(x)是区间[1,5]上的连续函数,则该函数一定 A A.在区间[1,5]上可积 B 在区间(1,5)上有最小值 C.在区间(1,5)上可导 D.在区间(1,5)上有最大值 解:连续必定可积。
3.π0cos x xdx ⎰= DA. 0B.1C.-1D.-2解:000cos sin sin sin cos 2x xdx xd x x x xdx x πππππ==-==-⎰⎰⎰4.由曲线y =y x =所围成的平面图形的面积是 D A.3/2 B.1/2 C.1/3 D.1/6 解:交点为()()0,0,1,1,)13122002121132326S x dx x x ⎛⎫==-=-= ⎪⎝⎭⎰5.二阶微分方程263sin cos x y y y e x x '''+-=,则其特解的形式为B A 2(cos sin )x e a x b x + B.)2sin 2cos (2x b x a e x +C.2(cos sin )x xe a x b x +D.2(cos 2sin 2)xxe a x b x + 解:22363sin cos sin 22xx y y y e x x e x '''+-==,齐次方程的特征方程为:212603,2r r r r +-=⇒=-=,而2λ=,所以22ϖ±不是特征根,故选择B非选择题部分注意事项:1.用黑色字迹的签字笔或钢笔将答案写在答题纸上,不能答在试题卷上。
浙江省高中数学竞赛试题及解答

2013年浙江省高中数学竞赛试题解答一、选择题(本大题共有10小题,每题只有一个正确答案,将正确答案的序号填入题干后的括号里,多选、不选、错选均不得分,每题5分,共50分)1. 集合{,11P x x R x =∈-<},{,1},Q x x R x a =∈-≤且P Q ⋂=∅,则实数a 取值范围为( )A. 3a ≥B. 1a ≤-.C. 1a ≤-或 3a ≥D. 13a -≤≤答案 C {02},{11},P x x Q x a x a =<<=-<<+要使P Q ⋂=∅,则12a -≥或10a +≤。
解得1a ≤-或 3a ≥。
2. 若,,R αβ∈ 则90αβ+=o是sin sin 1αβ+>的( ) A. 充分而不必要条件 B. 必要而不充分条件 C. 充要条件 D. 既不充分也不必要条件 答案 D 若0,90sin sin 1αβαβ==⇒+=o。
当60sin sin 1αβαβ==⇒+=>o ,但90αβ+≠o。
3. 已知等比数列{an}:,31=a 且第一项至第八项的几何平均数为9,则第三项是( )A. D.答案 B 计算得2733,q a ==4. 已知复数(,,z x yi x y R i =+∈为虚数单位),且28z i =,则z =( ) A.22z i =+ B. 22z i =-- C. 22,z i =-+或22z i =- D. 22,z i =+或22z i =-- 答案 D5. 已知直线AB 与抛物线24y x =交于,A B 两点,M 为AB 的中点,C 为抛物线上一个动点,若0C 满足00min{}C A C B CA CB •=•u u u u r u u u u r u u u r u u u r,则下列一定成立的是( )。
A. 0C M AB ⊥B. 0,C M l ⊥其中l 是抛物线过0C 的切线C. 00C A C B ⊥D. 012C M AB =答案 B2()()()CA CB CM AM CM BM CM CM AM BM AM BM •=-•-=-++•u u u r u u u r u u u u r u u u u r u u u u r u u u u r u u u u r u u u u r u u u u r u u u u r u u u u r u u u u r 22min min{}CM AM CA CB CM CM l =-⇒•=⇔⊥u u u u u r u u u u r u u u u r u u u r u u u r。
浙江省高等数学竞赛试题与答案

(1) 若数列{yn} 满足条件
(a)
yn
>
0 ;(b) lim n→∞
yn
=
0 ;(c)
yn
=
a1 yn+1
+ a2 yn+2 , n
= 1, 2,3,L
证明 a1 + a2 > 1。
(2)若 a1 + a2 > 1,证明存在满足条件(a)、(b)、(c)的数列{yn} 。
5
证 设数列{yn} 满足条件(a)、(b)、(c),
n3π 1+ n
2
− nπ
⎞ ⎟ ⎠
=
∞
(−1)n+1an ,其中 an
n=1
=
sin
1
nπ + n2
→0
( ) 记
g(x)
=
sin
xπ 1+ x2
,
x
>
1 ,则因
g ′( x)
=
π
1− x2 1+ x2
2
xπ cos 1+ x2
<
0 ,故 an+1
<
an ,因此
∑ ∑ ∑ ∑ ∞
n=1
(−1)n+1an
2
22
22 2
5.假设立体 I 由1− z = x2 + y2 与 z = 0 围成,密度为 ρ ;立体 II 由1+ z = x2 + y2 与
z = 0 围成,密度为 1。若立体 I 和立体 II 组成的立体其重心位于原点 (0, 0, 0) ,求 ρ 的值。
∫∫∫ ρ z d x d y d z + ∫∫∫ z d x d y d z
浙江省2013年高考数学真题及答案

2013年普通高等学校招生全国统一考试(浙江卷)数 学(理科)选择题部分(共50分)注意事项:1.答题前,考生务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔分别填写在试卷和答题纸规定的位置上.2.每小题选出答案后,用2B 铅笔把答题纸上对应题目的答案标号涂黑,如需改动,用橡皮擦干 净后,再选涂其它答案标号。
不能答在试题卷上.参考公式:如果事件A ,B 互斥,那么 柱体的体积公式()()()P A B P A P B +=+ V Sh =如果事件A ,B 相互独立,那么 其中S 表示柱体的底面积,h 表示柱体的高 ()()()P A B P A P B ⋅=⋅ 锥体的体积公式如果事件A 在一次试验中发生的概率是p ,那么 13V Sh =n 次独立重复试验中事件A 恰好发生k 次的概率 其中S 表示锥体的底面积,h 表示锥体的高()()()1,0,1,2,,n k k k n n P k C p p k n -=-= 球的表面积公式台体的体积公式 24πS R =()1213V h S S = 球的体积公式 其中12,S S 分别表示台体的上底、下底面积, 34π3V R = h 表示台体的高 其中R 表示球的半径一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1, 已知i 是虚数单位,则()()12i i -+-=A ,3i -+B ,13i -+C ,33i -+D ,1i -+2, 设集合{}{}22,340S x x T x x x =>-=+-≤,则()R C S T =U A ,(]2,1- B ,(],4-∞- C ,(],1-∞ D ,[)1,+∞3,已知,x y 为正实数,则A ,lg lg lg lg 222x y x y +=+ B ,()lg lg lg 222x y x y +=g C ,lg lg lg lg 222x yx y =+g D ,()lg lg lg 222xy x y =g 4,已知函数()()()cos 0,0,f x A x A R ωϕωϕ=+>>∈,则“()f x 是奇函数”是“2πϕ=”的A ,充分不必要条件B ,必要不充分条件C ,充分必要条件D ,既不充分也不必要条件5,某程序框图如图所示,若该程序运行后输出的值是95,则 A ,4a = B ,5a = C ,6a = D ,7a =6,已知,sin 2cos R ααα∈+=,则tan 2α= A ,43 B ,34 C ,34- D ,43- 7,设∆ABC ,0P 是边AB 上一定点,满足014P B AB =,且对于边 AB 上任一点,恒有PB PC ≥00P B P C .则A ,90ABC ∠=oB ,90BAC ∠=o C ,AB AC =D ,AC BC =8,已知e 为自然对数的底数,设函数()()()()111,2k x f x e x k =--=,则A ,当1k =时,()f x 在1x =处取到极小值B ,当1k =时,()f x 在1x =处取到极大值C ,当2k =时,()f x 在1x =处取到极小值D ,当2k =时,()f x 在1x =处取到极大值9,如图,12,F F 是椭圆221:14x C y +=与双曲线2C 的公共焦点,,A B 分别是12,C C 在第二、四象限的公共点,若四边形12AF BF 为矩形,则2C 的离心率是A B C ,32 D ,210,在空间中,过点A 作平面π的垂线,垂足为B ,记().B f A π=设,αβ是两个不同的平面,对空间任意一点P ,()()12,Q f f P Q f f P βααβ⎡⎤==⎡⎤⎣⎦⎣⎦,恒有12PQ PQ =,则A ,平面α与平面β垂直B ,平面α与平面β所成的(锐)二面角为45oC ,平面α与平面β平行D ,平面α与平面β所成的(锐)二面角为60o2013年普通高等学校招生全国统一考试(浙江卷)数 学(理科)非选择题部分(共100分)注意事项:1.用黑色字迹的签字笔或钢笔将答案写在答题纸上,不能答在试题卷上.2.在答题纸上作图,可先使用2B 铅笔,确定后必须使用黑色字迹的签字笔或钢笔描黑.11,设二项式5的展开式中常数项为A ,则A = 12,某几何体的三视图(单位:cm )如图所示,则此几何体的体积等于 3cm13,设z kx y =+,其中,x y 满足20240240x y x y x y +-≥⎧⎪-+≥⎨⎪--≤⎩,若z 的最大值为12,则实数k =14,将,,,,,A B C D E F六个字母排成一排,且,A B 均在C 的同侧,则不同的排法共有 种(用数字作答)15,设F 为抛物线2:4C y x =的焦点,过点()1,0P -的直线l 交抛物线C 于,A B 两点,点Q 为线段AB 的中点,若2FQ =,则直线l 的斜率等于16,在ABC V 中,90C ∠=o ,M 是BC 的中点。
浙江省历年高数竞赛试题及解答

浙江省首届数学分析竞赛试题(2002.12.7)一.计算题(每小题5分,共30分)1.求极限limx →。
2.求积分|1|Dxy dxdy -⎰⎰,11{(,)2,2}22D x y x y =≤≤≤≤。
3.设2x y x e =是方程hx y ay by ce '''++=的一个解,求常数,,,a b c h 。
4.设()f x 连续,且当1x >-时,2()[()1]2(1)xx xe f x f t dt x +=+⎰,求()f x 。
5.设211arctan2nnk S k ==∑,求lim n n S →∞。
6.求积分12121(1)x x x e dx x++-⎰。
二. (15分)求平面221x y z +-=含在椭圆柱体22149x y +=内的面积。
三. (20分)证明:20)0x dx >。
四.(20分)设二元函数(,)f x y 有一阶连续的偏导数,且(0,1)(1,0)f f =。
证明:单位圆周上至少存在两点满足方程(,)(,)0yf x y x f x y x y∂∂-=∂∂。
五.(15分)设11a =,21a =,2123n n n a a a ++=+,1n ≥,求1nn n a x ∞=∑的收敛半径,收敛域及和函数。
2002年浙江省高等数学竞赛试题及解答一、计算题 1. 求极限x →解:原式())()01cos 1lim1xx x ex→-+=-()201cos 2lim1x x x x xe →-=-12112=⋅⋅=. 2. 求积分1D I xy dxdy =-⎰⎰,()11,:2,222D x y x y ⎧⎫=≤≤≤≤⎨⎬⎩⎭.解:记(){}1,:,1D x y xy D xy =∈≥,(){}2,:,1D x y xy D xy =∈≤,()()1211D D I xy dxdy xy dxdy =-+-⎰⎰⎰⎰()()1222111122211x xdx xy dy dx xy dy =-+-⎰⎰⎰⎰222112222211111111222222x dx x dx x x x x ⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=---+--- ⎪ ⎪ ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦⎰⎰2211221111222822x dx x dx x x ⎛⎫⎛⎫=+-++- ⎪ ⎪⎝⎭⎝⎭⎰⎰212171582x dx x ⎛⎫=+- ⎪⎝⎭⎰2217111512l n 2l n 2822222⎛⎫⎛⎫⎛⎫=⋅-+--- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭152ln 264=+. 3. 设2xy x e =是方程hxy ay by ce '''++=的一个解,求常数a ,b ,c ,h .解:()22x y x x e '=+,()242x y x x e ''=++,代入方程,得()()21422x hxa b x a x e ce ⎡⎤+++++=⎣⎦, 于是 1242010h c a a b =⎧⎪=⎪⎨+=⎪⎪++=⎩,故2a =-,1b =,2c =,1h =.4. 设()f x 连续,且当1x >-时,()()()20121xxxe f x f t dt x ⎡⎤+=⎢⎥⎣⎦+⎰,求()f x . 解:由条件可知()00f =,()()()2211xx f t dt xe x -'⎡⎤+=+⎢⎥⎣⎦⎰,()()()()21111x xt f t dt te d t -+-=-+⎰⎰()11xxt xe x e dt -=-++⎰()111xxxe x e -=-++-11x e x=-+, ()()211xxe f t dt x +=+⎰,()01x f t dt +=⎰()()23221xxef x x =±+.5、 设211arctan2nnk S k==∑,求lim n n S →∞. 解:利用公式arctan arctan arctan1x yx y xy--=+,2111arctan arctan arctan 22121k k k =--+,211arctan 2nn k S k ==∑111arctan arctan 2121nk k k =⎛⎫=- ⎪-+⎝⎭∑1a r c t a n 1a r c t a n 21n =-+,lim 4n n S π→∞=;211arctan 24k k π∞==∑. 由2211arctanarctan arctan 441222k k k k=--+-, 得2221arctan arctan 4412k k k ∞==-+∑. 6. 计算积分121211x x I x e dx x +⎛⎫=+- ⎪⎝⎭⎰.解法一 因为111x x x e x +⎛⎫+- ⎪⎝⎭111x x x x e x e x ++⎛⎫=+- ⎪⎝⎭1x x xe +'⎛⎫= ⎪⎝⎭,所以1212x xI xedx +'⎛⎫= ⎪⎝⎭⎰ 21521232x x xe e +⎛⎫== ⎪⎝⎭. 解法二112211221x x xx I edx x e dx x ++⎛⎫=+- ⎪⎝⎭⎰⎰11221122x x xxedx xde++=+⎰⎰211122111222x x x xxx edx xee dx +++⎛⎫=+- ⎪⎝⎭⎰⎰5232e =.解法三 分析:观察被积函数的特点,令1u x=做代换,利用定积分的“递推方法”求I , 令1u x=,则11222111u u I u e du u u +⎛⎫⎛⎫=+-- ⎪ ⎪⎝⎭⎝⎭⎰112211u u u e d e u ⎛⎫⎛⎫=+- ⎪ ⎪⎝⎭⎝⎭⎰1111112222222111111u u u u u u u e e u e e du e e du u u u ⎡⎤⎛⎫⎛⎫⎛⎫=+--+----⎢⎥ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎣⎦⎰⎰1111522222211311u u u u e u e du e du u u ++⎛⎫⎛⎫=--+--- ⎪ ⎪⎝⎭⎝⎭⎰⎰11152221221131u u u u e u e du e d u u u ++⎛⎫⎛⎫=--+-+ ⎪ ⎪⎝⎭⎝⎭⎰⎰1152223u u e I e +⎛⎫=-- ⎪⎝⎭523e I =-,所以5232I e =.二、求平面221x y z +-=含在椭圆柱体22149x y +=内的面积.解:112z x y =+-,()22,:149x y D x y ⎧⎫=+≤⎨⎬⎩⎭,DS =D=32D d x d y =⎰⎰ 32392ππ=⋅⋅⋅=.三、证明:()200x dx >.证明:令2xu =,则()22sin x dx u π=⎰2012πππ⎛⎫=+ ⎪⎝⎭⎰⎰00sin 12t πππ+⎛⎫=+ ⎪⎝⎭⎰⎰0012ππ⎛⎫=+ ⎪⎝⎭⎰⎰01sin 2u du π=-⎰ 0>. 同理可证20sin 0xdx xπ>⎰. 四、设二元函数(),f x y 有一阶连续的偏导数,且()()0,11,0f f =,证明:在单位圆周上至少存在两点满足方程()(),,0y f x y x f x y x y∂∂-=∂∂. 证明:令cos x θ=,sin y θ=,()()cos ,sin F f θθθ=,()02θπ≤≤;因为(),f x y 有一阶连续的偏导数,所以()F θ可导.()()sin cos f f f fF y x x y x yθθθ∂∂∂∂'=-+=-+∂∂∂∂, 由条件,得()()01,0Ff =,()0,12F f π⎛⎫= ⎪⎝⎭,()()21,0F f π=, ()02F F π⎛⎫= ⎪⎝⎭,()22F F ππ⎛⎫= ⎪⎝⎭,利用罗尔中值定理,得 存在10,2πθ⎛⎫∈ ⎪⎝⎭,使得()10F θ'=, 存在2,22πθπ⎛⎫∈ ⎪⎝⎭,使得()20F θ'=,即得在单位圆周上至少存在两点满足方程()(),,0y f x y x f x y x y∂∂-=∂∂. 五、设11a =,21a =,2123n n n a a a ++=+,()1,2,n =,求1nn n a x ∞=∑的收敛半径,收敛域及和函数. 解:由条件可知, ()2113n n n n a a a a ++++=+,()21133n n n n a a a a +++-=--,于是()2121332n n n n a a a a +++=+=,()()()212131321nnn n a a a a ++-=--=--,从而()()14231nn n a +=+-,()()11312nnn a +=+-,()1,2,n = 因此()()111312n n n a --=+-,()1,2,n =.因为()111133lim lim3113nn n n n n naa -+-→∞→∞-+==⎛⎫+- ⎪⎝⎭,所以收敛半径13r=; ()111111312n nn n n n n n n a x x x ∞∞∞--===⎛⎫=+- ⎪⎝⎭∑∑∑的收敛域为11,33⎛⎫- ⎪⎝⎭; ()11111111312n nn n n n n n n a x x x x ∞∞∞----===⎛⎫=+- ⎪⎝⎭∑∑∑ 1112131x x x ⎛⎫=+ ⎪-+⎝⎭.(五)、设{}n a ,{}n b 为满足1n n ab n e a e +=+,()1,2,n =的两个实数列,已知0na >,()1,2,n =,且1n n a ∞=∑收敛. 证明:1n n b ∞=∑也收敛.证明:由1nn a∞=∑收敛,得lim 0nn a →∞=,由1nn b a n e e a +=-,得 lim 0n n b →∞=,由1n n n a b b n e a e e +=+>,得 1n n a b +>,显然()111n na b nn n eea+∞∞==-=∑∑收敛,因为111lim lim 1n n n n n a b n n a b e e eξ++→∞→∞-==-,所以()11n n n ab ∞+=-∑收敛,()11n n n n b a a b ++=--,11n n n n b a b a ++≤-+,于是1nn b∞=∑收敛,1nn b∞=∑收敛.或者()()1ln ln 1n nb b n n n n a e a b a e -+=+=++,()1ln 1limlim 1nb n n n n n nna e ab a a -+→∞→∞+-==,()11n n n a b ∞+=-∑收敛,从而1n n b ∞=∑收敛.(五)、设0na >,()1,2,n =,且nna b n ea e=+,()1,2,n =,若1n n a ∞=∑收敛.,试证1nn nb a ∞=∑收敛.证明:由1nn a∞=∑收敛,得lim 0nn a →∞=,由nn b a n ee a =-,得 lim 0n n b →∞=,因为()22ln lim lim lim n na n n nn n n n n nb e a a b a a a →∞→∞→∞-==()20ln 1lim 2x x e x x +→-==, 又1n n a ∞=∑收敛,所以1nn nb a ∞=∑收敛.(五) 、设0na >,()1,2,n =,1n n a ∞=∑收敛,且nn n aa b n e a e +=+,()1,2,n =,证明:1nn b∞=∑也收敛.证明:由1nn a∞=∑收敛,得lim 0nn a →∞=,再由nn n a a b n e a e +=+,得 lim 0n n b →∞=,()ln n a n n na b e a +=-,()ln n a n n n b e a a =--,()()10ln ln limlim 0n a xnn x ne a ex a x++→∞→--==,()1ln na nn ea ∞=-∑收敛,所以1nn b∞=∑收敛,1nn b∞=∑收敛.()ln n a n n na b e a +=-,因为2limlim n nn n n n n n na b a a ba a →∞→∞++=()()220ln ln 1limlim 2n a xnn x ne a ex a x +→∞→--===,所以1nnn n a b a ∞=+∑收敛,1nn nb a ∞=∑发散.2004年浙江省大学生高等数学(微积分)竞赛试题(工科类) 一. 计算题(每小题15分,满分60分)1. 计算:()()200cos 2lim tan 1x tx x e tdt x x x →----⎰。
2009年浙江省高等数学(微积分)竞赛试题及参考答案[1]
![2009年浙江省高等数学(微积分)竞赛试题及参考答案[1]](https://img.taocdn.com/s3/m/4f22eb3010661ed9ad51f316.png)
2009年浙江省高等数学(微积分)竞赛试题及参考答案(文专类)一、计算题(每小题12分,满分60分)1.求极限211lim sin n n i i i n n π→∞=∑解 211l i m s i n n n i i i n n π→∞=∑=10sin x xdx π⎰=11cos xd x ππ-⎰=11001(cos cos )x x xdx πππ--⎰=111(1sin )x πππ---=1π2.计算不定积分解=43-⎰=C3.设2100()(tan1)[(tan2)(tan100)]444xx x f x πππ=---L ,求(1)f '解 2100()(tan1)[(tan2)(tan100)]444xx x f x πππ=---L21002()sec[(tan2)(tan100)]4444xx x f x ππππ'=--L2100(tan1)[(tan2)(tan100)]444xx x πππ'+---L2(1)sec [(12)(1100)]44f ππ'=--L =99!2π-⨯4.设cot cos 2sin x tt y t =⎧⎪⎨=⎪⎩,(0,)t π∈,求此曲线的拐点解csc cot 2cos dy t t t dt =--,2csc dx t dt =- 2cos (12sin )dy t t dx =+,2323sin cos 2d y t t dx=-令220d ydx=得123,44t t ππ==当04t π<<时,220d ydx<,当344t ππ<<时,220d ydx>, 当34t ππ<<时,220d ydx<, 因此拐点为(1,0),(1,0)-5.已知极限212lim()1x x x e ax bx →++=,求常数的值,a b解 212lim()xx x e ax bx →++=221lim(1)x x e ax bx x e →++-⋅= 0(2)lim2x x e ax b x e→++=1于是0lim(2)0xx e ax b →++=,1b =-由0(2)lim02x x e a →+=,得12a =- 另解 2222111221lim()lim(11)x xe ax bx x xx eax bx x x x e ax bx e ax bx ++-++-→→++=+++-221limx x e ax bx x e -++-==12222220011()112lim lim xx x x x o x ax bx e ax bx x x --+++++-++-= 22201(1)()()12lim 0,12x b x a x o x a b x -++++==⇒=-=- 二、(满分20分)设(0)0,0()1f f x '=<<,证明:当0x >时,230(())()xxf t dt f t dt >⎰⎰证 设230()(())()xxF x f t dt f t dt =-⎰⎰则(0)0F =,20()()[2()()]xF x f x f t dt f x '=-⎰,由(0)0f =且0()1f x '<<,知当0x >时,()0f x >。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2013浙江省高等数学(微积分)竞赛试题数学类一、计算题(每小题14分,满分70分)1.求极限()2221sin lim ln sin ln nn k k kn k k n n →+∞=-⎡⎤+--⎣⎦∑。
2.求异面面直线1:L 511431x y z --+==-与2224:292x y z L +--==-的公垂线L 的方程。
装订线3.求积分()()sin sin x a dx x b ++⎰,其中为,a b 常数。
4.设()cos xf x e x =,证明()()02n nn f x +∞=∑收敛并求和函数。
5.已知二元函数(),u x y 满足20u ux y y∂∂+=∂∂∂,且20,x uy ==1cos y ux ==,求(),u x y 的表达式。
二、(满分20)设()ln n n f x x x =,证明极限()11lim !n n n f n n →+∞⎛⎫⎪⎝⎭存在。
三、(满分20分)设f 在[]0,1上连续,在()0,1上可导,()()010f f ==,证明:() 0,1 x ∀∈()()()0,1 f f x ξξ'∃∈=。
四、(满分20分)证明:()()1 01x f x x αβαβ-=>>-在()0,1上严格单调增。
五、(满分20分)设数列{}n x 满足:11x =,()0,/2n x π∈,1sin cos n n n x x x +=,1,2,n = 证明:1)lim 0n n x →+∞= ;2)级数1nn x+∞=∑收敛。
2013浙江省高等数学(微积分)竞赛试题数学类参考答案一、计算题(每小题14分,满分70分)1.求极限()2221sin lim ln sin ln nn k k kn k k n n →+∞=-⎡⎤+--⎣⎦∑。
解:记()ln(1)f x x x =+, 11,k k k x x n n -=∆= 1k k x ξ-<2s i n k k kx n-=< ()()22211sin ln sin ln nnk k k k k k n k k n f x n ξ==-⎡⎤+--=∆⎣⎦∑∑ 原极限10ln(1)x x dx =+=⎰210111ln 22214x dx x =-=+⎰ 2.求异面面直线1:L 511431x y z --+==-与2224:292x y z L +--==-的公垂线L 的方程。
解:{}1253,2,6l l ⨯=--,公垂线L 法矢量为l = {}3,2,6-过公垂线L 与1L 的平面1π,其法矢量为{}1116,27,17n l l =⨯=取1L 上点()15,1,1M -,则方程为 ()()()1652711710x y z -+-++= 即1π:16271790x y z ++=同理可得过公垂线L 与2L 的平面2π的方程为:5863120x y z ++= 所以公垂线L 的方程为162717905863120x y z x y z ++=⎧⎨++=⎩3.求积分()()sin sin x a dx x b ++⎰,其中为,a b 常数。
解:()()()()()sin sin cos cos sin x a x b a b x b a b +=+-++-()()()()()()sin cos cos sin sin sin x a x b dx a b x a b dx x b x b ++=-+-++⎰⎰ ()()()cos sin ln sin a b x a b x b c =-+-++4.设()cos xf x e x =,证明()()02n nn f x +∞=∑收敛并求和函数。
解:()()cos sin cos /4x xx f x e x e x x π'=-=+所以 ()()()cos /4nn x fx e x n π=+()()n nxfx e ≤ 所以()()02n xnn n f x +∞+∞==≤∑收敛。
且()()2n nn f x +∞=∑()()()/410Re Re 1cos sin x ix in x i x n e i e x x π+∞+=⎡⎤==+=-⎣⎦ 5.已知二元函数(),u x y 满足20u ux y y∂∂+=∂∂∂,且20,x uy ==1co s y ux ==求(),u x y 的表达式。
解: ()x u u c x += ()()()()xx x x x x eu u e c x e u e c x ⇒+=⇒=()()()()x x x e u e c x dx g y u f x e g y -⇒=+⇒=+⎰ ,f g 为为任意函数()()()()222000x uy f g y y g y y f ==⇒+=⇒=- 1cos y ux ==()()()()1cos cos 1x x f x e g x f x x e g --⇒+=⇒=-()()()()22cos 01cos 1x x x u x e y e f g x e y ---=+-+=+-二、(满分20)设()ln n n f x x x =,求()11lim()!n n n n f n →+∞解:()11ln n n n f x nx x x --'=+()()()()(1)1111(())ln (())1!n n n n n n n f x nx x x n f x n -----=+=+-()()()11111(())(())!1!n n n n f x f x n n n --=+-()121111ln 1!n nk k f x x k k=='=+=+∑∑ 记()()11!nn n n n x f =11ln nk n k ==-∑ 则11111ln01n n n n n x x dx n n n x ---=-=-<-⎰ 且111111111ln ln n k n n kk x x dx n dx n x n n n-+=>+-=+-=∑⎰⎰ 即{}n x 单调减有下界所以{}n x 收敛 所以()()11!lim n nn n n f c →+∞= 欧拉常数 三、(满分20分)设f 在[]0,1上连续,在()0,1上可导,()()010f f ==,证明:() 0,1 x ∀∈()()()0,1 f f x ξξ'∃∈=。
解:() 0,1 x ∀∈若 ()=0 f x 则由罗尔定理 ()()()0,1 0f f x ξξ'∃∈==若 ()0 f x ≠ 则考虑函数 ()()()g t f t tf x =-()()()()2110g x g x f x =--< 所以(),1 x η∃∈()0g η= 又()00g =所以 ()()0, 0g ξηξ'∃∈= 即()() 0f f x ξ'-=四、(满分20分)证明:()()1 01x f x xαβαβ-=>>-在()0,1上严格单调增。
解:()f x 严格单调增等价于()1 (=1)1t h t t λαλβ-=>-的严格单调增记()1g t t λ=- 则 ()2(1)0g t tλλλ-''=--< 从而 ()g t 是凸函数所以12 1t t ∀<< 2212112121111 0 011t t tt t t t λλλλ--=+⨯=>=>-- ()()()21121g t g t g λλ>+()21111t g t t -=- ()()212111g t g t t t ⇒>--()()12h t h t < 所以()f x 严格单调增。
五、(满分20分)设11x =,1sin cos n n n x x x += ()10,/2n x π+∈,证明: 1)lim 0n n x →+∞= 。
2)级数1nn x+∞=∑收敛解:由微分中值定理 得()0,1ξ∃∈ 使2sin1sin 0cos cos x ξ-==21x ξ⇒=< 一般地1sin sin0cos cos n n n n x x x x ξ+-==11n n x x ξ+⇒=<<3sin /6n n n x x x >- 24111cos 1/2/24n n n x x x +++<-+3/6n n x x ⇒-()24111/2/24n n n x x x ++<-+24211/12/3n n n x x x ++⇒-<因为1n x < 所以()()2222111111/121/12/32n n n n n n x x x x x x ++++-<-<⇒<1n n x -⇒≤ 所以1)lim 0n n x →+∞= 2)级数111n n n n x +∞+∞-==≤∑∑收敛。
