浙江省名校新高考研究联盟Z联盟届第一次联考信息技术答案
浙江省名校新高考研究联盟Z联盟新届第一次联考信息技术答案完整版

浙江省名校新高考研究联盟Z联盟新届第一次联考信息技术答案HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】浙江省名校新高考研究联盟(Z20联盟)2019届第一次联考技术参考答案第一部分信息技术(共50分)一、选择题(本大题共12小题,每小题2分,共24分)二、非选择题(本大题共5小题,其中第13小题4分,第14小题5分,第15小题8分,第16小题3分,第17小题6分,共26分)13.(1)= 110*(D3-E3)*C3 (1分)(2)F8 (1分)(3)A2:E3 (1分)(4)B (1分)14.(1)Btn (不区分大小写) (1分)(2)①n = Len(s) 或n = Len (1分)②n1 + n2 + n3 < n-1 or n2 = 0 or n3 = 0 (2分)或 n1 + n2 + n3 <>n-1 or n2 * n3 = 0(3)不合法(1分)15.(1)A (1分)(2)动画补间 (或其他等价答案) (1分)(3)将“诗人”图层第12帧复制到第1帧 (或其他等价答案) (1分)(4)load main end (1分)(5)AD (2分)(6)getURL(""); stopAllSounds(); (2分)16.(1)count = 1 (1分)(2)a(j) = a(j - 1) + 1 (或其他等价答案) (2分)17.(1)70007 (1分)(2)①p <= n 或 val(p)<=val(n)(1分)②i=i-1 (2分)③ln Mod 2 = 0 Or i < (ln + 1) \ 2 (2分)或not (ln Mod 2 = 1 and i =(ln + 1) \ 2。
浙江省名校新高考研究联盟2024-2025学年高三上学期第一次联考(暑假返校考)数学试题(解析版)

Z20名校联盟(浙江省名校新高考研究联盟)2025届高三第一次联考数学试题卷(答案在最后)考生须知:1.本卷满分150分,考试时间120分钟.2.答题前务必将自己的姓名,准考证号用黑色字迹的签字笔或钢笔分别填写在试题卷和答题纸规定的地方.3.答题时,请按照答题纸上“注意事项”的要求,在答题纸相应的位置上规范答题,在本试卷纸上答题一律无效.4.考试结束后,只需上交答题卷.第Ⅰ卷一、单选题:本题共8小题,每小题5分,共40分.在每小题给出的选项中,只有一项是符合题目要求的.1.已知集合{}220,{230}A x x xB x x =--≤=-<∣∣,则A B = ()A.[]2,1- B.31,2⎡⎫-⎪⎢⎣⎭C.3,2⎛⎫-∞ ⎪⎝⎭D.(],1-∞-【答案】B 【解析】【分析】根据题意求集合,A B ,再结合交集运算求解.【详解】由题意可得:{}3|12,|2A x x B x x ⎧⎫=-≤≤=<⎨⎬⎩⎭,所以3|12A B x x ⎧⎫⋂=-≤<⎨⎬⎩⎭.故选:B .2.7212x x ⎛⎫- ⎪⎝⎭的展开式中21x 项的系数是()A.672B.420- C.84D.560-【答案】D【解析】【分析】根据题意结合二项式定理可得()7731712C rr rr r T x --+=-⋅⋅⋅,令732r -=-运算求解即可.【详解】由题意可知:7212x x ⎛⎫- ⎪⎝⎭的展开式通项为()()777317721C 212C ,0,1,,7rrr rr rr r T x x r x ---+⎛⎫=-=-⋅⋅⋅=⋅⋅⋅ ⎪⎝⎭,令732r -=-,解得3r =,所以21x项的系数是()343712C 560-⋅⋅=-.故选:D .3.已知等差数列{}n a 前n 项和为n S ,若751213a a =,则139SS =()A.913B.1213 C.75D.43【答案】D 【解析】【分析】根据给定条件,利用等差数列前n 项和公式、等差数列性质计算即得.【详解】在等差数列{}n a 中,由751213a a =,得113137199513()131312429()991332a a S a a a S a +===⨯=+.故选:D4.已知随机变量X 的分布列如下表所示,则()21E X +=()X123P13a16A.116B.113C.143D.223【答案】C 【解析】【分析】根据分布列的性质可得12a =,进而可得11()6E X =,再根据期望的性质分析求解.【详解】由分布列可得11136++=a ,解得12a =,则11111()1233266E X =⨯+⨯+⨯=,所以14(21)2()13E X E X +=+=.故选:C .5.已知函数22)()log ,(f x x ax a =-∈R ,则“2a ≤”是“函数()f x 在(1,)+∞上单调递增”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】B 【解析】【分析】根据给定条件,求出函数()f x 在(1,)+∞上单调递增等价条件,再利用充分条件、必要条件的定义判断即得.【详解】由函数()f x 在(1,)+∞上单调递增,得1210a a ⎧≤⎪⎨⎪-≥⎩,解得1a ≤,所以“2a ≤”是“函数()f x 在(1,)+∞上单调递增”的必要不充分条件.故选:B6.函数π()cos(0)6f x x ωω=+>的图象在区间(0,1)上恰有一个对称中心,则ω的取值范围为()A.π2π(,]63 B.π4π(,]63C.π4π(,33D.π7π(,]33【答案】C 【解析】【分析】求出相位的范围,结合余弦函数的性质列出不等式求解即得.【详解】由(0,1)x ∈,得πππ666x ωω<+<+,由()f x 的图象在区间(0,1)上恰有一个对称中心,得ππ3π262ω<+≤,所以π4π33ω<≤.故选:C7.若某圆台有内切球(与圆台的上下底面及每条母线均相切的球),且母线与底面所成角的余弦值为13,则此圆台与其内切球的体积之比为()A.74B.2C.32D.53【答案】A 【解析】【分析】将圆台还原成圆锥,作出圆锥的轴截面,再结合给定角求出圆锥底面圆半径、高与内切球半径的关系即可计算得解.【详解】将圆台母线延长交于点S ,得圆锥1SO ,作圆锥1SO 的轴截面,等腰梯形ABCD 为圆台的轴截面,截内切球O 得大圆,并且是梯形ABCD 的内切圆,令SA 切圆O 于T,如图,设底面圆直径2AB R =,依题意,11cos 3SAO ∠=,3SA R =,1SO =,设内切球半径为r ,则12OT OO OO r ===,1cos 3SOT ∠=,3SO r =,14SO r ==,于是=R ,且2O 为1SO 的中点,而内切球体积314π3V r =,圆台的体积222321111117π7πππ())43322243V R SO R SO r r =⋅-⋅=⋅=,所以圆台与其内切球的体积比为2174V V =.故选:A8.设函数2π()(1)1,()cos 22xf x a xg x ax =--=-,若函数()()()h x f x g x =-在区间(1,1)-上存在零点,则实数a 的取值范围是()A.2a ≤B.112a <≤C.122a <≤ D.12a <≤【答案】C【解析】【分析】利用函数零点的定义,转化为函数2()1F x ax a =+-,π()cos 2xG x =在(1,1)-上的图象有公共点求解.【详解】由()()()0h x f x g x =-=,得2π(1)1cos22xa x ax --=-,依题意,2π1cos2x ax a +-=在(1,1)-上有解,记2()1F x ax a =+-,π()cos 2x G x =,因此函数(),()F x G x 在(1,1)-上的图象有公共点,0()1G x <≤,如图,当0a ≤时,2()11F x ax a =+-≤-,显然函数(),()F x G x 在(1,1)-上的图象无公共点,当0a >时,函数(),()F x G x 图象都关于y 对称,得(0)(0)(1)(1)F G F G ≤⎧⎨>⎩,即11210a a -≤⎧⎨->⎩,解得122a <≤,所以实数a 的取值范围是122a <≤.故选:C【点睛】方法点睛:函数零点个数判断方法:(1)直接法:直接求出f (x )=0的解;(2)图象法:作出函数f (x )的图象,观察与x 轴公共点个数或者将函数变形为易于作图的两个函数,作出这两个函数的图象,观察它们的公共点个数.二、多选题:本题共3小题,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对得6分,部分选对得部分分,有选错的得0分.9.已知正实数,,a b c 满足2510a b c ==,则()A.b c a +=B.a b c >>C.111a b c+= D.49a b c+≥【答案】BCD 【解析】【分析】对于A :举反例说明即可;对于B :设25101a b c t ==>=,可得2510log ,log ,log a t b t c t ===,结合对数函数性质分析判断;对于C :利用换底公式分析判断;对于D :可得111c a b ⎛⎫+= ⎪⎝⎭,结合基本不等式运算求解.【详解】对于选项A :若1,2510a b c ===,则25log 10,log 10a b ==,则25log 10log 101a b c =≠+=+,故A 错误;对于选项B :因为0a b c >,,,设25101a b c t ==>=,则2510ln ln ln log ,log ,log ln 2ln 5ln10t t t a t b t c t ======,又ln 0,0ln 2ln 5ln10t ><<<,可得ln ln ln ln 2ln 5ln10t t t>>,所以a b c >>,故B 正确;对于选项C :因为111log 2,log 5,log 10t t t a b c===,所以111log 2log 5log 10t t t a b c+=+==,故C 正确;对于选项D :因为111a b c +=,即111c a b ⎛⎫+= ⎪⎝⎭,可得1144(4)1459b a a b c a b c c c a b a b ⎛⎛⎫⎛⎫+=++=+++≥+= ⎪ ⎪ ⎝⎭⎝⎭⎝,当且仅当4b aa b=,即2a b =时,等号成立,所以49a b c +≥,故D 正确.故选:BCD.10.若直线()y kx k =∈R 与圆()()22:111C x y -+-=交于不同的两点,A B O 、为坐标原点,则()A.当2k =时,AB =B.CA CB ⋅的取值范围为[]1,1-C.1OA OB ⋅=D.线段AB 【答案】AC 【解析】【分析】对于A :求圆心()1,1C 到直线20x y -=的距离,结合垂径定理运算求解;对于B :根据数量积可得cos CA CB ACB ⋅=∠uu r uu r,进而可得结果;对于C :分析可得221OA OB OC r ⋅=-=,即可得结果;对于D :分析可知点M 的轨迹是以OC 为直径的半圆(除去,E F ),即可得结果.【详解】由题意可知:圆()()22:111C x y -+-=的圆心为()1,1C ,半径为1r =,且直线()y kx k =∈R 过定点0,0,设线段AB 中点为M ,对于选项A :当2k =时,则直线为2y x =,即20x y -=,圆心()1,1C 到直线20x y -=的距离为55d CM ===,所以||2||AB AM ==A 正确;对于选项B :因为cos cos CA CB CA CB ACB ACB ⋅=⋅∠=∠,因为点,A B 不重合,所以cos 1ACB ∠<,故B 错误;对于选项C :因为()()·OA OB OM MA OM MA⋅=+-()222222OM MA OC d r d =-=---221OC r =-=,所以1OA OB ⋅=,故C 正确;对于选项D :因为线段AB 中点M 满足OM CM ⊥,设OC 的中点为N ,圆C 与x 、y 分别切于点E 、F ,可知圆N 过点E 、F ,且90ECF ∠=︒,可知点M 的轨迹是以OC 为直径的半圆(除去,E F ),所以轨迹长为1222ππ222⨯⨯=,故D 错误.故选:AC.11.若函数()cos 1cos ,Z f x nx n =-∈,则下列说法正确的是()A.若2n =,则函数()f x 的最大值为2B.若3n =,则函数()f x 为奇函数C.存在Z n ∈,使得()sin 1sin f x nx =-D.若()()sin cos 2f x f x +=,则42,Z n k k =+∈【答案】ACD 【解析】【分析】对于A :整理可得[]2()22,1,1f x x x =-∈-,结合二次函数求最值;对于B :举反例说明即可;对于C :取1n =,代入检验即可;对于D :根据题意结合诱导公式可得()πcos cos 2ππ,2n nx nx k k ⎛⎫-=--∈ ⎪⎝⎭Z ,进而可得π2ππ,2n k k =+∈Z ,运算求解即可.【详解】因为[]cos 1,1x ∈-,可知()f x 的定义域为[]1,1-,对于选项A :当2n =时,2(cos )1cos 222cos f x x x =-=-,可得[]2()222,1,1f x x x =-≤∈-,当且仅当0x =时,等号成立,所以函数()f x 的最大值为2,故A 正确;对于选项B :当3n =时,则()cos 1cos3f x x =-,令π2x =,则π3πcos cos022==,可得()010f =≠,所以函数()f x 不为奇函数,故B 错误;对于选项C :当1n =时,(cos )1cos f x x =-,则[]()1,1,1f x x x =-∈-,且对任意R x ∈,则[]sin 1,1x ∈-,所以(sin )1sin f x x =-,故C 正确.对于选项D :因为πππ(sin )cos 1cos 1cos 222n f x f x n x nx ⎡⎤⎛⎫⎛⎫⎛⎫=-=--=--⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦,若π(sin )(cos )1cos 1cos 22n f x f x nx nx ⎛⎫+=--+-= ⎪⎝⎭,可得()πcos cos cos 2ππ,Z 2n nx nx nx k k ⎛⎫-=-=--∈ ⎪⎝⎭,则π2ππ,Z 2n k k =+∈,解得42,Z n k k =+∈,故D 正确.故选:ACD.【点睛】关键点点睛:对于BC :对于直接说明比较麻烦的问题时,常取特值,举例说明即可.第Ⅱ卷三、填空题:本题共3小题,共15分.12.已知,a b 是两个单位向量,若()3a b b -⊥ ,则向量,a b 夹角的余弦值为______.【答案】13【解析】【分析】根据垂直条件及数量积运算律,再由夹角公式即可求解.【详解】由(3)a b b -⊥ ,得231a b b ⋅== ,则1cos ,3|||a b a b a b ⋅〈〉== .故答案为:1313.若复数z 满足2,2z z z z +=⋅=,则2z z -=__________.【答案】【解析】【分析】根据给定条件,设出复数z 的代数形式,结合复数相等、共轭复数及模的意义计算得解.【详解】设i,,R z a b a b =+∈,则i z a b =-,22z z a +==,解得1a =,由2z z ⋅=,得222a b +=,解得21b =,又23i z z a b -=-+,所以|2|z z -=.14.如图,设双曲线G22−22=1>0,>0的左焦点为F ,过F 作倾斜角为60o 的直线l 与双曲线C 的左支交于,A B 两点,若4AF FB =,则双曲线C的渐近线方程为__________.【答案】5y x =±【解析】【分析】利用双曲线定义,结合余弦定理求出,a b 的关系即可得解【详解】令双曲线的右焦点为F ',半焦距为c ,设||BF t =,则||4AF t =,由双曲线定义得||2BF t a '=+,||42AF t a '=+,由直线AB 倾斜角为60o ,得60120BFF AFF ⎧∠=⎨∠='⎩' ,由余弦定理得222222|||2|cos 60|||2|cos120BF BF FF BF FF AF AF FF AF FF ⎧=+''''''-⎪⎨=+-⎪⎩,即222222(2)42(42)1648t a t c tc t a t c tc ⎧+=+-⎨+=++⎩,整理得2222(2)22(42)a c t c a a c t c a ⎧+=-⎨-=-⎩,于是65ca =,5b a =,所以双曲线C 的渐近线方程为5y x =±.故答案为:5y x =±【点睛】关键点点睛:求出双曲线渐近线方程,关键是由给定条件,结合余弦定理求出b a值.四、解答题:本题共5小题,共77分.解答应写出文字说明,证明过程或演算步骤.15.已知三棱锥,A BCD AD -⊥底面,,2BCD BC CD AD BC CD ⊥===,点P 是AD 的中点,点Q 为线段BC 上一动点,点M 在线段DQ 上.(1)若PM ∥平面ABC ,求证:M 为DQ 的中点;(2)若Q 为BC 的中点,求直线DQ 与平面ABC 所成角的正弦值.【答案】(1)证明见详解(2)105【解析】【分析】(1)由线面平行的性质可得//PM AQ ,即可得结果;(2)方法一:建系标点,利用空间向量求线面夹角;方法二:做辅助线,可证DN⊥平面ABC ,进而可得线面夹角;方法三:利用等体积法求D 到平面ABC 的距离,进而可得线面夹的正弦值.【小问1详解】连结AQ ,因为PM ∥平面,ABC PM ⊂平面ADQ ,平面ADQ 平面ABC AQ =,则//PM AQ ,又因为P 是AD 的中点,所以M 是DQ 中点.【小问2详解】方法一:因为AD ⊥底面,BCD BC CD ⊥,如图建立坐标系,则(2,0,0)D ,(0,2,0)B ,(2,0,2)A ,(0,1,0)Q ,可得(2,1,0)DQ =-uuu r,(2,0,2)CA = ,(0,2,0)CB = ,设平面ABC 的法向量为(,,)n x y z = ,则22020n CA x z n CB y ⎧⋅=+=⎪⎨⋅==⎪⎩,令1x =-,则0,1y z ==,可得(1,0,1)n =-,则cos ,5DQ n DQ n DQ n⋅==⋅,因此直线DQ 与平面ABC所成角的正弦值为5;方法二:取AC 中点N,因为DA DC =,则DN AC ⊥,因为AD ⊥底面BCD ,⊂BC 底面BCD ,则AD BC ⊥,且BC CD ⊥,AD CD D = ,,AD CD ⊂平面ACD ,则⊥BC 平面ACD ,由DN ⊂平面ACD ,可得BC DN ⊥,且AC BC C = ,,AC BC ⊂平面ABC ,所以DN ⊥平面ABC ,可知DQN ∠即为直线DQ 与平面ABC 所成角,且DN DQ ==10sin5DN DQN DQ ∠===.所以直线DQ 与平面ABC 所成角的正弦值为5;方法三:设D 到平面ABC 的距离为d ,可得1242333A BCD BCD V AD S -=⋅=⨯=△,则12ABC S BC AC =⋅=△即1433A BCD D ABC ABC V V d S --==⋅==△,解得d =则DQ =所有直线DQ 与平面ABC 所成角的正弦值5d DQ ==.16.在ABC V 中,内角,,A B C 所对的边分别为,,a b c ,满足cos 2a cB c-=.(1)若π3A =,求B ;(2)若ABC V 是锐角三角形,且4c =,求b 的取值范围.【答案】(1)4π9B =(2)(【解析】【分析】(1)根据利用正弦定理结合三角恒等变换可得2B C =,结合π3A =即可得结果;(2)由锐角三角形可得ππ64C <<,利用正弦定理运算求解即可.【小问1详解】因为cos 2a cB c -=,由正弦定理可得sin sin cos 2sin A C B C-=,则2sin cos sin sin sin()sin sin cos sin cos sin C B A C B C C B C C B C =-=+-=+-,整理得sin sin cos sin cos sin()C B C C B B C =-=-,因为(),0,πB C ∈,则()π,πB C -∈-,则C B C =-,即2B C =,由π3A =,得23π3B C C +==,则2π9C =,4π9B =.【小问2详解】因为ABC V 是锐角三角形,则π22π32B C B C C ⎧=<⎪⎪⎨⎪+=>⎪⎩,解得ππ64C <<,则cos 2C <<由正弦定理得sin sin c bC B =,得sin 4sin 28cos sin sin c B C b C C C===,可得b <<b的取值范围为(.17.已知椭圆G22+22=1>>0的离心率为12e =,左、右顶点分别为,,A B O 为坐标原点,M 为线段OA 的中点,P 为椭圆上动点,且MPB △.(1)求椭圆E 的方程;(2)延长PM 交椭圆于Q ,若6BP BQ ⋅=,求直线PQ 的方程.【答案】(1)22143x y +=(2)1)y x =+【解析】【分析】(1)根据离心率和面积关系列式求,,a b c ,进而可得方程;(2)设直线()()1122:(1),,,,PQ y k x P x y Q x y =+,联立方程,利用韦达定理结合数量积的坐标运算求解即可,注意讨论直线的斜率是否存在.【小问1详解】由条件得12c e a ==,即2a c=,则b =,则12OM a c ==,()2max 13333()222BMP S b a c c =+==,解得2,1a b c ===,所以椭圆E 的方程为22143x y +=.【小问2详解】由题意可知:()()2,0,2,0A B -,则()1,0M -,且直线PQ与椭圆必相交,若直线PQ 的斜率不存在,可知1PQ x =-:,联立方程221143x x y =-⎧⎪⎨+=⎪⎩,解得32y =±,不妨取331,,1,22P Q ⎛⎫⎛⎫--- ⎪ ⎪⎝⎭⎝⎭,则333,,3,22BP BQ ⎛⎫⎛⎫=-=-- ⎪ ⎪⎝⎭⎝⎭ ,可得9279644BP BQ ⋅=-=≠ ,不合题意;若直线PQ 的斜率存在,设直线()()1122:(1),,,,PQ y k x P x y Q x y =+,则()112,BP x y =- ,()222,BQ x y =-,与椭圆联列方程得22(1)3412y k x x y =+⎧⎨+=⎩,消去y 得()22223484120k x k x k +++-=,可得221212228412,3434k k x x x x k k-+=-=++,则212121212(2)(2)(2)(2)(1)(1)BP BQ x x y y x x k x x ⋅=--+=--+++()()()()()()2222222212122214128212443434k k k kkx x k x x kkk k +--=++-+++=-++++2227634k k==+,可得26k =,解得k =所以直线PQ的方程为1)y x =+;综上所述:直线PQ 的方程为)1y x =+.【点睛】方法点睛:与相交有关的向量问题的解决方法在解决直线与圆锥曲线相交,所得弦端点的有关的向量问题时,一般需利用相应的知识,将该关系转化为端点坐标满足的数量关系,再将其用横(纵)坐标的方程表示,从而得到参数满足的数量关系,进而求解.18.已知函数()()ln 0f x x x x =>;(1)设函数()()()1g x f x f x =+-,求函数()g x 的极值;(2)若不等式()(),f x ax b a b ≥+∈R 当且仅当在区间[)e,+∞上成立;求ab 的最大值(3)实数,m n 满足0m n <<,求证:()()ln 1ln 1f n f m m n n m-+<<+-.【答案】(1)极小值ln 2-,无极大值(2)e4(3)证明见解析【解析】【分析】(1)求出函数()g x 的导函数并判断出其单调性,即可得出极值;(2)结合函数图象将不等式恒成立转化为图象之间位置关系,得出等量关系并求得ab 的表达式利用二次函数性质可求出结论;(3)分别对不等式左右两边利用作差法并构造函数,由导函数求得其单调性即可证明得出结论.【小问1详解】()()(1)ln (1)ln(1),01g x f x f x x x x x x =+-=+--<<,令()()()1ln ln 11ln ln 1x x x x g x +---=-=-',令()0g x '=,得12x =,当10,2x ⎛⎫∈ ⎪⎝⎭时,()0g x '<,当1,12x ⎛⎫∈ ⎪⎝⎭时,()0g x '>,可得()g x 在10,2⎛⎫ ⎪⎝⎭上单调递减,在1,12⎛⎫⎪⎝⎭上单调递增,所以()g x 有极小值1ln 22g ⎛⎫=- ⎪⎝⎭,无极大值.【小问2详解】()1ln 0f x x '=+=,得1ex =,易知()f x 在10,e ⎛⎫ ⎪⎝⎭上单调递减,在1,e⎛⎫+∞ ⎪⎝⎭上单调递增,即可得在[)e,+∞上()f x 单调递增;易知()f x 在()e,e 处的切线方程为()e 2e y x -=-,即2e y x =-;若不等式()(),f x ax b a b ≥+∈R 当且仅当在区间[)e,+∞上成立;结合()f x 及y ax b =+的图象可知,需满足(e)e e 2f a ba ==+⎧⎨≤⎩,可得e e b a =-,2a ≤.于是21e e (1)e 24ab a a a ⎛⎫=-=--+ ⎪⎝⎭,易知当12a =时,取得最大值,故()maxe 4ab =.【小问3详解】先证明左边:作差()()ln ln ln ln ln f n f m n n m m n m m mm n m n m ---+-=--(ln ln )ln 1nn n m n m n n m m m-==--;因为0m n <<,令1n t m=>,则(ln ln )ln ln 111n n m t tt n m t t-==---;令()()ln 1,1ln 1ln h t t t t h t tt '=-+=+-=当1t >时,()0h t '>,函数()h t 在(1,)+∞上是增函数,所以()ln 1(1)0h t t t t h =-+>=,因此ln 1t t t >-,所以ln 11t tt >-,即()()ln 1f n f m m n m -->-,故()()ln 1f n f m m n m ->+-;对于右边()()ln ln ln ln ln f n f m n n m m n n m nn n m n m---+-=--(ln ln )1ln1m n m n n n m m m-==--令(ln ln )ln 1,11n m n m t t m n m t -=>=<--,令()ln 1t t φt =-+,则()1110φt t tt-=='-<恒成立;所以()t ϕ在()1,+∞上单调递减,可得()()10t ϕϕ<=,即()ln 10t t t ϕ=-+<,所以ln 1t t <-,即ln 11tt <-,即()()ln 1f n f m n n m --<-,故()()ln 1f n f m n n m-<+-.综上得()()ln 1ln 1f n f m m n n m-+<<+-.【点睛】关键点点睛:在证明不等式时关键是先利用作差法再根据表达式特征,构造函数并利用导数求出函数单调性及其最值,即可得出结论.19.混沌现象普遍存在于自然界和数学模型中,假设在一个混沌系统中,用n x 来表示系统在第n 个时刻的状态值,且该系统下一时刻的状态值1n x +满足1()n n x f x +=,已知初始状态值0(0,1)x ∈,其中2()()f x ax ax a =-∈R ,这样每一时刻的状态值012,,,,n x x x x 构成数列{}()n x n ∈N .(1)若数列{}n x 为等比数列,求实数a 的取值范围;(2)若01,12x a ==-,证明:①11112n nx x +<-≤;②212(2)ni i n x n =+≤+∑.【答案】(1)1a <-;(2)①证明见解析;②证明见解析.【解析】【分析】(1)根据给定条件,利用等比数列定义,结合0(0,1)x ∈求解即得.(2)①把1a =-代入,变形得11111n n nx x x +-=-,再探讨n x 的符号及数列{}n x 的单调性推理得证;②由已知结合累加法得21012nin i xx +==-∑,再由①结合累加法求得1124n x n +≥+即可推理得证.【小问1详解】由{}n x 是等比数列,得212n n n x x x ++=,且120,0n n n x x x a ++⋅⋅≠≠,依题意,21n n n x ax ax +=-,则22111(())n n n n n n x ax ax x ax ax +++-=-,于是1n n ax a ax a +-=-,即21n n n n x x ax ax +==-,整理得01n a x x a+==,因此101a a +<<,即110a-<<,解得1a <-,所以实数a 的取值范围是1a <-.【小问2详解】①由1a =-知,211)1111,11(n n n n n n n nx x x x x x x x ++=-+==+--,则11111n n n x x x +-=-,由210n n n x x x +-=-<,得数列{}n x 是递减数列,则011111,221n n n nx x x x x +≤=-=≤-;又110n n n x x x +=->,则1,n n x x +同号,有n x 与0x 同号,即0n x >,于是111111n n nx x x +-=>-,所以11112n nx x +<-≤.②由21nn n x x x +=-,得2101101(2)n nin n n n i i x x x x x x +++===-=-=-∑∑,由①知,1112n n x x +-≤,则10112(1)24n n n x x +≤++=+,又0n x >,因此1124n x n +≥+,所以210111122242(2)ni n i n x x n n +=+=-≤-=++∑.【点睛】思路点睛:涉及给出递推公式探求数列性质的问题,认真分析递推公式并进行变形,可借助累加、累乘求通项的方法分析、探讨项间关系而解决问题.。
浙江省名校新高考研究联盟(Z20名校联盟)2021届高三第一次联考试题 信息技术 Word版含答案

绝密★考试结束前(高三暑假返校联考)Z20名校联盟(浙江省名校新高考研究联盟)2021届第一次联考技术试题卷第一部分:信息技术(共50分)一、选择题(本大题共12小题,每小题2分,共24分。
每小题给出的四个选项中,只有一个符合题目要求,不选、多选、错选均不得分)1.下列有关信息和信息技术的说法中,错误..的是A.传感器技术已经在智能手机中广泛使用B.计算机中所有的字符都采用ASCII码编码C.声音数字化的基本方法是采样和量化D.数据压缩技术提高了多媒体信息存储、处理和传输的效率2.下列有关网站和网页的说法中,正确的是A.使用“添加到收藏夹”功能可将网址收藏到指定的文件夹中B.使用搜索引擎搜索时,关键词越多,搜索结果越多C.网站内各个网页之间均需相互链接D.以“网页全部(*.htm;*.html)”类型保存网页,网页中的图像不会被保存3.在设计某校园一卡通管理系统时,使用Access软件创建的数据表部分界面如图所示。
下列说法正确的是A.该一卡通系统属于数据库管理系统B.同一身份证号不能同时办理两张校园卡C.当前不能对数据表“充消记录表”进行重命名操作D.“用户身份”的字段值可以输入“是”或“否”4.将下列数转换为十进制数,除以8后余数为1的是A.B50HB.100111BC.F59HD.111000B5.使用Goldwave软件打开某音频文件,选中其中一段音频后的部分界面如图所示。
下列说法正确的是A.当前状态下执行“删除”操作,则两个声道的2~4秒均为静音B.当前状态下执行“裁剪”操作,保持其他参数不变直接保存,存储容量约为344.5KBC.把音频文件“素材.wav”重命名为“素材.mp3”,可以实现声音格式的转换D.当前状态下执行“插入6秒静音”操作,音频的时长不变6.使用Photoshop软件编辑“算术.psd”,部分界面如图所示。
则当前文档的图像大小为A.300*400像素B.520*1000像素C.450*800像素D.1116*1400像素7.在VB中,若x、y都是正整数且表达式x Mod y=1为真,则下列关系表达式值一定为真的是A.x>yB.x\y=0C.x\y<>x/yD.x*y Mod 2=08.如第8题图是求112122++的流程图,则图中①处应填入的内容是A.A←1+12AB.A←2+1AC.A←112A+D.A←12A+9.有如下VB程序段:数组元素a(1)到a(5)的值依次为“1,3,4,2,3”,执行该程序段后,变量s的值为A.6B.7C.10D.1310.有如下VB程序段:执行该程序段后,变量c的值是A.abcdefB.abcdefghC.ghabcdefD.hgabcdef11.某冒泡排序算法的VB程序段如下:执行完上述程序段后,实现a数组元素有序排列,则划线处的代码可以是①n To n + 2- i Step –i ②n To i + 1 Step -1 ③2 To i ④2 To n-iA.②③B.②④C.①④D.①③12.某同学将对分查找程序进行了改编,程序运行时,自动产生9个[10,99]之间的不重复随机数并降序排列,在文本框Text1中显示。
浙江省Z20名校联盟2024届高三第一次联考数学试题及参考答案

20Z 名校联盟(浙江省名校新高考研究联盟)2024届高三第一次联考数学试题卷一、单选题1.已知集合(){}2{2,1,0,1,2},|ln 56A B x y x x =--==--,则A B = A.{2,1,0,1,2}-- B.{2}- C.{0,1,2}D.{2,1,0}--2.已知复数1z i =-(i 为虚数单位),则574z=-A.1 C.3D.43.已知向量||5||4a b a b a ==,,,,与b 的夹角为120︒,若(2)()ka b a b -⊥+,则k =A.45-B.35-C.45D.354.已知等轴双曲线Γ经过点(3,2)A ,则Γ的标准方程为A.22155x y -= B.22155y x -= C.221y x -= D.221x y -=5.已知等差数列{}n a ,记n S 为数列{}n a 的前n 项和,若17515a S a ==,,则数列{}n a 的公差d =A.1B.2C.-1D.-26.已知函数1()ln 1x x e f x e +=-,则[(3)]f f =A.ln 3B.3C.3eD.3ln 3e 7.已知1sin cos 05αααπ-=≤≤,,则sin 24πα⎛⎫-=⎪⎝⎭A.50- B.50C.50-D.508.在三棱锥P ABO -中,PO ⊥平面ABO OB BA OH BP ⊥⊥,,于||4H AP C =,,为PA 中点,则三棱锥P HOC -的体积的最大值为A.263B.23C.63D.22二、多选题9.已知()*N nx n ⎛∈ ⎝的展开式中含有常数项,则n 的可能取值为A.4B.6C.8D.1010.已知圆22:(1)(2)25C x y -+-=,直线:(21)(1)740l m x m y m +++--=,则下列说法正确的是A.直线l 恒过定点(3,1)B.直线l 被圆C 截得的弦最长时,13m =-C.直线l 被圆C 截得的弦最短时,34m =-D.直线l 被圆C截得的弦最短弦长为11.设数列{}{}n n a b ,都是等比数列,则A.若n n n c a b =,则数列{}n c 也是等比数列B.若nn na db =,则数列{}n d 也是等比数列C.若{}n a 的前n 项和为n S ,则232n n n n n S S S S S --,,也成等比数列D.在数列{}n a 中,每隔k 项取出一项,组成一个新数列,则这个新数列仍是等比数列12.定义在(0,)+∞上的函数()f x 满足如下条件:①()()()f xy xf y yf x =+;②当1x >时,()0f x >:则下列结论中正确的是A.(1)0f =B.()()()f xy f x f y =C.()f x 在(1,)+∞上单调递增D.不等式33()22xf x x f x ⎛⎫⎛⎫-≥- ⎪ ⎪⎝⎭⎝⎭的解集为[2,)+∞三、填空题13.已知成对样本数据()()()1122,,,,,,(3)n n x y x y x y n ≥ 中12,,,n x x x 互不相等,且所有样本点()1,(1,2,,)i x y i n = 都在直线112y x =-+上,则这组成对样本数据的样本相关系数r =.14.中国茶文化博大精深,茶水的口感与茶叶类型和水的温度有关,经验表明,某种绿茶用80C ︒的开水泡制,再等茶水温度降至35C ︒时饮用,可以产生最佳口感.若茶水原来的温度是0C T ︒,经过一定时间min t 后的温度C T ︒,则可由公式()01ha a T T T T e ⎛⎫-=-⋅ ⎪⎝⎭求得,其中a T 表示室温,h 是一个随着物体与空气的接触状况而定的正常数,现有一杯80C ︒的绿茶放在室温为20C ︒的房间中,已知茶温降到50C ︒需要10min .那么在20C ︒室温下,用80C ︒的开水刚泡好的茶水大约需要放定时间min ,才能达到最佳饮用口感.15.杭州亚运会举办在即,主办方开始对志愿者进行分配.已知射箭场馆共需要6名志愿者,其中3名会说韩语,3名会说日语.目前可供选择的志愿者中有4人只会韩语,5人只会日语,另外还有1人既会韩语又会日语,则不同的选人方案共有种.(用数字作答)16.已知椭圆2222:1(0)x y C a b a b +=>>的右焦点为F ,过点F 作倾斜角为4π的直线交椭圆C 于,A B 两点,弦AB 的垂直平分线交x 轴于点P ,若||1||4PF AB =,则椭圆C 的离心心e =.四、解答题17.(10分)已知函数()2sin()0,||2f x x πωϕωϕ⎛⎫=+>< ⎪⎝⎭的周期为π,且图像经过点,26π⎛⎫⎪⎝⎭.(1)求函数()f x 的单调递增区间;(2)在ABC ∆中,角A B C ,,所对的边分别是a b c ,,,若2426ABC C af c b c S π∆⎛⎫++=== ⎪⎝⎭,,求a 的值.18.(12分)如图,在长方体1111ABCD A B C D -中,点,E F 分别在棱11AA CC ,上,且1133AE EA CF FC ==,.(1)证明:1//BE D F ;(2)若1124AB AD AA ===,,,求平面DEF 与平面BDF 夹角的余弦值.19.(12分)在数列{}n a 中,()(){}*111N 2(1)1n n n n na a a n a n na +==∈++,,的前n 项为n S .(1)求证:1n na ⎧⎫⎨⎩⎭为等差数列,并求{}n a 的通项公式;(2)当2n ≥时,1116n n n a S a λ-+≥恒成立,求λ的取值范围.20.(12分)已知函数(ln )()a x a f x x+=.(1)当1a =时,求函数()f x 的单调区间;(2)求证:当0a >时,22()a f x e -≤.21.(12分)2023年中央一号文件指出,民族要复兴,乡村必振兴.为助力乡村振兴,某电商平台准备为某地的农副特色产品开设直播带货专场.直播前,此平台用不同的单价试销,并在购买的顾客中进行体验调查问卷.已知有(30)N N >名热心参与问卷的顾客,此平台决定在直播中专门为他们设置两次抽奖活动,每次抽奖都是由系统独立、随机地从这N 名顾客中抽取20名顾客,抽中顾客会有礼品赠送,若直播时这N 名顾客都在线,记两次抽中的顾客总人数为X (不重复计数).(1)若甲是这N 名顾客中的一人,且甲被抽中的概概为925,求N ;(2)求使(30)P X =取得得大值时的整数N .22.(12分)已知抛物线2:E y x =与圆222:(4)(0)M x y r r +-=>相交于A B C D ,,,四个点.(1)当2r =时,求四边形ABCD 的面积;(2)四边形ABCD 的对角线交点是否可能为M ,若可能,求出此时r 的值;若不可能,请说明理由;(3)当四边形ABCD 的面积最大时,求圆M 的半径r 的值.Z20名校联盟(浙江省名校新高考研究联盟)2024届高三第一次联考数学参考答案选择题填空题13.−1 14.20 15.140 16.21 部分小题详解:7.解析:将−=αα5sin cos 1平方得−=αα2512sin cos 1,所以=αα252sin cos 24,则∈απ2(0,)。
技术答案(1-5卷)-2019年1月创新卷

《浙江省名校联盟新高考创新卷》2019年1月卷技术参考答案(一)第一部分信息技术一、选择题二、非选择题13.(1)=(SUM(B3:I3)-MIN(B3:I3)-MAX(B3:I3))/6······1分(其他等价公式亦可)(2)B······1分(3)A3:A12,J3:J12······1分(4)B······1分14.(1.1)num > 0······1分(其他等价公式亦可)(1.2)k = k - 1 ······2分(2)E······1分(3)A······1分15.(1)D······1分(2)形状补间······1分(3)乐······1分;stop(); ······1分(4)on (press) { gotoAndPlay(5);} ······2分(5)选中“按钮”图层的第5帧,然后将其转换为空白关键帧······2分16.(1)step_value = (-1) ^ i······1分(其他等价答案亦可)(2)start = start + step_value······2分(其他等价答案亦可)17.(1.1)i = 1 To n - 1 ······2分(1.2)a(t - n) = 1······2分(其他等价答案亦可)(1.3)check(n) ······1分(其他等价答案亦可)(2)29,33,34·····1分(编号间分隔符随意)说明:为使程序具有较高的通用性,建议别把n写成6!第二部分通用技术(共50分)一、选择题(本大题共 13 小题,每小题 2 分,共 26 分。
浙江省名校新高考研究联盟(Z20名校联盟)2025届高三上学期第一次联考试题 英语 含答案

绝密★暑假返校联考结束前Z20名校联盟(浙江省名校新高考研究联盟)2025 届高三第一次联考英语试题卷命题:平湖中学曹丽燕、陆晴雯磨题:临平中学李瑾义乌中学方波临安中学宋昕祎校稿:殷沈华、陈淑君考生须知1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)。
满在答题卷和机读卡的相应位置上。
第Ⅰ卷(选择题部分)第一部分:听力(共两节,满分30分)分为150分,考试时间为120分钟。
2.请用黑色签字笔将学校、班级、姓名、考号分别填写第一节:(共5小题;每小题1.5分,满分7.5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1.What does the man advise the woman to do?A.Buy a new refrigerator. B.Clean the refrigerator. C.Have the refrigerator fixed. 2.What does the man plan to do tomorrow?A.Have a rest. B.Attend a meeting. C.Watch a match.3.How does the woman sound?A.Angry. B.Disappointed. C.Excited.4.What does the woman mean?A.She isn’t feeling well. B.She likes gymnastics a lot. C.She is unable to join the team. 5.When does the conversation probably take place?A.In the morning. B.At noon. C.In the afternoon.第二节:(共15小题;每小题1.5分,满分22.5分)听下面5段对话或独白。
浙江省名校新高考研究联盟(Z20联盟)2024届第一次联考(附答案)

绝密★考试结束前(高三8月返校联考)浙江省名校新高考探讨联盟(Z20联盟)2024届第一次联考物理试题卷命题:长兴中学颜艳、叶银审题:平湖中学沈金林元济高级中学王建锋校对:魏俊枭考生须知:1.本卷满分100分,考试时间90分钟;2.答题前,在答题卷指定区域填写班级、姓名、考场、座位号及准考证号(填涂);3.全部答案必需写在答题卷上,写在试卷上无效;一、选择题I(本题共13小题,每小题3分,共39分,每小题列出的四个选项中只有一个是符合题目要求的,不选、多选、错选均不得分)1.下列仪器中不能干脆测量出国际单位制中基本物理量的是A.B.C.D.2.下列说法正确的是A.法拉第首次发觉了电流的磁效应B.卡文迪许利用扭称试验测量出了万有引力常量C.第谷依据天文观测资料,提出了行星沿椭圆轨道运动D.牛顿创建了把试验和逻辑推理有机地结合起来的科学探讨方法3.一位女士由于驾车超速而被警察挡住,警察走过来对她说:“太太,您刚才的车速是60公里每小时!”这位女士反对说:“不行能的!我才开了6分钟,还不到一小时,怎么可能走了60公里呢?”依据以上对话及右图下列说法正确的是A.女士说的6分钟是时间,60公里是位移B.警察说的60公里每小时是指平均速度C.图中的○50指的是瞬时速度D.图中的○50指汽车在1小时内行驶的路程不能超过50公里第3题图第4题图第5题图60°ALB4.如图所示是火箭点火放射的某一瞬间,下列说法正确的是 A .火箭受重力、地面推力、空气阻力作用 B .火箭加速升空过程中处于失重状态C .发动机喷出气体对火箭的作用力等于火箭所受的重力D .发动机喷出气体对火箭的作用力等于火箭对喷出气体的作用力5.如图所示,一质量为m 、电荷量为Q 的小球A 系在长为L 的绝缘轻绳下端,另一电荷量也为Q 的小球B 位于悬挂点的正下方(A 、B 均视为点电荷),轻绳与竖直方向成60°角,小球A 、B 静止于同一高度。
Z20 名校联盟(浙江省名校新高考研究联盟)2023 届高三第一次联考参考答案

Z20名校联盟(浙江省名校新高考研究联盟)2023届高三第一次联考数学参考答案(后附评分细则)一、单选题(共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)8.解法一:不妨设()()1,0,2,0a b =−=,(),c x y =,因为12c a c b −=−,=即2240x x y ++=,由图可知,向量c b −与a 夹角的最大值是6π. 解法二:∵2c a c b −=−,∴2c b b a c b −+−=−,又∵2b a =−,∴()23c b a c b −−=−, 则()()()222469c b a c b a c b ⎡⎤−−⋅−+=−⎢⎥⎣⎦, 即()()28120c b a c b −−⋅−+=,即()()2128c b a c b−+⋅−=,所以()()()()22212123cos ,288c b a c b c b a c b a c bc bc b−⋅−−+<−>==≥=−−−, 向量c b −与a 夹角的最大值是6π.二、多选题(本大题共4小题,每小题5分共20分.每小题列出的四个选项中有多个是符合题目要求的,全部选对得5分,部分选对得2分,有选错的得0分)11.解析:如图,过A 、B 作准线1y =−的垂线,垂足分别为H 、G ,设线段AB 的中点为C ,C 在准线上的射影为D .当线段AB 为通径时长度最小为24p =,故A 正确;y xOac bc b −因为1212AB x x k p+==,故B 正确; 因为直线1y =−为抛物线准线,由抛物线定义可知弦AB 的中点到准线的距离CD 等于()11||||||22BG AH AB +=, 故圆与直线1y =−相切,所以点M 在该圆的圆上或者圆外,故C 错误;由题意(0,1)M −,设211(,)4x A x ,222(,)4x B x ,直线AB 方程为1y mx =+, 则214y mx x y=+⎧⎪⎨=⎪⎩可得2440x mx −−=,所以12124,4x x m x x +==−, 2212121122111144,44MA MB x x x x k k x x x x ++==+==+,1212121212121211044444MA MB x x x xx x x x x x k k x x x x ++++∴+=+++=+=−=,所以直线MA 与直线MB 的斜率互为相反数,直线倾斜角互补,所以∠AMO =∠BMO , 故D 正确(D 选项也可用平面几何三角形相似得到), 故选:ABD.12.解析:∵ln ()x f x x =,∴21ln ()x f x x −'=,()f x ∴在(0,e)上单调递增,在(e,)+∞上单调递减, 又∵2211ln ln e ex x x k x ==, ∴当0k >时,要使12x x +越小,则取21e 1x x =→,故有121x x +>,故A 正确; 又21e x x 与均可趋向于+∞,故B 错误;当0k <,21e x x =,且1(0,1)x ∈,1211ln 1x x x x ∴+=+<,故C 正确; 21e e kk x k x ⋅=,令()e ,0k g k k k =<,'()(1)e k g k k =+, ()g k ∴在(,1)−∞−单调递减,在(1,0)−单调递增,1()(1)eg k g ∴≥−=−,故D 正确,故选:ACD.三、填空题(本大题有4小题,单空每空4分,多空每空3分,共20分) 13.π;14.122n +−;15.63;16.132a −±=.16.解析:直线l 的方程可化为()3230a x y x y −−++−=,由23030x y x y +−=⎧⎨−−=⎩,解得直线l 的恒过定点()2,1−,又点C 到直线l 的距离为d ==,因为2211sin 2=222ABC S r BCA r r ∆=∠≤=⇒, 则当ABC ∆的面积最大为2时,ABC ∆为等腰直角三角形, 圆心C到直线l的距离为d =解得 a =四、解答题(本大题有6小题,共70分.解答应写出必要的文字说明,证明过程或演算步骤) 17.解: (1)()()3sin cos cosbA C c aB −=−,)()sin cos sin sincos BA C C AB ∴−=−,()sinsin sin cos A B B C A B =+−sin sin sin cos A B A A B =−, sin 0,cos 1,A B B ≠+=即有1sin(),62B π+=7(,),666B πππ+∈23B π∴=; 5分(2)若选①O 为ABC ∆的重心,111sin 3324OAC BAC S S ac B ∆∆===; 10分若选②O 为ABC ∆的内心,∵2222cos 49b ac ac B =+−=,∴7b =, 设内切圆半径为r ,则有1()24ABC a b c r S ∆++==, 则有2r =,此时124OAC S br ∆==; 10分若选③O 为ABC ∆的外心,∵2222cos 49b a c ac B =+−=,∴7b =,设外接圆半径为R ,则2R sin b B =,解得 R 3=,如图,23AOC π∠=, AB CE FD O ABCO此时,21R sin 2OACSAOC =∠=. 10分18.解: (I=N n *∈且2n ≥),∴n a =∴当2n ≥时,1n n S S −−∴=+,又∵0n a >0,1(2)n =≥,∴数列1==为首项,公差为1的等差数列,1(1)1n n =+−⨯=,所以2n S n =. 4分 ∴当2n ≥时,121n a n n n =+−=−,又∵11a =满足上式,∴数列{}n a 的通项公式为21n a n =−. 6分 另解:当2n ≥时,221(1)21n n n a S S n n n −=−=−−=−, 当1n =时,11a =,满足上式,所以{}n a 的通项公式为21n a n =−. 6分 (II )当2n ≥时,221111114441n a n n n n ⎛⎫==− ⎪−−−⎝⎭, 故22211111111111111141223144n a a n n n ⎛⎫⎛⎫++=⨯−+−++−=⨯−< ⎪ ⎪−−−⎝⎭⎝⎭, 所以对,2n N n *∈≥,都有222111114n a a ++<−−. 12分 19.解:(I )方法一:延长,CB DA 交于点F ,连接PF ,在CDF ∆中, ∵BD 是ADC ∠的平分线,且BD BC ⊥, ∴点B 是CF 的中点,又∵E 是PC 的中点,∴BE ∥PF ,又PF ⊂平面PAD ,BE ⊄平面PAD ,∴直线BE ∥平面PAD . 6分方法二:取CD 的中点为G ,连接GE , ∵E 为PC 的中点,∴GE ∥PD , 又PD ⊂平面PAD ,GE ⊄平面PAD ,F P AB CD E∴GE ∥平面PAD ,① 又在四边形ABCD 中,2AD =,4BD =,AB =则90,60BAD BDA BDC ∠=∠=∠=,又因为BD BC ⊥,G 为CD 的中点,所以60DBG BDA ∠=∠=,所以AD ∥BG ,可得BG ∥平面PAD ,②由①②得平面BEG ∥平面PAD ,又BE ⊂平面BEG ,BE ⊄平面PAD ,∴直线BE ∥平面PAD .(II )在ABD ∆中,2AD =,4BD =,AB =则90BAD ∠=,即BA AD ⊥,由已知得60BDC BDA ∠=∠=,8CD =,又平面PAD ⊥平面ABCD ,BA ⊂平面ABCD ,所以BA ⊥平面PAD ,即BA PA ⊥, 所以PAD ∠为二面角P AB D −−的的平面角,所以60PAD ∠=, 又2PA AD ==,所以PAD ∆为正三角形,取AD 的中点为O ,连OP ,则OP AD ⊥,OP 如图建立空间直角坐标系,则()(()1,0,0,1,23,0,,1,0,0,A B C D P −−, 所以()()()1,0,3,2,23,0,DP BD DC ==−−=−,设()()111222,,,,,m x y z n x y z ==分别为平面PBD 和平面PCD 的法向量,则 0m DP m BD ⎧⋅=⎪⎨⋅=⎪⎩,即1111020x x ⎧+=⎪⎨−−=⎪⎩,取11y =−,则()3,1,1m =−−,n DP n DC ⎧⋅=⎪⎨⋅=⎪⎩,即222204430x x ⎧+=⎪⎨−+=⎪⎩,取21y =,则()3,1,1n =−,所以3cos ,5m n m n m n⋅==⋅, 则平面PBD 和平面PCD 所成夹角的余弦值为35. 12分20.解: (I )由题意得45670.20.30.40.55.5,0.3544x y ++++++====,又4170.560.450.340.8.22i ii x y==⨯+⨯+⨯+⨯=∑,PA B CDE G∴4148.24 5.50.350.5i ii x y x y =−⋅=−⨯⨯=∑∵42222217654126,ii x==+++=∑ ∴4222141264 5.55ii xx ==−−⨯=∑∴41422140.5ˆ0.154i ii ii x y xybxx ==−===−∑∑, 所以0.35ˆˆ0.1 5.50.2a y bx=−=−⨯=−, 故得y 关于x 的线性回归方程为0.10.2y x =−. 5分 (II )(ⅰ)将8x =代入0.10.20.180.20.6y x =−=⨯−=,估计该省要发放补贴的总金额为0.610000.5300⨯⨯=(万元) 7分(ⅱ)设小浙、小江两人中选择考研的的人数为X ,则X 的所有可能值为0,1,2;2(0)(1)(23)352P X p p p p ==−−=−+,2(1)(1)(31)(23)661P X p p p p p p ==−−+−=−+−, 2(2)(31)3P X p p p p ==−=−,∴()()()222()0352********E X p p p p p p p =⨯−++−+−⨯+−⨯=−,5(0.5)0.5(41)0.758E X p p =⨯−≤⇒≤, 1031113p p ∴≤−≤∴≤≤,,1385p ∴≤≤,故p 的取值范围为15,38⎡⎤⎢⎥⎣⎦. 12分注:p 的取值范围未取等不符不扣分 21.解: (I)因为c e a ==222243c a a b ==+,即223a b =,又点(在双曲线()2222:10,0x y C a b a b−=>>图象上,所以22921a b −=,即229213b b−=,解得221,3b a ==,所以双曲线22:13x C y −=. 4分(II )由已知点,A B 在以OP 为直径的圆22220000224x y x y x y +⎛⎫⎛⎫−+−= ⎪ ⎪⎝⎭⎝⎭上,又点,A B 在221x y +=上,则有方程组2222000022,2241,x y x y x y x y ⎧+⎛⎫⎛⎫−+−=⎪ ⎪ ⎪⎨⎝⎭⎝⎭⎪+=⎩ 解得直线AB 的方程为001x x y y +=, 设直线AB与渐近线,y y x ==的交点分别为,M N ,由001,,x x y y y +=⎧⎪⎨⎪⎩解得M ,由001,,x x y y y x +=⎧⎪⎨=⎪⎩解得N ,所以2200313MN x y ==−, 又点O 到直线AB的距离为d =,则三角形MON的面积222200001113112233S MN d x y x y =⋅=⨯=−−, 又因为220013x y −=,所以201833S y =+0=,由已知S =,解得203y =,即0y =,因为点P在双曲线右支上,解得0x =,即点(P或(P . 12分22.解: (I )当22e a =时,()22211ln ln 1e e f x x x x x x x x ⎛⎫=−−=−− ⎪⎝⎭, 要证()0f x ≤,即证21ln 10ex x −−≤,设()21ln 1,0eg x x x x =−−>,令()2110eg x x '=−=,解得2e x =,所以()g x 在()20,e 上递增,在()2e ,+∞上递减, 则()()2222max1e ln e1e 0eg x g ==−−⨯=, 所以()0g x ≤,即21ln 10ex x −−≤成立, 所以()0f x ≤成立. 5分(II ) 因为对任意的0,()x H x >在(0,)+∞上单调递减,所以()0H x '≤恒成立,即e ln 1x x x a x−−≤在(0,)+∞上恒成立,解法一:令e ln 1()(0)x x x F x x x −−=>,则22e ln ()x x xF x x +'=, 令2()e ln x h x x x =+,则()21()2e 0xh x x x x'=++>, 所以()h x 在(0,)+∞上为增函数,又因为11e2e 21e (1)e 0,1e 10e eh h −⎛⎫=>=−=−< ⎪⎝⎭, 所以01,1e x ⎛⎫∃∈ ⎪⎝⎭,使得()00h x =,即0200e ln 0x x x +=, 当00x x <<时,()0h x <,可得()0F x '<,所以()F x 在()00,x 上单调递减; 当0x x >时,()0h x >,可得()0F x '>,所以()F x 在()0,x +∞上单调递增, 所以()000min00e ln 1()x x x F x F x x −−==,由0200e ln 0x x x +=,可得01ln 000000ln 111e ln ln e x x x x x x x x ⎛⎫=−== ⎪⎝⎭,令()e x t x x =,则()001ln t x t x ⎛⎫= ⎪⎝⎭,又由()(1)e 0x t x x '=+>,所以()t x 在(0,)+∞上单调递增, 所以001lnx x =,可得00ln x x =−,所以001e x x =,即00e 1x x =, 所以()0000min000e ln 111()1x x x x F x F x x x −−+−====,即得1a ≤. 12分解法二: 先证e 1x x ≥+(0x ≥),设函数()e 1x h x x =−−,令()e 10xh x '=−=,解得0x =, ∴()h x 在[)0,+∞上单调递增,∴()()00h x h ≥=,即e 1x x ≥+成立. 设()ln k x x x =+(0x >), ∵()110k x x'=+>,∴()k x 在()0,+∞上单调递增, ∵()1110,110e e k k ⎛⎫=−+<=> ⎪⎝⎭,∴存在()00,x ∈+∞,使得00ln 0x x +=.令e ln 1()(0)x x x F x x x−−=>, 则()ln ln e e ln 1e ln 1ln 1ln 11x x x x x x x x x F x x x x+−−−−++−−==≥=, 当ln 0x x +=时,即0x x =时,取等号. ∴()min 1F x =,即得1a ≤. 12分Z20名校联盟(浙江省名校新高考研究联盟)2023届高三第一次联考数学试卷阅卷细则13-16.(每题5分,共20分)以数值正确为准, 注:第16题给出一个正确数值得3分. 17.(本题满分10分) (Ⅰ)5分1、有正确结论,23B π=,有过程,5分(无过程,3分) 2、无正确结论,找得分点:○1 ()sin sin sin cos A B B C A B =+− , 2分○21sin()62B π+=,2分 ○323B π=,1分 (Ⅱ)5分1、有正确结论,有过程,5分(无过程,3分)2、无正确结论,找得分点:①1sin 2ABCS ac B ==2分 15334OACABCSS ==,3分 ② ∵2222cos 49b a c ac B =+−=,∴7b =,2分解得内切圆半径2r =,2分124OAC S br ∆==,1分③∵2222cos 49b a c ac B =+−=,∴7b =,2分解得R 3=,,2分解得21sin 2OAC S R AOC ∆=∠,1分 18.(本题满分12分)(Ⅰ)6分1、有正确结论,得21n a n =−,有过程,6分(无过程,2分)2、无正确结论,找得分点:○1n a =2分○22nS n =,2分 ○321na n =−,2分 (Ⅱ)6分1、有正确证明过程,6分(无过程,不得分)2、证明有误,找得分点: ①221111114441n a n n n n ⎛⎫==− ⎪−−−⎝⎭,3分 ②22211111111111111141223144n a a n n n ⎛⎫⎛⎫++=⨯−+−++−=⨯−< ⎪ ⎪−−−⎝⎭⎝⎭,3分 19.(本题满分12分)(Ⅰ)6分1、有证明过程,6分(无过程,不得分)2、证明有误,找得分点:方法一:○1BD BC ⊥,2分 ○2BE ∥PF ,2分 ○3直线BE ∥平面PAD ,2分 方法二:○1取CD 的中点为G ,GE ∥PD ,2分 ○2AD ∥BG ,2分 ○3由平面BEG ∥平面PAD 得直线BE ∥平面PAD ,2分(Ⅱ)6分1、有正确结论35,有过程,6分(无过程,3分) 2、无正确结论,找得分点:①60PAD ∠=,1分②有建系思想,1分○3 求出法向量()3,1,1m =−−,()3,1,1n =−,2分 (法向量计算错误但有法向量计算公式的给1分)④解得余弦值为35,2分(结论错误但有法向量夹角计算公式的给1分) 其他证法酌情给分20.(本题满分12分)(Ⅰ)5分1、有正确结论:0.10.2y x =−,有过程,5分(无过程,2分)2、无正确结论,找得分点:①∵4148.24 5.50.350.5i i i x y x y =−⋅=−⨯⨯=∑, 4222141264 5.55i i xx ==−−⨯=∑,∴41422140.5ˆ0.154i ii i i x y xy b xx ==−===−∑∑,3分 ②0.35ˆˆ0.1 5.50.2a y bx=−=−⨯=−,1分 ③得0.10.2y x =−,1分(Ⅱ)7分(ⅰ)1、有正确结论:300万元,有过程,2分(无过程,1分)2、无正确结论,找得分点:将8x =代入0.10.20.180.20.6y x =−=⨯−=,1分(ⅱ)1、有正确结论:300万元,有过程,5分(无过程,2分)2、无正确结论,找得分点:①2(0)(1)(23)352P X p p p p ==−−=−+,2(1)(1)(31)(23)661P X p p p p p p ==−−+−=−+−,2(2)(31)3P X p p p p ==−=−,()()()222()0352********E X p p p p p p p =⨯−++−+−⨯+−⨯=−,3分 ②解1358p ≤≤,2分(1358p <≤或1358p ≤<或1358p <<均得2分) 21.(本题满分12分)(Ⅰ)4分1、有正确结论:双曲线22:13x C y −=,有过程,4分(无过程,2分) 2、无正确结论,找得分点:①得223a b =, 1分②点(代入()2222:10,0x y C a b a b −=>>,得22921a b−=, 1分 ③解得221,3b a ==,双曲线22:13x C y −=, 2分 (Ⅱ)8分1、有正确结论:点(P或(P ,有过程,8分(无过程,3分,只写出一个坐标的扣1分)2、无正确结论,找得分点:①解得直线AB 的方程为001x x y y +=, 1分②由001,,x x y y y +=⎧⎪⎨=⎪⎩解得M ,1分由001,,3x x y y y x +=⎧⎪⎨=⎪⎩解得N ,1分③2200313MN x y ==−, 点O 到直线AB的距离为d =,三角形MON 的面积222200001113112233S MN d x y x y =⋅=⨯=−−0,3分 ○4点(P或(P ,2分 本小题其他解法酌情给分22.(本题满分12分)(Ⅰ)5分找得分点累加:①要证()0f x ≤,即证21ln 10e x x −−≤,1分 ②设()21ln 1,0e g x x x x =−−>,得()g x 在()20,e 上递增,在()2e ,+∞上递减,2分 ③()()2222max 1e ln e 1e 0e g x g ==−−⨯=,即21ln 10e x x −−≤成立,2分(Ⅱ)7分1、有正确结论:1a ≤,有过程,7分(无过程,2分)2、无正确结论,找得分点:①由()0H x '≤恒成立,得e ln 1x x x a x −−≤,2分 ②令e ln 1()(0)x x x F x x x−−=>,得()F x 在()00,x 上单调递减;在()0,x +∞上单调递增,2分③01,1e x ⎛⎫∃∈ ⎪⎝⎭,使得0200e ln 0x x x +=,1分 ④求得()0000min 000e ln 111()1x x x x F x F x x x −−+−====,即1a ≤,2分 本小题其他解法酌情给分。
2024届Z20名校联盟(浙江省名校新高考研究联盟)高三第一次联考 英语答案 (1)

Z20名校联盟(浙江省名校新高考研究联盟)2024届高三第一次联考英语参考答案第一部分:听力(每小题1.5分,满分30分)1-5 ACBCA 6-10 CABAC 11-15 CBACC 16-20 BACBC第二部分:阅读理解(每小题2.5分,满分50分)21-23 CDB 24-27 BACD 28-31 DADB 32-35 DBCA36-40 CDFAG第三部分:语言运用(共两节,满分30分)第一节:完形填空(每小题1分,满分15分)41-45 BDACD 46-50 DABAC 51-55 ADCDB第二节:语法填空(每小题1.5分,满分15分)56. was compiled 57. to 58. the 59. which 60. being61. to love 62. However/Yet 63. meaningless 64. guidance 65. while第四部分:写作(共两节,满分40分)第一节:应用文写作(满分15分)一、评分原则1.本题总分为15分,按5个档次给分。
2.评分时,先根据文章的内容和语言初步确定其所属档次,然后以该档次的要求来衡量,确定或调整档次,最后给分。
3.词数少于60和多于100,从总分中减去2分。
4.评分时,应注意的主要方面为:内容要点、应用词汇和语法结构的丰富性和准确性以及上下文的连贯性。
5.拼写与标点符号是语言准确性的一个方面,应视其对交际的影响程度予以考虑。
英、美拼及词汇用法均可接受。
6.若书写较差,以至影响交际,将分数降低一个档次。
二、各档次的给分范围和要求第五档(13~15分)—完全完成了试题规定的任务。
—覆盖所有内容要点;—应用了较多的语法结构和词汇;—语法结构或词汇方面有些许错误,但为尽力使用较复杂结构或较高级词汇所致;具备较强的语言应用能力;—有效地使用了语句间的连接成分,使全文结构紧凑;—完全达到了预期的写作目的。
第四档(10~12分)—完全完成了试题规定的任务。
【校级联考】浙江省高三上学期第一次联考信息技术试题(解析版)

第一部分 信息技术(共50分)一、选择题(本大题共12小题,每小题2分,共24分。
每小题列出的四个备选项中只有一个是符合题目要求的,不选、多选、错选均不得分)1. 以下说法正确的是A. 信息的表示、传播、存储必须依附于某种载体B. 在公共场所上网时,应尽量把表单上的用户名和密码设置为自动完成C. 文字出现以后,才能进行传递信息D. “盲人摸象”体现了信息的时效性【答案】A【解析】【分析】【详解】本题主要考查信息的特征和信息技术的发展。
信息具有载体依附性,因此A 选项正确;从信息安全考虑,公共场所上网,一般不要保存用户名和密码,因此B 选项错误;信息可以依附于文字、声音、图像等多种载体传播,因此C 选项错误;“盲人摸象”体现了信息的不完全性,因此D 选项错误。
2. 以下软件中,不属于...浏览器的是 A. Internet ExplorerB. FirefoxC. Google ChromeD. CuteFTP【答案】D【解析】【分析】【详解】本题主要考查浏览器知识点。
Internet Explorer 是微软的IE 浏览器,Firefox 是火狐浏览器,Google Chrome 是谷歌浏览器,CuteFTP 是文件传输工具,故本题选D 选项。
3. 使用Word 软件编辑某文档,部分界面如下图所示下列说法正确的是(▲ )A. 共有两处修订,两处批注B. 文档中图片的文字环绕方式为“嵌入型”C. 用户t1 和用户s2 添加了批注D. 拒绝所有修订后,第一句文字是“记者从今天浙江省政府新闻信息办召开的新闻发布会上了解到”【答案】A【解析】【分析】【详解】略4. 已知英文小写字母比对应的大写字母ASCII码大32(十进制),某数据加密方法描述如下:(1)将字符的ASCII码值加20(十进制);(2)以字节为单位进行加密处理;(3)将1个字节的8位二进制数左移一位,最低位用左移出的最高位填充;(4)将处理后的8位二进制数分割成前4位与后4位两个二进制数;(5)分别将上述两个4位二进制数转换为十六进制数;(6)所得两个十六进制数码交换顺序后连接,即为该字节的密文。
浙江省浙南名校朕盟2023-2024学年高三上学期第一次联考技术试题含解析

【答案】D
【解析】
【详解】本题考查数据安全相关内容。信息系统不断电并不意味着没有安全漏洞,不能免除被攻击,A 选
项错误;杀毒软件能预防病毒感染,但不能有效避免未知病毒感染,B 选项错误;数据进行定期备份可以
增强数据安全性,但也不能完全避免数据丢失的可能,C 选项错误。对系统用户进行应严格的身份验证,
种数字内容和服务。选项 C 错误,无线网络中的数据通信仍然需要传输介质,如无线信号传输介质。数据
通过无线信号传输,而不需要物理电缆,但仍然需要传输介质。选项 D 正确,数据通信、资源共享和分布
处理是网络的三个主要功能。这是网络的基本功能之一,网络的主要目的之一是允许计算机之间的数据通
信,同时还支持资源共享和分布处理。故答案为 D 选项。
D. 系统自动生成餐厅年月日报表
【答案】B
【解析】
【详解】本题考查人工智能技术的引用。A 选项,二维码和条形码本身只是物体标记技术,主要用于物流,
不体现人工智能技术;B 选项,语音识别属于人工智能技术;C 选项,在线支付是一种通过第三方提供的与
银行之间的支付接口进行支付的方式,不体现人工智能技术;D 选项系统自动生成餐厅年月日报表属于系
对订单信息进行统计分析,自动生成餐厅年月日的报表。
下列关于信息系统安全和信息社会责任的说法,正确的是( )
A. 只要不停电,信息系统就不会有任何安全隐患
B. 只要安装了杀毒软件,信息系统就不会被病毒感染
C. 只要对数据进行定期备份,系统数据就不会有任何丢失
D. 只要对系统用户有严格的身份认证,系统就能提升数据的访问安全
执行该部分流程,若依次输入的数据为 2、-3、5、-1、2、1、-3、0,则输出 m 的值为( )
2024届Z20名校联盟(浙江省名校新高考研究联盟)高三第一次联考 英语答案

Z20 名校联盟(浙江省名校新高考研究联盟)2024 届高三第一次联考英语参考答案和解析阅读理解详解21-23 CDB21. C. 【细节理解题】根据第二款电动自行车的介绍可知, Temples 的专属零部件更少, 因此可在任何自行车店得到维修服务。
而另两款VanMoofs 和Cowboys 虽然也比较时尚, 但是他们要得到后续支持和服务会更加复杂, 故答案为C。
D. 【细节理解题】根据第三款电动自行车介绍的第一句话可知,这是一个注重细节的典型例子,在功能性、舒适性和实用性方面提供高质量的体验--如果你负担得起的话。
故答案为D。
23. B. 【推理判断题】通读全文,本文介绍了Cycling Electric 所推荐的三款各具特色的电动自行车,应出自生活杂志专栏,故答案为B.24-27 BACD24. B. 【细节理解题】根据文章第二段最后一句话I saw it as an art that combines tradition and modernity ,which was mostly the reason that I liked it 可知喜爱原因为传统中国风舞蹈是传统和现代的结合,故答案为B。
25. A. 【写作手法题】根据文章第五段最后一句话可知,作者采用列数字的方式说明Filippi 的视频点击量高,受人们欢迎,故答案为A。
26. C 。
【推理判断题】根据文章最后一段可知,Filippi 相信了解不同的文化是无价的,把它看做是一种个人成长方式,故答案为C.27. D. 【主旨大意题】本文介绍了一位意大利舞者对传统中国风舞蹈的喜爱与热情,故答案为D.28-31 DADB28. D. 【细节理解题】根据文章第二段最后一句"The flakes that the macaques unintentionally produced looked a lot like the oldest stone tools that were intentionally made byhominins ”可知,这些猕猴无意中产生的尖锐薄片,看起来和人类有意识制造的最古老的石器工具很像,故选D。
浙江省Z20名校联盟(名校新高考研究联盟)2022届高三上学期通用技术8月第一次联考试卷
浙江省Z20名校联盟(名校新高考研究联盟)2022届高三上学期通用技术8月第一次联考试卷一、选择题(本大题共13小题,每小题2分,共26分。
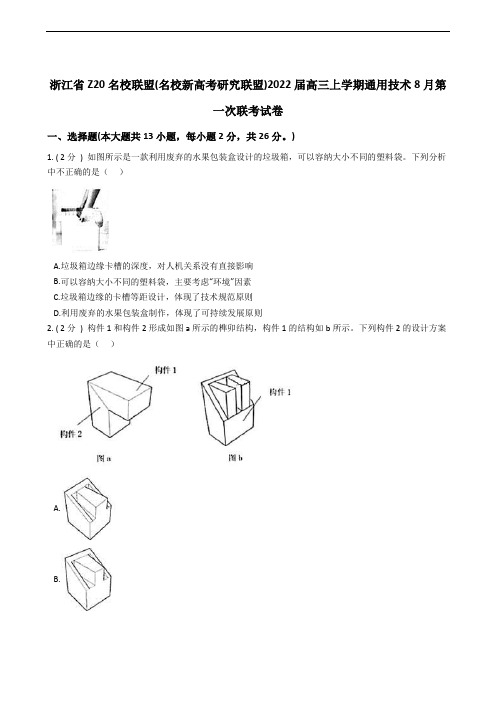
)1. ( 2分) 如图所示是一款利用废弃的水果包装盒设计的垃圾箱,可以容纳大小不同的塑料袋。
下列分析中不正确的是()A.垃圾箱边缘卡槽的深度,对人机关系没有直接影响B.可以容纳大小不同的塑料袋,主要考虑“环境”因素C.垃圾箱边缘的卡槽等距设计,体现了技术规范原则D.利用废弃的水果包装盒制作,体现了可持续发展原则2. ( 2分) 构件1和构件2形成如图a所示的榫卯结构,构件1的结构如b所示。
下列构件2的设计方案中正确的是()A.B.C.D.3. ( 6分) 通用技术课上,小明设计了如图所示的零件(图中R25的圆弧与直线相切),请根据图完成下面小题。
(1)图中漏标的尺寸共有()A.3处B.4处C.5处D.6处(2)用厚度为8mm、大小合适的钢板制作该零件,下列说法中不合理的是()A.在平口钳上钻孔时应集中注意力并戴上防护眼镜B.冲眼时,须用台虎钳夹持牢固,否则容易滑动C.正式锯割时,推锯加压、回拉不加压D.可用半圆锉锉削加工R48的圆弧(3)加工该零件时需吸用到一些钳工工具,下列钳工工具指配或使用不合理的是()A.B.C.D.4. ( 2分) 如图所示为某连杆机构,连杆2、连杆3与滑槽1连接。
电动机带动曲柄转动使滑块1、和滑块2在滑槽内上下移动,下列关于该连杆机构的分析中不正确的()A.电机转轴与曲柄之间的连接属于刚连接B.图示转动状态下曲柄受弯曲、连杆I受拉C.图示转动状态下滑块1、滑块2都向上运动D.连杆2、连杆3应选用抗弯曲能力较强的材料制作5. ( 2分) 如图所示为某化工厂“污染土壤(含有受热易挥发的有机污染物)处理系统工艺流程。
下列关于该工艺流程的分析不正确的是()A.预加热滚简加热和急冷装置冷却属于串行环节B.往热解吸滚筒中通天然气的日的是确保污染土壤加热到足够的温度,使有机污染物从土壤中得以挥发出米或被焚烧C.一级除尘和二级除尘环节不可以颠倒D.设计该工艺流程的主要H的是获取达标尼气6. ( 4分) 如下图所示为伺服电机控制系统,转角和速度检测元件检测伺服电机的转动角度和速度,并反馈到伺服控制器(PLC)与设定值比较,伺服控制器根据偏差值发出运动信号,伺服驱动器将运动信号转变成相应的电流信号驱动伺服电机转动。
浙江省高中技术第一次选考联考试题

浙江省高中技术第一次选考联考试题技术试题卷第一部分信息技术一、选择题( 本大题共12小题, 每小题2分, 共24分。
每小题给出的四个选项中,只有一个符合题目要求, 不选、多选、错选均不得分)1.下列有关信息的说法,不正确...的是A.因特网上的任意信息应尽可能的经过甄别后再使用B.网页中使用文字、图像、表格、超链接等方式表达信息C.在微信朋友圈分享自己的旅行见闻,这一过程主要属于信息的获取D.设置邮箱,限制邮件大小、类型以及过滤垃圾邮件,主要是为了提高信息的安全性2.使用浏览器软件打开某网页文件如第2题图所示。
第2题图下列说法正确的是A.该网页文件名为“冬季养生食物.htm” B.该网页文件本质上是文本文件C.页面中图像被保存在djyssp.htm文件中 D.页面中图像上没有超链接3.评价某网络新闻的部分界面如第3题图所示。
第3题图图中包含的评价方式有A.个人推荐、统计评价B.个人推荐、核心刊物评价C.核心刊物评价、统计评价D.专家推荐、核心刊物评价编号书名作者书价出版时间出版社SN-7208061644 追风筝的人卡勒德·胡赛尼¥28.90 2014-01-01 上海人民出版社则该数据表对应的结构恰当的是A .B .C .D .5.计算s = 2+4+6+…+10的算法流程图如第5题图所示。
若要计算s =2×4×6×…×10,则上述流程图中的“ ”应改为A .B .C .D .6.使用WinHex 软件观察字符“MP4播放器”的内码,结果如第6题图所示。
则大写字符“O ”的二进制内码是 A .1001001 B .00110001 C .1001111 D .010011117.某软件运行部分界面如第7图所示。
该软件能连续记录并及时反馈了用户在步行过程中的步数、距离和消耗的热量。
这主要体现了多媒体技术的A .安全性B .集成性C .实时性D .交互性 8. 某Photoshop 文件的图层面板如第8题图所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
浙江省名校新高考研究联盟Z联盟届第一次联考信息技术答案
Document number【SA80SAB-SAA9SYT-SAATC-SA6UT-
浙江省名校新高考研究联盟(Z20联盟)2019届第一次联考技术
答案
第一部分信息技术(共50分)
一、选择题(本大题共12小题,每小题2分,共24分)
二、非选择题(本大题共5小题,其中第13小题4分,第14小题5分,第15小题8
分,第16小题3分,第17小题6分,共26分)
13.(1)= 110*(D3-E3)*C3 (1分)
(2)F8 (1分)
(3)A2:E3 (1分)
(4)B (1分)
14.(1)Btn (不区分大小写) (1分)
(2)①n = Len(s) 或n = Len (1分)
②n1 + n2 + n3 < n-1 or n2 = 0 or n3 = 0 (2分)
或 n1 + n2 + n3 <>n-1 or n2 * n3 = 0
(3)不合法(1分)
15.(1)A (1分)
(2)动画补间 (或其他等价答案) (1分)
(3)将“诗人”图层第12帧复制到第1帧 (或其他等价答案) (1分)
(4)load main end (1分)
(5)AD (2分)
(6)getURL(""); stopAllSounds(); (2分)
16.(1)count = 1 (1分)
(2)a(j) = a(j - 1) + 1 (或其他等价答案) (2分)
17.(1)70007 (1分)
(2)①p <= n 或 val(p)<=val(n)(1分)
②i=i-1 (2分)
③ln Mod 2 = 0 Or i < (ln + 1) \ 2 (2分)
或not (ln Mod 2 = 1 and i =(ln + 1) \ 2。
