2016年高考数学冲刺卷01 理(新课标Ⅱ卷)答案
2016年高考数学冲刺卷02 理(山东卷)答案

2016年高考数学冲刺卷02 理(山东卷)答案第Ⅰ卷(共50分)一、选择题:本大题共10个小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.【命题意图】本题考查集合的真子集的概念、方程的解法等基础知识,考查数据处理能力以及基本运算能力. 【答案】C【试题解析】由于{}2|02A x ⎧⎫===⎨⎬⎩⎭,所以集合A 只有一个元素,有1211-=个真子集;故选C.2.【命题意图】本题考查复数的几何意义、直线方程等基础知识,考查学生的基本运算能力. 【答案】B.【试题解析】复数z 对应的点为(1,3)a -,则有312a =-+,所以2a =;故选B.3.【命题意图】本题考查指数不等式、对数不等式以及充分条件和必要条件的判定等知识,意在考查学生的逻辑思维能力. 【答案】B4.【命题意图】本题考查平面向量垂直的判定和四边形的面积等知识,意在考查学生的逻辑思维能力和基本计算能力. 【答案】C【试题解析】∵0OB AC ⋅=,∴OA BC ⊥,∴152OABC S OB AC ==,故选C . 5.【命题意图】本题考正态分布、正态分布密度曲线和定积分的几何意义等基础知识,意在考查学生的逻辑思维能力和基本计算能力. 【答案】A【试题解析】因为随机变量X 服从正态分布,其正态分布密度曲线为函数()()222x f x --=的图象,所以2μ=,即函数()f x 的图象关于直线2x =对称,因为21()3f x dx =⎰,所以()1023P X <≤=,所以()1243P X <≤=,因为()()12442P X P X <≤+>=, 所以()()14242P X P X >=-<≤111236=-=;故选A .6.【命题意图】本题考查程序框图的应用和三角函数的周期性,意在考查学生的逻辑思维能力和基本计算能力. 【答案】B【试题解析】由框图知输出的结果π2π2016πsin sin sin333s =+++,因为函数πsin 3y x =的周期是6,所以π2π6π336(sinsin sin)333s =+++00336=⨯=,故选B. 7.【命题意图】本题考查简单的线性规划和数形结合思想的应用,意在考查学生的逻辑思维能力和基本运算能力. 【答案】B8.【命题意图】本题以新定义为载体考查不足近似值或过剩近似值等基础知识,意在考查学生的审题能力和基本运算能力. 【答案】A 【试题解析】令3149π1015<<,则第一次用“调日法”后得16 3.2π5=>是π的更为精确的过剩近似值,即3116π105<<;第二次用“调日法”后得47π15<是π的更为精确的不足近似值,即4716π155<<;第三次用“调日法”后得63π20>是π的更为精确的过剩近似值,即4763π1520<<;第四次用“调日法”后得72235110=是π的更为精确的过剩近似值,即第四次用“调日法”后可得π的近似分数为722;故选A . 9.【命题意图】本题考查双曲线的定义和几何性质、抛物线的几何性质和平面向量的数量积等基础知识,意在考查学生的逻辑思维能力和基本运算能力. 【答案】B10.【命题意图】本题考查函数的性质的应用以及利用导数研究函数的单调性等基础知识,意在考查学生的逻辑思维能力、基本运算能力和解决问题的综合能力. 【答案】B【试题解析】令221)()(x x f x g -=,因为x ∀∈R ,有2()()f x f x x -+=, 所以021)(21)()()(22=-+--=+-x x f x x f x g x g ,即函数)(x g 为奇函数,因为在(0,)+∞上()f x x '<,所以0)()(''<-=x x f x g ,即函数)(x g 在(0,)+∞上单调递减,在)0,(-∞上单调递减,又0)0(=g ,)(x g ∴在R 上单调递减,由(4)()84f m f m m --≥-,得2211(4)()(84)(4)(4)[()](84)(4)()022f m f m mg m m g m m m g m g m ----=-+--+--=--≥,即(4)()g m g m -≥,所以m m ≤-4,解得2≥m ;故选B .第Ⅱ卷(共100分)二、填空题(每题5分,满分25分,将答案填在答题纸上)11.【命题意图】本题考查全称命题的否定,意在考查学生的逻辑思维能力.【答案】“0x ∃∈R ,0sin 1x ≥”【试题解析】命题“x ∀∈R ,sin 1x <”的否定是“0x ∃∈R ,0sin 1x ≥”.12.【命题意图】本题考查空间几何体的三视图、组合体的体积等知识,意在考查学生的空间想象能力和基本计算能力. 【答案】36π288+【试题解析】由三视图,知该几何体是由底面圆的半径为3,高为8的半圆柱和长为8,宽为6,高为6的长方体的组合体,所以该几何体的体积是21π3886636π2882V =⨯⨯⨯+⨯⨯=+. 13.【命题意图】本题考查排列组合应用题,意在考查学生的逻辑思维能力和基本计算能力. 【答案】3614.【命题意图】本题考查正弦定理、三角形的面积公式以及两角差的正弦公式的应用,意在考查学生的逻辑思维能力和基本计算能力.【试题解析】由正弦定理得:2sin b R B =,2sin c R C =,因为cos cos b C c B =,所以sin cos sin cos B C C B =,即()sin cos sin cos sin 0B C C B C B -=-=,所以C B =,即1c b ==,所以a 边上的高是12=,所以ABC ∆的面积是1122= 15.【命题意图】本题考查利用数列的递推式求数列的通项公式以及利用基本不等式求最值等知识,意在考查学生的逻辑思维能力、基本运算能力和解决问题的综合能力. 【答案】229【试题解析】因为数列}{n a 满足601=a ,*12()n n a a n n +-=∈N ,所以)1(24260)()()(123121-+⋅⋅⋅+++=-+⋅⋅⋅+-+-+=-n a a a a a a a a n n n602)11)(1(2602+-=-+-⨯+=n n n n则160602-+=+-=nn n n n n a n ,当7=n 时,7414160=-+n n ,当8=n 时, 229160=-+n n ,所以n a n 的最小值为229;故填229.三、解答题 (本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.) 16. (本小题满分12分)【命题意图】本题考查三角函数的图象与性质、三角恒等变换以及余弦定理的应用,意在考查学生分析问题、解决问题的能力和基本的计算能力.(Ⅱ)由1cos 22A f A ⎛⎫-=⎪⎝⎭,可得1sin cos 62A A π⎛⎫+-= ⎪⎝⎭,11cos 22A A -= , …………………………………7分 化简得1sin 62A π⎛⎫-= ⎪⎝⎭, …………………………………8分50666A A ππππ<<∴-<-<…………………………………9分 ,663A A πππ∴-=∴=, …………………………………10分又1bc =,3b c +=,由余弦定理可得()22222cos 36a b c bc A b c bc =+-=+-=, …………………………………11分a ∴=…………………………………12分17. (本小题满分12分)【命题意图】本题考查等差数列、等比数列的通项和前n 项和公式以及数学归纳法、裂项抵消法的应用,意在考查学生分析问题、解决问题的能力和基本的计算能力.(Ⅱ)因为)121121(1142114141414222+--+=-+=-+=-+=n n n n n a a c n n n ,所以1211)121121()7151()5131()311(+-+=+--+⋅⋅⋅+-+-+-+=n n n n n S n .因为2016<n S ,所以20161211<+-+n n ,即2015121<+-n n ,所以使2016<n S 的最大 自然数n 为2015. ………………12分 18. (本小题满分12分)【命题意图】本题考查独立性检验思想的应用、几何概型的概率公式、超几何分布的分布列和期望等知识,意在考查学生的应用数学能力和准确的计算能力.【试题解析】(Ⅰ)由表中数据得2K 的观测值()225022128850 5.556 5.024*********K ⨯⨯-⨯==≈>⨯⨯⨯所以根据统计在犯错误的概率不超过0.025的前提下认为视觉和空间能力与性别有关;.……………4分(Ⅲ)由题可知在选择做几何题的8名女生中任意抽取两人,抽取方法有2828C =种,其中甲、乙两人没有一个人被抽到有2615C =种;恰有一人被抽到有1126=12C C ⋅种; 两人都被抽到有221C =种X ∴可能取值为0,1,2,15(0)28P X ==,123(1)287P X ===,1(2)28P X == X 的分布列为:151211()0+1+22828282E X ∴=⨯⨯⨯=.………………12分19. (本小题满分12分)【命题意图】本题考查空间中垂直关系的转化、空间向量在立体几何中的应用以及同角三角函数基本关系式等知识,意在考查学生的空间想象能力和严密的逻辑推理能力.【试题解析】(Ⅰ)由题意,菱形11ACC A 中,1112,60AC AA AAC ==∠=111,DA DC DC DA ∴===又1BAC ∆中,12BA BC ==1,BD AC BD ∴⊥=222BCD BC DB DC ∴∆=+中,BD DC ∴⊥又11DC AAC C ⊂面,且1DC AC D =11BD AAC C ∴⊥面………………6分20. (本小题满分13分)【命题意图】本题考查导数的几何意义、利用导数研究不等式恒成立问题,意在考查学生的化归与转化思想的应用、运算求解能力.【试题解析】(Ⅰ)()()00ln 011f e =++=,()11x f x e x '=++,()010201f e '=+=+, ∴()y fx =在点()()0,0f 处的切线方程为()120y x -=-,即210x y -+=.…5分(Ⅱ)令()()1g x f x ax =--,则()()11x g x f x a e a x ''=-=+-+,令()11xh x e x =++,则()()211x h x e x '=-+,21. (本小题满分14分)【命题意图】本题考查椭圆的标准方程和几何性质、直线与椭圆的位置关系以及对称问题,意在考查学生逻辑推理能力和分析问题、解决问题的综合能力.【试题解析】(Ⅰ)因为椭圆C 的左顶点在圆22:12O x y +=上,所以a =. …………1分又离心率为23,所以23=a c ,所以3=c …………………2分 所以2223b a c =-=, …………………3分所以椭圆C 的方程为221123x y +=. …………………………4分(Ⅱ)(i )设11(,)M x y ,22(,)N x y .直线l 与椭圆C 方程联立223,1,123x my x y =+⎧⎪⎨+=⎪⎩化简并整理得22(4)630m y my ++-=,∴12264m y y m +=-+,12234y y m =-+ …………………………………………6分 ∴2121222624()6644m x x m y y m m +=++=-+=++,222212121222231836123()99444m m m x x m y y m y y m m m -=+++=--+=+++.因为OM ON ⊥,∴0OM ON ⋅=,即12120x x y y +=,代入,得22236123044m m m --=++,解得2114m =,所以m =. ………………8分故PMN ∆的面积存在最大值,最大值为1. ……………………………14分。
2016年高考数学中难题

2016年高考数学中难题一.选择题(共9小题)1.(2016•新课标Ⅱ)已知函数f(x)(x∈R)满足f(﹣x)=2﹣f(x),若函数y=与y=f(x)图象的交点为(x1,y1),(x2,y2),…,(x m,y m),则(x i+y i)=()A.0 B.m C.2m D.4m2.(2016•新课标Ⅱ)已知F1,F2是双曲线E:﹣=1的左,右焦点,点M在E上,MF1与x轴垂直,sin∠MF2F1=,则E的离心率为()A.B.C.D.23.(2016•新课标Ⅲ)在封闭的直三棱柱ABC﹣A1B1C1内有一个体积为V的球,若AB⊥BC,AB=6,BC=8,AA1=3,则V的最大值是()A.4πB. C.6πD.4.(2016•新课标Ⅲ)已知O为坐标原点,F是椭圆C:+=1(a>b>0)的左焦点,A,B分别为C的左,右顶点.P为C上一点,且PF⊥x轴,过点A的直线l与线段PF交于点M,与y轴交于点E.若直线BM经过OE的中点,则C的离心率为()A.B.C.D.5.(2016•新课标Ⅲ)定义“规范01数列”{a n}如下:{a n}共有2m项,其中m项为0,m项为1,且对任意k≤2m,a1,a2,…,a k中0的个数不少于1的个数,若m=4,则不同的“规范01数列”共有()A.18个B.16个C.14个D.12个6.(2016•浙江)如图,点列{A n}、{B n}分别在某锐角的两边上,且|A n A n+1|=|A n+1A n+2|,A n≠A n+1,n ∈N*,|B n B n+1|=|B n+1B n+2|,B n≠B n+1,n∈N*,(P≠Q表示点P与Q不重合)若d n=|A n B n|,S n为△A n B n B n+1的面积,则()A.{S n}是等差数列B.{S n2}是等差数列C.{d n}是等差数列 D.{d n2}是等差数列7.(2016•浙江)已知实数a,b,c.()A.若|a2+b+c|+|a+b2+c|≤1,则a2+b2+c2<100B.若|a2+b+c|+|a2+b﹣c|≤1,则a2+b2+c2<100C.若|a+b+c2|+|a+b﹣c2|≤1,则a2+b2+c2<100D.若|a2+b+c|+|a+b2﹣c|≤1,则a2+b2+c2<1008.(2016•四川)设直线l1,l2分别是函数f(x)=图象上点P1,P2处的切线,l1与l2垂直相交于点P,且l1,l2分别与y轴相交于点A,B,则△PAB的面积的取值范围是()A.(0,1) B.(0,2) C.(0,+∞)D.(1,+∞)9.(2016•四川)在平面内,定点A,B,C,D满足==,•=•=•=﹣2,动点P,M满足=1,=,则||2的最大值是()A.B.C. D.二.填空题(共21小题)10.(2016•新课标Ⅰ)设等比数列{a n}满足a1+a3=10,a2+a4=5,则a1a2…a n的最大值为.11.(2016•新课标Ⅰ)某高科技企业生产产品A和产品B需要甲、乙两种新型材料.生产一件产品A 需要甲材料1.5kg,乙材料1kg,用5个工时;生产一件产品B需要甲材料0.5kg,乙材料0.3kg,用3个工时,生产一件产品A的利润为2100元,生产一件产品B的利润为900元.该企业现有甲材料150kg,乙材料90kg,则在不超过600个工时的条件下,生产产品A、产品B的利润之和的最大值为元.12.(2016•新课标Ⅱ)若直线y=kx+b是曲线y=lnx+2的切线,也是曲线y=ln(x+1)的切线,则b=.13.(2016•新课标Ⅲ)已知f(x)为偶函数,当x<0时,f(x)=ln(﹣x)+3x,则曲线y=f(x)在点(1,﹣3)处的切线方程是.14.(2016•新课标Ⅲ)已知直线l:mx+y+3m﹣=0与圆x2+y2=12交于A,B两点,过A,B分别作l 的垂线与x轴交于C,D两点,若|AB|=2,则|CD|=.15.(2016•浙江)如图,在△ABC中,AB=BC=2,∠ABC=120°.若平面ABC外的点P和线段AC上的点D,满足PD=DA,PB=BA,则四面体PBCD的体积的最大值是.16.(2016•浙江)已知向量,,||=1,||=2,若对任意单位向量,均有|•|+|•|≤,则•的最大值是.17.(2016•浙江)设数列{a n}的前n项和为S n,若S2=4,a n+1=2S n+1,n∈N*,则a1=,S5=.18.(2016•山东)已知函数f(x)=,其中m>0,若存在实数b,使得关于x的方程f(x)=b有三个不同的根,则m的取值范围是.19.(2016•北京)双曲线﹣=1(a>0,b>0)的渐近线为正方形OABC的边OA,OC所在的直线,点B为该双曲线的焦点.若正方形OABC的边长为2,则a=.20.(2016•北京)设函数f(x)=.①若a=0,则f(x)的最大值为;②若f(x)无最大值,则实数a的取值范围是.21.(2016•四川)若函数f(x)是定义R上的周期为2的奇函数,当0<x<1时,f(x)=4x,则f(﹣)+f(2)=.22.(2016•上海)方程3sinx=1+cos2x在区间[0,2π]上的解为.23.(2016•上海)已知点(3,9)在函数f(x)=1+a x的图象上,则f(x)的反函数f﹣1(x)=.24.(2016•上海)在正四棱柱ABCD﹣A1B1C1D1中,底面ABCD的边长为3,BD1与底面所成角的大小为arctan,则该正四棱柱的高等于.25.(2016•上海)设a>0,b>0,若关于x,y的方程组无解,则a+b的取值范围为.26.(2016•江苏)定义在区间[0,3π]上的函数y=sin2x的图象与y=cosx的图象的交点个数是.27.(2016•江苏)如图,在平面直角坐标系xOy中,F是椭圆+=1(a>b>0)的右焦点,直线y=与椭圆交于B,C两点,且∠BFC=90°,则该椭圆的离心率是.28.(2016•江苏)设f(x)是定义在R上且周期为2的函数,在区间[﹣1,1)上,f(x)=,其中a∈R,若f(﹣)=f(),则f(5a)的值是.29.(2016•江苏)已知实数x,y满足,则x2+y2的取值范围是.30.(2016•江苏)在锐角三角形ABC中,若sinA=2sinBsinC,则tanAtanBtanC的最小值是.2016年高考数学中难题参考答案与试题解析一.选择题(共9小题)1.(2016•新课标Ⅱ)已知函数f(x)(x∈R)满足f(﹣x)=2﹣f(x),若函数y=与y=f(x)图象的交点为(x1,y1),(x2,y2),…,(x m,y m),则(x i+y i)=()A.0 B.m C.2m D.4m【解答】解:函数f(x)(x∈R)满足f(﹣x)=2﹣f(x),即为f(x)+f(﹣x)=2,可得f(x)关于点(0,1)对称,函数y=,即y=1+的图象关于点(0,1)对称,即有(x1,y1)为交点,即有(﹣x1,2﹣y1)也为交点,(x2,y2)为交点,即有(﹣x2,2﹣y2)也为交点,…则有(x i+y i)=(x1+y1)+(x2+y2)+…+(x m+y m)=[(x1+y1)+(﹣x1+2﹣y1)+(x2+y2)+(﹣x2+2﹣y2)+…+(x m+y m)+(﹣x m+2﹣y m)]=m.故选:B.2.(2016•新课标Ⅱ)已知F1,F2是双曲线E:﹣=1的左,右焦点,点M在E上,MF1与x轴垂直,sin∠MF2F1=,则E的离心率为()A.B.C.D.2【解答】解:由题意,M为双曲线左支上的点,则丨MF1丨=,丨MF2丨=,∴sin∠MF2F1=,∴=,可得:2b4=a2c2,即b2=ac,又c2=a2+b2,可得e2﹣e﹣=0,e>1,解得e=.故选:A.3.(2016•新课标Ⅲ)在封闭的直三棱柱ABC﹣A1B1C1内有一个体积为V的球,若AB⊥BC,AB=6,BC=8,AA1=3,则V的最大值是()A.4πB. C.6πD.【解答】解:∵AB⊥BC,AB=6,BC=8,∴AC=10.故三角形ABC的内切圆半径r==2,又由AA1=3,故直三棱柱ABC﹣A1B1C1的内切球半径为,此时V的最大值=,故选:B.4.(2016•新课标Ⅲ)已知O为坐标原点,F是椭圆C:+=1(a>b>0)的左焦点,A,B分别为C的左,右顶点.P为C上一点,且PF⊥x轴,过点A的直线l与线段PF交于点M,与y轴交于点E.若直线BM经过OE的中点,则C的离心率为()A.B.C.D.【解答】解:由题意可设F(﹣c,0),A(﹣a,0),B(a,0),设直线AE的方程为y=k(x+a),令x=﹣c,可得M(﹣c,k(a﹣c)),令x=0,可得E(0,ka),设OE的中点为H,可得H(0,),由B,H,M三点共线,可得k BH=k BM,即为=,化简可得=,即为a=3c,可得e==.另解:由△AMF∽△AEO,可得=,由△BOH∽△BFM,可得==,即有=即a=3c,可得e==.故选:A.5.(2016•新课标Ⅲ)定义“规范01数列”{a n}如下:{a n}共有2m项,其中m项为0,m项为1,且对任意k≤2m,a1,a2,…,a k中0的个数不少于1的个数,若m=4,则不同的“规范01数列”共有()A.18个B.16个C.14个D.12个【解答】解:由题意可知,“规范01数列”有偶数项2m项,且所含0与1的个数相等,首项为0,末项为1,若m=4,说明数列有8项,满足条件的数列有:0,0,0,0,1,1,1,1;0,0,0,1,0,1,1,1;0,0,0,1,1,0,1,1;0,0,0,1,1,1,0,1;0,0,1,0,0,1,1,1;0,0,1,0,1,0,1,1;0,0,1,0,1,1,0,1;0,0,1,1,0,1,0,1;0,0,1,1,0,0,1,1;0,1,0,0,0,1,1,1;0,1,0,0,1,0,1,1;0,1,0,0,1,1,0,1;0,1,0,1,0,0,1,1;0,1,0,1,0,1,0,1.共14个.故选:C.6.(2016•浙江)如图,点列{A n}、{B n}分别在某锐角的两边上,且|A n A n+1|=|A n+1A n+2|,A n≠A n+1,n ∈N*,|B n B n+1|=|B n+1B n+2|,B n≠B n+1,n∈N*,(P≠Q表示点P与Q不重合)若d n=|A n B n|,S n为△A n B n B n+1的面积,则()A.{S n}是等差数列B.{S n2}是等差数列C.{d n}是等差数列 D.{d n2}是等差数列【解答】解:设锐角的顶点为O,|OA1|=a,|OB1|=c,|A n A n+1|=|A n+1A n+2|=b,|B n B n+1|=|B n+1B n+2|=d,由于a,c不确定,则{d n}不一定是等差数列,{d n2}不一定是等差数列,设△A n B n B n+1的底边B n B n+1上的高为h n,由三角形的相似可得==,==,两式相加可得,==2,即有h n+h n+2=2h n+1,由S n=d•h n,可得S n+S n+2=2S n+1,﹣S n+1=S n+1﹣S n,即为S n+2则数列{S n}为等差数列.另解:可设△A1B1B2,△A2B2B3,…,A n B n B n+1为直角三角形,且A1B1,A2B2,…,A n B n为直角边,即有h n+h n+2=2h n+1,由S n=d•h n,可得S n+S n+2=2S n+1,﹣S n+1=S n+1﹣S n,即为S n+2则数列{S n}为等差数列.故选:A.7.(2016•浙江)已知实数a,b,c.()A.若|a2+b+c|+|a+b2+c|≤1,则a2+b2+c2<100B.若|a2+b+c|+|a2+b﹣c|≤1,则a2+b2+c2<100C.若|a+b+c2|+|a+b﹣c2|≤1,则a2+b2+c2<100D.若|a2+b+c|+|a+b2﹣c|≤1,则a2+b2+c2<100【解答】解:A.设a=b=10,c=﹣110,则|a2+b+c|+|a+b2+c|=0≤1,a2+b2+c2>100;B.设a=10,b=﹣100,c=0,则|a2+b+c|+|a2+b﹣c|=0≤1,a2+b2+c2>100;C.设a=100,b=﹣100,c=0,则|a+b+c2|+|a+b﹣c2|=0≤1,a2+b2+c2>100;故选:D.8.(2016•四川)设直线l1,l2分别是函数f(x)=图象上点P1,P2处的切线,l1与l2垂直相交于点P,且l1,l2分别与y轴相交于点A,B,则△PAB的面积的取值范围是()A.(0,1) B.(0,2) C.(0,+∞)D.(1,+∞)【解答】解:设P1(x1,y1),P2(x2,y2)(0<x1<1<x2),当0<x<1时,f′(x)=,当x>1时,f′(x)=,∴l1的斜率,l2的斜率,∵l1与l2垂直,且x2>x1>0,∴,即x1x2=1.直线l1:,l2:.取x=0分别得到A(0,1﹣lnx1),B(0,﹣1+lnx2),|AB|=|1﹣lnx1﹣(﹣1+lnx2)|=|2﹣(lnx1+lnx2)|=|2﹣lnx1x2|=2.联立两直线方程可得交点P的横坐标为x=,∴|AB|•|x P|==.∵函数y=x+在(0,1)上为减函数,且0<x1<1,∴,则,∴.∴△PAB的面积的取值范围是(0,1).故选:A.9.(2016•四川)在平面内,定点A,B,C,D满足==,•=•=•=﹣2,动点P,M满足=1,=,则||2的最大值是()A.B.C. D.【解答】解:由==,可得D为△ABC的外心,又•=•=•,可得•(﹣)=0,•(﹣)=0,即•=•=0,即有⊥,⊥,可得D为△ABC的垂心,则D为△ABC的中心,即△ABC为正三角形.由•=﹣2,即有||•||cos120°=﹣2,解得||=2,△ABC的边长为4cos30°=2,以A为坐标原点,AD所在直线为x轴建立直角坐标系xOy,可得B(3,﹣),C(3,),D(2,0),由=1,可设P(cosθ,sinθ),(0≤θ<2π),由=,可得M为PC的中点,即有M(,),则||2=(3﹣)2+(+)2=+==,当sin(θ﹣)=1,即θ=时,取得最大值,且为.故选:B.二.填空题(共21小题)10.(2016•新课标Ⅰ)设等比数列{a n}满足a1+a3=10,a2+a4=5,则a1a2…a n的最大值为64.【解答】解:等比数列{a n}满足a1+a3=10,a2+a4=5,可得q(a1+a3)=5,解得q=.a1+q2a1=10,解得a1=8.则a1a2…a n=a1n•q1+2+3+…+(n﹣1)=8n•==,当n=3或4时,表达式取得最大值:=26=64.故答案为:64.11.(2016•新课标Ⅰ)某高科技企业生产产品A和产品B需要甲、乙两种新型材料.生产一件产品A 需要甲材料1.5kg,乙材料1kg,用5个工时;生产一件产品B需要甲材料0.5kg,乙材料0.3kg,用3个工时,生产一件产品A的利润为2100元,生产一件产品B的利润为900元.该企业现有甲材料150kg,乙材料90kg,则在不超过600个工时的条件下,生产产品A、产品B的利润之和的最大值为216000元.【解答】解:(1)设A、B两种产品分别是x件和y件,获利为z元.由题意,得,z=2100x+900y.不等式组表示的可行域如图:由题意可得,解得:,A(60,100),目标函数z=2100x+900y.经过A时,直线的截距最大,目标函数取得最大值:2100×60+900×100=216000元.故答案为:216000.12.(2016•新课标Ⅱ)若直线y=kx+b是曲线y=lnx+2的切线,也是曲线y=ln(x+1)的切线,则b=1﹣ln2.【解答】解:设y=kx+b与y=lnx+2和y=ln(x+1)的切点分别为(x1,kx1+b)、(x2,kx2+b);由导数的几何意义可得k==,得x1=x2+1再由切点也在各自的曲线上,可得联立上述式子解得;从而kx1+b=lnx1+2得出b=1﹣ln2.13.(2016•新课标Ⅲ)已知f(x)为偶函数,当x<0时,f(x)=ln(﹣x)+3x,则曲线y=f(x)在点(1,﹣3)处的切线方程是2x+y+1=0.【解答】解:f(x)为偶函数,可得f(﹣x)=f(x),当x<0时,f(x)=ln(﹣x)+3x,即有x>0时,f(x)=lnx﹣3x,f′(x)=﹣3,可得f(1)=ln1﹣3=﹣3,f′(1)=1﹣3=﹣2,则曲线y=f(x)在点(1,﹣3)处的切线方程为y﹣(﹣3)=﹣2(x﹣1),即为2x+y+1=0.故答案为:2x+y+1=0.14.(2016•新课标Ⅲ)已知直线l:mx+y+3m﹣=0与圆x2+y2=12交于A,B两点,过A,B分别作l 的垂线与x轴交于C,D两点,若|AB|=2,则|CD|=4.【解答】解:由题意,|AB|=2,∴圆心到直线的距离d=3,∴=3,∴m=﹣∴直线l的倾斜角为30°,∵过A,B分别作l的垂线与x轴交于C,D两点,∴|CD|==4.故答案为:4.15.(2016•浙江)如图,在△ABC中,AB=BC=2,∠ABC=120°.若平面ABC外的点P和线段AC上的点D,满足PD=DA,PB=BA,则四面体PBCD的体积的最大值是.【解答】解:如图,M是AC的中点.①当AD=t<AM=时,如图,此时高为P到BD的距离,也就是A到BD的距离,即图中AE,DM=﹣t,由△ADE∽△BDM,可得,∴h=,V==,t∈(0,)②当AD=t>AM=时,如图,此时高为P到BD的距离,也就是A到BD的距离,即图中AH,DM=t﹣,由等面积,可得,∴,∴h=,∴V==,t∈(,2)综上所述,V=,t∈(0,2)令m=∈[1,2),则V=,∴m=1时,V max=.另解:由于PD=DA,PB=BA,则对于每一个确定的AD,都有△PDB绕DB在空间中旋转,则PD⊥AC时体积最大,则只需考察所有PD⊥AC时的最大,设PD=DA=h,则V=Sh=h•sin30°•(2﹣h)•2,底二次函数求最值可知h=时体积最大为.故答案为:.16.(2016•浙江)已知向量,,||=1,||=2,若对任意单位向量,均有|•|+|•|≤,则•的最大值是.【解答】解:由绝对值不等式得≥|•|+|•|≥|•+•|=|(+)•|,于是对任意的单位向量,均有|(+)•|≤,∵|(+)|2=||2+||2+2•=5+2•,∴|(+)|=,因此|(+)•|的最大值≤,则•≤,下面证明:•可以取得,(1)若|•|+|•|=|•+•|,则显然满足条件.(2)若|•|+|•|=|•﹣•|,此时|﹣|2=||2+||2﹣2•=5﹣1=4,此时|﹣|=2于是|•|+|•|=|•﹣•|≤2,符合题意,综上•的最大值是,法2:由于任意单位向量,可设=,则|•|+|•|=||+||≥||+|=||=|+|,∵|•|+|•|≤,∴|+|≤,即(+)2≤6,即||2+||2+2•≤6,∵||=1,||=2,∴•≤,即•的最大值是.法三:设=,=,=,则=+,=﹣,|•|+|•|=||+||=||≤||,由题设当且仅当与同向时,等号成立,此时(+)2取得最大值6,由于|+|2+|﹣|)2=2(||2+||2)=10,于是(﹣)2取得最小值4,则•=,•的最大值是.故答案为:.17.(2016•浙江)设数列{a n}的前n项和为S n,若S2=4,a n+1=2S n+1,n∈N*,则a1=1,S5=121.【解答】解:由n=1时,a1=S1,可得a2=2S1+1=2a1+1,又S2=4,即a1+a2=4,即有3a1+1=4,解得a1=1;=S n+1﹣S n,可得由a n+1S n+1=3S n+1,由S2=4,可得S3=3×4+1=13,S4=3×13+1=40,S5=3×40+1=121.故答案为:1,121.18.(2016•山东)已知函数f(x)=,其中m>0,若存在实数b,使得关于x的方程f(x)=b有三个不同的根,则m的取值范围是(3,+∞).【解答】解:当m>0时,函数f(x)=的图象如下:∵x>m时,f(x)=x2﹣2mx+4m=(x﹣m)2+4m﹣m2>4m﹣m2,∴y要使得关于x的方程f(x)=b有三个不同的根,必须4m﹣m2<m(m>0),即m2>3m(m>0),解得m>3,∴m的取值范围是(3,+∞),故答案为:(3,+∞).19.(2016•北京)双曲线﹣=1(a>0,b>0)的渐近线为正方形OABC的边OA,OC所在的直线,点B为该双曲线的焦点.若正方形OABC的边长为2,则a=2.【解答】解:∵双曲线的渐近线为正方形OABC的边OA,OC所在的直线,∴渐近线互相垂直,则双曲线为等轴双曲线,即渐近线方程为y=±x,即a=b,∵正方形OABC的边长为2,∴OB=2,即c=2,则a2+b2=c2=8,即2a2=8,则a2=4,a=2,故答案为:220.(2016•北京)设函数f(x)=.①若a=0,则f(x)的最大值为2;②若f(x)无最大值,则实数a的取值范围是(﹣∞,﹣1).【解答】解:①若a=0,则f(x)=,则f′(x)=,当x<﹣1时,f′(x)>0,此时函数为增函数,当x>﹣1时,f′(x)<0,此时函数为减函数,故当x=﹣1时,f(x)的最大值为2;②f′(x)=,令f′(x)=0,则x=±1,若f(x)无最大值,则,或,解得:a∈(﹣∞,﹣1).故答案为:2,(﹣∞,﹣1)21.(2016•四川)若函数f(x)是定义R上的周期为2的奇函数,当0<x<1时,f(x)=4x,则f(﹣)+f(2)=﹣2.【解答】解:∵函数f(x)是定义R上的周期为2的奇函数,当0<x<1时,f(x)=4x,∴f(2)=f(0)=0,f(﹣)=f(﹣+2)=f(﹣)=﹣f()=﹣=﹣=﹣2,则f(﹣)+f(2)=﹣2+0=﹣2,故答案为:﹣2.22.(2016•上海)方程3sinx=1+cos2x在区间[0,2π]上的解为或.【解答】解:方程3sinx=1+cos2x,可得3sinx=2﹣2sin2x,即2sin2x+3sinx﹣2=0.可得sinx=﹣2,(舍去)sinx=,x∈[0,2π]解得x=或.故答案为:或.23.(2016•上海)已知点(3,9)在函数f(x)=1+a x的图象上,则f(x)的反函数f﹣1(x)=log2(x﹣1)(x>1).【解答】解:∵点(3,9)在函数f(x)=1+a x的图象上,∴9=1+a3,解得a=2.∴f(x)=1+2x,由1+2x=y,解得x=log2(y﹣1),(y>1).把x与y互换可得:f(x)的反函数f﹣1(x)=log2(x﹣1).故答案为:log2(x﹣1),(x>1).24.(2016•上海)在正四棱柱ABCD﹣A1B1C1D1中,底面ABCD的边长为3,BD1与底面所成角的大小为arctan,则该正四棱柱的高等于2.【解答】解:∵正四棱柱ABCD﹣A1B1C1D1的侧棱D1D⊥底面ABCD,∴∠D1BD为直线BD1与底面ABCD所成的角,∴tan∠D1BD=,∵正四棱柱ABCD﹣A1B1C1D1中,底面ABCD的边长为3,∴BD=3,∴正四棱柱的高=3×=2,故答案为:2.25.(2016•上海)设a>0,b>0,若关于x,y的方程组无解,则a+b的取值范围为(2,+∞).【解答】解:∵关于x,y的方程组无解,∴直线ax+y=1与x+by=1平行,∵a>0,b>0,∴≠,即a≠1,b≠1,且ab=1,则b=,由基本不等式有:a+b=a+≥2=2,当且仅当a=1时取等,而a的范围为a>0且a≠1,不满足取等条件,∴a+b>2,故答案为:(2,+∞).26.(2016•江苏)定义在区间[0,3π]上的函数y=sin2x的图象与y=cosx的图象的交点个数是7.【解答】解:法1:画出函数y=sin2x与y=cosx在区间[0,3π]上的图象如下:由图可知,共7个交点.法2:依题意,sin2x=cosx,即cosx(2sinx﹣1)=0,故cosx=0或sinx=,因为x∈[0,3π],故x=,,,,,,,共7个,故答案为:7.27.(2016•江苏)如图,在平面直角坐标系xOy中,F是椭圆+=1(a>b>0)的右焦点,直线y=与椭圆交于B,C两点,且∠BFC=90°,则该椭圆的离心率是.【解答】解:设右焦点F(c,0),将y=代入椭圆方程可得x=±a=±a,可得B(﹣a,),C(a,),由∠BFC=90°,可得k BF•k CF=﹣1,即有•=﹣1,化简为b2=3a2﹣4c2,由b2=a2﹣c2,即有3c2=2a2,由e=,可得e2==,可得e=,另解:设右焦点F(c,0),将y=代入椭圆方程可得x=±a=±a,可得B(﹣a,),C(a,),=(﹣a﹣c,),=(a﹣c,),•=0,则c2﹣a2十b2=0,因为b2=a2﹣c2,代入得3c2=2a2,由e=,可得e2==,可得e=.故答案为:.28.(2016•江苏)设f(x)是定义在R上且周期为2的函数,在区间[﹣1,1)上,f(x)=,其中a∈R,若f(﹣)=f(),则f(5a)的值是﹣.【解答】解:f(x)是定义在R上且周期为2的函数,在区间[﹣1,1)上,f(x)=,∴f(﹣)=f(﹣)=﹣+a,f()=f()=|﹣|=,∴a=,∴f(5a)=f(3)=f(﹣1)=﹣1+=﹣,故答案为:﹣29.(2016•江苏)已知实数x,y满足,则x2+y2的取值范围是[,13] .【解答】解:作出不等式组对应的平面区域,设z=x2+y2,则z的几何意义是区域内的点到原点距离的平方,由图象知A到原点的距离最大,点O到直线BC:2x+y﹣2=0的距离最小,由得,即A(2,3),此时z=22+32=4+9=13,点O到直线BC:2x+y﹣2=0的距离d==,则z=d2=()2=,故z的取值范围是[,13],故答案为:[,13].30.(2016•江苏)在锐角三角形ABC中,若sinA=2sinBsinC,则tanAtanBtanC的最小值是8.【解答】解:由sinA=sin(π﹣A)=sin(B+C)=sinBcosC+cosBsinC,sinA=2sinBsinC,可得sinBcosC+cosBsinC=2sinBsinC,①由三角形ABC为锐角三角形,则cosB>0,cosC>0,在①式两侧同时除以cosBcosC可得tanB+tanC=2tanBtanC,又tanA=﹣tan(π﹣A)=﹣tan(B+C)=﹣②,则tanAtanBtanC=﹣•tanBtanC,由tanB+tanC=2tanBtanC可得tanAtanBtanC=﹣,令tanBtanC=t,由A,B,C为锐角可得tanA>0,tanB>0,tanC>0,由②式得1﹣tanBtanC<0,解得t>1,tanAtanBtanC=﹣=﹣,=()2﹣,由t>1得,﹣≤<0,因此tanAtanBtanC的最小值为8,另解:由已知条件sinA=2sinBsinc,sin(B十C)=2sinBsinC,sinBcosC十cosBsinC=2sinBcosC,两边同除以cosBcosC,tanB十tanC=2tanBtanC,∵﹣tanA=tan(B十C)=,∴tanAtanBtanC=tanA十tanB十tanC,∴tanAtanBtanC=tanA十2tanBtanC≥2,令tanAtanBtanC=x>0,即x≥2,即x≥8,或x≤0(舍去),所以x的最小值为8.当且仅当t=2时取到等号,此时tanB+tanC=4,tanBtanC=2,解得tanB=2+,tanC=2﹣,tanA=4,(或tanB,tanC互换),此时A,B,C均为锐角.。
高考逆袭卷01-2024年高考数学最后冲刺大题秒杀技巧及题型专项训练(新高考新题型专用)(原卷版)

2024年高考考前逆袭卷(新高考新题型)01数学(考试时间:120分钟试卷满分:150分)全国新高考卷的题型会有所调整,考试题型为8(单选题)+3(多选题)+3(填空题)+5(解答题),其中最后一道试题是新高考地区新增加的题型,主要涉及集合、数列,导数等模块,以解答题的方式进行考查。
预测2024年新高考地区数列极有可能出现在概率与统计大题中,而结构不良型题型可能为集合或导数模块中的一个,出现在19题的可能性较大,难度中等偏上,例如本卷第19题。
第I 卷(选择题)一、选择题:本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合要求的。
1.已知样本数据12100,,,x x x 的平均数和标准差均为4,则数据121001,1,,1x x x ------ 的平均数与方差分别为()A .5,4-B .5,16-C .4,16D .4,42.已知向量()1,2a = ,3b = ,2a b -= ,则向量a 在向量b 上的投影向量的模长为()A .6B .3C .2D .53.已知在等比数列{}n a 中,23215a a +=,234729a a a =,则n n S a -=()A .1232n -⨯-B .()11312n --C .23n n ⨯-D .533n ⨯-4.已知三棱锥A BCD -中,6,3,AB AC BC ===三棱锥A BCD -的体积为2,其外接球的体积为500π3,则线段CD 长度的最大值为()A .7B .8C .D .105.一个信息设备装有一排六只发光电子元件,每个电子元件被点亮时可发出红色光、蓝色光、绿色光中的一种光.若每次恰有三个电子元件被点亮,但相邻的两个电子元件不能同时被点亮,根据这三个被点亮的电子元件的不同位置以及发出的不同颜色的光来表示不同的信息,则这排电子元件能表示的信息种数共有()A .60种B .68种C .82种D .108种6.已知 1.12a -=,1241log log 33b c ==,,则()A .a b c <<B .c b a <<C .b a c <<D .b c a <<7.纯电动汽车是以车载电源为动力,用电机驱动车轮行驶,符合道路交通、安全法规各项要求的车辆,它使用存储在电池中的电来发动.因其对环境影响较小,逐渐成为当今世界的乘用车的发展方向.研究发现电池的容量随放电电流的大小而改变,1898年Peukert 提出铅酸电池的容量C 、放电时间t 和放电电流I 之间关系的经验公式:C I t λ=,其中λ为与蓄电池结构有关的常数(称为Peukert 常数),在电池容量不变的条件下,当放电电流为7.5A 时,放电时间为60h ;当放电电流为25A 时,放电时间为15h ,则该蓄电池的Peukert 常数λ约为(参考数据:lg 20.301≈,lg 30.477≈)()A .1.12B .1.13C .1.14D .1.158.已知双曲线22122:1(0,0)x y C a b a b-=>>与抛物线22:2(0)C y px p =>,抛物线2C 的准线过双曲线1C 的焦点F ,过点F 作双曲线1C 的一条渐近线的垂线,垂足为点M ,延长FM 与抛物线2C 相交于点N ,若34ON OF OM += ,则双曲线1C 的离心率等于()A1+BCD1二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9.在复平面内,下列说法正确的是()A .若复数1i 1i-=+z (i 为虚数单位),则741z =-B .若复数z 满足z z =,则z ∈RC .若120z z =,则10z =或20z =D .若复数z 满足112z z -++=,则复数z 对应点的集合是以坐标原点O 为中心,焦点在x 轴上的椭圆10.设直线系:cos sin 1n m M x y θθ+=(其中0,m ,n 均为参数,02π≤≤θ,{},1,2m n ∈),则下列命题中是真命题的是()A .当1m =,1n =时,存在一个圆与直线系M 中所有直线都相切B .存在m ,n ,使直线系M 中所有直线恒过定点,且不过第三象限C .当m n =时,坐标原点到直线系M 中所有直线的距离最大值为1,最小值为2D .当2m =,1n =时,若存在一点()0A a ,,使其到直线系M 中所有直线的距离不小于1,则0a ≤11.如图所示,一个圆锥SO 的底面是一个半径为3的圆,AC 为直径,且120ASC ∠=︒,点B 为圆O 上一动点(异于A ,C 两点),则下列结论正确的是()A .SAB ∠的取值范围是ππ,62⎡⎤⎢⎣⎦B .二面角S BC A --的平面角的取值范围是ππ,62⎛⎫ ⎪⎝⎭C .点A 到平面SBC 的距离最大值为3D .点M 为线段SB 上的一动点,当SA SB ⊥时,6AM MC +>第II 卷(非选择题)三、填空题:本题共3小题,每小题5分,共15分.12.设集合{}2|60A x x x =--<,{|}B x a x a =-≤≤,若A B ⊆,则实数a 的取值范围是.13.已知三棱柱111ABC A B C -中,ABC 是边长为2的等边三角形,四边形11ABB A 为菱形,160A AB ∠=︒,平面11ABB A ⊥平面ABC ,M 为AB 的中点,N 为1BB 的中点,则三棱锥11C A MN -的外接球的表面积为.14.已知对任意()12,0,x x ∈+∞,且当12x x <时,都有:()212112ln ln 11a x x x x x x -<+-,则a 的取值范围是.四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15.(13分)在ABC 中,内角A ,B ,C 所对的边分别a ,b ,c ,其中2,a b c =+=,且sin A C =.(1)求c 的值;(2)求tan A 的值;(3)求cos 24A π⎛⎫+ ⎪⎝⎭的值.16.(15分)如图,在三棱锥-P ABC 中,M 为AC 边上的一点,90APC PMA ∠=∠=︒,cosCAB ∠=2AB PC =PA =(1)证明:AC ⊥平面PBM ;(2)设点Q 为边PB 的中点,试判断三棱锥P ACQ -的体积是否有最大值?如果有,请求出最大值;如果没有,请说明理由.17.(15分)近年来,某大学为响应国家号召,大力推行全民健身运动,向全校学生开放了,A B 两个健身中心,要求全校学生每周都必须利用课外时间去健身中心进行适当的体育锻炼.(1)该校学生甲、乙、丙三人某周均从,A B 两个健身中心中选择其中一个进行健身,若甲、乙、丙该周选择A 健身中心健身的概率分别为112,,233,求这三人中这一周恰好有一人选择A 健身中心健身的概率;(2)该校学生丁每周六、日均去健身中心进行体育锻炼,且这两天中每天只选择两个健身中心的其中一个,其中周六选择A 健身中心的概率为12.若丁周六选择A 健身中心,则周日仍选择A 健身中心的概率为14;若周六选择B 健身中心,则周日选择A 健身中心的概率为23.求丁周日选择B 健身中心健身的概率;(3)现用健身指数[]()0,10k k ∈来衡量各学生在一个月的健身运动后的健身效果,并规定k 值低于1分的学生为健身效果不佳的学生,经统计发现从全校学生中随机抽取一人,其k 值低于1分的概率为0.12.现从全校学生中随机抽取一人,如果抽取到的学生不是健身效果不佳的学生,则继续抽取下一个,直至抽取到一位健身效果不佳的学生为止,但抽取的总次数不超过n .若抽取次数的期望值不超过23,求n 的最大值.参考数据:2930310.980.557,0.980.545,0.980.535≈≈≈.18.(17分)已知椭圆2222:1(0)x y C a b a b+=>>的上下顶点分别为12,B B ,左右顶点分别为12,A A ,四边形1122A B A B 的面积为C 上的点到右焦点距离的最大值和最小值之和为6.(1)求椭圆C 的方程;(2)过点()1,0-且斜率不为0的直线l 与C 交于,P Q (异于12,A A )两点,设直线2A P 与直线1AQ 交于点M ,证明:点M 在定直线上.19.(17分)给定整数3n ≥,由n 元实数集合P 定义其随影数集{},,Q x y x y P x y =-∈≠∣.若()min 1Q =,则称集合P 为一个n 元理想数集,并定义P 的理数t 为其中所有元素的绝对值之和.(1)分别判断集合{}{}2,1,2,3,0.3,1.2,2.1,2.5S T =--=--是不是理想数集;(结论不要求说明理由)(2)任取一个5元理想数集P ,求证:()()min max 4P P +≥;(3)当{}122024,,,P x x x = 取遍所有2024元理想数集时,求理数t 的最小值.注:由n 个实数组成的集合叫做n 元实数集合,()()max ,min P P 分别表示数集P 中的最大数与最小数.。
2016年高考全国2卷理科数学及答案

绝密★启用前2016年普通高等学校招生全国统一考试理科数学 全国II 卷(全卷共12页)(适用地区:贵州,甘肃,青海,西藏,黑龙江,吉林,辽宁,宁夏,新疆,内蒙古,云南,重庆,陕西,海南)注意事项:1. 本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分。
2. 答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
3. 回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号,回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
4.考试结束后,将本试卷和答案卡一并交回。
第I 卷一、 选择题:本题共12小题,每小题5分。
在每个小题给出的四个选项中, 只有一项是符合题目要求的。
(1) 已知i m m z )1()3(−++=在复平面内对应的点在第四象限,则实数m 的取值范围是(A )(3−,1) (B )(1−,3) (C )(1,∞+) (D )(∞−,3−) (2) 已知集合{}3,2,1=A ,{}Z x x x x B∈<−+=,0)2)(1(,则=B A(A ){}1 (B ){}2,1 (C ){}3,2,1,0 (D ){}3,2,1,0,1− (3) 已知向量),1(m a =,)2,3(−=b 且b b a ⊥+)(,则=m(A )8− (B )6− (C )6 (D )8 (4) 圆0138222=+−−+y x y x的圆心到直线01=−+y ax 的距离为1,则=a(A )34−(B )43− (C )3 (D )2(5) 如图,小明从街道的E 处出发,先到F 处与小红会合,再一起到位于G 处的老年公寓参加志愿者活动,则小明到老年公寓可以选择的最短路径条数为 (A )24 (B )18 (C )12 (D )9(6) 右图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为(A )20π (B )24π (C )28π (D )32π(7) 若将函数x y 2sin 2=的图像向左平移12π个单位长度,则平移后图像的对称轴为 (A ))(62Z k k x ∈−=ππ (B ))(62Z k k x ∈+=ππ(C ))(122Z k k x ∈−=ππ (D ))(122Z k k x ∈+=ππ(8) 中国古代有计算多项式值的秦九韶算法,右图是实现该算法的程序框图.执行该程序框图,若输入的2=x ,2=n ,依次输入的a 为2,2,5,则输出的=s(A )7 (B )12(C )17 (D )34(9) 若53)4cos(=−απ,则=α2sin(A )257(B )51(C )51− (D )257−(10) 以从区间[]1,0随机抽取n 2个数n n y y y x x x ,⋯⋯,,,,,,2121,构成n 个数对),(),,(),,(2211n n y x y x y x ,⋯,其中两数的平方和小于1的数对共有m 个,则用随机模拟的方法得到的圆周率π的近似值为 (A )n 4 (B )n 2 (C )m 4 (D )m 2否是 0,0==s kn k >输入n x ,输出s开始 结束输入a1+=+⋅=k k ax s s(11) 已知21,F F 是双曲线E :12222=−by a x 的左,右焦点,点M 在E 上,1MF 与x 轴垂直,31sin 12=∠F MF ,则E 的离心率为 (A )2 (B )23(C )3 (D )2(12) 已知函数))((R x x f ∈满足)(2)(x f x f −=−,若函数xx y 1+=与)(x f y =图像的交点为),(,),,(),,(2211m m y x y x y x ⋯,则=+∑=mi i i y x 1)((A )0 (B )m (C )m 2 (D )m 4第Ⅱ卷本卷包括必考题和选考题两部分。
普通高等学校招生全国统一考试文科数学冲刺试题二参考答案(新课标全国1卷).docx

2016年普通高等学校招生全国统一考试·冲刺试题二 参考答案文科数学(新课标全国Ⅰ卷)一、选择题1—5 CDDAC 6—10 BCBAB 11—12 AD6、解析:设标准差为s ,则解得s=.8、【答案】B【解析】这是一个等差数列问题,不妨设从低到高的每个人所得的金为:1021,..,,a a a ,依题意有:7874243364431110984321=⇒⎩⎨⎧=+=+⇒⎩⎨⎧=++=+++d d a d a a a a a a a a .二、填空题13、2)(x x f = 14、9715、2016,8222=⋅s16、三、解答题17、解:(Ⅰ)∵由正弦定理得:,…3分再由余弦定理知:所以………………6分(Ⅱ)因为,由(1)知,所以,……………… 7分又因为成等比数列,所以,因为数列为等差数列,所以,………………………9分又因为公差,所以解得,所以数列的通项公式设,则数列的通项公式,所以前项和………… 10分………… 12分18、19、证明:(Ⅰ)因为在△AA 1C 中,AA 1=A 1C ,D 为AC 中点,所以A 1D ⊥AC ; ----------2分 因为侧面AA 1C 1C 底面ABC , --------3分 侧面AA 1C 1C ∩底面ABC = AC , -----------4分C 1B 1A 1FEDACB所以A 1D ⊥平面ABC ; -----------5分(Ⅱ)设B 1C 1的中点为G ,连结FG ,GB , ---------------6分在四边形FGBE 中FG ∥A 1B 1,且FG =12A 1B 1,又因为EB ∥A 1B 1,且EB =12A 1B 1, 所以FG 与EB 平行且相等,所以四边形FGBE 为平行四边形; 所以EF ∥BG , ------------8分 又因为BG 在平面BB 1C 1C 内,EF 不在平面BB 1C 1C 内, 所以EF ∥平面BB 1C 1C . --------------10分 (Ⅲ)四棱锥A 1-BB 1C 1C 的体积为233. -------------12分 20、解:(Ⅰ)设直线的方程为,,由 ∴,∴. (Ⅱ)根据题意,直线斜率存在,故设,, 由, l :1l x ty =+1122(,),(,)P x y Q x y 214x ty y x=+⎧⎨=⎩2440y ty ⇒--=124y y =-121x x =12123OP OQ x x y y ⋅=+=-12123x x y y =+=-,AB CD 1:,:AB x my t CD x y t m=+=-+11223344(,),(,),(,),(,)A x y B x y C x y D x y 24x my ty x=+⎧⎨=⎩2440y my t ⇒--=∴,得,同理可得 ∴, ∴当且仅当时,面积取最小值4. 21、(Ⅰ)由题意()1f x a x '=+,令()0f x '=解得1x a =-因为1,a e ⎛⎫∈-∞ ⎪⎝⎭,所以10e a<-<, 由()0f x '>解得10x a <<-,由()0f x '<解得1x e a -<< 从而()f x 的单调递增区间为10,a ⎛⎫-⎪⎝⎭,减区间为1,e a ⎛⎫- ⎪⎝⎭所以,()max 1111ln 4f x f a a ⎛⎫⎛⎫=-=--+-=- ⎪ ⎪⎝⎭⎝⎭,解得2a e =-.-------5分 (Ⅱ)函数()()ln 2xb g x f x x =--存在零点,即方程()ln 2x bf x x =+有实数根, 由已知,函数()f x 的定义域为{}0x x >,当1a e =-时,()1ln xf x x e=--+, 所以()11x ef x e x ex-'=-+=-,------7分 当0x e <<时,()0f x '>;当x e >时,()0f x '<,所以()f x 的单调增区间为()0,e ,减区间为(),e +∞,所以()()max 1f x f e ==-,所以()1f x ≥.令()ln 2x b h x x =+,则()21ln xh x x-'=.当0x e <<时,()0h x '>; 当x e >时,从而()()h x g x 在()0,e 上单调递增,在(),e +∞上单调递减,212122222y y x x m m t ++=⇒=+2(2,2)M m t m +222(,)N t m m+-4224421TM m m m m =+=+22424421TN m m m m=+=+112()42TMN S TM TN m m∆==+≥1m =所以()()max 12b h x h e e ==+,要使方程()ln 2x b f x x =+有实数根, 只需()()max 112b h x h e e ==+≥即可,则22b e≥-.-------12分选做题:22、解:(Ⅰ) AB 是圆O 的直径,BD AD ⊥∴,即︒=∠90ADM又MN 垂直BA 的延长线于点N ,即︒=∠90ANM∴M 、N 、A 、D 四点共圆,∴NAM MDN ∠=∠MDN BDC BDC BAC NAM BAC ∠=∠∴∠=∠∠=∠,,由于︒=∠=∠90ADB ADM ,所以ADN ADC ∠=∠ 所以DA 是CDN ∠的角分线(5分)(Ⅱ) M 、N 、A 、D 四点共圆, ∴BD BM NB AB ⋅=⋅①B 、C 、A 、D 四点共圆,∴MC MA MB MD ⋅=⋅②① +②有ANAB AC MA AB MA BM AN AB AB AC MA MA BM BN AB MC MA BD MB MB MD ⋅+⋅++=+⋅++⋅=⋅+⋅=⋅+⋅2222)()( B 、C 、M 、N 四点共圆,所以AN AB AC MA ⋅=⋅所以2222BM AB AM AB AN =++⋅(10分)23、解析: (Ⅰ)曲线1C 的参数方程为2x t y t⎧=⎨=⎩(t 为参数)普通方程为2y x =将cos sin x y ρθρθ=⎧⎨=⎩代入上式化简得2sin cos ρθθ=即1C 的极坐标方程为2sin cos 0ρθθ-= (5分) (Ⅱ)曲线2C 的极坐标方程22cos 40ρρθ+-=化为平面直角坐标方程为22240x y x ++-=将2y x =代入上式得2340x x +-=,解得1,4x x ==-(舍去)当1x =时,1y =±,所以1C 与2C 交点的平面直角坐标为(1,1),(1,1)A B -∵112,112A B ρρ=+==+=,tan 1,tan 1A B θθ==-,0,02ρθπ≥≤< ∴7,44A B ππθθ==故1C 与2C 交点的极坐标72,,2,44A B ππ⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭(10分)24、(Ⅰ)由题()(2)f x f x +-1(2)1ax a x =++-+ 1212ax a ax a =++--≥,可见,21a ≥,即12a ≥或12a ≤-…………………………………………5分 (Ⅱ)由111()()()4a b c f f f a a a---++=知4a b c ++=, 而222111()()()a b c f f f a a a---++222a b c =++,………………………………7分因为222216()222a b c a b c ab ac bc =++=+++++,又222ab a b ≤+,222ac a c ≤+,222cb c b ≤+,所以,222163()a b c ≤++,即222163a b c ++≥,等号成立当且仅当a b c ==. 因此,222111()()()a b c f f f a a a ---++的最小值是163.………………………10分。
2016年高考化学复习试题:专题十 重要的有机化合物 冲刺卷 含答案

专题十重要的有机化合物冲刺卷[本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共60分,考试时间50分钟]可能用到的相对原子质量:H—1C—12N—14O—16Na—23Mg—24Al—27S—32Mn—55Fe—56第Ⅰ卷(选择题共24分)不定项选择题(本题共6小题,每小题4分。
在每小题给出的四个选项中,有一个或两个选项符合题目要求)1.莱克多巴胺是一种对人体有害的瘦肉精,自2011年12月5日起已在中国境内禁止生产和销售。
下列有关莱克多巴胺说法中正确的是()A.分子式为C18H24NO3B.在一定条件下可发生加成、取代、消去、氧化等反应C.分子中有2个手性碳原子,且所有碳原子不可能共平面D.1 mol 莱克多巴胺最多可以消耗4 mol Br2、3 mol NaOH2.蜂胶的主要活性成分CPAE可由咖啡酸和苯乙醇在一定条件下反应制得:下列叙述正确的是()A.苯乙醇属于芳香醇,它与邻甲基苯酚互为同系物B.1 mol CPAE最多可与3 mol 氢氧化钠发生化学反应C.用FeCl3溶液可以检测上述反应中是否有CPAE生成D.咖啡酸、苯乙醇及CPAE都能发生取代反应和加成反应,苯乙醇还能起消去反应3.某药物中间体的合成路线如下。
下列说法正确的是()中间体A.对苯二酚在空气中能稳定存在B.1 mol该中间体最多可与11 mol H2反应C.2,5-二羟基苯乙酮能发生加成、水解、缩聚反应D.该中间体分子中含有1个手性碳原子4.一种抗高血压的药物甲基多巴的结构简式如右图所示,下列说法正确的是()A.1 mol甲基多巴的分子中含有4 mol双键B.每个甲基多巴分子中含有一个手性碳原子C.1 mol甲基多巴最多能与2 mol Br2发生取代反应D.甲基多巴既能与盐酸反应,又能与氢氧化钠溶液反应5.雷美替胺是首个没有列为特殊管制的非成瘾失眠症治疗药物,合成该有机物过程中涉及如下转化,下列说法正确的是()A.可用溴水区分化合物Ⅱ和化合物ⅢB.化合物Ⅰ、Ⅱ、Ⅲ均能与NaHCO3溶液发生反应C.1 mol化合物Ⅰ最多能与3 mol H2发生加成反应D.与化合物Ⅰ互为同分异构体,且分子中含有2个醛基的芳香族化合物有10种6.某种合成药物中间体X的结构简式如图所示。
2016年高考理科数学全国新课标Ⅱ卷答案及解析

一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知 在复平面内对应的点在第四象限,则实数m的取值范围是
(A) (B) (C) (D)
2.已知集合 , ,则
(A) (B)
(C) (D)
3.已知向量 ,且 ,则m=
(A) (B) (C)6(D)8
(A) (B) (C) (D)2
12.已知函数 满足 ,若函数 与 图像的交点
为 , ,⋯, ,则 ()
(A)0(B)m(C)2m(D)4m
第Ⅱ卷
本卷包括必考题和选考题两部分.第13~21题为必考题,每个试题考生都必须作答。第22~24题为选考题。考生根据要求作答。
二、选择题:本题共4小题,每小题5分。
∴
∴
∵ ,
∴
∴
∴
∴
∴ .
∴B,C,G,F四点共圆.
(Ⅱ)∵E为AD中点, ,
∴ ,
∴在 中, ,
连接 , ,
∴ .
23.【解析】解:⑴整理圆的方程得 ,
由 可知圆 的极坐标方程为 .
记直线的斜率为 ,则直线的方程为 ,
由垂径定理及点到直线距离公式知: ,
即 ,整理得 ,则 .
24.【解析】解:⑴当 时, ,若 ;
由图得 , ,由勾股定理得: ,
,
故选C.
7.【解析】B
平移后图像表达式为 ,
令 ,得对称轴方程: ,
故选B.
8.【解析】C
第一次运算: ,
第二次运算: ,
第三次运算: ,
故选C.
9.【解析】D
∵ , ,
故选D.
10.【解析】C
由题意得: 在如图所示方格中,而平方和小于1的点均在
2016年高考数学(理)冲刺卷(新课标Ⅰ卷) 02(解析版) Wo

全卷满分150分 考试时间120分钟第Ⅰ卷(共60分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.若集合{}|128xP x =≤<,{}1,2,3Q =,则P Q = ( )A .{}1,2B .{}1C .{}2,3D .{}1,2,3 【命题意图】本题考查不等式解法、集合的交集运算,容易题. 【答案】A【解析】由128x≤<,解得03x ≤<,所以{}|03P x x =≤<,所以{}1,2P Q = ,故选A .2.若复数z 满足11z i i i -=-+(),则z 的实部为( )A .12 B 1 C .1 D .12【命题意图】本题考查复数的运算与几何意义,容易题. 【答案】A3.等差数列{}n a 的前n 项和为n S ,若532S =,则3a =( )A .325 B .2 C . D .532【命题意图】本题考查等差数列的前n 项和与性质,容易题. 【答案】A【解析】根据等差数列的性质,535S a =,所以533255S a ==,故选A . 4.“0a =”是“函数1()sin f x x a x=-+为奇函数”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件【命题意图】本题考查函数奇偶性、充要条件判断,容易题. 【答案】C 【解析】1()s i n f x x ax =-+为奇函数⇔()()0f x f x -+=⇔11sin sin 0x a x a xx-+++-+= ⇔0a =,故“0a =”是“函数1()sin f x x a x=-+为奇函数”的充要条件,故选C . 5.在样本频率分布直方图中,共有9个小长方形,若中间一个小长方形的面积等于其他8个长方形面积和的25,且样本容量为140,则中间一组的频数为( ) A .28 B .40 C .56 D . 60 【命题意图】本题考频率分布直方图及性质,容易题. 【答案】B【解析】设中间一个长方形的面积为x ,则其他8个小长方形面积和为52x ,则512x x +=,所以27x =,所以中间一组的频数为2140407⨯=,故选B . 6.在平面直角坐标系xOy 中,满足221,0,0x y x y +≤≥≥的点(,)P x y 的集合对应的平面图形的面积为4π;类似的,在空间直角坐标系O xyz -中,满足2221,0,0,0x y z x y z ++≤≥≥≥,的点(,,)P x y z 的集合对应的空间几何体的体积为( ) A .8π B .6π C .4π D .3π 【命题意图】本题考查推理与证明、球的体积,中档题. 【答案】B7.登山族为了了解某山高()y km 与气温()x C ︒之间的关系,随机统计了4次山高与相应的气温,并制作了对照表:由表中数据,得到线性回归方程2()y x aa R =-+∈,由此请估计出山高为72(km )处气温的度数为( )A .10-B .8-C .4-D .6- 【命题意图】本题考查线性回归的基本思想,中档题.【答案】D【解析】由题意可得18131012434386410,4044x y ++-+++====,代入到线性回归方程 2y x a =-+,可得 60,260a y x =∴=-+,由 26072y x =-+=,可得6x =-,故选D .8.阅读如下图所示程序框图,运行相应的程序,则程序运行后输出的结果为( )A .7B .9C .10D .11【命题意图】本题考查程序框图、对数运算,中档题. 【答案】B【解析】11,lg lg31,3i S ===->-否;1313,l g+l g l g l g51,355i S ====->-否;1515,l g +l g l g l g 71,577i S ====->-否;1717,l g +l g l g l g 91,799i S ====->-否;1919,l g +l g l g l g 111,91111i S ====-<-是,输出9,i =故选B . 9.已知y x ,满足约束条件34y xy x x y ≤⎧⎪≥⎨⎪+≤⎩,则下列目标函数中,在点(3,1)处取得最小值的是( )A .2z x y =-B .2z x y =-+C .y x z --=21D .2z x y =+ 【命题意图】本题考查线性规划问题,中档题. 【答案】B10.P 是ABC ∆所在平面上一点,满足2PA PB PC AB ++=,若12ABC S ∆=,则PAB ∆的面积为( )A .4B .6C .8D .16【命题意图】本题考查平面向量的几何意义、平行关系,中档题. 【答案】A【解析】由()22PA PB PC AB PB PA ++==-,得3PA PB PC CB =-= ,所以PA BC ,且13PA BC =,ABC ∆的边AB 上的高是ABP ∆边AB 上的高的3倍,所以13ABP ABC S S ∆∆=,由12,4ABC ABP S S ∆∆=∴=,故选A . 11.已知12,F F 分别为双曲线2222:1(0,0)x y C a b a b-=>>的左右焦点,过1F 的直线l 与双曲线C 的左右两支分别交于,A B 两点,若22::3:4:5AB BF AF =,则双曲线的离心率为( )A B C .2 D 【命题意图】本题考查双曲线的定义与几何意义,中档题. 【答案】A12.函数()f x 是定义在(0,)+∞上的单调函数,且对定义域内的任意x ,均有3(()ln )2f f x x x --=,则()f e =( )A .31e +B .32e +C )31e e ++D .32e e ++ 【命题意图】本题考查函数的单调性、复合函数,较难题. 【答案】B第Ⅱ卷(共90分)二、填空题(本大题共4小题,每小题5分,共20分)13.二项式6(x的展开式中的常数项是___________. 【命题意图】本题考查二项式定理,容易题. 【答案】15【解析】由题意得,二项式的展开式662166((1)r r rrr r rr T C xC x ---+==-,当4r =时,常数项为446(1)15C -=.14.某几何体的三视图如图所示,其中侧视图的下半部分曲线为半圆弧,则该几何体的表面积为___________.【命题意图】本题考查三视图、棱柱与圆柱的体积计算,中档题. 【答案】32165++π【解析】由三视图可知该几何体是一个正三棱柱和一个半圆柱的组合体,三棱柱的两个侧面面积之和为16242=⨯⨯,两个底面面积之和为3232212=⨯⨯⨯;半圆柱的侧面积为ππ44=⨯,两个底面面积之和为ππ=⨯⨯⨯21212,所以几何体的表面积为32165++π.15.已知,M N 是圆22:20A x y x +-=与圆22:240B x y x y ++-=的公共点,则BMN∆的面积为________.【命题意图】本题考查两圆位置关系、直线与圆的位置关系,中档题. 【答案】3216.已知数列3n n a =,记数列{n a }的前n 项和为n T ,若对任意的 *n N ∈ ,3()362n T k n +≥-恒成立,则实数k 的取值范围___________. 【命题意图】本题考查等比数列的前n 项和、不等式恒成立问题,较难题.【答案】272≥k 【解析】()2323313131++-=--=n n n T ,所以23231+=+n n T ,将不等式转化为()n n n n k 32232)63(1-⨯=⨯-≥+恒成立,所以只需求数列nn 342-的最大值.因为当1=n 时,n n 342-=23-,当2=n 时,n n 342-=0,当3=n 时,nn 342-=272,当4=n 时,nn 342-=814,即数列值是先增后减,当3=n 时,取得最大值272,所以272≥k .三、解答题(解答应写出文字说明、证明过程或演算步骤)17.(本小题满分12分)已知函数2()2sin cos f x x x x =+.(1)求函数()f x 的最小正周期和单调减区间;(2)已知ABC ∆的三个内角A ,B ,C 的对边分别为a ,b ,c ,其中7a =,若锐角A满足()26A f π-=sin sin B C +=,求bc 的值. 【命题意图】本题考查三角恒等变换、三角函数的性质、正弦定理与余弦定理的应用,以及考查转化能力、逻辑思维能力、运算求解能力、整体思想的应用.18.如图,在梯形ABCD 中,//AB CD ,1,60AD DC CB ABC ===∠= ,四边形ACFE为矩形,平面ACFE ⊥平面ABCD ,1CF =. (1)求证:BC ⊥平面ACFE ;(2)点M 在线段EF 上运动,设平面M A B 与平面FCB 所成二面角的平面角为(90)θθ≤ ,试求cos θ的取值范围.【命题意图】本题考查空间直线和平面间的垂直关系、二面角、空间向量的应用,以及考查空间想象能力、逻辑推证能力、运算求解能力、转化的思想.19.(本小题满分12分)2015年高中学业水平考试之后,为了调查同学们的考试成绩,随机抽查了某高中的高二一班的10名同学的语文、数学、英语成绩,已知其考试等级分为,,A B C ,现在对他们的成绩进行量化:A 级记为2分,B 级记为1分,C 级记为0分,用(),,x y z 表示每位同学的语文、数学、英语的得分情况,再用综合指标x y zω=++的值评定该同学的得分等级:若4ω≥,则得分等级为一级;若23ω≤≤,则得分等级为二级;若01ω≤≤,则得分等级为三级,得到如下结果: 人员编号1A 2A 3A 4A 5A 6A 7A 8A 9A 10A(),,x y z()1,1,2()2,1,1()2,2,2()0,0,1()1,2,1()1,2,2()1,1,1()1,2,2()1,2,1()1,1,1(2)从得分等级是一级的同学中任取一人,其综合指标为a ,从得分等级不是一级的同学中任取一人,其综合指标为b ,记随机变量X a b =-,求X 的分布列及其数学期望.【命题意图】本题考查古典概型的概率、离散型随机变量分布列与期望,以及考查分类讨论思想、运算求解能力、数据处理能力.(2)计算10名同学的综合指标,可得下表: 人员编号 1A 2A3A4A5A6A7A8A9A10A综合指标4 461453543其中综合指标是一级的4≥有1235689,,,,,,A A A A A A A ,共7名, 综合指标不是一级的()4ω<有1710,,A A A 共3名. ………………(7分) 随机变量X 的所有可能取值为:1,2,3,4,5.()114211738121C C P X C C ===,()()11111122411211117373462,32121C C C C C C P X P X C C C C +======, ()()1111121111117373214,52121C C C C P X P X C C C C ======,………………(9分)所以X 的分布列为:所以12345212121212121EX =⨯+⨯+⨯+⨯+⨯=.………………(12分) 20.(本小题满分12分)已知椭圆M :2221(0)3x y a a +=>的一个焦点为(1,0)F -,左右顶点分别为,A B ,经过点F 的直线l 与椭圆M 交于,C D 两点. (1)求椭圆方程,并求当直线l 的倾斜角为45︒时,求线段CD 的长; (2)记ABD ∆与ABC ∆的面积分别为1S 和2S ,求12||S S -的最大值.【命题意图】本题考查椭圆的方程与几何性质、直线与椭圆的位置关系,以及考查方程思想、逻辑思维能力、运算求解能力.(2)设直线l 的方程为:1-=my x ()R m ∈,则由⎪⎩⎪⎨⎧=+-=134122y x my x ,得()0964322=--+my y m.设()11y ,x C ,()22y ,x D ,则436221+=+m m y y ,0439221<+-=⋅m y y . 所以,2121y AB S ⋅=,1221y AB S ⋅=,()21122142121y y y y AB S S +⨯⨯=-=-43122+=m m ………………(8分) 当0m ≠时,=-21S S 343212431222=⨯≤+=mmm m ()R m ∈. 由432=m ,得 332±=m ; 当0=m 时,3021<=-S S 从而,当332±=m 时,21S S -取得最大值3.………………(12分) 21.已知函数32()(63)x f x x x x t e =-++,t R ∈.(1)若函数()y f x =有三个不同的极值点,求t 的值;(2)若存在实数[]0,2t ∈,使对任意的[]1,x m ∈,不等式()f x x ≤恒成立,求正整数m的最大值.【命题意图】本题考查利用导数研究函数的单调性与极值、不等式恒成立问题,以及考查等价转化思想、方程思想、逻辑思维能力、运算求解能力.(2)不等式()f x x ≤,即32(63)x x x x t e x -++≤,即3263xt x e x x x -≤⋅-+-,转化为存在实数[]0,2t ∈,使对任意的[]1,x m ∈,不等式3263xt xex x x -≤-+-恒成立,即不等式32063xxe x x x -≤-+-在[]1,x m ∈上恒成立.………………(7分)设2()63xx ex x ϕ-=-+-,则'()26x x e x ϕ-=--+.设()'()26xr x x e x ϕ-==--+,则'()2x r x e -=-.因为1x m ≤≤,有'()0r x <,故()r x 在区间[]1,m 上是减函数.又1(1)4r e -=-0>,2(2)20r e -=->,3(3)0r e -=-<,故存在()02,3x ∈,使得00()'()0r x x ϕ==.当01x x ≤<时,有'()0x ϕ>;当0x x >时,有'()0x ϕ<,从而()y x ϕ=在区间[]01,x 上递增,在区间[)0,x +∞上递减.………………(10分) 又1(1)40e ϕ-=+>,2(2)50e ϕ-=+>,3(3)60e ϕ-=+>,4(4)50e ϕ-=+>,5(5)20e ϕ-=+>,6(6)30e ϕ-=-<,所以当15x ≤≤时,恒有()0x ϕ>;当6x ≥时,恒有()0x ϕ<;故使命题成立的正整数m 的最大值为5.………………(12分)请考生在第22、23、24题中任选一题做答,如果多做,则按所做的第一题计分。
2016年高考理科数学全国卷2(含详细答案)

第Ⅰ卷
一、选择题
1.【答案】A
【解析】z(m3)(m1)i在复平面内对应的点在第四象限,可得m30,m10,解得3m1.
【提示】利用复数对应点所在象限,列出不等式组求解即可.
【考点】复数的代数表示法及其几何意义
2.【答案】C
--------------------
()
A.0.8B.0.75C.0.6D.0.45
12.设函数f(x)3sinπ
000
范围是()
A.(,6)(6,)B.(,4)(4,)
C.(,2)(2,)D.(,1)(1,)
效
数学试卷第1页(共39页)
数学试卷第2页(共39页)
数学试卷第3页(共39页)
18.(本小题满分12分)
如图,四棱锥PABCD中,底面ABCD为矩形,PA平面ABCD,E为PD的中点.
(Ⅰ)证明:PB平面AEC;
(Ⅱ)设二面角DAEC为60,AP1,AD3,求三棱锥EACD的体积.
20.(本小题满分12分)
y2
12a2b21(ab0)的左、右焦点,M是C上一点且MF2与
x轴垂直,直线MF与C的另一个交点为N.
1
(Ⅰ)若直线MN的斜率为3
(Ⅱ)若直线MN在y轴上的截距为2,且|MN|5|FN|,求a,b.
1
请考生在第22、23、24题中任选一题作答,如果多做,则按所做的第一题计分,作答时
填写试题号.
22.(本小题满分10分)选修4—1:几何证明选讲
如图,P是O外一点,PA是切线,A为切点,割线PBC与O相交于点B,C,
PC2PA,D为PC的中点,AD的延长线交O于点E.证明:
(Ⅰ)BEEC;
(Ⅱ)ADDE2PB2.
2021年高考数学冲刺卷02 理(新课标Ⅰ卷)

绝密★启用前2016年高考冲刺卷(2)(新课标Ⅰ卷)理科数学试卷全卷满分150分 考试时间120分钟第Ⅰ卷(共60分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.若集合{}|128x P x =≤<,{}1,2,3Q =,则PQ =( )A .{}1,2B .{}1C .{}2,3D .{}1,2,3 2.若复数z 满足11z i i i -=-+(),则z 的实部为( )A .212-B .21-C .1D .212+3.等差数列{}n a 的前n 项和为n S ,若532S =,则3a =( )A .325 B .2 C .42 D .5324.“0a =”是“函数1()sin f x x a x=-+为奇函数”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件5.在样本频率分布直方图中,共有9个小长方形,若中间一个小长方形的面积等于其他8个长方形面积和的25,且样本容量为140,则中间一组的频数为( ) A .28 B .40 C .56 D .606.在平面直角坐标系xOy 中,满足221,0,0x y x y +≤≥≥的点(,)P x y 的集合对应的平面图形的面积为4π;类似的,在空间直角坐标系O xyz -中,满足2221,0,0,0x y z x y z ++≤≥≥≥,的点(,,)P x y z 的集合对应的空间几何体的体积为( ) A .8π B .6π C .4π D .3π 7.登山族为了了解某山高()y km 与气温()x C ︒之间的关系,随机统计了4次山高与相应的气温,气温x C ︒() 18 13 10 -1 山高y km ()24343864由表中数据,得到线性回归方程2()y x a a R =-+∈,由此请估计出山高为72(km )处气温的度数为( )A .10-B .8-C .4-D .6-8.阅读如下图所示程序框图,运行相应的程序,则程序运行后输出的结果为( )A .7B .9C .10D .119.已知y x ,满足约束条件34y xy x x y ≤⎧⎪≥⎨⎪+≤⎩,则下列目标函数中,在点(3,1)处取得最小值的是( )A .2z x y =-B .2z x y =-+C .y x z --=21D .2z x y =+ 10.P 是ABC ∆所在平面上一点,满足2PA PB PC AB ++=,若12ABC S ∆=,则PAB ∆的面积为( )A .4B .6C .8D .1611.已知12,F F 分别为双曲线2222:1(0,0)x y C a b a b-=>>的左右焦点,过1F 的直线l 与双曲线C 的左右两支分别交于,A B 两点,若22::3:4:5AB BF AF =,则双曲线的离心率为( ) A 13 B 15 C .2 D 312.函数()f x 是定义在(0,)+∞上的单调函数,且对定义域内的任意x ,均有3(()ln )2f f x x x --=,则()f e =( )A .31e +B .32e +C )31e e ++D .32e e ++第Ⅱ卷(共90分)二、填空题(本大题共4小题,每小题5分,共20分)13.二项式61()x x-的展开式中的常数项是___________. 14.某几何体的三视图如图所示,其中侧视图的下半部分曲线为半圆弧,则该几何体的表面积为___________. 15.已知,M N 是圆22:20A x y x +-=与圆22:240B x y x y ++-=的公共点,则BMN ∆的面积为________.16.已知数列3nn a =,记数列{n a }的前n 项和为n T ,若对任意的 *n N ∈ ,3()362n T k n +≥-恒成立,则实数 k 的取值范围___________.三、解答题(解答应写出文字说明、证明过程或演算步骤)17.(本小题满分12分)已知函数2()2sin cos 23cos 3f x x x x =+-.(1)求函数()f x 的最小正周期和单调减区间;(2)已知ABC ∆的三个内角A ,B ,C 的对边分别为a ,b ,c ,其中7a =,若锐角A 满足()326A f π-=,且133sin sin 14B C +=,求bc 的值. 18.如图,在梯形ABCD 中,//AB CD ,1,60AD DC CB ABC ===∠=,四边形ACFE 为矩形,平面ACFE ⊥平面ABCD ,1CF =.(1)求证:BC ⊥平面ACFE ;(2)点M 在线段EF 上运动,设平面MAB 与平面FCB 所成二面角的平面角为(90)θθ≤,试求cos θ的取值范围.19.(本小题满分12分)2015年高中学业水平考试之后,为了调查同学们的考试成绩,随机抽查了某高中的高二一班的10名同学的语文、数学、英语成绩,已知其考试等级分为,,A B C ,现在对他们的成绩进行量化:A 级记为2分,B 级记为1分,C 级记为0分,用(),,x y z 表示每位同学的语文、数学、英语的得分情况,再用综合指标x y z ω=++的值评定该同学的得分等级:若4ω≥,则得分等级为一级;若23ω≤≤,则得分等级为二级;若01ω≤≤,则得分等级为三级,得到如下结果: 人员编号1A 2A 3A 4A 5A 6A 7A 8A 9A 10A(),,x y z ()1,1,2 ()2,1,1 ()2,2,2 ()0,0,1 ()1,2,1 ()1,2,2 ()1,1,1 ()1,2,2 ()1,2,1 ()1,1,1(1)在这10名同学中任取两人,求这两位同学英语得分相同的概率;(2)从得分等级是一级的同学中任取一人,其综合指标为a ,从得分等级不是一级的同学中任取一人,其综合指标为b ,记随机变量X a b =-,求X 的分布列及其数学期望.20.(本小题满分12分)已知椭圆M :2221(0)3x y a a +=>的一个焦点为(1,0)F -,左右顶点分别为,A B ,经过点F 的直线l 与椭圆M 交于,C D 两点.(1)求椭圆方程,并求当直线l 的倾斜角为45︒时,求线段CD 的长; (2)记ABD ∆与ABC ∆的面积分别为1S 和2S ,求12||S S -的最大值. 21.已知函数32()(63)xf x x x x t e =-++,t R ∈.(1)若函数()y f x =有三个不同的极值点,求t 的值;(2)若存在实数[]0,2t ∈,使对任意的[]1,x m ∈,不等式()f x x ≤恒成立,求正整数m 的最大值.请考生在第22、23、24题中任选一题做答,如果多做,则按所做的第一题计分。
高考数学考前冲刺卷(二)

考前冲刺卷(二)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分.考试时间120分钟.第Ⅰ卷一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知函数f(x)=ax2+x+a,命题p:∃x0∈R,f(x0)=0,若p为假命题,则实数a的取值范围是( C )(A)[-,](B)(-,)(C)(-∞,-)∪(,+∞)(D)(-∞,-]∪[,+∞)解析:因为p为假命题,所以¬p为真命题,即不存在x0∈R,使f(x0)=0, 故Δ=1-4a2<0,解得a>或a<-,故选C.2.欧拉公式e iθ=cos θ+isin θ(e是自然对数的底数,i是虚数单位)是由瑞士著名数学家欧拉发现的.它将三角函数的定义域扩大到复数,建立了三角函数和指数函数的关系,它在复变函数论里占有非常重要的地位,当θ=π时,就有e iπ+1=0.根据上述背景知识试判断表示的复数在复平面对应的点位于( C )(A)第一象限 (B)第二象限(C)第三象限 (D)第四象限解析:由题意,=cos(-)+isin(-)=cos -isin =--i,则表示的复数在复平面对应的点为(-,-),位于第三象限,故选C.3.已知θ∈(,),则2cos θ+等于( A )(A)sin θ+cos θ(B)sin θ-cos θ(C)cos θ-sin θ(D)3cos θ-sin θ解析:因为θ∈(,),所以2cos θ+=2cos θ+ =2cos θ+=2cos θ+sin θ-cos θ=sin θ+cos θ.故选A.4.若(x+2)(-x)5展开式的常数项等于-80,则a等于( A )(A)-2 (B)2 (C)-4 (D)4解析:(-x)5的展开式的通项为T k+1=()5-k·(-x)k=(-1)k a5-k·x2k-5, 当2k-5=-1,即k=2时,T3=a3·x-1,当2k-5=0,即k=不成立,则多项式的常数项为x·a3·x-1=10a3=-80,得a3=-8,得a=-2,故选A.5.已知抛物线C1:y=x2的焦点F也是椭圆C2:+=1(m>0,n>0)的焦点,记C1与C2在第一象限内的交点为A,且|AF|=,则椭圆离心率为( A )(A)(B)(C)(D)3解析:因为抛物线C1:y=x2的焦点坐标为(0,1),可得n-m=1,因为抛物线C1的准线方程是y=-1,且A是抛物线与椭圆在第一象限内的交点,由|AF|=及|AF|=y A+1可知y A=,x A=,故A(,),代入椭圆方程可知+=1,解得m=3,n=4.所以椭圆的离心率为e===.故选A.6.已知数列{a n}是公比不为1的等比数列,S n为其前n项和,满足a2=2,且16a1,9a4,2a7成等差数列,则S3等于( C )(A)5 (B)6 (C)7 (D)9解析:数列{a n}是公比q不为1的等比数列,满足a2=2,且16a1,9a4,2a7成等差数列,可得a1q=2,18a4=16a1+2a7,即9a1q3=8a1+a1q6,解得q=2,a1=1,则S3==7.故选C.7.下列函数既是奇函数,又在[-1,1]上单调递增的是( C )(A)f(x)=|sin x|(B)f(x)=ln(C)f(x)=(e x-e-x)(D)f(x)=ln(-x)解析:对于A,由于函数f(x)=|sin x|为偶函数,不符合题意;对于B,f(x)=ln 的定义域为(-e,e),且f(-x)=ln =-ln =-f(x)为奇函数,设t==-1+,在(-e,e)上为减函数,而y=ln t为增函数,则f(x)=ln 在(-e,e)上为减函数,不符合题意;对于C,由f(x)=(e x-e-x)得f(-x)=-(e x-e-x)=-f(x)为奇函数,且f′(x)=(e x+e-x)>0,则f(x)=(e x-e-x)在R上为增函数,符合题意;对于D,f(x)=ln(-x)的定义域为R,f(-x)=ln(+x)=ln()=-ln(-x)=-f(x)为奇函数,设t=-x=,在R上为减函数,而y=ln t为增函数,则f(x)=ln(-x)在R上为减函数,不符合题意;故选C.8.已知坐标平面xOy中,点F1,F2分别为双曲线C:--y2=1(a>0)的左、右焦点,点M在双曲线C的左支上,MF2与双曲线C的一条渐近线交于点D,且D为MF2的中点,点I为△OMF2的外心,若O、I、D三点共线,则双曲线C的离心率为( C )(A) (B)3 (C) (D)5解析:设点M在第二象限,设M(m,n),F2(c,0),由D为MF2的中点,O,I,D三点共线知,直线OD垂直平分MF2,则直线OD的方程为y=x,故有=-a,且·n=·,解得m=,n=. 将M(,),即(,)代入双曲线的方程可得-=1,化简得c2=5a2,即e=.当M在第三象限时同理可得e=.故选C.二、多项选择题(本大题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求,全部选对的得5分,部分选对的得3分,有选错的得0分)9.已知集合A={1,2},集合B={0,2},设集合C={z|z=xy,x∈A,y∈B},则下列结论中不正确的是( ABD )(A)A∩C= (B)A∪C=C(C)B∩C=B (D)A∪B=C解析:因为A={1,2},B={0,2},所以C={0,2,4}.所以A∩C={2},A∪C={0,1,2,4},A∪B={0,1,2},B∩C=B.故选ABD.10.已知圆锥的侧面展开图为四分之三个圆面,设圆锥的底面半径为r,母线长为l,有以下结论,正确的是( ABD )(A)l∶r=4∶3(B)圆锥的侧面积与底面面积之比为4∶3(C)圆锥的轴截面是锐角三角形(D)圆锥轴截面是钝角三角形解析:A,由题得=π,所以=,所以l∶r=4∶3,所以该结论正确;B,由题得===,所以圆锥的侧面积与底面面积之比为4∶3,所以该结论正确;C,由题得轴截面的三角形的三边长分别为r,r,2r,顶角最大,其余弦为cos α==-<0,所以顶角为钝角,所以轴截面三角形是钝角三角形,所以该结论错误;D正确.故选ABD.11.将函数y=cos(2x+)的图象向左平移个单位后,得到f(x)的图象,则下列说法错误的是( ACD )(A)f(x)=-sin 2x(B)f(x)的图象关于x=-对称(C)f()=(D)f(x)的图象关于(,0)对称解析:将函数y=cos(2x+)的图象向左平移个单位后,得到f(x)=cos[2(x+)+]=cos(2x+)=-sin(2x+)的图象,故A符合题意; 当x=-时,f(x)=1,为最大值,故f(x)的图象关于x=-对称,故B不符合题意;f()=-sin =-sin =-,故C符合题意;当x=时,f(x)=-sin =-≠0,故f(x)的图象不关于(,0)对称,故D 符合题意.故选ACD.12.已知函数f(x)=-lo x,若0<a<b<c,且满足f(a)f(b)f(c)<0(0<a<b<c),则下列说法一定正确的是( AB )(A)f(x)有且只有一个零点(B)f(x)的零点在(0,1)内(C)f(x)的零点在(a,b)内(D)f(x)的零点在(c,+∞)内解析:因为y=,y=-lo x均为(0,+∞)上的单调增函数,故f(x)为(0,+∞)上的增函数.因为f(1)>0,f()<0,由零点存在定理可知f(x)有且只有一个零点且零点在(,1)内,故AB正确.因为f(a)f(b)f(c)<0,故f(a),f(b),f(c)的符号为两正一负或全负,而0<a<b<c且f(x)为(0,+∞)上的增函数,故f(a)<0,f(b)<0,f(c)<0或者f(a)<0,f(b)>0,f(c)>0.若f(a)<0,f(b)<0,f(c)<0,则零点在(c,+∞)内,若f(a)<0,f(b)>0,f(c)>0,则零点在(a,b)内.故CD错误.故选AB.第Ⅱ卷本卷包括填空题与解答题两部分,共90分.三、填空题(本大题共4小题,每小题5分,共20分)13.设函数f(x)=则f(f())= .解析:因为函数f(x)=所以f()=2-1=1,所以f(f())=f(1)=2.答案:214.已知向量a,b满足|a|=2,|b|=1,a,b的夹角为,则|a+2b|= ;a与a-2b的夹角为.解析:因为|a|=2,|b|=1,a,b的夹角为,所以|a+2b|====2,|a-2b|====2,所以cos<a,a-2b>====.因此<a,a-2b>=.答案:215.某校高三年级学生一次数学诊断考试成绩(单位:分)X服从正态分布N(110,102),从中抽取一个同学的数学成绩ξ,记该同学的成绩90<ξ≤110为事件A,记该同学的成绩80<ξ≤100为事件B,则在A事件发生的条件下B事件发生的概率P(B|A)= .(结果用分数表示)附:X满足:P(μ-σ<X≤μ+σ)=0.68;P(μ-2σ<X≤μ+2σ)=0.95;P(μ-3σ<X≤μ+3σ)=0.99.解析:由题意,P(A)=0.475,P(B)=×(0.99-0.68)=0.155,P(AB)=×(0.95-0.68) =0.135,所以P(B|A)==.答案:16.已知一正四棱柱(底面为正方形的直四棱柱)内接于底面半径为1,高为2的圆锥,当正四棱柱体积最大时,该正四棱柱的底面边长为.解析:如图为过正四棱柱的圆锥的轴截面,设正四棱柱的高为h,底面边长为a,则O,O1分别为AC,A1C1的中点,所以A 1C1=a,EF=2,△SA1C1∽△SEF,所以=,即=,所以a=(2-h)(0<h<2).因此正四棱柱的体积V=a2h=[(2-h)]2h=(h3-4h2+4h).令V′=(3h2-8h+4)=(h-2)(3h-2)=0,得h=,或者h=2(舍).当0<h<时,V′>0,当<h<2时,V′<0,故当h=时,V有最大值,此时a=(2-)=.答案:四、解答题(本大题共70分.解答应写出文字说明、证明过程或演算步骤)17.(本小题满分10分)已知数列{a n}的前n项和为S n,且满足2S n=-a n+n(n∈N*).(1)求证:数列{a n-}为等比数列;(2)求数列{a n-1}的前n项和T n.(1)证明:2S n=-a n+n,当n≥2时,2S n-1=-a n-1+n-1,两式相减,得2a n=-a n+a n-1+1,即a n=a n-1+.所以a n-=(a n-1-),所以数列{a n-}为等比数列.(2)解:由2S1=-a1+1,得a1=.由(1)知,数列{a n-}是以-为首项,为公比的等比数列.所以a n-=-()n-1=-()n,所以a n=-()n+.所以a n-1=-()n-.所以T n=-=[()n-1]-.18.(本小题满分12分)在某电视台举行的跑男节目中,某次游戏比赛分两个阶段,只有上一阶段的通过者,才能继续参加下一阶段的比赛,否则就被淘汰,每组选手每通过一个阶段,本组积分加10分,否则为0分.甲、乙两组明星选手参加了这次游戏比赛,已知甲组选手每个阶段通过的概率均为,乙组选手每个阶段通过的概率均为.(1)求甲、乙两组选手都取得10分就被淘汰的概率;(2)设甲、乙两组选手的最后积分之和为X,求X的分布列和数学期望. 解:(1)记“甲、乙两组选手都取得10分就被淘汰”为事件A,则P(A)=×(1-)××(1-)=.(2)X所有可能取值为0,10,20,30,40,且P(X=0)=(1-)×(1-)=,P(X=10)=×(1-)×(1-)+(1-)××(1-)=+=,P(X=20)=(1-)×()2+×(1-)××(1-)+()2×(1-)=++=,P(X=30)=()2××(1-)+×(1-)×()2=+==,P(X=40)=()2×()2=.则X的分布列为X 0 10 20 30 40P所以X的数学期望E(X)=0×+10×+20×+30×+40×=.19.(本小题满分12分)如图,在多面体ABCDEF中,平面ADEF⊥平面ABCD,四边形ADEF为正方形,四边形ABCD为梯形,且AD∥BC,△ABD是边长为1的等边三角形,M 为线段BD中点,BC=3.(1)求证:AF⊥BD;(2)求直线MF与平面CDE所成角的正弦值.(1)证明:因为四边形ADEF为正方形,所以AF⊥AD.又因为平面ADEF⊥平面ABCD,且平面ADEF∩平面ABCD=AD,所以AF⊥平面ABCD.所以AF⊥BD.(2)解:取AD中点O,EF中点K,连接OB,OK.于是在△ABD中,OB⊥OD,在正方形ADEF中OK⊥OD,又平面ADEF⊥平面ABCD,故OB⊥平面ADEF,进而OB⊥OK,即OB,OD,OK两两垂直,分别以OB,OD,OK所在直线为x轴,y轴,z轴建立如图所示的空间直角坐标系.则B(,0,0),D(0,,0),C(,3,0),E(0,,1),M(,,0),F(0,-,1),所以=(-,-,1),=(-,-,0),=(0,0,1),设平面CDE的一个法向量为n=(x,y,z),则令x=-5,则y=,则n=(-5,,0).设直线MF与平面CDE所成角为θ,则直线MF与平面CDE所成角的正弦值为sin θ=|cos<,n>|===.20.(本小题满分12分)如图,直线l为经过市中心O的一条道路,B,C是位于道路l上的两个市场,在市中心O正西方向的道路较远处分布着一些村庄,为方便村民生活,市政府决定从村庄附近的点A处修建两条道路AB,AC,l与OA 的夹角为(OA>3 km,∠OAC为锐角).已知以2 km/h的速度从O点到达B,C的时间分别为t,(1+)t(单位:h).(1)当t=1时:①设计AB的长为3 km,求此时OA的长;②修建道路AB,AC的费用均为a元/km,现需要使工程耗费最少,直接写出所需总费用的最小值;(2)若点A与市中心O相距(6+4)km,铺设时测量出道路AC,AB的夹角为,求时间t的值.解:(1)①当t=1时,OB=2,OC=2(1+)=2+6.因为AB=3,∠AOC=,在△AOB中,由余弦定理可得AB2=OA2+OB2-2OA·OBcos ,即27=OA2+12-2OA·2×,解得OA=3+.②在△AOC中,由余弦定理可知AC2=OA2+OC2-2OA·OCcos = (3+)2+(2+6)2-2(3+)(2+6)×=63+18-18,所以AC=.所以修建道路AB,AC的总费用的最小值为(+3)a元.(2)设∠BAO=θ,在△ABO中,由正弦定理可得==.同理在△ABC中,=,且BC=BO,∠ACB=-θ.所以=.所以=,整理可得sin θcos θ=,θ∈(0,),tan θ∈(0,),sin θ≠0,cos θ≠0.所以==,解得tan θ=2-.在△ABO中,BO====2.所以t==1 h.21.(本小题满分12分)椭圆C:+=1(a>b>0)的离心率e=,过点A1(-a,0)和B2(0,b)的直线与原点间的距离为.(1)求椭圆C的方程;(2)若方程为y=kx+m的直线L与椭圆C相交于不同两点A,B,设点M(2,0),直线AM与BM的斜率分别为k1,k2且k1+k2=0,判断直线L是否过定点?若过定点,求出该定点的坐标.解:(1)由题意可知,直线A1B2的方程为bx-ay+ab=0.依题意得解得a2=2,b2=1,所以椭圆C的方程为+y2=1.(2)联立消去y可得(2k2+1)x2+4kmx+2m2-2=0,Δ=16k2m2-4(2k2+1)(2m2-2)=16k2-8m2+8>0,设A(x1,y1),B(x2,y2),则x1+x2=-,x1x2=,所以k1+k2=+==0,所以x2y1+x1y2-2(y1+y2)=0,即x2(kx1+m)+x1(kx2+m)-2(kx1+kx2+2m)=0,即2k·-(m-2k)·-4m==0,所以k+m=0,故直线L的方程为y=kx-k=k(x-1),所以直线L过定点(1,0).22.(本小题满分12分)已知函数f(x)=x2-+axln x,其中e为自然对数的底数.(1)当a≥0时,求证:x≥1时,f(x)>0;(2)当a≥-时,讨论函数f(x)的极值点个数.(1)证明:由f′(x)=x-+a(ln x+1),易知f′()=0,设g(x)=f′(x),则g′(x)=,当a≥0时,g′(x)>0,又f′()=g()=0,所以0<x<时,g(x)<0;x>时,g(x)>0,即f(x)在(0,)上递减,在(,+∞)上递增;所以当x≥1时,f(x)≥f(1)=->0.(2)解:由(1)可得,①当a≥0时,f(x)当且仅当在x=处取得极小值,无极大值,故此时极值点个数为1;②当-≤a<0时,易知g(x)在(0,-a)上递减,在(-a,+∞)上递增,所以g(x)min=g(-a)=-+aln(-a),又设h(a)=-+aln(-a),其中-≤a<0,则h′(a)=1+ln(-a)≤0,对-≤a<0恒成立,所以h(a)单调递减,h(a)≤h(-)=0(当且仅当a=-时取等号),所以(ⅰ)当a=-时,g(x)≥0,即f(x)在(0,+∞)上单调递增,故此时极值点个数为0;(ⅱ)当-<a<0时,>-a>0,g(x)在(-a,+∞)上递增,又g()=0,所以当-a≤x<时g(x)<0,当x>时,g(x)>0,即f(x)总在x=处取得极小值;又当x→0且x>0时,g(x)→+∞,所以存在唯一x0∈(0,-a)使得g(x0)=0,且当0<x<x0时,g(x)>0,当x0<x<-a时,g(x)<0,则f(x)在x=x0处取得极大值;故此时极值点个数为2,综上,当a=-时,f(x)的极值点个数为0;当-<a<0时,f(x)的极值点个数为2;当a≥0时,f(x)的极值点个数为1.。
2016届高考数学(理)冲刺卷(新课标Ⅱ卷)03(考试版)

绝密★启用前2016年高考冲刺卷(3)(新课标Ⅱ卷)理科数学试卷第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知{}⎭⎬⎫⎩⎨⎧=+===12|,|222y x x N x y y M ,则=⋂N M ( ) A .{})1,1(),1,1(- B .{}1 C .]2,0[ D .[]1,0 2. 复数1z ,2z 在复平面内对应的点关于直线y x =对称,且132z i =+,则2z =( )A .32i -B .23i -C .32i --D .23i +3.已知等差数列{}n a 的公差为2,若1a 、3a 、4a 成等比数列,则6a 等于( )A .-2B .-4C .0D .24.已知向量a ,b 满足()2a b a ⋅+=,且||1a =,||2b =,则a 与b 的夹角为( )A .6πB .5πC .4πD .3π5.阅读如图所示的程序框图,运行相应的程序,则输出的结果是( )A..0CD .33366.某几何体的三视图如图所示,则该几何体的表面积为( )第8题图A.7+ B.7+.4+ D.4+7.两圆222240x y ax a +++-=和2224140x y by b +--+=恰有三条公切线,若,a R b R ∈∈且0ab ≠,则2211a b +的最小值为( ) A .1 B .3 C .19 D .498. 已知x ,y 满足约束条件1,1,49,3,x y x y x y ≥⎧⎪≥-⎪⎨+≤⎪⎪+≤⎩,若24m ≤≤,则目标函数+z y mx =的最大值的变化范围是( )A .[]1,3B .[]4,6C .[]4,9D .[]5,99. 若函数2(2)()m x f x x m-=+的图象如图所示,则m 的范围为( ) O-11y xA .)1,(--∞B .)2,1(-C .)2,0(D .)2,1(10. 已知椭圆()2222:10x y E a b a b+=>>的右焦点为()3,0F ,过点F 的直线交椭圆E 于,A B 两点,若AB 的中点坐标为(1,-1),则E 的方程为( ) A .2214536x y += B .2213627x y += C .2212718x y += D .221189x y +=11.已知在三棱锥P ABC -中,P ABC V -=4APC π∠=,3BPC π∠=,PA AC ⊥,PB BC ⊥,且平面PAC ⊥平面PBC ,那么三棱锥P ABC -外接球的体积为( )A .43πB D .323π 12. 已知函数()=x a f x x e -+,()()ln 24a x g x x e -=+-,其中e 为自然对数的底数,若存在实数0x ,使00()()3f x g x -=成立,则实数a 的值为( )A .ln 21--B .1+ln2-C .ln 2-D .ln 2第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.曲线2y x =与直线y x =所围成的封闭图形的面积为 .14.若21()n x x-展开式的二次项系数之和为128,则展开式中2x 的系数为 .15.已知x ,R y ∈,满足22246x xy y ++=,则224z x y =+的最小值为 .16.对R α∀∈,[0,2]n ∈,(23cos ,3sin )e n n αα=+-的长度不超过6的概率为________. 三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17. (本小题满分12分)已知函数()2sin()(0,||)f x x ωϕωϕπ=+><经过点7(,2),(,2)1212ππ-,且在区间7(,)1212ππ上为单调函数. (Ⅰ)求,ωϕ的值; (Ⅱ)设*()()3n n a nf n N π=∈,求数列{}n a 的前30项和30S .18. (本小题满分12分)甲、乙两位同学从A B C D 、、、共(2,)n n n N +≥∈所高校中,任选两所参加自主招生考试(并且只能选两所高校),但同学特别喜欢A 高校,他除选A 高校外,再在余下的1n -所中随机选1所;同学乙对n 所高校没有偏爱,在n 所高校中随机选2所. 若甲同学未选中D 高校且乙选中D 高校的概率为310. (I )求自主招生的高校数n ;(II )记X 为甲、乙两名同学中未参加D 高校自主招生考试的人数,求X 的分布列和数学期望.19.(本小题满分12分)如图,菱形ABCD 与正三角形BCE 的边长均为2,它们所在平面互相垂直,FD ⊥平面ABCD ,且FD =.(I )求证://EF 平面ABCD ;(II )若060CBA ∠=,求钝二面角A FB E --的余弦值.20.(本小题满分12分)已知12,F F 分别为椭圆22122:1y x C a b+=的上、下焦点,1F 是抛物线22:4C x y =的焦点,点M 是1C 与2C 在第二象限的交点,且15||3MF =.(I )求椭圆1C 的方程;(II )与圆22(1)1x y ++=相切的直线:(),0l y k x t kt =+≠交椭圆1C 于,A B ,若椭圆1C 上一点P 满足OA OB OP λ+=,求实数λ的取值范围. 21. (本小题满分12分)已知函数221()x ax bx f x e++=(e 为自然对数的底数). (I ) 若21=a ,求函数)(x f 的单调区间; (II ) 若1)1(=f ,且方程1)(=x f 在)1,0(内有解,求实数a 的取值范围.请考生在第(22)、(23)、(24)三题中任选一题作答.注意:只能做所选定的题目.如果多做,则按所做的第一个题目计分.22.(本题满分10分) 选修41-:几何证明选讲如图,O 的半径OC 垂直于直径AB ,M 为BO 上一点,CM 的延长线交O 于N ,过N 点的切线交AB 的延长线于P .(I )求证:2PM PB PA =⋅;(II )若O 的半径为,OB =,求:MN 的长.23. (本题满分10分) 选修4-4:坐标系与参数方程在直角坐标系xOy 中,直线l 的方程是8y =,圆C 的参数方程是22cos 2sin x y ϕϕ=+⎧⎨=⎩(ϕ为参数),以O 为极点,x 轴的非负半轴为极轴建立极坐标系.(Ⅰ)求直线l 和圆C 的极坐标方程;(Ⅱ)射线:OM θα=(其中02πα<<)与圆C 交于O ,P 两点,与直线l 交于点M ,射线:2ON πθα=+与圆C 交于O ,Q 两点,与直线l 交于点N ,求OPOQOM ON ⋅的最大值.24. (本题满分10分)选修4-5:不等式选讲(I )已知函数()13f x x x =-++,求x 的取值范围,使()f x 为常函数;(II )若222,,z R,x 1x y y z ∈++=,求m =++的最大值.。
2016年高考数学冲刺卷02 理(新课标Ⅰ卷)答案

2016年高考数学冲刺卷02 理(新课标Ⅰ卷)答案全卷满分150分 考试时间120分钟第Ⅰ卷(共60分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.【命题意图】本题考查不等式解法、集合的交集运算,容易题.【答案】A【解析】由128x ≤<,解得03x ≤<,所以{}|03P x x =≤<,所以{}1,2P Q = ,故选A . 2.【命题意图】本题考查复数的运算与几何意义,容易题.【答案】A【解析】由(1)|1|z i i i i -=-+=,得)(1)1(1)(1)22i i i z i i i i +===+--+,则z 的实A . 3.【命题意图】本题考查等差数列的前n 项和与性质,容易题.【答案】A【解析】根据等差数列的性质,535S a =,所以533255S a ==. 4.【命题意图】本题考查函数奇偶性、充要条件判断,容易题.【答案】C5.【命题意图】本题考频率分布直方图及性质,容易题.【答案】B【解析】设中间一个长方形的面积为x ,则其他8个小长方形面积和为52x ,则512x x +=,所以27x =,所以中间一组的频数为2140407⨯=,故选B . 6.【命题意图】本题考查推理与证明、球的体积,中档题.【答案】B【解析】所求的空间几何体是以原点为球心,1为半径的球位于第一象限的部分,体积为3141836ππ⨯⨯⨯=,故选B . 7.【命题意图】本题考查线性回归的基本思想,中档题.【答案】D【解析】由题意可得18131012434386410,4044x y ++-+++====,代入到线性回归方程2y x a =-+,可得 60,260a y x =∴=-+,由 26072y x =-+=,可得6x =-,故选D .8.【命题意图】本题考查程序框图、对数运算,中档题.【答案】B 【解析】11,l g l g 31,3i S ===->-否;1313,l g +l g l g l g5355i S ====->-否;1515,l g +l g l g l g 71,577i S ====->-否;1717,l g +l g l g799i S ====->-否;1919,l g+l g l g lg111,91111i S ====-<-是,输出9,i =故选B . 9.命题意图】本题考查线性规划问题,中档题.【答案】B10.【命题意图】本题考查平面向量的几何意义、平行关系,中档题.【答案】A【解析】由()22PA PB PC AB PB PA ++==-,得3PA PB PC CB =-= ,所以PA BC ,且13PA BC =,ABC ∆的边AB 上的高是ABP ∆边AB 上的高的3倍,所以13ABP ABC S S ∆∆=,由12,4A B C A B PS S ∆∆=∴=. 11.【命题意图】本题考查双曲线的定义与几何意义,中档题.【答案】A【解析】由题意不妨设223,4,5AB BF AF ===,因为22222AB BF AF +=,所以290ABF ∠= ,又由双曲线的定义得12122,2BF BF a AF AF a -=-=,所以1113453AFAF AF +-=-⇒=,所以1222BF BF a -==,所以1a =,在直角12BF F ∆中,222121252F F BF BF =+=,因为22124F F c =,所以2452c =,所以c =,所以双曲线的离心率为ce a==A . 12.【命题意图】本题考查函数的单调性、复合函数,较难题. 【答案】B第Ⅱ卷(共90分)二、填空题(本大题共4小题,每小题5分,共20分) 13.【命题意图】本题考查二项式定理,容易题.【答案】15【解析】由题意得,二项式的展开式662166((1)r r rrr r rr T C xC x ---+==-,当4r =时,常数项为446(1)15C -=.14.【命题意图】本题考查三视图、棱柱与圆柱的体积计算,中档题.【答案】32165++π【解析】由三视图可知该几何体是一个正三棱柱和一个半圆柱的组合体,三棱柱的两个侧面面积之和为16242=⨯⨯,两个底面面积之和为3232212=⨯⨯⨯;半圆柱的侧面积为ππ44=⨯,两个底面面积之和为ππ=⨯⨯⨯21212,所以几何体的表面积为32165++π. 15.【命题意图】本题考查两圆位置关系、直线与圆的位置关系,中档题.【答案】3216.【命题意图】本题考查等比数列的前n 项和、不等式恒成立问题,较难题.【答案】272≥k 【解析】()2323313131++-=--=n n n T ,所以23231+=+n n T ,将不等式转化为()n n n n k 32232)63(1-⨯=⨯-≥+恒成立,所以只需求数列n n 342-的最大值.因为当1=n 时,nn 342-=23-,当2=n 时,n n 342-=0,当3=n 时,n n 342-=272,当4=n 时,nn 342-=814,即数列值是先增后减,当3=n 时,取得最大值272,所以272≥k . 三、解答题(解答应写出文字说明、证明过程或演算步骤)17.【命题意图】本题考查三角恒等变换、三角函数的性质、正弦定理与余弦定理的应用,以及考查转化能力、逻辑思维能力、运算求解能力、整体思想的应用.【解析】(1)2()2sin cos sin2f x x x x x x =+= 2sin(2)3x π=+,因此()f x 的最小正周期为22T ππ==.………………(3分) 因为3222232k x k πππππ≤≤+++, 所以,()f x 的单调递减区间为7[,]1212x k k ππππ∈++()k Z ∈.………………(5分)(2) 由()2sin(2())2sin 26263A A f A πππ-=-+==, 又∵A 为锐角,∴3A π=.………………(7分)由正弦定理可得2sin a R A ===,sin sin 2b c B C R ++==,………………(9分)则1314b c +==. 由余弦定理可知,22222()21cos 222b c a b c bc a A bc bc +-+--===, 整理,得40bc =.………………(12分)18.【命题意图】本题考查空间直线和平面间的垂直关系、二面角、空间向量的应用,以及考查空间想象能力、逻辑推证能力、运算求解能力、转化的思想.(2)由(1)可建立分别以直线,,CA CB CF 为轴轴轴,z y x ,,建立如图所示的空间直角坐标系,令)30(≤≤=λλFM ,则)0,0,3(),0,0,0(A C ,()()1,0,,0,1,0λM B ,∴ ()()1,1,,0,1,3-=-=λBM AB .………………(7分)设1(,,)n x y z =为平面MAB 的一个法向量,由1100n AB n BM ⎧=⎪⎨⋅=⎪⎩,联立得⎩⎨⎧=+-=+-003z y x y x λ ,取1=x ,则1n ()λ-=3,3,1.…………(9分) ∵()21,0,0n =是平面FCB 的一个法向量,∴=θcos 1212||||||n n n n ⋅⋅=10分)∵0λ≤≤ ∴ 当0λ=时,θcosλ=θcos 有最大值12,∴1cos 2θ⎤∈⎥⎣⎦.………………(12分)19.【命题意图】本题考查古典概型的概率、离散型随机变量分布列与期望,以及考查分类讨论思想、运算求解能力、数据处理能力.(2)计算10名同学的综合指标,可得下表:其中综合指标是一级的4≥有1235689,,,,,,A A A A A A A ,共7名, 综合指标不是一级的()4ω<有1710,,A A A 共3名. ………………(7分) 随机变量X 的所有可能取值为:1,2,3,4,5.()114211738121C C P X C C ===,()()11111122411211117373462,32121C C C C C C P X P X C C C C +======, ()()1111121111117373214,52121C C C C P X P X C C C C ======,………………(9分)所以X 的分布列为:所以12345212121212121EX =⨯+⨯+⨯+⨯+⨯=.………………(12分) 20.【命题意图】本题考查椭圆的方程与几何性质、直线与椭圆的位置关系,以及考查方程思想、逻辑思维能力、运算求解能力.(2)设直线l 的方程为:1-=my x ()R m ∈,则由⎪⎩⎪⎨⎧=+-=134122y x my x ,得()0964322=--+my y m .设()11y ,x C ,()22y ,x D ,则436221+=+m m y y ,0439221<+-=⋅m y y . 所以,2121y AB S ⋅=,1221y AB S ⋅=, ()21122142121y y y y AB S S +⨯⨯=-=-43122+=m m ………………(8分) 当0m ≠时,=-21S S 343212431222=⨯≤+=mmm m ()R m ∈. 由432=m ,得 332±=m ; 当0=m 时,3021<=-S S 从而,当332±=m 时,21S S -取得最大值3.………………(12分) 21.【命题意图】本题考查利用导数研究函数的单调性与极值、不等式恒成立问题,以及考查等价转化思想、方程思想、逻辑思维能力、运算求解能力.请考生在第22、23、24题中任选一题做答,如果多做,则按所做的第一题计分。
2016年高考数学(理)冲刺卷(新课标Ⅱ卷) 01(解析版) 含解析

第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合{}1,1M =-,120N x x⎧⎫=-<⎨⎬⎩⎭,则下列结论正确的是( )A .N M ⊆B .N M =∅C .M N ⊆D .MN =R【命题意图】本题主要考查集合运算及分式不等式的解法,其中解不等式120x-<易忽略x 的取值为负值的情况。
【答案】C .2.若复数z 满足()1i 1i i z -=-+,则z 的实部为( ) A 21- B 21 C.1 21+ 【命题意图】本题主要考查复数的有关概念及复数的运算,属基础题。
【答案】A【解析】由()1i 1i i z -=-+2i,得()()()()2i 1i 2i 1i1i 1i z +==--+ =2121i 22+,所以z 21-,故选A .3。
若()(),,,A a b B c d 是()ln f x x =图象上不同两点,则下列各点一定在()f x图象上的是( )A.(),a c b d ++B.()a c bd +, C 。
(),ac b d + D 。
(),ac bd【命题意图】本题主要考查对数的运算法则及分析问题解决问题的能力.【答案】C【解析】因为()(),,,A a b B c d 在()ln f x x =图象上,所以ln b a = ,ln ,d c = 所以ln ln ln b d a c ac +=+=,因此(),ac b d +在()ln f x x =图象上,故选C .4。
“牟合方盖”是我国古代数学家刘徽在研究球的体积的过程中构造的一个和谐优美的几何体.它由完全相同的四个曲面构成,相对的两个曲面在同一个圆柱的侧面上,好似两个扣合(牟合)在一起的方形伞(方盖).其直观图如下左图,图中四边形是为体现其直观性所作的辅助线.当其主视图和侧视图完全相同时,它的俯视图可能是( )[ 学图】本题将三视图与我国古代数学成就有机结合在一起,主要考查三视图的画法及空间想象能力。
2016年高考数学冲刺卷02 文(新课标Ⅰ卷)答案

2016年高考数学冲刺卷02 文(新课标Ⅰ卷)答案全卷满分150分 考试时间120分钟第Ⅰ卷(共60分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.【命题意图】本题考查不等式解法、集合的交集运算,容易题.【答案】C【解析】由题意,得{|02}A x x =≤≤,所以{0,1}A B = ,故选C . 2.【命题意图】本题考查复数的运算与几何意义,容易题.【答案】C【解析】由题意得,2(1)2(1)111i ii i i i i--==--=--++,故对应的点在第三象限,故选C . 3.【命题意图】本题考查平面向量的几何意义,容易题.【答案】D【解析】1322BD AD AB AC CD AB AC AB AB AC AB =-=+-=--=-,故选D .4.【命题意图】本题考查古典概型,容易题.【答案】A5.【命题意图】本题考查线性规划问题,容易题.【答案】C【解析】作出不等式组表示的平面区域如图,目标函数23z y x =-化为斜截式为322zy x =+,所以当直线322zy x =+的截距最大时max z ,所以当直线23z y x =-过点()0,2时,max =4z ,故选C .6.【命题意图】本题考查分段函数、函数单调性与不等式,中档题.【答案】D【解析】根据函数的解析式可知,函数是定义域R 上的增函数,所以2(2)()f x f x ->的等价条件是22x x ->,解得(2,1)x ∈-,故选D .7.【命题意图】本题考查推理与证明、球的体积,中档题.【答案】B8.【命题意图】本题考查程序框图、对数运算,中档题.【答案】B 【解析】11,l g l g 31,3i S ===->-否;1313,l g +l g l g l g 5355i S ====->-否;1515,l g +l g lg l g 71,577i S ====->-否;1717,l g +l g l g799i S ====->-否;1919,l g+l g l g lg111,91111i S ====-<-是,输出9,i =故选B . 9.【命题意图】本题考查函数解析式与图象,中档题.【答案】A【解析】根据题意得101231()12445152422xx f x x x x x ⎧<<⎪⎪⎪=-≤<⎨⎪⎪-≤<⎪⎩f (x )=,分段函数图象分段画即可,故选A .10.【命题意图】本题考查三角函数的图象与性质、诱导公式,中档题.【答案】A【解析】因为两个函数关于x a =对称,则函数sin(2)3y x π=-关于x a =的对称函数为sin(2(2))3y a x π=--,利用诱导公式将其化为余弦表达式为c o s [(2(2))]23y a x ππ=---=5cos(24)6x a π+-,令25cos(2)cos(24)36y x x a ππ=+=+-,则24a π=,故选A .11.【命题意图】本题考查双曲线的定义与几何意义、抛物线的方程与几何性质,中档题.【答案】A12.【命题意图】本题考查不等式性质与解法、导数与函数单调性,难度大.【答案】C【解析】()()0f x xf x '+>⇒()0xf x '>⎡⎤⎣⎦.设()()()2ln g x xf x x x b ==+-,若存在1,22x ⎡⎤∈⎢⎥⎣⎦,使得()()0fx x f x '+>,则函数()g x 在区间1,22⎡⎤⎢⎥⎣⎦上存在子区间使得()0g x '>成立,()()212212x bx g x x b x x -+'=+-=,设()2221h x xb x =-+,则()20h >或102h ⎛⎫> ⎪⎝⎭,即8410b -+>或1102b -+>,得94b <,故选C .第Ⅱ卷(共90分)二、填空题(本大题共4小题,每小题5分,共20分) 13.【命题意图】本题考查直线与圆的位置关系,容易题.【答案】±2【解析】由题,得直线方程为y x a =+,即0x y a -+==,解2a =±.14.【命题意图】本题考查三视图、棱柱与圆柱的体积计算,中档题.【答案】32165++π【解析】由三视图可知该几何体是一个正三棱柱和一个半圆柱的组合体,三棱柱的两个侧面面积之和为16242=⨯⨯,两个底面面积之和为3232212=⨯⨯⨯;半圆柱的侧面积为ππ44=⨯,两个底面面积之和为ππ=⨯⨯⨯21212,所以几何体的表面积为32165++π. 15.【命题意图】本题考查线性回归的基本思想,中档题.【答案】68度【解析】回归直线过()y x ,,根据题意()1041101318=-+++=x ,40464383424=+++=y ,代入()6010240=⨯--=a,所以4-=x 时,()()686042=+-⨯-=y ,所以用电量的度数是68度.16.【命题意图】本题考查正弦定理、余弦定理的应用,较难题.【答案】8三、解答题(解答应写出文字说明、证明过程或演算步骤)17.【命题意图】本题考查等差数列的通项公式、裂项法求和;以及考查转化能力、逻辑思维能力、运算求解能力、分类讨论的思想的应用. 【解析】(1)设数列{}n a 的公差为d ,由题意2142S S S =,即2111(46)(2)a a d a d +=+,∵11a =,0d ≠,∴2d =,∴21n a n =-.………………(5分) (2)由(1)得2n S n =,∴21n b n =. 当1n =时,112b =<成立;………………(7分) 当2n ≥时,()2111111n b n n n n n=<=---, ∴12n b b b +++< (11111111)1122223341n n n+-+-+-++-=-<-…成立, 所以对任意的正整数n ,不等式成立.………………(12分)18.【命题意图】本题考查空间直线和平面间的平行与垂直关系、棱锥的体积,以及考查空间想象能力、逻辑推证能力、转化的思想.19.【命题意图】本题考查样本估计总体、抽样方法、古典概型,以及考查分类讨论思想、运算求解能力、数据处理能力.【解析】(Ⅰ)∵被调查的所有女生的平均得分为8.25分, ∴5301010608.25203060x x +⨯+⨯=+++,解得90x =.………………(3分)现从所有答卷中抽取一份,共有结果10253520903060270y y +++++++=+()(), ∴抽到男生且得分是15分得概率127010y y =+,解得30y =,………………(6分)(Ⅱ)从得分是15分的学生中用分层抽样的方法抽取6人,则抽样比例为=,∴女生抽取4人,记为a,b,c,d,男生抽取2人,记为A,B,从这6人中随机抽取2人的种数,,,,,,,,,,,,,,AB Aa Ab Ac Ad Ba Bb Bc Bd ab ac ad bc bd cd共15种,………………(9分)其中所抽取的2人中至少有1名男生,,,,,,,,AB Aa Ab Ac Ad Ba Bb Bc Bd共9种,故所抽取的2人中至少有1名男生的概率93155P==.………………(12分)20.【命题意图】本题考查椭圆的方程与几何性质、直线与椭圆的位置关系、平面向量数量积,以及考查方程思想、逻辑思维能力、运算求解能力.21.【命题意图】本题考查导数几何意义、利用导数研究函数的单调性与极值,以及考查等价转化思想、方程思想、分类讨论思想、逻辑思维能力、运算求解能力.请考生在第22、23、24题中任选一题做答,如果多做,则按所做的第一题计分。
高考数学重难点全真模拟试卷01(新高考专用)(老师专用)(解析版)

新高考数学重难点全真模拟试卷01(考试时间:120分钟试卷满分:150分)注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答第Ⅰ卷时,选出每小题答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
写在本试卷上无效。
3.回答第Ⅱ卷时,将答案写在答题卡上。
写在本试卷上无效。
4.考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求.1.(2022秋·天津南开·高三南开翔宇学校校考期末)设全集为{}270U x N x x =∈-<,{}2,3,5U A =ð,{}2,5,6B =,则()U A B = ð()A.{}1,4B.{}2,5C.{}6D.{}1,3,4,6【答案】A【分析】把{}270U x N x x =∈-<化简,分别求出集合A ,U B ð,然后求解()U A B ∩ð.【解析】{}{}{}270071,2,3,4,5,6U x N x x U x N x =∈-<∴=∈<<= 又{}{}2,3,51,4,6U A A =∴= ð,又{}{}2,5,61,3,4U B B =∴= ð(){}1,4U A B ∴= ð,故选:A2.(2023秋·河北·高三统考阶段练习)复数()()231i 1i --在复平面内对应的点在()A.第一象限B.第二象限C.第三象限D.第四象限【答案】D【分析】根据复数的四则运算法则化简后,即可确定复数()()231i 1i --在复平面内对应的点的坐标,进而判断其所在象限.【解析】()()()()()232221i 1i 1i i 12i i 2i 1i 2i 2i 2i 2----==-⋅=+=+---,则复数()()231i 1i --在复平面内对应的点的坐标为()2,2-,位于第四象限,故选:D.3.(2023秋·黑龙江牡丹江·高三牡丹江市第三高级中学校考阶段练习)已知向量a ,b满足1a = ,2b = ,且a b += a 与b 的夹角为()A.π6B.2π3C.5π6D.π3【答案】B【分析】先求得数量积1a b ⋅=-,再利用向量夹角公式即可求得a 与b 的夹角.【解析】因为a b += ()22222523a b a b a b a b a b +=+=++⋅=+⋅= ,则1a b ⋅=- .则11cos ,122a b a b a b ⋅-===-⨯⋅.又因为[],0,π∈ a b ,所以2,π3a b = ,即a 与b的夹角为2π3.故选:B.4.(2023秋·天津南开·高三崇化中学校考期末)我国著名数学家华罗庚曾说过:“数无形时少直观,形无数时难入微;数形结合百般好,隔离分家万事休”.函数()32sin22xx x f x +=的部分图像大致为()A.B.C.D.【答案】A【分析】根据函数的奇偶性和特殊点的函数值,即可得解.【解析】∵()32sin22xx x f x +=,x ∈R ,33||||()2sin(2)2sin 2()()22x x x x x xf x f x --+-+-==-=-,则()f x 是奇函数,其图像关于原点对称,排除选项B、D;对12sin 2(1)02f +=>故可排除选项C.故选:A.5.(2022秋·宁夏吴忠·高三青铜峡市高级中学校考期末)已知等差数列{}n a 前9项的和为1027,8a =,则90a =()A.87B.89C.88D.90【答案】C【分析】根据已知条件求得公差d ,从而求得正确答案.【解析】设等差数列{}n a 的公差为d ,因为()199195927,22a a S aa a +⨯==+=,所以53a =.又因为108a =,所以1051105a a d -==-.故()90109010188a a =+-⨯=.故选:C6.(2023秋·山西吕梁·高三统考期末)已知3ππ,2α⎛⎫∈ ⎪⎝⎭,若22sin 291cos 2αα+=-,则cos sin cos sin αααα+=-()A.3-B.3C.97D.97-【答案】B【分析】由题知sin 0,cos 0αα<<,进而结合二倍角公式整理得sin cos 3sin ααα+=,即2sin cos αα=,再代入求解即可.【解析】因为3ππ,2α⎛⎫∈ ⎪⎝⎭,sin 0,cos 0αα<<,()()()()222221sin 2212sin cos sin cos 22sin 291cos 22sin sin 112sin αααααααααα++++====---,所以sin cos 3sin ααα+=,即2sin cos αα=所以cos sin 2sin sin 3cos sin 2sin sin αααααααα++==--.故选:B 7.(2023·全国·郑州中学校考模拟预测)设120231e 2023a =,2024ln2023b =,sin(0.2023)c =︒,则()A.c b a >>B.a b c >>C.b a c >>D.c a b>>【答案】D【分析】构造函数()()()e ln 1,0,1xf x x x x =-+∈,利用导数确定函数的单调性可得()12023111e ln 100202320232023f f ⎛⎫⎛⎫=-+>= ⎪ ⎪⎝⎭⎝⎭,即可判断,a b 大小关系;估计实数12023与0.2023π0.2023180︒=的大小关系及大致倍数关系,构造函数()1e sin 6,0,1000xh x x x x ⎛⎫=-∈ ⎪⎝⎭,利用导数确定单调性可得()12023111e sin 600202320232023h h ⎛⎫⎛⎫=-⨯<= ⎪ ⎪⎝⎭⎝⎭,从而结合正弦函数的单调性可比较,a c 大小,即可得结论.【解析】设()()()e ln 1,0,1x f x x x x =-+∈,则()()11e 1xf x x x =+-+',设()()()11e 1x g x f x x x==+-+',则()()()212e 01x g x x x =++>+'恒成立,所以()f x '在()0,1上单调递增,所以()()00f x f ''>=恒成立,则()f x 在()0,1上单调递增,故()12023111e ln 100202320232023f f ⎛⎫⎛⎫=-+>= ⎪ ⎪⎝⎭⎝⎭,即12023112024e ln 1ln 202320232023⎛⎫>+= ⎪⎝⎭,所以a b >;因为10.000494322023≈,0.2023π0.20230.0035308160.00049432180︒=≈>⨯,则10.202362023︒>⨯,设()1e sin 6,0,1000xh x x x x ⎛⎫=-∈ ⎪⎝⎭,则()()1e 6cos6x h x x x '=+-,又设()()()1e 6cos6xm x h x x x ==-'+,故()()2e 12sin 60xm x x x =++>'恒成立,所以()h x '在10,1000x ⎛⎫∈ ⎪⎝⎭上单调递增,所以()110001111e 6cos 0100010001000h x h ⎛⎫⎛⎫<=+-< ⎪ ⎪⎝'⎭⎝⎭'恒成立,则()h x 在10,1000⎛⎫ ⎪⎝⎭上单调递减,则()12023111e sin 600202320232023h h ⎛⎫⎛⎫=-⨯<= ⎪ ⎪⎝⎭⎝⎭,1202311e sin 620232023⎛⎫<⨯ ⎪⎝⎭又()1sin 6sin 0.20232023⎛⎫⨯<︒ ⎪⎝⎭,则()120231e sin 0.20232023<︒,即c a >;综上,c a b >>.故选:D.8.(2022·全国·统考高考真题)已知球O 的半径为1,四棱锥的顶点为O ,底面的四个顶点均在球O 的球面上,则当该四棱锥的体积最大时,其高为()A.13B.12D.22【答案】C【分析】方法一:先证明当四棱锥的顶点O 到底面ABCD 所在小圆距离一定时,底面ABCD 面积最大值为22r ,进而得到四棱锥体积表达式,再利用均值定理去求四棱锥体积的最大值,从而得到当该四棱锥的体积最大时其高的值.【解析】[方法一]:【最优解】基本不等式设该四棱锥底面为四边形ABCD ,四边形ABCD 所在小圆半径为r ,设四边形ABCD 对角线夹角为α,则2111sin 222222ABCD S AC BD AC BD r r rα=⋅⋅⋅≤⋅⋅≤⋅⋅=(当且仅当四边形ABCD 为正方形时等号成立)即当四棱锥的顶点O 到底面ABCD 所在小圆距离一定时,底面ABCD 面积最大值为22r 又设四棱锥的高为h ,则22r h 1+=,2123O ABCDV r h -=⋅⋅=≤=当且仅当222r h =即h [方法二]:统一变量+基本不等式由题意可知,当四棱锥为正四棱锥时,其体积最大,设底面边长为a ,底面所在圆的半径为r则2r a=,所以该四棱锥的高h =13V a=(当且仅当22142a a=-,即243a=时,等号成立)所以该四棱锥的体积最大时,其高h==.故选:C.[方法三]:利用导数求最值由题意可知,当四棱锥为正四棱锥时,其体积最大,设底面边长为a,底面所在圆的半径为r则22r a=,所以该四棱锥的高h=13V a=令2(02)a t t=<<,V=()322t tf t=-,则()2322tf t t-'=,43t<<,()0f t'>,单调递增,423t<<,()0f t'<,单调递减,所以当43t=时,V最大,此时h=.故选:C.【整体点评】方法一:思维严谨,利用基本不等式求最值,模型熟悉,是该题的最优解;方法二:消元,实现变量统一,再利用基本不等式求最值;方法三:消元,实现变量统一,利用导数求最值,是最值问题的常用解法,操作简便,是通性通法.二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.9.(2023秋·山西吕梁·高三统考期末)近年来、新冠疫情波及到千家万户,人们的生活方式和习惯不得不发生转变,短视频成了观众空闲时娱乐活动的首选.某电影艺术中心为了解短视频平台的观众年龄分布情况,向各大短视频平台的观众发放了线上调查问卷,共回收有效样本4000份,根据所得信息制作了如图所示的频率分布直方图,则下列说法正确的是()A.图中0.028a=B.在4000份有效样本中,短视频观众年龄在10~20岁的有1320人C.估计短视频观众的平均年龄为32岁D.估计短视频观众年龄的75%分位数为39岁【答案】CD【分析】根据频率和为1可构造方程求得a ,知A 错误;由频率和频数的关系可求得观众年龄在10~20岁的人数,知B 正确;由平均数和百分位数的估计方法可验证知CD 正确.【解析】对于A,()0.0150.0330.0110.011101a ++++⨯= ,0.03a ∴=,A 错误;对于B,由频率分布直方图知:短视频观众年龄在10~20岁的人对应频率为0.15,∴短视频观众年龄在10~20岁的有40000.15600⨯=人,B 错误;对于C,平均年龄()0.015150.033250.03350.011450.011551032x =⨯+⨯+⨯+⨯+⨯⨯=,C 正确;对于D,设75%分位数为x ,则()0.015100.03310300.030.75x ⨯+⨯+-⨯=,解得:39x =,D 正确.故选:CD.10.(2023·全国·高三专题练习)(多选题)如图,在正方体1111ABCD A B C D -中,点P 在线段1BC 上运动,给出下列判断正确的是()A.直线1B D ⊥平面1ACD ;B.1A P ∥平面1ACD ;C.异面直线1A P 与1AD 所成角的范围是π0,3⎛⎤⎥⎝⎦;D.三棱锥1D APC -的体积不变【答案】ABD【分析】对于A,利用线面垂直的判定定理证明判断;对于B,利用线面平行和面面平行的判定定理证明判断;对于C,分P 与线段1BC 的B 端和1C 端以及线段1BC 的中点重合判断;对于D,由11D APC P ACD V V --=,结合1BC ∥平面1AD C 判断.【解析】对于A,如图所示:连接BD ,根据正方体的性质,∵1BB ⊥平面ABCD ,且AC ⊂面ABCD ,∴1BB AC ⊥,又∵BD AC ⊥,且1BD BB B ⋂=,∴AC ⊥面1BB D ,∴1AC B D ⊥,连接1A D ,根据正方体的性质,∵11A B ⊥平面11A D DA ,且1AD ⊂面11A D DA ,∴111A B AD ⊥;又∵11AD A D ⊥,且1111A B A D A = ,∴1AD ⊥面11A B D ,∴11AD B D ⊥,且1AC AD A =I ,∴直线1B D ⊥平面1ACD ,故A 正确对于B,如图所示:连接111,A B A C ,在正方体中,∵AC ∥11AC ,且AC ⊂平面1ACD ,11A C ⊂/平面1ACD ,∴11AC ∥平面1ACD ,同理可证1BC ∥平面1ACD ,又∵11AC 、1BC ⊂平面11BA C ,且1111=A C BC C ,∴平面11//BA C 平面1ACD ,又∵1A P ⊂平面11BA C ,∴1//A P 平面1ACD ,故B 正确;对于C,当P 与线段1BC 的B 端重合时,异面直线1A P 与1AD 所成角为11A BC ∠,∵11A BC 为等边三角形,∴11π3BC A =∠;当P 与线段1BC 的1C 端重合时,异面直线1A P 与1AD 所成角为11A C B ∠,∵11A BC 为等边三角形,∴11π3AC B ∠=;∴当P 与线段1BC 的中点重合时,1A P 与1AD 所成角取最大值,∴11A PC ∠为异面直线1A P 与1AD 所成角,又∵111A B A C =,且P 为线段1BC 的中点,∴11π2A PC ∠=,故1A P 与1AD 所成角的范围是ππ,32⎡⎤⎢⎥⎣⎦,故C 错误;对于D,11D APC P ACD V V --=,∵1BC ∥1AD ,且1BC ⊂/平面1AD C ,1AD ⊂平面1AD C ,∴1BC ∥平面1AD C ,∴点P 到平面1ACD 的距离不变,且1ACD △的面积不变,所以三棱锥1P ACD -的体积不变,故D 正确;故选:ABD.11.(2023秋·河北·高三统考阶段练习)已知函数21e 1()ex x f x +-=,()f x '为()f x 的导函数,则()A.方程()f x x =只有一个实根B.()f x '的最小值为2eC.函数()()()f x G x f x '=的值域为(1,1)-D.函数()()()F x f x f x '=⋅为偶函数【答案】BC【分析】由零点存在定理可知方程()f x x =不止一个实根;利用()f x ''的正负,求出()f x '的单调性,进而求得()f x '的最小值;利用分离常数法,求得2()1e 21x G x =+-,根据指数函数及不等式的性质即可求出函数的值域;2222()e e x x F x ---=-,而()()F x F x -=-不符合偶函数的定义.【解析】对于A,方程()f x x =,即2111e 1e e 0ex x x x x x ---+---==-,显然0x =是方程的一个根,令()11ee x x x g x ---=--,由于()0201e e 1g --=-<,()1302e e 2g --=->,根据零点存在定理可知,函数()g x 在()1,2上有一个零点,因此方程()f x x =不只有一个实根,A 选项错误;对于B,2111e 1()e e ex x x x f x ---+-=-=,则()1111()e e e 1e 1+x x x x f x ------'⋅-⋅=-=,()1111()e 11e e e x x x x f x ------'==-'⋅+⋅-,令()0f x ''=,即110e e x x ----=,解得0x =,当0x <时,()0f x ''<,所以()f x '在(),0∞-上单调递减,当0x >时,()0f x ''>,所以()f x '在()0,∞+上单调递增,因此()f x '的最小值为112+e(0)e e f --'==,B 选项正确;对于C,1122112221122+111()e e e e ()1()e e e e e x x x x x x x x x f x G x f x --------+-'====+-++=,22222122011010220e 11e e e e 1x x x x x >⇒+>⇒<<⇒<<⇒-<-<+++ ,则2111e 21x -<-<+,所以函数()G x 的值域为(1,1)-,C 选项正确;对于D,()()11112222()()()e e e e ee +x x x x x x F xf x f x ---------'-==-⋅=而()22222222()ee e e ()x x x x F x F x ------=-==----,所以函数()()()F x f x f x '=⋅不是偶函数,D 选项错误;故选:BC.12.(2023·湖南岳阳·统考一模)已知抛物线23y x =上的两点()00,A x y ,()()000,0B x y x -≠及抛物线上的动点(),P x y ,直线PA ,PB 的斜率分别为1k ,2k ,坐标轴原点记为O ,下列结论正确的是()A.抛物线的准线方程为32x =-B.三角形AOB为正三角形时,它的面积为C.当0y 为定值时,1211k k -为定值D.过三点()000,A y ,()000,B y -,()()000,00C x x ≠的圆的周长大于3π【答案】BCD【分析】由抛物线方程判断A,根据正三角形求出直线OA 斜率,联立抛物线求点A 坐标即可判断B,直接计算1211k k -结合,A P 在抛物线方程上化简可判断C,根据题意及圆的性质求出半径,结合点A 在抛物线上可得出半径范围,即可判断D.【解析】对A,由抛物线23y x =知准线方程为34x =-,故A 错误;对B,当三角形AOB 为正三角形时,不妨设A 在第一象限,则π6AOx ∠=,直线AO 方程为33y x =,联立23y x =,可得009,x y ==故0||22AB y ==⨯=23||4AOB S AB ==△,故B 正确;对C,001200,y y y y k k x x x x -+==--,当0y 为定值时00000000022000020103((122)2)2)()()()331(x x x x y y x x y x x y x x y y y y k y y y y y k y x x -----===-+-+---=-=为定值,故C 正确;对D,因为圆过三点()000,A y ,()000,B y -,()()000,00C x x ≠,所以可设圆心为(,0)a ,则0R x a =-=22000()()2y x ax =-,故20003()2x x ax =-,因为00x ≠,所以0230x a =+>,即32a >-,故0332R x a a =-=+>,所以圆的周长32π2π3π2R >⨯=,故D 正确.故选:BCD第Ⅱ卷三、填空题:本题共4小题,每小题5分,共20分13.(2023秋·广东·高三校联考阶段练习)()8111x x ⎛⎫-+ ⎪⎝⎭的展开式中2x 项的系数为___.(用数字作答)【答案】28-【分析】由二项式展开式的通项公式求解即可【解析】()81x +的展开式通项为818C r rr T x-+=,所以22867C 28T x x ==,53368C 56T x x ==.故所求2x 的系数为1285628⨯-=-.14.(2023·广西梧州·统考一模)直线:l y x =与圆()()()222:120C x y a a -+-=>交A ,B 两点,若ABC 为等边三角形,则a 的值为______.【分析】结合几何关系和点到直线的距离即可求解.【解析】由条件和几何关系可得圆心C 到直线:l y x ==3a =.15.(2022秋·宁夏吴忠·高三青铜峡市高级中学校考期末)已知()2e ex xmf x -=满足()()0f x f x -+=,且()f x 在()(),n f n 处的切线与21y x =+平行,则m n +=__________.【答案】1【分析】根据()()0f x f x -+=,可得函数()f x 是R 上的奇函数,从而可求得m ,再根据导数的几何意义可得()2f n '=,从而可求得n ,即可得出答案.【解析】函数()2e e x xmf x -=的定义域为R ,因为()()0f x f x -+=,所以函数()f x 是R 上的奇函数,所以()010f m =-=,解得1m =,经检验成立所以()2e 1e x xf x -=,则()()22222e e e 1e e 1e e x x x xx xxf x ⋅--+'==,因为()f x 在()(),n f n 处的切线与21y x =+平行,所以()2e 12e n nf n +'==,解得0n =,所以1m n +=.16.(2022秋·江苏徐州·高三期末)已知椭圆C :()222210x y a b a b+=>>,经过原点O 的直线交C 于A ,B 两点.P 是C 上一点(异于点A ,B ),直线BP 交x 轴于点D .若直线AB ,AP的斜率之积为49,且BDO BOD ∠=∠,则椭圆C 的离心率为______.【分析】设点的坐标,求斜率,由题知220022222211x y a b m n a b ⎧+=⎪⎪⎨⎪+=⎪⎩,两式相减,化简得22AP BP b k k a ⋅=-,结合BDO BOD ∠=∠,知2249AP ABb k k a ⋅==,再利用222c a b =-及离心率公式即可求解.【解析】设()00,P x y ,(),A m n ,(),B m n --,则直线AP 的斜率为00y n x m --,BP 的斜率为00y nx m++,由题知220022222211x y a b m n ab ⎧+=⎪⎪⎨⎪+=⎪⎩,两式相减得22220022x m y n a b --=-,即200200x m y n a y n b x m +-=-⨯+-,即221AP BP a k k b =-⨯,即22AP BP b k k a⋅=-,又BDO BOD ∠=∠,则AB BP k k =-,即22AP AB b k k a⋅=,即2249b a =,则2249b a =,所以2222224599c a b a a a =-=-=,即2259c a =,则椭圆C的离心率为c a =四、解答题:本小题共6小题,共70分。
2016年高考数学冲刺卷02 理(四川卷)答案

2016年高考数学冲刺卷02 理(四川卷)答案第Ⅰ卷(共50分)一、选择题:(本大题共10个小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的。
)1.【命题意图】本题主要考查集合交集的运算,是容易题. 【答案】B【解析】由题意,知{|0}M y y =≥,{|N x x =≤≤,所以M N =⎡⎣,故选B .2.【命题意图】本题主要考查了复数的概念及除法,是容易题. 【答案】A 【解析】因为6(6)(3)18633(3)(3)1010ai ai i a a i i i i +++-+==+--+,则由题意,得18631010a a-+=,解得3a =,故选A .【一题多解】设复数z b bi =+,则由题意,得63aib bi i++=-,即()(3)6b bi i ai +-=+,即42b bi +=6ai +,由复数相等的条件,得462b b a =⎧⎨=⎩,解得323b a ⎧=⎪⎨⎪=⎩,故选A .3.【命题意图】本题主要考查了充分条件、必要条件,是容易题. 【答案】B【解析】0φ=时()cos f x x =是偶函数,但2φπ=时,()cos(2)cos f x x πx =+=也是偶函数,因此“()=cos(+)f x x ϕ()x R ∈为偶函数” 是“=0ϕ”的必要而不充分条件.故选B . 4.【命题意图】本题主要考查了抛物线及其性质,是容易题. 【答案】C5.【命题意图】本题主要考查了排列组合,是容易题. 【答案】B【解析】根据题意可知,第一组分3人有312C 种选择,第二组分3人有38C 种选择,第三组分3人有36C 种选择,第四组分3人有33C 种选择;第一组选择一名组长有3种选择,第二组选择一名组长有3种选择,第三组选择一名组长有3种选择,第四组选择一名组长有3种选择;根据分布计数原来,可知满足题目要求的种数有33334333412963129633C C C C C C C =种,故选B .6.【命题意图】本题主要考查线性规划,意在考查考生的数形结合的能力,是容易题. 【答案】B7.【命题意图】本题主要考查程序框图中的条件结构,属于基本知识的考查,意在考查考生的逻辑分析能力,是容易题. 【答案】A【解析】第一次循环,得1844,14b a =-==;第二次循环,得14410,4a b =-==;第三次循环,得1046,4a b =-==;第四次循环,得642,4a b =-==;第五次循环,得422,2b a =-==,此时2a b ==,不满足循环条件,退出循环,输出2a =,故选A .8.【命题意图】本题主要考查向量数量积及最值问题,属于基本知识的考查,意在考查考生的基本运算能力,是中档题. 【答案】D【解析】因(1,2,3),(2,1,2),(1,1,2)A Q P ,所以由点Q 在直线OP 上可得:存在实数λ,使得(,,2)OQ OP λλλλ→→==,则(,,2)Q λλλ,所以(1,2,32),(2,1,22),QA QB λλλλλλ→→=---=---,所以2(1)(2)(2)(1)(22)(32)2(385)QA QB λλλλλλλλ→→⋅=--+--+--=-+,根据二次函数的性质可得当43λ=时,取得最小值23-,此时448(,,)333Q ,故应选D . 9.【命题意图】本题主要考查双曲线的定义、直线与圆相切的性质和三角形中位线等知识,意在考查考生的逻辑分析能力与数形结合的能力,是中档题. 【答案】A10.【命题意图】本题主要考查了分段函数的图像以及函数恒成立问题,同时考查了考生的数形结合能力,是中档题. 【答案】D【解析】[)0,1x ∈时, ()22111,0244f x x x x ⎛⎫⎡⎤=-=--∈- ⎪⎢⎥⎝⎭⎣⎦,当[)1,2x ∈时,()()1.50.51,x f x -⎡=-∈-⎢⎣⎦,所以[)0,2x ∈时, ()min 1f x =-.()()22f x f x += ,()()()112424f x f x f x ∴=+=+, 所以当[)4,2x ∈--时,()min 14f x =-,于是要使[)4,2x ∈--时,()142t f x t≥-恒成立,只需11442t t-≥-即可. 又()()21110442t t t t t+--≥-⇔≤,解得2t ≤-或01t <≤.故D 正确. 第Ⅱ卷(共100分)二、填空题(本大题共4小题,每小题5分,共25分)11.【命题意图】本题主要考查二项式展开式等基础知识,考查学生的计算能力.【答案】35【解析】由题意,知2128n =,解得7n =,所以21()n x x -展开式的通项公式为27171()()r rr T C x r x-+=-=14317(1)r r r r T C x -+=-,0,1,,7r = ,令1432r -=,解得4r =,所以展开式中2x 的系数为447(1)35C -=.12.【命题意图】本题主要考查简单随机抽样等基础知识,考查学生的计算能力. 【答案】56 【解析】试题分析:求出样本间隔即可得到结论. 解:∵样本容量为5, ∴样本间隔为60÷5=12,∵编号为4,a ,28,b ,52号学生在样本中, ∴a=16,b=40, ∴a+b=56, 故答案为:5613. 【命题意图】本题考查三视图、几何体体积等基础知识,意在考查学生空间想象能力和基本运算能力.14.【命题意图】本题考查直线与圆的位置关系等基础知识,意在考查学生基本运算能力. 【答案】18【解析】由题意得,圆心到两直线距离相等,且等于222=r ,因此2==,即1a =,1b =或1,1b a == ,即2218a b +=.15.【命题意图】本题主要考查新定义函数问题,意在考查学生的综合分析能力和逻辑推理能力. 【答案】②③【解析】因)0(111≠+≠+m mx m x ,故①不是m 函数;②是,因=+=+)(2)(m x m x f )(2m x + )()(22m f x f m x +=+=;③是,因)sin()(m x m x f +=+,m x m f x f sin sin )()(+=+,若πk m 2= k 为不为0的整数,则=+=+)sin()(m x m x f x k x sin )2sin(=+π,m x m f x f sin sin )()(+=+ x k x sin 2sin sin =+=π,故)()()(m f x f m x f +=+;若)1(ln ln )ln(>=+⇔+=+m xm m x m x m x显然此式要恒成立则1=m 且0=m ,无解,故④不是三、解答题 (本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.)16.【命题意图】本题考查倍角公式与诱导公式化简、正余弦定理,解三角形等基础知识,意在考查学生转化与化归能力、综合分析问题解决问题的能力以及运算求解能力.【答案】(1)0,4π⎛⎤⎥⎝⎦和3,4ππ⎡⎫⎪⎢⎣⎭;(2.17.【命题意图】本题主要考查离散型随机变量的分布列和数学期望等基础知识,考查学生分析问题解决问题的能力、转化能力、计算能力.【答案】(1)0.56;(2)分布列见解析,53()30E ξ=. 【解析】(1)因为调查的50人中达到实际的水平有:36664328+++++=(人), 所求的概率为280.5650P ==. (2)调查的4人中高考成绩没有达到实际水平的人数为ξ,则0,1,2,3ξ=当221122143243432222646417(0);(1)515C C C C C C C p p C C C C ξξ+====== 221112123243232222646431(2),(3)1030C C C C C C C p p C C C C ξξ+====== 所求的分布列为3153()0123515103030E ξ=⨯+⨯+⨯+⨯=18.【命题意图】本小题主要考查空间直线与平面垂直判定及线面角等基础知识,考查空间想象能力、推理 论证能力、运算求解能力,考查数形结合思想、化归与转化思想. 【答案】(1)见解析;(2)(3)不存在,理由见解析. (3)假设在线段EB 上存在一点P ,使得平面1A DP ⊥平面1A B C ,设(,0,0)(02)P t t ≤≤,则1(,0,2)A P t =- ,12)A D =- ,设平面1ADP 的法向量为111(,,)p x y z =,由10A D p ⋅= ,10A P p ⋅= ,得11112020z tx z ⎧-=⎪⎨-=⎪⎩,令12x =,得(2,p t = ,∵平面1A DP ⊥平面1A BC ,∴0m p ⋅= ,即0=,解得3t =-, ∵02t ≤≤,∴在线段EB 上不存在点P ,使得平面1A DP ⊥平面1A BC .(12分 )19.【命题意图】本题考查已知数列前n 项和求通项以及分段数列前n 项和的求法等基础知识, 意 在考查学生转化与化归能力、推理能力和运算求解能力. 【答案】(Ⅰ)3n a n =(Ⅱ)272m ≥(Ⅲ)821t ≥要使m T n ≤对于一切的正整数n 恒成立,只需272m ≤, ∴272m ≥. (Ⅲ)38(18)828(81)187n nnnn n b B -==⇒==--, 将n B 代入11116n nn n B tb B tb ++-<+,化简得,()+18818178816+877n nn t t ⨯--⨯<⎛⎫- ⎪⎝⎭(﹡) ∵0t >,∴+188+877n t ⎛⎫>⎪⎝⎭, 所以(﹡)化为()+1+1816818+1387n n n t ⎡⎤⨯--<⨯⎣⎦,整理得()+1+1816818+1218n n n t ⎡⎤⨯--⎣⎦>⨯,∴+18151218n t ⎛⎫>- ⎪⎝⎭对一切的正整数n 恒成立, 易知+11518n -随n 的增大而增大,且+18158121821n ⎛⎫-< ⎪⎝⎭, ∴821t ≥. 20.【命题意图】本题考查椭圆的方程,直线与椭圆的位置关系,构建代数方法解决几何问题等基础知识,意在考查学生转化与化归能力,综合分析问题解决问题的能力,推理能力和运算能力.【答案】(1)()22104x y x +=≠; (2)直线CD 恒过定点(1,0).(2)设00(4,)(0)P y y ≠,又(2,0)A -,则()()12f x f x -≥,故直线AP 的方程为:0(2)6y y x =+,代入椭圆方程并整理得:()242121x a x a x x ---+≤+-。
(完整word)2016年安徽省合肥市高考数学二模试卷(理科)(解析版)
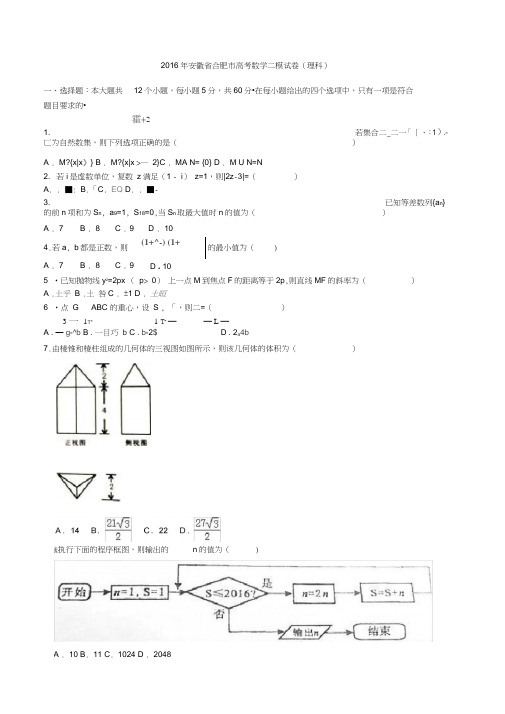
2016年安徽省合肥市高考数学二模试卷(理科)一、选择题:本大题共12个小题,每小题5分,共60分•在每小题给出的四个选项中,只有一项是符合题目要求的•霍+21. 若集合二_二一「丨、:1).-匸为自然数集,则下列选项正确的是()A . M?{x|x》}B . M?{x|x >—2}C . MA N= {0}D . M U N=N2. 若i是虚数单位,复数z满足(1 - i)z=1,则|2z-3|=()A. . ■:B.「C. EQD. . ■-3. 已知等差数列{a n}的前n项和为S n, a9=1, S18=0,当S n取最大值时n的值为()A . 7B . 8C . 9D . 104.若a, b都是正数,则(1+^-) (1+的最小值为()A . 7B . 8C . 9D . 105 •已知抛物线y2=2px (p> 0)上一点M到焦点F的距离等于2p,则直线MF的斜率为()A .土乎B .土咎C . ±1D . 土晅6 •点G ABC 的重心,设S , 「,则二=()3 一1T* 1 T-——L—A . —g-^bB . 一目巧bC . b-2$D . 2a4b7.由棱锥和棱柱组成的几何体的三视图如图所示,则该几何体的体积为()&执行下面的程序框图,则输出的n的值为()A . 10 B. 11 C. 1024 D . 20489.在三棱锥P - ABC 中,PA 丄平面ABC , _|■- - ■ ':J_',则三棱锥P- ABC12. 定义在R 上的偶函数f (x )的导函数为f '(x ),若对任意的实数 x ,都有2f (x ) +xf '(x )v 2恒成 立,则使x 2f ( x )- f (1)v x 2- 1成立的实数x 的取值范围为()A . {x|x 工±}B . ( - s,- 1) U ( 1, + s)C . (- 1, 1)D . (- 1, 0) U (0, 1) 二、填空题(每题 5分,满分20分,将答案填在答题纸上)13. ________________________________________ 命题灯咒>0,冥%>1”的否定是 .214. 双曲线M: 的左,右焦点分别为 F 1, F 2,记|F 1F 2|=2C ,以坐标原点 O 为圆心,c 为半径的圆与双曲线 M 在第一象限的交点为 P ,若|PF 1|=C +2 ,贝V P 点的横坐标为 __________ .2 o15. ______________________________________________________________________________________ 已知各项均为正数的数列{a n }前n 项和为S n ,若S ]二2・3片 一泊就1片二弘+1,则a n = _________________ 16. ____________________________________________________________________ 若函数f (x ) =x 2 (x - 2) 2- a|x -1|+a 有4个零点,贝V a 的取值范围为 ______________________________________ . 三、解答题(本大题共 5小题,共70分•解答应写出文字说明、证明过程或演算步骤 •) 17.在厶ABC 中,三个内角A, B , C 所对的边分别为 a, b,c,已知函数• ■ i - _ / - ■为偶函数,2F ( +) (1 )求 b ;(2 )若a=3,求△ ABC 的面积S.18. 某品牌手机厂商推出新款的旗舰机型,并在某地区跟踪调查得到这款手机上市时间( 占有率(y% )的几组相关对应数据;的外接球的表面积为()A . 20 nB . 24 nC . 28 nD . 32 nfx- y+l>010.已知实数x , y 满足{掘一3¥-1恋0,L<i若z=kx - y 的最小值为- 5,则实数k 的值为(A . - 3B . 3 或-5C . - 3 或-5D . ±311.某校组织由5名学生参加的演讲比赛, 采用抽签法决定演讲顺序, B 不是最后一个出场”的前提下,学生C 第一个出场的概率为(在学生A 和B 都不是第一个出场, )B .C .20x 个月)和市场(2)根据上述回归方程,分析该款旗舰机型市场占有率的变化趋势,并预测自上市起经过多少个月,该款旗舰机型市场占有率能超过 0.5% (精确到月)0.020.050.1(1)根据上表中的数据,用最小二乘法求出0.15 0.18y 关于x 的线性回归方程; 附:19. 如图,六面体ABCDHEFG 中,四边形ABCD为菱形,AE , BF , CG, DH都垂直于平面ABCD,若DA=DH=DB=4 , AE=CG=3(1)求证:EG丄DF;(2)求BE与平面EFGH所成角的正弦值.20. 已知椭圆Ei ~+~^l(a>b>0)经过点(2),且离心率为芈,F i, F2是椭圆E的左,右焦点(1)求椭圆E的方程;(2)若点A , B是椭圆E上关于y轴对称两点(A , B不是长轴的端点),点P是椭圆E上异于A , B的一点,且直线PA, PB分别交y轴于点M, N,求证:直线MF i与直线NF2的交点G在定圆上.21 .已知函数g (x) =ax3+x2+x (a为实数)(1)试讨论函数g (x)的单调性;(2)若对?x € (0, +x)恒有二’•「:心,「-“;一^,求实数a的取值范围.请考生在22、23、24三题中任选一题作答,如果多做,则按所做的第一题记分22.如图,PA为四边形ABCD外接圆的切线,CB的延长线交PA于点P, AC与BD相交于点M , PA// BD(1)求证:/ ACB= / ACD ;23.在直角坐标系xOy 中,曲线(a为参数),在以0为极点, x轴的非负半轴为(2 )若PA=3, PC=6, AM=1,求AB 的长.24.已知函数f (x) =|x - 4|+|x-a| (a€ R)的最小值为a极轴的极坐标系中,直线I: p sin+p cos 0 =m(1 )若m=0,判断直线l与曲线C的位置关系;(2)若曲线C上存在点P到直线I的距离为-求实数m的取值范围.1)求实数a 的值;(2)解不等式f (x)有.2016年安徽省合肥市高考数学二模试卷(理科)答案与解析一、选择题1.若集合二丄匚「丨、:'匸为自然数集,则下列选项正确的是()A . M?{x|x 羽}B . M?{x|x >— 2}C . MA N={0}D . M U N=N解:J'『J I"':=[ - 2,1), N 为自然数集,故 M?{x|x > 1错误;M?{x|x >- 2}错误;Mn N={0}正确;M U N=N 错误;选C 2•若i 是虚数单位,复数 z 满足(1 - i ) z=1,则|2z -3|=( A •二 B . 「 C. ., D . . 7z= (1 - i ) (a+bi ) =1, + (b - a ) i=1 , a - b=0, ,则 |2z - 3|=|2 (丄+〒i )- 3|=| -2+i|= _ :选3.已知等差数列{a n }的前n 项和为S n , a 9=1, S 18=0,当S n 取最大值时n 的值为()A . 7B . 8C . 9D . 10解:设等差数列{a n }的公差为d , T a 9=1, S 18=0 ,118X17…a 1+8d=1 , 18a 1+ d=0 ,可得:a 1=17 , d= - 2.•- a n =17 - 2 (n - 1) =19 - 2n , 出/111由a n >0解得:―二当S n 取最大值时n 的值为9 .选C4.若a , b 都是正数,则 )的最小值为( )A . 7B . 8C . 9D . 10解:T a , b 都是正数,则寸牛)=5+号+辛》5+^^严,当且仅当b=2a >0时取等号 选C 5 .已知抛物线y 2=2px ( p > 0) 上一点M 到焦点F 的距离等于2p ,则直线MF 的斜率为( )A .土晳B . 土号C . ±1D . - V3解:设 z=a+bi , 则(1 - i ) ••• (a+b) ••• a+b=1, • a =b =-解:抛物线的焦点为 F (二-, T 点M 到焦点F 的距离等于y M = ± ';p .6 •点GABC 的重心,设 BG =刃,GC =卫,则忑=()A . 2苏B .C . b -萬D . 2且十b解:由题意知, F3+ -=「匚, 即丄—+7•由棱锥和棱柱组成的几何体的三视图如图所示,则该几何体的体积为(T \ I t A1A . 14C . 22 D.-解:由三视图可知:该几何体的体积0),准线方程为 2p , ••• M 到准线2p .1:.选 DV 〒—■ 二•: ■疋=14 .选 A不满足条件S <2016,退出循环,输出 n 的值为1024.选C 9.在三棱锥 P -ABC 中,PA 丄平面ABC, - »'■ ' = - ■:J :,则三棱锥 P - ABC的外接球的表面积为()A . 20 nB . 24 nC . 28 nD . 32 n解:•/ AB=AC=2 :, / BAC=60 , •••由余弦定理可得BC=2 .二,273 设厶ABC 外接圆的半径为r ,则2r= 一 =4 ,• r =2,设球心到平面 ABC 的距离为d ,则由勾股定理可得 R 2=d 2+22=22+ ( 2 -d ) 2 , •- d=1, R 2=5 ,•三棱锥P - ABC 的外接球的表面积为 4 nR =20 n 选ACx- y+l>010 .已知实数x , y 满足■:-厂% 'n=1, S=1满足条件S W 2016 n=2, 满足条件S W 2016 n=4, 满足条件S W 2016 n=8, 满足条件S W 2016 n=16, 满足条件S W 2016 n=32, 满足条件 S W 2016 n=64 , 满足条件 S W 2016 n=128 满足条件 S W 2016 n=256 满足条件 S W 2016 n=512S=1+2=3 S=3+4=7 S=7+8=15 S=15+16=31 S=31+32=63 S=63+64=127 ,S=127+128=255 ,S=255+256=511 ,S=511+512=1023满足条件S W 2016 n=1024, S=1023+1024=2047 若z=kx - y 的最小值为- 5,贝U 实数k 的值为(&执行下面的程序框图,则输出的 n 的值为( )解:模拟执行程序框图,可得L<iA . - 3 B. 3 或-5 C. - 3 或-5D. ±3联立「孙“解得B 2,7, 化 z=kx - y 为 y=kx - z ,由图可知,当k v 0时,直线过A 时在y 轴上的截距最大,z 有最小值为k - 2= - 5,即k= - 3; 当k >0时,直线过B 时在y 轴上的截距最大,z 有最小值-2k+仁-5,即k=3. 综上,实数k 的值为±3 •选D11. 某校组织由5名学生参加的演讲比赛, 采用抽签法决定演讲顺序,B 不是最后一个出场”的前提下,学生C 第一个出场的概率为( 1I 3g D. -20解:方法一: 学生A 和B 都不是第一个出场,B 不是最后一个出场”的出场顺序为:分为两类.第一类:A 最后一个出场,从除了 B 之外的3人选1人安排第一个,其它的任意排,故有 AjA 33=18种, 第二类:A 不是最后一个出场,从除了 A , B 之外的3人选2人安排在,第一个或最后一个,其余 3人 任意排,故有A 32A 33=36种,故学生A 和B 都不是第一个出场,B 不是最后一个出场的种数 18+36=54种,学生A 和B 都不是第一个出场,B 不是最后一个出场”的前提下,学生 C 第一个出场的”的出场顺序为: 分为两类 第一类:学生C 第一个出场,A 最后一个出场,故有 A 33=6种,第二类:学生C 第一个出场,A 不是最后一个出场,从除了 A , B 之外的2人选1人安排在最后一个, 其余3人任意排,故有 A 21A 33=12种,故在 学生A 和B 都不是第一个出场,B 不是最后一个出场 种,方法二: 先排B ,有A 31 (非第一与最后),再排A 有A 31 (非第一)种方法,其余三个自由排,共有A 31A 31A 33=54这是总结果;18 154 :=3故学生C 第一个出场的概率为在学生A 和B 都不是第一个出场, )C . 的前提下,学生C 第一个出场的种数 6+12=18学生C 第一个出场,先排 B ,有A 31 (非第一与最后),再排A 有A 31, C 第一个出场,剩余 2人自由排, 故有 A 31A 31A 22=18 种,故学生C 第一个出场的概率为上二=丄,选A54 312. 定义在R 上的偶函数f ( x )的导函数为f '(x ),若对任意的实数 x ,都有2f (x ) +xf '(x )v 2恒成 立,则使x 2f ( x )- f (1)v x 2- 1成立的实数x 的取值范围为() A . {x|x 工土}B . ( - s,-1) U (1 ,+〜C . (- 1 ,1)D . (- 1 ,0) U (0, 1)解:当x > 0时,由2f (x ) +xf ' (x )- 2v 0可知:两边同乘以 x 得: 2xf (x )- x 2f ( x )- 2x v 0 设:g (x ) =x 2f (x )- x 2则 g' (x ) =2xf (x ) +X 2f'(x )- 2x v 0,恒成立: ••• g (x )在(0, +s)单调递减, 由 x 2f (x )- f (1) v x 2- 1• x 2f (x )- x 2v f ( 1 )- 1 即 g (x )v g (1)即 x > 1 ;当x v 0时,函数是偶函数,同理得:x v- 1综上可知:实数x 的取值范围为(-s,- 1) U (1, +s),选B 二、填空题 13.命题 灯艾>0, _________________________ 買召■乂>1”的否定是 .解:因为全称命题的否定是特称命题,所以,命题 W 工>0, /匕> 1”的否定是:F 1, F 2,记|F 1F 2|=2C ,以坐标原点 O 为圆心,c 为半径的圆与双曲线 M 在第一象限的交点为P ,若|PF 1|=C +2 ,贝V P 点的横坐标为 ________ 解:坐标原点O 为圆心,C 为半径的圆的方程为 X 2+y 2=c 2,2,22丘-c--■,解得由 |PF 1|=C +2 ,由双曲线的定义可得|PF 2|=|PF 1|- 2a=c+2 - 2=C ,在直角三角形PF 1F 2中,可得C 2+ ( C +2) 2=4C 2, 解得c=1+ .二x 2=cW b 2-Kl14.双曲线的左,右焦点分别为由c2=a2+b2=1+b2,可得b2=3+2 二可得P的横坐标为」「•答案:5 g15. 已知各项均为正数的数列{a n}前n项和为S n,若厂,■.,则a n= 解:由S i=2,得a i=S i=2,由3叮- 2且血片二曰田勺得恋/二的口+齢1)2,又a n> 0,--2S n=S n+a n+1,即S n=a n+1 ,当n》2时,S n- i=a n,两式作差得:a n=a n+1 - a n,即卩----- Z又由3S n - ^a rrt-l S n=a n+l,求得a2=2,•••当n》2时,务二尹7.验证n=1时不成立,辽,iTl[产1. n>216. ______________________________________________________________________________ 若函数f (x) =x2(x - 2) 2- a|x- 1|+a有4个零点,贝V a的取值范围为_____________________________________ .解:函数 f (x) =x2(x- 2) 2- a|x- 1|+a 有 4 个零点,转化为:x2(x - 2) 2- a|x- 1|+a=0 由 4 个根,I »自宣問乞直二即y=x2(x - 2) 2; y=a|x- 1| - a= '..两个函数的图象有4个交点,[a(.x — 2 J ? 1/1在同一个直角坐标系中画出两个函数的图象,如图:当a v0时,如图中蓝色的折线,函数有4个零点,可得-1 v a v 0;当a>0时,如图中的红色折线,此时函数有4个零点•满足题意.综上:a€ (- 1, 0) U (0, +〜4/• A= 当A= —或一::或兀 时,则C=n - 兀兀兀 362,△ ABC 的面积 S= ■ _ 一■= 一,.=,△△ ABC 的面积 S= : •-':=三、解答题17.在△ ABC 中,三个内角A,B ,C 所对的边分别为 a, b,c,已知函数,■ i -_ - ■为偶函数, (1 )求 b ;(2 )若a=3,求△ ABC 的面积S.解:(1)在厶ABC 中,7T 7C所以 f Ci)=2cos2s : b 二F :—片五…asinBb2二由正弦定理得sinA=兀兀由f (X )为偶函数可知■ ■,所以k 兀 » k £ Z又0 v B v n,故 当时,贝U C=n-(2) 根据上述回归方程,分析该款旗舰机型市场占有率的变化趋势,并预测自上市起经过多少个月,该 款旗舰机型市场占有率能超过0.5% (精确到月)b 二斗;----------- ,a=y _ bxEL =1X (0.02+0.05+0.1+0.15+0.18 ) =0.1;i A i 1X0. 02+2X0. 05+3X0. 1+4X0.15+5X 0. 13- 5X3X0.=0.1 - 0.042 X = - 0.026,所以线性回归方程为I -・「:;…(2 )由上面的回归方程可知,上市时间与市场占有率正相关, 即上市时间每增加1个月,市场占有率都增加0.042个百分点;m I. -: 7:-- I.:-,解得 X 》13预计上市13个月时,市场占有率能超过0.5%.-18•某品牌手机厂商推出新款的旗舰机型, 占有率(y% )的几组相关对应数据;x 1 y0.02(1) 根据上表中的数据,用最小二乘法求出并在某地区跟踪调查得到这款手机上市时间( 2 3 4 0.05 0.10.15y 关于x 的线性回归方程; 5 0.18x 个月)和市场附: 解:(1)根据表中数据,计算4X (1+2+3+4+5)=3,12+22+32+4^52 YX 护=0.042,19. 如图,六面体ABCDHEFG 中,四边形ABCD为菱形,AE , BF , CG, DH都垂直于平面ABCD,若DA=DH=DB=4 , AE=CG=3(1) 求证:EG丄DF ;(2) 求BE与平面EFGH所成角的正弦值.解:(1)连接AC ,•••四边形ABCD 为菱形,••• AC 丄BD , •/ BF 丄平面 ABCD , AC?平面 ABCD , • AC 丄BF ,又 BD?平面 BDF , BF?平面 BDF , BD A BF=B , • AC 丄平面BDF , •/ AE // CG , AE=CG , •四边形AEGC 是平行四边形, • EG // AC ,• EG 丄平面BDF ,又DF?平面BDF , • EG 丄DF .(2)设 AS BD=O , EGH HF=P ,•/四边形ABCD 为菱形,AE 丄平面ABCD ,BF 丄平面ABCD , • AD // BC , AE // BF , •平面ADHE //平面BCGF ,• EH // FG , 同理可得:EH // HG ,•四边形EFGH 为平行四边形, 又 O 为 AC 的中点,• OP // AE , AE=OP ,• OP 丄平面ABCD ,又OA 丄OB ,所以OA , OB , OP 两两垂直,(BF+DH ) , • BF=2 .以O 为原点建立空间直角坐标系 O - xyz ,•••△ ABD 是等边三角形,AB=4 , • OA=2 :';.• E (2, 0 , 3), P ( 0 , 0 , 3), F ( 0 , 2 , 2), B( 0 , 2 , 0).•屈=(2 .「;, - 2 ,3),二 £= (2. ; , 0 , 0),平=(0 ,2 , - 1).,令 y=i ,得1 -二设BE 与平面EFGH 所成角为• P 为EG 的中点, 设平面EFGH 的一个法向量为4^520.已知椭圆B : (&>b> 0)经过点(2近,2),且离心率为- 右焦点 (1) 求椭圆E 的方程;(2)若点A , B 是椭圆E 上关于y 轴对称两点(A , B 不是长轴的端点),点P 是椭圆E 上异于A , B 的 一点,且直线PA , PB 分别交y 轴于点M , N ,求证:直线 MF i 与直线NF 2的交点G 在定圆上.2 2解: (1) T 椭圆 B J2=1 (r>b> Q)经过点(2^21 2),且离心率为a £亠解得 a=4, b=c=272, 2 2•椭圆C 的方程訂K 证明:(2)设 B (x o , y o ), P ( x i , y i ),则 A (- x o , y o )故灿Xiy n *卞仍同理可得J "■' ,Ki)-(-2^xi^x o2 2,F i , F 2是椭圆E 的左,直线PA 的方程为V y(乂 -垃]),令x=0,得尸K l +xO话(逅沁尹5硏(■碍迪亠,1 *0- 2 2 _ 2 2 工1厲 矶厂—_ L?4 X 1 y O•••由条件=巧坎呻-沽)r职欧卅肯〉--g-------------------------- ---------------- ------------- 空一=-E+8=0x i ~ K o•- F i M丄F2N,•直线F i M与直线F2N交于点G在以F1F2为直径的圆上.21 .已知函数g (x ) =ax 3+x 2+x (a 为实数)(1) 试讨论函数g (x )的单调性;(2) 若对?x €( 0, +〜 恒有百3£皿乜,求实数a 的取值范围.解:(1) g' (x ) =3ax 2+2x+1(i) 当 a=0时,g (x )在 (-0 —寺)单调减和(一 * 8 单调增;(ii) 当 a ^0寸,△ =4 - 12a , g (x )在R 单调增;当 Q<a<—时,由 g' (x ) =3ax 2+2x+ 仁0 得,J - 1 ■ 3a-[+寸1 - 3a 十3a ? - 3a g (乂)在(X1, X2)单调减,在(-汽X1)和(X2, +8)单调增;当a v 0时,g (乂)在(X2, X1)单调增,在(-8, X2)和(X1, +8)单调减;(2)令 f Cx)=lnx+-^,则 F 【工〕二:—■—J"K s x因此,f (X )在(0, 1)单调减,在(1 , +8)单调增fmin (X ) =f ( 1) =1当 a >- 1 时,g (1) =a+2> 仁f (1),显然,对? x € (0, +8)不恒有 f (x ) >g (x ); 当a<- 1时,由(1)知,g (乂)在(0,禺)单调增,在(X1, +8)单调减,二1壬(衣]十1)尸⑹ 1]1 ? 1所以気做⑺十D ,即满足对?x € (0, +8)恒有f (X ) >g (x )综上,实数a € (- 8,- 1].22.如图,PA 为四边形ABCD 外接圆的切线,CB 的延长线交PA 于点P , AC 与BD 相交于点M , PA // BD(1)求证:/ ACB= / ACD ;(2 )若 PA=3, PC=6, AM=1,求 AB 的长.3日就[2-F2K 2+1=0,即所以,在(0, +8) 上, g' (x ) =3ax 2+2x+1亘成立,此时(1)证明:•/ PA 为切线,•••/PAB= / ACB .•/ PA / BD , PAB= / ABD= / ACD ,•••/ ACB= / ACD ・(2 )解:已知 PA=3, PC=6, AM=1,由切割线定理 PA 2=PB?PC 得:BC =—, •/ PA // BD ,得AB ACAM "AB所以 AB 2=AM?AC=4,所以 AB=2极轴的极坐标系中,直线(1 )若m=0,判断直线 I : p sin+B p cos 0 =m I 与曲线C 的位置关系;解:(1)曲线匚 宴二寸©8岂口+1y=-/2sin CC +1|1+1 - TO |由已知可得:圆心 C 到直线Ix+y=m 的距离d — 解得-K m<524.已知函数f (x ) =|x - 4|+|x - a| (a € R )的最小值为 a(1)求实数a 的值;(2 )解不等式f (x )有.解:(1) f (x ) =|x - 4|+|x - a| 羽 | a|=a ,从而解得a=2…(2 )由(1)知,f ( x ) =|x - 4|+|x - 2|= .「 ,综合函数y=f (x )的图象知,解集为{訂寺©<*}23•在直角坐标系xOy 中,曲线C- (a 为参数),在以O 为极点,x 轴的非负半轴为(2)若曲线C 上存在点 P 到直线I 的距离为,求实数m 的取值范围. 曲线 直线 C 的直角坐标方程为:(x - 1) I : p sin 0 + p cos,0可得直线I 的直角坐标方程为: 2+ (y - 1) 2=2,是 「个圆;圆心(1, 1),半径为:V2 x+y=0圆心 C 到直线I 的距离\ ',所以直线I 与圆C 相切 又知△ AMB 〜△ ABC ,所以 (a 为参数), (2)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2016年高考数学冲刺卷01 理(新课标Ⅱ卷)答案第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.【命题意图】本题主要考查集合运算及分式不等式的解法,其中解不等式120x-<易忽略x 的取值为负值的情况. 【答案】C . 【解析】∵1212000x x x x --<⇒>⇒<或12x >,∴()1,0,2N ⎛⎫=-∞+∞ ⎪⎝⎭,又∵{1,1}M =-,∴M N ⊆,故选C.2.【命题意图】本题主要考查复数的有关概念及复数的运算,属基础题. 【答案】A3.【命题意图】本题主要考查对数的运算法则及分析问题解决问题的能力. 【答案】C【解析】因为()(),,,A a b B c d 在()ln f x x =图象上,所以ln b a = ,ln ,d c = 所以l n l n l n b d a c a c +=+=,因此(),ac b d +在()ln f x x =图象上,故选C . 4.【命题意图】本题将三视图与我国古代数学成就有机结合在一起,主要考查三视图的画法及空间想象能力. 【答案】B【解析】由直观图可知俯视图应为正方形,排除A,C,又上半部分相邻两曲面的交线看得见,在俯视图中应为实线,故选B.5.【命题意图】本题主要考查直线与圆的位置关系及利用同角三角函数的关系式求值,意在考查基本运算能力. 【答案】B【解析】圆1C 与圆2C 都关于直线210x y --=对称,则两圆的圆心,02a ⎛⎫-⎪⎝⎭、1,tan 2a θ⎛⎫-- ⎪⎝⎭都在直线210x y --=,由此可得1,a =- tan 2θ=-,所以sin cos θθ=22sin cos sin cos θθθθ+=2tan tan 1θθ+=25-,故选B. 6. 【命题意图】本题主要考查条件概率的计算及学生对概率模型的识别. 【答案】C【解析】设某次射中目标为事件A ,下一次射中为事件B ,则()0.7P A =,()P AB =0.4,则已知某次射中,则随后一次射中的概率是()()()4/7P AB P B A P A ==.7.【命题意图】本题在知识点交汇处命题,主要考查三角函数的图像、三角函数求值及三角函数的导函数,意在考查识图能力及分析问题解决问题的能力. 【答案】C8.【命题意图】本题主要考查学生对程序框图的理解,及分段函数求值问题,意在考查分类讨论思想. 【答案】A【解析】由题意可得如下混合组:①21350x x x ≤⎧⎨++=⎩ ,②15230x x <≤⎧⎨-=⎩ ,③25log 0x x x >⎧⎨+=⎩,①②③均无解,故选A.9.【命题意图】本题主要考查分段函数图像、函数与方程及含参数的不等式不等式问题,意在考查利用图像解决问题的能力 【答案】D【解析】若0b ≠,由()()00,20f f ==知22[()]()0f x af x b +-<不可能只有1个整数解,所以0b =,由选项均为正数,不妨设0a >,由不等式2[()]()0f x af x +<可得()0a f x -<<,结合()f x 图象可知()0a f x -<<的整数解应为3,所以()()43f a f ≤-< ,∴38a <≤,故选D .10.【命题意图】本题主要考查利用抽象函数的导函数研究函数单调性,意在考查构造函数解决问题的能力 【答案】B11.【命题意图】本题以集合为载体综合考查圆锥曲线问题,意在考查学生对新概念的理解能力,及应用新概念处理问题的能力. 【答案】C .【解析】分析题意可知,所有满足题意的有序实数对(,)λμ所构成的集合为{(,)|11,11}λμλμ-≤≤-≤≤,将其看作点的集合,其区域为中心在原点,以(1,1)-,(1,1)--,(1,1)-,(1,1)为顶点的正方形及其内部,A,B,D 选项分别表示直线,圆,双曲线,与该正方形及其内部无公共点,选项C 为抛物线,有公共点(0,1)-,故选C .12. 【命题意图】本题主要考查数量积的坐标运算,意在考查转化与化归思想、函数思想及数形结合思想. 【答案】C .第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.【命题意图】本题属于基础题,主要考查定积分的求法、二项式系数的性质及简单的运算与变形能力. 【答案】20【解析】∵ee 111d ln 1x x x==⎰,∴1,a = ()()63331111x x x x ⎛⎫-=- ⎪⎝⎭--,设()61x -的展开式的通项为1r T +,则()616C 1rr rr T x -+=⋅-,令63r -=,则()61x -的展开式中含3x 项的系数为:332020x x ⎛⎫--= ⎪⎝⎭. 14.【命题意图】本题在知识交汇处设计问题,主要考查学生对全称量词、特称量词的理解及函数值域求法与基本不等式的应用. 【答案】[4,)+∞.【解析】由题意得,问题等价于当0x >时,4y x a x =+-可取遍所有正数,而4y a a ≥=-, ∴404a a -≤⇒≥,即实数a 的取值范围是[4,)+∞,故填:[4,)+∞.15.【命题意图】本题主要考查线性规划知识及构造斜率模型求范围的基本方法,意在考查化归思想在解题中的应用. 【答案】[01],【解析】易知1a ≤,不等式表示的平面区域如图所示,设(20)Q ,,平面区域内动点()P x y ,,则2PQ y k x =-,当P 是x a =与1x y -=交点时,PQ 的斜率最大,为12a a -- 当P 是x a =与1x y +=交点时, PQ 的斜率最小,为12a a --,由1122a a -≥--且1122a a -≤-得02a ≤≤,又1a ≤,所以[]0,1a ∈.16.【命题意图】本题主要考查抛物线及一元二次方程根与系数的关系,意在考查计算能力及分析问题解决问题的能力 【答案】(2,)+∞.三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.【命题意图】本题考查等差数列通项及前n 项和的求法,裂项求和的方法,意在考查方程思想求通项及分析问题、解决问题的能力、基本运算能力.【解析】(1)1432141=+=+d a a a ,由127,,a a a 成等比数列得()()21116a a d a d +=+ ,整理得214d a d =,∵0d ≠,∴14d a =,14d a =与12314a d +=联立解得11,4a d == ,(4分)∴34)1(1-=-+=n d n a a n ,n n S n -=22(6分)18.【命题意图】本小题主要考查统计与概率的相关知识,包括独立性检验、离散型随机变量的分布列以及数学期望和方差的求法. 本题主要考查学生对数据处理的能力. 【解析】(1) 由题意可得关于商品和服务评价的22⨯列联表:22200(80104070)11.11110.8281505012080K ⨯⨯-⨯=≈>⨯⨯⨯,可以在犯错误概率不超过0.1%的前提下,认为商品好评与服务好评有关. (6分)(2) 每次购物时,对商品和服务都好评的概率为25,且X 的取值可以是0,1,2,3,4,5. 其中53(0)()5P X ==;14523(1)()()55P X C ==;223523(2)()()55P X C ==;332523(3)()()55P X C ==;441523(4)()()55P X C ==;52(5)()5P X ==.X 的分布列为:由于~(5,)5X B ,则525EX =⨯=;2265(1)555DX =⨯⨯-=. (12分)19.【命题意图】本题主要考查空间向量的应用、线面垂直的判断及二面角的求法.意在考查逻辑推理能力及运算能力(2)平面PBD 的法向量为(1,1,0)BC =-, (0,2,1)PC =- ,设PQ PC λ=,(0,1)λ∈所以(0,2,1)Q λλ-,设平面QBD 的法向量为(,,)a b c n =,(1,1,0)DB = ,(0,2,1)DQ λλ=-, 由0DB ⋅=n ,0DQ ⋅= n ,得2(1)0a b b c λλ+=⎧⎨+-=⎩, 令1b =所以2(1,1,)1λλ--n =,所以cos 45BC BC⋅===n n 注意到(0,1)λ∈,得1λ=.所以在线段PC 上存在一点Q ,使得二面角Q BD P --为45,此时1PQ PC= (12分)20.【命题意图】本题以椭圆为载体考查圆锥曲线中的基础知识,意在运算能力及分析问题解决问题的能力,同时考查函数思想与方程思想的应用.(2)①当直线MN 的斜率不存在时,易得OMN ∆的面积为1 ②当直线MN 的斜率存在时,设直线MN 的方程为y kx t =+()()2222211484104x y k x ktx t y kx t ⎧+=⎪⇒+++-=⎨⎪=+⎩由1122(,),(,)M x y N x y ,可得()2121222418,1414t ktx x x x k k--+==++, ()()()2222121212122414t k y y kx t kx t k x x kt x x x t k-=++=+++=+ 又121214OM ON y y k k x x ⋅==-,可得22241t k =+因为12MN x x =-, 点O 到直线MN的距离d =12122OMNt S MN d x x ∆=⋅⋅=⋅-2t =12t ==综上:OMN ∆的面积为定值1.(12分)21.【命题意图】本题主要考查导数的应用及不等式恒成立问题,同时考查转化与化归思想的应用.(解法一)转化为,函数ln y x =与函数yax =的图象在(0,)+∞上有两个不同交点,如图.可见,若令过原点且切于函数ln y x =图象的直线斜率为k ,只须0a k <<.令切点00A(,ln )x x ,所以001|x x k y x ='==,又00ln x k x =,所以000ln 1x x x =,解得0e x =, 于是1e k =,所以10ea <<.(6分)所以()g x 的草图如下, 可见,要想函数ln ()xg x x=与函数y a =的 图象在(0,)+∞上有两个不同交点, 只须10ea <<.(6分)(解法三)令()ln g x x ax =-,从而转化为函数()g x 有两个不同零点, 而11()ax g x ax x x-'=-=(0x >) 若0a ≤,可见()0g x '>在(0,)+∞上恒成立,所以()g x 在(0,)+∞单调增, 此时()g x 不可能有两个不同零点.若0a >,在10x a<<时,()0g x '>,在1x a >时,()0g x '<,所以()g x 在1(0,)a 上单调增,在1(,)a +∞上单调减,从而1()()g x g a =极大1ln 1a=-又因为在0x →时,()g x →-∞,在x →+∞时,()g x →-∞,于是只须:()0g x >极大,即1ln10a ->,所以10ea <<.综上所述,10e a <<.(6分)(2)因为112e x x λλ+<⋅等价于121ln ln x x λλ+<+.由(1)可知12,x x 分别是方程ln 0x ax -=的两个根,即11ln x ax =,22ln x ax =所以原式等价于121ax ax λλ+<+12()a x x λ=+,因为0>λ,120x x <<, 所以原式等价于121a x x λλ+>+.又由11ln x ax =,22ln x ax =作差得,1122ln ()x a x x x =-,即1212ln x x a x x =-. 所以原式等价于121212ln 1x x x x x x λλ+>-+,因为120x x <<,原式恒成立,即112212(1)()ln xx x x x x λλ+-<+恒成立. 令12x t x =,(0,1)t ∈, 则不等式(1)(1)ln t t t λλ+-<+在(0,1)t ∈上恒成立. 令(1)(1)()ln t h t t t λλ+-=-+, 又221(1)()()h t t t λλ+'=-+22(1)()()t t t t λλ--=+,当21λ≥时,可见(0,1)t ∈时,()0h t '>,所以()h t 在(0,1)t ∈上单调增,又(1)0h =,()0h t <在(0,1)t ∈恒成立,符合题意.当21λ<时,可见2(0,)t λ∈时,()0h t '>,2(,1)t λ∈时()0h t '<,所以()h t 在2(0,)t λ∈时单调增,在2(,1)t λ∈时单调减,又(1)0h =,所以()h t 在(0,1)t ∈上不能恒小于0,不符合题意,舍去.综上所述,若不等式112e x x λλ+<⋅恒成立,只须21λ≥,又0λ>,所以1λ≥.(12分)请考生在第(22)、(23)、(24)三题中任选一题作答.注意:只能做所选定的题目.如果多做,则按所做的第一个题目计分.22.【命题意图】本小题主要考查相似三角形的判断,直线与圆的位置关系的判断,意在考查学生利用平面几何知识推理证明的能力和逻辑思维能力.23.【命题意图】本小题主要考查参数方程、极坐标方程与普通方程的互化及圆的方程和和几何性质.同时考查运算能力.【解析】(1)消去参数α得曲线1C 的普通方程02:221=-+x y x C . (1)将曲线θρsin 4:2=C 化为直角坐标方程得04:222=-+y y x C (2)由)2()1(-得024=-x y ,即为直线AB 的方程,故直线AB 的斜率为21(5分) (2)由1)1(:221=+-y x C 知曲线1C 是以)(0,11C 为圆心,半径为1的圆; 由4)2(:222=-+y x C 知曲线2C 是以)(2,02C 为圆心,半径为2的圆. 因为1122||||||||AB AC C C BC ≤++, 所以当AB 取最大值时,圆心21,C C 在直线AB 上,所以直线AB (即直线21C C )的方程为:22=+y x .因为O 到直线AB 的距离为55252==d ,又此时12||||123AB C C =++=所以AOB ∆的面积为1553)53(55221+=+⋅⋅=S (10分) 24.【命题意图】本小题主要考查利用基本不等式证明不等式、利用柯西不等式求最值及简单绝对值不等式的解法,意在考查逻辑推理能力及运算能力.。
