2018年高中数学必修2期末考试
人教版高中数学必修二期末考试试题

人教版高中数学必修二期末考试试题一、选择题1. 若函数 $f(x)=x^3-3x^2+bx+c$ 的图像过点 $(1,5)$,则$b=$()A.$-1$ B.$-2$ C.$-3$ D.$-4$2. 函数 $y=\frac{x+1}{x-1}$ 的图象关于直线 $y=-x$ 对称。
3. 从集合 $\{1,2,3,4,5,6\}$ 中取两个不同的元素组成一个二元组,则其中不含 $3$ 的二元组的数目为()。
A.$20$ B.$10$ C.$15$ D.$18$4. 已知集合$A=\{x\mid 2x-1\in \mathbb{N}\}$,则$A=$()。
A.$\bigl\{\frac{1}{2},\frac{3}{2},\frac{5}{2},\cdots\bigr\}$ B .$\bigl\{\frac{1}{2},\frac{3}{2},\frac{5}{2},\cdots,b\bigr\}$C.$\bigl\{1,2,3,\cdots\bigr\}$ D.$\bigl\{\cdots,-\frac{1}{2},\frac{1}{2},\frac{3}{2},\frac{5}{2},\cdots\bigr\}$5. 如图所示,大三角形的三个点坐标分别为 $A(-2,0)$,$B(0,2)$,$C(2,-4)$,以 $C$ 为顶点小三角形顶点的坐标为()。
A.$(-\frac{7}{5},-\frac{14}{5})$ B.$(\frac{7}{5},\frac{6}{5})$C.$(\frac{2}{5},-\frac{18}{5})$ D.$(\frac{6}{5},-\frac{4}{5})$二、填空题6. 下列各组数中互为相反数的是()。
$${1\over3},-{1\over3};\qquad {\sqrt{10}},-\sqrt{10};\qquad -3,3\sqrt{2}$$7. 容量为 $500 \rm mL$ 的杯中盛满水,再加进糖水搅拌,这时每 $100 \rm mL$ 的液体中含糖 $10\%$。
高中数学必修二期末考试试卷(含答案)

高中数学必修一期末考试试卷(一)(时间:120分钟满分:150分)一、选择题(本大题共12小题,每小题5分,共60分)1.下面多面体中有12条棱的是()A.四棱柱B.四棱锥C.五棱锥D.五棱柱2.棱锥的侧面和底面可以都是()A.三角形B.四边形C.五边形D.六边形3.如图,Rt△O′A′B′是一平面图的直观图,斜边O′B′=2,则这个平面图形的面积是()A.22 B.1C. 2D.2 24.如图,正方形ABCD的边长为1,CE所对的圆心角∠CDE=90°,将图形ABCE绕AE所在直线旋转一周,形成的几何体的表面积为()A.5πB.4πC.3πD.2π5.以长为8 cm,宽为6 cm的矩形的一边为旋转轴旋转而成的圆柱的底面面积为()A.64π cm2B.36π cm2C.64π cm2或36π cm2D.48π cm26.将若干毫升水倒入底面半径为2 cm的圆柱形器皿中,量得水面高度为6 cm,若将这些水倒入轴截面是正三角形的倒圆锥形器皿中,则水面高度为()A.6 3 cmB.6 cmC.2318 cmD.3312 cm7.如图所示,△A′B′C′是水平放置的△ABC的斜二测直观图,其中O′C′=O′A′=2O′B′,则以下说法正确的是()A.△ABC是钝角三角形B.△ABC是等腰三角形,但不是直角三角形C.△ABC 是等腰直角三角形D.△ABC 是等边三角形8.过球的一条半径的中点,作垂直于该半径的平面,则所得截面的面积与球的表面积的比为( ) A.316 B.916 C.38 D.9329.如图,圆锥形容器的高为h ,圆锥内水面的高为h 1,且h 1=13h ,,若将圆锥形容器倒置,水面高为h 2,则h 2等于( )A.23hB.1927hC.363h D.3193h 10.若在棱长为1的正方体上,分别用过共顶点的三条棱中点的平面去截该正方体,则截去8个三棱锥后,剩下的凸多面体的体积是( ) A.23 B.16 C.56 D.1311.若三棱锥的三条侧棱两两垂直,且其长度分别为1,2,3,则此三棱锥的外接球的表面积为( ) A.3π B.6π C.18πD.24π12.《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺,问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米约有( )A.14斛B.22斛C.36斛D.66斛二、填空题(本大题共4小题,每小题5分,共20分)13.若一个圆台的母线长为l ,上、下底面半径分别为r 1,r 2,且满足2l =r 1+r 2,其侧面积为8π,则l =________. 14.三棱锥P -ABC 中,D ,E 分别为PB ,PC 的中点.记三棱锥D -ABE 的体积为V 1,P -ABC 的体积为V 2,则V 1V 2=________.15.一块正方形薄铁皮的边长为4,以它的一个顶点为圆心,剪下一个最大的扇形,用这块扇形铁皮围成一个圆锥,则这个圆锥的容积为________.(铁皮厚度忽略不计)16.已知一个球与一个正三棱柱的三个侧面和两个底面都相切,且这个球的体积是323π,那么这个三棱柱的体积是________.三、解答题(本大题共6小题,共70分)17.(10分)如图,长方体ABCD -A 1B 1C 1D 1中,AB =16,BC =10,AA 1=8,点E ,F 分别在A 1B 1,D 1C 1上,A1E=D1F=4.过点E,F的平面α与此长方体的面相交,交线围成一个正方形.(1)在图中画出这个正方形(不必说明画法和理由);(2)求平面α把该长方体分成的两部分体积的比值.18.(12分)如图所示,在多面体FE-ABCD中,已知ABCD是边长为1的正方形,且△ADE,△BCF均为正三角形,EF∥AB,EF=2,求该多面体的体积V.19.(12分)如图所示是一个圆台形的纸篓(有底无盖),它的母线长为50 cm,两底面直径分别为40 cm和30 cm.求纸篓的表面积.20.(12分)有一盛满水的圆柱形容器,内壁底面半径为5,高为2,现将一个半径为3的玻璃小球缓慢浸没于水中.(1)求圆柱的体积;(2)求溢出水的体积.21.(12分)如图所示,一个圆锥形的空杯子上面放着一个半球形的冰淇淋,如果冰淇淋融化了,会溢出杯子吗?请用你的计算数据说明理由.22.(12分)如图所示,在正三棱柱ABC-A1B1C1中,AB=3,AA1=4,M为AA1的中点,P是BC上的一点,且由P沿棱柱侧面经过棱CC1到M的最短路线为29.设这条最短路线与CC1的交点为N,求:(1)该三棱柱的侧面展开图的对角线的长;(2)PC和NC的长.高中数学必修一期末考试试卷(一)答案(时间:120分钟 满分:150分)一、选择题(本大题共12小题,每小题5分,共60分) 1.答案 A解析 ∵n 棱柱共有3n 条棱,n 棱锥共有2n 条棱,∴四棱柱共有12条棱;四棱锥共有8条棱;五棱锥共有10条棱;五棱柱共有15条棱.故选A. 2.答案 A解析 三棱锥的侧面和底面均为三角形. 3.答案 D解析 ∵Rt △O ′A ′B ′是一平面图形的直观图,斜边O ′B ′=2, ∴直角三角形的直角边长是2, ∴直角三角形的面积是12×2×2=1,∴原平面图形的面积是1×22=2 2.故选D. 4.答案 A解析 由题意知,形成的几何体是组合体:上面是半球、下面是圆柱, ∵正方形ABCD 的边长为1,∠CDE =90°, ∴球的半径是1,圆柱的底面半径是1,母线长是1,∴形成的几何体的表面积S =π×12+2π×1×1+12×4π×12=5π.5.答案 C解析 分别以长为8 cm ,宽为6 cm 的边所在的直线为旋转轴,即可得到两种不同大小的圆柱,显然C 选项正确. 6.答案 B解析 设圆锥中水的底面半径为r cm ,由题意知 13πr 2×3r =π×22×6, 得r =23,∴水面的高度是3×23=6(cm). 7.答案 C 8.答案 A解析 设球的半径为R ,所得的截面为圆M ,圆M 的半径为r . 画图可知(图略),R 2=14R 2+r 2,∴34R 2=r 2.∴S 球=4πR 2,截面圆M 的面积为πr 2=34πR 2,则所得截面的面积与球的表面积的比为34πR 24πR 2=316.故选A.9.答案 D解析 设圆锥形容器的底面积为S , 则未倒置前液面的面积为49S ,∴水的体积V =13Sh -13×49S (h -h 1)=1981Sh ,设倒置后液面面积为S ′,则S ′S =⎝⎛⎭⎫h 2h 2,∴S ′=Sh 22h2.∴水的体积V =13S ′h 2=Sh 323h 2,∴1981Sh =Sh 323h2, 解得h 2=319h3,故选D. 10.答案 C解析 易知V =1-8×13×12×12×12×12=56.11.答案 B解析 将三棱锥补成边长分别为1,2,3的长方体,则长方体的体对角线是外接球的直径,所以2R =6,解得R =62,故S =4πR 2=6π. 12.答案 B解析 米堆的体积即为四分之一的圆锥的体积, 设圆锥底面半径为r ,则14×2πr =8,得r =16π,所以米堆的体积为13×14πr 2×5≈3209(立方尺),3209÷1.62≈22(斛). 二、填空题(本大题共4小题,每小题5分,共20分) 13.答案 2解析 S 圆台侧=π(r 1+r 2)l =2πl 2=8π,所以l =2. 14.答案 14解析 如图,设点C 到平面P AB 的距离为h ,则点E 到平面P AD 的距离为12h .∵S △DAB =12S △P AB ,∴V1V2=13S△DAB·12h13S△PAB·h=13×12S△P AB·12h13S△P AB·h=14.15.答案15π3解析如图所示,剪下最大的扇形的半径即圆锥的母线长l等于正方形的边长4,扇形的弧长=14×(2π×4)=2π,即为圆锥的底面周长,设圆锥的底面半径为r,高为h,则2πr=2π,所以r=1,所以h=l2-r2=15,所以圆锥的容积为13πr2h=15π3.16.答案48 3解析设球的半径为r,则43πr3=323π,得r=2,柱体的高为2r=4.又正三棱柱的底面三角形的内切圆半径与球的半径相等,所以底面正三角形的边长为43,所以正三棱柱的体积V=34×(43)2×4=48 3.三、解答题(本大题共6小题,共70分)17.解(1)交线围成的正方形EHGF如图所示.(2)如图,作EM⊥AB,垂足为M,则AM=A1E=4,EB1=12,EM=AA1=8.因为四边形EHGF为正方形,所以EH=EF=BC=10.于是MH=EH2-EM2=6,AH=10,HB=6.故S四边形A1EHA=12×(4+10)×8=56,S四边形EB1BH=12×(12+6)×8=72.因为长方体被平面α分成两个高为10的直棱柱,所以其体积的比值为97(79也正确).18.解如图所示,分别过A,B作EF的垂线AG,BH,垂足分别为G,H.连接DG,CH,容易求得EG=HF =12.所以AG =GD =BH =HC =32, S △AGD =S △BHC =12×22×1=24,V =V E -ADG +V F -BHC +V AGD -BHC =⎝⎛⎭⎫13×12×24×2+24×1=23.19解 根据题意可知,纸篓底面圆的半径r ′=15 cm ,上口的半径r =20 cm ,设母线长为l , 则纸篓的表面积S =πr ′2+(2πr ′+2πr )l2=π(r ′2+r ′l +rl )=π(152+15×50+20×50)=1 975π(cm 2).20.(12分)有一盛满水的圆柱形容器,内壁底面半径为5,高为2,现将一个半径为3的玻璃小球缓慢浸没于水中.(1)求圆柱的体积; (2)求溢出水的体积.解 (1)∵内壁底面半径为5,高为2,∴圆柱体积V =π×52×2=50π. (2)溢出水的体积为43×π×33=36π.21解 由题图可知半球的半径为4 cm , 所以V 半球=12×43πR 3=12×43π×43=1283π(cm 3),V 圆锥=13πR 2h =13π×42×12=64π(cm 3).因为V 半球<V 圆锥,所以如果冰淇淋融化了,不会溢出杯子. 22.解 (1)该三棱柱的侧面展开图是宽为4,长为9的矩形, 所以对角线的长为42+92=97.(2)将该三棱柱的侧面沿棱BB 1展开,如图所示. 设PC 的长为x ,则MP 2=MA 2+(AC +x )2.因为MP =29,MA =2,AC =3,所以x =2(负值舍去),即PC 的长为2. 又因为NC ∥AM ,所以PC P A =NC AM ,即25=NC 2,所以NC =45.。
高中数学选择性必修二 高二上学期数学期末测试卷(A卷 夯实基础)同步单元AB卷(含答案)

班级 姓名 学号 分数高二上学期数学期末测试卷(A 卷·夯实基础)注意事项:本试卷满分150分,考试时间120分钟.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.一、单项选择题(本大题共8小题,每小题5分,共40分)1.过两点()()5,,3,1A y B -的直线的倾斜角是135°,则y 等于( ) A .2 B .2- C .3 D .3-【答案】D 【详解】因为斜率tan1351k ︒==-,所以1153y k +==--,得3y =-. 故选:D.2.40y --=,经直线10x y +-=反射,则反射光线所在直线的方程是( ) A50y ++= B.40x += C.50x += D.0x +=【答案】C 【详解】40y --=,令0x =,解得4y =-, 设()0,4A -,关于直线10x y +-=的对称点为(),B m n , 则4141022n mm n +⎧=⎪⎪⎨-⎪+-=⎪⎩,解得51m n =⎧⎨=⎩,即()5,1B ,40y --=,令x =1y =-,设)1C-,关于直线10x y +-=的对称点为(),D a b ,则11102b =--=,解得21a b =⎧⎪⎨=⎪⎩(2,1D ,BD k ==直线BD:)15y x -=-,即50x =。
故选:C3.已知异面直线,a b 的方向向量分别是()()2,1,3,1,3,2m n --==,则,a b 夹角的大小是( ) A .56πB .34π C .3π D .6π【答案】C 【详解】异面直线,a b 的方向向量分别是()()2,1,3,1,3,2m n --==∴21132371cos ,1424m n m n m n⨯+⨯-+⨯-⋅-====-, 异面直线,a b 所成角为范围为02πθ<≤,,a b ∴夹角的大小是3π故选:C4.设数列{}n a 的前n 项和S n =n 2,则a 8的值为( ) A .15 B .16C .49D .64【答案】A 【详解】878644915a S S =-=-= 故选:A5.已知在等比数列{}n a 中,3544a a a =,等差数列{}n b 的前n 项和为n S ,且74b a =,则13S =( ) A .26 B .52 C .78 D .104【答案】B 【详解】因为在等比数列{}n a 中,3544a a a =,可得2444a a =,40a ≠,解得44a =,又因为数列{}n b 是等差数列,744b a ==,则()13113711313134522S b b b =⨯+==⨯=.故选:B.6.直三棱柱111ABC A B C -中,90BCA ∠=,M 、N 分别是11A B 、11A C 的中点,1BC CA CC ==,则BM 与NA 所成的角的余弦值为( )A .BCD . 【答案】C 【详解】由题意可知1CC ⊥平面ABC ,且90BCA ∠=,以点C 为坐标原点,CA 、CB 、1CC 所在直线分别为x 、y 、z 轴建立如下图所示的空间直角坐标系,设12BC CA CC ===,则()2,0,0A 、()0,2,0B 、()1,0,2N 、()1,1,2M ,()1,0,2AN =-,()1,1,2BM =-,30cos ,56AN BM AN BM AN BM⋅<>===⨯⋅故BM 与NA 30故选:C.7.设抛物线C :y 2=4x 的焦点为F ,M 为抛物线C 上一点,N (2,2),则MF MN +的最小值为( ) A .3 B .2C .1D .4【答案】A 【详解】因为抛物线C :y 2=4x 的焦点为F (1,0),准线为1x =-, 根据抛物线定义可知MF =1M x +,所以当MN 垂直抛物线准线时,MF MN +最小, 最小值为:13N x +=. 故选:A .8.已知椭圆C :2222x y a b +=1(a >b >0)的左、右焦点分别为F 1、F 2,离心率为34,点P 为椭圆上一点,若∠F 1PF 2=π2,且F 1PF 2内切圆的半径为1,则C 的方程为( ) A .22167x y +=1B .223214x y +=1C .24x +y 2=1D .22447x y +=1【答案】A 【详解】易知F 1PF 2中,内切圆半径r =1212-2PF PF F F +=a -c =1,又离心率为34c a =,解得a =4,c =3,所以椭圆C 的方程为22167x y +=1. 故选:A二、多项选择题(本大题共4小题,每小题5分,共20分.全部选对的得5分,部分选对的得3分,有选错的得0分)9.已知等差数列{}n a 的公差为d ,前n 项和为n S ,316a =,512a =,则( ) A .2d =- B .124a =C .2628a a +=D .n S 取得最大值时,11n =【答案】AC 【详解】解法一:由题可得11216,412a d a d +=⎧⎨+=⎩,解得120,2,a d =⎧⎨=-⎩故选项A 正确,选项B 错误;易知()()2012222n a n n =+-⨯-=-+,则26181028a a +=+=,选项C 正确.因为1020a =>,110a =,1220a =-<,所以当10n =或11时,n S 取得最大值(技巧:由0d <得数列{}n a 递减,进而判断n S 最大时的临界项) 选项D 错误. 故选:AC解法二:对于A :易知53212164d a a =-=-=-,所以2d =-,选项A 正确;对于B :()132162220a a d =-=-⨯-=,选项B 错误; 对于C :263528a a a a +=+=,选项C 正确;对于D :易知()()2012222n a n n =+-⨯-=-+,1020a =>,110a =,1220a =-<(技巧:由0d <得数列递减,进而判断n S 最大时的临界项)所以当10n =或11时,n S 取得最大值,所以选项D 错误. 故选:AC10.已知直线:440l kx y k -+-=与圆22:4440M x y x y +--+=,则下列说法中正确的是( )A .直线l 与圆M 一定相交B .若0k =,则直线l 与圆M 相切C .当1k =时,直线l 被圆M 截得的弦最长D .圆心M 到直线l的距离的最大值为【答案】BCD【详解】22:4440M x y x y +--+=,即()()22224x y -+-=,是以()2,2为圆心,以2为半径的圆,A.因为直线:440l kx y k -+-=,直线l 过()4,4,2244444440+-⨯-⨯+>,则()4,4在圆外,所以直线l 与圆M 不一定相交,故A 错误;B.若0k =,则直线:4l y =,直线l 与圆M 相切,故B 正确;C.当1k =时,直线l 的方程为0x y -=,过圆M 的圆心,即直线l 是直径所在直线,故C 正确;D.由圆的性质可知当直线l 与过点()4,4的直径垂直时,圆心M 到直线l 的距离的最大,此时=故D 正确,故选:BCD.11.已知点P 在双曲线22:1169x y C -=上,1F ,2F 分别为双曲线的左、右焦点,若12PF F △的面积为20,则下列说法正确的是( ) A .点P 到x 轴的距离为4 B .12523PF PF += C .12PF F △为钝角三角形 D .1260F PF ∠=︒【答案】AC 【详解】由双曲线的方程可得4a =,3b =,则5c =,由12PF F △的面积为20,得112102022P P c y y ⨯⨯=⨯⨯=,解得4P y =,即点P 到x 轴的距离为4,故A 选项正确; 将4P y =代入双曲线方程可得203P x =,根据双曲线的对称性可设20,43P ⎛⎫⎪⎝⎭,则2133PF =,由双曲线的定义知1228PF PF a -==,则11337833PF =+=, 则12133750333PF PF +=+=,故B 选项错误; 在12PF F △中,12371321033PF c PF =>=>=, 则24012020553PF k -==>-,21PF F ∠为钝角,则12PF F △为钝角三角形,故C 选项正确;()2222121212121212122100cos 22PF PF PF PF PF PF F F F PF PF PF PF PF -+-+-∠==13376410021891331133713372233-+⨯⨯⨯==-≠⨯⨯⨯, 则1260F PF ∠=︒错误, 故选:AC.12.已知函数()2ln f x x x =,下列说法正确的是( )A .当1x >时,()0f x >;当01x <<时,()0f x <B .函数()f x的减区间为(,增区间为)+∞C .函数()f x 的值域1,2e ⎡⎫-+∞⎪⎢⎣⎭D .()1f x x ≥-恒成立 【答案】ACD 【详解】对于选项A ,当01x <<时,ln 0x <;当1x >时,ln 0x >,故选项A 正确; 对于选项B ,2ln 2ln 1fxx x x x x ,令()0f x '>可得2ln 10x ,有x >知函数()f x 的减区间为⎛⎝,增区间为⎫+∞⎪⎭,故选项B 错误;对于选项C ,由上可知()min 11e 2e f x f ===-,x →+∞时,()f x →+∞,故选项C 正确;对于选项D ,()22111ln 10ln 0f x x x x x x x x ≥-⇔-+≥⇔-+≥,令()211ln g x x x x=-+,有()()()22333121212x x x x x g x x x x x '-++--===+,令()0g x '>可得1x >,故函数()g x 的增区间为()1,+∞,减区间为()0,1,可得()()min 10g x g ==,故选项D 正确. 故选:ACD .三、填空题(本大题共4小题,每小题5分,共20分)13.与直线3250x y -+=的斜率相等,且过点()4,3-的直线方程为_________ 【答案】392y x =+【详解】直线3250x y -+=的斜率为32,故所求直线方程为()3342-=+y x ,即392y x =+.故答案为:392y x =+. 14.数列{}n a 中,11a =,()*12,2nn n a a n N a +=∈+,则5a =___________ 【答案】13【详解】 122nn n a a a +=+,11a =, 则1212223a a a ==+,2322122a a a ==+,3432225a a a ==+,4542123a a a ==+. 故答案为:13.15.若函数()ln f x x x =+在x =1处的切线与直线y =kx 平行,则实数k =___________. 【答案】2 【详解】∵()ln f x x x =+, ∴1()1f x x '=+,1(1)121f '=+=,又函数()ln f x x x =+在x =1处的切线与直线y =kx 平行, ∴2k =. 故答案为:2.16.设5(4P -是双曲线2222:1(0,0)x y C a b a b -=>>上一点,1(2,0)F -是C 的左焦点,Q 是C右支上的动点,则C 的离心率为______,1PQF △面积的取值范围是_______. 【答案】2)+∞ 【详解】双曲线C 的右焦点为2(2,0)F,则13||2PF =,27||2PF ,因点P 在双曲线C 上,则由双曲线定义得2122a PF PF =-=,即1a =,又2c =, 所以双曲线C 的离心率为2ce a==;因直线PF 1的斜率1PF k =ba=1PF 与双曲线C 在第一、三象限的渐近线平行,则这条渐近线与直线1PF 0y -+的距离d ==上的点Q 到直线PF 1距离h d >=,于是得11113222PQF SPF h =⋅⋅>⨯所以1PQF △面积的取值范围是)+∞.故答案为:2;)+∞ 四、解答题(本大题共6小题,共70分)17.已知圆()22:20C x y mx y m R ++-=∈,其圆心在直线0x y +=上.(1)求m 的值;(2)若过点()1,1的直线l 与C 相切,求l 的方程. 【答案】 (1)2m =(2)20x y +-=或0x y -= 【详解】 (1)圆C 的标准方程为:222(1)124m m x y ⎛⎫++-=+⎪⎝⎭, 所以,圆心为,12m ⎛⎫- ⎪⎝⎭由圆心在直线0x y +=上,得2m =. 所以,圆C 的方程为:22(1)(1) 2.x y ++-=(2)由题意可知直线l 的斜率存在,设直线l 的方程为:()11y k x -=-, 即10,kx y k --+=由于直线l 和圆C解得:1k =±所以,直线方程为:20x y +-=或0x y -=.18.如图,在三棱锥P -ABC 中,△ABC 是以AC 为底的等腰直角三角形,PA =PB =PC =AC =4,O 为AC 的中点.(1)证明:PO ⊥平面ABC .(2)若点M 在棱BC 上,且二面角M -PA -C 为30°,求直线PC 与平面PAM 所成角的正弦值. 【答案】 (1)证明见解析. (2【详解】 (1)证明:连接BO,AB BC ==O 是AC 的中点,BO AC ∴⊥,且 2BO =,又 2PA PC PB AC ====,,PO AC PO ∴⊥=222PB PO BO =+,则PO OB ⊥,OB AC O =,OB ⊂平面ABC ,AC ⊂平面ABC ,PO ∴⊥平面ABC ,(2)解:建立以 O 为坐标原点,,,OB OC OP 分别为,,x y z 轴的空间直角坐标系如图所示,则()0,2,0A -,(0,0,P ,()0,2,0C ,()2,0,0B ,设(2,2,0)BM BC λλλ==-()01λ≤≤,则()()(2,2,0)2,2,022,22,0AM BM BA λλλλ=-=----=-+,所以PC 与平面PAM 所成角的正弦值为则平面PAC 的法向量为() 1,0,0m =, 设平面MPA 的法向量(,,),n x y z =则(0,2,PA =--20,n PA y ⋅=--= ()()22220n AM x y λλ⋅=-++=,令1z =,则y =(11x λλ+=-,二面角M PA C --为30︒,∴3cos302m n m n︒⋅==⋅, 即=13λ= 或 3λ=( 舍),设平面MPA的法向量(23,n =,(0,2,PC =-,设PC 与平面PAM 所成的角为θ,则|sin |cos ,|12PC n θ-=<>==+19.已知椭圆与双曲线221169x y -=具有共同的焦点1F 、2F ,点P 在椭圆上,12PF PF ⊥,____________①椭圆过点(),②椭圆的短轴长为10,③(①②③中选择一个) (1)求椭圆的标准方程; (2)求12PF F △的面积. 【答案】(1)条件选择见解析,椭圆方程为2215025x y += (2)1225PF F S=【详解】 (1)解:设椭圆方程()222222210,x y a b c a b a b+=>>=-.因为椭圆与双曲线221169x y -=具有共同的焦点,则225c =.选①:由已知可得a =225b =,椭圆方程为2215025x y +=; 选②:由已知可得5b =,则250a =,椭圆方程为2215025x y +=;选③得c a =,则250a =,椭圆方程为2215025x y +=. (2)解:由椭圆定义知122PF PF a +==, 又12PF PF ⊥,222124100PF PF c ∴+==②,由①可得2212121221002200PF PF PF PF PF PF ++⋅=+⋅=,解得1250PF PF ⋅=, 因此,12121252PF F SPF PF =⋅=. 20.设函数()322f x x x x =--++.(1)求()f x 在2x =-处的切线方程;(2)求()f x 的极大值点与极小值点;(3)求()f x 在区间[]5,0-上的最大值与最小值.【答案】(1)7100x y ++=;(2)极小值点为1x =-,极大值点为13x =; (3)()min 1f x =,()max 97f x =.【详解】(1)由题意得:()2321f x x x '=--+,则()212417f '-=-++=-,又()284224f -=--+=,()f x ∴在2x =-处的切线方程为()472y x -=-+,即7100x y ++=; (2)令()23210f x x x '=--+=,解得:1x =-或13x =, 则()(),,x f x f x '变化情况如下表:()f x ∴的极小值点为1x =-,极大值点为3x =; (3)由(2)知:()f x 在[)5,1--上单调递减,在(]1,0-上单调递增; 又()5125255297f -=--+=,()02f =,()111121f -=--+=, ()()min 11f x f ∴=-=,()()max 597f x f =-=.21.已知椭圆C 的离心率e =()1A ,)2A (1)求椭圆C 的方程;(2)设动直线:l y kx b =+与曲线C 有且只有一个公共点P ,且与直线2x =相交于点Q ,求证:以PQ 为直径的圆过定点()1,0N .【答案】(1)2212x y +=; (2)证明见解析.【详解】(1)椭圆长轴端点在x 轴上,∴可设椭圆方程为()222210x y a b a b+=>>,由题意可得:222a b c c e a a ⎧=+⎪⎪==⎨⎪⎪=⎩,解得:11a b c ⎧=⎪=⎨⎪=⎩,∴椭圆C 的方程为:2212x y +=; (2) 由2212x y y kx b ⎧+=⎪⎨⎪=+⎩得:()222124220k x kbx b +++-=,曲线C 与直线l 只有一个公共点,()228120k b ∴=+-=,即2221b k =+,设(),P P P x y ,则()22422212P kb kb k x b b k =-=-=-+, 222221p P k b k y kx b b b b b-∴=+=-+==,21,k P b b ⎛⎫∴- ⎪⎝⎭; 由2y kx b x =+⎧⎨=⎩得:22x y k b =⎧⎨=+⎩,即()2,2Q k b +; ()1,0N ,211,k NP bb ⎛⎫∴=-- ⎪⎝⎭,()1,2NQ k b =+, 2210k k b NP NQ b b+∴⋅=--+=,即NP NQ ⊥, ∴以PQ 为直径的圆恒过定点()1,0N .22.已知函数()ln xe f x ax a x x=-+. (1)若a e =,求()f x 的极值点;(2)若()0f x ≥,求a 的取值范围.【答案】(1)极小值点为1,无极大值点(2)(,]e -∞【详解】(1)解:(1)()f x 定义域为(0,)+∞,222(1)(1)(1)()()x x x x xe e e x e e x x e ex f x e x x x x x -----'=-+=-=, 令(),(0,)x g x e ex x =-∈+∞,则()x g x e e '=-,当01x <<时,()0g x '<,当1x >时,()0g x '>,所以函数()g x 在()0,1上递减,在()1,+∞上递增,所以()()10g x g ≥=,即0x e ex -≥,当01x <<时,()0f x '<,当1x >时,()0f x '>,所以函数()f x 在()0,1上递减,在()1,+∞上递增,()f x ∴的极小值点为1,无极大值点;(2)由()0f x ≥得ln (ln )x x e a x x --≥,令ln ,(0,)t x x x =-∈+∞,则t e at ≥,111x t x x-'=-=, 当01x <<时,0t '<,当1x >时,0t '>,所以函数ln ,(0,)t x x x =-∈+∞在()0,1上递减,在()1,+∞上递增,所以当1x =时,min 1t =,[1+t ∴∈∞,),te a t∴≤, 令(),[1,)te m t t t =∈+∞,则2(1)()0t e t m t t -'=≥, 所以函数()t e m t t=在[1,)t ∈+∞上递增,所以min ()(1)m t m e ==, 所以a e ≤,所以a 的取值范围为(,]e -∞.。
【易错题】高中必修二数学下期末试题(含答案)

故选 D. 【点睛】 本题考查三视图求几何体的表面积,由三视图正确复原几何体是解题的关键,考查空间想 象能力.
6.D
解析:D 【解析】
试题分析: AB 2a, AC 2a b , AC AB b ,b AC AB BC .
由题意知 b
2, a b
a b cos120
1
2
1 2
棱 CC1 的中点,则异面直线 AB1 和 BM 所成的角为( )
A.
B.
C.
D.
2
3
11.已知 f x 是定义在 R 上的奇函数,当 x 0 时, f x 3 2x ,则不等式
f x 0 的解集为( )
A.
,
3 2
0,
3 2
B.
,
3 2
3 2
,
C.
3 2
,
3 2
【详解】
因为 b 在 a 上的投影(正射影的数量)为 2 ,
所以| b | cos a, b 2 ,
即
|
b
|
cos
2 a,
b
,而
1
cos
a,
b
0
,
所以| b | 2 ,
因为
a
2b
2
(a
2b)2
2
a
4a b
2
4b
|
a
|2
4
|
a
||
b|
cos
a, b
4
| b|2
=16 4 4 (2) 4 | b |2 48 4 | b |2
16.在四面体 ABCD中, AB=AD 2, BAD 60,BCD 90,二面角 A BD C 的大小为150 ,则四面体 ABCD 外接球的半径为__________.
高中数学必修2立体几何期末试卷及答案
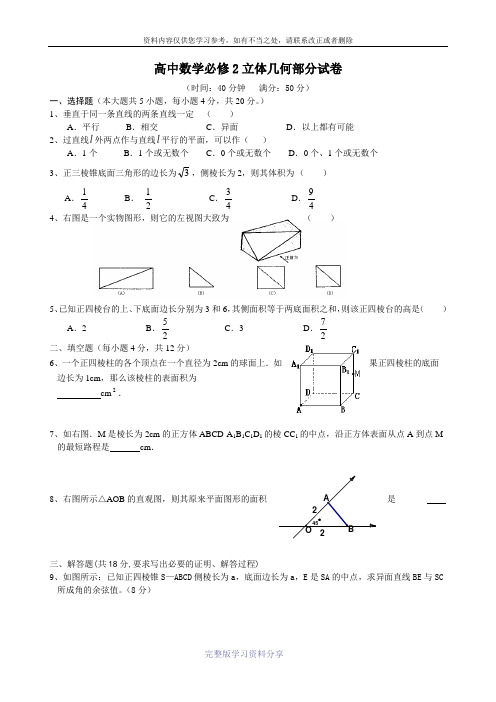
高中数学必修2立体几何部分试卷(时间:40分钟 满分:50分)一、选择题(本大题共5小题,每小题4分,共20分。
)1、垂直于同一条直线的两条直线一定 ( )A .平行B .相交C .异面D .以上都有可能2、过直线l 外两点作与直线l 平行的平面,可以作( )A .1个B .1个或无数个C .0个或无数个D .0个、1个或无数个3、正三棱锥底面三角形的边长为3,侧棱长为2,则其体积为 ( )A .41B . 21C .43D .49 4、右图是一个实物图形,则它的左视图大致为 ( )5、已知正四棱台的上、下底面边长分别为3和6,其侧面积等于两底面积之和,则该正四棱台的高是( )A .2B .25C .3D .27 二、填空题(每小题4分,共12分) 6、一个正四棱柱的各个顶点在一个直径为2cm 的球面上.如果正四棱柱的底面边长为1cm ,那么该棱柱的表面积为cm 2.7、如右图.M 是棱长为2cm 的正方体ABCD-A 1B 1C 1D 1的棱CC 1的中点,沿正方体表面从点A 到点M 的最短路程是 cm .8、右图所示△AOB 的直观图,则其原来平面图形的面积是_______三、解答题(共18分,要求写出必要的证明、解答过程)9、如图所示:已知正四棱锥S —ABCD 侧棱长为a ,底面边长为a ,E 是SA 的中点,求异面直线BE 与SC 所成角的余弦值。
(8分) 45B O A 2210、如下的三个图中,左边的是一个长方体截去一个角所得多面体的直观图,它的正视图和侧视图在右边画出(单位:cm )。
(1)画出该多面体的俯视图;(2)按照给出的尺寸,求该多面体的体积;(3)在所给直观图中连结'BC ,证明:'BC ∥面EFG 。
(10分)必修2立体几何部分试卷答案题号 12 3 4 5 答案 D D C D A6、2+427、 178、 49、解:连接AC 、BD 交于点0,连接EO.224侧视图正视图624G F C'B'D'C A D∵E 为SA 的中点,O 为AC 的中点,∴EO ∥SC (3分)∴∠BEO 为异面直线BE 、SC 所成的角(或其补角) (1分) 又∵正四棱锥S —ABCD 侧棱长为a ,底面边长为a∴EO=21SC=21a, BE=23a, OB=22a 在△EBO 中 EO 2+OB 2=BE 2 ∴△EBO 为Rt △. (2分) COS ∠BEO=33=BE OE (1分) ∴异面直线BE 、SC 所成的角的余弦值为33。
高三数学-2018学年度第二学期期末考试及答案 精品

2018——2018学年度第二学期期末考试高二级数学科试题姓名: __________班别:__________学号:__________考试说明:本试卷共8页,其中第一卷(第1~4页)为单选题和填空题,第二卷(第5~8页)为选择题和填空题的答题卡和解答题。
考试时间为120分钟,试卷满分为100分。
第一卷一、单选题(每小题3分,共36分。
请把正确的答案选项写在第二卷的答题卡上。
) 1、下列命题中正确的是( )A 、垂直于同一平面的两个平面平行。
B 、若一条直线和另一条直线平行,则它就和经过另一条直线的任何平面平行。
C 、平行于同一个平面的两条直线互相平行。
D 、若一条直线上的两点在一个平面内,则这条直线上所有的点都在这个平面内。
2、满足21=-z 复数z 在复平面上对应的点的集合是( )A 、以点(1,0)为圆心,半径为2的圆。
B 、以点(1,0)为圆心,半径为2的圆。
C 、以点(0,1)为圆心,半径为2的圆。
D 、以点(0,1)为圆心,半径为2的圆。
3、以下四个命题中正确的是( )A 、统计中的假设检验通常是假设随机变量不服从正态分布。
B 、如果随机变量),(~2σμξN ,则)1,0(~2N σμξη-=。
C 、标准正态曲线在0=x 时位于最高点。
D 、△ABC 为直角三角形的充要条件是0=⋅4、某12人的兴趣小组中,有5名“三好生”,现从中任意选6人参加竞赛,用ξ表示这6人中“三好生”的人数,则下列概率中等于6123735C CC 的是( )A .P (ξ=2)B .P (ξ=3)C .P (ξ≤2)D .P (ξ≤3)5、已知ξ~B(n ,p),E ξ=8,D ξ=1.6,则n 与p 的值分别是( )A .100和0.18B .20和0.4C .10和0.2D .10和0.86、满足i y x y x i y x )()1(12--+-=++-y x 、的的值是( )A .2,3==y xB .2,3-==y xC .2,3=-=y xD .2,3-=-=y x7、已知向量a = (2,4,x),b = (2,y ,2) ,若a=6,且a b ⊥ ,则x+y 的值为( )A .-3或1B .3或-1C .-3D .18、在正方形321G G SG 中,F E 、分别是3221G G G G 及的中点,D 是EF 的中点,现沿EF SF SE 、及、把这个正方形折成一个四面体,使321G G G 、、三点重合记为G ,则必有( )A 、EFG SD 平面⊥B 、EFG SG 平面⊥C 、SEF GF 平面⊥D 、SEF GD 平面⊥9、把边长为a 的正三角形ABC 沿高线AD 折成一个二面角B —AD —C ,若B 、C 两点间的距离为a 23,则这个二面角的大小为( ) A .︒120 B .︒90 C .︒60 D .︒3010. 在北纬45°的纬度圈上有甲、乙两地,两地经度差为90°,则甲、乙两地最短距离为(设地球半径为R )( ) A. R π42 B. R 3π C. R 2π D. 3R11、已知凸多面体每个面都是五边形,每个顶点都有三条棱相交,则该凸多面体的面数F 、顶点V 、棱数E 分别为( ) A 、E=20,F=12、 V=30 B 、E=12,F=20、V=30 C 、E=30,F=12、V=20 D 、E=30,F=20、V=1212、如图,棱长都为2的直平行六面体ABCD —A 1B 1C 1D 1中,∠BAD=60°,则对角线A 1C与侧面DCC 1D 1所成角的正弦值为( )A .21B .22C .23D .43二、填空题(每小题4分,共16分,请把正确的答案写在第二卷的答题卡上。
高中数学必修二期末试卷及答案

一、选择题:本大题共14小题,每小题4分,共56分.在每小题给出的四个选项中,只有一项是符合要求的.1.在直角坐标系中,已知A(-1,2),B(3,0),那么线段AB中点的坐标为中点的坐标为(().A.(2,2)B.(1,1)C.(-2,-2)D.(-1,-1) 2.右面三视图所表示的几何体是.右面三视图所表示的几何体是(().A.三棱锥.三棱锥B.四棱锥.四棱锥C.五棱锥.五棱锥D.六棱锥.六棱锥3.如果直线x+2y-1=0和y=kx互相平行,则实数k的值为的值为(().A.2 B.21C.-2 D.-214.一个球的体积和表面积在数值上相等,则该球半径的数值为.一个球的体积和表面积在数值上相等,则该球半径的数值为(().A.1 B.2 C.3 D.4 5.下面图形中是正方体展开图的是.下面图形中是正方体展开图的是(().6.圆x2+y2-2x-4y-4=0的圆心坐标是的圆心坐标是(().A.(-2,4) B.(2,-4) C.(-1,2) D.(1,2)7.直线y=2x+1关于y轴对称的直线方程为轴对称的直线方程为(().A.y=-2x+1 B.y=2x-1 C.y=-2x-1 D.y=-x-1 8.已知两条相交直线a,b,a∥平面 a,则b与a 的位置关系是的位置关系是(().A.bÌ平面a B.b⊥平面aC.b∥平面a D.b与平面a相交,或b∥平面a9.在空间中,a,b是不重合的直线,a,b是不重合的平面,则下列条件中可推出是不重合的平面,则下列条件中可推出a∥b的是的是(().A.aÌa,bÌb,a∥b B.a∥a,bÌbC.a⊥a,b⊥a D.a⊥a,bÌa10.圆x2+y2=1和圆x2+y2-6y+5=0的位置关系是的位置关系是(().正视图正视图 侧视图侧视图俯视图俯视图(第2题)11.如图,正方体ABCD —A'B'C'D'中,直线D'A 与DB 所成的角可以表示为所成的角可以表示为(( ). A .∠D'DB B .∠AD' C' C .∠ADBD .∠DBC'12. 圆(x -1)2+(y -1)2=2被x 轴截得的弦长等于轴截得的弦长等于(( ). A . 1 B .23C . 2 D . 3 13.如图,三棱柱A 1B 1C 1—ABC 中,侧棱AA 1⊥底面A 1B 1C 1,底面三角形A 1B 1C 1是正三角形,E 是BC 中点,则下列叙述正确的是中点,则下列叙述正确的是(( ).A .CC 1与B 1E 是异面直线是异面直线 B .AC ⊥平面A 1B 1BAC .AE ,B 1C 1为异面直线,且AE ⊥B 1C 1D .A 1C 1∥平面AB 1E14.有一种圆柱体形状的笔筒,底面半径为4 4 cm cm ,高为12 12 cm cm .现要为100个这种相同规格的笔筒涂色个这种相同规格的笔筒涂色((笔筒内外均要涂色,笔筒厚度忽略不计要涂色,笔筒厚度忽略不计)). 如果每0.5 kg 涂料可以涂1 m 2,那么为这批笔筒涂色约需涂料.,那么为这批笔筒涂色约需涂料.A .1.23 kg B .1.76 kg C .2.46 kg D .3.52 kg 二、填空题:本大题共4小题,每小题4分,共16分.把答案填在题中横线上.分.把答案填在题中横线上. 15.坐标原点到直线4x +3y -12=0的距离为的距离为 .16.以点A (2,0)为圆心,且经过点B (-1,1)的圆的方程是 .17.如图,在长方体ABCD —A 1B 1C 1D 1中,棱锥A 1——ABCD 的体积与长方体的体积之比为_______________.18.在平面几何中,有如下结论:三边相等的三角形内任意一点到三边的距离之和为定值.拓展到空间,类比平面几何的上述结论,可得:四个面均为等边三角形的四面体内任意一点_______________________________________.三、解答题:本大题共3小题,共28分.解答应写出文字说明,证明过程或演算步骤.分.解答应写出文字说明,证明过程或演算步骤. 19.已知直线l 经过点经过点((0,-2),其倾斜角是60°. (1)求直线l 的方程;的方程;(2)求直线l 与两坐标轴围成三角形的面积.与两坐标轴围成三角形的面积. 20.如图,在三棱锥P —ABC 中,PC ⊥底面ABC , AB ⊥BC ,D ,E 分别是AB ,PB 的中点.的中点.(1)求证:DE ∥平面P AC ;CBAD A ¢ B ¢C ¢D ¢(第11题)A 1 B 1 C 1 ABEC(第13题)ABC DD1 C 1 B 1 A 1 (第17题)ACPE(2)求证:AB ⊥PB ;21.已知半径为5的圆C 的圆心在x 轴上,圆心的横坐标是整数,且与直线4x +3y -29=0相切.相切. (1)求圆C 的方程;的方程;(2)设直线ax -y +5=0与圆C 相交于A ,B 两点,求实数a 的取值范围;的取值范围;(3) 在(2)的条件下,是否存在实数a ,使得过点P (-2,4)的直线l 垂直平分弦AB ?若存在,求出实数a 的值;若不存在,请说明理由.存在,请说明理由.22.为C 的圆经过点A(1,1)和B(2,-2)且圆心C 在直线L:x-y+1=0上,求圆心为C 的圆的标准方程 23.知圆22:68210C x y x y +--+=和直线:430l kx y k --+=.⑴ 证明:不论证明:不论k 取何值,直线l 和圆C 总相交;总相交;⑵ 当当k 取何值时,圆C 被直线l 截得的弦长最短?并求最短的弦的长度截得的弦长最短?并求最短的弦的长度24知圆C 同时满足下列三个条件:①与y 轴相切;②在直线y =x 上截得弦长为27;③圆心在直线x -3y =0上. 求圆C 的方程. 25,已知△ABC 是正三角形,EA 、CD 都垂直于平面ABC ,且EA=AB=2a,DC=a,F 是BE 的中点,求证:(1) FD ∥平面ABC; (2) AF ⊥平面EDB.26.图,在正方体ABCD-A 1B 1C 1D 1中,E 、F 、G 分别是CB 、CD 、CC 1的中点,的中点, (1) 求证:平面A B 1D 1∥平面EFG; (2) 求证:平面AA 1C ⊥面EFG.F EDCBAM FGE C1D1A1B1DC ABPD 1B 1D B。
2017-2018学年高中数学必修二期末考试(附答案)
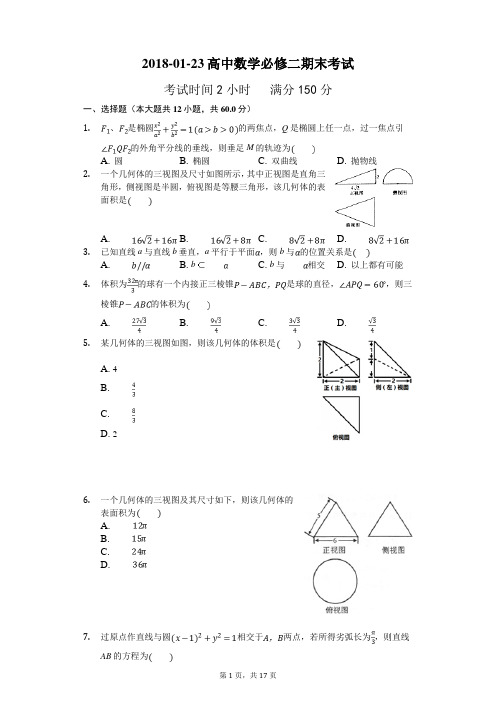
2018-01-23高中数学必修二期末考试考试时间2小时满分150分一、选择题(本大题共12小题,共60.0分)1.、是椭圆的两焦点,Q是椭圆上任一点,过一焦点引的外角平分线的垂线,则垂足M的轨迹为A. 圆B. 椭圆C. 双曲线D. 抛物线2.一个几何体的三视图及尺寸如图所示,其中正视图是直角三角形,侧视图是半圆,俯视图是等腰三角形,该几何体的表面积是A. B. C. D.3.已知直线a与直线b垂直,a平行于平面,则b与的位置关系是A. B. b C. b与相交 D. 以上都有可能4.体积为的球有一个内接正三棱锥是球的直径,,则三棱锥的体积为A. B. C. D.5.某几何体的三视图如图,则该几何体的体积是A. 4B.C.D. 26.一个几何体的三视图及其尺寸如下,则该几何体的表面积为A.B.C.D.7.过原点作直线与圆相交于两点,若所得劣弧长为,则直线AB的方程为A. B. C. D.8.直线与曲线有且仅有一个公共点,则的取值范围是A. B. 或C. D.9.若l为一条直线,为三个互不重合的平面,给出下面三个命题:,则;,则;,则,则其中正确的命题有A. 0个B. 1个C. 2个D. 3个10.若直线与圆相切,则点的位置是A. 在圆上B. 在圆外C. 在圆内D. 以上皆有可能11.一个正方体被一个平面截去一部分后,剩余部分的三视图如图所示,则截去部分体积与剩余部分体积的比值为A.B.C.D.12.已知点是:内一点,则以点M为中点的圆O的弦长为A.B. C. D. 6二、填空题(本大题共4小题,共20.0分)13.已知一个三棱锥的俯视图与侧左视图如图所示,俯视图是边长为2的正三角形,侧视图是有一条直角边长为1的直角三角形,则该三棱锥的表面积为______ .14.一个棱长为的正方体被一个平面截去一部分后,剩余部分的三视图如图所示,则此剩余部分的体积为______.15.表面红色的正方体木块,棱长为5个长度单位,现将其分割为若干个棱长一个长度单位的正方体小木块,其中两面红色的个数为;16.下列条件中,能判断两个平面平行的是一个平面内的一条直线平行于另一个平面一个平面内的两条直线平行于另一个平面一个平面内有无数条直线平行于另一个平面一个平面内任何一条直线都平行于另一个平面三、解答题(本大题共6小题,共70.0分)17.如图,在直三棱柱中,M为的中点,为等边三角形.Ⅰ证明:平面;Ⅱ若,求点到平面的距离.18.已知圆O:和点.若过点M有且只有一条直线与圆O相切,求实数a的值,并求出切线方程;若,求过点M的最短弦AC与最长弦BD所在的直线方程并求此时的.19.本小题满分14分如图,三角形PDC所在的平面与长方形ABCD所在的平面垂直,点E是CD边的中点,点分别在线段上,且.证明:求二面角的正切值求直线PA与直线FG所成角的余弦值.20.本题满分10分在平面直角坐标系中,各顶点的坐标分别为:求点到直线的距离;求边的高所在直线的方程.21.如图,直三棱柱,,点分别为和的中点。
【易错题】高中必修二数学下期末试卷(带答案)(2)

【易错题】高中必修二数学下期末试卷(带答案)(2)一、选择题1.设集合{}1,2,4A =,{}240B x x x m =-+=.若{}1A B ⋂=,则B =( ) A .{}1,3-B .{}1,0C .{}1,3D .{}1,52.某程序框图如图所示,若输出的S=57,则判断框内为 A .k >4? B .k >5? C .k >6?D .k >7?3.在ABC ∆中,2AB =2AC =,E 是边BC 的中点.O 为ABC ∆所在平面内一点且满足222OA OB OC ==u u u v u u u v v ,则·AE AO u u u v u u u v 的值为( )A .12B .1C .22D .324.已知不等式220ax bx ++>的解集为{}12x x -<<,则不等式220x bx a ++<的解集为( ) A .112x x ⎧⎫-<<⎨⎬⎩⎭B .112x x x ⎧⎫<->⎨⎬⎩⎭或 C .{}21x x -<<D .{}21x x x <->或5.已知函数()y f x =为R 上的偶函数,当0x ≥时,函数()()210216()122xx x f x x ⎧≤≤⎪⎪=⎨⎛⎫⎪> ⎪⎪⎝⎭⎩,若关于x 的方程[]()2()()0,f x af x b a b R ++=∈有且仅有6个不同的实数根,则实数a 的取值范围是( )A .51,24⎛⎫-- ⎪⎝⎭B .11,24⎛⎫-- ⎪⎝⎭C .1111,,2448⎛⎫⎛⎫---- ⎪ ⎪⎝⎭⎝⎭U D .11,28⎛⎫-- ⎪⎝⎭6.要得到函数2sin 2y x x =+2sin 2y x =的图象( ) A .向左平移3π个单位 B .向右平移3π个单位 C .向左平移6π个单位 D .向右平移6π个单位7.若||1OA =u u u v ,||OB u u u v 0OA OB ⋅=u u u v u u u v,点C 在AB 上,且30AOC ︒∠=,设OC mOA nOBu u u v u u u v u u u v =+(,)m n R ∈,则mn的值为( )A .13B .3C .3D 8.已知01a b <<<,则下列不等式不成立...的是 A .11()()22ab>B .ln ln a b >C .11a b> D .11ln ln a b> 9.有5支彩笔(除颜色外无差别),颜色分别为红、黄、蓝、绿、紫.从这5支彩笔中任取2支不同颜色的彩笔,则取出的2支彩笔中含有红色彩笔的概率为 A .45B .35 C .25D .1510.设函数,则()sin 2cos 244f x x x ππ⎛⎫⎛⎫=+++ ⎪ ⎪⎝⎭⎝⎭,则( ) A .()y f x =在0,2π⎛⎫⎪⎝⎭单调递增,其图象关于直线4x π=对称B .()y f x =在0,2π⎛⎫⎪⎝⎭单调递增,其图象关于直线2x π=对称 C .()y f x =在0,2π⎛⎫⎪⎝⎭单调递减,其图象关于直线4x π=对称D .()y f x =在0,2π⎛⎫⎪⎝⎭单调递减,其图象关于直线2x π=对称11.1()xf x e x=-的零点所在的区间是( )A .1(0,)2B .1(,1)2C .3(1,)2D .3(,2)212.如图,点N 为正方形ABCD 的中心,ECD ∆为正三角形,平面ECD ⊥平面,ABCD M 是线段ED 的中点,则( )A .BM EN =,且直线,BM EN 是相交直线B .BM EN ≠,且直线,BM EN 是相交直线C .BM EN =,且直线,BM EN 是异面直线D .BM EN ≠,且直线,BM EN 是异面直线二、填空题13.在平面直角坐标系xOy 中, 已知圆C 1 : x 2 + y 2=8与圆C 2 : x 2+y 2+2x +y -a =0相交于A ,B 两点.若圆C 1上存在点P ,使得△ABP 为等腰直角三角形,则实数a 的值组成的集合为______.14.如图,在正方体1111ABCD A B C D -中,E 、F 分别是1DD 、DC 上靠近点D 的三等分点,则异面直线EF 与11A C 所成角的大小是______.15.如图是抛物线形拱桥,当水面在l 时,拱顶离水面2米,水面宽4米,水位下降1米后,水面宽 米.16.已知圆的方程为x 2+y 2﹣6x ﹣8y =0,设该圆过点(3,5)的最长弦和最短弦分别为AC 和BD ,则四边形ABCD 的面积为17.已知点()M a b ,在直线3415x y +=22a b +_______. 18.若a 10=12,a m =22,则m =______. 19.设α为锐角,若4cos()65πα+=,则sin(2)12πα+的值为______. 20.若两个向量a v 与b v 的夹角为θ,则称向量“a b ⨯v v”为向量的“外积”,其长度为sin a b a b θ⨯=v v v v .若已知1a =v ,5b =v ,4a b ⋅=-v v ,则a b ⨯=v v .三、解答题21.已知:a b c v v v、、是同一平面内的三个向量,其中()1,2a =v(1)若25c =v ,且//c a v v ,求c v的坐标;(2)若5b =v2a b +v v 与2a b -v v 垂直,求a v 与b v 的夹角θ. (3)若()1,1b =v ,且a v 与a b λ+v v的夹角为锐角,求实数λ的取值范围.22.设ABC ∆的内角A 、B 、C 所对的边分别为a 、b 、c ,且4cos ,25B b ==. (1)当π6A =时,求a 的值; (2)当ABC ∆的面积为3时,求a+c 的值.23.已知数列{}n a 满足11a =,()121n n na n a +=+,设nn a b n=. (1)求123b b b ,,; (2)判断数列{}n b 是否为等比数列,并说明理由; (3)求{}n a 的通项公式.24.已知ABC ∆中,内角,,A B C 所对边分别为,,a b c ,若()20a c cosB bcosC --=. (1)求角B 的大小;(2)若2b =,求a c +的取值范围. 25.已知数列{a n }满足a 1=1,1114n na a +=-,其中n ∈N *.(1)设221 nnba=-,求证:数列{b n}是等差数列,并求出{a n}的通项公式.(2)设41nnacn=+,数列{c n c n+2}的前n项和为T n,是否存在正整数m,使得11nm mTc c+<对于n∈N*,恒成立?若存在,求出m的最小值;若不存在,请说明.26.以原点为圆心,半径为r的圆O222:()0O x y r r+=>与直线380x y--=相切.(1)直线l过点(2,6)-且l截圆O所得弦长为43求直线l l的方程;(2)设圆O与x轴的正半轴的交点为M,过点M作两条斜率分别为12,k k12,k k的直线交圆O于,A B两点,且123k k⋅=-,证明:直线AB恒过一个定点,并求出该定点坐标.【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【解析】∵集合{}124A,,=,{}2|40B x x x m=-+=,{}1A B⋂=∴1x=是方程240x x m-+=的解,即140m-+=∴3m=∴{}{}{}22|40|43013B x x x m x x x=-+==-+==,,故选C2.A解析:A【解析】试题分析:由程序框图知第一次运行112,224k S=+==+=,第二次运行213,8311k S=+==+=,第三次运行314,22426k S=+==+=,第四次运行4154,52557k S =+=>=+=,输出57S =,所以判断框内为4?k >,故选C.考点:程序框图.3.D解析:D 【解析】 【分析】根据平面向量基本定理可知()12AE AB AC =+u u u v u u u v u u u v,将所求数量积化为1122AB AO AC AO ⋅+⋅u u uv u u u v u u u v u u u v ;由模长的等量关系可知AOB ∆和AOC ∆为等腰三角形,根据三线合一的特点可将AB AO ⋅u u u v u u u v 和AC AO ⋅u u u v u u u v 化为212AB u u uv 和212AC u u u v ,代入可求得结果.【详解】E Q 为BC 中点 ()12AE AB AC ∴=+u u u v u u u v u u u v()111222AE AO AB AC AO AB AO AC AO ∴⋅=+⋅=⋅+⋅u u u v u u u v u u u v u u u v u u u v u u u v u u u v u u u v u u u v222OA OB OC ==u u u v u u u v u u u v Q AOB ∴∆和AOC ∆为等腰三角形211cos 22AB AO AB AO OAB AB AB AB ∴⋅=∠=⋅=u u u v u u u v u u u v u u u v u u u v u u u v u u u v ,同理可得:212AC AO AC ⋅=u u u v u u u v u u u v22111314422AE AO AB AC ∴⋅=+=+=u u u v u u u v u u u v u u u v本题正确选项:D 【点睛】本题考查向量数量积的求解问题,关键是能够利用模长的等量关系得到等腰三角形,从而将含夹角的运算转化为已知模长的向量的运算.4.A解析:A 【解析】 【分析】根据一元二次不等式的解集与一元二次方程根的关系,结合韦达定理可构造方程求得,a b ;利用一元二次不等式的解法可求得结果.【详解】220ax bx ++>Q 的解集为{}12x x -<<1∴-和2是方程220ax bx ++=的两根,且0a <1212122baa⎧-=-+=⎪⎪∴⎨⎪=-⨯=-⎪⎩,解得:11a b =-⎧⎨=⎩ 222210x bx a x x ∴++=+-< 解得:112x -<<,即不等式220x bx a ++<的解集为112x x ⎧⎫-<<⎨⎬⎩⎭故选:A 【点睛】本题考查一元二次不等式的解法、一元二次不等式的解集与一元二次方程根的关系等知识的应用;关键是能够通过一元二次不等式的解集确定一元二次方程的根,进而利用韦达定理构造方程求得变量.5.B解析:B 【解析】 【分析】作出函数()y f x =的图像,设()f x t =,从而可化条件为方程20t at b ++=有两个根,利用数形结合可得114t =,2104t <<,根据韦达定理即可求出实数a 的取值范围. 【详解】由题意,作出函数()y f x =的图像如下,由图像可得,10()(2)4f x f ≤≤=Q 关于x 的方程[]()2()()0,f x af x b a b R ++=∈有且仅有6个不同的实数根,设()f x t =,20t at b ∴++=有两个根,不妨设为12,t t ;且114t =,2104t << 又12a t t -=+Q11,24a ⎛⎫∴∈-- ⎪⎝⎭故选:B 【点睛】本题主要考查函数与方程、由方程根的个数求参数的取值范围,考查学生运用数形结合思想解决问题的能力,属于中档题.6.C解析:C 【解析】 【分析】化简函数2sin 2y x x =+-. 【详解】依题意2ππsin 22sin 22sin 236y x x x x ⎡⎤⎛⎫⎛⎫=+=+=+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,故只需将函数2sin 2y x =的图象向左平移6π个单位.所以选C. 【点睛】本小题主要考查三角函数降次公式和辅助角公式,考查三角函数图象变换的知识,属于基础题.7.B解析:B 【解析】 【分析】利用向量的数量积运算即可算出. 【详解】解:30AOC ︒∠=Qcos ,2OC OA ∴<>=u u u r u u u rOC OA OC OA⋅∴=u u u r u u u r u u u r u u u r()2mOA nOB OA mOA nOBOA+⋅∴=+u u u r u u u ru u u r u u u r u u u r u u u r=1OA =Q,OB =,0OA OB ⋅==229m n∴=又CQ在AB上m∴>,0n>3mn∴=故选:B【点睛】本题主要考查了向量的基本运算的应用,向量的基本定理的应用及向量共线定理等知识的综合应用.8.B解析:B【解析】【分析】根据指数函数、对数函数的单调性,以及不等式的性质,对选项逐一分析,由此得出不等式不成立的选项.【详解】依题意01a b<<<,由于12xy⎛⎫= ⎪⎝⎭为定义域上的减函数,故11()()22a b>,故A选项不等式成立.由于lny x=为定义域上的增函数,故ln ln0a b<<,则11ln lna b>,所以B选项不等式不成立,D选项不等式成立.由于01a b<<<,故11a b>,所以C选项不等式成立.综上所述,本小题选B.【点睛】本小题主要考查指数函数和对数函数的单调性,考查不等式的性质,属于基础题.9.C解析:C【解析】选取两支彩笔的方法有25C种,含有红色彩笔的选法为14C种,由古典概型公式,满足题意的概率值为142542105CpC===.本题选择C选项.考点:古典概型名师点睛:对于古典概型问题主要把握基本事件的种数和符合要求的事件种数,基本事件的种数要注意区别是排列问题还是组合问题,看抽取时是有、无顺序,本题从这5支彩笔中任取2支不同颜色的彩笔,是组合问题,当然简单问题建议采取列举法更直观一些.10.D解析:D 【解析】()sin(2)cos(2))2442f x x x x x πππ=+++=+=,由02,x π<<得02x π<<,再由2,x k k Z ππ=+∈,所以,22k x k Z ππ=+∈. 所以y=f(x)在()y f x =在(0,)2π单调递减,其图象关于直线2x π=对称,故选D.11.B解析:B 【解析】函数f (x )=e x ﹣1x 是(0,+∞)上的增函数,再根据f (12)2<0,f (1)=e ﹣1>0,可得f (12)f (1)<0,∴函数f (x )=e x ﹣1x 的零点所在的区间是(12,1),故选B .点睛:判定函数的零点所在区间,只需计算区间端点处的函数值,并判断是否异号,只要异号,则区间内至少有一个零点存在.12.B解析:B 【解析】 【分析】利用垂直关系,再结合勾股定理进而解决问题. 【详解】如图所示, 作EO CD ⊥于O ,连接ON ,过M 作MF OD ⊥于F . 连BF ,Q 平面CDE ⊥平面ABCD .,EO CD EO ⊥⊂平面CDE ,EO ∴⊥平面ABCD ,MF ⊥平面ABCD ,MFB ∴∆与EON ∆均为直角三角形.设正方形边长为2,易知12EO ON EN ===,5,2MF BF BM ==∴=BM EN ∴≠,故选B .【点睛】本题考查空间想象能力和计算能力, 解答本题的关键是构造直角三角性.二、填空题13.【解析】【分析】先求得直线为:再分别讨论或和的情况根据几何性质求解即可【详解】由题则直线为:当或时设到的距离为因为等腰直角三角形所以即所以所以解得当时经过圆心则即故答案为:【点睛】本题考查圆与圆的位 解析:{}8,825,825-+【解析】 【分析】先求得直线AB 为:280x y a ++-=,再分别讨论90PAB ∠=︒或90PBA ∠=︒和90APB ∠=︒的情况,根据几何性质求解即可 【详解】由题,则直线AB 为:280x y a ++-=,当90PAB ∠=︒或90PBA ∠=︒时,设1C 到AB 的距离为d , 因为ABP △等腰直角三角形, 所以12d AB =,即2182d d =-,所以2d =, 228221a d -==+,解得825a =±当90APB ∠=︒时,AB 经过圆心1C ,则80a -=,即8a =, 故答案为:{}8,825,825-+ 【点睛】本题考查圆与圆的位置关系的应用,考查点到直线距离公式的应用,考查分类讨论思想和数形结合思想14.【解析】【分析】连接可得出证明出四边形为平行四边形可得可得出异面直线与所成角为或其补角分析的形状即可得出的大小即可得出答案【详解】连接在正方体中所以四边形为平行四边形所以异面直线与所成的角为易知为等 解析:60o【解析】 【分析】连接1CD ,可得出1//EF CD ,证明出四边形11A BCD 为平行四边形,可得11//A B CD ,可得出异面直线EF 与11A C 所成角为11BA C ∠或其补角,分析11A BC ∆的形状,即可得出11BA C ∠的大小,即可得出答案.【详解】连接1CD 、1A B 、1BC ,113DEDF DD DC ==Q,1//EF CD ∴, 在正方体1111ABCD A B C D -中,11//A D AD ,//AD BC ,11//A D BC ∴, 所以,四边形11A BCD 为平行四边形,11//A B CD ∴, 所以,异面直线EF 与11A C 所成的角为11BA C ∠.易知11A BC ∆为等边三角形,1160BA C ∴∠=o.故答案为:60o . 【点睛】本题考查异面直线所成角的计算,一般利用平移直线法,选择合适的三角形求解,考查计算能力,属于中等题.15.2米【解析】【分析】【详解】如图建立直角坐标系设抛物线方程为将A (2-2)代入得m=-2∴代入B 得故水面宽为米故答案为米考点:抛物线的应用解析:6米 【解析】 【分析】 【详解】如图建立直角坐标系,设抛物线方程为2x my =, 将A (2,-2)代入2x my =, 得m=-2,∴22x y =-,代入B ()0,3x -得06x =故水面宽为266 考点:抛物线的应用16.20【解析】【分析】根据题意可知过(35)的最长弦为直径最短弦为过(35)且垂直于该直径的弦分别求出两个量然后利用对角线垂直的四边形的面积等于对角线乘积的一半求出即可【详解】解:圆的标准方程为(x ﹣解析:6 【解析】 【分析】根据题意可知,过(3,5)的最长弦为直径,最短弦为过(3,5)且垂直于该直径的弦,分别求出两个量,然后利用对角线垂直的四边形的面积等于对角线乘积的一半求出即可. 【详解】解:圆的标准方程为(x ﹣3)2+(y ﹣4)2=52, 由题意得最长的弦|AC |=2×5=10,根据勾股定理得最短的弦|BD |=2251-=6,且AC ⊥BD , 四边形ABCD 的面积S =|12AC |•|BD |12=⨯10×6=6. 故答案为6. 【点评】考查学生灵活运用垂径定理解决数学问题的能力,掌握对角线垂直的四边形的面积计算方法为对角线乘积的一半.17.3【解析】【分析】由题意可知表示点到点的距离再由点到直线距离公式即可得出结果【详解】可以理解为点到点的距离又∵点在直线上∴的最小值等于点到直线的距离且【点睛】本题主要考查点到直线的距离公式的应用属于解析:3 【解析】 【分析】22a b +()0,0到点(),a b 的距离,再由点到直线距离公式即可得出结果.【详解】()0,0到点(),a b的距离,又∵点(),M a b在直线:3425l x y+=()0,0到直线34150x y+-=的距离,且3d==.【点睛】本题主要考查点到直线的距离公式的应用,属于基础题型.18.5【解析】解析:5【解析】5,52a m====19.【解析】试题分析:所以考点:三角恒等变形诱导公式二倍角公式同角三角函数关系【思路点晴】本题主要考查二倍角公式两角和与差的正弦公式题目的已知条件是单倍角并且加了我们考虑它的二倍角的情况即同时求出其正弦解析:50【解析】试题分析:247cos(2)213525πα⎛⎫+=⋅-=⎪⎝⎭,24sin(2)325πα+=,所以sin(2)sin(2)1234πππαα+=+-2472252550⎫=-=⎪⎝⎭.考点:三角恒等变形、诱导公式、二倍角公式、同角三角函数关系.【思路点晴】本题主要考查二倍角公式,两角和与差的正弦公式.题目的已知条件是单倍角,并且加了6π,我们考虑它的二倍角的情况,即247cos(2)213525πα⎛⎫+=⋅-=⎪⎝⎭,同时求出其正弦值24sin(2)325πα+=,而要求的角sin(2)sin(2)1234πππαα+=+-,再利用两角差的正弦公式,就能求出结果.在求解过程中要注意正负号.20.3【解析】【分析】【详解】故答案为3【点评】本题主要考查以向量的数量积为载体考查新定义利用向量的数量积转化是解决本题的关键解析:3【解析】【分析】【详解】44 155a b a b a b cos cos a b θθ⋅-⋅∴-⨯v v v v v vv v Q ====33[0sin 15355sin a b a b θπθθ∈∴⨯=⨯⨯v v Q v v ,),=,==故答案为3. 【点评】本题主要考查以向量的数量积为载体考查新定义,利用向量的数量积转化是解决本题的关键,三、解答题21.(1)(2,4)或(-2,-4) (2)π (3)()5,00,3⎛⎫-⋃+∞ ⎪⎝⎭【解析】 【分析】(1)设(,)c x y =r,根据条件列方程组解出即可;(2)令(2)(2)0a b a b +⋅-=r rr r 求出a b ⋅r r ,代入夹角公式计算;(3)利用()0a a b λ+>⋅r r r ,且a r 与a λb +r r 不同向共线,列不等式求出实数λ的取值范围.【详解】 解:设(,)c x y =r,∵c =r //c a r r,∴222020y x x y -=⎧⎨+=⎩,解得24x y =⎧⎨=⎩或24x y =-⎧⎨=-⎩, ∴(2,4)c =r 或(2,4)c =--r;(2)∵2a b +r r 与2a b -r r垂直,∴(2)(2)0a b a b +⋅-=r rr r ,即222320a a b b +⋅-=r r r r ,∴52a b ⋅=-r r ,∴5cos 1||||a ba b θ-⋅===-r r r r ,∴a r与b r的夹角为π;(3)a r Q 与a λb +r r的夹角为锐角则()0a a b λ+>⋅r r r ,且a r 与a λb +rr 不同向共线,()25(12)0a aa ab b λλλ+==+>∴⋅++⋅r r r r rr ,解得:53λ>-, 若存在t ,使()a b a t λ=+r r r,0t > ()()1,21,1(1,2)a b λλλλ+=+=++r rQ则()1,2(1,2)t λλ=++,122t t t t λλ+=⎧∴⎨+=⎩,解得:10t λ=⎧⎨=⎩, 所以53λ>-且0λ≠, 实数λ的取值范围是()5,00,3⎛⎫-⋃+∞ ⎪⎝⎭. 【点睛】本题考查了平面向量的数量积运算,利用数量积研究夹角,注意夹角为锐角,数量积大于零,但不能同向共线,夹角为钝角,数量积小于零,但不能反向共线,本题是中档题. 22.(1)53a =(2)a c +=【解析】试题分析:(1)利用同角三角函数的基本关系式,求出sin B ,利用正弦定理求出a 即可.(2)通过三角形的面积求出ac 的值,然后利用余弦定理即可求出a +c 的值. 试题解析: 解:(1)43cos ,sin 55B B =∴=Q . 由正弦定理得10,sin sin 3sin 6a b a A B π==可得. 53a ∴=. (2)ABC ∆Q 的面积13sin ,sin 25S ac B B ==, 33,1010ac ac ∴==. 由余弦定理2222cos b a c ac B =+-, 得4=22228165a c ac a c +-=+- ,即2220a c +=.∴()()22220,40a c ac a c +-=+=,∴a c +=点睛:解三角形问题,多为边和角的求值问题,这就需要根据正、余弦定理结合已知条件灵活转化边和角之间的关系,从而达到解决问题的目的.其基本步骤是:第一步:定条件,即确定三角形中的已知和所求,在图形中标出来,然后确定转化的方向. 第二步:定工具,即根据条件和所求合理选择转化的工具,实施边角之间的互化. 第三步:求结果.23.(1)11b =,22b =,34b =;(2){}n b 是首项为1,公比为2的等比数列.理由见解析;(3)12n n a n -=⋅.【解析】 【分析】(1)根据题中条件所给的数列{}n a 的递推公式()121n n na n a +=+,将其化为()121n n n a a n++=,分别令1n =和2n =,代入上式求得24a =和312a =,再利用nn a b n=,从而求得11b =,22b =,34b =; (2)利用条件可以得到121n na a n n+=+,从而 可以得出12n n b b +=,这样就可以得到数列{}n b 是首项为1,公比为2的等比数列;(3)借助等比数列的通项公式求得12n n a n-=,从而求得12n n a n -=⋅.【详解】(1)由条件可得()121n n n a a n++=.将1n =代入得,214a a =,而11a =,所以,24a =. 将2n =代入得,323a a =,所以,312a =. 从而11b =,22b =,34b =;(2){}n b 是首项为1,公比为2的等比数列. 由条件可得121n na a n n+=+,即12n n b b +=,又11b =, 所以{}n b 是首项为1,公比为2的等比数列; (3)由(2)可得11122n n nn a b n--==⨯=,所以12n n a n -=⋅. 【点睛】该题考查的是有关数列的问题,涉及到的知识点有根据数列的递推公式确定数列的项,根据不同数列的项之间的关系,确定新数列的项,利用递推关系整理得到相邻两项之间的关系确定数列是等比数列,根据等比数列通项公式求得数列{}n b 的通项公式,借助于{}n b 的通项公式求得数列{}n a 的通项公式,从而求得最后的结果. 24.(1)3B π=;(2)(]2,4.【解析】 【分析】(1)利用正弦定理化简()20a c cosB bcosC --=得:() 2sinA sinC cosB sinBcosC -=,再由正弦两角和差公式和化为:()2sinAcosB sinBcosC cosBsinC sin B C =+=+,再由()sin B C sinA +=得出cos B的值即可;(2)由sin 3b B =得出a A =,c C =,得到a c A C +=+,进而得到sin 6a c A π+=+⎛⎫ ⎪⎝⎭,再根据角的范围得到sin 6A π⎛⎫ ⎪⎝⎭+的范围即可.【详解】(1)Q 由()20a c cosB bcosC --=, 可得:() 2sinA sinC cosB sinBcosC -=,2sinAcosB sinBcosC cosBsinC ∴=+,可得:()2sinAcosB sin B C sinA =+=,(0,)A π∈Q ,0sinA >,∴可得12cosB =, 又由(0,)B π∈得:3B π=,(2)sin b B =Qa A =,c C =, Q 23A C π+=,]sin sin sin()333a c A C A A B ∴+=+=++1sin sin()sin sin 32A A A A A π⎤⎤=++=+⎥⎥⎦⎣⎦14cos 4sin()26A A A π⎤=+=+⎥⎣⎦,203A π<<Q ,5666A πππ<+<, 可得:1sin ,162A π⎛⎫⎛⎤+∈ ⎪ ⎥⎝⎭⎝⎦, ∴a c +的取值范围(]2,4.【点睛】本题主要考查解三角形,侧重考查正弦定理的应用,考查辅助角公式的运用,考查逻辑思维能力和运算能力,属于中档题. 25.(1)12n n a n+=;(2)3 【解析】 试题分析:(1)结合递推关系可证得b n +1-b n =2,且b 1=2,即数列{b n }是首项为2,公差为2的等差数列,据此可得数列{}n a 的通项公式为12n n a n+=. (2)结合通项公式裂项有21122n n c c n n ,+⎛⎫=-⎪+⎝⎭求和有111213212n T n n ⎛⎫=+--< ⎪++⎝⎭.据此结合单调性讨论可得正整数m 的最小值为3. 试题解析: (1)证明:b n +1-b n 1222121n n a a +=---222112114n n a a =--⎛⎫-- ⎪⎝⎭ 4222121n n n a a a =-=--. 又由a 1=1,得b 1=2,所以数列{b n }是首项为2,公差为2的等差数列,所以b n =2+(n -1)×2=2n ,由221n n b a =-,得12n n a n+=. (2)解:2n c n =,()2411222n n c c n n n n +⎛⎫==- ⎪++⎝⎭所以111213212n T n n ⎛⎫=+--< ⎪++⎝⎭.依题意,要使11n m m T c c +<对于n ∈N *恒成立,只需()134m m +≥,解得m ≥3或m ≤-4.又m >0,所以m ≥3,所以正整数m 的最小值为3.26.(1)2x =-或20x +-=100x +-=;(2)(2,0). 【解析】分析:(1)先由直线和圆相切得到圆的方程,再由垂径定理列式,分直线斜率存在与不存在两种情况得到结果;(3)联立直线和圆,由韦达定理得到交点的坐标,由这两个点写出直线方程,进而得到直线过定点. 详解:(1)∵圆222:(0)O x y r r +=>与直线0x y -+=80x --=相切, ∴圆心O到直线的距离为4d ==,∴圆O 的方程为:2216x y +=若直线l 的斜率不存在,直线l 为2x =- 1x =, 此时直线l截圆所得弦长为若直线l 的斜率存在,设直线l为()2y k x =+()1y k x =-,由题意知,圆心到直线的距离为1d == 2d =,解得:k = 此时直线l为100x +-=,则所求的直线l 为2x =-或20x +-=-100x += (2)由题意知,()4,0M ()2,0A -,设直线()1:4MA y k x =-,与圆方程联立得:()12224y k x x y ⎧=+⎨+=⎩ ()122416y k x x y ⎧=-⎨+=⎩, 消去y 得:()()222211114440k x k x k +++-= ()22221111816160k x k x k +-+-=,∴()21211611M A k x x k -=+∴()2121411Ak xk -=+,12181Ak yk -=+ 用13k -换掉1k 得到B 点坐标 ∴21213649B k x k -=+,121249B k y k =+ 12141B k y k =+ ∴直线AB 的方程为21112221118444131k k k y x k k k ⎛⎫-+=- ⎪+-+⎝⎭整理得:()121423k y x k =-- 则直线AB 恒过定点为()2,0.点睛:本题主要考查直线与圆锥曲线位置关系,所使用方法为韦达定理法:因直线的方程是一次的,圆锥曲线的方程是二次的,故直线与圆锥曲线的问题常转化为方程组关系问题,最终转化为一元二次方程问题,故用韦达定理及判别式是解决圆锥曲线问题的重点方法之一,尤其是弦中点问题,弦长问题,可用韦达定理直接解决,但应注意不要忽视判别式的作用.。
高中数学 第四章 圆与方程章末综合测评2(含解析)新人教A版必修2(2021年最新整理)

2017-2018学年高中数学第四章圆与方程章末综合测评2(含解析)新人教A版必修2编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2017-2018学年高中数学第四章圆与方程章末综合测评2(含解析)新人教A版必修2)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2017-2018学年高中数学第四章圆与方程章末综合测评2(含解析)新人教A版必修2的全部内容。
(四) 圆与方程(时间120分钟,满分150分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.在空间直角坐标系中,点A(-3,4,0)与点B(2,-1,6)的距离是( )A.243 B.2错误!C.9 D。
86【解析】由空间直角坐标系中两点间距离公式得:|AB|=错误!=错误!。
【答案】D2.当圆x2+y2+2x+ky+k2=0的面积最大时,圆心坐标是()A.(0,-1)B.(-1,0)C.(1,-1) D.(-1,1)【解析】圆的标准方程得:(x+1)2+错误!错误!=1-错误!,当半径的平方1-错误!取最大值为1时,圆的面积最大.∴k=0,即圆心为(-1,0).【答案】B3.圆O1:x2+y2-4x-6y+12=0与圆O2:x2+y2-8x-6y+16=0的位置关系是()A.相交B.相离C.内含D.内切【解析】把圆O1:x2+y2-4x-6y+12=0与圆O2:x2+y2-8x-6y+16=0分别化为标准式为(x-2)2+(y-3)2=1和(x-4)2+(y-3)2=9,两圆心间的距离d=错误!=2=|r1-r2|,所以两圆的位置关系为内切,故选D。
高中数学必修二期末考试试卷(三)(含答案解析)

高中数学必修二期末考试试卷(三)(含答案解析)(时间:120分钟 满分:150分)一、选择题(本大题共12小题,每小题5分,共60分) 1.直线l 经过原点和(1,-1),则l 的倾斜角是( ) A.45° B.-45° C.135° D.45°和135° 答案 C解析 ∵直线l 经过坐标原点和点(1,-1),∴直线l 的斜率k =-11=-1,∴直线l 的倾斜角α=135°,故选C.2.已知过点M (-2,a ),N (a,4)的直线的斜率为-12,则|MN |等于( )A.10B.180C.6 3D.6 5考点 两点间的距离公式 题点 求两点间的距离 答案 D 解析 k MN =a -4-2-a=-12,解得a =10,即M (-2,10),N (10,4),所以|MN |=(-2-10)2+(10-4)2=65,故选D.3.设点A (2,-3),B (-3,-2),直线过P (1,1)且与线段AB 相交,则l 的斜率k 的取值范围是( )A.k ≥34或k ≤-4B.-4≤k ≤34C.-34≤k ≤4D.以上都不对考点 直线的图象特征与倾斜角、斜率的关系 题点 倾斜角和斜率关系的其他应用 答案 A解析 建立如图所示的直角坐标系.由图可得k ≥k PB 或k ≤k P A .∵k PB =34,k P A =-4,∴k ≥34或k ≤-4.4.若光线从点P (-3,3)射到y 轴上,经y 轴反射后经过点Q (-1,-5),则光线从点P 到点Q 走过的路程为( ) A.10 B.5+17 C.4 5D.217考点 对称问题的求法 题点 光路可逆问题 答案 C解析 Q (-1,-5)关于y 轴的对称点为Q 1(1,-5),易知光线从点P 到点Q 走过的路程为|PQ 1|=42+(-8)2=4 5.5.到直线3x -4y -1=0的距离为2的直线方程是( ) A.3x -4y -11=0B.3x -4y -11=0或3x -4y +9=0C.3x -4y +9=0D.3x -4y +11=0或3x -4y -9=0 答案 B解析 直线3x -4y -11=0与3x -4y +9=0到直线3x -4y -1=0的距离均为2, 又因为直线3x -4y +11=0到直线3x -4y -1=0的距离为125,故不能选择A ,C ,D ,所以答案为B.6.过两点(-1,1)和(3,9)的直线在x 轴上的截距为( ) A.-32 B.-23 C.25 D.2考点 直线的两点式方程 题点 利用两点式求直线方程 答案 A解析 由两点式y -19-1=x +13+1,得y =2x +3,令y =0,得x =-32,即为在x 轴上的截距.7.若直线mx +ny +2=0平行于直线x -2y +5=0,且在y 轴上的截距为1,则m ,n 的值分别为( ) A.1和2 B.-1和2 C.1和-2D.-1和-2 考点 直线的一般式方程与直线的平行关系 题点 根据平行求参数的值答案 C解析 由已知得直线mx +ny +2=0过点(0,1),则n =-2,又因为两直线平行,所以-m n =12,解得m =1.8.若直线(2m -3)x -(m -2)y +m +1=0恒过某个点P ,则点P 的坐标为( ) A.(3,5) B.(-3,5) C.(-3,-5) D.(3,-5)答案 C解析 方程(2m -3)x -(m -2)y +m +1=0可整理得m (2x -y +1)-(3x -2y -1)=0,联立⎩⎪⎨⎪⎧ 2x -y +1=0,3x -2y -1=0,得⎩⎪⎨⎪⎧x =-3,y =-5.故P (-3,-5).9.若直线l 1:y =k (x -4)与直线l 2关于点(2,1)对称,则直线l 2过定点( ) A.(0,4) B.(0,2) C.(-2,4)D.(4,-2)考点 对称问题的求法 题点 直线关于点的对称问题 答案 B解析 ∵l 1:y =k (x -4)过定点M (4,0), 而点M 关于点(2,1)的对称点为N (0,2), 故直线l 2过定点(0,2).10.直线y =ax +1a的图象可能是( )考点 直线的斜截式方程 题点 直线斜截式方程的应用 答案 B解析 根据斜截式方程知,斜率与直线在y 轴上的纵截距同正负.11.若直线x -2y +5=0与直线2x +my -6=0互相垂直,则实数m 等于( ) A.-1 B.1 C.12 D.-12考点 直线的一般式方程与直线的垂直关系 题点 根据垂直求参数的值 答案 B解析 由两直线垂直,得12×⎝⎛⎭⎫-2m =-1,解得m =1. 12.已知直线x -2y +m =0(m >0)与直线x +ny -3=0互相平行,且两者之间的距离是5,则m +n 等于( ) A.-1 B.0 C.1 D.2考点 两条平行直线间的距离公式及应用 题点 利用两条平行直线间的距离求参数的值 答案 B解析 由题意知,所给两条直线平行,∴n =-2. 由两条平行直线间的距离公式,得d =|m +3|12+(-2)2=|m +3|5=5,解得m =2或m =-8(舍去),∴m +n =0.二、填空题(本大题共4小题,每小题5分,共20分)13.过点(-2,-3)且在x 轴,y 轴上的截距相等的直线方程为____________. 考点 直线的截距式方程 题点 利用截距式求直线方程 答案 x +y +5=0或3x -2y =0解析 当直线过原点时,所求直线的方程为3x -2y =0;当直线不过原点时,所求直线的方程为x +y +5=0.14.过两直线x -3y +1=0和3x +y -3=0的交点,并且与原点的最短距离为12的直线的方程为________.答案 x =12或x -3y +1=0解析 易求得两直线交点的坐标为⎝⎛⎭⎫12,32,当斜率不存在时,显然直线x =12满足条件.当斜率存在时,设过该点的直线方程为y -32=k ⎝⎛⎭⎫x -12, 化为一般式得2kx -2y +3-k =0, 因为直线与原点的最短距离为12,所以|3-k |4+4k 2=12,解得k =33,所以所求直线的方程为x -3y +1=0.15.已知直线x -2y -2k =0与两坐标轴围成的三角形的面积不大于1,则实数k 的取值范围是________________. 答案 [-1,0)∪(0,1]解析 令x =0,得y =-k ,令y =0,得x =2k , ∴三角形的面积S =12|xy |=k 2.又S ≤1,即k 2≤1.∴-1≤k ≤1.又当k =0时,直线过原点,与两坐标轴构不成三角形,故应舍去. ∴实数k 的取值范围是[-1,0)∪(0,1].16.已知直线l 与直线y =1,x -y -7=0分别相交于P ,Q 两点,线段PQ 的中点坐标为(1,-1),那么直线l 的斜率为________. 考点 中点坐标公式 题点 求过中点的直线方程 答案 -23解析 设P (x,1),则Q (2-x ,-3),将点Q 的坐标代入x -y -7=0,得2-x +3-7=0. ∴x =-2,∴P (-2,1),∴k l =-23.三、解答题(本大题共6小题,共70分)17.(10分)已知点M 是直线l :3x -y +3=0与x 轴的交点,将直线l 绕点M 旋转30°,求所得直线l ′的方程. 考点 直线的一般式方程题点 求直线的一般式方程及各种方程的互化 解 在3x -y +3=0中,令y =0,得x =-3, 即M (-3,0).∵直线l 的斜率k =3,∴其倾斜角θ=60°. 若直线l 绕点M 逆时针方向旋转30°, 则直线l ′的倾斜角为60°+30°=90°, 此时斜率不存在,故其方程为x =- 3.若直线l 绕点M 顺时针方向旋转30°,则直线l ′的倾斜角为60°-30°=30°,此时斜率为tan 30°=33, 故其方程为y =33(x +3),即x -3y +3=0. 综上所述,所求直线方程为x +3=0或x -3y +3=0.18.(12分)已知直线l 经过点(0,-2),其倾斜角的大小是60°. (1)求直线l 的方程;(2)求直线l 与两坐标轴围成的三角形的面积.解 (1)由直线的点斜式方程得直线l 的方程为y +2=tan 60°·x ,即3x -y -2=0. (2)设直线l 与x 轴、y 轴的交点分别为A ,B , 令y =0得x =233;令x =0得y =-2.所以S △AOB =12|OA |·|OB |=12×233×2=233,故所求三角形的面积为233.19.(12分)已知直线l 1的方程为x +2y -4=0,若l 2在x 轴上的截距为32,且l 1⊥l 2.(1)求直线l 1与l 2的交点坐标;(2)已知直线l 3经过l 1与l 2的交点,且在y 轴上的截距是在x 轴上的截距的2倍,求l 3的方程. 解 (1)设l 2的方程为2x -y +m =0, 因为l 2在x 轴上的截距为32,所以3-0+m =0,m =-3, 即l 2:2x -y -3=0.联立⎩⎪⎨⎪⎧ x +2y -4=0,2x -y -3=0得⎩⎪⎨⎪⎧x =2,y =1.直线l 1与l 2的交点坐标为(2,1). (2)当l 3过原点时,l 3的方程为y =12x .当l 3不过原点时,设l 3的方程为x a +y2a =1(a ≠0),又直线l 3经过l 1与l 2的交点, 所以2a +12a =1,得a =52,l 3的方程为2x +y -5=0.综上,l 3的方程为x -2y =0或2x +y -5=0.20.(12分)已知点A (5,1)关于x 轴的对称点为B (x 1,y 1),关于原点的对称点为C (x 2,y 2). (1)求△ABC 中过AB ,BC 边上中点的直线方程; (2)求△ABC 的面积. 考点 中点坐标公式 题点 与中位线有关的问题解 (1)∵点A (5,1)关于x 轴的对称点为B (x 1,y 1),∴B (5,-1), 又∵点A (5,1)关于原点的对称点为C (x 2,y 2), ∴C (-5,-1),∴AB 的中点坐标是(5,0),BC 的中点坐标是(0,-1).过(5,0),(0,-1)的直线方程是y -0-1-0=x -50-5, 整理得x -5y -5=0.(2)易知|AB |=|-1-1|=2,|BC |=|-5-5|=10,AB ⊥BC , ∴△ABC 的面积S =12|AB |·|BC |=12×2×10=10.21.(12分)已知直线l 1:y =-k (x -a )和直线l 2在x 轴上的截距相等,且它们的倾斜角互补,又知直线l 1过点P (-3,3).如果点Q (2,2)到直线l 2的距离为1,求l 2的方程. 考点 直线的一般式方程题点 求直线的一般式方程及各种方程的互化 解 由题意,可设直线l 2的方程为y =k (x -a ), 即kx -y -ak =0,∵点Q (2,2)到直线l 2的距离为1,∴|2k -2-ak |k 2+1=1,①又∵直线l 1的方程为y =-k (x -a ), 且直线l 1过点P (-3,3),∴ak =3-3k .② 由①②得|5k -5|k 2+1=1,两边平方整理得12k 2-25k +12=0,解得k =43或k =34.∴当k =43时,代入②得a =-34,此时直线l 2的方程为4x -3y +3=0;当k =34时,代入②得a =1,此时直线l 2的方程为3x -4y -3=0.综上所述,直线l 2的方程为4x -3y +3=0或3x -4y -3=0.22.(12分)已知直线l :y =4x 和点P (6,4),点A 为第一象限内的点且在直线l 上,直线P A 交x 轴的正半轴于点B ,(1)当OP ⊥AB 时,求AB 所在直线的方程;(2)求△OAB 面积的最小值,并求当△OAB 面积取最小值时点B 的坐标. 考点 点到直线的距离题点 与点到直线的距离有关的最值问题解 (1)∵点P (6,4),∴k OP =23.又∵OP ⊥AB ,∴k AB =-32.∵AB 过点P (6,4),∴直线AB 的方程为y -4=-32(x -6),化为一般式可得3x +2y -26=0.(2)设点A (a,4a ),a >0,点B 的坐标为(b,0),b >0,当直线AB 的斜率不存在时,a =b =6,此时△OAB 的面积S =12×6×24=72.当直线AB 的斜率存在时,有4a -4a -6=0-4b -6,解得b =5aa -1, 故点B 的坐标为⎝⎛⎭⎫5a a -1,0,故△OAB 的面积S =12·5a a -1·4a =10a 2a -1,即10a 2-Sa +S =0.①由题意可得方程10a 2-Sa +S =0有解, 故判别式Δ=S 2-40S ≥0,∴S ≥40,故S 的最小值为40,此时①为a 2-4a +4=0,解得a =2. 综上可得,△OAB 面积的最小值为40, 当△OAB 面积取最小值时,点B 的坐标为(10,0).。
2018年高中数学必修2期末考试

2018年高中数学必修二期末考试考试时间:2小时满分150分一、选择题(本大题共12小题,共60.0分)1.若是两条不同的直线,是两个不同的平面,则下列命题正确的是A. 若,则B. 若,则C. 若,则D. 若,则2.平面平面,它们之间的距离为,,点,点C是点B在的射影,且,则CD的最小值是A. 2B. 3C.D.3.经过点且在两坐标轴上的截距相等的直线方程是A. B.C. 或D. 或4.已知几何体的三视图如图所示,则该几何体是A. 体积为2的三棱锥B. 体积为2的四棱锥C. 体积为4的三棱锥D. 体积为4的四棱锥5.已知长方形的一组邻边长分别是,沿对角线AC折成一个三棱锥,则该三棱锥外接球的表面积是A. B. C. D.6.已知的一个顶点,, , 的角平分线方程分别是则的直线方程为A. B. C. D.7.以,为端点的线段的垂直平分线的方程是A. B. C. D.8.在平面直角坐标系xoy中,圆C的方程为,若直线上存在一点P,且过P作圆的两条切线相互垂直,则实数b的取值范围是A. B. C. D.9.圆:与圆:的位置关系是A. 内切B. 外离C. 内含D. 相交10.如图,已知,点C在内,且,若半径为1的圆C与的两边没有交点,点分别在射线上异于O的动点,则的最小值是A.B. 4C. 3D.11.在平面直角坐标系xoy中,已知AB是圆直径,若直线上存在点P,连接AP与圆O交于点Q,且满足,则实数k的取值范围是A. B. C. D.12.已知直线︰,动直线︰,则下列结论错误的是A. 存在k,使得的倾斜角为B. 对任意的,与都有公共点C. 对任意的,与都不重合D. 对任意的,与都不垂直二、填空题(本大题共4小题,共20.0分)13.如图所示,水平放置的的斜二测直观图是图中的,已知,则AB边的实际长度是________.14.已知圆,点P是直线上的动点,若在圆M上存在点Q,使得,则点P横坐标的取值范围是______.15.已知,点P在圆上运动,则的最小值是________.16.如图,正方体的棱长为4,动点P在正方形及其内部运动,且保持,在点P运动中,线段AP扫过的曲面的面积等于_________.三、解答题(本大题共6小题,共70.0分)17.已知曲线:.Ⅰ若曲线是一个圆,且点,在圆外,求实数m的取值范围;Ⅱ当时,曲线关于直线对称的曲线为设P为平面上的点,满足:存在过P点的无穷多对互相垂直的直线,它们分别与曲线和曲线相交,且直线被曲线截得的弦长与直线被曲线截得的弦长总相等.求所有满足条件的点P的坐标;若直线被曲线截得的弦为MN,直线被曲线截得的弦为RS,设与的面积分别为与,试探究是否为定值?若是,求出该定值;若不是,请说明理由.18.已知平行四边形ABCD对角线的交点是,AB边所在直线的方程为,AD边所在直线的方程为.Ⅰ求BC边所在的直线的方程;Ⅱ求平行四边形ABCD的面积.19.今有边长为12尺的正方形水池的中央生长着芦苇,长出水面的部分为2尺,将芦苇牵引向池岸,恰巧与水岸齐接。
高中数学必修二 期末模拟卷03(无答案)

期末模拟卷3一.选择题(共8小题)1.复数z满足z(1+i)=1﹣i,则z的虚部等于()A.﹣i B.﹣1C.0D.12.在一个随机试验中,彼此互斥的事件A,B,C,D发生的概率分别为0.1,0.1,0.4,0.4,则下列说法正确的是()A.A与B+C是互斥事件,也是对立事件B.B+C与D是互斥事件,也是对立事件C.A+B与C+D是互斥事件,但不是对立事件D.A+C与B+D是互斥事件,也是对立事件3.已知△ABC中,AB=2,BC=3,AC=,则cos B=()A.B.C.D.4.如图,非零向量,,且BC⊥OA,C为垂足,若,则λ=()A.B.C.D.5.某班统计一次数学测验的平均分与方差,计算完毕以后才发现有位同学的卷子还未登分,只好重算一次.已知原平均分和原方差分别为、s2,新平均分和新方差分别为、s12,若此同学的得分恰好为,则()A.=,s2=s12B.=,s2<s12C.=,s2>s12D.<,s2=s126.如图所示,一个水平放置的平面图形的斜二测直观图是等腰梯形OA'B'C',且直观图OA'B'C'的面积为2,则该平面图形的面积为()A.2B.4C.4D.27.某实验单次成功的概率为0.8,记事件A为“在实验条件相同的情况下,重复3次实验,各次实验互不影响,则3次实验中至少成功2次”,现采用随机模拟的方法估计事件A的概率:先由计算机给出0~9十个整数值的随机数,指定0,1表示单次实验失败,2,3,4,5,6,7,8,9表示单次实验成功,以3个随机数为组,代表3次实验的结果经随机模拟产生了20组随机数,如表:752029714985034437863694141469037623804601366959742761428261根据以上方法及数据,估计事件A的概率为()A.0.384B.0.65C.0.9D.0.9048.已知三棱锥P﹣ABC的各顶点都在同一球面上,且P A⊥平面ABC,AB=2,AC=1,∠ACB=90°,若该棱锥的体积为,则此球的表面积为()A.16πB.20πC.8πD.5π二.多选题(共4小题)9.某公司生产三种型号的轿车,产量分别为1500辆,6000辆和2000辆.为检验该公司的产品质量,公司质监部要抽取57辆进行检验,则下列说法正确的是()A.应采用分层随机抽样抽取B.应采用抽签法抽取C.三种型号的轿车依次应抽取9辆,36辆,12辆D.这三种型号的轿车,每一辆被抽到的概率都是相等的10.下列叙述中,正确的是()A.若||=0,则=0B.若||=0,则∥C.若∥,∥,则∥D.若=,=,则=11.雷达图是以从同一点开始的轴上表示的三个或更多个定量变量的二维图表的形式显示多变量数据的图形方法.为比较甲,乙两名学生的数学学科素养的各项能力指标值(满分为5分,分值高者为优),绘制了如图所示的六维能力雷达图,例如图中甲的数学抽象指标值为4,乙的数学抽象指标值为5,则下面叙述正确的是()A.甲的逻辑推理能力指标值优于乙的逻辑推理能力指标值B.甲的数学建模能力指标值优于乙的直观想象能力指标值C.乙的六维能力指标值整体水平优于甲的六维能力指标值整体水平D.甲的数学运算能力指标值优于甲的直观想象能力指标值12.如图,棱长为2的正方体ABCD﹣A1B1C1D1中,P在线段BC1(含端点)上运动,则下列判断正确的是()A.A1P⊥B1DB.三棱锥D1﹣APC的体积不变,为C.A1P∥平面ACD1D.A1P与D1C所成角的范围是三.填空题(共4小题)13.如表为武汉市2018年月平均降水量:月份123456789101112月平均降水量/cm5.8 4.8 5.3 4.6 5.6 5.6 5.17.1 5.6 5.36.4 6.6则武汉市2018年月平均降水量的三个四分位数分别为cm,cm,cm .14.已知i是虚数单位,则=.15.已知等边△ABC,D 为BC中点,若点M是△ABC 所在平面上一点,且满足,则=.16.某广场设置了一些石凳供大家休息,这些石凳是由正方体截去八个一样大的四面体得到的(如图).则该几何体共有个面;如果被截正方体的棱长是50cm,那么石凳的表面积是cm2.四.解答题(共6小题)17.设=(2,0),=(1,).(1)若(﹣λ)⊥,求实数λ的值;(2)若=x+y(x,y∈R),且||=2,与的夹角为,求x,y的值.18.甲,乙,丙三名射击运动员分别对一目标射击1次,甲射中的概率为0.90,乙射中的概率为0.95,丙射中的概率为0.95.求:(1)三人中恰有一人没有射中的概率;(2)三人中至少有两人没有射中的概率.(精确到0.001)19.如图,在三棱锥V﹣ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC=,O,M分别为AB,VA的中点.(1)求证:VB∥平面MOC;(2)求证:平面MOC⊥平面VAB.20.请从下面三个条件中任选一个,补充在下面的横线上,并作答.①=;②2c cos C=a cos B+b cos A;③△ABC的面积为c(a sin A+b sin B﹣c sin C).已知△ABC的内角A,B,C的对边分别为a,b,c,且_____.(1)求C;(2)若D为AB中点,且c=2,CD=,求a,b.21.“肥桃”因产于山东省泰安市肥城市境内而得名,已有1100多年的栽培历史.明代万历十一年(1583年)的《肥城县志》载:“果亦多品,惟桃最著名”.2016年3月31日,原中华人民共和国农业部批准对“肥桃”实施国家农产品地理标志登记保护.某超市在旅游旺季销售一款肥桃,进价为每个10元,售价为每个15元销售的方案是当天进货,当天销售,未售出的全部由厂家以每个5元的价格回购处理.根据该超市以往的销售情况,得到如图所示的频率分布直方图:(1)估算该超市肥桃日需求量的平均数(同一组中的数据用该组区间的中点值代表);(2)已知该超市某天购进了150个肥桃,假设当天的需求量为x个(x∈N,0≤x≤240),销售利润为y元.(ⅰ)求y关于x的函数关系式;(ⅱ)结合上述频率分布直方图,以频率估计概率的思想,估计当天利润y不小于650元的概率.22.《九章算术》是中国古代的一部数学专著,是《算经十书》中最重要的一部,成于公元一世纪左右.它是一本综合性的历史著作,是当时世界上最简练有效的应用数学,它的出现标志着中国古代数学形成了完整的体系.《九章算术》中将由四个直角三角形组成的四面体称为“鳖臑”,已知在三棱锥P﹣ABC中,P A⊥平面ABC.(1)从三棱锥P﹣ABC中选择合适的两条棱填空:⊥,则三棱锥P﹣ABC 为“鳖臑”;(2)如图,已知AD⊥PB,垂足为D,AE⊥PC,垂足为E,∠ABC=90°.(ⅰ)证明:平面ADE⊥平面P AC;(ⅱ)设平面ADE与平面ABC的交线为l,若P A=2,AC=2,求二面角E﹣l﹣C的大小.。
2018年高中数学必修二期末考试

2018年高中数学必修二期末考试考试时间 2小时满分150分一、选择题(本大题共12小题,共60.0分)1.一个体积为8cm3的正方体的顶点都在球面上,则球的表面积是( )A. 8πcm2B. 12πcm2C. 16πcm2D. 20πcm22.已知某个几何体的三视图如图所示,根据图中标出的尺寸(单位:cm),可得几何体的体积是( )cm3.A. 4B. 3C. 6D. 53.若圆x2+y2+Dx+Ey+F=0(D2+E2−4F>0)关于直线x−y=0对称,则可得到()A. D=EB. D=FC. E=FD. D=E且F≠04.已知双曲线C的右焦点F与抛物线y2=8x的焦点相同,若一点F为圆心,为半径的圆与双曲线相切,则双曲线方程为()A. B. C. D.5.如图,已知一个八面体的各条棱长均为1,四边形ABCD为正方形,给出下列命题:①不平行的两条棱所在的直线所成的角是60∘或90∘;②四边形AECF是正方形;③点A到平面BCE的距离为1.其中正确的命题有( )A. 0个B. 1个C. 2个D. 3个6.已知圆O1:(x−1)2+(y+3)2=4,圆O2:(x−2)2+(y+1)2=1,则两圆的位置关系是( )A. 相交B. 内切C. 内含D. 外切7.“a=1”是“方程x2+y2−2x+2y+a=0表示圆”的( )A. 充分而不必要条件B. 必要而不充分条件C. 充要条件D. 既不充分也不必要条件8.设A={(x,y)|y=1+√4−x2},B={(x,y)|y=k(x−2)+4},若A∩B中含有两个元素,则实数k的取值范围是( )A. [512,+∞) B. (512,34] C. (512,54] D. [13,34]9.直线3x+y+1=0和直线6x+2y+1=0的位置关系是( )A. 重合B. 平行C. 垂直D. 相交但不垂直10.如图,已知长方体的长和宽都是6cm,高是cm,则下列结论中正确的个数是()①BC和A′C′所成的角是45∘②AA′和BC′所成的角是30∘③A′B′和DD′的距离是6 ④B′C′和CD的距离是6A. 1B. 2C. 3D. 411.设m,n是两条不同的直线,α,β是两个不同的平面,下列命题中正确的是( )A. 若m⊥α,m//n,n//β,则α⊥βB. 若α//β,m⊂α,n⊂β,则m//nC. 若m⊥n,m⊂α,n⊂β,则α⊥βD. 若α⊥β,m⊂α,n⊂β,则m⊥n12.若直线l1:(m+3)x+4y+3m−5=0与l2:2x+(m+5)y−8=0平行,则m的值为( )A. −7B. −1或−7C. −6D. −133二、填空题(本大题共4小题,共20.0分)13.给出下列命题:①如果,是两条直线,且//,那么平行于经过的任何平面;②如果平面不垂直于平面,那么平面内一定不存在直线垂直于平面;③若直线,是异面直线,直线,是异面直线,则直线,也是异面直线;④已知平面⊥平面,且∩=,若⊥,则⊥平面;⑤已知直线⊥平面,直线在平面内,//,则⊥.其中正确命题的序号是.14.已知圆的极坐标方程为ρ=2sinθ,若直线{x=4t+ay=3t,(t为参数)与圆相切,则满足条件的整数a的值为______.15.已知一个空间几何体的三视图如下图所示,则该几何体的体积为cm3.16.直线l与圆x2+y2=1交于P、Q两点,P、Q的横坐标为x1,x2,△OPQ的面积(O为坐标原点),则x12+x22=______ .为12三、解答题(本大题共6小题,共70.0分)17.已知正方体ABCD−A′B′C′D′,P是线段上的异于端点B、B′的点,设PA∩A′B=E,PC∩BC′=F.(1)当P是BB′中点时,异面直线PC、AD所成角的正切值;(2)求证:EF//面ABCD.18.如图,已知正四棱锥V−ABCD中,AC与BD交于点M,VM是棱锥的高,若AC=6cm,VC=5cm,求正四棱锥V−ABCD的体积.19.如图1,在Rt△ABC中,∠ABC=90∘,∠BAC=60∘,AB=2,D,E分别为AC,BD的中点,连接AE并延长BC于F,将△ABD沿BD折起,使平面ABD⊥平面BCD,如图2,所示,(1)求证:AE⊥平面BCD;(2)求平面AEF与平面ADC所成的锐角二面角的余弦值;(3)在线段AF上是否存在点M使得EM//平面ADC?若存在,请指出点M的位置;若存在,请指出点M的位置;若不存在,说明理由.20.已知圆C:(x−3)2+(y−4)2=4和直线l:x+2y+2=0,直线m,n都经过圆C外定点A(1,0).(Ⅰ)若直线m与圆C相切,求直线m的方程;(Ⅱ)若直线n与圆C相交于P,Q两点,与l交于N点,且线段PQ的中点为M,求证:|AM|⋅|AN|为定值.21.如图,已知斜三棱柱ABC−A1B1C1中,AB=AC,D为BC的中点.(1)若平面ABC⊥平面BCC1B1,求证:AD⊥DC1;(2)求证:A1B//平面ADC1.22.如图,四边形ABCD为梯形,,求图中阴影部分绕AB旋转一周形成的几何体的表面积和体积23.答案和解析【答案】1. B2. A3. A4. B5. C6. A7. A8. B9. B10. B11. A12. A13. ②⑤.14. −315. 7π316. 117. 解:(1)在正方体正方体ABCD−A′B′C′D′中,∵BC//AD,∴∠PCB即为异面直线PC,AD所成角,在△PBC中,∵P是BB′中点,∴PB=12BB′=12BC,∴tan∠PCB=PBBC =12.(2)∵AA′//BB′,∴△PEB∽,同理有PFFC =PBCC′,∵A′A=C′C,∴PBA′A =PBCC′,∴在△PAC中,有PEEA =PFFC.∴EF//AC,又EF⊂面ABCD,AC⊆面ABCD,∴EF//面ABCD.18. 解:∵正四棱锥V−ABCD中,底面ABCD是正方形,且对角线AC=6cm∴BD=6cm,且AC⊥BD∴S ABCD=12×AC×BD=12×6×6=18(cm2)∵VM是棱锥的高,且VC=5cm∴Rt△VMC中,VM=√VC2−MC2=√52−32=4(cm)∴正四棱锥V−ABCD的体积为V=13S ABCD×VM=13×18×4=24(cm3)19. (Ⅰ)证明:在Rt△ABC中,∠ABC=90∘,D为AC的中点,∴AD=BD=DC,又∠BAC=60∘,∴△ABD为等边三角形,∵E是BD的中点,∴AE⊥BD,∵平面ABD⊥平面BCD,交线为BD,又在△ABD中,AE⊥BD于E,AE⊂平面ABD∴AE ⊥平面BCD .(Ⅱ)解:由(Ⅰ)结论AE ⊥平面BCD ,∴AE ⊥EF . 由题意知EF ⊥BD ,又AE ⊥BD .如图,以E 为坐标原点,分别以EF ,ED ,EA 所在直线为x 轴,y 轴,z 轴,建立空间直角坐标系E −xyz , 由(Ⅰ)知AB =BD =DC =AD =2,BE =ED =1. 由图1条件计算得则AE =√3,BC =2√3,EF =√33,则E(0,0,0),D(0,1,0),A(0,0,√3),F(√33,0,0),C(√3,2,0).则DC ⃗⃗⃗⃗⃗ =(√3,1,0),AD⃗⃗⃗⃗⃗⃗ =(0,1,−√3), 易知,平面AEF 的一个法向量为ED⃗⃗⃗⃗⃗ =(0,1,0). 设平面ADC 的法向量为n ⃗ =(x ,y ,z), 则{n⃗ ⋅DC ⃗⃗⃗⃗⃗ =0n ⃗ ⋅AD⃗⃗⃗⃗⃗⃗ =0,即{√3x +y =0y −√3z =0 令z =1,得y =√3,x =−1, 即n ⃗ =(−1,√3,1), ∴cos <n ⃗ ,ED⃗⃗⃗⃗⃗ >=√31×√5=√155, 即平面AEF 与平面ADC 所成的锐角二面角的余弦值为√155.(Ⅲ)解:设AM ⃗⃗⃗⃗⃗⃗ =λAF ⃗⃗⃗⃗⃗ ,其中λ∈[0,1]. ∵AF⃗⃗⃗⃗⃗ =(√33,0,−√3),∴AM⃗⃗⃗⃗⃗⃗ =λAF ⃗⃗⃗⃗⃗ =λ(√33,0,−√3),∴EM ⃗⃗⃗⃗⃗⃗ =EA ⃗⃗⃗⃗⃗ +AM ⃗⃗⃗⃗⃗⃗ =(√33λ,0,(1−λ)√3), 由EM ⃗⃗⃗⃗⃗⃗ ⋅n ⃗ =0,得√33λ−(1−λ)√3=0,解得λ=34∈[0,1].∴在线段AF 上是否存在点M 使得EM//平面ADC 且AM :AF =3:4. 20. 解:(Ⅰ)①若直线m 的斜率不存在,即直线是x =1,符合题意.②若直线m 斜率存在,设直线m 为y =k(x −1),即kx −y −k =0. 由题意知,圆心(3,4)到已知直线l 1的距离等于半径2, 即:|3k−4−k|√k 2+1=2,解之得k =34.所求直线方程是x =1,3x −4y −3=0. (II)用几何法,如图所示, △AMC∽△ABN ,则AMAB =ACAN ,可得|AM|⋅|AN|=|AC|⋅|AB|=2√5⋅3√5=6, 是定值.21. (本小题满分14分)证明:(1)因为AB=AC,D为BC的中点,所以AD⊥BC.因为平面ABC⊥平面BCC1B1,平面ABC∩平面BCC1B1=BC,AD⊂平面ABC,所以AD⊥平面BCC1B1.…(5分)因为DC1⊂平面BCC1B1,所以AD⊥DC1.…(7分)(2)(证法一)连接A1C,交AC1于点O,连接OD,则O为A1C的中点.因为D为BC的中点,所以OD//A1B.…(11分)因为OD⊂平面ADC1,A1B⊄平面ADC1,所以A1B//平面ADC1.…(14分)(证法二)取B1C1的中点D1,连接A1D1,DD1,D1B.则D1C1‖BD.所以四边形BDC1D1是平行四边形.所以D1B//C1D.因为C1D⊂平面ADC1,D1B⊄平面ADC1,所以D1B//平面ADC1.同理可证A1D1//平面ADC1.因为A1D1⊂平面A1BD1,D1B⊂平面A1BD1,A1D1∩D1B=D1,所以平面A1BD1//平面ADC1.…(11分)因为A1B∉平面A1BD1,所以A1B//平面ADC1.…(14分)22. ,【解析】1. 解:正方体体积为8,可知其边长为2,体对角线为√4+4+4=2√3,即为球的直径,所以半径为√3,表面积为4π(√3)2=12π.故选B.先根据正方体的顶点都在球面上,求出球的半径,然后求出球的表面积.本题考查学生的空间想象能力,以及对球的体积和表面积公式的考查,是基础题.2. 解:三视图复原的几何体是底面为直角梯形,一条侧棱垂直直角梯形的直角顶点的四棱锥,所以几何体的体积为:13×1+32×2×3=4故选:A.三视图复原的几何体是底面为直角梯形,一条侧棱垂直直角梯形的直角顶点的四棱锥,结合三视图的数据,求出几何体的体积.本题是基础题,考查几何体的三视图,几何体的表面积的求法,准确判断几何体的形状是解题的关键.3. 圆关于直线对称,即此直线是圆的对称轴,从而圆心在此直线上,即圆心坐标()应满足直线方程x−y=0,于是得到D=E.4. 本题考查了圆与双曲线的位置关系,考查了抛物线与双曲线的性质,解题的关键是利用代入验证法.解:抛物线的焦点为(2,0),即所求双曲线的右焦点为(2,0),故排除A,D答案.圆的方程为,B选项中,,可得,代入整理得,解得(舍去)或,即只有一根,故B选项符合题意,故选B.5. 解:因为八面体的各条棱长均为1,四边形ABCD为正方形,所以在四棱锥E−ABCD中,相邻两条侧棱所成的角为60∘,而像AE与CE所成的角为90∘,因为AE=CE=1,AC=√2,满足勾股定理的逆定理,所以AE⊥CE,同理AF⊥CF,AE⊥AF,所以四边形AECF是正方形;故①②正确;设点A到平面BCE的距离h,由V E−ABCD=2V A−BCE,所以13×1×1×√22=2×13×√34ℎ,解得ℎ=√63;所以点A到平面BCE的距离√63;故③错误;故选:C.利用直线和直所成的角以及利用等积法求点A到平面BCE的距离.本题考查了立体几何中线线关系以及线面关系,利用了等积法求点到平面的距离.6. 解:圆O1的圆心为O(1,−3),半径等于2,圆O2的圆心为(2,−1),半径等于1,它们的圆心距等于√(2−1)2+(−1+3)2=√5,因为2−1<√5<2+1,故两个圆相交,故选:A.先求出两个圆的圆心和半径,再根据它们的圆心距与半径之和、差的关系,可得两圆的位置关系.本题主要考查圆的标准方程,圆和圆的位置关系的判定方法,属于中档题.7. 解:方程x 2+y 2−2x +2y +a =0表示一个圆,则(−2)2+22−4a >0, ∴a <2,又a =1⇒a <2,反之不成立,∴a =1是方程x 2+y 2−2x +2y +a =0表示圆的充分不必要条件 故选:A .先由二元二次方程表示圆的条件得到a 的不等式,解不等式即可得方程x 2+y 2−2x +2y +a =0表示圆的充要条件,再看条件:“a =1”与此充要条件的关系,即可得到结果.本题考查二元二次方程表示圆的条件、必要条件、充分条件与充要条件的判断,属基础知识的考查,本题解题的关键是看清楚所表示的二元二次方程的各个系数之间的关系. 8. 解:由y =1+√4−x 2,平方化简得x 2+(y −1)2=4(y ≥1),∴集合A 表示以C(0,1)为圆心,半径为2的圆的上半圆.∵y =k(x −2)+4的图象是经过定点P(2,4)的一条直线,∴当直线与半圆有两个公共点时,集合C =A ∩B 中有两个元素.由直线y =k(x −2)+4与半圆相切时,圆心到直线的距离等于半径, 得|−2k+3|√k 2+1=2,解之得k =512(舍负)又∵直线经过半圆的左端点A(−2,1)时,它们有两个交点, 此时k =1−4−2−2=34,∴当直线夹在PA 到PB 之间(可与PA 重合,不与PB 重合)时, 直线y =k(x −2)+4与半圆有两个公共点,可得k ∈(512,34].故选:B根据题意,集合A 对应的图形是以C(0,1)为圆心、半径为2的圆的上半圆;集合B 对应的图形是经过定点P(2,4)的一条直线.A ∩B 中有两个元素,说明直线与圆有两个公共点,由此利用点到直线的距离公式和斜率公式加以计算,并观察直线倾斜角的变化,可得本题答案.本题给出两个集合的交集有两个元素,求参数k 的范围,着重考查了直线的方程、圆的方程、直线与圆的位置关系和点到直线的距离公式等知识,属于中档题.9. 解:∵直线3x +y +1=0即y =−3x −1,它的斜率k 1=−3,在y 轴上的截距是b 1=−1,直线6x +2y +1=0即y =−3x −12,此直线的斜率k 2=−3,在y 轴上的截距是b 2=−12, ∴k 1=k 2,b 1≠b 2,∴直线3x +y +1=0和直线6x +2y +1=0的位置关系是平行; 故选B .根据两直线的斜率相等,而在y 轴上的截距不同的两直线平行的定理来确定该题的答案.当直线y 1=k 1x +b 1与直线y 2=k 2x +b 2①平行时:k 1=k 2,b 1≠b 2;②重合时:k 1=k 2,b 1=b 2;③垂直时:k 1⋅k 2=−1.10. 解析:①③正确,②④不正确.答案:B11. 解:A ,若m ⊥α,m//n ,则n ⊥α,因为n//β,所以 α⊥β,正确; B ,α//β,m ⊂α,n ⊂β,m ,n 共面时,m//n ,不正确;C ,m ⊥n ,m ⊂α,n ⊂β,则α、β平行或相交,不正确;D ,若α⊥β,m ⊂α,n ⊂β,则m ,n 平行、相交、或异面,不正确;故选A .对四个选项分别进行判断,即可得出结论.本题考查空间直线与直线、直线与平面,平面与平面的位置关系,考查学生分析解决问题的能力,属于中档题.12. 解:直线l 1的斜率一定存在,为m+3−4,但当m =−5时,l 2的斜率不存在,两直线不平行. 当m ≠−5时,l 2的斜率存在且等于−2m+5,由两直线平行,斜率相等得m+3−4=−2m+5,解得m =−1或−7.当m =−1时,两直线重合,故不满足条件;经检验,m =−7满足条件,故选A . 直线l 1的斜率一定存在,为m+3−4,所以,当两直线平行时,l 2的斜率存在,求出l 2的斜率,利用它们的斜率相等解出m 的值.本题考查两直线平行的条件,两直线平行时,它们的斜率相等或者都不存在. 13. 试题分析:①错,a ,b 可能共面;②正确.若平面内一定存在直线垂直于平面,则平面垂直于平面.③错:a ,c 可能相交,也可能异面,也可能平行.④错.因为不一定在平面内.⑤正确.因为⊥平面,//,所以b ⊥平面,又因为在平面内,所以⊥. 因而正确的有②⑤.考点:线线,线面,面面平行与垂直的条件.点评:掌握线线,线面,面面平行与垂直的判定定理是解决这类小题的关键,因而要把这些有关的定理记熟.14. 解:把圆的极坐标方程为ρ=2sinθ,化为直角坐标方程为x 2+(y −1)2=1, 表示以(0,1)为圆心、半径等于1的圆.把直线{x =4t +a y =3t,(t 为参数)消去参数化为普通方程为3x −4y −3a =0, 根据圆心到直线的距离等于半径可得√9+16=1,求得整数a =−3,故答案为:−3.把直线的参数方程、圆的极坐标方程化为直角坐标方程,根据根据圆心到直线的距离等于半径,利用点到直线的距离公式求得整数a 的值.本题主要考查把参数方程、极坐标方程化为直角坐标方程的方法,点到直线的距离公式的应用,属于基础题.15. 【分析】本题考查了由三视图求几何体的体积,解题的关键是判断几何体的形状及数据所对应的几何量.由三视图知几何体是一圆柱挖去一个半球,且圆柱的高为3,圆柱与球的半径都是1,代入体积公式求出圆柱的体积与半球的体积相减.【解答】解:由三视图知几何体是一圆柱挖去一个半球,且圆柱的高为3,圆柱与球的半径都是1,∴几何体的体积V =π×12×3−23π×13=7π3.故答案是7π3. 16. 解:当直线l 斜率存在时,设直线方程为y =kx +b ,和圆的方程联立消y 并整理得(1+k 2)x 2+2kbx +b 2−1=0,由韦达定理可得x 1+x 2=−2kb 1+k 2,x 1x 2=b 2−11+k 2, ∵△OPQ 的面积为12,∴12×1×1×sin∠POQ =12,∴sin∠POQ =1,∠POQ =90∘,∴OP ⃗⃗⃗⃗⃗ ⋅OQ⃗⃗⃗⃗⃗⃗ =x 1x 2+y 1y 2=x 1x 2+(kx 1+b)(kx 2+b) =(1+k 2)x 1x 2+kb(x 1+x 2)+b 2=(1+k 2)b 2−11+k 2+kb −2kb 1+k 2+b 2=0,化简可得2b 2=k 2−1,∴x 12+x 22=(x 1+x 2)2−2x 1x 2=2b 2(k 2−1)+2(1+k 2)(1+k 2)2=1验证可得当直线斜率不存在时,仍有x 12+x 22=1故答案为:1当直线l 斜率存在时,设直线方程为y =kx +b ,联立方程由韦达定理可得x 1+x 2=−2kb1+k 2,x 1x 2=b 2−11+k 2,由三角形的面积可得∠POQ =90∘,进而可得OP ⃗⃗⃗⃗⃗ ⋅OQ ⃗⃗⃗⃗⃗⃗ =0,可得2b 2=k 2−1,代入x 12+x 22=(x 1+x 2)2−2x 1x 2,化简可得.本题考查直线和圆的位置关系,涉及三角形的面积公式和韦达定理以及向量的垂直,属中档题.17. (1)根据BC//AD ,判定∠PCB 即为异面直线PC ,AD 所成角,在△PBC 中求其正切值. (2)利用三角形相似,判断线段成比例,来证明EF//AC ,在有线线平行证线面平行. 本题考查了线面平行的判定,考查了异面直线所成的角,考查了学生的空间想象能力,逻辑推理能力.18. 分别求正四棱锥棱锥的底面积和高即可求体积本题考查求几何体的体积,关键是求底面积和高,有些题可以用割补法,把原几何体构造成比较规则的几何体后再求体积,也有些题可以用等积转化求体积.属简单题 19. (Ⅰ)由已知条件推导出AE ⊥BD 于E ,由此能证明AE ⊥平面BCD .(Ⅱ)以E 为坐标原点,分别以EF ,ED ,EA 所在直线为x 轴,y 轴,z 轴,建立空间直角坐标系E −xyz ,利用向量法能求出二面角的余弦值.(Ⅲ)根据线面平行的判定定理,利用向量法建立共线共线,设AM ⃗⃗⃗⃗⃗⃗ =λAF⃗⃗⃗⃗⃗ ,解方程即可. 本题考查直线与平面垂直的证明,考查二面角的余弦值的求法,考查满足条件的点是否存在的判断,解题时要认真审题,注意向量法的合理运用,综合性较强,运算量较大. 20. (Ⅰ)①当直线m 的斜率不存在,即直线是x =1,成立,②当直线m 斜率存在,设直线m 为y =k(x −1),由圆心到直线的距离等于半径求解.(II)用几何法,作出直线与圆的图象,根据三角形相似,将|AM|⋅|AN|转化为|AC|⋅|AB|验证求解.本题主要考查直线与圆的位置关系及其方程的应用,主要涉及了直线与圆相切,直线与圆相交时构造三角形及三角形相似的应用.21. (1)由D为等腰三角形底边BC的中点,利用等腰三角形的性质可得AD⊥BC,再利用已知面面垂直的性质即可证出.(2)证法一:连接A1C,交AC1于点O,再连接OD,利用三角形的中位线定理,即可证得A1B//OD,进而再利用线面平行的判定定理证得.证法二:取B1C1的中点D1,连接A1D1,DD1,D1B,可得四边形BDC1D1及D1A1AD是平行四边形.进而可得平面A1BD1//平面ADC1.再利用线面平行的判定定理即可证得结论.22. 【解析】试题分析:直角梯形绕直角腰旋转一周形成的是圆台,四分之一圆绕半径所在的直线旋转一周,形成的是半球,所以阴影部分绕旋转一周形成的是组合体,圆台挖去半球,,.试题解析:解:圆中阴影部分是一个圆台,从上面挖出一个半球S半球=×4π×22=8πS圆台侧=π×(2+5)×5=35πS圆台底=25π故所求几何体的表面积S表=8π+35π+25π=68π5分V圆台=V半球=.故所求几何体的体积V=V圆台−V半球=10分.考点:简单组合体的表面积和体积.。
高2018级高二下期期末试题数学(理科)

高2018级高二下期期末考试数学试题理 科一、选择题:本大题共12小题,每小题5分,共60分.1.已知集合,,则( )A .B .C .D .2.已知复数满足,则( ) A .B .C .D .3.为了得到函数的图象,只需把函数的图象( ) A .向左平移个长度单位 B .向左平移个长度单位 C .向右平移个长度单位 D .向右平移个长度单位 4.已知为等差数列的前项和,,,则( ) A . B . C . D .5.已知非零向量,满足且,则与的夹角为( ) A .B .C .D .6.如图所示的程序框图输出的是,则图中空白框中应填入( ){}24A x x x =≤{}230B x x =-<A B =I 302x x ⎧⎫≤≤⎨⎬⎩⎭342x x ⎧⎫<≤⎨⎬⎩⎭342x x ⎧⎫≤≤⎨⎬⎩⎭302x x ⎧⎫≤<⎨⎬⎩⎭z i 1i z =-z =1i --1i -1i -+1i +πsin(2)3y x =-πsin(2)6y x =+π4π2π4π2n S }{n a n 515S =612a =332n a n =+36n a n =-2312n S n n =-227n S n n =-ab |||=a b (3)-⊥a b b a b π3π62π35π6S30A .B .C .D .7.已知m 为非零实数,则“1m<-1”是“m >-1”的 ( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件8.已知圆的半径为,在圆内随机取一点,则过点的所有弦的长度都大于( ) A .B .C .D.9.已知某几何体的三视图如图所示,则该几何体的体积为( )A .B .C .D .10.已知,为椭圆()的两个焦点,为椭圆短轴上的一个顶点,,则椭圆的离心率的取值范围为( )A .B .C .D . 11.已知二次不等式ax 2+2x +b >0的解集为⎩⎨⎧x ⎪⎪⎪⎭⎬⎫x ≠-1a 且a >b ,则a 2+b 2a -b的最小值为( )A.2 B. 2 2 C. 4 2 D. 8 212.知函数f(x )=2ax 3-3ax 2+1,g (x )=-a 4x +32,若任意给定的x 0∈[0,2],总存在两个不同的x i (i =1,2)∈[0,2],使得f (x i )=g (x 0)成立,则实数a 的取值范围是( )A .(-∞,-1)B .(1,+∞)C .(-∞,-1)∪(1,+∞)D .[-1,1]2S S n =+22S S n =+2nS S =+S S n =+C 2C M M 1π3414129π182+9π362+18π18+18π36+1F 2F 22221x y a b+=0a b >>B 21212||BF BF F F ⋅≥u u u r u u u u r u u u u r ,1)3(0,3(0,66二、填空题:本大题共4小题,每小题5分,共20分.13.已知一组样本数据(x 1,y 1),(x 2,y 2),(x 3,y 3),…,(x 6,y 6),用最小二乘法得到其线性回归方程为y^=-2x +4,若x 1,x 2,x 3,…,x 6的平均数为1,则y 1+y 2+y 3+…+y 6=14.设为等比数列的前项和,若且,则 . 15.若变量x ,y 满足⎩⎪⎨⎪⎧x +y ≤2,2x -3y ≤9,x ≥0,则x 2+y 2的最大值是16.在正三棱锥中,侧面、侧面、侧面两两垂直,且侧棱, 则正三棱锥外接球的表面积为_________.三、解答题:本大题共6个大题,共70分.解答应写出文字说明、证明过程或演算步骤.17.(12分)在中,内角,,所对的边为,,,且满足.(1)求; (2)若,求. 18.(12分)2019年,我国施行个人所得税专项附加扣除办法,涉及子女教育、继续教育、大病医疗、住房贷款利息或者住房租金、赡养老人等六项专项附加扣除.某单位老、中、青员工分别有72,108,120人,现采用分层抽样的方法,从该单位上述员工中抽取25人调查专项附加扣除的享受情况. (1)应从老、中、青员工中分别抽取多少人?(2)抽取的25人中,享受至少两项专项附加扣除的员工有6人,分别记为A ,B ,C ,D ,E ,F .享受情况如下表,其中“○”表示享受,“×”表示不享受.现从这6人中随机抽取2人接受采访.②设M 为事件“抽取的2人享受的专项附加扣除至少有一项相同”,求事件M 发生的概率.n S {}n a n 114a =24643a a =5S =S ABC -SAB SAC SBC SA =S ABC -ABC △A B C a b c sin sin sin sin A C B Ab a c---=+C 4cos 5B =()cos B A -19.(12分)如图,在三棱锥中,,,两两垂直且相等,过的中点作平面,且分别交,于,,交,的延长线于,.(1)求证:平面;(2)若,求二面角的余弦值.20.(12分)已知椭圆()2222:10x y C a b a b +=>>,两焦点与短轴的一个端点的连线构成的(1)求椭圆C 的方程; (2)设与圆O :2234x y +=相切的直线l 交椭圆C 于A ,B 两点(O 为坐标原点),求△AOB 面积的最大值。
人教版高中数学必修二期末测试题一及答案

高中数学必修二期末测试题一一、选择题(本大题共2道小题,每小题5分,共60分。
)1、下图(1)所示的圆锥的俯视图为 ( )2、直线:30l y ++=的倾斜角α为 ( )A 、30o ;B 、60o ;C 、120o ;D 、150o 。
3、边长为a 正四面体的表面积是 ( )A3; B3a ; C2; D2。
4、对于直线:360l x y -+=的截距,下列说法正确的是 ( )A 、在y 轴上的截距是6;B 、在x 轴上的截距是6;C 、在x 轴上的截距是3;D 、在y 轴上的截距是3-。
5、已知,a b αα⊂//,则直线a 与直线b 的位置关系是 ( )A 、平行;B 、相交或异面;C 、异面;D 、平行或异面。
6、已知两条直线12:210,:40l x ay l x y +-=-=,且12l l //,则满足条件a 的值为 ( )A 、12-; B 、12; C 、2-; D 、2。
7、在空间四边形ABCD 中,,,,E F G H 分别是,,,AB BC CD DA 的中点。
若AC BD a ==,且AC 与BD 所成的角为60o,则四边形EFGH 的面积为 ( )A2; B2; C2; D2。
图(1)ABCD8、已知圆22:260C x y x y +-+=,则圆心P 及半径r 分别为 ( )A 、圆心()1,3P ,半径10r =;B 、圆心()1,3P ,半径r =C 、圆心()1,3P -,半径10r =;D 、圆心()1,3P -,半径r =。
9、下列叙述中错误的是 ( )A 、若P αβ∈I 且l αβ=I ,则P l ∈;B 、三点,,A BC 确定一个平面;C 、若直线a b A =I ,则直线a 与b 能够确定一个平面;D 、若,A l B l ∈∈且,A B αα∈∈,则l α⊂。
10、两条不平行的直线,其平行投影不可能是 ( )A 、两条平行直线;B 、一点和一条直线;C 、两条相交直线;D 、两个点。
2018年高中数学必修二期末考试
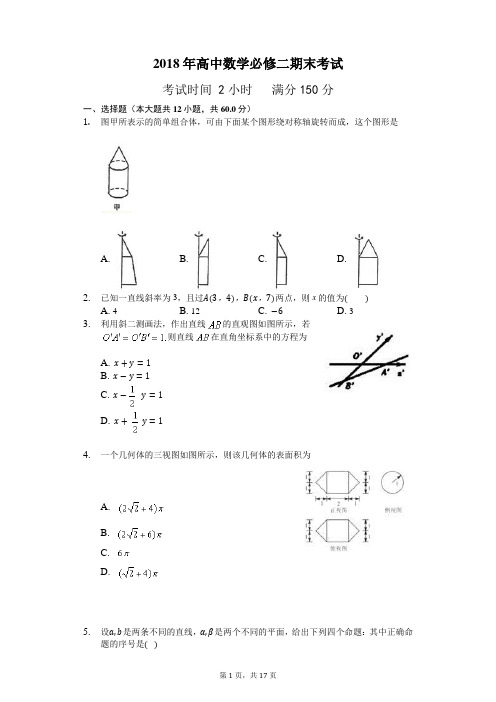
2018年高中数学必修二期末考试考试时间2小时满分150分一、选择题(本大题共12小题,共60.0分)1.图甲所表示的简单组合体,可由下面某个图形绕对称轴旋转而成,这个图形是A. B. C. D.2.已知一直线斜率为3,且过A(3,4),B(x,7)两点,则x的值为( )A. 4B. 12C. −6D. 33.利用斜二测画法,作出直线的直观图如图所示,若则直线在直角坐标系中的方程为A. x+y=1B. x−y=1C. x−y=1D. x+y=14.一个几何体的三视图如图所示,则该几何体的表面积为A.B.C.D.5.设a,b是两条不同的直线,α,β是两个不同的平面,给出下列四个命题:其中正确命题的序号是()①如果,那么a//b;②如果a//β,a⊂α,b⊂β,那么a//b;③如果,那么a⊥β;④如果a⊥β,a//b,,那么A. ①B. ②C. ③D. ④6.设是三个不重合的平面,l是直线,则下列结论正确的是A. 若,则B. 若C. 若//,且//,则//D. 若l上存在两点到的距离相等,则7.已知、是不同的平面,、是不同的直线,则下列命题不正确的是A. 若,m//n,,则B. 若m//,,则m//nC.若m//n,,则D.若,,则//8.直线的倾斜角为A. 30∘B. 60∘C. 120∘D. 150∘9.已知直线l过圆x2+(y−3)2=4的圆心,且与直线x+y+1=0垂直,则l的方程是A. x−y+3=0B. x−y−2=0C. x+y−3=0D. x+y−2=010.已知圆M:x2+y2−2ay=0(a>0)截直线x+y=0所得线段的长度是22,则圆M与圆N:(x−1)2+(y−1)2=1的位置关系是A. 外离B. 相切C. 相交D. 内含11.两条平行线与间的距离为A. 1B.C.D.12.如果直线与直线,互相平行,则a的值等于A. 1B. −1C. 1,−1D. 1,0,−1二、填空题(本大题共4小题,共20.0分)13.正方体的棱长为2,则它的外接球的表面积为_____________.14.将一副斜边长相等的直角三角板拼接成如图所示的空间图形,其中AD=BD=,∠BAC=300.若它们的斜边AB重合,让三角板ABD以AB为轴转动,则下列说法正确的是_________________.①当平面ABD⊥平面ABC时,C、D两点间的距离为;②在三角板ABD转动过程中,总有AB⊥CD;③在三角板ABD转动过程中,三棱锥D−ABC的体积最大可达.15.16、如图,两个正方形所在平面互相垂直,设M,N分别是的中点,那么其中正确结论的序号是。
高中数学选择性必修二 期末模块检测(基础卷)(含答案)

选择性必修第二册 期末模块检测试卷 基础A 卷解析版学校:___________姓名:___________班级:___________考号:___________题型:8(单选)+4(多选)+4(填空)+6(解答),满分150分,时间:120分钟一、单选题1.已知等比数列{}n a 中,1212a a +=,3134a a -=,则4=a ( )A .18- B .18C .4-D .4【答案】A 【分析】根据题意,将条件表示为1,a q 的形式,计算出1,a q ,再计算4a 即可. 【详解】∵等比数列{}n a 中,1212a a +=,3134a a -=,∴112111234a a q a a q ⎧+=⎪⎪⎨⎪-=⎪⎩,解得111,2a q ==-, ∴341311128a a q ⎛⎫=⨯-=-⎪⎝⎭= .故选:A.2.已知等差数列{}n a 的前n 项和为n S ,3a =5,则5S =( ) A .5B .25C .35D .50【答案】B 【分析】根据等差中项及等差数列求和公式即可求解. 【详解】由题意可知,{}n a 为等差数列,所以15355()5252525222a a a S +⨯⨯⨯==== 故选:B3.古代数学著作《九章算术》有如下问题:“今有女子善织,日自倍,五日五尺,问日织几何?”意思是:“女子善于织布,每天织的布都是前一天的2倍,已知她5天共织布5尺,问这名女子每天分别织布多少?”某数学兴趣小组依托某制造厂用织布机完全模拟上述情景,则从第一天开始,要使织布机织布的总尺数为165尺,则所需的天数为( ) A .7 B .8 C .9 D .10【答案】D 【分析】设该女子第一天织布x 尺,根据题意,求得531x =尺,结合等比数列的求和公式,列出方程,即可求解. 【详解】设该女子第一天织布x 尺,则5天共织布5(12)512x -=-,解得531x =尺,在情境模拟下,设需要n天织布总尺数达到165尺,则有5(12)3116512n -=-,整理得21024n=,解得10n =.故选:D . 4.观察下列式子:213122+<,221151233++<,222111712344+++<,…,则可归纳出()2221111231n +++⋅⋅⋅++小于( )A .1n n + B .211n n -+ C .211n n ++ D .21nn + 【答案】C 【分析】根据已知式子分子和分母的规律归纳出结论. 【详解】由已知式子可知所猜测分式的分母为1n +,分子第1n +个正奇数,即21n ,()2221112112311n n n ++++⋅⋅⋅+<++∴. 故选:C.5.设曲线1e x y ax -=-在点1x =处的切线方程为2y x =,则a =( ) A .0 B .1C .2D .3【答案】D 【分析】利用12x y ='=可求得答案. 【详解】1e x y a -'=-,∵112x y a ==-=',则3a =.故选:D6.已知数列{}n a ,{}n b 都是等差数列,记n S ,n T 分别为{}n a ,{}n b 的前n 项和,且713n n S n T n-=,则55a b =( ) A .3415B .2310C .317D .6227【答案】D 【分析】利用等差数列的性质以及前n 项和公式即可求解. 【详解】由713n n S n T n-=, ()()19551991955199927916229239272a a a a a a Sb b b b b b T ++⨯-======++⨯. 故选:D7.已知函数()331xf x x e =++,其导函数为()f x ',则()()()()2020202020212021f f f f ''+-+--的值为( )A .1B .2C .3D .4【答案】C 【分析】求得可得()'f x 的解析式,求出()f x '-解析式,可得()f x '为偶函数,即可求出()()20212021f f ''--的值,再求()()3f x f x +-=,即可求得()()20202020f f +-的值,即可求得答案. 【详解】()()22331xxe f x x e-'=++,()()()2222333()311xxxxe ef x x x ee----'-=+-=+++,所以()f x '为偶函数,所以()()202120210f f ''--=,因为()()33333331111x x x x x e f x f x x x e e e e -+-=++-=+=++++,所以()()202020203f f +-=,所以()()()()20202020202120213f f f f ''+-+--=. 故选:C .8.已知函数()()()22210,0x ax x x f x e ax e x ⎧-+<⎪=⎨-+-≥⎪⎩有两个零点,则实数a 的取值范围是( ) A .(),e +∞ B .()2e ,+∞C .()20,eD .()0,e【答案】B 【分析】分离变量,利用导函数应用得到函数在0x <无零点,则0x >有两个零点,利用函数最值得到参数范围 【详解】当0x =时,()201e f =--,∴0x =不是函数()f x 的零点.当0x <时,由()0f x =,得221x a x -=,设()221x h x x -=,()()3210x h x x-'=<,则()h x 在(),0-∞上单调递减,且()0h x <.所以0x <时无零点当0x >时,()0f x =等价于2x e e a x +=,令()2x e e g x x +=,()22x x xe e e g x x --'=,得()g x 在()0,2上单调递减,在()2,+∞上单调递增,()2min (2)g x g e ==,()2g x e ≥.因为()f x 有2个零点,所以2a e >. 故选:B. 【点睛】分离变量法,利用导数求函数的单调性,极值是解题关键.二、多选题9.已知递减的等差数列{}n a 的前n 项和为n S ,57S S =,则( ) A .60a >B .6S 最大C .130S >D .110S >【答案】ABD 【分析】转化条件为670a a +=,进而可得60a >,70a <,再结合等差数列的性质及前n 项和公式逐项判断即可得解. 【详解】因为57S S =,所以750S S -=,即670a a +=,因为数列{}n a 递减,所以67a a >,则60a >,70a <,故A 正确; 所以6S 最大,故B 正确;所以()113137131302a a S a+⨯==<,故C 错误;所以()111116111102a a S a+⨯==>,故D 正确.故选:ABD.10.已知定义在R 上的函数()f x ,其导函数()f x '的大致图象如图所示,则下列叙述不正确的是( )A .()()()f a f e f d >>B .函数()f x 在[],a b 上递增,在[],b d 上递减C .函数()f x 的极值点为c ,eD .函数()f x 的极大值为f b 【答案】ABD 【分析】对A ,B 由导数与函数单调性的关系,即可判断()f a ,()f b ,()f c 的大小以及()f x 的单调性,对C ,D 由极值的定义即可判断. 【详解】解:由题图知可,当(),x c ∈-∞时,()0f x '>,当(),x c e ∈时,()0f x '<,当(),x e ∈+∞时,()0f x '>, 所以()f x 在(),c -∞上递增, 在(),c e 上递减,在(),e +∞上递增, 对A ,()()f d f e >,故A 错误;对B ,函数()f x )在[],a b 上递增,在[],b c 上递增,在[],c d 上递减,故B 错误;对C ,函数()f x 的极值点为c ,e ,故C 正确; 对D ,函数()f x 的极大值为()f c ,故D 错误. 故选:ABD.11.在《增减算法统宗》中有这样一则故事:“三百七十八里关,初行健步不为难;次日脚痛减一半,如此六日过其关”.则下列说法正确的是( ) A .此人第六天只走了5里路B .此人第一天走的路程比后五天走的路程多6里C .此人第二天走的路程比全程的14还多1.5里 D .此人走的前三天路程之和是后三天路程之和的8倍 【答案】BCD 【分析】设此人第n 天走n a 里路,则{}n a 是首项为1a ,公比为12q = 的等比数列,由6S 求出1a ,然后求出相应的项,判断各选项. 【详解】解:根据题意此人每天行走的路程成等比数列, 设此人第n 天走n a 里路,则{}n a 是首项为1a ,公比为12q =的等比数列. 所以611611()(1)23781112a a q S q ⎡⎤-⎢⎥-⎣⎦===--,解得1192a =.选项A :55611192()62a a q ==⨯=,故A 错误,选项B :由1192a =,则61378192186S a -=-=,又1921866-=,故B 正确.选项C :211192962a a q ==⨯=,而6194.54S =,9694.5 1.5-=,故C 正确.选项D :2123111(1)192(1)33624a a a a q q ++=++=⨯++=, 则后3天走的路程为37833642-=, 而且336428÷=,D 正确. 故选:BCD . 【点睛】关键点点睛:本题考查等比数列的应用,解题关键是引入等比数列{}n a ,n a 表示第n 天行走的路程,根据前6项的和求出首项1a ,然后可得通项公式,从而判断出结论.12.已知数列{}n a 的前n 项和为2n 33S n n =-,则下列说法正确的是( )A .342n a n =-B .16S 为n S 的最小值C .1216272a a a +++=D .1230450a a a +++=【答案】AC 【分析】利用和与项的关系,分1n =和2n ≥分别求得数列的通项公式,检验合并即可判定A; 根据数列的项的正负情况可以否定B;根据前16项都是正值可计算判定C;注意到121617193300()a a a S a a a +++=+----16302S S =-可计算后否定D.【详解】1133132a S ==-=,()()()2213333113422n n n a S S n n n n n n -=-=---+-=-≥,对于1n =也成立,所以342n a n =-,故A 正确;当17n <时,0n a >,当n=17时n a 0=,当17n >时,n a 0<,n S ∴只有最大值,没有最小值,故B 错误;因为当17n <时,0n a >,∴21216163316161716272a a a S +++==⨯-=⨯=,故C 正确; 121617193300()a a a S a a a +++=+----2163022272(333030S S =-=⨯-⨯-)54490454=-=,故D 错误. 故选:AC. 【点睛】本题考查数列的和与项的关系,数列的和的最值性质,绝对值数列的求和问题,属小综合题.和与项的关系()()1112n nn S n a S S n -⎧=⎪=⎨-≥⎪⎩,若数列{}n a 的前 k 项为正值,往后都是小于等于零,则当n k ≥时有122n k n a a a S S ++⋯+=-,若数列{}n a 的前 k 项为负值,往后都是大于或等于零,则当n k ≥时有122n k n a a a S S ++⋯+=-+.若数列的前面一些项是非负,后面的项为负值,则前n 项和只有最大值,没有最小值,若数列的前面一些项是非正,后面的项为正值,则前n 项和只有最小值,没有最大值.三、填空题13.已知()2()21f x x xf =+',则()1f '等于__________.(用数字作答)【答案】-2【分析】求出()f x 的导函数,代入1x =即可求解.【详解】()2()21f x x xf =+',()()221f x x f ''∴=+,()()12121f f ''∴=⨯+,解得()12f '=-.故答案为:2-.14.()f x 对任意x ∈R 都有()()112f x f x +-=.数列{}n a 满足:()120n a f f f n n ⎛⎫⎛⎫=+++ ⎪ ⎪⎝⎭⎝⎭()11n f f n -⎛⎫++ ⎪⎝⎭,则n a =__________. 【答案】14n + 【分析】采用倒序相加法即可求得结果.【详解】由题意得:()()1012f f +=,1112n f f n n -⎛⎫⎛⎫+= ⎪ ⎪⎝⎭⎝⎭,2212n f f n n -⎛⎫⎛⎫+= ⎪ ⎪⎝⎭⎝⎭,……, ()()12101n n a f f f f f n n n -⎛⎫⎛⎫⎛⎫=+++⋅⋅⋅++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭, ()()12110n n n a f f f f f n n n --⎛⎫⎛⎫⎛⎫=+++⋅⋅⋅++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭, 122n n a +∴=,解得:14n n a +=.故答案为:14n +. 【点睛】本题考查利用倒序相加法求和的问题,属于基础题.15.已知32()263f x x x =-+,对任意的2][2x ∈-,都有()f x a ≤,则a 的取值范围为_______. 【答案】[3)+∞,【分析】利用导数研究函数的单调性,进而求得在给定区间上的最大值,根据不等式恒成立的意义即得实数a 的取值范围.【详解】由2()6120f x x x '=-=得0x =或2x =,在区间[-2,0)上()'0f x >,()f x 单调递增;在(0,2)内时()()'0,f x f x <单调递减. 又(2)37f -=-,(0)3f =,(2)5f =-,∴max ()3f x =,又()f x a ≤对于任意的x ∈[-2,2]恒成立,∴3a ≥,即a 的取值范围是[)3,+∞故答案为:[)3,+∞.【点睛】本题考查利用导数研究函数的在闭区间上的最值进而求不等式恒成立中的参数范围,属基础题,关键在于利用导数研究函数的单调性,求得在给定区间上的最大值.16.古代埃及数学中有一个独特现象:除23用一个单独的符号表示以外,其他分数都可写成若干个单分数和的形式.例如2115315=+,可这样理解:假定有两个面包,要平均分给5个人,如果每人12,不够,每人13,余13,再将这13分2成5份,每人得115,这样每人分得11315+.形如)*2(3,21n n N n ∈-的分数的分解:2115315=+,2117428=+,2119545=+,按此规律,则221n =-________()*3,n n N ∈. 【答案】2112n n n+- 【分析】 根据21123133(231)=+⨯-⨯⨯-,21124144(241)=+⨯-⨯⨯-,21125155(251)=+⨯-⨯⨯-,…进行归纳推理. 【详解】 由题意得,2115315=+,即21123133(231)=+⨯-⨯⨯-, 2117428=+,即21124144(241)=+⨯-⨯⨯-, 2119545=+,即21125155(251)=+⨯-⨯⨯-, 由此归纳出)*211(3,21(21)n n N n n n n =+∈⨯--. 经验证112112(21)(21)21n n n n n n n -++==---,结论成立, ∴2211212n n n n=+--. 故答案为:2112n n n +-. 【点睛】方法点睛:由数列的前n 项归纳通项公式时,首先要分析项的结构,然后再探究结构中的各部分与项的序号n 间的函数关系,进而求得通项公式.四、解答题17.已知数列{}n a 各项均为正数,其前n 项和为n S ,且满足()241n n S a =+. (1)求数列{}n a 的通项公式.(2)设11n n n b a a +=,求数列{}n b 的前n 项和n T . 【答案】(1)21n a n =-;(2)21n n T n =+. 【分析】(1)由=1n 可得11a =,再由2n ≥时,()21141n n S a --=+与条件作差可得12n n a a --=,从而利用等差数列求通项公式即可; (2)由n b 1(21)(21)n n =-+利用裂项相消求和即可. 【详解】(1)∵()241n n S a =+,∴()21141a a =+,解得11a =,当2n ≥时,由()241n n S a =+①可得, ()21141n n S a --=+②,①-②:()()1120n n n n a a a a --+--=,∵0n a >,∴10n n a a -+≠,∴120n n a a ---=,即∴12n n a a --=,∴{}n a 是以11a =为首项,以2d =为公差的等差数列,∴1(1)12(1)21n a a n d n n =+-=+-=-综上所述,结论是:21n a n =-.(2)由(1)可得11n n n b a a +=1(21)(21)n n =-+11122121n n ⎛⎫=- ⎪-+⎝⎭∴2n a n T b b b =+++111111123352121n n ⎛⎫=-+-++- ⎪-+⎝⎭ 11122121n n n ⎛⎫=-= ⎪++⎝⎭, 综上所述,21n n T n =+. 18.在①133a a b +=,②254b S b +=-,③194a a +=-这三个条件中任选两个,补充在下面的问题中.若问题中的m 存在,求出m 的值;若不存在,请说明理由.设等差数列{}n a 的前n 项和为n S ,{}n b 是各项均为正数的等比数列,设前n 项和为n T ,若 , ,且1422,5b T T ==.是否存在大于2的正整数m ,使得134,,m S S S 成等比数列?(注:如果选择多个条件分别解答,按第一个解答计分.)【答案】答案见解析.【分析】由等比数列的条件,求得2q ,可得等比数列的通项公式.然后分别选取条件①②,条件①③,条件②③,列出关于等差数列首项与公差的方程组,求得首项与公差,得到等差数列的通项公式及前n 项和,再由14S ,3S ,m S 成等比数列列式求解m 值即可.【详解】解:设{}n a 的 公差为d ,{}n b 的公比为(0)q q >,由题意知1q ≠,所以421142(1)(1)5511b q b q T T q q--===--, 整理得215q +=,因为0q >,所以2q ,所以2n n b =.(1)当选取的条件为①②时,有1358416a a S +=⎧⎨+=-⎩,所以1122824a d a d +=⎧⎨+=-⎩, 解得1128a d =⎧⎨=-⎩. 所以2820,416n n a n S n n =-+=-+.所以21312,12,416m S S S m m ===-+,若134,,m S S S 成等比数列,则2314m S S S =,所以241630m m -+=,解得2m = 因为m 为正整数,所以不符合题意,此时m 不存在.(2)当选取的条件为①③时,有131984a a a a +=⎧⎨+=-⎩,所以11228284a d a d +=⎧⎨+=-⎩, 解得162a d =⎧⎨=-⎩. 所以228,7n n a n S n n =-+=-+.所以2136,12,7m S S S m m ===-+,若134,,m S S S 成等比数列,则2314m S S S =,所以2760m m -+=,解得6m =或1m =(舍去)此时存在正整数6m =满足题意.(3)当选取的条件为②③时,有1954416a a S +=-⎧⎨+=-⎩,所以1128424a d a d +=-⎧⎨+=-⎩, 解得161a d =-⎧⎨=⎩. 所以2137,2n n n n a n S -=-=. 所以213136,15,2m m m S S S -=-=-=, 若134,,m S S S 成等比数列,则2314m S S S =,即22524m S =-,所以2452750m m -+=,解得132m =, 因为m 为正整数,所以不符合题意,此时m 不存在.【点睛】等比数列基本量的求解是等比数列中的一类基本问题,解决这类问题的关键在于熟练掌握等比数列的有关公式并能灵活运用,尤其需要注意的是,在使用等比数列的前n 项和公式时,应该要分类讨论,有时还应善于运用整体代换思想简化运算过程.19.已知数列{}n a 中,11a =,()*13n n n a a n N a +=∈+ (1)证明:数列112n a ⎧⎫+⎨⎬⎩⎭是等比数列 (2)若数列{}n b 满足()312n n n n n b a -=⋅,求数列{}n b 的前n 项和nT . 【答案】(1)证明见解析 ;(2)1242n n n T -+=-. 【分析】(1)由()*13n n n a a n N a +=∈+可得11111322n n a a +⎛⎫+=+ ⎪⎝⎭,然后可得答案; (2)由(1)可算出231n n a =-,12n n n b -=,然后用错位相减法可算出答案. 【详解】 (1)证明:由()*13n n n a a n N a +=∈+,知11111322n n a a +⎛⎫+=+ ⎪⎝⎭又111322a +=,∴112n a ⎧⎫+⎨⎬⎩⎭是以32为首项,3为公比的等比数列 (2)解:由(1)知111333222n n n a -+=⨯=,∴231n n a =-,12n n n b -= 0122111111123(1)22222n n n T n n --=⨯+⨯+⨯++-⨯+⨯ 211111112(1)22222n n n T n n -=⨯+⨯++-⨯+⨯ 两式相减得012111111222222222n n n nT n n -+=++++-⨯=- ∴1242n n n T -+=- 20.已知函数()()x x f x a a R e=-∈ (1)求函数()f x 的单调区间;(2)若方程()f x =0有两个不相等的实数根,求实数a 的取值范围.【答案】(1)()f x 的单调递增区间是(,1)-∞,单调递减区间是(1,)+∞.(2)10a e <<【分析】(1)首先求出函数的导函数,再解不等式即可得到函数的单调区间;(2)由()0x x f x a e =-=得x x a e =, 将此方程的根看作函数x x y e=与y a =的图象交点的横坐标,结合(1)中相关性质得到函数的图象,数形结合即可得到参数的取值范围;【详解】解:(1)∵()()x x f x a a R e=-∈ 所以21()()x x x x e xe x f x e e--'== ∴当1x <时,()0f x '>,当1x >时,()0f x '<;即()f x 的单调递增区间是(,1)-∞,单调递减区间是(1,)+∞.(2)由()0x x f x a e =-=得xx a e =, 将此方程的根看作函数x x y e =与y a =的图象交点的横坐标, 由(1)知函数x x y e =在1x =时有极大值1e,作出其大致图象,∴实数a 的取值范围是10a e<<. 【点睛】 本题考查利用导数研究函数的单调性及函数的零点问题,属于基础题.21.设函数()21x f x e ax x =---,a R ∈. (1)0a =时,求()f x 的最小值.(2)若()0f x ≥在[)0,+∞恒成立,求a 的取值范围.【答案】(1)0;(2)1(,]2-∞.【分析】(1)当0a =时,求导可得()1xf x e '=-,令()0f x '=,解得0x =,分别讨论(),0x ∈-∞和()0,∞+时,()'f x 的正负,即可得()f x 的单调性,即可求得答案;(2)求导可得()21x f x e ax '=--,设()21(0)x h x e ax x =--≥,分别讨论12a ≤和12a >时()h x '的正负,可得()h x 的单调性,进而可得()f x 的单调性,综合分析,即可得答案.【详解】(1)当0a =时,()1x f x e x =--,则()1xf x e '=-, 令()0f x '=,解得0x =,当(),0x ∈-∞时,()0f x '<,所以()f x 在(),0-∞单调递减函数;当()0,x ∈+∞时,()0f x '>,所以()f x 在()0,∞+单调递增函数;所以()()min 00f x f ==.(2)()21x f x e ax x =---,则()21xf x e ax '=--, 设()21(0)xh x e ax x =--≥,则()2x h x e a '=-, 当12a ≤时,()0h x '≥,所以()h x 在[)0,+∞上为增函数, 又(0)0h =,所以()(0)0h x h ≥=,即()0f x '≥,所以()f x 在在[)0,+∞上为增函数,又(0)0f =,所以()(0)0f x f ≥=,满足题意; 当12a >时,令()0h x '=,解得ln2x a =, 当(0,ln 2)x a ∈时,()0h x '<,所以()h x 在(0,ln 2)a 为减函数,所以当[0,ln 2)x a ∈时,()(0)0h x h ≤=,即()0f x '≤,所以()f x 在[0,ln 2)x a ∈为减函数,又(0)0f =所以()(0)0f x f ,不满足题意,综上:a 的取值范围是1(,]2-∞【点睛】解题的关键是熟练掌握利用导数求解函数单调性,极(最)值的方法,若处理恒成立问题时,需满足min ()0f x ≥,若处理存在性问题时,需满足max ()0f x ≥,需仔细审题,进行求解,属中档题. 22.已知2()2ln f x x x a x =-+.(1)若函数()f x 在2x =处取得极值,求实数a 的值;(2)若()()g x f x ax =-,求函数()g x 的单调递增区间;(3)若2a =,存在正实数12,x x ,使得()()1212f x f x x x +=+成立,求12x x +的取值范围.【答案】(1)4-;(2)答案见解析;(3)32⎡⎫++∞⎪⎢⎪⎣⎭. 【分析】(1)由题意结合极值的概念可得(2)0f '=,解得4a =-后,验证即可得解;(2)求导得(1)(2)()(0)x x a g x x x--'=>,按照0a ≤、02a <<、2a =、2a >分类讨论,求得()0g x '>的解集即可得解;(3)转化条件得()()()212121212322ln x x x x x x x x +-+=-,令12t x x =,()22ln (0)t t t t ϕ=->,求导确定()t ϕ的单调性和值域即可得解.【详解】(1)222()22(0)a x x a f x x x x x-+-+'==>, ∵函数()f x 在2x =处取得极值,∴84(2)0a f x -+'==,解得4a =-, 当4a =-时,()2222(1)(2)()x x x x f x x x'--+-==. ∴当02x <<时,()0f x '<,()f x 单调递减;当2x >时,()0f x '>,()f x 单调递增;∴当4a =-时,函数()f x 在2x =处取得极小值;(2)2()()(2)ln g x f x ax x a x a x =-=-++, ∴22(2)(1)(2)()2(2)(0)a x a x a x x a g x x a x x x x-++--'=-++==>, 令()0f x '=,则1x =或2a x =, ①当0a ≤时,令()0g x '>可得1x >,∴函数()g x 的单调递增区间为(1,)+∞;②当02a <<时,令()0g x '>可得02a x <<或1x >, ∴函数()g x 的单调递增区间为0,,(1,)2a ⎛⎫+∞ ⎪⎝⎭; ③当2a =时,()0g x '≥在(0,)x ∈+∞上恒成立,∴函数()g x 的单调递增区间为(0,)+∞;④当2a >时,令()0g x '>可得01x <<或2a x >,∴函数()g x 的单调递增区间为(0,1),,2a⎛⎫+∞ ⎪⎝⎭; (3)2a =,∴2()22ln f x x x x =-+,()()1212f x f x x x +=+,∴()()221212121222ln x x x x x x x x +-++=+,整理可得()()()212121212322ln x x x x x x x x +-+=-,令12t x x =,()22ln (0)t t t t ϕ=->, 12(1)()21t tt tϕ-⎛⎫'=-= ⎪⎝⎭,令()0t ϕ'=,解得1t =, 当01t <<时,()0t ϕ'<,()t ϕ单调递减;当1t >时,()0t ϕ'>,()t ϕ单调递增; ∴当1t =时,()t ϕ取得极小值即最小值为()12ϕ=,∴()()2121232x x x x +-+≥即()()21212320x x x x +-+-≥,解得1232x x +≤(舍去)或1232x x +≥,∴12x x +的取值范围为⎫+∞⎪⎪⎣⎭. 【点睛】本题考查了导数的综合应用,考查了运算求解能力、逻辑推理能力、分类讨论思想,属于中档题.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018年高中数学必修2期末考试考试时间 2小时满分150分一、选择题(本大题共12小题,共60.0分)1.若m,n是两条不同的直线,α,β是两个不同的平面,则下列命题正确的是()A. 若α⊥β,m⊥β,则m//αB. 若m//α,n//α,m⊂β,n⊂β,则α//βC. 若m//α,n⊥m,则n⊥αD. 若m//β,m⊂α,α⋂β=n,则m//n2.平面α//平面β,它们之间的距离为12,A,B∈α,点D∈β,点C是点B在β的射影,且AB=2,AD=13,则CD的最小值是()A. 2B. 3C. √21D. √293.经过点M(1,1)且在两坐标轴上的截距相等的直线方程是()A. x−y=0B. x+y−2=0C. x+y−2=0或x−y=0D. x=1或y=14.过点且平行于直线的直线方程为()A. B. C. D.5.已知几何体的三视图如图所示,则该几何体是( )A. 体积为2的三棱锥B. 体积为2的四棱锥C. 体积为4的三棱锥D. 体积为4的四棱锥6.已知长方形ABCD的一组邻边长分别是1,√3,沿对角线AC折成一个三棱锥B−ACD,则该三棱锥外接球的表面积是()A. 4πB. 3πC. 2πD. π7.已知ΔABC的一个顶点A(3,−1),∠B,∠C的角平分线方程分别是x=0,y=x,则BC的直线方程为()A. 2x−y+3=0B. 2x−y+5=0C. 3x−y+5=0D. 2x+3y−5=08.在平面直角坐标系xoy中,圆C的方程为x2+y2−4x+2y=0,若直线y=3x+b上存在一点P,且过P作圆的两条切线相互垂直,则实数b的取值范围是()A. [−11,−3]B. [3,11]C. [−17,3]D. [−3,17]9.圆O1:x2+y2−4x−6y+12=0与圆O2:x2+y2−8x−6y+16=0的位置关系是( )A. 内切B. 外离C. 内含D. 相交10.已知是两条不同的直线,是两个不同的平面,则下列说法正确的()A. 若//,//,则//B. 若,,,则C. 若,,则//D. 若//,,则//11.如图,已知∠AOB=60∘,点C在∠AOB内,且OC=5,若半径为1的圆C与∠AOB的两边没有交点,点X,Y分别在射线OA,OB上异于O的动点,则|PX|+|PY|+|XY|的最小值是()A. 2√3B. 4C. 3D. 4√312.在平面直角坐标系xoy中,已知AB是圆O:x2+y2=1直径,若直线l:kx−y−3k+1=0上存在点P,连接AP与圆O交于点Q,且满足BP//OQ,则实数k的取值范围是()A. k≥−34B. k≥−43C. k≤−34D. k≤−43二、填空题(本大题共4小题,共20.0分)13.如图所示,水平放置的ΔABC的斜二测直观图是图中的,已知,则AB边的实际长度是________.14.已知圆M:x2+y2−2x−2y−2=0,点P是直线x+y−6=0上的动点,若在圆M上存在点Q,使得∠OPQ=30∘,则点P横坐标的取值范围是______.15.已知A(4,3),B(4,−3),点P在圆x2+y2=4上运动,则的最小值是________.16.如图,正方体ABCD−A1B1C1D1的棱长为4,动点P在正方形及其内部运动,且保持AP=AC,在点P运动中,线段AP扫过的曲面的面积等于_________.三、解答题(本大题共6小题,共70.0分)17.已知点P(2,2),圆C:x2+y2−8x=0,过点P的动直线l与圆C交于A,B两点,线段AB的中点为M,O为坐标原点.(Ⅰ)求M的轨迹方程;(Ⅱ)当|OP|=|OM|时,求直线l的方程.18.已知曲线C1:x2+y2−2x−4y+m=0.(Ⅰ)若曲线C1是一个圆,且点P(1,1)在圆C1外,求实数m的取值范围;(Ⅱ)当m=2时,曲线C1关于直线x+1=0对称的曲线为C2.设P为平面上的点,满足:存在过P点的无穷多对互相垂直的直线l1,l2,它们分别与曲线C1和曲线C2相交,且直线l1被曲线C1截得的弦长与直线l2被曲线C2截得的弦长总相等.(ⅰ)求所有满足条件的点P的坐标;(ⅰ)若直线l1被曲线C1截得的弦为MN,直线l2被曲线C2截得的弦为RS,设∆PMR与∆PNS的面积分别为S1与S2,试探究S1·S2是否为定值?若是,求出该定值;若不是,请说明理由.19.已知平行四边形ABCD对角线的交点是M(−1,−1),AB边所在直线的方程为x+y−1=0,AD边所在直线的方程为2x−y−2=0.(Ⅰ)求BC边所在的直线的方程;(Ⅱ)求平行四边形ABCD的面积.20.今有边长为12尺的正方形水池的中央生长着芦苇,长出水面的部分为2尺,将芦苇牵引向池岸,恰巧与水岸齐接。
如图,记正方形水池的剖面图为矩形ABCD,芦苇根部O为池底AB的中点,顶端为P(注:芦苇与水面垂直),在牵引顶端P向水岸边点D的过程中,当芦苇经过DF的三等分点E(靠近D点)时,设芦苇的顶端为Q,(Ⅰ)以AB所在的直线为x轴,OP所在的直线为y轴,建立平面直角坐标系,求圆弧DP的方程;(Ⅱ)求点Q在水面上的投影离水岸边点D的距离(精确到0.01尺)(参考数据:√5≈2.236,√3≈1.732)21.22.答案和解析【答案】1. D2. B3. C4. A5. B6. A7. B8. C 9. A 10. D 11. D 12. A13. 1014. [1,5] 15. 26 16. 4√2π17. 解:(I)圆C 的方程可化为(x −4)2+y 2=16,所以圆心为C(4,0),半径为4,设M(x ,y),则CM ⃗⃗⃗⃗⃗⃗ =(x −4,y),MP ⃗⃗⃗⃗⃗⃗ =(2−x ,2−y), 由题设知CM ⃗⃗⃗⃗⃗⃗ ⋅MP ⃗⃗⃗⃗⃗⃗ =0,故(x −4)(2−x)+y(2−y)=0, 即(x −3)2+(y −1)2=2. 由于点P 在圆C 的内部,所以M 的轨迹方程是(x −3)2+(y −1)2=2.(II)由(1)可知M 的轨迹是以点N(3,1)为圆心,√2为半径的圆. 由于|OP|=|OM|,故O 在线段PM 的垂直平分线上, 又P 在圆N 上,从而ON ⊥PM . 因为ON 的斜率为13,所以l 的斜率为−3,故l 的方程为y −2=−3(x −2),即为3x +y −8=0. 18. 解:(Ⅰ)依题意得{4+16−4m >02−2−4+m >0,解得4<m <5,即实数的取值范围是(4,5)(Ⅱ)当m =2时,圆:(x −1)2+(y −2)2=3,圆心C 1(1,2),半径r 1=√3,圆C 2:(x +3)2+(y −2)2=3,圆心C 2(−3,2),半径r 2=√3. (ⅰ)因为要存在存在过点的无穷多对互相垂直的直线l 1,l 2,所以必有无穷多对的斜率存在.设直线l 1的斜率为k ,P(m,n)则直线l 1:kx −y −mk +n =0,同理直线l 2:x +ky −m −kn =0,由于两圆半径相等, 要使得直线l 1被曲线截得的弦长与直线l 2被曲线截得的弦长总相等,即d C 1−l 1=d c 2−l 2,即,即|k −2−mk +n|=|−3+2k −m −kn|,所以k −2−mk +n =−3+2k −m −kn 或整理得k(n −m −1)+(n +m +1)=0或k(3−m −n)+(n −m −5)=0 因为对无穷个k 都成立,所以{n −m −1=0n +m +1=0或{3−m −n =0n −m −5=0,解得{m =−1n =0或{m =−1n =4即P 1(−1,0),P 2(−1,4) (ⅰ)设C 1到MN 的距离为d ,则,所以同理所以S 1⋅S 2=(12PM ⋅PN)⋅(12PR ⋅PS)=254(定值)19. 解:(Ⅰ)联立{x +y −1=02x −y −2=0解得{x =1y =0,即A(1,0),因为AC 中点为M ,则C(−3,−2) 又因为BC//AD ,所以BC 所在的直线方程为y +2=2(x +3),即2x −y +4=0, (Ⅱ)联立{x +y −1=02x −y +4=0解得{x =−1y =2,即B(−1,2),所以|BC|=2√5, 点M 到BC 的距离为√5=√5,则A 点到BC 的距离为2√5, 则S △ABC =12√52√5=6, 所以平行四边形ABCD 的面积是12.20. 解:(Ⅰ)设水深为x 尺,则x2+62 =(x +2)2,解得,x =8.∴水深为8尺,芦苇长为10尺,以AB 所在的直线为x 轴,芦苇所在的直线为y 轴, 建立如图所示的平面直角坐标系,在牵引过程中,P 的轨迹是以O 为圆心,半径为10的圆弧,其方程为x 2 +y 2=100(−6≤x ≤0,8≤y ≤10) (Ⅱ)E 点的坐标为(−4,8),∴OE 所在的直线方程为y =−2x ,设Q 点坐标为(x ,y),联立{x 2+y 2=100y =−2x 解得x =−2√5,DG =6−2√5≈1.53故点Q 在水面上的投影离水岸边点D 的的距离为1.53尺.21. 解:(1)∵四边形DCBE 为平行四边形,∴∵DC 平面ABC ∴ 平面ABC∴为AE 与平面ABC 所成的角,即=由R t△ABE 为等腰直角三角形,又 得∵AB 是圆O 的直径 ∴∴∴∴(2)在CD 上存在点 ,使得MO//平面 ,该点 为的中点.证明:如图,取的中点,连MO、MN、NO,∵M、N、O分别为CD、BE、AB的中点,∴MN//DE.∵平面ADE,平面ADE,∴MN//平面ADE同理可得NO//平面ADE.∵,∴平面MNO//平面ADE.∵平面MNO,∴MO//平面ADE.22.【解析】1. 【分析】此题考查空间线面垂直、线面平行、面面垂直的判定,逐项判断真假即可,可利用举反例判断为假,属基础题.【解答】解:A.若α⊥β,m⊥β,m可能在α内,故错误;B.若m//α,n//α,m⊂β,n⊂β,少了m与n相交的条件,故错误;C.若m//α,n⊥m,n在α内也可与m异面垂直,故错误;D.若m//β,m⊂α,α⋂β=n,由线面平行的性质可得m//n,故正确.故选D.2. 【分析】本题考查了空间中两点间的距离问题,考查了数形结合解题能力,考查了空间想象能力,为中档题.本题关键为D点在面β上的轨迹为为圆心,以5为半径的圆.【解答】解:作图如下:过A做垂直β面,垂足为,可知,,,则D点在面β上的轨迹为为圆心,以5为半径的圆,∴当D落在的反向延长线上时,CD最短,即为5−2=3.故选B.3. 【分析】因为过点A(1,1)且在两坐标轴上的截距相等的直线的方程,要分截距为零,或者截距不为零两种情况来解决.【解答】解:当直线过原点时,方程为y=x.当直线不过原点时,设直线的方程为x+y=k,把点A(1,1)代入直线的方程可得k=2,故直线方程是x+y−2=0.综上,所求的直线方程为x+y−2=0,或y=x,故选C.4. 【分析】此题考查利用直线平行的判断求直线方程,关键是利用待定系数法.【解答】解:因为直线平行于x−2y+3=0,所以设直线方程为x−2y+c=0,因为直线过点(−1,3),所以−1−2×3+c=0,所以c=7,直线方程为x−2y+7=0.故选A.5. 【分析】本题考查由三视图还原几何体,求其体积,为基础题.考查学生空间想象能力.借助正方体为背景还原原几何体.【解答】解:正方体中还原为下图:原图为以A为顶点,CED1D为底的四棱锥,V=13×2×(2+1)2×2=2.故选B.6. 【分析】本题考查了三棱锥的外接球的表面积,为中档题,考查学生空间想象能力.本题关键为求外接球的半径,由直径所对的圆周角为直角的理论可知,三棱锥B−ACD 外接球的球心为AC的中点.【解答】解:由题意可知A、C、B三点都在球面上,∠B为直角∴三棱锥B−ACD外接球的球心为AC的中点,=1,三棱锥外接球的半径r=√3+12故三棱锥外接球的表面积S=4π×12=4π.故选A.7. 【分析】本题是基础题,考查点关于直线对称点的求法,直线方程的求法,考查计算能力,发现问题解决问题的能力,常考题型.分析题意,求出A关于x=0,y=x,的对称点的坐标,都在直线BC上,利用两点式方程求解即可.【解答】解:∵∠B、∠C的平分线分别是x=0,y=x,∴AB与BC对于x=0对称,AC与BC 对于y=x对称.A(3,−1)关于x=0的对称点在直线BC上,A关于y=x的对称点也在直线BC上.由两点式,所求直线BC的方程:y= 2x+5.故选B.8. 【分析】本题考查了直线与圆的位置关系,转化为圆心与直线的距离来研究,考查学生的问题转化能力.过P作圆的两条切线相互垂直,令切点分别为A、B则四边形CAPB是正方形,转化为≤√10.圆心C到直线y=3x+b的距离d=√10【解答】解:圆C:(x−2)2+(y+1)2=5,过P作圆的两条切线相互垂直,令切点分别为A、B则四边形CAPB是正方形,且CP=√2r=√10,≤√10,则圆心C到直线y=3x+b的距离d=√10解得−17≤b≤3.故选C.9. 【分析】本题考查了两圆的位置关系,根据圆心距与半径之间的大小关系可判断,首先把两圆化为标准形式,得到两圆的圆心坐标及半径,即可判断结果.【解答】解:∵圆C1:(x−2)2+(y−3)2=1,圆C2:(x−4)2+(y−3)2=9,∴圆C1:圆心(2,3),半径r1=1,圆C2:圆心(4,3),半径r2=3,∴圆心距为2,r2−r1=2,∴两圆内切.故选A.10. 【分析】本题考查了空间中直线与直线,直线与平面,平面与平面之间的位置关系,注意面面垂直,线线垂直,线面垂直的判定定理以及性质定理的应用.【解答】解:A命题中平行于同一平面的两条直线可以相交,异面,平行;B命题中两条直线可以相交,平行,异面,垂直;C命题不正确,直线可以在平面内;D命题正确.故选D.11. 【分析】本题考查了和圆有关的最值问题,圆外一点与圆上一点的距离转化为圆外一点与圆心的距离加减半径,为中档题.本题关键为作P关于OB的对称点M,作P关于OA的对称点N,连接MN,则|PX|+|PY|+ |XY|最小值是|MN|.【解答】解:如图作P关于OB的对称点M,作P关于OA的对称点N,连接MN,则|PX|+|PY|+|XY|最小值是|MN|,在ΔMON中,OM=ON=OP,∠MON=120∘,|MN|=√3|OM|=√3|OP|,因为,所以|PX|+|PY|+|XY|最小值是4√3.故选D.12. 【分析】本题考查了直线与圆的位置关系,考查了学生转化问题的能力,为中档题.由题意可知P的轨迹是以B为圆心,半径为2的圆即(x−1)2+y2=2,由于P为直线l与圆B的交点,转化为B到l的距离小于等于2.【解答】解:设A(−1,0),B(1,0),连接AP与圆O交于点Q,且满足BP//OQ可得OQ为△ABP的中位线,即||BP|=2|OQ|=2,所以P的轨迹是以B为圆心,半径为2的圆即(x−1)2+y2=2,所以P为直线l与圆B的交点,即d B−l≤2,即,.解得k≥−34故选A.13. 【分析】本题考查了斜二测画法直观图的应用问题,掌握斜二测画法直观图与原图中的线段关系是解答的关键.根据直观图中A′C′与B′C′,得出原平面图形是Rt△,并由勾股定理求出AB的值.【解答】解:直观图中的△A′B′C′,A′C′=6,B′C′=4,所以原图形是Rt△ABC,且AC=6,BC=8由勾股定理得AB=10.故答案为10.14. 【分析】本题考查了直线与圆的位置关系,为中档题.考查学生转化问题能力,若在圆M上存在点Q,使得∠OPQ=300,则直线PQ与圆M相交或相切,在转化为|PM|≤4,可求P横坐标的取值范围.【解答】解:依题意得M:(x−1)2+(y−1)2=4,若在圆M上存在点Q,使得∠OPQ=300,则直线PQ与圆M相交或相切,则d m−PQ≤r,即|PM|≤4,设P(x0,6−x0),则(x0−1)2+(6−x0−1)2≤16,解得1≤x0≤5.故答案为[1,5].15. 【分析】本题考查了与圆有关的最值问题,转化为两点之间的距离,用函数来研究,为中档题.【解答】解:令P坐标为(m,n),有m2+n2=4,(−2≤m≤2)则|PA|2+|PB|2=(m−4)2+(n−3)2+(m−4)2+(n+3)2=2m2−16m+32+2n2+18=2×4+32+18−16m=58−16m,又∵−2≤m≤2,则58−16m的最小值为58−32=26,则|PA|2+|PB|2的最小值是26.故答案为26.16. 【分析】本题考查了圆锥的侧面积,考查了学生的空间想象能力,为中档题.本题关键为线段AP扫过的曲面的面积是圆锥在正方体内的部分【解答】解:线段AP扫过的曲面的面积是圆锥在正方体内的部分,即1个圆锥的侧面积,如图所示,4所以线段AP扫过的曲面的面积.故答案为4√2π.17. 本题考查点的轨迹方程的求法,考查直线方程的求法,解题时要认真审题,注意圆的方程和性质的合理运用.(I)圆C 的方程可化为(x −4)2+y 2=16,由此能求出圆心为C(4,0),半径为4,设M(x ,y),求出向量CM ,MP 的坐标,由CM ⃗⃗⃗⃗⃗⃗ ⋅MP ⃗⃗⃗⃗⃗⃗ =0,运用向量的数量积的坐标表示,化简整理求出M 的轨迹方程;(II)由(Ⅰ)知M 的轨迹是以点N(3,1)为圆心,√2为半径的圆.由于|OP|=|OM|,故O 在线段PM 的垂直平分线上,可得ON ⊥PM ,由直线垂直的条件:斜率之积为−1,再由点斜式方程可得直线l 的方程.18. 本题考查圆的方程,考查了直线与圆位置关系的应用,考查数学转化思想方法,训练了计算能力,是中档题.(Ⅰ)依题意列关于m 的不等式组,求解不等式组得答案;(Ⅱ)当m =2时,求出圆C 1的方程,得到圆心坐标和半径,进一步求出关于x +y =0对称的圆C 2方程,得到C 2(−3,2).(i)要存在无穷多对直线L 1与L 2,必有无穷多对的斜率都存在,设L 1的斜率为k ,P(m ,n),则L 2的斜率为−1k ,求出L 1,L 2的方程,由两圆半径都相等,因此,若相交弦长相等,则两圆心到对应直线的距离必相等,列式可得(m −n −1)k −(m +n +1)=0或(3−m −n)k +(n −m −5)=0对无穷多个k 值成立.由此求得m 值,得到 点P 的坐标;(ii)设C 1到MN 的距离为d ,则,同理PR ⋅PS ,代入S 1⋅S 2=(12PM ⋅PN)⋅(12PR ⋅PS)=254得S 1⋅S 2为定值254. 19. 本题考查了点斜式求直线方程与平行四边形的面积,为基础题.(1)求C 点坐标C(−3,−2),又因为BC//AD ,由点斜式求直线方程;(2)平行四边形ABCD 的面积,拆成两个三角形的面积,以BC 为底,A 到BC 的距离为高,求面积.20. 本题为与圆相关的应用题,考查学生建模解决实际问题的能力,为中档题. (Ⅰ)以AB 所在的直线为x 轴,OP 所在的直线为y 轴,建立平面直角坐标系,在牵引过程中,P 的轨迹是以O 为圆心,半径为10的圆弧,注意范围;(Ⅱ)OE 所在的直线方程为y =−2x ,直线和圆联立方程组,求交点坐标,数形结合,转化为求DG 的长.21. (1)由于EB 也是圆面的垂线,所以三棱锥看成以EB 为高的,△ABC 为底的,线面角指线与它在面内的射影所成的角,所以可知即AE 与面ABC 所成的角,即 = ,即可在△ABE 中求得EB ,由AB 为直径可知△ABC 为直角三角形,所以易求得面积,即可求出三棱锥体积.(2)因为O 为中点,所以可先猜测M 是否为中点,要证MO 与面ADE 平行,可先证得MO 所在的面与面ADE 平行,可继续找中点,找EB 的中点,利用中位线证得线线平行,再证得线面平行,再证得平面MNO//平面ADE平行即可得面MNO内的直线MO与面ADE平行.22. 本题主要考察的是通过直线斜率判定两直线平行与垂直,对于有参数时要考虑直线斜率是否存在.①平行时,应考虑是否重合.②垂直时,应考虑斜率为0的情况.。
