匀变速直线运动的全部公式
匀变速直线运动公式 推论推导 及规律总结

匀变速直线运动公式推论推导及规律总结一、基本规律:1.基本公式:平均速度 v = s/t加速度 a = (v - v0)/t2.瞬时速度公式:瞬时速度 v = v0 + at初速度 v0 = 03.位移公式:s = vt + 1/2at^2二、匀变速直线运动的推论及推理掌握运用匀变速直线运动公式的推论是解决特殊问题的重要手段。
1.推论1:做匀变速直线运动的物体在中间时刻的即时速度等于这段时间的平均速度,即 v = S/t2.推论2:做匀变速直线运动的物体在一段位移的中点的即时速度 v = (v0 + vt)/23.推论3:做匀变速直线运动的物体,在连续相等的时间间隔 t 内的位移分别为 S1、S2、S3……Sn,加速度为 a,则ΔS = S2 - S1 = S3 - S2 = ……= Sn - Sn-1 = at^2推论6:对于初速度为零的匀变速直线运动,从开始运动算起,物体经过连续相等的位移所用的时间之比为(a(2(n-1)S)^(1/2))]×(n-n+1)/2=a(n-n+1)/(2(n-1)S),代入可得推论7:对于初速度为零的匀加速直线运动,第一个s末、第二个s末、……第n个s末的速度之比为自由落体运动和竖直上抛运动的公式和推论如下:自由落体运动:平均速度v=gt/2瞬时速度vt=gt位移公式s=1/2gt^2重要推论2gs=vt^2竖直上抛运动:瞬时速度vt=v-gt位移公式s=vt-1/2gt^2重要推论-2gs=vt-v作为匀变速直线运动应用的竖直上抛运动,其处理方法有两种:其一是分段法。
将上升阶段看做末速度为零,加速度大小为g的匀减速直线运动;将下降阶段看做初速度为零,加速度大小为g的匀加速直线运动。
其二是通过将竖直上抛运动的轨迹分解为水平和竖直两个方向运动的合成,分别处理水平和竖直两个方向的运动。
高中物理——匀变速直线运动公式总结

● 匀变速直线运动1、平均速度:()01=2t s v v v t =+2、有用推论:2202t v v as -=3、中间时刻速度:()/2012t t v v v v ==+4、末速度:0t v v at =+5、中间位置速度:/2s v =6、位移:20122t v s v t at vt t =+== 7、 加速度:0t v v a t-=8、实验用推论:2S aT ∆=✓ 1m/s=3.6km/h; ✓ 平均速度是矢量;✓ 匀变速直线运动中连续相等的时间间隔内的位移差是一个恒量,设时间间隔为T ,加速度为a ,连续相等的时间间隔内的位移分别为:S 1, S 2, …,S N ,则有:221321...N N S S S S S S S aT -∆=-=-==-=;✓ 无论是匀加速还是匀减速,总有:/2/2t s v v < ✓ 说明:(1)以上公式只适用于匀变速直线运动.(2)四个公式中只有两个是独立的,即由任意两式可推出另外两式.四个公式中有五个物理量,而两个独立方程只能解出两个未知量,所以解题时需要三个已知条件,才能有解.(3)式中v0、vt 、a 、x 均为矢量,方程式为矢量方程,应用时要规定正方向,凡与正方向相同者取正值,相反者取负值;所求矢量为正值者,表示与正方向相同,为负值者表示与正方向相反.通常将v0的方向规定为正方向,以v0的位置做初始位置.(4)以上各式给出了匀变速直线运动的普遍规律.一切匀变速直线运动的差异就在于它们各自的v0、a 不完全相同,例如a =0时,匀速直线运动;以v0的方向为正方向; a >0时,匀加速直线运动;a <0时,匀减速直线运动;a =g 、v0=0时,自由落体应动;a =g 、v0≠0时,竖直抛体运动.(5)对匀减速直线运动,有最长的运动时间t=v0/a ,对应有最大位移x=v02/2a ,若t >v0/a ,一般不能直接代入公式求位移。
匀变速直线运动公式

匀变速直线运动匀变速直线运动,速度均匀变化的直线运动,即加速度不变的直线运动。
其速度时间图像是一条倾斜的直线,表示在任意相等的时间内速度的变化量都相同,即速度(v)的变化量与对应时间(t)的变化量之比保持不变(加速度不变),这样的运动是变速运动中最简单的运动形式,叫做匀变速直线运动。
速度时间公式:匀变速直线运动试验的纸带其中a为加速度,为初速度, 为末速度,t为该过程所用时间,x为该过程中的位移。
V=V0+at条件: 物体作匀变速直线运动须同时符合下述两条:(1)所受合外力不为零,且保持不变;(2)合外力与初速度在同一直线上。
分类: 在匀变速直线运动中,如果物体的速度随着时间均匀增加,这个运动叫做匀加速直线运动;如果物体的速度随着时间均匀减小,这个运动叫做匀减速直线运动。
若速度方向与加速度方向相同(即同号),则是加速运动;若速度方向与加速度方向相反(即异号),则是减速运动。
一、位移公式推导:由于匀变速直线运动的速度是均匀变化的,故平均速度=(初速度+末速度)/2=中间时刻的瞬时速度而匀变速直线运动的位移=平均速度×时间,故利用位移公式和平均速度公式,得平均速度为典型应用:自由落体运动一、概念物体只在重力的作用下从静止开始下落的运动。
1、运动学特点:其大小、方向均不变。
2、受力特点:在真空中物体只受重力,或者在空气中,物体所受空气阻力很小,和物体重力相比可忽略。
3、运动性质:自由落体运动是初速度为零的匀加速直线运动。
所以匀变速直线运动的所有规律和初速度为零的匀加速直线运动中的各种比例关系都可用于自由落体运动。
4、自由落体的加速度:在同一地点,一切物体在自由落体运动中的加速度都相同,这个加速度叫重力加速度,用g表示,地球上不同的纬度,g值不同。
其方向为竖直向下。
通常计算时取9.8 粗略计算时,取10二、规律自由落体运动是初速度为零,加速度为g的匀加速直线运动,其运动规律如下:1、三个基本公式:2、三个特殊公式:(1)在连续相等的时间(T)内位移之差为一恒定值,即(2)某段时间内中间时刻的瞬时速度等于这段时间内的平均速度,即(3)某段位移中间位置的瞬时速度与这段位移的初、末速度和的关系是3、四个比例公式(参照上述比例关系)竖直上抛运动物体具有竖直向上的初速度,加速度始终为重力加速度g的匀变速运动,可分为上抛时的匀减速运动和下落时的自由落体运动的两过程。
高一物理匀变速直线运动公式

匀变速直线运动公式、规律总结一.基本规律:v =ts 1. 公式a =tv v t 0-a =t vtv =2v1v2/v1+v2 (2)平均速度v =t v 21 at v v t +=0 at v t =021at t v s +=221at s =t v v s t 20+= t vs t 2= 2022v v as t -= (6)重要推论22t v as =注意:基本公式中(1)式适用于一切变速运动,其余各式只适用于匀变速直线运.................................动.。
二.匀变速直线运动的两个重要规律:1.匀变速直线运动中某段时间内中间时刻的瞬时速度等于这段时间内的平均速度: 即2t v =v ==ts 20tv v + 2.匀变速直线运动中连续相等的时间间隔内的位移差是一个恒量:设时间间隔为T ,加速度为a ,连续相等的时间间隔内的位移分别为S 1,S 2,S 3,……S N ;则∆S=S 2-S 1=S 3-S 2= …… =S N -S N -1= aT 2注意:设在匀变速直线运动中物体在某段位移中初速度为0v ,末速度为t v ,在位移中点的瞬时速度为2s v ,则中间位置的瞬时速度为2s v =2220t v v +无论匀加速还是匀减速总有2t v =v =20t v v +<2s v =2220t v v +三.自由落体运动和竖直上抛运动:v=2tvgtvt=s=212gt22tvgs=总结:自由落体运动就是初速度v=0,加速度a=g的匀加速直线运动.gtvvt-=2.竖直上抛运动2021gttvs-=222vvgst-=-总结:竖直上抛运动就是加速度ga-=的匀变速直线运动.四.初速度为零的匀加速直线运动规律:设T为时间单位,则有:(1)1s末、2s末、3s末、…… ns末的瞬时速度之比为:v1∶v2∶v3∶……:vn=1∶2∶3∶……∶n同理可得:1T末、2T末、3T末、…… nT末的瞬时速度之比为:v1∶v2∶v3∶……:vn=1∶2∶3∶……∶n(2)1s内、2s内、3s内……ns内位移之比为:S1∶S2∶S3∶……:S n=12∶22∶32∶……∶n2同理可得:1T内、2T内、3T内……nT内位移之比为:S1∶S2∶S3∶……:S n=12∶22∶32∶……∶n2(3)第一个1s内,第二个2s内,第三个3s内,……第n个1s内的位移之比为:SⅠ∶SⅡ∶SⅢ∶……:S N=1∶3∶5∶……∶(2n-1)同理可得:第一个T内,第二个T内,第三个T内,……第n个T内的位移之比为:SⅠ∶SⅡ∶SⅢ∶……:S N=1∶3∶5∶……∶(2n-1)(4)通过连续相等的位移所用时间之比为:t1∶t2∶t3∶……:t n=1∶(12-)∶(23-)∶………∶(1--nn)。
匀变速直线运动的公式及推论

匀变速直线运动的公式及推论匀变速直线运动的公式较多,而这些公式在不同的条件下,又可以衍生许多推论,有些推论对于灵活、便捷地处理实际问题非常有用,本文就此作一介绍。
一、 基本公式:(1) 速度与时间关系公式 at v v t +=0(2) 位移与时间关系公式 2021at t v x +=(3) 速度与位移关系公式 ax v v t 2202=-以上三个公式只有两个是独立的,因此匀变速直线运动中五个物理量初速度v0、末速度v 、加速度a 、位移x 、时间t ,只有知道三个,才能求出另外两个。
例1、一辆卡车行驶速度为54千米/小时,紧急刹车时的加速度的大小是5 m/s 2。
那么刹车4s 后卡车行驶的距离是多少?解析:此题表面看三个已知是初速度、加速度、时间t ,其实时间是伪条件,卡车3s 已经停下来了,这里真正一个隐含条件是末速度为0。
应该用公式,ax v v t 2202=- 求得m x 5.22=二、关于速度的几个公式(1)平均速度原始公式t x v ∆∆=或t x v = (2)平均速度特殊公式()000221v v v v v v v v t t t +=+=或 (3)中间时刻速度公式()v v v v t t =+=0221 (4) 中点位置速度公式22022v v v t s += 公式适用任何变速直线运动,其它公式都只适用匀变速直线运动。
不管匀加速直线运动还是匀减速直线运动,一定。
例2、一个质点做匀变速直线运动,依次经过A 、C 、B 三点,其中C 是A 、B 的中点,已知AC 段的平均速度为3m\s,BC 段的平均速度为6m\s,求质点通过C 点的瞬时速度。
解析:此题若用基本公式求解,相当复杂.现在用平均速度特殊公式和中点位置速度公式来求解,相当明了. 由()c a ac v v v +=21 ()c b bc v v v +=21 ① ax v v t 2202=- ② 22022v v v t s += ③ 解①②③得vc=5m/s 。
匀变速直线运动公式整理

匀变速直线运动公式整理匀变速直线运动可是高中物理中的一个重要知识点哦。
咱们先来说说匀变速直线运动的基本公式,这就像打开这扇知识大门的钥匙。
首先,速度公式:v = v₀ + at 。
这里的 v 是末速度,v₀是初速度,a 是加速度,t 是时间。
打个比方,就像你骑着自行车从静止开始加速,初始速度 v₀是 0 ,假如加速度 a 是 1m/s²,骑了 5 秒,那末速度 v 就是 0 + 1×5 = 5m/s 。
接着是位移公式:x = v₀t + 1/2at²。
假设还是刚才骑自行车的例子,初速度 v₀为 0 ,加速度 a 是 1m/s²,骑了 5 秒,那位移 x 就是 0×5 +1/2×1×5² = 12.5 米。
还有一个推论公式:v² - v₀² = 2ax 。
比如说一辆汽车以 10m/s 的初速度加速行驶,加速度为 2m/s²,当末速度达到 20m/s 时,我们就可以通过这个公式算出行驶的位移 x 。
在学习匀变速直线运动公式的时候,我想起了之前带过的一个学生。
那时候我们正在做一道有关匀变速直线运动的题目,题目说一个小球从高处自由下落,经过 3 秒落地,让求下落的高度。
这孩子一开始有点懵,不知道从哪儿下手。
我就引导他,先分析题目,确定这是一个匀变速直线运动,初速度 v₀为 0 ,加速度 a 是重力加速度 g 约等于10m/s²,时间 t 是 3 秒。
然后让他想想用哪个公式来求解,他想了一会儿,说用位移公式 x = v₀t + 1/2at²。
接着他就动手计算,算出位移 x是 45 米。
当得出正确答案的那一刻,他脸上那种恍然大悟又带着兴奋的表情,我到现在都记得清清楚楚。
在实际应用这些公式的时候,一定要注意加速度的方向和正负。
如果加速度与速度方向相同,那加速度就是正的;如果相反,就是负的。
匀变速直线运动公式、规律总结

匀变速直线运动公式、规律总结一.基本规律:v 2s v ,三.初速度为零的匀加速直线运动规律:设T为时间单位,则有:(1)1s末、2s末、3s末、……ns末的瞬时速度之比为:v1∶v2∶v3∶……:vn=1∶2∶3∶……∶n同理可得:1T末、2T末、3T末、……nT末的瞬时速度之比为:v1∶v2∶v3∶……:vn=1∶2∶3∶……∶n(2)1s内、2s内、3s内……ns内位移之比为:SSSSt1例1(1(2(3(4(5例2例3:甲乙两辆汽车都从静止出发做加速直线运动,加速度方向一直不变。
在第一段时间间隔内,两辆汽车加速度大小不变,汽车乙的加速度是甲的两倍;在接下来的相同时间间隔内,汽车甲的加速度大小增加为原来的两倍,汽车乙的加速度大小减小为原来的一半。
求甲乙两车各自在这两段时间间隔内走过的总路程之比。
例4:如图所示,在水平面上固定着三个完全相同的木块,一子弹以水平初速度v射入木块,若子弹在木块中做匀减速运动,当穿透第三个木块时速度恰好为0,则子弹依次射入每个木块时的速度比和穿过每个木块所用时间比分别为()A.B.C.D.例5:质点做直线运动的位移x与时间t的关系为x=5t+t2(各物理量均采用国际单位制单位),则该质点() A.第1 s内的位移是5 mB.前2 s内的平均速度是6 m/sC.任意相邻的1 s内位移差都是1 mD.任意1 s内的速度增量都是2 m/s例6:一物体做匀加速直线运动,通过一段位移所用的时间为t1,紧接着通过下一段位移所用的时间为t2.则物体运动的加速度为:()A.B.C.D.例7:一质点由A点出发沿直线AB运动,行程的第一部分是加速度为a的匀加速运动;接着又以a’做匀减速运动,到达B恰好停止,若AB长为S,则质点走完AB所用的时间是()A.B.C.D.例8:一个小石块从空中a点自由落下,先后经过b点和c点,不计空气阻力.已知它经过b点时的速度为v,经过c点时的速度为3v.则ab段与ac段位移之比为( )A.1∶3 B.1∶5 C.1∶8 D.1∶9例9:个质点正在做匀加速直线运动,用固定在地面上的照相机对该质点进行闪光照相,相邻两次闪光的时间间隔为1s.分析照片发现,质点在第1 次、第2次闪光的时间间隔内移动了2m;在第3次、第4次闪光的时间间隔内移动了8m.由此,算不出来的物理量是:()A.第1次闪光时质点的速度.B.质点运动的加速度.C.从第2次闪光到第3次闪光这段时间内质点通过的位移.D.质点运动的初速度.例10:一个做匀变速直线运动的质点,初速度为0.5 m/s,第9 s内的位移比第5 s内的位移多4 m,则该质点的加速度、9 s末的速度和质点在9 s内通过的位移分别是()A.a=1 m/s2,v9=9 m/s,x9=40.5 m B.a=1 m/s2,v9=9 m/s,x9=45 mC.a=1 m/s2,v9=9.5 m/s,x9=45 m D.a=0.8 m/s2,v9=7.7 m/s,x9=36.9 m例11:甲乙丙三辆汽车以相同的速度同时经过某一个路标,从此开始甲车一直匀速运动,乙车先加速后减速,丙车先减速后加速,它们经过下一个路标时速度又相等,则()A. 甲车先通过下一个路标B. 乙车先通过下一个路标C. 丙车先通过下一个路标D. 条件不足,无法判断。
匀变速直线运动基本公式与推论

匀变速直线运动基本公式与推论匀变速直线运动是在物体运动过程中速度不断变化的情况下沿直线方向运动的一种运动形式。
在匀变速直线运动中,物体在单位时间内的位移不是恒定的,而是随着时间的变化而发生变化。
为了描述匀变速直线运动,我们引入基本公式和推论来进行分析和计算。
一、匀变速直线运动的基本公式1.位移-时间关系位移(s)是物体从其中一位置移动到另一位置的长度,通常用向量表示。
匀变速直线运动中,位移与时间之间的关系可以由如下公式表示:s = v0t + 1/2at^2其中,s为位移,v0为起始速度,t为时间,a为加速度。
2.速度-时间关系速度(v)是物体在单位时间内移动的位移长度,通常用向量表示。
在匀变速直线运动中,速度与时间之间的关系可以由如下公式表示:v = v0 + at其中,v为速度,v0为起始速度,t为时间,a为加速度。
3.加速度-时间关系加速度(a)是速度变化的速率,通常用标量表示。
在匀变速直线运动中,加速度与时间之间的关系可以由如下公式表示:a=(v-v0)/t其中,a为加速度,v为结束速度,v0为起始速度,t为时间。
二、匀变速直线运动的推论基于上述基本公式,我们可以得到该运动的一些推论,主要有距离-速度关系、时间-位移关系以及位移-速度关系。
1.距离-速度关系由速度-时间关系公式可得:v = v0 + at整理得:v - v0 = at左右两数乘以时间t,得:(v - v0) t = at^2移项得:at^2 = vt - v0t由位移-时间关系公式可得:s = v0t + 1/2at^2将上面的等式代入,得:s = v0t + 1/2(vt - v0t)整理化简,可得:s = v0t + 1/2vt - 1/2v0t化简合并同类项,可得:s=(v0+v)t/2这个推论说明了在匀变速直线运动中,物体在其中一时间段内的位移与物体的起始速度、结束速度以及时间的关系。
2.时间-位移关系由位移-时间关系公式可得:s = v0t + 1/2at^2将速度-时间关系公式代入,得:s=v0t+1/2(v-v0)t整理化简,可得:s=(v0+v)t/2和上述的推论1相同,这个推论也说明了在匀变速直线运动中,物体在其中一时间段内的位移与物体的起始速度、结束速度以及时间的关系。
匀变速运动的基本公式

匀变速运动的基本公式1.三个基本公式速度公式:v t=v0+at;位移公式:s=v0t+12at2;位移速度关系式:v t2-v02=2as.2.三个推论(1)连续相等的相邻时间间隔T内的位移差等于恒量,即s2-s1=s3-s2=…=s n-s(n-1)=aT2.(2)做匀变速直线运动的物体在一段时间内的平均速度等于这段时间初末时刻速度矢量和的一半,还等于中间时刻的瞬时速度.平均速度公式:v=v0+v t2=vt2.(3)匀变速直线运动的某段位移中点的瞬时速度v s2=v02+v t22.3.初速度为零的匀加速直线运动的特殊规律(1)在1T末,2T末,3T末,…nT末的瞬时速度之比为v1∶v2∶v3∶…∶v n=1∶2∶3∶…∶n.(2)在1T内,2T内,3T内,…,nT内的位移之比为s1∶s2∶s3∶…∶s n=12∶22∶32∶…∶n2.(3)在第1个T内,第2个T内,第3个T内,…,第n个T内的位移之比为sⅠ∶sⅡ∶sⅢ∶…∶s n=1∶3∶5∶…∶(2n-1).(4)从静止开始通过连续相等的位移所用时间之比为t1∶t2∶t3∶…∶t n=1∶(2-1)∶(3-2)∶…∶(n-n-1).(5)从静止开始通过连续相等的位移时的速度之比为v1∶v2∶v3∶…∶v n=1∶2∶3∶…∶n.一.匀变速直线运动规律公式的三性(1)条件性:速度公式和位移公式的适应条件必须是物体做匀变速直线运动.(2)矢量性:位移公式和速度公式都是矢量式.(3)可逆性:由于物体运动条件的不同,解题时可进行逆向转换.限时训练1.(2009·江苏单科)图1-2-3如图1-2-3所示,以8 m/s匀速行驶的汽车即将通过路口,绿灯还有2 s就熄灭,此时汽车距离停车线18 m.该车加速时最大加速度大小为2 m/s2,减速时最大加速度大小为5m/s2.此路段允许行驶的最大速度为12.5 m/s.下列说法中正确的有().①如果立即以最大加速度做匀加速运动,在绿灯熄灭前汽车可能通过停车线②如果立即以最大加速度做匀加速运动,在绿灯熄灭前通过停车线汽车一定超速③如果立即以最大加速度做匀减速运动,在绿灯熄灭前汽车一定不能通过停车线④如果距停车线5 m处以最大加速度减速,汽车能停在停车线处A.①②B.③④C.①③D.②④2.(2010·课标全国,24)短跑名将博尔特在北京奥运会上创造了100 m和200 m短跑项目的新世界纪录,他的成绩分别是9.69 s和19.30 s.假定他在100m比赛时从发令到起跑的反应时间是0.15 s,起跑后做匀加速运动,达到最大速率后做匀速运动.200 m比赛时,反应时间及起跑后加速阶段的加速度和加速时间与100 m比赛时相同,但由于弯道和体力等因素的影响,以后的平均速率只有跑100 m时最大速率的96%.求:(1)加速所用时间和达到的最大速率;(2)起跑后做匀加速运动的加速度.(结果保留两位小数)3.(2011·重庆卷,14)某人估测一竖直枯井深度,从井口静止释放一石头并开始计时,经 2 s听到石头落底声.由此可知井深约为(不计声音传播时间,重力加速度g取10 m/s2)().A.10 m B.20 mC.30 m D.40 m4.(2011·安徽卷,16)一物体做匀加速直线运动,通过一段位移Δx所用的时间为t1,紧接着通过下一段位移Δx所用的时间为t2,则物体运动的加速度为().A.2Δx(t1-t2)t1t2(t1+t2)B.Δx(t1-t2)t1t2(t1+t2)C.2Δx(t1+t2)t1t2(t1-t2)D.Δx(t1+t2)t1t2(t1-t2).5.(2011·天津卷)质点做直线运动的位移x与时间t的关系为x=5t+t2(各物理量均采用国际单位制单位),则该质点().A.第1 s内的位移是5 mB.前2 s内的平均速度是6 m/sC.任意相邻的1s内位移差都是1 mD.任意1 s内的速度增量都是2 m/s答案 1 C 2.(1)1.29S 11.24M/S (2)8.71 3.B 4.A 5.D。
高中物理匀变速直线运动公式大全
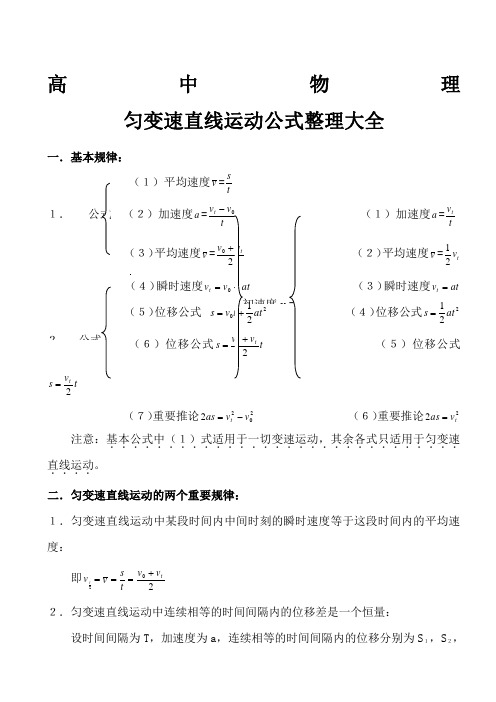
高中物理匀变速直线运动公式整理大全一.基本规律:(1)平均速度v =ts1. (2)加速度a (1)加速度a =t v t(3)平均速度 (2)平均速度v =t v 21(4) (3)瞬时速度at v t = (5)(4)位移公式221at s =(5)位移公式t2(7)重要推论2022v v as t -= (6)重要推论22t v as = 注意:基本公式中(1)式适用于一切变速运动,其余各式只适用于匀变速..............................直线运动....。
二.匀变速直线运动的两个重要规律:1.匀变速直线运动中某段时间内中间时刻的瞬时速度等于这段时间内的平均速度:即2tv =v ==t s 20tv v + 2.匀变速直线运动中连续相等的时间间隔内的位移差是一个恒量:设时间间隔为T ,加速度为a ,连续相等的时间间隔内的位移分别为S 1,S 2,S 3,……S N ;则∆S=S 2-S 1=S 3-S 2= …… =S N -S N -1= aT 2注意:设在匀变速直线运动中物体在某段位移中初速度为0v ,末速度为t v ,在位移中点的瞬时速度为2s v ,则中间位置的瞬时速度为2s v =2220t v v +无论匀加速还是匀减速总有2t v =v =20t v v +<2s v =2220t v v +三.自由落体运动和竖直上抛运动:(1)平均速度v =2tv (2)瞬时速度gt v t =(3)位移公式s =212gt(4)重要推论22t v gs =总结:自由落体运动就是初速度0v =0,加速度a =g 的匀加速直线运动. (1)瞬时速度gt v v t -=0 (2)位移公式2021gt t v s -= (3)重要推论2022v v gs t -=-总结:竖直上抛运动就是加速度g a -=的匀变速直线运动. 四.初速度为零的匀加速直线运动规律:设T 为时间单位(可能是分钟、或小时、天、周)则有: (1)1s 末、2s 末、3s 末、…… ns 末的瞬时速度之比为:v1∶v2∶v3∶…… :vn =1∶2∶3∶…… ∶n同理可得:1T 末、2T 末、3T 末、…… nT 末的瞬时速度之比为:v1∶v2∶v3∶…… :vn =1∶2∶3∶…… ∶n(2)1s 内、2s 内、3s 内…… ns 内位移之比为:S 1∶S 2∶S 3∶…… :S n =12∶22∶32∶…… ∶n 2同理可得:1T 内、2T 内、3T 内…… nT 内位移之比为:S 1∶S 2∶S 3∶…… :S n =12∶22∶32∶…… ∶n 2(3)第一个1s 内,第二个2s 内,第三个3s 内,…… 第n 个1s 内的位移之比为:S Ⅰ∶S Ⅱ∶S Ⅲ∶…… :S N =1∶3∶5∶…… ∶(2n -1)同理可得:第一个T 内,第二个T 内,第三个T 内,…… 第n 个T 内的位移之比为:S Ⅰ∶S Ⅱ∶S Ⅲ∶…… :S N =1∶3∶5∶…… ∶(2n -1)(4)通过连续相等的位移所用时间之比为:t 1∶t 2∶t 3∶…… :t n =1∶(12-)∶(23-)∶……… ∶(1--n n )。
匀变速直线运动公式

匀变速直线运动公式
匀加速直线运动的速度和时间公式为:v(t)=v(0)+at;匀加速直线运动的位移和时间公式为:s=v(0)t+1/2at^2;匀加速直线运动的位移和速度公式为:v(t)^2-v(0)^2=2as。
其中a为加速度,v(0)为初速度,v(t)为t秒时的速度 s(t)为t秒时的位移。
物体作匀变速直线运动须同时符合下述两条:
1、受恒外力作用;
2、合外力与初速度在同一直线上。
加速度公式推论:
由于匀变速直线运动的速度是均匀变化的,故平均速度=(初速度+末速度)/2=中间时刻的瞬时速度。
坯变速箱直线运动的路程s=平均速度*时间,故s=[(v0+v)/2]* t
利用速度公式v=v0+at,得s=[(v0+v0+at)/2]*t=[v0+at/2]*t=v0*t+1/2at^2
平均速度=(初速度+末速度)/2=中间时刻的瞬时速度
△x=at^2(△x代表相邻相等时间段内位移差,t代表相邻相等时间段的时间长度)
x为加速度,v为末速度,vo为初速度。
在匀变速直线运动中,如果物体的速度随着时间均匀增加,这个运动叫做匀加速直线运动;如果物体的速度随着时间均匀减小,这个运动叫做匀减速直线运动。
若速度方向与加速度方向同向(即为同号),则就是加速运动;若速度方向与加速度方向恰好相反(即为异号),则就是减速运动
速度无变化(a=0时),若初速度等于瞬时速度,且速度不改变,不增加也不减少,则运动状态为,匀速直线运动;若速度为0,则运动状态为静止。
匀变速直线运动公式、圆周运动、万有引力总结

1.自由落体运动
①末速度: ②下落高度:
③下落时间:
2.竖直下抛运动
①末速度: ②下落高度:
3.竖直上抛运动
①末速度: ②下落高度:
③上升时间: ④总时间:
⑤最大高度:
曲线运动
(1)①条件:v0与 不共线②速度方向:切线方向
③弯曲方向:总是从v0的方向转向 的方向
7.平抛运动
②合速度:
(1)在连续相等的时间间隔(T)内的位移之差等于一个恒量,即Δs=aT2⑤
(2)某段时间内中间时刻的瞬时速度等于这段时间内的平均速度,即: ⑥
(3)某段位移内中间位置的瞬时速度v中与这段位移初、末速度v0和vt关系: ⑦
注意:无论匀加速还是匀减速总有 = = < =
4、初速度为零的匀加速直线运动的一些特殊比例式(从t=0开始),设T为时间单位,则有:
20.中心天体质量:
21.中心天体密度:
22.卫星的运行速度:
23.地球表面的重力加速度:
24.第一宇宙速度(环绕速度):
第二宇宙速度(脱离速度):11.2km/s
第三宇宙速度(逃逸速度):16.7km/s
③速度方向:
⑤位移方向:
⑥飞行时间: ,与v0无关
8.斜抛运动
③飞行时间:
④射程: ⑤射高:
圆周运动
1.线速度: 2.角速度:
3.线速度与角速度的关系:
4.周期与频率的关系: 5.转速与频率的关系:
6.向心力:7.向心Fra bibliotek速度:8.竖直平面内圆周运动最高点的临界速度:
万有引力
18.开普勒第三定律:
19.万有引力定律: ,G=6.67×10-11
依题意可得:vt=0,t=3s,a=-6m/s2
匀变速直线运动的公式及推论

匀变速直线运动的五个公式及其选用原则时间(t )、位移(x )、速度(v 0、v )、加速度(a )是描述运动的几个重要物理量,它们可以组成许多运动学公式.在匀变速直线运动中,以下这五个公式是最基本的,记好、理解好这几个公式,对于学好物理学是至关重要的!一、两个基本公式1.位移公式:x =v 0t +12at 2 2.速度公式:v =v 0+at二、三个推导公式1.速度位移公式:v 2-v 20=2ax2.平均速度公式:v =v 0+v 2=v t 23.位移差公式:Δx =aT 2三、公式的选用原则1.能用推导公式求解的物理量,用基本公式肯定可以求解,但有些问题往往用推导公式更方便些.2.这五个公式适用于匀变速直线运动,不仅适用于单方向的匀加速或匀减速(末速度为零)直线运动,也适用于先做匀减速直线运动再反方向做匀加速直线运动而整个过程是匀变速直线运动(如竖直上抛运动)的运动.3.使用公式时注意矢量(v 0、v 、a 、x )的方向性,通常选v 0的方向为正方向,与v 0相反的方向为负方向.对点例题 一个滑雪运动员,从85 m 长的山坡上匀加速滑下,初速度为1.8 m /s ,末速度为5.0 m/s ,他通过这段山坡需要多长时间?解题指导 解法一:利用公式v =v 0+at 和x =v 0t +12at 2求解. 由公式v =v 0+at ,得at =v -v 0,代入x =v 0t +12at 2有:x =v 0t +(v -v 0)t 2,故t =2x v +v 0=2×855.0+1.8s =25 s解法二:利用公式v 2-v 20=2ax 和v =v 0+at 求解.由公式v 2-v 20=2ax 得,加速度a =v 2-v 202x =5.02-1.822×85m /s 2=0.128 m/s 2. 由公式v =v 0+at 得,需要的时间t =v -v 0a =5.0-1.80.128s =25 s 解法三:利用平均速度公式v =v 0+v 2及v =x t求解. 由v =v 0+v 2得v =1.8+5.02m /s =3.4 m/s 再由v =x t 得t =x v =853.4s =25 s 答案 25 s从车站开出的汽车,做匀加速直线运动,行驶了12 s 时,发现还有乘客没上来,于是立即做匀减速运动至停车,总共历时20 s ,行进了50 m ,求汽车的最大速度.答案 5 m/s解析 解法一:(基本公式法)设最大速度为v max ,由题意得,x =x 1+x 2=12a 1t 21+v max t 2-12a 2t 22,t =t 1+t 2, v max =a 1t 1,0=v max -a 2t 2,解得v max =2xt 1+t 2=2×5020 m /s =5 m/s. 解法二:(平均速度法)由于汽车在前后两段均做匀变速直线运动,故前后段的平均速度均为最大速度v max 的一半,即v =0+v max 2=v max 2,x =v t 得v max =2x t 总=5 m/s.。
匀变速直线运动的公式

匀变速直线运动的公式一、基本公式:1、速度公式:0t a t υυ=+⋅2、位移公式:2012s t at υ=+二、推论:1、平均速度公式:02tυυυ+=2、速度——位移公式:2202t as υυ-=推导:0t a t υυ=+⋅,22200122t s t at as υυυ=+⇒-= 3、中时速公式:022ttυυυυ 推导:00002222tttυυυυt t υυa υυt4、中位速公式:22022t Sυυυ。
(22ts υυ)推导:(1)22220000221222222t t t s S sa t t υυυυυυυυυ-+--==⋅⋅⋅⋅=⇒=2222022222s t S s a as υυυυυ-=-=⇒=或,(2)22222022()04sttst υυυυυυ三、匀变速直线运动的特殊规律1、初速为零的匀加速直线运动的特点:(1)从运动开始,在1T 末、2T 末、3T 末……nT 末的速度之比:υ1::υ2:υ3:…:υn =1:2:3:…:n (提示:t a t υ=⋅)(2)从运动开始,在1T 内、2T 内、3T 内……nT 内的位移之比:S 1:S 2:S 3:……:S n =12: 22: 32:……:n 2(提示:212s at)(3)从运动开始,在第1个T 内,第二个T 内,第3个T 内……第n 个T 内的位移之比:S Ⅰ:S Ⅱ:S Ⅲ:……:S N =1:3:5:……:(2N -1) (提示:S Ⅰ=S 2-S 1)(4)从运动开始,通过连续相等的位移所用时间之比:① t Ⅰ:t Ⅱ:t Ⅲ:……:t N =1:1):2):……:1n )② t 总t Ⅰ2、做匀变速直线运动的物体,如果在各个连续相等的时间T 内的位移分别为S Ⅰ,S Ⅱ,S III ……S N ,则△S =S Ⅱ-S Ⅰ= S III -S Ⅱ=……= S N -S N -1=aT 2=恒量推论:第n个T时间内的位移和第m个T时间内的位移之差:S n-S m=(n-m)aT2。
高中物理——匀变速直线运动公式总结

高中物理——匀变速直线运动公式总结-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN匀变速直线运动1、平均速度:()01=2t s v v v t =+2、有用推论:222t v v as -= 3、中间时刻速度:()/2012t t v v v v ==+4、末速度:0t v v at =+5、中间位置速度:220/22t s v v v +=6、位移:20122t v s v t at vt t =+==7、 加速度:0t v v a t-=8、实验用推论:2S aT ∆=✓ 1m/s=3.6km/h; ✓ 平均速度是矢量;✓ 匀变速直线运动中连续相等的时间间隔内的位移差是一个恒量,设时间间隔为T ,加速度为a ,连续相等的时间间隔内的位移分别为:S 1, S 2, …,S N ,则有:221321...N N S S S S S S S aT -∆=-=-==-=;✓ 无论是匀加速还是匀减速,总有:/2/2t s v v <自由落体运动1、初速度:00v =;末速度:t v gt =2、下落高度:212h gt =3、有用推论:22t v gh =● 竖直上抛运动1、位移:2012s v t gt =-2、末速度:0t v v gt =-3、有用推论:222t v v gs -=-4、上升最大高度:22v h g =5、往返时间:02v t g=✓ 全过程处理:是匀减速直线运动,以向上为正方向,加速度取负值; ✓ 分段处理:向上为匀减速直线运动,向下为自由落体运动,具有对称性; ✓ 上升与下落过程具有对称性,如在同点速度等值反向等。
● 平抛运动1、水平、竖直方向速度:0x v v =;y v gt = 3、水平方向位移:0x v t = 4、竖直方向位移:212y gt =5、运动时间:t ==6、合速度:t v == 7、合速度与水平方向夹角:tan y xv gt v v β==7、合位移:s =8、位移与水平方向夹角:tan 2y gt x v α== 9、水平、竖直方向加速度:0x a =;y a g =✓ 平抛运动是匀变速曲线运动,加速度为g ,通常可看作是水平方向的匀速直线运与竖直方向的自由落体运动的合成;✓ 运动时间由下落高度h (y )决定与水平抛出速度无关; ✓ θ与β的关系为tan β=2tan α; ✓ 在平抛运动中时间t 是解题关键;✓ 做曲线运动的物体必有加速度,当速度方向与所受合力(加速度)方向不在同一直线上时,物体做曲线运动。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
匀变速直线运动的全部公式
1.匀变速直线运动的基本方程:(1) (2) at v v +=02
02
1at t v X +
=2、联立两式消去t 和a 可得二个导出式:(1) (2) aX v v 22
02
=-t v
v X 2
0+=
3、三个推论:
(1)任意相邻相等时间内的位移之差相等——ΔX=X n -X n-1=aT 2。
(2)中间时刻的瞬时速度等于该段运动的平均速度—— 2
02
v
v v t
+=
(3)某段位移中点的瞬时速度——2
2
202
v v v X +=
4、特例:
(1)初速度为零(或末速度为零)的匀变速直线运动: , , , at v =221at X =
aX v 22=t v X 2
=(2)自由落体运动(初速度为零,加速度为g ):
, , , gt v =221gt h =
gh v 22=t v h 2
=5、初速为零的匀变速直线运动中几个常用结论:
①第1秒末、第2秒末、第3秒末……内的速度之比为:1∶2∶3∶……n
②前1秒、前2秒、前3秒……内的位移之比为:1∶4∶9∶……n 2
③第1秒、第2秒、第3秒……内的位移之比为:1∶3∶5∶……(2n-1)④第1米、第2米、第3米…所用的时间之比为:1∶
()12-∶(
)∶……
23-1
--n n 小结:教师辅助总结、强调、归纳:知三必求二;用时查缺量;三同两必同;注意正负向。
说明:
(1)以上五个公式中共有五个物理量:X 、t 、a 、v 0、v ,这五个物理量中只有三个是独立的,可以任意选定。
只要其中三个物理量确定之后,另外两个就唯一确定了。
(2)每个公式中只有其中的四个物理量,当已知某三个而要求另一个时,我们看缺哪一个往往就选定一个公式就可以了。
(3)如果两个匀变速直线运动有三个物理量对应相等,那么另外的两个物理量也一定对应相等。
(举例:从静止开始匀加速运动一段时间后以同样大小的加速度减速停下,有三量v 0、v t 、a 相同,那么t 、s 也一定相同。
)
(4)以上五个物理量中,除时间外,s 、v 0、v t 、a 均为矢量。
一般以v 0的方向为正方向,以t =0时刻的位移为零,这时s 、v t 和a 的正负就都有了确定的物理意义。
常用的有七大公式:一般来讲这七个公式可以解决匀变速直线运动的所有题目;公式多,往往解题方法也很多,因此我们在解题要学会选择最直接、最便捷的方法和公式解题。
