第一章&第二章算法题
大学第一章原文及翻译

⼤学第⼀章原⽂及翻译⼤学第⼀章原⽂及翻译 《⼤学》是⼀篇论述儒家修⾝治国平天下思想的散⽂,原是《⼩戴礼记》第四⼗⼆篇,相传为曾⼦所作,实为秦汉时儒家作品,是⼀部中国古代讨论教育理论的重要著作。
以下是⼤学第⼀章原⽂及翻译,欢迎阅读。
《⼤学》第⼀章原⽂ 作者:曾参 ⼤学之道,在明明德,在亲民,在⽌于⾄善。
知⽌⽽后有定,定⽽后能静,静⽽后能安,安⽽后能虑,虑⽽后能得。
物有本末,事有终始。
知所先后,则近道矣。
古之欲明明德于天下者,先治其国;欲治其国者,先齐其家;欲齐其家者,先修其⾝;欲修其⾝者,先正其⼼;欲正其⼼者,先诚其意;欲诚其意者,先致其知。
致知在格物。
物格⽽后知⾄,知⾄⽽后意诚,意诚⽽后⼼正,⼼正⽽后⾝修,⾝修⽽后家齐,家齐⽽后国治,国治⽽后天下平。
⾃天⼦以⾄于庶⼈,壹是皆以修⾝为本。
其本乱,⽽末治者否矣。
其所厚者薄,⽽其所薄者厚,未之有也。
译⽂ ⼤学的宗旨在于弘扬光明正⼤的品德,在于使⼈弃旧图新,在于使⼈达到最完善的境界。
知道应达到的境界才能够志向坚定;志向坚定才能够镇静不躁;镇静不躁才能够⼼安理得;⼼安理得才能够思虑周祥;思虑周祥才能够有所收获。
每样东西都有根本有枝末,每件事情都有开始有终结。
明⽩了这本末始终的道理,就接近事物发展的规律了。
古代那些要想在天下弘扬光明正⼤品德的⼈,先要治理好⾃⼰的国家;要想治理好⾃⼰的国家,先要管理好⾃⼰的家庭和家族;要想管理好⾃⼰的家庭和家族,先要修养⾃⾝的品性;要想修养⾃⾝的品性,先要端正⾃⼰的⼼思;要想端正⾃⼰的⼼思,先要使⾃⼰的意念真诚;要想使⾃⼰的意念真诚,先要使⾃⼰获得知识;获得知识的途径在于认识、研究万事万物。
通过对万事万物的认识、研究后才能获得知识;获得知识后意念才能真诚;意念真诚后⼼思才能端正;⼼思端正后才能修养品性;品性修养后才能管理好家庭和家族;管理好家庭和家族后才能治理好国家;治理好国家后天下才能太平。
上⾃国家元⾸,下⾄平民百姓,⼈⼈都要以修养品性为根本。
第一章绪论

(1)农业的本质特征——自然再生产与经济再生产相交织
农业具有生产对象具有其固有的生长、发育、繁殖的规律;土地是必不可少的、重要的生产资料农业生产与外界自然环境关系密切;农业内部各生产门类之间相互依存;农业生产时间与劳动时间不一致;农产品具有消费资料与生产资料的双重属性;农产品具有鲜活易腐烂且体积大等一般特征。
由于农业是人类直接利用生物、太阳能、土壤、气候等自然力的生产活动,农业生产一方面是人类劳动产品、劳动力和生产关系等经济现象的再生产过程,同时又是生物的生长和繁衍及其与自然界进行物质和能量相互转换的自然现象的再生产过程。因此,经济再生产与自然再生产相交织是农业的根本特性。
自然再生产---指生物依靠自然环境和自身的生活机能而进行的自然生长发育过程(生物的自然生长发育过程),即生物有机体同自然环境之间不断进行物质、能量交换和转化的过程。自然再生产过程是生物通过自身的代谢活动而实现的,它是农业再生产的自然基础。亦可理解为:作为农业生产对象的动、植物(和微生物)通过自身的生长、发育、繁殖而自行增殖的过程。
社会功能包括为农民提供谋生手段和就业机会、提供生活和社交场所;有助于形成和维持农村生活模式及社区活动;减少农村人口盲目向城市流动,保持社会稳定,形成社会资本;在发展中国家,农业还可以消除贫困,替代社会福利保障。
粮食安全功能指所有人在人任何时候都在经济上有能力并且可以获得足够数量卫生安全和营养的食物。其构成要素为充足的供给、供给的稳定性、粮食的可获得性、食物的卫生安全、质量和偏好等。其实现途径为依靠自己生产(自给自足)、依靠进口及二者结合。开放贸易有助于稳定世界农产品市场,反之又有利于稳定粮食进口国的价格和保障其国家粮食安全。
农业除了确保粮食和其它农产品的供给之外,还要发挥防止洪涝灾害、涵养水源、防止土壤侵蚀和水土流失、处理有机废弃物、净化空气、提供绿色景观和自然景观,以及传统文化的继承等多方面的作用。目前,欧盟、日本和韩国等国,已经将农业的多功能性作为保护其国内农业和农产品市场,维持其高度农业保护政策的口实。
第一章 我究竟为谁而活

第一章我究竟为谁而活?倚靠财富,像秋天落叶;义人繁茂,如夏季绿叶。
(箴言书11:28,现代中文译本)但倚靠耶和华,以耶和华为他所信赖的,这人是有福的。
他必像一棵树,栽种在水边,树根伸进河里;炎热来到,并不害怕,树叶仍然繁茂;在荒旱之年,它不挂虑,并且不断结果子。
(耶利米书17:7-8,圣经新译本)〖第1天万物皆由神开始〗因为万有都是靠他造的,无论是天上的、地上的、能看见的,不能看见的,或是有位的、主治的、执政的、掌权的,一概都是藉着他造的,又是为他造的。
(西1:16)因为一切,——全然的一切,不论天上地下,可见或不可见的一切。
都是从他开始,并且在他里面才可寻获最终目的。
除非你假定有一位神,否则探讨人生目的这问题是毫无意义的。
人生目的不是从你开始的。
生命的重心不是在你。
若把目光放在自己身上,我们将永远无法找出人生目的。
人生的目的不单是追求个人的满足和喜乐,它远比你的家庭、事业、甚至比你最疯狂的梦想与抱负意义更大深远。
若要知道你活在这世上的原因,你必须从神开始,因为你是因他的目的而生,也是为他的目的而活。
数千年来,找寻人生目的一直是个困扰人的问题。
因为我们往往错误的以自己为起点来开始。
我们问一些自我为中心的问题,比如:我要做什么样的人?我该如何运用我的人生?我的人生目标、我的雄心大志、我的梦想、我的将来是什么?专注在自我中心的想法永远无法显示我们人生的目的。
圣经说:“神指引他所造万物的生命,每一个生命都在他的权柄下。
”与一般畅销书籍、电影、讲座所标榜的正好相反,你不可能从自己的内在去寻求生命的意义,或许你已经尝试过了,你不是自己的创造者,怎能知道自己被造的目的?假若我交给你一件你从未见过的新发明,你不会知道它的作用,那物件也不能告诉你。
你只有从其创造者或它的使用说明书,才能知道这物件的功用。
有一次,我在山里迷了路。
当我停下来询问前往露营区的方向时,人家告诉我说:“你不能从这里到那里,你必须从山的另一面开始!”同样地,你不能以自我为出发点去寻找生命的目的。
第一章第一节心理发展及其主要观点

(一)心理发展的内涵什么是心理发展?所谓心理发展就是指个体从胚胎期经由出生、成熟、衰老一直到死亡的整个生命过程中所发生的持续而稳定的内在心理变化过程。
不过,并不是所有的心理变化都可以称之为心理发展,如由于病理原因而导致的心理变化就不属于发展的范畴。
个体心理发展的变化过程是渐进、连续而有规律的。
它既有量的积累,又有质的变化;既表现为某种心理品质成长、成熟的前进过程,又表现为某些心理品质的衰退和消亡过程;既包括语言和认知的发展,也包括情感、个性和社会性的发展。
因此,心理发展反映的是个体心理随年龄增长而出现的持续而稳定的系列变化过程,主要包括认知发展和人格发展两大方面。
其中,认知发展是个体自出生后在适应环境的活动中,对事物的认识以及面对问题情境时的思维方式与能力表现随年龄增长而逐渐改变的历程(张春兴,1996),也就是在个体与环境相互作用的过程中,其感觉、知觉、注意、记忆、思维、言语等认知的功能系统不断发展并趋于完善的变化过程,具体表现为,一是各种不同认知成份由低级到高级、由简单到复杂、由不完整到完整,不断发展;二是各种认知成份的关系逐渐趋于相互协调。
人格发展则是指个体自出生经成年到老年的整个生命全程中人格特征或个性心理形成、发展和表现的过程。
个体心理发展是个体生命全程发展和毕生变化的过程。
这一思想首先由美国心理学家何林渥斯(H.Z.Hollingworth,1930)提出,到20世纪70年代逐步系统化。
强调心理发展是涵盖人的整个一生,每一个年龄阶段都在发展和变化;强调个体自身在其发展中的重要作用,认为个体心理的发展过程就是通过树立目标、作出选择和创造策略来应付各种发展的挑战,以此控制他们机体的、社会情绪的和人格的发展(Nurmi,1997)。
个体心理发展是个体社会化的过程。
个体的社会化过程(Socialization Process)就是指在一定社会文化环境中,个体的生理和心理随年龄增长而逐渐变化,借以发展个体的社会属性、参与社会生活的过程。
第一章 地球概况

(2)海岭
海岭:一般海底山脉称为海岭。其中,位于大洋中间,常发生地震和地 壳运动较强烈的海岭称为洋脊或洋中脊。洋脊或洋中脊为海底线状隆起 地带,呈一系列鱼 状山脉,其中部最高,中央部位常有一条巨大的裂谷, 称为中央裂谷,谷深1 2km,谷宽可达13-48km。太平洋洋中脊因其裂 称为中央裂谷,谷深1-2km,谷宽可达13-48km。太平洋洋中脊因其裂 谷不明显而称之为洋隆或洋中隆。 (3)海沟:平行于岛弧或沿着大陆边缘呈断续延伸的两壁较陡、狭长 的水深大于6000m的深海槽称为海沟。海沟是地球表面最低洼的地区。 的水深大于6000m的深海槽称为海沟。海沟是地球表面最低洼的地区。 海沟的一个重要特点是在其靠近大陆的一侧有一条与其平行的隆起地形。 (4)深海盆地:深海盆地是海洋中另一类大型地形单元,它是介于大 陆边缘及洋中脊之间的平坦地带,是海底地形的主体,约占海洋面积的 43%,平均深度在海平面以下4000-5000m,深海盆地中主要有三种地 43%,平均深度在海平面以下4000-5000m,深海盆地中主要有三种地 形。 丘陵: 深海平原:是被来自大陆的沉积物覆盖的靠近大陆边缘的乎连续地形。 海山:海山是深海底部孤立或比较孤立的隆起地形,相对高度在1000m 海山:海山是深海底部孤立或比较孤立的隆起地形,相对高度在1000m 以上,隐没于水下或露出海面。其中有一类呈锥状者,称为海峰。
1、陆地地形
大陆按高程特征,可分为高山、丘陵、平原、高 原、盆地和洼地等地形单元。其中,低于1000米 原、盆地和洼地等地形单元。其中,低于1000米 的平原、丘陵、盆地面积最大,占地球表面的 20.8%。 20.8%。 海拔高程在600米以上,表面较平坦或略有起伏 海拔高程在600米以上,表面较平坦或略有起伏 600 的广阔地区称为高原。 此外尚有四周为山系或高原限制的低地,因其外 形似盆地称为盆地。 介于山地和平原之间的高低不平、连绵不断的低 矮浑圆的小山丘地形称为丘陵,一般高程在海拔 500米以下,相对高差多在数十米,最大高差不 500米以下,相对高差多在数十米,最大高差不 超过200米。河”,是一个巨型旋窝状星系, 正面呈旋窝形,侧面呈扁平型。 银河系包含1.5× 银河系包含1.5×103多亿颗行星。 银河系的直径约100000万光年,是太阳系直径的 银河系的直径约100000万光年,是太阳系直径的 8.0×107倍,中心厚约15000光年,边沿厚°约 8.0× 倍,中心厚约15000光年,边沿厚° 3000-6000光年。太阳距银河系中心约27700光年。 3000-6000光年。太阳距银河系中心约27700光年。 银河系的主要成员是恒星。恒星由巨大质量炽热 气体组成的能自己发光发热的球状天体。
第一章 机械运动

测量时: 放:零刻度线对准被测物体的一端,有刻 度线的一边紧靠被测物体且与被测物边保 持平行。 读数:视线要正对刻度线。 记录:不仅要记录数值,还必须注明测量 单位。
长度测量的特殊方法
化整为零:测一根长的铁丝长度 测多算少:测一根铁丝的直径 化直为曲:用车轮测某段道路长度
时间的测量
计算不止要写公式和数字,还要有文字说 明 数字后面要写上正确的单位
一些常见物体的运动速度
人步行速度约为1.1m/s 骑自行车的速度约为5m/s 高速路上运动的小轿车的速度约为33m/s
专题训练时间、路程、速度的计算
1.认真审题,找出各个运动阶段的已知条件 和待求的物理量,用准确的字母符号以及 角标 2.统一单位 3.根据物理概念选用物理公式,并进行公式 变换,同时应有必要的文字说明 4.代入计算,求解,数值后面要写上正确的 单位
中考题
15年株洲 甲同学骑自行车去看望乙同学,得知消息后, 乙同学步行去迎接,接到后同车返回。整个过 程他们的位置与时间关系如图所示,据图可知 () A.两同学在t=10min 时相遇 B.相遇前甲的速度是乙同学的4倍 C.相遇后乙的速度是原来的1.5倍 D.整个过程甲的平均速度是乙的2倍
第一章 机械运动
本章内容
第一节长度和时间的测量 第二节 运动的描述 第三节 运动的快慢 第四节 测量平均速度
第一节长度和时间的测量
长度的单位 长度的测量 时间的测量 误差
长度的单位
测量物理量前必须规定单位。 物理量的单位都有国际通用的符号 长度的国际单位制是米。
童年第一章主要内容

童年第一章主要内容童年第一章主要内容(一)昨天,哥哥借给我了一本书——高尔基笔下的《童年》。
想必大家都听说过这本书吧!我今天刚刚读完了第一章,下面我就来给大家讲一讲吧!第一章主要讲了:“我”在狭小的房子里,静静地看着父亲离我而去,我却没有丝毫的伤感,外祖母边哭边嘲笑我是一个可笑的人。
因为别人都大滴大滴的泪水往下落,我却无动于衷。
就在这时,母亲就生下了我的小弟弟,可在不久之后,他却也离我们而去。
这是我的母亲的心情落到了底谷,便远离了我和外祖母。
在处理丧事之后,我们三个踏上了回故乡的轮船。
我们在轮船上度过可两天两夜,终于抵达了故乡。
外祖父来接我们,舅舅舅妈们也来了,可是一家人为了那点财产没有停止过争吵,本来和和气气的一家人,一下子闹僵了。
其实,当我看到高尔基的童年时那么样的悲惨的时候,怜悯之心油然而生。
我并没有想到过,高尔基的童年的家会是那样的不和。
没关系了,这只是第一章么,下面肯定还会有更精彩的内容,尽请期待吧!童年第一章主要内容(二)第一章的中心人物是外祖母。
她善良、聪明、能干、充满爱心,是千千万万俄罗斯女性的优秀代表,对“我”的一生有着非常大的影响。
本章末尾用充满诗意的美好语言描写了外祖母的肖像和人品,塑造了一个光彩照人的平凡而伟大的人物形象。
年过花甲的外婆跟三、四岁的“我”见面时的第一次“对话”生动活泼,风趣盎然。
早已过不惑之年的高尔基,以三、四岁儿童的口吻、眼光、心理、行为,真实而生动地描写、反映当时的客观现实,深刻而准确地表达自己十分成熟的思想、观点和感情。
语言简洁生动,非常口语化,非常适合人物的口吻和当时的语言环境;情节画龙点睛,人物栩栩如生。
不仅本章,而且全部《童年》,具有这个显着的特点和优点。
《童年》开篇就写得十分精彩。
它可以摘出来绝不止一篇优美的散文。
从译者加的标题就可以大体知道本章内容:一、“外祖母的出现”;二、“父亲的去世和弟弟的降生”;三、“父亲的安葬”;四、“伏尔加河上的风光”。
语言学(第一章)

• 2.“两线” • (1)上古时期的两线斗争 • 名实关系:名由人定(参差)-名实相应 (整齐) • (2)中古时期的两线斗争 • 重程式化形式(理论)-重实际用法(材 料) • (3)近古时期的两线斗争 • 普遍唯理语法(内部研究)-经验主义 (外部研究) • (4)现当代时期的两线斗争 • 谱系论-波浪说
• (二)语言学的意义
• • • • 1、语言学是一门领先学科 2、语言教学与研究离不开语言学 3、制定和理解语文政策需要语言学 4、指导语言运用和文学创作、欣赏、研究 和翻译
第二节 语言和言语的对立统一
• 一、语言和言语的定义 • 言语就是个人讲话(写作)的行为和结果;语言是 人们所说(写)和存在于所说(所写)中的音义结 合的词汇系统和语法系统。 • 二、语言和言语的关系 • (一)二者的区别 • 1、语言是稳定的,具有相对静止状态;言语是自由 结合的,具有运动状态。 • 2、语言是社会共有的交际工具;言语除了社会因素 外,还具有个人因素。 • 3、语言系统的各个结构成分是有限的,但可以用它 们说出无限多的句子来。
• ห้องสมุดไป่ตู้ • • • •
(二)二者的联系 1、言语是第一性的,语言是第二性的。 2、语言来源于言语,又反作用于言语。 三、区分语言和言语的意义 1、明确了语言研究的不同领域。 2、为语言的学习和研究提供了一个模式: 言语-语言-言语
第三节 语言的社会功能
• • • • 一、语言是人类独有的最重要的交际工具 (一)语言是交际工具 交际功能是语言最根本的功能 (二)语言是最重要的交际工具
• • • •
(三)语言的混合和融合 1. 语言的混合 克里奥耳语、“洋泾浜”语。 2. 语言的融合
• 一种语言战胜了另一种语言或一种语言被 另一种语言吞噬的现象,叫做语言的融合。 • 语言的融合有自愿融合与被迫融合两种。 历史上鲜卑族的魏孝文帝所谓“断诸北语, 一从正音”的改革就是自愿融合,金朝的 女真语则是被迫融合。
第一章_多项式

8、一个数域必包含哪两个元素? 高 问题: 等 9、最小的数域是什么? 代 定理1.1.2:任何数域都包含有理数域Q。 数 证明:设F是一个数域,则 a F , a 0.
于是 a a 0 F , a a 1 F.
1 1 2,1 2 3,1 3 4,, N F
2016/5/25 高等代数
式
高则S是一个数环。 特别,当a=2时,S是全体偶数组成的数环。 等 S 0,即只包含一个零组成的数 代 当a=0时, 数 环,这是最小的数环,称为零环。
问题:3、一个数环是否一定包含0元? 4、除了零环外,是否还有只含有限个元素的 数环? 1
例2:证明 Z i a bi a, b Z , i 2 1 是一个数环。
多 项 式
2016/5/25
都不是多项式。
高等代数
高 等 代 数
定义2: f x , g x 是两个多项式, f x g x
最高次项, 亦称为首项。 除系数为0的项之外,同次项的系数都相等。 多项式的表法唯一。 方程 a0 a1x an xn 0 是一个条件等式而不是 1 两个多项式相等。
f x 3, f x 0
零次多项式:次数为0的多项式即非零常数。 零多项式:系数全为0的多项式。对零多项式不 定义次数,因此,在谈论多项式的次数时,意味着这 个多项式不是零多项式。 首一多项式:首项系数为1的多项式。 二、多项式的运算 定义4: 设 f x a0 a1x an xn
在多项式中,每个单项式叫做多项式的项。这是 形式表达式。
1
后来又把多项式定义为R上的函数:
f x a0 a1x an x
第一章 国际贸易概述

第一章国际贸易概述第一节国际贸易的基本概念一、对外贸易与国际贸易对外贸易(Foreign Trade)是指一个国家(地区)与另一个国家(地区)之间的商品、服务和技术的交换活动。
国际贸易(International Trade)是指世界上不同国家(地区)间的商品、服务和技术的交换活动。
区别:前者是以一国(地区)为主体,从一个国家(地区)的角度来看这些交换活动;后者是从整个国际范围或从全球角度来看。
二、货物贸易、服务贸易与技术贸易货物贸易(Commodity Trade)是指物质性商品的进出口,也称有形贸易(Tangible Trade)。
服务贸易(Service Trade)是指一国(地区)劳动者向另一国(地区)的消费者提供服务,并相应获取外汇收入的过程。
也称无形贸易(Intangible Trade)。
注:按WTO的分类,国际服务贸易有四大类:过境交付、境外消费、商业存在、自然人流动。
具体可分为商业、通讯、建筑及工程、销售、教育、环境、金融、健康与社会、旅游、文化与体育、运输及其他等12类155个项目。
技术贸易(Technology Trade)是指纯技术知识以及与技术转让相关的机器设备的贸易。
主要内容是专利、商标和专有技术。
货物贸易需要经过海关手续,反映在一国海关的贸易统计上;服务贸易则不需要经过海关手续,在国际收支表中只得到部分反映。
三、出口贸易、进口贸易与过境贸易出口贸易(Export Trade)是指一国把本国生产和加工的商品运往国外市场销售。
进口贸易(Import Trade)是指将外国生产和加工的商品输入国内市场销售。
过境贸易(Transit Trade):凡甲国经过丙国向乙国运送商品,对丙国来说是过境贸易。
另:复出口(Re- Export Trade )、复进口(Re- Import Trade )、净出口(Net Export)、净进口(Net Import)四、直接贸易、间接贸易与转口贸易直接贸易(Direct Trade)是指货物生产国(地区)A与货物消费国(地区)B直接买卖商品的贸易行为。
财务会计第一章

1.某企业 某企业2007年3月25日销售商品一批,款 日销售商品一批, 某企业 年 月 日销售商品一批 元收存银行。 项10 000元收存银行。 元收存银行 ——归属本期收入,款项收到 归属本期收入, 归属本期收入 2.某企业 某企业2007年3月25日销售商品一批,款 日销售商品一批, 某企业 年 月 日销售商品一批 元尚未收到。 项10 000元尚未收到。 元尚未收到 ——归属本期收入,款项尚未收到 归属本期收入, 归属本期收入 3.某企业 某企业2007年3月25日预收到一笔销售商 年 月 日预收到一笔销售商 某企业 品款项10 元存银行。 品款项 000元存银行。 元存银行 ——不归属本期收入,本期收到款项 不归属本期收入, 不归属本期收入
3、从提供信息的跨度来看:财务会计主 要是定期反映企业作为一个整体的财务 状况、经营成果以及现金流量的情况。 4、从工作程序的约束来看:财务会计主 要受外在统一的会计规范的约束。 5、从会计程序和方法来看:财务会计有 一套比较科学、统一、定型的会计处理 与方法。
三、企业会计准则
1、西方国家会计准则产生的社会经济背 景 2、我国的企业会计准则
(二)会计六要素 资产、负债、所有者权益、收入、费用、 利润。
1.资产 资产 资产,是指企业过去的交易或者事项形成的、 资产,是指企业过去的交易或者事项形成的、由企 业拥有 或者控制的、预期会给企业带来经济利益的资源。 或者控制的、预期会给企业带来经济利益的资源。 2.负债 负债 负债,是指企业过去的交易或者事项形成的、 负债,是指企业过去的交易或者事项形成的、预期会 导致经济利益流出企业的现时义务。 导致经济利益流出企业的现时义务。 3.所有者权益 所有者权益 所有者权益,是指企业资产扣除负债后, 所有者权益,是指企业资产扣除负债后,由所有者 享有的剩余权益。公司的所有者权益又称为股东权益。 享有的剩余权益。公司的所有者权益又称为股东权益。
第一章运动的描述
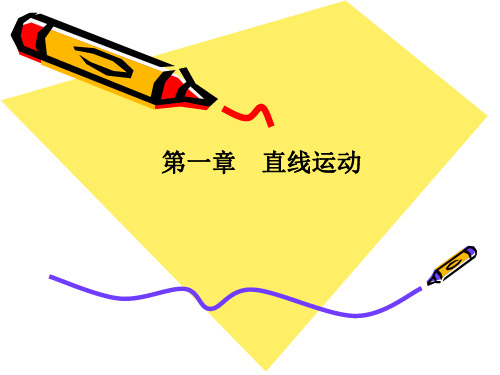
D. 10R,C 指向 A ;5πR 2
解析:选 C 如图,物体沿两个半径为 R 的圆弧由 A 运动到 C,路程 s=πR+3×2πR 4
=5πR,位移由 A 指向 C,x= 3R 2+R2= 10R,故选项 C 正确。 2
例题5、(多选)小明在玩“跳跳鼠”手机游戏时, 让跳跳鼠在手机屏幕上由点(0,0)出发,沿直线运动 到点(3,1),吃到一次食物。然后又由点(3,1)沿直 线运动到点(1,4),接着又由点(1,4)沿直线运动到 点(5,5),最后又由点(5,5)沿直线运动到点(2,2), 各吃到一次食物。平面坐标系横、纵坐标轴的单位 长度为1 cm,则( )
【答案】 B
四、位置、位移、路程
1.位置
质点的位置可以用规定的坐标系中的点表 示.在一维、二维、三维的坐标系中分别表示为
S(x)、S(x,y)、S(x,y,z).
2.位移
物体位置的变化,用始位置指向末位置的有 向线段表示.位移是矢量,国际单位是 “米”.位移的大小与路径无关,位移的方向是 由初位置指向末位置.位移的方向不一定是质点 运动的方向.
的点的科学抽象,与几何中的点不是一 回事.
例题1、(多选)研究下列各种运动情况时(如图), 哪些情况可以将研究对象视为质点( )
【答案】 BC
例题2、子弹沿水平方向射出,如果要计算子弹从
枪口飞到靶心所需时间,能否把子弹看做质点?如果要 计算子弹穿过一张薄纸所需的时间,能否把子弹看做质 点?
【答案】 计算子弹从枪口到靶心的时间,子弹可 以看做质点;射穿一张白纸不能将子弹看做质点.
第一章 直线运动
第1单元 运动学的基本概念
运动学的七个基本概念 一、机械运动
一个物体相对于另一个物体位置的改变, 叫做机械运动,简称运动,它包括平动、转动和 振动等运动形式.
第一章(新版09) 反对外国侵略的斗争

从皇帝到满朝贵族奉行的是“防民甚于防寇”
的政治路线,这是半殖民地中国屡战屡败的根本
原因,反动统治者从官吏到军队对人民欺压、害 怕、憎恨,处于尖锐对立的地位。把人民的反抗 看作“心腹之害”,对外敌只要不赶其下台,也 认为是患,但只是“肘腋之患”,大多采取“先
安内,后攘外”方针,从清帝到蒋介石皆如此。
林则徐的战略思想:
“民心可用”,利 用民众力量御敌。
林则徐的战略战术: “以守为战、以逸 待劳、诱敌深入、坚壁 清野、出奇设伏、水陆 夹攻”。 林则徐
1840年6月,鸦片战争爆发后,由于广东防守严 密,使英军无懈可击。英军北犯侵占定海,逼近大 沽,威胁清廷。直隶总督琦善乘机诬陷打击林则徐, 10月林被革职。1841年3月被派往浙江,到镇海后 立即与两江总督裕谦筹划海防、积极备战。 1841年5月,“广州和约”签订,清廷把战败 责任归于林则徐,把他流放新疆伊犁,途中写下悲 愤之句:“苟利国家生死以,岂因祸福趋避之”。 在新疆建议伊犁将军布彦泰:“屯垦耕战”,有备 无患。他曾预言:“终为中国之患者,其俄罗斯 乎!”在新疆推广“坎儿井”,至今流传“林公井” 的故事。
1894年中日甲午战争中,日军越过鸭绿江,一路 杀到辽东半岛,杀人数十万,旅顺一城,仅剩36人。
1900年八国联军入侵,拥有100万人口的天津,在 经历烧杀后仅剩10万人,八国联军进入北 京, 见人就杀,仅在庄王府就杀1700多人。
1900年7月,沙俄军警在东北制造了两起惨案, 一是海兰泡大惨案,遇难者达七千多人;另一起 是血洗江东六十四屯,被杀中国居民3万多人。 1931年日军占领东北,驱使青壮年为其服劳工。 一项工程完工后,即将所有劳工杀掉,埋入“万 人坑”,这种“万人坑”现已发现80多处,挖出 尸骨70多万具,仅在东北一地,日寇用各种方式 杀害的中国劳工达200多万人。
读者第一章内容概括

读者第一章内容概括
摘要:
1.介绍读者第一章的基本内容
2.分析第一章的主要角色和故事背景
3.概括第一章的情节发展和亮点
4.展望后续章节的发展趋势
正文:
作为一名职业写手,我有幸阅读了读者第一章的内容,并在此为大家带来一篇概括性的文章。
第一章以引人入胜的笔触为整个故事奠定了基础,让读者对接下来的情节充满期待。
首先,第一章通过生动的描绘,向读者介绍了故事的主要角色。
这些角色各具特色,有的热情洋溢,有的内敛沉稳,他们的性格和价值观在第一章中得到了充分的体现。
同时,角色之间的互动也富有张力,让读者对他们之间的友情、亲情和爱情充满好奇。
故事背景设定在一个充满竞争与挑战的世界,让读者能够感受到其中的紧迫感。
在这个世界中,角色们为了实现自己的目标,不得不付出艰辛的努力。
第一章为这个背景做了充分的铺垫,让读者能够更好地理解角色的动机和行为。
在情节发展方面,第一章展现了角色们从相识到相互信任的过程。
他们在面对困境时,展现出了不屈不挠的精神和团队合作意识。
这种情感的升华成为了故事的一大亮点,让人感叹不已。
同时,第一章还设置了一些悬念,为后续
情节的发展埋下了伏笔。
展望后续章节,随着角色们不断深入探索这个世界的秘密,他们之间的关系也将发生更多的变化。
面对未知的挑战和困境,他们将如何应对?角色之间的情感又将如何发展?这些都成为了读者继续阅读的动力。
总之,读者第一章以丰富的角色刻画、紧张的情节发展和深刻的主题内涵,为整个故事开了一个好头。
相信在接下来的章节中,作者将会带给读者更多的惊喜和感动。
第一章教材分析

[第一章教材分析]《第一章开启化学之门》教材分析一、地位和结构中国人常说“善始者,事半成,第一章教材分析。
”,初中化学课是学校教育中中学生系统学习化学的启蒙阶段,本章是初中化学课的开头一章,它带有绪言的性质。
正如章名所写,本章的学习内容旨在为学生打开化学的大门,使他们在学习伊始,初步了解化学这门课将要学些什么,学了化学有什么用,怎样学习化学;此外还要让学生了解一些最基本的化学概念和最基本的学习方法,为化学入门学习做好准备。
简而言之,本章在整个教材体系中,具有启明星的作用,为学生的学和教师的教指明了方向。
兴趣是学习的最好老师。
开启化学的大门,就要使学生真切地体验到化学学习和研究的内容是生动有趣、丰富多彩的;是引人入胜、富有魅力的。
为此本章以“化学给我们带来什么?”、“化学研究什么?”、“怎样学习和研究化学”为主题,通过约53幅插图和11个实验介绍一些古代、近代和现代的化学成就及其应用、日常生活和生产以及科学实验中的化学事实、现象及应用,让学生直观地领会到:化学事实和现象就在自己的身边和体内,化学科学内容丰富多彩、有趣有用,从而把学生要求学习的“胃口”充分调动起来。
基于化学是一门以实验为基础的自然科学,且新的化学课程倡导从学生和社会发展的需要出发,发挥学科自身的优势,将科学探究作为课程改革的突破口,激发学生的主动性和创新意识,促使学生积极主动地学习,使获得化学知识和技能的过程也成为理解化学、进行科学探究、联系社会生活和形成科学价值观的过程。
因此培养学生掌握“以观察、实验、实践为主的探究活动”这一学习化学的重要方法尤为重要。
本章第一节以26幅插图、4个《观察与思考》、2个《交流与讨论》和1个《活动与探究》,第二节以27幅插图、1个《观察与思考》、1个《交流与讨论》、1个《联想和启示》和3个《活动与探究》,第三节以1个《交流与讨论》和2个《活动与探究》;力求使学生通过简单的探究活动,体验探究的乐趣,初步体会到观察的重要性、实验的实证性和什么是科学研究。
第一章1.2充分条件与必要条件

为方程的两根).所以方程ax2+bx+c=0有两个相异实根,且两 根异号, 即方程ax2+bx+c=0有一正根和一负根.综上所 述,一元二次方程ax2+bx+c=0有一正根和一负根的充要条件 是ac<0.
返回
[类题通法] 充要条件的证明思路 (1)在证明有关充要条件的问题时,通常从“充分性” 和“必要性”两个方面来证明.在证明时,要注意:若证明 “p的充要条件是q”,那么“充分性”是q⇒p,“必要性” 是p⇒q;若证明“p是q的充要条件”,则与之相反.
解析:∵a⊥b,a⊥c时,a· b=a· c,但b与c不一定相 等,∴a· b=a· c⇒/ b=c;反之,b=c⇒a· b=a· c.
)
答案:B
返回
3.已知M={x|0<x≤3},N={x|0<x≤2},那么“a∈M”是“a ∈N”的________条件.
解析:∵由a∈M⇒/ a∈N,但a∈N⇒a∈M, ∴“a∈M”是“a∈N”的必要不充分条件.
返回
(2)令A={x|x2-2x-8=0}={x|x=-2或x=4}={- 2,4}, B={x|x=-2或x=4}={-2,4}. ∵A=B, ∴p⇔q, 即p是q的充要条件.
返回
[活学活用] 一元二次方程ax2+2x+1=0(a≠0)有一个正根和一个负根 的充分不必要条件是 A.a<0 C.a<-1 B.a>0 D.a<1 ( )
返回
a a (4)由于a<b,当b<0时, b >1;当b>0时, b a a <1,故若a<b,不一定有 b <1;当a>0,b>0, b <1 a 时,可以推出a<b;当a<0,b<0, b <1时,可以推 出a>b.因此p是q的既不充分也不必要条件.
论语第一章原文及翻译

论语第一章原文及翻译论语第一章原文及翻译导语:《学而》是《论语》第一篇的篇名。
《论语》中各篇一般都是以第一章的前二三个字作为该篇的篇名。
《学而》一篇包括16章,内容涉及诸多方面。
其中重点是“吾日三省吾身”;“节用而爱人,使民以时”;“礼之用,和为贵”以及仁、孝、信等道德范畴。
下面由小编为大家整理的论语第一章原文及翻译,欢迎大家阅读与借鉴!【原文】1·1 子曰(1):“学(2)而时习(3)之,不亦说(4)乎?有朋(5)自远方来,不亦乐(6)乎?人不知(7),而不愠(8),不亦君子(9)乎?”【注释】(1)子:中国古代对于有地位、有学问的男子的尊称,有时也泛称男子。
《论语》书中“子曰”的子,都是指孔子而言。
(2)学:孔子在这里所讲的“学”,主要是指学习西周的礼、乐、诗、书等传统文化典籍。
(3)时习:在周秦时代,“时”字用作副词,意为“在一定的时候”或者“在适当的时候”。
但朱熹在《论语集注》一书中把“时”解释为“时常”。
“习”,指演习礼、乐;复习诗、书。
也含有温习、实习、练习的意思。
(4)说:音yuè,同悦,愉快、高兴的意思。
(5)有朋:一本作“友朋”。
旧注说,“同门曰朋”,即同在一位老师门下学习的叫朋,也就是志同道合的人。
(6)乐:与说有所区别。
旧注说,悦在内心,乐则见于外。
(7)人不知:此句不完整,没有说出人不知道什么。
缺少宾语。
一般而言,知,是了解的意思。
人不知,是说别人不了解自己。
(8)愠:音yùn,恼怒,怨恨。
(9)君子:《论语》书中的君子,有时指有德者,有时指有位者。
此处指孔子理想中具有高尚人格的人。
【译文】孔子说:“学了又时常温习和练习,不是很愉快吗?有志同道合的人从远方来,不是很令人高兴的吗?人家不了解我,我也不怨恨、恼怒,不也是一个有德的君子吗?”【原文】1·2 有子(1)曰:“其为人也孝弟(2),而好犯上者(3),鲜(4)矣;不好犯上,而好作乱者,未之有也(5)。
第一章-孔子的教育思想PPT课件

2021/3/12
26
• (三)诲人不倦
• 教育是高尚的事业,需要对学生有高度责任 心、对社会有高度责任心的人来为其服务。教
师以教为业,也以教为乐,要树立“诲人不倦” 的精神,孔丘自己就是这样的人
• (四)以身作则
• 孔丘认为教师对学生进行教育的方式,不仅
有言教,还有身教,言教在说理,以提高道德
认识;身教在示范,实际指导行为方法。教师
• (六)教学相长
• 孔丘已认识到教学过程中教师对学生 不是单方面的知识传授,而是可以教学 相长的。他在 教学活动中为学生答疑解 惑,经常共同进行学问切磋。
2021/3/12
1
• 二、教育家教育思想
• 从孔子、孟子等诸子百家的教育思想到 朱熹、王守仁、再到蔡元培、陶行知等 教育家
• 从教育理论与政治、宗教、礼仪等融合 在一起到独立成系统的教育理论
• 特别是大家都知道的孔子的教育理论让 世界为之折服,让我们受益无穷
2021/3/12
2
第一章 孔子的教育思想
孔子一生中有一大半的时间,是从事 传道、授业、解惑的教育工作。他 创造了卓有成效的教育、教学方法; 总结、倡导了一整套正确的学习原 则;形成了比较完整的教学内容体 系;提出了一系列有深远影响的教 育思想;树立了良好的师德典范。
• 学习知识的方式:提倡多复习、练习, 才能牢固掌握。
2021/3/12
12
• 2、学思结合思想。单纯的学或单纯的思 都是片面的。学是基础,有了学才能进 行思考, 使认识加深,抓住事物的本 质。——揭示了学习与思考的辩证关系
• 教师不仅要努力鼓励学生努力学习知识, 还要引导学生积极思考,培养思维能力, 不仅知其然还要知其所以然。要弄清事 实的形成和形成这种事实的原因。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.4、试编写算法,求一元多项式P n(x)=a0+a1x+a2x2+a3x3+…a n x n的值P n(x0),并确定算法中的每一语句的执行次数和整个算法的时间复杂度,要求时间复杂度尽可能小,规定算法中不能使用求幂函数。
注意:本题中的输入a i(i=0,1,…,n),x和n,输出为P n(x0)。
通常算法的输入和输出可采用下列两种方式之一:(1)通过参数表中的参数显式传递。
(2)通过全局变量隐式传递。
试讨论这两种方法的优缺点,并在本题算法中以你认为较好的一种方式实现输入和输出【解答】(1)通过参数表中的参数显式传递优点:当没有调用函数时,不占用内存,调用结束后形参被释放,实参维持,函数通用性强,移置性强。
缺点:形参须与实参对应,且返回值数量有限。
(2)通过全局变量隐式传递优点:减少实参与形参的个数,从而减少内存空间以及传递数据时的时间消耗缺点:函数通用性降低,移植性差算法如下:通过全局变量隐式传递参数PolyValue(){ int i,n;float x,a[],p;printf(“\nn=”);scanf(“%f”,&n);printf(“\nx=”);scanf(“%f”,&x);for(i=0;i<n;i++)scanf(“%f ”,&a[i]); /*执行次数:n次*/p=a[0];for(i=1;i<=n;i++){ p=p+a[i]*x; /*执行次数:n次*/x=x*x;}printf(“%f”,p);}算法的时间复杂度:T(n)=O(n)通过参数表中的参数显式传递float PolyValue(float a[ ], float x, int n){float p,s;int i;p=x;s=a[0];for(i=1;i<=n;i++){s=s+a[i]*p; /*执行次数:n次*/p=p*x;}return(p);}算法的时间复杂度:T(n)=O(n)[techer's]#include <stdio.h>#define MAXSIZE 10float pnx(float a[],float x,int n){ int j;float sum=0.0;for(j=n;j>0;j--) /*a[0]=a0,[a1]=a1,...*/sum=(sum+a[j])*x;sum=sum+a[0];return(sum);}void main(){int n,i;float a[MAXSIZE],x,result;printf("Input the value of x:\n");scanf("%f",&x);printf("\n");printf("Input The n:\n");scanf("%d",&n);printf("\n");printf("Input a0,a1,...an:");for(i=0;i<=n;i++) scanf("%f",&a[i]);printf("\n");result=pnx(a,x,n);printf("The result is:%f\n",result);}2.4 已知线性表L递增有序。
试写一算法,将X插入到L的适当位置上,以保持线性表L的有序性。
Status Insert_SqList(SqList &va,int x)//把x插入递增有序表va中{if(va.length+1>va.listsize) return ERROR;va.length++;for(i=va.length-1;va.elem[i]>x&&i>=0;i--)va.elem[i+1]=va.elem[i];va.elem[i+1]=x;return OK;}//Insert_SqList[teacher's]int InsList_Sort(SeqList *L,elemtype e){int i;if(L->last>=MAXSIZE-1) {printf("表已满无法插入!");return(0);}i=L->last;while((i>=0)&&(e<L->elem[i]))/*寻找插入位置并移动元素*/{ L->elem[i+1]=L->elem[i];i--;}L->elem[i+1]=e;/*即使L为空,处理也相同*/L->last++;return (1);}2.5 写一算法,从顺序表中删除自第i个元素开始的k个元素。
[提示]:注意检查i和k的合法性。
(集体搬迁,“新房”、“旧房”)< 方法1 > 以待移动元素下标m(“旧房号”)为中心,计算应移入位置(“新房号”):for ( m= i-1+k; m<= L->last; m++)L->elem[ m-k ] = L->elem[ m ];< 方法2 > 同时以待移动元素下标m和应移入位置j为中心:< 方法2 > 以应移入位置j为中心,计算待移动元素下标:[teacher's]int DelList_k(SeqList *L,int i,int k){ /*假定从i往后的元素个数不足k个时,仅删除其后的所有元素*/int count,j;if ((i>L->last+1)||(k<1)) return(0);count=L->last-i+1;/*计算i后的元素个数*/j=i+k-1;while(j<=L->last)/*将i+k位置以后的元素向前移动*/{ L->elem[j-k]=L->elem[j];j++;/*原算法中的count--;去掉*/}if(count>=k) L->last=L->last-k;/*改变指向尾元的位置值*/else L->last=L->last-count;/*被删元素数少于k个时*/return (1);}2.6已知线性表中的元素(整数)以值递增有序排列,并以单链表作存储结构。
试写一高效算法,删除表中所有大于mink且小于maxk的元素(若表中存在这样的元素),分析你的算法的时间复杂度(注意:mink 和maxk是给定的两个参变量,它们的值为任意的整数)。
Status Delete_Between(Linklist &L,int mink,int maxk)//删除元素递增排列的链表L中值大于mink且小于maxk的所有元素{p=L;while(p->next->data<=mink) p=p->next; //p是最后一个不大于mink的元素if(p->next) //如果还有比mink更大的元素{q=p->next;while(q->data<maxk) q=q->next; //q是第一个不小于maxk的元素p->next=q;}}//Delete_Between2.7试分别以不同的存储结构实现线性表的就地逆置算法,即在原表的存储空间将线性表(a1, a2..., a n)逆置为(a n, a n-1,..., a1)。
(1)以一维数组作存储结构,设线性表存于a(1:arrsize)的前elenum个分量中。
(2)以单链表作存储结构。
[方法1]:在原头结点后重新头插一遍[方法2]:可设三个同步移动的指针p, q, r,将q的后继r改为p[teacher's]#include <stdio.h> //2.7.1#define MAXSIZE 10void createdata(int x[],int n){int i;if(n>=MAXSIZE) {printf("ERROR!");exit();}for(i=0;i<n;i++) x[i]=i+i;}void reverse1(int x[],int n){ int tmp,i,k;if(n>=MAXSIZE) {printf("OverFlow!");exit();}k=0;for(i=n-1;i>=n/2;i--){tmp=x[i];x[i]=x[k];x[k]=tmp;k++;}}void disparray(int x[],int n){int i;if(n>=MAXSIZE) {printf("ERROR!");exit();}for(i=0;i<n;i++) printf("%d ",x[i]);}void main(){int a[MAXSIZE];createdata(a,8);reverse1(a,8);disparray(a,8);}#include <stdio.h> //2.7.2typedef struct node{ int x;struct node *next;}snode,*Linklist;Linklist create(){ snode *head,*rear,*s;int y;head=(Linklist)malloc(sizeof(snode));rear=head;scanf("%d",&y);while(y!=-1){ s=(Linklist)malloc(sizeof(snode));s->x=y;rear->next=s;rear=s;scanf("%d",&y);}rear->next=NULL;return(head);}Linklist reverse2(snode *head){ Linklist p,q;p=head->next;head->next=NULL;while(p){ q=p;/*采用头插法,q指向待插节点,p指向下一个*/p=p->next;q->next=head->next;head->next=q;}return(head);}main(){ Linklist h,p;h=create();p=h->next;while(p){ printf("%5d",p->x);p=p->next;}h=reverse(h);printf("\n");p=h->next;while(p){ printf("%5d",p->x);p=p->next;}}2.8假设两个按元素值递增有序排列的线性表A和B,均以单链表作为存储结构,请编写算法,将A表和B表归并成一个按元素值递减有序的排列的线性表C,并要求利用原表(即A表和B表的)结点空间存放表C.[teacher's]/*ch2_8合并并逆置链表*/#include <stdio.h>typedef struct node{ int x;struct node *next;}snode,*Linklist;Linklist create(){ snode *head,*rear,*s;int y;head=(Linklist)malloc(sizeof(snode));rear=head;scanf("%d",&y);while(y!=-1){ s=(Linklist)malloc(sizeof(snode));s->x=y;rear->next=s;rear=s;scanf("%d",&y);}rear->next=NULL;return(head);}Linklist merge(snode *head1,snode *head2){ Linklist head,p,q,s;p=head1->next;/*指向A的首元节点*/q=head2->next;/*指向B的首元节点*/head=head1; /*以链表A的头节点做C的头节点*/head->next=NULL;free(head2); /*释放B的头节点*/while(p!=NULL&&q!=NULL)/*用头插法挑选元素插入*/ { if(p->x<q->x){ s=p;p=p->next;}else{s=q;q=q->next;}s->next=head->next;head->next=s;}if(p==NULL) p=q;while(p){ s=p;p=p->next;s->next=head->next;head->next=s;} return(head);}main(){ Linklist h,h1,h2,p,q;h1=create();h2=create();printf("\n******************************\n");p=h1->next;while(p) /*显示链表A的数据*/{ printf("%5d",p->x);p=p->next;}printf("\n******************************\n");q=h2->next;while(q) /*显示链表B的数据*/{ printf("%5d",q->x);q=q->next;}h=merge(h1,h2);p=h->next;printf("\n******************************\n");while(p) /*显示链表C的数据*/{printf("%5d",p->x);p=p->next;}}2.9假设有一个循环链表的长度大于1,且表中既无头结点也无头指针。
