北师大版七年级上册4.3.角课件

合集下载

(2024秋新版本)北师大版七年级数学上册《角》PPT课件

C. ∠AOB的边是两条射线 D. ∠AOB与∠BOA表示同一个角
课堂检测
基础巩固题
3.甲、乙、丙、丁，四名学生在判断钟表的分针和时针互相垂直的时刻时，每人说了两个时刻，说法都对的是（ D ） A．甲：“3时整和3时30分” B．乙说“6时15分和6时45分” C．丙说“9时整和12时15分” D．丁说：“3时整和9时整”
课堂检测
基础巩固题
1. 下列语句正确的是 ( D ) A. 两条直线相交，组成的图形叫做角 B. 两条有公共端点的线段组成的图形叫做角 C. 两条有公共点的射线组成的图形叫做角 D. 从同一点引出的两条射线组成的图形叫做角
2. 下列说法不正确的是 ( B )
A. ∠AOB 的顶点是O B. 射线BO，AO分别是∠AOB的两条边
1. 度量法
探究新知
2. 叠合法
想一想你能用图形和几何语言说明两个角的大小关系吗？ (两个角分别记作∠AOB，∠A'O'B')
B
B（B'）
B
'B
B
'
O（O'） A（ A' ） O（O'） A（A'） O（O'） A（A'）
∠AOB<∠A'O'B' ∠AOB =∠A'O'B' ∠AOB>∠A'O'B'
课堂检测 4. 如图所示：
基础巩固题
(1) 图中共有多少个角？请写出能用一个字母表示的角；
A
答案：8个；∠A，∠O.
(2) 把图中所有的角都表示出来.
O
1
3
答案：∠A，∠O，∠1，

北师大版七年级数学上册：4.3 角公开课一等奖优秀课件

（2）能用一个大写字母表示的角有几个？
B
D
C
图1
（3）以点A为顶点的角有哪几个？
以点D为顶点的角呢？
（4）图中共有多少个角？是哪些角？
4.如图2，用大写字母表示图中用希腊字母标注的角.
∠ α =___ ∠ γ =___
∠ β=____ ∠ θ=_____
A D γα E
β B
图2
θ CF
5.判断题
角的度量工具：量角器
想一想做一做
1°的角怎么定义？怎样画出1°的角？
角的度量
把一个周角360等分，每一份就是
一度的角记作 “ 1° ” 。
1°
角的度量单位：度，分，秒
角的度量
把一周角分成360等分，每一份所对的角叫做1度的角，记作 “1°” 。
把1度的角60等分，每一份所对的角叫做 1 分的角．记作 “1′ ” 。
练习：
(1) 32°21′＋ 68°48′； (2) 90°－25°32′； (3) 15°23′8″×4；
开动脑筋
1.确定相应钟表上时针与分针所成的角度。
120° 30° 120°
2.每经过1小时，时针转过多少度？每经过1分钟，分针转过多少度？
3.8时30分，时针与分针所成的角是多少？
（1）直线是一个平角
（×）
（2）如图（1），点P不在∠AOB的内部
（×）
A O
A
P
D
· · B
· B
EC
（3）如图（2）， ∠ABC与∠DBE是同一个角(√ ）
图1中有个角，它们是
．
图2中有个角，它们是
．
D
E
D

北师大版七年级数学上册《第四章基本平面图形4.3角》说课稿

北师大版七年级数学上册《第四章基本平面图形4.3角》说课稿一. 教材分析北师大版七年级数学上册《第四章基本平面图形4.3角》这一节的内容，主要介绍了角的定义、分类和性质。

通过这一节的学习，使学生能够理解角的概念，掌握角的分类和性质，能够运用角的知识解决一些简单的问题。

在教材的处理上，我将以角的定义和分类为主线，通过对角的性质的探究，使学生能够深入理解角的概念，掌握角的分类和性质。

在教学过程中，我会注重学生的参与，通过观察、思考、讨论等方式，使学生能够主动地参与到学习中来，提高学生的学习兴趣和学习效果。

二. 学情分析面对的是一群刚从小学升入初中的学生，他们对数学的基础知识有一定的掌握，但对于角的概念和性质可能还比较陌生。

因此，我需要通过一些简单的实例和生活中的实际问题，引导学生理解角的概念，掌握角的分类和性质。

同时，学生的学习习惯和学习方法可能还不够成熟，我需要通过引导和示范，使学生能够掌握科学的学习方法和思考方式，提高他们的学习效率和解决问题的能力。

三. 说教学目标1.知识与技能：理解角的概念，掌握角的分类和性质，能够运用角的知识解决一些简单的问题。

2.过程与方法：通过观察、思考、讨论等方式，培养学生的观察能力、思考能力和解决问题的能力。

3.情感态度与价值观：激发学生对数学的兴趣，培养学生的参与意识和团队精神。

四. 说教学重难点1.重点：理解角的概念，掌握角的分类和性质。

2.难点：对角的概念的深入理解，对角的分类和性质的灵活运用。

五. 说教学方法与手段1.教学方法：采用引导法、讨论法、实例法等，引导学生主动参与学习，提高学生的学习兴趣和学习效果。

2.教学手段：利用多媒体课件、实物模型等，直观地展示角的概念和性质，帮助学生理解和掌握知识。

六. 说教学过程1.导入：通过一些生活中的实际问题，引导学生思考角的概念，激发学生的学习兴趣。

2.新课导入：介绍角的定义和分类，引导学生理解角的概念，掌握角的分类。

2024年秋季新北师大版七年级上册数学教学课件 4.2.3 尺规作角

2．如图，已知∠AOB，请用尺规作∠A′O′B′，使∠A′O′B′＝2∠AOB。
作图如下：
小组展示
越展越优秀
提疑惑：你有什么疑惑？
知识点1：利用尺规作一个角等于已知角(重难点)
(1)作射线O′A′；(2)以点O为圆心，以任意长为半径作弧，交OA于点 C，交OB于点D；(3)以点O′为圆心，以OC的长为半径作弧，交O′A′ 于点C′；(4)以点C′为圆心，以CD的长为半径作弧，交前面的弧于点 D′；(5)过点D′作射线O′B′。∠A′O′B′就是所要作的角。
作法：如上图，(1)作射线O′A′。(2)以点______为O圆心，以 __任__意___长_为半径作弧，交OA于点C，交OB于点D。(3)以点___O__′_ 为圆心，以___O__C_的长为半径作弧，交O′A′于点C′。
(4)以点___C__′_为圆心，以_____C_D的长为半径作弧，交前面的弧于点D′。 (5)过点______作射D线′ _____。∠OA′′BO′′B′就是所要作的角。
2角
第3课时尺规作角
1．会用尺规作图作一个角等于已知角，培养学生的动手操作能力。 2．会通过尺规作图比较两个角的大小，培养学生的观察能力和总
结能力。 3．通过尺规作图，规范学生的作图步骤，培养学生的规范性。
旧知回顾 1．角的大小的比较方法有哪些？
度量法，叠合法 2．角的和差怎么表示？
略
问题导入
我们已经知道可以通过移动其中一个角的方法比较两个角的大小。如何移动一个角，使两个角的一条边重合呢？
图片导入打台球时，球的反射角总是等于入射角。
如右图。红球能否被击入右下角的袋中？你能画出红球在第一次反弹后的运动路线吗？
视频导入
请同学们阅读教材124－125页，思考并回答以下问题。

4.3.多边形和圆的初步认识课件+2024-2025学年北师大版(2024)数学七年级上册

解：共12个扇形。分析：除了图中一目了然的4个小扇形外，由相邻两个扇形组成的扇形有4个，由相邻三个扇形组成的扇形还有4个，因而共12 个。
当堂达标
5．如图所示，把一个圆分成四个扇形，求每个扇形的圆心角的度数。
解：因为一个周角为360°，
所以分成的四个扇形的圆心角分别是∠AOB＝∠BOC＝360°×25%＝90°； ∠COD＝360°×30%＝108°； ∠DOA＝360°×20%＝72°。
E
A
D
你还能画出图
中其他的对角
B
C
线吗？
新知初探
活动1：多边形边、顶点、内角的关系
…
n边形
多边形名称
三角形
四边形
五边形
六边形
八边形
……
n
顶点 3 4
568
n
边
34
5
6
8
n
内角
3
4
5
68
n
归纳：n边形有n个顶点、n条边、n个内角.
新知初探
活动2：多边形边、对角线的关系
问题1：过n边形的每一个顶点有几条对角线？可以分割成多少个三角形？
思考：这些图形是由什么样的线按怎样的方式组成的？
新知初探
多边形的相关概念
由若干条不在同一直线上的线段首尾顺次相连组
成的封闭平面图形叫作多边形。
组成多边形的各条线段叫作多边形的边。
每相邻两条边的公共端点叫作多边形的顶点。
在多边形中，连接不相邻两个顶点的线段
叫作多边形的对角线。
提示：我们平常所说的多边形都是指凸多边形，即多边形总在其任意一条边所在直线的同一侧。
问题2：n边形一共有多少条对角线？

北师大版七年级数学上册《基本平面图形——角的比较》教学PPT课件(4篇)

角的大小的比较方法： (1)如果已知角是锐角、直角、钝角、平角、周角几类中不同类的角，就可以直接由它们之间的关系比较出它们的大小； (2)可以通过量角器进行量度来比较角的大小； (3)可以根据各角在同一图中的位置关系比较角的大小．
角的平分线
活动：大家在练习本上画一个角，然后把角的两边对折，展开以后你会发现折痕把角分成了两个角，这两个角有什么关系呢，它们又和原来的角有着怎样的等量关系？
4.4 角的比较
知识回顾比较两条线段的长短的方法？ 1、度量法：用刻度尺测量线段的长度的方法。 2、叠合法：将其中一条线段移到另一条线段上作比较。
猜想：比较两个角的大小方法？
获取新知
问题:有一天学生张虎和王鹏各带了一把折扇(如图),下面是他们的一段对话:
张:我的折扇大一些,所以我的折扇的角也大一些.
2
2
2
(2)结合(1)的结论可求出∠DOE的度数，从而求出∠BOE的度数
解：(1)因为OC平分∠AOD，
1 所以∠DOC＝ 2 ∠AOD.
因为OE平分∠BOD，
1
所以∠DOE＝ 2∠BOD.
所以∠COE＝∠DOC＋∠DOE＝
1
(∠AOD＋∠BOD)
= 1 ∠AOB＝ 1 ×130°＝65°.
2
2
2
2. 已知，如图，∠AOB = 130°，∠AOD = 30°，∠BOC = 70° ，问：OC 是∠AOB 的平分线吗？OD 是∠AOC 的平分线吗？
解： OC不是∠AOB 的平分线 OD是∠AOC 的平分线 B
C D
A O
3. 如图，直线 m 外有一定点 O，A 是 m 上的一个动点，当点 A 从左向右运动时，观察∠α 和 ∠β 是如何变化的，∠α 和 ∠β 之间有关系吗？

北师大版(2024)数学七年级上册 4.2.1 角的认识课件(共23张PPT)

情境引入
在小学我们学习过角，请说说你对角的认识。你能在图4-16中找到角吗？
图4-16
获取新知
探究点1：角、平角、周角的概念
角由两条具有公共端点的射线组成(如图4-17)。角也可以看成是由一条射线绕着它的端点旋转而成的(如图4-18)。
A
边
顶点
O
边
B
图4-17
图4-18
角的大小与边的长短无关。
文化馆幼儿园
图书馆
游乐园超市
课堂小结
这节课，你有什么收获？
课堂小结
角的定义
有公共端点的两条射线组成的图形一条射线绕着它的端点旋转而形成的图形
平角、周角的定义
一条射线绕它的端点旋转，当终边和始边成一条直线时，所成的角叫作平角。终边继续旋转，当它又和始边重合时，所成的角叫作周角。
角
用三个大写字母或一个大写字母表示
B C
A
图4-21
D
解：（1）∠BAC,∠BAD和∠CAD
(2)∵以点A为顶点的角有3个 ∴∠BAC，∠BAD和∠CAD不能用∠A来表示
例题讲解
例2 下列四个图中，能用∠1、∠AOB、∠0三种方法表示同一个角的是( D )
[解析]A、图中的∠AOB 不能用∠0 表示，故本选项错误; B、图中的∠1和∠AOB不是表示同一个角，故本选项错误; C、图中的∠1 和∠AOB 不是表示同一个角，故本选项错误; D、图中∠1、∠AOB、∠O 表示同一个角，故本选项正确;
角的表示方法用一个数字加弧线表示
用一个小写希腊字母加弧线表示
角的度量方位角
度、分、秒 1°=60′，1′=60″
课堂小结
这节课，你有什么困惑？

七年级数学上册(北师大版习题课件)：4.3.角

7．下列计算错误的是( D ) A．0.25°＝900″ B．1.5°＝90′ C．1000″＝(158)° D．125.45°＝125°45′
8．时钟上的时刻从上午 8 时 15 分到 8 时 30 分，时针转了( A ) A．7.5° B．10° C．15° D．90°
9．计算： (1)51°37′42″＋29°58′53″；解：81°36′35″
17．(1)将31.24°化成用度、分、秒表示的形式；解：31°14′24″
(2)将38°37′12″化成以度为单位的形式．解：38.62°
18．如图，货轮O在航行过程中，发现灯塔A在它南偏东60°的方向上，同时，在它北偏东40°，南偏西10°，西北(即北偏西45°)方向上又分别发现了客轮B，货轮C和海岛D，仿照表示灯塔方位的方法画出表示客轮B，货轮C和海岛D方向的射线．
20．观察图形，回答问题： (1)在图①中有几个角？ (2)在图②中有几个角？ (3)在图③中有几个角？ (4)依此类推，如图④所示，若一个角内有n条射线，此时共有多少个角？
解：(1)1 个 (2)3 个 (3)6 个
（n＋1）（n＋2）
(4)
2
个
Байду номын сангаас
11．下列各角中，________是钝角．( B ) A.41周角 B.23平角 C．平角 D.41平角
12．下列说法正确的是( C ) A．两条射线组成的图形叫做角 B．角的大小在放大镜下会发生改变 C．角的大小与角的两边画出部分的长短无关 D．直线是一个角
13．如图，∠1＋∠2等于( B ) A．60° B．90° C．110° D．180° 14．如图，AOB是直线，图中小于180°的角共有( C ) A．7个 B．8个 C．9个 D．10个

北师大版七年级数学上册第4章第3节角(共30张PPT)

解:60′×1.45 =87′,
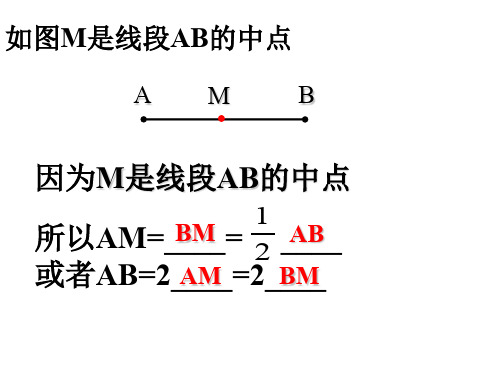
1.45°=87′=5220″.
例2 1800″等于多少分? 等
于多少度?
解: 1
( 60 ) ′× 1800= 30′,
1
( 60
) ° × 30 = 0.5°,
即 1800″=30′=0.5°.
0.25°等于多少分? 等于多少秒?
书解本：6P0′1×160.2随5 =堂15练′ 习第2题 P6101″7× 习15 题=49.30第0″ 2题
起始位置的射线叫做这个角的始边。
终边终止位置的射线叫做这个角的终边。
始边
一条射线绕它的端点旋转，当终边和始边成一条直线时，所成的角叫做平角.
终边继续旋转，当它和始边重合时，所成的角叫做周角.
角的表示方法
A
O
α
BO
1
O
四种
表
记作： ∠AOB 或 ∠BOA
记作 ∠α
记作∠1 示方
∠O
法
如图M是线段AB的中点
AM
B
因为M是线段AB的中点所或以者AABM==2__B_A_M_M___==212_B__A_M_B___
你能在图中找到角吗？
你能描述这些角的共同特征吗？
角的定义
边
顶点
边
角是由两条具有公共端点的射线组成的.
角的顶点角的边
角的第二种定义
角也可以看成一条射线绕着它的端点旋转而形成的。
Back
0° Back
120°
Back
90°
Back
（2）每过1h时针转过多少度？每过1min，分针转过多少度？
30° 6°
（3）10:10，时针与分针的夹角为多少度？

北师大版七年级上册数学4.3 多边形和圆的初步认识PPT课件

4. 如图是地球表面积统计图的一部分，扇形A表示地球某几种水域的面积，则此扇形的圆心角为___1_4_4___度.
课堂检测
能力提升题
从多边形的某一个顶点出发，分别连接这个顶点与
其余各顶点，把这个多边形分成10个三角形，那么这个
多边形是（ A ）
A. 十二边形
B.十一边形
C. 九边形
D.八边形
课堂检测
连接中考
1. 下列图形为正多边形的是（ D ）
A.
B.
C.
D.
2. 一个扇形的半径是6，圆心角是120°，该扇形的面积是（ C ）
A. 2π B. 4π
C. 12π
D.24π
课堂检测
基础巩固题
1. 如图所示的图形中，属于多边形的有几个( A )
A.3个
B.4个
C.5个
D.6个
课堂检测
基础巩固题
（2）圆心角的度数与周角的比与扇形的面积与圆的面积比有怎样的关系？
结论：扇形的圆心角与周角的比等于扇形面积与圆的面积比.
即S扇形=
圆心角周角
× S圆=
nπr2 360°
探究新知
做一做画一个半径是2厘米的圆，并在其中画一个圆心角为60°的扇形，你会计算这个扇形的面积吗？小组交流.
S扇形=
60° 360°
你能在我们生活周围找出这些平面图形吗？
探究新知找出我们生活中基本的平面图形
探究新知
找出我们生活中基本的平面图形
探究新知找出我们生活中基本的平面图形
探究新知
多边形的概念
定义：多边形是由一些不在同一条直线上的线段首尾顺次相连组成的封闭平面图形.
【注意】 ①组成多边形的线段在“同一平面内”; ②线段必须“不在同一直线上”且线段条数不少于3条; ③首尾顺次相连; ④封闭图形. 我们平常所说的多边形都是指凸多边形，即多边形总在任何一条边所在直线的同一侧.

北师大七年级数学上册--第四单元 4.3 《角》课件 (3)

A B
C O
角基础知识
问题：把一个周角7等分，每一份是多少度的角？
计算： 2518 6226 2317 4
7814 5638 1520 6
角例题讲解
【例1】65.32等于几度几分几秒？17524 等于几度？
【解析】几分几秒化成度，从秒开始，除以进率60 ；度化成几分几秒，从分开始，乘以进率60.
角基础知识
问题：如图，现实生活中有很多角的形象，你知道数学上怎怎样给角定义的吗？
角：公共端点的两条射线组成的图形叫做角．如下图，这个公共端点是角的顶点（点Ｏ），这两条射线是角的两条边（射线ＯＡ，ＯＢ）.
角基础知识
角的表示方法：角通常用如下的方法来表示
问题：① 一个角有几种表示方法？ ②如右图中有几个角？ AOB可以用 O来表示吗？为什么？
492852 4
6.①把1275830用度表示出来. ②把 83.35用度、分、秒表示出来.
角习题精选
A
7.根据下列语句画图:
E
(1)画∠AOB=10ຫໍສະໝຸດ °;BC(2)在∠AOB的内部画射线OC,使∠BOC=50°;
(3)在∠AOB的外部画射线OD,使∠DOA=40°;
(4)在射线OD上取E点,在射线OA上取F,使∠OEF=90°.
【答案】
65. 32° 65° 0.32° 65° 0.32 ×60 65° 19.2 65° 19 0.2 65° 19 0.2 ×60 65°1912
17524 17 5 (24) 17 5.4 17 (5.4) 17 0.09 17.09
60
60
角习题精选
角课堂总结
我们本节课从角的定义开始学习，角是由公共端点的两条射线组成的图形，然后学习角的表示方法，以及利用量角器度量一个角的度数，进行有关角的加、减、乘、除运算.

北师大版七年级数学上册《角的比较》课件(共19张PPT)

A
一
（ AOC为 1 和 2 的和
边
记作 AOC = 1 + 2 ）
重
合
B
21
C
O
A
（ AOC为 1 和 2 的差
记作 AOC = 1 – 2 ）
D A
C ( 1 ) DAB = DAC+ CAB
( 2 ) ACB = DCB – DCA B
看图填空
A
D
B
C
（ 1 ） ABC = ABD +
（ 2 ） BDC = ADC –
A
BC
D
5 CM
3 CM
AB > CD
一、叠合(从“形”出发）（1）以知 ABC与 DEF 如图：
C F
B
A
E
D
•1、“手和脑在一块干是创造教育的开始，手脑双全是创造教育的目的。” •2、一切真理要由学生自己获得，或由他们重新发现，至少由他们重建。 •3、反思自我时展示了勇气，自我反思是一切思想的源泉。 •4、好的教师是让学生发现真理，而不只是传授知识。 •5、数学教学要“淡化形式，注重实质.
1.根据图形会比较角的大小 2.理解角的和差概念 3.掌握角平分线的概念
线段的比较方法
1.从“形”出发，利用线段移动叠合的方法
A
BA
C
2.以“数” 出发，通过度量长度进行数值大小比较。
A （AB > AC） C B
经
过
叠AB (ຫໍສະໝຸດ )合（AB = AC）
A
B
C
（AB < AC）
二、度量以“数” 出发，通过度量长度进行数值大小比较。
F ∴∠EOC=1／2∠AOC, ∠COF=1／2∠COB（角平分线的意义）

七年级数学上册第四章 3角例题与讲解北师大版

七年级数学上册第四章 3角例题与讲解北师大版1．角的定义(1)静态定义：由两条具有公共端点的射线组成的几何图形叫做角．如图甲．角的有关概念：顶点：两条射线的公共端点．边：组成角的两条射线．(2)动态定义：角也可以看成是由一条射线绕着它的端点旋转所形成的几何图形．如图乙．谈重点角的理解(1)角有两个特征：①角是由两条射线组成的；②这两条射线有公共的端点．(2)角的大小与角的两边的长短无关：由于角的两边是射线，而射线是向一方无限延伸的，所以角的大小与角的两边的长短无关，只与两条射线张开的程度有关．【例1】下列说法错误的有( )．①有公共点的两条射线形成的图形是角②从一点引出的两条射线形成的图形是角③角的大小与两边所画的长度有关④线段绕着一个端点旋转也可以形成角A．1个B．2个C．3个D．4个解析：①×公共点与公共端点不同②√具备角的两个基本元素③×角的大小不因为两边的长短而改变④×角的两边是射线答案：C2．角的表示方法及画法角的表示方法有四种．(1)三个大写英文字母表示法：用角的两边上的两个大写字母和顶点的字母表示角，如图(1)中的角，可记为∠AOB，注意顶点的字母写在中间，每条边上的一点A，B写在两旁．(2)顶点字母表示法：当角的顶点处只有一个角时，也可以只用顶点的字母表示角，如图(1)中的∠AOB也可记为∠O.(3)阿拉伯数字表示法：在角的顶点处加上弧线标上数字，就可以用这个数字来表示角，如图(2)中的∠AOB可记为∠1.(4)希腊字母表示法：在角的顶点处加上弧线标上小写希腊字母(α，β，γ等)，就可以用这个小写希腊字母来表示角，如图(2)中的∠BOC可记为∠α.这种方法与数字表示法实际上是一样的．释疑点表示角时的注意事项①以上四种表示方法的前面必须加上角的符号“∠”．②表示角所用的符号“∠”，不能写成小于号“<”．③当一个顶点处有两个以上的角时，不能用顶点字母表示法来表示角，如图(2)中以O为顶点的角有∠1，∠α，∠AOC ，就不能用∠O 来表示了．否则，就会产生混乱．3．平角、周角(1)平角：一条射线绕它的端点旋转，当终边和始边成一条直线时，所成的角叫做平角，平角是180°，如图1.(2)周角：如图2，一条射线绕它的端点旋转一周，当终边与始边重合时，所成的角叫做周角．周角等于360°.(3)平角与周角的关系：一周角等于两平角．平角的两边成一条直线，周角的两边重合后成一条射线，但不能认为一条直线就是平角或认为一条射线就是周角．角必须有顶点和两边．【例3】下列说法是否正确，为什么？①平角是一条直线；②钟表上的分针经过1小时形成一个周角．分析：可根据平角和周角的形成定义判断．解：①错．因为平角是一条射线绕着它的端点旋转到反方向位置时形成的图形，平角有顶点、边这些基本元素，而直线没有，故是错误的； ②正确．因为分针经过1小时会旋转一周，所以分针经过1小时会回到初始位置，即能形成一个周角．4．度、分、秒的换算(1)角的单位及意义角的单位是度、分、秒．意义：①把一个平角180等分，每一份就是一度的角，记作1°；②把一度的角60等分，每一份就是一分的角，记作1′；③把一分的角60等分，每一份就是一秒的角，记作1″.(2)度、分、秒的进率及换算方法度、分、秒的进率是60.即1°＝60′，1′＝60″，1°＝60′＝3 600″.度6060⨯÷分6060⨯÷秒(3)度、分、秒有关的计算度、分、秒的进率是六十进制，不同于十进制．在运算中满60才向高位进1，而借1则表示低位的60.在进行度、分、秒的加减法或乘除法的运算时，要按级进行，即分别按度、分、秒计算，不够减、不够除的要借位．从高位借的，单位要化为低位的单位后才能进行运算．在相乘或相加时，当低位大于或等于60时，要向高位进位．【例4－1】 (1)用度、分、秒表示48.13°为__________；(2)用度表示23°9′36″为__________．解析：(1)先把0.13°化成分：60′×0.13＝7.8′，再把0.8′化成秒：60″×0.8＝48″，所以48.13°＝48°7′48″；(2)先把36″化成分：⎝ ⎛⎭⎪⎫160′×36＝0.6′，再把9.6′化成度：⎝ ⎛⎭⎪⎫160°×9.6＝0.16°，所以23°9′36″＝23.16°.答案：(1)48°7′48″ (2)23.16°【例4－2】计算：(1)13°29′＋78°37″； (2)61°39′－22°5′32″；(3)23°53′×3； (4)107°43′÷5.分析：先将相同单位相加减，注意进位和借位；乘法要先乘低位，再乘高位；除法是先除高位，高位余数换算成低位数后，再除低位．解：(1)13°29′＋78°37″＝91°29′37″.(2)61°39′－22°5′32″＝61°38′60″－22°5′32″＝39°33′28″.(3)23°53′×3＝69°159′＝71°39′.(4)107°43′÷5＝(105°＋2°43′)÷5＝105°÷5＋163′÷5＝21°＋(160′＋180″)÷5＝21°＋160′÷5＋180″÷5＝21°32′36″.5.角的计数方法数角的个数与数线段的条数的方法基本上相同，都要按一定的方法去数．常用的有两种方法：①始边计数法：先以某条边为始边(固定一边)，按顺时针方向或逆时针方向找到与之构成的所有的角，然后再以另一条射线为边，重复上面的过程，最后把所有的角的个数加起来，就是构成角的总个数．②分类计数法：先数清基本的角，再数由两个基本角组成的角，由三个基本角组成的角……【例5】如图，图中共有多少个角？用字母分别表示出来．分析：要确定有多少个角，需要先确定始边与终边的条数．可以用始边计数法数角的个数．即先以OA为始边，则能与它组成角的边有3条，就有3个角；再以OB为始边，按逆时针数出角的个数，依次类推．解：以OA为一边的角有∠AOB，∠AOC，∠AOD；以OB为一边且不重复的角有∠BOC，∠BOD；以OC为一边且不重复的角有∠COD.因此图中共有6个角，它们分别为：∠AOB，∠AOC，∠AOD，∠BOC，∠BOD，∠COD.6．角的应用角在生活和生产中随处可见．本节的有关角的应用主要是钟表中的角．钟面上共有12个大格，把周角平均分，即360°÷12＝30°.钟表面上有60个小格，360°÷60＝6°.因此，时针每小时转动30°，分针每分钟转动6°.时针与分针的夹角的求法：先确定时针与分针之间有几个大格，即有多少个30°.用30°乘大格数．特别注意：①从时针开始数，所形成的角有时需要按顺时针数，如3：40；有时需要按逆时针数，如2：50.②从时针开始，按顺时针形成的角，两个度数相减；按逆时针形成的角度数相加．③时针每分钟转30°÷60＝0.5°.【例6】如图是部分节目的播出时间，分别确定出钟表上时针与分针所成的最小的角的度数．分析：确定钟表上时针与分针所成的最小角的度数，需要先确定时针与分针形成的角中包含几个大格和小格．节目时间大格度数小格度数夹角新闻联播19：0030°×50°150°新闻30分12：000°0°0°今日说法12：3530°×535×0.5°相加电视剧20：0030°×40°120°解：新闻30分：0°；今日说法：30°×5＋35×0.5°＝167.5°；电视剧：30°×4＝120°.。

角第1课时角的概念及表示方法课件 2024-2025学年北师大版(2024)七年级数学上册

2.其他的方位角常以正南、正北为基准，向东或向西旋转的角度表示方向。如图2所示：①OA表示北偏西50°方向；②OB表示南偏东30°方向。
ห้องสมุดไป่ตู้
当堂达标
当堂达标
1.下列语句正确的是（ D）
A.两条直线相交，组成的图形叫做角
B.两条有公共端点的线段组成的图形叫角
C.两条有公共点的射线组成的图形叫角
D.从同一点引出的两条射线组成的图形叫角
60
新知初探
度分秒进率关系图
度
÷60
分 ×60
秒
新知初探
例1 计算： (1)1.45°等于多少分？等于多少秒？ (2)1800''等于多少分？等于多少度？
解：(1)1.45°=1.45×60'=87'， 1.45°=87'=87×60''=5220''.
(2)1800''=(1800÷60)'=30'，
条直线时，所成的角叫做平角；
终边继续旋转，当它又和始边重合时，所成的角叫做周角.
1平角＝180°，1周角＝360°
新知初探
想一想：怎么知道一个角的大小？
角的度量工具：量角器角的度量单位：度，分，秒
1°的 1 为1分，记作“1′”，即1°＝60′
60
1′的 1 为1秒，记作“1″”，即1′＝60″
解： (1)0.72°=0.72×60′=43.2′，0.2′=0.2×60″=12″，所以 25.72°=25°43′12″。 (2)30″=30×(610)′=0.5′，12.5′=12.5×(610)°≈0.21°，所以 45°12′30″=45.21°。