C++函数、递推、递归(课堂PPT)
合集下载
C++函数、递推、递归ppt课件

i = 7 s1 = 2 * (s2 + 1) ; s2 = s1 ;
// S(7) = 2 * (S(8) + 1) // s2 = s1 = S(7)
i = 6 s1 = 2 * (s2 + 1) ; s2 = s1 ;
// S(6) = 2 * (S(7) + 1) // s2 = s1 = S(6)
看一个简单的例子:
1 4
第九讲——函数、递推、递归
递归
有 5 个人坐在一起,问第 5 个人多少岁? 他说比第 4 个人 大两岁。问第 4 个人岁数,他说比第 3 个人大两岁。问第 3 个人,又说比第 2 个人大两岁。问第 2 个人,说比第 1 个人 大两岁。最后问第 1 个人,他说是 10 岁。请问第 5 个人多 大?
3
第九讲——函数、递推、递归
解题思路:
假设用 S(i) 表示第 i 天没吃之前的桃子数目;
则
S(1) 即为第 1 天所摘的桃子数; S(2) = S(1) * 1/2 – 1 第 2 天没吃之前的桃子数
S(3) = S(2) * 1/2 - 1 第 3 天没吃之前的桃子数
…
…
S(9) = S(8) * 1/2 - 1 第 9 天没吃之前的桃子数
= age(2) + 2 + 2 + 2 // c = age(2) + 2
= age(1) + 2 + 2 + 2 + 2;// c = 10;
2 2
计算年龄程序
第九讲——函数、递推、递归
2 3
第九讲——函数、递推、递归
递归算例(2)
用递归方法计算 n! 算法思路:
《c语言递归算法》课件

《C语言递归算法》PPT 课件
C语言递归算法是一种强大的编程技巧,通过函数自身调用实现问题的解决。 本课件将介绍递归算法的概念、实现方式、应用场景、优缺点以及与循环的 区别,同时还会通过案例演示帮助理解。
什么是递归算法?
基本概念
递归是指函数直接或间接地调用自身的过程。
递归特点
递归算法需要有基准条件和递推关系,用于结 束递归和推进递归过程。
递归算法的实现方式
递归函数
通过函数自身调用实现递归,需要定义递归函数和 递归终止条件。
递归流程图
通过流程图展示递归算法的执行过程,帮助理解递 归逻辑。
递归算法的应用场景
1 数学计算
递归算法可以用于解决数学问题,如斐波那契数列、阶乘等。
2 数据结构
递归算法在树、图等数据结构的遍历和搜索中有广泛应用。
递归算法的优点和缺点
优点
• 简化问题复杂度 • 代码结构清晰
缺点
• 执行效率较低 • 内存占用较高
递归算法与循环的区别
1
循环
2
迭代操作
3
递归
函数自身调用
区别
递归更直观,但消耗资源较多;循环更 高效,但代码可读性差。
递归算法的注意事项
1 递归终止条件
保证递归过程能够结束,否则可能导致死循 环。
2 堆栈溢出
过深的递归调用可能导致堆栈溢出,需要注 意递归深度。
递归算法的案例演示
斐波那契数列
通过递归实现斐波那契数列的计算。
二叉树遍历
通过递归遍历二叉树的各种方式。
C语言递归算法是一种强大的编程技巧,通过函数自身调用实现问题的解决。 本课件将介绍递归算法的概念、实现方式、应用场景、优缺点以及与循环的 区别,同时还会通过案例演示帮助理解。
什么是递归算法?
基本概念
递归是指函数直接或间接地调用自身的过程。
递归特点
递归算法需要有基准条件和递推关系,用于结 束递归和推进递归过程。
递归算法的实现方式
递归函数
通过函数自身调用实现递归,需要定义递归函数和 递归终止条件。
递归流程图
通过流程图展示递归算法的执行过程,帮助理解递 归逻辑。
递归算法的应用场景
1 数学计算
递归算法可以用于解决数学问题,如斐波那契数列、阶乘等。
2 数据结构
递归算法在树、图等数据结构的遍历和搜索中有广泛应用。
递归算法的优点和缺点
优点
• 简化问题复杂度 • 代码结构清晰
缺点
• 执行效率较低 • 内存占用较高
递归算法与循环的区别
1
循环
2
迭代操作
3
递归
函数自身调用
区别
递归更直观,但消耗资源较多;循环更 高效,但代码可读性差。
递归算法的注意事项
1 递归终止条件
保证递归过程能够结束,否则可能导致死循 环。
2 堆栈溢出
过深的递归调用可能导致堆栈溢出,需要注 意递归深度。
递归算法的案例演示
斐波那契数列
通过递归实现斐波那契数列的计算。
二叉树遍历
通过递归遍历二叉树的各种方式。
C++函数、递推、递归ppt课件

i = 7 s1 = 2 * (s2 + 1) ; s2 = s1 ;
// S(7) = 2 * (S(8) + 1) // s2 = s1 = S(7)
i = 6 s1 = 2 * (s2 + 1) ; s2 = s1 ;
// S(6) = 2 * (S(7) + 1) // s2 = s1 = S(6)
3 0
第九讲——函数、递推、递归
一般形式: S(i-1) = 2 * (S(i) + 1), i = 2,3,4,…,10
则 S(1) 即为第 1 天所摘的桃子数; S(1) = 2 * (S(2) + 1) S(2) = 2 * (S(3) + 1) … S(8) = 2 * (S(9) + 1) S(10) = 1
i = 9 s1 = 2 * (s2 + 1) ; s2 = s1 ;
i = 8 s1 = 2 * (s2 + 1) ; s2 = s1 ;
// S(9) = 2 * (S(10) + 1) // s2 = s1 = S(9)
// S(8) = 2 * (S(9) + 1) // s2 = s1 = S(8)
例: 王小二自称刀工不错,有人放一张大的煎饼在砧板上,问他:
“饼不许离开砧板,切 100 刀最多能分成多少块?”
1 0
分析:
第九讲——函数、递推、递归
切一刀
切二刀
切三刀
切四刀
令 q(n) 表示切 n 刀能分成的块数,由上图可知
q(1) = 1 + 1 = 2 q(2) = 1 + 1 + 2 = 4 q(3) = 1 + 1 + 2 + 3 = 7 q(4) = 1 + 1 + 2 + 3 + 4 = 11
PPT-06函数递推和递归

例:
bool checkprime( int );
15
函数的定义
函数返回值的类型 函数名(类型名 形式参数1,
类型名 形式参数2,. . . )
{
// 函数体
说明部分
语句部分
} 例: bool checkprime( int af )
checkprime 为函数名,要以英文字母开头
bool 是函数值的数据类型,这里是布尔型
18
被调用函数嵌套在 if 语句中,a 是实在参数
if ( checkprime( a ) )主函数 调用
checkprime( af ) 子函数 形式参数
19
实在参数是一个具有确定值的表达式
一个函数在调用子函数时,要将实在参数 赋给形式参数
调用时
17 实在参数 a
17 形式参数 af
实在参数的个数及类型应与形式参数一致。 赋值时前后对应关系不会改变。
两者配合得天衣无缝。
13
在checkprime( int af ) 函数 中,有return 0 和 return 1 两处 不同。
如果先有return 0了,后面 一条return 1 就不起作用了。
不会既执行return 0又执行 return 1。
14
函数的说明
要放在主函数之前,告诉系统 有自定义的子函数可以被调用。
for(i=1; i<=m; i=i+1 )
// 计数循环 i
sum=sum+power( i, l ); // 累加
return sum;
// 返回值sum给函数SOP(n, k)
}
// 自定义函数体结束
31
// 以下函数是被函数SOP(n, k)调用的函数 // 功能:计算p的q次幂
bool checkprime( int );
15
函数的定义
函数返回值的类型 函数名(类型名 形式参数1,
类型名 形式参数2,. . . )
{
// 函数体
说明部分
语句部分
} 例: bool checkprime( int af )
checkprime 为函数名,要以英文字母开头
bool 是函数值的数据类型,这里是布尔型
18
被调用函数嵌套在 if 语句中,a 是实在参数
if ( checkprime( a ) )主函数 调用
checkprime( af ) 子函数 形式参数
19
实在参数是一个具有确定值的表达式
一个函数在调用子函数时,要将实在参数 赋给形式参数
调用时
17 实在参数 a
17 形式参数 af
实在参数的个数及类型应与形式参数一致。 赋值时前后对应关系不会改变。
两者配合得天衣无缝。
13
在checkprime( int af ) 函数 中,有return 0 和 return 1 两处 不同。
如果先有return 0了,后面 一条return 1 就不起作用了。
不会既执行return 0又执行 return 1。
14
函数的说明
要放在主函数之前,告诉系统 有自定义的子函数可以被调用。
for(i=1; i<=m; i=i+1 )
// 计数循环 i
sum=sum+power( i, l ); // 累加
return sum;
// 返回值sum给函数SOP(n, k)
}
// 自定义函数体结束
31
// 以下函数是被函数SOP(n, k)调用的函数 // 功能:计算p的q次幂
c语言--函数的递归调用PPT参考幻灯片

第机作业:num(n)= 2* (num(n+1)+1) (n<10)
❖ 说有一只调皮的小猴子,摘了一堆水果,第一天 吃了水果的一半,又多吃了一个;第二天吃了剩 下水果的一半,又多吃了一个;依次类推….到第 十天,发现只剩下了10个水果,请问这只猴子到 底摘了多少个水果?
16
可以看到: 1)、3)为同一问题,都为n –1个盘子借助于一个 空塔移至另一塔上。
10
计
例11 Hanoi问题
第五章 函数
A
B
C
11
计
12
程序如下:
A
B
C
A
B
C
A
B
C
A
B
C
第五章 函数
void move(char getone, char putone) {printf("%c--->%c\n",getone,putone); }
1
第五章 函数
张福祥 主编
辽宁大学出版社
1
计
2
第五章 函数
我们先看这样一个例子:
❖ 说有一只调皮的小猴子,摘了一堆水果,第一天 吃了水果的一半,又多吃了一个;第二天吃了剩 下水果的一半,又多吃了一个;依次类推….到第 十天,发现只剩下了1个水果,请问这只猴子到 底摘了多少个水果?
2
计
3
第五章 函数
第五章 函数
age(int n) { int c;
if(n==1) c=10; else c = age(n-1)+2; return(c) ; }
age(5)
n=5
n=4
n=3
n=2
n=1
C++函数、递推、递归

s2 = s1 ;
s1 = 2 * (s2 + 1) ;
s2 = s1 ;
s1 = 2 * (s2 + 1) ; s2 = s1 ;
s1 = 2 * (s2 + 1) ; s2 = s1 ;
s1 = 2 * (s2 + 1) ;
s2 = s1 ;
// S(5) = 2 * (S(6) + 1) // s2 = s1 = S(5) // S(4) = 2 * (S(5) + 1) // s2 = s1 = S(4) // S(3) = 2 * (S(4) + 1) // s2 = s1 = S(3)
•fact(1) = 1 (边界条件)
精品PPT
第九讲——函数(hánshù)、递推、递 归
递推算(tuī suàn)例(3)
递推算法程序实现: 有了通项公式和边界条件后,采用循环结构,从边
界条件出 发,利用通项公式通过若干步递推过程就可以求出结果;
例: 王小二自称刀工不错,有人放一张大的煎饼在砧板上,问他: “饼不许离开砧板,切 100 刀最多能分成多少块?”
借助循环结构采用递推方法求解!
精品PPT
第九讲——函数(hánshù)、递推、 递归
一般(yībān) 形式a:ge(n) = 10
age(n) = age(n-1) + 2
(n=1)
(n>2)
精品PPT
第九讲——函数(hánshù)、递推、递 归
分析: 上述求解是从求解目标出发,即将第 n 个人的年龄表示第 (n-1) 个人的年龄,再回溯到第 (n-2)个人的年龄 …… 直 到第 1 个人的年龄;(回溯阶段) 然后,采用递推方法,从第 1 个人的已知年龄推算第 2 个 人的年龄,在推算第 3 个人的年龄,直到推算出第 5 个 人的 年龄;(递推阶段) 这是一个递归问题,对它的求解可以分成 回溯 和 递推 两 个阶段;显而易见,如果不希望递归过程无限制的进行 下去, 必须有一个结束(jiéshù)递归过程的条件;如: age(1) = 10
s1 = 2 * (s2 + 1) ;
s2 = s1 ;
s1 = 2 * (s2 + 1) ; s2 = s1 ;
s1 = 2 * (s2 + 1) ; s2 = s1 ;
s1 = 2 * (s2 + 1) ;
s2 = s1 ;
// S(5) = 2 * (S(6) + 1) // s2 = s1 = S(5) // S(4) = 2 * (S(5) + 1) // s2 = s1 = S(4) // S(3) = 2 * (S(4) + 1) // s2 = s1 = S(3)
•fact(1) = 1 (边界条件)
精品PPT
第九讲——函数(hánshù)、递推、递 归
递推算(tuī suàn)例(3)
递推算法程序实现: 有了通项公式和边界条件后,采用循环结构,从边
界条件出 发,利用通项公式通过若干步递推过程就可以求出结果;
例: 王小二自称刀工不错,有人放一张大的煎饼在砧板上,问他: “饼不许离开砧板,切 100 刀最多能分成多少块?”
借助循环结构采用递推方法求解!
精品PPT
第九讲——函数(hánshù)、递推、 递归
一般(yībān) 形式a:ge(n) = 10
age(n) = age(n-1) + 2
(n=1)
(n>2)
精品PPT
第九讲——函数(hánshù)、递推、递 归
分析: 上述求解是从求解目标出发,即将第 n 个人的年龄表示第 (n-1) 个人的年龄,再回溯到第 (n-2)个人的年龄 …… 直 到第 1 个人的年龄;(回溯阶段) 然后,采用递推方法,从第 1 个人的已知年龄推算第 2 个 人的年龄,在推算第 3 个人的年龄,直到推算出第 5 个 人的 年龄;(递推阶段) 这是一个递归问题,对它的求解可以分成 回溯 和 递推 两 个阶段;显而易见,如果不希望递归过程无限制的进行 下去, 必须有一个结束(jiéshù)递归过程的条件;如: age(1) = 10
C++函数、递推、递归ppt课件

递归调用
在调用一个函数的过程中又出现直接或间接地调用该 函数本身,称为函数的递归(recursive)调用; C++允许函数的递归调用;
例:
int f(int x) {
int y, z;
z = f(y);
return 2 * z;
}
大连理工大学 盘锦校区基础教学部
19
递归调用
第九讲——函数、递推、递归
大连理工大学 盘锦校区基础教学部
23
第九讲——函数、递推、递归
递归算例(2)
用递归方法计算 n! 算法思路:
若 n = 10, 则 n! = 10 * 9! 定义函数 fact(n) 表示计算 n!的函数,则有
fact(n) = n * fact(n-1), n > 1
fact(n) = 1,
n = 0, n = 1;
然后,采用递推方法,从第 1 个人的已知年龄推算第 2 个 人的年龄,在推算第 3 个人的年龄,直到推算出第 5 个人的 年龄;(递推阶段)
这是一个递归问题,对它的求解可以分成 回溯 和 递推 两 个阶段;显而易见,如果不希望递归过程无限制的进行下去, 必须有一个结束递归过程的条件;如:age(1) = 10
大连理工大学 盘锦校区基础教学部
12
递推算例(3 ) 参考程序:
第九讲——函数、递推、递归
大连理工大学 盘锦校区基础教学部
13
递归
第九讲——函数、递推、递归
递归算法在可计算理论中占有重要地位,它是算法设计的有 力工具,对于拓展编程思路非常有用。 就递归算法而言不涉及高深数学知识,只不过初学者建立起递 归概念不太容易。
大连理工大学 盘锦校区基础教学部
C语言递归算法PPT演示课件

for (k=1;k<=10;k++)
cin>>a[k];
cin>>x;
search(x,L,R);
system("pause");
} void search(int x,int top,int bot) //二分查找递归过程
{
int mid;
if (top<=bot)
{ mid=(top+bot)/2;
an加入到k个子集中的任一个中去,共有k种加入方式,这样对
于an的每一种加入方式,都可以使集合划分为k个子集,因此
根据乘法原理,划分数共有k * S(n-1,k)个。
•16
综合上述两种情况,应用加法原理,得出n个元素的集合 {a1,a2,……,an}划分为k个子集的划分数为以下递归公 式:S(n,k)=S(n-1,k-1) + k * S(n-1,k) (n>k,k>0)。
确定n个元素a1 ,a2 ,……,an 放入k个无标号盒子中去
的划分数S(n,k)。
【输入样例】setsub.in
23 7
【输出样例】setsub.out
4382641999117305
•15
【算法分析】
先举个例子,设S={1,2,3,4},k=3,不难得出S有 6种不同的划分方案,即划分数S(4,3)=6,具体方案为:
int s(int n, int k)
//数据还有可能越界,请用高精度计算
{
if ((n < k) || (k == 0)) return 0;
//满足边界条件,退出
if ((k == 1) || (k == n)) return 1;
第6章--函数递推递归(C++版)PPT课件

函数原型和函数定义在返回值类型、函数名和参数个数与类型必 须完全一致,否则,就会发生编译错误。下面对max()函数原型声明 是合法的。
int max(int x, int y); 也可以:
int max(int , int ); 可以看到函数原型声明与函数定义时的第一行类似,只多了一个 分号,成为了一个声明语句而已。
• 例6.4 定义一个函数check(n,d),让它返回一个布尔值。如果数字d 在正整数n的某位中出现则送回true,否则送回false。
• 3.函数的返回值
在组成函数体的各类语句中,值得注意的是返回语句return。它 的一般形式是:
➢ return(表达式);
其功能是把程序流程从被调函数转向主调函数并把表达式的值带 回主调函数,实现函数的返回。所以,在圆括号表达式的值实际上就 是该函数的返回值。其返回值的类型即为它所在函数的函数类型。当 一个函数没有返回值时,函数中可以没有return语句(在TC++和VC++ ,函数类型定义为void,可以没有return语句;函数类型定义为int ,必须有返回值),直接利用函数体的右花括号“}”,作为没有返 回值的函数的返回。也可以有return语句,但return后没有表达式。 返回语句的另一种形式是:
在一个程序中可以只有主程序而没有子程序(本章以前都是如此) ,但不能没有主程序,也就是说不能单独执行子程序。
在此之前,我们曾经介绍并使用了C++提供的各种标准函数,如 abs(),sqrt()等等,这些系统提供的函数为我们编写程序提供了很大 的方便。比如:求sin(1)+ sin(2)+...+sin(100)的值。但这些函 数只是常用的基本函数,编程时经常需要自定义一些函数。
int max(int x, int y); 也可以:
int max(int , int ); 可以看到函数原型声明与函数定义时的第一行类似,只多了一个 分号,成为了一个声明语句而已。
• 例6.4 定义一个函数check(n,d),让它返回一个布尔值。如果数字d 在正整数n的某位中出现则送回true,否则送回false。
• 3.函数的返回值
在组成函数体的各类语句中,值得注意的是返回语句return。它 的一般形式是:
➢ return(表达式);
其功能是把程序流程从被调函数转向主调函数并把表达式的值带 回主调函数,实现函数的返回。所以,在圆括号表达式的值实际上就 是该函数的返回值。其返回值的类型即为它所在函数的函数类型。当 一个函数没有返回值时,函数中可以没有return语句(在TC++和VC++ ,函数类型定义为void,可以没有return语句;函数类型定义为int ,必须有返回值),直接利用函数体的右花括号“}”,作为没有返 回值的函数的返回。也可以有return语句,但return后没有表达式。 返回语句的另一种形式是:
在一个程序中可以只有主程序而没有子程序(本章以前都是如此) ,但不能没有主程序,也就是说不能单独执行子程序。
在此之前,我们曾经介绍并使用了C++提供的各种标准函数,如 abs(),sqrt()等等,这些系统提供的函数为我们编写程序提供了很大 的方便。比如:求sin(1)+ sin(2)+...+sin(100)的值。但这些函 数只是常用的基本函数,编程时经常需要自定义一些函数。
C语言递推与递归PPT课件
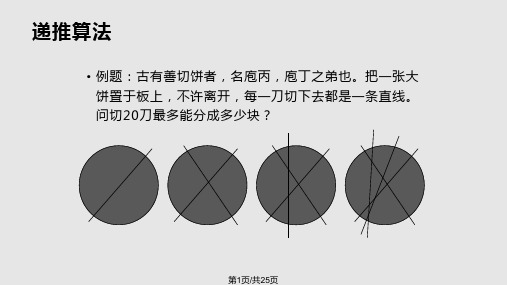
• 使用递归函数编程
• void qsort(int array[], int start, int end) • 把数组下标为start到end的元素进行快速排序第18页/共25页快速排序问题5
7
3
8
1
4
2
6
2
7
3
8
1
4
5
6
2
5
3
8
1
4
7
6
2
4
3
8
1
5
7
6
2
4
3
5
1
8
7
6
2
4
3
1
5
8
7
6
1
4
3
2
第16页/共25页
汉诺塔问题
第17页/共25页
快速排序问题
• 快速排序思路如下
• 将要排序的数据放在数组array中 • 取a[0]变在变量m中,通过分区处理把m排在适当的位置,使
m左边的数都比m小,m右边的数都比m大 • 按照常上面的思路分别处理m左边和右边的数据 • 如果分区长度是1,停止处理
• 思路提示
• m个球取出来的n个,包含两种情况:n在其中和n不在其中
• 编程实现
• 使用递归思想 • 编写递归函数 int cmn(int m, int n)
第12页/共25页
计算组合数
第13页/共25页
汉诺塔问题
• 据说在古代印度bramah神庙中,有个和尚整天把3根 柱子上的金盘倒来倒去。初始在柱子A上有64个盘子串 在一起,每一个盘子都比它下面的盘子小,可以在ABC 三个柱子之间互相移动,最终要全部移动到柱子C上。 移动规则如下:每次只允许移动一个,且较大的盘子永 远不能放在较小的盘子上。
• void qsort(int array[], int start, int end) • 把数组下标为start到end的元素进行快速排序第18页/共25页快速排序问题5
7
3
8
1
4
2
6
2
7
3
8
1
4
5
6
2
5
3
8
1
4
7
6
2
4
3
8
1
5
7
6
2
4
3
5
1
8
7
6
2
4
3
1
5
8
7
6
1
4
3
2
第16页/共25页
汉诺塔问题
第17页/共25页
快速排序问题
• 快速排序思路如下
• 将要排序的数据放在数组array中 • 取a[0]变在变量m中,通过分区处理把m排在适当的位置,使
m左边的数都比m小,m右边的数都比m大 • 按照常上面的思路分别处理m左边和右边的数据 • 如果分区长度是1,停止处理
• 思路提示
• m个球取出来的n个,包含两种情况:n在其中和n不在其中
• 编程实现
• 使用递归思想 • 编写递归函数 int cmn(int m, int n)
第12页/共25页
计算组合数
第13页/共25页
汉诺塔问题
• 据说在古代印度bramah神庙中,有个和尚整天把3根 柱子上的金盘倒来倒去。初始在柱子A上有64个盘子串 在一起,每一个盘子都比它下面的盘子小,可以在ABC 三个柱子之间互相移动,最终要全部移动到柱子C上。 移动规则如下:每次只允许移动一个,且较大的盘子永 远不能放在较小的盘子上。
C语言递归算法ppt课件

因此,我们可以得出划分数S(n,k)的递归关系式为:
S(n,k)=S(n-1,k-1) + k * S(n-1,k) (n>k,k>0)
S(n,k)=0
(n<k)或(k=0)
S(n,k)=1
(k=1)或(k=n)
ppt课件完整
18
【参考程序】
#include<iostream>
using namespace std;
}
int fac(int n)
{
if (n==1) return 1;
return(fac(n-1)+n);
/p/p调t课用件完下整一层递归
3
}
运行程序,当T=5时,输出结果:S=15,其递归调用执行过程是: (设T=3)
递归调用过程,实质上是不断调用过程或函数的过程,由于递归调 用一次,所有子程序的变量(局部变量、变参等)、地址在计算机内部 都有用特殊的管理方法——栈(先进后出)来管理,一旦递归调用结束, 计算机便开始根据栈中存储的地址返回各子程序变量的值,并进行相应 操作。
mov过程中出现了自己调用自己的情况,在Pascal中称为递归调用,这 是Pascal语言的一个特色。对于没有递归调用功能的程序设计语言,则需 要将递归过程重新设计为非递归过程的程序。
ppt课件完整
13
【例4】用递归的方法求斐波那契数列中的第N个数
【参考程序】 #include<iostream> using namespace std; int a[11]; int fib(int); int main() { int m; cin>>m; cout<<"fib("<<m<<")="<<fib(m); }
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例: 王小二自称刀工不错,有人放一张大的煎饼在砧板上,问他: “饼不许离开砧板,切 100 刀最多能分成多少块?”
1 0
分析:
第九讲——函数、递推、递归
切一刀
切二刀
切三刀
切四刀
令 q(n) 表示切 n 刀能分成的块数,由上图可知
q(1) = 1 + 1 = 2 q(2) = 1 + 1 + 2 = 4 q(3) = 1 + 1 + 2 + 3 = 7 q(4) = 1 + 1 + 2 + 3 + 4 = 11
S(10) = S(9) * 1/2 – 1 第 10 天没吃之前的桃子数
4
第九讲——函数、递推、递归
一般形式: S(i) = S(i-1) * 1/2 – 1,
i = 2, 3, …, 10;
这个公式可用于知第 1 天没吃之前的桃子 数推算第 2 天 没吃之前的,再推算第 3 天没吃之前的,…….。现在要求的是 第 1 天没吃之前的。能否倒过来,先知 第 10 天没吃之前的 的再反推第 9天没吃之 的,……,直到第 1 天没吃之前的。为 此将上式改写为:
《C++语言程序设计》
第九讲 函数、递推、递 归
1
递推
第九讲——函数、递推、递归
递推是计算机数值计算中的一个重要算法。
思路:通过数学推导,将复杂的运算化解为若干重复 的简单运算,以充分发挥计算机长于重复运算的特点;
递推法特点:从一个已知的事实出发,按一定规律推 出下一个事实,再从这个新的已知事实出发,再向下 推出一个新的事实。
1!,2!,3!,…,(n-1)!, n!
另fact(n) 为 n 阶乘,依据后项与前项的关系可以写出递推公
式:
fact(n) = n * fact(n-1) (通项公式)
fact(1) = 1 (边界条件)
9
第九讲——函数、递推、递归
递推算例(3)
递推算法程序实现: 有了通项公式和边界条件后,采用循环结构, 从边界条件出 发,利用通项公式通过若干步递推过程就可以求 出结果;
2
第九讲——函数、递推、递归
递推举例(1)
例: (猴子吃桃问题)
猴子第1天摘下若干桃子,当即吃了一半,还不过瘾, 又多吃了一个。第2天早上又将剩下的桃子吃掉一半, 又多吃了一个。以后每天早上都吃了前一天剩下的一 半另加一个。到第10天早上想再吃时,就只剩下一个 桃子了。问第1天猴子共摘了多少桃子?
个人, 岁。
大?age(3) = age(2) + 2;
i = 4 s1 = 2 * (s2 + 1) ; s2 = s1 ;
i = 3 s1 = 2 * (s2 + 1) ; s2 = s1 ;
i = 2 s1 = 2 * (s2 + 1) ; s2 = s1 ;
i = 1 s1 = 2 * (s2 + 1) ; s2 = s1 ;
// S(5) = 2 * (S(6) + 1) // s2 = s1 = S(5) // S(4) = 2 * (S(5) + 1) // s2 = s1 = S(4) // S(3) = 2 * (S(4) + 1) // s2 = s1 = S(3)
s2 = s1 ;
// s2 = s1 = S(7)
i = 6 s1 = 2 * (s2 + 1) ; s2 = s1 ;
// S(6) = 2 * (S(7) + 1) // s2 = s1 = S(6)
7
第九讲——函数、递推、递归
i = 5 s1 = 2 * (s2 + 1) ; s2 = s1 ;
1 1
分析:
第九讲——函数、递推、递归
切一刀
切二刀
切三刀
切四刀
在切法上是让每两条线都有交点。用归纳法可得出
q(n) = q(n-1) + n q(0) = 1 (边界条件)
1 2
递推算例(3) 参考程序:
第九讲——函数、递推、递归
1 3
递归
第九讲——函数、递推、递归
递归算法在可计算理论中占有重要地位,它是算法设计的有 力工具,对于拓展编程思路非常有用。 就递归算法而言不涉及高深数学知识,只不过初学者建立起递 归概念不太容易。
3
第九讲——函数、递推、递归
解题思路:
假设用 S(i) 表示第 i 天没吃之前的桃子数目;
则
S(1) 即为第 1
天所摘的桃子数;
S(2) = S(1) * 1/2 – 1 第 2 天没吃之前的桃子数
S(3) = S(2) * 1/2 - 1 第 3 天没吃之前的桃子数
…
…
S(9) = S(8) * 1/2 - 1 第 9 天没吃之前的桃子数
// S(2) = 2 * (S(3) + 1) // s2 = s1 = S(2)
// S(1) = 2 * (S(2) + 1) // s2 = s1 = S(1)
8
第九讲——函数、递推、递归
递推举例(2)
递推数列 一个数列从某一项起,它的任何一项都可以用它前
面的若干项 来确定,这样的数列称为递推数列,表示某项与其 前面的若干 项的关系就称为递推公式。例如自然数 1,2,…,n 的 阶乘就可 以形成如下数列:
看一个简单的例子:
1 4
第九讲——函数、递推、递归
递归
有 5 个人坐在一起,问第 5 个人多少岁? 他说比第 4 个人
大两岁。问第
4个
人岁数,他说比第 3 个人大两岁。问第 3
个人,又说比第 2
个人
大两岁。问第 2
个人,
说比第 1
个人
大两岁。最后问第 1 他说ag是e(51)0= age(4) + 2; 请问ag第e(45) 个= 人ag多e(3) + 2;
i = 8 s1 = 2 * (s2 + 1) ; s2 = s1 ;
// S(9) = 2 * (S(10) + 1) // s2 = s1 = S(9)
// S(8) = 2 * (S(9) + 1) // s2 = s1 = S(8)
i = 7 s1 = 2 * (s2 + 1) ; // S(7) = 2 * (S(8) + 1)
5
程序:
大连理工大学 盘锦校区基础教学部
第九讲——函数、递推、递归
6
6
第九讲——函数、递推、递归
分析:
一般形式:S(i-1) = 2 * (S(i) + 1), i = 10, 9, 8,…, 2;
初始:s2 = 1 ; // S(10) = 1
i = 9 s1 = 2 * (s2 + 1) ; s2 = s1 ;
1 0
分析:
第九讲——函数、递推、递归
切一刀
切二刀
切三刀
切四刀
令 q(n) 表示切 n 刀能分成的块数,由上图可知
q(1) = 1 + 1 = 2 q(2) = 1 + 1 + 2 = 4 q(3) = 1 + 1 + 2 + 3 = 7 q(4) = 1 + 1 + 2 + 3 + 4 = 11
S(10) = S(9) * 1/2 – 1 第 10 天没吃之前的桃子数
4
第九讲——函数、递推、递归
一般形式: S(i) = S(i-1) * 1/2 – 1,
i = 2, 3, …, 10;
这个公式可用于知第 1 天没吃之前的桃子 数推算第 2 天 没吃之前的,再推算第 3 天没吃之前的,…….。现在要求的是 第 1 天没吃之前的。能否倒过来,先知 第 10 天没吃之前的 的再反推第 9天没吃之 的,……,直到第 1 天没吃之前的。为 此将上式改写为:
《C++语言程序设计》
第九讲 函数、递推、递 归
1
递推
第九讲——函数、递推、递归
递推是计算机数值计算中的一个重要算法。
思路:通过数学推导,将复杂的运算化解为若干重复 的简单运算,以充分发挥计算机长于重复运算的特点;
递推法特点:从一个已知的事实出发,按一定规律推 出下一个事实,再从这个新的已知事实出发,再向下 推出一个新的事实。
1!,2!,3!,…,(n-1)!, n!
另fact(n) 为 n 阶乘,依据后项与前项的关系可以写出递推公
式:
fact(n) = n * fact(n-1) (通项公式)
fact(1) = 1 (边界条件)
9
第九讲——函数、递推、递归
递推算例(3)
递推算法程序实现: 有了通项公式和边界条件后,采用循环结构, 从边界条件出 发,利用通项公式通过若干步递推过程就可以求 出结果;
2
第九讲——函数、递推、递归
递推举例(1)
例: (猴子吃桃问题)
猴子第1天摘下若干桃子,当即吃了一半,还不过瘾, 又多吃了一个。第2天早上又将剩下的桃子吃掉一半, 又多吃了一个。以后每天早上都吃了前一天剩下的一 半另加一个。到第10天早上想再吃时,就只剩下一个 桃子了。问第1天猴子共摘了多少桃子?
个人, 岁。
大?age(3) = age(2) + 2;
i = 4 s1 = 2 * (s2 + 1) ; s2 = s1 ;
i = 3 s1 = 2 * (s2 + 1) ; s2 = s1 ;
i = 2 s1 = 2 * (s2 + 1) ; s2 = s1 ;
i = 1 s1 = 2 * (s2 + 1) ; s2 = s1 ;
// S(5) = 2 * (S(6) + 1) // s2 = s1 = S(5) // S(4) = 2 * (S(5) + 1) // s2 = s1 = S(4) // S(3) = 2 * (S(4) + 1) // s2 = s1 = S(3)
s2 = s1 ;
// s2 = s1 = S(7)
i = 6 s1 = 2 * (s2 + 1) ; s2 = s1 ;
// S(6) = 2 * (S(7) + 1) // s2 = s1 = S(6)
7
第九讲——函数、递推、递归
i = 5 s1 = 2 * (s2 + 1) ; s2 = s1 ;
1 1
分析:
第九讲——函数、递推、递归
切一刀
切二刀
切三刀
切四刀
在切法上是让每两条线都有交点。用归纳法可得出
q(n) = q(n-1) + n q(0) = 1 (边界条件)
1 2
递推算例(3) 参考程序:
第九讲——函数、递推、递归
1 3
递归
第九讲——函数、递推、递归
递归算法在可计算理论中占有重要地位,它是算法设计的有 力工具,对于拓展编程思路非常有用。 就递归算法而言不涉及高深数学知识,只不过初学者建立起递 归概念不太容易。
3
第九讲——函数、递推、递归
解题思路:
假设用 S(i) 表示第 i 天没吃之前的桃子数目;
则
S(1) 即为第 1
天所摘的桃子数;
S(2) = S(1) * 1/2 – 1 第 2 天没吃之前的桃子数
S(3) = S(2) * 1/2 - 1 第 3 天没吃之前的桃子数
…
…
S(9) = S(8) * 1/2 - 1 第 9 天没吃之前的桃子数
// S(2) = 2 * (S(3) + 1) // s2 = s1 = S(2)
// S(1) = 2 * (S(2) + 1) // s2 = s1 = S(1)
8
第九讲——函数、递推、递归
递推举例(2)
递推数列 一个数列从某一项起,它的任何一项都可以用它前
面的若干项 来确定,这样的数列称为递推数列,表示某项与其 前面的若干 项的关系就称为递推公式。例如自然数 1,2,…,n 的 阶乘就可 以形成如下数列:
看一个简单的例子:
1 4
第九讲——函数、递推、递归
递归
有 5 个人坐在一起,问第 5 个人多少岁? 他说比第 4 个人
大两岁。问第
4个
人岁数,他说比第 3 个人大两岁。问第 3
个人,又说比第 2
个人
大两岁。问第 2
个人,
说比第 1
个人
大两岁。最后问第 1 他说ag是e(51)0= age(4) + 2; 请问ag第e(45) 个= 人ag多e(3) + 2;
i = 8 s1 = 2 * (s2 + 1) ; s2 = s1 ;
// S(9) = 2 * (S(10) + 1) // s2 = s1 = S(9)
// S(8) = 2 * (S(9) + 1) // s2 = s1 = S(8)
i = 7 s1 = 2 * (s2 + 1) ; // S(7) = 2 * (S(8) + 1)
5
程序:
大连理工大学 盘锦校区基础教学部
第九讲——函数、递推、递归
6
6
第九讲——函数、递推、递归
分析:
一般形式:S(i-1) = 2 * (S(i) + 1), i = 10, 9, 8,…, 2;
初始:s2 = 1 ; // S(10) = 1
i = 9 s1 = 2 * (s2 + 1) ; s2 = s1 ;
