SPSS操作方法:判别分析报告例题
判别分析实验报告 SPSS
一、实验目的及要求:1、目的用SPSS软件实现判别分析及其应用.2、内容及要求用SPSS对实验数据利用Fisher判别法和贝叶斯判别法,建立判别函数并判定宿州、广安等13个地级市分别属于哪个管理水平类型。
二、仪器用具:三、实验方法与步骤:准备工作:把实验所用数据从Word文档复制到Excel,并进一步导入到SPSS 数据文件中,同时,由于只有当被解释变量是属性变量而解释变量是度量变量时,判别分析才适用,所以将城市管理的7个效率指数变量的变量类型改为“数值(N)”,度量标准改为“度量(S)”,以备接下来的分析。
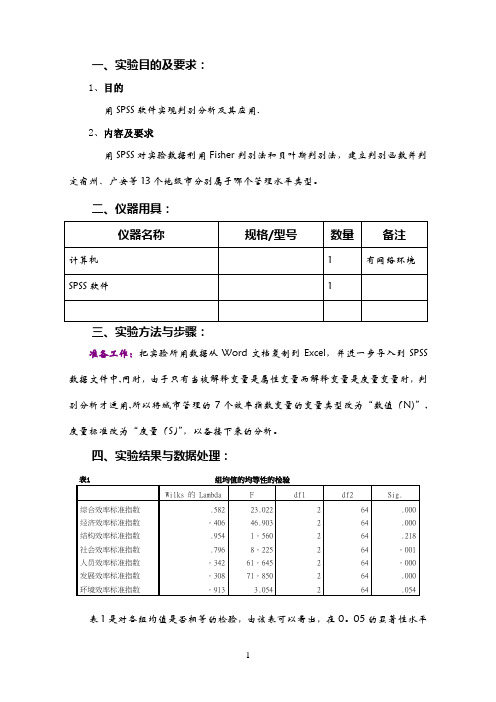
四、实验结果与数据处理:表1 组均值的均等性的检验Wilks 的 Lambda F df1 df2 Sig.综合效率标准指数.582 23.022 2 64 .000 经济效率标准指数。
406 46.903 2 64 .000 结构效率标准指数.954 1。
560 2 64 .218 社会效率标准指数.796 8。
225 2 64 。
001 人员效率标准指数。
342 61。
645 2 64 。
000 发展效率标准指数。
308 71。
850 2 64 .000 环境效率标准指数。
913 3.054 2 64 .054表1是对各组均值是否相等的检验,由该表可以看出,在0。
05的显著性水平上我们不能拒绝结构效率标准指数和环境效率标准指数在三组的均值相等的假设,即认为除了结构效率标准指数和环境效率标准指数外,其余五个标准指数在三组的均值是有显著差异的。
表2 对数行列式group 秩对数行列式1 6 —33.4102 6 -33.1773 6 —40。
584汇聚的组内 6 -32.308 打印的行列式的秩和自然对数是组协方差矩阵的秩和自然对数。
表3 检验结果箱的 M 140.196F 近似。
2。
498df1 42df2 1990.001Sig. .000 对相等总体协方差矩阵的零假设进行检验。
以上是对各组协方差矩阵是否相等的Box’M检验,表2反映协方差矩阵的秩和行列式的对数值。
2024版SPSS判别分析方法案例分析

01 查看判别分析的结果输出,包括判别函数系数、 结构矩阵、分类结果等。
02 根据输出结果,解读判别分析的结果,如判别函 数的贡献、分类准确率等。
03 结合专业知识和实际背景,对结果进行合理解释 和讨论。
05
案例分析:某公司客户流失预测 模型构建
案例背景及问题描述
01
某大型电信公司面临客户流失问题,需要构建客户流失
04
SPSS判别分析操作过程
导入数据并建立数据集
1
打开SPSS软件,选择“文件”->“打开”>“数据”,导入需要分析的数据文件。
2
在数据视图中检查数据的完整性和准确性,确保 数据质量。
3
根据需要,对数据进行预处理,如缺失值处理、 异常值处理等。
选择合适的判别分析方法
根据研究目的和数据特点,选择合适 的判别分析方法,如线性判别分析、 二次判别分析等。
决策树与随机森林
基于贝叶斯定理和多元正态分 布假设,通过最大化类间差异 和最小化类内差异来建立线性 判别函数。适用于正态分布且 各类别协方差矩阵相等的情况。
放宽了LDA的假设条件,允许各 类别具有不同的协方差矩阵。 通过构建二次判别函数进行分 类。适用于更一般的数据分布 情况。
基于距离度量的方法,将新样 本分配给与其最近的K个已知样 本中最多的类别。适用于多类 别、非线性可分问题。
数据变换与标准化
数据变换
根据分析需求,对数据进行适当的变换,如对数变换、平 方根变换等,以改善数据的分布形态或满足分析要求。
数据标准化
对数据进行标准化处理,消除量纲和数量级的影响,使不 同变量具有可比性。常用的标准化方法包括Z分数标准化、 最小最大标准化等。
数据离散化
SPSS操作方法:判别分析例题

1991 年 30 个省、市、自治区城镇居民月平均收人数据表
x2:人均国有经济单位职工工资
x3:人均来源于国有经济单位标准工资
x4:人均集体所有制工资收入
x5:人均集体所有制职工标准工资
样品序 地区 x1
类 号序
G1 6 7
G2 6 7
G3 1
1号 北 京 170.03 110.2
2
3
4
5
8
9
天 津 141.55 82.58
1
2
3
4
5
8
9
山 西 102.49 71.72
内蒙古 106.14 7
黑龙江 103.34 62.99
江 西 98.089 69.45
河 南 104.12 72.23 贵 州 108.49 80.79
陕 西 113.99 75.6
甘 肃 114.06 84.31
实验指导之二
判别分析的 SPSS 软件的基本操作
[实验例题] 为研究 1991 年中国城镇居民月平均收入状况,按标准化欧氏平方
距离、离差平方和聚类方法将 30 个省、市、自治区.分为三种类型。试建立判
别函数,判定广东、西藏分别属于哪个收入类型。判别指标及原始数据见表 9-
4。
人
x1:人均生活费收入 体)
10 青 海 108.80 80.41
11 宁 夏 115.96 88.2l
辽 宁 128.46 68.91
x2
x3
59.76 50.98 53.39 60.24 52.30 53.02 48.18 45.60 50.13 50.57 69.70 47.72 46.19 44.60 42.95 43.04 47.31 47.52 50.88 52.78 50.45 51.85 43.4l
SPSS数据的判别分析

W [y
( 1 2 ) 1 ] ( 1 2 ) 2
1 W是关于y的线性函数, 是已知的p维向量,是W的判别系数 ( 1 2)
2016/9/11 14 zf
2、总体协方差已知,且不相等:
判别函数:
d 2 (y, G2 ) d 2 (y, G1 )
1 1 (y 2 ) 2 (y 2 ) (y 1 )1 (y 1 )
2016/9/11
18 zf
例:下表是某金融机构客户的个人资料,这些资料对一个金融机 构来说,对于客户信用度的了解至关重要,因为利用这些资料, 可以挖掘出许多的信息,建立客户的信用度评价体系。所选变量 为: x1: 月收入 x2:月生活费支出 x3:虚拟变量,住房的所有权,自己的为‚1‛,租用的‚0‛ x4:目前工作的年限 x5:前一个工作的年限 x6:目前住所的年限 x7:前一个住所的年限 X8: 家庭赡养的人口数 X9:信用程度,‚5‛的信用度最高,‚1‛的信用度最低。
距离判别缺点:没有 考虑到每个总体出现 的机会大小,即先验 概率,没有考虑到错 判的损失
设有个K总体,分别有均值向量 u i (i=1,2,…,k)和协方差阵∑i= ∑ , 又设Y是一个待判样品。则Y与各总体的距离为(即判别函数):
d d22((y y,,G Gii)) ((y y ii)) 11((y y ii)) y y 11y y 2 2y y 11 ii ii 11 ii y y'' 11y y 2 2((y y 11 ii 0 0..5 5 ii 11 ii))
判别法则:
y G1 , 如d 2 y,G1 d 2 y,G2 , 2 2 y G2 , 如d y,G2 d y,G1 待判, 如d 2 ( y, G ) d 2 ( y, G ) 1 2
判别分析实验报告SPSS

判别分析实验报告SPSS实验目的:判别分析(Discriminant Analysis)是一种经典的多元统计分析方法,用于解释和预测分类变量。
该实验旨在使用SPSS软件进行判别分析,探索一组变量对分类结果的贡献和预测能力。
实验步骤:1.数据收集:从一些公司的人力资源数据库中随机选择了200个员工作为样本,收集了以下变量:性别(男、女)、教育程度(本科、研究生、博士)、工龄(年)、绩效评分(0-5)、离职与否(是、否)。
2.数据清洗:检查数据中是否存在缺失值,并对缺失值进行处理。
删除离职与否变量中缺失值。
3.数据探索:使用SPSS进行描述性统计分析,了解样本的基本情况。
分别计算男女性别比例和各教育程度及离职状态的分布情况。
4. 变量选择:使用SPSS进行判别分析,将离职与否作为分类变量,性别、教育程度、工龄和绩效评分作为预测变量。
使用Wilks' Lambda检验选择预测变量,确定对分类结果的贡献。
5.判别函数计算:根据选择的预测变量,计算判别函数。
使用判别函数对样本进行分类,并计算分类结果的准确率。
实验结果:1.数据探索结果显示,样本中男女性别比例约为1:1,教育程度主要集中在本科和研究生,离职比例为14%。
2. 判别分析结果显示,Wilks' Lambda检验结果为0.632,p值小于0.05,说明选取的预测变量对分类结果有统计上显著的贡献。
3.计算得到的判别函数为D=-0.311(性别)+0.236(教育程度)+0.011(工龄)+0.585(绩效评分)。
4.使用判别函数对样本进行分类,分类准确率为81.5%。
其中,离职样本的分类准确率为75%,非离职样本的分类准确率为82%。
实验结论:通过判别分析实验,我们得出以下结论:1.性别、教育程度、工龄和绩效评分这四个变量对员工的离职与否有显著的预测能力。
2.预测变量中绩效评分对离职结果的贡献最大,说明绩效评分较低的员工更容易离职。
spss教程_13-1(判别分析)

具体操作 Save: 保存新变量 Predicted group membership : 建立新变量,表明预测的类成员 Discriminant score:建立新变量, 表明判别分数 Probabilities of group membership : 建立新变量.表明样品属于某一类的概率
Wilk’s λ最小法
U统计量 λ=组内平方和/总平方和,每一步都是统计量 最小的进入判别函数 容许度=1-Ri2 (Ri2为偏相关系数)
1 p F引 p 1 p
p 1
ng p g 1
p 1 1 p n g p F剔 p 1 g 1 p
判别分析
分类: 1、按判别的组数来分,有两组判别分析和多 组判别分析 2、按区分不同总体所用的数学模型来分,有 线性判别和非线性判别 3、按判别对所处理的变量方法不同有逐步判 别、序贯判别。 4、按判别准则来分,有费歇尔判别准则、贝 叶斯判别准则
判别分析
判别分析和前面的聚类分析有什么不同呢? 主要不同点就是,在聚类分析中一般人们事 先并不知道或一定要明确应该分成几类,完 全根据数据来确定。 而在判别分析中,至少有一个已经明确知道 类别的“训练样本”,利用这个数据,就可 以建立判别准则,并通过预测变量来为未知 类别的观测值进行判别了。
Casewise:逐步输出每个样品的分类结果 limit cases to:最大样品数 Summary table:分类概括表 Leave-one-out classification 剔除一个样品 后用其他样品得到的该样品的分类结果
具体操作
Plot: 输出统计图 Combined-groups:各类输出在同一张散点图中 Separate-groups:每类输出一张散点图中 Territorial mao:分类区域图
判别分析的SPSS实现

第五节判别分析判别分析是根据观察或测量到的若干变量值,判断研究对象如何分类的方法。
判别函数一般形式是:F1= a i1x1+a i2x2+a i3x3...+a in x nF2= a i1x1+a i2x2+a i3x3...+a in x n: :F m= a m1x1+a m2x2+a m3x 3...+a mn x nSPSS提供的判别分析过程是Discriminant过程。
【例3-9】浙江北部地区1950~1982年小麦赤霉病发生程度与气象因子研究,总结出上年12月降雨量(x1)、上年10月下旬至11月中旬和当年1~2月总降雨(x2)、上年10月下旬至11月上旬日照时数(x3)、上年10月下旬至12月中旬和当年2月总雨量(x4)以及当年3月中旬平均温度(x5)等5个因子,并将赤霉病情分为轻中重三级(y,分别用1、2、3表示)。
用这些数据建立气象因子与小麦赤霉病发生程度的判别模型。
年份x1x2x3x4x5y195014.3107.3140.0105.3 6.91 195146.5129.1154.191.311.91 195243.0143.183.9157.413.02 195371.2280.582.5317.413.93 1954.769.3145.669.511.31 1955123.9297.364.6307.213.73 195685.4115.439.4144.711.11 195738.477.394.6143.213.92 195879.696.885.499.09.62 195933.474.7129.5103.49.91 196048.195.9155.392.010.511955123.9297.364.6307.213.73 195685.4115.439.4144.711.11 195738.477.394.6143.213.92 195879.696.885.499.09.62 195933.474.7129.5103.49.91 196048.195.9155.392.010.51 19617.7116.3158.2148.115.11 19628.9225.3104.2195.513.81 196334.8150.7165.0124.611.91 196444.4147.288.3158.712.72 196574.2232.794.1154.613.53 1966.180.9148.881.311.01 1967119.6208.070.9217.813.83 196894.0130.249.2176.211.02 196932.983.6115.3135.713.82 197065.588.1126.9102.59.71 197131.359.3105.182.910.01 197252.393.3173.791.210.01 19737.298.2154.3120.715.01 1974 5.3245.8100.4200.213.711准备分析数据在SPSS数据管理窗口,定义变量名x1、x2、x3、x4、x5、y分别表示表中对应变量。
专题16用SPSS进行判别分析

专题16 用SPSS进行判别分析1 用默认方法作判别分析2 选项的设置简介1 用默认方法作判别分析用默认方法作判别分析,可按如下步骤进行。
①建立或读入数据文件在数据窗中输入待分析的数据,或利用File菜单中的Open功能打开已存在的数据文件。
②展开主对话框在SPSS主界面中依次逐层选择“Analyze”、“Classify”、“Discriminant”,展开判别分析主对话框(如图)。
③选择分类变量及其取值范围在如图14.1的主对话框左边的矩形框中选定分类变量,并用上面一个箭头按钮将其移到“Grouping Variable”框中。
然后用其下面的“Define Range”按钮打开如图14.2的对话框。
分别在“Minimum”和“Maximum”后面的矩形框中键入分类变量的最大值与最小值,然后按“Continue”按钮返回主对话框。
分类变量须是数值型的,其值必须是整数,每个值代表一类,如1代表健将、2代表一级运动员、3代表二级运动员。
④选择判别变量在主对话框左边的矩形框中选择判别变量,并用下面一个箭头按钮将它们移到“Independents”矩形框中。
⑤选择是否作逐步判别若不用逐步判别筛选变量,在主对话框中选择“Enter independents together”。
若作逐步判别,则选择“Use stepwise method”。
⑥运行程序检查所选变量是否有误,若选择有误,则选定错误变量,用边上的箭头按钮将其移出。
若变量选择无误,按“OK”按钮即可运行程序。
返回2 选项的设置简介①在主对话框中单击“Statistics”按钮可以打开选择输出统计量的对话框。
●选定“Means”可得到各类的均数、标准差等统计量●选定“Univariate ANOVAs”可得到各单变量的方差分析●选定“Box’s M”可得到各类协差阵相等性的Box检验●选择“Fisher’s”可得到费歇的线性分类函数●选定“Unstandardized”可以得到非标准化的典型判别函数系数●选定“Within-groups covariance”可以得到合并组内协差阵。
SPSS操作方法:判别分析例题

SPSS操作方法:判别分析例题为研究1991年中国城镇居民月平均收入状况,按标准化欧氏平方距离、离差平方和聚类方法将30个省、市、自治区.分为三种类型。
试建立判别函数,判定广东、西藏分别属于哪个收入类型。
判别指标及原始数据见表9-4。
1991年30个省、市、自治区城镇居民月平均收人数据表单位:元/人 x1:人均生活费收入 x6:人均各种奖金、超额工资(国有+集体) x2:人均国有经济单位职工工资 x7:人均各种津贴(国有+集体)x3:人均来源于国有经济单位标准工资x8:人均从工作单位得到的其他收入x4:人均集体所有制工资收入 x9:个体劳动者收入5贝叶斯判别的SPSS操作方法:1. 建立数据文件2.单击Analyze→ Classify→ Discriminant,打开Discriminant Analysis 判别分析对话框如图1所示:图1 Discriminant Analysis判别分析对话框3.从对话框左侧的变量列表中选中进行判别分析的有关变量x1~x9进入Independents 框,作为判别分析的基础数据变量。
从对话框左侧的变量列表中选分组变量Group进入Grouping Variable 框,并点击Define Range...钮,在打开的Discriminant Analysis: Define Range对话框中,定义判别原始数据的类别数,由于原始数据分为3类,则在Minimum(最小值)处输入1,在Maximum(最大值)处输入3(见图2)。
选择后点击Continue按钮返回Discriminant Analysis主对话框。
图2 Define Range对话框4、选择分析方法Enter independent together 所有变量全部参与判别分析(系统默认)。
本例选择此项。
Use stepwise method 采用逐步判别法自动筛选变量。
单击该项时Method 按钮激活,打开Stepwise Method对话框如图3所示,从中可进一步选择判别分析方法。
判别分析实验报告 SPSS

判别分析实验报告 SPSS一、实验目的判别分析是一种用于分类和预测的统计方法。
本次实验旨在通过使用 SPSS 软件,掌握判别分析的基本原理和操作流程,能够运用判别分析方法对实际数据进行分类,并对分类结果进行评估和解释。
二、实验数据本次实验使用的数据集包含了两个类别(类别 A 和类别 B)的样本,每个样本具有若干个特征变量,如年龄、收入、教育程度等。
数据集共有 200 个样本,其中类别 A 有 100 个样本,类别 B 有 100 个样本。
三、实验步骤1、数据导入首先,打开 SPSS 软件,选择“文件”菜单中的“打开”选项,将实验数据文件导入到 SPSS 中。
2、变量定义在 SPSS 数据视图中,对各个变量进行定义,包括变量名称、变量类型、变量标签等。
3、判别分析操作选择“分析”菜单中的“分类”子菜单,然后点击“判别分析”选项。
在弹出的判别分析对话框中,将类别变量选入“分组变量”框中,将其他特征变量选入“自变量”框中。
4、选择判别方法SPSS 提供了多种判别方法,如费希尔判别法、贝叶斯判别法等。
本次实验选择费希尔判别法。
5、模型评估在判别分析结果中,查看判别函数的系数、判别函数的显著性检验、分类结果的准确性等指标,以评估模型的性能。
四、实验结果与分析1、判别函数系数判别函数的系数反映了各个自变量对判别函数的贡献程度。
通过查看系数的大小和符号,可以了解各个变量在区分不同类别中的重要性。
例如,年龄变量的系数为正,说明年龄越大,越有可能属于某个类别;而收入变量的系数为负,说明收入越低,越有可能属于另一个类别。
2、判别函数的显著性检验通过对判别函数的显著性检验,可以判断判别函数是否能够有效地区分不同的类别。
如果检验结果显著,说明判别函数具有统计学意义,可以用于分类。
3、分类结果SPSS 会给出每个样本的分类结果,以及分类的准确性。
通过比较实际类别和预测类别,可以评估模型的分类效果。
如果分类准确性较高,说明模型能够较好地对样本进行分类;如果分类准确性较低,则需要进一步分析原因,可能是数据质量问题、变量选择不当或者判别方法不合适等。
判别分析的一般步骤及SPSS实现

判别分析的SPSS实现
表7.3 Bayes判别法的输出结果
C l as si fic ati on Fu ncti o n C oe ffi ci e n ts
GROUP
1.00
X1
-14 3.85 1
X2
15 3.13 6
6
2
2 1.000
.469 9.674
.231
7
2
2 1.000
.868 8.332 -.613
8
2
2 1.000
5.98 5 10 .1 28 -2.51 8
9
2
2 1.000
4.793 8.342 1.760
10
2
2 1.000
.101 9.491 -.145
11
3
3 1.000
.139 -6.687 -.394
Dist a nce t o Funct ion Funct ion
Cent roid
1
2
.297 -2.177 1.364
2
1
1 1.000
.236 -2.270 1.375
3
1
1 1.000
.117 -2.741 1.323
4
1
1 .998
.507 -3.199
.638
5
1
1 1.000
.418 -2.582
标准化的典型判别函数是由标准化的自变量通过Fisher判别法得到的,所以 要得到标准化的典型判别得分,代入该函数的自变量必须是经过标准化的。
2. Canonical Discriminant Function Coefficients(给出未标准化的典型判别 函数系数)
聚类分析及判别分析案例

一、案例背景随着现代人力资源管理理论的迅速开展,绩效考评技术水平也在不断提高。
绩效的多因性、多维性,要求对绩效实施多标准大样本科学有效的评价。
对企业来说,对上千人进展多达50~60个标准的考核是很常见的现象。
但是,目前多标准大样本大型企业绩效考评问题仍然困扰着许多人力资源管理从业人员。
为此,有必要将当今国际上最流行的视窗统计软件SPSS应用于绩效考评之中。
在分析企业员工绩效水平时,由于员工绩效水平的指标很多,各指标之间还有一定的关联性,缺乏有效的方法进展比拟。
目前较理想的方法是非参数统计方法。
本文将列举某企业的具体情况确定适当的考核标准,采用主成分分析以及聚类分析方法,比拟出各员工绩效水平,从而为企业绩效管理提供一定的科学依据。
最后采用判别分析建立判别函数,同时与原分类进展比拟。
聚类分析二、绩效考评的模型建立1、为了分析某企业绩效水平,按照综合性、可比性、实用性和易操作性的选取指标原那么,本文选择了影响某企业绩效水平的成果、行为、态度等6个经济指标(见表1)。
2、对某企业,搜集整理了28名员工2021年第1季度的数据资料。
构建1个28×6维的矩阵(见表2)。
3、应用SPSS数据统计分析系统首先对变量进展及主成分分析,找到样本的主成分及各变量在成分中的得分。
去结果中的表3、表4、表5备用。
表 5成份得分系数矩阵a成份1 2Zscore(X1) .227Zscore(X2) .228Zscore(X3) .224Zscore(X4) .177Zscore(X5) .186 .572Zscore(X6) .185 .587提取方法 :主成份。
构成得分。
a. 系数已被标准化。
4、从表3中可得到前两个成分的特征值大于1,分别为3.944和1.08,所以选取两个主成分。
根据累计奉献率超过80%的一般选取原那么,主成分1和主成分2的累计奉献率已到达了83.74%的水平,说明原来6个变量反映的信息可由两个主成分反映83.74%。
spss判别分析案例详解

spss判别分析案例详解SPSS判别分析案例详解。
在统计学中,判别分析是一种用于确定不同组别之间差异的统计方法。
它可以帮助我们理解不同变量之间的关系,以及这些变量在预测和分类方面的作用。
在本文中,我们将通过一个实际的案例来详细介绍如何使用SPSS进行判别分析。
案例背景:假设我们是一家电子商务公司的数据分析师,我们想要确定哪些因素对于用户购买高价值产品的决策具有影响力。
我们收集了一些用户的个人信息和他们的购买行为数据,希望通过判别分析找出影响用户购买高价值产品的关键因素。
数据准备:首先,我们需要将收集到的数据导入SPSS软件中。
在导入数据后,我们可以对数据进行初步的检查,确保数据的完整性和准确性。
接下来,我们需要选择判别分析作为我们的分析方法,并将购买高价值产品作为分类变量,个人信息和购买行为数据作为判别变量。
分析步骤:1. 设定判别分析的目的和假设,在进行判别分析之前,我们需要明确分析的目的是什么,以及我们的假设是什么。
在这个案例中,我们的目的是找出影响用户购买高价值产品的关键因素,我们的假设是个人信息和购买行为数据会对用户的购买决策产生影响。
2. 进行判别分析,在设定好目的和假设后,我们可以开始进行判别分析。
SPSS 会根据我们选择的分类变量和判别变量,自动进行变量选择和模型拟合,得出判别函数和判别系数。
通过判别函数和判别系数,我们可以了解每个判别变量对于不同组别的影响程度,以及它们对于用户购买高价值产品的预测能力。
3. 结果解释,在得出判别函数和判别系数后,我们需要对结果进行解释。
我们可以通过判别函数的系数来理解每个判别变量对于用户购买高价值产品的影响程度,以及它们之间的相互关系。
同时,我们还可以通过判别系数的大小来评估判别模型的预测能力和区分能力。
案例分析:通过对案例数据的判别分析,我们得出了以下结论:1. 个人收入、年龄和教育程度是影响用户购买高价值产品的重要因素,其中个人收入对用户购买高价值产品的影响最大,其次是年龄和教育程度。
spss进行判别分析步骤_spss判别分析结果解释_spss判别分析案例详解

spss进⾏判别分析步骤_spss判别分析结果解释_spss判别分析案例详解1.Discriminant Analysis判别主对话框如图 1-1 所⽰图 1-1 Discriminant Analysis 主对话框(1)选择分类变量及其范围在主对话框中左⾯的矩形框中选择表明已知的观测量所属类别的变量(⼀定是离散变量),按上⾯的⼀个向右的箭头按钮,使该变量名移到右⾯的Grouping Variable 框中。
此时矩形框下⾯的Define Range 按钮加亮,按该按钮屏幕显⽰⼀个⼩对话框如图1-2 所⽰,供指定该分类变量的数值范围。
图 1-2 Define Range 对话框在Minimum 框中输⼊该分类变量的最⼩值在Maximum 框中输⼊该分类变量的最⼤值。
按Continue 按钮返回主对话框。
(2)指定判别分析的⾃变量图 1-3 展开 Selection Variable 对话框的主对话框在主对话框的左⾯的变量表中选择表明观测量特征的变量,按下⾯⼀个箭头按钮。
把选中的变量移到Independents 矩形框中,作为参与判别分析的变量。
(3)选择观测量图 1-4 Set Value ⼦对话框如果希望使⽤⼀部分观测量进⾏判别函数的推导⽽且有⼀个变量的某个值可以作为这些观测量的标识,则⽤Select 功能进⾏选择,操作⽅法是单击Select 按钮展开Selection Variable。
选择框如图1-3 所⽰。
并从变量列表框中选择变量移⼊该框中再单击Selection Variable 选择框右侧的Value按钮,展开Set Value(⼦对话框)对话框,如图1-4 所⽰,键⼊标识参与分析的观测量所具有的该变量值,⼀般均使⽤数据⽂件中的所有合法观测量此步骤可以省略。
(4)选择分析⽅法在主对话框中⾃变量矩形框下⾯有两个选择项,被选中的⽅法前⾯的圆圈中加有⿊点。
这两个选择项是⽤于选择判别分析⽅法的l Enter independent together 选项,当认为所有⾃变量都能对观测量特性提供丰富的信息时,使⽤该选择项。
SPSS处理多元判别分析
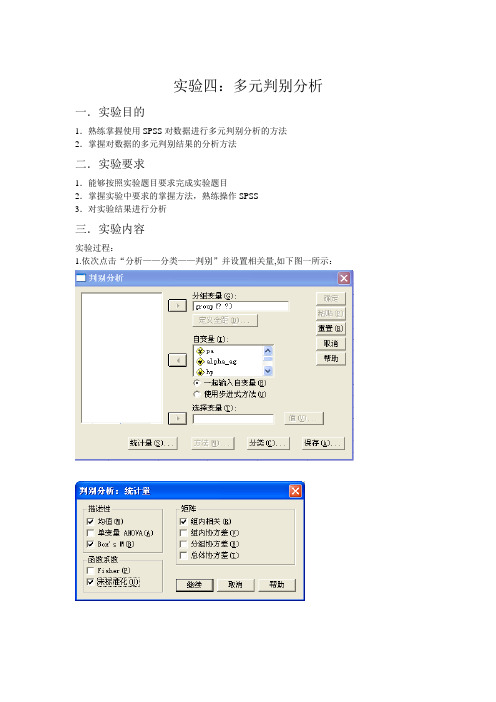
实验四:多元判别分析一.实验目的1.熟练掌握使用SPSS对数据进行多元判别分析的方法2.掌握对数据的多元判别结果的分析方法二.实验要求1.能够按照实验题目要求完成实验题目2.掌握实验中要求的掌握方法,熟练操作SPSS3.对实验结果进行分析三.实验内容实验过程:1.依次点击“分析——分类——判别”并设置相关量,如下图一所示:【图一】分析的结果如表一所示:【表一】判别分析案例处理摘要未加权案例N 百分比有效100 100.0 排除的缺失或越界组代码0 .0至少一个缺失判别变量0 .0缺失或越界组代码还有至少一个缺失判别变量0 .0合计0 .0 合计100 100.0组统计量group 均值标准差有效的 N(列表状态)未加权的已加权的正常人pa 28.2136 4.70056 25 25.000alpha_ag 67.5780 16.75241 25 25.000 hp 257.1212 126.27684 25 25.000 alpha_at 282.1680 30.83337 25 25.000肝癌,AFP检测阳性pa 15.8555 10.21072 40 40.000 alpha_ag 120.7943 62.04790 40 40.000 hp 321.8357 249.33407 40 40.000 alpha_at 492.4633 151.32253 40 40.000肝癌,AFP检测阴性pa 16.3145 7.80152 20 20.000 alpha_ag 55.2980 26.12832 20 20.000 hp 91.4700 126.45050 20 20.000 alpha_at 313.3080 55.59623 20 20.000肝硬化pa 21.9793 8.47264 15 15.000 alpha_ag 69.6187 50.46477 15 15.000hp 297.1527 210.05123 15 15.000alpha_at 314.7287 72.52736 15 15.000 合计pa 19.9554 9.77612 100 100.000 alpha_ag 86.7146 53.67732 100 100.000hp 255.8815 212.46384 100 100.000alpha_at 377.3982 140.18786 100 100.000汇聚的组内矩阵pa alpha_ag hp alpha_at相关性pa 1.000 -.112 .119 -.290alpha_ag -.112 1.000 .456 .528hp .119 .456 1.000 .484alpha_at -.290 .528 .484 1.000分析 1协方差矩阵的均等性的箱式检验对数行列式group 秩对数行列式正常人 4 25.055肝癌,AFP检测阳性 4 32.930肝癌,AFP检测阴性 4 26.634肝硬化 4 29.759汇聚的组内 4 30.930打印的行列式的秩和自然对数是组协方差矩阵的秩和自然对数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验指导之二判别分析的SPSS软件的基本操作[实验例题]为研究1991年中国城镇居民月平均收入状况,按标准化欧氏平方距离、离差平方和聚类方法将30个省、市、自治区.分为三种类型。
试建立判别函数,判定、分别属于哪个收入类型。
判别指标及原始数据见表9-4。
1991年30个省、市、自治区城镇居民月平均收人数据表单位:元/人x1:人均生活费收入x6:人均各种奖金、超额工资(国有+集体)x2:人均国有经济单位职工工资x7:人均各种津贴(国有+集体)x3:人均来源于国有经济单位标准工资x8:人均从工作单位得到的其他收入x4:人均集体所有制工资收入x9:个体劳动者收入6 湖南124.00 84.66 44.05 13.5 7.47 19.11 20.49 10.3 1.76待判1 广东211.30 114.0 41.44 33.2 11.2 48.72 30.77 14.9 11.12 西藏175.93 163.8 57.89 4.22 3.37 17.81 82.32 15.7 0.00贝叶斯判别的SPSS操作方法:1. 建立数据文件2.单击Analyze→Classify→Discriminant,打开Discriminant Analysis判别分析对话框如图1所示:图1 Discriminant Analysis判别分析对话框3.从对话框左侧的变量列表中选中进行判别分析的有关变量x1~x9进入Independents 框,作为判别分析的基础数据变量。
从对话框左侧的变量列表中选分组变量Group进入Grouping Variable 框,并点击Define Range...钮,在打开的Discriminant Analysis: Define Range 对话框中,定义判别原始数据的类别数,由于原始数据分为3类,则在Minimum(最小值)处输入1,在Maximum(最大值)处输入3(见图2)。
选择后点击Continue按钮返回Discriminant Analysis主对话框。
图2 Define Range对话框4、选择分析方法✧Enter independent together 所有变量全部参与判别分析(系统默认)。
本例选择此项。
✧Use stepwise method 采用逐步判别法自动筛选变量。
单击该项时Method 按钮激活,打开Stepwise Method对话框如图3所示,从中可进一步选择判别分析方法。
图3 Stepwise Method对话框✧Method栏,选择变量的统计量方法Wilks’lambda (默认)按统计量Wilks λ最小值选择变量;Unexplained variance :按照所有组方差之和最小值选择变量;Mahalanobis’distance:按照相邻两组的最大马氏距离选择变量;Smallest F ratio:按组间最小F值比的最大值选择变量;Rao’s V按照统计量Rao V最大值选择变量。
✧Criteria 选择逐步回归的标准(略)选择系统默认项。
5.单击Statistics 按钮,打开Statistics对话框如图4所示,从中指定输出的统计量。
✧Descriptives描述统计量栏Means -各类中各自变量的均值,标准差std Dev 和各自变量总样本的均值和标准差(本例选择)。
Univariate ANOV----对各类中同一自变量均值都相等的假设进行检验,输出单变量的方差分析结果(本例选择)。
Box’s M --对各类的协方差矩阵相等的假设进行检验(本例选择)。
图4 Statistics对话框✧Function coefficients 选择输出判别函数系数Fisherh’s 给出贝叶斯判别函数系数(本例选择)Unstandardized 给出未标准化的典型判别(也称典则判别)系数(费舍尔判别函数)。
✧Matrices 栏选择给出的自变量系数矩阵Within-groups correlation 合并类相关系数矩阵(本例选择)Within-groups covariance 合并类协方差矩阵(本例选择)Separate-groups covariance 各类协方差矩阵(本例选择)Total covariance 总协方差矩阵(本例选择)6.单击Classify按钮,打开Classify对话框如图5所示:图5 Classify对话框✧Prior Probabilities栏,选择先验概率。
All groups equal 各类先验概率相等(系统默认);Compute from groups sizes 各类的先验概率与其样本量成正比. (本例选择)✧Use Covariance Matrix 栏,选择使用的协方差矩阵Within-groups --使用合并类协方差矩阵进行分类(系统默认)(本例选择)Separate-groups --使用各类协方差矩阵进行分类✧Display栏,选择生成到输出窗口中的分类结果Casewise results 输出每个观测量包括判别分数实际类预测类(根据判别函数求得的分类结果)和后验概率等。
Summary table 输出分类的小结给出正确分类观测量数(原始类和根据判别函数计算的预测类相同)和错分观测量数和错分率(本例选择)。
Leave-one-out classification 输出交互验证结果。
✧Plots栏,要求输出的统计图Combined-groups 生成一包括各类的散点图(本例选择);Separate-groups 每类生成一个散点图;Territorial map 根据生成的函数值把各观测值分到各组的区域图。
(本例选择)6.单击Save 按钮,打开Save对话框,见图6.图6 Save对话框✧Predicted group membership 建立一个新变量,系统根据判别分数,把观测量按后验概率最大指派所属的类;(本例选择)✧Discriminant score 建立表明判别得分的新变量,该得分是由未标准化的典则判别函数计算。
(本例选择)Probabilities of group membership 建立新变量表明观测量属于某一类的概率。
有m 类,对一个观测量就会给出m 个概率值,因此建立m 个新变量。
(本例选择)全部选择完成后,点击OK,得到输出结果如下:Group Statistics 各类统计分析个体劳动者收入 1.3845 .73428 11 11.000 3 人均生活费收入(元/人)133.5150 17.11642 6 6.000人均国有经济单位职工工资76.1700 6.06280 6 6.000 人均来源于国有经济单位标准工资44.3033 .91825 6 6.000 人均集体所有制工资收入20.3333 4.09031 6 6.000 人均集体所有制职工标准工资12.4783 3.04592 6 6.000 人均各种奖金、超额工资(国有+集体) 20.3033 5.39344 6 6.000人均各种津贴(国有+集体) 13.2732 4.34722 6 6.000 均从工作单位得到的其他收入10.1500 2.80907 6 6.000个体劳动者收入 1.9233 1.11631 6 6.000 Total 人均生活费收入(元/人)125.4796 22.22549 28 28.000 人均国有经济单位职工工资82.7143 12.09003 28 28.000 人均来源于国有经济单位标准工资49.4636 6.09033 28 28.000 人均集体所有制工资收入12.3282 5.36546 28 28.000 人均集体所有制职工标准工资7.7046 3.54143 28 28.000 人均各种奖金、超额工资(国有+集体) 16.5630 6.10883 28 28.000 人均各种津贴(国有+集体) 15.9147 5.54104 28 28.000均从工作单位得到的其他收入9.0811 2.98513 28 28.000 个体劳动者收入 1.6136 1.26601 28 28.000a The covariance matrix has 25 degrees of freedom.3 人均生活费收入(元/人)292.972 38.451 14.013 37.178 13.567 78.758 -8.776 29.547 16.466 人均国有经济单位职工工资38.451 36.758 2.665 -13.730 -14.286 16.990 19.297 3.658 4.120人均来源于国有经济单位标准工资14.013 2.665 .843 1.649 .400 4.905 -.783 1.806 .732人均集体所有制工资收入37.178 -13.730 1.649 16.731 11.802 8.488 -15.180 5.753 .532人均集体所有制职工标准工资13.567 -14.286 .400 11.802 9.278 1.340 -11.632 3.026 -.549人均各种奖金、超额工资(国有+集体)78.758 16.990 4.905 8.488 1.340 29.089 -3.967 10.556 4.171人均各种津贴(国有+集体)-8.776 19.297 -.783 -15.180 -11.632 -3.967 18.898 -2.998 1.312 均从工作单位得到的其他收入29.547 3.658 1.806 5.753 3.026 10.556 -2.998 7.891 .680个体劳动者收入16.466 4.120 .732 .532 -.549 4.171 1.312 .680 1.246Tot al人均生活费收入(元/人)493.973 182.382 51.722 40.606 15.154 123.390 24.245 39.841 1.513 人均国有经济单位职工工资182.382 146.169 52.685 -20.328 -19.362 40.532 42.118 11.447 2.648 人均来源于国有经济单位标准工资51.722 52.685 37.092 -12.222 -7.958 7.157 5.158 -.595 -.133人均集体所有制工资收入40.606 -20.328 -12.222 28.788 18.414 15.043 -11.572 5.872 -.720人均集体所有制职工标准工资15.154 -19.362 -7.958 18.414 12.542 6.755 -10.523 2.711 -1.031 人均各种奖金、超额工资(国有+集体)123.390 40.532 7.157 15.043 6.755 37.318 1.737 13.194 .106人均各种津贴(国有+集体)24.245 42.118 5.158 -11.572 -10.523 1.737 30.703 .708 2.548 均从工作单位得到的其他收入39.841 11.447 -.595 5.872 2.711 13.194 .708 8.911 .335 个体劳动者收入 1.513 2.648 -.133 -.720 -1.031 .106 2.548 .335 1.603a The total covariance matrix has 27 degrees of freedom.标准文案Box's Test of Equality of Covariance Matrices 协方差矩阵相等的检验Log Determinants分类RankLog Determinant1914.087291.5733.(a).(b)Pooled within-groups915.603The ranks and natural logarithms of determinants printed are those of the group covariance matrices.a Rank < 6b Too few cases to be non-singular Test Results(a)检验结果Box's M FApprox.195.630 2.155df145df21314.073Sig..000Tests null hypothesis of equal population covariance matrices.a Some covariance matrices are singular and the usual procedure will not work. The non-singular groups will betested against their own pooled within-groups covariance matrix. The log of its determinant is 17.611.注意,检验没有通过,即各类的协方差相等的假设在显著性水平下是不成立的。
