三角形与四边形的综合题

合集下载

中考数学解答题压轴题突破重难点突破十一三角形、四边形综合题类型三：与平移有关的问题

11 ∴△ENP≌△HGP(AAS)，∴PG＝PN＝2NG＝2AB＝3.
证明：如答图①，过点 B 作 BC⊥AO 于点 ቤተ መጻሕፍቲ ባይዱ，则四边形 OCBM 为矩形， ∴BC＝OM，∠CBM＝∠ABP＝∠ACB ＝∠PMB＝90°. ∴∠CBP＋∠PBM＝∠ABC＋∠CBP＝90°， ∴∠ABC＝∠PBM，
AB OM ∴△ABC∽△PBM，∴PB＝BM.
(3)若 AO＝2 6，且当 MO＝2PO 时，请直接写出 AB 和 PB 的长．【分层分析】由于点 P 的位置不确定，故需要分情况进行讨论，共两种情况，第一种情况是点 P 在点 O 的左侧，第二种情况是点 P 在点 O 的右侧，然后利用相似三角形的性质即可求出答案．
Ⅱ)若∠HEF＝30°，求 EH 的长；解：作 HI⊥EF 于点 I， ∵∠HEF＝30°＝∠HFE， ∴IE＝IF，由(1)知 EF＝2AB＝12，∴IE＝6， ∴IH＝2 3，∴EH＝4 3.
Ⅲ)判断 PG 的长度在等边三角形 ABC 平移的过程中是否会发生变化？如果不变，请求出 PG 的长；如果变化，请说明理由．解：不变．由Ⅰ)知△EBN≌△HAG，∴NE＝GH，
解：分两种情况：Ⅰ)如答图②，当点 P 在点 O 左边时，设 PO＝x，则 BC＝MO＝2x，PM＝PO＋MO＝3x，由(2)知△ABC∽△PBM，
AC BC 6 2x ∴PM＝BM，即3x＝ 6. 解得 x1＝1，x2＝－1(舍去)， ∴AB＝ AC2＋BC2＝ 10，PB＝ PM2＋BM2＝ 15；
类型三：与平移有关的问题
(贵港：2022T26， 2018T26)
(2018·贵港)如图，已知：A，B 两点在直线 l的同一侧，线段 AO，BM
均是直线 l的垂线段，且 BM 在 AO 的右边，AO＝2BM，将 BM 沿直线 l 向右平移，在平移过程中，始终保持∠ABP＝90°不变，BP 边与直线 l 相交于点 P.

【十年中考真题系列】嘉兴、舟山卷第四章三角形与四边形

【十年中考真题系列】嘉兴、舟山卷第四章三角形与四边形1．长度分别为2，7，x 的三条线段能组成一个三角形，x 的值可以是（）（A ）4 （B ）5 （C ）6 （D ）9 2．已知一个正多边形的内角是140°，则这个正多边形的边数是（）（A ）6 （B ）7 （C ）8 （D ）93．如图，AB //CD ，EF 分别为交AB ，CD 于点E ，F ，∠1＝50°，则∠2的度数为（）（A ）50° （B ）120° （C ）130° （D ）150°（第3题）（第4题）（第5题）（第6题）4．如图，已知AD 为△ABC 的角平分线，DE ∥AB 交AC 于E ，如果 AE EC ＝ 2 3 ，那么 AB AC＝（）（A ） 13（B ）2 3（C ）2 5（D ）3 55．如图，边长为4的等边△ABC 中，DE 为中位线，则四边形BCED 的面积为（）（A ）2 3 （B ）3 3 （C ）4 3 （D ）6 36．如图，A 、B 两点在河的两岸，要测量这两点之间的距离，测量者在与A 同侧的河岸边选定一点C ，测出AC ＝a 米，∠A ＝90°，∠C ＝40°，则AB 等于（）米．（A ）a sin40°（B ）a cos40°（C ）a tan40°（D ）atan40°7．已知△ABC 中，∠B 是∠A 的2倍，∠C 比∠A 大20°，则∠A 等于（）（A ）40° （B ）60° （C ）80° （D ） 90°8．如图，直线l 1∥l 2∥l 3，直线AC 分别交l 1，l 2，l 3于点A ，B ，C ；直线DF 分别交l 1，l 2，l 3于点D ，E ，F . AC 与DF 相交于点G ，且AG ＝2，GB ＝1，BC ＝5，则 DEEF 的值为（）（A ） 1 2（B ）2（C ）2 5（D ）3 5（第8题）（第9题）（第10题）（第11题）9．欧几里得的《原本》记载，形如x 2＋ax ＝b 2的方程的图解法是；画Rt △ABC ，使∠ACB ＝90°，BC ＝a 2 ，AC ＝b ，再在斜边AB 上截取BD ＝ a2 ．则该方程的一个正根是（）（A ）AC 的长（B ）AD 的长（C ）BC 的长（D ）CD 的长10．如图，在平面直角坐标系xOy 中，已知点A （2，0），B （1，1）．若平移点A 到点C ，使以点O ，A ，C ，B 为顶点的四边形是菱形，则正确的平移方法是（）（A ）向左平移1个单位，再向下平移1个单位ABCDFA BC DE（B ）向左平移（22－1）个单位，再向上平移1个单位（C ）向右平移2个单位，再向上平移1个单位（D ）向右平移1个单位，再向上平移1个单位11．如图，矩形ABCD 中，AD ＝2，AB ＝3，过点A ，C 作相距为2的平行线段AE ，CF ，分别交CD ，AB 于点E ，F ，则DE 的长是（）（A ） 5（B ）13 6（C ）1（D ）5 612．用尺规在一个平行四边形内作菱形ABCD ，下列作法中错误的是（）（A ）（B ）（C ）（D ）13．一张矩形纸片ABCD ，已知AB ＝3，AD ＝2，小明按所给图步骤折叠纸片，则线段DG 长为（）（A ） 2（B ）2 2（C ）1（D ）2（第13题）（第14题）14．数学活动课上，四位同学围绕作图问题：“如图，已知直线l 和l 外一点P ，用直尺和圆规作直线PQ ，使PQ ⊥l 于点Q ”. 分别作出了下列四个图形.其中作法错误的是（）（A ）（B ）（C ）（D ）15．如图，在一张矩形纸片ABCD 中，AD ＝4 cm ，点E ，F 分别是CD 和AB 的中点．现将这张纸片折叠，使点B 落在EF 上的点G 处，折痕为AH ．若HG 的延长线恰好经过点D ，则CD 的长为（）（A ）2 cm（B ）2 3 cm （C ）4 cm （D ）3 3cm（第15题）（第16题）（第17题）（第18题）16．如图，等腰△ABC 中，底边BC ＝a ，∠A ＝36°，∠ABC 的平分线交AC 于D ，∠BCD 的平分线交BD 于E ，设k ＝5－12，则DE ＝（）（A ）k 2a（B ）k 3a（C ）a k 2（D ）a k 317．如图，已知C 是线段AB 上的任意一点（端点除外），分别以AC 、BC 为斜边并且在AB 的同一侧作等腰直角△ACD 和△BCE ，连结AE 交CD于点M ，连结BD 交CE 于点N ，给出以下三个结论：①ADEBMN∥AB；②1MN＝1AC＋1BC；③MN≤14AB，其中正确结论的个数是（）（A）0 （B）1 （C）2 （D）318．如图，①②③④⑤五个平行四边形拼成一个含30°内角的菱形EFGH（不重叠无缝隙）．若①②③④四个平行四边形面积的和为14 cm2，四边形ABCD面积是11 cm2，则①②③④四个平行四边形周长的总和为（）（A）48 cm （B）36 cm （C）24 cm （D）18 cm19．如图，在△ABC中，AB=AC，∠A＝40°，则△ABC的外角∠BCD＝_______度．D（第19题）（第20题）（第21题）（第22题）20．如图，AD∥BC，BD平分∠ABC，且∠A＝110°，则∠D＝_______．21．在直角△ABC中，∠C＝90°，AD平分∠BAC交BC于点D，若CD＝4，则点D到斜边AB的距离为_________．22．如图，一张三角形纸片ABC，AB＝AC＝5. 折叠该纸片，使点A落在BC的中点上，折痕经过AC上的点E，则AE的长为__________．23．如图，在地面上的点A处测得树顶B的仰角为α度，AC＝7米，则树高BC为______米．（第23题）（第24题）（第25题）（第26题）24．如图，直线l1∥l2∥l3，直线AC交l1，l2，l3，于点A，B，C；直线DF交l1，l2，l3于点D，E，F，已知ABAC＝13，则EFDE＝________．25．如图，已知菱形ABCD的一个内角∠BAD＝80º，对角线AC、BD相交于点O，点E在AB上且BE ＝BO，则∠BAD＝_______．26．如图，正方形ABCD的边长为3，点E，F分别在边AB，BC上，AE＝BF＝1，小球P从点E出发沿直线向点F运动，每当碰到正方形的边时反弹，反弹时反射角等于入射角．当小球P第一次碰到点E时，小球P与正方形的边碰撞的次数为______，小球P所经过的路程为_________．27．如图，把n个边长为1的正方形拼接成一排，求得tan∠BA1C＝1，tan∠BA2C＝13，tan∠BA3C＝17，计算tan∠BA4C＝，……按此规律，写出tan∠BA n C＝（用含n的代数式表示）．FEDCAA DCB（第27题）（第28题）28．如图，已知△ABC和△DEC的面积相等，点E在BC边上，DE∥AB交AC于点F，AB＝12，EF＝9，则DF的长是__________．29．如图，在矩形ABCD中，AB＝4，AD＝2，点E在CD上，DE＝1，点F是边AB上一动点，以EF 为斜边作Rt△EFP．若点P在矩形ABCD的边上，且这样的直角三角形恰好有两个，则AF的值是__________．（第29题）（第30题）（第31题）30．一副含30°和45°角的三角板ABC和DEF叠合在一起，边BC与EF重合，BC＝EF＝12 cm（如图1），点G为边BC（EF）的中点，边FD与AB相交于点H，此时线段BH的长是．现将三角板DEF绕点G按顺时针方向旋转（如图2），在∠CGF从0°到60°的变化过程中，点H相应移动的路径长共为．（结果保留根号）31．如图，在Rt△ABC中，∠ABC＝90°，BA＝BC．点D是AB的中点，连接CD，过点B作BG丄CD，分别交GD、CA于点E、F，与过点A且垂直于的直线相交于点G，连接DF．给出以下四个结论：①AGAB＝FGFB；②点F是GE的中点；③AF＝23AB；④S△ABC＝S△BDF，其中正确的结论序号是___________．32．在四边形ABCD中，∠D＝60°，∠B比∠A大20°，∠C是∠A的2倍，求∠A，∠B，∠C的大小．33．如图，已知△ABC，∠B＝40°．（1）在图中，用尺规作出△ABC的内切圆O，并标出⊙O与边AB，BC，AC的切点D，E，F（保留痕迹，不必写作法）；（2）连接EF，DF，求∠EFD的度数．34．如图，在□ABCD中，已知点E在AB上，点F在CD上且AE＝CF．（1）求证：DE＝BF；（2）连结BD，并写出图中所有的全等三角形．（不要求证明）35．如图，已知菱形ABCD的对角线相交于点O，延长AB至点E，使BE＝AB，连接CE．（1）求证：BD＝EC；（2）若∠E＝50°，求∠BAO的大小．36．如图，△ABC与△DCB中，AC与BD交于点E，且∠A＝∠D，AB＝DC．（1）求证：△ABE≌DCE；（2）当∠AEB＝50°，求∠EBC的度数？37．已知：如图，在□ABCD中，O为对角线BD的中点，过点O的直线EF分别交AD，BC于E，F两点，连结BE，DF．（1）求证：△DOE≌△BOF；（2）当∠DOE等于多少度时，四边形BFDE为菱形？请说明理由．38．如图，正方形ABCD中，点E，F分别在AB，BC上，AF＝DE，AF和DE相交于点G．（1）观察图形，写出图中所有与∠AED相等的角；（2）选择图中与∠AED相等的任意一个角，并加以证明．39．已知：在△ABC 中，AB ＝AC ，D 为AC 的中点，DE ⊥AB ，DF ⊥BC ，垂足分别为点E ，F ，且DE＝DF ．求证：△ABC 是等边三角形．40．如图，在平行四边形ABCD 中，AE ⊥BC 于E ，AF ⊥CD 于F ，BD 与AE 、AF 分别相交于G 、H ．（1）求证：△ABE ∽△ADF ；（2）若AG ＝AH ，求证：四边形ABCD 是菱形．41．如图，已知⊙O 的半径为1，PQ 是⊙O 的直径，n 个相同的正三角形沿PQ 排成一列，所有正三角形都关于PQ 对称，其中第一个△A 1B 1C 1的顶点A 1与点P 重合，第二个△A 2B 2C 2的顶点A 2是B 1C 1与PQ 的交点，…，最后一个△A n B n C n 的顶点B n 、C n 在圆上．（1）如图1，当n ＝1时，求正三角形的边长a 1；（2）如图2，当n ＝2时，求正三角形的边长a 2；（3）如题图，求正三角形的边长a n （用含n 的代数式表示）．ADCBGHF图1图242．以四边形ABCD 的边AB 、BC 、CD 、DA 为斜边分别向外侧作等腰直角三角形，直角顶点分别为E 、F 、G 、H ，顺次连结这四个点，得四边形EFGH ．（1）如图1，当四边形ABCD 为正方形时，我们发现四边形EFGH 是正方形；如图2，当四边形ABCD为矩形时，请判断：四边形EFGH 的形状（不要求证明）；（2）如图3，当四边形ABCD 为一般平行四边形时，设∠ADC ＝α（0°＜α＜90°），① 试用含α的代数式表示∠HAE ； ② 求证：HE =HG ；③ 四边形EFGH 是什么四边形？并说明理由．43．将△ABC 绕点A 按逆时针方向旋转θ度，并使各边长变为原来的n 倍，得△AB ′C ′，即如图①，我们将这种变换记为[θ，n ]．（1）如图①，对△ABC 作变换[60°，3]得△AB ′C ′，则S △AB ′C ′：S △ABC ＝_____；直线BC 与直线B ′C ′所夹的锐角为_____度；（2）如图②，△ABC 中，∠BAC ＝30°，∠ACB ＝90°，对△ABC 作变换[θ，n ]得△AB 'C '，使点B 、C 、C ′在同一直线上，且四边形ABB 'C '为矩形，求θ和n 的值；（3）如图③，△ABC 中，AB ＝AC ，∠BAC ＝36°，BC ＝l ，对△ABC 作变换[θ，n ]得△AB ′C ′，使点B 、C 、B ′在同一直线上，且四边形ABB 'C '为平行四边形，求θ和n 的值．A BCDHEFG（图2）E BFGDHAC（图3）（图1）A BCDH EFG44．类比梯形的定义，我们定义：有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”．（1）已知：如图1，四边形ABCD是“等对角四边形”，∠A≠∠C，∠A＝70°，∠B＝80°．求∠C，∠D的度数．（2）在探究“等对角四边形”性质时：①小红画了一个“等对角四边形”ABCD(如图2)，其中∠ABC＝∠ADC，AB＝AD，此时她发现CB＝CD成立．请你证明此结论；②由此小红猜想：“对于任意‘等对角四边形’，当一组邻边相等时，另一组邻边也相等”．你认为她的猜想正确吗?若正确，请证明；若不正确，请举出反例．（3）已知：在“等对角四边形"ABCD中，∠DAB＝60°，∠ABC＝90°，AB＝5，AD＝4．求对角线AC的长．45．类比等腰三角形的定义，我们定义：有一组邻边相等的凸四边形叫做“等邻边四边形”.（1）概念理解：如图1，在四边形ABCD中，添加一个条件，使得四边形ABCD是“等邻边四边形”，请写出你添加的一个条件；（2）问题探究：①小红猜想：对角线互相平分的“等邻边四边形”是菱形，她的猜想正确吗？请说明理由；②如图2，小红画了一个Rt△ABC，其中∠ABC＝90°，AB＝2，BC＝1，并将Rt△ABC沿∠B的平分线BB′方向平移得到△A′B′C′，连结A A′，BC′. 小红要使平移后的四边形ABC′A′是“等邻边四边形”，应平移多少距离（即线段BB′的长）？（3）应用拓展：如图3，“等邻边四边形”ABCD中，AB＝AD，∠BAD＋∠BCD＝90°，AC，BD为对角线，AC ＝2AB．试探究BC，CD，BD的数量关系．46．我们定义：有一组邻角相等的凸四边形叫做“等邻角四边形”．（1）概念理解：请你根据上述定义举一个等邻角四边形的例子；（2）问题探究：如图1，在四边形ABCD 中，BE 平分∠ABC 交CD 于点E ，AD ∥BE ，∠D ＝80°，∠C ＝40° ，探究四边形ABCD 是否为等邻角四边形，并说明理由；（3）应用拓展：如图2，在Rt △ABC 与Rt △ABD 中，∠C ＝∠D ＝90°，BC ＝BD ＝3，AB ＝5，将Rt △ABD 绕着点A 顺时针旋转角α（0°＜∠α＜∠BAC ），得到Rt △AB 'D '（如图3），当凸四边形AD 'BC 为等邻角四边形时，求出它的面积．47．我们定义：如果一个三角形一条边上的高等于这条边，那么这个三角形叫做“等高底”三角形，这条边叫做这个三角形的“等底”．（1）概念理解：如图1，在△ABC 中，AC ＝6，BC ＝3，∠ACB ＝30°，试判断△ABC 是否是“等高底”三角形请说明理由．（2）问题探究：如图2，△ABC 是“等高底”三角形，BC 是“等底”，作△ABC 关于BC 所在直线的对称图形得到△A 'BC ，连结AA '交直线BC 于点D ．若点B 是△AA 'C 的重心，求ACBC的值．（3）应用拓展：如图3．已知l 1∥l 2，l 1与l 2之间的距离为2．“等高底”△ABC 的“等底”BC 在直线l 1上，点A 在直线l 2上，有一边的长是BC 的2倍．将△ABC 绕点C 按顺时针方向旋转45° 得到△A 'B 'C ，AC 所在直线交l 2于点D ．求CD 的值．图1D'D 图2BDCE48．如图，AM 是△ABC 的中线，D 是线段AM 上一点（不与点A 重合）．DE ∥AB 交AC 于点F ，CE ∥AM ，连结AE ．（1）如图1，当点D 与M 重合时，求证：四边形ABDE 是平行四边形；（2）如图2，当点D 不与M 重合时，（1）中的结论还成立吗？请说明理由. （3）如图3，延长BD 交AC 于点H ，若BH ⊥AC ，且BH ＝AM ．①求∠CAM 的度数；②当FH ＝3，DM ＝4时，求DH 的长．49．如图1，已知点E ，F ，G ，H 分别是四边形ABCD 各边AB ，BC ，CD ，DA 的中点，根据以下思路可以证明四边形EFGH 是平行四边形：（1）如图2，将图1中的点C 移动至与点E 重合的位置，F ，G ，H 仍是BC ，CD ，DA 的中点，求证：四边形CFGH 是平行四边形；（2）如图3，在边长为1的小正方形组成的5×5网格中，点A ，C ，B 都在格点上，在格点上找一点D ，使点C 与BC ，CD ，DA 的中点F ，G ，H 组成的四边形CFGH 是正方形．画出点D ，并求正方形CFGH 的边长．图3图1 图2EH EH FG50．如图，已知A、B是线段MN上的两点，MN＝4，MA＝1，MB＞1．以A为中心顺时针旋转点M，以B为中心逆时针旋转点N，使M、N两点重合成一点C，构成△ABC，设AB＝1．（1）求x的取值范围；（2）若△ABC为直角三角形，求x的值；（3）探究：△ABC的最大面积？51．小明在做课本“目标与评定”中的一道题：如图1，直线a，b所成的角跑到画板外面去了，你有什么办法量出这两条直线所成的角的度数？小明的做法是：如图2，画PC∥a，量出直线b与PC的夹角度数，即直线a，b所成角的度数．（1）请写出这种做法的理由；（2）小明在此基础上又进行了如下操作和探究（如图3）：①以P为圆心，任意长为半径画圆弧，分别交直线b，PC于点A，D；②连结AD并延长交直线a于点B，请写出图3中所有与∠PAB相等的角，并说明理由；（3）请在图3画板内作出“直线a，b所成的跑到画板外面去的角”的平分线（画板内的部分），只要求作出图形，并保留作图痕迹．11。

中考数学冲刺专题训练(附答案)：三角形与四边形

精品基础教育教学资料，仅供参考，需要可下载使用！中考数学冲刺专题训练（附答案）：三角形与四边形一、选择题（本大题共8个小题，每小题5分，共40分．在每小题给出的四个选项中，只有一个选项是符合题目要求的）1．一个等腰三角形的底边长是6，腰长是一元二次方程28150x x -+=的一根，则此三角形的周长是（） A ．16 B ．12C ．14D ．12或16【答案】A 【解析】解方程28150x x -+=，得：3x =或5x =，若腰长为3，则三角形的三边为3、3、6，显然不能构成三角形；若腰长为5，则三角形三边长为5、5、6，此时三角形的周长为16，故选：A ．2．如图，在△ABC 中，BE 是∠ABC 的平分线，CE 是外角∠ACM 的平分线，BE 与CE 相交于点E ，若∠A =60°，则∠BEC 是（）A ．15°B ．30°C ．45°D ．60°【答案】B 【解析】∵BE 是∠ABC 的平分线， ∴∠EBM=12∠ABC ， ∵CE 是外角∠ACM 的平分线， ∴∠ECM=12∠ACM ，则∠BEC=∠ECM-∠EBM=12×（∠ACM-∠ABC ）=12∠A=30°，故选：B ．3．如图，在△ABC 中，∠C ＝90°，AC ＝12，AB 的垂直平分线EF 交AC 于点D ，连接BD ，若cos ∠BDC ＝57，则BC 的长是（）A ．10B ．8C ．3D ．6【答案】D 【解析】∵∠C ＝90°，cos ∠BDC ＝57，设CD ＝5x ，BD ＝7x ， ∴BC ＝6x ，∵AB 的垂直平分线EF 交AC 于点D ， ∴AD ＝BD ＝7x ， ∴AC ＝12x ， ∵AC ＝12， ∴x ＝1， ∴BC ＝6；故选D.4．一个菱形的边长为6，面积为28，则该菱形的两条对角线的长度之和为( ) A ．8 B ．12C ．16D ．32【答案】C 【解析】如图所示：四边形ABCD 是菱形，12AO CO AC ∴==， 12DC BO BD ==，AC BD ⊥，面积为28，∴12282AC BD OD AO ⋅=⋅=① 菱形的边长为6，2236OD OA ∴+=②，由①②两式可得：222()2362864OD AO OD OA OD AO +=++⋅=+=，8OD AO ∴+=，2()16OD AO ∴+=，即该菱形的两条对角线的长度之和为16，故选C ．5．如图，点B 、F 、C 、E 在一条直线上，AB ∥ED ，AC ∥FD ，那么添加下列一个条件后，仍无法判定△ABC ≌△DEF 的是（）A ．AB =DE B ．AC =DF C ．∠A =∠D D ．BF =EC【答案】C 【解析】解：选项A 、添加AB=DE 可用AAS 进行判定，故本选项错误；选项B 、添加AC=DF 可用AAS 进行判定，故本选项错误；选项C 、添加∠A=∠D 不能判定△ABC ≌△DEF ，故本选项正确；选项D 、添加BF=EC 可得出BC=EF ，然后可用ASA 进行判定，故本选项错误．故选C ．6．如图，ABCD 中，对角线AC 、BD 相交于点O ，OE BD ⊥交AD 于点E ，连接BE ，若ABCD 的周长为28，则ABE ∆的周长为（）A ．28B ．24C ．21D ．14【答案】D 【解析】∵四边形ABCD 是平行四边形， ∴OB OD =，AB CD =，AD BC =， ∵平行四边形的周长为28， ∴14AB AD += ∵OE BD ⊥，∴OE 是线段BD 的中垂线， ∴BE ED =，∴ABE ∆的周长14AB BE AE AB AD =++=+=，故选：D ．7．如图，在ABCD 中，将ADC ∆沿AC 折叠后，点D 恰好落在DC 的延长线上的点E 处．若=60B ︒∠，=3AB ，则ADE ∆的周长为（）A ．12B ．15C ．18D ．21【答案】C 【解析】由折叠可得，90ACD ACE ︒∠=∠=，90BAC ︒∴∠=，又60B ︒∠=，30ACB ︒∴∠=，26BC AB ∴==，6AD ∴=，由折叠可得，60E D B ︒∠=∠=∠=，60DAE ︒∴∠=，ADE ∴∆是等边三角形， ADE ∴∆的周长为6318⨯=，故选：C ．8．如图，在正方形ABCD 中，E 、F 分别是BC 、CD 上的点，且∠EAF ＝45°，AE 、AF 分别交BD 于M 、N ，连按EN 、EF 、有以下结论：①AN ＝EN ，②当AE ＝AF 时，BEEC＝2﹣2，③BE+DF ＝EF ，④存在点E 、F ，使得NF ＞DF ，其中正确的个数是（）A ．1B ．2C ．3D ．4【答案】B 【解析】 ①如图1，∵四边形ABCD 是正方形，∴∠EBM ＝∠ADM ＝∠FDN ＝∠ABD ＝45°，∵∠MAN＝∠EBM＝45°，∠AMN＝∠BME，∴△AMN∽△BME，∴AM MN BM EM=，∵∠AMB＝∠EMN，∴△AMB∽△NME，∴∠AEN＝∠ABD＝45°∴∠NAE＝∠AEN＝45°，∴△AEN是等腰直角三角形，∴AN＝EN，故①正确；②在△ABE和△ADF中，∵AB ADABE ADF90 AE AF︒=⎧⎪∠=∠=⎨⎪=⎩，∴Rt△ABE≌Rt△ADF（HL），∴BE＝DF，∵BC＝CD，∴CE＝CF，假设正方形边长为1，设CE＝x，则BE＝1﹣x，如图2，连接AC，交EF于H，∵AE＝AF，CE＝CF，∴AC是EF的垂直平分线，∴AC⊥EF，OE＝OF，Rt △CEF 中，OC ＝12EF ＝22x ， △EAF 中，∠EAO ＝∠FAO ＝22.5°＝∠BAE ＝22.5°， ∴OE ＝BE ， ∵AE ＝AE ，∴Rt △ABE ≌Rt △AOE （HL ）， ∴AO ＝AB ＝1， ∴AC ＝2＝AO+OC ，∴1+22x ＝2， x ＝2﹣2，∴BE EC ＝1(22)22---＝(21)(22)2-+＝22；故②不正确； ③如图3，∴将△ADF 绕点A 顺时针旋转90°得到△ABH ，则AF ＝AH ，∠DAF ＝∠BAH ， ∵∠EAF ＝45°＝∠DAF+∠BAE ＝∠HAE ， ∵∠ABE ＝∠ABH ＝90°， ∴H 、B 、E 三点共线，在△AEF 和△AEH 中，AE AE FAE HAE AF AH =⎧⎪∠=∠⎨⎪=⎩，∴△AEF ≌△AEH （SAS ）， ∴EF ＝EH ＝BE+BH ＝BE+DF ，故③正确；④△ADN 中，∠FND ＝∠ADN+∠NAD ＞45°， ∠FDN ＝45°， ∴DF ＞FN ，故存在点E 、F ，使得NF ＞DF ，故④不正确；故选B ．二、填空题（本大题共4个小题，每小题6分，共24分）9．如图，在△ABC 中，以点B 为圆心，以BA 长为半径画弧交边BC 与点D ，连结AD ，若∠B =40°，∠C =36°，则∠DAC 的度数是____________．【答案】34° 【解析】由作图过程可知BD=BA ， ∵∠B=40°， ∴∠BDA=∠BAD=12(180°-∠B)=70°， ∴∠DAC=∠BDA-∠C=70°-36°=34°. 故答案为34°. 10．如图，在矩形ABCD 中，1AB =，BC a =，点E 在边BC 上，且35BE α=．连接AE ，将ABE ∆沿AE 折叠，若点B 的对应点B '落在矩形ABCD 的边上，则 a 的值为________．【答案】53或53【解析】分两种情况：①当点B '落在AD 边上时，如图1．四边形ABCD 是矩形，90BAD B ︒∴∠=∠=，将ABE ∆沿AE 折叠，点B 的对应点B '落在AD 边上，1452BAE B AE BAD '︒∴∠=∠=∠=，AB BE ∴=，315a ∴=， 53a ∴=；②当点B '落在CD 边上时，如图2． ∵四边形ABCD 是矩形，90BAD B C D ︒∴∠=∠=∠=∠=，AD BC a ==．将ABE ∆沿AE 折叠，点B 的对应点B '落在CD 边上，90B AB E '︒∴∠=∠=，1AB AB '==，35EB EB a '==，2221DB B A AD a ''∴=-=-，3255EC BC BE a a =-=-=．在ADB '∆与B CE '∆中，90A 90B AD EBC B DD C ︒︒⎧∠=∠=-∠'''⎨∠=∠=⎩， ADB B CE ''∴∆⋃∆，DB AB CE B E'''∴=，即2112355a a a -=，解得153a =，20a =（舍去）．综上，所求a 的值为53或53．故答案为53或53． 11．如图，正方形ABCD 的边长为4，点E 是CD 的中点，AF 平分BAE ∠交BC 于点F ，将ADE ∆绕点A 顺时针旋转90°得ABG ∆，则CF 的长为_____．【答案】6-25 【解析】作FM AD M FN AG N ⊥⊥于，于，如图，易得四边形CFMD 为矩形，则4FM ＝∵正方形ABCD的边长为4，点是的中点，2DE ∴＝，∴224225AE =+=∵△ADE 绕点A 顺时针旋转90°得△ABG ，∴252349090AG AE BG DE GAE ABG D ∠∠∠︒∠∠︒＝＝，＝＝，＝，＝，＝＝而90ABC ∠︒＝， ∴点G 在CB 的延长线上，∵AF 平分∠BAE 交BC 于点F ，∴∠1＝∠2，∴∠2+∠4＝∠1+∠3，即F A 平分∠GAD ， ∴FN ＝FM ＝4， ∵11••22AB GF FN AG ＝, ∴425254GF ⨯==, ∴4225625CF CG GF +=-＝﹣＝﹣ ．故答案为6-25．12．如图，在平面直角坐标系中，OA ＝1，以OA 为一边，在第一象限作菱形OAA 1B ，并使∠AOB ＝60°，再以对角线OA 1为一边，在如图所示的一侧作相同形状的菱形OA 1A 2B 1，再依次作菱形OA 2A 3B 2，OA 3A 4B 3，……，则过点B 2018，B 2019，A 2019的圆的圆心坐标为_____．【答案】（-32018，3）2019）【解析】过A 1作A 1C ⊥x 轴于C ，∵四边形OAA1B是菱形，∴OA＝AA1＝1，∠A1AC＝∠AOB＝60°，∴A1C＝32，AC＝12，∴OC＝OA+AC＝32，在Rt△OA1C中，OA1＝2213OC AC+=，∵∠OA2C＝∠B1A2O＝30°，∠A3A2O＝120°，∴∠A3A2B1＝90°，∴∠A2B1A3＝60°，∴B1A3＝23，A2A3＝3，∴OA3＝OB1+B1A3＝33＝（3）3∴菱形OA2A3B2的边长＝3＝（3）2，设B1A3的中点为O1，连接O1A2，O1B2，于是求得，O1A2＝O1B2＝O1B133）1，∴过点B1，B2，A2的圆的圆心坐标为O1（0，23，∵菱形OA3A4B3的边长为333，∴OA4＝934，设B2A4的中点为O2，连接O2A3，O2B3，同理可得，O2A3＝O2B3＝O2B2＝3＝（3）2，∴过点B2，B3，A3的圆的圆心坐标为O2（﹣3，33），…以此类推，菱形OA2019A2020B2019的边长为（3）2019，OA2020＝（3）2020，设B2018A2020的中点为O2018，连接O2018A2019，O2018B2019，求得，O2018A2019＝O2018B2019＝O2018B2018＝（3）2018，∴点O2018是过点B2018，B2019，A2019的圆的圆心，∵2018÷12＝168…2，∴点O2018在射线OB2上，则点O2018的坐标为（﹣（3）2018，（3）2019），即过点B2018，B2019，A2019的圆的圆心坐标为：（﹣（3）2018，（3）2019），故答案为：（﹣（3）2018，（3）2019）．三、解答题（本大题共3个小题，每小题12分，共36分．解答应写出文字说明、证明过程或演算步骤）13．如图，矩形EFGH的顶点E，G分别在菱形ABCD的边AD，BC上，顶点F、H在菱形ABCD的对角线BD上.=；（1）求证：BG DEFH=，求菱形ABCD的周长。

平行四边形和三角形的面积复习课综合练习题

平行四边形和三角形的面积复习课综合练习题一、基本练习填空（1）如下图一个平行四边形花圃，它的面积是（）平方米。

（2）如图，阴影部分的面积是20平方米，平行四边形的面积是（）平方米；如果平行四边形的面积是20平方米，则阴影部分的面积是（）平方米。

（3）一个三角形的面积比与它等底等高的平行四边形的面积少15平方分米，平行四边形的面积是（）平方分米，三角形的面积是（）平方分米。

【这样设计练习的目的在于加深学生对三角形与它等底等高的平行四边形面积关系的理解：三角形面积是平行四边形面积的一半，平行四边形是与它等底等高的三角形面积的2倍。

】二、综合练习 1、判断题（1）平行四边形的面积是三角形面积的2倍。

（）（2）下图是两个完全一样的长方形中，甲、乙两个阴影部分面积大小相等。

（）米（3）两个面积相等的三角形一定可以拼在成一个平行四边形。

（）（4）如右图用手捏住用硬纸条长方形的对角拉成一个平行四边形，周长和面积都变小了。

（5）如下图中，长方形面积大于平行四边形的面积。

2、操作题：（每在下面的方格纸中分别画出面积是8平方厘米的一个平行四行四边形和一个三角形。

个方格的边长表示1厘米）【本道题是一道开放性的练习，设计的目的在于加深通过动手画相同面积的平行四边形，加深理解平行四边形面积与三角形面积之间的联系。

在学生独立思考和小组合作交流的基础上进行动手操作，教师注意加强指导和引导。

】三、解决问题（1）如右图，如果正方形的周长是14分米，请你求出平行四边形的面积。

（2）如图一个交通标志牌的面积是36平方分米，求它的高是多少分米？【本题的设计是根据乘除法的互逆关系灵活运用三角形面积公式。

引导学生注意在根据三角形面积和底求高时，不要忘记三角形的面积先要乘2，同时还对学生进行交通常识的教育。

】（3）如图一个平行四边形花圃，底5米，高6米。

①如果每平方米种4棵玫瑰花，一共可以种多少棵玫瑰花？②如果每棵玫瑰花占地0.25平方米，一共可以种多少棵玫瑰花？四、拓展练习：如上题中的一个平行四边形花圃，底5米，高6米。

苏教版四年级数学下册第七单元《三角形、平行四边形和梯形》专项精选试卷附答案

苏教版四年级数学下册单元综合素质评价第七单元三角形、平行四边形和梯形一、填空。

(每空1分，共24分)1．照相机的支架有三条腿，这是利用了三角形的( )性；电动伸缩门是利用平行四边形( )的特性设计的。

2．一个三角形的两个内角的度数分别是75°和30°，另一个内角的度数是( )°；按边分，这个三角形是( )三角形。

3．在能围成三角形的三根小棒下面画“√”，不能的画“×”。

(1)(2) (3)4．把一根24厘米长的铁丝围成一个等边三角形，每条边的长是( )厘米；如果围成其他三角形，那么最长边的长度要小于( )厘米。

5．如图，在平行四边形中，30厘米长的底边上的高是( )厘米，20厘米长的底边上的高是( )厘米。

6．如图，∠1＝( )°，∠2＝( )°。

7．一个梯形的下底长度是上底长度的4倍，如果将上底延长6厘米，那么这个梯形就变成了一个平行四边形，则这个梯形的上底是( )厘米，下底是( )厘米。

8．两个完全相同的直角三角形可以拼成一个大三角形，这个大三角形的内角和是( )°；如果拼成一个平行四边形，那么这个平行四边形的内角和是( )°。

一个六边形的内角和是( )°。

9．用铁丝做一个长方形，再拉成一个平行四边形(如右图)，这个平行四边形的底( )长方形的长，平行四边形的高( )长方形的宽，平行四边形的周长( )长方形的周长，平行四边形的面积( )长方形的面积。

(填“大于”“小于”或“等于”)10．用三个完全一样的等腰三角形可以拼成一个等腰梯形(如图)。

已知每个等腰三角形的周长是16厘米，等腰梯形的周长是24厘米，那么这个等腰梯形的上底是( )厘米，腰长是( )厘米。

二、选择。

(每小题2分，共10分)1．小明要给一块地围上篱笆，( )的围法更牢固些。

2．下列选项表示的是各种三角形之间的关系，正确的一项是( )。

3．在一个等腰梯形中画一条线段，可以将它分割成两个完全一样的( )。

初二三角形与四边形的综合题

三角形与四边形的综合题知识梳理教学重、难点作业完成情况典题探究1．用两个全等的直角三角形拼下列图形：①矩形；②菱形；③正方形；④平行四边形；⑤等腰三角形；⑥等腰梯形．其中一定能拼成的图形是（）．（A）①②③（B）①④⑤（C）①②⑤（D）②⑤⑥2．把“直角三角形、等腰三角形、•等腰直角三角形”填入下列相应的空格上：（1）正方形可以由两个能够完全重合的_________拼合而成；（2）菱形可以由两个能够完全重合的_________拼合而成；（3）矩形可以由两个能够完全重合的________拼合而成．3．一张矩形纸片按如图甲或乙所示对折，然后沿着图丙中的虚线剪下，得到①，•②两部分，将①展开后得到的平面图形是（）．（A ）三角形（B ）矩形（C ）菱形（D ）梯形4．小许拿了一张正方形的纸片如图甲，沿虚线对折一次得图乙．•再对折一次得图丙．然后用剪刀沿图丙中的虚线（虚线与底边平行）剪去一个角．打开后的形状是（• ）．演练方阵A 档（巩固专练）1.用一把刻度尺来判定一个零件是矩形的方法是 .2．如果边长分别为4cm 和5cm 的矩形与一个正方形的面积相等，那么这个正方形的边长为______cm ．3．如图，正方形ABCD 的边长为4cm ，则图中阴影部分的面积为 cm 2．4．如图1，DE∥BC，DF∥AC，EF∥AB，图中共有_______个平行四边形． 5若四边形ABCD 是平行四边形，请补充条件A BCD(写一个即可)，使四边形ABCD 是菱形．6．，在平行四边形ABCD 中，已知对角线AC 和BD 相交于点O ，△ABO 的周长为17，AB ＝6，那么对角线AC ＋BD ＝⒎以正方形ABCD 的边BC 为边做等边△BCE，则∠AED 的度数为 . 8．延长正方形ABCD 的边AB 到E ，使BE ＝AC ，则∠E＝ °9．已知菱形ABCD 的边长为6，∠A＝60°，如果点P 是菱形内一点，且PB ＝PD ＝2那么AP 的长为．10．在平面直角坐标系中，点A 、B 、C 的坐标分别是A(－2，5)， B(－3，－1)，C(1，－1)，在第一象限内找一点D ，使四边形 ABCD 是平行四边形，那么点D 的坐标是．B 档（提升精练）1如图1，在四边形ABCD 中，AB CD =，E F 、分别是BC AD 、的中点，连结EF 并延长，分别与BA CD 、的延长线交于点M N 、，则BME CNE ∠=∠（不需证明）．（温馨提示：在图1中，连结BD ，取BD 的中点H ，连结HE HF 、，根据三角形中位线定理，证明HE HF =，从而12∠=∠，再利用平行线性质，可证得BME CNE ∠=∠．）问题一：如图2，在四边形ADBC 中，AB 与CD 相交于点O ，AB CD =，E F 、分别是BC AD 、的中点，连结EF ，分别交DC AB 、于点M N 、，判断OMN △的形状，请直接写出结论．问题二：如图3，在ABC △中，AC AB >，D 点在AC 上，AB CD =，E F 、分别是BC AD 、的中点，连结EF 并延长，与BA 的延长线交于点G ，若60EFC ∠=°，连结GD ，判断AGD △的形状并证明．AC DFE NM O BC DH A F NM 1 2 图1图2 图3ABDF GE2已知Rt ABC △中，90AC BC C D ==︒，∠，为AB 边的中点，90EDF ∠=°，EDF ∠绕D 点旋转，它的两边分别交AC 、CB （或它们的延长线）于E 、F ．当EDF ∠绕D 点旋转到DE AC ⊥于E 时（如图1），易证12DEFCEF ABC S S S +=△△△．当EDF ∠绕D 点旋转到DE AC 和不垂直时，在图2和图3这两种情况下，上述结论是否成立？若成立，请给予证明；若不成立，DEF S △、CEF S △、ABC S △又有怎样的数量关系？请写出你的猜想，不需证明．3已知：ABC △的高AD 所在直线与高BE 所在直线相交于点F ．（1）如图l ，若ABC △为锐角三角形，且45ABC ∠=°，过点F 作FG BC ∥，交直线AB 于点G ，求证：FG DC AD +=；（2）如图 2，若135ABC ∠=°，过点F 作FG BC ∥，交直线AB 于点G ，则FG 、DC 、AD 之间又有怎样的数量关系？请写出你的猜想，不需证明．AE CF BD图1图3ADFECBADBCE 图2FAE CDG BF（图1）AE CB DFG（图2）4已知：正方形ABCD 中，45MAN ∠=，MAN ∠绕点A 顺时针旋转，它的两边分别交CB DC ，（或它们的延长线）于点M N ，．当MAN ∠绕点A 旋转到BM DN =时（如图1），易证BM DN MN +=．（1）当MAN ∠绕点A 旋转到BM DN ≠时（如图2），线段BM DN ，和MN 之间有怎样的数量关系？写出猜想，并加以证明．（2）当MAN ∠绕点A 旋转到如图3的位置时，线段BM DN ，和MN 之间又有怎样的数量关系？请直接写出你的猜想．5已知：如图，BD 、CE 分别是△ABC 的外角平分线，过点A 作AF ⊥BD ，AG ⊥CE ，垂足分别为F 、G ，连结FG ，延长AF 、AG 与直线BC 相交，易证：)(21AC BC AB FG ++=，若：（1）BD 、CE 分别是△ABC 的内角平分线（如图2）；（2）BD 为△ABC 的内角平分线，CE 为△ABC 的外角平分线（如图3），则在图2、图3两种情况下，线段FG 与△ABC 三边又有怎样的数量关系？请写出你的猜测，并对其中的一种情况进行证明。

(最新)2020年中考数学复习专题6 四边形与三角形的综合(精讲)试题

专题六四边形与三角形的综合毕节中考备考攻略纵观近4年毕节中考数学试卷,四边形与三角形的综合是每年的必考考点,其中2015年第24题综合考查平行四边形和直角三角形；2016年第25题综合考查菱形和三角形全等；2017年第24题综合考查平行四边形与三角形相似、解直角三角形；2018年第24题综合考查平行四边形、三角形和菱形.预计2019年将继续综合考查四边形与三角形.熟练掌握特殊四边形的性质与判定、特殊三角形的性质、全等三角形的判定与性质、相似三角形的判定与性质,掌握三角形中位线和梯形中位线性质的推导和应用,会画出四边形全等变换后的图形.解决问题时必须充分利用几何图形的性质及在题设的基础上挖掘几何图形中隐含的数量关系和位置关系,在复杂的“背景”下辨认、分解基本图形,通过添加辅助线补全或构造基本图形,并善于联想所学知识,突破思维障碍,合理运用各种数学方法.中考重难点突破四边形与特殊三角形例1 如图,在四边形ABCD 中,AB ∥DC,AB ＝AD,对角线AC,BD 交于点O,AC 平分∠BAD ,过点C 作CE⊥AB 交AB 的延长线于点E,连接OE.(1)求证：四边形ABCD 是菱形； (2)若AB ＝5,BD ＝2,求OE 的长.【解析】(1)先判断出∠OAB＝∠DCA,进而判断出∠DAC＝∠DCA ,得出CD ＝AD ＝AB,即可得出结论； (2)先判断出OE ＝OA ＝OC,再求出OB ＝1,利用勾股定理求出OA,即可得出结果. 【答案】(1)证明：∵AB∥CD ,∴∠CAB ＝∠ACD. ∵AC 平分∠BAD ,∴∠CAB ＝∠CAD , ∴∠CAD ＝∠ACD ,∴AD ＝CD. 又∵AD＝AB,∴AB ＝CD.又∵AB∥CD ,∴四边形ABCD 是平行四边形. 又∵AB＝AD,∴四边形ABCD 是菱形； (2)解：∵四边形ABCD 是菱形,∴AC ⊥BD,OA ＝OC ＝12AC,OB ＝OD ＝12BD ＝1.在Rt △AOB 中,∠AOB ＝90°,∴OA ＝AB 2－OB 2＝2. ∵CE ⊥AB,∴∠AEC ＝90°. 在Rt △AEC 中,O 为AC 中点, ∴OE ＝12AC ＝OA ＝2.四边形与三角形全等例2 (2018·张家界中考)在矩形ABCD 中,点E 在BC 上,AE ＝AD,DF ⊥AE,垂足为点F. (1)求证：DF ＝AB ；(2)若∠FDC＝30°,且AB ＝4,求AD.【解析】(1)利用“AAS ”证△ADF≌△EAB 即可得证；(2)由∠ADF＋∠FDC＝90°,∠DAF ＋∠ADF＝90°得∠FDC＝∠DAF＝30°,据此知AD ＝2DF,根据DF ＝AB 可得答案.【答案】(1)证明：在矩形ABCD 中,AD ∥BC, ∴∠AEB ＝∠DAF.又∵DF⊥AE ,∴∠DFA ＝90°,∴∠DFA ＝∠B. 又∵AD＝EA,∴△ADF ≌△EAB,∴DF ＝AB ；(2)解：∵∠ADF＋∠FDC ＝90°,∠DAF ＋∠ADF＝90°,∴∠FDC ＝∠DAF＝30°,∴AD ＝2DF.∵DF ＝AB ＝4,∴AD ＝2AB ＝8.四边形与三角形相似例3 (2018·资阳中考)已知：如图,在Rt △ABC 中,∠ACB ＝90°,点M 是斜边AB 的中点,MD ∥BC,且MD ＝CM,DE ⊥AB 于点E,连接AD,CD.(1)求证：△MED∽△BCA； (2)求证：△AMD≌△CMD；(3)设△MDE 的面积为S 1,四边形BCMD 的面积为S 2,当S 2＝175S 1时,求cos ∠ABC 的值.【解析】(1)易证∠DME＝∠CBA ,∠ACB ＝∠DE M ＝90°,从而可证明△MED∽△BCA；(2)由∠ACB＝90°,点M 是斜边AB 的中点,可知BM ＝CM ＝AM,又由MD∥BC 可证明∠AMD＝∠CMD ,从而可利用全等三角形的判定方法证明△AMD≌△CMD；(3)易证DM ＝12AB,由(1)可知△MED∽△BCA ,所以S 1S △ACB ＝⎝ ⎛⎭⎪⎫DM AB 2＝14,所以S △MCB ＝12S △ACB ＝2S 1,从而可求出S △EBD ＝S 2－S △MCB －S 1＝25S 1,由于S 1S △EBD ＝ME EB ,从而可知ME BE ＝52,设ME ＝5x,EB ＝2x,从而用x 表示出AB,BC,最后根据锐角三角函数的定义即可求出答案.【答案】(1)证明：∵MD∥BC ,∴∠DME ＝∠CBA. ∵∠ACB ＝∠DEM＝90°,∴△MED ∽△BCA ； (2)证明：∵∠ACB＝90°,点M 是斜边AB 的中点, ∴BM＝CM ＝AM,∴∠MCB ＝∠MBC. ∵∠DMB ＝∠MBC , ∴∠MCB ＝∠DMB＝∠MBC. ∵MD ∥BC,∴∠CMD ＝180°－∠MCB. 又∵∠AMD＝180°－∠DMB , ∴∠AMD ＝∠CMD. 在△AMD 与△CMD 中, ⎩⎪⎨⎪⎧MD ＝MD ，∠AMD ＝∠CMD，AM ＝CM ，∴△AMD ≌△CMD(SAS )；(3)解：∵DM＝CM,∴AM ＝CM ＝DM ＝BM, ∴DM ＝12AB.由(1)可知△MED∽△BCA ,∴S 1S △ACB ＝⎝ ⎛⎭⎪⎫DM AB 2＝14,∴S △ACB ＝4S 1. ∵CM 是△ACB 的中线,∴S △MCB ＝12S △ACB ＝2S 1,∴S △EBD ＝S 2－S △MCB －S 1＝25S 1,∴S 1S △EBD ＝ME EB ,∴S 125S 1＝ME EB ,∴ME EB ＝52. 设ME ＝5x,EB ＝2x,则BM ＝7x, ∴AB ＝2BM ＝14x. ∵MD AB ＝ME BC ＝12,∴BC ＝10x, ∴cos ∠ABC＝BC AB ＝10x 14x ＝57.1.(2018·贺州中考)如图,在△ABC 中,∠ACB ＝90°,O,D 分别是边AC,AB 的中点,过点C 作CE ∥AB 交DO 的延长线于点E,连接AE.(1)求证：四边形AECD 是菱形；(2)若四边形AECD 的面积为24,tan ∠BAC ＝34,求BC 的长.(1)证明：∵点O 是AC 的中点,∴OA ＝OC.∵CE ∥AB,∴∠DAO ＝∠ECO. 又∵∠AOD＝∠COE ,∴△AOD ≌△COE(ASA ),∴AD ＝CE, ∴四边形AECD 是平行四边形. 又∵CD 是Rt △ABC 斜边AB 上的中线, ∴CD ＝AD ＝12AB,∴四边形AECD 是菱形；(2)由(1)知,四边形AECD 是菱形,∴AC ⊥ED.在Rt △AOD 中,tan ∠DAO ＝OD OA ＝tan ∠BAC ＝34,可设OD ＝3x,OA ＝4x, 则ED ＝2OD ＝6x,AC ＝2OA ＝8x.由题意可得12·6x·8x＝24,∴x ＝1,∴OD ＝3.∵O,D 分别是AC,AB 的中点, ∴OD 是△ABC 的中位线, ∴BC ＝2OD ＝6.2.(2018·盐城中考)在正方形ABCD 中,对角线BD 所在的直线上有两点E,F 满足BE ＝DF,连接AE,AF,CE,CF,如图.(1)求证：△AB E≌△ADF；(2)试判断四边形AECF 的形状,并说明理由. (1)证明：∵四边形ABCD 是正方形,∴AB ＝AD, ∴∠ABD ＝∠ADB ,∴∠ABE ＝∠ADF. 在△ABE 与△ADF 中,⎩⎪⎨⎪⎧AB ＝AD ，∠ABE ＝∠ADF，BE ＝DF ，∴△ABE ≌△ADF(SAS )； (2)解：四边形AECF 是菱形. 理由：连接AC,交BD 于点O. ∵四边形ABCD 是正方形, ∴OA ＝OC,OB ＝OD,AC ⊥EF, ∴OB ＋BE ＝OD ＋DF,即OE ＝OF. ∵OA ＝OC,OE ＝OF,∴四边形AECF 是平行四边形, 又∵AC⊥EF ,∴四边形AECF 是菱形.3.(2018·湖州中考) 已知在Rt △ABC 中,∠BAC ＝90°,AB ≥AC,D,E 分别为AC,BC 边上的点(不包括端点),且DC BE ＝ACBC＝m,连接AE,过点D 作DM ⊥AE,垂足为点M,延长DM 交AB 于点F. (1)如图1,过点E 作EH⊥AB 于点H,连接DH.①求证：四边形DHEC 是平行四边形； ②若m ＝22,求证：AE ＝DF ； (2)如图2,若m ＝35,求DFAE的值.(1)证明：①∵EH⊥AB ,∠BAC ＝90°, ∴EH ∥CA,∴△BHE ∽△BAC,∴BE BC ＝HEAC .∵DC BE ＝AC BC ,∴BE BC ＝DC AC ,∴HE AC ＝DC AC, ∴HE ＝DC.∵EH ∥DC,∴四边形DHEC 是平行四边形； ②∵AC BC ＝22,∠BAC ＝90°,∴AC ＝AB.∵DC BE ＝22,HE ＝DC,∴HE BE ＝22. 又∵∠BHE＝90°,∴BH ＝HE. ∵HE ＝DC,∴BH ＝CD,∴AH ＝AD. ∵DM ⊥AE,EH ⊥AB, ∴∠EHA ＝∠AMF＝90°,∴∠HAE ＋∠HEA＝∠HAE＋∠AFM＝90°, ∴∠HEA ＝∠AFD.∵∠EHA ＝∠FAD＝90°,∴△HEA ≌△AFD,∴AE ＝DF ； (2)解：过点E 作EG⊥AB 于点G.∵CA ⊥AB,∴EG ∥CA,∴△EGB ∽△CAB, ∴EG CA ＝BE BC ,∴EG BE ＝CA BC ＝35. ∵CD BE ＝35,∴EG ＝CD. 设EG ＝CD ＝3x,AC ＝3y,则BE ＝5x,BC ＝5y, ∴BG ＝4x,AB ＝4y. ∵∠EGA ＝∠AMF＝90°, ∴∠GEA ＋∠EAG＝∠EAG＋∠AFM ,∴∠AFM＝∠AEG.∵∠FAD＝∠EGA＝90°,∴△FAD∽△EGA,∴DFAE＝ADAG＝3y－3x4y－4x＝34.毕节中考专题过关 1.(2018·乌鲁木齐中考)如图,在四边形ABCD 中,∠BAC ＝90°,E 是BC 的中点,AD ∥BC,AE ∥DC,EF ⊥CD 于点F.(1)求证：四边形AECD 是菱形；(2)若AB ＝6,BC ＝10,求EF 的长.(1)证明：∵AD∥BC ,AE ∥DC,∴四边形AECD 是平行四边形.∵∠BAC ＝90°,E 是BC 的中点,∴AE ＝CE ＝12BC,∴四边形AECD 是菱形；(2)解：过A 作AH⊥BC 于点H.∵∠BAC ＝90°,AB ＝6,BC ＝10,∴AC ＝102－62＝8.∵S △ABC ＝12BC·AH＝12AB·AC ,∴AH ＝6×810＝245.∵点E 是BC 的中点,BC ＝10,四边形AECD 是菱形,∴CD ＝CE ＝5.∵S ▱AECD ＝CE·A H ＝CD·EF ,∴EF ＝AH ＝245.2.(2018·青岛中考)已知：如图,▱ABCD 的对角线AC 与BD 相交于点E,点G 为AD 的中点,连接CG,CG 的延长线交BA 的延长线于点F,连接FD.(1)求证：AB ＝AF ；(2)若AG ＝AB,∠BCD ＝120°,判断四边形ACDF 的形状,并证明你的结论.(1)证明：∵四边形ABCD 是平行四边形,∴AB ∥CD,AB ＝CD,∴∠AFG ＝∠DCG.又∵GA＝GD,∠AGF ＝∠CGD ,∴△AGF ≌△DGC,∴AF ＝CD.∴AB ＝AF ；(2)解：四边形ACDF 是矩形.证明：∵AF＝CD,AF ∥CD,∴四边形ACDF 是平行四边形.∵四边形ABCD 是平行四边形,∴∠BAD ＝∠BCD＝120°.∴∠FAG ＝60°.∵AB ＝AG ＝AF,∴△AFG 是等边三角形,∴AG ＝GF.∵四边形ACDF 是平行四边形,∴FG ＝CG,AG ＝DG.∴AD＝CF.∴四边形ACDF 是矩形.3.已知：如图,四边形ABCD 中,AD ∥BC,AD ＝CD,E 是对角线BD 上一点,且EA ＝EC.(1)求证：四边形ABCD 是菱形；(2)如果BE ＝BC,且∠CBE∶∠BCE＝2∶3,求证：四边形ABCD 是正方形.证明：(1)在△ADE 与△CDE 中,⎩⎪⎨⎪⎧AD ＝CD ，DE ＝DE ，EA ＝EC ，∴△ADE ≌△CDE,∴∠ADE ＝∠CDE.∵AD ∥BC,∴∠ADE ＝∠CBD ,∴∠CDE ＝∠CBD ,∴BC ＝CD.∵AD ＝CD,∴BC ＝AD,∴四边形ABCD 为平行四边形.∵AD ＝CD,∴四边形ABCD 是菱形；(2)∵BE＝BC,∴∠BCE ＝∠BEC.∵∠CBE ∶∠BCE ＝2∶3,∴∠CBE ＝180×22＋3＋3＝45°. ∵四边形ABCD 是菱形,∴∠ABE ＝∠CBE＝45°,∴∠ABC ＝90°,∴四边形ABCD 是正方形.4.(2018·眉山中考)如图①,在四边形ABCD 中,AC ⊥BD 于点E,AB ＝AC ＝BD,点M 为BC 的中点,N 为线段AM 上的点,且MB ＝MN.(1)求证：BN 平分∠ABE；(2)若BD ＝1,连接DN,当四边形DNBC 为平行四边形时,求线段BC 的长；(3)如图②,若点F 为AB 的中点,连接FN,FM,求证：△MFN∽△BDC.(1)证明：∵AB＝AC,∴∠ABC ＝∠ACB.∵M 为BC 的中点,∴AM ⊥BC.在Rt △ABM 中,∠MAB ＋∠ABC＝90°.在Rt △CBE 中,∠EBC ＋∠ACB＝90°,∴∠MAB ＝∠EBC.又∵MB ＝MN,∴△MBN 为等腰直角三角形,∴∠MNB ＝∠MBN＝45°,∴∠EBC ＋∠NBE＝45°,∠MAB ＋∠ABN＝∠MNB＝45°,∴∠NBE ＝∠ABN ,即BN 平分∠ABE；(2)解：设BM ＝CM ＝MN ＝a.当四边形DNBC 是平行四边形时,DN ＝BC ＝2a.在△ABN 和△DBN 中,⎩⎪⎨⎪⎧AB ＝DB ，∠NBD ＝∠NBA，BN ＝BN ，∴△ABN ≌△DBN(SAS ),∴AN ＝DN ＝2a.在Rt △ABM 中,由AM 2＋BM 2＝AB 2,得(2a ＋a)2＋a 2＝1,解得a ＝±1010(负值舍去),∴BC ＝2a ＝105；(3)证明：在Rt △MAB 中,F 是AB 的中点,∴MF ＝AF ＝BF,∴∠MAB ＝∠FMN.又∵∠MAB＝∠CBD ,∴∠FMN ＝∠DBC. ∵MFAB ＝MNBC ＝12,∴MF BD ＝MN BC ＝12,∴△MFN ∽△BDC.5.(2018·枣庄中考)如图,将矩形ABCD 沿AF 折叠,使点D 落在BC 边的点E 处,过点E 作EG∥CD 交AF 于点G,连接DG.(1)求证：四边形EFDG 是菱形；(2)探究线段EG,GF,AF 之间的数量关系,并说明理由；(3)若AG ＝6,EG ＝25,求BE 的长.(1)证明：∵GE∥DF ,∴∠EGF ＝∠DFG.由翻折的性质可知DG ＝EG,DF ＝EF,∠DGF ＝∠EGF ,∴∠DGF ＝∠DFG ,∴DG ＝DF,∴DG ＝EG ＝DF ＝EF,∴四边形EFDG 是菱形；(2)解：EG 2＝12GF·AF.理由：连接DE,交AF 于点O.∵四边形EFDG 是菱形,∴GF ⊥DE,OG ＝OF ＝12GF.∵∠DOF ＝∠ADF＝90°,∠OFD ＝∠DFA , ∴△DOF ∽△ADF,∴DF AF ＝OF DF ,即DF 2＝OF·AF.∵OF ＝12GF,DF ＝EG,∴EG 2＝12GF·AF；(3)解：过点G 作GH⊥DC ,垂足为点H. ∵EG 2＝12GF·AF ,AG ＝6,EG ＝25,即GF 2＋6GF －40＝0,解得GF ＝4,GF ＝－10(舍去).∵DF ＝EG ＝25,AF ＝AG ＋GF ＝10, ∴AD ＝AF 2－DF 2＝4 5.∵GH ⊥DC,AD ⊥DC,∴GH ∥AD, ∴△FGH ∽△FAD,∴GH AD ＝GF AF ,即GH 45＝410,∴GH ＝855.∴BE ＝AD －GH ＝45－855＝1255.。

中考数学平面几何压轴(三角形与四边形)训练15题(精选无答案)

中考平面几何压轴（三角形与四边形）训练15题（精选）1.如图，四边形ABCD 是平行四边形，且对角线AC , BD 交于点O ，点M , N 分别在AD , BC 上，且AM = CN ,点E ，F 分别是BD 与AN ，CM 的交点.(1)求证:OE = OF ;(2)连接BM 交AC 于点H ,连接HE ，HF ;(i)如图2，若HE ∥AB ,求证: FH ∥AD ;(ii)如图3,若四边形ABCD 为菱形且DM = 2AM ,∠EHF=60°，求AC BD 的值.2.(1)如图①，在矩形ABCD 的AB 边上取一点E ，将ΔADE 沿DE 翻折，使点A 落在BC 上的A′处，若AB =6，BC =10，求AEEB 的值；(2)如图②，在矩形ABCD 的BC 上取一点E ，将四边形ABED 沿DE 翻折，使点B 落在DC 的延长线上B′处，若BC ·CE =24，AB =6，求BE 的值；(3)如图③，在ΔABC 中，∠BAC =45°，AD ⊥BC ，垂足为点D ，AD =10，AE =6，过点E 作EF ⊥AD 交AC 于点F ，连接DF ，且满足∠DFE =2∠DAC ，直接写出BD+53EF 的值.3. 在正方形ABCD 中，AB =10, AC 是对角线，点O 是AC 的中点，点E 在AC 上，连接DE ，点C 关于DE 的对称点是C',连接DC' ,EC'.(1) 如图1，若DC'经过点O ,求证:OC ′CE = √22. (2) 如图2，连接CC'，BC',若∠ADC' = 2∠CBC',求CC'的长;(3) 当点B , C', E 三点共线时，直接写出CE 的长.4.如图，正方形ABCD中，点M在边BC上，点E是AM的中点，连接ED，EC．（1）求证：ED= EC；（2）将BE绕点E逆时针旋转，使点B的对应点B′落在AC上，连接MB′．当点M在边BC上运动时（点M不与B，C 重合），判断△CMB′的形状，并说明理由．（3）在（2）的条件下，已知AB= 1，当∠DEB′=45°时，求BM的长．5.如图，在正方形ABCD中，点M、N在直线BD上，连接AM，AN并延长交BC、CD于点E、F，连接EN.(1)如图1，若M，N都在线段BD上，且AN = NE，求∠MAN;(2)如图2.当点M在线段DB 延长线上时,AN = NE,(1)中∠MAN的度数不变，判断BM，DN，MN之间的数量关系并证明;(3)如图3,若点M在DB的延长线上,N在BD的延长线上,且∠MAN=135°(i)AB=√6,MB=√3,求DN.(ii)求证:2AM2 - MB 2= MN2 - BN2.6.如图，在RtΔABC与RtΔBDE中,∠BAC=∠BDE=90°,∠ABC=∠DBE=α.（1)如图1,当α= 60°,且点E为BC的中点时,若AB=2,连接AD.求AD的长度；（2)如图2,若α≠ 60°,且点E为BC中点时,取CE中点F,连接AF、DF。

真题精选：三角形和四边形(二)

《三角形与四边形》真题精选1.（2012·上海市文来中学分班卷）∠l、∠2、∠3是三角形的三个内角。

∠2的度数是∠1的2倍，∠3的度数是∠1的3倍。

这个三角形是（）三角形。

2．（2012·南京市南师附中仙林学校初中部招生卷）一根长60 cm的铁丝围成一cm。

个长方形，如果长和宽都是质数，它的面积最大是（）23．（2012·杭州市采荷实验学校分班卷）如图，梯形上底与下底的比是2:3，阴影三角形的面积为18平方厘米，空白三角形的面积是（）平方厘米。

4．（2012·苏州市迎春中学招生卷）如下图，∠1＝（）。

5.（2011·青岛市青开四中分班卷）下图的长方形中，三角形的面积比梯形的面积小35平方厘米，则梯形的上底长为（）厘米。

6.（2011·广州市六中珠江中学招生卷）如下图，每相邻三个点所形成的三角形都是面积为12cm 的正三角形，则△ABC 的面积为（）2cm 。

7.（2012·长沙市沙坪中学分班卷）三条边长分别是6㎝、8㎝、10㎝的直角三角形，将它的最短边对折使它与斜边相重合（如图），重叠后的三角形即阴影部分的面积是（）2cm 。

8.（2012·北京市三帆中学分班卷）一个等腰三角形底和高的比是8:3，把它沿底边上的高剪开，拼成一个长方形，这个长方形面积是192平方厘米。

那么这个长方形的周长是（）厘米。

9.（2011·天津市培杰中学分班卷）如下图，在长方形ABCD 中，三角形ABP 的面积为45平方厘米，三角形CPQ 的面积为60平方厘米，则四边形EPFQ 的面积为（）平方厘米。

10．（2011·太原市山大附中招生卷）如图，在三角形ABC中，EF和AB互相平行，DE和BC互相平行。

四边形BDEF的面积是120平方厘米。

三角形AEF（阴影部分）的面积是（）平方厘米。

11．（2012·上海市文绮中学招生卷）如下图，将四条边长为16 cm、宽为 2 cm 的方形纸条垂直相交平放在桌面上，则桌面被盖住的面积是（）。

小学四年级三角形和四边形图形与几何专题(附答案)

小学四年级三角形和四边形图形与几何专题(附答案)图形与几何专题一、填空题1、三角形的内角和是180°，一个等腰三角形，它的一个底角是26°，它的顶角是128°。

2、长5厘米，8厘米，13厘米的三根小棒不能围成一个三角形。

3、三角形具有三边性。

4、一个三角形中有一个角是45°，另一个角是它的2倍，第三个角是90°，这是一个直角三角形。

5、按角的大小，三角形可以分为钝角三角形、锐角三角形、直角三角形。

6、在三角形中，∠1=30°，∠2=70°，∠3=80°，它是锐角三角形。

7、有两组对边平行的四边形是平行四边形。

8、在一个直角三角形中，有一个角是30°,另两个角分别是60°、90°。

9、长方形正方形是特殊的四边形。

10、将一个大三角形分成两个小三角形，其中一个小三角形的内角和是90度。

11、三角形的两个内角之和是85°，这个三角形是钝角三角形，另一个角是95度。

12、一个等边三角形的边长是9厘米，它的周长是27厘米。

13、数一数下图中有5个角。

二、判断题1、√2、√3、×4、√5、×6、×7、√8、×9、×10、√11、√12、√三、选择题1、A2、C3、B4、A5、1个。

一、数学题6、一条红领巾，它的顶角是100°，它的一个底角是多少度？答：80度7、把一个10°的角先扩大6倍后，再用6倍的放大镜来看，看到的角是多少度？答：60度8、一个三角形的两条边分别是40厘米、50厘米，第三条边的长度只能选哪个？答：90厘米9、下面说法，正确的是：答：等腰三角形都是锐角三角形。

10、如果一个三角形中，一个角是另一个角的2倍，那么这个三角形一定不是哪种三角形？答：等腰直角三角形11、直角三角形的内角和是锐角三角形的内角和的哪个关系？答：小于12、下面分别是三角形的三条边长度，不能围成三角形的是哪个？答：5cm、6cm、7cm二、画图题4、我是小画家。

中考数学几何压轴题(有关三角形、四边形)的综合专题(含答案解析)

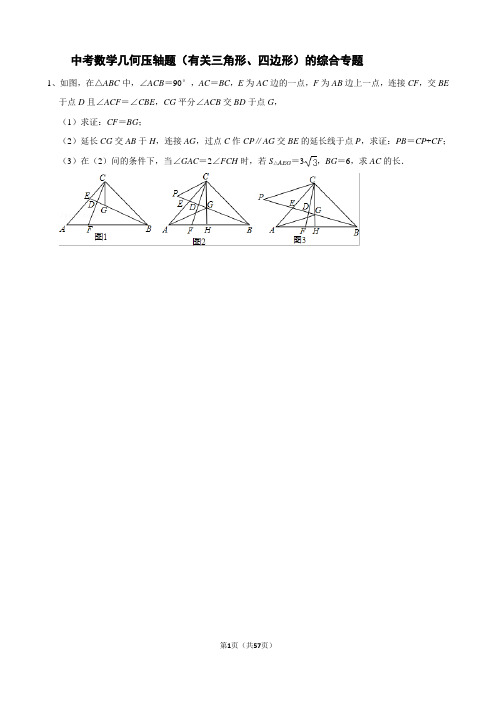
中考数学几何压轴题（有关三角形、四边形）的综合专题1、如图，在△ABC中，∠ACB＝90°，AC＝BC，E为AC边的一点，F为AB边上一点，连接CF，交BE于点D且∠ACF＝∠CBE，CG平分∠ACB交BD于点G，（1）求证：CF＝BG；（2）延长CG交AB于H，连接AG，过点C作CP∥AG交BE的延长线于点P，求证：PB＝CP+CF；（3）在（2）问的条件下，当∠GAC＝2∠FCH时，若S△AEG＝3，BG＝6，求AC的长．2、[问题背景]如图1所示，在△ABC中，AB＝BC，∠ABC＝90°，点D为直线BC上的一个动点（不与B、C重合），连结AD，将线段AD绕点D按顺时针方向旋转90°，使点A旋转到点E，连结EC．[问题初探]如果点D在线段BC上运动，通过观察、交流，小明形成了以下的解题思路：过点E作EF⊥BC 交直线BC于F，如图2所示，通过证明△DEF≌△，可推证△CEF是三角形，从而求得∠DCE＝．[继续探究]如果点D在线段CB的延长线上运动，如图3所示，求出∠DCE的度数．[拓展延伸]连接BE，当点D在直线BC上运动时，若AB＝，请直接写出BE的最小值．3、（2019秋•锦江区校级期末）在Rt△ABC中，∠ACB＝90°，∠A＝30°，BD是△ABC的角平分线．（1）如图1，求证：AD＝2DC．（2）如图2，作∠CBD的角平分线交线段CD于点M，若CM＝1，求△DBM的面积；（3）如图3，过点D作DE⊥AB于点E，点N是线段AC上一点（不与C、D重合），以BN为一边，在BN的下方作∠BNG＝60°，NG交DE延长线于点G，试探究线段ND，DG与AD之间的数量关系，并说明理由．4、（2019•镇平县三模）如图1，已知直角三角形ABC，∠ACB＝90°，∠BAC＝30°，点D是AC边上一点，过D作DE⊥AB于点E，连接BD，点F是BD中点，连接EF，CF．（1）发现问题：线段EF，CF之间的数量关系为；∠EFC的度数为；（2）拓展与探究：若将△AED绕点A按顺时针方向旋转α角（0°＜α＜30°），如图2所示，（1）中的结论还成立吗？请说明理由；（3）拓展与运用：如图3所示，若△AED绕点A旋转的过程中，当点D落到AB边上时，AB边上另有一点G，AD＝DG＝GB，BC＝3，连接EG，请直接写出EG的长度．5、（2017春•西城区校级期末）如图1，在等腰△ABC中，AB＝AC，∠BAC＝a，点P是线段AB的中点，点E是线段CB延长线上一点，且PE＝PC，将线段PC绕点P顺时针旋转α得到PD，连接BD．（1）如图2，若α＝60°，其他条件不变，先补全图形，然后探究线段BD和BC之间的数量关系，并说明理由．（2）如图3，若α＝90°，其他条件不变，探究线段BP、BD和BC之间的等量关系，并说明理由．6、【发现问题】如图1，已知△ABC，以点A为直角顶点、AB为腰向△ABC外作等腰直角△ABE．请你以A为直角顶点、AC为腰，向△ABC外作等腰直角△ACD（不写作法，保留作图痕迹）．连接BD、CE．那么BD与CE的数量关系是BD＝CE．【拓展探究】如图2，已知△ABC，以AB、AC为边向外作正方形AEFB和正方形ACGD，连接BD、CE，试判断BD与CE之间的数量关系，并说明理由．【解决问题】如图3，有一个四边形场地ABCD，∠ADC＝60°，BC＝15，AB＝8，AD＝CD，求BD的最大值．7、（1）如图1，点C为线段AB外一个动点，已知AB＝a，AC＝b．当点C位于BA的延长线上时，线段BC取得最大值，则最大值为（用含a，b的式子表示）；（2）如图2，点C为线段AB外一个动点，若AB＝10，AC＝3，分别以AC，BC为边，作等边三角形ACD和等边三角形BCE，连接AE，DB．①求证：AE＝DB；②请直接写出线段AE的最大值；（3）如图3，AB＝6，点M为线段AB外一个动点，且AM＝2，MB＝MN，∠BMN＝90°，请直接写出线段AN的最大值．8、【初步探索】（1）如图1：在四边形ABC中，AB＝AD，∠B＝∠ADC＝90°，E、F分别是BC、CD上的点，且EF ＝BE+FD，探究图中∠BAE、∠F AD、∠EAF之间的数量关系．小王同学探究此问题的方法是：延长FD到点G，使DG＝BE．连接AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出结论，他的结论应是；【灵活运用】（2）如图2，若在四边形ABCD中，AB＝AD，∠B+∠D＝180°．E、F分别是BC、CD上的点，且EF＝BE+FD，上述结论是否仍然成立，并说明理由；【拓展延伸】（3）如图3，已知在四边形ABCD中，∠ABC+∠ADC＝180°AB＝AD，若点E在CB的延长线上，点F在CD的延长线上，如图3所示，仍然满足EF＝BE+FD，请写出∠EAF与∠DAB的数量关系，并给出证明过程．9、（2018•大东区一模）如图，在Rt△ABC中，∠ACB＝90°，∠A＝30°，点O为AB中点，点P为直线BC上的动点（不与点B、点C重合），连接OC、OP，将线段OP绕点P逆时针旋转60°，得到线段PQ，连接BQ．（1）如图1，当点P在线段BC上时，请直接写出线段BQ与CP的数量关系．（2）如图2，当点P在CB延长线上时，（1）中结论是否成立？若成立，请加以证明；若不成立，请说明理由；（3）如图3，当点P在BC延长线上时，若∠BPO＝45°，AC＝，请直接写出BQ的长．10、模型发现：同学们知道，三角形的两边之和大于第三边，即如图1，在△ABC中，AB+AC＞BC．对于图1，若把点C看作是线段AB外一动点，且AB＝c，AC＝b，则线段BC的长会因为点C的位置的不同而发生变化．因为AB、AC的长度固定，所以当∠BAC越大时，BC边越长．特别的，当点C位于时，线段BC的长取得最大值，且最大值为（用含b，c的式子表示）（直接填空）.模型应用：点C为线段AB外一动点，且AB＝3，AC＝2，如图2所示，分别以AC，BC为边，作等边三角形ACD 和等边三角形BCE，连接BD，AE．（1）求证：BD＝AE．（2）线段AE长的最大值为．模型拓展：如图3，在平面直角坐标系中，点A是y轴正半轴上的一动点，点B是x轴正半轴上的一动点，且AB ＝8．若AC⊥AB，AC＝3，试求OC长的最大值．11、已知：△ABC中，∠ACB＝90°，AC＝BC．（1）如图1，点D在BC的延长线上，连AD，过B作BE⊥AD于E，交AC于点F．求证：AD＝BF；（2）如图2，点D在线段BC上，连AD，过A作AE⊥AD，且AE＝AD，连BE交AC于F，连DE，问BD与CF有何数量关系，并加以证明；（3）如图3，点D在CB延长线上，AE＝AD且AE⊥AD，连接BE、AC的延长线交BE于点M，若AC ＝3MC，请直接写出的值．12、已知在△ABC中，AB＝AC，射线BM、BN在∠ABC内部，分别交线段AC于点G、H．（1）如图1，若∠ABC＝60°，∠MBN＝30°，作AE⊥BN于点D，分别交BC、BM于点E、F．①求证：∠1＝∠2；②如图2，若BF＝2AF，连接CF，求证：BF⊥CF；（2）如图3，点E为BC上一点，AE交BM于点F，连接CF，若∠BFE＝∠BAC＝2∠CFE，求的值．13、已知，△ABC中，AB＝AC，∠BAC＝90°，E为边AC任意一点，连接BE．（1）如图1，若∠ABE＝15°，O为BE中点，连接AO，且AO＝1，求BC的长；（2）如图2，F也为AC上一点，且满足AE＝CF，过A作AD⊥BE交BE于点H，交BC于点D，连接DF交BE于点G，连接AG；①若AG平分∠CAD，求证：AH＝AC；②如图3，当G落在△ABC外时，若将△EFG沿EF边翻折，点G刚好落在AB边上点P，直接写出AG与EF的数量关系．14、如图所示，Rt△ABC中，∠ACB＝90°，E为AC中点，作ED⊥AC交AB于D，连接CD；（1）如图1，求证：AB＝2CD；（2）如图2，作CF⊥AB交AB于F，点G为CF上一点，点H为DE延长线上一点，分别连接AH、GH，若∠AHG＝2∠B，求证：AH＝GH；（3）如图3，在（2）的条件下，连接DG，且有DE＝BF，∠EDG＝90°，若AC＝6，求AH的长度．15、【问题情境】一节数学课后，老师布置了一道课后练习题：如图：已知在Rt△ABC中，AC＝BC，∠ACB＝90°，CD⊥AB于点D，点E、F分别在A和BC上，∠1＝∠2，FG⊥AB于点G，求证：△CDE≌△EGF．（1）阅读理解，完成解答本题证明的思路可用下列框图表示：根据上述思路，请你完整地书写这道练习题的证明过程；（2）特殊位置，证明结论若CE平分∠ACD，其余条件不变，求证：AE＝BF；（3）知识迁移，探究发现如图，已知在Rt△ABC中，AC＝BC，∠ACB＝90°，CD⊥AB于点D，若点E是DB的中点，点F在直线CB上且满足EC＝EF，请直接写出AE与BF的数量关系．（不必写解答过程）16、在正方形ABCD和等腰直角△BGF中，∠BGF＝90°，P是DF的中点，连接PG、PC．（1）如图1，当点G在BC边上时，延长GP交DC于点E．求证：PG＝PC；（2）如图2，当点F在AB的延长线上时，（1）中的结论是否成立？请证明你的结论；（3）如图3，若四边形ABCD为菱形，且∠ABC＝60°，△BGF为等边三角形，点F在CB的延长线上时，线段PC、PG又有怎样的数量关系，请直接写出你的结论，并画出论证过程中需要添加的辅助线．17、在△ABC中，∠BAC＝60°，点D、E分别在边AC、AB上，AD＝AE，连接CE、BD相交于点F，且∠BEC＝∠ADF，连接AF．（1）如图1，连接ED，求证：∠ABD＝∠CED；（2）如图2，求证：EF+FD＝AF；（3）如图3，取BC的中点G，连接AG交BD于点H，若∠GAC＝3∠ABD，BH＝7，求△ABH的面积．18、点D，E分别在△ABC的边AC，BD上，BD，CE交于点F，连接AF，∠F AE＝∠F AD，FE＝FD．（1）如图1，若∠AEF＝∠ADF，求证：AE＝AD；（2）如图2，若∠AEF≠∠ADF，FB平分∠ABC，求∠BAC的度数；（3）在（2）的条件下，如图3，点G在BE上，∠CFG＝∠AFB若AG＝6，△ABC的周长为20，求BC长．中考数学几何压轴题（有关三角形、四边形）的综合专题参考答案1、如图，在△ABC中，∠ACB＝90°，AC＝BC，E为AC边的一点，F为AB边上一点，连接CF，交BE于点D且∠ACF＝∠CBE，CG平分∠ACB交BD于点G，（1）求证：CF＝BG；（2）延长CG交AB于H，连接AG，过点C作CP∥AG交BE的延长线于点P，求证：PB＝CP+CF；（3）在（2）问的条件下，当∠GAC＝2∠FCH时，若S△AEG＝3，BG＝6，求AC的长．证明：（1）如图1，∵∠ACB＝90°，AC＝BC，∴∠A＝45°，∵CG平分∠ACB，∴∠ACG＝∠BCG＝45°，∴∠A＝∠BCG，在△BCG和△CAF中，∵，∴△BCG≌△CAF（ASA），∴CF＝BG；（2）如图2，∵PC∥AG，∴∠PCA＝∠CAG，∵AC＝BC，∠ACG＝∠BCG，CG＝CG，∴△ACG≌△BCG，∴∠CAG＝∠CBE，∵∠PCG＝∠PCA+∠ACG＝∠CAG+45°＝∠CBE+45°，∠PGC＝∠GCB+∠CBE＝∠CBE+45°，∴∠PCG＝∠PGC，∴PC＝PG，∵PB＝BG+PG，BG＝CF，∴PB＝CF+CP；（3）解法一：如图3，过E作EM⊥AG，交AG于M，∵S△AEG＝AG•EM＝3，由（2）得：△ACG≌△BCG，∴BG＝AG＝6，∴×6×EM＝3，EM＝，设∠FCH＝x°，则∠GAC＝2x°，∴∠ACF＝∠EBC＝∠GAC＝2x°，∵∠ACH＝45°，∴2x+x＝45，x＝15，∴∠ACF＝∠GAC＝30°，在Rt△AEM中，AE＝2EM＝2，AM＝＝3，∴M是AG的中点，∴AE＝EG＝2，∴BE＝BG+EG＝6+2，在Rt△ECB中，∠EBC＝30°，∴CE＝BE＝3+，∴AC＝AE+EC＝2+3+＝3+3．解法二：同理得：∠CAG＝30°，AG＝BG＝6，如图4，过G作GM⊥AC于M，在Rt△AGM中，GM＝3，AM＝＝＝3，∵∠ACG＝45°，∠MGC＝90°，∴GM＝CM＝3，∴AC＝AM+CM＝3+3．2、[问题背景]如图1所示，在△ABC中，AB＝BC，∠ABC＝90°，点D为直线BC上的一个动点（不与B、C重合），连结AD，将线段AD绕点D按顺时针方向旋转90°，使点A旋转到点E，连结EC．[问题初探]如果点D在线段BC上运动，通过观察、交流，小明形成了以下的解题思路：过点E作EF⊥BC 交直线BC于F，如图2所示，通过证明△DEF≌△ADB，可推证△CEF是等腰直角三角形，从而求得∠DCE＝135°．[继续探究]如果点D在线段CB的延长线上运动，如图3所示，求出∠DCE的度数．[拓展延伸]连接BE，当点D在直线BC上运动时，若AB＝，请直接写出BE的最小值．解：[问题初探]如图2，过点E作EF⊥BC交直线BC于F，∴∠DFE＝90°＝∠ABD，∴∠EDF+∠DEF＝90°，由旋转知，AD＝DE，∠ADE＝90°，∴∠ADB+∠EDF＝90°，∴∠ADB＝∠DEF，∴△ABD≌△DFE（AAS），∴BD＝EF，DF＝AB，∵AB＝BC，∴BC＝DF，∴BD＝CF，∴EF＝CF，∴△CEG是等腰直角三角形，∴∠ECF＝45°，∴∠DCE＝135°，故答案为：ADB，等腰直角，135；[继续探究]如图3，过点E作EF⊥BC于F，∴∠DFE＝90°＝∠ABD，∴∠EDF+∠DEF＝90°，由旋转知，AD＝DE，∠ADE＝90°，∴∠ADB+∠EDF＝90°，∴∠ADB＝∠DEF，∴△ABD≌△DFE（AAS），∴BD＝EF，DF＝AB，∵AB＝BC，∴BC＝DF，∴BD＝CF，∴EF＝CF，∴△CEG是等腰直角三角形，∴∠ECF＝45°，∴∠DCE＝45°；[拓展延伸]如图4，在△ABC中，∠ABC＝90°，AB＝BC＝，∴∠ACB＝45°当点D在射线BC上时，由[问题初探]知，∠BCM＝135°，∴∠ACM＝∠BCM﹣∠ACB＝90°，当点D在线段CB的延长线上时，由[继续探究]知，∠BCE＝45°，∴∠ACN＝∠ACB+∠BCM＝90°，∴点E是过点C垂直于AC的直线上的点，∴当BE⊥MN时，BE最小，∵∠BCE＝45°，∴∠CBE＝45°＝∠BCE，∴BE＝CE，∴BE最小＝BC＝，即：BE的最小值为．3、在Rt△ABC中，∠ACB＝90°，∠A＝30°，BD是△ABC的角平分线．（1）如图1，求证：AD＝2DC．（2）如图2，作∠CBD的角平分线交线段CD于点M，若CM＝1，求△DBM的面积；（3）如图3，过点D作DE⊥AB于点E，点N是线段AC上一点（不与C、D重合），以BN为一边，在BN的下方作∠BNG＝60°，NG交DE延长线于点G，试探究线段ND，DG与AD之间的数量关系，并说明理由．证明：（1）如图1，过点D作DE⊥AB，∵BD是△ABC的角平分线，DE⊥AB，∠ACB＝90°，∴DC＝DE，∵∠A＝30°，DE⊥AB，∴AD＝2DE，∴AD＝2DC；（2）如图2，过点M作ME∥BD，∵∠ACB＝90°，∠A＝30°，∴∠ABC＝60°，∵BD是△ABC的角平分线，∴∠ABD＝∠DBC＝30°，∵BM平分∠CBD，∴∠CBM＝15°＝∠DBM，∵ME∥BD，∴∠MEC＝∠CBD＝30°，∠EMB＝∠DBM＝∠MBE，∴ME＝BE，∵∠MEC＝30°，∠C＝90°∴CE＝MC＝，ME＝2MC＝2＝BE，∴BC＝+2，∵∠CBD＝30°，∠C＝90°，∴BC＝CD，∴CD＝1+，∴DM＝，∴△DBM的面积＝××（+2）＝1+；（3）若点N在CD上时，AD＝DG+DN，理由如下：如图3所示：延长ED使得DW＝DN，连接NW，∵∠ACB＝90°，∠A＝30°，BD是△ABC的角平分线，DE⊥AB于点E，∴∠ADE＝∠BDE＝60°，AD＝BD，∵DN＝DW，且∠WDN＝60°∴△WDN是等边三角形，∴NW＝DN，∠W＝∠WND＝∠BNG＝∠BDN＝60°，∴∠WNG＝∠BND，在△WGN和△DBN中，∴△WGN≌△DBN（SAS），∴BD＝WG＝DG+DN，∴AD＝DG+DN．（3）若点N在AD上时，AD＝DG﹣DN，理由如下：如图4，延长BD至H，使得DH＝DN，连接HN，由（1）得DA＝DB，∠A＝30°．∵DE⊥AB于点E．∴∠2＝∠3＝60°．∴∠4＝∠5＝60°．∴△NDH是等边三角形．∴NH＝ND，∠H＝∠6＝60°．∴∠H＝∠2．∵∠BNG＝60°，∴∠BNG+∠7＝∠6+∠7．即∠DNG＝∠HNB．在△DNG和△HNB中，∴△DNG≌△HNB（ASA）．∴DG＝HB．∵HB＝HD+DB＝ND+AD，∴DG＝ND+AD．∴AD＝DG﹣ND．4、如图1，已知直角三角形ABC，∠ACB＝90°，∠BAC＝30°，点D是AC边上一点，过D作DE⊥AB于点E，连接BD，点F是BD中点，连接EF，CF．（1）发现问题：线段EF，CF之间的数量关系为EF＝CF；∠EFC的度数为120°；（2）拓展与探究：若将△AED绕点A按顺时针方向旋转α角（0°＜α＜30°），如图2所示，（1）中的结论还成立吗？请说明理由；（3）拓展与运用：如图3所示，若△AED绕点A旋转的过程中，当点D落到AB边上时，AB边上另有一点G，AD＝DG＝GB，BC＝3，连接EG，请直接写出EG的长度．解：（1）如图1中，∵DE⊥AB，∴∠BED＝90°，∵∠BCD＝90°，BF＝DF，∴FE＝FB＝FD＝CF，∴∠FBE＝∠FEB，∠FBC＝∠FCB，∴∠EFC＝∠EFD+∠CFD＝∠FBE+∠FEB+∠FBC+∠FCB＝2（∠FBE+∠FBC）＝2∠ABC＝120°，故答案为：EF＝CF，120°．（2）结论成立．理由：如图2中，取AB的中点M，AD的中点N，连接MC，MF，ED，EN，FN．∵BM＝MA，BF＝FD，∴MF∥AD，MF＝AD，∵AN＝ND，∴MF＝AN，MF∥AN，∴四边形MFNA是平行四边形，∴NF＝AM，∠FMA＝∠ANF，在Rt△ADE中，∵AN＝ND，∠AED＝90°，∴EN＝AD＝AN＝ND，同理CM＝AB＝AM＝MB，在△AEN和△ACM中，∠AEN＝∠EAN，∠MCA＝∠MAC，∵∠MAC＝∠EAN，∴∠AMC＝∠ANE，又∵∠FMA＝∠ANF，∴∠ENF＝∠FMC，在△MFC和△NEF中，，∴△MFC≌△NEF（SAS），∴FE＝FC，∠NFE＝∠MCF，∵NF∥AB，∴∠NFD＝∠ABD，∵∠ACB＝90°，∠BAC＝30°，∴∠ABC＝60°，△BMC是等边三角形，∠MCB＝60°∴∠EFC＝∠EFN+∠NFD+∠DFC＝∠MCF+∠ABD+∠FBC+∠FCB＝∠ABC+∠MCB＝60°+60°＝120°．（3）如图3中，作EH⊥AB于H．在Rt△ABC中，∵∠BAC＝30°，BC＝3，∴AB＝2BC＝6，在Rt△AED中，∠DAE＝30°，AD＝2，∴DE＝AD＝1，在Rt△DEH中，∵∠EDH＝60°，DE＝1，∴EH＝ED•sin60°＝，DH＝ED•cos60°＝，在Rt△EHG中，EG＝＝．5、如图1，在等腰△ABC中，AB＝AC，∠BAC＝a，点P是线段AB的中点，点E是线段CB延长线上一点，且PE＝PC，将线段PC绕点P顺时针旋转α得到PD，连接BD．（1）如图2，若α＝60°，其他条件不变，先补全图形，然后探究线段BD和BC之间的数量关系，并说明理由．（2）如图3，若α＝90°，其他条件不变，探究线段BP、BD和BC之间的等量关系，并说明理由．解：（1）BC＝2BD，理由：如图2，连接CD，由旋转可得，CP＝DP，∠CPD＝60°，∴△CDP是等边三角形，∴∠CDP＝60°＝∠PCD，又∵P是AB的中点，AB＝AC，∠A＝60°，∴等边三角形ABC中，∠PCB＝30°，CP⊥AB，∴∠BCD＝30°，即BC平分∠PCD，∴BC垂直平分PD，∴∠BDC＝∠BPC＝90°，∴Rt△BCD中，BC＝2BD．（2）如图3，取BC中点F，连接PF，∵∠A＝90°，AB＝AC，∴△ABC是等腰直角三角形，∵P是AB的中点，F是BC的中点，∴PF是△ABC的中位线，∴PF∥AC，∴∠PFB＝∠ACB＝45°，∠BPF＝∠A＝90°，∴△BPF是等腰直角三角形，∴BF＝BP，BP＝PF，∵∠DPC＝∠BPF＝90°，∴∠BPD＝∠FPC，又∵PD＝PC，∴△BDP≌△FCP，∴BD＝CF，∵BC＝BF+FC，∴BC＝BD+BP．6、【发现问题】如图1，已知△ABC，以点A为直角顶点、AB为腰向△ABC外作等腰直角△ABE．请你以A为直角顶点、AC为腰，向△ABC外作等腰直角△ACD（不写作法，保留作图痕迹）．连接BD、CE．那么BD与CE的数量关系是BD＝CE．【拓展探究】如图2，已知△ABC，以AB、AC为边向外作正方形AEFB和正方形ACGD，连接BD、CE，试判断BD与CE之间的数量关系，并说明理由．【解决问题】如图3，有一个四边形场地ABCD，∠ADC＝60°，BC＝15，AB＝8，AD＝CD，求BD的最大值．【发现问题】解：延长CA到M，作∠MAC的平分线AN，在AN上截取AD＝AC，连接CD，即可得到等腰直角△ACD；连接BD、CE，如图1所示：∵△ABE与△ACD都是等腰直角三角形，∴AB＝AE，AD＝AC，∠BAE＝∠CAD＝90°，∴∠BAD＝∠EAC，在△BAD和△EAC中，，∴△BAD≌△EAC（SAS），∴BD＝CE，【拓展探究】解：BD＝CE；理由如下：∵四边形AEFB与四边形ACGD都是正方形，∴AB＝AE，AD＝AC，∠BAE＝∠CAD＝90°，∴∠BAD＝∠EAC，在△BAD和△EAC中，，∴△BAD≌△EAC（SAS），∴BD＝CE；【解决问题】解：以AB为边向外作等边三角形ABE，连接CE，如图3所示：则∠BAE＝60°，BE＝AB＝AE＝8，∵AD＝CD，∠ADC＝60°，∴△ACD是等边三角形，∴∠CAD＝60°，AC＝AD，∴∠CAD+∠BAC＝∠BAE+∠BAC，即∠BAD＝∠EAC，在△BAD和△EAC中，，∴△BAD≌△EAC（SAS），∴BD＝CE；当C、B、E三点共线时，CE最大＝BC+BE＝15+8＝23，∴BD的最大值为23．7、如图1，点C为线段AB外一个动点，已知AB＝a，AC＝b．当点C位于BA的延长线上时，线段BC取得最大值，则最大值为a+b（用含a，b的式子表示）；（2）如图2，点C为线段AB外一个动点，若AB＝10，AC＝3，分别以AC，BC为边，作等边三角形ACD和等边三角形BCE，连接AE，DB．①求证：AE＝DB；②请直接写出线段AE的最大值；（3）如图3，AB＝6，点M为线段AB外一个动点，且AM＝2，MB＝MN，∠BMN＝90°，请直接写出线段AN的最大值．（1）解：∵点C为线段AB外一动点，且AC＝b，AB＝a，∴当点C位于BA的延长线上时，线段BC的长取得最大值，且最大值为AC+AB＝a+b，（2）①证明：如图2中，∵△ACD与△BCE是等边三角形，∴CD＝AC，CB＝CE，∠ACD＝∠BCE＝60°，∴∠DCB＝∠ACE，在△CAD与△EAB中，，∴△CAD≌△EAB（SAS），∴AE＝BD．②∵线段AE长的最大值＝线段BD的最大值，由（1）知，当线段BD的长取得最大值时，点D在BA的延长线上，∴最大值为AD+AB＝3+10＝13；（3）如图3中，连接BN，∵将△AMN绕着点M顺时针旋转90°得到△PBM，连接AP，则△APM是等腰直角三角形，∴MA＝MP＝2，BP＝AN，∴P A＝2，∵AB＝6，∴线段AN长的最大值＝线段BP长的最大值，∴当P在线段BA的延长线时，线段BP取得最大值最大值＝AB+AP＝6+2．8、【初步探索】（1）如图1：在四边形ABC中，AB＝AD，∠B＝∠ADC＝90°，E、F分别是BC、CD上的点，且EF ＝BE+FD，探究图中∠BAE、∠F AD、∠EAF之间的数量关系．小王同学探究此问题的方法是：延长FD到点G，使DG＝BE．连接AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出结论，他的结论应是∠BAE+∠F AD＝∠EAF；【灵活运用】（2）如图2，若在四边形ABCD中，AB＝AD，∠B+∠D＝180°．E、F分别是BC、CD上的点，且EF＝BE+FD，上述结论是否仍然成立，并说明理由；【拓展延伸】（3）如图3，已知在四边形ABCD中，∠ABC+∠ADC＝180°AB＝AD，若点E在CB的延长线上，点F在CD的延长线上，如图3所示，仍然满足EF＝BE+FD，请写出∠EAF与∠DAB的数量关系，并给出证明过程．解：（1）∠BAE+∠F AD＝∠EAF．理由：如图1，延长FD到点G，使DG＝BE，连接AG，根据SAS可判定△ABE≌△ADG，进而得出∠BAE＝∠DAG，AE＝AG，再根据SSS可判定△AEF≌△AGF，可得出∠EAF＝∠GAF＝∠DAG+∠DAF＝∠BAE+∠DAF．故答案为：∠BAE+∠F AD＝∠EAF；（2）仍成立，理由：如图2，延长FD到点G，使DG＝BE，连接AG，∵∠B+∠ADF＝180°，∠ADG+∠ADF＝180°，∴∠B＝∠ADG，又∵AB＝AD，∴△ABE≌△ADG（SAS），∴∠BAE＝∠DAG，AE＝AG，∵EF＝BE+FD＝DG+FD＝GF，AF＝AF，∴△AEF≌△AGF（SSS），∴∠EAF＝∠GAF＝∠DAG+∠DAF＝∠BAE+∠DAF；（3）∠EAF＝180°﹣∠DAB．证明：如图3，在DC延长线上取一点G，使得DG＝BE，连接AG，∵∠ABC+∠ADC＝180°，∠ABC+∠ABE＝180°，∴∠ADC＝∠ABE，又∵AB＝AD，∴△ADG≌△ABE（SAS），∴AG＝AE，∠DAG＝∠BAE，∵EF＝BE+FD＝DG+FD＝GF，AF＝AF，∴△AEF≌△AGF（SSS），∴∠F AE＝∠F AG，∵∠F AE+∠F AG+∠GAE＝360°，∴2∠F AE+（∠GAB+∠BAE）＝360°，∴2∠F AE+（∠GAB+∠DAG）＝360°，即2∠F AE+∠DAB＝360°，∴∠EAF＝180°﹣∠DAB．9、如图，在Rt△ABC中，∠ACB＝90°，∠A＝30°，点O为AB中点，点P为直线BC上的动点（不与点B、点C重合），连接OC、OP，将线段OP绕点P逆时针旋转60°，得到线段PQ，连接BQ．（1）如图1，当点P在线段BC上时，请直接写出线段BQ与CP的数量关系．（2）如图2，当点P在CB延长线上时，（1）中结论是否成立？若成立，请加以证明；若不成立，请说明理由；（3）如图3，当点P在BC延长线上时，若∠BPO＝45°，AC＝，请直接写出BQ的长．解：（1）CP＝BQ，理由：如图1，连接OQ，由旋转知，PQ＝OP，∠OPQ＝60°⊅∴△POQ是等边三角形，∴OP＝OQ，∠POQ＝60°，在Rt△ABC中，O是AB中点，∴OC＝OA＝OB，∴∠BOC＝2∠A＝60°＝∠POQ，∴∠COP＝∠BOQ，在△COP和△BOQ中，，∴△COP≌△BOQ（SAS），∴CP＝BQ，（2）CP＝BQ，理由：如图2，连接OQ，由旋转知，PQ＝OP，∠OPQ＝60°∴△POQ是等边三角形，∴OP＝OQ，∠POQ＝60°，在Rt△ABC中，O是AB中点，∴OC＝OA＝OB，∴∠BOC＝2∠A＝60°＝∠POQ，∴∠COP＝∠BOQ，在△COP和△BOQ中，，∴△COP≌△BOQ（SAS），∴CP＝BQ，（3）如图3，在Rt△ABC中，∠A＝30°，AC＝，∴BC＝AC•tan∠A＝，过点O作OH⊥BC，∴∠OHB＝90°＝∠BCA，∴OH∥AB，∵O是AB中点，∴CH＝BC＝，OH＝AC＝，∵∠BPQ＝45°，∠OHP＝90°，∴∠BPQ＝∠PQH，∴PH＝OH＝，∴CP＝PH﹣CH＝﹣＝，连接BQ，同（1）的方法得，BQ＝CP＝．10、模型发现：同学们知道，三角形的两边之和大于第三边，即如图1，在△ABC中，AB+AC＞BC．对于图1，若把点C看作是线段AB外一动点，且AB＝c，AC＝b，则线段BC的长会因为点C的位置的不同而发生变化．因为AB、AC的长度固定，所以当∠BAC越大时，BC边越长．特别的，当点C位于线段BA的延长线上时，线段BC的长取得最大值，且最大值为b+c（用含b，c的式子表示）（直接填空）模型应用：点C为线段AB外一动点，且AB＝3，AC＝2，如图2所示，分别以AC，BC为边，作等边三角形ACD 和等边三角形BCE，连接BD，AE．（1）求证：BD＝AE．（2）线段AE长的最大值为5．模型拓展：如图3，在平面直角坐标系中，点A是y轴正半轴上的一动点，点B是x轴正半轴上的一动点，且AB ＝8．若AC⊥AB，AC＝3，试求OC长的最大值．解：当点C位于线段BA的延长线上时，线段BC的长取得最大值，最大值为b+c，故答案为：线段BA的延长线上；b+c；模型应用：（1）证明：∵△ACD、△BCE都是等边三角形，∴CD＝CA＝AD，CB＝CE，∠ACD＝60°，∠BCE＝60°，∴∠DCB＝∠ACE，在△DCB和△ACE中，，∴△DCB≌△ACE（SAS）∴BD＝AE；（2）当点D位于线段BA的延长线上时，线段BD的长取得最大值，最大值为AB+AD＝AB+AC＝3+2＝5，∵AE＝BD，∴线段AE长的最大值为5，模型拓展：取AB的中点G，连接OG、CG，在Rt△AOB中，G为AB的中点，∴OG＝AB＝4，在Rt△CAG中，CG＝＝＝5，当点O、G、C在同一条直线上时，OC最大，最大值为4+5＝9．11、已知：△ABC中，∠ACB＝90°，AC＝BC．（1）如图1，点D在BC的延长线上，连AD，过B作BE⊥AD于E，交AC于点F．求证：AD＝BF；（2）如图2，点D在线段BC上，连AD，过A作AE⊥AD，且AE＝AD，连BE交AC于F，连DE，问BD与CF有何数量关系，并加以证明；（3）如图3，点D在CB延长线上，AE＝AD且AE⊥AD，连接BE、AC的延长线交BE于点M，若AC ＝3MC，请直接写出的值．（1）证明：如图1中，∵BE⊥AD于E，∴∠AEF＝∠BCF＝90°，∵∠AFE＝∠CFB，∴∠DAC＝∠CBF，∵BC＝CA，∴△BCF≌△ACD，∴BF＝AD．（2）结论：BD＝2CF．理由：如图2中，作EH⊥AC于H．∵∠AHE＝∠ACD＝∠DAE＝90°，∴∠DAC+∠ADC＝90°，∠DAC+∠EAH＝90°，∴∠DAC＝∠AEH，∵AD＝AE，∴△ACD≌△EHA，∴CD＝AH，EH＝AC＝BC，∵CB＝CA，∴BD＝CH，∵∠EHF＝∠BCF＝90°，∠EFH＝∠BFC，EH＝BC，∴△EHF≌△BCF，∴FH＝CF，∴BD＝CH＝2CF．（3）如图3中，同法可证BD＝2CM．∵AC＝3CM，设CM＝a，则AC＝CB＝3a，BD＝2a，∴＝＝．12、已知在△ABC中，AB＝AC，射线BM、BN在∠ABC内部，分别交线段AC于点G、H．（1）如图1，若∠ABC＝60°，∠MBN＝30°，作AE⊥BN于点D，分别交BC、BM于点E、F．①求证：∠1＝∠2；②如图2，若BF＝2AF，连接CF，求证：BF⊥CF；（2）如图3，点E为BC上一点，AE交BM于点F，连接CF，若∠BFE＝∠BAC＝2∠CFE，求的值．（1）①证明：如图1中，∵AB＝AC，∠ABC＝60°∴△ABC是等边三角形，∴∠BAC＝60°，∵AD⊥BN，∴∠ADB＝90°，∵∠MBN＝30°，∠BFD＝60°＝∠1+∠BAF＝∠2+∠BAF，∴∠1＝∠2②证明：如图2中，在Rt△BFD中，∵∠FBD＝30°，∴BF＝2DF，∵BF＝2AF，∴BF＝AD，∵∠BAE＝∠FBC，AB＝BC，∴△BFC≌△ADB，∴∠BFC＝∠ADB＝90°，∴BF⊥CF（2）在BF上截取BK＝AF，连接AK．∵∠BFE＝∠2+∠BAF，∠CFE＝∠4+∠1，∴∠CFB＝∠2+∠4+∠BAC，∵∠BFE＝∠BAC＝2∠EFC，∴∠1+∠4＝∠2+∠4∴∠1＝∠2，∵AB＝AC，∴△ABK≌CAF，∴∠3＝∠4，S△ABK＝S△AFC，∵∠1+∠3＝∠2+∠3＝∠CFE＝∠AKB，∠BAC＝2∠CEF，∴∠KAF＝∠1+∠3＝∠AKF，∴AF＝FK＝BK，∴S△ABK＝S△AFK，∴＝2．13、已知，△ABC中，AB＝AC，∠BAC＝90°，E为边AC任意一点，连接BE．（1）如图1，若∠ABE＝15°，O为BE中点，连接AO，且AO＝1，求BC的长；（2）如图2，F也为AC上一点，且满足AE＝CF，过A作AD⊥BE交BE于点H，交BC于点D，连接DF交BE于点G，连接AG；①若AG平分∠CAD，求证：AH＝AC；②如图3，当G落在△ABC外时，若将△EFG沿EF边翻折，点G刚好落在AB边上点P，直接写出AG与EF的数量关系．（1）解：如图1中，在AB上取一点M，使得BM＝ME，连接ME．在Rt△ABE中，∵OB＝OE，∴BE＝2OA＝2，∵MB＝ME，∴∠MBE＝∠MEB＝15°，∴∠AME＝∠MBE+∠MEB＝30°，设AE＝x，则ME＝BM＝2x，AM＝x，∵AB2+AE2＝BE2，∴（2x+x）2+x2＝22，∴x＝（负根已经舍弃），∴AB＝AC＝（2+）•，∴BC＝AB＝+1．方法二：作EH⊥BC于H，求出BH，CH即可解决问题．（2）证明：如图2中，作CP⊥AC，交AD的延长线于P，GM⊥AC于M．∵BE⊥AP，∴∠AHB＝90°，∴∠ABH+∠BAH＝90°，∵∠BAH+∠P AC＝90°，∴∠ABE＝∠P AC，在△ABE和△CAP中，，∴△ABE≌△CAP，∴AE＝CP＝CF，∠AEB＝∠P，在△DCF和△DCP中，，∴△DCF≌△DCP，∴∠DFC＝∠P，∴∠GFE＝∠GEF，∴GE＝GF，∵GM⊥EF，∴FM＝ME，∵AE＝CF，∴AF＝CE，∴AM＝CM，在△GAH和△GAM中，，∴△AGH≌△AGM，∴AH＝AM＝CM＝AC（3）解：结论：AG＝EF．理由：如图3中，作CM⊥AC交AD的延长线于M，连接PG交AC于点O．由（2）可知△ACM≌△BAE，△CDF≌△CDM，∴∠AEB＝∠M＝∠GEF，∠M＝∠CFD＝∠GFE，AE＝CM＝CF，∴∠GEF＝∠GFE，∴GE＝GF，∵△EFP是由△EFG翻折得到，∴EG＝EP＝GF＝PF，∴四边形EGFP是菱形，∴PG⊥AC，OE＝OF，∵AE＝CF，∴AO＝OC，∵AB∥OP，∴BP＝PC，∵PF∥BE，∴EF＝CF＝AE，∵PB＝PC，AO＝OC，∴PO＝OG＝AB，∴AB＝PG，AB∥PG，∴四边形ABPG是平行四边形，∴AG∥BC，∴∠GAO＝∠ACB＝45°，设EO＝OF＝a，则OA＝OG＝3a，AG＝3a，∴＝＝，∴AG＝EF14、如图所示，Rt△ABC中，∠ACB＝90°，E为AC中点，作ED⊥AC交AB于D，连接CD；（1）如图1，求证：AB＝2CD；（2）如图2，作CF⊥AB交AB于F，点G为CF上一点，点H为DE延长线上一点，分别连接AH、GH，若∠AHG＝2∠B，求证：AH＝GH；（3）如图3，在（2）的条件下，连接DG，且有DE＝BF，∠EDG＝90°，若AC＝6，求AH的长度．解：（1）∵E为AC中点，作ED⊥AC交AB于D，∴AD＝CD，∵∠ACB＝90°，∴BC∥DE，∴AD＝BD，∴CD＝BD，∴AB＝2CD；（2）如图2，连接CH，∵点E是AC的中点，∴AE＝CE，∵DE⊥AC，∴CH＝AH，∴∠ACH＝∠CAH，∵∠ACB＝90°，∴∠B+∠BAC＝90°，∵CF⊥AB，∴∠BAC+∠ACF＝90°，∴∠ACF＝∠B，∴∠HCG＝∠ACH+∠ACF＝∠CAH+∠B，∠AHG＝2∠B∴在四边形AHGF中，∠AFG+∠FGH+∠AHG+∠F AH＝360°，∴∠FGH＝360°﹣（∠AFG+∠AHG+∠F AH）＝360°﹣（90°+2∠B+∠CAH+∠BAC）＝360°﹣（90°+2∠B+∠CAH+90°﹣∠B）＝360°﹣（180°+∠B+∠CAH）＝180°﹣（∠B+∠CAH），∵∠CGH＝180°﹣∠FGH＝∠B+∠CAH＝∠HCG，∴CH＝GH，∵CH＝AH，∴AH＝GH；（3）如图3，由（1）知，DE∥BC，∴∠B＝∠ADE，在△BFC和△DEA中，，∴△BFC≌△DEA，∴BC＝AD，∵AD＝BD＝CD，∴BC＝BD＝CD，∴△BCD是等边三角形，∴∠B＝60°，在Rt△ABC中，AC＝6，∴BC＝2，AB＝4，∵CF⊥BD，∴DF＝，CF＝3，∵∠BAC＝30°，∴∠ADE＝60°，∵∠EDG＝90°，∠FDG＝30°，在Rt△DFG中，DF＝，∴FG＝1，DG＝2，∴CG＝CF﹣FG＝2过点H作HN⊥CF，由（2）知，CH＝GH，∴NG＝CG＝1，∴FN＝NG+FG＝2，过点H作HM⊥AB，∴∠FMH＝∠NFM＝∠HNF＝90°，∴四边形NFMH是矩形，∴HM＝FN＝2，在Rt△DMH中，∠ADE＝60°，HM＝2，∴DH＝，在Rt△HDG中，根据勾股定理得，HG＝＝．15、【问题情境】一节数学课后，老师布置了一道课后练习题：如图：已知在Rt△ABC中，AC＝BC，∠ACB＝90°，CD⊥AB于点D，点E、F分别在A和BC上，∠1＝∠2，FG⊥AB于点G，求证：△CDE≌△EGF．（1）阅读理解，完成解答本题证明的思路可用下列框图表示：根据上述思路，请你完整地书写这道练习题的证明过程；（2）特殊位置，证明结论若CE平分∠ACD，其余条件不变，求证：AE＝BF；（3）知识迁移，探究发现如图，已知在Rt△ABC中，AC＝BC，∠ACB＝90°，CD⊥AB于点D，若点E是DB的中点，点F在直线CB上且满足EC＝EF，请直接写出AE与BF的数量关系．（不必写解答过程）（1）证明：∵AC＝BC，∠ACB＝90°，∴∠A＝∠B＝45°，∵CD⊥AB，∴∠CDB＝90°，∴∠DCB＝45°，∵∠ECF＝∠DCB+∠1＝45°+∠1，∠EFC＝∠B+∠2＝45°+∠2，∠1＝∠2，∴∠ECF＝∠EFC，∴CE＝EF，∵CD⊥AB，FG⊥AB，∴∠CDE＝∠EGF＝90°，在△CDE和△EGF中，，∴△CDE≌△EGF（AAS）；（2）证明：由（1）得：CE＝EF，∠A＝∠B，∵CE平分∠ACD，∴∠ACE＝∠1，∵∠1＝∠2，∴∠ACE＝∠2，在△ACE和△BEF中，，∴△ACE≌△BEF（AAS），∴AE＝BF；（3）AE＝BF，作EH⊥BC与H，如图3所示：设DE＝x，根据题意得：BE＝DE＝x，AD＝BD＝2x，CD＝AD＝2x，AE＝3x，根据勾股定理得：BC＝AC＝2x，∵∠ABC＝45°，EH⊥BC，∴BH＝x，∴CH＝BC﹣BH＝x，∵EC＝EF，∴FH＝CH＝x，∴BF＝x﹣x＝x，∴＝，∴AE＝．16、在正方形ABCD和等腰直角△BGF中，∠BGF＝90°，P是DF的中点，连接PG、PC．（1）如图1，当点G在BC边上时，延长GP交DC于点E．求证：PG＝PC；（2）如图2，当点F在AB的延长线上时，（1）中的结论是否成立？请证明你的结论；（3）如图3，若四边形ABCD为菱形，且∠ABC＝60°，△BGF为等边三角形，点F在CB的延长线。

初中数学四边形、三角形几何综合题目汇总(动点、旋转)大全

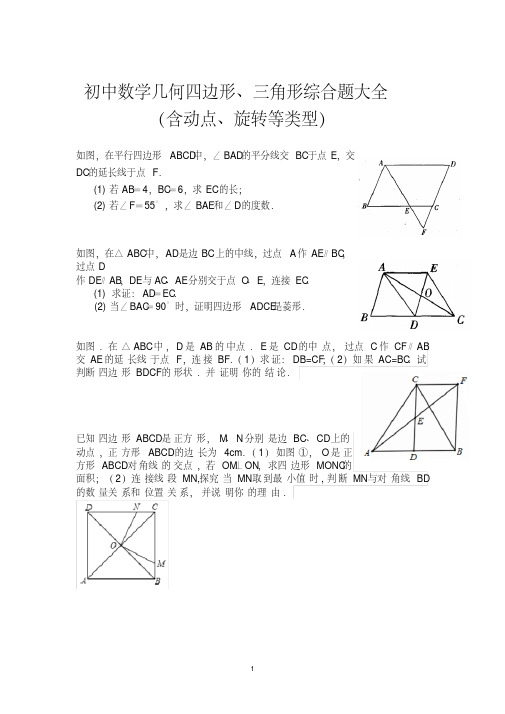
初中数学几何四边形、三角形综合题大全（含动点、旋转等类型）如图，在平行四边形ABCD中，∠BAD的平分线交BC于点E，交DC的延长线于点F．(1)若AB＝4，BC＝6，求EC的长；(2)若∠F＝55°，求∠BAE和∠D的度数．如图，在△ABC中，AD是边BC上的中线，过点A作AE∥BC，过点D作DE∥AB，DE与AC、AE分别交于点O、E，连接EC．(1)求证：AD＝EC．(2)当∠BAC＝90°时，证明四边形ADCE是菱形．如图．在△ABC中，D是AB的中点．E是CD的中点，过点C作CF∥AB 交AE的延长线于点F，连接BF．（1）求证：DB=CF；（2）如果AC=BC．试判断四边形BDCF的形状．并证明你的结论．已知四边形ABCD是正方形，M、N分别是边BC、CD上的动点，正方形ABCD的边长为4cm．（1）如图①，O是正方形ABCD对角线的交点，若OM⊥ON，求四边形MONC的面积；（2）连接线段MN,探究当MN取到最小值时,判断MN与对角线BD 的数量关系和位置关系，并说明你的理由．已知四边形ABCD 是边长为2的菱形，∠BAD =60°，对角线AC 与BD 交于点O ，过点O 的直线EF 交AD 于点E ，交BC 于点F ．（1）求证：△AOE ≌△COF ；（2）若∠EOD =30°，求CF 的长．已知，如图，在Rt △ABC 中，CD 是斜边上的中线，DE ⊥AB 交BC 于点F ，交AC 的延长线于点E ．(1)△ADE ∽△FDB 吗?为什么?(2)你能推出结论CD 2=DE ·DF 吗?请试一试．如图，在四边形ABCD 中，AC 、BC 相交于点O ，∠ABD=∠ACD ，试找出图中的相似三角形，并加以证明．如图，E 、F 是□ABCD 的对角线AC 上的两点，且AE =CF ．请你以点F 为一个端点与图中已标明字母的某一点连成一条线段，猜想并说明它与图中已有的某一条线段相等（只需说明一组线段相等即可）．（1）连结；（2）猜想：=；（3）证明：如图，将?ABCD 的边DC 延长到点E ，使CE=DC ，连接AE ，交BC 于点F ．（1）求证：△ABF ≌△ECF ；（2）若∠AFC=2∠D ，连接AC 、BE ，求证：四边形ABEC 是矩形．ODCBABCDE FA在平行四边形ABCD中，过点D作DE⊥AB于点E，点F 在边CD上，DF=BE，连接AF，BF．（1）求证：四边形BFDE是矩形；（2）若CF=3，BF=4，DF=5，求证：AF平分∠DAB如图，在四边形ABCD中，∠ABC=90°，AC=AD，M，N分别为AC，AD的中点，连接BM，MN，BN．(1)求证：BM=MN；(2) ∠BAD=60°，AC平分∠BAD ，AC=2，求BN的长。

专题21 与三角形四边形相关的压轴题-2022年中考数学真题分项汇编(全国通用)(第2期)(解析版)

专题21 与三角形、四边形相关的压轴题解答题1．（2022·黑龙江）如图，在平面直角坐标系中，平行四边形ABCD 的边AB 在x 轴上，顶点D 在y 轴的正半轴上，M 为BC 的中点，OA 、OB 的长分别是一元二次方程27120x x -+=的两个根()OA OB <，4tan 3DAB ∠=，动点P 从点D 出发以每秒1个单位长度的速度沿折线DC CB -向点B 运动，到达B 点停止．设运动时间为t 秒，APC △的面积为S ．(1)求点C 的坐标；(2)求S 关于t 的函数关系式，并写出自变量t 的取值范围；(3)在点P 的运动过程中，是否存在点P ，使CMP 是等腰三角形？若存在，请直接写出点P 的坐标；若不存在，请说明理由．【答案】(1)点C 坐标为()7,4 (2)()()14207149871255t t S t t ⎧-≤<⎪=⎨-<≤⎪⎩(3)存在点P ()4,4或9,42⎛⎫ ⎪⎝⎭或59,412⎛⎫ ⎪⎝⎭，使CMP 是等腰三角形【分析】（1）先求出方程的解，可得3OA =，4OB =，再由4tan 3DAB ∠=，可得4OD =，然后根据四边形ABCD 是平行四边形，可得CD =7，90ODC AOD ∠=∠=︒，即可求解；（2）分两种情况讨论：当07t <时，当712t <时，过点A 作AF BC ⊥交CB 的延长线于点F ，即可求解；（3）分三种情况讨论：当CP =PM 时，过点M 作MF ⊥PC 于点F ；当52PC CM ==时；当PM =CM 时，过点M 作MG ⊥PC 于点G ，即可求解．(1)解：27120x x -+=，解得13x =，24x =，∵OA OB <，∴3OA =，4OB =， ∵4tan 3DAB ∠=， ∴43OD OA =， ∴4OD =，∵四边形ABCD 是平行四边形，∴347DC AB ==+=，DC AB ∥，∴点C 坐标为()7,4；(2)解：当07t <时，()117414222S CP OD t t =⋅=-⋅=-，当712t <时，过点A 作AF BC ⊥交CB 的延长线于点F ，如图，5AD ，∵四边形ABCD 是平行四边形，∴5BC AD ==，∵BC AF AB OD ⋅=⋅，∴574AF ⋅=⨯， ∴285AF =， ∴()11281498722555S CP AF t t =⋅=-⋅=-， ∴()()14207149871255t t S t t ⎧-≤<⎪=⎨-<≤⎪⎩；(3)解：存在点P ，使CMP 是等腰三角形，理由如下：根据题意得：当点P 在CD 上运动时，CMP 可能是等腰三角形，∵四边形ABCD 是平行四边形，∴∠C =∠BAD ，BC =AD =5， ∴4tan tan 3C DAB =∠=， ∵点M 为BC 的中点，∴52CM =，当CP =PM 时，过点M 作MF ⊥PC 于点F ，∴3,22CF FM ==，设PC =PM =a ，则PD =7-a ，32PF a =-， ∵PF 2+FM 2=PM 2， ∴222322a a ⎛⎫-+= ⎪⎝⎭，解得：2512a =， ∴59712DP PC =-=， ∴此时点P 59,412⎛⎫ ⎪⎝⎭；当52PC CM ==时，∴972PD PC =-=， ∴此时点P 9,42⎛⎫ ⎪⎝⎭；当PM =CM 时，过点M 作MG ⊥PC 于点G ，则32CG =，∴23PC CG ==，∴PD =7-PC =4，∴此时点P ()4,4；综上所述，存在点P ()4,4或9,42⎛⎫ ⎪⎝⎭或59,412⎛⎫ ⎪⎝⎭，使CMP 是等腰三角形【点睛】本题主要考查了平行四边形的性质，坐标与图形，等腰三角形的性质，解直角三角形，熟练掌握相关知识点，并利用数形结合思想解答是解题的关键．2．（2022·贵州黔东南）阅读材料：小明喜欢探究数学问题，一天杨老师给他这样一个几何问题：如图，ABC 和BDE 都是等边三角形，点A 在DE 上．求证：以AE 、AD 、AC 为边的三角形是钝角三角形．(1)【探究发现】小明通过探究发现：连接DC ，根据已知条件，可以证明DC AE =，120ADC =∠︒，从而得出ADC 为钝角三角形，故以AE 、AD 、AC 为边的三角形是钝角三角形．请你根据小明的思路，写出完整的证明过程．(2)【拓展迁移】如图，四边形ABCD 和四边形BGFE 都是正方形，点A 在EG 上．①试猜想：以AE 、AG 、AC 为边的三角形的形状，并说明理由．②若2210AE AG +=，试求出正方形ABCD 的面积．【答案】(1)钝角三角形；证明见详解(2)①直角三角形；证明见详解；②S 四边形ABCD =5【分析】（1）根据等边三角形性质得出，BE =BD ，AB =CB ，∠EBD =∠ABC =60°，再证△EBA ≌△DBC （SAS ）∠AEB =∠CDB =60°，AE =CD ，求出∠ADC =∠ADB +∠BDC =120°，可得△ADC 为钝角三角形即可；（2）①以AE 、AG 、AC 为边的三角形是直角三角形，连结CG ，根据正方形性质，得出∠EBG =∠ABC ，EB =GB ，AB =CB ，∠BEA =∠BGE =45°，再证△EBA ≌△GBC （SAS ）得出AE =CG ，∠BEA =∠BGC =45°，可证△AGC 为直角三角形即可；②连结BD ，根据勾股定理求出AC面积公式求解即可．(1)证明：∵△ABC 与△EBD 均为等边三角形，∴BE =BD ，AB =CB ，∠EBD =∠ABC =60°，∴∠EBA +∠ABD =∠ABD +∠DBC ，∴∠EBA =∠DBC ，在△EBA 和△DBC 中，EB DB EBA DBC AB CB =⎧⎪∠=∠⎨⎪=⎩，∴△EBA ≌△DBC （SAS ），∴∠AEB =∠CDB =60°，AE =CD ，∴∠ADC =∠ADB +∠BDC =120°，∴△ADC 为钝角三角形，∴以AE 、AD 、AC 为边的三角形是钝角三角形．(2)证明：①以AE 、AG 、AC 为边的三角形是直角三角形．连结CG ，∵四边形ABCD 和四边形BGFE 都是正方形，∴∠EBG =∠ABC ，EB =GB ，AB =CB ，∵EG 为正方形的对角线，∴∠BEA =∠BGE =45°，∴∠EBA +∠ABG =∠ABG +∠GBC =90°，∴∠EBA =∠GBC ，在△EBA 和△GBC 中，G EB B EBA GBC AB CB =⎧⎪∠=∠⎨⎪=⎩，∴△EBA ≌△GBC （SAS ），∴AE =CG ，∠BEA =∠BGC =45°，∴∠AGC =∠AGB +∠BGC =45°+45°=90°，∴△AGC 为直角三角形，∴以AE 、AG 、AC 为边的三角形是直角三角形；②连结BD ，∵△AGC 为直角三角形，2210AE AG +=，∴AC∴四边形ABCD 为正方形，∴AC =BD∴S 四边形ABCD =211522AC BD AC ⋅==．【点睛】本题考查等边三角形的性质，三角形全等判定与性质，正方形的性质，勾股定理，掌握等边三角形的性质，三角形全等判定与性质，正方形的性质，勾股定理是解题关键．3．（2022·海南）如图1，矩形ABCD 中，6,8AB AD ==，点P 在边BC 上，且不与点B 、C 重合，直线AP 与DC 的延长线交于点E ．(1)当点P 是BC 的中点时，求证：ABP ECP △≌△；(2)将APB △沿直线AP 折叠得到APB '，点B '落在矩形ABCD 的内部，延长PB '交直线AD 于点F ． ①证明FA FP =，并求出在（1）条件下AF 的值；②连接B C '，求PCB '△周长的最小值；③如图2，BB '交AE 于点H ，点G 是AE 的中点，当2EAB AEB ∠=∠''时，请判断AB 与HG 的数量关系，并说明理由．【答案】(1)见解析(2)①见解析；132AF =；②12,；③2AB HG =，见解析【分析】（1）根据矩形的性质得到AB DE ∥，再结合P 是BC 的中点证明ABP ECP △≌△；（2）①设FA x =，在Rt AB F '中，表示出三角形的其他两边，再由勾股定理列方程计算即可； ②当点B '恰好位于对角线AC 上时，CB AB '+'最小，利用勾股定理计算即可；③过点B '作B M DE '∥，交AE 于点M ，证明B M EM AB AB ===''，再由11()22HG AG AH AE AM EM =-=-=即可得到12HG AB =． (1)解：如图9-1，在矩形ABCD 中，AB DC ，即AB DE ∥，∴1,2E B ∠=∠∠=∠．∵点P 是BC 的中点，∴BP CP =．∴(AAS)ABP ECP △≌△．(2)①证明：如图9-2，在矩形ABCD 中，AD BC ∥，∴3FAP ∠=∠．由折叠可知34∠=∠，∴4FAP ∠=∠．∴FA FP =．在矩形ABCD 中，8BC AD ==，∵点P 是BC 的中点， ∴118422BP BC ==⨯=．由折叠可知6,4AB AB PB PB ==='='，90B AB P AB F ∠=∠=∠=''︒．设FA x =，则FP x =．∴4FB x '=-．在Rt AB F '中，由勾股定理得222AF B A B F '+'=，∴2226(4)x x =+-，∴132x =，即132AF =． ②解：如图9-3，由折叠可知6A B B A '==，B P BP '=．∴8PCB C CP PB CB CB CB CB '''=+'+=+=+'△．由两点之间线段最短可知，当点B '恰好位于对角线AC 上时，CB AB '+'最小．连接AC ，在Rt ADC 中，90D ∠=︒，∴10AC ==，∴1064CB AC AB =-'='-=最小值， ∴88412PCB C CB '=+'=+=最小值．③解：AB 与HG 的数量关系是2AB HG =．理由是：如图9-4，由折叠可知16,,AB AB BB AE ∠=∠=⊥''．过点B '作B M DE '∥，交AE 于点M ，∵AB DE ∥，∴AB DE B M '∥∥，∴165AED ∠=∠=∠=∠．∴AB B M AB ''==，∴点H 是AM 中点．∵2EAB AEB ∠=∠''，即628∠=∠，∴528∠=∠．∵578∠=∠+∠，∴78∠=∠．∴B M EM '=．∴B M EM AB AB ===''．∵点G 为AE 中点，点H 是AM 中点， ∴11,22AG AE AH AM ==． ∴11()22HG AG AH AE AM EM =-=-=． ∴12HG AB =． ∴2AB HG =．【点睛】此题考查了矩形的性质、折叠问题、勾股定理、全等三角形的判定、等腰三角形的性质，关键是作出辅助线，根据等腰三角形的性质证明．4．（2022·吉林）如图，在ABC 中，90ACB ∠=︒，30A ∠=︒，6cm =AB ．动点P 从点A 出发，以2cm/s 的速度沿边AB 向终点B 匀速运动．以PA 为一边作120APQ ∠=︒，另一边PQ 与折线AC CB -相交于点Q ，以PQ 为边作菱形PQMN ，点N 在线段PB 上．设点P 的运动时间为(s)x ，菱形PQMN 与ABC 重叠部分图形的面积为2()cm y ．(1)当点Q 在边AC 上时，PQ 的长为 cm ；（用含x 的代数式表示）(2)当点M 落在边BC 上时，求x 的值；(3)求y 关于x 的函数解析式，并写出自变量x 的取值范围．【答案】(1)2x(2)1(3)22201312332x y x x ⎧⎪≤≤⎪⎪=-+-≤⎨⎪⎪-+≤≤⎪⎩＜【分析】（1）先证明∠A =∠AQP =30°，即AP =PQ ，根据题意有AP =2x ，即PQ =2x ；（2）当M 点在BC 上，Q 点在AC 上，在（1）中已求得AP =PQ =2x ，再证明△MNB 是等边三角形，即有BN =MN ，根据AB =6x =6cm ，即有x =1（s ）；（3）分类讨论：当01x ≤＜时，此时菱形PQMN 在△ABC 的内部，此时菱形PQMN 与△ABC 重叠的面积即是菱形PQMN 的面积，过Q 点作QG ⊥AB 于G 点，求出菱形的面积即可；当x ＞1，且Q 点在线段AC 上时，过Q 点作QG ⊥AB 于G 点，设QM 交BC 于F 点，MN 交BC 于E 点，过M 点作NH ⊥EF 于H 点，先证明△ENB 是等边三角形、△MEF 是等边三角形，重叠部分是菱形PQMN 的面积减去等边△MEF 的面积，求出菱形PQMN 的面积和等边△MEF 的面积即可，此时需要求出当Q 点在C 点时的临界条件；当332x ≤＜时，此时Q 点在线段BC 上，此时N 点始终与B 点重合，过Q 点作QG ⊥AB 于G 点，重叠部分的面积就是△PBQ 的面积，求出等边△PBQ 的面积即可．(1)当Q 点在AC 上时，∵∠A =30°，∠APQ =120°，∴∠AQP =30°，∴∠A =∠AQP ，∴AP =PQ ，∵运动速度为每秒2cm ，运动时间为x 秒，∴AP =2x ，∴PQ =2x ；(2)当M 点在BC 上，Q 点在AC 上，如图，在（1）中已求得AP =PQ =2x ，∵四边形QPMN 是菱形，∴PQ =PN =MN =2x ，PQ MN ∥，∵∠APQ =120°，∴∠QPB =60°，∵PQ MN ∥，∴∠MNB =∠QPB =60°，∵在Rt △ABC 中，∠C =90°，∠A =30°，∴∠B =60°，∴△MNB 是等边三角形，∴BN =MN ，∴AB =AP +PN +BN =2x ×3=6x =6cm ，∴x =1（s ）；(3)当P 点运动到B 点时，用时6÷2=3（s ），即x 的取值范围为：03x ≤≤，当M 点刚好在BC 上时，在（2）中已求得此时x =1，分情况讨论，即当01x ≤＜时，此时菱形PQMN 在△ABC 的内部，∴此时菱形PQMN 与△ABC 重叠的面积即是菱形PQMN 的面积，过Q 点作QG ⊥AB 于G 点，如图，∵∠APQ =120°，∴∠QPN =60°，即菱形PQMN 的内角∠QPN =∠QMN =60°，∴QG =PQ ×sin ∠QPN =2x ，∴重叠的面积等于菱形PQMN 的面积为，即为：22y PN QG x =⨯==；当x ＞1，且Q 点在线段AC 上时，过Q 点作QG ⊥AB 于G 点，设QM 交BC 于F 点，MN 交BC 于E 点，过M 点作NH ⊥EF 于H 点，如图，∵PQ MN ∥，∴∠MNB =∠QPN =60，∵∠B =60°，∴△ENB 是等边三角形，同理可证明△MEF 是等边三角形∴BN =NE ，∠MEF =60°，ME =EF ，∵AP =PQ =PN =MN =2x ，AB =6，∴BN =6-AN =6-4x ，∴ME =MN -NE =2x -BN =6x -6，∵MH ⊥EF ，∴MH =ME ×sin ∠MEH =(6x -6)×sin60°=(3x -∴△MEF 的面积为：2(3311(66)1)22MEF S EF MH x x x =⨯⨯=-⨯-⨯=-△，QG =PQ ×sin ∠QPN =2x ，∵菱形PQMN 的面积为22PN QG x ⨯==，∴重叠部分的面积为2221)MEF PQMN y S S x =-=--=-+-△菱形当Q 点与C 点重合时，可知此时N 点与B 点重合，如图，∵∠CPB =∠CBA =60°，∴△PBC 是等边三角形，∴PC =PB ，∵AP =PQ =2x ，∴AP =PB =2x ，∴AB =AP +PB =4x =6，则x =32，即此时重合部分的面积为：2y =-+-312x ≤＜；当332x ≤＜时，此时Q 点在线段BC 上，此时N 点始终与B 点重合，过Q 点作QG ⊥AB 于G 点，如图，∵AP =2x ，∴PB =AB -AP =6-2x ，∵∠QPB =∠ABC =60°，∴△PQB 是等边三角形，∴PQ =PB ，同时印证菱形PQMN 的顶点N 始终与B 点重合，∴QG =PQ ×sin ∠QPN =(6-2x )x -，∴211(62))22PBQ S x PB QG x =⨯⨯=⨯---=+△∴此时重叠部分的面积2PBQ y S ==-+△综上所述：22201312332x y x x ⎧⎪≤≤⎪⎪=-+-≤⎨⎪⎪-+≤≤⎪⎩＜．【点睛】本题考查了一次函数的应用、菱形的性质、等边三角形的判定与性质、等腰三角形的判定与性质、解直角三角形等知识，理清运动过程中Q 点的位置以及菱形PQMN 的位置是解答本题的关键．解答本题需要注意分类讨论的思想．5．（2022·黑龙江牡丹江）在菱形ABCD 和正三角形BGF 中，60ABC ∠=︒，P 是DF 的中点，连接PG 、PC ．(1)如图1，当点G 在BC 边上时，写出PG 与PC 的数量关系．（不必证明）(2)如图2，当点F 在AB 的延长线上时，线段PC 、PG 有怎样的数量关系，写出你的猜想，并给予证明；(3)如图3，当点F 在CB 的延长线上时，线段PC 、PG 又有怎样的数量关系，写出你的猜想（不必证明）．【答案】(1)PG =(2)PG =，证明见解析(3)PG =【分析】（1）延长GP 交DC 于点E ，利用()PED PGF SAS △≌△，得出PE PG =，DE FG =，得到CE CG =，CP 是EG 的中垂线，在Rt CPG 中，60PCG ∠=︒，利用正切函数即可求解；（2）延长GP 交DA 于点E ，连接EC ，GC ，先证明()DPE FPG ASA △≌△，再证明()CDE CBG SAS △≌△，利用在Rt CPG 中，60PCG ∠=︒，即可求解；（3）延长GP 到H ，使PH PG =，连接CH ，CG ，DH ，作FE ∥DC ，先证GFP HDP △≌△，再证HDC GBC ≌△△，利用在Rt CPG 中，60PCG ∠=︒，即可求解．(1)解：如图1，延长GP 交DC 于点E ，∵P 是DF 的中点，∴PD=PF ，∵BGF 是正三角形，∴60BGF ∠=︒，∵60ABC ∠=︒，∴BGF ABC ∠=∠，∴AB GF ，∵四边形ABCD 是菱形，∴AB CD ，∴CD GF ∥，∴CDP PFG ∠=∠，在PED 和PGF 中，DPE FPG DP PFCDP PFG ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∴()PED PGF SAS △≌△，∴PE PG =，DE FG =，∵BGF 是正三角形，∴FG BG =，∵四边形ABCD 是菱形，∴CD CB =，CE CG ∴=，CP ∴是EG 的中垂线，在Rt CPG 中，60PCG ∠=︒，tan tan 60PG PCG PC PC ∴=∠⋅=︒⋅= ．(2)解：PG =，理由如下：如图2，延长GP 交DA 于点E ，连接EC ，GC ，60ABC ∠=︒，BGF 正三角形，∴GF BC AD ，EDP GFP ∴∠=∠，在DPE 和FPG 中，EDP GFP DP FPDPE FPG ∠=∠⎧⎪=⎨⎪∠=∠⎩()DPE FPG ASA ∴△≌△PE PG ∴=，DE FG BG ==，60CDE CBG ∠=∠=︒，CD CB =，在CDE △和CBG 中，60CD CB CDE CBG CD CB =⎧⎪∠=∠=︒⎨⎪=⎩()CDE CBG SAS ∴△≌△CE CG ∴=，DCE BCG ∠=∠，120ECG DCB ∴∠=∠=︒，PE PG =，CP PG ∴⊥，1602PCG ECG ∠=∠=︒(3)解：猜想：PG = ．证明：如图3，延长GP 到H ，使PH PG =，连接CH ，CG ，DH ，作FE DC ，P 是线段DF 的中点，FP DP ∴=，GPF HPD ∠=∠，GFP HDP ∴△≌△，GF HD ∴=，GFP HDP ∠=∠，120GFP PFE ∠+∠=︒，PFE PDC ∠=∠，120CDH HDP PDC ∴∠=∠+∠=︒，四边形ABCD 是菱形，CD CB ∴=，60ADC ABC ∠=∠=︒，点A 、B 、G 又在一条直线上，120GBC ∴∠=︒，四边形BEFG 是菱形，GF GB ∴=，HD GB ∴=，HDC GBC ∴△≌△，CH CG ∴=，DCH BCG ∠=∠，120DCH HCB BCG HCB ∴∠+∠=∠+∠=︒，即120HCG ∠=︒CH CG =，PH PG =，PG PC ∴⊥，60GCP HCP ∠=∠=︒，【点睛】本题主要考查了等边三角形的性质、菱形的性质、全等三角形的判定和性质、解直角三角形． 6．（2022·内蒙古呼和浩特）下面图片是八年级教科书中的一道题：如图，四边形ABCD 是正方形，点E 是边BC 的中点，90AEF ∠=︒，且EF 交正方形外角的平分线CF 于点F ．求证AE EF =．（提示：取AB 的中点G ，连接EG ．）(1)请你思考题中“提示”，这样添加辅助线的意图是得到条件：；(2)如图1，若点E 是BC 边上任意一点（不与B 、C 重合），其他条件不变．求证：AE EF =；(3)在（2）的条件下，连接AC ，过点E 作EP ⊥AC ，垂足为P ．设=BE k BC，当k 为何值时，四边形ECFP 是平行四边形，并给予证明．【答案】(1)AG=CE (2)过程见解析(3)13，证明过程见解析【分析】对于（1），根据点E 是BC 的中点，可得答案；对于（2），取AG=EC ，连接EG ，说明△BGE 是等腰直角三角形，再证明△GAE ≌△CEF ，可得答案；对于（3），设BC=x ，则BE =kx ，则GE =，(1)EC k x =-，再利用等腰直角三角形的性质表示EP 的长，利用平行四边形的判定得只要EP=FC ，即可解决问题．(1)解：∵E 是BC 的中点，∴BE=CE ．∵点G 是AB 的中点，∴BG=AG ，∴AG=CE ．故答案为：AG=CE ；(2)取AG=EC ，连接EG ．∵四边形ABCD 是正方形， ∴AB=BC ，∠B =90°．∵AG=CE ，∴BG=BE ，∴△BGE 是等腰直角三角形， ∴∠BGE=∠BEG=45°，∴∠AGE =135°．∵四边形ABCD 是正方形， ∴∠BCD=90°．∵CF 是正方形ABCD 外角的平分线， ∴∠DCF=45°，∴∠ECF=90°+45°=135°． ∵AE ⊥EF ，∴∠AEB +∠FEC =90°．∵∠BAE +∠AEB =90°，∴∠BAE=∠CEF ，∴△GAE ≌△CEF ，∴AE=EF ；(3)当13k =时，四边形PECF 是平行四边形．如图．由（2）得，△GAE ≌△CEF ， ∴CF=EG ．设BC=x ，则BE =kx ，∴GE =，(1)EC k x =-． ∵EP ⊥AC ，∴△PEC 是等腰直角三角形，∴∠PEC=45°，∴∠PEC+∠ECF =180°，)PE k x =-． ∴PE CF ∥，当PE=CF 时，四边形PECF 是平行四边形，)k x -=，解得13k =．【点睛】这是一道关于四边形的综合问题，主要考查了正方形的性质，全等三角形的性质和判定，平行四边形的判定等知识．7．（2022·福建）已知ABC DEC ≌△△，AB ＝AC ，AB ＞BC ．(1)如图1，CB 平分∠ACD ，求证：四边形ABDC 是菱形；(2)如图2，将（1）中的△CDE 绕点C 逆时针旋转（旋转角小于∠BAC ），BC ，DE 的延长线相交于点F ，用等式表示∠ACE 与∠EFC 之间的数量关系，并证明；(3)如图3，将（1）中的△CDE 绕点C 顺时针旋转（旋转角小于∠ABC ），若BAD BCD ∠=∠，求∠ADB 的度数．【答案】(1)见解析(2)180ACE EFC ∠+∠=︒，见解析(3)30°【分析】（1）先证明四边形ABDC 是平行四边形，再根据AB ＝AC 得出结论；（2）先证出ACF CEF ∠=∠，再根据三角形内角和180CEF ECF EFC ∠+∠+∠=︒，得到180ACF ECF EFC ∠+∠+∠=︒，等量代换即可得到结论；（3）在AD 上取一点M ，使得AM ＝CB ，连接BM ，证得ABM CDB △△≌，得到MBA BDC ∠=∠，设BCD BAD α∠=∠=，BDC β∠=，则ADB αβ∠=+，得到α+β的关系即可．(1)∵ABC DEC ≌△△，∴AC ＝DC ，∵AB ＝AC ，∴∠ABC ＝∠ACB ，AB ＝DC ，∵CB 平分∠ACD ，∴ACB DCB ∠=∠，∴ABC DCB ∠=∠，∴AB CD ∥，∴四边形ABDC 是平行四边形，又∵AB ＝AC ，∴四边形ABDC 是菱形；(2)结论：180ACE EFC ∠+∠=︒．证明：∵ABC DEC ≌△△，∴ABC DEC ∠=∠，∵AB ＝AC ，∴A ABC CB =∠∠，∴ACB DEC ∠=∠，∵180ACB ACF DEC CEF ∠+∠=∠+∠=︒，∴ACF CEF ∠=∠，∵180CEF ECF EFC ∠+∠+∠=︒，∴180ACF ECF EFC ∠+∠+∠=︒，∴180ACE EFC ∠+∠=︒；(3)在AD 上取一点M ，使得AM ＝CB ，连接BM ，∵AB ＝CD ，BAD BCD ∠=∠，∴ABM CDB △△≌，∴BM ＝BD ，MBA BDC ∠=∠，∴ADB BMD ∠=∠，∵BMD BAD MBA ∠=∠+∠，∴ADB BCD BDC ∠=∠+∠，设BCD BAD α∠=∠=，BDC β∠=，则ADB αβ∠=+，∵CA ＝CD ，∴2CAD CDA αβ∠=∠=+，∴2BAC CAD BAD β∠=∠-∠=， ∴()1180902ACB BAC β∠=︒-∠=︒-， ∴()90ACD βα∠=︒-+，∵180ACD CAD CDA ∠+∠+∠=︒，∴()()9022180βααβ︒-+++=︒，∴30αβ+=︒，即∠ADB ＝30°．【点睛】本题考查了菱形的判定定理、全等三角形的判定和性质、三角形内角和定理等，灵活运用知识，利用数形结合思想，做出辅助线是解题的关键．8．（2022·湖南衡阳）如图，在菱形ABCD 中，4AB =，60BAD ∠=︒，点P 从点A 出发，沿线段AD 以每秒1个单位长度的速度向终点D 运动，过点P 作PQ AB ⊥于点Q ，作PM AD ⊥交直线AB 于点M ，交直线BC 于点F ，设PQM 与菱形ABCD 重叠部分图形的面积为S （平方单位），点P 运动时间为t （秒）．(1)当点M 与点B 重合时，求t 的值；(2)当t 为何值时，APQ 与BMF 全等；(3)求S 与t 的函数关系式；(4)以线段PQ 为边，在PQ 右侧作等边三角形PQE ，当24t ≤≤时，求点E 运动路径的长．【答案】(1)2t = (2)4t =或43t =(3)())220224t S t ≤≤=⎨⎪+-<≤⎪⎩【分析】（1）画出图形，根据30°直角三角形求解即可；（2）根据全等的性质计算即可，需要注意分类讨论；（3）利用面积公式计算即可，需要根据M 在B 点左边和右边分类讨论；（4）先确定E 点的运动轨迹是一条直线，再根据24t ≤≤求点E 运动路径的长．(1)M 与B 重合时，∵60A ∠=︒， ∴122PA AB ==， ∴2t =.(2)①当02t ≤≤时，∵2AM t =，∴42BM t =-，∵APQ BMF △≌△，∴AP BM =，∴42t t =-， ∴43t =. ②当24t <≤，∵2AM t =，∴24BM t =-，∵APQ BMF △≌△，∴AP BM =，∴24t t =-，∴4t =.∴4t =或43t =.(3)①当02t ≤≤时，PQ =， ∴32MQ t =，∴2PQM S S ==△. ②当24t <≤时，∵2BF t =-，)2MF t -，∴22)BFM S t =-△，∴2PQM BFM S S S =-=+-△△∴22,0224t S t ≤≤=⎨⎪+-<≤⎪⎩. (4)连接AE .∵PQE 为正三角形，∴PE =，在Rt △APE 中，2tan PE PAE PA t ∠=== ∴PAE ∠为定值.∴E 的运动轨迹为直线，AE =，当2t =时AE =当4t =时=AE∴E 的运动路径长为=【点睛】本题属于四边形的综合问题，考查了菱形的性质，30°直角三角形的性质，全等三角形的性质，锐角三角函数等知识，综合程度较高，考查学生灵活运用知识的能力．9．（2022·浙江金华）如图，在菱形ABCD 中，310,sin 5AB B ==，点E 从点B 出发沿折线B C D --向终点D 运动．过点E 作点E 所在的边（BC 或CD ）的垂线，交菱形其它的边于点F ，在EF 的右侧作矩形EFGH ．(1)如图1，点G 在AC 上．求证：FA FG =．(2)若EF FG =，当EF 过AC 中点时，求AG 的长．(3)已知8FG =，设点E 的运动路程为s ．当s 满足什么条件时，以G ，C ，H 为顶点的三角形与BEF 相似（包括全等）？【答案】(1)见解析(2)7AG=或5(3)1s=或3225s=或327s=或1012s≤≤【分析】（1）证明△AFG是等腰三角形即可得到答案；（2）记AC中点为点O．分点E在BC上和点E在CD上两种情况进行求解即可；（3）过点A作AM BC⊥于点M，作AN CD⊥于点N．分点E在线段BM上时，点E在线段MC上时，点E 在线段CN上，点E在线段ND上，共四钟情况分别求解即可．(1)证明：如图1，∵四边形ABCD是菱形，∴BA BC=，∴BAC BCA∠=∠．∵FG BC，∴FGA BCA∠=∠，∴BAC FGA∠=∠，∴△AFG是等腰三角形，∴FA FG=．(2)解：记AC中点为点O．①当点E在BC上时，如图2，过点A作AM BC⊥于点M，∵在Rt ABM 中，365AM AB ==，∴8BM ==．∴6,2FG EF AM CM BC BM ====-=，∵,OA OC OE AM =∥， ∴112122CE ME CM ===⨯=， ∴1AF ME ==，∴167AG AF FG =+=+=．②当点E 在CD 上时，如图3，过点A 作AN CD ⊥于点N ．同理，6,2FG EF AN CN ====，112AF NE CN ===， ∴615AG FG AF =-=-=．∴7AG =或5．(3)解：过点A 作AM BC ⊥于点M ，作AN CD ⊥于点N ．①当点E 在线段BM 上时，08s <≤．设3EF x =，则4,3BE x GH EF x ===，ⅰ）若点H 在点C 的左侧，810s +≤，即02s <≤，如图4，10(48)24CH BC BH x x =-=-+=-．∵GHC FEB △∽△， ∴GH CH EF BE =， ∴GH EF CH BE =， ∴33244x x =-，解得14x =，经检验，14x =是方程的根， ∴41s x ==．∵GHC BEF △∽△， ∴GH CH BE EF =， ∴GH BE CH EF =， ∴34243x x =-，解得825x =，经检验，825x =是方程的根， ∴32425s x ==． ⅰ）若点H 在点C 的右侧，810s +>，即28s <≤，如图5，(48)1042CH BH BC x x =-=+-=-．∵GHC FEB △∽△， ∴GH CH EF BE =， ∴GH EF CH BE =， ∴33424x x =-，此方程无解．∵GHC BEF △∽△， ∴GH CH BE EF =， ∴GH BE CH EF =， ∴34423x x =-，解得87x =，经检验，87x =是方程的根， ∴3247s x ==． ②当点E 在线段MC 上时，810s <≤，如图6，6,8,EF EH BE s ===．∴8,2BH BE EH s CH BH BC s =+=+=-=-．∵GHC FEB △∽△， ∴GH CH EF BE =， ∴GH EF CH BE =， ∴662s s=-，此方程无解．∵GHC BEF △∽△， ∴GH CH BE EF =， ∴GH BE CH EF =， ∴626s s =-，解得1s =经检验，1s =∵810s <≤，∴1s =±③当点E 在线段CN 上时，1012s ≤≤，如图7，过点C 作⊥CJ AB 于点J ，在Rt BJC △中，10,6,8BC CJ BJ ===．8,EH BJ JF CE ===，∴BJ JF EH CE +=+，∴CH BF =，∵,90GH EF GHC EFB =∠=∠=︒，∴GHC EFB △≌△，符合题意，此时，1012s ≤≤．④当点E 在线段ND 上时，1220s <<，∵90EFB ∠>︒，∴GHC 与BEF 不相似．综上所述，s 满足的条件为：1s =或3225s =或327s =或1012s ≤≤．【点睛】此题考查了相似三角形的性质、菱形的性质、勾股定理、等腰三角形的判定和性质、矩形的性质、锐角三角函数等知识，分类讨论方法是解题的关键．10．（2022·四川南充）如图，在矩形ABCD 中，点O 是AB 的中点，点M 是射线DC 上动点，点P 在线段AM 上（不与点A 重合），12OP AB =．(1)判断ABP △的形状，并说明理由．(2)当点M 为边DC 中点时，连接CP 并延长交AD 于点N ．求证：PN AN =．(3)点Q 在边AD 上，85,4,5AB AD DQ ===，当90CPQ ∠=︒时，求DM 的长．【答案】(1)ABP △为直角三角形，理由见解析(2)见解析 (3)43或12 【分析】（1）由点O 是AB 的中点，12OP AB =可知OP OA OB ==，由等边对等角可以推出90APB APO BPO ∠=∠+∠=︒；（2）延长AM ，BC 交于点E ，先证EC BC =，结合（1）的结论得出PC 是直角BPE 斜边的中线，推出12PC BE CE ==，进而得到34∠=∠，再通过等量代换推出21∠=∠，即可证明PN AN =；（3）过点P 作AB 的平行线，交AD 于点F ，交BC 于点G ，得到两个K 型，证明BPG FAP ∆∆，CPG PQF ∆∆，利用相似三角形对应边成比例列等式求出QF ，FP ，再通过AFP ADM ∆∆即可求出DM ．(1)解：ABP △为直角三角形，理由如下：∵点O 是AB 的中点，12OP AB =， ∴OP OA OB ==，∴APO PAO ∠=∠，BPO PBO ∠=∠，∵ 180APO PAO BPO PBO ∠+∠+∠+∠=︒， ∴1180=902APO BPO ∠+∠=⨯︒︒， ∴90APB ∠=︒，∴ABP △为直角三角形；(2)证明：如图，延长AM ，BC 交于点E ，由矩形的性质知：//AD BE ，90ADM ECM ∠=∠=︒，∴14∠=∠，∵ 点M 为边DC 中点，∴DM CM =，在ADM △和ECM 中，14ADM ECM DM CM ∠=∠⎧⎪∠=∠⎨⎪=⎩∴(AAS)ADM ECM ≅△△，∴EC AD =，∵BC AD =，∴EC BC =，即C 点为BE 的中点，由（1）知90APB ∠=︒，∴90BPE ∠=︒，即BPE 为直角三角形， ∴12PC BE CE ==， ∴34∠=∠，又∵23∠∠=，14∠=∠，∴21∠=∠，∴PN AN =；(3)解：如图，过点P 作AB 的平行线，交AD 于点F ，交BC 于点G ，由已知条件85,4,5AB AD DQ ===，设QF a =，FP x =，则8124455GB AF DQ QF a a ==--=--=-，5PG x =-，85CG a =+． ∵AB AD ⊥，AB BC ⊥，//FG AB ，∴FG AD ⊥，FG BC ⊥，∴90AFP PGB ∠=∠=︒，∴90FAP FPA ∠+∠=︒，∵90APB ∠=︒，∴90BPG FPA ∠+∠=︒，∴BPG FAP ∠=∠，∴BPG FAP ∆∆， ∴GB PG FP AF =，即1255125a x x a --=-， ∴212(5)()5x x a -=-．同理，∵ 90QFP ∠=︒，∴90FQP FPQ ∠+∠=︒，∵90CPQ ∠=︒，∴90CPG FPQ ∠+∠=︒，∴CPG FQP ∠=∠，∴CPG PQF ∆∆， ∴CG PG FP QF =，即855a x x a+-=， ∴8(5)()5x x a a -=+． ∴2128()()55a a a -=+，解得910a =， ∴12352AF a =-=，将910a =代入8(5)()5x x a a -=+得989(5)()10510x x -=⨯+，整理得242090x x -+=，解得12x =或92x =． ∵FAP DAM ∠=∠，AFP ADM ∠=∠，∴AFP ADM ∆∆， ∴FP AF DM AD =，即324x DM =， ∴83DM x =， ∴当12x =时，814323DM =⨯=，当92x =时，891232DM =⨯=，此时点M 在DC 的延长线上，综上，DM 的长为43或12．【点睛】本题考查矩形的性质，直角三角形斜边中线的性质，相似三角形的判定与性质等，第3问有一定难度，解题关键是作辅助线构造K 字模型．11．（2022·湖北武汉）已知CD 是ABC 的角平分线，点E ，F 分别在边AC ，BC 上，AD m =，BD n =，ADE 与BDF 的面积之和为S ．(1)填空：当90ACB ∠=︒，DE AC ⊥，DF BC ⊥时，①如图1，若45B ∠=︒，m =n =_____________，S =_____________；②如图2，若60B ∠=︒，m =n =_____________，S =_____________；(2)如图3，当90ACB EDF ∠=∠=︒时，探究S 与m 、n 的数量关系，并说明理由：(3)如图4，当60ACB ∠=︒，120EDF ∠=︒，6m =，4n =时，请直接写出S 的大小．【答案】(1)①25；②4；(2)S =12mn(3)S =【分析】（1）①先证四边形DECF 为正方形，再证△ABC 为等腰直角三角形，根据CD 平分∠ACB ，得出CD ⊥AB ，且AD =BD =m ,然后利用三角函数求出BF=BD cos45°=5，DF =BD sin45°=5，AE =AD cos45°=5即可；②先证四边形DECF 为正方形，利用直角三角形两锐角互余求出∠A =90°-∠B =30°，利用30°直角三角形先证求出DE =1122AD =⨯=AE =ADcos 30°=6，DF =DE =BF =DF tan30°=2，BD =DF ÷sin60°=4即可；（2）过点D 作DH ⊥AC 于H ，DG ⊥BC 于G ，在HC 上截取HI =BG ，连接DI ，先证四边形DGCH 为正方形，再证△DFG ≌△DEH （ASA ）与△DBG ≌△DIH （SAS ），然后证明∠IDA =180°-∠A -∠DIH =90°即可；（3）过点D 作DP ⊥AC 于P ，DQ ⊥BC 于Q ，在PC 上截取PR =QB ，连接DR ，过点A 作AS ⊥DR 于S ，先证明△DQF ≌△DPE ，△DBQ ≌△DRP ，再证△DBF ≌△DRE ，求出∠ADR =∠ADE +∠BDF =180°-∠FDE =60°即可．(1)解：①∵90ACB ∠=︒，DE AC ⊥，DF BC ⊥，CD 是ABC 的角平分线，∴四边形DECF 为矩形，DE =DF ，∴四边形DECF 为正方形，∵45B ∠=︒，∴∠A =90°-∠B =45°=∠B ，∴△ABC 为等腰直角三角形，∵CD 平分∠ACB ，∴CD ⊥AB ，且AD =BD =m ,∵m =∴BD =n =∴BF =BDcos 45°=5，DF =BDsin 45°=5，AE =ADcos 45°=5，ED =DF =5，∴S = 1155552522ADE BDF S S ∆+=⨯⨯+⨯⨯=；故答案为25；②∵90ACB ∠=︒，DE AC ⊥，DF BC ⊥，CD 是ABC 的角平分线，∴四边形DECF 为矩形，DE =DF ，∴四边形DECF 为正方形，∵60B ∠=︒，∴∠A =90°-∠B =30°，∴DE =1122AD =⨯AE =AD cos30°=6，DF =DE = ∵∠BDF =90°-∠B =30°，∴BF =DF tan30°=2，∴BD =DF ÷sin60°=4，∴BD =n =4，∴S=116222ADE BDF S S ∆+=⨯+⨯⨯ 故答案为：4；(2)解：过点D 作DH ⊥AC 于H ，DG ⊥BC 于G ，在HC 上截取HI =BG ，连接DI ，∴∠DHC =∠DGC =∠GCH =90°，∴四边形DGCH 为矩形，∵CD 是ABC 的角平分线，DH ⊥AC ，DG ⊥BC ，∴DG =DH ，∴四边形DGCH 为正方形，∴∠GDH =90°，∵90EDF ∠=︒，∴∠FDG +∠GDE =∠GDE +∠EDH =90°，∴∠FDG =∠EDH ，在△DFG 和△DEH 中，FDG EDH DG DHDGF DHE ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∴△DFG ≌△DEH （ASA ）∴FG =EH ，在△DBG 和△DIH 中，DG DH DGB DHI BG IH =⎧⎪∠=∠⎨⎪=⎩，∴△DBG ≌△DIH （SAS ），∴∠B =∠DIH ，DB =DI =n ，∵∠DIH +∠A =∠B +∠A =90°，∴∠IDA =180°-∠A -∠DIH =90°，∴S △ADI =1122AD DI mn ⋅=， ∴S =12ADE BDF ADE HDI ADI S S SS S mn ∆∆∆+=+==；(3)过点D 作DP ⊥AC 于P ，DQ ⊥BC 于Q ，在PC 上截取PR =QB ，连接DR ，过点A 作AS ⊥DR 于S ， ∵CD 是ABC 的角平分线，DP ⊥AC ，DQ ⊥BC ，∴DP =DQ ，∵∠ACB=60°∴∠QDP =120°，∵120EDF ∠=︒，∴∠FDQ +∠FDP =∠FDP +∠EDP =120°，∴∠FDQ =∠EDP ，在△DFQ 和△DEP 中，FDQ EDP DQ DPDQF DPE ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∴△DFQ ≌△DEP （ASA ）∴DF =DE ，∠QDF =∠PDE ，在△DBQ 和△DRP 中，DQ DP DQB DPR BQ RP =⎧⎪∠=∠⎨⎪=⎩，∴△DBQ ≌△DRP （SAS ），∴∠BDQ =∠RDP ，DB =DR ，∴∠BDF =∠BDQ +∠FDQ =∠RDP +∠EDP =∠RDE ，∵DB =DE ，DB =DR ，∴△DBF ≌△DRE ，∴∠ADR =∠ADE +∠BDF =180°-∠FDE =60°，∴S =S △ADR=111sin 6064222AS DR AD DR ⋅=︒⨯=⨯=．【点睛】本题考查等腰直角三角形判定与性质，正方形判定与性质，三角形全等判定与性质，直角三角形判定，三角形面积，角平分线性质，解直角三角形，掌握等腰直角三角形判定与性质，正方形判定与性质，三角形全等判定与性质，直角三角形判定，三角形面积，角平分线性质，解直角三角形是解题关键． 12．（2022·山东临沂）已知ABC 是等边三角形，点B ，D 关于直线AC 对称，连接AD ，CD ．(1)求证：四边形ABCD 是菱形；(2)在线段AC 上任取一点Р（端点除外），连接PD ．将线段PD 绕点Р逆时针旋转，使点D 落在BA 延长线上的点Q 处．请探究：当点Р在线段AC 上的位置发生变化时，DPQ ∠的大小是否发生变化？说明理由．(3)在满足（2）的条件下，探究线段AQ 与CP 之间的数量关系，并加以证明．【答案】(1)见解析(2)DPQ ∠大小不变，理由见解析(3)CP AQ =，证明见解析【分析】（1）连接BD ，由等边三角形的性质可得AC 垂直平分BD ，继而得出AB BC CD AD ===，便可证明；（2）连接PB ，过点P 作PE CB ∥交AB 于点E ，PF ⊥AB 于点F ，可证明APE 是等边三角形，由等腰三角形三线合一证明APF EPF ∠=∠，QPF BPF ∠=∠，即可求解；（3）由等腰三角形三线合一的性质可得AF = FE ，QF = BF ，即可证明．(1)连接BD ， ABC 是等边三角形，AB BC AC ∴==，点B ，D 关于直线AC 对称，∴AC 垂直平分BD ，,DC BC AD AB ∴==，AB BC CD AD ∴===，∴四边形ABCD 是菱形；(2)当点Р在线段AC 上的位置发生变化时，DPQ ∠的大小不发生变化，始终等于60°，理由如下：将线段PD 绕点Р逆时针旋转，使点D 落在BA 延长线上的点Q 处，PQ PD ∴=， ABC 是等边三角形，,60AB BC AC BAC ABC ACB ∴==∠=∠=∠=︒，连接PB ，过点P 作PE CB ∥交AB 于点E ，PF ⊥AB 于点F ，则60,60APE ACB AEP ABC ∠=∠=︒∠=∠=︒，60APE BAC AEP ∴∠=∠=︒=∠，APE ∴是等边三角形，AP EP AE ∴==，PF AB ⊥，APF EPF ∴∠=∠，点B ，D 关于直线AC 对称，点P 在线段AC 上，∴PB = PD ，∠DP A =∠BP A ，∴PQ = PD ，PF AB ⊥，QPF BPF ∴∠=∠，∴∠QPF -∠APF =∠BPF -∠EPF ，即∠QP A = ∠BPE ，∴∠DPQ =∠DP A - ∠QP A =∠BP A -∠BPE = ∠APE = 60°；(3)AQ = CP ，证明如下：AC = AB ，AP = AE ，∴AC - AP = AB – AE ，即CP = BE ，AP = EP ，PF ⊥AB ，∴AF = FE ，PQ = PD ，PF ⊥AB ，∴QF = BF ，∴ QF - AF = BF – EF ，即AQ = BE ，∴AQ = CP ．【点睛】本题考查了图形的旋转，等边三角形的判定和性质，等腰三角形的性质，菱形的判定等，熟练掌握知识点是解题的关键．13．（2022·江西）问题提出：某兴趣小组在一次综合与实践活动中提出这样一个问题：将足够大的直角三角板()90,60PEF P F ∠=︒∠=︒的一个顶点放在正方形中心O 处，并绕点O 逆时针旋转，探究直角三角板PEF 与正方形ABCD 重叠部分的面积变化情况（已知正方形边长为2）．(1)操作发现：如图1，若将三角板的顶点P 放在点O 处，在旋转过程中，当OF 与OB 重合时，重叠部分的面积为__________；当OF 与BC 垂直时，重叠部分的面积为__________；一般地，若正方形面积为S ，在旋转过程中，重叠部分的面积1S 与S 的关系为__________；(2)类比探究：若将三角板的顶点F 放在点O 处，在旋转过程中，,OE OP 分别与正方形的边相交于点M ，N ． ①如图2，当BM CN =时，试判断重叠部分OMN 的形状，并说明理由；②如图3，当CM CN =时，求重叠部分四边形OMCN 的面积（结果保留根号）；(3)拓展应用：若将任意一个锐角的顶点放在正方形中心O 处，该锐角记为GOH ∠（设GOH α∠=），将GOH ∠绕点O 逆时针旋转，在旋转过程中，GOH ∠的两边与正方形ABCD 的边所围成的图形的面积为2S ，请直接写出2S 的最小值与最大值（分别用含α的式子表示），（参考数据：sin15tan152︒=︒=︒= 【答案】(1)1,1，114S S =(2)①OMN 1 (3)tan ,1tan 4522αα⎛⎫-︒- ⎪⎝⎭ 【分析】（1）如图1，若将三角板的顶点P 放在点O 处，在旋转过程中，当OF 与OB 重合时，OE 与OC重合，此时重叠部分的面积=△OBC的面积=14正方形ABCD的面积=1；当OF与BC垂直时，OE⊥BC，重叠部分的面积=14正方形ABCD的面积=1；一般地，若正方形面积为S，在旋转过程中，重叠部分的面积S1与S的关系为S1=14S．利用全等三角形的性质证明即可；（2）①结论：△OMN是等边三角形．证明OM=ON，可得结论；②如图3中，连接OC，过点O作OJ⊥BC于点J．证明△OCM≌△OCN（SAS），推出∠COM=∠CON=30°，解直角三角形求出OJ，即可解决问题；（3）如图4-1中，过点O作OQ⊥BC于点Q，当BM=CN时，△OMN的面积最小，即S2最小．如图4-2中，当CM=CN时，S2最大．分别求解即可．(1)如图1，若将三角板的顶点P放在点O处，在旋转过程中，当OF与OB重合时，OE与OC重合，此时重叠部分的面积=△OBC的面积=14正方形ABCD的面积=1；当OF与BC垂直时，OE⊥BC，重叠部分的面积=14正方形ABCD的面积=1；一般地，若正方形面积为S，在旋转过程中，重叠部分的面积S1与S的关系为S1=14 S．理由：如图1中，设OF交AB于点J，OE交BC于点K，过点O作OM⊥AB于点M，ON⊥BC于点N．∵O是正方形ABCD的中心，∴OM=ON，∵∠OMB=∠ONB=∠B=90°，∴四边形OMBN是矩形，∵OM=ON，∴四边形OMBN是正方形，∴∠MON=∠EOF=90°，∴∠MOJ=∠NOK，∵∠OMJ=∠ONK=90°，∴△OMJ≌△ONK（AAS），∴S△PMJ=S△ONK，∴S四边形OKBJ=S正方形OMBN=14S正方形ABCD，∴S1=14 S．故答案为：1，1，S1=14 S．(2)①如图2中，结论：△OMN是等边三角形．理由：过点O作OT⊥BC，∵O是正方形ABCD的中心，∴BT=CT，∵BM=CN，∴MT=TN，∵OT⊥MN，∴OM=ON，∵∠MON=60°，∴△MON是等边三角形；②如图3中，连接OC，过点O作OJ⊥BC于点J．。

三角形与四边形重难点题型-三年中考数学真题分项汇编(原卷版)

三角形与四边形重难点题型共23道题一、单选题1．（2022·浙江温州）如图，在Rt ABC 中，90ACB ∠=︒，以其三边为边向外作正方形，连结CF ，作GM CF ⊥于点M ，BJ GM ⊥于点J ，⊥AK BJ 于点K ，交CF 于点L ．若正方形ABGF 与正方形JKLM 的面积之比为5，102CE =CH 的长为（）A 5B 35+C ．2D 102．（2020·浙江湖州）四边形具有不稳定性，对于四条边长确定的四边形．当内角度数发生变化时，其形状也会随之改变．如图，改变正方形ABCD 的内角，正方形ABCD 变为菱形ABC ′D ′．若∠D ′AB ＝30°，则菱形ABC ′D ′的面积与正方形ABCD 的面积之比是（）A ．1B ．12C ．22D 33．（2020·浙江温州）如图，在Rt △AB C 中，∠ACB ＝90°，以其三边为边向外作正方形，过点C 作CR ∠FG 于点R ，再过点C 作PQ ∠CR 分别交边DE ，BH 于点P ，Q ．若QH ＝2PE ，PQ ＝15，则CR 的长为（）A ．14B ．15C ．83D ．54．（2020·浙江台州）把一张宽为1cm 的长方形纸片ABCD 折叠成如图所示的阴影图案，顶点A ，D 互相重合，中间空白部分是以E 为直角顶点，腰长为2cm 的等腰直角三角形，则纸片的长AD （单位：cm ）为（）A ．732+B ．742+C ．832+D ．842+二、填空题5．（2022·浙江绍兴）如图，10AB =，点C 在射线BQ 上的动点，连接AC ，作CD AC ⊥，CD AC =，动点E 在AB 延长线上，tan 3QBE ∠=，连接CE ，DE ，当CE DE =，CE DE ⊥时，BE 的长是______．6．（2021·浙江绍兴）如图，在平面直角坐标系中，正方形ABCD 的顶点A 在x 轴正半轴上，顶点B ，C 在第一象限，顶点D 的坐标5(,2)2．反比例函数ky x=（常数0k >，0x >）的图象恰好经过正方形ABCD 的两个顶点，则k 的值是_______．7．（2021·浙江杭州）如图是一张矩形纸片ABCD ，点M 是对角线AC 的中点，点E 在BC 边上，把DCE 沿直线DE 折叠，使点C 落在对角线AC 上的点F 处，连接DF ，EF ．若MF AB =，则DAF ∠=_____度．8．（2021·浙江金华）如图1是一种利用镜面反射，放大微小变化的装置．木条BC 上的点P 处安装一平面镜，BC 与刻度尺边MN 的交点为D ，从A 点发出的光束经平面镜P 反射后，在MN 上形成一个光点E ．已知,, 6.5AB BC MN BC AB ⊥⊥=，4,8BP PD ==．（1）ED 的长为____________．（2）将木条BC 绕点B 按顺时针方向旋转一定角度得到BC '（如图2），点P 的对应点为P '，BC '与MN 的交点为D′，从A 点发出的光束经平面镜P '反射后，在MN 上的光点为E '．若5DD '=，则EE '的长为____________．9．（2020·21的矩形纸片剪成四个等腰三角形纸片（无余纸片），各种剪法剪出的等腰三角形中，其中一个等腰三角形的腰长可以是下列数中的_____（填序号）． 2，∠1，2﹣1，33 10．（2021·浙江宁波）在平面直角坐标系中，对于不在坐标轴上的任意一点(),A x y ，我们把点11,B x y ⎛⎫⎪⎝⎭称为点A 的“倒数点”．如图，矩形OCDE 的顶点C 为()3,0，顶点E 在y 轴上，函数()20=>y x x的图象与DE 交于点A ．若点B 是点A 的“倒数点”，且点B 在矩形OCDE 的一边上，则OBC 的面积为_________．三、解答题11．（2022·浙江湖州）已知在Rt ∠AB C 中，∠ACB ＝90°，a ，b 分别表示∠A ，∠B 的对边，a b >．记∠ABC 的面积为S ．(1)如图1，分别以AC ，CB 为边向形外作正方形ACDE 和正方形BGF C ．记正方形ACDE 的面积为1S ，正方形BGFC 的面积为2S ． ∠若19S =，216S =，求S 的值；∠延长EA 交GB 的延长线于点N ，连结FN ，交BC 于点M ，交AB 于点H ．若FH ∠AB （如图2所示），求证：212S S S -=．(2)如图3，分别以AC ，CB 为边向形外作等边三角形ACD 和等边三角形CBE ，记等边三角形ACD 的面积为1S ，等边三角形CBE 的面积为2S ．以AB 为边向上作等边三角形ABF （点C 在∠ABF 内），连结EF ，CF ．若EF ∠CF ，试探索21S S -与S 之间的等量关系，并说明理由．12．（2022·浙江宁波）(1)如图1，在ABC 中，D ，E ，F 分别为,,AB AC BC 上的点，,,DE BC BF CF AF =∥交DE 于点G ，求证：DG EG =．(2)如图2，在（1）的条件下，连接,CD CG ．若,6,3⊥==CG DE CD AE ，求DEBC的值． (3)如图3，在ABCD 中，45,︒∠=ADC AC 与BD 交于点O ，E 为AO 上一点，EG BD ∥交AD 于点G ，⊥EF EG 交BC 于点F ．若40,︒∠=EGF FG 平分,10∠=EFC FG ，求BF 的长．13．（2021·浙江宁波）【证明体验】（1）如图1，AD 为ABC 的角平分线，60ADC ∠=︒，点E 在AB 上，AE AC =．求证：DE 平分ADB ∠．【思考探究】（2）如图2，在（1）的条件下，F 为AB 上一点，连结FC 交AD 于点G ．若FB FC =，2DG =，3CD =，求BD 的长．【拓展延伸】（3）如图3，在四边形ABCD 中，对角线AC 平分,2BAD BCA DCA ∠∠=∠，点E 在AC 上，EDC ABC ∠=∠．若5,25,2BC CD AD AE ===，求AC 的长．14．（2021·浙江湖州）已知在ACD △中，Р是CD 的中点，B 是AD 延长线上的一点，连结,BC AP ．（1）如图1，若90,60,,3ACB CAD BD AC AP ︒∠=︒∠===BC 的长．（2）过点D 作//DE AC ，交AP 延长线于点E ，如图2所示．若60,CAD BD AC ∠︒==，求证：2BC AP =．（3）如图3，若45CAD ∠=︒，是否存在实数m ，当BD mAC =时，2BC AP =？若存在，请直接写出m 的值；若不存在，请说明理由．15．（2020·浙江绍兴）问题：如图，在∠AB D中，BA＝B D．在BD的延长线上取点E，C，作∠AEC，使EA ＝EC，若∠BAE＝90°，∠B＝45°，求∠DAC的度数．答案：∠D AC＝45°思考：（1）如果把以上“问题”中的条件“∠B＝45°”去掉，其余条件不变，那么∠DAC的度数会改变吗？说明理由；（2）如果把以上“问题”中的条件“∠B＝45°”去掉，再将“∠BAE＝90°”改为“∠BAE＝n°”，其余条件不变，求∠DAC的度数．16．（2020·浙江舟山）为了测量一条两岸平行的河流宽度，三个数学研究小组设计了不同的方案，他们在河南岸的点A处测得河北岸的树H恰好在A的正北方向．测量方案与数据如下表：课题测量河流宽度测量工测量角度的仪器，皮尺等具测量小第一小组第二小组第三小组组测量方案示意图说明点B，C在点A的正东方向点B，D在点A的正东方向点B在点A的正东方向，点C在点A的正西方向．测量数据BC＝60m，∠ABH＝70°，∠ACH＝35°．BD＝20m，∠ABH＝70°，∠BCD＝35°．BC＝101m，∠ABH＝70°，∠ACH＝35°．（1）哪个小组的数据无法计算出河宽？（2）请选择其中一个方案及其数据求出河宽（精确到0.1m）．（参考数据：sin70°≈0.94，sin35°≈0.57，tan70°≈2.75，tan35°≈0.70）17．（2020·浙江衢州）如图1，在平面直角坐标系中，∠ABC的顶点A，C分别是直线y=﹣83x+4与坐标轴的交点，点B的坐标为（﹣2，0），点D是边AC上的一点，DE∠BC于点E，点F在边AB上，且D，F两点关于y轴上的某点成中心对称，连结DF，EF．设点D的横坐标为m，EF2为l，请探究：∠线段EF长度是否有最小值．∠∠BEF能否成为直角三角形．小明尝试用“观察﹣猜想﹣验证﹣应用”的方法进行探究，请你一起来解决问题．（1）小明利用“几何画板”软件进行观察，测量，得到l随m变化的一组对应值，并在平面直角坐标系中以各对应值为坐标描点（如图2）．请你在图2中连线，观察图象特征并猜想l与m可能满足的函数类别．（2）小明结合图1，发现应用三角形和函数知识能验证（1）中的猜想，请你求出l关于m的函数表达式及自变量的取值范围，并求出线段EF长度的最小值．（3）小明通过观察，推理，发现∠BEF能成为直角三角形，请你求出当∠BEF为直角三角形时m的值．18．（2020·浙江湖州）已知在△AB C中，AC＝BC＝m，D是AB边上的一点，将∠B沿着过点D的直线折叠，使点B落在AC边的点P处（不与点A，C重合），折痕交BC边于点E．AC；（1）特例感知如图1，若∠C＝60°，D是AB的中点，求证：AP＝12（2）变式求异如图2，若∠C＝90°，m＝2，AD＝7，过点D作DH∠AC于点H，求DH和AP的长；（3）化归探究如图3，若m＝10，AB＝12，且当AD＝a时，存在两次不同的折叠，使点B落在AC边上两个不同的位置，请直接写出a的取值范围．19．（2020·浙江金华）如图，在∠AB C中，AB=42∠B=45°，∠C=60°．（1）求BC边上的高线长．（2）点E为线段AB的中点，点F在边AC上，连结EF，沿EF将∠AEF折叠得到∠PEF．∠如图2，当点P落在BC上时，求∠AEP的度数．∠如图3，连结AP，当PF∠AC时，求AP的长．20．（2022·浙江绍兴）如图，在矩形ABCD 中，6AB =，8BC =，动点E 从点A 出发，沿边AD ，DC 向点C 运动，A ，D 关于直线BE 的对称点分别为M ，N ，连结MN ．(1)如图，当E 在边AD 上且2DE =时，求AEM ∠的度数．(2)当N 在BC 延长线上时，求DE 的长，并判断直线MN 与直线BD 的位置关系，说明理由．(3)当直线MN 恰好经过点C 时，求DE 的长．21．（2021·浙江衢州）【推理】如图1，在正方形ABC D 中，点E 是CD 上一动点，将正方形沿着BE 折叠，点C 落在点F 处，连结BE ，CF ，延长CF 交AD 于点G ．（1）求证：BCE CDG △△≌．【运用】（2）如图2，在【推理】条件下，延长BF 交AD 于点H ．若45HD HF =，9CE =，求线段DE 的长．【拓展】（3）将正方形改成矩形，同样沿着BE 折叠，连结CF ，延长CF ，BF 交直线AD 于G ，两点，若AB k BC =，45HD HF =，求DE EC 的值（用含k 的代数式表示）．22．（2021·浙江绍兴）问题：如图，在ABCD 中，8AB =，5AD =，DAB ∠，ABC ∠的平分线AE ，BF 分别与直线CD 交于点E ，F ，求EF 的长．答案：2EF =．探究：（1）把“问题”中的条件“8AB =”去掉，其余条件不变．∠当点E 与点F 重合时，求AB 的长；∠当点E 与点C 重合时，求EF 的长．（2）把“问题”中的条件“8AB =，5AD =”去掉，其余条件不变，当点C ，D ，E ，F 相邻两点间的距离相等时，求AD AB的值．23．（2020·浙江金华）如图，在平面直角坐标系中，正方形ABOC 的两直角边分别在坐标轴的正半轴上，分别过OB ，OC 的中点D ，E 作AE ，AD 的平行线，相交于点F ，已知OB =8．（1）求证：四边形AEFD 为菱形．（2）求四边形AEFD 的面积．（3）若点P 在x 轴正半轴上(异于点D )，点Q 在y 轴上，平面内是否存在点G ，使得以点A ，P ， Q ，G 为顶点的四边形与四边形AEFD 相似？若存在，求点P 的坐标；若不存在，试说明理由．。

押成都卷第26题(几何(三角形与四边形)综合压轴)(解析版)-备战2024年中考数学

押成都卷第26题押题方向一：几何（三角形与四边形）综合压轴3年成都真题考点命题趋势2023年成都卷第25题等腰三角形性质、全等（相似）的判定与性质、轨迹问题等从近年成都中考来看，几何综合压轴主要以三角形或四边形为背景，从全等过渡到相似，从定点过渡到动点，求线段长度、比值，探究数量关系等，整体难度极高，是高分段学生尽量要攻克的难点；预计2024年成都卷还将重视几何综合压轴的考查。

2022年成都卷第25题矩形的性质、等腰三角形性质、相似的判定与性质、勾股定理2021年成都卷第27题等腰三角形性质与判定、相似的判定与性质、旋转的性质、中位线1．（2023·四川成都·中考真题）探究式学习是新课程倡导的重要学习方式，某兴趣小组拟做以下探究．在Rt ABC △中，90,C AC BC ∠=︒=，D 是AB 边上一点，且1AD BD n=（n 为正整数），E 是AC 边上的动点，过点D 作DE 的垂线交直线BC 于点F ．【初步感知】(1)如图1，当1n =时，兴趣小组探究得出结论：22AE BF AB +=，请写出证明过程．【深入探究】(2)①如图2，当2n =，且点F 在线段BC 上时，试探究线段AE BF AB ，，之间的数量关系，请写出结论并证明；②请通过类比、归纳、猜想，探究出线段AE BF AB ，，之间数量关系的一般结论（直接写出结论，不必证明）【拓展运用】(3)如图3，连接EF ，设EF 的中点为M ．若22AB =E 从点A 运动到点C 的过程中，点M 运动的路径长（用含n 的代数式表示）．【答案】(1)见解析(2)①1223AE BF AB +=，证明过程略；②当点F 在射线BC 上时，121AE BF AB n n +=+，当点F 在CB 延长线上时，121AE BF AB n n -=+(3)21n +【分析】（1）连接CD ，当1n =时，1AD BD=，即AD BD =，证明AD CD =，从而得到ADE CDF V V ≌即可解答；（2）①过BD 的中点G 作BC 的平行线，交DF 于点J ，交AC 于点H ，当2n =时，AD DG =，根据GH BC ∥，可得AHG 是等腰直角三角形，12JG FB =，根据（1）中结论可得22AE JG AG +=，再根据12JG FB =，23AG AB =，即可得到1223AE BF AB +=；②分类讨论，即当点F 在射线BC 上时；当点F 在CB 延长线上时，画出图形，根据①中的原理即可解答；（3）如图，当1E 与A 重合时，取11E F 的中点1M ，当2E 与C 重合时，取22E F 的中点2M ，可得M 的轨迹长度即为12M M 的长度，可利用建系的方法表示出1122,,,E F E F 的坐标，再利用中点公式求出12,M M ，最后利用勾股定理即可求出12M M 的长度．【详解】（1）证明：如图，连接CD ，当1n =时，1AD BD=，即AD BD =，90,C AC BC ∠=︒= ，∴45A B ∠=∠=︒，CD AB ⊥，1452FCD ACB ∠=∠=︒,CD AD ∴=，2AB BC =，即22BC AB =，DE FD ⊥ ，90ADE EDC FDC EDC ∴∠+∠=∠+∠=︒，ADE CDF\Ð=Ð在ADE V 与CDF 中，ADE CDF DA DC DAE DCF ∠=∠⎧⎪=⎨⎪∠=∠⎩，()ASA ADE CDF ∴ ≌，AE CF ∴=，22BC CF BF AE BF AB ∴=+=+=；（2）①1223AE BF AB +=证明：如图，过BD 的中点G 作BC 的平行线，交DF 于点J ，交AC 于点H ，当2n =时，12AD DB =，即2AD DB =， G 是DB 的中点，AD DG ∴=，23AG AB =， HG BC ∥，90AHG C ∴∠=∠=︒，45HGA B ∠=∠=︒，45A ∠=︒ ，∴AHG 是等腰直角三角形，且DJG DBF △∽△，12JG DG FB DB ∴==，根据（1）中的结论可得22AE JG AG +=，1222222323AE JG AE FB AG AB AB ∴+=+==⨯=；故线段AE BF AB ，，之间的数量关系为1223AE BF AB +=；②解：当点F 在射线BC 上时，如图，在DB 上取一点G 使得AD DG =，过G 作BC 的平行线，交DF 于点J ，交AC 于点H ，同①，可得22AE JG AG +=，1AD BD n= ，AD DG =，1DG BD n ∴=，21AG AB n =+，同①可得1JG DG FB DB n ==，122222121AE JG AE FB AG AB AB n n n ∴+=+==⨯=++，即线段AE BF AB ，，之间数量关系为121AE BF AB n n +=+；当点F 在CB 延长线上时，如图，在DB 上取一点G 使得AD DG =，过G 作BC 的平行线，交DF 于点J ，交AC 于点H ，连接HD ；同（1）中原理，可证明()ASA DHE DGJ △≌△，可得22AE GJ AG -=，1AD BD n = ，AD DG =，1DG BD n ∴=，21AG AB n =+，同①可得1JG DG FB DB n==，122222121AE JG AE FB AG AB AB n n n ∴-=-==⨯=++即线段AE BF AB ，，之间数量关系为121AE BF AB n n -=+,综上所述，当点F 在射线BC 上时，121AE BF AB n n +=+；当点F 在CB 延长线上时，121AE BF AB n n -=+；（3）解：如图，当1E 与A 重合时，取11E F 的中点1M ，当2E 与C 重合时，取22E F 的中点2M ，可得M 的轨迹长度即为12M M 的长度，如图，以点D 为原点，1DF 为y 轴，DB 为x 轴建立平面直角坐标系，过点2E 作AB 的垂线段，交AB 于点G ，过点2F 作AB 的垂线段，交AB 于点H ，122,AD AB DB n == ，221AD n ∴=+，221n DB n =+，122,01E n ⎛⎫∴- ⎪ ⎪+⎝⎭，145F BD ∠=︒ ，1F D BD ∴=，1220,1n F n ⎛⎫∴ ⎪ ⎪+⎝⎭，1M 是11E F 的中点，122,11n M n n ⎛⎫∴- ⎪ ⎪++⎝⎭，122GB GC AB === ，221n DG DB BG n -+∴=-=+，222,21n E n ⎛⎫-+∴ ⎪ ⎪+⎝⎭，根据（2）中的结论22121AE BF AB n n -=+，22222211n n BF n AE AB n n ⎛⎫-∴=-= ⎪ ⎪++⎝⎭，22222221n n BH F H BF n -∴===+，2DH DB BH n ∴=+=，22222,1n n F n n ⎛⎫-∴- ⎪ ⎪+⎝⎭，22222222222,2222n n n n M n n ⎛⎫+--++∴ ⎪ ⎪++⎝⎭，2121M M n ∴=+．【点睛】本题考查了等腰三角形的性质，全等三角形的判定及性质，相似三角形的判定及性质，平行线的性质，正确地画出图形，作出辅助线，找对边之间的关系是解题的关键．()与A ，D 重合），连接BE ，以BE 为边在直线BE 的右侧作矩形EBFG ，使得矩形EBFG ∽矩形ABCD ，EG 交直线CD 于点H ．(1)【尝试初探】在点E 的运动过程中，ABE 与DEH △始终保持相似关系，请说明理由．(2)【深入探究】若2n =，随着E 点位置的变化，H 点的位置随之发生变化，当H 是线段CD 中点时，求tan ABE ∠的值．(3)【拓展延伸】连接BH ，FH ，当BFH △是以FH 为腰的等腰三角形时，求tan ABE ∠的值（用含n 的代数式表示）．【答案】(1)见解析(2)222-或222+(3)2n 或21n -【分析】（1）根据题意可得∠A =∠D =∠BEG =90°，可得∠DEH =∠ABE ，即可求证；（2）根据题意可得AB =2DH ，AD =2AB ，AD =4DH ，设DH =x ，AE =a ，则AB =2x ，AD =4x ，可得DE =4x -a ，再根据△ABE ∽△DEH ，可得()222a x +=或()222a -，即可求解；（3）根据题意可得EG =nBE ，然后分两种情况：当FH =BH 时，当FH =BF =nBE 时，即可求解．【详解】（1）解：根据题意得：∠A =∠D =∠BEG =90°，∴∠AEB +∠DEH =90°，∠AEB +∠ABE =90°，∴∠DEH =∠ABE ，∴△ABE ∽△DEH ；（2）解：根据题意得：AB =2DH ，AD =2AB ，∴AD =4DH ，设DH =x ，AE =a ，则AB =2x ，AD =4x ，∴DE =4x -a ，∵△ABE ∽△DEH ，∴AB AE DE DH =，∴24x a x a x =-，解得：()222a x +=或()222a -，∴()22AB a =+或()22a -，∴22tan 2AE ABE AB -∠==或222+；（3）解：∵矩形EBFG ∽矩形ABCD ，()1AD nAB n =>，∴EG =nBE ，如图，当FH =BH 时，∵∠BEH =∠FGH =90°，BE =FG ，∴Rt △BEH ≌Rt △FGH ，∴EH =GH=12EG ，∴2n EH BE =，∵△ABE ∽△DEH ，∴2DE EH n AB BE ==，即2n DE AB =，∴2n AE AD DE AB =-=，∴tan 2AE n ABE AB ∠==；如图，当FH =BF =nBE 时，222211HG FH FG n FG n BE =-=-=-，∴()21EH EG HG n n BE =-=--，∵△ABE ∽△DEH ，∴21DE EH n n AB BE ==--，即()21DE n n AB =--，∴21AE AD DE n AB =-=-，∴2tan 1AE ABE ABn ==-∠；综上所述，tan ABE ∠的值为2n 或21n -．【点睛】本题主要考查了相似三角形的判定和性质，矩形的性质，等腰三角形的性质，勾股定理等知识，熟练掌握相似三角形的判定和性质，矩形的性质，等腰三角形的性质，勾股定理等知识是解题的关键．3．（2021·四川成都·中考真题）在Rt ABC 中，90,5,3ACB AB BC ∠=︒==，将ABC 绕点B 顺时针旋转得到A BC ''△，其中点A ，C 的对应点分别为点A '，C '．（1）如图1，当点A '落在AC 的延长线上时，求AA '的长；（2）如图2，当点C '落在AB 的延长线上时，连接CC '，交A B '于点M ，求BM 的长；（3）如图3，连接,AA CC ''，直线CC '交AA '于点D ，点E 为AC 的中点，连接DE ．在旋转过程中，DE 是否存在最小值？若存在，求出DE 的最小值；若不存在，请说明理由．【答案】（1）8AA '=；（2）1511BM =；（3）存在，最小值为1【分析】（1）根据题意利用勾股定理可求出AC 长为4．再根据旋转的性质可知AB A B '=，最后由等腰三角形的性质即可求出AA '的长．（2）作CD AC '⊥交AC '于点D ，作//CE A B '交AC '于点E ．由旋转可得A BC ABC ''∠=∠，3BC BC '==．再由平行线的性质可知CEB A BC ''∠=∠，即可推出CEB ABC ∠=∠，从而间接求出3CE BC BC '===，DE DB =．由三角形面积公式可求出125CD =．再利用勾股定理即可求出185BE =，进而求出335C E '=．最后利用平行线分线段成比例即可求出BM 的长．（3）作//AP A C ''且交CD '延长线于点P ，连接A C '．由题意易证明BCC BC C ''∠=∠，90ACP BCC '∠=︒-∠，90A C D BC C '''∠=︒-∠，即得出ACP A C D ''∠=∠．再由平行线性质可知APC A C D ''∠=∠，即得出ACP APC ∠=∠，即可证明AP AC A C ''==，由此即易证()APD A C D AAS ''≅ ，得出AD A D '=，即点D 为AA '中点．从而证明DE 为ACA ' 的中位线，即12DE A C '=．即要使DE 最小，A C '最小即可．根据三角形三边关系可得当点A C B '、、三点共线时A C '最小，且最小值即为=A C A B BC ''-，由此即可求出DE 的最小值．【详解】（1）在Rt ABC 中，2222534AC AB BC =-=-=．根据旋转性质可知AB A B '=，即ABA '△为等腰三角形．∵90ACB ∠=︒，即BC AA '⊥，∴4A C AC '==，∴8AA '=．（2）如图，作CD AC '⊥交AC '于点D ，作//CE A B '交AC '于点E ．由旋转可得ABC ABC ''∠=∠，3BC BC '==．∵//CE A B '，∴CEB A BC ''∠=∠，∴CEB ABC ∠=∠，∴3CE BC BC '===，DE DB =．∵1122ABC S AB CD AC BC == ，即543CD ⨯=⨯，∴125CD =．在Rt BCD △中，2295DB BC CD =-=，∴185BE =．∴335C E BE BC ''=+=．∵//CE A B '，∴BM BC CE C E '='，即33335BM =，∴1511BM =．（3）如图，作//AP A C ''且交C D '延长线于点P ，连接A C '．∵BC BC '=，∴BCC BC C ''∠=∠，∵180ACP ACB BCC '∠=︒-∠-∠，即90ACP BCC '∠=︒-∠，又∵90A C D BC C '''∠=︒-∠，∴ACP A C D ''∠=∠．∵//AP A C ''，∴APC A C D ''∠=∠，∴ACP APC ∠=∠，∴AP AC =，∴AP A C ''=．∴在APD △和AC D '' 中ADP A DC APD A C D AP A C '''∠=∠⎧⎪∠=∠'''⎨⎪=⎩，∴()APD A C D AAS ''≅ ，∴AD A D '=，即点D 为AA '中点．∵点E 为AC 中点，∴DE 为ACA ' 的中位线，∴12DE A C '=，即要使DE 最小，A C '最小即可．根据图可知A C A B BC ''≥-，即当点A C B '、、三点共线时A C '最小，且最小值为==53=2A C A B BC ''--．∴此时1=12DE A C '=，即DE 最小值为1．【点睛】本题为旋转综合题．考查旋转的性质，勾股定理，等腰三角形的判定和性质，平行线的性质，平行线分线段成比例，全等三角形的判定和性质，中位线的判定和性质以及三角形三边关系，综合性强，为困难题．正确的作出辅助线为难点也是解题关键．常见考点：直角、等腰、全等、相似三角形的性质与判定；特殊的四边形的性质与判定；勾股定理与逆定理；锐角三角形函数；三大几何变换；线段的垂直平分线与角平分线的性质等。

2024 河北数学中考备考重难专题：三角形、四边形综合题平移问题(课件)

练习题图①
解：(Ⅰ)如图，设B′C′与AC交于点E， ∵CC′＝m，四边形OABC为正方形， ∴BB′＝CC′＝C′E＝m，B′E＝AB′＝6－m， ∴S＝m(6－m)＝6m－m2(0≤m≤6)；
E
练习题图
练习 (2022天津逆袭卷)在平面直角坐标系中，O为坐标原点，四边形OABC 为正方形，点A，点C分别在x轴正半轴、y轴正半轴上，B(6，6)，连接AC.将 △ABC沿y轴平移至△A′B′C′，设△A′B′C′与△OAC重叠部分的面积为S. (Ⅱ)当S＝8时，求CC′的长； (Ⅱ)当S＝8时，令6m－m2＝8，解得m＝2或m＝4， ∴CC′的长为2或4；
练习题图③
在Rt△DEF中，∵∠EDF＝90°，∠DFE＝30°，∴tan 30°＝ DE 3 ，
DF 3
∴DF＝ 3 DE，
又∵AB＝DE，AF＝DF，∴AF＝ 3 AB，
∴在Rt△ABF中，BF＝ AF 2 AB2 ((2022山西逆袭卷)综合与实践问题情境：
按照本地区考情及考法选题，针对性强，有效提高老师备课效率 2.贴近学生实际解题情境，形式符合教学习惯
审题时对题目数字、符号、辅助线、动图等关键信息进行题图批注，帮助学生梳理关键信息，激发学生兴趣，调动积极性 3.含解题思路引导与方法总结，提高课堂互动性
通过问题启发式解题思路点拨，激发学生数学思考与探索. 方法总结使学生复习一类题，会一类题，取得有效的复习成果三、课件使用场景适用于中考专题复习或题位复习
梯形+ 扫过的面积 (ii)点D为圆心，PQ为半径，圆心角50°
12 直角 ②求点在三的扇形面积
三角角形区域内 ②时长为平移过程时长和旋转过程时长
形的时长
之和。平移过程中K在△PQM内的距离长

三角形、平行四边形、梯形的面积综合练习题35932

梯形的面积练习题：一、求下面梯形的面积：上底2米下底3米高5米上底4分米下底5分米高2分米上底48米，下底56米，高35米。

上底124米，下底76米，高82米。

上底80米，下底50米，高60米。

上底15分米，下底9分米，高比下底长1分米。

下底24厘米，上底是下底的一半，高1分米。

上底5厘米，下底8厘米，高6厘米上底2.4分米，下底7.6分米，高8分米二、填空：1、两个完全一样的梯形可以拼成一个（）形，这个拼成的图形的底等于梯形的（）与（）的和，高等于梯形的（），每个梯形的面积等于拼成的平行四边形面积的（）。

2、梯形的上底是a，下底是b,高是c,则它的面积＝（）3、一个梯形上底与下底的和是15米，高是4米，面积是（）平方米。

4、一个梯形的面积是8平方厘米，如果它的上底、下底和高各扩大2倍，它的面积是（）平方厘米。

5、用两个完全一样的梯形拼成一个平行四边形，已知每个梯形的面积是24平方分米，拼成的平行四边形的面积是多少平方分米？三、判断：1、梯形的面积等于平行四边形的面积的一半。

（）2、两个完全相同的直角梯形，可以拼成一个长方形。

（）3、一个上底是5厘米，下底是8厘米，高是3厘米的梯形，它的面积是12平方厘米。

（）4、一个梯形的上底是３分米，下底是５分米，高是４分米，面积就是32平方分米。

（）四、应用题1、一座小型拦河坝，横截面的上底5米，下底131米，高21米。

这座拦河坝的横截面积是多少？2、一块梯形稻田，上底长8米，下底比上底长1.2米，高是上底的2倍。

这块稻田的面积是多少平方米？3、一块梯形草坪的面积是90平方米，上底是6米，下底是12米，高是多少米？4、一块梯形的果园，它的上底是160米，下底是120米，高30米。

如果每棵果树占地10平方米，这个果园共有树多少棵？5、用65米长的篱笆沿墙边围一个直角梯形的鸡舍，梯形的直角边是15米，你能计算出围成的鸡舍的面积吗？6、一块三角形地，底长38米，高是27米，如果每平方米收小麦0.7千克，这块地可以收小麦多少千克？1、有一块梯形地，上底长64米，比下底短16米，高50米。

2018年四年(下册)三角形和四边形知识点总结和练习试题

第二单元：认识三角形和四边形知识点及测试题1、图形分为：立体图形和平面图形。

2、平面图形：a、圆（由曲线围成的图形）b、三角形、四边形、多边形（由线段围成的图形）3、三角形内角和是180°。

锐角：小于90°的角是锐角。

钝角：大于90°的角是钝角。

直角：等于90°的角是直角。

平角=180°；周角=360°4、等腰三角形相等的两条边叫做腰。

等腰三角形两腰间的夹角叫顶角。

腰与底边的夹角叫底角。

两个底角相等。

5、等腰三角形包含：等腰三角形、等边三角形（又叫正三角形）、等腰直角三角形。

等边三角形是特殊的等腰三角形，它的每个内角都是60°。

6、三角形不易变形具有稳定性。

四边形易变形具有不稳定性、直角三角形（有一个直角两个锐角）按角分锐角三角形（三个角都是锐角）钝角三角形（有一个钝角两个锐角）7 、三角形（有三条边）等边三角形（三条边都相等）是对称图形，有三条对称轴按边分等腰三角形（有两条边相等）是对称图形，有一条对称轴8、三角形任意两边之和大于第三边。

（第三边大于两边之差，第三边小于两边之和。

最长边小于三角形周长的一半。

）9、由四条线段围成的封闭图形叫四边形四边形内角和是360°。

10、正方形是特殊的长方形。

长方形和正方形是特殊的平行四边形。

11、平行四边形：两组对边分别平行且相等的四边形。

12、梯形：只有一组对边平行的四边形。

13、平行的两条边叫做梯形的底边，上面的一条叫上底，下面一条叫下底。

14、梯形的周长：上底+下底+腰+腰15、等腰三角形的两个底角相等。

等边三角形是特殊的等腰三角形。

一般平行四边形平行四边形：（两组对边分别平行且相等的四边形） 16、四边形一般四边形：（有四条边）（两组对边都不平行的四边形）梯形：等腰梯形：两条腰相等，同一底上的两个底角相等。

（只有一组对边平行的四边形）直角梯形：一条腰垂直于的的梯形。

人教版五年级平行四边形和三角形专题练习题

人教版五年级平行四边形和三角形专题练习题一、填空题1、一个平行四边形的底是14厘米.高是9厘米.它的面积是（）；与它等底等高的三角形面积是（）。

2、一个三角形比与它等底等高的平行四边的面积少30平方厘米.则这个三角形的面积是（）。

3、一个三角形的面积是4.5平方分米.底是5分米.高是（）分米。

4、在推导平行四边形面积计算公式时.可把平行四边形通过割补平移转化为( )形去推导.推导三角形面积计算公式时.可把两个完全一样的三角形拼成一个( )形去推导.推导梯形面积计算公式时.可把两个完全一样的梯形拼成一个( )形进行推导。

5、两个一样的三角形通过（）、（）可以拼成平行四边形.平行四边形的面积（）两个三角形面积的和。

6、同底同高的平行四边形的面积是三角形面积的（）倍。

7、一个三角形底5dm.高6dm.面积是（）.与它等底等高的平行四边形面积是（）8、直角三角形的两条直角边长分别为3厘米和4厘米.这个直角三角形面积是( )平方厘米。

9、一个三角形的面积是25平方厘米.和它等底等高的平行四边形的面积是( )平方厘米。

10、一个平行四边形的底是6厘米.高是14厘米.它的面积是（）平方厘米.与它等底等高的三角形面积是（）平方厘米。

11、一块平行四边形田地.底是25米.高是17米.这块田地的面积是( )平方米。

12、一个直角三角形的面积是48平方米.一条直角边6米.另一条直角边( )米。

二、判断题1.三角形面积是平行四边形面积的一半。

( )2.平行四边形可以由两个完全相同的三角形拼成。

( )3.周长相等的平行四边形面积也相等。

( )4.面积相等的三角形一定等底等高。

( )5.等底等高的三角形面积是平行四边形面积的一半。

（）四、应用题1、一块三角形钢板.底边长3.6 dm.高1.5dm。

这种钢板每平方分米重1.8 kg.这块钢板重多少kg？2、在一块底边长8 m.高6.5 m的平行四边形菜地里种萝卜。

如果每m2收萝卜7.5 kg.这块地可收萝卜多少kg？3、一个平行四边形的面积是8cm2.与它等底等高的三角形的面积是多少平方厘米？4、一块平行四边形的菜地的面积是600平方米.它的底是150米.这块菜地的高是多少面？5、一块三角形的玻璃.它的底是24cm.高是15cm.这块玻璃的面积是多少平方厘米？如果每平方分米的玻璃0.6元.买这块玻璃需要多少元？6、一块三角形地.底边长20米.高是35米.如果平均每平方米可以收6.5千克小麦.这块地一共可以收多少千克小麦？7、一块平行四边形菜地一次共收蔬菜440千克.已知它的底是12.5米.高是5.5米．这次平均每平方米收蔬菜多少千克？8、一个平行四边形的苗圃.底长8.6米.高是底的一半.种了1849棵苗.平均每棵苗占地多少？。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。