双模压缩真空场与N型四能级原子双光子跃迁相互作用系统中光场的量子特性

合集下载

【国家自然科学基金】_偶极-偶极相互作用_基金支持热词逐年推荐_【万方软件创新助手】_20140802

偶氮苯封端偶极相互作用偶极滤波魔角旋转nmr 主客体配合物主客体相互作用不对称光敏gemini表面活性剂 ω -亚烷基吡啶(ω =2 y2o3 x射线激发发射 w纠缠态 tb3+掺杂硅酸盐玻璃 tavis-cummings模型 rddi monte carlo模拟 milburn理论 ln(ln=tb,tm,eu)纳米晶体 licabo3 kerr介质 eu~(2+) enso循环 dy3+ concurrence cdte/cds bell基测量 8 6 4 2-乙二胺 1hnmr技术 10)
科研热词推荐指数量子光学 4 荧光光谱法 3 牛血清白蛋白 3 部分转置矩阵负本征值 2 纠缠动力学 2 相互作用 2 人血清白蛋白 2 tavis-cummings模型 2 键合 1 量子纠缠 1 量子干涉 1 重离子加速器 1 酮-(对二甲氨基苯亚甲基)-四氢萘1 远程控制 1 近偶极-偶极相互作用 1 近代物理研究所 1 超冷里德堡原子 1 负折射率 1 表面吸附 1 补骨脂素 1 蛋白质阻抗 1 蛋白质 1 荧光光谱 1 自组装 1 自旋阻挫 1 自旋液体 1 自旋冰 1 能量转移 1 聚集 1 耗散环境 1 纠缠突然死亡与突然产生 1 纠缠猝死 1 纠缠度 1 纠缠原子 1 紫外-可见吸收光谱 1 稠密介质 1 磺酸甜菜碱 1 磷钼酸 1 磁性纳米粒子 1 硼酸盐 1 矮共振 1 真空库 1 相对论 1 相对熵 1 电磁诱导 1 电流变液 1 电场强度 1 生物传感 1 理论框架 1 热库 1 热带印度洋 1 海表面风场 1
推荐指数 2 2 2 2 2 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1

激光原理与技术_电子科技大学中国大学mooc课后章节答案期末考试题库2023年

激光原理与技术_电子科技大学中国大学mooc课后章节答案期末考试题库2023年1.在锁模激光器中，被锁定的模式数量越多，脉冲周期越短。

参考答案:错误2.对于对称共焦腔，其傍轴光线在腔内往返传输次即可自行闭合，其自再现模式为高斯光束。

参考答案:2##%_YZPRLFH_%##二##%_YZPRLFH_%##两3.谐振腔损耗越大，品质因子越高。

参考答案:错误4.有激光输出时，激活介质不是处于热平衡条件。

参考答案:正确5.在主动锁模激光器中，调制器应该放到谐振腔的一端。

参考答案:正确6.为得到高转化效率的光学倍频，要实现匹配，使得基频波和倍频波的折射率要相等，在他们相互作用过程中，两个基频光子湮灭，产生一个倍频光子。

参考答案:相位7.尽量增加泵浦功率有利于获得单模激光输出。

参考答案:错误8.在调Q激光器中，随着Dni/Dnt的增大，峰值光子数增加，脉冲宽度。

参考答案:变窄##%_YZPRLFH_%##变小##%_YZPRLFH_%##减小9.关于基模高斯光束的特点，下面描述不正确的是。

参考答案:基模高斯光束在激光腔内往返传播时没有衍射损耗10.KDP晶体沿z轴加电场时，折射率椭球的主轴绕z轴旋转了度角。

参考答案:45##%_YZPRLFH_%##四十五11.稳定谐振腔是指。

参考答案:谐振腔对旁轴光线的几何偏折损耗为零12.形成激光振荡的充分条件是。

参考答案:光学正反馈条件和增益阈值条件13.关于谐振腔的自再现模式，下面那个说法是正确的？参考答案:自再现模式与谐振腔的稳定性有关14.三能级激光器的激光下能级是基态，需至少将原子总数的通过泵浦过程转移到激光上能级，才能实现受激辐射光放大。

参考答案:一半##%_YZPRLFH_%##1/2##%_YZPRLFH_%##50%##%_YZPRLFH_%##二分之一##%_YZPRLFH_%##百分之五十15.谱线加宽是指的光谱展宽。

参考答案:自发辐射16.关于自发辐射和受激辐射说法正确的是。

电磁诱导吸收的研究进展

电磁诱导吸收的研究进展张连水;李晓莉;赵静宜;刘芳怡【摘要】电磁诱导吸收是光与物质相互作用中表现出来的奇特的非线性效应,对其形成机理及非线性特性的研究具有重要的理论意义和巨大的潜在应用价值.本工作以简并二能级、N型四能级系统和近似简并的Λ型能级系统的研究结果为基础,探讨了电磁诱导吸收的产生条件和本质.结果表明,原子相干对吸收的相长干涉产生电磁诱导吸收,而且其色散谱线在对应频率位置出现了变化剧烈的反常色散,可以引起探测光的群速增快甚至出现负群速,其应用前景正在进一步研究中.【期刊名称】《河北大学学报（自然科学版）》【年(卷),期】2010(030)006【总页数】6页(P719-724)【关键词】电磁诱导吸收;简并二能级系统;N型四能级系统;近似简并的Λ型能级系统【作者】张连水;李晓莉;赵静宜;刘芳怡【作者单位】河北大学,物理科学与技术学院,河北,保定,071002;河北大学,物理科学与技术学院,河北,保定,071002;河北大学,物理科学与技术学院,河北,保定,071002;河北大学,物理科学与技术学院,河北,保定,071002【正文语种】中文【中图分类】O562.3+2光与物质相互作用的非线性效应是近年来物理学的主要研究方向之一,其目的就是深入揭示光波场与原子系统相互作用的物理本质.近年来,在应用激光光学方面出现了许多奇特的现象,其中电磁诱导透明(EIT)和电磁诱导吸收(EIA)是一对性质相对立的相干现象,它们分别基于原子相干对吸收的相消干涉和相长干涉,使介质的吸收和色散特性发生完全不同的变化.目前,国内外关于EIT的研究已趋于成熟,对影响EIT 线宽的诸多因素以及外加驱动场对EIT的影响规律都进行了比较深入的研究,但关于EIA的研究尚处于起步阶段,国内外学者在此方向的研究成果还为数不多.电磁诱导吸收现象(EIA)出现在外加驱动场作用下的多能级系统中,通常认为是由激发态相干到基态相干的自发转移产生的,对其物理本质和形成条件的更准确的解释尚在进一步讨论中.目前对EIA的量子解释主要集中于简并二能级、N型四能级以及近似简并的Λ型能级模型.虽然3种模型之间存在一些差异,但它们最终得到了非常一致的结论,而且按照提出时间的先后顺序也是越来越完善.由于EIA具有显著的光学特性,如介质的线性吸收增强,色散增强;具有显著的非线性效应;而且EIA通常具有极窄的光谱线宽,其色散谱线在对应位置出现折射率的突变,可以引起探测光的群速增快甚至出现负群速,所以对EIA的研究将大大促进超光速等应用领域的发展.随着科学技术的发展,EIA的非线性效应很有可能被应用在超光速通信、超光速旅行以及光延迟线、光存储、量子计算机等领域之中.1998年,Kuhn等人[1]在研究脉冲激光使NO气体的粒子数布居发生转移时,首次观察到吸收曲线上出现了1个线宽极窄的超强吸收,对其进行了命名,即电磁诱导吸收(electromagnetically induced absorp tion),简称EIA,并认为EIA现象的产生与精细结构能级之间的相干作用有关.之后,各研究小组开始对EIA现象进行深入的研究.1998年,A kulshin等[2]在铷原子气室中观察到了EIA现象,认为是原子相干对吸收的相长干涉产生EIA.同时对其色散曲线进行了相应的理论研究,并于1999年提出了在简并二能级系统中实现EIA必须满足的3个基本条件,但对EIA的相干机制并没有给出明确的解释[3].2000年,Dancheva等人[4]在铷原子气室中通过单模和双模激光的激励作用也观察到了EIA现象,并得到了和A kulshin等人类似的结论,是精细结构中Zeeman子能级之间的相干作用导致了EIA.同年,Taichenachev[5]利用激发态相干到基态相干的自发转移解释了EIA,他对Akulshin等人的实验结果进行了分析,从中简化出1个N型四能级模型,给出了EIA的物理图像:EIA是由耦合光场导致的激发态Zeeman子能级的相干自发转移到基态Zeeman子能级所引起的,即是由激发态到基态的光诱导导致的自发转移产生的;EIA吸收谱线的线宽可以反映出基态Zeeman子能级间相干时间的长短,这种相干是处于同一个某态超精细能级中的Zeeman子能级相互之间作用的结果.他还推导出当铷原子气室的气体密度非常低时,弱探测场的强度和EIA的吸收强度成线性关系.2003年,Failache等[6]通过实验对Taichenachev的结论进行了证实,简并二能级系统中出现的EIA是由于粒子从激发态到基态的相干转移引起的.此实验为Hanle构型,在只含有Rb蒸气和缓冲气体(Ne)的密室中观测Rb原子D1线(F=1→F′=2)的共振吸收情况时观察到了EIA.2001年,Kim等人[7]在铯原子中观察到EIA,并研究了耦合场的强度及频率失谐对EIA的影响.2004年,王彦华研究小组[8]报道了室温下多普勒展宽背景中铯原子62S1/2(F=4)和62S3/2(F′=5)超精细能级循环跃迁构成的简并二能级系统中的EIA现象.在此简并二能级系统中,在一束较强的耦合光作用下,借助于弱探测光的吸收光谱观察到了EIA现象.实验中还研究了耦合光的强度和失谐对EIA的影响,分析了简并二能级系统中Zeeman子能级间的光抽运作用以及Zeeman子能级在耦合、探测光场作用下由自发跃迁引起的多个简并二能级系统间的相干作用.结果表明,Zeeman子能级间的相干时间越长,得到EIA的线宽越窄;耦合光的强度影响着Zeeman子能级上的布居数以及参与耦合的二能级的原子数,使Zeeman子能级间的相干时间发生了变化,从而影响了EIA的增强峰线宽,而耦合光的失谐则影响着EIA的吸收强度,由于耦合光的失谐,耦合光与原子之间的相互作用强度被减弱,使得EIA的强度与耦合场完全共振时相比要弱一些;此外,探测光及耦合光的线宽和铯原子气室中磁屏蔽后的剩余磁场对Zeeman子能级的转移,也影响了EIA的线宽. 2004年,王丽等[9]对N型四能级系统中的EIA现象展开了理论研究.系统包括2个简并基态能级和2个简并激发态能级,根据选择定则,|1＞⇔|4＞跃迁是偶极禁止的.1个弱耦合场同时驱动|1＞⇔|2＞跃迁和|3＞⇔|4＞跃迁,在|2＞⇔|3＞跃迁之间利用1个更弱的场进行探测,3个电偶极跃迁构成N型链,中间跃迁为探测跃迁,利用缀饰态理论,说明此系统中是缀饰态原子相干对吸收的相长干涉产生了EIA现象.随后,他们又对此N型四能级系统中耦合场线宽的影响进行了研究,结果表明耦合场的线宽抑制EIA的强度,即耦合场的线宽破坏EIA的相干作用.2006年,王丽等[10]对N型四能级系统中的EIA现象展开了新的理论研究.依然是3个电偶极跃迁构成N 型链,中间跃迁为探测跃迁,不同的是,两边分别为耦合跃迁和控制跃迁,即原子受到3个光场的作用,耦合场驱动|1＞⇔|2＞跃迁,控制场驱动|3＞⇔|4＞跃迁,探测场扫描|2＞⇔|3＞跃迁,通过研究介质对探测光的吸收,揭示了在N型四能级系统中,既可产生EIA又可产生EIT,这不仅取决于非相干转移率的大小而且还取决于耦合场、控制场的强度和第4个简并能级的衰减速率大小.2008年,王丽等[11]研究了激光场线宽对N型四能级系统中EIA的影响,结果表明,随着激光场线宽增大,原子相干将会减弱,从而抑制EIA.2004年,Liu等人[12]对基态近似简并的Λ型三能级系统中出现的EIA现象进行了理论研究.通常认为,在Λ型三能级系统中,当耦合场和探测场满足双光子共振条件时,会出现EIT现象,但研究表明,当考虑近似简并的两低能级之间的相干失相速率时,由于自发辐射诱导相干效应,系统中会出现EIA现象.同时还研究了耦合场和探测场之间的位相差对系统出现EIA或EIT的影响,通过调谐两场之间的位相差,可以使EIA和EIT相互转化.2007年,Zhang等[13]实验研究了具有Λ型三能级构型的冷Rb原子系统中的原子相干效应.频率可调谐的耦合场和探测场为双光子Raman跃迁提供了多条途径,不同的Ram an跃迁使系统呈现不同的光谱特性,可通过探测场的位相来控制.在原子共振频率附近,建设性相干导致EIT,破坏性相干导致EIA.2008年,笔者[14-15]对光学-射频双光子耦合作用下的基态和激发态都近似简并的Λ型四能级系统中EIA和EIT的相互转化进行了理论研究,结果表明,当双光子耦合场与原子能级共振时出现EIA,失谐时则使系统在与其频率失谐量相对应的探测频率位置出现EIT,而且EIA和EIT的线宽随着耦合场拉比频率的增大而增加.通过缀饰态理论分析,得到了与Taichenachev相似的结论:EIA是由双光子耦合场导致的激发态精细结构能级的相干自发转移到基态精细结构能级所引起的,本系统可简化为2个Λ型三能级系统的相干作用,它们相对于双光子耦合场具有大小相同的调谐频率而符号相反,在探测场的中心频率处感应形成EIA.根据相干的两重性,原子相干既然能够抑制吸收,同样也应该能够增强吸收.首先看一下Akulshin等提出的简并二能级模型,如图1所示.在这个系统中,能级|g＞是简并基态能级,能级|e＞是简并激发态能级.基态能级的总角动量为Fg,激发态能级的总角动量为Fe.Γb为激发态|e＞自发衰减到基态|g＞的粒子数衰减速率,Γ(1-b)为激发态|e＞到其他能级的粒子数弛豫速率,γ为激发态到基态的非相干转移速率,即热弛豫速率,通常认为γ<<Γ.耦合场E1和探测场E2均与|e ＞⇔|g＞跃迁发生耦合作用,同时还外加了磁场B,使系统的基态能级|g＞和激发态能级|e＞分裂成多个Zeeman子能级.Akulshin等认为是原子相干对吸收的相长干涉产生了EIA,并于1999年提出了实现EIA必须满足的3个基本条件:1)Fe=Fg+1,其中Fg和Fe分别为基态和激发态的总角动量;2)基态Fg到激发态Fe的跃迁是封闭的循环跃迁,即3)基态必须是简并的,即Fg≥1,在零磁场情况下有2 Fg+1个简并的Zeeman子能级.然而条件2)和3)并非必要条件,Kim小组己在实验中实现了Fg↔Fe=Fg-1和Fg↔Fe=Fg跃迁也可以获得EIA信号[16].Taichenachev[5]利用激发态相干到基态相干的自发转移解释了EIA,他对A kulshin等人的实验结果进行了分析,给出了EIA的物理图像:EIA是由耦合光场导致的激发态Zeeman子能级的相干自发转移到基态Zeeman子能级所引起的,即是由激发态到基态的光诱导导致的自发转移产生的;EIA吸收谱线的线宽可以反映出基态Zeeman子能级间相干时间的长短,这种相干是处于同一个某态超精细能级中的Zeeman子能级相互之间作用的结果.由于Akulshin等人提出的简并二能级模型过于简单,没有对系统中具体的原子相干过程进行阐述,因此王丽等人在简并二能级模型基础上构建出能够直观反映原子相干过程的N型四能级系统模型,如图2所示.在裸态能级图上,3个电偶极跃迁构成N型链的四能级系统,其中,中间跃迁为探测跃迁,两边的跃迁为耦合跃迁.在这个系统中,激发态能级的总角动量大于基态能级的总角动量,能级|1＞和|3＞是没有弛豫的简并基态能级,能级|2＞和|4＞是简并激发态能级.根据选择定则,|1＞⇔|4＞跃迁是偶极禁止的,1个弱耦合场(拉比频率为2Ω1)同时驱动|1＞⇔|2＞跃迁和|3＞⇔|4＞跃迁,在|2＞⇔|3＞跃迁之间利用1个更弱的场(拉比频率为2Ω2)进行探测.γ21和γ23分别为激发态|2＞自发衰减到|1＞和|3＞的粒子数衰减速率,γ43为激发态|4＞自发衰减到|3＞的粒子数衰减速率,γ0为激发态到基态的非相干转移速率.由于弱耦合场的作用,在缀饰态表象中探测跃迁分裂成4个相互耦合的跃迁.其中|1＞|2＞|3＞|4＞分别表示缀饰态能级,γ24,γ14,γ23,γ13分别为缀饰态之间的粒子数衰减速率,|2＞⇔|3＞,|1＞⇔|4＞,|1＞⇔|3＞,|2＞⇔|4＞跃迁的拉比频率分别为2a1,2a2,2a3,2a4.利用缀饰态理论,得到介质对光场的吸收表现为4个跃迁的相干叠加.这4个跃迁相互耦合,且源自4种不同因素导致的耦合,一部分源自激发态的自发辐射,即正比于γ23,对所有4个探测跃迁产生相同符号的耦合,均为负号,此时缀饰态相干表现为抑制吸收.另一部分源自激发态到基态的自发相干转移,即正比于γ0,对其中2个探测跃迁(|1＞⇔|3＞,|2＞⇔|4＞)产生正号的耦合,对另2个探测跃迁(|2＞⇔|3＞,|1＞⇔|4＞)产生负号的耦合.这些正负参半的耦合显著改变了缀饰态相干对吸收的贡献,使之由抑制吸收改变为增强吸收.换而言之,原子相干的自发转移使缀饰态相干由抑制吸收改变为增强吸收,从而导致EIA.因此,王丽等人得到的结论与A kulshin等人得出的EIA是由耦合光场导致的激发态Zeeman子能级的相干自发转移到基态Zeeman子能级所引起的结论完全吻合,而且王丽等人将简并二能级系统细化为基态和激发态均包括2个简并能级的N型四能级系统,并通过缀饰态理论对系统中的相干过程进行了阐述,最终得出了更加详细而且深刻的结论.虽然王丽等人对A kulshin提出的简并二能级模型进行了细化,并通过分析系统中的原子相干过程得出了原子相干的自发转移产生了EIA的结论,对Akulshin等人的结论进行了印证,但是王丽等人提出的N型四能级系统模型比较特殊,系统中的能级分布和激光场激发频率均具有高度对称的特性,不能反映出原子相干过程的一般性规律.因此,笔者构建了能级分布和激光场激发频率更贴近于真实原子系统的近似简并的Λ型四能级系统模型,如图3所示.在裸态能级图中,|1＞和|2＞能级属基态精细结构能级,|3＞和|4＞能级属激发态精细结构能级.频率为ωc的光学耦合场激励|2＞⇔|3＞跃迁,频率为ωrf的射频场激励|3＞⇔|4＞跃迁,可视为级联型的光学-射频双光子耦合场,而频率为ωp的探测场通过扫描|1＞⇔|4＞跃迁获得探测吸收谱.三场的拉比频率分别为Ωc,Ωrf和Ωp.在缀饰态模型中,由于射频场与|3＞⇔|4＞能级发生共振相互作用,由其产生的动态Stark劈裂效应使能级|4＞劈裂为2条对称分布的缀饰态能级|+＞和|-＞.当光学-射频双光子耦合场与|2＞⇔|4＞能级共振,形成跃迁路径1,如图3 b所示.而当双光子耦合场与|2＞⇔|+＞能级共振,形成跃迁路径2,如图3 c所示.在跃迁路径1中包含着2种形式的跃迁,即原子从能级|2＞跃迁到能级|+＞上和从能级|2＞跃迁到能级|-＞上,并构成2个新的Λ型三能级系统,这2个Λ型三能级系统相对于双光子耦合场具有大小相同的调谐频率而符号相反,它们之间形成量子相干,在探测场的中心频率处感应形成EIA.而跃迁路径2是一条单纯的跃迁路径,双光子耦合场将原子直接从能级|2＞激发到能级|+＞上并构成一个Λ型三能级系统,则形成EIT.因此,得出与Taichenachev相似的结论:EIA是由双光子耦合场导致的激发态精细结构能级的相干自发转移到基态精细结构能级所引起的. 为了使系统更具有一般性,分析了频率为ωrf的射频场不仅仅会激励激发态精细结构能级|3＞⇔|4＞的跃迁,也有可能激励基态精细结构能级|1＞⇔|2＞跃迁的情况,结果发现,如果射频场ωrf也与|1＞⇔|2＞跃迁发生相互作用,则会削弱EIA,同时增强EIT,这也从另一个侧面反映了EIA是由激发态精细结构能级的相干自发转移到基态精细结构能级所引起的.目前,在应用激光光学方面出现的非线性现象中,最具代表性的是电磁诱导透明(EIT)和电磁诱导吸收(EIA)现象,它们分别基于原子相干对吸收的相消干涉和相长干涉,使介质出现奇特的吸收和色散特性,并分别在慢光速和超光速等信息存储领域具有广阔的应用前景.由于EIT的研究起步较早,而且涉及的量子相干过程较EIA更简单一些,因此对EIT的研究已趋于成熟,但是关于EIA的研究尚处于起步阶段,而且对导致EIA的量子相干机理的解释还存在争议,甚至在一些实际原子系统中出现的EIA还无法用现在的理论给出解释.因此,EIA还属于量子光学领域里全新的研究课题,对其形成机理的探讨不仅具有重要的理论意义,而且对超光速等应用领域的发展具有重要指导意义.通过对简并二能级、N型四能级以及近似简并的Λ型能级3种模型的阐述,解释了产生EIA的量子相干过程.虽然3种模型之间存在一些差异,但它们最终得到了非常一致的结论,即EIA是由激发态相干到基态相干的自发转移产生的,而且3种模型按照提出时间的先后顺序也是越来越完善.随着对EIA研究的深入,将有更完善的理论模型被提出,并对实际原子系统中出现的EIA给出完美解释.【相关文献】[1]KUHN A,STEUERWALD S,BERGMANN K.Coherent population transfer in NO w ith pulsed lasers:the consequences of hyperfine structure,Dopp ler broadening and electromagnetically induced abso rption[J].Eur Phys JD,1998,1(1):57-70.[2]AKULSH IN A M,BARREIRO S,LEZAMA A.Electromagnetically induced abso rption and transparency due to resonant two-field excitation of quasidegenerate levels in Rb vapor[J].Phys Rev A,1998,57(4):2996-3002.[3]LEZAMA A,BARREIRO S,AKULSH IN A M.Electromagnetically induced absorption[J].Phys Rev A,1999,59(6):4732-4735.[4]DANCHEVA Y,ALZETTA G,CARTALEVA S,et al.Coherent effectson the Zeeman sublevelsof hyperfine states in optical pumping of Rb by monomode diode laser[J].Opt Commun,2000,178(1-3):103-110.[5]TA ICHENACHEV A V,TUMA IKIN A M,YUD IN V I.Electromagnetically induced abso rp tion in a four-state system[J].Phys Rev A,2000,61(1):011802(1-4).[6]FA ILACHE H,VALENTE P,BAN G,et al.Inhibition of electromagnetically induced abso rption due to excited-state decoherence in Rb vapor[J].Phys Rev A,2003,67(4):043810(1-7).[7]KIM K,KWON M,PARK H D,et al.Electromagnetically induced abso rption spectra depending on intensitiesand detunings of the coup ling field in Cs vapour[J].J Phys B:A t Mol Op t Phys,2001,34(23):4801-4808.[8]王彦华,闫树斌,王军民.铯原子气室中简并二能级系统的电磁诱导吸收[J].中国激光,2004,31(9):1065-1069.[9]王丽,胡响明.相长干涉:电磁诱导吸收[J].物理学报,2004,53(8):2544-2550.[10]王丽,宋海珍.四能级原子系统中的电磁诱导吸收[J].物理学报,2006,55(8):4145-4149.[11]王丽,杨兴强,肖绍武,激光场线宽对电磁诱导吸收效应的影响[J].量子光学学报,2008,14(3):267-272.[12]L IU C P,GONG SQ,FAN X J,et al.Electromagnetically induced abso rption via spontaneously generated coherence of aΛsystem[J].Op t Commun,2004,231(1-6):289-295.[13]ZHANGJiepeng,XU Jun,HERNANDEZ G,et al.Polychromatic-field-induced transparency and abso rption in a threelevelΛsyste m[J].Phys Rev A,2007,75(4):043810(1-4).[14]FU Guangsheng,L IXiaoli,ZHUANG Zhonghong,et al.Electromagnetically induced abso rption and transparency in an optical-rf two-pho ton coup ling configuration[J].Phys Lett A,2008,372(2):176-180.[15]张连水,李晓莉,王健.光学-射频双光子耦合作用下的电磁诱导透明和电磁诱导吸收[J].物理学报,2008,57(8):4921-4925.[16]KIM S K,MOON H S,KIM K,et al.Observation of electromagnetically induced abso rp tion in open system s regardless of angular momentum[J].Phys RevA,2003,68(6):063813(1-5).[17]A KULSH IN A M,LEZAMA A,SIDOROV A I,et al.‘Storage of light’in an atomicmedium using electromagneticallyinduced abso rption[J].J Phys B:A t Mol Opt Phys,2005,38:L365-L 374.。

自发参量下转换与双模压缩真空态-概述说明以及解释

自发参量下转换与双模压缩真空态-概述说明以及解释1.引言1.1 概述概述在量子光学领域，自发参量下转换和双模压缩是两个重要的研究课题，它们在光子的生成和控制过程中发挥着关键作用。

本文将结合这两个主题，探讨它们在真空态中的应用和意义。

首先，我们将介绍自发参量下转换的基本原理和特点，以及其在量子信息领域中的应用。

接着，我们将探讨双模压缩的概念和实验方法，以及在量子通信和量子计算中的潜在应用。

最后，我们将研究真空态的特性和量子行为，探讨其在量子信息科学中的重要性。

通过对这三个主题的深入探讨，我们希望能够加深对量子光学中自发参量下转换和双模压缩的理解，并为未来的量子技术发展提供一定的启示和指导。

文章结构部分内容如下：1.2 文章结构本文将分为三个部分来阐述自发参量下转换与双模压缩真空态的相关内容。

首先将在第二部分中介绍自发参量下转换的基本概念和原理，包括其在量子物理中的应用及最新研究进展。

接着，第二部分将详细探讨双模压缩的理论基础和实验现象，以及其与自发参量下转换的联系和区别。

最后，在第二部分中将介绍真空态的概念和性质，以及其在量子信息领域中的重要作用。

通过对这三个主要内容的详细讨论，本文旨在帮助读者更全面地了解自发参量下转换与双模压缩真空态的研究现状和未来发展方向。

1.3 目的目的部分的内容应该清晰地表达本文的研究目标和意义。

在这篇文章中，我们的目的是探讨自发参量下转换与双模压缩真空态之间的关系，从而深入研究这两个物理现象在量子力学中的应用和影响。

通过对这些现象的探讨，我们可以更深入地理解量子系统的行为，并为未来的研究和应用工作提供理论基础和启示。

同时，本文也旨在为读者提供对于这些复杂现象的简明解释，以便让更多人了解并深入研究这一领域的知识。

通过本文的阐述，我们希望能够推动量子物理学领域的发展，促进其在科学研究和技术应用中的进一步应用。

2.正文2.1 自发参量下转换自发参量下转换是一种常见的光学效应，它描述了光子在非线性介质中相互转换的现象。

跃迁类型和选择定则

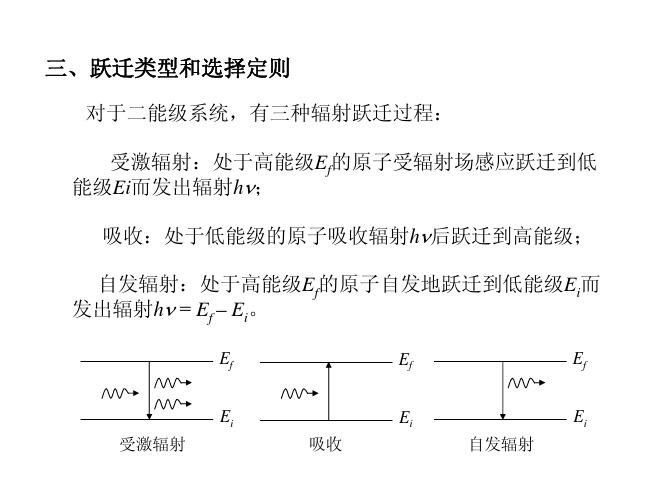
例如，氦原子的21S0和 23S1态，无法通过电偶极跃迁到基态11S0 (偶极禁戒)，这两个状态为亚稳态。
ns1S
20×104
np1Po
nd1D
ns3S
np3Po
nd3D
. ..
5(0) 515.6 4(0)
5047.7 184859.06 18×104 7281.3 3964.7 520 166271.70 16×104 0 584.3
这就是电偶极近似。与这一部分对应的跃迁称为电偶极跃迁(用E1表示)。
e
− ik ⋅r
1 = 1 − (ik ⋅ r ) + (ik ⋅ r ) 2 − 2!
第二项包含两部分，分别含有来源于电荷运动的电流产生的磁偶极矩和电荷分布产生的电四极矩，相应的辐射是磁偶极辐射（M1）和电四极辐射（E2）。第二项之后还有磁四极辐射（M2）和电八极辐射（E3）等。我们把除电偶极辐射之外的辐射称为禁戒辐射。这里的禁戒指的是对电偶极辐射禁戒，它可以通过其它种辐射跃迁，只是跃迁概率比电偶极辐射小很多。
同样，氦的21S0到基态11S0也不能进行电和磁的单光子跃迁，它们之间主要的是双光子跃迁过程。在激光的强相干场中，双光子过程才变得重要。现在经常利用功率较大的可调频率激光器来研究双光子和多光子跃迁等极小概率过程。
P = Pf / Pi=(-1) j 对Ej =(-1) j+1 对Mj
后三个选择定则是近似成立的。定则4只对所涉及的每个态都能用单一电子组态描述才成立，定则5和定则6适用于多电子原子的LS耦合。氢原子基态12S1/2的两条超精细劈裂能级之间的跃迁是磁偶极辐射的一个例子，它们的所有量子数都满足磁偶极辐射的选择定则，定则3和定则4使电偶极辐射禁戒。

【国家自然科学基金】_双光子相互作用_基金支持热词逐年推荐_【万方软件创新助手】_20140731

2009年序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
科研热词黏附高能重离子碰撞血管内皮细胞细胞膜流动性直接光子椭圆流星型八极矩分子平均自由程小檗碱双光子吸收不对称因子 zindo-sos方法 pg细胞 2,1,3-苯并噻二唑 1,3,4-嘑二唑
推荐指数 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2010年序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
科研热词量子干涉量子光学腔场谱二项式光场转让超导量子干涉仪腔量子电动力学结合方式纠缠度纠缠原子突然死亡真空场诱导相干相互作用电磁诱导透明概率克隆机梯形四能级原子系统双阳离子咔唑衍生物双光子细胞核荧光探针双光子参数范围动力学共振偶极相互作用 t-c模型 s模型 kerr效应
2012年序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
科研热词推荐指数相对论重离子碰撞 2 双轻子产生 2 双光子相互作用 2 钙成像 1 血液动力学 1 脑成像 1 纠缠态 1 系统药理学 1 相互作用 1 激光诱导 1 激光激发 1 定态 1 双光子跃迁 1 双光子显微镜 1 动力学演化 1 制备 1 共振相互作用 1 光操纵 1 two-photon interaction relativistic 1 heavy ion col two-mode entanglement, atomic 1 coherence, resonant rydberg原子 1 rabi频率 1 dilepton production 1

半导体物理学(刘恩科)第七版-完整课后题答案

第一章习题1．设晶格常数为a 的一维晶格，导带极小值附近能量E c (k)和价带极大值附近能量E V (k)分别为：E c =0220122021202236)(,)(3m k h m k h k E m k k h m k h V -=-+ 0m 。

试求：为电子惯性质量，nm a ak 314.0,1==π（1）禁带宽度;（2）导带底电子有效质量; （3）价带顶电子有效质量;（4）价带顶电子跃迁到导带底时准动量的变化解：（1）eV m k E k E E E k m dk E d k m kdk dE Ec k k m m m dk E d k k m k k m k V C g V V V c 64.012)0()43(0,060064338232430)(2320212102220202020222101202==-==<-===-==>=+===-+ 因此：取极大值处，所以又因为得价带：取极小值处，所以：在又因为：得：由导带：043222*83)2(1m dk E d mk k C nC===sN k k k p k p m dk E d mk k k k V nV/1095.7043)()()4(6)3(25104300222*11-===⨯=-=-=∆=-== 所以：准动量的定义：2. 晶格常数为0.25nm 的一维晶格，当外加102V/m ，107 V/m 的电场时，试分别计算电子自能带底运动到能带顶所需的时间。

解：根据：t k hqE f ∆∆== 得qEk t -∆=∆ sat sat 137192821911027.810106.1)0(1027.810106.1)0(----⨯=⨯⨯--=∆⨯=⨯⨯--=∆ππ补充题1分别计算Si （100），（110），（111）面每平方厘米内的原子个数，即原子面密度（提示：先画出各晶面内原子的位置和分布图）Si 在（100），（110）和（111）面上的原子分布如图1所示：（a ）(100)晶面（b ）(110)晶面（c ）(111)晶面补充题2一维晶体的电子能带可写为)2cos 81cos 87()22ka ka ma k E +-= （，式中a 为晶格常数，试求（1）布里渊区边界；（2）能带宽度；（3）电子在波矢k 状态时的速度；（4）能带底部电子的有效质量*n m ；（5）能带顶部空穴的有效质量*p m解：（1）由0)(=dk k dE 得 an k π= （n=0，±1，±2…）进一步分析an k π)12(+= ，E （k ）有极大值，214221422142822/1083.7342232212414111/1059.92422124142110/1078.6)1043.5(224141100cm atom a a a cm atom a a a cm atom a a ⨯==⨯+⨯+⨯⨯==⨯⨯+⨯+⨯=⨯==⨯+-）：（）：（）：（222)mak E MAX =（ ank π2=时，E （k ）有极小值所以布里渊区边界为an k π)12(+=(2)能带宽度为222)()ma k E k E MIN MAX =-（ (3）电子在波矢k 状态的速度)2sin 41(sin 1ka ka ma dk dE v -== （4）电子的有效质量)2cos 21(cos 222*ka ka mdkEd m n-== 能带底部 an k π2=所以m m n 2*= (5)能带顶部 an k π)12(+=，且**n p m m -=，所以能带顶部空穴的有效质量32*mm p =半导体物理第2章习题1. 实际半导体与理想半导体间的主要区别是什么？答：（1）理想半导体：假设晶格原子严格按周期性排列并静止在格点位置上，实际半导体中原子不是静止的，而是在其平衡位置附近振动。

量子光学华师

五、量子光学在交叉学科中的应用
量子信息科学；冷原子物理。
由于篇幅所限，本章对量子光学只作选择性的介绍：已相当成熟且自成体系的内容不予介绍（如第二部分内容）；虽然基本或活跃但占篇幅较大的内容不予介绍（如第一部分中的阻尼的量子理论、第五部分中的冷原子物理、以及第四部分中的大部分内容）。另外，我们不一定按上列次序进行介绍，有些内容将穿插进行。在本章最后，我们将给出各部分的参考文献，以供有兴趣的读者参考。
k
k
k
k
（2）算符的表象变换
∑ Fmn ( B) = Bm F Bn = Bm Ak
k ,l
Ak F Al
∑ ( ) Al Bn = Smk Fkl A Sn*l
k ,l
即 F ( B) = SF ( A) S +
表明算符在不同表象的变换为相似变换。
4．幺正变换的性质
用U （unitary）代替 S 表示幺正矩阵，带‘号和不带‘号分别表示不同的表象。
3
量子光学
—— Mars
量子力学（QM）基础
一、QM 的历史背景
1900，Planck，黑体辐射，能量量子化： ε = hν
1905，Einstein, 光电效应，光量子——光子
E = hν ， p = h λ （ p = E c = hν c = h λ ）
1913， Bohr, 原子光谱和原子结构，定态、；量子跃迁及频率条件：
则测量力学量 A 得到相应的本征值 An ，测量后系统仍处于本征态 ψ n ；若系
∑ 统处于任意态 ψ = cn ψ n ，则测量力学量 A 时以概率 cn 2 得到本征值 n
An ，若测量得到本征值 An ，则测量后系统塌缩到相应的本征态 ψ n 。

四原子Tavis-Cummings模型中两体及多体纠缠的研究

顿量可表示为
Ｈ ∑ ＋ａ＋ ∑（＋）＝ｗｇａ
示为
（）２
假设二原子开处于能级始都基态ｌ）腔处于粒态ｌ，此，统ｇ，场子数１因系所处的量子ｏ可表）初始态（））
ｌ）ｇｌ）。）２））（＝）［ｌ０ｇｇｇ
众所周知量子纠缠是量子信息发展过程中重要的量子资源之一，它是众多量子协议得以实现的重要依托ｎＱＤ腔提供一个很好的操控量子纠缠和展示量子信息过程的平台ｎ。中，ｃ。而Ｅ，。其４Ｊ模型就是人 — 们最熟悉和引用最广的场与原子相互作用的模型之一，ｃＪ模型展示的是量子化的场与量子化的二能级原 —
的下降算符；Ｗ为二能级原子的跃迁频率；口ａ，为原子的产生和湮灭算符；ｗ为腔场的频率。系统模型为４个二能级原子与１单模腔场的相互作用系统，中原子间个其
距离足够大，原子间相互作用可忽略。如图１因此。
收稿日期：０１４１２１－．７０图１四个二能级原子与一个单模场相互作用系统
２ｃｎｕｒｎｅＤａｇｅｏｃｒｅｃ￣ｎｌ的运算及比较ｔ
●
摘要：首先，究４研个二能级原子与１个单模腔场相互作用下量子系统的演化情况，此基础上，在再运用ｃｎｕｒｎｅｔｇｅｏｃｒｃ和ａｌｅｎ两种度量对４个二能级原子之间及与腔场的相互纠缠的周期性演化进行计算并对其结果进行讨论和分析。通过比较两种度
量之间的关系发现此量子系统只存在两体纠缠，而不存在多体之间的纠缠，另外，在恰当选择时间的情况下，以产生四原可

拉曼共振四能级原子系统中的有效交叉Kerr非线性

拉曼共振四能级原子系统中的有效交叉Kerr非线性王利强;查新未;李永放【摘要】A theoretical investigation is put forward for obtaining effective cross-Kerr nonlinearity of the four-level atom interacting with three electromagnetic ing density-matrix equations and perturbation iterative method,the variation dependence of the third-order susceptibility on the detunings of the applied electromagnetic fields is derived.The results show that a large cross-Kerr nonlinearity can be generated when the detunings of the two weak probe fields are Raman resonant,and the corresponding linear susceptibility and self-Kerr interactions vanish.The realization of the effective Kerr nonlinearity with vanishing absorption is possible in a Raman resonant four-level system.%提出了利用四能级原子系统与三个电磁场相互作用获取有效交叉Kerr非线性的方案.应用微扰理论和密度矩阵方法,得到了三阶极化率与外加电磁场失谐量的变化关系.结果表明：当两个弱探测场的失谐量达到拉曼共振时,可以获得一个大的交叉Kerr非线性磁化率,且自Kerr 非线性极化率和线性极化率为零.证明了在具有拉曼共振的四能级原子系统中获得无吸收有效交叉Kerr非线性的可行性.【期刊名称】《陕西师范大学学报（自然科学版）》【年(卷),期】2011(039)006【总页数】4页(P27-30)【关键词】非线性光学;三阶极化率;交叉Kerr非线性;拉曼共振【作者】王利强;查新未;李永放【作者单位】陕西师范大学物理学与信息技术学院,陕西西安710062;西安邮电学院理学院,陕西西安710061;西安邮电学院理学院,陕西西安710061;陕西师范大学物理学与信息技术学院,陕西西安710062【正文语种】中文【中图分类】O437.3光克尔效应是指光通过非线性光学介质时其偏振方向会随着其他光的作用而变化的现象，它反映了物质的非线性光学性能.光学克尔效应存在着广泛的应用，如纠缠浓缩［1－2］、量子传输［3］、量子门转换［4］和量子非破坏性测量［5］以及光调制器和光偏转器、光开关、光双稳态器件的制作.近年来，由于弱吸收增强的非线性极化率可以在弱光条件下研究非线性光学，其中基于电磁感应透明（Electromagnetic induced)和拉曼共振（Raman resonant)的介质来获得增强的光学克尔非线性效应引起人们极大的关注.Lukin等通过理论研究指出，利用四能级原子EIT产生的巨大交叉克尔非线性系数，有可能使一个单光子脉冲导致另一个单光子脉冲产生π相移，从而实现两个单光子脉冲的量子纠缠和量子相位门［6］.Yan等在冷原子N型四能级系统中也观察到EIT增强的交叉克尔非线性效应和双光子吸收［7－8］.不仅EIT过程可导致介质的线性和非线性极化率发生很大的变化［9－11］，Raman跃迁也可以极大地改变介质的极化率.在Raman过程中，由于原子相干导致的强色散效应会引起强的克尔非线性效应［12－16］.利用原子之间的相干性可以产生一个纯的交叉克尔效应已经被理论［17－18］和实验证实［19］.但对大多数材料来说，交叉克尔效应总是伴随不可忽略的非线性效应，例如自克尔效应，差频以及和频的产生［20］.本文在一个N型四能级Rb原子系统中，通过调谐探测场和泵浦场的失谐量达到Raman共振时，获得了一个较大的纯交叉克尔非线性系数，但对探测光的吸收为零.在旋波近似下，系统的密度矩阵运动方程为上式中2γ1、2γ3 分别表示能级｜2〉→｜1〉和｜4〉→｜3〉的自发衰减系数.下面讨论原子对入射光的线性和非线性响应情况.介质对两个弱的探测光ωa、ωc响应的极化强度可以表示为上式中的极化强度包括线性和非线性极化强度，例如频率为ωa的极化强度可以表示为式中的χ（1)和χ（3)表征介质对光极化特性的极化张量.而介质对光的响应是电偶极振子在光电场作用下振动所产生的极化，其极化强度是P＝－Ner（t)，N为单位体积内的振子数.对电偶极矩，取量子平均，得到极化强度与密度矩阵的关系式：上式中的第一项对应于介质对频率为ωa的响应，第二项对应于介质对频率为ωb 的响应，第三项对应于介质对频率为ωc的响应.本文所考虑的模型中，主要研究｜1〉和｜2〉之间的相干辐射作用，所以只考虑P（ωa)＝N（μ21ρ12)项，即将（5)式中的反对角元ρ12按Ωa、Ωc的泰勒形式展开，得到线性极化率χ（1)、自克尔极化率和交叉克尔极化率的表达式分别为图2、3给出了线性极化率的实部Re［χ（1)］、虚部Im［χ（1)］和表示自克尔非线性效应的三阶极化率的实部 Re［χs（3 )］、虚部Im［χs（3)］随探测场Ωa 的失谐量Δa变化曲线.取参量γ1＝7MHz，γ3＝7MHz，Ωb＝4MHz.由图2可以发现，当强泵浦场的失谐量Δb＝0时，出现了类似于Λ型次能级原子系统所呈现的电磁感应透明窗口，在拉曼共振Δa＝Δb＝0处，系统形成一个原子暗态，极化率的实部和虚部都为零.在相同条件下，图3给出了自克尔非线性极化率随探测场失谐量的变化曲线，可以发现，自克尔非线性极化率的虚部曲线显示出三个电磁感应透明点，而且对应的电磁感应透明窗口比线性极化率所对应的窗口要窄.同时发现自克尔非线性极化率的强度要比线性极化率的强度弱好几个数量级.图4给出了在满足拉曼共振Δa＝Δb＝0条件下，交叉克尔非线性极化率随探测场Ωc的失谐量Ωc的变化曲线.从图中我们可以明显的发现，在远离共振区，交叉克尔非线性极化率的实部曲线衰减比虚部慢得多.因此，当选择探测场Ωc远离共振时，可以获得一个相当大的交叉克尔非线性极化率的实部，并且由图2和图3可知，在拉曼共振条件下所对应的线性极化率和自克尔非线性极化率均为零，即可以获得无吸收有效的纯交叉克尔非线性.例如在图4中，当Δc＝100MHz时，通过计算交叉克尔极化率的实部大约为10－8 m2 V－2，而此时线性极化率和自克尔非线性极化率为零，并且交叉克尔非线性极化率的虚部小到可以忽略不计.而由交叉克尔效应诱导探测场Ωa的相位偏移，可以利用下式得到上式中，l为相互作用的长度，λ0为探测场Ωa在真空中的波长.由图4所给的参量可以得到Δφ＝0.1rad的光学相位偏移.本文在N型四能级原子系统中，提出一个获得有效交叉克尔非线性效应的方案.利用密度矩阵方程和微扰理论，导出了线性极化率和非线性极化率的具体表达式，给出了它们随3个电磁场失谐量变化关系.在一般条件，光与物质相互作用获得的交叉克尔非线性效应总是伴随着线性和自克尔非线性效应，但是在本文所提出的模型中，在满足拉曼共振Δa＝Δb＝0条件下，原子对光只存有交叉克尔响应，线性极化率和自克尔非线性极化率均等于零.虽然在此条件下所对应的交叉克尔非线性吸收不可忽略，但若探测场Ωc远离共振，仍可以获得一个大的交叉克尔非线性，同时交叉克尔非线性吸收部分小到可以忽略不计.因此在拉曼共振Δa＝Δb＝0条件下，通过适当选择探测场Ωc的失谐量，可以获得一个无吸收的有效的纯交叉克尔非线性.【相关文献】［1］Jaromir F，Ladislav M，Radim F.Entanglement concentration of continuous-variable quantum states［J］.Physical Review：A，2003，67：022304-022308.［2］David M，Natalia K.Procrustean entanglement concentration of continuous-variable states of light［J］.Physical Review：A，2006，74：042315-042320.［3］David V，Mauro F，Paolo plete Quantum Teleportation with a Kerr nonlinearity［J］.Physical Review Letters，2000，85：445-448.［4］Clausen J，Knoll L，Welsch D G.Quantum state conversion by cross-Kerr interaction ［J］.Journal of Optics Quantum and Semiclassical Optics，2002，4：155-163.［5］Munro W J，Nemoto K，Beausoleil R G，et al.High-efficiency quantum-nondemolition single-photon-mumberresolving detector［J］，Physical Review：A，2003，71：033819-033822.［6］Lukin M D，Imamoglu A.Nonlinear optics and quantum entanglement of ultra-slow single photons［J］.Physical Review Letters，2000，84：1419-1422.［7］Yan M，Rickey E，Zhu Y.Observation of absorptive photon switching by Quantum interference［J］.Physical Review：A，2001，64：041801-041806.［8］Yan M，Rickey E，Zhu Y.Nonlinear absorption by Quantum interference in cold atoms［J］.Optics Letters，2001，26：548-551.［9］Yan Xiang′an，Wang Liqiang，Yin Baoyin，et al.Enhancement of nonlinear susceptibility in a four-level tripod scheme［J］.Chinese Optics Letters，2010（8)：795-799.［10］Yan Xiang′an，Wang Liqiang，Yin Baoyin，et al.Enhanced self-Kerr nonlinearity in spontaneous emission［J］.Journal of the Optical Society of America B-optical Physics，2009，26：1862-1868.［11］Yan Xiang′an，Wang Liqiang，Yin Baoyin，et al.Effect of spontaneously generated coherence on Kerr nonlinearity in a four-level atomic system ［J］.Physical Letters：A，2008，372：6456-6460.［12］武海斌，常宏，马杰，等.Λ型三能级原子系统中Raman跃迁增强的Kerr非线性效应［J］.物理学报，2005，54：3632-3636.［13］任立庆，仇旭，樊荣，等.光脉冲Λ－在三能级介质中传输的解析分析［J］.陕西师范大学学报：自然科学版，2009，37（3)：28-32.［14］Payne M G，Deng L.Extremely slow propagation of a light pulse in an ultracold atomic vapor：A Raman scheme without electromagnetically induced transparency［J］，Physics Letters：A，2001，64：031802-031805.［15］Deng L，Hagley E W，Kozuma M，et al.Achieving very-low-loss group velocity reduction without electromagnetically induced transparency［J］，Applied Physics Letters，2002，81：1168-1170.［16］Wang L J，Kuzmich A，Dogariu A.Gain-assisted superluminal light propagation［J］，Nature，2000，406：277-279.［17］Schmidt H，Imamoglu A.Giant Kerr nonlinearities obtained by electromagnetically induced transparency［J］.Optics Letters，1996，21：1936-1938.［18］Kang H，Zhu Y.Observation of Large Kerr nonlinearity at low light intensities ［J］.Physics Review Letters，2003，91：093601-093604.［19］Wang Z B，Maralin K P，Sanders B rge crossphase modulation between slow copropagating weak pulses in 87Rb［J］.Physical Review Letters，2006，97：063901-063904.［20］石顺祥，陈国夫，赵卫，等，非线性光学［M］.北京：高等教育出版社，2003：113-197.。

光场与物质间的相互作用

（第四章）
物理与光电信息科技学院

《激光原理与技术》
➢描述光谱线加宽特性的物理量：线型函数和线宽
自发辐射功率 I 为频率的函数。设总的辐射功率为I0,有：

I0 I (v)d
线型函数 g ,(给0 定了光谱线的轮廓或形状) ：
g
度为光谱线宽度(FWHM)记作：
g

0

2
,
0

g 0 , 0
2
用波数差或波长差也可标记谱线宽度:
2
c
1 c
（第四章）
物理与光电信息科技学院

《激光原理与技术》
p(z,t)
m
eiwt
2w0 (w0 w) iw0
忽略原子间的相互作用，整个介质的宏观感应电极化强度为
ne2 E(z)
P(z,t) np(z,t)
m
eiwt
2w0 (w0 w) iw0
n为单位体积工作物质中的原子数，即原子密度。
（第四章）
物理与光电信息科技学院

《激光原理与技术》
在线性极化下，介质的感应电极化强度也可表示成：
P(z,t) 0E(z,t)
介质的线性电极化系数，通过比较为：
ne2
1
0m 2w0 (w0 w) iw0
令 / i // ，得到电极化系数实部和虚部为：
/

ne2
mw0 0
2w0 (w0 w) 1
《激光原理与技术》
光场与物质间的相互作用
1. 经典理论：将构成物质的原子系统和电磁场均做经典处理。光场服从麦克斯韦运动规律，原子服从经典力学运动规律的电偶极振子，该理论成功地解释了物质对光的吸收和色散作用，定性地说明了物质的自发辐射及其谱线宽，对解释光和物质相互作用中的某些物理现象有一定帮助，并对解释光和物质的非共振相互作用也起一定作用。

半导体物理刘恩科考研复习总结

1。

半导体中的电子状态金刚石与共价键（硅锗IV族）:两套面心立方点阵沿对角线平移1/4套构而成闪锌矿与混合键（砷化镓III—V族）：具有离子性，面心立方+两个不同原子纤锌矿结构：六方对称结构（AB堆积）晶体结构：原子周期性排列（点阵+基元）共有化运动:原子组成晶体后，由于电子壳层的交叠,电子不再完全局限在某一个原子上，可以由一个原于转移到相邻的原子上去，电子可以在整个晶体中运动。

能带的形成：组成晶体的大量原子的相同轨道的电子被共有化后，受势场力作用，把同一个能级分裂为相互之间具有微小差异的极其细致的能级,这些能级数目巨大，而且堆积在一个一定宽度的能量范围内，可以认为是连续的。

能隙(禁带）的起因:晶体中电子波的布喇格反射－周期性势场的作用.（边界处布拉格反射形成驻波,电子集聚不同区域，造成能量差）自由电子与半导体的E-K图：自由电子模型：半导体模型：导带底:E(k）〉E(0)，电子有效质量为正值;价带顶:E(k）<E（0)，电子有效质量为负值;能带越窄，k=0处的曲率越小，二次微商就小,有效质量就越大。

正负与有效质量正负有关。

空穴：共价键上流失一个电子而出现空位置，认为这个空状态带正电。

波矢为k的电子波的布喇格衍射条件：一维情况（布里渊区边界满足布拉格）：第一布里渊区内允许的波矢总数=晶体中的初基晶胞数N－每个初基晶胞恰好给每个能带贡献一个独立的k值；－直接推广到三维情况考虑到同一能量下电子可以有两个相反的自旋取向，于是每个能带中存在2N个独立轨道。

－若每个初基晶胞中含有一个一价原子，那么能带可被电子填满一半;－若每个原子能贡献两个价电子,那么能带刚好填满；初基晶胞中若含有两个一价原子,能带也刚好填满。

杂质电离：电子脱离杂质原子的的束缚成为导电电子的过程。

脱离束缚所需要的能力成为杂质电离能。

杂质能级：1）替位式杂质(3、5族元素，5族元素释放电子，正电中心，称施主杂质；3族元素接收电子，负电中心，受主杂质。

光场与N型四能级原子相互作用系统中原子布居的时间演化特性

文章编号：１０．３４２０）２０２ — ５０００６（０２０ —２１０
光场与Ｎ型四能级原子相互作用系统中
原子布居的时间演化特・ｆ＝生
黄春佳，文立
＿
（长沙电力学院物理与信息工程系．秒４０７２益阳师范高等々科学校物理系，阳４３４１长１０７；益１０９
当于具有双层精细结构的二能级原子，且在一定而的条件下可退化为Ｖ型或Ａ型三能级原子或简单二能级原子。因此，场与Ｎ型四能级原子相互作光用系统无疑是简单Ｊｙｅ～ｕａｎｓｍｍｉｓ模型的一种有Ｃｎｇ实际意义的推广。车文采用全量子理论，确求解精了单模光场与型四能级原子相互作用系统的波
（）～（）中。２３式和 “分别为光场的产生算符和湮设算符；和ｃ为原子第ｉｉ＝ｄ，Ｃｄ）能级ｃ（ｂ，，个粒子的产生算符和湮没算符，０相应能级的能量为
本征值（＝１；＝ｌ２３ｈ）Ｅ（，，）为原子与光场的耦合系数。然．ｅ — ０或ｅ — ０时，统将分别退显当１３系
关键词：能级厢子；四单模光岛；子粒子数布居原
中国分ห้องสมุดไป่ตู้类号：３０｝１２

热光场下双原子Jaynes-Cummings模型的动力学特征

第２卷第３１期
２０年９月出版０８
大
学
物
理
实
验
％ｆ２ｌ Ⅳ０．．３
Ｓｐ．２０ｅ０８
ｐＨＹｓＣＬＥＸＰＥＲＭＥＮＴｏＦＣｏＬＩＩＬＥＧＥ
文章编号：０７９４２０）３０５５１０ —２３（０８０ —０１ —０
模型直至 Ⅳ 能级原子的 ’ ，ｃ模型中相继地发现了特征各异的崩坍一复活现象［— ｌ１３。
１８９７年Ｒｍｅ等人在实验上已观察到崩坍一复活现象，得对ｅｐ使
于理论上的兴趣。近年来仍有不少人在研究［］。但至今，两个二能级原子（双原子）与
Ｑ０
ｎ
：
０Ｑ
Ｑ
０
０
（）２
式中，＝（ｎｎ＋１Ｑ，＝－矗）
和＝ｖ
最后求解Ｈｉｎｅｅｅｂｇ运动方程，们得到双原子模型耦合系统时间演化算符Ｕ（）ｓｒ我ｔ
在流形￡上的４× ４矩阵表示：
已知流形ｅ（ｎ一于空间）一般存在四个相应的本征矢：１ ” ｌｅ，，Ｉ＞＝Ｉ，Ｉｎ＞，２＞＝ｌ】ｅｌ ” ＿，ｅｇ，２ｎ＋１ｌ＞：Ｉｌｅ，＞，３ ” ，２ｎ十１ｌｌ１ｇ，，２＞。并且用它们作为流形ｅｇ＞，４＞，２／＋ｇ７的基矢，么我们得到整个耦合系统哈密顿函数（）的矩阵表示为：那１式

量子光学第二讲,相干态与压缩态

* 平移特性：对算符 a (a + ) 的作用相当于使其平移一个复数量 α ( α )
D + ( α ) aD ( α ) = a + α D + ( α ) a +D ( α ) = a + + α*
•
对于任一的算符函数 f (a, a + ) 有
D + ( α ) f ( a, a + ) D ( α ) = f ( a + α, a + + α* )
坐标表象中高阶本征函数可以写成
φn ( q ) = =
(a + )
n
n! 1
n
φ0 ( q ) =
1
1 1 ∂ ⎞n ⎛ ⎟ φ0 ( q ) n ⎜ ωq − ⎟ ⎜ ∂q ⎠ n ! (2 ω ) 2 ⎝
(2 n !)
2
H n ( ω q ) φ0 ( q )
其中 H n 为Hermite多项式，波函数满足正交归一化条件，因此
9
相干态物理性质
几率密度随时间的变化为
ω ψ ( q, t ) = π
2
( )
1
2
ω exp ⎡⎢ − ( q − q 0 cos ωt )2 ⎤⎥ ⎣ ⎦
该波包在谐振子势场中来回做简谐振动而形状不变，因此是相干的。该波包具有最小测不准关系，是最接近经典单模场的量子力学表述形式。相干的最小测不准波包可以写成
( )
( )
( )
( )
2004 © Dr. Shutian Liu, Department of Physics, Harbin Institute of Technology
12

双模光场与三能级原子的相互作用哈密顿量

双模光场与三能级原子的相互作用哈密顿量概述1. 光场与原子的相互作用是量子光学和原子物理中的重要研究领域。

双模光场是一种特殊的光场，其光子分布可以描述为两个不同的模式之间的转换。

而三能级原子是一种具有三个能级的原子系统，其能级结构的复杂性使得与光场的相互作用具有一定的特殊性。

本文将着重讨论双模光场与三能级原子的相互作用哈密顿量的推导和性质分析。

双模光场的描述2. 根据量子光学理论，双模光场可以由两个模式下的产生和湮灭算符$a_1, a_2, a_1^{\dagger}, a_2^{\dagger}$来描述。

在相干态的定义下，双模光场的描述可以通过其密度矩阵$\hat{\rho}$和期望值$\langle \hat{A} \rangle$来进行。

3. 双模光场与三能级原子的相互作用可以通过相互作用哈密顿量进行描述，该哈密顿量可以表示为$H_{int} = -\vec{d} \cdot \vec{E}$，其中$\vec{d}$为偶极子算符，$\vec{E}$为电场。

在考虑双模光场的情况下，我们可以将相互作用哈密顿量表示为$H_{int} = \sum_{i=1,2} g_i (a_i e^{-i\omega_i t} + a_i^{\dagger} e^{i\omega_i t})\vec{d}\cdot \vec{E}_i$，其中$g_i$为相互作用强度，$\omega_i$为频率，$\vec{E}_i$为电场。

三能级原子的描述4. 三能级原子由三个能级组成，分别为基态$|1\rangle$，第一激发态$|2\rangle$和上带态$|3\rangle$。

在外场作用下，原子之间可以发生跃迁，这些跃迁可以由跃迁矩阵元$V_{ij}$来描述。

在光学腔中，原子的跃迁可以受到光场的影响，从而导致原子的能级结构发生变化。

相互作用哈密顿量的推导5. 要描述双模光场与三能级原子的相互作用，我们需要推导相互作用哈密顿量。

四能级系统激光产生的原理

四能级系统激光产生的原理1.引言1.1 概述概述四能级系统激光是一种基于四个能级的激光系统，其原理基于原子或分子能级的跃迁。

在这种激光系统中，激发光源将原子或分子从基态激发到第一激发态，然后通过跃迁到第二激发态，并进一步跃迁到亚稳态。

最后，在亚稳态和基态之间的跃迁释放出具有特定波长和相干性的激光光子。

四能级系统激光在许多领域中都有广泛的应用，包括激光切割、激光雷达、医学治疗和科学研究等。

它具有高度的激光效率和较长的寿命，可以提供强大且稳定的激光输出。

本文将介绍四能级系统激光的基本原理，包括能级结构和激发跃迁过程。

此外，还将探讨四能级系统激光的应用前景以及它所面临的优势和挑战。

通过深入理解四能级系统激光的原理和特性，我们可以更好地利用它的优势，并克服潜在的挑战，推动激光技术的进一步发展。

(字数: 175)1.2文章结构文章结构部分的内容应该包括以下信息：在文章结构部分，我们将介绍四能级系统激光产生的原理。

本章将分为三个部分来阐述：引言、正文和结论。

引言部分将对四能级系统激光进行概述，介绍其基本概念和重要性。

我们将讨论四能级系统激光在各个领域中的应用，并对本文的目的进行说明。

正文部分将详细介绍四能级系统激光的基本原理。

我们将解释四能级激光器的工作原理和发射过程，并着重介绍其能级结构。

通过对能级结构的分析，我们将深入探讨四能级系统激光的产生机制和特点。

结论部分将对四能级系统激光的应用前景进行讨论。

我们将探讨该技术在通信、医学、材料科学等领域的潜在应用，并分析四能级系统激光的优势和挑战。

最后，我们将总结本文的主要内容，并展望未来对于四能级系统激光研究的重要方向。

通过以上结构，本文将全面介绍四能级系统激光产生的原理，希望读者能够通过本文的阅读，对该领域有更深入的了解。

1.3 目的本文的目的是探讨四能级系统激光产生的原理。

随着科技的飞速发展，激光技术已经成为许多领域不可或缺的重要工具，如光通信、医疗、材料加工等。

第二节受激辐射

第二节受激辐射、受激吸收与自发辐射黑体辐射场，可以理解为组成黑体的原子和光场（或电磁波）相互作用的结果。

光波的产生和传播过程都不可避免涉及光和原子之间的相互作用。

在电磁场理论中，证明了电磁辐射来源于具有加速度的带电物体。

这个结论我们可以从很多方面得到验证。

医院的X 光机利用高能电子快速减速辐射X 射线；高能电子加速器所产生的电磁辐射就来源于具有加速度的电子；电真空微波器件输出的微波也来源于具有加速度的电子辐射。

光在物质中传播时，原子中的正电荷和负电荷受光场中电场作用，向相反方向运动，形成电偶极子，电偶极子向空间辐射光，和入射光场叠加在一起，形成物质中的总光波。

电磁场理论这些结论在用于宏观物质时，没有出现问题。

但用于解释原子发光过程时，却出项了难以调和的矛盾。

二十世纪初，通过实验已经知道电子是物质的基本组成部分，电子带负电，但物质都是电中性的，所以物质中一定还有带正电的部分。

通过测量电子的荷质比（m e /），知道电子质量比原子质量小得多。

很重的带正电的部份称为原子核。

在这个基础上，物理学家开始猜想原子模型。

最早的原子模型是汤姆孙（J.J.Thomson ）提出的，他设想原子就是带正电荷的那一部分均匀分布为一个胶状的球体，带负电的电子镶嵌在这个胶体上，原子就像一个面上有芝麻的面包。

原子发光的频率（光谱）就是这样一个球体的振动频率。

这个模型被后来的电子散射和α粒子的散射实验证明是不对的。

卢瑟福（E.Rutherford ）1909年α粒子散射实验说明，原子大部分是空的，不是一个实心球。

所谓α粒子，就是由两粒带正电荷的质子和两粒中性的中子组成，相当于一个氦原子核。

在自然界内大部分的重元素（例如铀和镭，原子序数为82或以上）在衰变时辐射α粒子。

卢瑟福用α粒子去轰击铂薄片，按照汤姆孙模型，带正电的α粒子受到带正电的铂原子核的散射，α粒子应该偏离入射方向。

但实验发现，只有少量的α粒子发生大角度的偏转，大量原子直接穿过铂薄片，说明大量α粒子没有受到铂原子的作用，原子中的绝大部分空间空无一物。

稳态Y型和Ladder型双光子跃迁的对比

稳态Y型和Ladder型双光子跃迁的对比王德鑫;王伟浩;洪滔【摘要】在一个强耦合场和两个弱探测场相干驱动的四能级Y模型原子系统中实现双光子电磁感应透明.当耦合场与原子能级共振时,Y-型组态就可以等效成一个仅由两个弱的探测场驱动的四能级Ladder-型组态.Ladder模型原子的两个中间能级是精细结构能级(等效于Y模型中的坠饰能级).然而,当Y模型中的耦合场与原子能级之间有失谐时,则两个系统就不再等效.【期刊名称】《哈尔滨师范大学自然科学学报》【年(卷),期】2012(028)005【总页数】4页(P40-43)【关键词】电磁感应透明;量子相干;双光子跃迁;稳态光学响应【作者】王德鑫;王伟浩;洪滔【作者单位】哈尔滨师范大学;哈尔滨师范大学;哈尔滨师范大学【正文语种】中文0 引言目前，在激光场驱动的多能级量子系统中，由于量子相干效应导致的电磁感应透明(EIT)技术已经取得了相当大的成功，是激光诱导量子相消干涉中控制原子的吸收和色散［1－2］中的一项有效技术.EIT的本质就是调整激光场以满足光与物质共振相互作用时在相关的原子态间建立量子相干和关联.且在很多方面有重要应用，例如光存储和提取［3－4］，无粒子数反转光放大(LWI)［5－6］，控制自发辐射相干，全光快速开关［7－8］，量子信息编码操作［9－10］，等等.因此EIT在不同领域有这么广泛的研究，不仅自由空间［11］，近几年 EIT技术已经发展到光腔中［12－13］，利用腔模的强耦合性与原子作用.到目前为止，大多数EIT系统都是伴随单光子吸收和辐射的原子跃迁.作为单光子EIT的拓展，双光子EIT［14］自1996年由Agarwal和Harshawardhan提出引起了广大学者的关注.很快，高锦岳研究组就分别在钠原子和铷原子气体中成功的实现了由一个耦合场控制两个弱探测场吸收［15］，实验上验证了Agarwal的理论.随后，严敏在倒Y模型系统中实现了基于量子相干抑制双光子吸收［16］.近年来，对双光子EIT的特性及其相关应用的研究也得到了飞速的发展［17－18］.研究范围也已经由封闭的原子系统发展到开放的分子系统［19－20］.对印度学者Agarwal提出的模型及理论作了进一步的研究并设计一个新的模型与其进行对比.通过对数值结果及坠饰态理的分析，发现，这两种模型具有同样的光学响应.具体的结果和分析会在第二部分给出.1 理论模型和方程如图1所示，在三个激光场驱动的的四能级Y模型原子系统中，图1(a)，弱探测场Ep1和Ep2分别耦合|1〉↔|2〉和↔|4〉的跃迁，相应的激光场的频率为ωp1和ωp2.强耦合场Ec驱动|2〉↔|3〉的跃迁，其频率为ωc.在强耦合场作用下劈裂的坠饰态能级|2+〉和|2－〉(|2+〉= 如图1(b)所示.单光子失谐Δp1=ω21－ωp1，Δp2= ω42－ωp2，Δc=ω32－ωc为激光场频率和原子能级跃迁频率的差，其中ω21，ω32，ω42是原子的跃迁频率.定义为拉比频率 = 是表征原子和激光场耦合强度的物理量.图1(c)是提出的一个四能级Ladder模型原子系统.其中，|2〉和|3〉是超精细结构的两个子能级.两个弱的激光场分别耦合了|1〉↔|2〉和|3〉↔|4〉的跃迁.为了方便，定义，相应的单光子失谐为Δp1=ω0－ω11－ωp1，Δp2=ω0－ω44－ωp2.同样拉比频率定义为Ωp1 = 在旋转波近似和偶极近似的条件下，Y 模型和Ladder模型系统在相互作用图像下的哈密顿量分别为:图1 系统模型(a)Y模型原子系统，(b)与Y模型等效的坠饰态结构，(c)Ladder模型原子系统将其带入密度矩阵方程其中，Λρ包括自发辐射弛豫速率和相干弛豫速率.这样，就可以通过数值求解分别得到两个系统中四能级上的粒子数，进而分析双光子跃迁的情况.在Y模型系统中，由于强场的耦合作用使得能级|2〉劈裂成两个坠饰能级.令方程(1)中的Ωp1=Ωp2=0，Δp1=Δp2=0，可以得到坠饰能级的本征值和本征态两个模型中的双光子吸收率分别为:2 数值计算与分析图2 双光子跃迁几率随探测场失谐Δp1的变化关系Δp2=0，Ωp1=Ωp2=0.01γ.黑色虚线，蓝实线和黑色实线分别对应Ladder模型中Δ1=10γ，30γ，50γ的情况，其中Γ21=Γ32=Γ42=Γ43=γ;红色虚线，粉色实线和橙色实线分别对应Y模型系统中Ωc=10γ，30γ，50γ的情况，其中Γ21=Γ32=Γ42=γ.如图2所示，在两个弱探测场共振时双光子吸收被很好的抑制(即Δp1=Δp2=0时).同时，发现Y模型系统和Ladder模型系统具有相同的双光子吸收谱线线型，只是谱线的高度略有差别.这可以用坠饰态理论清晰的解释.由方程(4)可知Y模型系统坠饰态能级差ΔEY=E+－E－=2Ωc.通过前面的定义很容易得到Ladder模型系统中两个中间态的能级差ΔELadder=2Δ.在ΔEY=ΔELadder的情况下，两个系统具有相同的光学响应.这样，强场劈裂的坠饰态就被两个超精细结构能级所代替.也就是，在共振的条件下同时满足坠饰能级差与超精细能级差相等，两个中间能级为超精细结构的四能级Ladder模型可以代替在一个强场驱动下的四能级Y模型系统实现控制双光子的吸收和透明.同样，还可以通过双光子吸收率来解释.从方程(6)和(7)可知，当ω41=ωp1+ωp2时，PY=PLadder=0，这就通过控制失谐实现了双光子透明.此时，Y模型中的两个跃迁通道|1〉→|2+〉→|4〉和|1〉→|2－〉→|4〉分别等效于Ladder模型中的|1〉→|2〉→|4〉和|1〉→|3〉→|4〉两个跃迁通道.只是由于强耦合场的作用Y系统中四能级上的粒子数略多于Ladder系统.因此，强场不仅可用来劈裂坠饰态还能够影响粒子数的分布.图3 光子跃迁几率随探测场失谐Δp1的变化关系黑色实线和黑色虚线分别对应Ladder模型中Δp2=Δ= 5γ，10γ的情况;红色实线，红色虚线分别对应Y模型系统中Δp2=Ωc=5γ，10γ的情况，其他参数与图2相同.下面研究另外一种情况Δp2=Ωc(Y模型中)和Δp2=Δ(Ladder模型中)，如图3所示.这两个模型中双光子吸收峰不再对称，但是吸收谱线仍具有相同的线型.且在Δp1=Δp2=0处(即满足共振条件又保证共振处于两个坠饰能级之间)双光子吸收依然能被很好的抑制.同时，发现双光子吸收峰(Δp1=－Δp2)远大于单光子吸收峰(Δp1=Δp2处)，也就是在Δp1=－Δp2处双光子吸收被增强.而且，随着Δp2增加和Ωp1场远离共振，单光子吸收也逐渐被抑制.图4 双光子跃迁几率随探测场失谐Δp1的变化关系(a)黑色、红色和蓝色实线分别对应Y模型中Δc=0.0γ，5γ，10γ的情况;(b)黑色、红色和蓝色虚线分别对应Ladder模型系统中Δp2=0.0γ，5γ，10γ的情况.相应参数Ωp2= Δ=Ωc=5.0γ，其他参数与图2相同.接下来，进一步研究双光子跃迁的吸收线型.将两个系统中第二个弱探测场换成强耦合场，并保证Ωp2=Δ=Ωc=5.0γ.如图4所示，同步改变Δc和Δp2的大小，发现这时两种模型仍具有相似的吸收谱线线型.但Δc=Δp2≠0吸收谱线出现了第三个峰.而且第三个峰的出现还是消失，在Y模型系统中取决于强场与原子的耦合程度.这是因为当Δc很大时，激光场与原子退耦合导致第三个峰消失.在Ladder模型系统中取决于第二个场的强度和两个超精细能级的差.3 结论主要利用数值模拟的方法在相应参量值相同的情况下，对比了Y模型系统和Ladder模型系统的稳态双光子跃迁谱线.具体考虑三种情况.第一种情况:Y模型中强耦合场劈裂的两个坠饰能级等效于Ladder模型中两个超精细能级，同步改变Ωc和Δ的大小，谱线具有对称的吸收和透射;第二种情况:考虑第二个弱探测场与原子不共振时，导致了吸收谱线的不对称;第三种情况:将第二个弱探测场变为强场，同时保证两个系统在广场作用下的中间坠饰能级差始终相等，这样谱线在Δc=Δp2≠0时出现了第三个吸收峰.总之，通过对理论计算和分析发现，这两种模型具有同样的光学响应.参考文献［1］ TewariSP，AgarwlGS.ControlofPhaseMatchingandNonlinearGenerationinDenseMedia byResonantFields［J］. PhysRevLett，1986，56:1811－1814.［2］ HarrisSE，FieldJE，ImamoLUA.NonlinearOptical ProcessesUsingElectromagneticallyInducedTransparency［J］.Phys.Rev.Lett.，1990，64:1107－1110.［3］ ChoiKS，DengH，LauratJ，etal.MappingPhotonicEntanglementintoandoutofaQuantumMemory ［J］.Nature(London)，2008，452:67－71.［4］ HamBS.ControlofPhotonStorageTimeUsingPhaseLoc－king ［J］.Optics Express，2010，18:1704－1713.［5］ Ling H Y.Theoretical Investigation of Phenomena in the Closed Raman－driven Four－level Symmetrical Model［J］. Phys Rev A，1994，49:2827－2838.［6］ Zibrov A S，Lukin M D，Nlkonov D E，et al.Experimental Demonstration of Laser Oscillation without Population Inversion via Quantum Interference in Rb［J］.Phys.Rev.Lett.，1995，75:1499－1502. ［7］ Yan M.，Edwar Dward G.Rickey，Zhu Y F.Observation of Absorptive Photon Switching by Quantum Interference［J］. Phys.Rev.A.，2001，64:041801R－1－4.［8］ Harris SE，Yamamoto Y.Photon Switching by Quantum Interference ［J］.Phys Rev Lett，1998，81:3611－3614.［9］ Yang G J，Qiu TH，Wang K，et al.Reversible Storage of a Weak Light Pulse in a Thermal Atomic Medium［J］.Physical Review A，2010，81:063817－1－8.［10］Fleischhauer M，Lukin M D.Dark－state Polaritons in Electromagnetically Induced Transparency［J］.Physical Review Letters，2000，84:5094－5097.［11］Xu JH，La Rocca GC，Bassani F，etal.Electromagnetically Induced One－photon and Two－photon Transparency in Rubidium Atoms ［J］.Opt Commun，2003，216:157－164.［12］Zhang JP，Hernandez G，Zhu Y F.Slow LightWith Cavity Electromagnetically Induced Transparency［J］.Opt Lett，2008，33:46－48. ［13］Hernandez G，Zhang JP，Zhu Y F.Vacuum Rabi Splitting and Intracavity Dark State in a Cavity－atom System［J］. Chin Phys B，2008，17:2885－2890.［14］Agarwal G S，Harshawardhan W.Inhibition and Enhancement ofTwo Photon Absorption［J］.Phys Rev Lett，1996，77: 1039－1042. ［15］Gao JY，Yang SH，Wang D，et al.Electromagnetically Induced Inhibition of Two－photon Absorption in Sodium Vapor［J］.Phys Rev A，2000，61:023401－1－3.［16］Yan M，Edward RG，Zhu Y F.Suppression of Two－photon Absorption by Quantum Interference［J］.Phys Rev A，2001，64:043807－1－4.［17］ Chen JF，Lu W X，Wang SY，etal.Two－photon Freeinduction Decay with Electromagnetically Induced Transparency［J］.Opt.Lett.，2010，35:1923－1925.［18］ Becerra F E，Willis R T，Rolston S L，et al.Two－photon Dichroic Atomic Vapor Laser Lock Using Electromagnetically Induced Transparency and Absorption［J］.J.Opt.Soc.Am. B，2009，26:1315－1320.［19］ Qi J，Spano F C，Kirova T，et al.Measurement of Transition Dipole Moments in Lithium Dimers Using Electromagnetically Induced Transparency［J］.Phys Rev Lett，2002，88: 173003－1－4.［20］Li L，Qi P，Lazoudis A，et al.Chem The Role of Doppler Broadening in Electromagnetically Induced Transparency and Autler－TownePhys Lett，2005，403，262.。