自动控制原理第7章习题解答
(仅供参考)自动控制原理第七章习题答案

第七章 线性离散系统的分析与校正7-1 试根据定义∑∞=-*=0)()(n nTs e nT e s E确定下列函数的)(s E *和闭合形式的)(z E :⑴ t t e ωsin )(=;⑵ ))()((1)(c s b s a s s E +++=,b a ≠,c a ≠,c b ≠。
解:Ts e z =;⑴ )()sin()(0z E enT s E n nTs==∑∞=-*ω;1)cos(2)sin(21}{21)(20+-=⎥⎦⎤⎢⎣⎡---=-=-∞=--∑z T z z T e z z e z z j e e e j z E T j T j n nTsjwnT jwnT ωωωω。
⑵ ))()((1))()((1))()((1)(c s c b c a b s b c b a a s a c a b s E +--++--++--=; ∑∑∑∞=--∞=--∞=--*--+--+--=000))((1))((1))((1)(n nTs cnT n nTsbnT n nTs anT e e c b c a e e b c b a e e a c a b s E ; ))()(())()(())()(()(cTbT aT e z c b c a ze z b c b a z e z a c a b z z E ------+---+---=; 记))()((c b c a b a ---=∆,∆-=b a k 1,∆-=ca k 2,∆-=cb k 3;))()(()()()()(3)(2)(12321cTbT aT T c b T c a T b a aT bT cT e z e z e z ze k e k e k z e k e k e k z E ---+-+-+-------+-++-=。
7-2 采样周期为T ,试求下列函数的Z 变换:⑴ n a nT e =)(; ⑵ t e t t e 32)(-=;⑶ 3!31)(t t e =; ⑷ 21)(ss s E +=;⑸ )1(1)(2+-=-s s e s E sT 。
(完整版)自动控制原理课后习题及答案

第一章 绪论1-1 试比较开环控制系统和闭环控制系统的优缺点.解答:1开环系统(1) 优点:结构简单,成本低,工作稳定。
用于系统输入信号及扰动作用能预先知道时,可得到满意的效果。
(2) 缺点:不能自动调节被控量的偏差。
因此系统元器件参数变化,外来未知扰动存在时,控制精度差。
2 闭环系统⑴优点:不管由于干扰或由于系统本身结构参数变化所引起的被控量偏离给定值,都会产生控制作用去清除此偏差,所以控制精度较高。
它是一种按偏差调节的控制系统。
在实际中应用广泛。
⑵缺点:主要缺点是被控量可能出现波动,严重时系统无法工作。
1-2 什么叫反馈?为什么闭环控制系统常采用负反馈?试举例说明之。
解答:将系统输出信号引回输入端并对系统产生控制作用的控制方式叫反馈。
闭环控制系统常采用负反馈。
由1-1中的描述的闭环系统的优点所证明。
例如,一个温度控制系统通过热电阻(或热电偶)检测出当前炉子的温度,再与温度值相比较,去控制加热系统,以达到设定值。
1-3 试判断下列微分方程所描述的系统属于何种类型(线性,非线性,定常,时变)?(1)22()()()234()56()d y t dy t du t y t u t dt dt dt ++=+(2)()2()y t u t =+(3)()()2()4()dy t du t ty t u t dt dt +=+ (4)()2()()sin dy t y t u t tdt ω+=(5)22()()()2()3()d y t dy t y t y t u t dt dt ++= (6)2()()2()dy t y t u t dt +=(7)()()2()35()du t y t u t u t dt dt =++⎰解答: (1)线性定常 (2)非线性定常 (3)线性时变 (4)线性时变 (5)非线性定常 (6)非线性定常 (7)线性定常1-4 如图1-4是水位自动控制系统的示意图,图中Q1,Q2分别为进水流量和出水流量。
自动控制原理第7章离散系统题库习题

⾃动控制原理第7章离散系统题库习题7-1已知下列时间函数()c t ,设采样周期为T 秒,求它们的z 变换()C z 。
(a )2()1()c t t t = (b )()()1()c t t T t =- (c )()()1()c t t T t T =-- (d )()1()atc t t te -=(e )()1()sin atc t t et ω-= (f )()1()cos atc t t te t ω-=7-2已知()x t 的拉⽒变换为下列函数,设采样周期为T 秒,求它们的z 变换()X z 。
(a )21()C s s = (b )()()aC s s s a =+(c )2()()aC s s s a =+(d )1()()()()C s s a s b s c =+++(e )2221()()C s s s a =+(f )()1()1sT C s e s-=-7-3求下列函数的z 反变换。
(a )0.5(1)(0.4)zz z --(b )2()()T T zz e z e ----(c )22(1)(2)z z z ++7-4已知0k <时,()0c k =,()C z 为如下所⽰的有理分式120121212()1nn nn b b z b z b z C z a z a z a z------++++=++++L L 则有0(0)c b =以及[]1()()nk i i c kT b a c k i T ==--∑式中k n >时,0k b =。
(a )试证明上⾯的结果。
(b )设23220.5()0.5 1.5z z C z z z z +-=-+-应⽤(a )的结论求(0)c 、()c T 、(2)c T 、(3)c T 、(4)c T 、(5)c T 。
7-5试⽤部分分式法、幂级数法和反演积分法,求下列函数的z 反变换:(a )10()(1)(2) zE z z z =--(b )1123()12z E z z z ----+=-+(c )2()(1)(31)zE z z z =++(d )2()(1)(0.5)zE z z z =-+7-6⽤z 变换法求下⾯的差分⽅程(2)3(1)2()0,(0)0,(1)1x k x k x k x x ++++===并与⽤迭代法得到的结果(0)x 、(1)x 、(2)x 、(3)x 、(4)x 相⽐较。
自动控制原理与应用第7章 自动控制系统的校正

综上所述:比例-微分校正将使系统的稳定性和快速性得到改善, 但抗高频干扰的能力明显下降。
7.2.3 比例-积分(PI)校正(串联相位滞后校正) 其传递函数为
Gc ( s ) K c ( i s 1) is
装置的可调参数为:比例系数Kc、积分时间常数 τi。装置的伯德图如图所示,其相位曲线为 0°→-90°间变化的曲线(故称相位滞后)。 如果系统的固有部分中不包含积分环节而 又希望实现无静差调节时,可在系统中串联比 例积分校正来实现。
G( s )
(1s 1)( 2 s 1) (1s 1)( 2 s 1) R1C2 s
(1s 1)( 2 s 1) (1s 1)( 2 s 1)
式中
1 R1C1 2 R2C2 1 2
伯德图
表7-2
PD调节器
常见有源校正装置
由以上分析可知,比例微分校正对系统的影响为: (1)比例微分校正装置具有使相位超前的作用,可以抵消系统中惯性环 节带来的相位滞后的影响,使系统的稳定性显著改善。 (2) 校正后系统对数幅频特性的穿越频率ωc增大,从而改善了系统的 快速性,使调整时间减少(ωc↑→ts↓)。 (3) 比例微分校正不直接影响系统的稳态误差。 (4) 由图中曲线Ⅱ可知,比例-微分校正使系统的高频增益增大,由于 很多干扰都是高频干扰,因此这种校正容易引入高频干扰。
7.1.2
系统校正的方式
工程实践中常用的校正方法,串联校正、反馈校正 和复合校正。
7.有源校正装置两类。
无源校正装置通常是由一些电阻和电容组成的两端口网络。根据它 们对系统频率特性相位的影响,又分为相位滞后校正,相位超前校正 和相位滞后-超前校正。表7-1为几种典型的无源校正装置及其传递函 数和对数频率特性(伯德图)。 无源校正装置线路简单、组合方便、无需外供电源,但本身没有增 益,只有衰减,且输入阻抗较低、输出阻抗较高,因此在实际应用时, 常常需要增加放大器或隔离放大器。本课程重点介绍有源校正装置.
自动控制原理胡寿松第七章解析

1、线性定理 齐次性 Z [ae (t)] aE(z ) Z[e1 (t) e 2 (t)] E1 (z ) E 2 (z ) 叠加性 2、实数位移定理
Z[e(t- kT )] z -k E(z)
Z [e(t kT)] z k [E(z)- e(nT)z -n ]
n 0
k -1
z变换实际上是采样函数拉氏变换的变形,
因此又称为采样拉氏变换
z变换只适用于离散函数,或者说只能表征
连续函数在采样时刻的特性,而不能反映其 在采样时刻之间的特性。
24
成都信息工程学院控制工程系
第七章 线性离散系统的分析与校正
25
成都信息工程学院控制工程系
第七章 线性离散系统的分析与校正
二、Z变换的性质
0T
*
采样器可以用一个周期性闭合的采样开关S来表示。
理想采样开关S: T (t ) (t nT )
n 0
11
成都信息工程学院控制工程系
第七章 线性离散系统的分析与校正
理想单位脉冲序列 采样过程可以看成是一个幅值调制过程。
12
成都信息工程学院控制工程系
第七章 线性离散系统的分析与校正
1 jns t T ( t ) e T n -
1 jns t * 代入采样信号表达式:e ( t ) e( t ) T (t ) e( t )e T n
对采样信号表达式取拉氏变换: 1 E* (s) E(s jns ) T n 采样信号的付氏变换: 1 E* ( j ) E[j( ns )] T n
T (t)的付氏级数形式:
T (t)
n -
(t - nT) C e
自动控制原理简明教程第二版课后答案第七章习题答案

s2(0.K2s +1)
= (1− z−1)Z
s2(5sK+ 5)
1
− (1 z
− 1
)
(z5−Tz1)2
= − 5(z5−(11−)(ez−−2Te)−z3T ) (z5−T1) = ((1z−−ee−−55TT )) z(4(+z −e−15)(T )z+−1e−−56T e) −5T
−
4.0067z + 0.96 = z2 − 1.0067z + 0.0067
7
胡寿松自动控制原理习题解答第七章 电三刘晓峰制作
G2(s) R(s) G1(s) - T Gh(s) G3(s) G4(s)
(b) D2(z) D1(z) T (c) 图 7-56 闭环离散系统 N(s) T Gh(s) G1(s) G2(s)
R(s) -
T T
G1(z)
解: (a)G12(z) =
2 2 z −5.0335z+ 3 2 z +
0.0035+ 3.0067Kz+ 0.9598K = 0
(3.0067K − 5.0335)z+ 0.0035 + 0.9598K = 0
10
胡寿松自动控制原理习题解答第七章 电三刘晓峰制作
(2)G(z) = (1− z−1)Z
z−1)Z
K s2(0. 2s +1) 5K s2( s + 5)
7-3 试用部分分式法、幂级数法和反演积分法,求下列函数的 z 反变换:
10z
(1)E(z) =
(z −1)(z − 2) − 3+ z−1
(2)E(z) = 1− 2z−1 + z−2
自动控制原理(孟华)第7章习题解答(含过程)

习 题7-1 根据定义*()e()enTsn E s nT ∞-==∑试求下列函数的E *(s )和闭合形式的E (z )。
(1) e (t ) = t ; (2) 2)(1)(a s s E +=解 (1) e (t ) = t 求解过程可分为以下三个步骤进行:① 求()e t 的采样函数*()e t :由()()|,0,1,2,t nT e nT e t nT n ==== ,得斜坡函数()e t 在各采样时刻的值()e nT 。
故采样函数为*00()(0)()()()()()()()()n n e t e t e T t T e nT t nT e nT t nT nT t nT δδδδδ∞=∞==+-++-+=-=-∑∑② 求*()e t 的拉氏变换式*()E s :*()e t 的拉氏变换式为*()E s*0223'2'''2()()02[][(1)]1111(1)nTsnTsn n Ts TsnTsTs TsTsnTsTsTsTsnTs TsTs Ts Ts Ts E s e nT enTeTe TenTe e e eeeeeeTe e e e e ∞∞--==-------------===+++++=-+++++=-+++++⎡⎤⎡⎤=-=-=⎢⎥⎢⎥---⎣⎦⎣⎦∑∑③ 求()E z :由*1ln ()()|s znE z E s ==,得2()(1)Tz E z z =-(2) 2)(1)(a s s E +=① 求()e t :()ate t te -=② 求*()e t*0()()(),()()|anTt nTn e t e nT t nT e nT e t nTeδ∞-===-==∑所以 *0()()anTn e t nTet nT δ∞-==-∑③ 求*()E s*()()nTsanTnTsn n E s e nT enTee∞∞---====∑∑④ 求()E s*1ln 012()()|[()2()()]anTns zn Tat atatnE s E s nTeze z e z n e z T∞--==---===++++∑令1()at e z y -=,则2123''2()(123)()1(1)n nE y y y nyyT y y y y yTy Ty yT y y -=+++++=+++++⎛⎫== ⎪--⎝⎭将1()at y e z -=代入上式,可得()E z 为 1122()()[1()]()ataT at aTT e z Tze E z e z z e----==--7-2 求下列函数的Z 变换X (z )。
自动控制原理参考答案-第7章

2 −ωn 6 =− 2ξωn + a a
& = 0) (c & < 0) (c
2 −ωn c − 1 −6 1 c+ = 2ξωn + a a a 相变量的方向场如图 & c
1 − 6
1 6
c
(3) 系统方程: && + 6c + 5 = 0 ⎧c ⎨ && − 6c + 5 = 0 ⎩c
题 7-2:试计算题 7-2 图所示非线性结构图的描述函数。
x
k
M
y
d
c
题 7-2 图
非线性串联环节
死区+继电的非线性特性的串联等效特性:
0 ≤ ωt ≤ ψ ⎧0 ⎪ y(t) = ⎨ π M ψ ≤ ωt ≤ ⎪ ⎩ 2 A1 = 0 1 2π B1 = ∫ y(t) sin ωt ⋅ dωt π 0 π 4 = ∫ 2 M sin ωt ⋅ dωt π ψ
2 ωn =1 ⎫ ⎪ ⎧ωn = 1 e ≥ 0 时, , 所以奇点为稳定焦点 ⎬⇒ ⎨ 2ξωn = 1⎪ ⎭ ⎩ξ = 0.5 < 1
等倾线斜率: β =
2 −ωn −1 = 2ξωn + a 1 + a
e < 0 时,系统特征方程 s 2 + s − 1 = 0 ⇒ s1,2 = −1.618, +0.618 , 所以奇点为鞍
闭环传函: T ( s ) =
5
& c
c
0 5
题 7-9~题 8-12:
(略)
第 7 章主要知识点
1 描述函数法是在满足一定的条件下,对元件的非线性特性进行谐波线性化处 理,使非线性系统变为一个近似的线性系统,从而可用奈氏稳定判据判别系统 的稳定性和是否有自激振荡产生。 2 描述函数法需对系统的非线性部分进行谐波线性化处理,而不需对系统的线 性部分进行简化。相平面法需将系统的线性部分简化为二阶系统,而不对非线 性环节进行任何处理。 3 描述函数是系统运动状态做周期运动的描述,一般没有考虑外界作用,所以 只用于分析系统稳定性和自激震荡,而不能得到系统的响应。 4 相平面法可给出系统零输入响应的特性,也可观察到系统是否存在自激振荡 (以极限环出现),但较难确定自激振荡的振幅和频率。
自动控制原理考试试题第七章习题与答案
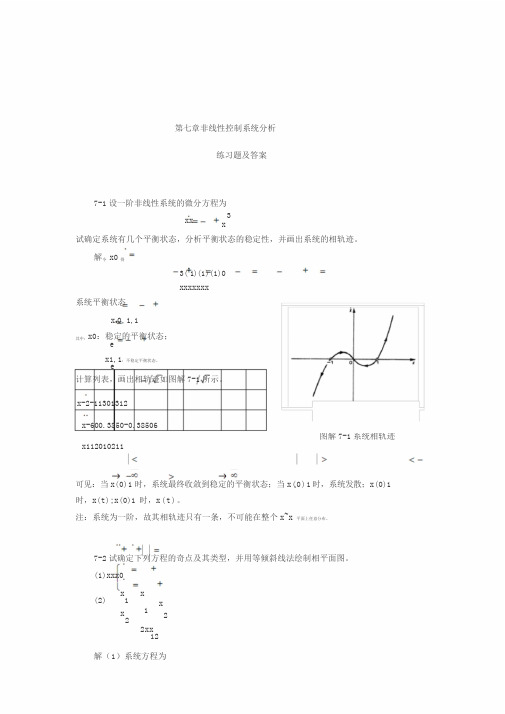
第七章非线性控制系统分析练习题及答案7-1设一阶非线性系统的微分方程为xx3 x试确定系统有几个平衡状态,分析平衡状态的稳定性,并画出系统的相轨迹。
解令x0得3(21)(1)(1)0xxxxxxx系统平衡状态x e0,1,1其中:x0:稳定的平衡状态;ex1,1:不稳定平衡状态。
e计算列表,画出相轨迹如图解7-1所示。
x-2-11301312x-600.3850-0.38506x112010211图解7-1系统相轨迹可见:当x(0)1时,系统最终收敛到稳定的平衡状态;当x(0)1时,系统发散;x(0)1 时,x(t);x(0)1时,x(t)。
注:系统为一阶,故其相轨迹只有一条,不可能在整个x~x平面上任意分布。
7-2试确定下列方程的奇点及其类型,并用等倾斜线法绘制相平面图。
(1)xxx0(2) x1x2xx122xx12解(1)系统方程为1:xxx0(x0):xxx0(x0)令xx0,得平衡点:x e0。
系统特征方程及特征根:132:ss10,sj(稳定的焦点)1,2222:ss10,s1.618,0.618(鞍点)1,2xf(x,x)xx, d xdxxxxdx dx 1xx,1xxx11I:1(x0)1II:1(x0)计算列表-∞-3-1-1/301/313∞x0:11-1-2/302-∞-4-2-4/3-1x0:11-1-4/3-2-4∞20-2/3-1用等倾斜线法绘制系统相平面图如图解7-2(a)所示。
2图解7-2(a)系统相平面图(2)xxx112①x22xx②12由式①:x2x1x1③式③代入②:(x1x1)2x1(x1x1)即x12x1x10④令x1x10得平衡点:x e0由式④得特征方程及特征根为2.4142ss2101,2(鞍点)0.414画相轨迹,由④式xx 11 d x1dxx12x1x1x 1 x1 2计算列表322.53∞11.52=1/(-2)∞210-1-2∞用等倾斜线法绘制系统相平面图如图解7-2(b)所示。
自动控制原理(第三版)第7章非线性控制系统(1)

自动控制原理
4)当非线性输入的信号为正弦作用时,由 于非线性其输出将不再是正弦信号,而包 含有各种谐波分量,发生非线性畸变。
大连民族学院机电信息工程学院
自动控制原理
5)混沌
大连民族学院机电信息工程学院
自动控制原理
非线性系统运动的特殊性
• 不满足叠加原理 — 线性系统理论原则上不能运用 (区别) • 稳定性问题 — 不仅与自身结构参数,且与输入, 初条件有关,平衡点可能不惟一,可以稳定且可以 在多个平衡点稳定,可能不稳定—发散、衰减等 nonlinear • 自振运动— 非线性系统特有的运动形式,产生自 持振荡 • 发生频率激变—频率响应的复杂性 — 跳频响应, 倍/分频响应,组合振荡
大连民族学院机电信息工程学院
自动控制原理
3、滞环(非单值特性)
) x 0 , 且y 0 k ( x a sgn x y =0 y x2 m sgn x
滞环特性会 使系统的相 角裕度减小, 动态性能恶 化,甚至产生 自持振荡。
x2
x2m
x2
x2m
a
0
x1
a
x2m
7.3 描述函数法 7.4 相平面法
7.5 Matlab 在本章中的应用
大连民族学院机电信息工程学院
自动控制原理
7.1 非线性控制系统概述
如果一个控制系统包含一个或一个以上具有非 线性特性的元件或环节,则此系统即为非线性系统。
• 前面研究的线性系统满足叠加性和齐次性; • 严格地说,由于控制元件或多或少地带有非线性特 性,所以实际的自动控制系统都是非线性系统; • 一些系统作为线性系统来分析: ①系统的非线性 不明显,可近似为线性系统。②某些系统的非线性 特性虽然较明显,但在某些条件下,可进行线性化 处理; • 但当系统的非线性特征明显且不能进行线性化处理 时,就必须采用非线性系统理论来分析。这类非线 大连民族学院机电信息工程学院 性称为本质非线性。
自动控制原理第7章习题及答案

习题7-1下面的微分方程代表了线性定常系统,请写出它们对应的状态空间表达(a ))(5)()(4)(22t r t c dtt dc dt t c d =++(b ))()()()(4)(5)(02233t r d c t c dtt dc dt t c d dt t c d t =++++⎰ττ (c )dtt dr t r t c dt t c d dt t c d )(4)()()(2)(2233+=++ 7-2 已知线性定常系统的状态方程为:Ax x =.,其中(1)⎥⎦⎤⎢⎣⎡-=2010A (2) ⎥⎦⎤⎢⎣⎡-=0110A (3)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=010100010A 试求系统统的状态转移矩阵At e答案:(1)⎥⎦⎤⎢⎣⎡-=--tt Ate e e2205.05.01 (2)⎥⎦⎤⎢⎣⎡-=t t t t e Atcos sin sin cos (3)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+--+-+-=------)(5.0)(5.00)(5.0)(5.001)(5.0)(5.01t t t t t t t t t t t t Ate e e e e e e e e e e e e 7-3 已知系统的状态方程为:u x x ⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡--=103210.,初始条件为⎥⎦⎤⎢⎣⎡=10)0(x ,试求单位阶跃收入时系统的时间响应x(t)答案:(1)求状态转移矩阵 先求出预解矩阵⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+++-+++-+-+++-++=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡++++-+++++=⎥⎦⎤⎢⎣⎡+-=---)2(2)1(1)2(2)1(2)2(1)1(1)2(1)1(2)2)(1()2)(1(2)2)(1(1)2)(1()3(321)(11s s s s s s s s s s s s s s s s s s s s A sI对上式进行拉式反变换,即可定出:⎥⎦⎤⎢⎣⎡+-+---=--------t t t t t t t t At2222e 2e e 2e 2e e e e 2e(2)求系统的时间响应()0022()2()()2()22()2()()2()022()e e ()d 002e e e e 2e e e e d 112e 2e e 2e 2e 2e e 2e 0.50.5tAt A t t t t t t t t t t t t t t t t t t t tx t x Bu e e ττττττττττττ---------------------------=+⎡⎤⎡⎤----⎡⎤⎡⎤=+⎢⎥⎢⎥⎢⎥⎢⎥-+-+-+-+⎣⎦⎣⎦⎣⎦⎣⎦⎡⎤-=⎢⎥⎣⎦⎰⎰7-4 已知矩阵:(1)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=t t t t t sin cos 0cos sin 0001)(ϕ (2)⎥⎦⎤⎢⎣⎡--+=-t t t t t t t e e e e e e e t 222222)(ϕ 试问:它们可能是某个系统的状态转移矩阵吗?为什么?答案:I =)0(ϕ时才是状态转移矩阵,所以上述两个矩阵均不是某个系统的状态转移矩阵。
自动控制原理第7章习题解——邵世凡

自动控制原理第7章习题解7-1 求下列采样的离散信号x *(t )及离散拉斯变换X *(s ) ① ()t te t x α-=; ② ()t e t x t ωαsin -=; ③()t t t x ωcos 2=; ④ ()t te t x 4-=; 解:① ()t te t x α-=()()[][]()211111011111--------+∞=----+∞=---=⎥⎦⎤⎢⎣⎡-====∑∑z e z Te z e dz d Tz z e dz d Tz ztekT x Z z X T T T k k kT k kkTααααα ② ()t e t x t ωαsin -=()()[][][]()()()()211cos 1sin sin sin ---∞+=-∞+=--+-====∑∑z e zekT z e kT zekT zkT ekT x Z z X kTkTkT k kkTk kkTαααααωωωω③()t t t x ωcos 2=()()[]()[]()()()()⎭⎬⎫⎩⎨⎧⎥⎦⎤⎢⎣⎡+--=⎭⎬⎫⎩⎨⎧⎥⎦⎤⎢⎣⎡====-------∞+=-----+∞=---+∞=-∑∑∑211111101111112cos 21cos 1cos cos cos z z kT z kT dz d Tz dz d Tz z kT dz d Tz dz d TzzkT kT dz dTzzkT kT kT x Z z X k k k kk kωωωωω ④ ()ttet x 4-=()()[][][]()21414141104114111-----+∞=----+∞=---=⎪⎭⎫ ⎝⎛-====∑∑z e z Te z e dz d Tz z e dz d Tz zkTekT x Z z X T T T k k kT k kkT7-2求下列函数的Z 变换。
①()kTe kT x α--=1; ②()kT ekT x kTωαcos -=;③()tet t x 52--=; ④()t t t x ωsin =;⑤()()a s s k s G +=; ⑥()()()211++=s s s s G⑦()211s s s e s G Ts +-=-;⑧()()15+=-s s e s G Ts解:① ()kTe kT x α--=1根据z 变换定义有:()()[][]11011111---+∞=--+∞=-+∞=-----=-=-==∑∑∑ze z z e zzekT x Z z X T k k kT k kk kkTααα ② ()kT e kT x kT ωαcos -= 根据欧拉公式有:()()kT j kT kTj kT kTj kT j kTkTe e e e ekT ekT x ωαωαωωααω--+----+=⎪⎪⎭⎫ ⎝⎛+==212cos 然后,再根据z 变换定义得:()()[]()()⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡+==∑∑∑+∞=---+∞=-+-+∞=---+-0002121k k kT j kT k k kT j kT k k kTj kT kT j kT z e z e z e e kT x Z z X ωαωαωαωα()()()21111cos 1cos 1111121-------+-+--=⎥⎦⎤⎢⎣⎡---=ze z e kT z e kT z e z e kT kT kT T j T T j T αααωαωαωω或者()()[][][]()()[]()()()2111cos 1cos 1cos cos ----∞+=-∞+=--+--====∑∑z e z e kT z e ze kT zekT zkT ekT x Z z X kTkTkTkTk kkTk kkTααααααωωωω③ ()t e t t x 52--= 根据z 变换定义有:()()[]()[]()()()15311220502521111-----∞+=--∞+=-∞+=-----+=-=-==∑∑∑z e z z z T z ezkT zekT kT x Z z X T k kkT k kk kkT其中,根据z 变换的性质有()()()⎭⎬⎫⎩⎨⎧⎥⎦⎤⎢⎣⎡==∑∑∑+∞=-----+∞=---+∞=-011110112k k k k k kz kT u dz d Tz dz d Tz z kT dz d Tz zkT ()()()()411121121111111111121111---------------⋅-+-=⎥⎥⎦⎤⎢⎢⎣⎡-=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-=z Tz z z T Tz z Tz dz d Tz z dz d Tz dzdTz ()()()()()()()()()311124111141214121211111111112221-----------------+=--+=--=--++-=z z z T z z z T Tz z z T Tzz z z z z T Tz④ ()t t t x ωsin = 根据z 变换的性质有()()[][][]⎥⎦⎤⎢⎣⎡-====∑∑∑+∞=----+∞=---+∞=-0110112sin sin k k kT j kT j k k k kz j e e dz d Tz z kT dz d Tz zkT kT kT x Z z X ωωωω()()⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛--+--=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛---=-------------1111111111111121111121z e z e z e z e j dz d Tz z e ze j dz d TzT j T j T j T j T j T j ωωωωωω()()⎪⎪⎭⎫ ⎝⎛+⋅-⋅=⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛++--=------------1cos 2sin 1211211112111z T z z T dz d Tz z e e z z e e j dz d TzT j T j T j T j ωωωωωω ()()[]()21211121121111cos 2cos 221cos 2sin 1cos 2sin +⋅---+⋅-⋅=⎪⎪⎭⎫ ⎝⎛+⋅-⋅=------------z T z T z z z T z T Tz z T z z T dz d Tzωωωωωω()()212111cos 21sin +⋅-⋅-⋅=----z T z z z T T ωω ⑤()()a s s ks G +=;方法是,首先将分式分解为部分分式,然后再利用留数方法确定其待定系数,最后通过查表可得Z 变换式。
自动控制原理考试题第七章习题与答案

第七章 非线性控制系统分析练习题及答案7-1 设一阶非线性系统的微分方程为3x x x+-= 试确定系统有几个平衡状态,分析平衡状态的稳定性,并画出系统的相轨迹。
解 令 x=0 得 -+=-=-+=x x x x x x x 321110()()()系统平衡状态x e =-+011,,其中:0=e x :稳定的平衡状态;1,1+-=e x :不稳定平衡状态。
计算列表,画出相轨迹如图解7-1所示。
可见:当x ()01<时,系统最终收敛到稳定的平衡状态;当x ()01>时,系统发散;1)0(-<x 时,x t ()→-∞; 1)0(>x 时,x t ()→∞。
注:系统为一阶,故其相轨迹只有一条,不可能在整个 ~xx 平面上任意分布。
7-2 试确定下列方程的奇点及其类型,并用等倾斜线法绘制相平面图。
(1)x x x ++=0 (2) ⎩⎨⎧+=+=2122112x x xx x x解 (1) 系统方程为x -2 -1 -13 0 13 1 2x-6 0 0.385 0 -0.385 0 6x 11 2 0 1 02 11图解7-1 系统相轨迹⎩⎨⎧<=-+I I >=++I )0(0:)0(0:x x x x x x x x令0x x ==,得平衡点:0e x =。
系统特征方程及特征根:21,221,21:10,()2:10, 1.618,0.618()s s s s s s I II ⎧++==-±⎪⎨⎪+-==-+⎩稳定的焦点鞍点(, ) , , x f x x x x dxdxxx x dx dx x x x x x==--=--==--=-+=ααβ111⎪⎪⎩⎪⎪⎨⎧<-=>--=)0(11:II )0(11:I x x βαβα计算列表用等倾斜线法绘制系统相平面图如图解7-2(a )所示。
图解7-2(a )系统相平面图(2) xx x 112=+ ① 2122x x x+= ② 由式①: x xx 211=- ③ 式③代入②: ( )( )x xx x x 111112-=+- 即 x x x 11120--= ④ 令 x x110== 得平衡点: x e =0 由式④得特征方程及特征根为 ⎩⎨⎧-==--414.0414.20122,12λs s (鞍点) 画相轨迹,由④式x xdxdx x x x 1111112===+α xx 112=-α 计算列表用等倾斜线法绘制系统相平面图如图解7-2(b )所示。
自动控制原理作业第七章参考答案【可编辑】

7.1 求下列矩阵的若尔当型及其变换矩阵(1)010001341⎡⎤⎢⎥⎢⎥⎢⎥---⎣⎦解:矩阵的特征值为:1230.78,0.11 1.95,0.11 1.95i i λλλ=-=-+=--,因此可化为对角线规范型:0.780.11 1.950.11 1.95ii -⎡⎤⎢⎥-+⎢⎥⎢⎥--⎣⎦变换矩阵为:1232221231111110.780.11 1.950.11 1.950.61-3.8 - 0.42i -3.8 + 0.42i P i i λλλλλλ⎡⎤⎡⎤⎢⎥⎢⎥==--+--⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦(2)540430461⎡⎤⎢⎥--⎢⎥⎢⎥-⎣⎦解:矩阵的特征值为:1231λλλ===,()2rank I A -=,表明1λ=的几何重数为3-()rank I A -=1,即该特征值对应一个若尔当块。
所以该矩阵的若尔当型为:11111⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦,变换矩阵0410404040P ⎡⎤⎢⎥=-⎢⎥⎢⎥--⎣⎦(3)421043521⎡⎤⎢⎥⎢⎥⎢⎥-⎣⎦解:矩阵的特征值为:1232, 2.21, 6.79λλλ=-==,因此可化为对角线规范型:2 2.21 6.79-⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦,变换矩阵为00.40.610.410.370.780.810.350.46P ⎡⎤⎢⎥=-⎢⎥⎢⎥--⎣⎦(4)010001340⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦解:矩阵的特征值为:1232.3,1, 1.3λλλ==-=-,因此可化为对角线规范型:2.31 1.3⎡⎤⎢⎥-⎢⎥⎢⎥-⎣⎦,变换矩阵为30.1 2.130.25 2.7530.583.58P -⎡⎤⎢⎥=-⎢⎥⎢⎥-⎣⎦7.2已知系统状态方程,求状态变换阵P ,使系统变为对角线型(假设系统的特征值为123,,λλλ)(1)012010001x x a a a ⎡⎤⎢⎥=⎢⎥⎢⎥---⎣⎦解:123222123111P λλλλλλ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦(2)123100100a x a x a -⎡⎤⎢⎥=-⎢⎥⎢⎥-⎣⎦解:系统的特征方程为:32123det()00I A a a a λλλλ-=⇒+++= 设变换矩阵123[,,],i i i i P v v v v Av v λ==满足设123[,,]Ti i i i v v v v =,则有:11212132313(1)(2)(3)i i i i i i i i i i i a v v v a v v v a v v λλλ-+=⎧⎪-+=⎨⎪-=⎩ 由(1)得211()(4)i i i v a v λ=+由(2)(4)得23121()(5)i i i i v a a v λλ=++ 代入(3)得321123()0i v a a a λλλ+++=所以1i v 是任意常数,取为1,则21i i v a λ=+,2312i i i v a a λλ=++所以112131222111221223132111P a a a a a a a a a λλλλλλλλλ⎡⎤⎢⎥=+++⎢⎥⎢⎥++++++⎣⎦7.3证明:对于具有互相不同特征值12,,,n λλλ 的矩阵1211000010000010000n n a a A a a --⎡⎤⎢⎥-⎢⎥⎢⎥=⎢⎥-⎢⎥⎢⎥-⎣⎦能将其变换为对角矩阵形式的变换矩阵为:11122111212121211111111n n n n n n n n n n n a a P a a a a a a a a λλλλλλλλλλ------⎡⎤⎢⎥++⎢⎥⎢⎥=++++⎢⎥⎢⎥⎢⎥++++++⎣⎦证明:系统的特征方程为:111det()00nn n n I A a a a λλλλ---=⇒++++=设变换矩阵12[,,,],n i i i i P v v v v Av v λ== 满足设12[,,,]Ti i i in v v v v = ,则有:21111212213231211211111111()()()(1)0(2)i i i i i i i i i i i i i i i n n n i in i in ini i n i n i i in i in n i v a v a v v v a v v v v a a v a v v v v a a v a v v v a v λλλλλλλλλλ-----=+⎧-+=⎧⎪⎪-+==++⎪⎪⎪⎪⇒⎨⎨⎪⎪-+==+++⎪⎪-=⎪⎪+=⎩⎩将(1)代入(2)得11110n n i i n i n i a a a v λλλ--++++= 对比系统特征方程可知11i v =满足。
自动控制原理第二章到第七章课后习题答案

自动控制原理第二章到第七章课后习题答案第二章2-1试求下图所示电路的微分方程和传递函数。
解:(a )根据电路定律,列写出方程组:001Li R c L R C di L u u dtu R i i dt Ci i i ⋅+==⋅==+⎰消除中间变量可得微分方程:20002i d u du L L C u u dt R dt⋅⋅+⋅+=对上式两边取拉氏变换得:2000()()()()i LL C U s s U s s U s U s R⋅⋅⋅+⋅⋅+= 传递函数为022()1()()1i U s R G s L U s R Ls LCRs s LCs R ===++++ (b )根据电路定律,列写出方程组:12011()i i u i R R idt C u u i R =++-=⎰消除中间变量可得微分方程:121012i R R Ru u idt R R C+=-⎰ 对上式两边取拉氏变换得:2012()(1)()(1)i U s R Cs U s R Cs R Cs +=++传递函数为0212()1()()1i U s R CsG s U s R Cs R Cs+==++2-3求下图所示运算放大器构成的电路的传递函数。
解:(a )由图(a ),利用等效复数阻抗的方法得22111(s)1(s)()1o i R U R Cs Cs G U s R R Cs ++==-=-+(b )由图(b ),利用等效复数阻抗的方法得222121211221211111(s)()1(s)1()1o i R U C s R R C C s R C R C s G U s R C s R C s R C s++++==-=-+2-5试简化下图中各系统结构图,并求传递函数()()C s R s 。
2-6试求下图所示系统的传递函数11()()C s R s ,21()()C s R s ,12()()C s R s 及22()()C s R s 。
广西大学自动控制原理习题答案(本科)第7章

习题参考答案7-1 求如下信号的频谱|()|F i ω。
(1)1)(=t f(2)t e t f -=)( (3)t t f cos )(= (4)t t f =)( (5)t te t f -=)((6)t t t f cos )(=解:控制系统中的信号都是指0<t 时0)(=t f 函数。
以下信号不考虑频谱中的奇异信号。
(1)|1||)(|ωω=i F(2)211|11||)(|ωωω+=+=i i F (3)|1||)(|2ωωω-=i F(4)21|)(|ωω=i F(5)2)1(1|)(|ωω+=i F(6)222)1(1|)(|ωωω-+=i F7-2 对题7-1的信号进行采样,采样频率为T =0.1秒, (1)求采样信号的频谱*|()|F i ω。
(2)求采样信号的z 变换。
解:(1)1)(=t f∑∞=-=0*)1.0()(n n t t f δωωωωωω1.0cos 2211.0sin 1.0cos 1111)(1.001.0*-=+-=-==-∞=-∑i e e i F i n n i111)(1-=-=-z zz z F(2)t e t f -=)(∑∞=--=01.0*)1.0()(n n n t e t f δωωωωωω1.0cos 2111.0sin 1.0cos 1111)(1.02.01.01.01.01.001.01.0*------∞=---+=+-=-==∑e e ieee e i F i n n i n1.011.011)(----=-=ez zz e z F (3)t t f cos )(=∑∑∞=-∞=-+=-=01.01.00*)1.0()(21)1.0()1.0(cos )(n n i n i n n t e e n t n t f δδ*0.1(1)0.1(1)0.1(1)0.1(1)0.1(1)0.1(1)0.1(1)0.1(1)0.20.10.10.21()21112111221122cos1(note :cos10.54)212cos110.54c i n i nn n i i i i i i i i i i F i ee e e e e e e e e e e ωωωωωωωωωωωωω∞∞-+--==-+---+---+------=+=+----=--+-==-+-=∑∑os0.10.54sin 0.11 1.08cos0.1cos0.2(1.08sin 0.1sin 0.2)i i ωωωωωω+-+++=108.154.008.1154.01)(22211+--=+--=---z z zz z z z z F (4)t t f =)(∑∞=-=0*)1.0(1.0)(n n t n t f δωωωωωωω1.0cos 202011.0sin 1.0cos 11.01|1.0|1.0)(221.01.001.0*-=+-=-==--∞=-∑i ee nei F i i n n i2211)1(1.0)1(1.0)(-=-=--z zz z z F (5)t te t f -=)(∑∞=--=01.0*)1.0(1.0)(n n n t ne t f δ,ωωωωωωω1.0cos 20101011.0sin 1.0cos 11.01|1.0|1.0)(1.02.021.01.021.01.01.01.001.01.0*--------∞=---+=+-=-==∑e e ie ee e nei F i i n n i n21.01.0211.011.0)(1.0)1(1.0)(-------=-=e z ze z e z e z F 7-3 已知连续信号的拉普拉斯变换如下,对信号进行频率为T =0.1秒采样后,求采样信号的z 变换。
大连理工自动控制原理本科第7章习题

1习题7-1 已知采样器的采样周期为T 秒,连续信号为(1) x(t)=te –at (2) x(t)=e -at sin ωt (3) x(t)=t 2cos ωt (4) x(t)=ta 4t求采样的离散输出信号x *(t)及离散拉氏变换x *(s)。
7-2 求下列函数的Z 变换(1) x(kt)=1-e -akT (2) x(kt)=e -aktcos ωk T (3) x(t)=t 2e -5t (4) x(t)=tsin ωt (5) G(S)=)(a s s k + (6) G(S)=)2)(1(1++s s s(7) G(s)=2)1(1ss seT S+-- (8) G(S)=)1(5+-s s eTS7-3 求下列函数x(z)的原函数 (1) X(Z)=)5)(1(6++z z z(2) X(Z)=11+z(3) X(Z)=2)2)(1(++z z z(4) X(Z)=)1)(6.0(2--z z z7-4 求题图T=1秒。
Y(Z)s1题图7-1 题7-4的采样系统7-5 题 图7-2所示的采样系统采样周期T=1秒。
求 (1) 系统的脉冲传递函数G (Z )=)()(Z R Z Y(2) 当输入r (t )=1(t )时,求y*(t)y*(t)r (t) y (t)题图7-2 题7-5的采样系统7-6 对题图7-2所示采样系统计算T=0.1秒,T=0.5秒时采样系统的输出y*(t )。
7-7 求题图7-3所示系统的脉冲传递函数。
y*(t)r (t) y (t) 题图7-3 题7-7所示采样系统7-8 求题图7-4所示系统脉冲传递函数或输出Z 变换表达式。
y*(t)r (t) y (t)题图7-4 题7-8所示采样系统7-9 求题图7-5所示采样系统输出的Z 变换表达式Y (Z )。
y*(t) r (t) y (t)题图7-5 题7-9所示采样系统7-10 已知采样系统如题图7-6,采样周期T=0.5秒 (1) 判别系统稳定性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
c(0) = c(1) = 0
c* (t + 2T ) − 6c* (t + T ) + 8c* (t) = r * (t),
解:(1)将
变为如下形式
r(t) = 1(t), c* (t) = 0(t ≤ 0)
c(k + 2) − 6c(k + 1) + 8c(k) = r(k) 令 k = −1则 c(1) − 6c(0) + 8c(−1) = r(−1) 即 c(1) = 6c(0) = 0
∞
∑ E * (s) = sin(ωnT )e−nsT n=0
E(z) =
z sinωT
z 2 − 2z cosωT + 1
(2) E(s) =
1
(s + a)(s + b)(s + c)
e(t) =
e −at
+
e −bt
+
e −ct
(b − a)(c − a) (a − b)(c − b) (a − c)(b − c)
∑ E* (s)
=
∞ n=0
(b
e −anT − a)(c
−
a)
+
(a
e −bnT − b)(c
−
b)
+
(a
e −cnT − c)(b
−
c)
e
−nsT
E(z)
=
(b
−
a)(c
−
z a)(z
−
e −aT
)
+
(a
−
b)(c
z − b)(z
−
e −bT
)
+
(a
−
c)(b
z − c)(z
−
= −3 − 5z −1 − 7z −2 − 9z −3 − 11z −4 − 13z −5 − L
∞
e*(t) = −∑ (2n + 3)δ (t − nT ) n=0
7-4 试求下列函数的脉冲序列 e* (t) :
(1) E(z) =
z
(z + 1)(3z 2 + 1)
(2)
E(z)
=
(z
z −1)(z +
1 6
4n
δ
(t
−
nT )
7-9 设开环离散系统如图 7—55 所示,试求开环脉冲传递函数 G(z) 。
R(s)
2
s+2
5
C(s)
s+5
(a)
R(s)
2
s+2
5
C(s)
s+5
(b)
图 7-55 开环离散系统
解:
Z
s
2 +
2
=
z
2z − e−2T
Z
s
5 +
5
=
z
胡寿松自动控制原理习题解答第七章
7—1 试根据定义
∞
∑ E * (s) = e(nT )e−nsT n=0
确定下列函数的 E * (s) 和闭合形式的 E(z) : (1) e(t) = sinωt
(2) E(s) =
1
(s + a)(s + b)(s + c)
解:(1) e(t) = sin ωt
(z −1)(z − 2) (z − 2) (z −1)
e(nT ) = 10 × (2n −1)
∞
∑ e* (t) = 10(2n −1)δ (t − nT ) n=0 2
胡寿松自动控制原理习题解答第七章
(2)
E(
z)
=
1
−3 − 2z
+
−1
z −1 +z
−2
= z − 3z2 z2 − 2z +1
即: z 2C(z) − 6zC(z) + 8C(z) = z z −1
C(z)
=
z
z −1
z2
1 − 6z
+8
=
(z
− 1)( z
z − 2)(z
−
4)
=
1 3
z
z −1
−
1 2
z
z −
2
+
1 6
z
z −
4
4
胡寿松自动控制原理习题解答第七章
∑ c* (t)
=
∞ n=0
1 3
−
1 2
2n
+
k = 2 时 c(2) − 4c(3) + c(4) = 0 所以 c(4) = 4c(3) − c(2) = 60 − 4 = 56
7-8 试用 z 变换法求解下列差分方程:
c* (t + 2T ) − 6c* (t + T ) + 8c* (t) = r * (t),
(1)
r(t) = 1(t), c* (t) = 0(t ≤ 0) (2) c* (t + 2T ) + 2c* (t + T ) + c* (t) = r * (t),
7-7 已知差分方程为
c(k ) − 4c(k + 1) + c(k + 2) = 0
初始条件: c(0) = 0, c(1) = 1。试用迭代法求输出序列 c(k), k = 1,2,3,4 。
3
胡寿松自动控制原理习题解答第七章
解: 因为 c(k ) − 4c(k + 1) + c(k + 2) = 0 k = 0 时 c(0) − 4c(1) + c(2) = 0 所以 c(2) = 4c(1) − c(0) = 4 − 0 = 4 k = 1 时 c(1) − 4c(2) + c(3) = 0 所以 c(3) = 4c(2) − c(1) = 16 − 1 = 15
z z −1
=
z2
0.53z + 0.1 −1.37z + 0.37
= z − 0.47z z −1 z − 0.37
( ) ∞
c(nT ) = ∑ 1 − 0.47 × 0.37n δ (t − nT ) n=0
7—15 试判断下列系统的稳定性: (1) 已知闭环离散系统的特征方程为
6
胡寿松自动控制原理习题解答第七章
解:(1) D(z) = (z + 1)(z + 0.5)(z + 2) = 0
由特征方程得到: z1 = −1 z2 = −0.5
所以系统不稳定。
z3 = −2
(2) D(z) = z 4 + 0.2z 3 + z 2 + 0.36z + 0.8 = 0
列朱利阵列如下:
0.8 0.36 1 0.2 1 1 0.2 1 0.36 0.8
对差分方程的每一项进行变换,根据实数位移定理:
Z[c(k + 2)] = z 2C(z) − z 2c(0) − zc(1) = z 2C(z)
Z[c(k + 1)] = zC(z) − zc(0) = zC(z)
所以: Z[c(k + 2) − 6c(k + 1) + 8c(k)] = Z[r(k)]
E(z) = anz z −1
(2) e(t) = t e2 −3t
E(z) =
T 2 ze −3T (z − e−3T ) 2
+
2T 2 ze −6T (z − e−3T )3
(3) e(t) = 1 t 3 3!
E(z) = T 3 (z 2 + 4z + 1) 6(z −1)4
(4)
E(s)
=
c(0) = c(T ) = 0, r(nT ) = n, (n = 0,1,2,L) c(k + 3) + 6c(k + 2) + 11c(k + 1) + 6c(k) = 0
(3)
c(0) = c(1) = 1, c(2) = 0
(4)
c(k + 2) + 5c(k + 1) + 6c(k) = cos k 2 π
0.5) 2
解:(1)
E(z)
=
(z
z + 1)(3z2
+ 1)
7-5 试确定下列函数的终值:
(1)
E(z)
=
Tz −1 (1 − z −1 )2
(2) E(z) =
z2
(z − 0.8)(z − 0.1)
解:(1)
lim
n→∞
e(nT
)
=
lim(
z→1
z
−
1)E(
z)
=
lim(
z→1
z
−
1)
(
z
Tz − 1)2
=∞
(2) lim e(nT ) = lim(z − 1)E(z) = lim(z − 1)
z2
=0
n →∞
z→1
z→1
(z − 0.8)(z − 0.1)
7-6 已知 E(z) = Z[e(t)] ,试证明下列关系式成立:
(1)
Z[a ne(t)]
=
E
z a
(2) Z[te(t)] = −Tz dE(z) ,T 为采样周期。 dz
F(z)
=
Tz (z −1)2
−
z
z+ −1
