复数复习(公式及例题)
复数的四则运算及几何意义习题课

题型四:求复数式中的实参数值
练习已知复数z满足|z|=1,且
(z - m ) = 2m (m < 0) ,求m的值.
2
m = 1-
2
题型五:证明复数的有关性质
例10 已知复数z满足|z|=1,求证: 1 z+ R. z
题型五:证明复数的有关性质 例12 求证:复数z为纯虚数的充要 条件是z2<0.
复数的概念与运算典型题型分析
题型一:复数的混合运算
3 - 4i 15 8 例1 计算: + i - (1 + i ) 1 + 2i
-17-3i 3 2z + (4z + 6)i 练习设复数z=1-i,求
的值.
- 3z
1 -i
求
1 例3 已知复数z满足 z + - i = 0 , 2 z z - z + 1
.
1 x
变式1:若复数z满足|z+1|+|z-1|=4,则复数z所对应的 点表示什么图形? 以(1,0),(-1,0)为焦点,长轴长为4的椭圆 变式2:若复数z满足|z+1|-|z-1|=1,则复数z所对应的 点表示什么图形? 以(1,0),(-1,0)为焦点,实轴长为1的双曲线的右支
变式3:你能给出下列方程所表示的图形的复数 表达形式吗?
解:由条件|z-4i|=|z+2|知复数z 对应的点到点A(0,4)与点 B(-2,0)的距离相等,所以复数 z对应的点的集合是线段AB的垂直 平分线.由平面解析几何知识得x,y 满足x+2y=3,所以由均值不等式得
2 x 4 y 2 2 x 4 y 2 2 x2 y 4 2
y 4
2、思考题: (1)你能写出线段Z1Z2的垂直平分线的复数表达形式吗? (2)你能写出抛物线y2=2px(p>0)的复数表达形式吗?
复变函数总复习资料

性质: (1) Ln(z1 z2 ) Lnz1 Lnz2 ,
(2) Ln z1 z2
(3)Lnzn
Lnz1 nLnz
Lnz2 Ln n
, z
1
Lnz
n
(4) 在除去负实轴(包括原点)的复平面内, 主值支和其它各分支
处处连续, 处处可导, 且 (ln z) 1 , (Lnz) 1 .
z
z 15
3.乘幂与幂函数:ab、zb
乘幂 ab ebLna.
由于 Lna ln a i(arg a 2k ) 是多值的, 因而ab 也是多值的.
(1) b 为整数:
a e e e e b
bLna
b[ln a i(arga2k )]
b(ln a iarga)2kbi
ez的性质:
1. f (z) ez 0
2. ez ez 处处解析
3. 满足加法定理:ez1ez2 ez1z2
4. 周期性:周期为 2k i
14
2.对数函数:Ln z ln z iArg z ln z i arg z i2k
多值!
主值: ln z ln z i arg z arg z 分支: Ln z ln z 2k i k 1, 2
3、 复数运算
z1 x1 iy1 z2 x2 iy2
加法、减法: z1 z2 (x1 x2 ) i( y1 y2 )
乘法: 除法:
z1z2 (x1 i y1)(x2 i y2ห้องสมุดไป่ตู้)
(x1x2 y1y2 ) i(x1y2 x2 y1)
z
各分支在除去原点和负实轴的复平面内是解析的: (zb ) bzb1.
复变函数_期末基础知识复习_和_模拟试题

第一、二章
一、 复数的表示方法 (代数、三角、指数表示法) 及其运算公式。
二、函数可导和解析的充分必要条件,函数可导和
解析的充分条件。C-R方程。
三、初等函数(指数函数、三角函数、对数函数、
幂函数)的定义与性质。
华侨大学厦门工学院 09电子3班
虚轴
复数的模:
z x2 y 2 r
C C
华侨大学厦门工学院 09电子3班
x x(t ) 1 :光滑曲线C 的实参数方程为 ,t : , y y(t )
f ( z )dz
C
{u[ x(t ), y(t )] iv[ x(t ), y(t )]} {x(t ) iy(t )}dt
注:过z1与z2两点的直线的参数方程为: z z1 ( z2 z1 )t, t .
连接z1 x1 iy1与z2 x2 iy2的直线段的参数方程为:
z z1 t ( z2 z1 ),0 t 1
华侨大学厦门工学院 09电子3班
通过两点( x1 , y1 )与( x2 , y2 )的直线方程为
留数定理
C
k 1 华侨大学厦门工学院 09电子3班
f ( z )dz 2 i Re s[ f ( z ), zk ].
n
第八、九章 一、傅氏变换、拉氏变换及它们的逆变换的定义。 二、记住 函数的几个重要性质。 三、记住几个重要函数的积分变换。 四、记住积分变换的性质(线性、位移、相似、 微分、积分性质)。 五、会用二、三、四中的结论求某些函数的积分 变换或逆变换。 六、会求解简单的微分方程。
f ( z ) Cn ( z z0 )n ,
《复数的概念》考点讲解复习与同步训练
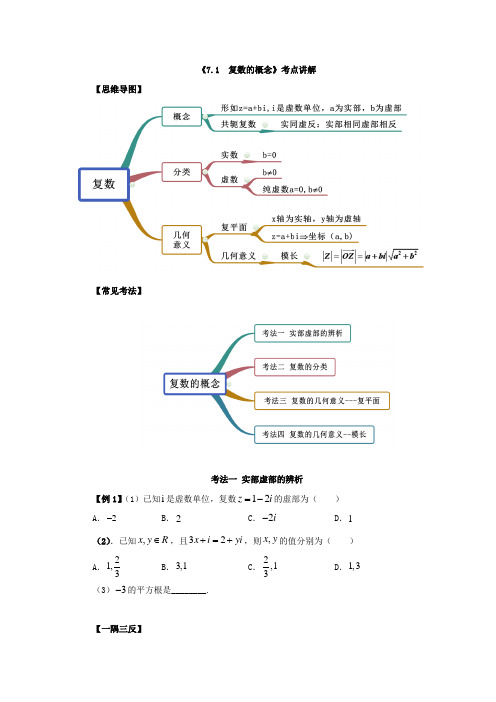
《7.1 复数的概念》考点讲解【思维导图】【常见考法】考法一 实部虚部的辨析【例1】(1)已知i 是虚数单位,复数12z i =-的虚部为( )A .2-B .2C .2i -D .1(2).已知,x y R ∈,且32x i yi +=+,则,x y 的值分别为( )A .21,3B .3,1C .2,13D .1,3(3)3-的平方根是________.【一隅三反】1. 1-的平方根为______.2.复数2(i 是虚数单位)的实部为( )A .2B .C .22-D .03.若复数1(1)2z i =-+,则z 的共轭复数的虚部是( ) A .12i - B .12i C .12- D .124.以2i -2+的实部为虚部的复数是( )A .2i +B .22i + CD .45i -考法二 复数的分类 【例2】已知复数()2262153m m z m m i m --=+--+(i 是虚数单位) (1)复数z 是实数,求实数m 的值;(2)复数z 是虚数,求实数m 的取值范围;(3)复数z 是纯虚数,求实数m 的值.【一隅三反】1.已知复数()()223183,z m m m m i m R =+-+-∈,其中i 为虚数单位.(1)若复数z 是实数,求实数m 的值;(2)若复数z 是纯虚数,求实数m 的值.2.复数()()()2152615z i m i m i =++-+-. (1)实数m 取什么数时,z 是实数;(2)实数m 取什么数时,z 是纯虚数;(3)实数m 取什么数时,z 对应的点在直线70x y ++=上.考法三 复数的几何意义--复平面【例3】(1)已知复数34z i =-+(i 虚单位),则复数z 在复平面内对应的点在( )A .第一象限B .第二象限C .第三象限D .第四象限 (2)在复平面内,若复数()()2246z m m m m i =-+--所对应的点在第二象限,则实数m 的取值范围是( )A .()0,3B .(),2-∞-C .()2,0-D .()3,4 【一隅三反】1.在复平面内,复数1i +的共轭复数所对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限 2.设复数2z i =+,则z 的共轭复数z 在复平面内对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限3.若()()11z m m i =++-(i 是虚数单位)在复平面内对应的点位于第四象限,则实数m 的取值范围为( )A .(),1-∞-B .(),1-∞C .()1,1-D .()1,-+∞考法四 复数的几何意义--模长【例4】(1)设i 虚数单位,复数12z i =+,则||z =( )A B .5 C .1 D .2(2)已知(26)12i x yi +=+,其中x 、y 是实数,则||x yi +=( )A .12B .32C .2D .2(3)设复数z 满足2z i -=,z 在复平面内对应的点为(),x y ,则( )A .()2214x y ++=B .()2212x y ++= C .()2214x y -+=D .()2214x y +-=【一隅三反】1.已知i 为虚数单位,实数x ,y 满足()3x i i y i +=-,则x yi +=( )A .10 BC .3D .12.复数12z i =-(其中i 为虚数单位),则3z i +=( )A .5 BC .2 D3.已知复数z 满足|2|1-+=z i ,则||z 的最小值为( )A1 B1 C1 D14.已知复数z 满足条件1z =,那么z i ++的最大值为______.《7.1 复数的概念(精讲)》考点讲解答案解析考法一 实部虚部的辨析【例1】(1)已知i 是虚数单位,复数12z i =-的虚部为( )B .2- B .2C .2i -D .1(2).已知,x y R ∈,且32x i yi +=+,则,x y 的值分别为( )A .21,3B .3,1C .2,13D .1,3(3)3-的平方根是________.【答案】(1)A (2)C (3)【解析】(1)复数12z i =-的虚部为2-.故选:A.(2)由题意知,321x y =⎧⎨=⎩,解得231x y ⎧=⎪⎨⎪=⎩,故选: C. (3)由()23=-得解.【一隅三反】1.1-的平方根为______.【答案】i ±【解析】()21i ±=-,因此,1-的平方根为i ±.故答案为i ±.2.复数2(i 是虚数单位)的实部为( )A .2B .C .2-D .0【答案】A【解析】根据复数的基本概念,可得复数22-的实部为2.故选:A . 3.若复数1(1)2z i =-+,则z 的共轭复数的虚部是( ) A .12i -B .12iC .12-D .12 【答案】D 【解析】因为复数111(1)222z i i =-+=--,所以z 的共轭复数1122z i =-+,虚部是12,故选:D .4.以2i -2+的实部为虚部的复数是( )A .2i +B .22i +CD .45i - 【答案】B【解析】22i i =的虚部为222+=+的实部为2,则复数为22z i =+故选:B.考法二 复数的分类【例2】已知复数()2262153m m z m m i m --=+--+(i 是虚数单位) (1)复数z 是实数,求实数m 的值;(2)复数z 是虚数,求实数m 的取值范围;(3)复数z 是纯虚数,求实数m 的值.【答案】(1)5m =;(2)5m ≠且3m ≠-;(3)3m =或2.【解析】(1)复数z 是实数,则2215030m m m ⎧--=⎨+≠⎩,解得5m =; (2)复数z 是虚数,则221503m m m ⎧--≠⎨≠-⎩,解得5m ≠且3m ≠-;(3)复数是纯虚数,则226032150m m m m m ⎧--=⎪≠-⎨⎪--≠⎩,解得3m =或2.【一隅三反】1.已知复数()()223183,z m m m m i m R =+-+-∈,其中i 为虚数单位.(1)若复数z 是实数,求实数m 的值;(2)若复数z 是纯虚数,求实数m 的值.【答案】(1)0或3;(2)6-.【解析】(1)若复数z 是实数,则230m m -=所以0m =或3m =. (2)若复数z 是纯虚数,则22303180m m m m ⎧-≠⎨+-=⎩所以6m =-. 2.复数()()()2152615z i m i m i =++-+-. (1)实数m 取什么数时,z 是实数;(2)实数m 取什么数时,z 是纯虚数;(3)实数m 取什么数时,z 对应的点在直线70x y ++=上.【答案】(1)5m =或3-;(2)2m =-;(3)12m =或2- 【解析】复数222(1)(52)(615)(56)(215)z i m i m i m m m m i =++-+-=+++--.(1)由22150m m --=,解得5m =或3-.5m ∴=或3-时,复数z 为实数.(2)由225602150m m m m ⎧++=⎨--≠⎩,解得2m =-.2m ∴=-时,复数z 为纯虚数.(3)由22(56)(215)70m m m m +++--+=.化为:22320m m +-=, 解得12m =或2-.12m ∴=或2-,z 对应点在直线70x y ++=上.考法三 复数的几何意义--复平面【例3】(1)已知复数34z i =-+(i 虚单位),则复数z 在复平面内对应的点在( )A .第一象限B .第二象限C .第三象限D .第四象限 (2)在复平面内,若复数()()2246z m m m m i =-+--所对应的点在第二象限,则实数m 的取值范围是( )A .()0,3B .(),2-∞-C .()2,0-D .()3,4【答案】(1)B (2)D【解析】(1)由复数的几何意义知,复数34z i =-+在复平面内对应的点为()3,4-,即在第二象限,故选:B(2)∵在复平面内,若复数()()2246z m m m m i =-+--所对应的点在第二象限, ∴224060m m m m ⎧-<⎨-->⎩解得34x <<∴实数m 的取值范围是()3,4故选:D. 【一隅三反】1.在复平面内,复数1i +的共轭复数所对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限 【答案】D 【解析】复数1i +的共轭复数为1i -,∴其对应的点()1,1-位于第四象限.故选:D.2.设复数2z i =+,则z 的共轭复数z 在复平面内对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限 【答案】D【解析】复数2z i =+的共轭复数2z i =-,则对应点的坐标为()2,1-,该点位于第四象限,故选:D.3.若()()11z m m i =++-(i 是虚数单位)在复平面内对应的点位于第四象限,则实数m 的取值范围为( )A .(),1-∞-B .(),1-∞C .()1,1-D .()1,-+∞【答案】C 【解析】()()11z m m i =++-对应的点为()1,1m m +-,因为对应的点位于第四象限,得1010m m +>⎧⎨-<⎩,解得11m -<<.故选:C.考法四 复数的几何意义--模长【例4】(1)(设i 虚数单位,复数12z i =+,则||z =( )A B .5 C .1 D .2(2)已知(26)12i x yi +=+,其中x 、y 是实数,则||x yi +=( )A .12B .32C .2D .2(3)设复数z 满足2z i -=,z 在复平面内对应的点为(),x y ,则( )A .()2214x y ++=B .()2212x y ++=C .()2214x y -+=D .()2214x y +-= 【答案】(1)A (2)C (3)D【解析】(1)||z == A(2)因为2612x xi yi +=+,所以21x =,62x y =,解得12x =,332y x ==,所以x yi +==,故选:C. (3)z 在复平面内对应的点为(),x y ,则复数()=,z x yi x y R +∈, 则()=12z i x y i -=+-,由复数的模长公式可得()22+1=4x y -,故选:D 【一隅三反】1.已知i 为虚数单位,实数x ,y 满足()3x i i y i +=-,则x yi +=( )A .10BC .3D .1【答案】B【解析】由(3)x i i y i +=-,得3xi y i -+=-,1x ∴=-,3y =-.则||x yi +故选:B .2.复数12z i =-(其中i 为虚数单位),则3z i +=( )A .5B C .2 D 【答案】B【解析】因为12z i =-,所以31231z i i i i +=-+=+所以3z i +==故选:B .3.已知复数z 满足|2|1-+=z i ,则||z 的最小值为( )A 1B 1C 1D 1 【答案】A【解析】设z a bi =+,则()2211a bi i a b i +-+=-++==, 由()()22211x y -++=,表示为以()2,1-为圆心,1为半径的圆,1,因为z =1,故选:A.4.已知复数z 满足条件1z =,那么z i ++的最大值为______.【答案】4【解析】因为1z =,所以复数z 对应的点在单位圆上,z i +表示复数z 对应的点与复数i -对应的点()1M --之间的距离,而3OM ==.所以z i +的最大值为14OM r OM +=+=.故答案为:4《7.1 复数的概念(精练)》同步练习【题组一 实部虚部辨析】1.若(2)x i i y i +=+,其中,x y R ∈,i 为虚数单位,则复数z x yi =+的虚部为( )A .1B .iC .2-D .2i -2.设i 为虚数单位,则复数55z i =-的实部为( )A .5-B .5i -C .5D .5i3.复数3z i =-的虚部是( )A .1B .iC .-1D .i -4.数24i z =--的虚部是( )A .2-B .2C .4-D .45.已知复数1z i =-,其中i 是虚数单位,则复数z 的虚部为( )A .iB .i -C .1-D .1【题组二 复数的分类】1.已知复数()()1i 1i z m =--+是纯虚数,则实数m =( )A .-2B .-1C .0D .1 2. i 为虚数单位,已知复数21(1)a a i -+-是纯虚数,则a 等于( )A .±1B .1C .1-D .03.设复数i z a b =+(其中a b R ∈、,i 为虚数单位),则“0a =”是“z 为纯虚数”的( )A .充分非必要条件B .必要非充分条件C .充要条件D .既非充分又非必要条件4.已知a 为实数,若复数()24(2)z a a i =-++为纯虚数,则复数z 的虚部为( )A .2B .4iC .2±D .4 5.已知i 为虚数单位,a R ∈,复数()242a a i -+-是纯虚数,则a =( )A .2B .-2C .4D .-2或26.若复数(1)(2)z m m i =++-(m ∈R )是纯虚数,则m =______ 7.已知复数223(3)z m m m i =--+-为纯虚数,则实数m =_____________8.实数m 取怎样的值时,复数()22153m m z i m --=-+是: (1)实数? (2)虚数? (3)纯虚数?9.已知复数()()11z m m i m R =++-∈. (1)m 取什么值时,z 为实数; (2)m 取什么值时,z 为纯虚数.10.已知m 为实数,i 为虚数单位,设复数()()2256253z m m m m i =++++-. (1)当复数z 为纯虚数时,求m 的值;(2)当复数z 对应的复点在直线70x y -+=的右下方,求m 的取值范围.【题组三 复数的几何意义--复平面】1.在复平面内,复数1i -+所对应的点位于( ) A .第一象限B .第二象限C .第三象限D .第四象限2.若,a b ∈R ,则复数()()224526a a b b i -++-+-表示的点在( ) A .在第一象限 B .在第二象限 C .在第三象限D .在第四象限3.复数()()2lg 2221()x xz x i x R -=-+-+-∈在复平面内对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限4.设复数1z ,2z 在复平面内对应的点关于虚轴对称,且12z i =+,则2z =( ) A .2i +B .2i -+C .2i -D .2i --5.已知()()214Z m m i =++-在复平面内对应的点在第二象限,则实数m 的取值范围是____.6.已知复数()()22lg 223z m m m m i =-++-若复数z 是实数,则实数m =_____;若复数z 对应的点位于复平面的第二象限,则实数的取值范围为________.7.在复平面内,复数()()222z m m m i =++--对应的点在第一象限,求实数m 的取值范围是________.【题组四 复数的几何意义--模长】1.已知a R ∈,若有a i -=i 为虚数单位),则a =( ) A .1B .2-C .2±D .±12.设复数z 满足1z i -=,z 在复平面内对应的点为(),x y 则x ,y 满足的关系式为______.3.已知a ,b R ∈,()123ai b a i +=++,则a =______,3a bi +=______. 4.知i 是虚数单位,若1z i =+,则22z z -=________. 5.若z C ∈且342z i ++≤,则z 的取值范围为__________. 【题组五 复数综合应用】1.(多选)已知复数1z i =+(其中i 为虚数单位),则以下说法正确的有( )A .复数z 的虚部为iB .z =C .复数z 的共轭复数1z i =-D .复数z 在复平面内对应的点在第一象限2.若复数12z i =+(i 为虚数单位),则下列命题正确的是( )A .z 是纯虚数B .z 的实部为2C .z 的共轭复数为12i -+D .z 3.已知复数z 在复平面上对应的点为()1,1-,则( ) A .z i +是实数(i 为虚数单位) B .z i +是纯虚数(i 为虚数单位) C .1z +是实数 D .1z +是纯虚数4.关于复数3-4i 的说法正确的是( )①实部和虚部分别为3和-4;②复数模为5③在复平面内对应的点在第四象限;④共轭复数为3+4i A .①③ B .①②④C .①②③④D .①③④《7.1 复数的概念(精练)》同步练习答案解析【题组一 实部虚部辨析】1.若(2)x i i y i +=+,其中,x y R ∈,i 为虚数单位,则复数z x yi =+的虚部为( ) A .1 B .iC .2-D .2i -【答案】C【解析】由于(2)x i i y i +=+,则1x=且2y =-,所以12z x yi i =+=-,所以复数z 的虚部为2-.故选:C.2.设i 为虚数单位,则复数55z i =-的实部为( ) A .5- B .5i -C .5D .5i【答案】C【解析】复数55z i =-的实部为5.故选:C. 3.复数3z i =-的虚部是( ) A .1 B .iC .-1D .i -【答案】C【解析】由复数虚部的定义得复数3z i =-的虚部是1-.故选:C 4.复数24i z =--的虚部是( ) A .2- B .2C .4-D .4【答案】C【解析】因为24i z =--,所以由复数定义可知虚部是4-,故选:C. 5.已知复数1z i =-,其中i 是虚数单位,则复数z 的虚部为( ) A .i B .i -C .1-D .1【答案】C【解析】因为1z i =-,则虚部为1-.故选:C.【题组二 复数的分类】1.已知复数()()1i 1i z m =--+是纯虚数,则实数m =( ) A .-2 B .-1C .0D .1【答案】D【解析】()()()1i 1i 11i z m m m =--+=--+,因为z 为纯虚数且m 为实数,故1010m m -=⎧⎨+≠⎩,故1m =, 故选:D2. i 为虚数单位,已知复数21(1)a a i -+-是纯虚数,则a 等于( ) A .±1 B .1C .1-D .0【答案】C【解析】复数21(1)a a i -+-是纯虚数,所以21010a a ⎧-=⎨-≠⎩,得1a =-.故选:C.3.设复数i z a b =+(其中a b R ∈、,i 为虚数单位),则“0a =”是“z 为纯虚数”的( )A .充分非必要条件B .必要非充分条件C .充要条件D .既非充分又非必要条件【答案】B【解析】若复数i z a b =+是纯虚数,则0a =,0b ≠, 则0a =不能证得z 为纯虚数,z 为纯虚数可以证得0a =, 故“0a =”是“z 为纯虚数”的必要非充分条件, 故选:B.4.已知a 为实数,若复数()24(2)z a a i =-++为纯虚数,则复数z 的虚部为( ) A .2 B .4iC .2±D .4【答案】D【解析】2(4)(2)z a a i =-++为纯虚数,∴24020a a ⎧-=⎨+≠⎩,即2a =.∴复数z 的虚部为4.故选:D .5.已知i 为虚数单位,a R ∈,复数()242a a i -+-是纯虚数,则a =( )A .2B .-2C .4D .-2或2【答案】B【解析】因为复数()242a a i -+-是纯虚数,所以240,202a a a -=-≠∴=-故选:B6.若复数(1)(2)z m m i =++-(m ∈R )是纯虚数,则m =______ 【答案】-1【解析】复数(1)(2)z m m i =++-(m ∈R )是纯虚数,则1020m m +=⎧⎨-≠⎩,所以1m =-. 故答案为:-17.已知复数223(3)z m m m i =--+-为纯虚数,则实数m =_____________【答案】1-【解析】由题意,复数223(3)z m m m i =--+-为纯虚数,则满足223030m m m ⎧--=⎨-≠⎩,解得1m =-,即实数m 的值为1-.故答案为:1-.8.实数m 取怎样的值时,复数()22153m m z i m --=-+是: (1)实数? (2)虚数? (3)纯虚数?【答案】(1)5m =或3m =-;(2)5m ≠且3m ≠-;(3)3m =. 【解析】(1)若22150m m --=,则z 为实数,此时3m =-或者5m =. (2)若22150m m --≠,则z 为虚数,此时3m ≠-且5m ≠.(3)若2302150m m m -=⎧⎨--≠⎩ ,则z 为纯虚数,此时3m =.9.已知复数()()11z m m i m R =++-∈.(1)m 取什么值时,z 为实数; (2)m 取什么值时,z 为纯虚数. 【答案】(1)1m =(2)1m =-【解析】(1)复数()()11z m m i m R =++-∈,若z 为实数,则10m -=,即1m =(2)若z 为纯虚数,则1010m m +=⎧⎨-≠⎩,解得1m =-10.已知m 为实数,i 为虚数单位,设复数()()2256253z m m m m i =++++-. (1)当复数z 为纯虚数时,求m 的值;(2)当复数z 对应的复点在直线70x y -+=的右下方,求m 的取值范围. 【答案】(1)2-;(2)(4,4)-.【解析】(1)由题意得:225602530m m m m ⎧++=⎨+-≠⎩,解得2m =-;(2)复数z 对应的点的坐标为22(56,253)m m m m +++-, 直线70x y -+=的右下方的点的坐标(),x y 应满足70x y -+>, 所以22(56)(253)70m m m m ++-+-+>, 解得44m -<<,所以m 的取值范围为(4,4)-. 【题组三 复数的几何意义--复平面】1.在复平面内,复数1i -+所对应的点位于( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限【答案】B【解析】由题,1i -+在复平面内对应的点为()1,1-,在第二象限,故选:B 2.若,a b ∈R ,则复数()()224526a a b b i -++-+-表示的点在( ) A .在第一象限 B .在第二象限 C .在第三象限 D .在第四象限【答案】D【解析】因为()2245210a a a -+=-+>,()2226150b b b -+-=---<, 所以由复数的几何意义知该复数表示的点在第四象限.故选:D3.复数()()2lg 2221()x xz x i x R -=-+-+-∈在复平面内对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限【答案】C【解析】复数()()2lg 2221()x xz x i x R -=-+-+-∈的实部()2lg 2a x -=+、虚部()221x x b -=-+-.因为()22221lg 20x x +≥>⇒+>,所以0a <. 因为21122202x x x x --≥-+⇒≥>+,所以0b <. 所以复数z 在复平面内对应的点位于第三象限.故选:C4.设复数1z ,2z 在复平面内对应的点关于虚轴对称,且12z i =+,则2z =( ) A .2i + B .2i -+C .2i -D .2i --【答案】B 【解析】12z i =+,1z ∴在复平面内对应点的坐标为(2,1),由复数1z ,2z 在复平面内对应的点关于虚轴对称,可知2z 在复平面内对应的点的坐标为(2,1)-,22z i ∴=-+,故选:B .5.已知()()214Z m m i =++-在复平面内对应的点在第二象限,则实数m 的取值范围是____.【答案】(),2-∞-【解析】()()214Z m m i =++-在复平面内对应的点()21,4m m +-在第二象限,所以21040m m +<⎧⎨->⎩,解得2m <-,即实数m 的取值范围是(),2-∞-.故答案为:(),2-∞-6.已知复数()()22lg 223z m m m m i =-++-若复数z 是实数,则实数m =________;若复数z 对应的点位于复平面的第二象限,则实数的取值范围为________.【答案】3- 21m <<【解析】z 为实数,则2230m m +-=,解得1m =或3-,又220m m ->,所以3m =-.z对应点在第二象限,则22lg(2)0230m m m m ⎧-<⎨+->⎩,解得21m <<+.故答案为:3-;21m <<.7.在复平面内,复数()()222z m m m i =++--对应的点在第一象限,求实数m 的取值范围是________.【答案】()()2,12,--+∞【解析】根据题意得出22020m m m +>⎧⎨-->⎩,解得21m -<<-或>2m ,所以实数m 的取值范围是()()2,12,--+∞.故答案为:()()2,12,--+∞.【题组四 复数的几何意义--模长】1.已知a R ∈,若有a i -=i 为虚数单位),则a =( ) A .1 B .2-C .2±D .±1【答案】C【解析】因为a R ∈所以a i -==,即215a +=,解得2a =±,故选:C2.设复数z 满足1z i -=,z 在复平面内对应的点为(),x y 则x ,y 满足的关系式为______.【答案】22(1)1y x +-=【解析】由题意,设复数(,)z x yi x y R =+∈,因为1z i -=1=,整理得22(1)1y x +-=,即复数z 在复平面内对应的点为(),x y 则,x y 满足的关系式为22(1)1y x +-=.故答案为:22(1)1y x +-=.3.已知a ,b R ∈,()123ai b a i +=++,则a =______,3a bi +=______.【答案】3-【解析】∵()123ai b a i +=++∴123ba a =⎧⎨=+⎩,解得31a b =-⎧⎨=⎩,则333a bi i +=-+===故答案为:(1)3-;(2)4.已知i 是虚数单位,若1z i =+,则22z z -=________. 【答案】2【解析】根据复数模的计算公式得:22212+222z z i i i -=+--=.故答案为:2 5.若z C ∈且342z i ++≤,则z 的取值范围为__________. 【答案】[]3,7【解析】342z i ++≤的几何意义为复平面内动点Z 到定点()3,4A --的距离小于等于2的点的集合,z 表示复平面内动点Z 到原点的距离,∵||5OA ==,5252z ∴-≤≤+.∴z 的取值范围为[]3,7. 故答案为:[]3,7. 【题组五 复数综合应用】1.(多选)已知复数1z i =+(其中i 为虚数单位),则以下说法正确的有( )A .复数z 的虚部为iB .z =C .复数z 的共轭复数1z i =- D .复数z 在复平面内对应的点在第一象限【答案】BCD【解析】因为复数1z i =+, 所以其虚部为1,即A 错误;z ==B 正确;复数z 的共轭复数1z i =-,故C 正确;复数z 在复平面内对应的点为()1,1,显然位于第一象限,故D 正确. 故选:BCD.2.若复数12z i =+(i 为虚数单位),则下列命题正确的是( )A .z 是纯虚数B .z 的实部为2C .z 的共轭复数为12i -+D .z 【答案】D【解析】复数12z i =+(i 为虚数单位)显然不是纯虚数,12z i =+的实部是1,z 的共轭复数为12i -,z =D 正确,故选:D.3.已知复数z 在复平面上对应的点为()1,1-,则( ) A .z i +是实数(i 为虚数单位) B .z i +是纯虚数(i 为虚数单位) C .1z +是实数 D .1z +是纯虚数 【答案】D【解析】由题意可得,1z i =-+,则1z i +=为纯虚数,12z i i +=-+是虚数,但不是纯虚数,故选:D .4.关于复数3-4i 的说法正确的是( ) ①实部和虚部分别为3和-4;②复数模为5③在复平面内对应的点在第四象限;④共轭复数为3+4i A .①③ B .①②④C .①②③④D .①③④【答案】C【解析】复数3-4i 的实部和虚部分别为3和-4,①正确;复数模为5,②正确; 在复平面内对应的点为(3,4)-在第四象限,③正确;复数3-4i 的共轭复数为3+4i ,④正确.故选:C.。
复数讲义(含知识点和例题及解析)

数系的扩充与复数的引入1.复数的有关概念 (1)复数的概念:形如a +b i(a ,b ∈R )的数叫做复数,其中a ,b 分别是它的实部和虚部。
若b =0,则a +b i 为实数;若b ≠0,则a +b i 为虚数;若a =0且b ≠0,则a +b i 为纯虚数。
(2)复数相等:a +b i =c +d i ⇔a =c 且b =d (a ,b ,c ,d ∈R )。
(3)共轭复数:a +b i 与c +d i 共轭⇔a =c ,b =-d (a ,b ,c ,d ∈R )。
(4)复平面:建立直角坐标系来表示复数的平面,叫做复平面。
x 轴叫做实轴,y 轴叫做虚轴。
实轴上的点都表示实数;除原点外,虚轴上的点都表示纯虚数;各象限内的点都表示非纯虚数。
(5)复数的模:向量OZ →的模r 叫做复数z =a +b i(a ,b ∈R )的模,记作|z |或|a +b i|,即|z |=|a +b i|=a 2+b 2。
2.复数的几何意义 (1)复数z =a +b i――→一一对应复平面内的点Z (a ,b )(a ,b ∈R )。
(2)复数z =a +b i ――→一一对应平面向量OZ →(a ,b ∈R )。
3.复数的运算(1)复数的加、减、乘、除运算法则设z 1=a +b i ,z 2=c +d i(a ,b ,c ,d ∈R )则: ①加法:z 1+z 2=(a +b i)+(c +d i)=(a +c )+(b +d )i 。
②减法:z 1-z 2=(a +b i)-(c +d i)=(a -c )+(b -d )i 。
③乘法:z 1·z 2=(a +b i)·(c +d i)=(ac -bd )+(ad +bc )i 。
④除法:z 1z 2=a +b i c +d i =(ac +bd )+(bc -ad )i c 2+d 2(c +d i ≠0)。
(2)复数加法的运算定律复数的加法满足交换律、结合律,即对任何z 1,z 2,z 3∈C ,有z 1+z 2=z 2+z 1,(z 1+z 2)+z 3=z 1+(z 2+z 3)。
复数(基础+复习+习题+练习)

课题:复数考纲要求:(Ⅰ)复数的概念:①理解复数的基本概念;②理解复数相等的充要条件;③了解复数的代数表示法及其几何意义;(Ⅱ))复数的四则运算:①会进行复数的代数形式的四则运算;②了解复数代数形式的加、减运算的几何意义.教材复习 1.虚数单位i :()1它的平方等于1-,即 21i =-;()2实数可以与它进行四则运算,进行四则运算时,原有加、乘运算律仍然成立.2.i 与-1的关系: i 就是1-的一个平方根,即方程21x =-的一个根,方程21x =-的另一个根是i -.3.i 的周期性:41n i i +=, 421n i +=-, 43n i i +=-, 41n i =.4.复数的定义:形如(,)a bi a b R +∈的数叫复数,a 叫复数的实部,b 叫复数的虚部.全体复数所成的集合叫做复数集,用字母C 表示5.复数的代数形式: 复数通常用字母z 表示,即(,)z a bi a b R =+∈,把复数表示成a bi+的形式,叫做复数的代数形式.6.复数与实数、虚数、纯虚数及0的关系:对于复数(,)a bi a b R +∈,当且仅当0b =时,复数(,)a bi a b R +∈是实数a ;当0b ≠时,复数z a bi =+叫做虚数;当0a =且0b ≠时,z bi =叫做纯虚数;当且仅当0a b ==时,z 就是实数07.复数集与其它数集之间的关系:N Z Q R C 苘苘8.两个复数相等的定义:如果两个复数的实部和虚部分别相等,那么我们就说这两个复数相等.这就是说,如果a ,b ,c ,d R ∈,那么a bi c di +=+⇔a c =,b d = 9. 复平面、实轴、虚轴:复数(,)z a bi a b R =+∈与有序实数对(),a b 是一一对应关系.建立一一对应的关系.点Z 的横坐标是a纵坐标是b ,复数(,)z a bi a b R =+∈可用点(),Z a b 表示,这个 建立了直角坐标系来表示复数的平面叫做复平面,也叫高斯平面,x 轴叫做实轴,y 轴叫做虚轴.实轴上的点都表示实数.对于虚轴上的点要除原点外,因为原点对应的有序实数对为()是000z i =+=表示是实数.故除了原点外,虚轴上的点都表示纯虚数.这就是复数的一种几何意义.也就是复数的另一种表示方法,即几何表示方法.10.复数1z 与2z 的和的定义:12z z +=()()a bi c di +++=()()a c b d i +++11.复数1z 与2z 的差的定义:12z z -=()()a bi c di +-+=()()a c b d i -+- 12.复数的加法运算满足交换律:1221z z z z +=+13.复数的加法运算满足结合律: 123123()()z z z z z z ++=++ 14.乘法运算规则:设1z a bi =+,2z c di =+(a 、b 、c 、d R ∈)是任意两个复数,那么它们的积()()()()12z z a bi c di ac bd bc ad i =++=-++其实就是把两个复数相乘,类似两个多项式相乘,在所得的结果中把2i 换成1-,并且把实部与虚部分别合并.两个复数的积仍然是一个复数.15.乘法运算律:(1)()()123123z z z z z z = ()2123123()()z z z z z z ⋅⋅=⋅⋅()3()1231213z z z z z z z +=+3.复数除法定义:满足()()()c di x yi a bi ++=+的复数x yi +(x 、y R ∈)叫复数a bi +除以复数c di +的商,记为:()()a bi c di +÷+或者dic bia ++ 16.除法运算规则:①设复数a bi + (a 、b R ∈),除以c di + (c ,d R ∈),其商为x yi +(x 、y R ∈),即()()a bi c di x yi +÷+=+∵()()()()x yi c di cx dy dx cy i ++=-++ ∴()()cx dy dx cy i a bi -++=+由复数相等定义可知⎩⎨⎧=+=-.,b cy dx a dy cx 解这个方程组,得⎪⎪⎩⎪⎪⎨⎧+-=++=.,2222d c ad bc y d c bd ac x于是有: ()()a bi c di +÷+2222ac bd bc adi c d c d +-=+++②利用()()22c di c di c d +-=+于是将dic bia ++的分母有理化得:原式22()()[()]()()()a bi a bi c di ac bi di bc ad ic di c di c di cd ++-+⋅-+-===++-+ 222222()()ac bd bc ad i ac bd bc adi c d c d c d ++-+-==++++.∴(()()a bi c di +÷+=i dc adbc d c bd ac 2222+-+++ 点评:①是常规方法,②是利用初中我们学习的化简无理分式时,都是采用的分母有理化思想方法,而复数c di +与复数c di -,相当于我们初中学习的23+的对偶式23-,它们之积为1是有理数,而()()22c di c di c d +-=+是正实数.所以可以分母实数化. 把这种方法叫做分母实数化法.17.共轭复数:当两个复数的实部相等,虚部互为相反数时,这两个复数叫做互为共轭复数。
复变函数复习资料

(一)复数的概念1.复数的概念:z x iy =+,,x y 是实数, ()()Re ,Im x z y z ==.21i =-. 注:一般两个复数不比较大小,但其模(为实数)有大小. ①两个复数相等,当且仅当它们的实部与虚部分别相等。
②一个复数等于零,当且仅当它的实部与虚部同时等于零。
③称复数x+iy 和x-iy 互为共轭复数。
2.复数的表示1)模:z=2)幅角:在0z ≠时,矢量与x 轴正向的夹角,记为()Arg z (多值函数);主值()arg z 是位于[)π2,0中的幅角。
(()Arg z 有无穷个值,()arg z 是复数z 的辐角的主值()Arg z =()arg z +2k π3)()arg z 与arctan y x之间的关系如下: 当0,x > arg arctanyz x=;当0,arg arctan 0,0,arg arctan yy z x x y y z xππ⎧≥=+⎪⎪<⎨⎪<=-⎪⎩; 4)三角表示:)sin (cos z θθi r +=,其中)(r z g A =θ;注:中间一定是“+”号。
(r=|z|)5)指数表示:θi re =z ,其中)(r z g A =θ。
(二) 复数的运算 1.加减法:若111222,z x iy z x iy =+=+,则()()121212z z x x i y y ±=±+±··2.乘除法:1)若111222,z x iy z x iy =+=+,则()()1212122112z z x x y y i x y x y =-++;()()()()112211112121221222222222222222x iy x iy z x iy x x y y y x y x i z x iy x iy x iy x y x y +-++-===+++-++。
高中数学第七章复数经典大题例题(带答案)

高中数学第七章复数经典大题例题单选题1、已知z =2+i ,则z−i 1+i =( )A .1−2iB .2+2iC .2iD .−2i答案:D分析:根据共轭复数的定义及复数的除法法则即可求解.由z =2+i ,得z =2−i ,所以z−i 1+i =2−i−i 1+i =2(1−i )×(1−i )(1+i )×(1−i )=2×(1−2i+i 2)2=−2i .故选:D.2、设(−1+2i)x =y −1−6i ,x,y ∈R ,则|x −yi|=( )A .6B .5C .4D .3答案:B分析:根据复数实部等于实部,虚部等于虚部可得{x =−3y =4,进而求模长即可. 因为(−1+2i )x =y −1−6i ,所以{2x =−6−x =y −1,解得{x =−3y =4, 所以|x −yi |=|−3−4i|=√(−3)2+(−4)2=5.故选:B.3、已知下列三个命题:①若复数z 1,z 2的模相等,则z 1,z 2是共轭复数;②z 1,z 2都是复数,若z 1+z 2是虚数,则z 1不是z 2的共轭复数;③复数z 是实数的充要条件是z =z .则其中正确命题的个数为A .0个B .1个C .2个D .3个答案:C解析:运用复数的模、共轭复数、虚数等知识对命题进行判断.对于①中复数z 1和z 2的模相等,例如z 1=1+i ,z 2=√2i ,则z 1和z 2是共轭复数是错误的;对于②z 1和z 2都是复数,若z 1+z 2是虚数,则其实部互为相反数,则z 1不是z 2的共轭复数,所以②是正确的;对于③复数z 是实数,令z =a ,则z =a 所以z =z ,反之当z =z 时,亦有复数z 是实数,故复数z 是实数的充要条件是z =z 是正确的.综上正确命题的个数是2个.故选C小提示:本题考查了复数的基本概念,判断命题是否正确需要熟练掌握基础知识,并能运用举例的方法进行判断,本题较为基础.4、在复平面内,复数z =1+i 1−i +1−i 2对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限答案:A解析:由复数的运算求出z ,则可得其对应的点的坐标,从而得出结论.z =(1+i)2(1−i)(1+i)+1−i 2=2i 2+1−i 2=12+12i , 则z 在复平面内对应的点为(12,12),在第一象限,故选:A .5、z 1、z 2是复数,则下列结论中正确的是( )A .若z 12+z 22>0,则z 12>−z 22B .|z 1−z 2|=√(z 1+z 2)2−4z 1⋅z 2C .z 12+z 22=0⇔z 1=z 2=0D .|z 12|=|z 1|2答案:D解析:举反例z 1=2+i ,z 2=2−i 可判断选项A 、B ,举反例,z 2=i 可判断选项C ,设z 1=a +bi ,(a,b ∈R ),分别计算|z 12|、|z 1|2即可判断选项D ,进而可得正确选项.对于选项A :取z 1=2+i ,z 2=2−i ,z 12=(2+i )2=3+2i ,z 22=(2−i )2=3−2i ,满足z 12+z 22=6>0,但z 12与z 22是两个复数,不能比较大小,故选项A 不正确;对于选项B :取z 1=2+i ,z 2=2−i ,|z 1−z 2|=|2i |=2,而√(z 1+z 2)2−4z 1⋅z 2=√42−4(2+i )(2−i )=√16−20无意义,故选项B 不正确;对于选项C :取,z 2=i ,则z 12+z 22=0,但是z 1≠0,z 2≠0,故选项C 不正确;对于选项D :设z 1=a +bi ,(a,b ∈R ),则z 12=(a +bi )2=a 2−b 2+2abi11z =11z =|z 12|=√(a 2−b 2)2+4a 2b 2=√(a 2+b 2)2=a 2+b 2,z 1=a −bi ,|z 1|=√a 2+b 2,所以|z 1|2=a 2+b 2,所以|z 12|=|z 1|2,故选项D 正确.故选:D.6、已知i 为虚数单位,则i +i 2+i 3+⋅⋅⋅+i 2021=( )A .iB .−iC .1D .-1答案:A分析:根据虚数的运算性质,得到i 4n +i 4n+1+i 4n+2+i 4n+3=0,得到i +i 2+i 3+⋅⋅⋅+i 2021=i 2021,即可求解.根据虚数的性质知i 4n +i 4n+1+i 4n+2+i 4n+3=1+i −1−i =0,所以i +i 2+i 3+⋅⋅⋅+i 2021=505×0+i 2021=i .故选:A.7、已知正三角形ABC 的边长为4,点P 在边BC 上,则AP⃗⃗⃗⃗⃗ ⋅BP ⃗⃗⃗⃗⃗ 的最小值为( ) A .2B .1C .−2D .−1答案:D分析:选基底,用基向量表示出所求,由二次函数知识可得.记|BP⃗⃗⃗⃗⃗ |=x ,x ∈[0,4] 因为AP⃗⃗⃗⃗⃗ =BP ⃗⃗⃗⃗⃗ −BA ⃗⃗⃗⃗⃗ , 所以AP⃗⃗⃗⃗⃗ ⋅BP ⃗⃗⃗⃗⃗ =BP ⃗⃗⃗⃗⃗ 2−BA ⃗⃗⃗⃗⃗ ⋅BP ⃗⃗⃗⃗⃗ =|BP ⃗⃗⃗⃗⃗ |2−2|BP ⃗⃗⃗⃗⃗ |=x 2−2x =(x −1)2−1≥−1. 故选:D8、已知关于x 的方程(x 2+mx )+2x i =-2-2i (m ∈R )有实数根n ,且z =m +n i ,则复数z 等于( )A .3+iB .3-iC.-3-iD.-3+i答案:B分析:根据复数相等得出m,n的值,进而得出复数z. 由题意知(n2+mn)+2n i=-2-2i,即{n 2+mn+2=02n+2=0,解得{m=3,n=−1,∴z=3−i故选:B多选题9、已知复数z=21+i,则正确的是()A.z的实部为﹣1B.z在复平面内对应的点位于第四象限C.z的虚部为﹣iD.z的共轭复数为1+i答案:BD分析:根据复数代数形式的乘除运算化简,结合复数的实部和虚部的概念、共轭复数的概念求解即可.因为z=21+i =2(1−i)(1+i)(1−i)=1−i,所以z的实部为1,虚部为-1,在复平面内对应的点为(1,-1),在第四象限,共轭复数为z=1+i,故AC错误,BD正确.故选:BD10、复数z=1−i,则()A.z在复平面内对应的点的坐标为(1,−1)B.z在复平面内对应的点的坐标为(1,1)C.|z|=2D.|z|=√2答案:AD分析:利用复数的几何意义,求出复数对应的点坐标为(1,−1),即可得答案;z=1−i在复平面内对应的点的坐标为(1,−1),|z|=√2.故选:AD.11、已知复数z满足(1+i3)z=2,则下列说法中正确的有()A.z的虚部是iB.|z|=√2C.z⋅z=2D.z2=2答案:BC分析:根据复数的除法运算求出z,结合相关概念以及复数乘法运算即可得结果.z=21+i3=21−i=1+i,其虚部为1,|z|=√2,z⋅z=(1+i)(1−i)=2,z2=(1+i)2=2i≠2.故选:BC.12、已知复数z1=−2+i(i为虚数单位),复数z2满足|z2−1+2i|=2,z2在复平面内对应的点为,则()A.复数z1在复平面内对应的点位于第二象限B.1z1=−25−15iC.(x+1)2+(y−2)2=4D.|z2−z1|的最大值为3√2+2答案:ABD分析:利用复数的几何意义可判断A选项;利用复数的除法运算可判断B选项;利用复数的模长公式可判断C选项;利用复数模长的三角不等式可判断D选项.对于A选项,复数z1在复平面内对应的点的坐标为(−2,1),该点位于第二象限,A对;对于B选项,1z1=1−2+i=−2−i(−2+i)(−2−i)=−25−15i,B对;对于C选项,由题意可得z2−1+2i=(x−1)+(y+2)i,因为|z2−1+2i|=2,则(x−1)2+(y+2)2=4,C错;对于D选项,z1−1+2i=−3+3i,则|z1−1+2i|=√(−3)2+32=3√2,所以,|z2−z1|=|(z2−1+2i)−(z1−1+2i)|≤|z2−1+2i|+|z1−1+2i|=2+3√2,D对.(), M x y故选:ABD.13、若复数z 满足:z (z +2i )=8+6i ,则( )A .z 的实部为3B .z 的虚部为1C .zz =√10D .z 在复平面上对应的点位于第一象限答案:ABD分析:根据待定系数法,将z =a +bi (a,b ∈R )代入条件即可求解a =3,b =1,进而即可根据选项逐一求解. 设z =a +bi (a,b ∈R ),因为z (z +2i )=8+6i ,所以zz +2iz =8+6i ,所以(a 2+b 2−2b )+2ai =8+6i ,所以a 2+b 2−2b =8,2a =6,所以a =3,b =1,所以z =3+i ,所以z 的实部为3,虚部为1,故A ,B 正确;zz =|z |2=10,故C 不正确;z 在复平面上对应的点(3,1)位于第一象限,故D 正确.故选:ABD .填空题14、i 2 021=________.答案:i分析:利用周期性求得所求表达式的值.i 2021=i 505×4+1=i 1=i所以答案是:i15、设复数z ,满足|z 1|=1,|z 2|=2,z 1+z 2=√3−i ,则|z 1−z 2|=____________.答案:√6解析:根据复数的几何意义得到对应向量的表示,再结合向量的平行四边形法则以及余弦定理求解出|z 1−z 2|的值.设z 1,z 2在复平面中对应的向量为OZ 1⃗⃗⃗⃗⃗⃗⃗ ,OZ 2⃗⃗⃗⃗⃗⃗⃗ ,z 1+z 2对应的向量为OZ 3⃗⃗⃗⃗⃗⃗⃗ ,如下图所示:因为z 1+z 2=√3−i ,所以|z 1+z 2|=√3+1=2,所以cos∠OZ 1Z 3=12+22−221×2×2=14, 又因为∠OZ 1Z 3+∠Z 1OZ 2=180°,所以cos∠Z 1OZ 2=−cos∠OZ 1Z 3=−14,所以|Z 2Z 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ |2=OZ 12+OZ 22−2OZ 1⋅OZ 2⋅cos∠Z 1OZ 2=1+4+1=6, 所以|Z 2Z 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ |=√6,又|z 1−z 2|=|Z 2Z 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ |=√6,所以答案是:√6.小提示:名师点评复数的几何意义:(1)复数z =a +bi (a,b ∈R )一一对应↔复平面内的点Z (a,b )(a,b ∈R ); (2)复数z =a +bi (a,b ∈R ) 一一对应↔平面向量OZ ⃗⃗⃗⃗⃗ . 16、在复平面内,复数z 对应的点的坐标是(3,−5).则(1−i)z =___________.答案:−2−8i ##−8i −2分析:根据给定条件求出复数,再利用复数的乘法运算计算作答.在复平面内,复数z 对应的点的坐标是(3,−5),则z =3−5i ,所以(1−i)z =(1−i)(3−5i)=−2−8i .所以答案是:−2−8i解答题17、已知复数z 1=4-m 2+(m -2)i ,z 2=λ+2sin θ+(cos θ-2)i (其中i 是虚数单位,m ,λ,θ∈R ).(1)若z 1为纯虚数,求实数m 的值;(2)若z 1=z 2,求实数λ的取值范围.答案:(1)-2;(2)[2,6]分析:(1)z 1为纯虚数,则其实部为0,虚部不为0,解得参数值;(2)由z 1=z 2,实部、虚部分别相等,求得λ关于θ的函数表达式,根据sinθ的范围求得参数取值范围.(1)由z 1为纯虚数,则{4−m 2=0,m −2≠0,解得m =-2. (2)由z 1=z 2,得{4−m 2=λ+2sinθ,m −2=cosθ−2,∴λ=4-cos 2θ-2sin θ=sin 2θ-2sin θ+3=(sinθ−1)2+2. ∵-1≤sin θ≤1,∴当sin θ=1时,λmin =2,当sin θ=-1时,λmax =6,∴实数λ的取值范围是[2,6].18、已知m ∈R ,α、β是关于x 的方程x 2+2x +m =0的两根.(1)若|α−β|=2√2,求m 的值;(2)用m 表示|α|+|β|.答案:(1)−1或3;(2)|α|+|β|={2√m,m >12,0≤m ≤12√1−m,m <0.分析:(1)由α、β是关于x 的方程x 2+2x +m =0的两根.可得α+β=−2,αβ=m ,对α,β分为实数,与一对共轭虚根即可得出.(2)不妨设α⩽β,对m 及其判别式分类讨论,利用根与系数的关系即可得出.解:(1)∵α、β是关于x 的方程x 2+2x +m =0的两根.∴α+β=−2,αβ=m ,若α,β为实数,即Δ=4−4m ≥0,解得m ≤1时;则2√2=|α−β|=√(α+β)2−4αβ=√4−4m ,解得m =−1.若α,β为一对共轭复数,即Δ=4−4m <0,解得m >1时;则2√2=|α−β|=√(α+β)2−4αβ=|√4m −4i|,解得m =3.综上可得:m =−1或3.(2)因为x2+2x+m=0,不妨设α⩽β.Δ=4−4m⩾0,即m⩽1时,方程有两个实数根.α+β=−2,αβ=m,0⩽m⩽1时,|α|+|β|=|α+β|=2.m<0时,α与β必然一正一负,则|α|+|β|=−α+β=√(α+β)2−4αβ=2√1−m.Δ=4−4m<0,即m>1时,方程有一对共轭虚根.|α|+|β|=2|α|=2√α2=2√m综上可得:|α|+|β|={2√m,m>1 2,0⩽m⩽12√1−m,m<0.。
复变函数复习资料

复变函数复习重点(一)复数的概念1.复数的概念:z x iy =+,,x y 是实数, ()()Re ,Im x z y z ==.21i =-. 注:一般两个复数不比较大小,但其模(为实数)有大小.2.复数的表示1)模:z =2)幅角:在0z ≠时,矢量与x 轴正向的夹角,记为()Arg z (多值函数);主值()arg z 是位于(,]ππ-中的幅角。
3)()arg z 与arctan y x之间的关系如下: 当0,x > arg arctan y z x=;当0,arg arctan 0,0,arg arctan yy z xx y y z x ππ⎧≥=+⎪⎪<⎨⎪<=-⎪⎩; 当x=0 arg=+-二分之拍4)三角表示:()cos sin z z i θθ=+,其中arg z θ=;注:中间一定是“+” 5)指数表示:i z z e θ=,其中arg z θ=。
(二) 复数的运算1.加减法:若111222,z x iy z x iy =+=+,则()()121212z z x x i y y ±=±+±2.乘除法:1)若111222,z x iy z x iy =+=+,则()()1212122112z z x x y y i x y x y =-++;()()()()112211112121221222222222222222x i y x i y z x i y x x y y y x y x i z x i y x i y x i y x y x y+-++-===+++-++。
2)若121122,i i z z e z z e θθ==, 则()121212i z z z z eθθ+=;()121122i z z e z z θθ-= 3.乘幂与方根1)若(cos sin )i z z i z e θθθ=+=,则(cos sin )nnn in z z n i n z e θθθ=+=。
《复数》全章习题

《复数》全章习题 学习目标 1.巩固复数的概念和几何意义.2.理解并能进行复数的四则运算,并认识复数加减法的几何意义.知识点一 复数的四则运算若两个复数z 1=a 1+b 1i ,z 2=a 2+b 2i (a 1,b 1,a 2,b 2∈R ).(1)加法:z 1+z 2=(a 1+a 2)+(b 1+b 2)i ;(2)减法:z 1-z 2=(a 1-a 2)+(b 1-b 2)i ;(3)乘法:z 1·z 2=(a 1a 2-b 1b 2)+(a 1b 2+a 2b 1)i ;(4)除法:z 1z 2=a 1a 2+b 1b 2a 22+b 22+a 2b 1-a 1b 2a 22+b 22i(z 2≠0); (5)实数四则运算的交换律、结合律、分配律都适合于复数的情况;(6)特殊复数的运算:i n (n 为正整数)的周期性运算;(1±i)2=±2i ;若ω=-12±32i ,则ω3=1,1+ω+ω2=0. 知识点二 共轭复数与复数的模(1)若z =a +b i ,则z =a -b i ,z +z 为实数,z -z 为纯虚数(b ≠0).(2)复数z =a +b i 的模,|z |=a 2+b 2,且z ·z =|z |2=a 2+b 2.知识点三 复数加、减法的几何意义(1)复数加法的几何意义若复数z 1、z 2对应的向量OZ 1→、OZ 2→不共线,则复数z 1+z 2是以OZ 1→、OZ 2→为两邻边的平行四边形的对角线OZ →所对应的复数.(2)复数减法的几何意义复数z 1-z 2是连接向量OZ 1→、OZ 2→的终点,并指向Z 1的向量所对应的复数.类型一 复数的四则运算例1 (1)计算:-23+i 1+23i +⎝ ⎛⎭⎪⎫21+i 2 012+(4-8i )2-(-4+8i )211-7i; (2)已知z =1+i ,求z 2-3z +6z +1的模. 解 (1)原式=i (1+23i )1+23i +⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫21+i 2 1 006+(4-8i )2-(4-8i )211-7i=i +(-i)1 006+0=-1+i.(2)z 2-3z +6z +1=(1+i )2-3(1+i )+62+i =3-i 2+i=1-i , ∴z 2-3z +6z +1的模为 2. 反思与感悟 (1)复数的除法运算是复数运算中的难点,如果遇到(a +b i)÷(c +d i)的形式,首先应该写成分式的形式,然后再分母实数化.(2)虚数单位i 的周期性:①i 4n +1=i ,i 4n +2=-1,i 4n +3=-i ,i 4n =1(n ∈N *);②i n +i n +1+i n +2+i n +3=0(n ∈N *). 跟踪训练1 计算:1i (2+2i)5+(11+i )4+(1+i 1-i)7. 解 1i (2+2i)5+(11+i )4+(1+i 1-i)7 =-i·(2)5·[(1+i)2]2·(1+i)+[1(1+i )2]2+i 7 =162(-1+i)-14-i =-(162+14)+(162-1)i. 类型二 复数的几何意义例2 设复数z 满足|z |=1,求|z -(3+4i)|的最值.解 由复数的几何意义,知|z |=1表示复数z 在复平面内对应的点在以原点为圆心,1为半径的圆上,因而|z -(3+4i)|的几何意义是求此圆上的点到点C (3,4)的距离的最大值与最小值. 如图,易知|z -(3+4i)|max =|AC |=|OC |+1=32+42+1=6,|z -(3+4i)|min =|BC |=|OC |-1=4.反思与感悟 复数和复平面内的点,以原点为起点的向量一一对应;复数加减法符合向量运算的平行四边形法则和三角形法则:|z 1-z 2|表示复数z 1,z 2对应的两点Z 1,Z 2之间的距离. 跟踪训练2 已知点集D ={z ||z +1+3i|=1,z ∈C },试求|z |的最小值和最大值. 解 点集D 的图象为以点C (-1, -3)为圆心,1为半径的圆,圆上任一点P 对应的复数为z ,则|OP →|=|z |.由图知,当OP 过圆心C (-1,-3)时,与圆交于点A 、B ,则|z |的最小值|OA |=|OC |-1=(-1)2+(-3)2-1=2-1=1,即|z |min =1;|z |的最大值|OB |=|OC |+1=2+1=3,即|z |max =3.类型三 复数相等 例3 已知复数z 满足z +z ·z =1-2i 4,求复数z . 解 设z =x +y i(x ,y ∈R ),∵z +z ·z =1-2i 4, ∴x +y i +x 2+y 2=1-2i 4, 即⎩⎨⎧ x +x 2+y 2=14,y =-12,解得⎩⎪⎨⎪⎧ x =0,y =-12或⎩⎪⎨⎪⎧x =-1,y =-12.∴z =-12i 或z =-1-12i.反思与感悟 两个复数相等是解决复数问题的重要工具.“复数相等”可以得到两个实数等式,为应用方程提供了条件,常用于确定系数,解复数方程等问题.跟踪训练3 设复数z 满足z 2=3+4i(i 是虚数单位),则|z |=________.答案 5 解析 设z =a +b i ,∴z 2=(a 2-b 2)+2ab i.又∵z 2=3+4i ,∴a 2-b 2=3,2ab =4,解得a 2=4,b 2=1,∴|z |=a 2+b 2= 5.1.复数z =2+a i 1+i(a ∈R )在复平面内对应的点在虚轴上,则a 等于( ) A .2B .-1C .1D .-2答案 D解析 z =2+a i 1+i =(2+a i )(1-i )(1+i )(1-i )=(2+a )+(a -2)i 2在复平面内对应的点(2+a 2,a -22)在虚轴上,所以2+a =0,即a =-2. 2.已知复数z =1+2i 1-i,则1+z +z 2+…+z 2 014为( ) A .1+iB .1-iC .iD .1答案 C3.△ABC 的三个顶点对应的复数分别为z 1,z 2,z 3,若复数z 满足|z -z 1|=|z -z 2|=|z -z 3|,则z 对应的点为△ABC 的( )A .内心B .垂心C .重心D .外心 答案 D 解析 由几何意义知,复数z 对应的点到△ABC 三个顶点距离都相等,z 对应的点是△ABC 的外心.4.若|z -1|=2,则|z -3i -1|的最小值为________.答案 1解析 因为|z -1|=2,所以复数z 在复平面内对应的点在以(1,0)为圆心,2为半径的圆上.|z -3i -1|表示复数z 在复平面内对应的点到点(1,3)的距离,因此,距离的最小值1.5.设复数z 和它的共轭复数z 满足4z +2z =33+i ,求复数z .解 设z =a +b i(a ,b ∈R ).因为4z +2z =33+i , 所以2z +(2z +2z )=33+i.2z +2z =2(a +b i)+2(a -b i)=4a ,整体代入上式,得2z +4a =33+i.所以z =33-4a 2+i 2. 根据复数相等的充要条件,得⎩⎨⎧ a =33-4a 2,b =12,解得⎩⎨⎧ a =32,b =12,所以z =32+i 2.1.复数的四则运算按照运算法则和运算律进行运算,其中除法运算的关键是将分母实数化.2.复数的几何意义是数形结合思想在复数中的一大体现.3.利用两个复数相等可以解决求参数值(或取值范围)和复数方程等问题. 课时作业 一、选择题1.复数z 对应的点在第二象限,它的模为3,实部是-5,则z 是( )A .-5+2iB .-5-2i C.5+2iD.5-2i答案 B解析 设复数z 的虚部为b ,则z =-5+b i ,b >0,∵3=5+b 2,∴b =2,∴z =-5+2i ,则z 的共轭复数是-5-2i ,故选B.2.复数1-2+i +11-2i的虚部是( ) A.15i B.15 C .-15i D .-15答案 B解析 1-2+i +11-2i=-2-i 5+1+2i 5=-15+15i.故选B. 3.若z =1+2i ,则4i z z -1等于( ) A .1B .-1C .iD .-i 答案 C解析 z =1+2i ,则4i z z -1=4i (1+2i )(1-2i )-1=4i 5-1=i. 4.若复数z =cosπ12+isin π12(i 是虚数单位),复数z 2的实部,虚部分别为a ,b ,则下列结论正确的是( )A .ab <0B .a 2+b 2≠1 C.a b = 3 D.b a = 3 答案 C解析 ∵z =cosπ12+isin π12, ∴z 2=(cos π12+isin π12)2 =cos 2π12-sin 2π12+2cos π12sin π12i =cos π6+isin π6=32+12i , 则a =32,b =12,则a b=3,故选C. 5.向量OZ 1→对应的复数是5-4i ,向量OZ 2→对应的复数是-5+4i ,则向量Z 1Z 2—→对应的复数是( )A .-10+8iB .10-8iC .-8+10iD .8+(-10i)答案 A解析 向量OZ 1→对应的复数是5-4i ,可得Z 1(5,-4);向量OZ 2→对应的复数是-5+4i ,可得Z 2(-5,4);向量Z 1Z 2—→对应的点是(-10,8),即向量Z 1Z 2—→对应的复数是-10+8i.故选A.6.已知复数z 的模为2,则|z -i|的最大值为( )A .1B .2 C. 5 D .3 答案 D 解析 ∵|z |=2,则复数z 对应的轨迹是以圆心为原点,半径为2的圆,而|z -i|表示的是圆上一点到点(0,1)的距离,∴其最大值为圆上的点(0,-2)到点(0,1)的距离,最大的距离为3.二、填空题7.i 是虚数单位,复数z 满足(1+i)z =2,则z 的实部为________.答案 1解析 因为(1+i)z =2,所以z =21+i =1-i ,所以其实部为1. 8.如果z 1=-2-3i ,z 2=3-2i (2+i )2,则z 1z 2=________. 答案 4-3i解析 ∵z 1=-2-3i ,z 2=3-2i (2+i )2, ∴z 1z 2=(-2-3i )(2+i )23-2i =-i (3-2i )(2+i )23-2i=-i(2+i)2=-(3+4i)i =4-3i.9.若复数1+i 1-i+b (b ∈R )所对应的点在直线x +y =1上,则b 的值为________. 答案 0解析 复数1+i 1-i +b =(1+i )2(1-i )(1+i )+b =2i 2+b =b +i. ∵所对应的点(b,1)在直线x +y =1上,∴b +1=1,解得b =0.10.如图,在复平面内,点A 对应的复数为z 1,若z 2z 1=i(i 为虚数单位),则z 2=________.答案 -2-i解析 由图可知,z 1=-1+2i ,∴由z 2z 1=i ,得z 2=z 1i =(-1+2i)i =-2-i. 三、解答题11.已知复数z 1=(1+b i)(2+i),z 2=3+(1-a )i (a ,b ∈R ,i 为虚数单位).(1)若z 1=z 2,求实数a ,b 的值;(2)若b =1,a =0,求|z 1+z 21-2i|. 解 (1)复数z 1=(1+b i)(2+i)=2-b +(2b +1)i ,z 2=3+(1-a )i ,由z 1=z 2,可得⎩⎪⎨⎪⎧ 2-b =3,2b +1=1-a ,解得⎩⎪⎨⎪⎧a =2,b =-1, 所以实数a =2,b =-1.(2)若b =1,a =0,则z 1=1+3i ,z 2=3+i.|z 1+z21-2i |=|1+3i +3-i||1-2i|=42+221+(-2)2=2. 12.已知复数z 1满足z 1(1-i)=2(i 为虚数单位),若复数z 2满足z 1+z 2是纯虚数,z 1·z 2是实数,求复数z 2.解 ∵z 1(1-i)=2,∴z 1=21-i =2(1+i )(1-i )(1+i )=2(1+i )2=1+i. 设z 2=a +b i(a ,b ∈R ),∵z 1+z 2=1+a +(b +1)i 是纯虚数,∴⎩⎪⎨⎪⎧1+a =0,1+b ≠0, ∴a =-1,b ≠-1. ∴z 1·z 2=(1+i)(-1+b i)=(-1-b )+(b -1)i ,又z 1·z 2是实数,则b -1=0,∴b =1,∴z 2=-1+i.13.求虚数z ,使z +9z∈R ,且|z -3|=3. 解 设z =a +b i(a ,b ∈R 且b ≠0),则z +9z =a +b i +9a +b i =(a +9a a 2+b 2)+(b -9b a 2+b2)i. 由z +9z ∈R ,得b -9b a 2+b 2=0, 又b ≠0,故a 2+b 2=9.① 又由|z -3|=3,得(a -3)2+b 2=3.②由①②,得⎩⎨⎧a =32,b =±332,即z =32+332i 或z =32-332i. 四、探究与拓展14.若a 是复数z 1=(1-i)(3+i)的虚部,b 是复数z 2=1+i 2-i 的实部,则ab =________. 答案 -25解析 z 1=(1-i)(3+i)=4-2i ,由a 是复数z 1=(1-i)(3+i)的虚部,得a =-2.z 2=1+i 2-i =(1+i )(2+i )(2-i )(2+i )=1+3i 5=15+35i , 由b 是复数z 2=1+i 2-i的实部,得b =15. 则ab =-2×15=-25. 15.在复平面内A ,B ,C 三点对应的复数分别为1,2+i ,-1+2i. (1)求AB →,BC →,AC →对应的复数;(2)判断△ABC 的形状;(3)求△ABC 的面积.解 (1)AB →对应的复数为z B -z A =(2+i)-1=1+i ,BC →对应的复数为z C -z B =(-1+2i)-(2+i)=-3+i , AC →对应的复数为z C -z A =(-1+2i)-1=-2+2i.(2)由(1)知|AB →|=|1+i|=2,|BC →|=|-3+i|=10,|AC →|=|-2+2i|=22,∴|AB →|2+|AC →|2=|BC →|2.故△ABC 为直角三角形.(3)S △ABC =12|AB →|·|AC →|=12×2×22=2.。
《复变函数》复习大纲及例题

《复变函数》复习大纲及例题1.复数的简单加减乘除运算、共轭复数、模2.复数的三角表示式、指数表示式例:1-=;例:23i +=.3.复数的对数或乘幂运算例:对数()1Ln -+的主值为;i i 的主值为.4.幂级数的收敛半径例:幂级数n n ∞=的收敛半径为3.5.复数的幂或方根运算例5-1:求()131i -的值.解:例5-2:求)55i 的值.解:)56556322ieie ππ--⎛⎫= ⎪ ⎪⎝⎭=.6—9.灵活运用柯西-古萨基本定理、复合闭路定理、柯西积分公式、高阶求导公式、留数定理、留数的规则I、II、III求积分6.柯西-古萨基本定理例6-1沿指定曲线的正向计算积分:2cos ,:1Czzdz C z =⎰ .解:()2cos f z z z =在复平面内处处解析,由柯西—古萨基本定理可知2cos 0Cz zdz =⎰ .56552cos sin266i i e πππ⎛⎫+= ⎪⎝⎭3arctan 233cos arctan sin arctan 22i i e⎤⎛⎫⎛⎫+= ⎪ ⎪⎥⎝⎭⎝⎭⎣⎦ 5ln 26i π+2eπ-()11136432244cos sin ,0,1,2.3312k k i k i e πππππ-⎡⎤-+-+⎫⎢⎥+=⎪⎢⎥⎪⎭⎢⎥⎣⎦-==7.柯西积分公式(或留数定理、规则)例7-1沿指定曲线的正向计算积分:12,:322C dz C z z z i ⎛⎫+= ⎪+-⎝⎭⎰ .解:1211222262222C C Cdz dz dz i i i z z i z z i πππ⎛⎫+=+=+⋅=⎪+-+-⎝⎭⎰⎰⎰ 例7-2沿指定曲线的正向计算积分:,:212zCe dz C z z -=-⎰.解:法1(柯西积分公式)()22222zz z Ce dz i e e iz ππ==⋅=-⎰法2(留数定理)2z =是函数()2ze f z z =-的一级极点,则()()22Re ,2lim 22z z e s f z z e z →=-=⎡⎤⎣⎦-,由留数定理得()22Re ,222z Ce dz i sf z e i z ππ=⋅=⎡⎤⎣⎦-⎰.8.高阶导数公式(或留数定理、规则)例8-1沿指定曲线的正向计算积分:5,:1zCe dz C z z =⎰ .解:法1(高阶导数公式)()()4050224!4!12z z z C e i i idz e e z πππ=⎡⎤=⋅=⋅=⎢⎥⎣⎦⎰ .法2(留数定理)0z =是函数()5ze f z z =的五级极点,则()()455011Re ,0lim 4!24z z e s f z z z →⎛⎫=⋅=⎡⎤ ⎪⎣⎦⎝⎭,由留数定理得()52Re ,012z Ce i dz i sf z z ππ==⎡⎤⎣⎦⎰ .例8-2沿指定曲线的正向计算积分:()3sin ,:21Czdz C z z =-⎰ .解:法1(高阶导数公式)()()()231sin 2sin sin12!1z Czi dz z i z ππ=⎡⎤=⋅=-⎣⎦-⎰法2(留数定理)1z =是函数()()3sin 1zf z z =-的三级极点,则()()()()23311sin 1Re ,1lim 12!21z z s f z z z →⎛⎫=-⋅=-⎡⎤ ⎪⎣⎦ ⎪-⎝⎭,由留数定理得()()3sin 2Re ,1sin11Czdz i s f z i z ππ==-⎡⎤⎣⎦-⎰ .9.复合闭路定理联合柯西积分公式(或留数定理、规则)例9-1沿指定曲线的正向计算积分:21,:32Cz dz C z z z+=-⎰.解:法1()()21121010111222Cz z z z z dz dz dzz zz z z z =-=+++=+---⎰⎰⎰()1102210101121122222z z z z z z z z z z dz dz i i i zz z z πππ===-=++-++⎡⎤⎡⎤=+=⋅+⋅=⎢⎢--⎣⎦⎣⎦⎰⎰.法2(留数定理)()()21122z z f z z z z z ++==--,0z =,2z =均为函数()f z 的一级极点,则()()011Re ,0lim 22z z s f z z z z →+=⋅=-⎡⎤⎣⎦-,()()()213Re ,2lim 222z z s f z z z z →+=-⋅=⎡⎤⎣⎦-,由留数定理得()()212Re ,02Re ,222Cz dz i s f z i s f z i z zπππ+=+=⎡⎤⎡⎤⎣⎦⎣⎦-⎰.例9-2沿指定曲线的正向计算积分:2,:21zCe dz C z z =-⎰.解:()()()()21111101011111zzzCz z e e e dz dz z z z z z +=-==+-+-+-⎰⎰⎰1111111101011221111zzz zz z z z e e e e z z dz dz i i ie ie z z z z ππππ-=-=+=-=⎡⎤⎡⎤-+=+=⋅+⋅=-⎢⎥⎢⎥+--+⎣⎦⎣⎦⎰⎰.(留数定理同样可解)10.参数法求函数积分例10-1计算积分()2Cx iy dz +⎰,其中C 为直线y x =上原点到1i +的直线段.解:设z x iy =+,则积分曲线的参数方程为()01x z x ix ≤≤=+,所以()()()()()()()1211000132211212222Cx x iy dz x ix i dx i i xdx i i i ⎛⎫+=++=++=++=+ ⎪⎝⎭⎰⎰⎰例10-2计算积分Czdz ⎰,其中C 点i 到3i +的直线段.解:设z x iy =+,且点i 到3i +所在水平直线参数方程为()03x z x i ≤≤=+,则()()323009322C Cx zdz x i dz x i dx ix i ⎛⎫=-=-=-= ⎪⎝⎭⎰⎰⎰.11.原函数与不定积分例11-1计算积分:32iz ie dz ππ-⎰.解:()()333222112022ii iz z z i ii e dz e d z e ππππππ---===⎰⎰例11-2计算积分:1sin z zdz ⎰.解:()11110000sin cos cos cos sin1cos1z zdz zd z z z zdz ⎡⎤=-=--=-⎢⎥⎣⎦⎰⎰⎰.12.函数可导、解析的充要条件例12-1函数()2iy f x x -=何处可导,何处解析.解:由题得()()2,,,x y x v x y y u ==-,则2,1,0,0xyyxx uvuv∂∂∂∂==-==∂∂∂∂,故当且仅当21x =-时柯西黎曼方程,xy yxuv uv∂∂∂∂==-∂∂∂∂,解得21x -=,所以函数()f x 在直线21x -=上可导,但处处不解析.13.将函数展开成洛朗级数例13-1将函数()13f z z=-在圆环域01z <<内展开成洛朗级数.解:()1113313f z z z ==⋅--,101,0133z z <<∴<<< ,由间接法展开得()100111333313nn n n n z z f z z ∞∞+==⎛⎫ ⎪⎝⎭=⋅==-∑∑.14.复数运算公式证明例13-1证明1212z z z z ⋅=⋅.证:设111222,z x iy z x iy =+=+,则()()()()12121212121122z z x x y y i x y y x x iy x iy ⋅=-++++=,()()1212121212z z x x y y i x y y x ∴⋅--+=.又()()()()11221212121212x iy x iy x x y y i x y y x z z --==--+⋅ ,1212z z z z ∴⋅=⋅,等式得证.。
复变函数与积分变换复习提纲以及5套题

标准实用复变函数复习提纲(一)复数的概念1.复数的概念:z x iy =+,,x y 是实数,()()Re ,Im x z y z ==.21i =-. 注:两个复数不能比较大小. 2.复数的表示1)模:z =2)幅角:在0z ≠时,矢量与x 轴正向的夹角,记为()Arg z (多值函数);主值()arg z 是位于(,]ππ-中的幅角。
3)()arg z 与arctanyx之间的关系如下: 当0,x > arg arctan yz x=;当0,arg arctan 0,0,arg arctan yy z xx y y z xππ⎧≥=+⎪⎪<⎨⎪<=-⎪⎩; 4)三角表示:()cos sin z z i θθ=+,其中arg z θ=;注:中间一定是“+”号。
5)指数表示:i z z e θ=,其中arg z θ=。
(二) 复数的运算1.加减法:若111222,z x iy z x iy =+=+,则()()121212z z x x i y y ±=±+± 2.乘除法:1)若111222,z x iy z x iy =+=+,则()()1212122112z z x x y y i x y x y =-++;()()()()11221111212122222222222222222x iy x iy z x iy x x y y y x y i z x iy x iy x iy x y x y +-++-===+++-++。
2)若121122,i i z z e z z e θθ==, 则()121212i z z z z e θθ+=;()121122i z z e z z θθ-= 3.乘幂与方根1) 若(cos sin )i z z i z e θθθ=+=,则(c o s s i n )nnn in z z n in z e θθθ=+=。
高中数学《复数》基础知识及经典练习题(含答案解析)

高中数学《复数》基础知识及经典练习题(含答案解析)一、基础知识:复数题目通常在高考中有所涉及,题目不难,通常是复数的四则运算1、复数z 的代数形式为(),z a bi a b R =+∈,其中a 称为z 的实部,b 称为z 的虚部(而不是bi ),2、几类特殊的复数:(1)纯虚数:0,0a b =≠ 例如:5i ,i 等(2)实数: 0b =3、复数的运算:设()12,,,,z a bi z c di a b c d R =+=+∈(1)21i =−(2)()()12z z a c b d i ±=+++(3)()()()()212z z a bi c di ac adi bci bdi ac bd ad bc i ⋅=+⋅+=+++=−++ 注:乘法运算可以把i 理解为字母,进行分配率的运算。
只是结果一方面要化成标准形式,另一方面要计算21i =−(4)()()()()()()1222a bi c di ac bd bc ad i z a bi z c di c di c di c d +−++−+===++−+ 注:除法不要死记公式而要理解方法:由于复数的标准形式是(),z a bi a b R =+∈,所以不允许分母带有i ,那么利用平方差公式及21i =的特点分子分母同时乘以2z 的共轭复数即可。
4、共轭复数:z a bi =−, 对于z 而言,实部相同,虚部相反5、复数的模:z = 2z z z =⋅ (22z z ≠) 6、两个复数相等:实部虚部对应相等7、复平面:我们知道实数与数轴上的点一一对应,推广到复数,每一个复数(),a bi a b R +∈都与平面直角坐标系上的点(),a b 一一对应,将这个平面称为复平面。
横坐标代表复数的实部,横轴称为实轴,纵轴称为虚轴。
8、处理复数要注意的几点:(1)在处理复数问题时,一定要先把复数化简为标准形式,即(),z a bi a b R =+∈(2)在实数集的一些多项式公式及展开在复数中也同样适用。
(完整版)高三复数总复习知识点、经典例题、习题

复数.基本知识【1】复数的基本概念(1) 形如a + bi 的数叫做复数(其中a ,b R );复数的单位为i ,它的平 方等于一1,即i 21.其中a 叫做复数的实部,b 叫做虚部纯虚数:当a = 0且b(2) 两个复数相等的定义:0时的复数a+ b i 为纯虚数a bi c di a c 且b d (其中,a , b ,c ,d , R )特别地 a bi 0 a b 0(3) 共轭复数:z a bi 的共轭记作z a bi ; (4)复平面:建立直角坐标系来表示复数的平面叫复平面;z a bi ,对应点坐标为p a,b ;(象限的复习)实数:当b = 0时复数 a + bi 为实数 虚数:当b 0时的复数a + bi 为虚数;设z 1 a 1bj ,Z 2a 2b 2i(1) 加法: Z 1 Z 2 a 1 a 2 b 1b 2 i ;(2) 减法: Z 1 Z 2 a 1 a 2th b 2 i ;(3) 乘法: Z 1 : Z 2 a ia2t 1b 2a2^ a 1b 2i特别 z z a 2 b 2。
(4) 幕运算:・1i i i 231 i4i i1 i.5 6i i1【3】 复数的化简c zadi( abi ,b 是均不为 0的实数) ;的化简就是通过分母实数化的方法将分母 化为实数:zc di c di a biac bdad bc i a bi a bi a bi2 ab 2对于:c di z a bi-a b 0, 当cab 时z :为实数; 当z 为纯虚数是z 可设为复数的基本运算【2】(5)复数的模:对于复数z bi ,\ a 2 b 2 叫做复数z 的模;二. 例题分析【例11已知z a 1 b 4 i ,求(1) 当a,b 为何值时z 为实数 (2) 当a,b 为何值时z 为纯虚数 (3) 当a,b 为何值时z 为虚数(4)当a,b 满足什么条件时z 对应的点在复平面内的第二象限A. 1 B . 0 C 1 D2 2【变式21求实数m 的值,使复数(m 2m 3) (m 3m 4)i 分别是:(1)实数。
(完整版)高三复数总复习知识点、经典例题、习题

复数一.基本知识【1】复数的基本概念(1)形如a + b i 的数叫做复数(其中R b a ∈,);复数的单位为i ,它的平方等于-1,即1i 2-=.其中a 叫做复数的实部,b 叫做虚部实数:当b = 0时复数a + b i 为实数虚数:当0≠b 时的复数a + b i 为虚数;纯虚数:当a = 0且0≠b 时的复数a + b i 为纯虚数(2)两个复数相等的定义:00==⇔=+∈==⇔+=+b a bi a R d c b a d b c a di c bi a )特别地,,,,(其中,且(3)共轭复数:z a bi =+的共轭记作z a bi =-;(4)复平面:建立直角坐标系来表示复数的平面叫复平面;z a bi =+,对应点坐标为(),p a b ;(象限的复习)(5)复数的模:对于复数z a bi =+,把z =叫做复数z 的模;【2】复数的基本运算设111z a b i =+,222z a b i =+(1) 加法:()()121212z z a a b b i +=+++;(2) 减法:()()121212z z a a b b i -=-+-;(3) 乘法:()()1212122112z z a a b b a b a b i ⋅=-++ 特别22z z a b ⋅=+。
(4)幂运算:1i i =21i =-3i i =-41i =5i i =61i =-⋅⋅⋅⋅⋅⋅【3】复数的化简c di z a bi+=+(,a b 是均不为0的实数);的化简就是通过分母实数化的方法将分母化为实数:()()22ac bd ad bc i c di c di a bi z a bi a bi a bi a b ++-++-==⋅=++-+ 对于()0c di z a b a bi +=⋅≠+,当c d a b=时z 为实数;当z 为纯虚数是z 可设为c di z xi a bi+==+进一步建立方程求解二. 例题分析【例1】已知()14z a b i =++-,求(1) 当,a b 为何值时z 为实数(2) 当,a b 为何值时z 为纯虚数(3) 当,a b 为何值时z 为虚数(4) 当,a b 满足什么条件时z 对应的点在复平面内的第二象限。
复数的加、减运算及其几何意义

我们规定,复数的加法法则如下: 设z1=a+bi,z2=c+di(a,b,c,d RR )是两个任意复数, 那么它们的和
(a+bi)+(c+di)=(a+c)+(b+d)i
说明:(1)复数的加法运算法则是一种规定.当b=0,d=0时, 与实数加法法则保持一致;
(2)两个复数的和仍然是一个复数,对于复数的加法 可以推广到多个复数相加的情形.
知识一:复数的加法
探究:
设z1=a+bi,z2=c+di(a,b,c,d RR)是两个任意复数, 由于希望加法结合律成立,
z1+z2=(a+bi)+(c+di)=(a+c)+(bi+di)
由于希望乘法分配律成立,
z1+z2=(a+c)+(bi+di)=(a+c)+(b+d)i
这样就猜想出了复数的加法法则.
说明:(3)复数的加法法则:
(a+bi)+(c+di)=(a+c)+(b+d)i 如果将i 看作“变元”,a+bi中的实部和虚部 a,b看作常数,我们就可以将复数看成是 “一次二项式”,很容易发现两个复数相加与 两个一次二项式相加(合并同类项)一致. 这样,得到两个复数相加与两个多项式相加 相类似.
例题2
y
解:复平面内的点Z1(x1,y1),Z2(x2,y2) 对应的复数分别为z1=x1+y1i,z2=x2+y2i, 所以点Z1,Z2之间的距离为
Z2(x2,y2)
z2
z2-z1
Z1(x1,y1)
高考文科复数复习知识点+例题+练习

复数的概念及运算一. 知识回顾1. 复数的有关概念形如______________的数叫做复数,其中i 叫做虚数单位,满足_________,a 叫做_________,b 叫做________,复数集记作_______________________。
2. 复数的分类复数),(R b a bi a ∈+是实数的充要条件是_________;是纯虚数的充要条件是__________.3. 复数相等两个复数)(2,1R d c b a di c z bi a z ∈+=+=、、、,若21z z =,则____________。
4. 共轭复数如果两个复数实部________,而虚部___________,则这两个复数互为_____________,即复数bi a z +=的共轭复数为z =_________。
5. 复数的几何意义(1)建立了直角坐标系来表示复数的平面叫做复平面,在复平面内,x 轴叫做 ,y 轴叫做 ,x 轴的单位是1,y 轴的单位是i.显然,实轴上的点都表示 ;除原点以外,虚轴上的点都表示 。
(2)复数z =a +b i 、有序实数对(a ,b )、点Z (a ,b )是一一对应的.(3)设OZ →=a +b i ,则向量OZ →的长度叫做复数a +b i 的 (或 ),记作|a +b i|,且|a +b i|= .(4)复数的加法可以按照向量的加法来进行,这就是复数加法的几何意义.6. 复数的代数运算对于i 有i 4n =______,i 4n +1=_____,i 4n +2=_____,i 4n +3=_____(n∈Z).已知两个复数z1=a +bi ,z2=c +di(a 、b 、c 、d∈R),则z1±z2=______________,z1·z2=_______________ ,z1z2=a +bic +di =________________.特别地,若z =a +bi ,则z·z =a 2+b 2.二. 例题讲解已知复数z =a 2-7a +6a 2-1+(a 2-5a -6)i(a ∈R).求实数a 分别取什么值时,z 分别为:(1)实数;(2)虚数;(3)纯虚数.【解答】 (1)当z 为实数时,则⎩⎪⎨⎪⎧ a 2-5a -6=0,a 2-1≠0,∴⎩⎪⎨⎪⎧ a =-1或a =6,a ≠±1.故当a =6时,z 为实数.(2)当z 为虚数时,则有⎩⎪⎨⎪⎧ a 2-5a -6≠0,a 2-1≠0,∴⎩⎪⎨⎪⎧a ≠-1且a ≠6,a ≠±1,∴a ≠±1且a≠6.∴当a ∈(-∞,-1)∪(-1,1)∪(1,6)∪(6,+∞)时,z 为虚数.(3)当z 为纯虚数时,则有⎩⎪⎨⎪⎧ a2-5a -6≠0,a 2-7a +6a 2-1=0. ∴⎩⎪⎨⎪⎧a ≠-1且a ≠6,a =6且a ≠±1. ∴不存在实数a 使z 为纯虚数.若复数z =(x 2-1)+(x -1)i 为纯虚数,则实数x 的值为( )A.-1 B .0 C .1 D .-1或1计算:(1)2-i 31-2i ; (2)-23+i 1+23i +⎝ ⎛⎭⎪⎪⎫21-i 2011. 【解答】 (1)2-i 31-2i =2+i 1-2i =(2+i)(1+2i)(1-2i)(1+2i)=2i +i1+2=i.(2)-23+i 1+23i +⎝ ⎛⎭⎪⎪⎫21-i 2011=i(1+23i)1+23i +⎣⎢⎢⎡⎦⎥⎥⎤⎝ ⎛⎭⎪⎪⎫21-i 21005·21-i=i +⎝ ⎛⎭⎪⎪⎫2-2i 1005·21-i =i +i 1005·21-i=i +i·21-i =-22+⎝ ⎛⎭⎪⎪⎫22+1i.i 是虚数单位,若1+7i2-i =a +b i(a ,b ∈R),则乘积ab 的值是()A .-15B .-3C .3D .15复数综合练习题一.选择题1.湖南 复数21i=- ( ) A1+i B 1-i C-1+i D-1-i2.全国23()1i i-=+ ( ) A -3-4i B-3+4i C3-4i D3+4i3.陕西 复数Z= 1i i+在复平面内对应的点在 ( ) A 第一象限 B 第二象限 C 第三象限 D 第四象限4.辽宁 设a,b,c R ∈若121i i a bi+=++则 ( ) A a= 32 b= 12 B a=3 b=1 C a=12 b=32 D a=1 b=3 5.江西 已知)()(1,x i i y x y +-=则分别为 ( )A x=-1 y=1B x=-1 y=2C x=1 y=1D x=1 y=26.安徽 ()21i i =-=已知则 ( )A i =B i =C i =D i =7.浙江 已知i 为虚数单位则51i i-=+ ( ) 23A i -- B 23i -+ C 23i - D 23i +8.山东 已知2a i b i i+=+ ,a,b R ∈ 则a+b= ( ) A-1 B1 C2 D39.北京在复平面内,复数6+5i 与 -2+3i 对应的点分别为A , B.若C 为AB 的中点,则点C 对应的复数为 ( )A 4+8iB 8+2iC 2+4iD 4+i10.四川,设i 是虚数单位,计算23i i i ++= ( )A-1 B1 C-i Di11.天津,复数31i i+=- ( ) A1+2i B2+4i C-1-4i D2-i12.复数a+bi 与c+di 的积是实数的充要条件是 ( )A ad+bc=0B ac+bd=0C ac=bdD ad=bc13.当213m ﹤﹤时,复数m(3+i)-(2+i)在复平面内对应的点位于() A 第一象限 B 第二象限 C 第三象限 D 第四象限二.计算题1.一直复数Z 与)(228Z i +-都是纯虚数,求Z2.已知i 是虚数单位21mim R i -∈+且是纯虚数,求20112()2mi mi -+3. 设为共轭复数,且 ,求的值。
高中数学知识复习总结(复数)

复数知识复习总结1.虚数单位i 的性质(1)它的平方等于-1,即 21i =-; (2)实数可以与它进行四则运算,进行四则运算时,原有加、乘运算律仍然成立;(2)i 与-1的关系: i 就是-1的一个平方根,即方程x 2=-1的一个根,方程x 2=-1的另一个根是-i ;(3)i 的周期性:i 4n+1=i, i 4n+2=-1, i 4n+3=-i, 4n =1。
2.复数的定义与表示:(1)形如(,)a bi a b R +∈的数叫复数, a 叫复数的实部,b 叫复数的虚部全体复数所成的集合叫做复数集,用字母C 表示*(2)复数的代数形式: 复数通常用字母z 表示,即(,)z a bi a b R =+∈,把复数表示成a +bi 的形式,叫做复数的代数形式。
3 复数与实数、虚数、纯虚数及0的关系:对于复数(,)a bi a b R +∈,当且仅当b =0时,复数a +bi (a 、b ∈R )是实数a ;当b ≠0时,复数z =a +bi 叫做虚数;当a =0且b ≠0时,z =bi 叫做纯虚数;当且仅当a =b =0时,z 就是实数0 4.复数集与其它数集之间的关系:N Z Q R C[题目3]如果复数2(i)(1i)m m ++是实数,则实数m =____________[题目4]如果复数ibi212+-的实部与虚部互为相反数,那么实数b 等于________ [题目1] 23212123n n n n ii i i --+++++(n Z ∈)的值等于_______________[题目2] 计算2341234()n n i i i i n i --+-++-(*n N ∈)的值。
5.两个复数相等的定义:如果两个复数的实部和虚部分别相等,那么我们就说这两个复数相等即:如果a ,b ,c ,d ∈R ,那么a +bi =c +di ⇔a =c ,b =d 。
这是解决复数问题时进行虚实转化的工具:一般地,两个复数只能说相等或不相等,而不能比较大小如果两个复数都是实数,就可以比较大小, 也只有当两个复数全是实数时才能比较大小。
复变函数总复习

2
3
x
2π π arg z = , arg z = 3 3 在圆环内的点不是内点. 在圆环内的点不是内点.
o
2
3
x
例 函数 w = 1 z将 z平面上的下列曲线变成 w 平 面上的什么曲线? 面上的什么曲线?
(1) x2 + y2 = 9, (2) x = 2. 2 2 2 解 (1) 因为 x + y = z = 9
c c
复积分的性质 1、 ∫ f (z)dz = ∫ f (z)dz c c
2、 3、
∫ kf (z)dz = k∫
c c
c
f (z)dz f (z)dz ± ∫ g(z)dz
c
∫ [ f (z) ± g(z)]dz = ∫
c
4、 ∫c f (z)dz ≤ ∫c f (z) ds ≤ ML 曲线C的长度为L,函数在C上满足 f (z) ≤ M
(3)Ln(3) = ln 3 + iArg(3)
= ln3 + (2k + 1)πi.
(k = 0, ± 1, ± 2,L )
例 解
. 求1 2 和i i 的值
1 2 =e
2Ln1
= e2kπi
2
= cos(2 2kπ) + i sin(2 2kπ) 其中k = 0,±1,±2,L.
i =e
i
= ln 2 + 3i + iArg(2 + 3i)
1 3 = ln13 + i π arctan + 2kπ. 2 2
(k = 0, ± 1, ± 2,L )
(2)Ln(3 3i)
= ln 3 3i + iArg(3 3i)
