最优化方法练习题答案修改建议版本--删减版
最优化方法习题答案

最优化方法习题答案最优化方法习题答案最优化方法是数学中一门重要的学科,它研究如何找到使函数取得最大值或最小值的方法。
在实际问题中,最优化方法被广泛应用于经济学、工程学、管理学等领域。
本文将为读者提供一些最优化方法习题的答案,希望能够帮助读者更好地理解和应用这一学科。
一、单变量函数的最优化问题1. 求函数f(x) = x^2 - 2x + 1在区间[0, 3]上的最小值。
解:首先,我们需要找到函数f(x)的驻点。
计算f'(x) = 2x - 2,并令其等于零,得到x = 1。
然后,我们计算f''(x) = 2,发现在x = 1处,f''(x)大于零,说明该点是函数的极小值点。
接下来,我们需要检查区间的端点和驻点,找到函数f(x)在这些点的函数值。
f(0) = 1,f(1) = 0,f(3) = 4。
由于f(1)是最小的函数值,因此函数f(x)在区间[0, 3]上的最小值为0。
2. 求函数f(x) = e^x - 2x在整个实数轴上的最小值。
解:首先,我们计算f'(x) = e^x - 2,并令其等于零,得到x = ln(2)。
然后,我们计算f''(x) = e^x,发现在x = ln(2)处,f''(x)大于零,说明该点是函数的极小值点。
接下来,我们需要检查整个实数轴上的函数值。
由于函数f(x)在x趋近负无穷大时趋于负无穷大,而在x趋近正无穷大时趋于正无穷大,因此函数f(x)在整个实数轴上没有最小值。
二、多变量函数的最优化问题1. 求函数f(x, y) = x^2 + y^2 - 2x - 4y在闭区域D={(x, y)|0≤x≤2, 0≤y≤3}上的最小值。
解:首先,我们需要找到函数f(x, y)的驻点。
计算f_x(x, y) = 2x - 2和f_y(x, y) = 2y - 4,并令它们同时等于零,得到x = 1和y = 2。
最优化方法(试题+答案)

1.若 ,则 , .
2.设 连续可微且 ,若向量 满足,则它是 在 处的一个下降方向。
3.向量 关于3阶单位方阵的所有线性无关的共轭向量有.
4.设 二次可微,则 在 处的牛顿方向为.
5.举出一个具有二次终止性的无约束二次规划算法:.
6.以下约束优化问题:
的K-K-T条件为:
.
7.以下约束优化.证明:要证凸规划,即要证明目标函数是凸函数且可行域是凸集。
一方面,由于 二次连续可微, 正定,根据凸函数等价条件可知目标函数是凸函数。
另一方面,约束条件均为线性函数,若任意 可行域,则
故 ,从而可行域是凸集。
2.证明:要证 是 在 处的一个可行方向,即证当 , 时, ,使得 ,
解此线性规划(作图法)得 ,于是 .由线性搜索
得 .因此, .重复以上计算过程得下表:
0
1
1
2
(注:范文素材和资料部分来自网络,供参考。请预览后才下载,期待你的好评与关注。)
2.采用精确搜索的BFGS算法求解下面的无约束问题:
3.用有效集法求解下面的二次规划问题:
4.用可行方向算法(Zoutendijk算法或Frank Wolfe算法)求解下面的问题(初值设为 ,计算到 即可):
参考答案
一、填空题
1. 2. 3. , (答案不唯一)。4.
5. 牛顿法、修正牛顿法等(写出一个即可)
0
1/2
1
2
2
3.解:取初始可行点 求解等式约束子问题
得解和相应的Lagrange乘子
转入第二次迭代。求解等式约束子问题
得解
令
转入第三次迭代。求解等式约束子问题
得解和相应的Lagrange乘子
最优化设计 课后习题答案

最优化方法-习题解答张彦斌计算机学院2014年10月20日Contents1第一章最优化理论基础-P13习题1(1)、2(3)(4)、3、412第二章线搜索算法-P27习题2、4、643第三章最速下降法和牛顿法P41习题1,2,374第四章共轭梯度法P51习题1,3,6(1)105第五章拟牛顿法P73-2126第六章信赖域方法P86-8147第七章非线性最小二乘问题P98-1,2,6188第八章最优性条件P112-1,2,5,6239第九章罚函数法P132,1-(1)、2-(1)、3-(3),62610第十一章二次规划习题11P178-1(1),5291第一章最优化理论基础-P13习题1(1)、2(3)(4)、3、4 1.验证下列各集合是凸集:(1)S={(x1,x2)|2x1+x2≥1,x1−2x2≥1};需要验证:根据凸集的定义,对任意的x(x1,x2),y(y1,y2)∈S及任意的实数λ∈[0,1],都有λx+(1−λ)y∈S.即,(λx1+(1−λ)y1,λx2+(1−λ)y2)∈S证:由x(x1,x2),y(y1,y2)∈S得到,{2x1+x2≥1,x1−2x2≥12y1+y2≥1,y1−2y2≥1(1)1把(1)中的两个式子对应的左右两部分分别乘以λ和1−λ,然后再相加,即得λ(2x1+x2)+(1−λ)(2y1+y2)≥1,λ(x1−2x2)+(1−λ)(y1−2y2)≥1(2)合并同类项,2(λx1+(1−λ)y1)+(λx2+(1−λ)y2)≥1,(λx1+(1−λ)y1)−2(λx2+(1−λ)y2)≥1(3)证毕.2.判断下列函数为凸(凹)函数或严格凸(凹)函数:(3)f(x)=x21−2x1x2+x22+2x1+3x2首先二阶导数连续可微,根据定理1.5,f在凸集上是(I)凸函数的充分必要条件是∇2f(x)对一切x为半正定;(II)严格凸函数的充分条件是∇2f(x)对一切x为正定。
最优化方法习题答案
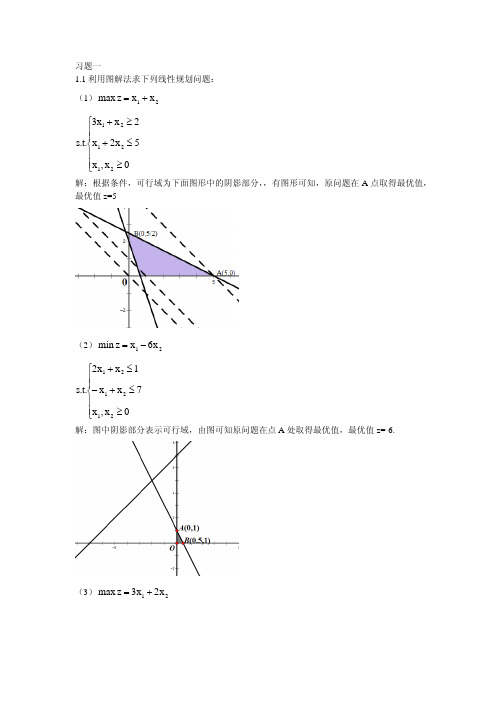
习题一1.1利用图解法求下列线性规划问题: (1)21x x z max +=⎪⎪⎩⎪⎪⎨⎧≥≤+≥+0x ,x 5x 2x 2x x 3.t .s 212121 解:根据条件,可行域为下面图形中的阴影部分,,有图形可知,原问题在A 点取得最优值,最优值z=5(2)21x 6x z min -=⎪⎪⎩⎪⎪⎨⎧≥≤+-≤+0x ,x 7x x 1x x 2.t .s 212121 解:图中阴影部分表示可行域,由图可知原问题在点A 处取得最优值,最优值z=-6.(3)21x 2x 3z max +=⎪⎪⎩⎪⎪⎨⎧≥-≥-≤+-0x ,x 4x 2x 1x x .t .s 212121 解:如图所示,可行域为图中阴影部分,易得原线性规划问题为无界解。
(4)21x 5x 2z min -=⎪⎪⎩⎪⎪⎨⎧≥≤+≥+0x ,x 2x x 6x 2x .t .s 212121 解:由图可知该线性规划可行域为空,则原问题无可行解。
1.2 对下列线性规划问题,找出所有的基解,基可行解,并求出最优解和最优值。
(1)4321x 6x 3x 2x 5z min -+-=⎪⎪⎩⎪⎪⎨⎧≥=+++=+++0x ,x ,x ,x 3x 2x x x 27x 4x 3x 2x .t .s 432143214321 解:易知1x 的系数列向量⎪⎪⎭⎫ ⎝⎛=21p 1,2x 的系数列向量⎪⎪⎭⎫ ⎝⎛=12p 2,3x 的系数列向量⎪⎪⎭⎫⎝⎛=13p 3,4x 的系数列向量⎪⎪⎭⎫⎝⎛=24p 4。
①因为21p ,p 线性无关,故有⎪⎩⎪⎨⎧--=+--=+43214321x 2x 3x x 2x 4x 37x 2x ,令非基变量为0x x 43==,得⎪⎪⎩⎪⎪⎨⎧=-=311x 31x 21,所以得到一个基解)0,0,311,31(x )1(-=是非基可行解; ②因为31p ,p 线性无关,可得基解)0,511,0,52(x)2(=,543z 2=;③因为41p ,p 线性无关,可得基解611,0,0,31(x )3(-=,是非基可行解;④因为32p ,p 线性无关,可得基解)0,1,2,0(x )4(=,1z 4-=;⑤因为42p ,p 线性相关,42x ,x 不能构成基变量; ⑥因为43p ,p 线性无关,可得基解)1,1,0,0(x )6(=,3z 6-=;所以)6()4()2(x ,x ,x是原问题的基可行解,)6(x 是最优解,最优值是3z -=。
最优化方法试题及答案

最优化方法试题及答案一、选择题1. 下列哪项不是最优化方法的特点?A. 目标性B. 可行性C. 多样性D. 随机性答案:D2. 在最优化问题中,约束条件的作用是什么?A. 限制解的可行性B. 增加问题的复杂性C. 提供额外的信息D. 以上都是答案:A3. 线性规划问题中,目标函数与约束条件之间的关系是什么?A. 无关B. 相等C. 线性D. 非线性答案:C二、简答题1. 简述最优化问题的基本构成要素。
答案:最优化问题的基本构成要素包括目标函数、决策变量、约束条件和解的可行性。
目标函数是衡量最优化问题解的质量的函数,决策变量是问题中需要确定的参数,约束条件是对决策变量的限制,解的可行性是指解必须满足所有约束条件。
2. 什么是局部最优解和全局最优解?请举例说明。
答案:局部最优解是指在问题的邻域内没有其他解比当前解更优的解,而全局最优解是指在整个解空间中最优的解。
例如,在山峰攀登问题中,局部最优解可能是到达了一个小山丘的顶部,而全局最优解是到达了最高峰的顶部。
三、计算题1. 假设一个农民有一块矩形土地,长为100米,宽为80米,他想在这块土地上建一个矩形的养鸡场,但只能沿着土地的长边布置。
如果养鸡场的一边必须靠在土地的长边上,另一边与土地的宽边平行,求养鸡场的最大面积。
答案:为了使养鸡场的面积最大,养鸡场的一边应该靠在土地的宽边上,另一边与土地的长边平行。
这样,养鸡场的长将是80米,宽将是100米,所以最大面积为80米 * 100米 = 8000平方米。
2. 一个工厂需要生产三种产品A、B和C,每种产品都需要使用机器X 和机器Y。
生产一个单位的产品A需要机器X工作2小时和机器Y工作1小时;产品B需要机器X工作3小时和机器Y工作2小时;产品C需要机器X工作1小时和机器Y工作3小时。
工厂每天有机器X总共300小时和机器Y总共200小时的使用时间。
如果工厂每天需要生产至少100单位的产品A,50单位的产品B和20单位的产品C,请问工厂应该如何安排生产以最大化产品的总产量?答案:设生产产品A的单位数为x,产品B的单位数为y,产品C的单位数为z。
最优化方法试卷及答案5套.docx

《最优化方法》1一、填空题:1. _______________________________________________________ 最优化问题的数学模型一般为:_____________________________________________ ,其中___________ 称为目标函数,___________ 称为约束函数,可行域D可以表示为_______________________________ ,若 ________________________________ ,称/为问题的局部最优解,若为问题的全局最优解。
2.设f(x)= 2斤+2“2-兀|+5花,则其梯度为__________ ^x = (l,2)r?6/ = (l,0)r,则f(x)在壬处沿方向d的一阶方向导数为___________ ,几何意义为_____________________________________ ,二阶方向导数为____________________ ,几何意义为_____________________________3.设严格凸二次规划形式为:min /(%) = 2兀]2 + 2x; - 2兀]-x2s.t. 2%! 4- x2 < 1> 0x2 > 0则其对偶规划为_______________________________________________min%(d ) = f (x k +ad k )的最优步长为务=—叫)F.d kT Gd k2. (10分)证明凸规划min/(x ),x G D (其中子(兀)为严格凸函数,D 是凸集)的最优解是唯一的3. (13分)考虑不等式约束问题min /(x )s.t. c i (x ) < 0, Z G / = {1,2,…,加}其中/(x ),6 (兀)a e /)具有连续的偏导数,设X 是约束问题的可行点,若在元处 d 满足巧(计<0,VC,(元)(可则d 是元处的可行下降方向。
最优化方法习题答案

习题一1.1利用图解法求下列线性规划问题: (1)21x x z max +=⎪⎪⎩⎪⎪⎨⎧≥≤+≥+0x ,x 5x 2x 2x x 3.t .s 212121 解:根据条件,可行域为下面图形中的阴影部分,,有图形可知,原问题在A 点取得最优值,最优值z=5(2)21x 6x z min -=⎪⎪⎩⎪⎪⎨⎧≥≤+-≤+0x ,x 7x x 1x x 2.t .s 212121 解:图中阴影部分表示可行域,由图可知原问题在点A 处取得最优值,最优值z=-6.(3)21x 2x 3z max +=⎪⎪⎩⎪⎪⎨⎧≥-≥-≤+-0x ,x 4x 2x 1x x .t .s 212121 解:如图所示,可行域为图中阴影部分,易得原线性规划问题为无界解。
(4)21x 5x 2z min -=⎪⎪⎩⎪⎪⎨⎧≥≤+≥+0x ,x 2x x 6x 2x .t .s 212121 解:由图可知该线性规划可行域为空,则原问题无可行解。
1.2 对下列线性规划问题,找出所有的基解,基可行解,并求出最优解和最优值。
(1)4321x 6x 3x 2x 5z min -+-=⎪⎪⎩⎪⎪⎨⎧≥=+++=+++0x ,x ,x ,x 3x 2x x x 27x 4x 3x 2x .t .s 432143214321 解:易知1x 的系数列向量⎪⎪⎭⎫ ⎝⎛=21p 1,2x 的系数列向量⎪⎪⎭⎫ ⎝⎛=12p 2,3x 的系数列向量⎪⎪⎭⎫⎝⎛=13p 3,4x 的系数列向量⎪⎪⎭⎫⎝⎛=24p 4。
①因为21p ,p 线性无关,故有⎪⎩⎪⎨⎧--=+--=+43214321x 2x 3x x 2x 4x 37x 2x ,令非基变量为0x x 43==,得⎪⎪⎩⎪⎪⎨⎧=-=311x 31x 21,所以得到一个基解)0,0,311,31(x )1(-=是非基可行解; ②因为31p ,p 线性无关,可得基解)0,511,0,52(x)2(=,543z 2=;③因为41p ,p 线性无关,可得基解611,0,0,31(x )3(-=,是非基可行解;④因为32p ,p 线性无关,可得基解)0,1,2,0(x )4(=,1z 4-=;⑤因为42p ,p 线性相关,42x ,x 不能构成基变量; ⑥因为43p ,p 线性无关,可得基解)1,1,0,0(x )6(=,3z 6-=;所以)6()4()2(x ,x ,x是原问题的基可行解,)6(x 是最优解,最优值是3z -=。
最优化方法习题答案
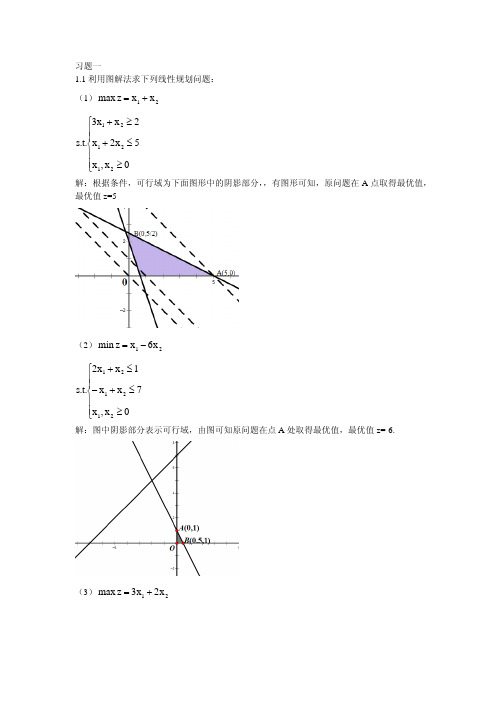
习题一1.1利用图解法求下列线性规划问题: (1)21x x z max +=⎪⎪⎩⎪⎪⎨⎧≥≤+≥+0x ,x 5x 2x 2x x 3.t .s 212121 解:根据条件,可行域为下面图形中的阴影部分,,有图形可知,原问题在A 点取得最优值,最优值z=5(2)21x 6x z min -=⎪⎪⎩⎪⎪⎨⎧≥≤+-≤+0x ,x 7x x 1x x 2.t .s 212121 解:图中阴影部分表示可行域,由图可知原问题在点A 处取得最优值,最优值z=-6.(3)21x 2x 3z max +=⎪⎪⎩⎪⎪⎨⎧≥-≥-≤+-0x ,x 4x 2x 1x x .t .s 212121 解:如图所示,可行域为图中阴影部分,易得原线性规划问题为无界解。
(4)21x 5x 2z min -=⎪⎪⎩⎪⎪⎨⎧≥≤+≥+0x ,x 2x x 6x 2x .t .s 212121 解:由图可知该线性规划可行域为空,则原问题无可行解。
1.2 对下列线性规划问题,找出所有的基解,基可行解,并求出最优解和最优值。
(1)4321x 6x 3x 2x 5z min -+-=⎪⎪⎩⎪⎪⎨⎧≥=+++=+++0x ,x ,x ,x 3x 2x x x 27x 4x 3x 2x .t .s 432143214321 解:易知1x 的系数列向量⎪⎪⎭⎫ ⎝⎛=21p 1,2x 的系数列向量⎪⎪⎭⎫ ⎝⎛=12p 2,3x 的系数列向量⎪⎪⎭⎫⎝⎛=13p 3,4x 的系数列向量⎪⎪⎭⎫⎝⎛=24p 4。
①因为21p ,p 线性无关,故有⎪⎩⎪⎨⎧--=+--=+43214321x 2x 3x x 2x 4x 37x 2x ,令非基变量为0x x 43==,得⎪⎪⎩⎪⎪⎨⎧=-=311x 31x 21,所以得到一个基解)0,0,311,31(x )1(-=是非基可行解; ②因为31p ,p 线性无关,可得基解)0,511,0,52(x)2(=,543z 2=;③因为41p ,p 线性无关,可得基解611,0,0,31(x )3(-=,是非基可行解;④因为32p ,p 线性无关,可得基解)0,1,2,0(x )4(=,1z 4-=;⑤因为42p ,p 线性相关,42x ,x 不能构成基变量; ⑥因为43p ,p 线性无关,可得基解)1,1,0,0(x )6(=,3z 6-=;所以)6()4()2(x ,x ,x是原问题的基可行解,)6(x 是最优解,最优值是3z -=。
最优化方法试卷及答案5套.docx

最优化⽅法试卷及答案5套.docx《最优化⽅法》1⼀、填空题:1. _______________________________________________________ 最优化问题的数学模型⼀般为:_____________________________________________ ,其中___________ 称为⽬标函数,___________ 称为约束函数,可⾏域D可以表⽰为_______________________________ ,若 ________________________________ ,称/为问题的局部最优解,若为问题的全局最优解。
2.设f(x)= 2⽄+2“2-兀|+5花,则其梯度为__________ ^x = (l,2)r?6/ = (l,0)r,则f(x)在壬处沿⽅向d的⼀阶⽅向导数为___________ ,⼏何意义为_____________________________________ ,⼆阶⽅向导数为____________________ ,⼏何意义为_____________________________3.设严格凸⼆次规划形式为:min /(%) = 2兀]2 + 2x; - 2兀]-x2s.t. 2%! 4- x2 < 1> 0x2 > 0则其对偶规划为_______________________________________________min%(d ) = f (x k +ad k )的最优步长为务=—叫)F.d kT Gd k2. (10分)证明凸规划min/(x ),x G D (其中⼦(兀)为严格凸函数,D 是凸集)的最优解是唯⼀的3. (13分)考虑不等式约束问题min /(x )s.t. c i (x ) < 0, Z G / = {1,2,…,加}其中/(x ),6 (兀)a e /)具有连续的偏导数,设X 是约束问题的可⾏点,若在元处 d 满⾜巧(计<0,VC,(元)(可则d 是元处的可⾏下降⽅向。
最优化方法课后习题答案

最优化方法课后习题答案最优化方法课后习题答案最优化方法是一门重要的数学学科,它旨在寻找给定问题的最佳解决方案。
在这门课程中,学生将学习各种最优化算法和技术,以解决不同类型的优化问题。
课后习题是巩固所学知识的重要方式,下面将为大家提供一些最优化方法课后习题的答案。
1. 线性规划问题的单纯形法是如何工作的?单纯形法是一种用于解决线性规划问题的常用方法。
其基本思想是通过不断迭代改进当前解决方案,直到找到最优解。
具体步骤如下:1) 初始解:选择一个可行解作为初始解,通常是通过求解一个相应的松弛问题得到。
2) 进入变量:选择一个进入变量,即使目标函数值增加最快的变量。
3) 离开变量:选择一个离开变量,即使约束条件仍然保持满足的变量。
4) 改进解:通过改变进入变量和离开变量的值,得到一个更好的解。
5) 终止条件:当无法找到更好的解时,算法终止。
2. 什么是凸优化问题?如何判断一个问题是否是凸优化问题?凸优化问题是指目标函数和约束条件都是凸函数的优化问题。
凸函数具有以下性质:1) 对于任意两个点x和y以及0≤λ≤1,有f(λx+(1-λ)y)≤λf(x)+(1-λ)f(y)。
2) 对于任意两个点x和y以及0≤λ≤1,有g(λx+(1-λ)y)≤λg(x)+(1-λ)g(y),其中g(x)表示约束函数。
要判断一个问题是否是凸优化问题,可以通过以下步骤:1) 检查目标函数和约束条件是否都是凸函数。
2) 检查约束条件是否满足凸集的定义,即对于任意两个点x和y以及0≤λ≤1,有λx+(1-λ)y满足所有约束条件。
如果以上两个条件都满足,则问题是凸优化问题。
3. 最小二乘法是如何解决无约束优化问题的?最小二乘法是一种常用的解决无约束优化问题的方法。
其基本思想是通过最小化目标函数和实际观测值之间的差距来找到最优解。
最小二乘法的步骤如下:1) 建立目标函数:根据实际观测值和模型假设,建立一个与待优化参数相关的目标函数。
2) 求解最优解:通过对目标函数求导,并令导数等于零,求解出最优解。
最优化习题

最优化方法部分课后习题解答习题一1.一直优化问题的数学模型为:22121122123142min ()(3)(4)5()02()50..()0()0f x x xg x x x g x x x s t g x x g x x =−+−⎧=−−≥⎪⎪⎪=−−+≥⎨⎪=≥⎪=≥⎪⎩试用图解法求出:(1)无约束最优点,并求出最优值。
(2)约束最优点,并求出其最优值。
(3)如果加一个等式约束,其约束最优解是什么?12()0h x x x =−=解:(1)在无约束条件下,的可行域在整个平面上,不难看出,当=(3,4)()f x 120x x *x 时,取最小值,即,最优点为=(3,4):且最优值为:=0()f x *x *()f x (2)在约束条件下,的可行域为图中阴影部分所示,此时,求该问题的最优点就是()f x 在约束集合即可行域中找一点,使其落在半径最小的同心圆上,显然,从图示中可12(,)x x 以看出,当时,所在的圆的半径最小。
*155(,)44x =()f x 其中:点为和的交点,令求解得到:1()g x 2()g x 1122125()02()50g x x x g x x x ⎧=−−=⎪⎨⎪=−−+=⎩1215454x x ⎧=⎪⎪⎨⎪=⎪⎩即最优点为:最优值为:=*155(,)44x =*()f x 658(3).若增加一个等式约束,则由图可知,可行域为空集,即此时最优解不存在。
2.一个矩形无盖油箱的外部总面积限定为S,怎样设计可使油箱的容量最大?试列出这个优化问题的数学模型,并回答这属于几维的优化问题.解:列出这个优化问题的数学模型为:该优化问题属于三维的优化问题。
123122313123max ()220..00f x x x x x x x x x x S x s t x x =++≤⎧⎪>⎪⎨>⎪⎪>⎩32123sx y z v⎛⎞=====⎜⎟⎝⎠习题二3.计算一般二次函数的梯度。
最优化方法试卷及答案5套

《最优化方法》1一、填空题:1.最优化问题的数学模型一般为:____________________________,其中___________称为目标函数,___________称为约束函数,可行域D 可以表示为_____________________________,若______________________________,称*x 为问题的局部最优解,若_____________________________________,称*x 为问题的全局最优解。
2.设f(x)= 212121522x x x x x +-+,则其梯度为___________,海色矩阵___________,令,)0,1(,)2,1(T T d x ==则f(x)在x 处沿方向d 的一阶方向导数为___________,几何意义为___________________________________,二阶方向导数为___________________,几何意义为____________________________________________________________。
3.设严格凸二次规划形式为:012..222)(min 2121212221≥≥≤+--+=x x x x t s x x x x x f则其对偶规划为___________________________________________。
4.求解无约束最优化问题:n R x x f ∈),(min ,设k x 是不满足最优性条件的第k 步迭代点,则:用最速下降法求解时,搜索方向k d =___________ 用Newton 法求解时,搜索方向k d =___________ 用共轭梯度法求解时,搜索方向k d =___________________________________________________________________________。
最优化方法试卷及答案5套

《最优化方法》1一、填空题:1.最优化问题的数学模型一般为:____________________________,其中 ___________称为目标函数,___________称为约束函数,可行域D 可以表示 为_____________________________,若______________________________, 称*x 为问题的局部最优解,若_____________________________________,称*x 为问题的全局最优解。
2.设f(x)= 212121522x x x x x +-+,则其梯度为___________,海色矩阵___________,令,)0,1(,)2,1(T T d x ==则f(x)在x 处沿方向d 的一阶方向导数为___________,几何意义为___________________________________,二阶 方向导数为___________________,几何意义为_________________________ ___________________________________。
3.设严格凸二次规划形式为:则其对偶规划为___________________________________________。
4.求解无约束最优化问题:n R x x f ∈),(min ,设k x 是不满足最优性条件的第k 步迭代点,则:用最速下降法求解时,搜索方向k d =___________ 用Newton 法求解时,搜索方向k d =___________ 用共轭梯度法求解时,搜索方向k d =___________________________________________________________________________。
二.(10分)简答题:试设计求解无约束优化问题的一般下降算法。
最优化方法习题答案
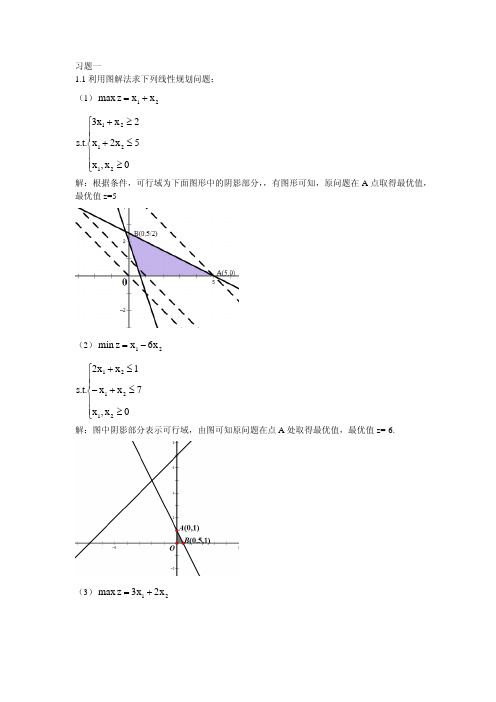
s.t.3x1 2x2 6 x1, x2 , x3 0
解:引入剩余变量 x 4 , x5 和人工变量 x6 , x7 ,利用两阶段法得到辅助线性规划 max w x6 x7 max z' 2x1 3x2 x3
x1 x2 x3 x4 1 s.t. x1 2x2 x5 4
xi 0,i 1,2,3,4,5
解:易知
x1
的系数列向量
p1
1
1
,
x2
的系数列向量
p2
1
2
,
x3
的系数列向量
p3
1
0
,
x4
的系数列向量 p4
1
0
,
x5 的系数列向量 p5
0
1
。
①因为 p1, p2
1 3 1
3
-M
0
0
0
5
3
-1
1
1
3
x1
x2
x3
x4
x5
0
x2
0
x1
1
0
1
2
1
1
2
0
1
2
3
3 M
-5.5
2
2
1
1
1.5
2
2
3 3
0.5
22
以 x 4 换入, x 2 换出有
x1
0
x4
0
x1
1
x2
x3
-3
-2
2
1
3
1
x4
x5
0
3M
-10
最优化方法测验及答案套

《最优化方法》1一、填空题:1.最优化问题的数学模型一般为:____________________________,其中 ___________称为目标函数,___________称为约束函数,可行域D 可以表示 为_____________________________,若______________________________, 称*x 为问题的局部最优解,若_____________________________________,称*x 为问题的全局最优解。
2.设f(x)= 212121522x x x x x +-+,则其梯度为___________,海色矩阵___________,令,)0,1(,)2,1(T T d x ==则f(x)在x 处沿方向d 的一阶方向导数为___________,几何意义为___________________________________,二阶 方向导数为___________________,几何意义为_________________________ ___________________________________。
3.设严格凸二次规划形式为:012..222)(min 2121212221≥≥≤+--+=x x x x t s x x x x x f则其对偶规划为___________________________________________。
4.求解无约束最优化问题:n R x x f ∈),(min ,设k x 是不满足最优性条件的第k 步迭代点,则:用最速下降法求解时,搜索方向k d =___________ 用Newton 法求解时,搜索方向k d =___________ 用共轭梯度法求解时,搜索方向k d =___________________________________________________________________________。
最优化方法习题1

《最优化方法》期末考试练习题声明:仅供复习时参考。
实际考试题型类似,题量小于本练习。
一. 选择题:略第一题主要考察基本概念、定理,算法的基本思想和matlab 命令。
二.简答题1. 写出线性规划问题;0, ,94 3 ,5 32 4 s.t. ,823 max 21321321321≥≥-+-≥+-+-x x x x x x x x x x x 的对偶规划。
2.如果求解某整数规划问题的松弛问题得到如下的最优单纯形表:求以1x ,2x 为源行生成的割平面方程。
3.在区间[0,3]上用黄金分割法求函数12)(3+-=t t t ϕ的极小点,只要求求出 初始的迭代点和保留区间及此时的近似最优解。
4. 用tx ex y 21-=拟合下列数据1.0,24.0,11,07.2,1=======-=y t y t y t y t写出非线性最小二乘问题三.计算题1.分别用最速下降方法和修正的牛顿法求解无约束问题 22214)(min x x x f +=。
取初始点()()Tx2,21=,.1.0=ε2.讨论约束极值问题⎪⎪⎩⎪⎪⎨⎧≥≥≤-≤++--+=0004..866)(min212121212221x x x x x x t s x x x x x f 的Kuhn-Tucker 点。
3.用外点法(外部惩罚函数法)求解2s.t.)3()1()(min 212221≤-+-+-=x x x x x f4.用内点法求解非线性规划03)( 03)( s.t. 296)(min 22112121≥-=≥-=++-=x x g x x g x x x x f5.用乘子法求解1s.t.6121)(min 212221=++=x x x x x f 6.用表格单纯形法求解线性规划⎪⎪⎩⎪⎪⎨⎧≥≥-≥-≤++++=0,,34623max 3213231321321x x x x x x x x x x x x x Z并根据最优单纯形表格写出该线性规划的最优基和最优基的逆。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
练习题一1、建立优化模型应考虑哪些要素? 答:决策变量、目标函数和约束条件。
2、讨论优化模型最优解的存在性、迭代算法的收敛性及停止准则。
答:针对一般优化模型()()min ()..0,1,2, 0,1,,i j f x s t g x i m h x j p≥===,讨论解的可行域D ,若存在一点*X D ∈,对于X D ∀∈ 均有*()()f X f X ≤则称*X 为优化模型最优解,最优解存在;迭代算法的收敛性是指迭代所得到的序列(1)(2)(),,,K X X X ,满足(1)()()()K K f X f X +≤,则迭代法收敛;收敛的停止准则有(1)()k k x x ε+-<,(1)()()k k k x x x ε+-<,()()(1)()k k f x f x ε+-<,()()()(1)()()k k k f x f x f x ε+-<,()()k f x ε∇<等等。
练习题二1、某公司看中了例2.1中厂家所拥有的3种资源R 1、R2、和R 3,欲出价收购(可能用于生产附加值更高的产品)。
如果你是该公司的决策者,对这3种资源的收购报价是多少?(该问题称为例2.1的对偶问题)。
解:确定决策变量 对3种资源报价123,,y y y 作为本问题的决策变量。
确定目标函数 问题的目标很清楚——“收购价最小”。
确定约束条件 资源的报价至少应该高于原生产产品的利润,这样原厂家才可能卖。
因此有如下线性规划问题:123min 170100150w y y y =++1231231235210..23518,,0y y y s t y y y y y y ++≥⎧⎪++≥⎨⎪≥⎩ *2、研究线性规划的对偶理论和方法(包括对偶规划模型形式、对偶理论和对偶单纯形法)。
答:略。
3、用单纯形法求解下列线性规划问题:(1)⎪⎪⎩⎪⎪⎨⎧≥≤+-≤++≤-++-=0,,43222..min32131321321321x x x x x x x x x x x t s x x x z ; (2)⎪⎪⎩⎪⎪⎨⎧=≥=++=+-=+-+-=)5,,2,1(052222..4min53243232132 i x x x x x x x x x x t s x x z i解:(1)引入松弛变量x 4,x 5,x 6123456min 0*0*0*z x x x x x x =-++++12341232 =22 5 =3..13 6=41,2,3,4,5,60x x x x x x x x s t x x x x x x x x x +-+⎧⎪+++⎪⎨-++⎪⎪≥⎩因检验数σ2<0,故确定x 2为换入非基变量,以x 2的系数列的正分量对应去除常数列,最小比值所在行对应的基变量x 4作为换出的基变量。
因检验数σ3<0,故确定x 3为换入非基变量,以x 3的系数列的正分量对应去除常数列,最小比值所在行对应的基变量x 5作为换出的基变量。
因检验数σj >0,表明已求得最优解:*(0,8/3,1/3,0,0,11/3)X =,去除添加的松弛变量,原问题的最优解为:*(0,8/3,1/3)X =。
(2)根据题意选取x 1,x 4,x 5,为基变量:⎪⎪⎩⎪⎪⎨⎧=≥=++=+-=+-+-=)5,,2,1(052222..4min53243232132 i x x x x x x x x x x t s x x z i因检验数σ2<0最小,故确定x 2为换入非基变量,以x 2的系数列的正分量对应去除常数列,最小比值所在行对应的基变量x 4作为换出的基变量。
因检验数σ3<0最小,故确定x 3为换入非基变量,以x 1的系数列的正分量对应去除常数列,最小比值所在行对应的基变量x 5作为换出的基变量。
因检验数σj >0,表明已求得最优解:*(9,4,1,0,0)X =。
8、某地区有A 、B 、C 三个化肥厂,供应本地甲、乙、丙、丁四个产粮区。
已知各化肥厂可供应化肥的数量和各产粮区对化肥的需要量,以及各厂到各区每吨化肥的运价如表2-28所示。
试制定一个使总运费最少的化肥调拨方案。
表2- 28解:设A 、B 、C 三个化肥厂为A 1、A 2、A 3,甲、乙、丙、丁四个产粮区为B 1、B 2、B 3、B 4;c ij为由A i 运化肥至B j 的运价,单位是元/吨;x ij 为由A i 运往B j 的化肥数量(i=1,2,3;j=1,2,3,4)单位是吨;z 表示总运费,单位为元,依题意问题的数学模型为:3411min ij ij i j z c x ===∑∑112131122232132333142434111213142122232431323334663..3787x x x x x x x x x s t x x x x x x x x x x x x x x x ++=⎧⎪++=⎪⎪++=⎪++=⎨⎪+++=⎪⎪+++=⎪+++=⎩ 该题可以用单纯形法或matlab 自带工具箱命令(linprog )求解。
*9、求解下列不平衡运输问题(各数据表中,方框的数字为单位价格ij c ,框外右侧的一列数为各发点的供应量i a ,框底下一行数是各收点的需求量j b ):(1) 5 1 7 10 要求收点3的需求必须正好满足。
6 4 6 803 2 5 1575 20 50(2) 5 1 0 20 要求收点1的需求必须由发点4供应。
3 2 4 10 7 5 2 15 9 6 0 155 10 15 解答略。
练习题三1、用0.618法求解问题12)(min 30+-=≥t t t t ϕ的近似最优解,已知)(t ϕ的单谷区间为]3,0[,要求最后区间精度0.5ε=。
答:t=0.8115;最小值-0.0886.(调用golds.m 函数) 2、求无约束非线性规划问题min ),,(321x x x f =123222124x x x x -++ 的最优解解一:由极值存在的必要条件求出稳定点:1122f x x ∂=-∂,228f x x ∂=∂,332fx x ∂=∂,则由()0f x ∇=得11x =,20x =,30x = 再用充分条件进行检验:2212f x ∂=∂,2228f x ∂=∂,2232f x ∂=∂,2120fx x ∂=∂∂,2130f x x ∂=∂∂,2230f x x ∂=∂∂即2200080002f ⎛⎫ ⎪∇= ⎪ ⎪⎝⎭为正定矩阵得极小点为T *(1,0,0)x =,最优值为-1。
解二:目标函数改写成min ),,(321x x x f =222123(1)41x x x -++- 易知最优解为(1,0,0),最优值为-1。
3、用最速下降法求解无约束非线性规划问题。
2221212122)(m in x x x x x x X f +++-=其中T x x X ),(21=,给定初始点T X )0,0(0=。
解一:目标函数()f x 的梯度112122()()142()122()()f x x x x f x x x f x x ∂⎡⎤⎢⎥∂++⎡⎤⎢⎥∇==⎢⎥-++∂⎢⎥⎣⎦⎢⎥∂⎣⎦(0)1()1f X⎡⎤∇=⎢⎥-⎣⎦令搜索方向(1)(0)1()1d f X -⎡⎤=-∇=⎢⎥⎣⎦再从(0)X 出发,沿(1)d 方向作一维寻优,令步长变量为λ,最优步长为1λ,则有(0)(1)0101X d λλλλ--⎡⎤⎡⎤⎡⎤+=+=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦故(0)(1)2221()()()2()2()2()f x f X d λλλλλλλλλϕλ=+=--+-+-+=-=令'1()220ϕλλ=-=可得11λ= (1)(0)(1)1011011X X d λ--⎡⎤⎡⎤⎡⎤=+=+=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦ 求出(1)X 点之后,与上类似地,进行第二次迭代:(1)1()1f X -⎡⎤∇=⎢⎥-⎣⎦ 令(2)(1)1()1d f X ⎡⎤=-∇=⎢⎥⎣⎦令步长变量为λ,最优步长为2λ,则有(1)(2)111111X d λλλλ--⎡⎤⎡⎤⎡⎤+=+=⎢⎥⎢⎥⎢⎥+⎣⎦⎣⎦⎣⎦ 故(1)(2)2222()()(1)(1)2(1)2(1)(1)(1)521()f x f X d λλλλλλλλλϕλ=+=--++-+-+++=--=令'2()1020ϕλλ=-=可得 215λ= (2)(1)(2)2110.8111 1.25X X d λ--⎡⎤⎡⎤⎡⎤=+=+=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦(2)0.2()0.2f X⎡⎤∇=⎢⎥-⎣⎦此时所达到的精度(2)()0.2828f X∇≈本题最优解11.5X*-⎡⎤=⎢⎥⎣⎦,()1,25f X*=-练习题四1、石油输送管道铺设最优方案的选择问题:考察网络图4-6,设A为出发地,F为目的地,B,C,D,E分别为四个必须建立油泵加压站的地区。
图中的线段表示管道可铺设的位置,线段旁的数字表示铺设这些管线所需的费用。
问如何铺设管道才能使总费用最小?图4- 6解:第五阶段:E1—F 4;E2—F 3;第四阶段:D1—E1 —F 7;D2—E2—F 5;D3—E1—F 5;第三阶段:C1—D1—E1 —F 12;C2—D2—E2—F 10;C3—D2—E2—F 8;C4—D3—E1—F 9;第二阶段:B1—C2—D2—E2—F 13;B2—C3—D2—E2—F 15;第一阶段:A—B1—C2—D2—E2—F 17;最优解:A—B1—C2—D2—E2—F 最优值:172、用动态规划方法求解非线性规划123123123max()27,,0f x x x xx x xx x x=++++=⎧⎨≥⎩解:1239,9,9x x x ===,最优值为9。
3、用动态规划方法求解非线性规划22112121212max 765..21039,0z x x x s t x x x x x x ⎧=++⎪+≤⎪⎨-≤⎪⎪≥⎩解:用顺序算法阶段:分成两个阶段,且阶段1 、2 分别对应12,x x 。
决策变量:12,x x状态变量:,i i v w 分别为第j 阶段第一、第二约束条件可供分配的右段数值。
1111*22211111111100(,)max {76}min{76,76}x v x w f v w x x v v w w ≤≤≤≤=+=++*111min{,}x v w =22*2*2222122220522222222222205(,)max{5(2,3)}max{5min{7(2)6(2),7(3)6(3)}}x x f v w x f v x w x x v x v x w x w x ≤≤≤≤=+-+=+-+-+++由于2210,9v w ==,2**222222222205(,)(10,9)max{min{33292760,68396621}x f v w f x x x x ≤≤==-+++可解的129.6,0.2x x ==,最优值为702.92。
