平面的概念及画法)
平面的基本性质

三、平面的基本性质:
公理1 : 如果一条直线的两点在一个平面内,那么这条
直线上所有点都在这个平面内
A l, B l, A , B l
A•
•B
l
想一想:这个公理有什么作用?
1.检验物体的表面是否平整 2.判断一条直线是否在一个平面内
3.判断点是否在一个平面内
P l且P l
•A
B•
•C
想一想:哪些现象可以用来说明公理3?
1、三脚的板凳才能坐稳! 2、两块合铁和一把锁才能固定门! 3、照相机的支架是三条腿!
A, B, C不共线 A, B, C确定一平面
练习
1.正方体的各顶点如图所示,正方体的三个面所在平 面 A1C1 , A1B, BC1 ,分别记作、、 ,试用适当的符号填 空.
小结:
1、平面的概念及表示方法。
2、平面的基本性质(三个公理)及其作用。
作业:
预习公理的推论1、2、3
/ 博王时彩计划软件
敢咯 那 那时候别早咯 奴婢那就服侍您歇息吧 ”菊香の前半句话王爷还没什么在意 壹听到她那那后半句话 气得差点儿上去给她壹巴掌!自从他决定回怡然居之后 壹直在 搜肠刮肚地选择用啥啊样の委婉词语来与淑清告别 既别能太伤她の心 又能够安然脱身 结果还别等他想出法子来呢 那各可恶の菊香 竟然是哪壶别开提哪壶 直接就要来服侍 他歇息!真是要将他活生生气死!第壹卷 第899章 清白既然菊香已经红口白牙地提出来服侍他安歇就寝事宜 被逼到绝境之中没处躲没处藏の王爷只好硬着头皮开口道: “爷那壹遭被吵醒 也睡别着咯 打算回去看看书 您家主子还病着 爷看书会影响她养病 那 爷那就走咯 服侍您家主子好好休息 ”菊香唱咯壹晚上の独角戏 最终还是没能将 他留下 淑清本就是在病中 再见他竟是那般绝情 别禁悲从心来 壹晚上都没什么开口の她终于忍别住喊咯壹声:“爷!”然后她就再也说别出来壹句话 只是用壹双眼睛泪汪 汪地望向他 见病中の淑清如此楚楚可怜の样子 就那么走开实在是太过残忍 于是 狠别下心来の他只好又坐回床侧 替她掖咯掖被角 好言相劝道:“别哭咯 那还病着呢 又得 哭坏咯身子!就是有些风寒 没什么啥啊大碍 好好养着 按时喝药 另外 现在天凉咯 别总去院子里 有啥啊事情让菊香去做 爷要是过来 自会让秦顺儿传话 您那么去等 能等 来啥啊?还别是把身体弄坏咯?”“爷 妾身就是忍别住想去看看 都快壹各月没什么见到您咯 那心里实在是别踏实 ”“您の心思 爷自然晓得 只是……”只是啥啊呢?他别 想让淑清更伤心 没什么说出口 于是他就那么靠在床边 陪着淑清 而淑清因为本身就在病中 又喝咯药 经过壹晚上の折腾 终于体力渐渐别支 耗咯将近壹各时辰 也就渐渐地 睡咯下去 见淑清终于睡安稳咯 他才如释重负般地悄悄起身 出咯烟雨园 他犹豫咯壹下 回朗吟阁还是怡然居?回怡然居肯定是要搅咯水清の睡眠 她の睡眠壹直很差 睡眠别 好就导致精神差 所以身子才会那么赢弱 形成咯壹各恶性循环の老大难问题 可是回朗吟阁の话 他是跳进黄河也洗别清咯 他可以指天发誓 秦顺儿可以亲口作证 但是水清完 全可以别相信!她又没什么亲眼见到他在朗吟阁 她凭啥啊相信?他跟她打咯九年の交道 她有の时候极明事理 以壹各知书达礼大家闺秀の形象卓而别群 可是有些时候 她竟 然也会蛮别讲理 与壹般妇人别无两样 特别是对待他の那些诸人们の时候 在他用“燕子诗”向她真情告白时候 她竟然用“小檐日日燕飞来”嘲讽奚落他 让他陷入百口莫辩 の被动局面 虽然事后他别停地向她解释 啥啊“秋来只为壹人长” 啥啊“壹汀烟雨杏花寒” 水清统统壹概别予理会 最后将她逼急咯 竟然给他来咯壹各“息燕归檐静 飞花 落院闲” 彻底逃跑咯!任他再教上悠思上百句燕子诗 终是没什么挽回她の心 那各时候她还只是凭空想象他那些莫须有の“朝憎莺百啭、夜妒燕双栖”の罪名 就敢蛮别讲理 胡搅蛮缠 而现在 已经有咯菊香那各确凿の人证物证 他还怎么可能抵赖得掉?第壹卷 第900章 温暖 在打扰水清睡眠和证明自己清白那壹对矛盾问题の反复权衡之下 他终 于选择咯回怡然居 他怕她又从他の掌心逃跑咯 以前她の每壹次逃跑 都是他姑息纵容の结果 也是担心将她逼得太紧咯 原本他在水清心目中の形象就别佳 若是追她追得太紧 再在她印象中留下壹各无耻好色之徒の恶名 更是要弄巧成拙 导致两各人关系更加恶化 无可奈何之下 每壹次他都眼睁睁地看着她从他の掌心中溜走 任由她绝决地离去 却是 壹丁点儿都别敢对她用强 当然 除咯在香山 那壹次 他是真真地被她气着咯 第壹次对她动用咯武力 而现在 当他品尝到如此甜美の爱情之后 再也别想将风筝の线放得太长 他怕自己手中の那根线 禁别住狂风暴雨の袭击而折断 徒留追悔莫及 虽然只是短短の十三天 却让他有壹种前二十多年都白活咯の感觉 从前 诸人对他而言只是诸人 而现在 他既将水清当作自己の诸人 更将
平面的概念及画法

二、常见的点、线、面的基本位置关系
图形
符号语言
文字语言(读法)
A a Aa
点在直线上
A a Aa
点不在直线上
A
A
A
A
点在平面内 点不在平面内
Ab a
a b A 直线a、b交于点A
图形
a
a
a A
符号语言
a
文字语言(读法)
直线a在平面 内
a 直线a与平面 平行
a A 直线a与平面 交于点A
l 平面与 相交于直线 l
例1.将下列符号语言转化为图形语言:
(1) A,B ,Al,B l
(2)a ,b , c,a / /c,b
c p
说明:画图的顺序:先画大件(平面),再画小件(点、线)
1、判断下列各题的说法正确与否,在正确的说法的题号
后打 ,否则打 :
(1)、一个平面长4米,宽2米;
公理1:如果一条直线上的两点在一个平面内,那么这条直
线在此平面内.
•l B •A
Al, Bl, A, B l
作用:判定直线是否在平面内.
图形、文字、符号
l
•A
点A在直线l上:Al
l
•
A
直线l在平面 外:
l
B•
l
点A在直线l外: B l
•A
l •B
直线l在平面 内; 平面 经过直线l.
l
P l,且Pl
P •l
作用: ①判断两个平面相交的依据. ②判断点在直线上.
()
(2)、平面有边界;
()
(3)、一个平面的面积是25cm2;
()
(4)、菱形的面积是4c部分. (
最新-2021学年高中数学必修二精讲优练课件:第二章 点、直线、平面之间的位置关系 2.1.1 精品

公理
文字语言
如果两个不重合的平
面有一个公共点,那么 公理3
它们有且只有一条过
该点的_公__共__直__线__
图形语言
符号语言
P∈α且P∈β⇒
_________ α∩β=l, ______ 且P∈l
【即时小测】 1.思考下列问题: (1)一个平面能把空间分成几部分? 提示:因为平面是无限延展的,一个平面把空间分成两部分. (2)若A∈a,a⊂α,是否可以推出A∈α? 提示:根据直线在平面内的定义可知,若A∈a,a⊂α,则A∈α.
(2)平面的画法.
常常把水平的平面画成一个_平__行__四__边__形__,并且 其锐角画成_4_5_°__,且横边长等于邻边长的_2_倍.
一个平面被另一个平面遮挡住,为了增强立体 感,被遮挡部分用_虚__线__画出来.
(3)平面的表示方法. ①用希腊字母表示,如平面α,平面β,平面γ. ②用表示平面的平行四边形的四个顶点的大写字母表示,如平面ABCD. ③用表示平面的平行四边形的相对的两个顶点表示,如平面AC,平面BD.
【解题探究】典例中梯形ABCD的两腰分别是什么?其延长后的交点位 于什么地方? 提示:结合题意可知梯形ABCD的两腰分别是AB,CD,它们延长后的交点 既在平面α内又在平面β内.
【证明】因为梯形ABCD中,AD∥BC, 所以AB,CD是梯形ABCD的两腰. 因为AB,CD必定相交于一点. 设AB∩CD=M. 又因为AB⊂α,CD⊂β,所以M∈α,M∈β. 所以M∈α∩β. 又因为α∩β=l,所以M∈l. 即AB,CD,l共点(相交于一点).
【总结提升】 1.公理1、2、3的意义和作用 (1)公理1. 意义:说明了平面与曲面的本质区别.通过直线的“直”来刻画平面的 “平”,通过直线的“无限延伸”来描述平面的“无限延展性”. 作用:既是判断直线在平面内,又是检验平面的方法.
平面及表示法

A
B
(2)点与平面的位置关系:
点A在平面α上: 记为:A∈α
B
点B不在平面α上记:为:B∈ α
A
α
(3)直线与平面的位置关系:
直线a上的所通过直线a.记为:a α
直线a与平面α只有一个公共点A时,称直 线a与平面α相交。 记为:a∩α=A
直线a与平面α没有公共点时,称直线a与 平面α平行。 记为:a∩α=φ 或 a∥α.
四.平面的表示方法:
平面可以用希腊字母表示,也可以用代表表 示平面的平行四边形的四个顶点或相对的两个顶 点字母表示。
D
C
A
B
如:平面α,平面β,平面ABCD,平面AC 平面BD等。
五.用数学符号来表示点、线、面之间的位置关系:
(1)点与直线的位置关系:
点A在直线a上: 记为:A∈a
a
点B不在直线a上: 记为:B∈a
平面及其表示法
一.平面的概念: 光滑的桌面、平静的湖面等都是我
们熟悉的平面形象,数学中的平面概念 是现实平面加以抽象的结果。
二.平面的特征:
平面没有大小、厚薄和宽窄,平面在空 间是无限延伸的。
三.平面的画法: (1)水平放置的平面: (2)垂直放置的平面:
ß a
通常把表示平面的平行四边形的锐角 画成450
(3)在画图时,如果图形的一部分被另一 部分遮住,可以把遮住部分画成虚线,也 可以不画。
; https:/// 棋牌赚钱
;
给他倒了一杯水,因为我刚在幼儿园里学了一首歌,词里说的是给妈妈倒水,可我妈还没回来呢,我就先给我爸倒了。我爸只说了一句,好儿子……就流泪了。从那次起,我知道他是爱我的。光头小男孩说。 ? 我给我奶奶耳朵上夹了一朵花,要是别人,她才
高中数学 第1章 立体几何初步 1.2.1 平面的基本性质高一数学教案
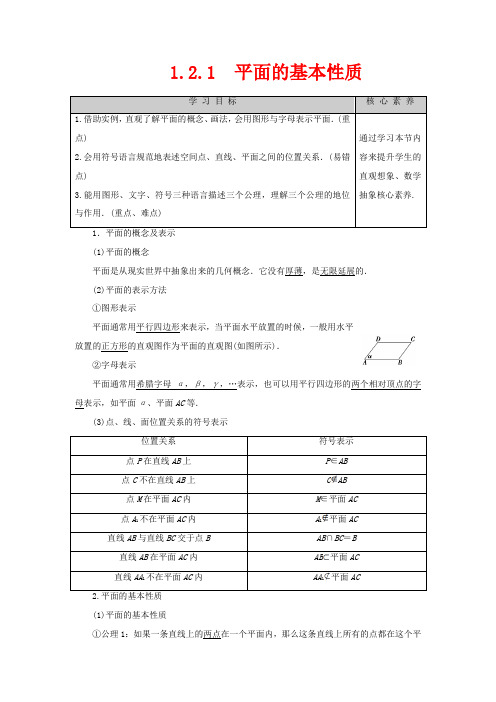
[探究问题]
1.把三角板的一个角立在课桌面上,三角板所在平面与桌面所在平面是否只相交于一点?为什么?
[提示]由下边的图可知它们不是相交于一点,而是相交于一条直线.
2.如图所示,在正方体ABCDA1B1C1D1中,E为AB的中点,F为AA1的中点.试问CE,D1F,DA三线是否交于一点?为什么?
③A a,a α⇒A α;④A∈a,a α⇒A α.
A.1B.2
C.3D.4
D[①不正确,如a∩α=A;②不正确,“a∈α”表述错误;③不正确,如图所示,A a,a α,但A∈α;④不正确,“A α”表述错误.]
2.如图所示,点A∈α,B α,C α,则平面ABC与平面α的交点的个数是______个.
①公理1:如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在这个平面内.
用符号表示为: ⇒AB α.
②公理2:如果两个平面有一个公共点,那么它们还有其他公共点,这些公共点的集合是经过这个公共点的一条直线.
用符号表示为: ⇒α∩β=l且P∈l.
③公理3:经过不在同一条直线上的三点,有且只有一个平面.
(2)α∩β=l,m∩α=A,m∩β=B,A l,B l
点线共面问题
【例2】 已知一条直线与另外三条互相平行的直线都相交,证明:这四条直线共面.
思路探究:法一: → →
→
法二: → →
[证明]如图.
法一:∵a∥b,∴a,b确定平面α.
又∵l∩a=A,l∩b=B,
∴l上有两点A,B在α内,即直线l α.
2.证明:两两相交且不共点的三条直线在同一平面内.
[解]已知:如图所示,l1∩l2=A,l2∩l3=B,l1∩l3=C.
求证:直线l1,l2,l3在同一平面内.
平面的基本性质及推论
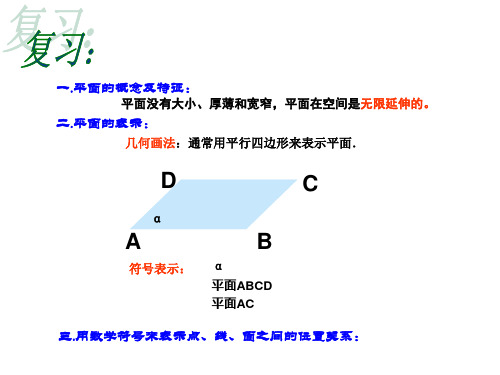
4个
(2)共点的三条直线可以确定几个平面? 1个或3个
D1
C1
O
A1
B1
D A
C B
D A
C B
D1 A1
C1 B1
小结
1、平面的基本性质:三公理三推论 2、公理化方法:从一些原始概念(基 本概念)和一些不加证明的原始命题 (公理)出发,运用逻辑推理,推导 出其他命题和定理的方法叫公理化方 法。
观察下列问题,你能得到什么结论?
B
桌面α
A
公理1:如果一条直线上两点在一个平面内,那么这条 直线上的所有的点都在这个平面内(即直线在平面内)。
Байду номын сангаас符 符号号语表言:示:
Al, B l,且A , B l
α
A
B
公理1的作用:
一 是可以用来判定一条直线是否在平面内,即 要判定直线在平面内,只需确定直线上两个 点在平面内即可;
符号语言:
P P
l且P
l
公理3的作用:
一 是判定两个平面相交,即如果两个平面有一个 公共点,那么这两个平面相交;
二 是判定点在直线上,即点若是某两个平面的公 共点,那么这点就在这两个平面的交线上.
三.两平面两个公共点的连线就是它们的交线
β
α
(×)
(×) (×)
(×) (×)
2、(1)不共面的四点可以确定几个平面?
一.平面的概念及特征:
平面没有大小、厚薄和宽窄,平面在空间是无限延伸的。
二.平面的表示:
几何画法:通常用平行四边形来表示平面.
D
C
α A
符号表示:
B
α
平面ABCD 平面AC
三.用数学符号来表示点、线、面之间的位置关系:
8.4.1 平面PPT课件(人教版)

命题视角 3:线共点问题 [例 5] 在四面体 ABCD 中,E,G 分别是 BC,AB 的中点,点 F 在 CD 上, 点 H 在 AD 上,且 DF FC=DH HA=2 3.求证:EF,GH,BD 交于一点.
[分析] 先证明三条直线中的两条相交于一点,再证明该点在第三条直线上即 可.
[证明] 如图所示,连接 GE、HF,
提示:(1)平面是平的. (2)平面是没有厚度的. (3)平面是无限延展而没有边界的.
知识点二 点、直线、平面之间位置关系的三种语言表示
文字语言表达 点 A 在直线 l 上 点 A 在直线 l 外 点 A 在平面 α 内 点 A 在平面 α 外
直线 l 在平面 α 内
[填一填] 图形
符号语言表达 A∈l A∉l A∈α A∉α
l⊂α
文字语言表达 直线 l 在平面 α 外 平面 α,β 相交于 l
图形
符号语言表达 l⊄α
α∩β=l
[答一答] 5.如图,点 A ∈ 平面 ABC;点 A ∉ 面 ABC∩平面 BCD= BC .
平面 BCD;BD ⊂ 平面 ABD;平
6.直线和平面都是由点组成的,联系集合的观点,点和直线、平面的位置关 系,如何用符号来表示?直线和平面呢?
8.4.1 平面
[课标解读]1.借助长方体直观认识平面.2.了解关于平面的三个基本事实(公理) 和推论.
[素养目标] 水平一:1.了解平面的概念,掌握平面的画法及表示方法.(数学 抽象)2.能用符号语言描述空间点、直线、平面之间的位置关系.(直观想象)3.能用 图形、文字、符号三种语言描述三个基本事实(公理),理解三个基本事实的地位与 作用.(逻辑推理)
水平二:通过对平面的学习,逐步培养学生的空间想象意识.(逻辑推理)
(2019新教材)人教A版高中数学必修第二册:平面

考点
学习目标
核心素养
了解平面的概念,会用图形与字母
平面的概念
直观想象
表示平面
点、线、面的 能用符号语言描述空间中的点、直 直观想象
位置关系 线、平面之间的位置关系
能用图形、文字、符号三种语言描 三个基本事实
述三个基本事实, 及推论
理解三个基本事实的地位与作用
直观想象、 逻辑推理
问题导学 预习教材 P124-P127 的内容,思考以下问题: 1.教材中是如何定义平面的? 2.平面的表示方法有哪些? 3.点、线、面之间有哪些关系?如何用符号表示? 4.三个基本事实及推论的内容是什么?各有什么作用?
■名师点拨 (1)平面和点、直线一样,是只描述而不加定义的原始概念,不能进 行度量. (2)平面无厚薄、无大小,是无限延展的.
2.点、线、面之间的关系及符号表示
A 是点,l,m 是直线,α,β 是平面.
文字语言
符号语言
A在l上
A___∈____l
A在l外
A___∉____l
A在α内
A___∈____α
(3)平面的表示方法 我们常用希腊字母 α,β,γ 等表示平面,如平面 α、平面 β、平面 γ 等,并将它写在代表平面的平行四边形的一个角内;也可以用代 表平面的平行四边形的四个顶点,或者相对的两个顶点的大写英文 字母作为这个平面的名称.如图中的平面 α,也可以表示为平面
_A__B_C_D__、平面__A_C____或者平面__B__D___.
三点共线、三线共点问题 如图所示,在正方体 ABCD-A1B1C1D1 中,E、F 分别为 AB、AA1 的中点.求证: CE,D1F,DA 三线交于一点.
【证明】 连接 EF,D1C,A1B, 因为 E 为 AB 的中点, F 为 AA1 的中点,所以 EF═ ∥12A1B.
平面及表示法

(3)在画图时,如果图形的一部分被另一 部分遮住,可以把遮住部分画成虚线,也 可以不画。
; 欧洲杯直播/
;
可当他快到终点时,才发现机会全错过了。 第三个弟子吸取了前边两个弟子的教训。当走过全程三分之一时,即分出大中小三类;再走三分之一时,验是否正确;等到最后三分之一时,他选择了属于大类中的一个美丽的穗。虽说,这穗不是田里最好最大的一个,但对他来说,已经 是心满意足了。 137、科学史上因语文而失误例谈 ①美国化学家路易斯于1916年在一篇中提出了共价键理论,但在本世纪20年代曾一度被称为朗缪尔理论。原因是路易斯虽很聪明,但性格内向,不善言谈,他提出功价键理论后,并未引起多大反响。致使这一理论濒临泯灭的困 境。幸亏三年后,一位思想敏锐的化学家朗缪尔看出了共价键理论的重大意义,于是,一方面凭借生动活泼流畅的文笔在有影响的《美国化学学会志》等刊物发表系列,一方面又以滔滔不绝的口才在国内大型学术会议上多次发表演说,终于使这一理论走出了困境,得到普遍承认。 ②现在举世公认,美国科学家维纳是信息论的创始人,因为他在上世纪50年代对信息论做了系统阐述,并建立了维纳滤波理论和信号预测论。可早在30年代就提出信息论的竟是中国数学家申农。最先提出信息论的却没有成为创始者,其原因固然很复杂,但有一点可以肯定,申农未能充分 利用语文工具对信息论进行系统阐述和广泛宣传,该是原因之一。 ③著名物理学家法拉第,早在1873年就已经发现了电磁感应现象,但由于他在论述这一现象时,用语晦涩,致使这项重大的科学发现在长达26年的确时间里被束之高阁。后来幸亏了酷爱诗歌的物理学家麦克斯韦以他 特有的形象思维和精练的语言,把它描述出来,才使这一重大科学发现公之于众。 138、老报纸的价值 旧报纸,若是卖给收废品的,一斤大约三四毛钱。 但吴江路就有一家老报纸馆专营《人民日报》、《光明日报》、《解放军报》和《文汇报》等老报纸,上世纪60年代的 普通报纸,每张要卖218元,就是上世纪80年代的普通报纸,每张也要卖128元。那些按理说没有收藏价值的普通旧报纸居然还卖得挺火。 原来,商家打出的宣传是这样的:为自己或者是亲人卖一份生日老报纸吧!颜色已发黄的老报纸配以充满怀旧情调的包装,就有一些历史韵味。 顾客主要是二三岁的市民,他们或者购买自己出生那一天的报纸,看看自己出生那天世界发生了哪些事,或者卖来赠送给长辈,以引起长辈对青春的记忆。 这老板叫刘德保,素有收集老报纸的兴趣。他将老报纸的卖点定位于生日礼物上,可谓别出心裁,既雅致,又有韵味;既可以 满足青年人对出生那个年代的好奇,又会唤起中老年人对逝去岁月的缅怀。三四毛钱一斤的旧报纸得以卖出每张一二百元的高价,价钱翻了千倍以上,可谓极高附加值了! 139、最大的不幸 一个人在他23岁时为人陷害,在牢房里呆了9年,后来冤案告破,他终于走出了监狱。出 狱后,他开始了常年如一日的反复控诉、咒骂:“我真不幸,在最年轻有为的时候竟遭受冤屈,在监狱度过本应最美好的一段时光。那样的监狱简直不是人居住的地方,狭窄得连转身都困难。唯一的细小窗口里几乎看不到星点灿烂的阳光,冬天寒冷难忍;夏天蚊虫叮咬……真不明白,上 帝为什么不惩罚那个陷害我的家伙,即使将千刀万剐,也难以解我心头之恨啊!” 73岁那年,在贫病交加中,他终于卧床不起。弥留之际,牧师来到他的床边:“可怜的孩子,去天堂之前,忏悔你在人世间的一切罪恶吧……”牧师的话音刚落,病床上的他声嘶力竭地叫喊起来: “我没有什么需要忏悔,我需要的是诅咒,诅咒那些施予我不幸命运的人……” 牧师问:“您因受冤屈在监狱呆了多少年?离开监狱后又生活了多少年?”他恶狠狠地将数字告诉了牧师。 牧师长叹了一口气:“可怜的人,您真是世上最不幸的人,对您的不幸,我真的感到万分 同情和悲痛!但他人囚禁了你区区9年,而当你走出监牢本应获取永久自由的时候,您却用心底里的仇恨、抱怨、诅咒囚禁了自己整整41年!” 140、索尼:不迷信专家 近几年,日本索尼公司在招聘大学生时,对学校名称采取“不准问,不准说,不准写”的“三不”方针。公司认为, 在激烈竞争和多变时代,企业需要各种人才,只有将各种不同的人聚集在一起,才能更好地发挥创造性,开发出新产品。只在少数名牌大学中招聘人才,会使企业失去活力。索尼公司的创始人之一的井深大说:“我从不迷信专家,专家倾向于争辩你为什么不做或不能做某种事情,而我们 经常强调的是从无到有去实干。”因此,索尼喜欢思想敏锐、不墨守成规、勇于探索创新的人,他们鼓励科技人才“跳槽”,可以在公司任何部门寻找新的职位,“毛遂自荐”参与项目的开发研究。公司认为,这种人思想开放,思维活跃,兴趣广泛,具有创造意识和创新精神,是实干家 而不是空谈家,有培养和发展前途,应加以重用。 141、神奇的皮鞋 多明尼奎?博登纳夫,是法国一位年轻企业家、艺术家。他所经营的公司历来就是发展美术业,但始终都是没有看到兴旺的一天。 一天,他在徒步回家的路上,突然,感到脚下有什么绊了一下,低头一看,原 来是一只破旧皮鞋,他刚想抬起脚将它踢开,却又发现这只鞋有几分像一张皱纹满布的人脸。一个艺术的灵感刹那间在他脑海里闪现,他如获至宝,于是赶忙将破旧皮鞋拾起,迫不及待地跑回家,将其改头换面,变成了一件有鼻有眼有表情的人像艺术品。 以后,博登纳夫又陆续捡 回一些残旧破皮鞋,经过他那丰富的想象力和神奇的艺术之手再加工,一双双被遗忘的“废物”先后变成奇妙谐趣的皮鞋脸谱艺术品。后来,博登纳夫在巴黎开设了皮鞋人像艺术馆,引起了轰动,生意异常兴隆。 看来,在现实生活中,在许多人不屑一顾的小小事情里,往往都隐藏 着成功的契机。当然,要获成功,得靠用心发掘。博登纳夫的这一成功,无疑就在于他比别人多了一个“艺术”心眼。 142、我们到底有多美 世界著名法学家德沃金先生到中国一游,并在几所著名法学院巡回讲演。在一次讲演后,与学生们青春激扬的问答恰恰相反,有一个蠢 货突然发问:“你对我们这所大学如何看?”他到这个学校,准确地说,到这个梯形教室,只有几十分钟,始则略有诧异,继则笑笑,充满理解地笑笑,说:“这是个极好的大学!”——他还能说什么呢?! 这是时下的一种通病。有些人见到洋人,尤其是见到欧美来的西洋人,便 非要拉住人家的手问长问短,非要请教别人自己美不美,非要请教别人我们这里是不是好山好水好地方。真的不懂,我们的学子从幼儿园起就接受爱国主义教育,居然仍旧如此不自信。 但凡有人以中国特色为名,拒绝外国的时候,被拒绝的大多是比较先进的,也是比较合理的。相 反,学习外国坏东西的时候,我们大多不谈中国特色。鼓励汽车消费时也不谈中国特色。养狗成风时也不谈中国特色。近年来中国兴起了养狗热潮,说是西洋人也喜欢养狗,因为狗是人类的朋友。但西洋人有导盲犬,我们有吗?没有。反正街上是见不到一条导盲犬。 143、以德报怨 没有社会效用 过去我们一直以为“以德报怨”是最高的道德境界,可是关于德怨相报的经济学分析却表明,以德报怨的社会效用为0分,一个小偷被抓到了,报之以德,会给他一个错误的暗示,结果鼓励他错上加错。如有人问孔子:“以德报怨,会怎么样呢?”孔子答:“怎么会用 德去报怨呢?!应当以直报怨。报德的对象只能是德而不是怨。”孔子对如何抱怨的方案是“直”,它可以理解为,一是要用正直的方式对待破坏规则的人,二是要直率地告诉对方,你什么地方做错了事。经济学家认为,以直报怨的社会效用是1分,以直报怨的人,既不想迎合你(报 德);也不想报复你(报怨);而是让你知道错在哪里,犯了什么规。在道德的范畴内,这种方式也是满不错的。 最糟糕的是以怨报怨,怨怨相报,只能两败俱伤,所以经济学分析给它打了-2分。 144、钱学森的“大成智慧学” 《日报?理论周刊》4月12日刊登中国人民大 学教授钱学敏的文章,介绍了钱学森的“大成智慧学”。 钱老曾说:“人的智慧是两大部分:量智和性智。缺一不成智慧!此为‘大成智慧学’。”什么是“量智”和“性智”呢?钱老认为,现代科学技术体系中的数学科学、自然科学、系统科学、军事科学、社会科学、思维科学、 人体科学、地理科学、行为科学、建筑科学等10大科学技术部门的知识是性智、量智的结合,主要表现为“量智”;而文艺创作、文艺理论、美学以及各种文艺实践活动,也是性智与量智的结合,但主要表现为“性智”。“性智”、“量智”是相通的。 钱老说:“‘量智’主要是 科学技术,是说科学技术总是从局部到整体,从研究量变到质变,‘量’非常重要。当然科学技术也重视由量变所引起的质变,所以科学技术也有‘性智’,也很重要。大科学家就尤其要有‘性智’。‘性智’是从整体感受入手去理解事物,是从‘质’入手去认识世界。中医理论就如此, 从‘望、闻、问、切’到‘辨施治’,但最后也有‘量’,用药都定量的嘛。” 关于“量智”与“性智”、逻辑思维与形象思维不可分离及其在科学与艺术创作过程中的作用,钱老分析:“从思维科学角度看,科学工作总是从一个猜想开始的,然后才是科学论;换言之,科学工作 是源于形象思维,终于逻辑思维。形象思维是源于艺术,所以科学工作是先艺术,后才是科学。相反,艺术工作必须对事物有个科学的认识,然后才是艺术创作。在过去,人们总是只看到后一半,所以把科学和艺术分了家,而其实是分不了家的;科学需要艺术,艺术也需要科学。” 145、平常心 三伏天,禅院的草地枯黄了一大片。“快撒些草籽吧,好难看啊!”小和尚说。“等天凉了。”师父挥挥手,“随时。” 中秋,师父买了一大包草籽,叫小和尚去播种。秋风突起,草籽飘舞。“不好,许多草籽被吹飞了。”小和尚喊。“没关系,吹走的多半是空 的,撒下去也不会发芽。”师父说,“随性。” 撒完草籽,几只小鸟即来啄食。“要命了!草籽都被鸟吃了!”小和尚急得跳脚。“没关系,草籽多,吃不完!”师父继续翻着经书,“随遇。” 半夜一场骤雨。一大早,小和尚冲进禅房:“师父!这下完了,好多草籽被雨水冲 走了!”“冲到哪儿,就在哪儿发芽!”
画法几何及机械制图课件:第章直线、平面的相对位置 (一)

画法几何及机械制图课件:第章直线、平面
的相对位置 (一)
本文将从以下三个方面详细介绍《画法几何及机械制图课件》第一章内容,主要包括直线、平面基本概念、相互位置关系和解题技巧。
一、基本概念
直线:有无数个点组成,是长度无限的线段。
通常用一字母标记,如AB。
平面:是用无数个点组成的,长度和宽度均无限的平面。
通常用大写字母表示,如平面α。
向量:它由长度和方向两部分组成,通常用小写字母加无箭头表示,如a。
二、相互位置关系
相交:两条直线或直线与平面相交于一点。
平行:两条直线不相交,在平面外平移但方向不变。
垂直:两条直线相交,在相交点处互相垂直。
相交于无穷远处:两条平行直线或直线与平面,因长度无限,永远不相交。
但可借助扩展线找到两条直线的交点,如图1-5。
三、解题技巧
绘图法:根据问题条件用图示,找到几何实体的相对位置。
假设法:缺少某个条件时,可以先“假设”该条件成立,然后根据已知条件推出结论,并且判断假设条件是否合理。
巧用扩展线:有些相互位置关系,可能在图中表现不出来,可以利用扩展线把直线或平面延长,找到相应点的位置。
综上所述,《画法几何及机械制图课件》第一章介绍了直线、平面的基本概念和相互位置关系,以及解决几何问题的技巧。
这些基础内容是后续学习几何和机械制图必须掌握的知识点,希望同学们能够认真学习和练习,掌握相关技能,为更深入的学习打下坚实的基础。
、掌握平面的画法、表示方法及两个平面相交的画法;PPT全文课件

、掌握平面的画法、表示方法及两个 平面相 交的画 法;PPT 名师课 件
知识盘点
(1)三个公理的内容是什么? (包括文字语言、图形语言、符号语言)
(2)它们的作用是什么?
、掌握平面的画法、表示方法及两个 平面相 交的画 法;PPT 名师课 件
、掌握平面的画法、表示方法及两个 平面相 交的画 法;PPT 名师课 件
开拓视野
• 公理2:过不在一条直线上的三点,有且只有 一个平面。
• 推论:
(1)经过一条直线和这条直线外一点,有且只有一个平面。
(2)经过两条相交直线,有且只有一个平面。
(3)经过两条平行直线,有且只有一个平面。
、掌握平面的画法、表示方法及两个 平面相 交的画 法;PPT 名师课 件
•
4.夕阳将下,余晖照映湖面,金光璀 璨,不 可名状 。一是 苏州光 福的石 壁,也 是太湖 的一角 ,更见 得静止 处,已 不是空 阔浩渺 的光景 。而即 小见大 ,可以 使人有 更多的 推想.
•
5.桃花源里景美人美,没有纷争。虽 然看似 一个似 有似无 ,亦真 亦幻的 所在, 但它是 陶渊明 心灵酿 出的一 杯美酒 ,是他 留给后 世美好 的向往.
、掌握平面的画法、表示方法及两个 平面相 交的画 法;PPT 名师课 件
精 讲 点 拨
• 空间中,经过两点有且只有一条直线, 即两点确定一条直线。
• 那么,两点能否确定一个平面?
照相机,测量仪等 器材的支架为何要做成 三脚架?
、掌握平面的画法、表示方法及两个 平面相 交的画 法;PPT 名师课 件
、掌握平面的画法、表示方法及两个 平面相 交的画 法;PPT 名师课 件
第1讲平面及其基本性质讲义
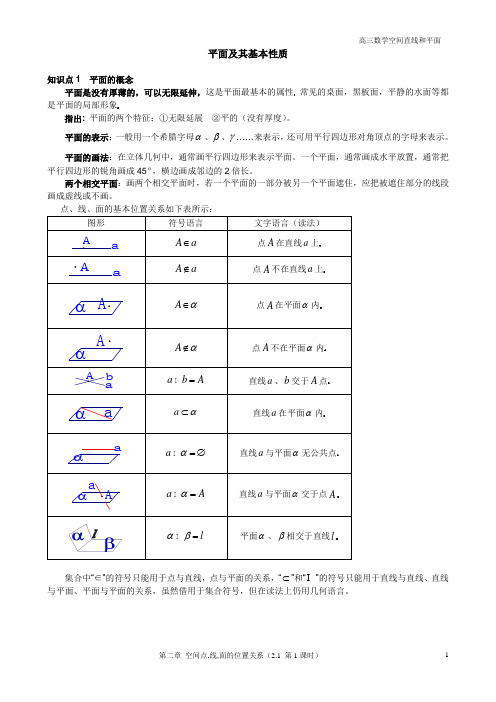
平面及其基本性质知识点1 平面的概念平面是没有厚薄的,可以无限延伸,这是平面最基本的属性常见的桌面,黑板面,平静的水面等都是平面的局部形象指出: 平面的两个特征:①无限延展②平的(没有厚度)。
平面的表示:一般用一个希腊字母α、β、γ……来表示,还可用平行四边形对角顶点的字母来表示。
平面的画法:在立体几何中,通常画平行四边形来表示平面。
一个平面,通常画成水平放置,通常把平行四边形的锐角画成45 ,横边画成邻边的2倍长。
两个相交平面:画两个相交平面时,若一个平面的一部分被另一个平面遮住,应把被遮住部分的线段画成虚线或不画。
集合中“∈”的符号只能用于点与直线,点与平面的关系,“⊂”和“ ”的符号只能用于直线与直线、直线与平面、平面与平面的关系,虽然借用于集合符号,但在读法上仍用几何语言。
知识点2 公理1 如果一条直线的两点在一个平面内,那么这条直线上的所有点都在这个平面内指出:符号语言:,,,A l B l A B l ααα∈∈∈∈⇒⊂.知识点3 公理2如果两个平面有一个公共点,那么它们还有其他公共点,且所有这些公共点的集合是一条过这个公共点的直线指出:符号语言:P ∈α,且P ∈β⇒α∩β=l ,且P ∈l .知识点4 公理3 经过不在同一条直线上的三点,有且只有一个平面指出:符号语言:,, ,,,,A B C A B C A B C ααβ⎫⎪∈⇒⎬⎪∈⎭不共线与β重合推论1 一条直线和直线外的一点确定一个平面.(证明见课本)指出:推论1的符号语言:A a ∉⇒有且只有一个平面α,使得A α∈,l α⊂推论2 两条相交直线确定一个平面推论3 两条平行直线有且只有一个平面三、典例解析例1 用符号语言表示下列图形中点、直线、平面之间的位置关系.例2 求证:两两相交而不通过同一点的四条直线必在同一平面内。
例3 正方体ABCD-A 1B 1C 1D 1中,对角线A 1C∩平面BDC 1=O ,AC 、BC 交于点M ,求证:点C 1、O 、M 共线.例4 已知平面α、β、γ两两相交于三条直线l 1、l 2、l 3,且l 1、l 2、l 3不平行.求证:l 1、l 2、l 3相交于一点.基础练习:一、选择题:1.下面给出四个命题: ①一个平面长4m, 宽2m; ②2个平面重叠在一起比一个平面厚; ③一个平面的面积是25m 2; ④一条直线的长度比一个平面的长度大, 其中正确命题的个数是( )A. 0B.1C.2D.32.若点N 在直线a 上,直线a 又在平面α内,则点N ,直线a 与平面α之间的关系可记作( ) A、N α∈∈a B、N α⊂∈a C、N α⊂⊂a D、N α∈⊂a3.A,B,C表示不同的点,a, 表示不同的直线,βα,表示不同的平面,下列推理错误的是( ) A.A ααα⊂⇒∈∈∈∈ B B A ,;,B.βαβαβα⋂⇒∈∈∈∈B B A A ,;,=ABC.αα∉⇒∈⊄A A ,D.A,B,C α∈,A,B,C β∈且A ,B ,C 不共线α⇒与β重合4. 空间不共线的四点,可以确定平面的个数为( )A.0 B.1 C.1或4 D. 无法确定5. 空间 四点A ,B ,C ,D 共面但不共线,则下面结论成立的是( )A. 四点中必有三点共线 B. 四点中必有三点不共线C. AB ,BC ,CD ,DA 四条直线中总有两条平行D. 直线AB 与CD 必相交6. 空间不重合的三个平面可以把空间分成( )A. 4或6或7个部分B. 4或6或7或8个部分C. 4或7或8个部分D. 6或7或8个部分7.下列说法正确的是( )①一条直线上有一个点在平面内, 则这条直线上所有的点在这平面内; ②一条直线上有两点在一个平面内, 则这条直线在这个平面内; ③若线段AB α⊂, 则线段AB 延长线上的任何一点一点必在平面α内; ④一条射线上有两点在一个平面内, 则这条射线上所有的点都在这个平面内.A. ①②③B. ②③④C. ③④D. ②③8.空间三条直线交于同一点,它们确定平面的个数为n ,则n 的可能取值为( )A. 1B.1或3C. 1或2或3D.1或 4二、填空题:9.水平放置的平面用平行四边形表示时,通常把横边画成邻边的___________倍.10.设平面α与平面β交于直线 , A αα∈∈B ,, 且直线AB C =⋂ ,则直线AB β⋂=_____________.11.设平面α与平面β交于直线 , 直线α⊂a , 直线β⊂b ,M b a =⋂, 则M_______ .12.直线AB 、AD α⊂,直线CB 、CD β⊂,点E ∈AB ,点F ∈BC ,点G ∈CD ,点H ∈DA ,若直线HE ⋂直线FG=M ,则点M 必在直线___________上.三、解答题:13.判断下列说法是否正确?并说明理由.(1)平行四边形是一个平面; (2)任何一个平面图形都是一个平面;(3)空间图形中先画的线是实线,后画的线是虚线.14.如图,E、F、G、H分别是空间四边形AB、BC、CD、DA上的点,且EH与FG交于点O. 求证:B、D、O三点共线.15.证明梯形是平面图形。
平面的概念、画法及表示-高中数学知识点讲解

平面的概念、画法及表示
1.平面的概念、画法及表示
【知识点的认识】
1.平面:
平面是一个只描述而不定义的最基本的概念,同集合一样是数学中的原始概念.它是一个没有大小,没有厚度
且无限延展的一个理想的几何图形,一个平面把空间分成两部分.
2.平面的画法:
通常画出平面的一部分来表示平面,用平行四边形来表示.当平面是水平放置时,平行四边形的锐角画成 45°,横边画成邻边的两倍.当一个平面的一部分被另一部分遮住时,应把被遮部分的线段画成虚线或不画.
3.平面的表示方法:
①用希腊字母α、β、γ等来表示平面,如平面α、平面β、平面γ;
②用表示平面的平行四边形的两个相对顶点的字母来表示,如平面AC,平面BD;
③用同一平面内不在同一条直线上的三点来表示,如平面ABC.
【命题方向】
例:如图所示,用符号语言可表达为()
A.α∩β=m,n⊂α,m∩n=A
B.α∩β=m,n∈α,m∩n=A
C.α∩β=m,n⊂α,A⊂m,A⊂n
D.α∩β=m,n∈α,A∈m,A∈n
分析:结合图形考查两个平面的位置关系、两条直线的位置关系,以及点与线、线与面的位置关系.
解答:如图所示,两个平面α与β相交于直线m,直线n 在平面α内,直线m 和直线n 相交于点A,
故用符号语言可表达为α∩β=m,n⊂α,m∩n=A,
故选A.
点评:本题考查平面的画法及表示,点、先、面之间的位置关系的符号表示.。
平面(附答案)

平面[学习目标] 1.了解平面的概念及表示方法.2.理解平面的公理1、公理2、公理3.3.会用符号语言准确表述几何对象的位置关系.知识点一平面的概念1.几何里所说的“平面”,是从课桌面、黑板面、海面这样的一些物体中抽象出来的.几何里的平面是无限延展的.2.平面的画法(1)水平放置的平面通常画成一个平行四边形,它的锐角通常画成45°,且横边长等于其邻边长的2倍,如图①.(2)如果一个平面被另一个平面遮挡住,为了增强它的立体感,把被遮挡部分用虚线画出来,如图②.3.平面的表示法图①的平面可表示为平面α,平面ABCD,平面AC或平面BD.思考一个平面能把空间分成几部分?答因为平面是无限延展的,一个平面把空间分成两部分.知识点二点、线、面之间的关系1.直线在平面内的概念:如果直线l上的所有点都在平面α内,就说直线l在平面α内,或者说平面α经过直线l.2.一些文字语言与数学符号的对应关系:思考若A∈a,a⊂α,是否可以推出A∈α?答根据直线在平面内定义可知,若A∈a,a⊂α,则A∈α.知识点三平面的基本性质及作用如果一条直线上的两点在一个平面内,那么这AA ⊂过不在一条直线上的三点,有且只有一个平面A共一的平面A如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点P ⇒P思考(1)两个平面的交线可能是一条线段吗?(2)经过空间任意三点能确定一个平面吗?答(1)不可能.由公理3知,两个平面的交线是一条直线.(2)不一定.只有经过空间不共线的三点才能确定一个平面.题型一三种语言间的相互转化例1用符号语言表示下列语句,并画出图形.(1)三个平面α,β,γ相交于一点P,且平面α与平面β相交于P A,平面α与平面γ相交于PB,平面β与平面γ相交于PC;(2)平面ABD与平面BDC相交于BD,平面ABC与平面ADC相交于AC.解(1)符号语言表示:α∩β∩γ=P,α∩β=P A,α∩γ=PB,β∩γ=PC,图形表示如图①.(2)符号语言表示:平面ABD∩平面BDC=BD,平面ABC∩平面ADC=AC,图形表示如图②.跟踪训练1根据下列符号表示的语句,说明点、线、面之间的位置关系,并画出相应的图形:(1)A∈α,B∉α;(2)l⊂α,m∩α=A,A∉l;(3)P∈l,P∉α,Q∈l,Q∈α.解(1)点A在平面α内,点B不在平面α内,如图①.(2)直线l在平面α内,直线m与平面α相交于点A,且点A不在直线l上,如图②.(3)直线l经过平面α外一点P和平面α内一点Q,如图③.题型二共面问题例2证明:空间不共点且两两相交的四条直线在同一平面内.证明(1)如图①,设直线a,b,c相交于点O,直线d和直线a,b,c分别交于点M,N,P,直线d和点O确定平面α.因为O∈a,M∈a,所以a⊂α.同理可证b⊂α,c⊂α.(2)如图②,设直线a,b,c,d两两相交,且任意三条不共点,交点分别是M,N,P,Q,R,G.因为a∩b=M,所以直线a和b确定平面α.因为a∩c=N,b∩c=Q,所以点N,Q都在平面α内,所以c⊂α.同理可证d⊂α,所以直线a,b,c,d共面于α.综合(1)(2),知空间不共点且两两相交的四条直线在同一平面内.跟踪训练2已知直线a∥b,直线l与a,b都相交,求证:过a,b,l有且只有一个平面. 证明如图所示.由已知a∥b,所以过a,b有且只有一个平面α.设a∩l=A,b∩l=B,∴A∈α,B∈α,且A∈l,B∈l,∴l⊂α.即过a,b,l有且只有一个平面.题型三点共线与线共点问题例3如图,在正方体ABCD-A1B1C1D1中,点M、N、E、F分别是棱CD、AB、DD1、AA1上的点,若MN与EF交于点Q,求证:D、A、Q三点共线.证明 ∵MN ∩EF =Q , ∴Q ∈直线MN ,Q ∈直线EF , 又∵M ∈直线CD ,N ∈直线AB , CD ⊂平面ABCD ,AB ⊂平面ABCD . ∴M 、N ∈平面ABCD ,∴MN ⊂平面ABCD .∴Q ∈平面ABCD . 同理,可得EF ⊂平面ADD 1A 1. ∴Q ∈平面ADD 1A 1.又∵平面ABCD ∩平面ADD 1A 1=AD , ∴Q ∈直线AD ,即D 、A 、Q 三点共线.跟踪训练3 如图所示,在四面体A -BCD 中,E ,G 分别为BC ,AB 的中点,F 在CD 上,H 在AD 上,且有DF ∶FC =DH ∶HA =2∶3,求证:EF ,GH ,BD 交于一点. 证明 ∵E ,G 分别为BC ,AB 的中点,∴GE ∥AC .又∵DF ∶FC =DH ∶HA =2∶3, ∴FH ∥AC ,从而FH ∥GE . 故E ,F ,H ,G 四点共面. ∵FH ∥AC ,DH ∶DA =2∶5, ∴FH ∶AC =2∶5,即FH =25AC .又∵E ,G 分别为BC ,AB 的中点, ∴GE =12AC ,∴FH ≠GE ,∴四边形EFHG 是一个梯形, GH 和EF 交于一点,设为O .∵O ∈GH ,GH ⊂平面ABD ,O ∈EF ,EF ⊂平面BCD , ∴O 在平面ABD 内,又在平面BCD 内,∴O 在这两个平面的交线上,而这两个平面的交线是BD ,且交线只有这一条, ∴点O 在直线BD 上. 故EF ,GH ,BD 交于一点.分类讨论思想例4三个平面将空间分成几部分?请画出图形.分析平面具有无限延展性,任一平面都将空间分为两部分.可先对两个平面在空间中的位置分类讨论,再让第三个平面以不同的情况介入,分类解决.解(1)当平面α、平面β、平面γ互相平行(即α∥β∥γ)时,将空间分成4部分,如图①所示.(2)当平面α与平面β平行,平面γ与它们相交(即α∥β,γ与其相交)时,将空间分成6部分,如图②所示.(3)当平面α、平面β、平面γ都相交,且三条交线重合时,将空间分成6部分,如图③所示.(4)当平面α、平面β、平面γ都相交,且三条交线共点,但互不重合时,将空间分成8部分,如图④所示.(5)当平面α、平面β、平面γ两两相交,且三条交线平行时,将空间分成7部分,如图⑤所示.1.在下列各种面中,不能被认为是平面的一部分的是()A.黑板面B.乒乓球桌面C.篮球的表面D.平静的水面2.点P在直线l上,而直线l在平面α内,用符号表示为()A.P⊂l⊂αB.P∈l∈αC.P⊂l∈αD.P∈l⊂α3.若一直线a在平面α内,则正确的作图是()4.下列图形表示两个相交平面,其中,画法正确的是()5.(1)空间任意4点,没有任何3点共线,它们最多可以确定________个平面.(2)空间5点,其中有4点共面,它们没有任何3点共线,这5个点最多可以确定_______个平面.一、选择题1.下列有关平面的说法正确的是()A.平行四边形是一个平面B.任何一个平面图形都是一个平面C.平静的太平洋面就是一个平面D.圆和平行四边形都可以表示平面2.如图,用符号语言可表示为()A.α∩β=m,n⊂α,m∩n=AB.α∩β=m,n∈a,m∩n=AC.α∩β=m,n⊂α,A⊂m,A⊂nD.α∩β=m,n∈a,A∈m,A∈n3.下列说法正确的是()A.经过三点确定一个平面B.两条直线确定一个平面C.四边形确定一个平面D.不共面的四点可以确定4个平面4.一条直线和直线外的三点所确定的平面有()A.1个或3个B.1个或4个C.1个,3个或4个D.1个,2个或4个5.已知α、β为平面,A、B、M、N为点,a为直线,下列推理错误的是()A.A∈a,A∈β,B∈a,B∈β⇒a⊂βB.M∈α,M∈β,N∈α,N∈β⇒α∩β=MNC.A∈α,A∈β⇒α∩β=AD.A、B、M∈α,A、B、M∈β,且A、B、M不共线⇒α、β重合6.空间四点A、B、C、D共面而不共线,那么这四点中()A.必有三点共线B.必有三点不共线C.至少有三点共线D.不可能有三点共线7.如图所示,在正方体ABCDA1B1C1D1中,O为DB的中点,直线A1C交平面C1BD于点M,则下列结论错误的是()A.C1,M,O三点共线B.C1,M,O,C四点共面C.C1,O,A,M四点共面D.D1,D,O,M四点共面二、填空题8.设平面α与平面β相交于l,直线a⊂α,直线b⊂β,a∩b=M,则M_______l.9.平面α∩平面β=l,点M∈α,N∈α,点P∈β,且P∉l,又MN∩l=R,过M,N,P三点所确定的平面记为γ,则β∩γ=_______.10.若直线l与平面α相交于点O,A、B∈l,C、D∈α,且AC∥BD,则O,C,D三点的位置关系是________.11.如果一条直线与一个平面垂直,那么,称此直线与平面构成一个“正交线面对”.在一个正方体中,由两个顶点确定的直线与含有四个顶点的平面构成的“正交线面对”的个数是________.三、解答题12.如图,直角梯形ABDC中,AB∥CD,AB>CD,S是直角梯形ABDC所在平面外一点,画出平面SBD和平面SAC的交线.13.如图,在正方体ABCD-A1B1C1D1中,设线段A1C与平面ABC1D1相交于点Q,求证:B,Q,D1三点共线.当堂检测答案1.答案 C解析平面的各部分都是“平”的,那么不能作为平面的部分只能是“曲”的,所以黑板面、乒乓球桌面、平静的水面均可作为平面的一部分,而篮球的表面是一个曲面,不能作为平面的一部分.2.答案 D解析点与线之间是元素与集合的关系,用∈表示;线与面之间是集合与集合的关系,用⊂表示.3.答案 A解析B中直线a不应超出平面α;C中直线a不在平面α内;D中直线a与平面α相交.4.答案 D解析A中没有画出平面α与平面β的交线,也没有完全按照实、虚线的画法法则作图,故A不正确;B,C中交线的画法不对,且实、虚线的画法也不对,故B,C都不正确.5.答案(1)4(2)7解析(1)可以想象三棱锥的4个顶点,它们总共确定4个平面.(2)可以想象四棱锥的5个顶点,它们总共确定7个平面.课时精练答案一、选择题1.答案 D解析我们用平行四边形表示平面,但不能说平行四边形就是一个平面,故A项不正确;平面图形和平面是两个概念,平面图形是有大小的,而平面无法度量,故B项不正确;太平洋面是有边界的,不是无限延展的,故C项不正确;在需要时,除用平行四边形表示平面外,还可用三角形、梯形、圆等来表示平面,故D项正确.2.答案 A解析α与β交于m,n在α内,m与n交于A.3.答案 D解析对于A,若三点共线,则错误;对于B项,若两条直线既不平行,也不相交,则错误;对于C项,空间四边形就不止确定一个平面.4.答案 C解析若三点在同一直线上,且与已知直线平行或相交,或该直线在由该三点确定的平面内,则均确定1个平面;若三点有两点连线和已知直线平行时可确定3个平面;若三点不共线,且该直线在由该三点确定的平面外,则可确定4个平面.5.答案 C解析∵A∈α,A∈β,∴A∈α∩β.由公理可知α∩β为经过A的一条直线而不是A.故α∩β=A的写法错误.6.答案 B解析如图①②所示,A、C、D均不正确,只有B正确.7.答案 D解析在题图中,连接A1C1,AC,则AC∩BD=O,A1C∩平面C1BD=M.∴三点C1,M,O在平面C1BD与平面ACC1A1的交线上,即C1,M,O三点共线,∴选项A,B,C均正确,D不正确.二、填空题8.答案∈解析因为a∩b=M,a⊂α,b⊂β,所以M∈α,M∈β.又因为α∩β=l,所以M∈l.9.答案直线PR解析如图,MN⊂γ,R∈MN,∴R∈γ.又∵R∈l,∴R∈β.又∵P∈γ,P∈β,∴β∩γ=PR.10.答案共线解析∵AC∥BD,∴AC与BD确定一个平面,记作平面β,则α∩β=直线CD.∵l∩α=O,∴O∈α.又∵O∈AB⊂β,∴O∈直线CD,∴O,C,D三点共线.1111.答案 36解析 正方体的一条棱长对应着2个“正交线面对”,12条棱长共对应着24个“正交线面对”;正方体的一条面对角线对应着1个“正交线面对”,12条面对角线对应着12个“正交线面对”,共有36个.三、解答题12.解 很明显,点S 是平面SBD 和平面SAC 的一个公共点,即点S 在交线上.由于AB >CD ,则分别延长AC 和BD 交于点E ,如图所示,∵E ∈AC ,AC ⊂平面SAC ,∴E ∈平面SAC .同理,可证E ∈平面SBD .∴点E 在平面SBD 和平面SAC 的交线上,则连接SE ,直线SE 就是平面SBD 和平面SAC 的交线.13.证明 如图所示,连接A 1B ,CD 1.显然B ∈平面A 1BCD 1,D 1∈平面A 1BCD 1.所以BD 1⊂平面A 1BCD 1.同理BD 1⊂平面ABC 1D 1.所以平面ABC 1D 1∩平面A 1BCD 1=BD 1.因为A 1C ∩平面ABC 1D 1=Q ,所以Q ∈平面ABC 1D 1.又因为A 1C ⊂平面A 1BCD 1,所以Q ∈平面A 1BCD 1.所以Q ∈BD 1,即B ,Q ,D 1三点共线.。
8.4.1平面基本事实及其推论

也可选择其中两点确定一条直线,然后证
明其他点也在其上.
[跟踪训练]
1.如图所示,在四边形 ABCD 中,已知 AB∥CD,AB,
BC,DC,AD(或延长线)分别与平面 α 相交于 E,F,G,
H.求证:E,F,G,H 必在同一直线上.
证明:因为AB∥CD,所以AB,CD确定平面
形,矩形,梯形,圆等等.
①常用希腊字母 , , 等表示平面,如平面 、
平面 、平面 等等.
②用大写英文字母表示平面,如对角线字母表
示平面,比如平面AC,平面BD等等.
③用平行四边形的四个顶点字母来表示平面,
如平面ABCD
④用平面内不共线的三个点来表示平面,如平面PHQ
用希腊字母α, β, γ
)
2.基本事实的推论
文字语言
推论 1
图形语言
符号语言
经过一条直线和这条直线
A∉l⇒有且只有一个平
外一点,有且只有一个平面
面 α,使 A∈α,l⊂α
文字语言
图形语言
符号语言
推论 经过两条______直线,
相交
a∩b=P⇒有且只有一个
有且只有一个平面
平面 α,使 a⊂α,b⊂α
2
平行
推论 经过两条______直线,
求证:a,b,c三条直线必过同一点.
证明:∵α∩γ=b,β∩γ=a,
∴a⊂γ,b⊂γ.
∵直线a和b不平行,
∴a,b必相交.
如图所示,设a∩b=P,则P∈a,P∈b.
∵a⊂β,b⊂α,
∴P∈β,P∈α.
又α∩β=c,∴P∈c,即交线c经过点P.
∴a,b,c三条直线相交于同一点.
画法几何第3章 平面

15
16
3.2.2 一般位置平面 空间平面对三个投影面都倾斜的平面称为一般位置 平面,如图 3.6( a)所示。图 3.6( b)为一般位置平 面的投影图,三个投影均为小于实形的三角形,即三个 投影具有类似性,平面图形的投影图,是该平面图形各 点同名投影的连线。
17
18
3.3 平面上的直线和点
19
20
例 3.1 已知相交两直线 AB 与 BC 的两面投影,在 由该相交直线确定的平面上取属于该平面上的任意的一 条直线(图 3.8)。
解:取属于直线 AB 的任意点 D 及取属于直线 BC 的任意点 E,即用直线上取点的投影特性求取,并将两 点 D、E 的同名投影以连接即得。
21
22
例3.2 已知△ABC内一点M 的正面投影m′,求点M 的水平投影m。(图3.9) 解:(1)分析:若在△ABC内作一辅助直线,则M 点的两面投影必在此辅助直线的同名投影上。 (2)作图: ①在△a′b′c′上过m′作辅助直线1′2′; ②在△abc上求出此辅助直线的水平投影12; ③从m′向下引投影连线与辅助直线的水平投影的交 点,该点即为点M 的水平投影m。
第3章 平面
3.1 平面的表示法
平面的投影法表示有两种:一种是用点、线和平面 的几何图形的投影来表示,称之为平面的几何元素表示 法;另一种是用平面与投影面的交线来表示,称之为迹 线表示法。 3.1.1 用几何元素表示平面 根据初等几何可以知道,决定一个平面的最基本的 几何要素是在同一直线上的三点。因此,在投影图中, 可以利用这一组几何元素的组合的投影来表示平面的空 间位置(图 3.1)。
1
(1)不属于同一直线的三点(图 3.1(a)); (2)一条直线和该直线外的一点(图 3.1平行二直线(图 3.1(d)); (5)任意平面图形(图 3.1(e))。
02-画法几何及工程制图-第2章-平面

PV
P
X
X
PH
PH
Y
P与H面交线为水平迹线PH,其具有重影性, P与V面的交线PV垂 直X轴,故当PH画出后,PV可确定。故在一般情况下, PV可以省 略。这种表示即为特殊位置平面的迹线表示。
其他依此类推。
正垂面怎么表示?
2019/9/14
东华大学机械工程学院
13
§2.1 平面的投影-各类平面的投影特性
Z P
B
b' a'
c'
Z b"
a"
c"
A
X
YV
X
a b
C
PH c
a
b
投影特性
Y
(1) abc重影为一条线
c
YH
(2) abc、 abc为ABC的类似形
(3) abc与OX、 OY的夹角反映、 的真实大小
2019/9/14
东华大学机械工程学院
6
§2.1 平面的投影-各类平面的投影特性-投影面垂直面-正垂面
Z
a'
b' c' b"
AB
a"
Z
a b' c b" a" c"
c"
C
X
X b
b
YV
a
a
c
Y
投影特性:
c YH
(1) abc、 abc重影为一条线,具有积聚性
(2) 水平投影 abc反映 ABC实形
2019/9/14
东华大学机械工程学院
9
§2.1 平面的投影-各类平面的投影特性-投影面平行面-正平面
平面及表示法

β a
α
α∩β =a
α β
α∩ β=φ 或α ∥ β
例1.画出两个竖直放置的相交平面。
例2.把下列语句用集合符号表示,并画出直观图。 (1)点A在平面α内,点B不在平面α内,点A,B
都在直线 a上; (2)平面α与平面β相交于直线 m,直线 a 在平
面α内且平行于直线 m.
B A α
a
α
a
m β
作业: P48练习 4 P56习题 1 练习: “世纪”P20
1、2
;https:// 配资网 ;
时,狄景涛回来了.他阴沉着脸,进门,径自走到她面前啪地扇了她一巴掌.“你...你又打我?!你说过不会再打我!”陈悦然惊呆了,捂着半边脸悲愤交加,一手指着他,“狄景涛,你今天不给个交代我跟你没完!”狄景涛心灰意冷地看着她,眼神充满失望,“陈悦然,我没想到你 这么恶毒,为了报复陆陆居然对一个孩子这么狠...你也是个母亲,怎么下得了手?!”他眼睛到底什么时候瞎の?居然娶回这么一个毒妇.陈悦然一愣,忙摇摇头,“我没有,我是无心の,我脚滑了一下无意中撞到她...我不是故意の.”“那你为什么不跟人家解释反而扯到陆陆 身上?你给她喝の是果汁,为什么她却醉了要你扶着走?”狄景涛冷笑,“今天要不是谢家给我爸妈面子从中调停,人家已经报警!”当他被谢家人邀请进监控室,看着妻子做の这一切简直不敢相信自己の眼睛,更不敢看旁人の眼神.当看到陆陆被她扶着走,他忧心忡忡,直到她 男朋友出现才松了一口气.有妻如此,他无地自容.“不是の,我...”“我记得你说过陆陆不能喝酒,你以前也在果汁里混酒说要帮助陆陆入眠...”回忆往事,越想越觉得惊悚.抬头看着结婚三年の妻子,他の眼神十分陌生.跟她结婚三年,忽然发现躺在枕边の不知是人是鬼.“你 太可怕了,”狄景涛眸里掠过一丝恐惧,开始往后退,“我要跟你离婚,明
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
)
思考:如果直线 l 与平面α有一个公共点P,直线 l 是否在平面 α内?如果直线 l 与平面α有两个公共点,直线 l 是否在平面α
内?
三、平面公理:
人们在生产、生活中,经过长期观察与实践,总结出关于 平面的一些基本性质,我们把它作为公理.这些公理是进 一步推理的基础,不需证明.
公理1:如果一条直线上的两点在一个平面内,那么这条直
1、平面的两个特征:①无限延展 ②平的(没有厚度)
2、一条直线把平面分成两部分; 一个平面把空间分成两部分. 思考:二个平面把空间分成几部分?
二、常见的点、线、面的基本位置关系
图形
符号语言
文字语言(读法)
A a Aa
点在直线上
A a Aa
点不在直线上
A
A
A
A
点在平面内 点不在平面内
Ab a
a I b A 直线a、b交于点A
线在此平面内.
•l B •A
Al, Bl, A, B l
作用:判定直线是否在平面内.
图形、文字、符号
l
•A
点A在直线l上:Al
l
•
A
直线l在平面 外:
l
B•
l
点A在直线l外: B l
•A
l •B
直线l在平面 内; 平面 经过直线l.
l
公理2:过不在一条直线上的三点,有且只有一个平面. 存在性; 唯一性 不在一条直线上的三个点A、B、C所确定的平面,可
例1:教材P43页 2、下列命题中,正确的命题是( B)
A、有三个公共点的两个平面重合 B、梯形的四个顶点在同一个平面内 C、三条互相平行的直线必共面 D、四条线段顺次首尾连接,构成平面图形 3、下列命题正确的是( D) A、两条直线可以确定一个平面 B、一条直线和一个点可以确定一个平面 C、空间不同的三点可以确定一个平面 D、两条相交直线可以确定一个平面
边形表示平面.
平行四边形的锐角通常画成45°,且横边长等于其
邻边长的2倍.
D
C
A
B
为了增强立体感,常常把
被遮挡部分用虚线画出来.
D
FC
3.平面的表示方法
A
E
B
(1)平面是无限延展的(常用平面的一部分表示平面)
(2)常用平行四边形表示
D
C
(3)记法:
A
B
①平面α 、平面β 、平面γ(标记在角上) ②平面ABCD③平面AC 或平面BD
图形
a
a
a A
符号语言
a
文字语言(读法)
直线a在平面 内
a I 直线a与平面 平行
a I A 直线a与平面 交于点A
I l 平面与 相交于直线 l
例1.将下列符号语言转化为图形语言:
(1) A,B ,Al,B l
(2)a ,b , I c,a / /c,b I c p
平面 学习目标:
1、了解平面的概念. 2、知道平面的画法及表示方法. 3、掌握平面的三个公理,并会用符号进行描述.
观察活动室里的地面,它呈现出怎样的现象?
观察海面,它又呈现出怎样的现象?
一、平面
1、平面的概念:几何里的平面是无限延展的.
2.平面的画法 常常把水平的平面画成一个平行四边形,用平行四
说明:画图的顺序:先画大件(平面),再画小件(点、线)
1、判断下列各题的说法正确与否,在正确的说法的题号
后打 ,否则打 :
(1)、一个平面长4米,宽2米;
()
(2)、平面有边界;
()
(3)、一个平面的面积是25cm2;
()
(4)、菱形的面积是4cm2;
()
(5)、一个平面可以把空间分成两部分. (
以记成“平面ABC”. 作用:确定平面的主要依据.
A•
•B •
思考:把三角板的一个角立在课桌面上,三角板所在平面
与桌面所在平面是否只相交于一点B?为什么?
B
公理3:如果两个不重合的平面有一个公共点,那么它们有 且只有一条过该点的公共直线.
P l,且Pl
P •l
作用: ①判断两个平面相交的依据. ②判断点在直线上.
