第四章 交通流特性
合集下载
交通流理论(详细版)
3
§4-1 概述
二、发展
• • • • • 在20世纪30年代才开始发展，概率论方法 概率论方法。 概率论方法 1933年，Kinzer.J.P泊松分布用于交通分析的可能性。 1936年，Adams.W.F发表数值例题。 1947年，Greenshields泊松分布用于交叉口分析。 20世纪50年代，跟驰理论 交通波理论 流体动力学 跟驰理论，交通波理论 跟驰理论 交通波理论(流体动力学 模拟)和车辆排队理论 车辆排队理论。 模拟 车辆排队理论 • 1975年丹尼尔(DanieL lG)和马休（Marthow，J.H） 出版了《交通流理论》一书。 • 1983年，蒋璜翻译为中文。人交出版社出版。
15
k=0,1,2,…n p=λt/n 一辆车到达的概率
k Pk = Cn p k (1 − p ) n − k
§4-2 交通流的统计分布特性
2.二项分布 2.二项分布
(3) 递推公式
P0 = (1 − p)
n
Pk = C p (1 − p )
k n k
n−k
n−k p Pk +1 = ⋅ ⋅ Pk k +1 1− p
?负指数分布移位负指数分布爱尔朗分布8?在一定的时间间隔内到达的车辆数或在一定的路段上分布的车辆数在一定的时间间隔内到达的车辆数或在一定的路段上分布的车辆数是所谓的随机变数描述这类随机变数的统计规律用的是离散型分布42交通流的统计分布特性二离散型分布泊松分布二项分布离散分布离散分布942交通流的统计分布特性1
N
18
§4-2 交通流的统计分布特性
三、连续型分布
• 车流到达的统计规律除了可用计数分布来描述外， 还可用车头时距分布来描述，这种分布属于连续 型分布。 负指数分布
城市道路交通调查与分析
瞬时地点车速行驶车速区间车速临界车速15位车速最低限制速度中位地点车速50位车速85位车速最高限制速度2交通流速度v车速2交通流速度v车速设计车速计算行车速度设计车速是指具有平均驾驶水平的驾驶员在道路交通与气候条件良好的情况下仅受道路条件限制所能保持的最大安全车速是道路线形几何设计的标准
第2章 城市道路交通调查与分析
一、交通流特性
2、三个交通流参数
交通量Q：某一特定时段内，通过道路某一地 点、某一断面或某一条车道的交通体的数量。 交通流速度V（车速） 交通密度K:某一瞬间，单位长度内某一车道、 某一方向或全部车道上的车辆数。
一、交通流特性
2、三个交通流参数
（1）交通量Q：某一特定时段内，通过道路某一 地点、某一断面或某一条车道的交通体的数量。
二、交通流统计分布 2、连续型分布——负指数分布
车头时距服从负指数分布的 车流特性见图，曲线是单调下降 的，说明车头时距愈短，出现的 概率愈大。
二、交通流统计分布 2、连续型分布
当负指数分布用于单车道交通流的车头时距分布时，理 论上会得出大量的0-1s的车头时距，但在实际中这种情 况不可能出现。因为车辆的车头至车头的间距至少为一 个车长加上前车尾部至后车头部的一定间隔。
二、交通流统计分布
交通流的统计分布特性是交通流特性预报的有效手段， 可使交通技术人员用少量的资料得出确切的预测结果。
交通的到达具有随机性，描述这种随机性的统计规律有 两种方法，即概率论中的离散型分布和连续性分布。
离散型分布又称计数分布，考查在一段固定长度的时间 内到达某场所的交通数量的波动性；连续型分布研究上述 事件发生的间隔时间的统计特性，如车头时距、车速和可 穿越空挡等的概率分布。
根据交通类型，可分为机动车交通量和非机动车交通量。
第2章 城市道路交通调查与分析
一、交通流特性
2、三个交通流参数
交通量Q：某一特定时段内，通过道路某一地 点、某一断面或某一条车道的交通体的数量。 交通流速度V（车速） 交通密度K:某一瞬间，单位长度内某一车道、 某一方向或全部车道上的车辆数。
一、交通流特性
2、三个交通流参数
（1）交通量Q：某一特定时段内，通过道路某一 地点、某一断面或某一条车道的交通体的数量。
二、交通流统计分布 2、连续型分布——负指数分布
车头时距服从负指数分布的 车流特性见图，曲线是单调下降 的，说明车头时距愈短，出现的 概率愈大。
二、交通流统计分布 2、连续型分布
当负指数分布用于单车道交通流的车头时距分布时，理 论上会得出大量的0-1s的车头时距，但在实际中这种情 况不可能出现。因为车辆的车头至车头的间距至少为一 个车长加上前车尾部至后车头部的一定间隔。
二、交通流统计分布
交通流的统计分布特性是交通流特性预报的有效手段， 可使交通技术人员用少量的资料得出确切的预测结果。
交通的到达具有随机性，描述这种随机性的统计规律有 两种方法，即概率论中的离散型分布和连续性分布。
离散型分布又称计数分布，考查在一段固定长度的时间 内到达某场所的交通数量的波动性；连续型分布研究上述 事件发生的间隔时间的统计特性，如车头时距、车速和可 穿越空挡等的概率分布。
根据交通类型，可分为机动车交通量和非机动车交通量。
行人交通流特性讲解
2.行人速度特性
(1)行人步行速度特性
步行速度分布范围较宽为0.5~1.5m/s，
成人一般集中在1.0~1.3m/s，
水平路段步行速度一般在0.5~1.5m/s
行人步行速度受诸多因素的影响，主要有：
①年龄和性别
青年的步速比中老年的大，男性比女性快。
②出行目的
换乘行人的步速一般在1.49m/s左右，
全体 0.62m
0.58m 0.59m 0.66人的身体在静止状态下所占的空间范
围，两肩的宽度和厚度是人行道空间和有关设施设计所必需
的基本尺寸，设计中肩宽、肩厚一般取为59.5cm和33cm。 行人动态空间需求可分为步幅区城（64cm）、感应区城（行 人知觉、心理和安全等因素影响）、行人视觉区城（2.1m） 以及避让与反应区域（自己前面预留一个可见的区域，以保 有足够的反应时间以便采取避让行为；0.48~0.6m）等。 心理缓冲空间：心理学家所做的人类心理缓冲区域测量实验，
行人过街特性中最主要的参数是行人过街速度，行 人的步行速度决定了他们与车辆交通相冲突的几率。
行人过街速度
m/s
性别
青年
中年
老年
男
女
1.32
1.21
1.28
1.28
1.10
1.01
3.行人步幅特性
步幅为步行者两脚先后着地，脚跟至脚跟或脚尖至脚
尖之间的距离，通常用m来表示。
步幅的分布区间因性别、年龄而稍有差别，95%的男
行人交通流特性
分析行人交通特性的目的：
• 步行交通是满足人们日常生活需要的一种基本交 通方式，行人出行活动是城市交通中的一个重要
组成成分。
• 准确分析行人交通特性，才能使行人和机动车可
第四章 交通流理论
各种类型的“顾客”按怎样的规律到达
定长输入：顾客等时距到达； 泊松输入：顾客到达时距符合负指数分布； 爱尔朗输入：顾客到达时距符合爱尔朗分布；
（2）排队规则
排 队 论 基 本 原 理
到达的“顾客”按怎样的次序接受服务
损失制：顾客到达时，若所有服务台被占，该顾
客就自动消失，永不再来；
第三节 排队论的应用
The Application of Queuing Theory
排 队 论 概 述
排队论也称随机服务系统理论，是研究“服务” 系统因“需求”拥挤而产生的等待行列或排队的 现象，以及合理协调“需求”与“服务”关系的 一种数学理论。是运筹学中以概率论为基础的一 个重要分支。 在交通工程中，排队论在研究车辆延误、通行能 力、信号配时以及停车场、收费厅、加油站等交 通设施的设计与管理诸方面得到广泛的应用。
Poisson distribution belongs to discrete function with only one parameter. In traffic engineering Poisson distribution equation is used to describe the arrivals of vehicles at intersections or toll booth, as well as number of accident (crash) Poisson distribution is appropriate to describe vehicle’s arrival when traffic volume is not high. When field data shows that the mean and variance have significant difference, we can no longer apply Poisson distribution.
交通流的特征
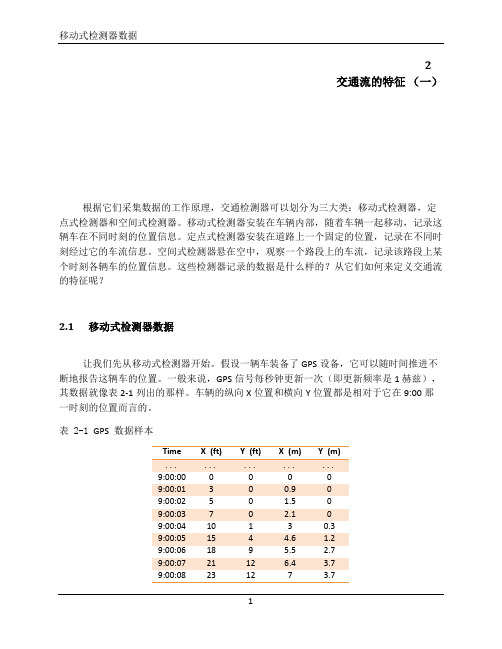
空间, x
道路
x v1 v2
hi vi vN
i
ti-1
ti T 时间, t
图 2-3 定点式检测器数据 4
定点式检测器数据 ������ = ������ ������
车头时距ℎ������ 定义为连续两辆车的车头（或车上同一参考点）通过同一观察点的时间 间隔，并以如下公式计算： ℎ������ = ������������ − ������������−1 如果忽略第一辆车和最后一辆车的不完整车头时距，观测时段 T 可以表示为：
tion
tioff
时间, t
图 2-4 感应线圈检测器数据
5
定点式检测器数据
当一辆车的前保险杠进入感应线圈检测器的检测区时，根据电磁学原理，检测器就 会产生一个信号。当这辆车的后保险杠驶出检测区时，该信号就会消失，如图所示。如果 我们设定一个合适的阈值，这个检测器就会输出两个信号：当车辆轧过线圈，输出是“开 (ON) ”信号，否则输出是“关 (OFF) ”信号。当线圈输出是“开”时，我们称这个线圈处 于“忙”的状态。有了这些铺垫，我们就可以来回顾一下以前定义的交通流特征，并定义 更多的交通流特征。 车流计数������：当出现“ON”状态时，检测器会有一个上升沿和一个下降沿，我们只 需要前后一致地数其中一个跃变就可以得到车流计数。 车头时距 ℎ������ ：如果我们取所有车辆上同一个点为参考点（比如说前保险杠），第 ������������ ������ − 1 辆车和 ������ 辆车之间的车头时距可以表示为ℎ������ = ������������������������ − ������������−1 ，它们之间的时间空档可以 ������ ������������ ������������������ 表示为������������ = ������������ − ������������−1 。 “开”时段 ������������ ：从一辆车的前保险杠进入检测区域到其后保险杠驶出检测区域所持 续的时间 ������������ = ������������������������������ − ������������������������ 。 车速 ������̇ ������ ：在“开”时段内，车辆 ������ 行驶的距离是 ������ + ������������ ，其中 ������ 是线圈的宽度（通 常为 6 英尺或 1.8 米），������������ 是这辆车的长度。因此，这辆车在观测点时的即时速度可以如 此计算： ������̇ ������ = ������ + ������������ ������ + ������������ = ������������������ ������������ ������������ − ������������������������
3_交通流特性
（2）不足1小时的变化 交通流特性常与短周期内交通流的波动有关，高峰小 时内的小时交通量与最大流率的比值，称为高峰小时系数
小时交通量 PHF 该小时的高峰流率
一般来说， PHF值在0.70到0.98之间，较低的值意味着流量变化较大。
5. 交通量空间分布特性：
1 方向分布
一条道路往返两个方向的交通量，在某一特定的时间内， 两方向上的交通量可能不同. K 方向不均衡性用方向分布系数 表示： D
平均日交通量（ADT）
1 n ADT Qi n i 1
周平均日交通量（Week Average Day Traffic, WADT）
月平均日交通量（Month Average Day Traffic, MADT）
1 7 WDAT Qi 7 i 1
一个月的日交通量之和 MDAT 本月的天数
数,K随着道路周围地区人口密度的增加而减少； K常取第30位小时交通 量系数值.
D ——在高峰小时内的总交通量中，高峰方向所占的 比例（%）.变化由 交通量的方向分布特性决定。
3.应用设计小时交通量计算路幅宽度：
DDHV n 2 C1 W W1 n
C1 每一车道的设计通行能力
n 车道数 W 路幅宽度 W1 一条车道的宽度
KD 主要行车方向交通量 100% 双向行车的总交通量
方向性分布是变通量的一个重要特性,发生在一个方 向上的交通量的饱和值必须在两个方向上都能用设 施予以满足 。
2 车道分布
当一个方向有多条车道时，各车道上交通量的分布是不同的， 慢车和较重车辆趋向于右侧车道。
在我国城市道路设计中，分析路段通行能力的影响因素时，认为 靠近路中心线的车道受影响小，而靠近路缘石的车道受影响大。 其影响用折减系数“ 条 ”表示。设靠近中心线为第1车道，其 折减系数 条 = 1, 则依次第二车道
交通流理论 第二章 第四节 交通流特性参数关系模型
279辆/英里，
最大流量为1400辆/小时。 （3）右边标尺为车间时距
二、流量－密度模型（flow－concentration model）
2、抛物线流量－密度模型（paraboli flow－concentration model）
根据Greenshields speed－concentration model
k u u f (1 ) kj
其中：uf为畅行交通流速度或自由流速度（free flow speed）； kj为jam density 阻塞密度
一、 速度和密度模型（speed－concentration model ）
（2）格林希尔治模型得到了现场数据的验证：●如图2－1所示 （P23） ●如下图所示
（3）该模型使用简便， 且发现该模型与现场数 据之间的相关性很好。 但是理论上与实践上的 各种原因，发现另外一 些模型更受欢迎。
一、 速度和密度模型（speed－concentration model ）
2、格林伯模型Greenberg speed－concerntration model
●格林伯运用理论的基本知识，提出了下列形式的速度－密度模型：
q ku kum ln(
则通过微分可以求出最大流量的条件：
kj k
)
qm um k j e
km
kj e
um um
该模型中um为一个参数，即um是按照规范规定的数值，用以确定其他特性。 图2－17（P25）表示这种拟合现场数据的模型。
二、流量－密度模型（flow－concentration model）
可以得到：
u u f (1
k ) kj
q ku ku f (1 k / k j ) u f k
交通流特性ppt
日交通量（veh）
中 原 工 学 院 交通工程概论
交通 量（ 辆/ h）
600 500 400 300 200 100
6
8 10 12 14 16 18 20 22 0
24
6 时间 （h）
中 原 工 学 院 交通工程概论
根据交通变化规律，用于表示交通时变化
特征的值有 高峰小时交通量（PHV）
Pinnacle Hour volume
长潭公路交通量周变图
120
100
80
60
4020ຫໍສະໝຸດ 0 周日AADT(%)
周一
周二
周三
周四
周五
周六
中 原 工 学 院 交通工程概论
3.小时交通量变化
一天24小时中每个小时的交通量不 断在变化，简称时变化。
中 原 工 学 院 交通工程概论
交通量小时变化曲线
100 80 60 40 20 0
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
统 计 时 间
5分 交 通 量
8：00 ~8： 05
118
8：05 ~8： 10
114
8： 10~ 8：15
112
8： 15~ 8：20
111
8： 20~ 8：25
114
8： 25~ 8：30
120
8： 30~ 8：35
115
8： 35~ 8：40
106
8： 40~ 8：45
104
8：45~ 8：50
PFHt
高峰小时交通量
60 高峰期间t分钟的最大交通量
t
中 原 工 学 院 交通工程概论
交通 量（ 辆/ h）
600 500 400 300 200 100
6
8 10 12 14 16 18 20 22 0
24
6 时间 （h）
中 原 工 学 院 交通工程概论
根据交通变化规律，用于表示交通时变化
特征的值有 高峰小时交通量（PHV）
Pinnacle Hour volume
长潭公路交通量周变图
120
100
80
60
4020ຫໍສະໝຸດ 0 周日AADT(%)
周一
周二
周三
周四
周五
周六
中 原 工 学 院 交通工程概论
3.小时交通量变化
一天24小时中每个小时的交通量不 断在变化，简称时变化。
中 原 工 学 院 交通工程概论
交通量小时变化曲线
100 80 60 40 20 0
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
统 计 时 间
5分 交 通 量
8：00 ~8： 05
118
8：05 ~8： 10
114
8： 10~ 8：15
112
8： 15~ 8：20
111
8： 20~ 8：25
114
8： 25~ 8：30
120
8： 30~ 8：35
115
8： 35~ 8：40
106
8： 40~ 8：45
104
8：45~ 8：50
PFHt
高峰小时交通量
60 高峰期间t分钟的最大交通量
t
交通工程学-第4章-道路交通流理论
连续流设施
间断流设施
无外部因素导致周期性中断。 高速公路、限制出入的一般公路路
段。
由于外部设备导致交通流周期性中断。 一般道路交叉口。
6
4.1 交通流特性
二、连续流特征(Characteristics of Uninterrupted Flow)
7
4.1 交通流特性
二、连续流特征(Characteristics of Uninterrupted Flow)
4
0.1954 0.6289
P(k8) 0.95
具有95%置信度的来车数不多于8辆。
32
4.2 概论统计模型
2、二项分布 ➢ ⑴ 基本公式
P (k)C n kpk(1p)nk
式中：
P（k）—在计数间隔t 内到达k 辆车的概率; λ—平均到车率（辆/s）；
t —每个计数间隔持续的时间（s）；
n—正整数 ；
计算机技术
交通规划 交通控制 交通工程设施设计
4
4.1 交通流特性
交通流定性和定量的特征称为交通流特性。它可用交通流 量、速度和交通密度三个基本参数来描述。
一、交通设施种类(Types of Facilities)
1、连续流设施：指在该设施下无外部因素而导致交通流周期性中断 的设施。
➢ (Uninterrupted-flow facilities are those on which no external factors cause periodic interruption to the traffic stream.)
p—二项分布参数， pt/n。
均值M和方差D分别为: :
33
4.2 概论统计模型
2、二项分布
交通流基本特性
交通流基本特性交通流是指在道路、公路或城市等交通网络中的车辆、行人等交通参与者的流动情况。
了解交通流的基本特性对于交通规划、交通管理以及道路设计都至关重要。
本文将介绍交通流的一些基本特性及其测量方法。
1. 交通流量交通流量是指在特定时间内通过某一路段或交叉口的车辆、行人等交通参与者的数量。
交通流量可以用每小时通过的车辆数（PCU）来衡量。
交通管理机构通常使用交通信号灯、交通监控设备等技术手段来测量交通流量。
交通密度是指在特定路段上单位长度上的车辆数量。
交通密度可以用车辆数（Vehicles）或车辆长度（Vehicle Length）来衡量。
交通密度的测量可以通过交通监控设备、视频监控等方式进行。
3. 平均速度平均速度是指交通流中所有车辆或交通参与者的平均速度。
平均速度可以通过路段上的测速设备来测量。
路段上的平均车速对于评估交通流的通畅程度、拥堵情况等具有重要意义。
4. 交通流稳定性交通流稳定性是指交通流在时间和空间上的稳定程度。
交通流稳定性主要通过交通监控设备、视频监控等手段来进行评估。
交通流的稳定性可以影响交通规划和交通管理的决策。
交通流模型是用来描述交通流行为和交通流特性的数学模型。
交通流模型可以用于预测交通流量、交通运行状态等。
常见的交通流模型包括瓶颈模型、微观交通模型等。
6. 交通流的影响因素交通流的特性受到多种因素的影响。
常见的影响因素包括道路条件、交通信号灯、交通管制等。
了解交通流的影响因素对于优化交通流、提高交通效率等具有重要意义。
7. 交通拥堵交通拥堵是指交通流在某一路段或交叉口出现停车等异常情况。
交通拥堵会导致交通流的速度下降、通行时间延长等问题。
交通拥堵对于城市交通运输和居民出行都带来了很大的不便。
交通流控制是指通过交通信号灯、交通指示牌、交通安全设施等手段对交通流进行调控和管理。
交通流控制可以减缓交通拥堵、提高交通效率，保障道路交通的安全和顺畅。
结论了解交通流的基本特性对于交通规划、交通管理和道路设计都具有重要意义。
现代交通流理论
用 检验判别这两种分布拟和的优劣。 对于泊松分布，把理论频数小于5的到达数合并后，并成10组，可算得： =172/12.1+202/20.7+。。。142/9.8-232=20.04， DF=10-1-1=8 查表得： =15.51< 可见泊松分布拟合是不可接受的 同理计算负二项分布，负二项分布是可以接受的。
4.2 交通流特性的统计分布 离散型分布 1）泊松分布： ——递推公式：由参数m及数量k可递推出Pk+1 ； P0=e-m, Pk+1=mPk/k+1 ——分布的均值与方差皆等于t，这是判断交通流到达规律是否服从泊松分布的依据。试证明之。 ——运用模型时的留意点：关于参数 m 可理解为时间间隔 t 内的平均到达车辆数，也可以理解为距离 l 内的平均车辆数；
02
1）简述
4.3 排队论及其应用
2）排队论的基本原理及应用 (1)基本概念 排队：单指等待服务的，不包括正在服务的,排队系统，则包括两者 排队系统的三个组成部分 排队系统输 来自 过 程排 队 规 则
服 务 方 式
定 长 输 入(D)
泊松 输 入(M)
爱尔朗输入
损 失 制
等 待 制
主干道
优先
次干道
优先
07
停让
08
计算次干道通行能力
4.2 交通流特性的统计分布
连续型分布 2）移位负指数分布 (1)基本假定：不能超车的单列交通流和车流量低的车头时距分布 (2)基本模型：车流平均到达率为（辆/秒），最小车头时距为 时，到达的车头时距 h 大于 t 秒的概率为 P (h>t) = e- （t-） (3)分布的均值与方差： M=1/ + m(样本均值)； D=1/ 2 s 2 (样本方差)
交通流的特性
二. 连续流特征
1. 总体特征
交通量Q、行车速度 V s 、车流密度K是表征交通流 特性中：Q——平均流量(辆/h)； V s ——空间平均车速(km/h); K—平均密度(辆/km)。
能反映交通流特性的一些特征变量：
(1)极大流量Qm，就是Q－V曲线上的峰值。
例 4-1 V=88-1.6K ，如限制 车流的实际流量不大于最大流量的 0.8 倍，求速度的最低 值和密度的最高值?(假定车流的密度＜最佳密度Km)
解：由题意可知：
当K=0时，V=Vf=88km/h,当V=0时，K=Kj=55辆/km。 则：Vm=44Km/h,Km=27.5辆/km,Qm=VmKm=1210辆/h。 由Q=VK和V=88-1.6K，有Q=88K-1.6K2 (如图)。当Q=0.8Qm时， 由88K-1.6K2=0.8Qm=968，解得：KＡ＝15.2，ＫＢ＝39.8。 则有密度 KA和KB与之对应，又由题意可知，所求密度小于 Km， 故为KA。 故当密度为KA=15.2辆/km，其速度为： VA=88-1.6KA =88-1.6×15.2 =63.68km/h 即KA=15.2辆/km，VA=63.68km/h为所求密度最高值与速度最低值。
V V f (1 Kj )
当交通密度很大时，可以采用格林柏(Grenberg)提 出的对数模型： K
V Vm ln
j
K
式中：Vm—对应最大交通量时速度。 当密度很小时，可采用安德五德 (Underwood) 提出 K 的指数模型：
V Vf e
Km
式中：Km—为最大交通量时的速度。
(2)临界速度Vm，即流量达到极大时的速度。
(3)最佳密度Km，即流量达到极大时的密量。
交通流特性及通行能力
设计交通量
• AADT不适合直接作为设计交通量
• 小时交通量与AADT的关系
• 设计交通量
– 设计年的设计小时交通量 – 交通增长率 – பைடு நூலகம்计年限 – DHV与AADT的比值 – 方向系数 – 车道系数
交通密度与车头间距
• 某时段内一定路段长度上的车辆数 • 反映交通拥挤程度 • 密度低～自由流 • 密度高～强迫流 • 与交通量和行驶速度的关系
服务水平
• 反映道路使用质量的主观客观评价指标 • 不间断交通流：交通密度 • 间断交通流：停车延误 • 美国的分级Vs我国的分级 • 标准
影响因素
• 道路条件 • 交通条件 • 交通控制条件 • 设计速度影响 • 驾驶员总体特征影响
通行能力和服务水平分析
• 不间断流的分析
V V N f f f id
道路交通流特性及通行能力
内容
• 速度 • 交通量 • 交通密度与车头间距 • 通行能力与服务水平 • 道路通行能力和服务水平分析
速度
• 瞬时速度（点速度） • 行驶速度 • 行程速度
瞬时速度（地点速度）
V = ds / dt
行驶速度（技术速度）
s s
t V=s/t
行程速度（区间、综合、运送）
车头间距与车头时距
• 车头之间的平均间距～车头间距 • 各车辆间的平均时差～车头时距 • 反映了车辆在交通流中的纵向分布 • 用于估计交通延误、配时等等 • 采用泊松分布
通行能力
• 通行能力：交通流率能达到的最大值 • 交通量与行驶速度、交通密度的关系 • 绿灯饱和流率 • 平均车头间距和平均行驶速度确定 • 给定条件下的生产能力——通行能力
V=s/t
速度
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
三、交通量的时间分布特性。 交通量是一个随机的时空变量，具有时空分布特性。 1、交通量的月变化：月不均衡系数
2、交通量的周变化：周变化系数
3、交通量的小时变化：小时变化系数 高峰小时流量比：高峰小时交通量占全天交通量之比 称为高峰小时流量比，我国一般为9%--10%。 高峰小时系数：高峰小时交通量与高峰小时某时段交 通量扩大为高峰小时交通量之比。
观测路段上所有车辆车头时距的平均值称为平均 车头时距。
2、车头间距：同向行驶的一列车队中，前后相邻两车 的车头之间的空间间隔，在观测路段上所有车辆车头 间距的平均值称为平均车头间距。
三、空间占有率和时间占有率。 1、空间占有率：观测路段中行驶的车辆总长度占该路 段长度的百分比。
2、时间占有率：在某一测定时间段内车辆通过某一断 面的累积时间在该测定时间的百分比。
2、年平均日交通量（AADT）：一年的观测期内日交 通量的平均值，算法是一年的交通量总和与该年总天 数的比值，单位是veh/d，表达式为：
3、月平均日交通量（MADT）：一个月的观测期内日 交通量的平均值，算法是一个月的交通量总和与该月 总天数的比值，单位是veh/d，表达式为：
4、周平均日交通量（WADT）：一周的观测期内日交 通量的平均值，算法是一周的交通量总和与周天数的 比值，单位是veh/d，表达式为：
5、小时交通量：一小时内观测的交通量，单位是 veh/d。 高峰小时交通量（PHV）：全天交通量最大的一个小 时称为高峰小时，该小时内的交通量称为高峰小时交 通量，通常有早、晚高峰交通流量。 年最大小时交通量（HAHY）：一年内各个小时交通 量中最大的一个小时交通量。
年第30位小时交通量（30HV）：将一年内各个小时 的交通量按从大到小顺序排列的第30个小时所对应的 交通量。常用30位小时交通量作为设计小时交通量。 6、交通流率：将不足一小时观测所得的交通量换算成 一小时交通量所得的比值，简称流率。
二、行车速度的统计分布特性。
1、速度频率分布曲线和累计频率分布曲线。
速度频率分布曲线：
速度累计频率分布曲线：
2、行车速度统计分布的特征值： 中位车速：也称50%车速和中值车速，表示该速度以 下行驶的车辆数与在该速度以上行驶的车辆数相等。 85%车速：有85%的车辆行驶在此速度以下，只有 15%的车辆行驶速度高于此值，常用85%车速作为最 高限速。 15%车速：只有15%的车辆行驶在此速度以下，有 85%的车辆行驶速度高于此值，常用15%车速作为最 低限速。车速偏差反应车速波动幅度。
三、时间平均车速与区间平均车速。
1、时间平均车速：单位时间内通过道路横断面的各车 辆的地点车速的算术平均值。
2、区间平均车速：行驶于道路某一区段的全部车辆的 车速分布的平均值。
3、时间平均车速与区间平均车速的换算关系。
时间平均车速观测值的均方差。
时间平均车速观测值的均方差。
一、交通密度的概念。 交通密度又称车流密度，在某一瞬间单位道路长 度内的车辆数。 当交通量由零逐渐增大，接近或达到道路通行能 力的交通密度称为临界密度，临界密度反应交通流最 大时的密度，又称为最佳密度。 二、车头时距与车头间距。 1、车头时距： 同向行驶的一列车队中，前后相邻两车 的车头之间的时间间隔。
四、交通量的空间分布特性 1、城乡分布特性。 2、路段分布特性。 3、方向分布特性，方向分布系数。
4、车道分布特性。
一、行车速度分类。
1、地点车速（spot speed）：车辆通过某一地点时的 瞬时车速。 2、行驶车速（running speed）：车辆行驶某一区间的 距离与行驶这一区间距离所需的时间的比值。 3、行程车速（overall speed）：车辆通过某段路程与 车辆过过该路段所需总时间之比，也叫行程车速。 4、设计车速（design speed）：仅受道路设计条件限 制所能保持的最大安全车速，也叫计算行车速度。 5、临界车速（critical speed）：道路通行能力达到的 最大值时的车速。
一、 交通流是在道路上通行车流和人流的总称。 按照对象分：机动车流、非机动流等； 按照状态分：连续流、间断流、自由流、强制流等； 按照交汇方向：分流、合流、交织流等； 按照运送对象：客流、货物流。 二、描述交通流的三个基本参数： 交通量、行车速度、交通密度
ห้องสมุดไป่ตู้
一、交通量的定义。 交通量是指在单位时间段内，通过道路某一断面的 交通实体数量，也叫交通流量，简称流量。一条路上 的交通流是单向还是双向需要具体分析。 二、交通量的表示方法。 1、平均日交通量（ADT）：观测期内日交通量的平均 值， 算法是观测期内日交通量总和与观测天数的比值， 单位是veh/d，表达式为：
四、交通密度的应用。 通过交通密度可判定交通拥挤情况，从而决定 采取控制措施。
一、交通流基本参数的基本关系。 交通流量、行车速度、交通密度 是表征交通流特征的 三个基本参数。
二、速度与密度的关系。
三、交通量和密度的关系。
四、交通量与速度的关系。