2018管理类联考数学真题-张全军

合集下载

2018年管理类联考真题与答案解析

2018 届管理类专业硕士研究生全国联考真题一、问题求解：第1—15 小题, 每小题 3 分, 共 45 分. 下列每题给出的A、B、C、D、E 五个选项中 , 只有一项是符合试题要求的. 请在答题卡上将所选项的字母涂黑.1、学科竞赛设一等奖、二等奖和三等奖，比例为1：3：8，获奖率为30％、已知10 人获得一等奖，则参加竞赛的人数为（A ）300 （B）400（C）500 （D）550（E）600【答案】 B2、为了解某公司员工的年龄结构，按男、女人数的比例进行了随机抽样，结果如下：根据表中数据估计，该公司男员工的平均年龄与全体员工的平均年龄分别是（单位：岁）（A ）32，30 （B）32, 29.5（C）32, 27 （D）30, 27（E）29.5, 27【答案】 A3、某单位采取分段收费的方式收取网络流量（单位：GB ）费用：每月流量20（含）以内免费，流量20 到 30（含）的每GB 收费 1 元，流量30 到 40（含）的每GB 收费 3 元，流量 40 以上的每GB 收费 5 元，小王这个月用了45GB 的流量，则他应该交费（A ）45 元（B）65 元（C）75 元（D）85 元（E）135 元【答案】 B4、如图，圆O 是三角形ABC 的内切圆，若三角形ABC 的面积与周长的大小之比为1：2，则圆 O 的面积为【答案】 A（A ）π（B）2π（C）3π（D）4π（E）5π5、设实数, 满足| - | =2，| - | =26, 则+ =（A ）30 （B）22（C）15 （D）13（E）10【答案】 E6、甲、乙两人进行围棋比赛，约定先胜 2 盘者赢得比赛。

已知每盘棋甲获胜的概率是0.6，是0.4，若乙在第一盘获胜，则甲赢得比赛的概率为乙获胜的概率（A ）0.144 （B）0.288（C）0.36 （D）0.4（E）0.6【答案】 C7、如图，四边形平行四边形，, , , 分别是四四边的中点，依次下去。

2018年全国硕士研究生管理类联考真题

2018年全国硕士研究生管理类联考真题(总分：160.00，做题时间：150分钟)一、问题求解问题求解（本大题共5小题，每小题3分，共45分）下列每题给出5个选项中，只有一个是符合要求的，请在答题卡上将所选择的字母涂黑。

(总题数：15，分数：45.00)1.学科竞赛设一等奖、二等奖和三等奖，比例为1：3：8，获奖率为30%，已知10人获得一等奖，则参加竞赛的人数为（）。

A.300B.400 √C.500D.550E.600获奖总人数为:10×（1+3+8）=120参加竞赛人数为1203÷30%=4002.为了解某公司员工的年龄结构，按男、女人数的比例进行了随机抽样，结果如下：根据表中数据估计，该公司男员工的平均年龄与全体员工的平均年龄分别是( )(单位：岁)A.32,30 √B.32,29.5C.32,D.30,27E.29.5,27男员工平均年龄为：23+26+28+30+34+36+38+41/9=32;全部员工平均年龄为：23+26+28+30+32+34+36+38+41+23+25+27+29+31/15=30另解：观察男员工的数据，可得一前一后相加为64，所以男员工平均年龄为32，观察女员工数据可得一前一后相加为54，所以女员工平均年龄为27，可得全体员工的平均年龄为30.3.某单位采取分段收费的方式收取网络流量(单位：GB)费用：每月流量20(含)以内免费，流量20到30(含)的每GB收费1元，流量30到40(含)的每GB收费3元，流量40以上的每GB收费5元。

小王这个月用了45GB的流量，则他应该交费( ).A.45B.65 √C.75D.85E.135这个月小王应交费：10×1+10×3+5×5=654.如图，圆O是三角形ABC的内切圆，若三角形ABC的面积与周长的大小之比为1:2，则圆O的面积为( )。

A.π√B.2πC.3πD.4πE.5π5.。

2018年12月管理类联考数学真题-张全军

2019届(2018年12月)管理类联考数学真题-张全军张全军整理一、问题求解1.某车间计划10天完成一项任务，工作3天后因故停工2天，但仍需要按计划完成任务，则工作效率需要提高( ).(A)20%(B)30%(C)40%(D)50%(E)60%2.设函数2()2(0)af x x a x=+> 在(0,)+∞的最小值为0()12f x =，则0x =( ). (A)5(B)4(C)3(D)2(E)13.某影城统计了一季度的观众人数，如图1，则一季度的男女观众人数之比为( ).(A)3:4(B) 5:6(C) 12:13(D)13:12(E) 4:34.设实数,a b 满足6,||||6ab a b a b =++−=，则22a b +=( ). (A)10(B)11(C)12(D)13(E)145.设圆C 与圆22(5)2x y −+=关于2y x =对称，则圆C 的方程为( ).(A)22(3)(4)2x y −+−= (B)22(4)(3)2x y ++−= (C)22(3)(4)2x y −++= (D)22(3)(4)2x y +++= (E)22(3)(4)2x y ++−=6.将一批树苗种在一个正方形花园边上，四角都种，如果每隔3m 种一棵树，那么剩下10棵树苗，如果每隔2m 种一棵，那么恰好种满正方形3条边，则这批树苗有( )棵.(A)54(B)60(C)70(D)82(E)947.在分别标记1、2、3、4、5、6的6张卡片里，甲抽取1张，乙从余下的卡片中再抽取2张，乙的卡片的数字之和大于甲的卡片数字的概率为( ).(A)1160(B)1360(C)4360(D)4760(E)49608.十名同学的语文和数学成绩如下：1212(A)E1>E2, δ1>δ2(B)E1>E2, δ1<δ2(C)E1>E2, δ1=δ2(D)E1<E2, δ1>δ2(E)E1<E2,δ1<δ29.如图，正方体于半径为3m球内，且一面位于球的大圆上，则正方体的表面积最大为( ).(A)12(B)18(C)24(D)30(E)3610.在三角形ABC中，AB=4，AC=6，BC=8，D为BC的中点，则AD=( ).(C)3(D)11.某单位要铺设草坪，若甲乙两公司合作需6天完成，工时费共2.4万元；若甲公司单独做4天后由乙公司接着做9天完成，工时费共计2.35万元；若由甲公司单独完成该项目，则工时费共计( )万元.(A)2.25(B)2.35(C)2.4(D)2.45(E)2.512.如下图，六边形ABCDEF 是平面与棱长为2的正方体所截得到的，若A 、B 、D 、E 分别为相应棱的中点，则六边形ABCDEF 的面积为( ).(A)2(C)(D)(E)13.火车行驶72千米用时1小时，其速度v 与行驶时间t 的关系如图所示，则v 0= ( ).(A)72(B)80(C)90(D)95(E)9614.某中学的5个学科各推荐2名教师作为支教候选人，若从中选派来自不同学科的2人参加支教工作，则不同的选派方式有( ).(A)20(B)24(C)30(D)40(E)4515.设数列{}n a 满足110,21n n a a a +=−=，则100a =( ).(A)9921−(B)992(C)9921+(D)10021−(E)10021+二、条件充分性判断：16.甲、乙、丙三人各自拥有不超过10本图书，甲丙购入2本图书后，他们拥有的图书数量构成等比数列，则能确定甲拥有图书的数量.(1)已知乙拥有的图书数量.(2)已知丙拥有的图书数量.17.有甲、乙两袋奖券，获奖率分别为p 和q ，某人从两袋中各随机抽取1张奖券，则此人获奖的概率不小于34. (1)已知p +q =1.(2)已知14pq =.18.直线y kx =与圆22430x y x +−+=有两个交点.(1)0k <<.(2)02k <<.19.能确定小明年龄.(1)小明年龄是完全平方数.(2)20年后小明年龄是完全平方数.20.关于x 的方程210x ax b ++−=有实根.(1)0a b +=.(2)0a b −=.21.如图，已知正方形ABCD 面积，O 为BC 上一点，P 为AO 的中点，Q 为DO 上一点，则能确定三角形PQD 面积.(1)O 为BC 的三等分点.(2)Q 为DO 的三等分点.22.设n 为正整数，则能确定n 除以5的余数.(1)已知n 除以2的余数. (2)已知n 除以3的余数.23.某校理学院五个系每年的录取人数如下表：(1)数学系录取平均分提高了3分，生物系录取平均分降低了2分. (2)化学系录取平均分提高了1分，地学系录取平均分降低了4分.24.设{}n a 的前n 项和为n S ，则数列{}n a 为等差数列.(1)2=2,1,2,3,n S n n n +=.(2)2=21,1,2,3,n S n n n ++=.25.设三角形区域D 由直线8560x y +−=，6420x y −+=与860kx y k −+−=(0)k <组成，则对于任意的(,)x y D ∈，22lg()2x y +≤.(1)(,1]k ∈−∞−.(2)1[1,)8k ∈−−.。

2018考研：管理类综合联考(199)真题与解析

A. 9 种 B.18 种 C.24 种 D.36 种 E.72 种
【答案】D
12. 从标号位 1 到 10 的 10 张卡片中随机抽取 2 张，它们的标号之和能被 5 整除的概率为（）
A. 1
B. 1
C. 2
D. 2
E. 7
5
9
9
15
45
【答案】E
2
13. 某单位检查 3 个部门的工作，由 3 个部门的主任和外聘的 3 名人员组成检查组，分两人一组检查工作，
D、E 五个选项中，只有一项是符合试题要求的。请在答题卡上将所选项的字母涂黑。
26. 人民既是历史的创造者，也是历史的见证者；既是历史的“剧中人”，也是历史
的“剧作者”。离开人民，文艺就会变成无根的浮萍、无病的呻吟、无魂的躯壳。观照人
民的生活、命运、情感，表达人民的心愿、心情、心声，我们的作品才会在人民中传之久
类型
（B）由于所列城市并非我国的所有城市，所以上面所列的 9 类天气一定不是所有的天
气类型
（C）由于所列城市在同一天不一定展示所有的天气类型，所以上面所列的 9 类天气可
能不是所有的天气类型
（D）由于所列城市在同一天可能展示所有的天气类型，所以上面所列的 9 类天气一定
是所有的天气类型
5
（E）由于所列城市分处我国的东南西北中，所以上面所列的 9 类天气一定就是所有的天气类型
27. 盛夏时节的某一天，某市早报刊载了由该市专业气象台提供的全国部分城市当天
天气预报，择其内容列表如下：
天津
阴
上海
雷阵雨
昆明
小雨
呼和浩特
阵雨
哈尔滨
少云
乌鲁木齐
晴

2018年管理类综合联考真题

2018届管理类专业联考真题一、问题求解：第 1 —15小题,每小题3分,共45分.下列每题给出的 A B 、C 、D E 五个选项中，只有一项是符合试题要求的•请在答题卡上将所选项的字母涂黑 •(E ) 6002男员工年龄(岁〉 2326 28 30 32 34363841女员工年龄(岁) 232527272931根据表中数据估计，该公司男员工的平均年龄与全体员工的平均年龄分别是(单位：岁)(A) 32, 30 ( B ) 32, 29.5 (C) 32, 27 ( D ) 30, 27(E) 29.5, 273、某单位采取分段收费的方式收取网络流量(单位： GB )费用：每月流量 20 (含)以内免费，流量20到30 (含)的每 GB 收费1元，流量30到40 (含)的每 GB 收费3元，流量40以上的每GB 收费5元，小王这个月用了 45GB 的流量，则他应该交费 (A ) 45 元 (B ) 65 元 (C) 75 元 (D ) 85 元(E ) 135元1、学科竞赛设一等奖、二等奖和三等奖，比例为一等奖，则参加竞赛的人数为 (A) 300 (C) 500 1 : 3： 8，获奖率为30%、已知10人获得 (B) 400 (D) 5504、如图，圆O 是三角形ABC 的内切圆，若三角形 ABC 的面积与周长的大小之比为 1： 2,则圆O 的面积为(A) n (C ) 3 n (E ) 5 n(B) 2n(D) 4n5、设实数满足 I 一； -1 I =2, I / -I =26, 则” +「= (A) 30 (B) 22 (C ) 15 (D) 13(E ) 106、甲、乙两人进行围棋比赛，约定先胜 2盘者赢得比赛。

已知每盘棋甲获胜的概率是 0.6,乙获胜的概率是0.4,若乙在第一盘获胜，则甲赢得比赛的概率为(A)0.144 ( B)0.288(C)0.36 ( D)0.4(E)0.67、如图，四边形二二-1 r 平行四边形，三二，-一，一.分别是三「」四边的中点，辽，二,r ，•匕分别是\ -.四边的中点，依次下去。

2018年考研管理类联考试题及参考答案

2018年考研管理类联考试题及参考答案一、冋题求解：第L1列極费允共輻分悔题给出的•臥c.叭E 五个型页中.只有一顶是符合试鯉求內请在答軀卡上将ffift 顶的审母涂聽K 学科竟寒设一等奖、二等奖和三尊奖，比例为1：3： S,茯奖率为30%、已知10人获得 —等奖，则金力喳寒的人数为(A> 300 (B) 400 (C) 500 (D) 550(E) 6002、为了解某公司员工的年龄结村按钛女人数的比例进f 亍了随机抽样，结果如F ；男貝工年龄(岁)23 2620 30 3224362841女員工年龄(岁〉 23 2527272931根將表中数1B 估计，诙公司男员工的平均年龄与全体员工的平均年龄分別杲(单位：岁)(A) 32, 30 (B) 32. 29.5 (C) 32, 27 (D) 30, 27(E) 29_5, 273>某单位采馭分段吹務的方式收取朗络流量(单■位；GB)费用；每月流量其(创以内免魏，溢量加到30 ｛含)的埒GB 收我1元，浚量如到40 (含)的毎GBlft 费弐元，流量40以上的每GB 收费' 元小王这个月用了巧GB 的茨邑贝」他应该交費4$元 (B) 65元 (C) 75元 (D)阴元(E) 135 元斗.如凰圆O 是三角形ABC 的内切圆，若三角形ABC 的面积与周长的犬小之比为1： 23(B) 2JT (D) 47TCE) 57T5、设实数a 丄満足阳上|乜3-聞=迪则CAi 30 22 (C) 15 (D) 13CE) 100甲、乙两人曲亍围棋比第约定先胜2盘者蛊得比第已知毎盘楫甲茯胜的槪率是0®乙狂胜的探卒呈丄4,—盘狂匕川甲嬴唱比暮葩播举力3 K(C) 3HO) 0.144 (B) 0.2SS(C)0.36 (D) 0.4<E) 0.67、如團，四边形4耳G D、平行四边形，4 ，C「D】分别是£ § C】。

2018年考研管理类联考数学试题解析

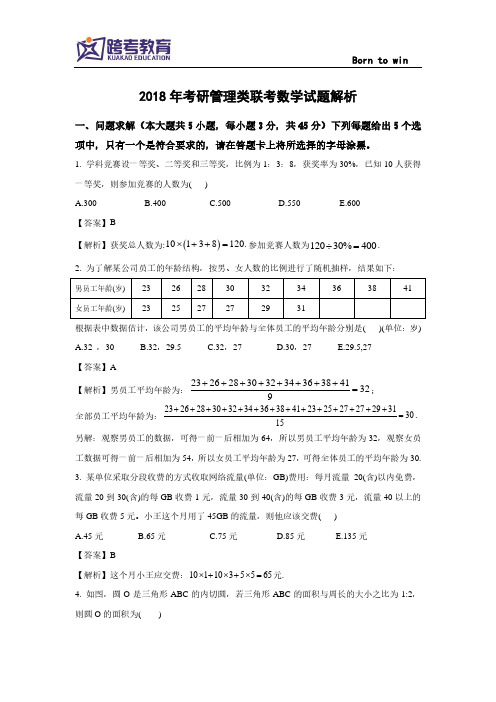
一等奖，则参加竞赛的人数为( )
A.300
B.400
C.500
D.550
E.600
【答案】B
【解析】获奖总人数为:10 1 3 8 120. 参加竞赛人数为120 30% 400 .
2. 为了解某公司员工的年龄结构，按男、女人数的比例进行了随机抽样，结果如下：
男员工年龄(岁) 23
26 28
全部员工平均年龄为： 23 26 28 30 32 34 36 38 41 23 25 27 27 29 31 30 . 15
另解：观察男员工的数据，可得一前一后相加为 64，所以男员工平均年龄为 32，观察女员
工数据可得一前一后相加为 54，所以女员工平均年龄为 27，可得全体员工的平均年龄为 30.
B.65 元
C.75 元
D.85 元
E.135 元
【答案】B
【解析】这个月小王应交费：101103 55 65 元.
4. 如图，圆 O 是三角形 ABC 的内切圆，若三角形 ABC 的面积与周长的大小之比为 1:2，
则圆 O 的面积为( )
Born to win
A
O
B
C
图.1
A.
【答案】A 【解析】
B. 2
C. 3
D. 4
A
a1
b1
E. 5
a2
rO
b2
B
c1
c2
C
S
1 2
a1r
1 2
b1r
1 2
a2r
1 2
b2r
1 2
c1r
1 2
c2r
1 2
r
a1
b1
a2
b2

2019管理类联考数学真题-张全军

2019届(2018年12月)管理类联考数学真题-张全军张全军整理一、问题求解1.某车间计划10天完成一项任务，工作3天后因故停工2天，但仍需要按计划完成任务，则工作效率需要提高( ). 解析请关注公众号“MBAliankaoshuxue ”MBA 联考数学.(A)20%(B)30%(C)40%(D)50%(E)60%2.设函数2()2(0)af x x a x=+> 在(0,)+∞的最小值为0()12f x =，则0x =( ). 解析请关注公众号“MBAliankaoshuxue ”MBA 联考数学.(A)5(B)4(C)3(D)2(E)13.某影城统计了一季度的观众人数，如图1，则一季度的男女观众人数之比为( ). 解析请关注公众号“MBAliankaoshuxue ”MBA 联考数学.(A)3:4(B) 5:6(C) 12:13(D)13:12(E) 4:34.设实数,a b 满足6,||||6ab a b a b =++−=，则22a b += ( ). 解析请关注公众号“MBAliankaoshuxue ”MBA 联考数学. (A)10 (B)11 (C)12 (D)13 (E)145.设圆C 与圆22(5)2x y −+=关于2y x =对称，则圆C 的方程为( ). 解析请关注公众号“MBAliankaoshuxue ”MBA 联考数学.(A)22(3)(4)2x y −+−= (B)22(4)(3)2x y ++−= (C)22(3)(4)2x y −++= (D)22(3)(4)2x y +++= (E)22(3)(4)2x y ++−=6.将一批树苗种在一个正方形花园边上，四角都种，如果每隔3m 种一棵树，那么剩下10棵树苗，如果每隔2m 种一棵，那么恰好种满正方形3条边，则这批树苗有( )棵. 解析请关注公众号“MBAliankaoshuxue ”MBA 联考数学.(A)54(B)60(C)70(D)82(E)947.在分别标记1、2、3、4、5、6的6张卡片里，甲抽取1张，乙从余下的卡片中再抽取2张，乙的卡片的数字之和大于甲的卡片数字的概率为( ). 解析请关注公众号“MBAliankaoshuxue ”MBA 联考数学.(A)1160(B)1360(C)4360(D)4760(E)49608.十名同学的语文和数学成绩如下：1212号“MBAliankaoshuxue”MBA联考数学.(A)E1>E2, δ1>δ2(B)E1>E2, δ1<δ2(C)E1>E2, δ1=δ2(D)E1<E2, δ1>δ2(E)E1<E2,δ1<δ29.如图，正方体于半径为3m球内，且一面位于球的大圆上，则正方体的表面积最大为( ). 解析请关注公众号“MBAliankaoshuxue”MBA联考数学.(A)12(B)18(C)24(D)30(E)3610.在三角形ABC中，AB=4，AC=6，BC=8，D为BC的中点，则AD=( ). 解析请关注公众号“MBAliankaoshuxue”MBA联考数学.(C)3(D)11.某单位要铺设草坪，若甲乙两公司合作需6天完成，工时费共2.4万元；若甲公司单独做4天后由乙公司接着做9天完成，工时费共计2.35万元；若由甲公司单独完成该项目，则工时费共计( )万元. 解析请关注公众号“MBAliankaoshuxue”MBA联考数学.(A)2.25(B)2.35(C)2.4(D)2.45(E)2.512.如下图，六边形ABCDEF 是平面与棱长为2的正方体所截得到的，若A 、B 、D 、E 分别为相应棱的中点，则六边形ABCDEF 的面积为( ). 解析请关注公众号“MBAliankaoshuxue ”MBA 联考数学.(A)2(C)(D)(E)13.火车行驶72千米用时1小时，其速度v 与行驶时间t 的关系如图所示，则v 0= ( ). 解析请关注公众号“MBAliankaoshuxue ”MBA 联考数学.(A)72(B)80(C)90(D)95(E)9614.某中学的5个学科各推荐2名教师作为支教候选人，若从中选派来自不同学科的2人参加支教工作，则不同的选派方式有( ). 解析请关注公众号“MBAliankaoshuxue ”MBA 联考数学.(A)20(B)24(C)30(D)40(E)4515.设数列{}n a 满足110,21n n a a a +=−=，则100a = ( ). 解析请关注公众号“MBAliankaoshuxue ”MBA 联考数学.(A)9921−(B)992(C)9921+(D)10021−(E)10021+二、条件充分性判断：16.甲、乙、丙三人各自拥有不超过10本图书，甲丙购入2本图书后，他们拥有的图书数量构成等比数列，则能确定甲拥有图书的数量. 解析请关注公众号“MBAliankaoshuxue ”MBA 联考数学.(1)已知乙拥有的图书数量.(2)已知丙拥有的图书数量.17.有甲、乙两袋奖券，获奖率分别为p 和q ，某人从两袋中各随机抽取1张奖券，则此人获奖的概率不小于34.解析请关注公众号“MBAliankaoshuxue ”MBA 联考数学. (1)已知p +q =1. (2)已知14pq =.18.直线y kx =与圆22430x y x +−+=有两个交点.解析请关注公众号“MBAliankaoshuxue ”MBA 联考数学.(1)03k −<<.(2)02k <<.19.能确定小明年龄. 解析请关注公众号“MBAliankaoshuxue ”MBA 联考数学.(1)小明年龄是完全平方数.(2)20年后小明年龄是完全平方数.20.关于x 的方程210x ax b ++−=有实根. 解析请关注公众号“MBAliankaoshuxue ”MBA 联考数学.(1)0a b +=.(2)0a b −=.21.如图，已知正方形ABCD 面积，O 为BC 上一点，P 为AO 的中点，Q 为DO 上一点，则能确定三角形PQD 面积. 解析请关注公众号“MBAliankaoshuxue ”MBA 联考数学.(1)O 为BC 的三等分点.(2)Q 为DO 的三等分点.22.设n 为正整数，则能确定n 除以5的余数. 解析请关注公众号“MBAliankaoshuxue ”MBA 联考数学.(1)已知n 除以2的余数. (2)已知n 除以3的余数.23.某校理学院五个系每年的录取人数如下表：“MBAliankaoshuxue ”MBA 联考数学.(1)数学系录取平均分提高了3分，生物系录取平均分降低了2分. (2)化学系录取平均分提高了1分，地学系录取平均分降低了4分.24.设{}n a 的前n 项和为n S ，则数列{}n a 为等差数列. 解析请关注公众号“MBAliankaoshuxue ”MBA 联考数学. (1)2=2,1,2,3,n S n n n +=.(2)2=21,1,2,3,n S n n n ++=.25.设三角形区域D 由直线8560x y +−=，6420x y −+=与860kx y k −+−=(0)k <组成，则对于任意的(,)x y D ∈，22lg()2x y +≤.解析请关注公众号“MBAliankaoshuxue ”MBA 联考数学.(1)(,1]k ∈−∞−.(2)1[1,)8k ∈−−.。

全国硕士研究生考试-管理类联考2018年数学真题

2018年全国硕士研究生招生考试管理类专业学位联考——数学一、问题求解：第1~15小题，每小题3分，共45分。

下列每题给出的A、B、C、D、E五个选项中，只有一项是符合试题要求的。

请在答题卡上将所选项的字母涂黑。

（2018-1）学科竞赛设一等奖、二等奖和三等奖，比例为1：3：8，获奖率为30%，已知10人获得一等奖，则参加竞赛的人数是（）（A）300 （B）400 （C）500 （D）550 （E）600 （2018-2）为了解某公司员工的年龄结构，按男、女人数的比例进行了随机抽样，结果如下：根据表中数据估计，该公司男员工的平均年龄与全体员工的平均年龄分别是（单位：岁）（A）32，30 （B）32，29.5 （C）32，27 （D）30，27 （E）29.5，27 （2018-3）某单位采取分段收费的方式收取网络流量（单位：GB）费用：每月流量20（含）以内免费，流量20到30（含）的每GB收费1元，流量30到40（含）的每GB收费3元，流量40以上的每GB收费5元。

小王这个月用了45GB的流量，则他应缴费（）（A）45元（B）65元（C）75元（D）85元（E）135元（2018-4）如图，圆O是三角形ABC的内切圆，若三角形ABC的面积与周长的大小之比为1：2，则圆O的面积为（）（A）（B）（C）（D）（E）（2018-5）设实数a，b满足︱a-b︱=2，︱a3-b3︱=26，则a2+b2=（）（A）30 （B）22 （C）15 （D）13 （E）10 （2018-6）有96位顾客至少购买了甲、乙、丙三种商品中的一种，经调查：同时购买了甲、乙两种商品的有8位，同时购买了甲、丙两种商品的有12位，同时购买了乙、丙两种商品的有6位，同时购买了三种商品的有2位，则仅购买了一种商品的顾客有（）B C（A ）70位（B ）72位（C ）74位（D ）76位（E ）82位（2018-7）如图，四边形A 1B 1C 1D 1是平行四边形，A 2，B 2，C 2，D 2分别是A 1B 1C 1D 1四边的中点，A 3B 3C 3D 3分别是A 2B 2C 2D 2四边的中点，依次下去，得到四边形序列A n B n C n D n （n=1，2，3，…），设A n B n C n D n 的面积为S n ，且S 1=12，则S 1+S 2+S 3+…=（）（A ）16 （B ）20（C ）24 （D ）28 （E ）30 （2018-8）将6张不同的卡片2张一组分别装入甲、乙、丙3个袋中，若指定的两张卡片要放在同一组，则不同的装法有（）（A ）12种（B ）18种（C ）24种（D ）30种（E ）36种（2018-9）甲、乙两人进行围棋比赛，约定先胜两盘者赢得比赛，已知每盘棋甲获胜的概率是0.6，乙获胜的概率是0.4.若乙在第一盘获胜，则甲赢得比赛的概率为（）（A ）0.14 （B ）0.288 （C ）0.36 （D ）0.4 （E ）0.6 （2018-10）已知圆C ：x 2+（y-a ）2=b ，若圆C 在点（1，2）处的切线与y 轴的交点为（0，3），则ab=（）（A ）-2 （B ）-1 （C ）0 （D ）1 （E ）2 （2018-11）羽毛球队有4名男运动员和3名女运动员，从中选出2对参加混双比赛，则不同的选派方式有（）（A ）9种（B ）18种（C ）24种（D ）36种（E ）72种（2018-12）从标号为1到10的10张卡片中随机抽取2张，它们的标号之和能被5整除的概率为（）（A ）1/5 （B ）1/9 （C ）2/9 （D ）1/15 （E ）7/45 （2018-13）某单位为检查3个部门的工作，由这3个部门的主任和外聘的3名人员组成检查组，分2人一组检查工作，每组有1名外聘成员，规定本部门主任不能检查本部门，则不同的安排方式有（）（A ）6种（B ）8种（C ）12种（D ）18种（E ）36种1 2 1（2018-14）如图，圆柱体的底面半径为2，高为3，垂直于底面的平面截圆柱体所得截面为矩形ABCD，若弦AB所对的圆心角是，则截掉部分（较小部分）的体积为（）（C）（D）（E）（2018-15）函数f（x）=max{x2，-x2+8}的最小值为（）（A）8 （B）7 （C）6 （D）5 （E）4二、条件充分性判断：第16~25小题，每小题3分，共30分。

2018年全国硕士研究生招生考试管理类综合真题及解析

2018年管理类专业硕士研究生全国联考真题一、问题求解：第1—15小题,每小题3分,共45分. 下列每题给出的A、B、C、D、E五个选项中, 只有一项是符合试题要求的. 请在答题卡上将所选项的字母涂黑.1、学科竞赛设一等奖、二等奖和三等奖，比例为1：3：8，获奖率为30％、已知10人获得一等奖，则参加竞赛的人数为（A）300 （B）400 （C）500 （D）550 （E）600【答案】2、为了解某公司员工的年龄结构，按男、女人数的比例进行了随机抽样，结果如下：根据表中数据估计，该公司男员工的平均年龄与全体员工的平均年龄分别是（单位：岁）（A）32，30 （B）32, 29.5 （C）32, 27 （D）30, 27（E）29.5, 27【答案】3、某单位采取分段收费的方式收取网络流量（单位：GB）费用：每月流量20（含）以内免费，流量20到30（含）的每GB收费1元，流量30到40（含）的每GB收费3元，流量40以上的每GB收费5元，小王这个月用了45GB 的流量，则他应该交费（A）45元（B）65元（C）75元（D）85元（E）135元【答案】4、如图，圆O是三角形ABC的内切圆，若三角形ABC的面积与周长的大小之比为1：2，则圆O的面积为（A）π（B）2π（C）3π（D）4π（E）5π【答案】5、设实数,满足|-|=2，|-|=26, 则+=（A）30 （B）22 （C）15 （D）13 （E）10【答案】6、甲、乙两人进行围棋比赛，约定先胜2盘者赢得比赛。

已知每盘棋甲获胜的概率是0.6，乙获胜的概率是0.4，若乙在第一盘获胜，则甲赢得比赛的概率为（A）0.144 （B）0.288 （C）0.36 （D）0.4 （E）0.6【答案】7、如图，四边形平行四边形，,,,分别是四边的中点，,,,分别是四边的中点，依次下去。

得到四边形序列（m=1，2，3…），设的面积为且=12，则+++…=（A）16 （B）20 （C）24 （D）28 （E）30【答案】8、已知圆+=b，若圆C在点（1.2）处的切线与y轴的交点为（0.3），则ab=（A）1-2 （B）-1 （C）0 （D）1 （E）2【答案】9、有96位顾客至少购买了甲、乙、丙三种商品中的一种，经调查：同时购买甲、乙两种商品的有8位，同时购买甲、丙两种商品的有12位，同时购买乙、丙两种商品的有6位，三种同时购买有2位，则仅购买一种商品的顾客有（A）70位（B）72位（C）74位（D）76位（E）82位【答案】10、将6张不同的卡片2张一组分别装入甲、乙、丙3个袋子中，若指定的两张卡片要在同一组，则不同的袋法有（A）12种（B）18种（C）24种（D）30种（E）36种【答案】11、某单位为检查3个部门的工作。

2018年管理类综合联考真题

2018 届管理类专业联考真题一、问题求解：第 1— 15 小题 , 每题 3 分 , 共 45 分. 以下每题给出的A、B、C、 D、E 五个选项中 , 只有一项为哪一项切合试题要求的 . 请在答题卡大将所选项的字母涂黑.1、学科比赛设一等奖、二等奖和三等奖，比率为1：3：8，获奖率为30％、已知 10 人获取一等奖，则参加比赛的人数为（A） 300 （ B） 400（C） 500 （ D） 550（E） 6002、为认识某企业员工的年纪构造，按男、女人数的比率进行了随机抽样，结果以下：依据表中数据预计，该企业男员工的均匀年纪与全体员工的均匀年纪分别是（单位：岁）（A） 32， 30 （ B） 32,（C） 32, 27 （ D） 30, 27（E） , 273、某单位采纳分段收费的方式收取网络流量（单位：GB）花费：每个月流量20（含）之内免费，流量 20 到 30（含）的每GB收费 1 元，流量30 到 40（含）的每GB收费 3 元，流量40 以上的每GB收费 5 元，小王这个月用了45GB的流量，则他应当交费（A） 45 元（B）65元（C） 75 元（D）85元（E） 135 元4、如图，圆O是三角形ABC的内切圆，若三角形ABC的面积与周长的大小之比为1：2，则圆 O的面积为（A）π（B）2π（C） 3π（D）4π（E） 5π5、设实数,知足|- |=2，|-|=26,则+ =（A） 30（B）22（C） 15（D）13（E） 106、甲、乙两人进行围棋比赛，商定先胜 2 盘者博得比赛。

已知每盘棋甲获胜的概率是，乙获胜的概率是，若乙在第一盘获胜，则甲博得比赛的概率为（A）（B）（C）（D）（E）7、如图，四边形平行四边形，,,,分别是四边的中点，,,,分别是四边的中点，挨次下去。

获取四边形序列（ m=1， 2， 3），设的面积为且=12 ，则+++ =（A）16（B）20（C）24（D）28（E）308、已知圆+=b ，若圆 C在点（）处的切线与y 轴的交点为（），则 ab= （A）1-2（B）-1（C）0（D）1（E）29、有96位顾客起码购置了甲、乙、丙三种商品中的一种，经检查：同时购置甲、乙两种商品的有8 位，同时购置甲、丙两种商品的有12 位，同时购置乙、丙两种商品的有 6 位，三种同时购置有 2 位，则仅购置一种商品的顾客有（A）70 位（B）72位（C）74位（D）76位（E）82位10、将 6 张不一样的卡片2 张一组分别装入甲、乙、丙3个袋子中，若指定的两张卡片要在同一组，则不一样的袋法有（A）12 种（B）18种（C）24种（D）30种（E）36种11、某单位为检查 3 个部门的工作。

2018年考研管理类联考数学试题解析

（1） EB 2FC
（2） ED EF
A
E
B
D
F
C
答案：D
解析：过 E 作 EG 垂直于 DC 交 DC 于 G，延长 EF、BC 交于点 H，只要能证明三角形 AED
全等于三角形 CFH 即可推出题干结论。
条件（1）可得 AE=DG=GF=CF，可得 AED EDG EGF CFH ，所以可以拼成
解析：设甲公司年终奖为 x ，乙公司年终奖为 y ，题干可得1.25x 0.9y x : y 18 : 25 ，
设甲、乙公司人数分别为 a,b
（1）可得 x y a : b x : y 18 : 25 ，充分。 ab
（2）可得 a : b x : y 18: 25 ，充分。
19. m, n 都是正整数，则能确定 m n 的值（1） 1 3 1
B. 2
C. 3
D. 4
A
a1
b1
E. 5
a2
rO
b2
B
c1
c2
C
S
1 2
a1r
1 2
b1r
1 2
a2r
1 2
b2r
1 2
c1r
1 2
c2r
1 2
r
a1
b1
a2
b2
c1
c2
1 2
r
L
S : L 1: 2,r 1 S圆 r2 .
另解:将三角形特殊化为等边三角形,设内切圆半径为 r , 可得三角形面积为 S 6 1 r 3r 3 3r2 ;三角形周长为 L 6 3r 6 3r ;
D. 0.4
E. 0.6
【答案】C
【解析】乙在第一盘获胜的情况下,甲要赢得比赛需后两局甲赢，

2018届管理类专业硕士研究生全国联考真题

2018届管理类专业硕士研究生全国联考真题一、问题求解：第1—15小题,每小题3分,共45分. 下列每题给出的A、B、C、D、E五个选项中, 只有一项是符合试题要求的. 请在答题卡上将所选项的字母涂黑.1、学科竞赛设一等奖、二等奖和三等奖，比例为1：3：8，获奖率为30％、已知10人获得一等奖，则参加竞赛的人数为（A）300 （B）400（C）500 （D）550（E）600【答案】B2、为了解某公司员工的年龄结构，按男、女人数的比例进行了随机抽样，结果如下：根据表中数据估计，该公司男员工的平均年龄与全体员工的平均年龄分别是（单位：岁）（A）32，30 （B）32, 29.5（C）32, 27 （D）30, 27（E）29.5, 27【答案】A3、某单位采取分段收费的方式收取网络流量（单位：GB）费用：每月流量20（含）以内免费，流量20到30（含）的每GB收费1元，流量30到40（含）的每GB收费3元，流量40以上的每GB收费5元，小王这个月用了45GB的流量，则他应该交费（A）45元（B）65元（C）75元（D）85元（E）135元【答案】B4、如图，圆O是三角形ABC的内切圆，若三角形ABC的面积与周长的大小之比为1：2，则圆O的面积为【答案】A（A）π（B）2π（C）3π（D）4π（E）5π5、设实数,满足|-|=2，|-|=26, 则+=（A）30 （B）22（C）15 （D）13（E）10【答案】E6、甲、乙两人进行围棋比赛，约定先胜2盘者赢得比赛。

已知每盘棋甲获胜的概率是0.6，乙获胜的概率是0.4，若乙在第一盘获胜，则甲赢得比赛的概率为（A）0.144 （B）0.288（C）0.36 （D）0.4（E）0.6【答案】C7、如图，四边形平行四边形，,,,分别是四边的中点，,, ,分别是四边的中点，依次下去。

得到四边形序列（m=1，2，3…），设的面积为且=12，则+++…=（A）16 （B）20 （C）24 （D）28 （E）30【答案】C8、已知圆+=b，若圆C在点（1.2）处的切线与y轴的交点为（0.3），则ab=（A）1-2 （B）-1 （C）0 （D）1 （E）2【答案】E9、有96位顾客至少购买了甲、乙、丙三种商品中的一种，经调查：同时购买甲、乙两种商品的有8位，同时购买甲、丙两种商品的有12位，同时购买乙、丙两种商品的有6位，三种同时购买有2位，则仅购买一种商品的顾客有（A）70位（B）72位（C）74位（D）76位（E）82位【答案】C10、将6张不同的卡片2张一组分别装入甲、乙、丙3个袋子中，若指定的两张卡片要在同一组，则不同的袋法有（A）12种（B）18种（C）24种（D）30种（E）36种【答案】B11、某单位为检查3个部门的工作。