2012年高考数学试卷三大压轴题目
2012年全国高考数学三大题型
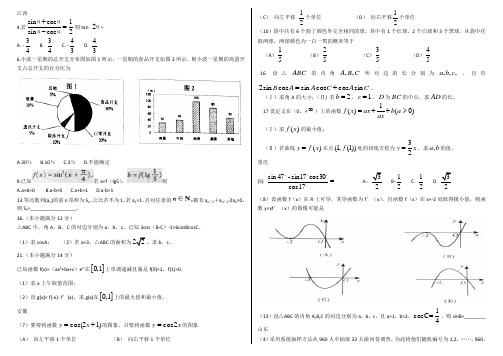
江西4.若sin cos 1sin cos 2+=-αααα则tan 2α= A. -34 B. 34 C. -43 D. 436.小波一星期的总开支分布图如图1所示,一星期的食品开支如图2所示,则小波一星期的鸡蛋开支占总开支的百分比为A.30%B.10%C.3%D.不能确定 9.已知若a=f (lg5),则A.a+b=0B.a-b=0C.a+b=1D.a-b=113.等比数列{a n }的前n 项和为S n ,公比若不为1。
若a 1=1,且对任意的都有a n +2+a n +1-2a n =0,则S 5=_________________。
16.(本小题满分12分)△ABC 中,角A ,B ,C 的对边分别为a ,b ,c 。
已知3cos (B-C )-1=6cosBcosC 。
(1)求cosA ; (2)若a=3,△ABC的面积为b ,c 。
21.(本小题满分14分) 已知函数f(x)=(ax 2+bx+c )e x在[]0,1上单调递减且满足f(0)=1,f(1)=0.(1)求a 上午取值范围; (2)设g(x)= f(-x)- f ′(x),求g(x)在[]0,1上的最大值和最小值。
安徽(7)要得到函数)12cos(+=x y 的图象,只要将函数x y 2cos =的图象(A ) 向左平移1个单位 (B ) 向右平移1个单位(C ) 向左平移12个单位 (D ) 向右平移12个单位(10)袋中共有6个除了颜色外完全相同的球,其中有1个红球,2个白球和3个黑球,从袋中任取两球,两球颜色为一白一黑的概率等于 (A )15 (B )25(C )35 (D )4516设△ABC的内角CB A ,,所对边的长分别为,,,c b a ,且有C A C A A B s i n c o s c o s s i n c o s s i n 2+=。
(Ⅰ)求角A 的大小;(Ⅱ) 若2b =,1c =,D 为BC 的中点,求AD 的长。
2012年北京市高考压轴卷 理科数学试题

2012年普通高校招生考试 数学(理)(北京卷)本试卷共5页,150分.考试时间长120分钟.考生务必将答案答在答题卡上,在试卷上作答无效.考试结束后,将本试卷和答题卡一并交回.第一部分(选择题 共40分)一、选择题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项. 1.若复数i x x z )1()1(2---=为纯虚数,则实数x 的值为( ) (A )1- (B )0 (C )1 (D )1-或12.设{}213A x x =-≤,{}0B x x a =->,若A B ⊆,则实数a 的取值范围是( ) (A )()-∞,-1 (B )(1]-∞-, (C )(2)-∞-, (D )(2]-∞-,3.已知函数⎩⎨⎧><=,,0,ln 0,)(x x x e x f x 则=)]1([e f f ( )(A )e1(B )e (C )e1-(D )e - 4.“不等式0)1(>-x x ”是“不等式11<x”成立的 ( ) (A )充分不必要条件 (B )必要不充分条件(C )充要条件 (D )既不充分也不必要条件5.已知直线l ,m 与平面αβγ,,满足//l l m βγαα=⊂ ,,,m γ⊥,则有( ) (A )αγ⊥且//m β (B )αγ⊥且l m ⊥ (C )//m β且l m ⊥ (D )//αβ且αγ⊥ 6.等差数列{}n a 中,10590,8S a ==,则4a =( )(A )16 (B )12 (C )8 (D )6 7.如下图,某几何体的正视图与侧视图都是边长为1的正方形,且体积是12,则该几何体的俯视图可以是( )8.已知函数()f x 的定义域为[1,5]-,部分对应值如下表,()f x 的导函数()y f x '=的图象如图,下列关于函数()f x 的命题: ①函数()y f x =是周期函数; ②函数()f x 在[0,2]上是减函数;③如果当[1,]x t ∈-时,()f x 的最大值是2,那么t 的最大值为4; ④当12a <<时,函数()y f x a =-有4个零点. 其中真命题的个数是( )(A )4个 (B )3个 (C )2个 (D )1个第二部分 (非选择题 共110分)二、填空题共6小题,每小题5分,共30分. 9.若tan 2,α=则sin cos αα= .10.某商场调查旅游鞋的销售情况,随机抽取了部分顾客的购鞋尺寸,整理得如下频率分布直方图,其中直方图从左至右的前3个小矩形的面积之比为1:2:3,则购鞋尺寸在[)39.5,43.5内的顾客所占百分比为______.11.执行如图所示的程序框图,若输出的b 的值为31,则图中判断框内①处应填12. 已知向量(1,2)a = ,(0,1)b = ,设,2u a kb v a b =+=-,若//u v ,则实数k 的值是13.设22(13)40a x dx =-+⎰,则二项式26()a x x +展开式中不含..3x 项的系数和是14.以下正确命题的为①命题“存在R x ∈,220x x --≥”的否定是:“不存在R x ∈,220x x --<”; ②函数x x x f )21()(31-=的零点在区间11(,)32内;③在极坐标系中,极点到直线:l πsin()4ρθ+= ④函数()x x f x ee -=-的图象的切线的斜率的最大值是2-;⑤线性回归直线 y bxa =+ 恒过样本中心(),x y ,且至少过一个样本点.三、解答题共6小题,共80分,解答应写出文字说明,演算步骤或证明过程. 15.(本小题共13分)已知函数2()sin cos f x x x x ωωω=⋅0>ω),直线1x x =,2x x =是)(x f y =图象的任意两条对称轴,且||21x x -的最小值为4π. (I )求()f x 的表达式;(Ⅱ)将函数()f x 的图象向右平移8π个单位后,再将得到的图象上各点的横坐标伸长为原来的2倍,纵坐标不变,得到函数()y g x =的图象,若关于x 的方程()0g x k +=,在区间0,2π⎡⎤⎢⎥⎣⎦上有且只有一个实数解,求实数k 的取值范围.16.(本小题共13分)已知等差数列}{n a 的前n 项和为n S ,且.62,546-=-=S a (1)求}{a n 通项公式; (2)求数列}a {n 的前n 项和.n T17.本小题共14分乒乓球单打比赛在甲、乙两名运动员间进行,比赛采用7局4胜制(即先胜4局者获胜,比赛结束),假设两人在每一局比赛中获胜的可能性相同.(Ⅰ)求甲以4比1获胜的概率;(Ⅱ)求乙获胜且比赛局数多于5局的概率; (Ⅲ)求比赛局数的分布列.18.(本小题共13分)如图,底面为平行四边形的四棱柱ABCD —A′B′C′D′,DD′⊥底面ABCD ,∠DAB =60°,AB =2AD ,DD′=3AD ,E 、F 分别是AB 、D′E 的中点.(Ⅰ)求证:DF ⊥CE ;(Ⅱ)求二面角A —EF —C 的余弦值.19.(本小题共14分) 已知函数()3213f x x ax bx =++()R a,b ∈. (Ⅰ)若曲线()C :y f x =经过点()12P ,,曲线C 在点P 处的切线与直线2140x y +-=垂直,求a,b 的值;(Ⅱ)在(Ⅰ)的条件下,试求函数()()()2713g x m f x x ⎡⎤=--⎢⎥⎣⎦(m 为实常数,1m ≠±)的极大值与极小值之差;(Ⅲ)若()f x 在区间()12,内存在两个不同的极值点,求证:02a b <+<.20.(本小题共13分)已知直线1:+=x y l ,23:22=+y x O 圆,直线l 被圆截得的弦长与椭圆)0(1:2222>>=+b a by a x C 的短轴长相等,椭圆的离心率23=e(Ⅰ) 求椭圆C 的方程;(Ⅱ) 过点M (0,13-)的动直线l 交椭圆C 于A 、B 两点,试问:在坐标平面上是否存在一个定点T ,使得无论l 如何转动,以A B 为直径的圆恒过定点T ?若存在,求出点T 的坐标;若不存在,请说明理由.参考答案一、选择题(共8小题,每小题5分,共40分)1.A 【解析】因为复数i x x z )1()1(2---=为纯虚数,所以⎩⎨⎧≠--=-0)1(012x x ,解得1-=x ,选A.2.A 【解析】集合}21{}3123{≤≤-=≤-≤-=x x x x A ,而}{a x x B >=,因为A B ⊆,所以1-<a ,选A.3.A 【解析】∵f (1e )=1ln e =—1< 0; ∴=)]1([e f f f (—1)=11e e-=. 4.C 【解析】不等式0)1(>-x x 的解为1>x 或0<x ;不等式11<x的解当0<x 时,成立,当0>x 时,得1>x ,所以不等式11<x的解为1>x 或0<x ,所以不等式0)1(>-x x ”是“不等式11<x”成立的充要条件,选C.5.B 【解析】m m αγαγ⊂⊥⇒⊥,,又l m l γ⊂⇒⊥.6.D 【解析】设等差数列的首项为1a ,公差为d ,9045102910101110=+=⨯+=d a d a S ,即18921=+d a ,又8415=+=d a a ,解 得2,01==d a ,,所以6314=+=d a a ,选D. 7.C 【解析】若俯视图为A,则几何体为边长为1的正方体,所以体积为1,不满足条件;若为B,则该几何体为底面直径为1,高为1的圆柱,此时体积为ππ411)21(2=⨯,不满足条件;若为D, 几何体为底面半径为1,高为1的圆柱的41部分,此时体积为ππ41141=⨯⨯,不满足条件,若为C ,该几何体为底面是直角三角形且两直角边为1,高为1的三棱柱,所以体积为211121=⨯⨯,满足条件,所以选C. 8.D 【解析】由导数图象可知,当01<<-x 或42<<x 时,0)('>x f ,函数单调递增,当20<<x 或54<<x ,0)('<x f ,函数单调递减,当0=x 和4=x ,函数取得极大值2)0(=f ,2)4(=f ,当2=x 时,函数取得极小值)2(f ,所以函数)(x f 不是周期函数,①不正确;②正确;因为在当0=x 和4=x ,函数取得极大值2)0(=f ,2)4(=f ,要使当],1[t x -∈函数)(x f 的最大值是4,当52≤≤t ,所以t 的最大值为5,所以③不正确;由a x f =)(知,因为极小值)2(f 未知,所以无法判断函数a x f y -=)(有几个零点,所以④不正确,所以真命题的个数为1个,选D.二、填空题(共6小题,每小题5分,共30分) 9.25 【解析】521421tan tan cos sin cos sin 222=+=+=+αααααα.10. 55% 【解析】后两个小组的频率为25.02125.02)0875.00375.0(=⨯=⨯+,所以前3个小组的频率为75.025.0-1=,又前3个小组的面积比为3:2:1,所以第三小组的频率为375.075.03213=⨯++,第四小组的频率为175.020875.0=⨯,所以购鞋尺寸在[)39.5,43.5的频率为%5555.0175.0375,0==+.11. 4 【解析】第一次运算为2,3==a b ,第二次运算为3,7==a b ,第三次运算为4,15==a b ,第四次运算为5,31==a b ,第五次运算不满足条件,输出31=b ,所以4≤a ,填4..12.12-【解析】)3,2()1,0()2,1(2=-=,)2,1()1,0()2,1(k k +=+=,因为//u v ,所以031)2(2=⨯-+k ,解得21-=k .13. 161 【解析】6)()31(203202-=-=-⎰x x dx x ,所以246-=+-=a ,二项式为62)2(xx -,展开式的通项为k kk k k k k xC xx C T )2()2()(31266261-=-=--+,令3312=-k ,即3=k ,所以33364)2(-=x C T ,所以3x 的系数为1602363-=-C ,令1=x ,得所有项的系数和为1,所以不含3x 项的系数和为161)160(1=--.14.②③④ 【解析】①命题的否定为“任意的R x ∈,220x x --<”,所以不正确;②因为x x x f )21()(31-=,又0)21()31()31(3131<-=f ,0)21()21()21(2131>-=f ,所以函数的零点在区间11(,)32,所以正确;③把极坐标方程化为普通方程,利用点到直线的距离公式求出2)1()('-≤+-=--=-x x x x ee e e xf ,当且仅当x xee 1=,即0,1==x e x 时取等号,所以正确;⑤线性回归直线 y bx a =+ 恒过样本中心(),x y ,但不一定过样本点,所以不正确,综上正确的为②③④.三、解答题(共6小题,共80分) 15.解:(Ⅰ)11()sin 2sin 22sin(2)223f x x x x x πωωωω==+=+,由题意知,最小正周期242T ππ=⨯=,222T πππωω===,所以2ω=, ∴()sin(4)3f x x π=+(Ⅱ)将()f x 的图象向右平移个8π个单位后,得到sin(4)6y x π=-的图象,再将所得图象所有点的横坐标伸长到原来的2倍,纵坐标不变,得到sin(2)6y x π=-的图象.()sin(2).6g x x π=-所以 令26x t π-=,∵02x π≤≤,∴566t ππ-≤≤()0g x k +=,在区间0,2π⎡⎤⎢⎥⎣⎦上有且只有一个实数解,即函数()y g x =与y k =-在区间0,2π⎡⎤⎢⎥⎣⎦上有且只有一个交点,由正弦函数的图像可知1122k -≤-<或1k -= ∴1122k -<≤或1k =-.16.解:(1)设等差数列}{n a 的公差为d ,则由条件得⎩⎨⎧-=+-=+62645511d a d a ,解得⎩⎨⎧=-=3201d a ,所以}{n a 通项公式)1(320-+-=n a n ,则233-=n a n(2)令0233≥-n ,则323≥n ,所以,当7≤n 时,0<n a ,当8≥n 时,0>n a .所以,当7≤n 时,]23)1(20[)(2121∙-+--=+++-=+++=n n n a a a b b b T n n n n n 263232+-= n n n a a a a a b b b T ++++++-=+++= 872121)(当8≥n 时,n a a a a a a a a ++++++++++-= 8721721)(2154263232+-=n n 所以⎪⎪⎩⎪⎪⎨⎧≥+-≤+-=8,154263237,2632322n n n n n n T n17.(Ⅰ)解:由已知,甲、乙两名运动员在每一局比赛中获胜的概率都是21. 记“甲以4比1获胜”为事件A ,则334341111()C ()()2228P A -==. (Ⅱ)解:记“乙获胜且比赛局数多于5局”为事件B .因为,乙以4比2获胜的概率为3353151115C ()()22232P -==, 乙以4比3获胜的概率为3363261115C ()()22232P -==,所以 125()16P B P P =+=. (Ⅲ)解:设比赛的局数为X ,则X 的可能取值为4,5,6,7.44411(4)2C ()28P X ===, 334341111(5)2C ()()2224P X -===, 335251115(6)2C ()()22216P X -==⋅=,336361115(7)2C ()()22216P X -==⋅=.比赛局数的分布列为:X 4 5 6 7 P18 14 516 51618.(Ⅰ),60AD AE DAE DAE =∠=∴△为等边三角形,设1AD =,则1,2,90DE CE CD DEC ==∴∠= ,即CE DE ⊥.DD '⊥底面ABCD , CE ⊂平面ABCD , 'CE DD ∴⊥. ''''CE DECE DD E CE DD CE DF DF DD E DE DD D ⊥⎫⎫⊥⎪⎪⊥⇒⇒⊥⎬⎬⊆⎪⎭⎪=⎭平面平面. (Ⅱ)取AE 中点H ,则12AD AE AB ==,又60DAE ∠= ,所以△DAE 为等边三角形. 则DH AB ⊥,DH CD ⊥.分别以'DH DC DD 、、所在直线为x y z 、、轴建立空间直角坐标系,设1AD =,则1113(0,0,0),,0),,0),'(0,0,3),,),(0,2,0)2242D E A D F C -.133(,),(0,1,0),,0)422EF AE CE =-==- .设平面AEF 的法向量为1(,,)n x y z =,则1304420x y z y ⎧--+=⎪⎨⎪=⎩,取1n =.平面CEF 的法向量为2(,,)n x y z =,则13042302x y z x y ⎧-+=⎪⎪-=,取2n =.13130401320,cos 21=⋅=>=<n n α. 所以二面角A EF C --的余弦值为13-.19.解:(Ⅰ)⇒()22f x x ax b '=++,直线2140x y +-=的斜率为12-,∴曲线C 在点P 处的切线的斜率为2, ()1122f a b '∴=++=……①曲线()C :y f x =经过点()12P ,, ()1123f a b ∴=++=……②由①②得:2,37.3a b ⎧=-⎪⎪⎨⎪=⎪⎩(Ⅱ)由(Ⅰ)知:()32127333f x x x x =-+,∴()()232123m g x x x -=-,()()2413g x m x x ⎛⎫'∴=-- ⎪⎝⎭, 由()00g x x '=⇒=,或43x =.当210m ->,即1m ,>或1m <-时,x ,()g x ',()g x 变化如下表由表可知:()()()403g x g x g g ⎛⎫-=- ⎪⎝⎭极大极小()()2232320118181m m ⎡⎤=---=-⎢⎥⎣⎦当210m ,-<即11m -<<时,x ,()g x ',()g x 变化如下表由表可知:()()()403g x g x g g ⎛⎫-=- ⎪⎝⎭极大极小()()2232321018181m m =---=--综上可知:当1m ,>或1m <-时,()()g x g x -=极大极小()232181m -; 当11m -<<时,()()g x g x -=极大极小()232181m -- (Ⅲ)因为()f x 在区间()12,内存在两个极值点 ,所以()0f x '=, 即220x ax b ++=在(1,2)内有两个不等的实根.∴2(1)120,(1)(2)440,(2)12,(3)4()0.(4)f a b f a b a a b '=++>⎧⎪'=++>⎪⎨<-<⎪⎪∆=->⎩由 (1)+(3)得:0a b +>,由(4)得:2a b a a +<+,由(3)得:21a -<<-,∴2211()224a a a +=+-<,∴2ab +<.故02a b <+<20.解: (Ⅰ)则由题设可知1=b ,又23=e 2=a 所以椭圆C 的方程是2212x y +=. (Ⅱ)解法一:假设存在点T (u, v ). 若直线l 的斜率存在,设其方程为13y kx =-,将它代入椭圆方程,并整理,得22(189)12160k x kx +--=. 设点A 、B 的坐标分别为1122(,),(,)A x y B x y ,则 12212212,18916.189k x x k x x k ⎧+=⎪⎪+⎨-⎪=⎪+⎩因为1122(,),(,)TA x u y v TB x u y v =--=-- 及112211,,33y kx y kx =-=-所以1212()()()()TA TB x u x u y v y v =--+--2221212121(1)()()339v k x x u k kv x x u v =+-+++++++222222(666)4(3325)62u v k ku u v v k +--+++-=+ 当且仅当0=⋅恒成立时,以AB 为直径的圆恒过定点T ,所以2222618180,0,33250.u v u u v v ⎧+-=⎪=⎨⎪++-=⎩解得0, 1.u v ==此时以AB 为直径的圆恒过定点T (0,1).当直线l 的斜率不存在,l 与y 轴重合,以AB 为直径的圆为221x y +=也过点T (0,1). 综上可知,在坐标平面上存在一个定点T (0,1),满足条件.解法二:若直线l 与y 轴重合,则以AB 为直径的圆是22 1.x y +=若直线l 垂直于y 轴,则以AB 为直径的圆是22116().39x y ++= 由22221,116().39x y x y ⎧+=⎪⎨++=⎪⎩解得01x y =⎧⎨=⎩. 由此可知所求点T 如果存在,只能是(0,1). 事实上点T (0,1)就是所求的点. 证明如下:当直线l 的斜率不存在,即直线l 与y 轴重合时,以AB 为直径的圆为221x y +=,过点T (0,1);当直线l 的斜率存在,设直线方程为13y kx =-,代入椭圆方程,并整理,得22(189)12160.k x kx +--=8分设点A 、B 的坐标为1122(,),(,)A x y B x y ,则12212212,18916.189k x x k x x k ⎧+=⎪⎪+⎨-⎪=⎪+⎩因为1122(,1),(,1)TA x y TB x y =-=-,21212121212416()1(1)()39TA TA x x y y y y k x x k x x =+-++=+-++222216161632160.189k k k k ---++==+ 所以TA TB ⊥,即以AB 为直径的圆恒过定点T (0,1). 综上可知,在坐标平面上存在一个定点T (0,1)满足条件.。
2012年高考数学压轴题19套

数学压轴题集1. 已知函数()ln ,()(0)af x xg x a x==>,设()()()F x f x g x =+ (1)求()F x 的单调区间; (2)若以()((0,3]y F x x =∈)图像上任意一点00(,)P x y 为切点的切线的斜率12k ≤恒成立, 求实数a 的最小值;(3)若对所有的[,)x e ∈+∞都有()xfx ax a ≥-成立,求实数a 的取值范围.解:(1)()()()ln (0),aF x f x g x x x x =+=+>'221()(0)a x a F x x x x x-=-=>.………2分 因为0a>由'()0(,)F x x a >⇒∈+∞,所以()F x 在上单调递增;由'()0(0,)F x x a <⇒∈,所以()F x 在(0,)a 上单调递减. ………………………………………………………………5分 (2)''0002201()(03),()(03)2x a x a F x x k F x x x x --=<≤==≤<≤恒成立,………7分 即200max 1(),2ax x ≥-+当01x =时取得最大值12。
所以,12a≥,所以min 12a =.……10分 (3)因为xe ≥,所以ln ln 1x x x x ax a a x ≥-⇔≤-,令ln (),[,)1x x h x x e x =∈+∞-,则'2ln 1()(1)x x h x x --=-.………………………………………………………………12分 因为当xe ≥时,'1(ln 1)10x x x--=->,所以ln 1ln 120x x e e e --≥--=->,所以'()0h x >,所以min()()1e h x h e e ==-,所以 1ea e ≤-.………………………16分 2.已知数列{}na 中,11=a, a a a a ,1(12≠-=为实常数),前n 项和n S 恒为正值,且当2≥n 时,1111+-=n n n a a S .(1)求证:数列{}nS 是等比数列;(2)设n a 与2+n a 的等差中项为A ,比较A 与1+n a 的大小;(3)设m 是给定的正整数,2=a.现按如下方法构造项数为m 2有穷数列{}n b :当m m m k2,,2,1 ++=时,1+⋅=k k k a a b ;当m k ,,2,1 =时,12+-=k m k b b .求数列{}nb 的前n 项和为),2(*∈≤N n m n T n .解:(1)当3≥n时, Nn n n n nnS S S S a a S ---=-=+-+11111111,化简得112+-=n n n S S S )3(≥n ,又由11=a ,12-=a a 得31111a a a--=, 解得)1(3-=a a a ,∴2321,,1a S a S S ===,也满足112+-=n n n S S S ,而n S 恒为正值,∴数列{}nS 是等比数列. 4 分(2){}nS 的首项为1,公比为a ,1-=n na S.当2≥n 时,21)1(---=-=n n n n a a S S a ,∴⎩⎨⎧≥-==-2,)1(1,12n a a n a n n . 当1=n 时,221312331333[()]222248n a a aa A a a a ++-+-=-==-+≥,此时1+>n a A .…6分当2≥n时, 12121)1(2)1()1(2--+++---+-=-+=-n nn n n n n a a a a a a a a a a A2)1(2)12()1(2322---=+--=n n a a a a a a .∵nS 恒为正值 ∴0>a 且1≠a ,若10<<a ,则01<-+n a A ,若1.>a ,则01>-+n a A .综上可得,当1=n 时, 1+>n a A ;当2≥n时,若10<<a ,则1+<n a A ,若1.>a ,则1+>n a A . 10 分(3)∵2=a∴⎩⎨⎧≥==-2,21,12n n a n n ,当m k m 21≤≤+时, 3212-+=⋅=k k k k a a b .若*∈≤N n m n ,,则由题设得1212221,,,+--===n m n m m b b b b b b=+++=+++=+--1212221n m m m n n b b b b b b T3)21(241)41(22222141341245434n m n m n m m m ----------=--=+++ .13 分 若*∈≤≤+N n m n m ,21,则n m m m n b b b T T ++++=++ 213212122142223)21(2-+---++++-=n m m m m 41)41(23)21(212214--+-=----m n m m m 3)12(2212-=-m m . 综上得⎪⎪⎩⎪⎪⎨⎧≤≤+-≤≤-=---m n m m n T m m n m n21,3)12(21,3)21(2212214. 16 分 3.A 是定义在[2,4]上且满足如下两个条件的函数()x Φ组成的集合:①对任意的[1,2]x ∈,都有(2)(1,2)x Φ∈; ②存在常数L (01)L <<,使得对任意的12,[1,2]x x ∈,都有1212(2)(2)x x L x x Φ-Φ≤-(1)设3()1,[2,4]x x x Φ=+∈,证明:()x A Φ∈;(2)设()x A Φ∈,如果存在0(1,2)x ∈,使得00(2)x x =Φ,那么,这样的0x 是唯一的;(3)设()x A Φ∈,任取1(1,2),x ∈令1(2),1,2,,n n x x n +=Φ=证明:给定正整数k ,对任意的正整数p ,不等式1211k k p k L x x x x L-+-≤--成立.证明:(1)对任意3[1,2],(2)12,[1,2],x x x x ϕ∈=+∈于是333(2)5x ϕ≤≤,…………2分又331352<<<,所以(2)(1,2)x ϕ∈。
2012高考数学压轴题精炼一

2012高考数学压轴题精炼一1.已知抛物线、椭圆和双曲线都经过点()1,2M ,它们在x 轴上有共同焦点,椭圆和双曲线的对称轴是坐标轴,抛物线的顶点为坐标原点.(Ⅰ)求这三条曲线的方程;(Ⅱ)已知动直线过点()3,0P ,交抛物线于,A B 两点,是否存在垂直于x 轴的直线l '被以AP 为直径的圆截得的弦长为定值?若存在,求出l '的方程;若不存在说明理由. 解:(Ⅰ)设抛物线方程为()220y px p =>,将()1,2M 代入方程得2p =24y x ∴= 抛物线方程为: …(1分) 由题意知椭圆、双曲线的焦点为()()211,0,1,0,F F -∴ c=1…………………(2分) 对于椭圆,1222a MF MF =+=+(222222211321a ab ac ∴=+=+=+∴=-=++= 椭圆方程为:………………………………(4分)对于双曲线,1222a MF MF '=-=2222221321a abc a '''''∴=∴=-=-=∴= 双曲线方程为:………………………………(6分)(Ⅱ)设AP 的中点为C ,l '的方程为:x a =,以AP 为直径的圆交l '于,D E 两点,DE 中点为H令()11113,,,22x y A x y +⎛⎫∴ ⎪⎝⎭ C ………………………………………………(7分)()1131123222x DC AP CH a x a +∴===-=-+ ()()()22222221111211323-2344246222DH DC CH x y x a a x a a a DH DE DH l x ⎡⎤⎡⎤∴=-=-+--+=-+⎣⎦⎣⎦'==-+=∴=== 当时,为定值; 的方程为: …………(12分)2.(14分)已知正项数列{}n a 中,16a =,点(n n A a 在抛物线21y x =+上;数列{}nb 中,点(),n n B n b 在过点()0,1,以方向向量为()1,2的直线上.(Ⅰ)求数列{}{},n n a b 的通项公式;(Ⅱ)若()()()n n a f n b ⎧⎪=⎨⎪⎩, n 为奇数, n 为偶数,问是否存在k N ∈,使()()274f k f k +=成立,若存在,求出k 值;若不存在,说明理由; (Ⅲ)对任意正整数n,不等式1120111111n n n a b b b +≤⎛⎫⎛⎫⎛⎫+++⎪ ⎪⎪⎝⎭⎝⎭⎝⎭成立,求正数a 的取值范围.解:(Ⅰ)将点(n n A a 代入21y x =+中得()11111115:21,21n n n n n n a a a a d a a n n l y x b n ++=+∴-==∴=+-⋅=+=+∴=+ 直线 …………………………………………(4分)(Ⅱ)()()()521n f n n ⎧+⎪=⎨+⎪⎩, n 为奇数, n 为偶数………………………………(5分) ()()()()()()27274275421,43527227145,24k k f k f k k k k k k k k k k ++=∴++=+∴=+∴++=+∴== 当为偶数时,为奇数, 当为奇数时,为偶数, 舍去综上,存在唯一的符合条件。
2012高考数学【理科】压轴题(三)

2012届高三理科数学压轴题(三)一、选择题:CABA ADAB二、填空题:9.76010.2711.-20 12.3613.(或等价方程)14.;15..三、解答题16.解:(1)∵-------------------------------2分∴函数的最小正周期-------------------------------------3分(2)函数的最大值和最小值分别为.----------------------------------5分(3)由得∴, -------------7分∴---------------------------------------9分∵,∴∴.-----------12分第17题答案18.(1)证明:依题意知图①折前,∴,----------------------------------------------2分∵∴平面-----------------------3分又∵平面∴-------------------------------------------4分(2)依题意知图①中AE=CF= ∴PE= PF=,在△BEF中,----5分在中,∴--------------------7分∴.-----------8分(3) 由(2)知又∴平面-------10分∴为DE与平面PDF所成的角,-------------------------------------------11分在中,∵,∴ ------14分19.(1)证明:由的两根得:是等差数列(2)由(1)知∴又也符合该式,(3)①②①—②得.20.(本小题满分14分)解:(1)因为满足, ……2分,解得,则椭圆方程为221553x y += ……4分 (2)①将代入221553x y +=中得 ……6分 , ……7分因为中点的横坐标为,所以,解得 …………9分 ②由(1)知,所以 ……………11分 …12分4222316549319k k k k ---=+++ …14分21. 解:(1)∵g (x )=ax 3+bx 2+cx +d (a ≠0)是R 上的奇函数,所以g (0)=0,又对任意x ∈R ,g (-x )=-g (x ),即a (-x )3+b (-x )2+c (-x )+d =-(ax 3+bx 2+cx +d ),∴bx 2+d =0对任意x ∈R 都成立,故b =d =0, 从而g (x )=ax 3+cx ,g ′(x )=3ax 2+c .又当x =1时,g (x )取得极值-2,∴⎩⎪⎨⎪⎧ g (1)=a +c =-2,g ′(1)=3a +c =0,解得⎩⎪⎨⎪⎧a =1,c =-3.∴g (x )=x 3-3x ,g ′(x )=3x 2-3=3(x -1)(x +1).∴当x ∈(-∞,1)∪(1,+∞)时,g ′(x )>0, 故g (x )在区间(-∞,-1],[1,+∞)上是增函数;当x ∈(-1,1)时,g ′(x )<0, 故g (x )在区间(-1,1)上是减函数. ∴当x =-1时,g (x )取得极大值2.(2)由f (x )≤g (x )⇔2x 2+x -k ≤x 3-3x ⇔k ≥-x 3+2x 2+4x , ∴原命题等价于k ≥-x 3+2x 2+4x 在x ∈[-1,3]上恒成立.令h (x )=-x 3+2x 2+4x ,x ∈[-1,3],则k ≥h (x )max .∵h ′(x )=-3x 2+4x +4=-(3x +2)(x -2),从而可得h ′(x ),h (x )的值随x 的变化如下表:↘↗↘max =h (2)=8,∴k 的取值范围为[8,+∞).(3)对任意x 1∈[-1,3],x 2∈[-1,3]都有f (x 1)≤g (x 2)成立,即f (x 1)max ≤g (x 2)min . f (x )=2x 2+x -k =2⎝⎛⎭⎫x +142-18-k , ∴当x 1∈[-1,3]时,f (x 1)max =f (3)=21-k , ∵g (x )=x 3-3x ,g ′(x )=3x 2-3=3(x -1)(x +1), ∴当x 2∈(-1,1)时,g ′(x 2)<0, 故g (x )在区间[-1,1]上是减函数;当x 2∈(1,3)时,g ′(x 2)>0, 故g (x 2)在区间(1,3]上是增函数; ∴当x =1时,g (x 2)取得最小值g (x 2)min =g (1)=-2.∴21-k ≤-2,k ≥23. ∴实数k 的取值范围是[23,+∞).温馨提示-专业文档供参考,请仔细阅读后下载,最好找专业人士审核后使用!。
江西省2012年高考数学压轴卷 理
2012年江西省高考压轴卷数学理一、选择题:本大题共10小题,每小题5分,共50分。
1.复数201121i i -(i 为虚数单位)的虚部是( )A .15i B .15C . 15i -D .15-2.设33tan ,,sin cos 32παπααα=<<-则的值( ) A .1322-+ B .1322-- C .1322+ D .1322-3.下列有关命题的说法正确的是( )A .命题“若21x =,则1x =”的否命题为:“若21x =,则1x ≠”.B .“1x =-”是“2560x x --=”的必要不充分条件.C .命题“存在x R ∈,使得210x x ++<”的否定是:“对任意x R ∈,均有210x x ++<”.D .命题“若αβ=,则sin sin αβ=”的逆否命题为真命题. 4.某圆柱被一平面所截得到的几何体如图(1)所示,若该几何体的正视图是等腰直角三角形,俯视图是圆(如右图),则它的侧视图是( )5.右面是“二分法”求方程3310x x -+=在区间(0,1)上的近似解的流程图.在图中①~④处应填写的内容分别是( ) A .()()0;f a f m a m <=;是;否 B .()()0;f b f m m b <=;是;否C .()()0;f b f m b m <=;是;否D .()()0;f b f m b m <=;否;是6.已知数列{}n a 的通项公式是21232n a n n =-+-,其前n 项和是n S ,对任意的,m n N *∈ 且m n <,则n m S S -的最大值是( )A .21-B .4C .8D .107.已知双曲线221(0,0)mx ny m n -=>>的离心率为2,则椭圆221mx ny +=的离心率为( )A .13B .33C .63D .2338.函数1cos y x x=⋅在坐标原点附近的图象可能是( )OABM NCP•9.如右图,给定两个平面向量OA 和OB ,它们的夹角为120︒,点C 在以O 为圆心的圆弧AB 上,且OC xOA yOB =+(其中,x y R ∈),则满足2x y +≥的概率为( )A .21-B .34C .4πD .3π10.已知函数()y f x =是定义在实数集R 上的奇函数,且当(,0)x ∈-∞时,()()xf x f x '<-成立(其中()()f x f x '是的导函数),若3(3)a f =,2211(lg3)(lg3),(log )(log )44b fc f ==,则,,a b c 的大小关系是( )A .c a b >>B .c b a >>C .a b c >>D .a c b >>二、填空题:本大题共4小题,每小题5分,共20分。
2012年上海市高考压轴卷 理科数学试题

绝密★启用前2012年普通高等学校招生全国统一考试上海 理科数学试卷考生注意:1.本考试设试卷和答题纸两部分,试卷包括试题与答题要求,所有答题必须涂(选择题)或写(非选择题)在答题纸上,做在试卷上一律不得分。
2.答题前,务必在答题纸上填写准考证号和姓名,并将核对后的条形码贴在指定位置上。
3.答题纸与试卷在试题编号上是一一对应的,答题时应特别注意,不能错位。
4.本试卷共有23道试题,满分150分.考试时间120分钟.一、填空题(56分)本大题共有14题,要求在答题纸相应题序的空格内直接填写结果,每个空格填对得4分,否则一律得零分. 1.已知复数z =(i 为虚数单位),则z z ⋅= .2.计算 =⎥⎥⎦⎤⎢⎢⎣⎡+-+⎪⎭⎫ ⎝⎛∞→n n n n 4132lim .3.函数)(x f y =的反函数为)0(1)1(log 2>++=x x y ,则=)(x f ._______4.若以⎪⎪⎭⎫⎝⎛1431a a 为增广矩阵的线性方程组有唯一一组解,则实数a 的取值范围为 . 5.532)23(xx -的二项展开式中,常数项的值是 .6.从一堆苹果中任取5只,称得它们的质量如下(单位:克):125,124,121,123,127.则该样本的标准差=s 克. 7.已知曲线12C C ,的极坐标方程分别为π4cos 002ρθρθ⎛⎫=<⎪⎝⎭,≥≤,cos 3ρθ=,则曲线1C 与2C 交点的极坐标为 .8.设定点)2,1(--A 、)2,1(B ,动点),(y x P 52=-,则动点P 的轨迹方程为 .9.设直线m 与平面α相交但不.垂直,则下列所有正确的命题序号是 . ①在平面α内有且只有一条直线与直线m 垂直; ②过直线m 有且只有一个平面与平面α垂直; ③与直线m 平行的直线不.可能与平面α垂直; ④与直线m 垂直的直线不.可能与平面α平行; ⑤与直线m 平行的平面不.可能与平面α垂直. 10.某校学生在上学路上要经过2个路口,假设在各路口是否遇到红灯是相互独立的,遇到红灯的概率都是13,遇到红灯时停留的时间都是2分钟.则该校某个学生在上学路上因遇到红灯停留的总时间ξ的均值等于 分钟.11.若关于x 的不等式)1(2+>+x b ax 的解集为}1|{<x x ,则b 的取值范围为 . 12.某城区从某年开始的绿化总面积y (万平方米)与时间x (年)的关系为x y 15.1=.则该城区绿化总面积从4万平方米到12万平方米所用的时间为 年.(四舍五入取整) 13.若212≥-+-a x x 对任意实数x 恒成立,则实数a 的取值范围为 . 14.对于任意的平面向量),(),,(2211y x y x ==,定义新运算⊕:),(2121y y x x +=⊕.若,,为平面向量,R ∈k ,则下列运算性质一定成立的所有序号是 .①=⊕⊕; ②)()(k k ⊕=⊕; ③)()()(k k k ⊕=⊕ ④⊕⊕=⊕⊕)()(; ⑤⊕+⊕=+⊕)(.二、选择题(20分)本大题共有4题,每题都给出四个结论,其中有且只有一个结论是正确的,必须把答题纸上相应题序内的正确结论代号涂黑,选对得5分,否则一律得零分. 15.如果命题“曲线C 上的点的坐标都是方程(,)0f x y =的解”是正确的,则下列命题中正确的是( )(A )曲线C 是方程(,)0f x y =的曲线;(B )方程(,)0f x y =的每一组解对应的点都在曲线C 上; (C )不满足方程(,)0f x y =的点(,)x y 不在曲线C 上; (D )方程(,)0f x y =是曲线C 的方程.16、若框图所给的程序运行的结果为90S =,那么判断框中应填入的关于k 的 判断条件错误..的是( ) (A )8k = (B )8k ≤ (C )9k < (D )9k =17.将若干水倒入底面半径为cm 2的圆柱器皿中(底面水平放置),量得水面的高度为cm 6.若将这些水倒入轴截面是正三角形的倒置的圆锥形器皿中,则水面的高度是( )A .cm 36B .cm 6C .cm 1823D .cm 1233 18.设}{n a 是公比为q 的等比数列,首项6411=a ,对于*∈N n ,n n a b 21log =,当且仅当4=n 时,数列{}n b 的前n 项和取得最大值,则q 的取值范围为 ( ) A .)32,3( B .)4,3( C .)4,22( D .)23,22(三、解答题(本题满分74分)本大题共有5题,解答下列各题必须在答题纸的规定区域(对应的题号)内写出必要的步骤.19.(本小题满分12分,第1小题满分6分,第2小题满分6分)如图,菱形ABCD 中,1==AC AB , 其对角线的交点为O ,现将ADC ∆沿对角线AC 向上翻折,使得OB OD ⊥.在四面体 ABCD 中,E 在AB 上移动,点F 在DC上移动,且)10(≤≤==a a CF AE . (1)求线段EF 的最大值与最小值; (2)当线段EF 的长最小时,求异面直线AC 与EF 所成角θ的大小.第16题图20.(本小题满分14分,第1小题满分7分,第2小题满分7分)已知函数2π()cos 12f x x ⎛⎫=+⎪⎝⎭,1()1sin 22g x x =+. (1)设0x 是函数()y f x =的一个零点,求0()g x 的值; (2)求函数()()()h x f x g x =+的单调递增区间.21.(本小题满分14分,第1小题满分7分,第2小题满分7分)某市一家庭一月份、二月份、三月份天然气用量和支付费用如下表所示:该市的家用天然气收费方法是:天然气费=基本费+超额费+保险费.现已知,在每月用气量不超过A 立方米时,只交基本费6元;每户的保险费是每月C 元)5(≤C ;用气量超过A 立方米时,超过部分每立方米付B 元.设当该家庭每月用气量x 立方米时,所支付费用为y 元.求y 关于x 的函数解析式.22.(本小题满分16分,第1小题满分8分,第2小题满分8分)设椭圆22222:b y x C =+(常数0>b )的左右焦点分别为12,F F ,,M N 是直线b x l 2:=上的两个动点,120FM F N ⋅= . (1)若12F M F N ==,求b 的值;(2)求MN 的最小值.23.(本小题满分18分,第1小题满分4分,第2小题满分8分,第2小题满分6分)如图,),(111y x P ,),(222y x P ,…,),(n n n y x P ,…是曲线)0(21:2≥=y x y C 上的点,)0,(11a A ,)0,(22a A ,…,)0,(n n a A ,… 是x 轴正半轴上的点,且110P A A ∆,221PA A ∆,…, n n n P A A 1-∆,… 均为斜边在x 轴上的等腰直角三角形(0A 为坐标原点).(1)写出1-n a 、n a 和n x 之间的等量关系,以及1-n a 、n a 和n y 之间的等量关系; (2)猜测并证明数列}{n a 的通项公式; (3)设nn n n n a a a a b 23211111++++=+++ ,集合{} ,,,,,321n b b b b B =,{}R 012|22∈<-+-=x a ax x x A ,,若φ=B A ,求实常数a 的取值范围.(理科数学)答案一、 1.5 2.1- 3.)1(121>--x x 4.13 5.1080 6.27.)6π8.)1(2≥=x x y 9.②③10.3411.),2(+∞ 12.8 13.),3[]1,(+∞--∞ 14.①④ 二、15.C . 16.D . 17.B . 18.C .三、19.解一:(1)以O 为坐标原点,如图建立空间直角坐标系xyz O -,……1分由已知可求得)0,21,23(--a a E ,)23,21,0(a a F -,…2分 222)23()21()21(a a a a a EF +--+-=53)52(252+-=a . ………………………2 所以,当52=a 时,线段EF 的最小值为515.……1分(2))53,53,53(=EF ,)0,1,0(=, ……2分.515151553cos =⨯==θ ……3分 所以,.515arccos=θ ……………………1分 解二:(1)如图,过点F 作DO FM //,则a FM 23=,…2分 在AEM ∆中,由余弦定理,得53)52(2560cos 22222+-=⋅-+=a AM AE AM AE EM .……3分 所以,当52=a 时,线段EF 的最小值为515. ………………1分 (2)过点E 作AC EN //,在EFN ∆中,可求得53=EN ,56=FN ,由余弦定理可求. 20.解:(1)由题设知1π()[1cos(2)]26f x x =++21-. 因为0x x =是函数()y f x =的一个零点,所以062cos 1=⎪⎭⎫⎝⎛++πx ,………………2分 162cos -=⎪⎭⎫ ⎝⎛+πx 即ππ125+=k x (k ∈Z ).………………………………………3分 所以.45652sin 211sin 211)(00=⎪⎭⎫ ⎝⎛++=+=ππk x x g …………………………………2分 (2)1π1()()()1cos 21sin 2262h x f x g x x x ⎡⎤⎛⎫=+=++++ ⎪⎢⎥⎝⎭⎣⎦1π3113cos 2sin 2sin 2262222x x x x ⎫⎡⎤⎛⎫=+++=++⎪ ⎪⎢⎥⎪⎝⎭⎣⎦⎝⎭ 1π3sin 2232x ⎛⎫=++ ⎪⎝⎭. ………………………………………………………………5分 当πππ2π22π232k x k -++≤≤,即5ππππ1212k x k -+≤≤(k ∈Z )时, 函数1π3()sin 2232h x x ⎛⎫=++ ⎪⎝⎭是增函数, 故函数()h x 的单调递增区间是5ππππ1212k k ⎡⎤-+⎢⎥⎣⎦,(k ∈Z ). ……………………2分 21.解:根据题意,⎩⎨⎧>+-+≤≤+= )2(.,)(6)1(,0,6A x C A x B A x C y …………………2分 因为50≤<C ,所以116≤+C .由表格知,二、三月份的费用大于11,因此,二、三月份的用气量均超过基本量A ,于是有⎩⎨⎧+-+=+-+= C A B C A B .)26(650,)20(638…………………………………………………………4分 解得.82,2C A B +== (3)……………………………………………………2分 假设一月份用气量超过了基本量,即A >4.将4=x 代入(2)得C A +=62与(3)矛盾.…………………………………2分 所以A ≤4,所以86=+C ,2=C . …………………………………………2分 因此,5=A ,2=B ,2=C .所以,⎩⎨⎧>-≤≤= .5,22,50,8 x x x y …………………………………………2分22.解:设),(1y b M ,),(2y b N ……………………………………………………1分 则),(),,3(2211y b F y b F ==由120FM F N ⋅=得2213b y y -= ①………………………………………………2分 (1)由12F M F N ==,得52)3(212=+y b ② ……………………………………………………1分52222=+y b ③ ……………………………………………………1分由①、②、③三式,消去12,y y ,并求得2=b . ……………………………………3分(2)易求椭圆C 的标准方程为:12422=+y x . …………………………………2分 解法一:22121212122212212124222)(b y y y y y y y y y y y y MN=-=--≥-+=-=,4分所以,当且仅当b y y 321=-=或b y y 312=-=时,MN 取最小值b 32. …2分解法二:222142122121269)(b b y b y y y MN ≥++=-=, ……………………………4分所以,当且仅当b y y 321=-=或b y y 312=-=时,MN 取最小值b 32.…2分 23.解:(1)依题意,有21n n n a a x +=-,21--=n n n a a y , ………………………4分(2)由n n x y 212=得212⎪⎭⎫ ⎝⎛-=-n n a a 2211n n a a +⨯=-, 即n n n n a a a a +=---121)(.猜测2)1(+=n n a n . …………………………………………………………2分 证明:①当1=n 时,可求得22121⨯==a ,命题成立; ……………………………1分②假设当k n =时,命题成立,即有2)1(+=k k a k , …………………………………1分则当1+=k n 时,由归纳假设及k k k k a a a a +=---121)(,得1212)1(2)1(++++=⎥⎦⎤⎢⎣⎡+-n k a k k k k a . 即0]2)2)(1([]2)1([)1()(1221=++⋅-+++-++k k k k a k k a k k 解得2)2)(1(1++=+k k a k (k k a k k a <-=+2)1(1不合题意,舍去) 即当1+=k n 时,命题成立. …………………………………………………………3分综上所述,对所有*∈N n ,2)1(+=n n a n . ……………………………………1分 (3)nn n n n a a a a b 23211111++++=+++ )12(22)3)(2(2)2)(1(2++++++++=n n n n n n 31221322122122+⎪⎭⎫ ⎝⎛+=++=+-+=n n n n n n n .……………………2分 因为函数xx x f 12)(+=在区间),1[+∞上单调递增,且0lim =∞→n n b ,所以⎥⎦⎤ ⎝⎛∈31,0n b .…………………………………………………………………………2分{}{})1,1(|,012|22+-∈=∈<-+-=a a x x R a a ax x x A由φ=B A ,有01≤+a 或311>-a , 故,(]⎪⎭⎫ ⎝⎛+∞-∈,341,0 a .………………………………………………………………2分。
江苏省2012年高考数学压轴卷

绝密★启用前2012年江苏省高考压轴卷数学试题第Ⅰ卷(必做题,共160分)一.填空题:本大题共14小题,每小题5分,共70分 .1.已知集合{1,2},{,},a A B a b ==若1{}2AB =,则A B 为___▲__.2.若命题“01)1(,2<+-+∈∃x a x R x 使得”是真命题,则实数a 的取值范围是 ▲3. 在棱长为2的正方体1111ABCD A BC D -中,点O 为底面ABCD 的中心,在正方体1111ABCD A BC D -内随机取一点P ,则点P 到点O 的距离大于1的概率为 ▲ . 4. 若抛物线22y px =的焦点与双曲线22163x y -=的右焦点重合,则p 的值为 ▲ . 5. 已知1tan 3α=-,cos β=,(0,)αβπ∈,则αβ+=___ ▲_____.6.已知实数,x y 满足不等式组001x y x y ≥⎧⎪≥⎨⎪+≤⎩,则2222x y x y +--的最小值为 ▲ .7. 按下图甲是某市有关部门根据对当地干部的月收入情况调查后画出的样本频率分布直方图,已知图甲中从左向右第一组的频数为4000. 在样本中记月收入在[)1000,1500,[1500,2000),[2000,2500),[2500,3000),[3000,3500),[3500,4000]的人数依次为1A 、2A 、……、6A .图乙是统计图甲中月工资收入在一定范围内的人数的算法流程图,则样本的容量n = ▲ ;图乙输出的S = ▲ .(用数字作答)Cy xO AB(第12题)8.已知直线m 、n ,平面α、β,给出下列命题:①若,m n αβ⊥⊥,且m n ⊥,则αβ⊥ ②若//,//m n αβ,且//m n ,则//αβ ③若,//m n αβ⊥,且m n ⊥,则αβ⊥ ④若,//m n αβ⊥,且//m n ,则//αβ 其中正确的命题的个数为 _▲_.9.若函数,0)(210)1,0)(2(log )(2>≠>+=x f a a x x x f a )内恒有,在区间(则f (x )的单调递增区间是 ▲ .10. 如图2所示的三角形数阵叫“莱布尼兹调和三角形”,它们是由整数的倒数组成的,第n 行有n 个数且两端的数均为1n()2n ≥,每个数是它下一行左右相邻两数 的和,如111122=+,111236=+,1113412=+,…,则第10行第4个数(从左往右数)为 ▲11.设函数54)(3++=x x x f 的图象在x=1处的切线为l ,则圆222288150x y x y +--+=上的点到直线l 的最短距离为 ▲ .12.如图,在平面直角坐标系xOy 中, 点A 为椭圆E :12222=+by a x(0>>b a )的左顶点, B ,C 在椭圆E 上,若四边形OABC 为 平行四边形,且∠OAB =30°,则椭圆E 的离心率等于 ▲ .13.当210≤≤x 时,21|2|3≤-x ax 恒成立,则实数a 的取值范围是___▲________. 14. 已知正项等比数列{}n a 满足7652a a a =+,若存在两项m n aa 、14a =,则14m n+的最小值是 ▲ .二、解答题:本大题共6小题,共90分.15.(本小题满分14分)已知复数1sin 2 z x i λ=+,2() (,,,)z m m x i m x R λ=+∈,且12z z =.(1)若0λ=且0x π<<,求x 的值;(2)设λ=()f x ,已知当x α=时,12λ=,试求cos(4)3πα+的值.16.(本小题满分14分)如图,已知空间四边形ABCD 中,,BC AC AD BD ==,E 是AB 的中点. 求证:(1)⊥AB 平面CDE ;(2)平面CDE ⊥平面ABC .(3)若G 为ADC ∆的重心,试在线段AE 上确定一点F, 使得GF//平面CDE .17.(本小题满分14分) 如图所示,某市政府决定在以政府大楼O 为中心,正北方向和正东方向的马路为边界 的扇形地域内建造一个图书馆.为了充分利用这块土地,并考虑与周边环境协调,设计要 求该图书馆底面矩形的四个顶点都要在边界上,图书馆的正面要朝市政府大楼.设扇形的 半径OM R = ,45MOP ∠=,OB 与OM 之间的夹角为θ. (1)将图书馆底面矩形ABCD 的面积S 表示成θ的函数. (2)求当θ为何值时,矩形ABCD 的面积S 有最大值? 其最大值是多少?(用含R 的式子表示)ABCD MOPQ F18. (本小题满分16分) 已知A 、B 分别是直线x y 33=和x y 33-=上的两个动点,线段AB 的长为32,P 是AB 的中点.(1)求动点P 的轨迹C 的方程;(2)过点)0,1(Q 任意作直线l (与x 轴不垂直),设l 与(1)中轨迹C 交于M N 、两点,与y 轴交于R 点.若RM MQ λ=,RN NQ μ=,证明:λμ+为定值.19.(本小题满分16分) 设数列}{n a 的通项是关于x 的不等式x n x x )12(2-<- 的解集中整数的个数.(1)求n a 并且证明}{n a 是等差数列; (2)设m 、k 、p ∈N *,m +p =2k ,求证:m S 1+pS 1≥k S 2; (3)对于(2)中的命题,对一般的各项均为正数的等差数列还成立吗?如果成立, 请证明你的结论,如果不成立,请说明理由.20.(本题满分16分)设函数23(),()ln .x f x g x x x-== (1)试判断当0,()()x g x f x >与的大小关系; (2)求证:23*(112)(123)[1(1)]()n n n e n N -+⋅+⋅++>∈;(3)设11(,)A x y 、2212(,)()B x y x x <是函数()y g x =的图象上的两点,且21021()(()())y y g x g x g x x x -''=-其中为的导函数,证明:012(,).x x x ∈第Ⅱ卷(附加题,共40分)21. A.(选修4-1:几何证明选讲)如图,在梯形ABCD中,AD∥BC,点E,F分别在边AB,CD上,设ED与AF相交于点G,若B,C,F,E四点共圆,求证:AG GF DG GE⋅=⋅.B.(选修4-2:矩阵与变换)已知M=1 -23,-2 11α⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦,试计算20MαGFEDCBA(第21—A题)C .(选修4-4:坐标系与参数方程)在极坐标系下,已知圆θθρsin cos :+=O 和直线:l 22)4sin(=-πθρ。
2012年高考数学压轴题精炼三

2012高考数学压轴题精练三1.(本小题满分13分) 如图,已知双曲线C:x a y ba b 2222100-=>>(),的右准线l 1与一条渐近线l 2交于点M ,F 是双曲线C 的右焦点,O 为坐标原点.(I )求证:OM MF →⊥→;(II )若||MF →=1且双曲线C 的离心率e =62,求双曲线C 的方程; (III )在(II )的条件下,直线l 3过点A (0,1)与双曲线C 右支交于不同的两点P 、Q 且P 在A 、Q 之间,满足AP AQ →=→λ,试判断λ的范围,并用代数方法给出证明.解:(I ) 右准线l 12:x a c=,渐近线l 2:y ba x =∴=+M a c ab c F c c a b ()()22220,,,, ,∴→=OM a c ab c ()2,MF c a c ab c b c abc →=--=-()()22,, OM MF a b c a b cOM MF →⋅→=-=∴→⊥→2222220……3分(II ) e b a e a b =∴=-=∴=621222222,, ||()MF b c a b c b b a cb a →=∴+=∴+=∴==1111142222222222,,, ∴双曲线C 的方程为:x y 2221-= ……7分 (III )由题意可得01<<λ……8分证明:设l 31:y kx =+,点P x y Q x y ()()1122,,,由x y y kx 22221-==+⎧⎨⎩得()1244022--+=k x kxl 3与双曲线C 右支交于不同的两点P 、Q∴-≠=+->+=->=-->⎧⎨⎪⎪⎪⎩⎪⎪⎪∴≠±<<-<⎧⎨⎪⎪⎪⎩⎪⎪⎪120161612041204120221012022212212222k k k x x k k x x k k k k k ∆() ∴-<<-122k……11分AP AQ x y x y →=→∴-=-λλ,,,()()112211,得x x 12=λ∴+=-=--∴+=--=-=+-()()()1412412116412421222122222222222λλλλx k k x k k k k k k ,-<<-∴<-<∴+>12202111422k k ,,()λλ∴+>∴-+>()1421022λλλλ∴λ的取值范围是(0,1)……13分2.(本小题满分13分)已知函数f x x n x n f n n x n n N ()()[()]()(*)=≤--+--<≤∈⎧⎨⎩00111,,数列{}a n 满足a f n n N n =∈()(*) (I )求数列{}a n 的通项公式;(II )设x 轴、直线x a =与函数y f x =()的图象所围成的封闭图形的面积为S a a ()()≥0,求S n S n n N ()()(*)--∈1;(III )在集合M N N k k Z ==∈{|2,,且10001500≤<k }中,是否存在正整数N ,使得不等式a S n S n n ->--10051()()对一切n N >恒成立?若存在,则这样的正整数N 共有多少个?并求出满足条件的最小的正整数N ;若不存在,请说明理由.(IV )请构造一个与{}a n 有关的数列{}b n ,使得lim()n n b b b →∞+++12 存在,并求出这个极限值. 解:(I ) n N ∈*∴=--+-=+-f n n n n f n n f n ()[()]()()111 ∴--=f n f n n ()()1……1分∴-=-=-=f f f f f f ()()()()()()101212323……f n f n n ()()--=1 将这n 个式子相加,得 f n f n n n ()()()-=++++=+012312f f n n n ()()()0012=∴=+∴=+∈a n n n N n ()(*)12……3分(II )S n S n ()()--1为一直角梯形(n =1时为直角三角形)的面积,该梯形的两底边的长分别为f n f n ()()-1,,高为1 ∴--=-+⨯=+-S n S n f n f n a a n n ()()()()112121=-++=12121222[()()]n n n n n……6分(III )设满足条件的正整数N 存在,则n n n nn ()+->⇔>⇔>12100522100520102 又M ={}200020022008201020122998,,,,,,,∴=N 201020122998,,……,均满足条件 它们构成首项为2010,公差为2的等差数列.设共有m 个满足条件的正整数N ,则2010212998+-=()m ,解得m =495 ∴M 中满足条件的正整数N 存在,共有495个,N min =2010 ……9分(IV )设b a n n=1,即b n n n n n =+=-+212111()()则b b b n n n n 122112121313141112111+++=-+-+-++-+=-+ [()()()()]() 显然,其极限存在,并且lim()lim[]n n n b b b n →∞→∞+++=-+=122112 ……10分 注:b c a n n=(c 为非零常数),b b q q n a n n an n n==<<++()(||)12012121,等都能使lim()n n b b b →∞+++12 存在.19. (本小题满分14分)设双曲线y ax 22231-=的两个焦点分别为F F 12、,离心率为2. (I )求此双曲线的渐近线l l 12、的方程;(II )若A 、B 分别为l l 12、上的点,且2512||||AB F F =,求线段AB 的中点M 的轨迹方程,并说明轨迹是什么曲线;(III )过点N ()10,能否作出直线l ,使l 与双曲线交于P 、Q 两点,且OP OQ →→=·0.若存在,求出直线l 的方程;若不存在,说明理由. 解:(I ) e c a =∴=2422, c a a c 22312=+∴==,,∴-=双曲线方程为y x 2231,渐近线方程为y x =±334分(II )设A x y B x y ()()1122,,,,AB 的中点()M x y ,[]2552522101033332233333331012121221221122121212121212122122||||||||()()()()()()AB F F AB F F c x x y y y x y x x x x y y y y y x x y y x x y y x x =∴==⨯=∴-+-===-=+=+∴+=--=+∴+++⎡⎣⎢⎤⎦⎥=又,,,, ∴+=+=321321007532512222()()y x x y ,即则M 的轨迹是中心在原点,焦点在x 轴上,长轴长为103,短轴长为1033的椭圆.(9分)(III )假设存在满足条件的直线l设l y k x l P x y Q x y :,与双曲线交于,、,=-()()()11122[] OP OQ x x y y x x k x x x x k x x x x i →→=∴+=∴+--=∴+-++=·00110101212122121221212()()()()由得则,y k x y x k x k x k x x k k x x k k ii =--=⎧⎨⎪⎩⎪--+-=+=-=--()()()13131633063133312222212221222 由(i )(ii )得k 230+=∴k 不存在,即不存在满足条件的直线l . 14分3. (本小题满分13分)已知数列{}a n 的前n 项和为S n N n ()*∈,且S m ma n n =+-()1对任意自然数都成立,其中m 为常数,且m <-1.(I )求证数列{}a n 是等比数列;(II )设数列{}a n 的公比q f m =(),数列{}b n 满足:b a b f b n n 11113==-,() ()*n n N ≥∈2,,试问当m 为何值时,lim (lg )lim (n b a n b b b b b b n n →∞=→∞+++3122334…+-b b n n 1)成立?解:(I )由已知S m ma n n ++=+-1111()()S m ma n n =+-()1 (2)由()()12-得:a ma ma n n n ++=-11,即()m a ma n n +=+11对任意n N ∈*都成立{} m m a a m m a n n n 为常数,且即为等比数列分<-∴=++1151(II )当n =1时,a m ma 111=+-()∴====+∴==+≥∈---a b I q f m m m b f b b b n n N n n n n 11111113112,从而由()知,()()()*∴=+-=∴⎧⎨⎩⎫⎬⎭∴=+-=+=+∈--1111111131212911b b b b b b n n b n n N n n n n n n n ,即为等差数列,分()()*a m m n n =+⎛⎝ ⎫⎭⎪-11∴→∞=→∞-++=+→∞+++=→∞-+-+++-+⎛⎝ ⎫⎭⎪=-lim (lg )lim lg lg lim ()lim n b a n n n m m mm n b b b b b b n n n n n n n 121133131414151112112231·……由题意知lgm m +=11,∴+=∴=-m m m 110109, 13分4.(本小题满分12分)设椭圆)0(12222>>=+b a by a x 的左焦点为F ,上顶点为A ,过点A 与AF 垂直的直线分别交椭圆和x 轴正半轴于P ,Q 两点,且P 分向量所成的比为8∶5.(1)求椭圆的离心率;(2)若过F Q A ,,三点的圆恰好与直线:033=++y x 相切,求椭圆方程. 解:(1)设点),0,(),0,(0c F x Q -其中),0(,22b A b a c -=.由P 分所成的比为8∶5,得)135,138(0b x P , 2分 ∴a x a x 231)135()138(022202=⇒=+.①, 4分而b x b c ⊥-==),,(),,(0,∴0=⋅.cb x b cx 2020,0==-∴.②, 5分由①②知0232,32222=-+∴=a ac c ac b .∴21.02322=∴=-+e e e . 6分 (2)满足条件的圆心为)0,2(22cc b O -', )0,(,2222222c O c c c c a c c b '∴=--=-, 8分 圆半径a ca cb r ==+=22222. 10分 由圆与直线:033=++y x 相切得,a c =+2|3|, 又3,2,1,2===∴=b a c c a .∴椭圆方程为13422=+y x . 12分5.(本小题满分14分)(理)给定正整数n 和正数b ,对于满足条件b a a n ≥-+211的所有无穷等差数列{}n a ,试求1221++++++=n n n a a a y 的最大值,并求出y 取最大值时{}n a 的首项和公差.(文)给定正整数n 和正数b ,对于满足条件b a a n =-+211的所有无穷等差数列{}n a ,试求1221++++++=n n n a a a y 的最大值,并求出y 取最大值时{}n a 的首项和公差.(理)解:设{}n a 公差为d ,则1111,a a nd nd a a n n -=+=++. 3分dn a n nd a d a a a a a y n n n n n n n )21()1()()(11111221+++++=+++++=+++=+++++++ d n n a n n 2)1()1(1+++=+ 4分 )2)(1()2)(1(1111a a a n nda n n n n -++=++=+++ )3(2111a a n n -+=+. 7分 又211211,++--≤-∴≥-n n a b a b a a .∴449449)23(332112111bb a b a a a a n n n n -≤-+--=-+-≤-++++,当且仅当231=+n a 时,等号成立. 11分 ∴8)49)(1()3(2111b n a a n y n -+≤-+=+. 13分 当数列{}n a 首项491+=b a ,公差n b d 434+-=时,8)49)(1(b n y -+=,∴y 的最大值为8)49)(1(b n -+. 14分(文)解:设{}n a 公差为d ,则1111,a a nd nd a a n n -=+=++. 3分)2)(1(2)1()1()21()1()()(1111111221nda n d n n a n d n a n nd a d a a a a a y n n n n n n n n n ++=+++=+++++=++++=+++=+++++++++)3(21)2)(1(11111a a n a a a n n n n -+=-++=+++, 6分又211211,++--=-∴=-n n a b a b a a .∴449449)23(332112111bb a b a a a a n n n n -≤-+--=-+-=-++++. 当且仅当231=+n a 时,等号成立. 11分 ∴8)49)(1()3(2111b n a a n y n -+=-+=+. 13分 当数列{}n a 首项491+=b a ,公差n b d 434+-=时,8)49)(1(b n y -+=.∴y 的最大值为8)49)(1(b n -+. 14分6.(本小题满分12分)垂直于x 轴的直线交双曲线2222=-y x 于M 、N 不同两点,A 1、A 2分别为双曲线的左顶点和右顶点,设直线A 1M 与A 2N 交于点P (x 0,y 0)(Ⅰ)证明:;22020为定值y x +(Ⅱ)过P 作斜率为02y x -的直线l ,原点到直线l 的距离为d ,求d 的最小值. 解(Ⅰ)证明:)0,2(),0,2(),,(),,(211111A A y x N y x M --- 则设)2(2111++=∴x x y y M A 的方程为直线 ①直线A 2N 的方程为)2(211---=x x y y ②……4分①×②,得)2(2221212---=x x y y分为定值的交点与是直线即822),(22),2(21,222020210022222121 =+∴=+--=∴=-y x N A M A y x P y x x y y x (Ⅱ)02222),(20020200000=-+=+--=-y y x x y x x x y x y y l 整理得结合的方程为 2220201222242y y y x d +=+=+=于是……10分11221122220202020≥+=∴≤+∴≤∴=+y d y y y x 当1,1,1200取最小值时d y y =±=……12分7.(本小题满分14分) 已知函数x x x f sin )(-= (Ⅰ)若;)(],,0[的值域试求函数x f x π∈ (Ⅱ)若);32(3)()(2:),,0(],,0[xf x f f x +≥+∈∈θθπθπ求证(Ⅲ)若)32(3)()(2,),)1(,(],)1(,[xf x f f Z k k k k k x ++∈+∈+∈θθππθππ与猜想的大小关系(不必写出比较过程).解:(Ⅰ)为增函数时当)(,0cos 1)(,),0(x f x x f x ∴>-='∈π分的值域为即求得所以上连续在区间又4],0[)()(0),()()0(],0[)( ππππx f x f f x f f x f ≤≤≤≤(Ⅱ)设)32(3)()(2)(x f x f f x g +-+-=θθ,32sin 3sin )(2)(xx f x g +++-=θθ即)32cos cos (31)(xx x g ++-='θ……6分θπθπθπ=='∈+∴∈∈x x g x x 得由,0)(),0(32),0(],,0[.)(,0)(,),0(为减函数时当x g x g x <'∈∴θ分为增函数时当8)(,0)(,),( x g x g x >'∈πθ分因而有对的最小值为则上连续在区间10)32(3)()(20)()(],0[)()(],0[)( xf x f fg x g x x g g x g +≥+=≥∈θθθπθπ(Ⅲ)在题设条件下,当k 为偶数时)32(3)()(2xf x f f +≥+θθ用心 爱心 专心 11 当k 为奇数时)32(3)()(2x f x f f +≤+θθ……14分。
2012年高考数学压轴题精炼一

2012高考数学压轴题精炼一1.(12分)已知抛物线、椭圆和双曲线都经过点()1,2M ,它们在x 轴上有共同焦点,椭圆和双曲线的对称轴是坐标轴,抛物线的顶点为坐标原点.(Ⅰ)求这三条曲线的方程;(Ⅱ)已知动直线l 过点()3,0P ,交抛物线于,A B 两点,是否存在垂直于x 轴的直线l '被以AP 为直径的圆截得的弦长为定值?若存在,求出l '的方程;若不存在,说明理由.[来源:学|科|网]解:(Ⅰ)设抛物线方程为()220y px p =>,将()1,2M 代入方程得2p =24y x ∴= 抛物线方程为: ………………………………………………(1分)由题意知椭圆、双曲线的焦点为()()211,0,1,0,F F -∴ c=1…………………(2分) 对于椭圆,1222a MF MF =+=+(222222211321a ab ac ∴=+∴=+=+∴=-=+∴= 椭圆方程为:………………………………(4分)对于双曲线,1222a MF MF '=-=2222221321a abc a '∴'∴=-'''∴=-=∴= 双曲线方程为:………………………………(6分)(Ⅱ)设AP 的中点为C ,l '的方程为:x a =,以AP 为直径的圆交l '于,D E 两点,DE 中点为H令()11113,,,22x y A x y +⎛⎫∴ ⎪⎝⎭ C ………………………………………………(7分)[来源:学科网ZXXK]()1112312322DC AP x CH a x a ∴=+=-=-+()()()2222221112121132344-23246222DH DC CH x y x a a x a aa DH DE DH l x ⎡⎤⎡⎤∴=-=-+--+⎣⎦⎣⎦=-+==-+=∴=='= 当时,为定值; 此时的方程为: …………(12分)2.(14分)已知正项数列{}n a 中,16a =,点(n n A a 在抛物线21y x =+上;数列{}nb 中,点(),n n B n b 在过点()0,1,以方向向量为()1,2的直线上.(Ⅰ)求数列{}{},n n a b 的通项公式;(Ⅱ)若()()()n na f nb ⎧⎪=⎨⎪⎩, n 为奇数, n 为偶数,问是否存在k N ∈,使()()274f k f k +=成立,若存在,求出k 值;若不存在,说明理由; (Ⅲ)对任意正整数n ,不等式1120111111n n n a b b b +-≤⎛⎫⎛⎫⎛⎫+++ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭成立,求正数a 的取值范围.解:(Ⅰ)将点(n n A a 代入21y x =+中得()11111115:21,21n n n n n n a a a a d a a n n l y x b n ++=+∴-==∴=+-⋅=+=+∴=+ 直线 …………………………………………(4分)(Ⅱ)()()()521n f n n ⎧+⎪=⎨+⎪⎩, n 为奇数, n 为偶数………………………………(5分)()()()()()()27274275421,42735227145,24k k f k f k k k k k k k k k k ++=∴++=+∴=+∴++=+∴== 当为偶数时,为奇数, 当为奇数时,为偶数, 舍去综上,存在唯一的符合条件。
数学- 2012高考数学压轴题集选(江苏)【2012高考复习必备】

1 1 S n an . 2 4
Tn , (n 2) , Tn 1
∴数列 bn 是以 2 为首项,以 1 为公差的等差数列, ∴ bn 2 ( n 1) n 1 ,∴ Tn
1 1 1 ,∴ a n 1 Tn 1 bn n 1 (20 21 22 2k 2 ) 2
当 k=10 时,其和是 55 210 2 1077 2011 当 k=11 时,其和是 66 211 2 2112 2011 又因为 2011-1077=934=467 2,是 2 的倍数
3 / 44
又∵ a2 3 , ∴( 10 分
p 2 ) 1 3 , ∴ p 4, ∴ an 2n 1 p2
……………………………
(3)由(2)得 bn log 2 2n ,即 bn n,(n N * ) , 数列 {Cn } 中, bk (含 bk 项)前的所有项的和是:
/
1 1 a . 1 a a
/
当 0 a 1 时, g ( a ) 0 ,在(0,1)上单调递增;当 a>1 时, g ( a ) 0 , 在 (1, ) 上单调递减. g max ( a ) g (1) 0 , g ( a ) =0 只有唯一解 a=1.
2 / 44
当 a 0 时,x (0, a ) 时, f ( x) 0 ,
/
在 (0, ) 上单调递增; 当 a 0 时, f ( x) 0 ,
/
在上单调递减; x ( a, ) 时, f ( x) 0 ,在 ( a , ) 上单调递增. 综上所述,当 a 0 时, f ( x ) 的单调递增区间为 (0, ) ; 当 a 0 时, f ( x ) 的单调递增区间为 ( a , ) ,单调递减区间为 (0, a ) . (2)充分性:a=1 时,由(1)知,在 x=1 处有极小值也是最小值, 即 f min ( x) f (1) 0 .而(0,1)在上单调递减,在 (1, ) 上单调递增, 在 (0, ) 上由唯一的一个零点 x=1. 必要性: f ( x ) =0 在 (0, ) 上有唯一解,且 a>0, 由(1)知,在 x=a 处有极小值也是 最小值 f(a), f(a)=0,即 ln a a 1 0 . 令 g ( a ) ln a a 1 , g / ( a )
2012高考数学压轴题(文科)及答案

2012高考数学压轴题(文科)及答案2012年江西省高考压轴卷数学文一、选择题 1、命题:若函数是幂函数,则函数的图像不经过第四象限.那么命题的逆命题、否命题、逆否命题这三个命题中假命题的个数是() 0 1 2 3 2.已知数据是江西普通职工个人的年收入,设这个数据的中位数为,平均数为,方差为,如果再加上世界首富的年收入,则这个数据中,下列说法正确的是() A.年收入平均数大大增大,中位数一定变大,方差可能不变 B.年收入平均数大大增大,中位数可能不变,方差变大 C.年收入平均数大大增大,中位数可能不变,方差也不变D.年收入平均数可能不变,中位数可能不变,方差可能不变。
3.设函数,对于任意不相等的实数,代数式的值等于() A. B. C.、中较小的数 D.、中较大的数 4.有下面四个判断:①命题:“设、,若,则”是一个假命题;②若“p或q”为真命题,则p、q均为真命题;③命题“ 、”的否定是:“ 、”;④若函数的图象关于原点对称,则其中正确的个数共有()A. 0个 B. 1个 C. 2个 D. 3个 5.数列的前n项和;(n∈N*);则数列的前50项和为()A.49 B.50 C.99 D.100 6.已知m>0,且mcosα-sinα= sin (α+),则tan =( ) A.-2 B.- C. D.2 7.一个几何体的三视图如右图所示,则该几何体的体积为( ) A. B. C. D. 8.若直线mx+ny=16和圆x2+y2=64没有交点,则过点(m,n)的直线与椭圆的交点个数为( ) A. 0 B.2个 C.1个 D.不确定 9.设变量满足约束条件:的最大值为( ) A.10 B.8 C.6 D.4 10.等比数列{ }中,a1=2,a8=4,f(x)=x(x-a1)(x-a2)…(x-a8),为函数f(x)的导函数,则=( ) A.0 B. C. D.二、填空题 11.某市有三所学校共有高三文科学生1500人,且三所学校的高三文科学生人数成等差数列,在三月进行全市联考后,准备用分层抽样的方法从所有高三文科学生中抽取容量为120的样本,进行成绩分析,则应从校学生中抽取________人. 12.已知如图所示的程序框图(未完成),设当箭头a指向①时,输出的结果为S=m,当箭头a指向②时,输出的结果为S=n,则m+n的值为. 13.某种产品的广告费支出x与销售额y之间有如下对应数据(单位:百万元). x 2 4 56 8 y 30 40[来 60 t 70 根据上表提供的数据,求出y关于x的线性回归方程为y^=6.5x+17.5,则表中t的值为. 14.已知△ABC 及其平面内一点P满足++=0,若实数λ满足+=λ.则λ=__________. 15. AB是半径为1的圆的直径,M为直径AB上任意一点,过点M作垂直于直径AB的弦,则弦长大于的概率是_____三、解答题 16 已知关于的一元二次函数(Ⅰ)设集合和,分别从集合和中随机取一个数作为和,求函数在区间[ 上是增函数的概率;(Ⅱ)设点是区域内的随机点,记有两个零点,其中一个大于,另一个小于 ,求事件发生的概率。
数学- 2012高考数学压轴题集选(江苏)【2012高考复习必备】

2012江苏高考数学压轴题集选1. 设n T 为数列{}n a 的前n 项之积,满足)(1*∈-=N n a Tn n.(1)设nn T b 1=,证明数列{}n b 是等差数列,并求n b 和n a ;(2)设22221n n T T T S +++= 求证:41211-≤<-+n n n a S a .解:(1)∵)2(,),(11≥=∈-=-*n T T a N n a T n n n n n ,∴数列{}n b 是以2为首项,以1为公差的等差数列, ∴1)1(2+=-+=n n b n ,∴111+==n b T nn ,∴1111+-=-=n T a n n(2)22222221)1(13121++++=+++=n T T T S n n ,∵2121)2)(1(1431321)1(13121222+-=++++⨯+⨯>++++n n n n 211-=+n a∴n n S a <-+211 ,当2≥n 时,)1(132121)1(131212222+++⨯+<++++n n n41112141-=+-+=n a n , 当1=n 时,41411211-===a T S , ∴41-≤n n a S .2.函数(1)()ln (0,)a x f x x x a R x-=->∈.(1)试求()f x 的单调区间;(2)当0a >时,求证:函数()f x 的图像存在唯一零点的充要条件是1a =; (3)求证:不等式111ln 12xx -<-对于(1,2)x ∈恒成立.解:(1)/221()(0)a x a f x x x xx-=-=>.当0a ≤时,/()0f x >,在(0,)+∞上单调递增; 当0a >时,(0,)x a ∈时,/()0f x <,在上单调递减; (,)x a ∈+∞时,/()0f x >,在(,)a +∞上单调递增. 综上所述,当0a ≤时,()f x 的单调递增区间为(0,)+∞;当0a >时,()f x 的单调递增区间为(,)a +∞,单调递减区间为(0,)a .(2)充分性:a =1时,由(1)知,在x =1处有极小值也是最小值, 即min ()(1)0f x f ==.而(0,1)在上单调递减,在(1,)+∞上单调递增, 在(0,)+∞上由唯一的一个零点x =1.必要性:()f x =0在(0,)+∞上有唯一解,且a >0, 由(1)知,在x =a 处有极小值也是最小值f (a ), f (a )=0,即ln 10a a -+=. 令()ln 1g a a a =-+, /11()1a g a a a-=-=.当01a <<时,/()0g a >,在(0,1)上单调递增;当a >1时,/()0g a <,在(1,)+∞上单调递减.m ax ()(1)0g a g ==,()g a =0只有唯一解a =1.∴(1)ln 2(1)0x x x +-->.∴111(12)ln 12x xx -<<<-.3. 已知数列{}na 的前n 项和为nS,且满足22n n S pa n =-,*n N ∈,其中常数2p >.(1)证明:数列{}1n a +为等比数列; (2)若23a =,求数列{}n a 的通项公式;(3)对于(2)中数列{}n a ,若数列{}n b 满足2log (1)n n b a =+(*n N ∈),在k b 与1k b +之间插入12k -(*k ∈N )个2,得到一个新的数列{}n c ,试问:是否存在正整数m ,使得数列{}n c 的前m 项的和2011m T =?如果存在,求出m 的值;如果不存在,说明理由.解:(1)∵22n n S pa n =-,∴1122(1)n n S pa n ++=-+,∴1122n n n a pa pa ++=--,∴1222n n p a a p p +=+--,∴11(1)2n n p a a p ++=+-, …………………………………4分 ∵1122a pa =-,∴102p a p =>-,∴110a +>∴11012n n a p a p ++=≠+-,∴数列{}1n a +为等比数列.(2)由(1)知1()2nn pa p +=-,∴()12nn pa p =-- ……………………………8分又∵23a =,∴2()132pp -=-,∴4p =,∴21n n a =- ……………………………10分(3)由(2)得2log 2n n b =,即*,()n b n n N =∈, 数列{C }n 中,k b (含k b 项)前的所有项的和是: 0122(1)123)(2222)2222k kk k k -++++++++++⨯=+-(…………………12分 当k=10 时,其和是10552210772011+-=<当k=11 时,其和是11662221122011+-=>又因为2011-1077=934=467⨯2,是2的倍数 ………………………………14分 所以当2810(1222)467988m =++++++= 时,T 2011m =,所以存在m=988使得T 2011m = ……………………………………16分4.已知函数2()1,()|1|f x xg x a x =-=-.(1)若关于x 的方程|()|()f x g x =只有一个实数解,求实数a 的取值范围; (2)若当x ∈R 时,不等式()()f x g x ≥恒成立,求实数a 的取值范围;(3)求函数()|()|()h x f x g x =+在区间[2,2]-上的最大值(直接写出结果......,不需给出演.....算步骤...).解:(1)方程|()|()f x g x =,即2|1||1|x a x -=-,变形得|1|(|1|)0x x a -+-=,显然,1x =已是该方程的根,从而欲原方程只有一解,即要求方程|1|x a +=, 有且仅有一个等于1的解或无解 ,结合图形得0a <. ……………………4分(2)不等式()()f x g x ≥对x ∈R 恒成立,即2(1)|1|x a x --≥(*)对x ∈R 恒成立, ①当1x =时,(*)显然成立,此时a ∈R ; ②当1x ≠时,(*)可变形为21|1|x a x -≤-,令21,(1),1()(1),(1).|1|x x x x x x x ϕ+>⎧-==⎨-+<-⎩ 因为当1x >时,()2x ϕ>,当1x <时,()2x ϕ>-, 所以()2x ϕ>-,故此时2a -≤.综合①②,得所求实数a 的取值范围是2a -≤. …………………………………8分(3)因为2()|()|()|1||1|h x f x g x x a x =+=-+-=2221,(1),1,(11),1,(1).x ax a x x ax a x x ax a x ⎧+--⎪--++-<⎨⎪-+-<-⎩≤≥…10分① 当1,22aa >>即时,结合图形可知()h x 在[2,1]-上递减,在[1,2]上递增,且(2)33,(2)3h a h a -=+=+,经比较,此时()h x 在[2,2]-上的最大值为33a +.② 当01,22a a 即0≤≤≤≤时,结合图形可知()h x 在[2,1]--,[,1]2a -上递减,在[1,]2a --,[1,2]上递增,且(2)33,(2)3h a h a -=+=+,2()124a ah a -=++,经比较,知此时()h x 在[2,2]-上的最大值为33a +. ③ 当10,02a a -<<即-2≤≤时,结合图形可知()h x 在[2,1]--,[,1]2a -上递减,在[1,]2a --,[1,2]上递增,且(2)33,(2)3h a h a -=+=+,2()124aah a -=++,经比较,知此时()h x 在[2,2]-上的最大值为3a +. ④ 当31,222a a -<-<-即-3≤≤时,结合图形可知()h x 在[2,]2a -,[1,]2a -上递减,在[,1]2a ,[,2]2a -上递增,且(2)330h a -=+<, (2)30h a =+≥,经比较,知此时()h x 在[2,2]-上的最大值为3a +. 当3,322aa <-<-即时,结合图形可知()h x 在[2,1]-上递减,在[1,2]上递增,故此时()h x 在[2,2]-上的最大值为(1)0h =. 综上所述,当0a ≥时,()h x 在[2,2]-上的最大值为33a +;当30a -<≤时,()h x 在[2,2]-上的最大值为3a +;当3a <-时,()h x 在[2,2]-上的最大值为0.…………………………………………16 5.已知函数2()4(0,,)f x ax x b a a b R =++∈且<.设关于x 的不等式()0f x >的解集为12,),x x (且方程()f x x =的两实根为,αβ.(1)若1αβ-=,求,a b 的关系式;(2)若,a b 都是负整数,且1αβ-=,求()f x 的解析式;(3)若12αβ<<<,求证:12(1)(1)7x x ++<.解:(1)由()f xx =,得230ax x b ++=,由已知得940ab ->,3,ba a αβαβ+=-=+ ∴()241αβαβαβ-=+-=,∴2941b aa-=.∴249a ab +=,∴a b 、的关系式为249a ab +=. ……………………………………5分 (2)∵a b 、是负整数,∴1,1a b ≤-≤-.由249a ab +=得:()49a b a +=,且4b a a +<.∴1,2a b =-=-,∴()242f x x x =-+-. ……………………………………10分(3)令()23g x ax x b=++,又0,12a αβ<<<<.∴()10,(2)0,g g >⎧⎪⎨<⎪⎩,即()130,(2)460,g a b g a b =++>⎧⎪⎨=++<⎪⎩ ……………………………………12分又12,x x 是方程240ax x b ++=的两根,∴12124,b x x x x a a +=-=.∴()()()121212111x x x x x x ++=+++=4411b b aa a--+=+由线性约束条件30,460,0.a b a b a ++>⎧⎪++<⎨⎪<⎩,画图可知. 4b a -的取值范围为()4,6-,…………14分∴431617b a--<+<+=.∴()()12117x x ++<.………………………………………………………………………16分6.已知函数)1,0(12)(2<≠++-=b a b ax ax x g ,在区间[]3,2上有最大值4,最小值1,设()()g x f x x=.(Ⅰ)求b a ,的值;(Ⅱ)不等式02)2(≥⋅-xxk f 在]1,1[-∈x 上恒成立,求实数k 的范围; (Ⅲ)方程0)3|12|2(|)12(|=--+-xx k f 有三个不同的实数解,求实数k 的范围.解:(Ⅰ)(1)2()(1)1g x a x b a =-++-当0>a 时,[]()2,3g x 在上为增函数故(3)296251(2)544220g a a b a g a a b b =-++==⎧⎧⎧⇒⇒⎨⎨⎨=-++==⎩⎩⎩当[]0()2,3a g x <时,在上为减函数故(3)296221(2)244253g a a b a g a a b b =-++==-⎧⎧⎧⇒⇒⎨⎨⎨=-++==⎩⎩⎩011==∴<b a b 即2()21g x x x =-+. ()12fx x x=+-.(Ⅱ)方程(2)20x xf k -⋅≥化为12222xxxk +-≥⋅2111()222xxk +-≥,令t x=21,221k t t ≤-+∵]1,1[-∈x ∴]2,21[∈t 记12)(2+-=t t t ϕ∴min ()0t ϕ= ∴0k ≤(Ⅲ)方程0)3|12|2(|)12(|=--+-xx k f 化为0)32(|12|21|12|=+--++-k k xx0)21(|12|)32(|12|2=++-+--k k x x ,0|12|x≠-令t x =-|12|, 则方程化为0)21()32(2=+++-k t k t (0t ≠) ∵方程0)32(|12|21|12|=+--++-k k xx 有三个不同的实数解,∴由|12|-=x t 的图像知,0)21()32(2=+++-k t k t 有两个根1t 、2t ,且21t 1t 0<<< 或 101<<t ,1t 2= 记)21()32()(2k t k t t +++-=ϕ则⎩⎨⎧<-=>+=0k )1(0k 21)0(ϕϕ 或 ⎪⎪⎩⎪⎪⎨⎧<+<=-=>+=12k3200k )1(0k 21)0(ϕϕ∴0k > 7.设二次函数2()f x ax bx c =++在区间[]2,2-上的最大值、最小值分别是M 、m ,集合{}|()A x f x x ==.(1)若{1,2}A =,且(0)2f =,求M 和m 的值;(2)若{1}A =,且1a ≥,记()g a M m =+,求()g a 的最小值.(1)由(0)22f c ==可知,……………………………1分又{}2A 1212(1)0.ax b x c =+-+=,,故,是方程的两实根 1-b 1+2=a ,c 2=a ⎧⎪⎪∴⎨⎪⎪⎩…………………3分 1,2a b ==-解得…………4分[]22()22(1)1,2,2f x x x x x ∴=-+=-+∈-min 1()(1)1,1x f x f m ====当时,即……………………………5分 max 2()(2)10,10.x f x f M =-=-==当时,即……………………………6分(2)2(1)0ax b x c +-+=由题意知,方程有两相等实根x=2, x=1∴ ⎪⎪⎩⎪⎪⎨⎧--=+a ca b 2111, 即⎩⎨⎧=-=a c a b 21 ……………………………8分∴f (x )=ax 2+(1-2a )x+a, x ∈[-2,2] 其对称轴方程为x==-aa 214-1a21又a≥1,故1-⎪⎭⎫⎢⎣⎡∈1,2121a ……………………………9分 ∴M=f (-2)=9a-2 …………………………10分 m=aaa f 411)212(-=- ……………………………11分g (a )=M+m=9a-a 41-1 ……………………………14分[)m in 63()1,1().4g a a g a +∞∴==又在区间上为单调递增的,当时,=431 ………16分8.已知函数22()242 f x axb b x=-+-⋅,2()1()(,)g x x a a b =---∈R .(1)当0b =时,若()(,2]f x -∞在上单调递减,求a 的取值范围;(2)求满足下列条件的所有整数对(,)a b :存在0x ,使得0()()f x f x 是的最大值,0()()g x g x 是 的最小值;(3)对满足(II )中的条件的整数对(,)a b ,试构造一个定义在{|D x x =∈R 且2,}x k k ≠∈Z上的函数()h x :使(2)()h x h x +=,且当(2,0)x ∈-时,()()h x f x =. 解:.1)当0b =时,()24f x ax x =-,…………………………………………………1分 若0a =,()4f x x =-,则()f x 在(],2-∞上单调递减,符合题意;………3分若0a ≠,要使()f x 在(],2-∞上单调递减,必须满足0,42,2a a>⎧⎪⎨≥⎪⎩……………………………………………………………………5分∴01a <≤.综上所述,a 的取值范围是[]0,1 …………………………………6分 (2)若0a =,()2242f x b b x =-+-,则()f x 无最大值,………………………7分故0a ≠,∴()f x 为二次函数,要使()f x 有最大值,必须满足20,420,a b b <⎧⎨+-≥⎩即0a <且1515b -≤≤+,…8分此时,2042b bx a+-=时,()f x 有最大值.………………………………………分又()g x 取最小值时,0x a =,………………………………………………………分 依题意,有242b ba a+-=∈Z ,则()2224251a b b b =+-=--,…………分∵0a <且1515b -≤≤+,∴()205a a <≤∈Z ,得1a =-,………………分 此时1b =-或3b =.∴满足条件的整数对(),a b 是()()1,1,1,3---.……………………………12分 (3)当整数对是()()1,1,1,3---时,()22f x x x =--(2)()h x h x += ,()h x ∴是以2为周期的周期函数,………………………分又当()2,0x ∈-时,,构造()h x 如下:当()22,2,x k k k ∈-∈Z ,则,()()()()()222222h x h x k fx k x k x k =-=-=----,故()()()()2222,22,2,.h x x k x k x k k k =----∈-∈Z9.已知函数()f x kx m =+,当[]11,x a b ∈时,()f x 的值域为[]22,ab ,当22[,]x a b ∈时,()f x 的值域为33[,]a b ,依次类推,一般地,当[]11,n n x a b --∈时,()f x 的值域为[],n n a b ,其中k 、m 为常数,且110,1a b == .(1)若k =1,求数列{}{},n n a b 的通项公式;(2)若0k >且1k ≠,问是否存在常数m ,使数列{}n b 是公比不为1的等比数列?请说明理由;(3)若0k <,设数列{}{},n n a b 的前n项和分别为,n nS T ,求()()1228122008T T T S S S+++-+++解:(1)因为()f x x m =+,当11[,]n n x a b --∈时,()f x 为单调增函数,所以其值域为11[,]n n a m b m --++,于是*11,(,2)n n n n a a m b b m n n --=+=+∈≥N . ……………… 又a 1=0, b 1=1, 所以(1)n a n m =-,1(1)n b n m =+-. ……………… (2)因为()(0)f x kx m k =+>,当11[,]n n x a b --∈时,()f x 为单调增函数,所以()f x 的值域为11[,]n n ka m kb m --++,所以*1(,2)n n b kb m n n -=+∈≥N .要使数列{b n }为等比数列,11n n n b mk b b --=+必须为与n 无关的常数. 又11,0,1b k k =>≠,故当且仅当0m =时,数列{}n b 是公比不为1的等比数列.(本题考生若先确定m =0,再证此时数列{}n b 是公比不为1的等比数列,给全分) (3)因为0k <,当11[,]n n x a b --∈时,()f x 为单调减函数, 所以()f x 的值域为11[,]n n kb m ka m --++, 于是*11,(,2)n n n n a kb m b ka m n n --=+=+∈≥N .所以211112211()()()()()()n n n n n n n n b a k b a k b a k b a k -------=--=--==--=- .111, 1,()()1(), 0, 1.1iij i i i jj j j i k T S ba k k k k k-===-⎧⎪-=-=-=⎨--<≠-⎪+⎩∑∑()()122008122008T T T S S S +++-+++20082008111()()iii j j i i j TS b a ====-=-∑∑∑200922017036, 1,20082009, 0, 1.(1)k k k k k k =-⎧⎪=+-⎨<≠-⎪+⎩1)因为()f x x m =+,当11[,]n n x a b --∈时,()f x 为单调增函数,所以其值域为11[,]n n a m b m --++,于是*11,(,2)n n n n a a m b b m n n --=+=+∈≥N . 又a 1=0, b 1=1, 所以(1)n a n m =-,1(1)n b n m =+-.10.已知二次函数g (x )对任意实数x 都满足()()21121g x g x xx -+-=--,且()11g =-令()19()ln (,0)28f x g x m x m x =+++∈>R(1)求 g (x )的表达式;(2)若0x ∃>使()0f x ≤成立,求实数m 的取值范围;(3)设1e m <≤,()()(1)H x f x m x =-+, 证明:对12[1]x x m ∀∈,,,恒有12|()()| 1.H x H x -<【解】 (1)设()2g x ax bx c =++,于是()()()()2211212212g x g x a x c x -+-=-+=--,所以121.a c ⎧=⎪⎨⎪=-⎩,又()11g =-,则12b =-.所以()211122g x x x =--. ……………………4分(2)()2191()ln ln (0).282f xg x m x x m x m x =+++=+∈>R ,当m >0时,由对数函数性质,f (x )的值域为R ; 当m =0时,2()02xf x =>对0x ∀>,()0f x >恒成立; ……………………6分当m <0时,由()0m f x x x m x'=+=⇒=-,列表:[]m in ()()ln .2mf x f m m m =-=-+-这时,[]minln 0()0e<0.20mm m f x m m ⎧-+->⎪>⇔⇒-<⎨⎪<⎩,……………………8分所以若0x ∀>,()0f x >恒成立,则实数m 的取值范围是(e 0]-,.故0x ∃>使()0f x ≤成立,实数m 的取值范围()(,e]0-∞-+∞ ,.……………… 10分(3)因为对[1]x m ∀∈,,(1)()()0x x m H x x --'=≤,所以()H x 在[1,]m 内单调递减.于是21211|()()|(1)()ln .22H x H x H H m m m m -≤-=--2121113|()()|1ln 1ln 0.2222H x H x m m m m m m-<⇐--<⇔--< ………………… 12分记13()ln (1e)22h m m m m m=--<≤,则()221133111()022332h'm m m m =-+=-+>,所以函数13()ln 22h m m m m =--在(1e],是单调增函数, ………………… 14分所以()()e 3e 1e 3()(e)1022e2eh m h -+≤=--=<,故命题成立. ………………… 16分11.已知二次函数1)(2++=bx ax x f 和函数bx a bx x g 21)(2+-=,(1)若)(x f 为偶函数,试判断)(x g 的奇偶性;(5分)(2)若方程()g x x =有两个不等的实根()2121,x x x x <,则①证明函数)(x f 在(-1,1)上是单调函数;(6分)②若方程0)(=x f 的有两实根为()4343,x x x x <,求使4213x x x x <<<成立的a 的取值范围.(5分)解:(1)∵)(x f 为偶函数,∴()()f x f x -=,∴0bx =,∴0b =∴21()g x a x=-,∴函数()g x 为奇函数;(2)①由x bx a bx x g =+-=21)(2得方程(*)0122=++bx x a 有不等实根x(0)m -,m- ()m -+∞,()f x ' - 0 + ()f x减极小 增∴△0422>-=a b 及0≠a 得12>ab 即1122b b aa-<-->或又)(x f 的对称轴()1,12-∉-=ab x故)(x f 在(-1,1)上是单调函数 ②21,x x 是方程(*)的根,∴011212=++bx x a ∴12121--=x a bx ,同理12222--=x a bx∴=)(1x f 222211111ax bx ax a x ++=-=212)(x a a - 同理=)(2x f 222)(x a a -要使4213x x x x <<<,只需⎪⎩⎪⎨⎧<<>0)(0)(021x f x f a 即⎩⎨⎧<->002a a a ,∴1>a 或⎪⎩⎪⎨⎧>><0)(0)(021x f x f a 即⎩⎨⎧>-<002a a a ,解集为φ 故a 的取值范围1>a12.已知函数)()0,1(),0()(x f y P t xt x x f =>+=作曲线过点的两条切线PM 、PN ,切点分别为M 、N . (1)当2=t 时,求函数)(x f 的单调递增区间; (2)设|MN |=)(t g ,试求函数)(t g 的表达式(3)在(2)的条件下,若对任意的正整数n ,在区间]64,2[n n +内,总存在m +1个数,,,,,121+m m a a a a 使得不等式)()()()(121+<+++m m a g a g a g a g 成立,求m 的最大值.解:(I )当,2)(,2xx x f t +==时 0221)(222>-=-='xx xx f 1分2,2-<>x x 或解得.则函数)(x f 有单调递增区间为),2(),2,(+∞--∞ 4分(II )设M 、N 两点的横坐标分别为1x 、2x ,)1(.02).1)(1()(0),0,1().)(1()(:,1)(12112111121112=-+--=+-∴--=+-∴-='t tx x x xt x t x P PM x x xt x t x y PM xt x f 即有过点切线又的方程为切线同理,由切线PN 也过点(1,0),得.02222=-+t tx x (2) 6分 由(1)、(2),可得02,221=-+t tx x x x 是方程的两根,(*).22121⎩⎨⎧-=⋅-=+∴t x x tx x 8分])1(1[)()()(||22122122211221x x t x x x t x x t x x x MN -+-=--++-=])1(1][4)[(22121221x x t x x x x -+-+把(*)式代入,得,2020||2t t MN +=因此,函数)0(2020)()(2>+=t t t t g t g 的表达式为 10分(III )易知]64,2[)(nn t g +在区间上为增函数,12121(2)()(1,2,,1).(2)()()().()()()(),i m m m g g a i m m g g a g a g a g a g a g a g a n +∴≤=+⋅≤++++++< 则对一切正整数成立恒成立对一切的正整数不等式n nn g g m )64()2(+<⋅∴ 13分,)64(20)64(2022022022nn nn m +++<⨯+⨯.3136.3136]1616[61)]64()64[(61,1664)]64()64[(61222<∴=+≥+++∴≥++++<m nn nn nn n nn nn m 恒成立对一切的正整数即由于m 为正整数,6≤∴m . 15分又当.,16,2,6121满足条件对所有的存在时n a a a a m m m ======+因此,m 的最大值为6. 16分13.已知函数x ax x x f ln )(2-+=, .a R ∈(1)若函数)(x f 在[]2,1上是减函数,求实数a 的取值范围;(2)令2)()(x x f x g -=,是否存在实数a ,当∈x ],0(e (e 是自然常数)时,函数)(x g 的最小值是3,若存在,求出a 的值;若不存在,说明理由;(3)当∈x ],0(e 时,证明: x x x x e ln )1(2522+>-解:(1)01212)(2'≤-+=-+=xax x xa x x f 在[]2,1上恒成立,令 12)(2-+=ax x x h ,有⎩⎨⎧≤≤0)2(0)1(h h 得,271⎪⎩⎪⎨⎧-≤-≤a a ……………………… 4分得27-≤a (5)分(2)假设存在实数a ,使x ax x g ln )(-=(],0(e x ∈)有最小值3,xa x g 1)('-=xax 1-=……………………………………………6分当0≤a 时,)(x g 在],0(e 上单调递减,31)()(min =-==ae e g x g ,ea 4=(舍去),②当e a<<10时,)(x g 在)1,0(a上单调递减,在],1(e a上单调递增∴3ln 1)1()(min =+==a ag x g ,2e a =,满足条件.③当e a ≥1时,)(x g 在],0(e 上单调递减,31)()(min =-==ae e g x g ,ea 4=(舍去),综上,存在实数2e a =,使得当],0(e x ∈时)(x g 有最小值3. ……………………10分(3)令x x e x F ln )(2-=,由(2)知,3)(min =x F .令25ln )(+=xx x ϕ,2'ln 1)(xx x -=ϕ,当e x ≤<0时,0)('≥x ϕ,()h x 在],0(e 上单调递增 ∴32521251)()(max =+<+==e e x ϕϕ ,25ln ln 2+>-∴xx x x e 即x x e 2522-x x ln )1(+>.………14分14.设函数322()f x x ax a x m =+-+(0)a >(1)若1a =时函数()f x 有三个互不相同的零点,求m 的范围; (2)若函数()f x 在[]1,1-内没有极值点,求a 的范围;(3)若对任意的[]3,6a ∈,不等式()1f x ≤在[]2,2x ∈-上恒成立,求实数m 的取值范围.解:(1)当1a =时32()f x x x x m =+-+,因为()f x 有三个互不相同的零点,所以32()0f x x x x m =+-+=, 即32m x x x =--+有三个互不相同的实数根。
陕西省2012年高考数学压轴卷试卷理

23 .
(2)设 cn an 2 an (n N ) , bn a2n 1 (n N ) , Sn 为数列 { bn } 前 n 项和,求 cn 的通
项,并求 Sn 取最小时的 n 值.
18.(本题 12 分)为拉动经济增长,某市决定新建一批重点工程,分别为基础设施工程、民
P 3! P( A1B2C3) 6P( A1) P(B2) P(C3 ) 6
. ----------
236 6
( 6 分)( 2)
用心
爱心
专心
4
记第 i 名工人选择的项目属于基础工程或产业建设工程分别为事件
Di , i 1,2,3 .
D1, D
,
即
P(
3
.
15. 选做题 (请考生在以下三个小题中任选一题做答,如果多做, 则按所做的第一题评阅记分)
A.(选修 4— 4 坐标系与参数方程)已知点 A 是曲线
2sin
上任意一点,则点 A 到直线 sin(
) 4的距离的最小值是
.
3
B.(选修 4— 5 不等式选讲)不等式 | x log 2 x | x | log 2 x | 的解集是 .
从而 f ( x)在( , 3),(0,3) 单调增加,在( 3,0),( 3, )单调减少……( 7 分)
(2) f '( x) (x3 3x2 ax b)e x (3x2 6x a)e x e x[ x3 (a 6) x b a]. 由条件得: f '(2) 0,即23 2( a 6) b a 0, 故b 4 a, 从而 f '(x) e x[ x3 (a 6) x 4 2a].
设平面 PMN的一个法向量为 m=( x, y,z), 1
2012年福建省高考压轴卷数学理试卷

2012年福建省高考压轴卷数学理本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题),第Ⅱ卷第21题为选考题,其它题为必考题.本试卷共6页,满分150分.考试时间120分钟. 注意事项:1.答题前,考生先将自己的姓名、准考证号填写在答题卡上.2.考生作答时,将答案答在答题卡上.请按照题号在各题的答题区域(黑色线框)内作答,超出答题区域书写的答案无效.在草稿纸、试题卷上答题无效.3.选择题答案使用2B 铅笔填涂,如需改动,用橡皮擦干净后,再选涂其它答案标号;非选择题答案使用0.5毫米的黑色中性(签字)笔或碳素笔书写,字体工整、笔迹清楚.4.做选考题时,考生按照题目要求作答,并用2B 铅笔在答题卡上把所选题目对应的题号涂黑.5.保持答题卡卡面清洁,不折叠、不破损.考试结束后,将本试卷和答题卡一并交回. 参考公式:样本数据1x 、2x 、…、n x 的标准差:s =x 为样本平均数; 柱体体积公式:V Sh =,其中S 为底面面积,h 为高;锥体体积公式:13V Sh =,其中S 为底面面积,h 为高; 球的表面积、体积公式:24S R π=,343V R π=,其中R 为球的半径.第Ⅰ卷(选择题 共50分)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1. 已知复数1cos23sin 23z i =+和复数2cos37sin37z i =+,则21z z ⋅为( )A .i 2321+B .i 2123+C .i 2321- D .i 2123-2. 已知{}n a 为等差数列,若9843=++a a a ,则9S =( ) A.24 B. 27 C. 15 D. 545. 在样本的频率分布直方图中, 共有9个小长方形, 若第一个长方形的面积为0.02, 前五个与后五个长方形的面积分别成等差数列且公差互为相反数,若样本容量为160, 则中间一组(即第五组)的频数为( )(A )12(B )24 (C )36 (D )484. 已知,a l 是直线,α是平面,且a α⊂,则“l a ⊥”是“l α⊥”的A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件5. 一个几何体的三视图如图所示(单位长度:cm), 则此几何体的表面积是A. (280cm + B. 284cmC. (296cm + D. 296cm6. 函数)0(sin 3>=ωωx y 在区间],0[π恰有2个零点,则ω的取值范围为()A .1≥ωB .21<≤ωC .31<≤ωD .3<ω7. 若b a c b a +===,2||,1||,且a c ⊥,则c b 与的夹角为( )A .30°B .60°C .120°D .150°8. 已知O 为坐标原点,点M 的坐标为(,1)a (0a >),点(,)N x y 的坐标x 、y 满足不等式组⎪⎩⎪⎨⎧≤≥-+≤-+1033032y y x y x . 若当且仅当30x y =⎧⎨=⎩时,OM ON ⋅取得最大值,则a 的取值范围是 ( ) A.1(0,)3 B.1(,)3+∞ C.1(0,)2 D.1(,)2+∞9.在平面直角坐标系中,定义1212(,)d P Q x x y y =-+-为两点11(,)P x y ,22(,)Q x y 之间的“折线距离”. 若O 为坐标原点,则O与直线20x y +-=上一点的“折线距离”的最小值是( )B. C.2 D. 4第6题图10. 已知234101()1234101x x x x f x x =+-+-+⋅⋅⋅+,234101()1234101x x x x g x x =-+-+-⋅⋅⋅-,若函数()f x 有唯一零点1x ,函数()g x 有唯一零点2x ,则有 ( ) A .12(0,1),(1,2)x x ∈∈ B .12(1,0),(1,2)x x ∈-∈ C .12(0,1),(0,1)x x ∈∈ D .12(1,0),(0,1)x x ∈-∈第Ⅱ卷(非选择题 共100分)二、填空题:本大题共5小题,每小题4分,共20分.将答案填在答题卡的相应位置. 11. 若集合M={}21m ,,集合N={}4,2,{}4,2,1=N M ,则实数m 的值的个数是_________12. 在区间[-3,5]上随机取一个数x ,则x ∈[1,3]的概率为_________13. 记2()nx x+的展开式中第k 项的系数为33,5,k a a a n =若则= _________14. 设双曲线的一个焦点为F ,虚轴的一个端点为B ,如果直线FB 与该双曲线的一条渐近线垂直,那么双曲线的离心率是_________15. 洛萨⋅科拉茨(Lothar Collatz,1910.7.6-1990.9.26)是德国数学家,他在1937年提出了一个著名的猜想:任给一个正整数n ,如果n 是偶数,就将它减半(即2n );如果n 是奇数,则将它乘3加1(即31n +),不断重复这样的运算,经过有限步后,一定可以得到1.如初始正整数为6,按照上述变换规则,我们得到一个数列:6,3,10,5,16,8,4,2,1.对科拉茨(Lothar Collatz )猜想,目前谁也不能证明,更不能否定.现在请你研究:如果对正整数n (首项)按照上述规则施行变换(注:1可以多次出现)后的第八项为1,则n 的所有可能的取值为_________三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. 16.(本小题满分13分)工人在包装某产品时不小心将两件不合格的产品一起放进了一个箱子,此时该箱子中共有外观完全相同的六件产品.只有将产品逐一打开检验才能确定哪两件产品是不合格的,产品一旦打开检验不管是否合格都将报废.记ξ表示将两件不合格产品全部检测出来后四件合格品中报废品的数量.(Ⅰ)求报废的合格品少于两件的概率; (Ⅱ)求ξ的分布列和数学期望.17.(本小题满分13分)已知函数43)3cos(sin 3)(++=πx x x f . (Ⅰ) 求函数)(x f 的单调递增区间;(Ⅱ) 已知ABC ∆中,角C B A ,,所对的边长分别为c b a ,,,若0)(=A f ,2,3==b a ,求ABC ∆的面积S .18.(本小题满分13分)已知椭圆122=+ny m x (常数m 、+∈R n ,且n m >)的左右焦点分别为21,F F ,M 、N为短轴的两个端点,且四边形F 1MF 2N 是边长为2的正方形.(Ⅰ)求椭圆方程;(Ⅱ)过原点且斜率分别为k 和-k (k ≥2)的两条直线与椭圆221x y m n+=的交点为A 、B 、C 、D (按逆时针顺序排列,且点A 位于第一象限内),求四边形ABCD 的面积S 的最大值.19. (本小题满分13分)在四棱锥P ABCD -中,侧面PCD ⊥底面ABCD ,PD CD ⊥,底面ABCD 是直角梯形,//AB CD ,ADC ∠=90°,1AB AD PD ===,2CD =. (Ⅰ)求证:BC ⊥平面PBD ; (Ⅱ)设E 为侧棱PC 上一点,PE PC λ=,试确定λ的 值,使得二面角P BD E --的大小为45°. 20.(本小题满分14分)设函数2()(1)f x x x =-,0x >. (Ⅰ)求()f x 的极值;(Ⅱ)设0a <≤1,记()f x 在(]0,a 上的最大值为()F a ,求函数()()F a G a a=的最小值; (Ⅲ)设函数2()ln 24g x x x x t =-++(t 为常数),若使()g x ≤x m +≤()f x 在(0,)+∞上恒成立的实数m 有且只有一个,求实数m 和t 的值.21. 本题有(1)、(2)、(3)三个选答题,每题7分,请考生任选2题作答,满分14分.如果多做,则按所做的前两题记分.作答时,先用2B 铅笔在答题卡上把所选题目对应的题号涂黑,并将所选题号填入括号中.作 (1)(本小题满分7分)选修4—2:矩阵与变换已知二阶矩阵M 有特征值3λ=及对应的一个特征向量111⎡⎤=⎢⎥⎣⎦e ,并且矩阵M 对应的变换将点(1,2)-变换成(9,15). 求矩阵M .(2)(本小题满分7分)选修4-4:坐标系与参数方程已知极点与原点重合,极轴与x 轴的正半轴重合.若曲线1C 的极坐标方程为:2sin ρ=θ,曲线2C的参数方程为:x 2cos y =θ⎧⎪⎨=θ⎪⎩(θ为参数),曲线1C 与2C 交于M ,N 两点,求M ,N 两点间的距离.(3)(本小题满分7分)选修4—5:不等式选讲不等式1t 1t 2x x 1++-≥+-对任意实数t 恒成立,试求实数x 的取值范围.2012年福建省高考压轴卷数学理答案第Ⅰ卷(选择题 共50分)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1. 已知复数1cos23sin 23z i =+和复数2cos37sin37z i =+,则21z z ⋅为( )A .i 2321+ B .i 2123+ C .i 2321- D .i 2123- 解析:A ;2. 已知{}n a 为等差数列,若9843=++a a a ,则9S =( ) A.24 B. 27 C. 15 D. 54解析:B ;5. 在样本的频率分布直方图中, 共有9个小长方形, 若第一个长方形的面积为0.02, 前五个与后五个长方形的面积分别成等差数列且公差互为相反数,若样本容量为160, 则中间一组(即第五组)的频数为( ) (A )12 (B )24 (C )36 (D )48 解析:C;4. 已知,a l 是直线,α是平面,且a α⊂,则“l a ⊥”是“l α⊥”的A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件解析:B ;5. 一个几何体的三视图如图所示(单位长度:cm), 则此几何体的表面积是A. (280cm + B. 284cmC. (296cm + D. 296cm 解析:A ;6. 函数)0(sin 3>=ωωx y 在区间],0[π恰有2个零点,则ω的取值范围为()A .1≥ωB .21<≤ωC .31<≤ωD .3<ω第6题图解析:B ;7. 若b a c b a +===,2||,1||,且a c ⊥,则c b 与的夹角为( )A .30°B .60°C .120°D .150° 解析:A ;8. 已知O 为坐标原点,点M 的坐标为(,1)a (0a >),点(,)N x y 的坐标x 、y 满足不等式组⎪⎩⎪⎨⎧≤≥-+≤-+1033032y y x y x . 若当且仅当30x y =⎧⎨=⎩时,OM ON ⋅取得最大值,则a 的取值范围是 ( ) A.1(0,)3 B.1(,)3+∞ C.1(0,)2 D.1(,)2+∞解析:D ;9.在平面直角坐标系中,定义1212(,)d P Q x x y y =-+-为两点11(,)P x y ,22(,)Q x y 之间的“折线距离”. 若O 为坐标原点,则O与直线20x y +-=上一点的“折线距离”的最小值是( )B. C.2 D. 4解析:A ;10. 已知234101()1234101x x x x f x x =+-+-+⋅⋅⋅+,234101()1234101x x x x g x x =-+-+-⋅⋅⋅-,若函数()f x 有唯一零点1x ,函数()g x 有唯一零点2x ,则有 ( ) A .12(0,1),(1,2)x x ∈∈ B .12(1,0),(1,2)x x ∈-∈ C .12(0,1),(0,1)x x ∈∈ D .12(1,0),(0,1)x x ∈-∈ 解析:B ;第Ⅱ卷(非选择题 共100分)二、填空题:本大题共5小题,每小题4分,共20分.将答案填在答题卡的相应位置. 11. 若集合M={}21m ,,集合N={}4,2,{}4,2,1=N M ,则实数m 的值的个数是_________解析:4.12. 在区间[-3,5]上随机取一个数x ,则x ∈[1,3]的概率为_________13. 记()nx x+的展开式中第k 项的系数为33,5,k a a a n =若则= _________解析:6.14. 设双曲线的一个焦点为F ,虚轴的一个端点为B ,如果直线FB 与该双曲线的一条渐近线垂直,那么双曲线的离心率是_________. 15. 洛萨⋅科拉茨(Lothar Collatz,1910.7.6-1990.9.26)是德国数学家,他在1937年提出了一个著名的猜想:任给一个正整数n ,如果n 是偶数,就将它减半(即2n );如果n 是奇数,则将它乘3加1(即31n +),不断重复这样的运算,经过有限步后,一定可以得到1.如初始正整数为6,按照上述变换规则,我们得到一个数列:6,3,10,5,16,8,4,2,1.对科拉茨(Lothar Collatz )猜想,目前谁也不能证明,更不能否定.现在请你研究:如果对正整数n (首项)按照上述规则施行变换(注:1可以多次出现)后的第八项为1,则n 的所有可能的取值为_________ 解析:{}2,3,16,20,21,128.三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. 16.(本小题满分13分)工人在包装某产品时不小心将两件不合格的产品一起放进了一个箱子,此时该箱子中共有外观完全相同的六件产品.只有将产品逐一打开检验才能确定哪两件产品是不合格的,产品一旦打开检验不管是否合格都将报废.记ξ表示将两件不合格产品全部检测出来后四件合格品中报废品的数量.(Ⅰ)求报废的合格品少于两件的概率; (Ⅱ)求ξ的分布列和数学期望. 解析:(Ⅰ) 12115155p =+=; (Ⅱ12141801234151551533E ξ=⨯+⨯+⨯+⨯+⨯= .17.(本小题满分13分)已知函数43)3cos(sin 3)(++=πx x x f . (Ⅰ) 求函数)(x f 的单调递增区间;(Ⅱ) 已知ABC ∆中,角C B A ,,所对的边长分别为c b a ,,,若0)(=A f ,2,3==b a ,求ABC ∆的面积S .解析:(Ⅰ)43)3sin sin 3cos(cos sin 3)(+-=ππx x x x f 43sin 23cos sin 232+-=x x x x x 2cos 432sin 43+=)32sin(23π+=x , 令Z k k x k ∈+≤+≤-,223222πππππ,得Z k k x k ∈+≤≤-,12125ππππ, 所以函数)(x f 的单调递增区间为Z k k k ∈⎥⎦⎤⎢⎣⎡+-,12,125ππππ; (Ⅱ) 0)(=A f ,0)32sin(23=+∴πA ,解得3π=A 或65π=A , 又b a <,故3π=A ,由B b A a sin sin =,得1sin =B ,则2π=B ,6π=C , 所以23sin 21==C ab S . 18.(本小题满分13分)已知椭圆122=+ny m x (常数m 、+∈R n ,且n m >)的左右焦点分别为21,F F ,M 、N为短轴的两个端点,且四边形F 1MF 2N 是边长为2的正方形.(Ⅰ)求椭圆方程;(Ⅱ)过原点且斜率分别为k 和-k (k ≥2)的两条直线与椭圆221x y m n+=的交点为A 、B 、C 、D (按逆时针顺序排列,且点A 位于第一象限内),求四边形ABCD 的面积S 的最大值.解析: (Ⅰ)依题意:42m n nm n -=⎧=⎧⎪∴⎨⎨==⎪⎩⎩,所求椭圆方程为22142x y +=.yx(Ⅱ)设A (x,y ).由22142y kxxy =⎧⎪⎨+=⎪⎩得A. 根据题设直线图象与椭圆的对称性,知2164().122kS k k==≥+ ∴16().122S k k k=≥+设1()2,M k k k =+则21()2,M k k '=-当2k ≥时,21()20M k k'=-> ∴()M k 在[)2,k ∈+∞时单调递增,∴[]min 9()(2),2M k M == ∴当2k ≥时,max 1632992S ==. 19. (本小题满分13分)在四棱锥P ABCD -中,侧面PCD ⊥底面ABCD ,PD CD ⊥,底面ABCD 是直角梯形,//AB CD ,ADC ∠=90°,1AB AD PD ===,2CD =.(Ⅰ)求证:BC ⊥平面PBD ; (Ⅱ)设E 为侧棱PC 上一点,PE PC λ=,试确定λ的 值,使得二面角P BD E --的大小为45°.解析:(Ⅰ)平面PCD ⊥底面ABCD ,PD ⊥CD ,所以PD ⊥平面ABCD , 所以PD ⊥AD. 如图,以D 为原点建立空间直角坐标系D —xyz . 则A (1,0,0),B (1,1,0),C (0,2,0), P (0,0,1)).0,1,1(),0,1,1(-==BC DB所以,,0DB BC ⊥=⋅又由PD ⊥平面ABCD ,可得PD ⊥BC , 所以BC ⊥平面PBD ;(Ⅱ)平面PBD 的法向量为),0,1,1(-=)1,0(,),1,2,0(∈=-=λλPC PE PC ,所以)1,2,0(λλ-E ,设平面QBD的法向量为n =(a ,b ,c ),)1,2,0(),0,1,1(λλ-==由n 0=⋅DB ,n 0=⋅,得 所以,⎩⎨⎧=-+=+0)1(20c b b a λλ,∴)12,1,1(--=λλn由CB n CB n ⋅=4cos π解得12-=λ。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2012年高考数学试卷三大压轴题目
上海
14.如图,AD 与BC 是四面体ABCD 中互相垂直的棱,2=BC ,
若c AD 2=,
且a CD AC BD AB 2=+=+,其中a 、c 为常数,则四面体
ABCD 的体积的最
大值是
17.设443211010≤<<<≤x x x x ,5510=x ,随机变量1ξ取值54321x x x x x 、、、、的
概率均为2.0,随机变量2ξ取值
2
22221554433221x x x x x x x x x x +++++、、、、的概率也均为2.0,若记21ξξD D 、分别为21ξξ、的方差,则( )
A .21ξξD D >
B .21ξξD D =
C .21ξξ
D D < D .1ξD 与2ξD 的大小关系与4321x x x x 、、、的取值有关
18.设25sin 1πn n a n =,n n a a a S +++= 21,在10021,,,S S S 中,正数的个数是( ) A .25 B .50 C .75 D .100
22.(4+6+6=16分)在平面直角坐标系xOy 中,已知双曲线1C :122
2=-y x .
(1)过1C 的左顶点引1C 的一条渐进线的平行线,求该直线与另一条渐进线及x 轴围成的三角形的面积; (2)设斜率为1的直线l 交1C 于P 、Q 两点,若l 与圆122=+y x 相切,求证:OQ OP ⊥;
(3)设椭圆2C :1422=+y x ,若M 、N 分别是1C 、2C 上的动点,且ON OM ⊥,求证:O 到直线MN 的距离是定值。
23.(4+6+8=18分)对于数集}1{21n x x x X ,,,, -=,其中n x x x <<<< 210,2≥n ,定义向量集},),,(|{X t X s t s a a Y ∈∈==,若对任意Y a ∈1,存在Y a ∈2,使得021=⋅a a ,则称X 具有性质P .例如}2,1,1{-具有性质P .
(1)若2>x ,且},2,1,1{x -具有性质P ,求x 的值;
(2)若X 具有性质P ,求证:X ∈1,且当1>n x 时,11=x ;
(3)若X 具有性质P ,且11=x 、q x =2(q 为常数),求有穷数列n x x x ,,, 21的通项公式。
天津
(8)设R n m ∈,,若直线02)1()1(=-+++y n x m 与圆1)1()1(22=-+-y x 相切,则m+n 的取值范围是
(A )]31,31[+- (B )),31[]31,(+∞+⋃--∞
(C )]222,222[+- (D )),222[]222,(+∞+⋃--∞(13)如图,已知AB 和AC 是圆的两条弦,过点B 作
圆的切线与AC 的延长线相交于点D. 过点C 作BD 的
平行线与圆相交于点E ,与AB 相交于点F ,AF=3,
FB=1,EF=2
3,则线段CD 的长为____________. (14)已知函数11
2--=x x y 的图象与函数2-=kx y 的图象恰有两个交点,则实数
k 的取值范围是_________.
(20)(本小题满分14分)
已知函数)ln()(a x x x f +-=的最小值为0,其中.0>a
(Ⅰ)求a 的值;
(Ⅱ)若对任意的),,0[+∞∈x 有)(x f ≤2kx 成立,求实数k 的最小值; (Ⅲ)证明∑=<+--n i n i 12)12ln(1
22(*N n ∈).
北京
14.已知f(x)=m(x-2m)(x+m+3),g(x)=错误!未找到引用源。
-2,若同时满足条件: ①错误!未找到引用源。
x ∈R ,f(x) <0或g(x) <0
②错误!未找到引用源。
x ∈(﹣∝, ﹣4),f(x)g(x) <0
则m 的取值范围是
20.(本小题共13分)
设A 是由m ×n 个实数组成的m 行n 列的数表,满足:每个数的绝对值不大于1,且所有数的和为零,记s(m ,n)为所有这样的数表构成的集合。
对于A ∈S(m,n),记r i (A)为A 的第ⅰ行各数之和(1≤ⅰ≤m ),C j (A)为A 的第j 列各数之和(1≤j ≤n ):
记K(A)为∣r 1(A)∣,∣R 2(A)∣,…,∣Rm(A)∣,∣C 1(A)∣,∣C 2(A)∣,…,∣Cn(A)∣中的最小值。
(1) 对如下数表A ,求K (A )的值; 1
1 -0.8 0.1
-0.3 -1
(2)设数表A ∈S (2,3)形如
1
1 c a b -1
求K (A )的最大值;
(3)给定正整数t ,对于所有的A ∈S (2,2t+1),求K (A )的最大值。
全国
(12)正方形ABCD 的边长为1,点E 在边AB 上,点F 在边BC 上,37
AE BF ==。
动点P 从E 出发沿直线向F 运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角,当点P 第一次碰到E 时,P 与正方形的边碰撞的次数为
(A )16 (B )14 (C )12 (D )10
(22)(本小题满分12分)(注意:在试卷上作答无效........
) 函数2()23f x x x =--,定义数列{}n x 如下:12x =,1n x +是过两点(4,5)P 、
(,())n n n Q x f x 的直线n PQ 与x 轴交点的横坐标。
(Ⅰ)证明:123n n x x +≤<<;
(Ⅱ)求数列{}n x 的通项公式。
新课标(10) 已知函数1()ln(1)f x x x
=+-,则()y f x =的图像大致为 (11)已知三棱锥S ABC -的所有顶点都在球O 的球面上,ABC ∆是边长为1的正三角形,SC 为球O 的直径,且2SC =,则此棱锥的体积为
(A )26 (B )36 (C )23 (D )22
(12)设点P 在曲线12x y e =
上,点Q 在曲线ln(2)y x =上,则||PQ 的最小值为 (A )1ln 2- (B )2(1ln 2)- (C )1ln 2+ (D )2(1ln 2)+
(16)数列{}n a 满足1(1)21n n n a a n ++-=-,则的前60项和为
(21)(本小题满分12分)
已知函数()f x 满足121()'(1)(0)2
x f x f e f x x -=-+ (Ⅰ)求()f x 的解析式及单调区间; (Ⅱ)若21()2
f x x ax b ≥++,求(1)a b +的最大值
(23)(本小题满分10分)选修4—4;坐标系与参数方程
已知曲线1C 的参数方程是12cos ,3sin ,x C y ϕϕ=⎧⎨=⎩
(ϕ为参数),以坐标原点为极点,x 轴的正
半轴为极轴建立坐标系,曲线2C 的极坐标方程是2ρ=,正方形ABCD 的顶点都在2C 上,且,,,A B C D 依逆时针次序排列,点A 的极坐标为(2,
)3π。
(Ⅰ)求点,,,A B C D 的直角坐标;
(Ⅱ)设P 为1C 上任意一点,求2222||||||||PA PB PC PD +++|的取值范围。
辽宁 (16)已知正三棱锥P -ABC ,点P ,A ,B ,C 都在半径为3的求面上,若PA ,PB ,PC 两
两互相垂直,则球心到截面ABC 的距离为________。
(21)(本小题满分12分) 设()ln(1)1(,,,)f x x x ax b a b R a b =+++++∈为常数,曲线()y f x =与 直线32
y x =在(0,0)点相切。
(Ⅰ)求,a b 的值。
(Ⅱ)证明:当02x <<时,9()6
x f x x <
+ (20)(本小题满分12分) 如图,椭圆0C :22
221(0x y a b a b
+=>>,a ,b 为常数),动圆22211:C x y t +=,1b t a <<。
点12,A A 分别为0C 的左,右顶点,1C 与0C 相交于A ,B ,C ,D 四点。
(Ⅰ)求直线1AA 与直线2A B 交点M 的轨迹方程;
(Ⅱ)设动圆22222:C x y t +=与0C 相交于////
,,,A B C D 四点,其中2b t a <<,
12t t ≠。
若矩形ABCD 与矩形////A B C D 的面积相等,证明:
2212
t t +为定值。
