在直角梯形ABCD中
初三数学四边形试题

初三数学四边形试题1.如图,梯形ABCD中,AD∥BC,点M是AD的中点,不添加辅助线,梯形满足条件时,有MB=MC(只填一个即可).【答案】AB=DC(或∠ABC=∠DCB、∠A=∠D)等【解析】当AB=DC时,∵梯形ABCD中,AD∥BC,则∠A=∠D,∵点M是AD的中点,∴AM=MD,又∵AB=DC,∴△ABM≌△△DCM(SAS),∴MB=MC,同理可得出:∠ABC=∠DCB、∠A=∠D时都可以得出MB=MC,【考点】1、梯形;2、全等三角形的判定.2.以下四个命题正确的是()A.任意三点可以确定一个圆B.菱形对角线相等C.直角三角形斜边上的中线等于斜边的一半D.平行四边形的四条边相等【答案】C【解析】A、不在同一直线上的三点确定一个圆,故A错误;B、菱形的对角线垂直但不一定相等,故B错误;C、正确;D、平行四边形的四条边不一定相等.故D错误故选C.【考点】命题与定理3.如图,在四边形ABCD中,对角线AC,BD交于点O,OA=OC,OB=OD,添加一个条件使四边形ABCD是菱形,那么所添加的条件可以是(写出一个即可).【答案】AB=AD(答案不唯一).【解析】利用菱形的判定定理添加邻边相等或对角线垂直即可判定该四边形是菱形.试题解析:∵OA=OC,OB=OD,∴四边形ABCD是平行四边形,∵邻边相等的平行四边形是菱形,∴添加的条件是AB=AD(答案不唯一).【考点】菱形的判定.4.下列多边形中,内角和与外角和相等的是()A.四边形B.五边形C.六边形D.八边形【答案】A.【解析】设多边形的边数是n,则(n-2)•180=360,解得n=4.故选A.【考点】多边形内角与外角.5.下列命题是假命题的是()A.平行四边形的对边相等B.四条边都相等的四边形是菱形C.矩形的两条对角线互相垂直D.等腰梯形的两条对角线相等【答案】C【解析】C项因为矩形的对角线相等但不一定垂直错误,是假命题;A、B、D选项正确,是真命题.6.若顺次连接四边形ABCD各边的中点所得四边形是矩形,则四边形ABCD一定是 ()A.矩形B.菱形C.对角线互相垂直的四边形D.对角线相等的四边形【答案】C【解析】已知:如图,四边形EFGH是矩形,且E、F、G、H分别AB、BC、CD、AD的中点,求证:四边形ABCD是对角线互相垂直的四边形.证明:由于E、F、G、H分别是AB、BC、CD、AD的中点,根据三角形中位线定理得:EH∥FG∥BD,EF∥AC∥HG;∵四边形EFGH是矩形,即EF⊥FG,∴AC⊥BD.7.如图,AD是△ABC的角平分线,过点D作DE∥AB,DF∥AC,分别交AC、AB于点E和F.(1)在图中画出线段DE和DF;(2)连接EF,则线段AD和EF互相垂直平分,这是为什么?【答案】(1)作图见解析;(2)证明见解析.【解析】(1)根据题目要求画出线段DE、DF即可;(2)首先证明四边形AEDF是平行四边形,再证明∠EAD=∠EDA,根据等角对等边可得EA=ED,由有一组邻边相等的平行四边形是菱形可证明四边形AEDF是菱形,再根据菱形的性质可得线段AD和EF互相垂直平分.试题解析:(1)如图所示;(2)∵DE∥AB,DF∥AC,∴四边形AEDF是平行四边形,∵AD是△ABC的角平分线,∴∠FAD=∠EAD,∵AB∥DE,∴∠FAD=∠EDA,∴∠EAD=∠EDA,∴EA=ED(等角对等边),∴平行四边形AEDF是菱形,∴AD与EF互相垂直平分.考点: 1.作图;2.菱形的判定与性质.8.如图,在Rt△ABC中,∠C =,AC = BC,AB = 30,矩形DEFG的一边DE在AB上,顶点G、F分别在AC、BC上,若DG︰GF = 1︰4,则矩形DEFG的面积是 .【答案】100【解析】又∵四边形DEFG是矩形,∴9.顺次连接一个四边形的各边中点,得到了一个矩形,则下列四边形中满足条件的是()①平行四边形;②菱形;③等腰梯形;④对角线互相垂直的四边形.A.①③B.②③C.③④D.②④【答案】D【解析】因为顺次连接任意一个四边形的各边中点,得到的是平行四边形,而要得到矩形,根据矩形的判定(有一个角是直角的平行四边形是矩形),所以该四边形的对角线应互相垂直,只有②④符合.10.已知平行四边形ABCD中,对角线AC和BD相交于点O,AC=10,BD=8.(1)若AC⊥BD,试求四边形ABCD的面积;(2)若AC与BD的夹角∠AOD=60°,求四边形ABCD的面积;(3)试讨论:若把题目中“平行四边形ABCD”改为“四边形ABCD”,且∠AOD=θ,AC=a,BD=b,试求四边形ABCD的面积(用含θ,a,b的代数式表示).【答案】(1)四边形ABCD的面积=40;(2)四边形ABCD的面积S=4S△AOD=20;(3)四边形ABCD的面积=absinθ.【解析】(1)因为AC⊥BD,所以四边形ABCD的面积等于对角线乘积的一半;(2)过点A分别作AE⊥BD,CF⊥BD,根据平行四边形对角线互相平分和正弦定理求出△AOD的面积,那么四边形ABCD的面积=4△AOD的面积;(3)作辅助线AE⊥BD,CF⊥BD,利用正弦定理求出△BCD、△ABD的高,那么四边形ABCD的面积=△BCD的面积+△ABD的面积.试题解析:(1)∵AC⊥BD,∴四边形ABCD的面积=AC•BD=40;(2)分别过点A,C作AE⊥BD,CF⊥BD,垂足分别为E,F.∵四边形ABCD为平行四边形,∴AO=CO=AC=5,BO=DO=BD=4.在Rt△AOE中,sin∠AOE=,∴AE=AO•sin∠AOE=AO×sin60°=5×=.∴S△AOD=OD•AE=×4××5=5.∴四边形ABCD的面积S=4S△AOD=20;(3)如图所示,过点A,C分别作AE⊥BD,CF⊥BD,垂足分别为E,F.在Rt△AOE中,sin∠AOE=,∴AE=AO•sin∠AOE=AO•sinθ.同理可得CF=CO•sin∠COF=CO×sinθ.∴四边形ABCD的面积S=S△ABD +S△CBD=BD•AE+BD•CF=BDsinθ(AO+CO)=BD•ACsinθ=absinθ.【考点】1.平行四边形的性质,2.三角形的面积,3.解直角三角形.11.如图,在直角梯形ABCD中,AD∥BC,AD⊥DC,点A关于对角线BD的对称点F刚好落在腰DC上,连接AF交BD于点E,AF的延长线与BC的延长线交于点G,M,N分别是BG,DF的中点.(1)求证:四边形EMCN是矩形;(2)若AD=2,S梯形ABCD=,求矩形EMCN的长和宽.【答案】解:(1)证明:∵点A、F关于BD对称,∴AD=DF,DE⊥AF。
高一数学立体几何综合试题

高一数学立体几何综合试题1.正方体的棱长为1,为的中点,为线段的动点,过的平面截该正方体所得的截面记为,则下列命题正确的是①当时,为四边形②当时,为等腰梯形③当时,与的交点满足④当时,为六边形⑤当时,的面积为【答案】①②③⑤【解析】如图,当时,,即Q为CC1中点,此时可得,故可得截面APQD1为等腰梯形,故②正确;由上图当点Q向C移动时,满足,只需在DD1上取点M满足AM∥PQ,即可得截面为四边形APQM,故①正确;③时,如图,延长DD1至N,使,连接AN交A1D1于S,连接NQ交C1D1于R,连接SR,可证,由1,可得,故可、得,故正确;④由③可知当时,只需点Q上移即可,此时的截面形状仍然上图所示的APQRS,显然为五边形,故错误;⑤当时,Q与C1重合,取A1D1的中点F,连接AF,可证,可知截面为APC1F为菱形,故其面积为,故正确.【考点】空间图形与平面图形的关系2.下列说法正确的是( )A.三点确定一个平面B.平面和有不同在一条直线上的三个交点C.梯形一定是平面图形D.四边形一定是平面图形【答案】C【解析】A中应为不共线的三点确定一个平面,B与公理2矛盾,D中有空间四边形,而C中梯形有一组对边平行,是平面图形,所以选C.【考点】平面的基本性质.3.等腰梯形,上底,腰,下底,以下底所在直线为x轴,则由斜二测画法画出的直观图的面积为_______.【答案】【解析】如上图,,,,因为,所以,所以,在直观图中,【考点】斜二测画法4.如图,在五面体中,四边形是正方形,平面∥(1)求异面直线与所成角的余弦值;(2)证明:平面;(3)求二面角的正切值。
【答案】(1);(2)略;(3)。
【解析】(1)因为四边形ADEF是正方形,所以FA∥ED.故∠CED为异面直线CE与AF所成的角.因为FA⊥平面ABCD,所以FA⊥CD.故ED⊥CD.在Rt△CDE中,CD=1,ED=2, CE==3,故cos∠CED==.所以异面直线CE和AF所成角的余弦值为。
中考数学总复习 基础讲练 第20讲 梯形(含答案点拨) 新人教版

考纲要求命题趋势1.了解梯形的有关概念与分类,掌握梯形的性质,会进行梯形的有关计算.2.掌握等腰梯形的性质与判定.3.能灵活添加辅助线,把梯形问题转化为三角形、平行四边形的问题来解决.等腰梯形的性质和判定是中考考查的内容,实际问题中往往和特殊三角形、特殊四边形的知识结合在一起综合运用.知识梳理一、梯形的有关概念及分类1.一组对边平行,另一组对边不平行的________叫做梯形.平行的两边叫做______,两底间的________叫做梯形的高.2.________相等的梯形叫做等腰梯形,有一个角是直角的梯形叫做直角梯形.3.梯形的分类:梯形⎩⎨⎧一般梯形特殊梯形⎩⎪⎨⎪⎧直角梯形等腰梯形4.梯形的面积=12(上底+下底)×高=中位线×高.二、等腰梯形的性质与判定1.性质:(1)等腰梯形的两腰相等,两底平行.(2)等腰梯形同一底上的两个角________.(3)等腰梯形的对角线________.(4)等腰梯形是轴对称图形,过两底中点的直线是它的对称轴.2.判定:(1)两腰相等的梯形是等腰梯形.(2)同一底上的两个角相等的________是等腰梯形.(3)对角线相等的________是等腰梯形.三、梯形的中位线1.定义:连接梯形两腰________的线段叫做梯形的中位线.2.性质:梯形的中位线平行于两底,且等于________的一半.四、梯形问题的解决方法梯形问题常通过――→转化辅助线三角形问题或平行四边形问题来解答,转化时常用的辅助线有:1.平移一腰,即从梯形的一个顶点作另一腰的平行线,把梯形分成一个平行四边形和一个三角形.2.过顶点作高,即从同一底的两端作另一底所在直线的垂线,把梯形转化成一个矩形和两个直角三角形.3.平移一条对角线,即从梯形的一个顶点作一条对角线的平行线,把梯形转化成平行四边形和三角形.4.延长梯形两腰使它们相交于一点,把梯形转化成三角形.5.过一腰中点作辅助线.(1)过此中点作另一腰的平行线,把梯形转化成平行四边形;(2)连接一底的端点与一腰中点,并延长与另一底的延长线相交,把梯形转化成三角形.自主测试1.若等腰梯形ABCD的上底长AD=2,下底长BC=4,高为2,那么梯形的腰DC的长为( )A.2 B. 3 C.3 D. 52.如图,在一块形状为直角梯形的草坪中,修建了一条由A→M→N→C的小路(M,N分别是AB,CD中点).极少数同学为了走“捷径”,沿线段AC行走,破坏了草坪,实际上他们仅少走了( )A.7米 B.6米 C.5米 D.4米3.如图,在直角梯形ABCD中,AD∥BC,∠B=90°,E为AB上一点,且ED平分∠ADC,EC平分∠BCD,则下列结论中,错误的是( )A.∠ADE=∠CDEB.DE⊥ECC.AD·BC=BE·DED.CD=AD+BC4.已知梯形的上底长为2,下底长为5,一腰长为4,则另一腰长x的取值范围是__________.考点一、一般梯形的性质【例1】如图,在梯形ABCD中,AD∥BC,BD=CD,∠BDC=90°,AD=3,BC=8,求AB的长.解:如图,作AE⊥BC于点E,DF⊥BC于点F.∴AE∥DF,∠AEF=90°.∵AD∥BC,∴四边形AEFD是矩形.∴EF=AD=3,AE=DF.∵BD =CD ,DF ⊥BC ,∴DF 是△BDC 边BC 上的中线.∵∠BDC =90°,∴DF =12BC =BF =4.∴AE =4,BE =BF -EF =4-3=1.在Rt △ABE 中,AB 2=AE 2+BE 2,∴AB =42+12=17.方法总结 遇到梯形问题,一般情况下通过作腰或对角线的平行线、高线、连对角线、延长两腰转化为三角形、平行四边形、直角三角形、矩形等问题来解决.触类旁通1 如图,在梯形ABCD 中,AD ∥BC ,AB ∥DE ,AF ∥DC ,E ,F 两点在边BC 上,且四边形AEFD 是平行四边形.(1)AD 与BC 有何等量关系?请说明理由.(2)当AB =DC 时,求证:四边形AEFD 是矩形. 考点二、等腰梯形的性质与判定【例2】如图,在等腰△ABC 中,点D ,E 分别是两腰AC ,BC 上的点,连接AE ,BD 相交于点O ,∠1=∠2.(1)求证:OD =OE ;(2)求证:四边形ABED 是等腰梯形.分析:(1)根据已知条件可知利用全等三角形证明BD =AE ,根据∠1=∠2可以证明OA =OB ,根据等式性质可知OD =OE ;(2)先证明四边形ABED 是梯形,然后证明两腰相等即可.证明:(1)∵△ABC 是等腰三角形,∴AC =BC . ∴∠BAD =∠ABE .又∵AB =BA ,∠2=∠1,∴△ABD ≌△BAE ,∴BD =AE . 又∵∠1=∠2,∴OA =OB .∴BD -OB =AE -OA ,即OD =OE .(2)由(1)知,OD =OE ,∴∠OED =∠ODE .∴∠OED =12(180°-∠DOE ).同理,∠1=12(180°-∠AOB ).∵∠DOE =∠AOB ,∴∠1=∠OED ,∴DE ∥AB . ∵AD 不平行于BE ,∴四边形ABED 是梯形, ∵AE =BD ,∴梯形ABED 是等腰梯形.方法总结 在证明一个四边形是等腰梯形时,必须先证明它是梯形,然后再通过两腰相等或同一底上的两个角相等,或者是对角线相等来证明梯形是等腰梯形.触类旁通2 如图,在矩形ABCD 中,对角线AC ,BD 交于点O ,M ,N 分别为AO ,DO 的中点,四边形BCNM是等腰梯形吗?为什么?考点三、有关梯形的计算【例3】如图,在梯形ABCD中,AD∥BC,AB⊥AC,∠B=45°,AD=2,BC=42,求DC的长.分析:由于△ABC是等腰直角三角形,且BC=42,可得出BC边上的高.只要通过平移腰CD,就可与BC边上的高构成直角三角形,从而求出CD.解:过点A作AE∥DC交BC于点E,过点A作AF⊥BC于点F,如图所示.∵AD∥BC,AE∥DC,∴四边形AECD为平行四边形.∴AE=DC,AD=EC= 2.又∵AB⊥AC,∠B=45°,BC=42,∴AB=AC=4.∴AF=BF=2 2.∴EF=BC-BF-EC= 2.在Rt△AFE中,AE=AF2+EF2=222+22=10,即DC=10.方法总结解决梯形问题作辅助线的方法要结合题目的条件和要证结论的需要灵活运用.若题中已知两对角线的条件,可考虑平移对角线,使两对角线在同一个三角形中;若已知两腰的某些条件,可考虑平移一腰;若已知两底角互余,可平移一腰或延长两腰构成直角三角形;若要求梯形的面积,常作出梯形的高.触类旁通3 如图所示,在等腰梯形ABCD中,AB∥CD,AD=BC,AC⊥BC,∠B=60°,BC=2 cm,则上底DC的长是__________cm.1.(2012山东临沂)如图,在等腰梯形ABCD中,AD∥BC,对角线AC,BD相交于点O,下列结论不一定正确的是( )A.AC=BDB.OB=OCC.∠BCD=∠BDCD.∠ABD=∠ACD2.(2012湖南长沙)下列四边形中,对角线一定不相等的是( )A.正方形 B.矩形C.等腰梯形 D.直角梯形3.(2012安徽)在一张直角三角形纸片的两直角边上各取一点,分别沿斜边中点与这两点的连线剪去两个三角形,剩下的部分是如图所示的直角梯形,其中三边长分别为2,4,3,则原直角三角形纸片的斜边长是( )A.10 B.4 5C.10或4 5 D.10或2174.(2012湖南长沙)如图,等腰梯形ABCD中,AD∥BC,AB=AD=2,∠B=60°,则BC 的长为__________.5.(2012四川内江)如图,四边形ABCD是梯形,BD=AC且BD⊥AC,若AB=2,CD=4,则S梯形ABCD=____________.6.(2012四川南充)如图,等腰梯形ABCD中,AD∥BC,点E是AD延长线上的一点,且CE=CD.求证:∠B=∠E.1.梯形的上底长为5,下底长为9,则梯形的中位线长等于( )A.6 B.7C.8 D.102.在等腰梯形ABCD中,AB∥CD,对角线AC平分∠BAD,∠B=60°,CD=2 cm,则梯形ABCD的面积为( )A.33cm2 B.6 cm2C.63cm2 D.12 cm23.如图,在梯形ABCD中,AB∥DC,∠D=90°,AD=DC=4,AB=1,F为AD的中点,则点F到BC的距离是( )A .4B .3C .2D .14.如图,在等腰梯形ABCD 中,AB ∥CD ,对角线AC ,BD 相交于O ,∠ABD =30°,AC ⊥BC ,AB =8 cm ,则△COD 的面积为( )A .433cm 2B .43cm 2C .233cm 2D .23cm 25.如图,等腰梯形ABCD 中,AD ∥BC ,AB ∥DE ,梯形ABCD 的周长为26,BE =4,则△DEC 的周长为__________.(第5题图)6.如图,在梯形ABCD 中,AB ∥DC ,∠ADC 的平分线与∠BCD 的平分线的交点E 恰在AB 上.若AD =7 cm ,BC =8 cm ,则AB 的长度是__________ cm.(第6题图)7.如图,在直角梯形ABCD 中,AD ∥BC ,AB ⊥BC ,AD =2,AB =3,BC =4,则梯形ABCD 的面积是__________.(第7题图)8.如图,在等腰梯形ABCD 中,AD ∥BC ,对角线AC ⊥BD 于点O ,AE ⊥BC ,DF ⊥BC ,垂足分别为E ,F ,AD =4,BC =8,则AE +EF =__________.(第8题图)9.如图,在菱形ABCD 中,∠DAB =60°,过点C 作CE ⊥AC 且与AB 的延长线交于点E ,求证:四边形AECD 是等腰梯形.参考答案导学必备知识 自主测试1.D 2.B 3.C 4.1<x <7 探究考点方法触类旁通1.解:(1)AD =13BC .理由如下:∵AD ∥BC ,AB ∥DE ,AF ∥DC ,∴四边形ABED 和四边形AFCD 都是平行四边形, ∴AD =BE ,AD =FC .又∵四边形AEFD 是平行四边形, ∴AD =EF ,∴AD =BE =EF =FC ,∴AD =13BC .(2)证明:∵四边形ABED 和四边形AFCD 都是平行四边形,∴DE =AB ,AF =DC . ∵AB =DC ,∴DE =AF .又∵四边形AEFD 是平行四边形, ∴四边形AEFD 是矩形.触类旁通2.解:是等腰梯形.根据三角形中位线定理有,MN ∥AD ∥BC ,且MN ≠BC ,∴四边形BCNM 为梯形.在矩形ABCD 中,AO =DO ,又M ,N 分别是AO ,DO 的中点,∴OM =ON ,∴CM =BN ,∴四边形BCNM 是等腰梯形.触类旁通3.2 ∠CAB =90°-60°=30°,∵等腰梯形ABCD 中,∠BAD =∠B =60°, ∴∠CAD =∠BAD -∠BAC =30°.又∵CD ∥AB ,∴∠DCA =∠CAB =30°=∠DAC . ∴CD =AD =BC =2 cm. 品鉴经典考题1.C 对于A ,∵四边形ABCD 是等腰梯形,∴AC =BD ,故本选项正确;对于B ,∵四边形ABCD 是等腰梯形,∴AB =DC ,∠ABC =∠DCB ,在△ABC 和△DCB 中,∵⎩⎪⎨⎪⎧AB =DC ,∠ABC =∠DCB ,BC =CB ,∴△ABC ≌△DCB (SAS),∴∠ACB =∠DBC ,∴OB =OC ,故本选项正确;对于C ,∵无法判定BC =BD ,∴∠BCD 与∠BDC 不一定相等,故本选项错误;对于D,∵∠ABC=∠DCB,∠ACB=∠DBC,∴∠ABD=∠ACD,故本选项正确.故选C.2.D 根据正方形、矩形、等腰梯形的性质,它们的两条对角线一定相等,只有直角梯形的对角线一定不相等.故选D.3.C 考虑两种情况.①如图:因为CD=22+42=25,点D是斜边AB的中点,所以AB=2CD=4 5.②如图:因为CE=32+42=5,点E是斜边AB的中点,所以AB=2CE=10,故原直角三角形纸片的斜边长是10或4 5.4.4 过点A作AE∥CD交BC于点E,∵AD∥BC,∴四边形AECD是平行四边形,∴AE=CD=2,AD=EC=2.∵∠B=60°,∴BE=AB=AE=2,∴BC=BE+CE=2+2=4.5.9 过点B作BE∥AC,交DC的延长线于点E,则AB=CE,BE=AC=BD.∵BD⊥AC,AB=2,CD=4,∴BD⊥BE,DE=6,∴梯形高为3,∴S梯形ABCD=(2+4)×3÷2=9.6.证明:∵CE=CD,∴∠CDE=∠E.∵AD∥BC,∴∠CDE=∠DCB.∴∠E=∠DCB.∵AB=DC,∴∠B=∠DCB.∴∠B=∠E.研习预测试题1.B 2.A 3.C 4.A 5.18 6.15 7.98.10 如图,过点D作DG∥AC,交BC的延长线于点G.易得四边形ACGD 为平行四边形,∴CG =AD =4,BG =BC +CG =8+4=12. ∵AC ⊥BD ,AC ∥DG ,∴BD ⊥DG .∵梯形ABCD 是等腰梯形,∴AC =BD =DG . ∴△BDG 为等腰直角三角形.又∵DF ⊥BC ,∴DF =12BG =6.∴AE +EF =DF +AD =6+4=10.9.证明:∵四边形ABCD 是菱形,∠DAB =60°,∴∠CAE =12∠DAB =30°.又∵CE ⊥AC ,∴∠E =60°=∠CBE .∴CE =BC =AD . ∵CD ∥AE ,AE =AB +BE =DC +BE ≠DC , ∴四边形AECD 是等腰梯形.。
2019-2020年八年级数学下册专题讲解+课后训练:梯形的辅助线 课后练习及详解
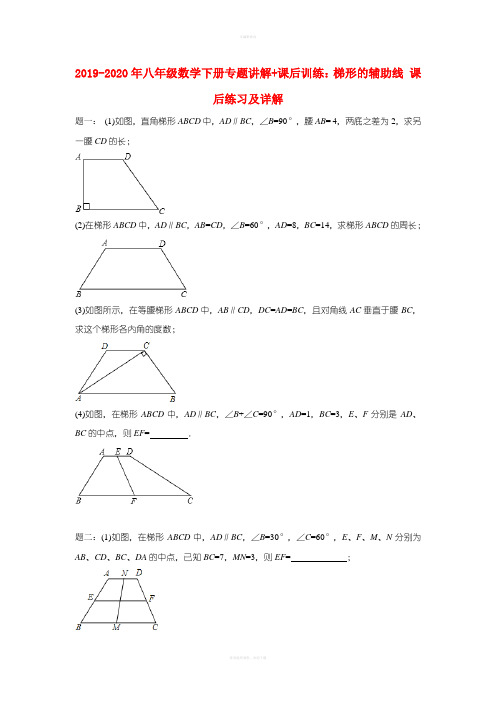
2019-2020年八年级数学下册专题讲解+课后训练:梯形的辅助线课后练习及详解题一:(1)如图,直角梯形ABCD中,AD∥BC,∠B=90°,腰AB= 4,两底之差为2,求另一腰CD的长;(2)在梯形ABCD中,AD∥BC,AB=CD,∠B=60°,AD=8,BC=14,求梯形ABCD的周长;(3)如图所示,在等腰梯形ABCD中,AB∥CD,DC=AD=BC,且对角线AC垂直于腰BC,求这个梯形各内角的度数;(4)如图,在梯形ABCD中,AD∥BC,∠B+∠C=90°,AD=1,BC=3,E、F分别是AD、BC的中点,则EF= .题二:(1)如图,在梯形ABCD中,AD∥BC,∠B=30°,∠C=60°,E、F、M、N分别为AB、CD、BC、DA的中点,已知BC=7,MN=3,则EF= ;(2)如图,在梯形ABCD中,AD=DC,AB=DC,∠D=120°,对角线CA平分∠BCD,且梯形的周长为20,则梯形ABCD的面积为;(3)如图,等腰梯形ABCD中,AD∥BC,AD=3,AB= 4,BC=7,求∠B的度数;(4)如图,梯形ABCD中,AD∥BC,AC⊥BD,AD=3,BC=7,E在BC上,CE=2,则DE= .题三:已知:等腰梯形的上底是2cm,腰长是4cm,一个底角是60°,则等腰梯形的下底是cm.题四:已知:等腰梯形的一个底角等于60°,它的两底分别为4cm和7cm,则它的周长为cm.题五:如图所示,在梯形ABCD中,AD∥BC,AB=CD,AC⊥BD,且AD= 4,BC=8,求AC的长.题六:如图,在梯形ABCD中,AD∥BC,对角线AC⊥BD,若AD=3,BC=7,求梯形ABCD 面积的最大值.题七:如图,梯形ABCD中,AD∥BC,点E在BC上,AE=BE,点F是CD的中点,且AF ⊥AB,若AD=2.7,AF=4,AB=6,求CE的长.题八:如图,在梯形ABCD中,AB∥CD,∠A+∠B=90°,CD=5,AB=11,点M、N分别为AB、CD的中点,求线段MN的长.题九:如图,在梯形ABCD中,AD∥BC,∠ABC=90°,AB= 4,AD=3,BC=5,点M是边CD的中点,连接AM、BM.求△ABM的面积.题十:如图,已知直角梯形ABCD中,AD∥BC(AD<BC),∠B=90°,AB=AD+BC.点E 是CD的中点,点F是AB上的点,∠ADF= 45°,FE=a,梯形ABCD的面积为m.(1)求证:BF=BC;(2)求△DEF的面积(用含a、m的代数式表示).题十一:以线段a=16,b=13为梯形的两底,c=10,d=6为腰画梯形,这样的梯形() A.只能画出一个B.能画出2个C.能画出无数个D.不能画出题十二:以线段a=5,b=10,c=15,d=20做梯形四边形,这样的梯形(不全等的)() A.至少能做3个B.恰好能做2个C.仅仅只能做1个D.一个也不能做梯形的辅助线课后练习参考答案题一:(1)2;(2)34;(3)60°,60°,120°,120°;(4)1.详解:(1)过D作DE⊥BC于E,∵AB⊥BC,DE⊥BC,AD∥BC,∴四边形ADEB是个矩形,∴AB=DE= 4,CE=BC AD=2,Rt△DEC中,CD===2;;(2)过A、D点作AE⊥BC于E,DF⊥BC于F,∵AB=CD,∠B=∠C,AE=DF,∴△ABE≌△DCF,∴BE=CF,∵AD=8,BC=14,BE=CF=3,又∵在Rt△ABE中,∠B=60°,∴AB=2BE=6,∴梯形ABCD的周长为8+14+6+6=34;(3)如图所示,过点C作CE∥AD,又DC∥AE,∴四边形AECD为平行四边形,又DC=AD=BC,∴四边形AECD为菱形,∴AE=CE=BC,∴∠EAC=∠ECA,∠CEB=∠B,∵∠B+∠CAB=90°,即3∠CAE=90°,∴∠CAE=30°,∴∠B=60°=∠DAB,∠D=∠DCB=120°;(4)过点E作AB、CD的平行线,与BC分别交于G,H,∵∠B+∠C=90°,∴∠EGH=∠B,∠EHG=∠C,∴∠EGH+∠EHG=90°,∴四边形ABGE和四边形CDEH都是平行四边形,△EGH为直角三角形,∵E、F分别是AD、BC的中点,∴BG=CH=0.5,GH=2,根据直角三角形中斜边上的中线是斜边的一半知,EF=GH=1,∴EF=1.题二:(1)4;(2)12;(3)60°;(4)5.详解:(1)过点N分别作NG∥AB,NH∥CD,得平行四边形ABGN和平行四边形DCHN,∴∠NGM+∠NHM=∠B+∠C=90°,GH=BC AD,MG=MH,∴GH=2MN=6,∴AD=76=1,∴EF= 4;(2)∵在梯形ABCD中,AB=DC,∴梯形ABCD是等腰梯形,∴∠D+∠DCB=180°,∵∠D=120°,∴∠B=∠DCB=60°,∵对角线CA平分∠BCD,∴∠ACB=30°,∵AD=DC,∴∠DAC=∠ACD=30°,∴∠BAC=90°,∴BC=2AB,∵梯形的周长为AD+DC+BC+AB=5AB=20,∴AB= 4,∴AC=4,BC=8,过点A作AE⊥BC于点E,∵AB= 4,AC=4,BC=8,∴AE=2,∴梯形ABCD的面积为(4+8)×2×=12;(3)过点A作AE∥DC交BC于E,∵AD∥BC,∴四边形AECD是平行四边形,∴EC=AD=3,DC=AE,∴BE=BC CE=73= 4,∴CD=AB= 4,∴AE=AB=BE= 4,∴△ABE是等边三角形,∴∠B=60°;(4)过D作DF∥AC交BC的延长线于F,∵AD∥BC,∴四边形ACFD是平行四边形,∴CF=AD=3,∵BC=7,∴BF=BC+CF=7+3=10,∵CE=2,∴BE=72=5,EF=2+3=5,∴BE=EF,又∵AC⊥BD,DF∥AC,∴∠BDF=90°,∴DE=BF=5.题三:6cm.详解:过D作DE∥AB交BC于E,∵DE∥AB,AD∥BC,∴四边形ABED是平行四边形,∴AD=BE=2cm,DE=AB=4cm,∠DEC=∠B=60°,AB=DE=DC,∴△DEC是等边三角形,∴EC=CD= 4cm,∴BC= 4cm+2cm=6cm.题四:17cm.详解:过上底顶点D作DE∥AB交BC于E,则四边形ABED是平行四边形,∴DE=AB,AD=BE,∵梯形的一个底角是60°,∴∠C=60°,又∵腰长AB=CD=DE,∴△CDE是等边三角形,∴CD=CE=BC BE=74=3cm,∴它的周长为3+7+3+4=17cm.题五:.详解:过D作DE∥AC交BC的延长线于E,∵AD∥BC,AB=CD,∴四边形ABCD是等腰梯形,∴ADEC是平行四边形,∴AD=CE,AC=DE,即可得出BE=BC+CE=BC+AD=12,又∵AC=BD,∴BD=ED,∴△BDE为等腰直角三角形,∴AC=BD=.题六:25.详解:过D作DE∥AC交BC延长线于E,∵AD∥BC,DE∥AC,∴四边形ACED是平行四边形,∴AD=CE,∴根据等底等高的三角形面积相等得出△ADC的面积等于△DCE的面积,即梯形ABCD的面积等于△BDE的面积,∵AC⊥BD,DE∥AC,∴∠BDE=90°,BE=3+7=10,∴此时△BDE的边BE边上的高越大,它的面积就越大,即当高是BE时最大,即梯形的最大面积是×10××10=25.题七:2.3.详解:延长AF、BC交于点G,∵AD∥BC,∴∠D=∠FCG,∠DAF=∠G,又DF=CF,∴△AFD≌△GFC,∴AG=2AF=8,CG=AD=2.7,∵AF⊥AB,AB=6,∴BG=10,∴BC=BG CG=7.3,∵AE=BE,∴∠BAE=∠B,∴∠EAG=∠AGE,∴AE=GE,∴BE=BG=5,∴CE=BC BE=2.3.题八:3.详解:如图,过D作DE∥BC,DF∥MN,∵在梯形ABCD中,AB∥CD,DE∥BC,∴CD=BE=5,AE=AB BE=115=6,∵M为AB的中点,∴MB=AM=AB=×11=5.5,ME=MB BE=5.55=0.5,∵N为DC的中点,∴DN=DC=×5=2.5,在四边形DFMN中,DC∥AB,DF∥MN,∴FM=DN=2.5,∴FE=FM+ME=2.5+0.5=3=AE,∴F为AE的中点,又∵DE∥BC,∴∠B=∠AED,∵∠A+∠B=90°,∴∠A+∠AED=90°,∴∠ADE=90°,即△ADE是直角三角形,∴DF=MN=AE=×6=3.题九:8.详解:延长AM交BC的延长线于点N,∵AD∥BC,∴∠DAM=∠N,∠D=∠MCN,∵点M是边CD的中点,∴DM=CM,∴△ADM≌△NCM(AAS),∴CN=AD=3,AM=MN=AN,∴BN=BC+CN=5+3=8,∵∠ABC=90°,∴S△ABN=×AB•BN=×4×8=16,∴S△ABM=S△ABN=8,即△ABM的面积为8.题十:见详解.详解:(1)∵四边形ABCD是直角梯形,∴∠A=90°,∵∠ADF=45°,∴∠AFD= 45°,∴AD=AF,∵AB=AF+BF,AB=AD+BC,∴BF=BC;(2)连接FC,设AD=AF=x,BC=BF=y,连接CF,作DH⊥BC于H,易证四边形ABHD为矩形、△CDF为直角三角形,又∵E是CD中点,∴CD=2EF=2a,由勾股定理得x2+y2=2a2…①,由直角梯形的面积公式可得:(x+y)2=2m…②,由②①,得xy=m a2,∵S△DFC=S梯形ABCD S△AFD S△BFC=(x+y)2 x2 y2 = xy,∴S△DEF=S△DFC=m a2.题十一:D.详解:如图,过点B作BE∥AD,则出现平行四边形ABED和一个△BEC,∵AB=13,CD=16,AD=10,BC=6∴CE=3,BE=10,∵3+6<10,∴BE,CE,BC不能构成三角形∴这样的梯形一个也不能作.故选D.题十二:C.详解:作DE∥AB,则DE=AB,①当a=5为上底,b=10为下底,c、d为腰时,105=5,与15,20不能构成三角形,故不满足题意;②当a=5为上底,b=15为下底,b、d为腰时,155=10,与10,20不能构成三角形,故不满足题意;③当a=5为上底,d=20为下底,b、c为腰时,205=15,与10,15可以构成三角形,故满足题意;④当b=10为上底,c=15为下底,a、d为腰时,1510=5,与5,20不能构成三角形,故不满足题意;⑤当b=10为上底,d=20为下底,a、c为腰时,2010=10,与5,15不能构成三角形,故不满足题意;⑥当c=15为上底,d=20 为下底,a、b为腰时,2015=5,与5,10不能构成三角形,故不满足题意;综上可得只有当a=5为上底,d=20为下底,b、c为腰时,满足题意,即以线段a=5,b=10,c=15,d=20做梯形四边形,这样的梯形(不全等的)只能做一个.故选C..。
初二数学下册证明题(中等难题 含答案)

一:已知:如图,在直角梯形ABCD 中,AD ∥BC ,∠ABC =90°,DE ⊥AC 于点F ,交BC 于点G ,交AB 的延长线于点E ,且AE AC =.(1)求证:BG FG =;(2)若2AD DC ==,求AB 的长.二:如图,已知矩形ABCD ,延长CB 到E ,使CE=CA ,连结AE 并取中点F ,连结AE 并取中点F ,连结BF 、DF ,求证BF ⊥DF 。
DCEBGAF三:已知:如图,在矩形ABCD 中,E 、F 分别是边BC 、AB 上的点,且EF=ED,EF ⊥ED.求证:AE 平分∠BAD.四、(本题7分)如图,△ABC 中,M 是BC 的中点,AD 是∠A 的平分线,BD ⊥AD 于D ,AB=12,AC=18,求DM 的长。
(第23题)EDBAF五、(本题8分)如图,四边形ABCD 为等腰梯形,AD ∥BC ,AB=CD ,对角线AC 、BD交于点O ,且AC ⊥BD ,DH ⊥BC 。
⑴求证:DH=21(AD+BC ) ⑵若AC=6,求梯形ABCD 的面积。
六、(6分) 、如图,P 是正方形ABCD 对角线BD 上一点,PE ⊥DC ,PF ⊥BC ,E 、F 分别为垂足,若CF=3,CE=4,求AP 的长.七、(8分)如图,等腰梯形ABCD 中,AD ∥BC ,M 、N 分别是AD 、BC 的中点,E 、F 分别是BM 、CM 的中点.(1)在不添加线段的前提下,图中有哪几对全等三角形?请直接写出结论; (2)判断并证明四边形MENF 是何种特殊的四边形?(3)当等腰梯形ABCD 的高h 与底边BC 满足怎样的数量关系时?四边形MENF 是正方形(直接写出结论,不需要证明).选择题:15、如图,每一个图形都是由不同个数的全等的小等腰梯形拼成的,梯形上、下底及腰长如图,依此规律第10个图形的周长为 。
……第一个图 第二个图 第三个图 16、如图,矩形ABCD 对角线AC 经过原点O ,B 点坐标为(―1,―3),若一反比例函数xky 的图象过点D ,则其 解析式为 。
例题2:在直角梯形ABCD中,角A=角B=90度,DC=4,BC=10,点

运动图形中的分类讨论尚文中学王伟庆九(3)一、教学目标:1、掌握利用所学的数学思想和方法对分类讨论的问题进行求解的一般的思路,逐步培养学生解综合题能力。
2、通过解数学综合题的过程,增强学生解题中分类讨论的意识,提高分析问题和解决问题的能力。
培养学生数学思维的全面性和周密性。
二、教学过程:1、例题演示(1):例题1:已知半圆O的直径DE=12,直角三角形ABC中,∠ACB=90度,AC=12,半圆O在三角形ABC的左侧,(1)若∠B A C=30度,半圆O在直线AC上从左向右运动求:在运动中ΔABC一边所在的直线与半圆O所在的圆能相切几次?(2)当半圆O运动到DE与AC重合时,设B是射线CB上的动点,半圆O与斜边AB交于P点,过P点作半圆O的切线交BC于F点,求证:1)BF=PF=FC2)若PF所在直线与AC所在的直线交于G点,设OG为X,BC为Y,求Y与X的函数解析式B2、探索分类讨论的思想(略)3、巩固练习例题2:在直角梯形ABCD中,∠C=∠B=90°点G是射线CB上一个动点,将三角板的直角顶点重合于点G,三角板两直角边中的一边始终经过D点,另一直角边交射线AB于点E。
求证:1)ΔEBGΔ∽ΔGCD2)若DC=10,BC=2,AB=4,设GC为X,BE为Y,求Y与X的函数解析式及定义域3)在上一小题的条件下,是否存在这样G点,使ΔEBG的周长是ΔGDC周长的一半,若存在求GC的值?(备用)4、变式思考:(紧接上题)4)当DC=10,BC=2,AB=4 动点P从点C出发,沿CD方向以每秒2个单位长的速度运动,动点Q从B出发,在线段BA 上以每秒一个单位的速度运动,连接AP,点P、Q同时出发,当Q点运动到A点后立即回到B点停止运动,而点P继续运动到D点停止运动,设运动时间为t秒求:当t为何值时,ΔAPQ为等腰三角形?5、总结全课、布置作业。
博识教育小学几何面积练习(1--10)

FBEDCA10厘米FEDCBA8厘米6厘米MPDCBAFEDCBA8CM26CM2小学几何面积问题一1..已知平行四边形ABCD 的面积是18平方厘米,AE=2EB,CF=2FB,求三角形DEF 的面积(阴影部分)是 平方厘米.2.在直角梯形ABCD 中AD=8厘米,DC=6厘米,BC=10厘米, 且S △ADE =S △AFB =S四AFCE 求三角形EFC 的面积为 平方厘米.3.已知P 是长方形ABCD 的对角线上一点,M 为线段PC 的中点,如果三角形APB 的面积是2平方厘米,那么三角形BMC 的面积是 平方厘米.4.长方形ABCD 的面积是48平方厘米。
S △ABE =8cm 2S △AFD =6cm 2求三角形EFC 的面积是 平方厘米. 5. 如图长方形ABCD 中,宽AD=6厘米,长DC=8厘米。
E 在DC 的延长线上,AE 交BC 于F 点,如果三角形BFE 的面8厘米6厘米FDCBAE8CM2D/C/B/A/DCBAGFDCEBA8105EDCFABFDCEBA积是8平方厘米。
求:阴影部分的面积是 平方厘米.6.把四边形ABCD 的各边延长一倍,得到一个大四边形A /B /C /D /,如果四边形ABCD 的面积是3平方厘米,那么大四边形A /B /C /D /的面积是 平方厘米.7.四边形ABCD 两条对角线交于E ,延长CA 到F ,使AF=AE; 延长DB 到E,使BE=DE.如果四边形ABCD 的面积是3平方厘米. 求三角形EFG 的面积为 平方厘米.8.如图△ABC 中BD=2DC,AE=2ED,如果FC=12厘米.那么:AF= 厘米.9.如图△ABC 中,△AEF,△ABE,△EBD 的面积分别是5cm 2,10cm 2,8cm 2 求四边形EDCF 的面积是 平方厘米.FEDCBAFEDCBAFEDCBAFEDCBA小学几何面积问题二1.如图长方形ABCD 中,AB=15厘米,BC=8厘米,三角形AFD 的面积比三角形FEC 的面积大30平方厘米,求CE 的长是 厘米.2. 如图正方形ABCD 中,边长为6厘米,三角形AFD 的面积比三角形FEC 的面积小6平方厘米,求CE 的长是 厘米.3.如图ABCD 是长方形,AD=4厘米,AB=9厘米,阴影部分(△DEF )的面积是6平方厘米,求梯形ABED 的面积是 平方厘米.4.如图,已知阴影部分的面积是120平方厘米,E,F 分别是AB,BC 的中点,长方形宽AB 为16厘米,那么,长方形的长AD 为 厘米.5.如图,ABCD 是梯形,BECE,AD=9厘米, BE ⊥EC ,BE=8厘米,EC=6厘米.EDCBAFEDCBAGFEDCBAGFEDCBA求这个梯形的面积是 平方厘米.6.长方形ABCD 中,E 为BC 的中点,阴影部分△AFD 的面积是4平方厘米.则这个长方形面积是 平方厘米.7.正方形ABCD 中,E 为BC 的中点,F 为DC 的中点已知正方形边长是5厘米.则阴影部分△AGD 的面积是 平方厘米.8. 正方形ABCD 中,E 为BC 上的四等份点,F 为DC 的中点已知正方形边长是4厘米.则阴影部分△AGB 的面积是 平方厘米.CDCABDOAB CBDO O BADC L 2L 1NA CBMHH小学几何面积问题三1.在梯形ABCD 中,AD//BC,图中阴影部分的面积为4,OC=2AO, 求 S 梯ABCD =2在梯形ABCD 中,AD//BC,S △BOC=14 OC=2AO 求 S 梯ABCD =3. 在梯形ABCD 中,AD//BC,S △AOB=14 OC=3AO 求 S 梯ABCD =4.在梯形ABCD 中,AD//BC,图中阴影部分的面积为30,OC=3AO,S △AOB =6求S 空=5.读一读:A 若直线L 1//L 2 (如图一)一.当高不变,底扩大(或缩小)K 倍。
六年级奥数题:图形提高(三(B)[1]
![六年级奥数题:图形提高(三(B)[1]](https://img.taocdn.com/s3/m/eac3b8ed0740be1e640e9ab7.png)
图形提高〔三〕【精典习题】1.如图,一长方形中画了些直线,已知其中的三块面积分别为13平方分米、35平方分米、49平方分米,问阴影部分面积是多少?2.长方形的长是8cm,宽是6cm,三角形AOB的面积为16cm2,求ODC∆的面积。
3.如图,在长方形ABCD中,AB长8厘米,BC长15厘米,四边形EFGH的面积是9平方厘米,那么阴影部分面积的和是平方厘米。
4.如下图,在平行四边形ABCD中,E、F与对角线B、D平行,问:与ADE∆的面积相等的三角形在图中共有几个?ABDEGFAEB49 35135.如下图,平行四边形ABCD中,ADG∆面积是5平方厘米,∆的面积是3平方厘米,问∆面积是6.2平方厘米,PHFDHC∆的面积是多少平方厘米?PEG6.如下图,O是平行四边形ABCD内的一点,AD=3DE。
已知三个空白三角形面积分别是19,20,35平方厘米,三角形BOC的面积是多少平方厘米?7.如下列图,ABCD是个长方形,DEFG是个平行四边形,E点在BC边上,FG过A点,已知,三角形AKF与三角形ADG面积之和等于5平方厘米。
DC=CE=5厘米。
求BEK∆的面积。
7.如图,ABCD是长方形,图中的数字是各部分的面积数,则图中阴影部分的面积为______。
8.如图,正方形中套着一个长方形,正方形的边长是12厘米,长方形的四个角的顶点把正方形的四边各分成两段,其中长的一段是9.有红、黄、绿三块大小一样的正方形纸片,放在一个正方形盒内,它们之间互相叠合〔如右图〕,已知露在外面的部分中,红色面积是24,黄色面积是14,绿色面积是10,那么正方形盒子的面积是多少?10.如图,下面△AOB和△ DOC的面积分别为20平方厘米和24平方厘米,长方形AODE的面积为30平方厘米,求△BOC的面积为多少平方厘米?10.这是一块正方形的地板砖示意图。
其中AA1=AA2=BB1=BB2=CC1=CC2=DD1=DD2。
动点问题(含答案)

动点问题(含答案)动点问题1. 如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AD=24cm,AB=8cm,BC=26cm,动点P从A开始沿AD边向D以1cm/s的速度运动;动点Q从点C开始沿CB边向B以3cm/s的速度运动.P、Q分别从点A、C同时出发,当其中一点到达端点时,另外一点也随之停止运动,设运动时间为ts.(1)当t为何值时,四边形PQCD为平行四边形?(2)当t为何值时,四边形PQCD为等腰梯形?(3)当t为何值时,四边形PQCD为直角梯形?点评:此题主要考查了平行四边形、等腰梯形,直角梯形的判定,难易程度适中.2. 如图,△ABC中,点O为AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的外角平分线CF于点F,交∠ACB内角平分线CE于E.(1)试说明EO=FO;(2)当点O运动到何处时,四边形AECF是矩形并证明你的结论;(3)若AC边上存在点O,使四边形AECF是正方形,猜想△ABC的形状并证明你的结论.点评:本题主要考查利用平行线的性质“等角对等边”证明出结论(1),再利用结论(1)和矩形的判定证明结论(2),再对(3)进行判断.解答时不仅要注意用到前一问题的结论,更要注意前一问题为下一问题提供思路,有相似的思考方法.是矩形的判定和正方形的性质等的综合运用.3. 如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,已知AD=AB=3,BC=4,动点P从B点出发,沿线段BC向点C作匀速运动;动点Q从点D出发,沿线段DA向点A作匀速运动.过Q 点垂直于AD的射线交AC于点M,交BC于点N.P、Q两点同时出发,速度都为每秒1个单位长度.当Q点运动到A点,P、Q两点同时停止运动.设点Q运动的时间为t秒.(1)求NC,MC的长(用t的代数式表示);(2)当t为何值时,四边形PCDQ构成平行四边形;(3)是否存在某一时刻,使射线QN恰好将△ABC的面积和周长同时平分?若存在,求出此时t的值;若不存在,请说明理由;(4)探究:t为何值时,△PMC为等腰三角形.点评:此题繁杂,难度中等,考查平行四边形性质及等腰三角形性质.考查学生分类讨论和数形结合的数学思想方法.4. 如图,在矩形ABCD中,BC=20cm,P,Q,M,N分别从A,B,C,D出发沿AD,BC,CB,DA方向在矩形的边上同时运动,当有一个点先到达所在运动边的另一个端点时,运动即停止.已知在相同时间内,若BQ=xcm(x≠0),则AP=2xcm,CM=3xcm,DN=x2cm.(1)当x为何值时,以PQ,MN为两边,以矩形的边(AD或BC)的一部分为第三边构成一个三角形;(2)当x为何值时,以P,Q,M,N为顶点的四边形是平行四边形;(3)以P,Q,M,N为顶点的四边形能否为等腰梯形?如果能,求x的值;如果不能,请说明理由.点评:本题主要考查梯形的性质及勾股定理.在解题(2)时,应注意分情况进行讨论,防止在解题过程中出现漏解现象.5. 直线y=- 34x+6与坐标轴分别交于A、B两点,动点P、Q同时从O点出发,同时到达A点,运动停止.点Q沿线段OA运动,速度为每秒1个单位长度,点P沿路线O⇒B⇒A运动.(1)直接写出A、B两点的坐标;(2)设点Q的运动时间为t(秒),△OPQ的面积为S,求出S与t之间的函数关系式;(3)当S= 485时,求出点P的坐标,并直接写出以点O、P、Q为顶点的平行四边形的第四个顶点M的坐标.点评:本题主要考查梯形的性质及勾股定理.在解题(2)时,应注意分情况进行讨论,防止在解题过程中出现漏解现象.○答○案1.分析:(1)四边形PQCD为平行四边形时PD=CQ.(2)四边形PQCD为等腰梯形时QC-PD=2CE.(3)四边形PQCD为直角梯形时QC-PD=EC.所有的关系式都可用含有t的方程来表示,即此题只要解三个方程即可.解答:解:(1)∵四边形PQCD平行为四边形∴PD=CQ∴24-t=3t解得:t=6即当t=6时,四边形PQCD平行为四边形.(2)过D作DE⊥BC于E则四边形ABED为矩形∴BE=AD=24cm∴EC=BC-BE=2cm∵四边形PQCD为等腰梯形∴QC-PD=2CE即3t-(24-t)=4解得:t=7(s)即当t=7(s)时,四边形PQCD为等腰梯形.(3)由题意知:QC-PD=EC时,四边形PQCD为直角梯形即3t-(24-t)=2解得:t=6.5(s)即当t=6.5(s)时,四边形PQCD为直角梯形.2.分析:(1)根据CE平分∠ACB,MN∥BC,找到相等的角,即∠OEC=∠ECB,再根据等边对等角得OE=OC,同理OC=OF,可得EO=FO.(2)利用矩形的判定解答,即有一个内角是直角的平行四边形是矩形.(3)利用已知条件及正方形的性质解答.解答:解:(1)∵CE平分∠ACB,∴∠ACE=∠BCE,∵MN∥BC,∴∠OEC=∠ECB,∴∠OEC=∠OCE,∴OE=OC,同理,OC=OF,∴OE=OF.(2)当点O运动到AC中点处时,四边形AECF是矩形.如图AO=CO,EO=FO,∴四边形AECF为平行四边形,∵CE平分∠ACB,∴∠ACE= ∠ACB,同理,∠ACF= ∠ACG,∴∠ECF=∠ACE+∠ACF= (∠ACB+∠ACG)= ×180°=90°,∴四边形AECF是矩形.(3)△ABC是直角三角形∵四边形AECF是正方形,∴AC⊥EN,故∠AOM=90°,∵MN∥BC,∴∠BCA=∠AOM,∴∠BCA=90°,∴△ABC是直角三角形.3.分析:(1)依据题意易知四边形ABNQ是矩形∴NC=BC-BN=BC-AQ=BC-AD+DQ,BC、AD已知,DQ 就是t,即解;∵AB∥QN,∴△CMN∽△CAB,∴CM:CA=CN:CB,(2)CB、CN已知,根据勾股定理可求CA=5,即可表示CM;四边形PCDQ构成平行四边形就是PC=DQ,列方程4-t=t即解;(3)可先根据QN平分△ABC的周长,得出MN+NC=AM+BN+AB,据此来求出t的值.然后根据得出的t的值,求出△MNC的面积,即可判断出△MNC的面积是否为△ABC面积的一半,由此可得出是否存在符合条件的t值.(4)由于等腰三角形的两腰不确定,因此分三种情况进行讨论:①当MP=MC时,那么PC=2NC,据此可求出t的值.②当CM=CP时,可根据CM和CP的表达式以及题设的等量关系来求出t的值.③当MP=PC时,在直角三角形MNP中,先用t表示出三边的长,然后根据勾股定理即可得出t的值.综上所述可得出符合条件的t的值.解答:解:(1)∵AQ=3-t∴CN=4-(3-t)=1+t在Rt△ABC中,AC2=AB2+BC2=32+42∴AC=5在Rt△MNC中,cos∠NCM= = ,CM= .(2)由于四边形PCDQ构成平行四边形∴PC=QD,即4-t=t解得t=2.(3)如果射线QN将△ABC的周长平分,则有:MN+NC=AM+BN+AB即:(1+t)+1+t= (3+4+5)解得:t= (5分)而MN= NC= (1+t)∴S△MNC= (1+t)2= (1+t)2当t= 时,S△MNC=(1+t)2= ≠ ×4×3∴不存在某一时刻t,使射线QN恰好将△ABC的面积和周长同时平分.(4)①当MP=MC时(如图1)则有:NP=NC即PC=2NC∴4-t=2(1+t)解得:t=②当CM=CP时(如图2)则有:(1+t)=4-t解得:t=③当PM=PC时(如图3)则有:在Rt△MNP中,PM2=MN2+PN2而MN= NC= (1+t)PN=NC-PC=(1+t)-(4-t)=2t-3∴[ (1+t)]2+(2t-3)2=(4-t)2解得:t1= ,t2=-1(舍去)∴当t= ,t= ,t= 时,△PMC为等腰三角形4.分析:以PQ,MN为两边,以矩形的边(AD或BC)的一部分为第三边构成一个三角形的必须条件是点P、N重合且点Q、M不重合,此时AP+ND=AD即2x+x2=20cm,BQ+MC≠BC即x+3x≠20cm;或者点Q、M重合且点P、N不重合,此时AP+ND≠AD即2x+x2≠20cm,BQ+MC=BC即x+3x=20cm.所以可以根据这两种情况来求解x的值.以P,Q,M,N为顶点的四边形是平行四边形的话,因为由第一问可知点Q只能在点M的左侧.当点P在点N的左侧时,AP=MC,BQ=ND;当点P在点N的右侧时,AN=MC,BQ=PD.所以可以根据这些条件列出方程关系式.如果以P,Q,M,N为顶点的四边形为等腰梯形,则必须使得AP+ND≠AD即2x+x2≠20cm,BQ+MC≠BC即x+3x≠20cm,AP=ND即2x=x2,BQ=MC即x=3x,x≠0.这些条件不能同时满足,所以不能成为等腰梯形.解答:解:(1)当点P与点N重合或点Q与点M重合时,以PQ,MN为两边,以矩形的边(AD或BC)的一部分为第三边可能构成一个三角形.①当点P与点N重合时,由x2+2x=20,得x1= -1,x2=- -1(舍去).因为BQ+CM=x+3x=4(-1)<20,此时点Q与点M不重合.所以x= -1符合题意.②当点Q与点M重合时,由x+3x=20,得x=5.此时DN=x2=25>20,不符合题意.故点Q与点M不能重合.所以所求x的值为-1.(2)由(1)知,点Q只能在点M的左侧,①当点P在点N的左侧时,由20-(x+3x)=20-(2x+x2),解得x1=0(舍去),x2=2.当x=2时四边形PQMN是平行四边形.②当点P在点N的右侧时,由20-(x+3x)=(2x+x2)-20,解得x1=-10(舍去),x2=4.当x=4时四边形NQMP是平行四边形.所以当x=2或x=4时,以P,Q,M,N为顶点的四边形是平行四边形.(3)过点Q,M分别作AD的垂线,垂足分别为点E,F.由于2x>x,所以点E一定在点P的左侧.若以P,Q,M,N为顶点的四边形是等腰梯形,则点F一定在点N的右侧,且PE=NF,即2x-x=x2-3x.解得x1=0(舍去),x2=4.由于当x=4时,以P,Q,M,N为顶点的四边形是平行四边形,所以以P,Q,M,N为顶点的四边形不能为等腰梯形.5.解答:解:(1)∵MD∥NC,当MD=NC,即15-t=2t,t=5时,四边形MNCD是平行四边形;(2)作DE⊥BC,垂足为E,则CE=21-15=6,当CN-MD=12时,即2t-(15-t)=12,t=9时,四边形MNCD是等腰梯形6.分析:(1)若过点P作PM⊥BC于M,则四边形PDCM为矩形,得出PM=DC=12,由QB=16-t,可知:s= PM×QB=96-6t;(2)本题应分三种情况进行讨论,①若PQ=BQ,在Rt△PQM中,由PQ2=PM2+MQ2,PQ=QB,将各数据代入,可将时间t求出;②若BP=BQ,在Rt△PMB中,由PB2=BM2+PM2,BP=BQ,将数据代入,可将时间t求出;③若PB=PQ,PB2=PM2+BM2,PB=PQ,将数据代入,可将时间t求出.解答:解:(1)过点P作PM⊥BC于M,则四边形PDCM为矩形.∴PM=DC=12,∵QB=16-t,∴s= •QB•PM= (16-t)×12=96-6t(0≤t≤ ).(2)由图可知,CM=PD=2t,CQ=t,若以B、P、Q为顶点的三角形是等腰三角形,可以分三种情况:①若PQ=BQ,在Rt△PMQ中,PQ2=t2+122,由PQ2=BQ2得t2+122=(16-t)2,解得;②若BP=BQ,在Rt△PMB中,PB2=(16-2t)2+122,由PB2=BQ2得(16-2t)2+122=(16-t)2,此方程无解,∴BP≠PQ.③若PB=PQ,由PB2=PQ2得t2+122=(16-2t)2+122得,t2=16(不合题意,舍去).综上所述,当或时,以B、P、Q为顶点的三角形是等腰三角形.7.分析:(1)分别令y=0,x=0,即可求出A、B的坐标;(2))因为OA=8,OB=6,利用勾股定理可得AB=10,进而可求出点Q由O到A的时间是8秒,点P的速度是2,从而可求出,当P在线段OB上运动(或0≤t≤3)时,OQ=t,OP=2t,S=t2,当P在线段BA上运动(或3<t≤8)时,OQ=t,AP=6+10-2t=16-2t,作PD⊥OA于点D,由相似三角形的性质,得PD=48-6t5,利用S= 12OQ×PD,即可求出答案;(3)令S= 485,求出t的值,进而求出OD、PD,即可求出P的坐标,利用平行四边形的对边平行且相等,结合简单的计算即可写出M的坐标.解答:解:(1)y=0,x=0,求得A(8,0)B(0,6),(2)∵OA=8,OB=6,∴AB=10.∵点Q由O到A的时间是81=8(秒),∴点P的速度是6+108=2(单位长度/秒).当P在线段OB上运动(或O≤t≤3)时,OQ=t,OP=2t,S=t2.当P在线段BA上运动(或3<t≤8)时,OQ=t,AP=6+10-2t=16-2t,如图,做PD⊥OA于点D,由PDBO=APAB,得PD= 48-6t5.∴S= 12OQ•PD=- 35t2+245t.(3)当S= 485时,∵485>12×3×6∴点P在AB上当S= 485时,- 35t2+245t= 485∴t=4∴PD= 48-6×45= 245,AD=16-2×4=8AD= 82-(245)2= 325∴OD=8- 325= 85∴P(85,245)M1(285,245),M2(- 125,245),M3(125,- 245)。
数学五年级上册梯形的面积解决问题复习题(含答案)

6.3梯形的面积1.已知如图是两个边长为10cm和8cm的正方形,求MN的长是多少厘米?2.一个直角梯形的周长是48米,两底之和与两腰之和的比是2:1,已知一腰是另一腰的,求这个直角梯形的面积.3.如图,一块长方形的草地中有一条平行四边形的小路,小路的底是1米,求草地的面积.(单位:米)4.三角形的面积为30cm2,求阴影部分的面积.5.各图形的面积是多少平方厘米?(每小格面积是1cm,不满一格算半格)6.直角梯形ABCD中,AD=3厘米,AB=4厘米,BC=6厘米,BE把梯形分成面积相等的两部分,DE长多少厘米?7.已知图中阴影部分的面积是9.6平方厘米,求梯形的面积.8.已知图中梯形ABCD的面积是27.5平方厘米,求阴影部分的面积.9.如图,在直角梯形ABCD中,已知AD=3cm,AB=4cm,CD=5cm,BC=6cm,BE将梯形分成面积相等的两部分.问DE的长是多厘米?10.看图计算:(1)已知正方形的面积为12平方厘米,阴影部分是一个圆,求圆的面积.(2)图中,BO=2DO,阴影部分的面积是4平方厘米,求梯形ABCD的面积.11.如图,一块梯形草地中有一条2米宽的长方形小路,已知小路的面积是16平方米,求草地的面积.12.右图的平行四边形中,三角形的面积是20平方分米,求阴影部分(梯形)的面积.13.如图所示,两个相同的直角三角形部分叠在一起.求阴影部分的面积.(单位:厘米)14.一块梯形地的面积是2400平方米,高60米,上底长27米,下底长多少米?(列方程解答)15.一个梯形花台,上底长12米,下底长18米,高10米.这个花台的占地面积是多少平方米?16.在图中画出与三角形面积相等的一个直角梯形.(2)如果把上图中的小方格看作边长是1厘米的正方形,请你计算出你画的这个梯形的面积.(要求列出算式)17.照下面的样子,用铁皮焊制一个盛水容器,求这个容器最多能装水多少立方厘米?(单位:厘米)18.已知如图梯形中阴影部分的面积是10平方厘米,试求梯形的面积.(单位:厘米)19.王叔叔用木栏杆靠墙一边围了一块菜地,围成的菜地木栏杆长76米,求出这块菜地的面积.20.一条长1500米的水渠横截面如图所示,求挖成这条水渠需要挖土多少立方米?21.求阴影部分的面积.(单位:厘米)22.量一量,画一画,算一算.(测量结果取整数,并标在相应位置)(l)量出∠A= 度.(2)作梯形的高.(3)测量出这个图形的上、下底和高,并计算面积.23.一块梯形棉花地,量得上底16米,下底23米,高28米.如果每平方米种棉花9棵,这块地一共可以种多少棵棉花?24.如图,李爷爷在自已的院墙边用篱笆围了一个牛栏,篱笆全长20.5米,求牛栏的占面积是多少?参考答案1.S△ABC=(10+8)×8÷2,=18×8÷2,=144÷2,=72(平方厘米);S△AMC=8×8÷2,=64÷2,=32(平方厘米);S△MBC=72﹣32=40(平方厘米);MN的长度为:40×2÷(10+8),=80÷18,=(平方厘米);答:MN的长是厘米.2.梯形的两底之和:48×=32(米),梯形的两腰之和:48﹣32=16(米),梯形的高:16×=6(米),梯形的面积:32×6÷2,=192÷2,=96(平方米);答:这个直角梯形的面积96平方米.3.(20﹣1)×10,=19×10,=190(平方米);答:草地的面积是190平方米.4.30×2÷(14﹣8),=30×2÷6,=10(厘米),(14+8)×10÷2,=22×10÷2,=110(平方厘米).答:阴影部分的面积是110平方厘米.5.(1)4×4×1=16(平方厘米);答:这个图形的面积是16平方厘米.(2)5×5×1﹣2×3÷2,=25﹣3,=22(平方厘米);答:这个图形的面积是22平方厘米.6.解:画图如下:BE把梯形分成相等的两部分,△BCE面积=梯形ABCD,所以6×EF×=(3+6)×4÷2÷2,3EF=9,3EF÷3=9÷3,EF=3,作EF⊥BC,DH⊥BC,在直角梯形ABCD中,所以EF∥DH,四边形ABHD是一个长方形,所以AD=BH=3cm,DH=AB=4cm,HC=BC﹣AD=3cm,在直角△DHC中,CD===5,因为EF∥DH,所以直角△CEF∽△DHC,即,=,所以CE=CD×EF÷DH,CE=5×3÷4=,DE=CD﹣CE=5﹣==1(厘米),答:DE 的长度是1厘米.7.解:由题意知,空白三角形的底是10厘米,高是4厘米,所以空白三角形的面积是:10×4÷2,=20(平方厘米),S 梯=S 阴影+S 三角形,=9.6+20,=29.6(平方厘米);答:梯形的面积是29.6平方厘米.8.解:设梯形的高为x 厘米,则:(7+4)×x÷2=27.5,11x÷2×2=27.5×2,11x=55,x=5;7×5÷2,=35÷2,=17.5(平方厘米);答:阴影部分的面积为17.5平方厘米.9.解:BE 将梯形分成面积相等的两部分,所以三角形BCE 的面积为:(3+6)×4÷2÷2=9,三角形DBE 的面积是:9﹣×3×4=9﹣6=3,在三角形DBE 与三角形BEC 中高相等,S △DBE :S △BEC =DE :EC ,即3:9=DE :EC ,设DE=x ,则3:9=x :(5﹣x ),9x=3(5﹣x ),9x=15﹣3x ,12x=15, x=,答:DE 的长是厘米.10.解:(1)设正方形的边长为d ,圆的半径为r ,那么d=2r ,d 2=12平方厘米,即(2r )2=12,4r 2=12,r2=3,圆的面积为:3.14×3=9.42(平方厘米);(2)因为BO=2DO,所以三角形CDO的面积=三角形BCO面积的一半,即三角形CDO的面积=2平方厘米;三角形BCD与三角形ACD同底等高,所以三角形BCD与三角形ACD的面积相等,三角形AOD的面积=三角形BCO的面积,即三角形AOD的面积=4平方厘米;BO=2DO,三角形ABO的面积是三角形AOD面积的2倍,即三角形AOB的面积=8平方厘米;梯形ABCD的面积为:4+2+4+8=18(平方厘米),答:(1)圆的面积为9.42平方厘米;(2)梯形ABCD的面积为18平方厘米.11.这块梯形草地的高是:16÷2,=8(米);这块梯形草地的面积是:[(4+6)+18﹣2]×8÷2,=26×8÷2,=104(平方米).答:草地的面积是104平方米.12.20×2÷5,=40÷5,=8(分米);8×8﹣20,=64﹣20,=44(平方分米);答:阴影部分的面积是44平方分米.13.[(8﹣3)+8]×5÷2,=(5+8)×5÷2,=13×5÷2,=65÷2,=32.5(平方厘米);答:阴影部分的面积是32.5平方厘米.14.解:设梯形的下底为x,(27+x)×60÷2=2400(27+x)×60=4800,27+x=80,x=53,答:设梯形的下底为53米.15.(12+18)×10×2,=30×10÷2,=150(平方米);答:这个花台的占地面积是150平方米.16.三角形面积=6×4÷2=12(个)格子面积,如图所示直角梯形与三角形面积相等:.(2)梯形面积:(2+4)×4÷2,=6×4÷2,=12(平方厘米);答:梯形面积为12平方厘米.17.(5+13)×3÷2×30,=18×3÷2×30,=54÷2×30,=27×30,=810(立方厘米);答:这个容器最多能装水810立方厘米.18.三角形的高为:10×2÷5=20÷5,=4(厘米);梯形的面积为:(5+10)×4÷2=15×4÷2,=60÷2,=30(平方厘米);答:梯形的面积为30平方厘米.19.(76-26)×26÷2=50×26÷2=1300÷2=650(平方米)答:这块菜地的面积是650平方米. 20.(1.2+4.8)×1.5÷2×1500,=6×1.5÷2×1500,=9÷2×1500,=4.5×1500,=6750(立方米);答:挖成这条水渠需要挖土6750立方米.21.(4+8)×4÷2﹣3.14×42×,=12×4÷2﹣3.14×4,=24﹣12.56,=11.44(平方厘米);答:阴影部分的面积是11.44平方厘米.22.(1)是得∠A=70度.(2)测量结果及画图如下:(3)梯形的面积:(2+5)×2÷2,=7×2÷2,=7(平方厘米).答:梯形的面积是7平方厘米.23.(16+23)×28÷2×9,=39×28÷2×9,=1092÷2×9,=546×9,=4914(棵);答:这块地一共可以种4914棵棉花.24.(20.5﹣8.5)×8.5÷2,=12×8.5÷2,=102÷2,=51(平方米);答:牛栏的占地面积是51平方米.。
中考数学动点问题专项训练
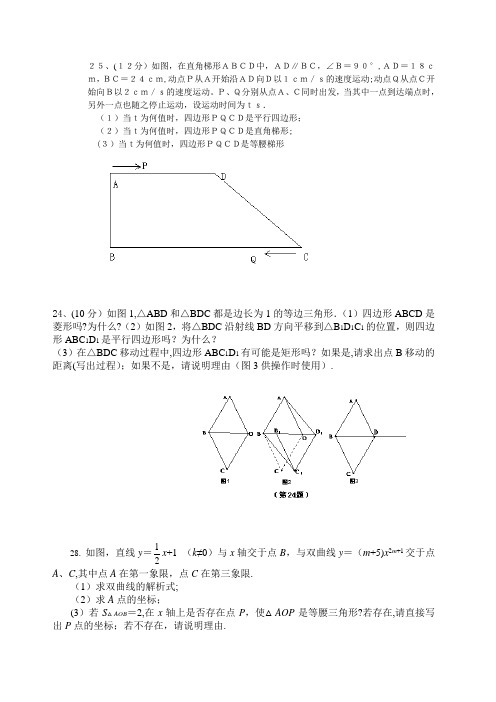
25、(12分)如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AD=18cm,BC=24cm,动点P从A开始沿AD向D以1cm/s的速度运动;动点Q从点C开始向B以2cm/s的速度运动。
P、Q分别从点A、C同时出发,当其中一点到达端点时,另外一点也随之停止运动,设运动时间为ts.(1)当t为何值时,四边形PQCD是平行四边形; (2)当t为何值时,四边形PQCD是直角梯形; (3)当t为何值时,四边形PQCD是等腰梯形24、(10分)如图1,△ABD 和△BDC 都是边长为1的等边三角形.(1)四边形ABCD 是菱形吗?为什么?(2)如图2,将△BDC 沿射线BD 方向平移到△B 1D 1C 1的位置,则四边形ABC 1D 1是平行四边形吗?为什么?(3)在△BDC 移动过程中,四边形ABC 1D 1有可能是矩形吗?如果是,请求出点B 移动的距离(写出过程);如果不是,请说明理由(图3供操作时使用).28. 如图,直线y =21x +1 (k ≠0)与x 轴交于点B ,与双曲线y =(m +5)x 2m +1交于点A 、C ,其中点A 在第一象限,点C 在第三象限.(1)求双曲线的解析式; (2)求A 点的坐标;(3)若S △AOB =2,在x 轴上是否存在点P ,使△AOP 是等腰三角形?若存在,请直接写出P 点的坐标;若不存在,请说明理由.22、(12分)如图,已知:梯形ABCD 中,AD ∥BC ,AB =CD ,E 、F 、G 、H 分别是AD 、BC 、BE 、CE 的中点。
(1)求证:△ABE ≌△DCE(2)四边形EGFH 是什么特殊四边形?并证明你的结论.(3)连接EF ,当四边形EGFH 是正方形时,线段EF 与BC 有什么关系?请说明理由.(满分10分)如下图,直角梯形ABCD 中,AD ∥BC ,AD=24cm ,BC=26cm ,∠B=90°,动点P 从A 开始沿AD 边向D 以1s cm /的速度运动,动点Q 从点C 开始沿CB 以3s cm /的速度向点B 运动.P 、Q 同时出发,当其中一点到达顶点时,另一点也随之停止运动,设运动时间为ts ,问t 为何值时,(1)四边形PQCD 是平行四边形.(2)当t 为何值时,四边形PQCD 为等腰梯形.7.(6分)如图,在等腰梯形ABCD 中,M BC AD ,//、N 分别为AD 、BC 的中点,E 、F 分别是BM 、CM 的中点.(1)求证:DCM ABM ∆≅∆。
【数学】学而思网校内部奥数习题集.中年级(第5-8套)

——第五套一、填空题:1.(32.8×91-16.4×92-1.75×656) ÷(0.2×0.2)=().2.有一列长00米的火车,每秒行驶5米。
它通过一座长850米的大桥需要()秒。
3.在下图所示除法竖式的每个方框中,填入适当的数字,使算式成立。
那么算式中的被除数是().4.如图,数表中的上、下两行都是等差数列,那么同一列中两个数的差(大数减小数)最小是().5.小明、小红、小玲共有3块糖。
如果小玲吃掉3块,那么小红与小玲的糖就一样多;如果小红给小明2块糖,那么小明的糖就是小红的糖的2倍。
小红有()块糖。
6.华侨小学某班有60人,在参加某个活动时,他们着装白色或黑色上衣,黑色或蓝色裤子。
其中有人穿白上衣蓝裤子,有34人穿黑裤子,29人穿黑上衣,那么穿黑上衣黑裤子的有()人。
7.下面是两个具有一定的规律的数列,请你按规律补填出空缺的项:(1)1,5,11,19,29,___,55;(2)1,2,6,16,44,___,328。
8.已知在每个正方体的个面上分别写着1,2,3,4,5,6这6个数,并且任意两个相对的面上所写的两个数的和都等于7。
如下图所示,现在把5个这样的正方体一个挨着一个连接起来,在紧挨着的两个面上的两个数之和都等于8,那么图中标有问号的那个面上所写的数是().79. 一个钝角三 角形的一条 边为 ,这条边上的 高为 ,那么这个三 角形的面积 是( )cm 210. 16支球队 进行淘汰赛 ,为了决出冠 军,要进行( )场比赛。
二、解答题:11. 李师傅某天 生产了一批 零件,他把它们分 成了甲、乙两堆。
如果从甲堆 零件中拿 5个放到乙 堆中,则两推零件 的个数相等 ;如果从乙堆 零件中拿 5个放到甲 堆中,则甲堆零件 的个数是乙 堆的3倍。
那么,甲堆原来有 零件多少个 ?李师傅这一 天共生产零 件多少个?12. 用绳测井深 ,把绳三折,井外余2米 ,把绳四折,还差1米不 到井口,那么井深多 少米?绳长多少米 ?13. 如图所示,在直角梯形 A BCD 中 ,三角形 E 和三角形 C DE 都是 等腰直角三 角形,且BC=20厘米,那么直角梯 形 的面积是( )cm 214. 学学和思思 分别从A 、B 两地同时 出发,相向而行。
中考总复习数学(人教版 全国通用)基础讲练 第20讲 梯形(含答案点拨)

第20讲 梯形考纲要求命题趋势1.了解梯形的有关概念与分类,掌握梯形的性质,会进行梯形的有关计算.2.掌握等腰梯形的性质与判定. 3.能灵活添加辅助线,把梯形问题转化为三角形、平行四边形的问题来解决.等腰梯形的性质和判定是中考考查的内容,实际问题中往往和特殊三角形、特殊四边形的知识结合在一起综合运用.知识梳理一、梯形的有关概念及分类1.一组对边平行,另一组对边不平行的________叫做梯形.平行的两边叫做______,两底间的________叫做梯形的高.2.________相等的梯形叫做等腰梯形,有一个角是直角的梯形叫做直角梯形. 3.梯形的分类:梯形⎩⎨⎧一般梯形特殊梯形⎩⎪⎨⎪⎧直角梯形等腰梯形4.梯形的面积=12(上底+下底)×高=中位线×高.二、等腰梯形的性质与判定 1.性质:(1)等腰梯形的两腰相等,两底平行. (2)等腰梯形同一底上的两个角________. (3)等腰梯形的对角线________.(4)等腰梯形是轴对称图形,过两底中点的直线是它的对称轴. 2.判定:(1)两腰相等的梯形是等腰梯形.(2)同一底上的两个角相等的________是等腰梯形. (3)对角线相等的________是等腰梯形. 三、梯形的中位线1.定义:连接梯形两腰________的线段叫做梯形的中位线. 2.性质:梯形的中位线平行于两底,且等于________的一半. 四、梯形问题的解决方法梯形问题常通过――→转化辅助线三角形问题或平行四边形问题来解答,转化时常用的辅助线有:1.平移一腰,即从梯形的一个顶点作另一腰的平行线,把梯形分成一个平行四边形和一个三角形.2.过顶点作高,即从同一底的两端作另一底所在直线的垂线,把梯形转化成一个矩形和两个直角三角形.3.平移一条对角线,即从梯形的一个顶点作一条对角线的平行线,把梯形转化成平行四边形和三角形.4.延长梯形两腰使它们相交于一点,把梯形转化成三角形. 5.过一腰中点作辅助线.(1)过此中点作另一腰的平行线,把梯形转化成平行四边形;(2)连接一底的端点与一腰中点,并延长与另一底的延长线相交,把梯形转化成三角形.自主测试1.若等腰梯形ABCD的上底长AD=2,下底长BC=4,高为2,那么梯形的腰DC的长为()A.2 B. 3 C.3 D. 52.如图,在一块形状为直角梯形的草坪中,修建了一条由A→M→N→C的小路(M,N分别是AB,CD中点).极少数同学为了走“捷径”,沿线段AC行走,破坏了草坪,实际上他们仅少走了()A.7米 B.6米 C.5米 D.4米3.如图,在直角梯形ABCD中,AD∥BC,∠B=90°,E为AB上一点,且ED平分∠ADC,EC平分∠BCD,则下列结论中,错误的是()A.∠ADE=∠CDEB.DE⊥ECC.AD·BC=BE·DED.CD=AD+BC4.已知梯形的上底长为2,下底长为5,一腰长为4,则另一腰长x的取值范围是__________.考点一、一般梯形的性质【例1】如图,在梯形ABCD中,AD∥BC,BD=CD,∠BDC=90°,AD=3,BC=8,求AB的长.∴AE∥DF,∠AEF=90°.∵AD∥BC,∴四边形AEFD是矩形.∴EF=AD=3,AE=DF.∵BD=CD,DF⊥BC,∴DF是△BDC边BC上的中线.∵∠BDC=90°,∴DF=12BC=BF=4.∴AE=4,BE=BF-EF=4-3=1.在Rt△ABE中,AB2=AE2+BE2,∴AB=42+12=17.方法总结遇到梯形问题,一般情况下通过作腰或对角线的平行线、高线、连对角线、延长两腰转化为三角形、平行四边形、直角三角形、矩形等问题来解决.触类旁通 1 如图,在梯形ABCD中,AD∥BC,AB∥DE,AF∥DC,E,F两点在边BC上,且四边形AEFD是平行四边形.(1)AD与BC有何等量关系?请说明理由.(2)当AB=DC时,求证:四边形AEFD是矩形.考点二、等腰梯形的性质与判定【例2】如图,在等腰△ABC中,点D,E分别是两腰AC,BC上的点,连接AE,BD 相交于点O,∠1=∠2.(1)求证:OD=OE;(2)求证:四边形ABED是等腰梯形.分析:(1)根据已知条件可知利用全等三角形证明BD=AE,根据∠1=∠2可以证明OA =OB,根据等式性质可知OD=OE;(2)先证明四边形ABED是梯形,然后证明两腰相等即可.证明:(1)∵△ABC是等腰三角形,∴AC=BC.∴∠BAD=∠ABE.又∵AB=BA,∠2=∠1,∴△ABD≌△BAE,∴BD=AE.又∵∠1=∠2,∴OA=OB.∴BD-OB=AE-OA,即OD=OE.(2)由(1)知,OD=OE,∴∠OED=∠ODE.∴∠OED=12(180°-∠DOE).同理,∠1=12(180°-∠AOB).∵∠DOE=∠AOB,∴∠1=∠OED,∴DE∥AB.∵AD不平行于BE,∴四边形ABED是梯形,∵AE=BD,∴梯形ABED是等腰梯形.方法总结在证明一个四边形是等腰梯形时,必须先证明它是梯形,然后再通过两腰相等或同一底上的两个角相等,或者是对角线相等来证明梯形是等腰梯形.触类旁通2 如图,在矩形ABCD中,对角线AC,BD交于点O,M,N分别为AO,DO的中点,四边形BCNM是等腰梯形吗?为什么?考点三、有关梯形的计算【例3】如图,在梯形ABCD中,AD∥BC,AB⊥AC,∠B=45°,AD=2,BC=42,求DC的长.分析:由于△ABC是等腰直角三角形,且BC=42,可得出BC边上的高.只要通过平移腰CD,就可与BC边上的高构成直角三角形,从而求出CD.解:过点A作AE∥DC交BC于点E,过点A作AF⊥BC于点F,如图所示.∵AD∥BC,AE∥DC,∴四边形AECD为平行四边形.∴AE=DC,AD=EC= 2.又∵AB⊥AC,∠B=45°,BC=42,∴AB=AC=4.∴AF=BF=2 2.∴EF=BC-BF-EC= 2.在Rt△AFE中,AE=AF2+EF2=(22)2+(2)2=10,即DC=10.方法总结解决梯形问题作辅助线的方法要结合题目的条件和要证结论的需要灵活运用.若题中已知两对角线的条件,可考虑平移对角线,使两对角线在同一个三角形中;若已知两腰的某些条件,可考虑平移一腰;若已知两底角互余,可平移一腰或延长两腰构成直角三角形;若要求梯形的面积,常作出梯形的高.触类旁通3 如图所示,在等腰梯形ABCD中,AB∥CD,AD=BC,AC⊥BC,∠B=60°,BC=2 cm,则上底DC的长是__________cm.A.AC=BDB.OB=OCC.∠BCD=∠BDCD.∠ABD=∠ACD2.(湖南长沙)下列四边形中,对角线一定不相等的是()A.正方形 B.矩形C.等腰梯形 D.直角梯形3.(安徽)在一张直角三角形纸片的两直角边上各取一点,分别沿斜边中点与这两点的连线剪去两个三角形,剩下的部分是如图所示的直角梯形,其中三边长分别为2,4,3,则原直角三角形纸片的斜边长是()A.10 B.4 5C.10或4 5 D.10或2174.(湖南长沙)如图,等腰梯形ABCD中,AD∥BC,AB=AD=2,∠B=60°,则BC 的长为__________.5.(四川内江)如图,四边形ABCD是梯形,BD=AC且BD⊥AC,若AB=2,CD=4,则S梯形ABCD=____________.6.(四川南充)如图,等腰梯形ABCD中,AD∥BC,点E是AD延长线上的一点,且CE=CD.求证:∠B =∠E .1.梯形的上底长为5,下底长为9,则梯形的中位线长等于( ) A .6 B .7 C .8 D .102.在等腰梯形ABCD 中,AB ∥CD ,对角线AC 平分∠BAD ,∠B =60°,CD =2 cm ,则梯形ABCD 的面积为( )A .33cm 2B .6 cm 2C .63cm 2D .12 cm 23.如图,在梯形ABCD 中,AB ∥DC ,∠D =90°,AD =DC =4,AB =1,F 为AD 的中点,则点F 到BC 的距离是( )A .4B .3C .2D .14.如图,在等腰梯形ABCD 中,AB ∥CD ,对角线AC ,BD 相交于O ,∠ABD =30°,AC ⊥BC ,AB =8 cm ,则△COD 的面积为( )A .433cm 2B .43cm 2C .233cm 2D .23cm 25.如图,等腰梯形ABCD 中,AD ∥BC ,AB ∥DE ,梯形ABCD 的周长为26,BE =4,则△DEC 的周长为__________.(第5题图)6.如图,在梯形ABCD 中,AB ∥DC ,∠ADC 的平分线与∠BCD 的平分线的交点E 恰在AB 上.若AD =7 cm ,BC =8 cm ,则AB 的长度是__________ cm.(第6题图)7.如图,在直角梯形ABCD 中,AD ∥BC ,AB ⊥BC ,AD =2,AB =3,BC =4,则梯形ABCD 的面积是__________.(第7题图)8.如图,在等腰梯形ABCD 中,AD ∥BC ,对角线AC ⊥BD 于点O ,AE ⊥BC ,DF ⊥BC ,垂足分别为E ,F ,AD =4,BC =8,则AE +EF =__________.(第8题图)9.如图,在菱形ABCD 中,∠DAB =60°,过点C 作CE ⊥AC 且与AB 的延长线交于点E ,求证:四边形AECD 是等腰梯形.参考答案导学必备知识 自主测试1.D 2.B 3.C 4.1<x <7 探究考点方法触类旁通1.解:(1)AD =13BC .理由如下:∵AD ∥BC ,AB ∥DE ,AF ∥DC ,∴四边形ABED 和四边形AFCD 都是平行四边形, ∴AD =BE ,AD =FC .又∵四边形AEFD 是平行四边形, ∴AD =EF ,∴AD =BE =EF =FC ,∴AD =13BC .(2)证明:∵四边形ABED 和四边形AFCD 都是平行四边形,∴DE =AB ,AF =DC . ∵AB =DC ,∴DE =AF .又∵四边形AEFD 是平行四边形, ∴四边形AEFD 是矩形.触类旁通2.解:是等腰梯形.根据三角形中位线定理有,MN ∥AD ∥BC ,且MN ≠BC ,∴四边形BCNM 为梯形.在矩形ABCD 中,AO =DO ,又M ,N 分别是AO ,DO 的中点,∴OM =ON ,∴CM =BN ,∴四边形BCNM 是等腰梯形.触类旁通3.2 ∠CAB =90°-60°=30°,∵等腰梯形ABCD 中,∠BAD =∠B =60°, ∴∠CAD =∠BAD -∠BAC =30°.又∵CD ∥AB ,∴∠DCA =∠CAB =30°=∠DAC . ∴CD =AD =BC = 2 cm. 品鉴经典考题1.C 对于A ,∵四边形ABCD 是等腰梯形,∴AC =BD ,故本选项正确;对于B ,∵四边形ABCD 是等腰梯形,∴AB =DC ,∠ABC =∠DCB ,在△ABC 和△DCB 中,∵⎩⎪⎨⎪⎧AB =DC ,∠ABC =∠DCB ,BC =CB ,∴△ABC ≌△DCB (SAS),∴∠ACB =∠DBC ,∴OB =OC ,故本选项正确; 对于C ,∵无法判定BC =BD ,∴∠BCD 与∠BDC 不一定相等,故本选项错误; 对于D ,∵∠ABC =∠DCB ,∠ACB =∠DBC , ∴∠ABD =∠ACD ,故本选项正确. 故选C.2.D 根据正方形、矩形、等腰梯形的性质,它们的两条对角线一定相等,只有直角梯形的对角线一定不相等.故选D.3.C 考虑两种情况. ①如图:因为CD =22+42=25,点D 是斜边AB 的中点, 所以AB =2CD =4 5. ②如图:因为CE=32+42=5,点E是斜边AB的中点,所以AB=2CE=10,故原直角三角形纸片的斜边长是10或4 5.4.4过点A作AE∥CD交BC于点E,∵AD∥BC,∴四边形AECD是平行四边形,∴AE=CD=2,AD=EC=2.∵∠B=60°,∴BE=AB=AE=2,∴BC=BE+CE=2+2=4.5.9过点B作BE∥AC,交DC的延长线于点E,则AB=CE,BE=AC=BD.∵BD⊥AC,AB=2,CD=4,∴BD⊥BE,DE=6,∴梯形高为3,∴S梯形ABCD=(2+4)×3÷2=9.6.证明:∵CE=CD,∴∠CDE=∠E.∵AD∥BC,∴∠CDE=∠DCB.∴∠E=∠DCB.∵AB=DC,∴∠B=∠DCB.∴∠B=∠E.研习预测试题1.B2.A3.C4.A5.186.157.98.10如图,过点D作DG∥AC,交BC的延长线于点G.易得四边形ACGD为平行四边形,∴CG=AD=4,BG=BC+CG=8+4=12.∵AC⊥BD,AC∥DG,∴BD⊥DG.∵梯形ABCD是等腰梯形,∴AC=BD=DG.∴△BDG为等腰直角三角形.又∵DF⊥BC,∴DF=12BG=6.∴AE+EF=DF+AD=6+4=10.9.证明:∵四边形ABCD是菱形,∠DAB=60°,∠DAB=30°.∴∠CAE=12又∵CE⊥AC,∴∠E=60°=∠CBE.∴CE=BC=AD. ∵CD∥AE,AE=AB+BE=DC+BE≠DC,∴四边形AECD是等腰梯形.。
重庆中考数学24题专题

重庆中考几何一、有关几何的基本量:线段、角度、全等、面积、四边形性质1、如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,E为AB延长线上一点,连接ED,与BC 交于点H.过E作CD的垂线,垂足为CD上的一点F,并与BC交于点G.已知G为CH的中点,且∠BEH=∠HEG.(1)若HE=HG,求证:△EBH≌△GFC;(2)若CD=4,BH=1,求AD的长.(1)证明:∵HE=HG,∴∠HEG=∠HGE,∵∠HGE=∠FGC,∠BEH=∠HEG,∴∠BEH=∠FGC,∵G是HC的中点,∴HG=GC,∴HE=GC,∵∠HBE=∠CFG=90°.∴△EBH≌△GFC;(2)解:过点H作HI⊥EG于I,∵G为CH的中点,∴HG=GC,∵EF⊥DC,HI⊥EF,∴∠HIG=∠GFC=90°,∠FGC=∠HGI,∴△GIH≌△GFC,∵△EBH≌△EIH(AAS),∴FC=HI=BH=1,∴AD=4-1=3.2、已知,Rt△ABC中,∠ACB=90°,∠CAB=30°.分别以AB、AC为边,向形外作等边△ABD 和等边△ACE.(1)如图1,连接线段BE、CD.求证:BE=CD;(2)如图2,连接DE交AB于点F.求证:F为DE中点.证明:(1)∵△ABD和△ACE是等边三角形,∴AB=AD,AC=AE,∠DAB=∠EAC=60°,∴∠DAB+∠BAC=∠EAC+∠BAC,即∠DAC=∠BAE,在△DAC和△BAE中,AC=AE ∠DAC=∠BAE AD=AB ,∴△DAC≌△BAE(SAS),∴DC=BE;(2)如图,作DG∥AE,交AB于点G,由∠EAC=60°,∠CAB=30°得:∠FAE=∠EAC+∠CAB=90°,∴∠DGF=∠FAE=90°,又∵∠ACB=90°,∠CAB=30°,∴∠ABC=60°,又∵△ABD为等边三角形,∠DBG=60°,DB=AB,∴∠DBG=∠ABC=60°,在△DGB和△ACB中,∠DGB=∠ACB ∠DBG=∠ABC DB=AB ,∴△DGB≌△ACB(AAS),∴DG=AC,又∵△AEC为等边三角形,∴AE=AC,∴DG=AE,在△DGF和△EAF中,∠DGF=∠EAF ∠DFG=∠EFA DG=EA ,∴△DGF≌△EAF(AAS),∴DF=EF,即F为DE中点.3、如图,在直角梯形ABCD中,AD⊥DC,AB∥DC,AB=BC,AD与BC延长线交于点F,G是DC延长线上一点,AG⊥BC于E.(1)求证:CF=CG;(2)连接DE,若BE=4CE,CD=2,求DE的长.解答:(1)证明:连接AC,∵DC ∥AB ,AB=BC ,∴∠1=∠CAB ,∠CAB=∠2, ∴∠1=∠2;∵∠ADC=∠AEC=90°,AC=AC , ∴△ADC ≌△AEC , ∴CD=CE ;∵∠FDC=∠GEC=90°,∠3=∠4, ∴△FDC ≌△GEC ,∴CF=CG .(2)解:由(1)知,CE=CD=2, ∴BE=4CE=8,∴AB=BC=CE+BE=10,∴在Rt △ABE 中,AE= AB 2-BE 2 =6, ∴在Rt △ACE 中,AC= AE 2+CE 2 =102 由(1)知,△ADC ≌△AEC , ∴CD=CE ,AD=AE ,∴C 、A 分别是DE 垂直平分线上的点, ∴DE ⊥AC ,DE=2EH ;(8分) 在Rt △AEC 中,S △AEC =21 AE •CE=21AC •EH , ∴EH=AC CEAE ⋅ =10226⨯ =5103∴DE=2EH=2×5103=5106 4、如图,AC 是正方形ABCD 的对角线,点O 是AC 的中点,点Q 是AB 上一点,连接CQ ,DP ⊥CQ 于点E ,交BC 于点P ,连接OP ,OQ ;求证:(1)△BCQ ≌△CDP ; (2)OP=OQ .证明:∵四边形ABCD 是正方形, ∴∠B=∠PCD=90°,BC=CD , ∴∠2+∠3=90°,又∵DP ⊥CQ , ∴∠2+∠1=90°, ∴∠1=∠3,在△BCQ 和△CDP 中,∠B=∠PCD BC=CD ∠1=∠3 . ∴△BCQ ≌△CDP . (2)连接OB . 由(1):△BCQ ≌△CDP 可知:BQ=PC , ∵四边形ABCD 是正方形, ∴∠ABC=90°,AB=BC , 而点O 是AC 中点, ∴BO=21AC=CO ,∠4=21∠ABC=45°=∠PCO , 在△BCQ 和△CDP 中, BQ=CP ∠4=∠PCO BO=CO∴△BOQ ≌△COP , ∴OQ=OP .5、在等腰梯形ABCD 中,AD ∥BC ,AB=AD=CD,∠ABC=60°,延长AD 到E,使DE=AD,延长DC 到F ,使DC=CF,连接BE 、BF 和EF.⑴求证:△ABE ≌△CFB; ⑵如果AD=6,tan ∠EBC 的值. 解:(1)证明:连结CE , 在△BAE 与△FCB 中,∵ BA=FC ,∠A=∠BCF ,, AE=BC , ∴△BAE ≌△FCB ;(2)延长BC 交EF 于点G ,作AH ⊥BG 于H ,作AM ⊥BG ,∵△BAE ≌△FCB ,∴∠AEB=∠FBG ,BE=BF ,∴△BEF 为等腰三角形,又∵AE ∥BC , ∴∠AEB=∠EBG ,∴∠EBG=∠FBG ,∴BG ⊥EF ,∵∠AMG=∠EGM=∠AEG=90°, ∴四边形AMGE 为矩形,∴AM=EG , 在Rt △ABM 中,AM=AB •sin60°=6×23=33 ,∴EG=AM=33, BG=BM+MG=6×2+6×cos60°=15,∴tan ∠EBC=531533==BG EG 6、如图,在梯形ABCD 中,AD ∥BC ,∠C=90°,E 为CD 的中点,EF ∥AB 交BC 于点F(1)求证:BF=AD+CF ;ABDECF(2)当AD=1,BC=7,且BE平分∠ABC时,求EF的长.(1)证明:如图(1),延长AD交FE的延长线于N∵∠NDE=∠FCE=90°∠DEN=∠FEC DE=EC∴△NDE≌△FCE ∴DN=CF ∵AB∥FN,AN∥BF∴四边形ABFN是平行四边形∴BF=AD+DN=AD+FC(2)解:∵AB∥EF,∴∠ABN=∠EFC,即∠1+∠2=∠3,又∵∠2+∠BEF=∠3,∴∠1=∠BEF,∴BF=EF,∵∠1=∠2,∴∠BEF=∠2,∴EF=BF,又∵BC+AD=7+1∴BF+CF+AD=8而由(1)知CF+AD=BF∴BF+BF=8∴2BF=8,∴BF=4,∴BF=EF=47、已知:AC是矩形ABCD的对角线,延长CB至E,使CE=CA,F是AE的中点,连接DF、CF分别交AB于G、H点(1)求证:FG=FH;(2)若∠E=60°,且AE=8时,求梯形AECD 的面积.(1)证明:连接BF∵ABCD为矩形∴AB⊥BC AB⊥AD AD=BC∴△ABE为直角三角形∵F是AE的中点∴AF=BF=BE∴∠FAB=∠FBA∴∠DAF=∠CBF∵AD=BC, ∠DAF=∠CBF ,AF=BF ,∴△DAF≌△CBF∴∠ADF=∠BCF∴∠FDC=∠FCD∴∠FGH=∠FHG ∴FG=FH ;(2)解:∵AC=CE ∠E=60° ∴△ACE 为等边三角形 ∴CE=AE=8 ∵AB ⊥BC ∴BC=BE=CE 21=4 ∴根据勾股定理AB=34 ∴梯形AECD 的面积=21×(AD+CE)×CD=21×(4+8)×34=3248、如图,直角梯形ABCD 中,AD ∥BC ,∠BCD=90°,且CD=2AD ,tan ∠ABC=2,过点D作DE ∥AB ,交∠BCD 的平分线于点E ,连接BE . (1)求证:BC=CD ;(2)将△BCE 绕点C ,顺时针旋转90°得到△DCG ,连接EG .求证:CD 垂直平分EG ; (3)延长BE 交CD 于点P .求证:P 是CD 的中点. 证明:(1)延长DE 交BC 于F ,∵AD ∥BC ,AB ∥DF ,∴AD=BF ,∠ABC=∠DFC . 在Rt △DCF 中,∵tan ∠DFC=tan ∠ABC=2, ∴CFCD=2, 即CD=2CF ,∵CD=2AD=2BF , ∴BF=CF , ∴BC=BF+CF=21CD+21CD=CD . 即BC=CD .(2)∵CE 平分∠BCD ,∴∠BCE=∠DCE , 由(1)知BC=CD , ∵CE=CE ,∴△BCE ≌△DCE , ∴BE=DE ,由图形旋转的性质知CE=CG ,BE=DG , ∴DE=DG ,∴C ,D 都在EG 的垂直平分线上, ∴CD 垂直平分EG . (3)连接BD , 由(2)知BE=DE , ∴∠1=∠2. ∵AB ∥DE ,∴∠3=∠2.∴∠1=∠3.∵AD ∥BC ,∴∠4=∠DBC .由(1)知BC=CD ,∴∠DBC=∠BDC ,∴∠4=∠BDP . 又∵BD=BD ,∴△BAD ≌△BPD(ASA)∴DP=AD . ∵AD=21CD ,∴DP=21CD .∴P 是CD 的中点. 9.(2011南岸二诊)如图,已知点P 是正方形ABCD 的对角线AC 上一点,过点P 作EF ⊥DP ,交AB 于点E ,交CD 于点G ,交BC 的延长线于点F ,连接DF .(1)若23=DF ,求DP 的长; (2)求证:CF AE =.10.如图,正方形CGEF 的对角线CE 在正方形ABCD 的边BC 的延长线上(CG >BC ),M 是线段AE 的中点,DM 的延长线交CE 于N . (1)线段AD 与NE 相等吗?请说明理由; (2)探究:线段MD 、MF 的关系,并加以证明.11、如图,梯形ABCD 中,AD ∥BC ,AB=DC=10cm ,AC 交BD 于G ,且∠AGD=60°,E 、F 分别为CG 、AB 的中点.(1)求证:△AGD 为正三角形; (2)求EF 的长度.G 24题图PFEDCBA解答:(1)证明:连接BE,∵梯形ABCD中,AB=DC,∴AC=BD,可证△ABC≌△DCB,∴∠GCB=∠GBC,又∵∠BGC=∠AGD=60°∴△AGD为等边三角形,(2)解:∵BE为△BCG的中线,∴BE⊥AC,在Rt△ABE中,EF为斜边AB上的中线,∴EF=AB=5cm.12、如图,梯形ABCD中,AD∥BC,DE=EC,EF∥AB交BC于点F,EF=EC,连接DF.(1)试说明梯形ABCD是等腰梯形;(2)若AD=1,BC=3,DC=,试判断△DCF的形状;(3)在条件(2)下,射线BC上是否存在一点P,使△PCD是等腰三角形,若存在,请直接写出PB的长;若不存在,请说明理由.解答:解:(1)证明:∵EF=EC,∴∠EFC=∠ECF,∵EF∥AB,∴∠B=∠EFC,∴∠B=∠ECF,∴梯形ABCD是等腰梯形;(2)△DCF是等腰直角三角形,证明:∵DE=EC,EF=EC,∴EF=CD,∴△CDF是直角三角形(如果一个三角形一边上的中线等于这条边的一半,那么这个三角形是直角三角形),∵梯形ABCD是等腰梯形,∴CF=(BC﹣AD)=1,∵DC=,∴由勾股定理得:DF=1,∴△DCF是等腰直角三角形;(3)共四种情况:∵DF⊥BC,∴当PF=CF时,△PCD是等腰三角形,即PF=1,∴PB=1;当P与F重合时,△PCD是等腰三角形,∴PB=2;当PC=CD=(P在点C的左侧)时,△PCD是等腰三角形,∴PB=3﹣;当PC=CD=(P在点C的右侧)时,△PCD是等腰三角形,∴PB=3+.故共四种情况:PB=1,PB=2,PB=3﹣,PB=3+.(每个1分)13.在梯形ABCD中,AD∥BC,AB=CD,且DE⊥AD于D,∠EBC=∠CDE,∠ECB=45°.⑴求证:AB=BE ;⑵延长BE ,交CD 于F .若CE =2,tan ∠CD E =31,求BF 的长. 13.⑴证明:延长DE ,交BC 于G .∵DE ⊥AD 于D ,∴∠ADE =90°又AD ∥BC , ∴∠DGC =∠BGE =∠ADE =90°, 而∠ECB =45°, ∴△EGC 是等腰直角三角形, ∴EG=CG在△BEG 和△DCG 中,EBG CDG EGB CGD EG CG ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△BEG ≌△DCG (AAS ) ∴BE=CD=AB ⑵连结BD .∵∠EBC=∠CDE ∴∠EBC +∠BCD =∠CDE +∠BCD =90°,即∠BFC =90° ∵CE=2,∴EG=CG=1又tan ∠CDE =31,∴13CG DG =,∴DG =3 ∵△BEG ≌△DCG ,∴BG=DG=3∴2210BE BG EG =+=∴CD=BE=10法一:∵1122BCDSBC DG CD BF ==,11431022BF ⨯⨯=⨯∴6105BF = 法二:经探索得,△BEG ∽△BFC ,∴BE BCBG BF=,∴1043BF = ∴6105BF = 14.如图,直角梯形ABCD 中,,90,45,AD BC ADC ABC AB ∠=∠=∥的垂直平分线EG 交BC 于F ,交DC 的延长线于.G求证:(1)CG CF =;(2).BC DG =AB CDEF证明:(1) ,AB EF ⊥ 45B ∠=904545EFB ∴∠=-=45CFG ∴∠=//,90AD BC ADC ∠=90FCG ∴∠=45,FCG ∴∠= CG CF =∴(2)连接AF , EF 是AB 的中垂线,AF BF FE AB ∴=⊥45=∠=∠∴BFE AFE90=∠∴AFB DCB AFB ∠=∠∴BC AD CD AF //,// ∴,AF DC BF DC ∴=∴=由(1)知CG CF = ,CG DC CF BF +=+∴即:DG BC =二、有关“截长补短”题型1、在ABCD 中,对角线,BD BC G BD ⊥为延长线上一点且ABG ∆为等边三角形,BAD ∠、CBD ∠的平分线相交于点E ,连接AE BD F 交于,连接GE 。
2019-2020学年市第六中学高一上学期期中数学试题(解析版)

2019-2020学年市第六中学高一上学期期中数学试题(解析版)2019-2020学年市第六中学高一上学期期中数学试题一、单选题1.设集合M=[1,2],N={x∈Z|-1A.[1,2]B.(-1,3)C.{1}D.{1,2}【答案】D【解析】集合N为整数集,所以先用列举法求出集合N,然后根据交集的定义求出即可.【详解】解:,.故选:D.【点睛】本题考查交集的概念和运算,解题的关键是先分析出集合中的代表元素是整数,属于基础题.2.已知集合A={x|x>2},B=,则B∩∁RA等于()A.{x|2≤x≤5}B.{x|-1≤x≤5}C.{x|-1≤x≤2}D.{x|x≤-1}【答案】C【解析】已知集合A,B,则根据条件先求出,然后根据交集的定义求出即可.【详解】解:集合A={x|x>2},所以,又集合,则.故选:C.【点睛】本题考查交集和补集的概念和计算,属于基础题.3.函数f(x)=+lg(3x+1)的定义域是()A.(-∞,1)B.C.【答案】B【解析】函数f(x)的定义域即:即被开方数大于等于0,分母不为0,且对数函数的真数有意义,根据条件列出方程组,解出的范围即为所求.【详解】解:函数f(x)=+lg(3x+1)的定义域是,解得:,所以函数f(x)的定义域是.故选:B.【点睛】本题考查求复合函数的定义域,解题的关键是保证每部分都有意义,属于基础题.4.已知f()=x-x2,则函数f(x)的解析式为()A.f(x)=x2-x4B.f(x)=x-x2C.f(x)=x2-x4(x≥0)D.f(x)=-x(x≥0)【答案】C【解析】令(),解出,利用换元法将代入解析式即可得出答案.【详解】解:令(),则,所以(),所以f(x)=x2-x4().故选:C.【点睛】本题考查利用换元法求函数解析式,解题的关键是注意换元之后的定义域,属于基础题.5.与函数相同的函数是()A.B.C.D.【答案】D【解析】试题分析:A中对应关系不同;B中定义域不同;C中定义域不同;D中对应关系,定义域均相同,是同一函数【考点】函数是同一函数的标准6.下列函数中,既是偶函数又在区间上单调递减的是()A.C.D.【答案】C【解析】试题分析:因为函数是奇函数,所以选项A不正确;因为函为函数既不是奇函数,也不是偶函数,所以选项B不正确;函数的图象抛物线开口向下,对称轴是轴,所以此函数是偶函数,且在区间上单调递减,所以,选项C正确;函数虽然是偶函数,但是此函数在区间上是增函数,所以选项D不正确;故选C。
八年级数学下册期末动点问题及压轴题带答案

1.(12分)已知:如图,平面直角坐标系中,A(0,4),B(0,2),点C是x轴上一点,点D为OC的中点.(1)求证:BD∥AC;(2)若点C在x轴正半轴上,且BD与AC的距离等于1,求点C的坐标;(3)如果OE⊥AC于点E,当四边形ABDE为平行四边形时,求直线AC的解析式.2.(12分)如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AD=24cm,BC=26cm.一动点P从点A开始沿AD边向点D以1cm/s的速度运动,动点Q从点C开始沿CB 边向点B以3cm/s的速度运动.P,Q分别从点A和点C同时出发,当其中一点到达端点时,另一点也随之停止运动.设运动时间为t s,则(1)t为何值时,四边形PQCD为平行四边形?(2)t为何值时,四边形PQCD为等腰梯形?(3)AB边的长是否存在一数值,使四边形PQCD为菱形.如果存在,请求出AB 边的长,如果不存在,请说出理由.3.(本题10分)已知:在正方形ABCD 中,AB =6,P 为边CD 上一点,过P 点作PE ⊥BD 于点E ,连接BP(1) O 为BP 的中点,连接CO 并延长交BD 于点F① 如图1,连接OE ,求证:OE ⊥OC② 如图2,若53=EF BF ,求DP 的长 (2) CP EP 22+=___________4.(本题12分)如图1,直线333+-=x y 分别与y 轴、x 轴交于点A 、点B ,点C 的坐标为(-3,0),D 为直线AB 上一动点,连接CD 交y 轴于点E(1) 点B 的坐标为__________,不等式0333>+-x 的解集为___________(2) 若S △COE =S △ADE ,求点D 的坐标(3) 如图2,以CD 为边作菱形CDFG ,且∠CDF =60°.当点D 运动时,点G 在一条定直线上运动,请求出这条定直线的解析式.5.(11分)如图1,在平面直角坐标系中,点O 是坐标原点,四边形ABCO 是菱形,点A 的坐标为(﹣3,4),点C 在x 轴的正半轴上,直线AC 交y 轴于点M ,AB 边交y 轴于点H ,连接BM .(1)菱形ABCO的边长是 ;(2)求直线AC 的解析式;(3)动点P 从点A 出发,沿折线ABC 方向以2个单位/秒的速度向终点C 匀速运动,设△PMB 的面积为S (S≠0),点P 的运动时间为t 秒.①求S 与t 之间的函数关系式;②在点P 运动过程中,当S =3,请直接写出t 的值.6.(11分)如图,在直角梯形ABCD 中,AD ∥BC ,∠B=90°,且AD=12cm ,AB=8cm ,DC=10cm ,若动点P 从A 点出发,以每秒2cm 的速度沿线段AD 向点D 运动;动点Q 从C 点出发以每秒3cm 的速度沿CB 向B 点运动,当P 点到达D 点时,动点P 、Q 同时停止运动,设点P 、Q 同时出发,并运动了t 秒,回答下列问题:(1)BC= cm ;(2)当t 为多少时,四边形PQCD 成为平行四边形?(3)当t 为多少时,四边形PQCD 为等腰梯形?(4)是否存在t ,使得△DQC 是等腰三角形?若存在,请求出t 的值;若不存在,说明理由.7、如图①,已知正方形ABCD的边长为1,点P是AD边上的一个动点,点A关于直线BP的对称点是点Q,连接PQ、D Q、CQ、BQ,设AP=x.(1)BQ+DQ的最小值是_______,此时x的值是_______;(2)如图②,若PQ的延长线交CD边于点E,并且∠CQD=90°.①求证:点E是CD的中点;②求x的值.(3)若点P是射线AD上的一个动点,请直接写出当△CDQ为等腰三角形时x 的值.8、如图1,平面直角坐标系中,直线AB:y=﹣x+b交x轴于点A(8,0),交y轴正半轴于点B.(1)求点B的坐标;(2)如图2,直线AC交y轴负半轴于点C,AB=BC,P为线段AB上一点,过点P 作y轴的平行线交直线AC于点Q,设点P的横坐标为t,线段PQ的长为d,求d与t之间的函数关系式;(3)在(2)的条件下,M为CA延长线上一点,且AM=CQ,在直线AC上方的直线AB上是否存在点N,使△QMN是以QM为斜边的等腰直角三角形?若存在,请求出点N的坐标及PN的长度;若不存在,请说明理由.1.【解答】解:(1)∵A(0,4),B(0,2),∴OA=4,OB=2,点B为线段OA的中点,又点D为OC的中点,即BD为△AOC的中位线,∴BD∥AC;(2)如图1,作BF⊥AC于点F,取AB的中点G,则G(0,3),∵BD∥AC,BD与AC的距离等于1,∴BF=1,∵在Rt△ABF中,∠AFB=90°,AB=2,点G为AB的中点,∴FG=BG=AB=1,∴△BFG是等边三角形,∠ABF=60°.∴∠BAC=30°,设OC=x,则AC=2x,根据勾股定理得:OA==x,∵OA=4,∴x=∵点C在x轴的正半轴上,∴点C的坐标为(,0);(3)如图2,当四边形ABDE为平行四边形时,AB∥DE,∴DE⊥OC,∵点D为OC的中点,∴OE=EC,∵OE⊥AC,∴∠OCA=45°,∴OC=OA=4,∵点C在x轴的正半轴上,∴点C的坐标为(4,0),设直线AC的解析式为y=kx+b(k≠0).将A(0,4),C(4,0)代入AC的解析式得:解得:∴直线AC的解析式为y=﹣x+4.2.【解答】解:(1)由运动知,AP=t,CQ=3t,∴DP=AD﹣AP=24﹣t,∵四边形PQCD为平行四边形,∴DP=CQ,∴24﹣t=3t,∴t=6;(2)如图2,过点D作DE⊥BC于E,过点P作PF⊥BC于F,∴四边形EFPD是矩形,∴DE=PF,[来源:Z|xx|]∵四边形PQCD是等腰梯形,∴∠PQC=∠DCQ,∵∠PFQ=∠DEC=90°,∴△PFQ≌△DEC,∴FQ=CE,∴BE=AD=24,∴CE=BC﹣BE=2,∵四边形PQCD为等腰梯形,∴CQ=DP+2CE,由运动知,AP=t,CQ=3t,∴DP=AD﹣AP=24﹣t,∴24﹣t+2×2=3t,∴t=7,(3)AB边的长是8时,四边形PQCD为菱形,理由:由(1)知,t=6时,四边形PQCD是平行四边形,∴DP=24﹣6=18,∵平行四边形PQCD是菱形,∴CD=DP=18,如图2,过点D作DE⊥BC于E,∴四边形ABED是矩形,∴AB=DE,在Rt△CDE中,CE=2,CD=18,∴DE==8.3.证明:(1) ① ∵∠PEB =∠PCB =90°,O 为BP 的中点∴OE =OB =OP =OC∴∠POE =2∠DBP ,∠POC =2∠CBP∴∠COE =∠POE +∠POC =2(∠DBP +∠CBP )=90°∴OE ⊥OC② 连接OE 、CE∵△COE 为等腰直角三角形∴∠ECF =45°在等腰Rt △BCD 中,BF 2+DE 2=EF 2设BF =3x ,EF =5x ,则DE =4x∴3x +4x +5x =26,解得x =22 ∴DP =2DE =424=x(2) ∵62==-+=+CD C DP CP EP ∴2322=+CP EP4.解:(1) (3,0)、x <3(2) ∵S △COE =S △ADE∴S △AOB =S △CBD 即33321621⨯⨯=⨯⨯D y ,y D =233 当y =233时,23233333==+-x x ,∴D (23323,) (3) 连接CF∵∠CDF =60°∴△CDF 为等边三角形连接AC∵AB =AC =BC =6∴△ABC 为等边三角形∴△CAF ≌△CBD (SAS )∴∠CAF =∠ACB =60°∴AF ∥x 轴设D (m ,333+-m )过点D 作DH ⊥x 轴于H∴BH =3-m ,DB =6-2m =AF∴F (2m -6,33)由平移可知:G (m -9,m 3-) 令⎪⎩⎪⎨⎧-=-=m y m x 39∴点G 在直线393--=x y 上6.解:根据题意得:PA=2t ,CQ=3t ,则PD=AD-PA=12-2t .(1)如图,过D 点作DE ⊥BC 于E ,则四边形ABED 为长方形,DE=AB=8cm ,AD=BE=12cm ,在直角△CDE 中,∵∠CED=90°,DC=10cm ,DE=8cm ,∴22DC DE -,∴BC=BE+EC=18cm .…………………………………………………………………2分(直接写出最后结果18cm 即可)(2)∵AD ∥BC ,即PD ∥CQ ,∴当PD=CQ 时,四边形PQCD 为平行四边形,即12-2t=3t ,解得t=125秒, 故当t=125秒时四边形PQCD 为平行四边形;………………………………………4分(3)如图,过D 点作DE ⊥BC 于E ,则四边形ABED 为长方形,DE=AB=8cm ,AD=BE=12cm ,当PQ=CD 时,四边形PQCD 为等腰梯形.过点P 作PF ⊥BC 于点F ,过点D 作DE ⊥BC 于点E ,则四边形PDEF 是长方形,EF=PD=12-2t ,PF=DE .在Rt △PQF 和Rt △CDE 中,PQ CD PF DE ==⎧⎨⎩, ∴Rt △PQF ≌Rt △CDE (HL ),∴QF=CE ,∴QC-PD=QC-EF=QF+EC=2CE ,即3t-(12-2t )=12,解得:t=245, 即当t=245时,四边形PQCD 为等腰梯形;……………………………………………8分(4)△DQC 是等腰三角形时,分三种情况讨论:①当QC=DC 时,即3t=10,∴t=103;②当DQ=DC时,36 2t=∴t=4;③当QD=QC时,3t×65 10=∴t=259.故存在t,使得△DQC是等腰三角形,此时t的值为103秒或4秒或259秒.………11分③在Rt△DMQ中,DQ2=DM2+QM2222 (3)8(38) t t=+-36t=100t=25 97.解:(1);-1;(2)①证明:在正方形ABCD中,AB=BC,∠A=∠BCD=90°∵Q点为A点关于BP的对称点∴AB=QB,∠A=∠PQB=90°∴QB=BC,∠BQE=∠BCE∴∠BQC=∠BCQ∴∠EQC=∠EQB-∠CQB=∠ECB-∠QCB=∠ECQ∴EQ=EC在Rt△ABC中∵∠QDE=90°-∠QCE,∠DQE=90°-∠EQC∴∠QDE=∠DQE∴EQ+ED∴CE=EQ=ED即E是CD的中点②(3)或或8.解:(1)∵y=﹣x+b交x轴于点A(8,0),∴0=﹣×8+b,b=6,∴直线AB解析式为y=﹣x+6,令x=0,y=6,B(0,6);(2)∵A(8,0),B(0,6),∴OA=8,OB=6,∵∠AOB=90°,∴AB=10=BC,∴OC=4,∴点C(0,﹣4),设直线AC解析式为y=kx+b’,∴,∴∴直线AC解析式为y=x﹣4,∵P在直线y=﹣x+6上,∴可设点P(t,﹣t+6),∵PQ∥y轴,且点Q在y=x﹣4 上,∴Q(t, t﹣4),∴d=(﹣t+6)﹣(t ﹣4)=﹣t+10;(3)过点M作MG⊥PQ于G,∴∠QGM=90°=∠COA,∵PQ∥y轴,∴∠OCA=∠GQM,∵CQ=AM,∴AC=QM,在△OAC与△GMQ中,,∴△OAC≌△GMQ,∴QG=OC=4,GM=OA=8,过点N作NH⊥PQ于H,过点M作MR⊥NH于点R,∴∠MGH=∠RHG=∠MRH=90°,∴四边形GHRM是矩形,∴HR=GM=8,可设GH=RM=k,∵△MNQ是等腰直角三角形,∴∠QMN=90°,NQ=NM,∴∠HNQ+∠HQN=90°,∴∠HNQ+∠RNM=90°,∴∠RNM=∠HQN,∴△HNQ≌△RMN,∴HN=RM=k,NR=QH=4+k,∵HR=HN+NR,∴k+4+k=8,∴k=2,∴GH=NH=RM=2,∴HQ=6,∵Q(t,t﹣4),∴N(t+2,t﹣4+6)即 N(t+2,t+2)∵N在直线AB:y=﹣x+6上,∴t+2=﹣(t+2)+6,∴t=2,∴P(2,),N(4,3),∴PH=,NH=2,∴PN==.。
中考数学易错题综合专题三(附答案详解)
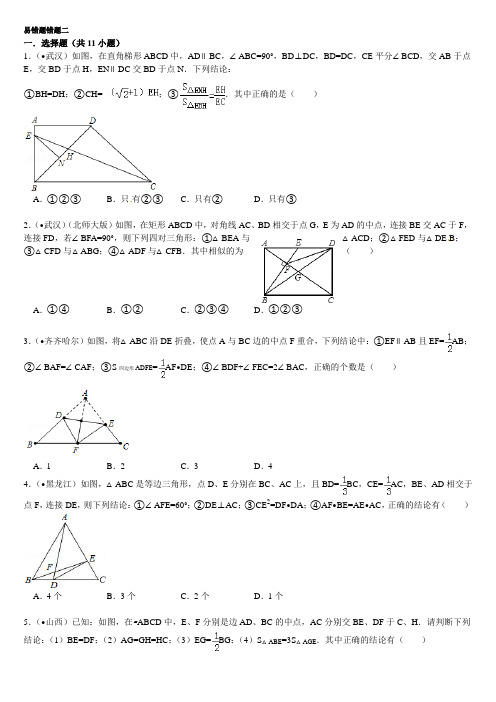
易错题错题二一.选择题(共11小题)1.(•武汉)如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,BD⊥DC,BD=DC,CE平分∠BCD,交AB于点E,交BD于点H,EN∥DC交BD于点N.下列结论:①BH=DH;②CH=;③.其中正确的是()A.①②③B.只有②③C.只有②D.只有③2.(•武汉)(北师大版)如图,在矩形ABCD中,对角线AC、BD相交于点G,E为AD的中点,连接BE交AC于F,连接FD,若∠BFA=90°,则下列四对三角形:①△BEA与△ACD;②△FED与△DE B;③△CFD与△ABG;④△ADF与△CFB.其中相似的为()A.①④B.①②C.②③④D.①②③3.(•齐齐哈尔)如图,将△ABC沿DE折叠,使点A与BC边的中点F重合,下列结论中:①EF∥AB且EF=AB;②∠BAF=∠CAF;③S四边形ADFE=AF•DE;④∠BDF+∠FEC=2∠BAC,正确的个数是()A.1B.2C.3D.44.(•黑龙江)如图,△ABC是等边三角形,点D、E分别在BC、AC上,且BD=BC,CE=AC,BE、AD相交于点F,连接DE,则下列结论:①∠AFE=60°;②DE⊥AC;③CE2=DF•DA;④AF•BE=AE•AC,正确的结论有()A.4个B.3个C.2个D.1个5.(•山西)已知:如图,在▱ABCD中,E、F分别是边AD、BC的中点,AC分别交BE、DF于C、H.请判断下列结论:(1)BE=DF;(2)AG=GH=HC;(3)EG=BG;(4)S△ABE=3S△AGE.其中正确的结论有()A.1个B.2个C.3个D.4个6.在课外活动课上,某同学做了一个对角线互相垂直的等腰梯形形状的风筝,其面积为450 cm2,则两条对角线共用的竹条至少需()A.30cm B.40cm C.60cm D.80cm7.(•兰州)如图,A、B、C三点在正方形网格线的交点处,若将△ABC绕着点A逆时针旋转得到△AC′B′,则tanB′的值为()A.B.C.D.8.在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB 交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1…按这样的规律进行下去,正方形ABCC2010的面积为()A.5×B.5×C.5×D.5×9.(•佳木斯)如图,已知▱ABCD中,∠BDE=45°,DE⊥BC于E,BF⊥CD于F,DE、BF相交于H,BF、AD的延长线相交于G,下面结论:①DB=BE;②∠A=∠BHE;③AB=BH;④△BHD∽△BDG.其中正确的结论是()A.①②③④B.①②③C.①②④D.②③④10.(•鸡西)在锐角△ABC中,∠BAC=60°,BD、CE为高,F是BC的中点,连接DE、EF、FD.则以下结论中一定正确的个数有()①EF=FD;②AD:AB=AE:AC;③△DEF是等边三角形;④BE+CD=BC;⑤当∠ABC=45°时,BE=DE.A.2个B.3个C.4个D.5个11.如图,ABCD、CEFG是正方形,E在CD上,直线BE、DG交于H,且HE•HB=,BD、AF交于M,当E在线段CD(不与C、D重合)上运动时,下列四个结论:①BE⊥GD;②AF、GD所夹的锐角为45°;③GD=;④若BE平分∠DBC,则正方形ABCD的面积为4.其中正确的结论个数有()A.1个B.2个C.3个D.4个二.填空题(共10小题)12.如图△ABC中,∠ACB=90°,BC=6cm,AC=8cm,动点P从A出发,以2cm/s的速度沿AB移动到B,则点P出发_________s时,△BCP为等腰三角形.13.如图,边长为1的正方形ABCD中,点E是对角线BD上的一点,且BE=BC,点P在EC上,PM⊥BD于M,PN⊥BC于N,则PM+PN=_________.14.(•眉山)如图,已知梯形ABCD中,AD∥BC,∠B=30°,∠C=60°,AD=4,AB=3,则下底BC的长为_________.15.在半径为5的⊙O中,有两平行弦AB.CD,且AB=6,CD=8,则弦AC的长为_________.16.如图,在平面直角坐标系上有个点P(1,0),点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(﹣1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,…,依此规律跳动下去,点P第100次跳动至点P100的坐标是_________.17.(•锦州)如图,在平面直角坐标系上有点A(1,0),点A第一次跳动至点A1(﹣1,1),第四次向右跳动5个单位至点A4(3,2),…,依此规律跳动下去,点A第100次跳动至点A100的坐标是_________.18.(•牡丹江)开学初,小明到某商场购物,发现商场正在进行购物返券活动,活动规则如下:购物每满100元,返购物券50元,此购物券在本商场通用,且用购物券购买商品不再返券.小明只购买了单价分别为60元、80元和120元的书包、T恤、运动鞋,在使用购物券参与购买的情况下,他的实际花费为_________元.19.⊙O的弦AB的长等于半径,那么弦AB所对的圆周角等于_________度.20.如图,将△ABC沿DE折叠,使点A与BC边的中点F重合,下列结论中:①EF∥AB且;②∠BAF=∠CAF ;③;④∠BDF+∠FEC=2∠BAC,正确结论的序号是___ .21.(•江西)如图,已知点F的坐标为(3,0),点A,B分别是某函数图象与x轴、y轴的交点,点P是此图象上的一动点.设点P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5﹣x(0≤x≤5),给出以下四个结论:①AF=2;②BF=5;③OA=5;④OB=3.其中正确结论的序号是_________.三.解答题(共4小题)22.在平面直角坐标系中,点A、B分别在2=0的两个实数根,C是线段AB的中点,OC=3,D在线段OC上,OD=2CD.(1)求OA、OB的长;(2)求直线AD的解析式;(3)P是直线AD上的点,在平面内是否存在点Q,使以O、A、P、Q为顶点的四边形是菱形?若存在,求出点Q的坐标;若不存在,请说明理由.23.(•朝阳)如图①,点A′,B′的坐标分别为(2,0)和(0,﹣4),将△A′B′O绕点O按逆时针方向旋转90°后得△ABO,点A′的对应点是点A,点B′的对应点是点B.(1)写出A,B两点的坐标,并求出直线AB的解析式;(2)将△ABO沿着垂直于x轴的线段CD折叠,(点C在x轴上,点D在AB上,点D不与A,B重合)如图②,使点B落在x轴上,点B的对应点为点E.设点C的坐标为(x,0),△CDE与△ABO重叠部分的面积为S.①试求出S与x之间的函数关系式(包括自变量x的取值范围);②当x为何值时,S的面积最大,最大值是多少?③是否存在这样的点C,使得△ADE为直角三角形?若存在,直接写出点C的坐标;若不存在,请说明理由.24.如图所示,在平面直角坐标系中,四边形OABC是等腰梯形.BC∥OA,∠COA=60°,OA、AB(OA>AB)是方程x2﹣11x+28=0的两个根.(1)求点B的坐标;(2)求线段AC的长;(3)在x轴上是否存在一点P,使以点P、A、C为顶点的三角形为等腰三角形?若存在,请接写出点P的坐标;若不存在,请说明理由.25.(•山西)在直角梯形OABC中,CB∥OA,∠COA=90°,CB=3,OA=6,BA=.分别以OA、OC边所在直线为x轴、y轴建立如图所示的平面直角坐标系.(1)求点B的坐标;(2)已知D、E分别为线段OC、OB上的点,OD=5,OE=2EB,直线DE交是(2)中直线DE上的一个动点,在、N 为顶点的四边形是菱形?若存在,请求出点N的坐标;若不存在,请说明理由.5月29龙江易错题错题二参考答案与试题解析一.选择题(共11小题)1.(•武汉)如图,在直角梯形A BCD中,AD∥BC,∠ABC=90°,BD⊥DC,BD=DC,CE平分∠BCD,交AB于点E,交BD于点H,EN∥DC交BD于点N.下列结论:①BH=DH;②CH=;③.其中正确的是()A.①②③B.只有②③C.只有②D.只有③考点:直角梯形.分析:①如图,过H作HM⊥BC于M,根据角平分线的性质可以得到DH=HM,而在Rt△BHM中BH>HM,所以容易判定①是错误的;②设HM=x,那么DH=x,由于∠ABC=90°,BD⊥DC,BD=DC,由此得到∠DBC=45°,而AD∥CB,由此可以证明△ADB是等腰直角三角形,又CE平分∠BCD,∠BDC=∠ABC=90°,由此可以证明△DCH∽△EBC,再利用相似三角形的性质可以推出∠BEH=∠DHC,然后利用对顶角相等即可证明∠BHC=∠BEH,接着得到BH=BE,然后即可用x分别表示BE、EN、CD,又由EN∥DC可以得到△DCH∽△NEH,再利用相似三角形的性质即可结论②;③利用(2)的结论可以证明△ENH∽△CBE,然后利用相似三角形的性质和三角形的面积公式即可证明结论③.解答:解:①如图,过H作HM⊥BC于M,∵CE平分∠BCD,BD⊥DC∴DH=HM,而在Rt△BHM中BH>HM,∴BH>HD,∴所以容易判定①是错误的;②∵CE平分∠BCD,∴∠DCE=∠BCE,而∠EBC=∠BDC=90°,∴∠BEH=∠DHC,而∠DHC=∠EHB,∴∠BEH=∠EHB,∴BE=BH,设HM=x,那么DH=x,∵BD⊥DC,BD=DC,∴∠DBC=∠ABD=45°,∴BH=x=BE,∴EN=x,∴CD=BD=DH+BH=(+1)x,即=+1,∵EN∥DC,∴△DCH∽△NEH,∴=+1,即CH=(+1)EH;③由②得∠BEH=∠EHB,∵EN∥DC,∴∠ENH=∠CDB=90°,∴∠ENH=∠EBC,∴△ENH∽△CBE,∴EH:EC=NH:BE,而,∴.所以正确的只有②③.故选B.点评:此题比较复杂,综合性很强,主要考查了梯形的性质,相似三角形的判定和性质以及等腰直角三角形的性质.2.(•武汉)(北师大版)如图,在矩形ABCD中,对角线AC、BD相交于点G,E为AD的中点,连接BE交AC于F,连接FD,若∠BFA=90°,则下列四对三角形:①△BEA与△ACD;②△FED与△DEB;③△CFD与△ABG;④△ADF 与△CFB.其中相似的为()A.①④B.①②C.②③④D.①②③解答:解:根据题意得:∠BAE=∠ADC=∠AFE=90°∴∠AEF+∠EAF=90°,∠DAC+∠ACD=90°∴∠AEF=∠ACD∴①中两三角形相似;容易判断△AFE∽△BAE,得=,又∵AE=ED,∴=而∠B ED=∠BED,∴△FED∽△DEB.故②正确;∵AB∥CD,∴∠BAC=∠GCD,∵∠ABE=∠DAF,∠EBD=∠EDF,且∠ABG=∠ABE+∠EBD,∴∠ABG=∠DAF+∠EDF=∠DFC;∵∠ABG=∠DFC,∠BAG=∠DCF,∴△CFD∽△ABG,故③正确;所以相似的有①②③.故选D.点评:此题考查了相似三角形的判定:①有两个对应角相等的三角形相似;②有两个对应边的比相等,且其夹角相等,则两个三角形相似;③三组对应边的比相等,则两个三角形相似.3.(•齐齐哈尔)如图,将△ABC沿DE折叠,使点A与BC边的中点F重合,下列结论中:①EF∥AB且EF=AB;②∠BAF=∠CAF;③S四边形ADFE=AF•DE;④∠BDF+∠FEC=2∠BAC,正确的个数是()A.1B.2C.3D.4分析:根据对折的性质可得AE=EF,∠DAF=∠DFA,∠EAF=∠AFE,∠BAC=∠DFE,据此和已知条件判断图中的相等关系.解答:解:①由题意得AE=EF,BF=FC,但并不能说明AE=EC,∴不能说明EF是△ABC的中位线,故①错;②题中没有说AB=AC,那么中线AF也就不可能是顶角的平分线,故②错;③易知A,F关于D,E对称.那么四边形ADFE是对角线互相垂直的四边形,那么面积等于对角线积的一半,故③对;④∠BDF=∠BAF+∠DFA,∠FEC=∠EAF+∠AFE,∴∠BDF+∠FEC=∠BAC+∠DFE=2∠BAC,故④对.正确的有两个,故选B.点评:翻折前后对应线段相等,对应角相等.4.(•黑龙江)如图,△ABC是等边三角形,点D、E分别在BC、AC上,且BD=BC,CE=AC,BE、AD相交于点F,连接DE,则下列结论:①∠AFE=60°;②DE⊥AC;③CE2=DF•DA;④AF•BE=AE•AC,正确的结论有()A.4个B.3个C.2个D.1个分析:本题是开放题,对结论进行一一论证,从而得到答案.①利用△ABD≌△BCE,再用三角形的一个外角等于与它不相邻的两个内角和,即可证∠AFE=60°;②从CD上截取CM=CE,连接EM,证△CEM是等边三角形,可证明DE⊥AC;③△BDF∽△ADB,由相似比则可得到CE2=DF•DA;④只要证明了△AFE∽△BAE,即可推断出AF•BE=AE•AC.解答:解:∵△ABC是等边三角形∴AB=BC=AC,∠BAC=∠ABC=∠BCA=60°∵BD=BC,CE=AC∴BD=EC∴△ABD≌△BCE∴∠BAD=∠CBE,∵∠ABE+∠EBD=60°∴∠ABE+∠CBE=60°∵∠AFE是△ABF的外角∴∠AFE=60°∴①是对的;如图,从CD上截取CM=CE,连接EM,则△CEM是等边三角形∴EM=CM=EC∵EC=CD∴EM=CM=DM∴∠CED=90°∴DE⊥AC,∴②是对的;由前面的推断知△BDF∽△ADB∴BD:AD=DF:DB∴BD2=DF•DA∴CE2=DF•DA∴③是对的;在△AFE和△BAE中,∠BAE=∠AFE=60°,∠AEB是公共角∴△AFE∽△BAE∴AF•BE=AE•AC∴④是正确的.故选A.点评:本题主要应用到了三角形外角与内角的关系,直角三角形的判定,全等三角形和相似三角形的判定及性质,内容较多,较为复杂.5.(•山西)已知:如图,在▱ABCD中,E、F分别是边AD、BC的中点,AC分别交BE、DF于C、H.请判断下列结论:(1)BE=DF;(2)AG=GH=HC;(3)EG=BG;(4)S△ABE=3S△AGE.其中正确的结论有()A.1个B.2个C.3个D.4个分析:(1)根据BF∥DE,BF=DE可证BEDF为平行四边形;(2)根据平行线等分线段定理判断;(3)根据△AGE∽△CGB可得;(4)由(3)可得△ABG的面积=△AGE面积×2.解答:解:(1)∵▱ABCD,∴AD=BC,AD∥BC.E、F分别是边AD、BC的中点,∴BF∥DE,BF=DE.∴BEDF为平行四边形,BE=DF.故正确;(2)根据平行线等分线段定理可得AG=GH=HC.故正确;(3)∵AD∥BC,AE=AD=BC,∴△AGE∽△CGB,AE:BC=EG:BG=1:2,∴EG=BG.故正确.(4)∵BG=2EG,∴△ABG的面积=△AGE面积×2,∴S△ABE=3S△AGE.故正确.故选D.点评:此题考查了平行四边形的判定及性质、相似三角形的判定及性质等知识点,难度中等.6.在课外活动课上,某同学做了一个对角线互相垂直的等腰梯形形状的风筝,其面积为450 cm2,则两条对角线共用的竹条至少需()A.30cm B.40cm C.60cm D.80cm考点:等腰梯形的性质.专题:应用题.分析:设对角线的长是x,根据面积公式可求得对角线的长,从而可得到两条对角线所用的竹条至少需要多少.解答:解:等腰梯形的对角线互相垂直且相等,可以设对角线的长是.故选C点评:对角线互相垂直的四边形的面积的计算方法是需要注意记忆的问题,两对角线长若是a,b则面积是ab.7.(•兰州)如图,A、B、C三点在正方形网格线的交点处,若将△ABC绕着点A逆时针旋转得到△AC′B′,则tanB′的值为()A.B.C.D.分析:过C点作CD⊥AB,垂足为D,根据旋转性质可知,∠B′=∠B,把求tanB′的问题,转化为在Rt△BCD中求tanB.解答:解:过C点作CD⊥AB,垂足为D.根据旋转性质可知,∠B′=∠B.在Rt△BCD中,tanB==,∴tanB′=tanB=.故选B.点评:本题考查了旋转的性质,旋转后对应角相等;三角函数的定义及三角函数值的求法.8.在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB 交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1…按这样的规律进行下去,正方形ABCC的面积为()A.5×B.5×C.5×D.5×分析:先利用ASA证明△AOD和△A1BA相似,根据相似三角形对应边成比例可以得到AB=2A1B,所以正方形A1B1C1C的边长等于正方形ABCD边长的以此类推,后一个正方形的边长是前一个正方形的边长的然后即可求出第个正方形的边长与第1个正方形的边长的关系,从而求出第个正方形的面积.解答:解:∵四边形ABCD是正方形,∴∠ABC=∠BAD=90°,AB=BC,∴∠ABA1=90°,∠DAO+∠BAA1=180°﹣90°=90°,又∵∠AOD=90°,∴∠ADO+∠DAO=90°,∴∠ADO=∠BAA1,在△AOD和A1BA中,∵,∴△AOD∽△A1BA,∴==2,∴BC=2A1B,∴A1C=BC,以此类推A2C1=A1C,A3C2=A2C1即后一个正方形的边长是前一个正方形的边长的倍,∴第个正方形的边长为()BC,∵A的坐标为(1,0),D点坐标为(0,2),∴BC=AD==,∴正方形ABCC的面积为[()BC]2=5×()4022=5×().故选D.点评:本题考查的是一次函数综合题,涉及到正方形的性质及直角三角形的性质、相似三角形的判定与性质,属规律性题目.9.(•佳木斯)如图,已知▱ABCD中,∠BDE=45°,DE⊥BC于E,BF⊥CD于F,DE、BF相交于H,BF、AD的延长线相交于G,下面结论:①DB=BE;②∠A=∠BHE;③AB=BH;④△BHD∽△BDG.其中正确的结论是()A.①②③④B.①②③C.①②④D.②③④分析:根据已知及相似三角形的判定方法对各个结论进行分析从而得到最后答案.解答:解:∵∠BDE=45°,DE⊥BC∴DB=BE,BE=DE∵DE⊥BC,BF⊥CD∴∠BEH=∠DEC=90°∵∠BHE=∠DHF∴∠EBH=∠CDE∴△BEH≌△DEC∴∠BHE=∠C,BH=CD∵▱ABCD中∴∠C=∠A,AB=CD∴∠A=∠BHE,AB=BH∴正确的有①②③故选B.点评:此题考查了相似三角形的判定和性质:①如果两个三角形的三组对应边的比相等,那么这两个三角形相似;②如果两个三角形的两条对应边的比相等,且夹角相等,那么这两个三角形相似;③如果两个三角形的两个对应角相等,那么这两个三角形相似.平行于三角形一边的直线截另两边或另两边的延长线所组成的三角形与原三角形相似.相似三角形的对应边成比例,对应角相等.10.(•鸡西)在锐角△ABC中,∠BAC=60°,BD、CE为高,F是BC的中点,连接DE、EF、FD.则以下结论中一定正确的个数有()①EF=FD;②AD:AB=AE:AC;③△DEF是等边三角形;④BE+CD=BC;⑤当∠ABC=45°时,BE=DE.A.2个B.3个C.4个D.5个分析:①EF、FD是直角三角形斜边上的中线,都等于BC的一半;②可证△ABD∽△ACE;③证明∠EFD=60°;④假设结论成立,在BC上取满足条件的点H,证明其存在性;⑤当∠ABC=45°时,EF不一定是BC边的高.解答:解:①∵BD、CE为高,∴△BEC、△BDC是直角三角形.∵F是BC的中点,∴EF=DF=BC.故正确;②∵∠ADB=∠AEC=90°,∠A公共,∴△ABD∽△ACE,得AD:AB=AE:AC.故正确;③∵∠A=60°,∴∠ABC+∠ACB=120°.∵F是BC的中点,∴EF=BF,DF=CF.∴∠ABF=∠BEF,∠ACB=∠CDF.∴∠BFE+∠CFD=120°,∠EFD=60°.又EF=FD,∴△DEF是等边三角形.故正确;④若BE+CD=BC,则可在BC上截取BH=BE,则HC=CD.∵∠A=60°,∴∠ABC+∠ACB=120°.又∵BH=BE,HC=CD,∴∠BHE+∠CHD=120°,∠EHD=60°.所以存在满足条件的点,假设成立,但一般情况不一定成立,故错误;⑤当∠ABC=45°时,在Rt△BCE中,BC=BE,在Rt△ABD中,AB=2AD,由B、C、D、E四点共圆可知,△ADE∽△ABC,∴==,即=,∴BE=DE,故正确;故此题选C.点评:此题考查了相似三角形的判定和性质,综合性很强.11.如图,ABCD、CEFG是正方形,E在CD上,直线BE、DG交于H,且HE•HB=,BD、AF交于M,当E在线段CD(不与C、D重合)上运动时,下列四个结论:①BE⊥GD;②AF、GD所夹的锐角为45°;③GD=;④若BE平分∠DBC,则正方形ABCD的面积为4.其中正确的结论个数有()A.1个B.2个C.3个D.4个分析:①由已知条件可证得△BEC≌△DGC,∠EBC=∠CDG,因为∠BDC+∠DBH+∠EBC=90°,所以∠BDC+∠DBH+∠CDG=90°,即BE⊥GD,故①正确;②若以BD为直径作圆,那么此圆必经过A、B、C、H、D五点,根据圆周角定理即可得到∠AHD=45°,所以②的结论也是正确的.③此题要通过相似三角形来解;由②的五点共圆,可得∠BAH=∠BDH,而∠ABD=∠DBG=45°,由此可判定△ABM∽△DBG,根据相似三角形的比例线段即可得到AM、DG的比例关系;④若BE平分∠DBC,那么H是DG的中点;易证得△ABH∽△BCE,得BD•BC=BE•BH,即BC2=BE•BH,因此只需求出BE•BH的值即可得到正方形的面积,可先求出BE、EH的比例关系,代入已知的乘积式中,即可求得BE•BH的值,由此得解.解答:解:①正确,证明如下:∵BC=DC,CE=CG,∠BCE=∠DCG=90°,∴△BEC≌△DGC,∴∠EBC=∠CDG,∵∠BDC+∠DBH+∠EBC=90°,∴∠BDC+∠DBH+∠CDG=90°,即BE⊥GD,故①正确;②由于∠BAD、∠BCD、∠BHD都是直角,因此A、B、C、D、H五点都在以BD为直径的圆上;由圆周角定理知:∠DHA=∠ABD=45°,故②正确;③由②知:A、B、C、D、H五点共圆,则∠BAH=∠BDH;又∵∠ABD=∠DBG=45°,∴△ABM∽△DBG,得AM:DG=AB:BD=1:,即DG=AM;故③正确;④过H作HN⊥CD于N,连接EG;若BH平分∠DBG,且BH⊥DG,易知:BH垂直平分DG;得DE=EG,H是DG中点,HN为△DCG的中位线;设CG=x,则:HN=x,EG=DE=x,DC=BC=(+1)x;∵HN⊥CD,BC⊥CD,∴HN∥BC,∴∠NHB=∠EBC,∠ENH=∠ECB,∴△BEC∽△HEN,则BE:EH=BC:HN=2+2,即EH=;∴HE•BH=BH•=4﹣2,即BE•BH=4;∵∠DBH=∠CBE,且∠BHD=∠BCE=90°,∴△DBH∽△CBE,得:DB•BC=BE•BH=4,即BC2=4,得:BC2=4,即正方形ABCD的面积为4;故④正确;因此四个结论都正确,故选D.点评:本题主要考查三角形相似和全等的判定及性质、正方形的性质以及圆周角定理等知识的综合应用,能够判断出A、B、C、D、H五点共圆是解题的关键.二.填空题(共10小题)12.如图△ABC中,∠ACB=90°,BC=6cm,AC=8cm,动点P从A出发,以2cm/s的速度沿AB移动到B,则点P 出发2,2.5,1.4s时,△BCP为等腰三角形.分析:根据∠ACB=90°,BC=6cm,AC=8cm,利用勾股定理求出AB的长,再分别求出BC=BP,BP=PC时,AP的长,然后利用P点的运动速度即可求出时间.解答:解;∵△ABC中,∠ACB=90°,BC=6cm,AC=8cm,∴AB===10,∵当BC=BP时,△BCP为等腰三角形,即BC=BP=6cm,△BCP为等腰三角形,∴AP=AB﹣BP=10﹣6=4,∵动点P从A出发,以2cm/s的速度沿AB移动,∴点P出发=2s时,△BCP为等腰三角形,当点P从A出发,以2cm/s的速度沿AB移动到AB的中点时,此时AP=BP=PC,则△BCP为等腰三角形,点P出发=2.5s时,△BCP为等腰三角形,当BC=PC时,过点C作CD⊥AB于点D,则△BCD∽△BAC,∴,解得:BD=3.6,∴BP=2BD=7.2,∴AP=10﹣7.2=2.8,∴点P出发1.4s时,△BCP为等腰三角形.故答案为:2;2.5;1.4.点评:此题主要考查勾股定理和等腰三角形的判定,解答此题的关键是首先根据勾股定理求出AB的长,然后再利用等腰三角形的性质去判定.13.如图,边长为1的正方形ABCD中,点E是对角线BD上的一点,且BE=BC,点P在EC上,PM⊥BD于M,PN⊥BC于N,则PM+PN=.分析:连接BP,作EF⊥BC于点F,由正方形的性质可知△BEF为等腰直角三角形,BE=1,可求EF,利用面积法得S△BPE+S△BPC=S△BEC,将面积公式代入即可.解答:由正方形的性质可知∠EBF=45°,∴△BEF为等腰直角三角形,又根据正方形的边长为1,得到BE=BC=1,在直角三角形BEF中,sin∠EBF=,即BF=EF=BEsin45°=1×=,又PM⊥BD,PN⊥BC,∴S△BPE+S△BPC=S△BEC,即BE×PM+×BC×PN=BC×EF,∵BE=BC,PM+PN=EF=;故答案为:.点评:解决本题的关键是作出辅助线,构造矩形和全等三角形,把所求的线段转移到正方形的对角线上.14.(•眉山)如图,已知梯形ABCD中,AD∥BC,∠B=30°,∠C=60°,AD=4,AB=3,则下底BC的长为10.分析:过A作AE∥CD,把梯形分成平行四边形和直角三角形,利用平行四边形的对边相等得到CE=AD,所以BE可以求出,在直角三角形中,根据∠B=30°,利用勾股定理求出BE,BC的长也就可以求出了.解答:解:如图,过A作AE∥CD交BC于点E,∵AD∥BC,∴四边形AECD是平行四边形,∴CE=AD=4,∵∠B=30°,∠C=60°,∴∠BAE=90°,∴AE=BE(直角三角形30°角所对的直角边等于斜边的一半),在Rt△ABE中,BE2=AB2+AE2,即BE2=(3)2+(BE)2,BE2=27+BE2,BE2=36,解得BE=6,∴BC=BE+EC=6+4=10.故答案为:10.点评:通过作腰的平行线,把梯形分成平行四边形和直角三角形,再利用直角三角形30°角所对的直角边等于斜边的一半和勾股定理求解,考虑本题的突破口在于两个已知角的和是90°.15.在半径为5的⊙O中,有两平行弦AB.CD,且AB=6,CD=8,则弦AC的长为或5.解答:解:利用垂径定理和勾股定理可知:OE=3,OF=4,①如图,∵4﹣3=1,(8﹣6)÷2=1,∴AC==;②如图,∵4+3=7,(8﹣6)÷2=1,∴AC==5.点评:本题综合考查了垂径定理和勾股定理的运用.16.如图,在平面直角坐标系上有个点P(1,0),点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(﹣1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,…,依此规律跳动下去,点P第100次跳动至点P100的坐标是(26,50).分析:解决本题的关键是分析出题目的规律,以奇数开头的相邻两个坐标的纵坐标是相同的,所以第100次跳动后,纵坐标为100÷2=50;其中4的倍数的跳动都在y轴的右侧,那么第100次跳动得到的横坐标也在y轴右侧.P1横坐标为1,P4横坐标为2,P8横坐标为3,依此类推可得到P100的横坐标.解答:解:经过观察可得:以奇数开头的相邻两个坐标的纵坐标是相同的,所以第100次跳动后,纵坐标为100÷2=50;其中4的倍数的跳动都在y轴的右侧,那么第100次跳动得到的横坐标也在y轴右侧.P1横坐标为1,P4横坐标为2,P8横坐标为3,依此类推可得到:P n的横坐标为n÷4+1(n是4的倍数).故点P100的横坐标为:100÷4+1=26,纵坐标为:100÷2=50,点P第100次跳动至点P100的坐标是(26,50).故答案填(26,50).点评:本题的关键是分析出题目的规律,找出题目中点的坐标的规律,总结规律是近几年出现的常见题目.17.(•锦州)如图,在平面直角坐标系上有点A(1,0),点A第一次跳动至点A1(﹣1,1),第四次向右跳动5个单位至点A4(3,2),…,依此规律跳动下去,点A第100次跳动至点A100的坐标是(51,50).考点:坐标与图形性质;规律型:图形的变化类.专题:规律型.分析:根据图形观察发现,第偶数次跳动至点的坐标,横坐标是次数的一半加上1,纵坐标是次数的一半,然后写出即可.解答:解:观察发现,第2次跳动至点的坐标是(2,1),第4次跳动至点的坐标是(3,2),第6次跳动至点的坐标是(4,3),第8次跳动至点的坐标是(5,4),…第2n次跳动至点的坐标是(n+1,n),∴第100次跳动至点的坐标是(51,50).故答案为:(51,50).点评:本题考查了坐标与图形的性质,以及图形的变化问题,结合图形得到偶数次跳动的点的横坐标与纵坐标的变化情况是解题的关键.18.(•牡丹江)开学初,小明到某商场购物,发现商场正在进行购物返券活动,活动规则如下:购物每满100元,返购物券50元,此购物券在本商场通用,且用购物券购买商品不再返券.小明只购买了单价分别为60元、80元和120元的书包、T恤、运动鞋,在使用购物券参与购买的情况下,他的实际花费为210或200元.分析:根据题意读懂商场的活动规则,应该分两种情况:让其先买120元的运动鞋,得50元购物券,再用购物券去买那两样东西,依此计算实际花费;若先购买120元和80元,可得到100元的购物券,那么60元的就不用再掏钱了.所以应该是200或210.解答:解:他的实际花费=120+60﹣50+80=210元或若现购买120元和80元,可得到100元的购物券,那么60元的就不用再掏钱了,即120+80=200(元).点评:本题旨在学生养成仔细读题的习惯.19.⊙O的弦AB的长等于半径,那么弦AB所对的圆周角等于30或150度.分析:一条弦所对的圆周角有两种情况:当圆周角的顶点在优弧上,圆周角应是一个锐角;当圆周角的顶点在劣弧上,圆周角是一个钝角.解答:解:∵弦AB的长等于半径,∴当把圆心分别与点A,B连接,可得等边三角形,等边三角形的内角是60°,∴弦AB所对的圆心角是60°,∴弦AB把圆分成60°和300°的两段弧,根据弧的度数等于它所对的圆心角的度数,而一条弧所对的圆周角的度数等于所对圆心角度数的一半,∴弦AB所对的圆周角等于30°或150°.故弦AB所对的圆周角等于30°或150°.点评:一条弦(非直径)把圆分成两条弧,两条弧对应两个不同度数的圆周角.20.如图,将△ABC沿DE折叠,使点A与BC边的中点F重合,下列结论中:①EF∥AB且;②∠BAF=∠CAF;③;④∠BDF+∠FEC=2∠BAC,正确结论的序号是③④.分析:根据折叠得到DE垂直平分AF,再根据对角线互相垂直的四边形的面积等于两条对角线的乘积的一半即可证明③,根据三角形的外角的性质即可证明④.解答:解:①要使EF∥AB且,则需EF是△ABC的中位线,根据折叠得AE=EF,显然本选项不一定成立;②要使∠BAF=∠CAF,则需AD=AE,显然本选项不一定成立;③根据折叠得到DE垂直平分AF,故本选项正确;④根据三角形的外角的性质,得∠BDF=∠DAF+∠AFD,∠CEF=∠EAF+∠AFE,又∠BAC=∠DFE,则∠BDF+∠FEC=2∠BAC,故本选项成立.故答案为③④.点评:此题综合考查了折叠的性质、对角线互相垂直的四边形的面积等于两条对角线的乘积的一半、三角形的外角的性质.21.(•江西)如图,已知点F的坐标为(3,0),点A,B分别是某函数图象与x轴、y轴的交点,点P是此图象上的一动点.设点P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5﹣x(0≤x≤5),给出以下四个结论:①AF=2;②BF=5;③OA=5;④OB=3.其中正确结论的序号是①②③.分析:一次函数与正比例函数动点函数图象的问题.解答:解:此题由解析式求点的坐标,再求线段长,是数形结合的典范.当x=5时,d=2=AF,故①正确;当x=0时,d=5=BF,故②正确;OA=OF+FA=5,故③正确.当x=0时,BF=5,OF=3,OB=4,故④错误.故答案为①②③.点评:本题是今年出现的一种新题型,以多选题的形式出现,从考生所填的项中,能看出学生思维层次上的差异,弥补了填空题的不足.答题时,不少学生选择④,有的考生甚至填入⑤,说明学生对这类新题型的缺乏答题策略,对没有把握的结论宁可少选,也不可乱选;即宁缺勿滥.三.解答题(共4小题)22.在平面直角坐标系中,点A、B分别在2=0的两个实数根,C是线段AB的中点,OC=3,D在线段OC上,OD=2CD.(1)求OA、OB的长;(2)求直线AD的解析式;(3)P是直线AD上的点,在平面内是否存在点Q,使以O、A、P、Q为顶点的四边形是菱形?若存在,求出点Q的坐标;若不存在,请说明理由.分析:(1)求出AB=2OC=6,根据OA+OB=2m+6,OA×OB=2m2,得出方程(2m+6)2﹣4m2=180,求出m的值,代入方程,求出方程的解即可;(2)过C作CM⊥OA于M,过D作DN⊥OA于N,求出C、D的坐标,设直线AD的解析式是y=kx+b,把A、D的坐标代入求出即可;(3)求出AD与y轴的交点F的坐标,求出AF,①以OA为一边时,共有4个点,根据A坐标和OP=OA即可求出R、T的坐标,K(3,﹣3),同理求出G、K的坐标;②以OA为对角线,作OA的垂直平分线交AD于P,交OA于M,在OA的下方作MP=MQ,把x=3代入y=﹣x+6求出y,即可得出此时Q的坐标.解答:解:(1)∵AB=2OC=6,∴OA2+OB2=AB2==180,∵OA+OB=2m+6,OA×OB=2m2,∴(OA+OB)2﹣2OA×OB=180,即(2m+6)2﹣4m2=180,∴m=6,即方程为x2﹣18x+72=0,∴x1=12,⊥OA于M,过D作DN⊥OA于N,∵CM∥OB,∴===,∵OA=6,OB=12,∴CM=6,AM=3,OM=3,∴C(3,6),∵OD=2CD,∴===,∴DN=4,ON=2,。
中考数学几何证明题--(专题练习 答案详解)

几何证明题专题1、如图,等腰梯形ABCD中,AD∥BC,AB=DC,E为AD中点,连接BE,CE(1)求证:BE=CE;(2)若∠BEC=90°,过点B作BF⊥CD,垂足为点F,交CE于点G,连接DG,求证:BG=DG+CD.2、如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,E为AB延长线上一点,连接ED,与BC交于点H.过E作CD的垂线,垂足为CD上的一点F,并与BC交于点G.已知G 为CH的中点.(1)若HE=HG,求证:△EBH≌△GFC;(2)若CD=4,BH=1,求AD的长.3、如图,梯形ABCD中,AB∥CD,AD=DC=BC,∠DAB=60°,E是对角线AC延长线上一点,F是AD延长线上的一点,且EB⊥AB,EF⊥AF.(1)当CE=1时,求△BCE的面积;(2)求证:BD=EF+CE.4、如图.在平行四边形ABCD中,O为对角线的交点,点E为线段BC延长线上的一点,且.过点E EF∥CA,交CD于点F,连接OF.(1)求证:OF∥BC;(2)如果梯形OBEF是等腰梯形,判断四边形ABCD的形状,并给出证明.5、如图,梯形ABCD中,AD∥BC,∠ABC=90°,BF⊥CD于F,延长BF交AD的延长线于E,延长CD交BA的延长线于G,且DG=DE,AB=,CF=6.(1)求线段CD的长;(2)H在边BF上,且∠HDF=∠E,连接CH,求证:∠BCH=45°﹣∠EBC.6、如图,直角梯形ABCD中,AD∥BC,∠B=90°,∠D=45°.(1)若AB=6cm,,求梯形ABCD的面积;(2)若E、F、G、H分别是梯形ABCD的边AB、BC、CD、DA上一点,且满足EF=GH,∠EFH=∠FHG,求证:HD=BE+BF.7、已知:如图, ABCD中,对角线AC,BD相交于点O,延长CD至F,使DF=CD,连接BF交AD于点E.(1)求证:AE=ED;(2)若AB=BC,求∠CAF的度数.8、已知:如图,在正方形ABCD中,点G是BC延长线上一点,连接AG,分别交BD、CD于点E、F.(1)求证:∠DAE=∠DCE;(2)当CG=CE时,试判断CF与EG之间有怎样的数量关系?并证明你的结论.9、如图,已知正方形ABCD,点E是BC上一点,点F是CD延长线上一点,连接EF,若BE=DF,点P是EF的中点.(1)求证:DP平分∠ADC;(2)若∠AEB=75°,AB=2,求△DFP的面积.10、如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,BD=BC,E为CD的中点,交BC的延长线于F;(1)证明:EF=EA;(2)过D作DG⊥BC于G,连接EG,试证明:EG⊥AF.11、如图,直角梯形ABCD中,∠DAB=90°,AB∥CD,AB=AD,∠ABC=60度.以AD 为边在直角梯形ABCD外作等边三角形ADF,点E是直角梯形ABCD内一点,且∠EAD=∠EDA=15°,连接EB、EF.(1)求证:EB=EF;(2)延长FE交BC于点G,点G恰好是BC的中点,若AB=6,求BC的长.12、如图,在梯形ABCD中,AD∥BC,AB=DC=AD,∠C=60°,AE⊥BD于点E,F是CD的中点,DG是梯形ABCD的高.(1)求证:AE=GF;(2)设AE=1,求四边形DEGF的面积.13、已知,如图在直角梯形ABCD中,AD∥BC,∠ABC=90°,DE⊥AC于点F,交BC于点G,交AB的延长线于点E,且AE=AC,连AG.(1)求证:FC=BE;(2)若AD=DC=2,求AG的长.14、如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,点E是AB边上一点,AE=BC,DE⊥EC,取DC的中点F,连接AF、BF.(1)求证:AD=BE;(2)试判断△ABF的形状,并说明理由.15、(2011•潼南县)如图,在直角梯形ABCD中,AB∥CD,AD⊥DC,AB=BC,且AE⊥BC.(1)求证:AD=AE;(2)若AD=8,DC=4,求AB的长.16、如图,已知梯形ABCD中,AD∥CB,E,F分别是BD,AC的中点,BD平分∠ABC.(1)求证:AE⊥BD;(2)若AD=4,BC=14,求EF的长.17、如图,在梯形ABCD中,AD∥BC,∠D=90°,BE⊥AC,E为垂足,AC=BC.(1)求证:CD=BE;(2)若AD=3,DC=4,求AE.18、如图,在梯形ABCD中,AD∥BC,AB⊥AC,∠B=45°,AD=1,BC=4,求DC的长.19、已知梯形ABCD中,AD∥BC,AB=BC=DC,点E、F分别在AD、AB上,且.(1)求证:BF=EF﹣ED;(2)连接AC,若∠B=80°,∠DEC=70°,求∠ACF的度数.20、如图,梯形ABCD中,AD∥BC,点E在BC上,AE=BE,且AF⊥AB,连接EF.(1)若EF⊥AF,AF=4,AB=6,求AE的长.(2)若点F是CD的中点,求证:CE=BE﹣AD.21、如图,四边形ABCD为等腰梯形,AD∥BC,AB=CD,对角线AC、BD交于点O,且AC⊥BD,DH⊥BC.(1)求证:DH=(AD+BC);(2)若AC=6,求梯形ABCD的面积.22、已知,如图,△ABC是等边三角形,过AC边上的点D作DG∥BC,交AB于点G,在GD的延长线上取点E,使DE=DC,连接AE,BD.(1)求证:△AGE≌△DAB;(2)过点E作EF∥DB,交BC于点F,连AF,求∠AFE的度数.23、如图,梯形ABCD中,AD∥BC,DE=EC,EF∥AB交BC于点F,EF=EC,连接DF.(1)试说明梯形ABCD是等腰梯形;(2)若AD=1,BC=3,DC=,试判断△DCF的形状;(3)在条件(2)下,射线BC上是否存在一点P,使△PCD是等腰三角形,若存在,请直接写出PB的长;若不存在,请说明理由.24、如图,在梯形ABCD中,AD∥BC,∠ABC=∠BCD=60°,AD=DC,E、F分别在AD、DC的延长线上,且DE=CF.AF交BE于P.(1)证明:△ABE≌△DAF;(2)求∠BPF的度数.25、如图,在梯形ABCD中,AD∥BC,AB=AD=DC,BD⊥DC,将BC延长至点F,使CF=CD.(1)求∠ABC的度数;(2)如果BC=8,求△DBF的面积?26、如图,梯形ABCD中,AD∥BC,AB=DC=10cm,AC交BD于G,且∠AGD=60°,E、F分别为CG、AB的中点.(1)求证:△AGD为正三角形;(2)求EF的长度.27、已知,如图,AD∥BC,∠ABC=90°,AB=BC,点E是AB上的点,∠ECD=45°,连接ED,过D作DF⊥BC于F.(1)若∠BEC=75°,FC=3,求梯形ABCD的周长.(2)求证:ED=BE+FC.28、(2005•镇江)已知:如图,梯形ABCD中,AD∥BC,E是AB的中点,直线CE交DA的延长线于点F.(1)求证:△BCE≌△AFE;(2)若AB⊥BC且BC=4,AB=6,求EF的长.29、已知:如图,在梯形ABCD中,AD∥BC,BC=DC,CF平分∠BCD,DF∥AB,BF 的延长线交DC于点E.求证:(1)△BFC≌△DFC;(2)AD=DE;(3)若△DEF的周长为6,AD=2,BC=5,求梯形ABCD的面积.30、如图,梯形ABCD中,AD∥BC.∠C=90°,且AB=AD.连接BD,过A点作BD的垂线,交BC于E.(1)求证:四边形ABED是菱形;(2)如果EC=3cm,CD=4cm,求梯形ABCD的面积.参考答案1、如图,等腰梯形ABCD中,AD∥BC,AB=DC,E为AD中点,连接BE,CE(1)求证:BE=CE;(2)若∠BEC=90°,过点B作BF⊥CD,垂足为点F,交CE于点G,连接DG,求证:BG=DG+CD.证明:(1)已知等腰梯形ABCD中,AD∥BC,AB=DC,E为AD中点,∴AB=DC,∠BAE=∠CDE,AE=DE,∴△BAE≌△CDE,∴BE=CE;(2)延长CD和BE的延长线交于H,∵BF⊥CD,∠HEC=90°,∴∠EBF+∠H=∠ECH+∠H=90°∴∠EBF=∠ECH,又∠BEC=∠CEH=90°,BE=CE(已证),∴△BEG≌△CEH,∴EG=EH,BG=CH=DH+CD,∵△BAE≌△CDE(已证),∴∠AEB=∠GED,∠HED=∠AEB,∴∠GED=∠HED,又EG=EH(已证),ED=ED,∴△GED≌△HED,∴DG=DH,∴BG=DG+CD.2、如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,E为AB延长线上一点,连接ED,与BC交于点H.过E作CD的垂线,垂足为CD上的一点F,并与BC交于点G.已知G 为CH的中点.(1)若HE=HG,求证:△EBH≌△GFC;(2)若CD=4,BH=1,求AD的长.(1)证明:∵HE=HG,∴∠HEG=∠HGE,∵∠HGE=∠FGC,∠BEH=∠HEG,∴∠BEH=∠FGC,∵G是HC的中点,∴HG=GC,∴HE=GC,∵∠HBE=∠CFG=90°.∴△EBH≌△GFC;(2)解:∵ED平分∠AEF,∠A=∠DFE=90°,∴AD=DF,∵DF=DC﹣FC,∵△EBH≌△GFC,∴FC=BH=1,∴AD=4﹣1=3.3、如图,梯形ABCD中,AB∥CD,AD=DC=BC,∠DAB=60°,E是对角线AC延长线上一点,F是AD延长线上的一点,且EB⊥AB,EF⊥AF.(1)当CE=1时,求△BCE的面积;(2)求证:BD=EF+CE.(2)过E点作EM⊥DB于点M,四边形FDME是矩形,FE=DM,∠BME=∠BCE=90°,∠BEC=∠MBE=60°,△BME≌△ECB,BM=CE,继而可证明BD=DM+BM=EF+CE.(1)解:∵AD=CD,∴∠DAC=∠DCA,∵DC∥AB,∴∠DCA=∠CAB,∴,∵DC∥AB,AD=BC,∴∠DAB=∠CBA=60°,∴∠ACB=180°﹣(∠CAB+∠CBA)=90°,∴∠BCE=180°﹣∠ACB=90°,∵BE⊥AB,∴∠ABE=90°,∴∠CBE=∠ABE﹣∠ABC=30°,在Rt△BCE中,BE=2CE=2,,∴…(5分)(2)证明:过E点作EM⊥DB于点M,∴四边形FDME是矩形,∴FE=DM,∵∠BME=∠BCE=90°,∠BEC=∠MBE=60°,∴△BME≌△ECB,∴BM=CE,∴BD=DM+BM=EF+CE…(10分)4、如图.在平行四边形ABCD中,O为对角线的交点,点E为线段BC延长线上的一点,且.过点E作EF∥CA,交CD于点F,连接OF.(1)求证:OF∥BC;(2)如果梯形OBEF是等腰梯形,判断四边形ABCD的形状,并给出证明.解答:(1)证明:延长EF交AD于G(如图),在平行四边形ABCD中,AD∥BC,AD=BC,∵EF∥CA,EG∥CA,∴四边形ACEG是平行四边形,∴AG=CE,又∵,AD=BC,∴,∵AD∥BC,∴∠ADC=∠ECF,在△CEF和△DGF中,∵∠CFE=∠DFG,∠ADC=∠ECF,CE=DG,∴△CEF≌△DGF(AAS),∴CF=DF,∵四边形ABCD是平行四边形,∴OB=OD,∴OF∥BE.(2)解:如果梯形OBEF是等腰梯形,那么四边形ABCD是矩形.证明:∵OF∥CE,EF∥CO,∴四边形OCEF是平行四边形,∴EF=OC,又∵梯形OBEF是等腰梯形,∴BO=EF,∴OB=OC,∵四边形ABCD是平行四边形,∴AC=2OC,BD=2BO.∴AC=BD,∴平行四边形ABCD是矩形.5、如图,梯形ABCD中,AD∥BC,∠ABC=90°,BF⊥CD于F,延长BF交AD的延长线于E,延长CD交BA的延长线于G,且DG=DE,AB=,CF=6.(1)求线段CD的长;(2)H 在边BF 上,且∠HDF=∠E ,连接CH ,求证:∠BCH=45°﹣∠EBC .(1)解:连接BD ,由∠ABC=90°,AD ∥BC 得∠GAD=90°,又∵BF ⊥CD ,∴∠DFE=90°又∵DG=DE ,∠GDA=∠EDF ,∴△GAD ≌△EFD ,∴DA=DF ,又∵BD=BD ,∴Rt △BAD ≌Rt △BFD (HL ),∴BF=BA=,∠ADB=∠BDF 又∵CF=6,∴BC=,又∵AD ∥BC ,∴∠ADB=∠CBD ,∴∠BDF=∠CBD ,∴CD=CB=8.(2)证明:∵AD ∥BC ,∴∠E=∠CBF ,∵∠HDF=∠E ,∴∠HDF=∠CBF ,由(1)得,∠ADB=∠CBD ,∴∠HDB=∠HBD ,∴HD=HB ,由(1)得CD=CB ,CBD CDBCBD HDF CDB CBH∴∠=∠∴∠-∠=∠-∠∠∠∴即BDH=HBDHB=HD∴△CDH ≌△CBH ,∴∠DCH=∠BCH ,∴∠BCH=∠BCD==.6、如图,直角梯形ABCD中,AD∥BC,∠B=90°,∠D=45°.(1)若AB=6cm,,求梯形ABCD的面积;(2)若E、F、G、H分别是梯形ABCD的边AB、BC、CD、DA上一点,且满足EF=GH,∠EFH=∠FHG,求证:HD=BE+BF.解:(1)连AC,过C作CM⊥AD于M,如图,在Rt△ABC中,AB=6,sin∠ACB==,∴AC=10,∴BC=8,在Rt△CDM中,∠D=45°,∴DM=CM=AB=6,∴AD=6+8=14,∴梯形ABCD的面积=•(8+14)•6=66(cm2);(2)证明:过G作GN⊥AD,如图,∵∠D=45°,∴△DNG为等腰直角三角形,∴DN=GN,又∵AD∥BC,∴∠BFH=∠FHN,而∠EFH=∠FHG,∴∠BFE=∠GHN,∵EF=GH,∴Rt△BEF≌Rt△NGH,∴BE=GN,BF=HN,∴DA=AN+DN=AN+DG=BF+BE.7、已知:如图,▱ABCD中,对角线AC,BD相交于点O,延长CD至F,使DF=CD,连接BF交AD于点E.(1)求证:AE=ED;(2)若AB=BC,求∠CAF的度数.(1)证明:如图.∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD.∵DF=CD,∴AB∥DF.∵DF=CD,∴AB=DF.∴四边形ABDF是平行四边形,∴AE=DE.(2)解:∵四边形ABCD是平行四边形,且AB=BC,∴四边形ABCD是菱形.∴AC⊥BD.∴∠COD=90°.∵四边形ABDF是平行四边形,∴AF∥BD.∴∠CAF=∠COD=90°.8、已知:如图,在正方形ABCD中,点G是BC延长线上一点,连接AG,分别交BD、CD于点E、F.(1)求证:∠DAE=∠DCE;(2)当CG=CE时,试判断CF与EG之间有怎样的数量关系?并证明你的结论.(1)证明:在△DAE和△DCE中,∠ADE=∠CDE(正方形的对角线平分对角),ED=DE(公共边),AE=CE(正方形的四条边长相等),∴△DAE≌△DCE(SAS),∴∠DAE=∠DCE(全等三角形的对应角相等);(2)解:如图,由(1)知,△DAE≌△DCE,∴AE=EC,∴∠EAC=∠ECA(等边对等角);又∵CG=CE(已知),∴∠G=∠CEG(等边对等角);而∠CEG=2∠EAC(外角定理),∠ECB=2∠CEG(外角定理),∴4∠EAC﹣∠ECA=∠ACB=45°,∴∠G=∠CEG=30°;过点C作CH⊥AG于点H,∴∠FCH=30°,∴在直角△ECH中,EH=CH,EG=2CH,在直角△FCH中,CH=CF,∴EG=2×CF=3CF.9、如图,已知正方形ABCD,点E是BC上一点,点F是CD延长线上一点,连接EF,若BE=DF,点P是EF的中点.(1)求证:DP平分∠ADC;(2)若∠AEB=75°,AB=2,求△DFP的面积.(1)证明:连接PC.∵ABCD是正方形,∴∠ABE=∠ADF=90°,AB=AD.∵BE=DF,∴△ABE≌△ADF.(SAS)∴∠BAE=∠DAF,AE=AF.∴∠EAF=∠BAD=90°.∵P是EF的中点,∴PA=EF,PC=EF,∴PA=PC.又AD=CD,PD公共,∴△PAD≌△PCD,(SSS)∴∠ADP=∠CDP,即DP平分∠ADC;(2)作PH⊥CF于H点.∵P是EF的中点,∴PH=EC.设EC=x.由(1)知△EAF是等腰直角三角形,∴∠AEF=45°,∴∠FEC=180°﹣45°﹣75°=60°,∴EF=2x,FC=x,BE=2﹣x.在Rt△ABE中,22+(2﹣x)2=(x)2解得x1=﹣2﹣2(舍去),x2=﹣2+2.∴PH=﹣1+,FD=(﹣2+2)﹣2=﹣2+4.=(﹣2+4)×=3﹣5.∴S△DPF10、如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,BD=BC,E为CD的中点,交BC的延长线于F;(1)证明:EF=EA;(2)过D作DG⊥BC于G,连接EG,试证明:EG⊥AF.(1)证明:∵AD∥BC,∴∠DAE=∠F,∠ADE=∠FCE.∵E为CD的中点,∴ED=EC.∴△ADE≌△FCE.∴EF=EA.(5分)(2)解:连接GA,∵AD∥BC,∠ABC=90°,∴∠DAB=90°.∵DG⊥BC,∴四边形ABGD是矩形.∴BG=AD,GA=BD.∵BD=BC,∴GA=BC.由(1)得△ADE≌△FCE,∴AD=FC.∴GF=GC+FC=GC+AD=GC+BG=BC=GA.∵由(1)得EF=EA,∴EG⊥AF.(5分)11、如图,直角梯形ABCD中,∠DAB=90°,AB∥CD,AB=AD,∠ABC=60度.以AD为边在直角梯形ABCD外作等边三角形ADF,点E 是直角梯形ABCD内一点,且∠EAD=∠EDA=15°,连接EB、EF.(1)求证:EB=EF;(2)延长FE交BC于点G,点G恰好是BC的中点,若AB=6,求BC的长.(1)证明:∵△ADF为等边三角形,∴AF=AD,∠FAD=60°(1分)∵∠DAB=90°,∠EAD=15°,AD=AB(2分)∴∠FAE=∠BAE=75°,AB=AF,(3分)∵AE为公共边∴△FAE≌△BAE(4分)∴EF=EB(5分)(2)解:如图,连接EC.(6分)∵在等边三角形△ADF中,∴FD=FA,∵∠EAD=∠EDA=15°,∴ED=EA,∴EF是AD的垂直平分线,则∠EFA=∠EFD=30°.(7分)由(1)△FAE≌△BAE知∠EBA=∠EFA=30°.∵∠FAE=∠BAE=75°,∴∠BEA=∠BAE=∠FEA=75°,∴BE=BA=6.∵∠FEA+∠BEA+∠GEB=180°,∴∠GEB=30°,∵∠ABC=60°,∴∠GBE=30°∴GE=GB.(8分)∵点G是BC的中点,∴EG=CG∵∠CGE=∠GEB+∠GBE=60°,∴△CEG为等边三角形,∴∠CEG=60°,∴∠CEB=∠CEG+∠GEB=90°(9分)∴在Rt△CEB中,BC=2CE,BC2=CE2+BE2∴CE=,∴BC=(10分);解法二:过C作CQ⊥AB于Q,∵CQ=AB=AD=6,∵∠ABC=60°,∴BC=6÷=4.12、如图,在梯形ABCD中,AD∥BC,AB=DC=AD,∠C=60°,AE⊥BD于点E,F是CD的中点,DG是梯形ABCD的高.(1)求证:AE=GF;(2)设AE=1,求四边形DEGF的面积.(1)证明:∵AB=DC,∴梯形ABCD为等腰梯形.∵∠C=60°,∴∠BAD=∠ADC=120°,又∵AB=AD,∴∠ABD=∠ADB=30°.∴∠DBC=∠ADB=30°.∴∠BDC=90°.(1分)由已知AE⊥BD,∴AE∥DC.(2分)又∵AE为等腰三角形ABD的高,∴E是BD的中点,∵F是DC的中点,∴EF∥BC.∴EF∥AD.∴四边形AEFD是平行四边形.(3分)∴AE=DF(4分)∵F是DC的中点,DG是梯形ABCD的高,∴GF=DF,(5分)∴AE=GF.(6分)(2)解:在Rt△AED中,∠ADB=30°,∵AE=1,∴AD=2.在Rt△DGC中∠C=60°,并且DC=AD=2,∴DG=.(8分)由(1)知:在平行四边形AEFD中EF=AD=2,又∵DG⊥BC,∴DG⊥EF,∴四边形DEGF的面积=EF•DG=.(10分)13、已知,如图在直角梯形ABCD中,AD∥BC,∠ABC=90°,DE⊥AC于点F,交BC于点G,交AB的延长线于点E,且AE=AC,连AG.(1)求证:FC=BE;(2)若AD=DC=2,求AG的长.解答:(1)证明:∵∠ABC=90°,DE⊥AC于点F,∴∠ABC=∠AFE.∵AC=AE,∠EAF=∠CAB,∴△ABC≌△AFE,∴AB=AF.∴AE﹣AB=AC﹣AF,即FC=BE;(2)解:∵AD=DC=2,DF⊥AC,∴AF=AC=AE.∴AG=CG,∴∠E=30°.∵∠EAD=90°,∴∠ADE=60°,∴∠FAD=∠E=30°,∴FC=,∵AD∥BC,∴∠ACG=∠FAD=30°,∴CG=2,∴AG=2.14、如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,点E是AB边上一点,AE=BC,DE⊥EC,取DC的中点F,连接AF、BF.(1)求证:AD=BE;(2)试判断△ABF的形状,并说明理由.(1)证明:∵AD∥BC,∴∠BAD+∠ABC=180°,∵∠ABC=90°,∴∠BAD=∠ABC=90°,∵DE⊥EC,∴∠AED+∠BEC=90°∵∠AED+∠ADE=90°,∴∠BEC=∠ADE,∵∠DAE=∠EBC,AE=BC,∴△EAD≌△EBC,∴AD=BE.(2)答:△ABF是等腰直角三角形.理由是:延长AF交BC的延长线于M,∵AD∥BM,∴∠DAF=∠M,∵∠AFD=∠CFM,DF=FC,∴△ADF≌△MFC,∴AD=CM,∵AD=BE,∴BE=CM,∵AE=BC,∴AB=BM,∴△ABM是等腰直角三角形,∵△ADF≌△MFC,∴AF=FM,∴∠ABC=90°,∴BF⊥AM,BF=AM=AF,∴△AFB是等腰直角三角形.15、(2011•潼南县)如图,在直角梯形ABCD中,AB∥CD,AD⊥DC,AB=BC,且AE⊥BC.(1)求证:AD=AE;(2)若AD=8,DC=4,求AB的长.解答:(1)证明:连接AC,∵AB∥CD,∴∠ACD=∠BAC,∵AB=BC,∴∠ACB=∠BAC,∴∠ACD=∠ACB,∵AD⊥DC,AE⊥BC,∴∠D=∠AEC=90°,∵AC=AC,∴,∴△ADC≌△AEC,(AAS)∴AD=AE;(2)解:由(1)知:AD=AE,DC=EC,设AB=x,则BE=x﹣4,AE=8,在Rt△ABE中∠AEB=90°,由勾股定理得:82+(x﹣4)2=x2,解得:x=10,∴AB=10.说明:依据此评分标准,其它方法如:过点C作CF⊥AB用来证明和计算均可得分.16、如图,已知梯形ABCD中,AD∥CB,E,F分别是BD,AC的中点,BD平分∠ABC.(1)求证:AE⊥BD;(2)若AD=4,BC=14,求EF的长.(1)证明:∵AD∥CB,∴∠ADB=∠CBD,又BD平分∠ABC,∴∠ABD=∠CBD,∴∠ADB=∠ABD,∴AB=AD,∴△ABD是等腰三角形,已知E是BD的中点,∴AE⊥BD.(2)解:延长AE交BC于G,∵BD平分∠ABC,∴∠ABE=∠GBE,又∵AE⊥BD(已证),∴∠AEB=∠GEB,BE=BE,∴△ABE≌△GBE,∴AE=GE,BG=AB=AD,又F是AC的中点(已知),所以由三角形中位线定理得:EF=CG=(BC﹣BG)=(BC﹣AD)=×(14﹣4)=5.答:EF的长为5.17、如图,在梯形ABCD中,AD∥BC,∠D=90°,BE⊥AC,E为垂足,AC=BC.(1)求证:CD=BE;(2)若AD=3,DC=4,求AE.(1)证明:∵AD∥BC,∴∠DAC=∠BCE,而BE⊥AC,∴∠D=∠BEC=90°,AC=BC,∴△BCE≌△CAD.∴CD=BE.(2)解:在Rt△ADC中,根据勾股定理得AC==5,∵△BCE≌△CAD,∴CE=AD=3.∴AE=AC﹣CE=2.18、如图,在梯形ABCD中,AD∥BC,AB⊥AC,∠B=45°,AD=1,BC=4,求DC的长.解:如图,过点D作DF∥AB,分别交AC,BC于点E,F.(1分)∵AB⊥AC,∴∠AED=∠BAC=90度.∵AD∥BC,∴∠DAE=180°﹣∠B﹣∠BAC=45度.在Rt△ABC中,∠BAC=90°,∠B=45°,BC=4,∴AC=BC•sin45°=4×=2(2分)在Rt△ADE中,∠AED=90°,∠DAE=45°,AD=1,∴DE=AE=.∴CE=AC﹣AE=.(4分)在Rt△DEC中,∠CED=90°,∴DC==.(5分)19、已知梯形ABCD中,AD∥BC,AB=BC=DC,点E、F分别在AD、AB上,且.(1)求证:BF=EF﹣ED;(2)连接AC,若∠B=80°,∠DEC=70°,求∠ACF的度数.证明:∵FC=F′C,EC=EC,∠ECF'=∠BCF+∠DCE=∠ECF,∴△FCE≌△F′CE,∴EF′=EF=DF′+ED,∴BF=EF﹣ED;(2)解:∵AB=BC,∠B=80°,∴∠ACB=50°,由(1)得∠FEC=∠DEC=70°,∴∠ECB=70°,而∠B=∠BCD=80°,∴∠DCE=10°,∴∠BCF=30°,∴∠ACF=∠BCA﹣∠BCF=20°.20、如图,梯形ABCD中,AD∥BC,点E在BC上,AE=BE,且AF⊥AB,连接EF.(1)若EF⊥AF,AF=4,AB=6,求AE的长.(2)若点F是CD的中点,求证:CE=BE﹣AD.解:(1)作EM⊥AB,交AB于点M.∵AE=BE,EM⊥AB,∴AM=BM=×6=3;∵∠AME=∠MAF=∠AFE=90°,∴四边形AMEF是矩形,∴EF=AM=3;在Rt△AFE中,AE==5;(2)延长AF、BC交于点N.∵AD∥EN,∴∠DAF=∠N;∵∠AFD=∠NFC,DF=FC,∴△ADF≌△NCF(AAS),∴AD=CN;∵∠B+∠N=90°,∠BAE+∠EAN=90°,又AE=BE,∠B=∠BAE,∴∠N=∠EAN,AE=EN,∴BE=EN=EC+CN=EC+AD,∴CE=BE﹣AD..21、如图,四边形ABCD为等腰梯形,AD∥BC,AB=CD,对角线AC、BD交于点O,且AC⊥BD,DH⊥BC.(1)求证:DH=(AD+BC);(2)若AC=6,求梯形ABCD的面积.解:(1)证明:过D作DE∥AC交BC延长线于E,(1分)∵AD∥BC,∴四边形ACED为平行四边形.(2分)∴CE=AD,DE=AC.∵四边形ABCD为等腰梯形,∴BD=AC=DE.∵AC⊥BD,∴DE⊥BD.∴△DBE为等腰直角三角形.(4分)∵DH⊥BC,∴DH=BE=(CE+BC)=(AD+BC).(5分)(2)∵AD=CE,∴.(7分)∵△DBE为等腰直角三角形BD=DE=6,∴.∴梯形ABCD的面积为18.(8分)注:此题解题方法并不唯一.22、已知,如图,△ABC是等边三角形,过AC边上的点D作DG∥BC,交AB于点G,在GD的延长线上取点E,使DE=DC,连接AE,BD.(1)求证:△AGE≌△DAB;(2)过点E作EF∥DB,交BC于点F,连AF,求∠AFE的度数.(1)证明:∵△ABC是等边三角形,DG∥BC,∴∠AGD=∠ABC=60°,∠ADG=∠ACB=60°,且∠BAC=60°,∴△AGD是等边三角形,AG=GD=AD,∠AGD=60°.∵DE=DC,∴GE=GD+DE=AD+DC=AC=AB,∵∠AGD=∠BAD,AG=AD,∴△AGE≌△DAB;(2)解:由(1)知AE=BD,∠ABD=∠AEG.∵EF∥DB,DG∥BC,∴四边形BFED是平行四边形.∴EF=BD,∴EF=AE.∵∠DBC=∠DEF,∴∠ABD+∠DBC=∠AEG+∠DEF,即∠AEF=∠ABC=60°.∴△AFE是等边三角形,∠AFE=60°.23、如图,梯形ABCD中,AD∥BC,DE=EC,EF∥AB交BC于点F,EF=EC,连接DF.(1)试说明梯形ABCD是等腰梯形;(2)若AD=1,BC=3,DC=,试判断△DCF的形状;(3)在条件(2)下,射线BC上是否存在一点P,使△PCD是等腰三角形,若存在,请直接写出PB的长;若不存在,请说明理由.解:(1)证明:∵EF=EC,∴∠EFC=∠ECF,∵EF∥AB,∴∠B=∠EFC,∴∠B=∠ECF,∴梯形ABCD是等腰梯形;(2)△DCF是等腰直角三角形,证明:∵DE=EC,EF=EC,∴EF=CD,∴△CDF是直角三角形(如果一个三角形一边上的中线等于这条边的一半,那么这个三角形是直角三角形),∵梯形ABCD是等腰梯形,∴CF=(BC﹣AD)=1,∵DC=,∴由勾股定理得:DF=1,∴△DCF是等腰直角三角形;(3)共四种情况:∵DF⊥BC,∴当PF=CF时,△PCD是等腰三角形,即PF=1,∴PB=1;当P与F重合时,△PCD是等腰三角形,∴PB=2;当PC=CD=(P在点C的左侧)时,△PCD是等腰三角形,∴PB=3﹣;当PC=CD=(P在点C的右侧)时,△PCD是等腰三角形,∴PB=3+.故共四种情况:PB=1,PB=2,PB=3﹣,PB=3+.(每个1分)24、如图,在梯形ABCD中,AD∥BC,∠ABC=∠BCD=60°,AD=DC,E、F分别在AD、DC的延长线上,且DE=CF.AF交BE于P.(1)证明:△ABE≌△DAF;(2)求∠BPF的度数.解答:(1)证明:∵在梯形ABCD中,AD∥BC,∠ABC=∠BCD=60°,∴AB=CD,∵AD=DC,∴BA=AD,∠BAE=∠ADF=120°,∵DE=CF,∴AE=DF,在△BAE和△ADF中,,∴△ABE≌△DAF(SAS).(2)解:∵由(1)△BAE≌△ADF,∴∠ABE=∠DAF.∴∠BPF=∠ABE+∠BAP=∠BAE.而AD∥BC,∠C=∠ABC=60°,∴∠BPF=120°.25、如图,在梯形ABCD中,AD∥BC,AB=AD=DC,BD⊥DC,将BC延长至点F,使CF=CD.(1)求∠ABC的度数;(2)如果BC=8,求△DBF的面积?解答:解:(1)∵AD∥BC,∴∠ADB=∠DBC,∵AB=AD,∴∠ADB=∠ABD,∴∠DBC=∠ABD,∵在梯形ABCD中AB=DC,∴∠ABC=∠DCB=2∠DBC,∵BD⊥DC,∴∠DBC+2∠DBC=90°∴∠DBC=30°∴∠ABC=60°(2)过点D作DH⊥BC,垂足为H,∵∠DBC=30°,BC=8,∴DC=4,∵CF=CD∴CF=4,∴BF=12,∵∠F+∠FDC=∠DCB=60°,∠F=∠FDC∴∠F=30°,∵∠DBC=30°,∴∠F=∠DBC,∴DB=DF,∴,在直角三角形DBH中,∴,∴,∴,即△DBF的面积为.26、如图,梯形ABCD中,AD∥BC,AB=DC=10cm,AC交BD于G,且∠AGD=60°,E、F分别为CG、AB的中点.(1)求证:△AGD为正三角形;(2)求EF的长度.(1)证明:连接BE,∵梯形ABCD中,AB=DC,∴AC=BD,可证△ABC≌△DCB,∴∠GCB=∠GBC,又∵∠BGC=∠AGD=60°∴△AGD为等边三角形,(2)解:∵BE为△BCG的中线,∴BE⊥AC,在Rt△ABE中,EF为斜边AB上的中线,∴EF=AB=5cm.27、已知,如图,AD∥BC,∠ABC=90°,AB=BC,点E是AB上的点,∠ECD=45°,连接ED,过D作DF⊥BC于F.(1)若∠BEC=75°,FC=3,求梯形ABCD的周长.(2)求证:ED=BE+FC.解:(1)∵∠BEC=75°,∠ABC=90°,∴∠ECB=15°,∵∠ECD=45°,∴∠DCF=60°,在Rt△DFC中:∠DCF=60°,FC=3,∴DF=3,DC=6,由题得,四边形ABFD是矩形,∴AB=DF=3,∵AB=BC,∴BC=3,∴BF=BC﹣FC=3﹣3,∴AD=DF=3﹣3,∴C=3×2+6+3﹣3=9+3,梯形ABCD答:梯形ABCD的周长是9+3.(2)过点C作CM垂直AD的延长线于M,再延长DM到N,使MN=BE,∴CN=CE,可证∠NCD=∠DCE,∵CD=CD,∴△DEC≌△DNC,∴ED=EN,∴ED=BE+FC.28、(2005•镇江)已知:如图,梯形ABCD中,AD∥BC,E是AB的中点,直线CE交DA的延长线于点F.(1)求证:△BCE≌△AFE;(2)若AB⊥BC且BC=4,AB=6,求EF的长.(1)证明:∵AD∥BC,E是AB的中点,∴AE=BE,∠B=∠EAF,∠BCE=∠F.∴△BCE≌△AFE(AAS).(2)解:∵AD∥BC,∴∠DAB=∠ABC=90°.∵AE=BE,∠AEF=∠BEC,∴△BCE≌△AFE.∴AF=BC=4.∵EF2=AF2+AE2=9+16=25,∴EF=5.29、已知:如图,在梯形ABCD中,AD∥BC,BC=DC,CF平分∠BCD,DF∥AB,BF 的延长线交DC于点E.(1)△BFC≌△DFC;(2)AD=DE;(3)若△DEF的周长为6,AD=2,BC=5,求梯形ABCD的面积.(1)∵DC=BC,∠1=∠2,CF=CF,∴△DCF≌△BCF.(2)延长DF交BC于G,∵AD∥BG,AB∥DG,∴四边形ABGD为平行四边形.∴AD=BG.∵△DFC≌△BFC,∴∠EDF=∠GBF,DF=BF.又∵∠3=∠4,∴△DFE≌△BFG.∴DE=BG,EF=GF.∴AD=DE.(3)∵EF=GF,DF=BF,∴EF+BF=GF+DF,即:BE=DG.∵DG=AB,∴BE=AB.∵C=DF+FE+DE=6,△DFE∴BF+FE+DE=6,即:EB+DE=6.∴AB+AD=6.又∵AD=2,∴AB=4.∴DG=AB=4.∵BG=AD=2,∴GC=BC﹣BG=5﹣2=3.又∵DC=BC=5,在△DGC中∵42+32=52∴DG2+GC2=DC2∴∠DGC=90°.=(AD+BC)•DG∴S梯形ABCD=(2+5)×430、如图,梯形ABCD中,AD∥BC.∠C=90°,且AB=AD.连接BD,过A点作BD的垂线,交BC于E.(1)求证:四边形ABED是菱形;(2)如果EC=3cm,CD=4cm,求梯形ABCD的面积.解答:解:(1)证明:∵AD∥BC,DE2=CD2+CE2=42+32=25,∴∠OAD=∠OEB,∴DE=5又∵AB=AD,AO⊥BD,∴AD=BE=5,=.∴OB=OD,∴S梯形ABCD又∵∠AOD=∠EOB,∴△ADO≌△EBO(AAS),∴AD=EB,又∵AD∥BE,∴四边形ABCD是平行四边形,又∵AB=AD∴四边形ABCD是菱形.(2)∵四边形ABCD是菱形,∴AD=DE=BE,。
六年级数轴动点问题

易通六年级数学 动点问题典型练习题:
1 数轴上A 点表示-30,B 点表示70
(1)点P 从A 向正半轴以每秒2个单位,点Q 从B 向负半轴运动,每秒5个单位 ①t 秒后,P 、Q 表示的数各是多少?
②几秒后,P,Q 相距30个单位,此时P 、Q 所表示的数各是多少?
(2)点P 从A 向负半轴运动,点Q 从B 向负半轴运动
①t 秒后,P 、Q 所表示的数是多少?
②几秒后, P 、Q 相距30个单位,此时P 、Q 所表示的数是各是多少?
2 长方形ABCD 中,AB =20,BC=10 。
P 从A 向B 运动,每秒2个单位,Q 从B 向C 运动,每秒1个单位 ⑴ t 秒后 AP=________ BP= ________ BQ=________ CQ=________ ⑵ 用含t 的代数式表示△DPQ 的面积
3 在直角梯形ABCD 中,AD=10, BC=30, AB=16, P 从A 延射线AD 运动,每秒1个单
位Q 从C 出发在线段BC 上运动,以每秒2个单位
⑴ t 秒后 AP=________ DP=________
BQ=________ CQ=________
⑵用含t 表示△BPQ 的面积
⑶多少秒后面积为208
⑷用含t 的代数式表示△BPQ 的面积
4 在直接梯形ABCD 中 AD=10, BC=30, AB=16 ,P 从A 出发一每秒2个单位延直线AB 运动
A
B D
C
A B C
D
⑴AP=________ BP=________
A D
⑵用含t表示的代数式表示△DPC的面积
B C。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
在直角梯形ABCD中,AD平行BC,角B=90度,AD=24cm,AB=8cm,BC26cm,动点P从A点开始沿AD边向D点以每秒1cm的速度运动,动点Q从C点出发沿CB边向B点以每秒3cm的速度运动,P,Q两点分别从A,C同时出发,当其中一点到达端点时,另一点也随之停止运动。
设运动时间为t秒,t分别为何值时,四边形PQCD为平行四边形,等腰梯形。
解:(1)平行四边形:因为动点P从A点开始沿AD边向D点以每秒1cm的速度运动,所以AP=tcm.因为AD=24cm所以PD=AD-AP=(24-t)cm.因为动点Q从C点出发沿CB边向B点以每秒3cm的速度运动,所以CQ=3tcm.因为在平行四边形PQCD中,PD=CQ,所以24-t=3t,解得t=6.
(2)过点D作BC的垂线交BC于点E.所以DE=8.因为AD=24,BC=26,所以CE=2.所以CD=2根号17.因为四边形PQCD为等腰梯形,所以PQ=CD=2根号17.过点P作线段BC的垂线交于点F,所以三角形QPF全等于三角形CDE,所以QF=CE=2.由第(1)题可知,DP=(24-t)cm,CQ=3tcm.所以EF=CQ-CE-QF=(3t-4)cm.因为PF垂直BC,DE垂直BC,所以PD=EF,所以(24-t)=(3t-4),解得,t=7.。
