不规则图形求面积·切割补
割补法求面积

3
10 4
12
方法总结
切割法:
把不规则的图形切割成已学图形,再把各部分面积加起来
拼补法:
把不规则的图形拼补成已学图形,再用总面积减去补上的图形面积
谢谢观看
练习
图形大世界
——割补法
REPORT
面积公式回顾
面积=边长×边长
面积=长×宽
面积=底×高
面积=底×高÷2
面积=(上底+下底)×高÷2
3cm 3cm
3cm 3cm
左侧图形的面积 该怎么求呢
3cm 3cm
3cm 3cm
我们学过哪些图形的面积公式呢?
可以将不规则的图形切割成两 个或多个已学图形,进行计算:
3×3+3×(3+3)=27(平方厘米)
3cm 3cm
3cm 3cm
我们学过哪些图形的面积公式呢?
可以将不规则的图形拼补成一 个或多个已学图形,进行计算:
(3+3)×(3+3)- 3×3=27(平方厘米)
10 3
3
这个图该
6 怎么求呢
单位:厘米
10 3
3
这个图该
6 怎么求呢
单位:厘米
切割法: 3×6×2+10×(3+6+3)=156(平方厘米)
10 3
3
这个图该
6 怎么求呢
单位:厘米
切割法: 3×10×2+(3+10+3)×6=156(平方厘米)
10 3
3
这个图该
6 怎么求呢
单位:厘米
拼补法: (10+3+3)×(3+6+3)- 3×3×4=156(平方厘米)
不规则图形面积的计算(实用课件)

8
“割”、“补”的方法是我们今后计算复 杂图形时常用的方法,方法越简单越好。
❖ 在进行图形计算割补时,要注意以下几点:
(1)要根据原来图形的特点进行思考。
(2)要便于利用已知条件计算简单图形的面积。
(3)可以用不同的方法进行割补。
不规则图形面积的计算(实用课件)
9
练一练:
1、校园里有一个花圃(如图),你能算出 它的面积是多少平方米?
❖
3×6÷2=9㎡
❖ 草坪的面积:120+9=129㎡
❖ 答:这块草坪的不面规则图积形面是积的1计2算(9实㎡用课件)
6
12m
方法三:分割法 4m
10m
15m
❖ 草坪的面积=梯形面积+三角形面积 ❖ 梯形的面积:(4+10)×12÷2=84㎡ ❖ 三角形的面积:10-4=6m,15×6÷2=45㎡ ❖ 草坪的面积:84+45=129㎡ ❖ 答:这块草坪的面积是129㎡
不规则图形面积的计算
感谢您的阅览
不规则图形面积的计算(实用课件)
你还记得吗?
长 方 形 的 面 积 = 长 ×宽
S=ab
正 方 形 的 面 积 = 边长×边长
S=a×a
平行四边形的面积= 底×高
S=ah
三 角 形 的 面 积 = 底×高÷2
S=ah÷2
梯 形 的 面 积 = (上底+下底)×高÷2 S=(a+b)h÷2
17
作业
课本23页练习四1到4题
不规则图形面积的计算(实用课件)
18
45cm 60cm
学校开运动会要制作一 些锦旗,式样如右图。 一面锦旗需要多少平方 厘米面料?
(60+45) ×(30÷2) ÷2×2 =105×15÷2×2 =1575(㎝²)
求不规则图形面积的五种方法

求不规则图形面积的五种方法
一、相加法:临方法是将不规则图形分解转化成几个基本规测图形,分别计算它们的面积,然后相加求出整个图形的面积。
二、相减法:这种方法是将所求的不规则图形的面积看成是若千个基本规则图形的面积之差.
三、直接求法:这种方法是根据已知条件,从整体出发直接求出不规则图形面积
四、重新组合法:这种方法是将不规则图形拆开,根据具体情况和计算上的需要,重新组合成一个新的图形,设法求出这个新图形面积即可4个角处,这时采用相减法就可求出其面积了.
五、割补法:这种方法是把原图形的受部分切割下来补在图形中的另部分使之成为基本规则图形,从而使问题得到解决。
五年级不规则图形面积计算

五年级不规那么图形面积计算我们曾经学过的三角形、长方形、正方形、平行四边形、梯形、菱形、圆和扇形等图形,一般称为根本图形或规那么图形.我们的面积及周长都有相应的公式直接计算.如下表:实际问题中,有些图形不是以根本图形的形状出现,而是由一些根本图形组合、拼凑成的,它们的面积及周长无法应用公式直接计算.一般我们称这样的图形为不规那么图形。
那么,不规那么图形的面积及周长怎样去计算呢?我们可以针对这些图形通过实施割补、剪拼等方法将它们转化为根本图形的和、差关系,问题就能解决了。
一、例题与方法指导例1 如右图,甲、乙两图形都是正方形,它们的边长分别是10厘米和12厘米.求阴影局部的面积。
思路导航:阴影局部的面积等于甲、乙两个正方形面积之和减去三个“空白〞三角形〔△ABG、△BDE、△EFG〕的面积之和。
例2 如右图,正方形ABCD的边长为6厘米,△ABE、△ADF与四边形AECF的面积彼此相等,求三角形AEF的面积. 思路导航:∵△ABE 、△ADF 与四边形AECF 的面积彼此相等,∴四边形 AECF 的面积与△ABE 、△ADF 的面积都等于正方形ABCD 的13。
在△ABE 中,因为AB=6.所以BE=4,同理DF=4,因此CE=CF=2, ∴△ECF 的面积为2×2÷2=2。
所以S △AEF=S 四边形AECF-S △ECF=12-2=10〔平方厘米〕。
例3 两块等腰直角三角形的三角板,直角边分别是10厘米和6厘米。
如右图那样重合.求重合局部〔阴影局部〕的面积。
思路导航:在等腰直角三角形ABC 中∵AB=10∵EF=BF=AB-AF=10-6=4,∴阴影局部面积=S △ABG-S △BEF=25-8=17〔平方厘米〕。
例4 如右图,A 为△CDE 的DE 边上中点,BC=CD ,假设△ABC 〔阴影局部〕面积为5平方厘米.求△ABD 及△ACE 的面积.B C思路导航:取BD中点F,连结AF.因为△ADF、△ABF和△ABC等底、等高,所以它们的面积相等,都等于5平方厘米.∴△ACD的面积等于15平方厘米,△ABD的面积等于10平方厘米。
求不规则面积的数学方法

求不规则面积的数学方法一、分割法。
1.1 原理阐述。
求不规则面积的时候啊,分割法是个挺不错的法子。
就是把那个不规则的图形啊,分割成咱们熟悉的图形,像三角形、长方形、正方形啥的。
这就好比把一个大难题啊,拆成一个个小问题,各个击破嘛。
就拿一块奇形怪状的地来说,咱们可以想象着用几条线把它切成几块规整的形状,就像切蛋糕似的。
1.2 实际例子。
比如说有个不规则的多边形,看着乱得很。
咱们仔细瞅瞅,从几个合适的点连线,把它分成了三个三角形和一个长方形。
三角形的面积公式咱都知道,底乘高除以二嘛,长方形面积就是长乘宽。
把这几个小图形的面积都算出来,然后一加,这个不规则多边形的面积就出来了。
这就像是把一群散兵游勇,按照不同的队伍编排好,再把每个队伍的人数一加,总数就清楚了。
二、填补法。
2.1 原理剖析。
填补法呢,和分割法有点相反。
要是遇到个不规则的图形,咱就想办法给它补上一块或者几块,让它变成一个咱们能轻松算面积的规则图形。
这就好比一个人衣服破了个洞,咱们补上一块布,让它完整起来。
等算出这个完整的规则图形的面积之后呢,再把咱们补上的那部分面积减掉,剩下的就是原来不规则图形的面积了。
2.2 举例说明。
就像有个图形,缺了一角,看着像个残缺不全的正方形。
咱们就给它补上那缺的一角,让它变成一个完整的正方形。
先算出这个正方形的面积,然后再算出补上的小三角形的面积。
正方形面积减去三角形面积,得嘞,原来那个不规则图形的面积就到手了。
这就像先把一个不完整的东西补全,再把多出来的部分去掉,就得到原本的东西了。
三、方格纸估算。
3.1 操作方法。
方格纸估算这个方法也很实用。
把这个不规则的图形画在方格纸上,每个方格的大小是一样的。
然后咱们就数这个图形占了多少个方格。
对于那些不满一格的,咱们就大概估算一下,是半格呢还是三分之一格之类的。
这就有点像咱们过日子,有时候大概估摸一下东西的数量。
3.2 实际操作。
比如说有个不规则的树叶形状的图形画在方格纸上。
五年级割补求面积问题

五年级奥数用割补法求面积在组合图形中,除了多边形外,还有由圆、扇形、弓形与三角形、矩形、平行四边形、梯形等图形组合而成的不规则图形,为了计算它们的面积,常常需要变动图形的位置或对图形进行分割、旋转、拼补,使它变成可以计算出面积的规则图形。
就是在多边形的组合图形中,为了计算面积,有时也要用到割补的方法。
例1求下列各图中阴影部分的面积:分析与解:(1)如左下图所示,将左下角的阴影部分分为两部分,然后按照右下图所示,将这两部分分别拼补在阴影位置。
可以看出,原题图的阴影部分等于右下图中AB弧所形成的弓形,其面积等于扇形OAB与三角形OAB的面积之差。
π×4×4÷4-4×4÷2=4.56。
(2)在题图虚线分割的两个正方形中,右边正方形的阴影部分是半径为5的四分之一个圆,在左边正方形中空白部分是半径为5的四分之一个圆。
如下图所示,将右边的阴影部分平移到左边正方形中。
可以看出,原题图的阴影部分正好等于一个正方形的面积,为5×5=25。
例2在一个等腰三角形中,两条与底边平行的线段将三角形的两条边等分成三段(见右图),求图中阴影部分的面积占整个图形面积的几分之几。
分析与解:阴影部分是一个梯形。
我们用三种方法解答。
(1)割补法从顶点作底边上的高,得到两个相同的直角三角形。
将这两个直角三角(2)拼补法将两个这样的三角形拼成一个平行四边形(下页左上图)。
积和平行四边行面积同时除以2,商不变。
所以原题阴影部分占整个图形面(3)等分法将原图等分成9个小三角形(见右上图),阴影部分占3个小三角形,注意,后两种方法对任意三角形都适用。
也就是说,将例题中的等腰三角形换成任意三角形,其它条件不变,结论仍然成立。
例3如左下图所示,在一个等腰直角三角形中,削去一个三角形后,剩下一个上底长5厘米、下底长9厘米的等腰梯形(阴影部分)。
求这个梯形的面积。
分析与解:因为不知道梯形的高,所以不能直接求出梯形的面积。
不规则图形的常用方法
不规则图形求面积的常用基本方法对于不规则图形面积的计算问题一般将它转化为若干基本规则图形的组合,分析整体与部分的和、差关系,问题便得到解决。
常用的基本方法有:一、相加法这种方法是将不规则图形分解转化成几个基本规则图形,分别计算它们的面积,然后相加求出整个图形的面积。
例如,下图要求整个图形的面积,只要先求出上面半圆的面积,再求出下面正方形的面积,然后把它们相加就可以了。
二、相减法这种方法是将所求的不规则图形的面积看成是若干个基本规则图形的面积之差。
例如,下图中,若求阴影部分的面积,只需先求出正方形面积再减去里面圆的面积即可。
三、直接求法这种方法是根据已知条件,从整体出发直接求出不规则图形面积。
如下图,欲求阴影部分的面积,通过分析发现它就是一个底是2、高是4的三角形,其面积直接可求为:。
四、重新组合法这种方法是将不规则图形拆开,根据具体情况和计算上的需要,重新组合成一个新的图形,设法求出这个新图形面积即可。
例如,欲求下图中阴影部分面积,可以把它拆开使阴影部分分布在正方形的4个角处,这时采用相减法就可求出其面积了。
五、辅助线法这种方法是根据具体情况在图形中添一条或若干条辅助线,使不规则图形转化成若干个基本规则图形,然后再采用相加、相减法解决即可。
如下图,求两个正方形中阴影部分的面积。
此题虽然可以用相减法解决,但不如添加一条辅助线后用直接法作更简便。
六、割补法这种方法是把原图形的一部分切割下来补在图形中的另一部分,使之成为基本规则图形,从而使问题得到解决。
例如,如下图,欲求阴影部分的面积,只需把右边弓形切割下来补在左边,这样整个阴影部分面积恰是正方形面积的一半。
七、平移法这种方法是将图形中某一部分切割下来平行移动到一恰当位置,使之组合成一个新的基本规则图形,便于求出面积。
例如,如下图,欲求阴影部分面积,可先沿中间切开把左边正方形内的阴影部分平行移到右边正方形内,这样整个阴影部分恰是一个正方形。
八、旋转法这种方法是将图形中某一部分切割下来之后,使之沿某一点或某一轴旋转一定角度贴补在另一图形的一侧,从而组合成一个新的基本规则的图形,便于求出面积,例如,欲求下图(1)中阴影部分的面积,可将左半图形绕B点逆时针方向旋转180°,使A与C重合,从而构成如下图(2)的样子,此时阴影部分的面积可以看成半圆面积减去中间等腰直角三角形的面积。
不规则图形面积的求法

不规求不规则图形面积的基本思路是通过分割、重叠、等积替换等方法把不规则图形转化为规则图形或规则图形面积的和差。
一、等积替换(1)三角形等积替换依据:等底等高的三角形面积相等或全等的三角形面积相等。
例1、如图1所示,半圆O 中,直径AB 长为4,C 、D 为半圆O 的三等分点.,求阴影部分的面积.解:连结OC 、OD , 由C 、D 为半圆O 的三等分点知:∠COD=60°,且∠ADC=∠DAB=30°, ∴CD ∥AB ,所以ODC ADC S S ∆∆=(同底等高的三角形面积相等) ∴==扇形阴影OCD S S ππ323602602=⨯⨯例2、如图2所示,在矩形ABCD 中,AB=1,以AD 为直径的 半圆与BC 切于M 点,求阴影部分面积.解:由AB =1,半圆与BC 相切,得AD =2 取AD 的中点O ,则OD =BM =1。
连结OM 交 BD 于E; 则△OED ≌△MEB∴MEB OED S S ∆∆= (全等三角形面积相等) ∴==扇形阴影OMD S S 43601902ππ=⨯⨯(2)弓形等积替换依据:等弧所对的弓形面积相等。
例3、 在RT △ABC 中,∠B=90°,AB=BC=4,AB 为直径的⊙O 交AC 于点D, 求图中两个阴影部分的面积之和.解:连结BD ,由AB 为⊙O 的直径得∠ADB =90°, RT △ABC 中∠B =90°AB =BC =4,得∠A =45°且AC=,AD =BD =CD=∴A D BnD S S 弓形m 弓形=∴C D B 11S C D B D 422S ∆⨯⨯⨯阴影===例4、点A、B、C、D是圆周上四点,且 AB + CD = A C + BD , 弦AB=8,CD=4,求两个阴影部分的面积之和。
解:作⊙ O 的直径BE 连结AE ,则∠BAE =90°,A B A E =+半圆;A图2图4又∵ AB + CD = A C + BD = 1A B C D A C B D 2(+++)=半圆, ∴ AE = C D ,所以A E C DS m n S 弓形弓形=,AE=CD=4。
不规则图形面积的计算(方法总结及详解)

不规则图形计算的方法总结总结:对于不规则图形面积的计算问题一般将它转化为若干基本规则图形的组合,分析整体与部分的和、差关系,问题便得到解决.常用的基本方法有:一、相加法:这种方法是将不规则图形分解转化成几个基本规则图形,分别计算它们的面积,然后相加求出整个图形的面积.例如,右图中,要求整个图形的面积,只要先求出上面半圆的面积,再求出下面正方形的面积,然后把它们相加就可以了.二、相减法:这种方法是将所求的不规则图形的面积看成是若干个基本规则图形的面积之差.例如,右图,若求阴影部分的面积,只需先求出正方形面积再减去里面圆的面积即可.三、直接求法:这种方法是根据已知条件,从整体出发直接求出不规则图形面积.如下页右上图,欲求阴影部分的面积,通过分四、重新组合法:这种方法是将不规则图形拆开,根据具体情况和计算上的需要,重新组合成一个新的图形,设法求出这个新图形面积即可.例如,欲求右图中阴影部分面积,可以把它拆开使阴影部分分布在正方形的4个角处,这时采用相减法就可求出其面积了.五、辅助线法:这种方法是根据具体情况在图形中添一条或若干条辅助线,使不规则图形转化成若干个基本规则图形,然后再采用相加、相减法解决即可.如右图,求两个正方形中阴影部分的面积.此题虽然可以用相减法解决,但不如添加一条辅助线后用直接法作更简便.六、割补法:这种方法是把原图形的一部分切割下来补在图形中的另一部分使之成为基本规则图形,从而使问题得到解决.例如,如右图,欲求阴影部分的面积,只需把右边弓形切割下来补在左边,这样整个阴影部分面积恰是正方形面积的一半.七、平移法:这种方法是将图形中某一部分切割下来平行移动到一恰当位置,使之组合成一个新的基本规则图形,便于求出面积.例如,如上页最后一图,欲求阴影部分面积,可先沿中间切开把左边正方形内的阴影部分平行移到右边正方形内,这样整个阴影部分恰是一个正方形。
八、旋转法:这种方法是将图形中某一部分切割下来之后,使之沿某一点或某一轴旋转一定角度贴补在另一图形的一侧,从而组合成一个新的基本规则的图形,便于求出面积.例如,欲求上图(1)中阴影部分的面积,可将左半图形绕B点逆时针方向旋转180°,使A与C重合,从而构成如右图(2)的样子,此时阴影部分的面积可以看成半圆面积减去中间等腰直角三角形的面积.九、对称添补法:这种方法是作出原图形的对称图形,从而得到一个新的基本规则图形.原来图形面积就是这个新图形面积的一半.例如,欲求右图中阴影部分的面积,沿AB在原图下方作关于AB为对称轴的对称扇形ABD.弓形CBD的面积的一半就是所求阴影部分的面积。
平面不规则图形面积求解策略

平面不规则图形面积求解策略浙江省金华市第四中学 童桂恒分析近几年中考的试题,我们可以看到:在中考客观性试题中常有一类平面不规则图形的面积问题,对这类试题由于图形的不规则使学生在求解时往往感到茫然,不知所措;然而这类试题又有较好的选拔功能,能体现对数学思想方法、思维能力素质的考查,符合“少考计算,多考思维”的中考改革思路,所以,它常常得到各地中考命题专家的青睐。
本文将结合实例谈谈平面不规则图形面积求解的若干策略。
一、割补法割补法是求解平面不规则图形面积问题最常用的方法之一,它包含三个方面的内容:一是分割原有图形成规则图形;二是粘补原有图形为规则图形;三是分割粘补兼而有之。
例1 如图1--1,ABCD 是边长为8的一个正方形, EF、 HG 、 EH 、 FG 都是半径为4的圆弧,且 EH、 FG 分别与AB 、AD 、BC 、DC 相切,则阴影部分的面积= .(05年内蒙古呼和浩特市中考题)略解,连结EG 、FH 相交于点O ,则扇形OEH 、BEF 、OGF 、DGH 全等,都是半径为4的41圆,把扇形OEH 割下,粘补到扇形BEF 上,再把扇形OGF 割下,粘补到扇形DGH 上(如图1—2所示),因此有S阴影=SBEOF正方形 +SDGOH正方形 =2×4×4=32.图1--1图1--2图2--1图2--2例2 当汽车在雨中行驶时,为了看清楚道路,司机要启动前方挡风玻璃上的雨刷器。
如图2--1是某汽车的一个雨刷器的示意图,雨刷器杆AB 与雨刷器CD 在B 处固定连接(不能转动),当杆AB 绕A 点转动90°时,雨刷CD 扫过的面积是多少呢?小明仔细观察了雨刷器的转动情况量得CD=80cm ,∠DBA=20°,端点C 、D 与点A 的距离分别是115cm 、35cm ,他经过认真思考只选用了其中的部分数据就求得了结果,你知道小明是怎样计算的吗?也请你算一算雨刷CD 扫过的面积 .cm 2 (π取3.14) (04年山东济南市中考题)略解,由于CD 和AB 在点B 处固定连接(不能转动),所以在整个运动过程中,就有AC=AC′=115cm ,AD=AD′=35cm ,CD=CD′=80cm ,因此△ACD ≌△AC′D′,把△AC′D′割下,粘补到△ACD 的位置(见图2--2),则雨刷CD 扫过的面积,就等于以A 为圆心,AC 、AD 为半径的两个41圆的面积差. 即41π (AC 2-AD 2)= 41×3.14×(1152-352)=9420cm 2. 注:在应用割补法求解问题时,往往要综合应用“分割”与“粘补”两种技能策略,对思维的灵活性和严密性有着较高的要求。
不规则四边形的面积计算公式

不规则四边形的面积计算公式摘要:一、不规则四边形的概念二、计算不规则四边形面积的方法1.割补法2.坐标法三、割补法的具体步骤1.将四边形分割成若干个小三角形2.计算小三角形的面积之和3.求得四边形的面积四、坐标法的具体步骤1.建立坐标系2.计算四边形各顶点的坐标3.计算四边形面积五、举例说明两种方法的应用1.割补法应用举例2.坐标法应用举例六、总结与展望正文:不规则四边形是指边形狀不规整的四边形。
计算不规则四边形的面积是数学中的一个常见问题,本文将介绍两种常用的计算方法:割补法和坐标法。
割补法是一种传统的方法,它的主要思路是将不规则四边形分割成若干个小三角形,然后计算这些小三角形的面积之和,从而得到四边形的面积。
具体步骤如下:首先,将四边形分割成若干个小三角形。
这可以通过将四边形的对角线连接起来,将四边形分割成若干个三角形来完成。
然后,计算这些小三角形的面积。
这可以通过使用海伦公式(Heron"s formula)来计算三角形的面积,或者通过直接计算三角形的底和高来得到。
最后,将所有小三角形的面积相加,得到的结果即为四边形的面积。
坐标法是一种基于几何坐标系的方法,它的主要思路是建立一个坐标系,然后计算四边形各顶点的坐标,从而得到四边形的面积。
具体步骤如下:首先,建立一个平面直角坐标系,并将四边形的四个顶点坐标标出。
然后,计算四边形的面积。
这可以通过计算四边形对角线在坐标轴上的投影长度,然后应用向量叉积公式来得到。
最后,得到的结果即为四边形的面积。
接下来,我们通过两个例子来说明这两种方法的应用。
例1:使用割补法计算一个不规则四边形的面积。
假设四边形的四个顶点坐标分别为A(2,3),B(5,3),C(5,1),D(2,1)。
首先,将四边形分割成若干个小三角形。
然后,计算每个小三角形的面积。
最后,将所有小三角形的面积相加,得到的结果即为四边形的面积。
例2:使用坐标法计算一个不规则四边形的面积。
不规则图形面积的解答方法之欧阳音创编

一、相加法:这种方法是将不规则图形分解转化成几个基本规则图形,分别计算它们的面积,然后相加求出整个图形的面积.例如,下图中,要求整个图形的面积,只要先求出上面半圆的面积,再求出下面正方形的面积,然后把它们相加就可以了。
二、相减法:这种方法是将所求的不规则图形的面积看成是若干个基本规则图形的面积之差.例如,下图,若求阴影部分的面积,只需先求出正方形面积再减去里面圆的面积即可。
三、直接求法:这种方法是根据已知条件,从整体出发直接求出不规则图形面积.如下图,欲求阴影部分的面积,通过分析发现它是一个底2,高4的三角形,就可以直接求面积了。
四、重新组合法:这种方法是将不规则图形拆开,根据具体情况和计算上的需要,重新组合成一个新的图形,设法求出这个新图形面积即可.例如,欲求下图中阴影部分面积,可以把它拆开使阴影部分分布在正方形的4个角处,这时采用相减法就可求出其面积了。
五、辅助线法:这种方法是根据具体情况在图形中添一条或若干条辅助线,使不规则图形转化成若干个基本规则图形,然后再采用相加、相减法解决即可.如下图,求两个正方形中阴影部分的面积.此题虽然可以用相减法解决,但不如添加一条辅助线后用直接法作更简便。
六、割补法:这种方法是把原图形的一部分切割下来补在图形中的另一部分使之成为基本规则图形,从而使问题得到解决.例如,如下图,欲求阴影部分的面积,只需把右边弓形切割下来补在左边,这样整个阴影部分面积恰是正方形面积的一半.七、平移法:这种方法是将图形中某一部分切割下来平行移动到一恰当位置,使之组合成一个新的基本规则图形,便于求出面积.例如,如下图,欲求阴影部分面积,可先沿中间切开把左边正方形内的阴影部分平行移到右边正方形内,这样整个阴影部分恰是一个正方形。
八、旋转法:这种方法是将图形中某一部分切割下来之后,使之沿某一点或某一轴旋转一定角度贴补在另一图形的一侧,从而组合成一个新的基本规则的图形,便于求出面积.例如,欲求下图(1)中阴影部分的面积,可将左半图形绕B点逆时针方向旋转180°,使A与C重合,从而构成如下图(2)的样子,此时阴影部分的面积可以看成半圆面积减去中间等腰直角三角形的面积.九、对称添补法:这种方法是作出原图形的对称图形,从而得到一个新的基本规则图形.原来图形面积就是这个新图形面积的一半.例如,欲求下图中阴影部分的面积,沿AB在原图下方作关于AB 为对称轴的对称扇形ABD.弓形CBD的面积的一半就是所求阴影部分的面积。
不规则四边形的面积计算公式

不规则四边形的面积计算公式摘要:一、不规则四边形的定义与特点二、不规则四边形面积计算的常用方法1.割补法2.投影法3.近似法三、具体步骤与实例演示四、注意事项与实用技巧正文:一、不规则四边形的定义与特点不规则四边形是指四边形的边长和角度都不规律的几何图形。
它的特点是形状各异,面积难以直接计算。
在工程技术、建筑设计等领域,不规则四边形的面积计算问题较为常见。
为了解决这一问题,我们需要掌握一些实用的计算方法。
二、不规则四边形面积计算的常用方法1.割补法割补法是将不规则四边形分割成若干个规则图形(如三角形、矩形等),然后计算这些规则图形的面积之和。
具体操作步骤如下:(1)找出不规则四边形的关键点,如顶点、边中点等。
(2)从关键点向对边作平行线,将不规则四边形分割成若干个规则图形。
(3)计算各个规则图形的面积,如三角形面积=底×高/2,矩形面积=长×宽等。
(4)将各个规则图形的面积相加,得到不规则四边形的总面积。
2.投影法投影法是将不规则四边形投影到某个方向上,计算投影面的面积,再根据投影与原图形的比例关系计算不规则四边形的面积。
具体操作步骤如下:(1)确定不规则四边形的一个投影面。
(2)计算投影面的面积,如矩形投影面积=长×高。
(3)根据投影与原图形的比例关系,计算不规则四边形的面积。
比例关系可通过平行四边形的面积与投影面积之比求得。
3.近似法近似法是将不规则四边形近似为一个相似的规则四边形,然后计算近似四边形的面积。
具体操作步骤如下:(1)选取一个合适的相似规则四边形(如矩形、平行四边形等)。
(2)计算相似四边形的边长比例。
(3)根据相似比例,计算不规则四边形的面积。
三、具体步骤与实例演示以下以一个具体实例演示不规则四边形面积计算的步骤:实例:计算一个不规则四边形的面积,已知边长分别为a=8cm,b=10cm,c=12cm,d=14cm,角度分别为α=60°,β=45°,γ=90°,δ=30°。
不规则面积计算公式

不规则面积计算公式(实用版)目录1.引言2.不规则面积计算公式的定义和原理3.计算不规则面积的常见方法和公式4.实际应用案例5.结论正文【引言】在数学和实际生活中,计算不规则形状的面积是一项常见的任务。
与规则形状(如矩形、圆形等)的面积计算公式不同,不规则形状的面积计算需要借助一些特殊的方法和公式。
本文将介绍不规则面积计算公式的定义、原理以及实际应用。
【不规则面积计算公式的定义和原理】不规则面积计算公式指的是用于计算不规则形状平面区域的面积的数学公式。
其原理主要基于积分和微积分的概念,将不规则形状分解为无数个微小元素,然后对这些元素的面积进行求和,最终得到整个不规则形状的面积。
【计算不规则面积的常见方法和公式】计算不规则面积的常见方法主要有以下几种:1.割补法:将不规则形状分割成若干个规则形状,通过计算这些规则形状的面积和来近似求得不规则形状的面积。
2.累加法:将不规则形状分解为无数个微小元素,对每个元素的面积进行累加求和,得到整个不规则形状的面积。
3.数值积分法:利用数值积分方法对不规则形状进行离散化处理,然后计算每个小区域的面积之和,得到整个不规则形状的面积。
【实际应用案例】计算不规则面积在实际生活中的应用非常广泛,例如:1.土地测绘:在土地资源管理、城市规划等领域,计算不规则土地面积是非常重要的任务。
2.物体表面积计算:在制造、建筑等领域,计算物体表面积有助于优化设计方案、降低成本。
3.计算不规则区域的统计数据:在环境科学、生态学等领域,计算不规则区域的面积有助于分析和研究相关数据。
【结论】不规则面积计算公式在数学和实际应用中具有重要意义。
通过掌握计算不规则面积的方法和公式,可以更好地解决实际生活中的一些问题。
不规则图形面积的求法

不规则图形面积的求法求不规则图形面积的基本思路是通过分割、重叠、等积替换等方法把不规则图形转化为规则图形或规则图形面积的和差。
一、等积替换(1)三角形等积替换依据:等底等高的三角形面积相等或全等的三角形面积相等。
例1、如图1所示,半圆O 中,直径AB 长为4,C 、D 为半圆O 的三等分点.,求阴影部分的面积.解:连结OC 、OD , 由C 、D 为半圆O 的三等分点知:∠COD=60°,且∠ADC=∠DAB=30°, ∴CD ∥AB ,所以ODC ADC S S ∆∆=(同底等高的三角形面积相等)∴==扇形阴影O CD S S ππ323602602=⨯⨯例2、如图2所示,在矩形ABCD 中,AB=1,以AD 为直径的半圆与BC 切于M 点,求阴影部分面积.解:由AB =1,半圆与BC 相切,得AD =2 取AD 的中点O ,则OD =BM =1。
连结OM 交 BD 于E; 则△OED ≌△MEB∴MEB OED S S ∆∆= (全等三角形面积相等)∴==扇形阴影O M D S S 43601902ππ=⨯⨯ (2)弓形等积替换依据:等弧所对的弓形面积相等。
例3、 在RT △ABC 中,∠B=90°,AB=BC=4,AB 为直径的⊙O 交AC 于点D, 求图中两个阴影部分的面积之和.解:连结BD ,由AB 为⊙O 的直径得∠ADB =90°, RT △ABC 中∠B =90°AB =BC =4,得∠A =45°且AC=AD =BD =CD=∴A D BnD S S 弓形m 弓形=∴CDB 11S CD BD 422S ∆⨯⨯⨯阴影===例4、点A、B、C、D是圆周上四点,且 AB + CD= AC + BD , 弦AB=8,CD=4,求两个阴影部分的面积之和。
解:作⊙ O 的直径BE 连结AE ,则∠BAE =90°,AB AE =+半圆;A图2图4又∵ AB + CD= AC + BD = 1AB CD AC BD 2(+++)=半圆, ∴ AE = CD ,所以A E C DS m n S 弓形弓形=,AE=CD=4。
五年级不规则图形面积计算

五年级不规则图形面积计算我们曾经学过的三角形、长方形、正方形、平行四边形、梯形、菱形、圆和扇形等图形,一般称为基本图形或规则图形.我们的面积及周长都有相应的公式直接计算.如下表:实际问题中,有些图形不是以基本图形的形状出现,而是由一些基本图形组合、拼凑成的,它们的面积及周长无法应用公式直接计算.一般我们称这样的图形为不规则图形。
那么,不规则图形的面积及周长怎样去计算呢?我们可以针对这些图形通过实施割补、剪拼等方法将它们转化为基本图形的和、差关系,问题就能解决了。
一、例题与方法指导例1 如右图,甲、乙两图形都是正方形,它们的边长分别是10厘米和12厘米.求阴影部分的面积。
思路导航:阴影部分的面积等于甲、乙两个正方形面积之和减去三个“空白”三角形(△ABG、△BDE、△EFG)的面积之和。
例2 如右图,正方形ABCD的边长为6厘米,△ABE、△ADF 与四边形AECF的面积彼此相等,求三角形AEF的面积.思路导航:∵△ABE、△ADF与四边形AECF的面积彼此相等,∴四边形 AECF的面积与△ABE、△ADF的面积都等于正方形ABCD 的13。
在△ABE中,因为AB=6.所以BE=4,同理DF=4,因此CE=CF=2,∴△ECF的面积为2×2÷2=2。
所以S△AEF=S四边形AECF-S△ECF=12-2=10(平方厘米)。
例3 两块等腰直角三角形的三角板,直角边分别是10厘米和6厘米。
如右图那样重合.求重合部分(阴影部分)的面积。
思路导航:在等腰直角三角形ABC中∵AB=10∵EF=BF=AB-AF=10-6=4,∴阴影部分面积=S△ABG-S△BEF=25-8=17(平方厘米)。
例4 如右图,A为△CDE的DE边上中点,BC=CD,若△ABC (阴影部分)面积为5平方厘米.求△ABD及△ACE的面积.B思路导航:取BD中点F,连结AF.因为△ADF、△ABF和△ABC等底、等高,所以它们的面积相等,都等于5平方厘米.∴△ACD的面积等于15平方厘米,△ABD的面积等于10平方厘米。
补形法求不规则图形的面积,到底是个什么道理?看过的都学会了
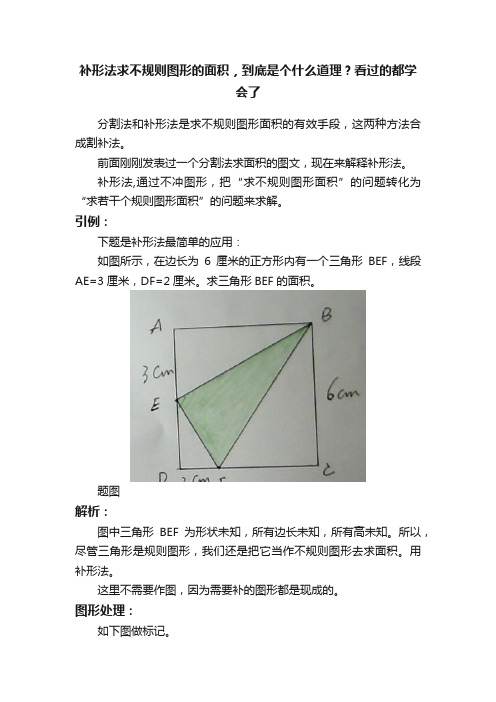
补形法求不规则图形的面积,到底是个什么道理?看过的都学会了分割法和补形法是求不规则图形面积的有效手段,这两种方法合成割补法。
前面刚刚发表过一个分割法求面积的图文,现在来解释补形法。
补形法,通过不冲图形,把“求不规则图形面积”的问题转化为“求若干个规则图形面积”的问题来求解。
引例:下题是补形法最简单的应用:如图所示,在边长为6厘米的正方形内有一个三角形BEF,线段AE=3厘米,DF=2厘米。
求三角形BEF的面积。
题图解析:图中三角形BEF为形状未知,所有边长未知,所有高未知。
所以,尽管三角形是规则图形,我们还是把它当作不规则图形去求面积。
用补形法。
这里不需要作图,因为需要补的图形都是现成的。
图形处理:如下图做标记。
很明显,正方形ABCD的面积=①+②+③+S,在这个等式中,正方形的面积和①、②、③所标示的三角形面积均可求,所以,我们可以通过移项,用这些可求的面积去表示阴影部分的面积S:S=正方形ABCD的面积-①-②-③标示处理后的图形补形法的应用举例:如图所示,长方形的长和宽分别是6厘米和4厘米,阴影部分的总面积是10平方厘米。
求四边形ABCD的面积。
题图解析:如下对图形进行标示处理。
标示处理后的图形因为四边形ABCD是个不规则四边形,所有边长未知,所有角度未知,所以直接求面积是不可能的。
在标示后的图形中,我们可以用三角形AFG的面积(①+②+③+S的和),减去①、②、③的和,即可的四边形ABCD 的面积S的值。
上图中,三角形CEF的面积+三角形CGH-阴影部分的总面积,即可得到①+②的值,而③的值等于三角形AFG的一半,也等于长方形EFGH的四分之一,很容易求出。
进而,S可求。
S=三角形AFG的面积-(①+②)-③=6×4÷2-(6×4 ÷2-10)-6×4÷2 ÷2=12-2-6=4(平方厘米)问题得解。
结束语数学中的思想方法本身往往很简单,但在实际使用中却很灵活,有时因为使用环境被过度包装,甚至看不出来题目的本质,需要进行等价转化后才能露出本来面目。
面积求解的九类方法

面积求解的九类方法一、相加法这种方法是将不规则图形转化成或割分成几个基本的规则图形,如三角形、四边形、扇形、半圆形或圆形,然后分别计算它们的面积,最后相加求出整个图形的面积。
例如求下图图形的面积。
解析:总面积=半圆的面积+正方形的面积二、相减法这种方法是将不规则图形看成是若干个基本规则图形的面积之差,然后分别计算它们的面积,最后相加减,得出所求图形的面积。
四、重新组合法这种方法是将不规则图形拆开并重组,根据具体情况和计算上的需要,重新组合成一个更容易求解的图形,这种思路可以理解为化零为整,如果在实际操作中,感觉拆分重组比较困难抽象,可以考虑单独求解每个独立的单元,然后利用相加法的思想求解。
例如求下图左侧图形阴影部分的面积。
解析:阴影部分面积=正方形的面积-圆形的面积五、辅助线法这种方法是根据图形的具体情况,在图形中添加一条或若干条辅助线,使不规则图形或一个动态图形通过平行、局部等面积转移,从而构造一个规则图形或一个面积固定的基本图形进行面积求解,通常这类题目涉及的知识点是等面积转化法,如同底等高,平行线转移顶点等,在中学阶段,这是一类难度相对较大的面积求解类问题。
例如求下图左侧图形阴影部分的面积。
解析:阴影部分面积=12ACxBH思路:连接BE,并过点B作BH⊥AC,交点为点H,因为AC、BE分别是两个正方形的对角线,所以AC∥BE,所以△ACE的面积与△ABC的面积相等。
六、割补法这种方法是将原图形的一部分切割下来补到图形中的另一部分使之成为基本规则图形,从而使问题得到解决。
这种方法的优点是构造完成后会很大程度上降低计算量,另外,割补法也是在初中阶段,计算二次函数图像或其它曲线围成的不规则图形进行求面积的唯一选择,但割补法对学生空间的想象能力有一定要求,在求解大多面积问题时,不要盲目强求通过割补,达到求解面积的目的,这样反而会在实际的考试中造成不必要的时间上浪费。
例如求下图图形阴影部分的面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【模块一】不规则图形求面积
【例1】图中是两个正方形,边长分别为8厘米和4厘米,那么阴影部分的面积是_____平方厘米。
【例2】一块矩形场地被一条路隔成甲、乙两块,甲、乙的面积之比为3∶8,尺寸如图所示,则甲
的面积是 。
【例3】如图所示,在四边形ABCD 中,线段BC 长为6厘米,角ABC 为直角,角BCD 为135°,而
且点A 到边CD 的垂线AE 的长为12厘米,线段ED 的长为5厘米,求四边形ABCD 的面积。
【例4】如图⑴,线段MN 将长方形纸分成面积相等的两部分。
沿MN 将这张长方形纸对折后得到图
⑵,将图⑵沿对称轴对折,得到图⑶,已知图⑶所覆盖的面积占长方形纸面积的3
10
,阴影部分面积为6平方厘米。
则长方形的面积是多少平方厘米?
【模块二】几何中的“差不变原理”
经典几何题解析及拓展
【例5】如下图,正方形ABCD的边长为8厘米,梯形AEBD的对角线交于点O,且△AOE的面积比△BOD的面积小16平方厘米,求梯形AEBD的面积。
【例6】如图,ABCG是4×7的长方形,DEFG是2×10的长方形,那么,三角形BCM的面积与三角形DEM的面积之差是________。
【例7】如图,四边形ABCD和四边形DEFG都是正方形,已知三角形AFH的面积为6平方厘米,求三角形CDH的面积。
【模块三】旋转与平移
【例8】如图所示,△ABC中,∠ABC=90°,AB=3,BC=5,以AC为一边向△ABC外作正方形ACD E,中心为O,求△OBC的面积。
【例9】如图,直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=3,将腰CD以D为中心逆时针旋转90°至ED,连接AE、CE,则△ADE的面积是_____。
【例10】如图,在四边形ABCD 中,∠ABC =∠ADB =105°,∠CDB =60°,∠CBD =75°,AB =
CD =15厘米,求四边形ABCD 的面积。
【模块四】利用“一半模型”巧解几何体
【例11】已知正方形的边长为10,EC =3,BF =2 ,则ABCD S 四边形 。
【例12】如图,过平行四边形ABCD 内的一点P 作边的平行线EF 、GH ,若△PBD 的面积为8平方
分米,求平行四边形PHCF 的面积比平行四边形PGAE 的面积大多少平方分米?
【例13】如右图所示,在梯形ABCD 中,E 、F 分别是其两腰AB 、CD 的中点,G 是EF 上的任意一
点,已知△ADG 的面积为15cm 2,而△BCG 的面积7
20
,则梯形ABCD 的面积是 cm 2。
【模块五】代数方法解几何问题
【例14】如图,已知CD=5,DE=7,EF=15,FG=6,线段AB将图形分成两部分,左边部分面积是38,右边部分面积是65,那么三角形ADG的面积是。
【例15】如图,长方形的长为8,宽为4,将长方形沿一条对角线折起压平,求重叠部分(阴影部分)的面积。
