内切球和外接球例题
2023年高考数学考法专练——外接球与内切球

2023年高考数学考法专练——外接球与内切球考法一、 墙角模型例1、长方体1111ABCD A B C D -的8个顶点在同一球面上,且12,3,1AB AD AA ===,则球面面积为( )A .83π B .43π C .4π D .8π例2、已知正三棱锥S -ABC 的三条侧棱两两垂直,2,则此三棱锥的外接球的表面积为( )A .πB .3πC .6πD .9π例32的正四面体的外接球体积为___________.跟踪练习1、长方体1111ABCD A B C D -的长、宽、高分别为2,2,1,其顶点都在球O 的球面上,则球O 的表面积为______.2、在三棱锥P ABC -中,已知PA ,PB ,PC 两两垂直,且1PA =,2PB =,3PC =,则三棱锥P ABC -的外接球的表面积为3、已知正四棱柱(底面为正方形且侧棱与底面垂直的棱柱)的底面边长为3,侧棱长为4,则其外接球的表面积为4、在四面体S ABC -中,SA ⊥平面ABC ,三内角B ,A ,C 成等差数列,2SA AC ==,1AB =,则该四面体的外接球的表面积为5、如图,在ABC 中,3AB AC ==1cos 3BAC ∠=-,D 是棱BC 的中点,以AD 为折痕把ACD △折叠,使点C 到达点C '的位置,则当三棱锥C ABD '-体积最大时,其外接球的表面积为6、在三棱锥P ABC -中,点A 在平面PBC 中的投影是PBC 的垂心,若ABC 是等腰直角三角形且1AB AC ==,3PC =,则三棱锥P ABC -的外接球表面积为7、已知三棱锥S ABC -的三条侧棱,,SA SB SC 两两互相垂直且13,5AC AB ==的表面积为14π,则BC =______________.8、三棱锥P ABC -中,PA ⊥平面ABC ,直线PB 与平面ABC 所成角的大小为30,AB =60ACB ∠=︒,则三棱锥P ABC -的外接球的表面积为________.9、已知三棱锥A BCD -的所有顶点都在球O 的球面上,且AB ⊥平面BCD ,AB =4AC AD ==,CD =O 的表面积为___________.10、已知长方体1111ABCD A B C D -的体积为1AA =,则当长方体1111ABCD A B C D -的表面积最小时,该长方体外接球的体积为__________.考法二、汉堡模型例1、《九章算术》中将四个面都为直角三角形的三棱锥称之为鳖臑.若三棱锥P ABC -为鳖臑,PA ⊥平面ABC ,2PA AB ==,4AC =,三棱锥P ABC -的四个顶点都在球O 的球面上,则球O 的表面积为( )A .12πB .20πC .24πD .32π例2、已知三棱锥A BCD -的所有顶点都在球O 的球面上,且AB ⊥平面BCD ,2AB =,CD =,AC AD ==O 的表面积为( )AB .2πC .3πD .6π例3、已知边长为3的正ABC 的顶点和点D 都在球O 的球面上.若6AD =,且AD ⊥平面ABC ,则球O 的表面积为( )A .B .48πC .24πD .12π跟踪练习1、已知各顶点都在同一球面上的正四棱柱的底面边长为a ,高为h ,球的体积为,则这个正四棱柱的侧面积的最大值为( )A .B .C .D .2、(多选)在四面体ABCD 中,AB AC ⊥,AC CD ⊥,直线AB ,CD 所成的角为60°,AB CD ==,4AC =,则四面体ABCD 的外接球表面积为( )A .π3B .52πC .80πD .208π3、已知四棱锥P ABCD -的五个顶点都在球О的球面上,PA ⊥平面ABCD ,底面ABCD 是高为12的等腰梯形,//AD BC ,1AD PA ==,2BC =,则球О的表面积为( )A .10πB .4πC .5πD .6π 4、在四棱锥P ABCD -中,已知PA ⊥底面,,ABCD AB BC AD CD ⊥⊥,且120,2BAD PA AB AD ∠=︒===,则该四棱锥外接球的体积为( )A .B .203πCD .5、设直三棱柱111ABC A B C -1AB AC AA ==,120BAC ∠=︒,则此直三棱柱的高是______ .6、已知正三棱柱的高与底面边长均为2,则该正三棱柱内半径最大的球与其外接球的表面积之比为( )A .17B .7C .37D .77、已知三棱锥P ABC ﹣的四个顶点都在球O 的表面上,PA ⊥平面ABC ,AB BC ⊥且8PA =,6AC =,则球O 的表面积为( )A .10πB .25πC .50πD .100π8、三棱锥P ABC -中,PA ⊥平面ABC ,30ABC ∠=︒,APC ∆的面积为3,则三棱锥P ABC -的外接球体积的最小值为( )A B C . D .9、已知四棱锥P ABCD -的顶点都在球O 的球面上,PA ⊥底面ABCD ,1AB AD ==,2BC CD ==,若球O 的表面积为9π,则四棱锥P ABCD -的体积为( )A .4B .43C .D .3考点三 斗笠模型例1、在三棱锥P ABC -中,PA PB PC ===AB AC BC ===,则三棱锥P ABC -外接球的表面积是( )A .9πB .15π2C .4πD .25π4例2、某圆锥的侧面展开后,是一个圆心角为23π的扇形,则该圆锥的体积与它的外接球的体积之比为( ) A .243256 B .128243 C .128729 D .256729例3、设圆锥的顶点为A ,BC 为圆锥底面圆O 的直径,点P 为圆O 上的一点(异于B 、C ),若BC =三棱锥A PBC -的外接球表面积为64π,则圆锥的体积为___________.跟踪练习1、已知圆锥的顶点和底面圆周都在球O 面上,圆锥的侧面展开图的圆心角为23π,面积为3π,则球O 的表面积等于( )A .818πB .812πC .1218πD .1212π 2、已知一个圆锥的底面半径为2,高为3,其体积大小等于某球的表面积大小,则此球的体积是( )A .BC .4πD .43π 3、正三棱锥P -ABC 底面边长为2,M 为AB 的中点,且PM ⊥PC ,则三棱锥P -ABC 外接球的体积为( )A .323πB .6πCD .34、已知在高为2的正四棱锥P ABCD -中,2AB =,则正四棱锥P ABCD -外接球的体积为( )A .4πB .92πC .274πD .83π 5、已知一个圆锥的底面面积为3π,侧面展开图是半圆,则其外接球的表面积等于___________. 考点四、垂面模型例1、在三棱锥P ABC -中,PAC △是等边三角形,平面PAC ⊥平面,ABC AB AC ==60CAB ∠=,则三棱锥P ABC -的外接球体积为( )A .43πBC .323πD .3例2、如图所示,在三棱锥A BCD -中,平面ACD ⊥平面BCD ,ACD △是以CD 为斜边的等腰直角三角形,AB BC ⊥,24AC CB ==,则该三棱锥的外接球的表面积为( )A .32πB .40πC .40103D .6423例3、已知三棱锥P ABC -的每个顶点都在球O 的球面上,平面ABC ⊥平面PBC ,AC BC ⊥,6AC =,8AB =,214PC PB ==,则三棱锥P ABC -外接球的表面积为( )A .503πB .533πC .100πD .32π跟踪练习1、在三棱锥D ABC -中,平面ABC ⊥平面ABD ,AB AD ⊥,4AB AD ==,6ACB π∠=,若三棱锥D ABC -的四个顶点都在同一个球面上,则该球的表面积为___________.2、在四面体ABCD 中,BCD △是边长为2的等边三角形,ABD △是以BD 为斜边的等腰直角三角形,平面ABD ⊥平面A BC ,则四面体ABCD 的外接球的表面积为__________.3、在四面体ABCD 中,已知平面ABD ⊥平面ABC ,且4AB AD DB AC CB =====,其外接球表面积为 ( )A .403πB .803πC .16πD .20π4、在三棱锥P ABC -中,平面PAB ⊥平面,23,90ABC PA PB AB BAC ===∠=︒,4AC =,则三棱锥P ABC -的外接球的表面积为( )A .20πB .643πC .32πD .80π5、已知三棱锥A BCD -中,平面ABD ⊥平面BCD ,若1AD DB BC CD ====,120ADB ∠=︒,则该三棱锥的外接球的表面积为( )A .7π3B .10π3C .20π3D .13π3考点五 矩形模型例1、若矩形ABCD 的面积是4,沿对角线AC 将矩形ABCD 折成一个大小是60°的二面角B -AC -D ,则四面体ABCD 的外接球的体积最小值为( )A .8πB .823C 6πD 1717例2、在三棱锥S ABC -中,2SAC SBC π∠=∠=,23ACB π∠=,1AC BC ==.若三棱锥S ABC -的体积为1,则该三棱锥外接球的表面积为( )A .13πB .373πC .49πD .52π例3、已知三棱锥,3,1,4,22A BCD AB AD BC BD -====A BCD -的体积最大时,则外接球的表面积为___________.跟踪练习1、四面体ABCD 中,90ABC BCD ∠=∠=︒,2AB BC CD ===,23AD =表面积为__________.2、在矩形ABCD 中23AB =2AD =,沿对角线BD 进行翻折,则三棱锥C ABD -外接球的表面积为( )A .4πB .6πC .12πD .16π3、将长、宽分别为4和3的长方形ABCD 沿对角线AC 折成直二面角,得到四面体A BCD -,则四面体A BCD -的外接球的表面积为( )A .25πB .50πC .5πD .10π4、中国古代数学家刘徽所注释的《九章算术》中,称四个面均为直角三角形的四面体为“鳖臑”.如图所示的鳖臑ABCD 中,AB ⊥面BCD ,CD BC ⊥,若1CD =,5AC =且顶点,,,A B C D 均在球O 上,则球O 的表面积为______. 考法六 、 怀表模型例1、已知S ,A ,B ,C 四点都在某个球表面上,ABC 与SBC 都是边长为1的正三角形,二面角A BC S --的大小为23π,则该球的表面积为( ) A .43π B .73π C .3π D .133π 例2、如图,菱形ABCD 的边长为6,3BAD π∠=,将其沿着对角线BD 折叠至直二面角A BD C --,连接AC ,得到四面体ABCD ,则此四面体的外接球的表面积为例3、已知菱形ABCD 的边长为4,对角线4BD =,将ABD △沿着BD 折叠,使得二面角A BD C --为120︒,则三棱锥A BCD -的外接球的表面积为___________.跟踪练习1、已知边长为ABCD 中,60A ∠=,现沿对角线BD 折起,使得二面角A BD C --为120︒,此时点A 、B 、C 、D 在同一个球面上,则该球的表面积为( ).A .20πB .28πC .32πD .36π2、在边长为3的菱形ABCD 中,BD =ABCD 沿其对角线AC 折成直二面角B AC D --,若,,,A B C D 四点均在某球面上,则该球的表面积为___________.考法七、 其他模型外接球例1、已知四棱锥P ABCD -中,ABD △是边长为2BC CD ==,60BPD ∠=,二面角P BD C --的余弦值为13-,当四棱锥的体积最大时,该四棱锥的外接球的体积为( )A .8πB .C .D .12π例2、已知三棱锥A BCD -中,===AB BD DA DC =,BC =A BD C --的大小为135︒,则三棱锥A BCD -外接球的表面积为( )A .64πB .52πC .40πD .32π例3、在四面体ABCD 中,2==AC BD ,AD BC ==AB CD ==___________.跟踪练习1、在三棱锥S ABC -中,90SBA SCA ∠=∠=︒,底面ABC 是等边三角形,三棱锥S ABC -则三棱锥S ABC -的外接球表面积的最小值是( )A .12πB .24πC .6πD .10π2、已知球O 的半径为R ,A ,B ,C 三点在球O 的球面上,球心O 到平面ABC 的距离为12R ,3AB AC ==,120BAC ∠=︒,则球O 的表面积为( )A .48πB .16πC .64πD .36π3、已知四面体ABCD 中,60BAD ∠=︒,90BCD ∠=︒,2AB AD ==,H 是BD 的中点,CH BD ⊥,120AHC ∠=︒,则四面体的外接球的表面积为( )A .275πB .3215πC .94πD .529π4、在棱长为8的正方体1111ABCD A B C D -中,P 为棱1DD 上一点,且P 到11C D 的距离与到AC 的距离相等,则四面体P ACD -的外接球的表面积为( )A .128πB .132πC .133πD .164π5、球O 的两个相互垂直的截面圆1O 与2O 的公共弦AB 的长度为2,若1O AB △是直角三角形,2O AB △是等边三角形,则球O 的表面积为( )A .9πB .12πC .16πD .20π6、如图是一个由6个正方形和8个正三角形围成的十四面体,其所有顶点都在球O 的球面上,若十四面体的棱长为1,则球O 的表面积为( )A .2πB .4πC .6πD .8π7、已知三棱锥P ABC -的四个顶点都在半径为R 的球面上,且3BAC π∠=,2BC =,若三棱锥P ABC-体积的最大值为32R ,则该球的表面积为( ) A .649π B .329π C .6427π D .169π 8、等边ABC 的边长为2,点D 为AC 的中点,将ABD △沿BD 折起到A BD ',使得23A DC π'∠=,若该三棱锥的所有顶点都在同一个球面上,则该球的表面积为______.考法八、 内切球例1、如图,在四棱锥P ABCD -中,O 是正方形ABCD 的中心,PO ⊥底面ABCD ,5PA =2AB =,则四棱锥P ABCD -内切球的体积为( )A 3πB 43πC 113πD 1253π 例2、已知球O 是棱长为24的正四面体ABCD 的内切球,球1O 与球O 外切且与正四面体的三个侧面都相切,则球1O 的表面积为( )A .24πB .12πC .8πD .6π例3、已知直三棱柱111ABC A B C -的底面ABC 为等边三角形,若该棱柱存在外接球与内切球,则其外接球与内切球表面积之比为( )A .25:1B . 1C .5:1D 1跟踪练习1、设球O 内切于正三棱柱111ABC A B C -,则球O 的体积与正三棱柱111ABC A B C -的体积的比值为________.2、已知球1O 是棱长为2的正方体1111ABCD A B C D -的内切球,球2O (在正方体1111ABCD A B C D -内部)与平面ABCD ,平面11ABB A 和平面11ADD A 都相切,并且与球1O 相切,则球1O 与球2O 的半径之比为___________.4、已知正三棱锥 P ABC -的底面边长为2,,PAB PBC 分别切于点,M N ,则MN 的长度为___________.5、《九章算术》中将四个面都为直角三角形的三棱锥称之为鳖臑,若三棱锥P ABC -为鳖臑, PA ⊥平面ABC ,4PA BC ,3AB =,AB BC ⊥,若三棱锥P ABC -有一个内切球O ,则球O 的体积为( ) A .92π B .94π C .916π D .9π6、阿基米德是古希腊伟大的数学家、物理学家、天文学家,是静态力学和流体静力学的奠基人,和高斯、牛顿并列为世界三大数学家,他在不知道球体积公式的情况下得出了圆柱容球定理,即圆柱内切球(与圆柱的两底面及侧面都相切的球)的体积等于圆柱体积的三分之二.那么,圆柱内切球的表面积与该圆柱表面积的比为( )A .12B .13C .23D .347、已知在三梭锥A BCD -中,2AB CD ==,3AD AC BC BD ====,则该三棱锥内切球的体积为( )A B C D。
立体几何外接球和内切球十大题型

立体几何外接球和内切球十大题型
立体几何中的外接球和内切球是常见的题型,下面我将列举十个常见的题型并进行解答。
1. 求立方体的外接球和内切球的半径。
外接球的半径等于立方体的对角线的一半,内切球的半径等于立方体的边长的一半。
2. 求正方体的外接球和内切球的半径。
外接球的半径等于正方体的对角线的一半,内切球的半径等于正方体的边长的一半。
3. 求圆柱体的外接球和内切球的半径。
外接球的半径等于圆柱体的底面半径,内切球的半径等于圆柱体的高的一半。
4. 求圆锥的外接球和内切球的半径。
外接球的半径等于圆锥的底面半径,内切球的半径等于圆锥的高的一半。
5. 求球的外接球和内切球的半径。
外接球的半径等于球的半径的根号3倍,内切球的半径等于球的半径的一半。
6. 求棱锥的外接球和内切球的半径。
外接球的半径等于棱锥的底面边长的一半,内切球的半径等于棱锥的高的一半。
7. 求棱柱的外接球和内切球的半径。
外接球的半径等于棱柱的底面边长的一半,内切球的半径等于棱柱的高的一半。
8. 求四面体的外接球和内切球的半径。
外接球的半径等于四面体的外接圆的半径,内切球的半径等
于四面体的内切圆的半径。
9. 求正六面体的外接球和内切球的半径。
外接球的半径等于正六面体的对角线的一半,内切球的半径等于正六面体的边长的一半。
10. 求正八面体的外接球和内切球的半径。
外接球的半径等于正八面体的对角线的一半,内切球的半径等于正八面体的边长的一半。
以上是关于立体几何中外接球和内切球的十个常见题型及其解答。
希望能对你有所帮助。
与球有关的内切、外接问题

(2)三棱锥A-BCD,侧棱长为2 5 ,底面是边长为2 3 的等边三角形, 125
则该三棱锥外接球的体积为___6__π__.
解析 如图所示,该三棱锥为正三棱锥,O为底面 BCD的中心且AO垂直于底面BCD,O′在线段AO上, O′为外接球球心, 令 O′A=O′D=R,OD=23DE=23×2 3× 23=2, AD=2 5,
(2) 三 棱 锥 A - BCD 的 四 个 面 都 是 直 角 三 角 形 , 且 侧 棱 AB 垂 直 于 底 面
BCD,BC⊥CD,AB=BC=2,且VA-BCD=
4 3
,则该三棱锥A-BCD外接
球的体积为__4___3_π__.
解析 因为AB⊥BC,BC⊥CD,构造如图所示的长方体, 则AD为三棱锥A-BCD的外接球的直径. 设外接球的半径为R. ∵VA-BCD=13×12×BC×CD×AB=16×2×CD×2=43, ∴CD=2,∴该长方体为正方体,∴AD=2 3,∴R= 3, 外接球体积为 V=43πR3=4 3π.
B,C,D都在同一球面上,则此球的体积为___3__.
解析 如图,设正四棱锥的底面中心为O1, ∴SO1垂直于底面ABCD,令外接球球心为O, ∴△ASC的外接圆就是外接球的一个轴截面圆, 外接圆的半径就是外接球的半径. 在△ASC 中,由 SA=SC= 2,AC=2,
得SA2+SC2=AC2. ∴△ASC是以AC为斜边的直角三角形. ∴A2C=1 是外接圆的半径,也是外接球的半径. 故 V 球=43π.
∴AO= AD2-OD2=4,∴OO′=4-R,
又OO′2+OD2=O′D2, ∴(4-R)2+4=R2,解得 R=52,∴V 球=43πR3=1625π.
反思 感悟
(完整版)高考外接球内切球专题练习

高考外接球与内接球专题练习(1)正方体,长方体外接球1. 如图所示,已知正方体ABCD ﹣A 1B 1C 1D 1的棱长为2,长为2的线段MN 的一个端点M 在棱DD 1上运动,另一端点N 在正方形ABCD 内运动,则MN 的中点的轨迹的面积为( )A. 4πB. 2πC. πD. 2π 2. 正方体的内切球与其外接球的体积之比为( ) A. 1:3 B. 1:3 C. 1:33 D. 1:93. 长方体ABCD ﹣A 1B 1C 1D 1的8个顶点在同一个球面上,且AB=2,AD=3,AA 1=1, 则该球的表面积为( )A. 4πB. 8πC. 16πD. 32π4. 底面边长为1,侧棱长为2的正四棱柱的各顶点均在同一球面上,则该球的体积为A. 323π B. 4π C. 2π D. 43π 5. 已知正三棱锥P ﹣ABC ,点P ,A ,B ,C 都在半径为3的球面上,若P A ,PB ,PC 两两垂直,则球心到截面ABC 的距离为 _________ .6. 在三棱椎A ﹣BCD 中,侧棱AB ,AC ,AD 两两垂直,△ABC ,△ACD ,△ADB 的 面积分别为22,32,62,则该三棱椎外接球的表面积为( ) A. 2π B. 6π C. 46π D. 24π7. 设A 、B 、C 、D 是半径为2的球面上的四点,且满足AB ⊥AC 、AD ⊥AC 、AB ⊥AD , 则S △ABC +S △ABD +S △ACD 的最大值为( )A. 4B. 8C. 12D. 168. 四面体ABCD 中,已知AB=CD=29,AC=BD=34,AD=BC=37,则四面体的 外接球的表面积为( )A. 25πB. 45πC. 50πD. 100π9. 如图,在三棱锥S ﹣ABC 中,M 、N 分别是棱SC 、BC 的中点,且MN ⊥AM ,若AB=22,则此正三棱锥外接球的体积是A. 12πB. 43πC. 433π D. 123π 10. 已知三棱锥P ABC -的顶点都在同一个球面上(球O ),且2,6PA PB PC ===, 当三棱锥P ABC -的三个侧面的面积之和最大时,该三棱锥的体积与球O 的体积的比值为( )A. 316πB. 38πC. 116πD. 18π (2)直棱柱外接球11. 已知三棱柱ABC ﹣A 1B 1C 1的6个顶点都在球O 的球面上,若AB=3,AC=4,AB ⊥AC , AA 1=12,则球O 的半径为A. 3172B. 210C. 132D. 310 12. 设三棱柱的侧棱垂直于底面,所有棱长都为a ,顶点都在一个球面上,则该球的表面 积为( )A. 2a πB. 273a πC. 2113a π D. 25a π 13. 直三棱柱ABC ﹣A 1B 1C 1的各顶点都在同一球面上,若AB=AC=AA 1=2,∠BAC=120°, 则此球的表面积等于_________ .14. 三棱锥S ﹣ABC 的所有顶点都在球O 的表面上,SA ⊥平面ABC ,AB ⊥BC ,又SA=AB=BC=1,则球O 的表面积为( )A. 32πB. 32π C. 3π D. 12π 15. 已知球O 的面上四点A 、B 、C 、D ,DA ⊥平面ABC ,AB ⊥BC ,DA=AB=BC=3, 则球O 的体积等于 _________ .(3)正棱锥外接球16. 棱长均相等的四面体ABCD 的外接球半径为1,则该四面体的棱长为___________17. 如图,在等腰梯形ABCD 中,AB=2DC=2,∠DAB=60°,E 为AB的中点,将△ADE 与△BEC 分别沿ED 、EC 向上折起,使A 、B重合于点P ,则P ﹣DCE 三棱锥的外接球的体积为( )A. 4327πB. 62π C. 68π D. 624π 18. 已知三棱锥P ABC -的所有顶点都在表面积为28916π的球面上,底面ABC 是边长为 3的等边三角形,则三棱锥P ABC -体积的最大值为__________19. 正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积 为( )A. 814π B. 16π C. 9π D. 274π 20. 已知正三棱锥P ﹣ABC 的顶点均在球O 上,且P A=PB=PC=25,AB=BC=CA=23, 则球O 的表面积为( )A. 25πB. 1256πC. 52π D. 20π21. 在球O 的表面上有A 、B 、C 三个点,且3AOB BOC COA π∠=∠=∠=,△ABC 的外接圆半径为2,那么这个球的表面积为( ) A. 48π B. 36π C. 24π D. 12π 22. 半径为2的半球内有一内接正六棱锥P ﹣ABCDEF ,则此正六棱锥的侧面积是 ____.23. 表面积为23的正八面体的各个顶点都在同一个球面上,则此球的体积为( )A. 23πB. 3π C. 23π D. 223π 24. 正四棱锥P ﹣ABCD 底面的四个顶点A 、B 、C 、D 在球O 的同一个大圆上,点P 在球面 上,如果163P ABCD V -=,则求O 的表面积为( ) A. 4π B. 8π C. 12π D. 16π(4)棱锥外接球25. 已知A ,B ,C ,D 在同一个球面上,AB ⊥平面BCD ,BC ⊥CD ,若AB=6,213AC =, AD=8,则此球的体积是 _________ .26. 在矩形ABCD 中,AB=4,BC=3,沿AC 将矩形ABCD 折成一个直二面角B ﹣AC ﹣D , 则四面体ABCD 的外接球的体积为( )A. 12512πB. 1259πC. 1256πD. 1253π 27. 点A ,B ,C ,D 在同一个球的球面上,AB=BC=2,AC=22,若四面体ABCD 体积 的最大值为43,则该球的表面积为( ) A. 163π B. 8π C. 9π D. 12π 28. 四棱锥S ﹣ABCD 的底面ABCD 是正方形,侧面SAB 是以AB 为斜边的等腰直角三角 形,且侧面SAB ⊥底面ABCD ,若AB=23,则此四棱锥的外接球的表面积为( )A. 14πB. 18πC. 20πD. 24π29. 三棱锥S ﹣ABC 的四个顶点都在球面上,SA 是球的直径,AC ⊥AB ,BC=SB=SC=2, 则该球的表面积为( )A. 4πB. 6πC. 9πD. 12π30. 已知四棱锥V ﹣ABCD 的顶点都在同一球面上,底面ABCD 为矩形,AC∩BD=G ,VG ⊥平面ABCD ,AB=3,AD=3,VG=3,则该球的体积为( )A. 36πB. 9πC. 123πD. 43π(5)内接球31. 一块石材表示的几何体的三视图如图所示,将该石材切削、打磨,加工成球,则能得到的最大球的半径等于( )A. 1B. 2C. 3D. 432. 在封闭的直三棱柱111ABC A B C -内有一个体积为V 的球,若AB BC ⊥,6,8AB BC ==,13AA =,则V 的最大值为A. 4πB. 92πC. 6πD. 323π 33. 已知球O 与棱长为4的正四面体的各棱相切,则球O 的体积为( ) A. 823π B. 833π C. 863π D. 1623π 34. 把一个皮球放入一个由8根长均为20的铁丝接成的四棱锥形骨架内,使皮球的表面 与8根铁丝都有接触点(皮球不变形),则皮球的半径为( )A. 103B. 10C. 102D. 3035. 棱长为23的正四面体内切一球,然后在正四面体和该球形成的空隙处各放入一个小 球,则这些球的最大半径为( )A. 2B. 22C. 24D. 2636. 如图,在四面体ABCD 中,截面AEF 经过四面体的内切球球心O ,且与BC ,DC 分别截于E 、F ,如果截面将四面体分成体积相等的两部分,设四棱锥A ﹣BEFD 与三棱锥A ﹣EFC的表面积分别是S 1,S 2,则必有( )A. S 1<S 2B. S 1>S 2C. S 1=S 2D. S 1,S 2的大小关系不能确定(6)球的截面问题37. 平面α截球O 的球面所得圆的半径为1,球心O 到平面α的距离为,则此球的体 积为( )A. 6πB. 43πC. 46πD. 63π38. 已知三棱锥S ﹣ABC 的所有顶点都在球O 的球面上,△ABC 是边长为1的正三角形, SC 为球O 的直径,且SC=2,则此棱锥的体积为( )A. 26B. 36C. 23D. 2239. 高为2的四棱锥S ﹣ABCD 的底面是边长为1的正方形,点S ,A ,B ,C ,D 均在半 径为1的同一球面上,则底面ABCD 的中心与顶点S 之间的距离为( )A. 102B. 232+C. 32D. 240. 已知三棱锥S ﹣ABC 的各顶点都在一个半径为r 的球面上,球心O 在AB 上,SO ⊥底面ABC ,AC =,则球的体积与三棱锥体积之比是( )A. πB. 2πC. 3πD. 4π41. 在半径为13的球面上有A ,B ,C 三点,AB=6,BC=8,CA=10,则(1)球心到平面ABC 的距离为 _________ ;(2)过A ,B 两点的大圆面与平面ABC 所成二面角为(锐角)的正切值为 ____.42. 设A 、B 、C 、D 是球面上的四个点,且在同一平面内,AB=BC=CD=DA=3,球心到 该平面的距离是球半径的一半,则球的体积是( )A. B. C. D.43. 已知过球面上A 、B 、C 三点的截面和球心的距离等于球半径的一半,且AB=BC=CA=2, 则球面面积是( ) A. 169π B. 83π C. 4π D. 649π 44. 已知OA 为球O 的半径,过OA 的中点M 且垂直于OA 的平面截球面得到圆M . 若圆M 的面积为3π,则球O 的表面积等于 _________ .45. 三棱锥P ﹣ABC 的各顶点都在一半径为R 的球面上,球心O 在AB 上,且有P A=PB=PC , 底面△ABC 中∠ABC=60°,则球与三棱锥的体积之比是 _________ .46. 已知H 是球O 的直径AB 上一点,:1:2AH HB =,AB ⊥平面α,H 为垂足,α截 球O 所得截面的面积为π,则球O 的表面积为__________(7)旋转体的外接内切47. 半径为4的球O 中有一内接圆柱.当圆柱的侧面积最大时,球的表面积与该圆柱的侧面 积之差是 _________ .48. 将4个半径都是R 的球体完全装入底面半径是2R 的圆柱形桶中,则桶的最小高度 是 _________ .1. D ;2. C ;3. B ;4. D ;5. 3; 6. B ; 7. B ; 8. C ; 9. B ;10. A ; 11. C ; 12. B ; 13. 20π; 14. C ; 15. 92π; 16. ;17. C ; 19. A ; 20. A ; 21. A ; 22. ; 23. A ; 24. D ; 25. 2563π; 26. C ; 27. C ; 28. D ; 29. B ; 30. D ; 31. B ; 32. B ; 33. A ; 34. B ; 35. C ; 36. C ; 37. B ; 38. A ; 39. A ; 40. D ;41. 12;3;42. A;43. D;44. 16π;45.3;46.92π47. 30π;48.(2R+;。
外接球内切球问题(含答案)

外接球内切球问题1. (陕西理•6)一个正三棱锥的四个顶点都在半径为1的球面上,其中底面的三个顶点在该球的一个大圆上,则该正三棱锥的体积是( )A .433 B .33 C .43 D .123 答案B 2. 直三棱柱111ABC A B C -的各顶点都在同一球面上,若12AB AC AA ===,120BAC ∠=︒,则此球的表面积等于。
解:在ABC ∆中2AB AC ==,120BAC ∠=︒,可得BC =由正弦定理,可得ABC ∆外接圆半径r=2,设此圆圆心为O ',球心为O ,在RT OBO '∆中,易得球半径R =故此球的表面积为2420R ππ=.3.正三棱柱111ABC A B C -内接于半径为2的球,若,A B 两点的球面距离为π,则正三棱 柱的体积为.答案 84.表面积为的正八面体的各个顶点都在同一个球面上,则此球的体积为A B .13π C .23π D 答案A【解析】此正八面体是每个面的边长均为a 的正三角形,所以由8=1a =A 。
5.已知正方体外接球的体积是π332,那么正方体的棱长等于( ) A.22 B.332 C.324 D.334 答案 D6.(2006山东卷)正方体的内切球与其外接球的体积之比为 ( )A .1∶3B .1∶3C .1∶33D .1∶9答案C7.(2008海南、宁夏理科)一个六棱柱的底面是正六边 形,其侧棱垂直底面.已知该六棱柱的顶点都在同一个球面上,且该六棱柱的体积为98,底面周长为3,则这个球的体积为. 答案34π 8. (2007天津理•12)一个长方体的各顶点均在同一球的球面上,且一个顶点上的三条棱 的长分别为1,2,3,则此球的表面积为.答案14π9.(2007全国Ⅱ理•15)一个正四棱柱的各个顶点在一个直径为2cm 的球面上。
如果正四 棱柱的底面边长为1cm ,那么该棱柱的表面积为cm 2.答案2+10.(2006辽宁)如图,半径为2的半球内有一内接正六棱锥P ABCDEF -,则此正六棱 锥的侧面积是________.答案11.(辽宁省抚顺一中2009届高三数学上学期第一次月考)棱长为2的正四面体的四个顶点都在同一个球面上,若过该球球心的一个截面如图,则图中三角形(正四面体的截面)的面积是.12.(2009枣庄一模)一个几何体的三视图如右图所示,则该几何体外接球的表面积为 ( )A .π3B .π2C .316πD .以上都不对答案C13.(吉林省吉林市2008届上期末)设正方体的棱长为233,则它的外接球的表面积为( ) A .π38B .2πC .4πD .π34答案C1 .(2012新课标理)已知三棱锥S ABC -的所有顶点都在球O 的求面上,ABC ∆是边长为1的正三角形,SC 为球O 的直径,且2SC =;则此棱锥的体积为 ( )FA .6B .6C .3D .225.(2012辽宁文)已知点P,A,B,C,D 是球O 表面上的点,PA ⊥平面ABCD,四边形ABCD 是边长为.若则△OAB 的面积为______________.。
高中数学《简单几何体的外接球与内切球问题》练习题

简单几何体的外接球与内切球问题一、外接球的问题:(一) 由球的定义确定球心在空间,如果一个定点与一个简单多面体的所有顶点的距离都相等,那么这个定点就是该简单多面体的外接球的球心.由上述性质,可以得到确定简单多面体外接球的球心的如下结论.结论1:正方体或长方体的外接球的球心其体对角线的中点.结论2:正棱柱的外接球的球心是上下底面中心的连线的中点.结论3:直三棱柱的外接球的球心是上下底面三角形外心的连线的中点.结论4:正棱锥的外接球的球心在其高上,具体位置可通过计算找到.结论5:若棱锥的顶点可构成共斜边的直角三角形,则公共斜边的中点就是其外接球的球心.例1、一个六棱柱的底面是正六边形,其侧棱垂直于底面,已知该六棱柱的顶点都在同一个球面上,且该六棱柱的体积为98,底面周长为3,则这个球的体积为 . 43π 例2、已知各顶点都在同一个球面上的正四棱柱的高为4,体积为16,则这个球的表面积是 .24π例3、在直三棱柱111C B A ABC -中,4,3,6,41====AA A AC AB π,则直三棱柱111C B A ABC -的外接球的表面积 .1603π例46 (二)构造正方体或长方体确定球心长方体或正方体的外接球的球心是在其体对角线的中点处.以下是常见的、基本的几何体补成正方体或长方体的途径与方法.途径1:正四面体、三条侧棱两两垂直的正三棱锥、四个面都是是直角三角形的三棱锥都分别可构造正方体.途径2:同一个顶点上的三条棱两两垂直的四面体、相对的棱相等的三棱锥都分别可构造长方体和正方体.途径3:若已知棱锥含有线面垂直关系,则可将棱锥补成长方体或正方体.途径4:若三棱锥的三个侧面两两垂直,则可将三棱锥补成长方体或正方体.例6、在三棱锥BCD A -中,BC CD BCD AB ⊥⊥,平面,543===CD BC AB ,,,则三棱锥BCD A -外接球的表面积 . 50π例7、在三棱锥BCD A -中,2,3,4AB CD AD BC AC BD ======,则三棱锥BCD A -外接球的体积 .(三) 由性质确定球心利用球心O 与截面圆圆心1O 的连线垂直于截面圆及球心O 与弦中点的连线垂直于弦的性质,确定球心.例6、正四棱锥S ABCD -S A B C D 、、、、都在同一球面上,则此球的体积为 . 43π 例8、三棱锥S_-ABC 中,SA ⊥面ABC ,SA=2。
空间几何体外接球内切球专题(50道大练习)

27.一只小球放入一长方体容器内,且与共点的三个面相接触.若小球上一点到这三个 面的距离分别为 4、5、5,则这只小球的半径是 ( ) A.3 或 8 B.8 或 11 C.5 或 8 D.3 或 11
28.在底面半径为 3,高为 4 2 3 的圆柱形有盖容器中,放入一个半径为 3 的大球后 再放入与球面、圆柱侧面及上底面均相切的小球,则放入的小球的个数最多的为 A.4 个 B.5 个 C. 6 个 D.7 个
)
AC 2 7 , PB BC 2 3 , PA 平面 PBC, 23. 已知四面体 P ABC 中, PA 4 ,
则四面体 P ABC 的内切球半径与外接球半径的比( )
A.
2 16
B.
3 2 8
C.
3 2 16
D.
2 8
试卷第 4 页,总 13 页
郭大侠的数学江湖
24 .已知三棱锥 D ABC 中, AB BC 1 , AD 2 , BD 5 , AC
每天一刻钟,数学点点通
7.已知点 在直径为
的球面上,过点 作球的两两垂直的三条弦 的最大值为(
C. D. 3
,若
,则
A. B.
)
8. 长方体的三个相邻面的面积分别是 2、 3、 6 , 这个长方体的顶点都在同一个球面上, 则这个球的表面积为( ) A.
7 2
B. 56
C. 14
D. 16
9.已知底面边长为 1,侧棱长为 2 的正四棱柱的各顶点均在同一个球面上,则该球的 体积为( ) B. 4 C. 2 D.
2 4
D.
2 6
17.已知四面体 ABCD 的一条棱长为 a ,其余棱长均为 2 3 ,且所有顶点都在表面积 为 20 的球面上,则 a 的值等于( A. 3 3 B. 2 5 ) C. 3 2 D. 3
经典三类球:外接球、内切球、棱切球(解析版)

经典三类球:外接球、内切球、棱切球1【考点预测】考点一:正方体、长方体外接球1.正方体的外接球的球心为其体对角线的中点,半径为体对角线长的一半.2.长方体的外接球的球心为其体对角线的中点,半径为体对角线长的一半.3.补成长方体(1)若三棱锥的三条侧棱两两互相垂直,则可将其放入某个长方体内,如图1所示.(2)若三棱锥的四个面均是直角三角形,则此时可构造长方体,如图2所示.(3)正四面体P -ABC 可以补形为正方体且正方体的棱长a =PA2,如图3所示.(4)若三棱锥的对棱两两相等,则可将其放入某个长方体内,如图4所示图1图2图3图4考点二:正四面体外接球如图,设正四面体ABCD 的的棱长为a ,将其放入正方体中,则正方体的棱长为22a ,显然正四面体和正方体有相同的外接球.正方体外接球半径为R =22a ⋅32=64a ,即正四面体外接球半径为R =64a .考点三:对棱相等的三棱锥外接球四面体ABCD 中,AB =CD =m ,AC =BD =n ,AD =BC =t ,这种四面体叫做对棱相等四面体,可以通过构造长方体来解决这类问题.如图,设长方体的长、宽、高分别为a ,b ,c ,则b 2+c 2=m 2a 2+c 2=n 2a 2+b 2=t2,三式相加可得a 2+b 2+c 2=m 2+n 2+t 22,而显然四面体和长方体有相同的外接球,设外接球半径为R ,则a 2+b 2+c 2=4R 2,所以R =m 2+n 2+t 28.直棱柱外接球如图1,图2,图3,直三棱柱内接于球(同时直棱柱也内接于圆柱,棱柱的上下底面可以是任意三角形)图1图2图3第一步:确定球心O 的位置,O 1是ΔABC 的外心,则OO 1⊥平面ABC ;第二步:算出小圆O 1的半径AO 1=r ,OO 1=12AA 1=12h (AA 1=h 也是圆柱的高);第三步:勾股定理:OA 2=O 1A 2+O 1O 2⇒R 2=h 22+r 2⇒R =r 2+h 2 2,解出R考点五:直棱锥外接球如图,PA ⊥平面ABC ,求外接球半径.解题步骤:第一步:将ΔABC 画在小圆面上,A 为小圆直径的一个端点,作小圆的直径AD ,连接PD ,则PD 必过球心O ;第二步:O 1为ΔABC 的外心,所以OO 1⊥平面ABC ,算出小圆O 1的半径O 1D =r (三角形的外接圆直径算法:利用正弦定理,得a sin A=b sin B =c sin C =2r ),OO 1=12PA ;第三步:利用勾股定理求三棱锥的外接球半径:①(2R )2=PA 2+(2r )2⇔2R =PA 2+(2r )2;②R 2=r 2+OO 12⇔R =r 2+OO 12.考点六:正棱锥外接球正棱锥外接球半径:R=r2+h22h.垂面模型如图1所示为四面体P-ABC,已知平面PAB⊥平面ABC,其外接球问题的步骤如下:(1)找出△PAB和△ABC的外接圆圆心,分别记为O1和O2.(2)分别过O1和O2作平面PAB和平面ABC的垂线,其交点为球心,记为O.(3)过O1作AB的垂线,垂足记为D,连接O2D,则O2D⊥AB.(4)在四棱锥A-DO1OO2中,AD垂直于平面DO1OO2,如图2所示,底面四边形DO1OO2的四个顶点共圆且OD为该圆的直径.图1图2考点八:锥体内切球方法:等体积法,即R=3V体积S表面积考点九:棱切球方法:找切点,找球心,构造直角三角形1【典型例题】1(2023春·天津宁河·高一校考期末)在三棱锥P-ABC中,AP=2,AB=3,PA⊥面ABC,且在△ABC中,C=60°,则该三棱锥外接球的表面积为()B.8πC.10πD.12πA.20π3【答案】B【解析】根据题意得出图形如右图:O为球心,N为底面△ABC截面圆的圆心,ON⊥面ABC,∵在三棱锥P-ABC中,AP=2,AB=3,PA⊥面ABC,且在△ABC中,C=60°=2r,解得r=1,∴根据正弦定理得出:3sin60°∵PA⊥面ABC,∴PA⎳ON,∵PA=2,AN=1,ON=d,∴OA=OP=R,∴根据等腰三角形得出:12+d2=(2-d)2+12,解得d=1,∴R=1+1=2∴三棱锥的外接球的表面积为4πR2=8π.故选:B.2(2023·辽宁沈阳·高一东北育才学校校考阶段练习)在正三棱锥S-ABC中,外接球的表面积为36π,M,N分别是SC,BC的中点,且MN⊥AM,则此三棱锥侧棱SA=()A.1B.2C.3D.23【答案】D【解析】取AC的中点E,连结BE、SE,∵三棱锥S-ABC正棱锥,∴SA=SC,BA=BC.又∵E为AC的中点,∴SE⊥AC且BE⊥AC∵SE、BE是平面SBE内的相交直线,∴AC⊥平面SBE,又SB在平面SBE内可得SB⊥AC又∵MN是△SBC的中位线,∴MN∥SB,可得MN⊥AC又∵MN ⊥AM ,又AM ,AC 是平面SAC 内的相交直线,∴MN ⊥平面SAC ,结合MN ∥SB ,可得SB ⊥平面SAC 又∵三棱锥S -ABC 是正三棱锥,∴∠ASB =∠BSC =∠ASC =90°,因此将此三棱锥补成正方体,则它们有相同的外接球,设球的半径为R ,可得4πR 2=36π,解得R =3,∴SA 2+SA 2+SA 2=2R =6,解之得SA =23故选:D3(2023春·河南南阳·高一校联考期末)《九章算术》是我国古代著名的数学著作,书中记载有几何体“刍甍”.现有一个刍甍如图所示,底面ABCD 为正方形,EF ∥平面ABCD ,四边形ABFE ,CDEF为两个全等的等腰梯形,EF =12AB =2,AE =23则该刍甍的外接球的体积为()A.642π3B.3πC.643π3D.642π【答案】A【解析】取AD ,BC 中点N ,M ,正方形ABCD 中心O ,EF 中点O 2,连接EN ,MN ,FM ,OO 2,如图,依题意,OO2⊥平面ABCD,EF⎳AB⎳MN,点O是MN的中点,MN=AB=4,等腰△AED中,AD⊥EN,EN=AE2-AN2=22,同理FM=22,因此,等腰梯形EFMN的高OO2=EN2-MN-EF22=7,由几何体的结构特征知,刍甍的外接球球心O1在直线OO2上,连O1E,O1A,OA,正方形ABCD外接圆半径OA= 22,则有O1A2=OA2+OO21O1E2=O2E2+O2O21,而O1A=O1E,O2E=12EF=1,当点O1在线段O2O的延长线(含点O)时,视OO1为非负数,若点O1在线段O2O(不含点O)上,视OO1为负数,即有O2O1=O2O+OO1=7+OO1,即(22)2+OO21=1+(7+OO1)2,解得OO1=0,因此刍甍的外接球球心为O,半径为OA=22,所以刍甍的外接球的体积为4π3×223=642π3.故选:A.4(2023·高一课时练习)已知圆台的上下底面半径分别为1和2,侧面积为35π,则该圆台的外接球半径为()A.1055B.654C.1854D.1054【答案】B【解析】设圆台的高和母线分别为h,l,球心到圆台上底面的距离为x,根据圆台的侧面积公式可得π1+2l=35π⇒l=5,因此圆台的高h=l2-2-12=2,当球心在圆台内部时,则12+x2=22+h-x2,解得x=74,故此时外接球半径为1+x2=65 16=65 4,当球心在圆台外部时,则12+x2=22+x-h2,x>h,解得x=74不符合要求,舍去,故球半径为65 4故选:B5(2023·高一课时练习)已知圆锥的底面半径为2,高为42,则该圆锥的内切球表面积为()A.4πB.42πC.82πD.8π【答案】D【解析】如图,圆锥与内切球的轴截面图,点O为球心,内切球的半径为r,D,E为切点,设OD=OE=r,即BE=BD=2由条件可知,AB=422+22=6,△ADO中,AO2=AD2+DO2,即42-r2=6-22+r2,解得:r=2,所以圆锥内切球的表面积S=4πr2=8π.故选:D6(2023·高一课时练习)一个正四棱柱的每个顶点都在球O的球面上,且该四棱柱的底面面积为3,高为10,则球O的体积为()A.16πB.32π3C.10π D.28π3【答案】B【解析】设该正四棱柱的底面边长为a,高为h,则a2=3,h=10,解得a=3,所以该正四棱柱的体对角线为球O的直径,设球O的半径为R,所以,2R=a2+a2+h2=3+3+10=4,即R=2,所以,球O的体积为4π3×23=32π3.故选:B7(2023·高一课时练习)正八面体是每个面都是正三角形的八面体.如图所示,若此正八面体的棱长为2,则它的内切球的表面积为()A.423π B.8327π C.83π D.163π【答案】C【解析】以内切球的球心为顶点、正八面体的八个面为底面,可将正八面体分为8个全等的正三棱锥,设内切球的半径为r ,则8V 三棱锥=V 正八面体=2V 正四棱锥,且正四棱锥的高为图中CO ,易得CO =2,即:8×13×12×2×2×32 ⋅r =2×13×2×2 ×2解得:r =63,所以,内切球的表面积为8π3.故选:C .8(2023·高一课时练习)已知A ,B ,C 三点均在球O 的表面上,AB =BC =CA =2,且球心O 到平面ABC 的距离等于球半径的13,则下列结论正确的为()A.球O 的外切正方体的棱长为6B.球O 的表面积为8πC.球O 的内接正方体的棱长为3D.球O 的半径为32【答案】A【解析】设球O 的半径为R ,△ABC 的外接圆半径为r ,则r =233,因为球心O 到平面ABC 的距离等于球O 半径的13,所以R 2-19R 2=43,得R 2=32,即R =62,故D 错误;球O 的外切正方体的棱长b 满足b =2R =6,故A 正确;所以球O 的表面积S =4πR 2=4π×32=6π,故B 错误;球O 的内接正方体的棱长a 满足3a =2R =6,即a =2,故C 错误.故选:A .9(2023·河南开封·开封高中校考模拟预测)已知某棱长为22的正四面体的各条棱都与同一球面相切,则该球与此正四面体的体积之比为()A.π2B.π3C.3π3D.2π2【答案】A【解析】如图,正方体ABCD -A 1B 1C 1D 1中,棱长为2,所以,四面体A 1BDC 1是棱长为22的正四面体,当正四面体的各条棱都与同一球面相切时,该球为正方体的内切球,半径为1,所以,该球的体积为4π3,因为正四面体的体积为8-4×13×12×2×2×2=8-163=83,所以,该球与此正四面体的体积之比为4π383=π2.故选:A10(2023·高一课时练习)正四面体ABCD 的棱长为a ,O 是棱AB 的中点,以O 为球心的球面与平面BCD 的交线和CD 相切,则球O 的体积是()A.16πa 3B.26πa 3 C.36πa 3 D.23πa 3【答案】D【解析】设点A 在平面BCD 内的射影为点E ,则E 为△BCD 的中心,取CD 的中点M ,连接BM ,则E ∈BM ,取线段BE 的中点F ,连接OF ,因为O 、F 分别为AB 、BE 的中点,则OF ⎳AE 且OF =12AE ,因为AE ⊥平面BCD ,则OF ⊥平面BCD ,因为BE ⊂平面BCD ,则AE ⊥BE ,正△BCD的外接圆半径为BE=a2sinπ3=33a,∴AE=AB2-BE2=63a,所以,OF=12AE=66a,易知球O被平面BCD所截的截面圆圆心为点F,且BF=EF=EM,故FM=BE=33a,因为△BCD为等边三角形,M为CD的中点,则BM⊥CD,因为以O为球心的球面与平面BCD的交线和CD相切,则切点为点M,则球O的半径为OM=OF2+FM2=22a,因此,球O的体积是V=43π×22a3=23πa3.故选:D.11(2023·高一课时练习)已知直三棱柱ABC-A1B1C1的底面为直角三角形,如图所示,∠BAC= 90°,AB=1,AC=2,AA1=3,则四面体A-A1BC的体积为,四棱锥A1-BCC1B1的外接球的表面积为.【答案】 1 14π【解析】由题意可得S△ABC=12×AB⋅AC=12×2×1=1,且h=AA1,则V A-A1BC=13S△ABC⋅h=13×1×3=1因为△ABC 外接圆的圆心即为BC 中点,设为O ,△A 1B 1C 1外接圆的圆心即为B 1C 1中点,设为O 1,则OO 1的中点到六个顶点的距离相等,则OO 1的中点M 为外接球的球心,即CM 为半径,OC =12BC =12AC 2+AB 2=52,OM =12AA 1 =32所以CM =OC 2+OM 2=54+94=142,即外接球的表面积为4πR 2=4π×144=14π故答案为:1,14π2【过关测试】一、单选题1(2023·高一课时练习)若正四面体的表面积为83,则其外接球的体积为()A.43πB.12πC.86πD.323π【答案】A【解析】设正四面体的棱长为a ,由题意可知:4×34a 2=83,解得:a =22,所以正四面体的棱长为22,将正四面体补成一个正方体,则正方体的棱长为2,正方体的体对角线长为23,因为正四面体的外接球的直径为正方体的体对角线长,所以外接球半径R =3,则外接球的体积为V =43πR 3=43π,故选:A .2(2023·陕西渭南·高一统考期末)在直三棱柱ABC -A 1B 1C 1中,AB =BC =2,AA 1=22,∠ABC =π2,则此三棱柱外接球的表面积为()A.4πB.8πC.16πD.24π【答案】C 【解析】因为AB=BC=2,∠ABC=π2,所以△ABC为等腰直角三角形,将直三棱柱ABC-A1B1C1补全为如图长方体ABCD-A1B1C1D1,则长方体的外接球即直三棱柱的外接球,因为AB=BC=2,AA1=22,所以外接球直径2R=AC1=22+22+222=4,所以外接球半径R=2,表面积S=4πR2=16π.故选:C.3(2023春·河北衡水·高一校考阶段练习)在正四棱锥P-ABCD中,AB=4,PA=26,则平面PAB截四棱锥P-ABCD外接球的截面面积是()A.65π5B.36π5C.12πD.36π【答案】B【解析】如图,作PO ⊥平面ABCD,垂足为O ,则O 是正方形ABCD外接圆的圆心,从而正四棱锥P-ABCD外接球的球心O在PO 上,取棱AB的中点E,连接O D,O E,OD,PE,作OH⊥PE,垂足为H.由题中数据可得O D=22,O E=2,PE=25,O P=4,设四棱锥P-ABCD外接球的半径为R,则R2=O D2+O O2=OP2=O P-O O2,即R2=8+O O2=4-O O2,解得R=3.由题意易证△OPH∽△EPO ,则PHO P=OPPE,故PH=65 5.故所求截面圆的面积是π⋅PH2=36π5.故选:B4(2023春·山西太原·高一校考阶段练习)在三棱锥P -ABC 中,PA =PB =PC =3,侧棱PA与底面ABC 所成的角为60°,则该三棱锥外接球的体积为()A.πB.π3C.4πD.4π3【答案】D【解析】设点P 在平面ABC 内的射影点为E ,如下图所示:由线面角的定义可知,直线PA 与底面ABC 所成的角为∠PAE =60°,所以,PE =3sin60°=32,AE =3cos60°=32,因为PE ⊥平面ABC ,BE 、CE ⊂平面ABC ,∴PE ⊥BE ,PE ⊥CE ,∴BE =PB 2-PE 2=32=PC 2-PE 2=CE ,所以,△ABC 的外接圆圆心为点E ,且其外接圆半径为32,所以,三棱锥P -ABC 的外接球球心O 在直线PE 上,设球O 的半径为r ,由几何关系可得OE 2+AE 2=OA 2,即32-r 2+322=r 2,解得r =1,因此,三棱锥P -ABC 外接球的体积为V =43πr 3=43π.故选:D .5(2023春·河南鹤壁·高一河南省浚县第一中学校考阶段练习)已知三棱锥P -ABC 的四个顶点均在同一个球面上,底面ABC 满足BA =BC =6,∠ABC =π2,若该三棱锥体积的最大值为3,则其外接球的体积为()A.323π B.32π C.16π D.823π【答案】A【解析】在△ABC中,BA=BC=6,∠ABC=π2,因此三棱锥P-ABC的外接球被平面ABC截得的截面小圆圆心是AC的中点O1,令三棱锥P-ABC的外接球球心为O,则OO1⊥平面ABC,而S△ABC=12AB⋅BC=3,O1A=3,因三棱锥P-ABC体积的最大值为3,则三棱锥P-ABC底面ABC上的高最大,设此最大高为h,由13×3h=3得h=3,要三棱锥P-ABC的体积最大,当且仅当球O上的点P到平面ABC的距离最大,则点P在线段O1O的延长线上,设球O半径为R,则有(h-R)2+O1A2=R2,即(3-R)2+(3)2=R2,解得R=2,所以三棱锥P-ABC的外接球体积为V=43πR3=323π.故选:A6(2023·高一课时练习)《九章算术》是我国古代数学名著,它在几何学中的研究比西方早1000多年.在《九章算术》中,将底面为矩形且一侧棱垂直于底面的四棱锥称为阳马.如图P-ABCD 是阳马,PA⊥平面ABCD,PA=5,AB=3,BC=4.则该阳马的外接球的表面积为()A.1252π3B.50π C.100π D.500π3【答案】B【解析】因PA⊥平面ABCD,AB⊂平面ABCD,AD⊂平面ABCD,则PA⊥AB,PA⊥AD,又因四边形ABCD为矩形,则AB⊥AD.则阳马的外接球与以PA,AB,AD为长宽高的长方体的外接球相同.又PA=5,AB=3,AD=BC=4.则外接球的直径为长方体体对角线,故外接球半径为:R=PA2+AB2+AD22=32+42+522=522,则外接球的表面积为:S=4πR2=4π⋅504=50π.故选:B7(2023·吉林·高一吉林一中校考阶段练习)如图,在△ABC中,AB=25,BC=210,AC=213,D ,E ,F 分别为三边中点,将△BDE ,△ADF ,△CEF 分别沿DE ,EF ,DF 向上折起,使A ,B ,C 重合为点P ,则三棱锥P -DEF 的外接球表面积为()A.72π B.7143π C.14π D.56π【答案】C【解析】由题意可知,PE =DF =10,PF =DE =13,PD =EF =5,即三棱锥P -DEF 的对棱相等,先将该三棱锥补充成长方体,如图所示:设FH =x ,HD =y ,HP =z ,则x 2+y 2=10,y 2+z 2=5,x 2+z 2=13,所以x 2+y 2+z 2=14,于是三棱锥P -DEF 的外接球直径为14,半径为142,所以该三棱锥外接球的表面积为:4π⋅142 2=14π.故选:C .8(2023·高一课时练习)如图,在等腰梯形ABCD 中,AB =2DC =2,∠DAB =60°,E 为AB 中点.将ΔADE 与ΔBEC 分别沿ED 、EC 折起,使A 、B 重合于点P ,则三棱锥P -DCE 的外接球的体积为()A.43π27B.6π2C.6π8D.6π24【答案】C【解析】易证所得三棱锥为正四面体,它的棱长为1,故其外接球与棱长为22的正方体的外接球一直,又正方体外接球半径为R=12+12+122=64故外接球的体积为43π633=68π故选C.9(2023·高一课时练习)边长为1的正四面体内切球的体积为()A.6π8B.212C.π6D.6π216【答案】D【解析】将棱长为1的正四面体ABCD补成正方体AECF-GBHD,则该正方体的棱长为22,V A-BCD=223-4V B-ACE=24-4×13×12×22 3=212,设正四面体ABCD的内切球半径为r,正四面体ABCD每个面的面积均为34×12=34,由等体积法可得V A-BCD=212=13r S△ABC+S△ACD+S△ABD+S△BCD=33r,解得r=612,因此,该正四面体的内切球的体积为V=43π×6123=6216π.故选:D.10(2023·高一课时练习)已知三棱锥S-ABC的所有顶点都在球O的球面上,SC是球O的直径.若平面SAC⊥平面SBC,SA=AC,SB=BC,球O的体积为36π,则三棱锥S-ABC的体积为()A.9B.18C.27D.36【答案】A【解析】如图,三棱锥S-ABC的所有顶点都在球O的球面上,SC是球O的直径O为SC中点,SA=AC,SB=BC∴AO⊥SC,BO⊥SC,∵平面SAC⊥平面SBC,平面SAC∩平面SBC=SC,BO⊂平面SBC,∴BO⊥平面SCA,设BO=r,由球O的体积为36π,可得43πr3=36π,∴r=3,则V S-ABC=V B-SCA=13S△SCA⋅BO=13×12×2r×r×r=13r3=9,∴三棱锥S-ABC的体积为9,故选∶A.11(2023·高一课时练习)如下图是一个正八面体,其每一个面都是正三角形,六个顶点都在球O 的球面上,则球O与正八面体的体积之比是()A.πB.4π3C.3π2D.2π【答案】A【解析】由题意得正方形ABCD的中心O即为外接球球心,设AB=a,则R=OA=22a,球O的体积为V1=43π×22a3=2π3a3,而h=OE=22a,故正八面体的体积V2=2×13×a2×22a=23a3,得V1V2=π,故选:A12(2023·高一课时练习)已知三棱柱ABC-A1B1C1所有的顶点都在球O的球面上,球O的体积是500π3,∠ABC =60°,AC =43,则AA 1=()A.3B.6C.4D.8【答案】B【解析】设球O 的半径为R ,△ABC 外接圆的半径为r ,则43πR 3=500π3,解得R =5,因为∠ABC =60°,AC =43,由正弦定理得,△ABC 外接圆的半径r =432sin60°=4,则AA 1=2R 2-r 2=2×3=6.故选:B二、多选题13(2023春·湖北襄阳·高一襄阳四中校考阶段练习)如图,线段AB 为圆O 的直径,点E ,F 在圆O 上,EF ⎳AB ,矩形ABCD 所在平面和圆O 所在平面垂直,且AB =2,EF =AD =1,则下列说法正确的是()A.OF ⎳平面BCEB.BF ⊥平面ADFC.三棱锥C -BEF 外接球的体积为5πD.三棱锥C -BEF 外接球的表面积为5π【答案】ABD【解析】选项A :由EF ⎳AB ,AB =2,EF =1,可得EF // OB 则四边形OBEF 为平行四边形,则OF ⎳BE又OF ⊄平面BCE ,BE ⊂平面BCE ,则OF ⎳平面BCE .判断正确;选项B :连接BF ,线段AB 为圆O 的直径,则BF ⊥AF 由平面ABCD ⊥平面ABEF ,平面ABCD ∩平面ABEF =AB AD ⊂平面ABCD ,AD ⊥AB ,则AD ⊥平面ABEF则AD ⊥BF ,又AF ∩AD =A ,AF ⊂平面ADF ,AD ⊂平面ADF 则BF ⊥平面ADF .判断正确;选项C :取CD 中点H ,连接OH由平面ABCD ⊥平面ABEF ,平面ABCD ∩平面ABEF =ABOH ⊥AB ,OH ⊂平面ABEF ,可得OH ⊥平面ABEF又点E ,F ,B 在圆O 上,则三棱锥C -BEF 外接球球心在直线OH 上,由OH ⎳BC ,OH ⊄平面BCE ,BC ⊂平面BCE可得OH ⎳平面BCE ,则三棱锥C -BEF 外接球球心到平面BCE 的距离为点O 到平面BCE 的距离由BC ⊥平面ABEF ,BC ⊂平面BCE ,可得平面BCE ⊥平面ABEF ,则点O 到平面BCE 的距离即点O 到直线BE 的距离,又点O 到直线BE 的距离为32,则三棱锥C -BEF 外接球球心到平面BCE 的距离为32在△BCE 中,BC ⊥BE ,BC =BE =1,则CE =2,则△BCE 外接圆半径为22则三棱锥C -BEF 外接球的半径R =22 2+32 2=52则三棱锥C -BEF 外接球的体积为43π⋅52 3=556π.判断错误;选项D :由三棱锥C -BEF 外接球的半径R =52则三棱锥C -BEF 外接球的表面积为4πR 2=4π⋅522=5π.判断正确.故选:ABD14(2023春·江苏无锡·高一江苏省江阴市第一中学校考阶段练习)我们把所有棱长都相等的正棱柱(锥)叫“等长正棱柱(锥)”,而与其所有棱都相切的称为棱切球,设下列“等长正棱柱(锥)”的棱长都为1,则下列说法中正确的有()A.正方体的棱切球的半径为2B.正四面体的棱切球的表面积为π2C.等长正六棱柱的棱切球的体积为4π3D.等长正四棱锥的棱切球被棱锥5个面(侧面和底面)截得的截面面积之和为7π12【答案】BCD 【解析】正方体的棱切球的直径为正方体的面对角线,正方体的棱切球的半径为面对角线的一半,即为22,选项A 错误;如图,四面体ABCD 为棱长为1的正四面体,把正四面体ABCD 放到正方体中,则正方体的棱长即为正四面体的棱切球的直径,所以正四面体的棱切球的半径为24,即正四面体的棱切球的表面积为π2,选项B 正确;如图,等长正六棱柱的棱切球的直径为AB ,即直径为2,半径为1,所以等长正六棱柱的棱切球的体积为4π3,选项C 正确;由棱切球的定义可知,棱切球被每一个面所截,截面为该面的内切圆,则等长正四棱锥的底面内切圆的面积为π×12 2=π4,每个侧面正三角形的内切圆的半径为正三角形高的13,即36,所以四个侧面正三角形的内切圆的面积为4×π×36 2=π3,所以等长正四棱锥的棱切球被棱锥5个面截得的截面面积之和为π4+π3=7π12,选项D 正确.故选:BCD .15(2023春·湖南邵阳·高一湖南省邵东市第三中学校考期中)已知正方体ABCD -A 1B 1C 1D 1的各棱长均为2,下列结论正确的是()A.该正方体外接球的直径为23B.该正方体内切球的表面积为4πC.若球O 与正方体的各棱相切,则该球的半径为2D.该正方体外接球的体积为43【答案】ABC【解析】若正方体的棱长为2,则:①若球为正方体的外接球,则外接球直径等于正方体体对角线,即2R =22+22+22=23,故A 正确,外接球体积为43πR 3=43π,故D 错误;②若球为正方体的内切球,则内切球半径为棱长的一半,故R =1,球的表面积为4πR 2=4π,故B 正确;③若球与正方体的各棱相切,则球的直径等于正方形对角线长,即R =22+22=22,球的半径为R =2,故C 正确.故本题选:ABC .三、填空题16(2023春·陕西汉中·高一校考期中)已知球O 是四棱锥P -ABCD 的外接球,四边形ABCD 是边长为1的正方形,点P 在球面上运动且PA =2,则当四棱锥P -ABCD 的体积最大时,球O 的表面积是.【答案】6π【解析】设PA 与平面ABCD 夹角为θ,则四棱锥P -ABCD 的体积为V =13S ABCD ⋅h =13×1×h =13×PA ×sin θ=23sin θ,当sin θ=1时,四棱锥P -ABCD 的体积最大,即θ=90°,此时PA ⊥平面ABCD ,将四棱锥P -ABCD 补成一个正四棱柱,如图所示,此时四棱锥P -ABCD 和该正四棱柱有相同的外接球O ,设球O 的半径为R ,则2R =PC =12+12+22=6,可得R =62,所以球O 的表面积为S =4πR 2=4π×622=6π.故答案为:6π17(2023·高一课时练习)、已知正方体外接球的体积是323π,那么正方体的棱长等于【答案】433【解析】设正方体的棱长为a ,则外接球的半径为3a 2,外接球的体积V =4π3R 3=4π3×3a 2 3=3πa 32=32π3,解得a =433,即正方体的棱长等于433.18(2023春·浙江宁波·高一余姚中学校考阶段练习)已知某圆锥的内切球的体积为32π3,则该圆锥的表面积的最小值为.【答案】32π【解析】设圆锥的内切球半径为r ,则43πr 3=32π3,解得r =2,设圆锥顶点为A ,底面圆周上一点为B ,底面圆心为C ,内切球球心为D ,内切球切母线AB 于E ,底面半径BC =R >2,∠BDC =θ,则tan θ=R 2,又∠ADE =π-2θ,由已知△BDE ,△BDC 为直角三角形,又DC =DE ,BD =BD ,所以△BDE ≅△BDC ,所以BE =BC =R ,∠BDE =∠BDC =θ,所以∠ADE =π-2θ,故AB=BE +AE =R +2tan π-2θ =R -2tan2θ,又tan2θ=2tan θ1-tan 2θ=R 1-R 24=4R 4-R 2,故AB =R -8R 4-R 2=R R 2+4 R 2-4,故该圆锥的表面积为S =πR 2R 2+4 R 2-4+πR 2=2πR 4R 2-4,令t =R 2-4>0,则S =2π(t +4)2t =2πt +16t +8 ≥2π2t ×16t +8 =32π,当且仅当t =16t,即t =4,R =22时取等号.故答案为:32π.19(2023·高一课时练习)如果圆柱、圆锥的底面直径和高都等于一个球的直径,则圆柱、球、圆锥的体积的比是.【答案】3:2:1【解析】设球的半径为r ,则球的体积为V 球=43πr 3,圆柱的体积为V 圆柱=πr 2⋅2r =2πr 3,圆锥的体积为V 圆锥=13πr 2⋅2r =2πr 33,因此,V 圆柱:V 球:V 圆锥=2:43:23=3:2:1.故答案为:3:2:1.20(2023·高一课时练习)已知A 、B 、C 是球面上三点,且AB =AC =4,∠BAC =90°,若球心O 到平面ABC 的距离为22,则该球表面积为.【答案】64π【解析】因为AB =AC =4,∠BAC =90°,所以BC 为平面ABC 截球所得小圆的直径,如图,设小圆的半径为r ,得2r =AB 2+AC 2=42,解得r =22,又球心O 到平面ABC 的距离d =22,根据球的截面圆性质,得球的半径R =r 2+d 2=4,所以球的表面积为S =4πR 2=64π.故答案为:64π.21(2023春·河南商丘·高一商丘市第一高级中学校考期中)已知正三棱锥S -ABC ,SA =SB =SC =23,AB =3,球O 与三棱锥S -ABC 的所有棱相切,则球O 的表面积为.【答案】(19-83)π【解析】取等边△ABC 的中心E ,连接SE ,则SE ⊥平面ABC ,连接AE 并延长,交BC 于点D ,则D 为BC 中点,且AD ⊥BC ,在SE 上找到棱切球的球心O ,连接OD ,则OD 即为棱切球的半径,过点O 作OF ⊥SA 于点F ,则OF 也是棱切球的半径,设OD =OF =R ,因为SA =SB =SC =23,AB =3,所以求得AD =332,AE =3,DE =32,由勾股定理得:SE =12-3=3,且∠ASE =30°,设OE =h ,OD =OE 2+ED 2=h 2+34,SO =3-h ,OF =123-h ,由题意得:h 2+34=123-h ,解得:h =3-1或-1-3,当h=3-1时,R2=h2+34=194-23,此时球O的表面积为(19-83)π;当棱切球的半径最大时,切点为A,B,C,由于∠ASE=30°,SA=SB=SC=23,可求得最大半径R=23tan30°=2,而当h=-3-1时,R2=h2+34=194+23>4,显然不成立,故h=-3-1舍去,综上:球O的表面积为(19-83)π故答案为:(19-83)π22(2023春·山东德州·高一德州市第一中学校考阶段练习)边长为2的正四面体内有一个球,当球与正四面体的棱均相切时,球的体积为.【答案】2 3π【解析】结合正四面体的性质:球心在正四面体的体高上,且为外接球的球心,如下图:取球心O,若OD⊥PA,则OD即为球的半径,而O 为底面中心,∴PO ⊥面ABC,若E为BC中点,则AE=PE=3,∴PO =263,PO=62,AO=233,由Rt△PDO∼Rt△PO A,则POPA=ODAO,故OD=22,∴球的体积为43π⋅OD3=23π.故答案为:23π23(2023春·广东江门·高一江门市培英高级中学校考期中)已知正方体的棱长为2,则与正方体的各棱都相切的球的表面积是.【答案】8π【解析】过正方体的对角面作截面如图,故球的半径r=2,∴其表面积S=4π×(2)2=8π.故答案为:8π.24(2023春·江苏苏州·高一江苏省苏州实验中学校考阶段练习)一个球被平面截下的一部分叫做球缺,截面叫做球缺的底面,垂直于截面的直径被截下的线段长叫做球缺的高,球缺的体积公式为V =π3(3R-h)h2,其中R为球的半径,h为球缺的高.若一球与一棱长为2的正方体的各棱均相切,则该球与正方体的公共部分的体积为.【答案】10-162 3π【解析】由题可得该球与正方体的公共部分球去掉6个球缺,则球的半径为R=22+222=2,球缺高h=2-1,则一个球缺的体积为π332-2-12-12=π342-5,则该球与正方体的公共部分的体积为4π3×23-6×π342-5=10-1623π.故答案为:10-162 3π.四、解答题25(2023·全国·高一专题练习)已知球与正四面体的六条棱都相切,求球与正四面体的体积之比.【解析】如图,设正四面体棱长为a,球半径为R,取AB的中点为E,CD中点F,连接AF,BF,EF,则AF=BF=32a,∴EF⊥AB,同理EF⊥CD,∴EF是AB,CD的公垂线,则EF的长是AB,CD的距离,EF=AF2-AE2=34a2-14a2=22a,又由球与正四面体的六棱都相切,得EF是该球的直径,即2R=22a,∴R3=232a3,V 球=43πR3=43π⋅232a3=224πa3,又V正四面体=13×S×h=13×12×a×a×sin60°×63a=212a3,故V球V正四面体=π226(2023·高一课时练习)有三个球,已知球O1内切于正方体,球O2与这个正方体各棱都相切,球O3过这个正方体的各个顶点,求球O1、球O2、球O3的表面积之比.【解析】设正方体的棱长为a.①球O1为正方体的内切球,球心O1是正方体的中心,切点是正方体六个面的中心,经过四个切点及球心作截面,如图1所示,设球O1的半径为r1,表面积为S1,则2r1=a,r1=a2,所以S1=4πr21=πa2.②球O2与正方体各棱的切点为各棱的中点,过正方体的两个相对面的面对角线作截面,如图2所示,设球O2的半径为r2,表面积为S2,则2r2=2a,r2=22a,所以S2=4πr22=2πa2.③球O3过正方体的各个顶点,即正方体的各个顶点都在球面上,过正方体的体对角线作截面,如图3所示,设球O3的半径为r3,表面积为S3,则2r3=3a,r3=32a,所以S3=4πr23=3πa2.故这三个球的表面积之比S1:S2:S3=πa2:2πa2:3πa2=1:2:3.图1 图2 图3。
内切圆与外接球专题含答案

内切球与外接球专题(1)1.已知S,A,B,C是球O表面上的点,SA⊥平面ABC,AB⊥BC,SA=AB=1,BC=√2,求球O的表面积.2.已知四棱锥S−ABCD的底面是等腰梯形,AB//CD,AD=DC=BC=1,AB=SA=2且SA⊥平面ABCD,则四棱锥S−ABCD的外接球的体积为_________.3.正三棱锥的高为1,底面边长为2√6,内有一个球与它的四个面都相切(如图).求:(1)这个正三棱锥的表面积;(2)这个正三棱锥内切球的表面积与体积.4.一个六棱柱的底面是正六边形,其侧棱垂直底面.已知该六棱柱的顶点都在同一个球面上,且该六棱柱的高为√3,底面周长为3,求这个球的体积.5.如图,正四棱锥P−ABCD底面的四个顶点A,B,C,D在球O的同一个大圆上,点P在球面上,如果V P−ABCD=16,则球O的表面积是______.36.将边长为2的正△ABC沿BC边上的高AD折成直二面角B—AD—C,则三棱锥B—ACD的外接球的表面积为________.7.四棱锥P−ABCD中,底面ABCD为正方形,PD⊥底面ABCD,AB=1,PD=√2,若点E为PB的中点,则四面体EPCD外接球的体积是_______.8.直三棱柱ABC−A1B1C1的各顶点都在同一球面上,若AB=AC=AA1=2,∠BAC=60°,则此球的表面积等于________.9.三棱锥D−ABC内接于球O,DC⊥平面ABC,∠ACB=30°,AB=2,DC=4,则三棱锥D−ABC外接球的体积为________.10.直角△ABC的三个顶点都在球O的球面上,且AB=AC=2,若三棱锥O—ABC的体积为2,则该球的表面积为________.11.已知一个圆锥内接于球O(圆锥的底面圆周及顶点均在球面上),圆锥的高为2,底面半径为1,则球O的表面积为________.12.“正四棱锥的顶点都在球O的球面上”,若该棱锥的高为4,底面边长为2,求该球的体积.答案和解析1.【答案】解:∵SA⊥平面ABC,AB⊥BC,∴四面体S−ABC的外接球半径等于以长宽高分别SA,AB,BC三边长的长方体的外接球的半径,∵SA=AB=1,BC=√2,∴2R=√SA2+AB2+BC2=2,∴球O的表面积S=4πR2=4π.2.【答案】【解析】【分析】本题考查了几何体的外接球、几何体外接球的体积计算.【解答】过点A,B,C,D作球O的截面如图1,设AB中点为O1,连接O1C,O1D,则CD=//O1A,所以四边形ADCO1平行四边形,所以O1C=1,同理O1D=1,所以O1A=O1B=O1C=O1D,所以O1是等腰梯形ABCD的外心,过S,A,B作球O的截面如图2,设BS的中点为O,连接O1O,OA,则O1O//SA,所以O1O⊥平面ABCD,所以OA=OB=OC=OD,又SA⊥AB,所以OA=OS,所以点O是四棱锥S−ABCD的外接球球心,OA为四棱锥S−ABCD外接球的半径,在中,AB=SA=2,∴OA=12BS=√2.3.【答案】解:(1)底面正三角形的中心到一边的距离为13×√32×2√6=√2,则正棱锥侧面的斜高为√12+(√2)2=√3,所以S侧=3×12×2√6×√3=9√2,所以S表=S侧+S底=9√2+12×√32×(2√6)2=9√2+6√3.(2)如图,设正三棱锥P−ABC的内切球球心为O,连结OP,OA,OB,OC,则O点到三棱锥的四个面的距离都为球的半径r,所以V P−ABC=V O−PAB+V O−PBC+V O−PAC+V O−ABC=13S侧·r+13S△ABC·r=13S表·r=(3√2+2√3)r.又V P−ABC=13×12×√32×(2√6)2×1=2√3,所以(3√2+2√3)r=2√3,即,所以,.4.【答案】解:∵正六边形的周长为3,得边长为12,故其主对角线为1,从而球的直径2R=√(√3)2+12=2,∴R=1,∴球的体积.5.【答案】16π【解析】解:如图,正四棱锥P−ABCD底面的四个顶点A,B,C,D在球O的同一个大圆上,点P在球面上,∴PO⊥底面ABCD,PO=R,S ABCD=2R2,VP−ABCD=163,所以13⋅2R2⋅R =163,解得:R =2,球O 的表面积:S =4πR 2=16π,故答案为:16π6.【答案】5π解:根据题意可知三棱锥B −ACD 的三条侧棱BD ,DC ,DA 两两互相垂直, 所以它的外接球就是它扩展为长方体的外接球,因为长方体的对角线的长为√1+1+√32=√5,所以球的半径为√52,所以三棱锥B −ACD 的外接球的表面积为4π×(√52)2=5π.故答案为5π.7.【答案】4π3解在四棱锥EPCD 中外接球球心为O , ∵已知PC =√CD 2+PD 2=√2+12=√3, 设外接球半径为x 则O 到P 、E 距离相等 可得:(x −12)2+(√32)2=x 2解得:x =1∴四棱锥P −ABCD 外接球的体积是43πx 3=4π38.【答案】28π3解:直三棱ABC −A 1B 1C 1的各顶点都在同一球面上,若AB =AC =AA 1=2,∠BAC =60°,如图,连接上下底面中心,O 为PQ 的中点,OP ⊥平面ABC ,则球的半径为OA ,由题意OP =1,AP =2√33,∴OA =√1+43=√73,所以球的表面积为:4πR 2=283π9.【答案】64√23π解:将三棱锥补全成三棱柱,则球心到底面的距离为DC2=2,又在△ABC 中,由正弦定理可知,2sin30°=2R =4,所以外接圆半径R =2, 所以由圆的截面性质可知,球的半径R′=√22+22=2√2,所以三棱锥S −ABC 外接球的体积,故答案为64√2π3. 10.【答案】44π解:设球心到平面ABC 的距离为d ,球的半径为r ,由题意得,V O−ABC =13×12×2×2×d =2,解得d =3,∵直角△ABC ,AB =AC =2,∴BC =2√2,∴r =√d 2+(BC2)2=√32+(√2)2=√11, ∴球的表面积为4πr 2=44π.故答案为44π.11.【答案】25π4解:设球的半径为R ,则OA =2−R ,则R 2=(2−R )2+1,解得R =54,则球O 的表面积为4πR 2=4π×(54)2=25π412.【答案】解:如图,设球心为O ,半径为r ,则在Rt △AOF 中,(4−r)2+(√2)2=r 2,解得r =94, 则球O 的体积V 球=43πr 3=43π×(94)3=243π16.。
空间几何体的外接球内切球问题

P DS CAO空间几何体的外接球、内切球问题外接球问题一.棱锥的外接球三棱锥都有外接球;底面有外接圆的任意棱锥都有外接球。
1.确定棱锥外接球球心的通法先找到棱锥底面的外接圆的圆心D ,过D 作底面的垂线DP交一侧棱的中垂面于O ,点O 即为外接球的球心。
练习:1.三棱锥S-ABC 的各顶点都在同一球面上,若SB ⊥平面ABC ,SB=6,AB=AC=2120BAC ∠=︒,则此球的表面积等于 。
2. 点A 、B 、C 、D 均在同一球面上,其中△ ABC 是正三角形,AD ⊥平面ABC ,AD=2AB=6则该球的体积为 。
3.四面体ABCD 的四个顶点在同一球面上,AB=BC=CD=DA=3,32=AC ,6=BD ,则该球的表面积为 ( )A . π14 B.π15 C.π16 D.π182.补成长方体或正方体,再利用体对角线是外接球直径这一结论求解。
练习:1.三棱锥O ABC -中,,,OA OB OC 两两垂直,且22OA OB OC a ===,则三棱锥O ABC -外接球的表面积为( )A .26a πB .29a πC .212a πD .224a π2.已知,,,S A B C 是球O 表面上的点,SA ABC ⊥平面,AB BC ⊥,1SA AB ==,BC =O 表面积等于(A )4π (B )3π (C )2π (D )π3.,四个顶点在同一个球面上,则此球的表面积为( )A.3πB.4πD.6π4.3.公共边所对的两个角为直角确定球心法 练习1.在矩形ABCD 中,4,3AB BC ==,沿AC 将矩形ABCD 折成一个直二面角B ACD --,则四面体ABCD 的外接球的体积为 A.12512π B.1259π C.1256π D.1253π2.空间四边形ABCD中,1,AB BC AD DC ====ABCD 的外接球的表面积为4.利用轴截面截球为大圆确定球半径正四、六、八棱锥的外接球的一个轴截面为大圆,该圆的半径等于外接球的半径. 练习:1.正四棱锥S ABCD -S A B C D 、、、、都在同一球面上,则此球的体积为 .2.正六棱锥EF S ABCD -的底面边长为1S A B C D 、、、、、E 、F 都在同一球面上,则此球的表面积为 .3.表面积为的正八面体的各个顶点都在同一个球面上,则此球的体积为_ C_ A_ O_ D _ BA.3B.13π C.23π D.3二.棱柱的外接球底面有外接圆的直棱柱才有外接球。
外接球与内切球问题5

外接球与内切球问题5一、单选题1.(2022·湖北·高三阶段练习)已知某圆台的体积为(9+,其上底面和下底面的面积分别为3π,6π,且该圆台两个底面的圆周都在球O 的球面上,则球O 的表面积为()A .25πB .26πC .27πD .28π【答案】D【解析】设该圆台的高为h ,则1(9(3π6π)3h +=+,解得3h =.由题意得:上底面圆的半径为BD =,下底面圆的半径为AC =,设球心O 到下底面的距离为t ,即OA t =,则3BO t =-,由勾股定理得:2222OA AC OB BD +=+,即22(3)t t +=-+,解得1t =,则球O 的半径R ==,故球O 的表面积为24π28πR =.故选:D2.(2022·甘肃·高台县第一中学模拟预测(文))已知A ,B ,C 均在球O 的球面上运动,且满足π3AOB ∠=,若三棱锥O ABC -体积的最大值为6,则球O 的体积为().A .12πB .48πC .D .643π3【答案】C【解析】如图所示,当点C 位于垂直于平面AOB 的直径端点时,三棱锥O ABC -的体积最大,设球O 的半径为R ,此时2311632212O ABC C AOB V V R R R --==⨯⨯==,故3R =O 的体积为34π3R V ==.故选:C .3.(2022·江苏南京·模拟预测)已知A ,B ,C ,D 为球O 的球面上的四点,记AB 的中点为E ,且()0AB OC λλ=>,四棱锥D AECO -O 的表面积为()A .8πB .12πC .16πD .20π【答案】C【解析】因()0AB OC λλ=>,则平面ABC 过球O 的球心O ,又AB 的中点为E ,则点E 是以AB 为直径的球的截面小圆圆心,连接OE ,如图,则OE AB ⊥,四边形AECO 为梯形,令球O 的半径为R ,设EA r =,则OE =四棱锥D AECO -体积最大,当且仅当梯形AECO 面积最大,并且点D 到平面AECO 的距离最大,显然球面上的点D 到平面AECO 的最大距离为R ,梯形AECO 面积1(2S R r =+令2223()()()()()f r R r R r R r R r =+-=+-,0r R <<,求导得:232()3()()()2()(2)f r R r R r R r R r R r '=+--+=+-,当102r R <<时,()0f r '>,当12R r R <<时,()0f r '<,即函数()f r 在1(0,)2R 上递增,在1(,)2R R 是递减,因此当12r R =时,4max 127()()216f r f R R ==,2max S =,于是得四棱锥D AECO -体积的最大值为213R =2R =,所以球O 的表面积为2416R ππ=.故选:C4.(2022·黑龙江·海伦市第一中学高三期中)已知四面体ABCD 的所有顶点在球O 的表面上,AB ⊥平面BCD ,AB =CD =,135CBD ∠=︒,则球O 的体积为()A B .763πC .283πD 【答案】D 【解析】如图,设底面BCD △的外接圆的圆心为'O ,外接圆的半径为r ,由正弦定理得24,2sin sin135CD r r CBD ︒===∴=∠,过'O 作底面BCD 的垂线,与过AC 的中点E 作侧面ABC 的垂线交于O ,则O 就是外接球的球心,并且'2ABOO ==,外接球的半径R OB ===,球O 的体积为343V R ππ=;故选:D.5.(2022·全国·高三阶段练习(文))已知正四棱锥的所有顶点都在体积为36π的球O 的球面上,若该正四棱锥的高为h ,且25h ≤≤,则该正四棱锥的体积的取值范围是()A .3250,33⎡⎤⎢⎥⎣⎦B .6418,3⎡⎤⎢⎥⎣⎦C .3264,33⎡⎤⎢⎥⎣⎦D .5064,33⎡⎤⎢⎥⎣⎦【答案】C【解析】设球O 的半径为R ,因为球O 的体积为36π,所以34363R ππ=,解得3R =.当35h <≤时,如图,设正四棱锥的底面边长为2a ,则有22232(3)a h =+-,整理得2226a h h =-.同理,当23h ≤≤时,有22232(3)a h =+-,整理得2226a h h =-.所以正四棱锥的体积()223211224643333V Sh a h h h h h h ==⨯⨯=⨯-⨯=-+.由2'280V h h =-+=,得4h =或0h =.因为25h ≤≤,当24h ≤<时,0V '>,所以函数()V h 在[2,4)上单调递增;当45h <≤时,0V '<,所以函数()V h 在(4,5]上单调递减.所以当4h =时,正四棱锥的体积V 取得最大值,最大值为()4V =643.又()3223V =,()5053V =,所以,该正四棱锥体积的取值范围是3264,33⎡⎤⎢⎥⎣⎦.故选:C.6.(2022·贵州·高三阶段练习(文))已知正三棱锥S ABC -的底面边长为6,体积为A ,B ,C 三点均在以S 为球心的球S 的球面上,P 是该球面上任意一点,则三棱锥-P ABC 体积的最大值为()A .B .C .D .【答案】D【解析】设三棱锥的高为SO h =,所以有113662322h h =⨯⨯⨯⇒=,在直角三角形SAO 中,62sin 60AO AO ︒==⇒=4SA ===,当,,P O S 共线时,三棱锥-P ABC 体积的最大,显然426PO PS SO =+=+=,如图所示:最大值为:11666322⨯⨯⨯=故选:D7.(2022·全国·高三阶段练习(理))已知体积为V 的正三棱柱111ABC A B C -的所有顶点都在球O 的球面上,当球O 的表面积S 取得最小值时,该正三棱柱的底面边长a 与高h 的比值为()A .12B C .2D .2【答案】D【解析】如图,设正三棱柱111ABC A B C -的上、下底面的中心分别为1O 和2O ,则12O O 的中点为O .设球O 的半径为R ,则OA R =.设AB BC AC a ===,1AA h =,则212OO h =,223O A ==,2ABC S a =△.所以正三棱柱111ABC A B C -的体积2V h ,所以23a h =.在2Rt OO A ∆中,222222221143R OA OO O A h a ==+=+,球O 的表面积222114π4π43S R h a ⎛⎫==+ ⎪⎝⎭.方法一:222222111114π4π4π43466S R a h a a ⎛⎫⎛⎫==+=++≥⎪ ⎪⎝⎭⎝⎭212233322223111114π312π12π4π46612123h a a a h V ⎛⎫⎛⎫⎛⎫⨯⨯⨯==⨯= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,当且仅当221146h a =,即a h =时,S 取得最小值.方法二:由2V h,得2a =,所以222221111114π4π4π4π4343349S R h a h h h h ⎛⎫⎛⎫⎛⎫==+=+⨯=+⨯ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.令()()21104h h h h ϕ=⨯>,则()211'2h h hϕ=⨯.令()'0h ϕ=,得1303h h ==,当()00,h h ∈时,()'0h ϕ<时,()h ϕ单调递减;当()0,2h h R ∈时,()0'h ϕ>,()h ϕ单调递增.所以当13233h V =时,S取得最小值,此时13a =,所以132a h ==.故选:D .8.(2022·福建·浦城县第三中学高三期中)《九章算术·商功》:“斜解立方,得两堑堵,其一为阳马,一为鳖臑,阳马居二,鳖臑居一.”下图解释了这段话中由一个长方体得到堑堵、阳马、鳖臑的过程.在一个长方体截得的堑堵和鳖臑中,若堑堵的内切球(与各面均相切)半径为1,则鳖臑体积的最小值为()A.2B.C.2D.【答案】C【解析】依题意,堑堵的内切球(与各面均相切)半径为1,所以直角三角形ABC 的内切圆半径为1,12AA =,设,AB b BC a ==,则AC =所以(11122a b ab ⨯+⨯=,(2ab a b =+≥=+当且仅当a b =时等号成立,26ab ≥≥+,所以鳖臑体积(11114226232333V ab ab ⎛⎫=⨯⨯=≥+=+ ⎪⎝⎭.故选:C二、多选题9.(2022·浙江·慈溪中学高三期中)已知棱长为1的正方体1111ABCD A B C D -,以正方体中心O 为球心的球O 与正方体的各条棱相切,点P 为球面上的动点,则下列说法正确的是()A .球O 在正方体外部分的体积为213-B .若点P 在球O 的正方体外部(含正方体表面)运动,则17,44PA PB ⎡⎤⋅∈-⎢⎥⎣⎦C .若点P 在平面ABCD 下方,则直线AP 与平面1111D C B AD .若点P 、M 、N 在球O 的正方体外部(含正方体表面)运动,则PM PN ⋅ 最小值为14-【答案】BD【解析】对于A ,正方体的棱切球O的半径2R =,如下图所示,球O在正方体外部的体积3411323O V V V π⎛>-=⋅-=- ⎝⎭球正方体,或者可根据球O 在平面1111D C B A 上方球缺部分的体积()221111533322222624V R h h πππ⎡⎤⎛⎫⎛⎫⎛⎫=-⋅=⋅--⋅-=-⎢⎥ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦,h 为球缺的高,所以球O在正方体外部的体积为55666244V ππ⎛⎫⎫=-=- ⎪⎪ ⎪⎭⎝⎭,A 选项错误;对于B ,取AB 中点E ,可知E 在球面上,可得12EB EA BA =-=,所以()()()()22214P PE EA PE EB PEEAP A E PB +⋅=+⋅=-=- ,点P 在球O 的正方体外部(含正方体表面)运动,所以0PE ≤ (当PE为直径时,PE =,所以17,44PA PB ⎡⎤⋅∈-⎢⎥⎣⎦,B 选项正确;对于C,若正方体上底面字母为ABCD ,则直线AP 与平面1111D C B A 所成角的正弦值最大时,如上图所示P 点位置,此时正弦值最大为1,若正方体下底面字母为ABCD ,设平面ABCD 的中心为1O ,直线AP 与平面1111D C B A 所成角即为直线AP 与平面ABCD 所成角,则直线AP 与平面1111D C B A 所成角最大时,直线AP 正好与平面ABCD 下方球O 相切,过A 作平面ABCD 下方球O 的切线,切点为P,将正方体及其棱切球的截面画出,如下图所示,可得2OA =,12O A OP ==,112O O =,190OO A APO ∠=∠= ,1APO OO A ≅ ,所以112O O AP ==,sin OPOAQ OA∠==1sin OO OAC OA ∠==所以直线AP 与平面1111D C B A 所成角最大时为CAQ ∠,()1sin sin 3CAQ OAQ OAC ∠=∠-∠==,C 选项错误;对于D ,()()()2PM PN OM OP ON OP OM ON OP OM ON OP ⋅=-⋅-=⋅-⋅++ ,记向量OP 与向量+ OM ON 的夹角为θ,2OP OM ON === ,因为()cos OP OM ON OP OM ON OP OM ON θ⋅+=⋅+≤⋅+ ,且()2222OM ONOM ON OM ON +=++⋅ ,所以()2122PM PN OM ON OP OM ON OP OM ON ⋅=⋅-⋅++≥⋅-,令t =,所以上式可化为221111222224t PM PN t -⋅=-+=-≥- ,当且仅当t 成立,此时14OM ON ⋅=- ,即2,3OM ON π= 时等号成立,根据题意可知此条件显然成立,D 选项正确.故选:BD.10.(2022·福建泉州·高三开学考试)已知正四棱台1111ABCD A B C D -的所有顶点都在球O 的球面上,11122,AB A B AA ===E 为1BDC 内部(含边界)的动点,则()A .1//AA 平面1BDC B .球O 的表面积为6πC .1EA EA +的最小值为D .AE 与平面1BDC 所成角的最大值为60°【答案】ACD【解析】对于A ,如图1,由棱台的结构特征易知1AA 与1CC 的延长线必交于一点,故11,,,A A C C 共面,又面1111//A B C D 面ABCD ,而面11AA C C 面111111A B C D AC =,面11AA C C 面ABCD AC =,故11//A C AC ,即112//AC AO ;由平面几何易得1121122A C AO AC ===⨯=,即112AC AO =;所以四边形112AAC O 是平行四边形,故112//AA C O ,而1AA ⊄面1BDC ,12⊂C O 面1BDC ,故1//AA 平面1BDC ,故A 正确;.对于B ,如图2,设1O 为11A C 的中点,O 为正四棱台外接球的球心,则1A O AO R ==,在等腰梯形11AAC C 中,易得()22222121111322O O AA AC A C ⎡⎤=--=-=⎢⎥⎣⎦⎝⎭,即122O O =,为方便计算,不妨设12,O O a O O b ==,则由2222221112A O a A O AO AO b +===+,即22222a b ⎛+=+ ⎝⎭,即2232a b -=,又12a b O O +=解得0a b ==,即O 与2O 重合,故R AO =故球O 的表面积为)22448R πππ=⨯=,故B 错误;.对于C ,由图2易得12BD O O ⊥,BD AC ⊥,122O O AC O ⋂=,12OO AC ⊂、面11AAC C ,故BD ⊥面11AAC C ,不妨设E 落在图3E '处,过E '作1//E E BD ',则1E E '⊥面11AAC C ,故11E E E A '⊥,故在1Rt AE E ' 中,1E A E A '<(勾股边小于斜边);同理,111E A E A '<,所以1111E A E A E A E A ''+<+,故动点E 只有落在1C O 上,1EA EA +才有可能取得最小值;再看图4,由11A C O C 关于对称点为可知,故1EA EA AC +≥=C 正确,.对于D ,由选项C 可知,BD ⊥面11AAC C ,BD ⊂面1BDC ,故面11AAC C ⊥面1BDC ,在面11AAC C 内过A 作1AF C O ⊥交1C O 于F ,如图5,则AF ⊂面11AAC C ,面11AAC C 面11BDC C O =,故AF ⊥面1BDC ,故AEF ∠为AE 与平面1BDC 所成角,在Rt AEF 中,sin AF AEF AE∠=,故当AE 取得最小值时,sin AEF ∠取得最大值,即AEF ∠取得最大值,显然,动点E 与O 重合时,AE 取得最小值,即AEF ∠取得最大值,且1AEF AOF C OC ∠=∠=∠,在1C OC △中,11C O AA ==11CC AA ==12OC AC ==故1C OC △为正三角形,即160C OC ∠=︒,即AE 与平面1BDC 所成角的最大值为60︒,故D 正确.故选:ACD.11.(2022·广东·铁一中学高三阶段练习)如图,已知圆锥顶点为P ,其轴截面PAB 是边长为6的为正三角形,1O 为底面的圆心,EF 为圆1O 的一条直径,球O 内切于圆锥(与圆锥底面和侧面均相切),点Q 是球O 与圆锥侧面的交线上一动点,则()A .圆锥的表面积是45πB .球O 的体积是C .四棱锥Q AEBF -体积的最大值为D .QE QF +的最大值为【答案】BCD 【解析】依题意,动点Q 的轨迹是圆,所在平面与圆锥底面平行,令其圆心为2O ,连接1PO ,如图,正PAB 内切圆即为球O 的截面大圆,球心O 、截面圆圆心2O 都在线段1PO 上,连2,OQ O Q ,1PO =O 的半径1OO =2,OQ PQ O Q PO ⊥⊥,60POQ ∠= ,221333,2222OO OQ O Q OQ ====,12332O O =,对于A ,圆锥的表面积是2211πππ3π3627πS O A O A PA =+⋅⋅=⨯+⨯⨯=,A 错误;对于B ,球O 的体积是3314π4π33V OO ==⨯=,B 正确;对于C ,因Q 到平面AEBF 的距离与截面圆圆心2O 到平面的距离相等,均为2,则当四边形AEBF Q AEBF -的体积最大,11sin 182AEBF S AB EF AO E =⋅∠≤,当且仅当190AO E ∠= ,即EF AB ⊥时取“=”,则四棱锥Q AEBF -体积的最大值为1183⨯C 正确;对于D ,因22212129QO QO O O =+=,则有1113QO EO FO ===,即QE QF ⊥,因此22236QE QF EF +==,由均值不等式得:2QE QF +≤=QE QF +≤QE QF =时取“=”,D 正确.故选:BCD12.(2022·湖南·长沙一中模拟预测)传说古希腊数学家阿基米德的墓碑上刻着一个圆柱,圆柱内有一个内切球,这个球的直径恰好与圆柱的高相等.“圆柱容球”是阿基米德最为得意的发现;如图是一个圆柱容球,12O O ,为圆柱上下底面的圆心,O 为球心,EF 为底面圆1O 的一条直径,若球的半径2r =,则()A .球与圆柱的表面积之比为12:B .平面DEF 截得球的截面面积最小值为165πC .四面体CDEF 的体积的取值范围为3203⎛⎤ ⎥⎝⎦,D .若P 为球面和圆柱侧面的交线上一点,则PE PF +的取值范围为2⎡+⎣【答案】BCD【解析】由球的半径为r ,可知圆柱的底面半径为r ,圆柱的高为2r ,则球表面积为24r π,圆柱的表面积222226r r r r πππ+⋅=,所以球与圆柱的表面积之比为23,故A 错误;过O 作1OG DO ⊥于G ,则由题可得12525OG ==,设O 到平面DEF 的距离为1d ,平面DEF 截得球的截面圆的半径为1r ,则1d OG ≤,22221114164455r r d d =-=-≥-=,所以平面DEF 截得球的截面面积最小值为165π,故B 正确;由题可知四面体CDEF 的体积等于12E DCO V -,点E 到平面1DCO 的距离(0,4]d ∈,又114482DCO S =⨯⨯= ,所以123228(0,33E DCO V d -=⨯∈,故C 正确;由题可知点P 在过球心与圆柱的底面平行的截面圆上,设P 在底面的射影为P ',则222,16PP PE PF P E P F '''==+=,设2t P E '=,则20,4t ⎡⎤∈⎣⎦,PE PF +=所以()2224PE PF +==+242448⎡⎤=++⎣⎦,所以2PE PF ⎡+∈+⎣,故D 正确.故选:BCD.13.(2022·全国·模拟预测)如图,在五面体PQABCD 中,底面ABCD 为矩形,ADP 和BCQ △均为等边三角形,//PQ 平面ABCD ,7AB =,AD =P AD C --和Q BC A --的大小均为((0,))θθ∈π.设五面体PQABCD 的各个顶点均位于球O 的表面上,则()A .有且仅有一个θ,使得五面体PQABCD 为三棱柱B .有且仅有两个θ,使得平面ADP ⊥平面BCQC .当1cos 4θ=-时,五面体PQABCD 的体积取得最大值D .当cos 0θ=时,球O 的半径取得最小值【答案】ABC【解析】对于选项A:∵//PQ 平面ABCD ,经过PQ 的平面PQBA 与平面ABCD 交于直线AB ,∴//PQ AB ,取,AD BC 的中点分别为,E F ,连接EF ,则////EF AB PQ连接,PE QF ,∵ADP 和BCQ △均为等边三角形,∴,PE AD QF BC ⊥⊥,又∵底面ABCD 为矩形,∴EF 垂直,AD BC ,故得二面角P AD C --的平面角为=PEF θ∠,二面角Q BC A --的平面角为=QFE θ∠,因为//AD BC ,,AD BC 分别在平面PAD 和平面QBC 中,平面PQEF 与平面PAD 和QBC 分别交于直线,PE QF ,所以当且仅当//PE QF 时,平面//PAD 平面QBC ,故当且仅当PEF PFE θθπ∠+∠=+=,即π2θ=时,平面//PAD 平面QBC ,即五面体PQABCD 为三棱柱,故A 正确;对于选项B:当平面PAD 和平面QBC 不平行时,它们的交线为l ,由于//AD BC ,BC ⊂平面QBC ,AD ⊄平面QBC ,∴//AD 平面QBC ,又∵AD ⊂平面PAD ,平面PAD ⋂平面QBC =直线l ,∴//AD l ,∴,PE l ⊥同理QF l ⊥,∴当且仅当PE QF ⊥时,平面PAD ⊥平面QBC ,由于四边形PQFE 为等腰梯形,∴当且仅当π4θ=或3π4θ=时,PE QF ⊥,∴当且仅当π4θ=或3π4θ=时,平面PAD ⊥平面QBC ,故B 正确;对于选项C:设PEF ∠的补角为απθ=-,过A 作直线AR 与直线PQ 垂直相交,垂足为R ,连接DR ,∵AD ⊥EF ,EF //PQ ,∴AD ⊥PQ ,又∵AD ∩AR =A ,AD ,AR ⊂平面ADF ,∴平面ADR ⊥直线PQ ,同理做出S ,得到平面SBC ⊥直线PQ ,,ADR BCS 为直三棱柱ADR BCS -的底面,且RS =EF 为直三棱柱的高,PR 、QS 为三棱锥P ADR -和Q BCS -的底面上的高因为()cos =cos π=cos α-θ-θ,3cos ,3sin .OG PG αα==所以五面体PQABCD 的体积为++P AED Q FCB ADE BCF V V V V ---=(如上图)或ADR BCS P ADR Q BCS V V V V -----=(如下图)两种情况下都有113sin 23cos +723V αα⎛⎫⨯⨯⨯ ⎪⎝⎭())2cos +72cos +7ααα,令=cos ,(0,π),t αα∈则()1,1t ∈-,所以()2+7V t ,对V 求导得V -+',令0V '=得=2t -(舍去)或14t =,1,14t ∈⎛⎫ ⎪⎝⎭0V '<,11,4t ∈-⎛⎫ ⎪⎝⎭,0,V '>故14t =时体积取得极大值也是最大值.所以()1cos =cos π=cos =4α-θ-θ,所以1cos =4θ-.五面体PQABCD 的体积取得最大值.故C 正确;对于D 项:取等边QBC 的中心1O ,EF 的中点2O ,过1O 作平面QBC 的垂线与过2O 的平面ABCD 的垂线的交点O 即为五面体PQABCD 的外接球的球心,如图所示,连接OB ,2BO ,则r OB ==∵四边形ABCD 为边长一定的矩形,∴2O B 为定值,∴当且仅当1OO 最小,即1,O O 重合时外接球的半径最小,此时θ为锐角,故D 不对.故选:ABC.14.(2022·全国·模拟预测)已知正三棱锥S ABC -的底面ABC 的面积为3,球1O ,2O 分别是三棱锥S ABC -的外接球与内切球,则下列说法正确的是()A .球1O 的表面积为493πB .二面角S ABC --的大小为30C .若点E 在棱SB 上,则AE CE +D .在三棱锥S ABC -中放入一个球3O ,使其与平面SAB 、平面SBC 、平面SAC 以及球2O 均相切,则球3O【答案】ACD【解析】依题意,234AB =,解得AB =S ABC -的高为h ,则三棱锥S ABC -的体积133V =⨯=,解得h =S 在底面ABC 内的投影为O ,1R 为球1O 的半径,连接BO ,则()22211h R BO R -+=,即)22114R R -+=,解得16R =,则球1O 的表面积2114943S R ππ==,故A 正确(对应下方右图).取棱AB 的中点D ,连接,SD OD ,由正三棱锥的性质,易知,SO AB CO AB ⊥⊥,于是SDO ∠即为二面角S AB C --的平面角,tan SDO ∠=,且0180SDO ︒≤∠≤︒,则60SDO ∠=,故B 错误.将侧面,SAB SBC 平面展开,使得,,,S A B C 四点共面,显然,A C 的连线就是AE CE +有最小值.SA SB SC ====SBC △中,22221cos27SB BC SC SBC SB BC +-∠===⋅,则sin SBC ∠=,故8212sin 27AC BC SBC =⋅∠=⨯,故C 正确(对应下方左图).三棱锥S -ABC 的表面积为132⨯=根据内切球半径r 和棱锥体积V ,棱锥表面积为S ,易知3Sr V =,设2R 为球2O 的半径,3R 为球3O 的半径,则2133⨯=,解得23R =,原三棱锥的高h =ABC ,去截原三棱锥,得到一个1233h =的棱台,那么剩余部分棱锥的高是原棱锥的13,根据相似关系,剩余棱锥的底面积为19,,表面积为19,体积为1119339⨯=,于是3111399R ⨯=,解得39R =,故D 正确.故选:ACD .三、填空题15.(2022·河南·高三阶段练习(文))已知四面体ABCD 的各顶点都在球O 的表面上,22AB CD ==,E ,F 分别为,AB CD 的中点,O 为EF 的中点.若AB CD ⊥,直线AC 与BD 所成的角为60︒,AB EF <,则球O 的表面积为____________.【答案】20π【解析】依题意,作出球O 的内接正四棱柱,IDJC AHBG AC GI K -= .因为GI BD ∥,所以60AKG ∠=︒或120︒,又AB EF <,则60AKG ∠=︒.因为22AB =,则2,23AG AI ==,在Rt AEO △中,3,2EO AE ==,则225AO AE EO =+=,则球O 的表面积24π20πS R ==.故答案为:20π16.(2022·四川·石室中学高三期中(文))已知ABC 的所有顶点都在球O 的表面上,1,120AB AC BAC ∠=== ,球O 的体积为32π3,若动点P 在球O 的表面上,则点P 到平面ABC 的距离的最大值为__________.【答案】23+【解析】因为1,120AB AC BAC ∠=== ,所以22211211cos1203BC =+-⨯⨯⨯= ,即3BC =设ABC 的外接圆的圆心为1,O ABC 的外接圆的半径为r ,球O 的半径为R ,则3221,sin sin120BC r r r BAC∠=⇒=⇒=332π4π233R R =⇒=,因为1OO ⊥平面ABC ,所以11OO O A ⊥,则1OO ==.延长1O O 与球O 交于点1P ,当点P 与点1P 重合时,点P 到平面ABC 的距离取得最大值2故答案为:217.(2022·贵州·贵阳一中高三阶段练习(理))在三棱锥-P ABC 中,已知π2π2,,,23PA AB AC PAB BAC D ∠∠=====是线段BC 上的点,2,BD DC AD PB =⊥.若三棱锥-P ABC 的各顶点都在球O 的球面上,则球O 的表面积为___________.【答案】20π【解析】如图所示,在ABC 中,因为2AB AC ==,2π3BAC ∠=,可得BC =.又因为2BD DC =,所以3BD =.由π6ABC ∠=,2AB =,可得233AD ==,可得222BD AB AD =+,所以AB AD ⊥.又由AD PB ⊥,PB AB B ⋂=且PB ,AB ⊂平面PAB ,所以AD ⊥平面PAB .又由PA ⊂平面PAB ,所以PA AD ⊥.由π2PAB ∠=,即PA AB ⊥,且AB AD A ⋂=,AD ,AB ⊂平面ABC ,可得PA ⊥平面ABC .设ABC 外接圆1O 的半径为r ,则24sin BC r BAC==∠,可得2r =,即12AO =.设三棱锥-P ABC 的外接球的半径为R ,可得22222221112152PA R AO OO AO ⎛⎫=+=+=+= ⎪⎝⎭,即R O 的半径为5,故表面积为24π(5)20πS =⨯=.故答案为:20π18.(2022·贵州·贵阳一中高三阶段练习(文))在三棱锥-P ABC 中,已知π2π2,,,23PA AB AC PAB BAC D ∠∠=====是线段BC 上的点,,AD AB AD PB ⊥⊥.若三棱锥-P ABC 的各顶点都在球O 的球面上,则球O 的表面积为______.【答案】20π【解析】如图,因为,,AD AB AD PB PB AB B ⊥⊥⋂=,且,PB AB ⊂平面PAB ,所以AD ⊥平面PAB .又PA ⊂平面PAB ,所以PA AD ⊥.因为π2∠=PAB ,即PA AB ⊥,且AB AD A ⋂=,,AB AD ⊂平面ABC ,所以PA ⊥平面ABC .在ABC 中,因为2π2,3AB AC BAC ∠===,可得222212cos 22222232BC AB AC AB AC BAC ∠⎛⎫=+-⋅⋅+-⨯⨯⨯-= ⎪⎝⎭设ABC 外接圆的半径为r ,则24sin BC r BAC∠==,可得2r =,即12AO =,设三棱锥-P ABC 的外接球的半径为R ,可得22222221112152PA R AO OO AO ⎛⎫=+=+=+= ⎪⎝⎭,即5R =O 524π(5)20πS =⨯=.故答案为:20π19.(2022·甘肃·高台县第一中学模拟预测(理))已知点A ,B ,C 均在球O 的球面上运动,且满足3AOB π∠=,若三棱锥O ABC -体积的最大值为6,则球O 的体积为___________.【答案】323π【解析】如图所示,当点C 位于垂直于面AOB 的直径端点时,三棱雉O ABC -的体积最大,设球O 的半径为R ,此时231133632212O ABC C AOB V V R R R --==⨯⨯⨯==,故3243R =,则球O 的体积为343233R V ππ==.故答案为:323π20.(2022·四川·成都市锦江区嘉祥外国语高级中学有限责任公司高三期中(理))如图,在三棱锥A PBC -中,已知π4APC ∠=,π3BPC ∠=,PA AC ⊥,PB BC ⊥,平面PAC ⊥平面PBC ,三棱锥A PBC -的体积3,若点P ,A ,B ,C 都在球O 的球面上,则球O 的表面积为____________.【答案】4π【解析】因为在三棱锥-P ABC 中,π4APC ∠=,π3BPC ∠=,PA AC ⊥,PB BC ⊥,所以PAC △和PBC 均为直角三角形,且斜边均为PC ,所以PC 为球O 的直径,PC 的中点为球心O ,设PA a =,则AC a =,PC =,22PB a =,BC a =,且PAC △的边PC 高为1222h PC a ==,因为平面PAC ⊥平面PBC ,根据面面垂直的性质定理可知PAC △的边PC 上的高h 即为三棱锥的高,因为三棱锥A PBC -的体积为111332PBC h S a =⨯⨯=⨯⨯⨯⨯⇒=V 所以球半径12PC R ==,所以球O 的表面积为224π4π14πS R ==⨯=.故答案为:4π.。
超全的外接球与内切球问题

第二章:外接球与内切球1.空间几何体的内切球几何体示例图像截面图对应性质圆柱r h 、分别为圆柱的底面圆半径和高,R 为内切球半径.R r =且2h R =;正三棱柱r h 、分别为柱体的底面三角形内切圆半径和高,R 为内切球半径.R r =且2h R =;正棱锥PE 为锥体的斜高,h r 、分别为锥体的高和底面内切圆半径,R 为内切球半径.1POF PEO △∽△可得R OP h R r PE PE -==“钻石”PE 为锥体的斜高,h r 、分别为锥体的高和底面内切圆半径,R 为内切球半径.在Rt POE △中,满足h rR PE⋅=一般三棱锥记R 为内切球半径,三棱锥的四个面面积分别为1234S S S S 、、、,则1234VR S S S S =+++【示例1】1.如图,在圆柱12O O 内有一个球O ,该球与圆柱的上、下底面及母线均相切,记圆柱12O O 的体积为1V ,球O 的体积为2V ,则12V V =__________.【解析】记内切球半径为R ,底面圆半径为r ,圆柱高为h ;则R r =且2h R =;则23122V h s r r r ππ=⋅=⋅=,3324433V R r ππ==;∴1232V V =2.如果一个球的外切圆锥的高是这个球的半径的3倍,则圆锥的侧面面积和球的表面积之比为__________.【解析】轴截面如右图,记h r 、为圆锥的高和底面圆半径,R 为内切球半径;由题意,3h R =,同时由1POF PEO △∽△可得1OP OFPE EO =;即R r==,得r =,则PE =.∴在圆锥1O P 中,2212S PE r R ππ=⋅=侧,2=4S R π球;则:3:1S S =侧球【例1】1.已知正方体的内切球(球与正方体的六个面都相切)的体积是323π,则该正方体的表面积为__________.2.如果一个八面体各个面都是全等的正三角形,如图所示,则这个几何体叫正八面体,则棱长为4的正八面体的内切球半径是__________.3.在封闭的直三棱柱111ABC A B C -内有一个体积为V 的球,若AB BC ⊥,6AB =,8BC =,13AA =,则V 的最大值是__________.4.天津滨海文化中心地处天津滨海新区开发区,是天津乃至京津冀地区的标志性文化工程.其中滨海图书馆建筑独具特色,被称为“滨海之眼”,如图1所示,中心球状建筑引起了小明的注意,为了测量球的半径,小明设计了两个方案,方案甲,构造正三棱柱侧面均与球相切如图2所示,底面边长约为30米,估计此时球的完整表面积为平方米;方案乙,测量球被地面截得的圆的周长约为16π米,地面到球顶部高度约为16米,估计此时球的完整体积为立方米,你认为哪种方案好呢?课堂练习1:1.一个球与一个正三棱柱的三个侧面和两个底面都相切,已知这个球的体积是32,那么3这个球的半径是,三棱柱的体积是.2.正四棱锥的高与底面边长相等且体积为83,(1)以底面中心为球心,经过四棱锥四条侧棱中点的球的表面积为__________;(2)该正四棱锥的内切球体积为__________.3.农历五月初五是端午节,民间有吃粽子的习惯,粽子又称粽籺,俗称“粽子”,古称“角黍”,是端午节大家都会品尝的食品,传说这是为了纪念战国时期楚国大臣、爱国主义诗人屈原.如图,平行四边形形状的纸片是由六个边长为1的正三角形构成的,将它沿虚线折起来,可以得到如图所示粽子形状的六面体,则该六面体的体积为;若该六面体内有一球,则该球体积的最大值为.2.柱体外接球问题概述具备外接球的柱体,一定是“直”的,即侧棱垂直于底面或圆柱体.其球心必在柱体上下底面外接圆圆心连线的中点.此时球心到柱体底面的距离d 等于柱体高h 的一半(即2h d =).示例图像圆柱长方体直三棱柱计算公式222224h R d r r =+=+22224R a b c =++2sin ar A=,222R d r =+问题设计①.先求出柱体高和底面相关信息,再求外接球半径;②.已知外接球半径,求柱体的高或底面相关变量.【示例2】1.如图,长方体1111ABCD A B C D -的底面是面积为2的正方形,该长方体的外接球体积为323π,点E 为棱AB 的中点,则三棱锥1D ACE -的体积是__________.【解析】Ⅰ.确定长方体的高→Ⅱ.求1D ACEV -3432233V R R ππ==→=球,则2222114222AB AD AA R AA AB AD ⎫++=⎪→=⎬==⎪⎭;∴在三棱锥1D ACE -中,122112ACE h AA S AE BC ⎧==⎪⎨=⋅=⎪⎩△;得112233D ACE ACE V h S -=⋅=△2.已知直三棱柱111ABC A B C -的外接球半径为4,同时BA BC ⊥,BA BC =则111ABC A B C -体积的最大值为__________.【解析】Ⅰ.找到侧棱和底面棱长的关系→Ⅱ.函数求最值显然Rt ABC △为等腰直角三角形,则22r AB =;此时212ABC S AB CB r =⋅=△;同时222224h R d r r =+=+可得22164h r =-;则()()23116640844ABCh V h S h h h h ⎛⎫=⋅=⋅-=-<< ⎪⎝⎭△;令()()36408f x x x x =-+<<,则()2364f x x '=-+;令()0f x '=得x =;∴()f x 在⎛ ⎝上递增,在⎫⎪⎭上递减,则()max 9f x f ==,则()max max14V f x ==【例2】1.若一个圆柱的轴截面是面积为4的正方形,则该圆柱的外接球的表面积为__________.2.在正方体1111ABCD A B C D -中,三棱锥11A B CD -的表面积为,则正方体外接球的体积为__________.3.已知直三棱柱的各棱长都相等,三棱柱的所有顶点都在球O 的表面上,若球O 的表面积为28π,则该三棱柱的体积为__________.4.如图,直三棱柱111ABC A B C -的六个顶点都在半径为1的半球面上,AB AC =,侧面11BCC B 是半球底面圆的内接正方形,则侧面11ABB A 的面积为__________.5.“迪拜世博会”于2021年10月1日至2022年3月31日在迪拜举行,中国馆建筑名为“华夏之光”,外观取型中国传统灯笼,寓意希望和光明.它的形状可视为内外两个同轴圆柱,某爱好者制作了一个中国馆的实心模型,已知模型内层底面直径为12cm ,外层底面直径为16cm ,且内外层圆柱的底面圆周都在一个直径为20cm 的球面上.此模型的体积为__________.课堂练习2:1.已知正方体的体积是8,则这个正方体的外接球的体积是__________.2.在正方体1111ABCD A B C D -中,三棱锥11A B CD -的表面积为,则正方体外接球的体积为__________.3.一直三棱柱的每条棱长都是2,且每个顶点都在球O 的表面上,则球O 的表面积为__________.4.已知一个体积为8的正方体内接于半球体,即正方体的上底面的四个顶点在球面上,下底面的四个顶点在半球体的底面圆内.则该半球体的体积为__________.3.侧棱垂直于底面的锥体外接球问题阐述若锥体有一条侧棱PA 满足PA ⊥底面ABC ,则该锥体必可还原成一个直棱柱.即侧棱垂直于底面的棱锥与还原之后的直棱柱具有相同的外接球.示例图像还原至长方体还原至长方体还原至直三棱柱对应条件AP AB AC 、、两两垂直AP AB BC 、、两两垂直PA ⊥面ABC 计算公式22224R AP AB AC =++22224R PA AB BC =++12sin AB r C =⋅且12d h =222R d r =+备注当锥体有三条棱两两垂直时,记这三条棱的棱长分别为a b c 、、,则22224R a b c =++.若锥体的底面不含直角,仅有侧棱垂直于底面时,用222R d r =+求出外接球半径【示例3】在三棱锥P ABC -中,90ACB ∠=︒,8AB =,PC ⊥面ABC 且6PC =,则该三棱锥外接球的表面积为__________.【解析】由题意可知CA CB CP 、、两两垂直;则222222222464410041006R CP CB CA CA CB AB R S R CP ππ⎫=++⎪+==→=→==⎬⎪=⎭【例3】1.在三棱锥A BCD -中,AB AC AD 、、两两垂直,且ACB ACD ABD △、△、△的面积分别为22A BCD -的外接球的表面积为__________.2.在三棱锥P ABC -中,PA ⊥平面ABC ,且ABC △为等边三角形,2AP AB ==,则三棱锥P ABC -的外接球的表面积__________.3.如图,PA ⊥面ABCE ,其中ABCD 为正方形,2AD =,1ED =.若三棱锥P ADE -的外接球的体积为92π.则四棱锥P ABCD -的外接球的表面积为__________.课堂练习3:1.在边长为2的等边三角形ABC 中,点D 是BC 的中点.以AD 为折痕,将ABC △折成直二面角B AD C --,则过A B C D 、、、四点的球的表面积为__________.2.在四面体S ABC -中,SA ⊥平面ABC ,120BAC ∠=︒,1AB =,2AC =,3SA =,则该四面体外接球面积为__________.3.在《九章算术》中,将底面为矩形且有一条侧棱与底面垂直的四棱锥称为阳马.已知四棱锥M ABCD -为阳马,侧棱MA ⊥底面ABCD ,且1MA =,2BC =,3AB =.若该四棱锥的顶在都在同一球面上,则该球的表面积为__________.4.正棱锥和圆锥的外接球补充:问题阐述①.正四面体内嵌于正方体,则两者具有相同的外接球.记正四面体的边长为a ,正方体的边长为b ,外接球半径为R ;②.两个具有相同底面,且顶点(P Q 、)在底面的射影均为底面外接圆圆心的锥体的外接球.记底面外接圆半径为r ,两个锥体的高分别为12h h 、,外接球半径为R示例图像对应计算①.2a b =且2243R b =;②.22342R a =①.122h h R +=且PA QA ⊥(PQ 为球的直径);②.212r h h =⋅(直角三角形内射影定理);【示例4】1.正三棱锥底面边长为3,侧棱与底面成60︒角,则其外接球的体积为__________.【解析】Ⅰ.确定正棱锥的高和底面外接圆半径ABC △是边长为3的等边三角形,则333r AB ==;在Rt POA △中,3360OA r OP h PAO ⎫==⎪→==⎬∠=︒⎪⎭;Ⅱ.求外接圆半径,并求其体积则2231243222633h r R V R h ππ+===→==2.两个圆锥的底面是一个球的同一截面,顶点均在球面上,若球的体积为323π,两个圆锥的高之比为1:3,则这两个圆锥的体积之和为__________.【解析】Ⅰ.求出12R h h r→→、3432233V R R ππ==→=球,显然PQ 是球O 的直径,则PA QA ⊥,则212r h h =⋅;121122243331h h R h r h h h +===⎫⎧→→=⎬⎨==⎭⎩Ⅱ.求锥体的体积则()21211233V h S h h r ππ=⋅=+⋅=【例4】1.若一个四面体的所有棱长均为1,四个顶点在同一个球面上,则此球的表面积为__________.2.如图,半球内有一内接正四棱锥S ABCD -,该四棱锥的体积为3,则该半球的体积为__________.3.已知圆锥的顶点和底面圆周都在球O 的球面上,圆锥的母线长为3,侧面展开图的面积为3π,则球O 的表面积等于__________.4.以ABC 为底的两个正三棱锥P ABC -和Q ABC -内接于同一个球,并且正三棱锥P ABC -的侧面与底面ABC 所成的角为45︒,记正三棱锥P ABC -和正三棱锥Q ABC -的体积分别为1V 和2V ,则12V V =__________.5.《九章算术》是我国古代的数学名著,其中有很多对几何体体积的研究,已知某囤积粮食的容器的下面是一个底面积为32π,高为h 的圆柱,上面是一个底面积为32π,高为h 的圆锥,若该容器有外接球,则外接球的体积为__________.6.已知三棱锥P ABC -的四个顶点在球O 的球面上,PA PB PC ==,ABC △是边长为2的正三角形,E F 、分别是PA AB 、的中点,90CEF ∠=︒,则球O 的体积为__________.课堂练习4:1.正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积为__________.2.底面是边长为1的正方形,侧面是等边三角形的四棱锥的外接球的体积为__________.3.已知正方体1111ABCD A B C D -的棱长为2,其各面中心分别为E F G H M N 、、、、、,则连接相邻各面中心构成的几何体的外接球表面积为__________.4.设A ,B ,C ,D 是同一个半径为4的球的球面上四点,ABC ∆为等边三角形且面积为D ABC -体积的最大值为__________.5.在正三棱锥P ABC -中,6AB BC AC ===,点D 是PA 的中点.若PB CD ⊥,则该三棱锥外接球的表面积为__________.5.其他模型问题阐述①.面ABC ⊥面BCD ;②.记12r r 、分别为ABC BCD △、△的外接圆半径,R 为三棱锥A BCD -外接球半径.①.三棱锥D ABC -中,AD 为外接球直径;②.记球面距1OO d =,ABC △的外接圆半径为r ,D ABC -的高为h .示例图像对应性质①.2h d =;②.2222124BC R r r =+-(BC 为交线长);①.AB DB AC DC ⊥⊥、(直径所对圆周角);②.222R d r =+且2h d =;解题步骤①.确定三棱锥A BCD -中的两个垂直平面;②.求出对应的外接圆半径和交线长;③.求外接球的半径;①.确定外接球的直径;②.求出底面三角形外接圆半径r ;③.22D ABC R r d h V --→→→;【示例5】1.将长、宽分别为4和3的长方形ABCD 沿对角线AC 折成直二面角,得到四面体A BCD -,则四面体A BCD -的外接球的表面积为__________.【解析】由题意,面ACD ⊥面ACB 且5AC =而ACD ACB △、△都是直角三角形,则12522AC r r ===;则2222122544AC R r r =+-=;得2425S R ππ==2.已知三棱锥S ABC -的所有顶点都在球O 的表面上,ABC △是边长为1的正三角形,SC 为球O 的直径,且2SC =,则此三棱锥的体积为__________.【解析】在ABC △中,2sin 3AB r C ==;同时112R SC ==,则d ==,则2h d ==∴111sin 33326V hS AB AC C ==⨯⋅⋅=【例5】1.已知三棱维A BCD -中,侧面ABC ⊥底面BCD ,ABC △是边长为6的正三角形,BCD ∆是直角三角形,且2BCD π∠=,4CD =,则此三棱锥外接球的表面积为__________.2.在三棱锥A BCD -中,BA AD ⊥,BC CD ⊥,且AD ==A BCD -外接球的体积为__________.3.已知球的直径4SC =,A ,B 是该球球面上的两点,AB =,30ASC BSC ∠=∠=︒,则棱锥S ABC -的体积为__________.4.已知球的直径4SC =,A ,B 是该球球面上的两点.2AB =,45ASC BSC ∠=∠=︒,则棱锥S ABC -的体积为__________.5.已知三棱锥S ABC -外接球的球心O 在线段SA 上,若ABC △与SBC △均为面积是的等边三角形,则三棱锥S ABC -外接球的体积为__________.6.已知三棱锥S ABC -的所有顶点都在球O 的球面上,SC 是球O 的直径.若平面SCA ⊥平面SCB ,SA AC =,SB BC =,三棱锥S ABC -的体积为9,则球O 的表面积为__________.课后作业:1.已知圆锥的底面圆周及顶点均在球面上,若圆锥的轴截面为正三角形,则圆锥的体积与球的体积之比为__________.2.已知一个圆柱的高是底面半径的2倍,且其上、下底面的圆周均在球面上,若球的体积为323π,则圆柱的体积为__________.3.已知在ABC ∆中,角A B C 、、所对的边分别为a b c 、、,且2a =,6A π=,又点A B C 、、都在球O 的球面上,且点O 到平面ABC ,则球O 的体积为__________.4.一个正三棱锥的底面边长等于一个球的半径,该正三棱锥的高等于这个球的直径,则球的体积与正三棱锥体积的比值为__________.5.正四面体A BCD -的棱长为4,点E 为BC 边上的中点,过点E 做其外接球的截面,则截面圆的面积最小值为__________.6.已知一个正三棱柱所有棱长均为3,若该正三棱柱内接于半球体,即正三棱柱的上底面的三个顶点在球面上,下底面的三个顶点在半球体的底面圆内,则该半球体的体积为__________.7.所有棱长都是3的直三棱柱111ABC A B C -的六个顶点都在同一球面上,则该球的表面积是__________.8.已知圆柱1OO 的两底面圆周上的所有点都在球C 的表面,且圆柱1OO 的底面半径为1,高为,则球C 的表面积为__________.9.已知某圆柱的轴截面为正方形,则此圆柱的表面积与此圆柱外接球的表面积之比为__________.10.已知直三棱柱111ABC A B C -的6个顶点都在球O 的球面上,若1AB =,AC =,AB AC ⊥,14AA =,则球O 的表面积为__________.11.已知正三棱台的高为1,上、下底面边长分别为和,其顶点都在同一球面上,则该球的表面积为__________.12.已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为__________.13.正三棱柱111ABC A B C -内接于半径为2的球,若A ,B 两点的球面距离为π,则正三棱柱的体积为__________.14.直三棱柱111ABC A B C -的各顶点都在同一球面上,若12AB AC AA ===,120BAC ∠=︒,则此球的表面积等于__________.15.已知矩形ABCD 的顶点都在半径为2的球O 的球面上,且AB =,BC =,过点D作DE 垂直于平面ABCD ,交球O 于点E ,则棱锥E ABCD -的体积为__________.16.在三棱锥P ABC -中,PA ⊥平面ABC ,AB BC ⊥,3AB =,4BC =,5PA =,则三棱锥P ABC -的外接球的表面积为__________.17.《九章算术》中,将四个面都为直角三角形的三棱锥称之为鳖臑.若三棱锥P ABC-为鳖臑,PA⊥平面ABC,2==,4PA AB-的四个顶点都在球O的球AC=,三棱锥P ABC面上,则球O的表面积为__________.18.已知在半径为2的球面上有A、B、C、D四点,若2==,则四面体ABCD的AB CD体积的最大值为().A B C.D19.已知四棱锥P ABCD=====,且底面ABCD为正方形,则-满足2PA PB PC PD AB该四棱锥的外接球的体积为__________.20.已知三棱锥P ABC -的四个顶点在球O 的球面上,PA PB PC ==,ABC ∆是边长为2的正三角形,PA PC ⊥,则球O 的体积为__________.21.高为1的圆锥内接于半径为1的球,则该圆锥的体积为__________.22.已知正四棱锥P ABCD -的高为2,AB =,过该棱锥高的中点且平行于底面ABCD的平面截该正四棱锥所得截面为1111A B C D ,若底面ABCD 与截面1111A B C D 的顶点在同一球面上,则该球的表面积为__________.23.已知正四棱锥的侧棱长为l ,其各顶点都在同一球面上.若该球的体积为36π,且3l ≤≤,则该正四棱锥体积的取值范围是__________.24.已知球O 的半径为1,四棱锥的顶点为O ,底面的四个顶点均在球O 的球面上,则当该四棱锥的体积最大时,其高为__________.25.已知四棱锥S ABCD -的所有棱长均相等,且底面是边长为的正方形,其5个顶点都在直径为10的球面上,则该四棱锥的体积为__________.26.已知1111ABCD A B C D -是边长为1的正方体,S ABCD -是高为1的正四棱锥,若点1111S A B C D 、、、、在同一球面上,则该球的表面积为__________.27.已知三棱锥S ABC -的底面是以AB 为斜边的等腰直角三角形,2SA SB SC AB ====,设S ,A ,B ,C 四点均在以O 为球心的某个球面上,则O 到平面ABC 的距离为__________.28.现有一副斜边长相等的直角三角板.若将它们的斜边AB 重合,其中一个三角板沿斜边折起形成三棱锥A BCD -,如图所示,已知6DAB π∠=,4BAC π∠=,三棱锥的外接球的表面积为4π,该三棱锥的体积的最大值为().A B C D 29.已知三棱锥A BCD -的四个顶点A ,B ,C ,D 都在球O 的表面上,BC CD ⊥,AC ⊥平面BCD ,且AC =,2BC CD ==,则球O 的表面积为__________.30.已知各顶点都在一个球面上的正四棱柱高为4,体积为16,则这个球的表面积是__________.31.已知矩形ABCD的顶点都在半径为2的球O的球面上,且AB=,BC=,过点D 作DE垂直于平面ABCD,交球O于点E,则棱锥E ABCD-的体积为().32.已知圆锥底面圆的直径为3,圆锥的高为,该圆锥的内切球也是棱长为a的正四面2体的外接球,则此正四面体的棱长a为__________.33.设P,A,B,C为球O表面上的四个点,PA,PB,PC两两垂直,且3PB=,PA=,6三棱锥P ABC-的体积为18,则球O的体积为__________.34.已知六棱锥P ABCDEFPA=,PA⊥底面-的七个顶点都在球O的表面上,若2ABCDEF,且六边形ABCDEF是边长为1的正六边形,则球O的体积为__________.35.已知一个正方体的所有顶点在一个球面上,若这个正方体的表面积为18,则这个球的体积为__________.36.如图,圆形纸片的圆心为O,半径为5cm,该纸片上的等边三角形ABC的中心为O.D、∆分别是以BC,CA,AB为底边的等腰三E、F为圆O上的点,DBC∆,ECA∆,FAB角形.沿虚线剪开后,分别以BC,CA,AB为折痕折起DBC∆,使得D、∆,FAB∆,ECAcm的最大E、F重合,得到三棱锥.当ABC△的边长变化时,所得三棱锥体积(单位:3)值为__________.37.已知底面边长为1的正四棱柱的各顶点均在同一球面上,则该球的体积为__________.38.已知S ,A ,B ,C 是球O 表面上的点,SA ⊥平面ABC ,AB BC ⊥,1SA AB ==,BC =O 的表面积等于__________.39.已知在半径为2的球面上有A 、B 、C 、D 四点,若2AB CD ==,则四面体ABCD 的体积的最大值为__________.40.已知点P A B C D 、、、、是球O 表面上的点,PA ⊥平面ABCD ,四边形ABCD 是边长为正方形.若PA =,则OAB ∆的面积为__________.41已知四面体P ABC -的外接球的球心O 在AB 上,且OP ⊥面ABC ,2AC =.若32P ABC V -=,则该球的体积为__________.。
外接球和内切球(精心整理)
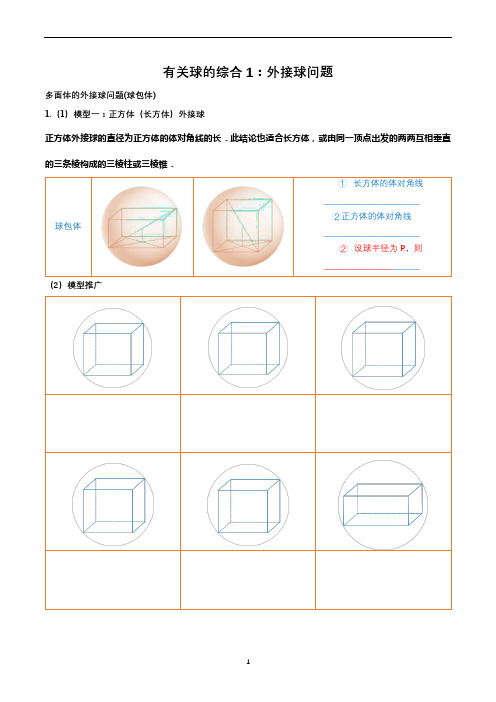
有关球的综合1:外接球问题多面体的外接球问题(球包体)1.(1)模型一:正方体(长方体)外接球正方体外接球的直径为正方体的体对角线的长.此结论也适合长方体,或由同一顶点出发的两两互相垂直的三条棱构成的三棱柱或三棱锥.(2)模型推广例1:已知一个正方体的所有顶点在一个球面上,若这个正方体的表面积为18,则这个球的体积为________.例2:设三棱柱ABC−A1B1C1的侧棱垂直于底面,AB=AC=2,∠BAC=90°,AA1=2,且三棱柱的所有顶点都在同一球面上,则该球的表面积为___________.例3:在球面上有四个点P、A、B、C,如果PA、PB、PC两两垂直,且PA=PB=PC=2,则该球的表面积为___________.例4.《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称为阳马;将四个面都为直接三角形的三棱锥称为鳖臑。
若三棱锥P-ABC为鳖臑,PA⊥平面ABC,PA=AB=2,AC=4,三棱锥P-ABC的四个顶点都在球O的球面上,则球O的表面积为_______.例5:已知正四面体的棱长为√2,则该四面体的外接球的体积为___________.例6.在三棱锥A-BCD中,AB=CD=2,AD=BC=√,AC=BD=√7,则该三棱锥的外接球表面积是_________.2.模型2:球包柱求三角形外接圆半径的方法例7:(1)设三棱柱ABC−A1B1C1的侧棱垂直于底面,AB=AC=2,∠BAC=120°,AA1=2,且三棱柱的所有顶点都在同一球面上,则该球的表面积为___________.(2)(2018·河北衡水调研)一个直六棱柱的底面是边长为2的正六边形,侧棱长为3,则它的外接球的表面积为________.例8:三棱锥D-ABC中,AD⊥平面ABC,AC=√3,BC=1,COS∠ACB=√3sin∠ACB,AD=2,则该三棱锥外接球的表面积为( )A.8π B.12πC.16πD.20π例9:如图,网格纸上小正方形的边长为l ,粗实线画出的是某几何体的三视图,该几何体是由一个三棱柱切割得到的,则该几何体外接球的表面积为( )A.π20B. π18C.π16D. π8例10:如图,网格纸上正方形的边长为1,图中粗线画出的是某三棱锥的三视图,则该三棱锥的外接球的表面积为_______________.模型3:球包锥(顶点连心锥)例11:一个圆锥的轴截面是边长为2的正三角形,其外接球的表面积为_____________例12:(1)正三棱锥P-ABC 中,侧棱长为1,底面三角形ABC _________.(2)正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积为( ) A.81π4B .16πC .9π D.27π4例13:在三棱锥P-ABC中,PA=PB=PC=2,AB=AC=1,BC=√3,则该三棱锥的外接球的表面积为()3.模型4:两圆定心法例14.(1)三棱锥P-ABC中,平面PAC⊥平面ABC,AB⊥AC,PA=PC=AC=2,AB=4,则三棱锥P-ABC 的外接球表面积为( )A.23πB.23π4C.64π3D.64π(2)三棱锥P-ABC中,△ABC和△PBC都是等边三角形,侧面PBC⊥底面ABC,AB=2√3,则三棱锥P-ABC的外接球表面积为__________.例15:(1)(2018惠州模拟)在三棱锥S-ABC中,△ABC是边长为3的等边三角形,SA=√3,SB=2√3,二面角S-AB-C 的大小为120°,则该三棱锥外接球的表面积为_____________(2)已知边长为2√3的菱形ABCD 中,∠BAD =60°,现沿对角线BD 折起,使得二面角A-BD-C 为120°,点A 、B 、C 、D 都在同一个球面上,则该球的表面积为__________.有关球的综合2:内切球问题平面基础:求三角形内切圆的半径1、等边三角形:设等边三角形边长为a ,则其内切圆半径为________.r=2、直角三角形:设直角三角形两直角边分别为,a b ,斜边为c ,则其内切圆的半径为__________.r=3、任意三角形:设三角形三边分别为,,,a b c 则其内切圆半径_______.r=1. 模型1:球切柱问题(1)球内切于正方体、内切于圆柱的问题,请看下表(2)球内切三棱柱的问题例1、直三棱柱111ABC A B C-内有一个的球,,AB6BC8==,且AB BC⊥.(1)若球与侧面底面均相切,求侧柱1AA;(2)若1AA3=,求球的体积V的最大值.2. 模型2:球切锥类型一:球切圆锥例2:(1)一个圆锥的母线长为2,圆锥的母线与底面夹角为π4,则该圆锥的内切球的表面积为()A.8π B.4(2−√2)2π C.4(2+√2)2π D.32(4−√2)249π(2)将半径为3,圆心角为2π3的扇形围成一个圆锥,则该圆锥的内切球的体积为()A.√2π3B. √3π3C. 4π3D.2π类型二:三棱锥的内切球例3(1):已知三棱锥P-ABC中,PA⊥底面ABC,AC=4,BC=3,AB=5,PA=3,则该三棱锥的内切球的体积为__________.(2)已知一个三棱锥的所有棱长均为√2,则该三棱锥的内切球的体积为__________.。
十种题型搞定多面体的外接球,内切球问题

十种题型搞定多面体的外接球,内切球问题题型一 直角四面体的外接球 补成长方体,长方体对角线长为球的直径1.三棱锥P ABC -中,ABC ∆为等边三角形,2PA PB PC ===,PA PB ⊥,三棱锥P ABC -的外接球的表面积为( )A .48πB .12πC .D .2.在正三棱锥A BCD -中,,E F 分别是,AB BC 的中点,EF DE ⊥,若BC =A BCD -外接球的表面积为A πB 2πC 3πD 4π3.在正三棱锥S ABC -中,,M N 分别是,SC BC 的中点,且MN AM ⊥,若侧棱SA =,则正三棱锥S ABC -外接球的表面积为A 12πB 32πC 36πD 48π 4.(2019全国1理12).已知三棱锥P −ABC 的四个顶点在球O 的球面上,P A =PB =PC ,△ABC 是边长为2的正三角形,E ,F 分别是P A ,AB 的中点,∠CEF =90°,则球O 的体积为A .B .C . D5.设A ,B ,C ,D 是半径为2的球面上的四个不同点,且满足AB →·AC →=0,AD →·AC →=0,AB →·AD →=0,用S 1、S 2、S 3分别表示△ABC 、△ACD 、△ABD 的面积,则S 1+S 2+S 3的最大值是________.题型二 等腰四面体的外接球 补成长方体,长方体相对面的对角线为等腰四面体的相对棱1.在四面体ABCD 中,若AB CD ==,2AC BD ==,AD BC ==ABCD 的外接球的表面积为( ) A .2πB .4πC .6πD .8πA B C D ,,,四点在半径为225的球面上,且5AC BD ==, AD BC ==,AB CD =,则三棱锥D ABC -的体积是____________.3.在三棱锥S ﹣ABC 中,底面△ABC 的每个顶点处的三条棱两两所成的角之和均为180°,△ABC 的三条边长分别为AB=3,AC=5,BC=6, 则三棱锥ABC S -的体积( )A .22B . 10C .232D .234 题型三 有公共斜边的两个直角三角形组成的三棱锥 ,球心在公共斜边的中点处1.在矩形ABCD 中,AB =4,BC =3,沿AC 将矩形ABCD 折成一个直二面角D AC B --,则四面体ABCD 的外接球的体积为A. π12125B.π9125C.π6125D.π31252.三棱锥S ABC -的所有顶点都在球O 的球面上,且SA AC SB BC ====4SC =,则该球的体积为A2563π B 323π C 16π D 64π3.在四面体S ABC -中,,2AB BC AB BC SA SC ⊥====,二面角S AC B --的余弦值是3-)A. B .6π C .24π D4.在平面四边形ABCD 中,1AB AD CD ===,2BD =,BD CD ⊥,将其沿对角线BD 折成四面体'A BCD -,使平面'A BD ⊥平面BCD ,若四面体'A BCD -顶点都在同一个球面上,则该球的体积为A 32πB 3πC 23π D 2π 5.平行四边形ABCD 中,AB ·BD =0,沿BD 将四边形折起成直二面角A 一BD -C ,且4222=+BD AB ,则三棱锥A -BCD 的外接球的表面积为( ) A .2π B .4π C .π4 D .2π6已知直角梯形ABCD ,AB AD ⊥,CD AD ⊥,222AB AD CD ===,沿AC 折叠成三棱锥,当三棱锥体积最大时,三棱锥外接球的体积为 .题型四 侧棱垂直于地面或侧面垂直于地面 过底面外心做垂线,球心有垂线上 1.已知四面体P ABC -,其中ABC ∆是边长为6的等边三角形,PA ⊥平面ABC ,4PA =,则四面体P ABC -外接球的表面积为________.2. 一个几何体的三视图如图所示,其中正视图是一个正三角形,则这个几何体的( )外接球的半径为33B .表面积为137++C .体积为3D .外接球的表面积为π4. 题型五 其中一条侧棱满足某个特殊的条件1.已知三棱锥BCD A -中,2====CD BD AC AB ,AD BC 2=,直线AD 底面BCD 所成的角是3π,则此时三棱锥外接球的体积是 ( ) A π8 B π32 C π324 D π328 答案。
正四面体的外接球和内切球

E
O C O1 B
所以PO1 4r
6 易求PO1 2 6, 所以r . 2
应用探究
(1) 解:设球半径原来为R,扩大后 为R/,则R/=nR,则S/:S= (nR)2:R2=n2:1,即球的表面积扩大到原 来的n2倍. (2) 解:设球半径原来为R,扩大后 为R/,由条件V/:V= (R/)3:R3=8:1,即 (R/):R=2:1,所以S/:S= (R/)2:R2=4:1,球 的表面积扩大3倍.
2
2、若正四体的棱长都为6,内有一球与四个面都相 切,求球的表面积。
解法2:连结OA、OB、OC、 OP,那么
P
VP ABC VOPAB VOPBC VOPCA VO ABC 4VO ABC
VO ABC
因VP ABC
1 S ABC OO1 , 3
1 SABC PO1 , 3
D 6л
C1 B1
解法2 构造棱长为1的正方 体,如图。则A1、C1、B、D是 棱长为 2 的正四面体的顶点。 正方体的外接球也是正四面体 的外接球,此时球的直径 为 3 , 3 2 S球 =4 ( ) 3 , 选A 2
D A B
C
2、若正四体的棱长都为6,内有一球与四个面都相 切,求球的表面积。
·
M
●
D
2 在RtBOO1中,由O1B2 BO2 OO 得 1
2
C
2 2 3 2 R ( R) , 解得R , 所以S球 4 R2 3 . 3 2 3
1、一个四面体的所有的棱都为 2 ,四个顶点在同 一球面上,则此球的表面积( )
A 3л
B 4л
C 3 3
D1 A1
外接球内切球

类型一:直棱柱1.一个正四棱柱的各个顶点在一个直径为2cm 的球面上.如果正四棱柱的底面边长为1cm,那么该棱柱的表面积为cm².2.长方体ABCD-A1B1C1D1的8个顶点都在球O的表面上,E为AB的中点,CE=3,cos∠ACE=5√3/9,且四边形ABB1A1为正方形,则球O的直径为3.已知底面边长为1,侧棱长为√2的正四棱柱的各顶点均在同一个球面上,则该球的体积为4.设三棱柱的侧棱垂直于底面,所有棱长都为a,顶点都在一个球面上,则该球的表面积为5.直三棱柱ABC-A1B1C1的各顶点都在同一球面上,若AB=AC=AA1=2,∠BAC=120°,则此球的表面积等于6.已知正三棱柱(底面是正三角形,侧棱与底面垂直)的体积为3√3cm³,所有顶点都在球O的球面上,则球O的表面积的最小值为cm2。
7.已知直三棱柱ABC-A1B1C1的6个顶点都在球0的球面上.若AB=3,AC=4,AB⊥AC,AA1=12,则球0的半径为8.在直三棱柱ABC-A1B1C1中,AB=BC=2,∠ABC=π/2,若该直三棱柱的外接球表面积为16π,则此直三棱柱的高为9.在三棱柱ABC-A1B1C1,AA1⊥面ABC,∠BAC=2π/3,AA1=4,AB=AC=2√3,则三棱柱ABC-A1B1C1的外接球的表面积为10.若一个底面边长为√6/2,侧棱长为√6的正六棱柱的所有顶点都在一个球的面上,则此球的体积为类型二:圆柱1. 如图,在圆柱O1O2内有一个球O,该球与圆柱的上、下底面及母线均相切,记圆柱O1O2的体积为V1,球O的体积为V2,则V1∶V2的值是2.(2017·新课标全国三·8·新课)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为2.如图所示,球O半径为R,圆柱O1O2内接于球O,当圆柱体积最大时,圆柱的体积V=则R=类型三:三棱锥1.已知正四面体S- ABC的外接球表面积为6π,则正四面体S- ABC的体积为2.一个四面体的所有棱长都为√2,四个顶点在同一球面上,则此球的表面积为3.一个棱长为5的正四面体(棱长都相等的三棱锥)纸盒内放一个小正四面体,若小正四面体在纸盒内可以任意转动,则小正四面体的棱长的最大值为4.如图所示,在正四面体A- BCD中,E是棱AD的中点,P是棱AC上一动点,BP+PE的最小值为√7,则该正四面体的外接球的体积是5. 正三棱锥的四个顶点都在同一球面上,若该棱锥的底面边长为2√3,侧棱与侧棱所成角的余弦值为1/4则该球的表面积为6. 已知三棱锥A- BCD 满足∶AB=AC=AD ,△BCD 是边长为2的等边三角形.三棱锥A- BCD 的外接球的球心0满足∶OB ⃑⃑⃑⃑⃑ +OC ⃑⃑⃑⃑⃑ +OD⃑⃑⃑⃑⃑⃑ =0,则该三棱锥的体积为7. 已知三棱锥S- ABC 的所有顶点都在球O 的球面上,△ABC 是边长为1的正三角形,SC 为球O 的直径,且SC=2,则此棱锥的体积为8. 在球面上有四个点P ,A ,B ,C ,如果PA ,PB ,PC 两两互相垂直,且PA=PB=PC=a ,那么这个球面的面积是9. 在三棱锥P- ABC 中,PA ,PB ,PC 两两相互垂直,PA=PB=PC=1,则此三棱锥内切球的半径为10. 正三角形ABC 的边长为2,将它沿高AD 折叠,使点B 与点C 间的距离为√3,则四面体ABCD 外接球的表面积为11. 正三棱锥S- ABC 中,M 、N 分别是棱SC 、BC 的中点,且AM ⊥MN ,若侧棱SA=2√3,则正三棱锥S- ABC 外接球的表面积是12. 已知三棱锥P- ABC 的四个顶点在球0的球面上,PA=PB=PC ,△ABC 是边长为2的正三角形,E ,F 分别是PA ,AB 的中点,∠CEF=90°,则球0的体积为13.如图,已知球O表面上四点A,B,C,D,DA⊥平面ABC,AB⊥BC,DA=AB=BC=√3,则球O 的体积等于14.已知S,A,B,C是球O表面上的点,SA⊥平面ABC,AB⊥BC,SA=AB=1,BC=√2,则球O的体积等于15.如图,在三棱锥P一ABC中,PA⊥平面ABC,AC⊥BC,AB=2,AP=√5,则三棱锥P—ABC的外接球的体积为16.已知在三棱椎P- ABC中、PC⊥平面ABC、PC=2CB=2.∠BAC=π/6,则三棱锥P- ABC外接球的表面积为17.在三棱锥P- ABC中,AB⊥平面PAC,PA=PC=AC=AB,三棱锥P- ABC的体积为18√3,已知三棱锥P一ABC它的顶点都在球O的球面上,则球O的表面积为18.在三棱锥A- BCD中,AB⊥平面BCD,△BCD是边长为3的等边三角形,AB=√3,则该三棱锥的外接球的表面积为19.三棱锥A- BCD中,AB=CD=6,AC=BD=AD=BC=5,则三棱锥的外接球的表面积为20.三棱锥A- BCD中,AB=CD=4,AC=BD=AD=BC=3,则该三棱锥的内切球的表面积为21.三棱锥A- BCD中,AB=CD=2,AD=BC=3,AC=BD=4,则三棱锥A- BCD外接球的表面积为22.已知三棱锥A- BCD,三组对棱两两相等,且AB=CD=1,AD=BC=√3,若三棱锥A- BCD的外接球表面积为9π/2,则AC=23.将边长为2√3,锐角为60°的菱形沿较短的对角线折叠成120°的二面角,若该菱形折叠后所得到三棱锥内接于球,则该球的表面积为24.在三棱锥S- ABC中,△ABC是边长为3的等边三角形,SA=√3,SB=2√3,二面角S-AB-C的大小为120°,则此三棱锥的外接球的表面积为25.在四面体S- ABC中,AB⊥BC,AB=BC=√2,SA=SC=2,二面角S-AC-B的余弦值是-√3/3,则该四面体外接球的表面积是26.已知A- BCD是球0的内接三棱锥,AB=AC=BC=BD=CD=6,AD=9,则球0的表面积为27.三棱锥P- ABC中,△ABC与△PBC都是等边三角形,侧面PBC⊥底面ABC,AB=2√3,则该三棱锥的外接球的表面积为28.球O的球面上有四点S,A,B,C,其中O,A,B,C四点共面,△ABC是边长为2的正三角形,面SAB⊥面ABC,则棱锥S- ABC的体积的最大值为29.已知三棱锥P- ABC中,PA=1,PB=3,AB=2√2,CA=CB=√5,面PAB⊥面ABC,则此三棱锥的外接球的表面积为30.已知二面角P-AB-C的大小为120°,且∠PAB=∠ABC=90°,AB=AP,AB+BC=6.若点P,A,B,C都在同一个球面上,则该球的表面积的最小值为31.在四面体ABCD中,若AD=DC=AC=CB=1,则当四面体ABCD的体积最大时,其外接球的表面积为32.平面四边形ABCD中,AB=AD=√2,CB=CD=√10,AC=4,沿直线AC将△ACD翻折成△ACD',当三棱锥D′-ABC的体积取得最大值时,该三棱锥的外接球的表面积是33.已知三棱锥P- ABC的顶点都在球0的球面上,AC⊥BC,AC=2,BC=4.若三棱锥P- ABC的体积的最大值为20/3,则球0的体积为34.设A,B,C,D是同一个半径为4的球的球面上四点,△ABC为等边三角形且其面积为9√3,则三棱锥D- ABC 体积的最大值为35.在菱形ABCD中,∠BAD=π/3 ,沿BD将△ABD折起到△PBD的位置,得到三棱锥P- BCD,若三棱锥P -BCD的体积最大时PC=√6,则此时三棱锥P- BCD的外接球的表面积为类型四:四棱锥1.正四棱锥S- ABCD的底面边长和各侧棱长都为√2,点S,A,B,C,D都在同一个球面上,则该球的体积为2.正四棱锥的顶点都在同一球面上.若该棱锥的高为4,底面边长为2,则该球的表面积为3.已知正方体ABCD一A1B1C1D1的棱长为1,点P是线段A1C1上的动点,则四棱锥P一ABCD的外接球半径R的取值范围是4.粽子古称“角黍”,是中国传统的节庆食品之一,由粽叶包裹糯米等食材蒸制而成.因各地风俗不同,粽子的形状和味道也不同,某地流行的“五角粽子”,其形状可以看成所有棱长均为8cm的正四棱锥,则这个粽子的表面积为cm²,现在需要在粽子内部放入一颗咸蛋黄,蛋黄的形状近似地看成球,则当这个蛋黄的体积最大时,其半径与正四棱锥的高的比值为类型五:圆锥1.已知圆锥的底面半径为1,母线长为3,则该圆锥内半径最大的球的体积为2.某圆锥的侧面展开图的面积为12π,圆心角a(α属于(0,π))的正切值为-√3,若圆锥的体积为V1,其外接球的体积为V2,则V1∶V2=3.设球的半径为3/4,该球的内接圆锥(顶点在球面上,底面为某平面与球的截面)的体积为V,则V的最大值为类型六:组合体1.如右图,是由正四棱锥和长方体拼接而成的组合体,其顶点都在半径为R的球面上,记r为ABCD的外接圆半径.若该正四棱锥和长方体体积相等,则r∶R=类型七:球的截面问题1.平面α截球O的球面所得圆的半径为1,球心O到平面α的距离为√2,则此球的体积为2.一平面截一球得到直径是6cm的圆面,球心到这个平面的距离是4cm,则该球的体积是3.已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为4.用平面a截半径为R的球,如果球心到截面的距离为R/2,那么截得小圆的面积与球的表面积的比值为5.圆O1是以R为半径的球O的小圆,若圆O1 的面积S1和球O的表面积S的比为S1∶S=2∶9,则圆心O1到球心O的距离与球半径的比OO1∶R=6.已知H是球O的直径AB上一点,AH∶HB=1∶2,AB⊥平面a,H为垂足,a截球O 所得截面的面积为π,则球O的表面积为7.设A,B,C,D是球面上的四个点,且在同一平面内,AB=BC=CD=DA=3,球心到该平面的距离是球半径的一半,则球的体积是8.已知矩形ABCD的顶点都在半径为4的球O的球面上,且AB=6,BC=2√3,则棱锥O- ABCD的体积为9.已知球的表面积为20π,球面上有A,B,C三点,如果AB=AC=BC=2√3,则球心到平面ABC的距离为10.已知过球面上A,B,C三点的截面和球心的距离等于球半径的一半,且AB=BC=CA=2,则球面面积是。
(秒杀)外接球与内切球问题

球的切接问题【类型一——外接球问题】题型一:长方体模型、正方体模型、墙角模型(有一条或以上的侧棱垂直于底面)(锥、柱体都适用)公式: 2222h R r ⎛⎫=+ ⎪⎝⎭(r :底面外接圆半径 h :侧棱的高度)例1.已知P ,A ,B ,C ,D 是球O 的球面上的五个点,四边形ABCD 为梯形,//AD BC ,2AB DC AD ===,4BC PA ==,PA ⊥面ABCD ,则球O 的体积为_______.题型二、对棱相等模型(补形为长方体) 公式: 22228x y z R ++=例2.已知一个三棱锥P ABC -,4PA PB BC AC ====,3PC AB ==,则它的外接球的表面积为______.题型三、共斜边的两个直角三角形,则球心在斜边的中点上 公式:2R =斜边长例3.在矩形ABCD 中,42AB AD ==,,现将矩形ABCD 沿对角线BD 折起,则所得三棱锥A BCD -外接球的体积是________.题型四、正多面体模型(上顶点在下底面投影点为底面外接圆圆心) 公式:R =r 2+h 22h(r :底面外接圆半径 h :棱锥的高度)例4.在三棱锥P ABC -中, 25PA PB PC === 23AB AC BC ===锥P ABC -外接球的体积是___________题型五、面面垂直模型 公式: 222212()2l R r r =+- (r 1,r 2:垂直的两个平面各自的外接圆半径 L:两个平面交线的长度)例 5.已知EAB ∆所在的平面与矩形ABCD 所在的平面互相垂直,︒=∠===60,2,3AEB AD EB EA ,则多面体ABCD E -的外接球的表面积为R 2=题型六、二面角模型m 2+n 2−2mncosθs 2inθ+(l 2)2(m ,n :分别表示两个平面外接圆圆心到交线l 的距离; θ:二面角)例6.在三棱锥S ABC -中,2,1SA SB AC BC SC =====,二面角S AB C --的大小为60︒,则三棱锥S ABC -的外接球的表面积为_______________O O 2M AO 1类型六、锥体的内切球问题等体积法:r=3V体S表例7.试求出棱全长为a的正四面体的内切球半径_____________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
内切球和外接球例题 Company number:【0089WT-8898YT-W8CCB-BUUT-202108】
高考数学中的内切球和外接球问
题
一、直接法(公式法)
1、求正方体的外接球的有关问题 例1若棱长为3的正方体的顶点都在同一球面上,则该球的表面积为______________ .27π.
例2 一个正方体的各顶点均在同一球的球面上,若该正方体的表面积为
24,则该球的体积为
______________.
.
2、求长方体的外接球的有关问题 例3 (2007年天津高考题)一个长方体的各顶点均在同一球面上,且一个顶点上的三条棱长分别为1,2,3,则此球的表面积为 .14π.
例4、(2006年全国卷I )已知各顶点都在一个球面上的正四棱柱高为4,体积为16,则这个球的表面积为( ). C.
A. 16π
B. 20π
C. 24π
D. 32π
3.求多面体的外接球的有关问题 例5. 一个六棱柱的底面是正六边形,其侧棱垂直于底面,已知该六棱柱
的顶点都在同一个球面上,且该六棱柱
的体积为9
8,底面周长为3,则这个球
的体积为 .
解 设正六棱柱的底面边长为x ,高
为h
,则有263,1,296,84x x x h h =⎧⎧
=⎪⎪
∴⎨⎨
=⨯
⎪⎪=⎩⎩ ∴
正六棱柱的底面圆的半径
1
2r =
,球心到
底面的距离
d =
.
∴外接球的半径
1R ==.43V π
∴=
球.
二、构造法(补形法)
1、构造正方体
例5 (2008年福建高考题)若三棱
锥的三条侧棱两两垂直,且侧棱长均为
,则其外接球的表面积是
_______________.9π
解 据题意可知,该三棱锥的三条侧棱两两垂直,∴把这个三棱锥可以补成
一个棱长为3的正方体,于是正方体的外接球就是三棱锥的外接球.设其外接球的半径为R ,则有
()
()()()
2
2
2
2
23339
R =
++=.∴
29
4R =
.故其外接球的表面积
249S R ππ==.
小结 一般地,若一个三棱锥的三条侧棱两两垂直,且其长度分别为
a b c 、、,则就可以将这个三棱锥补成
一个长方体,于是长方体的体对角线的
长就是该三棱锥的外接球的直径.设其外
接球的半径为R ,则有222
2R a b c =++.
出现“墙角”结构利用补形知识,联系长方体。
【例题】:在四面体中,共
顶点的三条棱两两垂直,其长度分别为
,若该四面体的四个顶点在一
个球面上,求这个球的表面积。
解:因为:长方体外接球的直径为
长方体的体对角线长所以:四面体外接
球的直径为
的长即:
所以球的
表面积为
例 6.一个四面体的所有棱长都为
2,四个顶点在同一球面上,则此球的
表面积为( )
A. 3π
B. 4π
C. 33π
D.
6π
解析:一般解法,需设出球心,作出高线,构造直角三角形,再计算球的
半径.在此,由于所有棱长都相等,我们
联想只有正方体中有这么多相等的线
段,所以构造一个正方体,再寻找棱长
相等的四面体,四面体A BDE -满足条件,即
AB=AD=AE=BD=DE 2BE ==可求得正方体的棱长为1,体对角线为
33,所以
此球的表面积便可求得,故选A. 例7.在等腰梯形ABCD 中,
AB=2DC=2,0DAB=60∠,E 为AB 的
中点,将ADE ∆与BEC ∆分布沿ED 、
EC 向上折起,使A B 、重合于点P ,则三棱锥P-DCE 的外接球的体积为( ).
A. 27
B. 2
C. 8
D. 24
解析: 因为AE=EB=DC=1,
0DAB=CBE=DEA=60∠∠∠,所以
AE=EB=BC=DC=DE=CE=1AD =,即三
棱锥P-DCE 为正四面体,至此,这与例
6就完全相同了,故选C.
例8 .已知球O 的面上四点A 、B 、C 、D ,DA ABC ⊥平面,AB BC ⊥
,
O 的体积等
于 .
解析:本题同样用一般方法时,需要找出球心,求出球的半径.而利用长方体模型很快便可找到球的直径,由于
DA ABC ⊥平面,AB BC ⊥,联想长方
体中的相应线段关系,构造长方体,又
因为方体,所以CD 长即为外接球的直径,
利用直角三角形解出CD=3.故球O 的体
积等于9
2π.
2、构造长方体
例9.已知点A 、B 、C 、D 在同一个球面上,B BCD A ⊥平面,BC DC ⊥,
若6,AB =,则球的体积是 .
解析:首先可联想到例8,构造下
面的长方体,于是AD 为球的直径,O
为球心,OB=OC=4为半径,要求B 、C 两点间的球面距离,只要求出BOC ∠即可,在Rt ABC ∆中,求出=4BC ,所以
0C=60BO ∠,故B 、C 两点间的球面距
离是43π.
三.多面体几何性质法
例1 0.已知各顶点都在同一个球面上的正四棱柱的高为4,体积为16,则这个球的表面积是
A.16π
B.20π
C.24π
D.32π
解 设正四棱柱的底面边长为x ,外
接球的半径为R ,则有
2416x =,解得2x =.
∴
2R R ==∴= .∴
这个球的表面积是2
424R ππ=.选C.小
结 本题是运用“正四棱柱的体对角线的长等于其外接球的直径”这一性质来求解的.
四.寻求轴截面圆半径法
例11.正四棱锥S ABCD -的底面边
,点
S A B C D 、、、、都在同一球面上,则此球的体积为 .
解 设正四棱锥的底面中心为1O ,外接球的球心为O ,如图1所示.∴由球的截面的性质,可得1OO ABCD ⊥平面.
又1SO ABCD ⊥平面,∴球心O 必在
1SO 所在的直线上.
∴ASC ∆的外接圆就是外接球的一个轴截面圆,外接圆的半径就是外接球的半径.在ASC ∆
中,由
2SA SC AC ===,得
222SA SC AC +=.∴
ASC AC ∆∆是以为斜边的Rt .∴1
2AC
=是
外接圆的半径,也是外接球的半径.故
43V π=
球.
五 .确定球心位置法
例11.在矩形ABCD 中,
4,3AB BC ==,沿AC 将矩形ABCD 折
成一个直二面角B AC D --,则四面体
ABCD 的外接球的体积为
A.125
12π
B.125
9π C.1256π
D.125
3π
解 设矩形对角线的交点为O ,则由矩形对角线互相平分,可知
OA OB OC OD ===.∴点O 到四面体的四个顶点A B C D 、、、的距离相等,即点O 为四面体的外接球的球心,∴外接
C
D A
S
O 1图3
球的半径
52R OA ==
.故
3412536V R ππ
==球.选C.
【例题】:已知三棱锥的四个顶点都在球
的球面上,且,,,
,求球的体积。
解:且,,
,, 因为 所以知所以
所以可得图形为:
在
中斜边为,在中斜边为
,取斜边的中点
,在
中
,在
中
所以在几何体中
,即为该四面
体的外接球的球心, ,所
以该外接球的体积为。
