八上第11讲 期中专题一 将军饮马类题型全覆盖
八年级将军饮马问题例题讲解

八年级将军饮马问题例题讲解哎呀,今天咱们聊聊八年级的将军饮马问题,听名字就觉得特别有意思,对吧?咱们先来个开门见山,将军带着他的军队,经过一条河,得给马喝水。
这问题看似简单,但其实里面藏着不少小玄机,真的是个大考验,脑袋瓜得动一动。
想象一下,这将军带着一帮士兵,行军走到河边,嗨,口渴得不行,马儿们更是想喝水。
可是,问题来了,河边的水不深,能让马儿们喝到,但不让它们掉进水里。
将军一边心急如焚,一边得想办法。
怎么让这些马儿在喝水的时候不掉进河里呢?这时候就得用到一些小技巧了。
咱们可以想象一下,马儿们得排队,得一个一个地喝水。
将军心里想着,得控制好马儿的喝水速度,别让它们都挤在一起,这样容易出事。
也许能用一些方法,比如说把马儿们牵得远一些,慢慢地让它们喝,像是在参加比赛一样,嘿嘿,真是有意思的场景。
想想马儿们排成一队,乖乖的,一个个慢慢走过来喝水,真是可爱。
这时候就得算一算了,马儿们得喝多少水,每匹马喝水的速度又有多快。
嘿,可能是三两口就满足了,也可能是急着想喝个痛快,一口气喝个干净。
将军得根据情况来调整策略,真是够麻烦的。
不过,思来想去,最好的办法还是得让马儿们分批来,排着队,井然有序。
然后,咱们再来想象一下,如果马儿们不听话,乱跑,那可就麻烦了。
想象一下将军那个急得直挠头的样子,心里想着:这马儿也太不听话了!要不就得用点小办法,比如说放一块香饽饽在河边,吸引它们过来,嘿嘿,果然,马儿们就乖乖走过来喝水了。
就像小朋友看到喜欢的玩具一样,立马就冲过去了,真是太可爱了。
接着咱们来讨论一下,假设这条河不宽,马儿们很快就能喝到水,那将军得加快速度,不能让马儿们等太久。
想想那画面,马儿们都急得不行,口水都快流下来了,哈哈,真是个搞笑的场景。
将军这时候就得使出浑身解数,调整路线,确保马儿们能尽快喝水。
但是,事情总是没那么简单。
马儿喝水喝得急,可能还会打架,踩到脚,这可就不好了。
所以,将军得一边指挥,一边安抚,真是一场心力交瘁的战斗。
初二数学将军饮马相关题目及解答

这是总纲:【序号一】文章引言- 对“初二数学将军饮马相关题目及解答”进行简单介绍和解释。
【序号二】初步理解将军饮马问题- 对问题进行初步描述,解释将军饮马问题的背景和相关概念。
- 分析将军饮马问题中的关键因素和要点,引导读者初步理解问题。
【序号三】盘点各类将军饮马问题- 总结各类将军饮马问题,包括常见的类型、变种及相关的难点。
- 分析各类问题的特点和难点,并介绍解题的一般思路和方法。
【序号四】深度解析具体的将军饮马问题- 选取一到两个典型的将军饮马问题进行详细分析,展示深度解题的过程和技巧。
- 重点突出解题思路和方法,引导读者掌握解决具体问题的技巧和策略。
【序号五】对将军饮马问题的个人理解和观点- 共享个人对将军饮马问题的理解和感悟,探讨解题过程中的心得和体会。
- 提出对将军饮马问题的个人见解和观点,展示对问题的深刻理解和思考。
【序号六】总结和回顾- 对全文进行总结和回顾,强调将军饮马问题的重要性和解题的技巧。
- 突出对变种问题的解题策略和技巧,鼓励读者深入探索相关问题,提升解题能力。
【序号七】结语- 对全文进行简短的结语,表达对将军饮马问题的重视和对读者的鼓励。
假设最终文章大致如下:序号一:文章引言在初二数学学习中,将军饮马问题一直是一个经典而又充满挑战的题目。
它不仅考验着学生的数学思维和逻辑能力,同时也对解题技巧和方法提出了很高的要求。
在接下来的文章中,我们将对将军饮马问题进行全面的探讨和分析,并共享解题的一般思路和方法。
序号二:初步理解将军饮马问题将军饮马问题是一个著名的逻辑问题,通常以丰富的形式出现在中学数学教科书中。
它涉及到将军与士兵、马与草地之间的复杂关系,要求学生通过数学方法解决实际问题,锻炼逻辑推理和数学建模的能力。
让我们来看一下一个常见的例子。
假设有一名将军带着三十个士兵和三十匹马要过草原。
草原上有三十个不同的点,它们是将军要经过的地方。
将军每次只能带十匹马经过,但他有几个条件:1. 每匹马每次必须有骑手骑着; 2. 每个地点只能经过一次; 3. 带着马过草地时必须带上骑手;问题是,如何保证士兵、马、将军都能安全地过草地?透过这个简单的例子,我们初步了解了将军饮马问题的背景和相关概念。
初二将军饮马练习题及答案

初二将军饮马练习题及答案题目一:将军饮马练习阅读下面的短文,然后根据短文内容回答问题。
春秋时期,楚国的将军薛将军因在战场上立下赫赫战功,受到国王的嘉奖,被封为将军。
薛将军深感自己取得的成就来之不易,为了更好地提升自己的军事才能,他经常利用业余时间练习骑射。
一天,他饮酒之后,心血来潮,决定骑马练习。
他醉醺醺地骑在马背上,手握弓箭,身姿挺拔。
突然,他抬头目视远方的鹰,大声喊道:“马儿,你好生奔放,将你的速度发挥到极致。
”马儿似乎听懂了薛将军的话,使出浑身解数奔驰起来。
薛将军稳稳地坐在马背上,准备放箭。
问题:1. 薛将军为什么经常练习骑射?2. 为什么薛将军喊马儿将速度发挥到极致?3. 薛将军的骑射练习中有哪些亮点?答案:1. 薛将军经常练习骑射是为了提升自己的军事才能。
2. 薛将军喊马儿将速度发挥到极致是为了更好地测试自己的骑射技巧。
3. 薛将军的骑射练习中的亮点包括:饮酒后决定进行练习,以更高难度的状态来挑战自己;喊马儿将速度发挥到极致,考验自己的射击准确性和反应能力。
题目二:将军饮马练习答案解析问题:1. 薛将军为什么经常练习骑射?答案解析:薛将军经常练习骑射是为了更好地提升自己的军事才能。
他深感自己在战场上立下的赫赫战功来之不易,因此希望通过练习骑射来增强自己的战斗力。
2. 为什么薛将军喊马儿将速度发挥到极致?答案解析:薛将军喊马儿将速度发挥到极致是为了更好地测试自己的骑射技巧。
他希望在马儿飞驰的情况下,能够准确地射箭,展现出自己的高超技艺。
3. 薛将军的骑射练习中有哪些亮点?答案解析:薛将军的骑射练习中的亮点包括:a) 饮酒后决定进行练习:饮酒之后,薛将军心血来潮,决定骑马练习。
这展现了他的勇气和自信,也体现了他对自己技艺的自豪感。
b) 喊马儿将速度发挥到极致:薛将军对马儿的速度要求极高,希望它能够发挥出最快的速度。
这要求他自己的反应能力和射击准确性都必须达到非常高的水平。
总结:薛将军通过练习骑射来提升自己的军事才能,展示了他在战场上立下的赫赫战功所带来的成就感。
将军饮马问题例题

将军饮马问题例题
例题:一个将军饮马,有三个酒坛,其中一个酒坛里装着毒酒,另外两个酒坛里装着普通的酒。
这三个酒坛外观相同,将军无法通过外观来判断哪个酒坛是有毒的。
在喝下一杯毒酒后,将军将会立即死亡。
现在将军有一匹马,这匹马可以闻出毒酒,如果马喝下一杯毒酒,它将会在30分钟后死亡。
将军只有30
分钟的时间来确定哪个酒坛里装着毒酒,并且不允许酒坛之间进行任何类型的测量。
解法:将军可以按照以下步骤确定毒酒所在的酒坛:
1. 为了节省时间,将将军的马分成三组,每组10匹马。
标记
这三组马为A、B、C。
2. 让A组的马尝试第一个酒坛,让B组尝试第二个酒坛,C
组尝试第三个酒坛。
3. 让所有的马者都喝下一杯酒。
4. 等待15分钟。
5. 如果A组的马中有马死亡,那么第一个酒坛是有毒的;如
果B组的马中有马死亡,那么第二个酒坛是有毒的;如果C
组的马中有马死亡,那么第三个酒坛是有毒的。
6. 如果在15分钟内没有任何马死亡,那么第一个酒坛是安全的,因此第二个酒坛是有毒的;如果A和B组的马都没有死
亡,那么第三个酒坛是有毒的。
这样,将军可以在30分钟内确定哪个酒坛里装着毒酒。
中考复习:“将军饮马”类题型大全

“将军饮马”类题型大全一.求线段和最值1(一)两定一动型例1:如图,AM⊥EF,BN⊥EF,垂足为M、N,MN=12m,AM=5m,BN=4m, P是EF 上任意一点,则PA+PB的最小值是______m.分析:这是最基本的将军饮马问题,A,B是定点,P是动点,属于两定一动将军饮马型,根据常见的“定点定线作对称”,可作点A关于EF的对称点A’,根据两点之间,线段最短,连接A’B,此时A’P+PB即为A’B,最短.而要求A’B,则需要构造直角三角形,利用勾股定理解决.解答:作点A关于EF的对称点A’,过点A’作A’C⊥BN的延长线于C.易知A’M=AM=NC=5m,BC=9m,A’C=MN=12m,在Rt△A’BC中,A’B=15m,即PA+PB的最小值是15m.变式:如图,在边长为2的正三角形ABC中,E,F,G为各边中点,P为线段EF上一动点,则△BPG周长的最小值为_________.分析:考虑到BG为定值是1,则△BPG的周长最小转化为求BP+PG的最小值,又是两定一动的将军饮马型,考虑作点G关于EF的对称点,这里有些同学可能看不出来到底是哪个点,我们不妨连接AG,则AG⊥BC,再连接EG,根据“直角三角形斜边中线等于斜边的一半”,可得AE=EG,则点A就是点G关于EF的对称点.最后计算周长时,别忘了加上BG的长度.解答:连接AG,易知PG=PA,BP+PG=BP+PA,当B,P,A三点共线时,BP+PG=BA,此时最短,BA=2,BG=1,即△BPG周长最短为3.2(二)一定两动型例2:如图,在△ABC中,AB=AC=5,D为BC中点,AD=5,P为AD上任意一点,E 为AC上任意一点,求PC+PE的最小值.分析:这里的点C是定点,P,E是动点,属于一定两动的将军饮马模型,由于△ABC 是等腰三角形,AD是BC中线,则AD垂直平分BC,点C关于AD的对称点是点B,PC+PE=PB+PE,显然当B,P,E三点共线时,BE更短.但此时还不是最短,根据“垂线段最短” 只有当BE⊥AC时,BE最短.求BE时,用面积法即可.解答:作BE⊥AC交于点E,交AD于点P,易知AD⊥BC,BD=3,BC=6,则AD·BC=BE·AC,4×6=BE·5,BE=4.8变式:如图,BD平分∠ABC,E,F分别为线段BC,BD上的动点,AB=8,△ABC的周长为20,求EF+CF的最小值________.分析:这里的点C是定点,F,E是动点,属于一定两动的将军饮马模型,我们习惯于“定点定线作对称”,但这题这样做,会出现问题.因为点C的对称点C’必然在AB上,但由于BC长度未知,BC’长度也未知,则C’相对的也是不确定点,因此我们这里可以尝试作动点E关于BD的对称点.解答:如图,作点E关于BD的对称点E’,连接E’F,则EF+CF=E’F+CF,当E’,F,C三点共线时,E’F+CF=E’C,此时较短.过点C作CE’’⊥AB于E’’,当点E’ 与点E’’重合时,E’’C最短,E’’C为AB边上的高,E’’C=5.(三)两定两动型例3:如图,∠AOB=30°,OC=5,OD=12,点E,F分别是射线OA,OB上的动点,求CF+EF+DE的最小值.分析:这里的点C,点D是定点,F,E是动点,属于两定两动的将军饮马模型,依旧可以用“定点定线作对称”来考虑.作点C关于OB的对称点,点D关于OA的对称点.解答:作点C关于OB的对称点C’,点D关于OA的对称点D’,连接C’D’. CF+EF+DE=C’F+ EF+D’E,当C’,F, E,D’四点共线时,CF+EF+DE=C’D’最短.易知∠D’OC’=90°,OD’=12,OC’=5,C’D’=13,CF+EF+DE最小值为13.变式:(原创题)如图,斯诺克比赛桌面AB宽1.78m,白球E距AD边0.22m,距CD 边1.4m,有一颗红球F紧贴BC边,且距离CD边0.1m,若要使白球E经过边AD,DC,两次反弹击中红球F,求白球E运动路线的总长度.分析:本题中,点E和点F是定点,两次反弹的点虽然未知,但我们可以根据前几题的经验作出,即分别作点E关于AD边的对称点E’,作点F关于CD边的对称点F’,即可画出白球E的运动路线,化归为两定两动将军饮马型.解答:作点E关于AD边的对称点E’,作点F关于CD边的对称点F’,连接E’F’,交AD于点G,交CD于点H,则运动路线长为EG+GH+HF长度之和,即E’F’长,延长E’E交BC于N,交AD于M,易知E’M=EM=0.22m,E’N=1.78+0.22=2m,NF’=NC+CF’=1.4+0.1=1.5m,则Rt△E’NF’中,E’F’=2.5m,即白球运动路线的总长度为2.5m.小结:以上求线段和最值问题,几乎都可以归结为“两定一动”“一定两动”“两定两动”类的将军饮马型问题,基本方法还是“定点定线作对称”,利用“两点之间线段最短”“垂线段最短”的2条重要性质,将线段和转化为直角三角形的斜边,或者一边上的高,借助勾股定理,或者面积法来求解.当然,有时候,我们也需学会灵活变通,定点对称行不通时,尝试作动点对称.(二)求角度例1:P为∠AOB内一定点,M,N分别为射线OA,OB上一点,当△PMN周长最小时,∠MPN=80°.(1)∠AOB=_____°(2)求证:OP平分∠MPN分析:这又是一定两动型将军饮马问题,我们应该先将M,N的位置找到,再来思考∠AOB 的度数,显然作点P关于OA的对称点P’,关于OB的对称点P’’,连接P’P’’,其与OA交点即为M,OB交点即为N,如下图,易知∠DPC与∠AOB互补,则求出∠DPC的度数即可.解答:(1)法1:如图,∠1+∠2=100°,∠1=∠P’+∠3=2∠3,∠2=∠P’’+∠4=2∠4,则∠3+∠4=50°,∠DPC=130°,∠AOB=50°.再分析:考虑到第二小问要证明OP平分∠MPN,我们就连接OP,则要证∠5=∠6,显然很困难,这时候,考虑到对称性,我们再连接OP’,OP’’,则∠5=∠7,∠6=∠8,问题迎刃而解.解答:(1)法2:易知OP’=OP’’,∠7+∠8=∠5+∠6=80°,∠P’OP’’=100°,由对称性知,∠9=∠11,∠10=∠12,∠AOB=∠9+∠10=50°(2)由OP’=OP’’,∠P’OP’’=100°知,∠7=∠8=40°,∠5=∠6=40°,OP平分∠MPN.变式:如图,在五边形ABCDE中,∠BAE=136°,∠B=∠E=90°,在BC、DE上分别找一点M、N,使得△AMN的周长最小时,则∠AMN+∠ANM的度数为________.分析:这又是典型的一定两动型将军饮马问题,必然是作A点关于BC、DE的对称点A′、A″,连接A′A″,与BC、DE的交点即为△AMN周长最小时M、N的位置.解答:如图,∵∠BAE=136°,∴∠MA′A+∠NA″A=44°由对称性知,∠MAA′=∠MA′A,∠NAA″=∠NA″A,∠AMN+∠ANM=2∠MA′A+2∠NA″A=88°思考题:1.(2017·安顺)如图所示,正方形ABCD的边长为6,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为_______.2.(2017·安徽改编)如图,在矩形ABCD中,AB=4,AD=3.P为矩形ABCD内一点,若矩形ABCD面积为△PAB面积的4倍,则点P到A,B两点距离之和PA+PB 的最小值为________.。
【中考数学】最全“将军饮马”类问题(类型大全+分类汇编)总复习
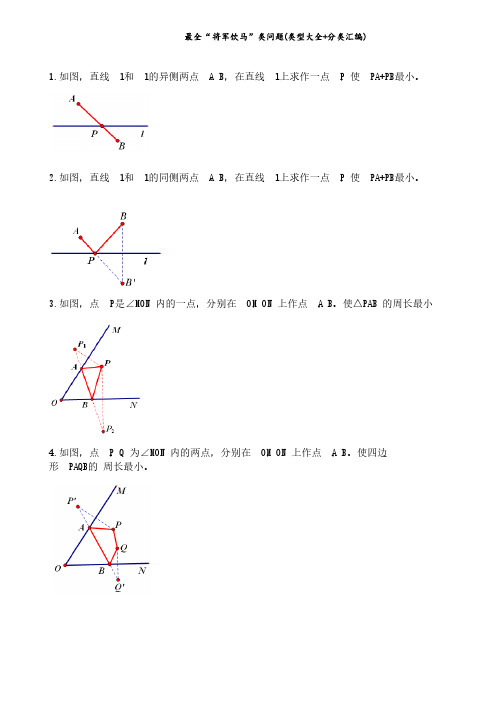
最全“将军饮马”类问题(类型大全+分类汇编)1.1.如图,直线如图,直线如图,直线 l l 和 l 的异侧两点的异侧两点的异侧两点 A A 、B ,在直线,在直线 l l 上求作一点上求作一点上求作一点 P P ,使,使,使 PA+PB PA+PB 最小。
最小。
最小。
2.2.如图,直线如图,直线如图,直线 l l 和 l 的同侧两点的同侧两点的同侧两点 A A 、B ,在直线,在直线 l l 上求作一点上求作一点上求作一点 P P ,使,使,使 PA+PB PA+PB 最小。
最小。
最小。
3.3.如图,点如图,点如图,点 P P 是∠是∠是∠MON MON 内的一点,分别在内的一点,分别在 OM OM ,ON 上作点上作点 A A ,B 。
使△。
使△PAB PAB 的周长最小的周长最小4.4.如图,点如图,点如图,点 P P ,Q 为∠为∠MON MON 内的两点,分别在内的两点,分别在 OM OM ,ON 上作点上作点 A A ,B 。
使四边形 PAQB 的 周长最小。
周长最小。
5.5.如图,点如图,点如图,点 A A 是∠是∠是∠MON MON 外的一点,在射线外的一点,在射线 OM OM 上作点上作点上作点 P P ,使,使,使 PA PA 与点与点与点 P P 到射线到射线到射线 ON ON 的距离的距离之和最小之和最小6. .如图,点如图,点如图,点 A A 是∠是∠是∠MON MON 内的一点,在射线内的一点,在射线 OM OM 上作点上作点上作点 P P ,使,使,使 PA PA 与点与点与点 P P 到射线到射线到射线 ON ON 的距的距离之和最小离之和最小EMME HM30°二、常见题型三角形问题1.如图,在等边△如图,在等边△ABC ABC ABC 中,中,中,AB = 6AB = 6AB = 6,,AD AD⊥⊥BC BC,,E E 是是 AC AC 上的一点,上的一点,上的一点,M M M 是是 AD AD 上的一点,若上的一点,若上的一点,若 AE = 2 AE = 2 AE = 2,求,求,求 EM+EC EM+EC EM+EC 的最小值的最小值 A解:∵点解:∵点 C C C 关于直线关于直线关于直线 AD AD AD 的对称点是点的对称点是点的对称点是点 B B B,,A∴连接∴连接 BE BE BE,交,交,交 AD AD AD 于点于点于点 M M M,则,则,则 ME+MD ME+MD 最小,过点过点 B B B 作作 BH BH⊥⊥AC AC 于点于点于点 H H H,, 则 EH = AH EH = AH –– AE = 3 AE = 3 –– 2 = 1,BH = BC2 - CH2 = 62 - 32 = 3 3在直角△在直角△BHE BHE BHE 中,中,中,BE = BE = BH2 + HE2B=(3 3)2 + 12 = 2 7DCBDC2.如图,在锐角△如图,在锐角△ABC ABC ABC 中,中,中,AB = 4 2AB = 4 2AB = 4 2,∠,∠,∠BAC BAC BAC=45°,∠=45°,∠=45°,∠BAC BAC BAC 的平分线交的平分线交的平分线交 BC BC BC 于点于点于点 D D D,,M 、N N 分别是分别是分别是 AD AD AD 和和 AB AB 上的动点,上的动点,则 BM+MN BM+MN 的最小值是的最小值是 .解:作点解:作点 B B B 关于关于关于 AD AD AD 的对称点的对称点 B'B',,过点过点 B' B' B'作作 B'E B'E⊥⊥AB AB 于点于点 E ,交,交 AD AD AD 于点于点于点 F F F,, 则线段则线段 B'E B'E B'E 的长就是的长就是的长就是 BM BM BM+MN的最小值+MN的最小值 在等腰等腰 Rt Rt Rt△△AEB'AEB'中,中, 根据勾股定理得到,根据勾股定理得到,B'E B'E = 4CB'M FDAN EB3.如图,△如图,△ABC ABC ABC 中,中,中,AB=2AB=2AB=2,∠BAC=30°,若在,∠BAC=30°,若在,∠BAC=30°,若在 AC AC AC、、AB AB 上各取一点上各取一点上各取一点 M M M、、N ,使,使 BM+MN BM+MN BM+MN 的值最小,则这个最小值的值最小,则这个最小值C解:作解:作 AB AB AB 关于关于关于 AC AC AC 的对称线段的对称线段 AB'AB',,过点过点 B' B' B'作作 B'N B'N⊥⊥AB AB,垂足为,垂足为,垂足为 N N N,交,交,交 AC AC AC 于点于点 M , 则 B'N = MB'+MN = MB+MN B'N B'N 的长就是的长就是的长就是 MB+MN MB+MN MB+MN 的最小值的最小值则∠则∠B'AN = 2B'AN = 2B'AN = 2∠∠BAC= 60BAC= 60°,°,°,AB' = AB = 2AB' = AB = 2AB' = AB = 2,, ∠ANB'= 90ANB'= 90°,∠°,∠°,∠B' = 30B' = 30B' = 30°。
将军饮马问题例题及应用
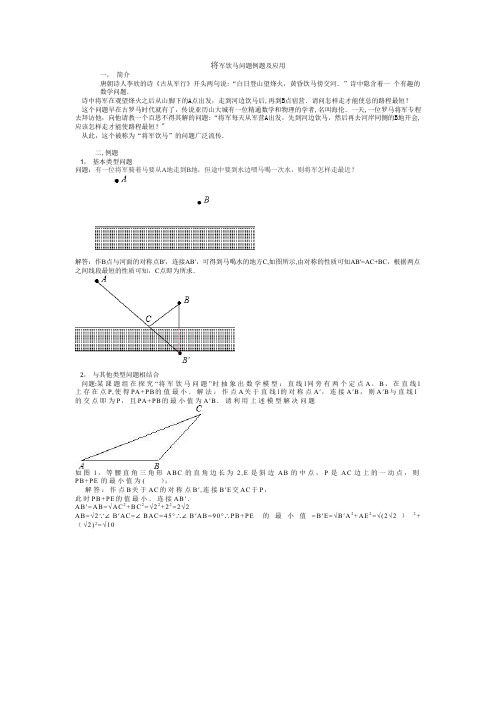
将军饮马问题例题及应用一,简介唐朝诗人李欣的诗《古从军行》开头两句说:“白日登山望烽火,黄昏饮马傍交河.”诗中隐含着一个有趣的数学问题.诗中将军在观望烽火之后从山脚下的A点出发,走到河边饮马后,再到B点宿营.请问怎样走才能使总的路程最短?这个问题早在古罗马时代就有了,传说亚历山大城有一位精通数学和物理的学者,名叫海伦.一天,一位罗马将军专程去拜访他,向他请教一个百思不得其解的问题:“将军每天从军营A出发,先到河边饮马,然后再去河岸同侧的B地开会,应该怎样走才能使路程最短?"从此,这个被称为“将军饮马”的问题广泛流传.二,例题1,基本类型问题问题:有一位将军骑着马要从A地走到B地,但途中要到水边喂马喝一次水,则将军怎样走最近?解答:作B点与河面的对称点B′,连接AB′,可得到马喝水的地方C,如图所示,由对称的性质可知AB′=AC+BC,根据两点之间线段最短的性质可知,C点即为所求.2,与其他类型问题相结合问题:某课题组在探究“将军饮马问题”时抽象出数学模型:直线l同旁有两个定点A、B,在直线l 上存在点P,使得PA+PB的值最小.解法:作点A关于直线l的对称点A′,连接A′B,则A′B与直线l 的交点即为P,且PA+PB的最小值为A′B.请利用上述模型解决问题如图1,等腰直角三角形A B C的直角边长为2,E是斜边AB的中点,P是AC边上的一动点,则PB+PE的最小值为( );解答:作点B关于AC的对称点B′,连接B′E交AC于P,此时PB+PE的值最小.连接AB′.AB′=AB=√AC2+B C2=√22+22=2√2AB=√2∵∠B′AC=∠B AC=45°∴∠B′AB=90°∴PB+PE的最小值=B′E=√B′A2+AE2=√(2√2)2+(√2)2=√10。
将军饮马问题例题及应用
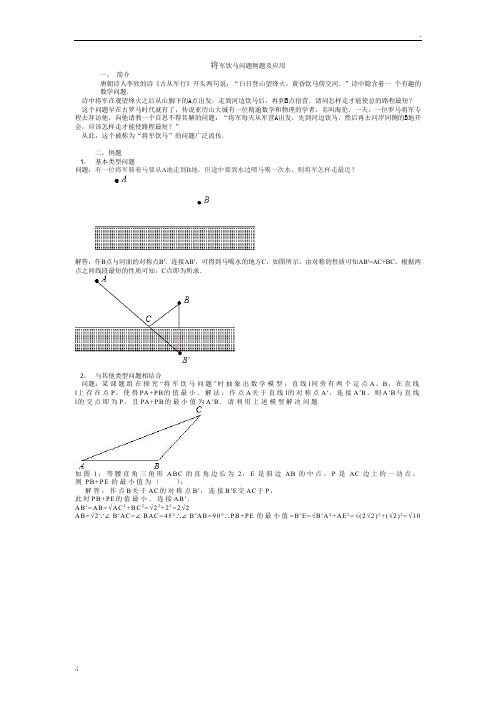
..; 将军饮马问题例题及应用一, 简介唐朝诗人李欣的诗《古从军行》开头两句说:“白日登山望烽火,黄昏饮马傍交河.”诗中隐含着一 个有趣的数学问题.诗中将军在观望烽火之后从山脚下的A 点出发,走到河边饮马后,再到B 点宿营.请问怎样走才能使总的路程最短? 这个问题早在古罗马时代就有了,传说亚历山大城有一位精通数学和物理的学者,名叫海伦.一天,一位罗马将军专程去拜访他,向他请教一个百思不得其解的问题:“将军每天从军营A 出发,先到河边饮马,然后再去河岸同侧的B 地开会,应该怎样走才能使路程最短?”从此,这个被称为“将军饮马”的问题广泛流传.二,例题1, 基本类型问题问题:有一位将军骑着马要从A 地走到B 地,但途中要到水边喂马喝一次水,则将军怎样走最近?解答:作B 点与河面的对称点B ′,连接AB ′,可得到马喝水的地方C ,如图所示,由对称的性质可知AB ′=AC+BC ,根据两点之间线段最短的性质可知,C 点即为所求.2, 与其他类型问题相结合问题:某课题组在探究“将军饮马问题”时抽象出数学模型:直线l 同旁有两个定点A 、B ,在直线l 上存在点P ,使得PA+PB 的值最小.解法:作点A 关于直线l 的对称点A ′,连接A ′B ,则A ′B 与直线l 的交点即为P ,且PA+PB 的最小值为A ′B .请利用上述模型解决问题如图1,等腰直角三角形A B C 的直角边长为2,E 是斜边AB 的中点,P 是AC 边上的一动点,则PB +PE 的最小值为( );解答:作点B 关于AC 的对称点B ′,连接B ′E 交AC 于P ,此时PB +PE 的值最小.连接AB ′.AB ′=AB =√AC 2+B C 2=√22+22=2√2AB =√2∵∠B ′AC =∠B AC =45°∴∠B ′AB =90°∴PB +PE 的最小值=B ′E=√B ′A 2+AE 2=√(2√2)2+(√2)2=√10。
将军饮马问题(解析版)

将军饮马问题模型的概述:唐朝诗人李颀的诗《古从军行》开头两句说:“白日登山望烽火,黄昏饮马傍交河.”诗中隐含着一个有趣的数学问题:将军在观望烽火之后从山脚下的A点出发,走到河边让战马饮水后再到B 点宿营。
问如何行走才能使总的路程最短。
模型一(两点在河的异侧):将军在观望烽火之后从山脚下的A点出发,走到河边让战马饮水后再到B 点宿营,将在何处渡河使行走距离最短并求最短距离。
方法:如右图,连接AB,与线段L交于点M,在M处渡河距离最短,最短距离为线段AB的长。
模型二(两点在河的同侧):将军在观望烽火之后从山脚下的A点出发,需先走到河边让战马饮水后再到B点宿营,将在何处渡河使行走距离最短并求最短距离。
方法:如右图,作点B关于直线L的对称点B',连接AB',与直线L的交点即为所求的渡河点,最短距离为线段AB'的长。
模型三:如图,将军同部队行驶至P处,准备在此驻扎,但有哨兵发现前方为两河AB、BC的交汇处,为防止敌军在对岸埋伏需派侦察兵到河边观察,再返回P处向将军汇报情况,问侦察兵在AB、BC何处侦查才能最快完成任务并求最短距离。
数学描述:如图在直线AB、BC上分别找点M、N,使得∆PMN周长最小。
方法:如右图,分别作点P关于直线AB、BC的对称点P'、P'',连接P'P'',与两直线的交点即为所求点M、N,最短距离为线段P'P''的长。
模型四如图,深夜为防止敌军在对岸埋伏,将军又派一队侦察兵到河边观察,并叮嘱观察之后先去存粮位置点Q处查看再返回P处向将军汇报情况,问侦察在AB、BC何处侦查才能最快完成任务并求最短距离。
数学描述:如图在直线AB、BC上分别找点M、N,使得四边形PQNM周长最小。
方法:如右图,分别作点P、点Q关于直线AB、BC的对称点P'、Q',连接P'Q',与两直线的交点即为所求点M、N,最短距离为线段(PQ+P'Q')的长。
中考复习:将军饮马类题型大全

“将军饮马”类题型大全一.求线段和最值1(一)两定一动型例1:如图,AM⊥EF,BN⊥EF,垂足为M、N,MN=12m,AM=5m,BN=4m,P是EF上任意一点,则PA+PB的最小值是______m.分析:这是最基本的将军饮马问题,A,B是定点,P是动点,属于两定一动将军饮马型,根据常见的“定点定线作对称”,可作点A关于EF的对称点A’,根据两点之间,线段最短,连接A’B,此时A’P+PB即为A’B,最短.而要求A’B,则需要构造直角三角形,利用勾股定理解决.解答:作点A关于EF的对称点A’,过点A’作A’C⊥BN的延长线于C.易知A’M =AM=NC=5m,BC=9m,A’C=MN=12m,在Rt△A’BC中,A’B=15m,即PA+PB的最小值是15m.变式:如图,在边长为2的正三角形ABC中,E,F,G为各边中点,P为线段EF上一动点,则△BPG周长的最小值为_________.分析:考虑到BG为定值是1,则△BPG的周长最小转化为求BP+PG的最小值,又是两定一动的将军饮马型,考虑作点G关于EF的对称点,这里有些同学可能看不出来到底是哪个点,我们不妨连接AG,则AG⊥BC,再连接EG,根据“直角三角形斜边中线等于斜边的一半”,可得AE=EG,则点A就是点G关于EF的对称点.最后计算周长时,别忘了加上BG的长度.解答:连接AG,易知PG=PA,BP+PG=BP+PA,当B,P,A三点共线时,BP+PG =BA,此时最短,BA=2,BG=1,即△BPG周长最短为3.2(二)一定两动型例2:如图,在△ABC中,AB=AC=5,D为BC中点,AD=5,P为AD上任意一点,E为AC上任意一点,求PC+PE的最小值.分析:这里的点C是定点,P,E是动点,属于一定两动的将军饮马模型,由于△ABC 是等腰三角形,AD是BC中线,则AD垂直平分BC,点C关于AD的对称点是点B,PC+PE=PB+PE,显然当B,P,E三点共线时,BE更短.但此时还不是最短,根据“垂线段最短”只有当BE⊥AC时,BE最短.求BE时,用面积法即可.解答:作BE⊥AC交于点E,交AD于点P,易知AD⊥BC,BD=3,BC=6,则AD·BC=BE·AC,4×6=BE·5,BE=4.8变式:如图,BD平分∠ABC,E,F分别为线段BC,BD上的动点,AB=8,△ABC的周长为20,求EF+CF的最小值________.分析:这里的点C是定点,F,E是动点,属于一定两动的将军饮马模型,我们习惯于“定点定线作对称”,但这题这样做,会出现问题.因为点C的对称点C’必然在AB上,但由于BC长度未知,BC’长度也未知,则C’相对的也是不确定点,因此我们这里可以尝试作动点E关于BD的对称点.解答:如图,作点E关于BD的对称点E’,连接E’F,则EF+CF=E’F+CF,当E’,F,C三点共线时,E’F+CF=E’C,此时较短.过点C作CE’’⊥AB于E’’,当点E’与点E’’重合时,E’’C最短,E’’C为AB边上的高,E’’C=5.(三)两定两动型例3:如图,∠AOB=30°,OC=5,OD=12,点E,F分别是射线OA,OB上的动点,求CF+EF+DE的最小值.分析:这里的点C,点D是定点,F,E是动点,属于两定两动的将军饮马模型,依旧可以用“定点定线作对称”来考虑.作点C关于OB的对称点,点D关于OA 的对称点.解答:作点C关于OB的对称点C’,点D关于OA的对称点D’,连接C’D’.CF +EF+DE=C’F+EF+D’E,当C’,F,E,D’四点共线时,CF+EF+DE=C’D’最短.易知∠D’OC’=90°,OD’=12,OC’=5,C’D’=13,CF+EF+DE最小值为13.变式:(原创题)如图,斯诺克比赛桌面AB宽1.78m,白球E距AD边0.22m,距CD边1.4m,有一颗红球F紧贴BC边,且距离CD边0.1m,若要使白球E经过边AD,DC,两次反弹击中红球F,求白球E运动路线的总长度.分析:本题中,点E和点F是定点,两次反弹的点虽然未知,但我们可以根据前几题的经验作出,即分别作点E关于AD边的对称点E’,作点F关于CD边的对称点F’,即可画出白球E的运动路线,化归为两定两动将军饮马型.解答:作点E关于AD边的对称点E’,作点F关于CD边的对称点F’,连接E’F’,交AD于点G,交CD于点H,则运动路线长为EG+GH+HF长度之和,即E’F’长,延长E’E交BC于N,交AD于M,易知E’M=EM=0.22m,E’N=1.78+0.22=2m,NF’=NC+CF’=1.4+0.1=1.5m,则Rt△E’NF’中,E’F’=2.5m,即白球运动路线的总长度为2.5m.小结:以上求线段和最值问题,几乎都可以归结为“两定一动”“一定两动”“两定两动”类的将军饮马型问题,基本方法还是“定点定线作对称”,利用“两点之间线段最短”“垂线段最短”的2条重要性质,将线段和转化为直角三角形的斜边,或者一边上的高,借助勾股定理,或者面积法来求解.当然,有时候,我们也需学会灵活变通,定点对称行不通时,尝试作动点对称.(二)求角度例1:P为∠AOB内一定点,M,N分别为射线OA,OB上一点,当△PMN周长最小时,∠MPN=80°.(1)∠AOB=_____°(2)求证:OP平分∠MPN分析:这又是一定两动型将军饮马问题,我们应该先将M,N的位置找到,再来思考∠AOB的度数,显然作点P关于OA的对称点P’,关于OB的对称点P’’,连接P’P’’,其与OA交点即为M,OB交点即为N,如下图,易知∠DPC 与∠AOB互补,则求出∠DPC的度数即可.解答:(1)法1:如图,∠1+∠2=100°,∠1=∠P’+∠3=2∠3,∠2=∠P’’+∠4=2∠4,则∠3+∠4=50°,∠DPC=130°,∠AOB=50°.再分析:考虑到第二小问要证明OP平分∠MPN,我们就连接OP,则要证∠5=∠6,显然很困难,这时候,考虑到对称性,我们再连接OP’,OP’’,则∠5=∠7,∠6=∠8,问题迎刃而解.解答:(1)法2:易知OP’=OP’’,∠7+∠8=∠5+∠6=80°,∠P’OP’’=100°,由对称性知,∠9=∠11,∠10=∠12,∠AOB=∠9+∠10=50°(2)由OP’=OP’’,∠P’OP’’=100°知,∠7=∠8=40°,∠5=∠6=40°,OP平分∠MPN.变式:如图,在五边形ABCDE中,∠BAE=136°,∠B=∠E=90°,在BC、DE上分别找一点M、N,使得△AMN的周长最小时,则∠AMN+∠ANM的度数为________.分析:这又是典型的一定两动型将军饮马问题,必然是作A点关于BC、DE的对称点A′、A″,连接A′A″,与BC、DE的交点即为△AMN周长最小时M、N的位置.解答:如图,∵∠BAE=136°,∴∠MA′A+∠NA″A=44°由对称性知,∠MAA′=∠MA′A,∠NAA″=∠NA″A,∠AMN+∠ANM=2∠MA′A+2∠NA″A=88°思考题:1.(2017·安顺)如图所示,正方形ABCD的边长为6,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为_______.2.(2017·安徽改编)如图,在矩形ABCD中,AB=4,AD=3.P为矩形ABCD 内一点,若矩形ABCD面积为△PAB面积的4倍,则点P到A,B两点距离之和PA+PB的最小值为________.。
第11讲 “将军饮马”问题探究(教师版)

知识导航
①作定点关于动点所在直线的对称点,构造轴对称图形
②等腰三角形、角分线模型是天然的轴对称模型
经典例题
1
三角板、刻度尺作图,保留作图痕迹,不写作法.
2
如图,正方形
3
如图,正方形4
在
直线、射线、线段问题>题型:动点与线段-无数轴1
三角板、刻度尺作图,保留作图痕迹,不写作法:
2
如图,在
3
如图,在知识导航
经典例题1
如图,直线2
如图,
知识导航
经典例题
1
如图,在一组平行线
2
如图,直线
3
如图,在正方形
设汽车行驶到公路上点的位置时,距离村庄最近,行驶到点的位置时,距离村庄上分别画出、的位置;
行驶时,在公路的哪一段上距离、两村都越来越近?在哪一段两村都越来越
关于直
三角形
>等腰三角形>等腰等边综合如图,四边形中,。
初中将军饮马问题题型总结(全)

初中将军饮马问题题型总结(全)题型一:将军饮马之单动点1.三角形中的将军饮马题目描述:在等腰三角形ABC中,AB=AC,AD、CE是三角形ABC的两条中线,P是AD上的一个动点,则下列线段的长度等于BP+EP最小值的是()解析:连接PC,由于AB=AC,BD=CD,AD垂直于BC,所以PB=PC。
因此,PB+PE=PC+PE,PE+PC>CE,当P、C、E共线时,PB+PE的值最小,最小值为CE的长度,故选B.2.等边三角形中的将军饮马题目描述:在等边三角形ABC中,AB=2,AD是BC边上的高,E是AC的中点,P是AD上的一个动点,则PE+PC的最小值为()解析:连接BE交AD于点P',AD、BE分别是等边三角形ABC边BC、AC的垂直平分线,P'B=P'C,P'E+P'C=P'E+P'B=BE。
根据两点之间线段最短,点P在点P'时,PE+PC有最小值,最小值即为BE的长。
因此,BE=BC/2-CE/2=3,所以P'E+P'C的最小值为3,故选C.3.等腰三角形中的将军饮马题目描述:在等腰三角形ABC中,AB=AC,BC=4,面积是16,AC的垂直平分线EF分别交AC、AB边于E、F点,若点D为BC边的中点,点M为线段EF上一动点,则△CDM周长的最小值为()解析:连接AD、AM,由于△ABC是等腰三角形,点D是BC边的中点,AD垂直于BC,所以S△ABC=1/2×4×AD=16,解得AD=8.EF是线段AC的垂直平分线,所以点C关于直线EF的对称点为点A,MA=MC,AD=AM+MD,因此AD的长为CM+MD的最小值。
且AC6,BM3,因为BM AD,故BM AC,所以BM是AC的中线,故CM3。
又因为AC是菱形的对角线,所以AC平分DAB,即DAM30。
又因为AM MD,所以ADM75。
中考复习:“将军饮马”类题型大全(K12教育文档)

中考复习:“将军饮马”类题型大全(word版可编辑修改)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(中考复习:“将军饮马”类题型大全(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为中考复习:“将军饮马”类题型大全(word版可编辑修改)的全部内容。
“将军饮马”类题型大全一.求线段和最值1(一)两定一动型例1:如图,AM⊥EF,BN⊥EF,垂足为M、N,MN=12m,AM=5m,BN=4m, P是EF上任意一点,则PA+PB的最小值是______m.分析:这是最基本的将军饮马问题,A,B是定点,P是动点,属于两定一动将军饮马型,根据常见的“定点定线作对称”,可作点A关于EF的对称点A’,根据两点之间,线段最短,连接A’B,此时A’P+PB即为A’B,最短.而要求A’B,则需要构造直角三角形,利用勾股定理解决.解答:作点A关于EF的对称点A’,过点A'作A'C⊥BN的延长线于C.易知A'M=AM=NC =5m,BC=9m,A’C=MN=12m,在Rt△A’BC中,A’B=15m,即PA+PB的最小值是15m.变式:如图,在边长为2的正三角形ABC中,E,F,G为各边中点,P为线段EF上一动点,则△BPG周长的最小值为_________.分析:考虑到BG为定值是1,则△BPG的周长最小转化为求BP+PG的最小值,又是两定一动的将军饮马型,考虑作点G关于EF的对称点,这里有些同学可能看不出来到底是哪个点,我们不妨连接AG,则AG⊥BC,再连接EG,根据“直角三角形斜边中线等于斜边的一半",可得AE=EG,则点A就是点G关于EF的对称点.最后计算周长时,别忘了加上BG的长度.解答:连接AG,易知PG=PA,BP+PG=BP+PA,当B,P,A三点共线时,BP+PG=BA,此时最短,BA=2,BG=1,即△BPG周长最短为3。
题型01 最值问题之将军饮马-2023年中考数学重难点专题最后冲刺之最值问题(全国通用)(解析版)

最值问题之将军饮马模型精讲基础模型:如图,在直线上找一点P 使得PA +PB 最小?模型解析:作点A 关于直线的对称点A ’,连接PA ’,则PA ’=PA ,所以PA +PB =PA’+PB当A ’、P 、B 三点共线的时候,PA ’+PB =A’B ,此时为最小值(两点之间线段最短)模型变式:1、两定一动之点点在OA 、OB 上分别取点M 、N ,使得△PMN 周长最小.此处M 、N 均为折点,分别作点P 关于OA (折点M 所在直线)、OB (折点N 所在直线)的对称点,化折线段PM +MN +NP 为P ’M +MN +NP ’’,当P ’、M 、N 、P ’’共线时,△PMN 周长最小.2、两定两动之点点在OA 、OB 上分别取点M 、N 使得四边形PMNQ 的周长最小。
BBBB考虑PQ 是条定线段,故只需考虑PM +MN +NQ 最小值即可,类似,分别作点P 、Q 关于OA 、OB 对称,化折线段PM +MN +NQ 为P ’M +MN +NQ ’,当P ’、M 、N 、Q ’共线时,四边形PMNQ 的周长最小。
3、一定两动之点线在OA 、OB 上分别取M 、N 使得PM +MN 最小。
此处M 点为折点,作点P 关于OA 对称的点P ’,将折线段PM +MN 转化为P ’M +MN ,即过点P ’作OB 垂线分别交OA 、OB 于点M 、N ,得PM +MN 最小值(点到直线的连线中,垂线段最短)针对训练一、单选题1.如图,正方形ABCD 的边长为4,点M 在DC 上,且DM =1,N 是AC 上一动点,则DN +MN 的最小值为( )A .4B.C.D .5【答案】D【详解】∵四边形ABCD 是正方形,∴点B 与D 关于直线AC 对称,∴DN =BN ,连接BD ,BM 交AC 于N′,连接DN′,∴当B 、N 、M 共线时,DN +MN 有最小值,则BM 的长即为DN +MN的最小值,∴AC 是线段BD 的垂直平分线,BB2.如图所示,在△ABC 中,,BD 平分,P 为线段BD 上一动点,为边AB 上一动点,当AP PQ +的值最小时,APB Ð的度数是( )A .118°B .125°C .136°D .124°∵BD 平分ABC Ð,ABC Ð∴12ABD CBD ABC Ð=Ð=Ð∵BP BP =,∴()SAS PBQ PBE V V ≌,∵90AEB Ð=°,34CBD Ð=°,∴124APB AEB CBD Ð=Ð+Ð=°.故选:D .3.如图,Rt △ABC 中,9043C AC BC Ð==°=,,,点P 为AC 边上的动点,过点P 作PD AB ^于点D ,则PB PD +的最小值为( )A .154B .245C .5D .203根据对称性的性质,可知:BP 在Rt △ABC 中,90,ACB AC Ð=°225AB AC BC \=+=,根据对称性的性质,可知:V 2S S S S \=+=4.如图所示,已知A (1,y 1),B (2,y 2)为反比例函数y 2=x图象上的两点,动点P (x ,0)在x 轴正半轴上运动,当线段AP 与线段BP 之差达到最大值时,点P 的坐标是( )A.(3,0)B.(72,0)C.(53,0)D.(52,0)P PB 与x轴分别交于A,B两点,若点A、点B关于原点O对称,则AB的最小值为()A .3B .4C .5D .6【答案】D【详解】解:连接OP ,PA PB ^Q ,90APB \Ð=°,AO BO =Q ,2AB PO \=,若要使AB 取得最小值,则PO 需取得最小值,连接OM ,交⊙M 于点P ¢,当点P 位于P ¢位置时,OP ¢取得最小值,过点M 作MQ x ^轴于点Q ,则3OQ =、4MQ =,5OM \=,又2MP ¢=Q ,3OP \¢=,26AB OP \=¢=,故选:D .6.如图,等边△ABC 的边长为6,AD 是BC 边上的中线,M 是AD 上的动点,E 是边AC 上一点,若AE =2,则EM +CM 的最小值为( )A B.C.D.的最小值为()A.2B C D.1【答案】B【详解】解:连接AM、AC,AM交BD于P,PPB PE y+=,当点P从A向点C运动时,y与x的函数关系如图2所示,其中点M是函数图象的最低点,则点M的坐标是()A.(B.(C.(D.(【答案】AP小值为()A.5B.C.D.10【答案】A【详解】连接EC,交BD于P点∵四边形ABCD为正方形∴A点和C点关于BD对称\=PA PC\+=+=PA PE PC PE EC根据“两点之间线段最短”,可知PA PE+的最小值即为线段EC的长.10.如图,在矩形ABCD 边上一动点,连接PD 、PE ,则PD PE +的最小值为( )A .8B .C .10D .2点E 在以BC 为直径的半圆O 上运动,作半圆点E 的对称点为1E ,连接1'O E ∴当点D 、P 、1E 、'O 共线时,如图所示,在Rt 'DCO V 中,CD 22'8610DO \=+=,又1'2O E =Q ,11''8DE DO O E \=-=,即PD PE +的最小值为8,故选:A .二、填空题11.如图,在△ABC 中,90BAC Ð=°,3AB =,4AC =,EF 垂直平分BC ,点P 为直线EF 上任意一点,则AP BP +的最小值是______.【答案】4【详解】解:连接PC .∵EF 是BC 的垂直平分线,∴BP PC =,∴PA BP AP PC +=+,∴当点A ,P ,C 在一条直线上时,PA BP +有最小值,最小值为4AC =.故答案为:4.12.如图,在等边△ABC 中,BD AC ^于D ,3cm =AD .点,P Q 分别为,AB AD 上的两个定点且1cm BP AQ ==,点M 为线段BD 上一动点,连接,PM QM ,则PM QM +的最小值为______cm .^∵△ABC是等边三角形,BD AC为500m,天黑前牧童从A处将牛牵到河边饮水,再赶回家,那么牧童最少要走______.【答案】1300m14.如图,菱形草地ABCD 中,沿对角线修建60米和80米两条道路,M 、N 分别是草地边BC 、CD 的中点,在线段BD 上有一个流动饮水点P ,若要使PM PN +的距离最短,则最短距离是 _____米.【答案】50【详解】解:作M 关于BD 的对称点Q ,连接NQ ,交BD 于P ¢,连接MP ¢,当P 点与P ¢重合时,MP NP MP NP NQ ¢¢+=+=的值最小,Q 四边形ABCD 是菱形,AC BD \^,QBP MBP Ð=Ð,即Q 在AB 上,MQ BD ^Q ,15.在平面直角坐标系中,点,点,若有一点,当BA BO+的值最小时,=a ________.【答案】1 216.如图,直线4y x =+与x 轴,y 轴分别交于A 和B ,点C 、D 分别为线段AB 、OB 的中点,P 为OA 上一动点,当PC PD +的值最小时,点P 的坐标为 ___________.【答案】()10-,【详解】解:作点D 关于x 轴的对称点D ¢,连接CD ¢交x 轴于点P ,此时PC PD +值最小,最小值为CD ¢,如图.令4y x =+中0x =,则4y =,∴点B 的坐标为()04,;令4y x =+中0y =,则40x +=,解得:4x =-,∴点A 的坐标为()40-,.∵点C 、D 分别为线段AB 、OB 的中点,∴点()22C -,,点()02D ,.∵点D ¢和点D 关于x 轴对称,∴点D ¢的坐标为()02-,.设直线CD ¢的解析式为y kx b =+,∵直线CD ¢过点()22C -,,()02D ¢-,,∴222k b b -+=ìí=-î,解得22k b =-ìí=-î,∴直线CD ¢的解析式为22y x =--.令0y =,则022x =--,解得:1x =-,∴点P 的坐标为()10-,.故答案为:()10-,.17.如图,点P 是AOB Ð内任意一点,3cm OP =,点M 和点N 分别是射线OA 和射线OB 上的动点,30AOB Ð=°,则△PMN 周长的最小值是______.【答案】3cm【详解】解:分别作点P 关于OA OB 、的对称点C 、D ,连接CD ,分别交OA OB 、于点M 、N ,连接OP OC OD PM PN 、、、、.∵点P 关于OA 的对称点为C ,关于OB 的对称点为D ,∴PM CM OP OC COA POA ==Ð=Ð,,;∵点P 关于OB 的对称点为D ,∴PN DN OP OD DOB POB ==Ð=Ð,,,∴3cm OC OD OP ===,22260COD COA POA POB DOB POA POB AOB Ð=Ð+Ð+Ð+Ð=Ð+Ð=Ð=°,∴COD △是等边三角形,∴()3cm CD OC OD ===.∴△PMN 的周长的最小值3cm PM MN PN CM MN DN CD =++=++³=.故答案为:3cm .18.如图,在周长为12的菱形ABCD 中,1DE =,2DF =,若P 为对角线AC 上一动点,则EP FP +的最小值为______.【答案】3【详解】解:作F 点关于BD 的对称点F ¢,则PF PF ¢=,连接'EF 交BD 于点P .EP FP EP P F \+¢+=.由两点之间线段最短可知:当E 、P 、F'在一条直线上时,EP FP +的值最小,此时F EP FP EP P E F ¢+==¢+.Q 四边形ABCD 为菱形,周长为12,3AB BC CD DA \====,AB CD ∥,2AF =Q ,1AE =,1DF AE \==,\四边形AE D F ¢是平行四边形,3E D F A \¢==.EP FP \+的最小值为3.故答案为:3.19.如图,在Rt ABC △中,90ACB Ð=°,AC BC =,点C 在直线MN 上,30BCN Ð=°,点P 为MN 上一动点,连接AP ,BP .当AP BP +的值最小时,CBP Ð的度数为__________度.【答案】15【详解】如图,作B 关于MN 的对称点D ,连接,,AD BD CD ,AP BP +Q 的值最小,则MN 交AD 于P ,由轴对称可知:20.如图,抛物线43y x x =-+与x 轴分别交于,A B 两点(点A 在点B 的左侧),与轴交于点C ,在其对称轴上有一动点M ,连接,,MA MC AC ,则MAC △周长的最小值是______.21.如图,抛物线2y x bx c =++与x 轴交于()()1030A B -,,,两点.(1)求该抛物线的解析式;(2)观察函数图象,直接写出当x 取何值时,0y >?(3)设(1)题中的抛物线交y 轴于C 点,在该抛物线的对称轴上是否存在点Q ,使得QAC △的周长最小?若存在,求出Q 点的坐标;若不存在,请说明理由.∴1k =,∴直线BC 的解析式为3y x =-,把1x =代入上式,∴=2y -,∴Q 点坐标为()12-,.22.教材呈现:下图是华师版八年级下册数学教材第111页的部分内容.(1)问题解决:请结合图①,写出例1的完整解答过程.(2)问题探究:在菱形ABCD 中,对角线AC 、BD 相交于点O ,AB =4,∠BAD =2∠ABC .过点D 作DE //AC 交BC 的延长线于点E .如图②,连结OE ,则OE 的长为____.(3)如图③,若点P 是对角线BD 上的一个动点,连结PC 、PE ,则PC +PE 的最小值为_____.(3,0),B(0,4),D为边OB的中点.(1)若E为边OA上的一个动点,求CDE(2)若E、F为边OA上的两个动点,且EF=1,当四边形CDEF的周长最小时,求点E、F的坐标.∵在矩形OACB 中,∴D (0,2),C (设直线CD ¢为y 得34k b =+,b ∴直线CD ¢为y 理由如下:∵四边形CDEF 的周长为∴DE +CF 最小时,四边形轴于点D,且:4:3CD AD=,反比例函数kyx=的图象经过A、B两点.(1)求反比例函数的解析式.(2)点P为直线AC上一动点,求BP OP+的最小值.∵BC AC ^,FC BC =,∴AC 垂直平分BF ,∴BP FP =,∴BP OP FP OP OF +=+=,由“两点间线段最短”可得BP 由(1)得A 、B 关于原点对称,∴()7,3B -,∵C 为线段BF 的中点,25.如图,已知抛物线(1)求抛物线的解析式;(2)点P是抛物线对称轴上一点,当PB+PC的值最小时,求点P的坐标;(3)点M在抛物线上运动,点N在y轴上运动,是否存在点M,N,使得90Ð=o且以点C,M,N为顶点CMN的三角形与OACV相似?若存在,求出点M和点N的坐标;若不存在,说明理由.∵对于2246y x x =+-,令∴C (0,-6),26.如图,直线1l 经过9,02A æöç÷èø、()2,5B -两点,直线2:3l y x =-+与直线1l 交于点C ,与x 轴交于点D .(1)求点C的坐标;(2)点P是y轴上一点,当四边形PDCB的周长最小时,求四边形PDCB的面积;(3)把直线1l沿y轴向上平移9个单位长度,得到新直线3l与直线2l交于点E,试探究在x轴上是否存在点Q,在平面内存在点F使得以点D,Q,E,F为顶点的四边形是菱形(含正方形)?若存在,直接写出符合条件的点Q的坐标;若不存在,说明理由.27.如图,已知一次函数y=kx+b的图像经过A(1,4),B(4,1)两点,并且交x轴于点C,交y轴于点D.(1)求该一次函数的表达式;(2)若y轴存在一点P使PA+PB的值最小,求此时点P的坐标及PA+PB的最小值;(3)在x轴上是否存在一点M,使△MOA的面积等于△AOB的面积;若存在请直接写出点M的坐标,若不存在请说明理由.)∴154M x =或154M x =-,∴M (154,0)或(154-,0),∴存在一点M ,使△MOA 的面积等于△AOB 的面积,且M 点的坐标为(154,0)或(154-,0).28.如图,在平面直角坐标系中,直线AB 分别与x 轴的负半轴、y 轴的正半轴交于A 、B 两点,其中OA =2,S △ABC =12,点C 在x 轴的正半轴上,且OC =OB .(1)求直线AB 的解析式;(2)将直线AB 向下平移6个单位长度得到直线l 1,直线l 1与y 轴交于点E ,与直线CB 交于点D ,过点E 作y 轴的垂线l 2,若点P 为y 轴上一个动点,Q 为直线l 2上一个动点,求PD +PQ +DQ 的最小值;(3)若点M为直线AB上的一点,在y轴上是否存在点N,使以点A、D、M、N为顶点的四边形为平行四边形,若存在,请直接写出点N的坐标;若不存在,请说明理由.∴D'(﹣2,2),D''(2,﹣6),设直线D'D''解析式为y=sx+t,则2262s ts t=-+ìí-=+î,解得22st=-ìí=-î,∴直线D'D'解析式为y=﹣2x﹣2,令x=0得y=﹣2,即P(0,﹣2),令y=﹣2得x=0,即Q(0,﹣2),∴此时PD=25,PQ=0,DQ=25,∴PD+PQ+DQ的最小值为45.(3)存在,理由如下:此时AD中点即为MN中点,∴2200224pp q-+=+ìí+=++î,解得2pq=ìí=-î,∴N(0,﹣2);②以AM、DN为对角线,如图:同理可得:2200242p p q -+=+ìí++=+î,解得410p q =ìí=î,∴N (0,10);③以AN 、DM 为对角线,如图:同理可得2020224p q p -+=+ìí+=++î,解得42p q =-ìí=-î,∴N (0,﹣2),综上所述,以点A 、D 、M 、N 为顶点的四边形为平行四边形,N 的坐标为(0,﹣2)或(0,10).29.在Rt △ABC 中,AB =BC ,在Rt△CEH 中,∠CEH =45°,∠ECH =90°,连接AE .(1)如图1,若点E在CB延长线上,连接AH,且AH=6,求AE的长;∠HBF=45°时,求证:(2)如图2,若点E在AC上,F为AE的中点,连接BF、BH,当BH=2BF,∠EHB+12AE=CE;(3)如图3,若点E在线段AC上运动,取AE的中点F,作FH'∥BC交AB于H,连接BE并延长到D,使得BE =DE,连接AD、CD;在线段BC上取一点G,使得CG=AF,并连接EG;若点E在线段AC上运动的过程中,当ACD的周长取得最小值时,△AED的面积为25,请直接写出GE+BH′的值.,连接,作。
将军饮马(最完整讲义)
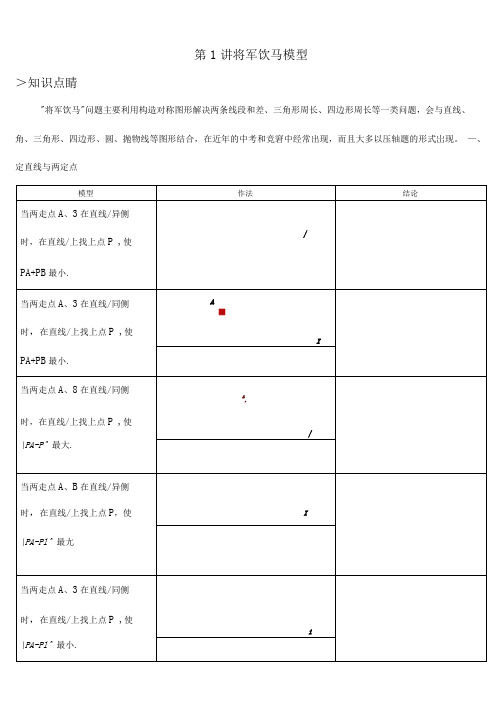
第1讲将军饮马模型>知识点睛"将军饮马"问题主要利用构造对称图形解决两条线段和差、三角形周长、四边形周长等一类问题,会与直线、角、三角形、四边形、圆、抛物线等图形结合,在近年的中考和竞窘中经常出现,而且大多以压轴题的形式岀现。
—、定直线与两定点>精讲精练例1 :如图,点P是乙AOB内任意一点f"O於30° r OP=8,点〃和点AZ分别是射线Q4和射线OB上的动点,贝ZPMN周长的最小值・例2 :如图,正方形ABCD 的边长是4 , 〃在DC 上,且DM", /V 是力0边上的一动点,贝4DMN 周长的最小 值.例3 :如图,在R2ABO 中.zO 必=90° " ( 4,4 ),点。
在边ABA L ^AC.CB^.3,点Z?为OB 的中点,点P 为边OA 上的动点,当点P 在OA 上移动时,使四边形PWU 周长最小的点P 的坐标为( )例4 :如图,在汀中r AC=BC^ACB=^ .点D 在BC 上f BD=3 . DC=\ ,点Q 是力0上的动点,则PC+PD 的最小值为()A.4例5 :如图,在等边卫力中,AB=6 , /V 为AB±-点且BN=2AN t 的高线力。
交EC 于点D t 〃是AD±_的动点■连结BM. MN.则3/W+/14/V 的最小值是 ______________ .A ・(2,2)D M8. 3>/3 C. 2>/6 0・ 4.5例6 :如图,在R2ABD 中,力於6 , z24Q=30° , zZ?=90° r /V 为力0上一点且BN=2AN. 〃是力。
上的动点, 连结BM t MN.则劭升/14/V 的最小值・例7 :如图,在 ^ABC 中,z/l«=90°, AC=6・力於12 r 力。
平分z04/点尸是力。
的中点,点F 是AD±_的 动点,则QF+FF 的最小值为()例8 :如图,在锐角三角形力中,BC=4 t z/I^C=60° , BD 平分zABC,交MU 于点D, M 、/V 分别是BD, BC 上的动点,则CM+ MN 的最小值是()A ・ VJB . 2C. 2 JID . 4例9 :如图,在菱形ABCD 中r AC= 6^2 , BD=6 , F 是BC 的中点,P 、M 分别是AC^力0上的动点,连接PE 、如,则PF+加的最小值是()B ・ 4 D ・ 2s/3第7题图 第8题图例10 :如图r矩形ABOC的顶点力的坐标为(45 ) , Q是03的中点,F是OC上的一点,当出力%的周长最小时,点F的坐标是(4A ・(0.-)B • 2>/10例12:如图f ABCD中/於10/U5,点£ F、G、〃分别在矩形力02各边上,旦AE=CG, BF=DH,则四边形"6片周长的最小值为()力.5>/5 B ・C・ 10j亍 D • \5長例13 :如图,zMO於60° f点P是乙AOB内的走点且OP= 73 ,若点M、/V分别是射线04 03上异于点O的动点,贝ZPMN周长的最小值是(力•迹B•巫2 2)C. 6D. 3C • (0,2) D.(O.y) 例11 :如图,在矩形ABCD中z AB=6 , AD=3 .动点P满足片刑第10题图例14 :如图,乙AOB的边02与"轴正半轴重合点P是04上的一动点,点/V( 3,0 )是03上的一定点,点M 是O/V的中点,zAO8=30°.要使PW+P/V最小,则点P的坐标为________________________ .例15 :如图,已知正比例函数y=kx( £>0 )的图像与x轴相交所成的锐角为70°,走点力的坐标为(0,4) , P 为F轴上的f 动点,M、/V为函数y^kx ( k>0 )的图像上的两个动点r则AM±MP+PN的最小值为第15题图例16 :如图,在平面直角坐标系中,矩形ABCD的顶点B在原点,点4 U在坐楙由上r点Z?的坐标为(6,4), F为CO的中点,点只Q为边上两个动点,且Pg2 ,要使四边形APQE的周长最小r则点P的坐示应为例17 :如图,矩形ABCD中,A»2 t AB=4 , MU为对角线,E、F分别为边AB、CQ上的动点,且EFrAC于点连接CF,求AF+CE的最小值.例18 :如图,正方形ABCD的面积是12 r心ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,求PD + PE的最小值。
(完整word版)中考复习:“将军饮马”类题型大全

“将军饮马”类题型大全一.求线段和最值1(一)两定一动型例1:如图,AM⊥EF,BN⊥EF,垂足为M、N,MN=12m,AM=5m,BN=4m, P是EF 上任意一点,则PA+PB的最小值是______m.分析:这是最基本的将军饮马问题,A,B是定点,P是动点,属于两定一动将军饮马型,根据常见的“定点定线作对称”,可作点A关于EF的对称点A’,根据两点之间,线段最短,连接A’B,此时A’P+PB即为A’B,最短.而要求A’B,则需要构造直角三角形,利用勾股定理解决.解答:作点A关于EF的对称点A’,过点A’作A’C⊥BN的延长线于C.易知A’M=AM=NC=5m,BC=9m,A’C=MN=12m,在Rt△A’BC中,A’B=15m,即PA+PB的最小值是15m.变式:如图,在边长为2的正三角形ABC中,E,F,G为各边中点,P为线段EF上一动点,则△BPG周长的最小值为_________.分析:考虑到BG为定值是1,则△BPG的周长最小转化为求BP+PG的最小值,又是两定一动的将军饮马型,考虑作点G关于EF的对称点,这里有些同学可能看不出来到底是哪个点,我们不妨连接AG,则AG⊥BC,再连接EG,根据“直角三角形斜边中线等于斜边的一半”,可得AE=EG,则点A就是点G关于EF的对称点.最后计算周长时,别忘了加上BG的长度.解答:连接AG,易知PG=PA,BP+PG=BP+PA,当B,P,A三点共线时,BP+PG=BA,此时最短,BA=2,BG=1,即△BPG周长最短为3.2(二)一定两动型例2:如图,在△ABC中,AB=AC=5,D为BC中点,AD=5,P为AD上任意一点,E 为AC上任意一点,求PC+PE的最小值.分析:这里的点C是定点,P,E是动点,属于一定两动的将军饮马模型,由于△ABC 是等腰三角形,AD是BC中线,则AD垂直平分BC,点C关于AD的对称点是点B,PC+PE=PB+PE,显然当B,P,E三点共线时,BE更短.但此时还不是最短,根据“垂线段最短” 只有当BE⊥AC时,BE最短.求BE时,用面积法即可.解答:作BE⊥AC交于点E,交AD于点P,易知AD⊥BC,BD=3,BC=6,则AD·BC=BE·AC,4×6=BE·5,BE=4.8变式:如图,BD平分∠ABC,E,F分别为线段BC,BD上的动点,AB=8,△ABC的周长为20,求EF+CF的最小值________.分析:这里的点C是定点,F,E是动点,属于一定两动的将军饮马模型,我们习惯于“定点定线作对称”,但这题这样做,会出现问题.因为点C的对称点C’必然在AB上,但由于BC长度未知,BC’长度也未知,则C’相对的也是不确定点,因此我们这里可以尝试作动点E关于BD的对称点.解答:如图,作点E关于BD的对称点E’,连接E’F,则EF+CF=E’F+CF,当E’,F,C三点共线时,E’F+CF=E’C,此时较短.过点C作CE’’⊥AB于E’’,当点E’ 与点E’’重合时,E’’C最短,E’’C为AB边上的高,E’’C=5.(三)两定两动型例3:如图,∠AOB=30°,OC=5,OD=12,点E,F分别是射线OA,OB上的动点,求CF+EF+DE的最小值.分析:这里的点C,点D是定点,F,E是动点,属于两定两动的将军饮马模型,依旧可以用“定点定线作对称”来考虑.作点C关于OB的对称点,点D关于OA的对称点.解答:作点C关于OB的对称点C’,点D关于OA的对称点D’,连接C’D’. CF+EF+DE=C’F+ EF+D’E,当C’,F, E,D’四点共线时,CF+EF+DE=C’D’最短.易知∠D’OC’=90°,OD’=12,OC’=5,C’D’=13,CF+EF+DE最小值为13.变式:(原创题)如图,斯诺克比赛桌面AB宽1.78m,白球E距AD边0.22m,距CD 边1.4m,有一颗红球F紧贴BC边,且距离CD边0.1m,若要使白球E经过边AD,DC,两次反弹击中红球F,求白球E运动路线的总长度.分析:本题中,点E和点F是定点,两次反弹的点虽然未知,但我们可以根据前几题的经验作出,即分别作点E关于AD边的对称点E’,作点F关于CD边的对称点F’,即可画出白球E的运动路线,化归为两定两动将军饮马型.解答:作点E关于AD边的对称点E’,作点F关于CD边的对称点F’,连接E’F’,交AD于点G,交CD于点H,则运动路线长为EG+GH+HF长度之和,即E’F’长,延长E’E交BC于N,交AD于M,易知E’M=EM=0.22m,E’N=1.78+0.22=2m,NF’=NC+CF’=1.4+0.1=1.5m,则Rt△E’NF’中,E’F’=2.5m,即白球运动路线的总长度为2.5m.小结:以上求线段和最值问题,几乎都可以归结为“两定一动”“一定两动”“两定两动”类的将军饮马型问题,基本方法还是“定点定线作对称”,利用“两点之间线段最短”“垂线段最短”的2条重要性质,将线段和转化为直角三角形的斜边,或者一边上的高,借助勾股定理,或者面积法来求解.当然,有时候,我们也需学会灵活变通,定点对称行不通时,尝试作动点对称.(二)求角度例1:P为∠AOB内一定点,M,N分别为射线OA,OB上一点,当△PMN周长最小时,∠MPN=80°.(1)∠AOB=_____°(2)求证:OP平分∠MPN分析:这又是一定两动型将军饮马问题,我们应该先将M,N的位置找到,再来思考∠AOB 的度数,显然作点P关于OA的对称点P’,关于OB的对称点P’’,连接P’P’’,其与OA交点即为M,OB交点即为N,如下图,易知∠DPC与∠AOB互补,则求出∠DPC的度数即可.解答:(1)法1:如图,∠1+∠2=100°,∠1=∠P’+∠3=2∠3,∠2=∠P’’+∠4=2∠4,则∠3+∠4=50°,∠DPC=130°,∠AOB=50°.再分析:考虑到第二小问要证明OP平分∠MPN,我们就连接OP,则要证∠5=∠6,显然很困难,这时候,考虑到对称性,我们再连接OP’,OP’’,则∠5=∠7,∠6=∠8,问题迎刃而解.解答:(1)法2:易知OP’=OP’’,∠7+∠8=∠5+∠6=80°,∠P’OP’’=100°,由对称性知,∠9=∠11,∠10=∠12,∠AOB=∠9+∠10=50°(2)由OP’=OP’’,∠P’OP’’=100°知,∠7=∠8=40°,∠5=∠6=40°,OP平分∠MPN.变式:如图,在五边形ABCDE中,∠BAE=136°,∠B=∠E=90°,在BC、DE上分别找一点M、N,使得△AMN的周长最小时,则∠AMN+∠ANM的度数为________.分析:这又是典型的一定两动型将军饮马问题,必然是作A点关于BC、DE的对称点A′、A″,连接A′A″,与BC、DE的交点即为△AMN周长最小时M、N的位置.解答:如图,∵∠BAE=136°,∴∠MA′A+∠NA″A=44°由对称性知,∠MAA′=∠MA′A,∠NAA″=∠NA″A,∠AMN+∠ANM=2∠MA′A+2∠NA″A=88°思考题:1.(2017·安顺)如图所示,正方形ABCD的边长为6,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为_______.2.(2017·安徽改编)如图,在矩形ABCD中,AB=4,AD=3.P为矩形ABCD内一点,若矩形ABCD面积为△PAB面积的4倍,则点P到A,B两点距离之和PA+PB 的最小值为________.。
中学数学 “将军饮马”类问题 (含答案)

最全“将军饮马”类问题(类型大全+分类汇编)1.如图,直线 l 和 l 的异侧两点 A、B,在直线 l 上求作一点 P,使 PA+PB 最小。
2.如图,直线 l 和 l 的同侧两点 A、B,在直线 l 上求作一点 P,使 PA+PB 最小。
3.如图,点 P 是∠MON 内的一点,分别在 OM,ON 上作点 A,B。
使△PAB 的周长最小4.如图,点 P,Q 为∠MON 内的两点,分别在 OM,ON 上作点 A,B。
使四边形 PAQB 的周长最小。
5.如图,点 A 是∠MON 外的一点,在射线 OM 上作点 P,使 PA 与点 P 到射线 ON 的距离之和最小6. .如图,点 A 是∠MON 内的一点,在射线 OM 上作点 P,使 PA 与点 P 到射线 ON 的距离之和最小E MMEHM30°二、常见题型三角形问题1.如图,在等边△ABC 中,AB = 6,AD⊥BC,E 是 AC 上的一点,M 是 AD 上的一点,若 AE = 2,求 EM+EC 的最小值A解:∵点 C 关于直线 AD 的对称点是点 B,A∴连接 BE,交 AD 于点 M,则 ME+MD 最小,过点 B 作 BH⊥AC 于点 H,则 EH = AH – AE = 3 – 2 = 1,BH = BC2 - CH2 = 62 - 32 = 3 3在直角△BHE 中,BE = BH2 + HE2 B= (3 3)2 + 12 = 2 7D C B D C2.如图,在锐角△ABC 中,AB = 4 2,∠BAC=45°,∠BAC 的平分线交 BC 于点 D,M、N 分别是 AD 和 AB 上的动点,则 BM+MN 的最小值是.解:作点 B 关于 AD 的对称点B',过点 B'作 B'E⊥AB 于点E,交 AD 于点 F,则线段 B'E 的长就是 BM+MN的最小值在等腰 Rt△AEB'中,根据勾股定理得到,B'E = 4CB'M F D A N E B3.如图,△ABC 中,AB=2,∠BAC=30°,若在 AC、AB 上各取一点 M、N,使 BM+MN 的值最小,则这个最小值C 解:作 AB 关于 AC 的对称线段AB',过点 B'作 B'N⊥AB,垂足为 N,交 AC 于点M,则 B'N = MB'+MN = MB+MNB'N 的长就是 MB+MN 的最小值则∠B'AN = 2∠BAC= 60°,AB' = AB = 2,∠ANB'= 90°,∠B' = 30°。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
时间飞逝,下周将进入考试周,考前计划两讲内容,第一讲,主要是对初二阶段将军饮马专题再作一个归纳,第二讲,主要对常考易错知识点进一步辨析.
今天我们主要是对“将军饮马”专题中求线段和最值与求角度做整理.
一.求线段和最值
1
(一)两定一动型
例1:
如图,AM⊥EF,BN⊥EF,垂足为M、N,MN=12m,AM=5m,BN=4m,P是EF上任意一点,则PA+PB的最小值是______m.
分析:
这是最基本的将军饮马问题,A,B是定点,P是动点,属于两定一动将军饮马型,根据常见的“定点定线作对称”,可作点A关于EF的对称点A’,根据两点之间,线段最短,连接A’B,此时A’P+PB即为A’B,最短.而要求A’B,则需要构造直角三角形,利用勾股定理解决.
解答:
作点A关于EF的对称点A’,过点A’作A’C⊥BN的延长线于C.易知A’M =AM=NC=5m,BC=9m,A’C=MN=12m,在Rt△A’BC中,A’B=15m,即PA+PB的最小值是15m.
变式:
如图,在边长为2的正三角形ABC中,E,F,G为各边中点,P为线段EF上一动点,则△BPG周长的最小值为_________.
分析:
考虑到BG为定值是1,则△BPG的周长最小转化为求BP+PG的最小值,又是两定一动的将军饮马型,考虑作点G关于EF的对称点,这里有些同学可能看不出来到底是哪个点,我们不妨连接AG,则AG⊥BC,再连接EG,根据“直角三角形斜边中线等于斜边的一半”,可得AE=EG,则点A就是点G关于EF的对称点.最后计算周长时,别忘了加上BG的长度.
解答:
连接AG,易知PG=PA,BP+PG=BP+PA,当B,P,A三点共线时,BP+PG=BA,此时最短,BA=2,BG=1,即△BPG周长最短为3.
2
(二)一定两动型
例2:
如图,在△ABC中,AB=AC=5,D为BC中点,AD=5,P为AD上任意一点,E为AC上任意一点,求PC+PE的最小值.
这里的点C是定点,P,E是动点,属于一定两动的将军饮马模型,由于△ABC 是等腰三角形,AD是BC中线,则AD垂直平分BC,点C关于AD的对称点是点B,PC+PE=PB+PE,显然当B,P,E三点共线时,BE更短.但此时还不是最短,根据“垂线段最短” 只有当BE⊥AC时,BE最短.求BE时,用面积法即可.
解答:
作BE⊥AC交于点E,交AD于点P,易知AD⊥BC,BD=3,BC=6,
则AD·BC=BE·AC,
4×6=BE·5,BE=4.8
变式:
如图,BD平分∠ABC,E,F分别为线段BC,BD上的动点,AB=8,△ABC的周长为20,求EF+CF的最小值________.
这里的点C是定点,F,E是动点,属于一定两动的将军饮马模型,我们习惯于“定点定线作对称”,但这题这样做,会出现问题.因为点C的对称点C’必然在AB上,但由于BC长度未知,BC’长度也未知,则C’相对的也是不确定点,因此我们这里可以尝试作动点E关于BD的对称点.
解答:
如图,作点E关于BD的对称点E’,连接E’F,则EF+CF=E’F+CF,当E’,F,C三点共线时,E’F+CF=E’C,此时较短.过点C作CE’’⊥AB于E’’,当点E’ 与点E’’重合时,E’’C最短,E’’C为AB边上的高,E’’C =5.
3
(三)两定两动型
例3:
如图,∠AOB=30°,OC=5,OD=12,点E,F分别是射线OA,OB上的动点,求CF+EF+DE的最小值.
分析:
这里的点C,点D是定点,F,E是动点,属于两定两动的将军饮马模型,依旧可以用“定点定线作对称”来考虑.作点C关于OB的对称点,点D关于OA 的对称点.
解答:
作点C关于OB的对称点C’,点D关于OA的对称点D’,连接C’D’.CF +EF+DE=C’F+EF+D’E,当C’,F,E,D’四点共线时,CF+EF +DE=C’D’最短.易知∠D’OC’=90°,OD’=12,OC’=5,C’D’=13,CF+EF+DE最小值为13.
变式:
(原创题)如图,斯诺克比赛桌面AB宽1.78m,白球E距AD边0.22m,距CD边1.4m,有一颗红球F紧贴BC边,且距离CD边0.1m,若要使白球E经过边AD,DC,两次反弹击中红球F,求白球E运动路线的总长度.
分析:
本题中,点E和点F是定点,两次反弹的点虽然未知,但我们可以根据前几题的经验作出,即分别作点E关于AD边的对称点E’,作点F关于CD边的对称点F’,即可画出白球E的运动路线,化归为两定两动将军饮马型.
解答:
作点E关于AD边的对称点E’,作点F关于CD边的对称点F’,连接E’F’,交AD于点G,交CD于点H,则运动路线长为EG+GH+HF长度之和,即E’F’长,延长E’E交BC于N,交AD于M,易知E’M=EM=0.22m,E’N=1.78+0.22=2m,NF’=NC+CF’=1.4+0.1=1.5m,则Rt△E’NF’中,E’F’=2.5m,即白球运动路线的总长度为2.5m.
小结:
以上求线段和最值问题,几乎都可以归结为“两定一动”“一定两动”“两定两动”类的将军饮马型问题,基本方法还是“定点定线作对称”,利用“两点之间
线段最短”“垂线段最短”的2条重要性质,将线段和转化为直角三角形的斜边,或者一边上的高,借助勾股定理,或者面积法来求解.
当然,有时候,我们也需学会灵活变通,定点对称行不通时,尝试作动点对称.
(二)求角度
例1:
P为∠AOB内一定点,M,N分别为射线OA,OB上一点,当△PMN周长最小时,∠MPN=80°.
(1)∠AOB=_____°
(2)求证:OP平分∠MPN
分析:
这又是一定两动型将军饮马问题,我们应该先将M,N的位置找到,再来思考∠AOB的度数,显然作点P关于OA的对称点P’,关于OB的对称点P’’,连接P’P’’,其与OA交点即为M,OB交点即为N,如下图,易知∠DPC 与∠AOB互补,则求出∠DPC的度数即可.
解答:
(1)法1:
如图,∠1+∠2=100°,∠1=∠P’+∠3=2∠3,∠2=∠P’’+∠4=2∠4,则∠3+∠4=50°,∠DPC=130°,∠AOB=50°.
再分析:
考虑到第二小问要证明OP平分∠MPN,我们就连接OP,则要证∠5=∠6,显然很困难,这时候,考虑到对称性,我们再连接OP’,OP’’,则∠5=∠7,∠6=∠8,问题迎刃而解.
解答:
(1)法2:
易知OP’=OP’’,∠7+∠8=∠5+∠6=80°,∠P’OP’’=100°,由对称性知,∠9=∠11,∠10=∠12,∠AOB=∠9+∠10=50°
(2)
由OP’=OP’’,∠P’OP’’=100°知,∠7=∠8=40°,∠5=∠6=40°,OP平分∠MPN.
变式:
如图,在五边形ABCDE中,∠B AE=136°,∠B=∠E=90°,在BC、DE上分别找一点M、N,使得△AMN的周长最小时,则∠AMN+∠ANM的度数为________.
分析:
这又是典型的一定两动型将军饮马问题,必然是作A点关于BC、DE的对称点A′、A″,连接A′A″,与BC、DE的交点即为△AMN周长最小时M、N的位置.解答:
如图,
∵∠BAE=136°,
∴∠MA′A+∠NA″A=44°
由对称性知,
∠MAA′=∠MA′A,
∠NAA″=∠NA″A,
∠AMN+∠ANM
=2∠MA′A+2∠NA″A=88°
本讲思考题:
1.(2017·安顺)如图所示,正方形ABCD的边长为6,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD PE的和最小,则这个最小值为_______.
本讲思考题:
2.(2017·安徽改编)如图,在矩形ABCD中,AB=4,AD=3.P为矩形ABCD 内一点,若矩形ABCD面积为△PAB面积的4倍,则点P到A,B两点距离之和PA PB的最小值为________.。
