中考数学旋转综合练习题含答案解析
中考数学压轴题专题复习——初中数学 旋转的综合含详细答案

中考数学压轴题专题复习——初中数学旋转的综合含详细答案一、旋转1.已知正方形ABCD中,E为对角线BD上一点,过E点作EF⊥BD交BC于F,连接DF,G为DF中点,连接EG,CG.(1)请问EG与CG存在怎样的数量关系,并证明你的结论;(2)将图①中△BEF绕B点逆时针旋转45°,如图②所示,取DF中点G,连接EG,CG.问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.(3)将图①中△BEF绕B点旋转任意角度,如图③所示,再连接相应的线段,问(1)中的结论是否仍然成立?(请直接写出结果,不必写出理由)【答案】(1)证明见解析(2)证明见解析(3)结论仍然成立【解析】【分析】(1)利用直角三角形斜边上的中线等于斜边的一半,可证出CG=EG.(2)结论仍然成立,连接AG,过G点作MN⊥AD于M,与EF的延长线交于N点;再证明△DAG≌△DCG,得出AG=CG;再证出△DMG≌△FNG,得到MG=NG;再证明△AMG≌△ENG,得出AG=EG;最后证出CG=EG.(3)结论依然成立.【详解】(1)CG=EG.理由如下:∵四边形ABCD是正方形,∴∠DCF=90°.在Rt△FCD中,∵G为DF的中点,∴CG=12FD,同理.在Rt△DEF中,EG=12FD,∴CG=EG.(2)(1)中结论仍然成立,即EG=CG.证法一:连接AG,过G点作MN⊥AD于M,与EF的延长线交于N点.在△DAG与△DCG中,∵AD=CD,∠ADG=∠CDG,DG=DG,∴△DAG≌△DCG(SAS),∴AG=CG;在△DMG与△FNG中,∵∠DGM=∠FGN,FG=DG,∠MDG=∠NFG,∴△DMG≌△FNG (ASA),∴MG=NG.∵∠EAM=∠AEN=∠AMN=90°,∴四边形AENM是矩形,在矩形AENM中,AM=EN.在△AMG与△ENG中,∵AM=EN,∠AMG=∠ENG,MG=NG,∴△AMG≌△ENG(SAS),∴AG=EG,∴EG=CG.证法二:延长CG至M,使MG=CG,连接MF,ME,EC.在△DCG与△FMG中,∵FG=DG,∠MGF=∠CGD,MG=CG,∴△DCG≌△FMG,∴MF=CD,∠FMG=∠DCG,∴MF∥CD∥AB,∴EF⊥MF.在Rt△MFE与Rt△CBE中,∵MF=CB,∠MFE=∠EBC=90°,EF=BE,∴△MFE≌△CBE∴∠MEF=∠CEB,∴∠MEC=∠MEF+∠FEC=∠CEB+∠CEF=90°,∴△MEC为直角三角形.∵MG=CG,∴EG=1MC,∴EG=CG.2(3)(1)中的结论仍然成立.理由如下:过F作CD的平行线并延长CG交于M点,连接EM、EC,过F作FN垂直于AB于N.由于G为FD中点,易证△CDG≌△MFG,得到CD=FM,又因为BE=EF,易证∠EFM=∠EBC,则△EFM≌△EBC,∠FEM=∠BEC,EM=EC∵∠FEC+∠BEC=90°,∴∠FEC+∠FEM=90°,即∠MEC=90°,∴△MEC是等腰直角三角形.∵G为CM中点,∴EG=CG,EG⊥CG【点睛】本题是四边形的综合题.(1)关键是利用直角三角形斜边上的中线等于斜边的一半解答;(2)关键是利用了直角三角形斜边上的中线等于斜边的一半的性质、全等三角形的判定和性质解答.2.已知正方形ABCD的边长为4,一个以点A为顶点的45°角绕点A旋转,角的两边分别与BC、DC的延长线交于点E、F,连接EF,设CE=a,CF=b.(1)如图1,当a=42时,求b的值;(2)当a=4时,在图2中画出相应的图形并求出b的值;(3)如图3,请直接写出∠EAF绕点A旋转的过程中a、b满足的关系式.【答案】(1)42;(2)b=8;(3)ab=32.【解析】试题分析:(1)由正方形ABCD的边长为4,可得AC=42,∠ACB=45°.再CE=a=42,可得∠CAE=∠AEC,从而可得∠CAF的度数,既而可得 b=AC;(2)通过证明△ACF∽△ECA,即可得;(3)通过证明△ACF∽△ECA,即可得.试题解析:(1)∵正方形ABCD的边长为4,∴AC=42,∠ACB=45°.∵CE=a=42,∴∠CAE=∠AEC=452︒=22.5°,∴∠CAF=∠EAF-∠CAE=22.5°,∴∠AFC=∠ACD-∠CAF=22.5°,∴∠CAF=∠AFC,∴b=AC=CF=42;(2)∵∠FAE=45°,∠ACB=45°,∴∠FAC+∠CAE=45°,∠CAE+∠AEC=45°,∴∠FAC =∠AEC.又∵∠ACF=∠ECA=135°,∴△ACF∽△ECA,∴AC CFEC CA=,∴4242=,∴CF=8,即b=8.(3)ab=32.提示:由(2)知可证△ACF∽△ECA,∴∴AC CFEC CA=,∴4242a=,∴ab=32.3.如图1,在□ABCD中,AB=6,∠B= (60°<≤90°). 点E在BC上,连接AE,把△ABE沿AE折叠,使点B与AD上的点F重合,连接EF.(1)求证:四边形ABEF是菱形;(2)如图2,点M是BC上的动点,连接AM,把线段AM绕点M顺时针旋转得到线段MN,连接FN,求FN的最小值(用含的代数式表示).【答案】(1)详见解析;(2)FE·sin(-90°)【解析】【分析】(1)由四边形ABCD是平行四边形得AF∥BE,所以∠FAE=∠BEA,由折叠的性质得∠BAE=∠FAE,∠BEA=∠FEA,所以∠BAE=∠FEA,故有AB∥FE,因此四边形ABEF是平行四边形,又BE=EF,因此可得结论;(2)根据点M在线段BE上和EC上两种情况证明∠ENG=90°-,利用菱形的性质得到∠FEN=-90°,再根据垂线段最短,求出FN的最小值即可.【详解】(1)∵四边形ABCD是平行四边形,∴AD∥BC,∴∠FAE=∠BEA,由折叠的性质得∠BAE=∠FAE,∠BEA=∠FEA, BE=EF,∴∠BAE=∠FEA,∴AB∥FE,∴四边形ABEF是平行四边形,又BE=EF,∴四边形ABEF是菱形;(2)①如图1,当点M在线段BE上时,在射线MC上取点G,使MG=AB,连接GN、EN.∵∠AMN=∠B=,∠AMN+∠2=∠1+∠B∴∠1=∠2又AM=NM,AB=MG∴△ABM≌△MGN∴∠B=∠3,NG=BM∵MG=AB=BE∴EG=AB=NG∴∠4=∠ENG= (180°-)=90°-又在菱形ABEF中,AB∥EF∴∠FEC=∠B=∴∠FEN=∠FEC-∠4=- (90°-)=-90°②如图2,当点M在线段EC上时,在BC延长线上截取MG=AB,连接GN、EN.同理可得:∠FEN=∠FEC-∠4=- (90°-)=-90°综上所述,∠FEN=-90°∴当点M在BC上运动时,点N在射线EH上运动(如图3)当FN⊥EH时,FN最小,其最小值为FE·sin(-90°)【点睛】本题考查了菱形的判定与性质以及求最短距离的问题,解题的关键是分类讨论得出∠FEN =-90°,再运用垂线段最短求出FN的最小值.4.在平面直角坐标系中,已知点A(0,4),B(4,4),点M,N是射线OC上两动点(OM<ON),且运动过程中始终保持∠MAN=45°,小明用几何画板探究其中的线段关系.(1)探究发现:当点M,N均在线段OB上时(如图1),有OM2+BN2=MN2.他的证明思路如下:第一步:将△ANB绕点A顺时针旋转90°得△APO,连结PM,则有BN=OP.第二步:证明△APM≌△ANM,得MP=MM.第一步:证明∠POM=90°,得OM2+OP2=MP2.最后得到OM2+BN2=MN2.请你完成第二步三角形全等的证明.(2)继续探究:除(1)外的其他情况,OM2+BN2=MN2的结论是否仍然成立?若成立,请证明;若不成立,请说明理由.(3)新题编制:若点B是MN的中点,请你编制一个计算题(不标注新的字母),并直接给出答案(根据编出的问题层次,给不同的得分).【答案】(1)见解析;(2)结论仍然成立,理由见解析;(3)见解析.【解析】【分析】(1)将△ANB绕点A顺时针旋转90°得△APO,连结PM,则有BN=OP.证明△APM≌△ANM,再利用勾股定理即可解决问题;(2)如图2中,当点M,N在OB的延长线上时结论仍然成立.证明方法类似(1);(3)如图3中,若点B是MN的中点,求MN的长.利用(2)中结论,构建方程即可解决问题.【详解】(1)如图1中,将△ANB绕点A顺时针旋转90°得△APO,连结PM,则有BN=OP.∵点A(0,4),B(4,4),∴OA=AB,∠OAB=90°,∵∠NAP=∠OAB=90°,∠MAN=45°,∴∠MAN=∠MAP,∵MA=MA,AN=AP,∴△MAN≌△MAP(SAS).(2)如图2中,结论仍然成立.理由:如图2中,将△ANB绕点A顺时针旋转90°得△APO,连结PM,则有BN=OP.∵∠NAP=∠OAB=90°,∠MAN=45°,∴∠MAN=∠MAP,∵MA=MA,AN=AP,∴△MAN≌△MAP(SAS),∴MN=PM,∵∠ABN=∠AOP=135°,∠AOB=45°,∴∠MOP=90°,∴PM2=OM2+OP2,∴OM2+BN2=MN2;(3)如图3中,若点B是MN的中点,求MN的长.设MN=2x,则BM=BN=x,∵OA=AB=4,∠OAB=90°,∴OB=42,∴OM=42﹣x,∵OM2+BN2=MN2.∴(42﹣x)2+x2=(2x)2,解得x=﹣22+26或﹣22﹣26(舍弃)∴MN=﹣42+46.【点睛】本题属于几何变换综合题,考查了等腰直角三角形的性质和判定,全等三角形的判定和性质,勾股定理等知识,解题的关键是学会利用旋转法添加辅助线,构造全等三角形解决问题,属于中考压轴题.5.如图1,△ABC是边长为4cm的等边三角形,边AB在射线OM上,且OA=6cm,点D 从O点出发,沿OM的方向以1cm/s的速度运动,当D不与点A重合时,将△ACD绕点C 逆时针方向旋转60°得到△BCE,连结DE.(1)求证:△CDE是等边三角形;(2)如图2,当6<t<10时,△BDE的周长是否存在最小值?若存在,求出△BDE的最小周长;若不存在,请说明理由;(3)如图3,当点D在射线OM上运动时,是否存在以D、E、B为顶点的三角形是直角三角形?若存在,求出此时t的值;若不存在,请说明理由.【答案】(1)见解析(2)见解析(3)存在【解析】试题分析:(1)由旋转的性质得到∠DCE=60°,DC=EC,即可得到结论;(2)当6<t<10时,由旋转的性质得到BE=AD,于是得到C△DBE=BE+DB+DE=AB+DE=4+DE,根据等边三角形的性质得到DE=CD,由垂线段最短得到当CD⊥AB时,△BDE的周长最小,于是得到结论;(3)存在,①当点D于点B重合时,D,B,E不能构成三角形,②当0≤t<6时,由旋转的性质得到∠ABE=60°,∠BDE<60°,求得∠BED=90°,根据等边三角形的性质得到∠DEB=60°,求得∠CEB=30°,求得OD=OA-DA=6-4=2,于是得到t=2÷1=2s;③当6<t<10s 时,此时不存在;④当t>10s时,由旋转的性质得到∠DBE=60°,求得∠BDE>60°,于是得到t=14÷1=14s.试题解析:(1)证明:∵将△ACD绕点C逆时针方向旋转60°得到△BCE,∴∠DCE=60°,DC=EC,∴△CDE是等边三角形;(2)存在,当6<t<10时,由旋转的性质得,BE=AD,∴C△DBE=BE+DB+DE=AB+DE=4+DE,由(1)知,△CDE是等边三角形,∴DE=CD,∴C△DBE=CD+4,由垂线段最短可知,当CD⊥AB时,△BDE的周长最小,此时,CD cm,∴△BDE的最小周长=CD;(3)存在,①∵当点D与点B重合时,D,B,E不能构成三角形,∴当点D与点B重合时,不符合题意;②当0≤t<6时,由旋转可知,∠ABE=60°,∠BDE<60°,∴∠BED=90°,由(1)可知,△CDE是等边三角形,∴∠DEB=60°,∴∠CEB=30°,∵∠CEB=∠CDA,∴∠CDA=30°,∵∠CAB=60°,∴∠ACD=∠ADC=30°,∴DA=CA=4,∴OD=OA﹣DA=6﹣4=2,∴t=2÷1=2s;③当6<t<10s时,由∠DBE=120°>90°,∴此时不存在;④当t>10s时,由旋转的性质可知,∠DBE=60°,又由(1)知∠CDE=60°,∴∠BDE=∠CDE+∠BDC=60°+∠BDC,而∠BDC>0°,∴∠BDE>60°,∴只能∠BDE=90°,从而∠BCD=30°,∴BD=BC=4,∴OD=14cm,∴t=14÷1=14s.综上所述:当t=2或14s时,以D、E、B为顶点的三角形是直角三角形.点睛:在不带坐标的几何动点问题中求最值,通常是将其表达式写出来,再通过几何或代数的方法求出最值;像第三小问这种探究性的题目,一定要多种情况考虑全面,控制变量,从某一个方面出发去分类.6.如图,点P是正方形ABCD内的一点,连接PA,PB,PC.将△PAB绕点B顺时针旋转90°到△P'CB的位置.(1)设AB的长为a,PB的长为b(b<a),求△PAB旋转到△P'CB的过程中边PA所扫过区域(图中阴影部分)的面积;(2)若PA=2,PB=4,∠APB=135°,求PC的长.【答案】(1) S阴影=(a2-b2);(2)PC=6.【解析】试题分析:(1)依题意,将△P′CB逆时针旋转90°可与△PAB重合,此时阴影部分面积=扇形BAC的面积-扇形BPP'的面积,根据旋转的性质可知,两个扇形的中心角都是90°,可据此求出阴影部分的面积.(2)连接PP',根据旋转的性质可知:BP=BP',旋转角∠PBP'=90°,则△PBP'是等腰直角三角形,∠BP'C=∠BPA=135°,∠PP'C=∠BP'C-∠BP'P=135°-45°=90°,可推出△PP'C是直角三角形,进而可根据勾股定理求出PC的长.试题解析:(1)∵将△PAB绕点B顺时针旋转90°到△P′CB的位置,∴△PAB≌△P'CB,∴S△PAB=S△P'CB,S阴影=S扇形BAC-S扇形BPP′=(a2-b2);(2)连接PP′,根据旋转的性质可知:△APB≌△CP′B,∴BP=BP′=4,P′C=PA=2,∠PBP′=90°,∴△PBP'是等腰直角三角形,P'P2=PB2+P'B2=32;又∵∠BP′C=∠BPA=135°,∴∠PP′C=∠BP′C-∠BP′P=135°-45°=90°,即△PP′C是直角三角形.PC==6.考点:1.扇形面积的计算;2.正方形的性质;3.旋转的性质.7.在平面直角坐标系中,O为原点,点A(0,4),点B(﹣2,0),把△ABO绕点A逆时针旋转,得△AB′O′,点B、O旋转后的对应点为B′、O′.(1)如图①,若旋转角为60°时,求BB′的长;(2)如图②,若AB′∥x轴,求点O′的坐标;(3)如图③,若旋转角为240°时,边OB上的一点P旋转后的对应点为P′,当O′P+AP′取得最小值时,求点P′的坐标(直接写出结果即可)【答案】(1)252)点O′8545);(3)点P′的坐标为(﹣83 5,365.【解析】分析:(1)由点A、B的坐标可得出AB的长度,连接BB′,由旋转可知:AB=AB′,∠BAB′=60°,进而可得出△ABB′为等边三角形,根据等边三角形的性质可求出BB′的长;(2)过点O′作O′D⊥x轴,垂足为D,交AB′于点E,则△AO′E∽△ABO,根据旋转的性质结合相似三角形的性质可求出AE、O′E的长,进而可得出点O′的坐标;(3)作点A关于x轴对称的点A′,连接A′O′交x轴于点P,此时O′P+AP′取最小值,过点O′作O′F⊥y轴,垂足为点F,过点P′作PM⊥O′F,垂足为点M,根据旋转的性质结合解直角三角形可求出点O′的坐标,由A、A′关于x轴对称可得出点A′的坐标,利用待定系数法即可求出直线A′O′的解析式,由一次函数图象上点的坐标特征可得出点P的坐标,进而可得出OP的长度,再在Rt△O′P′M中,通过解直角三角形可求出O′M、P′M的长,进而可得出此时点P′的坐标.详解:(1)∵点A(0,4),点B(﹣2,0),∴OA=4,OB=2,∴AB22OA OB5.在图①中,连接BB′.由旋转可知:AB =AB ′,∠BAB ′=60°,∴△ABB ′为等边三角形,∴BB ′=AB =25. (2)在图②中,过点O ′作O ′D ⊥x 轴,垂足为D ,交AB ′于点E . ∵AB ′∥x 轴,O ′E ⊥x 轴,∴∠O ′EA =90°=∠AOB .由旋转可知:∠B ′AO ′=∠BAO ,AO ′=AO =4,∴△AO ′E ∽△ABO ,AE AO ='O E BO ='AO AB,即4AE ='2O E =25,∴AE =85,O ′E =45,∴O ′D =45+4,∴点O ′的坐标为(8545,+4). (3)作点A 关于x 轴对称的点A ′,连接A ′O ′交x 轴于点P ,此时O ′P +AP ′取最小值,过点O ′作O ′F ⊥y 轴,垂足为点F ,过点P ′作PM ⊥O ′F ,垂足为点M ,如图3所示. 由旋转可知:AO ′=AO =4,∠O ′AF =240°﹣180°=60°,∴AF =12AO ′=2,O ′F =32AO ′=23,∴点O ′(﹣23,6).∵点A (0,4),∴点A ′(0,﹣4).设直线A ′O ′的解析式为y =kx +b ,将A ′(0,﹣4)、O ′(﹣23,6)代入y =kx +b ,得: 4236b k b =-⎧⎪⎨-+=⎪⎩,解得:534k b ⎧=-⎪⎨⎪=-⎩,∴直线A ′O ′的解析式为y =﹣53x ﹣4. 当y =0时,有﹣53x ﹣4=0,解得:x =﹣43,∴点P (﹣43,0),∴OP =O ′P ′=43. 在Rt △O ′P ′M 中,∠MO ′P ′=60°,∠O ′MP ′=90°,∴O ′M =12O ′P ′=23,P ′M =32O ′P ′=65,∴点P ′的坐标为(﹣23+235,6+65),即(﹣833655,).点睛:本题考查了函数图象及旋转变换、待定系数法求一次函数解析式、等边三角形的判定与性质、一次函数图象上点的坐标特征以及解直角三角形,解题的关键是:(1)利用等边三角形的性质找出BB′的长;(2)通过解直角三角形求出AE、O′E的长;(3)利用两点之间线段最短找出当O′P+AP′取得最小值时点P的位置.8.如图1,△ACB、△AED都为等腰直角三角形,∠AED=∠ACB=90°,点D在AB上,连CE,M、N分别为BD、CE的中点.(1)求证:MN⊥CE;(2)如图2将△AED绕A点逆时针旋转30°,求证:CE=2MN.【答案】(1)证明见解析;(2)证明见解析.【解析】试题分析:(1)延长DN交AC于F,连BF,推出DE∥AC,推出△EDN∽△CFN,推出DE EN DN==,求出DN=FN,FC=ED,得出MN是中位线,推出MN∥BF,证CF CN NF△CAE≌△BCF,推出∠ACE=∠CBF,求出∠CBF+∠BCE=90°,即可得出答案;(2)延长DN到G,使DN=GN,连接CG,延长DE、CA交于点K,求出BG=2MN,证△CAE≌△BCG,推出BG=CE,即可得出答案.试题解析:(1)证明:延长DN交AC于F,连BF,∵N为CE中点,∴EN=CN,∵△ACB和△AED是等腰直角三角形,∠AED=∠ACB=90°,DE=AE,AC=BC,∴∠EAD=∠EDA=∠BAC=45°,∴DE ∥AC ,∴△EDN ∽△CFN , ∴DE EN DN CF CN NF== , ∵EN=NC ,∴DN=FN ,FC=ED , ∴MN 是△BDF 的中位线,∴MN ∥BF ,∵AE=DE ,DE=CF ,∴AE=CF ,∵∠EAD=∠BAC=45°,∴∠EAC=∠ACB=90°,在△CAE 和△BCF 中,CA BC CAE BCF AE CF ⎧⎪∠∠⎨⎪⎩=== , ∴△CAE ≌△BCF (SAS ),∴∠ACE=∠CBF ,∵∠ACE+∠BCE=90°,∴∠CBF+∠BCE=90°,即BF ⊥CE ,∵MN ∥BF ,∴MN ⊥CE .(2)证明:延长DN 到G ,使DN=GN ,连接CG ,延长DE 、CA 交于点K ,∵M 为BD 中点,∴MN 是△BDG 的中位线,∴BG=2MN ,在△EDN 和⊈CGN 中,DN NG DNE GNC EN NC ⎧⎪∠∠⎨⎪⎩===,∴△EDN ≌△CGN (SAS ),∴DE=CG=AE ,∠GCN=∠DEN ,∴DE ∥CG ,∴∠KCG=∠CKE ,∵∠CAE=45°+30°+45°=120°,∴∠EAK=60°,∴∠CKE=∠KCG=30°,∴∠BCG=120°,在△CAE 和△BCG 中,AC BC CAE BCG AE CG ⎧⎪∠∠⎨⎪⎩=== , ∴△CAE ≌△BCG (SAS ),∴BG=CE ,∵BG=2MN ,∴CE=2MN .【点睛】考查了等腰直角三角形性质,全等三角形的性质和判定,三角形的中位线,平行线性质和判定的应用,主要考查学生的推理能力.9.已知:如图1,将两块全等的含30º角的直角三角板按图所示的方式放置,∠BAC=∠B 1A 1C =30°,点B ,C ,B 1在同一条直线上.(1)求证:AB =2BC(2)如图2,将△ABC 绕点C顺时针旋转α°(0<α<180),在旋转过程中,设AB 与A 1C 、A 1B 1分别交于点D 、E ,AC 与A 1B 1交于点F .当α等于多少度时,AB 与A 1B 1垂直?请说明理由.(3)如图3,当△ABC 绕点C 顺时针方向旋转至如图所示的位置,使AB ∥CB 1,AB 与A 1C 交于点D ,试说明A 1D=CD .【答案】(1)证明见解析(2)当旋转角等于30°时,AB 与A 1B 1垂直.(3)理由见解析【解析】试题分析:(1)由等边三角形的性质得AB =BB 1,又因为BB 1=2BC ,得出AB =2BC ;(2) 利用AB 与A 1B 1垂直得∠A 1ED=90°,则∠A 1DE=90°-∠A 1=60°,根据对顶角相等得∠BDC=60°,由于∠B=60°,利用三角形内角和定理得∠A 1CB=180°-∠BDC-∠B=60°,所以∠ACA 1=90°-∠A 1CB=30°,然后根据旋转的定义得到旋转角等于30°时,AB 与A 1B 1垂直;(3)由于AB ∥CB 1,∠ACB 1=90°,根据平行线的性质得∠ADC=90°,在Rt △ADC 中,根据含30度的直角三角形三边的关系得到CD=12AC ,再根据旋转的性质得AC=A 1C ,所以CD=12A 1C ,则A 1D=CD . 试题解析: (1)∵△ABB 1是等边三角形;∴ AB =BB 1∵ BB 1=2BC∴AB =2BC(2)解:当AB 与A 1B 1垂直时,∠A 1ED=90°,∴∠A 1DE=90°-∠A 1=90°-30°=60°,∵∠B=60°,∴∠BCD=60°,∴∠ACA 1=90°-60°=30°,即当旋转角等于30°时,AB 与A 1B 1垂直.(3)∵AB ∥CB 1,∠ACB 1=90°,∴∠CDB=90°,即CD 是△ABC 的高,设BC=a ,AC=b ,则由(1)得AB=2a ,A 1C=b , ∵1122ABC S BC AC AB CD ∆=⨯=⨯, 即11222ab a CD =⨯⨯ ∴12CD b =,即CD=12A 1C , ∴A 1D=CD. 【点睛】本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了含30度的直角三角形三边的关系.10.如图,△ABC 是等边三角形,AB=6cm ,D 为边AB 中点.动点P 、Q 在边AB 上同时从点D 出发,点P 沿D→A 以1cm/s 的速度向终点A 运动.点Q 沿D→B→D 以2cm/s 的速度运动,回到点D停止.以PQ为边在AB上方作等边三角形PQN.将△PQN绕QN的中点旋转180°得到△MNQ.设四边形PQMN与△ABC重叠部分图形的面积为S(cm2),点P运动的时间为t(s)(0<t<3).(1)当点N落在边BC上时,求t的值.(2)当点N到点A、B的距离相等时,求t的值.(3)当点Q沿D→B运动时,求S与t之间的函数表达式.(4)设四边形PQMN的边MN、MQ与边BC的交点分别是E、F,直接写出四边形PEMF 与四边形PQMN的面积比为2:3时t的值.【答案】(1)(2)2(3)S=S菱形PQMN=2S△PNQ=t2;(4)t=1或【解析】试题分析:(1)由题意知:当点N落在边BC上时,点Q与点B重合,此时DQ=3;(2)当点N到点A、B的距离相等时,点N在边AB的中线上,此时PD=DQ;(3)当0≤t≤时,四边形PQMN与△ABC重叠部分图形为四边形PQMN;当≤t≤时,四边形PQMN与△ABC重叠部分图形为五边形PQFEN.(4)MN、MQ与边BC的有交点时,此时<t<,列出四边形PEMF与四边形PQMN的面积表达式后,即可求出t的值.试题解析:(1)∵△PQN与△ABC都是等边三角形,∴当点N落在边BC上时,点Q与点B重合.∴DQ=3∴2t=3.∴t=;(2)∵当点N到点A、B的距离相等时,点N在边AB的中线上,∴PD=DQ,当0<t<时,此时,PD=t,DQ=2t∴t=2t∴t=0(不合题意,舍去),当≤t<3时,此时,PD=t,DQ=6﹣2t∴t=6﹣2t,解得t=2;综上所述,当点N到点A、B的距离相等时,t=2;(3)由题意知:此时,PD=t,DQ=2t当点M在BC边上时,∴MN=BQ∵PQ=MN=3t,BQ=3﹣2t∴3t=3﹣2t∴解得t=如图①,当0≤t≤时,S△PNQ=PQ2=t2;∴S=S菱形PQMN=2S△PNQ=t2,如图②,当≤t≤时,设MN、MQ与边BC的交点分别是E、F,∵MN=PQ=3t,NE=BQ=3﹣2t,∴ME=MN﹣NE=PQ﹣BQ=5t﹣3,∵△EMF是等边三角形,∴S△EMF=ME2=(5t﹣3)2.;(4)MN、MQ与边BC的交点分别是E、F,此时<t<,t=1或.考点:几何变换综合题11.如图1,矩形ABCD中,E是AD的中点,以点E直角顶点的直角三角形EFG的两边EF,EG分别过点B,C,∠F=30°.(1)求证:BE=CE(2)将△EFG绕点E按顺时针方向旋转,当旋转到EF与AD重合时停止转动.若EF,EG分别与AB,BC相交于点M,N.(如图2)①求证:△BEM≌△CEN;②若AB=2,求△BMN面积的最大值;③当旋转停止时,点B恰好在FG上(如图3),求sin∠EBG的值.【答案】(1)详见解析;(2)①详见解析;②2;62【解析】【分析】(1)只要证明△BAE≌△CDE即可;(2)①利用(1)可知△EBC是等腰直角三角形,根据ASA即可证明;②构建二次函数,利用二次函数的性质即可解决问题;③如图3中,作EH⊥BG于H.设NG=m,则BG=2m,3,6m.利用面积法求出EH,根据三角函数的定义即可解决问题.【详解】(1)证明:如图1中,∵四边形ABCD是矩形,∴AB=DC,∠A=∠D=90°,∵E是AD中点,∴AE=DE,∴△BAE≌△CDE,∴BE=CE.(2)①解:如图2中,由(1)可知,△EBC是等腰直角三角形,∴∠EBC=∠ECB=45°,∵∠ABC=∠BCD=90°,∴∠EBM=∠ECN=45°,∵∠MEN=∠BEC=90°,∴∠BEM=∠CEN,∵EB=EC,∴△BEM≌△CEN;②∵△BEM≌△CEN,∴BM=CN,设BM=CN=x,则BN=4-x,∴S△BMN=12•x(4-x)=-12(x-2)2+2,∵-12<0,∴x=2时,△BMN的面积最大,最大值为2.③解:如图3中,作EH⊥BG于H.设NG=m,则BG=2m,3m,6m.∴EG=m+3m=(1+3)m ,∵S △BEG =12•EG•BN=12•BG•EH , ∴EH=3?(13) m m +=3+3m , 在Rt △EBH 中,sin ∠EBH=3+36226m EH EB m+==. 【点睛】本题考查四边形综合题、矩形的性质、等腰直角三角形的判定和性质、全等三角形的判定和性质、旋转变换、锐角三角函数等知识,解题的关键是准确寻找全等三角形解决问题,学会添加常用辅助线,学会利用参数解决问题,12.在平面直角坐标系中,四边形AOBC 是矩形,点(0,0)O ,点(5,0)A ,点(0,3)B .以点A 为中心,顺时针旋转矩形AOBC ,得到矩形ADEF ,点O ,B ,C 的对应点分别为D ,E ,F .(Ⅰ)如图①,当点D 落在BC 边上时,求点D 的坐标;(Ⅱ)如图②,当点D 落在线段BE 上时,AD 与BC 交于点H .①求证ADB AOB △△≌;②求点H 的坐标.(Ⅲ)记K 为矩形AOBC 对角线的交点,S 为KDE △的面积,求S 的取值范围(直接写出结果即可).【答案】(Ⅰ)点D 的坐标为(1,3).(Ⅱ)①证明见解析;②点H 的坐标为17(,3)5.(Ⅲ)303343033444S -+≤≤. 【解析】分析:(Ⅰ)根据旋转的性质得AD=AO=5,设CD=x ,在直角三角形ACD 中运用勾股定理可CD 的值,从而可确定D 点坐标;(Ⅱ)①根据直角三角形全等的判定方法进行判定即可;②由①知BAD BAO ∠=∠,再根据矩形的性质得CBA OAB ∠=∠.从而BAD CBA ∠=∠,故BH=AH ,在Rt △ACH 中,运用勾股定理可求得AH 的值,进而求得答案;(Ⅲ)3033430334S -+≤≤.详解:(Ⅰ)∵点()5,0A ,点()0,3B ,∴5OA =,3OB =.∵四边形AOBC 是矩形,∴3AC OB ==,5BC OA ==,90OBC C ∠=∠=︒.∵矩形ADEF 是由矩形AOBC 旋转得到的,∴5AD AO ==.在Rt ADC V 中,有222AD AC DC =+,∴22DC AD AC =- 22534=-=.∴1BD BC DC =-=.∴点D 的坐标为()1,3.(Ⅱ)①由四边形ADEF 是矩形,得90ADE ∠=︒.又点D 在线段BE 上,得90ADB ∠=︒.由(Ⅰ)知,AD AO =,又AB AB =,90AOB ∠=︒,∴Rt ADB Rt AOB V V ≌.②由ADB AOB V V ≌,得BAD BAO ∠=∠.又在矩形AOBC 中,//OA BC ,∴CBA OAB ∠=∠.∴BAD CBA ∠=∠.∴BH AH =.设BH t =,则AH t =,5HC BC BH t =-=-.在Rt AHC V 中,有222AH AC HC =+,∴()22235t t=+-.解得175t=.∴175BH=.∴点H的坐标为17,3 5⎛⎫ ⎪⎝⎭.(Ⅲ)3033430334S-+≤≤.点睛:本大题主要考查了等腰三角形的判定和性质,勾股定理以及旋转变换的性质等知识,灵活运用勾股定理求解是解决本题的关键.13.如图,是边长为的等边三角形,边在射线上,且,点从点出发,沿的方向以的速度运动,当不与点重合是,将绕点逆时针方向旋转得到,连接.(1)求证:是等边三角形;(2)当时,的周长是否存在最小值?若存在,求出的最小周长;若不存在,请说明理由.(3)当点在射线上运动时,是否存在以为顶点的三角形是直角三角形?若存在,求出此时的值;若不存在,请说明理由.【答案】(1)详见解析;(2)存在,2+4;(3)当t=2或14s时,以D、E、B为顶点的三角形是直角三角形.【解析】试题分析:(1)由旋转的性质得到∠DCE=60°,DC=EC,即可得到结论;(2)当6<t<10时,由旋转的性质得到BE=AD,于是得到C△DBE=BE+DB+DE=AB+DE=4+DE,根据等边三角形的性质得到DE=CD,由垂线段最短得到当CD⊥AB时,△BDE的周长最小,于是得到结论;(3)存在,①当点D与点B重合时,D,B,E不能构成三角形,②当0≤t<6时,由旋转的性质得到∠ABE=60°,∠BDE<60°,求得∠BED=90°,根据等边三角形的性质得到∠DEB=60°,求得∠CEB=30°,求得OD=OA﹣DA=6﹣4=2,于是得到t=2÷1=2s;③当6<t<10s时,此时不存在;④当t>10s时,由旋转的性质得到∠DBE=60°,求得∠BDE>60°,于是得到t=14÷1=14s.试题解析:(1)证明:∵将△ACD绕点C逆时针方向旋转60°得到△BCE,∴∠DCE=60°,DC=EC,∴△CDE是等边三角形;(2)存在,当6<t<10时,由旋转的性质得,BE=AD,∴C△DBE=BE+DB+DE=AB+DE=4+DE,由(1)知,△CDE是等边三角形,∴DE=CD,∴C△DBE=CD+4,由垂线段最短可知,当CD⊥AB时,△BDE的周长最小,此时,CD=2cm,∴△BDE的最小周长=CD+4=2+4;(3)存在,①∵当点D与点B重合时,D,B,E不能构成三角形,∴当点D与点B重合时,不符合题意,②当0≤t<6时,由旋转可知,∠ABE=60°,∠BDE<60°,∴∠BED=90°,由(1)可知,△CDE是等边三角形,∴∠DEB=60°,∴∠CEB=30°,∵∠CEB=∠CDA,∴∠CDA=30°,∵∠CAB=60°,∴∠ACD=∠ADC=30°,∴DA=CA=4,∴OD=OA﹣DA=6﹣4=2,∴t=2÷1=2s;③当6<t<10s时,由∠DBE=120°>90°,∴此时不存在;④当t>10s时,由旋转的性质可知,∠DBE=60°,又由(1)知∠CDE=60°,∴∠BDE=∠CDE+∠BDC=60°+∠BDC,而∠BDC >0°,∴∠BDE >60°,∴只能∠BDE=90°,从而∠BCD=30°,∴BD=BC=4,∴OD=14cm ,∴t=14÷1=14s ,综上所述:当t=2或14s 时,以D 、E 、B 为顶点的三角形是直角三角形.考点:旋转与三角形的综合题.14.如图,已知Rt △ABC 中,∠ACB =90°,AC =BC ,D 是线段AB 上的一点(不与A 、B 重合).过点B 作BE ⊥CD ,垂足为E .将线段CE 绕点C 顺时针旋转90︒,得到线段CF ,连结EF .设∠BCE 度数为α.(1)①补全图形;②试用含α的代数式表示∠CDA .(2)若3EF AB = ,求α的大小. (3)直接写出线段AB 、BE 、CF 之间的数量关系.【答案】(1)①答案见解析;②45α︒+;(2)30α=︒;(3)22222AB CF BE =+.【解析】试题分析:(1)①按要求作图即可;②由∠ACB=90°,AC=BC ,得∠ABC=45°,故可得出结论;(2)易证FCE ∆∽ ACB ∆,得3CF AC =FA ,得△AFC 是直角三角形,求出∠ACF=30°,从而得出结论;(3)222A 22B CF BE =+.试题解析:(1)①补全图形.②∵∠ACB=90°,AC=BC ,∴∠ABC=45°∵∠BCE=α ∴∠CDA=45α︒+(2)在FCE ∆和ACB ∆中,45CFE CAB ∠=∠=︒ ,90FCE ACB ∠=∠=︒ ∴ FCE ∆∽ ACB ∆ ∴ CF EF AC AB = Q 3EF AB = ∴ 32CF AC = 连结FA .Q 90,90FCA ACE ECB ACE ∠=︒-∠∠=︒-∠∴ FCA ECB ∠=∠=α在Rt CFA ∆中,90CFA ∠=︒,3cos FCA ∠= ∴ 30FCA ∠=︒即30α=︒.(3)22222AB CF BE =+15.已知△ABC 是边长为4的等边三角形,边AB 在射线OM 上,且OA =6,点D 是射线OM 上的动点,当点D 不与点A 重合时,将△ACD 绕点C 逆时针方向旋转60°得到△BCE ,连接DE .(1)如图1,求证:△CDE 是等边三角形.(2)设OD =t ,①当6<t <10时,△BDE 的周长是否存在最小值?若存在,求出△BDE 周长的最小值;若不存在,请说明理由.②求t为何值时,△DEB是直角三角形(直接写出结果即可).【答案】(1)见解析;(2) ①见解析; ②t=2或14.【解析】【分析】(1)由旋转的性质得到∠DCE=60°,DC=EC,即可得到结论;(2)①当6<t<10时,由旋转的性质得到BE=AD,于是得到C△DBE=BE+DB+DE=AB+DE=4+DE,根据等边三角形的性质得到DE=CD,由垂线段最短得到当CD⊥AB时,△BDE的周长最小,于是得到结论;②存在,当点D与点B重合时,D,B,E不能构成三角形;当0≤t<6时,由旋转的性质得到∠ABE=60°,∠BDE<60°,求得∠BED=90°,根据等边三角形的性质得到∠DEB=60°,求得∠CEB=30°,求得OD=OA-DA=6-4=2=t;当6<t<10时,此时不存在;当t>10时,由旋转的性质得到∠DBE=60°,求得∠BDE>60°,于是得到t=14.【详解】(1)∵将△ACD绕点C逆时针方向旋转60°得到△BCE,∴∠DCE=60°,DC=EC,∴△CDE是等边三角形;(2)①存在,当6<t<10时,由旋转的性质得,BE=AD,∴C△DBE=BE+DB+DE=AB+DE=4+DE,由(1)知,△CDE是等边三角形,∴DE=CD,∴C△DBE=CD+4,由垂线段最短可知,当CD⊥AB时,△BDE的周长最小,此时,CD=3,∴△BDE的最小周长=CD+4=3;②存在,∵当点D与点B重合时,D,B,E不能构成三角形,∴当点D与点B重合时,不符合题意;当0≤t<6时,由旋转可知,∠ABE=60°,∠BDE<60°,∴∠BED=90°,由(1)可知,△CDE是等边三角形,∴∠DEB=60°,∴∠CEB=30°,∵∠CEB=∠CDA,∴∠CDA=30°,∵∠CAB=60°,∴∠ACD=∠ADC=30°,∴DA=CA=4,∴OD=OA﹣DA=6﹣4=2,∴t=2;当6<t<10时,由∠DBE=120°>90°,∴此时不存在;当t>10时,由旋转的性质可知,∠DBE=60°,又由(1)知∠CDE=60°,∴∠BDE=∠CDE+∠BDC=60°+∠BDC,而∠BDC>0°,∴∠BDE>60°,∴只能∠BDE=90°,从而∠BCD=30°,∴BD=BC=4,∴OD=14,∴t=14,综上所述:当t=2或14时,以D、E、B为顶点的三角形是直角三角形.【点睛】本题考查了旋转的性质,等边三角形的判定和性质,三角形周长的计算,直角三角形的判定,熟练掌握旋转的性质是解题的关键.。
中考数学《旋转》专题练习含答案解析

旋转一、选择题(共6小题,每小题4分,满分24分)1.下列图形中,你认为既是中心对称图形又是轴对称图形的是()A.B.C.D.2.如图,所给的图案由△ABC绕点O顺时针旋转()前后的图形组成的.A.45°、90°、135°B.90°、135°、180°C.45°、90°、135°、180°、225° D.45°、180°、225°3.如图,边长为1的正方形ABCD绕点A逆时针旋转30°到正方形AB′C′D′,图中阴影部分的面积为()A.B.C.1﹣D.1﹣4.如图,P是等边三角形ABC内一点,∠APB,∠BPC,∠CPA的大小之比为5:6:7,则以PA,PB,PC为边的三角形三内角大小之比(从小到大)是()A.2:3:4 B.3:4:5C.4:5:6 D.以上结果都不对5.下列图形中,是中心对称图形的是()A.菱形B.等腰梯形C.等边三角形D.等腰直角三角形6.在平面直角坐标系中,点P(2,﹣3)关于原点对称的点的坐标是()A.(2,3)B.(﹣2,3)C.(﹣2,﹣3)D.(﹣3,2)二、填空题(共6小题,每小题5分,满分30分)7.在平面直角坐标系中,已知点P0的坐标为(1,0),将点P0绕着原点O按逆时针方向旋转60°得点P1,延长OP1到点P2,使OP2=2OP1再将点P2绕着原点O按逆时针方向旋转60°得点P3,则点P3的坐标是.8.如图所示,△ABC中,∠BAC=90°,AB=AC=5,△ABC按逆时针方向旋转一个角度后,成为△ACD,则旋转中心是点、旋转角是.9.如图,设P是等边三角形ABC内任意一点,△ACP′是由△ABP旋转得到的,则PA PB+PC(选填“>”、“=”、“<”)10.如图,E、F分别是正方形ABCD的边BC、CD上一点,且BE+DF=EF,则∠EAF=度.11.如图,O是等边△ABC内一点,将△AOB绕A点逆时针旋转,使得B,O两点的对应分别为C,D,则旋转角为度,图中除△ABC外,还有等边三形是△.12.如图,Rt△ABC中,P是斜边BC上一点,以P为中心,把这个三角形按逆时针方向旋转90°得到△DEF,图中通过旋转得到的三角形还有.三、解答题13.已知:正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB、DC(或它们的延长线)于点M、N.当∠MAN绕点A旋转到BM=DN时(如图1),易证BM+DN=MN.(1)当∠MAN绕点A旋转到BM≠DN时(如图2),线段BM、DN和MN之间有怎样的数量关系?写出猜想,并加以证明;(2)当∠MAN绕点A旋转到如图3的位置时,线段BM、DN和MN之间又有怎样的数量关系?请直接写出你的猜想.14.如图,正方形ABCD的边长为1,AB,AD上各有一点P,Q,如果△APQ的周长为2,求∠PCQ的度数.15.有两张完全重合的矩形纸片,小亮同学将其中一张绕点A顺时针旋转90°后得到矩形AMEF(如图1),连接BD、MF,若此时他测得BD=8cm,∠ADB=30°.(1)请直接写出AF的长;(2)小红同学用剪刀将△BCD与△MEF剪去,与小亮同学继续探究.他们将△ABD绕点A顺时针旋转得△AB1D1,AD1交FM于点K(如图2),设旋转角为β(0°<β<90°),当△AFK为等腰三角形时,求△AFK的面积(保留根号).旋转参考答案与试题解析一、选择题(共6小题,每小题4分,满分24分)1.下列图形中,你认为既是中心对称图形又是轴对称图形的是()A.B.C.D.【考点】中心对称图形;轴对称图形.【分析】根据轴对称图形与中心对称图形的概念求解.【解答】解:既是中心对称图形又是轴对称图形的只有A.故选A.【点评】掌握好中心对称与轴对称的概念.轴对称的关键是寻找对称轴,两边图象沿对称轴折叠后可重合,中心对称是要寻找对称中心,图形旋转180度后与原图重合.2.如图,所给的图案由△ABC绕点O顺时针旋转()前后的图形组成的.A.45°、90°、135°B.90°、135°、180°C.45°、90°、135°、180°、225° D.45°、180°、225°【考点】旋转的性质.【专题】计算题.【分析】根据旋转的性质,把旋转后的图形看作为正八边形,依次得到旋转的角度.【解答】解:把△ABC绕点O顺时针旋转45°,得到△HEF;顺时针旋转180°,得到△ADC;顺时针旋转225°,得到△HGF;故选D.【点评】本题考查了旋转的性质:旋转前后的两个图形全等,对应点与旋转中心的连线段的夹角等于旋转角,对应点到旋转中心的距离相等.3.如图,边长为1的正方形ABCD绕点A逆时针旋转30°到正方形AB′C′D′,图中阴影部分的面积为()A.B.C.1﹣D.1﹣【考点】旋转的性质;正方形的性质.【分析】设B′C′与CD的交点为E,连接AE,利用“HL”证明Rt△AB′E和Rt△ADE全等,根据全等三角形对应角相等∠DAE=∠B′AE,再根据旋转角求出∠DAB′=60°,然后求出∠DAE=30°,再解直角三角形求出DE,然后根据阴影部分的面积=正方形ABCD的面积﹣四边形ADEB′的面积,列式计算即可得解.【解答】解:如图,设B′C′与CD的交点为E,连接AE,在Rt△AB′E和Rt△ADE中,,∴Rt△AB′E≌Rt△ADE(HL),∴∠DAE=∠B′AE,∵旋转角为30°,∴∠DAB′=60°,∴∠DAE=×60°=30°,∴DE=1×=,∴阴影部分的面积=1×1﹣2×(×1×)=1﹣.故选:C.【点评】本题考查了旋转的性质,正方形的性质,全等三角形判定与性质,解直角三角形,利用全等三角形求出∠DAE=∠B′AE,从而求出∠DAE=30°是解题的关键,也是本题的难点.4.如图,P是等边三角形ABC内一点,∠APB,∠BPC,∠CPA的大小之比为5:6:7,则以PA,PB,PC为边的三角形三内角大小之比(从小到大)是()A.2:3:4 B.3:4:5C.4:5:6 D.以上结果都不对【考点】旋转的性质;三角形内角和定理;等边三角形的性质.【专题】计算题.【分析】将△APB绕A点逆时针旋转60°得△AP′C,显然有△AP′C≌△APB,连PP′,则AP′=AP,∠P′AP=60°,得到△AP′P是等边三角形,PP′=AP,所以△P′CP的三边长分别为PA,PB,PC;再由∠APB+∠BPC+∠CPA=360°,∠APB:∠BPC:∠CPA=5:6:7,得到∠APB=100°,∠BPC=120°,∠CPA=140°,这样可分别求出∠PP′C=∠AP′C﹣∠AP′P=∠APB ﹣∠AP′P=100°﹣60°=40°,∠P′PC=∠APC﹣∠APP′=140°﹣60°=80°,∠PCP′=180°﹣(40°+80°)=60°,即可得到答案.【解答】解:如图,将△APB绕A点逆时针旋转60°得△AP′C,显然有△AP′C≌△APB,连PP′,∵AP′=AP,∠P′AP=60°,∴△AP′P是等边三角形,∴PP′=AP,∵P′C=PB,∴△P′CP的三边长分别为PA,PB,PC,∵∠APB+∠BPC+∠CPA=360°,∠APB:∠BPC:∠CPA=5:6:7,∴∠APB=100°,∠BPC=120°,∠CPA=140°,∴∠PP′C=∠AP′C﹣∠AP′P=∠APB﹣∠AP′P=100°﹣60°=40°,∠P′PC=∠APC﹣∠APP′=140°﹣60°=80°,∠PCP′=180°﹣(40°+80°)=60°,∴∠PP′C:∠PCP′:∠P′PC=2:3:4.故选A.【点评】本题考查了旋转的性质:旋转前后的两个图形全等,对应点与旋转中心的连线段的夹角等于旋转角,对应点到旋转中心的距离相等.也考查了等边三角形的性质.5.下列图形中,是中心对称图形的是()A.菱形B.等腰梯形C.等边三角形D.等腰直角三角形【考点】中心对称图形.【分析】旋转180°后与原图重合的图形是中心对称图形.【解答】解:菱形,等腰梯形,等边三角形,等腰直角三角形都是轴对称图形;菱形既是轴对称图形,又是中心对称图形.故选A.【点评】运用轴对称和中心对称图形概念,找出符合条件的图形.【链接】如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴.如果一个图形绕某一点旋转180°后能够与自身重合,那么这个图形就叫做中心对称图形,这个点叫做对称中心.6.在平面直角坐标系中,点P(2,﹣3)关于原点对称的点的坐标是()A.(2,3)B.(﹣2,3)C.(﹣2,﹣3)D.(﹣3,2)【考点】关于原点对称的点的坐标.【分析】根据“平面直角坐标系中任意一点P(x,y),关于原点的对称点是(﹣x,﹣y)”解答.【解答】解:根据中心对称的性质,得点P(2,﹣3)关于原点对称的点的坐标是(﹣2,3).故选B.【点评】关于原点对称的点坐标的关系,是需要识记的基本问题.记忆方法是结合平面直角坐标系的图形记忆.二、填空题(共6小题,每小题5分,满分30分)7.在平面直角坐标系中,已知点P0的坐标为(1,0),将点P0绕着原点O按逆时针方向旋转60°得点P1,延长OP1到点P2,使OP2=2OP1再将点P2绕着原点O按逆时针方向旋转60°得点P3,则点P3的坐标是(﹣1,).【考点】坐标与图形变化﹣旋转.【专题】压轴题.【分析】已知将点P0绕着原点O按逆时针方向旋转60°得点P1,则OP1=1,P1点的坐标是(.则P2的坐标是;再将点P2绕着原点O按逆时针方向旋转60°得点P3,则点P3与P2关于y轴对称,因而点P3的坐标就很容易求出.【解答】解:∵点P0绕着原点O按逆时针方向旋转60°得点P1,∴P1点的坐标是(,∴P2的坐标是,又∵点P3与P2关于y轴对称,∴点P3的坐标是(﹣1,).【点评】解决本题的关键是正确理解题目,按题目的叙述一定要把各点的大致位置确定,正确地作出图形.8.如图所示,△ABC中,∠BAC=90°,AB=AC=5,△ABC按逆时针方向旋转一个角度后,成为△ACD,则旋转中心是点A、旋转角是∠CAD,是90°.【考点】旋转的性质.【分析】确定图形的旋转时首先要确定旋转前后的对应点,即可确定旋转中心.【解答】解:旋转中心是点A、旋转角是∠CAD,是90°.【点评】本题主要考查了旋转的定义,正确确定旋转中的对应点,是确定旋转中心,旋转角的前提.9.如图,设P是等边三角形ABC内任意一点,△ACP′是由△ABP旋转得到的,则PA<PB+PC(选填“>”、“=”、“<”)【考点】旋转的性质;三角形三边关系;等边三角形的判定.【分析】此题只需根据三角形的任意两边之和大于第三边和等边三角形的性质,进行分析即可.【解答】解:根据三角形的三边关系,得:BC<PB+PC.又AB=BC>PA,∴PA<PB+PC.【点评】本题结合旋转主要考查了三角形的三边关系:两边之和大于第三边,两边之差小于第三边.10.如图,E、F分别是正方形ABCD的边BC、CD上一点,且BE+DF=EF,则∠EAF=45度.【考点】旋转的性质;正方形的性质.【分析】根据BE+DF=EF,则延长FD到G,使DG=BE,则FG=EF,可以认为是把△ABE 绕点A逆时针旋转90度,得到△ADG,根据旋转的定义即可求解.【解答】解:如图:延长FD到G,使DG=BE,则FG=EF,在△ABE和△ADG中,,∴△ABE≌△ADG(SAS),∴AE=AG又∴AF=AF,GF=EF∴△AGF≌△AEF∴∠EAF=∠GAF=×90°=45°.【点评】本题考查旋转的性质.旋转变化前后,对应点到旋转中心的距离相等以及每一对对应点与旋转中心连线所构成的旋转角相等.要注意旋转的三要素:①定点﹣旋转中心;②旋转方向;③旋转角度.11.如图,O是等边△ABC内一点,将△AOB绕A点逆时针旋转,使得B,O两点的对应分别为C,D,则旋转角为60度,图中除△ABC外,还有等边三形是△AOD.【考点】旋转的性质;等边三角形的性质;等边三角形的判定.【分析】根据旋转的性质及全等三角形的性质作答.【解答】解:∵将△AOB绕A点逆时针旋转,使得B,O两点的对应分别为C,D,∴△AOB≌△ADC,∴OA=AD,∠BAO=∠DAC,∴∠BAO+∠OAC=∠DAC+∠OAC=∠BAC=60°,即∠OAD=60°,所以旋转角为60°.∵OA=AD,∠OAD=60°,∴△AOD为等边三角形.【点评】此题主要考查了图形旋转的性质:旋转变化前后,对应线段、对应角分别相等,图形的大小、形状都不改变.12.如图,Rt△ABC中,P是斜边BC上一点,以P为中心,把这个三角形按逆时针方向旋转90°得到△DEF,图中通过旋转得到的三角形还有△EPQ.【考点】旋转的性质.【分析】旋转中心是P,旋转方向为逆时针,旋转角是90度,已确定,再通过观察发现全等三角形,判断是否符合本题的旋转规律.【解答】解:根据旋转的性质可知,旋转中心是P,旋转角是90度,图中通过旋转得到的三角形还有△EPQ.【点评】本题考查旋转两相等的性质,即对应点到旋转中心的距离相等以及每一对对应点与旋转中心连线所构成的旋转角相等.三、解答题13.已知:正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB、DC(或它们的延长线)于点M、N.当∠MAN绕点A旋转到BM=DN时(如图1),易证BM+DN=MN.(1)当∠MAN绕点A旋转到BM≠DN时(如图2),线段BM、DN和MN之间有怎样的数量关系?写出猜想,并加以证明;(2)当∠MAN绕点A旋转到如图3的位置时,线段BM、DN和MN之间又有怎样的数量关系?请直接写出你的猜想.【考点】旋转的性质;全等三角形的判定与性质;正方形的性质.【专题】计算题;压轴题.【分析】(1)BM+DN=MN成立,证得B、E、M三点共线即可得到△AEM≌△ANM,从而证得ME=MN.(2)DN﹣BM=MN.证明方法与(1)类似.【解答】解:(1)BM+DN=MN成立.证明:如图,把△ADN绕点A顺时针旋转90°,得到△ABE,则可证得E、B、M三点共线(图形画正确).∴∠EAM=90°﹣∠NAM=90°﹣45°=45°,又∵∠NAM=45°,∴在△AEM与△ANM中,∴△AEM≌△ANM(SAS),∴ME=MN,∵ME=BE+BM=DN+BM,∴DN+BM=MN;(2)DN﹣BM=MN.在线段DN上截取DQ=BM,在△ADQ与△ABM中,∵,∴△ADQ≌△ABM(SAS),∴∠DAQ=∠BAM,∴∠QAN=∠MAN.在△AMN和△AQN中,∴△AMN≌△AQN(SAS),∴MN=QN,∴DN﹣BM=MN.【点评】本题考查了旋转的性质,解决此类问题的关键是正确的利用旋转不变量.14.如图,正方形ABCD的边长为1,AB,AD上各有一点P,Q,如果△APQ的周长为2,求∠PCQ的度数.【考点】正方形的性质;全等三角形的判定与性质.【专题】计算题.【分析】简单的求正方形内一个角的大小,首先从△APQ的周长入手求出PQ=DQ+BP,然后将△CDQ逆时针旋转90°,使得CD、CB重合,然后利用全等来解.【解答】解:如图所示,△APQ的周长为2,即AP+AQ+PQ=2①,正方形ABCD的边长是1,即AQ+QD=1,AP+PB=1,∴AP+AQ+QD+PB=2②,①﹣②得,PQ﹣QD﹣PB=0,∴PQ=PB+QD.延长AB至M,使BM=DQ.连接CM,△CBM≌△CDQ(SAS),∴∠BCM=∠DCQ,CM=CQ,∵∠DCQ+∠QCB=90°,∴∠BCM+∠QCB=90°,即∠QCM=90°,PM=PB+BM=PB+DQ=PQ.在△CPQ与△CPM中,CP=CP,PQ=PM,CQ=CM,∴△CPQ≌△CPM(SSS),∴∠PCQ=∠PCM=∠QCM=45°.【点评】熟练掌握正方形的性质,会运用正方形的性质进行一些简单的运算.15.有两张完全重合的矩形纸片,小亮同学将其中一张绕点A顺时针旋转90°后得到矩形AMEF(如图1),连接BD、MF,若此时他测得BD=8cm,∠ADB=30°.(1)请直接写出AF的长;(2)小红同学用剪刀将△BCD与△MEF剪去,与小亮同学继续探究.他们将△ABD绕点A顺时针旋转得△AB1D1,AD1交FM于点K(如图2),设旋转角为β(0°<β<90°),当△AFK为等腰三角形时,求△AFK的面积(保留根号).【考点】锐角三角函数的定义;旋转的性质.【专题】操作型.【分析】(1)根据旋转的性质可知△AFM≌△ADB,则AF=AD=BD•cos∠ADB=8×=4cm;(2)当△AFK为等腰三角形时,由于AM<AF,那么A不能是等腰△AFK的顶点,则分两种情况:①K为顶点,即AK=FK时;②F为顶点,即AF=FK.针对每一种情况,利用三角形的面积公式,可分别求出△AFK的面积.【解答】解:(1)AF=;(2)△AFK为等腰三角形时,分两种情况:①当AK=FK时,如图.过点K作KN⊥AF于N,则KN⊥AF,AN=NF=AF=2cm.在直角△NFK中,∠KNF=90°,∠F=30°,∴KN=NF•tan∠F=2cm.∴△AFK的面积=×AF×KN=;②当AF=FK时,如图.过点K作KP⊥AF于P.在直角△PFK中,∠KPF=90°,∠F=30°,∴KP=KF=2cm.∴△AFK的面积=×AF×KP=12cm2.【点评】本题考查旋转的性质,旋转变化前后,对应线段、对应角分别相等,图形的大小、形状都不改变.注意(2)中需分情况讨论△AFK为等腰三角形时的不同分类,不要漏解.。
中考数学《旋转的综合》专项训练及答案

一、旋转真题与模拟题分类汇编(难题易错题)1.(1)发现:如图1,点A为线段BC外一动点,且BC=a,AB=b.填空:当点A位于时,线段AC的长取得最大值,且最大值为(用含a,b的式子表示) (2)应用:点A为线段BC外一动点,且BC=4,AB=1,如图2所示,分别以AB,AC为边,作等边三角形ABD和等边三角形ACE,连接CD,BE.①请找出图中与BE相等的线段,并说明理由;②直接写出线段BE长的最大值.(3)拓展:如图3,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(6,0),点P 为线段AB外一动点,且PA=2,PM=PB,∠BPM=90°,请直接写出线段AM长的最大值及此时点P的坐标.【答案】(1)CB的延长线上, a+b;(2)①CD=BE,理由见解析;②BE长的最大值为5;(3)满足条件的点P坐标(222)或(222),AM的最大值为2+4.【解析】【分析】(1)根据点A位于CB的延长线上时,线段AC的长取得最大值,即可得到结论;(2)①根据已知条件易证△CAD≌△EAB,根据全等三角形的性质即可得CD=BE;②由于线段BE长的最大值=线段CD的最大值,根据(1)中的结论即可得到结果;(3)连接BM,将△APM绕着点P顺时针旋转90°得到△PBN,连接AN,得到△APN是等腰直角三角形,根据全等三角形的性质得到PN=PA=2,BN=AM,根据当N在线段BA的延长线时,线段BN取得最大值,即可得到最大值为2+4;如图2,过P作PE⊥x轴于E,根据等腰直角三角形的性质即可求得点P的坐标.如图3中,根据对称性可知当点P在第四象限时也满足条件,由此求得符合条件的点P另一个的坐标.【详解】(1)∵点A为线段BC外一动点,且BC=a,AB=b,∴当点A位于CB的延长线上时,线段AC的长取得最大值,且最大值为BC+AB=a+b,故答案为CB的延长线上,a+b;(2)①CD=BE,理由:∵△ABD与△ACE是等边三角形,∴AD=AB,AC=AE,∠BAD=∠CAE=60°,∴∠BAD+∠BAC=∠CAE+∠BAC,即∠CAD=∠EAB,在△CAD与△EAB中,AD ABCAD EAB AC AE=⎧⎪∠=∠⎨⎪=⎩,∴△CAD≌△EAB(SAS),∴CD=BE;②∵线段BE长的最大值=线段CD的最大值,由(1)知,当线段CD的长取得最大值时,点D在CB的延长线上,∴最大值为BD+BC=AB+BC=5;(3)如图1,∵将△APM绕着点P顺时针旋转90°得到△PBN,连接AN,则△APN是等腰直角三角形,∴PN=PA=2,BN=AM,∵A的坐标为(2,0),点B的坐标为(6,0),∴OA=2,OB=6,∴AB=4,∴线段AM长的最大值=线段BN长的最大值,∴当N在线段BA的延长线时,线段BN取得最大值,最大值=AB+AN,∵AN=2AP=22,∴最大值为22+4;如图2,过P作PE⊥x轴于E,∵△APN是等腰直角三角形,∴PE=AE2,∴OE=BO﹣AB﹣AE=6﹣42=22,∴P(2﹣2,2).如图3中,根据对称性可知当点P在第四象限时,P(2﹣2,﹣2)时,也满足条件.综上所述,满足条件的点P坐标(2﹣2,2)或(2﹣2,﹣2),AM的最大值为22+4.【点睛】本题综合考查了全等三角形的判定和性质,等腰直角三角形的性质,最大值问题,旋转的性质.正确的作出辅助线构造全等三角形是解题的关键.2.如图:在△ABC中,∠ACB=90°,AC=BC,∠PCQ=45°,把∠PCQ绕点C旋转,在整个旋转过程中,过点A作AD⊥CP,垂足为D,直线AD交CQ于E.(1)如图①,当∠PCQ在∠ACB内部时,求证:AD+BE=DE;(2)如图②,当CQ在∠ACB外部时,则线段AD、BE与DE的关系为_____;(3)在(1)的条件下,若CD=6,S△BCE=2S△ACD,求AE的长.【答案】(1)见解析(2)AD=BE+DE (3)8【解析】试题分析:(1)延长DA到F,使DF=DE,根据线段垂直平分线上的点到线段两端点的距离相等可得CE=CF,再求出∠ACF=∠BCE,然后利用“边角边”证明△ACF和△BCE全等,根据全等三角形的即可证明AF=BE,从而得证;(2)在AD上截取DF=DE,然后根据线段垂直平分线上的点到线段两端点的距离相等可得CE=CF,再求出∠ACF=∠BCE,然后利用“边角边”证明△ACF和△BCE全等,根据全等三角形的即可证明AF=BE,从而得到AD=BE+DE;(3)根据等腰直角三角形的性质求出CD=DF=DE,再根据等高的三角形的面积的比等于底边的比求出AF=2AD,然后求出AD的长,再根据AE=AD+DE代入数据进行计算即可得解.试题解析:(1)证明:如图①,延长DA到F,使DF=DE.∵CD⊥AE,∴CE=CF,∴∠DCE=∠DCF=∠PCQ=45°,∴∠ACD+∠ACF=∠DCF=45°.又∵∠ACB=90°,∠PCQ=45°,∴∠ACD+∠BCE=90°﹣45°=45°,∴∠ACF=∠BCE.在△ACF和△BCE中,∵CE CFACF BCEAC BC=⎧⎪∠=∠⎨⎪=⎩,∴△ACF≌△BCE(SAS),∴AF=BE,∴AD+BE=AD+AF=DF=DE,即AD+BE=DE;(2)解:如图②,在AD上截取DF=DE.∵CD⊥AE,∴CE=CF,∴∠DCE=∠DCF=∠PCQ=45°,∴∠ECF=∠DCE+∠DCF=90°,∴∠BCE+∠BCF=∠ECF=90°.又∵∠ACB=90°,∴∠ACF+∠BCF=90°,∴∠ACF=∠BCE.在△ACF和△BCE中,∵CE CFACF BCEAC BC=⎧⎪∠=∠⎨⎪=⎩,∴△ACF≌△BCE(SAS),∴AF=BE,∴AD=AF+DF=BE+DE,即AD=BE+DE;故答案为:AD=BE+DE.(3)∵∠DCE=∠DCF=∠PCQ=45°,∴∠ECF=45°+45°=90°,∴△ECF是等腰直角三角形,∴CD=DF=DE=6.∵S△BCE=2S△ACD,∴AF=2AD,∴AD =112+×6=2,∴AE=AD+DE=2+6=8.点睛:本题考查了全等三角形的判定与性质,线段垂直平分线上的点到线段两端点的距离相等的性质,等腰直角三角形的性质,综合性较强,但难度不是很大,作辅助线构造出全等三角形是解题的关键.3.如图1,是边长分别为6和4的两个等边三角形纸片ABC和CD1E1叠放在一起.(1)操作:固定△ABC,将△CD1E1绕点C顺时针旋转得到△CDE,连接AD、BE,如图2.探究:在图2中,线段BE与AD之间有怎样的大小关系?并请说明理由;(2)操作:固定△ABC,若将△CD1E1绕点C顺时针旋转30°得到△CDE,连接AD、BE,CE 的延长线交AB于点F,在线段CF上沿着CF方向平移,(点F与点P重合即停止平移)平移后的△CDE设为△PQR,如图3.探究:在图3中,除三角形ABC和CDE外,还有哪个三角形是等腰三角形?写出你的结论(不必说明理由);(3)探究:如图3,在(2)的条件下,设CQ=x,用x代数式表示出GH的长.【答案】(1)BE=CD.理由见解析;(2)△CHQ是等腰三角形;(3)2-x.【解析】试题分析:(1)根据等边三角形的性质可得AB=BC,CD=CE,∠ACB=∠ECD=60°,然后求出∠ACD=∠BCE,再利用“边角边”证明△ACD和△BCE全等,根据全等三角形对应边相等证明即可;(2)求出∠ACF=30°,再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠CHQ=30°,从而得到∠ACF=∠CHQ,判断出△CHQ是等腰三角形;(3)求出∠CGP=90°,然后利用∠ACF的余弦表示出CG,再根据等腰三角形的性质表示出CH,然后根据GH=CG-CH整理即可得解.试题解析:(1)BE=CD.理由如下:∵△ABC与△CDE是等边三角形,∴AC=BC,CE=CD,∠ACB=∠ECD=60°.∴∠ACB-∠ACE=∠ECD-∠ACE,即∠BCE=∠ACD.在△ACD和△BCE中,∴△ACD≌△BCE(SAS),∴BE=AD;(2)∵旋转角为30°,∴∠BCF=30°,∴∠ACF=60°-30°=30°,∴∠CHQ=∠RQP-∠ACF=60°-30°=30°,∴∠ACF=∠CHQ,∴△CHQ是等腰三角形;(3)∠CGP=180°-∠ACF-∠RPQ=180°-30°-60°=90°,∴CG=CP•cos30°=(x+4),∵△CHQ是等腰三角形,∴CH=2•CQcos30°=2x•=x,∴GH=CG-CH=(x+4)-x=2-x.考点:几何变换综合题.4.如图是两个可以自由转动的转盘,甲转盘被等分成3个扇形,乙转盘被等分成4个扇形,每一个扇形上都标有相应的数字.同时转动两个转盘,当转盘停止后,计算指针所指区域内的数字之和.如果指针恰好指在分割线上,那么重转一次,直到指针指向一个数字为止.(1)请你通过画树状图或列表的方法分析,并求指针所指区域内的数字和小于10的概率;(2)小亮和小颖小亮和小颖利用它们做游戏,游戏规则是:指针所指区域内的数字和小于10,小颖获胜;指针所指区域内的数字之和等于10,为平局;指针所指区域内的数字之和大于10,小亮获胜.你认为该游戏规则是否公平?请说明理由;若游戏规则不公平,请你设计出一种公平的游戏规则.【答案】(1)13;(2)不公平.【解析】试题分析:(1)依据题意先用列表法或画树状图法分析所有等可能的出现结果,然后根据概率公式求出该事件的概率.(2)判断游戏的公平性,首先要计算出游戏双方赢的概率,概率相等则公平,否则不公平.试题解析:(1)共有12种等可能的结果,小于10的情况有4种,所以指针所指区域内的数字和小于10的概率为13.(2)不公平,因为小颖获胜的概率为;小亮获胜的概率为512.小亮获胜的可能性大,所以不公平.可以修改为若这两个数的和为奇数,则小亮赢;积为偶数,则小颖赢.考点:1.游戏公平性;2.列表法与树状图法.5.在△ABC中,AB=AC,将线段AC绕着点C逆时针旋转得到线段CD,旋转角为,且,连接AD、BD.(1)如图1,当∠BAC=100°,时,∠CBD 的大小为_________;(2)如图2,当∠BAC=100°,时,求∠CBD的大小;(3)已知∠BAC的大小为m(),若∠CBD 的大小与(2)中的结果相同,请直接写出的大小.【答案】(1)30°;(2)30°;(3)α=120°-m°,α=60°或α=240-m°.【解析】试题分析:(1)由∠BAC=100°,AB=AC,可以确定∠ABC=∠ACB=40°,旋转角为α,α=60°时△ACD是等边三角形,且AC=AD=AB=CD,知道∠BAD的度数,进而求得∠CBD的大小.(2)由∠BAC=100°,AB=AC,可以确定∠ABC=∠ACB=40°,连结DF、BF.AF=FC=AC,∠FAC=∠AFC=60°,∠ACD=20°,由∠DCB=20°案.依次证明△DCB≌△FCB,△DAB≌△DAF.利用角度相等可以得到答案.(3)结合(1)(2)的解题过程可以发现规律,求得答案.试题解析:(1)30°;(2)30°;(2)如图作等边△AFC,连结DF、BF.∴AF=FC=AC,∠FAC=∠AFC=60°.∵∠BAC=100°,AB=AC,∴∠ABC=∠BCA=40°.∵∠ACD=20°,∴∠DCB=20°.∴∠DCB=∠FCB=20°.①∵AC=CD,AC=FC,∴DC=FC.②∵BC=BC,③∴由①②③,得△DCB≌△FCB,∴DB=BF,∠DBC=∠FBC.∵∠BAC=100°,∠FAC=60°,∴∠BAF=40°.∵∠ACD=20°,AC=CD,∴∠CAD=80°.∴∠DAF=20°.∴∠BAD=∠FAD=20°.④∵AB=AC,AC=AF,∴AB=AF.⑤∵AD=AD,⑥∴由④⑤⑥,得△DAB≌△DAF.∴FD=BD.∴FD=BD=FB.∴∠DBF=60°.∴∠CBD=30°.(3)α=120°-m°,α=60°或α=240-m°.考点:1.全等三角形的判定和性质;2.等边三角形的判定和性质.6.如图1,矩形ABCD中,E是AD的中点,以点E直角顶点的直角三角形EFG的两边EF,EG分别过点B,C,∠F=30°.(1)求证:BE=CE(2)将△EFG绕点E按顺时针方向旋转,当旋转到EF与AD重合时停止转动.若EF,EG分别与AB,BC相交于点M,N.(如图2)①求证:△BEM≌△CEN;②若AB=2,求△BMN面积的最大值;③当旋转停止时,点B恰好在FG上(如图3),求sin∠EBG的值.【答案】(1)详见解析;(2)①详见解析;②2;62【解析】【分析】(1)只要证明△BAE≌△CDE即可;(2)①利用(1)可知△EBC是等腰直角三角形,根据ASA即可证明;②构建二次函数,利用二次函数的性质即可解决问题;③如图3中,作EH⊥BG于H.设NG=m,则BG=2m,BN=EN=3m,EB=6m.利用面积法求出EH,根据三角函数的定义即可解决问题.【详解】(1)证明:如图1中,∵四边形ABCD是矩形,∴AB=DC,∠A=∠D=90°,∵E是AD中点,∴AE=DE,∴△BAE≌△CDE,∴BE=CE.(2)①解:如图2中,由(1)可知,△EBC是等腰直角三角形,∴∠EBC=∠ECB=45°,∵∠ABC=∠BCD=90°,∴∠EBM=∠ECN=45°,∵∠MEN=∠BEC=90°,∴∠BEM=∠CEN,∵EB=EC,∴△BEM≌△CEN;②∵△BEM≌△CEN,∴BM=CN,设BM=CN=x,则BN=4-x,∴S△BMN=12•x(4-x)=-12(x-2)2+2,∵-12<0,∴x=2时,△BMN的面积最大,最大值为2.③解:如图3中,作EH⊥BG于H.设NG=m,则BG=2m,3m,6m.∴EG=m+3m=(1+3)m , ∵S △BEG =12•EG•BN=12•BG•EH , ∴EH=3?(13)2m m m +=3+32m ,在Rt △EBH 中,sin ∠EBH=3+362246mEHEB m+==. 【点睛】本题考查四边形综合题、矩形的性质、等腰直角三角形的判定和性质、全等三角形的判定和性质、旋转变换、锐角三角函数等知识,解题的关键是准确寻找全等三角形解决问题,学会添加常用辅助线,学会利用参数解决问题,7.如图,在Rt △ABC 中,∠ACB =90°,∠A =30°,点O 为AB 中点,点P 为直线BC 上的动点(不与点B 、点C 重合),连接OC 、OP ,将线段OP 绕点P 顺时针旋转60°,得到线段PQ ,连接BQ .(1)如图1,当点P 在线段BC 上时,请直接写出线段BQ 与CP 的数量关系.(2)如图2,当点P 在CB 延长线上时,(1)中结论是否成立?若成立,请加以证明;若不成立,请说明理由;(3)如图3,当点P 在BC 延长线上时,若∠BPO =15°,BP =4,请求出BQ 的长.【答案】(1)BQ =CP ;(2)成立:PC =BQ ;(3)434-. 【解析】试题分析:(1)结论:BQ =CP .如图1中,作PH ∥AB 交CO 于H ,可得△PCH 是等边三角形,只要证明△POH ≌△QPB 即可;(2)成立:PC =BQ .作PH ∥AB 交CO 的延长线于H .证明方法类似(1);(3)如图3中,作CE ⊥OP 于E ,在PE 上取一点F ,使得FP =FC ,连接CF .设CE =CO =a ,则FC =FP =2a ,EF =3a ,在Rt △PCE 中,表示出PC ,根据PC +CB =4,可得方程(62)24a a ++=,求出a 即可解决问题;试题解析:解:(1)结论:BQ =CP .理由:如图1中,作PH ∥AB 交CO 于H .在Rt △ABC 中,∵∠ACB =90°,∠A =30°,点O 为AB 中点,∴CO =AO =BO ,∠CBO =60°,∴△CBO 是等边三角形,∴∠CHP =∠COB =60°,∠CPH =∠CBO =60°,∴∠CHP =∠CPH =60°,∴△CPH 是等边三角形,∴PC =PH =CH ,∴OH =PB ,∵∠OPB =∠OPQ +∠QPB =∠OCB +∠COP ,∵∠OPQ =∠OCP =60°,∴∠POH =∠QPB ,∵PO =PQ ,∴△POH ≌△QPB ,∴PH =QB ,∴PC =BQ .(2)成立:PC =BQ .理由:作PH ∥AB 交CO 的延长线于H .在Rt △ABC 中,∵∠ACB =90°,∠A =30°,点O 为AB 中点,∴CO =AO =BO ,∠CBO =60°,∴△CBO 是等边三角形,∴∠CHP =∠COB =60°,∠CPH =∠CBO =60°,∴∠CHP =∠CPH =60°,∴△CPH 是等边三角形,∴PC =PH =CH ,∴OH =PB ,∵∠POH =60°+∠CPO ,∠QPO =60°+∠CPQ ,∴∠POH =∠QPB ,∵PO =PQ ,∴△POH ≌△QPB ,∴PH =QB ,∴PC =BQ .(3)如图3中,作CE ⊥OP 于E ,在PE 上取一点F ,使得FP =FC ,连接CF .∵∠OPC =15°,∠OCB =∠OCP +∠POC ,∴∠POC =45°,∴CE =EO ,设CE =CO =a ,则FC =FP =2a ,EF =3a ,在Rt △PCE 中,PC =22PE CE + =22(23)a a a ++ =(62)a +,∵PC +CB =4,∴(62)24a a ++=,解得a =4226-,∴PC =434-,由(2)可知BQ =PC ,∴BQ =434-.点睛:此题考查几何变换综合题、旋转变换、等边三角形的判定和性质全等三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.8.如图1,O 为直线AB 上一点,过点O 作射线OC ,AOC 30∠=,将一直角三角板()M 30∠=的直角顶点放在点O 处,一边ON 在射线OA 上,另一边OM 与OC 都在直线AB 的上方.()1将图1中的三角板绕点O 以每秒5的速度沿逆时针方向旋转一周.如图2,经过t 秒后,ON 落在OC 边上,则t =______秒(直接写结果).()2如图2,三角板继续绕点O 以每秒5的速度沿逆时针方向旋转到起点OA 上.同时射线OC 也绕O 点以每秒10的速度沿逆时针方向旋转一周,①当OC 转动9秒时,求MOC ∠的度数.②运动多少秒时,MOC 35∠=?请说明理由.【答案】(1)6;(2)①45;②11秒或25秒,理由见解析. 【解析】【分析】(1)因为∠AOC=30°,所以ON 落在OC 边上时,三角板旋转了30°,即可求出旋转时间;(2)在整个旋转过程中,可以看做这样一个追及问题更容易理解,即:ON 绕点O 以每秒5°的速度沿逆时针方向旋转,同时射线OC 也绕O 点以每秒10°的速度沿逆时针方向旋转; ①9秒时,∠NOC=45°,而OC 旋转了90°,所以∠MOC 的度数就是45°; ②∠MOC=35°时,应分OC 与OM 重合前35°与重合后35°两种情况考虑,分别进行求解即可.【详解】()1AOC 30∠=,而三角板每秒旋转5,∴当ON 落在OC 边上时,有5t 30=,得t 6=,故答案为6;()2①当OC 转动9秒时,COA 30109120∠=+⨯=, 而MOA 309059165∠=++⨯=,又MOC MOA COA ∠∠∠=-,即:MOC 16512045∠=-=,答:当OC 转动9秒时,MOC ∠的度数为45;②设OC 运动起始位置为射线OP(如图1),运动t 秒时,MOC 35∠=,则MOP 905t ∠=+,COP 10t ∠=,当MOC 35∠=时,有()905t 10t 35+-=或()10t 905t 35-+=,得t 11=或t 25=,因为三角板与射线OC 都只旋转一周,所以不考虑再次追及的情况,故当运动11秒或25秒时,MOC 35∠=.【点睛】本题考查的是用方程的思想解决角的旋转的问题,找准等量关系,正确列出一元一次方程是解题的关键.。
中考数学旋转综合题及详细答案

则∠ AFG=90°. ∵ ∠ ABH=∠ G=60°,AB=a,AG=2a,
∴ AH=AB×sin60°= 3 a,AF=AG×sin60°= 3 a. 2
∴ 点 F 到 BC 的最大距离为 3 a+ 3 a= 3 3 a. 22
∴ S△ BCF= 1 ×2a× 3 3 a= 3 3 a2.
2
22
PC=
=6.
考点:1.扇形面积的计算;2.正方形的性质;3.旋转的性质.
3.如图 1, ABCD 和 AEFG 是两个能完全重合的平行四边形,现从 AB 与 AE 重合时开 始,将 ABCD 固定不动, AEFG 绕点 A 逆时针旋转,旋转角为 α(0°<α<360°), AB=a,BC=2a;并发现:如图 2,当 AEFG 旋转到点 E 落在 AD 上时,FE 的延长线恰好通过 点 C.
(2)根据面积公式得出 S△ GHK=S 四边形 CKGH-S△ CKH= 1 x2-3x+9,根据△ GKH 的面积恰好等于 2
△
ABC 面积的
5
,代入得出方程 1
x2-3x+9=
5
1
×
×6×6,求出即可.
12
2
12 2
解:(1)BH 与 CK 的数量关系:BH=CK,理由是:
连接 OC,
由直角三角形斜边上中线性质得出 OC=BG, ∵ AC=BC,O 为 AB 中点,∠ ACB=90°, ∴ ∠ B=∠ ACG=45°,CO⊥AB, ∴ ∠ CGB=90°=∠ KGH, ∴ 都减去∠ CGH 得:∠ BGH=∠ CGK, 在△ CGK 和△ BGH 中
∴
1
x2﹣3x+9=
5
1
×
最新九年级数学中考复习:旋转综合压轴题(角度问题)含答案

2023年九年级数学中考复习:旋转综合压轴题(角度问题)1.如图① ,在①ABC 中,AB =AC =4,①BAC =90°,AD ①BC ,垂足为D .(1)S △ABD = .(直接写出结果)(2)如图①,将①ABD 绕点D 按顺时针方向旋转得到①A′B′D ,设旋转角为α (α<90°),在旋转过程中: 探究一:四边形APDQ 的面积是否随旋转而变化?说明理由; 探究二:当α=________时,四边形APDQ 是正方形.2.如图,在等腰Rt ABC 和等腰Rt CDE 中,90ACB DCE ∠=∠=︒.(1)观察猜想:如图1,点E 在BC 上,线段AE 与BD 的关系是_________;(2)探究证明:把CDE △绕直角顶点C 旋转到图2的位置,(1)中的结论还成立吗?说明理由; (3)拓展延伸:把CDE △绕点C 在平面内转动一周,若10AC BC ==,5CE CD ==,AE 、BD 交于点P 时,连接CP ,直接写出BCP 最大面积_________.3.如图1,在Rt △ABC 中,①A =90°,AB =AC ,点D ,E 分别在边AB ,AC 上,AD =AE ,连接DC ,点M ,P ,N 分别为DE ,DC ,BC 的中点.(1)观察猜想:图1中,请判断线段PM 与PN 的数量关系和位置关系,并说明理由;(2)探究证明:把△ADE 绕点A 逆时针方向旋转到图2的位置,连接MN ,BD ,CE ,判断△PMN 的形状,并说明理由;(3)拓展延伸:把△ADE 绕点A 在平面内自由旋转,若AD =3,AB =7,请直接写出△PMN 面积的最大值.4.如图1,①ABC 为等腰直角三角形,①BAC =90°,AB =AC ,点D 在AB 边上,点E 在AC 边上,AD =AE ,连接DE ,取BC 边的中点O ,连接DO 并延长到点F ,使OF =OD ,连接CF . (1)请判断①CEF 的形状,并说明理由;(2)将(1)中①ADE 绕点A 旋转,连接CE ,(1)中的结论是否仍然成立,若成立,请仅就图2所示情况给出证明,若不成立,请说明理由;(3)若AB =6,AD =4,将①ADE 由图1位置绕点A 旋转,当点B ,E ,D 三点共线时,请直接写出①CEF 的面积.5.如图,在Rt ABC 中,90BAC ∠=︒,AB AC =,点D 是AB 外一动点,连接AD ,把AD 绕点A 逆时针旋转90°,得到AE ,连接CE ,DE ,BC 与DE 交于点F ,且AB BD ⊥.(1)如图1,若CB =6CE =,求DE 的长;(2)如图2,若点H 、G 分别为线段CF 、AE 的中点,连接HG ,求证:12HG BF =;(3)如图3,在(2)的条件下,若CE =4CF =,将BDF 绕点F 顺时针旋转角3(060)αα︒<≤︒,得到B D F '',连接B G ',取B G '中点Q ,连接BQ ,当线段BQ 最小时,请直接写出BQB '的面积.6.如图1,矩形ABCD 中,15,20AB BC ==,将矩形ABCD 绕着点A 顺时针旋转,得到矩形BEFG .(1)当点E 落在BD 上时,则线段DE 的长度等于________; (2)如图2,当点E 落在AC 上时,求BCE 的面积;(3)如图3,连接AE CE AG CG 、、、,判断线段AE 与CG 的位置关系且说明理由,并求22CE AG +的值;(4)在旋转过程中,请直接写出BCE ABG S S +△△的最大值.7.在平面直角坐标系中,O 为原点,点(4,0)A -,点(0,3),B ABO 绕点B 顺时针旋转,得A BO ''△,点A O 、旋转后的对应点为A O ''、,记旋转角为α.(1)如图①,90α=︒,边OA 上的一点M 旋转后的对应点为N ,当1OM =时,点N 的坐标为_____; (2)90α=︒,边OA 上的一点M 旋转后的对应点为N ,当O M BN '+取得最小值时,在图①中画出点M 的位置,并求出点N 的坐标.(3)如图①,P 为AB 上一点,且:2:1PA PB =,连接PO PA ''、,在ABO 绕点B 顺时针旋转一周的过程中,PO A ''的面积是否存在最大值和最小值,若存在,请求出;若不存在,请说明理由.8.如图1,①ABC 和①DEC 均为等腰三角形,且①ACB =①DCE =90°,连接BE ,AD ,两条线段所在的直线交于点P .(1)线段BE 与AD 有何数量关系和位置关系,请说明理由. (2)若已知BC =12,DC =5,①DEC 绕点C 顺时针旋转, ①如图2,当点D 恰好落在BC 的延长线上时,求AP 的长;①在旋转一周的过程中,设①P AB 的面积为S ,求S 的最值.9.如图,在菱形ABCD 中,2AB =,60BAD ∠=,过点D 作DE AB ⊥于点E ,DF BC ⊥于点F .()1如图1,连接AC 分别交DE 、DF 于点M 、N ,求证:13MN AC =; ()2如图2,将EDF 以点D 为旋转中心旋转,其两边'DE 、'DF 分别与直线AB 、BC 相交于点G 、P ,连接GP ,当DGP 的面积等于10.如图1,一副直角三角板满足AB=BC ,AC=DE ,①ABC=①DEF=90°,①EDF=30°操作:将三角板DEF 的直角顶点E 放置于三角板ABC 的斜边AC 上,再将三角板DEF 绕点E 旋转,并使边DE 与边AB 交于点P ,边EF 与边BC 于点Q . 探究一:在旋转过程中, (1)如图2,当1CEEA=时,EP 与EQ 满足怎样的数量关系?并给出证明; (2)如图3,当2CEEA=时,EP 与EQ 满足怎样的数量关系?并说明理由; (3)根据你对(1)、(2)的探究结果,试写出当CEm EA=时,EP 与EQ 满足的数量关系式为 ,其中m 的取值范围是 .(直接写出结论,不必证明) 探究二:若2CEEA=且AC=30cm ,连接PQ ,设△EPQ 的面积为S (cm 2),在旋转过程中: (1)S 是否存在最大值或最小值?若存在,求出最大值或最小值;若不存在,说明理由. (2)随着S 取不同的值,对应△EPQ 的个数有哪些变化,求出相应S 的值或取值范围.11.如图1,在①ABC中,①BAC=90°,AB=AC,点D在边AC上,CD①DE,且CD=DE,连接BE,取BE的中点F,连接DF.(1)请直接写出①ADF的度数及线段AD与DF的数量关系;(2)将图1中的△CDE绕点C按逆时针旋转,①如图2,(1)中①ADF的度数及线段AD与DF的数量关系是否仍然成立?请说明理由;①如图3,连接AF,若AC=3,CD=1,求S△ADF的取值范围.12.已知点E是正方形ABCD的边AB上一点,AB=BE=2.以BE为边向右侧作正方形BEFG,将正方形BEFG绕点B顺时针旋转α度(0≤α≤90°),连结AE,CG(如图).(1)求证:①ABE①①CBG.(2)当点E在BD上时,求CG的长.(3)当90∠时,正方形BEFG停止旋转,求在旋转过程中线段AE扫过的面积.(参考数据:AEB=︒sin28︒≈,sin62︒≈tan28︒≈tan62︒≈)13.如图,矩形ABCD 中,5,6,==AB BC BCG 为等边三角形.点E ,F 分别为,AD BC 边上的动点,且EF AB ∥,P 为EF 上一动点,连接BP ,将线段BP 绕点B 顺时针旋转60︒至BM ,连接,,,PA PC PM GM .(1)求证:=GM PC ;(2)当,,PB PC PE 三条线段的和最小时,求PF 的长;(3)若点E 以每秒2个单位的速度由A 点向D 点运动,点P 以每秒1个单位的速度由E 点向F 点运动.E ,P 两点同时出发,点E 到达点D 时停止,点P 到达点F 时停止,设点P 的运动时间为t 秒. ①求t 为何值时,AEP △与CFP 相似; ①求BMP 的面积S 的最小值.14.如图1,在Rt ABC 中,90,5∠=︒==C AC BC ,点D 是边BC 上的一点,且BD =,过点D 做BC 边的垂线,交AB 边于点E ,将BDE 绕点B 顺时针方向旋转,记旋转角为()0360αα︒≤<︒.(1)【问题发现】当0α=︒时,AECD的值为________,直线,AE CD 相交形成的较小角的度数为________; (2)【拓展探究】试判断:在旋转过程中,(1)中的两个结论有无变化?请仅就图2的情况给出证明; (3)【问题解决】当BDE 旋转至A ,D ,E 三点在同一条直线上时,请直接写出ACD △的面积.15.在中Rt ABC △中.90ABC ∠=︒,AB BC =,点E 在射线CB 上运动.连接AE ,将线段AE 绕点E 顺时针旋转90°得到EF ,连接CF .(1)如图1,点E在点B的左侧运动;①当2BE=,BC=EAB∠=_________°;①猜想线段CA,CF与CE之间的数量关系为_________.(2)如图2,点E在线段CB上运动时,第(1)间中线段CA,CF与CE之间的数量关系是否仍然成立如果成立,请说明理由;如果不成立,请求出它们之间新的数量关系.=,以A,E,C,F为顶点的四边形面积为y,请直接写出(3)点E在射线CB上运动,BC=,设BE xy与x之间的函数关系式(不用写出x的取值范围).16.如图,在①ABC中,AB=,①A=45°,AC=C作直线平行AB,将①ABC绕点A顺时针旋转得到①AB C''(点B,C的对应点分别为B',C'),射线AB',AC'分别交直线l于点P、Q.(1)如图1,求BC的长;(2)如图2,当点C为PQ中点时,求tan①APQ;(3)如图3,当点P,Q分别在线段AB',AC'上时,试探究四边形PQC B''的面积是否存在最大值.若存在,求出其最大值;若不存在,请说明理由.17.已知Rt△ABC中,AC=BC,①C=90°,D为AB边的中点,①EDF=90°,①EDF绕D点旋转,它的两边分别交AC、CB(或它们的延长线)于E、F.(1)如图1,当①EDF 绕D 点旋转到DE ①AC 于E 时,易证S △DEF +S △CEF 与S △ABC 的数量关系为__________;(2)如图2,当①EDF 绕D 点旋转到DE 和AC 不垂直时,上述结论是否成立?若成立,请给予证明; (3)如图3,这种情况下,请猜想S △DEF 、S △CEF 、S △ABC 的数量关系,不需证明.18.面直角坐标系中,O 为原点,点(12,0)A ,点(0,5)B ,线段AB 的中点为点C .将ABO 绕着点B 逆时针旋转,点O 对应点为1O ,点A 的对应点为1A .(1)如图①,当点1O 恰好落在AB 上时, ①此时1CO 的长为__________;①点P 是线段OA 上的动点,旋转后的对应点为1P ,连接11,BP PO ,试求11BP PO +最小时点P 的坐标; (2)如图①,连接11,CA CO ,则在旋转过程中,11CAO △的面积是否存在最大值?若存在,直接写出最大值,若不存在,说明理由.19.如图,在Rt ABC 中,90C ∠=︒,5AB =,3sin 5A =.点P 从点A 出发,以每秒4个单位长度的速度向终点B 匀速运动,过点P 作PD AB ⊥交折线AC ,CB 于点D ,连结BD ,将DBP 绕点D 逆时针旋转90︒得到DEF .设点P 的运动时间为t (秒).(1)用含t 的代数式表示线段PD 的长. (2)当点E 落在AB 边上时,求AD 的长. (3)当点F 在ABC 内部时,求t 的取值范围.(4)当线段DP 将ABC 的面积分成1:2 的两部分时,直接写出t 的值.20.如图1,在Rt ABC △中,90B ∠=︒,AB BC =,AO 是BC 边上的中线,点D 是AO 上一点,DE EO ⊥,E 是垂足,DEO 可绕着点O 旋转,点F 是点E 关于点O 的对称点,连接AD 和CF .(1)问题发现:如图2,当1ADDO=时,则下列结论正确的是_______.(填序号)①BE CF =;①点F 是OC 的中点:①AO 是BAC ∠的角平分线;①AD .(2)数学思考:将图2中DEO 绕点O 旋转,如图3,则AD 和CF 具有怎样的数量关系?请给出证明过程;(3)拓展应用:在图1中,若ADx DO=,将DEO 绕着点O 旋转. ①则AD =_______CF ;①若4AB =,1x =,在DEO 旋转过程中,如图4,当点D 落在AB 上时,连结BE ,EC ,求四边形ABEC 的面积.答案21.(1)4(2)四边形APDQ 的面积不会随旋转而变化,理由见详解;当45α=︒时,四边形APDQ 是正方形.22.(1)AE BD =,AE BD ⊥; (2)结论仍成立23.(1)PM =PN ,PM ①PN . (2)△PMN 是等腰直角三角形. (3)S △PMN 最大=25224.(1) ①CEF 是等腰直角三角形;(2)成立,(3)18-18+25.(1)(3)8 26.(1)10;(2)42;(3) AE ①CG 221250CE AG =+;(4)30027.(1)(-3,4);(2)N (-3,92);(3)最大值为283,最小值为8328.(1)BE =AD ,BE 与AD 互相垂直,(2)①AP =8413;①最小47,最大72 29.(2)顺时针或逆时针旋转60.30.探究一:(1)EP=EQ ;证明见解析;(2)1:2,(3)EP :EQ=1:m ,①0<(1)当50cm 2;当75cm 2.(2)50<S≤62.5时,这样的三角形有2个;当S=50或62.5<S≤75时,这样的三角形有一个.31.(1)①ADF =45°,AD (2)①成立,;①1≤S △ADF ≤4.32.(3)3145S π=33.(3)①73;①34.,45︒;(2)无变化(3)121235.(1)①30;①AC +CF CE ;(2)CA -CF;(3)当点E 在点B 左侧运动时,y =21322x +;当点E 在点B 右侧运动时,y 32+.36.(3)存在;21-37.(1)S △DEF +S △CEF =12S △ABC(2)上述结论S △DEF +S △CEF =12S △ABC 成立(3)S △DEF -S △CEF =12S △ABC38.(1)①1.5 ①20,07⎛⎫ ⎪⎝⎭ (2)存在最大值,最大值为6939.(1)3t (2)258 (3)355374t ≤≤40.(1)①①①(2)AD =,①465。
中考数学折叠,旋转问题专题含答案

【经典例题1】如图,CD是⊙O的直径,AB是⊙O的弦,AB⊥CD,垂足为G,OG:OC=3:5,AB=8.(1)求⊙O的半径;(2)点E为圆上一点,∠ECD=15°,将沿弦CE翻折,交CD于点F,求图中阴影部分的面积.【解析】(1)连接AO,如右图1所示,∵CD为⊙O的直径,AB⊥CD,AB=8,∴AG==4,∵OG:OC=3:5,AB⊥CD,垂足为G,∴设⊙O的半径为5k,则OG=3k,∴(3k)2+42=(5k)2,解得,k=1或k=﹣1(舍去),∴5k=5,即⊙O的半径是5;(2)如图2所示,将阴影部分沿CE翻折,点F的对应点为M,∵∠ECD=15°,由对称性可知,∠DCM=30°,S阴影=S弓形CBM,连接OM,则∠MOD=60°,∴∠MOC=120°,过点M作MN⊥CD于点N,∴MN=MO•sin60°=5×,∴S阴影=S扇形OMC﹣S△OMC==,即图中阴影部分的面积是:.练习1-1如图,在⊙O中,点C在优弧上,将弧沿BC折叠后刚好经过AB 的中点D,连接AC,CD.则下列结论中错误的是()A.AC=CD B.+=C.OD⊥AB D.CD平分∠ACB 【解析】A、过D作DD'⊥BC,交⊙O于D',连接CD'、BD',由折叠得:CD=CD',∠ABC=∠CBD',∴AC=CD'=CD,故①正确;B、∵AC=CD',∴,由折叠得:,∴=,故②正确;C、∵D为AB的中点,∴OD⊥AB,故③正确;D、延长OD交⊙O于E,连接CE,∵OD⊥AB,∴∠ACE=∠BCE,∴CD不平分∠ACB,故④错误;故选:D.练习1-2如图,AB是⊙O的弦,点C在上,点D是AB的中点.将在沿AC 折叠后恰好经过点D,若⊙O的半径为2,AB=8.则AC的长是()A.6B.C.2D.4【解析】如图,延长BO交⊙O于E,连接AE,OA,OD,OC,BC,作CH⊥AB 于H.∵AD=DB,∴OD⊥AB,∴∠ADO=90°,∵OA=2,AD=DB=4,∴OD==2,∵BE是直径,∴∠BAE=90°,∵AD=DB,EO=OB,∴OD∥AE,AE=2OD=4,∴AE=AD,∴=,∴=,∴∠CAE=∠CAH=45°,∴∠BOC=2∠CAB=90°,∴BC=OC=2,∵CH⊥AB,∴∠CAH=∠ACH=45°,∴AH=CH,设AH=CH=x,则BH=8﹣x,在Rt△BCH中,∵CH2+BH2=BC2,∴x2+(8﹣x)2=(2)2,∴x=6或2(舍弃),在Rt△ACH中,∵AC=,∴AC=6.故选:A.练习1-3在扇形AOB中,∠AOB=75°,半径OA=12,点P为AO上任一点(不与A、O重合).(1)如图1,Q是OB上一点,若OP=OQ,求证:BP=AQ.(2)如图2,将扇形沿BP折叠,得到O的对称点O'.①若点O'落在上,求的长.②当BO'与扇形AOB所在的圆相切时,求折痕的长.(注:本题结果不取近似值)【解析】(1)证明:∵BO=AO,∠O=∠O,OP=OQ,∴△BOP≌△AOQ(SAS).∴BP=AQ.(2)解:①如图1,点O'落在上,连接OO',∵将扇形沿BP折叠,得到O的对称点O',∴OB=O'B,∵OB=OO',∴△BOO'是等边三角形,∴∠O'OB=60°.∵∠AOB=75°,∴∠AOO'=15°.∴的长为.②BO'与扇形AOB所在的圆相切时,如图2所示,∴∠OBO'=90°.∴∠OBP=45°.过点O作OC⊥BP于点C,∵OA=OB=12,∠COB=∠OBP=45°,∴.又∵∠AOB=75°,∠COB=45°,∴∠POC=30°,∴.∴.∴折痕的长为.旋转类【经典例题2】如图1,在锐角△ABC中,AB=5,AC=42,∠ACB=45∘. 计算:求BC的长;操作:将图1中的△ABC绕点B按逆时针方向旋转,得到△A1BC1.如图2,当点C1在线段CA的延长线上时。
中考数学真题《图形的旋转》专项测试卷(附答案)

中考数学真题《图形的旋转》专项测试卷(附答案)学校:___________班级:___________姓名:___________考号:___________(30题)一 、单选题1.(2023·江苏无锡·统考中考真题)如图,ABC 中 55BAC ∠=︒ 将ABC 逆时针旋转(055),αα︒<<︒得到ADE DE 交AC 于F .当40α=︒时 点D 恰好落在BC 上 此时AFE ∠等于( )A .80︒B .85︒C .90︒D .95︒2.(2023·天津·统考中考真题)如图,把ABC 以点A 为中心逆时针旋转得到ADE 点B C 的对应点分别是点D E 且点E 在BC 的延长线上 连接BD 则,下列结论一定正确的是( )A .CAE BED ∠=∠B .AB AE =C .ACE ADE ∠=∠D .CE BD =3.(2023·四川宜宾·统考中考真题)如图,ABC 和ADE 是以点A 为直角顶点的等腰直角三角形 把ADE 以A 为中心顺时针旋转 点M 为射线BD CE 的交点.若3AB 1AD =.以下结论: ①BD CE = ①BD CE ⊥ ①当点E 在BA 的延长线上时 33MC -=①在旋转过程中 当线段MB 最短时 MBC 的面积为12. 其中正确结论有( )A .1个B .2个C .3个D .4个4.(2023·山东聊城·统考中考真题)如图,已知等腰直角ABC 90ACB ∠=︒ 2AB = 点C 是矩形ECGF 与ABC 的公共顶点 且1CE = 3CG = 点D 是CB 延长线上一点 且2CD =.连接BG DF 在矩形ECGF 绕点C 按顺时针方向旋转一周的过程中 当线段BG 达到最长和最短时 线段DF 对应的长度分别为m 和n 则,mn的值为( )A .2B .3C 10D 13二 填空题5.(2023·江苏连云港·统考中考真题)以正五边形ABCDE 的顶点C 为旋转中心 按顺时针方向旋转 使得新五边形A B CD E ''''的顶点D 落在直线BC 上则,正五边ABCDE 旋转的度数至少为______°.6.(2023·湖南张家界·统考中考真题)如图,AO 为BAC ∠的平分线 且50BAC ∠=︒ 将四边形ABOC 绕点A 逆时针方向旋转后 得到四边形AB O C ''' 且100OAC '∠=︒则,四边形ABOC 旋转的角度是______.7.(2023·湖南常德·统考中考真题)如图1 在Rt ABC △中 90ABC ∠=︒ 8AB = 6BC = D 是AB 上一点 且2AD = 过点D 作DE BC ∥交AC 于E 将ADE 绕A 点顺时针旋转到图2的位置.则图2中BDCE的值为__________.8.(2023·江苏无锡·统考中考真题)已知曲线12C C 、分别是函数2(0),(0,0)ky x y k x x x=-<=>>的图像 边长为6的正ABC 的顶点A 在y 轴正半轴上 顶点B C 在x 轴上(B 在C 的左侧) 现将ABC 绕原点O 顺时针旋转 当点B 在曲线1C 上时 点A 恰好在曲线2C 上则,k 的值为__________.9.(2023·辽宁·统考中考真题)如图,线段8AB = 点C 是线段AB 上的动点 将线段BC 绕点B 顺时针旋转120°得到线段BD 连接CD 在AB 的上方作Rt DCE ∆ 使90,30DCE E ∠=∠= 点F 为DE 的中点 连接AF 当AF 最小时 BCD ∆的面积为___________.10.(2023·江西·统考中考真题)如图,在ABCD 中 602B BC AB ∠=︒=, 将AB 绕点A 逆时针旋转角α(0360α︒<<︒)得到AP 连接PC PD .当PCD 为直角三角形时 旋转角α的度数为_______.11.(2023·上海·统考中考真题)如图,在ABC 中 35C ∠=︒ 将ABC 绕着点A 旋转(0180)αα︒<<︒ 旋转后的点B 落在BC 上 点B 的对应点为D 连接AD AD ,是BAC ∠的角平分线则,α=________.12.(2023·湖南郴州·统考中考真题)如图,在Rt ABC △中 90BAC ∠=︒ 3cm AB = =60B ∠︒.将ABC 绕点A 逆时针旋转 得到AB C ''△ 若点B 的对应点B '恰好落在线段BC 上则,点C 的运动路径长.....是___________cm (结果用含π的式子表示).13.(2023·内蒙古·统考中考真题)如图,在Rt ABC △中 90,3,1ACB AC BC ∠=︒== 将ABC 绕点A 逆时针方向旋转90︒ 得到AB C ''△.连接BB ' 交AC 于点D 则,ADDC的值为________.14.(2023·黑龙江绥化·统考中考真题)已知等腰ABC 120A ∠=︒ 2AB =.现将ABC 以点B 为旋转中心旋转45︒ 得到A BC ''△ 延长C A ''交直线BC 于点D .则A D '的长度为_______. 15.(2023·浙江嘉兴·统考中考真题)一副三角板ABC 和DEF 中90304512C D B E BC EF ∠=∠=︒∠=︒∠=︒==,,,.将它们叠合在一起 边BC 与EF 重合 CD 与AB 相交于点G (如图1) 此时线段CG 的长是___________ 现将DEF 绕点()C F 按顺时针方向旋转(如图2)边EF 与AB 相交于点H 连结DH 在旋转0︒到60︒的过程中 线段DH 扫过的面积是___________.三 解答题16.(2023·北京·统考中考真题)在ABC 中 ()045B C αα∠=∠=︒<<︒ AM BC ⊥于点M D 是线段MC 上的动点(不与点M C 重合) 将线段DM 绕点D 顺时针旋转2α得到线段DE .(1)如图1 当点E 在线段AC 上时 求证:D 是MC 的中点(2)如图2 若在线段BM 上存在点F (不与点B M 重合)满足DF DC = 连接AE EF 直接写出AEF ∠的大小 并证明.17.(2023·四川自贡·统考中考真题)如图1 一大一小两个等腰直角三角形叠放在一起 M N 分别是斜边DE AB 的中点 2,4DE AB ==.(1)将CDE 绕顶点C 旋转一周 请直接写出点M N 距离的最大值和最小值(2)将CDE 绕顶点C 逆时针旋转120︒(如图2) 求MN 的长.18.(2023·四川达州·统考中考真题)如图,网格中每个小正方形的边长均为1 ABC 的顶点均在小正方形的格点上.(1)将ABC 向下平移3个单位长度得到111A B C △ 画出111A B C △ (2)将ABC 绕点C 顺时针旋转90度得到222A B C △ 画出222A B C △ (3)在(2)的运动过程中请计算出ABC 扫过的面积.19.(2023·辽宁·统考中考真题)在Rt ABC ∆中 90°ACB ∠= CA CB = 点O 为AB 的中点 点D 在直线AB 上(不与点,A B 重合) 连接CD 线段CD 绕点C 逆时针旋转90° 得到线段CE 过点B 作直线l BC ⊥ 过点E 作EF l ⊥ 垂足为点F 直线EF 交直线OC 于点G .(1)如图,当点D 与点O 重合时 请直接写出线段AD 与线段EF 的数量关系 (2)如图,当点D 在线段AB 上时 求证:2CG BD BC +=(3)连接DE CDE 的面积记为1S ABC 的面积记为2S 当:1:3EF BC =时 请直接写出12S S 的值.20.(2023·四川乐山·统考中考真题)在学习完《图形的旋转》后 刘老师带领学生开展了一次数学探究活动【问题情境】刘老师先引导学生回顾了华东师大版教材七年级下册第121页“探索”部分内容:如图,将一个三角形纸板ABC 绕点A 逆时针旋转θ到达AB C ''△的位置 那么可以得到:AB AB '=AC AC '= BC B C ''= BAC B AC ''∠=∠ ABC AB C ''∠=∠ ACB AC B ''∠=∠( )刘老师进一步谈到:图形的旋转蕴含于自然界的运动变化规律中 即“变”中蕴含着“不变” 这是我们解决图形旋转的关键 故数学就是一门哲学. 【问题解决】(1)上述问题情境中“( )”处应填理由:____________________(2)如图,小王将一个半径为4cm 圆心角为60︒的扇形纸板ABC 绕点O 逆时针旋转90︒到达扇形纸板A B C '''的位置.①请在图中作出点O①如果=6cm BB '则,在旋转过程中 点B 经过的路径长为__________ 【问题拓展】小李突发奇想 将与(2)中完全相同的两个扇形纸板重叠 一个固定在墙上 使得一边位于水平位置 另一个在弧的中点处固定 然后放开纸板 使其摆动到竖直位置时静止 此时 两个纸板重叠部分的面积是多少呢?如图所示 请你帮助小李解决这个问题.21.(2023·浙江绍兴·统考中考真题)在平行四边形ABCD 中(顶点,,,A B C D 按逆时针方向排列) 12,10,AB AD B ==∠为锐角 且4sin 5B =.(1)如图1 求AB 边上的高CH 的长.(2)P 是边AB 上的一动点 点,C D 同时绕点P 按逆时针方向旋转90︒得点,C D ''. ①如图2 当点C '落在射线CA 上时 求BP 的长. ①当AC D ''△是直角三角形时 求BP 的长.22.(2023·四川南充·统考中考真题)如图,正方形ABCD 中 点M 在边BC 上 点E 是AM 的中点 连接EDEC .(1)求证:ED EC =(2)将BE 绕点E 逆时针旋转 使点B 的对应点B '落在AC 上 连接MB '.当点M 在边BC 上运动时(点M 不与B C 重合) 判断CMB '的形状 并说明理由.(3)在(2)的条件下 已知1AB = 当45DEB ∠'=︒时 求BM 的长.23.(2023·江苏扬州·统考中考真题)【问题情境】在综合实践活动课上 李老师让同桌两位同学用相同的两块含30︒的三角板开展数学探究活动 两块三角板分别记作ADB 和,90,30A D C ADB A D C B C ∠=∠=︒∠''''=∠=︒△ 设2AB =. 【操作探究】如图1 先将ADB 和A D C ''的边AD A D ''重合 再将A D C ''绕着点A 按顺时针...方向旋转 旋转角为()0360αα︒≤≤︒ 旋转过程中ADB 保持不动 连接BC .(1)当60α=︒时 BC =________ 当22BC = α=________︒ (2)当90α=︒时 画出图形 并求两块三角板重叠部分图形的面积(3)如图2 取BC 的中点F 将A D C ''绕着点A 旋转一周 点F 的运动路径长为________. 24.(2023·湖南·统考中考真题)(1)[问题探究]如图1 在正方形ABCD 中 对角线AC BD 、相交于点O .在线段AO 上任取一点P (端点除外) 连接PD PB 、.①求证:PD PB =①将线段DP 绕点P 逆时针旋转 使点D 落在BA 的延长线上的点Q 处.当点P 在线段AO 上的位置发生变化时 DPQ ∠的大小是否发生变化?请说明理由 ①探究AQ 与OP 的数量关系 并说明理由. (2)[迁移探究]如图2 将正方形ABCD 换成菱形ABCD 且60ABC ∠=︒ 其他条件不变.试探究AQ 与CP 的数量关系 并说明理由.25.(2023·湖北随州·统考中考真题)1643年 法国数学家费马曾提出一个著名的几何问题:给定不在同一条直线上的三个点A B C 求平面上到这三个点的距离之和最小的点的位置 意大利数学家和物理学家托里拆利给出了分析和证明 该点也被称为“费马点”或“托里拆利点” 该问题也被称为“将军巡营”问题. (1)下面是该问题的一种常见的解决方法 请补充以下推理过程:(其中①处从“直角”和“等边”中选择填空 ①处从“两点之间线段最短”和“三角形两边之和大于第三边”中选择填空 ①处填写角度数 ①处填写该三角形的某个顶点)当ABC 的三个内角均小于120︒时如图1 将APC △绕 点C 顺时针旋转60︒得到A P C '' 连接PP '由60PC P C PCP ''=∠=︒, 可知PCP '△为 ① 三角形 故PP PC '= 又P A PA ''= 故PA PB PC PA PB PP A B '''++=++≥由 ① 可知 当B P P ' A 在同一条直线上时 PA PB PC ++取最小值 如图2 最小值为A B ' 此时的P 点为该三角形的“费马点” 且有APC BPC APB ∠=∠=∠= ①已知当ABC 有一个内角大于或等于120︒时 “费马点”为该三角形的某个顶点.如图3 若120BAC ∠≥︒则,该三角形的“费马点”为 ① 点.(2)如图4 在ABC 中 三个内角均小于120︒ 且3430AC BC ACB ==∠=︒,, 已知点P 为ABC 的“费马点” 求PA PB PC ++的值(3)如图5 设村庄A B C 的连线构成一个三角形 且已知4km 23km 60AC BC ACB ==∠=︒,,.现欲建一中转站P 沿直线向A B C 三个村庄铺设电缆 已知由中转站P 到村庄A B C 的铺设成本分别为a 元/km a 元/km 2a 元/km 选取合适的P 的位置 可以使总的铺设成本最低为___________元.(结果用含a 的式子表示)26.(2023·四川·统考中考真题)如图1 已知线段AB AC 线段AC 绕点A 在直线AB 上方旋转 连接BC 以BC 为边在BC 上方作Rt BDC 且30DBC ∠=︒.(1)若=90BDC ∠︒ 以AB 为边在AB 上方作Rt BAE △ 且90AEB ∠=︒ 30EBA ∠=︒ 连接DE 用等式表示线段AC 与DE 的数量关系是(2)如图2 在(1)的条件下 若DE AB ⊥ 4AB = 2AC = 求BC 的长(3)如图3 若90BCD ∠=︒ 4AB = 2AC = 当AD 的值最大时 求此时tan CBA ∠的值.27.(2023·湖北黄冈·统考中考真题)【问题呈现】CAB △和CDE 都是直角三角形 90,,ACB DCE CB mCA CE mCD ∠=∠=︒== 连接AD BE 探究ADBE 的位置关系.(1)如图1 当1m =时 直接写出AD BE 的位置关系:____________(2)如图2 当1m ≠时 (1)中的结论是否成立?若成立 给出证明 若不成立 说明理由. 【拓展应用】(3)当3,7,4m AB DE ===时 将CDE 绕点C 旋转 使,,A D E 三点恰好在同一直线上 求BE 的长.28.(2023·内蒙古赤峰·统考中考真题)数学兴趣小组探究了以下几何图形.如图① 把一个含有45︒角的三角尺放在正方形ABCD 中 使45︒角的顶点始终与正方形的顶点C 重合 绕点C 旋转三角尺时 45︒角的两边CM CN 始终与正方形的边AD AB 所在直线分别相交于点M N 连接MN 可得CMN .【探究一】如图① 把CDM 绕点C 逆时针旋转90︒得到CBH 同时得到点H 在直线AB 上.求证:CNM CNH ∠=∠【探究二】在图①中 连接BD 分别交CM CN 于点E F .求证:CEF CNM △∽△【探究三】把三角尺旋转到如图①所示位置 直线BD 与三角尺45︒角两边CM CN 分别交于点E F .连接AC 交BD 于点O 求EFNM的值.29.(2023·湖南·统考中考真题)问题情境:小红同学在学习了正方形的知识后 进一步进行以下探究活动:在正方形ABCD 的边BC 上任意取一点G 以BG 为边长向外作正方形BEFG 将正方形BEFG 绕点B 顺时针旋转.特例感知:(1)当BG 在BC 上时 连接DF AC ,相交于点P 小红发现点P 恰为DF 的中点 如图①.针对小红发现的结论 请给出证明(2)小红继续连接EG 并延长与DF 相交 发现交点恰好也是DF 中点P 如图① 根据小红发现的结论 请判断APE 的形状 并说明理由 规律探究:(3)如图① 将正方形BEFG 绕点B 顺时针旋转α 连接DF 点P 是DF 中点 连接AP EP AEAPE 的形状是否发生改变?请说明理由.30.(2023·贵州·统考中考真题)如图① 小红在学习了三角形相关知识后 对等腰直角三角形进行了探究 在等腰直角三角形ABC 中 ,90CA CB C =∠=︒ 过点B 作射线BD AB ⊥ 垂足为B 点P 在CB 上.(1)【动手操作】如图① 若点P 在线段CB 上 画出射线PA 并将射线PA 绕点P 逆时针旋转90︒与BD 交于点E 根据题意在图中画出图形 图中PBE ∠的度数为_______度 (2)【问题探究】根据(1)所画图形 探究线段PA 与PE 的数量关系 并说明理由 (3)【拓展延伸】如图① 若点P 在射线CB 上移动 将射线PA 绕点P 逆时针旋转90︒与BD 交于点E 探究线段,,BA BP BE 之间的数量关系 并说明理由.参考答案一 单选题1.(2023·江苏无锡·统考中考真题)如图,ABC 中 55BAC ∠=︒ 将ABC 逆时针旋转(055),αα︒<<︒得到ADE DE 交AC 于F .当40α=︒时 点D 恰好落在BC 上 此时AFE ∠等于( )A .80︒B .85︒C .90︒D .95︒【答案】B【分析】根据旋转可得B ADB ADE ∠=∠=∠ 再结合旋转角40α=︒即可求解. 【详解】解:由旋转性质可得:55BAC DAE ∠=∠=︒ AB AD = ①40α=︒①15DAF ∠=︒ 70B ADB ADE ∠=∠=∠=︒ ①85AFE DAF ADE ∠=∠+∠=︒故选:B .【点睛】本题考查了几何—旋转问题 掌握旋转的性质是关键.2.(2023·天津·统考中考真题)如图,把ABC 以点A 为中心逆时针旋转得到ADE 点B C 的对应点分别是点D E 且点E 在BC 的延长线上 连接BD 则,下列结论一定正确的是( )A .CAE BED ∠=∠B .AB AE =C .ACE ADE ∠=∠D .CE BD = 【答案】A【分析】根据旋转的性质即可解答. 【详解】根据题意 由旋转的性质可得AB AD = AC AE = BC DE = 故B 选项和D 选项不符合题意=ABC ADE ∠∠=ACE ABCBAC∴=ACE ADEBAC 故C 选项不符合题意=ACB AED =ACB CAECEA=AED CEA BED∴=CAE BED 故A 选项符合题意故选:A .【点睛】本题考查了旋转的性质 熟练掌握旋转的性质和三角形外角运用是解题的关键.3.(2023·四川宜宾·统考中考真题)如图,ABC 和ADE 是以点A 为直角顶点的等腰直角三角形 把ADE 以A 为中心顺时针旋转 点M 为射线BD CE 的交点.若3AB 1AD =.以下结论: ①BD CE = ①BD CE ⊥ ①当点E 在BA 的延长线上时 33MC -=①在旋转过程中 当线段MB 最短时 MBC 的面积为12.其中正确结论有( )A .1个B .2个C .3个D .4个【答案】D【分析】证明BAD CAE ≌即可判断① 根据三角形的外角的性质得出① 证明DCM ECA ∠∠∽得出313-= 即可判断① 以A 为圆心 AD 为半径画圆 当CE 在A 的下方与A 相切时 MB 的值最小 可得四边形AEMD 是正方形 在Rt MBC 中22MC BC MB -21 然后根据三角形的面积公式即可判断①.【详解】解:①ABC 和ADE 是以点A 为直角顶点的等腰直角三角形 ①,,90BA CA DA EA BAC DAE ==∠=∠=︒ ①BAD CAE ∠=∠ ①BAD CAE ≌①ABD ACE ∠=∠ BD CE = 故①正确 设ABD ACE α∠=∠= ①45DBC α∠=︒-,①454590EMB DBC BCM DBC BCA ACE αα∠=∠+∠=∠+∠+∠=︒-+︒+=︒ ①BD CE ⊥ 故①正确当点E 在BA 的延长线上时 如图所示①DCM ECA ∠=∠ 90DMC EAC ∠=∠=︒ ①DCM ECA ∠∠∽①MC CDAC EC= ①3AB = 1AD =.①31CD AC AD =-= 222CE AE AC =+= 313-=①33MC -=故①正确 ①如图所示 以A 为圆心 AD 为半径画圆①90BMC ∠=︒ ①当CE 在A 的下方与A 相切时 MB 的值最小 90ADM DAE AEM ∠=∠=∠=︒①四边形AEMD 是矩形 又AE AD =①四边形AEMD 是正方形 ①1MD AE ==①222BD EC AC AE =- ①21MB BD MD =-= 在Rt MBC 中 22MC BC MB -①PB 取得最小值时 222MC AB AC MB +-()2332121+--①)()1112121222BMCSMB MC =⨯==故①正确 故选:D .【点睛】本题考查了旋转的性质 相似三角形的性质 勾股定理 切线的性质 垂线段最短 全等三角形的性质与判定 正方形的性质 熟练掌握以上知识是解题的关键.4.(2023·山东聊城·统考中考真题)如图,已知等腰直角ABC 90ACB ∠=︒ 2AB = 点C 是矩形ECGF与ABC 的公共顶点 且1CE = 3CG = 点D 是CB 延长线上一点 且2CD =.连接BG DF 在矩形ECGF 绕点C 按顺时针方向旋转一周的过程中 当线段BG 达到最长和最短时 线段DF 对应的长度分别为m 和n 则,mn的值为( )A .2B .3C 10D 13【答案】D【分析】根据锐角三角函数可求得1AC BC == 当线段BG 达到最长时 此时点G 在点C 的下方 且BC G 三点共线 求得4BG = 5DG = 根据勾股定理求得26DF = 即26m = 当线段BG 达到最短时 此时点G 在点C 的上方 且B C G 三点共线则,2BG = 1DG = 根据勾股定理求得2DF 即2n = 即可求得13mn【详解】①ABC 为等腰直角三角形 2AB = ①2sin 4521AC BC AB ==⋅︒== 当线段BG 达到最长时 此时点G 在点C 的下方 且B C G 三点共线 如图:则4BG BC CG =+= 5DG DB BG =+=在Rt DGF △中 22225126DF DG GF =++ 即26m =当线段BG 达到最短时 此时点G 在点C 的上方 且B C G 三点共线 如图:则2BG CG BC =-= 1DG BG DB =-=在Rt DGF △中 2222112DF DG GF =++ 即2n = 故26132m n == 故选:D .【点睛】本题考查了锐角三角函数 勾股定理等 根据旋转推出线段BG 最长和最短时的位置是解题的关键.二 填空题5.(2023·江苏连云港·统考中考真题)以正五边形ABCDE 的顶点C 为旋转中心 按顺时针方向旋转 使得新五边形A B CD E ''''的顶点D 落在直线BC 上则,正五边ABCDE 旋转的度数至少为______°.【答案】72【分析】依据正五边形的外角性质 即可得到DCF ∠的度数 进而得出旋转的角度. 【详解】解:①五边形ABCDE 是正五边形①530726DCF ∠÷=︒=︒①新五边形A B CD E ''''的顶点D 落在直线BC 上则,旋转的最小角度是72︒故答案为:72.【点睛】本题主要考查了正多边形 旋转性质 关键是掌握正多边形的外角和公式的运用.6.(2023·湖南张家界·统考中考真题)如图,AO 为BAC ∠的平分线 且50BAC ∠=︒ 将四边形ABOC 绕点A 逆时针方向旋转后 得到四边形AB O C ''' 且100OAC '∠=︒则,四边形ABOC 旋转的角度是______.【答案】75︒【分析】根据角平分线的性质可得25BAO OAC ==︒∠∠ 根据旋转的性质可得50BAC B AC ''∠=∠=︒ 25B AO O AC ''''==︒∠∠ 求得75OAO '∠=︒ 即可求得旋转的角度.【详解】①AO 为BAC ∠的平分线 50BAC ∠=︒①25BAO OAC ==︒∠∠①将四边形ABOC 绕点A 逆时针方向旋转后 得到四边形AB O C '''①50BAC B AC ''∠=∠=︒ 25B AO O AC ''''==︒∠∠①1002575OAO OAC O AC ''''∠=∠-∠=︒-︒=︒故答案为:75︒.【点睛】本题考查了角平分线的性质 旋转的性质 熟练掌握以上性质是解题的关键.7.(2023·湖南常德·统考中考真题)如图1 在Rt ABC △中 90ABC ∠=︒ 8AB = 6BC = D 是AB 上一点 且2AD = 过点D 作DE BC ∥交AC 于E 将ADE 绕A 点顺时针旋转到图2的位置.则图2中BDCE的值为__________.【答案】45【分析】首先根据勾股定理得到2210AC AB BC += 然后证明出ADE ABC △△∽ 得到AD AEAB AC= 进而得到ADABAE AC = 然后证明出ABD ACE ∽ 利用相似三角形的性质求解即可.【详解】①在Rt ABC △中 90ABC ∠=︒ 8AB = 6BC = ①2210AC AB BC +①DE BC ∥①90ADE ABC ∠=∠=︒ AED ACB ∠=∠①ADE ABC △△∽ ①ADAEAB AC = ①ADABAE AC =①BAC DAE ∠=∠①BAC CAD DAE CAD ∠+∠=∠+∠①BAD CAE ∠=∠①ABD ACE ∽ ①84105BD AB CD AC ===. 故答案为:45.【点睛】此题考查了相似三角形的性质和判定 解题的关键是熟练掌握相似三角形的性质和判定定理.8.(2023·江苏无锡·统考中考真题)已知曲线12C C 、分别是函数2(0),(0,0)k y x y k x x x=-<=>>的图像 边长为6的正ABC 的顶点A 在y 轴正半轴上 顶点B C 在x 轴上(B 在C 的左侧)现将ABC 绕原点O 顺时针旋转 当点B 在曲线1C 上时 点A 恰好在曲线2C 上则,k 的值为__________.【答案】6【分析】画出变换后的图像即可(画AOB 即可) 当点A 在y 轴上 点B C 在x 轴上时 根据ABC 为等边三角形且AO BC ⊥ 可得3OB OA = 过点A B 分别作x 轴垂线构造相似则,BFO OEA ∽ 根据相似三角形的性质得出3AOE S =△ 进而根据反比例函数k 的几何意义 即可求解.【详解】当点A 在y 轴上 点B C 在x 轴上时 连接AOABC 为等边三角形且AO BC ⊥则,30BAO ∠=︒∴tan tan30BAO ∠=︒=3OB OA = 如图所示 过点,A B 分别作x 轴的垂线 交x 轴分别于点,E FAO BO ⊥ 90BFO AEO AOB ∠=∠=∠=︒∴90BOF AOE EAO ∠=︒-∠=∠∴BFO OEA ∽ ∴213BFO AOE S OB SOA ⎛⎫== ⎪⎝⎭ ∴212BFO S -==∴3AOE S =△∴6k =.【点睛】本题考查了反比例函数的性质 k 的几何意义 相似三角形的性质与判定 正确作出辅助线构造相似三角形是解题关键.9.(2023·辽宁·统考中考真题)如图,线段8AB = 点C 是线段AB 上的动点 将线段BC 绕点B 顺时针旋转120°得到线段BD 连接CD 在AB 的上方作Rt DCE ∆ 使90,30DCE E ∠=∠= 点F 为DE 的中点 连接AF 当AF 最小时 BCD ∆的面积为___________.3【分析】连接CF BF , BF ,CD 交于点P 由直角三角形的性质及等腰三角形的性质可得BF 垂直平分CF 60ABF ∠=︒为定角 可得点F 在射线BF 上运动 当AF BF ⊥时 AF 最小 由含30度角直角三角形的性质即可求解.【详解】解:连接CF BF , BF ,CD 交于点P 如图,①90DCE ∠= 点F 为DE 的中点①FC FD =①30E ∠=①60FDC ∠=︒,①FCD 是等边三角形①60DFC FCD ∠=∠=︒①线段BC 绕点B 顺时针旋转120°得到线段BD①BC BD =①FC FD =①BF 垂直平分CF 60ABF ∠=︒①点F 在射线BF 上运动①当AF BF ⊥时 AF 最小此时9030FAB ABF ∠=︒-∠=︒ ①142BF AB == ①1302BFC DFC ∠=∠=︒ ①90FCB BFC ABF ∠=∠+∠=︒①122BC BF == ①112PB BC == ①由勾股定理得223PC BC PB - ①223CD PC == ①11231322BCD S CD PB =⋅=⨯△3【点睛】本题考查了等腰三角形性质 含30度直角三角形的性质 斜边中线性质 勾股定理 线段垂直平分线的判定 勾股定理 旋转的性质 确定点F 的运动路径是关键与难点.10.(2023·江西·统考中考真题)如图,在ABCD 中 602B BC AB ∠=︒=, 将AB 绕点A 逆时针旋转角α(0360α︒<<︒)得到AP 连接PC PD .当PCD 为直角三角形时 旋转角α的度数为_______.【答案】90︒或270︒或180︒【分析】连接AC 根据已知条件可得90BAC ∠=︒ 进而分类讨论即可求解.【详解】解:连接AC 取BC 的中点E 连接AE 如图所示①在ABCD 中 602B BC AB ∠=︒=, ①12BE CE BC AB ===①ABE 是等边三角形①60BAE AEB ∠=∠=︒ AE BE =①AE EC = ①1302EAC ECA AEB ∠=∠=∠=︒ ①90BAC ∠=︒①AC CD ⊥如图所示 当点P 在AC 上时 此时90BAP BAC ∠=∠=︒则,旋转角α的度数为90︒当点P 在CA 的延长线上时 如图所示则,36090270α=︒-︒=︒当P 在BA 的延长线上时则,旋转角α的度数为180︒ 如图所示①PA PB CD == PB CD ∥①四边形PACD 是平行四边形①AC AB ⊥①四边形PACD 是矩形①90PDC ∠=︒即PDC △是直角三角形综上所述 旋转角α的度数为90︒或270︒或180︒故答案为:90︒或270︒或180︒.【点睛】本题考查了平行四边形的性质与判定 等边三角形的性质与判定 矩形的性质与判定 旋转的性质 熟练掌握旋转的性质是解题的关键.11.(2023·上海·统考中考真题)如图,在ABC 中 35C ∠=︒ 将ABC 绕着点A 旋转(0180)αα︒<<︒ 旋转后的点B 落在BC 上 点B 的对应点为D 连接AD AD ,是BAC ∠的角平分线则,α=________.【答案】1103⎛⎫︒ ⎪⎝⎭【分析】如图,AB AD = BAD ∠=α 根据角平分线的定义可得CAD BAD α∠=∠= 根据三角形的外角性质可得35ADB α∠=︒+ 即得35B ADB α∠=∠=︒+ 然后根据三角形的内角和定理求解即可.【详解】解:如图,根据题意可得:AB AD = BAD ∠=α①AD 是BAC ∠的角平分线①CAD BAD α∠=∠=①35ADB C CAD α∠=∠+∠=︒+ AB AD =①35B ADB α∠=∠=︒+则在ABC 中 ①180C CAB B ∠+∠+∠=︒①35235180αα︒++︒+=︒ 解得:1103α⎛⎫=︒ ⎪⎝⎭故答案为:1103⎛⎫︒ ⎪⎝⎭【点睛】本题考查了旋转的性质 等腰三角形的性质 三角形的外角性质以及三角形的内角和等知识 熟练掌握相关图形的性质是解题的关键.12.(2023·湖南郴州·统考中考真题)如图,在Rt ABC △中 90BAC ∠=︒ 3cm AB = =60B ∠︒.将ABC 绕点A 逆时针旋转 得到AB C ''△ 若点B 的对应点B '恰好落在线段BC 上则,点C 的运动路径长.....是___________cm (结果用含π的式子表示).3π【分析】由于AC 旋转到AC ' 故C 的运动路径长是CC '的圆弧长度 根据弧长公式求解即可.【详解】以A 为圆心作圆弧CC ' 如图所示.在直角ABC 中 =60B ∠︒则,30C ∠=︒则()2236cm BC AB ==⨯=. ①)22226333cm AC BC AB =--.由旋转性质可知 AB AB '= 又=60B ∠︒①ABB '是等边三角形.①60BAB '∠=︒.由旋转性质知 60CAC '∠=︒.故弧CC '的长度为:()602333cm 3603AC πππ⨯⨯⨯=⨯ 3π【点睛】本题考查了含30︒角直角三角形的性质 勾股定理 旋转的性质 弧长公式等知识点 解题的关键是明确C 点的运动轨迹.13.(2023·内蒙古·统考中考真题)如图,在Rt ABC △中 90,3,1ACB AC BC ∠=︒== 将ABC 绕点A 逆时针方向旋转90︒ 得到AB C ''△.连接BB ' 交AC 于点D 则,AD DC 的值为________.【答案】5【分析】过点D 作DF AB ⊥于点F 利用勾股定理求得10AB根据旋转的性质可证ABB ' DFB △是等腰直角三角形 可得DF BF = 再由1122ADB SBC AD DF AB =⨯⨯=⨯⨯ 得=10AD DF 证明AFD ACB 可得DF AF BC AC = 即3AF DF = 再由=10AF DF 求得10=DF 从而求得52AD = 12CD = 即可求解. 【详解】解:过点D 作DF AB ⊥于点F①90ACB ∠=︒ 3AC = 1BC = ①223110AB +①将ABC 绕点A 逆时针方向旋转90︒得到AB C ''△ ①==10AB AB ' 90BAB '∠=︒①ABB '是等腰直角三角形①45ABB '∠=︒又①DF AB ⊥①45FDB ∠=︒①DFB △是等腰直角三角形①DF BF = ①1122ADB S BC AD DF AB =⨯⨯=⨯⨯ 即=10AD DF ① 90C AFD ∠=∠=︒ CAB FAD ∠=∠①AFD ACB ①DF AF BC AC= 即3AF DF = 又①=10AF DF ①10=DF ①105=10=2AD 51=3=22CD - ①52==512AD CD 故答案为:5.【点睛】本题考查旋转的性质 等腰三角形的判定与性质 相似三角形的判定与性质 三角形的面积 熟练掌握相关知识是解题的关键.14.(2023·黑龙江绥化·统考中考真题)已知等腰ABC 120A ∠=︒ 2AB =.现将ABC 以点B 为旋转中心旋转45︒ 得到A BC ''△ 延长C A ''交直线BC 于点D .则A D '的长度为_______. 【答案】423423+-或【分析】根据题意 先求得23BC = 当ABC 以点B 为旋转中心逆时针旋转45︒ 过点B 作BE A B '⊥交A D '于点E 当ABC 以点B 为旋转中心顺时针旋转45︒ 过点D 作DF BC '⊥交BC '于点F 分别画出图形 根据勾股定理以及旋转的性质即可求解.【详解】解:如图所示 过点A 作AM BC ⊥于点M①等腰ABC 120BAC ∠=︒ 2AB =. ①30ABC ACB ∠=∠=︒ ①112AM AB == 223BM CM AB AM =- ①23BC =如图所示 当ABC 以点B 为旋转中心逆时针旋转45︒ 过点B 作BE A B '⊥交A D '于点E①120BAC ∠=︒①60DA B '∠=︒ 30A EB '∠=︒在Rt A BE '中 24A E A B ''== 2223BE A E A B ''-= ①等腰ABC 120BAC ∠=︒ 2AB =. ①30ABC ACB ∠=∠=︒①ABC 以点B 为旋转中心逆时针旋转45︒ ①45ABA '∠=︒①180********DBE ∠=︒-︒-︒-︒=︒ 1804530105A BD '∠=︒-︒-︒=︒ 在A BD '中 1801806010515D DA B A BD ∠=︒-∠-∠=︒-︒-︒=''︒, ①D EBD ∠=∠ ①23EB ED ==①423A D A E DE ''=+=+如图所示 当ABC 以点B 为旋转中心顺时针旋转45︒ 过点D 作DF BC '⊥交BC '于点F在BFD △中 45BDF CBC ∠'=∠=︒ ①DF BF =在Rt DC F '中 30C '∠=︒ ①3'DF ①33BC BF BF ==①33DF BF ==①2623DC DF '==-①6232423A D C D A C ''''=-=-=- 综上所述 A D '的长度为423-423+ 故答案为:43-43+【点睛】本题考查了旋转的性质 勾股定理 含30度角的直角三角形的性质 熟练掌握旋转的性质 分类讨论是解题的关键.15.(2023·浙江嘉兴·统考中考真题)一副三角板ABC 和DEF 中90304512C D B E BC EF ∠=∠=︒∠=︒∠=︒==,,,.将它们叠合在一起 边BC 与EF 重合 CD 与AB 相交于点G (如图1) 此时线段CG 的长是___________ 现将DEF 绕点()C F 按顺时针方向旋转(如图2) 边EF 与AB 相交于点H 连结DH 在旋转0︒到60︒的过程中 线段DH 扫过的面积是___________.【答案】6662 1218318π-【分析】如图1 过点G 作GH BC ⊥于H 根据含30︒直角三角形的性质和等腰直角三角形的性质得出3BH GH = GH CH = 然后由12BC =可求出GH 的长 进而可得线段CG 的长 如图2 将DEF 绕点C 顺时针旋转60︒得到11D E F 1FE 与AB 交于1G 连接1D D 1AD 22D E F 是DEF 旋转0︒到60︒的过程中任意位置 作1DN CD ⊥于N 过点B 作1BM D D ⊥交1D D 的延长线于M 首先证明1CDD 是等边三角形 点1D 在直线AB 上 然后可得线段DH 扫过的面积是弓形12D D D 的面积加上1D DB 的面积 求出DN 和BM 然后根据线段DH 扫过的面积111121D DBCD DD DBD D D CD D S SS SS=+=-+弓形扇形列式计算即可.【详解】解:如图1 过点G 作GH BC ⊥于H①3045ABC DEF DFE ∠=︒∠=∠=︒, 90GHB GHC ∠=∠=︒ ①3BH GH = GH CH = ①312BC BH CH GH GH =+=+= ①36GH =①()226366662CG GH ===如图2 将DEF 绕点C 顺时针旋转60︒得到11D E F 1FE 与AB 交于1G 连接1D D 由旋转的性质得:1160E CB DCD ∠=∠=︒ 1CD CD = ①1CDD 是等边三角形①30ABC ∠=︒ ①190CG B ∠=︒ ①112CG BC =①1CE BC =①1112CG CE = 即AB 垂直平分1CE①11CD E 是等腰直角三角形 ①点1D 在直线AB 上连接1AD 22D E F 是DEF 旋转0︒到60︒的过程中任意位置 则线段DH 扫过的面积是弓形12D D D 的面积加上1D DB 的面积 ①12BC EF == ①22DC DB === ①1162DC D D == 作1DN CD ⊥于N 则,132ND NC == ①()()222211623236DN D D ND =-=-过点B 作1BM D D ⊥交1D D 的延长线于M 则,90M ∠=︒ ①160D DC ∠=︒ 90CDB ∠=︒①118030BDM D DC CDB ∠=︒-∠-∠=︒ ①1322BM BD == ①线段DH 扫过的面积112D DBD D D S S =+弓形111CD DD DBCD D S S S=-+扇形(260621123623236022π⋅=-⨯⨯ 1218318π=-故答案为:6662 1218318π-.【点睛】本题主要考查了旋转的性质 含30︒直角三角形的性质 二次根式的运算 解直角三角形 等边三角形的判定和性质 勾股定理 扇形的面积计算等知识 作出图形 证明点1D 在直线AB 上是本题的突破点 灵活运用各知识点是解题的关键.三 解答题16.(2023·北京·统考中考真题)在ABC 中 ()045B C αα∠=∠=︒<<︒ AM BC ⊥于点M D 是线段MC 上的动点(不与点M C 重合) 将线段DM 绕点D 顺时针旋转2α得到线段DE .(1)如图1 当点E 在线段AC 上时 求证:D 是MC 的中点(2)如图2 若在线段BM 上存在点F (不与点B M 重合)满足DF DC = 连接AE EF 直接写出AEF ∠的大小 并证明. 【答案】(1)见解析 (2)90AEF ∠=︒ 证明见解析【分析】(1)由旋转的性质得DM DE = 2MDE α∠= 利用三角形外角的性质求出C DEC α∠=∠= 可得DE DC = 等量代换得到DM DC =即可(2)延长FE 到H 使FE EH = 连接CH AH 可得DE 是FCH 的中位线 然后求出B ACH ∠∠= 设DM DE m == CD n = 求出2BF m CH == 证明()SAS ABF ACH ≅ 得到AF AH = 再根据等腰三角形三线合一证明AE FH ⊥即可.。
中考数学旋转(大题培优)含答案解析

【解析】 试Biblioteka 分析:(1)如图 1,证明△ ADC≌ △ BDF(AAS),可得 BF=AC; (2)如图 2,由折叠得:MD=DC,先根据三角形中位线的推论可得:AE=EC,由线段垂直 平分线的性质得:AB=BC,则∠ ABE=∠ CBE,结合(1)得:△ BDF≌ △ ADM,则
MN∥ AE,MN= AE,利用三角形全等证出 AE=AF,而 DM= AF,从而得到 DM,MN 数量相 等的结论,再利用三角形外角性质和三角形全等,等腰三角形性质以及角角之间的数量关 系得到∠ DMN=∠ DGE=90°.从而得到 DM、MN 的位置关系是垂直. 试题解析:(1)∵ 四边形 ABCD 是正方形,∴ AB=AD=BC=CD,∠ B=∠ ADF=90°,∵ △ CEF 是等腰直角三角形,∠ C=90°,∴ CE=CF,∴ BC﹣CE=CD﹣CF,即 BE=DF, ∴ △ ABE≌ △ ADF,∴ AE=AF,∴ △ AEF 是等腰三角形;(2)DM、MN 的数量关系是相等, DM、MN 的位置关系是垂直;∵ 在 Rt△ ADF 中 DM 是斜边 AF 的中线,∴ AF=2DM,∵ MN 是△ AEF 的中位线,∴ AE=2MN,∵ AE=AF,∴ DM=MN;∵ ∠ DMF=∠ DAF+∠ ADM, AM=MD,∵ ∠ FMN=∠ FAE,∠ DAF=∠ BAE,∴ ∠ ADM=∠ DAF=∠ BAE, ∴ ∠ DMN=∠ FMN+∠ DMF=∠ DAF+∠ BAE+∠ FAE=∠ BAD=90°,∴ DM⊥MN;(3)(2)中的
由(1)可知△ EAB≌ △ GAC, ∴ ∠ 1=∠ 2,BE=CG, ∵ BD=DC,∠ BDE=∠ CDM,DE=DM, ∴ △ EDB≌ △ MDC, ∴ EM=CM=CG,∠ EBC=∠ MCD, ∵ ∠ EBC=∠ ACF, ∴ ∠ MCD=∠ ACF, ∴ ∠ FCM=∠ ACB=∠ ABC, ∴ ∠ 1=3=∠ 2, ∴ ∠ FCG=∠ ACB=∠ MCF, ∵ CF=CF,CG=CM, ∴ △ CFG≌ △ CFM, ∴ FG=FM, ∵ ED=DM,DF⊥EM, ∴ FE=FM=FG, ∵ AE=AG,AF=AF, ∴ △ AFE≌ △ AFG,
2022年中考数学复习:旋转类综合体专项训练(含答案)

2022年中考数学复习:旋转综合体专项训练1.如图,在Rt ABC 中,90ABC ∠=︒,30ACB ∠=︒,将ABC 绕点C 顺时针旋转一定的角度α得到DEC ,点A ,B 的对应点分别是点D ,E .(1)如图①,当点E 恰好在AC 边上时,连接AD ,求①ADE 的度数;(2)如图①,当60α=时,若点F 为AC 边上的动点,当①FBC 为何值时,四边形BFDE 为平行四边形?请说出你的结论并加以证明2.综合与实践问题:如图1,已知点G 在正方形ABCD 的对角线AC 上,GE ⊥BC ,GF ⊥CD ,垂足为F .证明与推断(1)①四边形CEGF 的形状是 ;②AGBE的值为 ; 【探究与证明】(2)在图1的基础上,将正方形CEGF 绕点C 按顺时针方向旋转α角(0°<α<45°),如图2所示,并说明理由;【拓展与运用】(3)如图3,在(2)的条件下,正方形CEGF 在旋转过程中,AG 和GE 的位置关系是 .3.若①ABC ,①ADE 为等腰三角形,AC =BC ,AD =DE ,将①ADE 绕点A 旋转,连接BE ,F 为BE 中点,连接CF ,DF .(1)若①ACB =①ADE =90°,如图1,试探究DF 与CF 的关系并证明; (2)若①ACB =60°,①ADE =120°,如图2,请直接写出CF 与DF 的关系.4.在平面直角坐标系中,点(0,0)O ,点A ,点)(0),30B m m AOB >∠=︒.以点O 为中心,逆时针旋转OAB ,得到OCD ,点,A B 的对应点分别为,C D .记旋转角为α.(1)如图①,当点C 落在OB 上时,求点D 的坐标;(2)如图①,当45α=︒时,求点C 的坐标;(3)在(2)的条件下,求点D 的坐标(直接写出结果即可).5.如图,30HAB ∠=︒,点B 与点C 关于射线AH 对称,连接AC .D 点为射线AH 上任意一点,连接CD .将线段CD 绕点C 顺时针旋转60°,得到线段CE ,连接BE .(1)求证:直线EB 是线段AC 的垂直平分线;(2)点D 是射线AH 上一动点,请你直接写出ADC ∠与ECA ∠之间的数量关系.6.已知如图,等腰△ABC 中,AB=AC ,△BAC=α(α>90︒),F 为BC 中点,D 为BC 延长线上一点,以点A 为中心,将线段AD 逆时针旋转α得到线段AE ,连接CE ,DE .(1)补全图形并比较△BAD 和△CAE 的大小; (2)用等式表示CE ,CD ,BF 之间的关系,并证明;(3)过F 作AC 的垂线,并延长交DE 于点H ,求EH 和DH 之间的数量关系,并证明.7.一副三角尺(分别含30°,60°,90°和45°,45°,90°)按如图所示摆放,边OB ,OC 在直线l 上,将三角尺ABO 绕点O 以每秒10°的速度顺时针旋转,当边OA 落在直线l 上时停止运动,设三角尺ABO 的运动时间为t 秒.(1)如图,①AOD = °= ′; (2)当t =5时,①BOD = °; (3)当t = 时,边OD 平分①AOC ;(4)若在三角尺ABO 开始旋转的同时,三角尺DCO 也绕点O 以每秒4°的速度逆时针旋转,当三角尺ABO 停止旋转时,三角尺DCO 也停止旋转.在旋转过程中,是否存在某一时刻使①AOC =2①BOD ,若存在,请直接写出的值;若不存在,请说明理由.8.如图,正方形ABCO 的边OA 、OC 在坐标物上,点B 坐标为()3,3.将正方形ABCO 绕点A 顺时针旋转角度()090αα︒<<︒,得到正方形ADEF ,ED 交线段OC 于点G ,ED 的延长线交线段BC 于点P .连AP 、AG .(1)求证:AOG①ADG;∠的度数;并判断线段OG、PG、BP之间的数量关系,说明理由;(2)求PAG(3)当12∠=∠时,求直线PE的解析式(可能用到的数据:在Rt中,30°内角对应的直角边等于斜边的一半).(4)在(3)的条件下,直线PE上是否存在点M,使以M、A、G为顶点的三角形是等腰三角形?若存在,请直接写出M点坐标;若不存在,请说明理由.9.如图,等腰Rt①ABC中,AB=AC,D为线段BC上的一个动点,E为线段AB上的一个动点,使得CD=.连接DE,以D点为中心,将线段DE顺时针旋转90°得到线段DF,连接线段EF,过点D作射线DR①BC交射线BA于点R,连接DR,RF.(1)依题意补全图形;(2)求证:①BDE①①RDF;(3)若AB=AC=2,P为射线BA上一点,连接PF,请写出一个BP的值,使得对于任意的点D,总有①BPF为定值,并证明.10.在①ABC中,AB=AC,①BAC=90°,D为平面内的一点.(1)如图1,当点D在边BC上时,BD=2,且①BAD=30°,AD=;(2)如图2,当点D在①ABC的外部,且满足①BDC﹣①ADC=45°,求证:BD AD;(3)如图3,若AB =4,当D 、E 分别为AB 、AC 的中点,把①DAE 绕A 点顺时针旋转,设旋转角为α(0<α≤180°)直线BD 与CE 的交点为P ,连接P A ,直接出①P AB 面积的最大值 .11.已知:①ABC 为等边三角形,且AB =4,点D 在直线BC 上运动,线段DA 绕着点D 顺时针旋转60°得到线段DE ,连接AE 和BE ,直线AE 交直线BC 于点F . (1)如图,当点D 在点C 左侧时,求证:CD =BE ;(2)若①ABC 的面积等于①ABF 面积的4倍,直接写出线段CD 的长;(3)在(2)的条件下,若点E 关于直线AD 的对称点为点G ,连接DG 交线段AC 于点M ,DE 交线段AB 于点N ,连接MN ,直接写出线段MN 的长.12.已知在①ABC 中,90ACB ∠=︒,AC =BC =(1)如图1,以点A 为原点,AB 所在直线为x 轴建立平面直角坐标系,直接写出点B ,C 的坐标; (2)如图2,过点C 作①MCN =45°交AB 于点M ,N ,且AM =1,求MN 的长度;(3)如图3,过点C 作①MCN =45°,当点M ,N 分布在点B 异侧时,线段AM ,BN 和MN 满足怎样的数量关系?并给予证明.13.如图,在①ABC 中,AC = BC ,①ACB = 90°,D 是线段AC 延长线上一点,连接BD ,过点A 作AE ①BD 于E .(1)求证:①CAE =①CBD ;(2)将射线AE 绕点A 顺时针旋转45°后,所得的射线与线段BD 的延长线交于点F ,连接CE . ①依题意补全图形;①用等式表示线段EF ,CE ,BE 之间的数量关系,并证明.14.把两个等腰直角ABC 和ADE 按如图1所示的位置摆放,将ADE 绕点A 按逆时针方向旋转,如图2,连接BD ,EC ,设旋转角为α(0360α︒<<︒).(1)如图1,BD 与EC 的数量关系是___________,BD 与EC 的位置关系是___________;(2)如图2,(1)中BD 和EC 的数量关系和位置关系是否仍然成立,若成立,请证明;若不成立请说明理由.(3)如图3,当点D 在线段BE 上时,BEC ∠=___________. (4)当旋转角α=__________时,ABD △的面积最大.15.如图,在Rt ①ABC 中,BC =4,AC =2,①ACB =90°,矩形BDEF 的边BF =1,BD =2,矩形BDEF 可以绕点B 在平面内旋转,连接AE 、BE 、CD . (1)证明:①ABE ①①CBD ;(2)当A 、E 、F 三点共线时,求CD 的长;(3)设AE 的中点为M ,连接FM ,直接写出FM 的最大值.16.在平面直角坐标系中,四边形AOBC 是矩形,点A 的坐标为()5,0,点B 的坐标为()0,3,以点A 为中心,顺时针旋转矩形AOBC ,得到矩形ADEF ,点O ,B ,C 的对应点分别为D ,E ,F .(1)如图①,当点D 落在BC 边上时,求点D 的坐标;(2)如图①,当点D 落在线段BE 上时,连接AB ,AD 与BC 交于点H . ①求证:ADB AOB ≅△△; ①求点H 的坐标.(3)点K 为矩形AOBC 对角线的交点,S 为KDE 得面积,直接写出S 的取值范围.17.如图,P 是正三角形ABC 内的一点,且6,8,10PA PB PC ===,若将PAC △绕点A 顺时针旋转后得到P AB '△,(1)求旋转角的度数;(2)求点P 与点P '之间的距离; (3)求APB ∠的度数.18.如图在平面直角坐标系中,点O 为坐标原点,直线y 34=-x +b 分别交x 轴,y 轴于点A 、B ,OA =4,①OBA 的外角平分线交x 轴于点D .(1)求点D 的坐标;(2)点P 是线段BD 上一点(不与B 、D 重合),过点P 作PC ①BD 交x 轴于点C ,设点P 的横坐标为t ,△BCD 的面积为S ,求S 与t 之间的函数解析式(不要求写出自变量t 的取值范围);(3)在(2)的条件下,PC 的延长线交y 轴于点E ,当PC =PB 时,将射线EP 绕点E 旋转45°交直线AB 于点F ,求F 点坐标.19.如图,在菱形ABCD 中,60ABC ∠=︒,E 为对角线AC 上一点,将线段DE 绕点D 逆时针旋转60︒,点E 的对应点为F ,连接BE ,AF ,CF .(1)求证:B ,C ,F 三点共线;(2)若点G 为BE 的中点,连接AG ,求证:2AF AG =.20.如图,在四边形ABCD中,BC=CD,△BCD=α°,△ABC+△ADC=180°,AC、BD交于点E.将△CBA 绕点C顺时针旋转α°得到△CDF(点B、A的对应点分别为点D、F).(1)画出旋转之后的图形(不要求写画法,保留画图痕迹);(2)求证:△CAB=△CAD;(3)若△ABD=90°,AB=3,BD=4,△BCE的面积为1S,△CDE的面积为2S,求1S:2S的值.参考答案:1.解:①将ABC绕点C顺时针旋转一定的角度α得到①DEC,E点在AC上,①CA=CD,①ECD=①BCA=30︒,(180︒−30︒)=75︒,①①CAD=①CDA=12又①①DEC=①ABC=90︒,①①ADE=90°-75︒=15︒;(2)①FBC=30︒时,四边形BFDE为平行四边形,①①FBC=①ACB=30︒,①①ABF=①A=60︒,①BF=CF=AF,①ABF是等边三角形,①BF=AB,①将ABC绕点C顺时针旋转60︒得到DEC,①DE=AB,BCE是等边三角形,①DEC=①ABC=90︒,①①CBE=①BEC=60︒,①①EBF=①EBC-①FBC=30︒,①①DEB+①EBF=180︒,①DE=BF,//DE BF,①四边形BFDE为平行四边形.2.①正方形;.理由:如图1中,∵四边形ABCD 是正方形,∴∠BCD =90°,∠BCA =45°,∵GE ⊥BC 、GF ⊥CD ,∴∠CEG =∠CFG =∠ECF =90°,∴四边形CEGF 是矩形,∠CGE =∠ECG =45°,∴EG =EC ,∴四边形CEGF 是正方形,∵AC BC ,,∴AG =AC ﹣CGBC ﹣EC ,∴AG BE(2)结论:AG ,理由:如图2中,连接CC ,∵四边形ABCD 是正方形,∴∠ABC =90°,AB =BC ,∴△ABC 为等腰直角三角形,∴AC BC由①得四边形GECF 是正方形,∴∠GEC =∠ECF =90°,GE =EC ,∴△EGC 为等腰直角三角形.∴CG CE∴AC CG BC EC=∴△ACG ∽△BCE ,∴AG CG BE EC∴线段AG 与BE 之间的数量关系为AG ;(3)如图3中,连接CG ,∵∠CEF =45°,点B 、E ,∴∠BEC =135°.∵△ACG ∽△BCE ,∴∠AGC =∠BEC =135°.∴∠AGF =∠AGC +∠CGF =135°+45°=180°,∴点A ,G ,F 三点共线,∴∠AGE =∠AGF ﹣∠EGF =180°﹣90°=90°,∴AG ⊥GE ,故答案为:AG ⊥GE .3.(1)DF =CF 且DF ①CF ;延长CF 至点M ,使CF =FM ,连接ME ,MD ,CD ,延长DE 交CB 延长线于点N ,如图1,①BF=EF,CF=FM,①BFC=①EFM,①①BFC①①EFM(SAS),①EM=BC=AC,①FME=①FCB,①BC①EM,①①N=①MEN,在四边形ACND中,①ACB=①ADE=90°,①①N+①CAD=360°-(①ACB+①ADE)=180°,又①①MEN+①MED=180°,①①MED=①CAD,又AD=DE,EM=AC,①①MED①①CAD(SAS),①DM=DC,①MDE=①CDA,①①MDC=①NDC+①MDE=①NDC+①CDA=①ADE=90°,①①DCM为等腰直角三角形,①点F是CM中点,CM=CF,DF①CF;①DF=12(2)DF①CF且CF;延长CF至点M,使CF=FM,连接ME,MD,CD,延长ED交BC延长线于点N,如图2,①BF=EF,CF=FM,①BFC=①EFM,①①BFC①①EFM(SAS),①EM =BC =AC ,①FME =①FCB ,①BC //EM ,①①N =①NER ,①①ACB =60°,①①ACN =120°,①①ADE =120°,①①ADN =60°,①①N +①CAD =360°-(①ACN +①ADN )=180°,①①DER +①DEM =180°,①①DEM =①CAD ,又 AD =DE ,EM =AC ,①①MED ①①CAD (SAS ),①DM =DC ,①MDE =①CDA ,①①DCM 为等腰三角形,①①CDM =①ADE =120°,①F 是CM 的中点,①DF ①CF①60CDF ∠=︒①30DCF ∠=︒①CD =2DE由勾股定理得,222CE DE CD +=①2224CE DE DE +=解得,CF (负值舍去)①DF ①CF 且CF .4.(1)如图,过点D 作DE OA ⊥,垂足为E .① 0A ,B m )0m (>),① AB OA ⊥,OA =AB m =.① 30AOB ∠=︒,① 22OB AB m ==.在Rt OAB 中,由222OA AB OB +=,得2234m m +=.解得1m =.① 1AB =,2OB =.① OCD 是由OAB 旋转得到的,① 2OD OB ==,30DOC AOB ∠=∠=︒.① 60DOE DOC BOA ∠=∠+∠=︒.① 9030ODE DOE ∠=︒-∠=︒.① 112OE OD ==. 在Rt OED 中,DE =① 点D 的坐标为(.(2)如图,过点C 作CT OA ⊥,垂足为T .由已知,得45COT ∠=︒.① 9045OCT COT ∠=︒-∠=︒.① OT CT=.① OCD是由OAB旋转得到的,① OC OA==在Rt OTC△中,由222T TO C OC+=,得OT CT=① 点C的坐标为.(3)如图①中,过点D作DJ①OA于点J,在DJ上取一点K,使得DK=OK,设OJ=m.①①DOC=30°,①COT=45°,①①DOJ=75°,①①ODJ=90°-75°=15°,①KD=KO,①①KDO=①KOD=15°,①①OKJ=①KDO+①KOD=30°,①OK=DK=2m,KJ,①OD2=OJ2+DJ2,①22=m2+(2m)2,解得m=,①OJ DJ①D⎫⎪⎪⎝⎭.5.(1)证明:连接AE,DB,CB①点B 与点C 关于射线AH 对称,30HAB ∠=︒ ①CD BD =,AC AB =①30HAB HAC ∠∠==︒①260CAB HAC ∠∠==︒①ABC 为等边三角形,60ACB ∠=︒ ①60DCE ∠=︒①DCE ACD ACB ACD ∠∠∠∠-=- ECA DCB ∠=∠①在ECA △和DCB 中,EC DC ECA DCB AC BC =⎧⎪∠=∠⎨⎪=⎩①()ECA DCB SAS ≅△△①BD EA =①DC BD EC ==,①AE EC =又AB BC =①EB 垂直平分AC(2)分两种情况来讨论:第一种情况,如图,当点D 在ABE △内部时:①点B 与点C 关于射线AH 对称,①90CFA ∠=︒①90ADC CFA DCB DCB ∠=∠+∠=︒+∠ ①ECA DCB ∠=∠①90ADC ECA ∠=︒+∠第二种情况,如图,当点D 在ABC 外部时: ①点B 与点C 关于射线AH 对称,①90CFA ∠=︒①90ADC CFA DCB DCB ∠=∠-∠=︒-∠ ①ECA DCB ∠=∠①90ADC ECA ∠=︒-∠6.如图,即为补全的图形,根据题意可知BAC DAE α∠=∠=,①BAC CAD DAE CAD ∠+∠=∠+∠,即BAD CAE ∠=∠.(2)由旋转可知AD AE =,①在BAD 和CAE 中AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩,①()BAD CAE SAS ≅,①BD CE =.①BD BC CD =+,①CE BC CD =+.①点F 为BC 中点,①2BC BF =,①2CE BF CD =+,即2CE CD BF -=.(3)如图,连接AF ,作AN DE ⊥,①AB=AC ,F 为BC 中点,①90AFD ∠=︒,12FAB FAC α∠=∠=. 根据作图可知90AND ∠=︒,①180AFD AND ∠+∠=︒,①A 、F 、D 、N 四点共圆,①AFN ADN ∠=∠.①AD AE =,AN DE ⊥,①EN DN =,11(180)9022AFN ADN DAE α∠=∠=︒-∠=︒-. ①11909022AFN FAC αα∠+∠=︒-+=︒. ①90AFH FAC ∠+∠=︒,且点H 在线段DE 上,①点H 与点N 重合,①EH DH =.7.(1)①180AOD AOB COD ∠=︒-∠-∠,3045AOB COD ∠=︒∠=︒,,①10510560=6300AOD '∠=︒=⨯.故答案为:105,6300;(2)当5t =时,即三角尺ABO 绕点O 顺时针旋转了51050⨯︒=︒,如图,ABO 即为旋转后的图形.由旋转可知50BOM ∠=︒,①180180455085BOD COD BOM ∠=︒-∠-∠=︒-︒-︒=︒,故答案为85;(3)当三角尺绕点O 顺时针旋转到如图所示的ABO 的位置时,边OD 平分①AOC .①224590AOC COD ∠=∠=⨯︒=︒,①90AOM ∠=︒①90903060BOM AOB ∠=︒-∠=︒-︒=︒, ①60610t ==; 故答案为:6;(4)①当边OA 落在直线l 上时停止运动时, ①180150=1510t -≤. 当OA 和OC 重合时,即有10418030t t +=︒-︒, 解得:757t =. ①当757t ≤时,1801030415014AOC t t t ∠=︒--︒-=︒-, 当757t >时,1030418014150AOC t t t ∠=+︒+-︒=-︒. 当OB 和OD 重合时,即有10418045t t +=︒-︒, 解得:13514t =①当13514t ≤时,1801045413514BOD t t t ∠=︒--︒-=︒-, 当13514t >时,1045418014225BOD t t t ∠=+︒+-︒=-︒. ①可根据2AOC BOD ∠=∠分类讨论,①当13514t ≤时,有15014=2(13514)t t ︒-︒-, 解得:607t =,符合题意; ①当13575147t <≤时,即有150142(14225)t t ︒-=-︒ 解得:1007t =,符合题意; ①当757t >时,即有141502(14225)t t -︒=-︒解得:150157t =>,不符合题意舍; 综上,可知当607t =或1007t =时,2AOC BOD ∠=∠. 8.(1)证明:在Rt△AOG 和Rt△ADG 中,AO AD AG AG=⎧⎨=⎩ ①AOG ①ADG (HL ).(2)在Rt ①ADP 和Rt ①ABP 中,AD AB AP AP=⎧⎨=⎩ ΔΔADP ABP ∴≅(HL ), 则DAP BAP ∠=∠;ΔΔAOG ADG ≅,1DAG ∴∠=∠;又190DAG DAP BAP ∠+∠+∠+∠=︒,2290DAG DAP ∴∠+∠=︒,45DAG DAP ∴∠+∠=︒,PAG DAG DAP ∠=∠+∠,45∴∠=︒PAG ;ΔΔAOG ADG ≅,DG OG ∴=,ΔΔADP ABP ≅,DP BP ∴=,PG DG DP OG BP ∴=+=+.(3)解:ΔΔAOG ADG ≅,AGO AGD ∴∠=∠,又190AGO ∠+∠=︒,290PGC ∠+∠=︒,12∠=∠,AGO PGC ∴∠=∠,又AGO AGD ∠=∠,AGO AGD PGC ∴∠=∠=∠,又180AGO AGD PGC ∠+∠+∠=︒,180360AGO AGD PGC ∴∠=∠=∠=︒÷=︒,12906030∴∠=∠=︒-︒=︒;∴在Rt ΔAOG 中,2,3AG OG OA ==,222AG OG OA =+∴222(2)3OG OG =+ 解得OGG ∴点坐标为0),3CG =在Rt ΔPCG 中,2PG CG =,222PG CG PC =+∴222(2)CG CG PC =+, ∴3PC =,P ∴点坐标为:(3,3),设直线PE 的解析式为:y kx b =+,则033b k b +=+=⎪⎩,解得3k b ⎧=⎪⎨=-⎪⎩∴直线PE 的解析式为3y =-.(4)①如图1,当点M 在x 轴的负半轴上时,AG MG =,点A 坐标为(0,3),∴点M 坐标为(0,3)-.①如图2,当点M 在EP 的延长线上时,由(3),可得60AGO PGC ∠=∠=︒,EP ∴与AB 的交点M ,满足AG MG =,A 点的横坐标是0,GM ∴的横坐标是3,∴点M 坐标为3).综上,可得点M 坐标为(0,3)-或3).9.(1)如图,(2)DR ①BC90RDB ∴∠=︒将线段DE 顺时针旋转90°得到线段DF ,90,EDF ED FD ∴∠=︒=BDR EDF ∴∠=∠即BDE EDR EDR RDF ∠+∠=∠+∠BDE RDF ∴∠=∠ ABC 是等腰直角三角形90BDR ∠=︒45BRD ∴∠=︒BRD ∴是等腰直角三角形BD DR ∴=∴①BDE ①①RDF ;(2)如图,当24PB AB ==时,使得对于任意的点D ,总有①BPF 为定值,证明如下,ABC 是等腰直角三角形,2AB AC ==BC ∴=DC =设DE a =,则CD =,①BDE ①①RDF ,DR BD ∴==,FR BR a == ABC 是等腰直角三角形,45EBD ∴∠=︒DR BC ⊥45BRD ∴∠=︒BDR ∴是等腰直角三角形,42BR a ∴==-()4422PR BP BR a a ∴=-=--=①BDE ①①RDF ,45FRD EBD ∴∠=∠=︒90BRF BRD DRF ∴∠=∠+∠=︒1tan 22RF a BPF RP a ∴∠=== BPF ∴∠为定值10.证明:(1)如图1,将①ABD 沿AB 折叠,得到①ABE ,连接DE ,①AB =AC ,①BAC =90°,①①ABC =45°,①将①ABD 沿AB 折叠,得到①ABE ,①①ABD ①①ABE ,①AE =AD ,BE =BD ,①ABE =①ABD =45°,①BAD =①BAE =30°,①①DBE =90°,①DAE =60°,且AD =AE ,BE =BD ,①①ADE 是等边三角形,DE =,①AD =DE =故答案为:(2)如图2,过点A 作AE ①AD ,且AE =AD ,连接DE ,①AE ①AD ,①①DAE =①BAC =90°,①①BAE =①DAC ,且AD =AE ,AB =AC ,①①BAE ①①CAD (SAS )①①ACD=①ABE,①①ACD+①DCB+①ABC=90°,①①DCB+①ABC+①ABE=90°,①①BOC=90°,①AE=AD,AE①AD,①DE=,①ADE=45°,①①BDC﹣①ADC=45°,①①BDC=①ADC+45°=①EDC,且DO=DO,①DOB=①DOE=90°,①①DOB①①DOE(ASA)①BD=DE,①BD=;(3)如图3,连接PC交AB于G点①①DAE绕A点旋转①AD=AE,AB=AC,①①DAE=①BAC=90°①①DAB=①EAC①①DAB①①EAC①①DBA=①ECA①①PGB=①AGC①①BPC=①GAC=90°①①BPC为直角三角形①点P在以BC中点M为圆心,BM为半径的圆上,连接PM交AB所在直线于点N,当PM①AB时,点P到直线AB的距离最大,①①BAC=90°①A 、P 、B 、C 四点共圆①PM ①AB ,①N 是AB 的中点①M 是BC 的中点①MN =122AC = ①AB =AC =4,①CB =22442,①BM =PM =12BC =,①PN =2 ,①点P 到AB 所在直线的距离的最大值为:PN =2 . ①①P AB的面积最大值为12AB ×PN =4. 11.(1)证明:ABC 是等边三角形60,BAC AB AC ∴∠=︒=线段DA 绕着点D 顺时针旋转60°得到线段DE , 60,DAE DA DE ∴∠=︒=ADE ∴是等边三角形DAC DAE CAE BAC CAE EAB ∴∠=∠-∠=∠-∠=∠ 即DAC EAB ∠=∠∴ADC AEB △≌△∴CD BE =(2)ABC 是等边三角形,AB =4,则60BAC ∠=︒过点A 作AM BC ⊥,则1302BAH BAC ∠=∠=︒ Rt ABH 中,122BH AB ==AH ∴=142ABC S ∴=⨯⨯△①ABC 的面积等于①ABF 面积的4倍ABF S ∴=△11sin 60422ABF S BF AB =⋅⨯︒=⨯=△ 1BF ∴= ①当F 点在B 点的左侧时,如图,60ACB ABC ∠=∠=︒120ACD ∴∠=︒ADC AEB △≌△ADC AEB ∴∠=∠,BE DC =60ABC ∠=︒60EBF ABE ABC ∴∠=∠-∠=︒60FBE FCA ∴∠=∠=︒又AFC EFB ∠=∠AFC EFB ∴∽FB BE FC AC∴= 4,1AC BC AB BF ====413FC ∴=-=14433FB AC BE FC ⋅⨯∴=== 43CD EB ∴==①当F 点在B 点的右侧时,如图,ADC AEB △≌△60ACD EBA ∴∠=∠=︒60ABC ∠=︒18060EBF ABC ABE ∴∠=︒-∠-∠=︒BE AC ∴∥FEB FAC ∴∽FB BE FC AC∴= 1,4,145FB AC FC BC BF ===+=+=45FB AC BE FC ⨯∴== 45CD EB ∴==综上所述CD 的长为43或45(3)如图,点E 关于直线AD 的对称点为点G ,ADE 是等边三角形60ADE ADG ∴∠=∠=︒,AE AD =AEN ADM ∴∠=∠60=︒60,60MAD DAB CAB EAB DAB DAE ∠+∠=∠=︒∠+∠=∠=︒MAD NAE ∴∠=∠MAD NAE ∴=AM AN ∴=60MAN ∠=︒AMN ∴是等边三角形MN AN ∴=由(2)可得45BE =,FEB FAC ∽ 445525EF BF BF AF FC BC BF ∴====+过点A 作AH BC ⊥,则AH =,2CH HB ==,3HF HB BF =+=AF ∴=425EF AF ∴==AE AF EF ∴=-==60,ABE AEN EAB NAE ∠=∠=︒∠=∠∴BEA ENA ∽BE BA EN EA∴= 则BE EA EN BA ⨯=60,ADN ABE AND ENB ∠=∠=︒∠=∠ADN EBN ∴∽AD AN EB EN∴= 即AN EB EN AD ⨯= BE EA AN EB BA AD ⨯⨯∴= EA AD AN AB⨯∴=AE AD =,4AB =2926142500AN ⎝⎭∴== 即92612500MN =12. 解:(1)如图1,过点C 作CD ①x 轴于D ,①在①ABC 中,90ACB ∠=︒,AC =BC=①4AB = ,①点B (4,0),①CD ①AB ,①AD =CD =12AB =12×4=2,①点C 的坐标为(2,2);(2)如图,把①ACM 绕点C 逆时针旋转90°得到①BCM ′,连接M ′N ,①90ACB ∠=︒,AC =BC ,①①ABC 是等腰直角三角形,①①CAB =①CBA =45°,由旋转的性质得,45AM BM CM CM CAM CBM ACM BCM '''==∠=∠=︒∠=∠'、、,,①454590M BN ABC CBN ∠'=∠+∠'=︒+︒=︒ ,①①MCN =45°,①90904545M CN BCN BCM BCN ACM MCN ∠'=∠+∠'=∠+∠=︒-∠=︒-︒=︒ , ①MCN M CN ∠=∠' ,在①MCN 和①M ′CN 中,①CM CM MCN M CN CN CN ''=⎧⎪∠=∠⎨⎪=⎩,①MCN M CN SAS '≌(), ①MN M N =' ,在Rt M NB ' 中,222BM BN M N +='' ,①222AM BN MN += ,1AM =,①3MN BN AB AM +=-=,1BM '= ,设MN x =,则BN =3x -,()22213-x x ∴+=,解得:53x =, 53MN ∴=; (3)AM 2+BN 2=MN 2,证明如下:如图3,把①BCN 绕点C 顺时针旋转90°得到ACN ' ,①90ACB ∠=︒,AC =BC ,①①ABC 是等腰直角三角形,①①CAB =①CBA =45°,由旋转的性质得,135AN BN CN CN CAN CBN '='=∠'=∠=︒,, , ①1354590MAN ∠'=︒-︒=︒,①点N '在y 轴上,①①MCN =45°,①904545MCN ∠'=︒-︒=︒,①MCN MCN ∠=∠' ,在①MCN 和①MCN ′中,①CN CN MCN MCN CM CM =''⎧⎪∠=∠⎨⎪=⎩,①()MCN MCN SAS ≅' ,①MN MN =' ,在Rt AMN ' 中,222AM AN MN +''= ,①222AM BN MN += .13.(1)如图1,①90ACB ∠=︒,AE BD ⊥,①90ACB AEB ∠=∠=︒,又①12∠=∠,①CAE CBD ∠=∠;(2)①补全图形如图2;①EF BE =.理由如下:在AE 上截取AM ,使AM BE =.又①AC CB =,CAE CBD ∠=∠,①ΔΔACM BCE ≌,①CM CE =,ACM BCE ∠=∠,又①90ACB ACM MCB ∠=∠+∠=︒,①90MCE BCE MCB ∠=∠+∠=︒,①ME =,又①射线AE 绕点A 顺时针旋转45︒,后得到AF ,且90AEF ∠=︒,①EF AE AM ME BE ==+=.14.解:(1)如图:BD 与EC 的数量关系是相等,理由如下:,AB AC AD AE ==,AB AD AC AE ∴-=-,BD EC ∴=;BD 与EC 的位置关系是垂直,理由如下:AB AC ⊥, 又点,D E 分别在,AB AC 上,BD EC ⊥;(2)成立:理由分别如下:如图:根据旋转的性质可得:,,AD AE AB AC BAD CAE ==∠=∠, ()ABD ACE SAS ∴≌,BD EC ∴=,作BD 的延长线交EC 于点F ,交AC 于点G ,如下图:由ABD ACE SAS △≌△()可知,ABD ACE ∠=∠,AGB FGC ∠=∠,AGB FGC ∴∽,90GAB GFC ∴∠=∠=︒,GF CF ∴⊥,即BD EC ⊥;(3)当点D 在线段BE 上时,90BAD BAC DAC DAC ∠=∠-∠=︒-∠,90CAE DAE DAC DAC ∠=∠-∠=︒-∠,BAD CAE ∴∠=∠,又AB AC =,AD AE =,()BAD CAE SAS ∴∆≅∆,180135ADB AEC ADE ∴∠=∠=︒-∠=︒,451354590BEC AEC ∴∠=∠-︒=︒-︒=︒;(4)由题意知,点D 的轨迹在以A 为圆心,AD 为半径的圆, 在ABD ∆中,当AB 为底时,点D 到AB 的距离最大时,ABD ∆的面积最大, 故如图所示,当AD AB ⊥时,ABD ∆的面积最大,∴旋转角为90︒或270︒,故答案为:90︒或270︒.15.解:(1)在Rt ①ABC 中,BC =4,AC =2,①ACB =90°,AB ∴=在Rt ①BDE 中,BF =1,BD =2,BE ∴=121tan ,tan 242ED AC EBD ABC BD BC ∴∠==∠=== EBD ABC ∴∠=∠EBD ABD ABC ABD ∴∠-∠=∠-∠ABE CBD ∴∠=∠24AB BE BC BD ===∴①ABE ①①CBD ;(2)当A 、E 、F 三点共线时,分两种情况讨论: ①90AED ∠=︒,如图,在Rt ①AFB 中,222AB BF AF =+21(2)20AE ∴++=2(2)19AE ∴+=2AE ∴=①ABE ①①CBDAE CD ∴=CD ∴= ①如图,90AFB ∠=︒在Rt ①AFB 中,22220119AF AB BF =-=-=AF ∴=2AE AF EF ∴=+=EBD ABC ∠=∠90EBF ABC ∴∠+∠=︒EBF ABC FBC DBF FBC ∴∠+∠+∠=∠++∠24AB BE BC BD ===∴①ABE ①①CBDAE CD ∴=CD ∴=综上所述,CD =CD =(3)如图,延长EF 至点G ,使得EF =FG ,连接BG ,此时①BEG 是等腰三角形, 当G B A 、、三点共线,此时FM 最大//BD GEG DBA ∴∠=∠9090180DBA FBD GBF G FBD GBF ∴∠+∠+∠=∠+∠+∠=︒+︒=︒, 此时,G B A 、、三点共线,F M 、分别是BE 、AE 的中点,FM ∴是①EGA 的中位线,111==()222FM AG AB BG ∴+==16.解:(1)如图①中,(5,0)A ,(0,3)B ,5OA ∴=,3OB =,四边形AOBC 是矩形,3AC OB ∴==,5OA BC ==,90OBC C ∠=∠=︒,矩形ADEF 是由矩形AOBC 旋转得到,5AD AO ∴==,在Rt ADC 中,4CD ,1BD BC CD ∴=-=,(1,3)D ∴.(2)①如图①中,由四边形ADEF 是矩形,得到90ADE ∠=︒,点D 在线段BE 上,90ADB ∴∠=︒,由(①)可知,AD AO =,又AB AB =,90AOB ∠=︒,()Rt ADB Rt AOB HL ∴≌.①如图①中,由ADB AOB ∆≅∆,得到BAD BAO ∠=∠,又在矩形AOBC 中,//OA BC ,CBA OAB ∴∠=∠,BAD CBA ∴∠=∠,BH AH ∴=,设AH BH m ==,则5HC BC BH m =-=-,在Rt AHC 中,222AH HC AC =+,2223(5)m m ∴=+-,175m ∴=, 175BH ∴=, 17(5H ∴,3). (3)如图①中,当点D 在线段BK 上时,DEK ∆的面积最小,最小值113(522DE DK ==⨯⨯=当点D 在BA 的延长线上时,①D E K ''的面积最大,最大面积113(522D E KD =⨯''⨯'=⨯⨯=. 17.解:(1)∵P AB ∆'由PAC ∆绕点A 旋转得到,∴P AB PAC ∆≅∆',∴P AB PAC ∠=∠',P A PA '=,∵60BAC PAC PAB ∠=∠+∠=︒,∴60P AB PAB ∠+∠='︒,即:60P AP ∠='︒,∴旋转角度数为60︒;(2)如图所示,连接P P ',∵60P AP ∠='︒,P A PA '=,∴P AP ∆'为等边三角形,∴6P P PA '==,即点P 与点P '之间的距离为6;(3)在P PB ∆'中,由(1)得:10P B PC ='=,6P P '=,8PB =,∴222P B P P PB ''=+,∴P PB ∆'为直角三角形,∴90P PB ∠='︒,由(1)得60APP ∠='︒,∴150APB P PB APP ∠=∠+='∠'︒,∴APB ∠的度数为150︒.18.( 1 )①OA =4,①A (4,0),把A (4,0)代入34y x b =-+, 得:b =3,过点D 作DH ①AB 于点H ,则DH =DO ,BH =BO ,①当x =0时,y =3,①B (0,3),①OA =4,BO =BH =3,在Rt OAB 中,①5AB ,AD =DO +OA =DH +4, ①1122ABD S AD OB AB DH =⋅⋅=⋅⋅, ①()1143522DH DH ⨯+⨯=⨯⋅, 解得:DH =6,①OD =6,①点D 的坐标为(﹣6,0),(2)过点P 作PE ①OD 于点E ,则△DPE ①①DBO ,①点P 在直线BD 上,且点P 的横坐标为t ,①DE =t +6,①OD =6,OB =3,在Rt OBD △中,BD ==①①DPE ①①DBO , ①DP DE DB DO =,66t +,解得:)6DP t =+, ①PC ①BD , ①①PDC ①①ODB , ①PC DP OB OD=,①)6236t PC +=,①)6PC t =+,①)()1115154566=22884BCD S BD PC t t t =⋅⋅=⨯+=++; (3)作PH 垂直于x 轴于点H ,设射线EP 绕点E 逆时针旋转45°交x 轴于点K ,顺时针旋转45°交x 轴于点G .①①BPC =90°,①BOC =90°①B ,P ,C ,O 四点共圆,①PC PB =,①45PCB PBC ∠=∠=︒,①①POC =①PBC =45°,①90PHO ∠=︒,①45HPO POC ∠=∠=︒,①PH =HO ,①DH =6﹣HO =6﹣PH ,①DHP DOB ∽, ①663PH DO PH BO -==, 得PH =2,①HC =CO =1,①OE =2,①点(0,2)E -,①①KEP =①DBC ,①PEB =①BDC ,①①KEP +①PEB =①DBC +①BDC ,即①KEO =①BCO ,①OE :GK =CO :BO =1:3,①GK =6,①K (﹣6,0),设直线KE 的解析式为:y kx b =+,则62y k b b =-+⎧⎨-=⎩,解得:132k b ⎧=-⎪⎨⎪=-⎩,, ①直线KE 为:y 13=-x ﹣2, 联立方程组:123334y x y x ⎧=--⎪⎪⎨⎪=-+⎪⎩解得x =12,y =﹣6,①F 1(12,﹣6),①①KEP +①PEG =90°,①①DEG =90°,①①OEG =①ODE ,①OG :OE =OE :OD =1:3,①OG 23=; ①G (23,0), 设直线EG 的解析式为:y mx n =+, 则20=32m n n⎧+⎪⎨⎪-=⎩,解得:32m n =⎧⎨=-⎩, ①直线EG 的解析式为:y =3x ﹣2, 联立方程组:32334y x y x =-⎧⎪⎨=-+⎪⎩, 解得x 43=,y =2, ①F 2(43,2), 综上所述:F 的坐标为(12,﹣6)或(43,2). 19.证明:(1)①四边形ABCD 是菱形,①ABC =60°, ①AB =BC =AD =CD ,①ADC =①ABC =60°,①①ADC 是等边三角形,①AD =AC =AB =BC ,①①ACB 是等边三角形,①①ACB =①ACD =60°,①①ADC =①EDF =60°,①①ADE =①CDF ,①将线段DE 绕点D 逆时针旋转60︒,点E 的对应点为F , ①DE DF =,在①ADE 和①CDF 中,DA DC ADE CDF DE DF =⎧⎪∠=∠⎨⎪=⎩①①ADE ①①CDF (AAS ),①60DCF DAE ∠=∠=︒,①180DCF BCD ∠+∠=︒,①B ,C ,F 三点共线;(2)如图,过点B 作BH ①AC ,交AG 的延长线于点H ,①BH ①AC ,①①H =①GAE ,①ABH +①BAC =180°,①①ABH =120°=①ACF ,①点G 为BE 的中点,①BG =GE ,在①AGE 和①HGB 中,H GAE AGE BGH BG GE ∠=∠⎧⎪∠=∠⎨⎪=⎩,①①AGE ①①HGB (AAS ),由(1)得AE CF =,①AE =BH =CF ,AG =GH =12AH ,在①ABH 和①ACF 中,AB AC ABH ACF BH CF =⎧⎪∠=∠⎨⎪=⎩,①①ABH ①①ACF (SAS ),①AF =AH ,①AF =2AG .20.(1)如图①CDF 即为旋转之后的图形;(2)证明:由旋转旋转可知:①CAB ①①CFD ,①①CDF =①CBA ,①F =①CAB ,CA =CF ,①①CBA +①CDA =180°,①①CDF +①CDA =180°,①A 、D 、F 三点共线,①AC =CF ,①①F =①CAD ,①①CAB =①CAD ;(3)过点E 作EM ①AF 于点M ,过点C 作CN ①BD 于点N , ①①ABE =①AME =90°,在①ABE 和①AME 中,EAB EAM ABE AME AE AE ∠=∠⎧⎪∠=∠⎨⎪=⎩, ①①ABE ①①AME (AAS ),①AM =AB =3,BE =ME ,①①ABD =90°,AB =3,BD =4,①5AD ==,①DM =2,设BE EM x ==,则4DN x =-,①()222x 24x +=-,解得 1.5x =,①BE =1.5,DE =2.5, ①12113::225S S BE CN DE CN =⋅⋅=.。
中考数学专题复习旋转的综合题及详细答案

【答案】(1)证明见解析;(2)45°或 135°;(3) . 【解析】 试题分析:(1)根据正方形的性质可得 AB=AD,AE=AG,∠ BAD=∠ EAG=90°,再求出 ∠ BAE=∠ DAG,然后利用“边角边”证明△ ABE 和△ ADG 全等,根据全等三角形对应边相等 证明即可. (2)当点 C 在直线 BE 上时,可知点 E 与 C 重合或 G 点 C 与重合,据此求解即可.
∵ PE2+AE2=AP2, ∴ △ PEA 是直角三角形 ∴ ∠ PEA=90°, ∴ ∠ CEA=135°, 又∵ △ CPB≌ △ CEA ∴ ∠ BPC=∠ CEA=135°. 【点睛】 考点:几何变换综合题;平行线平行线分线段成比例.
6.如图,在 Rt△ ABC 中,∠ ACB=90°,∠ A=30°,点 O 为 AB 中点,点 P 为直线 BC 上的动 点(不与点 B、点 C 重合),连接 OC、OP,将线段 OP 绕点 P 顺时针旋转 60°,得到线段 PQ,连接 BQ. (1)如图 1,当点 P 在线段 BC 上时,请直接写出线段 BQ 与 CP 的数量关系. (2)如图 2,当点 P 在 CB 延长线上时,(1)中结论是否成立?若成立,请加以证明;若 不成立,请说明理由; (3)如图 3,当点 P 在 BC 延长线上时,若∠ BPO=15°,BP=4,请求出 BQ 的长.
【答案】(1)详见解析;(2)FE·sin( -90°) 【解析】 【分析】 (1)由四边形 ABCD 是平行四边形得 AF∥ BE,所以∠ FAE=∠ BEA,由折叠的性质得 ∠ BAE=∠ FAE,∠ BEA=∠ FEA,所以∠ BAE=∠ FEA,故有 AB∥ FE,因此四边形 ABEF 是平行四 边形,又 BE=EF,因此可得结论; (2)根据点 M 在线段 BE 上和 EC 上两种情况证明∠ ENG=90°- ,利用菱形的性质得到
最新中考数学几何旋转综合题专题练习(含答案)
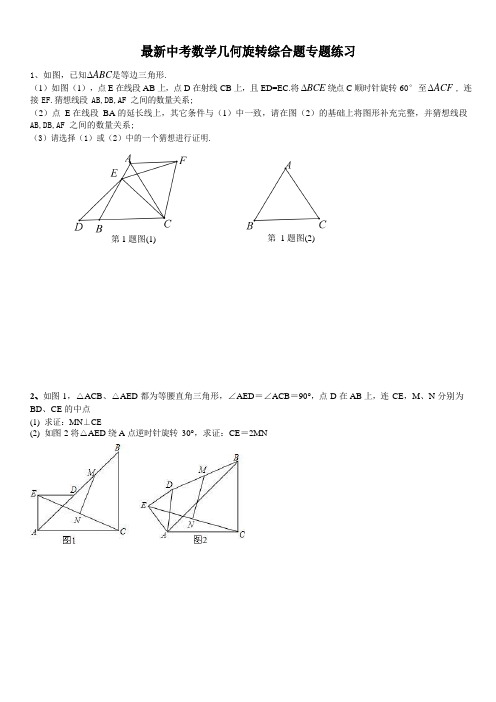
最新中考数学几何旋转综合题专题练习1、如图,已知∆ABC是等边三角形.(1)如图(1),点E 在线段AB 上,点D 在射线CB 上,且ED=EC.将∆BCE 绕点C 顺时针旋转60°至∆ACF , 连接 EF.猜想线段 AB,DB,AF 之间的数量关系;(2)点E 在线段BA 的延长线上,其它条件与(1)中一致,请在图(2)的基础上将图形补充完整,并猜想线段AB,DB,AF 之间的数量关系;(3)请选择(1)或(2)中的一个猜想进行证明.第 1 题图(2)第1 题图(1)2、如图1,△ACB、△AED 都为等腰直角三角形,∠AED=∠ACB=90°,点D 在AB 上,连CE,M、N 分别为BD、CE 的中点(1)求证:MN⊥CE(2)如图2 将△AED 绕A 点逆时针旋转30°,求证:CE=2MNPA C 1 1O C图 3B 1A 1O图 2C A 13、在等腰 Rt △A B C 和等腰 Rt △A 1B 1C 1 中,斜边 B 1C 1 中点 O 也是 B C 的中点。
(1)如图 1,则 AA 1 与 CC 1 的数量关系是 ;位置关系是 。
(2)如图 2,将△A 1B 1C 1 绕点 O 顺时针旋转一定角度,上述结论是否仍然成立,请证明你的结论。
(3)如图 3,在(2)的基础上,直线 AA 1、CC 1 交于点 P ,设 A B =4,则 P B 长的最小值是。
AAABB 1O图 1BCC 1C B1B 14、已知,正方形 ABCD 的边长为 4,点 E 是对角线 BD 延长线上一点,AE =BD .将△ABE 绕点 A 顺时针旋转α度 (0°<α<360°)得到△AB ′E ′,点 B 、E 的对应点分别为 B ′、E ′ (1) 如图 1,当α=30°时,求证:B ′C =DE(2) 连接 B ′E 、DE ′,当 B ′E =DE ′时,请用图 2 求α的值 (3) 如图 3,点 P 为 AB 的中点,点 Q 为线段 B ′E ′上任意一点,试探究,在此旋转过程中,线段 PQ 长度的取值范围为14 PF ABFPF5、如图 P 为等边△ABC 外一点,AH 垂直平分 PC 于点 H ,∠BAP 的平分线交 PC 于点 D (1) 求证:DP =DB(2) 求证:DA +DB =DC(3) 若等边△ABC 边长为 ,连接 BH ,当△BDH 为等边三角形时,请直接写出 CP 的长度为6、如图,四边形 ABCD 为正方形,△BEF 为等腰直角三角形(∠BFE=900,点 B 、E 、F ,按逆时针排列),点 P 为 DE 的中点,连 PC ,PF(1)如图①,点 E 在 BC 上,则线段 PC 、PF 有何数量关系和位置关系?请写出你的结论,并证明.(2)如图②,将△BEF 绕点 B 顺时针旋转 a(O<a<450),则线段 PC ,PF 有何数量关系和位置关系?请写出你的结论,并证明.(3)如图③,若 AB=1,△AEF 为等腰直角三角形,且∠A EF=90°,△AEF 绕点 A 逆时针旋转过程中,能使点 F 落在 BC 上,且 AB 平分 EF ,直接写出 AE 的值是 .ADADDEBCBECE图① 图② 图③C2 7、已知等腰 Rt △ABC 和等腰 Rt △EDF ,其中 D 、G 分别为斜边 AB 、EF 的中点,连 CE ,又 M 为 BC 中点,N 为 CE 的中点,连 MN 、MG(1) 如图 1,当 DE 恰好过 M 点时,求证:∠NMG =45°,且 MG = MN(2) 如图 2,当等腰 Rt △EDF 绕 D 点旋转一定的度数时,第(1)问中的结论是否仍成立,并证明 (3) 如图 3,连 BF ,已知 P 为 BF 的中点,连 CF 与 PN ,直接写出PN=CF8、已知:如图,在 Rt △ABC 中,AC=BC ,CD ⊥AB 于 D ,AB=10,将 CD 绕着 D 点顺时针旋转 a (0°<a<90°) 到 DP 的位置,作 PQ ⊥CD 于 Q ,点 I 是△PQD 角平分线的交点,连 IP ,IC ,(1)如图 1,在 PD 旋转的过程中,线段 IC 与 IP 之间是否存在某种确定不变的关系?请证明你的猜想。
中考数学旋转(大题培优易错难题)及答案

一、旋转真题与模拟题分类汇编〔难题易错题〕1 .在由△ ABC中,AB=BC=5, Z B=90%将一块等腰直角三角板的直角顶点放在斜边AC的中点.处,将三角板绕点0旋转,三角板的两直角边分别交AB, BC或其延长线于E, F两点,如图①与②是旋转三角板所得图形的两种情况.〔1〕三角板绕点0旋转,△OFC是否能成为等腰直角三角形?假设能,指出所有情况〔即给出△OFC是等腰直角三角形时BF的长〕:假设不能,请说明理由:〔2〕三角板绕点0旋转,线段0E和OF之间有什么数量关系?用图①或②加以证实:〔3〕假设将三角板的直角顶点放在斜边上的点P处〔如图③〕,当AP:AC=L4时,PE和PF 有怎样的数量关系?证实你发现的结论.【解析】【小题1】由题意可知,①当F为BC的中点时,由AB=BC=5,可以推出CF和OF的长度,即可推出BF的长度,②当B与F重合时,根据直角三角形的相关性质,即可推出OF 的长度,即可推出BF 的长度;【小题2】连接0B,由己知条件推出△ OEB合么OFC,即可推出OE=OF:【小题3]过点P做PM±AB, PN±BC,结合图形推出△ PNF~ & PME, △ APM- △ PNC,继而推出PM: PN=PE: PF, PM: PN=AP: PC,根据条件即可推出PA: AC=PE: PF=1: 4.2 .在平面直角坐标中,边长为2的正方形OA8C的两顶点A、C分别在y轴、X轴的正半轴上,点.在原点.现将正方形.48c绕.点顺时针旋转,当A点一次落在直线y=x上时停止旋转,旋转过程中,A5边交直线〕'='于点M边交汇轴于点N 〔如图〕.〔1〕求边04在旋转过程中所扫过的面积;〔2〕旋转过程中,当和AC平行时,求正方形O43C旋转的度数:(3)设AM3N的周长为P,在旋转正方形O45C的过程中,〃值是否有变化?请证实你的结论. 【答案】(1)n/2(2) 22.5.⑶周长不会变化,证实见解析【解析】试题分析:(1)根据扇形的面积公式来求得边0A在旋转过程中所扫过的面积:(2)解决此题需利用全等,根据正方形一个内角的度数求出NAOM的度数:(3)利用全等把△ MBN的各边整理到成与正方形的边长有关的式子.试题解析:(1) TA点第一次落在直线y=x上时停止旋转,直线y=x与y轴的夹角是45.,/. 0A 旋转了45°.0A在旋转过程中所扫过的面积为土」=-.360 2(2) •/ MNII AC,・•. Z BMN=Z BAC=45% Z BNM=Z BCA=45°./. Z BMN=Z BNM. /. BM=BN.又YBA=BC, A AM=CN.又;OA=OC, Z OAM=Z OCN, △ OAM合△ OCN./. Z A0M=Z CON=- (Z AOC-Z MON ) =- (90°-45°) =22.5°.2 2旋转过程中,当MN和AC平行时,正方形OABC旋转的度数为45.-22.5.=22.5..(3)在旋转正方形OABC的过程中,p值无变化.证实:延长BA交y轴于E点,那么N AOE=45°-Z AOM, Z CON=90°-45°-Z AOM=450-Z AOM,・•. Z AOE=Z CON.又:OA=OC, Z OAE=180o-90o=90°=Z OCN.:, & OAE2 A OCN.「.OE=ON, AE=CN.文:Z MOE=Z MON=45°, 0M=0M,「・△ OME2△ OMN. /. MN=ME=AM+AE.・•, MN=AM+CN,/. p=MN+BN+BM=AM+CN+BN+BM=AB+BC=4...・在旋转正方形OABC的过程中,p值无变化.考点:旋转的性质.3.己知:如图1,将两块全等的含30.角的直角三角板按图所示的方式放置,N 84c=N 8MiC=30°,点8, C, 8]在同一条直线上.(1)求证:AB=2BC(2)如图2,将△ABC绕点C顺时针旋转凌.(0Va<180),在旋转过程中,设AB与AiC. AiB】分别交于点D、E, AC与A】Bi交于点F.当骏等于多少度时,AB与A X B工垂直?请说明理由.〔3〕如图3,当△ABC绕点C顺时针方向旋转至如下图的位置,使ABIICBi,AB与AK 交于点D,试说明A1D=CD.【答案】〔1〕证实见解析〔2〕当旋转角等于30.时,AB与AiBa垂直.〔3〕理由见解析【解析】试题分析:⑴由等边三角形的性质得八8=88],又由于8B1=2BC,得出A8=28C;⑵利用AB与AiBi垂直得N AiED=90°,那么N AQE=90°-N Ai=60°,根据对顶角相等得Z BDC=60.,由于N B=60°,利用三角形内角和定理得N A1CB=180°-Z BDC-Z B=60°,所以N ACA】=90.-/AiCB=30.,然后根据旋转的定义得到旋转角等于30.时,AB与AiBi垂直:⑶由于ABIICB], N ACBF90.,根据平行线的性质得N ADC=90.,在由△ ADC中,根据含30度的直角三角形三边的关系得到CD=L AC,再根据旋转的性质得AC=AC 所以2CD=-AiC,贝ljAiD=CD.2试题解析:(1).「△488]是等边三角形;AB=BBi•/ 881=2BCAB=2BC〔2〕解:当AB 与AiBi垂直时,Z AiED=90%・•, Z A1DE=90°-Z A F900-30°=60°,Z B=60% ?. Z BCD=60%/. Z ACAi=90°-60c=30°,即当旋转角等于30.时,AB与A】B,垂直.〔3〕 ABII CBi, Z ACBi=90%/. Z CDB=90°,即CD 是△ ABC 的高,设BC=.,AC=.,贝lj由〔1〕得AB=2fl, ,7 ^WRC = — BCxAC = — ABxCD.UBC 2 2即[=k2axeO2 2CD = -b 9即CD=-!-AiC,2 2/. AiD=CD.【点睛】此题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中央的距离相等: 对应点与旋转中央的连线段的夹角等于旋转角.也考查了含30度的直角三角形三边的关系.4.:在△ ABC中,BC=a, AC=b,以AB为边作等边三角形ABD.探究以下问题:〔1〕如图1,当点D与点C位于直线AB的两侧时,a=b=3,且N ACB=60.,那么CD=—: 〔2〕如图2,当点D与点C位于直线AB的同侧时,a=b=6,且N ACB=90.,那么CD=_;〔3〕如图3,当NACB 变化,且点D与点C位于直线AB的两侧时,求CD的最大值及相应的N ACB的度数.【答案】〔1〕3\产:〔2〕 3、伸-3\4 ㈠〕当NA CB=120.时,CD有最大值是a+b.【解析】【分析】〔1〕a=b=3,且NACB=60.,△ ABC是等边三角形,且CD是等边三角形的高线的2倍,据此即可求解;〔2〕 a=b=6,且NACB=90.,△ ABC是等腰直角三角形,且CD是边长是6的等边三角形的高长与等腰直角三角形的斜边上的高的差:〔3〕以点D为中央,将△ DBC逆时针旋转60.,那么点B落在点A,点C落在点E.连接AE, CE,当点E、A、C在一条直线上时,CD有最大值,CD=CE=a+b.【详解】(1)/ a=b=3,且NACB=60°,「. △ ABC是等边三角形,3//. 0C= 2 ,/. CD=3、3:(2)石-3©〔3〕以点D 为中央,将△ DBC 逆时针旋转60., 那么点B 落在点A,点C 落在点E.连接AE, CE, CD 有最大值是a+b.此题主要考查了等边三角形的性质,以及轴对称的性质,正确理解CD 有最大值的条件, 是解题的关键.5.在△ ABC 中,AB=AC, Z A=30°,将线段BC 绕点B 逆时针旋转60.得到线段BD,再将线 段BD 平移到EF,使点E 在AB 上,点F 在AC 上.〔1〕如图1,直接写出N ABD 和NCFE 的度数;〔2〕在图1中证实:AE=CF ;〔3〕如图2,连接CE,判断4CEF 的形状并加以证实.□ 1 口2【答案】(1)15% 45.: (2)证实见解析:(3) 4CEF 是等腰直角三角形,证实见解析.【解析】试题分析:(1)根据等腰三角形的性质得到N ABC 的度数,由旋转的性质得到/ DBC 的度 数,从・•・A CDE 为等边三角CE=CD.当点E 、A 、C 不在一条直线上时,有 CD=CE<AE+AC=a+b ;当点E 、A 、C 在一条直线上时,CD 有最大值,CD=CE=a+b :只有当N ACB=120°时,Z CAE=180%即A 、C 、E 在一条直线上,此时AE 最大【点/. Z ACB=120°, 因此当N ACB=120°时,而得到NABD的度数;根据三角形外角性质即可求得NCFE的度数.(2)连接CD、DF,证实△ BCD是等边三角形,得到CD=BD,由平移的性质得到四边形BDFE是平行四边形,从而ABH FD,证实△ AEF合△ FCD即可得AE=CF.(3)过点E作EG J_CF于G,根据含30度直角三角形的性质,垂直平分线的判定和性质即可证实△ CEF是等腰直角三角形.(1) :在△ ABC 中,AB=AC, ZA=30% Z ABC=75°.•将线段BC绕点B逆时针旋转60.得到线段BD,即NDBC=60..NABD=15../. Z CFE=Z A+Z ABD=45°.(2)如图,连接CD、DF.线段BC绕点B逆时针旋转60得到线段BD, /. BD=BC, Z CBD=60°. △ BCD是等边三角形.「・CD=BD.・「线段BD平移到EF,・・.EFII BD, EF=BD.四边形BDFE是平行四边形,EF=CD.「AB = AC, Z A=30°, /. Z ABC=Z ACB=75°. /. Z ABD=Z ACD=15°.,•,四边形BDFE是平行四边形…♦・ABH FD. /. Z A=Z CFD.:■ & AEF合△ FCD (AAS)./. AE=CF.(3) ZkCEF是等腰直角三角形,证实如下:如图,过点E作EG_LCF于G,: Z CFE =45°, /. Z FEG=45°. /. EG=FG.1EG =耳AEZ A=30°, NAGE=90°,「・2・1 1EG = £:F FG = KFV AE=CF,「. 2 . /. 2.・.G为CF的中点.「.EG为CF的垂直平分线.EF=EC./. Z CEF=Z FEG=90°.・•.△ CEF是等腰直角三角形.考点:1 •旋转和平移问题:2.等腰三角形的性质;3.三角形外角性质;4.等边三角形的判定和性质:5.平行四边形的判定和性质:6.全等三角形的判定和性质;7.含30度直角三角形的性质:8.垂直平分线的判定和性质:9.等腰直角三角形的判定.6.边长为2的正方形ABCD的两顶点A、C分别在正方形EFGH的两边DE、DG上〔如图1〕.现将正方形ABCD绕D点顺时针旋转,当A点第一次落在DF上时停止旋转,旋转过程中,AB 边交DF于点M, BC边交DG于点N.〔1〕求边DA在旋转过程中所扫过的面积:〔2〕旋转过程中,当MN和AC平行时〔如图2〕,求正方形ABCD旋转的度数;〔3〕如图3,设AMBN的周长为p,在旋转正方形ABCD的过程中,p值是否有变化?清证实你的结论.71【答案】〔1〕2 〔2〕 225°;〔3〕不变化,证实见解析.【解析】试题分析:〔1〕将正方形ABCD绕D点顺时针旋转,当A点第一次落在DF上时停止旋转,旋转过程中,DA旋转了45°,从而根据扇形面积公式可求DA在旋转过程中所扫过的面积.〔2〕旋转过程中,当MN和AC平行时,根据平行的性质和全等三角形的判定和性质可求正方形ABCD旋转的度数为22.5.〔3〕延长BA交DE轴于H点,通过证实/D4〃三4DCN和/DM〃三4DMN可得结论.〔1〕;A点第一次落在DF上时停止旋转,「.DA旋转了45°.457r x 22 7TDA在旋转过程中所扫过的而积为360― 一2〔2〕 ,/ MN II AC, = ^-BAC = 45° Z./7/VM = ZBC4=45°.乙BMN =乙BNM . BM = BN・•・• • •T7.. BA = BC . AM = CN • ,・・•T7..DA = DC,4AM =乙DCN . ADAM=ADCN• /• • •1"DM = k〔900 - 45°〕 = 22.5°.L ADM=乙CDN . 2••• ・• •厂.旋转过程中,当MN和AC平行时,正方形ABCD旋转的度数为45°-22.5.= 22.5.⑶不变化,证实如下:如图,延长BA交DE轴于H点,那么LADE = 45° - LADM L CDN = 900 - 45° - L ADM = 450 - L ADM,,.LADE =乙CDN•• •T7.. DA = DC^DAH = 1800-90° = 90° = LDCN . ADAH^ADCN • •• • •.DH = DN f AH = CN•• ♦..〔MDE =乙MDN = 45°刀M = DM . ADMHwADMNv.MN = MH = AM + AH . MN = AM + CNp = MN + BN + BM = AM + CN + BN + BM = AB + BC = 4,在旋转正方形ABCD的过程中,P值无变化.考点:1 ,而动旋转问题:2.正方形的性质:3,扇形面积的计算:4.全等三角形的判定和性质.7.思维启迪:(1)如图1, A, B两点分别位于一个池塘的两端,小亮想用绳子测量A, B 间的距离,但绳子不够长,聪明的小亮想出一个方法:先在地上取一个可以直接到达B点的点C,连接BC,取BC的中点P (点P可以直接到达A点),利用工具过点C作CDII AB,思维探索:(2)在4ABC 和4ADE 中,AC=BC. AE = DE,且AE<AC,Z ACB = Z AED =90.,将△ ADE绕点A顺时针方向旋转,把点E在AC边上时△ ADE的位置作为起始位置 (此时点B和点D位于AC的两侧),设旋转角为a,连接BD,点P是线段BD的中点,连接PC, PE.①如图2,当△ ADE在起始位置时,猜测:PC与PE的数量关系和位置关系分别是;②如图3,当a = 90.时,点D落在AB边上,请判断PC与PE的数量关系和位置关系,并证实你的结论:③当a=150.时,假设BC = 3, DE=I,请直接写出PC?的值.【答案】(1) 200: (2)①PC=PE, PC_LPE:②PC与PE的数量关系和位置关系分别是PC=PE, PC±PE,见解析:@PC2=-1()+ 3-.2【解析】【分析】(1)由CDIIAB,可得NC=NB,根据N APB=N DPC即可证实△ ABP2△ DCP,即可得AB = CD,即可解题.(2)①延长EP交BC于F,易证△ FBP合△ EDP (SAS)可得△ EFC是等腰直角三角形,即可证实PC=PE, PCXPE.②作BFII DE,交EP延长线于点F,连接CE、CF,易证△ FBP合△ EDP (SAS),结合得BF = DE=AE,再证实△FBCW △ EAC (SAS),可得△ EFC是等腰直角三角形,即可证实PC = PE, PC±PE.③作BFII DE,交EP延长线于点F,连接CE、CF,过E点作EH_LAC交CA延长线于H 点,由旋转旋转可知,Z CAE = 150", DE与BC所成夹角的锐角为30.,得N FBC = N EAC, 同②可证可得PC=PE, PC_LPE,再由己知解三角形得J. EC2=CH2+HE2=1O + 3JJ,即可求出尸C2=9EC2 = 1()-3丫’3 2 2【详解】(1)解:丁CDII AB, J Z C=Z B,在仆ABP和aDCP中,BP = CPZAPB = NDPC,/B = /C:■ & ABP合△ DCP (SAS),DC=AB.AB = 200 米.・•・CD=200米,故答案为:200.(2)①PC与PE的数量关系和位置关系分别是PC=PE, PCXPE.理由如下:如解图1,延长EP交BC于F,同(1)理,可知,△ FBP合 & EDP (SAS),/. PF=PE, BF = DE,又,.,AC=BC, AE = DE,FC=EC,又•・・Z ACB = 90\EFC是等腰直角三角形,・/ EP = FP,・・.PC=PE, PCJLPE.®PC与PE的数量关系和位置关系分别是PC = PE, PC±PE.理由如下:如解图2,作BFII DE,交EP延长线于点F,连接CE、CF, 同①理,可知△ FBP2△ EDP (SAS),・・.BF = DE. PE = PF=-EF, 2・/ DE=AE,/. BF = AE,・••当a=90.时,Z EAC=90°,ED II AC, EAII BCFBII AC, Z FBC=90,・•・ Z CBF=Z CAE,在^ FBC和^ EAC中,BF = AE< NCBE = NCAE ,BC = AC:■ & FBC合 ' EAC (SAS),・•. CF = CE, Z FCB = Z EC A,•/ Z ACB = 90°,/. Z FCE = 90°,△ FCE是等腰直角三角形,・/ EP = FP,CP±EP, CP = EP=-EF.2③如解图3,作BFII DE,交EP延长线于点F,连接CE、CF,过E点作EH_LAC交CA延长线于H点,当a=150.时,由旋转旋转可知,Z CAE = 150°, DE与BC所成夹角的锐角为30.,・•・ Z FBC=Z EAC=a=150°同②可得^ FBP24 EDP (SAS),同②△ FCE是等腰直角三角形,CPJ_EP, CP = EP=』±CE,2在RSAHE 中,NEAH = 30.,AE=DE=1,HE=- , AH=叵,2 2又< AC=AB=3,/. CH=3+正,2・•, EC2=CH2+HE2=IO +3>/3【点睛】此题考查几何变换综合题,考查了旋转的性质、全等三角形的判定和性质,等腰直角三角形性质、勾股定理和30.直角三角形性质等知识,解题的关键是正确寻找全等三角形解决问题,属于压轴题.8.小明合作学习小组在探究旋转、平移变换.如图△ ABC, △ DEF均为等腰直角三角形, 各顶点坐标分别为 A (1, 1) , B (2, 2) , C (2, 1) , D ( 0) , E( 2五,0),〔1〕他们将△ ABC绕C点按顺时针方向旋转45.得到△ AiBiC.请你写出点A],Bi的坐标,并判断A】C和DF的位置关系:〔2〕他们将△ ABC绕原点按顺时针方向旋转45.,发现旋转后的三角形恰好有两个顶点落在抛物线y = 2g?+bx+c±.请你求出符合条件的抛物线解析式:〔3〕他们继续探究,发现将△ ABC绕某个点旋转45,假设旋转后的三角形恰好有两个顶点落在抛物线y = x?上,那么可求出旋转后三角形的直角顶点P的坐标.请你直接写出点P的所有坐标.A】C和DF的位置关系是平行.〔2〕•/ △ ABC绕原点按顺时针方向旋转45.后的三角形即为^ DEF,2 应x〔扃+>/Ib + c = O①当抛物线经过点D、E时,根据题意可得:{, ,解得2 应x〔2 回一+ 2回+ c=0b = -12(=8万A y = 2>/2x2-12x+8x/2 .2 五x(近忘b + c = o②当抛物线经过点D、F时,根据题意可得:{(3①丫372 点,解得I 2 J 2 2b = -llL = 7-72y = 2V2x2-llx+7>/2.2耳〔2⑸+2岳+ c = 0③当抛物线经过点E、F时,根据题意可得:{〔30丫35/22ax --- +---b + c =-2 2J 乙b = -13'c = 10 应y = 2x/2x2-13x + 10x/2 .〔3〕在旋转过程中,可能有以下情形:①顺时针旋转45.,点A、B落在抛物线上,如答图1所示,易求得点p坐标为〔o, Lz叵〕. 2②顺时针旋转45.,点B、C落在抛物线上,如答图2所示,设点夕,.的横坐标分别为右,X2,易知此时BC与一、三象限角平分线平行,.•.设直线BC的解析式为y=x+b.联立丫f2与丫=乂+1〕得:x2=x+b,即X? — x-b = 0,「. X]+x? =1,X t x2 =-b ..•.根据题意易得:|x「x」=走,.J 〔Xi-xJ?=:,即 2 2\2 IX] +X2〕 -4x^2 =-..1- l + 4b = i,解得b =一2 8x2-x + - = 0,解得x = ^^x 或x = ^^.8 4 4••1点c的横坐标较小,x = 三口 .42 - *\/2 . 9 3-2近1IX = ------------- 时,y = x = ---------------------- .4 8.p f 2-5/2 3-2V2 .4 8③顺时针旋转45.,点C、A落在抛物线上,如答图3所示,设点C, A,的横坐标分别为4, X2.易知此时C7V与二、四象限角平分线平行,.•.设直线C7V的解析式为y = -x + b.联立y=x?与y = lX + b 得:x° =-x + b ,即+ x - b = 0 , /. X. +x?=一1, x,x, ="b .••・UA'=1, .•.根据题意易得:|x「x」= WI, ... 〔x「X2〕2 =;,即2 2.1- l+4b = l,解得b =一 2 8, 2 I ] 八-2 + y/2 T -2 - V2..X- + X + —= 0 , 解得X = ------------------ x 或X = ---------------- -8 4 4•・•点C的横坐标较大,「. x = "2+V,2 .4w + V? . 2 3 -2>/2ix = --------------- 时,y = x = ----------------------- .4 8*〕.4 8④逆时针旋转45.,点A、B落在抛物线上.由于逆时针旋转45.后,直线AB与y轴平行,由于与抛物线最多只能有一个交点,故此种情形不存在.⑤逆时针旋转45.,点B、C落在抛物线上,如答图4所示,与③同理,可求得:P 〔二2 一退,3二2巫〕.4 8⑥逆时针旋转45.,点C、A落在抛物线上,如答图5所示,与②同理,可求得:p 〔2y,,一y.〕.综上所述,点P的坐标为:〔0,上叵〕,〔三叵,3-2立〕,p〔―2 +点,2 4 8 43-2>/2 2 + 72 3 + 20\8 4 8等图I 答医2 硝; 1 答& 等国【解析】〔1〕由旋转性质及等腰直角三角形边角关系求解.〔2〕首先明确△ ABC绕原点按顺时针方向旋转45.后的三角形即为ADEF,然后分三种情况进行讨论,分别计算求解.〔3〕旋转方向有顺时针、逆时针两种可能,落在抛物线上的点有点A和点B、点B和点C、点C和点D三种可能,因此共有六种可能的情形,需要分类讨论,防止漏解.考点:旋转变换的性质,曲线上点的坐标与方程的关系,平行线的性质,等腰直角三角形的性质,分类思想的应用.。
中考数学初中数学 旋转-经典压轴题附答案解析

中考数学初中数学 旋转-经典压轴题附答案解析一、旋转1.在△ABC 中,AB=AC ,∠BAC=α(︒<<︒600α),将线段BC 绕点B 逆时针旋转60°得到线段BD 。
(1)如图1,直接写出∠ABD 的大小(用含α的式子表示); (2)如图2,∠BCE=150°,∠ABE=60°,判断△ABE 的形状并加以证明; (3)在(2)的条件下,连结DE ,若∠DEC=45°,求α的值。
【答案】(1)1302α︒-(2)见解析(3)30α=︒【解析】解:(1)1302α︒-。
(2)△ABE 为等边三角形。
证明如下:连接AD ,CD ,ED ,∵线段BC 绕点B 逆时针旋转60︒得到线段BD , ∴BC=BD ,∠DBC=60°。
又∵∠ABE=60°,∴1ABD 60DBE EBC 302α∠=︒-∠=∠=︒-且△BCD 为等边三角形。
在△ABD 与△ACD 中,∵AB=AC ,AD=AD ,BD=CD ,∴△ABD ≌△ACD (SSS )。
∴11BAD CAD BAC 22α∠=∠=∠=。
∵∠BCE=150°,∴11BEC 180(30)15022αα∠=︒-︒--︒=。
∴BEC BAD ∠=∠。
在△ABD 和△EBC 中,∵BEC BAD ∠=∠,EBC ABD ∠=∠,BC=BD , ∴△ABD ≌△EBC (AAS )。
∴AB=BE 。
∴△ABE 为等边三角形。
(3)∵∠BCD=60°,∠BCE=150°,∴DCE 1506090∠=︒-︒=︒。
又∵∠DEC=45°,∴△DCE 为等腰直角三角形。
∴DC=CE=BC 。
∵∠BCE=150°,∴(180150)EBC 152︒-︒∠==︒。
而1EBC 30152α∠=︒-=︒。
∴30α=︒。
(1)∵AB=AC ,∠BAC=α,∴180ABC 2α︒-∠=。
初中数学中考专题旋转解答题(含答案)

2019-2020旋转解答题中考专题(含答案)1.如图1,点E 是正方形ABCD 边CD 上任意一点,以DE 为边作正方形DEFG ,连接BF ,点M 是线段BF 中点,射线EM 与BC 交于点H ,连接CM .(1)请直接写出CM 和EM 的数量关系和位置关系;(2)把图1中的正方形DEFG 绕点D 顺时针旋转45°,此时点F 恰好落在线段CD 上,如图2,其他条件不变,(1)中的结论是否成立,请说明理由;(3)把图1中的正方形DEFG 绕点D 顺时针旋转90°,此时点E 、G 恰好分别落在线段AD 、CD 上,如图3,其他条件不变,(1)中的结论是否成立,请说明理由.2.请认真阅读下面的数学小探究系列,完成所提出的问题:()1探究1:如图1,在等腰直角三角形ABC 中,90ACB ∠=o ,BC a =,将边AB 绕点B 顺时针旋转90o 得到线段BD ,连接.CD 求证:BCD V 的面积为21.(2a 提示:过点D 作BC 边上的高DE ,可证ABC V ≌)BDE V()2探究2:如图2,在一般的Rt ABC V 中,90ACB ∠=o ,BC a =,将边AB 绕点B 顺时针旋转90o 得到线段BD ,连接.CD 请用含a 的式子表示BCD V 的面积,并说明理由.()3探究3:如图3,在等腰三角形ABC 中,AB AC =,BC a =,将边AB 绕点B 顺时针旋转90o 得到线段BD ,连接.CD 试探究用含a 的式子表示BCD V 的面积,要有探究过程. 3.已知:≌ABC 和≌ADE 均为等边三角形,连接BE ,CD ,点F ,G ,H 分别为DE ,BE ,CD 中点. (1)当≌ADE 绕点A 旋转时,如图1,则≌FGH 的形状为 ,说明理由;(2)在≌ADE 旋转的过程中,当B ,D ,E 三点共线时,如图2,若AB =3,AD =2,求线段FH 的长; (3)在≌ADE 旋转的过程中,若AB =a ,AD =b (a >b >0),则≌FGH 的周长是否存在最大值和最小值,若存在,直接写出最大值和最小值;若不存在,说明理由.4.在平面直角坐标系中,O 为原点,点A (8,0),点B (0,6),把≌ABO 绕点B 逆时针旋转得≌A′B′O′,点A 、O 旋转后的对应点为A′、O′,记旋转角为α.(1)如图1,若α=90°,则AB= ,并求AA′的长;(2)如图2,若α=120°,求点O′的坐标;(3)在(2)的条件下,边OA 上的一点P 旋转后的对应点为P′,当O′P+BP′取得最小值时,直接写出点P′的坐标.5.如图,在Rt≌ABC中,≌ACB=90°,≌A=30°,点O为AB中点,点P为直线BC上的动点(不与点B、点C重合),连接OC、OP,将线段OP绕点P顺时针旋转60°,得到线段PQ,连接BQ.(1)如图1,当点P在线段BC上时,请直接写出线段BQ与CP的数量关系.(2)如图2,当点P在CB延长线上时,(1)中结论是否成立?若成立,请加以证明;若不成立,请说明理由;(3)如图3,当点P在BC延长线上时,若≌BPO=15°,BP=4,请求出BQ的长.6.(1)发现如图,点A为线段BC外一动点,且BC=a,AB=b.填空:当点A位于____________时,线段AC的长取得最大值,且最大值为_________.(用含a,b的式子表示)(2)应用点A为线段BC外一动点,且BC=3,AB=1.如图所示,分别以AB,AC为边,作等边三角形ABD和等边三角形ACE,连接CD,BE.≌找出图中与BE相等的线段,并说明理由;≌直接写出线段BE长的最大值.(3)拓展如图,在平面直角坐标系中,点A的坐标为(2 , 0),点B的坐标为(5 , 0),点P为线段AB外一动点,且PA=2,PM=PB,∠BPM=90°,求线段AM长的最大值及此时点P的坐标.7.(10分)如图1,在Rt≌ABC中,≌B=90°,BC=2AB=8,点D,E分别是边BC,AC的中点,连接DE. 将≌EDC绕点C按顺时针方向旋转,记旋转角为α.(1)问题发现≌ 当时,;≌ 当时,(2)拓展探究试判断:当0°≤α<360°时,的大小有无变化?请仅就图2的情况给出证明.(3)问题解决当≌EDC旋转至A、D、E三点共线时,直接写出线段BD的长.8.如图,≌ABC中,AB=AC=1,≌BAC=45°,≌AEF是由≌ABC绕点A按顺时针方向旋转得到的,连接BE,CF相交于点D。
中考数学专题训练---旋转的综合题分类附详细答案

一、旋转真题与模拟题分类汇编(难题易错题)1.两块等腰直角三角板△ABC和△DEC如图摆放,其中∠ACB=∠DCE=90°,F是DE的中点,H是AE的中点,G是BD的中点.(1)如图1,若点D、E分别在AC、BC的延长线上,通过观察和测量,猜想FH和FG的数量关系为______和位置关系为______;(2)如图2,若将三角板△DEC绕着点C顺时针旋转至ACE在一条直线上时,其余条件均不变,则(1)中的猜想是否还成立,若成立,请证明,不成立请说明理由;(3)如图3,将图1中的△DEC绕点C顺时针旋转一个锐角,得到图3,(1)中的猜想还成立吗?直接写出结论,不用证明.【答案】(1)相等,垂直.(2)成立,证明见解析;(3)成立,结论是FH=FG,FH⊥FG.【解析】试题分析:(1)证AD=BE,根据三角形的中位线推出FH=12AD,FH∥AD,FG=12BE,FG∥BE,即可推出答案;(2)证△ACD≌△BCE,推出AD=BE,根据三角形的中位线定理即可推出答案;(3)连接BE、AD,根据全等推出AD=BE,根据三角形的中位线定理即可推出答案.试题解析:(1)解:∵CE=CD,AC=BC,∠ECA=∠DCB=90°,∴BE=AD,∵F是DE的中点,H是AE的中点,G是BD的中点,∴FH=12AD,FH∥AD,FG=12BE,FG∥BE,∴FH=FG,∵AD⊥BE,∴FH⊥FG,故答案为相等,垂直.(2)答:成立,证明:∵CE=CD,∠ECD=∠ACD=90°,AC=BC,∴△ACD≌△BCE∴AD=BE,由(1)知:FH=12AD ,FH ∥AD ,FG=12BE ,FG ∥BE , ∴FH=FG ,FH ⊥FG ,∴(1)中的猜想还成立.(3)答:成立,结论是FH=FG ,FH ⊥FG . 连接AD ,BE ,两线交于Z ,AD 交BC 于X , 同(1)可证∴FH=12AD ,FH ∥AD ,FG=12BE ,FG ∥BE , ∵三角形ECD 、ACB 是等腰直角三角形, ∴CE=CD ,AC=BC ,∠ECD=∠ACB=90°, ∴∠ACD=∠BCE , 在△ACD 和△BCE 中AC BC ACD BCE CE CD ⎧⎪∠∠⎨⎪⎩=== , ∴△ACD ≌△BCE , ∴AD=BE ,∠EBC=∠DAC ,∵∠DAC+∠CXA=90°,∠CXA=∠DXB , ∴∠DXB+∠EBC=90°, ∴∠EZA=180°﹣90°=90°, 即AD ⊥BE , ∵FH ∥AD ,FG ∥BE , ∴FH ⊥FG , 即FH=FG ,FH ⊥FG , 结论是FH=FG ,FH ⊥FG.【点睛】运用了等腰直角三角形的性质、全等三角形的性质和判定、三角形的中位线定理,旋转的性质等知识点的理解和掌握,能熟练地运用这些性质进行推理是解此题的关键.2.如图所示,△ABC 和△ADE 是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°,EC 的延长线交BD 于点P .(1)把△ABC绕点A旋转到图1,BD,CE的关系是(选填“相等”或“不相等”);简要说明理由;(2)若AB=3,AD=5,把△ABC绕点A旋转,当∠EAC=90°时,在图2中作出旋转后的图形,PD=,简要说明计算过程;(3)在(2)的条件下写出旋转过程中线段PD的最小值为,最大值为.【答案】(1)BD,CE的关系是相等;(2)53417或203417;(3)1,7【解析】分析:(1)依据△ABC和△ADE是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°,即可BA=CA,∠BAD=∠CAE,DA=EA,进而得到△ABD≌△ACE,可得出BD=CE;(2)分两种情况:依据∠PDA=∠AEC,∠PCD=∠ACE,可得△PCD∽△ACE,即可得到PD AE =CDCE,进而得到PD=53417;依据∠ABD=∠PBE,∠BAD=∠BPE=90°,可得△BAD∽△BPE,即可得到PB BEAB BD,进而得出PB=63434,PD=BD+PB=203417;(3)以A为圆心,AC长为半径画圆,当CE在⊙A下方与⊙A相切时,PD的值最小;当CE在在⊙A右上方与⊙A相切时,PD的值最大.在Rt△PED中,PD=DE•sin∠PED,因此锐角∠PED的大小直接决定了PD的大小.分两种情况进行讨论,即可得到旋转过程中线段PD的最小值以及最大值.详解:(1)BD,CE的关系是相等.理由:∵△ABC和△ADE是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°,∴BA=CA,∠BAD=∠CAE,DA=EA,∴△ABD≌△ACE,∴BD=CE;故答案为相等.(2)作出旋转后的图形,若点C在AD上,如图2所示:∵∠EAC=90°,∴CE=2234AC AE +=,∵∠PDA=∠AEC ,∠PCD=∠ACE , ∴△PCD ∽△ACE , ∴PD CDAE CE =, ∴PD=53417; 若点B 在AE 上,如图2所示:∵∠BAD=90°, ∴Rt △ABD 中,BD=2234AD AB +=,BE=AE ﹣AB=2,∵∠ABD=∠PBE ,∠BAD=∠BPE=90°,∴△BAD ∽△BPE , ∴PB BEAB BD=,即2334PB =, 解得PB=63434, ∴PD=BD+PB=34+63434=203417, 故答案为53417或203417; (3)如图3所示,以A 为圆心,AC 长为半径画圆,当CE 在⊙A 下方与⊙A 相切时,PD 的值最小;当CE 在在⊙A 右上方与⊙A 相切时,PD 的值最大. 如图3所示,分两种情况讨论:在Rt △PED 中,PD=DE•sin ∠PED ,因此锐角∠PED 的大小直接决定了PD 的大小. ①当小三角形旋转到图中△ACB 的位置时,在Rt△ACE中,CE=2253-=4,在Rt△DAE中,DE=225552+=,∵四边形ACPB是正方形,∴PC=AB=3,∴PE=3+4=7,在Rt△PDE中,PD=2250491DE PE-=-=,即旋转过程中线段PD的最小值为1;②当小三角形旋转到图中△AB'C'时,可得DP'为最大值,此时,DP'=4+3=7,即旋转过程中线段PD的最大值为7.故答案为1,7.点睛:本题属于几何变换综合题,主要考查了等腰直角三角形的性质、旋转变换、全等三角形的判定和性质、相似三角形的判定和性质、圆的有关知识,解题的关键是灵活运用这些知识解决问题,学会分类讨论的思想思考问题,学会利用图形的特殊位置解决最值问题.3.如图,正方形ABCD中,点E是BC边上的一个动点,连接AE,将线段AE绕点A逆时针旋转90°,得到AF,连接EF,交对角线BD于点G,连接AG.(1)根据题意补全图形;(2)判定AG与EF的位置关系并证明;(3)当AB=3,BE=2时,求线段BG的长.【答案】(1)见解析;(2)见解析;(3)5 2.【解析】【分析】(1)根据题意补全图形即可;(2)先判断出△ADF≌△ABE,进而判断出点C,D,F共线,即可判断出△DFG≌△HEG,得出FG=EG,即可得出结论;(3)先求出正方形的对角线BD,再求出BH,进而求出DH,即可得出HG,求和即可得出结论.【详解】(1)补全图形如图所示,(2)连接DF,由旋转知,AE=AF,∠EAF=90°,∵四边形ABCD是正方形,∴AB∥CD,AD=AB,∠ABC=∠ADC=BAD=90°,∴∠DAF=∠BAE,∴△ADF≌△ABE(SAS),∴DF=BE,∠ADF=∠ABC=90°,∴∠ADF+∠ADC=180°,∴点C,D,F共线,∴CF∥AB,过点E作EH∥BC交BD于H,∴∠BEH=∠BCD=90°,DF∥EH,∴∠DFG=∠HEG,∵BD是正方形ABCD的对角线,∴∠CBD=45°,∴BE=EH,∵∠DGF=∠HGE,∴△DFG≌△HEG(AAS),∴FG=EG∵AE=AF,∴AG⊥EF;(3)∵BD是正方形的对角线,∴22,由(2)知,在Rt△BEH中,22,∴2由(2)知,△DFG≌△HEG,∴DG=HG,∴HG=12DH=22,∴BG=BH+HG=22+22=522.【点睛】此题是四边形综合题,主要考查了旋转的性质,全等三角形的判定和性质,正方形的性质,勾股定理,作出辅助线是解本题的关键.4.已知:△ABC和△ADE均为等边三角形,连接BE,CD,点F,G,H分别为DE,BE,CD 中点.(1)当△ADE绕点A旋转时,如图1,则△FGH的形状为,说明理由;(2)在△ADE旋转的过程中,当B,D,E三点共线时,如图2,若AB=3,AD=2,求线段FH的长;(3)在△ADE旋转的过程中,若AB=a,AD=b(a>b>0),则△FGH的周长是否存在最大值和最小值,若存在,直接写出最大值和最小值;若不存在,说明理由.【答案】(1)△FGH是等边三角形;(2)612;(3)△FGH的周长最大值为32(a+b),最小值为32(a﹣b).【解析】试题分析:(1)结论:△FGH是等边三角形.理由如下:根据三角形中位线定理证明FG=FH,再想办法证明∠GFH=60°即可解决问题;、(2)如图2中,连接AF、EC.在Rt△AFE和Rt△AFB中,解直角三角形即可;(3)首先证明△GFH的周长=3GF=32BD,求出BD的最大值和最小值即可解决问题;试题解析:解:(1)结论:△FGH是等边三角形.理由如下:如图1中,连接BD、CE,延长BD交CE于M,设BM交FH于点O.∵△ABC和△ADE均为等边三角形,∴AB=AC,AD=AE,∠BAC=∠DAE,∴∠BAD=∠CAE,∴△BAD≌△CAE,∴BD=CE,∠ADB=∠AEC,∵EG=GB,EF=FD,∴FG=12BD,GF∥BD,∵DF =EF ,DH =HC ,∴FH =12EC ,FH ∥EC ,∴FG =FH ,∵∠ADB +∠ADM =180°,∴∠AEC +∠ADM =180°,∴∠DMC +∠DAE =180°,∴∠DME =120°,∴∠BMC =60° ∴∠GFH =∠BOH =∠BMC =60°,∴△GHF 是等边三角形,故答案为:等边三角形. (2)如图2中,连接AF 、EC .易知AF ⊥DE ,在Rt △AEF 中,AE =2,EF =DF =1,∴AF 2221-3,在Rt △ABF 中,BF 22AB AF -6,∴BD =CE =BF ﹣DF 61,∴FH =12EC =612. (3)存在.理由如下.由(1)可知,△GFH 是等边三角形,GF =12BD ,∴△GFH 的周长=3GF =32BD ,在△ABD中,AB =a ,AD =b ,∴BD 的最小值为a ﹣b ,最大值为a +b ,∴△FGH 的周长最大值为32(a +b ),最小值为32(a ﹣b ).点睛:本题考查等边三角形的性质.全等三角形的判定和性质、解直角三角形、三角形的三边关系、三角形的中位线的宽等知识,解题的关键是学会添加常用辅助线,正确寻找全等三角形解决问题,学会利用三角形的三边关系解决最值问题,属于中考压轴题.5.如图1,菱形ABCD ,AB 4=,ADC 120∠=,连接对角线AC 、BD 交于点O ,()1如图2,将AOD 沿DB 平移,使点D 与点O 重合,求平移后的A'BO 与菱形ABCD 重合部分的面积.()2如图3,将A'BO 绕点O 逆时针旋转交AB 于点E',交BC 于点F ,①求证:BE'BF 2+=; ②求出四边形OE'BF 的面积.【答案】()() 13?2①证明见解析3② 【解析】 【分析】(1)先判断出△ABD 是等边三角形,进而判断出△EOB 是等边三角形,即可得出结论; (2)先判断出 ≌△OBF ,再利用等式的性质即可得出结论; (3)借助①的结论即可得出结论. 【详解】()1四边形为菱形,ADC 120∠=,ADO 60∠∴=,ABD ∴为等边三角形,DAO 30∠∴=,ABO 60∠=,∵AD//A′O , ∴∠A′OB=60°,EOB ∴为等边三角形,边长OB 2=,∴重合部分的面积:3434⨯=,()2①在图3中,取AB 中点E ,由()1知,∠EOB=60°,∠E′OF=60°, ∴∠EOE′=∠BOF ,又∵EO=BO ,∴∠OEE′=∠OBF=60°, ∴△OEE′≌△OBF , ∴EE′=BF ,∴BE′+BF=BE′+EE′=BE=2;②由①知,在旋转过程中始终有△OEE′≌△OBF ,∴S△OEE′=S△OBF,∴S四边形OE′BF =OEBS3=.【点睛】本题考查了菱形的性质、全等三角形的判定与性质,等边三角形的判定与性质,综合性较强,熟练掌握相关内容、正确添加辅助线是解题的关键.6.已知Rt△DAB中,∠ADB=90°,扇形DEF中,∠EDF=30°,且DA=DB=DE,将Rt△ADB的边与扇形DEF的半径DE重合,拼接成图1所示的图形,现将扇形DEF绕点D按顺时针方向旋转,得到扇形DE′F′,设旋转角为α(0°<α<180°)(1)如图2,当0°<α<90°,且DF′∥AB时,求α;(2)如图3,当α=120°,求证:AF′=BE′.【答案】(1)15°;(2)见解析.【解析】试题分析:(1)∵∠ADB=90°,DA=DB,∴∠BAD=45°,∵DF′∥AB,∴∠ADF′=∠BAD=45°,∴α=45°﹣30°=15°;(2)∵α=120°,∴∠ADE′=120°,∴∠ADF′=120°+30°=150°,∠BDE′=360°﹣90°﹣120°=150°,∴∠ADF′=∠BDE′,在△ADF′和△BDE′中,,∴△ADF′≌△BDE′,∴AF′=BE′.考点:①旋转性质;②全等三角形的判定和性质.7.已知△ABC是等腰三角形,AB=AC.(1)特殊情形:如图1,当DE∥BC时,有DB EC.(填“>”,“<”或“=”)(2)发现探究:若将图1中的△ADE绕点A顺时针旋转α(0°<α<180°)到图2位置,则(1)中的结论还成立吗?若成立,请给予证明;若不成立,请说明理由.(3)拓展运用:如图3,P是等腰直角三角形ABC内一点,∠ACB=90°,且PB=1,PC=2,PA=3,求∠BPC的度数.【答案】(1)=;(2)成立,证明见解析;(3)135°.【解析】【分析】试题(1)由DE∥BC,得到DB ECAB AC=,结合AB=AC,得到DB=EC;(2)由旋转得到的结论判断出△DAB≌△EAC,得到DB=CE;(3)由旋转构造出△CPB≌△CEA,再用勾股定理计算出PE,然后用勾股定理逆定理判断出△PEA是直角三角形,在简单计算即可.【详解】(1)∵DE∥BC,∴DB ECAB AC=,∵AB=AC,∴DB=EC,故答案为=,(2)成立.证明:由①易知AD=AE,∴由旋转性质可知∠DAB=∠EAC,又∵AD=AE,AB=AC∴△DAB≌△EAC,∴DB=CE,(3)如图,将△CPB绕点C旋转90°得△CEA,连接PE,∴△CPB≌△CEA,∴CE=CP=2,AE=BP=1,∠PCE=90°,∴∠CEP=∠CPE=45°,在Rt△PCE中,由勾股定理可得,PE=2在△PEA中,PE2=(22)2=8,AE2=12=1,PA2=32=9,∵PE2+AE2=AP2,∴△PEA是直角三角形∴∠PEA=90°,∴∠CEA=135°,又∵△CPB≌△CEA∴∠BPC=∠CEA=135°.【点睛】考点:几何变换综合题;平行线平行线分线段成比例.8.如图1,点O为直线AB上一点,过O点作射线OC,使∠AOC:∠BOC=1:2,将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.(1)将图1中的三角板绕点O按逆时针方向旋转至图2的位置,使得ON落在射线OB 上,此时三角板旋转的角度为度;(2)继续将图2中的三角板绕点O按逆时针方向旋转至图3的位置,使得ON在∠AOC的内部.试探究∠AOM与∠NOC之间满足什么等量关系,并说明理由;(3)在上述直角三角板从图1逆时针旋转到图3的位置的过程中,若三角板绕点O按15°每秒的速度旋转,当直角三角板的直角边ON所在直线恰好平分∠AOC时,求此时三角板绕点O的运动时间t的值。
2024年中考数学高频考点专题复习——旋转综合题(含解析)

2024年中考数学高频考点专题复习——旋转综合题1.如图,△ABC 和△DEF 关于某点对称(1)在图中画出对称中心O ;(2)连结AF 、CD ,判断四边形ACDF 的形状,并说明理由.2.在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为1个单位.(1)画出关于原点O 的中心对称图形;(2)在(1)的条件下,请分别写出点A 、B 、C 的对应点、、的坐标.ABC ABC 111A B C 1A 1B 1C3.如图1,图2,△ABC 是等边三角形,D 、E 分别是AB 、BC 边上的两个动点(与点A 、B 、C 不重合),始终保持BD=CE.(1)当点D 、E 运动到如图1所示的位置时,求证:CD=AE.(2)把图1中的△ACE 绕着A 点顺时针旋转60°到△ABF 的位置(如图2),分别连结DF 、EF.①找出图中所有的等边三角形(△ABC 除外),并对其中一个给予证明;②试判断四边形CDFE 的形状,并说明理由.4.如图,矩形 中, ,将矩形 绕点C 顺时针旋转得到矩形 .设旋转角为 ,此时点 恰好落在边 上,连接 .(1)当 恰好是 中点时,此时 ;(2)若 ,求旋转角 及 的长.5.将线段AB 绕点A 逆时针旋转60°得到线段AC ,继续旋转α(0°<α<120°)得到线段AD ,连接CD 、BD .(1)如图,若α=80°,则∠BDC 的度数为 ;(2)请探究∠BDC 的大小是否与角α的大小有关,并说明理由.ABCD 4BC =ABCD A B C D ''''αB 'AD B B 'B 'AD α=75AB B ︒∠='αAB6.在平面直角坐标系中,小方格都是边长为1的正方形,△ABC ≌△DEF ,其中点A 、B 、C 、都在格点上,请你解答下列问题:(1)如图(a )在方格纸中,选择标有序号①②③④中的一个小正方形涂黑,与图中阴影部分构成中心对称图形,涂黑的小正方形的序号为 .(2)画出△ABC 关于y 轴对称的△A 1B 1C 1;画出△ABC 绕点P (1,﹣1)顺时针旋转90°后的△A 2B 2C 2;(3)△A 1B 1C 1与△A 2B 2C 2成中心对称吗?若成中心对称请你求出对称中心的坐标;若不成,则说明理由.7.图1是某小型汽车的侧面示意图,其中矩形 表示该车的后备箱,在打开后备箱的过程中,箱盖 可以绕点A 逆时针方向旋转,当旋转角为 时,箱盖 落在 的位置(将后备箱放大后如图2所示).已知 厘米, 厘米, 厘米.在图2中求: (1)点 到 的距离(结果保留根号);(2)E 、 两点的距离(结果保留根号).ABCD ADE 60︒ADE AD E ''90AD =30DE =40EC =D 'BC E '8.如图, 是等腰直角三角形, 是直角三角形, ,点 为边 中点将 绕点 顺时针旋转,旋转角记为 ,点 为边 的中点.(1)如图,求初始状态时 的大小;(2)如图,在旋转过程中,若点 构成平行四边形,请直接写出此时 的值;(3)在旋转过程中,若点 和点 重合,请在图中画出 并连接 ,判断此时是否有 ?如果成立,请证明;如果不成立,请说明理由.ABC 90,ABC BDE ∠=︒ 30E ∠=︒D BC BDE D (0360)αα<<︒F BE AEC ∠,,,B D F B 'a F B ,B DE ' AE AE ED ⊥9.如图,在菱形 中, ,将边 绕点 逆时针旋转至 ,记旋转角为 .过点 作 于点 ,过点 作 直线 于点 ,连接 .(1)(探索发现)填空:当 时, = .的值是 (2)(验证猜想)当 时,(1)中的结论是否仍然成立?若成立,请仅就图2的情形进行证明;若不成立,请说明理由;(3)(拓展应用)在(2)的条件下,若 ,当 是等腰直角三角形时,请直接写出线段 的长.ABCD 120BAD ∠= AB A 'AB αD DF BC ⊥F B BE ⊥'B D E EF 60α= 'EBB ∠ 'EF DB 0360α<< AB =BDE ∆EF10.如图(1),在△ABC中,AB=BC,P为AB边上一点,连接CP,以PA、PC为邻边作APCD,AC与PD 相交于点E,已知∠ABC=∠AEP= (0°< <90°).(1)求证: ∠EAP=∠EPA;(2)APCD是否为矩形?请说明理由;(3)如图(2),F为BC中点,连接FP,将∠AEP绕点E顺时针旋转适当的角度,得到∠MEN(点M、N分别是∠MEN的两边与BA、FP延长线的交点).猜想线段EM与EN之间的数量关系,并证明你的结论.αα11.定义:有一组邻边相等,且它们的夹角为60°的四边形叫做半等边四边形.(1)已知在半等边四边形ABCD 中,AB=AD ,∠BAD=60°,∠BCD=120°.①如图1,若∠B=∠D ,求证:BC=CD ;②如图2,连结AC ,探索线段AC 、BC 、CD 之间的数量关系,并说明理由;(2)如图3,已知∠MAC=30°,AC=10+10,点D 是射线AM 上的一个动点,记∠DCA=a ,点B 在直线AC 的下方,若四边形ABCD 是半等边四边形,且CB=CD .问:当点D 在15°≤a≤45°的变化过程中运动时,点B 也随之运动,请直接写出点B 所经过的路径长.12.已知,把45°的直三角板的直角顶点E 放在边长为6的正方形ABCD 的一边BC 上,直三角板的一条直角边经过点D ,以DE 为一边作矩形DEFG ,且GF 过点A ,得到图1.(1)求矩形DEFG 的面积;(2)若把正方形ABCD 沿着对角线AC 剪掉一半得到等腰直角三角形ABC ,把45°的直三角板的一个45°角的顶点与等腰直角三角形ABC 的直角顶点B 重合,直三角板夹这个45°角的两边分别交CA 和CA 的延长线于点H 、P ,得到图2.猜想:CH 、PA 、HP 之间的数量关系,并说明理由;(3)若把边长为6的正方形ABCD 沿着对角线AC 剪掉一半得到等腰直角三角形ABC ,点M 是Rt △ABC 内一个动点,连接MA 、MB 、MC ,设MA+MB+MC =y ,直接写出 的最小值.2y13.(1)观察猜想:如图①,在Rt △ABC 和Rt △BDE 中,∠ABC =∠EBD =90°,AB =BC ,BE =BD ,连接AE ,点F 是AE 的中点,连接CD 、BF ,当点D 、B 、C 三点共线时,线段CD 与线段BF 的数量关系是 ,位置关系是 .(2)探究证明:在(1)的条件下,将Rt △BDE 绕点B 顺时针旋转至图②位置时,(1)中的结论是否仍然成立?如果成立,请你就图②的情形进行证明;如果不成立,请说明理由;(3)拓展延伸:如图③,在Rt △ABC 和Rt △BDE 中,∠ABC =∠EBD =90°,BC =2AB =8,BD =2BE =4,连接AE ,点F 是AE 的中点,连结CD 、BF ,将△BDE 绕点B 在平面内自由旋转,请直接写出BF 的取值范围,14.请认真阅读下面的数学小探究系列,完成所提出的问题:(1)探究1,如图1,在等腰直角三角形ABC 中, , ,将边AB 绕点B 顺时针旋转90°得到线段BD ,连接CD ,过点D 作BC 边上的高DE ,则DE 与BC 的数量关系是 , 的面积为 ;(2)探究2,如图2,在一般的 中, ,( , ),将边AB 绕点B 顺时针旋转90°得到线段BD ,连接CD ,请用含m ,n 的式子表示 的面积,并说明理由.(3)探究3:如图3,在等腰三角形ABC 中, , ( ,, ),将边AB 绕点B 顺时针旋转90°得到线段BD ,连接CD ,试探究用含a ,b ,c 的式子表示 的面积,要有探究过程.90ACB ∠=︒5BC =BCD Rt ABC 90ACB ∠=︒22()()BC m n m n =+--0m >0n >BCD AB AC =BC a b c =++0a >0b >0c >BCD15.如图1,在△ABC中,∠A=120°,AB=AC,点D,E分别在边AB,AC上,AD=AE,连接BE,点M,N,P分别为DE,BE,BC的中点,连接NM,NP.(1)图1中,线段NM,NP的数量关系是 ,∠MNP的度数为 ;(2)把△ADE绕点A顺时针旋转到如图2所示的位置,连接MP.求证:△MNP是等边三角形;(3)把△ADE绕点A在平面内旋转,若AD=2,AB=5,请直接写出△MNP面积的最大值.16.(1)问题发现:如图①,正方形ABCD的边长为4,对角线AC、BD相交于点O,E是AB上点(点E不与A、B重合),将射线OE绕点O逆时针旋转90°,所得射线与BC交于点F,则四边形OEBF的面积为 .(2)问题探究:如图②,线段BQ=10,C为BQ上点,在BQ上方作四边形ABCD,使∠ABC=∠ADC=90°,且AD =CD,连接DQ,求DQ的最小值;(3)问题解决:“绿水青山就是金山银山”,某市在生态治理活动中新建了一处南山植物园,图③为南山植物园花卉展示区的部分平面示意图,在四边形ABCD中,∠ABC=∠ADC=90°,AD=CD,AC=600米.其中AB、BD、BC为观赏小路,设计人员考虑到为分散人流和便观赏,提出三条小路的长度和要取得最大,试求AB+BD+BC的最大值.17.如图14-1,在平面直角坐标系xOy 中,直线l 2:y=与x 轴交于点B ,与直线l 1交于点c ,c点到x 轴的距离CD 为2 ,直线1交x 轴于点A(-3,0) .(1)求直线l 1的函数表达式;(2)如图14-2,y 轴上的两个动点E 、F(E 点在F 点上方)满足线段EF 的长为 ,连接CE 、AF ,当线段CE+EF+AF 有最小值时,求出此时点F 的坐标,以及CE+EF+AF 的最小值;(3)如图14-3,将△ACB 绕点B 逆时针方向旋转60°,得到△BGH ,使点A 与点H 重合,点C 与点G 重合(C 、G 两点恰好关于x 轴对称),将ABGH 沿直线BC 平移,记平移中的△BGH 为△B'G'H',在平移过程中,设直线B'H'与x 轴交于点M ,是否存在这样的点M ,使得△B'MG'为等腰三角形?若存在,请直接写出此时点M 的坐标;若不存在,说明理由.18.如图(1)问题发现:如图1,已知点C 为线段 上一点,分别以线段 为直角边作两个等腰直角三角形, ,连接 ,线段 之间的数量关系为 ;位置关系为 .(2)拓展研究:如图2,把 绕点C 逆时针旋转,线段 交于点F ,则 之间的关系是否仍然成立,说明理由;x AB ,AC BC 90,,ACD CA CD CB CE ︒∠===,AE BD ,AE BD Rt ACD ∆,AF BD ,AE BD(3)解决问题:如图3,已知 ,连接 ,把线段AB 绕点A 旋转,若 ,请直接写出线段 的取值范围.19.如图1,在 中, , ,点 分别是 的中点,连接 .(1)探索发现:图1中,的值为 ; 的值为 ;(2)拓展探究若将 绕点 逆时针方向旋转一周,在旋转过程中的大小有无变化,请仅就图2的情形给出证明;(3)问题解决当 旋转至 三点在同一直线时,直接写出线段 的长.,,90AC CD BC CE ACD BCE ︒==∠=∠=,,AB AE AD 7,5AB AC ==AE ABC 2AB AC ==120BAC ∠=︒,D E ,AC BC DE AB BC AD BE CDE C AD BECDE ,,A D E BE20.有两个形状、大小完全相同的直角三角板ABC 和CDE ,其中∠ACB =∠DCE =90°.将两个直角三角板ABC 和CDE 如图①放置,点A ,C ,E 在直线MN 上.(1)三角板CDE 位置不动,将三角板ABC 绕点C 顺时针旋转一周,①在旋转过程中,若∠BCD =35°,则∠ACE = ▲ °;②在旋转过程中,∠BCD 与∠ACE 有怎样的数量关系?请依据图②说明理由.(2)在图①基础上,三角板ABC 和CDE 同时绕点C 顺时针旋转,若三角板ABC 的边AC 从CM 处开始绕点C 顺时针旋转,转速为12°/秒,同时三角板CDE 的边CE 从CN 处开始绕点C 顺时针旋转,转速为2°/秒,当AC 旋转一周再落到CM 上时,两三角板都停止转动.如果设旋转时间为t 秒,则在旋转过程中,当∠ACE =2∠BCD 时,t 为多少秒?21.我们做如下的规定:如果一个三角形在运动变化时保持形状和大小不变,则把这样的三角形称为三角形板.把两块边长为4的等边三角形板 和 叠放在一起,使三角形板 的顶点 与三角形板 的AC 边中点 重合,把三角形板 固定不动,让三角形板 绕点 旋转,设射线 与射线 相交于点M ,射线 与线段 相交于点N.ABC DEF DEF D ABC O ABC DEF O DE AB DF BC(1)如图1,当射线 经过点 ,即点N 与点 重合时,易证△ADM ∽△CND.此时,AM·CN= .(2)将三角形板 由图1所示的位置绕点 沿逆时针方向旋转,设旋转角为 .其中 ,问AM·CN 的值是否改变?说明你的理由.(3)在(2)的条件下,设AM= x ,两块三角形板重叠面积为 ,求 与 的函数关系式.(图2,图3供解题用)22.已知抛物线(,,是常数,)的顶点为,与轴相交于,两点(点在点的左侧),与轴相交于点.(1)若点,求点和点的坐标;(2)将点绕点逆时针方向旋转,点的对应点为,若,两点关于点中心对称,求点的坐标和抛物线解析式:(3)在(1)的条件下,点为直线下方抛物线上的一个动点,过点作轴,与相交于点,过点作轴,与轴相交于点,求的最大值及此时点的坐标.DF B B DEF O α090α<< y y x 2y ax bx c =++a b c 0a ≠()14M -,x A B A B y C ()03C -,A B A B 90︒A 1A A 1A M 1A P BC P PD x BC D P PE y x E PD PE +P答案解析部分1.【答案】(1)解:对称中心O 如图所示;(2)解:∵A 与F ,C 与D 是对应点,∴AO=DO ,CO =FO ,∴四边形ACDF 是平行四边形.2.【答案】(1)解:如图所示:(2)解:由图可知:,,.3.【答案】(1)证明:∵△ABC 是正三角形,∴BC=CA ,∠B=∠ECA=60°.又∵BD=CE ,∴△BCD ≌△CAE.∴CD=AE.(2)解:① 图中有2个正三角形,分别是△BDF ,△AFE.由题设,有△ACE ≌△ABF ,∴CE=BF ,∠ECA=∠ABF=60°又∵BD=CE ,∴BD=CE=BF ,∴△BDF 是正三角形,∵AF=AE ,∠FAE=60°,∴△AFE 是正三角形.1(12)A -,1(33)B -,1(40)C ,② 四边形CDFE 是平行四边形.∵∠FDB=∠ABC =60°∴FD ∥EC.又∵FD=FB=EC ,∴四边形CDFE 是平行四边形.4.【答案】(1)60°(2)解:∵四边形 是矩形,∴ ,∴ .由旋转的性质得 ,∴ ,∴ ,即旋转角 为30°.作 于点E.则 .5.【答案】(1)30°(2)解:无关.理由如下:由旋转变换可知:∠BAC=60°,∠CAD=α, = , AB=AC=AD ,∴ ,,ABCD //AD BC 75CBB AB B ︒'∠=∠='CB CB ='75CB B CBB ︒∠'=∠='180757530BCB ︒︒︒︒∠--='=αB E BC '⊥122AB B E CB '='==()1180602ADB α∠=︒-+︒⎡⎤⎣⎦1202α︒-()11802ADC α∠=︒-()11202ADB α︒∠=-∴∠BDC=∠ADC-∠ADB= - =30° ,∴∠BDC 的大小与ɑ的度数无关.6.【答案】(1)②(2)解:如图(3)解:如图所示:△A 1B 1C 1与△A 2B 2C 2成中心对称图形,对称中心的坐标为:(1,0).7.【答案】(1)解:过点 作 ,垂足为点H ,交 于点F .由题意得 (厘米), .∵四边形 是矩形,∴ , .在 中, 又∵ , ,∴ .∴ (厘米)答:点 到 的距离是 (厘米).(2)解:连结 、 、 .()11802α︒-()11202α︒-D 'D H BC '⊥AD 90AD AD =='60DAD ∠='︒ABCD AD BC 90AFD BHD ∠'=∠='︒Rt AD F ∆'sin 90sin 60D F AD DAD ︒=⋅∠=⋅='''40CE =30DE =70FH=70)D H D F FH ='++'=D 'BC ()70+AE AE 'EE '由题意得 , .∴ 是等边三角形.∴ .∵四边形 是矩形,∴ .在 中, , ,∴(厘米)答:E 、 两点的距离是厘米.8.【答案】(1)解:∵∠BED =30°,△BDE 是直角三角形,∴∠EBD =90°-∠BED =60°.又∵D 是BC 的中点,∴DE 是BC 的垂直平分线.∵BE =CE ,∠BEC =60°,∴△BCE 是等边三角形.∴BC =BE .∵△ABC 是等腰三角形,∠ABC =90°,∴AB =BC .∴BE =AB .∵AB ⊥BC ,DE ⊥BC ,∴AB ∥DE ,∴∠ABE =∠BED =30°.∴∠BAE =∠BEA = (180°-∠ABE)=75°.∴∠AEC =∠BAE +∠BEC =135°.(2)解:∵四边形BDFB '是平行四边形,∠FB 'D =60°∴B 'F ∥BD ,∴∠B D B '=∠FB 'D =60°AE AE ='60EAE ∠='︒AEE ∆'EE AE '=ABCD 90ADE ∠=︒Rt ADE ∆90AD =30DE =AE ===E '12即 =60°.(3)解:△B 'DE 如图所示,AE ⊥DE 不成立,理由如下:DE 与AB 相交于点G ,假设AE ⊥DE ,则△AEG ∽△DBG ,设BG =a ,∠BDG =30°,∴DG =2a ,BD = a ,AB =2 BD = a .∴AG =AB -BG =(-1)a ,B 'D =BD =a .∴DE = =3a.∴GE =DE -DG=3a -2a =a .∴ , .∴ 与假设矛盾.∴AE ⊥DE 不成立.9.【答案】(1)30(2)解:当 时, (1)中的结论仍然成立.证明:如图1,连接 .a tan 30B D'AG DG ==1GE a GB a ==AG GE DG GB≠0360α<< BD,, . , . . .,即 . ,, . .,(3)解:线段 的长为 或 .连接 , 交于点 .,, ,,∵DE=BE ,∠DEB=90°,∴∠EDB=∠EBD=45°,. ,∠B′EB=90°,, . , . .'AB AD AB == 1'(180)9022AB B αα∴∠=︒-=︒-1'[180(120)]3022AB D αα∠=︒-︒-=︒+'180''180(90)(306022EB B AB D AB B αα∴∠=︒-∠-∠=︒-︒--︒+=︒'30EBB ∴∠=︒11(180)3022CBD ABC BAD∠=∠=︒-∠=︒ 'EBB CBD ∴∠=∠'''EBB FBB CBD FBB ∴∠+∠=∠+∠'DBB EBF ∠=∠cos BF DBF BD ∠== cos ''BE EBB BB ∠=='BF BE BD BB ∴='DBB FBE ∆∆∽''EF BE DB BB ∴==EF 3+3-AC BD O AC DB ⊥ 1602BAO BAD ∠=∠=︒sin OB AB BAO ∴=⋅∠=2BD OB ∴==sin DE BE BD DBE ∴==⋅∠=='AB AD AB == 1'(180)9022AB B αα∴∠=︒-=︒-1'[180(120)]3022AB D αα∠=︒-︒-=︒+'180''180(90)(306022EB B AB D AB B αα∴∠=︒-∠-∠=︒-︒--︒+=︒'30EBB ∴∠=︒'tan '2EB BE EBB ∴=⋅∠==分两种情况: 如图,,∵∠B′BE=∠DBF=30°,∴cos ∠B′BE=cos ∠DBF=,又∵∠B′BE+∠EBD=∠EBD+∠DBF ,∴∠B′BD=∠EBF ,∴△B′BD ∽△EBF ,∴ , . 如图,.①''2B D DE BE =+=+EB FB B B DB ='=EB FB EF B B DB B D '='2)3EF D '∴==+=②''2B D DE B E =-=∵∠B′BE=∠DBF=30°,∴cos ∠B′BE=cos ∠DBF=,又∵∠B′BE-∠FBB′=∠DBF-∠FBB′,∴∠B′BD=∠EBF ,∴△B′BD ∽△EBF ,∴ ,.综上所述,线段 的长为或 .10.【答案】(1)证明:(1)在△ABC 和△AEP 中,∠ABC=∠AEP,∠BAC=∠EAP, ∠ACB=∠APE,在△ABC 中,AB=BC. ∠ACB=∠BAC,∠EPA=∠EAP,(2)解: APCD 是矩形.四边形APCD 是平行四边形,AC=2EA,PD=2EP.由(1)知, ∠EPA=∠EAP.EA=EP ,进而AC=PDAPCD 是矩形.(3)解:EM=ENEA=EP, ∠EPA=90° - ∠EAM=180°-∠EAP =180°-∠EPA= 180°-(90°-)=90°+ 由(2)知, ∠CPB=90°,F 是BC 的中点, FP=FB,∠FPB=∠ABC= ,∠EPN=∠EPA+∠APN=∠EPA+∠FPB=90° -+ =90°+ ∠EAM=∠EPN∠AEP 绕点E 顺时针旋转适当的角度,得到∠MEN ,EB FB B B DB ='=EB FB EF B B DB B D '='2)3EF B D ∴===-'EF 33 ∴∴∴ ∴∴∴ ∴12α∴12α12α∴∴α∴12αα12α∴∠AEP-∠AEN =∠MEN-∠AEN,即∠MEA=∠NEP.△EAM ≌△EPN,EM=EN.11.【答案】(1)解:①证明:连结AC ,∵∠A+∠B+∠C+∠D=360°,且∠A=60°,∠C=120°,∴∠B+∠D=180°,且∠B=∠D ,∴∠B=∠D=90°,∵AB=AD ,AC=AC ,∴△ABC ≌△ADC (HL ),∴BC=DC ;②解:延长CB ,使得CD=BE ,∵∠BAD=60°,∠BCD=120°,∴∠ABC+∠D=180°,且∠ABC+∠ABE=180°,∴∠D=∠ABE ,又∵AB=AD∴△ABE ≌△ADC ,∴AE=AC,∴∴∴∠BAE=∠DAC ,∴∠EAC=∠BAE+∠BAC=∠DAC+∠BAC=∠BAD=60°,∴△ACE 是等边三角形,∴AC=CE=CB+BE=CB+CD(2)解:如图,设∠ACD=15°,∠DCD‘=30°,作CM ⊥AD ,D‘H ⊥AC ,由旋转图形的特点可知,CB=CD ,CB‘=CD’,∠BCB'=DCD‘=30°,∴△∠BCB'≌△DCD‘,BB'=DD’,设D'H=x ,由勾股定理得:, HC=x,则,解得x=10, 即D'H=10,得,AD’=20,在Rt △AMC 中,∵,∠DAC=30°,∴,AM=(,-5,,∴DD’为D 点的运动路程,则BB‘的运动路程也为10 .12.【答案】(1)解:∵四边形ABCD 是正方形,∴∠ADC =∠DCE =90°,∵四边形DEFG 是矩形,∴∠AGD =∠GDE =90°,∴∠DCE =∠AGD =90°,∠ADC =∠GDE =90°,∴∠ADC ﹣∠ADE =∠GDE ﹣∠ADE ,∴∠EDC =∠ADG ,∵∠EDC =∠ADG ,∠DCE =∠AGD =90°,∴△ECD ∽△AGD ,∴ ,∴DG•DE =DC•DA =6×6=36,∴矩形DEFG 的面积=DG•DE =36;(2)解: ,证明:把△BAP 绕着点B 顺时针旋转90°得到△BCK ,连接KH ,由旋转得△BAP ≌△BCK ,∴BK =BP ,∠PBA =∠KBC ,∠BCK =∠BAP = ,∴∠HCK = = ,∴由勾股定理得, ,∵∠PBE =45°,∴∠PBA+∠ABE =45°,∵∠PBA =∠KBC ,∴∠KBC+∠ABE =45°,∵∠ABC =90°,∴∠HBK =45°,∵∠PBE =45°,∴∠HBK =∠PBE =45°,∵BK =BP ,∠HBK =∠PBE ,BH =BH ,∴△BHP ≌△BHK (SAS ),CD DE DG DA=222CH PA HP +=18045135︒-︒=︒BCK BCA ∠-∠1354590︒-︒=︒222CH PA KH +=∴HK =HP ,∵ ,∴ ;(3)解:把△BMC 绕着点B 顺时针旋转60°得到△BKN ,连接MK ,BN ,NC ,由旋转得,△BMC ≌△BKN ,∴MC =KN ,BM =BK ,∵BM =BK ,∠MBK =60°,∴△BKM 是等边三角形,∴MK =BM ,∴MA+MB+MC =AM+MK+KN ,当A ,M ,K ,N 四点共线时,AN 就是所求的MA+MB+MC 的最小值,过N 作NQ ⊥AB 交AB 的延长线于Q ,∵ ,∠BQN =90°,∴QN =BN•sin30°=6× =3,BQ =BN•cos30°= ,∴AQ =AB+BQ =,在Rt △AQN 中,由勾股定理得,,∴ 的最小值为 .13.【答案】(1)CD=2BF ;BF ⊥CD(2)解:BF ⊥CD ,CD=2BF 成立,证明:∵△ABC 与△DBE 都是等腰直角三角形,∴AB=BC ,DB=EB ,∠ABC=∠DBE=90°,222CH PA KH +=222CH PA HP +=180906030NBQ ∠︒-︒-︒=︒=126=6+(222226372AN AQ QN +=++=+=2y 72+如图②,将△ABE 绕点B 顺时针旋转90°得到△CBG ,点E 、F 的对应点分别是G 、H ,连BH , 则△ABE ≌△CBG ,BE=BG ,AE=CG ,BF=BH ,∠FBH=∠EBG=90°,AF=CH ,EF=GH , ∴BF ⊥BH ,∵AF=EF ,∴CH=GH ,∵∠DBE=90°,∴∠DBE+∠EBG=180°,∴D 、B 、G 三点共线,∴BH ∥CD ,,∴BF ⊥CD ,,即CD=2BF ,∴BF ⊥CD ,CD=2BF 成立;(3)14.【答案】(1)DE=BC ;12.5(2)解:过点D 作BC 边上的高DE ,如图,∵∠ABC+∠A=90°,∠ABC+∠DBE=90°,∴∠A=∠DBE ,又∵∠ACB=∠E=90°,AB=BD ,∴ ,∴,12BH CD =12BF CD =13BF ≤≤ACB BED ≌BC DE =又 .∴ 的面积为:.(3)解:作 于G ,过点D 作BC 边上的高DE ,如图,由(2)同理,可证 ,∴ ,又 ,∵AB=AC , ,∴ .∴ 的面积为: .15.【答案】(1)NM=NP ;60°(2)证明:由旋转得:∠BAD=∠CAE ,又∵AB=AC ,AD=AE ,∴△ABD ≌△ACE (SAS ),∴BD=CE ,∠ABD=∠ACE ,∵点M ,N ,P 分别为DE ,BE ,BC 的中点,∴MN= BD ,PN= CE ,MN ∥BD ,PN ∥CE ,∴MN=PN ,∠ENM=∠EBD ,∠BPN=∠BCE ,∴∠ENP=∠NBP+∠NPB=∠NBP+∠ECB ,∵∠EBD=∠ABD+∠ABE=∠ACE+∠ABE ,∴∠MNP=∠MNE+∠ENP=∠ACE+∠ABE+∠EBC+∠EBC+∠ECB=180°-∠BAC=60°,∴△MNP 是等边三角形;(322()()4mn BC m n m n =+--=BCD 221448m n 2mn mn ⨯⨯=AGB BED ≌BG DE =BC a b c =++BC a b c =++11()22BG BC a b c ==++BCD 2111()()()224a b c a b c a b c ⨯++⨯++=++121216.【答案】(1)4(2)解:如图②中,连接BD ,取AC 的中点O ,连接OB ,OD.∵∠ABD =∠ADC =90°,AO =OC ,∴OA =OC =OB =OD ,∴A ,B ,C ,D 四点共圆,∴∠DBC =∠DAC ,∵DA =DC ,∠ADC =90°,∴∠DAC =∠DCA =45°,∴∠DBQ =45°,根据垂线段最短可知,当QD ⊥BD 时,QD 的值最短,DQ 的最小值=BQ =5 .(3)解:如图③中,将△BDC 绕点D 顺时针旋转90°得到△EDA , ∵∠ABC+∠ADC =180°,∴∠BCD+∠BAD =∠EAD+BAD =180°,∴B ,A ,E 三点共线,∵DE =DB ,∠EDB =90°,∴BE = BD ,∴AB+BC =AB+AE =BE =BD,∴BC+BC+BD =( +1)BD ,∴当BD 最大时,AB+BC+BD 的值最大,∵A ,B ,C ,D 四点共圆,∴当BD 为直径时,BD 的值最大,∵∠ADC =90°,∴AC 是直径,∴BD =AC 时,AB+BC+BD 的值最大,最大值=600( +1).17.【答案】(1)解:∵点C 的纵坐标为2 ,点c 在直线l 2:y= ∴点C(-1,2 )设l 1的表达式为y= kx+ b将A(-3,0)、C(-1,2)代入, 解得故直线l 1的表达式为:y=x+3 (2)解:作点a关于y 轴的对称点A(3,0),将点a4向上平移个单位长度得E (3,)连接E'C 交y 轴于点E ,在E下方取EF= ,则点F是所求点,将点C 、E' 的坐标代入一次函数表达式,同理可得: CE' 的函数表达式为:y= 故点E(0,),点F(0,)CE+EF+4F 的最小值=FE+CE'= +.(3)M(5+8,0)或(5-8,0)或(-3,0)或(-19,0) x +03k bk b=-+⎧⎪⎨=-+⎪⎩k b ⎧=⎪⎨=⎪⎩x +18.【答案】(1)AE=BD ;AE ⊥BD(2)解: 仍然成立.由题意得,∵△ACD 和△BCE 是等腰直角三角形即 ,∴∴ .∴∴ .(3)解: 连接BD.由(2)可知,AE=BD ,在△ABD 中,且 ,所以 即 在AB 绕点A 旋转过程中,当A ,B ,D 三点在一条直线上时, 或者,AE BD AE BD =⊥90ACD DCE ECB DCE DCE ︒∴∠+∠=∠+∠=+∠,,ACE DCB AC CD EC CB ∠=∠==ACE DCB∆≅∆,12AE DB =∠=∠180(4512)90EFB ︒︒︒∠=--∠+∠=AE BD⊥77AE -≤≤7AD AB ===77BD <<+77AE -<<+7AE =7AE =∴ ≤AE≤ 19.【答案】(1(2)解:无变化,理由: 由(1)知,CD=1, ,∴,∴ ,由(1)知,∠ACB=∠DCE=30°,∴∠ACD=∠BCE,∴△ACD ∽△BCE,∴,(3)解:线段BE 的长为或 ,理由如下: 当点D 在线段AE 上时,如图2,过点C 作CF ⊥AE 于F,∠CDF=180°﹣∠CDE=60°,∴∠DCF=30°,∴ ,∴,7-7+CE BE ==CD CE =AC BC =CD AC CE BC ==AD AC BE BC ==1122DF CD ==CF ==在Rt △AFC 中,AC=2,根据勾股定理得, ,∴AD=AF+DF=,由(2)知, ,∴当点D在线段AE 的延长线上时,如图3,过点C 作CG ⊥AD 交AD 的延长线于G,∵∠CDG=60°,∴∠DCG=30°,∴ ,∴ ,在Rt △ACG 中,根据勾股定理得,,∴ ,由(2)知,,∴即:线段BE 的长为或.AF ==AD BE =BE ==1122DG CD ==CG ==AG =AD AG DG =-=AD BE =BE ==20.【答案】(1)①145;②∠BCD+∠ACE =180°,理由如下:∵∠ACE =∠ACB+∠BCE ,∴∠BCD+∠ACE =∠BCD+∠ACB+∠BCE =∠ACB+∠DCE =90°+90°=180°;(2)解:三角板ABC 和CDE 重合之前,∠ACE =180°-10°t ,∠BCD =10°t ,依题意有180°-10°t =2×10°t ,解得t =6;三角板ABC 和CDE 重合之后,∠ACE =10°t-180°,∠BCD =360°-10°t ,依题意有10°t-180°=2×(360°-10°t ),解得t =30.故当t =6或30秒时,有∠ACE =2∠BCD .故答案为:6或30.21.【答案】(1)4(2)解:AM•CN 的值不会改变.连接BD ,在△ADM 与△CND 中,∵∠A=∠C=60°,∠DNC=∠DBN+∠BDN=30°+α,∠ADM=30°+α,∴∠ADM=∠CND ,∴△ADM ∽△CND∴ ,∴AM•CN=AD•CD=2×2=4,∴AM•CN 的值不会改变;(3)解:情形1,当0°<α<60°时,1<AM <4,即1<x <4,此时两三角形板重叠部分为四边形AD AM CN CD如图2,过D 作DQ ⊥AB 于Q ,DG ⊥BC 于G ,∴DQ=DG= ,由(2)知,AM•CN=4,得CN=,于是y=(1<x <4); 情形2,当60°≤α<90°时,AM≥4时,即x≥4,此时两三角形板重叠部分为△DPN ,如图3,过点D 作DH ∥BC 交AM 于H ,易证△MBP ∽△MHD ,∴ ,又∵MB=x-4,MH=x-2,DH=2,∴BP=,∴PN=4- ,于是y= ,综上所述,1<x <4时,y=;x≥4时,y= 22.【答案】(1)解:设抛物线解析式为,将点代入得,4x 21122AB AM DQ CN DG x -⋅-⋅=BP MB DH MH=282x x --4282x x x ---114284222x PN DG x x -⎛⎫⋅=--= ⎪-⎝⎭x ()214y a x =--()03C -,解得:∴抛物线解析式为当时,解得:,∵点在点的左侧,∴,;(2)解:∵,抛物线,与轴相交于,两点∴,对称轴为直线,设,则,∴∵点绕点逆时针方向旋转得到,则点一定在第四象限,如图所示,则,,∵,两点关于点中心对称,∴解得:,则∴,1a =()214y x =--0y =()2140x --=1213x x =-=,A B ()10A -,()30B ,()14M -,2y ax bx c =++x A B 0a >1x =()0A m ,()20B m -,222AB m m m=--=-A B 90︒A 'A '22BA BA m ='=-()222A m m '--,A 1A M 228m -=-3m =-()58A '-,()30A -,()50B ,将点代入得,解得:∴抛物线解析式为;(3)解:如图所示,设交于点,由(1)可得,,设直线的解析式为,将点代入得,解得所以直线的解析式为,∵抛物线解析式为,设,则,∴,∵轴,轴,由∵则是等腰直角三角形,∴()30A -,()214y a x =--1640a -=14a =()21144y x =--PE BC F ()30B ,()03C -,BC 3y kx =-()30B ,330k -=1k =BC 3y x =-()221423y x x x =--=--()223P t t t --,()0E t ,()3F t t -,223233FP t t t t t =--++=-+223PE t t =-++PD x PE y OC OB=OCB 45FDP OBC ∠=∠=︒∴也是等腰直角三角形,∴∴∴当时,取得最大值此时,即.PDF PD PF=PD PE+22323t t t t =-+-++2253t t =-++252525232168t t ⎛⎫=--+++ ⎪⎝⎭2549248t ⎛⎫=--+ ⎪⎝⎭54t =PD PE +498225632314416t t ⎛⎫--=--=- ⎪⎝⎭563416P ⎛⎫- ⎪⎝⎭。
中考数学(旋转提高练习题)压轴题训练及答案解析(1)

一、旋转真题与模拟题分类汇编(难题易错题)1.(1)发现:如图1,点A为线段BC外一动点,且BC=a,AB=b.填空:当点A位于时,线段AC的长取得最大值,且最大值为(用含a,b的式子表示) (2)应用:点A为线段BC外一动点,且BC=4,AB=1,如图2所示,分别以AB,AC为边,作等边三角形ABD和等边三角形ACE,连接CD,BE.①请找出图中与BE相等的线段,并说明理由;②直接写出线段BE长的最大值.(3)拓展:如图3,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(6,0),点P 为线段AB外一动点,且PA=2,PM=PB,∠BPM=90°,请直接写出线段AM长的最大值及此时点P的坐标.【答案】(1)CB的延长线上, a+b;(2)①CD=BE,理由见解析;②BE长的最大值为5;(3)满足条件的点P坐标(222)或(222),AM的最大值为2+4.【解析】【分析】(1)根据点A位于CB的延长线上时,线段AC的长取得最大值,即可得到结论;(2)①根据已知条件易证△CAD≌△EAB,根据全等三角形的性质即可得CD=BE;②由于线段BE长的最大值=线段CD的最大值,根据(1)中的结论即可得到结果;(3)连接BM,将△APM绕着点P顺时针旋转90°得到△PBN,连接AN,得到△APN是等腰直角三角形,根据全等三角形的性质得到PN=PA=2,BN=AM,根据当N在线段BA的延长线时,线段BN取得最大值,即可得到最大值为2+4;如图2,过P作PE⊥x轴于E,根据等腰直角三角形的性质即可求得点P的坐标.如图3中,根据对称性可知当点P在第四象限时也满足条件,由此求得符合条件的点P另一个的坐标.【详解】(1)∵点A为线段BC外一动点,且BC=a,AB=b,∴当点A位于CB的延长线上时,线段AC的长取得最大值,且最大值为BC+AB=a+b,故答案为CB的延长线上,a+b;(2)①CD=BE,理由:∵△ABD与△ACE是等边三角形,∴AD=AB,AC=AE,∠BAD=∠CAE=60°,∴∠BAD+∠BAC=∠CAE+∠BAC,即∠CAD=∠EAB,在△CAD与△EAB中,AD ABCAD EAB AC AE=⎧⎪∠=∠⎨⎪=⎩,∴△CAD≌△EAB(SAS),∴CD=BE;②∵线段BE长的最大值=线段CD的最大值,由(1)知,当线段CD的长取得最大值时,点D在CB的延长线上,∴最大值为BD+BC=AB+BC=5;(3)如图1,∵将△APM绕着点P顺时针旋转90°得到△PBN,连接AN,则△APN是等腰直角三角形,∴PN=PA=2,BN=AM,∵A的坐标为(2,0),点B的坐标为(6,0),∴OA=2,OB=6,∴AB=4,∴线段AM长的最大值=线段BN长的最大值,∴当N在线段BA的延长线时,线段BN取得最大值,最大值=AB+AN,∵AN=2AP=22,∴最大值为22+4;如图2,过P作PE⊥x轴于E,∵△APN是等腰直角三角形,∴PE=AE2,∴OE=BO﹣AB﹣AE=6﹣42=22,∴P(2﹣2,2).如图3中,根据对称性可知当点P在第四象限时,P(2﹣2,﹣2)时,也满足条件.综上所述,满足条件的点P坐标(2﹣2,2)或(2﹣2,﹣2),AM的最大值为22+4.【点睛】本题综合考查了全等三角形的判定和性质,等腰直角三角形的性质,最大值问题,旋转的性质.正确的作出辅助线构造全等三角形是解题的关键.2.在Rt△ABC中,AB=BC=5,∠B=90°,将一块等腰直角三角板的直角顶点放在斜边AC的中点O处,将三角板绕点O旋转,三角板的两直角边分别交AB,BC或其延长线于E,F两点,如图①与②是旋转三角板所得图形的两种情况.(1)三角板绕点O旋转,△OFC是否能成为等腰直角三角形?若能,指出所有情况(即给出△OFC是等腰直角三角形时BF的长);若不能,请说明理由;(2)三角板绕点O旋转,线段OE和OF之间有什么数量关系?用图①或②加以证明;(3)若将三角板的直角顶点放在斜边上的点P处(如图③),当AP:AC=1:4时,PE和PF 有怎样的数量关系?证明你发现的结论.【答案】(1)△OFC是能成为等腰直角三角形,(2)OE=OF.(3)PE:PF=1:3.【解析】【小题1】由题意可知,①当F为BC的中点时,由AB=BC=5,可以推出CF和OF的长度,即可推出BF的长度,②当B与F重合时,根据直角三角形的相关性质,即可推出OF 的长度,即可推出BF的长度;【小题2】连接OB,由已知条件推出△OEB≌△OFC,即可推出OE=OF;【小题3】过点P做PM⊥AB,PN⊥BC,结合图形推出△PNF∽△PME,△APM∽△PNC,继而推出PM:PN=PE:PF,PM:PN=AP:PC,根据已知条件即可推出PA:AC=PE:PF=1:4.3.如图1,△ABC是边长为4cm的等边三角形,边AB在射线OM上,且OA=6cm,点D 从O点出发,沿OM的方向以1cm/s的速度运动,当D不与点A重合时,将△ACD绕点C 逆时针方向旋转60°得到△BCE,连结DE.(1)求证:△CDE是等边三角形;(2)如图2,当6<t<10时,△BDE的周长是否存在最小值?若存在,求出△BDE的最小周长;若不存在,请说明理由;(3)如图3,当点D在射线OM上运动时,是否存在以D、E、B为顶点的三角形是直角三角形?若存在,求出此时t的值;若不存在,请说明理由.【答案】(1)见解析(2)见解析(3)存在【解析】试题分析:(1)由旋转的性质得到∠DCE=60°,DC=EC,即可得到结论;(2)当6<t<10时,由旋转的性质得到BE=AD,于是得到C△DBE=BE+DB+DE=AB+DE=4+DE,根据等边三角形的性质得到DE=CD,由垂线段最短得到当CD⊥AB时,△BDE的周长最小,于是得到结论;(3)存在,①当点D于点B重合时,D,B,E不能构成三角形,②当0≤t<6时,由旋转的性质得到∠ABE=60°,∠BDE<60°,求得∠BED=90°,根据等边三角形的性质得到∠DEB=60°,求得∠CEB=30°,求得OD=OA-DA=6-4=2,于是得到t=2÷1=2s;③当6<t<10s 时,此时不存在;④当t>10s时,由旋转的性质得到∠DBE=60°,求得∠BDE>60°,于是得到t=14÷1=14s.试题解析:(1)证明:∵将△ACD绕点C逆时针方向旋转60°得到△BCE,∴∠DCE=60°,DC=EC,∴△CDE是等边三角形;(2)存在,当6<t<10时,由旋转的性质得,BE=AD,∴C△DBE=BE+DB+DE=AB+DE=4+DE,由(1)知,△CDE是等边三角形,∴DE=CD,∴C△DBE=CD+4,由垂线段最短可知,当CD⊥AB时,△BDE的周长最小,此时,CD3cm,∴△BDE的最小周长=CD;(3)存在,①∵当点D与点B重合时,D,B,E不能构成三角形,∴当点D与点B重合时,不符合题意;②当0≤t<6时,由旋转可知,∠ABE=60°,∠BDE<60°,∴∠BED=90°,由(1)可知,△CDE是等边三角形,∴∠DEB=60°,∴∠CEB=30°,∵∠CEB=∠CDA,∴∠CDA=30°,∵∠CAB=60°,∴∠ACD=∠ADC=30°,∴DA=CA=4,∴OD=OA﹣DA=6﹣4=2,∴t=2÷1=2s;③当6<t<10s时,由∠DBE=120°>90°,∴此时不存在;④当t>10s时,由旋转的性质可知,∠DBE=60°,又由(1)知∠CDE=60°,∴∠BDE=∠CDE+∠BDC=60°+∠BDC,而∠BDC>0°,∴∠BDE>60°,∴只能∠BDE=90°,从而∠BCD=30°,∴BD=BC=4,∴OD=14cm,∴t=14÷1=14s.综上所述:当t=2或14s时,以D、E、B为顶点的三角形是直角三角形.点睛:在不带坐标的几何动点问题中求最值,通常是将其表达式写出来,再通过几何或代数的方法求出最值;像第三小问这种探究性的题目,一定要多种情况考虑全面,控制变量,从某一个方面出发去分类.4.已知:在△ABC中,BC=a,AC=b,以AB为边作等边三角形ABD.探究下列问题:(1)如图1,当点D与点C位于直线AB的两侧时,a=b=3,且∠ACB=60°,则CD= ;(2)如图2,当点D与点C位于直线AB的同侧时,a=b=6,且∠ACB=90°,则CD= ;(3)如图3,当∠ACB变化,且点D与点C位于直线AB的两侧时,求 CD的最大值及相应的∠ACB的度数.【答案】(1);(2);(3)当∠ACB=120°时,CD有最大值是a+b.【解析】【分析】(1)a=b=3,且∠ACB=60°,△ABC是等边三角形,且CD是等边三角形的高线的2倍,据此即可求解;(2)a=b=6,且∠ACB=90°,△ABC是等腰直角三角形,且CD是边长是6的等边三角形的高长与等腰直角三角形的斜边上的高的差;(3)以点D为中心,将△DBC逆时针旋转60°,则点B落在点A,点C落在点E.连接AE,CE,当点E、A、C在一条直线上时,CD有最大值,CD=CE=a+b.【详解】(1)∵a=b=3,且∠ACB=60°,∴△ABC是等边三角形,∴OC=,∴CD=3;(2)3;(3)以点D为中心,将△DBC逆时针旋转60°,则点B落在点A,点C落在点E.连接AE,CE,∴CD=ED,∠CDE=60°,AE=CB=a,∴△CDE为等边三角形,∴CE=CD.当点E、A、C不在一条直线上时,有CD=CE<AE+AC=a+b;当点E、A、C在一条直线上时,CD有最大值,CD=CE=a+b;只有当∠ACB=120°时,∠CAE=180°,即A、C、E在一条直线上,此时AE最大∴∠ACB=120°,因此当∠ACB=120°时,CD有最大值是a+b.【点睛】本题主要考查了等边三角形的性质,以及轴对称的性质,正确理解CD有最大值的条件,是解题的关键.5.在△ABC中,AB=AC,将线段AC绕着点C逆时针旋转得到线段CD,旋转角为,且,连接AD、BD.(1)如图1,当∠BAC=100°,时,∠CBD 的大小为_________;(2)如图2,当∠BAC=100°,时,求∠CBD的大小;(3)已知∠BAC的大小为m(),若∠CBD 的大小与(2)中的结果相同,请直接写出的大小.【答案】(1)30°;(2)30°;(3)α=120°-m°,α=60°或α=240-m°.【解析】试题分析:(1)由∠BAC=100°,AB=AC,可以确定∠ABC=∠ACB=40°,旋转角为α,α=60°时△ACD是等边三角形,且AC=AD=AB=CD,知道∠BAD的度数,进而求得∠CBD的大小.(2)由∠BAC=100°,AB=AC,可以确定∠ABC=∠ACB=40°,连结DF、BF.AF=FC=AC,∠FAC=∠AFC=60°,∠ACD=20°,由∠DCB=20°案.依次证明△DCB≌△FCB,△DAB≌△DAF.利用角度相等可以得到答案.(3)结合(1)(2)的解题过程可以发现规律,求得答案.试题解析:(1)30°;(2)30°;(2)如图作等边△AFC ,连结DF 、BF .∴AF=FC=AC ,∠FAC=∠AFC=60°.∵∠BAC=100°,AB=AC ,∴∠ABC=∠BCA=40°.∵∠ACD=20°,∴∠DCB=20°.∴∠DCB=∠FCB=20°.①∵AC=CD ,AC=FC ,∴DC=FC .②∵BC=BC ,③∴由①②③,得△DCB ≌△FCB ,∴DB=BF ,∠DBC=∠FBC .∵∠BAC=100°,∠FAC=60°,∴∠BAF=40°.∵∠ACD=20°,AC=CD ,∴∠CAD=80°.∴∠DAF=20°.∴∠BAD=∠FAD=20°.④∵AB=AC ,AC=AF ,∴AB=AF .⑤∵AD=AD ,⑥∴由④⑤⑥,得△DAB ≌△DAF .∴FD=BD .∴FD=BD=FB .∴∠DBF=60°.∴∠CBD=30°.(3)α=120°-m°,α=60°或α=240-m°.考点:1.全等三角形的判定和性质;2.等边三角形的判定和性质.6.已知O 为直线MN 上一点,OP ⊥MN ,在等腰Rt △ABO 中,90BAO ∠=︒,AC ∥OP 交OM 于C ,D 为OB 的中点,DE ⊥DC 交MN 于E .(1) 如图1,若点B 在OP 上,则①AC OE (填“<”,“=”或“>”);②线段CA 、CO 、CD 满足的等量关系式是 ;(2) 将图1中的等腰Rt △ABO 绕O 点顺时针旋转α(045α︒<<︒),如图2,那么(1)中的结论②是否成立?请说明理由;(3) 将图1中的等腰Rt △ABO 绕O 点顺时针旋转α(),请你在图3中画出图形,并直接写出线段CA 、CO 、CD 满足的等量关系式 ;【答案】(1)①=;②AC2+CO2=CD2;(2)(1)中的结论②不成立,理由见解析;(3)画图见解析;OC-CA=2CD.【解析】试题分析:(1)①如图1,证明AC=OC和OC=OE可得结论;②根据勾股定理可得:AC2+CO2=CD2;(2)如图2,(1)中的结论②不成立,作辅助线,构建全等三角形,证明A、D、O、C四点共圆,得∠ACD=∠AOB,同理得:∠EFO=∠EDO,再证明△ACO≌△EOF,得OE=AC,AO=EF,根据勾股定理得:AC2+OC2=FO2+OE2=EF2,由直角三角形中最长边为斜边可得结论;(3)如图3,连接AD,则AD=OD证明△ACD≌△OED,根据△CDE是等腰直角三角形,得CE2=2CD2,等量代换可得结论(OC﹣OE)2=(OC﹣AC)2=2CD2,开方后是:OC﹣AC=CD.试题解析:(1)①AC=OE,理由:如图1,∵在等腰Rt△ABO中,∠BAO=90°,∴∠ABO=∠AOB=45°,∵OP⊥MN,∴∠COP=90°,∴∠AOC=45°,∵AC∥OP,∴∠CAO=∠AOB=45°,∠ACO=∠POE=90°,∴AC=OC,连接AD,∵BD=OD,∴AD=OD,AD⊥OB,∴AD∥OC,∴四边形ADOC是正方形,∴∠DCO=45°,∴AC=OD,∴∠DEO=45°,∴CD=DE,∴OC=OE,∴AC=OE;②在Rt△CDO中,∵CD2=OC2+OD2,∴CD2=AC2+OC2;故答案为AC2+CO2=CD2;(2)如图2,(1)中的结论②不成立,理由是:连接AD,延长CD交OP于F,连接EF,∵AB=AO,D为OB的中点,∴AD⊥OB,∴∠ADO=90°,∵∠CDE=90°,∴∠ADO=∠CDE,∴∠ADO﹣∠CDO=∠CDE﹣∠CDO,即∠ADC=∠EDO,∵∠ADO=∠ACO=90°,∴∠ADO+∠ACO=180°,∴A、D、O、C四点共圆,∴∠ACD=∠AOB,同理得:∠EFO=∠EDO,∴∠EFO=∠AOC,∵△ABO是等腰直角三角形,∴∠AOB=45°,∴∠DCO=45°,∴△COF和△CDE是等腰直角三角形,∴OC=OF,∵∠ACO=∠EOF=90°,∴△ACO≌△EOF,∴OE=AC,AO=EF,∴AC2+OC2=FO2+OE2=EF2,Rt△DEF中,EF>DE=DC,∴AC2+OC2>DC2,所以(1)中的结论②不成立;(3)如图3,结论:OC﹣CA=CD,理由是:连接AD,则AD=OD,同理:∠ADC=∠EDO,∵∠CAB+∠CAO=∠CAO+∠AOC=90°,∴∠CAB=∠AOC,∵∠DAB=∠AOD=45°,∴∠DAB﹣∠CAB=∠AOD﹣∠AOC,即∠DAC=∠DOE,∴△ACD≌△OED,∴AC=OE,CD=DE,∴△CDE是等腰直角三角形,∴CE2=2CD2,∴(OC﹣OE)2=(OC﹣AC)2=2CD2,∴OC﹣AC=CD,故答案为OC﹣AC=CD.考点:几何变换的综合题7.正方形ABCD和正方形AEFG的边长分别为2和22,点B在边AG上,点D在线段EA 的延长线上,连接BE.(1)如图1,求证:DG⊥BE;(2)如图2,将正方形ABCD绕点A按逆时针方向旋转,当点B恰好落在线段DG上时,求线段BE的长..【答案】(1)答案见解析;(2)26【解析】【分析】(1)由题意可证△ADG≌△ABE,可得∠AGD=∠AEB,由∠ADG+∠AGD=90°,可得∠ADG+∠AEB=90°,即DG⊥BE;(2)过点A作AM⊥BD,垂足为M,根据勾股定理可求MG的长度,即可求DG的长度,由题意可证△DAG≌△BAE,可得BE=DG.【详解】(1)如图,延长EB交GD于H∵四边形ABCD和四边形AEFG是正方形∴AD=AB,AG=AE,∠DAG=∠BAE=90°∴△ADG≌△ABE(SAS)∴∠AGD=∠AEB∵∠ADG+∠AGD=90°∴∠ADG+∠AEB=90°∴DG⊥BE(2)如图,过点A作AM⊥BD,垂足为M∵正方形ABCD和正方形AEFG的边长分别为2和22,∴AM=DM=2,∠DAB=∠GAE=90°∴MG=22-=6,∠DAG=∠BAEAG MA∴DG=DM+MG=2+6,由旋转可得:AD=AB,AG=AE,且∠DAG=∠BAE∴△DAG≌△BAE(SAS)+∴BE=DG=26【点睛】考查了旋转的性质,正方形的性质,全等三角形的判定和性质,勾股定理,熟练运用这些性质进行推理是本题的关键.8.如图,在△ABC中,∠CAB=70°,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,求∠BAB′的度数.【答案】40°.【解析】【分析】先根据平行线的性质,由CC′∥AB得∠AC′C=∠CAB=70°,再根据旋转的性质得AC=AC′,∠BAB′=∠CAC′,于是根据等腰三角形的性质有∠ACC′=∠AC′C=70°,然后利用三角形内角和定理可计算出∠CAC′=40°,从而得到∠BAB′的度数.【详解】∵CC′∥AB,∴∠A CC′=∠CAB=70°,∵△ABC绕点A旋转到△AB′C′的位置,∴AC=AC′,∠BAB′=∠CAC′,在△ACC′中,∵AC=AC′∴∠ACC′=∠AC′C=70°,∴∠CAC′=180°-70°-70°=40°,∴∠BAB′=40°.【点睛】本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.。
2023年中考数学【图形的旋转】真题汇编(共30题,解析版)

图形的旋转(30题)一、单选题江苏无锡·统考中考真题)如图,△ABC中,∠BAC=55°,将△ABC逆时针旋转α(0°<α< 55°),得到△ADE,DE交AC于F.当α=40°时,点D恰好落在BC上,此时∠AFE等于()A.80°B.85°C.90°D.95°【答案】B【分析】根据旋转可得∠B=∠ADB=∠ADE,再结合旋转角α=40°即可求解.【详解】解:由旋转性质可得:∠BAC=∠DAE=55°,AB=AD,∵α=40°,∴∠DAF=15°,∠B=∠ADB=∠ADE=70°,∴∠AFE=∠DAF+∠ADE=85°,故选:B.【点睛】本题考查了几何-旋转问题,掌握旋转的性质是关键.天津·统考中考真题)如图,把△ABC以点A为中心逆时针旋转得到△ADE,点B,C的对应点分别是点D,E,且点E在BC的延长线上,连接BD,则下列结论一定正确的是()A.∠CAE=∠BEDB.AB=AEC.∠ACE=∠ADED.CE=BD【答案】A【分析】根据旋转的性质即可解答.【详解】根据题意,由旋转的性质,可得AB=AD,AC=AE,BC=DE,故B选项和D选项不符合题意,∠ABC=∠ADE∵∠ACE=∠ABC+∠BAC∴∠ACE=∠ADE+∠BAC,故C选项不符合题意,∠ACB=∠AED∵∠ACB=∠CAE+∠CEA∵∠AED=∠CEA+∠BED∴∠CAE=∠BED,故A选项符合题意,故选:A .【点睛】本题考查了旋转的性质,熟练掌握旋转的性质和三角形外角运用是解题的关键.3(2023·四川宜宾·统考中考真题)如图,△ABC 和△ADE 是以点A 为直角顶点的等腰直角三角形,把△ADE 以A 为中心顺时针旋转,点M 为射线BD 、CE 的交点.若AB =3,AD =1.以下结论:①BD =CE ;②BD ⊥CE ;③当点E 在BA 的延长线上时,MC =3-32;④在旋转过程中,当线段MB 最短时,△MBC 的面积为12.其中正确结论有()A.1个B.2个C.3个D.4个【答案】D 【分析】证明△BAD ≌△CAE 即可判断①,根据三角形的外角的性质得出②,证明∠DCM ∽∠ECA 得出MC 3=3-12,即可判断③;以A 为圆心,AD 为半径画圆,当CE 在⊙A 的下方与⊙A 相切时,MB 的值最小,可得四边形AEMD 是正方形,在Rt △MBC 中MC =BC 2-MB 2=2+1,然后根据三角形的面积公式即可判断④.【详解】解:∵△ABC 和△ADE 是以点A 为直角顶点的等腰直角三角形,∴BA =CA ,DA =EA ,∠BAC =∠DAE =90°,∴∠BAD =∠CAE ,∴△BAD ≌△CAE ,∴∠ABD =∠ACE ,BD =CE ,故①正确;设∠ABD =∠ACE =α,∴∠DBC =45°-α,∴∠EMB =∠DBC +∠BCM =∠DBC +∠BCA +∠ACE =45°-α+45°+α=90°,∴BD ⊥CE ,故②正确;当点E 在BA 的延长线上时,如图所示∵∠DCM =∠ECA ,∠DMC =∠EAC =90°,∴∠DCM ∽∠ECA∴MC AC =CD EC ∵AB =3,AD =1.∴CD =AC -AD =3-1,CE =AE 2+AC 2=2∴MC 3=3-12∴MC =3-32,故③正确;④如图所示,以A 为圆心,AD 为半径画圆,∵∠BMC =90°,∴当CE 在⊙A 的下方与⊙A 相切时,MB 的值最小,∠ADM =∠DAE =∠AEM =90°∴四边形AEMD 是矩形,又AE =AD ,∴四边形AEMD 是正方形,∴MD =AE =1,∵BD =EC =AC 2-AE 2=2,∴MB =BD -MD =2-1,在Rt △MBC 中,MC =BC 2-MB 2∴PB 取得最小值时,MC =AB 2+AC 2-MB 2=3+3-2-1 2=2+1∴S △BMC =12MB ×MC =122-1 2+1 =12故④正确,故选:D .【点睛】本题考查了旋转的性质,相似三角形的性质,勾股定理,切线的性质,垂线段最短,全等三角形的性质与判定,正方形的性质,熟练掌握以上知识是解题的关键.4(2023·山东聊城·统考中考真题)如图,已知等腰直角△ABC ,∠ACB =90°,AB =2,点C 是矩形ECGF 与△ABC 的公共顶点,且CE =1,CG =3;点D 是CB 延长线上一点,且CD =2.连接BG ,DF ,在矩形ECGF 绕点C 按顺时针方向旋转一周的过程中,当线段BG 达到最长和最短时,线段DF 对应的长度分别为m 和n ,则m n的值为()A.2B.3C.10D.13【答案】D【分析】根据锐角三角函数可求得AC=BC=1,当线段BG达到最长时,此时点G在点C的下方,且B,C,G三点共线,求得BG=4,DG=5,根据勾股定理求得DF=26,即m=26,当线段BG达到最短时,此时点G在点C的上方,且B,C,G三点共线,则BG=2,DG=1,根据勾股定理求得DF=2,即n =2,即可求得mn=13.【详解】∵△ABC为等腰直角三角形,AB=2,∴AC=BC=AB⋅sin45°=2×22=1,当线段BG达到最长时,此时点G在点C的下方,且B,C,G三点共线,如图:则BG=BC+CG=4,DG=DB+BG=5,在Rt△DGF中,DF=DG2+GF2=52+12=26,即m=26,当线段BG达到最短时,此时点G在点C的上方,且B,C,G三点共线,如图:则BG=CG-BC=2,DG=BG-DB=1,在Rt△DGF中,DF=DG2+GF2=12+12=2,即n=2,故mn=262=13,故选:D.【点睛】本题考查了锐角三角函数,勾股定理等,根据旋转推出线段BG最长和最短时的位置是解题的关键.二、填空题5(2023·江苏连云港·统考中考真题)以正五边形ABCDE的顶点C为旋转中心,按顺时针方向旋转,使得新五边形A B CD E 的顶点D 落在直线BC上,则正五边ABCDE旋转的度数至少为°.【答案】72【分析】依据正五边形的外角性质,即可得到∠DCF的度数,进而得出旋转的角度.【详解】解:∵五边形ABCDE是正五边形,∴∠DCF=360°÷5=72°,∴新五边形A B CD E 的顶点D 落在直线BC上,则旋转的最小角度是72°,故答案为:72.【点睛】本题主要考查了正多边形、旋转性质,关键是掌握正多边形的外角和公式的运用.6(2023·湖南张家界·统考中考真题)如图,AO为∠BAC的平分线,且∠BAC=50°,将四边形ABOC 绕点A逆时针方向旋转后,得到四边形AB O C ,且∠OAC =100°,则四边形ABOC旋转的角度是.【答案】75°【分析】根据角平分线的性质可得∠BAO=∠OAC=25°,根据旋转的性质可得∠BAC=∠B AC =50°,∠B AO =∠O AC =25°,求得∠OAO =75°,即可求得旋转的角度.【详解】∵AO为∠BAC的平分线,∠BAC=50°,∴∠BAO=∠OAC=25°,∵将四边形ABOC绕点A逆时针方向旋转后,得到四边形AB O C ,∴∠BAC=∠B AC =50°,∠B AO =∠O AC =25°,∴∠OAO =∠OAC -∠O AC =100°-25°=75°,故答案为:75°.【点睛】本题考查了角平分线的性质,旋转的性质,熟练掌握以上性质是解题的关键.7(2023·湖南常德·统考中考真题)如图1,在Rt△ABC中,∠ABC=90°,AB=8,BC=6,D是AB上一点,且AD=2,过点D作DE∥BC交AC于E,将△ADE绕A点顺时针旋转到图2的位置.则图2中BDCE的值为.【答案】45【分析】首先根据勾股定理得到AC =AB 2+BC 2=10,然后证明出△ADE ∽△ABC ,得到AD AB =AE AC ,进而得到AD AE =AB AC ,然后证明出△ABD ∽△ACE ,利用相似三角形的性质求解即可.【详解】∵在Rt △ABC 中,∠ABC =90°,AB =8,BC =6,∴AC =AB 2+BC 2=10∵DE ∥BC ∴∠ADE =∠ABC =90°,∠AED =∠ACB∴△ADE ∽△ABC∴AD AB =AE AC ∴AD AE =AB AC∵∠BAC =∠DAE∴∠BAC +∠CAD =∠DAE +∠CAD∴∠BAD =∠CAE∴△ABD ∽△ACE∴BD CD =AB AC =810=45.故答案为:45.【点睛】此题考查了相似三角形的性质和判定,解题的关键是熟练掌握相似三角形的性质和判定定理.8(2023·江苏无锡·统考中考真题)已知曲线C 1、C 2分别是函数y =-2x (x <0),y =k x(k >0,x >0)的图像,边长为6的正△ABC 的顶点A 在y 轴正半轴上,顶点B 、C 在x 轴上(B 在C 的左侧),现将△ABC 绕原点O 顺时针旋转,当点B 在曲线C 1上时,点A 恰好在曲线C 2上,则k 的值为.【答案】6【分析】画出变换后的图像即可(画△AOB 即可),当点A 在y 轴上,点B 、C 在x 轴上时,根据△ABC 为等边三角形且AO ⊥BC ,可得OB OA =13,过点A 、B 分别作x 轴垂线构造相似,则△BFO ∽OEA ,根据相似三角形的性质得出S △AOE =3,进而根据反比例函数k 的几何意义,即可求解.【详解】当点A 在y 轴上,点B 、C 在x 轴上时,连接AO ,∵△ABC 为等边三角形且AO ⊥BC ,则∠BAO =30°,∴tan ∠BAO =tan30°=OB OA=33,如图所示,过点A ,B 分别作x 轴的垂线,交x 轴分别于点E ,F ,∵AO ⊥BO ,∠BFO =∠AEO =∠AOB =90°,∴∠BOF=90°-∠AOE=∠EAO,∴△BFO∽OEA,∴S△BFOS△AOE=OBOA2=13,∴S△BFO=-22=1,∴S△AOE=3,∴k=6.【点睛】本题考查了反比例函数的性质,k的几何意义,相似三角形的性质与判定,正确作出辅助线构造相似三角形是解题关键.9(2023·辽宁·统考中考真题)如图,线段AB=8,点C是线段AB上的动点,将线段BC绕点B顺时针旋转120°得到线段BD,连接CD,在AB的上方作RtΔDCE,使∠DCE=90°,∠E=30°,点F为DE的中点,连接AF,当AF最小时,ΔBCD的面积为.【答案】3【分析】连接CF,BF,BF,CD交于点P,由直角三角形的性质及等腰三角形的性质可得BF垂直平分CF,∠ABF=60°为定角,可得点F在射线BF上运动,当AF⊥BF时,AF最小,由含30度角直角三角形的性质即可求解.【详解】解:连接CF,BF,BF,CD交于点P,如图,∵∠DCE=90°,点F为DE的中点,∴FC=FD,∵∠E=30°,∴∠FDC=60°,∴△FCD是等边三角形,∴∠DFC=∠FCD=60°;∵线段BC绕点B顺时针旋转120°得到线段BD,∴BC=BD,∵FC=FD,∴BF垂直平分CF,∠ABF=60°,∴点F在射线BF上运动,∴当AF⊥BF时,AF最小,此时∠FAB=90°-∠ABF=30°,∴BF=12AB=4;∵∠BFC=12∠DFC=30°,∴∠FCB=∠BFC+∠ABF=90°,∴BC=12BF=2,∵PB=12BC=1,∴由勾股定理得PC=BC2-PB2=3,∴CD=2PC=23,∴S△BCD=12CD⋅PB=12×23×1=3;故答案为:3.【点睛】本题考查了等腰三角形性质,含30度直角三角形的性质,斜边中线性质,勾股定理,线段垂直平分线的判定,勾股定理,旋转的性质,确定点F的运动路径是关键与难点.10(2023·江西·统考中考真题)如图,在▱ABCD中,∠B=60°,BC=2AB,将AB绕点A逆时针旋转角α(0°<α<360°)得到AP,连接PC,PD.当△PCD为直角三角形时,旋转角α的度数为.【答案】90°或270°或180°【分析】连接AC,根据已知条件可得∠BAC=90°,进而分类讨论即可求解.【详解】解:连接AC,取BC的中点E,连接AE,如图所示,∵在▱ABCD中,∠B=60°,BC=2AB,∴BE=CE=12BC=AB,∴△ABE是等边三角形,∴∠BAE=∠AEB=60°,AE=BE,∴AE=EC∠AEB=30°,∴∠EAC=∠ECA=12∴∠BAC=90°∴AC⊥CD,如图所示,当点P在AC上时,此时∠BAP=∠BAC=90°,则旋转角α的度数为90°,当点P在CA的延长线上时,如图所示,则α=360°-90°=270°当P在BA的延长线上时,则旋转角α的度数为180°,如图所示,∵PA=PB=CD,PB∥CD,∴四边形PACD是平行四边形,∵AC⊥AB∴四边形PACD是矩形,∴∠PDC=90°即△PDC是直角三角形,综上所述,旋转角α的度数为90°或270°或180°故答案为:90°或270°或180°.【点睛】本题考查了平行四边形的性质与判定,等边三角形的性质与判定,矩形的性质与判定,旋转的性质,熟练掌握旋转的性质是解题的关键.11(2023·上海·统考中考真题)如图,在△ABC中,∠C=35°,将△ABC绕着点A旋转α(0°<α< 180°),旋转后的点B落在BC上,点B的对应点为D,连接AD,AD是∠BAC的角平分线,则α=.【答案】110 3°【分析】如图,AB=AD,∠BAD=α,根据角平分线的定义可得∠CAD=∠BAD=α,根据三角形的外角性质可得∠ADB=35°+α,即得∠B=∠ADB=35°+α,然后根据三角形的内角和定理求解即可.【详解】解:如图,根据题意可得:AB=AD,∠BAD=α,∵AD是∠BAC的角平分线,∴∠CAD=∠BAD=α,∵∠ADB=∠C+∠CAD=35°+α,AB=AD,∴∠B=∠ADB=35°+α,则在△ABC中,∵∠C+∠CAB+∠B=180°,∴35°+2α+35°+α=180°,解得:α=1103°;故答案为:110 3°【点睛】本题考查了旋转的性质、等腰三角形的性质、三角形的外角性质以及三角形的内角和等知识,熟练掌握相关图形的性质是解题的关键.12(2023·湖南郴州·统考中考真题)如图,在Rt△ABC中,∠BAC=90°,AB=3cm,∠B=60°.将△ABC绕点A逆时针旋转,得到△AB C ,若点B的对应点B 恰好落在线段BC上,则点C的运动路径长是cm(结果用含π的式子表示).【答案】3π【分析】由于AC 旋转到AC ,故C 的运动路径长是CC 的圆弧长度,根据弧长公式求解即可.【详解】以A 为圆心作圆弧CC ,如图所示.在直角△ABC 中,∠B =60°,则∠C =30°,则BC =2AB =2×3=6cm .∴AC =BC 2-AB 2=62-32=33cm .由旋转性质可知,AB =AB ,又∠B =60°,∴△ABB 是等边三角形.∴∠BAB =60°.由旋转性质知,∠CAC =60°.故弧CC 的长度为:60360×2×π×AC =π3×33=3πcm ;故答案为:3π【点睛】本题考查了含30°角直角三角形的性质、勾股定理、旋转的性质、弧长公式等知识点,解题的关键是明确C 点的运动轨迹.13(2023·内蒙古·统考中考真题)如图,在Rt △ABC 中,∠ACB =90°,AC =3,BC =1,将△ABC 绕点A 逆时针方向旋转90°,得到△AB C .连接BB ,交AC 于点D ,则ADDC的值为.【答案】5【分析】过点D 作DF ⊥AB 于点F ,利用勾股定理求得AB =10,根据旋转的性质可证△ABB 、△DFB 是等腰直角三角形,可得DF =BF ,再由S △ADB =12×BC ×AD =12×DF ×AB ,得AD =10DF ,证明△AFD ∼△ACB ,可得DF BC =AF AC,即AF =3DF ,再由AF =10-DF ,求得DF =104,从而求得AD=52,CD =12,即可求解.【详解】解:过点D 作DF ⊥AB 于点F ,∵∠ACB =90°,AC =3,BC =1,∴AB =32+12=10,∵将△ABC 绕点A 逆时针方向旋转90°得到△AB C ,∴AB=AB =10,∠BAB =90°,∴△ABB 是等腰直角三角形,∴∠ABB =45°,又∵DF⊥AB,∴∠FDB=45°,∴△DFB是等腰直角三角形,∴DF=BF,∵S△ADB=12×BC×AD=12×DF×AB,即AD=10DF,∵∠C=∠AFD=90°,∠CAB=∠FAD,∴△AFD∼△ACB,∴DF BC =AFAC,即AF=3DF,又∵AF=10-DF,∴DF=104,∴AD=10×104=52,CD=3-52=12,∴AD CD =5212=5,故答案为:5.【点睛】本题考查旋转的性质、等腰三角形的判定与性质、相似三角形的判定与性质、三角形的面积,熟练掌握相关知识是解题的关键.14(2023·黑龙江绥化·统考中考真题)已知等腰△ABC,∠A=120°,AB=2.现将△ABC以点B为旋转中心旋转45°,得到△A BC ,延长C A 交直线BC于点D.则A D的长度为.【答案】4+23或4-23【分析】根据题意,先求得BC=23,当△ABC以点B为旋转中心逆时针旋转45°,过点B作BE⊥A B交A D于点E,当△ABC以点B为旋转中心顺时针旋转45°,过点D作DF⊥BC 交BC 于点F,分别画出图形,根据勾股定理以及旋转的性质即可求解.【详解】解:如图所示,过点A作AM⊥BC于点M,∵等腰△ABC,∠BAC=120°,AB=2.∴∠ABC=∠ACB=30°,∴AM=1AB=1,BM=CM=AB2-AM2=3,2∴BC=23,如图所示,当△ABC以点B为旋转中心逆时针旋转45°,过点B作BE⊥A B交A D于点E,∵∠BAC=120°,∴∠DA B=60°,∠A EB=30°,在Rt△A BE中,A E=2A B=4,BE=A E2-A B2=23,∵等腰△ABC,∠BAC=120°,AB=2.∴∠ABC=∠ACB=30°,∵△ABC以点B为旋转中心逆时针旋转45°,∴∠ABA =45°,∴∠DBE=180°-90°-45°-30°=15°,∠A BD=180°-45°-30°=105°在△A BD中,∠D=180°-∠DA B-∠A BD=180°-60°-105°=15°,∴∠D=∠EBD,∴EB=ED=23,∴A D=A E+DE=4+23,如图所示,当△ABC以点B为旋转中心顺时针旋转45°,过点D作DF⊥BC 交BC 于点F,在△BFD中,∠BDF=∠CBC =45°,∴DF=BF在Rt△DC F中,∠C =30°FC'∴DF=33∴BC=BF+3BF=23∴DF=BF=3-3∴DC =2DF=6-23∴A D=C D-A C =6-23-2=4-23,综上所述,A D的长度为4-23或4+23,故答案为:4-23或4+23.【点睛】本题考查了旋转的性质,勾股定理,含30度角的直角三角形的性质,熟练掌握旋转的性质,分类讨论是解题的关键.15(2023·浙江嘉兴·统考中考真题)一副三角板ABC 和DEF 中,∠C =∠D =90°,∠B =30°,∠E =45°,BC =EF =12.将它们叠合在一起,边BC 与EF 重合,CD 与AB 相交于点G (如图1),此时线段CG 的长是,现将△DEF 绕点C (F )按顺时针方向旋转(如图2),边EF 与AB 相交于点H ,连结DH ,在旋转0°到60°的过程中,线段DH 扫过的面积是.【答案】66-62;12π-183+18【分析】如图1,过点G 作GH ⊥BC 于H ,根据含30°直角三角形的性质和等腰直角三角形的性质得出BH =3GH ,GH =CH ,然后由BC =12可求出GH 的长,进而可得线段CG 的长;如图2,将△DEF 绕点C 顺时针旋转60°得到△D 1E 1F ,FE 1与AB 交于G 1,连接D 1D ,AD 1,△D 2E 2F 是△DEF 旋转0°到60°的过程中任意位置,作DN ⊥CD 1于N ,过点B 作BM ⊥D 1D 交D 1D 的延长线于M ,首先证明△CDD 1是等边三角形,点D 1在直线AB 上,然后可得线段DH 扫过的面积是弓形D 1D 2D 的面积加上△D 1DB 的面积,求出DN 和BM ,然后根据线段DH 扫过的面积=S 弓形D 1D 2D +S △D 1DB =S 扇形CD 1D -S △CD 1D +S △D 1DB 列式计算即可.【详解】解:如图1,过点G 作GH ⊥BC 于H ,∵∠ABC =30°,∠DEF =∠DFE =45°,∠GHB =∠GHC =90°,∴BH =3GH ,GH =CH ,∵BC =BH +CH =3GH +GH =12,∴GH =63-6,∴CG =2GH =2×63-6 =66-62;如图2,将△DEF 绕点C 顺时针旋转60°得到△D 1E 1F ,FE 1与AB 交于G 1,连接D 1D ,由旋转的性质得:∠E 1CB =∠DCD 1=60°,CD =CD 1,∴△CDD 1是等边三角形,∵∠ABC =30°,∴∠CG 1B =90°,∴CG 1=12BC ,∵CE1=BC,∴CG1=12CE1,即AB垂直平分CE1,∵△CD1E1是等腰直角三角形,∴点D1在直线AB上,连接AD1,△D2E2F是△DEF旋转0°到60°的过程中任意位置,则线段DH扫过的面积是弓形D1D2D的面积加上△D1DB的面积,∵BC=EF=12,∴DC=DB=22BC=62,∴D1C=D1D=62,作DN⊥CD1于N,则ND1=NC=32,∴DN=D1D2-ND12=622-322=36,过点B作BM⊥D1D交D1D的延长线于M,则∠M=90°,∵∠D1DC=60°,∠CDB=90°,∴∠BDM=180°-∠D1DC-∠CDB=30°,∴BM=12BD=32,∴线段DH扫过的面积=S弓形D1D2D +S△D1DB,=S扇形CD1D -S△CD1D+S△D1DB,=60π⋅622360-12×62×36+12×62×32,=12π-183+18,故答案为:66-62,12π-183+18.【点睛】本题主要考查了旋转的性质,含30°直角三角形的性质,二次根式的运算,解直角三角形,等边三角形的判定和性质,勾股定理,扇形的面积计算等知识,作出图形,证明点D1在直线AB上是本题的突破点,灵活运用各知识点是解题的关键.三、解答题16(2023·北京·统考中考真题)在△ABC中、∠B=∠C=α0°<α<45°,AM⊥BC于点M,D是线段MC上的动点(不与点M,C重合),将线段DM绕点D顺时针旋转2α得到线段DE.(1)如图1,当点E在线段AC上时,求证:D是MC的中点;(2)如图2,若在线段BM上存在点F(不与点B,M重合)满足DF=DC,连接AE,EF,直接写出∠AEF的大小,并证明.【答案】(1)见解析(2)∠AEF=90°,证明见解析【分析】(1)由旋转的性质得DM=DE,∠MDE=2α,利用三角形外角的性质求出∠DEC=α=∠C,可得DE=DC,等量代换得到DM=DC即可;(2)延长FE到H使FE=EH,连接CH,AH,可得DE是△FCH的中位线,然后求出∠B=∠ACH,设DM=DE=m,CD=n,求出BF=2m=CH,证明△ABF≅△ACH SAS,得到AF=AH,再根据等腰三角形三线合一证明AE⊥FH即可.【详解】(1)证明:由旋转的性质得:DM=DE,∠MDE=2α,∵∠C=α,∴∠DEC=∠MDE-∠C=α,∴∠C=∠DEC,∴DE=DC,∴DM=DC,即D是MC的中点;(2)∠AEF=90°;证明:如图2,延长FE到H使FE=EH,连接CH,AH,∵DF=DC,∴DE是△FCH的中位线,∴DE∥CH,CH=2DE,由旋转的性质得:DM=DE,∠MDE=2α,∴∠FCH=2α,∵∠B=∠C=α,∴∠ACH=α,△ABC是等腰三角形,∴∠B=∠ACH,AB=AC,设DM=DE=m,CD=n,则CH=2m,CM=m+n,∴DF=CD=n,∴FM=DF-DM=n-m,∵AM⊥BC,∴BM=CM=m+n,∴BF=BM-FM=m+n-n-m=2m,∴CH=BF,在△ABF和△ACH中,AB=AC∠B=∠ACH BF=CH,∴△ABF≅△ACH SAS,∴AF =AH ,∵FE =EH ,∴AE ⊥FH ,即∠AEF =90°.【点睛】本题考查了等腰三角形的判定和性质,旋转的性质,三角形外角的性质,三角形中位线定理以及全等三角形的判定和性质等知识,作出合适的辅助线,构造出全等三角形是解题的关键.17(2023·四川自贡·统考中考真题)如图1,一大一小两个等腰直角三角形叠放在一起,M ,N 分别是斜边DE ,AB 的中点,DE =2,AB =4.(1)将△CDE 绕顶点C 旋转一周,请直接写出点M ,N 距离的最大值和最小值;(2)将△CDE 绕顶点C 逆时针旋转120°(如图2),求MN 的长.【答案】(1)最大值为3,最小值为1(2)7【分析】(1)根据直角三角形斜边上的中线,得出CM ,CN 的值,进而根据题意求得最大值与最小值即可求解;(2)过点N 作NP ⊥MC ,交MC 的延长线于点P ,根据旋转的性质求得∠MCN =120°,进而得出∠NCP =60°,进而可得CP =1,勾股定理解Rt △NCP ,Rt △MCP ,即可求解.【详解】(1)解:依题意,CM =12DE =1,CN =12AB =2,当M 在NC 的延长线上时,M ,N 的距离最大,最大值为CM +CN =1+2=3,当M 在线段CN 上时,M ,N 的距离最小,最小值为CN -CN =2-1=1;(2)解:如图所示,过点N 作NP ⊥MC ,交MC 的延长线于点P ,∵△CDE 绕顶点C 逆时针旋转120°,∴∠BCE =120°,∵∠BCN =∠ECM =45°,∴∠MCN =∠BCM -∠ECM =∠BCE =120°,∴∠NCP =60°,∴∠CNP =30°,∴CP =12CN =1,在Rt △CNP 中,NP =NC 2-CP 2=3,在Rt △MNP 中,MP =MC +CP =1+1=2,∴MN =NP 2+MP 2=3+4=7.【点睛】本题考查了直角三角形斜边上的中线等于斜边的一半,勾股定理,旋转的性质,含30度角的直角三角形的性质,熟练掌握旋转的性质,勾股定理是解题的关键.18(2023·四川达州·统考中考真题)如图,网格中每个小正方形的边长均为1,△ABC 的顶点均在小正方形的格点上.(1)将△ABC 向下平移3个单位长度得到△A 1B 1C 1,画出△A 1B 1C 1;(2)将△ABC 绕点C 顺时针旋转90度得到△A 2B 2C 2,画出△A 2B 2C 2;(3)在(2)的运动过程中请计算出△ABC 扫过的面积.【答案】(1)见解析(2)见解析(3)5+5π2【分析】(1)先作出点A 、B 、C 平移后的对应点A 1,B 1、C 1,然后顺次连接即可;(2)先作出点A 、B 绕点C 顺时针旋转90度的对应点A 2,B 2,然后顺次连接即可;(3)证明△ABC 为等腰直角三角形,求出S △ABC =12AB ×BC =52,S 扇形CAA 2=90π×10 2360=5π2,根据旋转过程中△ABC 扫过的面积等于△ABC 的面积加扇形CAA 1的面积即可得出答案.【详解】(1)解:作出点A 、B 、C 平移后的对应点A 1,B 1、C 1,顺次连接,则△A 1B 1C 1即为所求,如图所示:(2)解:作出点A 、B 绕点C 顺时针旋转90度的对应点A 2,B 2,顺次连接,则△A 2B 2C 2即为所求,如图所示:(3)解:∵AB =12+22=5,AC =32+12=10,BC =12+22=5,∴AB =BC ,∵5 2+5 2=10=10 2,∴AB 2+BC 2=AC 2,∴△ABC 为等腰直角三角形,∴S △ABC =12AB ×BC =52,根据旋转可知,∠ACA 2=90°,∴S 扇形CAA 2=90π×10 2360=5π2,∴在旋转过程中△ABC 扫过的面积为S =S △ABC +S 扇形CAA 2=5+5π2.【点睛】本题主要考查了平移、旋转作图,勾股定理逆定理,扇形面积计算,解题的关键是作出平移或旋转后的对应点.19(2023·辽宁·统考中考真题)在Rt ΔABC 中,∠ACB =90°,CA =CB ,点O 为AB 的中点,点D 在直线AB 上(不与点A ,B 重合),连接CD ,线段CD 绕点C 逆时针旋转90°,得到线段CE ,过点B 作直线l ⊥BC ,过点E 作EF ⊥l ,垂足为点F ,直线EF 交直线OC 于点G .(1)如图,当点D与点O重合时,请直接写出线段AD与线段EF的数量关系;(2)如图,当点D在线段AB上时,求证:CG+BD=2BC;(3)连接DE,△CDE的面积记为S1,△ABC的面积记为S2,当EF:BC=1:3时,请直接写出S1S2的值.【答案】(1)EF=22AD(2)见解析(3)59或17 9【分析】(1)可先证△BCD≌△BCE,得到BD=BE,根据锐角三角函数,可得到BE和EF的数量关系,进而得到线段AD与线段EF的数量关系.(2)可先证△ACD≌△GEC,得到DA=CG,进而得到CG+BD=DA+BD=AB,问题即可得证.(3)分两种情况:①点D在线段AB上,过点C作CN垂直于FG,交FG于点N,过点E作EM垂直于BC,交BC于点M,设EF=a,利用勾股定理,可用含a的代数式表示EC,根据三角形面积公式,即可得到答案.②点D在线段BA的延长线上,过点E作EJ垂直于BC,交BC延长线于点J,令EF交AC于点I,连接BE,设EF=b,可证△CDA≌△CEB,进一步证得△EBJ是等腰直角三角形,EJ=BJ,利用勾股定理,可用含b的代数式表示EC,根据三角形面积公式,即可得到答案【详解】(1)解:EF=22 AD.理由如下:如图,连接BE.根据图形旋转的性质可知CD=CE.由题意可知,△ABC为等腰直角三角形,∵CD为等腰直角三角形△ABC斜边AB上的中线,∴∠BCD=45°,AD=BD.又∠DCE=90°,∴∠BCE=45°.在△BCD和△BCE中,CD =CE∠BCD =∠BCEBC =BC∴△BCD ≌△BCE .∴BD =BE ,∠CBE =∠CBD =45°.∴∠EBF =45°.∴EF =BE ·sin ∠EBF =22BE .∴EF =22AD .(2)解:∵CO 为等腰直角三角形△ABC 斜边AB 上的中线,∴AO =BO .∵∠ACD +∠DCB =∠BCE +∠DCB =90°,∴∠ACD =∠BCE .∵BC ⊥l ,EF ⊥l ,∴BC ∥EF .∴∠G =∠OCB =45°,∠GEC =∠BCE .∴∠G =∠A ,∠ACD =∠GEC .在△ACD 和△GEC 中,∠ACD =∠GEC∠A =∠GCD =CE∴△ACD ≌△GEC .∴DA =CG .∴CG +BD =DA +BD =AB =2BC .(3)解:当点D 在线段AB 延长线上时,不满足条件EF :BC =1:3,故分两种情况:①点D 在线段AB 上,如图,过点C 作CN 垂直于FG ,交FG 于点N ;过点E 作EM 垂直于BC ,交BC 于点M .设EF =a ,则BC =AC =3a .根据题意可知,四边形BFEM 和CMEN 为矩形,△GCN 为等腰直角三角形.∴EF =BM =a ,CM =NE =2a .由(2)证明可知△ACD ≌△GEC ,∴AC =GE =3a .∴NG =NC =a .∴NC =EM =a .根据勾股定理可知CE =EM 2+CM 2=2a 2+a 2=5a ,△CDE 的面积S 1与△ABC 的面积S 2之比S 1S 2=12CE 212BC 2=125a 2123a2=59②点D 在线段BA 的延长线上,过点E 作EJ 垂直于BC ,交BC 延长线于点J ,令EF 交AC 于点I ,连接BE ,由题意知,四边形FBJE ,FBCI 是矩形,∵∠DCE =∠ACB =90°∴∠DCE -∠ACE =∠ACB -∠ACE即∠DCA =∠ECB又∵CD =CE ,CA =CB∴△CDA ≌△CEB∴∠DAC =∠EBC而∠DAC =180°-∠CAB =180°-45°=135°∴∠EBC =135°∠EBJ =180°-∠EBC =45°∴△EBJ 是等腰直角三角形,EJ =BJ设EF =b ,则BC =IF =3b ,EJ =BJ =CI =b∴EI =EF +IF =4b Rt △CIE 中,CE =CI 2+EI 2=b 2+(4b )2=17b△CDE 的面积S 1与△ABC 的面积S 2之比S 1S 2=12CE 212BC 2=1217b 2123b2=179【点睛】本题主要考查全等三角形的判定及性质、勾股定理以及图形旋转的性质,灵活利用全等三角形的判定及性质是解题的关键.20(2023·四川乐山·统考中考真题)在学习完《图形的旋转》后,刘老师带领学生开展了一次数学探究活动【问题情境】刘老师先引导学生回顾了华东师大版教材七年级下册第121页“探索”部分内容:如图,将一个三角形纸板△ABC绕点A逆时针旋转θ到达△AB C 的位置,那么可以得到:AB=AB ,AC =AC ,BC=B C ;∠BAC=∠B AC ,∠ABC=∠AB C ,∠ACB=∠AC B ()刘老师进一步谈到:图形的旋转蕴含于自然界的运动变化规律中,即“变”中蕴含着“不变”,这是我们解决图形旋转的关键;故数学就是一门哲学.【问题解决】(1)上述问题情境中“( )”处应填理由:;(2)如图,小王将一个半径为4cm,圆心角为60°的扇形纸板ABC绕点O逆时针旋转90°到达扇形纸板A BC 的位置.①请在图中作出点O;②如果BB =6cm,则在旋转过程中,点B经过的路径长为;【问题拓展】小李突发奇想,将与(2)中完全相同的两个扇形纸板重叠,一个固定在墙上,使得一边位于水平位置,另一个在弧的中点处固定,然后放开纸板,使其摆动到竖直位置时静止,此时,两个纸板重叠部分的面积是多少呢?如图所示,请你帮助小李解决这个问题.【答案】问题解决(1)旋转前后的图形对应线段相等,对应角相等(2)①见解析;②322πcm 问题拓展:83π-833cm 2【分析】问题解决(1)根据旋转性质得出旋转前后的图形对应线段相等,对应角相等;(2)①分别作BB 和AA 的垂直平分线,两垂直平分线的交点即为所求点O ;②根据弧长公式求解即可;问题拓展,连接PA ,交AC 于M ,连接PA ,PD ,AA ,由旋转得∠PA B =30°,PA =PA =4,在Rt △PAM 和Rt △A DM 中求出A M 和DM 的长,可以求出S 阴影部分B DP =S 扇形B A P -S △ADP ,再证明△ADP ≌△A DP ,即可求出最后结果.【详解】解:【问题解决】(1)旋转前后的图形对应线段相等,对应角相等(2)①下图中,点O 为所求②连接OB ,OB ,∵扇形纸板ABC 绕点O 逆时针旋转90°到达扇形纸板A B C 的位置,∴∠BOB =90°,OB =OB ,∵BB =6cm ,设OB =OB =xcm ,∴x 2+x 2=62,∴OB =OB =32cm ,在旋转过程中,点B 经过的路径长为以点O 为圆心,圆心角为90°,OB 为半径的所对应的弧长,∴点B 经过的路径长=90×π×32180=322πcm ;【问题拓展】解:连接PA ,交AC 于M ,连接PA ,PD ,AA 如图所示∴∠PAC =12∠BAC =30°.由旋转得∠PA B =30°,PA =PA =4. 在Rt △PAM 中,A M =PM =PA ⋅sin ∠PAM =4×sin30°=2.在Rt △A DM 中,∵∠DA M =12∠B A C =30°,∴A D =A M cos ∠DA M =2cos30°=433,DM =12A D =12×433=233. ∴S △A DP =12DM ⋅A P =12×233×4=433.S 扇形B A P =30×π×42360=43π.∴S 阴影部分B DP =S 扇形B A P -S △ADP =43π-433, 在△ADP 和△A DP 中,∵AD =AM -DM =23-233=433=A D ,又∵∠PAD =∠PA D =30°,PA =PA ,∴△ADP ≌△A DP .又∵S 扇形PAC =S 扇形B AP ,∴S 阴影部分BDP =S 阴影部分CDP ,∴S 阴影部分=2S 阴影部分BDP =2×43π-433 =83π-833 cm 2.【点睛】本题考查了旋转的性质,弧长公式,解直角三角形,三角形全等的性质与判定,解题的关键是抓住图形旋转前后的对应边相等,对应角相等,正确作出辅助线构造出直角三角形.21(2023·浙江绍兴·统考中考真题)在平行四边形ABCD 中(顶点A ,B ,C ,D 按逆时针方向排列),AB =12,AD =10,∠B 为锐角,且sin B =45.(1)如图1,求AB 边上的高CH 的长.(2)P 是边AB 上的一动点,点C ,D 同时绕点P 按逆时针方向旋转90°得点C ,D .①如图2,当点C 落在射线CA 上时,求BP 的长.②当△AC D 是直角三角形时,求BP 的长.【答案】(1)8(2)①BP =347;②BP =6或8±2【分析】(1)利用正弦的定义即可求得答案;(2)①先证明△PQC ≌△CHP ,再证明△AQC ∽△AHC ,最后利用相似三角形对应边成比例列出方程即可;②分三种情况讨论完成,第一种:C 为直角顶点;第二种:A 为直角顶点;第三种,D 为直角顶点,但此种情况不成立,故最终有两个答案.【详解】(1)在▱ABCD 中,BC =AD =10,在Rt △BCH 中,CH =BC sin B =10×45=8.(2)①如图1,作CH ⊥BA 于点H ,由(1)得,BH =BC 2-CH 2=6,则AH =12-6=6,作C Q ⊥BA 交BA 延长线于点Q ,则∠CHP =∠PQC =90°,∴∠C PQ +∠PC Q =90°.∵∠C PQ +∠CPH =90°∴∠PC Q =∠CPH .由旋转知PC =PC ,∴△PQC ≌△CHP .设BP =x ,则PQ =CH =8,C Q =PH =6-x ,QA =PQ -PA =x -4.∵C Q ⊥AB ,CH ⊥AB ,∴C Q ∥CH ,∴△AQC ∽△AHC ,∴C Q CH =QA HA ,即6-x 8=x -46,∴x =347,∴BP =347.②由旋转得△PCD ≌△PC D ,CD =C D ,CD ⊥C D ,又因为AB ∥CD ,所以C D ⊥AB .情况一:当以C 为直角顶点时,如图2.∵C D ⊥AB ,∴C 落在线段BA 延长线上.∵PC ⊥PC ,∴PC ⊥AB ,由(1)知,PC =8,∴BP =6.情况二:当以A 为直角顶点时,如图3.设C D 与射线BA 的交点为T ,作CH ⊥AB 于点H .∵PC ⊥PC ,∴∠CPH +∠TPC =90°,∵C D ⊥AT ,∴∠PC T +∠TPC =90°,∴∠CPH =∠PC T .又∵∠CHP =∠PTC =90°,PC =C P ,∴△CPH ≌△PC T ,∴C T =PH ,PT =CH =8.设C T =PH =t ,则AP =6-t ,∴AT =PT -PA =2+t∵∠C AD =90°,C D ⊥AB ,∴△ATD ∽△C TA ,∴AT TD =CT TA ,∴AT 2=C T ⋅TD ,∴(2+t )2=ι12-t ,化简得t 2-4t +2=0,解得t =2±2,∴BP =BH +HP =8±2.情况三:当以D 为直角顶点时,点P 落在BA 的延长线上,不符合题意.综上所述,BP =6或8±2.【点睛】本题考查了平行四边形的性质,正弦的定义,全等的判定及性质,相似的判定及性质,理解记忆相关定义,判定,性质是解题的关键.22(2023·四川南充·统考中考真题)如图,正方形ABCD 中,点M 在边BC 上,点E 是AM 的中点,连接ED ,EC .(1)求证:ED =EC ;(2)将BE 绕点E 逆时针旋转,使点B 的对应点B 落在AC 上,连接MB ′.当点M 在边BC 上运动时(点M 不与B ,C 重合),判断△CMB ′的形状,并说明理由.(3)在(2)的条件下,已知AB =1,当∠DEB ′=45°时,求BM 的长.【答案】(1)见解析(2)等腰直角三角形,理由见解析(3)BM =2-3【分析】(1)根据正方形的基本性质以及“斜中半定理”等推出△EAD ≌△EBC ,即可证得结论;(2)由旋转的性质得EB =EB =AE =EM ,从而利用等腰三角形的性质推出∠MB C =90°,再结合正方形对角线的性质推出B M =B C ,即可证得结论;(3)结合已知信息推出△CME ∽△AMC ,从而利用相似三角形的性质以及勾股定理进行计算求解即可.【详解】(1)证:∵四边形ABCD 为正方形,∴∠BAD =∠ABC =90°,AD =BC ,∵点E 是AM 的中点,∴EA =EB ,∴∠EAB =∠EBA ,∴∠BAD -∠EAB =∠ABC -∠EBA ,即:∠EAD =∠EBC ,在△EAD 与△EBC 中,EA =EB∠EAD =∠EBCAD =BC∴△EAD ≌△EBC SAS ,∴ED =EC ;。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、旋转真题与模拟题分类汇编(难题易错题)1.在正方形ABCD中,点E,F分别在边BC,CD上,且∠EAF=∠CEF=45°.(1)将△ADF绕着点A顺时针旋转90°,得到△ABG(如图①),求证:△AEG≌△AEF;(2)若直线EF与AB,AD的延长线分别交于点M,N(如图②),求证:EF2=ME2+NF2;(3)将正方形改为长与宽不相等的矩形,若其余条件不变(如图③),请你直接写出线段EF,BE,DF之间的数量关系.【答案】(1)证明见解析;(2)证明见解析;(3)EF2=2BE2+2DF2.【解析】试题分析:(1)根据旋转的性质可知AF=AG,∠EAF=∠GAE=45°,故可证△AEG≌△AEF;(2)将△ADF绕着点A顺时针旋转90°,得到△ABG,连结GM.由(1)知△AEG≌△AEF,则EG=EF.再由△BME、△DNF、△CEF均为等腰直角三角形,得出CE=CF,BE=BM,NF=DF,然后证明∠GME=90°,MG=NF,利用勾股定理得出EG2=ME2+MG2,等量代换即可证明EF2=ME2+NF2;(3)将△ADF绕着点A顺时针旋转90°,得到△ABG,根据旋转的性质可以得到△ADF≌△ABG,则DF=BG,再证明△AEG≌△AEF,得出EG=EF,由EG=BG+BE,等量代换得到EF=BE+DF.试题解析:(1)∵△ADF绕着点A顺时针旋转90°,得到△ABG,∴AF=AG,∠FAG=90°,∵∠EAF=45°,∴∠GAE=45°,在△AGE与△AFE中,,∴△AGE≌△AFE(SAS);(2)设正方形ABCD的边长为a.将△ADF绕着点A顺时针旋转90°,得到△ABG,连结GM.则△ADF≌△ABG,DF=BG.由(1)知△AEG≌△AEF,∴EG=EF.∵∠CEF=45°,∴△BME、△DNF、△CEF均为等腰直角三角形,∴CE=CF ,BE=BM,NF=DF,∴a﹣BE=a﹣DF,∴BE=DF,∴BE=BM=DF=BG,∴∠BMG=45°,∴∠GME=45°+45°=90°,∴EG2=ME2+MG2,∵EG=EF,MG=BM=DF=NF,∴EF2=ME2+NF2;(3)EF2=2BE2+2DF2.如图所示,延长EF交AB延长线于M点,交AD延长线于N点,将△ADF绕着点A顺时针旋转90°,得到△AGH,连结HM,HE.由(1)知△AEH≌△AEF,则由勾股定理有(GH+BE)2+BG2=EH2,即(GH+BE)2+(BM﹣GM)2=EH2又∴EF=HE,DF=GH=GM,BE=BM,所以有(GH+BE)2+(BE﹣GH)2=EF2,即2(DF2+BE2)=EF2考点:四边形综合题2.(1)如图①,在矩形ABCD 中,对角线AC 与BD 相交于点O ,过点O 作直线EF ⊥BD ,交AD 于点E ,交BC 于点F ,连接BE 、DF ,且BE 平分∠ABD .①求证:四边形BFDE 是菱形;②直接写出∠EBF 的度数;(2)把(1)中菱形BFDE 进行分离研究,如图②,点G 、I 分别在BF 、BE 边上,且BG=BI ,连接GD ,H 为GD 的中点,连接FH 并延长,交ED 于点J ,连接IJ 、IH 、IF 、IG.试探究线段IH 与FH 之间满足的关系,并说明理由;(3)把(1)中矩形ABCD 进行特殊化探究,如图③,当矩形ABCD 满足AB=AD 时,点E 是对角线AC 上一点,连接DE 、EF 、DF ,使△DEF 是等腰直角三角形,DF 交AC 于点G.请直接写出线段AG 、GE 、EC 三者之间满足的数量关系.【答案】(1)①详见解析;②60°.(2)IH =3FH ;(3)EG 2=AG 2+CE 2.【解析】【分析】(1)①由△DOE ≌△BOF ,推出EO =OF ,∵OB =OD ,推出四边形EBFD 是平行四边形,再证明EB =ED 即可.②先证明∠ABD =2∠ADB ,推出∠ADB =30°,延长即可解决问题.(2)IH =3FH .只要证明△IJF 是等边三角形即可.(3)结论:EG 2=AG 2+CE 2.如图3中,将△ADG 绕点D 逆时针旋转90°得到△DCM ,先证明△DEG ≌△DEM ,再证明△ECM 是直角三角形即可解决问题.【详解】(1)①证明:如图1中,∵四边形ABCD 是矩形,∴AD ∥BC ,OB =OD ,∴∠EDO =∠FBO ,在△DOE 和△BOF 中,EDO FBO OD OBEOD BOF ∠∠⎧⎪⎨⎪∠∠⎩=== , ∴△DOE ≌△BOF ,∴EO =OF ,∵OB =OD ,∴四边形EBFD 是平行四边形,∵EF ⊥BD ,OB =OD ,∴EB =ED ,∴四边形EBFD 是菱形.②∵BE 平分∠ABD ,∴∠ABE =∠EBD ,∵EB =ED ,∴∠EBD =∠EDB ,∴∠ABD =2∠ADB ,∵∠ABD +∠ADB =90°,∴∠ADB =30°,∠ABD =60°,∴∠ABE =∠EBO =∠OBF =30°,∴∠EBF =60°.(2)结论:IH=3FH .理由:如图2中,延长BE 到M ,使得EM =EJ ,连接MJ .∵四边形EBFD 是菱形,∠B =60°,∴EB =BF =ED ,DE ∥BF ,∴∠JDH =∠FGH ,在△DHJ 和△GHF 中,DHG GHF DH GHJDH FGH ∠∠⎧⎪⎨⎪∠∠⎩=== , ∴△DHJ ≌△GHF ,∴DJ =FG ,JH =HF ,∴EJ =BG =EM =BI ,∴BE =IM =BF ,∵∠MEJ =∠B =60°,∴△MEJ 是等边三角形,∴MJ =EM =NI ,∠M =∠B =60°在△BIF 和△MJI 中,BI MJ B M BF IM ⎧⎪∠∠⎨⎪⎩===,∴△BIF ≌△MJI ,∴IJ =IF ,∠BFI =∠MIJ ,∵HJ =HF ,∴IH ⊥JF ,∵∠BFI +∠BIF =120°,∴∠MIJ +∠BIF =120°,∴∠JIF =60°,∴△JIF 是等边三角形,在Rt △IHF 中,∵∠IHF =90°,∠IFH =60°,∴∠FIH =30°,∴IH=3FH .(3)结论:EG 2=AG 2+CE 2.理由:如图3中,将△ADG 绕点D 逆时针旋转90°得到△DCM ,∵∠FAD +∠DEF =90°,∴AFED 四点共圆,∴∠EDF =∠DAE =45°,∠ADC =90°,∴∠ADF +∠EDC =45°,∵∠ADF =∠CDM ,∴∠CDM +∠CDE =45°=∠EDG ,在△DEM 和△DEG 中,DE DE EDG EDM DG DM ⎧⎪∠∠⎨⎪⎩=== , ∴△DEG ≌△DEM ,∴GE =EM ,∵∠DCM =∠DAG =∠ACD =45°,AG =CM ,∴∠ECM =90°∴EC 2+CM 2=EM 2,∵EG =EM ,AG =CM ,∴GE 2=AG 2+CE 2.【点睛】考查四边形综合题、矩形的性质、正方形的性质、菱形的判定和性质,等边三角形的判定和性质,勾股定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形,学会转化的思想思考问题.3.平面上,Rt △ABC 与直径为CE 的半圆O 如图1摆放,∠B =90°,AC =2CE =m ,BC =n ,半圆O 交BC 边于点D ,将半圆O 绕点C 按逆时针方向旋转,点D 随半圆O 旋转且∠ECD 始终等于∠ACB ,旋转角记为α(0°≤α≤180°)(1)当α=0°时,连接DE ,则∠CDE = °,CD = ;(2)试判断:旋转过程中BD AE的大小有无变化?请仅就图2的情形给出证明; (3)若m =10,n =8,当α=∠ACB 时,求线段BD 的长; (4)若m =6,n =2,当半圆O 旋转至与△ABC 的边相切时,直接写出线段BD 的长.【答案】(1)90°,2n ;(2)无变化;(3)55;(4)BD=101143. 【解析】试题分析:(1)①根据直径的性质,由DE ∥AB 得CD CE CB CA =即可解决问题.②求出BD 、AE 即可解决问题.(2)只要证明△ACE ∽△BCD 即可.(3)求出AB 、AE ,利用△ACE ∽△BCD 即可解决问题.(4)分类讨论:①如图5中,当α=90°时,半圆与AC 相切,②如图6中,当α=90°+∠ACB 时,半圆与BC 相切,分别求出BD 即可.试题解析:(1)解:①如图1中,当α=0时,连接DE ,则∠CDE =90°.∵∠CDE =∠B =90°,∴DE ∥AB ,∴CE CD AC CB ==12.∵BC =n ,∴CD =12n .故答案为90°,12n . ②如图2中,当α=180°时,BD =BC +CD =32n ,AE =AC +CE =32m ,∴BD AE =n m .故答案为n m. (2)如图3中,∵∠ACB =∠DCE ,∴∠ACE =∠BCD .∵CD BC n CE AC m==,∴△ACE ∽△BCD ,∴BD BC n AE AC m ==.(3)如图4中,当α=∠ACB 时.在Rt △ABC 中,∵AC =10,BC =8,∴AB =22AC BC -=6.在Rt △ABE 中,∵AB =6,BE =BC ﹣CE =3,∴AE =22AB BE +=2263+=35,由(2)可知△ACE ∽△BCD ,∴BD BC AE AC =,∴35=810,∴BD =125.故答案为125. (4)∵m =6,n =42,∴CE =3,CD =22,AB =22CA BC -=2,①如图5中,当α=90°时,半圆与AC 相切.在Rt △DBC 中,BD =22BC CD +=224222+()()=210. ②如图6中,当α=90°+∠ACB 时,半圆与BC 相切,作EM ⊥AB 于M .∵∠M =∠CBM =∠BCE =90°,∴四边形BCEM 是矩形,∴342BM EC ME ===,,∴AM =5,AE =22AM ME +=57,由(2)可知DB AE =223,∴BD =21143. 故答案为210或21143.点睛:本题考查了圆的有关知识,相似三角形的判定和性质、勾股定理等知识,正确画出图形是解决问题的关键,学会分类讨论的思想,本题综合性比较强,属于中考压轴题.4.在平面直角坐标中,边长为2的正方形OABC 的两顶点A 、C 分别在y 轴、x 轴的正半轴上,点O 在原点.现将正方形OABC 绕O 点顺时针旋转,当A 点一次落在直线y x =上时停止旋转,旋转过程中,AB边交直线y x=于点M,BC边交x轴于点N(如图).(1)求边OA在旋转过程中所扫过的面积;(2)旋转过程中,当MN和AC平行时,求正方形OABC旋转的度数;(3)设MBN∆的周长为p,在旋转正方形OABC的过程中,p值是否有变化?请证明你的结论.【答案】(1)π/2(2)22.5°(3)周长不会变化,证明见解析【解析】试题分析:(1)根据扇形的面积公式来求得边OA在旋转过程中所扫过的面积;(2)解决本题需利用全等,根据正方形一个内角的度数求出∠AOM的度数;(3)利用全等把△MBN的各边整理到成与正方形的边长有关的式子.试题解析:(1)∵A点第一次落在直线y=x上时停止旋转,直线y=x与y轴的夹角是45°,∴OA旋转了45°.∴OA在旋转过程中所扫过的面积为24523602ππ⨯=.(2)∵MN∥AC,∴∠BMN=∠BAC=45°,∠BNM=∠BCA=45°.∴∠BMN=∠BNM.∴BM=BN.又∵BA=BC,∴AM=CN.又∵OA=OC,∠OAM=∠OCN,∴△OAM≌△OCN.∴∠AOM=∠CON=12(∠AOC-∠MON)=12(90°-45°)=22.5°.∴旋转过程中,当MN和AC平行时,正方形OABC旋转的度数为45°-22.5°=22.5°.(3)在旋转正方形OABC的过程中,p值无变化.证明:延长BA交y轴于E点,则∠AOE=45°-∠AOM,∠CON=90°-45°-∠AOM=45°-∠AOM,∴∠AOE=∠CON.又∵OA=OC,∠OAE=180°-90°=90°=∠OCN.∴△OAE≌△OCN.∴OE=ON,AE=CN.又∵∠MOE=∠MON=45°,OM=OM,∴△OME≌△OMN.∴MN=ME=AM+AE.∴MN=AM+CN,∴p=MN+BN+BM=AM+CN+BN+BM=AB+BC=4.∴在旋转正方形OABC的过程中,p值无变化.考点:旋转的性质.5.如图,点A是x轴非负半轴上的动点,点B坐标为(0,4),M是线段AB的中点,将点M绕点A顺时针方向旋转90°得到点C,过点C作x轴的垂线,垂足为F,过点B作y 轴的垂线与直线CF相交于点E,连接AC,BC,设点A的横坐标为t.(Ⅰ)当t=2时,求点M的坐标;(Ⅱ)设ABCE的面积为S,当点C在线段EF上时,求S与t之间的函数关系式,并写出自变量t的取值范围;(Ⅲ)当t为何值时,BC+CA取得最小值.【答案】(1)(1,2);(2)S=32t+8(0≤t≤8);(3)当t=0时,BC+AC有最小值【解析】试题分析:(I)过M作MG⊥OF于G,分别求OG和MG的长即可;(II)如图1,同理可求得AG和OG的长,证明△AMG≌△CAF,得:AG=CF=12t,AF=MG=2,分别表示EC和BE的长,代入面积公式可求得S与t的关系式;并求其t的取值范围;(III)证明△ABO∽△CAF,根据勾股定理表示AC和BC的长,计算其和,根据二次根式的意义得出当t=0时,值最小.试题解析:解:(I)如图1,过M作MG⊥OF于G,∴MG∥OB,当t=2时,OA=2.∵M是AB的中点,∴G是AO的中点,∴OG=12OA=1,MG是△AOB的中位线,∴MG=12OB=12×4=2,∴M(1,2);(II)如图1,同理得:OG=AG=12t.∵∠BAC=90°,∴∠BAO+∠CAF=90°.∵∠CAF+∠ACF=90°,∴∠BAO=∠ACF.∵∠MGA=∠AFC=90°,MA =AC ,∴△AMG ≌△CAF ,∴AG =CF =12t ,AF =MG =2,∴EC =4﹣12t ,BE =OF =t +2,∴S △BCE =12EC •BE =12(4﹣12t )(t +2)=﹣14t 2+32t +4; S △ABC =12•AB •AC =12•216t +•21162t +=14t 2+4,∴S =S △BEC +S △ABC =32t +8. 当A 与O 重合,C 与F 重合,如图2,此时t =0,当C 与E 重合时,如图3,AG =EF ,即 12t =4,t =8,∴S 与t 之间的函数关系式为:S =32t +8(0≤t ≤8); (III )如图1,易得△ABO ∽△CAF ,∴AB AC =OB AF =OA FC =2,∴AF =2,CF =12t ,由勾股定理得:AC =22AF CF +=22122t +()=2144t +,BC =22BE EC +=221242t t ++-()()=21544t +(),∴BC +AC =( 5+1)2144t +,∴当t =0时,BC +AC 有最小值.点睛:本题考查了几何变换综合题,知识点包括相似三角形、全等三角形、点的坐标、几何变换(旋转)、三角形的中位线等,解题的关键是正确寻找全等三角形或相似三角形解决问题,学会利用参数解决问题,属于中考压轴题.6.在正方形ABCD 中,连接BD .(1)如图1,AE ⊥BD 于E .直接写出∠BAE 的度数.(2)如图1,在(1)的条件下,将△AEB以A旋转中心,沿逆时针方向旋转30°后得到△AB′E′,AB′与BD交于M,AE′的延长线与BD交于N.①依题意补全图1;②用等式表示线段BM、DN和MN之间的数量关系,并证明.(3)如图2,E、F是边BC、CD上的点,△CEF周长是正方形ABCD周长的一半,AE、AF 分别与BD交于M、N,写出判断线段BM、DN、MN之间数量关系的思路.(不必写出完整推理过程)【答案】(1)45°;(2)①补图见解析;②BM、DN和MN之间的数量关系是BM2+MD2=MN2,证明见解析;(3)答案见解析.【解析】(1)利用等腰直角三角形的性质即可;(2)依题意画出如图1所示的图形,根据性质和正方形的性质,判断线段的关系,再利用勾股定理得到FB2+BM2=FM2,再判断出FM=MN即可;(3)利用△CEF周长是正方形ABCD周长的一半,判断出EF=EG,再利用(2)证明即可.解:(1)∵BD是正方形ABCD的对角线,∴∠ABD=∠ADB=45°,∵AE⊥BD,∴∠ABE=∠BAE=45°,(2)①依题意补全图形,如图1所示,②BM、DN和MN之间的数量关系是BM2+MD2=MN2,将△AND绕点D顺时针旋转90°,得到△AFB,∴∠ADB=∠FBA,∠BAF=∠DAN,DN=BF,AF=AN,∵在正方形ABCD中,AE⊥BD,∴∠ADB=∠ABD=45°,∴∠FBM=∠FBA+∠ABD=∠ADB+∠ABD=90°,在Rt△BFM中,根据勾股定理得,FB2+BM2=FM2,∵旋转△ANE得到AB1E1,∴∠E1AB1=45°,∴∠BAB1+∠DAN=90°﹣45°=45°,∵∠BAF=DAN,∴∠BAB1+∠BAF=45°,∴∠FAM=45°,∴∠FAM=∠E1AB1,∵AM=AM,AF=AN,∴△AFM≌△ANM,∴FM=MN,∵FB2+BM2=FM2,∴DN2+BM2=MN2,(3)如图2,将△ADF绕点A顺时针旋转90°得到△ABG,∴DF=GB,∵正方形ABCD的周长为4AB,△CEF周长为EF+EC+CF,∵△CEF周长是正方形ABCD周长的一半,∴4AB=2(EF+EC+CF),∴2AB=EF+EC+CF∵EC=AB﹣BE,CF=AB﹣DF,∴2AB=EF+AB﹣BE+AB﹣DF,∴EF=DF+BE,∵DF=GB,∴EF=GB+BE=GE,由旋转得到AD=AG=AB,∵AM=AM,∴△AEG≌△AEF,∠EAG=∠EAF=45°,和(2)的②一样,得到DN2+BM2=MN2.“点睛”此题是四边形综合题,主要考查了正方形的性质、旋转的性质,三角形的全等,判断出(△AFN≌△ANM,得到FM=MM),是解题的关键.7.如图1,在Rt△ABC中,∠ACB=90°,E是边AC上任意一点(点E与点A,C不重合),以CE为一直角边作Rt△ECD,∠ECD=90°,连接BE,AD.(1)若CA=CB,CE=CD①猜想线段BE,AD之间的数量关系及所在直线的位置关系,直接写出结论;②现将图1中的Rt△ECD绕着点C顺时针旋转锐角α,得到图2,请判断①中的结论是否仍然成立,若成立,请证明;若不成立,请说明理由;(2)若CA=8,CB=6,CE=3,CD=4,Rt△ECD绕着点C顺时针转锐角α,如图3,连接BD,AE,计算的值.【答案】(1)①BE=AD,BE⊥AD;②见解析;(2)125.【解析】试题分析:根据三角形全等的判定与性质得出BE=AD,BE⊥AD;设BE与AC的交点为点F,BE与AD的交点为点G,根据∠ACB=∠ECD=90°得出∠ACD=∠BCE,然后结合AC=BC,CD=CE得出△ACD≌△BCE,则AD=BE,∠CAD=∠CBF,根据∠BFC=∠AFG,∠BFC+∠CBE=90°得出∠AFG+∠CAD=90°,从而说明垂直;首先根据题意得出△ACD∽△BCE,然后说明∠AGE=∠BGD=90°,最后根据直角三角形的勾股定理将所求的线段转化成已知的线段得出答案.试题解析:(1)①解:BE=AD,BE⊥AD②BE=AD,BE⊥AD仍然成立证明:设BE与AC的交点为点F,BE与AD的交点为点G,如图1.∵∠ACB=∠ECD=90°,∴∠ACD=∠BCE ∵AC=BC CD=CE ∴△ACD≌△BCE∴AD=BE ∠CAD=∠CBF ∵∠BFC=∠AFG ∠BFC+∠CBE=90°∴∠AFG+∠CAD=90°∴∠AGF=90°∴BE⊥AD(2)证明:设BE与AC的交点为点F,BE的延长线与AD的交点为点G,如图2.∵∠ACB=∠ECD=90°,∴∠ACD=∠BCE ∵AC=8,BC=6,CE=3,CD=4 ∴△ACD∽△BCE∴∠CAD=∠CBE ∵∠BFC=∠AFG ∠BFC+∠CBE=90°∴∠AFG+∠CAD=90°∴∠AGF=90°∴BE⊥AD ∴∠AGE=∠BGD=90°∴,.∴.∵,,∴考点:三角形全等与相似、勾股定理.8.在正方形 ABCD 中,M 是 BC 边上一点,且点 M 不与 B、C 重合,点 P 在射线 AM 上,将线段 AP 绕点 A 顺时针旋转 90°得到线段 AQ,连接BP,DQ.(1)依题意补全图 1;(2)①连接 DP,若点 P,Q,D 恰好在同一条直线上,求证:DP2+DQ2=2AB2;②若点 P,Q,C 恰好在同一条直线上,则 BP 与 AB 的数量关系为:.【答案】(1)详见解析;(2)①详见解析;②BP=AB.【解析】【分析】(1)根据要求画出图形即可;(2)①连接BD,如图2,只要证明△ADQ≌△ABP,∠DPB=90°即可解决问题;②结论:BP=AB,如图3中,连接AC,延长CD到N,使得DN=CD,连接AN,QN.由△ADQ≌△ABP,△ANQ≌△ACP,推出DQ=PB,∠AQN=∠APC=45°,由∠AQP=45°,推出∠NQC=90°,由CD=DN,可得DQ=CD=DN=AB;【详解】(1)解:补全图形如图 1:(2)①证明:连接 BD,如图 2,∵线段 AP 绕点 A 顺时针旋转 90°得到线段 AQ,∴AQ=AP,∠QAP=90°,∵四边形 ABCD 是正方形,∴AD=AB,∠DAB=90°,∴∠1=∠2.∴△ADQ≌△ABP,∴DQ=BP,∠Q=∠3,∵在 Rt△QAP 中,∠Q+∠QPA=90°,∴∠BPD=∠3+∠QPA=90°,∵在 Rt△BPD 中,DP2+BP2=BD2,又∵DQ=BP,BD2=2AB2,∴DP2+DQ2=2AB2.②解:结论:BP=AB.理由:如图 3 中,连接 AC,延长 CD 到 N,使得 DN=CD,连接 AN,QN.∵△ADQ≌△ABP,△ANQ≌△ACP,∴DQ=PB,∠AQN=∠APC=45°,∵∠AQP=45°,∴∠NQC=90°,∵CD=DN,∴DQ=CD=DN=AB,∴PB=AB.【点睛】本题考查正方形的性质,旋转变换、勾股定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴。
