数字电路逻辑设计习题3
(完整版)数字电路与逻辑设计课后习题答案蔡良伟(第三版)

0 1 1 0
0 1 1 1
1 0 0 0
1 0 0 1
1 0 1 0
1 0 1 1
1 1 0 0
1 1 0 1
1 1 1 0
1 1 1 1
0 0 0 0
0 0 0 1
0 0 1 0
0 0 1 1
0 1 0 0
0 1 0 1
0 1 1 0
0 1 1 1
1 0 0 0
1 0 0 1
1 0 1 0
3-6
3-7
3-8
3-9
3-10
求减数的补码,然后与被减数相加即可。电路图如下:
3-11
3-12
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
3-13
(1)真值表:
(2)电路图
3-14
3-15
第四章习题
4-1
4-2
4-3
4-4
4-5
4-6
4-7
4-8
4-9
4-10
RSDRSJK RST
4-11
(1)转换真值表
1 1 0 1
1 1 1 0
1 1 1 1
1 0 1 0
0 0 0 0
0 0 0 1
0 0 1 0
00 11
0 1 0 0
0 1 0 1
0 1 1 0
0 1 1 1
1 0 0 0
1 0 0 1
××××
××××
××××
××××
××××
1×0×1×0×
0×0×0××1
0×0××1 1×
0×0××0×1
0××1 1×1×
数字电路第三章习题答案
数字电路第三章习题答案
3-10
F S 1 A S 0 B A S 0 B A B S 0 A B S 1 S 0 A B F F S 1 A S 0 B A S 0 B A B S 0 A B S 1 S 0 A B
数字电路第三章习题答案
3-11
试用六个与非门设计一个水箱控制电路。图为水箱示意图。A、B、C是三个电极。 当 电极被水浸没时,会有信号输出。水面在A,B间为正常状态,点亮绿灯G;水面在B、 C间或在A以上为异常状态,点亮黄灯Y;水面在C以下为危险状态.点亮红灯R。
3531736半加器的设计1半加器真值表2输出函数3逻辑图输入输出被加数a加数b4逻辑符号31837ab改为用与非门实现函数表达式变换形式
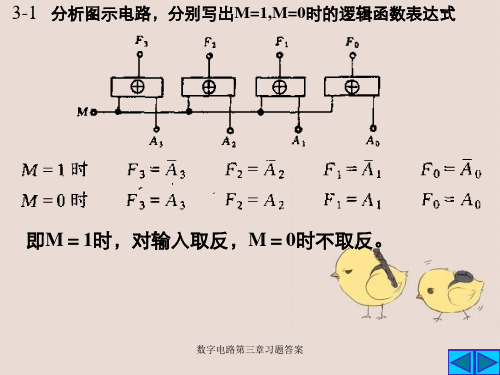
3-1 分析图示电路,分别写出M=1,M=0时的逻辑函数表达式
即M=1时,对输入取反,M=0时不取反。
数字电路第三章习题答案
3-2 分析图示补码电路,要求写出逻辑函数表达式,列出真值表。
3-10 试用与非门设计一个逻辑选择电路。
S1、S0为选择端,A、B为数据输入端。 选择电路的功能见下表。选择电路可 以有反变量输入。
数字电路第三章习题答案
3-10
F S 1 A S 0 B A S 0 B A B S 0 A B S 1 S 0 A B F F S 1 A S 0 B A S 0 B A B S 0 A B S 1 S 0 A B FS 1 S 0A B S 1 S 0(A B )S 1 S 0(A BA)B
数字电路第三章习题答案
3-5
Ai 0 0 0 0 1 1 1 1
Si Ai BiCi Ai BiCi Ai BiCi Ai BiCi
数字电路与逻辑设计试题 (1)

《数字电路与逻辑设计》试题3参考答案一. 填空题(10)1. 一个触发器有Q 和Q 两个互补的输出引脚,通常所说的触发器的输出端是指 Q ,所谓置位就是将输出端置成 1 电平,复位就是将输出端置成 0 电平。
2. 我们可以用逻辑函数来表示逻辑关系,任何一个逻辑关系都可以表示为逻辑函数的 与或 表达式,也可表示为逻辑函数的 或与 表达式。
3.计数器和定时器的内部结构是一样的,当对不规则的事件脉冲计数时,称为 计数 器,当对周期性的规则脉冲计数时,称为 定时 器。
4.当我们在计算机键盘上按一个标为“3”的按键时,键盘向主机送出一个ASCII 码,这个ASCII 码的值为 33H 。
5.在5V 供电的数字系统里,所谓的高电平并不是一定是5V ,而是有一个电压范围,我们把这个电压范围称为 高电平噪声 容限;同样所谓的低电平并不是一定是0V ,而也是有一个电压范围,我们把这个电压范围称为 低电平噪声 容限。
二. 选择题(10)1.在数字系统里,当某一线路作为总线使用,那么接到该总线的所有输出设备(或器件)必须具有 b结构,否则会产生数据冲突。
a. 集电极开路;b. 三态门;c. 灌电流;d. 拉电流2.TTL 集成电路采用的是 b 控制,其功率损耗比较大;而MOS 集成电路采用的是 a 控制,其功率损耗比较小。
a. 电压;b.电流;c. 灌电流;d. 拉电流3. 欲将二进制代码翻译成输出信号选用 b ,欲将输入信号编成二进制代码选用 a ,欲将数字系统中多条传输线上的不同数字信号按需要选择一个送到公共数据线上选用 c ,欲实现两个相同位二进制数和低位进位数的相加运算选用 e 。
a. 编码器;b. 译码器;c. 多路选择器;d. 数值比较器;e. 加法器;f. 触发器; g. 计数器; h. 寄存器4. 卡诺图上变量的取值顺序是采用 b 的形式,以便能够用几何上的相邻关系表示逻辑上的相邻。
a. 二进制码; b. 循环码; c. ASCII 码; d. 十进制码5. 根据最小项与最大项的性质,任意两个不同的最小项之积为 0 ,任意两个不同的最大项之和为1 。
习题3 组合逻辑电路分析与设计 数字电子技术 含答案

1习 题 3组合逻辑电路分析与设计数字电子技术[题3.1] 分析图题3.1所示电路,列出真值表,写出输出函数表达式,并说明电路的逻辑功能。
解:由电路图得真值表如下所示:所以:AB 时,11Y = A B 时,31Y = A B =时,21Y =电路实现比较器的功能。
A ,B 是输入;Y 1,Y 2,Y 3分别是A<B ,A=B ,A>B 时的输出。
[题3.2] 分析图题3.2所示电路,说明电路的逻辑功能。
2解:电路的逻辑函数表达式为:(10Y S EN A S EN B EN Y EN ⎧=⋅⋅+⋅⋅=⎪⎨=⎪⎩时);输出高阻态(时)电路的逻辑功能是:在使能条件EN=1且S=0时,输出A ;在使能条件EN=1且S=1时,输出B ;使能条件EN=0时,输出高阻态。
电路实现数据选择器的功能。
[题3.3] 图题3.3是一个密码锁控制电路。
开锁条件是必须将开锁开关闭合,且要拨对密码。
如果以上两个条件都得到满足,开锁信号为1,报警信号为0,即锁打开而不报警。
否则,开锁信号为0,报警信号为1。
试分析该电路的密码是多少。
解:1Y S ABCD =⋅2Y S ABCD =⋅分析电路可知:电路的密码是1001。
[题3.4] 图题3.4所示电路由4位二进制比较器7485和4位二选一数据选择器74157组成。
其中74157控制端B A /的控制作用为:B A /=0时,Y i =A i ,否则,Y i =B i 。
试分析图示电路的逻辑功能。
3解:当A B ≤时,输出A ;当A B 时,输出B ;所以电路的功能是输出A ,B 中较小的数。
[题3.5] 某建筑物的自动电梯系统有五个电梯,其中三个是主电梯(设为A 、B 、C ),两个备用电梯。
当上下人员拥挤,主电梯全被占用时,才允许使用备用电梯。
现需设计一个监控主电梯的逻辑电路,当任何两个主电梯运行时,产生一个信号(Y 1),通知备用电梯准备运行;当三个主电梯都在运行时,则产生另一个信号(Y 2),使备用电梯主电源接通,处于可运行状态。
《数字电路与逻辑设计》综合练习题及解答

《数字电路与逻辑设计》综合练习题及解答第一部分习题一、填空1.将十进制数转换成等值的二进制数、十六进制数。
10 = 2= 162.10= 余3BCD= 8421BCD 3.16= 24.一位二进制数只有2个数,四位二进制数有个数;为计64个数,需要位二进制数。
5.二进制数2的等值八进制数是8。
6.二进制数2的等值十进制数是10。
7.欲对100个对象进行二进制编码,则至少需要位二进制数。
8.二进制数为000000~111111能代表个十进制整数。
9.为将信息码10110010配成奇校验码,其配奇位的逻辑值为;为将信息码01101101配成偶校验码,其配偶位的逻辑值为。
10.格雷码的特点是。
11.n变量函数的每一个最小项有个相领项。
12.当ij时,同一逻辑函数的两个最小项mimj=。
2n113.n变量的逻辑函数,mi为最小项,则有mi=。
i014.逻辑函数FABCD的反函数F=。
15.逻辑函数FA(BC)的对偶函数F是。
16.多变量同或运算时,=0,则xi=0的个数必须为。
17.逻辑函数F(A,B,C)1C18. 逻辑函数F(A,B,C,D)( )。
19.逻辑函数F(A,B,C)(ABC)(ABC)的最简与或式为。
20.巳知函数的对偶式F(A,B,C,D)ABCDBC,则它的原函数F =。
* * * * * 21.正逻辑约定是、。
22.双极型三极管截止状态过渡到饱和状态所需的过渡时间称为时间,它时间和时间两部分组成,可用等式描述。
23.双极型三极管饱和状态过渡到截止状态所需的过渡时间称为时间,它时间和时间两部分组成,可用等式描述。
1。
AB的最小项表达式为F(A,B,C)=m(1,2,3,4,8,10)(0,12,14)的最简与或式为F=24.三极管反相器带灌电流负载时,负载电流的方向是从,此时反相器输出电平。
25.三极管反相器带拉电流负载时,负载电流的方向是从,此时反相器输出电平。
26.输入端的噪声容限说明。
《数字电路制作与测试》习题册(三)

《数字电路制作与测试》习题册(三)项⽬三计数器的设计与调试主要知识点:⼀、填空题1. 时序逻辑电路的输出不仅与有关,⽽且与有关。
2. 时序逻辑电路中的存储电路通常有两种形式:和。
3. 是构成时序逻辑电路中存储电路的主要元件。
4. 锁存器和触发器是构成时序逻辑电路中的主要元件。
5. 按逻辑功能分,触发器有、、、触发器等⼏种。
6. 触发器按照逻辑功能来分⼤致可分为种。
7. 触发器是构成逻辑电路的重要部分。
8. 触发器有两个互补的输出端Q 、Q ,定义触发器的0状态为,1状态为,可见触发器的状态指的是端的状态。
9. 触发器的两个输出端Q 、Q ,当0,1Q Q ==时,我们称触发器处于。
10. 触发器的状态指的是的状态,当1,0Q Q ==时,触发器处于。
11. 触发器有2个稳态,存储4位⼆进制信息要个触发器。
12. 因为触发器有个稳态,6个触发器最多能存储⼆进制信息。
13. ⼀个有与⾮门构成的基本RS 触发器,其约束条件是。
14. ⼀个基本R S 触发器在正常⼯作时,它的约束条件是R +S =1,则它不允许输⼊S = 且R = 的信号。
15. 与⾮门构成的基本RS 锁存器输⼊状态不允许同时出现R = S = 。
16. 与⾮门构成的基本RS 锁存器的特征⽅程是,约束条件是。
17. 由与⾮门构成的基本RS 锁存器其逻辑功能有种。
18. 由与⾮门构成的基本RS 锁存器正常⼯作时有三种状态,分别是01R S =输出为,10R S = 输出为,11R S =输出为。
(0状态/1状态/保持状态)。
19. 与⾮门构成的基本RS 锁存器当Q=1时,R = ,S = 。
20. 与⾮门构成的基本RS 锁存器当Q=0时,R = ,S = 。
21. 锁存器和触发器的区别在于其输出状态的变化是否取决于。
22. 触发器的输出状态变化除了由输⼊信号决定外还取决于。
23. 和共同决定了触发器输出状态的变化。
24. 钟控RS 触发器的约束条件是。
数字逻辑与系统设计习题(1-3)

第1章习题一.单选题:1.以下代码中为恒权码的是( )。
A )余3循环码B )5211码C )余3码D )右移码2.一位八进制数可以用( )位二进制数来表示。
A )1B )2C )3D )43.十进制数43用8421BCD 码表示为( )A )10011B )0100 0011C )1000011D )100114.A + BC =( )A )AB + AC B )ABC C )(A +B)(A + C)D )BC5.在函数L(A,B,C,D) = AB + CD 的真值表中,L=1的状态有( )A )2个B )4个C )6个D )7个6.已知两输入逻辑变量AB 和输出结果Y 的真值表如下表,则AB 的逻辑关系为( )A )同或B )异或C )与非D )或非 7.利用约束项化简逻辑函数时,约束项应看成( ) A )1B )2C )能使圈组大的看成1,其它看成0D )无所谓8.当逻辑函数有 n 个变量时,共有( )组变量取值组合A )nB )2nC )n 2D )2n9.利用卡诺图化简逻辑函数时,8个相邻的最小项可消去( )个变量。
A )1B )2C )3D )410.下面的卡诺图化简,应画( )个包围圈。
A )2B )3C )4D )511.卡诺图中,变量的取值按( )规律排列。
A )Ascii 码B )8421BCD 码C )余3码D )循环码12.4变量逻辑函数的真值表,表中的输入变量的取值应有( )种。
A )2B )4C )8D )1613.TTL 逻辑电路是以( )为基础的集成电路A )三极管B )二极管C )场效应管D )晶闸管14.CMOS 逻辑电路是以( )为基础的集成电路A )三极管B )NMOS 管C )PMOS 管D )NMOS 管和PMOS 管二.判断题:1.十进制数(64.5)10与(40.8)16等值。
( )2.在任一输入为1的情况下,"或非"运算的结果是逻辑0。
数字电路与逻辑设计(第二版)习题电子版

第一章 习题1-1 将下列十进制数转换为二进制数、八进制数和十六进制数。
(1)2210 (2)10810 (3)13.12510 (4)131.62510 1-2 将下列二进制数转换为十进制数、八进制数和十六进制数。
(1)1011012 (2)111001012 (3)101.00112 (4)100111.1012 1-3 将下列八进制数转换为十进制数、二进制数和十六进制数。
(1)168 (2)1728 (3)61.538 (4)126.7481-4 将下列十六进制数转换为十进制数、二进制数和八进制数。
(1)2A 16 (2)B2F 16 (3)D3.E 16 (4)1C3.F916 1-5用真值表证明下列逻辑函数等式。
(1) A(B+C)=AB+AC (2) A+BC=(A+B)(A+C)(3) A +B ̅̅̅̅̅̅̅̅=A B ̅ (4) AB̅̅̅̅=A +B ̅ (5) A+BC̅̅̅̅+A BC=1 (6) A B ̅+A B=AB +AB ̅̅̅̅̅̅̅̅̅̅̅̅ (7) A ⨁B=A ⨁B̅ (8) A B̅+B C +C A =A B+B ̅C+C A 1-6利用逻辑代数公式证明下列逻辑等式。
(1) A+A B+B ̅=1 (2) A+B A +CD ̅̅̅̅̅̅̅̅̅̅=A (3) AB+A C+B̅C =AB+C (4) A B ̅+A +C ̅̅̅̅̅̅̅̅+B ̅(D+E)C=A B ̅+A C (5) A ⨁B+AB=A+B(6) AB̅+BC +CA ̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅=A B ̅C +ABC (7) AB̅D ̅+B ̅C D+A D+A B ̅C+A B ̅CD ̅=A B ̅+A D+B ̅C (8) A ⨁B +B ⨁C +C ⨁D=A B̅+B C +C D ̅+D A 1-7 利用反演规则写出下列逻辑函数的反函数。
(1) F 1=A B̅C+A B C (2) F 2=A(B̅+C)+ C (B+D) (3) F 3=(A B+c D̅)(C+D ̅) (4) F 4=(A B +C D ̅)(B+A D ̅) (5) F 5=A B ̅+A C B +D ̅̅̅̅̅̅̅̅ (6) F 6=A +BC ̅̅̅̅̅̅̅̅̅̅+B ̅+CD ̅̅̅̅̅̅̅̅̅̅ (7) F 7=AC +BD ̅̅̅̅̅̅̅̅̅̅̅̅C +A +BD̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅ (8) F 8=(A +D ̅(B ̅+C)̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅+(A +C ̅̅̅̅̅̅̅̅+B)AB +CD̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅1-8 利用对偶规则写出下列逻辑函数的对偶函数。
数字电路与逻辑设计课后习题答案蔡良伟(第三版)

数字电路答案
00011100 0011 11111001
111000011.111110012 = 111000011.111110010= 703.7628
703
76 2
703.762 8 = 7*8 2 + 0*8 1 + 3*8 0 + 7*8 - 1 + 6*8 - 2 + 2*8 - 3 = 451.972610
00 0 0 1 0 01 0 0 1 1 11 1 1 1 1 10 1 1 1 1
8
数字电路答案
A B C DF A B C DF 0 0 0 00 1 0 0 00 0 0 0 10 1 0 0 11 0 0 1 01 1 0 1 01 0 0 1 11 1 0 1 11 0 1 0 01 1 1 0 00 0 1 0 11 1 1 0 10 0 1 1 01 1 1 1 00 0 1 1 11 1 1 1 10
1
1
1
1
0
1
1
1
1
1
3
数字电路答案
(3) A B A B
A 0 0 1 1 左式=右式,得证。
(4) AB A B
A 0 0 1 1 左式=右式,得证。
(5) A BC A BC 1
A 0 0 0 0 1 1 1 1 左式=右式,得证。
(6) AB AB AB A B
数电习题3
,习题三【试题3-1】 用74LS138设计一个能对32地址译码的译码电路。
【解题方法指导】构成32地址译码系统需要用4片74LS138译码器。
32地址对应5位二进制地址码A 4A 3A 2A 1A 0,低三位地址A 2A 1A 0为每一片译码器提供8个低位地址,高位地址A 4A 3作为译码器的使能信号。
A 4A 3=00时,74138-1译码输出;A 4A 3=01时,74138-2译码输出;A 4A 3=10时,74138-3译码输出;A 4A 3=11时,74138-4译码输出。
A 4A 3可以用2/4线译码器译码,为74138-1~74138-4提供使能信号。
考虑到74138有多个使能端;可利用使能端本身的译码功能。
由于74138只有一个高电平有效的使能端,所以A 4中A 3要有一个反相后接低电平有效的使能端,使A 4A 3=11时,74138-4译码输出。
【解答】能实现32地址译码的译码系统之一如图3-53所示。
》图3-53 74138实现32地址译码《【试题3-2】用74138和74151组成图3-54所示16通道数据传输系统,可将任一输入通道的输入数据从任一输出通道输出。
;图3-54【解题方法指导】本题实质是将8通道数据选择器和8通道数据分配器扩展为Y 24~Y 31A 3Y 8~Y 15A 4I I 1 I Y 0Y 1~Y16通道。
八选一数选器74151只有一个使能端,所以要用一个反相器使两片74151分别使能。
八通道数据分配器74138有三个使能端,一片74138用高电平使能,另一片74138则用低电平使能,剩余一个低电平使能端作为数据输入端。
因为,低电平使能端作为数据输入端,输入输出数据同相,所以,74151用高电平输出有效的输出端Y 。
【解答】能实现16通道数据传输系统之逻辑图如图3-55所示。
\:图3-55【试题3-3】用一片74LS48实现三位十进制数动态扫描显示。
数字逻辑练习题

数字逻辑练习题数字逻辑是计算机科学中的一个重要概念,它涉及到数字电路的设计与分析。
在数字逻辑中,我们需要理解二进制数系统、布尔代数和逻辑门等基础知识,以便解决各种数字电路的设计问题。
本文将提供一些数字逻辑练习题,旨在帮助读者巩固和加深对数字逻辑的理解。
练习题1:二进制加法请设计一个电路,实现两个4位二进制数的加法运算。
输入是两个4位的二进制数(A和B),输出是它们的和(S)。
要求使用逻辑门实现电路,不允许使用任何其他的辅助设备。
练习题2:二进制比较器请设计一个电路,比较两个4位二进制数的大小关系。
输入是两个4位的二进制数(A和B),输出是一个信号(C),当A大于B 时为1,当A小于或等于B时为0。
要求使用逻辑门实现电路。
练习题3:验证码验证假设你正在设计一个网站,需要用户输入一个四位的验证码。
请设计一个电路,验证用户输入的验证码是否正确。
输入是用户输入的四位二进制数(I),正确的验证码是固定的(C)。
如果输入与验证码匹配,输出为1,否则输出为0。
要求使用逻辑门实现电路。
练习题4:电梯控制请设计一个简单的电梯控制电路,实现电梯的上下控制。
输入是一个二进制数(D),代表电梯当前的楼层。
输出是两个信号(U 和D),当需求楼层大于当前楼层时,输出U为1,D为0;当需求楼层小于当前楼层时,输出D为1,U为0;当需求楼层等于当前楼层时,输出D和U都为0。
练习题5:疯狂打地鼠游戏假设你正在设计一个疯狂打地鼠的游戏,需要一个随机数生成器。
请设计一个电路,产生一个随机的3位二进制数作为地鼠出现的位置。
输出是一个3位的二进制数(R),代表地鼠出现的位置。
要求使用逻辑门实现电路。
以上是一些数字逻辑练习题,涵盖了基本的加法、比较、验证和控制等方面的问题。
通过解决这些练习题,读者可以加深对数字逻辑的理解,并提高解决数字电路设计问题的能力。
希望本文对读者在数字逻辑学习中有所帮助。
数字电路与逻辑设计习题及参考答案全套

数字电路与逻辑设计习题及参考答案一、选择题1. 以下表达式中符合逻辑运算法则的是 D 。
A.C ·C=C 2B.1+1=10C.0<1D.A+1=12. 一位十六进制数可以用 C 位二进制数来表示。
A . 1B . 2C . 4D . 163. 当逻辑函数有n 个变量时,共有 D 个变量取值组合?A. nB. 2nC. n 2D. 2n4. 逻辑函数的表示方法中具有唯一性的是 A 。
A .真值表 B.表达式 C.逻辑图 D.状态图5. 在一个8位的存储单元中,能够存储的最大无符号整数是 D 。
A .(256)10B .(127)10C .(128)10D .(255)106.逻辑函数F=B A A ⊕⊕)( = A 。
A.BB.AC.B A ⊕D. B A ⊕7.求一个逻辑函数F 的对偶式,不可将F 中的 B 。
A .“·”换成“+”,“+”换成“·”B.原变量换成反变量,反变量换成原变量C.变量不变D.常数中“0”换成“1”,“1”换成“0”8.A+BC= C 。
A .A+B B.A+C C.(A+B )(A+C ) D.B+C9.在何种输入情况下,“与非”运算的结果是逻辑0。
DA .全部输入是0 B.任一输入是0 C.仅一输入是0 D.全部输入是110.在何种输入情况下,“或非”运算的结果是逻辑1。
AA .全部输入是0 B.全部输入是1 C.任一输入为0,其他输入为1 D.任一输入为111.十进制数25用8421BCD 码表示为 B 。
A .10 101B .0010 0101C .100101D .1010112.不与十进制数(53.5)10等值的数或代码为 C 。
A .(0101 0011.0101)8421BCDB .(35.8)16C .(110101.11)2D .(65.4)813.以下参数不是矩形脉冲信号的参数 D 。
A.周期B.占空比C.脉宽D.扫描期14.与八进制数(47.3)8等值的数为: BA. (100111.0101)2B.(27.6)16C.(27.3 )16D. (100111.101)215. 常用的BCD码有 D 。
数字电路 第3章习题课

题3-15
A B C D
F 0 0 1 1 1 1 0 0 0 0 × × × × × ×
× ×
题3-15
解: F BC D0 0
F
四选一MUX D1 1 D2 1 D3 0 E
题3-16
用74LS138和与非门实现下列逻辑函数。
Y1 ABC A( B C )
+5V
0 0 1 F3 F 5 F 61 F 7 04 F 0 0 1 0 0 1 74138 1 1 1 0 A0 1 1 12 A1 A 0 0 0 0X0 0 X1 0 X2
题3-13
试用 74138 和 74151 构成两个四位二进制数相同 比较器。其功能为两个二进制数相等时输出为 1, 否则为 0。 解:74138 和 74151 地址端均为三变量输入,要 实现四位二进制数相同比较器,必须分别用两个芯 片级联扩展输入端,并分别将待比较的两个四位二 进制数输入到扩展后的输入端,就可得到两个四位 二进制数相同时,输出为 1 的功能。逻辑图如图 3-36 所示。
1 0 B F= A B+ A B 1 1 B 0 0 0 0 1 B F= AB
G1 G0 A
A2 F F A1 MUX A0 D D D D D D D 0 1 2 3 4 5 6 D7 1 1
B
1
1 1
1 0 B F= A B+A 1 1 1 = A +B
题3-5
列出图 3-58 所示电路的真值表。图中芯片为 8421 码二-十进制译码器,输出低电平有效。
0 1
D
题3-3
解:
F F0 F4 F5 F6 F8 F10 F12 F15 F0 F4 F5 F6 F8 F10 F12 F15 (0,4,5,6,8,10,12,15)
奥鹏北语14秋《数字电路与逻辑设计》作业3满分答案

一,单选题
1. A. A
B. B
C. C
D. D
?
正确答案:D
2.在下列逻辑电路中,不是组合逻辑电路的有()。
A.译码器
B.编码器
C.全加器
D.寄存器
?
正确答案:D
3. A. A
B. B
C. C
D. D
?
正确答案:C
4. 101键盘的编码器输出()位二进制代码。
A. 2
A.错误
B.正确
?
正确答案:A
4. A.错误
B.正确
?
正确答案:A
5.三态门的三种状态分别为:高电平、低电平、不高不低的电压。()
A.错误
B.正确
?
正确答案:A
C. C
D. D
?
正确答案:D
14.一个8选一数据选择器的数据输入端有()个。
A. 1
B. 2
C. 3
D. 8
?
正确答案:D
15.存储8位二进制信息要()个触发器。
A. 2
B. 3
C. 4
D. 8
?
正确答案:D
二,判断题
1. A.错误
B.正确
?
正确答案:A
2. A.错误
B.正确
?
正确答案:A
3.因为逻辑表达式A+B+AB=A+B成立,所以AB=0成立。()
A.主从JKF/F
B.主从DF/F
C.同步RSF/F
D.边沿DF/F
?
正确答案:C
10. A. A
B. B
C. C
D. D
?
数字电路与逻辑设计习题及参考答案

数字电路与逻辑设计习题及参考答案一、选择题1.以下表达式中符合逻辑运算法则的是D。
A.C·C=C2B.1+1=10C.0<1D.A+1=12.一位十六进制数可以用C位二进制数来表示。
A.1B.2C.4D.163.当逻辑函数有n个变量时,共有D个变量取值组合?A.nB.2nC.n2D.2n4.逻辑函数的表示方法中具有唯一性的是A。
A.真值表B.表达式C.逻辑图D.状态图5.在一个8位的存储单元中,能够存储的最大无符号整数是D。
A.(256)10B.(127)10C.(128)10D.(255)106.逻辑函数F=B A A⊕⊕)(=A。
A.BB.AC.B A⊕D.B A⊕7.求一个逻辑函数F的对偶式,不可将F中的B。
A.“·”换成“+”,“+”换成“·”B.原变量换成反变量,反变量换成原变量C.变量不变D.常数中“0”换成“1”,“1”换成“0”8.A+BC=C。
A.A+B B.A+C C.(A+B)(A+C) D.B+C9.在何种输入情况下,“与非”运算的结果是逻辑0。
D A.全部输入是0B.任一输入是0C.仅一输入是0D.全部输入是110.在何种输入情况下,“或非”运算的结果是逻辑1。
A A.全部输入是0 B.全部输入是1 C.任一输入为0,其他输入为1 D.任一输入为111.十进制数25用8421BCD码表示为B。
A.10101B.00100101C.100101D.1010112.不与十进制数(53.5)10等值的数或代码为C。
A.(01010011.0101)8421BCDB.(35.8)16C.(110101.11)2D.(65.4)813.以下参数不是矩形脉冲信号的参数D。
A.周期B.占空比C.脉宽D.扫描期14.与八进制数(47.3)8等值的数为:BA.(100111.0101)2B.(27.6)16C.(27.3)16D.(100111.101)215.常用的BCD码有D。
《数字电路逻辑设计》--逻辑函数及其化简练习题

《数字电路逻辑设计》练习题------ 逻辑函数及其化简一.用公式证明下列各等式。
1. AB AC (B C)D AB AC D 原式左边二AB AC BD CD=AB AC+BC+BCD=AB AC+D=右边2. A C A B A C D+BC A BC 原式左边A C(1+D)+A B+BC=A C + A B+BC=(C+B+BC =AB C+BC=A+BC=右边3. BCD BCD ACD+ABC D+A BCD +BC D+BCD BC BC+BD原式左边=BCD+A BCD BCD+BCD+ABC D+BC D+ACD=BCD+A BCD+BD+BC D+ACD=BCD+ACD+B CD+BD+B^ D=BCD+ACD+BD+DC+B^ D=BCD+BD+DC+B C D=C(D+B)+ B( D+C)=BC+BD+BC=右边2. F=AB+AB+BC=m (2,3,4,5,7)F m(0,1,6)F*= m(1,6,7)3. F=AB+C BD+A D B C=m(1,5,6,7,8,9,13,14,15 )F m(0,2,3,4,10,1,2 )F*= m(3 ,4,5,11,12,3,5)三.用公式法化简下列各式1. F=ABC+A CD+AC=A(BC+C)+A CD=AC AB A CD =C(A AD) A B=A C+C D+AET2. F=A C D+BC+BD+A B+AC+^ C =AC D+BC+BD+A B+AC+BC+^ C =ACD+BC+AC+B=AD+C+B3. F=(A+B)(A+B+C)(A+C)(B+C+D)Q F*= AB+ABC+AC+BCD=AB+AC+BCD=AB+ACF=(F*)*=(A+B)(A+C)=AC+AB —4. AB B+D CD+BC+A BD+A+CD=1原式左边=AB B+D C D BC+A BD A+C+D =(AB+ B+D+C D)(B+C)+C+D=(B+D)(B+C)+C+D =BC+BD+CD+C+D=1=右边二.写出下列各逻辑函数的最小项表达式及其对偶式、反演式的最小项表达式1. F=ABCD+ACD+BD= m( 4,6,11,12,14,15 )F m(0,1,2,3,5,7,8,9,10,13)F*= m(2,5,6,7,8,10,12,13,14,15) 4. F=AB+A B?BC+B CF AB+A B BC+B CAB+A B BC+B C ACAB BC B C AC AB B C5. F=AC+BC B(AC AC)F (A C)(B C) ABC ABCAB A C BC C ABC ABCAB C (A B)C AC BC四.用图解法化简下列各函数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3-1 分析题图3-1所示电路,写出电路输出Y 1和Y 2的逻辑函数表达式,列出真值表,说明它的逻辑功能。
解:由题图3-1从输入信号出发,写出输出Y 1和Y 2的逻辑函数表达式为1Y A B C =⊕⊕ ; 2()()Y A B C AB A B C A =⊕⋅⋅=⊕⋅+B将上式中的A 、 B 、C 取值000~111,分别求出Y 1和Y 2,可得出真值表如题解 表3-1所示。
题解 表3-1ABCA B ⊕()A B C ⊕⋅AB1Y2Y0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 1 0 1 0 0 1 0 0 1 1 1 1 0 0 1 1 0 0 1 0 0 1 0 1 0 1 1 1 0 0 1 1 1 0 0 0 1 0 1 111111综上,由题解 表3-1可以看出,该电路实现了一位全加器的功能。
其中,A 和B 分别是被加数及加数,C 为相邻低位来的进位数;Y1为本位和数,Y 2为相邻高位的进位数。
3-2 分析题图3-2所示电路,要求:写出输出逻辑函数表达式,列出真值表,画出卡诺图,并总结电路功能。
解:由题图3-2从输入信号出发,写出输出F 的逻辑函数表达式为()()F A B C D =:::将上式中的A 、 B 、C 、D 取值0000~1111,求出F ,可得真值表和卡诺图分别如题解 表3-2和题解 图3-1所示。
题解 表3-2A B C DA B : C D :F0 0 0 0 1 1 1 0 0 0 1 1 0 0 0 0 1 0 1 0 0 0 0 1 1 1 1 1 0 1 0 0 0 1 0 0 1 0 1 0 0 1 0 1 1 0 0 0 1 0 1 1 1 0 1 0 1 0 0 0 0 1 0 1 0 0 1 0 0 11 0 1 0 0 0 1 1 0 1 1 0 1 0 1 1 0 0 1 1 1 1 1 0 1 1 0 0 1 1 1 0 1 0 0 1 1 1 1 1 1 1综上,由题解 表3-2可以看出,当输入A 、 B 、C 、D 中含有偶数个“1”时,输出;否则,当输入A 、 B 、C 、D 中含有奇数个“1”时,输出。
1F =0F =3-3 分析题图3-3所示电路,要求:写出X 、Y 、Z 的逻辑表达式,列出真值表,并总结电路功能。
解:由题图3-3从输入信号出发,写出输出X 、 Y 、Z 的逻辑函数表达式为X AB = ; Y AB AB =+ ; Z AB =将上式中的A 、 B 取值00~11,分别求出X 、 Y 、Z ,可得真值表如题解 表3-3所示。
题解 表3-3AB 0 0 0 0 0 1 0 0 1 1 0 1 0 01 1 0 0 0 1 0 综上,由题解 表3-3可以看出,该电路实现了一位数值比较器的功能:当A B <时,输出1X =;当A B =时,输出1Y =;当A B >时,输出1Z =。
3-4 题图3-4 所示是某同学设计的代码转换电路。
当控制信号1K =时,可将输入的3位二进制码转换成循环码;0K =时能把输入的3位循环码转换成二进制码。
代码转换表见题表3-1。
试检查电路有无错误,若有错,请改正之。
题表3-1二进制码循环码B 2B 1B 0G 2G 1G 00 0 0 0 0 00 0 1 0 0 1 0 1 0 0 1 1 0 1 1 0 1 0 1 0 0 1 1 0 1 0 1 1 1 1 1 1 0 1 0 1 1 1 1 1 0 0解:由题图3-4从输入信号出发,写出输出Y 2、Y 1、Y 0的逻辑函数表达式为2Y X =22 ; ; 11Y X X =⊕()0112()Y KX K X X X =+⊕:0将K 、2X 、1X 、0X 取不同值,求出,填入真值表题解 表3-4中。
210Y YY 题解 表3-4由题解 表3-4可以看出,题图3-4所示电路在1K =时,可将输入的3位二进制码转换成循环码;但是,在0K =时并不能把输入的3位循环码转换成二进制码。
综上,若要电路实现预期功能,其真值表如表题解 3-5所示。
题解 表3-5K2X 1X 0X 2Y 1Y 0Y0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 1 1 0 1 0 0 0 1 0 0 1 1 0 1 1 0 1 0 0 0 1 1 1 1 0 1 0 1 0 1 1 1 0 0 1 0 0 1 1 1 1 0 0 0 0 0 0 1 0 0 1 0 0 1 1 0 1 0 0 1 1 1 0 1 1 0 1 0 1 1 0 0 1 1 0 1 1 0 1 1 1 1 1 1 1 0 1 0 1 1 1 1 1 1 0 0 由题解 表3-5可以写出输出Y 2、Y 1、Y 0的逻辑函数表达式分别如下22Y X =1210210210212102102102102121212112()()()()Y K X X X X X X X X X X X X 0K X X X X X X X X X X X X K X X X X K X X X X X X =+++++++=+++=⊕()()()0210210210210210210210210210210210210210101120()()()()()()Y K X X X X X X X X X X X X K X X X X X X X X X X X X K X X X X X X K X X X X X X K X X X K X X KX K X X X =+++++++⎡⎤⎡⎤=⊕++⊕+⊕⎣⎦⎣⎦=⊕⊕+⊕⎡⎤+⊕⊕⎣⎦:=根据输出Y 2、Y 1、Y 0的逻辑函数表达式,可以画出修正后的电路图如题图 解3-2所示。
3-5 用与非门设计下列函数,允许反变量输入。
(1)(,,,)(1,2,3,7,8,11)(0,9,10,12,13)md F A B C D =+∑∑ (2)(,,,)(0,2,4,5,9,10,13,14)MF A B C D =∏(3)(,,)F A B C AB ACD A C BC =+++解(1) 将填入卡诺图,并对“1”格圈圈合并,如题解 图3-3所示,得到最简与-或式为F (,,,)F A B C D B A CD =+两次取反(,,,)F A B C D B A CD B A CD B A CD =+=+=⋅用与非门实现的逻辑电路图如题解 图3-4所示。
解(2) 将填入卡诺图,并对“1”格圈圈合并,如题解 图3-5所示,得到最简与-或式为F(,,,)F A B C D CD ABD ABC ACD=+++两次取反(,,,)F A B C D CD ABD ABC ACD CD ABD ABC ACD=+++=⋅⋅⋅用与非门实现的逻辑电路图如题解 图3-6所示。
CD&解(3) 将填入卡诺图,并对“1”格圈圈合并,如题解 图3-7所示,得到最简与-或式为F(,,,)F A B C D C AB AD=++两次取反F A B C D C AB AD C AB AD=++=⋅⋅(,,,)用与非门实现的逻辑电路图如题解 图3-8所示。
3-6 用与非门设计能实现下列功能的组合电路。
(1)三变量表决电路——输出与多数变量的状态一致;(2)四变量判奇电路——4个变量中有奇数个1时输出为1,否则输出为0;(3)运算电路——当K=1时,实现一位全加器功能;当K=0时,实现一位全减器功能。
解(1):据题意,3个输入A、B、C在不同取值组合下的输出F被列在题解表3-6中。
题解 表3-6A B C F0 0 0 00 0 1 00 1 0 00 1 1 11 0 0 01 0 1 11 1 0 11 1 1 1由题解 表3-6可以得出输出F的逻辑函数表达式为=+++(,,)F A B C ABC ABC ABC ABC利用题解 图3-9所示卡诺图,得到输出F的最简与-或表达式,并两次取反变换成与非-与非表达式为=++=⋅⋅(,,)F A B C AB BC AC AB BC AC根据表达式,画出逻辑图如题解 图3-10所示。
解(2):据题意3个输入A、B、C、D在不同取值组合下的输出F被列在题解表3-7中。
题解表3-7A B C D F0 0 0 0 00 0 0 1 10 0 1 0 10 0 1 1 00 1 0 0 10 1 0 1 00 1 1 0 00 1 1 1 11 0 0 0 11 0 0 1 01 0 1 0 01 0 1 1 11 1 0 0 01 1 0 1 11 1 1 0 11 1 1 1 0利用题解 图3-11所示卡诺图,得到输出F的最简与-或表达式,并两次取反变换成与非-与非表达式为(,,,)F A B C D ABCD ABCD ABCD ABCD ABCD ABCD ABCD ABCDABCD ABCD ABCD ABCD ABCD ABCDABCD ABCD=+++++++=⋅⋅⋅⋅⋅⋅⋅根据表达式,画出逻辑图如题解 图3-12所示。
解(3):据题意4个输入K 、A 、B 、C 在不同取值组合下的输出F 和Y 被列在题解 表3-8中。
题解 表3-8K A B C F Y0 0 0 0 0 0 0 0 0 1 1 1 0 0 1 0 1 1 0 0 1 1 0 1 0 1 0 0 1 0 0 1 0 1 0 0 0 1 1 0 0 0 0 1 1 1 1 1 1 0 0 0 0 0 1 0 0 1 1 0 1 0 1 0 1 0 1 0 1 1 0 1 1 1 0 0 1 0 1 1 0 1 0 1 1 1 1 0 0 1 11111 1利用题解 图3-13所示卡诺图,得到输出F 和Y 的最简与-或表达式,并两次取反变换成与非-与非表达式为(,,,)F K A B C ABC ABC ABC ABCABC ABC ABC ABC=+++=⋅⋅⋅(,,,)Y K A B C BC K AC KAB K AB KACBC K A C KAB K AB KAC=++++=⋅⋅⋅⋅根据表达式,画出逻辑图如题解 图3-14所示。
3-7 用或非门设计下列函数,允许反变量输入。
(1)(,,,)(4,5,6,7,12,13)(8,9)md F A B C D =+∑∑(2)(,,,)(1,3,4,6,9,11,12,14)MF A B C D =∏(3)(,,,)()()() F W X Y Z W X Y Z W X Y Z W Y Z =++++++++()()W X Y Z W X Y Z ++++++解(1):将填入卡诺图,并对“0”格圈圈合并,如题解 图3-15所示,得到最简或-与式,并两次取反变换成或非-或非表达式为F (,,,)()F A B C D B A C B A C =+=++用或非门实现的逻辑电路图如题解 图3-16所示。
