初一数学提优训练101120

合集下载

七年级提优测试卷数学答案

一、选择题（每题3分，共30分）1. 下列数中，不是有理数的是（）A. 2.5B. -1/3C. √2D. 0答案：C解析：有理数包括整数和分数，而√2是一个无理数，不属于有理数。

2. 下列图形中，不是轴对称图形的是（）A. 正方形B. 等腰三角形C. 长方形D. 梯形答案：D解析：轴对称图形是指存在一条直线，使得图形关于这条直线对称。

梯形没有这样的对称轴。

3. 下列代数式中，合并同类项后结果是2x的是（）A. x + 2x + 3B. 3x - 4x + 5C. 2x - 3x + 4D. 5x - 2x + 1答案：B解析：合并同类项是将代数式中相同字母的项合并在一起。

在选项B中，合并同类项后得到 -1x，即 -x，与2x不符。

4. 下列方程中，解为x=2的是（）A. 2x - 4 = 0B. 2x + 4 = 0C. 2x - 6 = 0D. 2x + 6 = 0答案：A解析：将x=2代入选项A中的方程，得到22 - 4 = 0，等式成立。

5. 下列函数中，是反比例函数的是（）A. y = 2x + 3B. y = 3/xC. y = x^2D. y = 2x^3答案：B解析：反比例函数的形式是y = k/x（k为常数，且k≠0）。

在选项B中，函数形式符合反比例函数的定义。

二、填空题（每题5分，共25分）6. （3分）若a = -2，b = 5，则a + b = ________。

答案：3解析：将a和b的值代入a + b，得到-2 + 5 = 3。

7. （3分）若x^2 - 5x + 6 = 0，则x的值为_______。

答案：2或3解析：这是一个一元二次方程，可以通过因式分解或使用求根公式求解。

因式分解得到(x - 2)(x - 3) = 0，所以x的值为2或3。

8. （3分）若∠A = 45°，∠B = 90°，则∠C = _______。

答案：45°解析：在直角三角形中，两个锐角的和为90°，所以∠C也是45°。

2020-2021学年人教版七年级数学下册第10章《数据的收集、整理与描述》提优测试卷

人教版七年级数学下册第10章《数据的收集、整理与描述》提优测试卷题号一二三总分得分(时间:90分钟满分:120分)一、选择题(本大题共8小题,每小题3分,24分在每小题的4个选项中,只有一个选项是符合题目要求的)1.(2020云南昆明期末,1)下列调查中,调查方式选择合理的是( )A.为了了解某一品牌家具的甲醛含量,选择全面调查B.为了了解我市七年级学生的身高情况,选择抽样调查C.为了检测乘坐飞机的旅客是否携带违禁物品,选择抽样调查D.为了了解一批袋装食品是否含有防腐剂,选择全面调查2.(2020安徽铜陵期末,3)2020年5月20日,随着第一批考生经体温检测等流程后进入考点,铜陵市2020年初中学业水平体育考试正式拉开序幕据了解,铜陵市共有.7万名考生报名参加体育考试,为了了解考生体育成绩,从中抽取2000名考生的体育成绩进行统计,在这个问题中样本是( )A.1.7万名考生B.抽取的2000名考生C.1.7万名考生的体育成绩D.抽取的2000名考生的体育成绩3.(2019四川南充中考,4)在2019年南充市初中毕业升学体育与健康考试中,某校九年级(1)班体育委员对本班50名同学参加球类自选项目的情况做了统计,制作出扇形统计图(如图所示),则该班选考乒乓球的人比选考羽毛球的人多( )A.5人B.10人C.15人D.20人4.(2020陕西延安实验中学期末,6)为了了解某校七年级800名学生的跳绳情况(60秒跳绳的次数),随机对该年级50名学生进行了调查.根据收集的数据绘制了如图所示的频数分布直方图(每组数据包括左端值不包括右端值,如最左边第一组的次数x为60≤x<80),则以下说法正确的是( )A.最多的跳绳次数是160B.大多数学生跳绳次数在140～160范围内C.跳绳次数不少于100的占80%D.由样本可以估计全年级800人中跳绳次数在60～80范围内的有70人5.(2020北京丰台期末,6)小明统计了同学们5月份平均每天观看北京市“空中课堂”的时间,并绘制了统计图,如图所示(每组数据不包括左端值和右端值).下面有四个推断:①此次调查中,小明一共调查了100名学生；②此次调查中,平均每天观看时间不足30分钟的人数占调查总人数的10%；③此次调查中,平均每天观看时间超过60分钟的人数超过调查总人数的一半；④此次调查中,平均每天观看时间不足60分钟的人数少于平均每天观看时间在60～90分钟范围内的人数所有合理推断的序号是( )A.①②B.①④C.③④D.②③④6.(2020北京海淀期末,5)某调查机构对某地互联网行业从业情况进行调查统计,得到当地互联网行业从业人员年龄分布统计图和当地90后从事互联网行业岗位分布统计图对于以下四种说法,你认为正确的是( )①在当地互联网行业从业人员中,90后人数占总人数的一半以上②在当地互联网行业从业人员中,80前人数占总人数的13③在当地互联网行业中,从事技术岗位的90后人数超过总人数的20%；④在当地互联网行业中,从事设计岗位的90后人数比从事互联网行业的80前的总人数少A.①③B.②④C.①②D.③④7.(2020浙江嘉兴期末,8)5G移动通信网络将推动我国数字经济发展迈上新台阶,据预测,2020年到2025年中国直接经济产出和间接经济产出的情况如图所示,根据图中提供的信息,下列推断不正确的是( )A.2020年到2025年,5G间接经济产出和直接经济产出都呈增长趋势B.2020年到2022年,5G间接经济产出和直接经济产出共10.7万亿元C.2023年到2024年,5G间接经济产出和直接经济产出的增长率相同D.2020年到2025年,5G间接经济产出总量比直接经济产出总量多3万亿元8.(2018云南中考,13)2017年12月8日,2017带一路数字科技文化节·玉溪暨第10届全国三维数字化创新设计大赛总决赛在玉溪圆满闭幕某校为了解学生对这次大赛的了解程度,在全校1300名学生中随机抽取部分学生进行了一次问卷调查,并根据收集到的信息进行了统计,绘制了如图所示的两幅统计图下列四个选项中,说法错误的是( )A.抽取的学生人数为50B.“非常了解”的人数占抽取的学生人数的12%C.a＝72°D.估计全校“不了解”的人数为428二、填空题(本大题共8小题,每小题4分,共32分)9.(2020安徽马鞍山期末,9)下列调查:①调查人们在使用某款手机过程中容易出现的问题；②调查某县中学生对“D&”事件的看法；③调查某班学生的视力情况；④调乘坐飞机的旅客是否携带了违禁物品,其中,适宜采用抽样调查方式的有________10.(2020湖南株洲中考,14)王老师对本班40个学生所穿校服尺码的数据统计如下:则该班学生所穿校服尺码为“L”的人数为________11.(2019山东德州模拟,10)A班学生参加“垃圾分类知识竞赛,已知竞赛得分都是整数,竞赛成绩的频数分布直方图如图所示,那么成绩高于60分的学生占A班参赛人数的百分比为________12.(2019上海中考,14)小明为了解所在小区居民各类生活垃圾的投放情况,随机调查了该小区50户家庭某一天各类生活垃圾的投放量,统计得出这50户家庭各类生活垃圾的投放总量是100千克,并作出各类生活垃圾投放量分布情况的扇形统计图(如图所示),根据以上信息,估计该小区300户居民这一天投放的可回收垃圾共________13.(2018湖南邵阳中考,15)某市对九年级学生进行综合素质评价,评价结果分为A、B、C、D、E五个等级现随机抽取了500名学生的评价结果作为样本进行分析,绘制了如图所示的统计图已知图中从左到右的五个长方形的高之比为2:3:3:1:1,据此估算该市80000名九年级学生中综合素质评价结果为“A”的学生有________人14.(2019浙江宁波效实中学月考,13)某城市为了了解本市男、女青少年平均身高发育情况,随机调查了6岁18岁的男、女青少年各100人,制作成如图所示的不同年龄平均身高统计图,从图中可知,该城市的男性青少年的身高高于同年龄女性青少年的身高的年龄段大概是________15.(2020湖北十堰中考,13)某校即将举行30周年校庆,拟定了A,B,C,D四种活动方案,为了解学生对方案的意见,学校随机抽取了部分学生进行问卷调查(每人只能赞成一种方案),将调查结果进行统计并绘制成如图所示的两幅不完整的统计图.若该校有学生3000人,请根据以上统计结果估计该校学生赞成方案B的人数为________16.(2019云南中考,5)某中学九年级甲、乙两个班参加了一次数学考试,每班的考试人数都为40,每个班的考试成绩分为A、B、C、D、E五个等级,绘制的统计图如图所示:根据以上统计图提供的信息,D等级这一组人数较多的班是________三、解答题(本大题共7小题,共64分)17.(2020浙江金华中考,19)(6分)某市在开展线上教学活动期间,为更好地组织初中学生居家体育锻炼,随机抽取了部分初中学生对“最喜爱的体育锻炼项目进行线上问卷调查(每人必须只选其中一项),得到不完整的统计表和如图所示不完整的统计图.请根据图表信息回答下列问题:(1)求参与问卷调查的学生总人数；(2)在参与问卷调查的学生中,最喜爱“开合跳”的学生有多少人？(3)该市共有初中学生约8000人,估算该市初中学生中最喜爱“健身操”的人数18.(2020河北石家庄一模,19)(6分)“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和如图所示的部分频数分布直方图:请结合图表完成下列各题:(1)表中a的值为________；(2)将频数分布直方图补充完整；(3)若测试成绩不低于80分为优秀,则本次测试的优秀率是多少？19.(2020山东聊城中考,19)(9分)为了提高学生的综合素养,某校开设了五门手工活动课,按照类别分为A“剪纸”、B“沙画”、C“葫芦雕刻”、D“泥塑”、E“插花”为了了解学生对每种活动课的喜爱情况,随机抽取了部分同学进行调查,将调查结果绘制成如图所示的两幅不完整的统计图根据以上信息,回答下列问题:(1)本次调查的样本容量为________,统计图中的a＝________, b＝________。

七年级数学提优试卷

实验中学七年级数学学习检测题一、填空题：姓名1、如图：∠1的同位角有个，∠ABC 的同旁内角有个，∠EBC 的内错角有个。

2、如图：要使AD ∥BC ，只需再有（添加一个条件即可）。

3、如图：AB ∥CD ，且AE ⊥CE ，则∠A ＋∠C ＝ °。

4、如图：在ΔABC 中，OB 、OC 分别平分∠ABC 与∠ACB ，且∠A ＝40°，则∠BOC ＝ °。

5、如图：AD 、AE 分别是ΔABC 的角平分线和高，∠B ＝50°，∠C ＝70°，则∠BAD ＝，∠EAD ＝。

6、如图：ΔABC 是等边三角形，∠1＝20°，求∠E ＝。

7、等腰三角形的一边长是4cm ，另一边长是8cm ，则等腰三角形的周长为。

8、如果：6,10,m n a a ==则2m n a-= 。

9、如果：()15102b a b a mn =，求：222m mn n -+= 。

10、如果：24n x =，则：6n x = 。

二、选择题：11、下面说法正确的是----------------------------------------------------------------------------( )A 、()[]532a a -=- B 、()[]632a a -=- C 、()[]832a a -=- D 、()[]1535a a -=- 12、若：3m a =，28n =，则：()m n a =----------------------------------------------------( )A 、9B 、24C 、27D 、1113、若n 为正整数，计算：212(2)2(2)n n +-+⋅-的结果为--------------------------------( ) A 、212n + B 、212n +- C 、－1 D 、014、下列说法正确的是----------------------------------------------------------------------------( )A 、0(2)1x -=B 、()()22111-=--x x C 、13636-= D 、24(2)-=± 15、下列说法正确的是----------------------------------------------------------------------------( ) A 、332223-<- B 、332223> C 、332223< D 、01(3.14)1π-->16、一种花粉的直径约为450nm ，则这种花粉的直径用科学记数法表示为----------( )A 、945010-⨯mB 、74.510-⨯mC 、74.510-⨯mD 、114.510-⨯m17、如图所示：将等边三角形ABC 剪去一个角后，∠1＋∠2＝------------------------( )A 、120°B 、240°C 、300°D 、360°18、在三角形纸片ABC 中，∠A ＝65°，∠B ＝75°，将纸片的一角折叠，使点C落在ΔABC 内，则∠1＝20°，则∠2＝-------------------------------------------------- ( )A 、 60°B 、80°C 、20°D 、40°19、一个多边形的外角和与它的内角和的总和为2700°，则此多边形是--------------( )A 、13B 、9C 、15D 、1120、如图所示：图⑴互不重叠的三角形共4个，图⑵互不重叠的三角形共7个，图⑶互不重叠的三角形共10个………，则在第n 个图形中，互不重叠的三角形共-----------------------------------------------------------------------------------------( )A 、n 3个B 、()13+n 个C 、()13-n 个D 、()13+n 个三、计算题：21、①、÷-⨯3-20-111（-2）（-2）（-）（-）28 ②、82434()(2)m m m ÷⨯---43（-2m ）③、543()()()2x y x y y x --⋅-÷ ④、()()524232)(a a a -÷⋅⑤、（3）()123041323--⎪⎭⎫ ⎝⎛--+- ⑥、()a b -()3a b -()5b a -⑦、333)31()32()9(⨯-⨯- ⑧、3014225.0⨯-22、如果922)2(162=⋅n ，解关于x 的方程24=+nx 。

苏科版数学七年级上提优练习与答案(余角、补角、对顶角))

苏科版数学七年级上提优练习内容：余角、补角、对顶角1．(2020独家原创试题)如图6—3—1，A，0，B在一条直线上，∠1=∠2，∠3=∠4，则图中互余的角共有( )A．5对 B．4对 C．3对 D．2对2．如果∠α和互∠β补，且∠α＜∠β [0／<，下列式子：①900一∠α②∠β—900；③21(∠α+∠β)；④21(∠β -∠α )．中是∠α的余角的有 ( )A．1个 B．2个 C．3个 D．4个3．∠1和∠2互余，∠2和∠3互补，如果∠l=630．那么∠3= ．4．已知一个角韵补角比这个角的4倍大l5。

，求这个角的余角．5．(2020独家原创试题)如罔6—3—2，直线a，b相交与点0．因为∠l+∠2=1800，∠3+2∠=1800，所以∠1=∠3，这是根据 ( )A．同角的余角相等 B．等角的余角相等 c．同角的补角相等D．等角的补角相等6．如图6—3—3所示，点0在直线AB上，且∠AOC=∠BOC=900．∠EOF=900，试判断∠AOE，∠COE与∠BOF的关系．7．∠l与∠2是对顶角的是 ( )8．如图6—3—4，直线AB、CD相交于点0，∠AOC=67.50．OE把∠BOD分成两个角，且∠DOE:∠BOE=1:2．(1)求∠DOE的度数；(2)若OF平分A∠OE，试说明OA平分∠COF．9．(2020江苏南京江宁期未，15，★☆☆)如图6—3—5，∠AOB与∠AOC互余，∠AOD与∠AOC互补，OC平分∠BOD，则∠AOB的度数是 ( )10．(2019江苏泰州l姜堰期末，6，★☆☆)如图6—3—6所示，直线AB与CD相交于点0，0B平分∠DOE，若∠DOE=600．则∠AOE的度数是 ( )11．(2020江苏苏州I相城期末，10，★☆☆)大雁迁徙时常排成人字形．这个人字形的一边与其飞行方向夹角是54044/8//，从空气动力学角度看，这个角度对于大雁伍飞行最佳，所受阻力最小．54044/8//的补角是________________.12．(2019江苏徐州l云龙期末，15，★★☆)两条直线相交所成的四个角中，有两个角分别是(2x一l0)0和(110一x)0，则x=__________.13．(2019广东广州培正中学期未，23，★☆☆)如图6—3—7所示．直线AB与DF相交于点0，OC平分∠AOD，OE在∠BOD内，且∠DOE=∠AOD，∠COE=780．(1)求∠EOB的度数；(2)写出∠DOE的所有补角．14．(2018广西贺州中考，2，★☆☆)如图6-3-8，下列各组角中．互为对顶角的是( )15．(2017广东中考．3．★☆☆)已知∠A=700，则∠A的补角为 ( )A．1100 B．700 C．300 D．20016．(2019江苏常州中考，12，★☆☆)如果∠a=350，那么∠a的余角等于___________。

2020-2021学年苏科版数学七年级下学期计算专项练习提优

苏科版数学七年级下学期——计算专项练习提优一、计算(1) 20－2－2+(－2)2 (2) (－2a 3)2+(a 2)3－2a ·a 5 (3)（4）2(a 2)3－a 2·a 4＋(2a 4)2÷a 2 （5）2010201020)4()41()21()32(-⨯+---（6） 22710234)2()(2a a a a a ÷-+- （7）12011125.0221032-++⨯-⎪⎭⎫ ⎝⎛-（8）（3a 2）2﹣a 2•2a 2+（﹣2a 3）2+a 2．） (9) (－2a 3)2·3a 3＋6a 12÷(－2a 3)．(10) (x ＋y ＋3)(x ＋y －3). （11）(x －2y +4)(x +2y －4)(12) (3x +1)2－(3x －1)2 (13)(3x ＋2)(3x ＋1)－(3x ＋1)2. （14）()212--x （15）)2)(2(---x x （16）)2)(2(b a b a -+（17）))((22y x y x +- （18）()()b a b a 54+- （19）()()221212--+x x（20）()232y x +- （21）()22832y y x +-（22）()()()2b a b a b a +--+ （23）()()2233y y --+（24）)23)(32(m n n m --- （25）(2a+3b)(3b-2a) （26）()()2255+-t t （27）)2()2(a b b a -⋅--（28）()2223n m- （29）()()()y x x y y x -+--33322（30）)23)(32(22a b b a ++- （31）()()()()2212222-++---x x x x（32）)1)(1)(1(2++-x xx （33）)23)(23()59(+---x x x x（34）(a －2b ＋3)(a ＋2b －3) （35）()()()222223x x x x --+-+二、因式分解：(1)（x－y)－2b(y－x) (2) 2x(m－n)－(n－m) (3) 2x2+12xy+18y2 （4）2x2﹣8．（5）ax3－9ax；(6) x4－16(7)4224168x x y y-+(8)(x2＋x)2－(x＋1)2(9) (x2+y2)2－4x2y2（10）x2＋2x(x－3y)＋(x－3y)2 (11) (y＋2)(y＋4)＋1（12）4x2＋9y2－12xy（13）x3－2x2y＋5xy2（14）8mn2＋4m2n （15）(x－y)2－2(x－y) （16）x2－9y2（17）a2＋6ab＋9b2 （18）x4－16 （19）x3－2x2＋x （20）(3m－2n)2－(m＋3n)2（21）4m2－(m－3n)2 （22）4x2－4x(x－y)＋(x－y)2 （23）2a2－18（24）(3x－2y)2－(2x－3y)2 （25）(x2＋4)2－16x2 （26）4x(x－y)2＋3(y－x)3（27）a 2－12ab ＋36b 2 （28）25x 2＋10xy ＋y 2（29）－3＋6a －3a 2 （30）16a 4＋24a 2b 2＋9b 4（31）(x －y )2－10(x －y )＋25 （32）(x 2－1)2－6(x 2－1)＋9（33）(x 2＋y 2)2－4x 2 y 2 （36）－x 2＋8xy －16y 2 （37）(a 2＋4)2－16a 2（38）1－2x 2＋x 4 （39）2x 2－4x ＋2 （40）32244y y x xy --（41）1)2(2)2(222++++x x x x （42）2)(9)(124y x y x -+--（43）12a 3b 2－9a 2b ＋3ab 2 （44）mn mn n m 1892722-+-（45）222249147y x xy y x +-- （46）()()22916n m n m +--（47）35a a - （48）4416y x +-（49）a 2(x －y )－4b 2(x －y) （50）4(a +b )2－9(a －b )2三、化简求值（1）(x －2)2+2(x +2)( x －4)－(x －3)(x + 3)：其中x =－1．（2） (1)(2)3(3)2(2)(1)x x x x x x ---+++-，其中31=x(3) ()()()()21121x x x x x +-+-+- ，其中12x =-(4)(2a ＋b )2－(3a －b )2＋5a (a －b )，其中11,105a b ==（5）(a －b )2－2a (a ＋3b )＋(a ＋2b )(a －2b )，其中a ＝1，b ＝－3．（6）已知1ab =- ，求()()3222342a b a b a b -+⋅- 的值(7)已知与互为相反数，求的值(8)已知 1,3-==+xy y x ，求下列各式的值:1122=+y x ）（ 22-2y xy x +）（三、解方程组：(1) ⎩⎨⎧=+-=165383y x yx (2)⎩⎨⎧=+=-625143y x y x（3）⎩⎨⎧=-=+115332y x y x （4）⎩⎨⎧+=-+=-)5(3)1(55)1(3x y y x(5) ⎩⎨⎧=-+=-14)(423y x y y x (6) ⎩⎪⎨⎪⎧x ＋3y ＝0，x 3－y －12＝1；（7）⎪⎩⎪⎨⎧=--=+-132324)3(3y x y y x （8）⎪⎩⎪⎨⎧=+=+=++1323432z y z x z y x()2165x y --2x y ++22x y -（9）若方程组⎩⎨⎧=++=+ky x k y x 32253的解满足x+y =－2，求k 的值．（10）已知关于x 、y 的方程组⎩⎪⎨⎪⎧3x ＋4y ＝k ＋2，2x ＋5y ＝2k －1的解满足x －y ＝－1，求k 的值．（11）若关于x 、y 的方程组⎩⎪⎨⎪⎧2x ＋y ＝a －3，x －y ＝2a 的解满足x ＋3y ＜0，试求字母a 的取值范围．（12）已知关于x 、y 的方程组⎩⎪⎨⎪⎧x ＋y ＝m ＋2，4x ＋5y ＝6m –3的解是一对正数，求m 的取值范围．四、解一元一次不等式（组）（1）解不等式组：⎪⎩⎪⎨⎧->+-≥+13112x x x ，并把它的解集在数轴上表示出来.(2)解不等式组：35611 32x xx x-≤+⎧⎪⎨-<-⎪⎩，并将解集在数轴上表示出来．(3)312126+-<+xx; (4) ,⎪⎩⎪⎨⎧-≤-+<-2142151(3xxxx）并写出其最大整数解.（5）解不等式组⎩⎨⎧-≤--<-51)2(325xxxx（6）解不等式组⎪⎩⎪⎨⎧≥->+-+231223312xxx(7)求解不等式组⎪⎩⎪⎨⎧≥+->+13213)1(2xxx（8）解不等式组⎪⎩⎪⎨⎧-<--≤+-xxxx8)1(31323（9）解不等式组()112241xx x-⎧≤⎪⎨⎪-<+⎩，并写出不等式组的正整数解．（10）解不等式组⎪⎩⎪⎨⎧+-≥>+2321xxx。

提优测试卷七年级数学

一、选择题（每题4分，共20分）1. 下列数中，不是有理数的是（）A. 3.14B. 0C. √2D. -1/32. 已知x的平方等于4，则x的值为（）A. ±2B. ±4C. ±1D. ±33. 如果一个长方形的长是10cm，宽是5cm，那么它的面积是（）A. 50cm²B. 100cm²C. 25cm²D. 15cm²4. 下列图形中，属于轴对称图形的是（）A. 三角形B. 长方形C. 正方形D. 梯形5. 已知一个数的相反数是-5，那么这个数是（）A. 5B. -5C. 0D. 10二、填空题（每题4分，共20分）6. -2的相反数是______。

7. 0.25的分数表示是______。

8. 如果一个等腰三角形的底边长是6cm，那么它的腰长是______cm。

9. 圆的半径是r，那么它的直径是______。

10. 一个数是-3的5倍，这个数是______。

三、解答题（每题10分，共30分）11. 计算下列各题：（1）(3/4) × (2/3) + (1/2) × (3/4)（2）-5 + 3 - (-2)（3）(-1/3) × (-2/3) × (-3/4)12. 解下列方程：（1）2x - 5 = 3（2）3(x + 2) = 9（3）(2/3)x - 1 = 1/213. 一个等腰三角形的底边长是10cm，腰长是15cm，求这个三角形的周长。

四、应用题（每题10分，共20分）14. 小明去商店买文具，他带的钱可以买3支铅笔和2支钢笔，或者买4支铅笔和1支钢笔。

如果铅笔每支2元，钢笔每支3元，小明最多可以买多少支铅笔？15. 小华有一个正方形的花园，花园的边长是20米。

他在花园的一角建了一个小亭子，亭子到花园四边的距离相等。

求亭子到花园四边的距离。

五、拓展题（每题10分，共20分）16. 小明有一些钱，他决定用这些钱买一些笔记本和笔。

七年级数学第十二章《证明》提优训练

七年级数学第十二章《证明》提优训练第一篇：七年级数学第十二章《证明》提优训练七年级数学提优训练第十二章证明一，选择1.下列关于判断一个数学结论是否正确的叙述正确的是()A.只需观察得出B.只需依靠经验获得C.通过亲自实验得出D.必须进行有根据地推理.2.通过观察你能肯定的是()A.图形中线段是否相等;B.图形中线段是否平行C.图形中线段是否相交;D.图形中线段是否垂直3.下列问题你不能肯定的是()A.一支铅笔和一瓶矿泉水的体积大小关系;B.三角形的内角和C.n边形的外角和;D.三角形与矩形的面积关系4.下列问题用到推理的是()A.根据x=1,y=1 得x=y;B.观察得到四边形有四个内角;C.老师告诉了我们关于金字塔的许多奥秘;D.由公理知道过两点有且只有一条直线5.下列句子中,是命题的是()A.今天的天气好吗B.作线段AB∥CD;C.连结A、B两点D.正数大于负数6.下列命题是真命题的是()A.如果两个角不相等,那么这两个角不是对顶角;B.两互补的角一定是邻补角C.如果a2=b2,那么a=b;D.如果两角是同位角,那么这两角一定相等 7.下列命题是假命题的是()A.如果a∥b,b∥c,那么a∥c;B.锐角三角形中最大的角一定大于或等于60°C.两条直线被第三条直线所截,内错角相等;D.矩形的对角线相等且互相平分8.已知下列四个命题：（1）若直角三角形的两边长分别是3与4，则第三边长是5；（2）(a)2 a；（3）若点P（a,b）在第三象限，则点Q(-a,-b)在第一象限；（4）两边及第三边上的中线对应相等的两个三角形全等，其中正确的选项是（）A.只有（1）错误，其他正确B.（1）（2）错误，（3）（4）正确C.（1）（4）错误，（2）（3）正确D.只有（4）错误，其他正确二，填空9．有一正方体，将它各面上分别标出a、b、c、d、e、f。

有甲、乙、丙三个同学站在不同角度观察结果如图，问这个正方体各个面上的字母的对面各是什么字母，即a的对面为，b的对面为，c的对面为.10．某参观团依据下列约束条件，从A、B、C、D、E五个地方选定参观地点：（1）如果去A地，那么也必须去B地；（2）D、E两地至少去一处；（3）B、C两地只去一处；（4）C、D两地都去或都不去；（5）如果去E地，那么A、D两地也必须去依据上述条件，你认为参观团只能去__________________ 11．命题“两条对角线互相平分的四边形是平行四边形”的条件是：________________，结论是：___________________．12．如图，Rt△ABC中，∠C=90°，AD平分∠BAC，BD平分∠CBE，则∠ADB=______°．13．∠1、∠2、∠3分别是△ABC的3个外角，则∠1+∠2+∠3=_______°．14．下面的句子中是命题的有___________________．（1）我是扬州人；（2）你吃饭了吗？（3）对顶角相等；（4）内错角相等；（5）延长线段AB；（6）明天可能下雨；（7）若a2>b2则a>b.三，解答15．判断下列命题的真假：（1）同角的余角相等；（2）异号两数相加得零；（3）等腰梯形是轴对称图形；（4）鸦片战争是中国近代史的开端；（5）平行于同一条直线的两直线平行；（6）函数y= x+1的自变量x的取值范围是x≥-1；（7）在三角形中，两边之和小于第三边。

七年级上数学提优训练卷

七年级上数学提优训练卷对于刚刚踏入初中阶段的七年级学生来说，数学的学习开始逐渐展现出更丰富的层次和更高的要求。

这份七年级上数学提优训练卷，旨在帮助同学们进一步巩固基础，拓展思维，提升解决问题的能力。

一、选择题1、若有理数 a、b 满足 a ＋ b ＜ 0，ab ＜ 0，则（）A a ＞ 0，b ＞ 0B a ＜ 0，b ＞ 0C a、b 异号，且负数的绝对值较大 D a、b 异号，且正数的绝对值较大这道题考查了有理数的加法和乘法法则。

因为 ab ＜ 0，所以 a、b异号。

又因为 a ＋ b ＜ 0，所以负数的绝对值较大，答案选择 C。

2、下列式子中，正确的是（）A －5 （－3) ＝－8B （＋6) （－5) ＝ 1C －7 ｜－7| ＝ 0D ＋5 （－6) ＝ 11对于选项 A，－5 （－3) ＝－5 ＋ 3 ＝－2，所以 A 错误；选项 B，（＋6) （－5) ＝ 6 ＋ 5 ＝ 11，B 错误；选项 C，－7 ｜－7| ＝－7 7＝－14，C 错误；选项 D，＋5 （－6) ＝ 5 ＋ 6 ＝ 11，D 正确。

3、已知 a、b 互为相反数，c、d 互为倒数，m 的绝对值是 2，则式子 m² cd ＋＼（＼frac{a ＋ b}｛m}＼）的值为（）A －3B 3C －5D 3 或－5因为 a、b 互为相反数，所以 a ＋ b ＝ 0；c、d 互为倒数，所以 cd ＝ 1；m 的绝对值是 2，所以 m²＝ 4。

当 m ＝ 2 时，m² cd ＋＼（＼frac{a ＋ b}｛m}＼）＝ 4 1 ＋ 0 ＝ 3；当 m ＝－2 时，m² cd ＋＼（＼frac{a ＋ b}｛m}＼）＝ 4 1 ＋ 0 ＝ 3。

答案选择 B。

二、填空题1、比较大小：＼（＼frac{3}｛4}＼）＼（＼frac{4}｛5}＼）。

先通分，＼（＼frac{3}｛4}＼）＝＼（＼frac{15}｛20}＼），＼（＼frac{4}｛5}＼）＝＼（＼frac{16}｛20}＼），因为＼（＼frac{15}｛20}＼）＞＼（＼frac{16}｛20}＼），所以＼（＼frac{3}｛4}＼）＞＼（＼frac{4}｛5}＼）。

七年级数学期末复习培优提高训练(十)

七年级数学期末复习培优提高训练（十）（2020-2021学年）1、（10分）水浒中学要把420元奖学金分给22名获一、二等奖的学生，一等奖每人50元，二等奖每人10元。

获得一等奖的人，二等奖人.2、（10分）将一张长方形的纸对折,可得到一条折痕,继续对折,对折时每次折痕与上次的折痕保持平行,连续对折三次后,可以得到7条折痕,那么对折四次可以得到 15条折痕,如果对折n 次,可以得到条折痕.3、（10分）点A 在数轴上距原点5个单位长度，且位于原点的左侧，若将A 向右移动4个单位长度，再向左移动1个单位长度，此时点A 表示的数是__________；已知∠α与∠β互余，∠α=400，则∠β的补角是_______度.4、（10分）两个角大小的比为7﹕3，它们的差是72°，则这两个角的数量关系是（）A. 相等B. 互补C. 互余D. 无法确定5、（10分）图表示从上面看一个由相同小立方块搭成的几何体得到的平面图形，小正方形中的数字表示该位置上小立方块的个数，则从正面看该几何体得到的平面图形为（）6、（16分）我国宋朝数学家杨辉在他的著作《详解九章算法》中提出“杨辉三角”（如下图），此图揭示了 (a+b)n （n 为非负整数）展开式的项数及各项系数的有关规律．例如：0()1a b ，它只有一项，系数为1；1()a b a b ，它有两项，系数分别为1，1，系数和为2；222()2a b a ab b ，它有三项，系数分别为1，2，1，系数和为4；33223()33a b a a b ab b ，它有四项，系数分别为1，3，3，1，系数和为8；……根据以上规律，解答下列问题：1111111233 (1)21243第5题A ． B ．Ｃ．Ｄ．（1）4()a b 展开式共有项，系数分别为；（2）()n a b 展开式共有项，系数和为．7、计算：（每小题10分，共20分）（1） 1914726235|263131959| （2）522)2(32(3238、（14分）据《楚天都市报》消息，武汉市居民生活用水价格将进行自2020年以来的第四次调整,试行居民生活用水阶梯式计量水价.拟定城市居民用水户（户籍人口4人及以内）每月用水量在22立方米以内的，为第一级水量基数，按调整后的居民生活用水价格收取；超过22立方米且低于30立方米（含30立方米）的部分为第二级水量基数，按调整后价格的1.5倍收取；超过30立方米的部分为第三级水量基数，按调整后价格的2倍收取.已知调整后居民生活用水价格由现行的每立方米1.51元拟上涨到1.96元.市民张先生一家三口人,他按自己家庭月均用水量计算了一下,按目前新价格,他一个月要缴纳74.48元水费.请问张先生一家月均用水量是多少立方米?和调整前比较,他家每月平均多缴纳多少元水费?参考答案。

初一下数学提优题

初一学生数学提优的题目
1.已知一个三角形的两边分别为3和8，求第三边的取值范围。

2.有一个两位数，十位数字是个位数字的2倍。

如果把这两个数字的位置对调，那么所得的新数比原数小27。

求这个两位数。

3.已知a、b、c是三角形的三边长，化简：∣b+c−a∣+∣b−c−a∣。

4.某班学生去旅游，如果每辆汽车坐45人，则有15人没座位；如果每辆汽车坐60人，则恰有一辆汽车空着。

求该班学生人数和汽车辆数。

5.一列火车匀速行驶，经过一条长300米的隧道需要20秒的时间。

隧道的顶上有一盏灯，垂直向下发光，灯
光照在火车上的时间是10秒。

根据以上数据，你能否求出火车的长度？火车的速度是多少？。

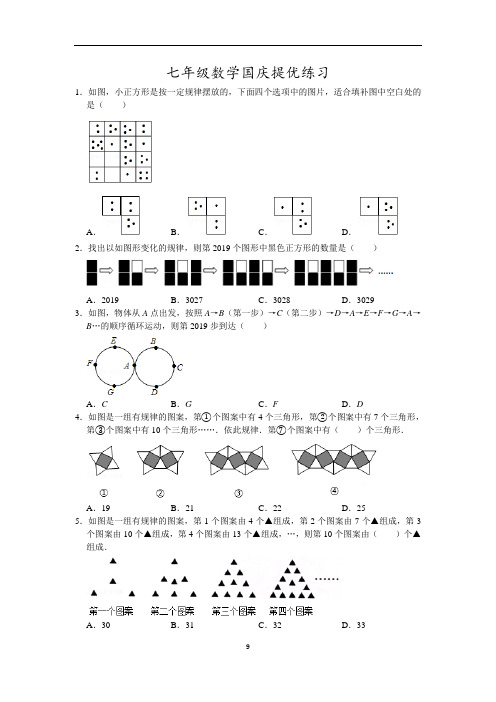
苏教版初一数学上册国庆提优练习(含答案)

七年级数学国庆提优练习1．如图，小正方形是按一定规律摆放的，下面四个选项中的图片，适合填补图中空白处的是（）A．B．C．D．2．找出以如图形变化的规律，则第2019个图形中黑色正方形的数量是（）A．2019B．3027C．3028D．30293．如图，物体从A点出发，按照A→B（第一步）→C（第二步）→D→A→E→F→G→A→B…的顺序循环运动，则第2019步到达（）A．C B．G C．F D．D4．如图是一组有规律的图案，第①个图案中有4个三角形，第②个图案中有7个三角形，第③个图案中有10个三角形……．依此规律．第⑦个图案中有（）个三角形．A．19B．21C．22D．255．如图是一组有规律的图案，第1个图案由4个▲组成，第2个图案由7个▲组成，第3个图案由10个▲组成，第4个图案由13个▲组成，…，则第10个图案由（）个▲组成．A．30B．31C．32D．336．观察下列图中所示的一系列图形，它们是按一定规律排列的，依照此规律，第2019个图形共有（）个〇．A．6055B．6056C．6057D．60587．下列图形都是由同样大小的黑色菱形纸片组成，其中第①个图中有3个黑色菱形纸片，第②个图中有5个黑色菱形纸片，第③个图中有7个黑色菱形纸片，…按此规律排列下去，第20个图中黑色菱形纸片的张数为（）A．38B．39C．40D．418．观察下列一组图形中点的个数，其中第一个图共有4个点，第2个图中共有10个点，第三个图中共有19个点，……，按此规律第100个图中共有点的个数是（）A．15000B．15001C．15151D．15129．如图所示，将形状、大小完全相同的“”和线段按照一定规律摆成下列图形，则第20幅图中的“”的个数为（）A．420B．440C．460D．48010．将正整数按如图所示的位置顺序排列：根据排列规律，则2017应在（）A．A处B．B处C．C处D．D处11．观察下列算式：31＝3，32＝9，33＝27，34＝81，35＝243，36＝729…通过观察，用你所发现的规律得出32019的末位数是（）A．1B．3C．7D．912．计算：31﹣1＝2，32﹣1＝8，33﹣1＝26，34﹣1＝80，35﹣1＝242，…，归纳各计算结果中的个位数字的规律，猜测32019﹣1的个位数字是（）A．2B．8C．6D．013．已知m≥2，n≥2，且m、n均为正整数，如果将m n进行如图所示的“分解”，那么下列四个叙述中正确的有（）①在25的“分解”中，最大的数是11．②在43的“分解”中，最小的数是13．③若m3的“分解”中最小的数是23，则m＝5．④若3n的“分解”中最小的数是79，则n＝5．A．1个B．2个C．3个D．4个14．定义：a是不为1的有理数，我们把称为a的差倒数．如：3的差倒数是＝﹣，﹣的差倒数是＝．已知a1＝2，a2是a1的差倒数，a3是a2的差倒数．a4是a3的差倒数，…，依此类推，则a10＝，若S n＝a1+a2+…+a n，则S2018＝15．如图，将一串有理数按下列规律排列，回答下列问题：（1）在A处的数是正数还是负数？（2）负数排在A、B、C、D中的什么位置？（3）第2019个数是正数还是负数？排在对应于A、B、C、D中的什么位置？16．探索规律：观察下面由组成的图案和算式，解答问题：1+3＝4＝221+3+5＝9＝321+3+5+7＝16＝421+3+5+7+9＝25＝52（1）请计算1+3+5+7+9+11＝；（2）请计算1+3+5+7+9+…+19＝；（3）请计算1+3+5+7+9+…+（2n﹣1）＝；（3）请用上述规律计算：21+23+25+ (99)17．仔细阅读下面的例题，找出其中规律，并解决问题：例：求1+2+22+23+24+…+22017的值．解：令S＝1+2+22+23+24+ (22017)则2S＝2+22+23+24+25+ (22018)所以2S﹣S＝22018﹣1，即S＝22018﹣1，所以1+2+22+23+24+…+22017＝22018﹣1仿照以上推理过程，计算下列式子的值：①1+5+52+53+54+…+5100②1﹣3+32﹣33+34﹣35+…+3201918．满足|ab|+|a－b|－1=0的整数对（a，b）共有（）个．A．4个B．5个C．6个D．7个19．已知（|x+1|+|x-2|）（|y-2|+|y+1|）（|z-3|+|z+1|）=36，求x+2y+3z的最大值和最小值．20．某服装厂生产一种夹克和T恤，夹克每件定价100元，T恤每件定价50元．厂方在开展促销活动期间，向客户提供两种优惠方案：①买一件夹克送一件T恤；②夹克和T恤都按定价的80%付款．现某客户要到该服装厂购买夹克30件，T恤x件（x＞30）．（1）若该客户按方案①购买需付款__________元（用含x的式子表示）；若该客户按方案②购买需付款____________元（用含x的式子表示）；（2）若x=50时，通过计算说明按方案①、方案②哪种方案购买较为合算？（3）当x=50时，你能给出一种更为省钱的购买方案吗？试写出你的购买方法．答案与解析1．如图，小正方形是按一定规律摆放的，下面四个选项中的图片，适合填补图中空白处的是（）A．B．C．D．【分析】根据题意知原图形中各行、各列中点数之和为10，据此可得．【解答】解：由题意知，原图形中各行、各列中点数之和为10，符合此要求的只有故选：D．【点评】本题主要考查图形的变化规律，解题的关键是得出原图形中各行、各列中点数之和为10．2．找出以如图形变化的规律，则第2019个图形中黑色正方形的数量是（）A．2019B．3027C．3028D．3029【分析】仔细观察图形并从中找到规律，然后利用找到的规律即可得到答案．【解答】解：∵当n为偶数时第n个图形中黑色正方形的数量为n+个；当n为奇数时第n个图形中黑色正方形的数量为n+个，∴当n＝2019时，黑色正方形的个数为2019+1010＝3029个．故选：D．【点评】本题考查了图形的变化类问题，解题的关键是仔细的观察图形并正确的找到规律．3．如图，物体从A点出发，按照A→B（第一步）→C（第二步）→D→A→E→F→G→A→B…的顺序循环运动，则第2019步到达（）A．C B．G C．F D．D【分析】根据物体的运动规律可知：每8步一个循环，结合2019＝8×252+3可知第2019步和第3步到达同一点，进而即可得出结论．【解答】解：根据物体的运动规律可知：每8步一个循环，∵2019＝8×252+3，∴第2019步到达D点．故选：D．【点评】本题考查了规律型：图形的变化类，根据物体的运动规律找出每8步一个循环是解题的关键．4．如图是一组有规律的图案，第①个图案中有4个三角形，第②个图案中有7个三角形，第③个图案中有10个三角形……．依此规律．第⑦个图案中有（）个三角形．A．19B．21C．22D．25【分析】由题意可知：第（1）个图案有3+1＝4个三角形，第（2）个图案有3×2+1＝7个三角形，第（3）个图案有3×3+1＝10个三角形，…依此规律，第n个图案有（3n+1）个三角形，代入n＝7即可求得答案．【解答】解：∵第（1）个图案有3+1＝4个三角形，第（2）个图案有3×2+1＝7个三角形，第（3）个图案有3×3+1＝10个三角形，…∴第n个图案有（3n+1）个三角形．当n＝7时，3n+1＝22，故选：C．【点评】此题考查图形的变化规律，找出图形之间的运算规律，利用规律解决问题．5．如图是一组有规律的图案，第1个图案由4个▲组成，第2个图案由7个▲组成，第3个图案由10个▲组成，第4个图案由13个▲组成，…，则第10个图案由（）个▲组成．A．30B．31C．32D．33【分析】仔细观察图形，结合三角形每条边上的三角形的个数与图形的序列数之间的关系发现图形的变化规律，利用发现的规律求解即可．【解答】解：观察发现：第一个图形有3×2﹣3+1＝4个三角形；第二个图形有3×3﹣3+1＝7个三角形；第一个图形有3×4﹣3+1＝10个三角形；…第n个图形有3（n+1）﹣3+1＝3n+1个三角形；当n＝10时，3n+1＝3×10+1＝31，故选B．故选：B．【点评】考查了规律型：图形的变化类，本题是一道找规律的题目，这类题型在中考中经常出现．对于找规律的题目首先应找出哪些部分发生了变化，是按照什么规律变化的．6．观察下列图中所示的一系列图形，它们是按一定规律排列的，依照此规律，第2019个图形共有（）个〇．A．6055B．6056C．6057D．6058【分析】设第n个图形有a n个〇（n为正整数），观察图形，根据各图形中〇的个数的变化可找出“a n＝1+3n（n为正整数）”，再代入a＝2019即可得出结论．【解答】解：设第n个图形有a n个〇（n为正整数），观察图形，可知：a1＝1+3×1，a2＝1+3×2，a3＝1+3×3，a4＝1+3×4，…，∴a n＝1+3n（n为正整数），∴a2019＝1+3×2019＝6058．故选：D．【点评】本题考查了规律型：图形的变化类，根据各图形中〇的个数的变化找出变化规律“a n＝1+3n（n为正整数）”是解题的关键．7．下列图形都是由同样大小的黑色菱形纸片组成，其中第①个图中有3个黑色菱形纸片，第②个图中有5个黑色菱形纸片，第③个图中有7个黑色菱形纸片，…按此规律排列下去，第20个图中黑色菱形纸片的张数为（）A．38B．39C．40D．41【分析】仔细观察图形知道第一个图形有3个正方形，第二个有5＝3+2×1个，第三个图形有7＝3+2×2个，由此得到规律求得第20个图形中正方形的个数即可．【解答】解：观察图形知：第一个图形有3个正方形，第二个有5＝3+2×1个，第三个图形有7＝3+2×2个，…故第20个图形有3+2×19＝41（个），故选：D．【点评】此题主要考查了图形的变化规律，是根据图形进行数字猜想的问题，关键是通过归纳与总结，得到其中的规律，然后利用规律解决一般问题．8．观察下列一组图形中点的个数，其中第一个图共有4个点，第2个图中共有10个点，第三个图中共有19个点，……，按此规律第100个图中共有点的个数是（）A．15000B．15001C．15151D．1512【分析】设第n个图中共有点的个数为a n个，观察图形找出部分a n点的个数，根据数的变化找出变化规律“a n＝+1”，此题得解．【解答】解：设第n个图中共有点的个数为a n个，观察图形可得：a1＝4＝1+3，a2＝10＝1+3+6，a3＝19＝1+3+6+9，…，∴a n＝1+3+6+…+3n＝+1．当n＝100时，＝15151故选：C．【点评】本题考查了规律型中得图形的变化类，根据图形中点的个数的变化找出变化规律“a n＝+1”是解题的关键．9．如图所示，将形状、大小完全相同的“”和线段按照一定规律摆成下列图形，则第20幅图中的“”的个数为（）A．420B．440C．460D．480【分析】由点的分布情况得出a n＝n（n+2），据此求解可得．【解答】解：由图知a1＝3＝1×3，a2＝8＝2×4，a3＝15＝3×5，a4＝24＝4×6，…，∴a n＝n（n+2），当n＝20时，a6＝20×22＝440，故选：B．【点评】本题主要考查图形的变化类，解题的关键是得出a n＝n（n+2）．10．将正整数按如图所示的位置顺序排列：根据排列规律，则2017应在（）A．A处B．B处C．C处D．D处【分析】除数字1外，每4个数一循环，然后用2016除以4得到504，于是可判断2017应在D处．【解答】解：2017﹣1＝2016，2016÷4＝504，所以2017应在D处．故选：D．【点评】本题考查了规律型：数字的变化类：认真观察、仔细思考，善用联想是解决这类问题的方法．11．观察下列算式：31＝3，32＝9，33＝27，34＝81，35＝243，36＝729…通过观察，用你所发现的规律得出32019的末位数是（）A．1B．3C．7D．9【分析】观察不难发现，3n的个位数字分别为3、9、7、1，每4个数为一个循环组依次循环，用2019÷4，根据余数的情况确定答案即可．【解答】解：∵31＝3，32＝9，33＝27，34＝81，35＝243，36＝729，…，∴个位数字分别为3、9、7、1依次循环，∵2019÷4＝504…3，∴32019的个位数字与循环组的第3个数的个位数字相同，是7．故选：C．【点评】本题考查了尾数特征，观察数据发现每4个数为一个循环组，个位数字依次循环是解题的关键．12．计算：31﹣1＝2，32﹣1＝8，33﹣1＝26，34﹣1＝80，35﹣1＝242，…，归纳各计算结果中的个位数字的规律，猜测32019﹣1的个位数字是（）A．2B．8C．6D．0【分析】由31﹣1＝2，32﹣1＝8，33﹣1＝26，34﹣1＝80，35﹣1＝242，…得出末尾数字以2，8，6，0四个数字不断循环出现，由此用2019除以4看得出的余数确定个位数字即可．【解答】解：∵2019÷4＝504…3，∴32019﹣1的个位数字是6，故选：C．【点评】本题考查了尾数的特征，关键是能根据题意得出个位数字循环的规律是解决问题的关键．13．已知m≥2，n≥2，且m、n均为正整数，如果将m n进行如图所示的“分解”，那么下列四个叙述中正确的有（）①在25的“分解”中，最大的数是11．②在43的“分解”中，最小的数是13．③若m3的“分解”中最小的数是23，则m＝5．④若3n的“分解”中最小的数是79，则n＝5．A．1个B．2个C．3个D．4个【分析】通过观察可知：底数是几，分解成的奇数的个数为几，且奇数的个数之和为幂，由此规律进一步分析探讨得出正确的答案．【解答】解：①在25的“分解”中，最大的数是25﹣1+1＝17，所以此叙述不正确；②在43的“分解”中最小的数是13，则其他三个数为15，17，19，四数的和为64，恰好为43，所以此叙述正确；③若m等于5，由53“分解”的最小数是2，1，则其余四个数为23，25，27，29，31，所以此叙述错误；④若3n的“分解”中最小的数是3n﹣1﹣2＝79，则n＝5，所以此叙述正确．故正确的有②④．故选：B．【点评】考查学生观察分析问题的能力，由观察可知底数是几，分解成的奇数的个数为几，且奇数的个数之和为幂．由此可以依次判断．14．定义：a是不为1的有理数，我们把称为a的差倒数．如：3的差倒数是＝﹣，﹣的差倒数是＝．已知a1＝2，a2是a1的差倒数，a3是a2的差倒数．a4是a3的差倒数，…，依此类推，则a10＝2，若S n＝a1+a2+…+a n，则S2018＝1009【分析】求出数列的前4项，继而得出数列的循环周期，然后求解可得．【解答】解：∵a1＝2，a2＝＝＝﹣1、a3＝＝＝、a4＝＝＝2、……∴这列数每3个数为一周期循环，∵10÷3＝3…1，∴a10＝a1＝2，2018÷3＝672……2，∴S2018＝672×（2﹣1+）+2﹣1＝1009，故答案为：2、1009．【点评】本题主要考查数字的变化规律，解决此类问题时通常需要确定数列与序数的关系或者数列的循环周期等，此题得出这列数每3个数为一周期循环是解题的关键．15．如图，将一串有理数按下列规律排列，回答下列问题：（1）在A处的数是正数还是负数？（2）负数排在A、B、C、D中的什么位置？（3）第2019个数是正数还是负数？排在对应于A、B、C、D中的什么位置？【分析】（1）根据A是向上箭头的上方对应的数解答；（2）根据箭头的方向与所对应的数的正、负情况解答；（3）根据4个数为一个循环组依次循环，用2017除以4，根据余数的情况确定所对应的位置即可．【解答】解：（1）A是向上箭头的上方对应的数，与4的符号相同，在A处的数是正数；（2）观察不难发现，向下箭头的上边的数是负数，下方是正数，向上箭头的下方是负数，上方是正数，所以，B和D的位置是负数；（3）∵2019÷4＝504…3，∴第2019个数排在C的位置，是负数．【点评】本题是对数字变化规律的考查，仔细观察图形，从箭头方向向下和向上两种情况对应的数的正负情况考虑求解是解题的关键．16．探索规律：观察下面由组成的图案和算式，解答问题：1+3＝4＝221+3+5＝9＝321+3+5+7＝16＝421+3+5+7+9＝25＝52（1）请计算1+3+5+7+9+11＝36；（2）请计算1+3+5+7+9+…+19＝100；（3）请计算1+3+5+7+9+…+（2n﹣1）＝n2；（3）请用上述规律计算：21+23+25+ (99)【分析】（1）（2）（3）根据已知得出连续奇数的和等于数字个数的平方，得出答案即可；（4）利用以上已知条件得出21+23+25+…+99＝（1+3+5+…+97+99）﹣（1+3+5+…+19），利用得出规律求出即可．【解答】解：（1）1+3+5+7+9+11＝62＝36；（2）1+3+5+7+9+…+19＝102＝100；（3）1+3+5+7+9+…+（2n﹣1）＝n2；（3）21+23+25+…+99＝（1+3+5+...+97+99）﹣（1+3+5+ (19)＝502﹣102＝2500﹣100＝2400．【点评】此题主要考查了数字变化规律，通过分析找到各部分的变化规律后用一个统一的式子表示出变化规律是此类题目的难点．17．（仔细阅读下面的例题，找出其中规律，并解决问题：例：求1+2+22+23+24+…+22017的值．解：令S＝1+2+22+23+24+ (22017)则2S＝2+22+23+24+25+ (22018)所以2S﹣S＝22018﹣1，即S＝22018﹣1，所以1+2+22+23+24+…+22017＝22018﹣1仿照以上推理过程，计算下列式子的值：①1+5+52+53+54+…+5100②1﹣3+32﹣33+34﹣35+…+32019【分析】①根据题目中的例子可以解答本题；②根据题目中的例子和本题的式子的特点可以解答本题．【解答】解：①令S＝1+5+52+53+54+ (5100)则5S＝5+52+53+54+…+5100+5101，∴5S﹣S＝5101﹣1，∴4S＝5101﹣1，∴S＝，即1+5+52+53+54+…+5100＝；②令S＝1﹣3+32﹣33+34﹣35+ (32019)则3S＝3﹣32+33﹣34+35﹣36+ (32020)∴S+3S＝1+32020，∴4S＝1+32020，∴2020134S+=，即1﹣3+32﹣33+34﹣35+ (32019)2020 134+．【点评】本题考查数字的变化类，有理数的混合运算，解答本题的关键是明确题目中的式子的特点，求出相应的结果．18．满足|ab|+|a－b|－1=0的整数对（a，b）共有（）个．A．4个B．5个C．6个D．7个【解答】解：∵|ab|+|a-b|=1，∴0≤|ab|≤1，0≤|a-b|≤1，∵a，b是整数，∴|ab|=0，|a-b|=1或|a-b|=0，|ab|=1①当|ab|=0，|a-b|=1时，Ⅰ、当a=0时，b=±1，∴整数对（a，b）为（0，1）或（0，-1），Ⅱ、当b=0时，a=±1，∴整数对（a，b）为（1，0）或（-1，0），②当|a-b|=0，|ab|=1时，∴a=b，∴a2=b2=1，∴a=1，b=1或a=-1，b=-1，∴整数对（a，b）为（1，1）或（-1，-1），即：满足|ab|+|a-b|=1的所有整数对（a，b）为（0，1）或（0，-1）或（1，0）或（-1，0）或（1，1）或（-1，-1）．∴满足|ab|+|a-b|-1=0的整数对（a，b）共有6个．故选：C．19．已知（|x+1|+|x-2|）（|y-2|+|y+1|）（|z-3|+|z+1|）=36，求x+2y+3z的最大值和最小值．【分析】直接利用绝对值的性质得出：|x+1|+|x-2|≥3，|y-2|+|y+1|≥3，|z-3|+|z+1|≥4，进而利用已知得出答案．【解答】解：∵|x+1|+|x-2|≥3，|y-2|+|y+1|≥3，|z-3|+|z+1|≥4，∴（|x+1|+|x-2|）（|y-2|+|y+1|）（|z-3|+|z+1|）≥36，∵（|x+1|+|x-2|）（|y-2|+|y+1|）（|z-3|+|z+1|）=36，∴|x+1|+|x-2|=3，|y-2|+|y+1|=3，|z-3|+|z+1|=4，∴-1≤x≤2，-1≤y≤2，-1≤z≤3，∴-1≤x≤2，-2≤2y≤4，-3≤3z≤9，∴-6≤x+2y+3z≤15，故最大值15，最小值-6．【点评】此题主要考查了绝对值，正确得出x，y，z的取值范围是解题关键．20．解：（1）1500+50x，2400+40x，故答案为：1500+50x；2400+40x；（2）当x=50，按方案①购买所需费用=1500+50×50=4000（元）；按方案②购买所需费用═2400+40×50=4400（元），所以按方案①购买较为合算；（3）先按方案①购买夹克30件，再按方案②购买T恤20件更为省钱．理由如下：先按方案①购买夹克30件所需费用=3000，按方案②购买T恤20件的费用=50×80%×20=800，所以总费用为3000+800=3800（元），小于4400元，所以此种购买方案更为省钱．。

七年级数学提优训练题

七年级数学提优训练题在七年级的数学学习中，掌握基础知识是重要的，但想要在数学上取得更优异的成绩，进行提优训练是必不可少的。

下面，就让我们一起来探索一些具有挑战性的七年级数学提优训练题。

一、有理数的运算有理数的运算是七年级数学的基础，也是容易出错的地方。

例如：计算－5 ＋ 2×（－3)÷（－1/3)。

这道题不仅考查了有理数的加、减、乘、除运算，还需要注意运算顺序。

先算乘除，后算加减。

2×（－3)＝－6，－6÷（－1/3) ＝ 18，所以－5 ＋ 18 ＝ 13。

再比如：比较大小－2/3 和－3/4。

这就需要将两个分数通分，化为同分母分数进行比较。

－2/3 ＝－8/12，－3/4 ＝－9/12，因为－8/12＞－9/12，所以－2/3 ＞－3/4 。

二、整式的加减在整式的加减中，同类项的合并是重点。

比如：化简 3x² 2xy ＋5y²（2x²＋ 3xy 4y²) 。

首先去括号，得到 3x² 2xy ＋ 5y² 2x² 3xy ＋4y²，然后合并同类项，最终结果为 x² 5xy ＋ 9y²。

还有这样的题目：已知 A ＝ 2x²＋ 3xy 5x ＋ 1 ，B ＝ x²＋ xy ＋ 2 ，求 A ＋ 2B 。

将 B 乘以 2 得到 2B ＝－2x²＋ 2xy ＋ 4 ，然后与 A 相加，得到 A ＋ 2B ＝ 2x²＋ 3xy 5x ＋ 1 ＋（－2x²＋ 2xy ＋ 4) ＝ 5xy 5x ＋5 。

三、一元一次方程一元一次方程的应用是提优训练中的常见题型。

例如：某商店将某种服装按进价提高 30%作为标价，又以九折优惠卖出，结果每件仍获利 17 元，问这种服装每件的进价是多少？设这种服装每件的进价是 x 元，标价为（1 ＋ 30%）x ＝ 13x 元，售价为 13x × 09 ＝ 117x 元。

2020-2021学年北师大版数学七年级下册第4章《三角形》章节提优练(解析)

2020-2021学年北师大版数学七年级下册章节提优练第4章《三角形》一．选择题1．（碑林区校级三模）如图，直线，的直角顶点落在直线上，点落在直线//a b Rt ABC ∆A a B 上，若，，则的大小为 b 115∠=︒225∠=︒ABC ∠()A ．B ．C ．D ．40︒45︒50︒55︒解：如图，作．//CK a，，//a b //CK a ，//CK b ∴，，13∴∠=∠42∠=∠，12152540ACB ∴∠=∠+∠=︒+︒=︒，90CAB ∠=︒ ，904050ABC ∴∠=︒-︒=︒故选：．C 2．（市中区校级期末）如图，有一块直角三角板放置在上，三角板的两条直角边XYZ ABC ∆XYZ 、改变位置，但始终满足经过、两点．如果中，则 XY XZ B C ABC ∆52A ∠=︒(ABX ACX ∠+∠=)A ．B ．C ．D ．38︒48︒28︒58︒解：连接，AX ，90BXC ∠=︒ ，360270AXB AXC BXC ∴∠+∠=︒-∠=︒，52A ∠=︒ ，52BAX CAX ∴∠+∠=︒，，180ABX BAX AXB ∠+∠+∠=︒ 180ACX CAX AXC ∠+∠+∠=︒，3602705238ABX ACX ∴∠+∠=︒-︒-︒=︒故选：．A3．（邓州市期末）如图，在中，，，在上取一点，使Rt ABC ∆90ACB ∠=︒5BC cm =AC E ，过点作，连接，使，若，则下列结论不正确的是 EC BC =E EF AC ⊥CF CF AB =12EF cm =()A ．B ．C ．平分D ．F BCF ∠=∠7AE cm =EF AB AB CF ⊥解：，，EF AC ⊥ 90ACB ∠=︒，90FEC ACB ∴∠=∠=︒，90F FCE FCE BCF ∴∠+∠=∠+∠=︒；故选项正确；F BCF ∴∠=∠A 在与中，，Rt ACB ∆Rt FEC ∆BC EC AB CF =⎧⎨=⎩，Rt ACB Rt FEC(HL)∴∆≅∆，，12AC EF ∴==5CE BC cm ==，故选项正确；7AE AC CE cm ∴=-=B ，Rt ACB Rt FEC ∆≅∆ ，A F ∴∠=∠，ADE EDF ∠=∠ ，90FED AEF ∴∠=∠=︒，故选项正确；AB CF ∴⊥D ，AED ACB ∠=∠ ，//DE BC ∴，∴75AD AE DB CE ==，AD DB ∴≠不平分，故选项错误，EF ∴AB C 故选：．C4．（大同期末）如图，在中，平分，，且分别交，，及ABC ∆AD BAC ∠EG AD ⊥AB AD AC 的延长线于点，，，，若，，则的度数为 BC E H F G 45B ∠=︒75ACB ∠=︒G ∠()A ．B ．C ．D ．15︒22.5︒27.5︒30︒解：平分，AD BAC ∠，BAD CAD ∴∠=∠，EG AD ⊥ ，90AMF ANE ∴∠=∠=︒，，90AEF BAD ∠+∠=︒ 90AFM CAD ∠+∠=︒，AEF AFM ∴∠=∠，，，ACB G CFG ∠=∠+∠ AEF B G ∠=∠+∠CFG AFE ∠=∠，ACB G B G ∴∠-∠=∠+∠，1()2G ACB B ∴∠=∠-∠，，45B ∠=︒ 75ACB ∠=︒，15G ∴∠=︒故选：．A5．（涞水县期末）如图，交于点，交于点，交于点，，EB AC M FC D AB FC N 90E F ∠=∠=︒，，给出下列结论：其中正确的结论有 B C ∠=∠AE AF =()①；12∠=∠②；BE CF =③；ACN ABM ∆≅∆④；CD DN =⑤．AFN AEM ∆≅∆A ．2个B ．3个C ．4个D ．5个解：，，，90E F ∠=∠=︒ B C ∠=∠AE AF =，()ABE ACF AAS ∴∆≅∆，，故②正确，BE CF ∴=AF AE =，BAE CAF ∠=∠，BAE BAC CAF BAC ∠-∠=∠-∠，故①正确，12∴∠=∠，ABE ACF ∆≅∆ ，AB AC ∴=又，BAC CAB ∠=∠B C∠=∠，故③正确，()ACN ABM ASA ∆≅∆不能证明成立，故④错误CD DN =，，，12∠=∠ F E ∠=∠AF AE =，故⑤正确，()AFN AEM ASA ∴∆≅∆故选：．C 6．（永春县期末）如图，是的角平分钱，，垂足为．若，AD ABC ∆CE AD ⊥F 30CAB ∠=︒，则的度数为 55B ∠=︒BDE ∠()A ．B ．C ．D ．35︒40︒45︒50︒解：，，30CAB ∠=︒ 55B ∠=︒，180305595ACB ∴∠=︒-︒-︒=︒，CE AD ⊥ ，90AFC AFE ∴∠=∠=︒是的角平分钱，AD ABC ∆，130152CAD EAD ∴∠=∠=⨯︒=︒又，AF AF = ()ACF AEF ASA ∴∆≅∆，AC AE ∴=，，AD AD = CAD EAD ∠=∠ ，ACD AED ∴∆≅∆()SAS ，DC DE ∴=，DCE DEC ∴∠=∠，901575ACE ∠=︒-︒=︒ ，957520DCE DEC ACB ACE ∴∠=∠=∠-∠=︒-︒=︒，202040BDE DCE DEC ∴∠=∠+∠=︒+︒=︒故选：．B 7．（新洲区期末）如图，，，过点作的垂线交的延长线于90ACB ∠=︒AC CD =D AB AB点．若，则的度数为 E 2AB DE =BAC ∠()A ．B ．C ．D ．45︒30︒22.5︒15︒解：连接，延长、交于，AD AC DE M ，，90ACB ∠=︒ AC CD =，45DAC ADC ∴∠=∠=︒，，90ACB ∠=︒ DE AB ⊥，90DEB ACB DCM ∴∠=︒=∠=∠，ABC DBE ∠=∠ 由三角形内角和定理得：，∴CAB CDM ∠=∠在和中ACB ∆DCM ∆CAB CDMAC CDACB DCM∠=∠⎧⎪=⎨⎪∠=∠⎩，()ACB DCM ASA ∴∆≅∆，AB DM ∴=，2AB DE = ，2DM DE ∴=，DE EM ∴=，DE AB ⊥ ，AD AM ∴=，114522.522BAC DAE DAC ∴∠=∠=∠=⨯︒=︒故选：．C 8．（肇庆期末）如图，在中，，是高，是中线，是角平分线，ABC ∆90BAC ∠=︒AD BE CF交于点，交于点，下面说法正确的是 CF AD G BE H ()①的面积的面积；②；③；④．ABE ∆BCE =∆AFG AGF ∠=∠2FAG ACF ∠=∠BH CH =A ．①②③④B ．①②③C ．②④D ．①③解：是中线，BE ，AE CE ∴=的面积的面积（等底等高的三角形的面积相等），故①正确；ABE ∴∆BCE =∆是角平分线，CF ，ACF BCF ∴∠=∠为高，AD ，90ADC ∴∠=︒，90BAC ∠=︒ ，，90ABC ACB ∴∠+∠=︒90ACB CAD ∠+∠=︒，ABC CAD ∴∠=∠，，AFG ABC BCF ∠=∠+∠ AGF CAD ACF ∠=∠+∠，故②正确；AFG AGF ∴∠=∠为高，AD ，90ADB ∴∠=︒，90BAC ∠=︒ ，，90ABC ACB ∴∠+∠=︒90ABC BAD ∠+∠=︒，ACB BAD ∴∠=∠是的平分线，CF ACB ∠，2ACB ACF ∴∠=∠，2BAD ACF ∴∠=∠即，故③正确；2FAG ACF ∠=∠根据已知条件不能推出，即不能推出，故④错误；HBC HCB ∠=∠BH CH =故选：．B9．（江油市期末）如图，等腰直角中，，于，的平分线分别ABC ∆90BAC ∠=︒AD BC ⊥D ABC ∠交、于、两点，为的中点，延长交于点，连接，．下列结论：AC AD E F M EF AM BC N DM NE ①；②；③是等边三角形；④，⑤．AE AF =AM EF ⊥AEF ∆DF DN =//AD NE 其中正确的结论有 ()A ．1个B ．2个C ．3个D ．4个解：，，，90BAC ∠=︒ AC AB =AD BC ⊥，，，45ABC C ∴∠=∠=︒AD BD CD ==90ADN ADB ∠=∠=︒，45BAD CAD ∴∠=︒=∠平分，BE ABC ∠，122.52ABE CBE ABC ∴∠=∠=∠=︒，9022.567.5BFD AEB ∴∠=∠=︒-︒=︒，67.5AFE BFD AEB ∴∠=∠=∠=︒，故①正确；③错误，AF AE ∴=为的中点，M EF ，故②正确；AM EF ∴⊥过点作于点，F FH AB ⊥H ，AM EF ⊥ ，90AMF AME ∴∠=∠=︒，9067.522.5DAN MBN ∴∠=︒-︒=︒=∠在和中，FBD ∆NAD ∆，FBD DAN BD ADBDF ADN ∠=∠⎧⎪=⎨⎪∠=∠⎩，()FBD NAD ASA ∴∆≅∆，故④正确；DF DN ∴=，67.5BAM BNM ∠=∠=︒ ，BA BN ∴=，，EBA EBN ∠=∠ BE BE =，()EBA EBN SAS ∴∆≅∆，90BNE BAM ∴∠=∠=︒，90ENC ADC ∴∠=∠=︒．故⑤正确，//AD EN ∴故选：．D 10．（黄岩区期末）如图，已知等边三角形，点为线段上一点，以线段为边向右侧ABC D BC DB 作，使，若，，则的度数是 DEB ∆DE CD =ADB m ∠=︒(1802)BDE m ∠=-︒DBE ∠()A ．B ．C ．D ．(60)m -︒(1802)m -︒(290)m -︒(120)m -︒解：如图，连接．AE 是等边三角形，ABC ∆，60C ABC ∴∠=∠=︒，，ADB m ∠=︒ (1802)BDE m ∠=-︒，，180ADC m ∴∠=︒-︒180ADE m ∠=︒-︒，ADC ADE ∴∠=∠，，AD AD = DC DE =，()ADC ADE SAS ∴∆≅∆，，60C AED ∴∠=∠=︒DAC DAE ∠=∠，DEA DBA ∴∠=∠，，，四点共圆，A ∴D EB ，(60)DBE DAE DAC m ∴∠=∠=∠=-︒故选：．A 二．填空题11．（哈尔滨模拟）如图，在中，为的中线，，，ABC ∆BD ABC ∆2DBA CAB ∠=∠25BD =，则的长为　66　．38CB =AB 解：延长至，使，作交于，连接、，如图所示：BD E DE DB =ADF CAB ∠=∠AB F AE DF 则，，DF AF =2DFB CAB ADF CAB ∠=∠+∠=∠，2DBA CAB ∠=∠ ，1252AF DF DB DE BE ∴=====，90BFE ∴∠=︒，90AFE ∴∠=︒为的中线，BD ABC ∆，AD CD ∴=在和中，，ADE ∆CDB ∆AD CD ADE CDB DE DB =⎧⎪∠=∠⎨⎪=⎩，()ADE CDB SAS ∴∆≅∆，38AE CB ∴==EF∴===，41BF∴===；66AB AF BF∴=+=故66．12．（琼山区校级期末）如图，和都是等腰三角形，且，当点ABC∆EBD∆100ABC EBD∠=∠=︒在边上时，　40　度．D AC BAE∠=解：，，，ABC ABD DBC∠=∠+∠EBD EBA ABD∠=∠+∠ABC EBD∠=∠，DBC EBA∴∠=∠和都是等腰三角形，ABC∆EBD∆，，BE BD∴=AB CB=在和中EAB∆DCB∆，EB DBABE CBDAB CB=⎧⎪∠=∠⎨⎪=⎩，()EAB DCB SAS∴∆≅∆，BAE BCD∴∠=∠，，100ABC∠=︒AB CB=，180100402BAE BCD︒-︒∴∠=∠==︒故40．13．（玉田县期末）如图，在中，，平分交于点，于Rt ABC∆90C∠=︒AD CAB∠BC D BE AD⊥点．若，则．E28DBE∠=︒CAB∠=56︒解：，BE AE ⊥ ，90E C ∴∠=∠=︒，ADC BDE ∠=∠ ，28CAD DBE ∴∠=∠=︒平分，AE CAB ∠，256CAB CAD ∴∠=∠=︒故答案为．56︒14．（滕州市期末）如图，将沿着平行于的直线折叠，点落在点，若，ABC ∆BC A 125C ∠=︒，则的度数为．15A ∠=︒A DB ∠'100︒解：，，125C ∠=︒ 15A ∠=︒，1801801512540B A C ∴∠=︒-∠-∠=︒-︒-︒=︒沿着平行于的直线折叠，点落到点，ABC ∆ BC A A '，40ADE B ∴∠=∠=︒，40A DE ADE ∴∠'=∠=︒．1804040100A DB ∴∠'=︒-︒-︒=︒故．100︒15．（下城区期末）如图，点是的重心，过点作，交于点，连结，G ABC ∆G //GE BC AC E GC 若的面积为1，则的面积为．ABC ∆GEC ∆19解：连接并延长交于，AG BC D 点是的重心，G ABC ∆，，BD CD ∴=21AG GD =，1122ABD ADC ABC S S S ∆∆∆∴===，//GE BC ，AGE ADC ∴∆∆∽，∴22213AG GE AE AD DC AC ====+，∴49AGE ADC S S ∆∆=4299AGE ADC S S ∆∆∴==，11212299GEC AGE S S ∆∆∴==⨯=16．（交城县期末）已知：如图，为的角平分线，且，为延长线上的一点，BD ABC ∆BD BC =E BD ，过作，为垂足，下列结论：BE BA =E EF AB ⊥F ①；②；③；④，其中正确的是　ABD EBC ∆≅∆180BCE BCD ∠+∠=︒AD EF EC ==AE EC =①②④　（填序号）解：①为的角平分线，BD ABC ∆，ABD CBD ∴∠=∠在和中，ABD ∆EBC ∆，BD BC ABD CBDBE BA =⎧⎪∠=∠⎨⎪=⎩，()ABD EBC SAS ∴∆≅∆①正确；∴②为的角平分线，，，BD ABC ∆BD BC =BE BA =，BCD BDC BAE BEA ∴∠=∠=∠=∠，ABD EBC ∆≅∆ ，BCE BDA ∴∠=∠，180BCE BCD BDA BDC ∴∠+∠=∠+∠=︒②正确；∴③，，，，BCE BDA ∠=∠ BCE BCD DCE ∠=∠+∠BDA DAE BEA ∠=∠+∠BCD BEA ∠=∠，DCE DAE ∴∠=∠为等腰三角形，ACE ∴∆，AE EC ∴=，ABD EBC ∆≅∆ ，AD EC ∴=，AD AE EC ∴==为的角平分线，，而不垂直与，BD ABC ∆EF AB ⊥EC BC ，EF EC ∴≠③错误；∴④由③知，AD AE EC ==④正确；∴综上所述，正确的结论是①②④．故答案是：①②④．17．（春•沙坪坝区校级期末）如图，在中，、分别为边，的中点，若ABC ∆D E BC AC ，则图中阴影部分的面积是　12　．48ABC S ∆=解：点为中点，D BC ，12DC BC ∴=与的，边上的高相同，ADC ∆ ABC ∆DC BC ，1242ADC ABC S S ∆∆∴==点为中点，E AC ，12AE AC ∴=与的，边上的高相同，ADC ∆ ADE ∆AC AE ，1122ADE ADC S S ∆∆∴==故12．18．（春•崇川区校级期末）如图，在中，，，为形外一点，ABC ∆40BAC ∠=︒60ACB ∠=︒D ABC ∆平分，且，求．DA BAC ∠50CBD ∠=︒DCB ∠=60︒解：如图，延长到，延长到，作于，于，于．AB P AC Q DH AP ⊥H DE AQ ⊥E DF BC ⊥F，，4060100PBC BAC ACB ∠=∠+∠=︒+︒=︒ 50CBD ∠=︒，DBC DBH ∴∠=∠，，DF BC ⊥ DH BP ⊥，DF DH ∴=又平分，，，DA PAQ ∠DH PA ⊥DE AQ ⊥，DE DH ∴=，DE DF ∴=平分，CD ∴QCB ∠，18060120QCB ∠=︒-︒=︒ ，60DCB ∴∠=︒故答案为．60︒19．（建邺区校级月考）如图，的平分线与的平分线交于点．，和ACD ∠ABD ∠E A ∠CEB ∠之间的数量关系是．D ∠2A CEB D ∠=∠+∠解：如图，延长交于．设，．AC BD M ABE EBD x ∠=∠=ACE ECD y ∠=∠=，，2AMD A ABD A x ∠=∠+∠=∠+ ECD CEB EBD D CEB x D ∠=∠+∠+∠=∠++∠，2222ACD ECD CEB x D ∴∠=∠=∠++∠，ACD AMD D ∠=∠+∠ 22222AMD CEB x D D CEB x D∴∠=∠++∠-∠=∠++∠，222A x CEB x D ∴∠+=∠++∠，2A CEB D ∴∠=∠+∠故．2A CEB D ∠=∠+∠三．解答题20．（福建模拟）如图，是的中线，延长，过点作交的延长线于点，AD ABC ∆AD B BE AD ⊥AD E 过点作于点．求证：．C CF AD ⊥F DE DF =证明：是的中线，AD ABC ∆，BD CD ∴=，，BE AD ⊥ CF AD ⊥，90BED CFD ∴∠=∠=︒在和中，BDE ∆CDF ∆，BED CFD BDE CDF BD CD ∠=∠⎧⎪∠=∠⎨⎪=⎩，()BDE CDF AAS ∴∆≅∆．DE DF ∴=21．（惠安县期末）如图，已知，点、在上，且，求证：AB AC =D E BC ADE AED ∠=∠．BD CE=证明：，AB AC = ，B C ∴∠=∠在和中，，ABE ∆ACD ∆B C AED ADE AB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩，()ABE ACD AAS ∴∆≅∆，BE CD ∴=．BD CE ∴=22．（麻城市期末）如图，是的边上的中线，，是的边上的AD ABC ∆BC CD AB =AE ABD ∆BD 中线．求证：．2AC AE =证明：延长至点，使，连接，如图所示：AE F EF AE =DF 是的边上的中线，AE ABD ∆BD ，BE DE ∴=在与中，，ABE ∆FDE ∆AE EF AEB FEDBE DE =⎧⎪∠=∠⎨⎪=⎩，()ABE FDE SAS ∴∆≅∆，，DF AB CD ∴==EDF B ∠=∠是的边上的中线，，AD ABC ∆BC CD AB =，AB BD ∴=，ADB BAD ∴∠=∠，ADC B BAD BDA EDF ADF ∴∠=∠+∠=∠+∠=∠在与中，，ADF ∆ADC ∆AD AD ADF ADC DF DC =⎧⎪∠=∠⎨⎪=⎩，()ADF ADC SAS ∴∆≅∆．2AC AF AE ∴==23．（海州区校级期末）如图，在中，，，点在线段上运动（点ABC ∆2AB AC ==36B ∠=︒D BC 不与点、重合），连接，作，交线段于点．D B C AD 36ADE ∠=︒DE AC E （1）当时，，；128BDA ∠=︒EDC ∠=16︒AED ∠=（2）线段的长度为何值时，？请说明理由；DC ABD DCE ∆≅∆（3）在点的运动过程中，的形状可以是等腰三角形吗？若可以，请直接写出的度D ADE ∆BDA ∠数；若不可以，请说明理由．解：（1），AB AC = ，36C B ∴∠=∠=︒，，36ADE ∠=︒ 128BDA ∠=︒，18016EDC ADB ADE ∠=︒-∠-∠=︒ ，163652AED EDC C ∴∠=∠+∠=︒+︒=︒故；；16︒52︒（2）当时，，2DC =ABD DCE ∆≅∆理由：，，2AB = 2DC =，AB DC ∴=，36C ∠=︒ ，144DEC EDC ∴∠+∠=︒，36ADE ∠=︒ ，144ADB EDC ∴∠+∠=︒，ADB DEC ∴∠=∠在和中，ABD ∆DCE ∆，ADB DEC B CAB DC ∠=∠⎧⎪∠=∠⎨⎪=⎩；()ABD DCE AAS ∴∆≅∆（3）当的度数为或时，的形状是等腰三角形，BDA ∠108︒72︒ADE ∆①当时，，DA DE =72DAE DEA ∠=∠=︒；7040108BDA DAE C ∴∠=∠+∠=︒+︒=︒②当时，，AD AE =36AED ADE ∠=∠=︒，108DAE ∴∠=︒此时，点与点重合，不合题意；D B ③当时，，EA ED =36EAD ADE ∠=∠=︒；363672BDA EAD C ∴∠=∠+∠=︒+︒=︒综上所述，当的度数为或时，的形状是等腰三角形．BDA ∠108︒72︒ADE ∆24．（洛阳期末）如图，是的外角的平分线，且交的延长线于点．CE ABC ∆ACD ∠CE BA E（1）若，，求的度数；35B ∠=︒25E ∠=︒BAC ∠（2）请你写出、、三个角之间存在的等量关系，并写出证明过程．BAC ∠B ∠E ∠解：（1），，，ECD B E ∠=∠+∠ 35B ∠=︒25E ∠=︒，60ECD ∴∠=︒平分，EC ACD ∠，60ACE ECD ∴∠=∠=︒．602585BAC ACE E ∴∠=∠+∠=︒+︒=︒（2）结论：．2BAC B E ∠=∠+∠理由：，BAC ACE E ∠=∠+∠ ，ECD ACE B E ∠=∠=∠+∠．2BAC B E E B E ∴∠=∠+∠+∠=∠+∠25．（涟源市期末）如图，在中，，为边上的任意点，为线段的中ABC ∆90BAC ∠=︒E BC D BE 点，，，．AB AE =EF AE ⊥//AF BC （1）求证：；DAE C ∠=∠（2）求证：．AF BC =证明：（1），为线段的中点，AB AE = D BE AD BC∴⊥，90C DAC ∴∠+∠=︒90BAC ∠=︒90BAD DAC ∴∠+∠=︒，C BAD ∴∠=∠，，AB AE = AD BE ⊥，BAD DAE ∴∠=∠DAE C∴∠=∠（2）//AF BCFAE AEB∴∠=∠AB AE= B AEB∴∠=∠，且，B FAE ∴∠=∠90AEF BAC ∠=∠=︒AB AE=()ABC EAF ASA ∴∆≅∆AC EF∴=26．（柯桥区期末）小明在学习过程中，对教材中的一个有趣问题做如下探究：【习题回顾】已知：如图1，在中，，是角平分线，是高，、相ABC ∆90ACB ∠=︒AE CD AE CD 交于点．求证：；F CFE CEF ∠=∠【变式思考】如图2，在中，，是边上的高，若的外角的平ABC ∆90ACB ∠=︒CD AB ABC ∆BAG ∠分线交的延长线于点，其反向延长线与边的延长线交于点，则与还相CD F BC E CFE ∠CEF ∠等吗？说明理由；【探究廷伸】如图3，在中，在上存在一点，使得，角平分线交于ABC ∆AB D ACD B ∠=∠AE CD 点．的外角的平分线所在直线与的延长线交于点．试判断与F ABC ∆BAG ∠MN BC M M ∠的数量关系，并说明理由．CFE ∠【习题回顾】证明：，是高，90ACB ∠=︒ CD ，，90B CAB ∴∠+∠=︒90ACD CAB ∠+∠=︒，B ACD ∴∠=∠是角平分线，AE ，CAF DAF ∴∠=∠，CFE CAF ACD CEF DAF B ∠=∠+∠∠=∠+∠ ；CEF CFE ∴∠=∠【变式思考】CEF CFE∠=∠证明：为的角平分线，AF BAG ∠，GAF DAF ∴∠=∠为边上的高，CD AB ，90ACB ∴∠=︒，又，90ADF ACE ∴∠=∠=︒CAE GAF ∠=∠ ；CEF CFE ∴∠=∠【探究思考】，90M CFE ∠+∠=︒证明：、、三点共线、为角平分线，C A G AE AN ，又，90EAN ∴∠=︒GAN CAM ∠=∠ ，90M CEF ∴∠+∠=︒，，，CEF EAB B ∠=∠+∠ CFE EAC ACD ∠=∠+∠ACD B ∠=∠，CEF CFE ∴∠=∠．90M CFE ∴∠+∠=︒27．（莱西市期末）如图，在中，是边上的中线，是的中点，过点作的ABC ∆AD BC E AD A BC 平行线交的延长线于点，连接．BE F CF （1）试判断四边形的形状，并证明；ADCF （2）若，试判断四边形的形状，并证明．AB AC ⊥ADCF （1）解：四边形是平行四边形，理由如下：CDAF 是的中点，E AD ，AE ED ∴=，//AF BC ，，AFE DBE ∴∠=∠FAE BDE ∠=∠在和中，AFE ∆DBE ∆，AFE DBE FAE BDEAE DE ∠=∠⎧⎪∠=∠⎨⎪=⎩，()AFE DBE AAS ∴∆≅∆，AF BD ∴=是边中线，AD BC ，CD BD ∴=，AF CD ∴=四边形是平行四边形；∴CDAF （2）四边形是菱形，ADCF ，是斜边的中线，AC AB ⊥ AD BC ，12AD BC DC ∴==四边形是平行四边形， ADCF 平行四边形是菱形．∴ADCF 28．（遂宁期末）如图所示，已知锐角及一点．AOB ∠P （1）过点作、的垂线，垂足分别是、；（只作图，保留作图痕迹，不写作法）P OA OB M N （2）猜想与之间的关系，并证明．MPN ∠AOB ∠解：（1）过点作、的垂线、如图所示；P OA OB PM PN（2）猜想：或．180MPN AOB ∠+∠=︒MPN AOB ∠=∠理由：左图中，在四边形中，，PMON 90PMO PNO ∠=∠=︒ ．180MPN AOB ∴∠+∠=︒右图中，，，PJM OJN ∠=∠ 90AMJ JNO ∠=∠=︒．MPN AOB ∴∠=∠29．（瑶海区期末）如图，和中，，，，连接ABC ∆EBD ∆90ABC DBE ∠=∠=︒AB CB =BE BD =，，与交于点，与交于点．AE CD AE CD M AE BC N（1）求证：；AE CD =（2）求证：；AE CD ⊥（3）连接，有以下两个结论：①平分；②平分．其中正确的有　②　BM BM CBE ∠MB AMD ∠（请写序号，少选、错选均不得分）．（1）证明：，ABC DBE ∠=∠ ，ABC CBE DBE CBE ∴∠+∠=∠+∠即，ABE CBD ∠=∠在和中，ABE ∆CBD ∆，AB CB ABE CBDBE BD =⎧⎪∠=∠⎨⎪=⎩，ABE CBD ∴∆≅∆．AE CD ∴=（2），ABE CBD ∆≅∆ ，BAE BCD ∴∠=∠，，180NMC BCD CNM ∠=︒-∠-∠ 180ABC BAE ANB ∠=︒-∠-∠又，CNM ABC ∠=∠，90ABC ∠=︒ ，90NMC ∴∠=︒．AE CD ∴⊥（3）结论：②理由：作于，于．BK AE ⊥K BJ CD ⊥J，ABE CBD ∆≅∆ ，，AE CD ∴=ABE CDB S S ∆∆=，∴1122AE BK CD BJ = ，作于，于，BK BJ ∴= BK AE ⊥K BJ CD ⊥J 平分．BM ∴AMD ∠不妨设①成立，则，则，显然可不能，故①错误．ABM DBM ∆≅∆AB BD =故答案为②．30．（勃利县期末）阅读探索题：（1）如图1，是的平分线，以为圆心任意长为半径作弧，分别交射线、于、OP MON ∠O ON OM C 两点，在射线上任取一点（点除外），连接、．求证：．B OP A O AB AC AOB AOC ∆≅∆（2）请你参考以上方法，解答下列问题：如图2，在中，，，平分，试判断和、之间的Rt ABC ∆90ACB ∠=︒60A ∠=︒CD ACB ∠BC AC AD数量关系并证明．（1）证明：在和中，，AOB ∆AOC ∆OB OC BOA COA OA OA =⎧⎪∠=∠⎨⎪=⎩．()AOB AOC SSS ∴∆≅∆（2）在上截取，CB CE CA =平分，CD ACB ∠，ACD BCD ∴∠=∠在和中，，ACD ∆ECD ∆AC CE ACD ECD CD CD =⎧⎪∠=∠⎨⎪=⎩，()ACD ECD SAS ∴∆≅∆，60CAD CED ∴∠=∠=︒，90ACB ∠=︒ ，30B ∴∠=︒，30EDB ∴∠=︒即，EDB B ∠=∠，DE EB ∴=，BC CE BE =+ ，BC AC DE ∴=+．BC AC AD ∴=+。

提优必刷卷七上数学答案

提优必刷卷七上数学答案题目：提优必刷卷七上数学答案本文提供提优必刷卷七上数学答案，以下是各章节的详细题目以及对应的答案。

第一章：集合1.已知集合A={1,2,3},B={2,4,6}，求A∪B和A∩B的值。

答案：A∪B={1,2,3,4,6}，A∩B={2}。

2. 记A={x|x为2的倍数且2<x<12}，B={x|x是4的倍数且4<x<16}，求A∩B的值。

答案：A={4,6,8,10},B={8,12}，故A∩B={8}。

第二章：函数1. 已知函数f(x)={2x-3(x≤3);x+1(x>3)}，求f(1)和f(4)的值。

答案：f(1)=-4，f(4)=5。

2.已知函数f(x)=ax^2+bx+c，且f(2)=7，f(-1)=1，f(1)=1，则求a，b，c的值。

答案：a=3，b=2，c=-1。

第三章：三角形1. 已知三角形ABC，AB=8，AC=6，BC=10，求∠A、∠B、∠C的大小。

答案：∠A=36.87°，∠B=53.13°，∠C=90°。

2. 已知三角形ABC，BC=5，AC=6，AB=7，求∠A、∠B、∠C的大小。

答案：∠A=36.87°，∠B=53.13°，∠C=90°。

第四章：平面向量1. 已知向量a=(1,2)，b=(-1,3)，求a+b和a-b。

答案：a+b=(0,5)，a-b=(2,-1)。

2. 已知向量a=(3,1)，b=(2,-2)，c=(-5,3)，求a+2b-3c的值。

答案：a+2b-3c=(19,-7)。

第五章：立体图形1. 已知正方体ABCD-EFGH，AB=4，求AG的长度。

答案：AG=4√2。

2. 已知正六面体ABCDEFG，AB=2，求AE的长度。

答案：AE=2√3。

以上是提优必刷卷七上数学答案的详细内容。

希望对同学们的学习有所帮助。

七年级数学下册提优班练习(一) 试题

币仍仅州斤爪反市希望学校新浦二零二零—二零二壹七年级数学下册提优班练习〔一〕苏科1、两条直线被第三条直线所截，总有〔〕A 、同位角相等B 、内错角相等C 、同旁内角互补D 、以上都不对2、如图，以下说法正确的选项是〔〕A 、假设AB ∥CD ，那么∠1=∠2 B 、假设AD ∥BC ，那么∠3=∠4C 、假设∠1=∠2，那么AB ∥CD D 、假设∠1=∠2，那么AD ∥BC〔2〕〔3〕〔4〕〔5〕3、如图，能使AB ∥CD 的条件是〔〕A 、∠1=∠B B 、∠3=∠AC 、∠1+∠2+∠B=180°D 、∠1=∠A4、如图AD ∥BC,BD 平分∠ABC ，假设∠A ＝100°，那么∠DBC 的度数等于〔〕A 、100°B 、850°C 、40°D 、50°5、如下列图，AC ⊥BC ，DE ⊥BC ，CD ⊥AB,∠ACD ＝40°，那么∠BDE 等于〔〕A 、40°B 、50°C 、60°D 、不能确定6、如下列图，直线L 1∥L 2，L 3⊥L 4，①∠1+∠3=90°，②∠2+•∠3=90°，③∠2=∠4．以下说法中，正确的选项是〔〕A 、只有①正确B 、只有②正确C 、①和③正确D 、①②③都正确〔6〕〔7〕〔8〕〔9〕1AEDCBF7、将直角三角尺的直角顶点靠在直尺上，且斜边与这把直尺平行，那么，•在形成的这个图中与∠α互余的角共有〔〕A ．4个B ．3个C ．2个D ．1个8、如图，图中共有同旁内角〔〕对A 、 4．B 、 5．C 、6．D 、7．9、如图，把矩形ABCD 沿EF 对折后使两局部重合，假设150∠=°，那么AEF ∠= 〔〕A 、110°B 、115°C 、120°D 、130°10、在同一平面内，有12条互不重合的直线，假设，2l ∥3l ，43l l ⊥，4l ∥5l ……以此类推，那么1l 和12l 的位置关系是〔〕A 、平行B 、垂直C 、平行或垂直D 、无法确定二、填一填〔每题3分，共24分〕11、如图，AB ∥CD ，AC ⊥BC ，图中与∠CAB 互余的角的个数有。

数学提优训练题

七年级数学提优训练题姓名得分一、选择题1．如图，数轴上A ，B ，C 三点表示的数分别为a ，b ，c ，则它们的大小关系（）（A ） a >b >c （B ） b >c >a （C ） c >a >b （D ） b >a >c2．根据图1和图2所示，对a b c ，，三种物体的重量判断不正确的是（）（A ）ac < （B ）B ．a b < （C ）a c > （D ）b c <3. 若x ＞y ，则下列不等式中成立的是 ( )（A ） x+a ＜ y+b （B ）ax ＜by （C ）a 2x ＞b 2y （D ）a-x ＜a-y4. 不等式260x ->的解集在数轴上表示正确的是（）5. 如图在数轴上表示某不等式组两个不等式的解集，则该不等式组的解集为（）（A ）x ＜4 （B ）x ＜2 （C ）2＜x ＜4 （D ）x ＞26. 关于x 的不等式2x －a ≤－1的解集如图所示，则a 的取值是（）（A ）0 （B ）－3 （C ）－2 （D ）－17．不等式组221x x -⎧⎨-<⎩≤的整数解共有（）A ．3个B ．4个C ．5个D ．6个8．若不等式组0,122x a x x +⎧⎨->-⎩≥有解，则a 的取值范围是( )(A)a ＞－1 (B)a ≥－1 (C)a ≤1 (D)a ＜1二、填空题9. x 与5的差不小于3，用不等式表示为． .10 . 关于x 的方程x kx 21=-的解为正实数，则k 的取值范围是．11. 当x 时，式子3x -5的值大于5x +3的值.12. 解集在数轴上表示为如图所示的不等式组是．13. 三个连续正整数的和不大于12.这样的正整数有组.14．已知不等式：①1x >，②4x >，③2x <，④21x ->-，从这四个不等式中取两个，构成正整数解是2的不等式组是．（A ）（B ）（C ）（D ） ( 第6题) ( 第1题)图1 图2 ( 第2题) ( 第5题)( 第12题)15、用不等式表示：x 是正数_________；b 不大于3_________；a 的2倍与5的差是非负数______________16、如果a>b ，2a_____2b ；2______2b a ；-2a____-2b. 17、当x____________时,代数式－3x+5的值不大于4．18、如右图所示的不等式的解集表示___________19、当a 时，不等式(a —1)x ＞1的解集是x ＜11-a .20、不等式2x>11x 成立的条件是．21、若| 4x-8 |=8-4x ，则x 的取值范围是______________。

提优试卷七年级上数学答案

#### 一、选择题（每题4分，共20分）1. 答案：C解析：绝对值表示一个数到0的距离，所以|-3| = 3，|5| = 5，|-2| = 2，|-1| = 1。

显然，5是最大的。

2. 答案：B解析：平方根是指一个数的平方等于原数，所以√16 = 4，√25 = 5，√9 = 3，√4 = 2。

显然，5是最大的。

3. 答案：A解析：有理数包括整数和分数，整数包括正整数、0和负整数，分数包括正分数和负分数。

所以，有理数包括正数、0和负数。

4. 答案：D解析：代数式是由数字、字母和运算符号组成的表达式，所以2x + 3是一个代数式。

5. 答案：B解析：算术平方根是指一个数的平方根，所以√(4x^2) = 2x，因为4x^2的平方根是2x。

#### 二、填空题（每题5分，共25分）6. 答案：-1解析：-3的相反数是3，3加上-3等于0。

7. 答案：2解析：-5和5的绝对值都是5，所以-5和5的绝对值的平均数是(5 + 5) / 2= 5。

8. 答案：x^2 - 2x + 1解析：这是一个完全平方公式，即(a - b)^2 = a^2 - 2ab + b^2，这里 a = x，b = 1。

9. 答案：8解析：3的立方是27，2的立方是8，所以3^3 - 2^3 = 27 - 8 = 19。

10. 答案：5解析：|x|表示x的绝对值，所以|x| + |y|表示x和y的绝对值之和，当x = 3，y = 2时，|x| + |y| = |3| + |2| = 3 + 2 = 5。

#### 三、解答题（每题10分，共30分）11. 题目：计算 (-2)^3 - 3 × (-4)^2。

答案：-2^3 - 3 × (-4)^2 = -8 - 3 × 16 = -8 - 48 = -56。

12. 题目：解方程 2(x - 3) = 5。

答案：2(x - 3) = 5，展开得 2x - 6 = 5，移项得 2x = 5 + 6，即 2x = 11，最后除以2得 x = 11 / 2。