西北工业大学机械原理课后答案第3章
机械原理第八版课后练习答案(西工大版)(孙恒等)ppt课件

VC2=0
aC2=0
(2 分)
VC3B=0 ω3=0 akC3C2=0
(3 分)
(b)
(2 分)
(2 分)
VC2=VB+VC2B=VC3+Vc2C3 ω3=ω2=0
(2 分) (1 分)
aB+anC2B+atC2B=aC3+akC2C3+arC2C3 (3 分) (c)
答:
.
(2 分)
VB3=VB2+VB3B2 (2 分)
解:
1> f 3628 2
2> f 3527 1
3> f 3426 1
2-23 图示为一内然机的机构运动简图,试计算自由度 t 并分析组成此机构的基本杆组。如在 该机构中改选 EG 为原动件,试问组成此机构的基本杆组是否与前者有所不同。
解:
f 37210 1
2-21
图示为一收放式折叠支架机构。该支架中的件 1 和 5 分别用木螺钉连接于固定
VC=VB3+VCB3
(2 分)
(1 分) a n B3+a Bt 3=aB2+a B3Bk2+arB3B2 (3 分) 3- 13 试判断在图示的两机构中.B 点足否都存在哥氏加速度?又在何位置哥氏加速度为零?
解 1)图 (a)存在哥氏加速度,图2vB2B3故ω3,vB2B3中只要有一项为零,则哥氏加速度为零。图 (a)中 B 点到达最高和最低点时构件 1,3.4 重合,此时 vB2B3=0,当构件 1 与构件 3 相互垂直.即 _f=;点到达最左及最右位置时ω2=ω3=0.故在此四个位置无哥氏加速度。图 (b)中无论在什 么位置都有ω2=ω3=0,故该机构在任何位置哥矢加速度都为零。
《机械原理》第七版西北工业大学习题答案 特别全答案详解

题 2-8 图示为一刹车机构。刹车时,操作杆 1 向右拉,通过构件 2、3、4、5、6 使两闸瓦刹住车轮。试计 算机构的自由度,并就刹车过程说明此机构自由度的变化情况。(注:车轮不属于刹车机构中的构件。)
解:1)未刹车时,刹车机构的自由度
n 6 pl 8 ph 0
F 3n 2 pl ph 3 6 28 0 2
F 3n 2 pl ph 35 2 7 0 1
所设计的一种假肢膝关节机构,该机构能 为机架,
自由度,并作出大腿弯曲 90 度时的机构
简图。大腿弯曲 90 度时的机构运动简图
题 2-6 试计算如图所示各机构的自由度。图
a、d 为齿轮-连杆组合机构;图 b 为凸轮-连
杆组合机构(图中在 D 处为铰接在 题2-5
移动副。 解法一:
n 13 pl 17 ph 4
虚约束:
因为 AB BC CD AD ,4 和 5,6 和 7、8 和 9 为不影响机构传递运动的重复部分,与连杆 10、
11、12、13 所带入的约束为虚约束。机构可简化为图 2-7(b)
重复部分中的构件数 n 10 低副数 pl 17 高副数 ph 3 局部自由度 F 3
p5 3 p4 1 F 1
5
F 6 mn i mpi F 6 3 3 5 3p5 4 3p4 F 1 i m1
F0 6n ipi F 6 3 5 3 411 2 将平面高副改为空间高副,可消除虚约束。
题 2-10 图示为以内燃机的机构运动简图,试计算自由度,并分析组成此机构的基本杆组。如在该机构中 改选 EG 为原动件,试问组成此机构的基本杆组是否与前者不同。 解:1)计算此机构的自由度
p 2 pl ph 3n 2 17 3 310 3 4 局部自由度 F 4
机械原理第2、3、4、6章课后答案西北工业大学(第七版)

第二章 机构的结构分析题2-11 图a 所示为一简易冲床的初拟设计方案。
设计者的思路是:动力由齿轮1输入,使轴A 连续回转;而固装在轴A 上的凸轮2与杠杆3组成的凸轮机构使冲头4上下运动,以达到冲压的目的。
试绘出其机构运动简图(各尺寸由图上量取),分析是否能实现设计意图,并提出修改方案。
解:1)取比例尺,绘制机构运动简图。
(图2-11a)2)要分析是否能实现设计意图,首先要计算机构的自由度。
尽管此机构有4个活动件,但齿轮1和凸轮2是固装在轴A 上,只能作为一个活动件,故 3=n 3=l p 1=h p01423323=-⨯-⨯=--=h l p p n F原动件数不等于自由度数,此简易冲床不能运动,即不能实现设计意图。
分析:因构件3、4与机架5和运动副B 、C 、D 组成不能运动的刚性桁架。
故需增加构件的自由度。
3)提出修改方案:可以在机构的适当位置增加一个活动构件和一个低副,或用一个高副来代替一个低副。
(1) 在构件3、4之间加一连杆及一个转动副(图2-11b)。
(2) 在构件3、4之间加一滑块及一个移动副(图2-11c)。
(3) 在构件3、4之间加一滚子(局部自由度)及一个平面高副(图2-11d)。
11(c)题2-11(d)5364(a)5325215436426(b)321讨论:增加机构自由度的方法一般是在适当位置上添加一个构件(相当于增加3个自由度)和1个低副(相当于引入2个约束),如图2-1(b )(c )所示,这样就相当于给机构增加了一个自由度。
用一个高副代替一个低副也可以增加机构自由度,如图2-1(d )所示。
题2-12 图a 所示为一小型压力机。
图上,齿轮1与偏心轮1’为同一构件,绕固定轴心O 连续转动。
在齿轮5上开有凸轮轮凹槽,摆杆4上的滚子6嵌在凹槽中,从而使摆杆4绕C 轴上下摆动。
同时,又通过偏心轮1’、连杆2、滑杆3使C 轴上下移动。
最后通过在摆杆4的叉槽中的滑块7和铰链G 使冲头8实现冲压运动。
机械原理孙恒西北工业大学版第3章11844

例 2 凸轮机构,求从动件3的移动速度υ ∵ 过高副元素的接触点K作公法线nn ,则
nn 与瞬心连线P12P13的交点即为瞬心P23, 即P23为2、3两构件的等速重合点。
④当已知构件上两点的速度时,则该构件上其 它任一点的速度便可用速度影像原理求出。
注意构件ω方向的求法:
大小:ω=VCB / lBC 方向:将代表VCB矢量的bc移至机构图
的C点,根据VCB的方向可知ω 为逆时针方向。
2)加速度分析
加速度关系中也存在和速度影像原理一致的加速 度影像原理。
1.2 两构件重合点间的速度和加速度 分析
⑤矢量的点积
e1 e2 cos12 cos( 2 1 )
e i ei cos
e j e j sin
2
ee e 1
⑥其它基本关系
eet 0 e en 1
e1 e2t sin( 2 1 )
e1 e2 n cos( 2 1 )
2.平面机构运动分析----解析法
三、瞬心位置的确定 * 如果两构件通过运动副连接在一起,瞬心 位置很容易直接观察确定。(图3-2) * 两构件不直接接触,则它们的瞬心位置要 借助于“三心定理” (图3-3)
转动副: 移动副:
转动中心 垂直导路 无穷远处
作纯滚动: 在接触点
既滚动且滑动:
在过接触点的 公发线上
四、速度瞬心在机构速度分析中的应用
i cos 90 j sin 90 e 90
en
( et
) e
d 2e
机械原理第八版课后练习答案(西工大版)(孙恒等)

解:
1> 2>
f 3 6 2 8 2 f 3 5 2 7 1
f 3 4 2 6 1 3> 2-23 图示为一内然机的机构运动简图,试计算自由度 t 并分析组成此机构的基本杆组。如在 该机构中改选 EG 为原动件,试问组成此机构的基本杆组是否与前者有所不同。
解:(1) n=11, p1=17, ph=0, p`=2p1`+ph-3n`=2, F`=0 F=3n-(2p1+ph-p`)-F`=3×11-(2×17+0-2)-0=1 (2) 去掉虚约束后 F=3n-(2pl+ph) =3×5-(2×7+0) =1 (d)A、B、C 处为复合铰链。自由度为:F=3n-(2p1+ph-p`)-F`=3×6-(2×7+3)-0=1
3) ω1/ω3= P36P13/P16P13=DK/AK 由构件 1、3 在 K 点的速度方向相同,可知ω3 与ω1 同向。 3-6 在图示的四杆机构中, LAB=60mm, LCD=90mm,LAD=LBC=120mm, ω2=10rad/s,试用瞬心法求: 1)当φ=165°时,点的速度 vc; 2)当φ=165°时,构件 3 的 BC 线上速度最小的一点 E 的位置及速度的大小; 3)当 VC=0 时,φ角之值(有两个解)。
1)图 (a)存在哥氏加速度,图 (b)不存在。 (2)由于 akB2B3==2ω2vB2B3 故ω3,vB2B3 中只要有一项为零,则哥氏加速度为零。图 (a)中 B 点到达最高和最低点时构件 1,3.4 重合,此时 vB2B3=0,当构件 1 与构件 3 相互垂直.即 _f=;点到达最左及最右位置时ω2=ω3=0.故在此四个位置无哥氏加速度。图 (b)中无论在什 么位置都有ω2=ω3=0,故该机构在任何位置哥矢加速度都为零。 (3)对。因为ω3≡ω2。 3-14 在图示的摇块机构中,已知 lAB=30mm,lAC=100mm,lBD=50 mm,lDE=40 mm,曲柄以等 角速度ωl=40rad/S 回转,试用图解法求机构在φ1=45º位置时,点 D 及 E 的速度和加速度, 以及构件 2 的角速度和角加速度。 解 (1)以μl 作机构运动简图 (a)所示。 (2)速度分析: 以 C 为重合点,有 vC2 = vB + vC2B = vC3 + vC2C3 大小 ?ω1lAB ? 0 ’ 方向 ? ┴AB ┴BC //BC 以μl 作速度多边形图 (b),再根据速度影像原理,作△bde∽/△BDE 求得 d 及 e,由图可得 vD=μvpd=0.23 m/s vE=μvpe=0.173m/s ω2=μvbc2/lBC=2 rad/s(顺时针) 解 (3)加速度分析: 以 C 为重合点,有 aC2 == aB + anC2B + atC2B == aC3 + akC2C3 + arC2C3 0 2ω3vC2C3 ? 大小 ω12lAB ω22lBC ? B—A C—B ┴BC ┴BC //BC 方向 其中 anC2B=ω22lBC=0.49 m/s2,akC2C3=2ω3vC2C3=0.7m/s2,以μa 作加速度多边形如图 (c) 所示,由图可得
机械原理第三章习题答案
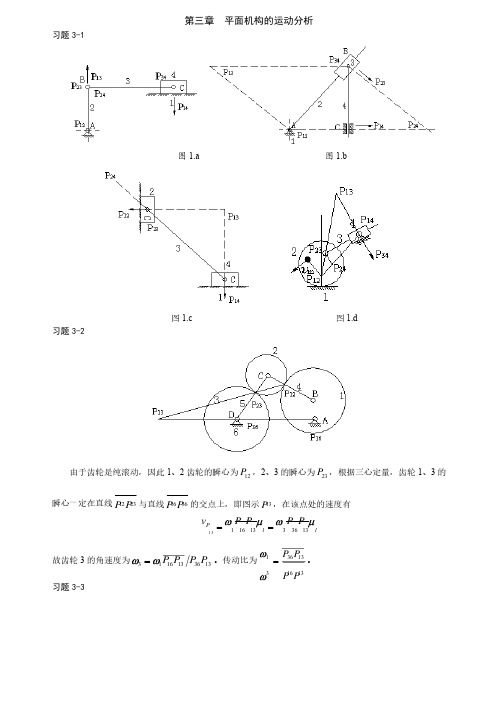
第三章平面机构的运动分析习题3-1 图1.a 图1.b 图1.c 图1.d 习题3-2 由于齿轮是纯滚动,因此1、2齿轮的瞬心为12P ,2、3的瞬心为23P ,根据三心定量,齿轮1、3的瞬心一定在直线2312P P与直线3616P P 的交点上,即图示13P ,在该点处的速度有ll P PP P P P v m w m w 133631316113==故齿轮3的角速度为1336131613P P P P w w =。
传动比为1316133631P P P P =w w 。
习题3-3答:1)三个瞬心中,14P、12P 为绝对瞬心,24P 为相对瞬心。
2)不利用其它的三个瞬心,因为它们全是相对瞬心。
3)构件2和4之间的转向关系可以根据瞬心24P 的瞬时绝对速度方向判断。
的瞬时绝对速度方向判断。
习题3-4取比例尺为mmm l 003.0=m ,作图如下,作图如下1) 由图上可知:l l P P P P P v m w m w 241442412224==,根据量得的长度,得,根据量得的长度,得s rad P P P P/455.414.72/14.32102414241224=´==w w 可计算出C 点的速度为:s m CD v l C /4.0003.030455.44=´´==m w2) 构件1、3的瞬心在点13P 处,且为绝对瞬心,因此构件3的角速度为的角速度为()s rad C P v l c /53.2)67.52003.0/(4.0133=´==mw 显然构件3上速度最小点在E 点,则其速度为点,则其速度为s m EP v l E /36.0003.04.4753.2133=´´==mw 3) 要使0=C v ,需瞬心12P 、24P 重合(如图),两位置分别为0126'=Ð=DAB j ,02227''=Ð=DAB j 。
机械原理第七版西北工业大学课后习题答(1-8章)
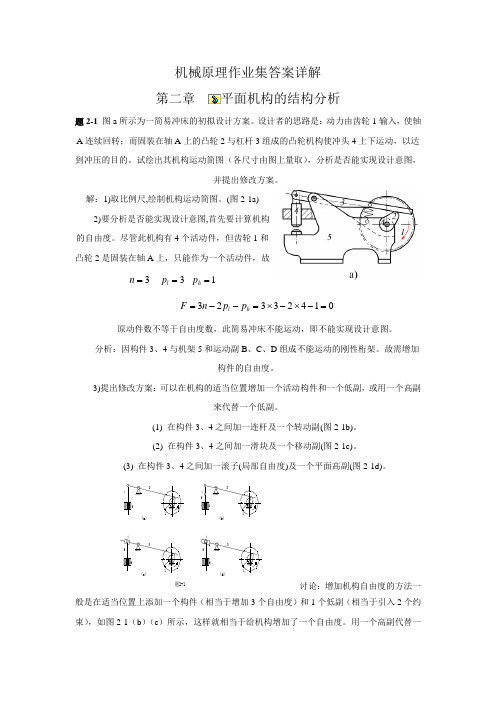
机械原理作业集答案详解 第二章平面机构的结构分析题2-1 图a 所示为一简易冲床的初拟设计方案。
设计者的思路是:动力由齿轮1输入,使轴A 连续回转;而固装在轴A 上的凸轮2与杠杆3组成的凸轮机构使冲头4上下运动,以达到冲压的目的。
试绘出其机构运动简图(各尺寸由图上量取),分析是否能实现设计意图,并提出修改方案。
解:1)取比例尺,绘制机构运动简图。
(图2-1a) 2)要分析是否能实现设计意图,首先要计算机构的自由度。
尽管此机构有4个活动件,但齿轮1和凸轮2是固装在轴A 上,只能作为一个活动件,故3=n 3=l p 1=h p01423323=-⨯-⨯=--=h l p p n F原动件数不等于自由度数,此简易冲床不能运动,即不能实现设计意图。
分析:因构件3、4与机架5和运动副B 、C 、D 组成不能运动的刚性桁架。
故需增加构件的自由度。
3)提出修改方案:可以在机构的适当位置增加一个活动构件和一个低副,或用一个高副来代替一个低副。
(1) 在构件3、4之间加一连杆及一个转动副(图2-1b)。
(2) 在构件3、4之间加一滑块及一个移动副(图2-1c)。
(3) 在构件3、4之间加一滚子(局部自由度)及一个平面高副(图2-1d)。
11(c)题2-1(d)54364(a)5325215436426(b)321讨论:增加机构自由度的方法一般是在适当位置上添加一个构件(相当于增加3个自由度)和1个低副(相当于引入2个约束),如图2-1(b )(c )所示,这样就相当于给机构增加了一个自由度。
用一个高副代替一个低副也可以增加机构自由度,如图2-1(d )所示。
题2-2 图a 所示为一小型压力机。
图上,齿轮1与偏心轮1’为同一构件,绕固定轴心O 连续转动。
在齿轮5上开有凸轮轮凹槽,摆杆4上的滚子6嵌在凹槽中,从而使摆杆4绕C 轴上下摆动。
同时,又通过偏心轮1’、连杆2、滑杆3使C 轴上下移动。
最后通过在摆杆4的叉槽中的滑块7和铰链G 使冲头8实现冲压运动。
机械原理_课后习题答案免费(全面)高教版 西北工大

2) 求vC2
v C 2 = v B + v C 2 B = v C 3 + vC 2 C 3
方向: 大小: ⊥AB
√
⊥BC ?
0 0
∥BC ?
取
μv = 0.005
m/s mm
作速度图
b
题3-10 解(续2)
[解] (2)速度分析
v B → vC 2 → v D , v E → ω 2
1) 求vB 2) 求vC2 3) 求vD 和求vE 用速度影像法
C
E
vC = v B + vCB v D = v B + v DB
(2) 求vE
D p(a, f )
v E = vC + v EC = v D + v ED
b d e c
题3-5 解
b) 解: 顺序 (1) 求vC
v B → vC → v E → v F
D B vB A E G F C
vC = v B + vCB
√
0 0
∥CD ?
b2 (b1) (b3)
其中 a B3B2 = 2ω2 v B3B2 = 0(∵ v B3B2 = 0)
a B1 ⎛ m / s 2 ⎞ 取 μa = ⎜ ⎟ 作加速度图 p ' b '1 ⎝ mm ⎠
题3-8 c) 解(续2)
[解] (3)加速度分析 a B 2 ( = a B1 ) → a B 3 → a C 3 1) 求aB2 A 1 ω1 2) 求aB3
取
√ v ⎛m/s⎞ μ v = B1 ⎜ ⎟ 作速度图 pb1 ⎝ mm ⎠
3) 求vC3 : 用速度影像法
v C 3 = 0 同时可求得 ω3 =
西北工业大学机械原理课后答案第3章

O OO OP 2P 3F 23(P 24Pl 3(P 34)(a)(b)Pl 3Pl 6A 1题3-6在图a 所示的四杆机构中,第三章平面机构的运动分析题3-3试求图示各机构在图示位置时全部瞬心的位置(用符号P j 直接标注在图上)解:题3-4在图示在齿轮-连杆机构中,试用瞬心法求齿轮1与齿轮3的传动比w1/w3.C 2P 12P 23St -解:1)计算此机构所有瞬心的数目K N (N1)2152) 为求传动比 < 3需求出如下三个瞬心 R 6、P 36、P 13如图3-2所示。
; 1 巳6只33) 传动比 仁3计算公式为: —3P 16P 13I AB =60mm , l cD =90mm , l AD =|Bc =120mm , w 2=10rad/s ,试用瞬心P134 C 4L CP 12AM B3P iP 34CBMF 24F 34P ?4(d)Pl 4法求:V B3I AB2IAB lBPI32.56rad sV ClCR 3 3 0.4m s量得 1 26.42 226.6P 3434B P 233 22A ,D- i Pl4P 12 1(a)P 131) 当0 =165。
时,点C 的速度Vc ;2) 当$ =165。
时,构件3的BC 线上速度最小的一点 E 的位置及速度的大小; 3) 当Vc=O 时,0角之值(有两个解)解:1)以选定比例尺,绘制机构运动简图。
(图3-3 )2)求V c ,定出瞬心P 13的位置。
如图 3-3 (a )3)定出构件3的BC 线上速度最小的点 E 的位置。
因为BC 线上速度最小的点必与 P 13点的距离最近,所以过 P 13点引BC 线延长线的垂线交于 E 点。
如图3-3 (a )v E1ER 3 3 0.375ms4)当V C 0时,P 13与C 点重合,即AB 与BC 共线有两个位置。
作出 V C 0的两个位置。
题3-12在图示的各机构中,设已知各构件的尺寸、原动件 1以等角速度3 1顺时针方向转动。
西工大版机械原理第3章

1 2
1
2 A(A1A2)
VA2、VA1为两构件上A点的绝对速度,VA2A1为相对速度
VA2A1方向为平行于导路方向。
(2)加速度分析
r aA2 aA1 ak a A2 A1 A2 A1
1 2
aA2、aA1为两构件上A点的绝对加速度
科氏加速度: a k A2 A1 21VA2 A1, 方向为将相对速度VA2 A1沿1转过90
大小 方向
? ⊥C P14 ?
?
⊥AB ⊥BC
vS 4 vC vS 4C vE vS 4 E
vS 4 vB vCB vS 4C vE vS 4 E
大小 方向
(1)用瞬心法确定C点方向
⊥AB
?
⊥CB
?
⊥SE
借助速度瞬心法
VC ?
= VB
+ VCB
P36 E • C G 3 5 A D 2 1 4 F B 6 即:VS3 = VB
vK 3 vK 2 2lOK
(2)用影像原理求vB
⊥OK
vC vB vCB
vB v pb
vC v pc 6 lCD lCD
例 3 – 3 图示为6杆(Ⅲ级)机构,已知2 ,作速度多边形
d
c p
b (2)利用特殊点S减少未知量
S
p14
e
vC vB vCB
n t k r aB3 aB 3 aB3 aB2 aB3B2 aB3B2
大小: 方向:
2 3 lBC
?
⊥BC
2 1 l AB
23VB3B 2
?
' ' b( ) 2 b1
西北工业大学机械原理课后答案第3章1
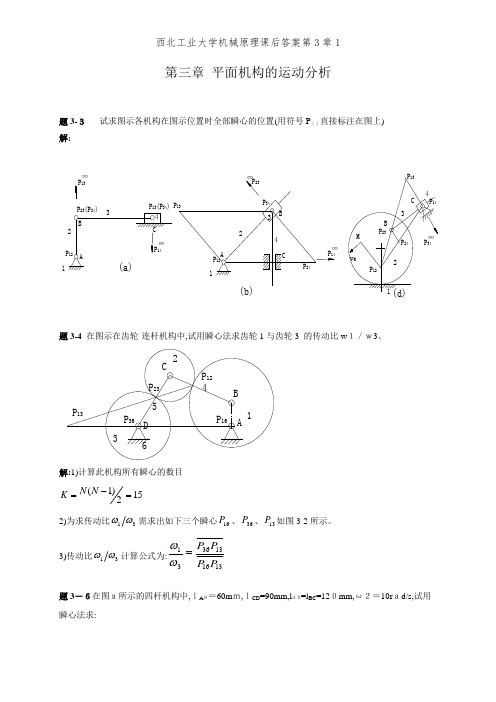
第三章 平面机构的运动分析题3-3 试求图示各机构在图示位置时全部瞬心的位置(用符号P ij直接标注在图上) 解:1P 13(P 34)13∞题3-4 在图示在齿轮-连杆机构中,试用瞬心法求齿轮1与齿轮3 的传动比w 1/w3、P 13P 23P 363D 652C 4B P 16A 1P 12解:1)计算此机构所有瞬心的数目152)1(=-=N N K2)为求传动比31ωω需求出如下三个瞬心16P 、36P 、13P 如图3-2所示。
3)传动比31ωω计算公式为:1316133631P P P P =ωω题3-6在图a所示的四杆机构中,lA B=60m m,lCD =90mm,l AD=l BC =120mm,ω2=10r ad/s,试用瞬心法求:231) 当φ=165°时,点C 的速度Vc;2) 当φ=165°时,构件3的BC 线上速度最小的一点E 的位置及速度的大小; 3) 当Vc=0时,φ角之值(有两个解)解:1) 以选定比例尺,绘制机构运动简图。
(图3-3 ) 2)求V C ,定出瞬心P13的位置。
如图3-3(a)s rad BP ll v l AB AB B 56.21323===μωω s m CP v l C 4.0313==ωμ 3)定出构件3的BC 线上速度最小的点E 的位置。
因为BC 线上速度最小的点必与P 13点的距离最近,所以过P 13点引BC 线延长线的垂线交于E 点。
如图3-3(a)s m EP v l E 375.0313==ωμ4)当0=C v 时,P 13与C点重合,即AB 与BC 共线有两个位置。
作出0=C v 的两个位置。
量得 ︒=4.261φ ︒=6.2262φ题3-12 在图示的各机构中,设已知各构件的尺寸、原动件1以等角速度ω1顺时针方向转动。
试用图解法求机构在图示位置时构件3上C 点的速度及加速度。
解:a)速度方程:32233C C C B C B C v v v v v +=+=加速度方程:r C C k C C C t B C n B C B t C nC a a a a a a a a 232323333++=++=+b) 速度方程:2323B B B B v v v +=加速度方程:r B B K B B B t B nB a a a a a 2323233++=+c) 速度方程:2323B B B B v v v +=加速度方程:r B B K B B B t B nB a a a a a 2323233++=+题3-14 在图示的摇块机构中,已知l AB =30mm,l AC=100mm,lBD =50mm,lDE =40mm 。
机械原理第八版课后练习答案(西工大版)(孙恒等)

解:(1) n=11, p1=17, ph=0, p`=2p1`+ph-3n`=2, F`=0 F=3n-(2p1+ph-p`)-F`=3×11-(2×17+0-2)-0=1 (2) 去掉虚约束后 F=3n-(2pl+ph) =3×5-(2×7+0) =1 (d)A、B、C 处为复合铰链。自由度为:F=3n-(2p1+ph-p`)-F`=3×6-(2×7+3)-0=1
(3 分)
3-8 机构中,设已知构件的尺寸及点 B 的速度 vB(即速度矢量 pb),试作出 各机构在图示位置时的速度多边形。
答:
(10 分) (b)
答:
答:
3—11 速度多边形和加速度多边彤有哪些特性?试标出图中的方向。 答 速度多边形和加速度多边形特性参见下图,各速度方向在图中用箭头标出。
3-12 在图示的机构中,设已知构件的尺寸及原动件 1 的角速度ω1 (顺时针),试用图解法求机 构在图示位置时 C 点的速度和加速度。 (a)
齿轮 3、5 和齿条 7 与齿轮 5 的啮合高副所提供的约束数目不同,因为齿轮 3、5 处只有一个 高副,而齿条 7 与齿轮 5 在齿的两侧面均保持接触,故为两个高副。 2-13 图示为一新型偏心轮滑阎式真空泵。其偏心轮 1 绕固定轴心 A 转动,与外环 2 固连在一 起的滑阀 3 在可绕固定轴心 C 转动的圆柱 4 中滑动。当偏心轮按图示方向连续回转时可将设 备中的空气吸入,并将空气从阀 5 中排出,从而形成真空。(1)试绘制其机构运动简图;(2) 计算其自由度。
解:
1> 2>
f 3628 2 f 3527 1
f 3426 1 3> 2-23 图示为一内然机的机构运动简图,试计算自由度 t 并分析组成此机构的基本杆组。如在 该机构中改选 EG 为原动件,试问组成此机构的基本杆组是否与前者有所不同。
西北工业大学机械原理习题答案

2-3在图a所示的四杆机构中,lAB=60mm,lCD=90mm,lAD=lBC=120mm,ω2=10rad/s,试用瞬心法求:
1)当φ=165°时,点C的速度vC;
2)当φ=165°时,构件3的BC线上速度最小的一点E的位置及速度的大小;
何进一步的认识?
1—4图a所示为一具有急回作用的冲床。图中绕固定轴心A转动的菱形盘1为原动件,其与滑块2在B点铰接,通过滑块2推动拨叉3绕固定轴心C转动,而拨叉3与圆盘4为同一构件。当圆盘4转动时,通过连杆5使冲头6实现冲压运动。试绘制其机构运动简图,并计算自由度。
解:1)选取适当比例尺μl,绘制机构运动简图(见图b)
10.平面机构是指组成机构的各个构件均在同一个平面上运动。
11.在平面机构中,平面低副提供2个约束,平面高副提供1个约束。
12.机构具有确定运动时所必须给定的独立运动参数的数目称为机构的自由度。
13.机构具有确定运动的条件是机构的原动件数目应等于机构的自由度的数目。
1—2试画出图示平面机构的机构示意图,并计算自由度(步骤:1)列出完整公式,2)带入数据,3)写出结果)。其中:
解:自由度计算:画出机构示意图:
n=3
pL=4pH=0
p'=0F'=0
F=3n-(2pl+ph-p′)-F′
=3×3-(2×4+0-0)-0
=1
1—3 试绘出图a)所示偏心回转油泵机构的运动简图(各部分尺寸由图中直接量取)。图中偏心轮1绕固定轴心A转动,外环2上的叶片a在可绕轴心c转动的圆柱3中滑动,将低压油从右湍吸入,高压油从左端排出。
2)分析是否能实现设计意图
n=3
西北工业大学机械原理课后答案第3章

西北工业大学机械原理课后答案第3章第3章课后习题参考答案3—1 何谓速度瞬心?相对瞬心与绝对瞬心有何异同点?答:参考教材30~31页。
3—2 何谓三心定理?何种情况下的瞬心需用三心定理来确定?答:参考教材31页。
3-3试求图示各机构在图示位置时全部瞬心的位置(用符号P,,直接标注在图上)(a)(b) 答:答:(10分)(d)(10分)3-4标出图示的齿轮一连杆组合机构中所有瞬心,并用瞬心法求齿轮1与齿轮3的传动比ω1/ω3。
(2答:1)瞬新的数目:K=N(N-1)/2=6(6-1)/2=152)为求ω1/ω3需求3个瞬心P16、P36、P13的位置3)ω1/ω3= P36P13/P16P13=DK/AK由构件1、3在K点的速度方向相同,可知ω3与ω1同向。
3-6在图示的四杆机构中,L AB=60mm,L CD=90mm,L AD=L BC=120mm, ω2=10rad/s,试用瞬心法求:1)当φ=165°时,点的速度vc;2)当φ=165°时,构件3的BC线上速度最小的一点E的位置及速度的大小;3)当V C=0时,φ角之值(有两个解)。
解:1)以选定的比例尺μ机械运动简图(图b)2)求vc定出瞬心p12的位置(图b)因p13为构件3的绝对瞬心,则有ω3=v B/lBp13=ω2l AB/μl.Bp13=10×0.06/0.003×78=2.56(rad/s)v c=μc p13ω3=0.003×52×2.56=0.4(m/s)(3(33)定出构件3的BC线上速度最小的点E的位置,因BC线上速度最小的点必与p13点的距离最近,故丛p13引BC线的垂线交于点E,由图可得v E=μl.p13Eω3=0.003×46.5×2.56=0.357(m/s) 4)定出vc=0时机构的两个位置(图c)量出φ1=26.4°φ2=226.6°3-8机构中,设已知构件的尺寸及点B的速度v B(即速度矢量pb),试作出各机构在图示位置时的速度多边形。
机械原理第八版课后练习答案(西工大版)(孙恒等)

解:1)以选定的比例尺μ机械运动简图(图 b) 2)求 vc 定出瞬心 p12 的位置(图 b) 因 p13为构件 3 的绝对瞬心,则有 ω3=vB/lBp13=ω2lAB/μl.Bp13=10×0.06/0.003×78=2.56(rad/s) vc=μcp13ω3=0.003×52×2.56=0.4(m/s)
(3 分)
3-8 机构中,设已知构件的尺寸及点 B 的速度 vB(即速度矢量 pb),试作出 各机构在图示位置时的速度多边形。
答:
(10 分) (b)
答:
答:
3—11 速度多边形和加速度多边彤有哪些特性?试标出图中的方向。 答 速度多边形和加速度多边形特性参见下图,各速度方向在图中用箭头标出。
3-12 在图示的机构中,设已知构件的尺寸及原动件 1 的角速度ω1 (顺时针),试用图解法求机 构在图示位置时 C 点的速度和加速度。 (a)
解:
f 33241 0不合理
∵ f 0,可改为
2-12 图示机构为一凸轮齿轮连杆组合机构,试绘制其机构示意简图并计算自由度。
解:
f 38210211
2-16 试计算图示凸轮-连杆组合机构的自由度 (a)
解: (b)
f 342511
A 为复合铰链
解:(1) 图示机构在 D 处的结构与图 2-1 所示者一致,经分析知该机构共有 7 个活动构件, 8 个低副(注意移动副 F 与 F’,E 与 E’均只算作一个移动副),2 个高副;因有两个滚子 2、4, 所以有两个局部自由度,没有虚约束,故机构的自由度为 F=3n- (2pl+ph- p’)- F’=3ⅹ7- (2ⅹ8+2-0)- 2=1 (2)如将 D 处结构改为如图 b 所示形式,即仅由两个移动副组成。注意,此时在该处 将带来一个虚约束。因为构件 3、6 和构件 5、6 均组成移动副,均要限制构件 6 在图纸平面 内转动,这两者是重复的,故其中有一个为虚约束。经分析知这时机构的活动构件数为 6, 低副数为 7,高副数和局部自由度数均为 2,虚约束数为 1,故机构的自由度为 F=3n- (2pl+ph- p’)- F’ =3×6- (2ⅹ7+2-1)- 2=1 上述两种结构的机构虽然自由度均为一,但在性能上却各有千秋:前者的结构较复杂,但没 有虚约束,在运动中不易产生卡涩现象;后者则相反,由于有一个虚约束,假如不能保证在 运动过程中构件 3、5 始终垂直,在运动中就会出现卡涩甚至卡死现象,故其对制造精度要求 较高。 (c)
机械原理课后答案3章
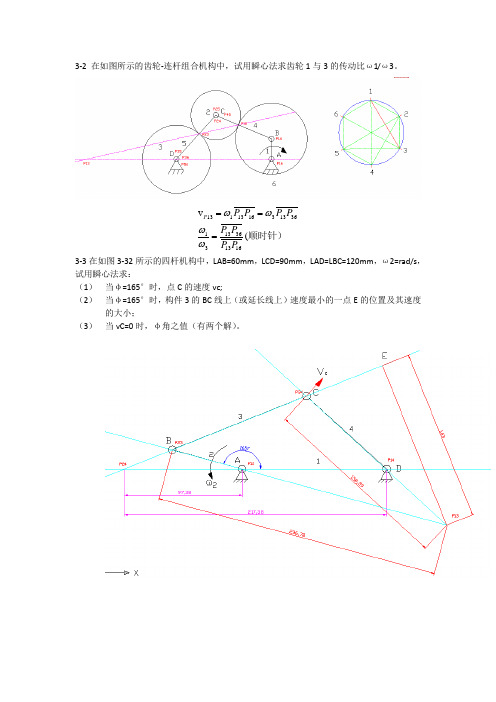
3-2 在如图所示的齿轮-连杆组合机构中,试用瞬心法求齿轮1与3的传动比ω1/ω3。
顺时针)(v 1613361331361331613113P P P PP P P P P ===ωωωω3-3在如图3-32所示的四杆机构中,LAB=60mm ,LCD=90mm ,LAD=LBC=120mm ,ω2=rad/s ,试用瞬心法求:(1) 当φ=165°时,点C 的速度vc;(2) 当φ=165°时,构件3的BC 线上(或延长线上)速度最小的一点E 的位置及其速度的大小;(3) 当vC=0时,φ角之值(有两个解)。
sm EP P P v P P v s m v s rad P P P P P P P P E C C CD C P /36.0143.055.2v (rad/s 55.2158.0403.0/403.009.048.4(/48.438.21738.9710v 133133431334341424122424142441224224=⨯=======⨯=⨯==⨯====ωωωωωωωω顺时针)顺时针)3-4在如图3-33所示的凸轮机构中,已知r=50mm ,LOA=30mm ,LAC=90mm ,φ1=90°,凸轮1以角速度ω1=10rad/s 逆时针转动。
试用瞬心法求从动件的角速度ω2。
顺时针)(/79.286.12486.3410v 2312131212231221312112s rad P P P P P P P P P =⨯====ωωωω 3-5在如图3-34所示的各机构中,已知各构件的尺寸及B 点的速度vB ,试作出其如图3-34所示位置时的速度多边形。
3-6在如图3-35所示的各机构中,已知各构件的尺寸,原动件1以等角速度ω1顺时针方向转动,试以图解法求机构在如图3-35所示位置时构件3上C 点的速度及角速度。
3-8A BCDEbk ec3。
机械原理第八版课后练习答案(西工大版)(孙恒等)

2-11 图示为一简易冲床的初拟设计方案。设计者的思路是:动力由齿轮 j 输入,使轴 A 连续 回转;而固装在轴^上的凸轮 2 与杠杆 3 组成的凸轮机构使冲头 4 上下运动,以达到冲压的目 的。试绘出其机构运动简图(各尺寸由图上量取),分析是否能实现设计意图,并提出修改方 案。
(3)对。因为ω3≡ω2。
3-14 在图示的摇块机构中,已知 lAB=30mm,lAC=100mm,lBD=50 mωl=40rad/S 回转,试用图解法求机构在φ1=45º位置时,点 D 及 E 的速度和加速度, 以及构件 2 的角速度和角加速度。
解 (1)以μl作机构运动简图 (a)所示。
解:1)以选定的比例尺μ机械运动简图(图 b) 2)求 vc 定出瞬心 p12 的位置(图 b) 因 p13为构件 3 的绝对瞬心,则有 ω3=vB/lBp13=ω2lAB/μl.Bp13=10×0.06/0.003×78=2.56(rad/s) vc=μcp13ω3=0.003×52×2.56=0.4(m/s)
VC2=0
aC2=0
(2 分)
VC3B=0 ω3=0
a kC3C2=0
(3 分)
(b)
答:
(2 分)
(2 分)
VC2=VB+VC2B=VC3+Vc2C3 ω3=ω2=0
(2 分) (1 分)
aB+anC2B+atC2B=aC3+akC2C3+arC2C3 (3 分) (c)
答:
(2 分)
VB3=VB2+VB3B2 (2 分)
3)定出构件 3 的 BC 线上速度最小的 点 E 的 位置,因 BC 线上速度最小的点必与 p13 点的距离 (3 分) 最近,故丛 p13 引 BC 线的垂线交于点 E,由图可得
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
答:
(1分) (1分)
Vc3=VB+VC3B=VC2+VC3C2(2分)
aC3=aB+anC3B+atC3B=aC2+akC3C2+arC3C2(3分)
VC2=0 aC2=0(2分)
VC3B=0 ω3=0 akC3C2=0(3分)
(b)
答:
(2分)
(2分)
VC2=VB+VC2B=VC3+Vc2C3(2分)
解:(1)以μl作机构运动简图如(a)所示。
(2)速度分斫:
此齿轮连杆机构可看作,ABCD受DCEF两个机构串联而成,则可写出:
vC=vB+vCB
vE=vC+vEC
以μv作速度多边形如图(b)所示.由图得
vE=μvpe m/S
取齿轮3与齿轮4的啮合点为k,根据速度影像原理,作△dck∽△DCK求得k点。然后分别以c,e为圆心,以ck.ek为半径作圆得圆g3和圆g4。圆g3代表齿轮3的速度影像,圆g4代表齿轮4的速度影像。
解1)以μl作机构运动简图.如图(a)。
2)利用瞬心多边形图(b)依次定出瞬心P36,P13.P15
vC=vP15=ω1AP15μl=1.24 m/S
3 -19图示齿轮一连杆组合机构中,MM为固定齿条,齿轮3的直径为齿轮4的2倍.设已知原动件1以等角速度ω1顺时针方向回转,试以图解法求机构在图示位置时E点的速度vE以及齿轮3,4的速度影像。
aD=μap`d`=0.6 4m/S2
aE=μap`e`=2.8m/s2
α2=atC2B/lBC=μan`2C`2/lBC=8.36rad/s2(顺时针) i
3- l5在图(a)示的机构中,已知lAE=70 mm,;lAB=40mm,lEF=60mm,
lDE==35 mm,lCD=75mm,lBC=50mm.原动件以等角速度ω1=10rad/s回转.试以图解法求机构在φ1=50。位置时.点C的速度Vc和加速度ac
(2)速度分析:
以C为重合点,有
vC2= vB+ vC2B= vC3+ vC2C3
大小?ω1lAB? 0’
方向? ┴AB ┴BC //BC
以μl作速度多边形图(b),再根据速度影像原理,作△bde∽/△BDE求得d及e,由图可得
vD=μvpd=0.23 m/s
vE=μvpe=0.173m/s
ω2=μvbc2/lBC=2 rad/s(顺时针)
继续作图。则矢量p`d5就代表了aE5。再利用加速度影像求得g’。
aG=μap`g`=0.53 m/S2
解:(1)以μl作机构运动简图(a)。
在图作出齿条2与齿轮3啮合摆动时占据的两个极限位置C’,C”可知摆程角φ如图所示:
(2)速度分析:
将构件6扩大到B点,以B为重合点,有
vB6= vB2+ vB6B2
大小?ω1lAB?
方向┴BD ┴AB∥BC
vB2=ωllAB= 0.01 8 m/s
以μv作速度多边形图(b),有
第3章课后习题参考答案
3—1何谓速度瞬心?相对瞬心与绝对瞬心有何异同点?
答:参考教材30~31页。
3—2何谓三心定理?何种情况下的瞬心需用三心定理来确定?
答:参考教材31页。
3-3试求图示各机构在图示位置时全部瞬心的位置(用符号P,,直接标注在图上)
(a)
(b)
答:
答:
(10分)
(d)
(10分)
3-4标出图示的齿轮一连杆组合机构中所有瞬心,并用瞬心法求齿轮1与齿轮3的传动比ω1/ω3。
提示:可先将机构进行高副低代,然后对其替代机构进行运动分析。
解(1)以μl作机构运动简图如图(a)所示。
(2)速度分析:先将机构进行高副低代,其替代机构如图(a)所示,并以B为重合点。有
VB2= vB4+ vB2B4
大小?ω1lAB?
方向┴ BD ┴ AB //|CD
以μv=0.005 rn/s2作速度多边形图如图(b),由图可得
vc=μcp13ω3=0.003×52×2.56=0.4(m/s)
3)定出构件3的BC线上速度最小的点E的位置,因BC线上速度最小的点必与p13点的距离最近,故丛p13引BC线的垂线交于点E,由图可得
vE=μl.p13Eω3=0.003×46.5×2.56=0.357(m/s)
4)定出vc=0时机构的两个位置(图c)量出
大小?ω12lABω22lBC?
方向//AC B-A C-B ┴BC
其中anB2=ω12lAB=0.8 m/s2
anC2B2=ωanC2B2=0.02 m/S2
以μa=0,01(rn/s2)/mm作加速度多边形图(c),再利用加速度影像求得e`2。然后利用重合点E建立方程
anE5十atE5=aE4+பைடு நூலகம்kE5E4+arE5E4
α= atB2/lBD=μan`2b`2/lBD=9.143 rad/s2:(顺时针)
3-18在图(a)所示的牛头刨机构中.lAB=200 mnl,lCD=960 mm,lDE=160 mm,设曲柄以等角速度ω1=5 rad/s.逆时针方向回转.试以图解法求机构在φ1=135º位置时.刨头点的速度vC。
ω3=ω2=0(1分)
aB+anC2B+atC2B=aC3+akC2C3+arC2C3(3分)
(c)
答:
(2分)
VB3=VB2+VB3B2(2分)
VC=VB3+VCB3(2分)
(1分)
anB3+atB3=aB2+akB3B2+arB3B2(3分)
3- 13试判断在图示的两机构中.B点足否都存在哥氏加速度?又在何位置哥氏加速度为零?怍出相应的机构位置图。并思考下列问题。
以μa作加速度多边形图(c),得f`4(f`5)点,再利用加速度影像求得b`及d’点。
根据aC=aB+anCB+atCB=aD+anCD+atCD
继续作图,则矢量p` c`就代表了aC.则求得
vC=μvpc=0.69 m/s
aC=μapc=3m/s2
3-16在图示凸轮机构中,已知凸轮1以等角速度ω1=10 rad/s转动,凸轮为一偏心圆,其半径R=25 mm,lAB=15mm.lAD=50 mm,φ1=90º,试用图解法求构件2的角速度ω2与角加速度α2。
ω2=ω6=vB6/lBD=μvpb6/μlBD=0.059rad/s(逆时针)
vB2B6=μvb2b6=0.018 45 rn/s
(3)加速度分析:
aB5= anB6+ atB6= anB2+ akB6B2+ arB6B2
大小ω26lBD?ω12lAB2ω2vB6B2?
方向B-D ┴BD B-A ┴BC∥BC
(3)加速度分析:
以C为重合点,有
aC2== aB+ anC2B+ atC2B== aC3+ akC2C3+ arC2C3
大小ω12lABω22lBC? 0 2ω3vC2C3?
方向B—A C—B ┴BC ┴BC //BC
其中anC2B=ω22lBC=0.49 m/s2,akC2C3=2ω3vC2C3=0.7m/s2,以μa作加速度多边形如图(c)所示,由图可得
以E为重合点vE5=vE4+vE5E4
大小? √ ?
方向┴EF√//EF
继续作图求得vE5,再根据速度影像原理,求得
vG=μvpg=0.077 m/ s
ω5=μvpg/lFG=0.86 rad/s(逆时针)
vE5E4=μve5e4=0.165 rn/s
(3)加速度分析:
aC2= anB2+ anC2B2+ atC2B2
(3)对。因为ω3≡ω2。
3-14在图示的摇块机构中,已知lAB=30mm,lAC=100mm,lBD=50 mm,lDE=40 mm,曲柄以等角速度ωl=40rad/S回转,试用图解法求机构在φ1=45º位置时,点D及E的速度和加速度,以及构件2的角速度和角加速度。
解(1)以μl作机构运动简图(a)所示。
解:1)速度分析:以F为重合点.有
vF4=vF5=vF1+vF5F1
以μl作速度多边形图如图(b)得,f4(f5)点,再利用速度影像求得b及d点
根据vC=vB+vCB=vD+vCD继续作速度图,矢量pc就代表了vC
2)加速度分析:根据aF4= anF4+ atF4= aF1+ akF5F1+ arF5F1
1)当φ=165°时,点的速度vc;
2)当φ=165°时,构件3的BC线上速度最小的一点E的位置及速度的大小;
3)当VC=0时,φ角之值(有两个解)。
解:1)以选定的比例尺μ机械运动简图(图b)
2) 求vc定出瞬心p12的位置(图b)
因p13为构件3的绝对瞬心,则有
ω3=vB/lBp13=ω2lAB/μl.Bp13=10×0.06/0.003×78=2.56(rad/s)
3-21图示为一汽车雨刷机构。其构件l绕固定轴心A转动,齿条2与构件1在B点处铰接,并与绕固定轴心D转动的齿轮3啮合(滚子5用来保征两者始终啮合),固连于轮3上的雨刷3’作往复摆动。设机构的尺寸为lAB=18 mm,轮3的分度圆半径r3=12 mm,原动件1以等角速度ω=l rad/s顺时针回转,试以图解法确定雨刷的摆程角和图示位置时雨刷的角速度和角加速度。
答:1)瞬新的数目:
K=N(N-1)/2=6(6-1)/2=15
2)为求ω1/ω3需求3个瞬心P16、P36、P13的位置
3)
ω1/ω3= P36P13/P16P13=DK/AK
