工具变量法的S命令及实例
工具变量法stata代码

工具变量法一、引言在社会科学研究中,研究目的往往是要了解某个因果关系的真实效应。
然而,由于存在内生性问题,观察到的相关性常常无法准确反映因果关系。
工具变量法作为一种常用的因果推断方法,在解决内生性问题上具有重要的作用。
本文将介绍工具变量法的基本原理、实施步骤以及在Stata软件中的具体操作。
二、工具变量法的基本原理工具变量法是通过引入外生性强的工具变量,来解决内生性问题。
内生性问题是指在观察数据中,因变量和解释变量之间存在系统性的关联,其关系与模型设定的相关性不同。
这种关联使得直接通过观察数据进行因果推断变得困难。
工具变量要求关联强,与内生解释变量相关,但与干扰项不相关。
通过工具变量法,我们可以利用工具变量对内生解释变量进行保证,从而得到更准确的因果效应估计。
三、工具变量法的实施步骤3.1 确定内生性问题在应用工具变量法之前,首先需要确定所研究的因果关系是否存在内生性问题。
内生性问题可以通过多种方式产生,比如遗漏变量、测量误差等。
在确定内生性问题后,我们需要找到与内生解释变量相关但与干扰项不相关的工具变量。
3.2 选择合适的工具变量选择合适的工具变量是工具变量法的关键步骤。
一个好的工具变量应该满足一定的条件,比如与内生解释变量的相关性、与干扰因素的无关性、外生性等。
常见的工具变量包括自然实验、随机分配等。
在选择工具变量时,需要结合具体研究对象与背景,寻找符合以上条件的工具变量。
3.3 估计工具变量法模型估计工具变量法模型的关键就是进行两步最小二乘法(Two-stage least squares, 2SLS)估计。
第一步,使用工具变量估计内生解释变量;第二步,将第一步估计得到的内生变量代入原始模型进行估计。
在Stata中,可以使用ivregress命令来估计工具变量法模型。
3.4 检验与解释结果在估计完成后,需要对结果进行检验与解释。
常见的检验方法包括工具变量的合理性检验、过度识别检验等。
在解释结果时,需要注意控制其他可能的干扰因素,确保结果的可信度与可靠性。
esttab导出工具变量法

esttab导出工具变量法
esttab 导出工具变量法是指使用 esttab 命令将回归结果导出为表格的方法。
其中,“工具变量法”是一种统计方法,用于控制或调整其他变量对因变量的影响。
下面是一个使用 esttab 导出工具变量法的示例:
```esttab
eststo olsbase: reg $y $c $f , vce(cluster idcode)
eststo olsmain: reg $y $x $c $f , vce(cluster idcode)
eststo olsint : reg $y c.${x}ib3.${m} $c $f , vce(cluster idcode)
eststo regivm : ivregress 2sls $y (${x} = ${z}) $c $f , vce(cluster idcode) eststo regivi : ivregress 2sls $y (${x} c.${x}#ib3.${m} = /// ${z} c.${z}#ib3.${m}) ib3.$m $c $f , vce(cluster idcode)
```
在上述代码中,“olsbase”、“olsmain”、“olsint”、“regivm”和“regivi”是回归结果的名称。
“$y”、“$x”、“$z”、“$m”和“$c$”是回归模型中的变量。
“vce(cluster idcode)”表示使用聚类稳健标准误。
你可以根据实际情况修改这些变量和名称,然后使用 esttab 命令将回归结果导出为表格。
stata中工具变量法

stata中工具变量法工具变量法(Instrumental Variable Method)是应用于计量经济学中的一种估计方法,其主要用途是解决回归分析中的内生性(endogeneity)问题。
内生性指的是自变量与误差项之间存在相关性,这种相关性会导致回归分析结果产生偏误和无效性。
在实践中,我们常常会遇到自变量与误差项之间存在内生性的情况。
一个常见的例子是研究教育对收入的影响,如果使用教育水平作为自变量,可能会出现教育水平与遗传因素等不可观测变量的内生性问题。
为了解决这个问题,可以使用工具变量法。
在Stata中,使用工具变量法进行估计有多种方法。
下面我们将介绍其中两种常见的方法。
第一种方法是使用Stata内置的ivregress命令。
该命令提供了一种简单的工具变量法估计的方式。
下面是一个使用ivregress命令进行工具变量法估计的示例:ivregress 2sls y (x = z)其中,y代表因变量,x代表内生自变量,z代表工具变量。
该命令会同时估计两个方程,第一个方程是自变量对因变量的影响,第二个方程是工具变量对内生自变量的影响。
通过估计这两个方程,可以得到调整后的内生自变量的估计值,从而解决内生性问题。
第二种方法是使用Stata的reg命令结合自定义工具变量进行估计。
这种方法相对于使用ivregress命令更加灵活,适用于一些特殊情况。
下面是一个使用reg命令进行工具变量法估计的示例:reg y (x = z)在这个示例中,y代表因变量,x代表内生自变量,z代表工具变量。
通过在reg命令中指定x和z之间的关系,可以实现工具变量法的估计。
需要注意的是,使用reg命令进行工具变量法估计需要确保工具变量满足一些假设条件,比如工具变量与误差项之间不应存在相关性。
总之,Stata中提供了多种方法进行工具变量法的估计。
根据实际问题的需求和假设条件的满足程度,可以选择合适的方法进行估计。
通过使用工具变量法可以有效解决回归分析中的内生性问题,提高估计结果的准确性和有效性。
工具变量法例子及解析

工具变量法例子及解析工具变量法是经济学中常用的一种回归分析方法,它的作用是削弱内生性问题对回归结果的影响。
本文将通过具体例子和分析,介绍工具变量法的原理、应用和重要性。
一、工具变量法原理工具变量法的核心思想是利用一个与内生变量有关的外生变量来代替内生变量,既能够在一定程度上削弱内生性问题,又能够保留回归模型的一般结构。
其原理可以简单归纳为以下几个步骤:1. 利用可靠性高的工具变量代替内生变量2. 使用工具变量回归得到内生变量的估计值3. 将内生变量的估计值代入原始回归模型,得出正确的回归效果。
通过以上三个步骤,工具变量法可以尽可能地消除内生性问题对回归分析的干扰,从而得到准确的分析结果。
二、工具变量法应用在实际经济研究中,工具变量法的应用非常广泛,以下是几个常见的应用:1. 教育和收入的关系分析这是一个非常经典的实证研究,研究者发现,教育与收入之间存在内生性问题,即教育水平可能受到家庭收入的影响。
为了解决这个问题,研究者使用父母教育程度作为工具变量,用它来代替受教育程度对收入的内生性影响,最终得出正确的研究结果。
2. 运动员收入与绩效的关系分析在研究运动员收入与绩效关系的时候,由于运动员自身的能力或健康状况等因素可能会影响分析结果,因此需要使用工具变量来解决内生性问题。
例如,研究者可以使用运动员所属的地理区域作为工具变量,用它来代替个人因素对收入和绩效的影响,从而得出更加准确的研究结果。
3. 货币政策与经济增长的关系分析在研究货币政策对经济增长的影响时,通常会使用实际利率作为工具变量来解决内生性问题。
由于实际利率受银行制度、资本市场以及政府债券利率等多种因素的影响,因此能够代替内生性较强的利率变量,得出更加准确的研究结果。
三、工具变量法的重要性工具变量法在经济学研究中具有非常重要的地位,它的主要作用在于解决内生性问题,从而得出更加准确的研究结果。
由于内生性问题可能会导致回归结果的偏误,因此如果不进行工具变量法处理,可能得出的结论会与实际情况有较大差距,这对于政策的制定和实施将会带来严重影响。
工具变量法2SLS与GMM

工具变量法2SLS与GMM1第 10 章工具变量,2SLS 与 GMM10.1 解释变量与扰动项相关的例子例农产品市场均衡模型q d = α + α p + u (需求)t 0 1 t t ? q s = β + β p + v(供给) t ? q d 0 1 t t = q s(均衡)tt令q ≡q d=q s,可得t t tq t =α0+α1 p t +u tq =β+βp +vt 0 1 t t两个方程中的被解释变量与解释变量完全一样。
如直接作回归q ?O?LS?→p,估计的是需求函数还是供给函数?t t2图10.1 需求与供给决定市场均衡341 1 1 11 1把线性方程组中的( p t , q t )看成是未知数(内生变量),把(u t , v t ) 看作已知,可求解( p t , q t )为(u t , v t ) 的函数:p = p (u ,v ) = β0 - α0 + v t - u t ? t t t t α - β α - β ? 1 1 1 1 ?q = q (u ,v ) = α1β0 - α0 β1 + α1v t - β1u t ?? t t t t α - β α - β由于 p t 为(u t , v t ) 的函数,故Cov( p t , u t ) ≠ 0,Cov( p t , v t ) ≠ 0。
OLS 估计值α?1, β? 不是α , β 的一致估计量。
称这种偏差为“联立方程偏差”(simultaneity bias)或“内生变量偏差”(endogen eity bias)。
1如能将内生变量分成两部分,一部分与扰动项相关,另一部分与扰动项不相关,可用与扰动项不相关的那部分得到一致估计。
这种分离常借助另一“工具变量”来实现。
假设在图10.1 中,存在某个因素(变量)使得供给曲线经常移动,而需求曲线基本不动,则可估计需求曲线,参见图10.2。
这个使得供给曲线移动的变量就是工具变量。
stata工具变量法案例

stata工具变量法案例Stata工具变量法是一种经济学研究中常用的方法,用于解决内生性问题。
它通过利用某些外生性强的变量作为工具变量,来估计内生变量与因果变量之间的关系。
下面是10个以Stata工具变量法案例为题的内容介绍。
1. 工具变量法的基本原理:介绍工具变量法的基本思想和理论基础,解释为什么需要使用工具变量来解决内生性问题。
2. 数据准备:讲解如何在Stata中导入和准备数据,包括变量的选择和处理,确保数据的质量和可用性。
3. 内生性问题的存在:说明内生性问题在经济学研究中的重要性和普遍存在性,以及内生性问题对实证结果的影响。
4. 工具变量的选择:介绍如何选择合适的工具变量,包括外生性、相关性和可用性等因素的考虑,以及常用的工具变量选择方法。
5. 工具变量法的估计:详细介绍Stata中的工具变量法估计命令,包括IVREG、IVREG2等命令的使用方法和参数解释。
6. 结果解读:解释工具变量法估计结果的含义和解读方法,包括工具变量估计量的一致性和有效性等统计性质。
7. 内生性检验:介绍如何在Stata中进行内生性检验,包括第一阶段回归、Hausman检验等常用的内生性检验方法。
8. IV回归的问题和限制:讨论工具变量法的局限性和可能存在的问题,如工具变量的有效性和外推性等问题。
9. 实证案例分析:以某个具体的经济学研究问题为例,使用Stata 进行实证分析,展示工具变量法的应用过程和结果。
10. 结论和讨论:总结工具变量法的优点和局限性,讨论工具变量法在经济学研究中的应用前景和发展方向。
以上是以Stata工具变量法案例为题的内容介绍,通过对工具变量法的原理、数据准备、工具变量选择、估计方法、结果解读、内生性检验、案例分析等方面的介绍,可以帮助读者更好地理解和应用Stata工具变量法。
计量经济学工具变量IVSLS

计量经济学工具变量IVSLS计量经济学中的工具变量(Instrumental Variable, IV)和两阶段最小二乘法(TwoStage Least Squares, 2SLS)是解决内生性问题的重要方法。
本文将从基本概念、理论依据、估计方法、应用实例和注意事项等方面,详细阐述IV和2SLS 的内容。
一、基本概念1. 内生性问题内生性问题是指模型中的解释变量与误差项存在相关性,导致普通最小二乘法(Ordinary Least Squares, OLS)估计结果有偏和不一致。
内生性问题的主要来源包括遗漏变量、双向因果关系和测量误差等。
2. 工具变量工具变量(IV)是指与内生解释变量具有相关性,但与误差项不相关的变量。
工具变量的选取应满足以下两个条件:(1)相关性:工具变量与内生解释变量具有相关性,即工具变量可以解释内生解释变量的变动。
(2)外生性:工具变量与误差项不相关,即工具变量不影响被解释变量的变动。
3. 两阶段最小二乘法(2SLS)两阶段最小二乘法(2SLS)是一种利用工具变量估计内生解释变量系数的方法。
2SLS估计过程分为两个阶段:第一阶段:用工具变量代替内生解释变量,对内生解释变量进行回归,得到拟合值。
第二阶段:将第一阶段得到的拟合值代入原模型,用OLS估计模型参数。
二、理论依据1. 内生性问题导致的估计偏误考虑一个简单的线性回归模型:Y = βX + ε其中,Y为被解释变量,X为解释变量,β为参数,ε为误差项。
如果X与ε相关,那么OLS估计的β将是有偏的。
2. 工具变量的有效性假设我们找到了一个工具变量Z,满足以下条件:(1)相关性:Cov(Z, X) ≠ 0(2)外生性:Cov(Z, ε) = 0那么,我们可以使用工具变量Z来估计β。
根据矩条件,我们有:E[(Z E(Z))ε] = 0这意味着Z与ε正交,可以用来消除ε对X的影响。
三、估计方法1. 第一阶段在第一阶段,我们将工具变量Z与内生解释变量X进行回归,得到拟合值X_hat:X_hat = Z (Z'Z)^(1)Z'X2. 第二阶段在第二阶段,我们将第一阶段得到的拟合值X_hat代入原模型,用OLS估计模型参数:Y = βX_hat + εβ_hat = (X_hat'X_hat)^(1)X_hat'Y四、应用实例以下是一个应用IV和2SLS估计的实例:考虑一个教育对收入影响的模型:Y = βX + ε其中,Y为收入,X为教育水平。
第10章-工具变量法,2SLS与GMM

8
同时对需求方程 qt 0 1 pt ut 两边求与 xt 的协方差:
Cov(qt , xt ) Cov( 0 1 pt ut , xt ) 1 Cov( pt , xt ) Cov(ut , xt ) 1 Cov( pt , xt )
3
把线性方程组中的 ( pt , qt ) 看成是未知数(内生变量),把 (ut , vt ) 看 作已知,可求解 ( pt , qt ) 为 (ut , vt ) 的函数:
0 0 vt ut ( , ) p p u v t t t t 1 1 1 1 q q (u , v ) 1 0 0 1 1vt 1ut t t t t 1 1 1 1
0 0 0
Var(u ) 0
故 OLS 不一致, 称为 “测量误差偏差”(measurement error bias)。 可确定此偏差的方向:
15
1 n ( xi x )( yi y ) ˆ n i 1 1 n 2 x x ( ) i n i 1 Cov( xi , yi ) Cov( xi* u , x* ) Var( xi ) Var( xi* u )
其中, v 为测量误差。代入可得:
y x ( v)
只要 Cov( x, v) 0 ,则 OLS 一致,但可能增大扰动项的方差。
18
10.2 工具变量法作为一种矩估计 1.矩估计 (Method of Moments,MM) 假设随机变量 x ~ N ( , 2 ) ,其中 , 2 为待估参数。 因 为 有 两 个 待 估 参 数 , 故 使 用 两 个 总 体 矩 条 件 (population moment conditions): 一阶矩: E( x) 二阶矩: E( x 2 ) Var( x) E( x) 2 2
stata中工具变量法

stata中工具变量法在Stata 中,工具变量法(Instrumental Variables, IV)是一种处理内生性(endogeneity)问题的方法,通常用于解决因果关系中的回归模型。
内生性问题指的是模型中的某些变量可能与误差项相关,从而导致OLS估计结果的偏误。
工具变量法通过引入一个或多个外生性足够相关但与误差项不相关的变量(称为工具变量)来解决这个问题。
以下是在Stata 中使用工具变量法的一般步骤:1. 确定内生性问题:确定模型中是否存在内生性问题,即某些解释变量与误差项相关。
2. 选择工具变量:选择足够相关但与误差项不相关的工具变量。
这些变量通常被认为是外生的,与误差项独立。
3. 估计工具变量模型:使用Stata 中的`ivregress` 命令估计工具变量模型。
语法如下:```stataivregress 2sls dependent_variable (endogenous_variable = instruments) other_exogenous_variables```其中,`dependent_variable` 是因变量,`endogenous_variable` 是内生变量,`instruments` 是工具变量,`other_exogenous_variables` 是其他外生变量。
例如:```stataivregress 2sls y (x = z) controls```4. 检验工具变量的有效性:使用`ivregress` 命令的`ivendog` 选项来检验工具变量的有效性。
```stataivregress 2sls y (x = z) controls, ivendog(x)```此命令将进行工具变量的内生性检验。
5. 诊断:进行模型诊断,检查模型的合理性和有效性。
高维回归stata工具变量法命令

高维回归stata工具变量法命令
在高维回归分析中,Stata工具变量法的命令是`ivregress`和`ivreg2`。
其中,`ivregress`是Stata自带的命令,支持两阶段最小二乘(2SLS)、广义矩估计(GMM)和有限信息最大似然估计(LIML)三种工具变量估计方法。
而`ivreg2`是一个更新的命令,支持更多的工具变量估计方法。
使用`ivregress`命令时,需要提供因变量、内生解释变量、工具变量和控制变量。
命令会自动进行两阶段最小二乘回归,第一阶段回归使用内生解释变量对工具变量和控制变量进行回归,得到拟合值,第二阶段回归使用被解释变量对第一阶段回归的拟合值和控制变量进行回归。
如果需要控制固定效应或进行聚类分析,可以使用选择项`absorb`和
`cluster`。
选择项`first`可以报告第一阶段回归的结果。
选择项`endog`可以检验内生解释变量是否为内生变量,即进行内生性检验。
请注意,使用工具变量法需要找到一个合适的工具变量并说明其合理性,这是工具变量法的难点。
另外,由于模型设定错误或数据问题,工具变量法可能无法完全消除内生性问题,因此在使用时需要谨慎。
工具变量法代码

工具变量法代码工具变量法(Instrumental Variables,简称IV)是一种常用的估计因果效应的方法。
它主要针对的是存在内生性问题的经济学模型,如回归分析中的自变量与误差项存在相关关系。
下文将介绍工具变量法的基本原理,以及其在实践中的使用方法和代码实现。
一、基本原理工具变量法的基本思想是利用一个或多个与内生性自变量相关但不受误差项影响的外生性变量(即工具变量)来代替内生性自变量,在保证模型符合经济学意义的前提下,得到更精确的因果效应估计。
具体来说,对于回归模型:y = α + βx + u其中,x为内生性自变量,u为误差项,我们考虑引入一个外生变量z作为工具变量,那么可以构建如下两个求解方程:x = δ + ρz + vy = α + β(δ + ρz + v) + u其中,δ和ρ是未知的系数。
第一个方程是用工具变量估计内生性自变量的回归式,第二个方程则是运用估计出的内生性自变量对y进行回归。
对于外生性工具变量z,我们可以假定它只会通过自变量x对y产生影响,而不会通过误差项u对y产生影响,即:Cov(z,u) = 0而通过IV估计,我们可以得到内生性自变量x在z上的部分效应(partial effect),从而得出因果效应的估计。
二、实践应用在实践中,工具变量法常常被用来研究各种经济学问题。
例如,研究教育水平对收入的影响、研究医疗保险对医疗消费的影响等。
下面以一个简单的例子来说明如何使用工具变量法。
假设我们想研究家庭收入对孩子的大学入学率的影响,但是我们发现家庭收入存在内生性问题,因为它与其他一些难以观测的因素(如家庭背景、社会阶层等)存在相关关系。
我们考虑使用父母的教育水平和收入作为工具变量,来估计家庭收入与大学入学率之间的因果关系。
代码实现在工具变量法的实现中,常常需要用到Python中的statsmodels(回归模型和统计测试)和pandas(数据处理)两个库。
我们假设有如下数据集:- family_income:家庭收入(千元) - education:父母教育水平(0-未受过教育,1-小学,2-初中,3-高中,4-大学) - college:是否考入本科(0-否,1-是)- random_var:随机变量,用于混淆我们首先看一下家庭收入与大学入学率是否存在内生性问题,可以通过构建回归模型来检验:import statsmodels.api as sm import pandas as pddf = pd.read_csv('data.csv')x = df[['family_income']] y = df[['college']] x = sm.add_constant(x) results = sm.OLS(y, x).fit() print(results.summary())运行上述代码后,我们可以得到回归模型的结果,其中P值可以判断内生性是否显著。
工具变量法工具变量法具体步骤

工具变量法工具变量法具体步骤工具变量法目录概念某一个变量与模型随机解释变量高度相关,但却不与为丛藓科扭口藓项相关,那么就可以用此变量与模型中相应回归系数的一个一致估计量,这个变量就称为方法变量,这种估计方法就叫工具基本原理变量法。
缺点工具变量法的关键是选择一个有效的优先选择工具变量,由于工具自变量变量可以选择中的困难,工具变量法本身存在两方面不足:一是由于工具变量不是惟一的,因而工具变量估计量有一定的任意性;其二由于误差项实际上是不可观测的,因而要寻找严格意义上与误差项无关的与所替代而随机解释变量高度相关的变量总的来说事实上是困难的。
工具变量法与内生解释变量可持续性解释变量会造成解读严重的后果:不一致性inconstent 和有偏biased ,因为频域不满足误差以解释线性为条件的期望值为0。
产生解释变量招盛纯一般有三个原因:一、遗漏变量二、测量误差三、联立性第三种情况是无法逐步解决的,前两种可以采用工具变量(IV )法。
IV 会带来的唯一坏处是估计方差的增大,也就是说同时采用OLS 和IV 估计,则前者的方差小于后者。
但IV 的应用是有前提条件的:1.IV 与内生解释函数相关,2.IV 与u 不相关。
在小样本情况下,一般用内生解释变量对IV 进行回归,如果R -sq 值很小的话,一般t值也很小,所以对IV 质量的评价没有大的风险问题,但是当采用大样本时,情况则相反,往往是t 值很大,而R -sq 很小,这时如果采用t 值进行关键问题评价则可能出现出现问题。
这时IV 与内生解释变量之间的若干程度不是阐释太大,但是如果与u 之间有轻微的相关机构的话,则:1、导致很小的不一致性;2、有偏性,并且这种有偏性随着R -sq趋于0而趋于OLS 的有偏性。
所以现在在采用IV 时最好采用R -sq 或F -sta 作为评价标准,另外为了观测IV 与u 的关系,可以将IV 作为解释变量放入方程进行回归,如果没有其他的系数没有多的变化,则说明IV 满足第二个条件。
工具变量法的系数

工具变量法(Instrumental Variables Method)是一种用于解决因果关系分析中的内生性问题(Endogeneity Problem)的方法。
在工具变量法中,我们使用一个或多个与内生解释变量相关,但与误差项无关的工具变量来估计因果效应。
关于工具变量法的系数,这里以二阶段最小二乘法(Two-Stage Least Squares)为例进行说明。
在二阶段最小二乘法中,我们首先使用工具变量和内生解释变量来预测内生解释变量的值,然后使用这个预测值和工具变量以及其他外生解释变量来进行回归分析,以估计因果效应。
假设我们的模型是:Y = β0 + β1*X + ε。
其中,X是内生解释变量,Y是因变量,ε是误差项。
我们选择了一个工具变量Z,它与X相关,但与误差项无关。
首先,我们使用Z和其他外生解释变量来预测X的值,得到预测值X_hat。
然后,我们在第二阶段进行回归分析,使用Y对X_hat和其他外生解释变量进行回归。
这个回归的系数就是我们想要估计的因果效应。
需要注意的是,工具变量必须满足与内生解释变量相关,但与误差项无关的条件。
否则,工具变量法将无法准确估计因果效应。
同时,
工具变量的选择也需要有一定的理论依据和实际背景的支持。
工具变量法经典例子

工具变量法经典例子
有了工具变量法,生活娱乐有了更多的想象力和无限的可能性,它为娱乐圈开
拓了无边的前景。
工具变量法是一种发掘娱乐圈非常完善的文化背景的独特方式,它可以引领我
们去探索傲视群雄的娱乐圈。
通过不断听取娱乐圈的观点,可以更好地理解并发挥娱乐圈独特文化背景,赋能娱乐圈不断发展。
工具变量法是一种跨文化的文化发展模式,它强调文化和艺术方面的能量,将
所有文化融合起来,使其成为一个独特的生活体验;弱化社会和文化的隔阂,交融大众化文化和原创形成一种工具变量法的艺术视角;变量的本质也决定了工具变量法引领的娱乐圈是一个发掘的好地方。
工具变量法的功能为人们提供广泛的娱乐选择和更加丰富的创意,它把人们从
传统的日常生活中解放出来,变成一种不同的人生态度,去体验和提升精彩的生活。
只要我们用心去寻求,娱乐圈便会成为一个无限可能的海洋。
只要结合工具变量法,一些想象不停、开放不止、未知运动的奇景就会在娱乐圈层出不穷。
工具变量法操作过程

工具变量法操作过程嘿,咱今儿就来唠唠工具变量法的操作过程哈。
你想啊,这工具变量法就像是一个巧妙的解题钥匙。
咱先得找到一个合适的工具变量,这可不容易哦,就跟找宝藏似的,得有一双火眼金睛。
这个工具变量得和咱关心的那个自变量有关系,还得满足一些特别的条件呢,可不能随随便便找一个。
然后呢,就开始建立模型啦。
这就好比搭积木,得一块一块稳稳地放上去。
把工具变量和其他相关的变量都放进去,看看它们能搭出个啥样的“建筑”来。
接下来就是进行估计啦。
这可不能马虎,得仔细着点儿。
就好像你在走一条不熟悉的路,得小心翼翼地试探着,看看怎么走才最靠谱。
在这过程中,你还得不断地检验呢。
检验啥?检验这个工具变量找得对不对呀,模型建得好不好呀。
这就像是给你的“作品”做个全面“体检”,有啥毛病赶紧找出来改掉。
你说这工具变量法是不是很有意思?它就像是一个魔法棒,能帮我们解决一些看似很难的问题。
比如说,我们想研究一个因素对另一个因素的影响,但中间可能有很多干扰因素。
这时候工具变量法就派上用场啦,它能帮我们把那些干扰因素给“过滤”掉,让我们更清楚地看到真正的关系。
而且哦,这工具变量法可不是随便谁都能玩好的,得有一定的专业知识和经验才行。
就像学骑自行车,一开始可能会摔倒,但多练几次就熟练啦。
你想想,如果没有工具变量法,我们很多研究不就没法进行啦?那得错过多少重要的发现呀!所以说,它可真是我们研究的好帮手呢。
咱再回过头来看看,找工具变量要细心,建模型要认真,估计要谨慎,检验要严格。
每一步都不能马虎,就跟盖大楼一样,根基得打牢了,每一层都得建得稳稳当当的。
总之呢,工具变量法是个很有用的方法,但要用好它可得下点功夫。
别嫌麻烦,等你真正掌握了,你就会发现它的魅力啦!就像学会了一门绝世武功,那感觉,倍儿爽!你还等啥,赶紧去试试吧!。
statas 变量 统计特征 命令

主题:统计学中的statas命令及其用法一、概述在统计学中,statas命令是一种用于描述和分析数据的工具。
通过使用statas命令,研究人员能够对数据进行各种统计特征的计算,并且能够进行相应的数据可视化和数据分析。
本文将介绍statas命令的基本用法及其常见的统计特征计算方法。
二、statas命令的基本结构1. statas命令的基本语法在使用statas命令时,需要使用特定的语法结构进行命令的输入。
一般而言,statas命令的语法结构包括命令名称、变量列表等部分。
对于描述性统计特征的计算,可以使用以下基本语法结构:``` statasummarize 变量名```其中,summarize是用于计算描述性统计特征的命令,变量名则是需要计算统计特征的变量名称。
2. statas命令的参数设置除了基本的命令语法之外,statas命令还可以使用一些参数来对命令进行进一步的设置。
在计算描述性统计特征时,可以使用det本人l参数来显示更详细的统计结果:``` statasummarize 变量名, det本人l```通过设置参数,可以对statas命令进行更加个性化的操作,从而得到符合需求的统计分析结果。
三、常见的statas命令及其用法1. 描述性统计特征计算描述性统计特征是对样本数据的基本特征进行总结和描述的指标,包括均值、标准差、中位数等。
在statas中,可以使用summarize命令对数据的描述性统计特征进行计算,并可以使用det本人l参数来显示更详细的统计结果。
2. t检验t检验是用于检验两组样本均值差异的统计方法。
在statas中,可以使用ttest命令对两组样本的均值差异进行检验,并可以使用不同的参数来对t检验的假设条件进行设置。
3. 方差分析方差分析是用于比较多组样本均值差异的统计方法。
在statas中,可以使用anova命令对多组样本的均值差异进行分析,并可以使用不同的参数来对方差分析的模型进行设置。
工具变量法的S命令及实例
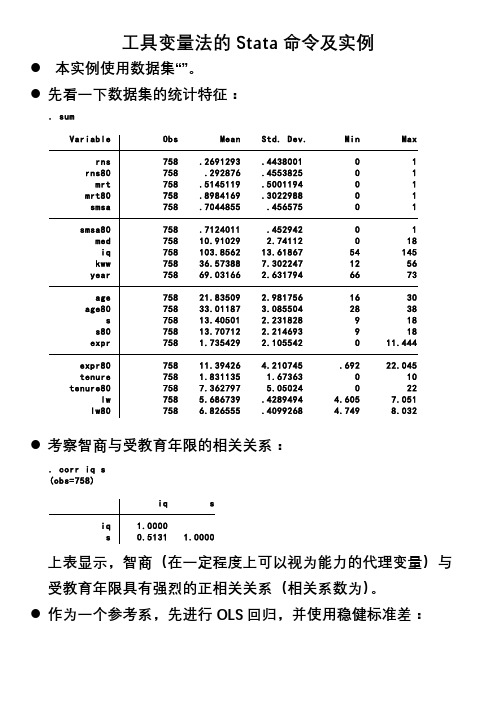
工具变量法的Stata命令及实例●本实例使用数据集“”。
●先看一下数据集的统计特征:. sumVariable Obs Mean Std. Dev. Min Maxrns 758 .2691293 .4438001 0 1rns80 758 .292876 .4553825 0 1mrt 758 .5145119 .5001194 0 1mrt80 758 .8984169 .3022988 0 1smsa 758 .7044855 .456575 0 1smsa80 758 .7124011 .452942 0 1med 758 10.91029 2.74112 0 18iq 758 103.8562 13.61867 54 145kww 758 36.57388 7.302247 12 56year 758 69.03166 2.631794 66 73age 758 21.83509 2.981756 16 30age80 758 33.01187 3.085504 28 38s 758 13.40501 2.231828 9 18s80 758 13.70712 2.214693 9 18expr 758 1.735429 2.105542 0 11.444expr80 758 11.39426 4.210745 .692 22.045tenure 758 1.831135 1.67363 0 10tenure80 758 7.362797 5.05024 0 22lw 758 5.686739 .4289494 4.605 7.051lw80 758 6.826555 .4099268 4.749 8.032●考察智商与受教育年限的相关关系:. corr iq s(obs=758)iq siq 1.0000s 0.5131 1.0000上表显示,智商(在一定程度上可以视为能力的代理变量)与受教育年限具有强烈的正相关关系(相关系数为)。
第七章工具变量、2SLS、GMM

任何随机向量x的函数f x 的期望E f x 都被称为 总体矩。事实上,OLS也是一种矩估计。利用解释 变量与扰动项的正交性,可以得到以下总体矩条件
E x i i =0
E x i yi =E x i x i
ˆ 渐近服从正态分布,即 进一步,工具变量估计量 IV
d ˆ - =S-1 ng ˆ ,其 n N 0 , AVar IV ZX IV -1 -1 ˆ 中渐近方差矩阵AVar IV = i i E zi x S E zi x
2、工具变量法作为一种矩估计
假设回归模型为 yi=1x i1+ + k-1x i,k-1+ k x ik+ i 假设只有最后一个解释变量x ik为内生变量,即 Cov x ik, i 0,因此OLS是不一致的。
假设有一个有效工具变量w满足Cov x ik,w i 0 (相关性),以及Cov w i, i =(外生性)。由于 0 x1, ,x k-1不是内生变量,故可以把自己作为自己 的工具变量(因为满足工具变量的两个条件)
公式,可得2SLS的最终表达式: -1 ˆ = XPX XPy
2SLS
= XZ ZZ ZX
-1
-1
XZ ZZ Zy
-1
四、有关工具变量的检验
在使用工具变量法时,必须对工具变量的有效性 进行检验。如果工具变量非有效,则可能导致估 计不一致,或估计量的方差过大。
ˆ ˆ 注意,第二阶段回归所得到的残差为e2 y-X 2SLS ˆ (这是正确的) 而原方程的残差却是e y-X
工具变量法(一):2SLS

工具变量法(一):2SLSGive me a lever long enough and a place to stand, and I will move the world. -- Archimedes实证研究的常见问题之一为“内生性”(endogeneity),即解释变量与扰动项相关。
研究者通常要花很大精力来解决内生性问题,而工具变量法则是解决内生性的常用利器。
内生性及其后果考虑最简单的一元线性回归模型:其中,为被解释变量,为解释变量,与为待估计的未知参数,下标表示个体(比如,第个企业),为随机扰动项(包含除外影响的所有其他因素),而为样本容量。
内生性意味着解释变量与扰动项相关,即如果存在内生性,则称解释变量为“内生变量”(endogenous variable);反之,则称为“外生变量”(exogenous variable)。
内生性的严重后果是使得OLS估计量不一致(inconsistent),即无论样本容量多大,OLS 估计量也不会收敛至真实的参数值。
工具变量的思想工具变量的思想其实很简单。
虽然内生变量是“坏” 的变量(与扰动项相关),但仍可能有“好” 的部分(与扰动项不相关的部分),正如坏人通常也有好的一面。
如果能将内生变量分解为内生部分与外生部分之和,则可能使用其外生部分得到一致估计。
而要实现这种分离,通常需要借助另一变量,比如,称为“工具变量”(Instrumental Variable,简记IV),因为它起着工具性的作用。
显然,并非任何变量都可以作为工具变量。
首先,变量要能够帮助内生变量分离出一个外生部分,则变量自身必须是“干净”的,即满足“外生性”(与扰动项不相关):其次,变量还须与有一定关系,即满足“相关性”(与相关):寻找内生变量的外生部分假设找到内生变量的有效工具变量,则可将对进行 OLS 回归,从而分离出的外生部分:此回归称为“第一阶段回归”(first stage regression)。
工具变量法代码

工具变量法代码
工具变量法是一种利用某个外生变量(工具变量)对内生变量进行估计的方法。
它可以解决内生性问题,即当自变量和误差项存在相关性时,OLS估计量会出现偏误。
下面是一段用工具变量法进行OLS 估计的Python代码:
```python
import numpy as np
import statsmodels.api as sm
# 生成随机数据
np.random.seed(0)
n = 500
x = np.random.normal(size=n)
y = 1 + 0.5*x + np.random.normal(size=n)
# 加入内生性
z = x + np.random.normal(size=n)
y = 1 + 0.5*z + np.random.normal(size=n)
# 定义工具变量(这里使用x的平方作为工具变量)
instrument = x**2
# 进行工具变量法估计
iv = sm.OLS(y, instrument).fit()
print(iv.summary())
```
以上代码中,我们首先生成了一个简单的线性模型,并在y和x 之间加入了内生性。
然后,我们定义了一个工具变量(这里使用x的平方作为工具变量),并用工具变量法进行OLS估计。
最后,我们输出了估计结果的摘要信息。
需要注意的是,工具变量法要求工具变量与内生变量相关但与误差项不相关。
因此,在实际应用中,我们需要对工具变量进行检验,以确保其满足这一要求。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
工具变量法的Stata命令及实例●本实例使用数据集“”。
●先看一下数据集的统计特征:. sumVariable Obs Mean Std. Dev. Min Maxrns 758 .2691293 .4438001 0 1rns80 758 .292876 .4553825 0 1mrt 758 .5145119 .5001194 0 1mrt80 758 .8984169 .3022988 0 1smsa 758 .7044855 .456575 0 1smsa80 758 .7124011 .452942 0 1med 758 10.91029 2.74112 0 18iq 758 103.8562 13.61867 54 145kww 758 36.57388 7.302247 12 56year 758 69.03166 2.631794 66 73age 758 21.83509 2.981756 16 30age80 758 33.01187 3.085504 28 38s 758 13.40501 2.231828 9 18s80 758 13.70712 2.214693 9 18expr 758 1.735429 2.105542 0 11.444expr80 758 11.39426 4.210745 .692 22.045tenure 758 1.831135 1.67363 0 10tenure80 758 7.362797 5.05024 0 22lw 758 5.686739 .4289494 4.605 7.051lw80 758 6.826555 .4099268 4.749 8.032●考察智商与受教育年限的相关关系:. corr iq s(obs=758)iq siq 1.0000s 0.5131 1.0000上表显示,智商(在一定程度上可以视为能力的代理变量)与受教育年限具有强烈的正相关关系(相关系数为)。
●作为一个参考系,先进行OLS回归,并使用稳健标准差:. reg lw s expr tenure rns smsa,rLinear regression Number of obs = 758 F(5, 752) = 84.05 Prob > F = 0.0000 R-squared = 0.3521 Root MSE = .34641Robustlw Coef. Std. Err. t P>|t| [95% Conf. Interval]s .102643 .0062099 16.53 0.000 .0904523 .1148338 expr .0381189 .0066144 5.76 0.000 .025134 .0511038 tenure .0356146 .0079988 4.45 0.000 .0199118 .0513173 rns -.0840797 .029533 -2.85 0.005 -.1420566 -.0261029 smsa .1396666 .028056 4.98 0.000 .0845893 .194744 _cons 4.103675 .0876665 46.81 0.000 3.931575 4.275775.其中expr, tenure, rns, smsa均为控制变量,而我们主要感兴趣的是变量受教育年限(s)。
回归的结果显示,教育投资的年回报率为%,这个似乎太高了。
可能的原因是,由于遗漏变量“能力”与受教育正相关,故“能力”对工资的贡献也被纳入教育的贡献,因此高估了教育的回报率。
引入智商iq作为能力的代理变量,再进行OLS回归:. reg lw s iq expr tenure rns smsa,rLinear regression Number of obs = 758 F(6, 751) = 71.89 Prob > F = 0.0000 R-squared = 0.3600 Root MSE = .34454Robustlw Coef. Std. Err. t P>|t| [95% Conf. Interval]s .0927874 .0069763 13.30 0.000 .0790921 .1064826 iq .0032792 .0011321 2.90 0.004 .0010567 .0055016 expr .0393443 .0066603 5.91 0.000 .0262692 .0524193 tenure .034209 .0078957 4.33 0.000 .0187088 .0497092 rns -.0745325 .0299772 -2.49 0.013 -.1333815 -.0156834 smsa .1367369 .0277712 4.92 0.000 .0822186 .1912553 _cons 3.895172 .1159286 33.60 0.000 3.667589 4.122754虽然教育的投资回报率有所下降,但是依然很高。
由于用iq作为能力的代理变量有测量误差,故iq是内生变量,考虑使用变量(med(母亲的受教育年限)、kww(在“knowledge of the World of Work”中的成绩)、mrt(婚姻虚拟变量,已婚=1)age(年龄))作为iq的工具变量,进行2SLS回归,并使用稳健的标准差:Instrumental variables (2SLS) regression Number of obs = 758 Wald chi2(6) = 355.73 Prob > chi2 = 0.0000 R-squared = 0.2002 Root MSE = .38336Robustlw Coef. Std. Err. z P>|z| [95% Conf. Interval]iq -.0115468 .0056376 -2.05 0.041 -.0225962 -.0004974 s .1373477 .0174989 7.85 0.000 .1030506 .1716449 expr .0338041 .0074844 4.52 0.000 .019135 .0484732 tenure .040564 .0095848 4.23 0.000 .0217781 .05935 rns -.1176984 .0359582 -3.27 0.001 -.1881751 -.0472216 smsa .149983 .0322276 4.65 0.000 .0868182 .2131479 _cons 4.837875 .3799432 12.73 0.000 4.0932 5.58255Instrumented: iqInstruments: s expr tenure rns smsa med kww mrt age在此2SLS回归中,教育回报率反而上升到%,而iq对工资的贡献居然为负值。
使用工具变量的前提是工具变量的有效性。
为此,进行过度识别检验,考察是否所有的工具变量均外生,即与扰动项不相关:. estat overidTest of overidentifying restrictions:Score chi2(3) = 51.5449 (p = 0.0000)结果强烈拒绝所有工具变量均外生的原假设。
考虑仅使用变量(med, kww)作为iq的工具变量,再次进行2SLS回归,同时显示第一阶段的回归结果:First-stage regressionsNumber of obs = 758 F( 7, 750) = 47.74 Prob > F = 0.0000 R-squared = 0.3066 Adj R-squared = 0.3001 Root MSE = 11.3931Robustiq Coef. Std. Err. t P>|t| [95% Conf. Interval]s 2.467021 .2327755 10.60 0.000 2.010052 2.92399 expr -.4501353 .2391647 -1.88 0.060 -.9196471 .0193766 tenure .2059531 .269562 0.76 0.445 -.3232327 .7351388 rns -2.689831 .8921335 -3.02 0.003 -4.441207 -.938455 smsa .2627416 .9465309 0.28 0.781 -1.595424 2.120907 med .3470133 .1681356 2.06 0.039 .0169409 .6770857 kww .3081811 .0646794 4.76 0.000 .1812068 .4351553 _cons 56.67122 3.076955 18.42 0.000 50.63075 62.71169Instrumental variables (2SLS) regression Number of obs = 758 Wald chi2(6) = 370.04 Prob > chi2 = 0.0000 R-squared = 0.2775 Root MSE = .36436Robustlw Coef. Std. Err. z P>|z| [95% Conf. Interval]iq .0139284 .0060393 2.31 0.021 .0020916 .0257653 s .0607803 .0189505 3.21 0.001 .023638 .0979227 expr .0433237 .0074118 5.85 0.000 .0287968 .0578505 tenure .0296442 .008317 3.56 0.000 .0133432 .0459452 rns -.0435271 .0344779 -1.26 0.207 -.1111026 .0240483 smsa .1272224 .0297414 4.28 0.000 .0689303 .1855146 _cons 3.218043 .3983683 8.08 0.000 2.437256 3.998831Instrumented: iqInstruments: s expr tenure rns smsa med kww上表显示,教育的回报率为%,较为合理,再次进行过度识别检验:. estat overidTest of overidentifying restrictions:Score chi2(1) = .151451 (p = 0.6972)接受原假设,认为(med,kww)外生,与扰动项不相关。
